Chương IV: Hành vi người tiêu dùng - lợi ích và thặng dư môn Kinh tế vi mô | Trường Đại học Kinh Tế Quốc Dân

CHƯƠNG IV : Hành vi người tiêu dùng
( Hộ gia đình – Household ) NỘI DUNG
1. Lý thuyết về lợi ích – đo được
2. Lý thuyết về lợi ích – có thể so sánh ( phân tích BÀNG QUAN – NGÂN SÁCH )
I.Các khái niệm và giả định
* Lợi ích ( U) : Sự thỏa mãn, hài lòng khi sử dụng, tiêu dùng dịch vụ, hàng hóa.
* Tổng lợi ích ( TU) : Lượng hàng hóa tiêu dùng -> TU( tổng lợi ích ) - Rời rạc Q 0 1 2 TU 0 3 6 - Hàm lợi ích
U = U (X, Y) (n = lượng hàng hóa ) ( U = X1/2Y1/2= √XY
! Đơn vị so sánh lợi ích giả định bằng 1 đơn vị trừu tượng gọi là Utils
* Lợi ích cận biên ( MU)
- TU tăng thêm khi tiêu dùng thêm 1 đơn vị hàng hóa - Lợi ích cận biên =
Thay đổi tổng lợi ích
Thay đổi lượng hàng hóa tiêu dùng MU =∆ T ∆ U Q = = (
)Q∆:delta change TU ' Nếu ; ∆ Q =1
MU =∆ TU =TU Q+1−TU Q
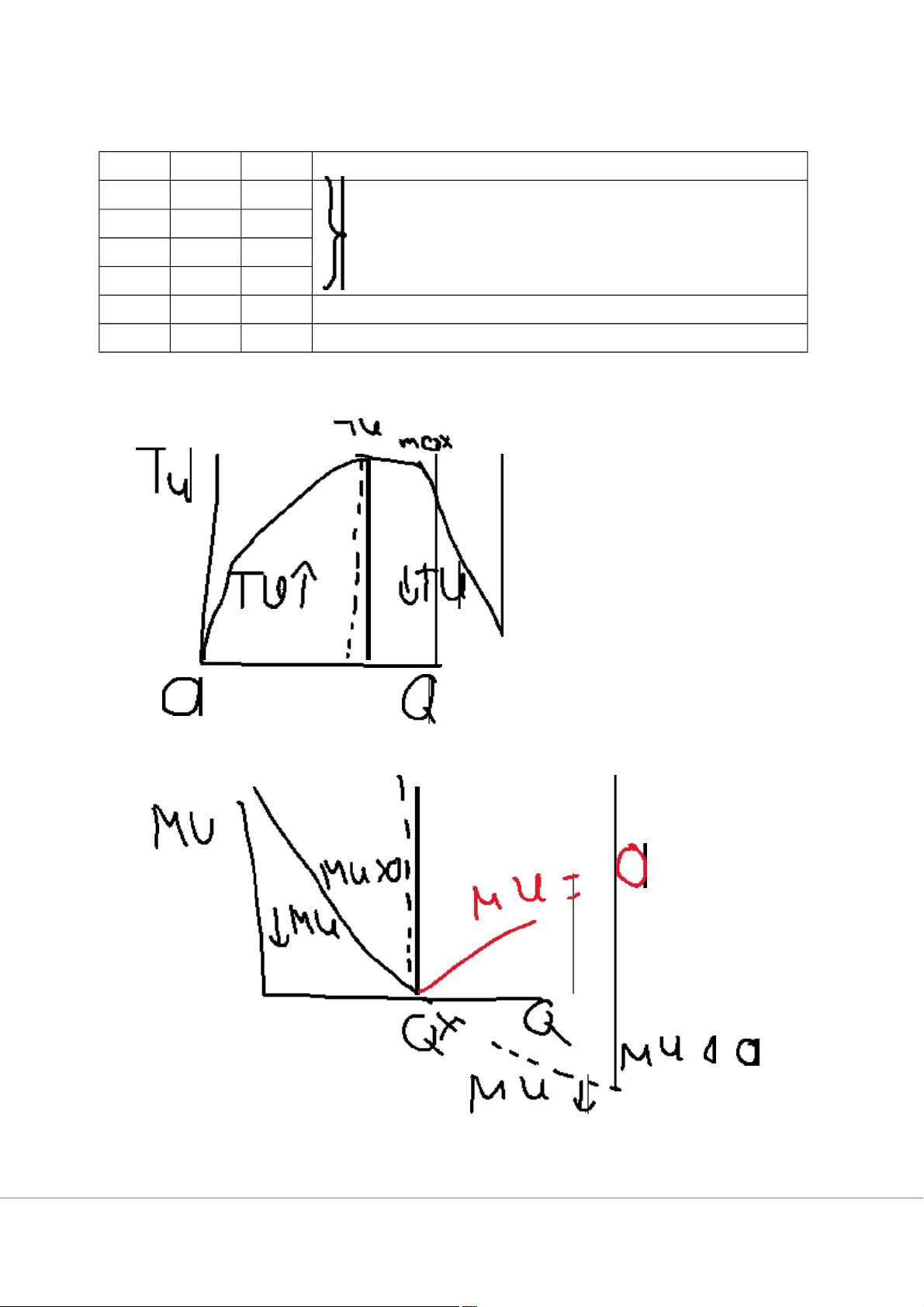
2. Quy luật lợi ích cận biên giảm dần ( MU giảm )
Ví dụ : Tiêu dùng n = 1 hàng hóa ( muốn gì ) Q TU MU Hành vi tiêu dùng hợp lý 0 0
MU >0 : Tăng Q vì TU vẫn tăng 1 3 3 2 5 2 3 6 1 4 6 0
Không còn giá trị vì MU = 0 đã là điểm tới hạn 5 5 -1
Phản lợi ích vì MU = -1 < 0 , giảm Q vì TU giảm K
hi tiêu dùng ngày càng nhiều hơn 1 hàng hóa nào đó( giả định giữ
nguyên mức tiêu dùng các hàng hóa khác) thì MU sẽ giảm dần ở 1 thời điểm
Quy luật MU giảm chỉ thích hợp trong thời gian ngắn
- Thời gian ngắn : khi liên tiếp sử dụng hàng hóa
3. Quy luật MU giảm dần và Đường cầu hàng hóa ( D)
3.1 Lựa chọn tiêu dùng tối ưa n =1 hàng hóa, với giá hàng hóa (P)
MU > P : mua thêm hàng hóa ( Tăng Q )
MU < P : giảm mua hàng hóa ( Giảm Q)
MU = P : Lượng hàng hóa tối ưu ( Q¿¿
Điều kiện cân bằng tiêu dùng Tổng quát với hàng hóa MU 1 P1=MU 2 P2=MU n P n
3.2 Rút ra đường cầu hàng hóa ( D) : dốc xuống KẾT LUẬN - (D) trùng MU >0
- Đường cầu hàng hóa chính là đường cận biên >0
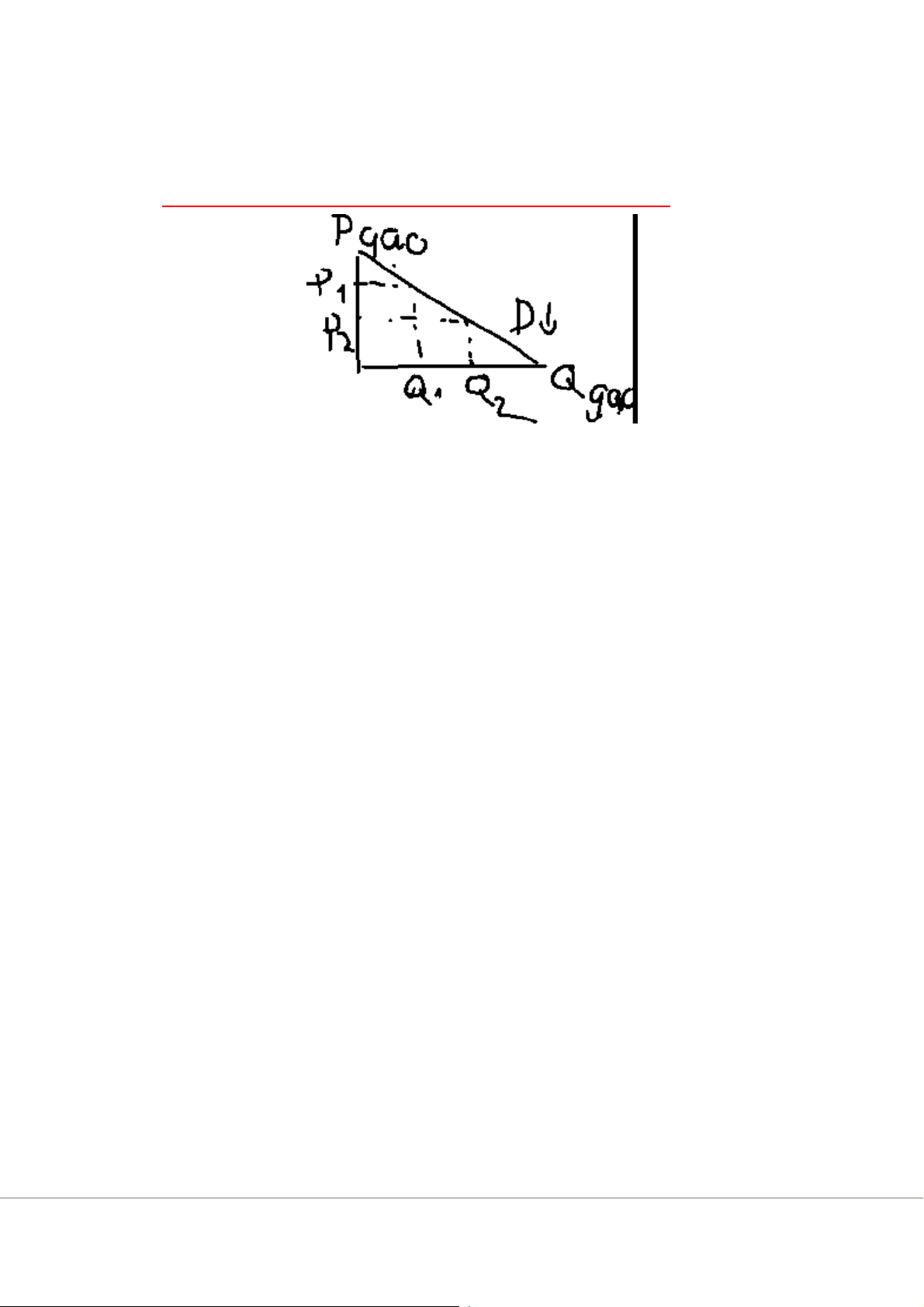
b) (D) dốc xuống do quy luật lợi ích cận biên giảm dần
4. Thặng dư của người tiêu dùng ( CS ): consumer supply CS = TU – TE
( rời rạc ) CS = ∑(MU −P) ĐỒ THỊ : Tính P0 thay Q=0 $P = 100 – Q0
TR ( tổng doanh thu người bán )= PQ = TE ( tổng giá trị người mua bỏ ra)
Q∗¿MUdQ=SPAQ0¿ TU = ∫ ¿ 0
TE=P∗Q∗−SPAQ 0
CS=TU −TE=SPAP CS =12¿ Ví dụ :
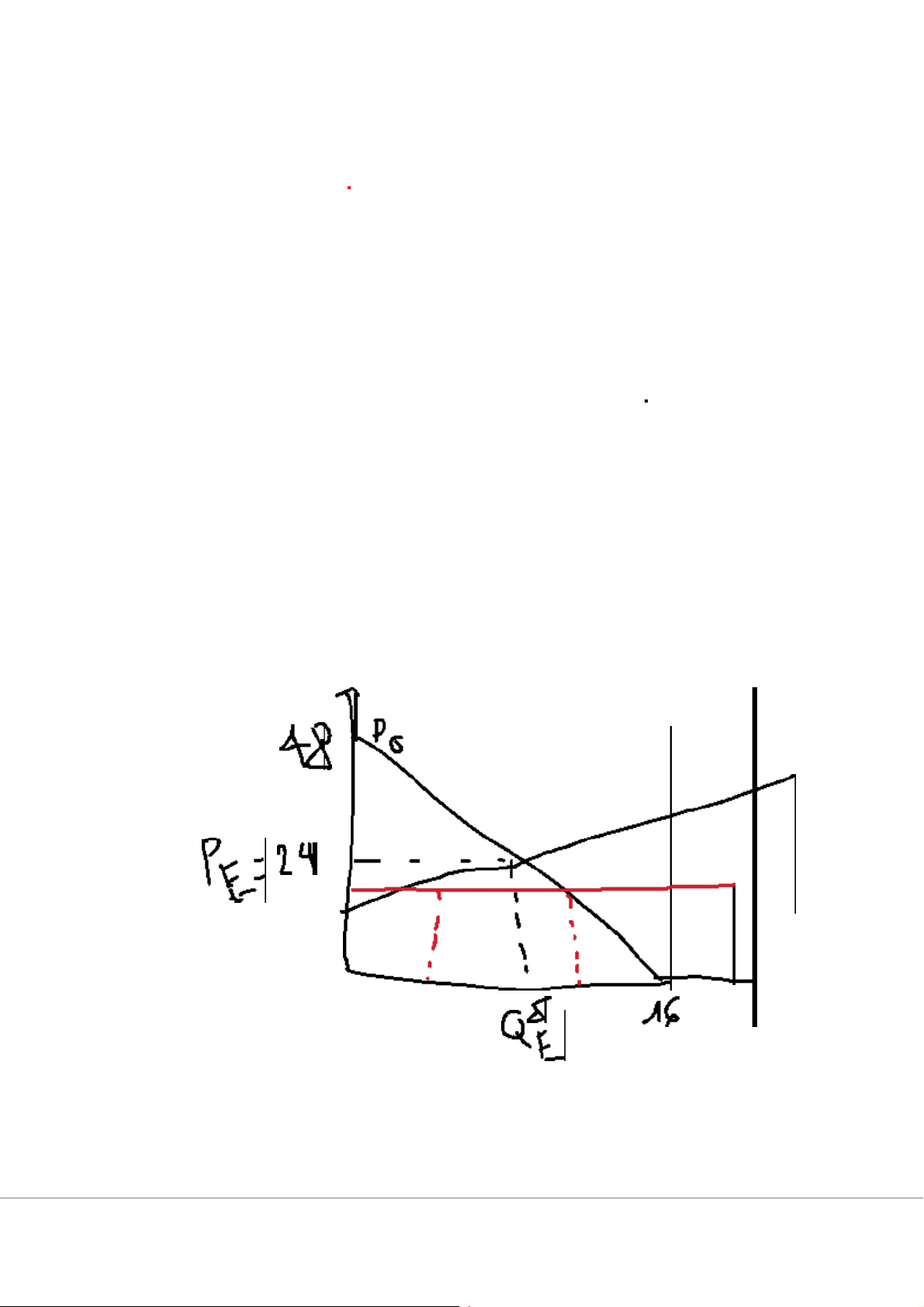
(D)$P = 48 – 3QD -> QD = 16- P/3 (1)
(S) $P = 16 + Qs -> Qs = P-16 (2) a) PE? QE? Giải (1) (2)
16-P/3 = P -16 <-> 4P= 96 -> PE= 24 , QE=8
C) CS , PE = 248 = diện tích tam giác P0EPE= ½ (48-24) x8 = 968
D) Giá trần Pc = 218 -> Thiếu hụt QD= 16-21/3 = 9/5 QS = 21 -16 = 5