Chương V_Bài 3_Phép cộng, phép trừ phân số | Bài giảng PowerPoint Toán 6 | Cánh diều
Bài giảng điện tử môn Toán 6 sách Cánh diều bao gồm đầy đủ các bài giảng trong cả năm học 2022 - 2023, được thiết kế dưới dạng file trình chiếu PowerPoint với nhiều hiệu ứng đẹp mắt.
Preview text:
CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC! KHỞI ĐỘNG
Thái Bình Dương bao phủ khoảng 1 bề mặt Trái Đất, 3
Đại Tây Dương bao phủ khoảng 1 bề mặt Trái Đất. 5
Thái Bình Dương và Đại Tây Dương
bao phủ khoảng bao nhiêu phần bề
mặt Trái Đất? Thái Bình Dương bao
phủ nhiều hơn Đại Tây Dương bao
nhiêu phần bề mặt Trái Đất? BÀI 3.
PHÉP CỘNG, PHÉP TRỪ PHÂN SỐ (3 tiết) NỘI DUNG
I. PHÉP CỘNG PHÂN SỐ
1. Quy tắc cộng hai phân số
2. Tính chất cộng hai phân số
II. PHÉP TRỪ PHÂN SỐ
1. Số đối của một phân số
2. Quy tắc trừ hai phân số I PHÉP CỘNG PHÂN SỐ
1. Quy tắc cộng hai phân số
Thực hiện cộng hai phân số sau:
Em hãy nhắc lại quy tắc cộng hai phân số cùng mẫu đã1 5 a) học + ở tiểu học? −1 5 7 7 b) + 7 7 Giải: 1 5 1+5 6 −1 5 −1+5 6 a) + = = b) + = = 7 7 7 7 7 7 7 7
Quy tắc cộng hai phân số cùng mẫu
Muốn cộng hai phân số có cùng mẫu
số ta cộng các tử và giữ nguyên mẫu:
𝒂 + 𝒃 = 𝒂+𝒃 𝒎 𝒎 𝒎 −𝟏 VD:
+ 𝟑 = −𝟏+𝟑 = 𝟐 𝟓 𝟓 𝟓 𝟓 11 5 Tính + −9 −6
Bước 1: Quy đồng mẫu hai phân số 11 −11 5 −5 = và = ; BCNN(9, 6) = 18 −9 9 −6 6 11 −11.2 −22 5 −5.3 = = và = = −15 −9 9.2 18 −6 6.3 18 11 5 Tính + −9 −6
Bước 2: Cộng các tử và giữ nguyên mẫu chung: −22 Ta có: + −15 = −22+ −15 = −37 18 18 18 18 Vậy 11 5 + = −37 −9 −6 18
Quy tắc cộng hai phân số không cùng mẫu
Muốn cộng hai phân số không cùng mẫu,
ta quy đồng mẫu những phân số đó rồi
cộng các tử và giữ nguyên mẫu chung.
Luyện tập 1. Tính: −3 2 −4 2 a) + ; b) + 7 7 9 −3 Giải: −3 2 −4 2 a) + b) + 7 7 9 −3 = −3+2 −4 −2 −4.1 −2.3 7 = + = + 9 3 9.1 3.3 = −1 7 −4 −6 −4+(−6) −10 = + = = 9 9 9 9
2. Tính chất của phép cộng phân số
Hãy nêu các tính chất của phép cộng số tự nhiên.
Giống như phép cộng số tự nhiên, phép cộng phân
số cũng có các tính chất giao hoán, kết hợp, cộng với số 0.
a) Tính chất giao hoán: 𝑎 𝑐 𝑐 𝑎 𝑏 + 𝑑 = 𝑑 + 𝑏
b) Tính chất kết hợp: 𝑎 𝑐 𝑝 𝑎 𝑐 𝑝
𝑏 + 𝑑 + 𝑞 = 𝑏 + 𝑑 + 𝑞 c) Cộng với số 0 𝑎 𝑎 𝑎 𝑏 + 0 = 0 + 𝑏 = 𝑏 Luyện tập 2. Tính một cách hợp lí: −5 −2 a) + 4 + 7 ; b) + 3 + −3 + 13. 9 11 11 5 8 5 8 Giải: −5 a) + 4 + 7 9 11 11 −2 b) + 3 + −3 + 13 5 8 5 8 = −5 + 4 + 7 9 11 11 = −2 + −3 + 3 + 13 5 5 8 8 = −5 + 1 −5 = −5 16 9 9 = + = −1 + 3 = 2 5 8
II. PHÉP TRỪ PHÂN SỐ 1. Số Hãy đối nêu của lại một các p khá h i â nin số ệm, tính chất hai số
nguyên đối nhau và cho ví dụ.
Giống như số nguyên, mỗi phân số đều có số đối
sao cho tổng của hai số đó bằng 0 3 VD: Phân số -
là số đối của phân số 3 5 5
Số đối của phân số 𝑎 kí hiệu −𝑎 . Ta có: 𝑏 𝑏 𝑎 𝑎 + (- ) = 0 𝑏 𝑏 𝑎 𝑎 −𝑎 Ta có: - = = , với a, b ∈ ℤ, b ≠ 0. 𝑏 −𝑏 𝑏 Số đối của 𝑎 𝑎 - là tức là: - − 𝑎 = 𝑎 𝑏 𝑏 𝑏 𝑏 3 5
Ví dụ : Tìm số đối của mỗi phân số sau: và - 4 6 Giải: −3
Số đối của phân số 3 là 4 4 5
Số đối của phân số −5 là - 6 6
2. Quy tắc trừ hai phân số
Hãy nhắc lại quy tắc trừ hai phân số cùng mẫu
Muốn trừ hai phân số có cùng mẫu, ta trừ tử của sốđã bị học trừ ở tiểu cho tử học
của.số trừ và giữ nguyên mẫu: 𝒂 𝒃 𝒂−𝒃 - = 𝒎 𝒎 𝒎 −1 3 −1−3 VD: - = = −4 5 5 5 5 13 7 Tính: - −9 −6 Để 7
tính hiệu hai phân số không cùng mẫu 13 - , −9 −6 ta làm như sau:
Bước 1. Quy đồng mẫu hai phân số 13 −13 7 −7 = và = ; −9 9 −6 6 BCNN(9, 6) = 18 13 −13.2 −26 7 −7.3 = = và = = −21 −9 9.2 18 −6 6.3 18
Bước 2. Trừ tử của số bị trừ cho tử của số trừ và giữ nguyên mẫu chung: −26 Ta có:
− −21 = −26− −21 = −5 18 18 18 18 Vậy 13 7 - = −5 −9 −6 18 Nhận xét
Muốn trừ hai phân số không cùng mẫu, ta
quy đồng những phân số đó rồi trừ tử
của số bị trừ cho tử của số trừ và giữ nguyên mẫu chung. Luyện tập 3. Tính: 7 9 - −10 10 Giải: −7 9 - = −7−9 10 10 10 = −16 = −8 10 5
a) Phân số 2 có phải là số đối của phân số 2 không? 5 −5 −3 2 −3 2
b) Tính và so sánh các kết quả sau: - và + 7 −5 7 5 Giải:
a) Phân số 2 là số đối của phân số 2 5 −5 −3 −3.5 b) – 2 = – −2.7 −3 2 −3.5 2.7 7 −5 7.5 5.7 + = + 7 5 7.5 5.7 −15 −1 = – −14 = −15 14 −1 35 35 35 = + = 35 35 35
Vậy −𝟑 – 𝟐 −𝟑 𝟐 = + 𝟕 −𝟓 𝟕 𝟓
* Quy tắc trừ hai phân số:
Muốn trừ hai phân số, ta cộng số bị trừ với số đối của số trừ: 𝑎 𝑐 𝑎 𝑐
𝑏 − 𝑑 = 𝑏 + − 𝑑 Luyện tập 7 −9 4. Tính: - 12 20 Giải: 7 – −9 7 9 = + 12 20 12 20 7.5 9.3 = + 12.5 20.3 35 27 = + 60 60 62 31 = = 60 30
III. QUY TẮC DẤU NGOẶC. E Q m uy hã tắ y c nhắc dấu quy tắc ngoặc đ dấu ối với ngoặc phân đối số với giốn số g nguyên như quy tắc
dấu ngoặc đối với số nguyên. Luyện tập −2 47
5. Tính một cách hợp lí: - + 5 49 49 −3 −2 47 −2 - + 5 = − 47 − 5 49 49 −3 49 49 −3 = −2−47 + 5 49 3 = −49 + 5 = −1 + 5 49 3 3 = −1.3+5 = 2 3 3 LUYỆN TẬP 1. Tính: −2 1 5 7 a) + 7 b) + 13 + −5 + 9 −9 −6 −15 c) −6 12 18 Giải: −2 1 5 7 a. + 7 b. + 13 c. + −5 + 9 −9 −6 −15 −6 12 18 −2 −5 −30 14 = + −7 = + −26 = + −15 + 9 9 30 30 36 36 36 −9 −31 −31 = = 1 = = 9 30 30
2. Tính một cách hợp lí: 2 −7 −11 −1 −5 13 2 a) + −3 + b) + 2 + c) + 12 + + 9 10 10 6 5 6 8 7 8 7 Giải: 2 −7 −11 −1 −5 13 2 a. + −3 + b. + 2 + c. + 12 + + 9 10 10 6 5 6 8 7 8 7 2 −11 2 −5 13 12 2 = + (−3 + −7) =( + −1) + = ( + ) + ( + ) 9 10 10 6 6 5 8 8 7 7 2 2 = - 1 = −2 + = 1 + 2 = 3 9 5 2 9 −7 −10+2 −8 = - = = = 9 9 9 5 5 6. Tìm x, biết: 5 1 3 −7 a) x - = b) - - x = 6 2 4 12 Giải: 5 1 a) x - = 3 −7 6 2 b) - - x = 4 12 1 5 x = + −3 −7 2 6 x = + 4 12 1 5 −9 −7 x = + x = + 2 6 12 12 4 −4 x = x = 3 3
7. Một xí nghiệp trong tháng Giêng đạt 3 kế hoạch của Quý I, 8
tháng Hai đạt 2 kế hoạch của Quý I. Tháng Ba xí nghiệp phải 7
đạt bao nhiêu phần kế hoạch của Quý I. Giải:
Một quý gồm 3 tháng. Coi số phần kế hoạch quý I là 1
Số phần kế hoạch tháng thứ ba phải đạt được là: 3 1 - − 2 = 19 (kế hoạch) 8 7 56 VẬN DỤNG
HOẠT ĐỘNG CẶP ĐÔI
Yêu cầu: Hai bạn cùng bàn thảo luận hoàn thành
các bài tập trong phiếu bài tập. Thời gian: 8 phút PHIẾU BÀI TẬP
Bài 1: Hai người cùng làm chung một công việc. Nếu làm riêng ,
người thứ nhất mất 3 giờ, người thứ hai mất 4 giờ. Hỏi nếu làm
chung thì mỗi giờ cả hai người làm dược mấy phần công việc?
Bài 2: Vòi nước A chảy đầy bể mất 6 giờ, vòi nước B chảy đầy bể
mát 8 giờ. Hỏi trong 1 giờ vòi A chảy nhiều hơn vòi B bao nhiêu phần bể? 𝟏
Bài 3: Tính: A = + 𝟏 + 𝟏 + 𝟏 𝟐.𝟑 𝟑.𝟒 𝟒.𝟓 𝟓.𝟔 TÌM TÒI MỞ RỘNG
Biểu diễn phân số trên trục số như thế nào?
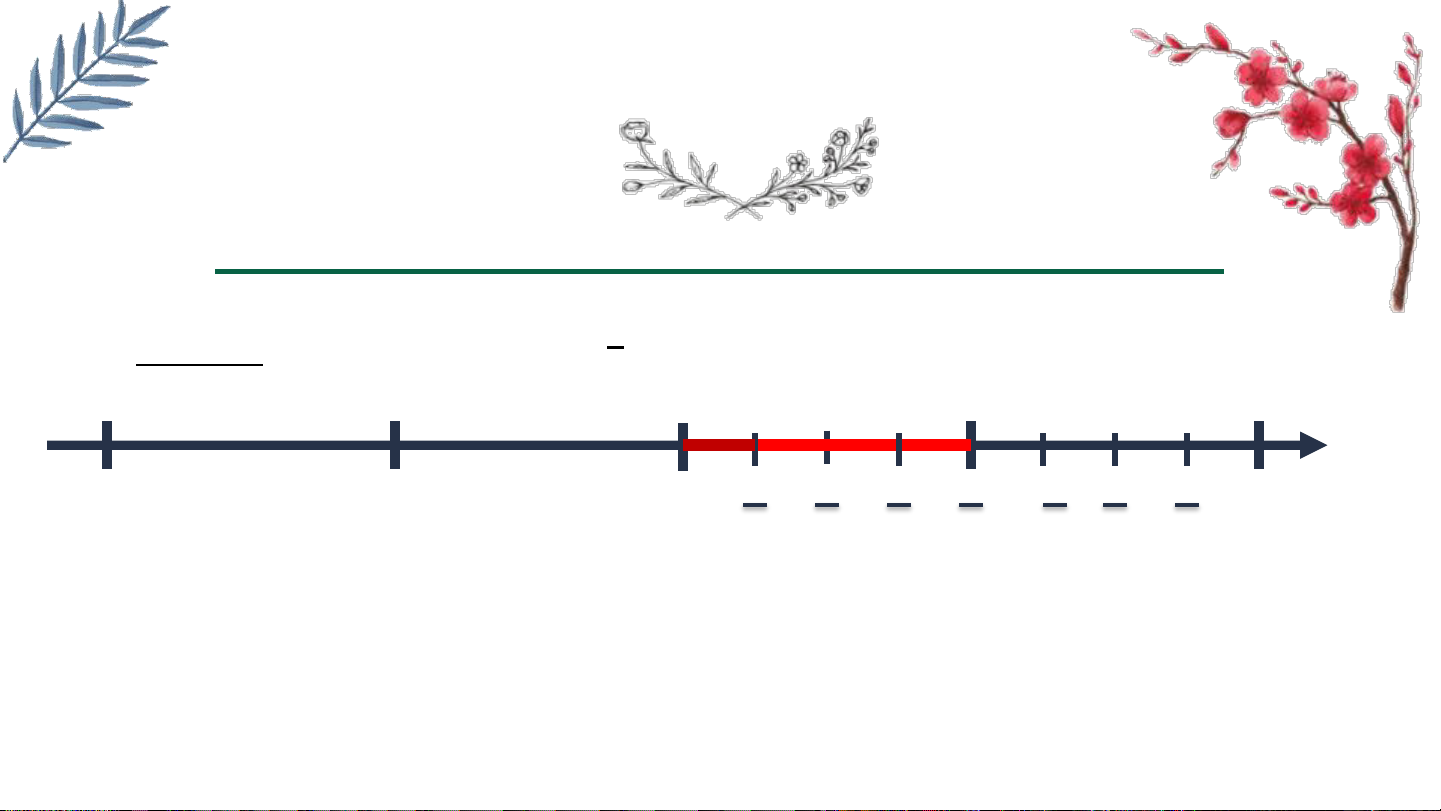
Ví dụ : Biểu diễn số hữu tỉ 5 trên trục số 4 -2 -1 0 1 2 3 4 5 6 7 2 4 4 4 4 4 4 4
Chia mỗi đoạn thẳng đơn vị cũ thành 4 phần bằng nhau rồi lấy 5 đơn vị mới. −3 5
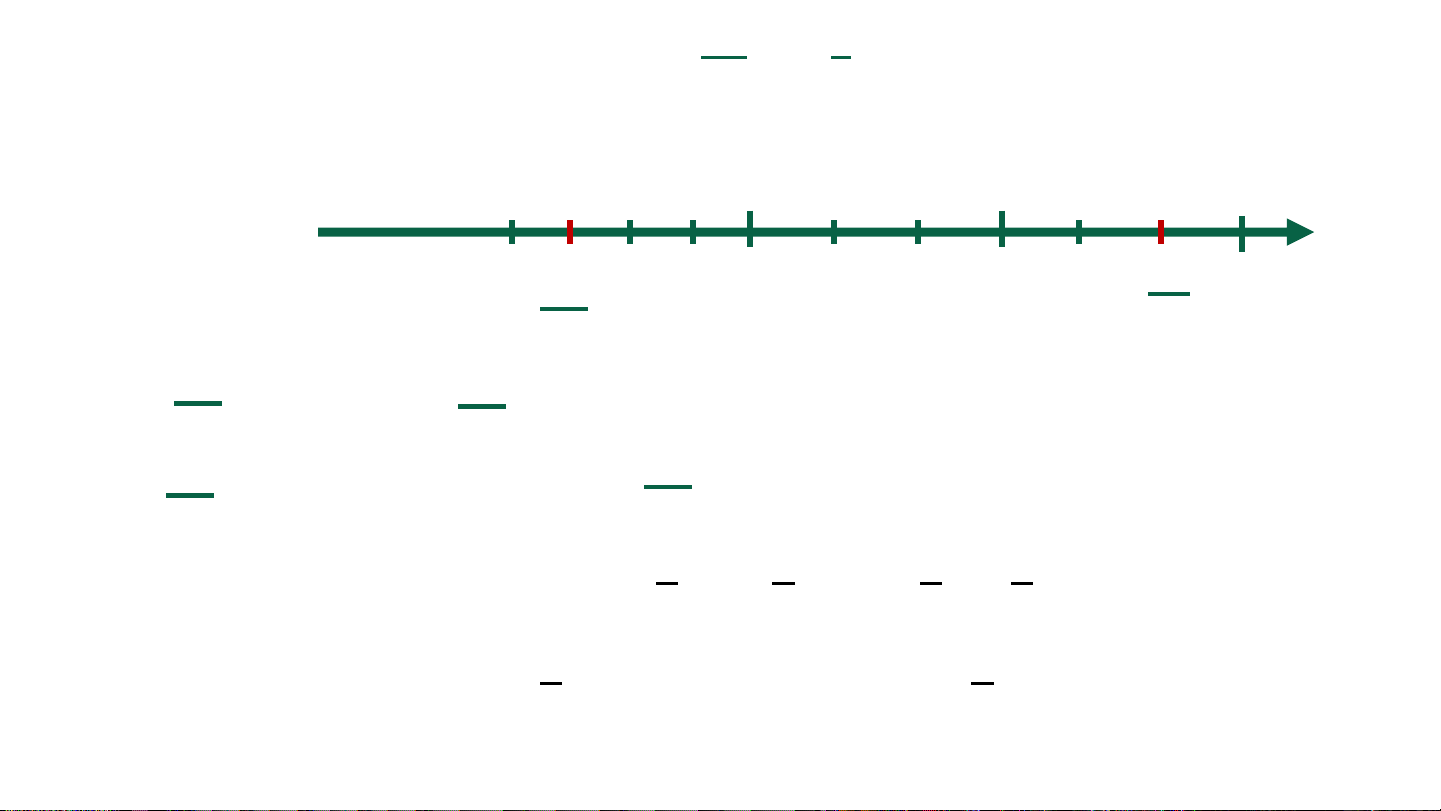
Hãy biểu diễn các phân số: và trên trục số. Nêu nhận 4 3
xét về vị trí hai số đó đối với nhau ? đối với 0 ? 5 -3 0 1 2 3 4 -3 5 ở bên trái trên trục số nằm ngang 4 3 -3 5 ở bên trái điểm 0 ; ở bên phải điểm 0. 4 3 Như vậy 𝒄 𝒄
hai phân số 𝒂 và
nếu 𝒂 < thì trên trục số 𝒃 𝒅 𝒃 𝒅
nằm ngang điểm 𝒂 ở bên trái điểm 𝒄 (cũng giống như 𝒃 𝒅
đối với hai số nguyên). CỦNG CỐ
Muốn cộng trừ hai phân số không
cùng mẫu, ta làm như thế nào?
* Lưu ý: Khi bỏ dấu ngoặc trong một biểu thức
cần lưu ý đến dấu xuất hiện trước dấu ngoặc
HƯỚNG DẪN VỀ NHÀ
- Hoàn thành bài tập còn lại trong SGK và các bài tập trong SBT.
- Chuẩn bị bài mới “Phép nhân, phép chia phân số”. CẢM ƠN CÁC EM ĐÃ CHÚ Ý BÀI GIẢNG