109 trang 3 lượt tải

Chuyên đề công thức lượng giác môn Toán 11 định hướng cấu trúc mới

6

Tài liệu gồm 109 trang, được biên soạn bởi thầy giáo Lê Bá Bảo, bao gồm lý thuyết và bài tập chuyên đề công thức lượng giác môn Toán 11 định hướng cấu trúc mới.

Chủ đề: Tài liệu chung Toán 11 85 tài liệu

Môn: Toán 11 3.6 K tài liệu

Tác giả:

Profile

Linh Đan

1 tháng trước
Danh sách Quiz
/109
CÔNG THỨC LƯỢNG GIÁC
TOÁN 11
LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ
Chuyên đề LƯỢNG GIÁC
LUYỆN THI THPT QUỐC GIA
CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
( )
sin sin cos cos sin a b a b a b+ = +
( )
sin sin cos cos sina b a b a b− = −
( )
cos cos cos sin sin a b a b a b+ = −
( )
cos cos cos sin sina b a b a b− = +
( )
tan tan
tan
tan tan1.
ab
ab
ab
−
−=
+
( )
tan tan
tan
tan tan1.
ab
ab
ab
+
+=
−
sin sin cos2 2 .a a a=
cos cos sin
cos
sin
22
2
2
2
21
12
a a a
a
a
=−
=−
=−
tan
tan
tan
2
2
2
1
a
a
a
=
−
( ) ( )
sin cos sin sin
1
.
2
a b a b a b

= − + +

( ) ( )
sin cos cos
1
sin .
2
a b a b a b

= − − +

( ) ( )
cos cos cos cos
1
.
2
a b a b a b

= − + +

sin sin sin cos2
22
a b a b
ab
+−
+=
sin sin cos sin2
22
a b a b
ab
+−
−=
cos cos cos cos2
22
a b a b
ab
+−
+=
cos cos sin sin2
22
a b a b
ab
+−
− = −
sin sin sin
3
3 3 4a a a=−
cos cos cos
3
3 4 3a a a=−
tan
2
a
t =
sin ; cos ; tan
2
2 2 2
2 1 2
1 1 1
t t t
a a a
t t t
−
= = =
+ + −
sin cos sin2
4
a a a

+ = +


cos sin cos2
4
a a a

− = +


( ) ( )
sin sin cos sin sin cos
22
1 2 1 2a a a a a a+ = + − = −
tan cot cot tan cot
sin
2
22
2
a a a a a
a
+ = − =
00
75
cos795 , sin18 , tan ,cot
12 8

0
0
11
cos290
3 sin250
A =+
( )( )
00
1 tan20 1 tan25B = + +
0 0 0 0
tan9 tan27 tan63 tan81C = − − +
22
22
sin sin sin sin
9 9 9 9
D
= + +
sin cos .cos .cos ;
32 32 16 8
A
=
sin10 .sin 30 .sin50 .sin70 ;B =
3
cos cos ;
55
C

=+
2 2 2
23
cos cos cos .
7 7 7
D
= + +
,

2
sin sin
2

+=
6
cos cos
2

+=
( )
cos

−
( )
sin

+
4
cos2
5
x =−
42
x


sin , cos , sin , cos 2
34
x x x x

+−
2
cos4 2 6sin

+=
2


tan 2
2 2 2 2
1 1 1 1
7
tan cot sin cos
+ + + =
cos4
sin cos cot
2

+=
0


2013
tan
2


+


( )
1
sin , tan 2tan
3
+ = = −
35
sin cos sin sin
8 8 12 12
A
= + + + − −
44
3 cos4
sin cos ;
44

+ = +
66
53
sin cos cos4 ;
88
+ = +
2
1 sin2
cot .
1 sin2 4


−
=+

+

0,
2
1 cos 1 cos 2sin ;
24



+ + − = +


1 cos 1 cos
tan .
24
1 cos 1 cos


+ + −
=+

+ − −

22
sin( ).sin( ) sin sin ;
+ − = −
cot cot 2
22

=
( )
sin sin 3sin , 2 , ;b k k
+ = + +
( )
( )
( )
sin sin cos
tan .
cos sin sin

++
=+
−+
x
2 2 2
22
cos cos cos ;
33
A

= + + + −
3
cos .cos cos .cos .
3 4 6 4
B
= − + + + +
cos 2cos2 cos3
;
sin sin2 sin3
a a a
A
a a a
++
=
++
cos cos
33
;
cot cot
2
aa
B
a
a

+ + −
=
−
( )
cos cos( ) cos( 2 ) ... cos( ) .C a a b a b a nb n= + + + + + + +
( ) ( )
sin 2cosa b a b+ = −
11
2 sin2 2 sin2
M
ab
=+
−−
,ab
0
2

2
2cot 1 cos2 ;

+
cot 1 cot 2 .

+
0
2

11
sin cos 2.
2cos 2sin


+ +
sin cos ;A x x=+
44
sin cos .B x x=+
2 2sin cos2A x x= − −
ABC
sin sin sin 4cos cos cos ;
2 2 2
A B C
A B C+ + =
2 2 2
sin sin sin 2(1 cos cos cos );A B C A B C+ + = +
sin2 sin2 sin2 4sin sin sin .A B C A B C+ + =
ABC
tan tan tan tan .tan .tan ;A B C A B C+ + =
cot .cot cot .cot cot .cot 1.A B B C C A+ + =
,ab
sin sin 2cos sin .
22
+−
−=
a b a b
ab
( )
cos cos cos sin sin .− = −a b a b a b
( )
sin sin cos cos sin .− = −a b a b a b
( ) ( )
2cos cos cos cos .= − + +a b a b a b
x
sin 2 2sin cosx x x=
sin 2 sin cosx x x=
sin 2 2 cosxx=
sin 2 2sinxx=
a
2
cos 2 1 2sinaa=−
22
sin 3 cos 3 3aa+=
sin 4 2sin 2 cos 2a a a=
( )
cos cos cos sin sina b a b a b− = +
a
2
cos 2 1 2sinaa=−
22
cos 2 cos sina a a=−
2
cos 2 1 2 cosaa=−
2
cos 2 2cos 1aa=−
a
cos 2 2cos 1aa=−
2
2sin 1 cos 2aa=−
( )
sin sin cos sin cosa b a b b a+ = +
sin 2 2sin cosa a a=
a
2
cos 2 1 2sinaa=−
cos 2 2sin cosa a a=
22
cos 2 cos sina a a=−
2
cos 2 2cos 1aa=−
a
22
cos 2 cos sina a a=−
2
cos 2 2cos 1aa=+
22
cos 2 cos sina a a=+
2
cos 2 2sin 1aa=−
,ab
tan( ) tana

−=
sin sin 2sin sin
22
a b a b
b
+−
+=
sin tan cos
=
cos( ) sin sin cos cosa b a b a b− = +
,ab
( ) ( )
1
sin sin cos cos
2
a b a b a b= − − +


( ) ( )
–cc
1
s
2
o cos cos osa b a bab +


=+
( ) ( )
cos cos cos
1
2
cosaa b a bb −


= + −
( ) ( )
1
sin cos sin – sin
2
a b a b a b


= + +
,ab
( )
sin sin sin cos cosa b a b a b+ = −
( )
sin sin cos cos sina b a b a b+ = −
( )
sin sin cos cos sina b a b a b+ = +
( )
sin sin sin cos cosa b a b a b+ = +
a
13
cos sin cos
3 2 2
a a a

+ = −


13
cos cos sin
3 2 2
a a a

+ = −


1
cos cos
32
aa

+ = +


31
cos sin cos
3 2 2
a a a

+ = −


44
3 cos4
sin cos .
44

+ = −
44
3 cos4
sin cos .
44

+ = +
44
3 cos4
sin cos
42

+ = +
44
3 cos4
sin cos
24

+ = −
x
44
31
sin cos cos 4
44
x x x+ = +
66
53
sin cos cos 4
84
x x x+ = +
44
sin cos cos 2− = −x x x
44
31
sin cos cos 4
44
x x x+ = −
44
sin ,

=+P cos
2
sin 2
3
=
1
3
1
9
7
7
9
sin
6
a

+


1
sin
2
+a
31
sin cos
22
+aa
31
sin cos
22
−aa
13
sin cos
22
−aa
( )
( )
sin
sin
ab
ab
+
−
sin sin
.
sin sin
+
−
ab
ab
sin sin
.
sin sin
−
+
ab
ab
tan tan
.
tan tan
+
−
ab
ab
cot cot
.
cot cot
+
−
ab
ab
sin .cos sin .cos
15 10 10 15
22
cos .cos sin .sin
15 5 15 5
+
−
1
1−
3
2
−
3
2
3
sin
4
=
cos 2
1
8
7
4
7
4
−
1
8
−
1
sin
3
=−
3
2


sin 2
7
9
42
9
42
9
−
2
3
−
3
cos
5
x =−
cos 2x
7
25
−
3
10
−
8
9
−
7
25
( )( )
1 3cos 2 2 3cos 2 ,

= − +P
2
sin .
3
=
49
.
27
50
27
48
.
27
42
27
1
sin cos
2
xx+ = −
sin 2x
3
4
−
3
4
1
2
1−
2
sin 2cos 1

+ = −
sin 2 α.
26
5
24
25
26
5
−
24
25
−
0
2

2
sin
3
=
1 sin 2 cos 2
sin cos
P


++
=
+
25
3
P =−
3
2
P =
25
3
P =
3
2
P =−
tan 2
=
tan
4

−


1
3
2
3
1
1
3
−
1
tan
7
=
3
tan
4
=

+
6
4
3
.
2
tan cot 2

+=
0
2




sin 2
2
1
1
3
−
2
2
4
sin
5
a =−
3
cos
5
b =
3
,0 ,
22
ab




( )
cos .ab−
7
.
25
0.
1.−
33
.
65
−
,

5
sin ,
13 2

=


3
cos , 0
52


=


( )
cos

−
16
65
18
65
−
18
65
16
65
−
tan
3

+


3
sin
52

=


48 25 3
11
+
8 5 3
11
−
83
11
−
48 25 3
11
−
sin sin
33
M x x

= − + +
3 sinMx=
cos3Mx=−
3 sinMx=−
cos3Mx=
tan 2=
π
tan
4

−


1
3
1
3
−
2
3
4
sin
5
a =
2
a

tan
6
a

−


48 25 3
11
−+
48 25 3
39
−+
48 25 3
11
+
48 25 3
39
+
5
tan
7
x =
5sin 2 7 cos 2P x x=+
13P =
7P =
2P =
9P =
sin cos m

+=
cos
4
P

=−


m
2
m
2
m
2m
2m
53
sin ,cos
13 5
ab= = −
0,
22
ab

( )
cos ab+
63
.
65
−
21
.
65
16
.
65
−
56
.
65
−
,

12
, ,sin , cos
2 3 3
= = −
( )
sin +

5 4 2
.
9
+
5 4 2
.
9
−
2 10 2
.
9
−
2 2 10
.
9
+
−
( )
tan 2 1 2ab+ + =
( )
tan 3 2024 10− + =ba
( )
tan 2023 5− a
8
21
−
7
15
8
21
7
15
−
ABC
( )
sin cos cos sin sinA B C B C+ = +
( ) ( ) ( ) ( )
cos 115 .cos –365 sin 115 .sin –365= + M
( )
cos 245M =−
( )
sin 480M =
( )
sin 245M =−
( )
cos 480M =
( ) ( )
sin cos cos sinA x y y x y y= − + −
cosAx=
sinAx=
sin .cos 2A x y=
cos .cos 2A x y=
1
sin cos
2
xx+=
sin 2x
3
4
3
8
2
2
3
4
−
2
1 sin
cos
4 2 2
aa
−

+=


2
1 sin
cos
4 2 2
aa
+

+=


2
1 cos
cos
4 2 2
aa
−

+=


2
1 cos
cos
4 2 2
aa
+

+=


2sin sin
44


+−
sin 2
cos 2
sin
cos
4cos .sin
63


−−
2
3 4sin
−+
2
4 3sin
+
2
3 4sin
−
2
sin
cos 2 m
=
m
22
2sin 4 cosA

=+
3Am=+
42Am=+
4Am=+
3Am=−
ABC
2sin .sin 1 cos ,A B C=+
ABC
.C
ABC
.A
ABC
.C
ABC
.A
ABC
sin 2sin cosA B C=
50 ,A =
60 .B =
75 .C =
65 .B =
55 .C =
tan 2,
=
2tan tan 2 .P

=+
8
.
3
P =
2
.
3
P =
4
.
3
P =
2.P =
1
sin cos ,
2

+=
3
sin2 .
8
=
3
sin2 .
4
=−
3
sin2 .
4
=
3
sin2 .
8
=−
5
cos .cos .
12 12
A

=
3
.
4
A =
1
.
2
A =
1
.
4
A =
3.A =
4
sin .cos 2 cos 4x a b x x= + +
, , .abc
.= + +S a b c
1S =
1S =−
4S =
0S =
;
2




1
sin .
5
=
sin
6

+


15 5
.
10
−
15 5
.
5
−
15 2 5
.
5
−
15 2 5
.
10
−
1
cos
3
=
1
cos
4
=
( ) ( )
cos .cos
−+
25
144
19
144
−
5
144
119
144
−
inx
2
2cos 1
s cos
x
A
x
−
=
+
sin cos .A x x=−
cos sin .A x x=+
sin cos .A x x= − −
cos sin .A x x=−
sin sin 3
2cos
xx
A
x
+
=
sin 4 .=Ax
sin .=Ax
sin 2 .=Ax
cos2 .=Ax
4sin 2 .cos 2
cos3 cos
xx
xx+
sin 2
cos
ax
bx
,,
a
ab
b
2
ab+
2
5−
5
3
cos cos5
sin 4 sin 2
aa
P
aa
−
=
+
sin 4 sin 2 0aa+
2cotPa=
2cosPa=
2 tanPa=
2sinPa=
2sin 2 sin 4
2sin 2 sin 4


−
+
2
tan
2
tan
−
2
tan 2
2
cot
sin sin3
2cos
+
=
xx
A
x
sin4=Ax
sin=Ax
sin2=Ax
cos2=Ax
sin 7 sin 5
sin 7 sin 5


−
+
tan 5 .tan

cos .sin

cos 2 .sin 3

cot 6 . tan

1
tan .
3
=x
cos5 cos3
.
sin 5 sin 3
+
=
−
xx
I
xx
1
3
I =
1
3
I =−
3I =
3I =−
sin sin 2 sin3
cos cos2 cos3
M
++
=
++
tan2 .M
=
cot2 .M
=
tan2 .M
=−
cot2 .M
=−
1 sin 4 cos 4
1 sin 4 cos 4


+−
++
2
cos
2
cot
2
tan
2
sin
sin 2 sin
1 cos cos 2
xx
P
xx
−
=
−+
cotPx=
tanPx=
cosPx=
sinPx=
1
1 .tan
cos 2
Bx
x

=+


tan 2x
cot 2x
cos 2x
sin x
2
1 cos cos 2 cos3
2cos cos 1

+ + +
+−
2 c os
−
cos
2 cos
2si n
2
sin 2 sin 5 sin 3
1 cos 2sin 2
a a a
A
aa
+−
=
+−
cosa
sin a
2 cos a
2sin a
( ) ( )
22
tan cot tan cot
cot tan
x x x x
A
xx
+ − −
=
−
2
cot 2
A
x
=
4A =
4
cot 2
A
x
=
8
cot 2
A
x
=
cos 2sin ,

=
1
tan .
2
=
1
sin .
5
=
cot 2.
=
45
sin2 .
5
=
,,
( )
tan .sin cos
+=
45
+ + =
60
+ + =
90
+ + =
120
+ + =
2
sin sin .
3
M


= + +


2.
3
.
2
3.
1.
47
sin cosxx+
2
2
1
2
1
sin 3cos

+
2
13−−
2−
0
,Mm
66
sin cosP

=+
40Mm+=
42Mm+=
44Mm+=
41Mm+=
0
2
x

44
sin cosP x x=+
1
1
2
1
4
0
ABC
2cos 2 cos 2 3 cos= + +P A B C
23
73
3
53
3
23
3
00
75
cos795 , sin18 , tan ,cot
12 8

0 0 0 0 0 0
795 75 2.360 30 45 2.360= + = + +
0 0 0 0 0 0
3 2 1 2 6 2
cos795 cos75 cos30 cos45 sin30 sin45 . .
2 2 2 2 4
−
= = − = − =
0 0 0
54 36 90+=
00
sin54 cos36=
( )
0 0 2 0
cos36 cos 2.18 1 2sin 18= = −
( ) ( ) ( )
0 2 0 0 2 0 0 2 0 0 2 0
sin18 . 1 2sin 18 2sin18 cos 18 sin18 . 1 2sin 18 2sin18 1 sin 18= − + = − + −
0 3 0
3sin18 4sin 18 .=−
( )( )
0 3 0 2 0 0 2 0 0
3sin18 4sin 18 1 2sin 18 sin18 1 4sin 18 2sin18 1 0− = − − + − =
0
sin18 1=
0
51
sin18
2
−
=
0
51
sin18
2
+
=
0
0 sin18 1
0
51
sin18
2
−
=
tan tan
7 3 1
34
tan tan 2 3
12 3 4
13
1 tan tan
34


+

+
= + = = = − −

−

−
5
cot cot tan .
8 2 8 8

= + = −


2
2tan
8
1 tan tan 2.
48
1 tan
8


= = =


−
22
1 tan 2tan tan 2tan 1 0
8 8 8 8
− = + − =
tan 1 2
8
= − −
tan 1 2
8
= − +
tan 0
8
tan 1 2.
8
= − +
5
cot 1 2.
8
=−
0
0
11
cos290
3 sin250
A =+
( )( )
00
1 tan20 1 tan25B = + +
0 0 0 0
tan9 tan27 tan63 tan81C = − − +
22
22
sin sin sin sin
9 9 9 9
D
= + +
( ) ( )
0 0 0 0 0 0 0
cos290 cos 180 90 20 cos 90 20 sin20= + + = − + =
( ) ( )
0 0 0 0 0 0 0
sin250 sin 180 90 20 sin 90 20 cos20= + − = − − = −
00
00
0
0 0 0 0 0
31
cos20 sin20
1 1 3 sin 20 sin20
22
4
sin20
3 cos20 3 sin20 .cos20 3.2.sin 20 .cos20
C
−
−
= − = =
0 0 0 0 0
00
sin60 cos20 cos60 sin20 4sin40 4 3
4.
3
3 sin40 3sin40
−
= = =
0 0 0 0 0 0
0 0 0 0
sin20 sin25 sin20 cos20 sin25 cos25
1 1 .
cos20 cos25 cos20 cos25
B
++
= + + =
0 0 0 0 0 0 0 0
00
sin20 cos45 cos20 sin45 sin25 cos45 cos25 sin45
2. . 2.
cos20 cos25
++
=
00
00
sin65 sin70
2 2.
cos20 cos25
==
( )
00
0 0 0
00
tan20 tan25
tan45 tan 20 50
1 tan20 tan25
+
= + =
−
00
0 0 0 0
00
tan20 tan25
1 tan20 tan25 tan20 tan25 1
1 tan20 tan25
+
= + + =
−
( )( )
00
1 tan20 1 tan25 2 + + =
2.B =
( )
0 0 0 0
tan9 tan81 tan27 tan63C = + − +
0 0 0 0 0 0 0 0
0 0 0 0
sin9 cos81 sin81 cos9 sin27 cos63 sin63 cos27
cos9 cos81 cos27 cos63
++
=−
( )
00
0 0 0 0 0 0 0 0
2 sin54 sin18
1 1 2 2
cos9 sin9 cos27 sin27 sin18 sin54 sin18 sin54
−
= − = − =
00
00
4cos36 .sin18
4
sin18 .sin54
==
2
22
2 2 2 2
sin sin sin sin sin sin sin sin
9 9 9 9 9 9 9 9
D

= + + = + −


2
2
1 1 1
2sin cos cos cos cos cos
6 18 2 3 9 18 2 2 9
1 cos
1 1 3
9
cos .
2 2 2 9 4
= + − = + −
+

= + − =


13
sin 3 cos 2 sin cos 2sin( )
2 2 3
x x x x x

= =



31
3 sin cos 2 sin cos 2sin( )
2 2 6
x x x x x

= =



11
sin cos 2 sin cos 2 sin( )
4
22
x x x x x

= =


sin cos .cos .cos ;
32 32 16 8
A
=
sin10 .sin30 .sin50 .sin70 ;B =
3
cos cos ;
55
C

=+
2 2 2
23
cos cos cos .
7 7 7
D
= + +
11
2sin cos .cos .cos sin .cos .cos
2 32 32 16 8 2 16 16 8
A

==


1 1 2
sin .cos sin
4 8 8 8 4 16
= = =
00
1
cos20 cos40 cos80
2
o
B =
0 0 0 0
16sin20 . 8sin20 cos20 cos40 cos80
o
B =
0 0 0 0 0
4sin40 cos40 cos80 2sin80 cos80 sin160 .
o
= = =
0
0
sin160 1
16
16sin20
B ==
2
2cos cos
55
C

=
sin 0
5
2 2 2 4
2sin . 4sin cos cos 2sin cos sin .
5 5 5 5 5 5 5
C
= = =
1
.
2
C =
2 4 6
1 cos 1 cos 1 cos
3 1 2 4 6
7 7 7
cos cos cos
2 2 2 2 2 7 7 7
D
+++

= + + = + + +


2 4 6
cos cos cos .
7 7 7
T
= + +
sin 0
7
2 4 6
2sin 2sin cos 2sin cos 2sin cos
7 7 7 7 7 7 7
T
= + +
3 5 3 5
sin sin sin sin sin sin sin .
7 7 7 7 7 7
= − + − + − = −
1
2
T =−
3 1 1 5
.
2 2 2 4
D

= + − =


,

2
sin sin
2

+=
6
cos cos
2

+=
( )
cos

−
( )
sin

+
22
21
sin sin sin sin 2sin sin
22
+ = + + =
22
63
cos cos cos cos 2cos cos
22
+ = + + =
( ) ( )
2 2 2 2
sin sin cos cos 2sin sin 2cos cos 2
2 2 sin sin cos cos 2 2cos 0
+ + + + + =
+ + = − =
( )
cos 0.

−=
( )( )
26
sin sin cos cos .
22
+ + =
( ) ( )
3
sin cos sin cos sin cos sin cos
2
13
sin2 sin2 sin
22
+ + + =
+ + + =
( ) ( )
sin2 sin2 2sin cos 0
+ = + − =
( )
cos 0

−=
( )
3
sin .
2

+=
4
cos2
5
x =−
42
x


sin , cos , sin , cos 2
34
x x x x

+−
42
x


sin 0, cos 0xx
2
1 cos2 9 3
sin sin ;
2 10
10
x
xx
−
= = =
2
1 cos2 1 1
cos cos .
2 10
10
x
xx
+
= = =
3
sin2 2sin cos .
5
x x x==
3 1 1 3 3 3
sin sin cos cos sin . . ;
3 3 3 2 2
10 10 2 10
x x x

+
+ = + = + =


4 2 2 3 2
cos 2 cos2 sin cos sin2 . . .
4 4 4 5 2 2 5 10
x x x

− = + = − + = −


2
cos4 2 6sin

+=
2


tan 2
( )
22
cos4 2 6sin 2cos 2 1 2 3 1 cos2
+ = − + = −
2
1
cos2
2cos 2 3cos2 2 0
2
cos2 2

=
+ − =
=−
1
cos2
2
=
cos2 2 0
+
22
22
11
1 tan 2 tan 2 1 3.
cos 2 cos 2


+ = = − =
22
2
sin2 0.
cos2 0
tan2 0.
tan2 3.
=−
2 2 2 2
1 1 1 1
7
tan cot sin cos
+ + + =
cos4
22
2 2 2 2 2 2
1 1 1 1 sin 1 cos 1
77
tan cot sin cos cos sin

++
+ + + = + =
( ) ( )
( )
( )
( )
2 2 2 2
22
4 4 2 2
2
2 2 2 2 2 2
2
22
2
sin sin 1 cos cos 1
7
sin cos
sin cos 1 7sin cos
sin cos 2sin cos 1 7sin cos
2 9sin cos 8 9 2sin cos
7
8 9sin 2 16 9 1 cos4 cos4 .
9

+ + +
=
+ + =
+ − + =
= =
= = − = −
7
cos4 .
9
=−
sin cos cot
2

+=
0


2013
tan
2


+


2
2
sin 2tan
22
sin 2sin cos 2cos .
2 2 2
cos tan 1
22


= = =
+
22
2 2 2
22
sin 1 tan
22
cos cos sin cos 1
2 2 2
cos tan 1
22



−

= − = − =


+


2
22
2tan 1 tan
1
22
sin cos cot
2
tan 1 tan 1 tan
2 2 2


−
+ = + =
++
2 2 3 2
2
tan 1 2tan tan 1 tan tan tan tan 1 0
2 2 2 2 2 2 2
tan 1 tan 1 0 tan 1
2 2 2

+ − = + − − + =


− + = =
00
22


tan 0
2
tan 1 cot 1
22

= =
2013
tan tan 2006 cot 1
2 2 2 2
+
= + + = − = −
2013
tan 1.
2


+
=−


sin ,cos ,tan ,cot
tan
2
t
=
22
2 2 2
2 1 2 1
sin ,cos ,tan ,cot
2
1 1 1
t t t t
t
t t t
−−
= = = =
+ + −
( )
1
sin , tan 2tan
3
+ = = −
35
sin cos sin sin
8 8 12 12
A
= + + + − −
( )
11
sin sin cos cos sin
33
+ = + =
tan 2tan sin cos 2sin cos
= − = −
( )
( )
2 2 2 2
2 2 2 2
1 1 1
cos sin cos sin 1 sin sin
3 9 9
2 4 4
sin cos sin cos sin 1 sin
3 9 9
= − = − =

= − = − =
( )
22
22
22
2
4 2 2 2
1
1 sin sin
11
9
1 sin sin
1
39
sin sin
3
2 1 1 1
sin sin 0 sin 0 sin .
3 9 3 3



−=

− − =


−=

− + = − = =


22
12
sin sin .
33

= + =
3 1 1 2
sin cos sin 2 sin cos2
8 8 2 2 4 2 2


+ + = + − = −





2
1 2 1 2 2 2 3 2
1 2sin 1 2.
2 2 2 3 2 12
+
= − − = − − = −
5 1 1 3
sin cos sin 2 sin cos2
12 12 2 2 3 2 2


− − = − + = − +





2
1 3 1 1 3 2 3 2
1 2sin 1 2.
2 2 2 3 2 12
−+
= − + + = − + + =
2 3 2 2 3 2 1
12 12 3
A
+ − +
= − + = −
44
3 cos4
sin cos ;
44

+ = +
66
53
sin cos cos4 ;
88
+ = +
2
1 sin2
cot .
1 sin2 4


−
=+

+

( )
2
4 4 2 2 2 2 2
1
sin cos sin cos 2sin cos 1 sin 2
2
+ = + − = −
1 cos4 3 cos4
1
4 4 4

−
= − = +
( ) ( ) ( )( )
33
6 6 2 2 2 2 4 2 2 4
sin cos sin cos sin cos sin sin cos cos
+ = + = + − +
( )
4 2 2 4 2 2 2
33
sin sin cos cos 1 3sin cos 1 sin 2 1 1 cos4
48
53
cos4 .
88
= − + = − = − = − −
=+
( )
( )
2
22
2 2 2
sin cos
1 sin 2 sin cos 2sin cos
1 sin2
sin cos 2sin cos
sin cos


−
− + −
==
+
++
+
2
2
2
2
2
2 cos
2cos
4
4
cot .
4
2sin
2 sin
4
4



+
+





= = = +





+

+





2
2
2
2
1 tan tan
1 cos sin 1 sin2
4
cot .
4 cos sin 1 sin2
tan tan
tan
4
4



−

−−

+ = = = =


++


+
+






0,
2
1 cos 1 cos 2sin ;
24



+ + − = +


1 cos 1 cos
tan .
24
1 cos 1 cos


+ + −
=+

+ − −

3
0
4 2 4 4

⎯⎯→ +
sin 0,sin 0
24


+


( )
2
2
1 cos 1 cos 4sin
24



+ + − = +


2
2 2 1 cos 1 cos 2 1 cos 1 cos sin
2


+ + − = − + − =




2 2 2 2
1 cos sin sin cos 1
− = + =
( )
( )( )
2
1 cos 1 cos
1 cos 1 cos 1 cos 1 cos
VT

+ + −
=
+ − − + + −
2
1 sin
2 2 1 cos . 1 cos 1 1 cos
.
2cos cos cos
+
+ + − + −
= = =
0


sin 0
2
22
22
sin cos
sin cos 2sin cos
22
1 sin
2 2 2 2
cos
cos sin
sin cos cos sin
22
2 2 2 2
VT



+
++

+

= = =
−
+−
2 sin
sin cos
24
22
tan
24
cos sin
2 cos
22
24
VP






+
+



= = = + =



−
+


22
sin( ).sin( ) sin sin ;
+ − = −
cot cot 2
22

=
( )
sin sin 3sin , 2 , ;b k k
+ = + +
( )
( )
( )
sin sin cos
tan .
cos sin sin

++
=+
−+
1
sin( ).sin( ) cos2 cos2
2

+ − =− −

( ) ( )
2 2 2 2
1
1 2sin 1 2sin sin sin
2

= − − − − = −

2sin cos 6sin cos
2 2 2 2
+ − + +
=
2 sin 0
2
k

+
+
cos 3cos
22
−+
=
cos cos sin sin 3 cos cos sin sin
2 2 2 2 2 2 2 2

+ = −


2sin sin cos cos
2 2 2 2
=
cot cot 2
22

=
( ) ( )
( ) ( )
( )
( )
1
sin sin 2 sin
sin sin 2
2
1 cos cos 2
cos cos 2 cos
2
VT

+ + + −
++

==

++

− − + − −



( ) ( )
( ) ( )
( )
2sin cos
tan
2cos cos
VP

+−
= = + =
+−
x
2 2 2
22
cos cos cos ;
33
A

= + + + −
3
cos .cos cos .cos .
3 4 6 4
B
= − + + + +
2 2 2
22
cos cos cos
33
A

= + + + −
1 4 4
3 cos2 cos 2 cos 2
2 3 3


= + + + + −


1 4 3
3 cos2 2cos cos2 .
2 3 2


= + + =


cos sin
6 3 2 6 3
+ = − + + = − −
3
cos sin
44


+ = − +
cos .cos sin .sin
3 4 3 4
B
= − + + − +
cos cos cos
3 4 3 4 3 4
1 2 3 2 2 6
cos cos sin sin . . .
3 4 3 4 2 2 2 2 4


= − − + = − − = +






−
= − = − =
cos 2cos2 cos3
;
sin sin2 sin3
a a a
A
a a a
++
=
++
cos cos
33
;
cot cot
2
aa
B
a
a

+ + −
=
−
( )
cos cos( ) cos( 2 ) ... cos( ) .C a a b a b a nb n= + + + + + + +
( )
( )
( )
( )
cos cos3 2cos2 2cos2 cos 1
2cos2 cos 2cos2
cot2
2sin2 cos 2sin2
sin sin3 2sin2 2sin2 cos 1
a a a a a
a a a
Aa
a a a
a a a a a
+ + +
+
= = = =
+
+ + +
cos cos 2cos cos cos
3 3 3
a a a a
+ + − = =
sin
cos sin cos cos sin sin
2
cos 1
2 2 2 2
cot cot .
2 sin sin
sin sin sin sin sin sin sin
2 2 2 2
a
a a a a
a
aa
aa
a
a a a a
aa
a a a

−
−−


− = − = = = = −
cos sin2
sin cos
1
2
sin
aa
B a a
a
= = − = −
−
.2sin 2sin cos 2sin cos( ) 2sin cos( 2 ) ... 2sin cos( )
2 2 2 2 2
b b b b b
C a a b a b a nb= + + + + + + +
( ) ( )
3 5 3
sin sin sin sin sin sin
2 2 2 2 2 2
2 1 2 1
... sin sin
22
b b b b b b
a a a a a a
n b n b
aa
= + + − + + + − − + + + − −
+−
+ + + + − −
( )
( )
21
sin sin 2sin 1 cos
2 2 2
nb
b nb
a a n b a

+
− + + = + −



( )
sin 1 cos
2
.
sin
2
nb
n b a
C
b

+−


=
( ) ( )
sin 2cosa b a b+ = −
11
2 sin2 2 sin2
M
ab
=+
−−
,ab
( )
( )( )
( )
( )
4 sin2 sin2 4 sin2 sin2
2 sin2 2 sin2 4 2 sin2 sin2 sin2 sin2
a b a b
M
a b a b a b
− + − +
==
− − − + +
( ) ( )
sin2 sin2 2sin cosa b a b a b+ = + −
( ) ( ) ( ) ( )
22
sin 2cos sin 4cosa b a b a b a b+ = − + = −
( ) ( ) ( ) ( )
22
cos2 cos2 1 2sin 2cos 1a b a b a b a b

+ − − = − + − − −

( ) ( ) ( )
2 2 2
2 2 sin cos 2 10cosa b a b a b

= − + + − = − −

( )
( ) ( )
( )
( )
22
2
22
4 4cos 4 4cos
4
.
1
3
3 3cos
4 8cos . 2 10cos
2
a b a b
M
ab
a b a b
− − − −
= = =
−−

− − − − −

0
2

2
2cot 1 cos2 ;

+
cot 1 cot 2 .

+
22
22
2 4 2
2
11
2 1 2cos 1 1 sin
sin sin
1
sin 2 sin 2sin 1 0
sin



− − −


+ − +
( )
2
2
sin 1 0
−

Tài liệu khác của Toán 11

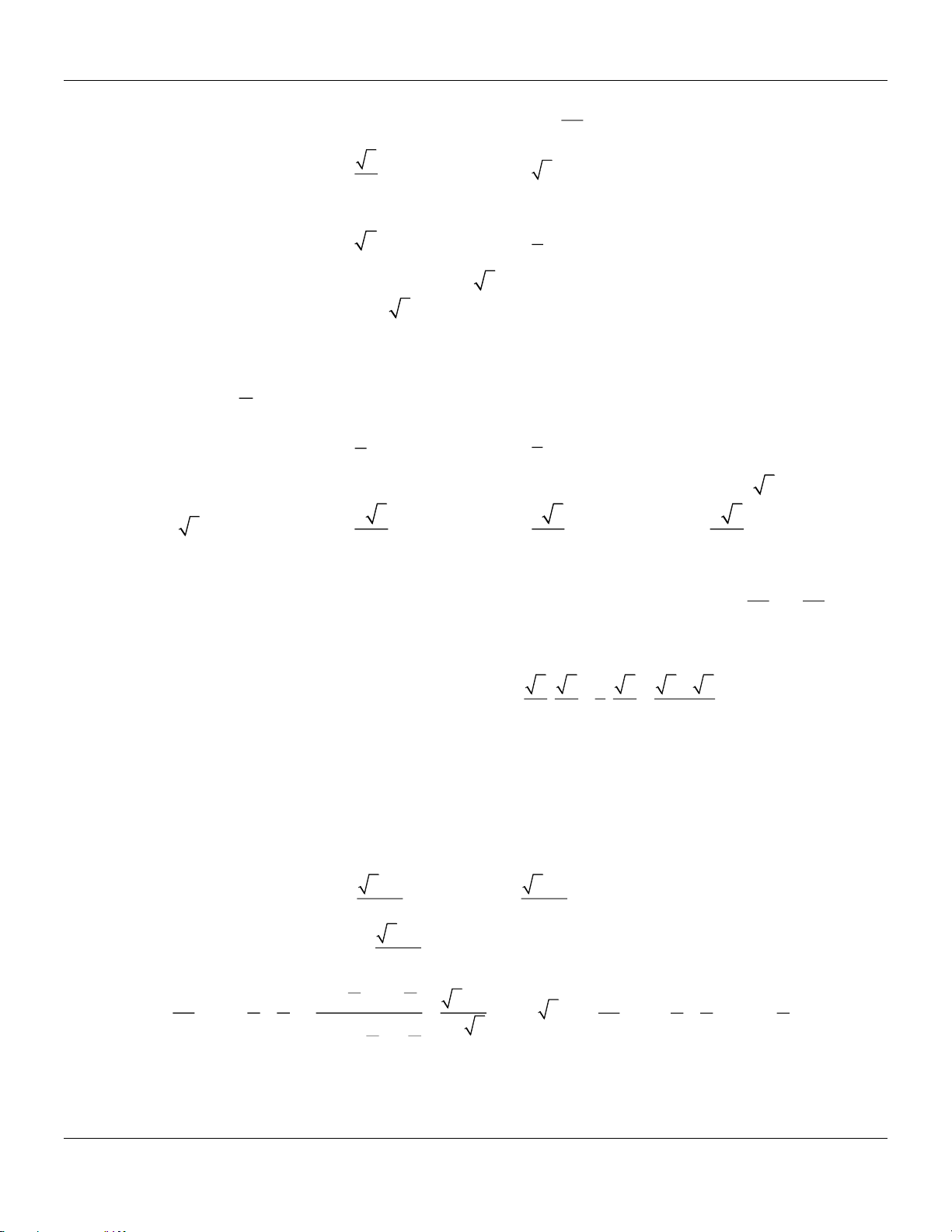
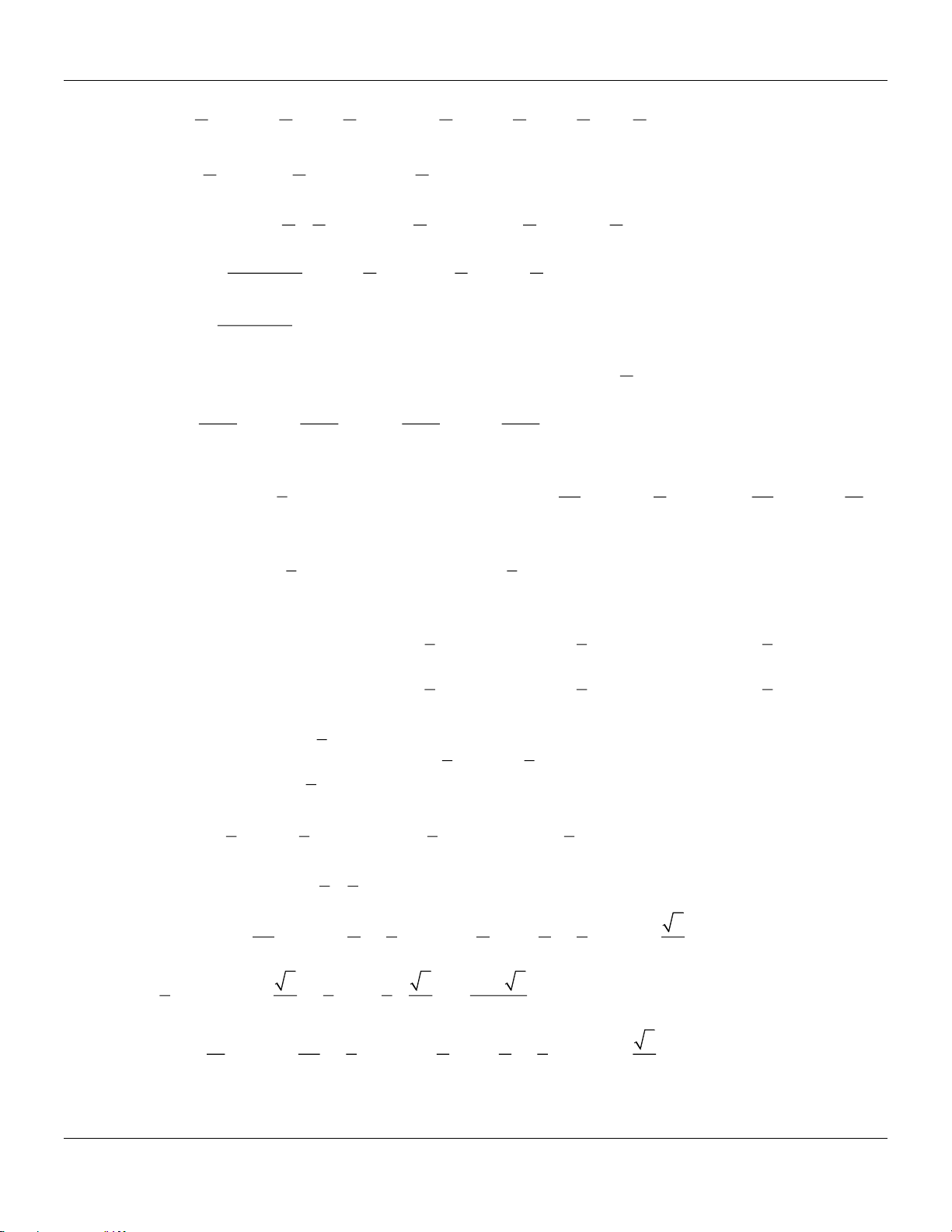
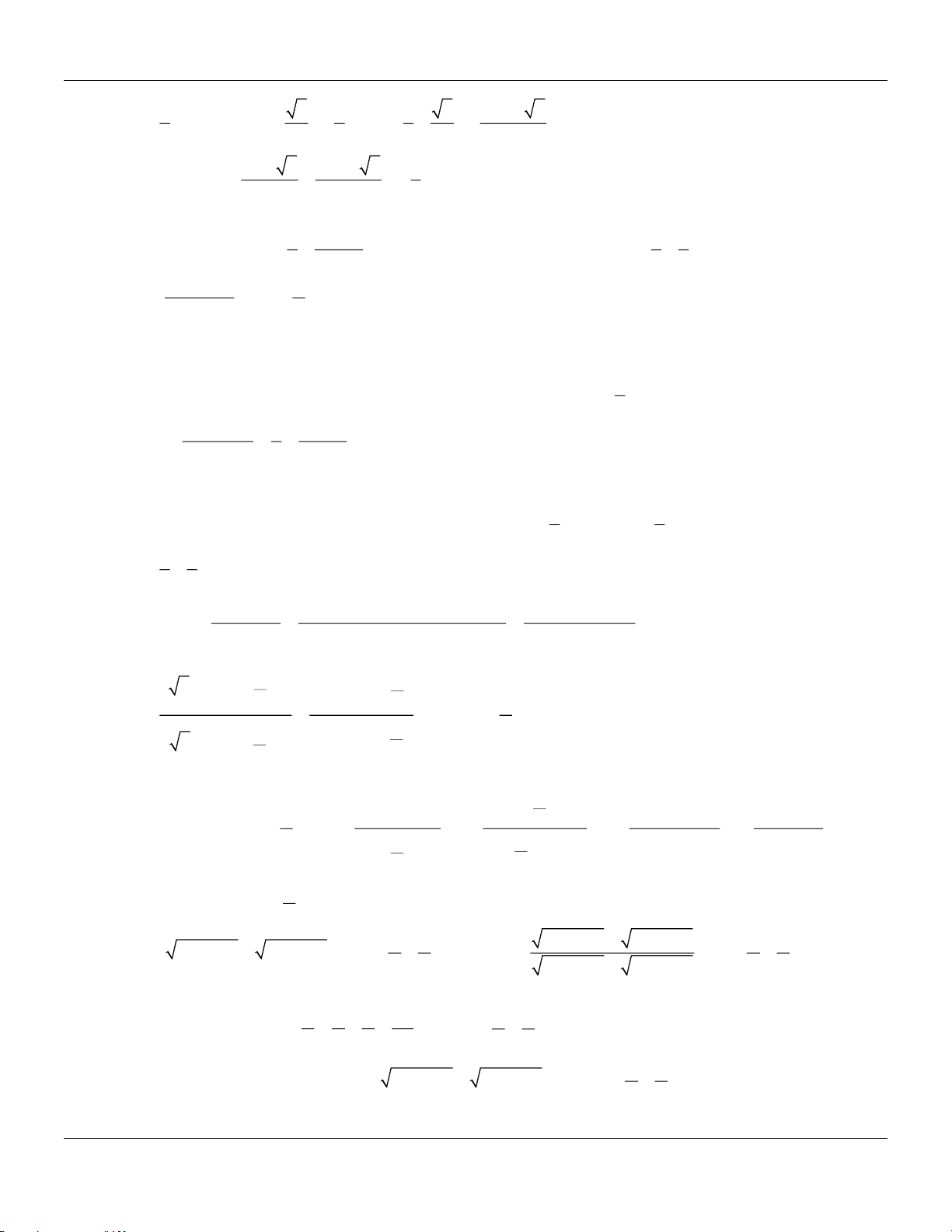
Preview text:

LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ TOÁN 11 Chuyên đề LƯỢNG GIÁC CÔNG THỨC LƯỢNG GIÁC
 LUYỆN THI THPT QUỐC GIA
 CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề LƯỢNG GIÁC Toán 11 KNTT CHƯƠNG I
HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC Chủ đề 2:
CÔNG THỨC LƯỢNG GIÁC I. TÓM TẮT LÝ THUYẾT 1. CÔNG THỨC CỘNG
sin (a + b) = sin c a osb + cos s a inb
sin (a − b) = sin c
a osb − cos sin a b
cos(a + b) = cos c a osb − sin s a inb
cos(a − b) = cos c a osb + sin s a inb a − b a + b (a−b) tan tan tan = (a+b) tan tan tan = 1 + tana ta . nb 1 − tana ta . nb
(giả sử các biểu thức đều có nghĩa)
2. CÔNG THỨC NHÂN ĐÔI sin2a = 2sina c . osa
cos2a = cos2a − sin2a = 2cos2a − 1 = 1 − 2sin2a 2tana tan2a = 1 − tan2a
(giả sử các biểu thức đều có nghĩa)
3. CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG 1 sina c . osb = sin 
(a −b)+sin(a+ b) 2 1 sin a s . inb = cos 
(a −b)−cos(a +b) 2 1 cosa c . osb = cos 
(a −b)+ cos(a +b) 2
4. CÔNG THỨC BIẾN ĐỔI TỔNG THÀNH TÍCH a + b a − b a + b a − b sina + sinb = s 2 in cos
sina − sinb = 2cos sin 2 2 2 2 a + b a − b a + b a − b
cosa + cosb = 2cos cos
cosa − cosb = − s 2 in sin 2 2 2 2
5. MỘT SỐ KẾT QUẢ CẦN LƯU Ý
1) sin a = sina − sin3 3 3 4 a cos a = cos3 3 4 a − 3cosa a 2 2t 1 − t 2t
2) Đặt t = tan . Lúc đó: sina = ; cosa = ; tana = 2 2 2 2 1 + t 1 + t 1 − t       3) sina + cosa = s 2 in a +  
cosa − sina = 2cos a +    4   4  2 2
1 + sin2a = (sina + cosa)
1 − sin2a = (sina − cosa)
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề LƯỢNG GIÁC Toán 11 KNTT 2 tana + cota =
cota − tana = 2cot2a sin2a
(giả sử các biểu thức đều có nghĩa)
II. BÀI TẬP MINH HỌA  
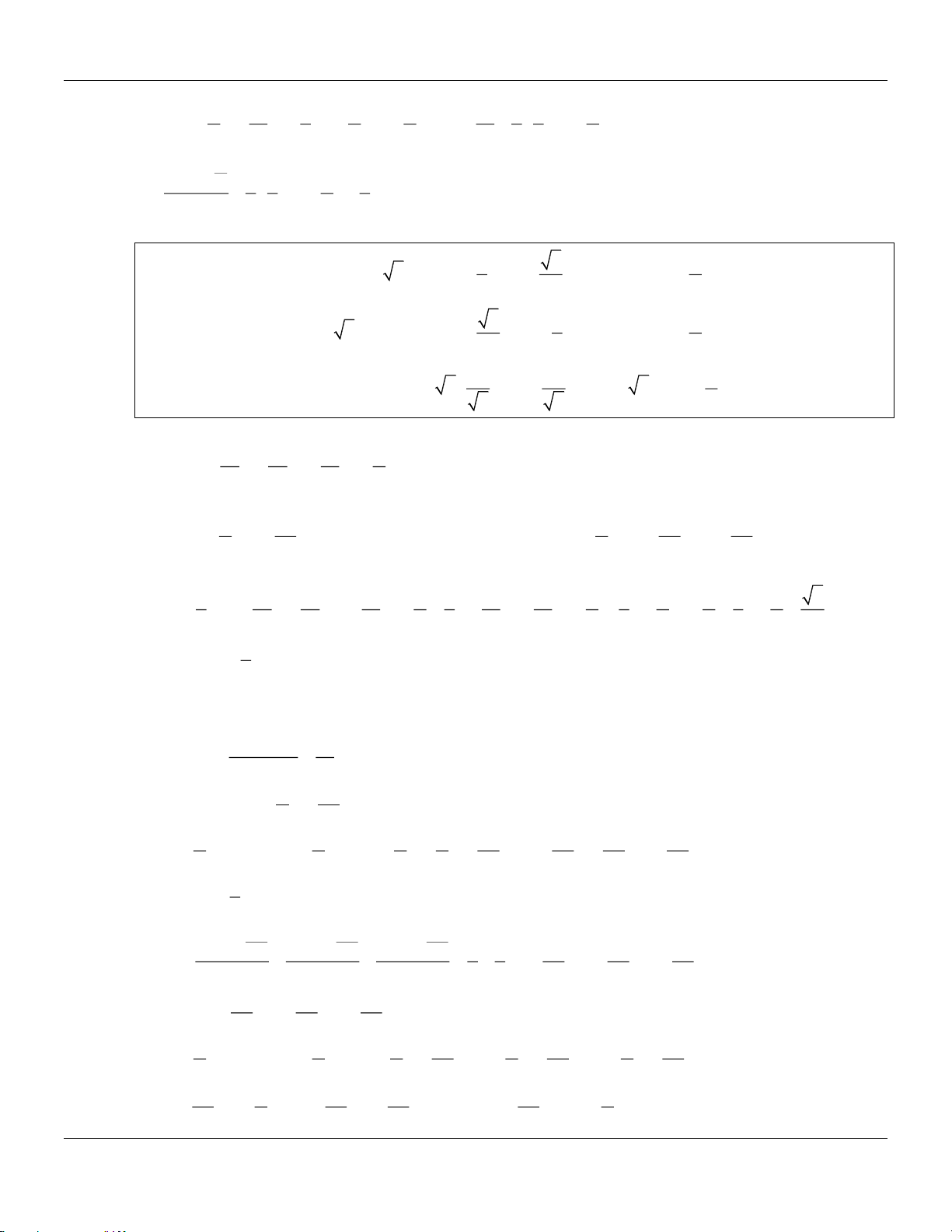
Câu 1: Không sử dụng máy tính, tính các giá trị lượng giác sau: 0 0 7 5 cos795 , sin18 , tan ,cot . 12 8
Câu 2: Không sử dụng máy tính, tính giá trị biểu thức lượng giác sau: 1 1 a) A = + b) B = ( 0 + )( 0 1 tan 20 1 + tan 25 ) 0 0 cos 290 3 sin 250     c) 0 0 0 0
C = tan 9 − tan 27 − tan 63 + tan 81 d) 2 2 2 2 D = sin + sin + sin sin 9 9 9 9
Câu 3: Không sử dụng máy tính, tính giá trị biểu thức lượng giác sau:     a) A = sin cos .cos .cos ; b) B = sin10 .  sin 30 .  sin 50 .sin70 ;  32 32 16 8  3  2 3 c) C = cos + cos ; d) 2 2 2 D = cos + cos + cos . 5 5 7 7 7 2 6
Câu 4: Cho  ,  thoả mãn sin + sin  = và cos + cos  =
. Tính cos( −  ) và sin( +  ) . 2 2 4        
Câu 5: Cho cos 2x = − , với
x  . Tính sin x, cos x, sin x + , cos 2x −     . 5 4 2  3   4   Câu 6: Cho 2
cos 4 + 2 = 6 sin  với
    . Tính tan 2 . 2 1 1 1 1 Câu 7: Cho + + + = 7 . Tính cos 4 . 2 2 2 2 tan  cot  sin  cos     + 2013 
Câu 8: Cho sin + cos = cot
với 0     . Tính tan  . 2  2   3      5     Câu 9: Cho ( + ) 1 sin = , tan = 2
− tan  . Tính A = sin  + cos  + + sin  − sin  −         . 3  8   8   12   12 
Câu 10: Chứng minh rằng với mọi góc lượng giác  làm cho biểu thức xác định thì  a) 4 4 3 cos 4 sin  + cos  = + ; b) 6 6 5 3 sin  + cos  = + cos4; 4 4 8 8 1 − sin 2    c) 2 = cot +  . 1 + sin 2  4  
Câu 11: Cho 0     ,  . Chứng minh rằng: 2   1 + cos + 1 − cos     a) 1 cos 1 cos   + + − = 2sin +  ; b) = tan +  .  2 4  1 + cos − 1 − cos  2 4 
Câu 12: Chứng minh rằng: a) 2 2
sin( +  ).sin( −  ) = sin  − sin  ;   b) cot cot
= 2 với sin + sin  = 3sin( +  ), + b k2 ,k ; 2 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề LƯỢNG GIÁC Toán 11 KNTT
sin + sin  cos( +  ) c) = +  −  ( + ) tan( ). cos sin sin
Câu 13: Chứng minh biểu thức sau không phụ thuộc vào x :  2   2  a) 2 2 2 A = cos  + cos + +   cos −  ;  3   3            3 
b) B = cos − .cos +  + cos + .cos + .  3   4   6   4 
Câu 14: Đơn giản biểu thức sau: (giả sử các biểu thức có nghĩa)       cos a + + cos a −    
cos a + 2cos 2a + cos 3a  3   3  a) A = ; b) B = ;
sin a + sin 2a + sin 3a a cot a − cot 2
c) C = cos a + cos(a + b) + cos(a + 2 )
b + ... + cos(a + nb) (n ). 1 1
Câu 15: Cho sin(a + b) = 2cos(a − b) . Chứng minh rằng biểu thức M = + không phụ 2 − sin 2a 2 − sin 2b
thuộc vào a,b . 
Câu 16: Chứng minh rằng với 0    thì 2 a) 2 2 cot   1 + cos 2 ; b) cot  1 + cot 2.   1  1 
Câu 17: Cho 0   
. Chứng minh rằng: sin + cos +     2. 2  2cos  2sin 
Câu 18: Tìm giá trị nhỏ nhất, lớn nhất của biểu thức sau:
a) A = sin x + cos x; b) 4 4 B = sin x + cos . x
Câu 19: Tìm giá trị nhỏ nhất, lớn nhất của biểu thức A = 2 − 2 sin x − cos 2x
Câu 20: Chứng minh trong mọi tam giác ABC ta đều có: A B C
a) sin A + sin B + sinC = 4cos cos cos ; 2 2 2 b) 2 2 2
sin A + sin B + sin C = 2(1 + cos Acos BcosC);
c) sin 2A + sin 2B + sin 2C = 4 sin Asin BsinC.
Câu 21: Chứng minh trong mọi tam giác ABC không vuông, ta đều có:
a) tan A + tan B + tanC = tan . A tan . B tanC; b) cot . A cot B + cot .
B cot C + cot C.cot A = 1.
III. BÀI TẬP TRẮC NGHIỆM
Câu 22: Với a,b là các góc bất kì, đẳng thức nào sau đây sai? + − A. sin − sin = a b a b a b 2cos sin .
B. cos (a − b) = cos a cos b − sin a sin . b 2 2
C. sin (a − b) = sin a cos b − cos a sin . b
D. 2 cos a cos b = cos (a − b) + cos (a + b).
Câu 23: Cho góc x bất kì, đẳng thức nào sau đây đúng?
A. sin 2x = 2sin x cos x . B. sin 2x = sin x cos x . C. sin 2x = 2 cos x .
D. sin 2x = 2 sin x .
Câu 24: Cho góc a bất kì, đẳng thức nào sau đây sai? A. 2
cos 2a = 1− 2sin a . B. 2 2
sin 3a + cos 3a = 3 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề LƯỢNG GIÁC Toán 11 KNTT
C. sin 4a = 2 sin 2a cos 2a .
D. cos (a − b) = cos a cosb + sin a sin b .
Câu 25: Cho góc a bất kì, đẳng thức nào sau đây sai? A. 2
cos 2a = 1− 2sin a . B. 2 2
cos 2a = cos a − sin a . C. 2
cos 2a = 1− 2 cos a . D. 2
cos 2a = 2 cos a −1.
Câu 26: Cho góc a bất kì, đẳng thức nào sau đây sai?
A. cos 2a = 2 cos a −1. B. 2
2sin a = 1− cos 2a .
C. sin (a + b) = sin a cos b + sin b cos a .
D. sin 2a = 2sin a cos a .
Câu 27: Cho góc a bất kì, đẳng thức nào sau đây sai? A. 2
cos 2a = 1− 2sin a .
B. cos 2a = 2sin a cos a C. 2 2
cos 2a = cos a − sin a . D. 2
cos 2a = 2 cos a −1.
Câu 28: Cho góc a bất kì, đẳng thức nào sau đây đúng? A. 2 2
cos 2a = cos a − sin a . B. 2
cos 2a = 2 cos a +1 . C. 2 2
cos 2a = cos a + sin a . D. 2
cos 2a = 2sin a −1 .
Câu 29: Với a,b là các góc bất kì, đẳng thức nào sau đây sai? (giả sử các biểu thức lượng giác đều có nghĩa) a b a b
A. tan(a −  ) = tan . B. sin + − + sin b = 2sin sin . 2 2
C. sin = tan cos .
D. cos(a − b) = sin a sin b + cos a cos b .
Câu 30: Với a,b là các góc bất kì, đẳng thức nào sau đây sai? 1 1
A. sin a sin b = cos 
(a −b)−cos(a +b) c s
o a cosb = cos a – b + cos a + b  . 2  . B.  ( ) ( ) 2  1 1
C. cos a cos b = cos 
(a +b)−cos(a −b) .
sin a cosb = sin a – b + sin a + b  2  D.  ( ) ( ) 2  .
Câu 31: Với a,b là các góc bất kì, đẳng thức nào sau đây đúng?
A. sin (a + b) = sin a sin b − cos a cos b .
B. sin (a + b) = sin a cos b − cos a sin b .
C. sin (a + b) = sin a cos b + cos a sin b .
D. sin (a + b) = sin a sin b + cos a cos b .
Câu 32: Cho góc a bất kì, đẳng thức nào sau đây đúng?    1 3    1 3 A. cos a + = sin a − cos a   . B. cos a + = cos a − sin a   .  3  2 2  3  2 2    1    3 1 C. cos a + = cos a +   . D. cos a + = sin a − cos a   .  3  2  3  2 2
Câu 33: Khẳng định nào sau đây đúng?   A. 4 4 3 cos 4 sin  + cos  = − . B. 4 4 3 cos 4 sin  + cos  = + . 4 4 4 4   C. 4 4 3 cos 4 sin  + cos  = + D. 4 4 3 cos 4 sin  + cos  = − 4 2 2 4
Câu 34: Cho góc x bất kì, đẳng thức nào sau đây sai? 5 3 A. 4 4 3 1
sin x + cos x = + cos 4x . B. 6 6
sin x + cos x = + cos 4x . 4 4 8 4 3 1 C. 4 4
sin x − cos x = − cos 2x . D. 4 4
sin x + cos x = − cos 4x . 4 4
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề LƯỢNG GIÁC Toán 11 KNTT 2
Câu 35: Tính giá trị của biểu thức 4 4
P = sin  + cos , biết sin 2 = . 3 1 9 7 A. . B. 1. C. . D. . 3 7 9   
Câu 36: Biểu thức sin a + 
 được viết lại thành  6  1 3 1 3 1 1 3 A. sin a + . B.
sin a + cos a . C.
sin a − cos a . D. sin a − cos a . 2 2 2 2 2 2 2 sin (a + b)
Câu 37: Biểu thức sin(a− bằng biểu thức nào sau đây? b) sin a + sin b sin a − sin b tan a + tan b cot a + cot b A. . B. . C. . D. . sin a − sin b sin a + sin b tan a − tan b cot a − cot b     sin .cos + sin .cos 15 10 10 15
Câu 38: Giá trị biểu thức 2  2  bằng cos .cos − sin .sin 15 5 15 5 3 3 A. 1. B. 1 − . C. − . D. . 2 2 3 Câu 39: Cho sin = . Tính cos 2 . 4 1 7 7 1 A. . B. . C. − . D. − . 8 4 4 8 1 3
Câu 40: Cho góc lượng giác  thỏa mãn sin = − , và     . Tính sin 2 . 3 2 7 4 2 4 2 2 A. . B. . C. − . D. − . 9 9 9 3 3
Câu 41: Cho cos x = − . Tính cos 2x . 5 7 3 8 7 A. − . B. − . C. − . D. . 25 10 9 25 2
Câu 42: Tính giá trị biểu thức P = (1− 3cos 2 )(2 + 3cos 2 ), biết sin = . 3 49 50 48 42 A. . B. . C. . D. . 27 27 27 27 1
Câu 43: Cho biết sin x + cos x = − . Tính sin 2x . 2 3 3 1 A. − . B. . C. . D. 1 − . 4 4 2 
Câu 44: Cho góc  thỏa mãn
    và sin + 2cos = 1
− . Tính giá trị sin 2α. 2 2 6 24 2 6 24 A. . B. . C. − . D. − . 5 25 5 25
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề LƯỢNG GIÁC Toán 11 KNTT  2 1+ sin 2 + cos 2
Câu 45: Cho góc  thỏa mãn 0    và sin = . Tính P = 2 3 sin + . cos 2 5 3 2 5 3 A. P = − . B. P = . C. P = . D. P = − . 3 2 3 2   
Câu 46: Cho tan = 2 . Giá trị tan  −   bằng  4  1 2 1 A. . B. . C. 1 . D. − . 3 3 3 1 3
Câu 47: Cho  và  là hai góc nhọn mà tan = và tan  =
. Góc  +  có giá trị bằng 7 4     A. . B. . C. . D. . 6 4 3 2   
Câu 48: Nếu tan + cot  = 2 , 0      thì sin 2 bằng  2   1 2 A. . B. 1. C. − . D. . 2 3 2 4 3    
Câu 49: Biết sin a = − , cos b = 3   a  ,0  b  
, tính cos(a − b). 5 5  2 2  7 33 A. . B. 0. C. −1. D. − . 25 65 5    3   
Câu 50: Cho hai góc  ,  thỏa mãn sin = ,     
 và cos  = , 0      . Tính giá trị 13  2  5  2 
đúng của cos ( −  ) . 16 18 18 16 A. . B. − . C. . D. − . 65 65 65 65    3   
Câu 51: Giá trị của tan  + 
 bằng bao nhiêu khi sin =       ?  3  5  2  48 + 25 3 8 − 5 3 8 − 3 48 − 25 3 A. . B. . C. . D. . 11 11 11 11      
Câu 52: Rút gọn biểu thức M = sin − x + sin +    x  ta được  3   3 
A. M = 3 sin x .
B. M = − 3 cosx .
C. M = − 3 sin x .
D. M = 3 cosx .  π 
Câu 53: Cho tan = 2 . Tính tan  −   .  4  1 1 2 A. . B. − . C. 1. D. . 3 3 3 4    
Câu 54: Cho sin a = với
a   . Tính tan − a   . 5 2  6  4 − 8 + 25 3 4 − 8 + 25 3 48 + 25 3 48 + 25 3 A. . B. . C. . D. . 11 39 11 39
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề LƯỢNG GIÁC Toán 11 KNTT 5
Câu 55: Cho biết tan x =
. Tính giá trị của biểu thức P = 5sin 2x + 7 cos 2x . 7 A. P = 13 . B. P = 7 . C. P = 2 . D. P = 9 .   
Câu 56: Biết sin + cos = m . Tính P = cos  −   theo m .  4  m m A. . B. . C. 2m . D. m 2 . 2 2 5 3  
Câu 57: Biết sin a =
,cosb = − với 0  a  ,  b   . Tính cos(a + b) . 13 5 2 2 63 21 16 56 A. − . B. . C. − . D. − . 65 65 65 65  1 2
Câu 58: Cho các góc  ,  thỏa
 ,    ,sin = ,cos  = − . Tính sin ( +  ) . 2 3 3 5 + 4 2 5 − 4 2 2 10 − 2 2 + 2 10 A. . B. . C. . D. − . 9 9 9 9
Câu 59: Cho tan (2a + b + )
1 = 2 ; tan (b − 3a + 2024) =10 . Giá trị của tan (2023 − 5a) bằng: 8 7 8 7 A. − . B. . C. . D. − . 21 15 21 15
Câu 60: Cho ABC nếu có quan hệ sin A(cos B + cosC) = sin B + sinC thì đó là tam giác gì? A. Tam giác đều. B. Tam giác cân.
C. Tam giác vuông cân. D. Tam giác vuông.
Câu 61: Rút gọn biểu thức M = cos (115).cos ( –365) + sin (115).sin (–365) . A. M = cos ( 24
− 5) . B. M = sin (480) . C. M = sin ( 2
− 45) . D. M = cos(480).
Câu 62: Rút gọn biểu thức A = sin ( x − y) cos y + cos ( x − y)sin y .
A. A = cos x .
B. A = sin x . C. A = sin .
x cos 2 y . D. A = cos . x cos 2y . 1
Câu 63: Nếu sin x + cos x = thì sin 2x bằng 2 3 3 2 3 A. . B. . C. . D. − . 4 8 2 4
Câu 64: Chọn đẳng thức đúng.
  a  1−sin a
  a  1+ sin a 2 2 A. cos + =   . B. cos + =   .  4 2  2  4 2  2
  a  1− cos a
  a  1+ cos a 2 2 C. cos + =   . D. cos + =   .  4 2  2  4 2  2      
Câu 65: Biểu thức 2sin + sin −     bằng  4   4  A. sin 2 . B. cos 2 . C. sin  . D. cos .      
Câu 66: Biểu thức 4 cos − .sin −     bằng  6   3  A. 2 3 − + 4sin  . B. 2 4 + 3sin  . C. 2 3 − 4sin  . D. 2 sin  .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề LƯỢNG GIÁC Toán 11 KNTT
Câu 67: Cho cos 2 = m . Tính theo m giá trị của biểu thức 2 2
A = 2sin  + 4 cos  .
A. A = 3 + m .
B. A = 4 + 2m .
C. A = 4 + m .
D. A = 3 − m .
Câu 68: Cho tam giác ABC thỏa mãn 2 sin .
A sin B = 1 + cosC, khẳng định nào sau đây đúng?
A. Tam giác ABC vuông tại C.
B. Tam giác ABC vuông tại A.
C. Tam giác ABC cân tại C.
D. Tam giác ABC cân tại A.
Câu 69: Cho tam giác ABC thỏa mãn sin A = 2 sin BcosC và A = 50, khẳng định nào sau đây đúng? A. B = 60 .  B. C = 75 .  C. B = 65 .  D. C = 55 . 
Câu 70: Cho góc  thỏa mãn tan = 2, tính giá trị biểu thức P = 2 tan + tan 2. 8 2 4
A. P = .
B. P = .
C. P = .
D. P = 2. 3 3 3 1
Câu 71: Cho sin + cos = , khẳng định nào sau đây đúng? 2 3 3 3 3
A. sin 2 = .
B. sin 2 = − .
C. sin 2 = .
D. sin 2 = − . 8 4 4 8  5
Câu 72: Tính giá trị A = cos .cos . 12 12 3 1 1 A. A = .
B. A = .
C. A = .
D. A = 3. 4 2 4 4
Câu 73: Cho biết sin x = a + .
b cos 2x + cos 4x với a, ,
b c  . Tính tổng S = a + b + . c A. S = 1 . B. S = −1 . C. S = 4 . D. S = 0 .    1   
Câu 74: Cho góc  thỏa mãn   ;  mà sin = . Tính sin  +    2  5  6  15 − 5 15 − 5 15 − 2 5 15 − 2 5 A. . B. . C. . D. . 10 5 5 10 1 1
Câu 75: Biết cos = , cos  =
. Tính cos ( −  ).cos ( +  ) . 3 4 25 19 − 5 119 − A. . B. . C. . D. . 144 144 144 144 2 2cos x − 1
Câu 76: Đơn giản biểu thức A =
ta được kết quả nào sau đây ? sinx + cos x
A. A = sin x − cos . x
B. A = cos x + sin . x
C. A = − sin x − cos .
x D. A = cos x − sin . x sin x + sin 3x
Câu 77: Rút gọn biểu thức A = 2cosx . A. A = sin 4 . x B. A = sin . x C. A = sin 2 . x D. A = cos2 . x 4sin 2 . x cos 2x
Câu 78: Rút gọn biểu thức
(với điều kiện biểu thức có nghĩa), ta được biểu thức có cos3x + cos x a sin 2x a dạng
với a,b  , tối giản. Giá trị của 2
a + b bằng b cos x b A. 2 . B. 5 − . C. 5 . D. 3 . cos a − cos5a
Câu 79: Rút gọn biểu thức P = a +
a  ) ta được: sin 4a + (với sin 4 sin 2 0 sin 2a
A. P = 2 cot a .
B. P = 2 cos a .
C. P = 2 tan a .
D. P = 2sin a .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề LƯỢNG GIÁC Toán 11 KNTT 2sin 2 − sin 4
Câu 80: Rút gọn biểu thức: bằng: 2sin 2 + sin 4 A. 2 tan  . B. 2 − tan  . C. 2 tan 2 . D. 2 cot  . sin + sin3
Câu 81: Rút gọn biểu thức = x x A . 2cosx
A. A = sin4x .
B. A = sinx .
C. A = sin2x .
D. A = cos2x . sin 7 − sin 5
Câu 82: Biến đổi thành tích biểu thức ta được sin 7 + sin 5 A. tan 5.tan  . B. cos.sin  . C. cos 2.sin 3 . D. cot 6.tan  . 1 cos5x + cos3x
Câu 83: Biết tan x = . Tính giá trị của biểu thức I = . 3
sin 5x − sin 3x 1 1 A. I = . B. I = − . C. I = 3 . D. I = −3 . 3 3 sin + sin 2 + sin 3
Câu 84: Giả sử biểu thức M =
có nghĩa, khẳng định nào sau đây đúng? cos + cos 2 + cos 3
A. M = tan 2.
B. M = cot 2.
C. M = −tan 2.
D. M = −cot 2. 1+ sin 4 − cos 4 Câu 85: Biểu thức
có kết quả rút gọn bằng 1+ sin 4 + cos 4 A. cos2 . B. cot2 . C. tan2 . D. sin2 . sin 2x − sin x
Câu 86: Rút gọn biểu thức P =
(với điều kiện biểu thức có nghĩa) ta được kết quả
1− cos x + cos 2x
A. P = cot x .
B. P = tan x .
C. P = cos x .
D. P = sin x .  1 
Câu 87: Biểu thức thu gọn của biểu thức B = +1 .tan x   là  cos 2x
A. tan 2x .
B. cot 2x .
C. cos 2x . D. sin x . 1+ cos + cos 2 + cos3
Câu 88: Rút gọn biểu thức bằng 2 2cos  + cos −1
A. −2 cos . B. cos . C. 2 cos . D. 2 sin  .
sin 2a + sin 5a − sin 3a
Câu 89: Rút gọn biểu thức A = 2 1+ cos a − . 2sin 2a A. cos a . B. sin a . C. 2 cos a . D. 2 sin a .
( x + x)2 −( x − x)2 tan cot tan cot
Câu 90: Với điều kiện xác định, hãy rút gọn biểu thức A = cot x − . tan x 2 4 8 A. A = .
B. A = 4 . C. A = . D. A = . cot 2x cot 2x cot 2x
Câu 91: Cho góc nhọn  thỏa mãn cos = 2 sin , khẳng định nào sau đây sai? 1 1 4 5 A. tan = . B. sin = . C. cot = 2. D. sin 2 = . 2 5 5
Câu 92: Nếu  ,  , là ba góc nhọn và thỏa mãn tan ( +  ).sin  = cos thì
A.  +  +  = 45 .
B.  +  +  = 60 .
C.  +  +  = 90 .
D.  +  +  = 120 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề LƯỢNG GIÁC Toán 11 KNTT  2 
Câu 93: Tìm giá trị lớn nhất của biểu thức M = sin + sin  +  .  3  3 A. 2. B. . C. 3. D. 1. 2
Câu 94: Giá trị lớn nhất của biểu thức 4 7
sin x + cos x là 1 A. 2 . B. 2 . C. . D. 1. 2
Câu 95: Tìm giá trị nhỏ nhất của biểu thức sin  + 3cos . A. 2 . B. −1− 3 . C. 2 − . D. 0 .
Câu 96: Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 6 6
P = sin  + cos  .
A. M + 4m = 0 .
B. M + 4m = 2 .
C. M + 4m = 4 .
D. M + 4m = 1. 
Câu 97: Cho 0  x
. Tìm giá trị nhỏ nhất của biểu thức 4 4
P = sin x + cos x . 2 1 1 A. 1. B. . C. . D. 0 . 2 4
Câu 98: Cho tam giác ABC . Tìm giá trị lớn nhất của biểu thức P = 2 cos A + 2 cos B + 2 3 cos C . 7 3 5 3 2 3 A. 2 3 . B. . C. . D. . 3 3 3
IV. LỜI GIẢI CHI TIẾT  
Câu 1: Không sử dụng máy tính, tính các giá trị lượng giác sau: 0 0 7 5 cos795 , sin18 , tan ,cot . 12 8 Lời giải: Vì 0 0 0 0 0 0
795 = 75 + 2.360 = 30 + 45 + 2.360 nên − 0 0 0 0 0 0 3 2 1 2 6 2
cos795 = cos75 = cos 30 cos 45 − sin 30 sin 45 = . − . = 2 2 2 2 4 Vì 0 0 0 54 + 36 = 90 nên 0 0 sin 54 = cos 36 Mà 0 = ( 0) 2 0 cos 36 cos 2.18 = 1 − 2sin 18 0 = ( 2 0 − ) 0 2 0 0 + = ( 2 0 − ) 0 + ( 2 0 sin18 . 1 2 sin 18 2 sin18 cos 18 sin18 . 1 2 sin 18 2 sin18 1 − sin 18 ) 0 3 0 = 3sin18 − 4sin 18 . Do đó 0 3 0 2 0 − = −  ( 0 − )( 2 0 0 3sin18 4 sin 18 1 2 sin 18 sin18
1 4 sin 18 + 2 sin18 − 1) = 0 − + 0  sin18 = 1 hoặc 0 5 1 sin18 = hoặc 0 5 1 sin18 = 2 2 − Vì 0 0  sin18  1 nên 0 5 1 sin18 = . 2   tan + tan 7     3 + 1 3 4 5      tan = tan + = = = 2 − −   3 ; cot = cot + = −   tan . 12  3 4    1 − 3 8  2 8  8 1 − tan tan 3 4
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề LƯỢNG GIÁC Toán 11 KNTT  2 tan     Ta lại có 8 1 = tan = tan 2. =   4  8   2 1 − tan 8       Suy ra 2 2 1 − tan = 2tan  tan + 2tan − 1 = 0  tan = 1 − − 2 hoặc tan = 1 − + 2 8 8 8 8 8 8   5 Do tan  0 nên tan = 1 − + 2. Vậy cot = 1 − 2. 8 8 8
Câu 2: Không sử dụng máy tính, tính giá trị biểu thức lượng giác sau: 1 1 a) A = + b) B = ( 0 + )( 0 1 tan 20 1 + tan 25 ) 0 0 cos 290 3 sin 250     c) 0 0 0 0
C = tan 9 − tan 27 − tan 63 + tan 81 d) 2 2 2 2 D = sin + sin + sin sin 9 9 9 9 Lời giải: a) Ta có 0 = ( 0 0 0 + + )= − ( 0 0 + ) 0 cos 290 cos 180 90 20 cos 90 20 = sin 20 0 = ( 0 0 0 + − )= − ( 0 0 − ) 0 sin 250 sin 180 90 20 sin 90 20 = −cos20 3 0 1 0 − 0 0 cos 20 sin 20 1 1 3 sin 20 − sin 20 2 2 C = − = = 4 0 0 0 0 0 0 sin 20 3 cos 20 3 sin 20 .cos 20 3.2.sin 20 .cos 20 0 0 0 0 0 sin 60 cos 20 − cos60 sin 20 4sin 40 4 3 = 4 = = . 0 0 3 sin 40 3 sin 40 3 0 0 0 0 0 0  sin 20  sin 25 
sin 20 + cos 20 sin 25 + cos 25
b) Cách 1: Ta có B = 1 + 1+  = . 0 0 0 0  cos 20  cos 25  cos 20 cos 25 0 0 0 0 0 0 0 0 sin 20 cos 45 + cos 20 sin 45 sin 25 cos 45 + cos 25 sin 45 0 0 = sin 65 sin70 2. . 2. = 2 = 2. 0 0 cos 20 cos 25 0 0 cos 20 cos 25 tan 20 + tan 25
Cách 2: Ta có tan 45 = tan(20 + 50 ) 0 0 0 0 0 = 0 0 1 − tan 20 tan 25 0 0 tan 20 + tan 25 Suy ra 0 0 0 0 1 =
 tan20 + tan25 + tan20 tan25 = 1  ( 0 + )( 0 1 tan 20 1 + tan 25 ) = 2 . 0 0 1 − tan 20 tan 25 Vậy B = 2. c) 0 0 C = + − ( 0 0 tan 9 tan 81 tan 27 + tan 63 ) 0 0 0 0 0 0 0 0 sin 9 cos81 + sin 81 cos9 sin 27 cos63 + sin 63 cos 27 = − 0 0 0 0 cos9 cos81 cos 27 cos63 2( 0 0 sin 54 − sin18 1 1 2 2 ) 0 0 = − = − = 4cos 36 .sin18 = = 4 0 0 0 0 0 0 0 0 cos9 sin 9 cos 27 sin 27 sin18 sin 54 sin18 sin 54 0 0 sin18 .sin 54 2           d) 2 2 2 2 2 2 D = sin + sin + sin sin = sin + sin −   sin sin 9 9 9 9  9 9  9 9
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề LƯỢNG GIÁC Toán 11 KNTT 2     1         2 1 1 = 2sin cos + cos − cos = cos + −      cos   6 18  2  3 9  18 2  2 9   1 + cos 1  1   3 9 = + − cos =   . 2 2  2 9  4
Lưu ý: Biến đổi sau thường xuyên được sử dụng:  1 3  
sin x  3 cos x = 2  sin x
cos x = 2sin(x  ) 2 2   3   3 1  
3 sin x  cos x = 2 
sin x  cos x = 2sin(x  )  2 2   6   1 1  
sin x  cos x = 2 sin x
cos x = 2 sin(x    ) .  2 2  4
Câu 3: Không sử dụng máy tính, tính giá trị biểu thức lượng giác sau:     a) A = sin cos .cos .cos ; b) B = sin10 .  sin 30 .  sin 50 .sin70 ;  32 32 16 8  3  2 3 c) C = cos + cos ; d) 2 2 2 D = cos + cos + cos . 5 5 7 7 7 Lời giải: 1       1    1   1  2 a) A = 2sin cos .cos .cos =   sin .cos .cos = sin .cos = sin = 2  32 32  16 8 2 16 16 8 4 8 8 8 4 16 1 b) Ta có 0 0 cos 20 cos 40 cos80o B = 2 Do đó: 0 0 0 0 16 sin 20 .
8 sin 20 cos 20 cos 40 cos 80o B = 0 0 o 0 0 0
= 4sin 40 cos40 cos80 = 2sin80 cos80 = sin160 . 0 sin160 1 Suy ra B = = . 0 16sin 20 16  2 c) Ta có C = 2cos cos . 5 5     2 2 2 4 Vì sin
 0 nên 2sin .C = 4sin cos cos = 2sin cos = sin . 5 5 5 5 5 5 5 5 1 Suy ra C = . 2 2 4 6 1 + cos 1 + cos 1 + cos 3 1  2 4 6  c) 7 7 7 D = + + = + cos + cos +  cos  2 2 2 2 2  7 7 7  2 4 6 Xét T = cos + cos + cos . 7 7 7    2  4  6 Vì sin
 0 nên 2sin T = 2sin cos + 2sin cos + 2sin cos 7 7 7 7 7 7 7 7  3    5 3   5   = sin − sin + sin − sin + sin − sin = −       sin .  7 7   7 7   7  7
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề LƯỢNG GIÁC Toán 11 KNTT 1 Suy ra T = − . 2 3 1  1  5 Vậy D = + . − =   . 2 2  2  4 2 6
Câu 4: Cho  ,  thoả mãn sin + sin  = và cos + cos  =
. Tính cos( −  ) và sin( +  ) . 2 2 Lời giải: 2 1 Ta có 2 2 sin + sin  =
 sin  + sin  + 2sin sin = (1) 2 2 6 2 2 3 cos + cos  =
 cos  + cos  + 2cos cos = (2) 2 2
Cộng vế với vế của (1) và (2) ta được: 2 2 2 2
sin  + sin  + cos  + cos  + 2sin sin  + 2cos cos  = 2
 2 + 2(sin sin + cos cos ) = 2  2cos( −  ) = 0
Vậy cos( −  ) = 0. (*) Từ giả thiết ta có (  +  )(  +  ) 2 6 sin sin cos cos = . 2 2 3
 sin cos + sin cos  + sin  cos + sin  cos  = 2 1  (  +  ) + ( +  ) 3 sin 2 sin 2 sin = 2 2
Mặt khác: sin 2 + sin 2 = 2sin ( +  )cos( −  ) = 0 (Do cos( −  ) = 0 từ (*)) Suy ra ( + ) 3 sin = . 2 4        
Câu 5: Cho cos 2x = − , với
x  . Tính sin x, cosx, sin x + , cos 2x −     . 5 4 2  3   4  Lời giải:   Vì
x  nên sin x  0, cos x  0 . 4 2 − x
Áp dụng công thức hạ bậc, ta có: 2 1 cos 2 9 3 sin x = =  sin x = ; 2 10 10 + 2 1 cos 2x 1 1 cos x = =  cosx = . 2 10 10 3
Ta có: sin 2x = 2sin xcos x = . 5
Theo công thức cộng, ta có:      3 1 1 3 3 + 3 sin x +
= sin xcos + cosxsin = . + . =   ;  3  3 3 10 2 10 2 2 10      4 2 2 3 2 cos 2x −
= cos2xsin + cos sin2x = − . + . = −   .  4  4 4 5 2 2 5 10
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề LƯỢNG GIÁC Toán 11 KNTT Câu 6: Cho 2
cos 4 + 2 = 6 sin  với
    . Tính tan 2 . 2 Lời giải: Ta có 2 2
cos 4 + 2 = 6 sin   2 cos 2 − 1 + 2 = 3(1 − cos 2 )  1 cos 2 = 2   1
2 cos 2 + 3cos 2 − 2 = 0  2    +   cos 2 = (Vì cos 2 2 0 )  2 cos2 = 2 − 1 1 Ta có: 2 2 1 + tan 2 =  tan 2 = − 1 = 3. 2 2 cos 2 cos 2  Vì
       2  2 nên sin 2  0. Mặt khác cos2  0 do đó tan 2  0. 2 Vậy tan 2 = − 3. 1 1 1 1 Câu 7: Cho + + + = 7 . Tính cos 4 . 2 2 2 2 tan  cot  sin  cos  Lời giải: 2 2 1 1 1 1 sin  + 1 cos  + 1 Ta có + + + = 7  + = 7 2 2 2 2 2 2 tan  cot  sin  cos  cos  sin  2 sin  ( 2 sin  + 1) 2 + cos  ( 2 cos  + 1)  = 7 2 2 sin  cos  4 4 2 2
 sin  + cos  + 1 = 7 sin  cos   (sin  + cos  )2 2 2 2 2 2 2
− 2sin  cos  + 1 = 7 sin  cos 
 2 = 9sin  cos   8 = 9(2sin cos )2 2 2 2  =   = ( −  ) 7 8 9 sin 2 16 9 1 cos 4  cos4 = − . 9 7 Vậy cos 4 = − . 9    + 2013 
Câu 8: Cho sin + cos = cot
với 0     . Tính tan  . 2  2  Lời giải:   sin 2 tan    Ta có 2 2 2 sin = 2 sin cos = 2cos . = 2 2 2   2 cos tan + 1 2 2     2 2 sin 1 −   tan    2 2 2 2 2 cos = cos − sin = cos 1 −  = 2 2 2    2  2  cos  tan + 1  2  2   2 2 tan 1 − tan  1 Do đó: 2 2 sin + cos = cot  + = 2    2 2 tan + 1 tan + 1 tan 2 2 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề LƯỢNG GIÁC Toán 11 KNTT          2 2 3 2  tan 1 + 2 tan − tan = 1+ tan  tan − tan − tan + 1 =   0 2  2 2  2 2 2 2 2         tan − 1 tan + 1 = 0  tan = 1       2   2  2     
Vì 0      0 
 do đó tan  0 nên tan = 1 cot = 1 2 2 2 2 2   + 2013       Ta có tan = tan + 2006 + = −cot = 1 −      2   2 2  2   + 2013  Vậy tan = 1 −   .  2  
Lưu ý: Ta có thể biểu diễn sin ,cos ,tan ,cot qua t = tan như sau: 2 2 2 2t 1 − t 2t 1 − t sin = ,cos = ,tan = ,cot = 2 2 2 1 + t 1 + t 1 − t 2t
(với  làm các biểu thức có nghĩa)  3      5     Câu 9: Cho ( + ) 1 sin = , tan = 2
− tan  . Tính A = sin  + cos  + + sin  − sin  −         . 3  8   8   12   12  Lời giải: Ta có ( + ) 1 1 sin
=  sin cos + cos sin  = (1) 3 3 và tan = 2
− tan   sin cos  = 2 − sin  cos (2)  1   2 2 1   = −   = ( 2 −  ) 2 1 cos sin cos sin 1 sin sin  =       Từ (1) và (2) ta được 3 9 9      2   2 2 4  2   = −   =  ( 2 −  ) 4 sin cos sin cos sin 1 sin =  3  9  9 ( 2 −  ) 2 1 1 sin sin  =  9   2 1 2 1  
 1− sin  − sin  =  2 2 1  3  9 sin  − sin  =  3 2   4 2 2 1 2 1 2 1
 sin  − sin  + = 0  sin  − = 0  sin  =   . 3 9  3  3 Do đó 2 2 1 2 sin  = sin  + = . 3 3  3     1       1  2  Ta có sin  +  cos  + =   sin 2 + −  sin  = cos2 −  8 8 2  2 4  2  2          1     + 2 2 1 2 2 2 3 2 = 1− 2sin  −  = 1− 2. −  = − 2  2  2  3 2  12         5  1       1  3  sin  −  cos  − =   sin 2 − +  sin  = −cos2 +   12   12  2   2  3  2  2  
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề LƯỢNG GIÁC Toán 11 KNTT 1     − + 2 3 1 1 3 2 3 2 =  1 − + 2sin  +  =  1 − + 2. +  = 2  2  2  3 2  12     2 + 3 2 2 − + 3 2 1 Do đó A = − + = − . 12 12 3
Câu 10: Chứng minh rằng với mọi góc lượng giác  làm cho biểu thức xác định thì  a) 4 4 3 cos 4 sin  + cos  = + ; b) 6 6 5 3 sin  + cos  = + cos4; 4 4 8 8 1 − sin 2    c) 2 = cot +  . 1 + sin 2  4  Lời giải: 1
a) Ta có sin  + cos  = (sin  + cos  )2 4 4 2 2 2 2 2
− 2sin  cos  = 1− sin 2 2 1 − cos 4 3 cos 4 = 1− = + 4 4 4 3 3 b) Ta có: 6 6  +
 = ( 2 ) + ( 2 ) = ( 2 2  +  )( 4 2 2 4 sin cos sin cos sin cos
sin  − sin  cos  + cos  ) 4 2 2 4 2 2 3 2 3
= sin  − sin  cos  + cos  = 1− 3sin  cos  = 1− sin 2 = 1− (1− cos4 ) 4 8 5 3 = + cos4. 8 8 1 − sin 2
sin  + cos  − 2 sin cos (sin −cos)2 2 2 c) Ta có = = 2 2 1 + sin 2
sin  + cos  + 2 sin cos (sin + cos)2 2        2  2 cos  +   2 cos  +     4   4     2 = = = cot  +  . 2        2  4  2 sin   2 sin  + +      4  4    2 2         − 2    1 tan tan  1   cos − sin  1 − sin 2 Cách khác: 2   4 cot + = =     = =   .  4           cos + sin  1 + sin 2  tan +     tan + tan   4  4     
Câu 11: Cho 0     ,  . Chứng minh rằng: 2   1 + cos + 1 − cos     a) 1 cos 1 cos   + + − = 2sin +  ; b) = tan +  .  2 4  1 + cos − 1 − cos  2 4  Lời giải:    3     a) Do 0     ⎯⎯ →  +  nên sin +  0,sin    0 4 2 4 4  2 4     
Đẳng thức tương đương với ( +  + −  )2 2 1 cos 1 cos = 4sin +    2 4 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề LƯỢNG GIÁC Toán 11 KNTT     2
 2 + 2 1+ cos 1− cos = 2 1  − cos  + 
  1− cos  = sin   2  2 2 2 2
 1 − cos  = sin   sin  + cos  = 1(luôn đúng) đ.p.c.m. ( +  + −  )2 1 cos 1 cos b) VT = (
1 + cos − 1 − cos )( 1+ cos + 1− cos ) 2
2 + 2 1 + cos . 1 − cos 1 + 1 − cos  1 + sin = = = . 2cos cos cos
Vì 0     nên sin  0 do đó 2         2 2 sin + + +  cos sin cos 2 sin cos  1 + sin  2 2 2 2 2 2  VT = = = cos          2 2 cos − sin sin + cos cos −   sin  2 2  2 2  2 2        2 sin sin cos + +    2 4 2 2      = = = tan + =   VP    đ.p.c.m.      2 4  cos − sin 2 cos +   2 2  2 4 
Câu 12: Chứng minh rằng: a) 2 2
sin( +  ).sin( −  ) = sin  − sin  ;   b) cot cot
= 2 với sin + sin  = 3sin( +  ), + b k2 ,k ; 2 2
sin + sin  cos( +  ) c) = +  −  ( + ) tan( ). cos sin sin Lời giải: 1
a) Ta có sin( +  ).sin( −  ) = − cos 2 − cos 2    2 1 = − ( 2 1 − 2sin  ) − ( 2 1 − 2sin  ) 2 2  = sin  − sin  2   +   −   +   + 
b) Từ giả thiết ta có 2sin cos = 6sin cos 2 2 2 2    −   +  Do   k2 + +   sin  0 suy ra cos = 3cos 2 2 2          
 cos cos + sin sin = 3 cos cos −  sin sin  2 2 2 2  2 2 2 2       
 2sin sin = cos cos  cot cot = 2  đ.p.c.m. 2 2 2 2 2 2 1 sin + sin  ( + 2 )+sin(  − ) sin + sin ( + 2 ) c) Ta có 2 VT = =  1   +  +  cos − −
cos( + 2 ) − cos(  −    ) cos cos( 2 )   2 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề LƯỢNG GIÁC Toán 11 KNTT 2sin( +  )cos(− ) = =
 +  = VP  đ.p.c.m.
2cos( +  )cos(− ) tan( )
Câu 13: Chứng minh biểu thức sau không phụ thuộc vào x :  2   2  a) 2 2 2 A = cos  + cos + +   cos −  ;  3   3            3 
b) B = cos − .cos +  + cos + .cos + .  3   4   6   4  Lời giải:  2   2  a) Ta có: 2 2 2 A = cos  + cos + +   cos −    3   3  1   4   4  = 3 + cos2 + cos +  2 +  cos −  2  2   3   3  1  4  3 = 3 + cos 2 + 2cos cos 2 = .   2  3  2            b) Vì  + =  − +  cos  + = −sin  −       6  3  2  6   3   3     và cos  + = −sin  +     nên  4   4             
B = cos − .cos +  + sin − .sin +   3   4   3   4               
= cos  −  −  +  =cos − − =   cos +     3   4   3 4   3 4      1 2 3 2 2 − 6 = cos cos − sin sin = . − . = . 3 4 3 4 2 2 2 2 4
Câu 14: Đơn giản biểu thức sau: (giả sử các biểu thức có nghĩa)       cos a + + cos a −    
cos a + 2cos 2a + cos 3a  3   3  a) A = ; b) B = ;
sin a + sin 2a + sin 3a a cot a − cot 2
c) C = cos a + cos(a + b) + cos(a + 2 )
b + ... + cos(a + nb) (n ). Lời giải:
(cosa+cos3a)+ 2cos2a 2cos2acosa+ 2cos2a 2cos2a(cosa+1) a) A = ( = = = a
sin a + sin 3a) + 2sin 2a a a + a
2sin 2a(cosa + 1) cot 2 2sin 2 cos 2sin 2        b) Ta có cos a + + cos a − = 2cosacos =     cos a  3   3  3  a a a a  sin a cos sin cos cos sin − −  a a a  −sin a cos a  2  1 và 2 2 2 2 cot a − cot = − = = = = − . 2 sin a a a a a sin a sin sin asin sin asin sin asin 2 2 2 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề LƯỢNG GIÁC Toán 11 KNTT cos a sin 2a Suy ra B =
= −sin acosa = − . 1 2 − sina b b b b b
c) Ta có C.2sin = 2sin cos a + 2sin cos(a + b) + 2sin cos(a + 2b) + ... + 2sin cos(a + nb) 2 2 2 2 2  b   b   3b   b   5b   3b  = sin + a + sin − a + sin
+ a + sin − − a + sin + a + sin − −            a  2   2   2   2   2   2   ( 2n + 1)b   (2n −1)b  ... + + sin + a + sin − − a  2   2       b   (2n+ )1b   nb  sin −  a +  sin
+ a = 2sin(n + ) 1 bcos −  a 2  2     2     nb  sin (n + 1)bcos −  a   2  Suy ra C = . b sin 2 1 1
Câu 15: Cho sin(a + b) = 2cos(a − b) . Chứng minh rằng biểu thức M = + không phụ 2 − sin 2a 2 − sin 2b
thuộc vào a,b . Lời giải:
4 − (sin 2a + sin 2b)
4 − (sin 2a + sin 2b) Ta có M = ( =
2 − sin 2a)(2 − sin 2b) 4 − 2(sin 2a + sin 2b) + sin 2asin 2b
Ta có sin 2a + sin 2b = 2sin (a + b)cos(a − b) Mà (a + b) = (a −b) 2  (a + b) 2 sin 2 cos sin
= 4cos (a − b) nên (a + b)− (a −b) 2 = − (a + b) 2 cos 2 cos 2 1 2 sin − 2cos 
(a −b)−1 2 = −  (a+ b) 2 + (a −b) 2 2 2 sin cos  = 2 −10cos  (a −b) 2
4 − 4 cos (a − b) 2
4 − 4 cos (a − b) 4 Suy ra M = = = . (đ.p.c.m). − a − b
4 − 8 cos (a − b) 1 − .2 − 10cos  (a −b) 2 2 2 3 3cos  ( ) 3 2  
Câu 16: Chứng minh rằng với 0    thì 2 a) 2 2 cot   1 + cos 2 ; b) cot  1 + cot 2. Lời giải:
a) Bất đẳng thức tương đương với  1  2 1 2 2 − 1  2cos   − 1  1−   sin  2 2  sin   sin  1 2 4 2 
+ sin   2  sin  − 2sin  + 1  0 2 sin   (  − )2 2 sin 1  0 (đúng) (đ.p.c.m).
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115

Tài liệu liên quan: