Chuyên Đề Dao Động Cơ Mức Vận Dụng Có Lời Giải Chi Tiết

Trọn bộ câu hỏi ôn tập dưới dạng trắc nghiệm ôn tập Chương 1: Dao động cơ (có đáp án) mức vận dụng. Giúp bạn ôn tập hiệu quả và đạt điểm cao !

Thông tin:
30 trang 11 tháng trước
Tác giả:
Student
Hải Yến
Đang cập nhật

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Chuyên Đề Dao Động Cơ Mức Vận Dụng Có Lời Giải Chi Tiết

Trọn bộ câu hỏi ôn tập dưới dạng trắc nghiệm ôn tập Chương 1: Dao động cơ (có đáp án) mức vận dụng. Giúp bạn ôn tập hiệu quả và đạt điểm cao !

90 45 lượt tải Tải xuống

Chủ đề: Chương 1: Dao động cơ

Môn: Vật Lí 12

Thông tin:

30 trang 11 tháng trước

Tác giả:

Profile Hải Yến
Trang 1
CHUYÊN ĐỀ ÔN TÂP MỨC ĐỘ 3 CHƯƠNG 1 DAO ĐỘNG CƠ HỌC
1. ĐẠI CƯƠNG DAO ĐỘNG ĐIỀU HÒA
Câu 1. Một vật nhỏ dao động điều hòa với chu kỳ T=1s. Tại thời điểm t
1
nào đó, li độ của vật là -2cm.
Tại thời điểm t
2
= t
1
+0.25s, vận tốc của vật có giá trị là:
A. 4 cm/s. B. -2 m/s. C. 2cm/s. D. - 4m/s.
Câu 2. Một dao động điều hoà với x=8cos(2t-
6
) cm. Thời điểm thứ 2023 vật qua vị trí có vận tốc v =
-8 cm/s có giá trị gần nhất là :
A. 1011,2s. B. 1011,3s. C. 1011,1s. D. 1011,5s.
Câu 3. Vật dao động điều hòa có vận tốc cực đại bằng 3m/s và gia tốc cực đại bằng 30 m/s
2
. Thời điểm ban
đầu vật có vận tốc 1,5m/s và thế năng đang tăng. Thời điểm vật có gia tốc bằng 15 m/s
2
là:
A. 0,10s. B. 0,15s. C. 0,20s. D. 0,05s.
Câu 4. Một vật dao động điều hòa, đi qua vị trị có vận tốc bằng không vào các thời điểm liên tiếp 4,25s
và 5,75s. Biết vào thời điểm ban đầu vật chuyển động theo chiều dương của trục tọa độ, và tốc độ lớn
nhất của vật trong quá trình dao động là 4 (cm/s). Vận tốc trung bình của vật trong khoảng từ thời điểm
0,75s đến thời điểm 2,25s là :
A. -4,00cm/s. B. 4,00cm/s. C. 0,00 cm/s. D. -4,25cm/s.
Câu 5. Một chất điểm dao động điều hòa với chu kì T. Gọi a
max
là gia tốc cực đại của vật. Khoảng thời
gian trong một chu kì để vật có độ lớn gia tốc lớn hơn
max
2
a
là :
A. T/3. B. 2T/3. C. T/6. D. T/2.
Câu 6. Hai chất điểm M, N dao động điều hòa dọc theo hai đường thẳng song song kề nhau và song
song với trục tọa độ Ox. Vị trí cân bằng của M và của N đều ở trên một đường thẳng qua gốc tọa độ và
vuông góc với Ox. Phương trình dao động của chúng lần lượt là x
1
= 10cos2πt cm và x
2
= 10 cos(2πt +
) cm. Hai chất điểm gặp nhau khi chúng đi qua nhau trên đường thẳng vuông góc với trục Ox. Thời
điểm lần thứ 2023 hai chất điểm gặp nhau là:
A. 16 phút 51,42s. B. 16 phút 51,92s. C. 16 phút 52,42s. D. 16 phút 50,92s.
Câu 7. Hai chất điểm dao động điều hòa cùng biên độ A, với tần số góc 3 Hz và 6 Hz. Lúc đầu hai vật
đồng thời xuất phát từ vị trí có li độ và đang chuyển động theo chiều dương. Khoảng thời gian
ngắn nhất để hai vật gặp nhau là:
A. . B. . C. . D. .
Câu 8. Một vật dao động điều hòa với phương trình Quãng đường vật đi
được từ thời điểm t
1
= 0,1 s đến t
2
= 6s là:
A. 84,4cm. B. 333,8cm. C. 331,4 cm. D. 337,5cm.
Câu 9. Một vật dao động điều hòa theo phương nằm ngang, khi li độ vật bằng 0 thì vận tốc có gia trị
31,4cm/s; khi li độ vật cực đại thì gia tốc có giá trị 4 m/s
2
. Lấy π
2
= 10. Thời gian ngắn nhất để vật chuyển
động từ li độ x = 0 đến x = 1,25cm là:
A. 1/12 s. B. 1/3 s. C. 1/6 s. D. 1/24 s.
Câu 10. Hai chất điểm M và N dao động điều hòa cạnh nhau, dọc theo trục Ox. Vị trí cân bằng của hai
chất điểm ở cùng gốc tọa độ O. Phương trình dao động của chúng lần lượt là
( ) ( )
1 1 2 2
cos , cos
36
x A t cm x A t cm


= + = −
. Biết
22
12
4
9 16
xx
+=
. Tại thời điểm t nào đó, chất
3
2
s
18
1
s
27
1
s
36
1
s
72
1
.)4/35cos(24 cmtx
−=
Trang 2
điểm M có li độ
1
3x cm=−
và vận tốc
1
30 3 /v cm s=−
. Khi đó, độ lớn vận tốc tương đối của chất
điểm này so với chất điểm kia xấp xỉ bằng:
A. 66 cm/s. B. 12 cm/s. C. 40 cm/s. D. 92 cm/s.
Câu 11. Một vật dao động điều hòa với phương trình
5cos 4
2
xt

=−


. Xác định thời gian ngắn nhất
để vật đi từ vị trí
2,5 cm
đến
2,5 cm−
.
A.
1
12
s
B.
1
s
10
C.
1
s
20
D.
1
6
s
Câu 12. Một chất điểm có khối lượng
320 g
dao động điều hòa dọc theo trục Ox. Biết đồ thị biểu diễn sự
phụ thuộc của động năng theo thời gian của chất điểm như hình vẽ và tại thời điểm ban đầu
(t 0)=
chất
điểm đang chuyển động ngược chiều dương. Phương trình dao động của chất điểm là
A.
x 5cos 2 t cm
6

=+


.
B.
5cos 4 cm
3
xt

=+


.
C.
5cos 2 t cm
6
x

=−


D.
x 5cos 4 t cm.
3

=−


Câu 13. Hình bên là đồ thị biểu diễn sự phụ thuộc li độ của hai dao
động điều hòa theo thời gian. Độ lệch pha của hai dao động này bằng
A.
3
.
8
B.
5
.
6
C.
3
.
4
D.
2
.
3
Câu 14. Một chất điểm dao động điều hòa có đồ thi biểu diễn sự
phụ thuộc của li độ x vào thời gian t như hình vẽ. Tại thời điểm t = 0,2s, chất có li độ 2 cm. Ở thời
điểm t = 0,9s, gia tốc của chất điểm có giá trị bằng:
A.
2
14,5cm / s
B.
2
57,0cm / s
C.
2
5,7m / s
D.
2
1,45m/ s
Câu 15. Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ có
dạng như hình vẽ bên. Phương trình dao động của li độ là
A.
2
10
33
x cos t


=−


(cm).
B.
2
10
33
x cos t


=+


(cm).
C.
22
10
33
x cos t


=+


(cm).
D.
10
33
x cos t


=−


(cm).
2. CON LẮC LÒ XO
Câu 16. Một vật dao động điều hòa với phương trình x = 10cos(πt + π/3) cm. Khoảng thời gian tính từ
lúc vật bắt đầu dao động (t = 0) đến khi vật đi được quãng đường 50 cm là
A. 7/3 s B. 2,4 s C. 4/3 s D. 1,5 s
Trang 3
Câu 17. Một con lắc lò xo gồm quả cầu nhỏ khối lượng 1 kg và lò xo có độ cứng 50 N/m. Cho con lắc
dao động điều hòa trên phương nằm ngang. Tại thời điểm vận tốc của quả cầu là 0,2 m/sthì gia tốc của nó
là
3−
m/s
2
. Cơ năng của con lắc là
A. 0,02 J. B. 0,05 J. C. 0,04 J D. 0,01 J
Câu 18. Một vật dao động điều hòa với tần số f =10 Hz. Tại thời điểm ban đầu vật đang ở li độ x = 2cm
và chuyển động theo chiều dương. Sau 0,25 (s) kể từ khi dao động thì vật ở li độ
A. x = 2 cm và chuyển động theo chiều đương.
B. x = 2 cm và chuyển động theo chiều âm.
C. x = −2 cm và chuyển động theo chiều âm.
D. x = −2 cm và chuyền động theo chiều dương.
Câu 19. Con lắc lò xo nằm ngang dao động điều hòa, lực đàn hồi cực đại tác đụng vào vật là 2 N, gia tốc
cực đại của vật là 2 m/s
2
. Khối lượng của vật là
A. 1 kg. B. 2 kg. C. 3 kg. D. 4 kg.
Câu 20. Một con lắc lò xo có độ cứng 50 N/m, dao động điều hòa với biên độ 4 cm. Chọn gốc tính thế
năng là vị trí cân bằng. Tổng động năng và thế năng của vật là
A. 25 mJ. B. 20 mJ. C. 40 mJ. D. 10 mJ.
Câu 21. Khi treo một vật nặng vào một lò xo, khi vật đứng yên lò xo dài thêm một đoạn 2,5 cm. Lấy g =
π
2
m/s
2
. Chu kì dao động tự do của con lắc bằng
A. 0,316 s. B. 0,317 s. C. 0,215 s. D. 0,291 s.
Câu 22. Một chất điểm dao động điều hòa có đồ thị như hình bên.
Thời điểm mà vận vận tốc v và li độ x thỏa mãn
( )
1
v
1,25 3 s
x
−
= −
lần thứ 2023 gần nhất với giá trị nào dưới đây?
A. 1618.12 s. B. 1617,94 s.
C. 1617.83 s. D. 1618,37 s.
x(cm)
t(s)
A
A−
1/ 3
31/30
O
thukhoadaihoc.vn
thukhoadaihoc.vn
Câu 23. Một vật dao động điều hòa với phương trình x = Acos(ωt + φ).
Hình bên là đồ thị biểu diễn sự phụ thuộc li độ x theo thời gian t. Tại
thời điểm t = 0, gia tốc của vật có giá trị là
A.
( )
22
5 2 cm /s−
B.
( )
22
5 3 cm /s−
C.
( )
22
5 2 cm/s
D.
( )
22
5 3 cm / s
t(s)
x(cm)
10
5
5−
O
0,5
1
1,5
thukhoadaihoc.vn
thukhoadaihoc.vn
Câu 24. Một vật dao động điều hòa với biên độ 5 cm, trong 1 phút thực hiện được 30 dao động toàn
phần. Quãng đường mà vật đi được trong 1 s là
A. 15 cm. B. 5 cm. C. 10 cm. D. 20 cm.
Câu 25. Một con lắc lò xo gồm lò xo và vật có khối lượng 80 g dao động
điều hòa trên mặt phẳng nằm ngang. Mốc tính thế năng tại vị trí cân bằng.
Hình bên là đồ thị biểu diễn sự phụ thuộc của thế năng đàn hồi của con
lắc W
t
vào thời gian t. Lấy π
2
= 10. Biên độ dao động của con lắc là
A.
22
cm. B. 2 cm.
C. 4 cm. D.
42
cm
( )
t
W mJ
t(s)
0,05
4
O
thukhoadaihoc.vn
thukhoadaihoc.vn
Câu 26. Một con lắc lò xo heo thẳng đứng (coi gia tốc trọng trường là 10 m/s
2
) quả cầu có khối lượng
120 g. Chiều dài tự nhiên của lò xo là 20 cm và độ cứng 40 N/m. Từ vị trí cân bằng, kéo vật thẳng đứng,
xuống dưới tới khi lò xo dài 26,5 cm rồi buông nhẹ cho nó dao động điều hòa Động năng của vật lúc lò
xo dài 25 cm là
A. 24,5 mJ. B. 22 mJ. C. 12 mJ. D. 16,5 mJ.
Trang 4
Câu 27. Một con lắc lò xo đang dao động điều hòa theo phương nằm ngang. Mốc thế năng ở vị trí cân
bằng. Biết động năng cực đại của con lắc là 80 mJ, lực kéo về cực đại tác dụng lên vật nhỏ của con lắc là
4 N. Khi vật qua vị trí có li độ 3 cm thì động năng của con lắc có giá trị là
A. 5 mJ. B. 75 mJ. C. 45 mJ. D. 35 mJ.
Câu 28. Một con lắc lò xo treo vào một điểm M cố định, đang dao động điều
hòa theo phương trình thẳng đứng. Hình bên là đồ thị biểu diễn sự phụ thuộc
của lực đàn hồi F
đh
mà lò xo tác dụng vào M theo thời gian t. Lấy
22
/g m s
=
. Độ dãn của lò xo khi con lắc ở vị trí cân bằng là
A.2 cm. B.4 cm.
C.6 cm. D.8 cm.
Câu 29. Một con lắc lò xo gồm vật nhỏ có khối lượng m=100 g, lò xo có
độ cứng k được treo thẳng đứng. Kích thích cho vật dao động điều hòa
với biên độ. Chọn gốc thế năng tại vị trí cân bằng của vật. Hình bên là
một phần đồ thị biểu diễn mối liên hệ giữa thế năng E
t
và độ lớn lực kéo
về |F
kv
| khi vật dao động. Chu kì dao động của vật là
A.0,222 s. B.0,314 s.
C.0,157 s. D.0,197 s.
Câu 30. Một con lắc lò xo dao động điều hòa theo phương ngang với lực đàn hồi lớn nhất của lò xo là 2
N và năng lượng dao động là 0,1 J. Thời gian trong một chu kì lực đàn hồi là lực kéo không nhỏ hơn 1 N
là 0,1 s. Tính tốc độ lớn nhất của vật.
A. 314,1 cm/s. B. 31,4 cm/s. C. 402,5 cm/s. D. 209,44 cm/s.
Câu 31. Con lắc lò xo có độ cứng k = 40 N/m treo thẳng đứng đang dao động điều hòa với tần số góc ω =
10 rad/s tại nơi có gia tốc trọng trường g = 10 m/s
2
. Khi lò xo không biến dạng thì vận tốc dao động của
vật triệt tiêu. Độ lớn lực của lò xo tác dụng vào điểm treo khi vật ở trên vị trí cân bằng và có tốc độ 80
cm/s là
A. 2,4 N. B. 2 N. C. 1,6 N. D. 3,2 N.
Câu 32. Một con lắc lò xo được treo thẳng đứng vào một điểm cố định đang dao động điều hòa theo
phương thẳng đứng. Hình bên là đồ thị biểu diễn sự phụ thuộc của lực đàn hồi mà lò xo tác dụng lên vật
nhỏ của con lắc theo thời gian . Lấy

. Biên độ dao động của con lắc lò xo là
A. 
C. 
Câu 33. Con lắc lò xo gồm vật nhỏ nặng 1 kg thực hiện đồng thời hai dao động điều hoà theo phương
thẳng đứng, theo các phương trình:
1
x 5 2 cos10t=
cm và
2
x 5 2 sin10t=
cm (Gốc tọa độ trùng với vị trí
cân bằng, t đo bằng giây và lấy gia tốc trọng trường g = 10 m/s
2
). Lực cực đại mà lò xo tác dụng lên vật là
A. 10N. B. 20 N. C. 25 N. D. 0,25 N.
Câu 34. Một con lắc lò xo treo vào một điểm cố định, dao động điều hòa theo phương thẳng đứng với
chu kì 1,2 s. Trong một chu kì, nếu tỉ số của thời gian lò xo giãn với thời gian lò xo nén bằng 2 thì thời
gian mà lực đàn hồi ngược chiều lực kéo về là
A. 0,2 s. B. 0,1 s. C. 0,3 s. D. 0,4 s.
Câu 35. Một con lắc lò xo gồm vật nhỏ khối lượng
0,2 kg
và lò xo có độ cứng
k 20 N / m=
. Vật nhỏ
được đặt trên giá cố định nằm ngang dọc theo trục lò xo. Hệ số ma sát trượt giữa giá đỡ và vật nhỏ là
0,01. Từ vị trí lò xo không biến dạng truyền cho vật vận tốc ban đầu
1 m / s
thì thấy con lắc dao động tắt
dần trong giới hạn đàn hồi của lò xo. Lấy
2
10 m / sg =
. Độ lớn lực đàn hồi cực đại của lò xo trong quá
trình dao động là
A.
2,2 N
. B.
19,8 N
. C.
1,5 N
D.
1,98 N
.
3. CON LẮC ĐƠN
Trang 5
Câu 36. Một con lắc đơn dao động điều hòa tại một địa điểm
A
. Nếu đem con lắc đến địa điểm
B
, biết
rằng chiều dài con lắc không đổi còn gia tốc trọng trường tại B bằng
81%
gia tốc trọng trường tại#A. So
với tần số dao động của con lắc tại
A
, tần số dao động của con lắc tại B sẽ
A. tăng
10%
. B. giảm
9%
. C. tăng
9%
D. giảm
10%
.
Câu 37. Một con lắc đơn dài
25 cm
, hòn bi có khối lượng
10 g
mang điện tích
4
q 10 C
−
=
. Cho
2
10 /g m s=
. Treo con lắc đơn giữa hai bản kim loại song song thẳng đứng cách nhau
20 cm
. Đặt hai bản
dưới hiệu điện thế một chiều
80 V
. Chu kì dao động của con lắc đơn với biên độ góc nhỏ là
A.
0,91 s
. B.
0,96 s
. C.
2,92 s
. D.
0,58 s
.
Câu 38. Trong bài thực hành đo gia tốc trọng trường
g
bằng
con lắc đơn, một nhóm học sinh tiến hành đo, xử lý số liệu và
vẽ được đồ thị biểu diễn sự phụ thuộc của bình phương chu kì
dao động điều hòa
( )
2
T
theo chiều dài
l
của con lắc như hình
bên. Lấy
3,14
=
. Giá trị trung bình của
g
đo được trong thí
nghiệm này là
A. 9,74 m/s B. 9,96 m/s
C. 9,58 m/s D.
2
9,42 m / s
Câu 39. Một con lắc đơn có chiều dài 1,92 m treo vào điểm T cố định. Từ vị
trí cân bằng O, kéo con lắc về bên phải đến A rồi thả nhẹ. Mỗi khi vật nhỏ đi từ
phải sang trái ngang qua B thì dây vướng vào đinh nhỏ tại D, vật dao động trên
quỹ đạo AOBC (được minh họa bằng hình bên). Biết TD = 1,28 m và
0
12
4

==
. Bỏ qua mọi ma sát. Lấy
22
g (m / s )
=
. Chu kì dao động của con
lắc là
A. 2,26 s. B. 2,61 s. C. 1,60 s. D. 2,77 s.
Câu 40. Con lắc lò xo M và con lắc đơn N có chu kỳ dao động riêng tương ứng là T
1
=0,4s và T
2
. Người
ta đưa cả hai con lắc ra biên của chúng (biên của con lắc lò xo tuỳ ý trong giới hạn đàn hồi, biên của con
lắc đơn tuỳ ý trong giới hạn góc bé). Ban đầu ta thả cho con lắc lò xo dao động, khi vật tới vị trí cân bằng
lần đầu thì người ta thả con lắc đơn cho dao động. Thấy rằng khi con lắc lò xo thực hiện đủ 10 dao động
thì con lắc đơn thực hiện đủ 2 dao động. Chu kỳ con lắc đơn T
2
là
A. 2s. B. 0,8 s. C. 1,95s. D. 1,78 s.
Câu 41. Hai con lắc đơn giống hệt nhau dài 1,44 m, con lắc
A
dao động trên Trái Đất và con lắc
B
dao
động trên Mặt Trăng. Cho biết gia tốc rơi tự do trên Mặt Trăng bằng 0,16 gia tốc rơi tự do trên Trái Đất
và bằng
22
0,16 m / s
. Giả sử hai con lắc được kích thích dao động điều hòa ở cùng một thời điểm thì sau
1 h
, con lắc
A
dao động nhiều hơn con lắc
B
là bao nhiêu dao động toàn phần?
A. 900. B. 800. C. 720. D. 640.
Câu 42. Hai con lắc đơn chiều dài
1
l
và
2
l
có chu kì dao động riêng lần lưọt là
1
T
và
12
2TT=
. Nếu cả hai
sợi dây cùng được cắt bớt đi 2 dm thì ta được hai con lắc đơn mới có chu kì dao động riêng tương ứng là
1
'T
và
21
''3TT=
. Chiều dài
1
l
có giá trị là
A.
8,4dm
. B.
4,6dm
. C.
3,2dm
. D.
12,8dm
.
Câu 43. Một con lắc đơn dao động với phương trình
0,1cos 10t rad,t
2

=−


đo bằng s tại nơi có gia
tốc rơi tự do
2
10 m / sg =
. Trong thời gian
1,2 s
đầu tiên kể từ
t0=
, vật nhỏ của con lắc đơn đi được
quãng đường là
A.
27,9 cm
. B.
12,1 cm
. C.
13,9 cm
. D.
26,1 cm
.
Trang 6
Câu 44. Ở một nơi trên Trái Đất, hai con lắc đơn có cùng khối lượng đang dao động điều hòa. Gọi
ℓ
1
, s
01
, F
1
và ℓ
2
, s
02
, F
2
lần lượt là chiều dài, biên độ, độ lớn lực kéo về cực đại của con lắc thứ nhất và của
con lắc thứ hai. Biết 



. Tỉ số
bằng
A.
. B.
. C.
. D.
.
Câu 45. Một con lắc đơn gồm vật nhỏ có khối lượng m treo vào một sợi dây dài 1 m. Từ vị trí cân bằng,
kéo vật theo chiều dương của trục tọa độ tới vị trí mà dây treo hợp với phương thẳng đứng góc α
0
= 6
0
rồi
thả không vận tốc đầu cho vật dao động điều hòa. Chọn mốc thời gian là lúc thả vật, gốc tọa độ là vị trí
cân bằng, lấy g = π
2
m/s
2
. Phương trình dao động của vật là
A.
s 6cos( t)(cm)=
. B.
s cos( t)(m)
30
=
.
C.
s cos( t )(m)
30
= +
. D.
s 6cos( t )(cm)
2
= +
.
Câu 46. Hai con lắc đơn có chiều dài hơn kém nhau
0,1 m
dao
động điều hòa tại một nơi nhất định. Hình vẽ bên là đồ thị phụ
thuộc thời gian của li độ góc của hai con lắc. Chiều dài con lắc 1
là?
A.
0,08 m
. B.
0,25 m
.
C.
0,15 m
. D.
0,18 m
.
Câu 47. Một con lắc đơn dao động điều hòa với biên độ góc
0
tại nơi có gia tốc trọng trường là g. Biết
gia tốc của vật ở vị trí biên gấp 8 lần gia tốc của vật ở vị trí cân bằng. Giá trị của
0
là
A.
.375,0 rad
B.
.062,0 rad
C.
.25,0 rad
D.
.125,0 rad
Câu 48. Một con lắc đơn có chiều dài l= 40cm, được treo tại nơi có g = 10m/s
2
. Bỏ qua sức cản không
khí. Đưa con lắc lệch khỏi VTCB một góc 0,1rad rồi truyền cho vật nặng vận tốc 20cm/s theo phương
vuông góc với dây hướng về VTCB. Chọn gốc tọa độ tại vị trí cân bằng của vật nặng, gốc thời gian lúc
gia tốc của vật nặng tiếp tuyến với quỹ đạo lần thứ nhất. Viết phương trình dao động của con lắc theo li
độ cong
A. 8cos(25t +) cm B. 4
2
cos(25t +) cm
C. 4
2
cos(25t +/2) cm D. 8cos(25t) cm
Câu 49. Một con lắc đơn dao động điều hoà theo phương trình li độ góc = 0,1cos(2t + /4) ( rad).
Trong khoảng thời gian 5,25s tính từ thời điểm con lắc bắt đầu dao động, có bao nhiêu lần con lắc có độ
lớn vận tốc bằng 1/2 vận tốc cực đại của nó?
A. 11 lần. B. 21 lần. C. 20 lần. D. 22 lần.
Câu 50. Một con lắc đơn gồm vật có khối lượng m, dây treo có chiều dài l = 2m, lấy g = π
2
. Con lắc dao
động điều hòa dưới tác dụng của ngoại lực có biểu thức F = F
0
cos(ωt + π/2)( N). Nếu chu kỳ T của ngoại
lực tăng từ 2s lên 4s thì biên độ dao động của vật sẽ:
A. tăng rồi giảm B. giảm rồi tăng C. chỉ giảm D. chỉ tăng
Câu 51. một con lắc đơn dao động điều hòa,nếu giảm chiều dài con lắc đi 44cm thì chu kì giảm đi
0,4s.lấy g=10m/s
2
.π
2
=10,coi rằng chiều dài con lắc đơn đủ lớn thì chu kì dao động khi chưa giảm chiều
dài là
A.1s B.2,4s C.2s D.1,8s
Câu 52. Một con lắc đơn gồm 1 vật nhỏ được treo vào đầu dưới của 1 sợi dây không dãn, đầu trên của sợi
dây được buộc cố định. Bỏ qua ma sát của lực cản của không khí. Kéo con lắc lệch khỏi phương thẳng
đứng một góc 0,1rad rồi thả nhẹ. Tỉ số độ lớn gia tốc của vật tại VTCB và độ lớn gia tốc tại vị trí biên
bằng:
A: 0,1. B. 0. C. 10. D. 1.
Trang 7
Câu 53. Một con lắc đơn gồm hòn bi nhỏ bằng kim loại được tích điện q > 0. Khi đặt con lắc vào trong
điện trường đều có véc tơ cường độ điện trường nằm ngang thì tại vị trí cân bằng dây treo hợp với
phương thẳng đứng một góc α, có tanα = 3/4; lúc này con lắc dao động nhỏ với chu kỳ T
1
. Nếu đổi chiều
điện trường này sao cho véctơ cường độ diện trường có phương thẳng đứng hướng lên và cường độ không
đổi thì chu kỳ dao động nhỏ của con lắc lúc này là:
A.
5
1
T
. B. T
1
5
7
C. T
1
7
5
. D. T
1
5
.
Câu 54. Con lắc đơn đang đứng yên trong điện trường đều nằm ngang thì điện trường đột ngột đổi chiều
(giữ nguyên phương và cường độ E) sau đó con lắc dao động điều hòa với biên độ góc α
0
. Gọi q và m là
điện tích và khối lượng của vật nặng; g là gia tốc trọng trường. Hệ thức liên hệ đúng là:
A. q.E = m.g.α
0
. B. q.E.α
0
= m.g. C. 2q.E = m.g.α
0
. D. 2q.E.α
0
= m.g.
Câu 55. Một con lắc đơn có chiều dài dây treo 50 cm và vật nhỏ có khối lượng 0,01 kg mang điện tích q
= 5.10
-6
C, được coi là điện tích điểm. Con lắc dao động điều hòa trong điện trường đều mà vectơ cường
độ điện trường có độ lớn E=10
4
V/m và hướng thẳng đứng xuống dưới. Lấy g=10 m/s
2
, π = 3,14. Xác
định chu kì dao động của con lắc.
A. 2,15 s. B. 3,15 s. C. 1,15 s. D. 4,15 s.
Câu 56. Có hai con lắc đơn giống nhau. Vật nhỏ của con lắc thứ nhất mang điện tích 2,45.10
-6
C, vật nhỏ
con lắc thứ hai không mang điện. Treo cả hai con lắc vào vùng điện trường đều có đường sức điện thẳng
đứng, và cường độ điện trường có độ lớn E = 4,8.10
4
V/m. Xét hai dao động điều hòa của con lắc, người
ta thấy trong cùng một khoảng thời gian, con lắc thứ nhất thực hiện được 7 dao động thì con lắc thứ hai
thực hiện được 5 dao động. Lấy g = 9,8 m/s
2
. Khối lượng vật nhỏ của mỗi con lắc là
A. 12,5 g. B. 4,054 g. C. 7,946 g. D. 24,5 g.
Câu 57. Khảo sát dao động điều hòa của một con lắc đơn, vật dao động nặng 200 g, tích điện q = −400
µC tại nơi có gia tốc trọng trường 10 m/s
2
. Khi chưa có điện trường chu kì dao động điều hòa là T. Khi có
điện trường đều phương thẳng đứng thì chu kì dao động điều hòa là 2T. Điện trường đều
A. hướng xuống và E = 7,5 kV/m. B. hướng lên và E = 7,5 kV/m.
C. hướng xuống và E = 3,75 kV/m. D. hướng lên và E = 3,75 kV/m.
Câu 58. Con lắc đơn gồm vật nặng có khối lượng 100 g, mang điện tích 10
−5
C đang dao động điều hòa
với biên độ góc 6°. Lấy g = 10 m/s
2
. Khi vật dao động đi qua vị trí cân bằng người ta thiết lập một điện
trường đều theo phưong thẳng đứng, hướng lên với độ lớn 25 kV/m thì biên độ góc sau đó là
A. 3° B.
43
°. C.
62
0
. D. 6°
4. TỔNG HỢP DAO ĐỘNG
Câu 59. Cho 2 dao động điều hòa x
1
; x
2
cùng phương, cùng tần số có đồ thị
như hình vẽ. Dao động tổng hợp của x
1
; x
2
có phương trình
A. x = 8
cos(πt -

) cm B. x = 8
cos(πt -
) cm
C. x = 8
cos(2πt -

) cm D. x = 8
cos(2πt -

) cm
Câu 60. Hai dao động điều hòa (1) và (2) cùng phương, cùng tần số và cùng biên độ 4 cm. Tại một thời
điểm nào đó, dao động (1) có li độ
23
cm, đang chuyển động ngược chiều dương, còn dao động (2) có li
độ 2 cm theo chiều dương. Lúc đó, dao động tổng hợp của hai dao động trên có li độ bao nhiêu và đang
chuyển động theo chiều nào?
A. x = 8 cm và chuyển động ngược chiều dương.
B. x = 5,46 và chuyển động ngược chiều dương
C. x = 5,46 cm và chuyển động theo chiều dương.
D. x = 8 cm và chuyển động theo chiều dương.
Trang 8
Câu 61. Một vật dao động điều hoà là tổng hợp của hai dao động cùng phương cùng tần số cùng, đồ thị li
độ thời gian của hai dao động thành phần như hình vẽ.. Tổng tốc độ của hai dao động có giá trị lớn nhất là
A. 280π (cm/s). B. 200π (cm/s)
C. 140π (cm/s). D. 160π (cm/s).
Câu 62. Một vật thực hiện đồng thời hai dao động cùng phương, cùng tần số 4Hz và cùng cùng biên độ 2
cm. Khi qua vị trí động năng của vật bằng 3 lần thế năng vật đạt tốc độ 24π (cm/s). Độ lệch pha giữa hai
dao động thành phần bằng
A. π/6. B. π/2. C. π/3. D. 2π/3.
Câu 63. Một chất điểm tham gia đồng thời hai dao động điều hòa trên cùng một trục Ox có phương trình:
x
1
= 4cos(ωt + π/3) cm, x
2
= A
2
cos(ωt + φ
2
) cm. Phương trình dao động tổng hợp x = 2cos(ωt + φ) cm.
Biết φ – φ
2
= π/2. Cặp giá trị nào của A
2
và φ sau đây là đúng?
A. 3/3 cm và 0. B. 2/3 cm và π/4. C. 3/3 cm và π/2. D.
23
cm và 0.
Câu 64. Hình vẽ bên là đồ thị biễu diễn sự phụ thuộc của li độ
x
vào thời gian
t
của hai dao động điều hòa cùng phương. Dao động
của vật là tổng hợp của hai dao động nói trên. Trong 0,20 s đầu
tiên kể từ
0t =
s, tốc độ trung bình của vật bằng
A.
40 3
cm/s. B. 40 cm/s.
C.
20 3
cm/s. D. 20 cm/s.
Câu 65. Một chất điểm dao động điều hòa là tổng hợp của hai dao
động cùng phương cùng cùng tần số với li độ lần lượt là x
1
và x
2
. Li độ của hai dao động thành phần thỏa
mãn điều kiện:
( )
2 2 2
12
1,5x 2x 18 cm+=
. Tính biên độ dao động tổng hợp của hai dao động trên.
A. 5cm. B. 2 cm. C. 4 cm. D. 5,4cm.
Câu 66. Một vật tham gia đồng thời 2 dao động diêu hoà cùng phương cùng tần số và vuông pha với
nhau. Nếu chỉ tham gia dao động thứ nhất thì cơ năng dao động là W
1
. Nếu chỉ tham gia dao động thứ hai
thì cơ năng dao động là W
2
. Nếu tham gia đồng thời 2 dao động thi cơ năng dao động là
A. 0,5(W
1
+ W
2
). B. (W
1
+ W
2
). C.
( )
0,5
22
12
W W .+
D.
( )
0,5
22
12
0,5 W W+
Câu 67. Một vật thực hiện đồng thời 2 dao động điều hòa cùng phương,
cùng chu kì 2s. Gốc tọa độ trùng với vị trí cân bằng. Đồ thị phụ thuộc thời
gian của các li độ được biểu diễn như hình vẽ. Biết t
2
– t
1
=
s. Biên độ dao
động tổng hợp gần giá trị nào nhất sau đây?
A.2 cm B.3,4 cm C.7,5 cm D.8 cm
Câu 68. Một vật m = 100 g thực hiện đồng thời hai dao động điều hòa
cùng phương được mô tả như hình vẽ. Lực kéo về cực đại tác dụng lên vật
gần giá trị nào nhất
A.1 N B.40 N C.10 N D.4 N
Câu 69. Đồ thị của hai dao động điều hòa cùng tần số có dạng như hình
vẽ. Phương trình nào sau đây là phương trình dao động tổng hợp của
chúng:
A. x = 5cos
cm B. x = cos󰇡
󰇢 cm
C. x = 5cos󰇡
󰇢 cm D. x = 5cos󰇡
󰇢 cm
Câu 70. Một chất điểm thực hiện đồng thời hai dao động điều hòa cùng
phương cùng chu kì T mà đồ thị x
1
và x
2
phụ thuộc thời gian biểu
diễn trên hình vẽ. Biết x
2
= v
1
T, tốc độ cực đại của chất điểm là 53,4
cm/s. Giá trị T gần giá trị nào nhất sau đây?
A.2,56 s B.2,99 s
C.2,75 s D.2,64 s
()x cm
O
6+
6−
()ts
0 , 3
0 , 1
0 , 2
Trang 9
Trang 10
HƯỚNG DẪN GIẢI
Câu 1. Một vật nhỏ dao động điều hòa với chu kỳ T=1s. Tại thời điểm t
1
nào đó, li độ của vật là -2cm.
Tại thời điểm t
2
= t
1
+0.25s, vận tốc của vật có giá trị là:
A. 4 cm/s. B. -2 m/s. C. 2cm/s. D. - 4m/s.
Hướng dẫn
Cách 1: Giả sử phương trình dao động của vật có dạng x = Acos t (cm)
x
1
= Acos t
1
(cm)
x
2
= Acos t
2
= Acos (t
1
+ ) = Acos( t
1
+ ) (cm) = - Asin t
1
v
2
= x’
2
= - Asin( t
1
+ ) = - Acos t
1
= 4 (cm/s). Đáp án: A
Cách 2: t
2
- t
1
=T/4
Đặt x
1
=Acosα (x
1
, α là li độ và pha tại thời điểm t
1
) suy ra vận tốc tại thời điểm t
2
là
v
2
=-wAsin(α+π/2)=-wAcosα.
Lập tỉ số x
1
/v
2
rút ra giá trị v
2
.
Câu 2. Một dao động điều hoà với x=8cos(2t-
6
) cm. Thời điểm thứ 2023 vật qua vị trí có vận tốc v =
-8 cm/s có giá trị gần nhất là :
A. 1011,2s. B. 1011,3s. C. 1011,1s. D. 1011,5s.
Hướng dẫn
T=1s.
Ta có
22
( ) 4 3
v
x A cm
= − =
.Vì v < 0 nên vật qua M
1
và M
2
Qua lần thứ 2023 thì phải quay 1011 vòng rồi đi từ M
0
đến M
1
. Góc quét  = 1011.2 + /3 t
=1011.T+ T/6=1011,1667 s. (Hình 7)
Câu 3. Vật dao động điều hòa có vận tốc cực đại bằng 3m/s và gia tốc cực đại bằng 30 m/s
2
. Thời điểm ban
đầu vật có vận tốc 1,5m/s và thế năng đang tăng. Thời điểm vật có gia tốc bằng 15 m/s
2
là:
A. 0,10s. B. 0,15s. C. 0,20s. D. 0,05s.
Hướng dẫn
v
max
= ωA= 3(m/s), a
max
= ω
2
A= 30π (m/s
2
) => ω = 10π --→ T = 0,2s
Khi t = 0 thì v = 1,5 m/s = v
max
/2→ Wđ
= W/4. Tức là tế năng W
t
=3W/4
2
2
0
0
33
2 4 2 2
kx
kA A
x= =
.
Do thế năng đang tăng, vật chuyển động theo chiều dương nên vị trí ban
đầu
x
0
=
3
2
A
Vật ở M
0
góc φ = -π/6.
(Có thể dùng trục tọa độ vận tốc để xác định M
0
nhanh hơn)
Thời điểm a = 15 (m/s
2
)= a
max
/2 =>
a=-ω
2
x>0 suy ra x = -A/2. Có 2 vị trí ứng với x = -A/2 là M và điểm đối xứng qua 0x. Tuy nhiên đáp án phù
hợp có trong 4 phương án là M ứng với thời điểm t = 3T/4 = 0,15s
(Điểm đối xứng M ứng với t=0,083s không có trong đáp án.)
Chọn B. 0,15s
Câu 4. Một vật dao động điều hòa, đi qua vị trị có vận tốc bằng không vào các thời điểm liên tiếp 4,25s
và 5,75s. Biết vào thời điểm ban đầu vật chuyển động theo chiều dương của trục tọa độ, và tốc độ lớn
T
2
T
2
T
2
T
2
4
T
T
2
2
T
2
T
2
T
2
2
T
2
T
2
43−
43
Hình
7
O
M
M
0
A
Trang 11
nhất của vật trong quá trình dao động là 4 (cm/s). Vận tốc trung bình của vật trong khoảng từ thời điểm
0,75s đến thời điểm 2,25s là :
A. -4,00cm/s. B. 4,00cm/s. C. 0,00 cm/s. D. -4,25cm/s.
Hướng dẫn
+ T/2 = 5,75 – 4,25 = 1,5 s => T = 3s (vị trị có vận tốc bằng không là VT biên)
+ v
max
= A => A = 6cm
+ t = 4,25s = T + T/4 + T/6
* Ở thời điểm 4,25s nếu vật ở VT biên dương thì khi t = 0 vật ở VT: x = -A
2
3
; v > 0 (nhận)
* Ở thời điểm 4,25s nếu vật ở VT biên âm thì khi t = 0 vật ở VT: x = A
2
3
; v < 0 (loại)
+ trong khoảng từ thời điểm 0,75s = T/6 + T/12 đến thời điểm 2,25s: t = 1,5s = T/2
=> vật từ x
1
=
#
A/2 đến x
2
= -#A/2
=> vận tốc: v = = = - 6/1,5 = - 4 cm/s
Câu 5. Một chất điểm dao động điều hòa với chu kì T. Gọi a
max
là gia tốc cực đại của vật. Khoảng thời
gian trong một chu kì để vật có độ lớn gia tốc lớn hơn
max
2
a
là :
A. T/3. B. 2T/3. C. T/6. D. T/2.
Hướng dẫn
Ta có : vị trí |a|=
max
2
a
tương ứng |x|=
2
A
Vẽ đường tròn, để |a|>
max
2
a
tương ứng |x|>
2
A
thì phần góc tương ứng là 45
0
.4 tương ứng thời gian
T/2. Đáp án D.
Câu 6. Hai chất điểm M, N dao động điều hòa dọc theo hai đường thẳng song song kề nhau và song
song với trục tọa độ Ox. Vị trí cân bằng của M và của N đều ở trên một đường thẳng qua gốc tọa độ và
vuông góc với Ox. Phương trình dao động của chúng lần lượt là x
1
= 10cos2πt cm và x
2
= 10 cos(2πt +
) cm. Hai chất điểm gặp nhau khi chúng đi qua nhau trên đường thẳng vuông góc với trục Ox. Thời
điểm lần thứ 2023 hai chất điểm gặp nhau là:
A. 16 phút 51,42s. B. 16 phút 51,92s. C. 16 phút 52,42s. D. 16 phút 50,92s.
Hướng dẫn
T=1s.
ta có x
2
= 10 cos(2πt + ) cm = - 10 sin(2πt)
x
1
= x
2
=> 10cos(2πt) = - 10 sin(2πt) => tan(2πt) = - => 2πt = - + kπ
=> t = - + (s) với k = 1; 2; 3.... vì t>0; hay có nghĩa là t = + với k = 0, 1,2...
Thời điểm lần đầu tiên hai chất điểm gặp nhau ứng với k = 0: t
1
= s.
Lần thứ 2013 chúng gặp nhau ứng với k = 2012 =>
t
2023
= 1011+ = 16 phút 51,4166s = 16 phút 51,42s Đáp án A
t
xx
−
12
2T
A−
3
2
3
2
3
3
3
1
6
12
1
2
k
12
5
2
k
12
5
12
5
x
-
A
0
T/6
A
T/4
-A
T/12
Trang 12
Câu 7. Hai chất điểm dao động điều hòa cùng biên độ A, với tần số góc 3 Hz và 6 Hz. Lúc đầu hai vật
đồng thời xuất phát từ vị trí có li độ và đang chuyển động theo chiều dương. Khoảng thời gian
ngắn nhất để hai vật gặp nhau là:
A. . B. . C. . D. .
Hướng dẫn
Vì cùng xuất phát từ x= và chuyển động theo chiều dương nên pha ban đầu của chúng - .
Do đó phương trình của chúng lần lượt là và
Khi gặp nhau: = => = = - +2kπ
t min thì k=0; .
Câu 8. Một vật dao động điều hòa với phương trình Quãng đường vật đi
được từ thời điểm t
1
= 0,1 s đến t
2
= 6s là:
A. 84,4cm. B. 333,8cm. C. 331,4 cm. D. 337,5cm.
Hướng dẫn
chu kỳ:
Thời gian đi: t
2
-t
1
= 6- 1/10= 5,9(s)
Ta có: Hay:
Quãng đường đi trong 14T là: S
1
=14.4A =56 A
Lúc t
1
= 0,1s vật ở tại M
1
, Lúc t
2
= 6s vật ở tại M
0
trùng lúc đầu.
Quãng đường đi trong 0,75T( Từ M
1
đến M
0
là ¾ vòng tròn) là:
S
2
=2(A - ) +2A = ( 4- )A
Quãng đường đi trong 14T+ 0,75T là: S =S
1
+S
2
331,4cm. Chọn C
Câu 9. Một vật dao động điều hòa theo phương nằm ngang, khi li độ vật bằng 0 thì vận tốc có gia trị
31,4cm/s; khi li độ vật cực đại thì gia tốc có giá trị 4 m/s
2
. Lấy π
2
= 10. Thời gian ngắn nhất để vật chuyển
động từ li độ x = 0 đến x = 1,25cm là:
A. 1/12 s. B. 1/3 s. C. 1/6 s. D. 1/24 s.
Hướng dẫn
Từ phương trình của vật dao động điều hòa.
Ta có:-Khi li độ bằng không thì vận tốc cực v
max
=
A
-Khi li độ cực đại thì gia tốc cực đại a
max
=
2
A =
v
max
-Tần số góc
= a
max
/ v
max
= 400/ 31,4 = 4
( rad/s)
biên độ A = v
max
/
= 10
/ 4
= 2,5 cm
Khi vật có li độ x = 1,25 cm
Từ phương trình li độ x = A cos (
t +
) = Acos
cos
= 1/2 = >
=
/ 3 và
= –
/3
Theo điều kiện đề cho xét thời gian vật đi từ x = 0 đến x = 1,25 cm
Khoảng thời gian tương ứng góc quay

=
/6
Thời gian tương ứng
t =

/
= 1/24 (s)
s
18
1
s
27
1
s
36
1
s
72
1
2
A
4
)
4
cos(
11
−= tAx
)
4
cos(
22
−= tAx
1
x
2
x
)
4
cos(
1
−tA
)
4
cos(
2
−tA
)
4
(
1
−t
)
4
(
2
−t
stt
36
1
4
2
)(
21
==+
.)4/35cos(24 cmtx
−=
22
0,4
5
Ts


===
21
5,9
14,75
0,4
tt
T
−
==
21
14,75 14 0,75t t T T T− = = +
2
M
0
X
O
A
X
2
x
1
-
A
Hình 6
-
M
1
– /3
O
1,2
5
2,
5
/
6
Trang 13
Câu 10. Hai chất điểm M và N dao động điều hòa cạnh nhau, dọc theo trục Ox. Vị trí cân bằng của hai
chất điểm ở cùng gốc tọa độ O. Phương trình dao động của chúng lần lượt là
( ) ( )
1 1 2 2
cos , cos
36
x A t cm x A t cm


= + = −
. Biết
22
12
4
9 16
xx
+=
. Tại thời điểm t nào đó, chất
điểm M có li độ
1
3x cm=−
và vận tốc
1
30 3 /v cm s=−
. Khi đó, độ lớn vận tốc tương đối của chất
điểm này so với chất điểm kia xấp xỉ bằng:
A. 66 cm/s. B. 12 cm/s. C. 40 cm/s. D. 92 cm/s.
Hướng dẫn
Nhận xét 2 dao động vuông pha.
+ Từ phương trình
2 2 2 2
1max
1
1 2 1 2
22
2 2max
6 ( / )
6
41
8 8 ( / )
9 16 6 8
v cm s
A cm
x x x x
A cm v cm s
=
=
+ = + =

==
+ Biểu diễn tương ứng hai dao động
vuông pha trên đường tròn.
=>Từ hình vẽ, ta có
1 1max
33
30 3 6 10 /
22
v v rad s

= − − = − =
+ Dao động thứ hai chậm pha hơn dao động thứ nhất một góc
0
90
=>Từ hình vẽ, ta có
2 2max
11
8 40 /
22
v v cm s
= = =
( )
21
40 30 3 91,96 /v v v cm s = − = − − =
= > đáp án D
Câu 11. Một vật dao động điều hòa với phương trình
5cos 4
2
xt

=−


. Xác định thời gian ngắn nhất
để vật đi từ vị trí
2,5 cm
đến
2,5 cm−
.
A.
1
12
s
B.
1
s
10
C.
1
s
20
D.
1
6
s
Lời giải.
Thời gian ngắn nhất là đi từ 2,5cm qua VTCB đến -2,5cm
min
1
2.
12 12
T
ts = =
Câu 12. Một chất điểm có khối lượng
320 g
dao động điều hòa dọc theo trục Ox. Biết đồ thị biểu diễn sự
phụ thuộc của động năng theo thời gian của chất điểm như hình vẽ và tại thời điểm ban đầu
(t 0)=
chất
điểm đang chuyển động ngược chiều dương. Phương trình dao động của chất điểm là
Trang 14
A.
x 5cos 2 t cm
6

=+


.
B.
5cos 4 cm
3
xt

=+


.
C.
5cos 2 t cm
6
x

=−


D.
x 5cos 4 t cm.
3

=−


Hướng dẫn
Tại
0t =
thì
2
max
max
4
16 2
d
Wv
v
v
Wv

= = = −


và
v
đang tăng
2
36
vx


= =
Tại
5
12
ts=
thì
00
d
Wv= → =
32
2
5/12


+
==
(rad/s)
( )
2
2 2 3 2
11
16.10 .0,32. 2 0,05 5
22
W m A A A m cm

−
= = =
. Chọn A
Câu 13. Hình bên là đồ thị biểu diễn sự phụ thuộc li độ của hai dao
động điều hòa theo thời gian. Độ lệch pha của hai dao động này bằng
A.
3
.
8
B.
5
.
6
C.
3
.
4
D.
2
.
3
Hướng dẫn
Chu kì T = 16 đơn vị
Hai thời điểm liên tiếp hai dao động có li độ bằng 0 là 3 đơn vị
23
. .3
16 8
t


= = =
Câu 14. Một chất điểm dao động điều hòa có đồ thi biểu diễn sự phụ thuộc của li độ x vào thời gian t
như hình vẽ. Tại thời điểm t = 0,2s, chất có li độ 2 cm. Ở thời điểm t = 0,9s, gia tốc của chất điểm có giá
trị bằng:
A.
2
14,5cm / s
B.
2
57,0cm / s
C.
2
5,7m / s
D.
2
1,45m/ s
Hướng dẫn
Chu kì T = 1,6s
Dùng vòng tròn lượng giác
Biên độ
2
sin
8
A
=
22
2
0.9 os .0,2
1.6
. 57 /
t x Ac
a x cm s
= → = −
= − =
Câu 15. Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc
vào thời gian của li độ có dạng như hình vẽ bên. Phương trình dao động của li độ
là
Trang 15
A.
2
10
33
x cos t


=−


(cm). B.
2
10
33
x cos t


=+


(cm).
C.
22
10
33
x cos t


=+


(cm). D.
10
33
x cos t


=−


(cm).
Hướng dẫn
( )
2
2.(4,25 2,75) 3
3
22
10 2,75 10
3 2 3 3
Ts
x cos t cos t
= − = =
= − + = +
Câu 16. Một vật dao động điều hòa với phương trình x = 10cos(πt + π/3) cm. Khoảng thời gian tính từ
lúc vật bắt đầu dao động (t = 0) đến khi vật đi được quãng đường 50 cm là
A. 7/3 s B. 2,4 s C. 4/3 s D. 1,5 s
Hướng dẫn
( )
2
7
3
s 50cm 5A t s
3
+
= = = = =

Câu 17. Một con lắc lò xo gồm quả cầu nhỏ khối lượng 1 kg và lò xo có độ cứng 50 N/m. Cho con lắc
dao động điều hòa trên phương nằm ngang. Tại thời điểm vận tốc của quả cầu là 0,2 m/sthì gia tốc của nó
là
3−
m/s
2
. Cơ năng của con lắc là
A. 0,02 J. B. 0,05 J. C. 0,04 J D. 0,01 J
Hướng dẫn
( )
k 50
5 2 rad / s
m1
= = =
( )
( )
2
2
a 3 3
xm
50
52
= − = =
( )
2
2 2 2
1 1 1 3 1
W kx mv .50. .1.0,2 0,05 J
2 2 2 50 2

= + = + =



Câu 18. Một vật dao động điều hòa với tần số f =10 Hz. Tại thời điểm ban đầu vật đang ở li độ x = 2cm
và chuyển động theo chiều dương. Sau 0,25 (s) kể từ khi dao động thì vật ở li độ
A. x = 2 cm và chuyển động theo chiều đương.
B. x = 2 cm và chuyển động theo chiều âm.
C. x = −2 cm và chuyển động theo chiều âm.
D. x = −2 cm và chuyền động theo chiều dương.
Hướng dẫn
( )
2 f 2 .10 20 rad / s = = =
t 20 .0,25 5 = = =
Ngược pha
x 2cm = −
Câu 19. Con lắc lò xo nằm ngang dao động điều hòa, lực đàn hồi cực đại tác đụng vào vật là 2 N, gia tốc
cực đại của vật là 2 m/s
2
. Khối lượng của vật là
A. 1 kg. B. 2 kg. C. 3 kg. D. 4 kg.
Hướng dẫn
F2
m 1kg
a2
= = =
Câu 20. Một con lắc lò xo có độ cứng 50 N/m, dao động điều hòa với biên độ 4 cm. Chọn gốc tính thế
năng là vị trí cân bằng. Tổng động năng và thế năng của vật là
A. 25 mJ. B. 20 mJ. C. 40 mJ. D. 10 mJ.
Hướng dẫn
Trang 16
( ) ( )
2
11
W kA .50.0,04 0,04 J 40 mJ
22
= = = =
Câu 21. Khi treo một vật nặng vào một lò xo, khi vật đứng yên lò xo dài thêm một đoạn 2,5 cm. Lấy g =
π
2
m/s
2
. Chu kì dao động tự do của con lắc bằng
A. 0,316 s. B. 0,317 s. C. 0,215 s. D. 0,291 s.
Hướng dẫn
0
2
0,025
T 2 2 0,316s
g
= =
Câu 22. Một chất điểm dao động điều hòa có đồ thị như hình bên.
Thời điểm mà vận vận tốc v và li độ x thỏa mãn
( )
1
v
1,25 3 s
x
−
= −
lần thứ 2023 gần nhất với giá trị nào dưới đây?
A. 1618.12 s. B. 1617,94 s.
C. 1617.83 s. D. 1618,37 s.
Hướng dẫn
2
5
3
31 1
t4
20 2

= = =
−
5 1 5 3
x Acos t Acos t
4 2 4 8
= − + = +


( )
( )
( )
2
22
2 2 2
2
2
22
5
Ax
Ax
vA
4
1,25 3 x
x x x 2

−

−


= = = − =


và
x trái dấu v
( )
5
2022
83
t 1618,37 s
5
4

+ +
= =
x(cm)
t(s)
A
A−
1/ 3
31/30
O
thukhoadaihoc.vn
thukhoadaihoc.vn
Câu 23. Một vật dao động điều hòa với phương trình x = Acos(ωt + φ).
Hình bên là đồ thị biểu diễn sự phụ thuộc li độ x theo thời gian t. Tại
thời điểm t = 0, gia tốc của vật có giá trị là
A.
( )
22
5 2 cm / s−
B.
( )
22
5 3 cm/ s−
C.
( )
22
5 2 cm / s
D.
( )
22
5 3 cm / s
t(s)
x(cm)
10
5
5−
O
0,5
1
1,5
thukhoadaihoc.vn
thukhoadaihoc.vn
Hướng dẫn
T
4
=
6 ô
( )
2
0,5s T 2s rad / s
T
= = = =
Góc quét từ t = 0 đến vị trí cân bằng lần dầu là
A2
t 0,25 x 5 2cm
2
 = = − = −
( )
2 2 2
a x 5 2 cm / s= − =
Câu 24. Một vật dao động điều hòa với biên độ 5 cm, trong 1 phút thực hiện được 30 dao động toàn
phần. Quãng đường mà vật đi được trong 1 s là
A. 15 cm. B. 5 cm. C. 10 cm. D. 20 cm.
Hướng dẫn
Trang 17
T
30T 60s 1s s 2A 2.5 10cm
2
= = = = =
Câu 25. Một con lắc lò xo gồm lò xo và vật có khối lượng 80 g dao động
điều hòa trên mặt phẳng nằm ngang. Mốc tính thế năng tại vị trí cân bằng.
Hình bên là đồ thị biểu diễn sự phụ thuộc của thế năng đàn hồi của con
lắc W
t
vào thời gian t. Lấy π
2
= 10. Biên độ dao động của con lắc là
A.
22
cm. B. 2 cm.
C. 4 cm. D.
42
cm
Hướng dẫn
( )
t
W mJ
t(s)
0,05
4
O
thukhoadaihoc.vn
thukhoadaihoc.vn
Dời trục hoành vào chính giữa đồ thị
( )
/
/
T
0,05s T 0,2s T 0,4s 5 rad / s
4
= = = =
( )
2
2 2 3 2
1 1 2
W m A 8.10 .0,08 5 A A m 2 2cm
2 2 50
−
= = = =
Câu 26. Một con lắc lò xo heo thẳng đứng (coi gia tốc trọng trường là 10 m/s
2
) quả cầu có khối lượng
120 g. Chiều dài tự nhiên của lò xo là 20 cm và độ cứng 40 N/m. Từ vị trí cân bằng, kéo vật thẳng đứng,
xuống dưới tới khi lò xo dài 26,5 cm rồi buông nhẹ cho nó dao động điều hòa Động năng của vật lúc lò
xo dài 25 cm là
A. 24,5 mJ. B. 22 mJ. C. 12 mJ. D. 16,5 mJ.
Hướng dẫn
( )
( )
( )
( )
CB 0 0
0 max CB
cb
0,23 m
mg 0,12.10
0,03 m A 0,265 0,23 0,035 m
k 40
x 0,25 0,23 0,02 m
= + =
= = = = − = − =
= − = − =
( )
( )
22
2 2 3
dt
kA kx 40
W W W 0,035 0,02 16,5.10 J
2 2 2
−
= − = − = − =
Câu 27. Một con lắc lò xo đang dao động điều hòa theo phương nằm ngang. Mốc thế năng ở vị trí cân
bằng. Biết động năng cực đại của con lắc là 80 mJ, lực kéo về cực đại tác dụng lên vật nhỏ của con lắc là
4 N. Khi vật qua vị trí có li độ 3 cm thì động năng của con lắc có giá trị là
A. 5 mJ. B. 75 mJ. C. 45 mJ. D. 35 mJ.
Hướng dẫn
max
,
d
W W 80 mJ 0 08 J= = =
;
max
max
.,
.,
2
1 1 2W 2 0 08
W kA F A A 0 04m 4cm
2 2 F 4
= = = = = =
max
/
,
F
4
k 100 N m
A 0 04
= = =
;
( ) ( )
. . , , ,
2 2 2 2
d
11
W k A x 100 0 04 0 03 0 035 J 35mJ
22
= − = − = =
Câu 28. Một con lắc lò xo treo vào một điểm M cố định, đang dao động điều
hòa theo phương trình thẳng đứng. Hình bên là đồ thị biểu diễn sự phụ thuộc
của lực đàn hồi F
đh
mà lò xo tác dụng vào M theo thời gian t. Lấy
22
/g m s
=
. Độ dãn của lò xo khi con lắc ở vị trí cân bằng là
A.2 cm. B.4 cm.
C.6 cm. D.8 cm.
Hướng dẫn
Từ đồ thị ta thấy chu kì của con lắc là:
( )
0,4Ts=
( ) ( )
2
2 0,4 2 0,04 4
ll
T l m cm
g


= = = =
Trang 18
Câu 29. Một con lắc lò xo gồm vật nhỏ có khối lượng m=100 g, lò xo có
độ cứng k được treo thẳng đứng. Kích thích cho vật dao động điều hòa
với biên độ. Chọn gốc thế năng tại vị trí cân bằng của vật. Hình bên là
một phần đồ thị biểu diễn mối liên hệ giữa thế năng E
t
và độ lớn lực kéo
về |F
kv
| khi vật dao động. Chu kì dao động của vật là
A.0,222 s. B.0,314 s.
C.0,157 s. D.0,197 s.
Hướng dẫn
󰇫

󰇫


k = 80 N/m
T = 2π



≈ 0,222 (s).
Câu 30. Một con lắc lò xo dao động điều hòa theo phương ngang với lực đàn hồi lớn nhất của lò xo là 2
N và năng lượng dao động là 0,1 J. Thời gian trong một chu kì lực đàn hồi là lực kéo không nhỏ hơn 1 N
là 0,1 s. Tính tốc độ lớn nhất của vật.
A. 314,1 cm/s. B. 31,4 cm/s. C. 402,5 cm/s. D. 209,44 cm/s.
Hướng dẫn
11
12
max
xF
1 A T
xt
A F 2 2 6
= = = =
Trong 1 chu kì thời gian lực kéo lớn hon 1 N là
( ) ( )
2
T
2t 0,1 s T 0,3 s
3
= = =
( ) ( ) ( )
2
max
max
kA
W 0,1
2
A 0,1 m 10 cm v A A 209,44 cm / s
2
T
F kA 2
==
= = = =
==
Câu 31. Con lắc lò xo có độ cứng k = 40 N/m treo thẳng đứng đang dao động điều hòa với tần số góc ω =
10 rad/s tại nơi có gia tốc trọng trường g = 10 m/s
2
. Khi lò xo không biến dạng thì vận tốc dao động của
vật triệt tiêu. Độ lớn lực của lò xo tác dụng vào điểm treo khi vật ở trên vị trí cân bằng và có tốc độ 80
cm/s là
A. 2,4 N. B. 2 N. C. 1,6 N. D. 3,2 N.
Hướng dẫn
Vì khi lò xo không biến dạng thì vận tốc dao động của vật triệt tiêu nên:
( )
0
2
mg g
A 0,1 m
k
= = = =
Li độ khi vật ớ trên vị trí cân bằng và có tốc độ 80 cm/s:
( ) ( )
2
22
2
v
x A x 6 cm 0,06 m+ = = =
Lực tác dụng của lò xo vào điểm treo chính là lực đàn hồi:
( ) ( )
dh 0
F k x 1,6 N= − =
Câu 32. Một con lắc lò xo được treo thẳng đứng vào một điểm cố
định đang dao động điều hòa theo phương thẳng đứng. Hình bên là
đồ thị biểu diễn sự phụ thuộc của lực đàn hồi mà lò xo tác dụng
lên vật nhỏ của con lắc theo thời gian . Lấy

.
Biên độ dao động của con lắc lò xo là
A. 
C. 
Hướng dẫn
Dời trục hoành lên 1 ô thì đồ thị lực đàn hồi chuyển thành đồ thị lực kéo về
5
F (N)
t (s)
O
0,4
Trang 19





󰇛

󰇜





.
Câu 33. Con lắc lò xo gồm vật nhỏ nặng 1 kg thực hiện đồng thời hai dao động điều hoà theo phương
thẳng đứng, theo các phương trình:
1
x 5 2 cos10t=
cm và
2
x 5 2 sin10t=
cm (Gốc tọa độ trùng với vị trí
cân bằng, t đo bằng giây và lấy gia tốc trọng trường g = 10 m/s
2
). Lực cực đại mà lò xo tác dụng lên vật là
A. 10N. B. 20 N. C. 25 N. D. 0,25 N.
Hướng dẫn
Biên độ dao động tổng hợp là:
2 2 2 2
1 2 1 2
2 cosΔ (5 2) (5 2) 10cm 0,1mA A A A A
= + + = + = =
Ta có:
0
22
0
10
Δ 0,1
Δ 10
gg
lm
l
= = = =
Lực cực đại mà lò xo tác dụng lên vật:
( ) ( )
22
max 0 0
Δ Δ 1 10 (0,1 0,1) 20F k l A m l A N
= + = + = + =
Câu 34. Một con lắc lò xo treo vào một điểm cố định, dao động điều hòa theo phương thẳng đứng với
chu kì 1,2 s. Trong một chu kì, nếu tỉ số của thời gian lò xo giãn với thời gian lò xo nén bằng 2 thì thời
gian mà lực đàn hồi ngược chiều lực kéo về là
A. 0,2 s. B. 0,1 s. C. 0,3 s. D. 0,4 s.
Hướng dẫn
Vì t
dãn
/t
nén
= 2 nên A = 2Δl
0
.
Lực đàn hồi và lực kéo về ngược hướng khi vật ở trong đoạn
0
0x
.
Khoảng thời gian cần tính chính
( )
0E
t 2t 2.T /12 0,2 s= = =
.
Câu 35. Một con lắc lò xo gồm vật nhỏ khối lượng
0,2 kg
và lò xo có độ cứng
k 20 N / m=
. Vật nhỏ
được đặt trên giá cố định nằm ngang dọc theo trục lò xo. Hệ số ma sát trượt giữa giá đỡ và vật nhỏ là
0,01. Từ vị trí lò xo không biến dạng truyền cho vật vận tốc ban đầu
1 m / s
thì thấy con lắc dao động tắt
dần trong giới hạn đàn hồi của lò xo. Lấy
2
10 m / sg =
. Độ lớn lực đàn hồi cực đại của lò xo trong quá
trình dao động là
A.
2,2 N
. B.
19,8 N
. C.
1,5 N
D.
1,98 N
.
Hướng dẫn:
0,01.0,2.10 0,02
ms
F mg
= = =
(N)
2 2 2 2
max max max
1 1 1 1
. .0,2.1 .20. 0,02. 0,099
2 2 2 2
max ms max
mv k l F l l l l m− = − =
max ax
20.0,099 1,98
dh m
F k l= = =
(N).
Câu 36. Một con lắc đơn dao động điều hòa tại một địa điểm
A
. Nếu đem con lắc đến địa điểm
B
, biết
rằng chiều dài con lắc không đổi còn gia tốc trọng trường tại B bằng
81%
gia tốc trọng trường tại#A. So
với tần số dao động của con lắc tại
A
, tần số dao động của con lắc tại B sẽ
A. tăng
10%
. B. giảm
9%
. C. tăng
9%
D. giảm
10%
.
Hướng dẫn:
Trang 20
1
2
1 0,81.
0.9
2
A
BA
g
f
l
g
ff
l
=
==
vậy tần số con lắc đặt tại B giảm 10
Câu 37. Một con lắc đơn dài
25 cm
, hòn bi có khối lượng
10 g
mang điện tích
4
q 10 C
−
=
. Cho
2
10 /g m s=
. Treo con lắc đơn giữa hai bản kim loại song song thẳng đứng cách nhau
20 cm
. Đặt hai bản
dưới hiệu điện thế một chiều
80 V
. Chu kì dao động của con lắc đơn với biên độ góc nhỏ là
A.
0,91 s
. B.
0,96 s
. C.
2,92 s
. D.
0,58 s
.
Hướng dẫn:
2
2
2 0,96
U
E
d
l
Ts
qE
g
m
=
==

+


Câu 38. Trong bài thực hành đo gia tốc trọng trường
g
bằng
con lắc đơn, một nhóm học sinh tiến hành đo, xử lý số liệu và
vẽ được đồ thị biểu diễn sự phụ thuộc của bình phương chu kì
dao động điều hòa
( )
2
T
theo chiều dài
l
của con lắc như hình
bên. Lấy
3,14
=
. Giá trị trung bình của
g
đo được trong thí
nghiệm này là
A. 9,74 m/s B. 9,96 m/s C. 9,58 m/s D.
2
9,42 m / s
( )
2
22
2 . 9,74 /
l
T g m s
g
= =
Hướng dẫn:
Câu 39. Một con lắc đơn có chiều dài 1,92 m treo vào điểm T cố định. Từ vị
trí cân bằng O, kéo con lắc về bên phải đến A rồi thả nhẹ. Mỗi khi vật nhỏ đi từ
phải sang trái ngang qua B thì dây vướng vào đinh nhỏ tại D, vật dao động trên
quỹ đạo AOBC (được minh họa bằng hình bên). Biết TD = 1,28 m và
0
12
4

==
. Bỏ qua mọi ma sát. Lấy
22
g (m / s )
=
. Chu kì dao động của con
lắc là
A. 2,26 s. B. 2,61 s. C. 1,60 s. D. 2,77 s.
Hướng dẫn:
Gọi
0
là biên độ góc của con lắc đơn có chiều dài l
( ) ( )
0 1 1 2
1 . . ( )mgl cos mg l TD cos CD cos
− = − − − +
Chu kì của con lắc là:
1
1
1
1
0
1
2sin
2
2
1
.2
2
cos
l
T
g
gg
l C D
−
−




= + +
Câu 40. Con lắc lò xo M và con lắc đơn N có chu kỳ dao động riêng tương ứng là T
1
=0,4s và T
2
. Người
ta đưa cả hai con lắc ra biên của chúng (biên của con lắc lò xo tuỳ ý trong giới hạn đàn hồi, biên của con
lắc đơn tuỳ ý trong giới hạn góc bé). Ban đầu ta thả cho con lắc lò xo dao động, khi vật tới vị trí cân bằng
lần đầu thì người ta thả con lắc đơn cho dao động. Thấy rằng khi con lắc lò xo thực hiện đủ 10 dao động
thì con lắc đơn thực hiện đủ 2 dao động. Chu kỳ con lắc đơn T
2
là
A. 2s. B. 0,8 s. C. 1,95s. D. 1,78 s.
Trang 21
Hướng dẫn:
1 2 2
1
10 2 1,95
4
T T T s

− = =


Câu 41. Hai con lắc đơn giống hệt nhau dài 1,44 m, con lắc
A
dao động trên Trái Đất và con lắc
B
dao
động trên Mặt Trăng. Cho biết gia tốc rơi tự do trên Mặt Trăng bằng 0,16 gia tốc rơi tự do trên Trái Đất
và bằng
22
0,16 m / s
. Giả sử hai con lắc được kích thích dao động điều hòa ở cùng một thời điểm thì sau
1 h
, con lắc
A
dao động nhiều hơn con lắc
B
là bao nhiêu dao động toàn phần?
A. 900. B. 800. C. 720. D. 640.
Hướng dẫn:
Từ:
2
2
1,44
2 2,
3
,
600 3600
2
4
1, 4
2 900
,4
6
6
4
26
01
A
B
T
l
T
g
s
sT
=
= − =
= =
=
.
Chọn A
Câu 42. Hai con lắc đơn chiều dài
1
l
và
2
l
có chu kì dao động riêng lần lưọt là
1
T
và
12
2TT=
. Nếu cả hai
sợi dây cùng được cắt bớt đi 2 dm thì ta được hai con lắc đơn mới có chu kì dao động riêng tương ứng là
1
'T
và
21
''3TT=
. Chiều dài
1
l
có giá trị là
A.
8,4dm
. B.
4,6dm
. C.
3,2dm
. D.
12,8dm
.
Hướng dẫn
22
11
2 1 2
2 1 1
22
11
2
4 0 12,8
2
9 16 3,2
2
3
2
Tl
Tl
l l l dm
l
T
l l l dm
g
Tl
Tl
==
− = =

=
− = − =
−

==
−
.
Chọn C
Câu 43. Một con lắc đơn dao động với phương trình
0,1cos 10t rad,t
2

=−


đo bằng s tại nơi có gia
tốc rơi tự do
2
10 m / sg =
. Trong thời gian
1,2 s
đầu tiên kể từ
t0=
, vật nhỏ của con lắc đơn đi được
quãng đường là
A.
27,9 cm
. B.
12,1 cm
. C.
13,9 cm
. D.
26,1 cm
.
Hướng dẫn:
2
10
1 100
10
g
l m cm
= = = =
0
100.0,1 10Al
= = =
(cm)
1,2 10. 217,42 180 37,42
o o o
t rad

= = = = +
10
2 sin37,42 26,1
A
o
S A A S cm
=
= + ⎯⎯⎯→
.
Chọn D
Câu 44. Ở một nơi trên Trái Đất, hai con lắc đơn có cùng khối lượng đang dao động điều hòa. Gọi
ℓ
1
, s
01
, F
1
và ℓ
2
, s
02
, F
2
lần lượt là chiều dài, biên độ, độ lớn lực kéo về cực đại của con lắc thứ nhất và của
con lắc thứ hai. Biết 



. Tỉ số
bằng
A.
. B.
. C.
. D.
.
Hướng dẫn:
F = mg.


.
O
37,42
°
-10
10
Trang 22
Chọn A
Câu 45. Một con lắc đơn gồm vật nhỏ có khối lượng m treo vào một sợi dây dài 1 m. Từ vị trí cân bằng,
kéo vật theo chiều dương của trục tọa độ tới vị trí mà dây treo hợp với phương thẳng đứng góc α
0
= 6
0
rồi
thả không vận tốc đầu cho vật dao động điều hòa. Chọn mốc thời gian là lúc thả vật, gốc tọa độ là vị trí
cân bằng, lấy g = π
2
m/s
2
. Phương trình dao động của vật là
A.
s 6cos( t)(cm)=
. B.
s cos( t)(m)
30
=
.
C.
s cos( t )(m)
30
= +
. D.
s 6cos( t )(cm)
2
= +
.
Hướng dẫn:
00
6ππ
S = lα = 1. =
180 30
m và kéo vật theo chiều dương, chọn mốc thời gian là lúc thả vật =>φ =0..
=>
s cos( t)(m)
30
=
Chọn B
Câu 46. Hai con lắc đơn có chiều dài hơn kém nhau
0,1 m
dao
động điều hòa tại một nơi nhất định. Hình vẽ bên là đồ thị phụ
thuộc thời gian của li độ góc của hai con lắc. Chiều dài con lắc 1
là?
A.
0,08 m
. B.
0,25 m
.
C.
0,15 m
. D.
0,18 m
.
Hướng dẫn:
Quan sát hai điểm đặc biệt cắt nhau của hai đồ thị trên trục hoành ta thấy:
22
2 1 2 1
0,1
1,5 2 1,5.2 0,18( ) 0,08( )
ll
T T l m l m
gg

−
= = = =
.
Chọn A
Câu 47. Một con lắc đơn dao động điều hòa với biên độ góc
0
tại nơi có gia tốc trọng trường là g. Biết
gia tốc của vật ở vị trí biên gấp 8 lần gia tốc của vật ở vị trí cân bằng. Giá trị của
0
là
A.
.375,0 rad
B.
.062,0 rad
C.
.25,0 rad
D.
.125,0 rad
Hướng dẫn:
gia tốc ở VTB là gia tốc tiếp tuyến còn gia tóc ở VTCB cua con lắc là gia tốc hướng tâm
a
tt
= g.sin
0
; tại VTCB a
ht
=2g(1-cos
)
0
radgg 125,08)cos1(16sin
0
2
0000
=→=→−=→
(
lấy sin
)
4
2cos1;
2
=−
Chọn D
Câu 48. Một con lắc đơn có chiều dài l= 40cm, được treo tại nơi có g = 10m/s
2
. Bỏ qua sức cản không
khí. Đưa con lắc lệch khỏi VTCB một góc 0,1rad rồi truyền cho vật nặng vận tốc 20cm/s theo phương
vuông góc với dây hướng về VTCB. Chọn gốc tọa độ tại vị trí cân bằng của vật nặng, gốc thời gian lúc
gia tốc của vật nặng tiếp tuyến với quỹ đạo lần thứ nhất. Viết phương trình dao động của con lắc theo li
độ cong
A. 8cos(25t +) cm B. 4
2
cos(25t +) cm
C. 4
2
cos(25t +/2) cm D. 8cos(25t) cm
Hướng dẫn:
Phương trình dao động của con lắc theo li độ cong có dạng
s = S
max
cos( t + )
Gọi
m
là biên độ góc của dao độngn của con lắc đơn
max
Trang 23
Khi đo biên độ của tọa độ cong S
max
=
m
l
0
= 0,1 rad.
Theo ĐL bảo toàn năng lượng ta có
mgl(1-cos
m
) = mgl(1-cos
0
) +
2
2
0
mv
<---->
mgl
2
2
max
= mgl
2
2
0
+
2
2
0
mv
<----->
2
max
=
2
0
+
gl
v
2
0
= 0,1
2
+ 0,01
max
= 0,141 = 0,1
2
(rad) <----> S
max
=
m
l = 0,04
2
(m) = 4
2
(cm) (*)
Tần số góc của dao động =
l
g
= 25 rad/s
Gốc thời gian t = 0 khi gia tốc của vật nặng tiếp tuyến với quỹ đạo lần thứ nhất tức là gia tốc hướng
tâm a
ht
= 0------> v = 0: tức là lúc vật ở biên âm (ở điểm A).
Khi t = 0 s = -S
max
----> = .
Vậy: Phương trình dao động của con lắc theo li độ cong s = S
max
cos( t + )
s = 4
2
cos( t +) (cm).
Chọn B
Câu 49. Một con lắc đơn dao động điều hoà theo phương trình li độ góc = 0,1cos(2t + /4) ( rad).
Trong khoảng thời gian 5,25s tính từ thời điểm con lắc bắt đầu dao động, có bao nhiêu lần con lắc có độ
lớn vận tốc bằng 1/2 vận tốc cực đại của nó?
A. 11 lần. B. 21 lần. C. 20 lần. D. 22 lần.
Hướng dẫn:
Trong một chu kì dao động có 4 lần v =
2
max
v
tại vị trí
W
đ
=
4
1
W-----> W
t
=
4
3
W
tmax
tức là lúc li độ
= ±
2
3
max
Chu kì của con lắc đơn đã cho T =
2
= 1 (s)
t = 5,25 (s) = 5T +
4
1
T
Khi t = 0:
0
= 0,1cos(/4) =
2
2
max
; vật chuyển động theo chiều âm về VTCB
Sau 5 chu kì vật trở lại vị trí ban đầu, sau T/4 tiếp vật chưa qua được vị trí = -
2
3
max
Do đó: Trong khoảng thời gian 5,25s tính từ thời điểm con lắc bắt đầu dao động, con lắc có độ lớn vận
tốc bằng 1/2 vận tốc cực đại của nó 20 lần.
Chọn C
Câu 50. Một con lắc đơn gồm vật có khối lượng m, dây treo có chiều dài l = 2m, lấy g = π
2
. Con lắc dao
động điều hòa dưới tác dụng của ngoại lực có biểu thức F = F
0
cos(ωt + π/2)( N). Nếu chu kỳ T của ngoại
lực tăng từ 2s lên 4s thì biên độ dao động của vật sẽ:
A. tăng rồi giảm B. giảm rồi tăng C. chỉ giảm D. chỉ tăng
Hướng dẫn:
Chu kỳ dao động riêng của con lắc đơn: T
0
= 2π
g
l
= 2π
2
2
= 2
2
(giây)
Khi chu kỳ T của ngoại lực tăng từ 2s lên 4s thì biên độ dao động của vật sẽ giảm
Vì khi T = 2s = T
0
----> f = f
0
thì biên độ đạt cực đại do có sự cộng hưởng; biên độ đạt cực đại.
A
O
M
0
0
Trang 24
Chọn A
Câu 51. một con lắc đơn dao động điều hòa,nếu giảm chiều dài con lắc đi 44cm thì chu kì giảm đi
0,4s.lấy g=10m/s
2
.π
2
=10,coi rằng chiều dài con lắc đơn đủ lớn thì chu kì dao động khi chưa giảm chiều
dài là
A.1s B.2,4s C.2s D.1,8s
Hướng dẫn:
T = 2
g
l
; T’ = 2
g
ll −
----->
T
T'
=
l
ll −
---->(
T
T'
)
2
=
l
ll −
---->(
T
TT '−
)
2
=
l
ll −
<---> 1 -
T
T2
+ (
T
T
)
2
= 1 -
l
l
<--->
T
T2
- (
T
T
)
2
=
l
l
(*)
T = 2
g
l
------> l =
2
2
4
gT
=
4
2
T
T
T2
- (
T
T
)
2
=
l
l
=
2
4
T
l
<----->
T
8,0
-
2
2
4,0
T
=
2
44,0.4
T
--->
T
8,0
=
2
92,1
T
--->
T
92,1
= 0,8 -----> T = 2,4 (s).
Chọn B
Câu 52. Một con lắc đơn gồm 1 vật nhỏ được treo vào đầu dưới của 1 sợi dây không dãn, đầu trên của sợi
dây được buộc cố định. Bỏ qua ma sát của lực cản của không khí. Kéo con lắc lệch khỏi phương thẳng
đứng một góc 0,1rad rồi thả nhẹ. Tỉ số độ lớn gia tốc của vật tại VTCB và độ lớn gia tốc tại vị trí biên
bằng:
A: 0,1. B: 0. C: 10. D: 1.
Hướng dẫn:
Xét thời điểm khi vật ở M, góc lệch của dây treo là
Vận tốc của vật tại M:
v
2
= 2gl( cos - cos
0
).----> v =
0
)cos2gl(cos
−
a =
22
ttht
aa +
a
ht
=
l
v
2
= 2g(cos - cos
0
)
a
tt
=
m
F
tt
=
m
P
sin
= g
Tại VTCB: = 0---> a
tt
= 0 nên a
0
= a
ht
= 2g(1-cos
0
) = 2g.2sin
2
2
0
= g
2
0
Tại biên: =
0
nên a
ht
=0 ----> a
B
= a
tt
= g
0
Do đó:
B
a
a
0
=
0
2
0
g
g
=
0
= 0,1.
Chọn A
Câu 53. Một con lắc đơn gồm hòn bi nhỏ bằng kim loại được tích điện q > 0. Khi đặt con lắc vào trong
điện trường đều có véc tơ cường độ điện trường nằm ngang thì tại vị trí cân bằng dây treo hợp với
phương thẳng đứng một góc α, có tanα = 3/4; lúc này con lắc dao động nhỏ với chu kỳ T
1
. Nếu đổi chiều
điện trường này sao cho véctơ cường độ diện trường có phương thẳng đứng hướng lên và cường độ không
đổi thì chu kỳ dao động nhỏ của con lắc lúc này là:
A.
5
1
T
. B. T
1
5
7
C. T
1
7
5
. D. T
1
5
.
A’
A
O
M
0
Trang 25
Hướng dẫn
Ta có Gia tốc do lực điện trường gây ra cho vật a =
m
F
=
m
Eq
( E là độ lớn cường độ điện trường)
Khi điện trường nằm ngang:
T
1
= 2π
1
g
l
Với g
1
=
22
ag +
. tanα =
P
F
=
g
a
=
4
3
----> a =
4
3
g
g
1
=
4
5
g
Khi điện trường hướng thẳng đứng lên trên
T
2
= 2π
2
g
l
Với g
2
= g –a = g -
4
3
g =
4
1
g
1
2
T
T
=
2
1
g
g
=
g
g
4
1
4
5
=
5
----> T
2
= T
1
5
.
Chọn D
Câu 54. Con lắc đơn đang đứng yên trong điện trường đều nằm ngang thì điện trường đột ngột đổi chiều
(giữ nguyên phương và cường độ E) sau đó con lắc dao động điều hòa với biên độ góc α
0
. Gọi q và m là
điện tích và khối lượng của vật nặng; g là gia tốc trọng trường. Hệ thức liên hệ đúng là:
A. q.E = m.g.α
0
. B. q.E.α
0
= m.g. C. 2q.E = m.g.α
0
. D. 2q.E.α
0
= m.g.
Hướng dẫn
- Lực điện có tác dụng làm dịch chuyển vị trí cân bằng.
- Giả sử lúc đầu F hướng sang phải như hình vẽ, thì ta có vị trí cân bằng O, dây
treo hợp với phương thẳng đúng 1 góc
.
Tại đây chưa dao động nên vật có vận tốc v
= 0.
- Khi đảo chiều điện trường thì ta lại có vị trí cân bằng mới là O
/
, dây treo vẫn hợp
với phương thẳng đứng 1 góc
(do điện trường có độ lớn không đổi).
- Tính từ O đến đến cân bằng mới O
/
thì góc lệch là
2
và lúc đầu v = 0 nên biên
độ lúc sau:
0
2. =
- Ta có: tan
F qE qE
P mg mg
= = =
, do nhỏ nên tan
qE
mg
=
=
0
/2 2qE = mg
0
=> Chọn C
Câu 55. Một con lắc đơn có chiều dài dây treo 50 cm và vật nhỏ có khối lượng 0,01 kg mang điện tích q
= 5.10
-6
C, được coi là điện tích điểm. Con lắc dao động điều hòa trong điện trường đều mà vectơ cường
độ điện trường có độ lớn E=10
4
V/m và hướng thẳng đứng xuống dưới. Lấy g=10 m/s
2
, π = 3,14. Xác
định chu kì dao động của con lắc.
A. 2,15 s. B. 3,15 s. C. 1,15 s. D. 4,15 s.
Hướng dẫn:
F = qE = 5.10
-6
.10
-4
= 0,05 (N)
a =


= 5 (m/s
2
)
g’ = g + a = 10 + 5 = 15 (m/s
2
)
T = 2π
󰆓



≈ = 1,15 s.
Chọn C
O’
F
P
A
O
Trang 26
Câu 56. Có hai con lắc đơn giống nhau. Vật nhỏ của con lắc thứ nhất mang điện tích 2,45.10
-6
C, vật nhỏ
con lắc thứ hai không mang điện. Treo cả hai con lắc vào vùng điện trường đều có đường sức điện thẳng
đứng, và cường độ điện trường có độ lớn E = 4,8.10
4
V/m. Xét hai dao động điều hòa của con lắc, người
ta thấy trong cùng một khoảng thời gian, con lắc thứ nhất thực hiện được 7 dao động thì con lắc thứ hai
thực hiện được 5 dao động. Lấy g = 9,8 m/s
2
. Khối lượng vật nhỏ của mỗi con lắc là
A. 12,5 g. B. 4,054 g. C. 7,946 g. D. 24,5 g.
Hướng dẫn
* 7T
1
= 5T
2
=> 7
'g
l
= 5
g
l
=> g’ =
g
25
49
=> g’ > g => lực điện F hướng xuống.
* P’ = P + F => g’ = g +

=> g +

=
g
25
49
=> m =
g
qE
24
25
= 0,0125kg
Chọn A
Câu 57. Khảo sát dao động điều hòa của một con lắc đơn, vật dao động nặng 200 g,
tích điện q = −400 µC tại nơi có gia tốc trọng trường 10 m/s
2
. Khi chưa có điện trường
chu kì dao động điều hòa là T. Khi có điện trường đều phương thẳng đứng thì chu kì
dao động điều hòa là 2T. Điện trường đều
A. hướng xuống và E = 7,5 kV/m. B. hướng lên và E = 7,5 kV/m.
C. hướng xuống và E = 3,75 kV/m. D. hướng lên và E = 3,75 kV/m.
Hướng dẫn:
Vì
g 3g
2 2.2 g' g
g' g 4 4
= = = −
Gia tốc trọng trường hiệu dụng giảm 0,75g nên
F qE=
hướng lên
(
E
hướng xuống) sao cho:
( )
6
qE
3g 3.10 400.10 .E
E 3750 V
4 m 4 0,2
−
= = =
Chọn C
Câu 58. Con lắc đơn gồm vật nặng có khối lượng 100 g, mang điện tích 10
−5
C đang dao động điều hòa
với biên độ góc 6°. Lấy g = 10 m/s
2
. Khi vật dao động đi qua vị trí cân bằng người ta thiết lập một điện
trường đều theo phưong thẳng đứng, hướng lên với độ lớn 25 kV/m thì biên độ góc sau đó là
A. 3° B.
43
°. C.
62
0
. D. 6°
Hướng dẫn:
* Tốc độ cực đại không đổi
'A' A =
nhưng
( )
2
qE
g' g 7,5 m / s
m
= − =
nên
0
''
max max max max
g' g g
. . 4 3
g'
= = =
Chọn B
Câu 59. Cho 2 dao động điều hòa x
1
; x
2
cùng phương, cùng tần số có đồ thị
như hình vẽ. Dao động tổng hợp của x
1
; x
2
có phương trình
A. x = 8
cos(πt -

) cm B. x = 8
cos(πt -
) cm
C. x = 8
cos(2πt -

) cm D. x = 8
cos(2πt -

) cm
Hướng dẫn:
Chu kỳ dao động T = 2 s ω = π rad/s
Ta có A
1
= A
2
= 8 cm
Tại t = 0, x
1
= 0 và đang chuyển động theo chiều dương φ
1
= -
x
1
= 8cos(πt -
) cm
Trong khi đó t = 0, x
2
= -8 cm φ
2
= π φ
2
= 8cos(πt + π) cm
Vậy x = x
1
+ x
2
= 8
cos(πt -

) cm Chọn A
P
F
E
q
Trang 27
Câu 60. Hai dao động điều hòa (1) và (2) cùng phương, cùng tần số và cùng biên độ 4 cm. Tại một thời
điểm nào đó, dao động (1) có li độ
23
cm, đang chuyển động ngược chiều dương, còn dao động (2) có li
độ 2 cm theo chiều dương. Lúc đó, dao động tổng hợp của hai dao động trên có li độ bao nhiêu và đang
chuyển động theo chiều nào?
A. x = 8 cm và chuyển động ngược chiều dương.
B. x = 5,46 và chuyển động ngược chiều dương
C. x = 5,46 cm và chuyển động theo chiều dương.
D. x = 8 cm và chuyển động theo chiều dương.
Hướng dẫn
Chọn thời điểm khảo sát là thời điểm han đầu t = 0 thì phương trình dao động của các chất điểm lần
lượt là:
1
2
x 4cos t
6
x 4cos t
3


= +


= −


Phương trình dao động tổng hợp (bằng phương pháp cộng các hàm lượng giác):
12
x x x 4cos t 4cos t
63

= + = + + −
x 2.4cos .cos t
4 12


= −


( )
x 4 2 cos t cm
12

= −


Tại thời điểm ban đầu li độ tổng hợp
0 01 02
x x x 2 3 2 5,46cm= + = +
. Pha ban đầu của dao động
tổng hợp
12
−
thuộc góc phần tư thứ IV nên vật đang chuyền
động theo chiều dương => Chọn B
3
−
6
6
2
6
23
1
A
2
A
A
2
23
Câu 61. Một vật dao động điều hoà là tổng hợp của hai dao động cùng phương cùng tần số cùng, đồ thị li
độ thời gian của hai dao động thành phần như hình vẽ.. Tổng tốc độ của hai dao động có giá trị lớn nhất là
A. 280π (cm/s). B. 200π (cm/s) C. 140π (cm/s). D. 160π (cm/s).
Hướng dẫn
Phương trình tổng tốc độ của các vật:
( )
( )( )
1
2
x 8cos 20 t cm
2
x 6cos 20 t cm

= −


= +
Phương trình vận tốc của các vật:
( )
( )( )
'
11
'
22
v x 160sin 10 t cm / s
2
v x 120sin 200 t cm / s

= = − −


= = − +
Trang 28
( )
( )
'
11
'
22
v x 160 cos20 t cm / s
v x 120 sin 20 t cm/ s
= =
= − =
Phương trình tổng tốc độ của các vật:
12
v v v 160 cos20 t 120 sin 20 t= + = +
( ) ( ) ( )
22
22
160 120 cos 20 t sin 20 t 200 cm / s + + =
Dấu bằng xảy ra khi
4
tan20 t
3
=
Chọn B
Câu 62. Một vật thực hiện đồng thời hai dao động cùng phương, cùng tần số 4Hz và cùng cùng biên độ 2
cm. Khi qua vị trí động năng của vật bằng 3 lần thế năng vật đạt tốc độ 24π (cm/s). Độ lệch pha giữa hai
dao động thành phần bằng
A. π/6. B. π/2. C. π/3. D. 2π/3.
Hướng dẫn
Khi W
đ
= 3W
t
( )
t
d
1
WW
4
3 3 3
W W v A 24 .8 A A 2 3 cm
4 4 4
=
= = = =
Mặt khác:
( )
2 2 2
1 2 1 2 2 1
A A A 2A A cos= + + −
22
12 2 2 2.2.2.cos
3
= + +   =
Chọn C
Câu 63. Một chất điểm tham gia đồng thời hai dao động điều hòa trên cùng một trục Ox có phương trình:
x
1
= 4cos(ωt + π/3) cm, x
2
= A
2
cos(ωt + φ
2
) cm. Phương trình dao động tổng hợp x = 2cos(ωt + φ) cm.
Biết φ – φ
2
= π/2. Cặp giá trị nào của A
2
và φ sau đây là đúng?
A. 3/3 cm và 0. B. 2/3 cm và π/4. C. 3/3 cm và π/2. D.
23
cm và 0.
Hướng dẫn
( )
( )
2 2 2
1 2 1 2
1 2 2 2
2 2 2
1 2 2 1` 2 1 1 1
A A A A A A A A A 2AA cos
A A A A A A A A A 2AA cos
= + = − = + − −
= + = − = + − −
( )
2
2 2 2
16 4 A 2.4.A cos A 2 3 cm
2
12 4 16 2.2.4cos
3
= + − =

= + − −


1
cos 0
32

− = =


Chọn D
3
1
A
A
2
A
Câu 64. Hình vẽ bên là đồ thị biễu diễn sự phụ thuộc của li độ
x
vào thời gian
t
của hai dao động điều
hòa cùng phương. Dao động của vật là tổng hợp của hai dao
động nói trên. Trong 0,20 s đầu tiên kể từ
0t =
s, tốc độ trung
bình của vật bằng
A.
40 3
cm/s. B. 40 cm/s.
C.
20 3
cm/s. D. 20 cm/s.
Hướng dẫn
Chọn B
+ Từ đồ thị, ta thấy rằng dao động thành phần ứng với đường liền nét có phương trình
1
10
4cos
33
xt


=+


cm.
+ Thành phần dao động ứng với đường nét đứt. Tại
0,05
12
T
t ==
s đồ thị đi qua vị trí
xA=−
→ tại
0t =
, thành phần dao động này đi qua vị trí
3
6
2
xA= − = −
cm →
43A =
cm.
()x cm
O
6+
6−
()ts
0 , 3
0 , 1
0 , 2
Trang 29
→
2
10 5
4 3cos
36
xt


=+


cm →
12
10 2
8cos
33
x x x t


= + = +


cm.
+ Tại
0t =
, vật đi qua vị trí
4x =−
cm theo chiều âm. Sau khoảng thời gian
0,2t=
s ứng với góc
quét
0
120t

= =
vật đến vị trí
4x =−
cm theo chiều dương.
→
44
40
0,2
tb
v
+
==
cm/s
Câu 65. Một chất điểm dao động điều hòa là tổng hợp của hai dao động cùng phương cùng cùng tần số
với li độ lần lượt là x
1
và x
2
. Li độ của hai dao động thành phần thỏa mãn điều kiện:
( )
2 2 2
12
1,5x 2x 18 cm+=
.
Tính biên độ dao động tổng hợp của hai dao động trên.
A. 5cm. B. 2 cm. C. 4 cm. D. 5,4cm.
Hướng dẫn
Từ
( )
2
2
2 2 2
12
12
xx
1,5x 2x 18 cm 1
3
12


+ = + =




( ) ( )
( )
12
22
12
12
xx
2
A A A 12 9 21 cm
A 12 cm ;A 3 cm
⊥  =
= + = + =
==
Chọn D
Câu 66. Một vật tham gia đồng thời 2 dao động diêu hoà cùng phương cùng tần số và vuông pha với
nhau. Nếu chỉ tham gia dao động thứ nhất thì cơ năng dao động là W
1
. Nếu chỉ tham gia dao động thứ hai
thì cơ năng dao động là W
2
. Nếu tham gia đồng thời 2 dao động thi cơ năng dao động là
A. 0,5(W
1
+ W
2
). B. (W
1
+ W
2
). C.
( )
0,5
22
12
W W .+
D.
( )
0,5
22
12
0,5 W W+
Hướng dẫn
Cả hai dao động vuông pha nên biên độ dao động tổng hợp:
22
12
A A A=+
Cơ năng dao động:
2 2 2 2 2 2
1 2 1 2
1 1 1
W m A m A m A W W
2 2 2
= = + = +
Chọn B
Câu 67. Một vật thực hiện đồng thời 2 dao động điều hòa cùng phương,
cùng chu kì 2s. Gốc tọa độ trùng với vị trí cân bằng. Đồ thị phụ thuộc thời
gian của các li độ được biểu diễn như hình vẽ. Biết t
2
– t
1
=
s. Biên độ dao
động tổng hợp gần giá trị nào nhất sau đây?
A.2 cm B.3,4 cm C.7,5 cm D.8 cm
Hướng dẫn:
Vì T = 2 s ω = π rad/s
Chọn gốc thời gian tại thời điểm t
1
→ x
1
= 6cos(ωt
1
+ φ
1
) = 6cosφ
1
= 0 φ
1
=
(vật chuyển động theo chiều âm) x
1
= 6cos(ωt +
)
cm
Với dao động 2 thì tại t
2
: x
2
= 6cos(ω(t
1
+
) + φ
2
) = 6 hay cos(π(0 +
) + φ
2
) = 1
→ φ
2
= -

→ x
2
= 6cos(ωt -

) cm
Vậy x = x
1
+ x
2
= 3,1cos(πt +


) cm → A ≈ 3,4 cm Chọn B
Câu 68. Một vật m = 100 g thực hiện đồng thời hai dao động điều hòa
cùng phương được mô tả như hình vẽ. Lực kéo về cực đại tác dụng lên vật
gần giá trị nào nhất
A.1 N B.40 N C.10 N D.4 N
Hướng dẫn:
Chu kì dao động T = 200 ms = 0,2 s → ω = 10π rad/s
Phương trình dao động: 󰇫

󰇛

󰇜

󰇡
󰇢
Trang 30
→ dao động tổng hợp x = x
1
+ x
2
=
cos(ωt – 0,588) cm
F
max
= k.A = mω
2
.A = 0,1.(10π)
2
.


≈ 3,56 N Chọn D
Câu 69. Đồ thị của hai dao động điều hòa cùng tần số có dạng như hình vẽ.
Phương trình nào sau đây là phương trình dao động tổng hợp của chúng:
A. x = 5cos
cm B. x = cos󰇡
󰇢 cm
C. x = 5cos󰇡
󰇢 cm D. x = 5cos󰇡
󰇢 cm
Hướng dẫn:
A
1
= 3 cm; tại t = 0 thì x = 0 và đang chuyển động theo chiều dương φ
1
= -
x
1
= 3cos(
t -
) cm
A
2
= 2 cm; tại t = 0 thì x = 0 và đang chuyển động theo chiều âm φ
2
=
x
2
= 2cos(
t +
) cm
Vậy x = x
1
+ x
2
= cos(
t -
) Chọn B
Câu 70: Một chất điểm thực hiện đồng thời hai dao động điều hòa
cùng phương cùng chu kì T mà đồ thị x
1
và x
2
phụ thuộc thời gian
biểu diễn trên hình vẽ. Biết x
2
= v
1
T, tốc độ cực đại của chất điểm là
53,4 cm/s. Giá trị T gần giá trị nào nhất sau đây?
A.2,56 s B.2,99 s
C.2,75 s D.2,64 s
Hướng dẫn:
Dễ thấy được hai dao động vuông pha (x
2
sớm hơn x
1
)
󰇫

󰇛

󰇜





→ A =






(1)
Áp dụng công thức vị trí gặp nhau x
0
ở bài toán trên (trường hợp vuông pha) ta được
|x
0
| =



=


=






T =

󰇛
󰇜

≈ 2,99 s Chọn B
| 1/30
| | Tải xuống

Tài liệu khác của Vật Lí 12

Preview text:

CHUYÊN ĐỀ ÔN TÂP MỨC ĐỘ 3 CHƯƠNG 1 DAO ĐỘNG CƠ HỌC
1. ĐẠI CƯƠNG DAO ĐỘNG ĐIỀU HÒA
Câu 1. Một vật nhỏ dao động điều hòa với chu kỳ T=1s. Tại thời điểm t1 nào đó, li độ của vật là -2cm.
Tại thời điểm t2 = t1+0.25s, vận tốc của vật có giá trị là: A. 4 cm/s. B. -2 m/s. C. 2cm/s. D. - 4m/s. 
Câu 2. Một dao động điều hoà với x=8cos(2t-
) cm. Thời điểm thứ 2023 vật qua vị trí có vận tốc v = 6
-8 cm/s có giá trị gần nhất là : A. 1011,2s. B. 1011,3s. C. 1011,1s. D. 1011,5s.
Câu 3. Vật dao động điều hòa có vận tốc cực đại bằng 3m/s và gia tốc cực đại bằng 30 m/s2. Thời điểm ban
đầu vật có vận tốc 1,5m/s và thế năng đang tăng. Thời điểm vật có gia tốc bằng 15 m/s2 là: A. 0,10s. B. 0,15s. C. 0,20s. D. 0,05s.
Câu 4. Một vật dao động điều hòa, đi qua vị trị có vận tốc bằng không vào các thời điểm liên tiếp 4,25s
và 5,75s. Biết vào thời điểm ban đầu vật chuyển động theo chiều dương của trục tọa độ, và tốc độ lớn
nhất của vật trong quá trình dao động là 4  (cm/s). Vận tốc trung bình của vật trong khoảng từ thời điểm
0,75s đến thời điểm 2,25s là : A. -4,00cm/s. B. 4,00cm/s. C. 0,00 cm/s. D. -4,25cm/s.
Câu 5. Một chất điểm dao động điều hòa với chu kì T. Gọi amax là gia tốc cực đại của vật. Khoảng thời a
gian trong một chu kì để vật có độ lớn gia tốc lớn hơn max là : 2 A. T/3. B. 2T/3. C. T/6. D. T/2.
Câu 6. Hai chất điểm M, N dao động điều hòa dọc theo hai đường thẳng song song kề nhau và song
song với trục tọa độ Ox. Vị trí cân bằng của M và của N đều ở trên một đường thẳng qua gốc tọa độ và
vuông góc với Ox. Phương trình dao động của chúng lần lượt là x1 = 10cos2πt cm và x2 = 10 3 cos(2πt +
 ) cm. Hai chất điểm gặp nhau khi chúng đi qua nhau trên đường thẳng vuông góc với trục Ox. Thời 2
điểm lần thứ 2023 hai chất điểm gặp nhau là:
A. 16 phút 51,42s.
B. 16 phút 51,92s.
C. 16 phút 52,42s. D. 16 phút 50,92s.
Câu 7. Hai chất điểm dao động điều hòa cùng biên độ A, với tần số góc 3 Hz và 6 Hz. Lúc đầu hai vật A 2
đồng thời xuất phát từ vị trí có li độ
và đang chuyển động theo chiều dương. Khoảng thời gian 2
ngắn nhất để hai vật gặp nhau là: 1 1 1 1 A. s . B. s . C. s . D. s . 18 27 36 72
Câu 8. Một vật dao động điều hòa với phương trình x = 4 2 cos(5 t  − 3 / 4) .
cm Quãng đường vật đi
được từ thời điểm t1 = 0,1 s đến t2 = 6s là: A. 84,4cm. B. 333,8cm. C. 331,4 cm. D. 337,5cm.
Câu 9. Một vật dao động điều hòa theo phương nằm ngang, khi li độ vật bằng 0 thì vận tốc có gia trị
31,4cm/s; khi li độ vật cực đại thì gia tốc có giá trị 4 m/s2. Lấy π2 = 10. Thời gian ngắn nhất để vật chuyển
động từ li độ x = 0 đến x = 1,25cm là: A. 1/12 s. B. 1/3 s. C. 1/6 s. D. 1/24 s.
Câu 10. Hai chất điểm M và N dao động điều hòa cạnh nhau, dọc theo trục Ox. Vị trí cân bằng của hai
chất điểm ở cùng gốc tọa độ O. Phương trình dao động của chúng lần lượt là       2 2 x x
x = A cos t +
cm , x = A cos t  − cm . Biết 1 2 +
= 4 . Tại thời điểm t nào đó, chất 1 1  ( ) 2 2  ( )  3   6  9 16 Trang 1
điểm M có li độ x = 3
− cm và vận tốc v = 30 −
3 cm / s . Khi đó, độ lớn vận tốc tương đối của chất 1 1
điểm này so với chất điểm kia xấp xỉ bằng: A. 66 cm/s. B. 12 cm/s. C. 40 cm/s. D. 92 cm/s.   
Câu 11. Một vật dao động điều hòa với phương trình x = 5cos 4 t − 
 . Xác định thời gian ngắn nhất  2 
để vật đi từ vị trí 2,5 cm đến −2,5 cm . 1 1 1 1 A. s B. s C. s D. s 12 10 20 6
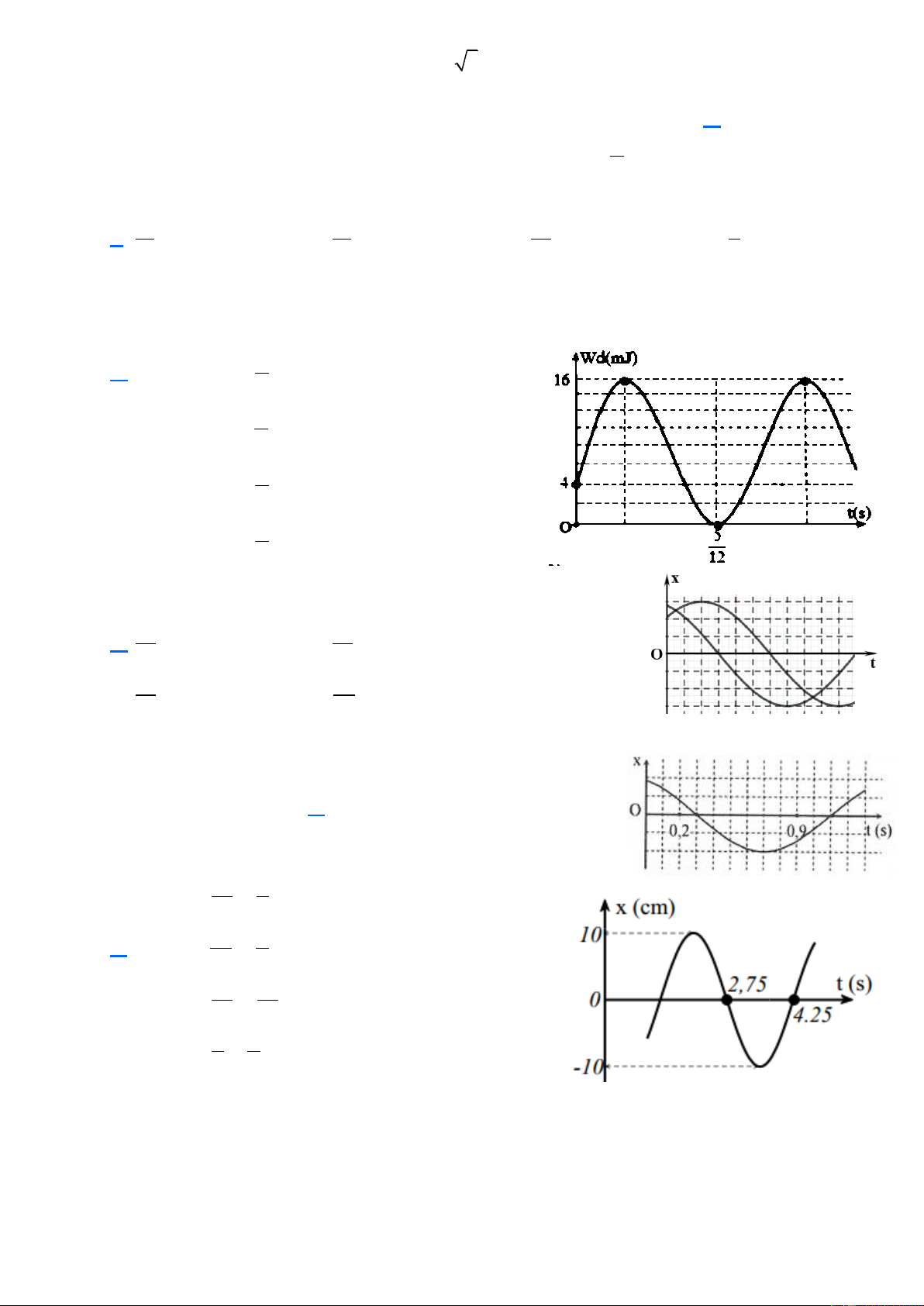
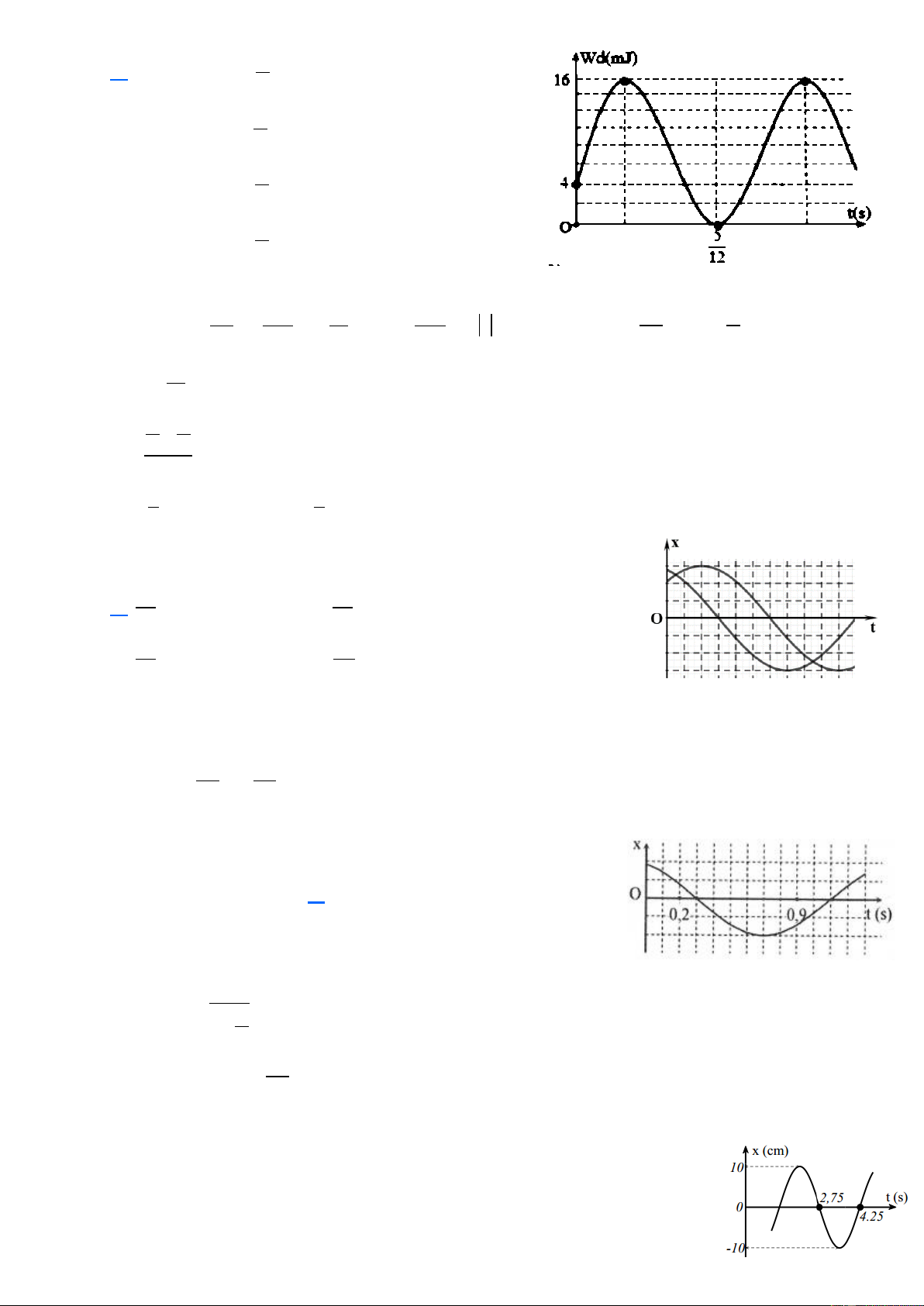
Câu 12. Một chất điểm có khối lượng 320 g dao động điều hòa dọc theo trục Ox. Biết đồ thị biểu diễn sự
phụ thuộc của động năng theo thời gian của chất điểm như hình vẽ và tại thời điểm ban đầu (t = 0) chất
điểm đang chuyển động ngược chiều dương. Phương trình dao động của chất điểm là    A. x = 5cos 2 t + cm   .  6    
B. x = 5cos 4 t + cm   .  3    
C. x = 5cos 2 t − cm    6     D. x = 5cos 4 t − cm.    3 
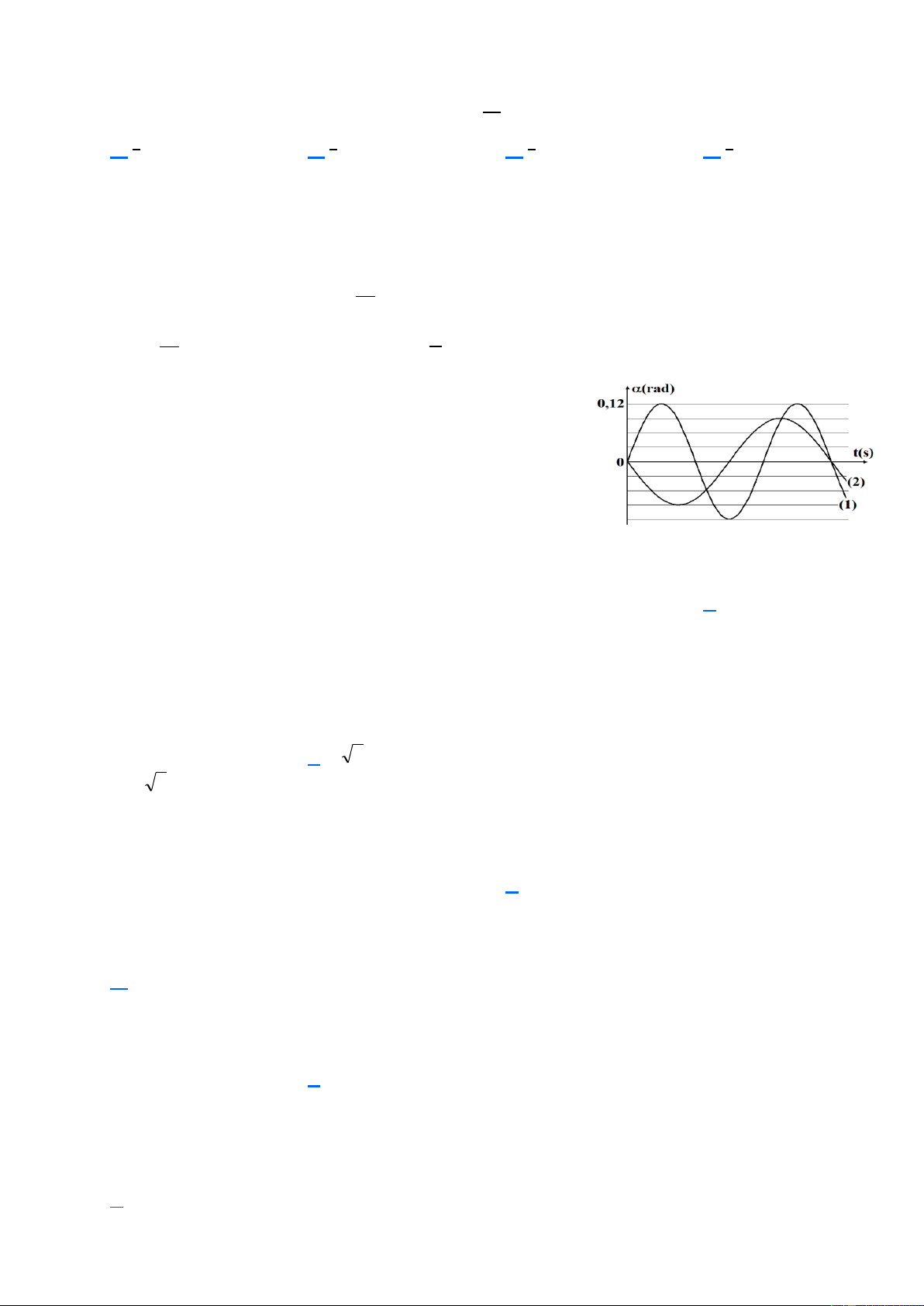
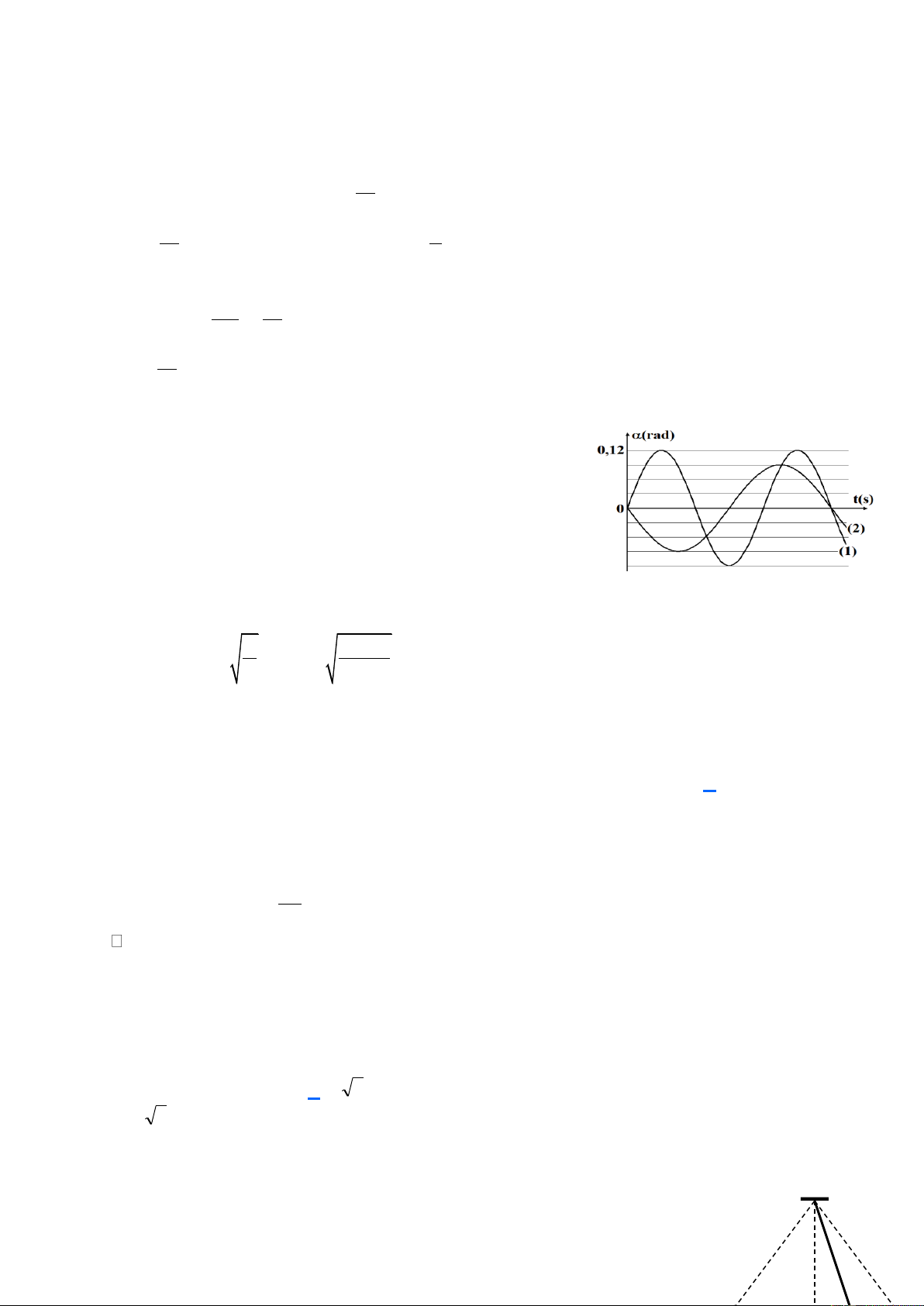
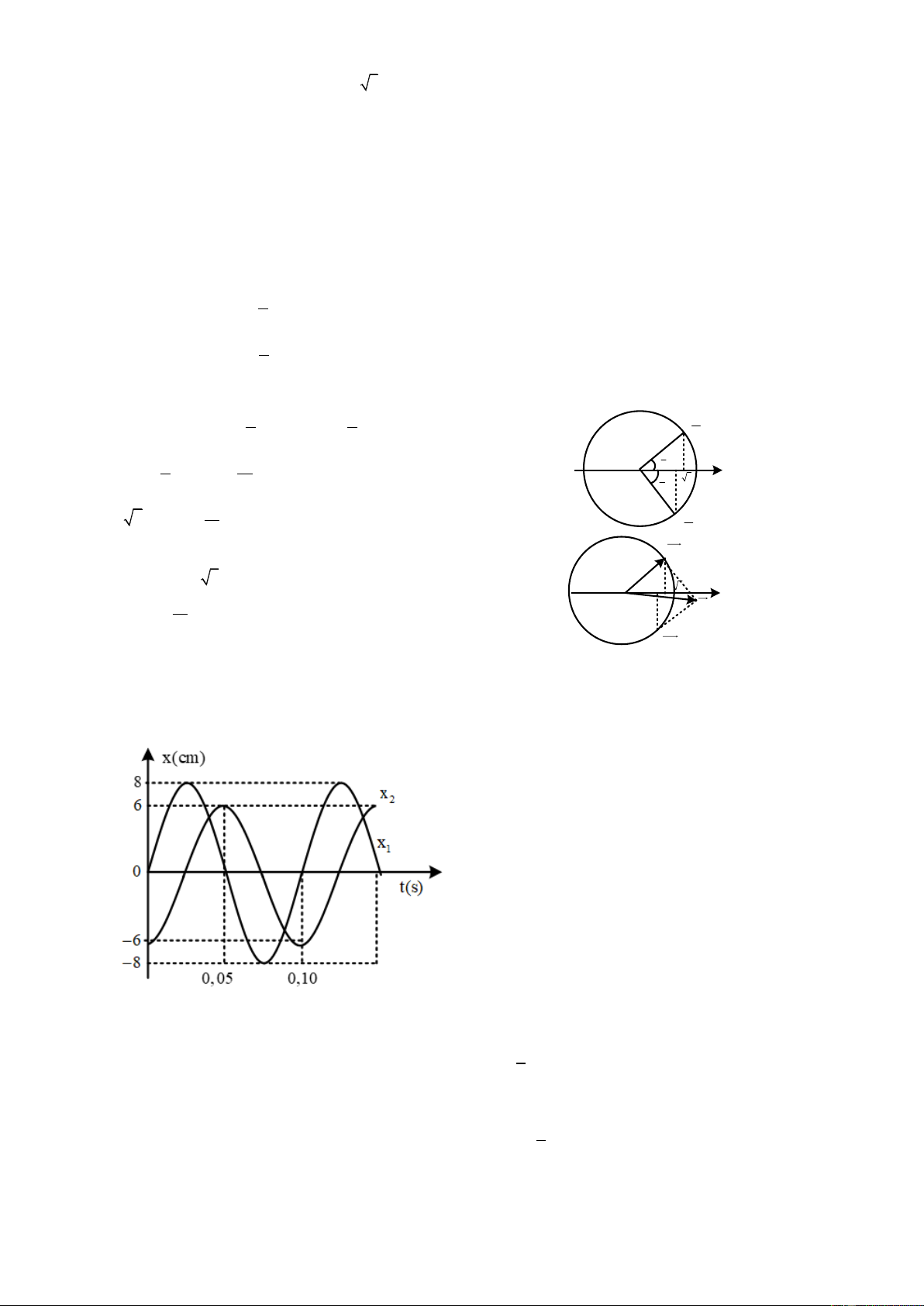
Câu 13. Hình bên là đồ thị biểu diễn sự phụ thuộc li độ của hai dao
động điều hòa theo thời gian. Độ lệch pha của hai dao động này bằng 3 5 A. . B. . 8 6 3 2 C. . D. . 4 3
Câu 14. Một chất điểm dao động điều hòa có đồ thi biểu diễn sự
phụ thuộc của li độ x vào thời gian t như hình vẽ. Tại thời điểm t = 0,2s, chất có li độ 2 cm. Ở thời
điểm t = 0,9s, gia tốc của chất điểm có giá trị bằng: A. 2 14, 5cm / s B. 2 57, 0 cm / s C. 2 5, 7m / s D. 2 1, 45 m/ s
Câu 15. Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ có
dạng như hình vẽ bên. Phương trình dao động của li độ là  2  
A. x = 10cos t −   (cm).  3 3   2  
B. x = 10cos t +   (cm).  3 3   2 2 
C. x = 10cos t +   (cm).  3 3     
D. x = 10cos t −   (cm).  3 3  2. CON LẮC LÒ XO
Câu 16. Một vật dao động điều hòa với phương trình x = 10cos(πt + π/3) cm. Khoảng thời gian tính từ
lúc vật bắt đầu dao động (t = 0) đến khi vật đi được quãng đường 50 cm là A. 7/3 s B. 2,4 s C. 4/3 s D. 1,5 s Trang 2
Câu 17. Một con lắc lò xo gồm quả cầu nhỏ khối lượng 1 kg và lò xo có độ cứng 50 N/m. Cho con lắc
dao động điều hòa trên phương nằm ngang. Tại thời điểm vận tốc của quả cầu là 0,2 m/sthì gia tốc của nó
là − 3 m/s2. Cơ năng của con lắc là A. 0,02 J. B. 0,05 J. C. 0,04 J D. 0,01 J
Câu 18. Một vật dao động điều hòa với tần số f =10 Hz. Tại thời điểm ban đầu vật đang ở li độ x = 2cm
và chuyển động theo chiều dương. Sau 0,25 (s) kể từ khi dao động thì vật ở li độ
A. x = 2 cm và chuyển động theo chiều đương.
B. x = 2 cm và chuyển động theo chiều âm.
C. x = −2 cm và chuyển động theo chiều âm.
D. x = −2 cm và chuyền động theo chiều dương.
Câu 19. Con lắc lò xo nằm ngang dao động điều hòa, lực đàn hồi cực đại tác đụng vào vật là 2 N, gia tốc
cực đại của vật là 2 m/s2. Khối lượng của vật là A. 1 kg. B. 2 kg. C. 3 kg. D. 4 kg.
Câu 20. Một con lắc lò xo có độ cứng 50 N/m, dao động điều hòa với biên độ 4 cm. Chọn gốc tính thế
năng là vị trí cân bằng. Tổng động năng và thế năng của vật là A. 25 mJ. B. 20 mJ. C. 40 mJ. D. 10 mJ.
Câu 21. Khi treo một vật nặng vào một lò xo, khi vật đứng yên lò xo dài thêm một đoạn 2,5 cm. Lấy g =
π2 m/s2. Chu kì dao động tự do của con lắc bằng A. 0,316 s. B. 0,317 s. C. 0,215 s. D. 0,291 s.
Câu 22. Một chất điểm dao động điều hòa có đồ thị như hình bên. x(cm) v −
Thời điểm mà vận vận tốc v và li độ x thỏa mãn = 1 − ,25 3( 1 s ) A x .vn .vn 1 / 3 ihoc
lần thứ 2023 gần nhất với giá trị nào dưới đây? O da ihoc oa 31 / 30 da t(s) A. 1618.12 s. B. 1617,94 s. oa C. 1617.83 s. D. 1618,37 s. −A thukh thukh
Câu 23. Một vật dao động điều hòa với phương trình x = Acos(ωt + φ). Hình bên là đồ x(cm)
thị biểu diễn sự phụ thuộc li độ x theo thời gian t. Tại .vn 10
thời điểm t = 0, gia tốc của vật có giá trị là ihoc 5 da .vn 1, 5 A. 2 −  ( 2 5 2 cm / s ) B. 2 −  ( 2 5 3 cm / s ) oa O ihoc da 0, 5 1 oa t(s) 5 − thukh C. 2  ( 2 5 2 cm / s ) D. 2  ( 2 5 3 cm / s ) thukh
Câu 24. Một vật dao động điều hòa với biên độ 5 cm, trong 1 phút thực hiện được 30 dao động toàn
phần. Quãng đường mà vật đi được trong 1 s là A. 15 cm. B. 5 cm. C. 10 cm. D. 20 cm.
Câu 25. Một con lắc lò xo gồm lò xo và vật có khối lượng 80 g dao động điề W mJ t ( )
u hòa trên mặt phẳng nằm ngang. Mốc tính thế năng tại vị trí cân bằng. Hình bên là đồ .vn
thị biểu diễn sự phụ thuộc của thế năng đàn hồi của con .vn ihoc lắc W da ihoc
t vào thời gian t. Lấy π2 = 10. Biên độ dao động của con lắc là oa da 4 oa A. 2 2 cm. B. 2 cm. thukh thukh C. 4 cm. D. 4 2 cm O 0,05 t(s)
Câu 26. Một con lắc lò xo heo thẳng đứng (coi gia tốc trọng trường là 10 m/s2) quả cầu có khối lượng
120 g. Chiều dài tự nhiên của lò xo là 20 cm và độ cứng 40 N/m. Từ vị trí cân bằng, kéo vật thẳng đứng,
xuống dưới tới khi lò xo dài 26,5 cm rồi buông nhẹ cho nó dao động điều hòa Động năng của vật lúc lò xo dài 25 cm là A. 24,5 mJ. B. 22 mJ. C. 12 mJ. D. 16,5 mJ. Trang 3
Câu 27. Một con lắc lò xo đang dao động điều hòa theo phương nằm ngang. Mốc thế năng ở vị trí cân
bằng. Biết động năng cực đại của con lắc là 80 mJ, lực kéo về cực đại tác dụng lên vật nhỏ của con lắc là
4 N. Khi vật qua vị trí có li độ 3 cm thì động năng của con lắc có giá trị là A. 5 mJ. B. 75 mJ. C. 45 mJ. D. 35 mJ.
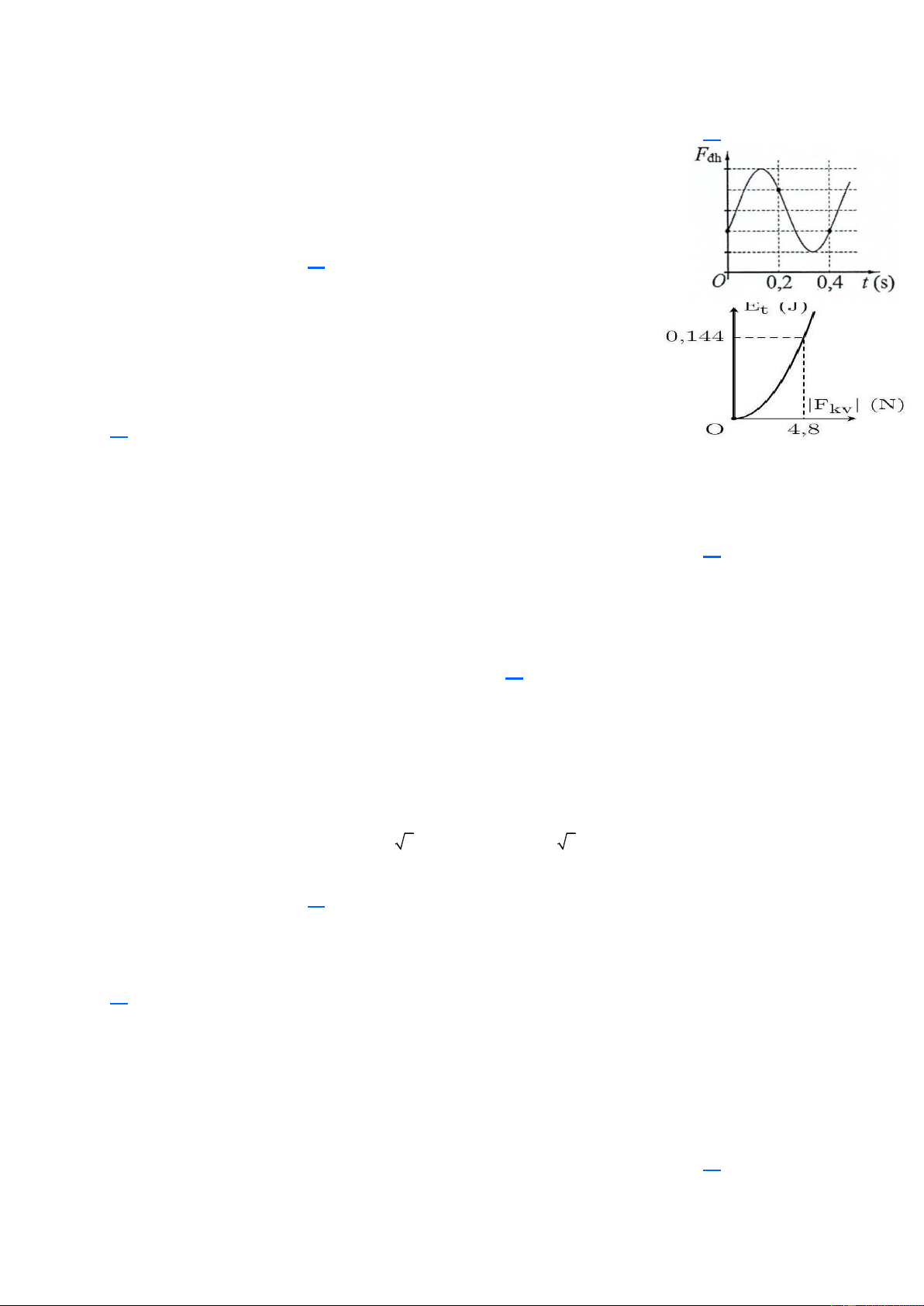
Câu 28. Một con lắc lò xo treo vào một điểm M cố định, đang dao động điều
hòa theo phương trình thẳng đứng. Hình bên là đồ thị biểu diễn sự phụ thuộc
của lực đàn hồi Fđh mà lò xo tác dụng vào M theo thời gian t. Lấy 2 2
g =  m / s . Độ dãn của lò xo khi con lắc ở vị trí cân bằng là A.2 cm. B.4 cm. C.6 cm. D.8 cm.
Câu 29. Một con lắc lò xo gồm vật nhỏ có khối lượng m=100 g, lò xo có
độ cứng k được treo thẳng đứng. Kích thích cho vật dao động điều hòa
với biên độ. Chọn gốc thế năng tại vị trí cân bằng của vật. Hình bên là
một phần đồ thị biểu diễn mối liên hệ giữa thế năng Et và độ lớn lực kéo
về |Fkv| khi vật dao động. Chu kì dao động của vật là A.0,222 s. B.0,314 s. C.0,157 s. D.0,197 s.
Câu 30. Một con lắc lò xo dao động điều hòa theo phương ngang với lực đàn hồi lớn nhất của lò xo là 2
N và năng lượng dao động là 0,1 J. Thời gian trong một chu kì lực đàn hồi là lực kéo không nhỏ hơn 1 N
là 0,1 s. Tính tốc độ lớn nhất của vật. A. 314,1 cm/s. B. 31,4 cm/s. C. 402,5 cm/s. D. 209,44 cm/s.
Câu 31. Con lắc lò xo có độ cứng k = 40 N/m treo thẳng đứng đang dao động điều hòa với tần số góc ω =
10 rad/s tại nơi có gia tốc trọng trường g = 10 m/s2. Khi lò xo không biến dạng thì vận tốc dao động của
vật triệt tiêu. Độ lớn lực của lò xo tác dụng vào điểm treo khi vật ở trên vị trí cân bằng và có tốc độ 80 cm/s là A. 2,4 N. B. 2 N. C. 1,6 N. D. 3,2 N.
Câu 32. Một con lắc lò xo được treo thẳng đứng vào một điểm cố định đang dao động điều hòa theo
phương thẳng đứng. Hình bên là đồ thị biểu diễn sự phụ thuộc của lực đàn hồi F mà lò xo tác dụng lên vật
nhỏ của con lắc theo thời gian 𝑡. Lấy 𝑔 = 𝜋2 = 10m/s2. Biên độ dao động của con lắc lò xo là
A. 1,44cm#𝐁. 8,64cm C. 5,76cm#. 7,2cm
Câu 33. Con lắc lò xo gồm vật nhỏ nặng 1 kg thực hiện đồng thời hai dao động điều hoà theo phương = =
thẳng đứng, theo các phương trình: x 5 2 cos10t x 5 2 sin10t 1 cm và 2
cm (Gốc tọa độ trùng với vị trí
cân bằng, t đo bằng giây và lấy gia tốc trọng trường g = 10 m/s2). Lực cực đại mà lò xo tác dụng lên vật là A. 10N. B. 20 N. C. 25 N. D. 0,25 N.
Câu 34. Một con lắc lò xo treo vào một điểm cố định, dao động điều hòa theo phương thẳng đứng với
chu kì 1,2 s. Trong một chu kì, nếu tỉ số của thời gian lò xo giãn với thời gian lò xo nén bằng 2 thì thời
gian mà lực đàn hồi ngược chiều lực kéo về là A. 0,2 s. B. 0,1 s. C. 0,3 s. D. 0,4 s.
Câu 35. Một con lắc lò xo gồm vật nhỏ khối lượng 0, 2 kg và lò xo có độ cứng k = 20 N / m . Vật nhỏ
được đặt trên giá cố định nằm ngang dọc theo trục lò xo. Hệ số ma sát trượt giữa giá đỡ và vật nhỏ là
0,01. Từ vị trí lò xo không biến dạng truyền cho vật vận tốc ban đầu 1 m / s thì thấy con lắc dao động tắt
dần trong giới hạn đàn hồi của lò xo. Lấy 2
g = 10 m / s . Độ lớn lực đàn hồi cực đại của lò xo trong quá trình dao động là 2, 2 N 19,8 N 1, 5 N 1, 98 N A. . B. . C. D. . 3. CON LẮC ĐƠN Trang 4
Câu 36. Một con lắc đơn dao động điều hòa tại một địa điểm A . Nếu đem con lắc đến địa điểm B , biết
rằng chiều dài con lắc không đổi còn gia tốc trọng trường tại B bằng 81% gia tốc trọng trường tại#A. So
với tần số dao động của con lắc tại A , tần số dao động của con lắc tại B sẽ A. tăng 10% . B. giảm 9% . C. tăng 9% D. giảm 10% . −
Câu 37. Một con lắc đơn dài 25 cm , hòn bi có khối lượng 10 g mang điện tích 4 q = 10 C . Cho 2
g = 10m / s . Treo con lắc đơn giữa hai bản kim loại song song thẳng đứng cách nhau 20 cm . Đặt hai bản
dưới hiệu điện thế một chiều 80 V . Chu kì dao động của con lắc đơn với biên độ góc nhỏ là A. 0, 91 s . B. 0, 96 s . C. 2, 92 s . D. 0, 58 s .
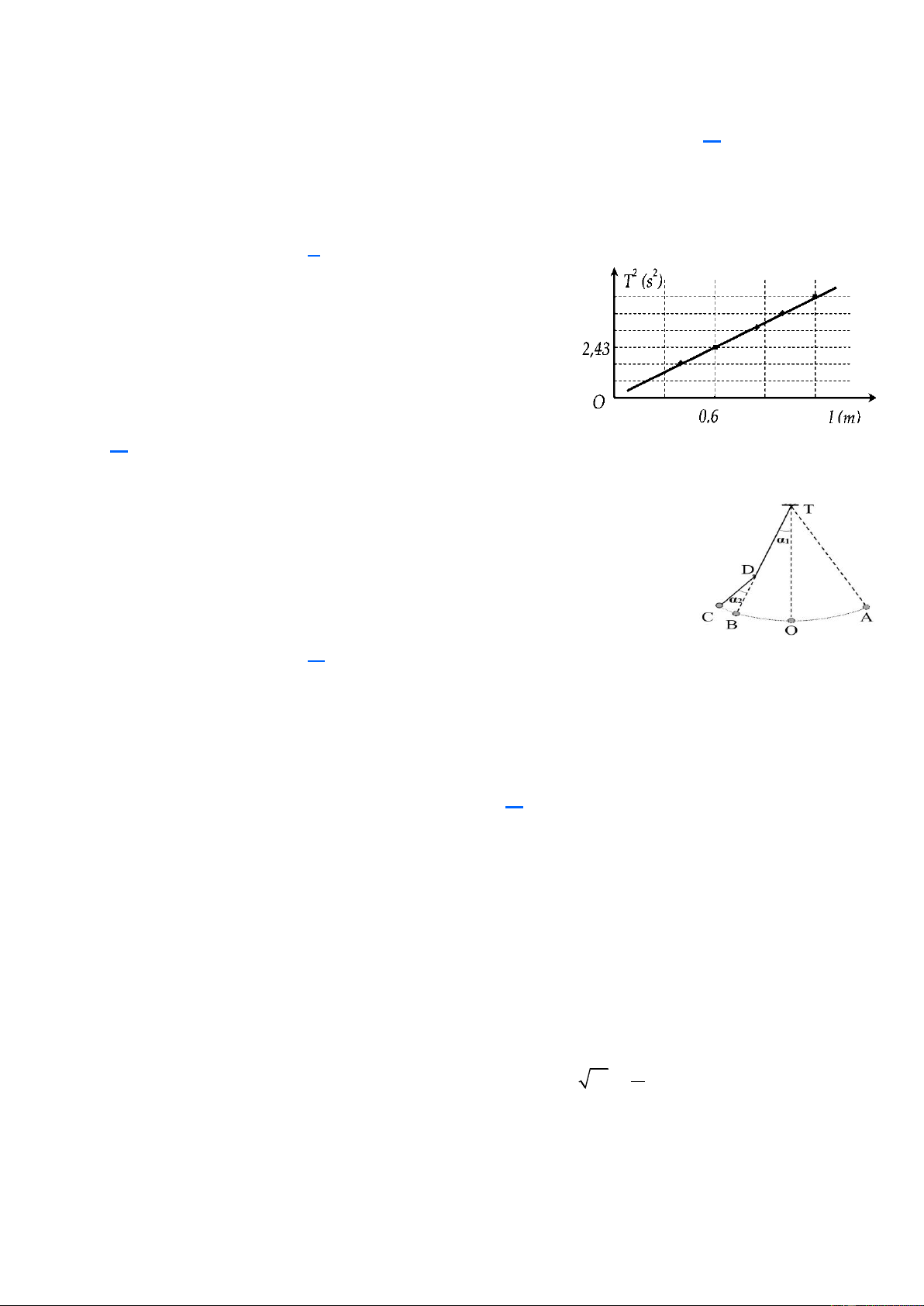
Câu 38. Trong bài thực hành đo gia tốc trọng trường g bằng
con lắc đơn, một nhóm học sinh tiến hành đo, xử lý số liệu và
vẽ được đồ thị biểu diễn sự phụ thuộc của bình phương chu kì dao động điều hòa ( 2
T ) theo chiều dài l của con lắc như hình
bên. Lấy  = 3,14 . Giá trị trung bình của g đo được trong thí nghiệm này là A. 9,74 m/s B. 9,96 m/s C. 9,58 m/s D. 2 9, 42 m / s
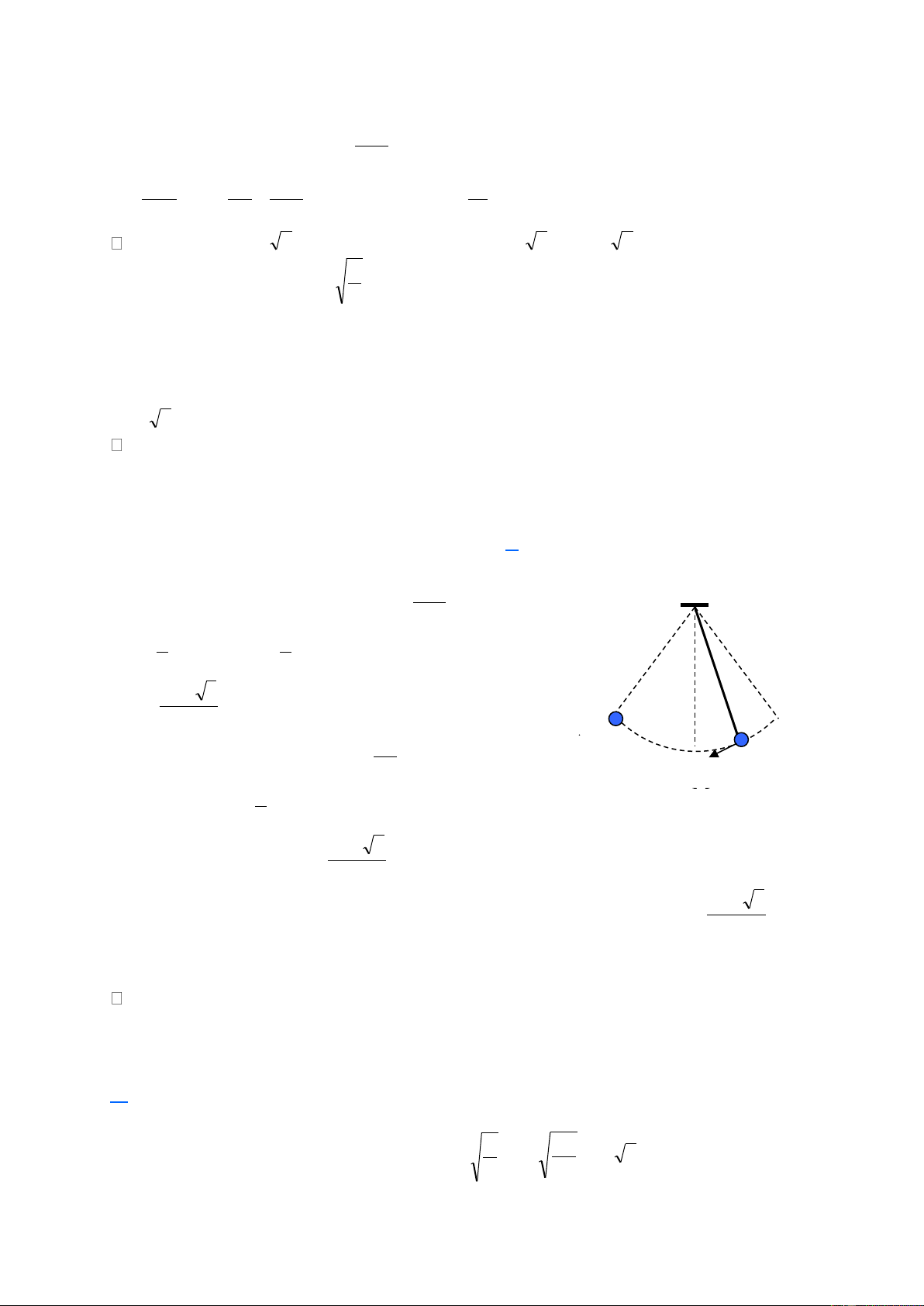
Câu 39. Một con lắc đơn có chiều dài 1,92 m treo vào điểm T cố định. Từ vị
trí cân bằng O, kéo con lắc về bên phải đến A rồi thả nhẹ. Mỗi khi vật nhỏ đi từ
phải sang trái ngang qua B thì dây vướng vào đinh nhỏ tại D, vật dao động trên
quỹ đạo AOBC (được minh họa bằng hình bên). Biết TD = 1,28 m và 0
 =  = 4 . Bỏ qua mọi ma sát. Lấy 2 2
g =  (m / s ) . Chu kì dao động của con 1 2 lắc là A. 2,26 s. B. 2,61 s. C. 1,60 s. D. 2,77 s.
Câu 40. Con lắc lò xo M và con lắc đơn N có chu kỳ dao động riêng tương ứng là T1=0,4s và T2. Người
ta đưa cả hai con lắc ra biên của chúng (biên của con lắc lò xo tuỳ ý trong giới hạn đàn hồi, biên của con
lắc đơn tuỳ ý trong giới hạn góc bé). Ban đầu ta thả cho con lắc lò xo dao động, khi vật tới vị trí cân bằng
lần đầu thì người ta thả con lắc đơn cho dao động. Thấy rằng khi con lắc lò xo thực hiện đủ 10 dao động
thì con lắc đơn thực hiện đủ 2 dao động. Chu kỳ con lắc đơn T2 là A. 2s. B. 0,8 s. C. 1,95s. D. 1,78 s.
Câu 41. Hai con lắc đơn giống hệt nhau dài 1,44 m, con lắc A dao động trên Trái Đất và con lắc B dao
động trên Mặt Trăng. Cho biết gia tốc rơi tự do trên Mặt Trăng bằng 0,16 gia tốc rơi tự do trên Trái Đất và bằng 2 2
0,16 m / s . Giả sử hai con lắc được kích thích dao động điều hòa ở cùng một thời điểm thì sau
1 h , con lắc A dao động nhiều hơn con lắc B là bao nhiêu dao động toàn phần? A. 900. B. 800. C. 720. D. 640.
Câu 42. Hai con lắc đơn chiều dài l và l có chu kì dao động riêng lần lưọt là T và T = 2T . Nếu cả hai 1 2 1 2 1
sợi dây cùng được cắt bớt đi 2 dm thì ta được hai con lắc đơn mới có chu kì dao động riêng tương ứng là
T ' và T ' = 3T '. Chiều dài l có giá trị là 1 2 1 1 A. 8, 4dm . B. 4, 6dm . C. 3, 2dm . D. 12,8dm . 
Câu 43. Một con lắc đơn dao động với phương trình    = 0,1cos 10t − rad, t  
đo bằng s tại nơi có gia  2  tốc rơi tự do 2
g = 10 m / s . Trong thời gian 1, 2 s đầu tiên kể từ t = 0 , vật nhỏ của con lắc đơn đi được quãng đường là A. 27, 9 cm . B. 12,1 cm . C. 13, 9 cm . D. 26,1 cm . Trang 5
Câu 44. Ở một nơi trên Trái Đất, hai con lắc đơn có cùng khối lượng đang dao động điều hòa. Gọi
ℓ1, s01, F1 và ℓ2, s02, F2 lần lượt là chiều dài, biên độ, độ lớn lực kéo về cực đại của con lắc thứ nhất và của F
con lắc thứ hai. Biết 3ℓ 2
2 = 2ℓ1, 2 s02 = 3 s01. Tỉ số bằng F1 9 3 4 2 A. . B. . C. . D. . 4 2 9 3
Câu 45. Một con lắc đơn gồm vật nhỏ có khối lượng m treo vào một sợi dây dài 1 m. Từ vị trí cân bằng,
kéo vật theo chiều dương của trục tọa độ tới vị trí mà dây treo hợp với phương thẳng đứng góc α0 = 60 rồi
thả không vận tốc đầu cho vật dao động điều hòa. Chọn mốc thời gian là lúc thả vật, gốc tọa độ là vị trí
cân bằng, lấy g = π2 m/s2. Phương trình dao động của vật là A. s = 6cos( t  )(cm) . B. s = cos( t  )(m) . 30   C. s = cos( t  + )
 (m) . D. s = 6cos( t  + )(cm) . 30 2
Câu 46. Hai con lắc đơn có chiều dài hơn kém nhau 0,1 m dao
động điều hòa tại một nơi nhất định. Hình vẽ bên là đồ thị phụ
thuộc thời gian của li độ góc của hai con lắc. Chiều dài con lắc 1 là? A. 0, 08 m . B. 0, 25 m . C. 0,15 m . D. 0,18 m .
Câu 47. Một con lắc đơn dao động điều hòa với biên độ góc  tại nơi có gia tốc trọng trường là g. Biết 0
gia tốc của vật ở vị trí biên gấp 8 lần gia tốc của vật ở vị trí cân bằng. Giá trị của  là 0 A. 3 , 0 75 rad. B. , 0 062 rad. C. , 0 25 rad. D. 1 , 0 25 rad.
Câu 48. Một con lắc đơn có chiều dài l= 40cm, được treo tại nơi có g = 10m/s2. Bỏ qua sức cản không
khí. Đưa con lắc lệch khỏi VTCB một góc 0,1rad rồi truyền cho vật nặng vận tốc 20cm/s theo phương
vuông góc với dây hướng về VTCB. Chọn gốc tọa độ tại vị trí cân bằng của vật nặng, gốc thời gian lúc
gia tốc của vật nặng tiếp tuyến với quỹ đạo lần thứ nhất. Viết phương trình dao động của con lắc theo li độ cong
A. 8cos(25t +) cm
B. 4 2 cos(25t +) cm
C. 4 2 cos(25t +/2) cm D. 8cos(25t) cm
Câu 49. Một con lắc đơn dao động điều hoà theo phương trình li độ góc  = 0,1cos(2t + /4) ( rad).
Trong khoảng thời gian 5,25s tính từ thời điểm con lắc bắt đầu dao động, có bao nhiêu lần con lắc có độ
lớn vận tốc bằng 1/2 vận tốc cực đại của nó? A. 11 lần. B. 21 lần. C. 20 lần. D. 22 lần.
Câu 50. Một con lắc đơn gồm vật có khối lượng m, dây treo có chiều dài l = 2m, lấy g = π2. Con lắc dao
động điều hòa dưới tác dụng của ngoại lực có biểu thức F = F0cos(ωt + π/2)( N). Nếu chu kỳ T của ngoại
lực tăng từ 2s lên 4s thì biên độ dao động của vật sẽ:
A. tăng rồi giảm
B. giảm rồi tăng C. chỉ giảm D. chỉ tăng
Câu 51. một con lắc đơn dao động điều hòa,nếu giảm chiều dài con lắc đi 44cm thì chu kì giảm đi
0,4s.lấy g=10m/s2.π2=10,coi rằng chiều dài con lắc đơn đủ lớn thì chu kì dao động khi chưa giảm chiều dài là A.1s B.2,4s C.2s D.1,8s
Câu 52. Một con lắc đơn gồm 1 vật nhỏ được treo vào đầu dưới của 1 sợi dây không dãn, đầu trên của sợi
dây được buộc cố định. Bỏ qua ma sát của lực cản của không khí. Kéo con lắc lệch khỏi phương thẳng
đứng một góc 0,1rad rồi thả nhẹ. Tỉ số độ lớn gia tốc của vật tại VTCB và độ lớn gia tốc tại vị trí biên bằng: A: 0,1. B. 0. C. 10. D. 1. Trang 6
Câu 53. Một con lắc đơn gồm hòn bi nhỏ bằng kim loại được tích điện q > 0. Khi đặt con lắc vào trong
điện trường đều có véc tơ cường độ điện trường nằm ngang thì tại vị trí cân bằng dây treo hợp với
phương thẳng đứng một góc α, có tanα = 3/4; lúc này con lắc dao động nhỏ với chu kỳ T1. Nếu đổi chiều
điện trường này sao cho véctơ cường độ diện trường có phương thẳng đứng hướng lên và cường độ không
đổi thì chu kỳ dao động nhỏ của con lắc lúc này là: T 7 5 A. 1 . B. T1 C. T1 . D. T1 5 . 5 5 7
Câu 54. Con lắc đơn đang đứng yên trong điện trường đều nằm ngang thì điện trường đột ngột đổi chiều
(giữ nguyên phương và cường độ E) sau đó con lắc dao động điều hòa với biên độ góc α0. Gọi q và m là
điện tích và khối lượng của vật nặng; g là gia tốc trọng trường. Hệ thức liên hệ đúng là:
A. q.E = m.g.α0.
B. q.E.α0 = m.g.
C. 2q.E = m.g.α0. D. 2q.E.α0 = m.g.
Câu 55. Một con lắc đơn có chiều dài dây treo 50 cm và vật nhỏ có khối lượng 0,01 kg mang điện tích q
= 5.10-6 C, được coi là điện tích điểm. Con lắc dao động điều hòa trong điện trường đều mà vectơ cường
độ điện trường có độ lớn E=104 V/m và hướng thẳng đứng xuống dưới. Lấy g=10 m/s2, π = 3,14. Xác
định chu kì dao động của con lắc. A. 2,15 s. B. 3,15 s. C. 1,15 s. D. 4,15 s.
Câu 56. Có hai con lắc đơn giống nhau. Vật nhỏ của con lắc thứ nhất mang điện tích 2,45.10-6C, vật nhỏ
con lắc thứ hai không mang điện. Treo cả hai con lắc vào vùng điện trường đều có đường sức điện thẳng
đứng, và cường độ điện trường có độ lớn E = 4,8.104 V/m. Xét hai dao động điều hòa của con lắc, người
ta thấy trong cùng một khoảng thời gian, con lắc thứ nhất thực hiện được 7 dao động thì con lắc thứ hai
thực hiện được 5 dao động. Lấy g = 9,8 m/s2. Khối lượng vật nhỏ của mỗi con lắc là A. 12,5 g. B. 4,054 g. C. 7,946 g. D. 24,5 g.
Câu 57. Khảo sát dao động điều hòa của một con lắc đơn, vật dao động nặng 200 g, tích điện q = −400
µC tại nơi có gia tốc trọng trường 10 m/s2. Khi chưa có điện trường chu kì dao động điều hòa là T. Khi có
điện trường đều phương thẳng đứng thì chu kì dao động điều hòa là 2T. Điện trường đều
A. hướng xuống và E = 7,5 kV/m.
B. hướng lên và E = 7,5 kV/m.
C. hướng xuống và E = 3,75 kV/m.
D. hướng lên và E = 3,75 kV/m.
Câu 58. Con lắc đơn gồm vật nặng có khối lượng 100 g, mang điện tích 10−5C đang dao động điều hòa
với biên độ góc 6°. Lấy g = 10 m/s2. Khi vật dao động đi qua vị trí cân bằng người ta thiết lập một điện
trường đều theo phưong thẳng đứng, hướng lên với độ lớn 25 kV/m thì biên độ góc sau đó là A. 3° B. 4 3 °. C. 6 2 0. D. 6°
4. TỔNG HỢP DAO ĐỘNG
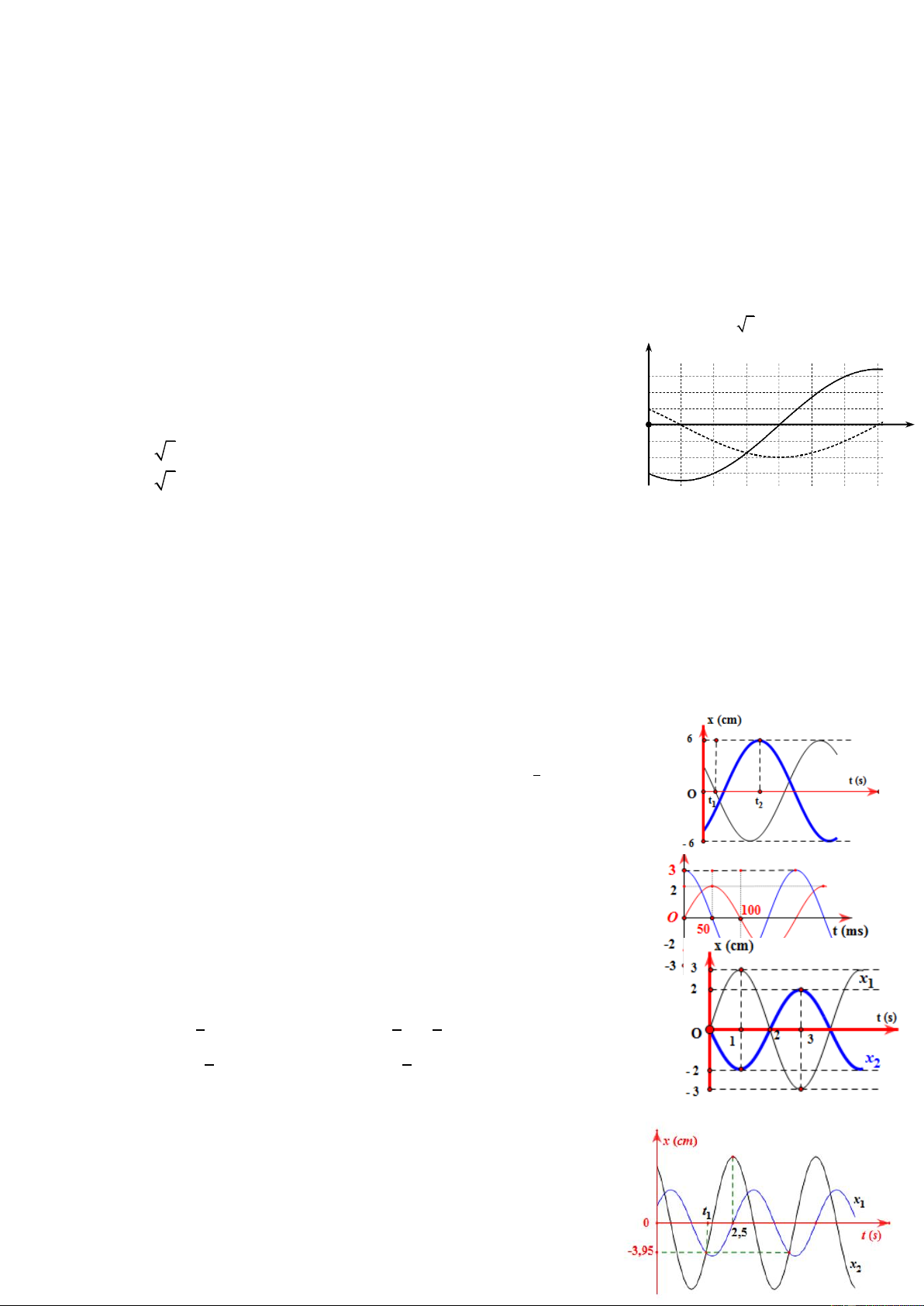
Câu 59. Cho 2 dao động điều hòa x1; x2 cùng phương, cùng tần số có đồ thị
như hình vẽ. Dao động tổng hợp của x1; x2 có phương trình 3π π
A. x = 8√2cos(πt - ) cm B. x = 8√2cos(πt - ) cm 4 4 3π
C. x = 8√2cos(2πt - ) cm D. x = 8√2cos(2πt - 4 5π) cm 4
Câu 60. Hai dao động điều hòa (1) và (2) cùng phương, cùng tần số và cùng biên độ 4 cm. Tại một thời
điểm nào đó, dao động (1) có li độ 2 3 cm, đang chuyển động ngược chiều dương, còn dao động (2) có li
độ 2 cm theo chiều dương. Lúc đó, dao động tổng hợp của hai dao động trên có li độ bao nhiêu và đang
chuyển động theo chiều nào?
A. x = 8 cm và chuyển động ngược chiều dương.
B. x = 5,46 và chuyển động ngược chiều dương
C. x = 5,46 cm và chuyển động theo chiều dương.
D. x = 8 cm và chuyển động theo chiều dương. Trang 7
Câu 61. Một vật dao động điều hoà là tổng hợp của hai dao động cùng phương cùng tần số cùng, đồ thị li
độ thời gian của hai dao động thành phần như hình vẽ.. Tổng tốc độ của hai dao động có giá trị lớn nhất là
A. 280π (cm/s).
B. 200π (cm/s)
C. 140π (cm/s). D. 160π (cm/s).
Câu 62. Một vật thực hiện đồng thời hai dao động cùng phương, cùng tần số 4Hz và cùng cùng biên độ 2
cm. Khi qua vị trí động năng của vật bằng 3 lần thế năng vật đạt tốc độ 24π (cm/s). Độ lệch pha giữa hai
dao động thành phần bằng A. π/6. B. π/2. C. π/3. D. 2π/3.
Câu 63. Một chất điểm tham gia đồng thời hai dao động điều hòa trên cùng một trục Ox có phương trình:
x1 = 4cos(ωt + π/3) cm, x2 = A2cos(ωt + φ2) cm. Phương trình dao động tổng hợp x = 2cos(ωt + φ) cm.
Biết φ – φ2 = π/2. Cặp giá trị nào của A2 và φ sau đây là đúng?
A. 3/3 cm và 0.
B. 2/3 cm và π/4.
C. 3/3 cm và π/2. D. 2 3 cm và 0.
Câu 64. Hình vẽ bên là đồ thị biễu diễn sự phụ thuộc của li độ x x(cm)
vào thời gian t của hai dao động điều hòa cùng phương. Dao động + 6
của vật là tổng hợp của hai dao động nói trên. Trong 0,20 s đầu
tiên kể từ t = 0 s, tốc độ trung bình của vật bằng O t ( s ) A. 40 3 cm/s. B. 40 cm/s. − 6 C. 20 3 cm/s. D. 20 cm/s. 0 , 1 0 , 2 0 , 3
Câu 65. Một chất điểm dao động điều hòa là tổng hợp của hai dao
động cùng phương cùng cùng tần số với li độ lần lượt là x1 và x2. Li độ của hai dao động thành phần thỏa mãn điều kiện: 2 2 1, 5x + 2x = 18( 2 cm
. Tính biên độ dao động tổng hợp của hai dao động trên. 1 2 ) A. 5cm. B. 2 cm. C. 4 cm. D. 5,4cm.
Câu 66. Một vật tham gia đồng thời 2 dao động diêu hoà cùng phương cùng tần số và vuông pha với
nhau. Nếu chỉ tham gia dao động thứ nhất thì cơ năng dao động là W1. Nếu chỉ tham gia dao động thứ hai
thì cơ năng dao động là W2. Nếu tham gia đồng thời 2 dao động thi cơ năng dao động là
A. 0,5(W1 + W2). B. (W1 + W2). C. (W + W )0,5 2 2 . D. 0,5(W + W 1 2 )0,5 2 2 1 2
Câu 67. Một vật thực hiện đồng thời 2 dao động điều hòa cùng phương,
cùng chu kì 2s. Gốc tọa độ trùng với vị trí cân bằng. Đồ thị phụ thuộc thời 2
gian của các li độ được biểu diễn như hình vẽ. Biết t2 – t1 = s. Biên độ dao 3
động tổng hợp gần giá trị nào nhất sau đây? A.2 cm B.3,4 cm C.7,5 cm D.8 cm
Câu 68. Một vật m = 100 g thực hiện đồng thời hai dao động điều hòa
cùng phương được mô tả như hình vẽ. Lực kéo về cực đại tác dụng lên vật
gần giá trị nào nhất A.1 N B.40 N C.10 N D.4 N
Câu 69. Đồ thị của hai dao động điều hòa cùng tần số có dạng như hình
vẽ. Phương trình nào sau đây là phương trình dao động tổng hợp của chúng: π π π
A. x = 5cos t cm
B. x = cos( t − ) cm 2 2 2 π π
C. x = 5cos( t + π) cm D. x = 5cos( t − π) cm 2 2
Câu 70. Một chất điểm thực hiện đồng thời hai dao động điều hòa cùng
phương cùng chu kì T mà đồ thị x1 và x2 phụ thuộc thời gian biểu
diễn trên hình vẽ. Biết x2 = v1T, tốc độ cực đại của chất điểm là 53,4
cm/s. Giá trị T gần giá trị nào nhất sau đây? A.2,56 s B.2,99 s C.2,75 s D.2,64 s Trang 8 Trang 9 HƯỚNG DẪN GIẢI
Câu 1. Một vật nhỏ dao động điều hòa với chu kỳ T=1s. Tại thời điểm t1 nào đó, li độ của vật là -2cm.
Tại thời điểm t2 = t1+0.25s, vận tốc của vật có giá trị là: A. 4 cm/s. B. -2 m/s. C. 2cm/s. D. - 4m/s. Hướng dẫn  2
Cách 1: Giả sử phương trình dao động của vật có dạng x = Acos t (cm) T  2 x1 = Acos t1 (cm) T  2  2 T  2   2 x2 = Acos t2 = Acos (t1+ ) = Acos( t1 + ) (cm) = - Asin t1 T T 4 T 2 T  2  2   2  2 v2 = x’2 = - Asin( t1 + ) = - Acos
t1 = 4 (cm/s). Đáp án: A T T 2 T T Cách 2: t2 - t1=T/4
Đặt x1=Acosα (x1, α là li độ và pha tại thời điểm t1) suy ra vận tốc tại thời điểm t2 là v2=-wAsin(α+π/2)=-wAcosα.
Lập tỉ số x1/v2 rút ra giá trị v2. 
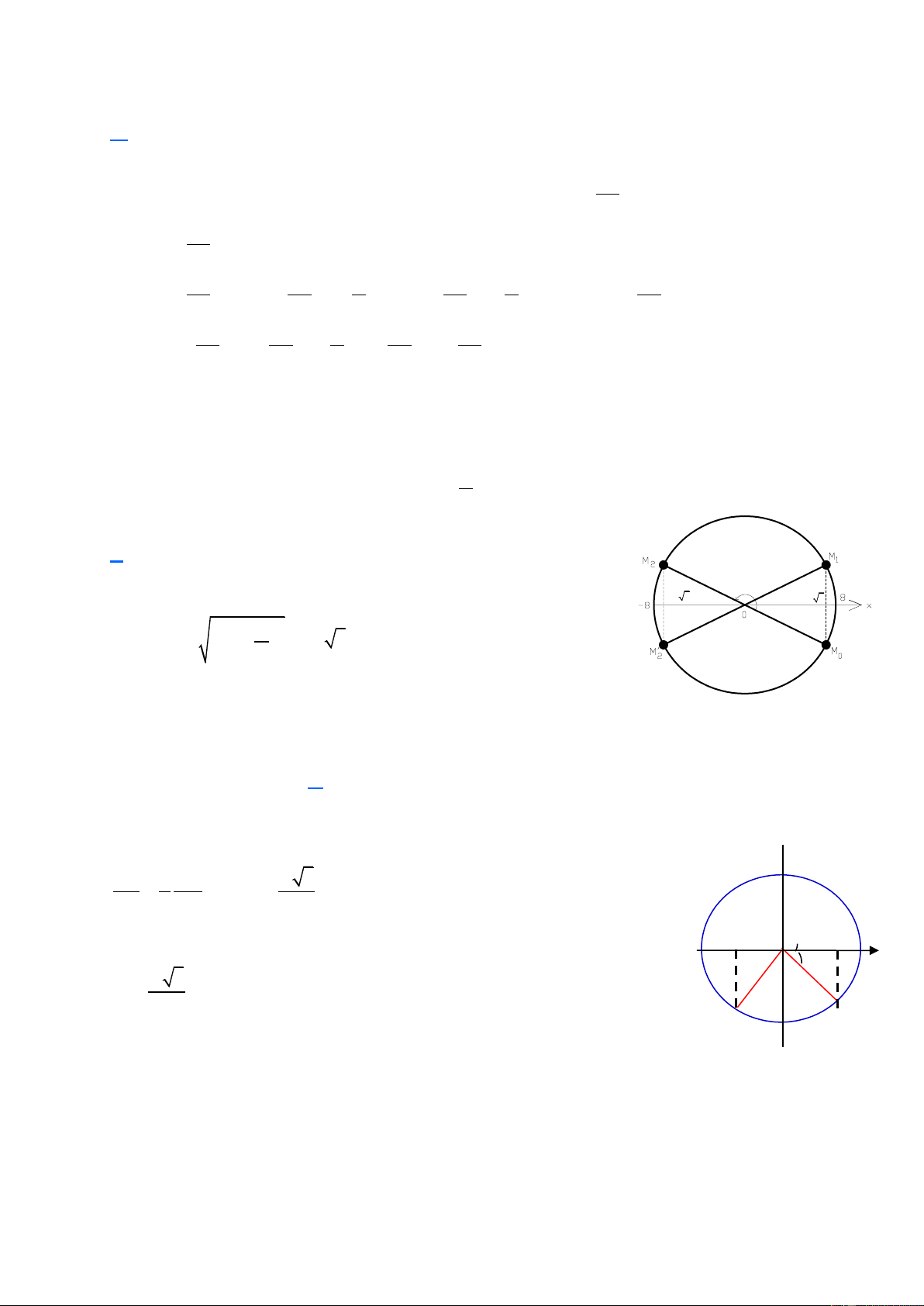
Câu 2. Một dao động điều hoà với x=8cos(2t-
) cm. Thời điểm thứ 2023 vật qua vị trí có vận tốc v = 6
-8 cm/s có giá trị gần nhất là : A. 1011,2s. B. 1011,3s. C. 1011,1s. D. 1011,5s. Hướng dẫn T=1s. −4 3 4 3 v Ta có 2 2
x =  A − ( ) = 4  3cm
.Vì v < 0 nên vật qua M1 và M2
Qua lần thứ 2023 thì phải quay 1011 vòng rồi đi từ M0 đến M1. Góc quét  = 1011.2 + /3  t
=1011.T+ T/6=1011,1667 s. (Hình 7) Hình 7
Câu 3. Vật dao động điều hòa có vận tốc cực đại bằng 3m/s và gia tốc cực đại bằng 30 m/s2. Thời điểm ban
đầu vật có vận tốc 1,5m/s và thế năng đang tăng. Thời điểm vật có gia tốc bằng 15 m/s2 là: A. 0,10s. B. 0,15s. C. 0,20s. D. 0,05s. Hướng dẫn
vmax = ωA= 3(m/s), amax = ω2A= 30π (m/s2) => ω = 10π --→ T = 0,2s
Khi t = 0 thì v = 1,5 m/s = vmax/2→ Wđ = W/4. Tức là tế năng Wt =3W/4 2 2 kx 3 kA A 3 0 =  x =  . 0 2 4 2 2
Do thế năng đang tăng, vật chuyển động theo chiều dương nên vị trí ban đầ O u A A 3 x0 =
Vật ở M0 góc φ = -π/6. 2 M
(Có thể dùng trục tọa độ vận tốc để xác định M M 0 nhanh hơn)
Thời điểm a = 15 (m/s2)= a 0 max/2 =>
a=-ω2x>0 suy ra x = -A/2. Có 2 vị trí ứng với x = -A/2 là M và điểm đối xứng qua 0x. Tuy nhiên đáp án phù
hợp có trong 4 phương án là M ứng với thời điểm t = 3T/4 = 0,15s
(Điểm đối xứng M ứng với t=0,083s không có trong đáp án.) Chọn B. 0,15s
Câu 4. Một vật dao động điều hòa, đi qua vị trị có vận tốc bằng không vào các thời điểm liên tiếp 4,25s
và 5,75s. Biết vào thời điểm ban đầu vật chuyển động theo chiều dương của trục tọa độ, và tốc độ lớn Trang 10
nhất của vật trong quá trình dao động là 4  (cm/s). Vận tốc trung bình của vật trong khoảng từ thời điểm
0,75s đến thời điểm 2,25s là : A. -4,00cm/s. B. 4,00cm/s. C. 0,00 cm/s. D. -4,25cm/s. Hướng dẫn
+ T/2 = 5,75 – 4,25 = 1,5 s => T = 3s (vị trị có vận tốc bằng không là VT biên) + vmax = A => A = 6cm + t = 4,25s = T + T/4 + T/6 -A T/12 3
* Ở thời điểm 4,25s nếu vật ở VT biên dương thì khi t = 0 vật ở VT - : x = -A ; v > 0 0 (nhận) A 2 x A 3
* Ở thời điểm 4,25s nếu vật ở VT biên âm thì khi t = 0 vật ở VT: x = A ; v < 0 T/6 T/4 (loại) 2
+ trong khoảng từ thời điểm 0,75s = T/6 + T/12 đến thời điểm 2,25s: t = 1,5s = T/2
=> vật từ x1 =#A/2 đến x2 = -#A/2 x − x − A => vận tốc: v = 2 1 = = - 6/1,5 = - 4 cm/s tT 2
Câu 5. Một chất điểm dao động điều hòa với chu kì T. Gọi amax là gia tốc cực đại của vật. Khoảng thời a
gian trong một chu kì để vật có độ lớn gia tốc lớn hơn max là : 2 A. T/3. B. 2T/3. C. T/6. D. T/2. Hướng dẫn a A
Ta có : vị trí |a|= max tương ứng |x|= 2 2 a A
Vẽ đường tròn, để |a|> max tương ứng |x|>
thì phần góc tương ứng là 450.4 tương ứng thời gian 2 2 T/2. Đáp án D.
Câu 6. Hai chất điểm M, N dao động điều hòa dọc theo hai đường thẳng song song kề nhau và song
song với trục tọa độ Ox. Vị trí cân bằng của M và của N đều ở trên một đường thẳng qua gốc tọa độ và
vuông góc với Ox. Phương trình dao động của chúng lần lượt là x1 = 10cos2πt cm và x2 = 10 3 cos(2πt +
 ) cm. Hai chất điểm gặp nhau khi chúng đi qua nhau trên đường thẳng vuông góc với trục Ox. Thời 2
điểm lần thứ 2023 hai chất điểm gặp nhau là:
A. 16 phút 51,42s.
B. 16 phút 51,92s.
C. 16 phút 52,42s. D. 16 phút 50,92s. Hướng dẫn T=1s.  ta có x2 = 10 3 cos(2πt + ) cm = - 10 3 sin(2πt) 2 1 
x1 = x2 => 10cos(2πt) = - 10 3 sin(2πt) => tan(2πt) = - => 2πt = - + kπ 3 6 1 k 5 k => t = - +
(s) với k = 1; 2; 3.... vì t>0; hay có nghĩa là t = + với k = 0, 1,2... 12 2 12 2 5
Thời điểm lần đầu tiên hai chất điểm gặp nhau ứng với k = 0: t1 = s. 12
Lần thứ 2013 chúng gặp nhau ứng với k = 2012 => 5 t2023 = 1011+
= 16 phút 51,4166s = 16 phút 51,42s Đáp án A 12 Trang 11
Câu 7. Hai chất điểm dao động điều hòa cùng biên độ A, với tần số góc 3 Hz và 6 Hz. Lúc đầu hai vật A 2
đồng thời xuất phát từ vị trí có li độ
và đang chuyển động theo chiều dương. Khoảng thời gian 2
ngắn nhất để hai vật gặp nhau là: 1 1 1 1 A. s . B. s . C. s . D. s . 18 27 36 72 Hướng dẫn A
Vì cùng xuất phát từ x=
và chuyển động theo chiều dương nên pha ban đầu của chúng - . 2 4  
Do đó phương trình của chúng lần lượt là x = Acos( t − ) và x = Acos( t − ) 1 1 4 2 2 4    
Khi gặp nhau: x = x => A cos( t −
) = A cos( t − )  ( t − ) = - ( t − ) +2kπ  1 2 1 4 2 4 1 4 2 4 2 1
t min thì k=0; ( +  t ) =  t = s . 1 2 4 36
Câu 8. Một vật dao động điều hòa với phương trình x = 4 2 cos(5 t  − 3 / 4) .
cm Quãng đường vật đi
được từ thời điểm t1 = 0,1 s đến t2 = 6s là: A. 84,4cm. B. 333,8cm. C. 331,4 cm. D. 337,5cm. Hướng dẫn 2 2 chu kỳ: T = = = 0,4s  5 Thời gian đi: t - 2 -t1 = 6- 1/10= 5,9(s) t − t 5, 9 Ta có: 2 1 =
=14,75 Hay: t − t =14,75T =14T + 0,75T T 0, 4 2 1 - A Quãng đường đi trong A 14T là: S x X 1 =14.4A =56 A O X
Lúc t1 = 0,1s vật ở tại M1, Lúc t2 = 6s vật ở tại M0 trùng lúc đầu. 1 2
Quãng đường đi trong 0,75T( Từ M1 đến M0 là ¾ vòng tròn) là: M M A 2 S 0 1 2 =2(A - ) +2A = ( 4- 2 )A 2
Quãng đường đi trong 14T+ 0,75T là: S =S Hình 6
1 +S2  331,4cm. Chọn C
Câu 9. Một vật dao động điều hòa theo phương nằm ngang, khi li độ vật bằng 0 thì vận tốc có gia trị
31,4cm/s; khi li độ vật cực đại thì gia tốc có giá trị 4 m/s2. Lấy π2 = 10. Thời gian ngắn nhất để vật chuyển
động từ li độ x = 0 đến x = 1,25cm là: A. 1/12 s. B. 1/3 s. C. 1/6 s. D. 1/24 s. Hướng dẫn
Từ phương trình của vật dao động điều hòa.
Ta có:-Khi li độ bằng không thì vận tốc cực vmax = A
-Khi li độ cực đại thì gia tốc cực đại amax = 2A = vmax
-Tần số góc  = amax / vmax = 400/ 31,4 = 4 ( rad/s) biên độ O 2, A = v 1,2
max /  = 10/ 4 = 2,5 cm  5
Khi vật có li độ x = 1,25 cm 5
Từ phương trình li độ x = A cos ( t + ) = Acos /
cos = 1/2 = >  = / 3 và  = – /3 6 – /3
Theo điều kiện đề cho xét thời gian vật đi từ x = 0 đến x = 1,25 cm
Khoảng thời gian tương ứng góc quay  = /6
Thời gian tương ứng t =  /  = 1/24 (s) Trang 12
Câu 10. Hai chất điểm M và N dao động điều hòa cạnh nhau, dọc theo trục Ox. Vị trí cân bằng của hai
chất điểm ở cùng gốc tọa độ O. Phương trình dao động của chúng lần lượt là       2 2 x x
x = A cos t +
cm , x = A cos t  − cm . Biết 1 2 +
= 4 . Tại thời điểm t nào đó, chất 1 1  ( ) 2 2  ( )  3   6  9 16
điểm M có li độ x = 3
− cm và vận tốc v = 30 −
3 cm / s . Khi đó, độ lớn vận tốc tương đối của chất 1 1
điểm này so với chất điểm kia xấp xỉ bằng: A. 66 cm/s. B. 12 cm/s. C. 40 cm/s. D. 92 cm/s. Hướng dẫn
Nhận xét 2 dao động vuông pha. + Từ phương trình 2 2 2 2 x x x xA = 6cmv = 6(cm / s) 1 1max 1 2 1 2 + = 4  + =1   
+ Biểu diễn tương ứng hai dao động 2 2 9 16 6 8 A = 8cm v = 8(cm / s)  2  2max
vuông pha trên đường tròn. 3 3
=>Từ hình vẽ, ta có v = − v  3 − 0 3 = −
6   = 10 rad / s 1 1max 2 2
+ Dao động thứ hai chậm pha hơn dao động thứ nhất một góc 0 90 1 1
=>Từ hình vẽ, ta có v = v
= 8 = 40cm / s 2 2max 2 2  v
 = v − v = 40 − 3
− 0 3 = 91,96cm / s 2 1 ( ) = > đáp án D   
Câu 11. Một vật dao động điều hòa với phương trình x = 5cos 4 t − 
 . Xác định thời gian ngắn nhất  2 
để vật đi từ vị trí 2,5 cm đến −2,5 cm . 1 1 1 1 A. s B. s C. s D. s 12 10 20 6 Lời giải.
Thời gian ngắn nhất là đi từ 2,5cm qua VTCB đến -2,5cm T 1 t  = 2. = s min 12 12
Câu 12. Một chất điểm có khối lượng 320 g dao động điều hòa dọc theo trục Ox. Biết đồ thị biểu diễn sự
phụ thuộc của động năng theo thời gian của chất điểm như hình vẽ và tại thời điểm ban đầu (t = 0) chất
điểm đang chuyển động ngược chiều dương. Phương trình dao động của chất điểm là Trang 13    A. x = 5cos 2 t + cm   .  6    
B. x = 5cos 4 t + cm   .  3    
C. x = 5cos 2 t − cm    6     D. x = 5cos 4 t − cm.    3  Hướng dẫn 2 Wv  4 v   Tại t = 0 thì d max =   =  v = − và v đang tăng 2   =   = W v 16 2  v 3 x 6 max  5 Tại t =
s thì W = 0 → v = 0 12 d   + 3 2  = = 2 (rad/s) 5 / 12 1 − 1 W = mA  16.10 = .0,32.(2 )2 2 2 3 2
A A  0, 05m = 5cm . Chọn A 2 2
Câu 13. Hình bên là đồ thị biểu diễn sự phụ thuộc li độ của hai dao
động điều hòa theo thời gian. Độ lệch pha của hai dao động này bằng 3 5 A. . B. . 8 6 3 2 C. . D. . 4 3 Hướng dẫn Chu kì T = 16 đơn vị
Hai thời điểm liên tiếp hai dao động có li độ bằng 0 là 3 đơn vị 2 3  = . t  = .3 = 16 8
Câu 14. Một chất điểm dao động điều hòa có đồ thi biểu diễn sự phụ thuộc của li độ x vào thời gian t
như hình vẽ. Tại thời điểm t = 0,2s, chất có li độ 2 cm. Ở thời điểm t = 0,9s, gia tốc của chất điểm có giá trị bằng: A. 2 14, 5cm / s B. 2 57, 0 cm / s C. 2 5, 7m / s D. 2 1, 45 m/ s Hướng dẫn Chu kì T = 1,6s
Dùng vòng tròn lượng giác Biên độ 2 A =  sin 8 2
t = 0.9 → x = − o Ac s .0, 2 1.6 2 2 a = 
− .x = 57cm / s
Câu 15. Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc
vào thời gian của li độ có dạng như hình vẽ bên. Phương trình dao động của li độ là Trang 14  2    2  
A. x = 10cos t −   (cm).
B. x = 10cos t +   (cm).  3 3   3 3   2 2     
C. x = 10cos t +   (cm).
D. x = 10cos t −   (cm).  3 3   3 3  Hướng dẫn 2
T = 2.(4, 25 − 2, 75) = 3s   = 3  2       x = cos (t − ) 2 10 2, 75 + =10cos t +      3 2   3 3 
Câu 16. Một vật dao động điều hòa với phương trình x = 10cos(πt + π/3) cm. Khoảng thời gian tính từ
lúc vật bắt đầu dao động (t = 0) đến khi vật đi được quãng đường 50 cm là A. 7/3 s B. 2,4 s C. 4/3 s D. 1,5 s Hướng dẫn  2 +  7 3 s = 50cm = 5A  t = = = (s)   3
Câu 17. Một con lắc lò xo gồm quả cầu nhỏ khối lượng 1 kg và lò xo có độ cứng 50 N/m. Cho con lắc
dao động điều hòa trên phương nằm ngang. Tại thời điểm vận tốc của quả cầu là 0,2 m/sthì gia tốc của nó
là − 3 m/s2. Cơ năng của con lắc là A. 0,02 J. B. 0,05 J. C. 0,04 J D. 0,01 J Hướng dẫn k 50  = = = 5 2 (rad / s) m 1 a 3 3 x = − = = m 2  ( )2 ( ) 50 5 2 2 1 1 1  3  1 2 2 2 W = kx + mv = .50.  + .1.0, 2 = 0,05(J)   2 2 2 50 2  
Câu 18. Một vật dao động điều hòa với tần số f =10 Hz. Tại thời điểm ban đầu vật đang ở li độ x = 2cm
và chuyển động theo chiều dương. Sau 0,25 (s) kể từ khi dao động thì vật ở li độ
A. x = 2 cm và chuyển động theo chiều đương.
B. x = 2 cm và chuyển động theo chiều âm.
C. x = −2 cm và chuyển động theo chiều âm.
D. x = −2 cm và chuyền động theo chiều dương. Hướng dẫn  = 2 f  = 2 .1  0 = 20(rad / s)  = t = 20 .0
 , 25 = 5  Ngược pha  x = −2cm 
Câu 19. Con lắc lò xo nằm ngang dao động điều hòa, lực đàn hồi cực đại tác đụng vào vật là 2 N, gia tốc
cực đại của vật là 2 m/s2. Khối lượng của vật là A. 1 kg. B. 2 kg. C. 3 kg. D. 4 kg. Hướng dẫn F 2 m = = =1kg a 2
Câu 20. Một con lắc lò xo có độ cứng 50 N/m, dao động điều hòa với biên độ 4 cm. Chọn gốc tính thế
năng là vị trí cân bằng. Tổng động năng và thế năng của vật là A. 25 mJ. B. 20 mJ. C. 40 mJ. D. 10 mJ. Hướng dẫn Trang 15 1 1 2 W kA .50.0, 04 = = = 0,04(J) = 40(mJ) 2 2
Câu 21. Khi treo một vật nặng vào một lò xo, khi vật đứng yên lò xo dài thêm một đoạn 2,5 cm. Lấy g =
π2 m/s2. Chu kì dao động tự do của con lắc bằng A. 0,316 s. B. 0,317 s. C. 0,215 s. D. 0,291 s. Hướng dẫn  0, 025 0 T = 2 = 2  0,316s 2 g 
Câu 22. Một chất điểm dao động điều hòa có đồ thị như hình bên. x(cm) v −
Thời điểm mà vận vận tốc v và li độ x thỏa mãn = 1 − ,25 3( 1 s ) A x .vn .vn 1 / 3 ihoc
lần thứ 2023 gần nhất với giá trị nào dưới đây? O da ihoc oa 31 / 30 da t(s) A. 1618.12 s. B. 1617,94 s. oa thukh C. 1617.83 s. D. 1618,37 s. −A thukh Hướng dẫn 2  5 3   = = = t  31 1 4 − 20 2 5  1    5 3  x = A cos t − +  = A cos t +        4  2    4 8  2  5  − 2    (A −x   v ) ( 2 2 2 2 2 A x )  4  = = = (−1,25 3)2 A  x =   và 2 2  x  x x 2 x trái dấu v 5  2022 + +  8 3 t = = 1618,37(s)  5 4
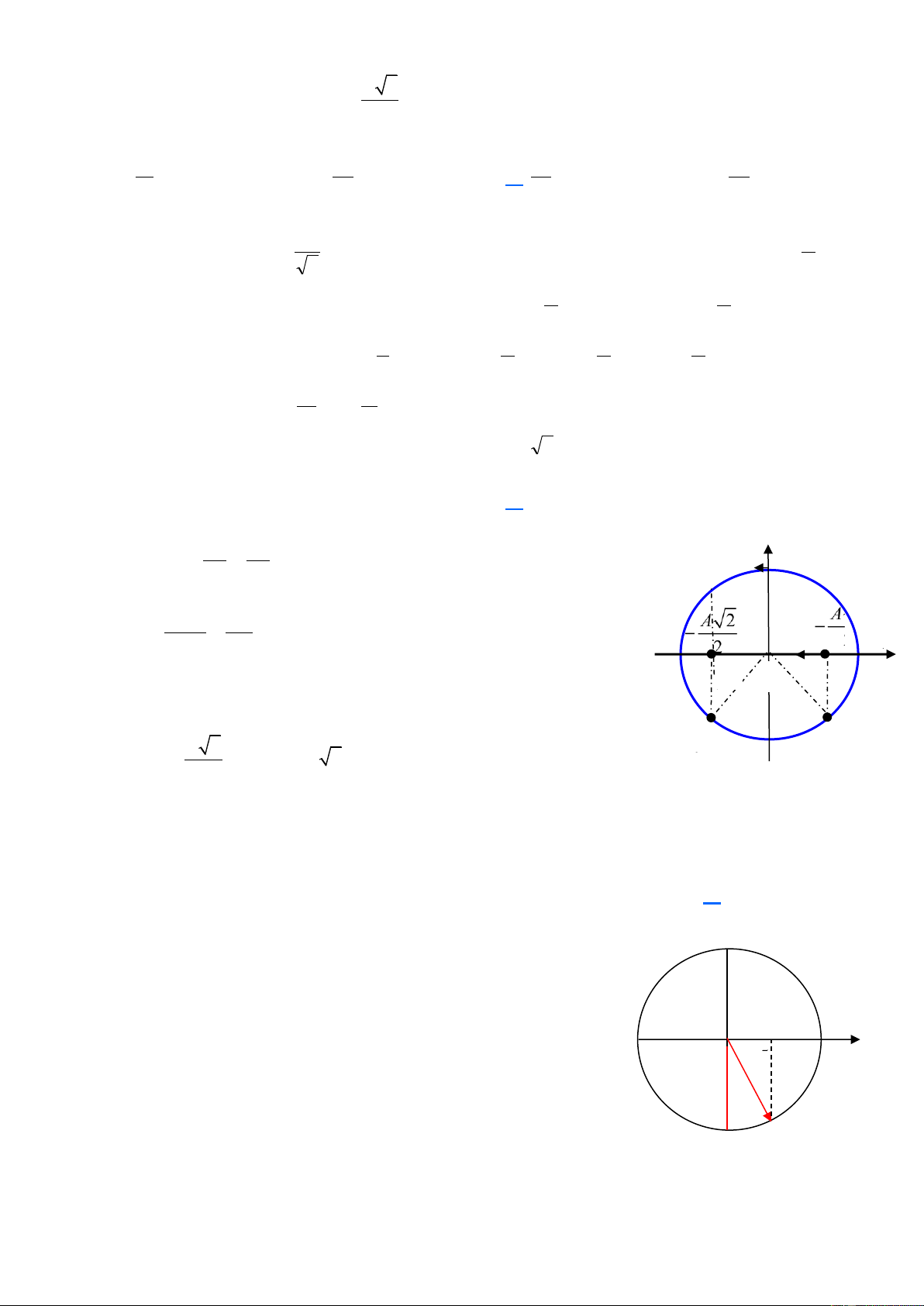
Câu 23. Một vật dao động điều hòa với phương trình x = Acos(ωt + φ). Hình bên là đồ x(cm)
thị biểu diễn sự phụ thuộc li độ x theo thời gian t. Tại .vn 10
thời điểm t = 0, gia tốc của vật có giá trị là ihoc 5 da .vn 1, 5 A. 2 −  ( 2 5 2 cm / s ) B. 2 −  ( 2 5 3 cm / s ) oa O ihoc da 0, 5 1 oa t(s) 5 − thukh C. 2  ( 2 5 2 cm / s ) D. 2  ( 2 5 3 cm / s ) thukh Hướng dẫn T  = 2
6 ô = 0,5s  T = 2s   = = (rad / s) 4 T A 2
Góc quét từ t = 0 đến vị trí cân bằng lần dầu là  t  = 0,25  x = − = 5 − 2cm 2 2 2 = − =  ( 2 a x 5 2 cm / s )
Câu 24. Một vật dao động điều hòa với biên độ 5 cm, trong 1 phút thực hiện được 30 dao động toàn
phần. Quãng đường mà vật đi được trong 1 s là A. 15 cm. B. 5 cm. C. 10 cm. D. 20 cm. Hướng dẫn Trang 16 T 30T = 60s  =1s  s = 2A = 2.5 =10cm 2
Câu 25. Một con lắc lò xo gồm lò xo và vật có khối lượng 80 g dao động điề W mJ t ( )
u hòa trên mặt phẳng nằm ngang. Mốc tính thế năng tại vị trí cân bằng. Hình bên là đồ .vn
thị biểu diễn sự phụ thuộc của thế năng đàn hồi của con .vn ihoc lắc W da ihoc
t vào thời gian t. Lấy π2 = 10. Biên độ dao động của con lắc là oa da 4 oa A. 2 2 cm. B. 2 cm. thukh thukh C. 4 cm. D. 4 2 cm O Hướng dẫn 0,05 t(s)
Dời trục hoành vào chính giữa đồ thị / T / 
= 0,05s  T = 0,2s  T = 0,4s   = 5(rad / s) 4 1 − 1 W = m A  8.10 = .0,08(5)2 2 2 2 3 2 A  A = m = 2 2cm 2 2 50
Câu 26. Một con lắc lò xo heo thẳng đứng (coi gia tốc trọng trường là 10 m/s2) quả cầu có khối lượng
120 g. Chiều dài tự nhiên của lò xo là 20 cm và độ cứng 40 N/m. Từ vị trí cân bằng, kéo vật thẳng đứng,
xuống dưới tới khi lò xo dài 26,5 cm rồi buông nhẹ cho nó dao động điều hòa Động năng của vật lúc lò xo dài 25 cm là A. 24,5 mJ. B. 22 mJ. C. 12 mJ. D. 16,5 mJ. Hướng dẫn  = +  = 0, 23 m CB 0 0 ( ) mg 0,12.10   = = = 0,03 m  A = − = 0, 265 − 0, 23 = 0,035 m 0 ( ) max CB ( ) k 40
x = − = 0,25−0,23 = 0,02 m  cb ( ) 2 2 kA kx 40 W W W ( 2 2 0, 035 0, 02 ) 3 16, 5.10− = − = − = − = J  d t ( ) 2 2 2
Câu 27. Một con lắc lò xo đang dao động điều hòa theo phương nằm ngang. Mốc thế năng ở vị trí cân
bằng. Biết động năng cực đại của con lắc là 80 mJ, lực kéo về cực đại tác dụng lên vật nhỏ của con lắc là
4 N. Khi vật qua vị trí có li độ 3 cm thì động năng của con lắc có giá trị là A. 5 mJ. B. 75 mJ. C. 45 mJ. D. 35 mJ. Hướng dẫn 1 1 2W 2 0 08 2 . , W = kA = F .A A = =
= 0,04 m = 4 cm W = W
= 80 mJ = 0,08 J max 2 2 F 4 d max ; max F 4 max 1 1 k = =
= 100 N / m W = k ( 2 2
A − x ) = .10 . 0 (0, 2 04 − 0, 2 03
= 0 035 J = 35 mJ d ) , A 0,04 ; 2 2
Câu 28. Một con lắc lò xo treo vào một điểm M cố định, đang dao động điều
hòa theo phương trình thẳng đứng. Hình bên là đồ thị biểu diễn sự phụ thuộc
của lực đàn hồi Fđh mà lò xo tác dụng vào M theo thời gian t. Lấy 2 2
g =  m / s . Độ dãn của lò xo khi con lắc ở vị trí cân bằng là A.2 cm. B.4 cm. C.6 cm. D.8 cm. Hướng dẫn
Từ đồ thị ta thấy chu kì của con lắc là: T = 0, 4 (s) llT = 2  0,4 = 2  l
 = 0,04 m = 4 cm 2 ( ) ( ) g Trang 17
Câu 29. Một con lắc lò xo gồm vật nhỏ có khối lượng m=100 g, lò xo có
độ cứng k được treo thẳng đứng. Kích thích cho vật dao động điều hòa
với biên độ. Chọn gốc thế năng tại vị trí cân bằng của vật. Hình bên là
một phần đồ thị biểu diễn mối liên hệ giữa thế năng Et và độ lớn lực kéo
về |Fkv| khi vật dao động. Chu kì dao động của vật là A.0,222 s. B.0,314 s. C.0,157 s. D.0,197 s. Hướng dẫn 1 𝐸 𝑘𝑥2 1 0,144 = . 𝑘𝑥2 { 𝑡 = 2  { 2  k = 80 N/m |𝐹𝑘𝑣| = 𝑘|𝑥| 4,8 = 𝑘|𝑥| 𝑚 T = 2π√ = 2𝜋√0,1 ≈ 0,222 (s). 𝑘 80
Câu 30. Một con lắc lò xo dao động điều hòa theo phương ngang với lực đàn hồi lớn nhất của lò xo là 2
N và năng lượng dao động là 0,1 J. Thời gian trong một chu kì lực đàn hồi là lực kéo không nhỏ hơn 1 N
là 0,1 s. Tính tốc độ lớn nhất của vật. A. 314,1 cm/s. B. 31,4 cm/s. C. 402,5 cm/s. D. 209,44 cm/s. Hướng dẫn x F 1 A T 1 1 = =  x =  t = 1 2 A F 2 2 6 max T
Trong 1 chu kì thời gian lực kéo lớn hon 1 N là 2t = = 0,1 s  T = 0,3 s 2 ( ) ( ) 3 2  kA W = = 0,1   2  = ( ) = ( ) 2 A 0,1 m 10 cm  v = A = A  209, 44 cm / s max ( ) T F = kA = 2  max
Câu 31. Con lắc lò xo có độ cứng k = 40 N/m treo thẳng đứng đang dao động điều hòa với tần số góc ω =
10 rad/s tại nơi có gia tốc trọng trường g = 10 m/s2. Khi lò xo không biến dạng thì vận tốc dao động của
vật triệt tiêu. Độ lớn lực của lò xo tác dụng vào điểm treo khi vật ở trên vị trí cân bằng và có tốc độ 80 cm/s là A. 2,4 N. B. 2 N. C. 1,6 N. D. 3,2 N. Hướng dẫn
Vì khi lò xo không biến dạng thì vận tốc dao động của vật triệt tiêu nên: mg g A =  = = = 0,1 m 0 ( ) 2 k 
Li độ khi vật ớ trên vị trí cân bằng và có tốc độ 80 cm/s: 2 v 2 2 x + = A  x = 6(cm) = 0,06(m) 2 
Lực tác dụng của lò xo vào điểm treo chính là lực đàn hồi: F = k  − x = 1,6 N  dh ( 0 ) ( ) F (N)
Câu 32. Một con lắc lò xo được treo thẳng đứng vào một điểm cố
định đang dao động điều hòa theo phương thẳng đứ 5 ng. Hình bên là
đồ thị biểu diễn sự phụ thuộc của lực đàn hồi F mà lò xo tác dụng
lên vật nhỏ của con lắc theo thời gian 𝑡. Lấy 𝑔 = 𝜋2 = 10m/s2. Biên độ O
dao động của con lắc lò xo là 0,4 t (s)
A. 1,44cm#𝐁. 8,64cm C. 5,76cm#. 7,2cm Hướng dẫn
Dời trục hoành lên 1 ô thì đồ thị lực đàn hồi chuyển thành đồ thị lực kéo về Trang 18 𝑇 2𝜋 25𝜋
+ 𝑇 = 3ô = 0,3𝑠 ⇒ 𝑇 = 0,24𝑠 → 𝜔 = = 𝑟𝑎𝑑/𝑠 4 𝑇 3 𝑔 𝜋2 𝛥𝑙0 = = = 0,0144𝑚 = 1,44𝑐𝑚 𝜔2 (25𝜋/3)2 𝑘𝐴 = 5𝑁 { ⇒ 𝐴 = 5𝛥𝑙 𝑘𝛥𝑙 0 = 5.1,44 = 7,2𝑐𝑚. 0 = 1𝑁
Câu 33. Con lắc lò xo gồm vật nhỏ nặng 1 kg thực hiện đồng thời hai dao động điều hoà theo phương
thẳng đứng, theo các phương trình: x = 5 2 cos10t x = 5 2 sin10t 1 cm và 2
cm (Gốc tọa độ trùng với vị trí
cân bằng, t đo bằng giây và lấy gia tốc trọng trường g = 10 m/s2). Lực cực đại mà lò xo tác dụng lên vật là A. 10N. B. 20 N. C. 25 N. D. 0,25 N. Hướng dẫn
Biên độ dao động tổng hợp là: 2 2 2 2 A =
A + A + 2A A  cos Δ = (5 2) + (5 2) = 10cm = 0,1m 1 2 1 2 g g 10  =  Δl = = = 0,1m 0 2 2 Δl  10 Ta có: 0
Lực cực đại mà lò xo tác dụng lên vật: F
= k (Δl + A) 2
= m (Δl + A) 2
= 110  (0,1+ 0,1) = 20N max 0 0
Câu 34. Một con lắc lò xo treo vào một điểm cố định, dao động điều hòa theo phương thẳng đứng với
chu kì 1,2 s. Trong một chu kì, nếu tỉ số của thời gian lò xo giãn với thời gian lò xo nén bằng 2 thì thời
gian mà lực đàn hồi ngược chiều lực kéo về là A. 0,2 s. B. 0,1 s. C. 0,3 s. D. 0,4 s. Hướng dẫn
Vì tdãn/tnén = 2 nên A = 2Δl0.
Lực đàn hồi và lực kéo về ngược hướng khi vật ở trong đoạn 0  x   0 . t = 2t = 2.T /12 = 0,2 s  0E ( )
Khoảng thời gian cần tính chính .
Câu 35. Một con lắc lò xo gồm vật nhỏ khối lượng 0, 2 kg và lò xo có độ cứng k = 20 N / m . Vật nhỏ
được đặt trên giá cố định nằm ngang dọc theo trục lò xo. Hệ số ma sát trượt giữa giá đỡ và vật nhỏ là
0,01. Từ vị trí lò xo không biến dạng truyền cho vật vận tốc ban đầu 1 m / s thì thấy con lắc dao động tắt
dần trong giới hạn đàn hồi của lò xo. Lấy 2
g = 10 m / s . Độ lớn lực đàn hồi cực đại của lò xo trong quá trình dao động là 2, 2 N 19,8 N 1,5 N 1, 98 N A. . B. . C. D. . Hướng dẫn: F
= mg = 0,01.0, 2.10 = 0,02 ms (N) 1 1 1 1 2 2 2 2 mv − k l  = F . l   .0,2.1 − .20. l  = 0,02. l   l   0,099m max ms max max max max 2 2 2 2 F = k l  = 20.0,099 =1,98 dh max m ax (N).
Câu 36. Một con lắc đơn dao động điều hòa tại một địa điểm A . Nếu đem con lắc đến địa điểm B , biết
rằng chiều dài con lắc không đổi còn gia tốc trọng trường tại B bằng 81% gia tốc trọng trường tại#A. So
với tần số dao động của con lắc tại A , tần số dao động của con lắc tại B sẽ A. tăng 10% . B. giảm 9% . C. tăng 9% D. giảm 10% . Hướng dẫn: Trang 19 1 g f = A 2 l
vậy tần số con lắc đặt tại B giảm 10% 1 0,81.g f = = 0.9 f B 2 Al
Câu 37. Một con lắc đơn dài 25 cm , hòn bi có khối lượng 10 g mang điện tích 4 q 10− = C . Cho 2
g = 10m / s . Treo con lắc đơn giữa hai bản kim loại song song thẳng đứng cách nhau 20 cm . Đặt hai bản
dưới hiệu điện thế một chiều 80 V . Chu kì dao động của con lắc đơn với biên độ góc nhỏ là A. 0, 91 s . B. 0, 96 s . C. 2, 92 s . D. 0, 58 s . Hướng dẫn: U E = d l T = 2 = 0,96s 2  qE  2 g +    m
Câu 38. Trong bài thực hành đo gia tốc trọng trường g bằng
con lắc đơn, một nhóm học sinh tiến hành đo, xử lý số liệu và
vẽ được đồ thị biểu diễn sự phụ thuộc của bình phương chu kì dao động điều hòa ( 2
T ) theo chiều dài l của con lắc như hình
bên. Lấy  = 3,14 . Giá trị trung bình của g đo được trong thí nghiệm này là A. 9,74 m/s B. 9,96 m/s C. 9,58 m/s D. 2 9, 42 m / s T = (  )2 l 2 2 2 .
g = 9,74m / s g Hướng dẫn:
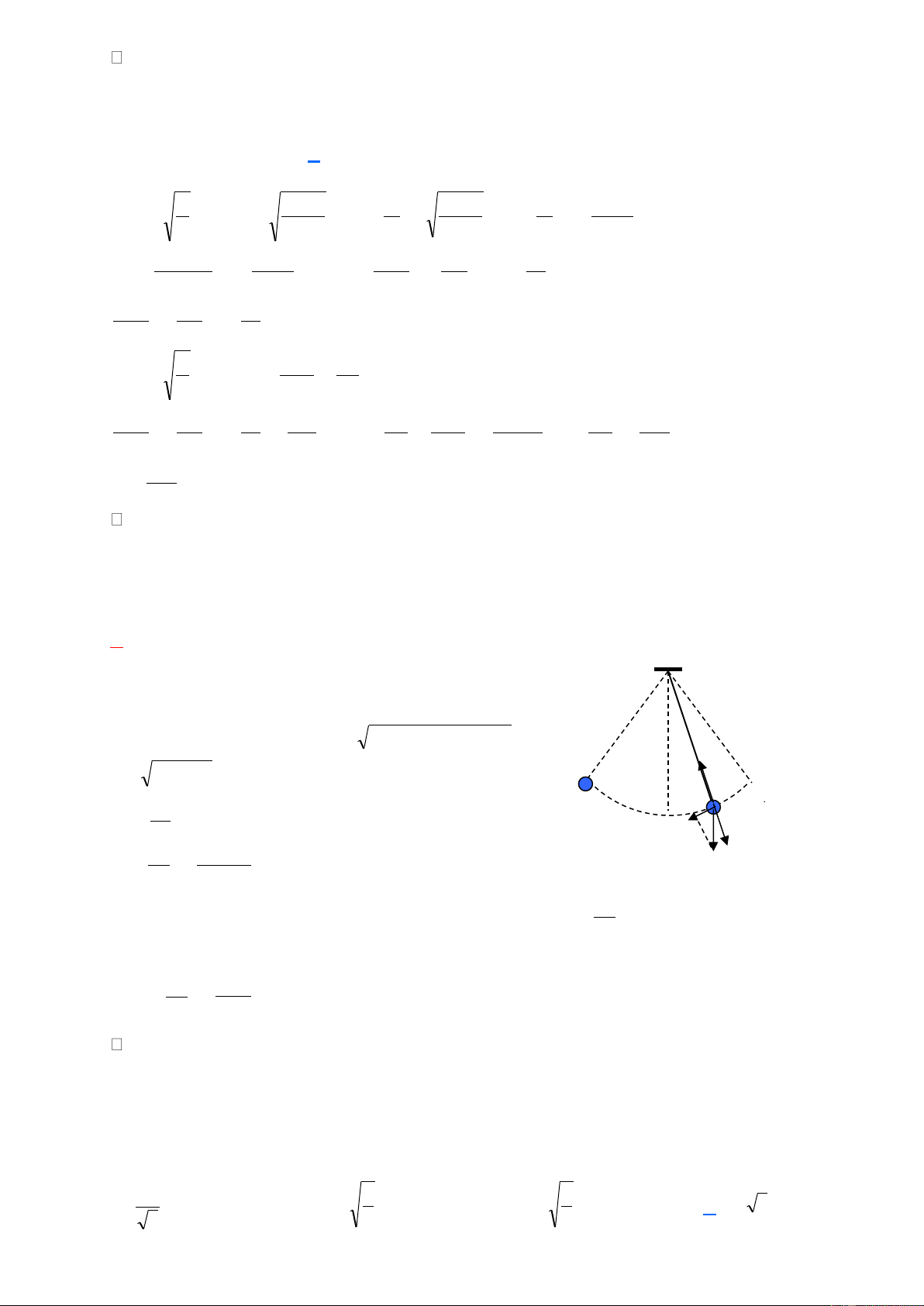
Câu 39. Một con lắc đơn có chiều dài 1,92 m treo vào điểm T cố định. Từ vị
trí cân bằng O, kéo con lắc về bên phải đến A rồi thả nhẹ. Mỗi khi vật nhỏ đi từ
phải sang trái ngang qua B thì dây vướng vào đinh nhỏ tại D, vật dao động trên
quỹ đạo AOBC (được minh họa bằng hình bên). Biết TD = 1,28 m và 0
 =  = 4 . Bỏ qua mọi ma sát. Lấy 2 2
g =  (m / s ) . Chu kì dao động của con 1 2 lắc là A. 2,26 s. B. 2,61 s. C. 1,60 s. D. 2,77 s. Hướng dẫn:
Gọi là biên độ góc của con lắc đơn có chiều dài l 0 mgl (1− cos = mg l − . TD cos − − .
CD cos( +  ) 0 ) ( 1 1 2 )     −  −  1 1 1 1 2 sin   2cos   1 l  2    
Chu kì của con lắc là: 0 1 T = .2 + + 2 g g g l CD
Câu 40. Con lắc lò xo M và con lắc đơn N có chu kỳ dao động riêng tương ứng là T1=0,4s và T2. Người
ta đưa cả hai con lắc ra biên của chúng (biên của con lắc lò xo tuỳ ý trong giới hạn đàn hồi, biên của con
lắc đơn tuỳ ý trong giới hạn góc bé). Ban đầu ta thả cho con lắc lò xo dao động, khi vật tới vị trí cân bằng
lần đầu thì người ta thả con lắc đơn cho dao động. Thấy rằng khi con lắc lò xo thực hiện đủ 10 dao động
thì con lắc đơn thực hiện đủ 2 dao động. Chu kỳ con lắc đơn T2 là A. 2s. B. 0,8 s. C. 1,95s. D. 1,78 s. Trang 20 Hướng dẫn:  1  10 −
T = 2T T = 1,95s   1 2 2  4 
Câu 41. Hai con lắc đơn giống hệt nhau dài 1,44 m, con lắc A dao động trên Trái Đất và con lắc B dao
động trên Mặt Trăng. Cho biết gia tốc rơi tự do trên Mặt Trăng bằng 0,16 gia tốc rơi tự do trên Trái Đất và bằng 2 2
0,16 m / s . Giả sử hai con lắc được kích thích dao động điều hòa ở cùng một thời điểm thì sau
1 h , con lắc A dao động nhiều hơn con lắc B là bao nhiêu dao động toàn phần? A. 900. B. 800. C. 720. D. 640. Hướng dẫn:  1, 44 T = 2 = 2, 4s A 2 l   3600 3600 Từ: T = 2    − = 900 . g  1, 4 4 2, 4 6 T = 2 = 6s B 2  , 0 16  Chọn A
Câu 42. Hai con lắc đơn chiều dài l và l có chu kì dao động riêng lần lưọt là T và T = 2T . Nếu cả hai 1 2 1 2 1
sợi dây cùng được cắt bớt đi 2 dm thì ta được hai con lắc đơn mới có chu kì dao động riêng tương ứng là
T ' và T ' = 3T '. Chiều dài l có giá trị là 1 2 1 1 A. 8, 4dm . B. 4, 6dm . C. 3, 2dm . D. 12,8dm . Hướng dẫn T l 2 2  = = 2 T l ll  − 4l = 0 l  = 12,8dm 1 1 2 1 2 T = 2       . g  − l − 9l = −16 l = 3, 2 T l 2 dm   2 1 1 2 2 = = 3 T l − 2  1 1 Chọn C
Câu 43. Một con lắc đơn dao động với phương trình    = 0,1cos 10t − rad, t  
đo bằng s tại nơi có gia  2  tốc rơi tự do 2
g = 10 m / s . Trong thời gian 1, 2 s đầu tiên kể từ t = 0 , vật nhỏ của con lắc đơn đi được quãng đường là A. 27, 9 cm . B. 12,1 cm . C. 13, 9 cm . D. 26,1 cm . Hướng dẫn: g 10 l = = =1m =100cm 2  10 37,42°
A = l = 100.0,1 = 10 (cm) 0 -10 O 10  =  =1,2 10.
= 217, 42o =180o + 37, 42o t rad o A 10 S 2 A Asin 37, 42 = = + ⎯⎯⎯
→ S  26,1cm . Chọn D
Câu 44. Ở một nơi trên Trái Đất, hai con lắc đơn có cùng khối lượng đang dao động điều hòa. Gọi
ℓ1, s01, F1 và ℓ2, s02, F2 lần lượt là chiều dài, biên độ, độ lớn lực kéo về cực đại của con lắc thứ nhất và của F
con lắc thứ hai. Biết 3ℓ 2
2 = 2ℓ1, 2 s02 = 3 s01. Tỉ số bằng F1 9 3 4 2 A. . B. . C. . D. . 4 2 9 3 Hướng dẫn: 𝑠 𝐹 𝑠 𝑙 3 3 9
F = mg. 0  2 = 02 . 1 = . = . 𝑙 𝐹1 𝑠01 𝑙2 2 2 4 Trang 21 Chọn A
Câu 45. Một con lắc đơn gồm vật nhỏ có khối lượng m treo vào một sợi dây dài 1 m. Từ vị trí cân bằng,
kéo vật theo chiều dương của trục tọa độ tới vị trí mà dây treo hợp với phương thẳng đứng góc α0 = 60 rồi
thả không vận tốc đầu cho vật dao động điều hòa. Chọn mốc thời gian là lúc thả vật, gốc tọa độ là vị trí
cân bằng, lấy g = π2 m/s2. Phương trình dao động của vật là A. s = 6cos( t  )(cm) . B. s = cos( t  )(m) . 30   C. s = cos( t  + )
 (m) . D. s = 6cos( t  + )(cm) . 30 2 Hướng dẫn: 6π π S = lα = 1. =
m và kéo vật theo chiều dương, chọn mốc thời gian là lúc thả vật =>φ =0.. 0 0 180 30  => s = cos( t  )(m) 30 Chọn B
Câu 46. Hai con lắc đơn có chiều dài hơn kém nhau 0,1 m dao
động điều hòa tại một nơi nhất định. Hình vẽ bên là đồ thị phụ
thuộc thời gian của li độ góc của hai con lắc. Chiều dài con lắc 1 là? A. 0, 08 m . B. 0, 25 m . C. 0,15 m . D. 0,18 m . Hướng dẫn:
Quan sát hai điểm đặc biệt cắt nhau của hai đồ thị trên trục hoành ta thấy: l l 0,1 2 2 T 1,5T 2 1,5.2 − =  =  l = 0,18( )
m l = 0, 08( ) m . 2 1 2 1 g g Chọn A
Câu 47. Một con lắc đơn dao động điều hòa với biên độ góc  tại nơi có gia tốc trọng trường là g. Biết 0
gia tốc của vật ở vị trí biên gấp 8 lần gia tốc của vật ở vị trí cân bằng. Giá trị của  là 0 A. 3 , 0 75 rad. B. , 0 062 rad. C. , 0 25 rad. D. 1 , 0 25 rad. Hướng dẫn:
gia tốc ở VTB là gia tốc tiếp tuyến còn gia tóc ở VTCB cua con lắc là gia tốc hướng tâm a   2 →  = −  → =  → = tt= g.sin ; tại VTCB a g sin 16 g 1 ( cos ) 8 125 , 0 rad ( 0 ht=2g(1-cos ) 0 0 0 0 0 0 2  lấy sin   1 ; − cos = 2 ) 4 Chọn D
Câu 48. Một con lắc đơn có chiều dài l= 40cm, được treo tại nơi có g = 10m/s2. Bỏ qua sức cản không
khí. Đưa con lắc lệch khỏi VTCB một góc 0,1rad rồi truyền cho vật nặng vận tốc 20cm/s theo phương
vuông góc với dây hướng về VTCB. Chọn gốc tọa độ tại vị trí cân bằng của vật nặng, gốc thời gian lúc
gia tốc của vật nặng tiếp tuyến với quỹ đạo lần thứ nhất. Viết phương trình dao động của con lắc theo li độ cong
A. 8cos(25t +) cm
B. 4 2 cos(25t +) cm
C. 4 2 cos(25t +/2) cm D. 8cos(25t) cm Hướng dẫn:
Phương trình dao động của con lắc theo li độ cong có dạng s = Smaxcos( t + )
Gọi m là biên độ góc của dao độngn của con lắc đơn Trang 22   max
Khi đo biên độ của tọa độ cong Smax = m l 0 = 0,1 rad.
Theo ĐL bảo toàn năng lượng ta có 2 mv mgl(1-cos 0 m) = mgl(1-cos0) + <----> 2 2  2  2 mv v2 mgl max = mgl 0 + 0 <-----> 2  = 2  + 0 = 0,12 + 0,01 2 2 2 max 0 gl
max = 0,141 = 0,1 2 (rad) <----> Smax = m l = 0,04 2 (m) = 4 2 (cm) (*) g
Tần số góc của dao động  = = 25 rad/s l
Gốc thời gian t = 0 khi gia tốc của vật nặng tiếp tuyến với quỹ đạo lần thứ nhất tức là gia tốc hướng
tâm aht = 0------> v = 0: tức là lúc vật ở biên âm (ở điểm A).
Khi t = 0 s = -Smax ---->  = .
Vậy: Phương trình dao động của con lắc theo li độ cong s = Smaxcos( t + )
s = 4 2 cos( t +) (cm). Chọn B
Câu 49. Một con lắc đơn dao động điều hoà theo phương trình li độ góc  = 0,1cos(2t + /4) ( rad).
Trong khoảng thời gian 5,25s tính từ thời điểm con lắc bắt đầu dao động, có bao nhiêu lần con lắc có độ
lớn vận tốc bằng 1/2 vận tốc cực đại của nó? A. 11 lần. B. 21 lần. C. 20 lần. D. 22 lần. Hướng dẫn: v
Trong một chu kì dao động có 4 lần v = max tại vị trí 2 1 3  Wđ = W-----> Wt = Wtmax tức là lúc li độ 4 4 0   3 = ± max 2  2 A
Chu kì của con lắc đơn đã cho T =  = 1 (s) O 1 M t = 5,25 (s) = 5T + T 0 4  2 Khi t = 0:  max 0 = 0,1cos(/4) =
; vật chuyển động theo chiều âm về VTCB 2  3
Sau 5 chu kì vật trở lại vị trí ban đầu, sau T/4 tiếp vật chưa qua được vị trí  = - max 2
Do đó: Trong khoảng thời gian 5,25s tính từ thời điểm con lắc bắt đầu dao động, con lắc có độ lớn vận
tốc bằng 1/2 vận tốc cực đại của nó 20 lần. Chọn C
Câu 50. Một con lắc đơn gồm vật có khối lượng m, dây treo có chiều dài l = 2m, lấy g = π2. Con lắc dao
động điều hòa dưới tác dụng của ngoại lực có biểu thức F = F0cos(ωt + π/2)( N). Nếu chu kỳ T của ngoại
lực tăng từ 2s lên 4s thì biên độ dao động của vật sẽ:
A. tăng rồi giảm
B. giảm rồi tăng C. chỉ giảm D. chỉ tăng Hướng dẫn: l 2
Chu kỳ dao động riêng của con lắc đơn: T0 = 2π = 2π g 2  = 2 2 (giây)
Khi chu kỳ T của ngoại lực tăng từ 2s lên 4s thì biên độ dao động của vật sẽ giảm
Vì khi T = 2s = T0----> f = f0 thì biên độ đạt cực đại do có sự cộng hưởng; biên độ đạt cực đại. Trang 23 Chọn A
Câu 51. một con lắc đơn dao động điều hòa,nếu giảm chiều dài con lắc đi 44cm thì chu kì giảm đi
0,4s.lấy g=10m/s2.π2=10,coi rằng chiều dài con lắc đơn đủ lớn thì chu kì dao động khi chưa giảm chiều dài là A.1s B.2,4s C.2s D.1,8s Hướng dẫn: l l − lT ' l − lT ' l − l  T = 2 ; T’ = 2 -----> = ---->( )2 = g g T l T l T − T  ' l − l  2 TTl  ---->( )2 = <---> 1 - + ( )2 = 1 - <---> T l T T l 2 TTl  - ( )2 = (*) T T l l 2 gT 2 T T = 2 ------> l = = g 2 4 4 2 TTl  4 l  8 , 0 2 , 0 4 4 , 0 . 44 8 , 0 92 , 1 - ( )2 = = <-----> - = ---> = T T l 2 T T 2 T 2 T T 2 T 92 , 1 --->
= 0,8 -----> T = 2,4 (s). T Chọn B
Câu 52. Một con lắc đơn gồm 1 vật nhỏ được treo vào đầu dưới của 1 sợi dây không dãn, đầu trên của sợi
dây được buộc cố định. Bỏ qua ma sát của lực cản của không khí. Kéo con lắc lệch khỏi phương thẳng
đứng một góc 0,1rad rồi thả nhẹ. Tỉ số độ lớn gia tốc của vật tại VTCB và độ lớn gia tốc tại vị trí biên bằng: A: 0,1. B: 0. C: 10. D: 1. Hướng dẫn:
Xét thời điểm khi vật ở M, góc lệch của dây treo là 
Vận tốc của vật tại M: 0 v2 = 2gl( cos - cos  −   0).----> v = 2gl(cos cos ) 0 a = 2 2 a + a ht tt v2 A’ A a ht = = 2g(cos - cos0) O l F M P sin  tt a tt = m = m = g 0 Tại VTCB: = 0---> a 
tt = 0 nên a0 = aht = 2g(1-cos0) = 2g.2sin2 2 = g 2 0
Tại biên:  = 0 nên aht =0 ----> aB = att = g0 a 2  g 0 Do đó 0 : = = ag 0 = 0,1. B 0 Chọn A
Câu 53. Một con lắc đơn gồm hòn bi nhỏ bằng kim loại được tích điện q > 0. Khi đặt con lắc vào trong
điện trường đều có véc tơ cường độ điện trường nằm ngang thì tại vị trí cân bằng dây treo hợp với
phương thẳng đứng một góc α, có tanα = 3/4; lúc này con lắc dao động nhỏ với chu kỳ T1. Nếu đổi chiều
điện trường này sao cho véctơ cường độ diện trường có phương thẳng đứng hướng lên và cường độ không
đổi thì chu kỳ dao động nhỏ của con lắc lúc này là: T 7 5 A. 1 . B. T1 C. T1 . D. T1 5 . 5 5 7 Trang 24 Hướng dẫn F Eq
Ta có Gia tốc do lực điện trường gây ra cho vật a = =
( E là độ lớn cường độ điện trường) m m
Khi điện trường nằm ngang: l F a 3 3 T 2 1 = 2π Với g1 = 2 g + a . tanα = = = ----> a = g g P g 4 4 1  5 g1 = g 4 A
Khi điện trường hướng thẳng đứng lên trên O’ l 3 1 T2 = 2π Với g2 = g –a = g - g = g F O g 4 4 2  5 g T g 2 = 1 = 4 = 5 ----> T P 2 = T1 5 . T g 1 1 2 g 4 Chọn D
Câu 54. Con lắc đơn đang đứng yên trong điện trường đều nằm ngang thì điện trường đột ngột đổi chiều
(giữ nguyên phương và cường độ E) sau đó con lắc dao động điều hòa với biên độ góc α0. Gọi q và m là
điện tích và khối lượng của vật nặng; g là gia tốc trọng trường. Hệ thức liên hệ đúng là:
A. q.E = m.g.α0.
B. q.E.α0 = m.g.
C. 2q.E = m.g.α0. D. 2q.E.α0 = m.g. Hướng dẫn
- Lực điện có tác dụng làm dịch chuyển vị trí cân bằng.
- Giả sử lúc đầu F hướng sang phải như hình vẽ, thì ta có vị trí cân bằng O, dây
treo hợp với phương thẳng đúng 1 góc .
 Tại đây chưa dao động nên vật có vận tốc v = 0.
- Khi đảo chiều điện trường thì ta lại có vị trí cân bằng mới là O/, dây treo vẫn hợp
với phương thẳng đứng 1 góc  (do điện trường có độ lớn không đổi).
- Tính từ O đến đến cân bằng mới O/ thì góc lệch là 2 và lúc đầu v = 0 nên biên độ lúc sau:  = 2 .  0 F qE qE qE - Ta có: tan  = = =
, do  nhỏ nên tan     = = 0/2 2qE = mg0 P mg mg mg => Chọn C
Câu 55. Một con lắc đơn có chiều dài dây treo 50 cm và vật nhỏ có khối lượng 0,01 kg mang điện tích q
= 5.10-6 C, được coi là điện tích điểm. Con lắc dao động điều hòa trong điện trường đều mà vectơ cường
độ điện trường có độ lớn E=104 V/m và hướng thẳng đứng xuống dưới. Lấy g=10 m/s2, π = 3,14. Xác
định chu kì dao động của con lắc. A. 2,15 s. B. 3,15 s. C. 1,15 s. D. 4,15 s. Hướng dẫn:
F = qE = 5.10-6.10-4 = 0,05 (N) F 0,05 a = = = 5 (m/s2) m 0,01
g’ = g + a = 10 + 5 = 15 (m/s2) T = 2π l
√ = 2π√0.5 ≈ = 1,15 s. g′ 15 Chọn C Trang 25
Câu 56. Có hai con lắc đơn giống nhau. Vật nhỏ của con lắc thứ nhất mang điện tích 2,45.10-6C, vật nhỏ
con lắc thứ hai không mang điện. Treo cả hai con lắc vào vùng điện trường đều có đường sức điện thẳng
đứng, và cường độ điện trường có độ lớn E = 4,8.104 V/m. Xét hai dao động điều hòa của con lắc, người
ta thấy trong cùng một khoảng thời gian, con lắc thứ nhất thực hiện được 7 dao động thì con lắc thứ hai
thực hiện được 5 dao động. Lấy g = 9,8 m/s2. Khối lượng vật nhỏ của mỗi con lắc là A. 12,5 g. B. 4,054 g. C. 7,946 g. D. 24,5 g. Hướng dẫn l l 49 * 7T1 = 5T2 => 7 = 5 => g’ =
g => g’ > g => lực điện F hướng xuống. g' g 25
* P’ = P + F => g’ = g + 𝑞𝐸 𝑞𝐸 49 qE 25 => g + = g => m = = 0,0125kg 𝑚 𝑚 25 24g P Chọn A q
Câu 57. Khảo sát dao động điều hòa của một con lắc đơn, vật dao động nặng 200 g, E
tích điện q = −400 µC tại nơi có gia tốc trọng trường 10 m/s2. Khi chưa có điện trường F
chu kì dao động điều hòa là T. Khi có điện trường đều phương thẳng đứng thì chu kì
dao động điều hòa là 2T. Điện trường đều
A. hướng xuống và E = 7,5 kV/m.
B. hướng lên và E = 7,5 kV/m.
C. hướng xuống và E = 3,75 kV/m.
D. hướng lên và E = 3,75 kV/m. Hướng dẫn: g 3g Vì 2 = 2.2  g ' = = g −
 Gia tốc trọng trường hiệu dụng giảm 0,75g nên F = qE hướng lên g ' g 4 4 6 3g q E 3.10 400.10− .E
( E hướng xuống) sao cho: =  =  E = 3750(V)  4 m 4 0, 2 Chọn C
Câu 58. Con lắc đơn gồm vật nặng có khối lượng 100 g, mang điện tích 10−5C đang dao động điều hòa
với biên độ góc 6°. Lấy g = 10 m/s2. Khi vật dao động đi qua vị trí cân bằng người ta thiết lập một điện
trường đều theo phưong thẳng đứng, hướng lên với độ lớn 25 kV/m thì biên độ góc sau đó là A. 3° B. 4 3 °. C. 6 2 0. D. 6° Hướng dẫn: qE
* Tốc độ cực đại không đổi 'A' = A  nhưng g ' = g − = 7,5( 2 m / s ) nên m 0 g ' g g ' '  .  = .    =  = 4 3  max max max max g ' Chọn B
Câu 59. Cho 2 dao động điều hòa x1; x2 cùng phương, cùng tần số có đồ thị
như hình vẽ. Dao động tổng hợp của x1; x2 có phương trình 3π π
A. x = 8√2cos(πt - ) cm B. x = 8√2cos(πt - ) cm 4 4 3π
C. x = 8√2cos(2πt - ) cm D. x = 8√2cos(2πt - 4 5π) cm
4 Hướng dẫn:
Chu kỳ dao động T = 2 s ω = π rad/s Ta có A1 = A2 = 8 cm 𝜋 𝜋 Tại t = 0, x 
1 = 0 và đang chuyển động theo chiều dương φ1 = - x1 = 8cos(πt - ) cm 2 2
Trong khi đó t = 0, x2 = -8 cm φ2 = π  φ2 = 8cos(πt + π) cm 3𝜋
Vậy x = x1 + x2 = 8√2cos(πt - ) cm  Chọn A 4 Trang 26
Câu 60. Hai dao động điều hòa (1) và (2) cùng phương, cùng tần số và cùng biên độ 4 cm. Tại một thời
điểm nào đó, dao động (1) có li độ 2 3 cm, đang chuyển động ngược chiều dương, còn dao động (2) có li
độ 2 cm theo chiều dương. Lúc đó, dao động tổng hợp của hai dao động trên có li độ bao nhiêu và đang
chuyển động theo chiều nào?
A. x = 8 cm và chuyển động ngược chiều dương.
B. x = 5,46 và chuyển động ngược chiều dương
C. x = 5,46 cm và chuyển động theo chiều dương.
D. x = 8 cm và chuyển động theo chiều dương. Hướng dẫn
Chọn thời điểm khảo sát là thời điểm han đầu t = 0 thì phương trình dao động của các chất điểm lần     x = 4 cos t  +  1   lượ   6  t là:      x = 4 cos t  − 2     3 
Phương trình dao động tổng hợp (bằng phương pháp cộng các hàm lượng giác):        x = x + x = 4 cos t  + + 4cos t  − 1 2      6   3  6      6 2 x = 2.4 cos .cos t  −    2 3 4  12  6     x = 4 2 cos t  −  (cm) −  12  3 Tại thời điểm ban đầu li độ tổng hợp A1 x = x
+ x = 2 3 + 2  5, 46cm . Pha ban đầu của dao động 0 01 02 2 2 3  tổng hợp −
thuộc góc phần tư thứ IV nên vật đang chuyền A 12
động theo chiều dương => Chọn B A2
Câu 61. Một vật dao động điều hoà là tổng hợp của hai dao động cùng phương cùng tần số cùng, đồ thị li
độ thời gian của hai dao động thành phần như hình vẽ.. Tổng tốc độ của hai dao động có giá trị lớn nhất là
A. 280π (cm/s). B. 200π (cm/s)
C. 140π (cm/s). D. 160π (cm/s). Hướng dẫn     x = 8 cos 20 t  − cm  1  ( )
Phương trình tổng tốc độ của các vật:   2  x = 6cos 20 t  +  cm  2 ( )( )     ' v = x = 160 − sin 10 t  − cm / s  1 1  ( )
Phương trình vận tốc của các vật:   2   ' v = x = 120 − sin 200 t  +  cm / s  2 2 ( )( ) Trang 27 ' v = x = 160cos 20 t  cm / s  1 1 ( )  ' v = −x = 120sin 20 t  cm / s  2 2 ( )
Phương trình tổng tốc độ của các vật: v = v + v = 160cos 20 t  + 120sin 20 t  1 2  ( )2 + ( )2 2 2 160 120 cos 20 t  + sin 20 t  = 200(cm / s) 4
Dấu bằng xảy ra khi tan 20 t  =  Chọn B 3
Câu 62. Một vật thực hiện đồng thời hai dao động cùng phương, cùng tần số 4Hz và cùng cùng biên độ 2
cm. Khi qua vị trí động năng của vật bằng 3 lần thế năng vật đạt tốc độ 24π (cm/s). Độ lệch pha giữa hai
dao động thành phần bằng A. π/6. B. π/2. C. π/3. D. 2π/3. Hướng dẫn  1 W = W  t  4 Khi Wđ = 3Wt   3 3 3 W = W  v = A   24 = .8 A   A = 2 3 cm d ( )  4 4 4 Mặt khác: 2 2 2
A = A + A + 2A A cos  −  1 2 1 2 ( 2 1)  2 2
 12 = 2 + 2 + 2.2.2.cos    =  Chọn C 3
Câu 63. Một chất điểm tham gia đồng thời hai dao động điều hòa trên cùng một trục Ox có phương trình:
x1 = 4cos(ωt + π/3) cm, x2 = A2cos(ωt + φ2) cm. Phương trình dao động tổng hợp x = 2cos(ωt + φ) cm.
Biết φ – φ2 = π/2. Cặp giá trị nào của A2 và φ sau đây là đúng?
A. 3/3 cm và 0.
B. 2/3 cm và π/4.
C. 3/3 cm và π/2. D. 2 3 cm và 0. Hướng dẫn 2 2 2 A = +  = −  = + −  −  1 A A2 1 A A A2 A A A 2AA cos  1 2 2 ( 2 ) A  1 2 2 2
A = A + A  A = A − A  A = A + A − 2AA cos  −   1 2 2 1` 2 1 1 ( 1 )    2 16 = 4 + A − 2.4.A cos  A = 2 3 cm  3 2 2 2 ( )  2      A 1
 2 = 4 +16 − 2.2.4cos  −     3     1  cos  − =   = 0    Chọn D A  3  2 2
Câu 64. Hình vẽ bên là đồ thị biễu diễn sự phụ thuộc của li độ x vào thời gian t của hai dao động điều
hòa cùng phương. Dao động của vật là tổng hợp của hai dao x(cm)
động nói trên. Trong 0,20 s đầu tiên kể từ t = 0 s, tốc độ trung + 6
bình của vật bằng A. 40 3 cm/s. B. 40 cm/s. O t ( s ) C. 20 3 cm/s. D. 20 cm/s. − 6 Hướng dẫn 0 , 1 0 , 2 0 , 3 Chọn B
+ Từ đồ thị, ta thấy rằng dao động thành phần ứng với đường liền nét có phương trình 10   x = 4 cos t + cm. 1    3 3  T
+ Thành phần dao động ứng với đường nét đứt. Tại t =
= 0,05 s đồ thị đi qua vị trí x = −A → tại 12 3
t = 0 , thành phần dao động này đi qua vị trí x = − A = 6 − cm → A = 4 3 cm. 2 Trang 28         → 10 5 10 2 x = 4 3 cos t +
cm → x = x + x = 8cos t + cm. 2      3 6  1 2  3 3 
+ Tại t = 0 , vật đi qua vị trí x = −4 cm theo chiều âm. Sau khoảng thời gian t = 0, 2 s ứng với góc quét 0   =  t
 = 120 vật đến vị trí x = −4 cm theo chiều dương. + → 4 4 v = = 40 cm/s tb 0, 2
Câu 65. Một chất điểm dao động điều hòa là tổng hợp của hai dao động cùng phương cùng cùng tần số
với li độ lần lượt là x 2 2 2
1 và x2. Li độ của hai dao động thành phần thỏa mãn điều kiện: 1, 5x + 2x = 18 cm . 1 2 ( )
Tính biên độ dao động tổng hợp của hai dao động trên. A. 5cm. B. 2 cm. C. 4 cm. D. 5,4cm. Hướng dẫn  x   x  Từ 1,5x + 2x = 18(cm ) 2 2 2 2 2 1 2  + = 1 1 2      12   3    x ⊥ x   =  1 2 2 2   2
 A = A + A = 12 + 9 = 21 cm Chọn D 1 2 ( ) A = 12 cm ;A = 3 cm  1 ( ) 2 ( )
Câu 66. Một vật tham gia đồng thời 2 dao động diêu hoà cùng phương cùng tần số và vuông pha với
nhau. Nếu chỉ tham gia dao động thứ nhất thì cơ năng dao động là W1. Nếu chỉ tham gia dao động thứ hai
thì cơ năng dao động là W2. Nếu tham gia đồng thời 2 dao động thi cơ năng dao động là
A. 0,5(W1 + W2). B. (W1 + W2). C. (W + W )0,5 2 2 . D. 0,5(W + W 1 2 )0,5 2 2 1 2 Hướng dẫn
Cả hai dao động vuông pha nên biên độ dao động tổng hợp: 2 2 A = A + A 1 2 Cơ năng dao độ 1 1 1 ng: 2 2 2 2 2 2 W = m A = m A +
m A = W + W  Chọn B 1 2 1 2 2 2 2
Câu 67. Một vật thực hiện đồng thời 2 dao động điều hòa cùng phương,
cùng chu kì 2s. Gốc tọa độ trùng với vị trí cân bằng. Đồ thị phụ thuộc thời 2
gian của các li độ được biểu diễn như hình vẽ. Biết t2 – t1 = s. Biên độ dao 3
động tổng hợp gần giá trị nào nhất sau đây? A.2 cm B.3,4 cm C.7,5 cm D.8 cm Hướng dẫn:
Vì T = 2 s ω = π rad/s
Chọn gốc thời gian tại thời điểm t1 → x 𝜋
1 = 6cos(ωt1 + φ1) = 6cosφ1 = 0  φ1 = (vật chuyển động theo chiều âm)  x1 = 6cos(ωt + 𝜋) 2 2 cm 2
Với dao động 2 thì tại t2: x2 = 6cos(ω(t1 + ) + φ2) = 6 hay cos(π(0 + 2) + φ2) = 1 3 3 → φ 2𝜋 2𝜋 2 = - → x2 = 6cos(ωt - ) cm 3 3
Vậy x = x1 + x2 = 3,1cos(πt + 11𝜋) cm → A ≈ 3,4 cm  Chọn B 12
Câu 68. Một vật m = 100 g thực hiện đồng thời hai dao động điều hòa
cùng phương được mô tả như hình vẽ. Lực kéo về cực đại tác dụng lên vật
gần giá trị nào nhất A.1 N B.40 N C.10 N D.4 N Hướng dẫn:
Chu kì dao động T = 200 ms = 0,2 s → ω = 10π rad/s
𝑥1 = 3 cos(𝜔𝑡) 𝑐𝑚 Phương trình dao động: { 𝜋
𝑥2 = 2 cos (𝜔𝑡 − ) 𝑐𝑚 2 Trang 29
→ dao động tổng hợp x = x1 + x2 = √13cos(ωt – 0,588) cm √13
Fmax = k.A = mω2.A = 0,1.(10π)2.
≈ 3,56 N  Chọn D 100
Câu 69. Đồ thị của hai dao động điều hòa cùng tần số có dạng như hình vẽ.
Phương trình nào sau đây là phương trình dao động tổng hợp của chúng: π π π
A. x = 5cos t cm
B. x = cos( t − ) cm 2 2 2 π π
C. x = 5cos( t + π) cm D. x = 5cos( t − π) cm 2 2 Hướng dẫn:
A1 = 3 cm; tại t = 0 thì x = 0 và đang chuyển động theo chiều dương φ1 𝜋 = - 2  𝜋 𝜋 x1 = 3cos( t - ) cm 2 2 𝜋
A2 = 2 cm; tại t = 0 thì x = 0 và đang chuyển động theo chiều âm φ2 = 2  𝜋 𝜋 x2 = 2cos( t + ) cm 2 2 𝜋 𝜋
Vậy x = x1 + x2 = cos( t - ) Chọn B 2 2
Câu 70: Một chất điểm thực hiện đồng thời hai dao động điều hòa
cùng phương cùng chu kì T mà đồ thị x1 và x2 phụ thuộc thời gian
biểu diễn trên hình vẽ. Biết x2 = v1T, tốc độ cực đại của chất điểm là
53,4 cm/s. Giá trị T gần giá trị nào nhất sau đây? A.2,56 s B.2,99 s C.2,75 s D.2,64 s Hướng dẫn: 𝜋
Dễ thấy được hai dao động vuông pha (x2 sớm hơn x1 ) 2  𝐴 𝑣
{ 𝑡ℎ = √𝐴2 + (2𝜋𝐴)2 = 𝐴√1 + 4𝜋2→ A = 𝑣𝑚𝑎𝑥 = 𝑚𝑎𝑥.𝑇 (1) 𝑣 𝜔√1+4𝜋2 2𝜋√1+4𝜋2
𝑚𝑎𝑥 = 𝜔. 𝐴𝑡ℎ = 𝜔𝐴. √1 + 4𝜋2
Áp dụng công thức vị trí gặp nhau x0 ở bài toán trên (trường hợp vuông pha) ta được 𝐴 2𝜋𝐴2 2𝜋 2𝜋 𝑣 |x 1𝐴2 𝑚𝑎𝑥.𝑇 0| = = = . 𝐴 = √ √ √ 𝐴√1+4𝜋2 1+4𝜋2 1+4𝜋2 2𝜋√1+4𝜋2 𝐴2 2 1+𝐴2  |𝑥
T = 0|(1+4𝜋2) ≈ 2,99 s Chọn B 𝑣𝑚𝑎𝑥 Trang 30