
























































































































Preview text:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 MỤC LỤC
PHẦN I – ĐỀ BÀI ............................................................................................................................... 4
GIỚI HẠN DÃY SỐ ........................................................................................................................... 4
A – LÝ THUYẾT VÀ PHƯƠNG PHÁP ............................................................................................. 4
B – BÀI TẬP ....................................................................................................................................... 4
DẠNG 1: TÍNH GIỚI HẠN BẰNG ĐỊNH NGHĨA ........................................................................ 4
DẠNG 2: TÌM GIỚI HẠN CỦA DÃY SỐ DỰA VÀO CÁC ĐỊNH LÝ VÀ CÁC GIỚI HẠN CƠ
BẢN ................................................................................................................................................ 7
GIỚI HẠN HÀM SỐ ......................................................................................................................... 15
A – LÝ THUYẾT TÓM TẮT ............................................................................................................ 15
B – BÀI TẬP ..................................................................................................................................... 15
DẠNG 1: TÍNH GIỚI HẠN DẠNG BẰNG ĐỊNH NGHĨA HOẶC TẠI MỘT ĐIỂM ................... 15 0
DẠNG 2: TÍNH GIỚI HẠN DẠNG VÔ ĐỊNH ........................................................................ 18 0
DẠNG 3: TÍNH GIỚI HẠN DẠNG VÔ ĐỊNH
....................................................................... 23
DẠNG 4: GIỚI HẠN MỘ BÊN VÀ CÁC DẠNG VÔ ĐỊNH KHÁC........................................... 27
DẠNG 5 : GIỚI HẠN LƯỢNG GIÁC ........................................................................................... 29
HÀM SỐ LIÊN TỤC ......................................................................................................................... 32
A – LÝ THUYẾT VÀ PHƯƠNG PHÁP ........................................................................................... 32
B – BÀI TẬP ..................................................................................................................................... 32
DẠNG 1: TÍNH LIÊN TỤC CỦA HÀM SỐ TẠI MỘT ĐIỂM ...................................................... 32
DẠNG 2: TÍNH LIÊN TỤC CỦA HÀM SỐ TRÊN TẬP XÁC ĐỊNH ........................................... 37
DẠNG 3: ÁP DỤNG TÍNH LIÊN TỤC XÉT SỐ NGHIỆM CỦA PHƯƠNG TRÌNH ................... 41
ÔN TẬP CHƯƠNG IV...................................................................................................................... 42
PHẦN II – HƯỚNG DẪN GIẢI ........................................................................................................ 50
GIỚI HẠN DÃY SỐ ......................................................................................................................... 50
A – LÝ THUYẾT VÀ PHƯƠNG PHÁP ........................................................................................... 50
B – BÀI TẬP ..................................................................................................................................... 50
DẠNG 1: TÍNH GIỚI HẠN BẰNG ĐỊNH NGHĨA ...................................................................... 50
DẠNG 2: TÌM GIỚI HẠN CỦA DÃY SỐ DỰA VÀO CÁC ĐỊNH LÝ VÀ CÁC GIỚI HẠN CƠ
BẢN .............................................................................................................................................. 55
GIỚI HẠN HÀM SỐ ......................................................................................................................... 78
A – LÝ THUYẾT TÓM TẮT ............................................................................................................ 78
B – BÀI TẬP ..................................................................................................................................... 78
DẠNG 1: TÍNH GIỚI HẠN DẠNG BẰNG ĐỊNH NGHĨA HOẶC TẠI MỘT ĐIỂM ................... 78
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 0
DẠNG 2: TÍNH GIỚI HẠN DẠNG VÔ ĐỊNH ........................................................................ 85 0
DẠNG 3: TÍNH GIỚI HẠN DẠNG VÔ ĐỊNH
....................................................................... 95
DẠNG 4: GIỚI HẠN MỘ BÊN VÀ CÁC DẠNG VÔ ĐỊNH KHÁC ......................................... 106
DẠNG 5 : GIỚI HẠN LƯỢNG GIÁC ......................................................................................... 110
HÀM SỐ LIÊN TỤC ....................................................................................................................... 118
A – LÝ THUYẾT VÀ PHƯƠNG PHÁP .......................................................................................... 118
B – BÀI TẬP ................................................................................................................................... 118
DẠNG 1: TÍNH LIÊN TỤC CỦA HÀM SỐ TẠI MỘT ĐIỂM .................................................... 118
DẠNG 2: TÍNH LIÊN TỤC CỦA HÀM SỐ TRÊN TẬP XÁC ĐỊNH ......................................... 126
DẠNG 3: ÁP DỤNG TÍNH LIÊN TỤC XÉT SỐ NGHIỆM CỦA PHƯƠNG TRÌNH ................. 135
ĐÁP ÁN ÔN TẬP CHƯƠNG IV ..................................................................................................... 136
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
PHẦN I – ĐỀ BÀI GIỚI HẠN DÃY SỐ
A – LÝ THUYẾT VÀ PHƯƠNG PHÁP
GIỚI HẠN HỮU HẠN GIỚI HẠN VÔ CỰC
1. Giới hạn đặc biệt:
1. Giới hạn đặc biệt: 1 1 k lim lim n lim n (k ) 0 ; lim 0 (k ) n n k n n lim n
q (q 1) lim n
q 0 ( q 1) ; lim C C 2. Định lí: n n 2. Định lí : 1 a) Nếu lim u lim 0 n thì a) Nếu lim u u n = a, lim vn = b thì n lim (un + vn) = a + b u lim (u b) Nếu lim u = 0 n – vn) = a – b
n = a, lim vn = thì lim n v lim (u n n.vn) = a.b u a
c) Nếu lim un = a 0, lim vn = 0 lim n (nếu b 0) u v b neáu . a v 0 n n thì lim n = v neáu . a v 0 b) Nếu u n n n 0, n và lim un= a
d) Nếu lim un = +, lim vn = a
thì a 0 và lim u a n neáu a 0 thì lim(u c) Nếu u v n.vn) = n n ,n và lim vn = 0 neáu a 0 thì lim un = 0 d) Nếu lim u
* Khi tính giới hạn có một trong các dạng vô n = a thì lim u a n 0
3. Tổng của cấp số nhân lùi vô hạn định: ,
, – , 0. thì phải tìm cách khử 0 u S = u dạng vô định. 1 + u1q + u1q2 + … = 1 q 1 1 q B – BÀI TẬP
DẠNG 1: TÍNH GIỚI HẠN BẰNG ĐỊNH NGHĨA Phương pháp:
Để chứng minh lim u 0 ta chứng minh với mọi số a 0 nhỏ tùy ý luôn tồn tại một số n sao n a
cho u a n n . n a
Để chứng minh limu l ta chứng minh lim(u l) 0 . n n
Để chứng minh lim u ta chứng minh với mọi số M 0 lớn tùy ý, luôn tồn tại số tự nhiên n
n sao cho u M n n . M n M
Để chứng minh lim u ta chứng minh lim(u ) . n n
Một dãy số nếu có giới hạn thì giới hạn đó là duy nhất.
Câu 1. Chọn mệnh đề đúng trong các mệnh đề sau:
A. Nếu lim u , thì lim u .
B. Nếu lim u , thì lim u . n n n n
C. Nếu lim u 0 , thì lim u 0 .
D. Nếu lim u a
, thì lim u a . n n n n
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1
Câu 2. Giá trị của lim bằng: n 1 A. 0 B. 1 C. 2 D. 3 1
Câu 3. Giá trị của lim (k * ) bằng: k n A. 0 B. 2 C. 4 D. 5 2 sin n
Câu 4. Giá trị của lim bằng: n 2 A. 0 B. 3 C. 5 D. 8
Câu 5. Giá trị của lim(2n 1) bằng: A. B. C. 0 D. 1 2 1 n
Câu 6. Giá trị của lim bằng: n A. B. C. 0 D. 1 2
Câu 7. Giá trị của lim bằng: n 1 A. B. C. 0 D. 1 cos n sin n
Câu 8. Giá trị của lim bằng: 2 n 1 A. B. C. 0 D. 1 n 1
Câu 9. Giá trị của lim bằng: n 2 A. B. C. 0 D. 1 3 3n n
Câu 10. Giá trị của lim bằng: 2 n A. B. C. 0 D. 1 2 n
Câu 11. Giá trị của lim bằng: n 1 A. B. C. 0 D. 1 2n 1
Câu 12. Giá trị của A lim bằng: n 2 A. B. C. 2 D. 1 2n 3
Câu 13. Giá trị của B lim bằng: 2 n 1 A. B. C. 0 D. 1 2 n 1
Câu 14. Giá trị của C lim bằng: n 1 A. B. C. 0 D. 1 n 2 n
Câu 15. Giá trị của A lim bằng: 2n 1 A. B. C. D. 1 2 2
n sin n 3n
Câu 16. Giá trị của B lim bằng: 2 n A. B. C. 3 D. 1
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1
Câu 17. Giá trị của C lim bằng: 2 n 2 n 7 A. B. C. 0 D. 1 4n 1
Câu 18. Giá trị của D lim bằng: 2 n 3n 2 A. B. C. 0 D. 4 n a
Câu 19. Giá trị của lim 0 bằng: n! A. B. C. 0 D. 1
Câu 20. Giá trị của lim n a với a 0 bằng: A. B. C. 0 D. 1
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
DẠNG 2: TÌM GIỚI HẠN CỦA DÃY SỐ DỰA VÀO CÁC ĐỊNH LÝ VÀ CÁC GIỚI HẠN CƠ BẢN Phương pháp:
Sử dụng các định lí về giới hạn, biến đổi đưa về các giới hạn cơ bản. f (n) Khi tìm lim
ta thường chia cả tử và mẫu cho k
n , trong đó k là bậc lớn nhất của tử và g(n) mẫu. Khi tìm lim k ( ) m f n
g(n) trong đó lim f (n) lim g(n) ta thường tách và sử dụng
phương pháp nhân lượng liên hơn.
+ Dùng các hằng đẳng thức:
a b a b a ; b 3 3
a b 3 2 3 3 2
a ab b a b
Dùng định lí kẹp: Nếu u v n
n ,n và lim vn = 0 thì lim un = 0
Khi tính các giới hạn dạng phân thức, ta chú ý một số trường hợp sau đây:
Nếu bậc của tử nhỏ hơn bậc của mẫu thì kết quả của giới hạn đó bằng 0.
Nếu bậc của từ bằng bậc của mẫu thì kết quả của giới hạn đó bằng tỉ số các hệ số của luỹ thừa
cao nhất của tử và của mẫu.
Nếu bậc của tử lớn hơn bậc của mẫu thì kết quả của giới hạn đó là + nếu hệ số cao nhất của tử
và mẫu cùng dấu và kết quả là – nếu hệ số cao nhất của tử và mẫu trái dấu. n u 1
Câu 1. Cho dãy số u với u và n 1
. Chọn giá trị đúng của lim u trong các số sau: n n 4n n u 2 n 1 1 A. . B. . C. 0 . D. 1. 4 2 n cos 2n
Câu 2. Kết quả đúng của lim 5 là: 2 n 1 1 A. 4. B. 5. C. –4. D. . 4 2n 1
Câu 3. Giá trị của. A lim bằng: 1 3n 2 A. B. C. D. 1 3 2 4n 3n 1
Câu 4. Giá trị của. B lim bằng: 2 (3n 1) 4 A. B. C. D. 1 9 2 n 2n 1
Câu 5. Kết quả đúng của lim là 4 3n 2 3 2 1 1 A. . B. . C. . D. . 3 3 2 2 4 3n n
Câu 6. Giới hạn dãy số u với u là: n n 4n 5
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 3 A. . B. . C. . D. 0 . 4 3 n 2n 5
Câu 7. Chọn kết quả đúng của lim : 3 5n 2 A. 5 . B. . C. . D. . 5 2 2n 3n 1
Câu 8. Giá trị của A lim bằng: 2 3n n 2 2 A. B. C. D. 1 3 2 n 2n
Câu 9. Giá trị của B lim bằng: 2 n 3n 1 1 A. B. C. 0 D. 1 3 2n 4 1 n 29 2
Câu 10. Giá trị của C lim bằng: 17 n 1 A. B. C. 16 D. 1 2 3 3
n 1 3n 2
Câu 11. Giá trị của D lim bằng: 4 4
2n n 2 n 3 1 3 A. B. C. D. 1 4 2 1 4 3 3n 1 n
Câu 12. Giá trị của C lim bằng: 4
2n 3n 1 n A. B. C. 0 D. 1 7 3
(n 2) (2n 1)
Câu 13. Giá trị của. F lim bằng: 2 5 (n 2) A. B. C. 8 D. 1 3 n 1
Câu 14. Giá trị của. C lim bằng: 2 n(2n 1) 1 A. B. C. D. 1 4 3 2 n 3n 2
Câu 15. Giá trị của. D lim bằng: 4 3 n 4n 1 A. B. C. 0 D. 1 3 n 2n 1
Câu 16. Giá trị của. E lim bằng: n 2 A. B. C. 0 D. 1 4 4
n 2n 1 2n
Câu 17. Giá trị của. F lim bằng: 3 3
3n n n 3 A. B. C. D. 1 3 3 1
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 2n 2
Câu 18. Cho dãy số u với u n
. Chọn kết quả đúng của lim u là: n 1 n 4 2 n n 1 n A. . B. 0 . C.1 . D. . 10 Câu 19. lim bằng : 4 2 n n 1 A. . B.10 . C. 0 . D. . n 1 4
Câu 20. Tính giới hạn: lim n 1 n 1 A.1. B. 0 . C. 1 D. . 2
1 3 5 .... 2n 1
Câu 21. Tính giới hạn: lim 2 3n 4 1 2 A. 0 . B. . C. . D.1. 3 3 2 n 1 1
Câu 22. Chọn kết quả đúng của lim 3 . 2 3 n 2n 1 A. 4 . B. 3 . C. 2 . D. . 2 k
a n ... a n a
Câu 23. Giá trị của k 1 0 D lim
(Trong đó k, p là các số nguyên dương; a b 0 ). p
b n ... b n b k p p 1 0 bằng: A. B. C. Đáp án khác D. 1 n2 2 5
Câu 24. Kết quả đúng của lim là: 3n 2.5n 5 1 5 25 A. . B. . C. . D. . 2 50 2 2 n n 1 3 4.2 3 Câu 25. lim bằng: 3.2n 4n A. . B. . C. 0 . D. 1. 3.2n 3n
Câu 26. Giá trị của C lim bằng: n 1 n 1 2 3 1 A. B. C. D. 1 3
Câu 27. Giá trị đúng của lim 3n 5n là: A. . B. . C. 2 . D. 2 . 3.2n 3n
Câu 28. Giá trị của. K lim bằng: n 1 n 1 2 3 1 A. B. C. 2 D. 1 3 5n 1 Câu 29. lim bằng : 3n 1 A. . B.1 . C. 0 D. .
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 n n 1 4 2 Câu 30. 4 lim bằng : n n2 3 4 1 1 A. 0 . B. . C. . D. . 2 4 3.3n 4n
Câu 31. Giá trị của. C lim bằng: n 1 n 1 3 4 1 A. B. C. 0 D. 1 2 2
1 a a ... n a
Câu 32. Cho các số thực a,b thỏa a 1; b 1. Tìm giới hạn I lim . 2
1 b b ... n b 1 b A. B. C. D. 1 1 a k k 1 a . n a n
... a n a
Câu 33. Tính giới hạn của dãy số k k 1 1 0 A lim với a b 0 . : p p 1 b . n b n
... b n b k p p p 1 1 0 A. B. C. Đáp án khác D. 1 n Câu 34. 2 3 lim n sin 2 n bằng: 5 A. . B. 0 . C. 2 . D. .
Câu 35. Giá trị của. M 2 lim
n 6n n bằng: A. B. C. 3 D. 1
Câu 36. Giá trị của. H 2 lim
n n 1 n bằng: 1 A. B. C. D. 1 2
Câu 37. Giá trị của B 2 lim
2n 1 n bằng: A. B. C. 0 D. 1
Bài 40. Giá trị của K n 2 lim
n 1 n bằng: 1 A. B. C. D. 1 2
Câu 38. Giá trị đúng của 2 2 lim
n 1 3n 2 là: A. . B. . C. 0 . D. 1.
Câu 39. Giá trị của A 2 lim
n 6n n bằng: A. B. C. 3 D. 1
Câu 40. Giá trị của B 3 3 2 lim
n 9n n bằng: A. B. C. 0 D. 3
Câu 41. Giá trị của D 2 3 3 2 lim
n 2n n 2n bằng: 1 A. B. C. D. 1 3
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
Câu 42. Giá trị của. M 3 2 3 lim
1 n 8n 2n bằng: 1 A. B. C. 0 D. 1 12
Câu 43. Giá trị của. N 2 3 3 lim
4n 1 8n n bằng: A. B. C. 0 D. 1
Câu 44. Giá trị của. K 3 3 2 2 lim
n n 1 3 4n n 1 5n bằng: 5 A. B. C. D. 1 12
Câu 45. Giá trị của. N 3 3 2 lim
n 3n 1 n bằng: A. B. C. 0 D. 1
Câu 46. Giá trị đúng của lim n n 1 n 1 là: A. 1. B. 0 . C. 1. D. .
Câu 47. Giá trị của. H n 3 3 2 lim
8n n 4n 3 bằng: 2 A. B. C. D. 1 3
Câu 48. Giá trị của A 2 lim
n 2n 2 n bằng: A. B. C. 2 D. 1 Câu 49. 5 5 2
lim 200 3n 2n bằng : A. 0 . B.1. C. . D. . 3
2n sin 2n 1
Câu 50. Giá trị của. A lim bằng: 3 n 1 A. B. C. 2 D. 1 n n!
Câu 51. Giá trị của. B lim bằng: 3 n 2n A. B. C. 0 D. 1 n 1
Câu 52. Giá trị của. D lim bằng: 2 2 2
n ( 3n 2 3n 1) 2 A. B. C. D. 1 3
Câu 53. Giá trị của. 2
E lim( n n 1 2n) bằng: A. B. C. 0 D. 1
Câu 54. Giá trị của. F lim n 1 n bằng: A. B. C. 0 D. 1 p
Câu 55. Giá trị của. k 2 2
H lim( n 1 n 1) bằng: A. B. C. Đáp án khác D. 1 1 1 1
Câu 56. Tính giới hạn của dãy số u ... : n 2 1 2 3 2 2 3
(n 1) n n n 1 A. B. C. 0 D. 1
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 3 3 3
(n 1) 1 2 ... n
Câu 57. Tính giới hạn của dãy số u : n 3 3n n 2 1 A. B. C. D. 1 9 1 1 1 n(n 1)
Câu 58. Tính giới hạn của dãy số u (1 )(1 )...(1
) trong đó T . : n T T T n 2 1 2 n 1 A. B. C. D. 1 3 3 3 3 2 1 3 1 n 1
Câu 59. Tính giới hạn của dãy số u . .... . : n 3 3 3 2 1 3 1 n 1 2 A. B. C. D. 1 3 n 2k 1
Câu 60. Tính giới hạn của dãy số u . : n k k 2 1 A. B. C. 3 D. 1
Câu 61. Tính giới hạn của dãy số 2
u q 2q ... n
nq với q 1 . : n q q A. B. C. D. q2 1 q2 1 n n
Câu 62. Tính giới hạn của dãy số u . : n 2 n k k 1 A. B. C. 3 D. 1 3 6 4
n n 1 4 n 2n 1
Câu 63. Tính giới hạn của dãy số B lim . : 2 (2n 3) 3 A. B. C. 3 D. 4
Câu 64. Tính giới hạn của dãy số C 2 lim
4n n 1 2n . : 1 A. B. C. 3 D. 4
Câu 65. Tính giới hạn của dãy số D 2 3 3 2 lim
n n 1 2 n n 1 n . : 1 A. B. C. D. 1 6 1
Câu 66. Cho dãy số (x ) xác định bởi 2 x , x
x x ,n 1 n 1 n 1 2 n n 1 1 1 Đặt S . Tính lim S . n n x 1 x 1 x 1 1 2 n A. B. C. 2 D. 1 1 2 k
Câu 67. Cho dãy (x ) được xác định như sau: x ... k k 2! 3! (k 1)!
Tìm lim u với u n x n x ... n n x . n n 1 2 2011
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 1 A. B. C. 1 D. 1 2012! 2012! u 2011 0 3 u
Câu 68. Cho dãy số (u ) được xác định bởi: 1 . Tìm lim n . n u u n 1 n n 2 un A. B. C. 3 D. 1 x 1 1
Câu 69. Cho dãy x 0 xác định như sau: f (x) . Tìm 0; . x A. B. C. 2010 D. 1 .
n 1 3 5 ... (2n 1)
Câu 70. Tìm lim u biết u n n 2 2n 1 1 A. B. C. D. 1 2 3
x 2 2x 1 khi x 1
Câu 71. Tìm lim u biết f (x) n x 1 3 m 2 khi x 1 3 6 A. B. C. 2 D. 2 x 1 1 khi x 0
Câu 72. Tìm lim u biết f (x) n x 2
2x 3m 1 khi x 0 A. B. C. 2 D. 1 2x 4 3 khi x 2
Câu 73. Tìm lim u biết f (x) trong đó x 1 . n x 1 khi x 2 2
x 2mx 3m 2 1 A. B. C. D. 1 3 n 1
Câu 74. Tìm lim u biết u n n 2 k 1 n k A. B. C. 3 D. 1
Câu 75. Tìm lim u biết u 2 2... 2 n n n dau can A. B. C. 2 D. 1
Câu 76. Gọi g(x) 0, x 2 là dãy số xác định bởi . Tìm lim f (x) lim x . 2 4 3 3 x2 x2 4 A. B. C. D. 1 3 2 2 1 1 1 Câu 77. Cho dãy số 2 2 2 2 A x x x x x x x x 3 0
được xác định như sau 1 1 2 1 2 2 1 2 2 4 2
x x . 1 2
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 3 Đặt x . Tìm 3
x 2x 3 3 2x 4 0 . 2 1 A. B. C. D. 1 2 Câu 78. Cho ,
a b , (a,b) 1; n ab 1, ab 2,..
. . Kí hiệu r là số cặp số (u, v) sao cho n r 1
n au bv . Tìm lim n . n n ab 1 A. B. C. D. ab 1 ab 1 u 1 2
Câu 79. Cho dãy số có giới hạn (un) xác định bởi :
. Tìm kết quả đúng của lim u . 1 n u , n 1 n 1 2 un 1 A. 0 . B.1. C. 1. D. 2 1 1 1 1
Câu 80. Tìm giá trị đúng của S 2 1 ... ....... . n 2 4 8 2 1 A. 2 1 . B. 2 . C. 2 2 . D. . 2 1 1 1
Câu 81. Tính giới hạn: lim .... 1.2 2.3 n n 1 3 A. 0 B.1. C. . D. Không có giới 2 hạn. 1 1 1
Câu 82. Tính giới hạn: lim .... 1.3 3.5 n 2n 1 2 A.1. B. 0 . C. . D. 2 . 3 1 1 1
Câu 83. Tính giới hạn: lim .... 1.3 2.4 n n 2 3 2 A. . B.1. C. 0 . D. . 4 3 1 1 1
Câu 84. Tính giới hạn: lim ... . 1.4 2.5 n(n 3) 11 3 A. . B. 2 . C. 1. D. . 18 2 1 1 1
Câu 85. Tính giới hạn: lim 1 1 ... 1 . 2 2 2 2 3 n 1 1 3 A. 1. B. . C. . D. . 2 4 2
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 GIỚI HẠN HÀM SỐ
A – LÝ THUYẾT TÓM TẮT
Giới hạn hữu hạn
Giới hạn vô cực, giới hạn ở vô cực
1. Giới hạn đặc biệt:
1. Giới hạn đặc biệt: lim x x lim c c 0 ;
neáu k chaün xx xx lim k x ; lim k x 0 0 x x neáu k leû (c: hằng số) c 2. Định lí: lim c c ; lim 0 k
a) Nếu lim f (x) L và lim g(x) M x x x xx xx 0 0 1 1 lim ; lim
thì: lim f (x) g(x) L M x 0 x x 0 x xx0 1 1
lim f (x) g(x) L M lim lim xx x x 0 x 0 x 0 lim f (x). (
g x) L.M 2. Định lí: xx0
Nếu lim f (x) L 0 và lim ( g x) thì: f (x) L xx xx 0 0 lim (nếu M 0) xx ( g x) M
neáu L vaø lim (
g x) cuøng daáu 0 xx0
b) Nếu f(x) 0 và lim f (x) L lim f (x) ( g x) xx neáu L vaø lim (
g x) traùi daáu xx 0 0 xx 0 thì L 0 và lim
f (x) L 0 neáu lim ( g x) xx0 xx 0 f (x)
c) Nếu lim f (x) L thì lim f (x) L lim neáu lim (
g x) 0 vaø L. ( g x) 0 xx xx xx ( g x) xx 0 0 0 0
3. Giới hạn một bên: neáu lim (
g x) 0 vaø L. ( g x) 0 xx
lim f (x) L 0 xx0 0
* Khi tính giới hạn có một trong các dạng vô định: ,
lim f (x) lim f (x) L 0 x x x x 0 0
, – , 0. thì phải tìm cách khử dạng vô định. B – BÀI TẬP
DẠNG 1: TÍNH GIỚI HẠN DẠNG BẰNG ĐỊNH NGHĨA HOẶC TẠI MỘT ĐIỂM Phương pháp:
+ Sử dụng định nghĩa chuyển giới hạn của hàm số về giới hạn của dãy số. + Nếu f ( )
x là hàm số cho bởi một công thức thì giá trị giới hạn bằng f (x ) 0 + Nếu f ( )
x cho bởi nhiều công thức, khi đó ta sử dụng điều kiện để hàm số có giới hạn ( Giới hạn
trái bằng giới hạn phải). 3 2 x 2x 1
Câu 1. Chọn kết quả đúng trong các kết quả sau của lim là: 5 x1 2x 1 1 1 A. 2 . B. . C. . D. 2 . 2 2
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 3 4x 1 Câu 2. lim bằng: 2 x 2
3x x 2 11 11 A . . B. . . C. . . D. . 4 4 x 1
Câu 3. Tìm giới hạn hàm số lim bằng định nghĩa. x 1 x 2 A. B. C. 2 D. 1
Câu 4. Tìm giới hạn hàm số lim 3 x 1 bằng định nghĩa. x2 A. B. C. 9 D. 1 x 3 2
Câu 5. Tìm giới hạn hàm số lim bằng định nghĩa. x 1 x 1 1 A. B. C. 2 D. 4 x 3
Câu 6. Tìm giới hạn hàm số lim bằng định nghĩa.
x x 2 A. B. C. 2 D. 1 2 2x x 1
Câu 7. Tìm giới hạn hàm số lim bằng định nghĩa. x x 2 A. B. C. 2 D. 1 3x 2
Câu 8. Tìm giới hạn hàm số lim bằng định nghĩa. x 1 2x 1 A. B. C. 5 D. 1 2 4x 3x
Câu 9. Cho hàm số f (x)
. Chọn kết quả đúng của lim f (x) : 2x 1 3 x 2 x 2 5 5 5 2 A. . B. . C. . D. . 9 3 9 9 x 4 2
Câu 10. Tìm giới hạn hàm số lim bằng định nghĩa. x0 2x 1 A. B. C. 2 D. 1 8 4x 3
Câu 11. Tìm giới hạn hàm số lim bằng định nghĩa. x 1 x 1 A. B. C. 2 D. 1 3x 1
Câu 12. Tìm giới hạn hàm số lim bằng định nghĩa. x 2 x 2 A. B. C. 2 D. 1 2 2x x 3
Câu 13. Tìm giới hạn hàm số lim bằng định nghĩa. x 1 x 1 A. B. 5 C. 2 D. 1 x 1
Câu 14. Tìm giới hạn hàm số lim bằng định nghĩa. x 2 x4 2 A. B. C. 2 D. 1
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 2 3x
Câu 15. Tìm giới hạn hàm số lim bằng định nghĩa. 2
x 2 x 1 3 A. B. C. D. 1 2
Câu 16. Tìm giới hạn hàm số 2
lim x x 1 bằng định nghĩa. x A. B. C. 2 D. 1 2 x 4
Câu 17. Tìm giới hạn hàm số lim bằng định nghĩa. x 2 4 x 1 2 x A. B. C. 0 D. 1 2 x 3x 2
Câu 18. Tìm giới hạn hàm số lim bằng định nghĩa. x 1 x 1 A. B. C. 2 D. 1 2 x x 1
Câu 19. Tìm giới hạn hàm số A lim bằng định nghĩa. x 1 x 1 1 A. B. C. D. 1 2 2 tan x 1
Câu 20. Tìm giới hạn hàm số B lim bằng định nghĩa. x sin x 1 6 4 3 6 A. B. C. D. 1 9
3 x 2 x 1
Câu 21. Tìm giới hạn hàm số C lim bằng định nghĩa. x0 3x 1 A. B. C. 3 2 1 D. 1 3 7x 1 1
Câu 22. Tìm giới hạn hàm số D lim bằng định nghĩa. x 1 x 2 A. B. C. 2 D. 3 x 1
Câu 23. Tìm giới hạn hàm số A lim bằng định nghĩa. 2
x2 x x 4 1 A. B. C. D. 1 6 2 sin 2x 3cos x
Câu 24. Tìm giới hạn hàm số B lim bằng định nghĩa. x tan x 6 3 3 9 A. B. C. D. 1 4 2 2 3
2x x 1 2x 3
Câu 25. Tìm giới hạn hàm số C lim bằng định nghĩa. 2 x 1 3x 2 3 3 9 A. B. C. D. 3 2 5 4 2 3x 1 2
Câu 26. Tìm giới hạn hàm số D lim bằng định nghĩa. 3 x 1 3x 1 2
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 A. B. C. D. 0 6 2
x 3 khi x 2
Câu 27. Cho hàm số f x
. Chọn kết quả đúng của lim f x : x 1 khi x 2 x2 A. 1. B. 0 . C. 1. D. Không tồn tại. 2
x ax 1 khi x 2
Câu 28. Tìm a để hàm số sau có giới hạn khi x 2 f (x) . 2
2x x 1 khi x 2 1 A. B. C. D. 1 2 2
5ax 3x 2a 1 khi x 0
Câu 29. Tìm a để hàm số sau có giới hạn tại x 0 f (x) . 2 1 x
x x 2 khi x 0 2 A. B. C. D. 1 2 2
5ax 3x 2a 1 khi x 0
Câu 30. Tìm a để hàm số. f (x)
có giới hạn tại x 0 2 1 x
x x 2 khi x 0 2 A. B. C. D. 1 2 2
x ax 1 khi x 1
Câu 31. Tìm a để hàm số. f (x)
có giới hạn khi x 1 . 2
2x x 3a khi x 1 1 A. B. C. D. 1 6 0
DẠNG 2: TÍNH GIỚI HẠN DẠNG VÔ ĐỊNH 0 P(x) 1. L = lim
với P(x), Q(x) là các đa thức và P(x0) = Q(x0) = 0 x 0 x Q(x)
Phân tích cả tử và mẫu thành nhân tử và rút gọn. Chú ý:
+ Nếu tam thức bậc hai 2
ax bx+c có hai nghiệm x , x thì ta luôn có sự phân tích 1 2 2
ax bx c a( x x )( x x ) . 1 2 + n n n 1 n2 n2 n 1 a b (a ) b (a a b ... ab b ) P(x) 2. L = lim
với P(x0) = Q(x0) = 0 và P(x), Q(x) là các biểu thức chứa căn cùng bậc x 0 x Q(x)
Sử dụng các hằng đẳng thức để nhân lượng liên hợp ở tử và mẫu.
Các lượng liên hợp:
+ ( a b )( a b ) a b 3 3 3 2 3 3 2 a b a + ( )(
ab b ) a b + n n n n 1 n n2 n n 1 ( a b )( a a b ... b ) a b P(x) 3. L = lim
với P(x0) = Q(x0) = 0 và P(x) là biêu thức chứa căn không đồng bậc x 0 x Q(x)
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
Giả sử: P(x) = m ( ) n ( ) m ( ) n u x v x vôùi u x
v(x ) a . 0 0
Ta phân tích P(x) = m ( ) n u x a a
v(x) .
Trong nhiều trường hợp việc phân tích như trên không đi đến kết quả ta phải phân tích như
sau: n ( ) m ( ) ( n ( ) ( )) (m u x v x u x m x v(x) (
m x)) , trong đó m(x) c . 2 x 2x 1
Câu 1. Chọn kết quả đúng trong các kết quả sau của lim là: 3 x1 2x 2 1 A. . B. 0 . C. . D. . 2 3 2 x 3x 2
Câu 2. Tìm giới hạn A lim : 2 x 1 x 4x 3 3 A. B. C. D. 1 2 4 2 x 5x 4
Câu 3. Tìm giới hạn B lim : 3 x2 x 8 1 A. B. C. D. 1 6 3 4
(1 3x) (1 4x)
Câu 4. Tìm giới hạn C lim : x0 x 1 A. B. C. D. 25 6 x 3
Câu 5. Cho hàm số f x
. Giá trị đúng của lim f x là: 2 x 9 x 3 A. . . B. 0. . C. 6.. D. .
(1 x)(1 2x)(1 3x) 1
Câu 6. Tìm giới hạn D lim : x0 x 1 A. B. C. D. 6 6 n x 1
Câu 7. Tìm giới hạn A lim (m, n * ) : 0 m x x 1 n A. B. C.
D. m n m n 1 ax 1
Câu 8. Tìm giới hạn B lim (n *
, a 0) : x0 x a n A. B. C. D. 1 n a n 1 ax 1
Câu 8. Tìm giới hạn A lim
với ab 0 : 0 m x 1 bx 1 am am A. B. C. D. 1 bn bn 3 4
1 x 1 x 1 x 1
Câu 9. Tìm giới hạn B lim
với 0 . : x0 x
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 19
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 A. B. C. B D. B 4 3 2 4 3 2 2 2x 5x 2
Câu 10. Tìm giới hạn A lim : 3 x2 x 3x 2 1 A. B. C. D. 1 3 4 x 3x 2
Câu 11. Tìm giới hạn B lim : 3 x 1 x 2x 3 1 A. B. C. D. 1 5 2x 3 x
Câu 12. Tìm giới hạn C lim : 2
x3 x 4x 3 1 A. B. C. D. 1 3 3 x 1 1
Câu 13. Tìm giới hạn D lim : 4 x0 2x 1 1 2 A. B. C. D. 1 3
3 4x 1 x 2
Câu 14. Tìm giới hạn E lim : 4 x7 2x 2 2 8 A. B. C. D. 1 27
(2x 1)(3x 1)(4x 1) 1
Câu 15. Tìm giới hạn F lim : x0 x 9 A. B. C. D. 1 2 3
1 4x 1 6x
Câu 16. Tìm giới hạn M lim : 2 x0 x 1 A. B. C. D. 0 3
m 1 ax n 1 bx
Câu 17. Tìm giới hạn N lim : x0 x a b a b A. B. C. D. m n m n m 1 n ax 1 bx 1
Câu 18. Tìm giới hạn G lim : x0 x a b a b A. B. C. D. m n m n n m
1 mx 1 nx
Câu 19. Tìm giới hạn V lim : 2 x0 x
mn n m
mn n m A. B. C. D. 2 2
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 20
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 x 3
1 x ...1 n x
Câu 20. Tìm giới hạn K lim : x n 1 x 1 1 1 A. B. C. D. 0 n! n n 2
1 x x 2 1 x x
Câu 21. Tìm giới hạn L lim : x0 x A. B. C. 2n D. 0 2 2x 5x 2
Câu 22. Tìm giới hạn A lim : 3 x2 x 8 1 A. B. C. D. 0 4 4 2 x 3x 2
Câu 23. Tìm giới hạn B lim : 3 x 1 x 2x 3 2 A. B. C. D. 0 5 2x 3 3
Câu 24. Tìm giới hạn C lim : 2 x 3 x 4x 3 1 A. B. C. D. 0 6 3 x 1 1
Câu 25. Tìm giới hạn D lim : x0 2x 1 1 1 A. B. C. D. 0 3
n (2x 1)(3x 1)(4x 1) 1
Câu 26. Tìm giới hạn F lim : x0 x 9 A. B. C. D. 0 n 3
1 4x 1 6x
Câu 27. Tìm giới hạn M lim : x0 1 cos 3x 4 A. B. C. D. 0 9
m 1 ax n 1 bx
Câu 28. Tìm giới hạn N lim : x0 1 x 1
2 an bm A. B. C. D. 0 mn n m
1 mx 1 nx
Câu 29. Tìm giới hạn V lim : 3 x0
1 2x 1 3x
2 an bm A. B. C.
D. mn n m mn
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 21
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 x 3
1 x ...1 n x
Câu 30. Tìm giới hạn K lim : x n 1 x 1 1 2 1 A. B. C. D. 0 n! 3
4x 1 2x 1
Câu 31. Tìm giới hạn A lim : x0 x 4 A. B. C. D. 0 3 4x 5 3
Câu 32. Tìm giới hạn B lim : 3 x 1 5x 3 2 4 2 A. B. C. D. 3 5 4 3
2x 3 2 3x
Câu 33. Tìm giới hạn C lim : x1 x 2 1 4 A. B. C. D. 3 3 x x 2
Câu 34. Tìm giới hạn D lim : 3
x2 x 3x 2 4 A. B. C. D. 1 3 3
1 2x 1 3x
Câu 35. Tìm giới hạn A lim : 2 x0 x 1 A. B. C. D. 0 2 3
5 4x 7 6x
Câu 36. Tìm giới hạn B lim : 3 2 x1
x x x 1 4 A. B. C. D. 1 3
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 22
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
DẠNG 3: TÍNH GIỚI HẠN DẠNG VÔ ĐỊNH Phương pháp: P(x) L = lim
trong đó P(x), Q(x) , dạng này ta còn gọi là dạng vô định .
x Q(x)
với P(x), Q(x) là các đa thức hoặc các biểu thức chứa căn.
– Nếu P(x), Q(x) là các đa thức thì chia cả tử và mẫu cho luỹ thừa cao nhất của x.
– Nếu P(x), Q(x) có chứa căn thì có thể chia cả tử và mẫu cho luỹ thừa cao nhất của x hoặc nhân lượng liên hợp.
Tương tự như cách khử dạng vô định ở dãy số. Ta cần tìm cách đưa về các giới hạn: + 2 lim k x ; 2k 1 lim x () . x x ( x) ( x) k + lim
0 (n 0; k 0) . n x x ( x) k
+ lim f (x) () lim 0 (k 0) . x 0 x
x x0 f (x) 5 Câu 1. lim bằng: x 3x 2 5 A. 0 . B. 1. C. . D. . 3 4 x 7
Câu 2. Giá trị đúng của lim là: 4
x x 1 A. 1 . B. 1. . C. 7. . D. . 2 2x 3x 2
Câu 3. Tìm giới hạn C lim : x 2 5x x 1 2 3 A. B. C. D. 0 6 2 2x 1 Câu 4. lim bằng: 2 x 3 x 1 1 A. 2 . B. . C. . D. 2 . 3 3 2 x 1
Câu 5. Cho hàm số f (x)
. Chọn kết quả đúng của lim f (x) : 4 2 2x x 3 x 1 2 A. . B. . C. 0 . D. . 2 2 1 3x Câu 6. lim bằng: x 2 2x 3 3 2 2 3 2 2 A. . B. . C. . D. . 2 2 2 2 3 4 6 1 x x
Câu 7. Tìm giới hạn D lim : x 3 4 1 x x
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 23
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 4 A. B. C. D. 1 3 x 1
Câu 8. Cho hàm số f x x 2
. Chọn kết quả đúng của lim f x : 4 2 x x 1 x 1 A. 0 . B. . C. 1. D. Không tồn tại. 2 2 x x 3 Câu 9. lim bằng: x 1 2 x 1 1 A. 3 . B. . C. 1. D. . 2 4 x 8x
Câu 10. Chọn kết quả đúng trong các kết quả sau của lim là: 3 2
x x 2x x 2 21 21 24 24 A. . B. . C. . D. . 5 5 5 5
Câu 12. Tìm giới hạn 2
E lim ( x x 1 x) : x 1 A. B. C. D. 0 2
Câu 13. Tìm giới hạn 2
F lim x( 4x 1 x) : x 4 A. B. C. D. 0 3
Câu 14. Chọn kết quả đúng trong các kết quả sau của 5 3
lim 4x 3x x 1 là: x A. . B. 0 . C. 4 . D. .
Câu 15. Chọn kết quả đúng trong các kết quả sau của 4 3 2 lim
x x x x là: x A. . B. 0 . C. 1. D. .
Câu 16. Tìm giới hạn B x x x : x 2 lim 1 4 A. B. C. D. 0 3
Câu 17. Tìm giới hạn 2 2
M lim ( x 3x 1 x x 1) : x 4 A. B. C. D. Đáp án khác 3
Câu 18. Tìm giới hạn N : x 3 3 lim 8x 2x 2x 4 A. B. C. D. 0 3
Câu 19. Tìm giới hạn H lim x x x : x 4 4 2 16 3 1 4 2 4 A. B. C. D. 0 3
Câu 20. Tìm giới hạn K x x x x : x 2 2 lim 1 2
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 24
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 A. B. C. D. 0 2 2 3x 5x 1
Câu 21. Tìm giới hạn A lim : 2
x 2x x 1 3 A. B. C. D. 0 2 n
a x ... a x a
Câu 22. Tìm giới hạn 0 n 1 B lim
n (a b 0) : m 0 0
x b x ... b x b 0 m 1 m 4 A. B. C. D. Đáp án khác 3 3 3 2
3x 1 2x x 1
Câu 23. Tìm giới hạn A lim : x 4 4 4x 2 3 3 2 A. B. C. D. 0 2 2
x x 1 2x 1
Câu 24. Tìm giới hạn B lim : x 3 3 2x 2 1 4 A. B. C. D. 0 3 3 4
(2x 1) (x 2)
Câu 25.Tìm giới hạn A lim : 7 x (3 2x) 1 A. B. C. D. 0 16 2
4x 3x 4 2x
Câu 26. Tìm giới hạn B lim : x 2
x x 1 x A. B. C. 2 D. 0 2 2x 3x 2
Câu 27. Tìm giới hạn C lim : x 2 5x x 1 2 3 A. B. C. D. 0 4 3 4 6 1 x x
Câu 28. Tìm giới hạn D lim : x 3 4 1 x x 4 A. B. C. D. 1 3
Câu 29. Tìm giới hạn A x x x x : x 2 3 3 lim 1 2 1 4 A. B. C. D. 0 3
Câu 30.Tìm giới hạn C x x x : x 2 lim 4 1 2 1 A. B. C. D. 0 2
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 25
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
Câu 31. Tìm giới hạn D x x x x : x 3 3 2 2 lim 1 1 1 A. B. C. D. 0 6
Câu 32. Tìm giới hạn A 2 2 lim
x x 1 2 x x x : x 3 A. B. C. D. 0 2
Câu 33.Tìm giới hạn 2 2
B lim x( x 2x 2 x x x) : x 1 A. B. C. D. 0 4 n
a x ... a x a
Câu 34. Tìm giới hạn 0 n 1 A lim
n , (a b 0) : m 0 0
x b x ... b x b 0 m 1 m 4 A. B. C. D. Đáp án khác 3 2 3 3
4x x 8x x 1
Câu 35. Tìm giới hạn B lim : x 4 4 x 3 4 A. B. C. D. 4 3 2 3 3
4x 2 x 1
Câu 36. Tìm giới hạn C lim : x 2 x 1 x 3 A. B. C. D. 0 2 2
x x 1 2x 1
Câu 37. Tìm giới hạn D lim : x 3 3
2x x 1 x 4 A. B. C. D. 0 3 2
Câu 38. Chọn kết quả đúng trong các kết quả sau của 2 lim x cos là: x0 nx A. Không tồn tại. B. 0 . C. 1. D. .
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 26
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
DẠNG 4: GIỚI HẠN MỘ BÊN VÀ CÁC DẠNG VÔ ĐỊNH KHÁC Phương pháp:
1. Giới hạn một bên : Áp dụng định lý giới hạn của một tích và một thương..
2. Dạng – : Giới hạn này thường có chứa căn
Ta thường sử dụng phương pháp nhân lượng liên hợp của tử và mẫu, Sau đó tìm cách biến đổi đưa về dạng . 3. Dạng 0.:
Ta cũng thường sử dụng các phương pháp như các dạng ở trên. 1 2
Câu 1. Chọn kết quả đúng của lim : 2 3 x0 x x A. . B. 0 . C. . D. Không tồn tại. 3 2 x x Câu 2. lim bằng: x 1 x 1 1 x A. 1. B. 0 . C. 1. D. . 2 x x 1 Câu 3. lim bằng: 2 x 1 x 1 A. –. B. –1. C. 1. D. +. x 3
Câu 4. Giá tri đúng của lim x 3 x 3 A. Không tồn tại. B. 0 . C. 1. D. .
Câu 5. Tìm giới hạn A 2 lim
x x 1 x : x 1 A. B. C. D. 0 2
Câu 6. Tìm giới hạn B x x x : x 2 lim 2 4 1 1 A. B. C. D. 0 4 1 1
Câu 7. Cho hàm số f (x)
. Chọn kết quả đúng của lim f 3 x : x 1 x 1 x 1 2 2 A. . B. . C. . D. . 3 3
Câu 8. Tìm giới hạn C lim [ n (x a )(x a )...(x a ) x] : 1 2 n x
a a ... a
a a ... a A. B. C. 1 2 n D. 1 2 n n 2n
Câu 9. Tìm giới hạn 2
A lim ( x x 1 x) : x 1 A. B. C. D. 0 2
Câu 10. Tìm giới hạn 2
B lim x( 4x 1 x) : x 1 A. B. C. D. 0 4
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 27
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
Câu 11. Tìm giới hạn 2 2
C lim ( x x 1 x x 1) : x 1 A. B. C. D. Đáp án khác 4
Câu 12. Tìm giới hạn 3 3
D lim ( 8x 2x 2x) : x 1 A. B. C. D. 0 4
Câu 13. Tìm giới hạn 4 4 2
E lim ( 16x 3x 1 4x 2) : x 1 A. B. C. D. 0 4
Câu 14. Tìm giới hạn 3 3
F lim (x 1 x ) : x 1 A. B. C. D. 0 4
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 28
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
DẠNG 5 : GIỚI HẠN LƯỢNG GIÁC Phương pháp:
Ta sử dụng các công thức lượng giác biến đổi về các dạng sau: sin x x tan x x lim lim 1, từ đây suy ra lim lim 1. x0 x0 x sin x x0 x0 x tan x sin u(x) tan u(x)
Nếu lim u(x) 0 lim 1 và lim 1. x 0 x x 0 x u(x) x 0 x u(x) 1 cos ax
Câu 1. Tìm giới hạn A lim : 2 x0 x a A. B. C. D. 0 2
1 sin mx cos mx
Câu 2. Tìm giới hạn A lim :
x0 1 sin nx cos nx m A. B. C. D. 0 n 1 cos . x cos 2 . x cos 3x
Câu 3. Tìm giới hạn B lim : 2 x0 x A. B. C. 3 D. 0 1 cos 2x
Câu 4.Tìm giới hạn A lim : x0 3x 2 sin 2 A. B. C. 1 D. 0
cos 2x cos 3x
Câu 5. Tìm giới hạn B lim :
x0 x(sin 3x sin 4x) 5 A. B. C. D. 0 2 2 tan 2x
Câu 6. Tìm giới hạn C lim : 3
x0 1 cos 2x A. B. C. 6 D. 0 2 x
Câu 7. Tìm giới hạn D lim : x0
1 x sin 3x cos 2x 7 A. B. C. D. 0 2 sin( m x )
Câu 8.Tìm giới hạn A lim . : 1 sin( n x x ) n A. B. C. D. 0 m
Câu 9. Tìm giới hạn B lim( x) tan x : x 2 2 5 A. B. C. D. 1 2
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 29
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1
Câu 10. Tìm giới hạn C lim x sin ( 0) : x0 x 5 A. B. C. D. 0 2
Câu 11.Tìm giới hạn D lim (sin x 1 sin x ) : x 5 A. B. C. D. 0 2
cos 3x cos 4x
Câu 12. Tìm giới hạn A lim :
x0 cos 5x cos 6 x 7 A. B. C. D. 0 11 3 1 1 2 sin 2 x
Câu 13. Tìm giới hạn B lim : x0 sin 3x 4 A. B. C. D. 0 9 2 sin 2x
Câu 14.Tìm giới hạn C lim : 3 4 x0 cos x cos x A. B. C. 9 6 D. 0 4 sin 2x
Câu 15.Tìm giới hạn D lim : 4 x0 sin 3x 16 A. B. C. D. 0 81 1 sin( cos x)
Câu 16.Tìm giới hạn 2 E lim : x0 sin(tan x) 5 A. B. C. D. 0 2
3sin x 2 cos x
Câu 17. Tìm giới hạn F lim : x x 1 x 5 A. B. C. D. 0 2
m cos ax m cos bx
Câu 18. Tìm giới hạn H lim : 2 x0 sin x b a A. B. C. D. 0 2n 2m 1 n cos ax
Câu 19.Tìm giới hạn M lim : 2 x0 x a A. B. C. D. 0 2n
cos 3x cos 4x
Câu 20.Tìm giới hạn A lim :
x0 cos 5x cos 6 x 7 A. B. C. D. 0 11
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 30
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 3 1 1 2 sin 2 x
Câu 21.Tìm giới hạn B lim : x0 sin 3x 4 A. B. C. D. 0 9 2 sin 2x
Câu 22. Tìm giới hạn C lim : 3 4 x0 cos x cos x A. B. C. 9 6 D. 0 4 sin 2x
Câu 23. Tìm giới hạn D lim : 4 x0 sin 3x 16 A. B. C. D. 0 81 1 sin( cos x)
Câu 24. Tìm giới hạn 2 E lim : x0 sin(tan x) A. B. C. 1 D. 0
3sin x 2 cos x
Câu 25.Tìm giới hạn F lim : x x 1 x 5 A. B. C. D. 0 2
m cos ax m cos bx
Câu 26. Tìm giới hạn H lim : 2 x0 sin x b a A. B. C. D. 0 2n 2m
3 1 3x 1 2x
Câu 27. Tìm giới hạn M lim : x0 1 cos 2x 1 A. B. C. D. 0 4 2
3x 5sin 2x cos x Câu 28. lim bằng: 2 x x 2 A. . B. 0 . C. 3 . D. .
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 31
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 HÀM SỐ LIÊN TỤC
A – LÝ THUYẾT VÀ PHƯƠNG PHÁP
1. Hàm số liên tục tại một điểm: y = f(x) liên tục tại x
lim f (x) f (x ) 0 0 x 0 x
Để xét tính liên tục của hàm số y = f(x) tại điểm x0 ta thực hiện các bước: B1: Tính f(x0).
B2: Tính lim f ( x) (trong nhiều trường hợp ta cần tính lim f (x) , lim f (x) ) x 0 x xx xx 0 0
B3: So sánh lim f ( x) với f(x0) và rút ra kết luận. x 0 x
2. Hàm số liên tục trên một khoảng: y = f(x) liên tục tại mọi điểm thuộc khoảng đó.
3. Hàm số liên tục trên một đoạn [a; b]: y = f(x) liên tục trên (a; b) và
lim f (x) f (a), lim f (x) f (b) xa xb
Hàm số đa thức liên tục trên R.
Hàm số phân thức, các hàm số lượng giác liên tục trên từng khoảng xác định của chúng.
Giả sử y = f(x), y = g(x) liên tục tại điểm x0. Khi đó:
Các hàm số y = f(x) + g(x), y = f(x) – g(x), y = f(x).g(x) liên tục tại x0. f ( x) Hàm số y =
liên tục tại x0 nếu g(x0) 0. g( x)
4. Nếu y = f(x) liên tục trên [a; b] và f(a). f(b)< 0 thì tồn tại ít nhất một số c (a; b): f(c) = 0.
Nói cách khác: Nếu y = f(x) liên tục trên [a; b] và f(a). f(b)< 0 thì phương trình f(x) = 0 có ít nhất một nghiệm c (a; b).
Mở rộng: Nếu y = f(x) liên tục trên [a; b]. Đặt m = min f (x) , M = max f (x) . Khi đó với mọi T (m; M) luôn tồn a;b a;b
tại ít nhất một số c (a; b): f(c) = T. B – BÀI TẬP
DẠNG 1: TÍNH LIÊN TỤC CỦA HÀM SỐ TẠI MỘT ĐIỂM Phương pháp:
Tìm giới hạn của hàm số y f (x) khi x x và tính f (x ) 0 0
Nếu tồn tại lim f (x) thì ta so sánh lim f (x) với f (x ) . 0 x 0 x x 0 x Chú ý:
1. Nếu hàm số liên tục tại x thì trước hết hàm số phải xác định tại điểm đó 0
2. lim f (x) l lim f (x) lim f (x) l . x 0 x xx xx 0 0
f (x) khi x x0
3. Hàm số y
liên tục tại x x lim f (x) k . k khi x 0 x x 0 x 0
f (x) khi x x 1 0
4. Hàm số f (x)
liên tục tại điểm x x khi và chỉ khi
f (x) khi x 0 x 2 0
lim f (x) lim f (x) f (x ) . 1 2 1 0 xx x x 0 0 Chú ý:
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 32
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
f (x) khi x x 0 Hàm số y
liên tục tại x x khi và chỉ khi k khi x 0 x0
lim f (x) k . x 0 x
f (x) khi x x 0 Hàm số y
liên tục tại x x khi và chỉ khi
g(x) khi x 0 x0
lim f (x) lim g(x) . xx xx 0 0 2 x 1
Câu 1. Cho hàm số f x và f 2
2 m 2 với x 2 . Giá trị của m để f x liên tục tại x 2 là: x 1 A. 3 . B. 3 . C. 3 . D. 3
Câu 2. Cho hàm số f x 2
x 4 . Chọn câu đúng trong các câu sau:
(I) f x liên tục tại x 2 .
(II) f x gián đoạn tại x 2 .
(III) f x liên tục trên đoạn 2 ; 2.
A. Chỉ I và III .
B. Chỉ I .
C. Chỉ II . D. Chỉ II và III 2 x 1 x 3; x 2
Câu 3. Cho hàm số f x 3
x x 6
. Tìm b để f x liên tục tại x 3 . b 3 x 3; b 2 3 2 3 A. 3 . B. 3 . C. . D. . 3 3 x 1
Câu 4. Cho hàm số f x
. Tìm khẳng định đúng trong các khẳng định sau: x 1
I f x gián đoạn tại x 1.
II f x liên tục tại x 1. 1
III lim f x x 1 2
A. Chỉ I .
B. Chỉ I .
C. Chỉ I và III . D. Chỉ II và III . 2x 8 2 x 2
Câu 5. Cho hàm số f x x 2
. Tìm khẳng định đúng trong các khẳng định sau: 0 x 2
I lim f x 0 . x 2
II f x liên tục tại x 2.
III f x gián đoạn tại x 2.
A. Chỉ I và III .
B. Chỉ I và II .
C. Chỉ I .
D. Chỉ I
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 33
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 2 4 x 2 x 2
Câu 6. Cho hàm số f x
. Tìm khẳng định đúng trong các khẳng định sau:. 1 x 2
I f x không xác định tại x 3.
II f x liên tục tại x 2.
III lim f x 2 x2
A. Chỉ I .
B. Chỉ I và II .
C. Chỉ I và III .
D. Cả I ; II ; III đều sai. sin 5x x 0
Câu 7. Cho hàm số f x 5x
. Tìm a để f x liên tục tại x 0. a 2 x 0 A. 1. B. 1. C. 2 . D. 2. x 2 1 , x 1
Câu 8.Cho hàm số f x 2
x 3 , x 1 . Tìm k để f x gián đoạn tại x 1. 2 k , x 1 A. k 2 . B. k 2 . C. k 2 . D. k 1 . x 2 khi x 4 Câu x 4
9.Cho hàm số f (x)
. Khẳng định nào sau đây đúng nhất 1 khi x 4 4
A. Hàm số liên tục tại x 4
B. Hàm số liên tục tại mọi điểm trên tập xác định nhưng gián đoạn tại x 4
C. Hàm số không liên tục tại x 4
D. Tất cả đều sai 2
x 3x 2 2 khi x 1
Câu 10. Cho hàm số f (x) x 1
. Khẳng định nào sau đây đúng nhất 2 3x x 1 khi x 1
A. Hàm số liên tục tại x 1
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục tại x 1
D. Tất cả đều sai x cos khi x 1
Câu 11. Cho hàm số 3. f x 2
. Khẳng định nào sau đây đúng nhất x 1 khi x 1
A. Hàm số liên tục tại tại x 1 và x 1 .
B. Hàm số liên tục tại x 1 , không liên tục tại điểm x 1 .
C. Hàm số không liên tục tại tại x 1 và x 1 .
D. Tất cả đều sai 2x 1 1
Câu 12. Chọn giá trị f (0) để các hàm số f (x)
liên tục tại điểm x 0 . x(x 1) A. 1 B. 2 C. 3 D. 4
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 34
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 3 2x 8 2
Câu 13. Chọn giá trị f (0) để các hàm số f (x)
liên tục tại điểm x 0 . 3x 4 2 2 1 A. 1 B. 2 C. D. 9 9
x x 2 khi x 1
Câu 14. Cho hàm số f (x) x 1
. Khẳng định nào sau đây đúng nhất 2x 3 khi x 1
A. Hàm số liên tục tại tại tại x 1 0
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục tại tại x 1 . 0
D. Tất cả đều sai 3
x 1 x 1 khi x 0
Câu 15. Cho hàm số 3. f (x) x
. Khẳng định nào sau đây đúng nhất 2 khi x 0
A. Hàm số liên tục tại x 0 0
B. Hàm số liên tục tại mọi điểm như gián đoạn tại x 0 0
C. Hàm số không liên tục tại x 0 0
D. Tất cả đều sai 3 x 1 khi x 1 Câu x 1
16. Cho hàm số f (x)
. Khẳng định nào sau đây đúng nhất 1 khi x 1 3
A. Hàm số liên tục tại x 1
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục tại tại x 1
D. Tất cả đều sai 2
x x 2 2x khi x 2
Câu 17. Cho hàm số f (x) x 2 2 x x 3 khi x 2
. Khẳng định nào sau đây đúng nhất
A. Hàm số liên tục tại x 2 0
B. Hàm số liên tục tại mọi điẻm
C. Hàm số không liên tục tại x 2 0
D. Tất cả đều sai
x 2a khi x 0
Câu 18. Tìm a để các hàm số f x
liên tục tại x 0 2
x x 1 khi x 0 1 1 A. B. C. 0 D. 1 2 4
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 35
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 4x 1 1 khi x 0
Câu 19. Tìm a để các hàm số 2
f (x) ax (2a 1)x
liên tục tại x 0 3 khi x 0 1 1 1 A. B. C. D. 1 2 4 6
3x 1 2 khi x 1 2 x 1
Câu 20.Tìm a để các hàm số f (x)
liên tục tại x 1 2 a(x 2) khi x 1 x 3 1 1 3 A. B. C. D. 1 2 4 4
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 36
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
DẠNG 2: TÍNH LIÊN TỤC CỦA HÀM SỐ TRÊN TẬP XÁC ĐỊNH Phương pháp:
+ Sử dụng các định lí về tính liên tục của hàm đa thức, lương giác, phân thức hữu tỉ …
+ Nếu hàm số cho dưới dạng nhiều công thức thì ta xét tính liên tục trên mỗi khoảng đã chia và tại các điểm chia của các khoảng đó.
Câu 1. Tìm khẳng định đúng trong các khẳng định sau: 1
I f x liên tục trên . 2 x 1 sin x
II f x
có giới hạn khi x 0. x
III f x 2
9 x liên tục trên đoạn 3 ; 3 .
A. Chỉ I và II .
B. Chỉ II và III .
C. Chỉ II .
D. Chỉ III .
Câu 2. Tìm khẳng định đúng trong các khẳng định sau: x 1
I . f x
liên tục với mọi x 1 . x 1
II . f x sin x liên tục trên . x
III . f x
liên tục tại x 1 . x
A. Chỉ I đúng.
B. Chỉ I và II .
C. Chỉ I và III .
D. Chỉ II và III . 2
x 3 , x 3
Câu 3. Cho hàm số f x x 3
. Tìm khẳng định đúng trong các khẳng định sau: 2 3 , x 3
I . f x liên tục tại x 3 .
II . f x gián đoạn tại x 3 .
III . f x liên tục trên .
A. Chỉ I và II .
B. Chỉ II và III .
C. Chỉ I và III .
D. Cả I , II , III đều đúng.
Câu 4. Tìm khẳng định đúng trong các khẳng định sau:
I . f x 5 2
x – x 1 liên tục trên . 1
II . f x
liên tục trên khoảng –1; 1 . 2 x 1
III . f x x 2 liên tục trên đoạn 2; .
A. Chỉ I đúng.
B. Chỉ I và II .
C. Chỉ II và III .
D. Chỉ I và III .
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 37
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
3 9 x , 0 x 9 x
Câu 5. Cho hàm số f x m , x 0
. Tìm m để f x liên tục trên 0; là. 3 , x 9 x 1 1 1 A. . B. . C. . D. 1. 3 2 6 2 x 1
Câu 6. Cho hàm số f (x)
.Khi đó hàm số y f x liên tục trên các khoảng nào sau đây? 2 x 5x 6 A. 3 ; 2 . B. 2 ; . C. ; 3 . D. 2;3 . 2
x 5x 6 khi x 2
Câu 7. Cho hàm số f x 3 2x 16
. Khẳng định nào sau đây đúng nhất. 2 x khi x 2
A. Hàm số liên tục trên
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục trên 2 :
D. Hàm số gián đoạn tại điểm x 2 . 3 x 1 khi x 1 x 1
Câu 8. Cho hàm số f (x)
. Khẳng định nào sau đây đúng nhất. 3
1 x 2 khi x 1 x 2
A. Hàm số liên tục trên
B. Hàm số không liên tục trên
C. Hàm số không liên tục trên 1:
D. Hàm số gián đoạn tại các điểm x 1 . tan x
, x 0 x
k , k
Câu 9. Cho hàm số f x x 2
. Hàm số y f x liên tục trên các khoảng 0 , x 0 nào sau đây? A. 0; . B. ; . C. ; . D. ; . 2 4 4 4 2 2 a x
, x 2, a
Câu 10. Cho hàm số f x
. Giá trị của a để f x liên tục trên là: 2 a 2 x , x 2 A. 1 và 2 . B. 1 và –1 . C. –1 và 2 . D. 1 và –2 . 2 x , x 1 3 2x
Câu 11. Cho hàm số f x
, 0 x 1 . Tìm khẳng định đúng trong các khẳng định sau: 1 x
x sin x , x 0
A. f x liên tục trên .
B. f x liên tục trên \ 0 .
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 38
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
C. f x liên tục trên \ 1 .
D. f x liên tục trên \ 0 ;1 . x 2
Câu 12. Cho hàm số f (x)
. Khẳng định nào sau đây đúng nhất. 2 x x 6
A. Hàm số liên tục trên
B. TXĐ : D \ 3;
2 .Ta có hàm số liên tục tại mọi x D và hàm số gián đoạn tại x 2, x 3
C. Hàm số liên tục tại x 2, x 3
D. Tất cả đều sai Câu 13. Cho hàm số 2
f (x) 3x 1 . Khẳng định nào sau đây đúng nhất.
A. Hàm số liên tục trên 1 1
B. Hàm số liên tục tại mọi điểm x ; ; 3 3 1 1
C. TXĐ : D ; ; 2 2 1 1
D. Hàm số liên tục tại mọi điểm x ; . 3 3
Câu 14. Cho hàm số f (x) 2 sin x 3 tan 2x . Khẳng định nào sau đây đúng nhất.
A. Hàm số liên tục trên
B. Hàm số liên tục tại mọi điểm
C. TXĐ : D \ k , k
D. Hàm số gián đoạn tại các điểm 2 2 x k , k 4 2 2
x 3x 2 khi x 1
Câu 15. Cho hàm số f x x 1
. Khẳng định nào sau đây đúng nhất. a khi x 1
A. Hàm số liên tục trên
B. Hàm số không liên tục trên
C. Hàm số không liên tục trên 1:
D. Hàm số gián đoạn tại các điểm x 1 . 2x 1 1 khi x 0
Câu 16. Cho hàm số f x x
. Khẳng định nào sau đây đúng nhất. 0 khi x 0
A. Hàm số liên tục trên
B. Hàm số không liên tục trên
C. Hàm số không liên tục trên 0;
D. Hàm số gián đoạn tại các điểm x 0 .
2x 1 khi x 0 Câu 17. Cho hàm số 3
f (x) (x 1) khi 0 x 2 . Khẳng định nào sau đây đúng nhất.
x 1 khi x 2
A. Hàm số liên tục trên
B. Hàm số không liên tục trên
C. Hàm số không liên tục trên 2;
D. Hàm số gián đoạn tại các điểm x 2 . 2
2x x 1 khi x 1
Câu 18. Cho hàm số f (x)
. Khẳng định nào sau đây đúng nhất. 3 x 1 khi x 1
A. Hàm số liên tục trên
B. Hàm số không liên tục trên
C. Hàm số không liên tục trên 2;
D. Hàm số gián đoạn tại các điểm x 1 .
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 39
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 sin x khi x 2
Câu 19. Xác định a, b để các hàm số f x liên tục trên
ax b khi x 2 2 2 1 2 a a a a A. B. C. D. b 1 b 2 b 0 b 0 3 2
x 3x 2x khi x(x 2) 0 x(x 2)
Câu 20. Xác định a, b để các hàm số f (x) a khi x 2 liên tục trên b khi x 0 a 10 a 11 a 1 a 12 A. B. C. D. b 1 b 1 b 1 b 1 3
x 2 2x 1 khi x 1
Câu 21. Tìm m để các hàm số f (x) x 1 liên tục trên 3 m 2 khi x 1 4 A. m 1 B. m C. m 2 D. m 0 3 x 1 1 khi x 0
Câu 22. Tìm m để các hàm số f (x) x liên tục trên 2
2x 3m 1 khi x 0 1 A. m 1 B. m C. m 2 D. m 0 6 2x 4 3 khi x 2
Câu 23. Tìm m để các hàm số f (x) x 1 liên tục trên khi x 2 2
x 2mx 3m 2 1 A. m 1 B. m C. m 5 D. m 0 6
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 40
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
DẠNG 3: ÁP DỤNG TÍNH LIÊN TỤC XÉT SỐ NGHIỆM CỦA PHƯƠNG TRÌNH Phương pháp :
Để chứng minh phương trình f (x) 0 có ít nhất một nghiệm trên D, ta chứng minh hàm số y f (x)
liên tục trên D và có hai số a, b D sao cho f (a). f (b) 0 .
Để chứng minh phương trình f (x) 0 có k nghiệm trên D, ta chứng minh hàm số y f (x) liên tục
trên D và tồn tại k khoảng rời nhau (a ; a ) (i=1,2,…,k) nằm trong D sao cho f (a ). f (a ) 0 . i i 1 i i 1
Câu 1. Tìm khẳng định đúng trong các khẳng định sau:
I. f x liên tục trên đoạn ;
a b và f a. f b 0 thì phương trình f x 0 có nghiệm.
II. f x không liên tục trên ;
a b và f a. f b 0 thì phương trình f x 0 vô nghiệm. A. Chỉ I đúng. B. Chỉ II đúng.
C. Cả I và II đúng. D. Cả I và II sai.
Câu 2. Tìm khẳng định đúng trong các khẳng định sau:
I f x liên tục trên đoạn ;
a b và f a. f b 0 thì tồn tại ít nhất một số c ;
a b sao cho f c 0 .
II f x liên tục trên đoạn ; a b và trên ;
b c nhưng không liên tục ; a c
A. Chỉ I .
B. Chỉ II .
C. Cả I và II đúng.
D. Cả I và II sai.
Câu 3. Cho hàm số f x 3 2
x – 1000x 0, 01. Phương trình f x 0 có nghiệm thuộc khoảng nào trong các khoảng sau đây? I. 1 ;0 . II. 0 ;1 . III. 1;2 . A. Chỉ I. B. Chỉ I và II. C. Chỉ II. D. Chỉ III.
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 41
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 ÔN TẬP CHƯƠNG IV
Câu 1. Dãy số nào sau đây có giới hạn khác 0 ? 1 1 n 1 sin n A. . B. . C. . D. . n n n n
Câu 2. Dãy số nào sau đây có giới hạn bằng 0 ? n n n n 4 4 5 1 A. . B. . C. . D. . 3 3 3 3
Câu 3. Dãy số nào sau đây có giới hạn bằng 0 ? n n n n A. 0, 999 . B. 1, 0 1 . C. 1, 0 1 . D. 2 , 00 1 .
Câu 4. Dãy số nào sau đây không có giới hạn? n n n n A. 0,99 . B. 1 . C. 0 , 99 . D. 0 ,89 . n 1 Câu 5.
có giá trị là bao nhiêu? n 3 1 1 A. . B. 1. C. 0 . D. . 3 4 3 4n Câu 6. lim
có giá trị là bao nhiêu? 5n 3 3 4 4 A. . B. . C. . D. . 5 5 5 5 2n 3n Câu 7. lim
có giá trị là bao nhiêu? 3n 2 5 A. 0 . B. 1. C. . D. . 3 3 cos 2n Câu 8. lim 4
có giá trị là bao nhiêu? n A. 0 . B. 2 . C. 2 . D. 4 . 3 3n 2n 1 Câu 9. lim
có giá trị là bao nhiêu? 4 4n 2n 1 3 2 A. 0 . B. . C. . D. . 4 7 4 3n 2n 3 Câu 10. lim
có giá trị là bao nhiêu? 4 4n 2n 1 3 4 A. 0 . B. . C. . D. . 4 7 2 4 2n 3n Câu 11. lim
có giá trị là bao nhiêu? 4 4n 5n 1 3 1 3 A. . B. 0 . C. . D. . 4 2 4 4 3n 2n 4 Câu 12. lim
có giá trị là bao nhiêu? 4 4n 2n 3 3 4 A. 0 . B. . C. . D. . 4 3
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 42
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 Câu 13. 3 2 lim 3
n 2n 5 có giá trị là bao nhiêu? A. 3 . B. 6 . C. . D. . Câu 14. 4 2
lim 2n n 5n có giá trị là bao nhiêu? A. . B. 0 . C. 2 . D. . 2
4n 5 n 4 Câu 15. lim có giá trị là bao nhiêu? 2n 1 A. 0 . B. 1. C. 2 . D. .
Câu 16. lim n 10 n có giá trị là bao nhiêu? A. . B. 10 . C. 10 . D. 0 . 2 3 2n 4n Câu 17. lim
có giá trị là bao nhiêu? 2 4n 5n 3 3 4 A. 0 . B. 1. C. . D. . 4 3
Câu 18. Nếu lim u L thì lim u 9 có giá trị là bao nhiêu? n n A. L 9 . B. L 3 . C. L 9 . D. L 3 . 1
Câu 19. Nếu lim u L thì lim
có giá trị là bao nhiêu? n 3 u 8 n 1 1 1 1 A. . B. . C. . D. . L 8 L 8 3 L 2 3 L 8 n 4 Câu 20. lim
có giá trị là bao nhiêu? n 1 A. 1. B. 2 . C. 4 . D. . 2 1 2n 2n Câu 21. lim
có giá trị là bao nhiêu? 2 5n 5n 3 1 2 2 A. 0 . B. . C. . D. . 5 5 5 4 10 n Câu 22. lim
có giá trị là bao nhiêu? 4 10 2n A. . B. 10000 . C. 5000 . D. 1.
1 2 3 ... n Câu 23. lim có giá trị là bao nhiêu? 2 2n 1 1 A. 0 . B. . C. . D. . 4 2 3 3 n n Câu 24. lim
có giá trị là bao nhiêu? 6n 2 1 1 3 2 A. . B. . C. . D. 0 . 6 4 6 Câu 25. n 2 2 lim
n 1 n 3 có giá trị là bao nhiêu? A. . B. 4 . C. 2 . D. 1 .
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 43
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 n sin 2n Câu 26. lim
có giá trị là bao nhiêu? n 5 2 1 A. . B. . C. 0 . D. 1. 5 5 Câu 27. 3
lim 3n 4n có giá trị là bao nhiêu? A. . B. 4 . C. 3 . D. .
Câu 28. Dãy số nào sau đây có giới hạn bằng 0 ? 2 n 2n 1 2n 2 1 2n 1 2n A. u . B. u . C. u . D. u . n 2 5n n n 5n 5 n 5n 5 n 2 5n 5n
Câu 29. Dãy số nào sau đây có giới hạn bằng ? A. 2 3
u 3n n . B. 2 3
u 3n n . C. 2
u 3n n . D. 2 3
u n 4n . n n n n
Câu 30. Dãy số nào sau đây có giới hạn bằng ? A. 4 3
u n 3n . B. 4 3
u n 3n . C. 2
u 3n n . D. 2 3
u n 4n . n n n n n 1 1 1 1
Câu 31. Tổng của cấp số nhân vô hạn ; ;...;
;... có giá trị là bao nhiêu? 2 4 2n 1 2 1 A. 1. B. . C. . D. . 3 3 3 n 1 1 1
Câu 32. Tổng của cấp số nhân vô hạn ; ;...;
;... có giá trị là bao nhiêu? 2 4 2n 1 1 2 A. . B. . C. . D. 1 . 3 3 3 n 1 1 1 1
Câu 33. Tổng của cấp số nhân vô hạn ; ;...;
;... có giá trị là bao nhiêu? 3 9 3n 1 1 3 3 A. . B. . C. . D. . 4 2 4 2 1 1 1
Câu 34. Tổng của cấp số nhân vô hạn ; ;...;
;... có giá trị là bao nhiêu? 1 2 6 2.3n 1 3 3 3 A. . B. . C. . D. . 3 8 4 2 n 1 1 1 1
Câu 35. Tổng của cấp số nhân vô hạn ; ;...;
;... có giá trị là bao nhiêu? n 1 2 6 2.3 8 3 2 3 A. . B. . C. . D. . 3 4 3 8 n 1 1 1 1
Câu 36. Tổng của cấp số nhân vô hạn 1; ; ;...;
;... có giá trị là bao nhiêu? n 1 2 4 2 2 2 3 A. . B. . C. . D. 2 . 3 3 2
Câu 37. Dãy số nào sau đây có giới hạn là ? 2 n 2n 1 2n 2 1 n 2 n 2 A. u . B. u . C. u . D. u . n 2 5n 5n n 5n 5 n 5n 5 n 3 5n 5n
Câu 38. Dãy số nào sau đâu có giới hạn là ?
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 44
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 2 9n 7n 2007 2008n A. u . B. u . n 2 n n n n 1 C. 2
u 2008n 2007n . D. 2 n 1. n
Câu 39. Trong các giới hạn sau đâu, giới hạn nào bằng 1? 2 2n 3 2 2n 3 2 2n 3 3 2n 3 A. lim . B. lim . C. lim . D. lim . 3 2 n 4 2 2 n 1 3 2 2 n 2n 2 2 n 1
Câu 40. Trong các giới hạn sau đâu, giới hạn nào bằng 0 ? 2 2n 3 2 3 2n 3n 2 4 2n 3n 3 3 2n A. lim . B. lim . C. lim . D. lim . 3 2 n 4 2 2 n 1 3 2 2 n 2n 2 2n 1
Câu 41. Trong các giới hạn sau đâu, giới hạn nào bằng ? 2 2n 3 3 2n 3n 2 4 2n 3n 3 3 2n A. lim . B. lim . C. lim . D. lim . 3 n 4 2 2 n 1 3 2 2 n 2n 2 2n 1 1
Câu 42. Dãy số nào sau đây có giới hạn nào bằng ? 5 2 n 2n 1 2n 2 1 2n 1 2n A. u . B. u . C. u . D. u . n 2 5n 5n n 5n 5 n 5n 5 n 2 5n 5n
Câu 43. lim 3 có giá trị là bao nhiêu? x 1 A. 2 . B. 1. C. 0 . D. 3 . Câu 44. lim 2
x 2x 3 có giá trị là bao nhiêu? x 1 A. 0 . B. 2 . C. 4 . D. 6 . Câu 45. lim 2
x 3x 5 có giá trị là bao nhiêu? x2 A. 1 5 . B. 7 . C. 3 . D. . 4 3x 2x 3 Câu 46. lim
có giá trị là bao nhiêu? 4
x 5x 3x 1 4 3 A. 0. B. . C. . D. . 9 5 4 5 3x 2x Câu 47. lim
có giá trị là bao nhiêu? 4
x 5x 3x 2 2 3 A. . B. . C. . D. . 5 5 2 5 3x x Câu 48. lim
có giá trị là bao nhiêu? 4
x x x 5 A. . B. 3. C. 1 . D. . 4 5 3x 2x Câu 49. lim
có giá trị là bao nhiêu? 4 6
x 5x 3x 1 3 2 A. . B. . C. . D. 0. 5 5 4 5 3x 2x Câu 50. lim
có giá trị là bao nhiêu? 4 6 x 1
5x 3x 1 1 3 2 2 A. . B. . C. . D. . 9 5 5 3
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 45
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 4 5 3x 2x Câu 51. lim
có giá trị là bao nhiêu? 4 2
x1 5x 3x 1 1 5 3 5 A. . B. . C. . D. . 3 9 5 3 4 5 3x x Câu 52. lim
có giá trị là bao nhiêu? 4
x1 x x 5 4 4 2 2 A. . B. . C. . D. . 5 7 5 7 4 3x 2x Câu 53. lim
có giá trị là bao nhiêu? 4 x 2 x 3x 2 13 7 11 13 A. . B. . C. . D. . 6 4 6 6 2 3 x x Câu 54. lim
có giá trị là bao nhiêu? 2
x2 x x 3 4 12 4 A. . B. . C. . D. . 9 5 3 4 5 x 2x Câu 55. lim
có giá trị là bao nhiêu? 4 5 x 1 2x 3x 2 1 1 2 1 A. . B. . C. . D. . 12 7 3 2 3 x x Câu 56. lim
có giá trị là bao nhiêu? 2
x2 x x 1 10 10 6 A. . B. . C. . D. . 7 3 7 Câu 57. 3
lim 4x 2x 3 có giá trị là bao nhiêu? x 1 A. 9. B. 5. C. 1. D. 5 . 4 5 3x 4x 3 Câu 58. lim
có giá trị là bao nhiêu? 5 4 x 9x 5x 1 1 3 2 A. 0. B. . C. . D. . 3 5 3 4 2 x 4x 3 Câu 59. lim
có giá trị là bao nhiêu? 2 x2 7x 9x 1 1 1 35 A. . B. . C. . D. . 15 3 9 4 2
x 4x 3x Câu 60. lim
có giá trị là bao nhiêu? 2 x 1 x 16x 1 1 3 3 A. . B. . C. . D. . 8 8 8 3 1 x Câu 61. lim
có giá trị là bao nhiêu? 2 x 1 3x x
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 46
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 1 A. 0. B. 1. C. . D. . 2 3 x 2 Câu 62. lim
có giá trị là bao nhiêu? x 1 x 1 1 1 A. . B. . C. . D. . 2 2 3 10 x Câu 63. lim
có giá trị là bao nhiêu? 2 x1 3x x 3 11 9 11 A. . B. . C. . D. . 2 4 2 2
Câu 64. lim x 3 x 5 có giá trị là bao nhiêu? x A. 0. B. 3 5. C. . D. . 4 3 2
2x x 2x 1 Câu 65. lim
có giá trị là bao nhiêu? 4 x x 2x A. 2 . B. 1 . C. 1. D. 2. Câu 66. x
có giá trị là bao nhiêu? 2 lim x 5 x x 5 5 A. . B. . C. 5. D. . 2 2 Câu 67. x
có giá trị là bao nhiêu? 2 lim x 1 x x 1 1 A. . B. 0. C. . D. . 2 2 4 y 1 Câu 68. lim
có giá trị là bao nhiêu? y 1 y 1 A. . B. 4. C. 2. D. . 4 4 y a Câu 69. lim
có giá trị là bao nhiêu? ya y a A. . B. 3 2a . C. 3 4a . D. 2 4a . 4 y 1 Câu 70. lim
có giá trị là bao nhiêu? 3 y 1 y 1 3 4 A. . B. 0. C. . D. . 4 3 2 4x 2 x 3 Câu 71. lim
có giá trị là bao nhiêu? x 2x 3 A. 0. B. 1. C. 2. D. . 2 4x 2 x 3 Câu 72. lim có giá trị là bao nhiêu? x 2x 3 1 A. 0. B. 1 . C. . D. . 2
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 47
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 2 x 3x 2 Câu 73. lim
có giá trị là bao nhiêu? x2 2x 4 3 1 1 A. . B. . C. . D. . 2 2 2 2 x 12x 35 Câu 74. lim
có giá trị là bao nhiêu? x2 x 5 A. . B. 5. C. 5 . D. 1 4. 2 x 12x 35 Câu 75. lim
có giá trị là bao nhiêu? x5 5x 25 1 2 2 A. . B. . C. . D. . 5 5 5 2 x 2x 15 Câu 76. lim
có giá trị là bao nhiêu? x 5 2x 10 1 A. 8 . B. 4 . C. . D. . 2 2 x 2x 15 Câu 77. lim
có giá trị là bao nhiêu? x5 2x 10 A. 4 . B. 1 . C. 4. D. . 2 x 9x 20 Câu 78. lim
có giá trị là bao nhiêu? x5 2x 10 5 3 A. . B. 2 . C. . D. . 2 2 4 5 3x 2x Câu 79. lim
có giá trị là bao nhiêu? 4
x 5x 3x 2 2 3 A. . B. . C. . D. . 5 5 3 x 1 Câu 80. lim
có giá trị là bao nhiêu? 2
x1 x x A. 3 . B. 1 . C. 0. D. 1. x Câu 81. lim x 2
có giá trị là bao nhiêu? 3 x x 1 A. . B. 0. C. 1. D. . 2 x 3x 2 Câu 82. lim
có giá trị là bao nhiêu? 3 x 1 x 1 1 1 A. . B. . C. 0. D. 1. 3 3 Câu 83.
lim x 3 x 5 có giá trị là bao nhiêu? x A. . B. 4. C. 0. D. . 2 3x 7x Câu 84. lim
có giá trị là bao nhiêu? x3 2x 3 3 A. . B. 2. C. 6. D. . 2
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 48
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 3 2
6x x x Câu 85. lim
có giá trị là bao nhiêu? x 1 x 2 8 4 8 A. . B. 2 . C. . D. . 3 3 3 2 x 1 Câu 86. lim
có giá trị là bao nhiêu? x 1 x 1 A. . B. 2. C. 1. D. .
x 2 2 x
Câu 87. Cho f x
với x 0 . Phải bổ sung thêm giá trị f 0 bằng bao nhiêu thì x
hàm số liên tục trên . 1 1 A. 0. B. 1. C. . D. . 2 2 2 x
Câu 88. Cho f x
với x 0 . Phải bổ sung thêm giá trị f 0 bằng bao nhiêu thì hàm x 1 1 số liên tục trên . A. 0. B. 1. C. 2. D. 2. 2 x 5x
Câu 89. Cho f x
với x 0 . Phải bổ sung thêm giá trị f 0 bằng bao nhiêu thì hàm số 3x liên tục trên . 5 1 5 A. . B. . C. 0. D. . 3 3 3 2 x
vôùi x 1, x 0 x
Câu 90. Cho hàm số f x 0 vôùi x 0
. Hàm số f x liên tục tại:
x vôùi x 1
A. mọi điểm thuộc .
B. mọi điểm trừ x 0.
C. mọi điểm trừ x 1.
D. mọi điểm trừ x 0 và x 1.
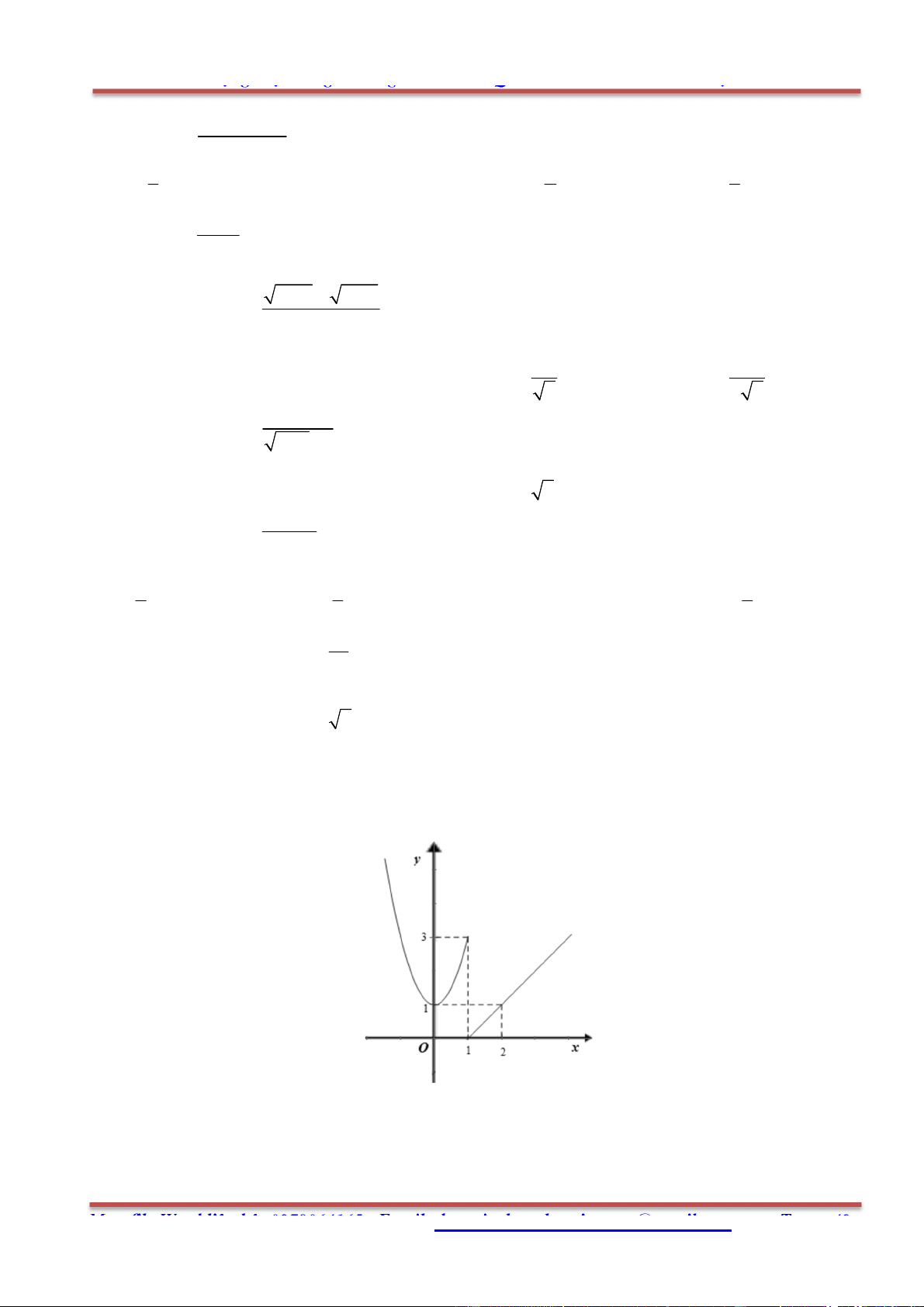
Câu 91. Hàm số f x có đồ thị như hình bên không liên tục tại điểm có hoành độ là bao nhiêu? A. x 0. B. x 1. C. x 2. D. x 3.
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 49
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
PHẦN II – HƯỚNG DẪN GIẢI GIỚI HẠN DÃY SỐ
A – LÝ THUYẾT VÀ PHƯƠNG PHÁP
GIỚI HẠN HỮU HẠN GIỚI HẠN VÔ CỰC
1. Giới hạn đặc biệt:
1. Giới hạn đặc biệt: 1 1 k lim lim n lim n (k ) 0 ; lim 0 (k ) n n k n n lim n
q (q 1) lim n
q 0 ( q 1) ; lim C C 2. Định lí: n n 2. Định lí : 1 a) Nếu lim u lim 0 n thì a) Nếu lim u u n = a, lim vn = b thì n lim (un + vn) = a + b u lim (u b) Nếu lim u = 0 n – vn) = a – b
n = a, lim vn = thì lim n v lim (u n n.vn) = a.b u a
c) Nếu lim un = a 0, lim vn = 0 lim n (nếu b 0) u v b neáu . a v 0 n n thì lim n = v neáu . a v 0 b) Nếu u n n n 0, n và lim un= a
d) Nếu lim un = +, lim vn = a
thì a 0 và lim u a n neáu a 0 thì lim(u c) Nếu u v n.vn) = n n ,n và lim vn = 0 neáu a 0 thì lim un = 0 d) Nếu lim u
* Khi tính giới hạn có một trong các dạng vô n = a thì lim u a n 0
3. Tổng của cấp số nhân lùi vô hạn định: ,
, – , 0. thì phải tìm cách khử 0 u S = u dạng vô định. 1 + u1q + u1q2 + … = 1 q 1 1 q B – BÀI TẬP
DẠNG 1: TÍNH GIỚI HẠN BẰNG ĐỊNH NGHĨA Phương pháp:
Để chứng minh lim u 0 ta chứng minh với mọi số a 0 nhỏ tùy ý luôn tồn tại một số n sao n a
cho u a n n . n a
Để chứng minh limu l ta chứng minh lim(u l) 0 . n n
Để chứng minh lim u ta chứng minh với mọi số M 0 lớn tùy ý, luôn tồn tại số tự nhiên n
n sao cho u M n n . M n M
Để chứng minh lim u ta chứng minh lim(u ) . n n
Một dãy số nếu có giới hạn thì giới hạn đó là duy nhất.
Câu 1. Chọn mệnh đề đúng trong các mệnh đề sau:
A. Nếu lim u , thì lim u .
B. Nếu lim u , thì lim u . n n n n
C. Nếu lim u 0 , thì lim u 0 .
D. Nếu lim u a
, thì lim u a . n n n n
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 50
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
Hướng dẫn giải: Chọn C.
Theo nội dung định lý. 1
Câu 2. Giá trị của lim bằng: n 1 A. 0 B. 1 C. 2 D. 3 Hướng dẫn giải:
Chọn A. 1 1 1 1
Với a 0 nhỏ tùy ý, ta chọn n 1 ta có
a n n nên có lim 0 . a a n 1 n 1 a n 1 a 1
Câu 3. Giá trị của lim (k * ) bằng: k n A. 0 B. 2 C. 4 D. 5 Hướng dẫn giải:
Chọn A. 1 1 1 1
Với a 0 nhỏ tùy ý, ta chọn n k ta có
a n n nên có lim 0 . a a k k a n n k n a 2 sin n
Câu 4. Giá trị của lim bằng: n 2 A. 0 B. 3 C. 5 D. 8 Hướng dẫn giải:
Chọn A. 1 2 sin n 1 1
Với a 0 nhỏ tùy ý, ta chọn n 2 ta có
a n n nên có a a n 2 n 2 n 2 a a 2 sin n lim 0 . n 2
Câu 5. Giá trị của lim(2n 1) bằng: A. B. C. 0 D. 1 Hướng dẫn giải:
Chọn A. M 1
Với mọi số dương M lớn tùy ý ta chọn n M 2
Ta có: 2n 1 2n 1 M n n lim(2n 1) . M M 2 1 n
Câu 6. Giá trị của lim bằng: n A. B. C. 0 D. 1 Hướng dẫn giải:
Chọn B. 2 n 1
Với mọi số dương M lớn tùy ý ta chọn n thỏa M M M nM 2 M M 4 n . M 2
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 51
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 2 2 n 1 n 1 Ta có:
M n n lim M n n 2 1 n Vậy lim . n 2
Câu 7. Giá trị của lim bằng: n 1 A. B. C. 0 D. 1 Hướng dẫn giải: Chọn C. 2
Với mọi a 0 nhỏ tùy ý, ta chọn n 1 1 a a 2 2 Suy ra
a n n lim 0 . n 1 a n 1 cos n sin n
Câu 8. Giá trị của lim bằng: 2 n 1 A. B. C. 0 D. 1 Hướng dẫn giải: Chọn C. cos n sin n 2 1 cos n sin n Ta có mà lim 0 lim 0 2 2 n n 2 2 n n 1 n 1
Câu 9. Giá trị của lim bằng: n 2 A. B. C. 0 D. 1 Hướng dẫn giải: Chọn C. 1
Với mọi số thực a 0 nhỏ tùy ý, ta chọn n 1 1 a 2 a n 1 1 n 1 Ta có:
a n n lim 0 . n 2 a n 1 n 2 3 3n n
Câu 10. Giá trị của lim bằng: 2 n A. B. C. 0 D. 1 Hướng dẫn giải: Chọn A. M
Với mọi M 0 lớn tùy ý, ta chọn n 1 M 3 3 3n n 1 Ta có: 3n
M n n 2 M n n 3 3n n Vậy lim . 2 n 2 n
Câu 11. Giá trị của lim bằng: n 1 A. B. C. 0 D. 1
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 52
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 Hướng dẫn giải: Chọn B. 2 1
Với mọi M 0 lớn tùy ý, ta chọn n 3 1 M a n 2 3 Ta có: n 1
1 n 3 M n nM 1 n n 1 2 n Suy ra lim . n 1 2n 1
Câu 12. Giá trị của A lim bằng: n 2 A. B. C. 2 D. 1 Hướng dẫn giải: Chọn C. 5
Với số thực a 0 nhỏ tùy ý, ta chọn n 2 2 a a 2n 1 5 5 Ta có: 2
a n n n 2 n 2 n 2 a a Vậy A 2 . 2n 3
Câu 13. Giá trị của B lim bằng: 2 n 1 A. B. C. 0 D. 1 Hướng dẫn giải: Chọn C. 2n 3
Với số thực a 0 nhỏ tùy ý, ta chọn n thỏa a a a 2 n 1 a 2
1 a 4a 13 n a a 2n 3 Ta có:
a n n B 0 . 2 n 1 a 2 n 1
Câu 14. Giá trị của C lim bằng: n 1 A. B. C. 0 D. 1 Hướng dẫn giải: Chọn D. 1
Với số thực a 0 nhỏ tùy ý, ta chọn n 1 a a 2 n 1 n 2 1 Ta có: 1 1
a n n n 1 n 1 n 1 a a Vậy C 1. n 2 n
Câu 15. Giá trị của A lim bằng: 2n 1 A. B. C. D. 1 2
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 53
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 Hướng dẫn giải: Chọn C. 2
n sin n 3n
Câu 16. Giá trị của B lim bằng: 2 n A. B. C. 3 D. 1 Hướng dẫn giải: Chọn C. 1
Câu 17. Giá trị của C lim bằng: 2 n 2 n 7 A. B. C. 0 D. 1 Hướng dẫn giải: Chọn C. 4n 1
Câu 18. Giá trị của D lim bằng: 2 n 3n 2 A. B. C. 0 D. 4 Hướng dẫn giải: Chọn D. n a
Câu 19. Giá trị của lim 0 bằng: n! A. B. C. 0 D. 1 Hướng dẫn giải: Chọn C.
Gọi m là số tự nhiên thỏa: m 1 a . Khi đó với mọi n m 1 m nm n a a a a a a a a Ta có: 0 . ... . ... . n! 1 2 m m 1 n m! m 1 nm a n a Mà lim 0 . Từ đó suy ra: lim 0 . m 1 n!
Câu 20. Giá trị của lim n a với a 0 bằng: A. B. C. 0 D. 1 Hướng dẫn giải: Chọn D.
Nếu a 1 thì ta có đpcm n
Giả sử a 1 . Khi đó: 1 n 1 n a a n a 1 a
Suy ra: 0 n a 1
0 nên lim n a 1 n 1 1
Với 0 a 1 thì 1 lim 1 lim n n a 1 . a a
Tóm lại ta luôn có: lim n a 1 với a 0 .
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 54
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
DẠNG 2: TÌM GIỚI HẠN CỦA DÃY SỐ DỰA VÀO CÁC ĐỊNH LÝ VÀ CÁC GIỚI HẠN CƠ BẢN Phương pháp:
Sử dụng các định lí về giới hạn, biến đổi đưa về các giới hạn cơ bản. f (n) Khi tìm lim
ta thường chia cả tử và mẫu cho k
n , trong đó k là bậc lớn nhất của tử và g(n) mẫu. Khi tìm lim k ( ) m f n
g(n) trong đó lim f (n) lim g(n) ta thường tách và sử dụng
phương pháp nhân lượng liên hơn.
+ Dùng các hằng đẳng thức:
a b a b a ; b 3 3
a b 3 2 3 3 2
a ab b a b
Dùng định lí kẹp: Nếu u v n
n ,n và lim vn = 0 thì lim un = 0
Khi tính các giới hạn dạng phân thức, ta chú ý một số trường hợp sau đây:
Nếu bậc của tử nhỏ hơn bậc của mẫu thì kết quả của giới hạn đó bằng 0.
Nếu bậc của từ bằng bậc của mẫu thì kết quả của giới hạn đó bằng tỉ số các hệ số của luỹ thừa
cao nhất của tử và của mẫu.
Nếu bậc của tử lớn hơn bậc của mẫu thì kết quả của giới hạn đó là + nếu hệ số cao nhất của tử
và mẫu cùng dấu và kết quả là – nếu hệ số cao nhất của tử và mẫu trái dấu. n u 1
Câu 1. Cho dãy số u với u và n 1
. Chọn giá trị đúng của lim u trong các số sau: n n 4n n u 2 n 1 1 A. . B. . C. 0 . D. 1. 4 2
Hướng dẫn giải: Chọn C.
Chứng minh bằng phương pháp quy nạp toán học ta có 2n n ,n n n n n n 1 1
Nên ta có : n 2 1 n n n n n 2 2 .2 2 4 2 n n 1 1 Suy ra : 0 u , mà lim 0 lim u 0 . n n 2 2 n cos 2n
Câu 2. Kết quả đúng của lim 5 là: 2 n 1 1 A. 4. B. 5. C. –4. D. . 4
Hướng dẫn giải: Chọn B. n n cos 2n n 2 2 2 n 1 n 1 n 1 n 1 1 n Ta có lim lim . 0 ; lim 0 2 2 n 1 n 11 / n 2 n 1 n cos 2n n cos 2n lim 0 lim 5 5 . 2 2 n 1 n 1
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 55
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 2n 1
Câu 3. Giá trị của. A lim bằng: 1 3n 2 A. B. C. D. 1 3 Hướng dẫn giải:
Chọn C. 2 4n 3n 1
Câu 4. Giá trị của. B lim bằng: 2 (3n 1) 4 A. B. C. D. 1 9 Hướng dẫn giải:
Chọn C. 2 n 2n 1
Câu 5. Kết quả đúng của lim là 4 3n 2 3 2 1 1 A. . B. . C. . D. . 3 3 2 2
Hướng dẫn giải: Chọn A. 2 2 1 2 / n 1 / 2 1 n n n 1 0 0 3 lim lim . 4 2 3n 2 3 2 / n 3 0 3 4 3n n
Câu 6. Giới hạn dãy số u với u là: n n 4n 5 3 A. . B. . C. . D. 0 . 4
Hướng dẫn giải: Chọn A. 4 3 3n n 3 / n 1 3 lim u lim lim n . n 4n 5 4 5 / n 3 3 / n 1 1 Vì 3 lim n ; lim . 4 5 / n 4 3 n 2n 5
Câu 7. Chọn kết quả đúng của lim : 3 5n 2 A. 5 . B. . C. . D. . 5
Hướng dẫn giải: Chọn D. 2 3 3 1 2 / n 5 / 2 5 n n n lim lim n. . 3 5n 3 / n 5 2 3
1 2 / n 5 / n 1 Vì lim n ; lim . 3 / n 5 5 2 2n 3n 1
Câu 8. Giá trị của A lim bằng: 2 3n n 2
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 56
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 2 A. B. C. D. 1 3 Hướng dẫn giải:
Chọn C. 3 1 2 2 2 Ta có: lim n n A . 1 2 3 3 2 n n 2 n 2n
Câu 9. Giá trị của B lim bằng: 2 n 3n 1 1 A. B. C. 0 D. 1 3 Hướng dẫn giải: Chọn D. 2 n n 1 1 n n 1 Ta có: B lim lim 2 n 3n 1 1 1 3 1 3 2 n n 2n 4 1 n 29 2
Câu 10. Giá trị của C lim bằng: 17 n 1 A. B. C. 16 D. 1 Hướng dẫn giải:
Chọn C. 1 2 1 2 8 4 9 9 4 9 n (2 ) .n (1 ) (2 ) .(1 ) 2 2 Ta có: lim n n lim n n C 16 1 1 17 n (1 ) 1 17 17 n n 2 3 3
n 1 3n 2
Câu 11. Giá trị của D lim bằng: 4 4
2n n 2 n 3 1 3 A. B. C. D. 1 4 2 1 Hướng dẫn giải:
Chọn C. 1 2 3 n 1 3 2 3 3 n n 1 3 Ta có: D lim . 4 1 2 2 1 4 n 2 1 3 4 n n 4 3 3n 1 n
Câu 12. Giá trị của C lim bằng: 4
2n 3n 1 n A. B. C. 0 D. 1
Hướng dẫn giải:
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 57
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 Chọn C. 3 1 1 4 5 8 n n n Chia cả tử và mẫu cho 2
n ta có được C lim 0 . 3 1 1 2 3 4 n n n 7 3
(n 2) (2n 1)
Câu 13. Giá trị của. F lim bằng: 2 5 (n 2) A. B. C. 8 D. 1 Hướng dẫn giải:
Chọn C. 7 3 2 1 1 2 n n Ta có: F lim 8 5 5 1 2 n 3 n 1
Câu 14. Giá trị của. C lim bằng: 2 n(2n 1) 1 A. B. C. D. 1 4 Hướng dẫn giải:
Chọn C. 3 2 n 3n 2
Câu 15. Giá trị của. D lim bằng: 4 3 n 4n 1 A. B. C. 0 D. 1 Hướng dẫn giải:
Chọn C. 3 n 2n 1
Câu 16. Giá trị của. E lim bằng: n 2 A. B. C. 0 D. 1 Hướng dẫn giải:
Chọn A. 4 4
n 2n 1 2n
Câu 17. Giá trị của. F lim bằng: 3 3
3n n n 3 A. B. C. D. 1 3 3 1 Hướng dẫn giải:
Chọn C. 2n 2
Câu 18. Cho dãy số u với u n
. Chọn kết quả đúng của lim u là: n 1 n 4 2 n n 1 n A. . B. 0 . C.1 . D. .
Hướng dẫn giải: Chọn B. 2n 2
Ta có: lim u lim n n 1 4 2 n n 1
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 58
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 n 2 1 2n 2 lim 4 2 n n 1 3 2
2n 2n 2n 2 lim 4 2 n n 1 ` 2 2 2 2 2 3 4 lim n n n n 0. 1 1 1 2 4 n n 10 Câu 19. lim bằng : 4 2 n n 1 A. . B.10 . C. 0 . D. .
Hướng dẫn giải: Chọn C. 10 10 Ta có: lim lim 4 2 n n 1 2 1 1 n 1 2 4 n n 1 1 10 Nhưng lim 1 1 và lim 0 2 4 n n 2 n 10 Nên lim 0. 4 2 n n 1 n 1 4
Câu 20. Tính giới hạn: lim n 1 n 1 A.1. B. 0 . C. 1 D. . 2
Hướng dẫn giải: Chọn B. 1 1 4 2 n 1 4 n n n 0 Ta có: lim lim 0 . n 1 n 1 1 1 1 2 n n
1 3 5 .... 2n 1
Câu 21. Tính giới hạn: lim 2 3n 4 1 2 A. 0 . B. . C. . D.1. 3 3
Hướng dẫn giải: Chọn B.
1 3 5 .... 2n 2 1 n 1 1 Ta có: lim lim lim . 2 2 3n 4 3n 4 4 3 3 2 n 2 n 1 1
Câu 22. Chọn kết quả đúng của lim 3 . 2 3 n 2n
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 59
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 A. 4 . B. 3 . C. 2 . D. . 2
Hướng dẫn giải: Chọn C. 1 2 1 n 1 1 2 1 1 lim 3 lim 3 n 3 0 2 2 3 n 2n 3 2n 1 1 2 n k
a n ... a n a
Câu 23. Giá trị của k 1 0 D lim
(Trong đó k, p là các số nguyên dương; a b 0 ). p
b n ... b n b k p p 1 0 bằng: A. B. C. Đáp án khác D. 1 Hướng dẫn giải: Chọn C.
Ta xét ba trường hợp sau a a k 1 0 a ... k k if a b 0 k p
k p . Chia cả tử và mẫu cho k n ta có: lim n n D . bp b if a b 0 0 ... k p pk k n n a a k 1 0 a ... k k a
k p . Chia cả tử và mẫu cho k n ta có: lim n n D k . b0 b b ... k k k n a a k 0 ... pk p
k p . Chia cả tử và mẫu cho p n : lim n n D 0 . b0 b ... p p n n2 2 5
Câu 24. Kết quả đúng của lim là: 3n 2.5n 5 1 5 25 A. . B. . C. . D. . 2 50 2 2
Hướng dẫn giải: Chọn B. 2 1 1 n2 0 2 5 n 1 5 25 25 lim lim . 3n 2.5n n 3 0 2 50 2. 5 n n 1 3 4.2 3 Câu 25. lim bằng: 3.2n 4n A. . B. . C. 0 . D. 1.
Hướng dẫn giải: Chọn C.
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 60
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 n n n 2 1 3 1 4. 3. n n 1 n n 3 3 3 4.2 3 3 2.2 3 lim lim lim 3.2n 4n 3.2n 4n n n 2 4 3. 1 4 n n 2 1 1 4. 3. n 3 3 3 lim 0 . 4 n 2 3. 1 4 3.2n 3n
Câu 26. Giá trị của C lim bằng: n 1 n 1 2 3 1 A. B. C. D. 1 3 Hướng dẫn giải:
Chọn C. n 2 3. 1 3.2n 3n 3 1 Ta có: C lim lim n 1 n 1 2 3 n 2 3 2. 3 3
Câu 27. Giá trị đúng của lim 3n 5n là: A. . B. . C. 2 . D. 2 .
Hướng dẫn giải: Chọn B. n n n n 3 lim 3 5 lim 5 1 . 5 n n 3 Vì lim 5 ; lim 1 1 . 5 3.2n 3n
Câu 28. Giá trị của. K lim bằng: n 1 n 1 2 3 1 A. B. C. 2 D. 1 3 Hướng dẫn giải:
Chọn A. n 2 3 1 3 1 K lim n 2 3 2 3 3 5n 1 Câu 29. lim bằng : 3n 1 A. . B.1 . C. 0 D. .
Hướng dẫn giải:
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 61
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 Chọn A. n 1 1 5n 1 5 Ta có: lim lim 3n 1 n n 3 1 5 5 n n n n n 1 3 1 3 1 Nhưng lim 1 1 0 , lim 0 và * 0 n 5 5 5 5 5 5n 1 Nên lim . 3n 1 n n 1 4 2 Câu 30. 4 lim bằng : n n2 3 4 1 1 A. 0 . B. . C. . D. . 2 4
Hướng dẫn giải: Chọn B. n 1 1 2. n n 1 4 2 1 1 2 n 2 1 Ta có: 4 lim . lim lim n n2 3 4 n 4 n 4 3 3 2 2 4 2 4 4 4 n n 1 3 Vì lim 0; lim 0. 2 4 3.3n 4n
Câu 31. Giá trị của. C lim bằng: n 1 n 1 3 4 1 A. B. C. 0 D. 1 2 Hướng dẫn giải:
Chọn B. 2
1 a a ... n a
Câu 32. Cho các số thực a,b thỏa a 1; b 1. Tìm giới hạn I lim . 2
1 b b ... n b 1 b A. B. C. D. 1 1 a Hướng dẫn giải:
Chọn C. n 1 a n 1 Ta có 2 1, , ,..., n a a
a là một cấp số nhân công bội a 2
1 a a ... a 1 a n 1 b n 1 Tương tự 2
1 b b ... b 1b n 1 1 a 1 b Suy ra lim 1 lim a I n 1 1 b 1 a 1 b
( Vì a 1, b 1 n 1 n 1 lim a lim b 0 ).
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 62
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 k k 1 a . n a n
... a n a
Câu 33. Tính giới hạn của dãy số k k 1 1 0 A lim với a b 0 . : p p 1 b . n b n
... b n b k p p p 1 1 0 A. B. C. Đáp án khác D. 1 Hướng dẫn giải: Chọn C.
Ta chia làm các trường hợp sau a a k 1 0 a ... k k a
TH 1: n k , chia cả tử và mẫu cho k n , ta được lim n n A k . bp 1 b b 0 b ... p p k n n a a k 1 0 a ... k k khi a b 0 k p
TH 2: k p , chia cả tử và mẫu cho k n , ta được lim n n A b b p p 1 b khi a b 0 0 ... k p k p k p 1 k n n n a a a k k 1 0 ... pk pk 1 p
TH 3: k p , chia cả tử và mẫu cho p n , ta được lim n n n A 0 . bp 1 b0 b ... p p n n n Câu 34. 2 3 lim n sin 2 n bằng: 5 A. . B. 0 . C. 2 . D. .
Hướng dẫn giải: Chọn C. n sin n 2 3 3 5 lim n sin 2n lim n 2 5 n n sin Vì 3 5 lim n ;lim 2 2 n n n sin sin 1 1 5 5 ; lim 0 lim 2 2 . n n n n
Câu 35. Giá trị của. M 2 lim
n 6n n bằng: A. B. C. 3 D. 1 Hướng dẫn giải:
Chọn C. 6n M lim 3 2
n 6n n
Câu 36. Giá trị của. H 2 lim
n n 1 n bằng: 1 A. B. C. D. 1 2
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 63
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 Hướng dẫn giải:
Chọn C. 1 1 n 1 1 Ta có: lim lim n H 2
n n 1 n 1 1 2 1 1 2 n n
Câu 37. Giá trị của B 2 lim
2n 1 n bằng: A. B. C. 0 D. 1 Hướng dẫn giải:
Chọn A. 1
Ta có: B lim n 2 1 n
Bài 40. Giá trị của K n 2 lim
n 1 n bằng: 1 A. B. C. D. 1 2 Hướng dẫn giải:
Chọn C.
Câu 38. Giá trị đúng của 2 2 lim
n 1 3n 2 là: A. . B. . C. 0 . D. 1.
Hướng dẫn giải: Chọn B. 2 2 n n n 2 2 lim 1 3 2 lim
11/ n 3 2 / n . Vì n 2 2 lim ; lim
11 / n 3 2 / n 1 3 0 .
Câu 39. Giá trị của A 2 lim
n 6n n bằng: A. B. C. 3 D. 1 Hướng dẫn giải:
Chọn C. 2 2
n 6n n Ta có A lim 2
n 6n n lim 2
n 6n n 6n 6 lim lim 3 2
n 6n n 6 1 1 n
Câu 40. Giá trị của B 3 3 2 lim
n 9n n bằng: A. B. C. 0 D. 3 Hướng dẫn giải: Chọn D. Ta có: B 3 3 2 lim
n 9n n
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 64
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 2 9n lim 3 2 n 9n 2 3 3 2 2 3
n n 9n n 9 lim 3 . 2 9 9 3 1 1 1 n n
Câu 41. Giá trị của D 2 3 3 2 lim
n 2n n 2n bằng: 1 A. B. C. D. 1 3 Hướng dẫn giải:
Chọn C. Ta có: D
2n n n 3 3 2 lim 2 lim
n 2n n 2 2n 2n lim lim 2 3 2 2 3 3 2 2 3
n 2n n
(n 2n ) n n 2n n 2 2 1 lim lim . 2 2 2 3 2 3 3 1 1 (1 ) 1 1 n n n
Câu 42. Giá trị của. M 3 2 3 lim
1 n 8n 2n bằng: 1 A. B. C. 0 D. 1 12 Hướng dẫn giải:
Chọn A. 2 1 n 1 Ta có: M lim 2 3 2 3 2 3 2 3 12
(1 n 8n ) 2n 1 n 8n 4n
Câu 43. Giá trị của. N 2 3 3 lim
4n 1 8n n bằng: A. B. C. 0 D. 1 Hướng dẫn giải:
Chọn C. Ta có: N
2n n 3 3 lim 4 1 2 lim
8n n 2n 1 Mà: lim 2
4n 1 2n lim 0 2 4n 1 2n n lim 3 2
8n n 2n lim 0 2 2 3 2 2
3 (8n n) 2n 8n n 4n Vậy N 0 .
Câu 44. Giá trị của. K 3 3 2 2 lim
n n 1 3 4n n 1 5n bằng: 5 A. B. C. D. 1 12
Hướng dẫn giải:
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 65
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 Chọn C. Ta có: K 3 3 2
n n n 2 lim 1 3lim
4n n 1 2n 1 1 Mà: lim 3 3 2
n n 1 n ; lim 2
4n n 1 2n 3 4 1 3 5 Do đó: K 3 4 12
Câu 45. Giá trị của. N 3 3 2 lim
n 3n 1 n bằng: A. B. C. 0 D. 1 Hướng dẫn giải:
Chọn D. 2 3n 1 N lim 1 3 2 2 3 3 2 2
3 (n 3n 1) .
n n 3n 1 n
Câu 46. Giá trị đúng của lim n n 1 n 1 là: A. 1. B. 0 . C. 1. D. .
Hướng dẫn giải: Chọn C.
n n n n n n 1 1 2 n lim 1 1 lim lim 1.
n 1 n 1
n 11/ n 11/ n
Câu 47. Giá trị của. H n 3 3 2 lim
8n n 4n 3 bằng: 2 A. B. C. D. 1 3 Hướng dẫn giải:
Chọn C. H lim n 2 3 3
8n n 2n lim n 2
4n 3 2n 3
Câu 48. Giá trị của A 2 lim
n 2n 2 n bằng: A. B. C. 2 D. 1 Hướng dẫn giải:
Chọn A. 2 2
Ta có A lim n 1 1 2 n n 2 2 Do lim n ; lim 1 1 2 . 2 n n Câu 49. 5 5 2
lim 200 3n 2n bằng : A. 0 . B.1. C. . D. .
Hướng dẫn giải: Chọn D. 200 2 Ta có: 5 5 2 5
lim 200 3n 2n lim n 3 5 3 n n
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 66
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 200 2 Nhưng 5 5 lim 3 3
0 và lim n 5 3 n n Nên 5 5 2
lim 200 3n 2n 3
2n sin 2n 1
Câu 50. Giá trị của. A lim bằng: 3 n 1 A. B. C. 2 D. 1 Hướng dẫn giải:
Chọn C. sin 2n 1 2 3 lim n A 2 1 1 3 n n n!
Câu 51. Giá trị của. B lim bằng: 3 n 2n A. B. C. 0 D. 1 Hướng dẫn giải:
Chọn C. n n ! n n n n Ta có: 0 B 0 3 3 3 n 2n n 2n n 2n n 1
Câu 52. Giá trị của. D lim bằng: 2 2 2
n ( 3n 2 3n 1) 2 A. B. C. D. 1 3 Hướng dẫn giải:
Chọn C.
Câu 53. Giá trị của. 2
E lim( n n 1 2n) bằng: A. B. C. 0 D. 1 Hướng dẫn giải:
Chọn B.
Câu 54. Giá trị của. F lim n 1 n bằng: A. B. C. 0 D. 1 Hướng dẫn giải:
Chọn A. p
Câu 55. Giá trị của. k 2 2
H lim( n 1 n 1) bằng: A. B. C. Đáp án khác D. 1 Hướng dẫn giải: Chọn C. Xét các trường hợp
TH1: k p H
TH 2: k p H
TH 3: k p H 0 . 1 1 1
Câu 56. Tính giới hạn của dãy số u ... : n 2 1 2 3 2 2 3
(n 1) n n n 1
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 67
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 A. B. C. 0 D. 1 Hướng dẫn giải:
Chọn D. 1 1 1 Ta có:
(k 1) k k k 1 k k 1 1 Suy ra u 1 lim u 1 n n n 1 3 3 3
(n 1) 1 2 ... n
Câu 57. Tính giới hạn của dãy số u : n 3 3n n 2 1 A. B. C. D. 1 9 Hướng dẫn giải:
Chọn C. 2
n(n 1) Ta có: 3 3 3
1 2 ... n 3 2 n(n 1) 1 Suy ra u lim u . n 3
3(3n n 2) n 9 1 1 1 n(n 1)
Câu 58. Tính giới hạn của dãy số u (1 )(1 )...(1
) trong đó T . : n T T T n 2 1 2 n 1 A. B. C. D. 1 3 Hướng dẫn giải:
Chọn C. 1 2
(k 1)(k 2) Ta có: 1 1 T k (k 1) k (k 1) k 1 n 2 1 Suy ra u . lim u . n 3 n n 3 3 3 3 2 1 3 1 n 1
Câu 59. Tính giới hạn của dãy số u . .... . : n 3 3 3 2 1 3 1 n 1 2 A. B. C. D. 1 3 Hướng dẫn giải:
Chọn C. 3 2 k 1
(k 1)(k k 1) Ta có 3 2 k 1
(k 1)[(k 1) (k 1) 1] 2 2 n n 1 2 Suy ra u . lim u n 3 (n 1) n n 3 n 2k 1
Câu 60. Tính giới hạn của dãy số u . : n k k 2 1 A. B. C. 3 D. 1 Hướng dẫn giải:
Chọn C.
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 68
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 1 1 1 1 2n 1 Ta có: u u ... n n 2 n 1 n 1 2 2 2 2 2 2 1 3 2n 1 u lim u 3 . n n 1 2 2 2 n
Câu 61. Tính giới hạn của dãy số 2
u q 2q ... n
nq với q 1 . : n q q A. B. C. D. q2 1 q2 1 Hướng dẫn giải: Chọn C. Ta có: 2 3 n n 1 u qu q q q ... q nq n n 1 n q n 1 q (1 q) u q nq . Suy ra lim u . n 1 q n 1 q2 n n
Câu 62. Tính giới hạn của dãy số u . : n 2 n k k 1 A. B. C. 3 D. 1 Hướng dẫn giải:
Chọn D. n n n 1 Ta có: n u n u 1 2 n 2 2 n 2 n n n 1 n 1 n 1 n u 1
0 lim u 1 . n 2 n 1 n 3 6 4
n n 1 4 n 2n 1
Câu 63. Tính giới hạn của dãy số B lim . : 2 (2n 3) 3 A. B. C. 3 D. 4 Hướng dẫn giải: Chọn D.
Chia cả tử và mẫu cho 2 n ta có được: 1 1 2 1 3 1 4 1 5 6 3 4 n n n n 1 4 3 B lim . 2 3 4 4 2 n
Câu 64. Tính giới hạn của dãy số C 2 lim
4n n 1 2n . : 1 A. B. C. 3 D. 4 Hướng dẫn giải:
Chọn D. 1 1 n 1 1 Ta có: lim lim n C 2
4n n 1 2n 1 1 4 4 2 2 n n
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 69
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
Câu 65. Tính giới hạn của dãy số D 2 3 3 2 lim
n n 1 2 n n 1 n . : 1 A. B. C. D. 1 6 Hướng dẫn giải:
Chọn C. Ta có: D
2n n n 3 3 2 lim 1 2 lim
n n 1 n 1 1 n 1 1 Mà: lim 2
n n 1 n lim lim n 2
n n 1 n 1 1 2 1 1 2 n n 2 n lim 1 3 3 2
n n 1 n lim 3 2 2 3 3 2 2
3 (n n 1) .
n n n 1 n 1 1 2 1 lim n 2 3 1 1 1 1 3 3 1 1 1 4 6 3 n n n n 1 2 1 Vậy D . 2 3 6 1
Câu 66. Cho dãy số (x ) xác định bởi 2 x , x
x x ,n 1 n 1 n 1 2 n n 1 1 1 Đặt S . Tính lim S . n n x 1 x 1 x 1 1 2 n A. B. C. 2 D. 1 Hướng dẫn giải: Chọn C.
Từ công thức truy hồi ta có: x
x , n 1, 2,... n 1 n
Nên dãy (x ) là dãy số tăng. n
Giả sử dãy (x ) là dãy bị chặn trên, khi đó sẽ tồn tại lim x x n n
Với x là nghiệm của phương trình : 2
x x x x 0 x vô lí 1
Do đó dãy (x ) không bị chặn, hay lim x . n n 1 1 1 1 Mặt khác: x x (x 1) x x 1 n 1 n n n n 1 1 1 Suy ra: x 1 x x n n n 1 1 1 1 1 Dẫn tới: S 2 lim S 2 lim 2 n n x x x x 1 n 1 n 1 n 1 1 2 k
Câu 67. Cho dãy (x ) được xác định như sau: x ... k k 2! 3! (k 1)!
Tìm lim u với u n x n x ... n n x . n n 1 2 2011
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 70
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 1 A. B. C. 1 D. 1 2012! 2012! Hướng dẫn giải:
Chọn C. k 1 1 1 Ta có: nên x 1 (k 1)! k ! (k 1)! k (k 1)! 1 1 Suy ra x x
0 x x k k 1 k k 1 (k 2)! (k 1)! Mà: n n x x n x ... n x n 2011x 2011 1 2 2011 2011 1 Mặt khác: lim lim n x 2011x x 1 2011 2011 2011 2012! 1 Vậy lim u 1 . n 2012! u 2011 0 3 u
Câu 68. Cho dãy số (u ) được xác định bởi: 1 . Tìm lim n . n u u n 1 n n 2 un A. B. C. 3 D. 1 Hướng dẫn giải: Chọn C.
Ta thấy u 0, n n 3 1 Ta có: 3 3 u u 3 (1) n 1 n 3 6 u u n n Suy ra: 3 3 3 3 u u
3 u u 3n (2) n n 1 n 0 1 1 1 1 Từ (1) và (2), suy ra: 3 3 3 u u 3 u 3 n 1 n 3 u 3n n u 3n 2 2 3 3n 9n 0 0 1 n 1 1 n 1 Do đó: 3 3
u u 3n (3) n 0 2 3 k k k 9 1 k 1 n 1 1 1 1 1 n 1 n 1 Lại có: 1 ... 2 2 . n 2 n 2 k n n n 2 k k k 1.2 2.3 ( 1) 1 k 1 k 1 2 2n Nên: 3 3 3
u 3n u u 3n 0 n 0 9 3 3 3 3 u u u 2 2 Hay 0 n 0 3 3 . n n n 9n 3 n 3 u Vậy lim n 3 . n x 1 1
Câu 69. Cho dãy x 0 xác định như sau: f (x) . Tìm 0; . x A. B. C. 2010 D. 1 Hướng dẫn giải:
Chọn C.
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 71
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 2 u u u u Ta có n n 1 u u n n n 1 n 2010 u .u 2010u n 1 n n 1 u 1 1 n 2010. u u u n 1 n n 1 u 1 1 1 Ta có 2010( ) 2010(1 ) n u u u u n 1 1 n 1 n 1
Mặt khác ta chứng minh được: lim u . n u Nên lim( ) 2010 u . un 1 .
n 1 3 5 ... (2n 1)
Câu 70. Tìm lim u biết u n n 2 2n 1 1 A. B. C. D. 1 2 Hướng dẫn giải:
Chọn C. 1 Ta có: 2
1 3 5 ... 2n 1 n nên lim u n 2 3
x 2 2x 1 khi x 1
Câu 71. Tìm lim u biết f (x) n x 1 3 m 2 khi x 1 3 6 A. B. C. 2 D. 2 Hướng dẫn giải:
Chọn D. n(n 1)
n(n 1)(2n 1)
Ta có: 1 2 ... n và 2 2 2
1 2 ... n 2 6 3 6 Nên lim u n 2 x 1 1 khi x 0
Câu 72. Tìm lim u biết f (x) n x 2
2x 3m 1 khi x 0 A. B. C. 2 D. 1 Hướng dẫn giải:
Chọn D. 1 1 1 1 Ta có: Suy ra u 1 lim u 1 n n
(k 1) k k k 1 k k 1 n 1 2x 4 3 khi x 2
Câu 73. Tìm lim u biết f (x) trong đó x 1 . n x 1 khi x 2 2
x 2mx 3m 2 1 A. B. C. D. 1 3
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 72
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 Hướng dẫn giải:
Chọn C. 1 2
(k 1)(k 2) 1 n 2 1 Ta có: 1 1 Suy ra u . lim u . T k (k 1) k (k 1) n 3 n n 3 k n 1
Câu 74. Tìm lim u biết u n n 2 k 1 n k A. B. C. 3 D. 1 Hướng dẫn giải:
Chọn D. 1 1 1 n n Ta có:
, k 1, 2,..., n Suy ra u n 2 2 2 n n n k n 1 2 2 n n n 1 n n Mà lim lim
1 nên suy ra limu 1. n 2 2 n n n 1
Câu 75. Tìm lim u biết u 2 2... 2 n n n dau can A. B. C. 2 D. 1 Hướng dẫn giải:
Chọn C. n n 1 1 1 1 1 ... 1 1 Ta có: 2 2 2 2n 2 u 2 2 ,nên 2 lim u lim 2 2 . n n
Câu 76. Gọi g(x) 0, x 2 là dãy số xác định bởi . Tìm lim f (x) lim x . 2 4 3 3 x2 x2 4 A. B. C. D. 1 3 Hướng dẫn giải:
Chọn C. 4 8 4 8
Ta có 0 u u u 3u
3u u nên dãy (u ) là dãy tăng. 1 2 3 1 2 3 9 9 9 9 n 4 4
Dễ dàng chứng minh được * u
,n .Từ đó tính được lim u . n 3 n 3 2 2 1 1 1 Câu 77. Cho dãy số 2 2 2 2 A x x x x x x x x 3 0
được xác định như sau 1 1 2 1 2 2 1 2 2 4 2
x x . 1 2 3 Đặt x . Tìm 3
x 2x 3 3 2x 4 0 . 2 1 A. B. C. D. 1 2 Hướng dẫn giải:
Chọn C. Ta có: 2 2 2 2 u
(u 3u )(u 3u 2) 1 (u 3u 1) n 1 n n n n n n 2
u 3u 1 n n
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 73
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 1 1 Suy ra: u
1 (u 1)(u 2) n 1 n n u 1 u 1 u 2 n 1 n n 1 1 1 Suy ra: u 2 u 1 u 1 n n n 1 n 1 1 1 1 1 1 Do đó, suy ra: v n u u u u u i 1 1 1 1 2 1 1 i i 1 1 n 1 n 1 Mặt khác, từ 2 u
u 3u 1 ta suy ra: u 3n . n 1 n n n 1 1 1 Nên lim 0 . Vậy lim v . u 1 n 2 n 1 Câu 78. Cho ,
a b , (a,b) 1; n ab 1, ab 2,..
. . Kí hiệu r là số cặp số (u, v) sao cho n r 1
n au bv . Tìm lim n . n n ab 1 A. B. C. D. ab 1 ab Hướng dẫn giải:
Chọn C. n 1 Xét phương trình 0; (1). n
Gọi (u , v ) là một nghiệm nguyên dương của (1). Giả sử (u, v) là một nghiệm nguyên dương khác 0 0
(u , v ) của (1). 0 0
Ta có au bv ,
n au bv n suy ra a(u u ) (
b v v ) 0 do đó tồn tại k nguyên dương sao cho 0 0 0 0 v 1
u u k ,
b v v ka . Do v là số nguyên dương nên 0
v ka 1 k . (2) 0 0 0 a
Ta nhận thấy số nghiệm nguyên dương của phương trình (1) bằng số các số k nguyên dương cộng với v 1 n u 1 1. Do đó 0 0 r 1 1. n a ab b a n u 1 n u 1
Từ đó ta thu được bất đẳng thức sau: 0 0 r 1. n ab b a ab b a 1 u 1 r 1 u 1 1 Từ đó suy ra : 0 n 0 . ab nb na n ab nb na n r 1
Từ đây áp dụng nguyên lý kẹp ta có ngay lim n . n n ab 1 u 1 2
Câu 79. Cho dãy số có giới hạn (un) xác định bởi :
. Tìm kết quả đúng của lim u . 1 n u , n 1 n 1 2 un 1 A. 0 . B.1. C. 1. D. 2
Hướng dẫn giải: Chọn B.
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 74
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 2 3 4 5 Ta có: u ; u ; u ; u ; u .;... 1 2 3 4 5 2 3 4 5 6 n Dự đoán u với * n n n 1
Dễ dàng chứng minh dự đoán trên bằng phương pháp quy nạp. n 1 Từ đó lim u lim lim 1. n n 1 1 1 n 1 1 1 1
Câu 80. Tìm giá trị đúng của S 2 1 ... ....... . n 2 4 8 2 1 A. 2 1 . B. 2 . C. 2 2 . D. . 2
Hướng dẫn giải: Chọn C. 1 1 1 1 1 Ta có: S 2 1 ... ....... 2. 2 2 . n 2 4 8 2 1 1 2 1 1 1
Câu 81. Tính giới hạn: lim .... 1.2 2.3 n n 1 3 A. 0 B.1. C. . D. Không có giới 2 hạn.
Hướng dẫn giải: Chọn B. Đặt : 1 1 1 1 1 1 1 1 1 n A .... 1 ... 1 1.2 2.3 n n 1 2 2 3 n n 1 n 1 n 1 1 1 1 n 1 lim .... lim lim 1 1.2 2.3 n n 1 n 1 1 1 n 1 1 1
Câu 82. Tính giới hạn: lim .... 1.3 3.5 n 2n 1 2 A.1. B. 0 . C. . D. 2 . 3
Hướng dẫn giải: Chọn B. Đặt
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 75
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 1 1 A .... 1.3 3.5 n 2n 1 2 2 2 2A .... 1.3 3.5 n 2n 1 1 1 1 1 1 1 1 2A 1 ... 3 3 5 5 7 n 2n 1 1 2n 2A 1 2n 1 2n 1 n A 2n1 1 1 1 n 1 1 Nên lim .... lim lim . 1.3 3.5 n 2n 1 2n 1 1 2 2 n 1 1 1
Câu 83. Tính giới hạn: lim .... 1.3 2.4 n n 2 3 2 A. . B.1. C. 0 . D. . 4 3
Hướng dẫn giải: Chọn A. 1 1 1 1 2 2 2 Ta có : lim .... lim .... 1.3 2.4 n n 2 2 1.3 2.4 n n 2 1 1 1 1 1 1 1 1 1 1 1 3 lim 1 ... lim 1 . 2 3 2 4 3 5 n n 2 2 2 n 2 4 1 1 1
Câu 84. Tính giới hạn: lim ... . 1.4 2.5 n(n 3) 11 3 A. . B. 2 . C. 1. D. . 18 2
Hướng dẫn giải: Chọn A. Cách 1: 1 1 1 1 1 1 1 1 1 1 1 lim ... lim 1 ... 1.4 2.5 n(n 3) 3 4 2 5 3 6 n n 3 1 1 1 1 1 1 lim 1 3 2 3 n 1 n 2 n 3 2 11 3n 12n 11 11 lim . 18 n
1 n 2 n 3 18 100 1
Cách 2: Bấm máy tính như sau:
và so đáp án (có thể thay 100 bằng số nhỏ hơn hoặc lớn x x 3 1 hơn).
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 76
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 1 1
Câu 85. Tính giới hạn: lim 1 1 ... 1 . 2 2 2 2 3 n 1 1 3 A. 1. B. . C. . D. . 2 4 2
Hướng dẫn giải: Chọn B. Cách 1: 1 1 1 1 1 1 1 1 1 lim 1 1 ... 1 lim 1 1 1 1 ... 1 1 2 2 2 2 3 n 2 2 3 3 n n 1 3 2 4 n 1 n 1 1 n 1 1 lim . . . ... . lim . 2 2 3 3 n n 2 n 2 100 1
Cách 2: Bấm máy tính như sau: 1
và so đáp án (có thể thay 100 bằng số nhỏ hơn hoặc lớn 2 x 2 hơn).
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 77
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 GIỚI HẠN HÀM SỐ
A – LÝ THUYẾT TÓM TẮT
Giới hạn hữu hạn
Giới hạn vô cực, giới hạn ở vô cực
1. Giới hạn đặc biệt:
1. Giới hạn đặc biệt: lim x x lim c c 0 ;
neáu k chaün xx xx lim k x ; lim k x 0 0 x x neáu k leû (c: hằng số) c 2. Định lí: lim c c ; lim 0 k
a) Nếu lim f (x) L và lim g(x) M x x x xx xx 0 0 1 1 lim ; lim
thì: lim f (x) g(x) L M x 0 x x 0 x xx0 1 1
lim f (x) g(x) L M lim lim xx x x 0 x 0 x 0 lim f (x). (
g x) L.M 2. Định lí: xx0
Nếu lim f (x) L 0 và lim ( g x) thì: f (x) L xx xx 0 0 lim (nếu M 0) xx ( g x) M
neáu L vaø lim (
g x) cuøng daáu 0 xx0
b) Nếu f(x) 0 và lim f (x) L lim f (x) ( g x) xx neáu L vaø lim (
g x) traùi daáu xx 0 0 xx 0 thì L 0 và lim
f (x) L 0 neáu lim ( g x) xx0 xx 0 f (x)
c) Nếu lim f (x) L thì lim f (x) L lim neáu lim (
g x) 0 vaø L. ( g x) 0 xx xx xx ( g x) xx 0 0 0 0
3. Giới hạn một bên: neáu lim (
g x) 0 vaø L. ( g x) 0 xx
lim f (x) L 0 xx0 0
* Khi tính giới hạn có một trong các dạng vô định: ,
lim f (x) lim f (x) L 0 x x x x 0 0
, – , 0. thì phải tìm cách khử dạng vô định. B – BÀI TẬP
DẠNG 1: TÍNH GIỚI HẠN DẠNG BẰNG ĐỊNH NGHĨA HOẶC TẠI MỘT ĐIỂM Phương pháp:
+ Sử dụng định nghĩa chuyển giới hạn của hàm số về giới hạn của dãy số.
+ Nếu f (x) là hàm số cho bởi một công thức thì giá trị giới hạn bằng f (x ) 0
+ Nếu f (x) cho bởi nhiều công thức, khi đó ta sử dụng điều kiện để hàm số có giới hạn ( Giới hạn
trái bằng giới hạn phải). 3 2 x 2x 1
Câu 1. Chọn kết quả đúng trong các kết quả sau của lim là: 5 x1 2x 1 1 1 A. 2 . B. . C. . D. 2 . 2 2
Hướng dẫn giải:
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 78
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 Chọn A. x 2x 1 3 1 2. 2 3 2 1 1 Cách 1: lim 2 5 x1 2x 1 2 5 1 1 3 2 x 2x 1
Cách 2: Bấm máy tính như sau: + CACL + 9 x 1 10 và so đáp án. 5 2x 1 3 2 x 2x 1
Cách 3: Dùng chức lim của máy VNCALL 570ES Plus: lim và so đáp án. 5 2x 1 9 x 1 10 3 4x 1 Câu 2. lim bằng: 2 x 2
3x x 2 11 11 A . . B. . . C. . . D. . 4 4 Hướng dẫn giải: Chọn B 3 4x 1 11 lim . 2
x2 3x x 2 4 x 1
Câu 3. Tìm giới hạn hàm số lim bằng định nghĩa. x 1 x 2 A. B. C. 2 D. 1 Hướng dẫn giải:
Chọn C. x 1 x 1
Với mọi dãy (x ) : lim x 1 ta có: lim n 2 Vậy lim 2 . n n x 2 x 1 x 2 n
Câu 4. Tìm giới hạn hàm số lim 3 x 1 bằng định nghĩa. x2 A. B. C. 9 D. 1 Hướng dẫn giải:
Chọn C. x 3 2
Câu 5. Tìm giới hạn hàm số lim bằng định nghĩa. x 1 x 1 1 A. B. C. 2 D. 4 Hướng dẫn giải:
Chọn D. x 3 2 1 lim x 1 x 1 4 x 3
Câu 6. Tìm giới hạn hàm số lim bằng định nghĩa.
x x 2 A. B. C. 2 D. 1 Hướng dẫn giải:
Chọn D. 2 2x x 1
Câu 7. Tìm giới hạn hàm số lim bằng định nghĩa. x x 2 A. B. C. 2 D. 1
Hướng dẫn giải:
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 79
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 Chọn B. 2 2x x 1 lim x x 2 3x 2
Câu 8. Tìm giới hạn hàm số lim bằng định nghĩa. x 1 2x 1 A. B. C. 5 D. 1 Hướng dẫn giải:
Chọn C. 3x 2 3x 2 3.1 2 Với mọi dãy x x ta có: lim lim n 5 n : lim 2 n x 1 2x 1 2x 1 2.11 n 2 4x 3x
Câu 9. Cho hàm số f (x)
. Chọn kết quả đúng của lim f (x) : 2x 1 3 x 2 x 2 5 5 5 2 A. . B. . C. . D. . 9 3 9 9 Hướng dẫn giải:
Chọn B. 2 2 4x 3x 4.2 3.2 5 Cách 1: lim x 2x 1 3 x 2 2.2 1 3 2 2 2 3 2 4x 3x
Cách 2: Bấm máy tính như sau: + CACL + 9 x 2 10 và so đáp án. 2x 1 3 x 2 2 4x 3x
Cách 3: Dùng chức lim của máy VNCALL 570ES Plus: lim và so đáp 2x 1 3 x 2 9 x 2 10 án. cos 5x
Cách 2: Bấm máy tính như sau: Chuyển qua chế độ Rad + + CACL + 9
x 10 và so đáp án. 2x cos 5x
Cách 3: Dùng chức lim của máy VNCALL 570ES Plus: chuyển chế độ Rad + lim và 9 2x x 10 so đáp án. x 4 2
Câu 10. Tìm giới hạn hàm số lim bằng định nghĩa. x0 2x 1 A. B. C. 2 D. 1 8 Hướng dẫn giải: Chọn B.
Với mọi dãy x x ta có: n : lim 0 n x 4 2 x 4 2 x 1 1 lim lim n lim n lim . x0 2x 2x 2 x 4 2 8 n 2x x n n 4 2 n 4x 3
Câu 11. Tìm giới hạn hàm số lim bằng định nghĩa. x 1 x 1 A. B. C. 2 D. 1
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 80
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 Hướng dẫn giải:
Chọn A. 4x 3 4x 3
Với mọi dãy (x ) : x 1, n và lim x 1 ta có: lim lim n . n n n x 1 x 1 x 1 n 3x 1
Câu 12. Tìm giới hạn hàm số lim bằng định nghĩa. x 2 x 2 A. B. C. 2 D. 1 Hướng dẫn giải:
Chọn B. 3x 1 3x 1
Với mọi dãy (x ) : x 2, n và lim x 2 ta có: lim lim n . n n n x 2 x 2 x 2 n 2 2x x 3
Câu 13. Tìm giới hạn hàm số lim bằng định nghĩa. x 1 x 1 A. B. 5 C. 2 D. 1 Hướng dẫn giải:
Chọn B. 2 2 2x x 3 2x x 3
Với mọi dãy (x ) : lim x 1 ta có: lim lim n n lim 2x 3 . n 5 n n x 1 x 1 x 1 n x 1
Câu 14. Tìm giới hạn hàm số lim bằng định nghĩa. x 2 x4 2 A. B. C. 2 D. 1 Hướng dẫn giải:
Chọn A. 2 3x
Câu 15. Tìm giới hạn hàm số lim bằng định nghĩa. 2
x 2x 1 3 A. B. C. D. 1 2 Hướng dẫn giải:
Chọn C. 2 3x 3 Đáp số: lim 2
x 2x 1 2
Câu 16. Tìm giới hạn hàm số 2
lim x x 1 bằng định nghĩa. x A. B. C. 2 D. 1 Hướng dẫn giải:
Chọn A. 2 x 4
Câu 17. Tìm giới hạn hàm số lim bằng định nghĩa. x 2 4 x 1 2 x A. B. C. 0 D. 1 Hướng dẫn giải:
Chọn C. 2 x 3x 2
Câu 18. Tìm giới hạn hàm số lim bằng định nghĩa. x 1 x 1
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 81
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 A. B. C. 2 D. 1 Hướng dẫn giải:
Chọn D. 2 x 3x 2 Do x 1
x 1 (x 1) . Đáp số: lim 1 . x 1 x 1 2 x x 1
Câu 19. Tìm giới hạn hàm số A lim bằng định nghĩa. x 1 x 1 1 A. B. C. D. 1 2 Hướng dẫn giải:
Chọn C. 2 x x 1 11 1 1 Ta có: A lim . x 1 x 1 11 2 2 tan x 1
Câu 20. Tìm giới hạn hàm số B lim bằng định nghĩa. x sin x 1 6 4 3 6 A. B. C. D. 1 9 Hướng dẫn giải:
Chọn C. 2 tan 1 2 tan x 1 4 3 6 Ta có 6 B lim . x sin x 1 9 6 sin 1 6
3 x 2 x 1
Câu 21. Tìm giới hạn hàm số C lim bằng định nghĩa. x0 3x 1 A. B. C. 3 2 1 D. 1 Hướng dẫn giải:
Chọn C.
3 x 2 x 1 Ta có: 3 C lim 2 1. x0 3x 1 3 7x 1 1
Câu 22. Tìm giới hạn hàm số D lim bằng định nghĩa. x 1 x 2 A. B. C. 2 D. 3 Hướng dẫn giải:
Chọn D. 3 3 7x 1 1 8 1 Ta có: D lim 3 . x 1 x 2 1 2 x 1
Câu 23. Tìm giới hạn hàm số A lim bằng định nghĩa. 2
x2 x x 4 1 A. B. C. D. 1 6 Hướng dẫn giải:
Chọn C.
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 82
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 2 sin 2x 3cos x
Câu 24. Tìm giới hạn hàm số B lim bằng định nghĩa. x tan x 6 3 3 9 A. B. C. D. 1 4 2 Hướng dẫn giải:
Chọn C. 2 3
2x x 1 2x 3
Câu 25. Tìm giới hạn hàm số C lim bằng định nghĩa. 2 x 1 3x 2 3 3 9 A. B. C. D. 3 2 5 4 2 Hướng dẫn giải:
Chọn D. 3x 1 2
Câu 26. Tìm giới hạn hàm số D lim bằng định nghĩa. 3 x 1 3x 1 2 1 A. B. C. D. 0 6 Hướng dẫn giải:
Chọn D. 2
x 3 khi x 2
Câu 27. Cho hàm số f x
. Chọn kết quả đúng của lim f x : x 1 khi x 2 x2 A. 1 . B. 0 . C. 1. D. Không tồn tại. Hướng dẫn giải:
Chọn C.
Ta có lim f x lim x 2 3 1 x2 x2
lim f x lim x 1 1 x 2 x 2
Vì lim f x lim f x 1 nên lim f x 1. x 2 x 2 x2 2
x ax 1 khi x 2
Câu 28. Tìm a để hàm số sau có giới hạn khi x 2 f (x) . 2
2x x 1 khi x 2 1 A. B. C. D. 1 2 Hướng dẫn giải: Chọn C. Ta có: 2
lim f (x) lim (x ax 2) 2a 6 . 2
lim f ( x) lim (2x x 1) 7 . x 2 x 2 x 2 x 2 1 1
Hàm số có giới hạn khi x 2 lim f (x) lim f (x) 2a 6 7 a . Vậy a là giá trị cần x 2 x 2 2 2 tìm. 2 5
ax 3x 2a 1 khi x 0
Câu 29. Tìm a để hàm số sau có giới hạn tại x 0 f (x) . 2 1 x
x x 2 khi x 0
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 83
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 2 A. B. C. D. 1 2 Hướng dẫn giải:
Chọn C. 2
Ta có lim f (x) 2a 1 1 2 lim f (x) a . x 0 x 0 2 2
5ax 3x 2a 1 khi x 0
Câu 30. Tìm a để hàm số. f (x)
có giới hạn tại x 0 2 1 x
x x 2 khi x 0 2 A. B. C. D. 1 2 Hướng dẫn giải:
Chọn C.
Ta có: lim f (x) lim
ax x a a 2 5 3 2 1 2 1 x0 x0
lim f (x) lim x x x x x 2 1 2 1 2 0 0 2
Vậy 2a 1 1 2 a . 2 2
x ax 1 khi x 1
Câu 31. Tìm a để hàm số. f (x)
có giới hạn khi x 1 . 2
2x x 3a khi x 1 1 A. B. C. D. 1 6 Hướng dẫn giải: Chọn D. Ta có: 2
lim f ( x) lim( x ax 2) a 3 . x 1 x 1 2
lim f (x) lim (2x x 3a) 3a 1 . x 1 x 1
Hàm số có giới hạn khi x 1 lim f (x) lim f (x) x 1 x 1
a 3 3a 1 a 1. Vậy a 1 là giá trị cần tìm.
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 84
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 0
DẠNG 2: TÍNH GIỚI HẠN DẠNG VÔ ĐỊNH 0 P(x) 1. L = lim
với P(x), Q(x) là các đa thức và P(x0) = Q(x0) = 0 x 0 x Q(x)
Phân tích cả tử và mẫu thành nhân tử và rút gọn. Chú ý:
+ Nếu tam thức bậc hai 2
ax bx+c có hai nghiệm x , x thì ta luôn có sự phân tích 1 2 2
ax bx c a(x x )(x x ) . 1 2 + n n n 1 n2 n2 n 1 a b (a ) b (a a b ... ab b ) P(x) 2. L = lim
với P(x0) = Q(x0) = 0 và P(x), Q(x) là các biểu thức chứa căn cùng bậc x 0 x Q(x)
Sử dụng các hằng đẳng thức để nhân lượng liên hợp ở tử và mẫu.
Các lượng liên hợp:
+ ( a b )( a b ) a b 3 3 3 2 3 3 2 a b a + ( )(
ab b ) a b + n n n n 1 n n2 n n 1 ( a b )( a a b ... b ) a b P(x) 3. L = lim
với P(x0) = Q(x0) = 0 và P(x) là biêu thức chứa căn không đồng bậc x 0 x Q(x)
Giả sử: P(x) = m ( ) n ( ) m ( ) n u x v x vôùi u x
v(x ) a . 0 0
Ta phân tích P(x) = m ( ) n u x a a
v(x) .
Trong nhiều trường hợp việc phân tích như trên không đi đến kết quả ta phải phân tích như
sau: n ( ) m ( ) ( n ( ) ( )) (m u x v x u x m x
v(x) m(x)) , trong đó m(x) c . 2 x 2x 1
Câu 1. Chọn kết quả đúng trong các kết quả sau của lim là: 3 x1 2x 2 1 A. . B. 0 . C. . D. . 2
Hướng dẫn giải: Chọn B. 2 2 x 2x 1 x 1 x 1 Cách 1: lim lim lim 0 3 x1 2x 2
x 2 x 1 2 1 x x 1 x 2 2 1 x x 1 2 x 2x 1
Cách 2: Bấm máy tính như sau: + CACL + 9 x 1 10 và so đáp án. 3 2x 2 2 x 2x 1
Cách 3: Dùng chức lim của máy VNCALL 570ES Plus: lim và so đáp án. 3 2x 2 9 x 1 10 3 2 x 3x 2
Câu 2. Tìm giới hạn A lim : 2 x 1 x 4x 3 3 A. B. C. D. 1 2 Hướng dẫn giải:
Chọn C.
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 85
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 3 2 2 x 3x 2
(x 1)(x 2x 2) 2 x 2x 2 3 Ta có: A lim lim lim . 2 x 1 x 1 x 4x 3
(x 1)(x 3) x 1 x 3 2 4 2 x 5x 4
Câu 3. Tìm giới hạn B lim : 3 x2 x 8 1 A. B. C. D. 1 6 Hướng dẫn giải:
Chọn D. 4 2 2 2 x 5x 4
(x 1)( x 4) 2
(x 1)(x 2)(x 2) 2
( x 1)( x 2) Ta có: B lim lim lim lim 1. 3 3 3 2 x2 x2 x 8 x 2
x2 ( x 2)( x 2x 4) 2 x2 x 2x 4 3 4
(1 3x) (1 4x)
Câu 4. Tìm giới hạn C lim : x0 x 1 A. B. C. D. 25 6 Hướng dẫn giải:
Chọn D. 3 4
(1 3x) (1 4x) Ta có: C lim x0 x 3 4 (1 3x) 1 (1 4x) 1 lim lim x0 x0 x x 2 2 3 [
x (1 3x) (1 3x) 1] 4
x(2 4x)[(1 4x) 1] lim lim x0 x0 x x 2 2
lim 3[(1 3x) (1 3x) 1] lim 4(2 4x)[(1 4x) 1] 25 x0 x0 x 3
Câu 5. Cho hàm số f x
. Giá trị đúng của lim f x là: 2 x 9 x 3 A. . . B. 0. . C. 6.. D. .
Hướng dẫn giải: Chọn B x 3 x 32 lim lim . 2 x 3 x3 x 9
x 3 x 3 x 3 lim 0 . x 3 x 3
(1 x)(1 2x)(1 3x) 1
Câu 6. Tìm giới hạn D lim : x0 x 1 A. B. C. D. 6 6 Hướng dẫn giải:
Chọn D. 3 2
(1 x)(1 2x)(1 3x) 1
6x 11x 6x Ta có: D lim lim 6 . x0 x0 x x
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 86
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 n x 1
Câu 7. Tìm giới hạn A lim (m, n * ) : 0 m x x 1 n A. B. C.
D. m n m Hướng dẫn giải:
Chọn C. n 1 n2 (x 1)(x x ... x 1) n 1 n2 x x ... x 1 n Ta có: A lim lim . m 1 m2
x0 (x 1)(x x ... x 1) m 1 m2 x0 x x ... x 1 m n 1 ax 1
Câu 8. Tìm giới hạn B lim (n *
,a 0) : x0 x a n A. B. C. D. 1 n a Hướng dẫn giải: Chọn C.
Cách 1: Nhân liên hợp Ta có: n n 1 n2
( 1 ax 1)( n (1 ax) n (1 ax)
... n 1 ax 1) B lim x0 n 1 n2
x( n (1 ax) n (1 ax)
... n 1 ax 1) a a B lim . x0 n 1 n2 n (1 ) n (1 ) ... n 1 1 n ax ax ax
Cách 2: Đặt ẩn phụ n t 1
Đặt t n 1 ax x
và x 0 t 1 a t 1 t 1 a B a lim a lim . n n 1 1 1 t 1 (t 1)( t n t t
t ... t 1) n n 1 ax 1
Câu 8. Tìm giới hạn A lim
với ab 0 : 0 m x 1 bx 1 am am A. B. C. D. 1 bn bn Hướng dẫn giải: Chọn C.
Áp dụng bài toán trên ta có: n 1 ax 1 x a m am A lim .lim . . 0 0 m x x x 1 bx 1 n b bn 3 4
1 x 1 x 1 x 1
Câu 9. Tìm giới hạn B lim
với 0 . : x0 x A. B. C. B D. B 4 3 2 4 3 2 Hướng dẫn giải:
Chọn C. Ta có: 3 4
1 x 1 x 1 x 1 3 4 3
1 x 1 x ( 1 x 1) 1 x (( 1 x 1) ( 1 x 1)
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 87
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 4 3 1 x 1 1 x 1 1 x 1 3
B lim( 1 x 1 x ) lim 1 x lim x0 x0 x x x0 x 2 2x 5x 2
Câu 10. Tìm giới hạn A lim : 3 x2 x 3x 2 1 A. B. C. D. 1 3 Hướng dẫn giải:
Chọn C.
(x 2)(2x 1) 1 Ta có: A lim 2
x2 (x 2)( x 2x 1) 3 4 x 3x 2
Câu 11. Tìm giới hạn B lim : 3 x 1 x 2x 3 1 A. B. C. D. 1 5 Hướng dẫn giải:
Chọn C. 3 2
(x 1)(x x x 2) 1 Ta có: B lim 2 x 1
(x 1)(x x 3) 5 2x 3 x
Câu 12. Tìm giới hạn C lim : 2
x3 x 4x 3 1 A. B. C. D. 1 3 Hướng dẫn giải:
Chọn C.
(x 3)(x 1) 1 Ta có: C lim x 3
(x 3)(x 1) 2x 3 x 3 3 x 1 1
Câu 13. Tìm giới hạn D lim : 4 x0 2x 1 1 2 A. B. C. D. 1 3 Hướng dẫn giải:
Chọn C. x 3 2 4 4 4
(2x 1) (2x 1) 2x 1 1 2 Ta có: D lim x0 x 2 3 3 x x 3 2 ( 1) 1 1
3 4x 1 x 2
Câu 14. Tìm giới hạn E lim : 4 x7 2x 2 2 8 A. B. C. D. 1 27 Hướng dẫn giải:
Chọn C.
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 88
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 3 3
4x 1 x 2 4x 1 3 x 2 3 Ta có: E lim lim lim A B 4 4 4 x7 x7 x7 2x 2 2 2x 2 2 2x 2 2
2 2x 2 2 2x 2 x 2 4 4 3 4 4 1 3 64 A lim lim 4 x7 x7 2x 2 2 3 4x 2 3 1 3 4x 1 9 27
2x 2 2 2x 2 x 2 4 4 4 2 3 8 B lim lim 4 x7 x7 2x 2 2 2 x 2 3 3 64 8 8
E A B 27 3 27
(2x 1)(3x 1)(4x 1) 1
Câu 15. Tìm giới hạn F lim : x0 x 9 A. B. C. D. 1 2 Hướng dẫn giải:
Chọn C. 3
1 4x 1 6x
Câu 16. Tìm giới hạn M lim : 2 x0 x 1 A. B. C. D. 0 3 Hướng dẫn giải:
Chọn D. 3
4x 1 (2x 1)
1 6x (2x 1) Ta có: M lim lim 0 2 2 x0 x0 x x
m 1 ax n 1 bx
Câu 17. Tìm giới hạn N lim : x0 x a b a b A. B. C. D. m n m n Hướng dẫn giải:
Chọn C. m 1 ax 1 n 1 bx 1 a b Ta có: N lim lim x0 x0 x x m n m 1 n ax 1 bx 1
Câu 18. Tìm giới hạn G lim : x0 x a b a b A. B. C. D. m n m n Hướng dẫn giải:
Chọn D.
m 1 ax n 1 bx 1 m 1 ax 1 b a Ta có: G lim lim x0 x0 x x n m
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 89
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 n m
1 mx 1 nx
Câu 19. Tìm giới hạn V lim : 2 x0 x
mn n m
mn n m A. B. C. D. 2 2 Hướng dẫn giải:
Chọn C.
(1 nx)m (1 mnx)
(1 mx)n (1 mnx) mn(n ) m Ta có: V lim lim . 2 2 x0 x0 x x 2 1 x 3
1 x ...1 n x
Câu 20. Tìm giới hạn K lim : x n 1 x 1 1 1 A. B. C. D. 0 n! Hướng dẫn giải:
Chọn C. 1 1 Ta có: K lim . x 1 3 2 3 n n 1 n! (1
x )( x x 1)...( x ... 1) n n 2
1 x x 2 1 x x
Câu 21. Tìm giới hạn L lim : x0 x A. B. C. 2n D. 0 Hướng dẫn giải:
Chọn C. n n 2 1 x x 1 2
1 x x 1 L lim 2n . n x 0 x 2 1 x x 2 2x 5x 2
Câu 22. Tìm giới hạn A lim : 3 x2 x 8 1 A. B. C. D. 0 4 Hướng dẫn giải:
Chọn C.
(2x 1)( x 2) 1 Ta có: A lim 2
x2 (x 2)(x 2x 4) 4 4 2 x 3x 2
Câu 23. Tìm giới hạn B lim : 3 x 1 x 2x 3 2 A. B. C. D. 0 5 Hướng dẫn giải:
Chọn C. 2 2
(x 1)(x 2) 2 Ta có: B lim 2 x 1
( x 1)( x x 3) 5
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 90
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 2x 3 3
Câu 24. Tìm giới hạn C lim : 2 x 3 x 4x 3 1 A. B. C. D. 0 6 Hướng dẫn giải:
Chọn C. 2(x 3) 1 Ta có: C lim
x3 (x 1)(x 3) 2x 3 3 6 3 x 1 1
Câu 25. Tìm giới hạn D lim : x0 2x 1 1 1 A. B. C. D. 0 3 Hướng dẫn giải:
Chọn C.
x 2x 1 1 1 Ta có: D lim x0 2 3 3 3 2x (x 1) x 1 1
n (2x 1)(3x 1)(4x 1) 1
Câu 26. Tìm giới hạn F lim : x0 x 9 A. B. C. D. 0 n Hướng dẫn giải:
Chọn C. Đặt n y
(2x 1)(3x 1)(4x 1) y 1 khi x 0 n y 1
(2x 1)(3x 1)(4x 1) 1 Và: lim lim 9 x0 x0 x x n y 1 9 Do đó: F lim x x n 1 n2 0 y y ... y 1 n 3
1 4x 1 6x
Câu 27. Tìm giới hạn M lim : x0 1 cos 3x 4 A. B. C. D. 0 9 Hướng dẫn giải:
Chọn C. 3 2
1 4x 1 6x x 2 4 Ta có: M lim . 2. . 2 x0 x 1 cos 3x 9 9
m 1 ax n 1 bx
Câu 28. Tìm giới hạn N lim : x0 1 x 1
2 an bm A. B. C. D. 0 mn
Hướng dẫn giải:
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 91
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 Chọn C.
m 1 ax 1 n 1 bx 1 x a b 2(an bm) Ta có: N lim . .2 . x0 x x 1 x 1 m n mn n m
1 mx 1 nx
Câu 29. Tìm giới hạn V lim : 3 x0
1 2x 1 3x
2 an bm A. B. C.
D. mn n m mn Hướng dẫn giải:
Chọn D. n 1 mx m 2 1 (1 nx) 1 x mn(n ) m Ta có: V lim
.2 mn(n m) . 2 2 3 x0 x x 1 2x 1 3 2 x 1 x 3
1 x ...1 n x
Câu 30. Tìm giới hạn K lim : x n 1 x 1 1 2 1 A. B. C. D. 0 n! Hướng dẫn giải:
Chọn C. 1 1 Ta có: K lim . x 1 3 2 3 n n 1 n! (1
x )( x x 1)...( x ... 1) 3
4x 1 2x 1
Câu 31. Tìm giới hạn A lim : x0 x 4 A. B. C. D. 0 3 Hướng dẫn giải:
Chọn C. 3 4x 1 1 2x 1 1 Ta có: A lim lim x0 x0 x x 4x 1 1 4x 4 Mà: lim lim lim 2 x0 x0 x
x 4x 1 x0 1 4x 1 1 3 2x 1 1 2x 2 lim lim x0 x0 2 x 3 3 3 x
(2x 1) 2x 1 1 2 4 Vậy A 2 . 3 3 4x 5 3
Câu 32. Tìm giới hạn B lim : 3 x 1 5x 3 2 4 2 A. B. C. D. 3 5 Hướng dẫn giải:
Chọn D.
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 92
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 2 3 3 4(x 1) (5x 3) 2 5x 3 4 2 3 3 4 (5x 3) 2 5x 3 4 2 Ta có: B lim lim . x 1
5(x 1) 4x 5 3 x 1 5 4x 5 3 5 4 3
2x 3 2 3x
Câu 33. Tìm giới hạn C lim : x1 x 2 1 4 A. B. C. D. 3 3 Hướng dẫn giải:
Chọn D. 4 3 2x 3 1 3x 2 1 Ta có: C lim lim x1 x1 x 2 1 x 2 1 4 3 2(x 1) 1 1 3(x 1) 1 1 2 1 x 1 x 1 4 lim lim 3 x1 x 1 1 1 (x 1) 1 1 (x 1) 1 1 2 2 x 1 x 1 x x 2
Câu 34. Tìm giới hạn D lim : 3
x2 x 3x 2 4 A. B. C. D. 1 3 Hướng dẫn giải:
Chọn D. 2 x x 2 2 3 2 3 x . x 3x 2 (3x 2) 2 3 2 3 x . x 3x 2 (3x 2) Ta có: D lim lim 1. x2 3
(x 3x 2) x x 2 x2
(x 1) x x 2 3
1 2x 1 3x
Câu 35. Tìm giới hạn A lim : 2 x0 x 1 A. B. C. D. 0 2 Hướng dẫn giải:
Chọn C. 3 t 1 Cách 1: Đặt 3
t 3x 1 x
và x 0 t 1 3 3 3 t 1 t 2 1 t t 3 3 Nên A lim 9 lim 2 2 2 2 t 1 3 t 1
(t 1) (t t 1) t 1 3 3 2 t 3t 2 3lim t 1 3 t 2 2 2 2
(t 1) (t t 1) t 3
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 93
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 2
(t 1) (t 2) 3lim t 1 3 t 2 2 2 2
(t 1) (t t 1) t 3 t 2 1 3lim . t 1 3 2 t 2 2 2
(t t 1) t 3 Cách 2: Ta có: 3
1 2x (1 x)
1 3x (1 x) A lim lim 2 2 x0 x0 x x 1 3 x lim lim x0 x0 2 3 3 2
1 2x 1 x
(1 3x) (1 x) 1 3x (1 x) 1 Do đó: A . 2 3
5 4x 7 6x
Câu 36. Tìm giới hạn B lim : 3 2 x 1
x x x 1 4 A. B. C. D. 1 3 Hướng dẫn giải:
Chọn D. 3
5 4x 7 6x Ta có: B lim x x 2 1 1 x 1
Đặt t x 1. Khi đó: 3 3
5 4x 7 6x
1 4t 1 6t lim lim x x 2 2 1 t 0 1 t 3
1 4t (2t 1)
1 6t (2t 1) lim lim 2 2 x0 t 0 t t 4 8t 12 lim lim 2 . t 0 t 0 2 2 2 3 3
1 4t 2t 1
(1 6t) (2t 1) (1 6t) (2t 1) Do đó: B 1 .
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 94
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
DẠNG 3: TÍNH GIỚI HẠN DẠNG VÔ ĐỊNH Phương pháp: P(x) L = lim
trong đó P(x), Q(x) , dạng này ta còn gọi là dạng vô định .
x Q(x)
với P(x), Q(x) là các đa thức hoặc các biểu thức chứa căn.
– Nếu P(x), Q(x) là các đa thức thì chia cả tử và mẫu cho luỹ thừa cao nhất của x.
– Nếu P(x), Q(x) có chứa căn thì có thể chia cả tử và mẫu cho luỹ thừa cao nhất của x hoặc nhân lượng liên hợp.
Tương tự như cách khử dạng vô định ở dãy số. Ta cần tìm cách đưa về các giới hạn: + 2 lim k x ; 2k 1 lim x () . x x ( x) ( x) k + lim
0 (n 0; k 0) . n x x ( x) k
+ lim f (x) () lim 0 (k 0) . x 0 x
x x0 f (x) 5 Câu 1. lim bằng: x 3x 2 5 A. 0 . B. 1. C. . D. . 3
Hướng dẫn giải: Chọn A. 5 5 Cách 1: lim lim x 0 x 3x 2 x 2 3 x 5
Cách 2: Bấm máy tính như sau: + CACL + 9
x 10 và so đáp án (với máy casio 570 VN Plus) 3x 2 5
Cách 3: Dùng chức lim của máy VNCALL 570ES Plus: lim và so đáp án. 9 3x 2 x 10 4 x 7
Câu 2. Giá trị đúng của lim là: 4
x x 1 A. 1 . B. 1. . C. 7. . D. .
Hướng dẫn giải: Chọn B 7 4 1 4 x 7 lim lim x 1. 4
x x 1 x 1 1 4 x 2 2x 3x 2
Câu 3. Tìm giới hạn C lim : x 2 5x x 1 2 3 A. B. C. D. 0 6
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 95
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
Hướng dẫn giải: 2 2 3 2 x 2 3 Ta có: C lim x 1 6 5 1 2 x 2 2x 1 Câu 4. lim bằng: 2 x 3 x 1 1 A. 2 . B. . C. . D. 2 . 3 3
Hướng dẫn giải: Chọn D. 1 2 2 2x 1 2 Cách 1: lim lim x 2 2 x 3 x x 3 1 2 x 2 2x 1
Cách 2: Bấm máy tính như sau: + CACL + 9
x 10 và so đáp án. 2 3 x 2 2x 1
Cách 3: Dùng chức lim của máy VNCALL 570ES Plus: lim và so đáp án. 2 3 x 9 x 10 2 x 1
Câu 5. Cho hàm số f (x)
. Chọn kết quả đúng của lim f (x) : 4 2 2x x 3 x 1 2 A. . B. . C. 0 . D. . 2 2
Hướng dẫn giải: Chọn C. 1 1 2 x 1 2 4 Cách 1: lim lim x x 0 4 2 x 2x x 3 x 1 3 2 2 4 x x 2 x 1
Cách 2: Bấm máy tính như sau: + CACL + 9
x 10 và so đáp án. 4 2 2x x 3 2 x 1
Cách 3: Dùng chức lim của máy VNCALL 570ES Plus: lim và so đáp án. 4 2 2x x 3 9 x 10 1 3x Câu 6. lim bằng: x 2 2x 3 3 2 2 3 2 2 A. . B. . C. . D. . 2 2 2 2
Hướng dẫn giải: Chọn A.
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 96
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 3 2 1 3x 3 2 Cách 1: lim lim x x 2 2x 3 x 3 2 2 2 x 1 3x
Cách 2: Bấm máy tính như sau: + CACL + 9
x 10 và so đáp án. 2 2x 3 1 3x
Cách 3: Dùng chức lim của máy VNCALL 570ES Plus: lim và so đáp án. 2 9 2x 3 x 1 0 3 4 6 1 x x
Câu 7. Tìm giới hạn D lim : x 3 4 1 x x 4 A. B. C. D. 1 3
Hướng dẫn giải: 2 1 1 3 x 1 6 2 x x Ta có: D lim 1 x 2 1 1 x 1 4 2 x x x 1
Câu 8. Cho hàm số f x x 2
. Chọn kết quả đúng của lim f x : 4 2 x x 1 x 1 A. 0 . B. . C. 1. D. Không tồn tại. 2
Hướng dẫn giải: Chọn A. 1 1 2 x 1 x 1 x 2 2 3 4 lim lim 2 lim lim x x x f x x 0 . 4 2 4 2 x x x x 1 x x x 1 x 1 1 1 2 4 x x 2 x x 3 Câu 9. lim bằng: x 1 2 x 1 1 A. 3 . B. . C. 1. D. . 2
Hướng dẫn giải: Chọn A. 1 3 1 3 1 3 2 x 1 x 1 1 2 2 2 x x 3 x x x x x x lim lim lim lim 3. . x 1 x 1 x 1 2 x 1 2x 1 1 x 1 1 x 2 2 x x 4 x 8x
Câu 10. Chọn kết quả đúng trong các kết quả sau của lim là: 3 2
x x 2x x 2 21 21 24 24 A. . B. . C. . D. . 5 5 5 5
Hướng dẫn giải:
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 97
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 Chọn C. 4 x 8x 4 x 8x lim thành lim 3 2
x x 2x x 2 3 2
x2 x 2x x 2 x x x x 2 2
x 2x 4 x 2 4 x 2x 4 8 24 lim lim lim . 3 2 x
x 2x x 2 x x 2 2 x 1 x 2 2 2 2 x 1 5
Câu 12. Tìm giới hạn 2
E lim ( x x 1 x) : x 1 A. B. C. D. 0 2
Hướng dẫn giải: x 1 1 Ta có: E lim x 2 2
x x 1 x
Câu 13. Tìm giới hạn 2
F lim x( 4x 1 x) : x 4 A. B. C. D. 0 3
Hướng dẫn giải: 1 Ta có: 2
F lim x 4 1 2 x x
Câu 14. Chọn kết quả đúng trong các kết quả sau của 5 3
lim 4x 3x x 1 là: x A. . B. 0 . C. 4 . D. .
Hướng dẫn giải: Chọn A. lim 3 1 1 5 3
4x 3x x 5 1 lim x 4 . . 2 4 5 x x x x x
Câu 15. Chọn kết quả đúng trong các kết quả sau của 4 3 2 lim
x x x x là: x A. . B. 0 . C. 1. D. .
Hướng dẫn giải: Chọn D. 1 1 1 4 3 2 4 lim
x x x x lim x 1 . . 2 3 x x x x x
Câu 16. Tìm giới hạn B x x x : x 2 lim 1 4 A. B. C. D. 0 3
Hướng dẫn giải: 1 1 1 1
Ta có: B lim x x 1
lim x 1 1 2 2 x x x x x x
Câu 17. Tìm giới hạn 2 2
M lim ( x 3x 1 x x 1) : x 4 A. B. C. D. Đáp án khác 3
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 98
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
Hướng dẫn giải: 4x 2 khi x Ta có: M lim x 2 2 2 khi x 3x 1 x x 1 x
Câu 18. Tìm giới hạn N : x 3 3 lim 8x 2x 2x 4 A. B. C. D. 0 3
Hướng dẫn giải: 2x Ta có: N lim 0 x 3 2 3 3 2
3 (8x 2x) 2x 8x 2x 4x
Câu 19. Tìm giới hạn H lim x x x : x 4 4 2 16 3 1 4 2 4 A. B. C. D. 0 3
Hướng dẫn giải: 4 2
16x 3x 1 (4x 2) Ta có: H lim x 4 4 2
16x 3x 1 4x 2 4 2 2
16x 3x 1 (4x 2) lim x 4 4 2
16x 3x 1 4x 2 4 2
16x 3x 1 4x 2 2
16x 3x 3 lim x 4 4 2
16x 3x 1 4x 2 4 2
16x 3x 1 4x 2 Suy ra H 0 .
Câu 20. Tìm giới hạn K x x x x : x 2 2 lim 1 2 1 A. B. C. D. 0 2
Hướng dẫn giải: 2 2 2
2x x 1 2 (x 1)(x x) Ta có: K lim x 2 2
x 1 x x 2x
4(x x x x) 2x x 2 4 3 2 2 1 lim x 2 2 x 1
x x 2x 2 2 2
2 (x 1)(x x) 2x x 1
4(x x x x) 2x x 2 4 3 2 2 1 lim x 2 2 x 1
x x 2x 2 2 2
2 (x 1)(x x) 2x x 1 3 2
8x 7x 2x 1 1 lim x 2 2
x x x x 2 2 2 x
x x x x 2 1 2 2 ( 1)( ) 2 1 2 3x 5x 1
Câu 21. Tìm giới hạn A lim : 2
x 2x x 1
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 99
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 3 A. B. C. D. 0 2
Hướng dẫn giải: 5 1 5 1 2 x (3 ) 3 2 2 3 Ta có: lim x x lim x x A x 1 1 x 1 1 2 2 x (2 ) 2 2 2 x x x x n
a x ... a x a
Câu 22. Tìm giới hạn 0 n 1 B lim
n (a b 0) : m 0 0
x b x ... b x b 0 m 1 m 4 A. B. C. D. Đáp án khác 3
Hướng dẫn giải: a a a n 1 n 1 x (a ... n ) 0 n 1 n Ta có: lim x x x B x b b b m 1 m 1 x (b ... m ) 0 m 1 m x x x a a a 1 n 1 a ... n 0 n 1 n a * Nếu x x x 0
m n B lim . x b b b 1 m 1 m b0 b ... 0 m 1 m x x x a a a 1 n 1 a ... n 0 n 1 n * Nếu lim x x x m n B 0 x b b b mn 1 m 1 x (b ... m ) 0 m 1 m x x x
( Vì tử a , mẫu 0 ). 0 * Nếu m n a a a nm 1 n 1 x (a ... n ) 0 n 1 n
khi a .b 0 0 0 lim x x x B . x b b b 1 m 1 m khi a b 0 0 0 b ... 0 m 1 m x x x 3 3 2
3x 1 2x x 1
Câu 23. Tìm giới hạn A lim : x 4 4 4x 2 3 3 2 A. B. C. D. 0 2
Hướng dẫn giải: 1 1 1 3 x 3 x 2 3 3 2 x x x 3 2 Ta có: A lim . x 2 2 4 x 4 4 x 2
x x 1 2x 1
Câu 24. Tìm giới hạn B lim : x 3 3 2x 2 1
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 100
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 4 A. B. C. D. 0 3
Hướng dẫn giải: 2 1 2 1 1 2 1 x ( 1 ) x( 1 ) 2 2 2 2 x x x x x x B lim x 2 1 2 1 3 3 x( 2 ) 2 3 3 x x x x (do tử , mẫu 3 2 ). 3 4
(2x 1) (x 2)
Câu 25.Tìm giới hạn A lim : 7 x (3 2x) 1 A. B. C. D. 0 16
Hướng dẫn giải: 3 4 1 2 2 1 x x 1 A lim 7 x 3 16 2 x 2
4x 3x 4 2x
Câu 26. Tìm giới hạn B lim : x 2
x x 1 x A. B. C. 2 D. 0
Hướng dẫn giải: 3 4 4 2 2 x x B lim 2 x 1 1 1 x 2 x x 2 2x 3x 2
Câu 27. Tìm giới hạn C lim : x 2 5x x 1 2 3 A. B. C. D. 0 4
Hướng dẫn giải: 2 2 3 2 x 2 3 C lim x 1 4 5 1 2 x 3 4 6 1 x x
Câu 28. Tìm giới hạn D lim : x 3 4 1 x x 4 A. B. C. D. 1 3
Hướng dẫn giải:
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 101
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 1 3 1 6 2 x x D lim 1 x 1 1 1 4 x x
Câu 29. Tìm giới hạn A x x x x : x 2 3 3 lim 1 2 1 4 A. B. C. D. 0 3
Hướng dẫn giải: 1 1 1 1 Ta có: 3
A lim x 1 x 2 2 2 3 x x x x x 1 1 1 1 3 lim x 1 2 2 2 3 x x x x x
Câu 30.Tìm giới hạn C x x x : x 2 lim 4 1 2 1 A. B. C. D. 0 2
Hướng dẫn giải: 1 x 1 1 1 x 1 x 1 Ta có: C lim lim lim x . x 2
4x x 1 2 x x 1 1 x 1 1 2 x 4 2x 4 2 2 x x 2 x x
Câu 31. Tìm giới hạn D x x x x : x 3 3 2 2 lim 1 1 1 A. B. C. D. 0 6 Hướng dẫn giải: Ta có: D 3 3 2
x x x x x x M N x 2 lim 1 lim 1 x 2 x 1 1 M lim x 3 2 2 3 3 2 2 3 3
(x x 1) . x
x x 1 x 1 1 x 1 1 lim lim x N x 2 x x 1 x x 1 1 2 1 1 2 x x 1 1 1 Do đó: B . 3 2 6
Câu 32. Tìm giới hạn A 2 2 lim
x x 1 2 x x x : x 3 A. B. C. D. 0 2
Hướng dẫn giải:
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 102
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
x x 1 x 4(x x) 2 2 2 2 2
Ta có: x x 1 2 x x x 2 2
x x 1 2 x x x 2 2
2x x x 1 1 5x 2x 2 2
x x 1 2 x x x 2x 2
x x 1 x 1 5x 2 2 2 2
x x 1 2 x x x
x x 1 2 x x x 2x(x 1) 2 2
x x 1 2 x x x 2
x x 1 x 1 5x . 2 2
x x 1 2 x x x 2 2 Do đó: lim x A x 1 1 1 1 1 1 2 1 1 1 1 2 2 x x x x x 1 5 1 5 3 lim x x 1 1 1 4 4 2 1 2 1 1 2 x x x
Câu 33.Tìm giới hạn 2 2
B lim x( x 2x 2 x x x) : x 1 A. B. C. D. 0 4
Hướng dẫn giải: 2 2 2
2x 2x 2x x 2x 4x 4x Ta có: 2 2
x 2x 2 x x x 2 2
x 2x 2 x x x 2
x 2x x 1 2x 2 2
x 2x 2 x x x 2x . 2 2 2
( x 2x 2 x x x)( x 2x x 1) 2 2 x Nên B lim x 2 2 2
( x 2x 2 x x x)( x 2x x 1) 2 1 lim . x 2 1 2 1 4 ( 1 2 1 1)( 1 1 ) x x x x n
a x ... a x a
Câu 34. Tìm giới hạn 0 n 1 A lim
n , (a b 0) : m 0 0
x b x ... b x b 0 m 1 m
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 103
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 4 A. B. C. D. Đáp án khác 3
Hướng dẫn giải: a a a n 1 n 1 x (a ... n ) 0 n 1 n Ta có: lim x x x A x b b b m 1 m 1 x (b ... m ) 0 m 1 m x x x a a a 1 n 1 a ... n 0 n 1 n a Nếu x x x 0
m n B lim . x b b b 1 m 1 m b0 b ... 0 m 1 m x x x a a a 1 n 1 a ... n 0 n 1 n Nếu lim x x x m n B 0 x b b b mn 1 m 1 x (b ... m ) 0 m 1 m x x x
( Vì tử a , mẫu 0 ). 0 a a a nm 1 n 1 x (a ... n ) 0 n 1 n
khi a .b 0
Nếu m n , ta có: 0 0 lim x x x B x b b b 1 m 1 m khi a b 0 0 0 b ... 0 m 1 m x x x 2 3 3
4x x 8x x 1
Câu 35. Tìm giới hạn B lim : x 4 4 x 3 4 A. B. C. D. 4 3
Hướng dẫn giải: 1 1 1 1 1 1 3 3 x 4 . x 8 4 8 2 3 2 3 x x x x x x Ta có: B lim lim 4 x 3 x 3 4 4 x 1 1 4 4 x x 2 3 3 4x 2 x 1
Câu 36. Tìm giới hạn C lim : x 2 x 1 x 3 A. B. C. D. 0 2
Hướng dẫn giải: 2 1 2 1 3 3 x 4 x 1 4 1 2 3 2 3 x x x x 3 Ta có: C lim lim x 1 x 1 2 x 1 x 1 1 2 2 x x 2
x x 1 2x 1
Câu 37. Tìm giới hạn D lim : x 3 3
2x x 1 x
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 104
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 4 A. B. C. D. 0 3
Hướng dẫn giải: 2 1 2 1 x 1 2 2 x x x Ta có: D lim . x 2 2 1 1 1 3 x 3 5 6 x x x x 2
Câu 38. Chọn kết quả đúng trong các kết quả sau của 2 lim x cos là: x0 nx A. Không tồn tại. B. 0 . C. 1. D. .
Hướng dẫn giải: Chọn B. 2 2 Cách 1: 2 2 0 cos 1 0 x cos x nx nx 2 Mà 2 lim x 0 nên 2 lim x cos 0 x0 x0 nx 2
Cách 2: Bấm máy tính như sau: Chuyển qua chế độ Rad + 2 x cos + CACL + 9 x 10 + n 10 và nx so
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 105
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
DẠNG 4: GIỚI HẠN MỘ BÊN VÀ CÁC DẠNG VÔ ĐỊNH KHÁC Phương pháp:
1. Giới hạn một bên : Áp dụng định lý giới hạn của một tích và một thương..
2. Dạng – : Giới hạn này thường có chứa căn
Ta thường sử dụng phương pháp nhân lượng liên hợp của tử và mẫu, Sau đó tìm cách biến đổi đưa về dạng . 3. Dạng 0.:
Ta cũng thường sử dụng các phương pháp như các dạng ở trên. 1 2
Câu 1. Chọn kết quả đúng của lim : 2 3 x0 x x A. . B. 0 . C. . D. Không tồn tại.
Hướng dẫn giải: Chọn C. 1 2 x 2 lim lim 2 3 3 x0 x0 x x x
lim x 2 2 0 x 0 Khi 3
x 0 x 0 x 0 x 2 Vậy lim . 3 x0 x 3 2 x x Câu 2. lim bằng: x 1 x 1 1 x A. 1 . B. 0 . C. 1. D. .
Hướng dẫn giải: Chọn C. 2 3 2 x x x x 1 x x 1 x lim lim lim lim 1. . x 1 x 1 x 1 1 x
x 1 x 2 x 1 1
x 11 x 1 x 1 1 x 1 2 x x 1 Câu 3. lim bằng: 2 x 1 x 1 A. –. B. –1. C. 1. D. +.
Hướng dẫn giải: Chọn D. 2 x x 1 lim
vì lim x x và lim x x . 2 2 1 0; 1 0 2 1 1 0 2 x 1 x 1 x 1 x 1 x 3
Câu 4. Giá tri đúng của lim x3 x 3 A. Không tồn tại. B. 0 . C. 1. D. .
Hướng dẫn giải: Chọn A.
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 106
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 x 3 x 3 lim lim 1 x3 x3 x x x 3 x 3 3 3 lim lim x3 x3 x 3 x 3 x 3 x 3 lim lim 1 x3 x3 x 3 x 3
Vậy không tồn tại giới hạn trên.
Câu 5. Tìm giới hạn A 2 lim
x x 1 x : x 1 A. B. C. D. 0 2 Hướng dẫn giải:
Chọn C. 2 2
( x x 1 x)( x x 1 x) Ta có: A lim x 2
x x 1 x 2 2
x x 1 x x 1 1 lim lim . x 2 x 2 2
x x 1 x
x x 1 x
Câu 6. Tìm giới hạn B x x x : x 2 lim 2 4 1 1 A. B. C. D. 0 4 Hướng dẫn giải:
Chọn C. 2 2
(2x 4x x 1)(2x 4x x 1) x 1 1 B lim lim . x 2
2x 4x x 1 x 2 4
2x 4x x 1 1 1
Câu 7. Cho hàm số f (x)
. Chọn kết quả đúng của lim f 3 x : x 1 x 1 x 1 2 2 A. . B. . C. . D. . 3 3
Hướng dẫn giải: Chọn A. 2
x x
lim f x lim 3 x 1 x 1 x 1
lim x x 2 2 x 1 Khi 3
x 1 x 1 x 1 0
Vậy lim f x . x 1
Câu 8. Tìm giới hạn C lim [ n (x a )(x a )...(x a ) x] : 1 2 n x
a a ... a
a a ... a A. B. C. 1 2 n D. 1 2 n n 2n Hướng dẫn giải:
Chọn C.
Đặt y n (x a )(x a )...(x a ) 1 2 n
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 107
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 n y n x n n n 1 n 1 n 1 y x ( y x)( y y x ... x
) y x n 1 n 1 n 1 y y x ... x n y n x
lim ( y x) lim n 1 n2 n 1 x x y y x ... x n y n x n 1 lim x C . n 1 n 1 n 1 x y y x ... x n 1 x n y n x b b b Mà 2 3 lim
lim (a a ... a ... n ) n 1 1 2 n 2 n 1 x x x x x x
a a ... a . 1 2 n k n 1 k y x n 1 n2 n 1 y y x ... x lim
1 k 0,..., n 1 lim n . n 1 x x n 1 x x
a a ... a Vậy 1 2 C n . n
Câu 9. Tìm giới hạn 2
A lim ( x x 1 x) : x 1 A. B. C. D. 0 2 Hướng dẫn giải:
Chọn C. x 1 1 A lim x 2 2
x x 1 x
Câu 10. Tìm giới hạn 2
B lim x( 4x 1 x) : x 1 A. B. C. D. 0 4 Hướng dẫn giải:
Chọn B.
Câu 11. Tìm giới hạn 2 2
C lim ( x x 1 x x 1) : x 1 A. B. C. D. Đáp án khác 4 Hướng dẫn giải:
Chọn D. x lim
x x x x x 2 2 2 1 1 lim 1 x 2 2
x x 1 x x 1 x lim
x x x x . x 2 2 2 1 1 lim 1 x 2 2
x x 1 x x 1
Câu 12. Tìm giới hạn 3 3
D lim ( 8x 2x 2x) : x 1 A. B. C. D. 0 4
Hướng dẫn giải:
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 108
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 Chọn D. 2x D lim 0 x 3 2 3 2 3 3
(8x 2x) 2x (8x 2x) 4x
Câu 13. Tìm giới hạn 4 4 2
E lim ( 16x 3x 1 4x 2) : x 1 A. B. C. D. 0 4 Hướng dẫn giải:
Chọn D. E lim x x x x x x 4 4 16 3 1 2 lim x 2 4 2 2 0
Câu 14. Tìm giới hạn 3 3
F lim (x 1 x ) : x 1 A. B. C. D. 0 4 Hướng dẫn giải:
Chọn D.
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 109
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
DẠNG 5 : GIỚI HẠN LƯỢNG GIÁC Phương pháp:
Ta sử dụng các công thức lượng giác biến đổi về các dạng sau: sin x x tan x x lim lim 1, từ đây suy ra lim lim 1. x0 x0 x sin x x0 x0 x tan x sin u(x) tan u(x)
Nếu lim u(x) 0 lim 1 và lim 1. x 0 x x 0 x u(x) x 0 x u(x) 1 cos ax
Câu 1. Tìm giới hạn A lim : 2 x0 x a A. B. C. D. 0 2 Hướng dẫn giải:
Chọn C. 2 2 ax ax 2 sin sin a a Ta có: 2 2 A lim lim . 2 x0 x0 x 2 ax 2 2
1 sin mx cos mx
Câu 2. Tìm giới hạn A lim :
x0 1 sin nx cos nx m A. B. C. D. 0 n Hướng dẫn giải:
Chọn C. 2 mx mx mx 2 sin 2 sin cos
1 sin mx cos mx Ta có: 2 2 2
1 sin nx cos nx nx nx nx 2 2 sin 2 sin cos 2 2 2 mx nx mx mx sin sin cos m 2 2 2 2 . . n mx nx nx nx sin sin cos 2 2 2 2 mx nx mx mx sin sin cos m 2 2 2 2 m A lim .lim .lim . x0 n mx x0 nx x0 nx nx n sin sin cos 2 2 2 2 1 cos . x cos 2 . x cos 3x
Câu 3. Tìm giới hạn B lim : 2 x0 x A. B. C. 3 D. 0 Hướng dẫn giải: Chọn C. Ta có: 1 cos . x cos 2 . x cos 3x
1 cos x cos x cos 2x(1 cos 3x) cos x(1 cos 2x) 2 x 2 x
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 110
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 cos x 1 cos 3x 1 cos 2x cos . x cos 2x cos x 2 2 2 x x x 1 cos x 1 cos 3x 1 cos 2x B lim lim cos . x cos 2x lim cos x 3 2 2 2 x0 x0 x0 x x x 1 cos 2x
Câu 4.Tìm giới hạn A lim : x0 3x 2 sin 2 A. B. C. 1 D. 0 Hướng dẫn giải:
Chọn D. 3x 2 sin sin x sin x 3 Ta có: 2 2 A lim lim x( ) . lim 0 . x0 3x x0 x0 x 2 3x sin 2 2
cos 2x cos 3x
Câu 5. Tìm giới hạn B lim :
x0 x(sin 3x sin 4x) 5 A. B. C. D. 0 2 Hướng dẫn giải:
Chọn C. 5x x 5x 2 sin sin sin 5 1 5 2 2 2 B lim lim( . ).lim . x0 7x x x0 2 5x x0 7x 2 2 x cos sin cos 2 2 2 2 2 tan 2x
Câu 6. Tìm giới hạn C lim : 3
x0 1 cos 2x A. B. C. 6 D. 0 Hướng dẫn giải:
Chọn C. 2 2 3 3 2 tan 2x
tan 2x(1 cos 2x cos 2x ) C lim lim 3 x0 x0 1 cos 2x 1 cos 2x 2 3 3 2
tan 2x(1 cos 2x cos 2x ) lim 2 x0 2sin x tan 2x x 2 2 3 3 2 2 lim( ) .(
) (1 cos 2x cos 2x). x0 2x sin x C 6 . 2 x
Câu 7. Tìm giới hạn D lim : x0
1 x sin 3x cos 2x 7 A. B. C. D. 0 2 Hướng dẫn giải:
Chọn C.
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 111
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 Ta có: D lim x0
1 x sin 3x cos 2x 2 x
1 x sin 3x cos 2x
1 x sin 3x 1 1 cos 2x Mà : lim lim lim 2 2 2 x0 x0 x0 x x x sin 3x 1 7 3lim( . ) 2 . x0 3x
1 x sin 3x 1 2 7 Vậy: D . 2 sin( m x )
Câu 8.Tìm giới hạn A lim. : 1 sin( n x x ) n A. B. C. D. 0 m Hướng dẫn giải:
Chọn C. sin (1 m x ) sin (1 m x ) (1 n x ) 1 n x A lim lim .lim .lim 1 n 1 m 1 n 1
sin (1 x ) (1 x )
sin (1 x ) 1 m x x x x x n n 1 n2 1 x (1 x)(x x ... 1) n lim lim . m m 1 m2 x 1 x 1 1 x (1 x)(x x ... 1) m
Câu 9. Tìm giới hạn B lim( x) tan x : x 2 2 5 A. B. C. D. 1 2 Hướng dẫn giải:
Chọn D. x sin x Ta có: 2 B lim( x) lim .lim sin x 1 . x 2 cos x x x 2 2 sin( x) 2 2 1
Câu 10. Tìm giới hạn C lim x sin ( 0) : x0 x 5 A. B. C. D. 0 2 Hướng dẫn giải:
Chọn D. 1 Ta có: 0 | x sin
| x . Mà lim x 0 x x0
Nên theo nguyên lí kẹp A 0 . 39
Câu 11.Tìm giới hạn D lim (sin x 1 sin x ) : x 5 A. B. C. D. 0 2
Hướng dẫn giải:
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 112
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 Chọn D.
Trước hết ta có: sin x x x 0 x 1 x x 1 x 1
Ta có: sin x 1 sin x 2sin .cos 2 2 x 1 x 1 Mà lim 0 nên D 0 . x x 1 x
cos 3x cos 4x
Câu 12. Tìm giới hạn A lim :
x0 cos 5x cos 6 x 7 A. B. C. D. 0 11 Hướng dẫn giải:
Chọn C. 7x x sin sin 7 Ta có: 2 2 A lim x0 11x x 11 sin sin 2 2 3 1 1 2 sin 2x
Câu 13. Tìm giới hạn B lim : x0 sin 3x 4 A. B. C. D. 0 9 Hướng dẫn giải:
Chọn C. 2 sin 2x 4 Ta có B lim x0 x 3 2 3 x x 9 sin 3 1 1 2sin 2 (1 2sin 2 ) 2 sin 2x
Câu 14.Tìm giới hạn C lim : 3 4 x0 cos x cos x A. B. C. 9 6 D. 0 Hướng dẫn giải:
Chọn C. 2 sin 2x 2 Ta có: lim x C 96 3 4 x0
cos x 1 1 cos x 2 2 x x 4 sin 2x
Câu 15.Tìm giới hạn D lim : 4 x0 sin 3x 16 A. B. C. D. 0 81 Hướng dẫn giải:
Chọn C. 1 sin( cos x)
Câu 16.Tìm giới hạn 2 E lim : x0 sin(tan x)
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 113
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 5 A. B. C. D. 0 2 Hướng dẫn giải:
Chọn D. 1 sin cos x 2 tan lim x E 0 x0 sin(tan x) tan x
3sin x 2 cos x
Câu 17. Tìm giới hạn F lim : x x 1 x 5 A. B. C. D. 0 2 Hướng dẫn giải:
Chọn D.
3sin x 2 cos x 1 Ta có: 0 0 khi x x 1 x x 1 x Vậy F 0 .
m cos ax m cos bx
Câu 18. Tìm giới hạn H lim : 2 x0 sin x b a A. B. C. D. 0 2n 2m Hướng dẫn giải:
Chọn C.
m cos ax 1 1 n cos bx 2 2 b a Ta có: lim x x H 2 x0 sin x 2n 2m 2 x 1 n cos ax
Câu 19.Tìm giới hạn M lim : 2 x0 x a A. B. C. D. 0 2n Hướng dẫn giải:
Chọn C. 1 cos ax
Ta có: 1 n cos ax n n 2 n n 1
1 cos ax ( cos ax) ... ( cos ax ) 1 cos x a 1 a 1 a M lim lim . . 2 n n 2 n n 1 x 0 x 0 x
1 cos ax ( cos ax) ... ( cos ax ) 2 n 2n
cos 3x cos 4x
Câu 20.Tìm giới hạn A lim :
x0 cos 5x cos 6 x 7 A. B. C. D. 0 11
Hướng dẫn giải:
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 114
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 Chọn C. 7x x sin sin 7 Ta có: 2 2 A lim x0 11x x 11 sin sin 2 2 3 1 1 2 sin 2x
Câu 21.Tìm giới hạn B lim : x0 sin 3x 4 A. B. C. D. 0 9 Hướng dẫn giải:
Chọn C. 2 sin 2x 4 Ta có B lim x0 x 3 2 3 x x 9 sin 3 1 1 2sin 2 (1 2sin 2 ) 2 sin 2x
Câu 22. Tìm giới hạn C lim : 3 4 x0 cos x cos x A. B. C. 9 6 D. 0 Hướng dẫn giải:
Chọn C. 2 sin 2x 2 Ta có: lim x C 96 3 4 x0
cos x 1 1 cos x 2 2 x x 4 sin 2x
Câu 23. Tìm giới hạn D lim : 4 x0 sin 3x 16 A. B. C. D. 0 81 Hướng dẫn giải:
Chọn C. 4 4
sin 2x 3x 16 16 Ta có: D lim . .
x0 2x sin 3x 81 81 1 sin( cos x)
Câu 24. Tìm giới hạn 2 E lim : x0 sin(tan x) A. B. C. 1 D. 0 Hướng dẫn giải:
Chọn D. 1 sin cos x 2 sin(tan x) Ta có: tan lim x E Mà lim 1; x0 sin(tan x) x0 tan x tan x
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 115
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 2 x sin 2 2 2sin 2 1 sin cos x 1 cos (1 cos x) 2 2 lim lim lim x0 x0 x0 tan x tan x tan x 2 x sin 2 2 sin 2 2 x sin x 2 lim . . x 0 x0 4 x x 2 2 tan x sin ( ) 2 2 2 Do đó: E 0 .
3sin x 2 cos x
Câu 25.Tìm giới hạn F lim : x x 1 x 5 A. B. C. D. 0 2 Hướng dẫn giải:
Chọn D.
3sin x 2 cos x 1 Ta có: 0 0 khi x x 1 x x 1 x Vậy F 0 .
3 1 3x 1 2x
Câu 26. Tìm giới hạn M lim : x0 1 cos 2x 1 A. B. C. D. 0 4 Hướng dẫn giải:
Chọn C.
3 3x 1 2x 1 1 2 1 Ta có: x 2 M lim . x0 1 cos 2x 2 4 2 x 2
3x 5sin 2x cos x Câu 27. lim bằng: 2 x x 2 A. . B. 0 . C. 3 . D. .
Hướng dẫn giải: Chọn B. 2 2
3x 5sin 2x cos x 3x 5sin 2x cos x lim lim lim lim 2 2 2 2 x x 2
x x 2 x x 2
x x 2 3 3x lim lim x A 0 1 2 x x 2 x 2 1 2 x
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 116
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 5 5sin 2x 5 lim 0 A lim lim 0 A 0 2 2 2 2 2
x x 2 x x 2
x x 2 2 0 cos x 1 lim 0 A lim lim 0 A 0 2 3 2 2 3
x x 2
x x 2
x x 2 2
3x 5sin 2x cos x Vậy lim 0 . 2 x x 2
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 117
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 HÀM SỐ LIÊN TỤC
A – LÝ THUYẾT VÀ PHƯƠNG PHÁP
1. Hàm số liên tục tại một điểm: y = f(x) liên tục tại x
lim f (x) f (x ) 0 0 x 0 x
Để xét tính liên tục của hàm số y = f(x) tại điểm x0 ta thực hiện các bước: B1: Tính f(x0).
B2: Tính lim f ( x) (trong nhiều trường hợp ta cần tính lim f (x) , lim f (x) ) x 0 x xx xx 0 0
B3: So sánh lim f ( x) với f(x0) và rút ra kết luận. x 0 x
2. Hàm số liên tục trên một khoảng: y = f(x) liên tục tại mọi điểm thuộc khoảng đó.
3. Hàm số liên tục trên một đoạn [a; b]: y = f(x) liên tục trên (a; b) và
lim f (x) f (a), lim f (x) f (b) xa xb
Hàm số đa thức liên tục trên R.
Hàm số phân thức, các hàm số lượng giác liên tục trên từng khoảng xác định của chúng.
Giả sử y = f(x), y = g(x) liên tục tại điểm x0. Khi đó:
Các hàm số y = f(x) + g(x), y = f(x) – g(x), y = f(x).g(x) liên tục tại x0. f ( x) Hàm số y =
liên tục tại x0 nếu g(x0) 0. g( x)
4. Nếu y = f(x) liên tục trên [a; b] và f(a). f(b)< 0 thì tồn tại ít nhất một số c (a; b): f(c) = 0.
Nói cách khác: Nếu y = f(x) liên tục trên [a; b] và f(a). f(b)< 0 thì phương trình f(x) = 0 có ít nhất một nghiệm c (a; b).
Mở rộng: Nếu y = f(x) liên tục trên [a; b]. Đặt m = min f (x) , M = max f (x) . Khi đó với mọi T (m; M) luôn tồn a;b a;b
tại ít nhất một số c (a; b): f(c) = T. B – BÀI TẬP
DẠNG 1: TÍNH LIÊN TỤC CỦA HÀM SỐ TẠI MỘT ĐIỂM Phương pháp:
Tìm giới hạn của hàm số y f (x) khi x x và tính f (x ) 0 0
Nếu tồn tại lim f (x) thì ta so sánh lim f (x) với f (x ) . 0 x 0 x x 0 x Chú ý:
1. Nếu hàm số liên tục tại x thì trước hết hàm số phải xác định tại điểm đó 0
2. lim f (x) l lim f (x) lim f (x) l . x 0 x xx xx 0 0
f (x) khi x x0
3. Hàm số y
liên tục tại x x lim f (x) k . k khi x 0 x x 0 x 0
f (x) khi x x 1 0
4. Hàm số f (x)
liên tục tại điểm x x khi và chỉ khi
f (x) khi x 0 x 2 0
lim f (x) lim f (x) f (x ) . 1 2 1 0 xx x x 0 0 Chú ý:
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 118
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
f (x) khi x x 0 Hàm số y
liên tục tại x x khi và chỉ khi k khi x 0 x0
lim f (x) k . x 0 x
f (x) khi x x 0 Hàm số y
liên tục tại x x khi và chỉ khi
g(x) khi x 0 x0
lim f (x) lim g(x) . xx xx 0 0 2 x 1
Câu 1. Cho hàm số f x và f 2
2 m 2 với x 2 . Giá trị của m để f x liên tục tại x 2 là: x 1 A. 3 . B. 3 . C. 3 . D. 3
Hướng dẫn giải: Chọn C
Hàm số liên tục tại x 2 lim f x f 2 . x2 2 x 1 Ta có lim lim x 1 1. x2 x2 x 1 m 3 Vậy 2 m 2 1 . m 3
Câu 2. Cho hàm số f x 2
x 4 . Chọn câu đúng trong các câu sau:
(I) f x liên tục tại x 2 .
(II) f x gián đoạn tại x 2 .
(III) f x liên tục trên đoạn 2 ; 2.
A. Chỉ I và III .
B. Chỉ I .
C. Chỉ II . D. Chỉ II và III
Hướng dẫn giải: Chọn B.
Ta có: D ; 2 2; . lim f x 2
lim x 4 0 . x2 x2 f 2 0 .
Vậy hàm số liên tục tại x 2 . 2 x 1 x 3; x 2
Câu 3. Cho hàm số f x 3
x x 6
. Tìm b để f x liên tục tại x 3 . b 3 x 3; b 2 3 2 3 A. 3 . B. 3 . C. . D. . 3 3
Hướng dẫn giải: Chọn D.
Hàm số liên tục tại x 3 lim f x f 3 . x 3
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 119
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 2 x 1 1 lim . 3 x3 x x 6 3
f 3 b 3 . 1 1 2 Vậy: b 3 b 3 . 3 3 3 x 1
Câu 4. Cho hàm số f x
. Tìm khẳng định đúng trong các khẳng định sau: x 1
I f x gián đoạn tại x 1.
II f x liên tục tại x 1. 1
III lim f x x 1 2
A. Chỉ I .
B. Chỉ I .
C. Chỉ I và III . D. Chỉ II và III .
Hướng dẫn giải: Chọn C. D \ 1 x 1 1 1 lim lim x 1 x 1 x 1 x 1 2
Hàm số không xác định tại x 1. Nên hàm số gián đoạn tại x 1. . 2x 8 2 x 2
Câu 5. Cho hàm số f x x 2
. Tìm khẳng định đúng trong các khẳng định sau: 0 x 2
I lim f x 0 . x 2
II f x liên tục tại x 2.
III f x gián đoạn tại x 2.
A. Chỉ I và III .
B. Chỉ I và II .
C. Chỉ I .
D. Chỉ I
Hướng dẫn giải: Chọn B. 2x 8 2 2x 8 4 2 x 2 lim lim lim 0 . x 2 x 2 x 2
2x 8 2 x 2 x 2 2x 8 2
Vậy lim f x f 2
nên hàm số liên tục tại x 2.. x 2 2 4 x 2 x 2
Câu 6. Cho hàm số f x
. Tìm khẳng định đúng trong các khẳng định sau:. 1 x 2
I f x không xác định tại x 3.
II f x liên tục tại x 2.
III lim f x 2 x2
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 120
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
A. Chỉ I .
B. Chỉ I và II .
C. Chỉ I và III .
D. Cả I ; II ; III đều sai.
Hướng dẫn giải: Chọn B. D 2; 2
f x không xác định tại x 3. 2 lim
4 x 0 ; f 2
0 . Vậy hàm số liên tục tại x 2. x2 lim f x 2 lim
4 x 0 ; lim f x 1. Vậy không tồn tại giới hạn của hàm số khi x 2.. x 2 x 2 x 2 sin 5x x 0
Câu 7. Cho hàm số f x 5x
. Tìm a để f x liên tục tại x 0. a 2 x 0 A. 1. B. 1. C. 2 . D. 2.
Hướng dẫn giải: Chọn B. sin 5x Ta có: lim
1; f 0 a 2 . x0 5x
Vậy để hàm số liên tục tại x 0 thì a 2 1 a 1 . x 2 1 , x 1
Câu 8.Cho hàm số f x 2
x 3 , x 1 . Tìm k để f x gián đoạn tại x 1. 2 k , x 1 A. k 2 . B. k 2 . C. k 2 . D. k 1 .
Hướng dẫn giải: Chọn A. TXĐ: D .
Với x 1 ta có f 2 1 k Với x 1 ta có
lim f x lim x
; lim f x lim x 2 1
4 suy ra lim f x 4 . 2 3 4 x 1 x 1 x 1 x 1 x 1
Vậy để hàm số gián đoạn tại x 1 khi lim f x 2 k 2
k 4 k 2 . x 1 x 2 khi x 4 Câu x 4
9.Cho hàm số f (x)
. Khẳng định nào sau đây đúng nhất 1 khi x 4 4
A. Hàm số liên tục tại x 4
B. Hàm số liên tục tại mọi điểm trên tập xác định nhưng gián đoạn tại x 4
C. Hàm số không liên tục tại x 4
D. Tất cả đều sai Hướng dẫn giải:
Chọn C.
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 121
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 x 2 1 1
Ta có : lim f ( x) lim lim f (4) x4 x4 x4 x 4 x 2 4
Hàm số liên tục tại điểm x 4 . 2
x 3x 2 2 khi x 1
Câu 10. Cho hàm số f (x) x 1
. Khẳng định nào sau đây đúng nhất 2 3x x 1 khi x 1
A. Hàm số liên tục tại x 1
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục tại x 1
D. Tất cả đều sai Hướng dẫn giải:
Chọn C.
(x 1)(x 2)
lim f (x) lim 2 2 x 1 x 1 x 1
lim f (x) lim x x f x 2 3 1 3 lim ( ) x 1 x 1 x 1
Hàm số không liên tục tại x 1 . x cos khi x 1
Câu 11. Cho hàm số 3. f x 2
. Khẳng định nào sau đây đúng nhất x 1 khi x 1
A. Hàm số liên tục tại tại x 1 và x 1 .
B. Hàm số liên tục tại x 1 , không liên tục tại điểm x 1 .
C. Hàm số không liên tục tại tại x 1 và x 1 .
D. Tất cả đều sai Hướng dẫn giải: Chọn B.
Hàm số liên tục tại x 1 , không liên tục tại điểm x 1 . 2x 1 1
Câu 12. Chọn giá trị f (0) để các hàm số f (x)
liên tục tại điểm x 0 . x(x 1) A. 1 B. 2 C. 3 D. 4 Hướng dẫn giải:
Chọn A. 2x 1 1 2x
Ta có : lim f (x) lim lim 1 x0 x0 x0 x(x 1)
x(x 1) 2x 1 1
Vậy ta chọn f (0) 1 3 2x 8 2
Câu 13. Chọn giá trị f (0) để các hàm số f (x)
liên tục tại điểm x 0 . 3x 4 2 2 1 A. 1 B. 2 C. D. 9 9 Hướng dẫn giải:
Chọn C.
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 122
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 2 3x 4 2 2
Ta có : lim f (x) lim x0 x0 2 3 3 x x 9 3 (2 8) 2. 2 8 4 2
Vậy ta chọn f (0) . 9
x x 2 khi x 1
Câu 14. Cho hàm số f (x) x 1
. Khẳng định nào sau đây đúng nhất 2x 3 khi x 1
A. Hàm số liên tục tại tại tại x 1 0
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục tại tại x 1 . 0
D. Tất cả đều sai Hướng dẫn giải:
Chọn C.
Ta có: f (1) 1 và lim f (x) lim 2x 3 1 x 1 x 1 2 x x 2 x x 2
lim f (x) lim lim x 1 x 1 x 1 x 1
(x 1)(x x 2) x 2 3 lim x 1 x x 2 2
Suy ra lim f (x) lim f ( x) x 1 x 1
Vậy hàm số không liên tục tại x 1 . 0 3
x 1 x 1 khi x 0
Câu 15. Cho hàm số 3. f (x) x
. Khẳng định nào sau đây đúng nhất 2 khi x 0
A. Hàm số liên tục tại x 0 0
B. Hàm số liên tục tại mọi điểm như gián đoạn tại x 0 0
C. Hàm số không liên tục tại x 0 0
D. Tất cả đều sai Hướng dẫn giải: Chọn C.
Ta có: f (0) 2 3 3 x 1 x 1 1 x 1
lim f ( x) lim lim 1 x0 x0 x0 x x 1 lim 1 2 f (0) 3 x0
1 x 1 x 1
Vậy hàm số liên tục tại x 0 .
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 123
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 3 x 1 khi x 1 Câu x 1
16. Cho hàm số f (x)
. Khẳng định nào sau đây đúng nhất 1 khi x 1 3
A. Hàm số liên tục tại x 1
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục tại tại x 1
D. Tất cả đều sai Hướng dẫn giải:
Chọn C. 3 x 1 1 1
Ta có : lim f (x) lim lim f (1) x 1 x4 x4 3 2 3 x 1 3 x x 1
Hàm số liên tục tại điểm x 1 . 2
x x 2 2x khi x 2
Câu 17. Cho hàm số f (x) x 2 2 x x 3 khi x 2
. Khẳng định nào sau đây đúng nhất
A. Hàm số liên tục tại x 2 0
B. Hàm số liên tục tại mọi điẻm
C. Hàm số không liên tục tại x 2 0
D. Tất cả đều sai Hướng dẫn giải:
Chọn C.
(x 1)(x 2)
Ta có : lim f (x) lim 2x 4 x 2 x 2 x 2
lim f (x) lim x x f x 2 3 5 lim ( ) x 2 x 2 x 2
Hàm số không liên tục tại x 2 . 0
x 2a khi x 0
Câu 18. Tìm a để các hàm số f x
liên tục tại x 0 2
x x 1 khi x 0 1 1 A. B. C. 0 D. 1 2 4 Hướng dẫn giải:
Chọn A. Ta có : 2
lim f (x) lim (x x 1) 1 x 0 x 0
lim f (x) lim (x 2a) 2a x 0 x 0 1
Suy ra hàm số liên tục tại x 0 a . 2 4x 1 1 khi x 0
Câu 19. Tìm a để các hàm số 2
f (x) ax (2a 1)x
liên tục tại x 0 3 khi x 0
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 124
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 1 1 A. B. C. D. 1 2 4 6 Hướng dẫn giải:
Chọn C. 4x 1 1
Ta có : lim f (x) lim x0
x0 x ax 2a 1 4 2 lim
x0 ax a
x 2a 1 2 1 4 1 1 2 1
Hàm số liên tục tại x 0 3 a . 2a 1 6
3x 1 2 khi x 1 2 x 1
Câu 20.Tìm a để các hàm số f (x)
liên tục tại x 1 2 a(x 2) khi x 1 x 3 1 1 3 A. B. C. D. 1 2 4 4 Hướng dẫn giải:
Chọn C. 3x 1 2 3
Ta có : lim f (x) lim 2 x 1 x 1 x 1 8 2 a( x 2) a
lim f ( x) lim x 1 x 1 x 3 2 a 3 3
Suy ra hàm số liên tục tại x 1 a . 2 8 4
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 125
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
DẠNG 2: TÍNH LIÊN TỤC CỦA HÀM SỐ TRÊN TẬP XÁC ĐỊNH Phương pháp:
+ Sử dụng các định lí về tính liên tục của hàm đa thức, lương giác, phân thức hữu tỉ …
+ Nếu hàm số cho dưới dạng nhiều công thức thì ta xét tính liên tục trên mỗi khoảng đã chia và tại các điểm chia của các khoảng đó.
Câu 1. Tìm khẳng định đúng trong các khẳng định sau: 1
I f x liên tục trên . 2 x 1 sin x
II f x
có giới hạn khi x 0. x
III f x 2
9 x liên tục trên đoạn 3 ; 3 .
A. Chỉ I và II .
B. Chỉ II và III .
C. Chỉ II .
D. Chỉ III .
Hướng dẫn giải: Chọn B.
Dễ thấy kđ (I) sai, Kđ (II) là lí thuyết.
Hàm số: f x 2
9 x liên tục trên khoảng 3
;3 . Liên tục phải tại 3 và liên tục trái tại 3 . Nên f x 2
9 x liên tục trên đoạn 3 ; 3 .
Câu 2. Tìm khẳng định đúng trong các khẳng định sau: x 1
I . f x
liên tục với mọi x 1 . x 1
II . f x sin x liên tục trên . x
III . f x
liên tục tại x 1 . x
A. Chỉ I đúng.
B. Chỉ I và II .
C. Chỉ I và III .
D. Chỉ II và III .
Hướng dẫn giải: Chọn D.
Ta có II đúng vì hàm số lượng giác liên tục trên từng khoảng của tập xác định. x , khi x 0 x x
Ta có III đúng vì f x . x x , khi x 0 x
Khi đó lim f x lim f x f 1 1. x 1 x 1 x
Vậy hàm số y f x
liên tục tại x 1 . x 2
x 3 , x 3
Câu 3. Cho hàm số f x x 3
. Tìm khẳng định đúng trong các khẳng định sau: 2 3 , x 3
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 126
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
I . f x liên tục tại x 3 .
II . f x gián đoạn tại x 3 .
III . f x liên tục trên .
A. Chỉ I và II .
B. Chỉ II và III .
C. Chỉ I và III .
D. Cả I , II , III đều đúng.
Hướng dẫn giải: Chọn C. 2 x 3 Với x
3 ta có hàm số f x
liên tục trên khoảng ;
3 và 3; , 1 . x 3 2 x 3 Với x
3 ta có f 3 2 3 và lim f x lim
2 3 f 3 nên hàm số liên tục tại x 3 x 3 x 3 x 3 , 2 Từ
1 và 2 ta có hàm số liên tục trên .
Câu 4. Tìm khẳng định đúng trong các khẳng định sau:
I . f x 5 2
x – x 1 liên tục trên . 1
II . f x
liên tục trên khoảng –1; 1 . 2 x 1
III . f x x 2 liên tục trên đoạn 2; .
A. Chỉ I đúng.
B. Chỉ I và II .
C. Chỉ II và III .
D. Chỉ I và III .
Hướng dẫn giải: Chọn D.
Ta có I đúng vì f x 5 2
x x 1 là hàm đa thức nên liên tục trên .
Ta có III đúng vì f x x 2 liên tục trên 2; và lim f x f 2 0 nên hàm số liên tục trên x 2 2; .
3 9 x , 0 x 9 x
Câu 5. Cho hàm số f x m , x 0
. Tìm m để f x liên tục trên 0; là. 3 , x 9 x 1 1 1 A. . B. . C. . D. 1. 3 2 6
Hướng dẫn giải: Chọn C.
TXĐ: D 0; .
Với x 0 ta có f 0 m . 3 9 x 1 1
Ta có lim f x lim lim . x 0 x 0 x x 0 3 9 x 6
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 127
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1
Vậy để hàm số liên tục trên 0; khi lim f x m m . x 0 6 2 x 1
Câu 6. Cho hàm số f (x)
.Khi đó hàm số y f x liên tục trên các khoảng nào sau đây? 2 x 5x 6 A. 3 ; 2 . B. 2 ; . C. ; 3 . D. 2;3 .
Hướng dẫn giải: Chọn B. x 3 Hàm số có nghĩa khi 2
x 5x 6 0 . x 2 2 x 1
Vậy theo định lí ta có hàm số f x
liên tục trên khoảng ; 3 ; 3 ; 2 và 2 ; . 2 x 5x 6 2
x 5x 6 khi x 2
Câu 7. Cho hàm số f x 3 2x 16
. Khẳng định nào sau đây đúng nhất. 2 x khi x 2
A. Hàm số liên tục trên
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục trên 2 :
D. Hàm số gián đoạn tại điểm x 2 . Hướng dẫn giải:
Chọn D.
TXĐ : D \ 2 2 x 5x 6
Với x 2 f (x) hàm số liên tục 3 2x 16
Với x 2 f (x) 2 x hàm số liên tục
Tại x 2 ta có : f (2) 0
lim f (x) lim 2 x 0 ; x 2 x 2
(x 2)(x 3) 1
lim f (x) lim lim f (x) 2 x 2 x 2 x 2
2( x 2)( x 2x 4) 24
Hàm số không liên tục tại x 2 . 3 x 1 khi x 1 x 1
Câu 8. Cho hàm số f (x)
. Khẳng định nào sau đây đúng nhất. 3
1 x 2 khi x 1 x 2
A. Hàm số liên tục trên
B. Hàm số không liên tục trên
C. Hàm số không liên tục trên 1:
D. Hàm số gián đoạn tại các điểm x 1 . Hướng dẫn giải: Chọn A.
Hàm số xác định với mọi x thuộc
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 128
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 x 2
Với x 1 f (x) hàm số liên tục x 2 3 x 1
Với x 1 f (x) hàm số liên tục x 1 2
Tại x 1 ta có : f (1) 3 3 x 1
(x 1)( x 1) 2
lim f (x) lim lim ; 3 2 x 1 x 1 x 1 3 x 1 3
(x 1)( x x 1) 1 x 2 2
lim f (x) lim
lim f (x) f (1) x 2 x 1 x 1 x 2 3
Hàm số liên tục tại x 1 .
Vậy hàm số liên tục trên . tan x
, x 0 x
k , k
Câu 9. Cho hàm số f x x 2
. Hàm số y f x liên tục trên các khoảng 0 , x 0 nào sau đây? A. 0; . B. ; . C. ; . D. ; . 2 4 4 4
Hướng dẫn giải: Chọn A. TXĐ: D \ k , k . 2
Với x 0 ta có f 0 0 . tan x sin x 1
lim f x lim lim .lim
1 hay lim f x f 0 . x0 x0 x x0 x0 x cos x x0
Vậy hàm số gián đoạn tại x 0 . 2 2 a x
, x 2, a
Câu 10. Cho hàm số f x
. Giá trị của a để f x liên tục trên là: 2 a 2 x , x 2 A. 1 và 2 . B. 1 và –1 . C. –1 và 2 . D. 1 và –2 .
Hướng dẫn giải: Chọn D. TXĐ: D . Với x
2 ta có hàm số f x 2 2
a x liên tục trên khoảng 2; . Với x
2 ta có hàm số f x a 2 2
x liên tục trên khoảng ; 2 . Với x 2 ta có f 2 2 2a .
lim f x lim 2 a 2
x 2 2 a ; lim f x 2 2 2
lim a x 2a . x 2 x 2 x 2 x 2
Để hàm số liên tục tại x
2 lim f x lim f x f 2 2
2a 2 2 a 2
a a 2 0 x 2 x 2 a 1 . a 2
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 129
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
Vậy a 1 hoặc a 2 thì hàm số liên tục trên . 2 x , x 1 3 2x
Câu 11. Cho hàm số f x
, 0 x 1 . Tìm khẳng định đúng trong các khẳng định sau: 1 x
x sin x , x 0
A. f x liên tục trên .
B. f x liên tục trên \ 0 .
C. f x liên tục trên \ 1 .
D. f x liên tục trên \ 0 ;1 .
Hướng dẫn giải: Chọn A. TXĐ: TXĐ: D .
Với x 1 ta có hàm số f x 2
x liên tục trên khoảng 1; . 1 3 2x
Với 0 x 1 ta có hàm số f x
liên tục trên khoảng 0 ;1 . 2 1 x
Với x 0 ta có f x x sin x liên tục trên khoảng ; 0 . 3 3 2x
Với x 1 ta có f
1 1; lim f x 2
lim x 1; lim f x lim 1 x 1 x 1 x 1 x 1 1 x
Suy ra lim f x 1 f 1 . x 1
Vậy hàm số liên tục tại x 1 . 3 2x sin x
Với x 0 ta có f 0 0 ; lim f x lim
0 ; lim f x lim . x sin x 2 lim x . lim 0 x 0 x 0 1 x x 0 x 0 x 0 x 0 x
suy ra lim f x 0 f 0 . x 0
Vậy hàm số liên tục tại x 0 . 4 Từ
1 , 2 , 3 và 4 suy ra hàm số liên tục trên . x 2
Câu 12. Cho hàm số f (x)
. Khẳng định nào sau đây đúng nhất. 2 x x 6
A. Hàm số liên tục trên
B. TXĐ : D \ 3;
2 .Ta có hàm số liên tục tại mọi x D và hàm số gián đoạn tại x 2, x 3
C. Hàm số liên tục tại x 2, x 3
D. Tất cả đều sai Hướng dẫn giải: Chọn B.
TXĐ : D \ 3; 2 .
Ta có hàm số liên tục tại mọi x D và hàm số gián đoạn tại x 2, x 3 Câu 13. Cho hàm số 2
f (x) 3x 1 . Khẳng định nào sau đây đúng nhất.
A. Hàm số liên tục trên 1 1
B. Hàm số liên tục tại mọi điểm x ; ; 3 3
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 130
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 1 1
C. TXĐ : D ; ; 2 2 1 1
D. Hàm số liên tục tại mọi điểm x ; . 3 3 Hướng dẫn giải:
Chọn B. 1 1 TXĐ : D ; ; 3 3 1 1
Ta có hàm số liên tục tại mọi điểm x ; ; 3 3 1 1 lim
f (x) 0 f
hàm số liên tục trái tại x 1 3 x 3 3 1 1 lim
f (x) 0 f
hàm số liên tục phải tại x 1 3 x 3 3 1 1
Hàm số gián đoạn tại mọi điểm x ; . 3 3
Câu 14. Cho hàm số f (x) 2 sin x 3 tan 2x . Khẳng định nào sau đây đúng nhất.
A. Hàm số liên tục trên B. Hàm số liên tục tại mọi điểm
C. TXĐ : D \ k , k
D. Hàm số gián đoạn tại các điểm 2 2 x k , k 4 2 Hướng dẫn giải:
Chọn D. TXĐ : D \ k , k 4 2
Ta có hàm số liên tục tại mọi điểm thuộc D và gián đoạn tại các điểm x k , k . 4 2 2
x 3x 2 khi x 1
Câu 15. Cho hàm số f x x 1
. Khẳng định nào sau đây đúng nhất. a khi x 1
A. Hàm số liên tục trên
B. Hàm số không liên tục trên
C. Hàm số không liên tục trên 1:
D. Hàm số gián đoạn tại các điểm x 1 . Hướng dẫn giải: Chọn D.
Hàm số liên tục tại mọi điểm x 1 và gián đoạn tại x 1
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 131
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 2x 1 1 khi x 0
Câu 16. Cho hàm số f x x
. Khẳng định nào sau đây đúng nhất. 0 khi x 0
A. Hàm số liên tục trên
B. Hàm số không liên tục trên
C. Hàm số không liên tục trên 0;
D. Hàm số gián đoạn tại các điểm x 0 . Hướng dẫn giải: Chọn D.
Hàm số liên tục tại mọi điểm x 0 và gián đoạn tại x 0
2x 1 khi x 0 Câu 17. Cho hàm số 3
f (x) (x 1) khi 0 x 2 . Khẳng định nào sau đây đúng nhất.
x 1 khi x 2
A. Hàm số liên tục trên
B. Hàm số không liên tục trên
C. Hàm số không liên tục trên 2;
D. Hàm số gián đoạn tại các điểm x 2 . Hướng dẫn giải: Chọn D.
Hàm số liên tục tại mọi điểm x 2 và gián đoạn tại x 2 2
2x x 1 khi x 1
Câu 18. Cho hàm số f (x)
. Khẳng định nào sau đây đúng nhất. 3 x 1 khi x 1
A. Hàm số liên tục trên
B. Hàm số không liên tục trên
C. Hàm số không liên tục trên 2;
D. Hàm số gián đoạn tại các điểm x 1 . Hướng dẫn giải: Chọn D.
Hàm số liên tục tại mọi điểm x 1
và gián đoạn tại x 1 . sin x khi x 2
Câu 19. Xác định a, b để các hàm số f x liên tục trên
ax b khi x 2 2 2 1 2 a a a a A. B. C. D. b 1 b 2 b 0 b 0 Hướng dẫn giải:
Chọn D.
a b 1 2 2 a
Hàm số liên tục trên a b 1 b 0 2
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 132
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 3 2
x 3x 2x khi x(x 2) 0 x(x 2)
Câu 20. Xác định a, b để các hàm số f (x) a khi x 2 liên tục trên b khi x 0 a 10 a 11 a 1 a 12 A. B. C. D. b 1 b 1 b 1 b 1 Hướng dẫn giải:
Chọn C. a 1
Hàm số liên tục trên . b 1 3
x 2 2x 1 khi x 1
Câu 21. Tìm m để các hàm số f (x) x 1 liên tục trên 3 m 2 khi x 1 4 A. m 1 B. m C. m 2 D. m 0 3 Hướng dẫn giải:
Chọn B.
3 x 2 2x 1
Với x 1 ta có f (x)
nên hàm số liên tục trên khoảng \ 1 x 1
Do đó hàm số liên tục trên khi và chỉ khi hàm số liên tục tại x 1
Ta có: f (1) 3m 2
3 x 2 2x 1
lim f ( x) lim x 1 x 1 x 1 3 x x 2 lim 1 x 1 (x 1) 2 3 2 3
x x x 2 (x 2) 2 x x 2 lim 1 2 x 1 2 3 2 3
x x x 2 (x 2) 4
Nên hàm số liên tục tại x 1 3m 2 2 m 3 4 Vậy m
là những giá trị cần tìm. 3 x 1 1 khi x 0
Câu 22. Tìm m để các hàm số f (x) x liên tục trên 2
2x 3m 1 khi x 0 1 A. m 1 B. m C. m 2 D. m 0 6 Hướng dẫn giải:
Chọn B.
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 133
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11 x 1 1
Với x 0 ta có f (x)
nên hàm số liên tục trên 0; x
Với x 0 ta có 2
f (x) 2x 3m 1 nên hàm số liên tục trên (; 0) .
Do đó hàm số liên tục trên khi và chỉ khi hàm số liên tục tại x 0
Ta có: f (0) 3m 1 x 1 1 1 1
lim f (x) lim lim x 0 x 0 x 0 x x 1 1 2
lim f (x) lim x m m 2 2 3 1 3 1 x0 x0 1 1
Do đó hàm số liên tục tại x 0 3m 1 m 2 6 1 Vậy m
thì hàm số liên tục trên . 6 2x 4 3 khi x 2
Câu 23. Tìm m để các hàm số f (x) x 1 liên tục trên khi x 2 2
x 2mx 3m 2 1 A. m 1 B. m C. m 5 D. m 0 6 Hướng dẫn giải: Chọn C.
Với x 2 ta có hàm số liên tục
Để hàm số liên tục trên thì hàm số phải liên tục trên khoảng ; 2 và liên tục tại x 2 .
Hàm số liên tục trên ; 2 khi và chỉ khi tam thức 2
g(x) x 2mx 3m 2 0, x 2 2
' m 3m 2 0 3 17 3 17 TH 1: m
g(2) m 6 0 2 2 2
m 3m 2 0 2
' m 3m 2 0 TH 2: m 2
x m ' 2 1 2 ' (m 2) 3 17 m 3 17 m 6 2 2 m 6 3 17 Nên
m 6 (*) thì g(x) 0, x 2 2
lim f (x) lim x 2 4 3 3 x2 x2 x 1 3
lim f (x) lim 2 x2 x2
x 2mx 3m 2 6 m 3
Hàm số liên tục tại x 2
3 m 5 (thỏa (*)) 6 m
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 134
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
DẠNG 3: ÁP DỤNG TÍNH LIÊN TỤC XÉT SỐ NGHIỆM CỦA PHƯƠNG TRÌNH Phương pháp :
Để chứng minh phương trình f (x) 0 có ít nhất một nghiệm trên D, ta chứng minh hàm số y f (x)
liên tục trên D và có hai số a, b D sao cho f (a). f (b) 0 .
Để chứng minh phương trình f (x) 0 có k nghiệm trên D, ta chứng minh hàm số y f (x) liên tục
trên D và tồn tại k khoảng rời nhau (a ; a ) (i=1,2,…,k) nằm trong D sao cho f (a ). f (a ) 0 . i i 1 i i 1
Câu 1. Tìm khẳng định đúng trong các khẳng định sau:
I. f x liên tục trên đoạn ;
a b và f a. f b 0 thì phương trình f x 0 có nghiệm.
II. f x không liên tục trên ;
a b và f a. f b 0 thì phương trình f x 0 vô nghiệm. A. Chỉ I đúng. B. Chỉ II đúng.
C. Cả I và II đúng. D. Cả I và II sai.
Hướng dẫn giải: Chọn A.
Câu 2. Tìm khẳng định đúng trong các khẳng định sau:
I f x liên tục trên đoạn ;
a b và f a. f b 0 thì tồn tại ít nhất một số c ;
a b sao cho f c 0 .
II f x liên tục trên đoạn ; a b và trên ;
b c nhưng không liên tục ; a c
A. Chỉ I .
B. Chỉ II .
C. Cả I và II đúng.
D. Cả I và II sai.
Hướng dẫn giải: Chọn D. KĐ 1 sai. KĐ 2 sai.
Câu 3. Cho hàm số f x 3 2
x – 1000x 0, 01. Phương trình f x 0 có nghiệm thuộc khoảng nào trong các khoảng sau đây? I. 1 ;0 . II. 0 ;1 . III. 1;2 . A. Chỉ I. B. Chỉ I và II. C. Chỉ II. D. Chỉ III.
Hướng dẫn giải: Chọn B. TXĐ: D .
Hàm số f x 3 2
x 1000x 0, 01 liên tục trên nên liên tục trên 1 ;0 , 0 ;1 và 1; 2, 1 . Ta có f
1 1000,99 ; f 0 0, 01 suy ra f
1 . f 0 0 , 2 . Từ
1 và 2 suy ra phương trình f x 0 có ít nhất một nghiệm trên khoảng 1 ;0 .
Ta có f 0 0, 01; f
1 999,99 suy ra f 0. f 1 0 , 3 . Từ
1 và 3 suy ra phương trình f x 0 có ít nhất một nghiệm trên khoảng 0 ;1 . Ta có f
1 999,99 ; f 2 3
9991, 99 suy ra f
1 . f 2 0 , 4 . Từ
1 và 4 ta chưa thể kết luận về nghiệm của phương trình f x 0 trên khoảng 1;2 .
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 135
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Giới hạn – ĐS> 11
ĐÁP ÁN ÔN TẬP CHƯƠNG IV Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 Câu 9 Câu 10 C D A B C D B C A C Câu 11 Câu 12 Câu 13 Câu 14 Câu 15 Câu 16 Câu 17 Câu 18 Câu 19 Câu 20 A B C D B D B C D A Câu 21 Câu 22 Câu 23 Câu 24 Câu 25 Câu 26 Câu 27 Câu 28 Câu 29 Câu 30 C C B A C D A D C B Câu 31 Câu 32 Câu 33 Câu 34 Câu 35 Câu 36 Câu 37 Câu 38 Câu 39 Câu 40 B B A C D B C D B A Câu 41 Câu 42 Câu 43 Câu 44 Câu 45 Câu 46 Câu 47 Câu 48 Câu 49 Câu 50 C A D D B C C D D A Câu 51 Câu 52 Câu 53 Câu 54 Câu 55 Câu 56 Câu 57 Câu 58 Câu 59 Câu 60 D A D C B A B D B B Câu 61 Câu 62 Câu 63 Câu 64 Câu 65 Câu 66 Câu 67 Câu 68 Câu 69 Câu 70 A C D A B B D B C D Câu 71 Câu 72 Câu 73 Câu 74 Câu 75 Câu 76 Câu 77 Câu 78 Câu 79 Câu 80 B A C C D B C B D A Câu 81 Câu 82 Câu 83 Câu 84 Câu 85 Câu 86 Câu 87 Câu 88 Câu 89 Câu 90 C A C B D A C D D A Câu 91 B
Mua file Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 136
Facebook: https://www.facebook.com/dongpay - Website: https://toanmath.com/




