




































































Preview text:
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
Chương IV. Giới hạn
Dạng 1.1. Câu hỏi lý thuyết A. PHƯƠNG PHÁP
I - GIỚI HẠN HỮU HẠN CỦA DÃY SỐ
Ta nói dãy số (u u
n ) có giới hạn là 0 khi n dần tới dương vô cực, nếu
n có thể nhỏ hơn một
số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi.
Kí hiệu: lim u = hay u → khi n → +∞ .Ta nói dãy số (v v
n ) có giới hạn là a (hay n 0 n 0 n→+∞ n
dần tới a ) khi n → +∞ , nếu lim (v − a = . n ) 0 n→+∞
Kí hiệu: lim v = a hay v → a khi n → +∞ . n n→+∞ n
Một vài giới hạn đặc biệt a) 1 lim = 0 ; 1 lim
= 0 với k nguyên dương; n→+∞ n k n→+∞ n b) lim n
q = 0 nếu | q |<1; n→+∞
c) Nếu u = c ( c là hằng số) thì lim u = c = c . n lim n n→+∞ n→+∞
Chú ý: Từ nay về sau thay cho lim u = a ta viết tắt là limu = a . →+~ n n n Định lí 1
a) Nếu limu = a và limv = b thì n n
- lim(u + v = a + b n n )
- lim(u − v = a − b n n )
- lim(u ⋅v = a ⋅b n n ) u a - lim n
= (nếu b ≠ 0) . v b n limu = a b) Nếu n
thì lim u = a n . u ≥ n ∀ n 0, a ≥ 0 II. GIỚI HẠN VÔ CỰC
Ta nói dãy số (u u
n ) có giới hạn là +∞ khi n → +∞ , nếu
có thể lớn hơn một số dương bất n
kì, kể từ một số hạng nào đó trở đi.
Kí hiệu: limu = +∞ hay u → +∞ khi n → +∞ . n n - Dãy số (u lim u − = +∞
n ) có giới hạn là −∞ khi n → +∞ , nếu ( n )
Kí hiệu: limu = −∞ hay u → −∞ khi n → +∞ . n n
Nhận xét: u = +∞ ⇔ u − = −∞ . n lim( n )
Một vài giới hạn đặc biệt a) lim k
n = +∞ với k nguyên dương. b) lim n
q = +∞ nếu q >1. Định lí 2
a) Nếu limu = a và limv = ±∞ thì un = . n n lim 0 vn Trang 1
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
b) Nếu limu = a > v = và v > n ∀ thì u = +∞. n 0, n 0,lim n 0 lim n vn
c) Nếu limu = +∞ và limv = a > thì limu v = +∞ . n. n 0 n n
B.2. Bài tập trắc nghiệm.
Câu 1. Phát biểu nào sau đây là sai ?
A. limu = c (u = c là hằng số ). B. lim n q = 0 ( q > ) 1 . n n C. 1 lim = 0 . D. 1 lim = 0 (k > ) 1 . n k n
Lời giải GVSB: Phạm Quốc Toàn; GVPB: Thúy Kiều Chọn B
Theo định nghĩa giới hạn hữu hạn của dãy số thì lim n q = 0 ( q < ) 1 .
Câu 2. Chọn mệnh đề đúng trong các mệnh đề sau?
A. Nếu lim u = +∞ , thì limu = +∞ .
B. Nếu lim u = +∞ , thì limu = −∞ . n n n n C. Nếu limu = u = u = −a u = a n 0 , thì lim . D. Nếu lim , thì lim . n 0 n n
Lời giải GVSB: Phạm Quốc Toàn; GVPB: Thúy Kiều Chọn C Ta có nếu limu = u = n 0 , thì lim . n 0
Câu 3. Trong các khẳng định sau, khẳng định nào đúng?
A. limv = nếu lim(v + a = .
B. limv = a nếu lim(v − a = . n ) 0 n ) 0 n 0 n
C. limv = nếu lim(v − a = .
D. limv = a nếu lim(v + a = . n ) 0 n ) 0 n 0 n
Lời giải GVSB: Phạm Quốc Toàn; GVPB: Thúy Kiều Chọn B
Theo định nghĩa giới hạn hữu hạn của dãy số
limv = a nếu lim(v − a = . n ) 0 n
Câu 4. Trong các kết quả sau, kết quả nào sai?
Nếu limu = a và limv = b thì n n u a
A. lim(u + v = a + b . B. lim n = . n n ) v b n
C. lim(u − v = a −b .
D. lim(u v = a b n. n ) . n n )
Lời giải GVSB: Phạm Quốc Toàn; GVPB: Thúy Kiều Chọn B u a
Theo định lý về giới hạn hữu hạn, ta có: lim n = (nếu b ≠ 0 ). v b n
Câu 5. Trong các khẳng định sau, khẳng định nào đúng?
A. Ta nói dãy số (u có giới hạn −∞ khi n → +∞ , nếu u có thể lớn hơn một số dương bất kì, n ) n
kể từ một số hạng nào đó trở đi. Trang 2
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
B. Ta nói dãy số (u có giới hạn +∞ khi n → +∞ , nếu u có thể nhỏ hơn một số dương bé n ) n
tùy ý, kể từ một số hạng nào đó trở đi.
C. Ta nói dãy số (u có giới hạn +∞ khi n → +∞ , nếu u có thể lớn hơn một số dương bất kì, n ) n
kể từ một số hạng nào đó trở đi.
D. Ta nói dãy số (u có giới hạn +∞ khi n → +∞ , nếu u có thể nhỏ hơn một số dương bất kì, n ) n
kể từ một số hạng nào đó trở đi.
Lời giải GVSB: Phạm Quốc Toàn; GVPB: Thúy Kiều Chọn C
Theo định nghĩa giới hạn vô cực
Ta nói dãy số (u có giới hạn +∞ khi n → +∞ , nếu u có thể lớn hơn một số dương bất kì, kể n ) n
từ một số hạng nào đó trở đi.
Câu 6. Cho limu = − , limv = và v > . Khi đó lim un bằng n 0 n 0 n 2 vn A. ∞ . B. −∞ . C. 0 . D. +∞ .
Lời giải GVSB: Phạm Quốc Toàn; GVPB: Thúy Kiều Chọn B
Ta có limu = − < , limv = và v > nên theo định lý về giới hạn vô cực ta có lim un = −∞ n 0 n 0 n 2 0 vn
Dạng 1.2 : Giới hạn dãy số đa thức,căn thức không liên hợp A. Phương pháp :
B1: Đặt n mũ cao nhất làm thừa số chung.
B2: Áp dụng quy tắc sau để tìm giới hạn
Nếu limu = ±∞ và limv = L ≠ thì lim(u v được cho trong bảng sau: n n ) n 0 n limu Dấu của L lim(u v n n ) n +∞ + +∞ +∞ − −∞ −∞ + −∞ −∞ − +∞ B. Bài tập.
B.1. Bài tập tự luận.
Bài 1. Tính giới hạn ( 2 lim n − 3n + ) 1 . Lời giải
GVSB: Phạm Thái; GVPB:Thúy Kiều Ta có ( 2 lim n − 3n + ) 1 2 3 1 lim n 1 = − + = +∞ . 2 n n
Bài 2. Tính giới hạn ( 2 lim 5n − n + ) 1 . Lời giải Trang 3
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
GVSB: Phạm Thái; GVPB: Thúy Kiều Ta có ( 2 n n ) 2 5 1 lim 5 1 lim n 1 − + = − + + = . −∞ 2 n n
Bài 3. Tính giới hạn ( 2
lim n − 2n + 3 + n).
Lời giải GVSB: Phạm Thái; GVPB: Thúy Kiều Ta có ( 2
lim n − 2n + 3 + n) 2 3 = lim n 1− + +1 = +∞ . 2 n n
B. 2. Bài tập trắc nghiệm.
Câu 1. Tính giới hạn L 2
lim 3n 5n 3 . A. L 3. B. L . C. L 5. D. L . Lời giải
GVSB: Phạm Thái; GVPB: Thúy Kiều Chọn D Ta có L
2n n 2 5 3 lim 3 5 3 lim n 2 . 2 n n Câu 2. ( 3 lim n − 2n + ) 1 bằng A. 0 . B. 1. C. −∞ . D. +∞ .
Lời giải GVSB: Phạm Thái; GVPB: Thúy Kiều Chọn D Ta có: ( 3n n ) 3 2 1 lim 2 1 lim n 1 − + = − + = +∞ . 2 3 n n Câu 3. ( 3 3
lim n − 8n + 3n + 2) bằng A. . +∞ B. . −∞ C. 1. − D. 0.
Lời giải GVSB: Phạm Thái; GVPB: Thúy Kiều Chọn B Ta có ( 3 3
lim n − 8n + 3n + 2) 3 2 = − 3 lim n 1 8 + + = −∞ 2 3 n n
Câu 4. Kết quả của giới hạn 5 5 2
lim 200 − 3n + 2n là: A. . +∞ B. 1. C. 0. D. . −∞ Lời giải
GVSB: Phạm Thái; GVPB: Thúy Kiều Chọn D 5 5 2 200 2 − + = 5 lim 200 3n 2n lim n − 3+ = −∞ . 5 3 n n Trang 4
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
Dạng 1.3 Giới hạn dãy phân thức hữu tỷ A. PHƯƠNG PHÁP P(n)
Giới hạn của (u trong đó u là một phân thức hữu tỉ dạng u = (trong đó n ) n n Q(n)
P(n),Q(n) là hai đa thức chứa của n ). Phương pháp:
Chia tử và mẫu cho k n với k
n là lũy thừa có số mũ lớn nhất của P(n) và Q(n) (hoặc là rút k n a
làm nhân tử) sau đó áp dụng các định lí về giới hạn hữu hạn và lim = 0(k > 0 để k ) n tính. B. BÀI TẬP.
B.1. Bài tập tự luận. 2 3 Câu 1. Tính n − 4 lim n . 3 2n + 5n − 2 Lời giải
GVSB: Nguyễn My; GVPB: Thúy Kiều 3 1 1 n − 4 2 3 − 4 Ta có: n − 4n n n 4 − lim = lim = lim = = 2 − . 3 2n + 5n − 2 5 2 5 2 3 2 n 2 + − 2 + − 2 3 2 3 n n n n 3 Câu 2. Tính n − 7 lim n . 2 1+ 2n Lời giải
GVSB: Nguyễn My; GVPB: Thúy Kiều 3 7 7 n 1 − 3 2 1− − Ta có: 2 n 7 lim n lim n = = lim . n n = +∞ . 2 1+ 2n 1 1 2 n + 2 + 2 2 2 n n 7 1 − Vì 2 n 1 lim
= > 0; lim n = +∞ . 1 + 2 2 2 n Câu 3. Tính n + 2 lim 2 n + n +1 Lời giải
GVSB: Nguyễn My; GVPB: Thúy Kiều 3 3 n1+ 1+ Ta có: n + 2 n 1 lim = lim = lim . n = 0 2 n + n +1 1 1 n 1 1 2 n 1+ + 1+ + 2 2 n n n n
B.2. Bài tập trắc nghiệm. Câu 1. Tính 2n − 3 I = lim 2 2n + 3n +1
A. I = −∞ .
B. I = +∞ . B. I =1.
D. I = 0. Lời giải Trang 5
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
GVSB: Nguyễn My; GVPB: Thúy Kiều Chọn D 2 2 3 n − 2 3 2n − 3 2 − 2 I = lim lim n n = = lim n n = 0 . 2 2n + 3n +1 3 1 2 3 1 n 2 + + 2 + + 2 n n 2 n n 3 2 Câu 2. Biết 2n + n − 4 1 lim
= với a là tham số. Khi đó 2 a − a bằng 3 an + 2 2 A. 0 . B. −12 . B. 6 − . D. 2 − . Lời giải
GVSB: Nguyễn My; GVPB: Thúy Kiều Chọn B 3 1 4 3 2 n 2 + − Ta có 3 2n + n − 4 n n 2 1 lim = lim = = . 3 an + 2 3 2 a 2 n a + 3 n
Suy ra a = 4 . Khi đó 2 2
a − a = 4 − 4 = −12 .
Câu 3. Cho dãy số (u với 1 1 1 u = + + + . Tính u . n ... n ) lim 1.3 3.5
(2n − )1(2n + )1 n A. 0 . B. 1 . C. 1 . D. 1. 4 2 Lời giải
GVSB: Nguyễn My; GVPB: Thúy Kiều Chọn C * Cách 1: Ta có 1 1 1 1 ( = − suy ra 2n ) 1 (2n ) 1
2 2n 1 2n 1 − + − + 1 1 1 1 = − 1.3 2 1 3 1 1 1 1 = − … 3.5 2 3 5 … 1 1 1 1 1 1 u = + + + = − nên 1 1 1 1 u = − = . n ... lim n lim 1.3 3.5 (2n ) 1 (2n ) 1 2 1 2n 1 − + + 2 1 2n 1 + 2 * Cách 2: Ta có 1 2 3
u = ; u = ; u = . Ta chứng minh n u = bằng qui nạp n (*) 1 2 3 3 5 7 2n +1
+ Với n =1, công thức (*) đúng. Trang 6
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 k +
+ Giả sử công thức (*) đúng với n = k ≥1⇒ u = . Ta cần chứng minh k 1 u = k 2k +1 k 1 + 2(k + ) 1 +1 . Thật vậy, ta có 1 2 u + + = + k 1 2k 3k 1 = + = + u k 1 k 2(k + ) 1 −1 2(k + ) 1 +1 2k +1 (2k + )
1 (2k + 3) (2k + ) 1 (2k + 3) (k + ) 1 (2k + ) 1 k +1 = n ( =
. Vậy công thức u = đúng với mọi * n∈ n (*) . 2k + )
1 (2k + 3) 2(k + ) 1 +1 2n +1 Khi đó n 1 limu = = . n lim 2n+1 2
Câu 4. Đặt f (n) = (n + n + )2 2 1 +1. f ( )
1 . f (3). f (5)... f (2n − ) 1
Xét dãy số (u sao cho = Tính lim n u . n . n ) un
f ( ) f ( ) f ( ) f ( n) . 2 . 4 . 6 . . 2 A. lim n u = B. 1 lim n u = C. lim n u = D. 1 lim n u = n . n 3. n . n 2. 3 2 Lời giải
GVSB: Nguyễn My; GVPB: Thúy Kiều Chọn D f 2n −1 (4n −2n+ )2 2 1 +1 Xét g (n) ( ) = ( ⇒ g n = . f 2n) ( ) (4n +2n+ )2 2 1 +1 ( 2 4n + )2 1 − 4n( 2 4n + ) 1 + ( 2 4n + ) 2 2 + − + − + g (n) 1
4n 1 4n 1 (2n ) 1 1 = ( = = 4n + )2 1 + 4n(4n + ) 1 + (4n + ) 2 2 2 2 1
4n +1+ 4n +1 (2n + )2 1 +1
2 10 26 (2n − 3)2 +1 (2n − )2 1 +1 2 ⇒ u = = n . . .... . 10 26 50 (2n − )2 1 +1 (2n + )2 1 +1 (2n + )2 1 +1 2 2n 1 ⇒ lim n u = = n lim . 2 4n + 4n + 2 2
Dạng 4.3. Giới hạn dãy phân thức (có mũ n) B. BÀI TẬP.
B.1. Bài tập tự luận. n−2 Bài 1. Tính giới hạn 2 − 5 lim . 3n + 2.5n Lời giải
GVSB: Nguyễn Hương Lan; GVPB: Bùi Hà Trang 7
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 1 n 1 2. − n−2 2 5 5 − 25 1 lim = lim = − . 3n + 2.5n 3 n 50 + 2 5 n+2 Bài 2. Tính giới hạn 3 − 5 lim . n+1 4 + 3.5n Lời giải
GVSB: Nguyễn Hương Lan; GVPB: Bùi Hà 1 n 3. − 25 n+2 3 − 5 3 − 25.5n 5 25 lim = lim = lim = − . n+1 4 + 3.5n 4.4n + 3.5n 4 n 3 4. + 3 5 2 n Bài 3.
Cho các số thực a,b thỏa + + + + a 1 a a ... a
< 1; b < 1. Tìm giới hạn I = lim . 2
1+ b + b + ... n + b Lời giải
GVSB: Nguyễn Hương Lan; GVPB: Bùi Hà n+1 Ta có: 2 1, , ,..., n a a
a là một cấp số nhân công bội a nên 2 n 1 1+ + + ... − a a a + a = . 1− a n+1 2 1, , ,..., n b b
b là một cấp số nhân công bội b nên 2 n 1 1+ + + ... − b b b + b = . 1− b n+1 1− a 2 n Suy ra
1+ a + a + ...+ a 1− a 1 I = lim = lim − b = . 2 n n+1
1+ b + b + ...+ b 1− b 1− a 1− b
Vì a < 1, b < 1 nên n+1 lim = lim n a b = 0.
B.2. Bài tập trắc nghiệm.
Câu 1. Kết quả của giới hạn 1 lim là 2n A. 0. B. 1. C. 1 . D. 1 . 2 4 Lời giải
GVSB: Nguyễn Hương Lan; GVPB: Bùi Hà Chọn A 1 1 n lim lim = = 0. 2n 2 n
Câu 2. Kết quả của giới hạn 3 −1 lim là 5n + 1 Trang 8
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 A. 0. B. 1 . C. 4 . D. 1. − 5 5 Lời giải
GVSB: Nguyễn Hương Lan; GVPB: Bùi Hà Chọn A 3 n 1 n − 3n −1 5 5 lim lim = = 0. 5n + 1 1 n 1 + 5 n n
Câu 3. Kết quả của giới hạn 3.2 − 3 lim là n+1 n+1 2 + 3 A. 1 − . B. 1 . C. 1. − D. 3 . 3 3 2 Lời giải
GVSB: Nguyễn Hương Lan; GVPB: Bùi Hà Chọn A 2 n 3. − 1 3.2n − 3n 3.2n − 3n 3 1 lim = lim = lim = − . n+1 n+1 2 + 3 2.2n + 3.3n 2 n 3 2. + 3 3 n n+1
Câu 4. Kết quả của giới hạn 4 + 2 4 lim là n n+2 3 + 4 A. 1 . B. 1 . C. 1 . D. 1 . 2 4 3 16 Lời giải
GVSB: Nguyễn Hương Lan; GVPB: Bùi Hà Chọn A 1 n 1 2. + n n+1 4 2 4n 2.2n 2 + + 1 4 4 lim = lim = lim = . n n+2 n n 4 3 + 4 3 + 16.4 3 n 2 + 16 4 B. BÀI TẬP.
B.1. Bài tập tự luận. 2
Bài 1. Tính giới hạn 2n + 3n + 5 − = lim n L . 2n −1 Lời giải
GVSB: Ân Trương; GVPB: Bùi Hà Trang 9
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 Ta có 3 5 n 2 1 3 5 2 2n + 3n + 5 − 2 n n 2 1 2 = lim n L lim 1 lim n n . 2n −1 1 1 n 2 2 2 n n 2 2
Bài 2. Tính giới hạn
9n + 2n −1 − 4n +1 L = lim .
1− 3n Lời giải
GVSB: Ân Trương; GVPB: Bùi Hà Ta có 2 + + 2 2n 3n 5 n − n 3 5 3 5 2 n 2 + + −1 2 + + −1 n 2 n n 2 n n L lim = lim = lim = 1 = − 1 n 3 − 1 1 3 n − 3 − 3 n n n
Bài 3. Tính giới hạn 2n +1 − n + 3 L = lim . 4n − 5 Lời giải
GVSB: Ân Trương; GVPB: Bùi Hà Ta có 1 3 + − + 2n +1 − n + 3 2 1 L + − + − = lim = lim n n 2 0 1 0 2 1 = = . 4n − 5 5 4 − 0 2 4 − n
B.2. Bài tập trắc nghiệm. 2 Câu 1. 4n +1 − n + 2 lim bằng 2n − 3 3 A. . B. 2 . C. 1. D. +∞ . 2 Lời giải
GVSB: Ân Trương; GVPB: Bùi Hà Chọn C 1 1 2 2 4 + − + 2 2 Ta có 4n +1 − n + 2 n n n 2 − 0 lim = lim = = 1. 2n − 3 3 2 2 − n 2 Câu 2. Cho 4n + 5 + = lim n I
. Khi đó giá trị của I là 2 4n − n +1 5 3 A. I =1. B. I = . C. 1. D. I = . 3 4 Lời giải
GVSB: Ân Trương; GVPB: Bùi Hà Chọn C Trang 10
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 5 2 4 + +1 2 Ta có 4n + 5 + = lim n = lim n I = 1. 2 4n − n +1 1 4 − 1+ 2 n Câu 3. Tìm
n 1+ 3+ 5 +…+ (2n −1) limu biết u = n n 2 2n +1 1 A. . B. +∞ . C. 1. D. −∞ . 2 Lời giải
GVSB: Ân Trương; GVPB: Bùi Hà Chọn A 2 2 + + +…+ − Ta có n 1 3 5 (2n 1) n n n 1 1 limu = = = = = . n lim lim lim lim 2 2 2 2n +1 2n +1 2n +1 1 2 2 + 2 n 2 2 3 2 Câu 4. Tính 1 + 2 + 3 +…+ lim n .
2n(n + 7)(6n + 5) 1 1 1 A. . B. . C. . D. +∞ . 6 2 6 2 Lời giải
GVSB: Ân Trương; GVPB: Bùi Hà Chọn A n n +1 2n +1 2 2 2 2 ( )( )
Ta có 1 + 2 + 3 +…+ n = . 6 1 1 1 2 + + 2 2 3 2 Khi đó 1 + 2 + 3 +…+ n
n(n +1)(2n +1) n n 1 lim = lim = lim = .
2n(n + 7)(6n + 5)
12n(n + 7)(6n + 5) 7 5 6 12 1+ 6 + n n Bài tập tự luận. Bài 1. Tính (3 3 2 2
lim 8n − 2n + 3n −1 − 4n + n −1) Lời giải
GVSB: ThienMinh Nguyễn; GVPB: Bùi Hà (3 3 2 2
lim 8n − 2n + 3n −1 − 4n + n −1) = (3 3 2
n − n + n − − n)+ ( 2 lim 8 2 3 1 2
lim 2n − 4n + n −1) 3 2 3 2 2
8n − 2n + 3n −1−8n
4n − 4n − n +1 = lim ( + lim 3 2 n n n )2 2 3 3 3 2 2
2n + 4n + n − − + − + − + − + 1 8 2 3 1 2 . n 8n 2n 3n 1 4n 2 2 − n + 3n −1 −n +1 = lim ( + lim 3 2 n n n )2 2 3 3 3 2 2
2n + 4n + n − − + − + − + − + 1 8 2 3 1 2 . n 8n 2n 3n 1 4n 3 1 1 2 − + − − + 2 1 = lim n n + lim n 2 1 1 2 3 1 2 3 1 3 3 2 + 4 8 2. 8 4 + − − + − + − + − + 2 2 3 2 3 n n n n n n n n Trang 11
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 2 − 1 − = ( ) + 2 3 3 2 + 4 8 + 2. 8 + 4 1 − 1 − 5 = + = − 6 4 12 2 3 6 Bài 2. Tính n + 1− lim n 4 2 4n +1 − 2n Lời giải
GVSB: ThienMinh Nguyễn; GVPB: Bùi Hà 2 3 6 n + 1− lim n 4 2 4n +1 − 2n ( 6 6 n +1− n )( 4 2 4n +1 + 2n ) = lim ( 4 4
4n +1− 4n ) 4 2 6
n − n . 1− n + ( 6 1− n )2 3 3 ( 4 2 4n +1 + 2n ) = lim 4 2 6
n − n . 1− n + ( 6 1− n )2 3 3 1 4 + + 2 4 n lim = 2 1 1 1 −.3 −1 + 3 −1 6 6 n n 4 = 3
Bài 3. Tính lim( n + 2021− n). n Lời giải
GVSB: ThienMinh Nguyễn; GVPB: Bùi Hà
lim( n + 2021− n). n 2021 = lim . n n + 2021 + n 2021 = lim n 2021 n 1+ +1 n 2021 = lim 2021 1+ +1 n 2021 = 2
B.2. Bài tập trắc nghiệm.
Câu 1. Trong các biến đổi sau, đâu là biến đổi đúng ? Trang 12
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 A. ( + − ) 2 2 n + 4 + lim 4 = lim n n n n n . 4n B. ( 2 + − ) 4 lim 4 = lim n n n n . 2
n + 4n + n C. ( 2
lim n + 4n − n) = lim(4n). D.
( 2n + n−n) 1 lim 4 = lim . 4n Lời giải
GVSB: ThienMinh Nguyễn; GVPB: Bùi Hà Chọn B ( 2 2 + − 2 n n n
lim n + 4n − n) 4 = lim 4 = lim n . 2
n + 4n + n 2
n + 4n + n Câu 2. Tính ( 2
lim n + n +1 − n) ? A. 0 . B. +∞ . C. 7 . D. 1. Lời giải
GVSB: ThienMinh Nguyễn; GVPB: Bùi Hà Chọn D ( 2
lim n + n +1 − n) n +1 = lim 2
n + n +1 + n 1 1+ = lim n = 1 1 1 1+ + +1 2 n n
Câu 3. Biết giới hạn 2 2 lim 9 + 3 − 9 + 2 a n n n = (a,b∈ )
là phân số tối giản. Khi đó giá và a b b trị của biểu thức 2
A = a + b là bao nhiêu ? A. 20 . B. 12. C. 98. D. 7 .
Lời giải GVSB: ThienMinh Nguyễn; GVPB: Bùi Hà Chọn D Ta có: 2 2 lim 9 + 3 − 9 + 2 a n n n = (a,b∈ ) . b Xét 2 2 lim n 9n 3 9n 2 + − + = lim n 2 2 9n + 3 + 9n + 2 1 1 = lim = 3 2 6 9 + + 9 + 2 2 n n Suy ra 2 2
a + b =1 + 6 = 7 Trang 13
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
Câu 4. Cho hai dãy số (un ),( n
v ) thỏa mãn n
v = un 1+ −un , n ∀ ≥ 1. Trong đó, 1 u =1 và ( n v ) là cấp số cộng có 3 2 1
v = 3 , công sai là 3. Đặt Sn = 1
u + u2 +...+ un . Tính lim( 2Sn −2n −n). Biết rằng: n(n + ) 1 2 2 2 n(n + ) 1 (2n + ) 1 1+ 2 +...+ n =
và 1 + 2 +...+ n = . 2 6 2 3 A. +∞ . B. − . C. . D. 1. 3 4 Lời giải
GVSB: ThienMinh Nguyễn; GVPB: Bùi Hà Chọn B Ta có: n
v = 1v + (n − )
1 d = 3+ 3n − 3 = 3n . Nên n
v 1− = 3n −3, n
v −2 = 3n − 6 , ...
Xét un = (un −un 1−) + (un 1− −un−2 ) +...+ (u2 − 1 u ) + 1 u un = n v 1− + n
v −2 +...+ 1v +1
un = (3n −3) +(3n −6) +...+3 +1
un = 3(n − )
1 + (n − 2) +...+1 +1
Đặt A = (n − ) 1 + (n − 2) +...+1 2 n n +1
n + n 2n n n −1
Nên A = (n − ) 1 + (n − 2) ( ) ( ) + ...+ 2 +1 = − n = − = 2 2 2 2 n(n − ) 2 1 Nên
3n − 3n + 2 3 2 3 un = 3 +1 = = n − n +1 2 2 2 2 Suy ra 3
u + u + u +...+ un = ( 2 2 2 3 1 2 3
1 + 2 +...+ n )− .(1+ 2+...+ n) + n 2 2 3 n(n + ) 1 (2n + ) 1 3 n(n + ) 1 1 u + u2 + 3 u +...+ un = . − . + n 2 6 2 2 3 2 2 2n 3n n 3n 3n 4n 1 u u2 3 u ... u + + − − + + + + + n = 4 3 3 2n 2n n n 1 u u2 3 u ... u + + + + + + n = = 4 2 3 Vậy n n S + n = 2 Suy ra lim(3 2
2Sn − 2n − n) = (3 3 2
lim n − 2n + n − n) 2 2 − + = lim n n ( 3 2
n − 2n + n )2 3 3 3 2 2 + .
n n − 2n + n + n 1 2 − + = lim n 2 2 1 2 1 3 1− + + 3 1− + +1 2 2 n n n n Trang 14
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 2 − = 3 Tự luận: 1 1 1 (− ) 1 n
Câu 1. Tính tổng cấp số nhân lùi vô hạn − ; ;− ;...; ;.... 2 4 8 2n Lời giải
GVSB: Nguyễn Ngọc Minh Châu; GVPB: Tuyet Trinh 1 1 1 (− ) 1 n
Ta có: Dãy số − ; ;− ;...;
;... là một cấp số nhân lùi vô hạn với 1 u = − và 1 q = − 2 4 8 2n 1 2 2 . 1 −
Do đó tổng của cấp số nhân lùi vô hạn trên là u 2 1 1 S = = = − . 1− q 1 3 1+ 2 Câu 2. Tính tổng 1 1 n 1 S = 1 − + − + ...+ 1 − + ... . 2 ( ) n 1 6 6 6 − Lời giải
GVSB: Nguyễn Ngọc Minh Châu; GVPB: Tuyet Trinh Ta có: Dãy số 1 1 n 1 1 − ; ;− ;...; 1 −
;... là một cấp số nhân lùi vô hạn với u = 1 − và công 2 ( ) n 1 6 6 6 − 1 bội 1 q = − . 6 Do đó u 1 − 6 1 S = = = − . 1− q 1 7 1+ 6
Câu 3. Tính tổng cấp số nhân lùi vô hạn (u biết u =1 và u ,u ,u theo thứ tự là ba số hạng n ) 1 1 3 4
liên tiếp trong một cấp số cộng. Lời giải
GVSB: Nguyễn Ngọc Minh Châu; GVPB: Tuyet Trinh
Gọi q là công bội của cấp số nhân (u với q <1. n ) Ta có: 2 3 u = ;
q u = q ;u = q . Do u ,u ,u theo thứ tự là ba số hạng liên tiếp trong một cấp 2 3 4 1 3 4 q =1(l) số cộng nên u + + u = 2u 3 2 ⇔ 1+ q = 2q 1 5 ⇔ (q − )( 2 1 q − q − ) 1 = 0 ⇔ q = (l) . 1 4 3 2 1− 5 q = (tm) 2
Vậy tổng cấp số nhân lùi vô hạn là: u 1 − 1 S = = 2 5 1 = = . 1− q 1− 5 1+ 5 2 1− 2 Trắc nghiệm:
Câu 1. (NB) Tính tổng cấp số nhân lùi vô hạn (u biết u =1 và 1 n ) q = − . 1 2 Trang 15
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 2 3 1 1 A. . B. . C. . D. . 3 2 3 2 Lời giải
GVSB: Nguyễn Ngọc Minh Châu; GVPB: Tuyet Trinh Chọn A
Tổng cấp số nhân lùi vô hạn là: u 1 2 1 S = = = . 1− q 1 3 1+ 2 Câu 2. (TH) Tổng 1 1 1 S = + + ...+ + ... có giá trị là: 2 3 3 3n 1 1 1 1 A. . B. . C. . D. . 9 4 3 2 Lời giải
GVSB: Nguyễn Ngọc Minh Châu; GVPB: Tuyet Trinh Chọn D Ta có: Dãy số 1 1 1
; ;...; ;... là một cấp số nhân lùi vô hạn với 1 u = và 1 q = . 2 3 3 3n 1 3 3 1 Do đó u 3 1 1 S = = = . 1− q 1 2 1− 3
Câu 3. (VD) Bạn A thả quả bóng cao su từ độ cao 10m theo phương thẳng đứng. Mỗi khi chạm
đất nó lại nảy lên theo phương thẳng đứng có độ cao bằng 3 độ cao trước đó. Tính tổng 4
quãng đường bóng đi được đến khi bóng dừng hẳn. A. 40m . B. 70m . C. 50m. D. 80m . Lời giải
GVSB: Nguyễn Ngọc Minh Châu; GVPB: Tuyet Trinh Chọn B
Đặt 10m = a .
Quãng đường đi được của quả bóng từ khi thả đến khi nảy lên cao nhất ở lần 1 là: 3
u = a + a . 1 4
Quãng đường đi được của quả bóng từ khi rơi xuống lần 2 đến khi nảy lên cao nhất ở lần 2 là: 3 3 3 3
u = a + . a = u . 2 1 4 4 4 4
Cứ lập luận như vậy ta được dãy số u ,u ,...,u
lập thành một cấp số nhân lùi vô hạn n ,... 1 2 với 3 35
u = a + a = m và công bội 3 q = . 1 4 2 4 35
Vậy tổng quãng đường bóng đi được từ khi thả đến khi dừng là: u1 2 S = = = 70m 1− q 3 1− 4 . Trang 16
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
Câu 4. (VDC) Cho hình vuông (C có cạnh bằng a . Người ta chia mỗi cạnh của hình vuông 1 )
thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông (C . 2 )
Từ hình vuông (C lại tiếp tục làm như trên ta nhận được dãy các hình vuông 2 )
C ,C ,C ,...C . Gọi S là diện tích hình vuông C (i∈{1;2;3; } ... ) . Đặt 1 2 3 n i i
T = S + S + S +...+ S + . Biết 32 T = , tính a ? n ... 1 2 3 3 5 A. 2 . B. . C. 2 . D. 2 2 . 2 Lời giải
GVSB: Nguyễn Ngọc Minh Châu; GVPB: Tuyet Trinh Chọn A 2 2
Cạnh của hình vuông (C là: 3 1 a 10 a = a + a = . Do đó diện tích 2 ) 2 4 4 4 5 2 5
S = a = S . 2 1 8 8 2 2
Cạnh của hình vuông (C là: 3 1 a 10 2 a = a + a = 5
= a . Do đó diện tích 3 ) 3 2 2 4 4 4 8 2 5 2 5 S = a =
S . Lập luận tương tự ta có các S , S , S ,..., S
tạo thành một dãy cấp n ,... 3 2 8 8 1 2 3 số nhân lùi vô hạn có 2
u = S = a và công bội 5 q = . 1 1 8 2 S 8a 2 8a 32 1 T = = . Với 32 T = ⇒ = 2
⇒ a = 4 ⇒ a = 2. 1− q 3 3 3 3 B. BÀI TẬP.
B.1. Bài tập tự luận.
Bài 1. Từ độ cao 55,8mcủa tháp nghiêng Pisa nước Italia người ta thả một quả bóng cao su chạm xuống 1
đất. Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng
độ cao mà quả bóng đạt trước 10
đó. Tính giới hạn tổng độ dài hành trình của quả bóng được thả từ lúc ban đầu cho đến khi nó
nằm yên trên mặt đất. Trang 17
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 .
Lời giải GVSB: Hồng Hà Nguyễn; GVPB: Tuyet Trinh
Gọi h là độ dài đường đi của quả bóng ở lần rơi xuống thứ ( * n n∈ ) . n
Gọi l là độ dài đường đi của quả bóng ở lần nảy lên thứ ( * n n∈ ) . n 1
Theo bài ra ta có h = 55,8 , l =
.55,8 = 5,58 và các dãy số (h , (l là các cấp số nhân lùi n ) n ) 1 1 10 1
vô hạn với công bội q = . 10
Từ đó ta suy ra giới hạn tổng độ dài đường đi của quả bóng là: h l 1 1 lim S = + = 68,2(m) 1 1 . 1− 1− 10 10
Bài 2. Để trang trí cho quán trà sữa sắp mở cửa của mình, bạn Việt quyết định tô màu một mảng tường
hình vuông cạnh bằng 1m . Phần tô màu dự kiến là các hình vuông nhỏ được đánh số lần lượt là
1,2,3...n,.. (các hình vuông được tô màu chấm bi), trong đó cạnh của hình vuông kế tiếp bằng
một nửa cạnh hình vuông trước đó (hình vẽ). Giả sử quá trình tô màu của Việt có thể tiến ra vô
hạn.Gọi u là diện tích của hình vuông được tô thứ
S = u + u +
+ u . Tính lim S . n ..... n n .Với 1 2 n n
Lời giải GVSB: Hồng Hà Nguyễn; GVPB: Tuyet Trinh
Diện tích của hình vuông lập thành cấp số nhân với số hạng đầu tiên là 1 1 u = ,q = . 1 4 4 n 1 −
Do đó số hạng tổng quát là 1 1 1 u = = n ≥ . n . n ( ) 1 4 4 4 1 Suy ra u 4 1 1 lim S = = = . n 1− q 1 3 1− 4 Trang 18
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
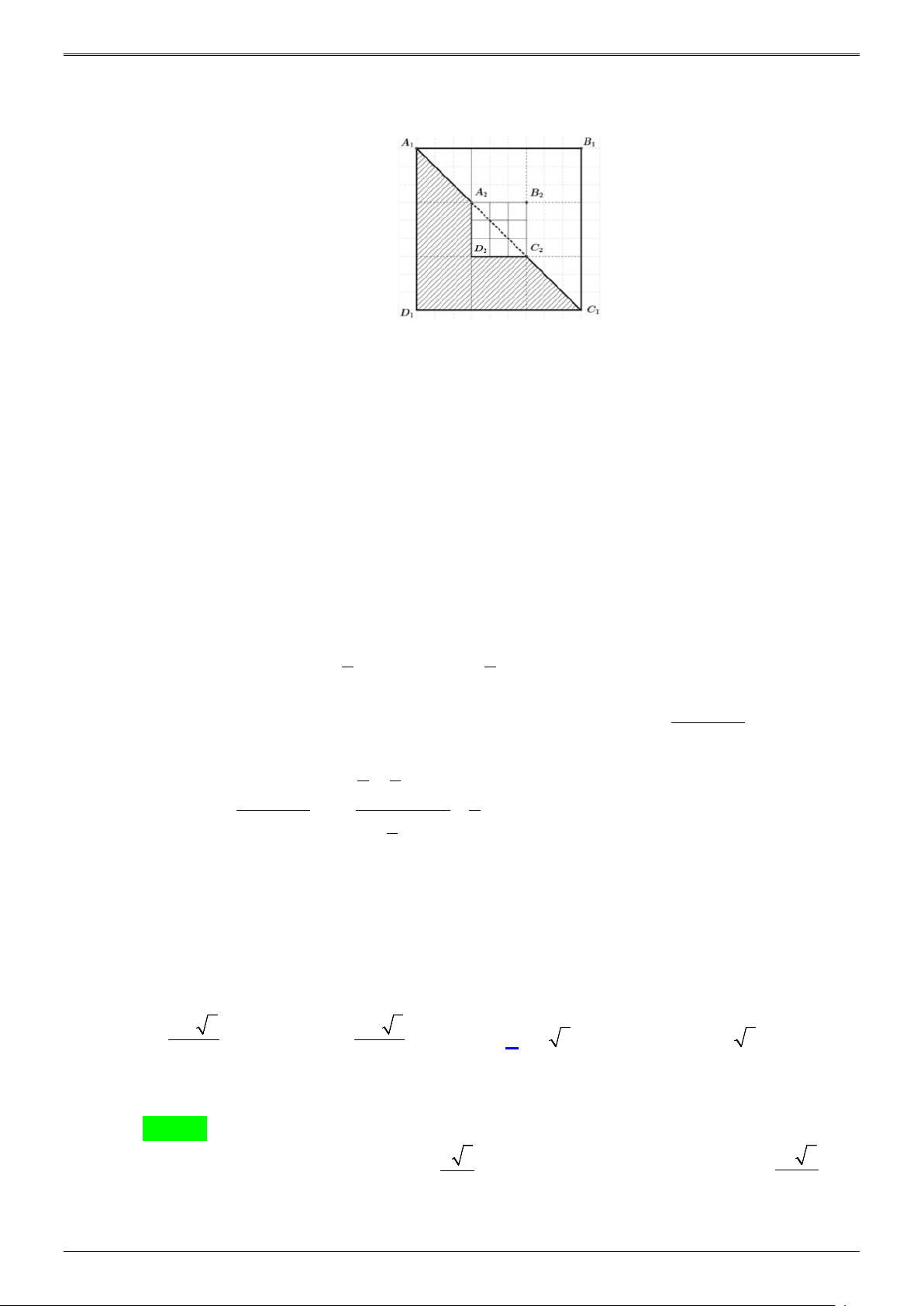
Bài 3. Với hình vuông A B C D như hình vẽ bên, cách tô màu như phần gạch sọc được gọi là cách tô 1 1 1 1
màu “đẹp”. Một nhà thiết kế tiến hành tô màu cho một hình vuông như hình bên, theo quy trình sau:
Bước 1: Tô màu “đẹp” cho hình vuông A B C D . 1 1 1 1
Bước 2: Tô màu “đẹp” cho hình vuông A B C D là hình vuông ở chính giữa khi chia hình 2 2 2 2
vuông A B C D thành 9 phần bằng nhau như hình vẽ. 1 1 1 1
Bước 3: Tô màu “đẹp” cho hình vuông A B C D là hình vuông ở chính giữa khi chia hình 3 3 3 3
vuông A B C D thành 9 phần bằng nhau. Cứ tiếp tục như vậy. 2 2 2 2
Gọi diện tích được tô màu ở mỗi bước là u , * n∈ n
Với S = u + u +
+ u . Tính lim S . n ..... 1 2 n n Lời giải
GVSB: Hồng Hà Nguyễn; GVPB: Tuyet Trinh
Do diện tích được tô màu ở mỗi bước là u , * n∈
u là một cấp số n
. Dễ thấy dãy các giá trị n 4 1
nhân với số hạng đầu u = và công bội q = . 1 9 9 n u q −1 1 ( )
Gọi S là tổng của k số hạng đầu trong cấp số nhân đang xét thì S = . k n q −1 4 1 n − 1 n u q −1 9 9 1 ( ) 1 lim S = = = . n lim lim q −1 1 2 −1 9
B.2. Bài tập trắc nghiệm.
Câu 1. Cho tam giác đều A B C cạnh a . Người ta dựng tam giác đều A B C có cạnh bằng đường cao 1 1 1 2 2 2
của tam giác A B C ; dựng tam giác đều A B C có cạnh bằng đường cao của tam giác A B C 1 1 1 3 3 3 2 2 2
và cứ tiếp tục như vậy. Tính tổng diện tích S của tất cả các tam giác đều A B C , A B C , A B C 1 1 1 2 2 2 3 3 3 … 2 3a 3 2 3a 3 A. . B. . C. 2 a 3 . D. 2 2a 3 . 4 2 Lời giải
GVSB: Hồng Hà Nguyễn; GVPB: Tuyet Trinh Chọn C a 3 2 a 3
Đường cao của tam giác đều cạnh a là
. Diện tích của tam giác đều cạnh a là . 2 4 Trang 19
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 a 3 Tam giác A B C ⇒ A B C ⇒
1 1 1 A B C có cạnh bằng a
tam giác 2 2 2 có cạnh bằng tam giác 1 1 1 2 2 n 1 − A B C 3 a ⇒ ⇒ A B C 3 a 3 3 3 có cạnh bằng
… tam giác n n n có cạnh bằng . 2 2 3 3 3 2 3 3 n 1 3 3 − Và 2 S = a 2 S = a 2 S a = 2 S a = A B C , A B C , A B C , …, A B C . 1 1 1 4 2 2 2 4 4 3 3 3 4 4 n n n 4 4 3 2 a Như vậy (S 3 q = 4 2 S + S +... = = 3a
n ) là một CSN lùi vô hạn với . Vậy 1 2 . 4 3 1− 4
Câu 2. Cho hình vuông (C có cạnh bằng 2 . Người ta chia mỗi cạnh của hình vuông thành bốn phần 1 )
bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông (C (Hình vẽ). 2 )
Từ hình vuông (C lại tiếp tục làm như trên ta nhận được dãy các hình vuông C ,C , C ,., 2 ) 1 2 3
C . Gọi S là diện tích của hình vuông C i ∈
T = S + S + S + S + i ( {1,2,3, } ..... ). Đặt ... . n ... n i 1 2 3 Tính limT ? 32 A. . B. 35 . C. 23 . D. 33 . 3 3 3 2 Lời giải
GVSB: Hồng Hà Nguyễn; GVPB: Tuyet Trinh Chọn A 2 2 Cạnh của hình vuông ( 3 1 10 C là: a = 5 5 .2 + .2 = . Do đó diện tích 2 S = 2 = 2 ) 2 4 4 2 2 8 2 5 = S . 1 8 2 2 2
Cạnh của hình vuông (C là: 3 1 a 10 10 2 a = a + a = = 2 . Do đó diện tích 3 ) 3 2 2 4 4 4 4 2 5 2 5 S = 2 =
S . Lý luận tương tự ta có các S , S , S ,...S . tạo thành một dãy cấp số n... 3 2 8 8 1 2 3 5
nhân lùi vô hạn có u = S và công bội q = . 1 1 8 S 32 1 limT = = . 1− q 3 Trang 20
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
Câu 3. Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác ABC được gọi là tam giác
trung bình của tam giác ABC . Ta xây dựng dãy các tam giác A B C , A B C , A B C ,... sao cho 1 1 1 2 2 2 3 3 3
A B C là một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương n ≥ 2, tam giác A B C là 1 1 1 n n n
tam giác trung bình của tam giác A
Với mỗi số nguyên dương n , kí hiệu S tương − B − C n n n− . 1 1 1 n
ứng là diện tích hình tròn ngoại tiếp tam giác A B C . Tính tổng S = S + S +...+ S + n ...? n n n 1 2 π π A. 15 S = .. B. S = 4π.. C. 9 S = . . D. S = 5π. 4 2 Lời giải
GVSB: Hồng Hà Nguyễn; GVPB: Tuyet Trinh Chọn B
Tam giác đều cạnh 3 có bán kính đường tròn ngoại tiếp là 3 3 2
= 3 ⇒ S = π r = 3π 3
Với mỗi tam giác đề bài cho, độ dài cạnh của tam giác sau bằng 1 độ dài cạnh của tam giác 2
trước nên diện tích đường tròn ngoại tiếp giảm đi 4 lần Khi đó 1 1 1 S S S ... S π = + + + + = + + + + n ... 3 1 ... .. 1 2 4 16 2n Khi 1
n → +∞ ⇒ S = 3π. = 4π. . 1 1− 4 Trang 21
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
Câu 1. [NB] Hàm số y = f (x) có giới hạn bằng a∈ khi x tiến đến x được kí hiệu là 0
A. lim f (x) = x .
B. lim f (x) = a .
C. lim f (x) = a .
D. lim f (x) = f (a) . 0 x→a x→a x→ 0 x x→ 0 x Lời giải
GVSB: Lưu Anh Bảo; GVPB: Tuyet Trinh Chọn C
Hàm số y = f (x) có giới hạn bằng a∈ khi x tiến đến x được kí hiệu là 0
lim f (x) = a . x→ 0 x
Câu 2. [NB] Hàm số y = f (x) có giới hạn bằng a∈ khi x tiến đến x khi và chỉ khi 0 A. lim f
( x) − a < 0 . B. lim f
( x) − a > 0
. C. lim f (x) = a . D. lim f
( x) − a = 0 . x→ 0x x→ 0x x→ 0x x→ 0x Lời giải
GVSB: Lưu Anh Bảo; GVPB: Tuyet Trinh Chọn D
lim f (x) = a ⇔ lim f
( x) − a = 0 . x→ 0x x→ 0x
Câu 3. [NB] Với c là hằng số cho trước , giá trị lim c bằng. x→ 0x A. 0 . B. c . C. x . D. +∞ . 0 Lời giải
GVSB: Lưu Anh Bảo; GVPB: Tuyet Trinh Chọn B
Công thức lim c = c . x→ 0x
Câu 4. [TH] Cho hàm số y = f (x) và y = g (x) thỏa: lim f (x) = a (a > 0,a∈) và x→ 0 x f (x)
lim g (x) = +∞ . Khi ấy, kết quả của giới hạn lim bằng x→ x→ 0x g ( x) 0 x A. 0 . B. +∞ . C. −∞ . D. 1. Lời giải
GVSB: Lưu Anh Bảo; GVPB: Tuyet Trinh Chọn A
Câu 5. [TH] Cho hàm số y = f (x) và y = g (x) thỏa: lim f (x) = a (a < 0,a∈) và x→ 0 x
lim g (x) = −∞ . Khi ấy, kết quả của giới hạn lim f (x).g (x) bằng x→ 0 x x→ 0x A. 0 . B. +∞ . C. −∞ . D. 1. Lời giải
GVSB: Lưu Anh Bảo; GVPB: Tuyet Trinh Chọn B
Câu 6. [TH] Cho hàm số y = f (x) và y = g (x) thỏa: lim f (x) = a và lim g (x) = b ( ; a b∈) . x→ 0 x x→ 0 x
Xét các mệnh đề sau: lim f
( x) + g ( x) = a + b ; lim f
( x) − g ( x) = a − b ; x→ 0x x→ 0x
f (x) a lim f
( x).g ( x) = ab ; lim = . x→ 0x x→ 0x g ( x) b Số mệnh đề đúng là A. 1. B. 2 . C. 3. D. 4 . Lời giải Trang 1
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
GVSB: Lưu Anh Bảo; GVPB: Tuyet Trinh Chọn A
Số mệnh đề đúng là: lim f
( x) + g ( x) = a + b ; lim f
( x) − g ( x) = a − b ; x→ 0x x→ 0x lim f
( x).g ( x) = ab . x→ 0x
f (x) a Mệnh đề lim
= chỉ đúng khi có thêm điều kiện b ≠ 0 . x→ 0x g ( x) b B. BÀI TẬP.
B.1. Bài tập tự luận. 2 Bài 1. Tìm giới hạn 2x + 3x − 2 lim . 2 x→ 1 − x − 4 Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Giang Trần 2 Ta có 2x + 3x − 2 lim = 1. 2 x→ 1 − x − 4 2
Bài 2. Tìm giới hạn x + x + 3 lim . 2 x→2 x + 4 Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Giang Trần 2 Ta có x + x + 3 lim 3 = . 2 x→2 x + 4 8 2
x + ax +1 khi x > 2
Bài 3. Tìm a để hàm số f (x) =
có giới hạn khi x → 2 . 2
2x − x +1 khi x ≤ 2 Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Giang Trần Ta có: 2
lim f (x) = lim (x + ax + 2) = 2a + 6 x 2+ x 2+ → → 2
lim f (x) = lim (2x − x +1) = 7 x 2− x 2− → →
Hàm số có giới hạn khi x 1
→ 2 ⇔ lim f (x) = lim f (x) ⇔ 2a + 6 = 7 ⇔ a = x 2+ x 2− → → 2 Vậy 1
a = là giá trị cần tìm. 2
B.2. Bài tập trắc nghiệm.
Nhận biết ( 3 câu) +
Câu 1. Tìm giới hạn x 1 lim
bằng định nghĩa. x 1 → x − 2 A. −∞ . B. 2 − . C. 1. D. +∞ . Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Giang Trần Chọn B + + Với mọi dãy (x x = ta có: x x 1 n 1 lim = 2 − . Vậy lim = 2 − . n ) : lim n 1 x − x 1 → x − 2 n 2 Trang 2
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 +
Câu 2. Tìm giới hạn x 1 A = lim . 2 x→ 2 − x + x + 4 A. +∞ . B. −∞ . C. 1 − . D. 1. 6 Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Giang Trần Chọn C Ta có x +1 1 A = lim = − . 2 x 2 →− x + x + 4 6 3 + − +
Câu 3. Tìm giới hạn x 2 x 1 C = lim . x→0 3x +1 A. +∞ . B. −∞ . C. 3 2 +1. D. 1. Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Giang Trần Chọn C 3 + − + Ta có x 2 x 1 3 C = lim = 2 +1. x→0 3x +1 Thông hiểu (2 câu) +
Câu 1. Tìm giới hạn 2 tan x 1 B = lim . π x→ sin x +1 6 + A. 4 3 6 . B. 1. C. +∞ . D. −∞ . 9 Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Giang Trần Chọn A π 2 tan +1 Ta có 2 tan x +1 6 4 3 + 6 B = lim = = . π → + π x sin x 1 9 6 sin +1 6
Câu 2. Tính giới hạn 4x +1 −1 K = lim . 2 x→0 x − 3x
A. K = 0. B. 2 K = − . C. 2 K = . D. 4 K = . 3 3 3 Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Giang Trần Chọn B Ta có 4x +1 −1 K = lim 4 = lim x 4 = lim 2 = − . 2 x→0 x − 3x
x→0 x ( x − ) 3 ( 4x +1 + ) 1 x→0 ( x − ) 3 ( 4x +1 + ) 1 3
GIỚI HẠN HÀM SỐ (TẠI MỘT ĐIỂM) – KHỬ VÔ ĐỊNH CHỈ TẠO NHÂN TỬ - 3 TỰ LUẬN + 4 TRẮC NGHIỆM TỰ LUẬN: 2 − x
Câu 1. Tính giới hạn 4 lim . x→ 2 − x + 2 Lời giải
GVSB: Dương Quang; GVPB: Giang Trần Trang 3
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 Ta có: 2 4 − x
(2 − x)(2 + x) lim = lim
= lim (2 − x) = 4 . x→ 2 − x→ 2 − x→ 2 x + 2 x + 2 −
Câu 2. Tính giới hạn 1 3 lim − . 3 x 1
→ 1− x 1− x Lời giải
GVSB: Dương Quang; GVPB: Giang Trần Ta có: 1 3 ( 2
1+ x + x ) −3 (x − ) 1 (x + 2) lim − = lim = lim 3 x→ 1− x 1 x→ − x (1− x)( 2 1+ x + x ) x→ (1− x)( 2 1 1 1 1+ x + x ) x + 2 lim = − = 1 − 2 x 1
→ 1+ x + x 2 Câu 3.
x + ax + b −
Tìm a,b biết giới hạn 1 3 lim = . 2 x 1 → x −1 2 Lời giải
GVSB: Dương Quang; GVPB: Giang Trần Đặt f (x) 2
= x + ax + b −1⇒ f ( ) 1 = 0 2
x + ax + b −1
x −1 x − x x −
Khi đó f (x) = (x − ) 1 (x − x ) ( )( 0 ) x 3 0 ⇒ lim = lim = lim = 0 2 2 x 1 → x 1 → x 1 x −1 x −1 → x +1 2 1− x 3 0 ⇔ = ⇒ x = 2
− ⇒ f x = x −1 x + 2 = x + x − 2 ⇒ a =1; b = 1 − . 0 ( ) ( )( ) 2 2 2 TRẮC NGHIỆM: 2 Câu 1. x − x + Giới hạn 3 2 lim bằng x→2 2x − 4 A. +∞ . B. 1 . C. 1 − . D. 3 . 2 2 2 Lời giải
GVSB: Dương Quang; GVPB: Giang Trần Chọn B 2 x − 3x + 2
(x − 2).(x − )1 x −1 1 lim = lim = lim = . x→2 x→2 2x − 4 2.(x − 2) x→2 2 2 2
x − (a + 2) x + a +1
Câu 2. Giới hạn lim bằng 3 x 1 → x −1 − − − A. a a a a 2 . B. 2 . C. − . D. . 3 3 3 3 Lời giải
GVSB: Dương Quang; GVPB: Giang Trần Chọn C 2 x − (a + 2) 2 x + a +1
x − x − (a + ) 1 x + a +1 Ta có lim = lim 3 x→ x −1 x→ (x − )1( 2 1 1 x + x + ) 1 x(x − ) 1 − (a + ) 1 (x − ) 1
(x − )1(x − a − )1 x − a −1 = lim a = = = − . x→ (x − )1( lim lim 2 x + x + ) 1 x→ ( x − ) 1 ( 2 1 1 x + x + ) 2 x 1 1 → x + x +1 3 2
3x − (3a + 2) x + b
Câu 3. Cho giới hạn lim
= 4 . Giá trị của biểu thức 2 2
T = a + b là: 2 x→2 x − 3x + 2 Trang 4
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
A. T = 90 .
B. T = 80 . C. T =16 .
D. T = 20. Lời giải
GVSB: Dương Quang; GVPB: Giang Trần Chọn D Đặt f (x) 2 = 3x + (2a + )
1 x + b ⇒ f (2) = 0 2
3x − 3a + 2 x + b
x − 2 3x − m
Khi đó: f (x) = (x − 2)(3x − m) ( ) ( )( ) ⇒ lim = lim = 4 2 x→2 x→2 x − 3x + 2
(x − 2)(x − ) 1 3x − ⇔ lim
m = 4 ⇔ 6−m = 4 ⇔ m = 2 x→2 x −1 a = 2
Suy ra f (x) = (x − 2)(3x − 2) 2
= 3x −8x + 4 ⇒ ⇒ T = 20 . b = 4 2018 2017 Câu 4. x + x + + x − Giới hạn ... 2018 lim bằng 2018 x 1 → x −1 A. 2018 . B. 2019 . C. 2019 . D. 2018 . 2018 2 2 Lời giải
GVSB: Dương Quang; GVPB: Giang Trần Chọn C x + x + ...+ x − 2018 ( 2018 x − ) 1 + ( 2017 2018 2017 x − ) 1 +...+ (x − ) 1 I = lim = lim 2018 2018 x 1 → x 1 x −1 → x −1 n x −1 (x − ) 1 ( n 1− n−2 x + x +...+ ) n 1 − n−2 1 x + x + + Xét ... 1 lim = lim = lim = n 2018 x→ x
−1 x→ (x − ) 1 ( 2017 2016 1 1 x + x + ...+ ) 2017 2016 x 1 1 → x + x + ...+1 2018 2019.2018 + + + Do đó 2018 2017 ... 1 2 2019 I = = = . 2018 2018 2
Dạng 2.4. Khử vô định – dùng liên hợp B. BÀI TẬP.
B.1. Bài tập tự luận. + − Bài 1. x 4 2 Tính lim x→0 x Lời giải
GVSB: Hoàng Văn Quảng; GVPB:Giang Trần Ta có: x + 4 − 2 x + 4 − 4 1 1 lim = lim = lim = x→0 x→0 x
x( x + 4 + 2) x→0 x + 4 + 2 4 x + 4 − 2 1 Vậy lim = . x→0 x 4 Bài 2. + − Tính 3x 1 4 lim
x→5 3 − x + 4 Lời giải Trang 5
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
GVSB: Hoàng Văn Quảng; GVPB:Giang Trần x (3x + ) 1 −16 + − (3 + x + 4 3 1 4 ) 3 − (3+ x + 4) Ta có lim = lim = lim = 18 9 − = − . x→5 x→5 3− x + 4 9 − (x + 4) ( 3x +1 + 4) x→5 3x +1 + 4 8 4 3 + − − Bài 3. 7x 1 5x 1
Tính giới hạn A = lim . x 1 → x −1 Lời giải
GVSB: Hoàng Văn Quảng; GVPB:Giang Trần
3 7x +1 − 2 − ( 5x −1 − 2) Ta có: A = lim x 1 → x −1 3 7x +1 − 2 5x −1 − 2 = lim − lim = I − J x 1 → x 1 x −1 → x −1 7(x − ) 1 I = lim x 1 → (x − ) 1 (3 (7x− )2 3 1 + 2 7x −1 + 4) 7 7 = lim = . x 1 → 3 ( x − )2 3 12 7 1 + 2 7x −1 + 4 5(x − ) 1 5 5 J = lim = lim = x 1 → ( x − )
1 ( 5x −1+ ) x 1 1 → 5x −1 +1 3 Vậy 2 A = − . 3
B.2. Bài tập trắc nghiệm. + − Câu 1. x 4 1 3 Tính giới hạn lim kết quả là 2 x→2 x − 4 A. 0. B. 1 . C. 2. D. -2. 6 Lời giải
GVSB: Hoàng Văn Quảng; GVPB:Giang Trần Chọn B x
( 4x+1−3)( 4x+1+ + − 3 4 1 3 ) 4x +1− 9 lim = lim = lim 2 x→2 x→2 x − 4
( 2x −4)( 4x+1+3) x→2 ( 2
x − 4)( 4x +1+3) 4x −8 = lim 4 1 = lim = . x→2 ( 2
x − 4)( 4x +1+3) x→2 (x + 2)( 4x +1+3) 6 + − Câu 2. x 2 5 1 Giới hạn của lim là 2 x→ 2 − x − 4 A. 1 − . B. 1 − . C. 1 − . D. 1. 2 4 3 3 Lời giải
GVSB: Hoàng Văn Quảng; GVPB:Giang Trần Chọn B Trang 6
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 x
( 2x+5− )1( 2x+5+ + − )1 2 5 1 2x + 4 lim = lim = lim 2 x→ 2 − x→ 2 x − 4 −
( 2x −4)( 2x+5 + ) x→ 2 1
− ( x − 2)( x + 2)( 2x + 5 + ) 1 2 1 = lim = − . x→ 2
− ( x − 2)( 2x + 5 + ) 1 4 3 + + Câu 3. x 1 1 Giới hạn của lim bằng bao nhiêu? x→ 2 − x + 2 A. 1 . B. 1. C. 1 . D. 2. 2 3 4 3 Lời giải
GVSB: Hoàng Văn Quảng; GVPB:Giang Trần Chọn B + + (1+ 1+ x) 1 1 x
(1− 1+x+ (1+x)2 3 3 3 3 ) + lim = lim x 2 1 = lim = x→ 2 − x→ 2 x + 2 − (x + 2)( 3 3
1− 1+ x + (1+ x)2 ) x→ 2 − (x + )( 3 3 −
+ x + ( + x)2 ) 3 2 1 1 1 2 3 + + − + Câu 4. x x x a Biết 2 7 1 2 lim =
+ c với a , b , c ∈ và a là phân số tối giản. Giá trị x 1 → 2 (x − ) 1 b b
của a + b + c bằng: A. 5. B. 37 . C. 13. D. 51. Lời giải
GVSB: Hoàng Văn Quảng; GVPB:Giang Trần Chọn C 2 3 2 3 x + x + − x +
x + x + − + − x + Ta có 2 7 1 2 2 2 7 1 lim = lim x 1 → 2 (x − ) x 1 1 → 2 (x − ) 1 2 3 x + x + 2 − 2 2 − 7x +1 = lim + lim = I + J . x 1 → 2 (x − ) x 1 1 → 2 (x − ) 1 2 2 Tính x + x + 2 − 2 x + x + 2 − 4 I = lim = lim x 1 → 2 (x − ) x 1 1 → 2 (x − )
1 ( 2x + x + 2 + 2) (x − )1(x + 2) x + 2 3 = lim = lim = . x 1 → 2 (x − )
1 ( 2x + x + 2 + 2) x 1→ 2( 2x + x + 2 + 2) 4 2 3 và 2 − 7x +1 8 − 7x −1 J = lim = x→ (x − ) lim 2 1 x→ 2 (x − ) 1 4 + 2 7x +1 + ( 7x+1)2 1 1 3 3 7 − 7 − = lim = . x→ + x + + ( x + )2 1 3 3 12 2 2 4 2 7 1 7 1 Trang 7
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 2 3 x + x + − x + Do đó 2 7 1 2 lim = I + J = x 1 → 2 (x − ) 1 12
Suy ra a =1, b =12 , c = 0 . Vậy a + b + c =13.
Chương IV. GIỚI HẠN
Dạng 2.4. Giới hạn tại điểm có kết quả là vô cực. A. PHƯƠNG PHÁP Dạng tích: Dạng thương: B. BÀI TẬP.
B.1. Bài tập tự luận.
Bài 1. Tính giới hạn x +1 lim .
x→− ( x + 2)2 2 Lời giải
GVSB: Trần Tín; GVPB: Phan Thanh Lộc Ta có: x +1 1 lim = lim . x +1 . 2 2 ( ) x→ 2 − ( x + 2) x→ 2 − ( x + 2) Do 1 lim = +∞ và lim (x + ) 1 = 1 − < 0 .
x→− ( x + 2)2 2 x→ 2 − Nên x +1 lim = −∞ .
x→− ( x + 2)2 2
Bài 2. Tính giới hạn 1− lim x . 3 2 x 1
→ x − 3x + 3x −1 Lời giải
GVSB: Trần Tín; GVPB: Phan Thanh Lộc Trang 8
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 Ta có: 1− x 1 − lim = lim . 3 2 x 1 → x 1
x − 3x + 3x −1 → ( x − )2 1 Do lim(− ) 1 = 1
− < 0 và lim(x − )2 1 = 0+ . x 1 → x 1 → Nên 1− lim x = −∞ . 3 2 x 1
→ x − 3x + 3x −1
Bài 3. Biết lim f (x) = 4. Tính giới hạn f (x) lim . x 1 →− x→− ( x + )4 1 1
Lời giải GVSB: Trần Tín; GVPB: Phan Thanh Lộc
Ta có: lim f (x) = 4 > 0 . x 1 →− Do lim(x + )4 1 = 0 và với x ∀ ≠ 1 − thì (x + )4 1 > 0. x 1 →− Suy ra f (x) lim = +∞ . x→− (x + )4 1 1
B.2. Bài tập trắc nghiệm. Câu 1. Giới hạn 5 lim bằng: x→ ( x − 3)2 3
A. L = −∞ . B. L = 5 − .
C. L = +∞ .
D. L = 5. Lời giải
GVSB: Trần Tín; GVPB: Phan Thanh Lộc Chọn C
Ta có: lim5 = 5 > 0 và lim(x −3)2 = 0+ . x→3 x→3 Vậy 5 lim = +∞ x→ ( x − 3)2 3 Câu 2. Giới hạn 1 1 lim − bằng:
x→− x −1 ( x + )2 1 1 1
A. L = −∞ .
B. L = − .
C. L = +∞ . D. 0 . 2 Lời giải
GVSB: Trần Tín; GVPB: Phan Thanh Lộc Chọn A 2 Ta có: 1 1 x + x + 2 lim − = lim
x→− x −1 ( x + )2
1 x→− (x − ) 1 (x + )2 1 1 1 2 Do x + x + 2 lim = 1
− < 0 và lim (x + )2 1 = 0+ . x→ 1 − (x − ) 1 x→ 1 − Vậy 1 1 lim − = −∞ .
x→− x −1 ( x + )2 1 1 + − Câu 3. Giới hạn x 4 2 lim bằng: 5 x→0 x 1
A. L = −∞ . B. L = .
C. L = +∞ . D. 4 . 4 Trang 9
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 Lời giải
GVSB: Trần Tín; GVPB: Phan Thanh Lộc Chọn C + − Ta có: x 4 2 x 1 lim = lim = lim 5 x→0 x→0 5 x
x ( x + 4 + 2) x→0 4x ( x + 4 + 2) Do 1 1 lim = > 0 và 4 lim x = 0+ .
x→0 ( x + 4 + 2) 4 x→0 + − Vậy x 4 2 lim = +∞ . 5 x→0 x 3 + − + Câu 4. Giới hạn x 4 x 6 lim bằng: 3 x→0 x 1 1
A. L = −∞ . B. L = .
C. L = +∞ . D. . 6 12
Lời giải GVSB: Trần Tín; GVPB: Phan Thanh Lộc Chọn C Ta có: 3
x + 4 − x −8 lim 3 x→0 x
x + 4 − 2 −(3 x+6 −2) lim = 3 x→0 x x x − x 4 2 ( + + x + 6)2 3 3 + 2 x + 6 + 4 = lim 3 x→0 x 1 1 − x 4 2 ( + + x + 6)2 3 3 + 2 x + 6 + 4 = lim 2 x→0 x Do 1 1 1 lim − = > và 2 lim x = 0+ .
x→ x 4 2 x→0 ( + + x + 6) 0 2 0 3 3 + + + 6 2 x 6 4 3 + − + Vậy x 4 x 6 lim = +∞ . 3 x→0 x
Dạng 2.6. Giới hạn của hàm số lượng giác A. PHƯƠNG PHÁP Định lý kẹp chặt.
Nếu g (x) ≤ f (x) ≤ h(x) và Lim g (x) = Lim h(x) = L thì Lim f (x) = L . x→ 0 x x→ 0 x x→ 0 x Trang 10
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
Giới hạn hàm lượng giác sinx lim = 1 x→0 x sin (ax)
Hệ quả: Nếu lim u (x) = 0 thì lim = 1 x→ 0 x x→0 ax
Tìm giới hạn của hàm số lượng giác có dạng 0 ta làm như sau: 0
- Biến đổi tổng thành tích
- Biến đổi để áp dụng giới hạn sin lim x =1 x→0 x B. BÀI TẬP.
B.1. Bài tập tự luận.
Bài 1. Tìm giới hạn sin 2 lim x . x→0 sin x2 Lời giải
GVSB: Hien Nguyen; GVPB: Phan Thanh Lộc sin 2x sin 2x sin 2x 2x 2x 2 lim = lim . = lim x .4 = 4. x→0 x x→0 x x x→0 sin sin sin x 2 2 2 2 x x 2 2
Bài 2. Tìm giới hạn
3− cos x − cos 2x − cos3 lim x . x→0
1− cos x Lời giải
GVSB: Hien Nguyen; GVPB: Phan Thanh Lộc
3− cos x − cos 2x − cos3 lim x x→0 1− cos x
1− cos x +1− cos 2x +1− cos3 lim x x→0 1− cos x 1− cos 2x 1− cos3 lim 1 x = + + x→0 1− cos x 1− cos x 2 3x 2 sin sin x 2 =1+ lim + lim x→0 x x→0 2 2 sin sin x 2 2 2 2 x x x 2 3 2 sin sin x 2 2 2 1 lim . .4 lim . .9 = + + =1+ 4 + 9 =14. 2 2 x→0 x x x→0 2 3x 2 sin sin x 2 2 2 2 Bài 3. Tìm giới hạn 1+ sin x − o c sx lim . 2 x→0 sin x Lời giải
GVSB: Hien Nguyen; GVPB: Phan Thanh Lộc Trang 11
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 2 2 2 2
1+ sin x − cos x
1+ sin x − cos x 2sin lim = lim = lim x 2 x→0 x→0 sin x ( 2
1+ sin x + cos x) 2 x→0 sin x ( 2
1+ sin x + cos x) 2 sin x 2 = lim = 1. x→0 ( 2
1+ sin x + cos x)
B.2. Bài tập trắc nghiệm. Câu 1. Tính x + sin x lim ? x→+∞ x A. 1 . B. +∞ . C. 1. D. 0 . 2 Lời giải
GVSB: Hien Nguyen; GVPB: Phan Thanh Lộc Chọn C Ta có x + sin x x sin x sin lim = lim + lim = 1+ lim x =1+0 =1. x→+∞ x→+∞ x→+∞ x x x x →+∞ x sin x ( Do 1
≤ khi x → ∞ , mà 1 sin lim = 0 ⇒ lim x = 0). x x x→+∞ x x →+∞ x 4
Câu 2. Tìm giới hạn sin 2 = lim x D ? 4 x→0 s in 3x A. +∞ . B. −∞ . C. 16 . D. 0 . 81 Lời giải
GVSB: Hien Nguyen; GVPB: Phan Thanh Lộc Chọn C 4 4
sin 2x 3x 16 16 D = lim . . = .
x→0 2x sin 3x 81 81 3
Câu 3. Tìm giới hạn 1+ 3x − 1+ 2 = lim x M ? x→0 1− cos 2x A. +∞ . B. −∞ . C. 1 − . D. 0 . 4 Lời giải
GVSB: Hien Nguyen; GVPB: Cô Long Chọn C 3 Ta có 1+ 3x − 1+ 2 = lim x M x→0 1− cos 2x 3 1+ 3x − 1+ 2 = lim x 2 x→0 2sin x Trang 12
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
3 1+ 3x − 1+ 2x 2 = lim x 2 x→0 2sin x 2 x 3 2 1+ 3x − 1+ 2 = lim x .lim x 2 2 x→0 x→0 x 2sin x
3 1+ 3x − (x + ) 1 + (x + ) 2 1 − 1+ 2x = lim .lim x 2 2 x→0 x→0 x 2sin x 3 1+ 3x − (x + ) 1 (x + ) 2 1 − 1+ 2x = lim + lim .lim x 2 2 2 x→0 x→0 x→0 x x 2sin x 2 −x (x + 3) 2 2 = lim + lim x .lim x x→0 2 3 x
(1+3x)2 +(x + ) 3
1 1+ 3x + (x + )2 x→0 1 x (x + ) 2 2 x→0 1 + 1+ 2x 2sin x −(x + 3) 2 1 = lim + lim .lim x x→ 3
(1+3x)2 +(x + )1 1+3x +(x + )2 3 1 x→ (x + ) 2 0 0 x→0 1 + 1+ 2x 2sin x 1 1 1 = 1 − + . = − . 2 2 4 π 1 sin cos x −
Câu 4. Tìm giới hạn 2 E lim = ? x→0 sin (tan x) A. +∞ . B. −∞ . C. 1. D. 0 . Lời giải
GVSB: Hien Nguyen; GVPB: Phan Thanh Lộc Chọn D π 1 sin cos x − 2 Ta có tan = lim x
E x→0 sin(tan x) tan x π 1 sin cos x − 2 sin (tan x) E lim = (vì lim = 1) x→0 sin (tan x) x→0 tan x π 1 cos (1 cos x) − − 2 lim = x→0 tan x Trang 13
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 2 2 2sin π sin x 2 lim = x→0 tan x 2 2 x 4 sin π sin sin x 2 2 2 x π 3 = lim . . .x = 0. 2 4 x→0 x
x tan x 8 2 π sin 2 2 Trang 14
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
Thiếu tóm tắt lí thuyết nha thầy
Dạng XX. Câu hỏi lí thuyết A. PHƯƠNG PHÁP
Giả sử hàm số f xác định trên khoảng (x ;b , (x ∈ R . Ta nói rằng hàm số 0 ) f có 0 )
giới hạn bên phải là số thực L khi x dần đến x (hoặc tại điểm x ) nếu với mọi dãy số bất 0 0
kì (x những số thuộc khoảng (x ;b mà lim x = x ta đều có lim f (x = L . Khi đó ta n ) 0 ) n ) n 0 viết
lim f (x) = L hoặc f (x) → L khi x x + → . x + → 0 0 x
Giả sử hàm số f xác định trên khoảng (a; x , (x ∈ R . Ta nói rằng hàm số 0 ) f có 0 )
giới hạn bên trái là số thực L khi x dần đến x (hoặc tại điểm x ) nếu với mọi dãy bất kì 0 0
(x những số thuộc khoảng ( ;
a x mà lim x = x ta đều có lim f (x = L Khi đó ta viết n ) 0 ) n ) n 0
lim f (x) = L hoặc f (x) → L khi x x − → . x − → 0 0 x
Các định nghĩa lim f ( x) = +∞ , lim f ( x) = −∞ , lim f ( x) = +∞ và lim f ( x) = −∞ x − → − + + 0 x x→ 0 x x→ 0 x x→ 0 x
được phát biểu tương tự
Các định lí về giới hạn của hàm số vẫn đúng khi thay x → x bởi x x − → hoặc 0 0 x x + → . 0
lim f (x) = L ⇔ lim f (x) = lim f (x) = L x + − → o x x→ o x x→ o x
B.2. Bài tập trắc nghiệm.
Câu 1. Chọn khẳng định đúng:
A. lim f (x) = L khi và chỉ khi lim f x lim f x x→ 0 x x 0 x x 0 x
B. lim f x L khi và chỉ khi lim f x L x 0 x x 0 x
C. lim f x L khi và chỉ khi lim f x L x 0 x x 0 x
D. lim f x L khi và chỉ khi lim f x lim f x L x 0 x x 0 x x 0 x Lời giải
GVSB: Hồ Minh Tường; GVPB: Phan Thanh Lộc Chọn D
Ta có: lim f x L khi và chỉ khi lim f x lim f x L . x 0 x x 0 x x 0 x
Câu 2. Cho hàm số f (x) thỏa mãn lim f (x) = 5 và lim f (x) = 5
− . Khẳng định nào sau đây là đúng?. x 3+ → x 3− →
A. lim f (x) = 5 .
B. lim f (x) = 0. x→3 x→3
C. Không tồn tại lim f (x).
D. lim f (x) = 5 − . x→3 x→3 Lời giải
GVSB: Hồ Minh Tường; GVPB: Phan Thanh Lộc Chọn C Ta có
lim f (x) ≠ lim f (x) , suy ra không tồn tại lim f (x). x 3+ x 3− → → x→3 Trang 1
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
Câu 3. Cho hàm số f (x) thỏa mãn lim f (x) = 2 và lim f (x) = a +1. Xác định giá trị của a sao cho x 1+ → x 1− →
tồn tại lim f (x). x 1 → A. a =1.
B. a = 3.
C. Không tồn tại a . D. a = 1 − . Lời giải
GVSB: Hồ Minh Tường; GVPB: Phan Thanh Lộc Chọn A Ta có
Để tốn tại lim f (x) thì lim f (x) = lim f (x) ⇔ 2 = a +1 ⇔ a =1. x 1 → x 1+ x 1− → →
Câu 4. Cho hàm số f (x) thỏa mãn lim f (x) = 2 và lim 3+ f (x) = m
. Xác định giá trị của m sao x 1+ → x 1− →
cho tồn tại lim f (x) x 1 →
A. m = 2 .
B. m = 5 .
C. Không tồn tại m . D. m = 1 − . Lời giải
GVSB: Hồ Minh Tường; GVPB: Phan Thanh Lộc Chọn B Ta có lim 3+ f
(x) = m ⇔ lim
(3)+ lim f (x) = m ⇔ lim f (x) = m −3. x 1− x 1− x 1− x 1− → → → →
Hàm số có giới hạn tại x =1 khi và chỉ khi lim f (x) = lim f (x) ⇔ 2 = m − 3 ⇔ m = 5. x 1+ x 1− → →
Câu 5. Cho hàm số f (x) thỏa mãn lim f (x) = m +1 và lim f (x) 2
= m −1. Tổng các giá trị của m sao x 2+ → x 2− →
cho tồn tại lim f (x) bằng. x→2 A. 1. B. 3. C. 0 . D. 2 . Lời giải
GVSB: Hồ Minh Tường; GVPB: Phan Thanh Lộc Chọn A Ta có m = −
lim f (x) = lim f (x) 1 2
⇔ m +1 = m −1 ⇔ . x 2+ x 2− → → m = 2
Tổng giá trị của m là: 1 − + 2 =1
x + m khi x < 0
Câu 6. Tìm các giá trị thực của tham số m để hàm số f (x) =
có giới hạn tại x = 0 . 2
x +1 khi x ≥ 0 A. 1. B. 3. C. 0 . D. 2 . Lời giải
GVSB: Hồ Minh Tường; GVPB: Phan Thanh Lộc Chọn A
Ta có: lim f (x) = 0 + m = m , lim f (x) 2 = 0 +1 =1 x 0− → x 0+ →
Hàm số có giới hạn tại x = 0 khi lim f (x) = lim f (x) ⇔ m =1. x 0− x 0+ → →
x + b khi x ≤ −
Câu 7. Biết hàm số y = f (x) 3 , 1 =
có giới hạn tại x = 1
− . Tính giá trị của a − b ?
x + a, khi x > 1 − A. 2 . B. 2 − . C. 4 . D. 1 − . Trang 2
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 Lời giải
GVSB: Hồ Minh Tường; GVPB: Phan Thanh Lộc Chọn B Tại điểm x = 1 − ta có
lim f (x) = lim (3x + b), lim f (x) = lim (x + a) = 1
− + a và f (− ) 1 = 3 − + b x ( ) 1 − x ( ) 1 − → − → − x ( ) 1 + x ( ) 1 + → − → −
Hàm số có giới hạn tại x = 1
− khi và chỉ khi lim f (x) = lim f (x) = f (− ) 1 x ( ) 1 − x ( ) 1 + → − → − ⇔ 3 − + b = 1
− + a ⇔ a − b = 2 − .
ax +1, khi x <1
Câu 8. Biết hàm số y = f (x) = x + 3, khi 1 ≤ x < 2 có giới hạn tại x =1 và x = 2 . Tính giá trị của
2x +b, khi x ≥ 2 4a + b ? A. 5 + 8. B. 5 + 4 . C. 5 . D. 5 − 4 . Lời giải
GVSB: Hồ Minh Tường; GVPB: Phan Thanh Lộc Chọn C
Tại điểm x =1 ta có
lim f (x) = lim (ax + )
1 = a +1, lim f (x) = lim x + 3 = 2 và f ( ) 1 = 1+ 3 = 2 x 1− x 1− → → x 1+ x 1+ → →
Hàm số có giới hạn tại x =1 khi và chỉ khi lim f (x) = lim f (x) = f ( )
1 ⇔ a +1 = 2 ⇔ a =1 x 1− x 1+ → →
Tại điểm x = 2 ta có
lim f (x) = lim x + 3 = 5 , lim f (x) = lim (2x + b) = b + 4 và f (2) = 2.2 + b = b + 4 . x (2)− x (2)− → → x (2)+ x (2)+ → →
Hàm số có giới hạn tại x = 2 khi và chỉ khi lim f (x) = lim f (x) x (2)− x (2)+ → →
⇔ b + 4 = 5 ⇔ b = 5 − 4.
Do đó: 4a + b = 5 .
1. Bài tập tự luận. 2 Bài 1. x + − Tính giới hạn sau: 3 1 lim x x ( ) 1 + → − x −1 Lời giải
GVSB: Lưu Thị Minh; GVPB:Phạm Tuyến 2 x + − x + Ta có: 3 1 4 1 3 lim = = − . x ( ) 1 + → − x −1 1 − −1 2
Bài 2. Tính giới hạn sau: 3 − x + 4 lim . x→3 x − 2 Lời giải
GVSB: Lưu Thị Minh; GVPB:Phạm Tuyến Trang 3
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 Ta có 3 − x + 4 3.3 − + 4 lim = = 5 − . x→3 x − 2 3− 2 5 2
x x x Bài 3. 3 2 1 Tính giới hạn sau: lim . x4 4 2x Lời giải
GVSB: Lưu Thị Minh; GVPB:Phạm Tuyến 5 2 5 2
x 3x 2x 1 4 3.4 2.4 1 983 Ta có lim . x4 4 2x 4 2.4 4
2. Bài tập trắc nghiệm.
Câu 1. Trong các mệnh đề sau, mệnh đề nào sai? A. 1 lim = +∞ . B. 1 1 lim = . C. 1 lim = +∞ . D. 1 lim = +∞ . x 2+ → x x 2+ → x 2 + 5 x→0 x x 0+ → x Lời giải
GVSB: Lưu Thị Minh; GVPB:Phạm Tuyến Chọn B Ta có: 1 1
lim = Vậy đáp án A đúng. x 2+ → x 2 Suy ra đáp án B sai.
Các đáp án C và D đúng. Giải thích tương tự đáp án A. − + Câu 2. x Giới hạn 2 1 lim bằng x 3+ → x −1 A. . +∞ B. − 5 C. 2 . D. 1. 2 3 3 Lời giải
GVSB: Lưu Thị Minh; GVPB:Phạm Tuyến Chọn B − x + Ta có 2 1 5 lim = − . x 2+ → x −1 2 Câu 3. Giới hạn 1 lim ,a ≠ 0 bằng: x 2a− → x − a A. 1 − . B. 0 . C. +∞ . D. 1 . 2a a Lời giải
GVSB: Lưu Thị Minh; GVPB:Phạm Tuyến Chọn D Ta có: 1 1 lim = . x 2a− → x − a a Trang 4
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
Câu 4. Giới hạn lim ( − 2) x x bằng: + 2 x→2 x − 4 A. 1 +∞ . B. 0 . C. . D. Kết quả khác. 2 Lời giải
GVSB: Lưu Thị Minh; GVPB:Phạm Tuyến Chọn B x x x − 2 Ta có lim (x − 2) = lim = 0 . + 2 x 2 − x 2 x 4 + → → x + 2 2 Câu 5. + Tính giới hạn x 1 lim . x 2− → x −1 A. 4 . B. 6 . C. 13 . D. 1. 2 Lời giải
GVSB: Lưu Thị Minh; GVPB:Phạm Tuyến Chọn C 2 2 x +1 5 +1 13 lim = = x→5 x −1 5 −1 2
Dạng 2.3. Khử dạng vô định – Giới hạn một bên A. PHƯƠNG PHÁP
Nếu giới hạn là hàm phân thức hữu tỉ thì ta phân tích thành nhân tử rồi khử dạng vô định.
Nếu giới hạn chứa dấu giá trị tuyệt đối thì ta khai triển bỏ dấu giá trị
tuyệt đối rồi khử dạng vô định.
Nếu giới hạn chứa căn thức thì ta nhân liên hợp để khử dạng vô định. B. BÀI TẬP.
B.1. Bài tập tự luận. x −1 x −1
Bài 1. Tính các giới hạn sau: lim , lim . x 1+ → x −1 x 1− → x −1 Lời giải
GVSB: Kieu Hung; GVPB: Phạm Tuyến
x −1 khi x ≥1 Ta có x −1 =
−x +1 khi x < 1 x −1 Do đó x −1 lim = lim = lim1 =1 x 1+ − x 1+ − x 1 x 1 x 1 + → → → x −1 −x +1 lim = lim = lim (− ) 1 = 1 − x 1− − x 1− − x 1 x 1 x 1 − → → → Trang 5
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 2
Bài 2. Tính giới hạn sau: x − 3x + 2 lim x + → (x − 2)2 2 Lời giải
GVSB: Kieu Hung; GVPB: Phạm Tuyến 2 x − 3x + 2 (x − ) 1 (x − 2) Ta có x −1 lim = lim = lim = +∞ x + (x − 2)2 x + (x − 2)2 2 2 x 2+ → → → x − 2 Vì lim (x − )
1 =1 > 0 , lim (x − 2) = 0 và x − 2 > 0, x ∀ > 2 . x 2+ → x 2+ → 2
Bài 3. Tính giới hạn sau: x − 5x + 6 lim x 2− →
x −1 −1 Lời giải
GVSB: Kieu Hung; GVPB: Phạm Tuyến 2 x x
(x − 2)(x −3) 5 6 ( x−1+ − + )1 Ta có lim = lim x 2− x 2 x −1 −1 − → →
( x−1− )1( x−1+ )1
(x − 2)(x −3)( x−1+ )1 = lim = lim (x − 3) − + = − − − ( x 1 )1 2 x→2 − x→2 x 2
B.2. Bài tập trắc nghiệm. 2
Câu 1. Tính giới hạn x + 2 lim x x 0+ → x A. 2 . B. +∞ . C. 0 . D. −∞ . Lời giải
GVSB: Kieu Hung; GVPB: Phạm Tuyến Chọn A 2 x + 2x x(x + 2) Ta có lim = lim = lim (x + 2) = 2 . x 0+ x 0+ x 0 x x + → → →
Câu 2. Tính giới hạn x −1 lim . x 1+ → x −1 A. +∞ . B. 2 . C. 0 . D. −∞ . Lời giải
GVSB: Kieu Hung; GVPB: Phạm Tuyến Chọn C Ta có x −1 lim = lim x −1 = 0 . x 1+ x 1 x −1 + → → 3 2
Câu 3. Tính giới hạn − lim x x x 1+ → x −1 +1− x A. 1 − . B. 1. C. 0 . D. +∞ . Lời giải
GVSB: Kieu Hung; GVPB: Phạm Tuyến Chọn B 3 2 Ta có x − x x x −1 lim = lim = lim x =1. x 1+ x 1 x −1 +1− x +
x −1(1− x −1) x 1+ → → → 1− x −1 x − 3
Câu 4. Tính giới hạn lim . x→3 x − 3 Trang 6
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 A. 1. B. 1 − . C. 0 .
D. Không tồn tại. Lời giải
GVSB: Kieu Hung; GVPB: Phạm Tuyến Chọn D x − 3 Ta có x − 3 lim = lim = lim1 =1 x 3+ − x 3+ − x 3 x 3 x 3 + → → → x − 3 −x + 3 lim = lim = lim (− ) 1 = 1 − x 3− − x 3− − x 3 x 3 x 3 − → → → x − 3 x − 3 x − 3 ⇒ lim ≠ lim
. Do đó không tồn tại lim . x 3+ − x 3 x 3 − → → x − 3 x→3 x − 3 1 3 − Õ >
Câu 5. Cho hàm số f (x) n u x 1 3
= x −1 x −1
. Tìm m để hàm số f (x) có giới hạn khi x →1 mx +3 n u Õ x ≤ 1 . A. m = 1 − .
B. m = 2 . C. m = 2 − . D. m =1. Lời giải
GVSB: Kieu Hung; GVPB: Phạm Tuyến Chọn C Ta có 2 + − − + f (x) 1 3 x x 2 (x ) 1 (x 2) x + 2 lim = lim − = lim = lim = lim = 1. + + 3 + 3 x→
x→ x −1 x −1 x→ x −1 x + → (x − ) 1 ( 2 1 1 1 1 x + x + ) + 2 x 1 1 → x + x +1
lim f (x) = lim (mx + 3) = m + 3 . x 1− x 1− → →
Hàm số có giới hạn khi x →1 khi lim f (x) = lim f (x) ⇔ 1= m + 3 ⇔ m = 2 − . x 1+ x 1− → →
Câu 6. Cho a,b là hai số thực khác 0 . Biết giới hạn lim a b − là hữu hạn. − 2 2
x→2 x − 6x + 8 x − 5x + 6
Tính giá trị nhỏ nhất của biểu thức 2 2
P = a − 2b + a − 6b −8 . A. 10 − . B. 8 − . C. 12 − . D. 5 − . Lời giải
GVSB: Kieu Hung; GVPB: Phạm Tuyến Chọn A Ta có lim a b − = lim a b − − 2 2 x 2 x 2 x
6x 8 x 5x 6 − → →
( x 2)( x 4) ( x 2)( x 3) − + − + − − − −
(a −b) x −3a + 4b = lim x 2− →
(x − 2)(x −3)(x − 4)
Theo giả thiết giới hạn lim a b −
là hữu hạn nên x = 2 là nghiệm của − 2 2
x→2 x − 6x + 8 x − 5x + 6
biểu thức (a −b) x −3a + 4b ⇒ a − 2b = 0 ⇒ a = 2b Do đó 2 2 2
P = a − 2b + a − 6b −8 = 2b − 4b −8 = 2(b − )2 1 −10 Có (b − )2 1 ≥ 0, b ∀ ⇒ P ≥ 1 − 0 . a = 2 Vậy min P = 1 − 0 khi . b =1 Trang 7
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
MỘT SỐ QUY ĐỊNH ĐÁNH MÁY (SẢN PHẨM PHẢI XÓA BỎ PHẦN HƯỚNG DẪN NÀY)
(có tham khảo chuẩn của BTN – cảm ơn thầy Trần Quốc Nghĩa) THÔNG THƯỜNG Diễn đàn GV Toán 1. Dấu độ 0 90
1. 90° Nhấn Ctrl Shiff K, buông ra nhấn D 2. Dấu phẩy d ' hoặc A'
2. d′ hoặc A′ Nhấn Ctrl Alt ‘
3. Cặp ngoặc tròn (3;4)
3. (3;4) Nhấn Ctrl (
4. Cặp ngoặc vuông [3;4]
4. [3;4] Nhấn Ctrl [
5. Tọa độ vectơ a (1;2)
5. a = (1;2) có dấu bằng. 6. Dấu song song
a / /b 6. a // b (Bôi đen dấu // rồi nhấn Ctrl Shift E) 7. Các tập số
N , Z , R …
7. , , (nhấn Ctrl D, buông ra nhấn Shift N)
8. Các chữ số tự nhiên không đi cùng bất kì kí tự nào khác có thể gõ bằng Word bình thường,
không cần gõ trong Mathtype.
9. Các biến số như x , y , t … và các chữ cái như a , b , m , A , B … đều phải được gõ trong Mathtype và in nghiêng.
10. Bảng biến thiên phải hóa ảnh, hình vẽ canh giữa trang, để chế độ In line with Text.
11. Đáp án đúng chỉ gạch chân chữ cái, không gạch chân dấu chấm. VD: A. chứ không phải là A.
12. Dấu chấm cuối 4 phương án là màu đen, không in đậm.
13. Màu xanh chuẩn cho các đáp án, chữ Bài, Lời giải, Chọn là màu xanh bên dưới
Quy định về gõ MATHTYPE
Font: Time New Roman Trang 8
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 Size: 12
3. GIỚI HẠN MỘT BÊN
Dạng 2.5. Giới hạn tại điểm có kết quả là vô cực A. PHƯƠNG PHÁP
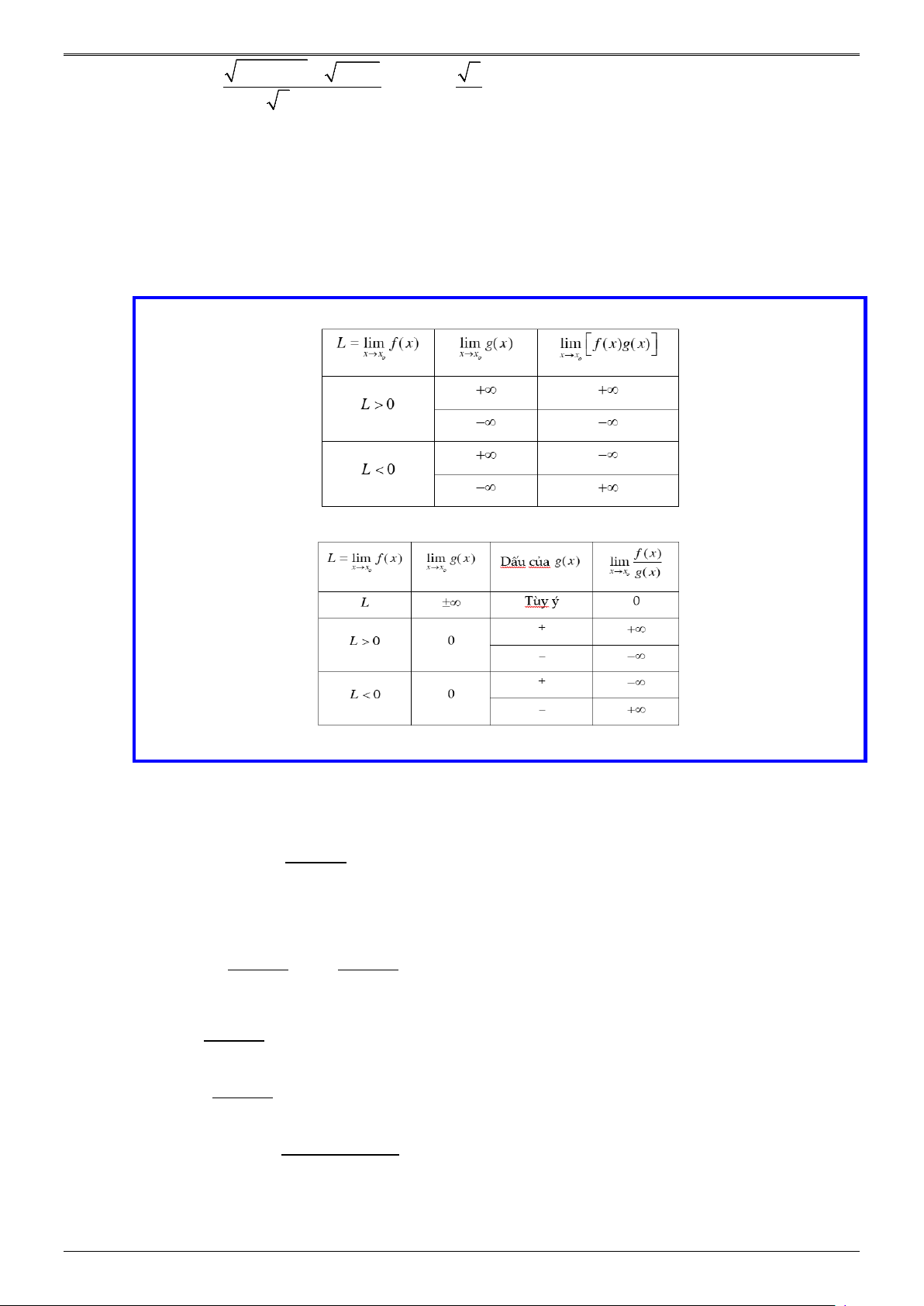
Quy tắc tìm giới hạn của tích f ( x).g ( x)
lim f (x) = L lim g (x)
lim f (x).g(x) x + → + + 0 x x→ 0 x x→ 0 x L > 0 +∞ +∞ L > 0 −∞ −∞ L < 0 +∞ −∞ L < 0 −∞ +∞ f (x)
Quy tắc tìm giới hạn của thương g (x) Trang 9
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
lim f (x) = L lim g (x) Dấu của g (x) f (x) x + → + 0 x x→ 0 x lim x + → 0 x g (x) L ±∞ Tùy ý 0 L > 0 0 + +∞ L > 0 0 − −∞ L < 0 0 + −∞ L < 0 0 − +∞ B. BÀI TẬP.
B.1. Bài tập tự luận.
Bài 1. Tìm giới hạn x −15 lim x 2+ → x − 2
Lời giải GVSB: Thúy Bình Đinh; GVPB: Phạm Tuyến lim (x −15) = 13 − < 0 x→2+ x −15
Vì lim (x − 2) = 0 ⇒ lim = . −∞ x→2+ x→2+ x − 2
x − 2 > 0 khi x → 2+ x + Bài 2. 2 Tìm giới hạn lim x 2+ → x − 2
Lời giải GVSB: Thúy Bình Đinh; GVPB: Phạm Tuyến
lim x + 2 = 2 > 0 x→2+ x + 2 lim x − 2 = 0 li ⇒ m = . +∞ x→2+ x→2+ x − 2
x − 2 > 0 khi x → 2+ 2 x − x − Bài 3. 3 4 Tìm giới hạn lim x→(− )− 2 1 1− x
Lời giải GVSB: Thúy Bình Đinh; GVPB: Phạm Tuyến 2 x − 3x − 4
(−x − )1(−x + 4) −x + 4 lim = lim = lim x ( )− 2 1 1− x x ( ) 1 −
(−x − )1(x − )1 x ( ) 1 − → − → − → −
−x −1(x − ) 1 Do
lim −x + 4 = 5 > 0 x→(− )1− − + − − − − − = ⇒ = −∞ ⇒ = −∞ . − ( 2 x (x )) x 4 x 3x 4 lim 1 1 0 lim lim x→(− ) x→(− )−
−x −1(x − ) x→(− )− 2 1 1 1 1 1− x
−x −1(x − )1 < 0, x ∀ < 1 −
B.2. Bài tập trắc nghiệm.
Câu 1. Mệnh đề nào sau đây sai? A. 1 − lim = +∞ . B. 1 lim = −∞ . C. 1 lim = +∞ . D. 1 lim = +∞ . + 3 x→0 x − 3 x→0 x x 0+ → x x 0+ → x Trang 10
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
Lời giải GVSB: Thúy Bình Đinh; GVPB: Phạm Tuyến Chọn B lim 1 = 1; 3 lim x = 0do + 3
x → 0 ⇒ x > 0 ⇒ x > 0 1 ⇒ lim = +∞ . x 0+ → x 0+ → + 3 x→0 x
lim 1 = 1; lim x = 0do x 0+ → ⇒ x > 0 1 ⇒ lim = +∞ . x 0+ → x 0+ → x 0+ → x
Vì lim 1 = 1; lim x = 0 do x 0+ →
⇒ x > 0 ⇒ x > 0 1 ⇒ lim = +∞ . x 0+ → x 0+ → x 0+ → x Vì lim (− ) 1 = 1 − ; 3 lim x = 0do − 3
x → 0 ⇒ x < 0 ⇒ x < 0 1 − ⇒ lim = +∞ . x 0− → x 0− → − 3 x→0 x 2 Câu 2. + −
Kết quả của giới hạn x x 3 lim là x 0− → x A. 0 . B. 1. C. 1 − . D. +∞ .
Lời giải GVSB: Thúy Bình Đinh; GVPB: Phạm Tuyến Chọn D lim + − = − < − ( 2 x x 3) 3 0 x→0 2 x + x − 3 lim x = 0 ⇒ lim = +∞ . x→0− x→0− x
x → 0− ⇒ x < 0 3 x − Câu 3. 2021 2022
Tính giới hạn I = lim x 1− → x −1 A. 2021. B. 2022 . C. −∞ . D. +∞ .
Lời giải GVSB: Thúy Bình Đinh; GVPB: Phạm Tuyến Chọn D lim − = − = − < − ( 3 2021x 2022) 3 2021.1 2022 1 0 x 1 → 3 − Ta có (x − ) 2021x 2022 lim 1 = 0 ⇒ lim = +∞ . x 1− → x 1− → x −1
x −1< 0 khi x →1−
Câu 4. Tính giới hạn 3 + 2 lim x x 2+ →− x + 2 A. −∞ . B. 2 . C. +∞ . D. 3 . 2
Lời giải GVSB: Thúy Bình Đinh; GVPB: Phạm Tuyến Chọn A lim (3+ 2x) = 1 − x→ 2+ − Do ( + ) 3+ 2 lim 2 = 0 ⇒ lim x x = −∞ . x→ 2+ − x→ 2+ − x + 2
x + 2 > 0 khi x > 2 − Trang 11
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 2 x +1 khi x < 1
Câu 5. Cho hàm số f (x) = 1− x
. Khi đó lim f (x) là x 1− →
2x − 2 khi x ≥ 1 A. +∞ . B. 2 . C. 4 . D. −∞ .
Lời giải GVSB: Thúy Bình Đinh; GVPB: Phạm Tuyến Chọn A Có lim ( 2
x + = > ; lim (1− x) = 0. − )1 2 0 x 1 → x 1− → 2 + Khi x 1−
→ ⇔ x <1 ⇔ 1− x > 0. Suy ra f (x) x 1 lim = lim = +∞ . x 1− x 1− → → 1− x +
Câu 6. Kết quả của giới hạn 1 x 1 lim − là: x 2+ → x − 2 x + 2 − 2 A. 11 − . B. 0 . C. +∞ . D. −∞ .
Lời giải GVSB: Thúy Bình Đinh; GVPB: Phạm Tuyến Chọn D + (x + ) 1 x ( x+2 +2) 1− (x + ) 1 ( x + 2 + 2 1 1 1 ) lim lim − = − = lim x 2+ − x 2+ + − − − x 2 x 2 x 2 2 x 2 x 2 + → → → x − 2 lim − + + + = − < + → (1 ( x ) 1 ( x 2 2) 11 0 x 2 1− (x + ) 1 ( x+2 +2) lim ( x − 2) = 0 ⇒ lim = −∞ . x→2+ x→2+ x − 2
x → 2+ ⇒ x > 2 ⇒ x − 2 > 0 1 x +1 ⇒ lim − = −∞ . x 2+ → x − 2 x + 2 − 2 Trang 12
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
2.1. Câu hỏi lí thuyết B. BÀI TẬP.
B.2. Bài tập trắc nghiệm.
Mức độ nhận biết
Câu 1. Giải sử ta có lim f (x) = a và lim g (x) = b . Trong các mệnh đề sau, mệnh đề nào sai ? x→+∞ x→+∞ f (x) A. lim f a
( x) − g ( x) = a − b . B. lim = . x→+∞
x→+∞ g ( x) b C. lim f
( x) + g ( x) = a + b . D. lim f
( x).g ( x) = . a b . x→+∞ x→+∞ Lời giải
GVSB: Nguyễn Loan; GVPB: Be Nho Chọn B f (x) Mệnh đề lim a
= sai vì thiếu điều kiện b ≠ 0 .
x→+∞ g ( x) b
Câu 2: Trong các mệnh đề sau, mệnh đề nào sai? A. 1 lim = 0 . B. 1 lim = −∞ . C. 1 lim = 0 . D. 1 lim = +∞ . x→+∞ x x 0+ → x 5 x→−∞ x x 0+ → x Lời giải
GVSB: Nguyễn Loan; GVPB: Be Nho Chọn B Ta có: 1
lim = +∞ do lim x = 0 và x > 0 . Vậy phương án 1 lim = +∞ đúng. x 0+ → x x 0+ → x 0+ → x Suy ra phương án 1 lim = −∞ sai. x 0+ → x Các phương án 1 lim = +∞ và 1 lim = +∞ đúng. + 5 x→0 x x 0+ → x
Giải thích tương tự phương án 1 lim = +∞ . x 0+ → x
Câu 3. Cho f (x) n n 1
= a x + a x − + + + với a ≠ n∈
. Khẳng định nào sau đây là đúng? n ( * 0 ) − a x a n n ... 1 1 0
A. lim f (x) = +∞ nếu n chẵn.
B. lim f (x) = +∞ nếu n lẻ và a < 0 . x→+∞ x→−∞ n
C. lim f (x) = +∞ .
D. lim f (x) = −∞ . x→+∞ x→−∞ Lời giải
GVSB: Nguyễn Loan; GVPB: Be Nho Chọn B Ta có:
lim f (x) = lim ( n n 1
a x + a x − + + + − a x a n n . . 1 1 0 ) x→−∞ x→−∞ Trang 1
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 n a − − a a n 1 n 1 1 0 = lim a x + x + + x +
= +∞ nếu n lẻ và a < 0 . n ... x→−∞ a a a n n n n
Mức độ thông hiểu
Câu 1: Cho các giới hạn: lim f (x) = 2 ; lim g (x) = 3. Khi đó, lim 3 f (x) − 4g (x) bằng x→+∞ x→+∞ x→+∞ A. 5. B. 2 . C. 6 − . D. 3. Lời giải
GVSB: Nguyễn Loan; GVPB: Be Nho Chọn C
Ta có lim 3 f (x) − 4g (x)
= lim 3 f ( x) − lim 4g ( x) = 3 lim f ( x) − 4 lim g ( x) = 6 − . x→+∞ x→+∞ x→+∞ x→+∞ x→+∞
Câu 2. Xét các mệnh đề sau:
(I ) lim kx = +∞, với k là số nguyên dương. x→+∞ (II ) 1 lim
= 0 , với k là số nguyên dương. k x→−∞ x
(III ) lim kx = −∞ , với k là số nguyên dương. x→−∞
A. (I ),(II ),(III ) đều đúng.
B. Chỉ (I ) đúng.
C. Chỉ (I ),(II ) đúng.
D. Chỉ (III ) đúng. Lời giải
GVSB: Nguyễn Loan; GVPB: Be Nho Chọn C
Mệnh đề đúng là (I ),(II ).
Mệnh đề (III ) sai vì với k là một số nguyên dương chẵn thì lim k x = +∞ . x→−∞
Câu 3. Xét các mệnh đề sau: (I ) 2 lim k
x = +∞ , với k là số nguyên. x→−∞ (II ) 2 1 lim k
x + = −∞ với k là số nguyên dương. x→−∞
(III ) lim k = −∞ , (k ≠ 0, n nguyên dương). n x→−∞ x
A. (I ),(II ),(III ) đều đúng.
B. Chỉ (II ) đúng.
C. Chỉ (I ),(II ) đúng.
D. Chỉ (III ) đúng. Lời giải
GVSB: Nguyễn Loan; GVPB: Be Nho Chọn B Trang 2
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
Mệnh đề (I ) sai vì với k là số nguyên âm thì 2 lim k x = 0 . x→−∞
Mệnh đề (II ) đúng.
Mệnh đề (III ) sai vì lim k = 0, ( k ≠ 0 , n nguyên dương). n x→−∞ x
2.2. Giới hạn tại vô cực của hàm đa thức A. PHƯƠNG PHÁP
Quy tắc tìm giới hạn tại vô cực . Cho lim f (x) = ;
±∞ lim g(x) = L ≠ 0. Ta có: x→ 0 x x→ 0 x lim f (x) Dấu của L
lim [ f (x).g(x)] x→ 0 x x→ 0 x +∞ ± ±∞ −∞ ± ∞
Phương pháp tìm giới hạn tại tại vô cực của hàm đa thức : lim ( n n 1 − n−2 a x + a + + +
(n∈*) − x a − x a n n n ....... 1 2 0 ) x→+∞
Bước 1: Rút x có lũy thừa bậc cao nhất ra làm nhân tử chung. lim ( n n 1 − n−2 a − a − a a x a + + + + = + + + + − x a − x a x a n n n ....... ) n n 1 n 2 0 lim n ....... 1 2 0 2 n x→+∞ x→+∞ x x x
Bước 2: Tìm các giới hạn + lim n
x = +∞ nếu n là số tự nhiên chẵn ; x→+∞ lim n
x = −∞ nếu n là số tự nhiên lẻ . x→+∞ + a − a − a n 1 n 2 0 lim a + + + + = a . n ....... 2 n n x→+∞ x x x
Bước 3: Áp dụng quy tắc tìm giới hạn tại vô cực suy ra kết quả.
( Tương tự khi tìm lim ( n n 1 − n−2 a x + a + + + ). − x a − x a n n n ....... 1 2 0 ) x→−∞ B. BÀI TẬP
B.1. Bài tập tự luận. Bài 1. Tìm giới hạn I 3
lim 2x 4x 5 x Lời giải
GVSB: Tô Thị Lan; GVPB: Be Nho I 3
x x 3 4 5 lim 2 4 5 lim x 2 . 2 3 x x x x 3 lim x . x 4 5 lim 2
2 0 0 2 0 . 2 3 x x x Trang 3
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 3 4 5
I lim x 2 . 2 3 x x x Bài 2. Tính giới hạn ( 4 2
lim 3x + 5x − 9 2x − . →−∞ ) 2021 x Lời giải
GVSB: Tô Thị Lan; GVPB: Be Nho ( 4 2
lim 3x + 5x − 9 2x − 4 1 1 1
= lim x 3+5 −9 2 − 2021 = +∞. →−∞ ) 2021 x 2 3 4 x→−∞ x x x 4 lim x = +∞ x→−∞ Vì 1 1 1 lim 3 5 9 2 2021 + − − = 3 > 0 2 3 4 x→−∞ x x x Bài 3.
Tính giới hạn lim (1− x)(1− 2x)(1− 3x)....(1− 2021x) . x→+∞ Lời giải
GVSB: Tô Thị Lan; GVPB: Be Nho
( − x)( − x)( − x) ( − x) 2021 1 1 1 1 lim 1 1 2 1 3 .... 1 2021 = lim x . − 1 − 2 − 3.... − 2021 = −∞ x→+∞ x→+∞ x x x x Vì: : 2021 lim x = +∞ x→+∞ 1 1 1 1 lim − 1 − 2 − 3.... − 2021 = (− ) 1 ( 2 − )( 3 − )...(− ) 2021 = −( ) 1.2.3....2021 < 0 x→+∞ x x x x
B.2. Bài tập trắc nghiệm.
Câu 1. Tính giới hạn ( 3 2 lim 2x − x + ) 1 x→−∞ A. + ∞ . B. −∞ . C. 2 . D. 0 . Lời giải
GVSB: Tô Thị Lan; GVPB: Be Nho Chọn B Ta có ( 3 2 x − x + ) 3 1 1 lim 2 1 = lim x 2− + = − ∞ 2 3 x→−∞ x→−∞ x x 3 lim x = −∞ x→−∞ vì 1 1 . lim 2 − + = 2 > 0 2 3 x→−∞ x x
Câu 2. Chọn kết quả đúng của ( 5 3 lim 4
− x + 3x + x + ) 1 . x→−∞ A. 0. B. +∞ . C. −∞ . D. 4 − . Lời giải Trang 4
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
GVSB: Tô Thị Lan; GVPB: Be Nho Chọn B Ta có ( 5 3
− x + x + x + ) 5 3 1 1 lim 4 3 1 = lim x 4 − + + + = +∞ . 2 4 5 x→−∞ x→−∞ x x x Vì 5 lim x = −∞ x→−∞ 3 1 1 . lim 4 − + + + = − 4 < 0 2 4 5 x→−∞ x x x
Câu 3. Giới hạn ( 4 2 lim −x + 3x + ) 2021 bằng x→−∞ A. −∞ . B. +∞ . C. 1. D. 0 . Lời giải
GVSB: Tô Thị Lan; GVPB: Be Nho Chọn A Ta có: ( 4 2
lim −x + 3x + 2018) 4 3 2021 = lim x 1 − + + = −∞ x→−∞ 2 4 x→−∞ x x Do 4 lim x = +∞ và 3 2021 lim 1 − + + = 1 − < 0. x→−∞ 2 4 x→−∞ x x
Câu 4. Giới hạn I 2021 lim 2x 4x 5 bằng x
A. I .
B. I . C. I 2. D. I 5. Lời giải
GVSB: Tô Thị Lan; GVPB: Be Nho Chọn A I 2021 x x 2021 4 5 lim 2 4 5 lim x 2 . 2020 2021 x x x x Vì 2021 lim x . x 4 5 lim 2
2 0 0 2 0 . 2020 2021 x x x 3 4 5 I lim x 2 . 2 3 x x x Câu 5. Giới hạn 3 2
I lim x 2x 4 x 5 x bằng
A. I .
B. I . C. I 0 . D. I 1. Lời giải Trang 5
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022
GVSB: Tô Thị Lan; GVPB: Be Nho Chọn A 3 2 I
x x x 3 2 lim 2 4 5 lim x
2x 4x 5 x x 3 2 4 5 lim x 1 . 2 3 x x x x Vì 2 4 5 3 lim x . và lim 1 1 0 . x 2 3 x x x x
Câu 6. Có bao nhiêu giá trị m nguyên thuộc đoạn [ 20 − ;20] để (m + ) ( 2 lim
x 2 m − 3x ) = −∞ x→−∞ A. 21 . B. 22 . C. 20 . D. 41. Lời giải
GVSB: Tô Thị Lan; GVPB: Be Nho Chọn A - Với m ≠ 0 , ( + ) ( 2 − ) 3 2 lim x 2 3x = lim m m m x m + − 3 2 x→−∞ x→−∞ x x 3 lim x = −∞ x→−∞ Vì 2 . lim m m + − 3 = 3 − m 2 x→−∞ x x Mà (m + ) ( 2 lim
x 2 m − 3x ) = −∞ x→−∞ . ⇒ 3
− m > 0 ⇔ m < 0 . Mà m∈[ 20 − ;20] ⇒ m∈{ 20 − ; 19 − ;....;− } 1 . - Với m = 0, (m + )( 2 m − ) = ( 2 lim x 2 3x lim 6 − x ) = −∞ . x→−∞ x→−∞ Vậy m∈{ 20 − ; 19 − ;....; 1 − ; } 0 .
2.3. Giới hạn tại vô cực của hàm phân thức A. PHƯƠNG PHÁP f (x) Tính lim
khi lim f (x) = lim g (x) = ∞ , trong đó f (x), g (x) là các đa thức.
x→∞ g ( x) x→∞ x→∞
Phương pháp giải: Chia cả tử và mẫu cho n
x với n là số mũ bậc cao nhất của biến số x trong mẫu thức. f x
Xét hàm số h(x) ( ) =
có hệ số của hạng tử bậc cao nhất của f (x), g (x) lần lượt là a,b. g (x) Trang 6
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 f (x)
• Nếu bậc cao nhất của f (x) lớn hơn bậc cao nhất của g (x) thì lim = ∞ .
x→∞ g ( x) f (x)
• Nếu bậc cao nhất của f (x) bằng bậc cao nhất của g (x) thì lim a = .
x→∞ g ( x) b f (x)
• Nếu bậc cao nhất của f (x) nhỏ hơn bậc cao nhất của g (x) thì lim = . →∞ g ( x) 0 x B. BÀI TẬP
B.1. Bài tập tự luận. 3 2 Bài 1. Tính
2x − 3x + 4x +1 A = lim . 4 3 2
x→+∞ x − 5x + 2x − x + 3 Lời giải
GVSB: Ngọc Lý; GVPB: Be Nho 2 3 4 1 3 2 − + + 2 3 4 Ta có:
2x − 3x + 4x +1 A x x x x 0 = lim = lim = = 0 . 4 3 2
x→+∞ x − 5x + 2x − x + 3 x→+∞ 5 2 1 3 1 1− + − + 2 3 4 x x x x 2 Bài 2. Tính giới hạn 1+ − lim x x x→−∞ x Lời giải
GVSB: Ngọc Lý; GVPB: Be Nho 2 1 1 2 1+ − x ( + −1) 2 lim x x = lim x x 1 1 lim x( 1) = + − = +∞ . x→−∞ x x→−∞ x 2 x→−∞ x x 3 Bài 3. Tính giới hạn 2x −10x − 3 lim . 3
x→−∞ x + 7x + 5 Lời giải
GVSB: Ngọc Lý; GVPB: Be Nho 10 3 3 2 − − 2 3 Ta có 2x −10x − 3 lim = lim x x = 2. 3
x→−∞ x + 7x + 5 x→+∞ 7 5 1+ + 2 3 x x 2 + + Bài 4. Tính x x 2 B = lim . x→−∞ 3 3 2 8x + x +1 Lời giải
GVSB: Ngọc Lý; GVPB: Be Nho 2 2 2 + + x + x 1+ 1− 1+ 2 2 Ta có: x x 2 B = lim = lim x x 0 = lim = = 0 . x→−∞ 3 3 2 8x + x +1 x→−∞ 1 1 x→−∞ 1 1 2 3 x 8 + + 3 8 + + 3 x x 3 x x x x x Bài 5. Tính 5 + 7.3 − 4 + 3 C = lim .
→+∞ 8.5x − 5.4x + 2x x Lời giải
GVSB: Ngọc Lý; GVPB: Be Nho Trang 7
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 3 x 4 x 3 1+ 7. − + x x x x Ta có 5 + 7.3 − 4 + 3 C 5 5 5 1 = lim = lim = .
→+∞ 8.5x − 5.4x + 2x x 4 x 2 x x→+∞ 8 8 − 5. + 5 5
B.2. Bài tập trắc nghiệm. 2
Câu 1: Kết quả của giới hạn 2x + 5x − 3 lim là 2
x→+∞ x + 6x + 3 A. 2 − . B. +∞ . C. 3 . D. 2 . Lời giải
GVSB: Ngọc Lý; GVPB: Be Nho Chọn D 5 3 2 2 + − 2 Ta có: 2x + 5x − 3 lim = lim x x = 2. 2
x→+∞ x + 6x + 3 x→+∞ 6 3 1+ + 2 x x 3 2 Câu 2: + −
Kết quả của giới hạn 2x 5x 3 lim là 2
x→−∞ x + 6x + 3 A. 2 − . B. +∞ . C. −∞ . D. 2 . Lời giải
GVSB: Ngọc Lý; GVPB: Be Nho Chọn C 5 3 3 2 + − 2 + − 3 Ta có: 2x 5x 3 lim = lim . x x x = −∞ . 2
x→−∞ x + 6x + 3 x→−∞ 6 3 1+ + 2 x x 3 2 Câu 3: − +
Kết quả của giới hạn 2x 7x 11 lim là 6 5
x→−∞ 3x + 2x − 5 A. 2 − . B. +∞ . C. 0 . D. −∞ . Lời giải
GVSB: Ngọc Lý; GVPB: Be Nho Chọn C 2 7 11 3 2 − + − + 3 4 6 Ta có: 2x 7x 11 lim = lim x x x = 0 . 6 5
x→−∞ 3x + 2x − 5 x→−∞ 2 5 3+ − 6 x x
(2x − )1(3x + 2)(4x −5)
Câu 4: Tính L = lim . 3 x→−∞ 8x + 2x + 7 A. L = 3. B. 3 L = . C. 4 L = . D. L = 3 − . 4 3 Lời giải
GVSB: Ngọc Lý; GVPB: Be Nho Chọn A 3 1 2 5 x 2 3 4 − + − 1 2 5 2 − 3+ 4 − lim x x x L = lim x x x = = 3. x→−∞ 3 2 7 x x→−∞ 2 7 8 + + 8 + + 2 3 x x 2 3 x x Trang 8
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 2 Câu 5: Cho hàm số + + f (x) 4x x 2 =
. Để hàm số có giới hạn bằng 2 khi x → +∞ thì giá trị của 2 ax + 5 a là A. a = 4 − . B. a = 4 . C. a = 3. D. a = 2 . Lời giải
GVSB: Ngọc Lý; GVPB: Be Nho Chọn D 1 2 2 4 + + + + = f (x) 2 4x x 2 x x 4 2 lim = lim = lim =
(a ≠ 0) ⇒ a = 2 . 2 x→+∞ x→+∞ ax + 5 x→+∞ 5 a a + 2 x
Câu 6: Trong bốn giới hạn sau đây, giới hạn nào bằng −∞ ? 2 2 A. 3 − x + 4 − + − + − + lim . B. 3x 4 lim . C. 3x 4 lim . D. 3x 4 lim . x→+∞ x − 2 x→−∞ x − 2 x→+∞ x − 2 x→−∞ x − 2 Lời giải
GVSB: Ngọc Lý; GVPB: Be Nho Chọn C 2 4 x 4 3 − + 2 2 − + 3 − + 2 Ta có: 3x 4 lim lim x = = lim . lim x x = −∞ . x→+∞ x − 2 x→+∞ 2 x→+∞ x→+∞ 2 x 1 − 1− x x 2 +
Câu 7: Gọi S là tập hợp các tham số nguyên a thỏa mãn 3x 2 2 lim
+ a − 4a = 0 . Tổng các phần 2
x→+∞ x + x − 2 tử của S bằng A. 4 . B. 3. C. 5. D. 2 . Lời giải
GVSB: Ngọc Lý; GVPB: Be Nho Chọn A 2 2 3+ + Ta có 2 3x 2 2 lim + − 4 = lim x a a + lim ( 2 a − 4a 2
= 3+ a − 4a = 0 2 )
x→+∞ x + x − 2 x→+∞ 1 2 1 x→+∞ + − 2 x x a =1 2
3+ a − 4a = 0 ⇔ ⇒ S = 4. a = 3
B.1. Bài tập tự luận 2 + Bài 1. Tính giới hạn 4x 1 K = lim . x→−∞ x +1 Lời giải
GVSB: Nguyễn Thành Thái; GVPB: Đỗ Hải Thu Trang 9
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 1 1 2 −x 4 + − 4 + 2 2 + Ta có: 4x 1 = lim = lim x = lim x K = 2 − . x→−∞ x +1 x→−∞ x +1 x→−∞ 1 1+ x 2 3 3 − + + Bài 2. Tìm giới hạn 4x 2 x 1 C = lim . x→−∞ 2 x +1 − x Lời giải
GVSB: Nguyễn Thành Thái; GVPB: Đỗ Hải Thu 2 1 2 1 − + 3 + − − + 3 x 4 x 1 4 1+ 2 3 2 3 Ta có: x x x x 1 C = lim = lim = . x→−∞ 1 x→−∞ 1 2 x 1+ − x − 1+ +1 2 2 x x Bài 3. Giới hạn I = + − − + . →+∞ ( 2 lim x 1 x x 2 x ) Lời giải
GVSB: Nguyễn Thành Thái; GVPB: Đỗ Hải Thu 2 2 − + − − Ta có: x x x 2 x 2 I = + − − + = lim +1 = lim +1 →+∞ ( 2 lim x 1 x x 2 x ) x→+∞ 2
x + x − x + 2 x→+∞ 2
x + x − x + 2 2 1− = lim x +1 3 = . x→+∞ 1 2 2 1+ 1− + 2 x x
B.2. Bài tập trắc nghiệm.
Câu 1. [NB] Tính giới hạn x +1 lim . 2022 x→+∞ x −1 A. 1 − . B. 1. C. 2 . D. 0 . Lời giải
GVSB: Nguyễn Thành Thái; GVPB: Đỗ Hải Thu Chọn D 1 1 + 2 x +1 1 lim = lim . x x = 0 . 2022 2021 x→+∞ x −1 x→+∞ x 1 1− 2021 x 2 + + Câu 2. [NB] Tính x 3x 5 lim . x→−∞ 4x −1 A. 1 − . B. 1. C. 0 . D. 1 . 4 4 Lời giải
GVSB: Nguyễn Thành Thái; GVPB: Đỗ Hải Thu Chọn A Trang 10
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 3 5 2 + + − 1+ + 2 Ta có x 3x 5 lim x x 1 = lim = − . x→−∞ 4x −1 x→−∞ 1 4 4 − x
Câu 3. [TH] Tìm giới hạn lim + − − . →+∞ ( x 1 x 3) x A. 0 . B. 2 . C. −∞ . D. +∞ . Lời giải
GVSB: Nguyễn Thành Thái; GVPB: Đỗ Hải Thu Chọn A + − + lim + − − x 1 x 3 = lim 4 = lim = 0 . →+∞ ( x 1 x 3) x x→+∞
x +1 + x − 3 x→+∞ x +1 + x − 3 2 − +
Câu 4. [TH] Tính giới hạn lim x x x . x→−∞ x +1 A. 1. B. 2 . C. 0 . D. −∞ . Lời giải
GVSB: Nguyễn Thành Thái; GVPB: Đỗ Hải Thu Chọn B 1 1 2 x + x 1+ 1+ 1+ − + Ta có: lim x x x = lim x = lim x = 2. x→−∞ x +1 x→−∞ x +1 x→−∞ 1 1+ x Câu 5. [VD] Cho ( 2 lim
x + ax + 5 + x = . Khi đó giá trị a là →−∞ ) 5 x A. 6 − . B. 10. C. 10 − . D. 6 . Lời giải
GVSB: Nguyễn Thành Thái; GVPB: Đỗ Hải Thu Chọn C 5 xa + + + + + ax 5 = lim lim x = →−∞ ( 2 lim x ax 5 x x
) x→−∞ 2x+ax+5−x x→−∞ a 5 x 1+ + − x 2 x x 5 a + = lim x a = − . x→−∞ a 5 2 − 1+ + −1 2 x x Vậy a = 10 − .
Câu 6. [VDC] Cho các số thực a , b , c thỏa mãn 2 c + a =18 và ( 2 lim
ax + bx − cx = − . Tính →+∞ ) 2 x
P = a + b + 5c . A. P =18 B. P =12 C. P = 9 D. P = 5. Trang 11
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC: 2021-2022 Lời giải
GVSB: Nguyễn Thành Thái; GVPB: Đỗ Hải Thu Chọn B ( 2 a − c ) 2 x + bx Ta có ( 2 lim
ax + bx − cx = − ⇔ lim = 2 − . →+∞ ) 2 x x→+∞ 2
ax + bx + cx 2
a − c = 0 (a, c > 0) Điều này xảy ra ⇔ b . = 2 − a + c
(Vì nếu c ≤ 0 thì + − = +∞ ). →+∞ ( 2 lim ax bx cx x ) Mặt khác, ta cũng có 2 c + a =18 . 2 a = c = 9 Do đó,
⇔ a = 9 , b = 12 − , c = 3. b = 2 − ( a + c)
Vậy P = a + b + 5c =12 . Trang 12
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC:2021-2022 HÀM SỐ LIÊN TỤC
Dạng 5.1. Các câu hỏi lý thuyết B. BÀI TẬP.
B.2. Bài tập trắc nghiệm
Câu 1. Cho hàm số y = f (x) có đồ thị như hình vẽ. Chọn khẳng định sai trong các khẳng định sau?
A. Hàm số y = f (x) liên tục tại x =1.
B. Hàm số y = f (x) gián đoạn tại x =1.
C. Hàm số y = f (x) liên tục tại x = 0 .
D. Hàm số y = f (x) liên tục tại x = 2 . Lời giải
GVSB: Nguyễn Hương Giang; GVPB: Đỗ Hải Thu Chọn A
Câu 2. Cho hàm số y = f (x) có đồ thị như hình vẽ. Chọn khẳng định đúng trong các khẳng định sau?
A. Hàm số y = f (x) liên tục trên .
B. Hàm số y = f (x) liên tục trên các khoảng ( ; −∞ − ) 1 ;( 1; − ) 1 và (1;+∞).
C. Hàm số y = f (x) liên tục trên \{ 1; − } 1 .
D. Hàm số y = f (x) liên tục trên các khoảng ( ;
−∞ 0);(0;2) và (2;+∞) . Lời giải
GVSB: Nguyễn Hương Giang; GVPB:Đỗ Hải Thu Chọn B
Câu 3. Cho y = f (x) và y = g (x) là hai hàm số liên tục tại điểm x . Chọn khẳng định đúng 0
trong các khẳng định sau?
A. Hàm số y = f (x) + g (x) liên tục tại điểm 2x . 0
B. Hàm số y = f (x) − g (x) không liên tục tại điểm x . 0
C. Hàm số y = f (x).g (x) liên tục tại điểm 2 x . 0
D. Hàm số y = f (x) + g (x) liên tục tại điểm x . 0 Trang1
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC:2021-2022 Lời giải
GVSB: Nguyễn Hương Giang; GVPB: Đỗ Hải Thu Chọn D
Câu 4. Tìm khẳng định đúng trong các khẳng định sau?
1. Nếu hàm số f (x) liên tục trên [a;b] và f (a). f (b) < 0 thì tồn tại ít nhất một điểm c∈[ ;
a b] sao cho f (c) = 0.
2. Hàm số f (x) liên tục trên ( ; a b) và ( ;
b c) thì liên tục trên ( ; a c) .
A. Chỉ 1 đúng.
B. Chỉ 2 đúng.
C. Cả 1 và 2 đều đúng.
D. Cả 1 và 2 đều sai. Lời giải
GVSB: Nguyễn Hương Giang; GVPB: Đỗ Hải Thu Chọn A
Câu 5. Cho hàm số f (x) liên tục trên [ ;
a b] và f (a). f (b) < 0. Khẳng định nào sau đây là sai?
A. Hàm số f (x) liên tục trên (a;b) .
B. Phương trình f (x) = 0 có ít nhất một nghiệm thuộc khoảng ( ; a b).
C. Hàm số f (x) liên tục tại điểm c∈(a;b) .
D. Phương trình f (x) = 0 có nhiều nhất một nghiệm thuộc khoảng ( ; a b). Lời giải
GVSB: Nguyễn Hương Giang; GVPB: Đỗ Hải Thu Chọn D
Câu 6. Hàm số nào trong các hàm số sau không liên tục trên ? A. 2
y = x + 2 . B. 3
y = x − 2x + 3 .
C. y = sin x . D. 1 y = . x Lời giải
GVSB: Nguyễn Hương Giang; GVPB: Đỗ Hải Thu Chọn D Hàm số 1
y = có tập xác định là D = ( ;
−∞ 0) ∪(0;+∞) nên hàm số đó không liên tục x trên
Dạng 5.2. Xét tính liên tục bằng đồ thị.
Dạng 5.3. Hàm số liên tục tại một điểm.
B.1. Bài tập tự luận. Bài 1.
Xét tính liên tục của hàm số f (x) = x tại x = 3 − . o Lời giải
GVSB: Lương Nguyên Thị; GVPB: Phạm văn Lãm
Tập xác định của hàm số f (x) là D = 0;+∞ ). Ta có 3 − ∉ D .
Vậy hàm số đã cho không liên tục tại x = 3 − . o Bài 2.
Xét tính liên tục của hàm số f (x) 2
= x + 2 tại x = 2 . o Lời giải
GVSB: Lương Nguyên Thị; GVPB: Phạm văn Lãm
Tập xác định của hàm số f (x) là D = . Ta có: Trang2
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC:2021-2022 f ( ) 2 2 = 2 + 2 = 6 . lim f (x) 2 2
= lim x + 2 = 2 + 2 = 6 . x→2 x→2
Do đó lim f (x) = f (2). x→2
Vậy hàm số đã cho liên tục tại x = 2 . o x + khi x ≠ − Bài 3.
Tìm giá trị của tham số m sao cho hàm số f (x) 3 1 1 = liên tục tại m khi x = 1 − x = 1 − . o Lời giải
GVSB: Lương Nguyên Thị; GVPB: Phạm văn Lãm
Tập xác định của hàm số f (x) là D = . Ta có: f (− ) 1 = m .
lim f (x) = lim (3x + ) 1 = 3.(− ) 1 +1 = 2 − . x→ 1 − x→ 1 −
Hàm số đã cho liên tục tại x = 1 − khi f (− )
1 = lim f (x) ⇔ m = 2 − . o x→ 1 − Vậy m = 2
− thỏa yêu cầu bài toán. 2. Trắc nghiệm
Câu 1. (NB) Cho hàm số 2
f (x) = 3+ x . Khẳng định nào sau đây đúng nhất ?
A. Hàm số liên tục tại x = 3.
B. Hàm số gián đoạn tại x = 3.
C. f (3) ≠ lim f (x) . x→3
D. lim f (x) ≠ lim f (x . + − ) x→3 x→3 Lời giải Chọn A
GVSB: Lương Nguyên Thị; GVPB: Phạm văn Lãm
Tập xác định của hàm số f (x) là D = . Ta có f ( ) 2 3 = 3 + 3 = 2 3 . lim f (x) 2 2
= lim 3 + x = 3 + 3 = 2 3 . x→3 x→3
Do đó lim f (x) = f (3) . x→3
Vậy hàm số đã cho liên tục tại x = 3. o
Câu 2. (TH) Cho hàm số f (x) 2
x − 4 khi x > 2 =
. Trong biều thức xác định f (x) , cần thay số 3 khi x ≤ 2
3 bởi số nào để hàm số liên tục tại x = o 2 A. 0 . B. 1. C. 2 . D. 3. Lời giải Chọn A
GVSB: Lương Nguyên Thị; GVPB: Phạm văn Lãm
Tập xác định của hàm số f (x) là D = . Ta có: Trang3
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC:2021-2022 lim f (x) 2 = lim x − 4 = 0 . x 2+ x 2+ → →
Hàm số liên tục tại x = . o
2 ⇔ lim f (x) = lim f (x) = f (2) = 0 x 2+ x 2− → →
Vậy cần thay số 3 bởi số 0 . 2 x −1 neáu ≠
Câu 3. (VD)Tìm giá trị của tham số m sao cho hàm số f (x) x 1 = x −1 liên tục tại 3
x −m neáu x =1 x = 1. o A. m = 5 − . B. m =1. C. m = 1 − .
D. m = 5. Lời giải Chọn B
GVSB: Lương Nguyên Thị; GVPB: Phạm văn Lãm
Tập xác định của hàm số f (x) là D = . Ta có: f ( ) 1 = 3− m . 2 f (x) x −1 lim = lim = lim(x + ) 1 = 2 . x 1 → x 1 → x −1 x 1 →
Hàm số f (x) liên tục tại điểm x =1 ⇔ lim f (x) = f ( )
1 ⇔ 3− m = 2 ⇔ m =1. x 1 →
Vậy m =1 thỏa yêu cầu bài toán. 2
ax − (a − 2)x − 2 khi x ≠ 1 Câu 4: (VDC)
Cho hàm số f (x) = x + 3 − 2
. Có tất cả bao nhiêu giá trị 2 8
+ a khi x = 1
của a để hàm số liên tục tại x =1? A. 1. B. 0 . C. 3. D. 2 . Lời giải Chọn D
GVSB: Lương Nguyên Thị; GVPB: Phạm văn Lãm
Tập xác định: D = [ 3 − ;+ ∞). 2
ax − (a − 2) x − 2 lim f (x) = lim . x 1 → x 1 → x + 3 − 2 (x − )
1 (ax + 2)( x +3 + 2) = lim . x 1 → x −1 = lim(ax + 2) + + = 4(a + 2) . → ( x 3 2) x 1 f ( ) 2 1 = 8 + a . a = 0
Hàm số đã cho liên tục tại x =1 khi lim f (x) = f ( ) 1 ⇔ (a + ) 2 4 2 = 8 + a ⇔ . x 1 → a = 4
Vậy có 2 giá trị của a để hàm số đã cho liên tục tại x =1. Trang4
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC:2021-2022
Dạng 5.4. Hàm số liên tục trên khoảng- đoạn. A. PHƯƠNG PHÁP
Để xét sự liên tục của hàm số f trên khoảng, ta áp dụng định nghĩa hoặc áp dụng định lý:
a) Nếu hai hàm số f và g liên tục tại điểm x thì các hàm số f ± g, fg,cf (c là một hằng số) 0
đều liên tục tại điểm x . 0
b) Hàm đa thức và hàm số phân thức hữu tỉ và các hàm lượng giác liên tục trên tập xác định của chúng. B. BÀI TẬP.
B.1. Bài tập tự luận. 2 x − 4x + 3 x >1
Bài 1. Chứng minh các hàm số f (x) = x −1
liên tục trên . − 5 − x x ≤1 Lời giải
GVSB: Trần Quang Thắng; GVPB: Phạm Văn Lãm 2 x − 4x + 3 > f (x) x 1 = x −1 . − 5 − x x ≤1
Tập xác định của f(x) là D = 2 2
Với mọi x ∈ 1;+∞ , ta có − + − + lim f (x)
x 4x 3 x 4x 3 0 0 = lim =
= f (x . Suy ra hàm số 0 ) 0 ( ) x→ 0 x x→ 0 x x −1 x −1 0
f (x) liên tục trên khoảng (1;+∞) ( ) 1 . Với mọi x ∈ ;1
−∞ , ta có lim f (x) = lim − − = − − = . Suy ra hàm số → → ( 5 x ) 5 x f x 0 ( 0) 0 ( ) x 0 x x 0 x
f (x) liên tục trên khoảng ( ) ;1 −∞ (2) .
Ta xét tính liên tục của f (x) tại x =1 0 2 x − 4x + 3 x −1 x − 3
Ta có: lim f (x) ( )( ) = lim = lim = lim (x − 3) = 2 − . x 1+ x 1+ − x 1+ − x 1 x 1 x 1 + → → → →
Ta có: lim f (x) = lim (− 5− x = − − − ) 2. x 1 → x 1 → Và có f ( ) 1 = − 5 −1 = 2 .
Vì lim f (x) = lim f (x) = f ( )
1 ⇒ Hàm số liên tục tại 1 (3) . x 1+ x 1− → → Từ ( ) 1 ,(2) và (
3) suy ra f (x) liên tục trên . 1 x ≤ 3
Bài 2. Cho hàm số f (x)
= ax + b 3 < x < 5. Xác định a, b để hàm số liên tục trên 7 x ≥ 5 Lời giải
GVSB: Trần Quang Thắng; GVPB: Phạm Văn Lãm
Ta có tập xác định của hàm số f (x) là D = .
Ta có: hàm số liên tục trên khoảng ( ;
−∞ 3),(3;5),(5;+∞) (vì là hàm đa thức). Trang5
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC:2021-2022
Do đó hàm số liên tục trên khi và chỉ khi hàm số liên tục tại các điểm x = 3 và x = 5 . + Tại x = 3 :
Ta có lim f (x) = lim1=1 và lim f (x) = lim (ax + b) = 3a + b và f (3) =1. x 3− x 3− → → x 3+ x 3+ → →
Do đó hàm liên tục tại x = 3 khi và chỉ khi
lim f (x) = lim f (x) = f (3) ⇔ 3a + b =1 ( ) 1 x 3− x 3+ → → + Tại x = 5
Ta có lim f (x) = 5a + b và lim f (x) = 7 = f (5). x 5− → x 5+ →
Do đó hàm số liên tục tại x = 5 khi và chỉ khi
lim f (x) = lim f (x) = f (5) ⇔ 5a + b = 7 (2) x 5− x 5+ → → 3 a + b =1 a = 3 Từ ( )
1 và (2) suy ra hàm số liên tục trên khi và chỉ khi: ⇔ . 5 a + b = 7 b = 8 −
Vậy với a = 3,b = 8
− thì hàm số liên tục trên . 3
x + 8 khi x > 2 − 2 x − 4
Bài 3. Cho hàm số f (x) = 3 − khi x = 2 −
. Tìm các khoảng, nửa khoảng mà trên
3+ x −5 khi −3≤ x < 2 −
đó hàm số f (x) liên tục. Lời giải
GVSB: Trần Quang Thắng; GVPB: Phạm Văn Lãm 3 Vì 2 x + − 4 ≠ 0 với mọi x 8 x > 2
− nên hàm số f (x) =
xác định trên khoảng ( 2; − +∞) . 2 x − 4 3 3 Ta có x ∀ ∈ 2; − +∞ thì + + lim f (x) x 8 x 8 0 = lim =
= f x nên hàm số f (x) liên tục 2 2 ( 0) 0 ( ) x→ 0 x x→ 0 x x − 4 x − 4 0 trên khoảng ( 2; − +∞) . Với mọi x∈[ 3 − ; 2
− ) thì 3+ x ≥ 0, do đó hàm số f (x) = 3+ x −5 xác định trên nửa khoảng [ 3 − ; 2 − ) . x ∀ ∈ 3 − ; 2
− , ta có lim f (x) = lim
+ − = 3+ x − 5 = f x nên hàm số f (x) 0 ( 0) → → ( 3 x 5) 0 [ ) x 0 x x 0 x
liên tục trên nửa khoảng [ 3 − ; 2 − ) . Tại x = 2 − , ta có f ( 2 − ) = 3
− . Và lim f (x) = lim + − = − ≠ − nên hàm số − − ( 3 x 5) 4 f ( 2) 0 x→ 2 − x→ 2 −
f(x) không liên tục tại x = 2 − .
Kết luận hàm số f (x) liên tục trên ( 2; − +∞) và trên [ 3 − ; 2 − ) .
A.2. Bài tập trắc nghiệm.
Câu 1. Cho hàm số y = f (x) liên tục trên (a;b). Điều kiện cần và đủ để hàm số liên tục trên
[a;b]là:
A. lim f (x) = f (a) và lim f (x) = f (b) . x a+ → x b+ →
B. lim f (x) = f (a) và lim f (x) = f (b) . x a+ → x b− → Trang6
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC:2021-2022
C. lim f (x) = f (a) và lim f (x) = f (b) . x a− → x b+ →
D. lim f (x) = f (a) và lim f (x) = f (b) . x a− → x b− → Lời giải
GVSB: Trần Quang Thắng; GVPB: Phạm Văn Lãm Chọn B
Hàm số y = f (x) liên tục trên (a;b). Điều kiện cần và đủ để hàm số liên tục trên [a;b]
là liên tục phải tại a và liên tục trái tại b, tức là lim f (x) = f (a) và lim f (x) = f (b) . x a+ → x b− →
Câu 2. Hàm số f (x) = 3+ x + 4 − x liên tục trên: A. (3;10) . B. [ 3 − ;4] . C. [ 3 − ;+∞) . D. ( ;4 −∞ ] . Lời giải
GVSB: Trần Quang Thắng; GVPB: Phạm Văn Lãm Chọn B
Tập xác định của hàm số [ 3 − ;4] . Vì với mọi x ∈ 3
− ;4 ta có lim f (x) = lim + + − = nên hàm số liên tục → → ( 3 x
4 x ) f (x0 ) 0 ( ) x 0 x x 0 x trên khoảng ( 3 − ;4). Ngoài ra ta có: lim f (x) = lim + + − = =
− nên hàm số liên tục phải tại x = 3 − + + ( 3 x 4 x ) 7 f ( 3) x→( 3 − ) x→( 3 − )
và lim f (x) = lim + + − = =
nên hàm số liên tục trái tại x = 4 . − − ( 3 x 4 x ) 7 f (4) x→(4) x→(4)
Do đó hàm số đã cho liên tục trên đoạn [ 3 − ;4] . 2 x − 5x + 6 khi x > 2
Câu 3. Cho hàm số f (x) = 4x +1 −3
. Tìm giá trị của tham số m để hàm số liên
2mx−1 khi x ≤ 2 tục trên ? A. 3 m − = . B. 1 m − = . C. 1 m = . D. 3 m = . 2 8 8 2 Lời giải
GVSB: Trần Quang Thắng; GVPB: Phạm Văn Lãm Chọn B
Tập xác định D = . 2 Khi x − +
∈(2;+∞) thì f (x) x 5x 6 =
là hàm sơ cấp xác định trên (2;+∞) nên hàm số 4x +1 − 3
f (x) liên tục trên (2;+∞) . Khi x∈( ;2
−∞ ) thì f (x) = 2mx −1 là hàm đa thức nên hàm số liên tục trên ( ;2 −∞ ) .
Do đó hàm số liên tục trên khi và chỉ khi hàm số liên tục tại x = 2 .
Ta có: f (2) = 4m −1 2 x x
(x − 2)(x −3)( 4x+1+3) (x −3)( 4x+1+ − + 3 5 6 ) f (x) 3 − lim = lim = lim = lim = . x 2+ x 2+ x 2 4x +1 − 3 + (4x +1−9) x 2+ → → → → 4 2 Trang7
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC:2021-2022
lim f (x) = lim (2mx − ) 1 = 4m −1. x 2− x 2− → →
Hàm số liên tục tại x = 2 khi và chỉ khi: f ( ) = f (x) = f (x) 3 − 1 − 2 lim lim ⇔ 4m −1 = ⇔ m = . x 2+ x 2− → → 2 8 1
+ cos x khi sin x ≥ 0
Câu 4. Hàm số f (x) =
có bao nhiêu điểm gián đoạn trên khoảng 3
− cos x khi sin x < 0 (0;2019)? A. Vô số. B. 320. C. 321. D. 319. Lời giải
GVSB: Trần Quang Thắng; GVPB: Phạm Văn Lãm Chọn C
Ta thấy hàm số liên tục với mọi x thỏa mãn sin x ≠ 0 . Ta chỉ cần xét tại
x = ⇔ x = kπ ( * sin 0
k ∈ ) , (Do x∈(0;2019) ).
+) Xét x = k π ( * 2 k ∈ )
lim f (x) = lim (1+ cosx) = 2 x→(k 2π )+ x→(k 2π )+
lim f (x) = lim (3− cosx) = 2 x→(k 2π )− x→(k 2π )− f (k2π ) = 2 .
Vì lim f (x) = lim f (x) = 2 ⇒ lim f (x) = 2 = f (k2π ) x (k 2π )+ x (k 2π )− → → x→k 2π
⇒ f (x)liên tục khi x = k π ( * 2 k ∈ ).
+) Xét x = π + k π ( * 2 k ∈ ) lim
f (x) = lim (1+ cosx) = 0
x→(π +k 2π )−
x→(π +k 2π )− lim
f (x) = lim (3− cosx) = 4
x→(π +k 2π )+
x→(π +k 2π )+ Vì lim f (x) ≠ lim
f (x), suy ra không tồn tại lim f (x) x (π k 2π )+ x (π k 2π )− → + → + x π → +k 2π
⇒ f (x)gián đoạn với x = π + k π ( * 2 k ∈ ) . Vì 1 2019 −π 1 2019 −π
0 < x < 2019 ⇒ 0 < π + k2π < 2019 ⇒ − < k < ⇒ − < k < < 320,9. 2 2π 2 2π
Mà k ∈ suy ra k ∈{0;1;2;....; }
320 . Do đó có 321 giá trị k thỏa mãn.
Dạng 5.5. Tìm m để hàm số liên tục tại 1 điểm.
B.1. Bài tập tự luận. 2 x − 7x +12 Bài 1. Cho hàm số khi x ≠ 3 y = x − 3
tìm giá trị của tham số m để hàm số liên tục tại 2m+1 khi x = 3 x = 3. Lời giải
Tập xác định: D = và x = 3∈ D . 0 Trang8
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC:2021-2022 2 x − 7x +12 Đặt ≠ y = f (x) khi x 3 = x − 3 . 2m+1 khi x = 3 f (3) = 2m +1. 2 x − x + x − x − lim f (x) 7 12 ( 3)( 4) = lim = lim
= lim(x − 4) = 3− 4 = 1 − . x→3 x→3 x→3 x→3 x − 3 x − 3
Hàm số liên tục tại x = 3 khi f (3) = lim f (x) ⇔ 2m +1= 1 − ⇔ m = 1 − . x→3 2
x − 25 khi x > 5
Bài 2. Tìm m để 2
f (x) = x − 4x −5
liên tục tại x 5. ( x −5)2 2 + m khi 5 x ≤ Lời giải
GVSB: Trần Thanh Toàn; GVPB: Thanh Hoa
Tập xác định: D = và x = 5∈ D . 0 f ( ) 2 5 = m .
lim f (x) = lim (x − 5)2 2 2 + m = m x 5− x 5− → → . ( 2x −25) (x −5)(x +5) (x +5) 10 5 lim f (x) = lim = lim = lim = = . + + 2 x 5 x 5 − − x 5 x 4x 5 − ( x + )
1 (x − 5) x 5− → → → → (x + ) 1 6 3
Để f (x) liên tục tại x = ⇔ f ( ) = f (x) = f (x) 2 5 15 5 2 lim lim ⇔ m = ⇔ m = . x 5− x 5+ → → 3 3 2 x − 3x + 2 x ≠ 2
Bài 3. Cho hàm số f (x) = x − 2
. Với giá trị nào của a thì hàm số đã cho liên a x = 2
tục tại điểm x = 2 ? 0 Lời giải
GVSB: Trần Thanh Toàn; GVPB: Thanh Hoa
Tập xác định: D = và x = 2∈ D . 0 2 x − 3x + 2 x −1 x − 2 Ta có lim f (x) ( )( ) = lim = lim = lim(x − ) 1 =1. x→2 x→2 x→2 x→2 x − 2 x − 2 f (2) = a .
Hàm liên tục tại x = 2 khi và chỉ khi lim f (x) = f (2) ⇔ a =1. x→2
Vậy hàm số đã cho liên tục tại x = 2 khi a =1.
B.2. Bài tập trắc nghiệm. 2
Câu 1: Cho hàm số f (x) x −1 = và f ( ) 2 2 = m − 2
x ≠ . Giá trị của m để f (x) liên tục tại x +1 với 2 x = 2 là: A. 3 . B. − 3 . C. ± 3 . D. 3 ± Lời giải
GVSB: Trần Thanh Toàn; GVPB: Thanh Hoa Chọn C Trang9
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC:2021-2022
Tập xác định: D = và x =1∈ D . 0
Hàm số liên tục tại x =1 ⇔ lim f (x) = f (2) . 0 x→2 2 Ta có x −1 lim = lim(x − ) 1 =1. x→2 x→2 x +1 m = 3 Vậy 2 m − 2 =1 ⇔ . m = − 3 2
2x − x − 6 Câu 2: Tìm tham số x ≠
m để hàm số f (x) khi 2 = x − 2
liên tục trên .
mx +3 khi x = 2 A. m = 1 − . B. m =1.
C. m = 2 . D. m = 4 . Lời giải
GVSB: Trần Thanh Toàn; GVPB: Thanh Hoa Chọn C
Tập xác định D = , x = 2∈ 0 . 2
+ Nếu x ≠ 2 thì hàm số f (x) 2x − x − 6 =
liên tục trên các khoảng ( ;2 −∞ ) và (2;+∞) . x − 2
+ Tại x = 2 : Ta có f (2) = 2m + 3. 2 x − x − x + x − lim f (x) 2 6 (2 3)( 2) = lim = lim = lim(2x + 3) = 7. x→2 x→2 x→2 x→2 x − 2 x − 2
Hàm số f (x) liên tục trên ⇔ f (x) liên tục tại điểm x = 2 ⇔ lim f (x) = f (2) x→2
⇔ 2m + 3 = 7 ⇔ m = 2. Vậy m = 2 . 3
x − 2 + 2x −1
Câu 3: Tìm tất cả các giá trị của m để hàm số khi x ≠ 1 f (x) = x −1
liên tục tại x = 1 0 3
m−2 khi x =1 ? A. 4 m = . B. m =1. C. m = 2 . D. 13 m = . 3 9 Lời giải
GVSB: Trần Thanh Toàn; GVPB: Thanh Hoa Chọn D
Tập xác định: D = và x =1∈ D . 0
Để hàm số liên tục tại x = 1 thì lim f (x) = f ( ) 1 . 0 x 1 → Ta có: f ( ) 1 = 3m − 2. Trang10
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC:2021-2022 ( ) 3 3
x − 2 + 2x −1 x − 2 + lim = lim = lim1 x f x + x 1 → x 1 → − x 1 x 1 → x − 1 3 x + x − 2 = lim 1+ x 1 → (x − ) 1 ( 2 3 3
x − x x − 2 + (x − 2)2 ) 2 x x 2 + + 7 = lim 1 + = . x 1 → 2 3 3
x − x x − + (x − )2 3 2 2
Nên hàm số liên tục tại 7 13
x =1 ⇔ 3m − 2 = ⇔ m = . 0 3 9 Vậy 13 m = là giá trị cần tìm. 9 2
x + ax + b
Câu 4: Cho a,b là hai số thực sao cho hàm số ≠ f (x) x 1 = x −1
liên tục tại x = 1. 0
2ax −1, x =1
Tính a − b A. 0 B. 1 − C. 5 − D. 7 Lời giải
GVSB: Trần Thanh Toàn; GVPB: Thanh Hoa Chọn D
Tập xác định: D = và x =1∈ D . 0 Ta có f ( ) 1 = 2a −1. 2
x + ax + b
Để hàm số liên tục tại x =1 thì phải tồn tại lim
và lim f (x) = f ( ) 1 . 0 x 1 → x −1 x 1 → 2
x + ax + b Để tồn tại lim thì ( 2
x + ax + b)(x − )
1 ⇒1+ a + b = 0 ⇒ b = −a −1. x 1 → x −1 2
x + ax + b (x − ) 1 (x + a + ) 1 Suy ra lim = lim = lim(x + a + ) 1 = a + 2. x 1 → − x 1 → − x 1 x 1 x 1 →
lim f (x) = f ( )
1 ⇔ a + 2 = 2a −1 ⇔ a = 3 x 1 →
Khi đó : b = −a −1 = 4 −
Do đó để hàm số liên tục tại x = 1 thì a −b = 3−( 4 − ) = 7 . 0
Dạng 5.6. Tìm m để hàm số liên tục trên khoảng- đoạn. B. BÀI TẬP.
B.1. Bài tập tự luận.
Bài 1. Tìm tất cả các giá trị của tham số thực m sao cho hàm số f (x) 2 x − m khi x ≥ 0 = mx + 2 khi x < 0
liên tục trên . Lời giải
GVSB: Đỗ Minh Vũ; GVPB: Thanh Hoa
Trên khoảng (0;+∞) hàm số f (x) = 2 x − m là hàm số liên tục. Trang11
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC:2021-2022 Trên khoảng ( ;0
−∞ ) hàm số f (x) = mx + 2 là hàm số liên tục.
Ta có lim f (x) = lim
x − m = −m = f
và lim f (x) = lim (mx + 2) = 2 . + + ( 2 ) (0) x→0 x→0 x 0− x 0− → →
Hàm số f (x) liên tục trên khi và chỉ khi
lim f (x) = lim f (x) = f (0) ⇔ −m = 2 ⇔ m = 2 − . x 0+ x 0− → → 2 x + 3x − 4 >
Bài 2. Cho hàm số f (x) khi x 1 = x −1
. Xác định a để hàm số liên tục trên . 2 − ax +1 khi x ≤1 Lời giải
GVSB: Đỗ Minh Vũ; GVPB: Thanh Hoa
Ta có hàm số liên tục trên các khoảng ( ) ;1 −∞ và (1;+ ∞).
Xét tính liên tục của hàm số tại x =1. Ta có f ( ) 1 =1− 2a
lim f (x) = lim ( 2 − ax + ) 1 =1− 2a x 1− x 1− → → 2 f (x) x + 3x − 4 lim = lim = lim (x + 4) = 5. x 1+ x 1+ x − x 1 1 + → → →
Hàm số đã cho liên tục trên khi và chỉ khi: f ( )
1 = lim f (x) = lim f (x) ⇔ 1− 2a = 5 ⇔ a = 2 − . x 1− x 1+ → → 3 2
x − 3x + 2x khi ( x x − 2) ≠ 0 ( x x − 2)
Bài 3. Xác định a,b để các hàm số f (x) = a khi x = 2
liên tục trên . b khi x = 0 Lời giải
GVSB: Đỗ Minh Vũ; GVPB: Thanh Hoa
Hàm số liên tục trên ( ;
−∞ 0) ∪(0;2) ∪(2;+∞) .
Xét tại x = 0 ta có: f (0) = b. 3 2 x − 3x + 2 lim ( ) = lim x f x = lim x −1 = 1 − . x→0 x→0 x(x − 2) ( ) x→0
Xét tại x = 2 ta có: f (2) = a . 3 2 ( ) x − 3x + 2 lim = lim x f x = lim x −1 =1. x→2 x→2 x(x − 2) ( ) x→2 lim f
(x) = f (0) = → a x 1
Hàm số liên tục trên khi và chỉ khi 0 ⇔
lim f ( x) = f (2) b = 1 − x→2
Vậy a = 1;b = 1 − .
B.2. Bài tập trắc nghiệm. Trang12
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC:2021-2022 x + khi x ≥ −
Câu 1. Cho hàm số y = f (x) 3 1 1 =
, m là tham số. Tìm m để hàm số liên tục
x + m khi x < 1 − trên . A. m = 3 − .
B. m = 5 . C. m = 1 − . D. m = 3 . Lời giải
GVSB: Đỗ Minh Vũ; GVPB: Thanh Hoa Chọn C
Ta có hàm số liên tục trên các khoảng ( ; −∞ − ) 1 và ( 1; − + ∞).
Xét tính liên tục của hàm số tại x = 1 − . Có f (− ) 1 = 2
− = lim f (x) và lim f (x) = 1 − + m. x 1+ →− x 1− →−
Để hàm số liên tục trên thì f (− )
1 = lim f (x) = lim f (x) ⇔ 2 − = 1
− + m ⇔ m = 1 − . x 1+ x 1− →− →− x −1 khi x >1
Câu 2. Cho hàm số f (x) x −1 =
, a là tham số. Tìm a để hàm số liên tục trên . 1
ax − khi x ≤1 2 A. 1 − . B. 1. C. 1 − . D. 1 . 2 2 Lời giải
GVSB: Đỗ Minh Vũ; GVPB: Thanh Hoa Chọn B
Ta có hàm số liên tục trên các khoảng ( ) ;1 −∞ và (1;+ ∞).
Xét tính liên tục của hàm số tại x =1. f ( ) 1 1 = a − 2 f (x) 1 1 lim = lim ax − = a − . x 1− x 1− → → 2 2 f (x) x −1 1 1 lim = lim = lim = . x 1+ x 1+ − x 1 x 1 + → → → x +1 2
Để hàm số liên tục trên 1 1 thì f ( )
1 = lim f (x) = lim f (x) ⇔ a − = ⇔ a =1. x 1− x 1+ → → 2 2 2 x − 5x + 6 khi x > 2
Câu 3. Cho hàm số f ( x) = 4x +1 − 3
. Tìm giá trị của tham số m để hàm số liên
2mx −1 khi x ≤ 2 tục trên . A. 3 m = . B. 3 m − = . C. 1 m − = . D. 1 m = . 2 2 8 8 Lời giải
GVSB: Đỗ Minh Vũ; GVPB: Thanh Hoa Chọn C Trang13
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC:2021-2022 2
Khi x ∈(2;+∞) thì f (x) x −5x + 6 =
là hàm sơ cấp xác định trên (2;+∞) nên hàm số 4x +1 − 3
f (x) liên tục trên (2;+∞) . Khi x∈( ;2
−∞ ) thì f (x) = 2mx −1 là hàm đa thức nên hàm số liên tục trên ( ;2 −∞ ) .
Do đó hàm số liên tục trên khi và chỉ khi hàm số liên tục tại x = 2 .
Ta có: f (2) = 4m −1 2 x x
(x − 2)(x −3)( 4x +1+3) (x −3)( 4x+1+ − + 3 5 6 ) f (x) 3 − lim = lim = lim = lim = . x 2+ x 2+ x 2 4x +1 − 3 + (4x +1−9) x 2+ → → → → 4 2
lim f (x) = lim (2mx − ) 1 = 4m −1. x 2− x 2− → →
Hàm số liên tục tại x = 2 khi và chỉ khi: f ( ) = f (x) = f (x) 3 − 1 − 2 lim lim ⇔ 4m −1 = ⇔ m = . x 2+ x 2− → → 2 8 2
2x − 7x + 6 khi x < 2
Câu 4. Cho hàm số y f (x) x − = = 2
. Biết a là giá trị để hàm số f (x) liên 1− x a + khi x ≥ 2 2+ x
tục trên , tìm số nghiệm nguyên của bất phương trình 2 7
−x + ax + > 0 . 4 A. 2 . B. 4 . C. 3. D. 1. Lời giải
GVSB: Đỗ Minh Vũ; GVPB: Thanh Hoa Chọn A
Ta có hàm số liên tục trên các khoảng ( ;2 −∞ ) và (2;+ ∞) .
Xét tính liên tục của hàm số tại x = 2 . Tại x = 2, ta có: 0 f ( ) 1 2 = a − 4 f (x) 1− x 1 lim = lim a + = a − . x 2+ x 2+ → → 2 + x 4 2 2x − 7x + 6
(x − 2)(2x −3)
−(x − 2)(2x − 3) lim f (x = lim = lim = lim − ) x→2 x 2− → x − 2 x 2− → x − 2 x 2− → x − 2
= − lim (2x − 3) = 1 − . x 2− →
Để hàm số liên tục trên 3
thì f (2) = lim f (x) = lim f (x) 1 ⇔ a − = 1 − ⇔ a = − . x 2+ x 2− → → 4 4 Với 3
a = − , xét bất phương trình 2 3 7
−x − x + > 0 7 ⇔ − < x <1 4 4 4 4
Mà x∈ nên x∈{ 1; − } 0 .
Vậy bất phương trình đã cho có 2 nghiệm nguyên. Trang14
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC:2021-2022
Dạng 5.7. Bài toán về số nghiệm của phương trình. B. BÀI TẬP.
B.1. Bài tập tự luận.
Câu 1. Cho hàm số f (x) liên tục trên đoạn [ 1; − 4] sao cho f (− )
1 = 2, f (4) = 7 . Có thể nói gì
về số nghiệm của phương trình f (x) = 5 trên đoạn [ 1; − 4] . Lời giải
GVSB: Lê Văn Quý; GVPB: Thanh Hoa
Ta có : f (x) = 5 ⇔ f (x) −5 = 0 . Đặt g (x) = f (x) −5. Khi đó g (− ) 1 = f (− ) 1 − 5 = 2 − 5 = 3 − ⇒ g (− ) 1 .g (4) < . g ( ) = f ( ) 0 4 4 − 5 = 7 − 5 = 2
Vậy phương trình g (x) = 0 có ít nhất một nghiệm thuộc khoảng ( 1; − 4) hay phương
trình f (x) = 5 có ít nhất một nghiệm thuộc khoảng ( 1; − 4) .
Câu 2. Chứng minh rằng với mọi m thì phương trình sau có nghiệm m(x − )
1 (x + 2) + 2x +1 = 0. Lời giải
GVSB: Lê Văn Quý; GVPB: Thanh Hoa
Đặt f (x) = m(x − )
1 (x + 2) + 2x +1.
Tập xác định: D = nên hàm số liên tục trên . Ta có: f ( ) 1 = 3; f ( 2 − ) = 3 − ⇒ f ( ) 1 ⋅ f ( 2 − ) < 0 .
Vậy phương trình đã cho có nghiệm với mọi m .
Câu 3. Cho hàm số ( ) 2
f x = ax + bx + c thỏa mãn 2a + 6b +19c = 0 . Chứng minh rằng phương trình 2
ax + bx + c = 0 có nghiệm trong 1 0; . 3 Lời giải
GVSB: Lê Văn Quý; GVPB: Thanh Hoa Hàm số ( ) 2
f x = ax + bx + c liên tục với mọi x∈ .
Ta có f (0) = c , 1 a b 1 = + + = (2 + 6 +18 ) c f c a b c = − . 3 9 3 18 18 2 Suy ra ( ) 1 0 . c f f = − . 3 18 f (0) = 0 Nếu c = 0 thì 1
, suy ra phương trình có nghiệm trong 1 0; . f = 0 3 3 2
Nếu c khác 0 thì ( ) 1 0 . c f f = − < 0 ⇒
phương trình có nghiệm thuộc 1 0; . 3 18 3 Vậy phương trình 2
ax + bx + c = 0 có nghiệm trong 1 0; . 3
B.2. Bài tập trắc nghiệm.
Câu 1: Cho hàm số f (x) 3 = 4
− x + 4x −1. Mệnh đề nào sau đây là sai?
A. Hàm số đã cho liên tục trên .
B. Phương trình f (x) = 0 không có nghiệm trên khoảng ( ) ;1 −∞ . Trang15
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC:2021-2022
C. Phương trình f (x) = 0 f (x) = 0 có nghiệm trên khoảng ( 2; − 0) .
D. Phương trình f (x) = 0 f (x) = 0 có ít nhất hai nghiệm trên khoảng 1 3; − . 2 Lời giải
GVSB: Lê Văn Quý; GVPB: Thanh Hoa Chọn D
(i) Hàm f (x) là hàm đa thức nên liên tục trên → A đúng. f (− ) 1 = 1 − < 0 (ii) Ta có →
= có nghiệm x trên ( 2; − ) 1 , f 1 (− ) f (x) 0 2 = 23 > 0 mà ( 2; − − ) 1 ⊂ ( 2; − 0) ⊂ (− ; ∞ ) 1 → B sai và C đúng. f (x) = 1 − < 0 (iii) Ta có 1 1
→ f (x) = 0 có nghiệm x thuộc 1 0;
. Kết hợp với (1) suy ra f = > 2 0 2 2 2
f (x) = 0 có các nghiệm x , x thỏa: 1 3 − < x < 1
− < 0 < x < → D đúng. 1 2 1 2 2
Câu 2: Cho phương trình 4 2
2x − 5x + x +1 = 0 . Mệnh đề nào sau đây là đúng?
A. Phương trình không có nghiệm trong khoảng ( 1; − ) 1 .
B. Phương trình không có nghiệm trong khoảng ( 2; − 0) .
C. Phương trình chỉ có một nghiệm trong khoảng ( 2; − ) 1 .
D. Phương trình có ít nhất hai nghiệm trong khoảng (0;2) . Lời giải
GVSB: Lê Văn Quý; GVPB: Thanh Hoa Chọn D
Hàm số f (x) 4 2
= 2x − 5x + x +1 là hàm đa thức có tập xác định là nên liên tục trên . Ta có f (0) =1 (i) ⇒ − < →
= có ít nhất một nghiệm x thuộc ( 1; − 0) . f 1 (− ) f ( ) 1 . f (0) 0 f (x) 0 1 = 3 − f (0) =1 (ii) ⇒ < →
= có ít nhất một nghiệm x thuộc (0; ) 1 . f 2 ( ) f (0). f ( ) 1 0 f (x) 0 1 = 1 − f ( ) 1 = 1 − (iii) ⇒ ⋅ < →
= có ít nhất một nghiệm x thuộc (1;2) . f 3 ( ) f ( ) 1 f (2) 0 f (x) 0 2 =15 Vậy phương trình
f (x) = 0 đã cho có các nghiệm x , x , x thỏa 1 2 3 1
− < x < 0 < x <1< x < 2 1 2 3 2 x + 4 x ∈ [0;2)
Câu 3. Cho hàm số f (x) =
. Phương trình f (x) = 7 có bao nhiêu ( x − 4 )2 + 6 x∈[2;4] nghiệm? A. 0 . B. 1 . C. 2 . D. 3 . Trang16
NHÓM CHUYÊN ĐỀ TỰ LUẬN TOÁN THPT NĂM HỌC:2021-2022 Lời giải
GVSB: Lê Văn Quý; GVPB: Thanh Hoa - Xét phương trình: 2 x + 4 = 7 trên [0;2). x = 3 (tho¶ m·n) Ta có: 2 2
x + 4 = 7 ⇔ x = 3 ⇔ . x = − 3 ( lo¹i)
- Xét phương trình: (x − )2 4 + 6 = 7 trên [2;4] . x = 3 tho¶ m·n Ta có: (x − 4)2 2 ( )
+ 6 = 7 ⇔ x −8x +15 = 0 ⇔ . x = 5 ( lo¹i)
Vậy phương trình f (x) = 7 có đúng hai nghiệm.
Câu 4. Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc khoảng ( 10 − ;10) để phương trình 3 2
x − 3x + (2m − 2) x + m −3 = 0 có ba nghiệm phân biệt x ; x ; x thỏa mãn 1 2 3 x < 1
− < x < x . 1 2 3 A. 19. B. 18. C. 4 . D. 3. Lời giải
GVSB: Lê Văn Quý; GVPB: Thanh Hoa Chọn C
Xét hàm số : f (x) 3 2
= x − 3x + (2m − 2) x + m −3 liên tục trên .
Giả sử phương trình có ba nghiệm phân biệt x ; x ; x thỏa mãn x < 1
− < x < x . Khi đó 1 2 3 1 2 3
f (x) = (x − x x − x x − x . 1 ) ( 2 ) ( 3 ) Ta có : f (− ) 1 = ( 1 − − x 1 − − x 1
− − x > 0 ( do x < 1
− < x < x ). 1 ) ( 2 ) ( 3 ) 1 2 3 Mà f (− )
1 = −m − 5 nên suy ra −m − 5 > 0 ⇔ m < 5 − .
Thử lại : với m < 5 − ta có :
lim f (x) = −∞ nên tồn tại a < 1
− sao cho f (a) < 0 ( ) 1 . x→−∞ Do m < 5 − nên f (− )
1 = −m − 5 > 0 (2) .
f (0) = m −3 < 0 (3) .
lim f (x) = +∞ nên tồn tại b > 0 sao cho f (b) > 0 (4) . x→+∞ Từ ( )
1 và (2) suy ra phương trình có nghiệm thuộc khoảng ( ; −∞ − ) 1 .
Từ (2) và (3) suy ra phương trình có nghiệm thuộc khoảng ( 1; − 0) .
Từ (3) và (4) suy ra phương trình có nghiệm thuộc khoảng (0;+∞). Vậy m < 5
− và m nguyên thuộc khoảng ( 10 − ;10) nên m∈{ 9 − ; 8 − ; 7 − ;− } 6 . Trang17
Document Outline
- CIV-1. GIỚI HẠN DÃY SỐ
- CIV-2. GIỚI HẠN HS TẠI MỘT ĐIỂM
- CIV-3. GIỚI HẠN MỘT BÊN
- CIV-4. GIỚI HẠN HS TẠI VÔ CỰC
- CIV-5. HÀM SỐ LIÊN TỤC
- Dạng 5.1. Các câu hỏi lý thuyết
- Dạng 5.2. Xét tính liên tục bằng đồ thị.
- Dạng 5.3. Hàm số liên tục tại một điểm.
- Dạng 5.4. Hàm số liên tục trên khoảng- đoạn.
- Dạng 5.5. Tìm m để hàm số liên tục tại 1 điểm.
- Dạng 5.6. Tìm m để hàm số liên tục trên khoảng- đoạn.
- Dạng 5.7. Bài toán về số nghiệm của phương trình.




