Chuyên đề giới hạn của dãy số – Huỳnh Ái Hằng

Tài liệu gồm 19 trang hướng dẫn giải các bài toán giới hạn của dãy số thông qua các ví dụ minh họa có lời giải chi tiết và các bài tập trắc nghiệm ôn luyện có đáp án.

I – Lý thuyết

39 20 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 5: Giới hạn. Hàm số liên tục (KNTT)

Môn: Toán 11

Thông tin:

19 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
[…Chuyên đề Trắc nghiệm Toán 11…] Chuyên đề: GIỚI HẠN
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 1 CLB Giáo viên trẻ TP Huế
Tác giả: HUỲNH ÁI HẰNG (Huế) Biên tập: Lê Bá Bảo (Huế)
CHUYÊN ĐỀ: GIỚI HẠN
Chủ đề 1:
I- LÝ THUYẾT:
1. ĐỊNH LÍ 1: Cho hai dãy số
,
nn
uv
. Nếu
;
*
lim 0
nn
n
u v n
v
thì
lim 0
n
u
.
2. CÁC PHÉP TOÁN: Giả sử
lim , lim
nn
u L v M 
và
c
là một hằng số. Khi đó:
*
* ;
* lim lim . .
* lim . . lim 0
n n n n
n
n
n
u v L M u v L M
u
L
c u c L M
vM
Định lý 1:NGUYÊN LÝ WEIERSTRASS
Một dãy số tăng và bị chặn trên ( hoặc giảm và bị chặn dưới ) thì có giới hạn.
Định lý 2: (ĐỊNH LÝ KẸP GIỮA)
Cho 3 dãy số
(( ), ( ), )
n n n
u v w
với:
;
*
.
n n n
v u w n
Lúc đó:
[…Chuyên đề Trắc nghiệm Toán 11…] Chuyên đề: GIỚI HẠN
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 2 CLB Giáo viên trẻ TP Huế
*CÁC KẾT QUẢ QUAN TRỌNG:
*
lim ,c c c
*
3
3
lim
lim
lim
n
n
n
uL
uL
uL

*
vµ
lim
0 lim
0
n
n
n
uL
L u L
un


* Tổng cấp số nhân lùi vô hạn
1q
:
2
1
1 1 1
...
1
u
S u u q u q
q
*
1
lim lim 0
n
n
u
u

*
3
1 1 1
lim 0; lim 0; lim 0;
n
nn
*
lim 0
n
q
nếu
1q
*
*
1
lim 0
k
k
n

Mở rộng:
lim 0
k
c
n
*
3
lim ; lim ; limn n n
*
lim
n
q 
nếu
1q
*
*
lim ,
k
nk 
3. MỘT VÀ QUY TẮC TÌM GIỚI HẠN DÃY SỐ:
lim , lim
nn
uv
lim , lim 0
nn
u v L
lim 0, lim 0
nn
u L v
lim
n
u
lim
n
v
lim .
nn
uv
lim
n
u
Dấu
L
lim .
nn
uv
Dấu
L
Dấu
n
v
lim
n
n
u
v
























II – BÀI TẬP TRẮC NGHIỆM MINH HỌA:
Câu 1. Với
k
là số nguyên dương thì
1
lim
k
n
bằng
A.

. B.

. C.
0
. D.
1
.
Hướng dẫn:
*
1
lim 0,
k
k
n

.
Lựa chọn đáp án C.
[…Chuyên đề Trắc nghiệm Toán 11…] Chuyên đề: GIỚI HẠN
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 3 CLB Giáo viên trẻ TP Huế
Câu 2. Trong các khẳng định sau, khẳng định nào sai?
A.
11
lim lim ;
k
k
n
n

. B.
lim 0
n
q
nếu
1q
.
C.
limcc
(
c
là hằng số). D.
33
lim lim
nn
uu
.
Hướng dẫn:
lim 0
n
q
nếu
1q
.
Lựa chọn đáp án B.
Câu 3. Cho dãy số
n
u
thỏa mãn
2
1
2
n
u
n

với mọi
n
. Khi đó,
lim
n
u
có giá trị bằng
A.
2
. B.
2
. C.
0
. D.
1
.
Hướng dẫn:
Vì
2
1
2
n
u
n

và
2
1
lim 0
n
nên
lim 2 0
n
u 
. Vậy
lim 2
n
u
.
Lựa chọn đáp án A.
Câu 4. Dãy số nào sau đây có giới hạn khác 0?
A.
1
1n
. B.
1
n
. C.
1
.
n
n
D.
cos n
n
.
Hướng dẫn:
11
lim lim 1 1 0
n
nn


.
Lựa chọn đáp án C.
Câu 5. Dãy số nào sau đây có giới hạn bằng 0?
A.
3
2
n


. B.
5
4
n


. C.
2
3
n


. D.
4
3
n


.
Hướng dẫn:
Vì
2
11
3
nên
2
lim 0
3
n


.
Lựa chọn đáp án C.
Câu 6. Dãy nào sau đây không có giới hạn?
A.
2
3
n


. B.
2
3
n


. C.
0,99
n
. D.
1
n
.
Hướng dẫn:
Nếu
n
chẵn thì
11
n

,
n
lẻ thì
11
n
. Do đó dãy số
1
n
không có giới hạn.
Lựa chọn đáp án D.
[…Chuyên đề Trắc nghiệm Toán 11…] Chuyên đề: GIỚI HẠN
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 4 CLB Giáo viên trẻ TP Huế
Câu 7.
1
lim
2
n
n
có giá trị bằng
A.
1
2
. B.
0
. C.
1
. D.
1
2
.
Hướng dẫn:
11
11
. Do lim 0 lim 0
22
nn
n n n n


.
Lựa chọn đáp án B.
Câu 8. Dãy số nào sau đây có giới hạn khác 0?
A.
1
.
3n
B.
1
.
n
n
C.
5
.
4
n


D.
2
2
.
n
Hướng dẫn:
Vì
5
1
4
nên
5
lim .
4
n



Lựa chọn đáp án C.
Câu 9.
12
lim
4
n
n
có giá trị bằng
A.
1
4
. B.
1
4
. C.
1
2
. D.
1
2
.
Hướng dẫn:
1
2
1 2 1
lim lim
4 4 2
n
n
n
.
Lựa chọn đáp án D.
Câu 10.
35
lim
5
nn
n
có giá trị bằng
A.
1
. B.
0
. C.
3
5
. D.
8
5
.
Hướng dẫn:
3
1
5
35
lim lim 1
1
5
n
nn
n



.
Lựa chọn đáp án A.
[…Chuyên đề Trắc nghiệm Toán 11…] Chuyên đề: GIỚI HẠN
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 5 CLB Giáo viên trẻ TP Huế
Câu 11.
1
7 5 1
lim
3.4 7
nn
nn

có giá trị bằng
A.
7
. B.
0
. C.
1
. D.
1
3
.
Hướng dẫn:
1
51
7
77
7 5 1 7.7 5 1
lim lim lim 7
3.4 7 3.4 7
4
3. 1
7
nn
n n n n
n n n n n











.
Lựa chọn đáp án A.
Câu 12.
2
22
32
lim
3 3 2
n n n
n n n
π
π


có giá trị bằng
A.
1
3
. B.
1
4
. C.

. D.
1
.
Hướng dẫn:
2
22
3
1
44
3 2 3 4 1
lim lim lim
4
3 3 2 3 3 4.4
3
34
44
nn
n n n n n n
n n n n n n n n
π
ππ
ππ
π
















.
Lựa chọn đáp án B.
Câu 13.
3
4
25
lim
22
nn
nn

có giá trị bằng
A.

. B.
2
. C.
0
. D.
6
.
Hướng dẫn:
3
34
4
34
2 1 5
25
lim lim 0
22
22
1
nn
n
nn
nn
nn




.
Lựa chọn đáp án C.
Câu 14. Gọi
sin 3
lim 4
n
L
n

thì
L
bằng số nào sau đây?
A.
0.
B.
2.
C.
2
. D.
4.
Hướng dẫn:
[…Chuyên đề Trắc nghiệm Toán 11…] Chuyên đề: GIỚI HẠN
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 6 CLB Giáo viên trẻ TP Huế
Ta có
sin 3 1n
nn
sin 3
lim 0
n
n

sin3
lim 4 4 2
n
L
n
.
Lựa chọn đáp án C.
Câu 15.
4
4
21
lim
32
nn
nn

có giá trị bằng
A.
0
. B.
2
3
. C.

. D.
2
5
.
Hướng dẫn:
4
34
4
3
11
2
2 1 2
lim lim
2
3
32
3
nn
nn
nn
n



.
Lựa chọn đáp án B.
Câu 16.
32
2
24
lim
23
nn
nn


có giá trị bằng
A.
2
. B.
0
. C.

. D.
2
.
Hướng dẫn:
3
32
3
3
2
2
2
2
14
14
2
2
24
lim lim lim
23
23
23
1
1
n
n
nn
n
n
n
n
nn
n
n
n
n
n













.
Lựa chọn đáp án C.
Câu 17.
2
2
23
lim
1 2 5
nn
nn


có giá trị bằng
A.
0
. B.
1
2
. C.
1
. D.

.
Hướng dẫn:
2
2
2
2
2 3 2 3
1 1 1 1
23
1
lim lim lim
2
1 5 1 5
1 2 5
1 2 1 2
nn
nn
n n n n
nn
nn
n n n n






.
Lựa chọn đáp án B.
Câu 18. Tổng của cấp số nhân lùi vô hạn
2
1 1 1
... ...
5
55
n
S
có giá trị bằng
A.
1
5
. B.
1
4
. C.
2
5
. D.
5
4
.
[…Chuyên đề Trắc nghiệm Toán 11…] Chuyên đề: GIỚI HẠN
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 7 CLB Giáo viên trẻ TP Huế
Hướng dẫn:
2
1 1 1
... ...
5
55
n
S
là tổng của cấp số nhân lùi vô hạn với
1
1
5
u
và
1
5
q
.
Khi đó,
1
1
5
1
4
1
5
S 
.
Lựa chọn đáp án B.
Câu 19. Cho các dãy số
, , ,
n n n n
u v w α
với
22
3 1 2
,
1 1 2
n
nn
n
n
uv
n


,
2017
4
n
n
w
,
41
2017 2
n
n
n
α
. Có bao nhiêu dãy số có giới hạn bằng
0
trong các dãy số trên?
A.
1
. B.
2
. C.
3
. D.
4
.
Hướng dẫn:
Có
3
dãy có giới hạn bằng
0
gồm
,,
n n n
u v w
.
Lựa chọn đáp án C.
Câu 20. Biết
41
lim
2
n
a
n
. Hỏi
a
là nghiệm của phương trình nào sau đây?
A.
2
40x 
. B.
2
5 4 0xx
. C.
2
5 4 0xx
. D.
2
4
0
54
x
xx

.
Hướng dẫn:
41
lim 4
2
n
aa
n
. Lần lượt thế
4a
vào các phương trình ở các phương án.
Lựa chọn đáp ánB.
Câu 21.
32
lim 3 1nn
có giá trị bằng
A.
2
. B.
1
. C.

. D.

.
Hướng dẫn:
3 2 3
3
11
lim 3 1 lim 3n n n
n
n



.
Lựa chọn đáp án C.
Câu 22.
22
lim 2n n n
có giá trị bằng
A.
0
. B.
1
. C.

. D.
1
2
.
Hướng dẫn:
[…Chuyên đề Trắc nghiệm Toán 11…] Chuyên đề: GIỚI HẠN
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 8 CLB Giáo viên trẻ TP Huế
22
22
2 2 2 2
2
2
lim 2 lim lim
22
n n n
n
n n n
n n n n n n
2
2
1
1
lim
2
12
11
n
n
n

.
Lựa chọn đáp án D.
Câu 23.
22
lim 2n n n
có giá trị bằng
A.
12
. B.

. C.
1
. D.

.
Hướng dẫn:
22
2
12
lim 2 lim 1 1n n n n
n
n







.
Lựa chọn đáp án D.
Câu 24.
2
2
2
lim
42
n n n
n n n


có giá trị bằng
A.
4
. B.
2
. C.
1
2
. D.
1
2
.
Hướng dẫn:
2 2 2
2 2 2
2
2
2 4 2
lim
4 4 2
2
lim
42
n n n n n n
n n n n n n
n n n
n n n
11
2 4 2 2 4 2
=
22
1 1 1 1
lim lim =4.
n
nn
n
nn


















Lựa chọn đáp án A.
Câu 25.
3
3
lim 1nn
có giá trị bằng
A.
0
. B.
1
. C.

. D.

.
Hướng dẫn:
2 2 2 2
3
3
33
33
33
11
lim lim 0lim 1
1 ( 1) 1 ( 1)
nn
nn
n n n n n n n n




Lựa chọn đáp án A.
[…Chuyên đề Trắc nghiệm Toán 11…] Chuyên đề: GIỚI HẠN
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 9 CLB Giáo viên trẻ TP Huế
Câu 26.
2
1 3 5 ... (2 1)
lim
32
n
n
có giá trị bằng
A.
0
. B.
1
. C.
1
3
. D.

.
Hướng dẫn:
1 3 5 ... (2 1)n
là tổng
n
số hạng đầu của cấp số cộng có
1
1, 2 1
n
u u n
và công
sai
2d
.
Do đó
2
1 3 5 ... (2 1) 1 2 1
2
n
n n n



.
Suy ra
2
22
2
1 3 5 ... (2 1) 1 1
lim lim lim
2
3
3 2 3 2
3
nn
nn
n

.
Lựa chọn đáp án C.
Câu 27.
1 1 1 1
lim ...
1.2 2.3 3.4
1nn


có giá trị bằng
A.
0
. B.
2
. C.
1
. D.
1.
Hướng dẫn:
Ta có:
1
1 1 1
.
1
11
kk
kk
k k k k


Do đó
1 1 1 1 1 1 1 1 1 1 1 1 1
... ... 1
1.2 2.3 3.4 1 2 2 3 3 4 1 1
1
n n n
nn

.
Suy ra
1 1 1 1 1
lim ... lim 1 1.
1.2 2.3 3.4 1
1
n
nn




Lựa chọn đáp án D.
Câu 28. Cho dãy
1
1
1
:
1
n
n
n
n
u
u
u
u
u
. Lúc đó,
lim
n
u
bằng
A.
0
. B.
2
. C.
1
. D.
1.
Hướng dẫn:
Dùng phương pháp quy nạp toán học, ta chứng minh được
1
lim 0.
nn
uu
n
Lựa chọn đáp án A.
[…Chuyên đề Trắc nghiệm Toán 11…] Chuyên đề: GIỚI HẠN
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 10 CLB Giáo viên trẻ TP Huế
III – BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN:
Câu 1. Trong các khẳng định sau, khẳng định nào là đúng?
A. Nếu
lim 0
n
u
thì
lim 0
n
u
. B. Nếu
lim
n
u 
thì
lim
n
u 
.
C. Nếu
lim
n
u 
thì
lim
n
u 
. D. Nếu
lim
n
ua
thì
lim
n
ua
.
Câu 2. Mệnh đề nào sau đây là mệnh đề đúng?
A. Một dãy số có giới hạn thì luôn luôn tăng hoặc luôn luôn giảm.
B. Nếu
n
u
là dãy số tăng thì
lim
n
u 
.
C. Nếu
lim
n
u 
và
lim
n
v
thì
lim 0
nn
uv
.
D. Nếu
n
n
ua
và
10a
thì
lim 0
n
u
.
Câu 3. Trong các khẳng định sau, khẳng định nào đúng?
A.
3
3
lim limf x g x f x g x



.
B.
3 3 3
lim lim limf x g x f x g x
.
C.
3 3 3
lim lim limf x g x f x g x
.
D.
3 3 3
lim limf x g x f x g x



.
Câu 4. Với
a
là một số thực, trong các khẳng định sau, khẳng định nào sai?
A. Nếu
lim
n
ua
và
lim
n
v
thì
lim 0
n
n
u
v
.
B. Nếu
lim
n
ua
và
lim
n
v 
thì
lim 0
n
n
u
v
.
C. Nếu
lim
n
ua
và
lim
n
v
thì
lim
nn
uv 
.
D. Nếu
lim 0
n
ua
và
lim 0
n
v
và
0
n
v
với mọi
n
thì
lim
n
n
u
v

.
Câu 5. Mệnh đề nào sau đây là đúng?
A. Mọi dãy dương đều có giới hạn.
B. Mọi dãy tăng đều có giới hạn.
C. Mọi dãy giảm đều có giới hạn.
D. Mọi dãy là dãy không đổi đều có giới hạn.
Câu 6. Mệnh đề nào sau đây là đúng?
A. Mọi dãy bị chặn đều có giới hạn.
B. Mọi dãy tăng và bị chặn trên đều có giới hạn.
C. Mọi dãy giảm và bị chặn trên có giới hạn.
D. Mọi dãy tăng và bị chặn dưới đều có giới hạn.
Câu 7. Cho
n
u
là một cấp số nhân lùi vô hạn với công bội
q
. Khẳng định nào sau đây là đúng?
A.
1q
.
[…Chuyên đề Trắc nghiệm Toán 11…] Chuyên đề: GIỚI HẠN
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 11 CLB Giáo viên trẻ TP Huế
B.
1
12
...
1
n
u
u u u
q
.
C.
2
1
1 1 2 1
... ...
1
n
u
u u q u q u q
q
.
D.
1
lim
1
n
u
S
q
.
Câu 8. Để tính
1
2.4 5 3
lim
25
n n n
nn

ta tiến hành
A. Chia cả tử và mẫu cho
2
n
. B. Chia cả tử và mẫu cho
3
n
.
C. Chia cả tử và mẫu cho
4
n
. D. Chia cả tử và mẫu cho
5
n
.
Câu 9.
1
1
5 2 1
lim
5.2 5 3
n
n
n
n


có giá trị bằng
A.
1
3
. B.
1
5
. C.
2
5
. D.
1
5
.
Câu 10.
23
32
23
lim
2 4 1
nn
nn

có giá trị bằng
A.
3
2
. B.
0
. C.
1
. D.
3
2
.
Câu 11.

23
lim
1
nn
n

có giá trị bằng
A.
0
. B.
1
3
. C.
1
. D.

.
Câu 12.


23
42
2 2 1 4 5
lim
3 1 3 7
n n n n
n n n
có giá trị bằng
A.
0
. B.
8
3
. C.
1
. D.

.
Câu 13.

32
4
2 3 1
lim
2 1 7
n n n
nn


có giá trị bằng
A.
1
. B.
3
. C.
3
2
. D.

.
Câu 14.

3
2
31
lim
1 1 2
nn
nn


có giá trị bằng
A.
0
. B.
1
. C.
1
2
. D.
1
4
.
[…Chuyên đề Trắc nghiệm Toán 11…] Chuyên đề: GIỚI HẠN
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 12 CLB Giáo viên trẻ TP Huế
Câu 15. Tổng
1 1 1
1 ... ...
24
2
n
S
bằng
A.
1
. B.
2
. C.
4
. D.
6
.
Câu 16. Tổng
1
1
1 1 1
+...+ ...
2 4 8
2
n
n
S


bằng
A.
1
. B.
1
3
. C.
3
.
4
D.
2
3
.
Câu 17. Với
k
là số nguyên dương thì
lim
k
n
bằng
A.

. B.

. C.
0
. D.
n
.
Câu 18.
32
lim 2 2 3nn
có giá trị bằng
A.
2
. B.
1
. C.

. D.

.
Câu 19.
42
lim 3 4 1n n n
có giá trị bằng
A.

. B.

. C.
3
. D.
7
.
Câu 20.
22
lim 4 1nn
có giá trị bằng
A.
3
. B.
1
. C.
0
. D.

.
Câu 21.
22
lim 2 1 2n n n n
có giá trị bằng
A.
12
. B.

. C.
1
. D.

.
Câu 22.
2
lim 2 3n n n
có giá trị bằng
A.
1
. B.
0
. C.

. D.
1
.
Câu 23.
2
92
lim
32
n n n
n
có giá trị bằng
A.
1
. B.
3
. C.
0
. D.

.
Câu 24.
23
1 1 1 1
lim ..
3
3 3 3
n



có giá trị bằng
A.
1
.
2
B.
1
.
24
C.

. D.
1
.
Câu 25.
22
lim 2 1 2 3 2n n n n
có giá trị bằng
A.
1
2
. B.
0
. C.

. D.

.
Câu 26.
11
lim
12nn



có giá trị bằng
A.
1
. B.
0
. C.
1
2
. D.

.
[…Chuyên đề Trắc nghiệm Toán 11…] Chuyên đề: GIỚI HẠN
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 13 CLB Giáo viên trẻ TP Huế
Câu 27.
2017 2016
2017 2015
lim
3
nn
nn
có giá trị bằng
A.
1
. B.
1
. C.
1
3
. D.

.
Câu 28.
1 1 1 1
lim ...
1.3 3.5 5.7
2 1 2 3nn





có giá trị bằng
A.
1
2
. B.
1
. C.
1
3
. D.

.
Câu 29.
lim 2 3n n n



có giá trị bằng
A.
1
. B.
0
. C.
5
2
. D.

.
Câu 30. Nếu
lim
n
uL
thì
3
lim 8
n
u
có giá trị bằng
A.
2L
. B.
3
8L
. C.
3
2L
. D.
8L
.
Câu 31. Nếu dãy
n
u
với
0,
n
un
và
lim
n
uL
thì
1
lim
9
n
u
có giá trị bằng
A.
1
3L
. B.
1
9L
. C.
1
3L
. D.
1
9L
.
Câu 32. Cho dãy số
n
u
với
lim 3
n
u
. Khi đó,
24
lim
1
n
n
u
u
có giá trị bằng
A.
4
. B.
2
. C.
5
. D.
1
2
.
Câu 33. Cho dãy số
n
u
với
lim
n
u 
. Khi đó,
2
2
lim
1
n
n
u
u
có giá trị bằng
A.
1
. B.

. C.
0
. D.
2
.
Câu 34. Cho dãy số
n
u
với
2
2 2 ... 2
n
n
u
. Chọn mệnh đề đúng trong các mệnh đề
sau:
A.
2
2
lim 2 2 ... 2 ...
12
n
n
u
.
B.
lim
n
u 
.
C.
lim
n
u 
.
D. Dãy số
n
u
không có giới hạn khi
n
.
Câu 35.
3
3
1
lim
8
n
n
có giá trị bằng
A.
1
. B.
1
2
. C.
1
8
. D.

.
[…Chuyên đề Trắc nghiệm Toán 11…] Chuyên đề: GIỚI HẠN
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 14 CLB Giáo viên trẻ TP Huế
Câu 36.
32
3
2
8 2 1
lim
21
nn
n

có giá trị bằng
A.
2
. B.
2
. C.
1
. D.

.
Câu 37.
1 1 1 1
lim ...
1.4 4.7 7.10
3 2 3 1nn





có giá trị bằng
A.
1
2
. B.
1
. C.
1
3
. D.

.
Câu 38.
3
1.2 2.3 3.4 ... 1
lim
2016 2017
nn
n
có giá trị bằng
A.
1
2017
. B.
1
2016
. C.

. D.

.
Câu 39.
3 ( 1) cos 3
lim
1
n
nn
n



có giá trị bằng
A.
3
2
. B.
3
. C.
5
. D.
1
.
Câu 40.
lim 3 5
n
n




có giá trị bằng
A.
3
. B.

. C.

. D.
5
.
Câu 41.
2
2
1
lim
2
nn
nn


có giá trị bằng
A.
1
. B.
2
. C.
0
. D.
1
.
Câu 42.
3
3
lim 2n n n
có giá trị bằng
A.
2
3
. B.
1
3
. C.
1
. D.
0
.
Câu 43.
3
23
lim n n n
có giá trị bằng
A.
1
3
. B.

. C.
1
. D.
0
.
Câu 44. Dãy số nào sau đây có giới hạn bằng 0?
A.
2
2
1
.
3
n
n
u
nn
B.
2
13
.
3
n
n
u
nn
C.
2
12
.
5
n
n
u
n
D.
12
.
5
n
n
u
n
Câu 45.
2
2 5 8 ... 3 1
lim
n
n
có giá trị bằng
A.
1
.
3
B.
0.
C.

. D.
3
.
[…Chuyên đề Trắc nghiệm Toán 11…] Chuyên đề: GIỚI HẠN
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 15 CLB Giáo viên trẻ TP Huế
Câu 46. Dãy số nào sau đây có giới hạn là
?
A.
2
2
2
.
33
n
nn
u
nn
B.
12
.
33
n
n
u
n
C.
2
2
.
33
n
n
u
n
D.
2
3
2
.
5
n
n
u
nn
Câu 47. Dãy số nào sau đây có giới hạn là
?
A.
2
2
3
.
2
n
nn
u
nn
B.
2018 2017
.
1
n
n
u
n
C.
2
2017 2016 .
n
u n n
D.
2
1.
n
un
Câu 48. Trong các giới hạn sau đây, giới hạn nào bằng
1?
A.
2
3
31
lim .
32
n
n

B.
3
3
23
lim .
21
n
n

C.
2
32
31
lim .
33
n
nn

D.
3
2
3
lim .
1
n
n

Câu 49. Trong các giới hạn sau đây, giới hạn nào bằng
0?
A.
2
3
52
lim .
54
n
n

B.
3
2
25
lim .
21
nn
n

C.
24
32
2
lim .
2
nn
nn

D.
3
2
35
lim .
1
n
n
Câu 50. Trong các giới hạn sau đây, giới hạn nào bằng
1
?
A.
2
3
2
lim .
4
n
n

B.
3
2
2
lim .
21
nn
n
C.
23
32
32
lim .
24
nn
nn

D.
4
2
32
lim .
21
n
n
Câu 51. Dãy số nào sau đây không có giới hạn?
A.
lim 1 sin
2
n
π
nπ







. B.
limsin nπ
.
C.
lim cos
2
π
nπ


. D.
limcos nπ
.
Câu 52. Dãy số nào sau đây có giới hạn bằng
1
?
A.
limsin nπ
. B.
limcos nπ
.
C.
2
lim sin
21
n
π
n


. D.
2
cos 2
lim
nn
n
.
Câu 53. Biết
41
lim
12
n
M
n
và
1
43
lim
24
nn
n
m
. Tích
.Mm
bằng
A.
2
. B.
2
. C.
1
2
. D.
1
2
.
[…Chuyên đề Trắc nghiệm Toán 11…] Chuyên đề: GIỚI HẠN
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 16 CLB Giáo viên trẻ TP Huế
Câu 54. Biết
2017
2017
lim 0
n
và
2017
2017
lim 0
n
. Khi đó,
2017
2017 sin 2017
lim
n
n
bằng
A.
2017
. B.
2017
. C.
1
. D.
0
.
Câu 55. Để tính
2
1 2 3 ...
lim
n
n
, một học sinh làm như sau:
Bước 1: Ta có
2 2 2 2 2
1 2 3 ... 1 2 3
...
nn
n n n n n
.
Bước 2: Suy ra
2 2 2 2 2
1 2 3 ... 1 2 3
lim lim ...
nn
n n n n n


Bước 3: Suy ra
2 2 2 2 2
1 2 3 ... 1 2 3
lim lim lim lim ... lim
nn
n n n n n
Bước 4: Suy ra
2
1 2 3 ...
lim 0 0 0 ... 0 0
n
n
.
Bạn học sinh đã giải đúng hay sai? Nếu sai thì sai thì bước nào?
A. Bước 1. B. Bước 2. C. Bước 3. D. Bài giải đúng.
Câu 56.
2
1 3 5 ... (2 1)
lim
54
n
n
có giá trị bằng
A.
0
. B.
1
4
. C.
1
5
. D.

.
Câu 57.
2
1 2 3 ...
lim
2
n
n
có giá trị bằng
A.
1
. B.

. C.
1
. D.
1
2
.
Câu 58.
2 2 2
lim ...
1.2 2.3
1nn


có giá trị bằng
A.
1
2
. B.
2
. C.
0
. D.

.
Câu 59. Cho dãy
1
*
1
2
:
1
2
n
n
n
u
u
un
u
. Lúc đó,
lim
n
u
bằng
A.
0
. B.
2
. C.
1
. D.
1.
Câu 60. Cho dãy
1
*
1
1
2
:
3
n
nn
u
u
u u n

. Lúc đó,
lim
n
u
bằng
A.

. B.
2
. C.

. D.
1.
Câu 61.
2 2 2 2
3
1 2 3 ...
lim
4 2017
n
n
có giá trị bằng
A.
1
.
3
B.
1
.
24
C.

. D.
3
.
[…Chuyên đề Trắc nghiệm Toán 11…] Chuyên đề: GIỚI HẠN
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 17 CLB Giáo viên trẻ TP Huế
Câu 62. Khẳng định nào sau đây là đúng?
A. Một dãy số có giới hạn thì luôn tăng hoặc luôn giảm.
B. Nếu
n
n
ua
và
1a
thì
lim 0
n
u
.
C. Nếu
lim 0
n
u
và
lim
n
v 
thì
lim( . ) 0
nn
uv
.
D. Nếu
lim
n
u 
thì
2017
lim 0
n
u
.
Câu 63. Khẳng định nào sau đây là sai?
A. Một dãy số tăng và bị chặn trên thì có giới hạn.
B. Một dãy số giảm và bị chặn dưới thì có giới hạn.
C. Nếu
lim
n
u 
và
lim
n
v 
thì
lim 1
n
n
u
v
.
D. Nếu
n
n
ua
và
2
1a
thì
lim 0
n
a
.
Câu 64. Khẳng định nào sau đây là sai?
A. Nếu
lim
n
ua
và
lim
n
vb
thì
lim( )
nn
u v a b
.
B. Nếu
lim
n
u 
và
lim
n
v 
thì
lim( ) 0
nn
uv
.
C. Nếu
0
n
u
với mọi
n
và
lim
n
va
thì
0a
.
D. Nếu
lim 2
n
u 
và
lim 2018
n
v
thì
lim 1009
n
n
v
u

.
Câu 65. Khẳng định nào sau đây là đúng?
A. Nếu
lim
n
ua
và
lim
n
vb
thì
lim
n
n
u
a
vb
.
B. Nếu
lim
n
ua
thì
lim
n
ua
.
C. Nếu
lim 5
n
u
và
lim 0
n
v
thì
lim
n
n
u
v

.
D. Nếu
n
n
ua
và
2a
thì
lim
n
u
.
Câu 66. Cho dãy số
n
u
với
3
2 4 6 ... 2
31
n
n
u
nn

. Khẳng định nào sau đây đúng?
A.
lim 0
n
u
. B.
lim 2
n
u
. C.
lim 3
n
u
. D.
lim
n
u 
.
Câu 67. Cho dãy số
n
u
với
2
1
1 2 2 ... 2
23
n
n
n
u
. Khẳng định nào sau đây đúng?
A.
1
lim
2
n
u
. B.
lim 1
n
u
. C.
lim
n
u 
. D.
lim
n
u 
.
Câu 68. Cho dãy số
n
u
với
7
5
2016
n
u
n

. Khẳng định nào sau đây đúng?
[…Chuyên đề Trắc nghiệm Toán 11…] Chuyên đề: GIỚI HẠN
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 18 CLB Giáo viên trẻ TP Huế
A.
lim 0
n
u
. B.
lim 5
n
u
. C.
lim 7
n
u
. D.
lim 2016
n
u
.
Câu 69. Cho
1 1 1
1 ... ...
24
2
n
S
. Khẳng định nào sau đây đúng?
A.
0S
. B.
1S
. C.
1
lim
2
n
u
. D.
lim
n
u 
.
Câu 70. Cho
2
1 2 2 ... 2 ...
n
S
. Khẳng định nào sau đây sai?
A.
S 
.
B.
2
lim(1 2 2 ... 2 )
n
S
.
C.
S
là tổng của cấp số nhân lùi vô hạn.
D.
S
là tổng vô hạn các phần tử của một cấp số nhân.
Câu 71. Cho dãy số
n
u
có
lim
n
u 
. Khẳng định nào sau đây sai?
A.
2
1
lim
22
n
n
u
u
. B.
2
2
1
1
lim
2
21
n
n
u
u
.
C.
lim 3 6
n
u 
. D.
2
1
1
lim
2 3 2
n
n
u
u


.
------- HẾT -------
[…Chuyên đề Trắc nghiệm Toán 11…] Chuyên đề: GIỚI HẠN
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 19 CLB Giáo viên trẻ TP Huế
ĐÁP ÁN CÂU HỎI TRẮC NGHIỆM TỰ LUYỆN
Câu
1
2
3
4
5
6
7
8
9
10
Đáp án
A
D
A
C
D
B
C
D
B
A
Câu
11
12
13
14
15
16
17
18
19
20
Đáp án
D
B
C
D
B
B
A
D
B
C
Câu
21
22
23
24
25
26
27
28
29
30
Đáp án
D
A
A
A
A
B
C
A
C
B
Câu
31
32
33
34
35
36
37
38
39
40
Đáp án
D
C
C
C
A
A
C
B
B
C
Câu
41
42
43
44
45
46
47
48
49
50
Đáp án
B
A
D
B
D
C
D
B
A
C
Câu
51
52
53
54
55
56
57
58
59
60
Đáp án
D
C
C
D
C
C
D
B
D
A
Câu
61
62
63
64
65
66
67
68
69
70
Đáp án
B
D
C
B
D
A
B
D
A
C
Câu
71
72
73
74
75
76
77
78
79
80
Đáp án
D
Trong tài liệu này, tác giả có sử dụng phần lí thuyết và một số câu hỏi của Thầy Lê
Bá Bảo (CLB Giáo viên trẻ TP Huế), Thầy Đặng Ngọc Hiền (TP Bà Rịa_Vũng Tàu) và sách
trắc nghiệm 2007, tài nguyên Page Toán học Bắc Trung Nam. Dù biên soạn rất kỹ, song
chắc chắn không tránh khỏi sai sót. Mong bạn đọc phản hồi để cùng tác giả hoàn thiện nội
dung trên. Xin cảm ơn! Xin tặng các Thầy Cô và các em học sinh chuyên đề này!
Tác giả: HUỲNH ÁI HẰNG
Địa chỉ: Tản Đà_Hương Sơ, TP Huế SĐT: 0935.905.892
Facebook: Ái Hằng Huỳnh Page: CLB GIÁO VIÊN TRẺ TP HUẾ
| 1/19
| | Tải xuống

Có thể bạn quan tâm:

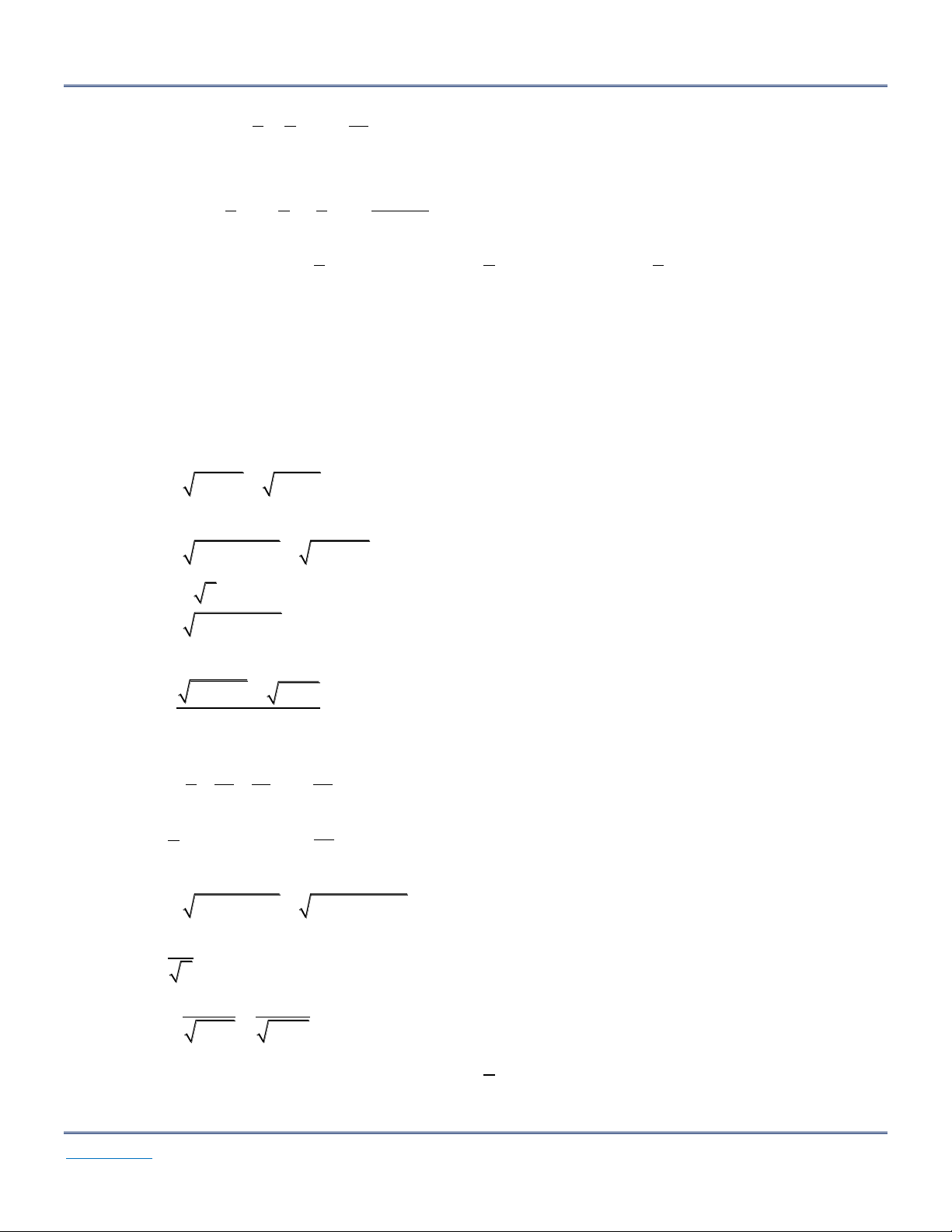
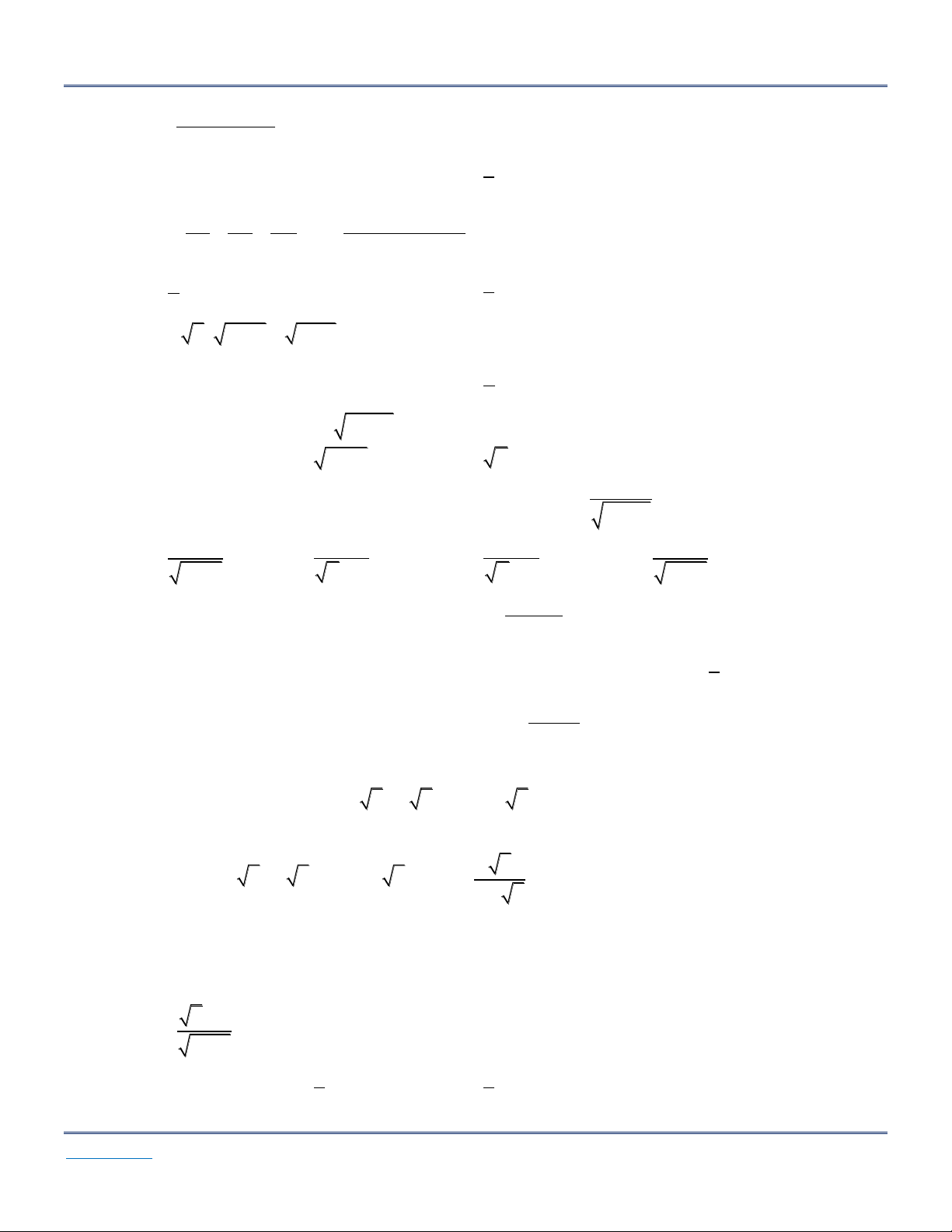
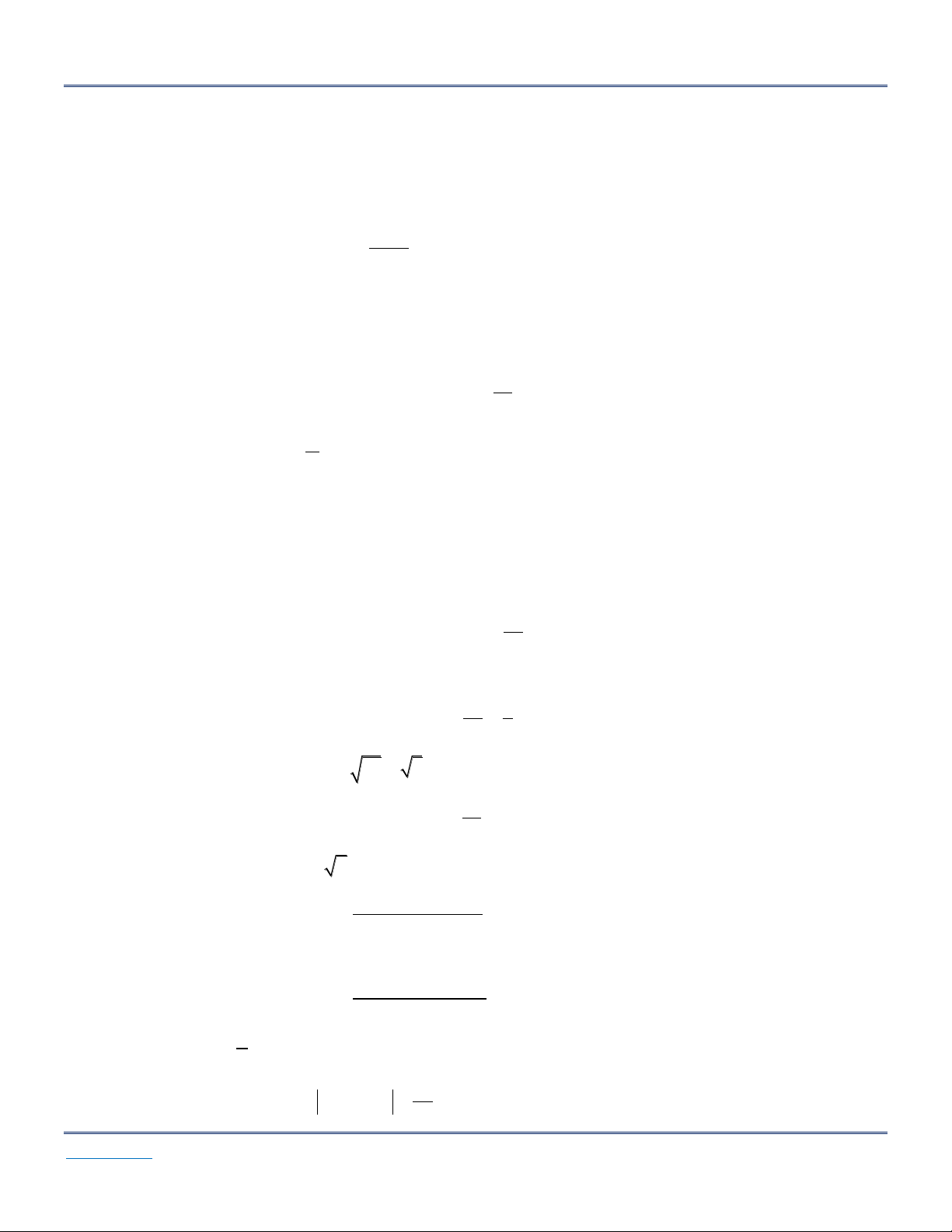
Preview text:

[…Chuyên đề Trắc nghiệm Toán 11…]
Chuyên đề: GIỚI HẠN
Tác giả: HUỲNH ÁI HẰNG (Huế)
Biên tập: Lê Bá Bảo (Huế)
CHUYÊN ĐỀ: GIỚI HẠN
Chủ đề 1: I- LÝ THUYẾT:
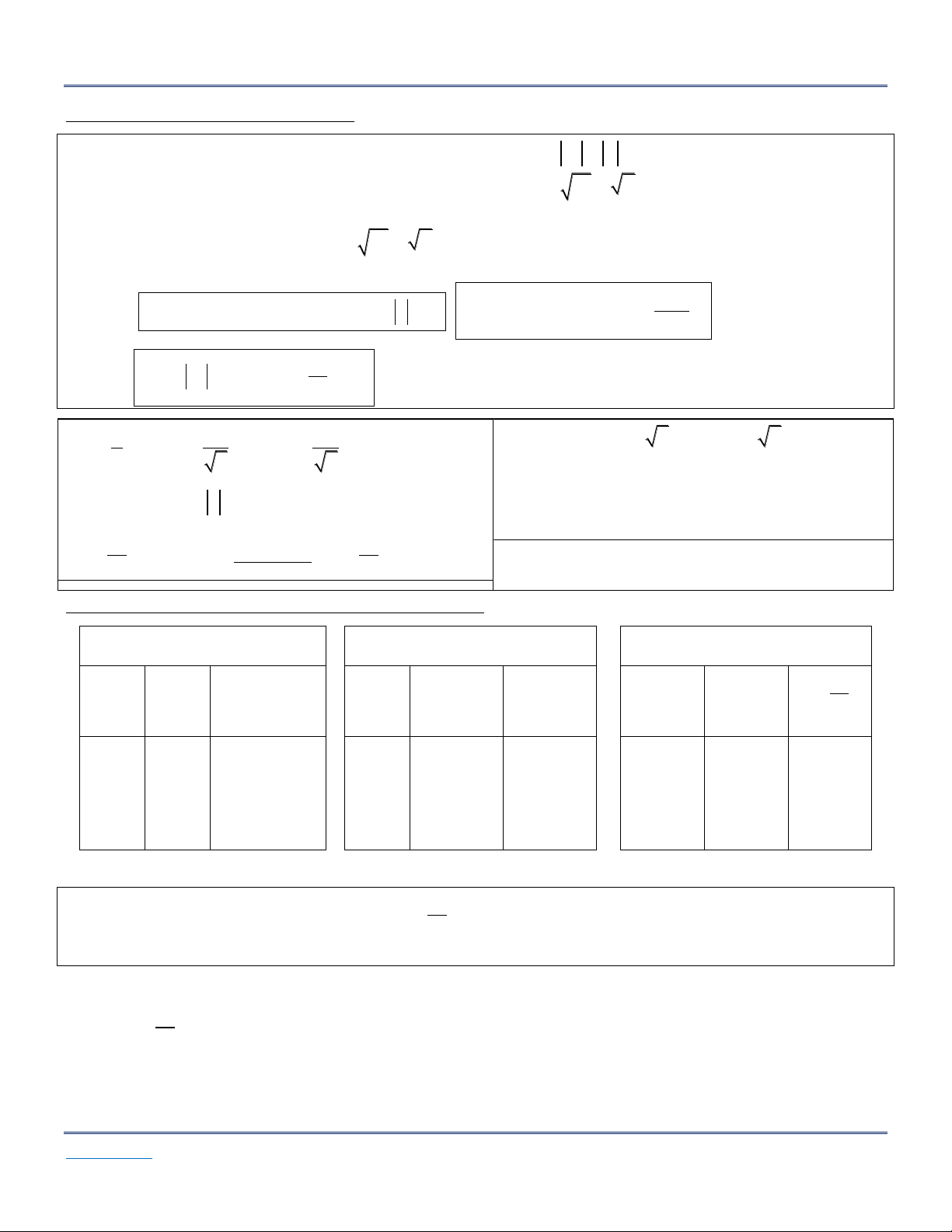
 u v ; * n   
1. ĐỊNH LÍ 1: Cho hai dãy số u  , v . Nếu n n
thì lim u  0 . nn lim v  0 nn
2. CÁC PHÉP TOÁN: Giả sử limu L, lim v M  và c là một hằng số. Khi đó: n n
* lim u v L M u vL M n n  * lim  . n n  . u L * lim  . c u c LM n  . * lim n ; 0 v M n
Định lý 1:NGUYÊN LÝ WEIERSTRASS
Một dãy số tăng và bị chặn trên ( hoặc giảm và bị chặn dưới ) thì có giới hạn.
Định lý 2: (ĐỊNH LÝ KẸP GIỮA)
Cho 3 dãy số (u ), (v ), (w ) với: v u w ; * n   . n n n n n n
lim v A Lúc đó: n   limu A lim n w A    n
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 1
CLB Giáo viên trẻ TP Huế
[…Chuyên đề Trắc nghiệm Toán 11…]
Chuyên đề: GIỚI HẠN
*CÁC KẾT QUẢ QUAN TRỌNG: lim u L  * lim c c, nc 
* lim u L   n 3 3 lim u Ln limu L * n
L  0 vµ lim u L u  0 n n   n u
* Tổng cấp số nhân lùi vô hạn q   1 : 2 1
S u u q u q  ...  1 1 1 1 q 1
* lim u    lim  0 n un 1 1 1       * lim  0; lim  0; lim  0; * n n 3 lim ; lim ; lim n 3 n n n * lim n
q   nếu q  1 * lim n
q  0 nếu q  1 * k n    * lim , k    1 c * lim
 0 k  Mở rộng: lim  0 k  *  n k n
3. MỘT VÀ QUY TẮC TÌM GIỚI HẠN DÃY SỐ:
limu  , lim v  
limu  , lim v L  0
limu L  0, lim v  0 n n n n n n lim u lim v lim u .v lim u Dấu L lim u .v Dấu L Dấu v u n n n n n n n n lim n vn                                    
II – BÀI TẬP TRẮC NGHIỆM MINH HỌA: 1 Câu 1.
Với k là số nguyên dương thì lim bằng k n A.  . B. . C. 0 . D. 1 . Hướng dẫn: 1 lim  0, k   . k  *  n
Lựa chọn đáp án C.
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 2
CLB Giáo viên trẻ TP Huế
[…Chuyên đề Trắc nghiệm Toán 11…]
Chuyên đề: GIỚI HẠN Câu 2.
Trong các khẳng định sau, khẳng định nào sai? 1 1 A. lim  lim ; k  . B. lim n
q  0 nếu q  1 . k n n
C. lim c c ( c là hằng số). D. 3 3
lim u  lim u . n n Hướng dẫn: lim n
q  0 nếu q  1.
Lựa chọn đáp án B. 1 Câu 3. Cho dãy số u thỏa mãn u 2 
với mọi n . Khi đó, lim u có giá trị bằng n n 2 n n A. 2 . B. 2  . C. 0 . D. 1 . Hướng dẫn: 1 1 Vì u 2  và lim
 0 nên limu   . Vậy limu  2. n  2 0 n 2 n 2 n n
Lựa chọn đáp án A. Câu 4.
Dãy số nào sau đây có giới hạn khác 0? 1 1 n1 cos n A. . B. . C. . D. . n 1 n n n Hướng dẫn: n1  1 lim  lim 1       1  0   . n n  
Lựa chọn đáp án C.
Câu 5. Dãy số nào sau đây có giới hạn bằng 0? nn n n 3  5 2  4 A.             . B.      . C.     . D.      . 2   4   3   3   Hướng dẫn: n 2 2 Vì 1    1 nên lim     0   . 3 3  
Lựa chọn đáp án C.
Câu 6. Dãy nào sau đây không có giới hạn? nn 2  2 n n A.         . B.      . C.  0  ,9  9 . D.   1 . 3   3   Hướng dẫn: n n n
Nếu n chẵn thì  
1  1 , n lẻ thì   1  1
 . Do đó dãy số   1 không có giới hạn.
Lựa chọn đáp án D.
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 3
CLB Giáo viên trẻ TP Huế
[…Chuyên đề Trắc nghiệm Toán 11…]
Chuyên đề: GIỚI HẠN  n 1 Câu 7. lim có giá trị bằng n  2 1 1 A. . B. 0 . C. 1  . D.  . 2 2 Hướng dẫn:  n n 1 1 1   1  . Do lim  0  lim  0 . n  2 n n n  2
Lựa chọn đáp án B.
Câu 8. Dãy số nào sau đây có giới hạn khác 0? n n 1   1 5 2 A. . B. . C.     .   D. . 3nn 4 2 n Hướng dẫn: n 5 5 Vì  1 nên lim      .    4 4  
Lựa chọn đáp án C. 1 2n Câu 9. lim có giá trị bằng 4n 1 1 1 1 A. . B.  . C. . D.  . 4 4 2 2 Hướng dẫn: 1 2 12n 1 lim  lim n   . 4n 4 2
Lựa chọn đáp án D. 3n  5n Câu 10. lim có giá trị bằng 5n 3 8 A. 1 . B. 0 . C. . D. . 5 5 Hướng dẫn: n 3     1    3n 5n 5 lim  lim  1. 5n 1
Lựa chọn đáp án A.
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 4
CLB Giáo viên trẻ TP Huế
[…Chuyên đề Trắc nghiệm Toán 11…]
Chuyên đề: GIỚI HẠN n 1 7  5n 1 Câu 11. lim có giá trị bằng 3.4n 7n 1 A. 7  . B. 0 . C. 1  . D. . 3 Hướng dẫn: n n 5    1 7       n 1           7  5n 1 7.7n 5n 1 7 7 lim  lim  lim  7  . 3.4n 7n 3.4n 7n n 4 3.    1   7
Lựa chọn đáp án A. n n 2 π  3  2 n Câu 12. lim có giá trị bằng n n 2n2 3π 3  2 1 1 A. . B. . C.  . D. 1  . 3 4 Hướng dẫn: n nπ 3         1 n n 2           π 3 2 n n π 3n 4n 4 4 1 lim  lim  lim  . n n 2n2 3π  3  2 3 n
π 3n  4.4n n n     4 π   3 3        4       4 4
Lựa chọn đáp án B. 3 2  n n5 Câu 13. lim có giá trị bằng 4 n 2n  2 A. . B. 2  . C. 0 . D. 6  . Hướng dẫn: 2  1 5   3 3 4 2  n n5 lim  lim n n n  0. 4 n  2n  2 2 2 1  3 4 n n
Lựa chọn đáp án C. sin 3n
Câu 14. Gọi L  lim 4 
thì L bằng số nào sau đây? n A. 0. B. 2. C. 2 . D. 4. Hướng dẫn:
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 5
CLB Giáo viên trẻ TP Huế
[…Chuyên đề Trắc nghiệm Toán 11…]
Chuyên đề: GIỚI HẠN sin 3n 1 n n Ta có  sin 3  lim  sin 3 0  L  lim 4  4  2 . n n n n
Lựa chọn đáp án C. 4 2n n 1 Câu 15. lim có giá trị bằng 4 3n  2n 2 2 A. 0 . B. . C.  . D. . 3 5 Hướng dẫn: 1 1   4 2 3 4 2n n 1 2 lim  lim n n  . 4 3n  2n 2 3 3  3 n
Lựa chọn đáp án B. 3 2 2n n  4 Câu 16. lim có giá trị bằng 2 n  2n3 A. 2 . B. 0 . C.  . D. 2  . Hướng dẫn:     3 1 4   1 4 n 2             3 2 3 2 3 2n n 4  n n        lim lim lim n n n     . 2  n  2n 3  2 3   2 3  2     n 1     1   2    2   n n   n n
Lựa chọn đáp án C.n  2  2 n   3 Câu 17. lim  có giá trị bằng 2 n   1 2n  5 1 A. 0 . B. . C. 1 . D.  . 2 Hướng dẫn:  2  3  2 3                   
n  n   2 2 n 1 n 1 1 1 2 3              n n n n 1 lim   lim  lim  . 2 n 12n  5          2 1   5   1   5   2 n 1   n2  1   2               n n n n
Lựa chọn đáp án B. 1 1 1
Câu 18. Tổng của cấp số nhân lùi vô hạn S   ... ... có giá trị bằng 2 5 5 5n 1 1 2 5 A. . B. . C. . D. . 5 4 5 4
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 6
CLB Giáo viên trẻ TP Huế
[…Chuyên đề Trắc nghiệm Toán 11…]
Chuyên đề: GIỚI HẠN Hướng dẫn: 1 1 1 1 1 S   ...
... là tổng của cấp số nhân lùi vô hạn với u  và q  . 2 5 5 5n 1 5 5 1 1 Khi đó, 5 S   . 1 4 1 5
Lựa chọn đáp án B. 3n 1 2n 2017
Câu 19. Cho các dãy số u , v , w , α với u  , v  , w  , n n nnn 2 n 2 1 n 1 2 n n 4n 4n 1 α
. Có bao nhiêu dãy số có giới hạn bằng 0 trong các dãy số trên? n 2017  2n A. 1 . B. 2 . C. 3 . D. 4 . Hướng dẫn:
Có 3 dãy có giới hạn bằng 0 gồm u , v , w . n nn
Lựa chọn đáp án C. 4n1 Câu 20. Biết lim
a . Hỏi a là nghiệm của phương trình nào sau đây? 2  n x 4 A. 2 x 4  0 . B. 2
x 5x  4  0 . C. 2
x  5x  4  0 . D.  0 . 2 x 5x  4 Hướng dẫn: 4n1 lim
a a  4 . Lần lượt thế a  4 vào các phương trình ở các phương án. 2  n
Lựa chọn đáp ánB. Câu 21.  3 2
lim 3n n   1 có giá trị bằng A. 2  . B. 1  . C.  . D. . Hướng dẫn:    3 2 n n  3 1 1 lim 3 1 lim n     3      . 3   n n  
Lựa chọn đáp án C. Câu 22.  2 2 lim
n n n  2 có giá trị bằng 1 A. 0 . B. 1 . C.  . D. . 2 Hướng dẫn:
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 7
CLB Giáo viên trẻ TP Huế
[…Chuyên đề Trắc nghiệm Toán 11…]
Chuyên đề: GIỚI HẠN
n n n  2  2 2
n n n    2   2  n 2 lim 2  lim  lim 2 2 2 2
n n n  2
n n n  2 2 1 1  lim n  . 1 2 2 1  1 2 n n
Lựa chọn đáp án D. Câu 23.  2 2 lim
n n n  2 có giá trị bằng A. 1 2 . B. . C. 1  . D.  . Hướng dẫn:        2 2 
n n n   1 2 lim
2  lim n 1  1       . 2    n n     
Lựa chọn đáp án D. 2
n  2n n Câu 24. lim có giá trị bằng 2
4n n 2n 1 1 A. 4 . B. 2 . C.  . D. . 2 2 Hướng dẫn: 2  2 2
n  2nn   
n  2n n  2 4n n 2  n lim  lim 2
4n n 2n  2 2
4n n4n  2 n  2n   n      1   1  2n 4   2   2 4   2     n      n   lim = lim =4.      2   2  n 1 1    1 1     n      n 
Lựa chọn đáp án A. Câu 25. lim3 3
n1 n có giá trị bằng A. 0 . B. 1 . C.  . D. . Hướng dẫn: n  n lim3 3 n1 n 1 1  lim    lim 0 3 n12 3
 (n1)n 3 n2 3 n12 3
 (n1)n 3 n2
Lựa chọn đáp án A.
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 8
CLB Giáo viên trẻ TP Huế
[…Chuyên đề Trắc nghiệm Toán 11…]
Chuyên đề: GIỚI HẠN
1 3  5 ...(2n1) Câu 26. lim có giá trị bằng 2 3n  2 1 A. 0 . B. 1 . C. . D.  . 3 Hướng dẫn:
1 3 5...(2n1) là tổng n số hạng đầu của cấp số cộng có u  1, u  2n1 và công 1 n sai d  2 . n
Do đó     n       n  2 1 3 5 ... (2 1) 1 2 1  n   2  . 2
1 3  5 ...(2n1) n 1 1 Suy ra lim  lim  lim  . 2 2 3n  2 3n  2 2 3 3  2 n
Lựa chọn đáp án C.    1 1 1 1  Câu 27. lim     ...     có giá trị bằng 1.2 2.3 3.4 nn  1  A. 0 . B. 2 . C. 1  . D. 1. Hướng dẫn: 1
k  1k 1 1   
Ta có: kk   1 k k   . 1 k k  1 1 1 1 1 1 1 1 1 1 1 1 1          1 Do đó   ...
                   . nn  ... 1 1.2 2.3 3.4 1 1 2 2 3 3 4 n n1 n 1    1 1 1 1   1  Suy ra lim     ...              nn  lim 1 1. 1.2 2.3 3.4 1    n 1
Lựa chọn đáp án D. u   1 
Câu 28. Cho dãy uu
. Lúc đó, lim u bằng n  1 : n u   n n1 u   1 n A. 0 . B. 2 . C. 1  . D. 1. Hướng dẫn: 1
Dùng phương pháp quy nạp toán học, ta chứng minh được u   limu  0. n n n
Lựa chọn đáp án A.
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 9
CLB Giáo viên trẻ TP Huế
[…Chuyên đề Trắc nghiệm Toán 11…]
Chuyên đề: GIỚI HẠN
III – BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN: Câu 1.
Trong các khẳng định sau, khẳng định nào là đúng?
A. Nếu limu  0 thì lim u  0 .
B. Nếu lim u   thì limu   . n n n n
C. Nếu lim u   thì limu  .
D. Nếu lim u a
 thì lim u a . n n n n Câu 2.
Mệnh đề nào sau đây là mệnh đề đúng?
A. Một dãy số có giới hạn thì luôn luôn tăng hoặc luôn luôn giảm.
B. Nếu u là dãy số tăng thì limu   . n n
C. Nếu limu   và lim v   thì limu v  . n n  0 n n D. Nếu n u a và 1
  a 0 thì limu  0 . n n Câu 3.
Trong các khẳng định sau, khẳng định nào đúng? A. 3 f   x g    3 lim x  lim f    x g  x   . B. 3 f   x g  3 x f   3 lim lim
x  lim g  x . C. 3 f   x g  3 x f   3 lim lim
x  lim g  x .   D. 3 f   x g  3 x f   3 lim lim x   g  x  .   Câu 4.
Với a là một số thực, trong các khẳng định sau, khẳng định nào sai? u
A. Nếu lim u a và lim v   thì lim n  0 . n n vn u
B. Nếu lim u a và lim v   thì lim n  0 . n n vn
C. Nếu lim u a và lim v   thì limu v   . n n n n u
D. Nếu limu a  0 và lim v  0 và v  0 với mọi n thì lim n   . n n n vn Câu 5.
Mệnh đề nào sau đây là đúng?
A. Mọi dãy dương đều có giới hạn.
B. Mọi dãy tăng đều có giới hạn.
C. Mọi dãy giảm đều có giới hạn.
D. Mọi dãy là dãy không đổi đều có giới hạn. Câu 6.
Mệnh đề nào sau đây là đúng?
A. Mọi dãy bị chặn đều có giới hạn.
B. Mọi dãy tăng và bị chặn trên đều có giới hạn.
C. Mọi dãy giảm và bị chặn trên có giới hạn.
D. Mọi dãy tăng và bị chặn dưới đều có giới hạn. Câu 7. Cho u
là một cấp số nhân lùi vô hạn với công bội q . Khẳng định nào sau đây là đúng? n  A. q  1.
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 10
CLB Giáo viên trẻ TP Huế
[…Chuyên đề Trắc nghiệm Toán 11…]
Chuyên đề: GIỚI HẠN u B. 1
u u ...u  . 1 2 n 1q u C. 2 n 1
u u q u q ...u q ...  . 1 1 2 1 1q u D. 1 lim S  . n 1 q
2.4n 5n  3n Câu 8. Để tính lim ta tiến hành n n 1 2 5 
A. Chia cả tử và mẫu cho 2n .
B. Chia cả tử và mẫu cho 3n .
C. Chia cả tử và mẫu cho 4n .
D. Chia cả tử và mẫu cho 5n .  n 5 n 1 2  1 Câu 9. lim có giá trị bằng n 5.2n  5 1 3 1 1 2 1 A.  . B. . C.  . D.  . 3 5 5 5 2 3 2n 3n Câu 10. lim có giá trị bằng 3 2 2n  4n 1 3 3 A.  . B. 0 . C. 1 . D. . 2 2 n  2 n  3 Câu 11. lim có giá trị bằng n1 1 A. 0 . B. . C. 1 . D.  . 3  2n 2  n  3 2n   1 4n  5 Câu 12. lim  có giá trị bằng 4 n 3n  1  2 3n 7 8 A. 0 . B. . C. 1 . D.  . 3  3 2nn  2 3n   1 Câu 13. lim  có giá trị bằng 2n  1  4 n 7 3 A. 1 . B. 3 . C.  . D.  . 2 3 n 3n 1 Câu 14. lim có giá trị bằng n  1 12 2 n 1 1 A. 0 . B. 1 . C.  . D. . 2 4
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 11
CLB Giáo viên trẻ TP Huế
[…Chuyên đề Trắc nghiệm Toán 11…]
Chuyên đề: GIỚI HẠN 1 1 1
Câu 15. Tổng S  1  ... ... bằng 2 4 2n A. 1 . B. 2 . C. 4 . D. 6 . n 1  1   1   1 1
Câu 16. Tổng S      +...+ ...   bằng 2 4   8 2n 1 3 2 A. 1 . B. . C. . D. . 3 4 3
Câu 17. Với k là số nguyên dương thì lim k n bằng A.  . B. . C. 0 . D. n . Câu 18.  3 2 lim 2
n 2n   3 có giá trị bằng A. 2  . B. 1  . C.  . D. . Câu 19.  4 2
lim 3n  4n n  1 có giá trị bằng A. . B.  . C. 3 . D. 7 . Câu 20.  2 2 lim
n  4  n 1 có giá trị bằng A. 3 . B. 1 . C. 0 . D.  . Câu 21.  2 2 lim
n  2n1  2n n có giá trị bằng A. 1 2 . B.  . C. 1  . D. . Câu 22.  2 lim
n 2n  3  
n có giá trị bằng A. 1  . B. 0 . C.  . D. 1 . 2
9n n n  2 Câu 23. lim có giá trị bằng 3n2 A. 1 . B. 3 . C. 0 . D.  .  1 1 1 1  Câu 24. lim    ..   có giá trị bằng 2 3  3 3 3 3n  1 1 A. . B. . C. . D. 1 . 2 24 Câu 25.  2 2 lim
2n n1  2n 3n 2 có giá trị bằng 1 A. . B. 0 . C.  . D.  . 2  1 1  Câu 26. lim      có giá trị bằng  n1 n  2  1 A. 1 . B. 0 . C. . D.  . 2
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 12
CLB Giáo viên trẻ TP Huế
[…Chuyên đề Trắc nghiệm Toán 11…]
Chuyên đề: GIỚI HẠN 2017 2016 nn Câu 27. lim có giá trị bằng 2017 2015 3nn 1 A. 1 . B. 1  . C. . D.  . 3  1 1 1 1  Câu 28. lim     ...   có giá trị bằng 1.3 3.5 5.7 
2n 12n3 1 1 A. . B. 1  . C. . D.  . 2 3   Câu 29. lim
nn2  n  3 có giá trị bằng   5 A. 1 . B. 0 . C. . D.  . 2
Câu 30. Nếu limu L thì 3
lim u  8 có giá trị bằng n n A. L  2 . B. 3 L  8 . C. 3 L  2 . D. L 8 . 1
Câu 31. Nếu dãy u với u  0, n
  và limu L thì lim có giá trị bằng n n n u  9 n 1 1 1 1 A. . B. . C. . D. . L  3 L  9 L  3 L  9 2u  4
Câu 32. Cho dãy số u
với lim u  3 . Khi đó, lim n có giá trị bằng n n u 1 n 1 A. 4  . B. 2 . C. 5 . D. . 2 u  2
Câu 33. Cho dãy số u
với limu  . Khi đó, lim n có giá trị bằng n n 2 u 1 n A. 1 . B.  . C. 0 . D. 2  . 2 n
Câu 34. Cho dãy số u với u  2   
. Chọn mệnh đề đúng trong các mệnh đề n  2 ...  2 n  sau: 2 n 2 A. lim u  2      . n
 2 ...  2 ... 1 2 B. limu   . n C. limu  . n D. Dãy số u
không có giới hạn khi n   . n  3 n 1 Câu 35. lim có giá trị bằng 3 n  8 1 1 A. 1 . B. . C. . D.  . 2 8
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 13
CLB Giáo viên trẻ TP Huế
[…Chuyên đề Trắc nghiệm Toán 11…]
Chuyên đề: GIỚI HẠN 3 3 2 8n  2n 1 Câu 36. lim có giá trị bằng 2 2n 1 A. 2 . B. 2 . C. 1 . D.  .  1 1 1 1  Câu 37. lim     ...   có giá trị bằng 1.4 4.7 7.10
3n23n  1 1 1 A. . B. 1  . C. . D.  . 2 3
1.2  2.3  3.4  ...  nn   1 Câu 38. lim có giá trị bằng 3 2016n  2017 1 1 A. . B. . C. . D.  . 2017 2016    3 ( 1  )n n cos 3nCâu 39. lim    có giá trị bằng    n 1  3 A. . B. 3 . C. 5 . D. 1  . 2 n
Câu 40. lim 3n  5   có giá trị bằng   A. 3 . B. . C.  . D.  5 . 2 n n 1 Câu 41. lim có giá trị bằng 2 n n  2 A. 1 . B. 2 . C. 0 . D. 1  . Câu 42. 3 3 lim n 2n  
n có giá trị bằng 2 1 A.  . B. . C. 1 . D. 0 . 3 3 Câu 43. 3 2 3 lim n n  
n có giá trị bằng 1 A. . B.  . C. 1 . D. 0 . 3
Câu 44. Dãy số nào sau đây có giới hạn bằng 0? 2 n 1 13n A. u  . B. u  . n 2 n  3n n 2 n  3n 2 1 2n 12n C. u  . D. u  . n n  5 n n  5
2  5  8  ...  3n 1 Câu 45. lim có giá trị bằng 2 n 1 A. . B. 0. C. . D. 3 . 3
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 14
CLB Giáo viên trẻ TP Huế
[…Chuyên đề Trắc nghiệm Toán 11…]
Chuyên đề: GIỚI HẠN
Câu 46. Dãy số nào sau đây có giới hạn là ? 2 n  2n 1 2n A. u  . B. u  . n 2 3n  3n n 3n  3 2 2  n 2 n  2 C. u  . D. u  . n 3n  3 n 3 n  5n
Câu 47. Dãy số nào sau đây có giới hạn là ? 2 n  3n 2018  2017n A. u  . B. u  . n 2 2n n n n 1 C. 2
u  2017n2016n . D. 2 u n 1. n n
Câu 48. Trong các giới hạn sau đây, giới hạn nào bằng 1?  2 3n 1 3 2n  3 A. lim . B. lim . 3 3  n  2 3 2  n 1 2 3n 1 3 n 3 C. lim . D. lim . 3 2 3  n  3n 2 n  1
Câu 49. Trong các giới hạn sau đây, giới hạn nào bằng 0? 2 5n  2 3 2n5n A. lim . B. lim . 3 5  n 4 2 2  n 1 2 4 2n n 3 3  5n C. lim . D. lim . 3 2 n   2n 2 n 1
Câu 50. Trong các giới hạn sau đây, giới hạn nào bằng 1 ? 2 n  2 3 2nn A. lim . B. lim . 3 n  4 2 2n 1 2 3 3n 2n 4 3  2n C. lim . D. lim . 3 2 2  n  4n 2 2n 1
Câu 51. Dãy số nào sau đây không có giới hạn?    n π A. lim  
1 sin  nπ    . B. lim sinn π . 2      π
C. lim cos  nπ  . D. lim cosn π . 2   
Câu 52. Dãy số nào sau đây có giới hạn bằng 1 ? A. lim sinn π . B. lim cosn π .  n2  ncos n2 C. lim sin π   . D. lim . 2n1  2 n 4n 1 4n  3n Câu 53. Biết lim  M và lim  m. Tích . M m bằng 12n n 1 24  1 1 A. 2 . B. 2  . C. . D.  . 2 2
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 15
CLB Giáo viên trẻ TP Huế
[…Chuyên đề Trắc nghiệm Toán 11…]
Chuyên đề: GIỚI HẠN 2017 2017  2017 sin2017  n Câu 54. Biết lim  0 và lim  0 . Khi đó, lim bằng 2017 n 2017 n 2017 n A. 2017 . B. 2017 . C. 1 . D. 0 .
1 2  3 ... n
Câu 55. Để tính lim
, một học sinh làm như sau: 2 n
1 2  3 ... n 1 2 3 n Bước 1: Ta có    ... . 2 2 2 2 2 n n n n n
1 2  3 ... n  1 2 3 n Bước 2: Suy ra lim lim     ...  2 2 2 2 2   n n n n n  
1 2  3 ... n 1 2 3 n Bước 3: Suy ra lim  lim lim lim ...lim 2 2 2 2 2 n n n n n
1 2  3 ... n Bước 4: Suy ra lim
 0 0 0 ...0  0 . 2 n
Bạn học sinh đã giải đúng hay sai? Nếu sai thì sai thì bước nào? A. Bước 1. B. Bước 2. C. Bước 3. D. Bài giải đúng.
1 3  5 ...(2n1) Câu 56. lim có giá trị bằng 2 5n 4 1 1 A. 0 . B.  . C. . D.  . 4 5
1 2  3 ... n Câu 57. lim có giá trị bằng 2 2n 1 A. 1  . B.  . C. 1 . D.  . 2    2 2 2  Câu 58. lim    ...     có giá trị bằng 1.2 2.3 nn  1  1 A. . B. 2 . C. 0 . D. . 2 u   2 1 
Câu 59. Cho dãy u
. Lúc đó, lim u bằng n  : 1 u  2  n   n n  * 1  un A. 0 . B. 2 . C. 1  . D. 1.  1 u  
Câu 60. Cho dãy u
. Lúc đó, lim u bằng n  1 : 2 n u   3u n nn   * 1  A.  . B. 2 . C. . D. 1. 2 2 2 2
1  2  3  ...  n Câu 61. lim có giá trị bằng 3 4n  2017 1 1 A. . B. . C. . D. 3 . 3 24
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 16
CLB Giáo viên trẻ TP Huế
[…Chuyên đề Trắc nghiệm Toán 11…]
Chuyên đề: GIỚI HẠN
Câu 62. Khẳng định nào sau đây là đúng?
A. Một dãy số có giới hạn thì luôn tăng hoặc luôn giảm. B. Nếu n
u a và a  1 thì lim u  0 . n n
C. Nếu limu  0 và lim v   thì lim(u .v )  0 . n n n n 2017
D. Nếu lim u   thì lim  0 . n un
Câu 63. Khẳng định nào sau đây là sai?
A. Một dãy số tăng và bị chặn trên thì có giới hạn.
B. Một dãy số giảm và bị chặn dưới thì có giới hạn. u
C. Nếu lim u   và lim v   thì lim n  1. n n vn 2 D. Nếu n u a và 
a  1 thì lim n a  0 . n
Câu 64. Khẳng định nào sau đây là sai?
A. Nếu lim u a và lim v b thì lim(u v )  a b . n n n n
B. Nếu lim u   và lim v   thì lim(u v )  0 . n n n n
C. Nếu u  0 với mọi n và lim v a thì a  0 . n n v D. Nếu limu  2
 và lim v  2018 thì lim n  1  009 . n n un
Câu 65. Khẳng định nào sau đây là đúng? u a
A. Nếu lim u a và lim v b thì lim n  . n n v b n
B. Nếu lim u a thì lim u a . n n u
C. Nếu limu  5 và lim v  0 thì lim n   . n n vn D. Nếu n
u a và a  2 thì lim n u   . n
2  4  6  ...  2n
Câu 66. Cho dãy số u với u
. Khẳng định nào sau đây đúng? n n 3 n  3n  1 A. lim u  0 . B. lim u  2 . C. lim u  3 . D. lim u   . n n n n 2
1 2  2  ...  2n
Câu 67. Cho dãy số u với u
. Khẳng định nào sau đây đúng? n n n1 2  3 1 A. lim u  . B. lim u  1. C. lim u   . D. lim u   . n 2 n n n 5
Câu 68. Cho dãy số u với u  2016 
. Khẳng định nào sau đây đúng? n n 7 n
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 17
CLB Giáo viên trẻ TP Huế
[…Chuyên đề Trắc nghiệm Toán 11…]
Chuyên đề: GIỚI HẠN A. lim u  0 . B. lim u  5 . C. lim u  7 . D. limu  2016 . n n n n 1 1 1
Câu 69. Cho S  1   ... 
 ... . Khẳng định nào sau đây đúng? 2 4 2n 1 A. S  0 . B. S  1 . C. lim u  . D. lim u   . n 2 n Câu 70. Cho 2 1 2 2 ... 2n S     
.... Khẳng định nào sau đây sai? A. S   . B. 2 lim(1 2 2 ... 2n S      ) .
C. S là tổng của cấp số nhân lùi vô hạn.
D. S là tổng vô hạn các phần tử của một cấp số nhân.
Câu 71. Cho dãy số u có limu   . Khẳng định nào sau đây sai? n n u  2 1 u n 2 1 1 A. lim n  . B. lim  . 2u 2 2 2u  1 2 n n 2 u   1 1 C. lim 3
u  6  . D. lim n   . n  2u  3 2 n ------- HẾT -------
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 18
CLB Giáo viên trẻ TP Huế
[…Chuyên đề Trắc nghiệm Toán 11…]
Chuyên đề: GIỚI HẠN
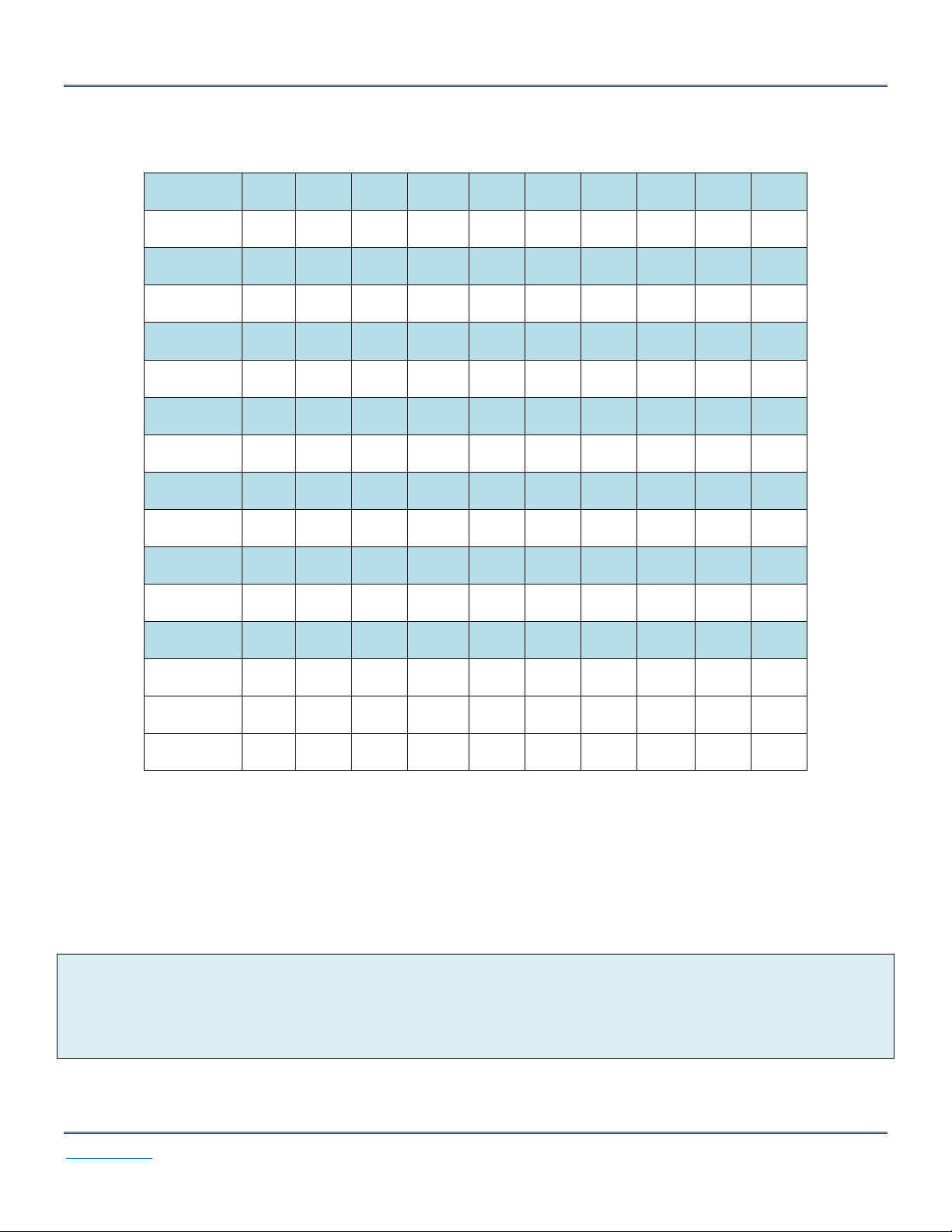
ĐÁP ÁN CÂU HỎI TRẮC NGHIỆM TỰ LUYỆN Câu 1 2 3 4 5 6 7 8 9 10 Đáp án A D A C D B C D B A Câu 11 12 13 14 15 16 17 18 19 20 Đáp án D B C D B B A D B C Câu 21 22 23 24 25 26 27 28 29 30 Đáp án D A A A A B C A C B Câu 31 32 33 34 35 36 37 38 39 40 Đáp án D C C C A A C B B C Câu 41 42 43 44 45 46 47 48 49 50 Đáp án B A D B D C D B A C Câu 51 52 53 54 55 56 57 58 59 60 Đáp án D C C D C C D B D A Câu 61 62 63 64 65 66 67 68 69 70 Đáp án B D C B D A B D A C Câu 71 72 73 74 75 76 77 78 79 80 Đáp án D
Trong tài liệu này, tác giả có sử dụng phần lí thuyết và một số câu hỏi của Thầy Lê
Bá Bảo (CLB Giáo viên trẻ TP Huế), Thầy Đặng Ngọc Hiền (TP Bà Rịa_Vũng Tàu) và sách
trắc nghiệm 2007, tài nguyên Page Toán học Bắc Trung Nam. Dù biên soạn rất kỹ, song
chắc chắn không tránh khỏi sai sót. Mong bạn đọc phản hồi để cùng tác giả hoàn thiện nội
dung trên. Xin cảm ơn! Xin tặng các Thầy Cô và các em học sinh chuyên đề này!
Tác giả: HUỲNH ÁI HẰNG
Địa chỉ: Tản Đà_Hương Sơ, TP Huế
SĐT: 0935.905.892
Facebook: Ái Hằng Huỳnh
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
Giáo viên: HUỲNH ÁI HẰNG…0935.905.892… 19
CLB Giáo viên trẻ TP Huế