








Preview text:
CHUYÊN ĐỀ: HIỆN TƯỢNG CẢM ỨNG ĐIỆN TỪ
A. LÍ THUYẾT VỀ HIỆN TƯỢNG CẢM ỨNG ĐIỆN TỪ
I. Từ thông qua diện tích S đặt trong một từ trường đều
+ Từ thông qua một mạch điện kín có diện tích S, đặt trong từ trường đều có vectơ cảm ứng
từ là B được xác định theo công thức:
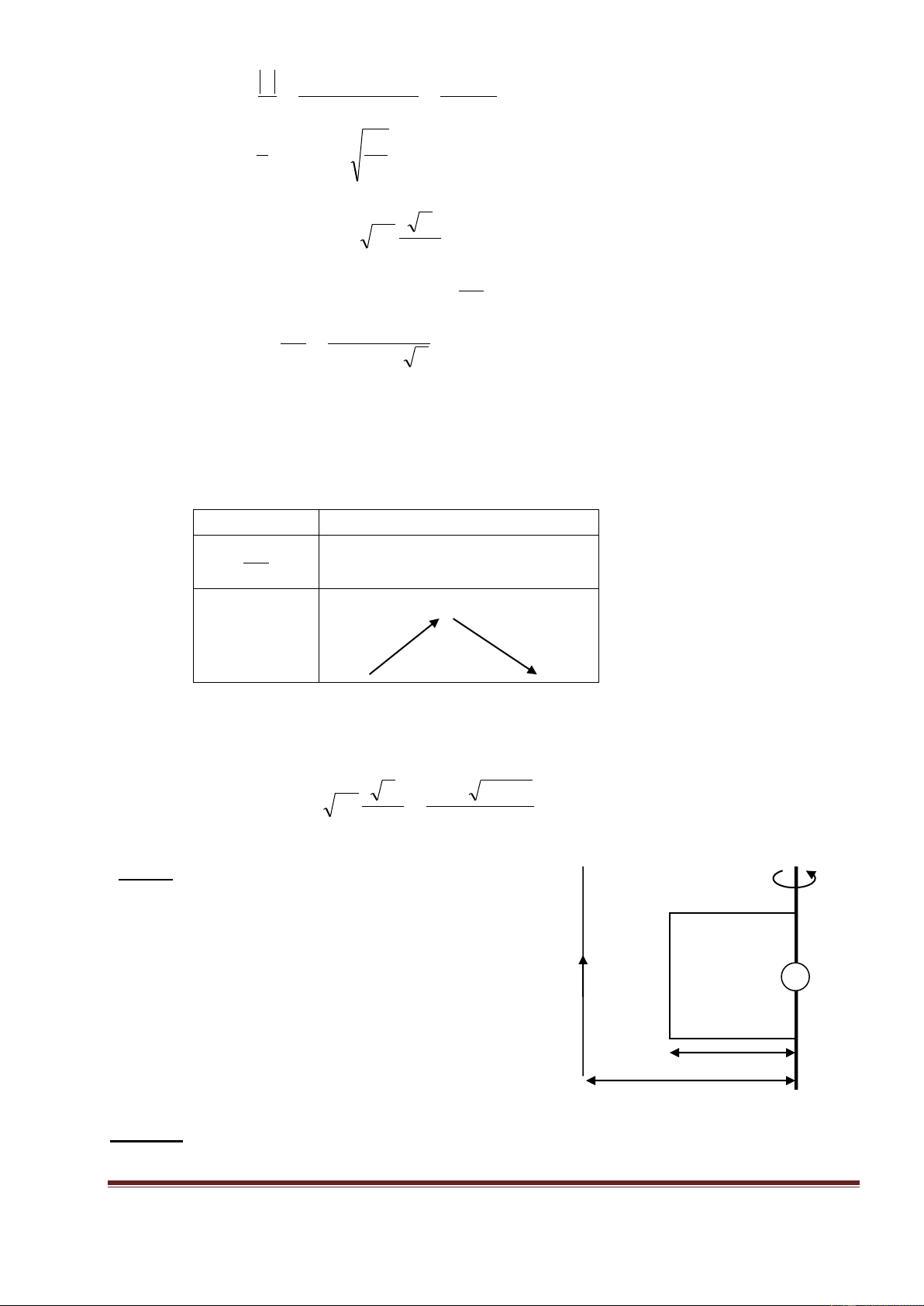
= BScos ; Trong đó = ( n ; B )
(Chiều của n tuỳ thuộc vào chiều (+) mà ta chọn cho khung dây kín)
II. Hiện tượng cảm ứng điện từ:
+ Khi từ thông qua một khung dây kín biến thiên thì trong ktg từ thông biến thiên trong
khung xuất hiện dòng điện cảm ứng
+ Khi một đoạn dây dẫn chuyển động cắt các đường cảm ứng thì trong đoạn dây xuất hiện
một suất điện động cảm ứng
III. Định luật Lenxơ về chiều dòng cảm ứng
+ Dòng cảm ứng có chiều chống lại nguyên nhân đã sinh ra nó
+ Dòng cảm ứng có chiều sao cho từ trường mà nó sinh ra chống lại sự biến thiên của từ thông sinh ra nó
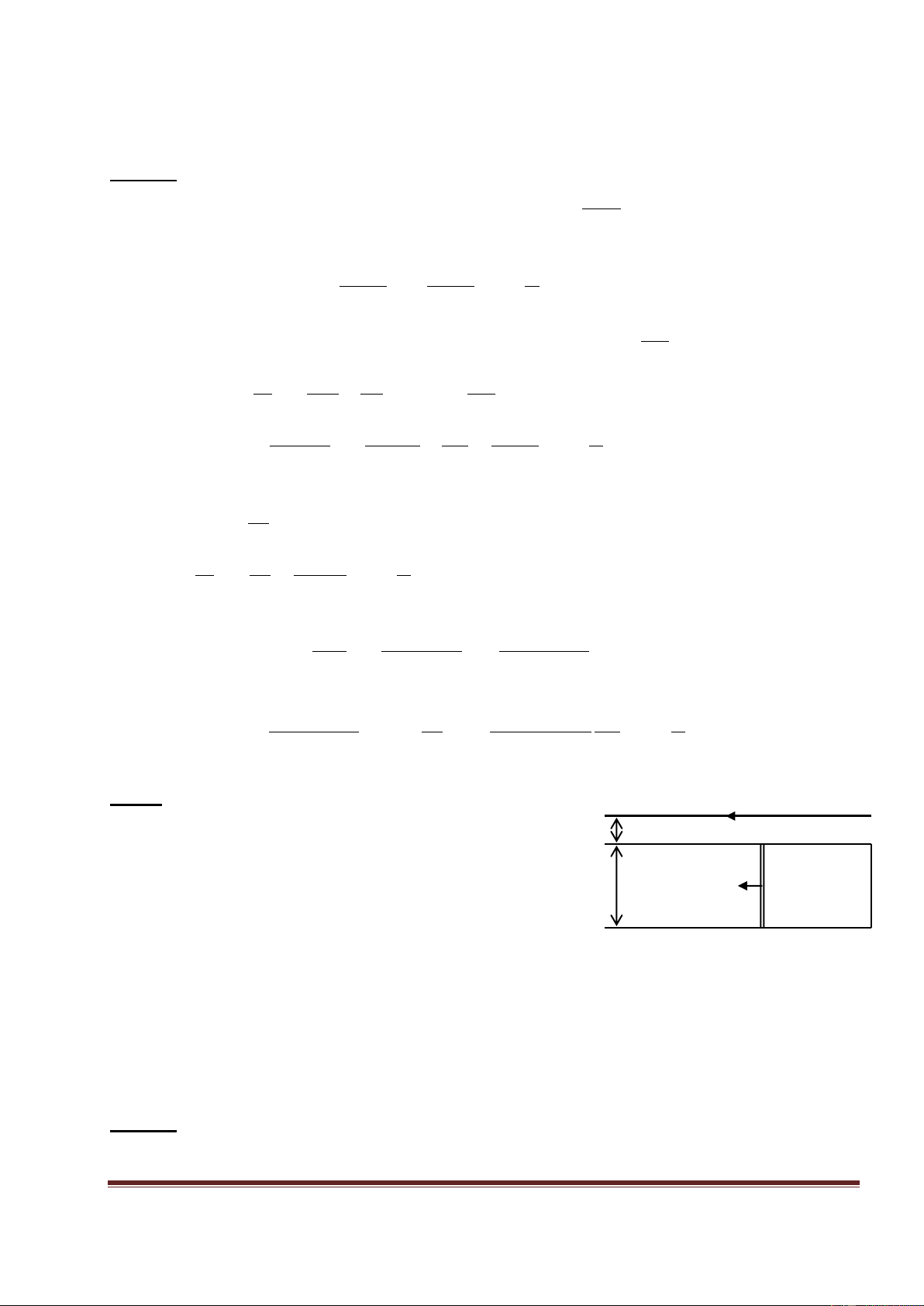
. Khi Bm tăng thì B và B ngược chiều m c
. Khi Bm giảm thì B và B cùng chiều m c
IV. Suất điện động cảm ứng:
* Định luật Farađây về cảm ứng điện từ:
Độ lớn suất điện động cảm ứng xuất hiện trong mạch kín tỉ lệ với tốc độ biến thiên từ thông qua mạch. ec = -N
(N là số vòng dây của khung) t
* Suất điện động cảm ứng xuất hiện trên đoạn dây dẫn chuyển động trong từ trường đều.
e = Blvsin c
+ v và B cùng vuông góc với đoạn dây và v tạo với B góc
+ Chiều của sđđ (từ cực (-) sang cực (+) tuân theo qui tắc BTP hoặc theo định luật Lenxơ
. Qui tắc BTP: Xoè bàn tay phải hứng đường cảm ứng, ngón tai cái choãi ra 900 chỉ
chiều v thì chiều
từ cổ tay đến 4 ngón còn lại chỉ chiều từ cực (-) sang cực (+) của nguồn cảm ứng
V. Suất điện động tự cảm:
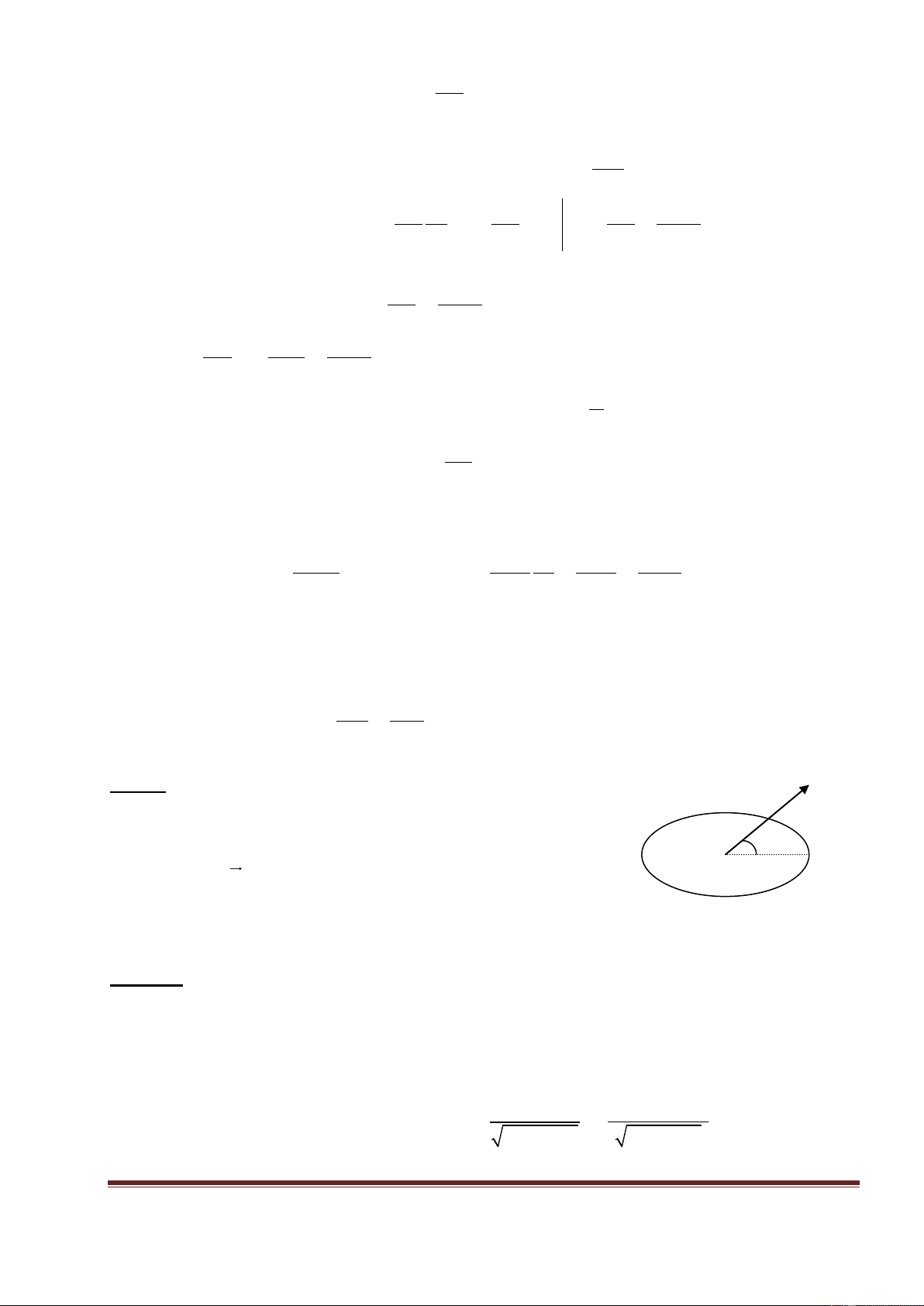
1. Từ thông tự cảm: = Li ( L = k.2 .n2V)
2. Suất điện động tự cảm: I etc = -L t 2
3. Năng lượng từ: 1 B V W =
LI2 suy ra trong cuộn dây: W = 2 4 k . 2
4. Mật độ năng lượng từ: B = 4 k . Trang 1
VI. Công của lực từ tác dụng lên một mạch điện kín chuyển động trong từ trường.
Khi một mạch điện chuyển động trong từ trường bất kì thì công của lực từ tác dụng lên
mạch điện được đo bằng tích của cường độ dòng điện với độ biến thiên từ thông qua mạch
trong quá trình chuyển động. A
= I.
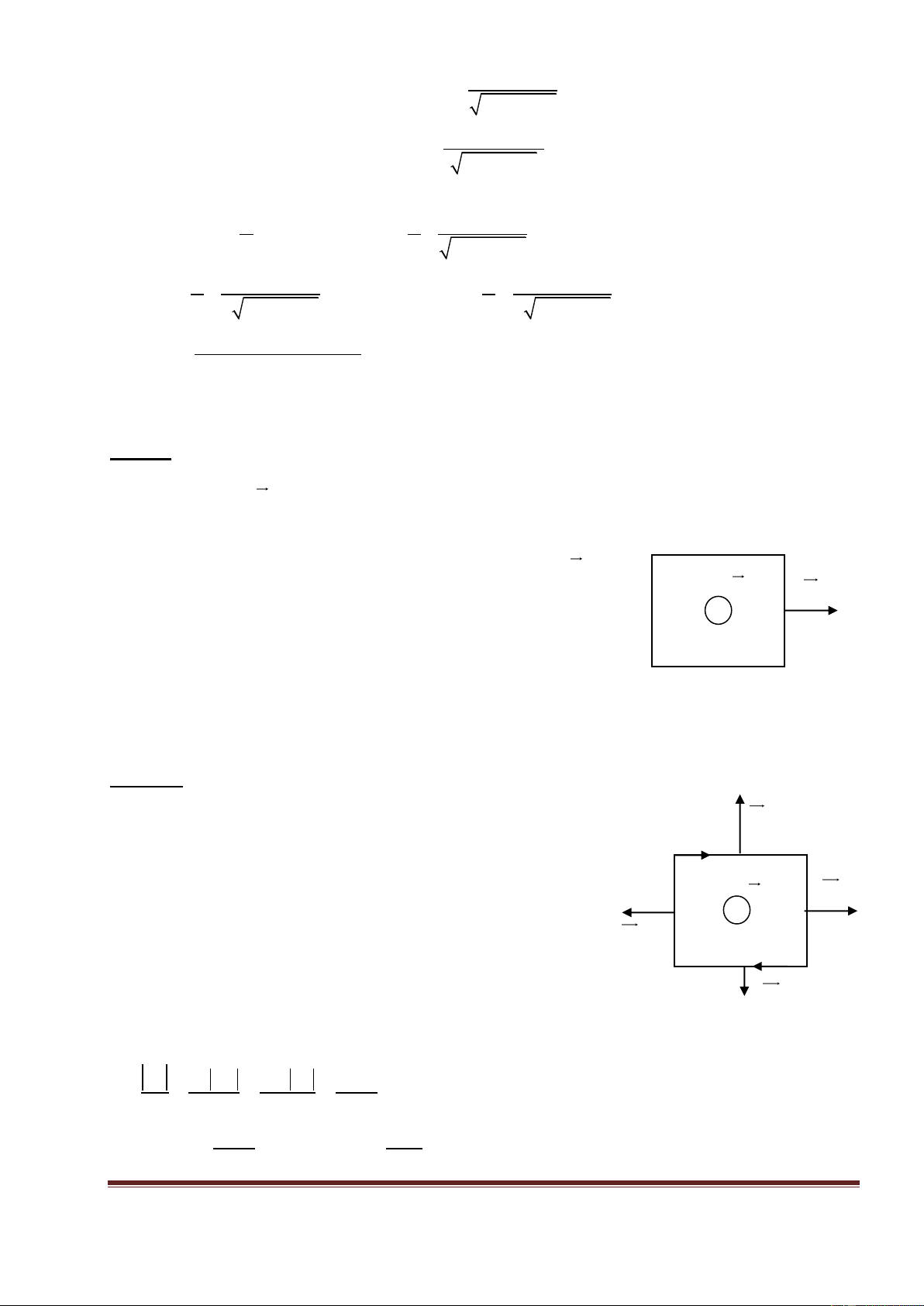
Ta có: F=BIl và F tạo với dịch chuyển x
một góc đúng bằng góc của vectơ pháp tuyến
khung tạo với vectơ từ cảm B .
Suy ra công của lực từ là : A = F. x
.cos = I.
B. MỘT SỐ BÀI TẬP VỀ HIỆN TƯỢNG CẢM ỨNG ĐIỆN TỪ
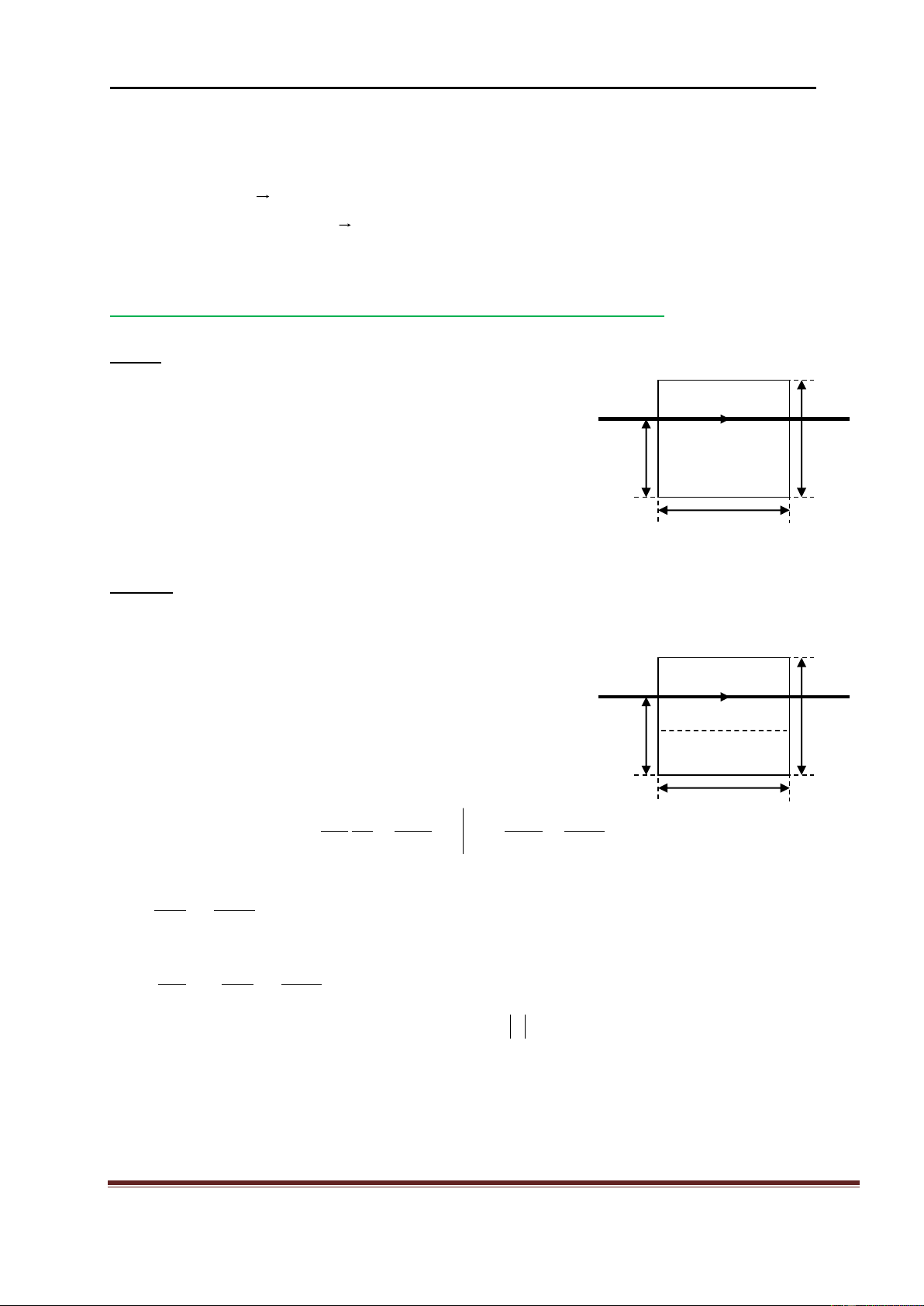
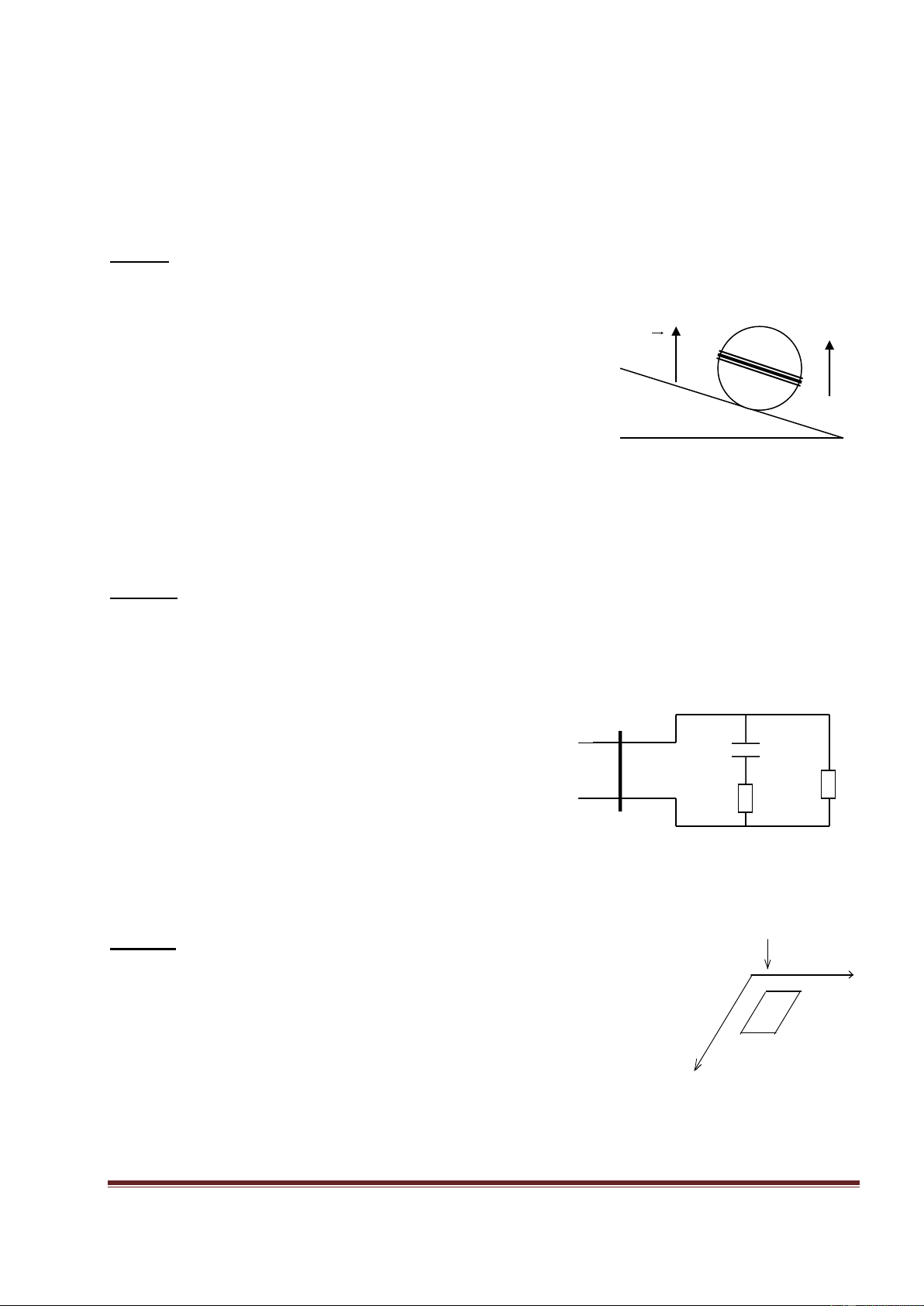
Bài 1: Một dòng điện chạy trên một dây dẫn thẳng dài qua
hai cạnh của một hình vuông ABCD, có cường độ dòng A B
điện i cho bởi biểu thức i = 4,5.t2 – 10.t; trong đó i tính
bằng A và t tính bằng s. Cho a = 12 cm; b = 16 cm (hình vẽ) i
(Giữa dây dẫn thẳng dài và hình vuông có cách điện) b
a.Tính suất điện động trong khung dây dẫn hình vuông a
ABCD tại thời điểm t = 3 s.
b. Xác định chiều của dòng điện cảm ứng trong khung tại D C thời điểm t=3s. b Lêi gi¶i
a. Tõ tr-êng B cña dßng ®iÖn i g©y ra cã ph-¬ng vu«ng gãc víi mÆt ph¼ng chøa khung d©y
ABCD, cã chiÒu ®i tõ sau ra tr-íc víi vïng ë phÝa trªn
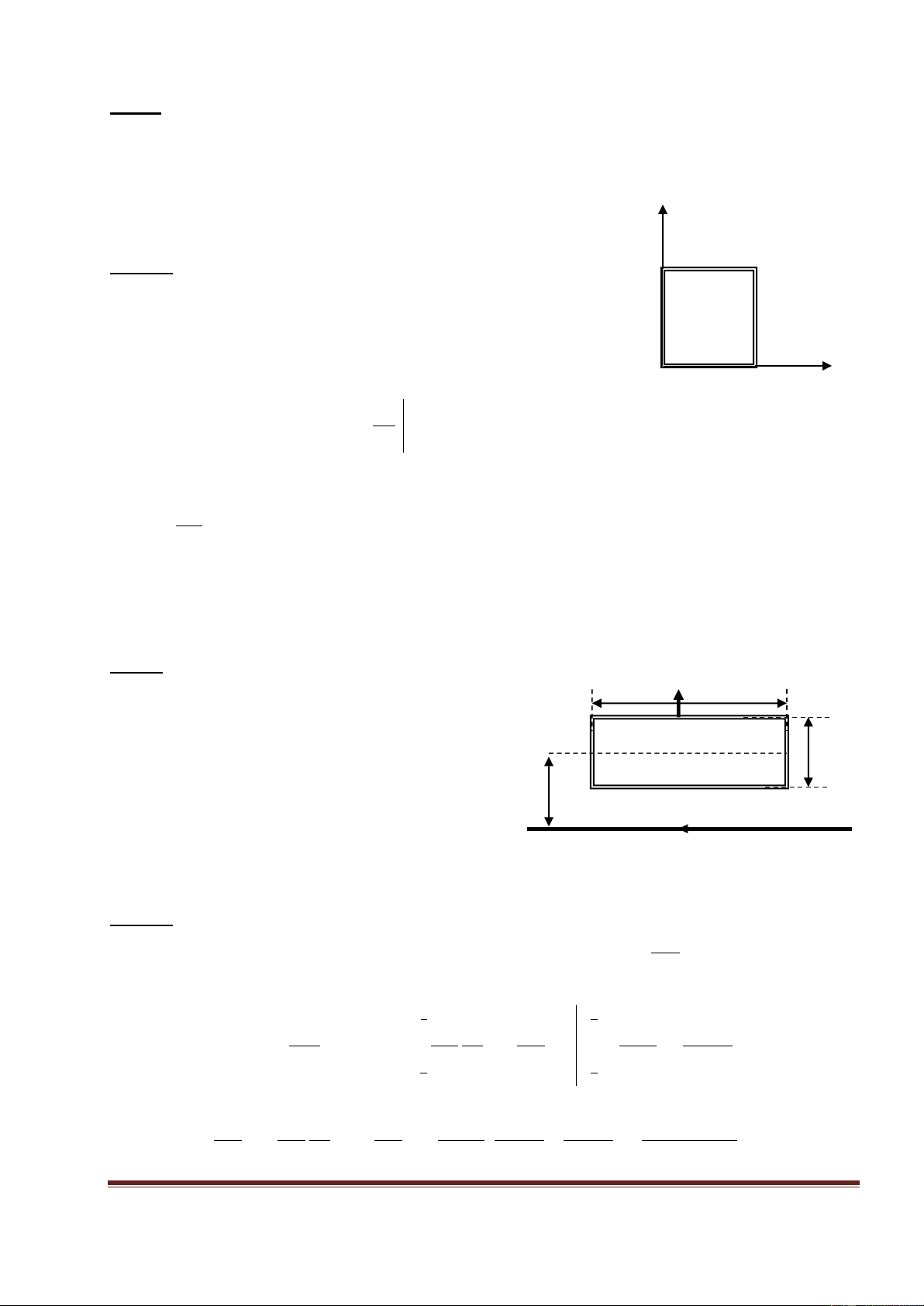
dßng ®iÖn vµ cã chiÒu tõ tr-íc ra sau ®èi víi vïng ë phÝa A B d-íi dßng ®iÖn. B M N
XÐt h×nh ch÷ nhËt A’B’NM ®èi xøng víi h×nh ch÷ nhËt
ABNM qua MN. V× lý do ®èi xøng nªn tõ th«ng göi qua i A B’ b
A’B’NM b»ng nh-ng tr¸i dÊu víi tõ th«ng göi qua ABNM, a ’
nªn tõ th«ng göi qua h×nh ch÷ nhËt ABCD chØ cßn b»ng tõ B
th«ng göi qua h×nh ch÷ nhËt A’B’CD vµ b»ng: D C a b i dr ib a bi a
= BdS = bBdr = b 0 = 0 ln r = 0 ln 2 r 2 − − 2 − b a b a b a
Thay i = 4,5.t2 – 10.t vµo biÓu thøc cña tõ th«ng ta ®-îc b a 0 = (ln )( . 5 , 4 2 t − . 10 t) 2 b − a
SuÊt ®iÖn ®éng c¶m øng trªn khung t¹i thêi ®iÓm t lµ d b a 0 = − = − (ln 9 )( t − ) 10 dt 2 b − a
T¹i thêi ®iÓm t = 3 s th× suÊt ®iÖn ®éng cã ®é lín 6 598 , 0 10 . − = V
b. T¹i thêi ®iÓm t = 3 s th× dßng ®iÖn i ®i qua d©y dÉn MN ®ang t¨ng theo thêi gian t tøc B
®ang t¨ng. Theo ®Þnh luËt Len-x¬ th× dßng ®iÖn c¶m øng ic ®i trong khung d©y ABCD ph¶i
cã chiÒu sao cho chèng l¹i sù t¨ng cña B trong khung A’B’CD, nghÜa lµ nã ph¶i sinh ra tõ
tr-êng c¶m øng B cã chiÒu ng-îc víi B . VËy i c
c ph¶i cã chiÒu ng-îc chiÒu quay cña kim
®ång hå t¹i thêi ®iÓm ®ã. Trang 2
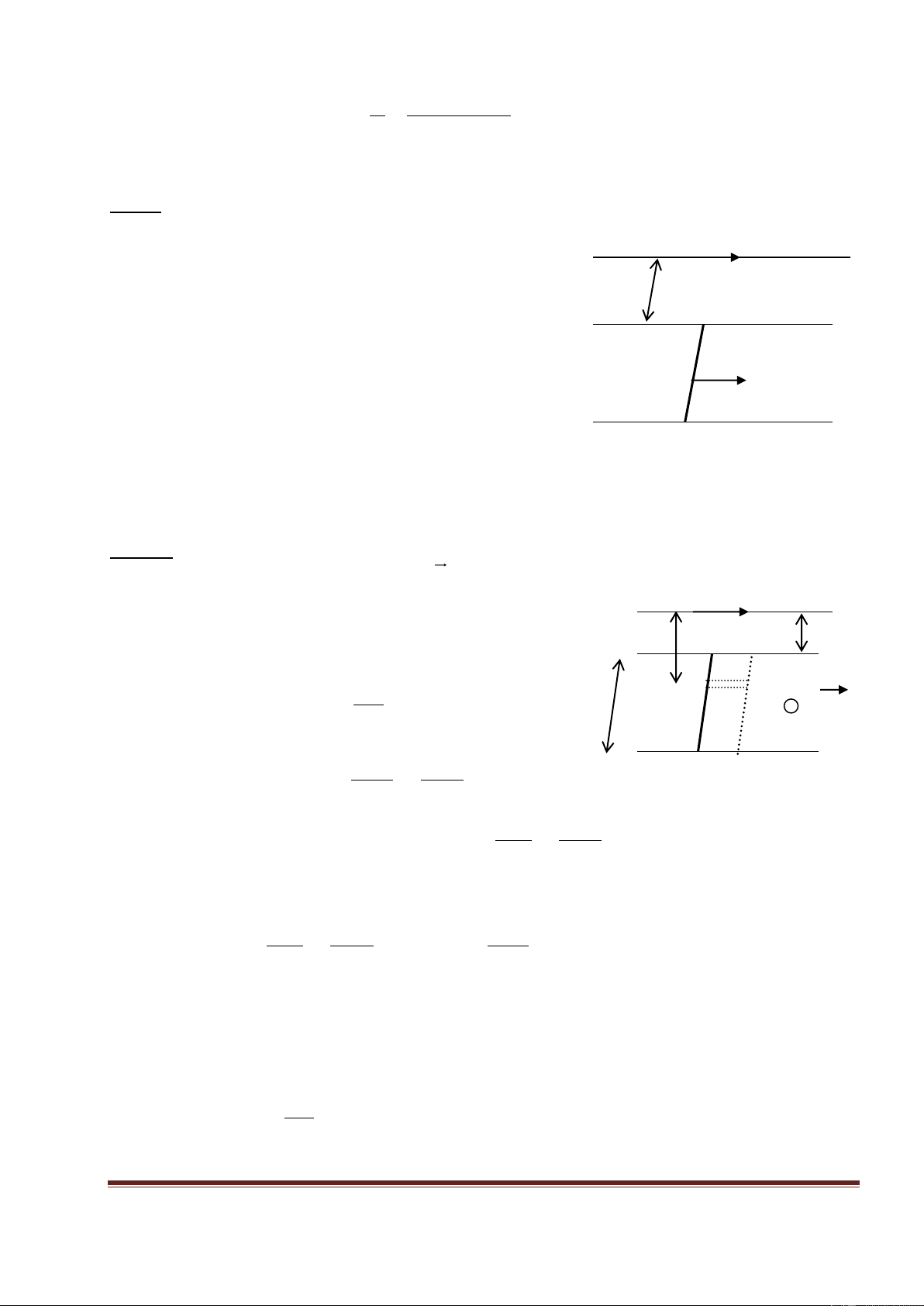
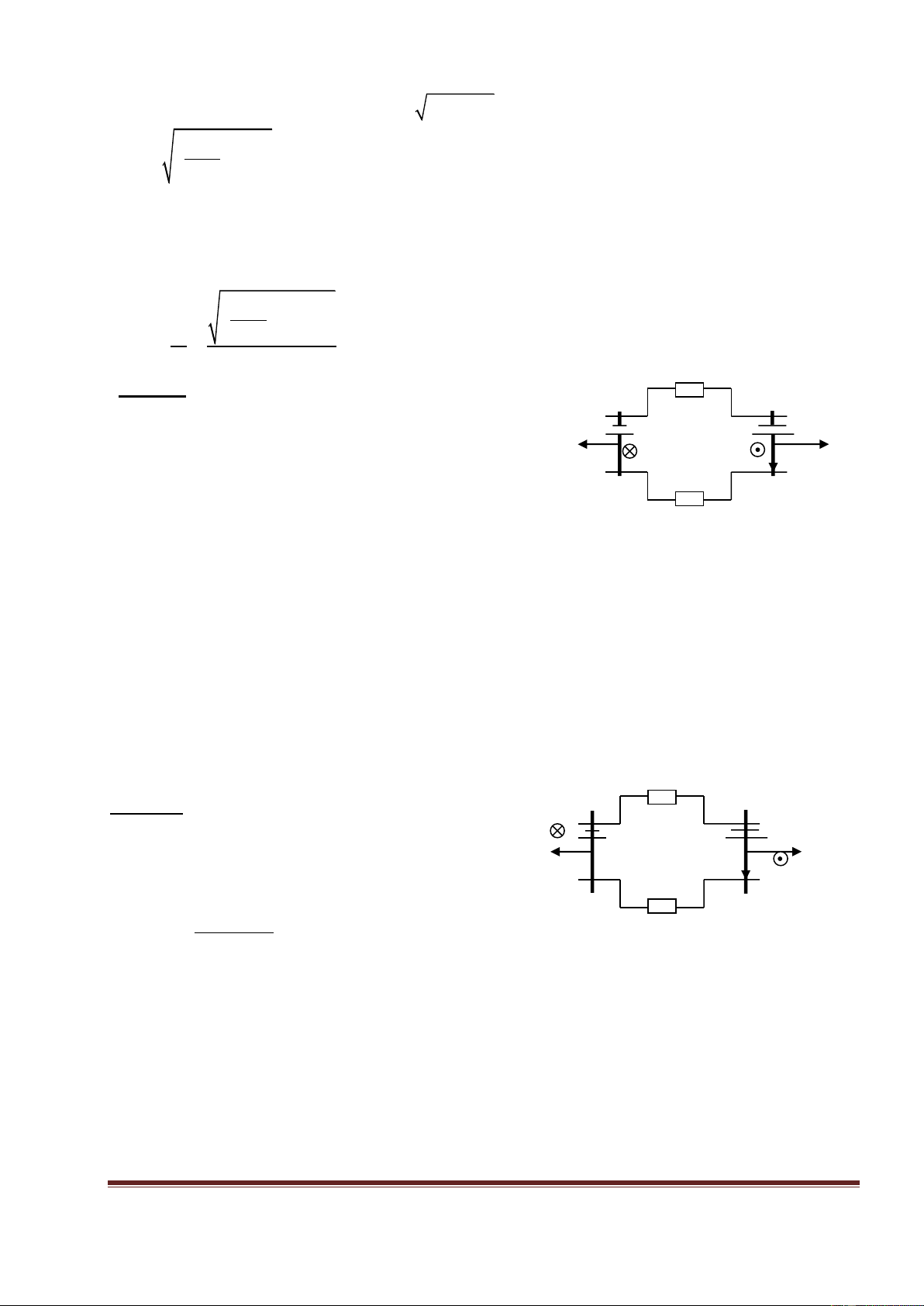
Bài 2: Một khung dây dẫn OABC nằm trong mặt phẳng Oxy có cạnh b=2cm. Từ trường B
vuông góc với mặt phẳng Oxy có chiều hướng từ trong ra ngoài và có độ lớn cho bởi công
thức B = 4t2y. Trong đó B tính bằng T, tính tính bằng s và y tính bằng m.
a. Xác định suất điện động cảm ứng trên khung dây tại thời điểm t = 2,5 s.
b. Xác định chiều của dòng cảm ứng chạy trong khung dây tại y thời điểm t=2,5s. Lêi gi¶i A B
a. Tõ th«ng göi qua bÒ mÆt bao bëi khung d©y h×nh ch÷ nhËt
cã c¹nh lµ b = 2 cm cã chiÒu cao lµ dy lµ: B
d = BdS = Bbdy = 4 2 t byd . y C
V× B = 4t2y lµ hµm cña hai biÕn t vµ y. Ta lÊy tÝch ph©n theo x O biÕn y b 2 y b 2 2 2 3 2
= 4t bydy = 4t b ydy = 4t b( ) = 2b t 2 0 0
SuÊt ®iÖn ®éng c¶m øng trªn khung d©y lµ: d = − = b3 4 − t dt
T¹i thêi ®iÓm t = 2,5 s, suÊt ®iÖn ®éng cã ®é lín lµ = 80.10-6 V
b. Khi t = 2,5 s th× B = 4yt2 ®ång biÕn víi t. VËy B cã chiÒu ng-îc chiÒu víi chiÒu cña B . c
Nªn dßng ®iÖn c¶m øng cã chiÒu ®i theo chiÒu quay cña kim ®ång hå.
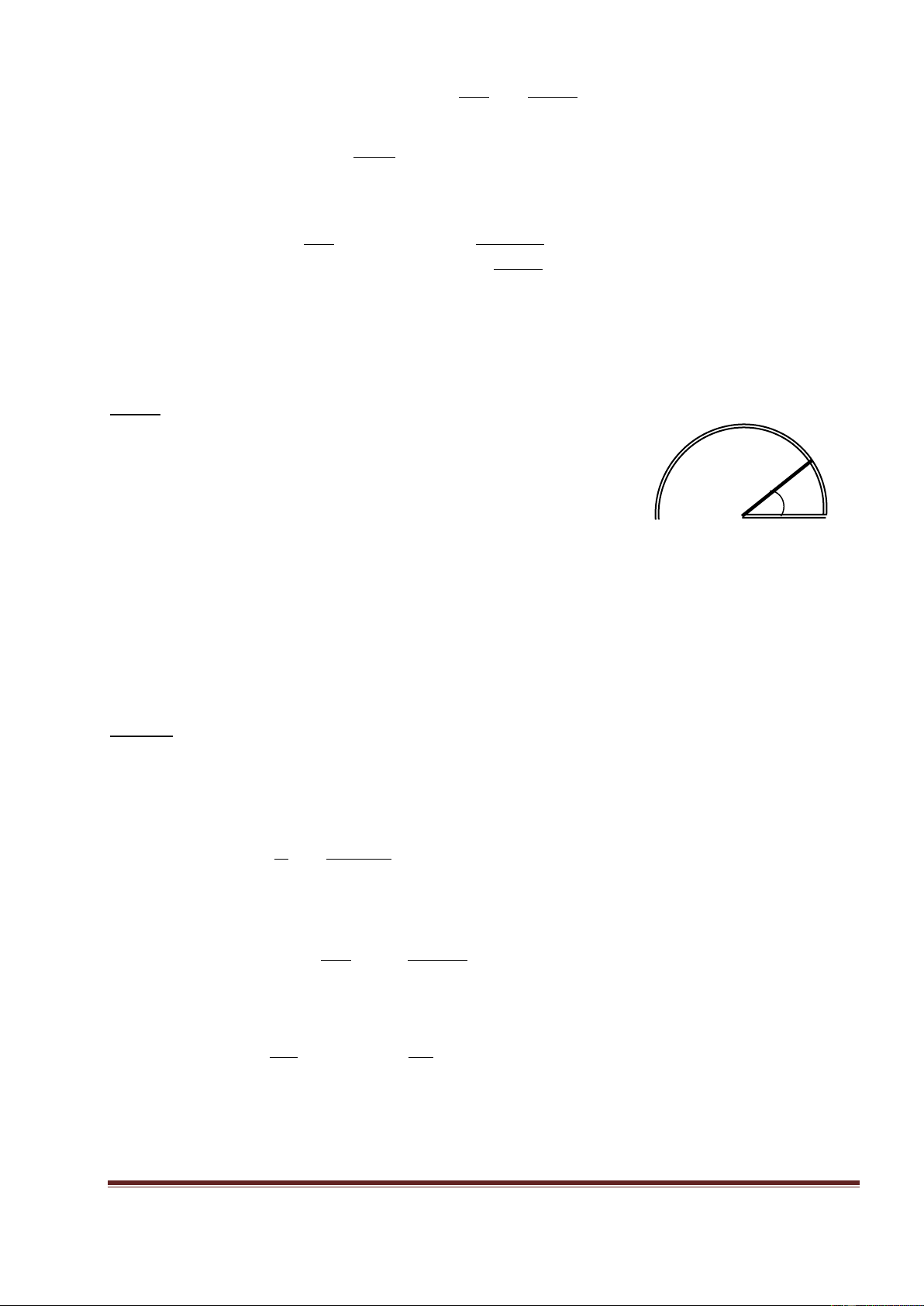
Bài 3: Một khung dây hình chữ nhật, có chiều
dài là a, chiều rộng là b, điện trở là R đặt gần v
một sợi dây dài vô hạn mang dòng điện i nh a
hình vẽ bên. Khoảng cách từ sợi dây dài đến
tâm của khung dây là r. Hãy tính. b
a. Độ lớn của từ thông gửi qua khung dây. r
b. Dòng điện cảm ứng trong khung dây i
khi khung dây chuyển động ra xa sợi dây dài với tốc độ v. Lêi gi¶i i
a. Tõ tr-êng B g©y ra bëi dßng ®iÖn th¼ng i ë kho¶ng c¸ch r lµ: B 0 = 2 r
Tõ th«ng göi qua khung d©y lµ: b b r + r + i a a i dr i a ia 2r + b 0 0 0 = BdS = drdx = dx = a ln 0 r = ln( ) . 2 r − b 2 r 2 b 2 2r b 0 r − r − a a
b. SuÊt ®iÖn ®éng c¶m øng trong khung d©y khi nã chuyÓn ®éng ra xa so víi d©y víi tèc ®é v d d dr d iav 2 2 2 abvi 0 = − = − = −v = − ( − ) 0 = dt dr dt dr 2 2r + b 2r − b (4 2 2 r − b ) Trang 3
C-êng ®é dßng ®iÖn c¶m øng ic ®i qua khung d©y lµ: 2 abvi 0 i = = c R R (4 2 2 r − b )
Bài 4: Trong cùng một mặt phẳng nằm ngang với dòng điện thẳng dài vô hạn có cường độ I
= 20A người ta đặt hai thanh trượt kim loại song song với dòng điện và thanh gần hơn cách
dòng điện một khoảng x0 = 1cm. Hai thanh trượt
cách nhau l = 2cm. Trên hai thanh trượt người ta I
lồng vào một đoạn dây dẫn MN dài x l .Cho dây dẫn 0
trượt tịnh tiến trên các thanh với vận tốc không đổi v M P
= 3m/s theo hướng song song với các thanh trượt.
a. Tìm hiệu điện thế xuất hiện giữa hai đầu v dây dẫn UMN.
b. Nối hai đầu P, Q của hai thanh trượt với
nhau bằng điện trở R = 0,2Ω để tạo thành mạch kín. Q N
Xác định độ lớn và điểm đặt lực kéo tác dụng lên
MN để nó chuyển động tịnh tiến đều như trên. Bỏ qua ma sát. Lêi gi¶i
Dòng I sinh ra từ trường có cảm ứng từ B như hình vẽ
Vì đoạn dây MN chuyển động trong từ trường nên trên I
nó xuất hiện suất điện động cảm ứng.Sau thời gian t kể X
từ lúc bắt đầu chuyển động,từ thông quét bởi đoạn dài M 0 P X
dx của dây (cách dòng I khoảng x) bàng: I dx dΦ = Bds = 0 vtdx l + B 2 x
Từ thông quét bởi cả đoạn dây MN bằng: x + 0 l
Ivt x + l Q N vt Φ = d = 0 ln 0 2 x x0 0
Iv x + l
Suất điện động cảm ứng có độ lớn: ε 0 0 c = /Φ’/ = ln 2 x0
Và cực của nguồn có dấu: N âm, M dương. Mạch hở
Iv x + l x + l U 0 0 0 MN = εc = ln =2.10-7Iv ln 2 x x 0 0
Thay số được UMN = 1,32.10-5 (V) Mạch kín .
Dòng điện qua đoạn dây MN có cường độ : Ic = εc / R = 6,6.10-5 (A)
*Lực từ tác dụng lên đoạn dài dx của dây dẫn MN : I dF = BI 0 cdx = Icdx 2 x Trang 4 X +l 0 + Các dF cùng hướng => I X l F = dF = 0 0 I ln 2 c X X 0 0 x + l Hay F = 2.10-7I.I 0 c ln = 2,9.10-10 (N) x0
Xác định điểm đặt của F .Giả sử G là điểm đặt của F . GM = XG X +l 0 I l X 0 GF =
XdF = Icl => XG = 2 X + = 1,82 (cm) l X 0 0 ln X 0
Suy ra G cách đầu M khoảng 0,82 cm.
Vậy lực kéo F' cân bằng với lực từ F F’= 2,9.10-10N và đặt tại G
Bài 5: Mét sîi d©y tiÕt diÖn ngang 1,2 mm2 vµ ®iÖn trë suÊt lµ 1,7.10-8 m ®-îc uèn thµnh
mét cung trßn cã t©m t¹i O, b¸n kÝnh r = 24 cm nh- h×nh vÏ bªn.
Mét ®o¹n d©y th¼ng kh¸c OP còng cïng lo¹i nh- trªn , cã thÓ quay P
quanh ®iÓm O vµ tr-ît cã tiÕp xóc víi cung trßn t¹i P. Sau cïng,
mét ®o¹n d©y th¼ng kh¸c OQ còng cïng lo¹i trªn, hîp víi hai ®o¹n B
d©y trªn thµnh mét m¹ch ®iÖn kÝn. Toµn bé hÖ nãi trªn ®Æt trong
mét tõ tr-êng B = 0,15 T, h-íng tõ trong ra ngoµi vu«ng gãc víi O Q
cung trßn. §o¹n d©y th¼ng OP tho¹t ®Çu n»m yªn t¹i vÞ trÝ = 0 vµ
nhËn mét gia tèc gãc b»ng 12 rad/s2.
a. TÝnh ®iÖn trë cña m¹ch kÝn OPQO theo .
b. TÝnh tõ th«ng qua m¹ch theo .
c. Víi gi¸ trÞ nµo cña th× dßng ®iÖn c¶m øng trong m¹ch ®¹t cùc ®¹i.
d. TÝnh gi¸ trÞ dßng ®iÖn c¶m øng cùc ®¹i trong m¹ch. Lêi gi¶i
a. §é dµi cña cung PQ lµ: PQ = r. Trong ®ã tÝnh b»ng rad
§é dµi cña m¹ch kÝn OPQO lµ:
l = OP + OQ + PQ = r + r + r = (2 + )r.
VËy ®iÖn trë cña m¹ch kÝnh OPQO lµ: l (2 + )r R = = S S
Thay sè ta ®-îc R = 3,4.10-3(2 + ) () = 3,4. (2 + ) m.
b. Tõ th«ng qua m¹ch kÝn OPQO lµ: r 2 2 ( , 0 ) 24 = BS = B = 15 , 0 = 10 . 32 , 4 −3 . (Wb) = . 32 , 4 mW 2 2
c. SuÊt ®iÖn ®éng c¶m øng trªn m¹ch kÝnh d − d 3 −3 −3 = − = − 10 . 32 , 4 = − 10 . 32 , 4 = − 10 . 32 , 4 t dt dt
Trong ®ã , t-¬ng øng lµ vËn tèc gãc vµ gia tèc gãc cña thanh OP.
Dßng ®iÖn c¶m øng ic trong khung lµ: Trang 5 − 10 . 32 , 4 3 t , 1 i = = = 271 t c − R , 3 10 . 4 3 (2 + ) 2 + 1 2 2 Víi
= t t = 2
Thay vµo biÓu thøc cña ic ta ®-îc i = , 1 . 271 2 c 2 + di
§Ó t×m gi¸ trÞ cùc ®¹i i c cmax cña ic ta ph¶ tÝnh d di − + 2 Ta cã c = d 2 ( 2 + ) 2
Kh¶o s¸t ic theo ta cã b¶ng biÕn thiªn 0 2 2 di c d + 0 - i
VËy khi = 2 rad th× ic ®¹t gi¸ trÞ cùc ®¹i.
d. C-êng ®é dßng ®iÖn c¶m øng cùc ®¹i trong m¹ch
Thay = 2 rad vµo biÓu thøc cña dßng ®iÖn c¶m øng ta ®-îc , 1 271 2 . 12 . 2 i = , 1 27 . 1 2 = = , 2 2A cMax 2 + (2 + ) 2
Bài 6: Một khung hình vuông làm bằng dây dẫn
quay đều quanh một trong số các cạnh của nó tại
gần một dây dẫn thẳng dài vô hạn có dòng điện
không đổi I đi qua (hình vẽ). Trục quay song song
với dây dẫn và khoảng cách giữa chúng bằng d, I
chiều dài cạnh khung bằng a. V
Tại vị trí mặt phẳng khung tạo với mặt phẳng chứa
dây dẫn và trục của khung một góc bằng bao
nhiêu thì vôn kế chỉ giá trị tuyệt đối cực đại tức a thời của điện áp? d Lời giải: Trang 6
Xét tại thời điểm t=0 khi khung dây trong C M
cùng mặt phẳng với dòng điện. O O2 1
Tại điểm M trên khung cách dòng điện đoạn
x, từ cảm do dòng điện gây ra tại M có độ lớn bằng: B kI M = x
Từ thông qua diện tích (a.dx) của khung là: k . Ia dx d =BM.a.dx = x D E
Xét tại thời điểm t=0 khung ở vị trí O2CDE
Tại thời điểm t, khung quay được góc = t
và ở vị trí O2C’D’E như hình 2.
Từ thông qua khung lúc này bằng từ thông C’ qua diện tích O
2AFE của khung khi =0, với O1A= O1C’= r C O1 O2 Xét tam giác O A 1C’O2: O + − 1C’=r = 2 2 d a 2da cos = O1A
Từ thông qua diện tích O2AFE là: d = d =...=kIa(lnd - ln 2 2
d + a − 2da cos ) r D’ 2 kIa d .sin( t) e = - ’ = 2 2
d + a − 2da cos(t) D E F e’ = 2 2 kIa d . 2 2
(d + a ).cost − 2ad 2 2 2
[d + a − 2da cos(t)] e’=0 khi cos 2ad = 2 2 d + a
Vậy tại vị trí mặt phẳng khung tạo với mặt phẳng chứa dây dẫn và trục của khung một góc 2ad thỏa mãn cos =
thì vôn kế chỉ giá trị tuyệt đối cực đại tức thời của điện áp 2 2 d + a
Bài 7: Một khung dây dẫn hình vuông chuyển động dọc theo trục x với vận tốc v0 đi vào
một bán không gian vô hạn (x>0) trong đó có một từ trường không đều hướng theo trục z:
Bz(x) = B0(1 + x) với B0 là hằng số dơng. Biết rằng hai cạnh của khung song song với trục
x, còn mặt phẳng của khung luôn vuông góc với trục z. Hỏi khung đã thâm nhập vào không
gian có từ trường một khoảng cách bằng bao nhiêu, nếu khối lượng của khung là m, chiều
dài cạnh của khung là b và biết rằng vào thời điểm khi các đường sức từ xuyên qua toàn bộ
mặt phẳng của khung, trong khung toả ra lượng nhiệt đúng bằng nhiệt lượng mà khung toả
ra trong chuyển động tiếp sau đó cho tới khi dừng hẳn.
Tính điện trở của khung. Bỏ qua hệ số tự cảm của O x
khung và coi b<<1. A D BZ Lời giải
Xét thời điểm cạnh CD có toạ độ là x và khung đang
thâm nhập vùng từ trường. Áp dụng định luật bảo toàn Trang 7 B C
năng lượng, nhiệt lượng toả ra trong khung bằng độ biến thiên động năng của khung: m 2 m dQ = v − (v + dv 2
) dQ = −mvdv (1) 2 2
Suất điện động cảm ứng xuất hiện trên cạnh CD là:
E = B bv = B 1 ( + x bv ) CD 0 E B 2 1 ( + x 2 ) b2v2dt B 2 2 1
( + 2 ) b2v2dt I =
dQ = I 2Rdt 0 0 = (2) R R R Từ (1) và (2) ta có: − Rmvdv = B2 1 ( + 2x b2 ) v2dt 0
−Rmdv = B2 1 ( + 2x b2 ) dx (3) 0
Gọi v1 là vận tốc của khung khi bắt đầu khung nằm trọn trong từ trường ta có: 2 2 mv mv 2 mv v 0 1 − Q = trong đó 0 0 Q = v = 2 2 4 1 2
Tích phân 2 vế phương trình (3) ta có: v1 b − Rmdv = B2 1 ( + 2x b2 ) dx 0 v 0 0 2 2 2 3 2 3
Rm(v − v ) = B b (b +b) = B b 1
( + b) B b 1 0 0 0 0 2 3 2 3 2B b ( 2 + ) 2 B b 0 0 R = = (*) mv ( 2 − ) 1 mv 0 0
Khi khung đã vào hẳn trong từ trường, cường độ dòng điện trong khung là: E − E B 1+ ( + ) − 1 ( + ) 2 CD 0 vb x b x B b v I AB 0 = = = R R R
Xét trong khoảng thời gian nhỏ dt: dQ I 2 = Rdt B2b4 2 v2dt 2 4 2 B b v dx dQ 0 = 0 = (4) R R +
Tích phân 2 vế phương trình (4) và thay R ở (*) vào ta được: ( 2 ) 1 s = 1 2 b
Khung đã vào trong từ trường được một đoạn là: 2 2 +1+ b2 2 +1
s = s + b = 1 2 b 2 b + 2 3 ( 2 + ) 2 B b Vậy 2 1 s = và 0 R = 2 b mv0
Bài 8: Cho một khung dây dẫn kín hình chữ nhật ABCD bằng kim loại, có điện trở R, có
chiều dài các cạnh là a và b. Một dây dẫn thằng dài vô hạn, nằm trong mặt phẳng của
khung dây, song song với cạnh AD và cách nó một đoạn d như hình vẽ bên. Trên dây dẫn
thẳng có dòng điện cường độ I0 chạy qua.
a. Tính từ thông qua khung dây.
b. Tính điện lượng chạy qua một tiết diện thẳng của khung a A
dây trong quá trình cường độ dòng điện trong dây dẫn thẳng giảm B đến 0. d b Trang 8 D C
c. Cho rằng cường độ dòng điện trong dây dẫn thẳng giảm tuyến tính theo thời gian
cho đến khi bằng 0, vị trí dây dẫn thẳng và vị trí khung dâykhông thay đổi. Hãy xác định
xung của lực từ tác dụng lên khung. Lời giải I
a. Cảm ứng từ tại điểm cách dây dẫn một đoạn r: B 0 0 = 2 r
Từ thông qua khung dây là:
d +a I b I b a 0 0 0 0 = dr = ln 1 ( + ) = 0 2 r 2 d d
b. Trong thời gian nhỏ dt trong khung có suất điện động d e = − , trong khung có dòng c dt điện cảm ứng e d dq d i c = = − = dq = −
lấy tích phân 2 vế ta được: R Rdt dt R − 0 − I b a q = − 0 = − 0 = 0 = 0 0 l 1 n( + ) R R R 2 R d
c. Gọi t là thời gian dòng điện giảm đều đến 0 thì: I = t I 1 ( −
);e = −' ; trong khung có dòng điện cảm ứng 0 c t e ' I b a i = c = − = 0 0 l 1 n( + ) = hằng số R R 2 R t d
Lực tác dụng lên khung là tổng hợp hai lực tác dụng lên các cạnh AD và BC: b b ab
F = B bi − B bi 0 = Ii 0 − Ii 0 = Ii 1 2 2 d 2 (d + a) 2 d (d + a)
Xung của lực tác dụng lên khung là: t t 2 2 2 ab I a X = Fdt = I abi 0 0 1(− t I )dt = 0 0 ln 1 ( + ) 2 d (d + a 0 ) t 4 2
d(d + a) 2R d 0 0
Bài 9: Một thanh có chiều dài L chuyển động với tốc độ
không đổi v dọc theo hai thanh ray dẫn điện nằm ngang. i
Hệ thống này được đặt trong từ trường của một dòng điện a
thẳng dài, song song với thanh ray cách thanh ray một
đoạn a, có cường độ dòng điện I chạy qua. Cho v =5 m/s, L v
a = 10 mm, L = 10 cm và I = 100 A.
a. Tính suất điện động cảm ứng trên thanh.
b. Tính cường độ dòng điện cảm ứng trong mạch. Biết rằng điện trở của thanh là 0,4
và điện trở của hai thanh ray và thanh ngang nối hai đầu thanh ray bên phải là không đáng kể.
c. Tính tốc độ sinh nhiệt trong thanh.
d. Phải tác dụng lên thanh một lực bằng bao nhiêu để duy trì chuyển động của nó.
e. Tính tốc độ cung cấp công từ bên ngoài lên thanh. Lời giải Trang 9 d
a. Suất điện động cảm ứng = − dt
Ta đi tính d = BdS = Bdrdxvới r là khoảng cách từ phần tử dS tới dòng điện i và x là
khoảng cách từ dS đến cạch nối hai đầu thanh ray, còn i B 0 = 2 r a+ L
a+ L i dr i a+ L i + Vậy a L d = dx Bdr = dx 0 = dx 0 ln(r) = 0 dx ln 2 r 2 2 a a a a
Do thanh L chuyển động với tốc độ không đổi v, nên: i a + L
dx = vdt d = 0 ln vdt 2 a + Vậy d iv a L = − = − 0 ln
Thay số vào ta được độ lớn của = 0,24 mV. dt 2 a
b. Dòng điện cảm ứng trong mạch có cường độ i = = 6 , 0 mA. c R
c. Tốc độ sinh nhiệt trên thanh là: dQ 2 −6 = Ri = 14 , 0 37 10 . W. c dt
d. Lực từ tác dụng lên dòng điện cảm ứng i = c trên thanh là F i dr B c Vì r
d vuông góc với B nên suy ra idr
a+ L ii dr ii a + L dF = i drB i 0 = F = dF 0 c 0 c = = ln c c 2 r 2 r 2 a a
Thay số vào ta được F=28,75.10-9 N.
Vậy để duy trì chuyển động cho thanh ta phải tác dụng lên thanh một ngoại lực bằng lực từ
tác dụng lên thanh F’ = 28,75.10-9 N.
e. Tốc độ cung cấp công từ bên ngoài chính là công suất của ngoại lực F’ dW Fdx = = F v −6 . = 14 , 0 37 10 . W . dt dt
Bài 10: Người ta đặt một vòng xuyến mảnh, đồng chất B
và dẫn điện bán kính r vào trong một từ trường đồng
nhất và biến đổi theo thời gian theo công thức B=B ocos t
. Điện trở của vòng xuyến là R và hệ số tự
cảm L. Vecto B tạo với mặt phẳng vòng xuyến góc .
Hãy tính momen trung bình của các lực tác dụng lên vòng xuyến? Lời giải:
Xét tại thời điểm t, từ thông qua vòng xuyến: = 2
r . sin .Bocos t
Suất điện động cảm ứng xuất hiện trong vòng xuyến là: e=- ’ = 2 r B o .sin .sin t
Ta có thể coi như trong vòng xuyến có một nguồn có sđđ bằng e, điện trở trong bằng 0 đang
cung cấp điện cho một mạch ngoài gồm điện trở thuần R nối tiếp với cuộn thuần cảm L 2
Cường độ dòng điện cực đại qua mạch là: I E r B .sin o o o = = 2 2 2 R + L 2 2 2 R + L Trang 10
Độ lệch pha của i với e là L : sin = e/i e/i 2 2 2 R + L 2
Biểu thức dòng qua vòng xuyến là: i = r B .sin o . sin( t - ) 2 2 2 e/i R + L
Momen ngẫu lực từ trung bình tác dụng lên vòng xuyến trong một chu kì là: 1 T 1 T 2 r B M 2 o 2 − TB = iB r os c .dt = .B r o c s .sin .sin( t ). o c s t.dt T T o 2 2 2 + o o R L 1 T 2 4 2 r B 1 T 2 4 2 r B = o o
c s.sin.sindt + o o
c s.sin.sin(2t −)dt T 2 2 2 + T 2 2 2 + o 2 R L o 2 R L 2 2 4 2
B r L sin. o c s = o 2 2 2 2(R + L )
Bài 11: Một khung dây dẫn phẳng, hình vuông cạnh a, khối lượng m, không biến dạng, điện
trở R. Khung được ném ngang từ độ cao h0 với vận tốc v0 (Hình 4) trong vùng có từ trường
với cảm ứng từ B có hướng không đổi, độ lớn phụ thuộc vào độ cao h theo quy luật
B = B + k.h , với k là hằng số, k 0 . 0
Lúc ném, mặt phẳng khung thẳng đứng vuông góc với B và
khung không quay trong suốt quá trình chuyển động. v a B 0 +
a. Tính tốc độ cực đại mà khung đạt được.
b. Khi khung đang chuyển động với tốc độ cực đại và
cạnh dưới của khung cách mặt đất một đoạn h1 thì mối hàn tại
một đỉnh của khung bị bung ra (khung hở). Bỏ qua mọi lực
cản. Xác định hướng của vận tốc của khung ngay trước khi chạm đất. Lời giải:
a. Tốc độ cực đại: F 1
- Chiều dòng điện cảm ứng (hình vẽ). I c
- Biểu diễn đúng lực từ tác dụng lên 4 cạnh. F
- Lực từ tổng hợp F có: phương thẳng đứng, hướng lên. B 4 F tăng theo v +
z đến lúc F = P khung sẽ chuyển động đều với vận tốc F v
trên phương thẳng đứng. 3 zmax
Khi khung CĐ đều, thế năng giảm, động năng không đổi,
xét trong khoảng thời gian t
, độ giảm thế năng đúng bằng F 2
nhiệt lượng tỏa ra trên khung. 2 mgv t = RI t z max 2 2 2 E c a B a k z a kvz I = = = = R R t R t R 2 2 ka v mgR z mgv t = R t v = ax zm R ax zm 2 4 k a Trang 11
Trên phương ngang khung CĐ đều vx = v0
Tốc độ cực đại của khung khi đó: 2 2 v = v + v a zm x 0 2 mgR 2 v = + v 2 4 0 k a
b. Hướng vận tốc ngay trước khi chạm đất:
- Khi chạm đất, vận tốc theo phương thẳng đứng 2 2 v ' = v + 2gh z z a m x 1
Góc hợp bởi vận tốc và phương ngang là: 2
mgR + 2gh ' 2 4 1 v k a tan z = = v v 0 0
Bài 12: Hai dây dẫn dài, mỗi dây có điện trở a c
R=0,41 được uốn thành hai đường ray nằm trong
mặt phẳng ngang như hình vẽ. Hai ray phía bên phải v2 Ft cách nhau l i
1=0,6m và nằm trong từ trường có cảm c
ứng từ B1=0,8T, hướng từ dưới lên. Hai thanh ray
bên trái cách nhau khoảng l d b 2=0,5m và nằm trong từ
trường B2=0,5T, hướng từ trên xuống.
Hai thanh kim loại nhẵn ab điện trở r1=0,41 và cd
điện trở r2=0,16 được đặt nằm trên các ray như
hình vẽ, mọi ma sát đều không đáng kể.
1. Tác dụng một lực kéo để ab chuyển động sang phải với vận tốc đều v1=10m/s; khi đó cd
cũng chịu tác dụng một ngoại lực và chuyển động sang trái với vận tốc đều v2=8m/s. Hãy tìm:
a. Độ lớn ngoại lực tác dụng lên cd, biết lực này nằm trong mặt phẳng ngang?
b. Hiệu điện thế giữa hai đầu c và d?
c. Công suất điện của mạch trên?
2. Nếu không có ngoại lực tác dụng vào cd thì nó sẽ chuyển động như thế nào? Lời giải: c a
1. Sđđ cảm ứng xuất hiện trên hai thanh: v2 . Trên ab: e Ft 1 = l1v1B1 = 4,8 (V) ic
. Trên cd: e2 = l2v2B2 = 2V < e1
ic có chiều như hình vẽ. d b e − e i 1 2 C = = 2,5 (A) 2R r + + r 1 2
a) Lực từ tác dụng lên cd: F2 = il2B2 = 0,625 (N) = Fk2 (Vì cd chuyển động đều) b) ucd = -e2-ir2 = -2,4 (V)
c) Công suất điện của cả mạch là: P = i2Rtđ = 7 (W)
2/ Nếu không có ngoại lực tác dụng vào cd.
Ngay khi ab chuyển động thì có dòng điện chạy qua cd theo chiều d-c có lực từ tác dụng
lên cd theo chiều hướng vào mạch điện, do đó cd sẽ chuyển động và lại xuất hiện trên cd
một suất điện động cảm ứng e2 có cực (+) nối với đầu c.
Xét tại thời điểm t, vận tốc của cd là v2, gia tốc là a. Trang 12 e − e v l B − v l B i = 1 2 = 1 1 1 2 2 2 2R r + + r 2R r + + r 1 2 1 2 − + + v l B v l B .( m 2R r r ) dv F 1 1 1 2 2 2 1 2 2 t=ma=il2B2= .l2B2 =v1l1B1 -l2B2v2 2R r + + r l B dt 1 2 2 2
Từ đó có thể tính quãng đường mà thanh đi được sau khoảng thời gian t =... hoặc tính v2.
@ Chú ý: Giải phương trình vi phân bậc nhất. x’ – kx = 0 dx dx x dx t x = kx = kdt
= k dt ln = k(t-t
k (t −t ) 0) x = xo 0 e dt x x x x 0 o to
+ Trở lại bài toán: .(
m 2R + r + r ) dv .(
m 2R + r + r ) 1 2 2 =v 1 2 1l1B1 -l2B2v2 (với k= - ) l B dt 2 2 l B 2 2 2 2 − Đặ dx
t : B1l1v1- B2l2v2 = x dx = -B2l2dv2 dv2= B l 2 2 .(
m 2R + r + r ) dx 2 2 B l Vậy: - 1 2 . = x (Đặt k= - 2 2 ) 2 2 l B dt
m(2R + r + r ) 2 2 1 2 x =x kt
o e (tại t=0 thì: v2=0 nên x0 = B1l1v1 Do đó: x = B kt
1l1v1. e v = B1v1l1(1- kt e )
* Tính quãng đường: + + Từ : .( m 2R r r ) dv 1 2 2 =v1l1B1 -l2B2v2 l B dt 2 2 .(
m 2R + r + r ) 1 2
dv2 = v1l1B1dt -l2B2v2dt = v1l1B1dt -l2Bds l B 2 2 + +
Tích phân hai vế được: .( m 2R r r ) 1 2
.v2 = v1l1B1.t -l2B.s s = .... l B 2 2
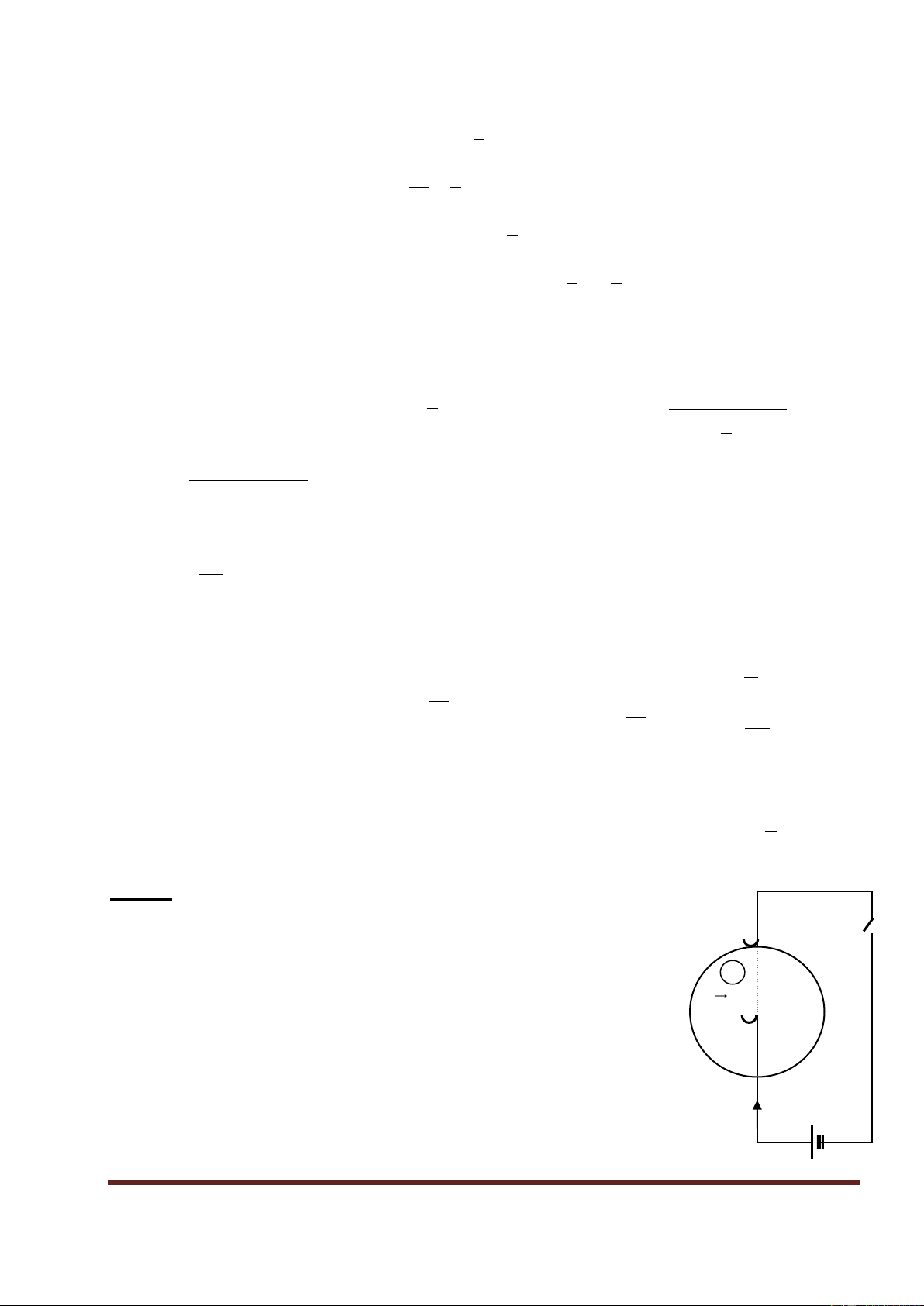
Bài 13: Cho hệ như hình vẽ, đĩa bằng đồng bán kính r có trục quay qua tâm đĩa và nằm
ngang, từ trường đều có B vuông góc với mặt đĩa, điện trở R tiếp xúc vành đĩa bằng chổi
quét kim loại, vật m treo bằng dây mảnh cách điện quấn quanh đĩa và dây không trượt trên
vành đĩa. Thả cho m chuyển động, hãy tính vận tốc quay cuối cùng của đĩa? Bỏ qua mọi ma sát. Lời giải:
Gọi momen quán tính của đĩa đối với trục quay là I
Xét tại thời điểm t khi vật m rơi được quãng đường S, B
nó có vận tốc là v, đĩa có vận tốc góc =v/r. Sau thời
gian rất nhỏ dt, một bán kính đĩa quét được góc
d = dt và bán kính đĩa quét một diện tích: dS = 1 1 R r. dt.R =
r2 dt. Suất điện động cảm ứng xuất m 2 2
hiện trên bán kính đĩa là: e= . B dS 1 = Br2 dt 2
Dòng điện xuất hiện trong mạch và trên bán kính đó Trang 13 e 2 Br là: i= = . R 2R
Bán kính đĩa chịu tác dụng của lực từ đặt vào trung điểm, cản trở chuyển động quay của đĩa 2 3 và có độ lớn: F B r t = Bi.r = (1) 2R
Gọi lực căng dây khi đó là T, gia tốc của m là a. Áp dụng định luật II Niuton cho vật m và
cho chuyển động quay của đĩa ta có: Mg – T = ma (2) a r a Tr - M(Ft) = I. Tr – Ft. = I. (3) r 2 r 2 4 B r mgr −
Từ (1), (2) và (3) suy ra: a= 4R I mr + r
Khi đĩa quay ổn định, vận tốc cuối cùng của đĩa ứng với a=0: =....
@ Giải lại bài toán nếu áp lực của chổi quét vào vành đĩa là F, hệ số ma sát k. Mg – T = ma (2) a r a Tr - M(Ft)- kF.r = I. Tr – Ft. - kF.r = I. (3) r 2 r 2 4 B r mgr − − kF.r
Từ (1), (2) và (3) suy ra: a= 4R I mr + r
@ Nếu điện trở R gắn vào đĩa thì không xuất hiện dòng điện qua R do đó m rơi xuống nhanh dần đều.
Bài 14: Trong một từ trường đồng nhất có cảm ứng từ biến đổi theo thời gian bởi
B=Bocos t (T). Một mẩu đồng có khối lượng riêng D, khối lượng M, điện trở suất được
kéo thành một dây dẫn dài L, tiết diện đồng đều, sau đó làm thành vòng kín đặt trong từ
trường. Có thể nhận được dòng điện cực đại khả dĩ trong dây dẫn đó bằng bao nhiêu? Lời giải: 2
Diện tích tiết diện dây là: S mD DL = điện trở dây: R= L = L S M
Gọi diện tích vòng dây là SV thì suất điện động xuất hiện trong khung là lớn nhất khi khung
được đặt vuông góc với các đường sức từ và có độ lớn là: e= dB S . = -S V V. Bosin( t) dt
Dòng điện trong khung có giá trị cực đại: I E S B o= o = V o R R 2 Vậy I L
o sẽ có giá trị lớn nhất có thể nếu khung được uốn thành vòng tròn để SVmax= . 2 4 → B M I o omax= 4 D Trang 14
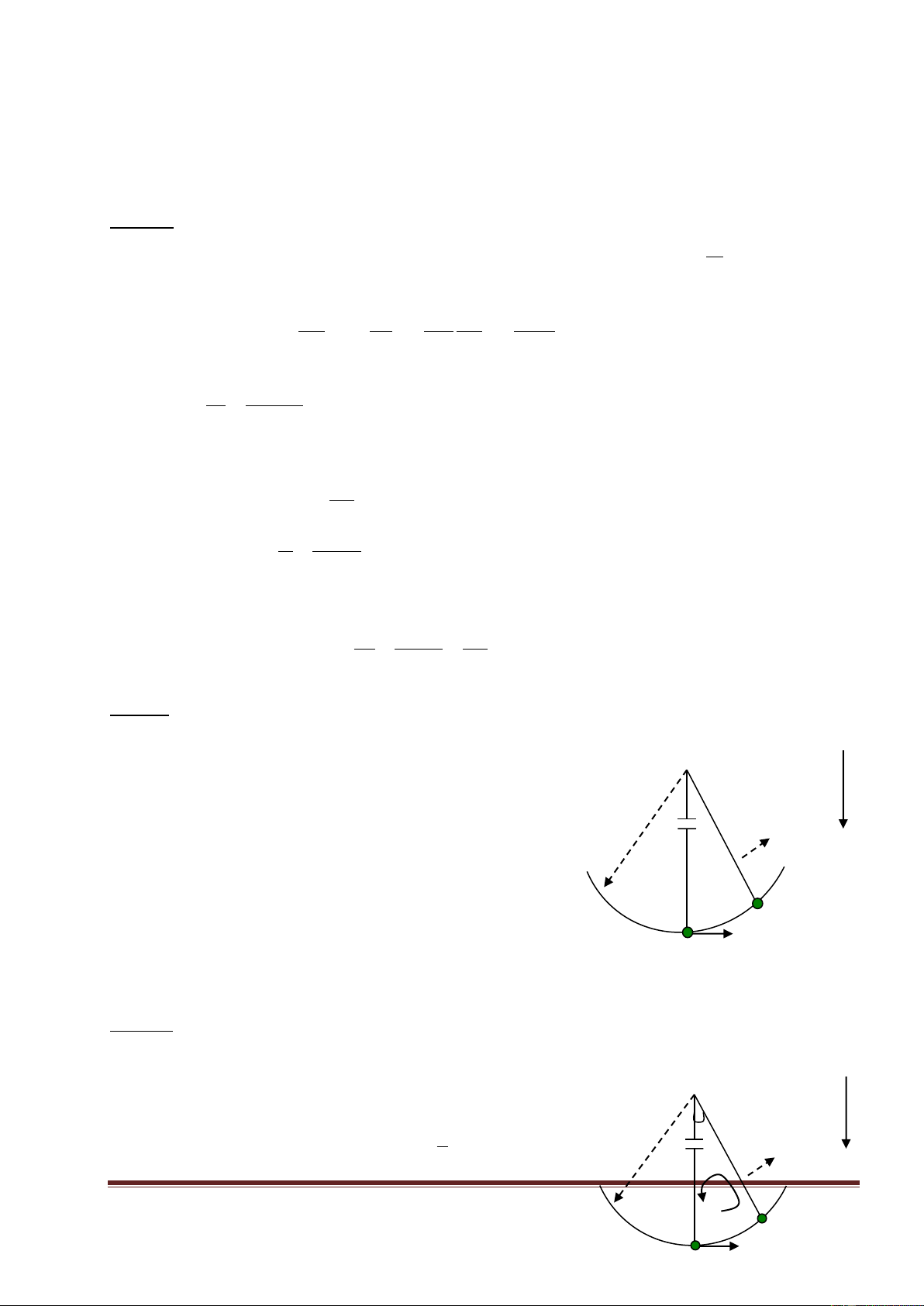
Bài 15 : Xét một con lắc đơn có khối lượng vật nặng là
m, chiều dài dây treo là l, thực hiện dao động nhỏ với
biên độ góc trong từ trường đều nằm ngang, từ 1
trường vuông góc với mặt phẳng dao động của con lắc.
Ngay tại thời điểm con lắc qua vị trí cân bằng, ta đặt
nhanh vào hai đầu dây treo con lắc một tụ điện bằng dây
dẫn mảnh, giả sử ngay khi mắc tụ, tụ kịp tích điện hoàn
toàn. Góc lệch cực đại của dây treo con lắc sau khi mắc
tụ là . Xác định điện dung C của tụ điện? 2 Lời giải
Ngay tại thời điểm con lắc qua vị trí cân bằng, vận tốc góc của dây treo là: v g = ax m = l 1 l
Sau thời gian rất nhỏ dt, dây treo quét góc: d = dt và quét một diện tích: ds= 1 l2. dt 2
Từ thông qua mạch biến thiên lượng: d 1 = Bds = B. l2. dt 2 2
Suất điện động trên dây là: e= d Bl g . = 1 dt 2 l 2
Hiệu điện thế tụ lúc đó là: U=e= Bl g . 1 (1) 2 l
* Khi dây lên cao dần, vận tốc giảm dần, suất điện động trên dây giảm dần và hiệu điện thế
tụ giảm dần. Khi con lắc lên cao nhất, vận tốc dây bằng 0, suất điện động trên dây bằng hiệu điện thế tụ bằng 0.
Vậy từ VTCB đến vị trí góc lệch cực đại năng lượng tụ giảm dần chuyển thành nhiệt tỏa 2
ra trên dây dẫn. Theo bảo toàn năng lượng ta có: 1 1 1 1 mgl 2 = Q+ mgl 2 = mgl 2 + CU2 (2) 2 1 2 2 2 2 2 2 2 −
Từ (1) và (2) suy ra: C= 4m( ) 1 2 2 2 2 B l 1
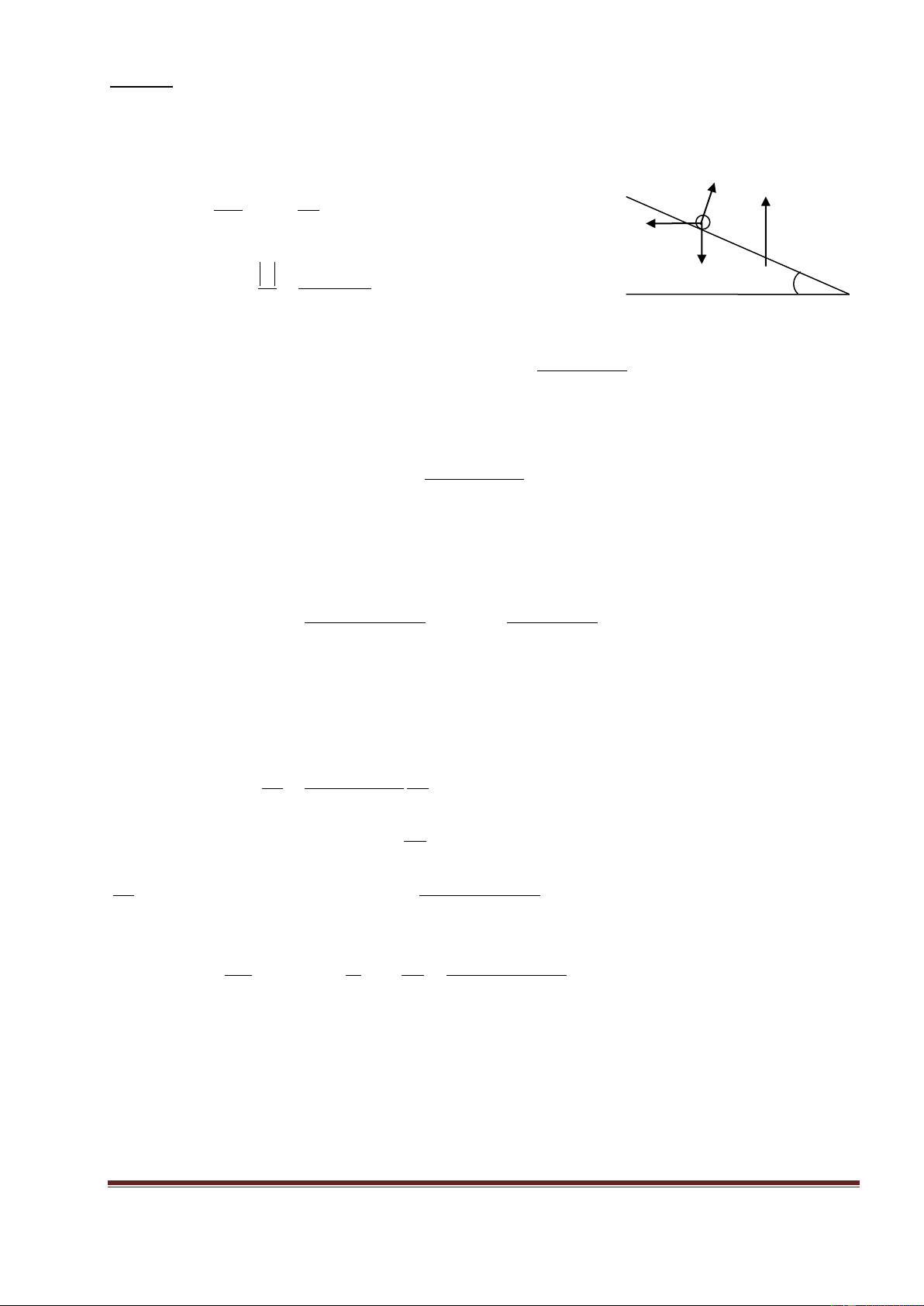
Bài 16 : Mét thanh dÉn ®iÖn cã chiÒu dµi l, khèi l-îng
m, ®iÖn trë R, tr-ît xuèng kh«ng ma s¸t trªn hai thanh B
ray ®iÖn trë kh«ng ®¸ng kÓ nh- trªn h×nh vÏ bªn. §Çu M’
d-íi cña hai thanh ®-îc nèi vµo nhau. MÆt ph¼ng cña l
hai thanh ray hîp víi mÆt ph¼ng ngang mét gãc . HÖ O’
th«ng ®Æt trong mét tõ tr-êng ®Òu cã c¸c ®-êng søc tõ
th¼ng ®øng, cã chiÒu h-íng lªn, c¶m øng tõ cã ®é lín M lµ B.
a. Chøng minh r»ng cuèi cïng thanh vËt dÉn sÏ O
®¹t tíi tèc ®é kh«ng ®æi mµ gi¸ trÞ cña nã b»ng: mgR sin v = 2 2 2 B l cos
b. Chøng minh r»ng tèc ®é sinh nhiÖt trªn thanh ®óng b»ng tèc ®é gi¶m thÕ n¨ng hÊp dÉn cña nã. Trang 15 Lêi gi¶i
a. Tõ th«ng göi qua bÒ mÆt ®îc t¹o bëi khung MOO’M’M lµ: = S B = BS co s = . B MM'.OM co s = Blxco s
SuÊt ®iÖn ®éng c¶m øng xuÊt hiÖn trªn thanh MM’ lµ: N d dx = − = −Bl c os = −Bvl c os B dt dt Dßng ®iÖn c¶m øng i F c trong m¹ch kÝn lµ: B P Bvl c os i = = c R R
Dßng ®iÖn c¶m øng ic ®-îc ®Æt trong tõ tr-êng B nªn chÞu t¸c dông cña lùc ®iÖn tõ: B2l 2v
F = i l B cã ®é lín F = i lB cos sin = i lB = B c B c c R
Nh- vËy thanh d©y dÉn chÞu t¸c dông cña 3 lùc P, F , N . Hîp lùc t¸c dông lªn ph-¬ng B
chuyÓn ®éng cña thanh d©y dÉn lµ: B2l 2v 2 cos
F = P − F = mg sin − t Bt R
Ta thÊy ban ®Çu thanh d©y dÉn MM’ chuyÓn ®éng nhanh dÇn, tøc lµ v t¨ng theo thêi gian t
vµ F gi¶m dÇn ®Õn kh«ng.
Gäi vmax lµ gi¸ trÞ lín nhÊt cña v ®¹t ®-îc øng víi lóc F = 0
Tõ biÓu thøc cña F ta cã: 2 2 2 B l v cos mgRsin 0= 0 = mg sin max − v = (§PCM) max 2 2 2 R B l cos
Khi v = vmax th× F = 0 khi ®ã thanh d©y dÉn MM’ chuyÓn ®éng th¼ng ®Òu, nªn v = vmax = const
b. XÐt tr-êng hîp khi thanh chuyÓn ®éng th¼ng ®Òu v = vmax = const khi ®ã F = 0 nªn: 2 2 2 cos dx B l v dx mg sin =
víi dxsin = dh lµ vi ph©n ®é cao dt R dt dh
VÕ tr¸i cña biÓu thøc trªn lµ mg
lµ tèc ®é gi¶m thÕ n¨ng hÊp dÉn cña thanh, v× dt dx 2 2 2 2 cos = B l v v
nªn vÕ ph¶i cña biÓu thøc lµ max max dt R
MÆt kh¸c ta cã tèc ®é sinh nhiÖt trªn thanh lµ: 2 dQ B2l 2v2 2 cos 2 2 = Ri = R max c = = dt R R R
VËy tèc ®é sinh nhiÖt trªn thanh MM” ®óng b»ng tèc ®é gi¶m thÕ n¨ng hÊp dÉn cña thanh ®ã. Trang 16
Bài 17 : Một đoạn dây dẫn thẳng chiều dài 2L được uốn thành một góc O
xOy = 2, đặt trong mặt phẳng nằm ngang. Một đoạn dây dẫn MN trượt
trên Ox, Oy và luôn tiếp xúc với Ox, Oy. Trong quá trình trượt, MN luôn
luôn vuông góc với đường phân giác của góc xOy, vận tốc trượt giữ B
không đổi và bằng v. Toàn bộ hệ thồng được đặt trong một từ trường đều M H N
có véc tơ cảm ứng từ B vuông góc với mặt phẳng xOy. Giả sử ban đầu x y
đoạn dây MN chuyển động từ O. Các dây dẫn trong mạch được làm từ
cùng một chất, đều cùng tiết diện và có điện trở trên mỗi đơn vị dài là r. Xác định :
a. Cường độ dòng điện chạy qua MN.
b. Nhiệt lượng tỏa ra trong toàn mạch khi MN đi hết Ox. Lêi gi¶i
Gọi H là trung điểm của MN, tại thời điểm t O
ta có : OH = vt ; MN = 2OH.tan = 2vt tan OH vt Có OM = ON = = cos cos
Suất điện động cảm ứng xuất hiện trên đoạn dây dẫn MN: B M H N = B.MN.v = 2Bv2t.tan Điện trở toàn mạch : x y 1+ sin
R = r(OM + ON + MN) = 2rvt( ) cos Bvsin
a. Cường độ dòng điện trong mạch là: I = = R r 1 ( + sin )
b. Nhiệt lượng tỏa ra trên toàn mạch: t0 2 2 2 t0 B v sin 1 sin 2 +
Q = dQ = I Rdt = 2rv ( t )dt 2 2 r 1 ( + sin ) cos 0 0 2 3 2 B v sin 2 Q = t với t 0 o = Lcos /v r 1 ( + sin ) cos 2 2 B vL sin 2 cos => Q = r 1 ( + sin )
Bài 18: Một khung dây dẫn hình vuông cạnh a, có khối lượng m và điện trở R, ban đầu nằm
trong mặt phẳng thẳng đứng xOz (các cạnh song song với trục Ox và Oz), trong một từ
trường có véc tơ cảm ứng từ B hướng theo trục Oy vuông góc với mặt phẳng xOz và có độ
lớn biến thiên theo tọa độ z (trục Oz hướng thẳng đứng xuống dưới) theo quy luật B = Bo +
kz, (Bo và k là các hằng số). Truyền cho khung một vận tốc ban đầu vo theo phương ngang
Ox và khung chuyển động trong mặt phẳng xOz. Người ta thấy sau một thời gian khung đạt
được vận tốc không đổi bằng v. Hãy tính vo. Lêi gi¶i
Ở thời điểm t khi tâm O của khung có tọa độ z, từ thông O
gửi qua khung bằng: = a2B = a2(Bo + kz)
Suất điện động cảm ứng trong khung (do vị trí của khung B M H Trang 17 N x y
tức tọa độ tâm G của khung biến đổi theo thời gian) là: d 2 dz = − = −a k
= −a2kv với v z
z là thành phần của vận dt dt
tốc v của khung theo phương Oz. a2kv
Dòng điện cảm ứng xuất hiện trong khung có cường độ I z = = và có chiều như R R
hình vẽ (khi khung chuyển động xuống dưới thì B tăng nên dòng điện cảm ứng sinh ra Bc có
chiều chống lại sự tăng tức là hướng ra ngoài => áp dụng quy tắc cái đinh ốc ta xác định
được chiều dòng điện cảm ứng)
Xét các lực điện từ tác dụng lên khung ta thấy các lực F2 và F4 tác dụng lên các cạnh NP và
QM triệt tiêu nhau còn các lực F1 và F3 ngược hướng nhau nên hợp lực điện từ tác dụng lên khung có độ lớn là: a3kv k 2a4v F = F z z
3 – F1 = (B3 – B1)Ia = k ( z − z ) = ( do z 3 1 3 – z1) = a ). R R
Lực F có hướng lên trên.
Theo định luật II Newton ta có:
P – F = 0 (tại thời điểm khung có vận tốc không đổi v) k 2a4v mgR => mg z = => v = R z 2 4 k a
Độ lớn của vận tốc là: v = v + v => 2 2 v = v + v 0 z 0 z
Bài 19: Dọc trên hai thanh kim loại đặt song song nằm ngang, khoảng
cách giữa chúng là l, có một thanh trượt MN, khối lượng m có thể trượt N
không ma sát. Các thanh được nối với một điện trở R và đặt trong một R
từ trường đều có véc tơ cảm ứng từ B thẳng đứng vuông góc với mặt v B o
phẳng khung. Biết đoạn dây MN trượt với vận tốc đầu vo như hình vẽ.
Tìm biểu thức cường độ dòng điện I chạy qua R. M Lêi gi¶i
MN chuyển động trong từ trường, cắt các đường cảm ứng từ, nên hai đầu của thanh
xuất hiện một suất điện động cảm ứng EC = Blv, do đó có dòng điện đi qua R đồng thời xuất
hiện lực từ F = iBl cản trở chuyển động nên vận tốc của MN giảm về tới 0. E Bvl B2l 2v N Có I C = = => F = R R R B
Theo định luật II Newton R vo F F dv B2l 2v dv B2l 2 i a = − = − => = − dt M m dt mR v mR v dv B 2l 2 t 2 2 v B l t Lấy tích phân hai vế : = − dt lnv = − v mR v0 mR v 0 0 2 2 B l t
=> v = v exp(− ) 0 mR 2 2 Blv B l t Blv => I = = I exp(− ) với I 0 = 0 R mR 0 R
Bài 20: Một thanh kim loại có chiều dài l nằm ngang, có thể quay quanh
trục thẳng đứng đi qua một đầu. Đầu kia của thanh được tựa trên một B Tran l g 18 o R
vòng dây dẫn nằm ngang có bán kính l. Vòng dây được nối với trục quay
(dẫn điện) qua một điện trở thuần R. Hệ được đặt trong một từ trường đều
hướng thẳng đứng xuống dưới. Hỏi lực cần thiết phải tác dụng vào thanh
để nó quay với vận tốc góc không đổi . Bỏ qua điện trở của vòng, trục
quay, các dây nối và ma sát. Áp dụng số: B = 0,8T, l = 0,5m, = 10rad/s. Lêi gi¶i 2
Xét khi thanh quay được một góc nhỏ d, diện tích nó quét được là: l dS = d 2
Suất điện động cảm ứng xuất hiện trên thanh: 2 2 d dS Bl d Bl e = − = −B = − = − dt dt 2 dt 2
Công suất tỏa nhiệt trên R (chính là công suất của mômen cản chuyển động quay của e2 B2l 4 2 thanh): P = = R 4R
Để thanh quay đều thì mômen lực tác dụng lên thanh phải bằng mômen cản: M = Mc d
Mặt khác: P = M = M c c dt P B2l 4 Suy ra M = = 4R
Lực cần thiết tác dụng lên thanh là nhỏ nhất khi lực đó được đặt vào đầu A của thanh (OA = l ): M B2l 3 , 0 2 F = = = min l 4R R
Bµi 21: Mét thanh kim lo¹i m¶nh, cøng, cã khèi l-îng nhá kh«ng ®¸ng kÓ, ë ®Çu cã g¾n
mét qu¶ cÇu kim lo¹i nhá (coi nh- chÊt ®iÓm) cã khèi l-îng b»ng m. Thanh cã thÓ dao ®éng
quanh trôc O n»m ngang nh- mét con l¾c. Qu¶ cÇu tiÕp
xóc víi mét sîi d©y dÉn K - L ®-îc uèn thµnh mét cung O
trßn cã b¸n kÝnh b. T©m cña sîi d©y nµy g¾n víi ®iÓm g
treo O qua mét tô ®iÖn cã ®iÖn dung C. TÊt c¶ c¬ cÊu b B
nµy ®-îc ®Æt trong mét tõ tr-êng ®Òu C B vu«ng gãc víi
mÆt ph¼ng dao ®éng cña thanh. T¹i thêi ®iÓm ban ®Çu
ng-êi ta truyÒn cho qu¶ cÇu (tõ vÞ trÝ c©n b»ng) vËn tèc K L
n»m trong mÆt ph¼ng h×nh vÏ vµ vu«ng gãc víi thanh.
Bá qua ma s¸t vµ ®iÖn trë cña thanh, cña d©y dÉn K-L V
vµ ®iÖn trë ë c¸c chç tiÕp xóc. O
a. Chøng minh qu¶ cÇu dao ®éng ®iÒu hoµ. T×m chu k× dao ®éng.
b. TÝnh n¨ng l-îng dao ®éng cña qu¶ cÇu. Lêi gi¶i
a)XÐt t¹i thêi ®iÓm t, thanh kim lo¹i hîp víi
ph-¬ng th¼ng ®øng gãc . Chän chiÒu d-¬ng cña dßng O
®iÖn trong m¹ch nh- h×nh vÏ. 1 B g
Tõ th«ng göi qua m¹ch ®iÖn lµ: = − b2 B 2 b C ( Trang 19 K L + ) d 1
SuÊt ®iÖn ®éng c¶m øng suÊt hiÖn trong m¹ch ®iÖn: E = − = b2 B dt 2 1
Khi ®ã, tô ®iÖn cã ®iÖn tÝch: q = CE = b2 BC . 2 dq 1
C-êng ®é dßng ®iÖn trong m¹ch: i = = b2 BC . dt 2 1
Lùc tõ t¸c dông lªn thanh kim lo¹i lµ: F = ibB = b3B 2 C . B 2 r 1
M« men cña lùc tõ t¸c dông lªn thanh lµ: M = −F . = − b4B2 C B B 2 4
M« men cña träng lùc t¸c dông lªn thanh: M = m − gbsin G
Víi c¸c gãc lÖch nhá cña thanh: sin , do ®ã: M = −mg b G
M« men qu¸n tÝnh cña qu¶ cÇu ®èi víi trôc quay ®i qua O: IO=mb2. 1 mgb
Cã: M + M = I −m gb − 4 2 b B C = mb 2 + = 0 G B O 4 2 1 4 2 mb + b B C 4 2 mgb §Æt =
, ta viÕt l¹i ph-¬ng tr×nh trªn nh- sau: 2 + = 0 1 mb2 + b4 B 2C 4
§ã lµ ph-¬ng tr×nh vi ph©n m« t¶ dao ®éng ®iÒu hoµ. Vậy qu¶ cÇu dao ®éng ®iÒu hoµ víi 2 chu k× T = .
b) Gi¶ sö ph-¬ng tr×nh dao ®éng cña qu¶ cÇu cã d¹ng: = Aco ( s t + ) → = −
A sin(t + ) Acos = 0 = V 2
T¹i thêi ®iÓm ban ®Çu: (0) = , 0 ( 0) 0 = 0 V → b A sin = 0 0 V 0 b A = b V 0
Vëy ph-¬ng tr×nh dao ®éng cña thanh lµ: = c os t + b 2 1
c) N¨ng l-îng cña dao ®éng b»ng ®éng n¨ng ban ®Çu cña thanh: 2 E = mV 0 2
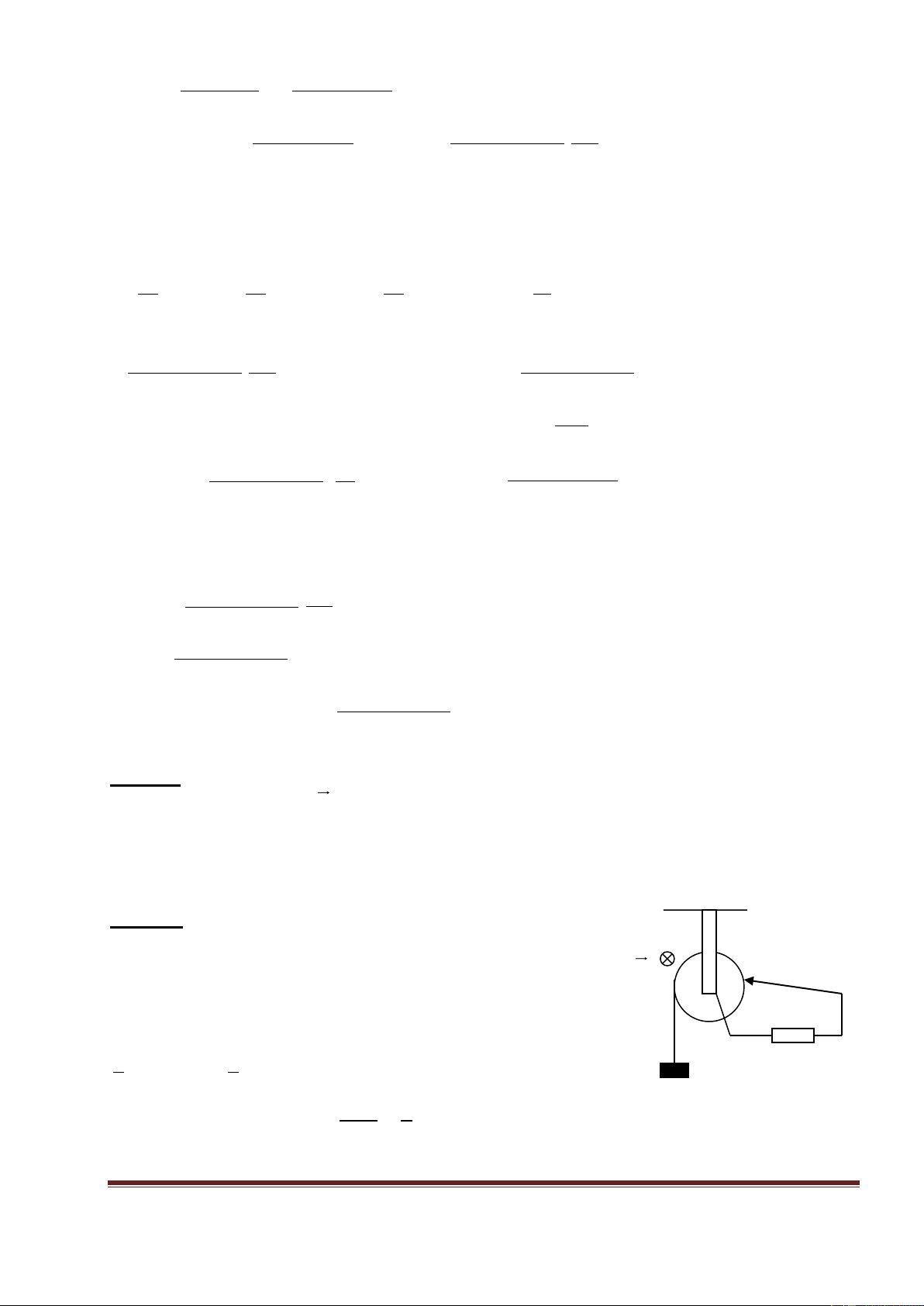
Bài 22: Một đĩa phẳng bằng đồng có bán kính r = 10cm, khối lượng
m = 0,4kg được đặt vuông góc với một từ trường đều có cảm ứng từ b K
B = 0,25T. Đĩa có thể quay tự do, không ma sát quanh trục đi qua tâm
và vuông góc với mặt phẳng của đĩa. Hai đầu ab của một bán kính có B a
đặt các tiếp điểm trượt (tiếp xúc với trục và mép đĩa) để cho dòng
điện chạy qua. Người ta nối hai tiếp điểm với nguồn điện áp một
chiều để cho dòng điện I = 5A chạy qua đĩa. I E
a. Hỏi sau bao lâu kể từ khi bắt đầu có dòng điện chạy qua, đĩa Trang 20 đạt tốc độ 5vòng/s.
b. Giả sử bánh xe quay nhanh dần đều tới tốc độ 5vòng/s rồi quay đều với tốc độ đó.
Hãy tìm công suất của động cơ.
c. Thiết bị trên có thể hoạt động như một máy phát điện. Giả sử ta không mắc nguồn
điện mà thay vào đó một điện trở R = 1. Khi bánh xe quay trong từ trường, trong mạch
xuất hiện suất điện động cảm ứng. Hỏi phải tác dụng vào bánh xe một mômen quay bằng
bao nhiêu để đĩa quay đều với tốc độ 5vòng/s. Tính công suất của máy trong trường hợp này. Lêi gi¶i
a. Khi đĩa đặt trong từ trường và có dòng điện chạy dọc theo bán kính sẽ chịu tác dụng của
lực từ F = BIr làm đĩa quay ngược chiều kim đồng hồ. 2
Mômen lực từ tác dụng lên đĩa: r Ir B M = F = . 2 2
- Phương trình ĐLH viết cho chuyển động quay của đĩa: 2 1 t t d BIr m 2 M = r m = dt = d 2 dt 2 BI 0 0 m t = = 8,4s. BI
b. Khi đĩa quay đều. Công lực từ thực hiện khi đĩa quay góc d : 2 r BIr dA = d F s = F d = d = d I . 2 2 2 Trong đó Br d =
d là từ thông mà bán kính ab quét được khi bánh xe quay góc d . 2 2 dA dA dA BIr - Công suất: P = = = = = 0,2355W dt d d 2
c. Khi bánh xe quay, bán kính cắt các đường cảm ứng từ nên giữa trục và một điểm trên
vành sẽ có một hiệu điện thế. Nếu ta nối điện trở với trục và vành bánh xe qua tiếp điểm
trượt ta có một mạch điện kín và trong mạch có dòng điện. Dòng điện này chính là dòng các
e chuyển động định hướng trong bánh xe dọc theo bán kính dưới tác dụng của lực từ. 2 2 r r
- Trong thời gian dt, bán kính quét diện tích: ds = d = d t. 2 2 2
Suất điện động cảm ứng: d r B = = . C dt 2 2 Dòng điện cảm ứng: r B C I = = = 0,04A R 2R
Khi dòng điện cảm ứng chạy dọc theo bán kính sẽ làm xuất hiện lực từ tác dụng lên đĩa. Theo
định luật Lentz, lực từ sẽ cản trở chuyển động quay của bánh xe. Muốn bánh xe quay đều, 2
phải tác dụng lên bánh xe một mômen có độ lớn: r BIr 5 M F 5.10− = = = (Nm) 2 2 Trang 21
- Công suất tỏa nhiệt trên điện trở R: P = I2R = 1,6.10-3W.
Bài 23: Một hình trụ tròn (C) dài l , bán kính R (R<< l), làm bằng vật liệu có
điện trở suất phụ thuộc vào khoảng cách tới trục theo công thức B 1 − 2 r = 1−
, trong đó là hằng số. Đặt vào hai đầu hình trụ một hiệu 0 2 2R 0
điện thế không đổi U.
a. Tìm cường độ dòng điện chạy qua hình trụ.
b. Tìm cảm ứng từ tại điểm M cách trục hình trụ đoạn x.
c. Ngắt hình trụ khỏi nguồn, sau đó đưa vào trong một từ trường đồng nhất hướng
dọc theo trục của hình trụ và biến đổi theo thời gian theo quy luật B = kt. Xác định cường
độ dòng điện cảm ứng xuất hiện trong hình trụ. Lêi gi¶i
a. Chia khối trụ thành những ống hình trụ cùng trục với khối trụ và có bề dày dr. Xét một
ống trụ có bán kính r, điện trở của ống trụ là:
dR = (r ) l l 0 = 2 dS r 1− 2 rdr 2 2R
- Cường độ dòng điện chạy qua mỗi ống: 2 U 2U r dI = = 1− rdr 2 dR l 2R 0
- Cường độ dòng điện chạy qua khối trụ có bán kính r < R là: r 2 2 2 2U r Ur r I = 1− rd r = 1− (1) r 2 2 l 2R l 4R 0 0 0 2 3UR
- Khi r = R ta tìm được dòng điện toàn phần chạy qua khối trụ: I = 4 l 0
b. Do tính đối xứng trụ nên các đường cảm ứng từ do dòng điện chạy qua khối trụ gây ra sẽ
là những đường tròn đồng tâm, tâm của các đường tròn nằm trên trục khối trụ.
- Chọn đường tròn, bán kính r, có tâm trên trục khối trụ. Áp dụng định lý Ampere có: Bd l = I 0 (c) 2 2 Ux x - Trường hợp x < R : .
B 2 x = I = 1− 0 x 0 2 l 4R 0 2 Ux x B = 1− 0 2 2 l 4R 0 Trang 22 - Trường hợp x > R: 2 2 3UR 3 UR 0 .2
B x = I = B = 0 0 4 l 8 lx 0 0
c. Từ thông gửi qua diện tích mỗi ống trụ: 2 = kt. r
- Suất điện động cảm ứng xuất hiện trong mỗi ống có độ lớn: = − ( ) 2
' t = k r
- Cường độ dòng điện cảm ứng xuất hiện trong mỗi ống trụ là: 2 3 2 2k r r dI = = 1− dr 2 dR l 2R 0
- Cường độ dòng điện cảm ứng toàn phần trong khối trụ là: 2 R 2 2k r 3 I = r 1− dr 2 l 2R 0 0 2 4
Thực hiện phép tính tích phân tìm được: k R I = 3 l 0
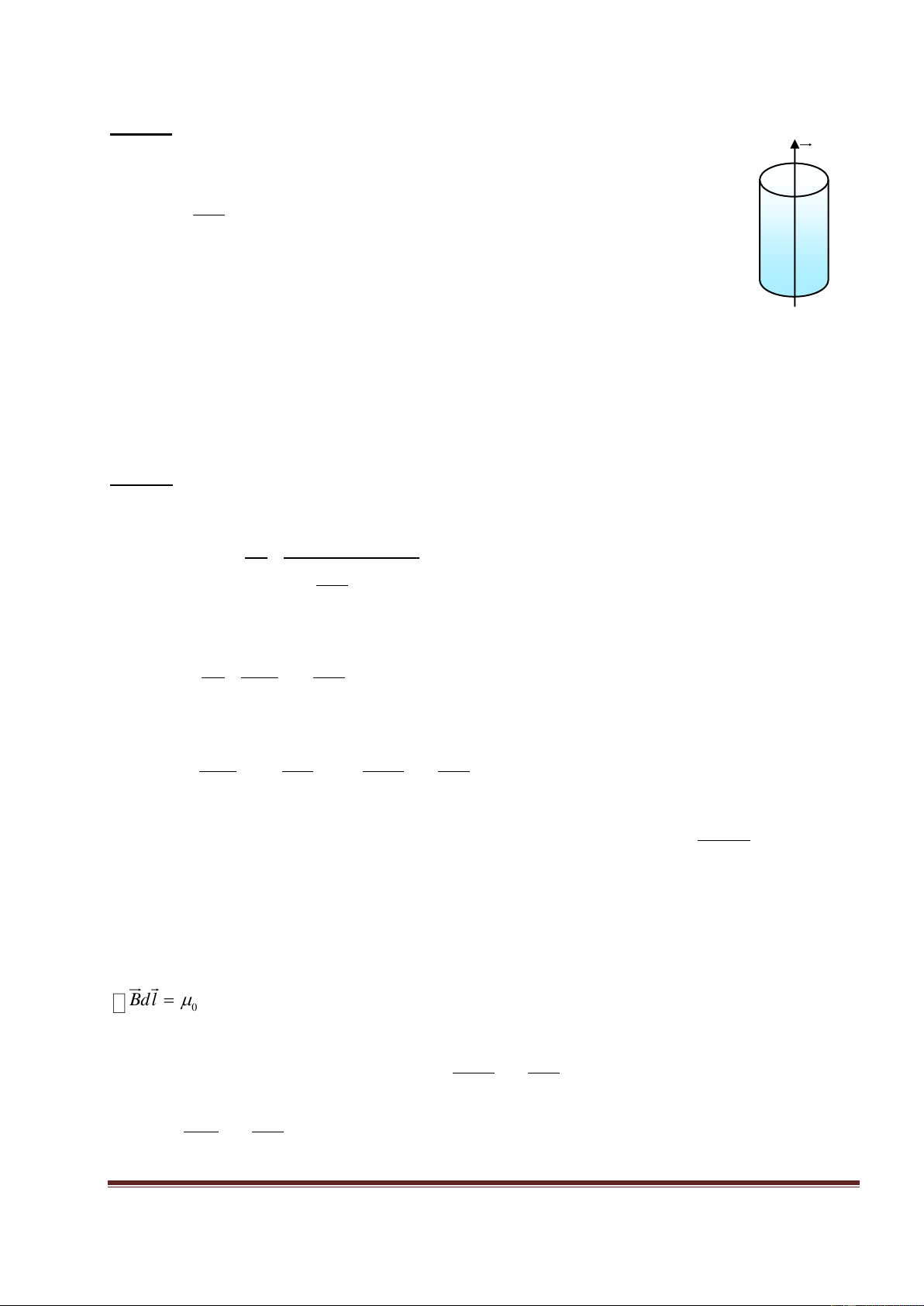
Bài 24: Một thanh kim loại OA khối lượng m, chiều dài a có thể quay tự do quanh trục
thẳng đứng Oz. Đầu A của thanh tựa trên một vòng kim loại hình tròn, tâm O, bán kính a,
đặt cố định nằm ngang. Đầu O của thanh và một điểm của vòng kim loại được nối với điện
trở thuần R, tụ điện C, khoá K và nguồn điện E tạo thành z
mạch điện như hình vẽ. Hệ thống được đặt trong một từ
trường đều, không đổi có véc tơ cảm ứng từ B hướng thẳng B
đứng lên trên. Bỏ qua điện trở của OA, điểm tiếp xúc, vòng A
dây và của nguồn điện. Bỏ qua hiện tượng tự cảm, mọi ma O
sát và lực cản không khí. Ban đầu K mở, tụ điện C chưa tích
điện.Tại thời điểm t = 0 đóng khoá K. R
a. Thiết lập hệ thức giữa tốc độ góc của thanh OA C
và điện tích q của tụ điện sau khi đóng khoá K. K
b. Tìm biểu thức và q theo thời gian t. Cho biết
mômen quán tính của thanh OA đối với trục quay Oz bằng E 1 dy 2 .
m a . Cho nghiệm của phương trình vi phân + ay = d 3 dx với y = y − d
(x) (d và a là hằng số) có dạng ax y = . A e + . a Lêi gi¶i
a. Sau khi đóng K có dòng điện trong mạch tích điện cho tụ. Khi đó thanh OA chị tác dụng
của lực điện từ, làm thanh quay quanh trục Oz. Khi thanh quay, trên thanh suất hiện suất
điện động cảm ứng. Gọi i là dòng điện chạy qua thanh OA. Lực điện từ dF tác dụng lên
đoạn dr của thanh là Bidr.
Mômen lực từ tác dụng lên thanh là: Trang 23 a 2 a M = ir B .dr=iB 2 0
Phương trình chuyển động quay của thanh: 2 2 d a 1 d a 2 I = iB ma = iB dt 2 3 dt 2 3B Suy ra: d = dq (1) 2m
Tích phân hai vế phương trình (1) và chú ý tại t = 0 thì = B 0 và q = 0 được: 3 = (2) 2mq
b. Suất điện động cảm ứng xuất hiện trên thanh OA: d 2 Ba E = − Suy ra E = C dt C 2
Áp dụng định luật Ôm: E – EC = uC + Ri 2 Ba q dq Suy ra: E − = + R (3) 2 C dt 2 2 Từ (2) và (3) : dq q 3B a C E + (1+ ) = (4) dt RC 4m R Đặt RC E t = và I = (5) 0 2 2 3B a C 0 R 1+ 4m t − Từ (4) ta tìm được: t0 q = Q e + I t 0 0 0
Biết t = 0, q = 0 suy ra Q0 = - I0t0 t − Vậy ta có: 0 = 1 t q I t − e 0 0 t 3BI t − Theo (2) 0 0 0 = 1 t − e 2m C. BÀI TẬP TỰ GIẢI
Bài 25: Từ một dây dẫn có chiều dài l = 2m và điện trở R = 4, người ta
hàn lại thành một hình vuông. Tại các cạnh của hình vuông người ta mắc B Trang 24
hai nguồn điện có suất điện động E1 = 10V và E2 = 8V theo hình 8. Mạch được đặt trong
một từ trường đều có hướng vuông góc với mặt phẳng hình vuông. Biết độ lớn của cảm ứng
từ B tăng theo quy luật B = kt, trong đó k = 16 T/s. Tính cường độ dòng điện trong mạch.
Bỏ qua điện trở trong của các nguồn.
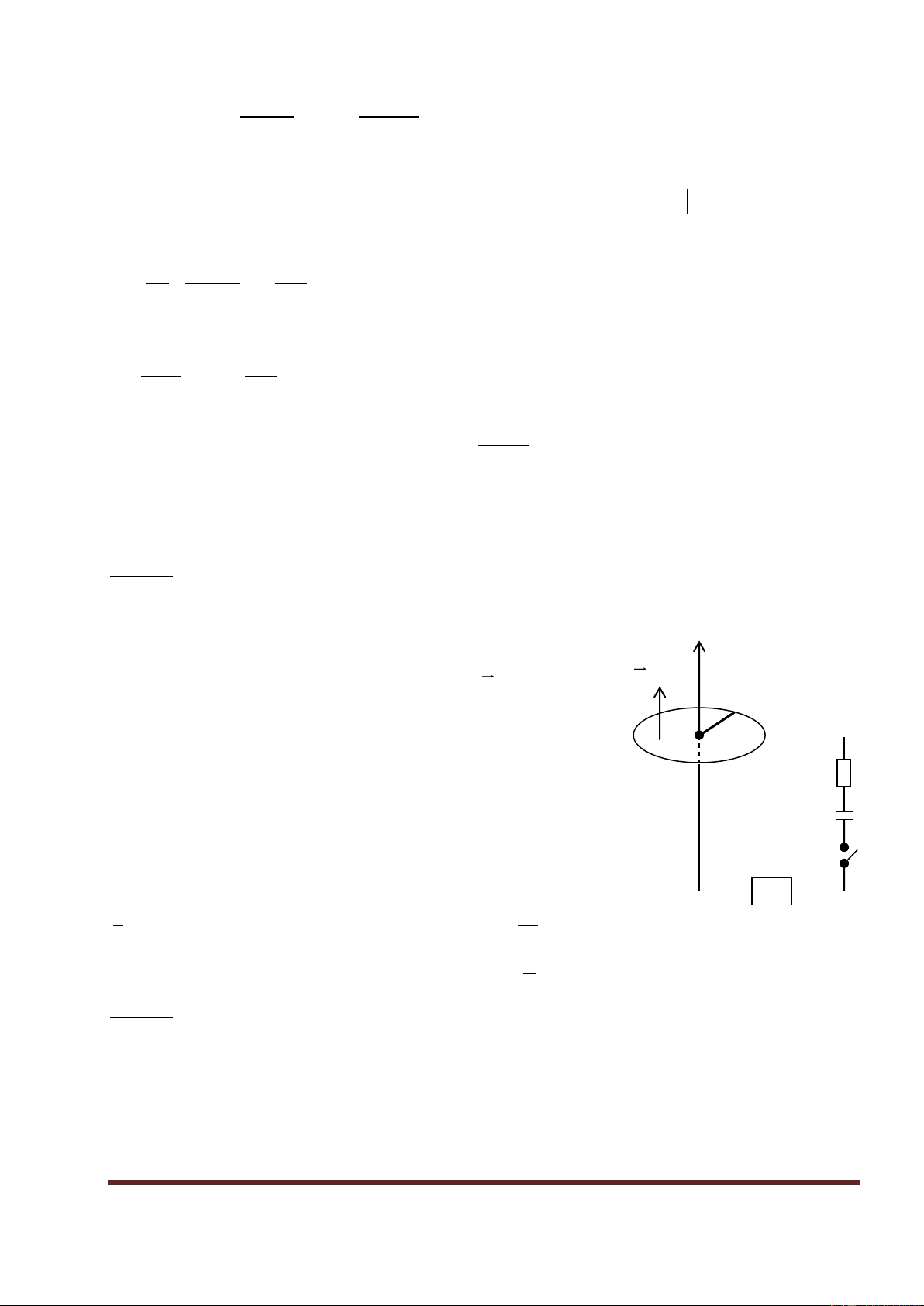
Bài 26: Một khối trụ bằng gỗ khối lượng m=250g dài
L=10cm, trên nó có quấn N=10 vòng dây hình chữ nhật sao
cho mặt phẳng vòng dây chia đôi khối trụ theo mặt phẳng B
chứa trục của khối gỗ. Hỏi dòng điện nhỏ nhất chạy qua
khung dây phải bằng bao nhiêu để nó có thể ngăn không
cho khối gỗ lăn xuống mặt phẳng nghiêng có góc nghiêng
bằng . Biết rằng có một từ trường đều đường sức thẳng
đứng hướng lên và từ cảm bằng B=0,5T và lúc đầu mặt phẳng khung dây song song với mặt phẳng nghiêng?
Bài 27: Trong hình bên, mn và xy là hai bản kim loại đặt vuông góc với mặt phẳng hình vẽ
và song song với nhau, chiều dài các bản rất lớn. Trong khoảng giữa hai bản có từ trường
đều B=0,8T vuông góc với mặt phẳng hình vẽ và hướng về phía sau. Thanh kim loại nhẹ ab
dài L=0,2m, điện trở Ro=0,1 luôn luôn tiếp xúc với hai bản kim loại và có thể chuyển
động không ma sát trong mặt phẳng hình vẽ.
R1 và R2 là hai điện trở có giá trị R1=R2=3,9 ,
tụ có điện dung C=10 F a m n
a. Khi ab chuyển động sang phải với vận
tốc đều v=2m/s thì ngoại lực tác dụng lên nó có
chiều nào, độ lớn bằng bao nhiêu? R1 y R 2
b. Nếu trong lúc chuyển động, thanh ab b
đột nhiên dừng lại thì ngay lúc đó lực từ tác
dụng vào ab sẽ có chiều nào? độ lớn bao nhiêu?
Bài 28: Trên mặt bàn phẳng nằm ngang nhẵn đặt một khung dây
dẫn hình chữ nhật có các cạnh là a và b (hình vẽ). Khung được đặt Bz x O
trong một từ trường có thành phần của cảm ứng từ dọc theo trục Oz N P
chỉ phụ thuộc vào tọa độ x theo quy luật : Bz = Bo(1 - x), trong đó
Bo và là các hằng số. Truyền cho khung một vận tốc vo dọc theo M Q
trục Ox. Bỏ qua độ tự cảm của khung dây, hãy xác định khoảng y
cách mà khung dây đi được cho tới khi dừng lại hoàn toàn. Biết
điện trở thuần của khung dây là R.
---------------- Hết ------------------ Trang 25 Trang 26




