HÌNH CHÓP ĐỀU
HÌNH CHÓP ĐỀU – HÌNH CHÓP CỤT ĐỀU
A.BÀI GIẢNG CỦNG CỐ KIẾN THỨC NỀN 1.HÌNH CHÓP
Định nghĩa: Hình chóp là hình có mặt đáy là một đa giác và các mặt bên là
các tam giác có chung đỉnh.
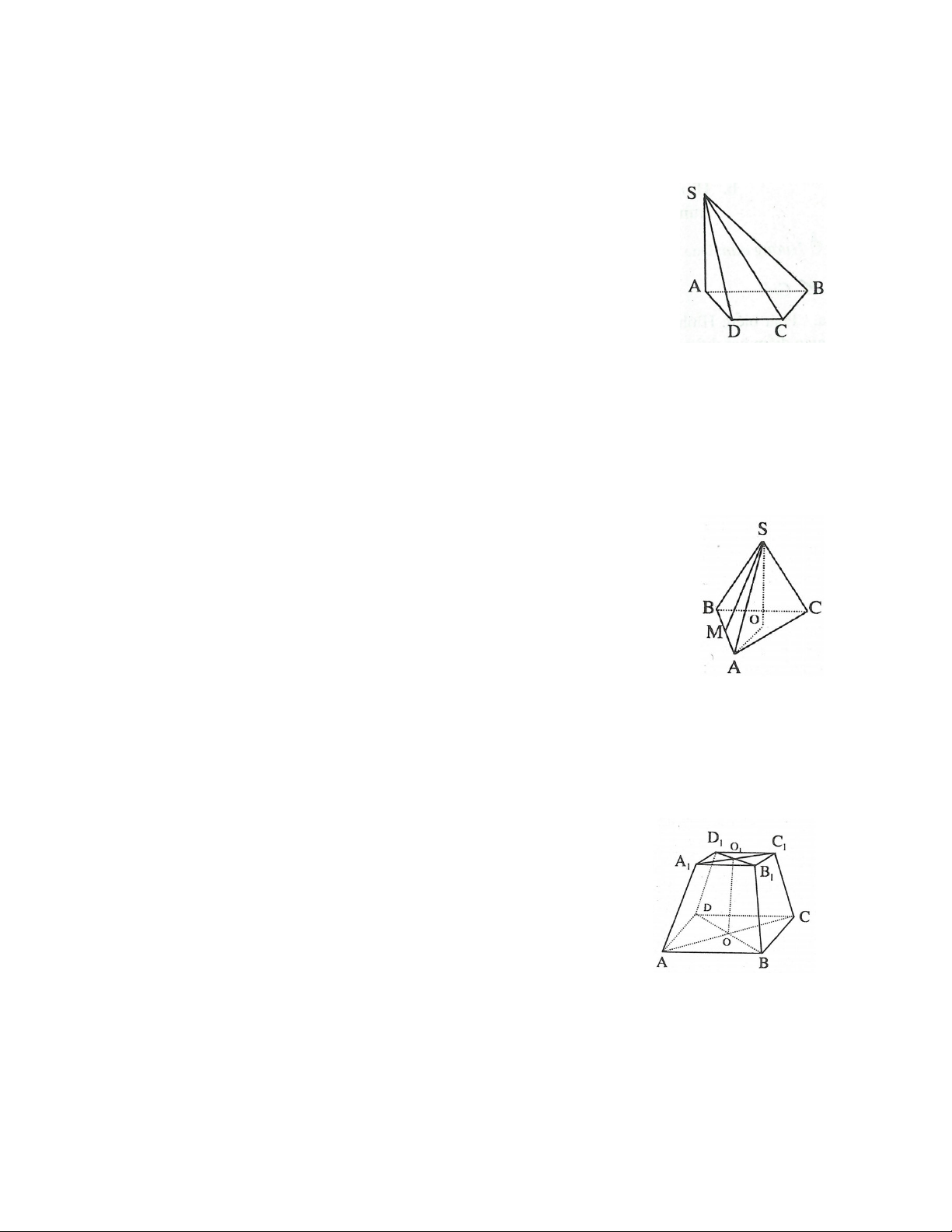
Hình bên cho ta hình ảnh của hình chóp S.ABCD, và ở đó:
1. Điểm S được gọi là đỉnh của hình chóp.
2. Các đoạn SA, SB, SC, SD được gọi là các cạnh bên của hình chóp.
3. Các tam giác SAB, SBC, SCD, SAD được gọi là các mặt bên của hình chóp.
4. Mặt ABCD là đáy của hình chóp.
5. Hình chóp này có đáy là tứ giác nên gọi là hình chóp tứ giác. 2. HÌNH CHÓP ĐỀU
Định nghĩa: Hình chóp đều là hình chóp có đáy là một đa giác đều, các mặt bên là tam giác cân bằng nhau có chung đỉnh.
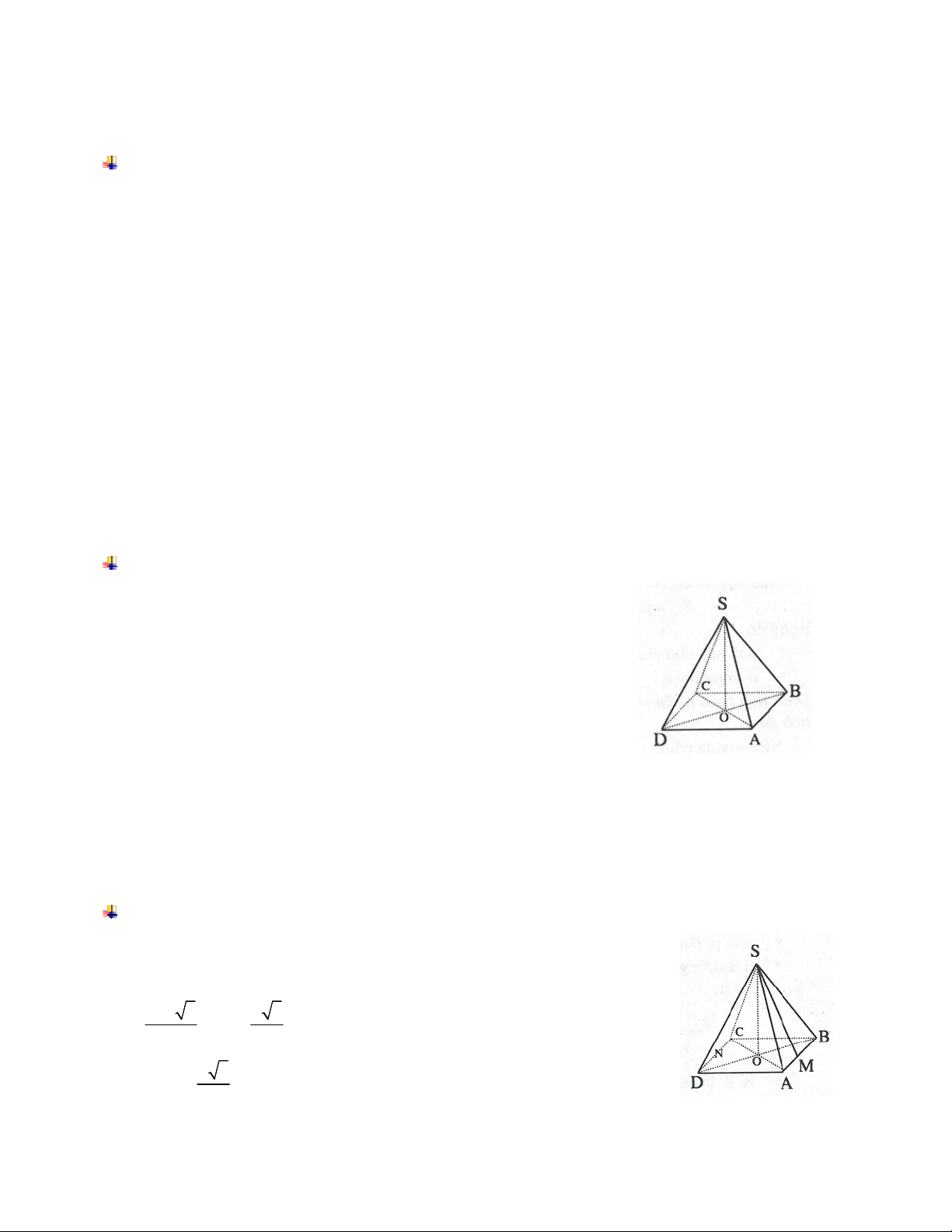
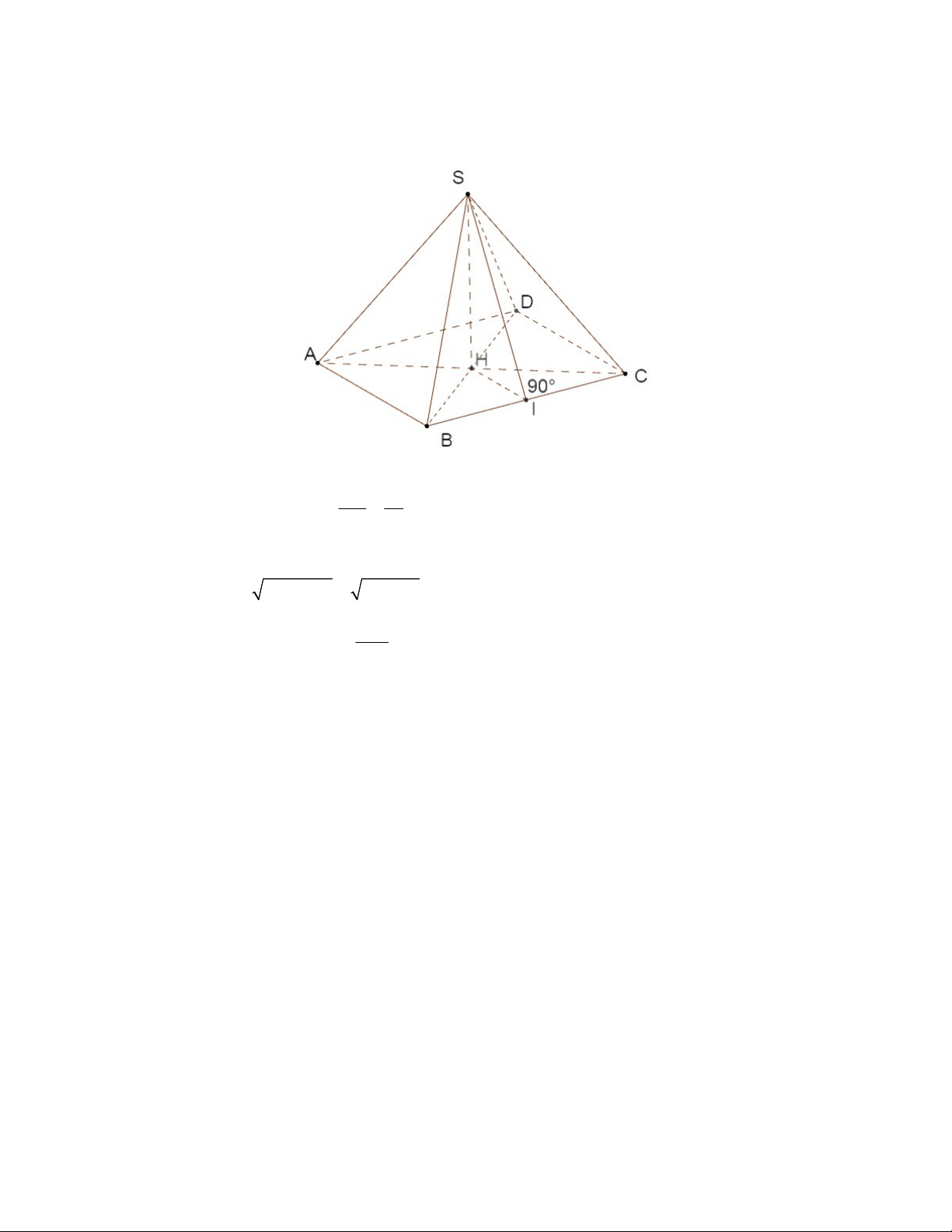
Hình bên cho ta hình ảnh của hình chóp tam giác đều S.ABC, và ở đó:
1. Điểm S được gọi là đỉnh của hình chóp.
2. Các đoạn SA, SB, SC bằng nhau được gọi là các cạnh bên của bên hình chóp.
3. Các tam giác SAB, SBC, SAC là các tam giác cân đỉnh S, chúng được gọi là
các mặt bên của hình chóp.
4. ABC là một tam giác đều và nó được gọi là đáy của hình chóp.
5. Đoạn SM (với M là trung điểm của AB) được gọi là trung đoạn.
6. Đoạn SO (với O là tâm của đáy ABC) được gọi là đường cao.
7. Hình chóp này có đáy là tam giác đều nên gọi là hình chóp tam giác đều. 3. HÌNH CHÓP CỤT ĐỀU
Định nghĩa: Cắt một hình chóp đều bằng một mặt phẳng song song với
đáy, phần hình chóp nằm giữa mặt phẳng đó và mặt phẳng đáy là một hình chóp cụt đều.
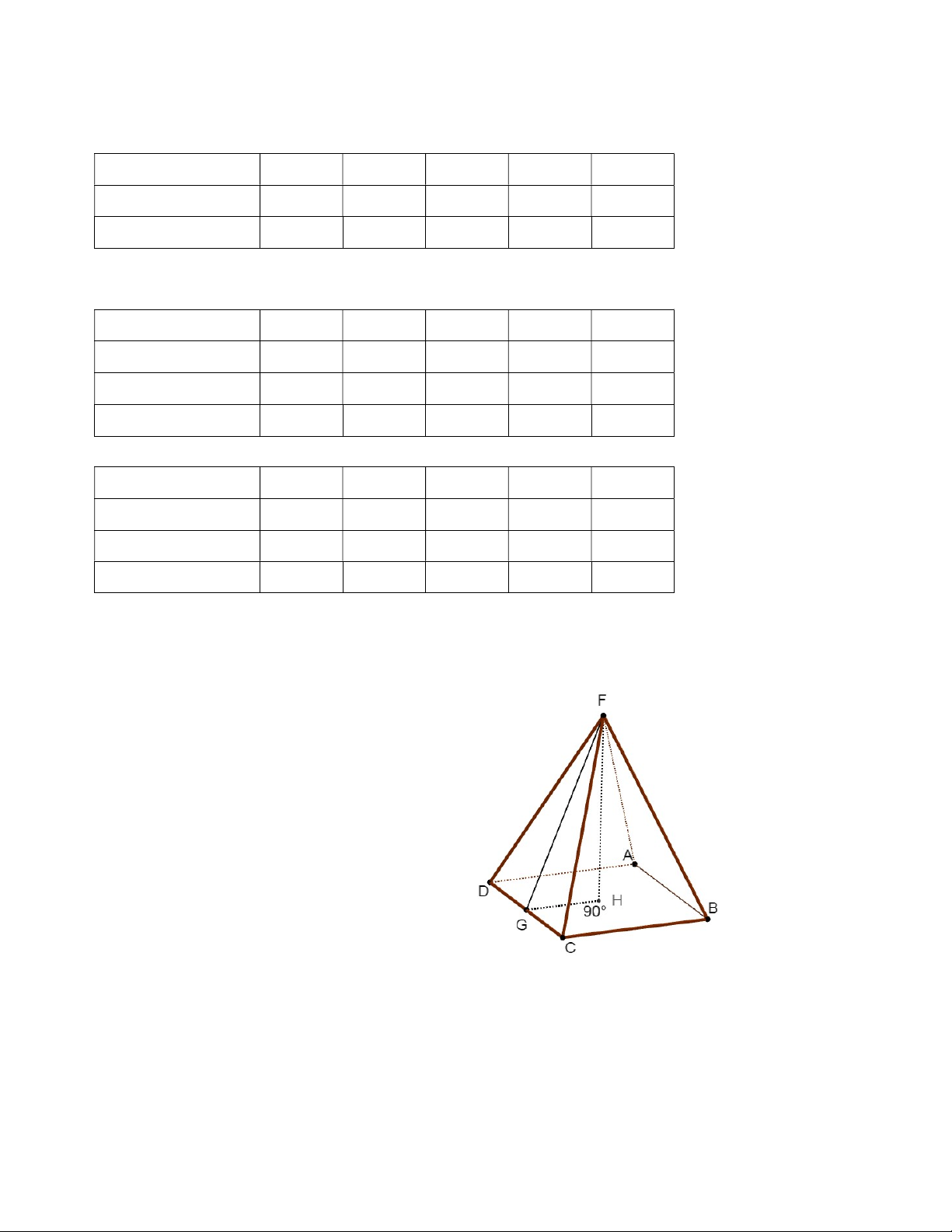
Hình bên cho ta hình ảnh của hình chóp cụt đều ABCDA B C D và ở đó 1 1 1 1
mỗi mặt bên của nó đều là những hình thang cân bằng nhau.
B. PHƯƠNG PHÁP GIẢI TOÁN
Ví dụ 1: Hãy xét sự đúng, sau của các phát biểu sau:
a. Hình chóp đều có đáy là hình thoi và chân đường cao trùng với giao điểm hai đường chéo của đáy.
b. Hình chóp đều có đáy là hình chữ nhật và chân đường cao trùng với giao điểm hai đường chéo của đáy.
 Hướng dẫn: Dựa vào định nghĩa của hình chóp đều. Giải:
a. Phát biểu: Hình chóp đều có đáy là hình thoi và chân đường cao trùng với giao điểm hai đường chéo của đáy là sai:
Vì hình thoi không phải là một đa giác đều nên hình chóp có đáy là hình thoi không phải là hình chóp đều.
b. Phát biểu: Hình chóp đều có đáy là hình chữ nhật và chân đường cao trùng với giao điểm hai đường chéo của đáy là sai.
Vì hình chữ nhật không phải là đa giác đều nên hình chóp có mặt đáy là hình chữ nhật không phải là hình chóp đều.
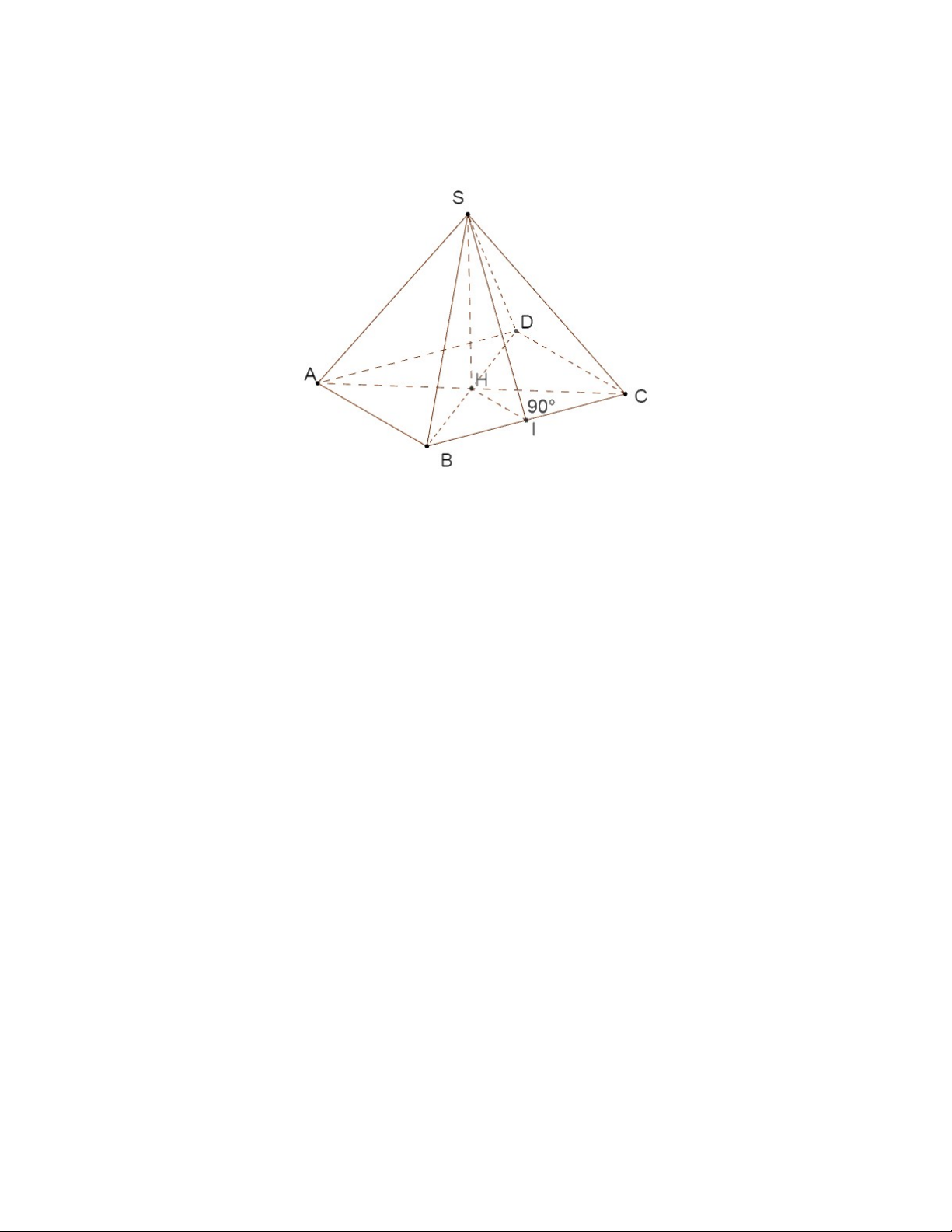
Ví dụ 2: Cho hình chóp tứ giác đều S.ABCD, gọi O là giao điểm của AC và BD.
a. Chứng minh rằng SO  (ABCD).
b. Chứng minh rằng (SAC)  (SBD).
 Hướng dẫn: Dựa vào định nghĩa của hình chóp đều. Giải: a. Ta lần lượt có:
 Trong SAC, ta có: SA  SC  S
 AC cân tại S  SO  AC (1)
 Trong SBD, ta có: SB  SD  S
 BD cân tại S  SO  BD (2)
Từ (1),(2) suy ra SO  (ABCD)
b. Từ kết quả câu a), ta có: SO  AC (3)
Mặt khác, vì ABCD là hình vuông nên BD  AC (4)
Từ (3) và (4) suy ra: (SBD)  AC  (SAC)  (SAC)  (SBD)
Ví dụ 3: Cho hình chóp tứ giác S.ABCD có chiều cao h và cạnh đáy bằng a. Gọi M, N theo thứ tự là
trung điểm của AB và CD. Tìm mối liên hệ giữa a và h để SMN là tam giác đều.
 Hướng dẫn: Sử dụng điều kiện về đường trung tuyến trong tam giác đều. Giải:
Trong SMN, ta có: MN  BC  a
Do đó, để SMN là tam giác đều điều kiện là: MN 3 a 3 SO   h  2 2 a 3 Vậy, với h 
thì SMN là tam giác đều. 2 PHIẾU BÀI TỰ LUYỆN
Dạng 1: Biến đổi công thức tính các đại lượng
Bài 1: Cho hình chóp có diện tích đáy và chiều cao. Em hãy điền vào ô trống Diện tích đáy 20 45 12 15 Chiều cao 15 18 30 V hình chóp 390 66 48
Bài 2: Cho hình chóp đều có đáy là tam giác đều . Điền vào ô trống Cạnh tam giác 10 24 15 Diện tích đáy 173.21 27.71 Chiều cao 12 15 20 V hình chóp 831.38 166.28
Bài 3: Cho hình chóp đều có đáy là hình vuông. Điền vào ô trống Cạnh hình vuông 15 25 30 Diện tích đáy 100 400 Chiều cao 12 18 V hình chóp 1050 2000 6300
Dạng 2 : Những bài toán về tự luận.
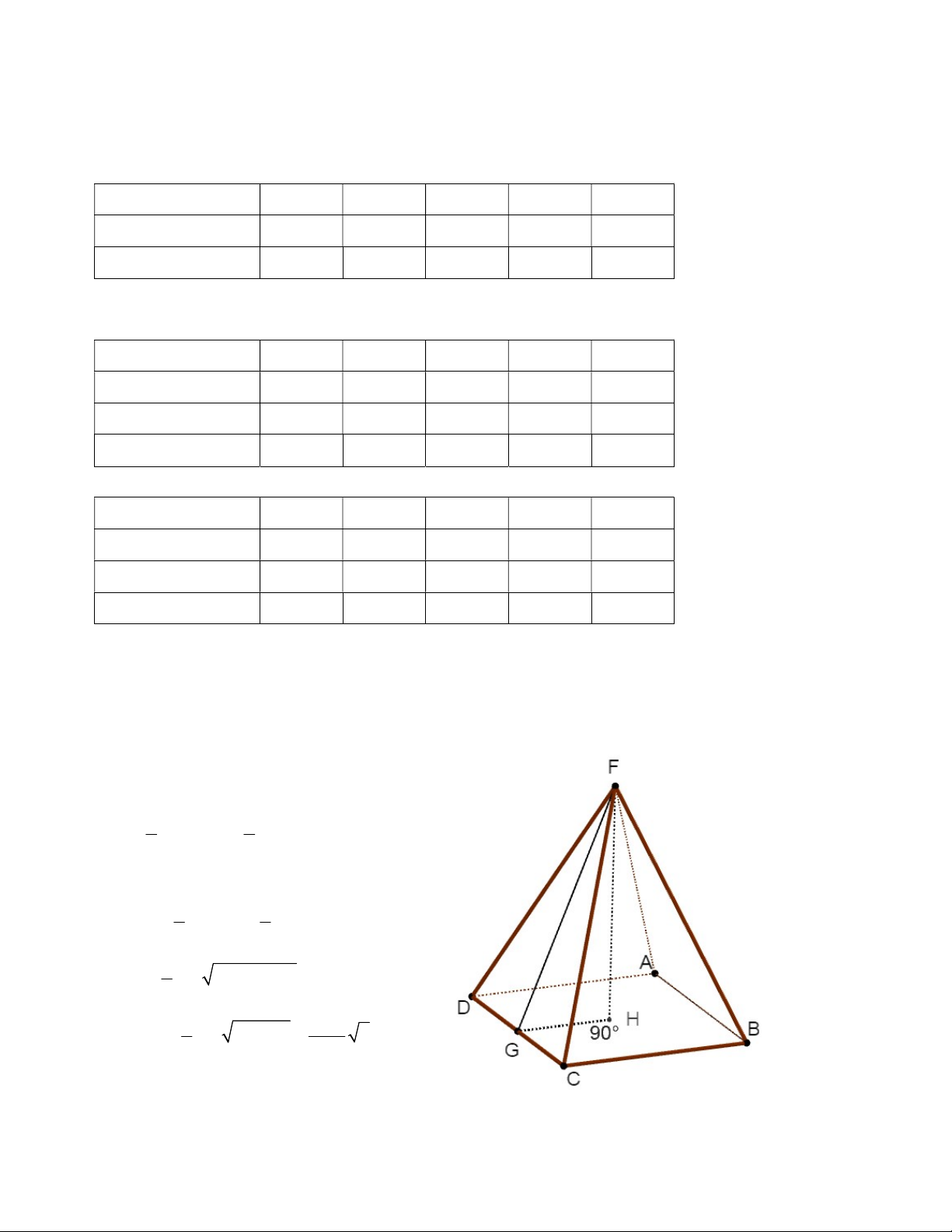
Bài 1: Cho AB  10cm , FG  15cm .
a) Tính diện tích xung quanh của hình chóp?
b) Tính thể tích của hình chóp?
Bài 2: Cho diện tích xung quanh bằng 2 6000m , GF  50 . m a) Tính Cạnh đáy AB ? b) Tính diện tích đáy?
c) Tính thể tích của hình chóp?
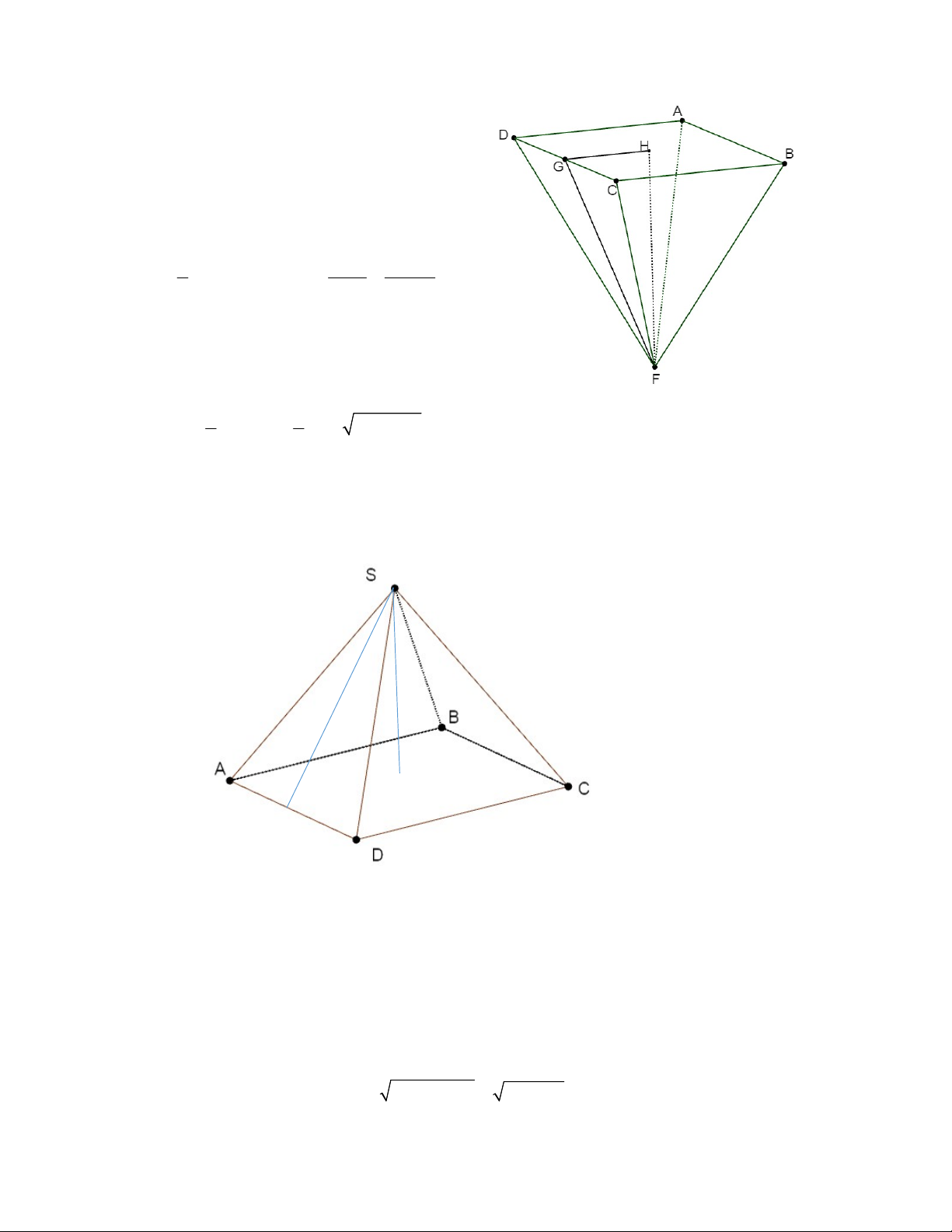
Bài 3: Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy là 12cm, cạnh bên SA 10c . m
a) Diện tích toàn phần hình chóp b) Thể tích hình chóp 10 cm 12 cm
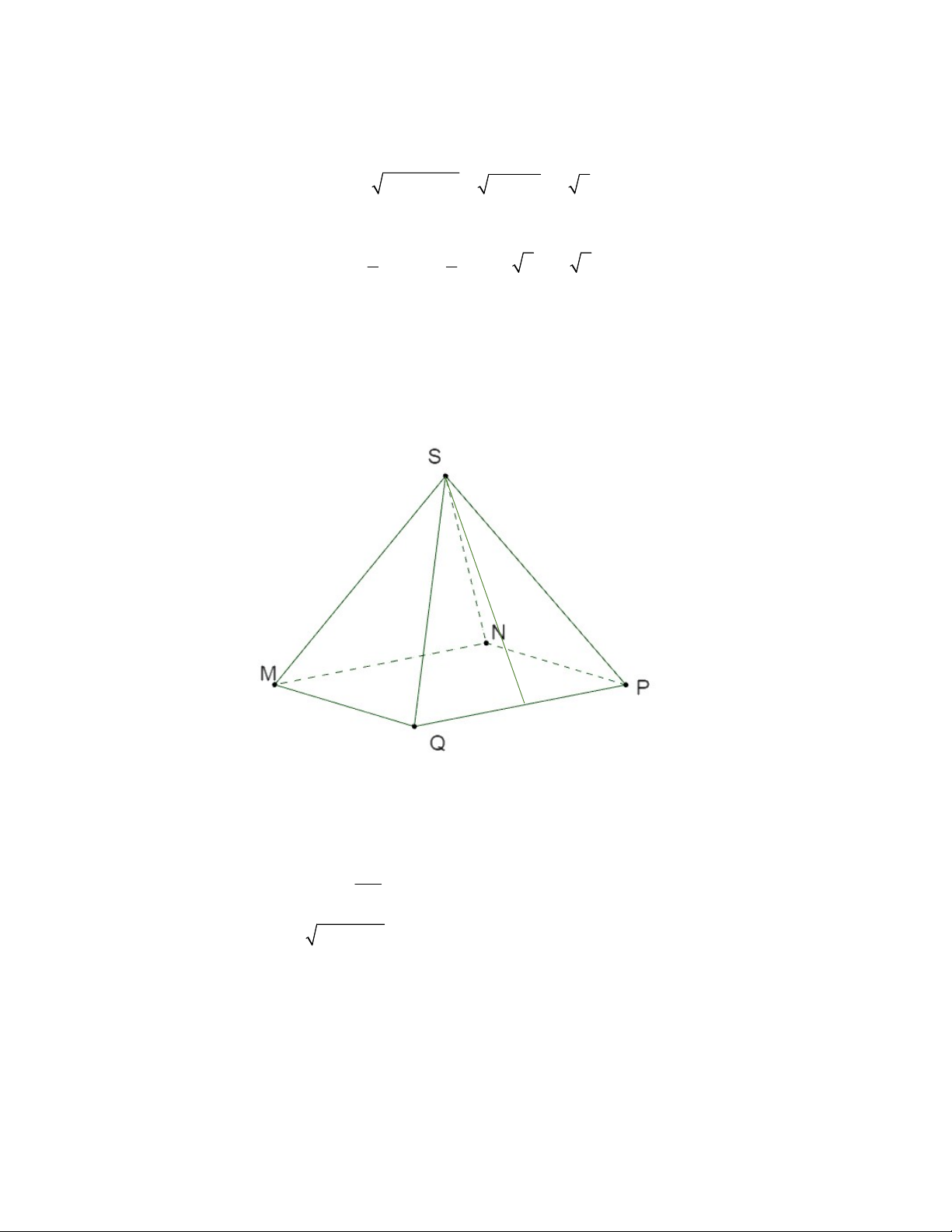
Bài 4: Một hình chóp tứ giác đều có độ dài cạnh bên bằng 30cm , đáy là hình vuông MNPQ cạnh 48c .
m Tính diện tích toàn phần của hình chóp.
Bài 5: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB  162cm , cạnh bên SA  15 cm . Tính
chiều cao và thể tích của hình chóp.
Bài 6: Một hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy là AB  12cm , cạnh bên SA  10cm .
Tính diện tích toàn phần của hình chóp.
LỜI GIẢI PHIẾU BÀI TỰ LUYỆN
Dạng 1: Biến đổi công thức tính các đại lượng
Bài 1: Cho hình chóp có diện tích đáy và chiều cao. Em hãy điền vào ô trống Diện tích đáy 20 45 11 12 15 Chiều cao 15 26 18 12 30 V hình chóp 100 390 66 48 150
Bài 2: Cho hình chóp đều có đáy là tam giác đều . Điền vào ô trống Cạnh tam giác 10 20 24 8 15 Diện tích đáy 43.3 173.21 249.42 27.71 97.43 Chiều cao 12 15 10 18 20 V hình chóp 173.21 866.03 831.38 166.28 649.52
Bài 3: Cho hình chóp đều có đáy là hình vuông. Điền vào ô trống Cạnh hình vuông 10 15 20 25 30 Diện tích đáy 100 225 400 625 900 Chiều cao 12 14 15 18 21 V hình chóp 400 1050 2000 3750 6300
Dạng 2 : Những bài toán tự luận
Bài 1: Cho hình chóp F.ABC .
D Có AB  10cm, FG  15c . m
a) Tính diện tích xung quanh của hình chóp?
b) Tính thể tích của hình chóp? Giải:
Diện tích xung quanh của hình chóp 1 1 S  FG.DC.4  15.10.4  2 300cm xq 2 2 Thể tích của hình chóp 1 1 V  S .h  2 AB .FH S.ABCD ABCD 3 3 1  2 2 10 . GF  2 HG 3 1 1000  2 2 10 . 15  2 5  3 2cm 3 3
Bài 2: Diện tích xung quanh hình chóp F.ABCD bằng 2 6000m , GF  50 . m a) Tính Cạnh đáy AB ? b) Tính diện tích đáy?
c) Tính thể tích của hình chóp? Giải a)Cạnh đáy AB dài 1 2.S 2.6000 S  FG.DC.4  DC  xq   60m xq 2 4.FG 4.50 b)Diện tích đáy S 2 2
đáy  AB  60.60  3600m c)Thể tích hình chóp 1 1 V  S .FH  2 3600 50  2 30  3 48000m S.ABCD day 3 3
Bài 3: Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy là 1 2cm , cạnh bên SA  10c . m
a) Diện tích toàn phần hình chóp b) Thể tích hình chóp 10 cm .I 12 cm H Giải Kẻ SH  DA Ta có S  AH  H Theo định lý Pytagoras 2 2 2 AH  HS  SA Hay  2  2 SH AS AH  100  36  8cm Kẻ SI   ABCD Ta có S  AI  I Theo định lý Pytagoras 2 2 2 IH  IS  SH Hay  2  2 SI HS IH  64  36  2 7cm Thể tích của hình chóp 1 1 V  S .SI  12.12.2 7  3 96 7cm S.ABCD day 3 3
Bài 4: Một hình chóp tứ giác đều có độ dài cạnh bên bằng 30cm, đáy là hình vuông MNPQ cạnh 48c .
m Tính diện tích toàn phần của hình chóp. Giải E
Gọi SE là một trung đoạn của hình chóp đều. Ta có S  PE  E
Theo định lý Py-ta-go, ta có: 2 2 2 SE  EP  SP 2  PQ SE2 2 2  2   SP – EP  SP    2 2  30  24  2  Nên:  2  2 SE 30 24  18cm
Diện tích xung quanh của hình chóp đều: 2 S  . p d  2.48.18  1728 xq cm Diện tích đáy là: 2 S  48.48  2304 d cm
Diện tích toàn phần của hình chóp đều: 2 1728  2304  4032 cm
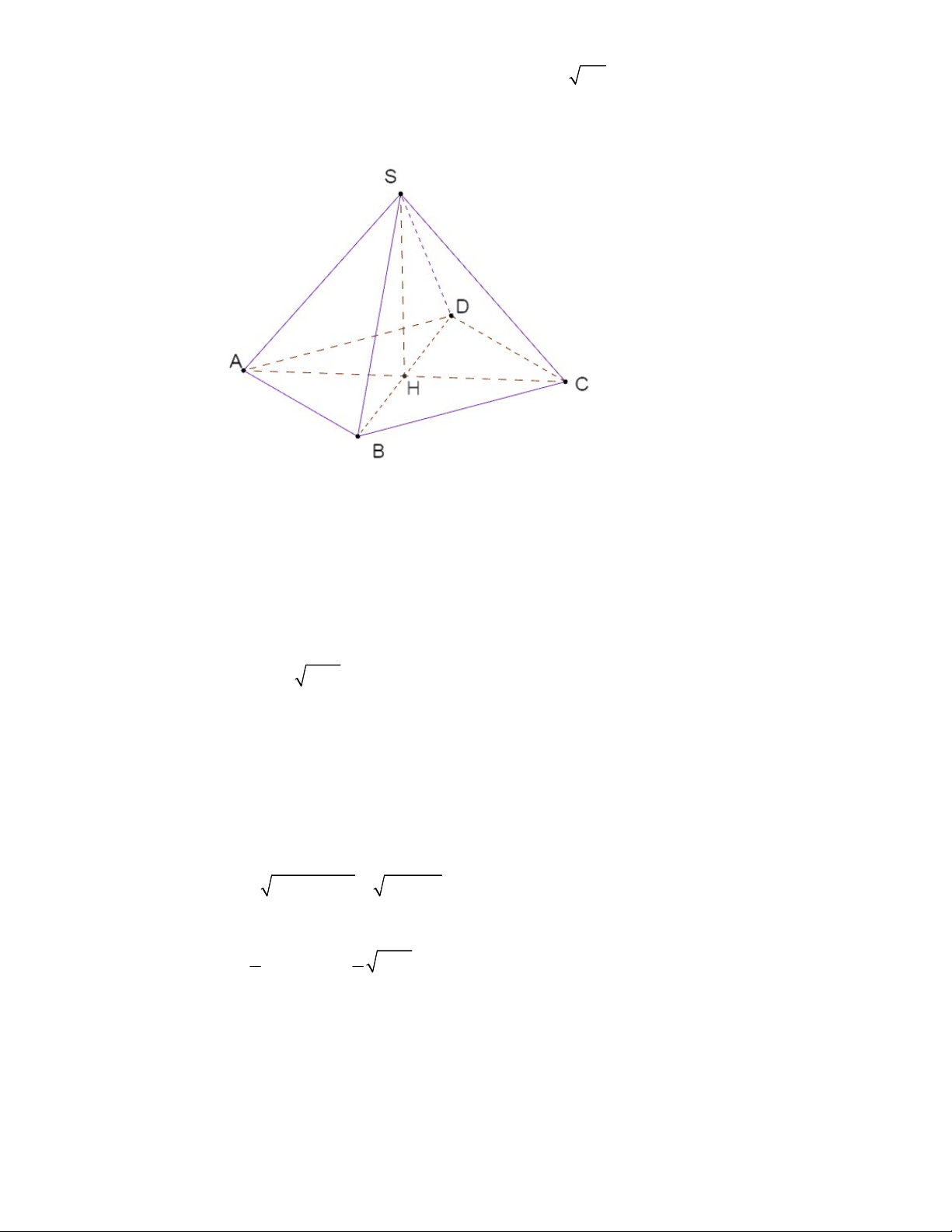
Bài 5: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB  162cm , cạnh bên SA  15 c . m Tính
chiều cao và thể tích của hình chóp. Giải: Ta có ABCD là hình vuông Nên AC  BD và AC  BD Ta có AHB  H Theo định lý Pytagoras 2 2 2 HA  HB  AB 2  2 2HA 162 2 HA  81 cm HA  9 cm SH  ABCD suy ra SH  AH
Trong tam giác vuông SHA ta có:  2  2  2  2 SH SA HA 15 9  12cm
Vậy chiều cao của hình chóp là 12 c . m 1 1 V  .S .SH  2 162 .12  3 648cm ABCD 3 3
Bài 6: Một hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy là AB  12cm , cạnh bên SA  10c . m
Tính diện tích toàn phần của hình chóp. Giải
Gọi SI là trung đoạn của hình chóp ta có: CD 12 DI  CI    6cm 2 2
Trong tam giác vuông SIB theo định lí Py-ta-go ta có: 2 2 2 2
SI  SB  BI  10  6  8cm 4.12 Vậy S  . .8 2  xq p d  192 cm 2 2 3
S  S  S  192 12  336 tp xq d cm .
========== TOÁN HỌC SƠ ĐỒ ==========