Chuyên đề ôn luyện bất phương trình và hệ bất phương trình bậc nhất hai ẩn

Tài liệu gồm 28 trang, được biên soạn bởi tác giả Trương Việt Long, bao gồm tóm tắt lý thuyết, bài tập tự luận và bài tập trắc nghiệm chuyên đề bất phương trình và hệ bất phương trình bậc nhất hai ẩn, giúp học sinh lớp 10 ôn luyện khi học chương trình Toán 10; tài liệu được biên soạn dựa trên nội dung Sách giáo khoa Toán 10 (tập 1) (Kết Nối Tri Thức Với Cuộc Sống).

112 56 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Ⓐ -

BT PHƯƠNG TRNH BC NHT HAI N

BIU DIN MIN NGHIM CA BT PHƯƠNG

TRNH BC NHT HAI N TRÊN MT PHNG

TA Đ

DNG 1: Xc đnh Bt phương trnh bc nht hai n

DNG 2: : Biu din min nghim ca bt phương trnh bc nht hai n

DNG 3: Bi ton thc t

Ⓑ

CHƯƠNG II: BT PHƯƠNG TRNH

V H BPT BC NHT NHIU N

DNG 1: : Tm nghim ca bt phương trnh bc nht hai n

DNG 2: Biu din tp nghim ca bt phương trnh bc nht hai n

Ⓒ

Ⓐ -

H BT PHƯƠNG TRNH BC NHT HAI N

BIU DIN MIN NGHIM CA H BT PHƯƠNG

TRNH BC NHT HAI N TRÊN MT PHNG

TA Đ

NG DNG CA H BT PHƯƠNG TRNH BC

NHT HAI N

DNG 1: Xc đnh H bt phương trnh bc nht hai n

DNG 2: : Biu din min nghim ca h bt phương trnh bc nht hai n

DNG 3: ng dng ca h bt phương trnh bc nht hai n

Ⓑ

DNG 1: : Tm nghim ca H bt phương trnh bc nht hai n

DNG 2: Min nghim ca H bt phương trnh bc nht hai n

DNG 3: ng dng ca h bt phương trnh bc nht hai n

Ⓒ

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

1. BT PHƯƠNG TRNH BC NHT HAI N

Chương

BT PHƯƠNG TRNH

V H BT PHƯƠNG TRNH

BC NHT HAI N

Bài BT PHƯƠNG TRNH BC NHT HAI N

TÓM TẮT LÝ THUYẾT

Định nghĩa

 Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là

(hoặc ; )

Trong đó a, b, c là các hệ số, a và b không đồng thời bằng 0, x và y là các ẩn số.

 Cặp số sao cho “ ” là mệnh đề đúng được gọi là một nghiệm của bất

phương trình .



,,ax by c ax by c ax by c

Nghiệm của các bất phương trình dạng cũng được định

nghĩa tương tự.

 Trong mặt phẳng tọa độ thì mỗi nghiệm của bất phương trình bậc nhất hai ẩn được biểu diễn

bởi một điểm và tập nghiệm của nó được biểu diễn bởi một tập hợp điểm. Ta gọi tập hợp điểm ấy

là miền nghim của bất phương trình.

V d: Ta có các bất phương trình bậc nhất hai ẩn như sau:

2 0xy

. d)

2 0xy

b) e)

2 3xy

2 2 1

x y x y

c) f)

ax by c+

ax by c+

;ax by c ax by c+  + 

( )

;xy

ax by c+

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

2. BIU DIN MIN NGHIM CA BPT BC NHT HAI N TRÊN MT PHNG TA Đ

Định nghĩa

 Định l :

:0d ax by c

Trong mặt phẳng tọa độ đường thẳng chia mặt phẳng thành hai nửa mặt

phẳng. Một trong hai nửa mặt phẳng ấy (không kể bờ (d)) gồm các điểm có tọa độ thỏa mãn

0ax by c

bất phương trình , nửa mặt phẳng còn lại (không kể bờ (d)) gồm các điểm có

0ax by c

tọa độ thỏa mãn bất phương trình .



0ax by c

Vậy để xác định miền nghiệm của bất phương trình , ta có quy tắc thực hành biểu

diễn hình học tập nghim (hay biểu diễn miền nghim) như sau:

 Bước 1.

(1)

0 ax by c

Vẽ đường thẳng (d): .

•

xx=

x =

Cho (Vi 1 giá trị nào đó ). Thay vào (1) ta tìm được giá trị .

( )

;A x y

( )

Vậy ta được điểm thuộc đường thẳng .

•

xx=

Tương tự: Cho . Thay vào (1) ta tìm được giá trị .

( )

;B x y

( )

Vậy ta được điểm thuộc đường thẳng .

( )

K đường thẳng đi qua A và B. Ta được đường thằng cn tìm.

⚠ Chú ý:

- Ta có thể cho y để tìm .

0x =

0y =

Thường thì ta sẽ cho để tìm y. Hoặc cho để tìm .

 Bước 2. Lấy một điểm không thuộc Δ (ta thường lấy gốc tọa độ O).

 Bước 3. Tính và so sánh vi c.

•

0ax by c

Nếu thì nửa mặt phẳng (không kể bờ (d)) chứa điểm M là miền nghiệm

0ax by c

của bất phương trình .

•

0ax by c

Nếu thì nửa mặt phẳng (không kể bờ (d)) không chứa điểm M là miền

0ax by c

nghiệm của bất phương trình .

⚠ Chú ý:

0ax by c

Đối vi các bất phương trình dạng hoặc thì miền nghiệm là

nửa mặt phẳng kể cả bờ.

( )

0 0 0

;M x y

ax by+

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 1: Xc đnh bt phương trnh bc nht 2 n

Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn:

2 3 6xy

20xy

21xy

2 3 6xy

là bất phương trình bậc nhất 2 ẩn. Vi

2; 3; 6.a b c= = =

2 0 4 0x y x y

là bất phương trình bậc nhất 2 ẩn. Vi

4 2; 1; 0.bc= = =

21xy

không phải là bất phương trình bậc nhất 2 ẩn. Vì chứa

( bậc hai )

Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn:

2 0xy

. b)

. c)

0xy

3 4 7xy

2 2 1

x y x y

Lời giải

.............................................................................................................................................................................................

BI TP T LUN

Ví dụ 1

BÀI GIẢI

Bài 1

BÀI TP RN LUYN

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Xác định miền nghiệm của bất phương trình :

2 0xy

Trong mặt phẳng tọa độ, vẽ đường thẳng

: 2 0d x y

Ta có

chia mặt phẳng thành hai nửa mặt phẳng.

Chọn một điểm bất kì không thuộc đường thẳng đó, chẳng hạn điểm

1;0M

Ta thấy (1; 0) là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cn tìm là nửa mặt phẳng chứa bờ (d)

và chứa điểm

1;0M

(Miền không được tô màu trên hình vẽ).

Xác định miền nghiệm của bất phương trình :

20xy

3 3 0xy

2 2 1

x y x y

Lời giải

.............................................................................................................................................................................................

Dạng 2: Biu din min nghim ca bt phương trnh bc nht hai n?

Ví dụ 1

BÀI GIẢI

Bài 2

BÀI TP RN LUYN

(

)

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 3: Bi ton thc t

Ông An muốn thuê một chiếc xe ô-tô ( có lái xe ) trong một tun. Giá thuê xe được cho như bảng sau:

Ph cố định

( Nghìn đồng/ngày )

Ph tnh theo quãng đường di chuyển

( Nghìn đồng/km )

T thứ Hai đến thứ Sáu

900

Thứ Bảy và Chủ nhật

1500

a) Gọi

và

ln lượt là số kilomet ông An đi trong các ngày t thứ Hai đến thứ Sáu và trong hai ngày cuối

tun. Viết bất phương trình biểu thị mối liên hệ gia

và

sao cho tổng số tiền ông An phải trả không quá

14 triệu đồng.

b) Biểu diễn miền nghiệm của bất phương trình ở câu a trên mặt phẳng tọa độ.

a) T thứ Hai đến thứ Sáu. 1 km di chuyển có chi ph là 8000 ( đồng ). Ông An đi hết

( km), vậy ông An sẽ

tốn chi ph là: 8000

( đồng ).

Tương tự : Vào hai ngày cuối tun, Ông An đi hết

( km), vậy ông An sẽ tốn chi ph là: 10000

( đồng ).

Vậy tổng số tiền ông An phải chi là: 8000

+ 10000

Theo bài ra ta có:

8000 10000 14.000.000 4 5 7000x y x y+   + 

b) Biểu diễn miền nghiệm của BPT ở câu a trên mặt phẳng tọa độ.

Ví dụ 3

BÀI GIẢI

BÀI TP RN LUYN

( )

: 4 5 7000d x y+=

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Một công ty kinh doanh thương mại chuẩn bị cho một đợt khuyến mại nhằm thu hút khách hàng bằng cách

tiến hành quảng cáo sản phẩm của công ty trên hệ thống phát thanh và truyền hình. Chi phí cho 1 phút quảng

cáo trên sóng phát thanh là 800.000 đồng, trên sóng truyền hình là 4.000.000 đồng. Công ty dự định chi tối

đa 16.000.000 đồng cho quảng cáo.

a) Gọi

và

ln lượt là số phút mà công ty thuê quảng cáo trên hệ thống phát thanh và truyền hình.

Viết bất phương trình biểu thị mối liên hệ gia

và

sao cho tổng số tiền công ty chi ph cho quảng cáo

không quá 16 triệu đồng.

b) Biểu diễn miền nghiệm của bất phương trình ở câu a trên mặt phẳng tọa độ.

Lời giải

.............................................................................................................................................................................................

Bài 3

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

distance

Dạng 1: Tm nghim ca BPT bc nht hai n

Phương pháp

 N󰈘 u

( )

;xy

là một nghiệm của

(1)

ax by c+

thì khi ta thay giá trị

;xy

vào biểu thức

( )

ta sẽ được một mệnh đề đúng.

CÂU 1: Trong các cặp số sau đây, cặp nào không là nghiệm của bất

phương trình

21xy+

( )

2;1−

. B.

( )

3; 7−

( )

0;1

. D.

( )

0;0

CÂU 2: Trong các cặp số sau đây, cặp nào không là nghiệm của bất

phương trình

4 5 0xy− + 

( )

5;0−

. B.

( )

2;1−

( )

1; 3−

. D.

( )

0;0

CÂU 3: Miền nghiệm của bất phương trình

( )

2 2 1 2 4x y x− + −  +

chứa điểm nào sau đây?

( )

1 ; 1 .A

( )

1; 5 .B

( )

4 ; 3 .C

( )

0 ; 4 .D

CÂU 4: Mệnh đề nào sau đây sai?

Miền nghiệm của bất phương trình

( ) ( )

2 2 2 2 1x y x− + + −  −

là nửa

mặt phẳng chứa điểm

( )

0;0

. B.

( )

1;1

( )

4;2

. D.

( )

1; 1−

CÂU 5: Mệnh đề nào sau đây đúng?

Miền nghiệm của bất phương trình

( ) ( )

3 1 4 2 5 3x y x− + −  −

là nửa

mặt phẳng chứa điểm

( )

0;0

. B.

( )

4;2−

( )

2;2−

. D.

( )

5;3−

Thà để giọt mồ hôi rơi trên

trang sách còn hơn để nước

mắt rơi ướt cả đề thi

distance

QUICK NOTE

.................................................

BI TP TRẮC NGHIM

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 6: Cho bất phương trình

2 4 5xy+

có tập nghiệm là

. Khẳng

định nào sau đây là khẳng định đúng ?

( )

1;1 S

. B.

( )

1;10 S

( )

1; 1 S−

. D.

( )

1;5 S

CÂU 7: Miền nghiệm của bất phương trình

3 2 0xy− + + 

không

chứa điểm nào sau đây?

( )

1 ; 2A

. B.

( )

2 ; 1B







. D.

( )

3 ; 1D

CÂU 8: Mệnh đề nào sau đây đúng?

Miền nghiệm của bất phương trình

( ) ( )

4 1 5 3 2 9x y x− + −  −

là nửa

mặt phẳng chứa điểm

( )

0;0

. B.

( )

1;1

( )

1;1−

. D.

( )

2;5

CÂU 9: Miền nghiệm của bất phương trình

( ) ( )

3 2 3 4 1 3x y x y+ +  + − +

là phần mặt phẳng chứa điểm nào?

( )

3;0

. B.

( )

3;1

( )

1;1

. D.

( )

0;0

CÂU 10: Cho bất phương trình

2 3 2 0xy− + + 

có tập nghiệm là

. Mệnh đề nào sau đây là đúng?

( )

1;1 S

. B.









( )

1; 2 S−

. D.

( )

1;0 S

CÂU 11: Cho bất phương trình

2 5 0xy− + 

có tập nghiệm là

Mệnh đề nào sau đây là đúng?

( )

2;2 S

. B.

( )

1;3 S

( )

2;2 S−

. D.

( )

2;4 S−

CÂU 12: Miền nghiệm của bất phương trình

3 2(2 5) 2(1 )x y x+ + +  −

không chứa điểm nào sau đây?

( )

1 ; 2A −−

. B.

;

11 11



−−





( )

0 ; 3C −

. D.

( )

4 ; 0D −

.................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 13: Miền nghiệm của bất phương trình

( )

5 2 9 2 2 7 x x y+ −  − +

là phần mặt phẳng không chứa điểm nào?

( )

2;1−

. B.

( )

2;3

( )

2; 1−

. D.

( )

0;0

CÂU 14: Miền nghiệm của bất phương trình

( ) ( )

1 3 1 3 2xy+ − − 

chứa điểm nào sau đây?

( )

1 ; 1A −

. B.

( )

1 ; 1B −−

( )

1; 1C −

. D.

( )

3 ; 3D −

CÂU 15: Miền nghiệm của bất phương trình

21xy+

không chứa

điểm nào sau đây?

( )

1 ; 1 .A

( )

2 ; 2B

( )

3 ; 3C

. D.

( )

1; 1D −−

CÂU 16: Cho bất phương trình

( ) ( )

3 1 4 2 5 3x y x− + −  −

. Khẳng

định nào dưới đây là khẳng định đúng?

A. Điểm

( )

0;0O

thuộc miền nghiệm của bất phương trình đã cho.

B. Điểm

( )

2;2B −

thuộc miền nghiệm của bất phương trình đã cho.

C. Điểm

( )

4;2C −

thuộc miền nghiệm của bất phương trình đã cho.

D. Điểm

( )

5;3D −

thuộc miền nghiệm của bất phương trình đã cho.

CÂU 17: Cho bất phương trình

( ) ( )

4 1 5 3 2 9x y x− + −  −

. Khẳng

định nào dưới đây là khẳng định đúng?

A. Điểm

( )

0;0O

thuộc miền nghiệm của bất phương trình đã cho.

B. Điểm

( )

1;1B

thuộc miền nghiệm của bất phương trình đã cho.

C. Điểm

( )

1;1C −

thuộc miền nghiệm của bất phương trình đã cho.

D. Điểm

( )

2;5D

thuộc miền nghiệm của bất phương trình đã cho.

CÂU 18: Cho bất phương trình

( ) ( )

3 2 2 5 2 1x y x+ + +  −

. Khẳng

định nào dưới đây là khẳng định sai?

A. Điểm

( )

3; 4A −−

thuộc miền nghiệm của bất phương trình đã cho.

B. Điểm

( )

2; 5B −−

thuộc miền nghiệm của bất phương trình đã cho.

C. Điểm

( )

1; 6C −−

thuộc miền nghiệm của bất phương trình đã cho.

D. Điểm

( )

0;0O

thuộc miền nghiệm của bất phương trình đã cho.

.................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 19: Cho bất phương trình

( ) ( )

− + + −  −2 2 2 2 1x y x

. Khẳng

định nào dưới đây là khẳng định sai?

A. Điểm

( )

0;0O

thuộc miền nghiệm của bất phương trình đã cho.

B. Điểm

( )

1;1B

thuộc miền nghiệm của bất phương trình đã cho.

C. Điểm

( )

4;2C

thuộc miền nghiệm của bất phương trình đã cho.

D. Điểm

( )

−1; 1D

thuộc miền nghiệm của bất phương trình đã cho.

CÂU 20: Bất phương trình

( )

3 – 2 – 1 0x y x +

tương đương với bất

phương trình nào sau đây?

–2 –2 0xy

. B.

5 –2 –2 0xy

5 –2 –1 0xy

. D.

4 –2 – 2 0xy

CÂU 21: Miền nghiệm của bất phương trình

( )

5 2 9 2 2 7x x y+ −  − +

không chứa điểm nào trong các điểm sau?

( )

0;0

. B.

( )

2; 1−

( )

2;1−

. D.

( )

2;3

CÂU 22: Cặp số nào sau đây không là nghiệm của bất phương trình

4 5 0xy− + 

( )

5;0−

. B.

( )

2;1−

( )

0;0

. D.

( )

1; 3−

CÂU 23: Cặp số nào sau đây không là nghiệm của bất phương trình

( )

5 2 1 0xy− − 

( )

0;1

. B.

( )

1;3

( )

–1;1

. D.

( )

–1;0

CÂU 24: Cặp số nào sau đây là nghiệm của bất phương trình

( )

–2 – 3x y y+

( )

4;–4

. B.

( )

2;1

( )

–1;–2

. D.

( )

4;4

CÂU 25: Điểm

( )

0;0O

thuộc miền nghiệm của bất phương trình

nào sau đây?

3 2 0xy+ + 

. B.

20xy+ + 

2 5 2 0xy+ − 

. D.

2 2 0xy+ + 

.................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 26: Cặp số

( )

2;3

là nghiệm của bất phương trình nào sau đây?

2 –3 –1 0xy

. B.

–0xy

43xy

. D.

–3 7 0xy+

CÂU 27: Cặp số

( )

1;–1

là nghiệm của bất phương trình nào sau

đây?

–3 0xy+

. B.

– – 0xy

3 1 0xy+ + 

. D.

– –3 –1 0xy

.................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 2: Biu din tp nghim ca BPT bc nht 2 n

Phương pháp

 󰉼󰉴󰉼󰈨 v󰉴 󰉼󰉴 󰈖 nêu trong b i t󰈨p T󰉼󰈨 lu󰈨n

CÂU 28: Miền nghiệm của bất phương trình

3 2 6xy+

là

A. B.

C. D.

CÂU 29: Miền nghiệm của bất phương trình

3 2 6xy− −

là

A. B.

C. D.

.................................................

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

1. H BT PHƯƠNG TRNH BC NHT HAI N

 Hệ bất phương trình bậc nhất hai ẩn l một h gm hai hoc nhiu bất phương trình bậc nhất hai.

 Nghiệm ca hệ bất phương trình bậc nhất hai ẩn l cp s

( )

;

tha mn tất c cc bất phương trình

c mt trong h đ cho.

 Miền nghiệm ca hệ là tập hợp cc điểm có tọa độ tha mãn mọi bất phương trình trong h.

Vậy min nghim của h là giao các min nghim của các bất phương trình trong h.

2. BIU DIN MIN NGHIM CA HPT BC NHT HAI N TRÊN MT PHNG TA Đ

 Để xc định min nghim của h, ta dùng phương php biểu diễn hình học như sau:

✓ Với mỗi BPT trong h, ta xc định min nghim của nó và gạch b (tô màu) min còn lại.

✓ Sau khi lm như trên lần lượt đi với tất c các bất phương trình trong h trên cùng một mt phẳng

tọa độ, min còn lại không bị gạch (tô màu) chính là min nghim của h bất phương trình đ cho.

3. NG DNG CA H BPT BC NHT HAI N

Phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức dạng

F ax by=+

( Trong đ x, y nghim đúng một h bất phương trình bậc nhất hai ẩn đ cho )

✓ Vẽ min nghim của h bất phương trình đ cho.

( Min nghim nhận được thường là một min đa gic )

✓ Tính giá trị của F ứng với là tọa độ cc đỉnh của min đa gic ni trên ri so sánh các kết

qu, từ đ suy ra gi trị lớn nhất, giá trị nh nhất của biểu thức.

( )

;xy

Bài H BT PHƯƠNG TRNH BC NHT HAI N

TÓM TẮT LÝ THUYẾT

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 1: Xc đnh h bt phương trnh bc nht hai n

H bất phương trình no sau đây l h BPT bậc nhất hai ẩn ?

0 0 2 3

) ) ) )

0 0

4 3 1

x x y z x y

a b c d



 + +  − + 



+





   



−

+







Ta c:

0 2 3

) )

4 3 1

x x y



 − + 









+





l h bất phương trình bậc nhất hai ẩn.

) )

x y z

+ + 



+







−



không phi l h bất phương trình bậc nhất hai ẩn vì:



+



−



chứa biến bậc hai

;

x y z

+ + 









chứa 3 ẩn

;;x y z

H bất phương trình no sau đây l h BPT bậc nhất hai ẩn ?

2 3 5

) 0 ) ) )

3 2 2

4 2 1 3

x y x

a y b c d

x y y

x y x





+  −



− + 

+

   



   

+

   

−  −

+  −





Lời giải

.............................................................................................................................................................................................

BI TP T LUN

Ví dụ 1

BÀI GIẢI

Bài 1.1

BÀI TP RN LUYN

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 2: Biu din tp nghim ca HBPT bc nht hai n trên mt phng ta đ

Biểu diễn min nghim của h bất phương trình hai ẩn

Vẽ cc đường thẳng và .

- Lấy điểm . Ta thấy tọa độ của tha mãn c bn bất

phương trình trong h.

- Min không bị gạch (min tứ giác OAIC, kể c bn cạnh của nó, với

, và , chứa điểm ) là min

Min biểu diễn nghim của h bất phương trình là một min đa gic.

Tính din tích S của đa gic đ.

Lời giải

.............................................................................................................................................................................................

+





+













( )

:3 6d x y+=

( )

:4d x y+=

( )

1;1M

( )

2;0A

( )

1;3I

( )

0;4C

−











+



Ví dụ 1

BÀI GIẢI

Bài 1.1

BÀI TP RN LUYN

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Biểu diễn nghim của h bất phương trình

2 3 6 0

2 3 1 0

+ − 





− − 









Lời giải

.............................................................................................................................................................................................

Biểu diễn nghim của h bất phương trình

2 2 10

2 4 12

+









+















Lời giải

.............................................................................................................................................................................................

Bài 1.2

Bài 1.3

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 3: ng dụng ca h bt phương trnh bc nht hai n

Một gia đình cần ít nhất 900 đơn vị protein v 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kg thịt bò chứa 800

đơn vị protein v 200 đơn vị lipit. Mỗi kg thịt lợn chứa 600 đơn vị protein v 400 đơn vị lipit. Biết rằng gia đình

này chỉ mua nhiu nhất 1,6 kg thịt bò và 1,1 kg thịt lợn, giá tin mỗi kg thịt bò là 250.000 đng, giá tin mỗi kg

thịt lợn l 85.000 đng. Hi chi phí ít nhất để mua thịt mỗi ngày của gia đình đ l bao nhiêu?

Gọi x và y lần lượt là s kg thịt bò và thịt lợn m gia đình đ mua mỗi ngy. Khi đ x và y phi tha mãn h bất

phương trình:

8 6 9

2 4 4

0 1,6

0 1,1

+





+













Lượng tin để mua thịt là:

250 85T x y=+

(nghìn đng).

Min nghim của h bất phương trình trên l min tứ giác ABCD với

( )

0,6;0,7A

( )

1,6;0,2B

( )

1,6;1,1C

và

( )

0,3;1,1D =

Tnh gi tr ca

250 85T x y=+

ti cc đnh A; B; C; D. Ta c: chi phí mua thịt ít nhất l 168.500 đng.

Ví dụ 1

BÀI GIẢI

BÀI TP RN LUYN

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Gọi a, b lần lượt là giá trị lớn nhất và giá trị nh nhất của biểu thức

L y x=−

, với x và y tha mãn h bất phương

trình

2 3 6 0

2 3 1 0

+ − 





− − 









. Tìm a, b?

Lời giải

.............................................................................................................................................................................................

Có ba nhóm máy A, B, C dùng để sn xuất ra hai loại sn phẩm I và II. Để sn xuất một đơn vị sn phẩm mỗi

loại phi lần lượt dùng các máy thuộc các nhóm khác nhau. S máy trong một nhóm và s máy của từng

nhóm cần thiết để sn xuất ra một đơn vị snphẩm thuộc mỗi loại được cho trong bng sau:

Mỗi đơn vị sn phẩm I li 3.000 đng,mỗi đơn vị

sn phẩm II li 5.000 đng. Để vic sn xuất hai

loại sn phẩm trên có lãi cao nhất thì cần dùng đến

mấy máy thuộc nhóm A?

Lời giải

.............................................................................................................................................................................................

Bài 1.1

Bài 1.2

Nhóm

S máy trong

mỗi nhóm

S máy trong từng nhm để sn

xuất ra một đơn vị sn phẩm

Loại I

Loại II

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

distance

Dạng 1: Tm nghim ca H BPT bc nht hai n

Phương pháp

 Bi󰈞 u di󰈞 n mi󰈚 n nghi󰈨m c󰈖 a h󰈨 BPT b󰈨c nh󰈘 t hai 󰈜 n trên m󰈨t

ph󰈤 ng t󰈨 a 󰈨.

✓ Ki󰈜 m tra  p  n n o thu󰈨c mi󰈚 n nghi󰈨m.

 G n 2 gi tr󰈨

( )

;xy

 đp n thnh 2 biến [v @trong MTCT.

✓ B󰈘 m t󰉼 ng BPT v ki󰈜 m tra.

CÂU 1: Câu nào sau đây đúng?.

Miền nghiệm ca hệ bất phương trình

2( 1) 4



+ − 



− + 











là phần mặt

phẳng chứa điểm

( )

2;1

. B.

( )

0;0

( )

1;1

. D.

( )

3;4

CÂU 2: Điểm nào sau đây không thuộc miền nghiệm ca hệ bất

phương trình

2 3 1 0

5 4 0

+ − 





− + 



( )

1;4−

. B.

( )

2;4−

( )

0;0

. D.

( )

3;4−

CÂU 3: Điểm nào sau đây thuộc miền nghiệm ca hệ bất phương

trình

2 5 1 0

2 5 0

− − 





+ + 





+ + 



( )

0;0

. B.

( )

1;0

( )

0; 2−

. D.

( )

0;2

Thà để giọt mồ hôi rơi trên

trang sch còn hơn để nước

mắt rơi ướt cả đề thi

distance

QUICK NOTE

....................................................

BI TP TRẮC NGHIM

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 4: Miền nghiệm ca hệ bất phương trình

3 3 0

−





− + 





+ − 



là phần

mặt phẳng chứa điểm

( )

5;3

. B.

( )

0;0

( )

1; 1−

. D.

( )

2;2−

CÂU 5: Miền nghiệm ca hệ bất phương trình

+





−





−







là phần

mặt phẳng chứa điểm

( )

0;0

. B.

( )

1;2

( )

2;1

. D.

( )

8;4

CÂU 6: Miền nghiệm ca bất phương trình

( ) ( )

3 2 3 4 1 3x y x y+ +  + − +

là phần mặt phẳng chứa điểm nào?

( )

3;0

. B.

( )

3;1

( )

1;1

. D.

( )

0;0

CÂU 7: Cho hệ bất phương trình

2 5 0

+





+



có tập nghiệm là

Khẳng đnh nào sau đây là khẳng đnh đúng?

( )

1;1 S

. B.

( )

1; 1 S− − 



−





. D.

;



−





CÂU 8: Cho hệ bất phương trình

3 1 0









+ + 





có tập nghiệm là

. Khẳng đnh nào sau đây là khẳng đnh đúng?

( )

1; 1 S−

. B.

( )

1; 3 S−

( )

1; 5 S−

. D.

( )

4; 3 S−

CÂU 9: Cho hệ bất phương trình

3 1 0









+ + 





có tập nghiệm là

. Khẳng đnh nào sau đây là khẳng đnh đúng?

( )

1;2 S−

. B.

( )

2;0 S

( )

1; 3 S−

. D.

( )

3;0 S

....................................................

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 10: Cho hệ bất phương trình

−







− + 





có tập nghiệm

Khẳng đnh nào sau đây là khẳng đnh đúng ?

( )

1; 2 S−

. B.

( )

2;1 S

( )

5; 6 S−

. D.

S =

CÂU 11: Cho hệ bất phương trình

4 3 2



−







−



có tập nghiệm

Khẳng đnh nào sau đây là khẳng đnh đúng ?



− − 





( )

 

; | 4 3 2S x y x= − =

C. Biểu diễn hình học ca

là nửa mặt phẳng chứa gốc tọa độ và kể

cả bờ

, với

là là đường thẳng

4 3 2xy−=

D. Biểu diễn hình học ca

là nửa mặt phẳng không chứa gốc tọa

độ và kể cả bờ

, với

là là đường thẳng

4 3 2xy−=

CÂU 12: Miền nghiệm ca hệ bất phương trình

−





+  −





−



chứa

điểm nào sau đây?

( )

1 ; 0A

. B.

( )

2 ; 3B −

( )

0 ; 1C −

. D.

( )

1; 0 .D −

CÂU 13: Miền nghiệm ca hệ bất phương trình

2 3 6 0

2 3 1 0

+ − 











− − 



chứa

điểm nào sau đây?

( )

1 ; 2 .A

( )

0 ; 2B

( )

1 ; 3C −

. D.

0 ; .



−





....................................................

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 14: Miền nghiệm ca hệ bất phương trình

2 1 0

3 5 0

−





− + 



chứa

điểm nào sau đây?

A. Không có. B.

; 2 .







( )

3 ; 1 .C −

; 10







CÂU 15: Miền nghiệm ca hệ bất phương trình

2 3 1 0

−





− + 



chứa

điểm nào sau đây?

( )

3 ; 4A

. B.

( )

4 ; 3B

( )

7 ; 4C

. D.

( )

4 ; 4 .D

CÂU 16: Miền nghiệm ca hệ bất phương trình

−





+  −



không

chứa điểm nào sau đây?

( )

1 ; 0 .A −

( )

1; 0 .B

( )

3 ; 4C −

. D.

( )

0 ; 3 .D

CÂU 17: Miền nghiệm ca hệ bất phương trình

3 2 6 0

2( 1) 4

− − 





− + 











không chứa điểm nào sau đây?

( )

2 ; 2A −

. B.

( )

3 ; 0 .B

( )

1 ; 1 .C −

( )

2 ; 3 .D −

CÂU 18: Miền nghiệm ca hệ bất phương trình

−





−  −





+



không

chứa điểm nào sau đây?

( )

3 ; 2 .A

( )

6 ; 3 .B

( )

6 ; 4 .C

( )

5 ; 4 .D

CÂU 19: Miền nghiệm ca hệ bất phương trình

−





+  −





+



không

chứa điểm nào sau đây?

( )

0 ; 1 .A

( )

1 ; 1 .B −

( )

3 ; 0 .C −

( )

3 ; 1 .D −

....................................................

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 2: Min nghim ca H BPT bc nht hai n

Phương pháp

 Bi󰈞 u di󰈞 n mi󰈚 n nghi󰈨m c󰈖 a h󰈨 BPT b󰈨c nh󰈘 t hai 󰈜 n trên m󰈨t

ph󰈤 ng t󰈨 a 󰈨. Ch󰈨 n  p  n.

 L󰈘 y 1 gi tr󰈨 thu󰈨c mi󰈚 n nghi󰈨m, thay v o ki󰈜 m tra c c b󰈘 t

ph󰉼󰉴nh trong h󰈨 󰉴󰈖  p  n.

CÂU 20: Cho hệ

2 3 5 (1)

5 (2)

+







+





. Gọi

là tập nghiệm ca bất

phương trình (1),

là tập nghiệm ca bất phương trình (2) và

là

tập nghiệm ca hệ thì

SS

SS=

SS

CÂU 21: Phần không gch chéo ở hình sau đây là biểu diễn miền

nghiệm ca hệ bất phương trình nào trong bốn hệ A, B, C, D ?

3 2 6







+



3 2 6







+  −



3 2 6







+



3 2 6







+  −



....................................................

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 22: Miền tam giác

ABC

kể cả ba cnh sau đây là miền nghiệm

ca hệ bết phương trình nào trong bốn bệ A, B, C, D ?

5 4 10







−





+



. B.

4 5 10

5 4 10







−





+



5 4 10

4 5 10







−





+



. D.

5 4 10

4 5 10







−





+



CÂU 23: Giá tr nhỏ nhất ca biết thức

F y x=−

trên miền xc đnh

bởi hệ

−





−





+



là.

min 1F =

khi

2, 3xy==

min 2F =

khi

0, 2xy==

min 3F =

khi

1, 4xy==

min 0F =

khi

0, 0xy==

CÂU 24: Giá tr nhỏ nhất ca biết thức

F y x=−

trên miền xc đnh

bởi hệ

+





−





+  −



là

min 3F =−

khi

1, 2xy= = −

min 0F =

khi

0, 0xy==

min 2F =−

khi

xy= = −

min 8F =

khi

2, 6xy= − =

....................................................

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 25: Cho hệ bất phương trình

3 5 15

−





+













. Khẳng đnh nào sau

đây là khẳng đnh sai ?

A. Trên mặt phẳng tọa độ

Oxy

, biểu diễn miền nghiệm ca hệbất

phương trình đã cho là miền tứ giác

ABCO

kể cả các cnh với

( )

0;3A

25 9

;







( )

2;0C

và

( )

0;0O

B. Đường thẳng

: x y m + =

c giao điểm với tứ giác

ABCO

kể cả

khi

m−  

C. Giá tr lớn nhất ca biểu thức

xy+

, với

và

thỏa mãn hệ bất

phương trình đã cho là

D. Giá tr nhỏ nhất ca biểu thức

xy+

, với

và

thõa mãn hệ bất

phương trình đã cho là 0.

....................................................

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 3: ng dụng ca H BPT bc nht hai n

Phương pháp

 Bi󰈞 u di󰈞 n mi󰈚 n nghi󰈨m c󰈖 a h󰈨 BPT b󰈨c nh󰈘 t hai 󰈜 n trên m󰈨t

ph󰈤 ng t󰈨 a 󰈨.

 Tnh gi tr󰈨 bi󰈜 u th󰉼 c

( )

;F x y

tại cc đỉnh của đa gic v kết luận.

CÂU 26: Giá tr lớn nhất ca biết thức

( )

;2F x y x y=+

với điều kiện

2 10 0













− − 



+ − 



là

. B.

. D.

CÂU 27: Giá tr nhỏ nhất ca biết thức

( )

;2F x y x y=−

với điều kiện













+ − 



− − 



là

10−

. B.

8−

. D.

6−

CÂU 28: Biểu thức

–F y x=

đt giá tr nhỏ nhất với điều kiện

− +  −





−





+







ti điểm

( )

;S x y

có to độ là

( )

4;1

. B.

( )

3;1

( )

2;1

. D.

( )

1;1

CÂU 29: Biểu thức

L y x=−

, với

và

thõa mãn hệ bất phương

trình

2 3 6 0

2 3 1 0

+ − 











− − 



, đt giá tr lớn nhất là

và đt giá tr nhỏ nhất

là

. Hãy chọn kết quả đúng trong cc kết quả sau:

a =

và

2b =−

. B.

2a =

và

b =−

3a =

và

0b =

. D.

3a =

và

−

....................................................

Bấm Tải xuống để xem toàn bộ.

| 1/28

| | Tải xuống

Preview text:

CHƯƠNG II: BẤT PHƯƠNG TRÌNH
VÀ HỆ BPT BẬC NHẤT NHIỀU ẨN Ⓐ -
1. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN 69
2. BIỂU DIỄN MIỀN NGHIỆM CỦA BẤT PHƯƠNG 70
TRÌNH BẬC NHẤT HAI ẨN TRÊN MẶT PHẲNG TỌA ĐỘ Ⓑ
DẠNG 1: Xác định Bất phương trình bậc nhất hai ẩn 71
DẠNG 2: : Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn 72
DẠNG 3: Bài toán thực tế 73 Ⓒ
DẠNG 1: : Tìm nghiệm của bất phương trình bậc nhất hai ẩn 75
DẠNG 2: Biểu diễn tập nghiệm của bất phương trình bậc nhất hai ẩn 80 Ⓐ -
1. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN 81
2. BIỂU DIỄN MIỀN NGHIỆM CỦA HỆ BẤT PHƯƠNG 81
TRÌNH BẬC NHẤT HAI ẨN TRÊN MẶT PHẲNG TỌA ĐỘ
3. ỨNG DỤNG CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC 81 NHẤT HAI ẨN Ⓑ
DẠNG 1: Xác định Hệ bất phương trình bậc nhất hai ẩn 82
DẠNG 2: : Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn 83
DẠNG 3: Ứng dựng của hệ bất phương trình bậc nhất hai ẩn 85 Ⓒ
DẠNG 1: : Tìm nghiệm của Hệ bất phương trình bậc nhất hai ẩn 87
DẠNG 2: Miền nghiệm của Hệ bất phương trình bậc nhất hai ẩn 91
DẠNG 3: Ứng dựng của hệ bất phương trình bậc nhất hai ẩn 94
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10 Chương
BẤT PHƯƠNG TRÌNH
2 VÀ HỆ BẤT PHƯƠNG TRÌNH
BẬC NHẤT HAI ẨN Bài 3
BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
A TÓM TẮT LÝ THUYẾT
1. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Định nghĩa
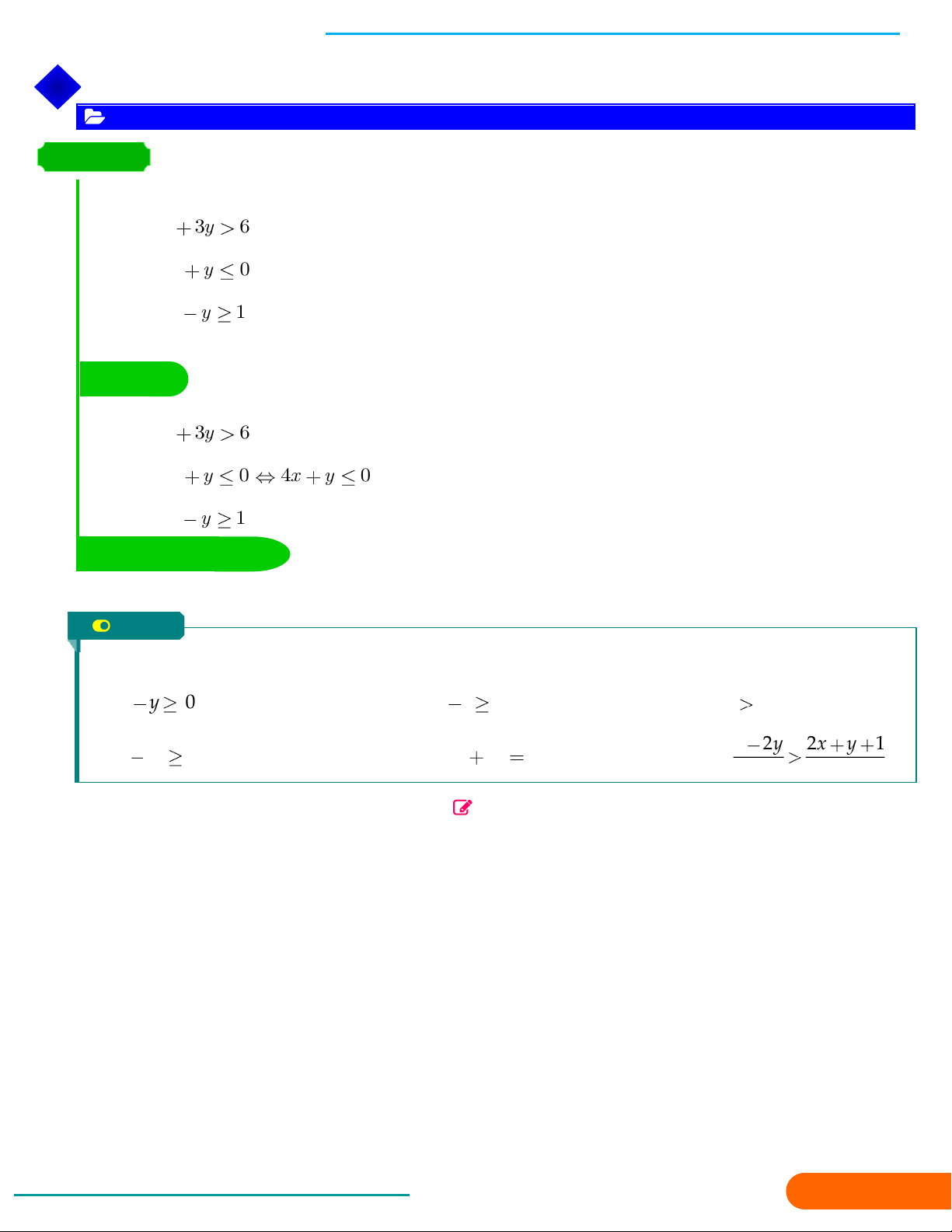
 Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là ax +by  c
(hoặc ax +by  c ; ax +by  ;
c ax +by  c )
Trong đó a, b, c là các hệ số, a và b không đồng thời bằng 0, x và y là các ẩn số.
 Cặp số ( x ; y
ax + by  c 0 0 ) sao cho “
” là mệnh đề đúng được gọi là một nghiệm của bất 0 0
phương trình ax +by  c .
 Nghiệm của các bất phương trình dạng ax by c,ax by c,ax by c cũng được định nghĩa tương tự.
 Trong mặt phẳng tọa độ thì mỗi nghiệm của bất phương trình bậc nhất hai ẩn được biểu diễn
bởi một điểm và tập nghiệm của nó được biểu diễn bởi một tập hợp điểm. Ta gọi tập hợp điểm ấy
là miền nghiệm của bất phương trình.
Ví dụ: Ta có các bất phương trình bậc nhất hai ẩn như sau: a) 2x y 0 . d) 2x y 0 b) 2x y 0 e) 2x y 0 x 2y 2x y 1 c) 2x y 3 f) 2 3 69
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
2. BIỂU DIỄN MIỀN NGHIỆM CỦA BPT BẬC NHẤT HAI ẨN TRÊN MẶT PHẲNG TỌA ĐỘ Định nghĩa
 Định lí : Trong mặt phẳng tọa độ đường thẳng d : ax by c 0 chia mặt phẳng thành hai nửa mặt
phẳng. Một trong hai nửa mặt phẳng ấy (không kể bờ (d)) gồm các điểm có tọa độ thỏa mãn
bất phương trình ax by c 0 , nửa mặt phẳng còn lại (không kể bờ (d)) gồm các điểm có
tọa độ thỏa mãn bất phương trình ax by c 0.
 Vậy để xác định miền nghiệm của bất phương trình ax by c 0, ta có quy tắc thực hành biểu
diễn hình học tập nghiệm (hay biểu diễn miền nghiệm) như sau:  Bước 1. (1)
Vẽ đường thẳng (d): ax by c 0 .
• Cho x = x (Với x = 1 giá trị nào đó ). Thay vào (1) ta tìm được giá trị y . 1 1 1
Vậy ta được điểm A(x ; y thuộc đường thẳng (d ) . 1 1 )
• Tương tự: Cho x = x . Thay vào (1) ta tìm được giá trị y . 2 2
Vậy ta được điểm B(x ; y thuộc đường thẳng (d ) . 2 2 )
Kẻ đường thẳng đi qua A và B. Ta được đường thằng (d ) cần tìm.
⚠ Chú ý: - Ta có thể cho y để tìm x .
- Thường thì ta sẽ cho x = 0 để tìm y. Hoặc cho y = 0 để tìm x .
 Bước 2. Lấy một điểm M x ; y 0 ( 0
0 ) không thuộc Δ (ta thường lấy gốc tọa độ O).
 Bước 3. Tính ax + by và so sánh ax + by với c. 0 0 0 0 • Nếu ax by c
0 thì nửa mặt phẳng (không kể bờ (d)) chứa điểm M là miền nghiệm 0 0
của bất phương trình ax by c 0. • Nếu ax by c
0 thì nửa mặt phẳng (không kể bờ (d)) không chứa điểm M là miền 0 0
nghiệm của bất phương trình ax by c 0.
⚠ Chú ý: Đối với các bất phương trình dạng ax by c 0 hoặc ax by c 0 thì miền nghiệm là
nửa mặt phẳng kể cả bờ. 70
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
B BÀI TẬP TỰ LUẬN
Dạng 1: Xác định bất phương trình bậc nhất 2 ẩn Ví dụ 1
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn: a) 2x 3y 6 b) 2 2 x y 0 c) 2 2x y 1 BÀI GIẢI a) 2x 3y
6 là bất phương trình bậc nhất 2 ẩn. Với a = 2;b = 3;c = 6. b) 2 2 x y 0 4x y
0 là bất phương trình bậc nhất 2 ẩn. Với 4 = 2;b =1;c = 0. c) 2 2x y
1 không phải là bất phương trình bậc nhất 2 ẩn. Vì chứa 2 x ( bậc hai )
BÀI TẬP RÈN LUYỆN Bài 1
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn: a) 2x y 0 . b) y 2 . c) x 0. x 2y 2x y 1 d) 2 x y 0 e) 3x 4y 7 f) 2 3 Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 71
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
Dạng 2: Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn? Ví dụ 1
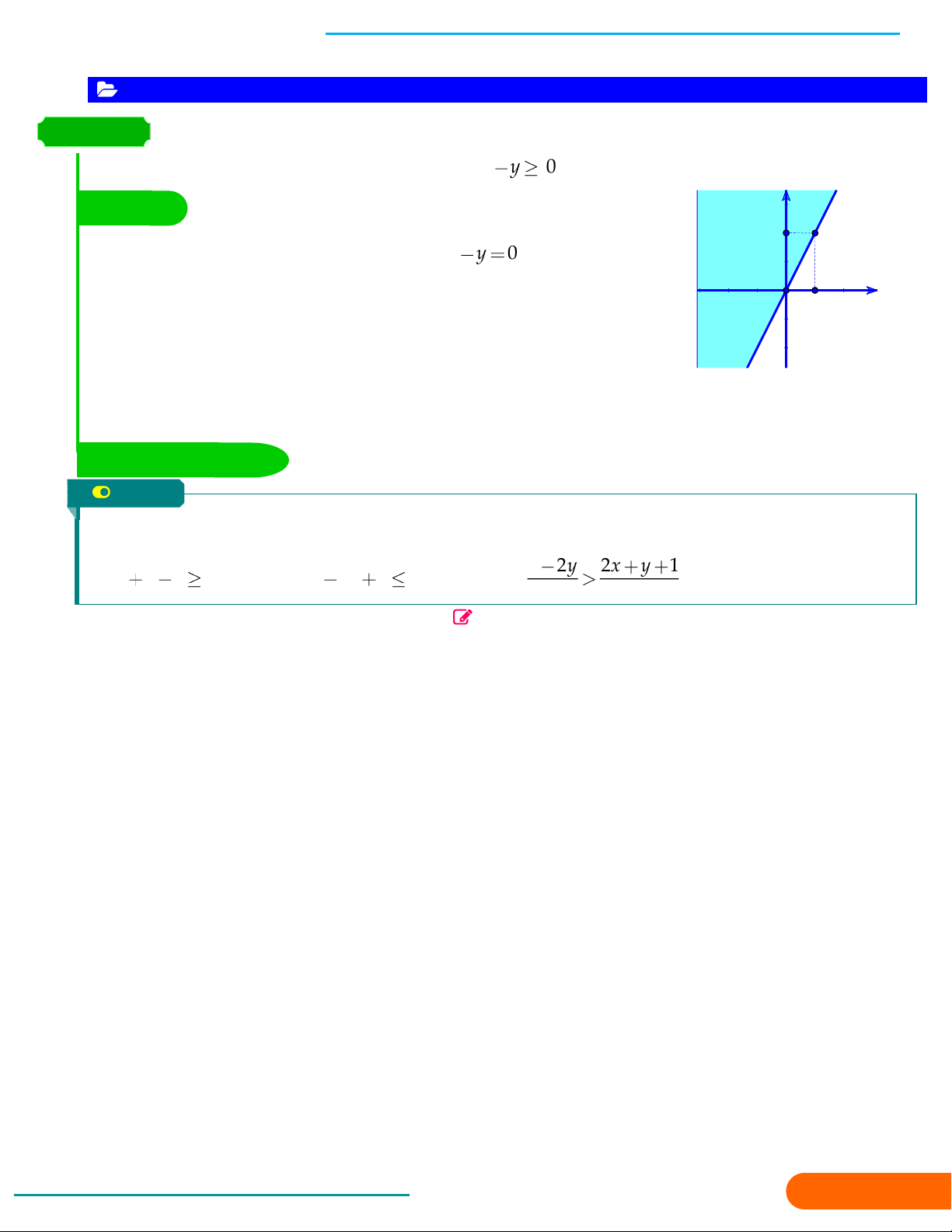
Xác định miền nghiệm của bất phương trình : 2x y 0 . y BÀI GIẢI 2
Trong mặt phẳng tọa độ, vẽ đường thẳng d : 2x y 0 .
Ta có d chia mặt phẳng thành hai nửa mặt phẳng. O 1 x
Chọn một điểm bất kì không thuộc đường thẳng đó, chẳng hạn điểm M 1;0 . (d)
Ta thấy (1; 0) là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng chứa bờ (d)
và chứa điểm M 1;0 (Miền không được tô màu trên hình vẽ).
BÀI TẬP RÈN LUYỆN Bài 2
Xác định miền nghiệm của bất phương trình : x 2y 2x y 1 a) x
y 2 0 b) x 3y 3 0 c) . 2 3 Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 72
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
Dạng 3: Bài toán thực tế Ví dụ 3
Ông An muốn thuê một chiếc xe ô-tô ( có lái xe ) trong một tuần. Giá thuê xe được cho như bảng sau: Phí cố định
Phí tính theo quãng đường di chuyển ( Nghìn đồng/ngày ) ( Nghìn đồng/km )
Từ thứ Hai đến thứ Sáu 900 8 Thứ Bảy và Chủ nhật 1500 10
a) Gọi x và y lần lượt là số kilomet ông An đi trong các ngày từ thứ Hai đến thứ Sáu và trong hai ngày cuối
tuần. Viết bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng.
b) Biểu diễn miền nghiệm của bất phương trình ở câu a trên mặt phẳng tọa độ. BÀI GIẢI
a) Từ thứ Hai đến thứ Sáu. 1 km di chuyển có chi phí là 8000 ( đồng ). Ông An đi hết x ( km), vậy ông An sẽ
tốn chi phí là: 8000 x ( đồng ).
Tương tự : Vào hai ngày cuối tuần, Ông An đi hết y ( km), vậy ông An sẽ tốn chi phí là: 10000 y ( đồng ).
Vậy tổng số tiền ông An phải chi là: 8000 x + 10000 y .
Theo bài ra ta có: 8000x +10000y 14.000.000 4x +5y  7000
b) Biểu diễn miền nghiệm của BPT ở câu a trên mặt phẳng tọa độ.
(d): 4x+5y = 7000
BÀI TẬP RÈN LUYỆN 73
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10 Bài 3
Một công ty kinh doanh thương mại chuẩn bị cho một đợt khuyến mại nhằm thu hút khách hàng bằng cách
tiến hành quảng cáo sản phẩm của công ty trên hệ thống phát thanh và truyền hình. Chi phí cho 1 phút quảng
cáo trên sóng phát thanh là 800.000 đồng, trên sóng truyền hình là 4.000.000 đồng. Công ty dự định chi tối
đa 16.000.000 đồng cho quảng cáo.
a) Gọi x và y lần lượt là số phút mà công ty thuê quảng cáo trên hệ thống phát thanh và truyền hình.
Viết bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền công ty chi phí cho quảng cáo
không quá 16 triệu đồng.
b) Biểu diễn miền nghiệm của bất phương trình ở câu a trên mặt phẳng tọa độ. Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 74
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
C BÀI TẬP TRẮC NGHIỆM distance
Dạng 1: Tìm nghiệm của BPT bậc nhất hai ẩn
Thà để giọt mồ hôi rơi trên Phương pháp
trang sách còn hơn để nước
 Nếu (x ; y là một nghiệm của (1)
ax + by  c thì khi ta thay giá trị
mắt rơi ướt cả đề thi 1 1 ) distance
x ; y vào biểu thức ( )
1 ta sẽ được một mệnh đề đúng. QUICK NOTE 1 1
.................................................
CÂU 1: Trong các cặp số sau đây, cặp nào không là nghiệm của bất .................................................
phương trình 2x + y 1?
.................................................
................................................. A. ( 2 − ; ) 1 . B. (3; 7 − ).
................................................. C. (0; ) 1 . D. (0;0) .
.................................................
.................................................
CÂU 2: Trong các cặp số sau đây, cặp nào không là nghiệm của bất .................................................
phương trình x − 4y +5  0?
.................................................
................................................. A. ( 5 − ;0). B. ( 2 − ; ) 1 .
................................................. C. (1; ) 3 − . D. (0;0) .
.................................................
.................................................
CÂU 3: Miền nghiệm của bất phương trình x − 2+ 2( y − )
1  2x + 4 .................................................
chứa điểm nào sau đây?
.................................................
................................................. A. A(1 ; ) 1 . B. B(1 ; ) 5 .
................................................. C. C(4 ; ) 3 .
D. D(0 ; 4).
.................................................
.................................................
CÂU 4: Mệnh đề nào sau đây sai?
.................................................
.................................................
Miền nghiệm của bất phương trình −x + 2 + 2( y − 2)  2(1− x) là nửa ................................................. mặt phẳng chứa điểm
................................................. A.
................................................. (0;0) . B. (1; ) 1 .
................................................. C. (4;2). D. (1; ) 1 − .
.................................................
.................................................
CÂU 5: Mệnh đề nào sau đây đúng?
.................................................
.................................................
Miền nghiệm của bất phương trình 3(x − )
1 + 4( y −2)  5x −3 là nửa .................................................
mặt phẳng chứa điểm
................................................. A. (0;0) . B. ( 4 − ;2) .
................................................. C.
................................................. ( 2 − ;2) . D. ( 5 − ; ) 3 .
.................................................
.................................................
................................................. 75
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
CÂU 6: Cho bất phương trình 2x +4y  5có tập nghiệm là S . Khẳng .................................................
định nào sau đây là khẳng định đúng ?
................................................. A.
................................................. (1; ) 1 S .
B. (1;10)S .
................................................. C. (1;− ) 1 S . D. (1; ) 5 S .
.................................................
.................................................
CÂU 7: Miền nghiệm của bất phương trình 3
− x + y +2  0 không .................................................
chứa điểm nào sau đây?
.................................................
A. A(1 ; 2). B. B(2 ; ) 1 .
.................................................  1 
................................................. C. C 1 ;  . D. D(3 ; ) 1 . 2   
.................................................
.................................................
CÂU 8: Mệnh đề nào sau đây đúng?
.................................................
Miền nghiệm của bất phương trình 4(x − ) 1 +5( y − )
3  2x −9 là nửa .................................................
.................................................
mặt phẳng chứa điểm
................................................. A. (0;0) . B. (1; ) 1 .
................................................. C. ( 1 − ; ) 1 . D. (2;5) .
.................................................
................................................. CÂU 9: Miền nghiệm của bất phương
trình ................................................. 3x + 2( y + ) 3  4(x + )
1 − y +3 là phần mặt phẳng chứa điểm nào?
................................................. A.
................................................. (3;0) . B. (3; ) 1 .
................................................. C. (1; ) 1 . D. (0;0) .
.................................................
.................................................
CÂU 10: Cho bất phương trình 2
− x + 3y + 2  0 có tập nghiệm là .................................................
S . Mệnh đề nào sau đây là đúng?
.................................................  
................................................. A. 2 (1; ) 1 S . B.  ;0S  . 2   
.................................................
................................................. C. (1; 2 − )S . D. (1;0)S .
................................................. CÂU 11:
.................................................
Cho bất phương trình x − 2y +5  0có tập nghiệm là S . .................................................
Mệnh đề nào sau đây là đúng?
.................................................
A. (2;2)S . B. (1; ) 3 S .
................................................. C. ( 2 − ;2)S . D. ( 2 − ;4)S .
.................................................
................................................. CÂU 12: Miền nghiệm của bất phương
trình .................................................
x +3+2(2y +5)  2(1− )
x không chứa điểm nào sau đây?
.................................................  1 2 
................................................. A. A( 1 − ; − 2). B. B − ; −  . 11 11  
.................................................
................................................. C. C(0 ; − ) 3 . D. D( 4 − ; 0).
................................................. 76
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10 CÂU 13: Miền nghiệm của bất phương
trình .................................................
.................................................
5(x + 2) −9  2x −2y +7 là phần mặt phẳng không chứa điểm nào? ................................................. A. ( 2 − ; ) 1 . B. (2; ) 3 .
................................................. C. (2; ) 1 − . D. (0;0) .
.................................................
.................................................
CÂU 14: Miền nghiệm của bất phương trình (1+ 3) x −(1− 3) y  2 .................................................
.................................................
chứa điểm nào sau đây?
................................................. A. A(1 ; − ) 1 . B. B( 1 − ; − ) 1 .
................................................. C.
................................................. C ( 1 − ; ) 1 .
D. D(− 3 ; 3).
.................................................
CÂU 15: Miền nghiệm của bất phương trình 2x + y 1 không chứa .................................................
.................................................
điểm nào sau đây?
................................................. A. A(1 ; ) 1 .
B. B(2 ; 2) .
................................................. C. C(3 ; ) 3 . D. D( 1 − ; − ) 1 .
.................................................
.................................................
CÂU 16: Cho bất phương trình 3(x − )
1 + 4( y −2)  5x −3. Khẳng .................................................
định nào dưới đây là khẳng định đúng?
................................................. A.
.................................................
Điểm O(0;0) thuộc miền nghiệm của bất phương trình đã cho.
................................................. B. Điểm B( 2
− ;2) thuộc miền nghiệm của bất phương trình đã cho. ................................................. C. Điểm C ( 4
− ;2) thuộc miền nghiệm của bất phương trình đã cho. .................................................
................................................. D. Điểm D( 5 − ; )
3 thuộc miền nghiệm của bất phương trình đã cho. ................................................. CÂU 17:
.................................................
Cho bất phương trình 4(x − ) 1 +5( y − )
3  2x −9 . Khẳng .................................................
định nào dưới đây là khẳng định đúng?
.................................................
A. Điểm O(0;0) thuộc miền nghiệm của bất phương trình đã cho. .................................................
B. Điểm B(1; )
1 thuộc miền nghiệm của bất phương trình đã cho.
.................................................
................................................. C. Điểm C( 1 − ; )
1 thuộc miền nghiệm của bất phương trình đã cho. .................................................
D. Điểm D(2;5) thuộc miền nghiệm của bất phương trình đã cho. .................................................
.................................................
CÂU 18: Cho bất phương trình x +3+ 2(2y +5)  2(1− x). Khẳng .................................................
định nào dưới đây là khẳng định sai?
................................................. A.
................................................. Điểm A( 3 − ; 4
− ) thuộc miền nghiệm của bất phương trình đã cho. ................................................. B. Điểm B( 2 − ; 5
− ) thuộc miền nghiệm của bất phương trình đã cho. ................................................. C. Điểm C( 1 − ; 6
− ) thuộc miền nghiệm của bất phương trình đã cho. .................................................
.................................................
D. Điểm O(0;0) thuộc miền nghiệm của bất phương trình đã cho. ................................................. 77
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10 CÂU 19:
.................................................
Cho bất phương trình −x + 2 + 2(y −2)  2(1− x) . Khẳng .................................................
định nào dưới đây là khẳng định sai?
.................................................
A. Điểm O(0;0) thuộc miền nghiệm của bất phương trình đã cho. .................................................
B. Điểm B(1; )
1 thuộc miền nghiệm của bất phương trình đã cho.
.................................................
.................................................
C. Điểm C(4;2) thuộc miền nghiệm của bất phương trình đã cho. .................................................
D. Điểm D(1;− )
1 thuộc miền nghiệm của bất phương trình đã cho. .................................................
.................................................
CÂU 20: Bất phương trình 3x – 2( y – x + )
1  0 tương đương với bất .................................................
phương trình nào sau đây?
................................................. A.
.................................................
x – 2y – 2  0.
B. 5x – 2y – 2  0 .
.................................................
C. 5x – 2y –1 0.
D. 4x – 2y – 2  0.
.................................................
CÂU 21: Miền nghiệm của bất phương trình 5(x + 2) −9  2x −2y +7 .................................................
.................................................
không chứa điểm nào trong các điểm sau?
................................................. A. (0;0) . B. (2; ) 1 − .
................................................. C. ( 2 − ; ) 1 . D. (2; ) 3 .
.................................................
.................................................
CÂU 22: Cặp số nào sau đây không là nghiệm của bất phương trình ................................................. x −4y +5 0?
................................................. A.
................................................. ( 5 − ;0). B. ( 2 − ; ) 1 .
................................................. C. (0;0) . D. (1; ) 3 − .
.................................................
.................................................
CÂU 23: Cặp số nào sau đây không là nghiệm của bất phương trình .................................................
5x − 2( y − ) 1  0 ?
................................................. A. (0; ) 1 . B. (1;3).
.................................................
................................................. C. (–1; ) 1 . D. (–1;0).
.................................................
CÂU 24: Cặp số nào sau đây là nghiệm của bất phương trình .................................................
–2(x – y) + y  3
................................................. ?
................................................. A. (4;–4) . B. (2; ) 1 .
.................................................
C. (–1;–2) . D. (4;4).
.................................................
.................................................
CÂU 25: Điểm O(0;0) thuộc miền nghiệm của bất phương trình .................................................
................................................. nào sau đây?
.................................................
A. x +3y +2  0.
B. x + y + 2  0.
.................................................
C. 2x +5y −2  0.
D. 2x+ y +2  0.
.................................................
................................................. 78
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10 CÂU 26:
................................................. Cặp số (2; )
3 là nghiệm của bất phương trình nào sau đây? .................................................
A. 2x –3y –1 0.
B. x – y  0.
.................................................
C. 4x  3y.
D. x –3y +7  0.
.................................................
.................................................
CÂU 27: Cặp số (1; – )
1 là nghiệm của bất phương trình nào sau ................................................. đây?
.................................................
A. x+ y –3 0.
B. –x – y  0.
................................................. C.
.................................................
x +3y +1 0.
D. –x –3y –1 0.
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
................................................. 79
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
Dạng 2: Biểu diễn tập nghiệm của BPT bậc nhất 2 ẩn
.................................................
................................................. Phương pháp
.................................................
 Tương tự với Phương pháp đả nêu trong bài tạ p Tự luạ n
................................................. CÂU 28:
.................................................
Miền nghiệm của bất phương trình 3x + 2y  6 là
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
................................................. A. B.
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
................................................. C. D.
.................................................
CÂU 29: Miền nghiệm của bất phương trình 3x −2y  6 − là
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
................................................. A. B.
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
.................................................
................................................. C. D.
.................................................
.................................................
.................................................
................................................. 80
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10 Bài 4
HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
A TÓM TẮT LÝ THUYẾT
1. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
 Hệ bất phương trình bậc nhất hai ẩn là một hệ gồm hai hoặc nhiều bất phương trình bậc nhất hai.
 Nghiệm của hệ bất phương trình bậc nhất hai ẩn là cặp số (x ; y thỏa mãn tất cả các bất phương trình o o )
có mặt trong hệ đả cho.
 Miền nghiệm của hệ là tập hợp các điểm có tọa độ thỏa mãn mọi bất phương trình trong hệ.
Vậy miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ.
2. BIỂU DIỄN MIỀN NGHIỆM CỦA HPT BẬC NHẤT HAI ẨN TRÊN MẶT PHẲNG TỌA ĐỘ
 Để xác định miền nghiệm của hệ, ta dùng phương pháp biểu diễn hình học như sau:
✓ Với mỗi BPT trong hệ, ta xác định miền nghiệm của nó và gạch bỏ (tô màu) miền còn lại.
✓ Sau khi làm như trên lần lượt đối với tất cả các bất phương trình trong hệ trên cùng một mặt phẳng
tọa độ, miền còn lại không bị gạch (tô màu) chính là miền nghiệm của hệ bất phương trình đã cho.
3. ỨNG DỤNG CỦA HỆ BPT BẬC NHẤT HAI ẨN
Phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức dạng F = ax +by .
( Trong đó x, y nghiệm đúng một hệ bất phương trình bậc nhất hai ẩn đã cho )
✓ Vẽ miền nghiệm của hệ bất phương trình đã cho.
( Miền nghiệm nhận được thường là một miền đa giác )
✓ Tính giá trị của F ứng với ( ;
x y) là tọa độ các đỉnh của miền đa giác nói trên rồi so sánh các kết
quả, từ đó suy ra giá trị lớn nhất, giá trị nhỏ nhất của biểu thức. 81
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
B BÀI TẬP TỰ LUẬN
Dạng 1: Xác định hệ bất phương trình bậc nhất hai ẩn Ví dụ 1
Hệ bất phương trình nào sau đây là hệ BPT bậc nhất hai ẩn ? 2 2 x  0 x + y  0
x + y + z  0  2 − x + y  3 a)  ) b  ) c  d)  2 y  0 y − x 1  y  0 4
 x +3y 1 BÀI GIẢI Ta có: 2 x  0  2 − x + y  3 a)  d) 
là hệ bất phương trình bậc nhất hai ẩn. 2 y  0
4 x +3y 1 2 x + y  0
x + y + z  0 ) b  c) 
không phải là hệ bất phương trình bậc nhất hai ẩn vì: y − x 1  y  0 2 x + y  0
x + y + z  0  chứa biến bậc hai 2 y ;  chứa 3 ẩn ; x ; y z y − x 1  y  0
BÀI TẬP RÈN LUYỆN Bài 1.1
Hệ bất phương trình nào sau đây là hệ BPT bậc nhất hai ẩn ? 2 x  0
x + 2 y  3x −5  x + 3  1   x +  0  5 − x + y  a) y  0 ) b  c) 1  2 d)  2 x + 1        −  −  2 t 1 3x 2y 2 2 y
4 x + 2y 1− 3x Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 82
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 2: Biễu diễn tập nghiệm của HBPT bậc nhất hai ẩn trên mặt phẳng tọa độ Ví dụ 1 3  x + y  6 x+ y  4
Biểu diễn miền nghiệm của hệ bất phương trình hai ẩn  x  0  y  0 BÀI GIẢI
Vẽ các đường thẳng (d :3x + y = 6
(d : x+ y = 4 2 ) 1 ) và . - Lấy điểm M 1;1 M 0 (
). Ta thấy tọa độ của thỏa mãn cả bốn bất 0 phương trình trong hệ.
- Miền không bị gạch (miền tứ giác OAIC, kể cả bốn cạnh của nó, với A(2;0) , I (1; )
3 và C (0;4), chứa điểm M ) là miền 0
BÀI TẬP RÈN LUYỆN Bài 1.1 y  2 − 
Miền biểu diễn nghiệm của hệ bất phương trình x  2
là một miền đa giác. 2x + y  8 
Tính diện tích S của đa giác đó. Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 83
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10 Bài 1.2
2x + 3y − 6  0 
Biểu diễn nghiệm của hệ bất phương trình 2x −3y −1 0 ? x  0  Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. Bài 1.3 2x + 2y 10 2y  4 
Biểu diễn nghiệm của hệ bất phương trình 2x + 4y 12 ? x  0  y  0  Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 84
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 3: Ứng dụng của hệ bất phương trình bậc nhất hai ẩn Ví dụ 1
Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kg thịt bò chứa 800
đơn vị protein và 200 đơn vị lipit. Mỗi kg thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình
này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn, giá tiền mỗi kg thịt bò là 250.000 đồng, giá tiền mỗi kg
thịt lợn là 85.000 đồng. Hỏi chi phí ít nhất để mua thịt mỗi ngày của gia đình đó là bao nhiêu? BÀI GIẢI
Gọi x và y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó mua mỗi ngày. Khi đó x và y phải thỏa mãn hệ bất 8  x + 6y  9
2x+4y  4 phương trình:  . 0  x 1,6 0 y1,1
Lượng tiền để mua thịt là: T = 250x +85y (nghìn đồng).
Miền nghiệm của hệ bất phương trình trên là miền tứ giác ABCD với A(0,6;0,7) , B(1,6;0,2) , C(1,6;1 ) ,1 và D = (0,3;1 ) ,1 .
Tính giá trị của T = 250x +85y tại các đỉnh A; B; C; D. Ta có: chi phí mua thịt ít nhất là 168.500 đồng. B
ÀI TẬP RÈN LUYỆN 85
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10 Bài 1.1
Gọi a, b lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức L = y − x , với x và y thỏa mãn hệ bất phương
2x + 3y − 6  0 
trình 2x −3y −1 0 . Tìm a, b? x  0  Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. Bài 1.2
Có ba nhóm máy A, B, C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản phẩm mỗi
loại phải lần lượt dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của từng
nhóm cần thiết để sản xuất ra một đơn vị sảnphẩm thuộc mỗi loại được cho trong bảng sau:
Mỗi đơn vị sản phẩm I lãi 3.000 đồng,mỗi đơn vị
Số máy trong từng nhóm để sản Số máy trong Nhóm
xuất ra một đơn vị sản phẩm
sản phẩm II lãi 5.000 đồng. Để việc sản xuất hai mỗi nhóm Loại I Loại II
loại sản phẩm trên có lãi cao nhất thì cần dùng đến A 10 2 2 mấy máy thuộc nhóm A? B 4 0 2 C 12 2 4 Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 86
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
C BÀI TẬP TRẮC NGHIỆM distance
Dạng 1: Tìm nghiệm của Hệ BPT bậc nhất hai ẩn
Thà để giọt mồ hôi rơi trên
trang sách còn hơn để nước Phương pháp
mắt rơi ướt cả đề thi
 Biễu diễn miền nghiê ̣m của hê ̣ BPT bậ c nhất hai ẩn trên mậ t distance QUICK NOTE phẩng tọa đo ̣.
....................................................
✓ Kiểm tra đấp ấn nầo thuo ̣c miền nghiê ̣m.
....................................................
 Gấn 2 giấ trị (x ; y ở đáp án thành 2 biến [và @trong MTCT.
.................................................... 1 1 )
....................................................
✓ Bấm từng BPT vầ kiểm tra.
....................................................
....................................................
CÂU 1: Câu nào sau đây đúng?.
....................................................
....................................................  x y + −1 0 
.................................................... 2 3 
....................................................  3y
Miền nghiệm của hệ bất phương trình 2(x −1) +
 4 là phần mặt .................................................... 2 
....................................................  x  0 
.................................................... 
....................................................
.................................................... phẳng chứa điểm
.................................................... A. (2; ) 1 . B. (0;0) .
....................................................
.................................................... C. (1; ) 1 . D. (3;4).
.................................................... CÂU 2:
....................................................
Điểm nào sau đây không thuộc miền nghiệm của hệ bất ....................................................
2x + 3y −1  0
.................................................... phương trình  ?
 5x − y + 4  0
....................................................
.................................................... A. ( 1 − ;4) . B. ( 2 − ;4) .
.................................................... C.
.................................................... (0;0) . D. ( 3 − ;4).
....................................................
CÂU 3: Điểm nào sau đây thuộc miền nghiệm của hệ bất phương ....................................................
....................................................
2x −5y −1 0 
....................................................
trình  2x + y + 5  0 ?
....................................................
 x + y +1 0 
....................................................
....................................................
A. (0;0) . B. (1;0) .
.................................................... C.
.................................................... (0; 2 − ) . D. (0;2) .
.................................................... 87
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
 x − y  0
.................................................... 
CÂU 4: Miền nghiệm của hệ bất phương trình x −3y + 3  0 là phần ....................................................
 x + y −5  0 
....................................................
.................................................... mặt phẳng chứa điểm
.................................................... A. (5; ) 3 . B. (0;0) .
.................................................... C. (1; ) 1 − . D. ( 2 − ;2) .
....................................................
.................................................... 3  x + y  9 
.................................................... x  y −3
CÂU 5: Miền nghiệm của hệ bất phương trình 
là phần .................................................... 2y  8 − x 
.................................................... y  6
.................................................... mặt phẳng chứa điểm
....................................................
A. (0;0) . B. (1;2) .
....................................................
.................................................... C. (2; ) 1 . D. (8;4).
.................................................... CÂU 6: Miền nghiệm của bất phương
trình .................................................... 3x + 2( y + ) 3  4(x + )
1 − y +3 là phần mặt phẳng chứa điểm nào?
....................................................
....................................................
A. (3;0). B. (3; ) 1 .
.................................................... C. (1; ) 1 . D. (0;0) .
.................................................... x + y  0
....................................................
CÂU 7: Cho hệ bất phương trình 
có tập nghiệm là S . .................................................... 2x + 5y  0
....................................................
Khẳng định nào sau đây là khẳng định đúng?
.................................................... A. (1; ) 1 S . B. ( 1 − ;− ) 1 S .
....................................................  1   1 2 
.................................................... C. 1;− S  . D. − ; S . 2     2 5  
....................................................
.................................................... x  0 CÂU 8: 
Cho hệ bất phương trình 
có tập nghiệm là S
....................................................
x + 3y +1 0
....................................................
. Khẳng định nào sau đây là khẳng định đúng?
.................................................... A.
.................................................... (1;− ) 1 S .
B. (1;− 3)S .
.................................................... C. ( 1 − ; 5)S . D. ( 4 − ; 3)S .
....................................................
.................................................... x  0 CÂU 9: 
Cho hệ bất phương trình 
có tập nghiệm là S
....................................................
x + 3y +1 0
....................................................
. Khẳng định nào sau đây là khẳng định đúng?
.................................................... A.
.................................................... ( 1 − ;2)S . B. ( 2;0)S .
....................................................
C. (1;− 3)S . D. ( 3;0)S .
....................................................
....................................................
.................................................... 88
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10 x − y  3 
....................................................
CÂU 10: Cho hệ bất phương trình  1
có tập nghiệm S . .................................................... 1− x + y  0  2
....................................................
....................................................
Khẳng định nào sau đây là khẳng định đúng ?
.................................................... A. (1; 2 − )S . B. (2; ) 1 S .
....................................................
.................................................... C. (5; 6 − )S . D. S = .
....................................................
....................................................  3 2x − y 1
....................................................
CÂU 11: Cho hệ bất phương trình  2 có tập nghiệm S . 
....................................................
4x −3y  2
....................................................
Khẳng định nào sau đây là khẳng định đúng ?
....................................................
....................................................  1  A. − ; 1 − S  .
.................................................... 4   
.................................................... B.
.................................................... S = (
 ;xy)|4x−3=  2 .
....................................................
C. Biểu diễn hình học của S là nửa mặt phẳng chứa gốc tọa độ và kể ....................................................
....................................................
cả bờ d , với d là là đường thẳng 4x −3y = 2 .
....................................................
D. Biểu diễn hình học của S là nửa mặt phẳng không chứa gốc tọa ....................................................
....................................................
độ và kể cả bờ d , với d là là đường thẳng 4x −3y = 2 .
....................................................
x − 2y  0
....................................................  CÂU 12:
....................................................
Miền nghiệm của hệ bất phương trình x + 3y  2 − chứa 
.................................................... y − x  3 
.................................................... điểm nào sau đây?
....................................................
.................................................... A. A(1 ; 0). B. B( 2 − ; ) 3 .
.................................................... C.
.................................................... C (0 ; − ) 1 . D. D( 1 − ; 0).
....................................................
2x + 3y − 6  0
....................................................  CÂU 13:
....................................................
Miền nghiệm của hệ bất phương trình x  0 chứa
2x −3y −1 0
.................................................... 
.................................................... điểm nào sau đây?
....................................................
.................................................... A. A(1 ; 2). B. B(0 ; 2).
....................................................  1 
.................................................... C. C( 1 − ; ) 3 . D. D 0 ; − . 
.................................................... 3  
....................................................
.................................................... 89
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10 2x −1 0 CÂU 14:
....................................................
Miền nghiệm của hệ bất phương trình  chứa  3 − x + 5  0
....................................................
.................................................... điểm nào sau đây?
....................................................  5 
.................................................... A. Không có. B. B ; 2 .  3   
....................................................
....................................................  1  C. C( 3 − ; ) 1 . D. D ; 10  .
.................................................... 2   
.................................................... 3  − y  0
....................................................
CÂU 15: Miền nghiệm của hệ bất phương trình 
chứa ....................................................
2x −3y +1  0
.................................................... điểm nào sau đây?
.................................................... A. A(3 ; 4) . B. B(4 ; ) 3 .
.................................................... C. C(7 ; 4) . D. D(4 ; 4).
....................................................
x − 2y  0
....................................................
CÂU 16: Miền nghiệm của hệ bất phương trình  không x + 3y  2 −
....................................................
....................................................
chứa điểm nào sau đây? A.
.................................................... A( 1 − ; 0). B. B(1 ; 0).
.................................................... C. C( 3 − ; 4). D. D(0 ; ) 3 .
.................................................... 3
 x − 2y − 6  0
....................................................  CÂU 17: 3y
....................................................
Miền nghiệm của hệ bất phương trình 2(x −1) +  4 2 
.................................................... x  0 
....................................................
không chứa điểm nào sau đây?
.................................................... A. A(2 ; −2). B. B(3 ; 0).
.................................................... C.
.................................................... C (1 ; − ) 1 . D. D(2 ; − ) 3 .
.................................................... x − y  0 
....................................................
CÂU 18: Miền nghiệm của hệ bất phương trình x −3y  3
− không .................................................... x + y  5 
....................................................
chứa điểm nào sau đây?
.................................................... A. A(3 ; 2). B. B(6 ; ) 3 .
.................................................... C.
.................................................... C (6 ; 4). D. D(5 ; 4).
.................................................... x −3y  0 
....................................................
CÂU 19: Miền nghiệm của hệ bất phương trình x + 2y  3
− không .................................................... y + x  2 
....................................................
chứa điểm nào sau đây?
.................................................... A. A(0 ; ) 1 . B. B( 1 − ; ) 1 .
.................................................... C.
.................................................... C ( 3 − ; 0). D. D( 3 − ; ) 1 .
....................................................
.................................................... 90
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 2: Miền nghiệm của Hệ BPT bậc nhất hai ẩn
....................................................
.................................................... Phương pháp
....................................................
 Biễu diễn miền nghiê ̣m của hê ̣ BPT bậ c nhất hai ẩn trên mậ t
....................................................
phẩng tọa đo ̣. Chọn đấp ấn.
....................................................
 Lấy 1 giấ trị thuo ̣c miền nghiê ̣m, thay vầo kiểm tra cấc bất
....................................................
phương trình trong hê ̣ ở đấp ấn.
....................................................
....................................................
....................................................
2x + 3y  5 (1)
....................................................  CÂU 20: Cho hệ  3
. Gọi S là tập nghiệm của bất .................................................... x + y  5 (2) 1  2
....................................................
....................................................
phương trình (1), S2 là tập nghiệm của bất phương trình (2) và S là ....................................................
tập nghiệm của hệ thì
....................................................
A. S  S
.................................................... 1 2 .
B. S  S
.................................................... 2 1 . C. S = S
.................................................... 2 . D.
.................................................... S  S 1 .
....................................................
CÂU 21: Phần không gạch chéo ở hình sau đây là biểu diễn miền ....................................................
nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D ?
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
.................................................... 
.................................................... y  0 A.  .
.................................................... 3  x + 2y  6
.................................................... y  0 B.  .
.................................................... 3  x + 2y  6 −
.................................................... x  0 C.
....................................................  . 3  x + 2y  6
.................................................... x  0
.................................................... D.  . 3  x + 2y  6 −
....................................................
.................................................... 91
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
CÂU 22: Miền tam giác ABC kể cả ba cạnh sau đây là miền nghiệm ....................................................
của hệ bết phương trình nào trong bốn bệ A, B, C, D ?
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
.................................................... y  0 x  0  
.................................................... A. 5
 x − 4y 10 .
B. 4x −5y 10 .
.................................................... 5  x+4y 10   5x + 4y 10 
.................................................... x  0 x  0
....................................................   C. 5
 x − 4y 10 . D. 5
 x − 4y 10 .
.................................................... 4x+5y 10   4x + 5y 10 
....................................................
....................................................
CÂU 23: Giá trị nhỏ nhất của biết thức F = y − x trên miền xác định ....................................................
y − 2x  2 
....................................................
bởi hệ 2y − x  4 là.
....................................................  x+ y  5 
.................................................... A.
....................................................
min F = 1 khi x = 2, y = 3.
....................................................
B. min F = 2 khi x = 0, y = 2.
....................................................
C. min F = 3 khi x =1, y = 4 .
....................................................
D. min F = 0 khi x = 0, y = 0.
.................................................... CÂU 24:
....................................................
Giá trị nhỏ nhất của biết thức F = y − x trên miền xác định ....................................................  2x + y  2 
....................................................
bởi hệ  x − y  2 là
.................................................... 5  x + y  4 − 
.................................................... A. min F = 3
− khi x =1, y = 2 − .
.................................................... B.
....................................................
min F = 0 khi x = 0, y = 0 .
.................................................... C. 4 2 min F = 2
− khi x = , y = − .
.................................................... 3 3
....................................................
D. min F = 8 khi x = 2 − , y = 6 .
....................................................
....................................................
....................................................
....................................................
.................................................... 92
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10 x − y  2
.................................................... 3
 x+5y 15
....................................................
CÂU 25: Cho hệ bất phương trình  . Khẳng định nào sau x  0 
.................................................... y  0
....................................................
....................................................
đây là khẳng định sai ?
....................................................
A. Trên mặt phẳng tọa độ Oxy , biểu diễn miền nghiệm của hệbất ....................................................
phương trình đã cho là miền tứ giác ABCO kể cả các cạnh với A(0; ) 3
....................................................  25 9 
.................................................... , B ; 
, C (2;0) và O(0;0) . 8 8   
....................................................
B. Đường thẳng : x + y = m có giao điểm với tứ giác ABCO kể cả .................................................... 17
.................................................... khi 1 −  m  . 4
....................................................
C. Giá trị lớn nhất của biểu thức x + y , với x và y thỏa mãn hệ bất .................................................... 17
.................................................... phương trình đã cho là . 4
....................................................
D. Giá trị nhỏ nhất của biểu thức x + y , với x và y thõa mãn hệ bất ....................................................
phương trình đã cho là 0.
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
....................................................
.................................................... 93
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 3: Ứng dụng của Hệ BPT bậc nhất hai ẩn
....................................................
.................................................... Phương pháp
....................................................
 Biễu diễn miền nghiê ̣m của hê ̣ BPT bậ c nhất hai ẩn trên mậ t
.................................................... phẩng tọa đo ̣.
....................................................
 Tính giấ trị biểu thức F ( ;
x y) tại các đỉnh của đa giác và kết luận.
....................................................
....................................................
....................................................
CÂU 26: Giá trị lớn nhất của biết thức F ( ;
x y) = x + 2y với điều kiện ....................................................  0  y  4
....................................................  x  0
....................................................  là
x − y −1 0 
....................................................
x+ 2y −10  0
....................................................
.................................................... A. 6 . B. 8 .
.................................................... C. 10. D. 12 .
....................................................
CÂU 27: Giá trị nhỏ nhất của biết thức F ( ;
x y) = x − 2y với điều kiện ....................................................  0  y  5
....................................................  x  0
....................................................  là
....................................................
x + y − 2  0  
....................................................
x − y − 2  0
.................................................... A. 10 − . B. 12.
.................................................... C. 8 − . D. 6 − .
....................................................
CÂU 28: Biểu thức F = y – x đạt giá trị nhỏ nhất với điều kiện ....................................................  2 − x + y  2 −
.................................................... 
....................................................
 x − 2y  2  tại điểm S ( ;
x y) có toạ độ là
.................................................... x + y  5 
....................................................  x  0
.................................................... A. (4; ) 1 . B. (3; ) 1 .
.................................................... C.
.................................................... (2; ) 1 . D. (1; ) 1 .
....................................................
CÂU 29: Biểu thức L = y − x , với x và y thõa mãn hệ bất phương ....................................................
2x + 3y − 6  0
....................................................  trình x  0
, đạt giá trị lớn nhất là a và đạt giá trị nhỏ nhất ....................................................
2x −3y −1 0 
....................................................
....................................................
là b . Hãy chọn kết quả đúng trong các kết quả sau:
.................................................... A. 25 11 a = và b = 2 − .
B. a = 2và b = − .
.................................................... 8 12
.................................................... − C. 9
a = 3và b = 0.
D. a = 3 và b = .
.................................................... 8
.................................................... 94
GV: Trương Việt Long – ĐT: 0569.59.79.99

Chuyên đề ôn luyện bất phương trình và hệ bất phương trình bậc nhất hai ẩn

Thông tin :

Tài liệu liên quan:

Các dạng toán bất phương trình và hệ bất phương trình bậc nhất hai ẩn thường gặp

Toán 10 Bài 3: Bất phương trình bậc nhất hai ẩn - Kết Nối Tri Thức

Toán 10 Bài 4: Hệ bất phương trình bậc nhất hai ẩn - Kết Nối Tri Thức

Toán 10 Bài tập cuối chương II - Kết nối tri thức với cuộc sống

Top 30 câu trắc nghiệm ôn tập các phép toán trên tập hợp (giải chi tiết)