Thông tin
Quiz

Chuyên đề ôn luyện mệnh đề toán học và tập hợp – Trương Việt Long

Tài liệu gồm 72 trang, được biên soạn bởi tác giả Trương Việt Long, bao gồm tóm tắt lý thuyết, bài tập tự luận và bài tập trắc nghiệm chuyên đề mệnh đề toán học và tập hợp, giúp học sinh lớp 10 ôn luyện khi học chương trình Toán 10;

Chủ đề:

Chương 1: Mệnh đề và tập hợp (KNTT) 31 tài liệu

Môn:

Toán 10 2.8 K tài liệu

Thông tin:

72 trang 1 năm trước

Tác giả:

Mai Nguyệt

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Chuyên đề ôn luyện mệnh đề toán học và tập hợp – Trương Việt Long

100 50 lượt tải Tải xuống

Ⓐ -

MNH Đ – MNH Đ CHA BIN

Mnh đ

Mnh đ cha bin

MNH Đ PH ĐNH

3. MNH Đ KO THEO – MNH Đ ĐO

Mnh đ ko theo

Mnh đ đo

4. MNH Đ TƯƠNG ĐƯƠNG

; 

5. MNH Đ CHA K HIU

DNG 1: Xc đnh mnh đ, tnh đng sai ca mnh đê

DNG 2: : Lp mnh đ ph đnh, v xt tnh đng sai ca mnh đ ph

đnh đ?

DNG 3: Lp mnh đ ko theo, mnh đ đo v xt tnh đng sai ca

mnh đ ph đnh đ?

DNG 4: Pht biu mnh đ tương đương

DNG 5: Dng k hiu ∀ v ∃ đ vit mnh đê

DNG 6: Pht biu mnh đ cha k hiu ∀ v ∃

DNG 7: Lp mnh đ ph đnh ca mnh đ cha k hiu ∀ v ∃

Ⓑ

CHƯƠNG I: MNH Đ TON HC – TP HP

MC LC

DNG 1: : Nhn bit mnh đ – Mnh đ cha bin

DNG 2: Xt tnh ĐNG – SAI ca mnh đê

DNG 3: Mnh đ cha bin

DNG 4: : Ph đnh mnh đê

DNG 5 : Mnh đ ko theo

DNG 6: Mnh đ đo

DNG 7: Mnh đ tương đương

DNG 8: : Dng k hiu ∀, ∃ đê viêt mênh đê

DNG 9: : Pht biu mnh đ cha k hiu ∀, ∃

DNG 10: Ph đnh mnh đ cha k hiu ∀, ∃

Ⓒ

Ⓐ -

CC KHI NIM CƠ BN V TP HP

Tp hp

Tp con

Hai tp hp bng nhau

CC TP HP S

Mi quan h gia cc tp hp s

Cc tp con thưng dng ca

3. CC PHP TON TRÊN TP HP

Giao ca hai tp hp

Hp ca hai tp hp

Hiu ca hai tp hp

DNG 1: Xc đnh tp hp bng cch lit kê tt c cc phn t

ca tp hp

DNG 2: Xc đnh tp hp bng cch ch ra tnh cht đc trung

DNG 3: Xc đnh tp con ca mt tp hp cho trưc

DNG 4: Cc php ton trên tp hp

( Không cha tp con ca ℝ )

DNG 5: S dụng biu đ Ven đ gii bi ton.

DNG 6: Chng minh tp hp bng nhau, tp con

DNG 7: Phân bit tp hp v tp con ca ℝ

Dạng 8: Cc php ton trên tp con ca ℝ

Ⓑ

DNG 1: Xc đnh s phn t ca tp hp

DNG 2: Xc đnh tp hp bng cch lit kê hoc ch ra tnh cht

đc trưng ca cc phn t thuc tp hp.

DNG 3: Tm tp con, s tp con ca mt tp hp cho trưc

DNG 4: Hai tp hp bng nhau.

DNG 5 : Giao ca cc tp hp (Không cha tp con ca ℝ)

DNG 6: Hp ca cc tp hp (Không cha tp con ca ℝ)

DNG 7: Hiu, phn b ca cc tp hp

(Không cha tp con ca ℝ)

DNG 8: : Vit cc tp con ca ℝ dưi dạng đoạn; khong;…

DNG 9: Cc php ton trên tp con ca ℝ

DNG 10: Tm điu kin ca tham s m đê đoạn; khong; na

khong tha mn điu kin cho trưc

Ⓒ

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

1. MNH Đ, MNH Đ CHA BIN

a. Mênh đ

b. Mnh đ cha bin

2. MNH Đ PH ĐNH

Chương

MNH Đ TON HC

TP HP

Bài MNH Đ TON HC

TÓM TẮT LÝ THUYT

Định nghĩa

Cho mnh đ

Mnh đ "không phải đưc gi l mnh đ phủ định của và kí hiu là

Nếu đúng thì sai, nếu sai thì đúng.

Định nghĩa

( )

; ; ;....x y n

Mệnh đề chứa biến là một câu khẳng định chứa biến nhận giá trị trong

một tập nào đó mà với mỗi giá trị của biến thuộc ta được một mệnh đề.

( )

;xy

( )

;P x y

Ta k hiu mnh đ cha biến l ; mnh đ cha biến l

Định nghĩa

Mnh đ l mt câu khẳng định đúng hoặc mt câu khẳng định sai.

Mt mnh đ Ton hc không thể vừa đúng, vừa sai.

; ; ;....; ; ; ;....A B C P Q R

Ngưi ta thưng s dng cc ch ci: để biểu thị cc mnh đ.

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

3. MNH Đ KO THEO, MNH Đ ĐO

a. Mnh đ ko theo

b. Mnh đ đo

4. MNH Đ TƯƠNG ĐƯƠNG

Định nghĩa

▶

.PQ

Mnh đ “ nếu v ch nếu ” đưc gi l mt mnh đ tương đương. K hiu:

 Nhân xt:

Nếu cả hai mnh để và đu đúng thì mnh đ tương đương đúng.

Mnh đ c thể pht biểu  nhng dng như sau:

P tương đương Q.

P l điu kin cn v đủ để c Q.

P khi v ch khi Q.

Định nghĩa

Cho mnh đ v

.PQ

Mnh đ "Nếu thì đưc gi l mnh đ kéo theo và kí hiu là:

Mnh đ ch sai khi đúng v sai.

Như vậy, ta ch cn xét tnh đúng sai của mnh đ khi đúng.

 Nhân xt:

.PQ

Cc định l ton hc l nhng mnh đ đúng v thưng pht biểu  dng

Khi đ ta ni:

P l giả thiết, Q l kết luận.

P l điu kin đủ để c Q.

Q l điu kin cn để c P.

Định nghĩa

▶ Mnh đ đo:

Cho mnh đ kéo theo

Mnh đ đưc gi l mnh đ đo

.PQ

của mnh đ

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

5. MNH Đ C CHA K HIU: ∀ , ∃

Dạng 1: Xc đnh mnh đ, tnh đng sai ca mnh đ

Cc câu sau đây, câu nào là mnh đ, câu nào không phải là mnh đ? Nếu là mnh đ hãy cho biết mnh đ

đ đúng hay sai.

(1) Ở đây đẹp quá!

(2) Phương trình

3 1 0xx

vô nghim

(3) 16 không là số nguyên tố

(4) Hai phương trình

4 3 0xx

và

3 1 0xx

có nghim chung.

(5) Số có lớn hơn

hay không?

(6) Italia vô địch Worldcup 2006

(7) Hai tam giác bằng nhau khi và ch khi chúng có din tích bằng nhau.(8) Mt t giác là hình thoi khi

và ch khi n c hai đưng chéo vuông góc với nhau.

Câu (1) và (5) không là mnh đ(vì là câu cảm thán, câu hỏi)

Các câu (3), (4), (6), (8) là nhng mnh đ đúng

Câu (2) và (7) là nhng mnh đ sai.

BI TP T LUN

Định nghĩa



• K hiu đc l: “Với mi”



• K hiu đc l: “Tn ti”.

Khi đ:

" ".xX

"Với mi thuc ", k hiu l:

" ".xX

"Tn ti thuc ", k hiu l:

" , ( )"x X P x

" , ( )".x X P x

Mnh đ phủ định của mnh đ là

" , ( )"x X P x

" , ( )".x X P x

Mnh đ phủ định của mnh đ là

Mnh đ cha đúng khi ta ch ra mt phn t đúng.

Mnh đ cha sai khi ta ch ra mt phn t sai.

Ví dụ 1

BÀI GIẢI

BÀI TP RN LUYN

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Các câu sau đây, câu nào là mệnh đề, câu nào không phải là mệnh đề? Nếu là mệnh đề hay cho

biết mệnh đề đó đúng hay sai.

a) Không được đi lối này!

b) Bây giờ là mấy giờ?

c) Chiến tranh thế giới lần thứ hai kết thúc năm 1946.

d) 16 chia 3 dư 1.

e) 2023 không là số nguyên tố.

là số vô tỉ.

g) Hai đường tròn phân biệt có nhiều nhất là hai điểm chung.

Lời giải

.............................................................................................................................................................................................

Bài 1

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Nêu mnh đ phủ định của các mnh đ sau, cho biết mnh đ ny đúng hay sai?

" Hình thoi c hai đưng chéo vuông góc với nhau"

" 6 là số nguyên tố"

" Tổng hai cnh của mt tam giác lớn hơn cnh còn li"

" Phương trình

2 2 0xx

có nghim "

Ta có các mnh đ phủ định là:

" Hai đưng chéo của hình thoi không vuông góc với nhau", mnh đ này sai.

" 6 không phải là số nguyên tố", mnh đ ny đúng.

" Tổng hai cnh của mt tam giác nhỏ hơn hoặc bằng cnh còn li", mnh đ này sai.

", mnh đ này sai.

" phương trình

2 2 0xx

vô nghim ", mnh đ ny đúng vì

4 2 2

2 2 1 1 0x x x

Nêu mệnh đề phủ định của các mệnh đề sau, cho biết mệnh đề này đúng hay sai?

" Trong tam giác tổng ba góc bằng 180

3 27

là số nguyên "

" Việt Nam vô địch Worldcup 2020"

" Bất phương trình

2013

2030x

vô nghiệm "

Lời giải

.............................................................................................................................................................................................

Dạng 2: Lp mnh đ ph đnh, v xt tnh đng sai ca mnh đ ph đnh đ?

Ví dụ 2

BÀI GIẢI

Bài 2

BÀI TP RN LUYN

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 3: Lp mnh đ ko theo, mnh đ đo v xt tnh đng sai ca mnh đ

ph đnh đ?

Phát biểu mnh đ

và phát biểu mnh đ đảo, xét tnh đúng sai của nó.

" T giác

ABCD

là hình thoi" và

" T giác

ABCD

AC và BD cắt nhau ti trung điểm mỗi đưng"

: "2 9"P

và

: "4 3"Q

" Tam giác

ABC

vuông cân ti A" và

" Tam giác

ABC

có

2AB

" Ngày 2 tháng 9 là ngày Quốc Khánh của nước Vit Nam" và

" Ngy 27 thng 7 l ngy thương

binh lit sĩ"

a) Mnh đ

là " Nếu t giác

ABCD

là hình thoi thì AC và BD cắt nhau ti trung điểm mỗi đưng",

mnh đ ny đúng.

Mnh đ đảo là

: "Nếu t giác

ABCD

có AC và BD cắt nhau ti trung điểm mỗi đưng thì

ABCD

là

hình thoi ", mnh đ này sai.

b) Mnh đ

là " Nếu

thì

", mnh đ ny đúng vì mnh đ

sai.

Mnh đ đảo là

: " Nếu

thì

", mnh đ ny đúng vì mnh đ

sai.

c) Mnh đ

là " Nếu tam giác

ABC

vuông cân ti A thì

2AB

", mnh đ ny đúng

Mnh đ đảo là

: " Nếu tam giác

ABC

có

2AB

thì nó vuông cân ti A", mnh đ này sai

d) Mnh đ

là " Nếu ngày 2 tháng 9 là ngày Quốc Khánh của nước Vit Nam thì ngày 27 tháng 7 là

ngy thương binh lit sĩ"

Mnh đ đảo là

: " Nếu ngy 27 thng 7 l ngy thương binh lit sĩ thì ngy 2 thng 9 l ngy Quốc

Khánh của nước Vit Nam"Hai mnh đ trên đu đúng vì mnh đ

,PQ

đu đúng

Ví dụ 3

BÀI GIẢI

BÀI TP RN LUYN

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Phát biểu mnh đ

và phát biểu mnh đ đảo, xét tnh đúng sai của nó.

“tam giác ABC đu” và

“tam giác ABC cân.”

“

12=

” và

“

12=

.”

“

32

” và

“

32xx

x

.”

“Số chia hết cho 6” và

“số chia hết cho 3 .”

“T giác ABCD là hình thoi” và

“Hai đưng chéo của nó vuông góc với nhau”

“Số chia hết cho 2”và

“số đ l số chẵn.”

“

ABC

c

AB BC CA==

” và

“

ABC

l tam gic đu.”

Lời giải

.............................................................................................................................................................................................

Bài 3

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 4: Pht biu mnh đ tương đương

Cho

ABC

. Xét cc mnh đ sau:

ABC

l tam gic vuông "

ABC

có mt góc bằng tổng hai góc còn li "

Pht biểu mnh đ

bằng 4 cch?

ABC

l tam gic vuông tương đương

ABC

có mt góc bằng tổng hai góc còn li.

ABC

l tam gic vuông l điu kin cn v đ đ

ABC

có mt góc bằng tổng hai góc còn li.

ABC

l tam gic vuông khi v ch khi

ABC

có mt góc bằng tổng hai góc còn li

ABC

l tam gic vuông nu v ch nu

ABC

có mt góc bằng tổng hai góc còn li

Phát biểu mnh đ

bằng bốn cch v v xét tnh đúng sai của nó.

"T giác

ABCD

là hình thoi" và

" T giác

ABCD

l hình bình hnh c hai đưng chéo vuông

góc với nhau"

" T giác ABCD là hình vuông" v

" T giác ABCD là hình ch nhật c hai đưng chéo bằng

vuông góc với nhau ".

Lời giải

.............................................................................................................................................................................................

Ví dụ 4

BÀI GIẢI

Bài 4

BÀI TP RN LUYN

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

.............................................................................................................................................................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 5: Dng k hiu ∀ v ∃ đ vit mnh đ

Dng k hiu ∀ v ∃ để viết cc mnh đ v mnh đ phủ định của cc mnh đ sau:

a) P: “Tích của ba số tự nhiên liên tiếp chia hết cho sáu.”

b) Q: “Có mt số nguyên mà bình phương của nó bằng chính nó.”

• Ta có

: , 1 2 6P n N n n n

, mnh đ phủ định là

: , 1 2P n N n n n 6

• Ta có

:,Q n Z n n

, mnh đ phủ định là

:,R n Z n n

Dng k hiu ∀ v ∃ để viết cc mnh đ v mnh đ phủ định của cc mnh đ sau:

" Với mi số thực bình phương của là mt số không âm."

" Có mt số hu t mà nghịch đảo của nó lớn hơn chnh n."

Lời giải

.............................................................................................................................................................................................

Ví dụ 5

BÀI GIẢI

Bài 5

BÀI TP RN LUYN

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 6: Pht biu mnh đ cha k hiu ∀ v ∃

Pht biểu cc mnh đ sau:

a) P: “

,0xx

.”

b) Q: “

.”

a) Cch 1: Với mi số thực

thì bình phương của

lớn hơn hoặc bằng 0.

Cch 2: Bình phương của mt số thực luôn l mt số không âm.

b) Cch 1: Tn ti số tự nhiên

sao cho

chia hết cho

1x +

Cch 2: Tn ti số tự nhiên

sao cho

1x +

l ước của

Pht biểu cc mnh đ sau v xét tnh đúng sai của n:

a) "

,1n n n

là hp số "

b) “

, 1 0x x x

”

,3xn

, 2 1 0qq

Lời giải

.............................................................................................................................................................................................

Ví dụ 6

BÀI GIẢI

Bài 6

BÀI TP RN LUYN

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 7: Lp mnh đ ph đnh ca mnh đ cha k hiu ∀ v ∃

Lập mnh đ phủ định của cc mnh đ sau v xét tnh đúng sai của cc mnh đ phủ định đ?

: " : 1".P x x

: " : 3".P x x

a) Mệnh đề phủ định của mệnh đề

là

: " : 1".P x x

Mệnh đề

là mệnh đề đúng.

b) Mệnh đề phủ định của mệnh đề

là

: " : 3".P x x

Mệnh đề

là mệnh đề sai.

Lập mnh đ phủ định của cc mnh đ sau v xét tnh đúng sai của cc mnh đ phủ định đ?:

: " : 0".P x x

: " : ".P x x x

: " : 4 1 0".P x x

: " : 7 0".P x x x

: " : 2 0".P x x x

: " : ( 1) ( 1)".P x x x

: " , 2P x x

hoặc

7".x

: " : 5 0".P x x

Lời giải

.............................................................................................................................................................................................

Ví dụ 7

BÀI GIẢI

Bài 7

BÀI TP RN LUYN

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

.............................................................................................................................................................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

distance

Dạng 1: Nhn bit mnh đ – Mnh đ cha bin

Phương pháp

 M󰉳t câu mà ch󰉞c ch󰉞󰉞c ch󰉞󰉳t

m󰉪󰉧

CÂU 1: Trong các câu sau, câu nào không phải là mệnh đề?

A. Buồn ngủ quá!

B. Hình thoi có hai đường chéo vuông góc với nhau.

C. 8 là số chính phương.

D. Băng Cốc là thủ đô của Mianma.

CÂU 2: Trong các câu sau, có bao nhiêu câu không phải là mệnh đề?

a) Huế là một thành phố của Việt Nam.

b) Sông Hương chảy ngang qua thành phố Huế.

c) Hãy trả lời các câu hỏi này!

5 19 24.+=

A. 1. B. 2. C. 3. D. 4.

CÂU 3: Trong các câu sau, có bao nhiêu câu là mệnh đề?

a) Hãy đi nhanh lên!

b) Hà Nội là thủ đô của Việt Nam.

c) Năm 2018 là năm nhuận.

2 4 5 6 11.

A. 1. B. 4. C. 3. D. 2.

CÂU 4: Cho các phát biểu sau, có bao nhiêu phát biểu là mệnh đề?

a) Hà Nội là thủ đô của Việt Nam.

, 2 5.xx

6 5.x

Phương trình

6 5 0xx

có nghiệm.

A. 1. B. 2. C. 3. D. 4.

CÂU 5: Câu nào trong các câu sau không phải là mệnh đề?

3 2 7+=

. B.

+1 > 0x

20x− − 

. D.

4 + x

CÂU 6: Câu nào trong các câu sau không phải là mệnh đề?

3 + 2 = 7.

x +1 > 0

2 - x < 0.

4 + x = 3.

QUICK NOTE

Thà để giọt mồ hôi rơi trên

trang sách còn hơn để nước

mắt rơi ướt cả đề thi

..................................................

BI TP TRẮC NGHIM

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 2: Xt tnh ĐNG – SAI ca mnh đ

Phương pháp

 S󰉼󰈖 d󰈨 ng c 󰈨nh l , tnh ch󰈘 󰈖 h󰈨 󰈜 nh󰈨n bi󰈘 t m󰈨󰈚  ng.

 L󰈘 y m󰈨t v i v d󰈨 c󰈨 th󰈜 󰈜 nh󰈨n bi󰈘 t m󰈨󰈚 sai.

CÂU 7: Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

A. Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số

đều là số chẵn.

B. Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều

là số chẵn.

C. Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều

là số lẻ.

D. Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là

số lẻ.

CÂU 8: Trong các câu sau, câu nào là mệnh đề đúng?

A. Nếu

thì

.ab

B. Nếu

chia hết cho 9 thì

chia hết cho 3.

C. Nếu em chăm chỉ thì em thành công.

D. Nếu một tam giác có một góc bằng

thì tam giác đó đều.

CÂU 9: Trong các phát biểu sau, phát biểu nào là mệnh đề đúng?

A. π là một số hữu tỉ.

B. Tổng của độ dài hai cạnh một tam giác lớn hơn độ dài cạnh thứ

ba.

C. Bạn có chăm học không?

D. Con thì thấp hơn cha.

CÂU 10: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?

2 4.

4 16.

23 5 2 23 2.5.

..................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 3: Mnh đ cha bin

Phương pháp

 M󰉪󰉧 ch󰉽a bi󰉦n là nh󰊀󰉼󰉠󰉬󰉼󰉹c tính

󰉼󰉵i m󰉲i giá tr󰉬 c󰉻a bi󰉦n s󰉥 cho ta m󰉳t m󰉪󰉧.

CÂU 11: Trong các câu sau, câu nào không là mệnh đề chứa biến?

A. 15 là số nguyên tố. B.

a b c+=

0xx+=

. D.

21n+

chia hết cho 3.

CÂU 12: Với giá trị thực nào của

mệnh đề chứa biến

( )

:2 1 0P x x −

là mệnh đề đúng?

. B.

. D.

CÂU 13: Cho mệnh đề chứa biến

( )

:" 15 "+P x x x

với

là số thực.

Mệnh đề nào sau đây là đúng:

( )

. B.

( )

. D.

( )

CÂU 14: Khẳng định nào sau đây sai?

A. “Mệnh đề” là từ gọi tắc của “mệnh đề logic”.

B. Mệnh đề là một câu khẳng đúng hoặc một câu khẳng định sai.

C. Mệnh đề có thể vừa đúng hoặc vừa sai.

D. Một khẳng định đúng gọi là mệnh đề đúng, một khẳng định sai

gọi là mệnh đề sai.

CÂU 15: Chọn khẳng định sai.

A. Mệnh đề

và mệnh đề phủ định

, nếu

đúng thì

sai và

điều ngược lại chắc đúng.

B. Mệnh đề

và mệnh đề phủ định

là hai câu trái ngược nhau.

C. Mệnh đề phủ định của mệnh đề

là mệnh đề không phải

được

kí hiệu là

D. Mệnh đề

: “



là số hữu tỷ” khi đó mệnh đề phủ định

là: “



là số vô tỷ”.

CÂU 16: Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

A. Nếu

ab

thì

ab

B. Nếu

chia hết cho

thì

chia hết cho

C. Nếu em chăm chỉ thì em thành công.

D. Nếu một tam giác có một góc bằng

thì tam giác đó là đều.

..................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 17: Trong các phát biểu sau, phát biểu nào là mệnh đề đúng:



là một số hữu tỉ.

B. Tổng của hai cạnh một tam giác lớn hơn cạnh thứ ba.

C. Bạn có chăm học không?

D. Con thì thấp hơn cha.

CÂU 18: Cho

là số tự nhiên, mệnh đề nào sau đây đúng?

( )

,1+n n n

là số chính phương.

( )

,1+n n n

là số lẻ.

( )( )

, 1 2 + +n n n n

là số lẻ.

( )( )

, 1 2 + +n n n n

là số chia hết cho

CÂU 19: Trong các mệnh đề sau, mệnh đề nào sai?



−  −  

. B.

4 16



  

23 5 2 23 2.5  

. D.

23 5 2 23 2.5  −  −

CÂU 20: Cho

là số thực. Mệnh đề nào sau đây đúng?

, 5 5 5      −x x x x

. B.

, 5 5 5   −  x x x

, 5 5    x x x

. D.

, 5 5 5      −x x x x

CÂU 21: Chọn mệnh đề đúng:

,1  −nn

là bội số của

. B.

,3  =xx

, 2 1  +

là số nguyên tố. D.

, 2 2   +

CÂU 22: Trong các mệnh đề nào sau đây mệnh đề nào sai?

A. Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một

góc bằng nhau.

B. Một tứ giác là hình chữ nhật khi và chỉ khi chúng có

góc vuông.

C. Một tam giác là vuông khi và chỉ khi nó có một góc bằng tổng hai

góc còn lại.

D. Một tam giác là đều khi và chỉ khi chúng có hai đường trung tuyến

bằng nhau và có một góc bằng

CÂU 23: Các mệnh đề sau, mệnh đề nào có mệnh đề đảo là đúng?

A. Nếu

và

cùng chia hết cho

thì

+ab

chia hết cho

B. Nếu hai tam giác bằng nhau thì diện tích bằng nhau.

C. Nếu

chia hết cho

thì

chia hết cho

D. Nếu một số tận cùng bằng

thì số đó chia hết cho

..................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 24: Mệnh đề nào sau đây sai?

A. Tứ giác

ABCD

là hình chữ nhật



tứ giác

ABCD

có ba góc vuông.

B. Tam giác

ABC

là tam giác đều



60A =

C. Tam giác

ABC

cân tại



=AB AC

D. Tứ giác

ABCD

nội tiếp đường tròn tâm



= = =OA OB OC OD

CÂU 25: Tìm mệnh đề đúng:

A. Đường tròn có một tâm đối xứng và có một trục đối xứng.

B. Hình chữ nhật có hai trục đối xứng.

C. Tam giác

ABC

vuông cân

45=A

D. Hai tam giác vuông

ABC

và

' ' 'A B C

có diện tích bằng nhau

' ' '  = ABC A B C

CÂU 26: Tìm mệnh đề sai:

chia hết cho



Hình vuông có hai đường chéo bằng nhau

và vuông góc nhau.

B. Tam giác

ABC

vuông tại

2 2 2

 = +C AB CA CB

C. Hình thang

ABCD

nội tiếp đường tròn

( )

O ABCD

là hình

thang cân.

chia hết cho



Hình bình hành có hai đường chéo vuông

góc nhau.

CÂU 27: Với giá trị thực nào của

mệnh đề chứa biến

( )

:2 1 0P x x −

là mệnh đề đúng:

. B.

. D.

CÂU 28: Cho mệnh đề chứa biến

( )

:" 15 "+P x x x

với

là số thực.

Mệnh đề nào sau đây là đúng:

( )

. B.

( )

. D.

( )

CÂU 29: Trong các mệnh đề sau, mệnh đề nào sai?

AA

. B.

A

AA

. D.

 

AA

CÂU 30: Cho biết

là một phần tử của tập hợp

, xét các mệnh đề

( )

: I x A

( )  

: II x A

( )

: III x A

( )  

:IV x A

Trong các mệnh đề sau, mệnh đề nào là đúng

và

. B.

và

III

và

. D.

và

..................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 31: Cho mệnh đề chứa biến

( )

:“ 1−P n n

chia hết cho 4” với

là số nguyên. Xét xem các mệnh đề

( )

và

( )

đúng hay sai?

( )

đúng và

( )

đúng. B.

( )

sai và

( )

sai.

( )

đúng và

( )

sai. D.

( )

sai và

( )

đúng.

CÂU 32: Cho tam giác

ABC

với

là chân đường cao từ

. Mệnh

đề nào sau đây sai?

A. “

ABC

là tam giác vuông ở

2 2 2

1 1 1

 = +

AH AB AC

”.

B. “

ABC

là tam giác vuông ở

.=BA BH BC

”.

C. “

ABC

là tam giác vuông ở

.=HA HB HC

”.

D. “

ABC

là tam giác vuông ở

2 2 2

 = +BA BC AC

”.

CÂU 33: Trong các mệnh đề sau, mệnh đề nào sai?

A. Để tứ giác

ABCD

là hình bình hành, điều kiện cần và đủ là hai

cạnh đối song song và bằng nhau.

B. Để

25=x

điều kiện đủ là

2=x

C. Để tổng

+ab

của hai số nguyên

,ab

chia hết cho 13, điều kiện cần

và đủ là mỗi số đó chia hết cho 13.

D. Để có ít nhất một trong hai số

,ab

là số dương điều kiện đủ là

0+ab

CÂU 34: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu tổng hai số

2+ab

thì có ít nhất một số lớn hơn 1.

B. Trong một tam giác cân hai đường cao bằng nhau.

C. Nếu tứ giác là hình vuông thì hai đường chéo vuông góc với nhau.

D. Nếu một số tự nhiên chia hết cho 6 thì nó chia hết cho 3.

CÂU 35: Mệnh đề nào sau là mệnh đề sai?

:2n n n  

. B.

:n n n  =

:0xx  

. D.

:x x x  

CÂU 36: Trong các mệnh đề sau tìm mệnh đề đúng?

:0  xx

. B.

:3xx

:0xx  − 

. D.

:  x x x

CÂU 37: Trong các mệnh đề sau, mệnh đề nào đúng?

,1  +nn

không chia hết cho

,3xx  

3x

( )

, 1 1  −  −x x x

,1nn  +

chia hết cho

..................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 4: Ph đnh mnh đ

Phương pháp

 Thêm (ho󰉢c b󰉵t) t󰉾 󰉢󰉘󰉼󰉵c v󰉬

ng󰊀 c󰉻a m󰉪󰉧 

 Ph󰈖 󰈨nh c󰈖 



” l “



”. V ngưc li.

 Ph󰈖 󰈨nh c󰈖 a “ = ” l “



”. V ngưc li.

 Ph󰈖 󰈨nh c󰈖 a “ > ” l “



”. V ngưc li……………

CÂU 38: Cho mệnh đề “Phương trình

4 4 0− + =xx

có nghiệm”.

Mệnh đề phủ định của mệnh đề đã cho là

A. Phương trình

4 4 0xx− + 

có nghiệm.

B. Phương trình

4 4 0− + =xx

có vô số nghiệm.

C. Phương trình

4 4 0− + =xx

có hai nghiệm phân biệt.

D. Phương trình

4 4 0− + =xx

vô nghiệm.

CÂU 39: Mệnh đề phủ định của mệnh đề “14 là số nguyên tố” là

mệnh đề:

A. 14 là số nguyên tố.

B. 14 chia hết cho 2.

C. 14 không phải là số nguyên tố.

D. 14 chia hết cho 7.

CÂU 40: Mệnh đề phủ định của mệnh đề: “

5 4 10+=

” là mệnh đề:

5 4 10+

. B.

5 4 10+

5 4 10+

. D.

5 4 10+

CÂU 41: Mệnh đề nào sau đây là phủ định của mệnh đề: “Mọi động

vật đều di chuyển”.

A. Mọi động vật đều không di chuyển.

B. Mọi động vật đều đứng yên.

C. Có ít nhất một động vật không di chuyển.

D. Có ít nhất một động vật di chuyển.

CÂU 42: Phủ định của mệnh đề: “Có ít nhất một số vô tỷ là số thập

phân vô hạn tuần hoàn” là mệnh đề nào sau đây:

A. Mọi số vô tỷ đều là số thập phân vô hạn tuần hoàn.

B. Có ít nhất một số vô tỷ là số thập phân vô hạn không tuần hoàn.

C. Mọi số vô tỷ đều là số thập phân vô hạn không tuần hoàn.

D. Mọi số vô tỷ đều là số thập phân tuần hoàn.

..................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 43: Cho mệnh đề

“

, 7 0x x x  − + 

” Mệnh đề phủ định

của

là:

, 7 0x x x  − + 

. B.

, 7 0x x x  − + 

C. Không tồn tại

: 7 0x x x− + 

. D.

, - 7 0x x x  + 

CÂU 44: Mệnh đề phủ định của mệnh đề

" 3 1 0"xx+ + 

với mọi

là:

A. Tồn tại

sao cho

3 1 0+ + xx

B. Tồn tại

sao cho

3 1 0+ + xx

C. Tồn tại

sao cho

3 1 0+ + =xx

D. Tồn tại

sao cho

3 1 0+ + xx

CÂU 45: Mệnh đề phủ định của mệnh đề

“

: 2 5 + +x x x

là số

nguyên tố” là :

: 2 5 + +x x x

không là số nguyên tố.

: 2 5 + +x x x

là hợp số.

: 2 5 + +x x x

là hợp số.

: 2 5 + +x x x

là số thực.

CÂU 46: Phủ định của mệnh đề

" ,5 3 1"x x x  − =

là:

" ,5 3 "x x x  −

. B.

" ,5 3 1"x x x  − =

" x ,5x 3 1"x  − 

. D.

" ,5 3 1"x x x  − 

CÂU 47: Cho mệnh đề

( )

:Px

" , 1 0"x x x  + + 

. Mệnh đề phủ

định của mệnh đề

( )

là:

" , 1 0"x x x  + + 

. B.

" , 1 0"x x x  + + 

" , 1 0"x x x  + + 

. D.

" 

, 1 0"x x x + + 

CÂU 48: Trong các mệnh đề sau, mệnh đề nào đúng?

A. Phủ định của mệnh đề “

2 1 2

  

” là mệnh đề “

2 1 2

  

”.

B. Phủ định của mệnh đề “

,1  + +k k k

là một số lẻ” là mệnh đề

“

,1  + +k k k

là một số chẵn”.

C. Phủ định của mệnh đề “

n

sao cho

1−n

chia hết cho 24” là

mệnh đề “

n

sao cho

1−n

không chia hết cho 24”.

D. Phủ định của mệnh đề “

, 3 1 0  − + x x x

” là mệnh đề “

, 3 1 0  − + x x x

”.

..................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 49: Cho mệnh đề

“ : ”=   xA xx

. Trong các mệnh đề sau,

mệnh đề nào là phủ định của mệnh đề

“ : ”  x x x

. B.

“ : ”  x x x

“ : ”  x x x

. D.

“ : ”  x x x

CÂU 50: Cho mệnh đề

“ : ”

=   +  −x x xA

. Lập mệnh đề phủ

định của mệnh đề

và xét tính đúng sai của nó.

“ : ”

=   +  −A x x x

. Đây là mệnh đề đúng.

“ : ”

=   +  −A x x x

. Đây là mệnh đề đúng.

“ : ”

=   +  −A x x x

. Đây là mệnh đề đúng.

“ : ”

=   +  −A x x x

. Đây là mệnh đề sai.

CÂU 51: Cho mệnh đề “phương trình

4 4 0− + =xx

có nghiệm”.

Mệnh đề phủ định của mệnh đề đã cho và tính đúng, sai của mệnh

đề phủ định là:

A. Phương trình

4 4 0− + =xx

có nghiệm. Đây là mệnh đề đúng.

B. Phương trình

4 4 0− + =xx

có nghiệm. Đây là mệnh đề sai.

C. Phương trình

4 4 0− + =xx

vô nghiệm. Đây là mệnh đề đúng.

D. Phương trình

4 4 0− + =xx

vô nghiệm. Đây là mệnh đề sai.

CÂU 52: Cho mệnh đề

“ :3 1=   +A n n

là số lẻ”, mệnh đề phủ định

của mệnh đề

và tính đúng, sai của mệnh đề phủ định là:

“ : 3 1=   +A n n

là số chẵn”. Đây là mệnh đề đúng.

“ : 3 1=   +A n n

là số chẵn”. Đây là mệnh đề sai.

“ : 3 1=   +A n n

là số chẵn”. Đây là mệnh đề sai.

“ : 3 1=   +A n n

là số chẵn”. Đây là mệnh đề đúng.

..................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 5: Mnh đ ko theo

Phương pháp: Xét mnh đ

.PQ

( Nếu P thì Q ).

 Khi đ

là giả thiết,

là kết luận.



l điu kin đủ để có

hoặc

l điu kin cn để có

CÂU 53: Cho mệnh đề: “Nếu

2ab+

thì một trong hai số

và

nhỏ hơn 1”. Phát biểu mệnh đề trên bằng cách sử dụng khái niệm

“điều kiện đủ”.

2ab+

là điều kiện đủ để một trong hai số

và

nhỏ hơn 1.

B. Một trong hai số

và

nhỏ hơn 1 là điều kiện đủ để

2ab+

C. Từ

2ab+

suy ra một trong hai số

và

nhỏ hơn 1

D. Tất cả các câu trên đều đúng.

CÂU 54: Cho mệnh đề: “Nếu một tứ giác là hình thang cân thì tứ

giác đó có hai đường chéo bằng nhau”. Phát biểu mệnh đề trên bằng

cách sử dụng khái niệm “điều kiện cần”.

A. Điều kiện cần để tứ giác là hình thang cân là tứ giác đó có hai

đường chéo bằng nhau.

B. Điều kiện cần để tứ giác có hai đường chéo bằng nhau là tứ giác

đó là hình thang cân.

C. Tứ giác là hình thang cân kéo theo tứ giác đó có hai đường chéo

bằng nhau.

D. Cả a, b đều đúng.

CÂU 55: Cho mệnh đề: “Nếu

ABC

là tam giác đều thì

ABC

là một

tam giác cân”. Tìm giả thiết và kết luận của định lí.

A. “

ABC

là tam giác cân” là giả thiết, “

ABC

là tam giác đều ” là kết

luận.

B. “

ABC

là tam giác đều” là giả thiết, “

ABC

là tam giác cân” là kết

luận.

C. “Nếu

ABC

là tam giác đều” là giả thiết, “thì

ABC

là tam giác cân”

là kết luận.

D. “Nếu

ABC

là tam giác cân” là giả thiết, “thì

ABC

là tam giác đều”

là kết luận.

..................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 56: Trong các mệnh đề sau, mệnh đề nào không phải là định lí?

, xx

chia hết cho



chia hết cho

, xx

chia hết cho



chia hết cho

, xx

chia hết cho



chia hết cho

, xx

chia hết cho

và



chia hết cho

CÂU 57: Trong các mệnh đề sau, mệnh đề nào là định lí?

, 2 4x x x   −  

, 2 4x x x    

, 4 2x x x    

D. Nếu

ab+

chia hết cho

thì

, ab

đều chia hết cho

CÂU 58: Cách phát biểu nào sau đây không thể dùng để phát biểu

mệnh đề:

AB

A. Nếu

thì

kéo theo

là điều kiện đủ để có

là điều kiện cần để có

..................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 6: Mnh đ đo

Phương pháp: Xét mnh đ

.PQ

( Nếu P thì Q ).

 Khi đ

là giả thiết,

là kết luận.



l điu kin đủ để có

hoặc

l điu kin cn để có

 Khi đó mnh đ

QP

gi l mnh đ đo ca mnh đ

.PQ

CÂU 59: Cho mệnh đề: “Nếu 2 góc ở vị trí so le trong thì hai góc đó

bằng nhau”. Trong các mệnh đề sau đây, đâu là mệnh đề đảo của

mệnh đề trên?

A. Nếu 2 góc bằng nhau thì hai góc đó ở vị trí so le trong.

B. Nếu 2 góc không ở vị trí so le trong thì hai góc đó không bằng

nhau.

C. Nếu 2 góc không bằng nhau thì hai góc đó không ở vị trí so le

trong.

D. Nếu 2 góc ở vị trí so le trong thì hai góc đó không bằng nhau.

CÂU 60: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo là

sai?

A. Tam giác cân có hai cạnh bằng nhau.

chia hết cho 6 thì

chia hết cho 2 và 3.

ABCD

là hình bình hành thì

song song với

ABCD

là hình chữ nhật thì

90 .A B C= = = 

..................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 7: Mnh đ tương đương

Phương pháp: Xét mnh đ

.PQ

( Nếu P thì Q ).

 Nếu cả hai mnh để

và

đu đúng thì mnh đ tương

đương đúng.

 Mnh đ

c thể pht biểu  nhng dng như sau:

P tương đương Q.

P l điu kin cn v đủ để c Q.

P khi v ch khi Q.

CÂU 61: Cho

a

. Mệnh đề nào dưới đây đúng?

và

6a

39aa

24aa

và

thì

18a

CÂU 62: Mệnh đề nào dưới đây sai?

A. Tứ giác

ABCD

là hình chữ nhật khi và chỉ khi

ABCD

có ba góc

vuông.

B. Tứ giác

ABCD

là hình bình hành khi và chỉ khi

ABCD

có hai cạnh

đối song song và bằng nhau.

C. Tứ giác

ABCD

là hình thoi khi và chỉ khi

ABCD

có hai đường chéo

vuông góc với nhau tại trung điểm mỗi đường.

D. Tứ giác

ABCD

là hình vuông khi và chỉ khi

ABCD

có bốn góc

vuông.

..................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 8: Dng k hiu ∀, ∃ đ vit mnh đ

Phương pháp:

 "Với mi

thuc ", k hiu l:

" ".xX

 "Tn ti

thuc ", k hiu l:

" ".xX

CÂU 63: Viết mệnh đề sau bằng cách sử dụng kí hiệu



hoặc



“Mọi số nhân với 1 đều bằng chính nó”.

, .1x x x  =

, .1x x x  =

CÂU 64: Viết mệnh đề sau bằng cách sử dụng kí hiệu



hoặc



“Mọi số cộng với số đối của nó đều bằng 0”.

( )

:0x x x  + − =

( )

:0x x x  + − =

,0x x x  − =

( )

,0x x x  + − =

CÂU 65: Các kí hiệu nào sau đây dùng để viết đúng mệnh đề “

là

một số tự nhiên”.

7 

7

7 

7 

CÂU 66: Kí hiệu nào sau đây dùng để viết đúng mệnh đề “

không

phải là số hữu tỉ”

2 

. B.

2 

2

. D.

không trùng với .

..................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 9: Pht biu mnh đ cha k hiu ∀, ∃

Phương pháp:

 K hiu đc l: “Với mi”

 K hiu



đc l: “Tn ti”.

CÂU 67: Mệnh đề

" , 3"xx  =

khẳng định rằng:

A. Bình phương của mỗi số thực bằng

B. Có ít nhất một số thực mà bình phương của nó bằng

C. Chỉ có một số thực có bình phương bằng

D. Nếu

là số thực thì

3=x

CÂU 68: Kí hiệu

là tập hợp các cầu thủ

trong đội tuyển bóng

rổ,

( )

là mệnh đề chứa biến “

cao trên

180 cm

”. Mệnh đề

" , ( )"x X P x

khẳng định rằng:

A. Mọi cầu thủ trong đội tuyển bóng rổ đều cao trên

180 cm

B. Trong số các cầu thủ của đội tuyển bóng rổ có một số cầu thủ cao

trên

180 cm

C. Bất cứ ai cao trên

180 cm

đều là cầu thủ của đội tuyển bóng rổ.

D. Có một số người cao trên

180 cm

là cầu thủ của đội tuyển bóng rổ.

CÂU 69: Mệnh đề

" , 3"xx  =

khẳng định rằng:

A. Bình phương của mỗi số thực bằng

B. Có ít nhất một số thực mà bình phương của nó bằng

C. Chỉ có một số thực có bình phương bằng

D. Nếu

là số thực thì

3=x

..................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 10: Ph đnh mnh đ cha k hiu ∀, ∃

Phương pháp:

 Mnh đ phủ định của mnh đ

" , ( )"x X P x

là

" , ( )".x X P x

 Mnh đ phủ định của mnh đ

" , ( )"x X P x

là

" , ( )".x X P x

CÂU 70: Mệnh đề nào sau đây là phủ định của mệnh đề: “Mọi động

vật đều di chuyển”.

A. Mọi động vật đều không di chuyển. B. Mọi động

vật đều đứng yên.

C. Có ít nhất một động vật không di chuyển. D. Có ít nhất

một động vật di chuyển.

CÂU 71: Phủ định của mệnh đề: “Có ít nhất một số vô tỷ là số thập

phân vô hạn tuần hoàn” là mệnh đề nào sau đây:

A. Mọi số vô tỷ đều là số thập phân vô hạn tuần hoàn.

B. Có ít nhất một số vô tỷ là số thập phân vô hạn không tuần hoàn.

C. Mọi số vô tỷ đều là số thập phân vô hạn không tuần hoàn.

D. Mọi số vô tỷ đều là số thập phân tuần hoàn.

CÂU 72: Cho mệnh đề

“

, 7 0x x x  − + 

” Mệnh đề phủ định

của

là:

, 7 0x x x  − + 

. B.

, 7 0x x x  − + 

C. Không tồn tại

: 7 0x x x− + 

. D.

, - 7 0x x x  + 

..................................................

CHUYÊN Đ ÔN LUYN KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

1. CC KHI NIM CƠ BN V TP HP

a. Tp hp

 Tập hợp là một khái niệm cơ bản của toán học, không định nghĩa mà chỉ mô tả.

 C hai cch xc định tập hợp:

▶ Liệt kê các phần tử: viết các phần tử của tập hợp trong hai dấu móc

{...;...;...;...}.

 Ví dụ:

{0; 1; 2; 3; 4}.X

▶ Chỉ ra tính chất đc trưng cho cc phần tử của tập hợp.

 Ví dụ:

{ | 3 36}.X n n

 Tập rỗng: là tập hợp không chứa phần tử nào, kí hiệu

 Ví dụ: Phương trình

10xx

không có nghiệm.

Ta nói tập hợp các nghiệm của phương trình này là tập hợp rỗng, tức

b. Tp hp con

 Cho 2 tập hợp :

;AB

▶ Nếu mọi phần tử của tập hợp

đu là phần tử của tập hợp

thì ta ni:

 Tập hợp

là một tập hợp con (tập con) của tập hợp

. Và k hiệu là

▶ Cch đọc khc:  Tập hợp

chứa trong tập hợp

 Tập hợp

chứa tập hợp

 Cch viết bng k hiệu:

( ).A B x A x B

Nhn xt: ▶

, AAA

và

, .AA

▶

, .A B B C A C

 Nếu tập

c

phần tử

có

tập hợp con.

 Ngưi ta thưng minh họa tập hợp bng một hình

phng, được bao quanh bi 1 đưng khp kn.

Gọi là biu đ Ven ( Hnh 1 )

Hnh 1

c. Hai tp hp bng nhau

 Nếu mi phần tử của tập hợp

đu là phần tử của tập hợp

v ngưc li thì ta ni:



và

là 2 tập hợp bng nhau. K hiệu:

Nhn xt:

Bài TP HP, CC PHP TON TRÊN TP HP

TÓM TẮT LÝ THUYẾT

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

2. CC TP HP S

a) Môi quan h gia cc tp hp s

 Tập hợp cc s t nhiên :



 

0;1;2;3;......=

 Tập hợp cc s t nhiên khc

không



 

1;2;3;......=

 Tập hợp cc s nguyên :



 

....; 3; 2; 1;0;1;2;3;......= − − −

 Tập hợp cc s hu tỉ :



; ; 0

a b b



=  





 Tập hợp cc s thc : g󰉰m

các s󰉯 h󰊀u t󰉫 và vô t󰉫.

 S󰈘 vô t󰈖 l c c s󰈘 th󰈨p phân

vô h󰈨 n không tu󰈚 n ho n.

b) Cc tp con thưng dng ca ℝ

 Khoảng

( ; ) { | }.a b x a x b

Ví dụ:

2 3 ( 2;3).xx

( ; ) { | }.a x x a

Ví dụ:

3 (3; ).xx

( ; ) { | }.b x x b

Ví dụ:

3 ( ;3).xx

 Đoạn

[ ; ] { | }.a b x a x b

 Nửa khoảng

[ ; ) { | }.a b x a x b

( ; ] { | }.a b x a x b

[ ; ) { | }.a x x a

( ; ] { | }.b x x b

Kí hiệu đọc là dương vô cc (cùng), kí hiệu đọc là âm vô cc (cùng).

Ta có th viết

( ; )

và gọi là khoảng

( ; ).

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

3. CC PHP TON TRÊN TP HP

a. Giao ca hai tp hp

 Tập hợp

gm các phần tử vừa thuộc

vừa thuộc

được gọi là giao của

và

 Kí hiệu

C A B

(phần gạch trong hình).

 Vậy

{|A B x x A

và

}.xB



x A B

(Cách nhớ: giao là lấy phần chung)

b. Hp ca hai tp hp

 Tập hợp

gm các phần tử thuộc

hoc thuộc

được gọi là hp của

và

 Kí hiệu:

C A B

(phần gạch chéo trong hình).

 Vậy

{|A B x x A

hoc

}.xB



x A B

(Cách nhớ: hợp là lấy hết)

c. Hiu ca hai tp hp

 Tập hợp

gm các phần tử thuộc

nhưng không thuộc

gọi là hiu của

và

 Kí hiệu

\C A B

(phần gạch chéo trong hình).

 Vậy

\ { |A B x x A

và

}.xB



x A B

(Cách nhớ: hiệu thuộc

mà không thuộc

 Khi

thì

\AB

gọi là phần bù của

trong

 Kí hiệu

C B A B

(phần gạch chéo trong hình).

Tổng kết: Giao

()AB

là lấy phần chung, hợp

()AB

là lấy hết, trừ

( \ )AB

là thuộc

mà không

thuộc

phần bù

C B A B

(dưới trừ trên và trên con dưới).

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 1: Xc đnh tp hp bng cch lit kê tt c cc phn t ca tp hp

Viết tập hợp sau bằng cách liệt kê các phần tử của nó:

{ | 20A x x

và

chia hết cho

3}.

Ta có:

{0; 3; 6; 9; 12; 15; 18}.A

Viết mỗi tập hợp sau bằng cách liệt kê các phần tử của nó..

{ | 2 10}.A x x

{ | 7 15}.A x x

{ |14 3 0}.A x x

{ | 15 2 0}.A x x

{ | 1 3}.A x x

{ | 5}.A x x

{ | 2 1}.A x x

A x x n

Lời giải

.............................................................................................................................................................................................

BI TP T LUN

Ví dụ 1

BÀI GIẢI

Bài 1.1

BÀI TP RN LUYN

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Viết mỗi tập hợp sau bằng cách liệt kê các phần tử của nó..

{ | (2 5 3)(4 ) 0}.A x x x x

{ |( 4 3)(2 1) 0}.A x x x x

{ | 2 7 5 0}.A x x x x

{ | 15 2 0}.A x x

4 2 2

{ |( 8 9)( 16) 0}.A x x x x

{ | 5}.A x x

{ | (3 4 7)(9 ) 0}.A x x x x

4 2 2

{ |( 3 4)( 25) 0}.A x x x x

Lời giải

.............................................................................................................................................................................................

Bài 1.2

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 2: Xc đnh tp hp bng cch ch ra tnh cht đc trung

Viết tập hợp sau bằng cách nêu tính chất đặc trưng của nó:

{2; 6; 12; 20; 30}.A

Cách 1:

{ ( 1) 1 5; }.A n n n n

Cách 2:

{ ( 1) 0< 6; }.A n n n n

Viết cc tập hợp sau bằng cách nêu tính chất đặc trưng của nó:

{1; 3; 5; 7}.A

0 ; 2; 4; 6;......B

C 0;5;10;15;20 .{}=

1 1 1 1 1

; ; ; ;

2 6 12 20 30

1 1 1 1 1

1; ; ; ; ;

3 9 27 81 234

1 1 1 1 1

; ; ; ;

2 6 12 20 30

 

G 4; 3; 2; 1;0;1;2;3;4 .= − − − −

{3; 6; 9; 12; 15}.G

Lời giải

.............................................................................................................................................................................................

Ví dụ 1

BÀI GIẢI

Bài 1.1

BÀI TP RN LUYN

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 3: Xc đnh tp con ca mt tp hp cho trưc

Tìm tất cả các tập hợp con của tập hợp sau: a)

{ ; }.A a b

{0;1;2}.B

a) Cc tập hợp con của tập hợp

{ ; }A a b

l:

; ; { }; { }.A a b

b) Cc tập hợp con của tập hợp

{0;1;2}.B

l:

; ; {1}; {2}; {3}; {1;2}; {1;3}; {2;3}.B

Tìm tất cả các tập hợp con của tập hợp sau:

 

1;2;3;Aa=

{Bx

sao cho

l ước của

8}.

}2{ 1 , C kkk

( ; ) | , , .

D x y x y y

1 1 1 1 1

1; ; ; ; ;

3 9 27 81 234

1 1 1 1 1

; ; ; ;

2 6 12 20 30

{ | 7 15}.G x x

H x x n

Lời giải

.............................................................................................................................................................................................

Ví dụ 1

BÀI GIẢI

Bài 1.1

BÀI TP RN LUYN

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Cho hai tập hợp

{ 4; 2; 1;2;3;4}A

và

{ | 4}.B x x

Tìm các tập hợp

sao cho

.A X B

Ta có:

4 4 4xx

và do

nên

{ 4; 3; 2; 1;0;1;2;3;4}.B

Theo đề

{ 4; 2; 1;2;3;4} { 4; 3; 2; 1;0;1;2;3;4}A X B X

nên tập hợp

là một

trong những tập hợp :

{ 4; 2; 1;2;3;4}, { 4; 3; 2; 1;2;3;4}, { 4; 2; 1;0;2;3;4},{ 4; 2; 1;1;2;3;4}, { 4; 2; 1;0;2;3;4},

{ 4; 3; 2; 1;1;2;3;4},

{ 4; 2; 1;0;1;2;3;4},

{ 4; 3; 2; 1;0;1;2;3;4}.

Cho

{1;2}A

và

{1;2;3;4;5}.B

Tìm các tập hợp

sao cho

.A X B

Lời giải

.............................................................................................................................................................................................

Ví dụ 2

BÀI GIẢI

BÀI TP RN LUYN

Bài 1.2

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 4: Cc php ton trên tp hp ( Không cha tp con ca ℝ )

Cho 2 tập hợp

{1; 2; 3}A

và

{1; 3; 5; 7}.B

Tm

Ta c:

{1;3}AB

Cho 2 tập hợp:

{1; 2; 3; 4; 5}A

và

{1; 3; 5; 7; 9; 11}.B

Xc đnh cc php ton sau:

Lời giải

..........................................................

........................................................ ……………

\AB

...........................................................

\BA

......................................................... ……………

( )\( )A B A B

..................................................................................................................... …………..

( \ ) ( \ )A B B A

........................................................................................................................................

Cho 2 tập hợp:

{1; 2; 3; 4}, {2; 4; 6; 8}AB

và

{3; 4; 5; 6}.C

Xc đnh cc php ton sau:

Lời giải

..........................................................

........................................................ ……………

..........................................................

........................................................ ……………

..........................................................

........................................................ ……………

\AB

...........................................................

\BC

......................................................... ……………

\CA

................................................................................................................................................... …..

( )A B C

.............................................................................................................................................. ..

Ví dụ 1

BÀI GIẢI

Bài 1.1

BÀI TP RN LUYN

Bài 1.2

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Xc đnh tập

v

đng thi tha mn:

{1;2;3}; \ {4;5}A B A B

và

\ {6;9}.BA

Vì

{1;2;3}AB

nên hai tập hợp

và

sẽ có ba phần tử:

1, 2, 3.

Vì

\ {4;5},AB

tức

4, 5 A

mà

4, 5 B

nên

{1; 2; 3; 4; 5}.A

Vì

\ {6;9},BA

……………………………………………………………………………………………………………………………………………

Xc đnh tập

v

đng thi tha mn:

{0; 1; 2; 3; 4}, \ { 3; 2}A B A B

và

\ {6; 9; 10}.BA

Lời giải

……………………………………………………………………………………………………………………………………………………………………………….

Xc đnh tập

v

đng thi tha mn:

\ {1; 5; 7; 8}, {3; 6; 9}A B A B

và

{ | 0 10}.A B x x

Lời giải

……………………………………………………………………………………………………………………………………………………………………………….

Ví dụ 2

BÀI GIẢI

Bài 1.1

BÀI TP RN LUYN

Bài 1.2

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 5: S dụng biu đ Ven đ gii bi ton.

Mỗi học sinh lớp

10C

đều chơi bng đ hoặc bóng chuyền. Biết rằng có

bạn chơi bng đ,

bạn

chơi bng chuyền và

bạn chơi cả 2 môn thể thao này. Hi lớp

10C

có bao nhiêu học sinh ?

Kí hiệu:

là tập các học sinh lớp

10C

chơi bng đ (c

ngưi).

là tập các học sinh lớp

10C

chơi bng chuyền (có

ngưi).

Vì mỗi bạn lớp

10C

đều chơi bng đ hoặc bóng chuyền

là tập các học sinh của lớp.

Để đếm số phần tử của

ta đếm số phần tử của

(25

phần tử) v đếm số phần tử của

(20B

phần tử), nhưng khi đ số phần tử của

được đếm 2 lần. (Nhng bạn chơi cả 2 môn th thao)

Tức số học sinh của lớp là

( ) ( ) ( ) ( ) 25 20 10 35n A B n A n B n A B

học sinh.

Trong số

học sinh lớp

10A

có

bạn được xếp loại học lực gii,

bạn xếp loại hạnh kiểm tốt,

trong đ c

bạn vừa học lực gii, vừa có hạnh kiểm tốt. Hi:

Lời giải

a) Lớp

10A

có bao nhiêu bạn được khen thưởng, biết rằng muốn được khen thưởng, bạn đ phải học

lực gii hoặc có hạnh kiểm tốt ?

................................................................................................................................................................................

..............................................................................................................................................................

bạn.

b) Lớp

10A

có bao nhiêu bạn chưa được xếp loại học lực gii v chưa c hạnh kiểm tốt ?

................................................................................................................................................................................

...............................................................................................................................................................

bạn.

Ví dụ 1

BÀI GIẢI

Bài 1.1

BÀI TP RN LUYN

10 bạn

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Trong lớp

10A

có 45 học sinh trong đ c 25 em thch môn Văn, 20 em thch môn Ton, 18 em thch môn Sử,

6 em không thích môn nào, 5 em thích cả ba môn. Hỏi s em thích chỉ một môn trong ba môn trên.

Gọi

,,a b c

theo thứ t là s học sinh chỉ thch môn Văn, Sử, Toán:

là s học sịnh chỉ thch hai môn là văn và ton.

là s học sịnh chỉ thích hai môn là Sử và toán

là s học sịnh chỉ thích hai môn là văn và Sử

Ta có s em thích ít nhất một môn là

45 6 39

Ta c biu đ Ven:

Da vào biu đ ven ta có hệ phương trình

5 25 (1)

5 18 (2)

5 20 (3)

5 39 (4)

a x z

b y z

c x y

x y z a b c

Cộng vế với vế (1), (2), (3) ta có:

2 15 63a b c x y z

(5)

Từ (4) và (5) ta có:

2 39 5 15 63a b c a b c

20a b c

Vậy chỉ có 20 em thích chỉ một môn trong ba môn trên.

Ví dụ 2

BÀI GIẢI

BÀI TP RN LUYN

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Trong lớp

10A

có 16 học sinh giỏi môn Toán, 15 học sinh giỏi môn Lý và 11 học sinh giỏi môn Hóa. Biết rng

có 9 học sinh vừa giỏi Toán và Lý, 6 học sinh vừa giỏi Lý và Hóa, 8 học sinh vừa giỏi Ha và Ton, trong đ

chỉ có 11 học sinh giỏi đúng hai môn. Hi c bao nhiêu học sinh của lớp:

Lời giải

a) Giỏi cả ba môn Toán, Lý, Hóa?

................................................................................................................................................................................

........................................................................................................................................................

học sinh.

b) Giỏi đúng một môn Toán, Lý hoc Hóa.?

................................................................................................................................................................................

.........................................................................................................................................................

học sinh.

Nhận xét: Với

,,A B C

là các tập bất kì khi đ ta luôn c

n A B n A n B n A B

( ) ( ) ( ) ( )n A B C n A n B n C n A B n B C n C n A B CA

Bài 1.2

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 6: Chng minh tp hp bng nhau, tp con

Cho

và

là hai tập hợp. Chứng minh rng:

\A B A

\A B A A B

a) Ta có

x x A B x A

. Suy ra

\A B A

b) Ta có

x A B A x B x

x B A

. Suy ra

\A B A

c) Ta có

x A B A x A B

x B A

Cho các tập hợp

,AB

và

. Chứng minh rng:

Lời giải

A B C A B A C

…………………………………………………………………………………………………………………….

A B C A B A C

…………………………………………………………………………………………………………………….

\\A B C A B C

…………………………………………………………………………………………………………………….

Ví dụ 1

BÀI GIẢI

Bài 1.1

BÀI TP RN LUYN

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 7: Phân bit tp hp v tp con ca ℝ

Hãy phân biệt các tập hợp sau:

{ 1;2}, [ 1;2], ( 1;2), [ 1;2), ( 1;2].

{ 1;2}

là tập hợp (dạng liệt kê) chỉ chứa

phần tử là số

và số

[ 1;2] { | 1 2}xx

là một đoạn từ

(lấy

và

( gm vô số các phần tử là số thực, chẳng hạn

1; 0,9; 0,89;.....;2.

)

( 1;2) { | 1 2}xx

là một khoảng

(không lấy

và

(gm vô số các phần tử là số thực, chẳng hạn

0,9999; 0,98;.....;1,888; 1,9,...,

nhưng không lấy

)

[ 1;2) { | 1 2}xx

là nửa khoảng……………………………………………………………...................................................

……………………………………………………………………………………………………………………………………………………………………………….

( 1;2]

……………………………………………………………...................................................……………………………………………………………..

……………………………………………………………………………………………………………………………………………………………………………….

Hãy phân biệt tập hợp sau:

{ | 2 3}A x x

và

{ | 2 3}.B x x

Lời giải

…………………………………………………………………………………………………………………….

Ví dụ 1

BÀI GIẢI

Bài 1.1

BÀI TP RN LUYN

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 8: Cc php ton trên tp con ca ℝ

Cho

[ 4;4), [1;7).AB

Hy xc đnh cc php ton sau v biểu din kết quả của php ton trên

trục số ?

Đ tìm

ta làm như sau:

- Sắp xếp theo thứ t tăng dần cc đim đầu mút của các tập hợp

,AB

lên trục s.

- Biu diễn các tập

,AB

trên trục s(phần nào không thuộc các tập đ thì gạch bỏ).

- Phần không bị gạch bỏ chính là giao của hai tập hợp

,AB

Đ tìm

ta làm như sau:

- Sắp xếp theo thứ t tăng dần cc đim đầu mút của các tập hợp

,AB

lên trục s.

- Tô đậm các tập

,AB

trên trục s.

- Phần tô đậm chính là hợp của hai tập hợp

,AB

Đ tìm

\AB

ta làm như sau:

- Sắp xếp theo thứ t tăng dần cc đim đầu mút của các tập hợp

,AB

lên trục s.

- Biu diễn tập

trên trục s(gạch bỏ phần không thuộc tập

), gạch bỏ phần thuộc tập

trên trục s .

- Phần không bị gạch bỏ chính là

\AB

[1;4),AB

biểu din trên trục số:

[ 4;7),AB

biểu din trên trục số: ……………………………………………………………………………………………………….

\ [ 4;1),AB

biểu din trên trục số: ……………………………………………………………………………………………………….

\ [4;7),BA

biểu din trên trục số: …………………………………………………………………………………………………………..

\ ( ; 4) [4; ) :C A A

…………………………………………………………………………………………………………...

\ ( ;1) [7; ) :C B B

……………………………………………………………………………………………………………...

Ví dụ 1

BÀI GIẢI

BÀI TP RN LUYN

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Cho

[3; ), (0;4).AB

Hy xc đnh cc php ton sau v biểu din kết quả của php ton trên

trục số ?

Lời giải

.................................................................................................................................................................................

.............................................................................................................................................................

\AB

..............................................................................................................................................................

\BA

..............................................................................................................................................................

...............................................................................................................................................................

Cho

( ;10), \[0;1]AB

Hy xc đnh cc php ton sau v biểu din kết quả của php

ton trên trục số ?

Lời giải

.................................................................................................................................................................................

.............................................................................................................................................................

\AB

..............................................................................................................................................................

\BA

..............................................................................................................................................................

...............................................................................................................................................................

Nhận xét: Tập

( ;10)A

cn c th viết dưới dạng:

...................................Ax

Bài 1.1

Bài 1.2

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Cho hai tập hợp

[ ; 2)A m m

và

(5;6), .Bm

a) Tìm

để

.AB

b) Tìm

để

.BA

c) Tìm

để

a) Tìm

để

.AB

• Để

5 2 6A B m m

2 6 4

b) Tìm

để

.BA

• Để

5 6 2B A m m

4 5.

2 6 4

c) Tìm

để

(Cố định tập

(5;6)B

thì tập

nằm bên trái hoặc bên phải).

……………………………………………………………………………………………………………………………………………………………………………….

Để

2 5 3

m+2

∞

m+2

∞

Ví dụ 2

BÀI GIẢI

BÀI TP RN LUYN

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Cho hai tập hợp

(3 1; 3 7)A m m

và

( 1;1), .Bm

Lời giải

a) Tìm

để

.BA

...........................................................................

..........................................................

2.m

b) Tìm

để

.AB

............................................................................

...........................................................................

.........................................................

4.m

Cho hai tập hợp

(2;7 )Am

và

( 1; ), .B m m

Lời giải

a) Tìm

để

.AB

...........................................................................

b) Tìm

để

.AB

............................................................................

...........................................................................

............................................................................

c) Tìm

để

(1; ).AB

............................................................................................................................................................................

……………………………………………………………………………………………………….

2.m

Bài 1.1

Bài 1.2

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Cho

, 2 , [2 1, )A B m

. Tìm m đ

A B R

Lời giải

............................................................................................................................................................................

………………………………………………………………………………………………………….

Tìm m đ

1; 2;m

Lời giải

............................................................................................................................................................................

………………………………………………………………………………………………………….

Viết tập A gm các phần tử x thỏa mãn điu kiện

dưới dạng tập s.

Lời giải

............................................................................................................................................................................

............................................................................................................................................................................ …

……………………………………………………………………………………………Vậy

1; 0 .A

Bài 1.3

Bài 1.4

Bài 1.5

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

distance

Dạng 1: Xc đnh s phn t ca tp hp

Phương pháp

 a  A: ph󰉚n t󰉿 a thu󰉳c vào t󰉝p h󰉹p A

 a  A: ph󰉚n t󰉿 a không thu󰉳c vào t󰉝p h󰉹p A

CÂU 1: Trong các tập hợp sau đây, tập hợp no c đúng một phần tử?

 

;xy

. B.

 

;x 

. D.



CÂU 2: Tập hợp

 

2;5X =

có bao nhiêu phần tử?

. B. Vô số.

. D.

CÂU 3: Cho tập hợp

 

|5A x x=  

. Tập hợp A được viết dưới dạng liệt kê các

phần tử là

 

1;2;3;4A=

. B.

 

1;2;3;4;5A=

 

0;1;2;3;4;5A=

. D.

 

0;1;2;3;4A=

CÂU 4: Cho tập hợp

. Trong các mệnh đề sau, mệnh đề nào sai?

A

. B.

 

AA

AA

. D.

AA

CÂU 5: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng?

 

/1x N x

. B.

 

/ 6 7 1 0x Z x x − + =

 

/ 4 2 0x Q x x − + =

. D.

 

/ 4 3 0x R x x − + =

CÂU 6: Trong các tập hợp sau đây, tập hợp no c đúng một phần tử?

 

;xy

. B.

 

;x 

. D.



CÂU 7: Tập hợp

 

2;5X =

có bao nhiêu phần tử?

. B. Vô số.

. D.

QUICK NOTE

Th để giọt m hôi

rơi trên trang sch

còn hơn để nước mắt

rơi ướt cả đề thi

distance

.....................................

BI TP TRẮC NGHIM

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 2: Xc đnh tp hp bng cch lit kê hoc ch ra tnh

cht đc trưng ca cc phn t thuc tp hp.

Phương pháp

 X 󰈨nh t󰈨p h󰉴󰈨 p b󰈢 ng c ch li󰈨t kê:

 Bước 1: Xc định điu kiện của

. (

thuộc tập s nào )

 Bước 2: Giải phương trình, tìm cc gi trị

. So snh với điu kiện đ chọn.

 X 󰈨nh t󰈨p h󰉴󰈨 p b󰈢 ng c ch ch󰈖 ra tnh ch󰈘 󰈨󰉼󰈖 a c c ph󰈚 n t󰉼󰈖 :

 Bước 1: Liệt kê ra một vài phần tử thuộc tập hợp đả cho  Đp n.

 Bước 2: Kim tra

CÂU 8: Hãy liệt kê các phần tử của tập

 

2 5 3 0 .xX x x= − + =

 

0.X =

 

1.X =







1; .







CÂU 9: Cho tập hợp

 

|5A x x=  

. Tập hợp A được viết dưới dạng liệt kê các

phần tử là

 

1;2;3;4A=

. B.

 

1;2;3;4;5A=

 

0;1;2;3;4;5A=

. D.

 

0;1;2;3;4A=

CÂU 10: Cho tập

( )

 

| 4 1 0X x x x=  − − =

. Tính tổng

các phần tử của tập

4S =

. B.

S =

9S =

. D.

1S =

CÂU 11: Liệt kê phân tử của tập hợp

 

| (2 )( 3 4) 0B x x x x x=  − − − =

 

1;0;4B =−

. B.

 

0;4B =

1; ;0;4



=−





. D.

 

0;1;4B =

CÂU 12: Cho

 

2 5 3 0X x R x x=  − + =

, khẳng đnh no sau đây đúng?

 

1X =

. B.













. D.

 

0X =

CÂU 13: Có bao nhiêu cách cho một tập hợp?

. B.

. D.

.....................................

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 14: Cho hai tập hợp

( )( )

 

| 2 3 4 0 , | 4 .A x x x x B x x=  − − − = =  

Viết lại các tập

và

bằng cách liệt kê các phần tử.

2; 1;2;



= − −





 

0;1;2;3B =

2; 1;2;



= − −





 

1;2;3;4B =

 

2; 1;2A= − −

 

0;1;2;3B =

 

2; 1;2A = − −

 

1;2;3B =

CÂU 15: Cho tập hợp

 

*22

,51A x x x=+ 

. Khi đ tập

bằng tập hợp nào

sau đây?

 

1;2;3;4A =

. B.

 

0;2;5A =

 

2;5A =

. D.

 

0;1;2;3;4;5A =

CÂU 16: Tìm số phần tử của tập hợp

( )( )

( )

 

/ 1 2 4 0A x x x x x=  − + − =

. B.

. D.

CÂU 17: Cho tập hợp

( )( )

 

| 2 5 2 16 0A x x x x=  + + − =

. Tập hợp

được

viết dưới dạng liệt kê là

4; ; 2; 4

−



−−





. B.

 

4; 2−−

 

4

. D.

 

4; 2; 4−−

CÂU 18: Hãy liệt kê các phần tử của tập hợp:

 

/ 2x 5 2 0X x x=  − + =

 

0X =

. B.







 

2X =

. D.







CÂU 19: Cho tập

( )

 

| 4 1 2 7 3 0X x x x x x=  − − − + =

. Tính tổng

các

phần tử của

S =

. B.

5S =

6S =

. D.

4S =

CÂU 20: Hãy liệt kê các phần tử của tập hợp

 

| 1 0X x x x=  + + =

X =

. B.

 

X =

 

0X =

. D.

0X =

.....................................

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 21: Cho

 

0;2;4;6A =

. Tập hợp

có bao nhiêu tập hợp con có

phần tử?

. B.

. D.

CÂU 22: Cho tập hợp

 

,,A a c e=

. Có bao nhiêu tập con của tập hợp

. B.

. D.

CÂU 23: Tính chất đặc trưng của tập hợp

 

1;2;3;4;5 .X =

 

5.xx

 

5.xx

 

5.xx

 

5.xx

CÂU 24: Tính chất đặc trưng của tập hợp

 

3; 2; 1;0;1;2;3 .X = − − −

 

3.xx

 

3.xx

 

3.xx

 

3 3 .xx −  

CÂU 25: Tính chất đặc trưng của tập hợp

1 1 1 1

; ; ; ;.... .

2 4 8 16







x x n



 = 





; * .

x x n



 = 





; * .

x x n



 = 





; * .

x x n



 = 



−



CÂU 26: Tính chất đặc trưng của tập hợp

1 1 1 1

; ; ; ;.... .

2 6 12 20







; * .

( 1)

x x n



 = 





; * .

( 1)

x x n



 = 





; * .

( 1)

x x n



 = 





; * .

( 1)

x x n



 = 





CÂU 27: Tìm các phần tử của tập hợp:

 

/ 2 5 3 0X x x x=  − + =

A. X =







. B. X =

 

C. X =







. D. X =

 

CÂU 28: Hãy liệt kê các phần tử của tập hợp

 

10X x x x=  + + =

0X =

. B.

 

0X =

X =

. D.

 

X =

.....................................

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 29: Cho

 

2 5 3 0X x x x=  − + =

, khẳng đnh no sau đây đúng:

 

0X =

 

1X =













CÂU 30: Cho tập hợp

( )( )

 

9 3 2 0B x R x x x=  − − + =

, tập hợp no sau đây l

đúng?

A. Tập hợp

 

3;9;1;2B =

B. Tập hợp

 

3; 9;1;2B = − −

C. Tập hợp

 

9;9;1;2B =−

D. Tập hợp

 

3;3;1;2B =−

CÂU 31: Cho tập hợp

 

2 15 0S x R x x=  − − =

. Hãy chọn kết quả đúng trong

các kết quả sau đây

 

3;5S =−

 

3; 5S =−

S =

SR=

.....................................

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 3: Tm tp con, s tp con ca mt tp hp cho trưc.

Phương pháp

 A  B  x (x  A  x  B).

 A  A, A.

 N󰉦u A  B và B  C thì A  C



A

, A.

 N󰉦u A c n phần tử thì A c

tập con.

CÂU 32: Hnh no sau đây minh họa tập

là con của tập

A. B.

C. D.

CÂU 33: Cho tập

 

2;3;4; 5 .X =

Hi tập

có bao nhiêu tập hợp con?

16.

CÂU 34: Cho hai tập hợp:



|X n n=

là bội số của 4 và 6} và



|Y n n=

là bội số của 12}. Trong các mệnh đề sau, tìm mệnh đề sai?

XY

. B.

YX

XY=

. D.

:n n X

và

nY

CÂU 35: Cho tập hợp

 

1;2;Aa=

 

1;2; ; ; ;B a b x y=

. Hi có bao nhiêu tập hợp

tha

A X B

. B.

. D.

CÂU 36: Cho A là tập hợp có hai phần tử, số tập hợp con của tập A là

. B.

C. vô số. D.

CÂU 37: Số tập con của tập hợp có

( )

1,nn

phần tử là

. B.

n−

. D.

CÂU 38: Cách viết no sau đây l đúng?

 

;.a a b

 

 

;.a a b

 

 

;.a a b

(



;.a a b

.....................................

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 39: Cho tập hợp

 

1;2;Aa=

 

1;2; ; ; ;B a b x y=

. Hi có bao nhiêu tập hợp

tha

A X B

CÂU 40: Cho A là tập hợp có hai phần tử, số tập hợp con của tập A là

C. vô số.

CÂU 41: Cho tập hợp

 

| 3 4B x x=  −  

. Tập hợp

có tất cả bao nhiêu tập

hợp con?

CÂU 42: Cho tập hợp

 

;;A x y z=

và

 

; ; ; ;B x y z t u=

. Có bao nhiêu tập

tha

mãn

A X B

CÂU 43: Có tất cả bao nhiêu tập

tha mãn

   

1;2 1;2;3;4;5X

CÂU 44: Trong các tập sau đây, tập hợp no c đúng hai tập hợp con?

 

;xy

 

; x

 

;; xy

.....................................

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 4: Hai tp hp bng nhau.

Phương pháp



( )

A B x A x B=     

CÂU 45: Hai tập hợp no dưới đây không bằng nhau?

| , ,

A x x k x= =  







và

1 1 1

;;

2 4 8







 

3;9;27;81A =

và

 

3 | ,1 4

B n n=   

 

| 2 3A x x=  −  

và

 

1;0;1;2;3B =−

 

|5A x x=  

và

 

0;1; 2; 3; 4B =

CÂU 46: Khẳng đnh no sau đây sai? Các tập

AB=

với

,AB

là các tập hợp sau?

( )( )

 

1;3 , 0} –1{=3A B x x x= =  −

 

1;3;5;7;9 , 2 1, ,0 4{}A B n n k k k= =  = +   

 

1;2 ,{ 0} 2 3A B x x x −= − = − =

 

, 1 0A B x x x=  =  + + =

.....................................

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 5: Giao ca cc tp hp (Không cha tp con ca ℝ)

Phương pháp



C A B x C

  



=     











CÂU 47: Cho hai tập hợp

   

7;0;5;7 , 3;5;7;13AB= − = −

khi đ tập

AB

là

 

5;7 .

 

7; 3;0;5;7;13 .−−

 

7;0 .−

 

13 .

CÂU 48: Cho hai tập hợp

 

2 3 1 0 , 3 2 9A x x x B x x=  − + = =  + 

khi đ:

 

2;5;7 .AB=

 

1.AB=

0;1;2; .



=





 

0;2 .AB=

CÂU 49: Cho hai tập hợp

 

=  − + − = =  −  + 

( 10 21)( ) 0 , 3 2 1 4A x x x x x B x x

khi đ tập

X A B=

là:

X =

. B.

 

3;7X =

 

1;0;1 .X =−

 

1;0;1;3;7X =−

CÂU 50: Cho ba tập hợp

 

=  − + =

4 3 0 ,A x x x

 

=  −  3 2 4 ,B x x

 

=  − =

0C x x x

khi đ tập

A B C

là:

 

1;3 .−

 

1;0;3 .−

 

1;3 .

 

CÂU 51: Cho

; ; ; ; , ; ; ; ;A a b c d m B c d m k l

. Tìm

;.A B a b

; ; .A B c d m

;.A B c d

; ; ; ; ; ; .A B a b c d m k l

CÂU 52: Cho

   

1;5 ; 1;3;5 .==AB

Chọn kết quả đúng trong các kết quả sau

 

1.=AB

 

1;3 .=AB

 

1;5 .=AB

 

1;3;5 .=AB

CÂU 53: Chọn khẳng đnh sai trong các khẳng đnh sau:

=

. B.

=

=

. D.

=

CÂU 54: Cho

. Trong các mệnh đề sau, mệnh đề nào sai?

.AA

.A A A

.....................................

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 6: Hp ca cc tp hp (Không cha tp con ca ℝ)

Phương pháp

 Nếu

C A B x C

  



=     











CÂU 55: Cho hai tập hợp

   

7;0;5;7 , 3;5;7;8AB= − = −

khi đ tập

AB

là

 

5;7 .

 

7; 3;0;5;7;8 .−−

 

7;0 .−

 

CÂU 56: Cho hai tập hợp

 

2 3 1 0 , 3 2 10A x x x B x x=  − + = =  + 

khi

đ:

0;1; ;2 .



=





 

1.AB=

 

0;1;2 .AB=

 

0;2 .AB=

CÂU 57: Cho hai tập hợp

 

=  − + − = =  −  + 

( 10 21)( ) 0 , 3 2 1 5A x x x x x B x x

khi đ tập

X A B=

là:

X =

. B.

 

3;7X =

 

1;0;1 .X =−

 

1;0;1;3;7X =−

CÂU 58: Cho ba tập hợp

 

=  − + = =  −   =  − =

2 5 4

5 4 0 , 3 2 4 , 0A x x x B x x C x x x

khi đ

tập

A B C

là:

 

1;4 .

 

1;0;1;4 .−

 

0;1 .

 

CÂU 59: Cho hai tập hợp

   

1;3;5;7 , 5;7AB==

. Tìm mệnh đề sai

.BA

.AB

.AA

.BB

CÂU 60: Cho tập hợp

 

= ;;A a b c

khi đ tập hợp A có tất cả bao nhiêu tập con.

. B.

10.

CÂU 61: Cho tập hợp

 

2 3 7A x x=  − 

. Tập hợp

có tất cả bao nhiêu tập

con khác rỗng.

.....................................

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 62: Cho tập hợp

 

1;2;3;4 .A

Tập hợp

có tất cả bao nhiêu tập con c đúng

3 phần tử.

16.

CÂU 63: Cho tập hợp

   

( )

 

1;3 , 0;1;3 , 4 3 0A B C x x x= = =  − + =

. Tập

mệnh đề đúng

.AB=

.AC=

.BC=

.A B C==

CÂU 64: Cho tập hợp

 

, 0;1;3 , (2 3)( 4) 0

A x x B C x x x



=   = =  − − =





. Khi đ

( )

A B C

là

 

0;1;2 .

 

2;0;1;2 .−

2; ;1;2 .



−





3; ;1;2 .







CÂU 65: Cho hai tập hợp

0;2A

và

0;1;2;3;4 .B

Có bao nhiêu tập hợp

tha mãn

.A XB

16.

CÂU 66: Cho ba tập hợp

 

( )( )

 

2 2 4

19 , 0;1; 3 , 4 3 16 0A x x B C x x x x=   = − =  − + − =

. Khi đ tập

hợp

( )

\X A B C=

 

0;1; 3X =−

 

1.X =

 

2;3 .X =

 

3;0;3X =−

.....................................

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 7: Hiu, phn b ca cc tp hp

(Không cha tp con ca ℝ)

Phương pháp

 Tập hợp

gm các phần tử thuộc

nhưng không thuộc

gọi là hiu của

và



\C A B

Nếu

thì











 Khi

thì

\AB

gọi là phần bù của

trong

Kí hiệu

C B A B

CÂU 67: Cho hai tập hợp

   

4; 2;5;6 , 3;5;7;8AB= − − = −

khi đ tập

\AB

là

 

3;7;8 .−

 

4; 2;6 .−−

 

2;6;7;8 .−

CÂU 68: Cho ba tập hợp

 

( )

 

=  − + = =  −   =  − − =

2 5 4

5 4 0 , 3 2 4 , 2 6 0A x x x B x x C x x x x

khi đ tập

( \ )\A B C

là:

 

1;4 .

 

1;0;1;4 .−

 

0;1 .

 

CÂU 69: Cho hai tập hợp

   

1;2;4;6 , 1;2;3;4;5;6;7;8AB==

khi đ tập

là

 

1;2;4;6 .

 

4;6 .

 

3;5;7;8 .

 

2;6;7;8 .

CÂU 70: Cho tập hợp

 

3 2 10A x x=  − 

khi đ:

 

1;2;3;4 .CA=

 

0;1;2;3;4 .CA=

 

1;2;3 .CA=

 

1;2;4 .CA=

CÂU 71: Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp

 

49A x x=   

 

4;9 .=A

(



4;9 .=A



)

4;9 .=A

( )

4;9 .=A

CÂU 72: Trong các khẳng đnh sau khẳng đnh no đúng:

\ =

. B.

=

=

. D.

=

CÂU 73: Cho tập hợp

 

30C x x=  −  

. Tập hợp C được viết dưới dạng nào?

( )

3;0C =−

. B.



)

3;0C =−

. C.

(



3;0C =−

. D.

 

3;0C =−

CÂU 74: Cho tập hợp

 

27C x R x=   

. Tập hợp

được viết dưới dạng no?

( )

2;7C =

. B.



)

2;7C =

(



2;7C =

. D.

 

2;7C =

CÂU 75: Cách viết no sau đây l đúng:

 

;a a b

. B.

 

 

;a a b

 

 

;a a b

. D.

(



;a a b

.....................................

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 8: Vit cc tp con ca ℝ dưi dạng đoạn; khong;…

Phương pháp



( ; ) { | }.a b x a x b



[ ; ] { | }.a b x a x b



[ ; ) { | }.a b x a x b

 (𝑎; 𝑏] = {𝑥 ∈ ℝ|𝑎 < 𝑥 ≤ 𝑏}.

 [𝑎; +∞) = {𝑥 ∈ ℝ|𝑥 ≥ 𝑎}.



( ; ] { | }.b x x b

CÂU 76: Sử dụng các kí hiệu khoảng, nửa khoảng, đoạn để viết tập hợp

 

49A x x=   

 

4;9 .=A

(



4;9 .=A



)

4;9 .=A

( )

4;9 .=A

CÂU 77: Cho các tập hợp:

| 3 |1 5 | 2 4A x R x B x R x C x R x

Hãy viết lại các tập hợp

, , A B C

dưới kí hiệu khoảng, nửa khoảng, đoạn.

;3 1;5 2;4A B C

CÂU 78: Cho tập hợp:

 

3 4 2=  +  +A x x x

. Hãy viết lại tập hợp

dưới kí

hiệu khoảng, nửa khoảng, đoạn.

1;A

. B.

1;A

. D.

;1A

CÂU 79: Cho các tập hợp:

|3B x x

Hãy viết lại các tập hợp

dưới kí hiệu khoảng, nửa khoảng, đoạn.

3;3B

. B.

3;3B

;3B

. D.

3;3B

.....................................

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 9: Cc php ton trên tp con ca ℝ

Phương pháp

 Đ tìm

ta làm như sau

 Sắp xếp theo thứ t tăng dần cc đim đầu mút của các tập hợp

,AB

lên trục

s

 Biu diễn các tập

,AB

trên trục s(phần nào không thuộc các tập đ thì

gạch bỏ)

 Phần không bị gạch bỏ chính là giao của hai tập hợp

,AB

 Đ tìm

ta làm như sau

 Sắp xếp theo thứ t tăng dần cc đim đầu mút của các tập hợp

,AB

lên trục

s

 Tô đậm các tập

,AB

trên trục s

 Phần tô đậm chính là hợp của hai tập hợp

,AB

 Đ tìm

\AB

ta làm như sau

 Sắp xếp theo thứ t tăng dần cc đim đầu mút của các tập hợp

,AB

lên trục

s

 Biu diễn tập

trên trục s(gạch bỏ phần không thuộc tập

), gạch bỏ

phần thuộc tập

trên trục s

 Phần không bị gạch bỏ chính là

\AB

CÂU 80: Khẳng đnh no sau đây sai?

CÂU 81: Cho hai tập hợp



)

1;5A =−

và

 

2;10B =

. Khi đ tập hợp

AB

bằng



)

2;5

. B.

 

1;10−

( )

2;5

. D.



)

1;10−

CÂU 82: Cho

(



;5M = −

và



)

2;6N =−

. Chọn khẳng đnh đúng

 

2;5MN = −

. B.

( )

;6MN = −

( )

2;5MN = −

. D.



)

2;6MN = −

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 83: Cho các khoảng

2;2 ; 1; ; ;

A B C

. Khi đ tập hợp

A B C

bằng:

CÂU 84: Cho các tập họp

   

 

3 3 ; 1 5 ; 2A x x B x x C x x=  −   =  −   =  

. Xc đnh các tập

hợp

A B C



)

2;3

. B.

( )

2;3



)

1;3−

. D. .

CÂU 85: Sử dụng kí hiệu khoảng để viết các tập hợp sau đây:

4; \ ;2E

4;9 .

1;8 .

4; .

CÂU 86: Cho

(



( )

;5 ; 0;AB= − = +

. Tập hợp

AB

là

(



0;5

. B.



)

0;5

( )

0;5

. D.

( )

;− +

CÂU 87: Cho hai tập hợp



)

9;8

CA=−

và

( ) ( )

; 7 8;

CB= − −  +

. Chọn khẳng

đnh đúng.

 

A8B=

. B.

A B =

A BR=

. D.



)

A 9; 7B = − −

CÂU 88: Cho

0;3 ; 1;5 ; 0;1A B C

. Khẳng đnh no sau đây sai?

.A B C

0;5 .A B C

\ 1;5 .A C C

\ 1;3 .A B C

CÂU 89: Tập hợp D =

( ;2] ( 6; )−  − +

là tập no sau đây?

( 6;2]−

( 4;9]−

( ; )− +

 

6;2−

CÂU 90: Cho tập hợp A =

(



;5−

, B =

 

/ 1 6x R x −  

. Khi đ

\AB

là

( )

;1− −

B. (-1;5]

(



;6−

(



;1− −

CÂU 91: Cho tập hợp D =

 

/ 2 4x R x −  

, E = [-3; 1]. Khi đ

DE

là:

A. (-2;1] B. [-3;4]

 

1;0;1−

 

0;1

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

CÂU 92: Cho tập hợp

2;A

. Khi đ, tập

là

CÂU 93: Cho

( ) ( )

= −  =  + = − −



5;1 ; 3; ; ; 2A B C

. Câu no sau đây đúng?

[ 5; 2]AC = − −

( 5; )AB = − +

( ; )BC = − +



=

CÂU 94: Cho

 

( ) ( )

1;4 ; 2;6 ; 1;2 .A B C= = =

Tìm

A B C

 

0;4 .



)

5; .+

( )

;1 .−

.

CÂU 95: Cho

(



( ) ( )

; 3 ; 2; ; 0;4A B C= − − = + =

. Khi đ

( )

A B C

là:

 

| 2 4xx  

 

| 2 4xx  

 

| 2 4xx  

 

| 2 4xx  

CÂU 96: Cho tập

)

( )

3; 8 ; 5;2 3; 11 .C A C B



= − = − 



Tập

( )

C A B

là:

( )

3; 3−



( )

5; 11−

( )

3;2 3; 8 .−

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Dạng 10: Tm điu kin ca tham s m đê đoạn; khong; na

khong tha mn điu kin cho trưc

Phương pháp:

 Bước 1: Minh họa cc tập đả cho trên trục s.

 Bước 2: Da vào yêu cầu bài ton. Xc định điu kiện của tham s.

Thưng thì ta s quy v việc giải BPT bậc nhất 1 n.

 Bước 3: Giải BPT, kết luận.

CÂU 97: Cho số thực

0a

.Điều kiện cần v đủ để

( )

;9 ;



−  +  





là

−  a

−  a

−  a

−  a

CÂU 98: Cho hai tập khác rỗng A = (m - 1;4] và B = (-2;2m + 2] với m thuộc R.

Xc đnh m để

AB  

( 2;5)−

( 2;5]−

[ 2;5]−

( 2;5]−

CÂU 99: Cho hai tập khác rỗng A = (m - 1;4] và B = (-2;2m + 2] với m thuộc R.

Xc đnh m để

BA

[-2;1)

( 2;1]−

[-2;1]

. D.

( 2;1)−

CÂU 100: Cho hai tập hợp

;Am

và

3 1;3 3B m m

. Tìm tất cả các giá tr

thực của tham số

để

A C B

100

CHUYÊN Đ DY HC KNTT 10

GV: Trương Vit Long – ĐT: 0569.59.79.99

Bấm Tải xuống để xem toàn bộ.

| 1/72

| | Tải xuống

Preview text:

CHƯƠNG I: MỆNH ĐỀ TOÁN HỌC – TẬP HỢP MỤC LỤC Ⓐ -
1. MỆNH ĐỀ – MỆNH ĐỀ CHỨA BIẾN 1 a. Mệnh đề
b. Mệnh đề chứa biến
2. MỆNH ĐỀ PHỦ ĐỊNH 1
3. MỆNH ĐỀ KÉO THEO – MỆNH ĐỀ ĐẢO 33 a. Mệnh đề kéo theo b. Mệnh đề đảo
4. MỆNH ĐỀ TƯƠNG ĐƯƠNG
5. MỆNH ĐỀ CHỨA KÍ HIỆU ;   Ⓑ
DẠNG 1: Xác định mệnh đề, tính đúng sai của mệnh đê 3
DẠNG 2: : Lập mệnh đề phủ định, và xét tính đúng sai của mệnh đề phủ 5 định đó?
DẠNG 3: Lập mệnh đề kéo theo, mệnh đề đảo và xét tính đúng sai của 6
mệnh đề phủ định đó?
DẠNG 4: Phát biểu mệnh đề tương đương 4
DẠNG 5: Dùng kí hiệu ∀ và ∃ để viết mệnh đê 10
DẠNG 6: Phát biểu mệnh đề chứa kí hiệu ∀ và ∃ 11
DẠNG 7: Lập mệnh đề phủ định của mệnh đề chứa kí hiệu ∀ và ∃ 12 Ⓒ
DẠNG 1: : Nhận biết mệnh đề – Mệnh đề chứa biến 14
DẠNG 2: Xét tính ĐÚNG – SAI của mệnh đê 15
DẠNG 3: Mệnh đề chứa biến 16
DẠNG 4: : Phủ định mệnh đê 20
DẠNG 5 : Mệnh đề kéo theo 23
DẠNG 6: Mệnh đề đảo 25
DẠNG 7: Mệnh đề tương đương 26
DẠNG 8: : Dùng kí hiệu ∀, ∃ đê viêt mênh đê 27
DẠNG 9: : Phát biểu mệnh đề chứa kí hiệu ∀, ∃ 28
DẠNG 10: Phủ định mệnh đề chứa kí hiệu ∀, ∃ 29 Ⓐ -
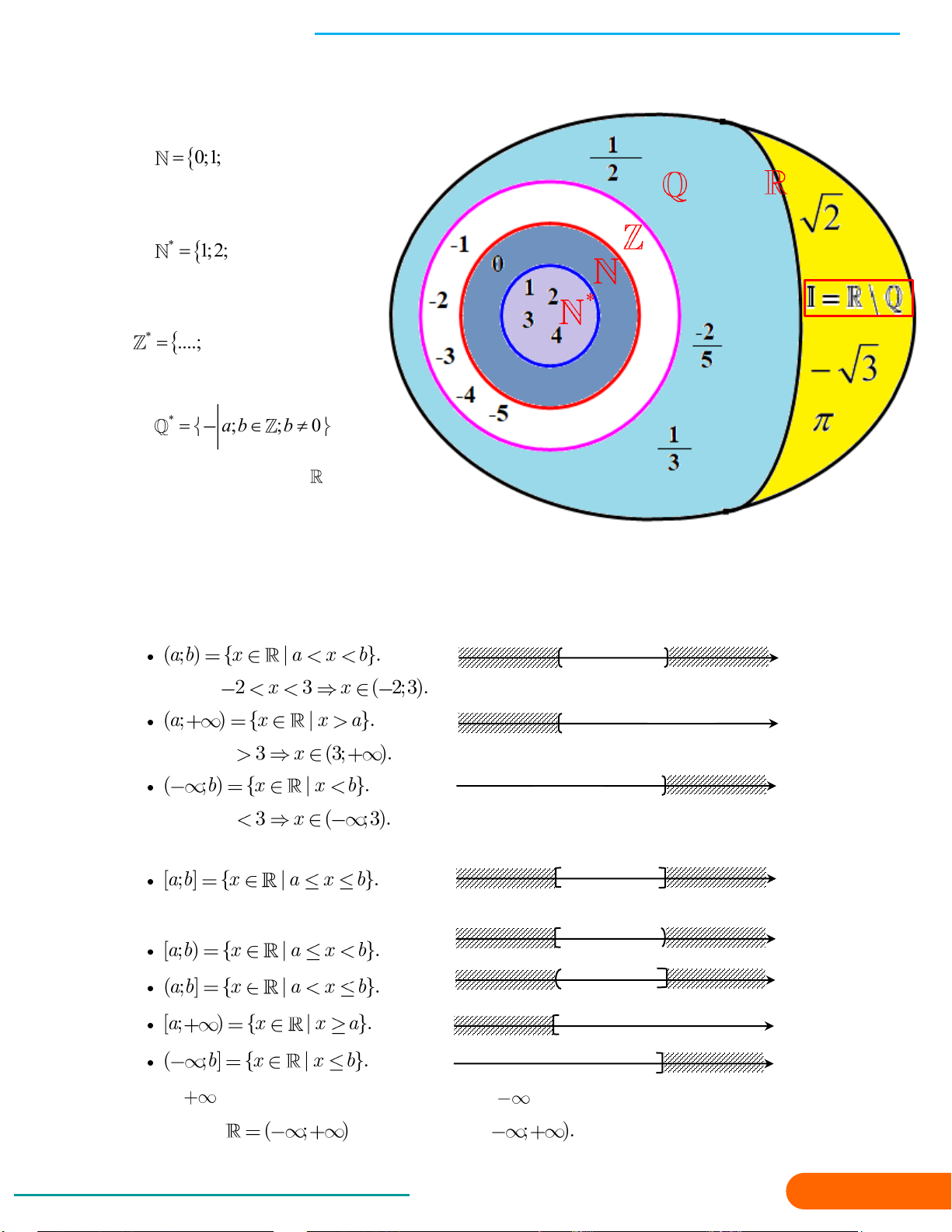
1. CÁC KHÁI NIỆM CƠ BẢN VỀ TẬP HỢP 31 a. Tập hợp b. Tập con
c. Hai tập hợp bằng nhau 2. CÁC TẬP HỢP SỐ 32
a. Mối quan hệ giữa các tập hợp số
b. Các tập con thường dùng của
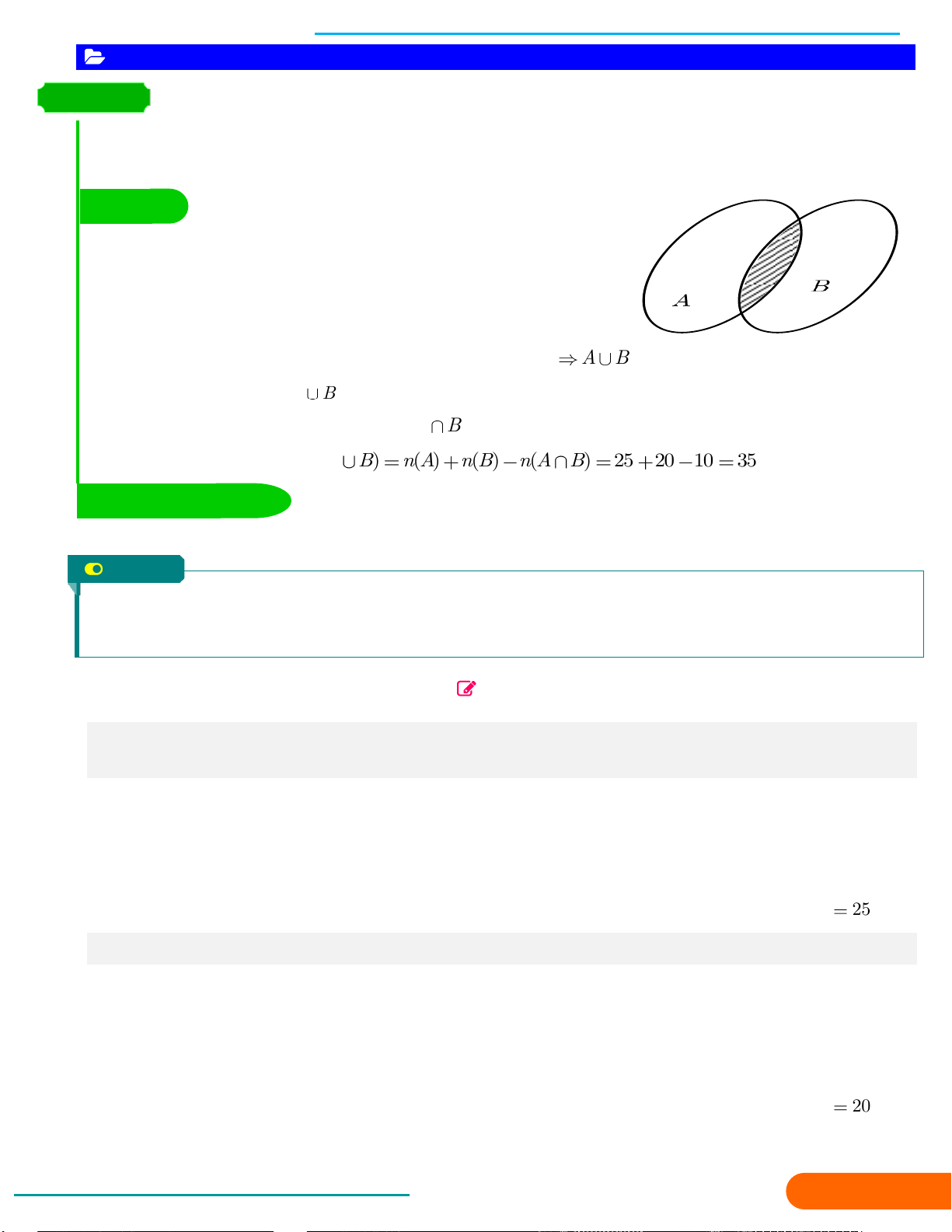
3. CÁC PHÉP TOÁN TRÊN TẬP HỢP 33
a. Giao của hai tập hợp
b. Hợp của hai tập hợp
c. Hiệu của hai tập hợp Ⓑ
DẠNG 1: Xác định tập hợp bằng cách liệt kê tất cả các phần tử 34 của tập hợp
DẠNG 2: Xác định tập hợp bằng cách chỉ ra tính chất đặc trung 36
DẠNG 3: Xác định tập con của một tập hợp cho trước 37
DẠNG 4: Các phép toàn trên tập hợp 39
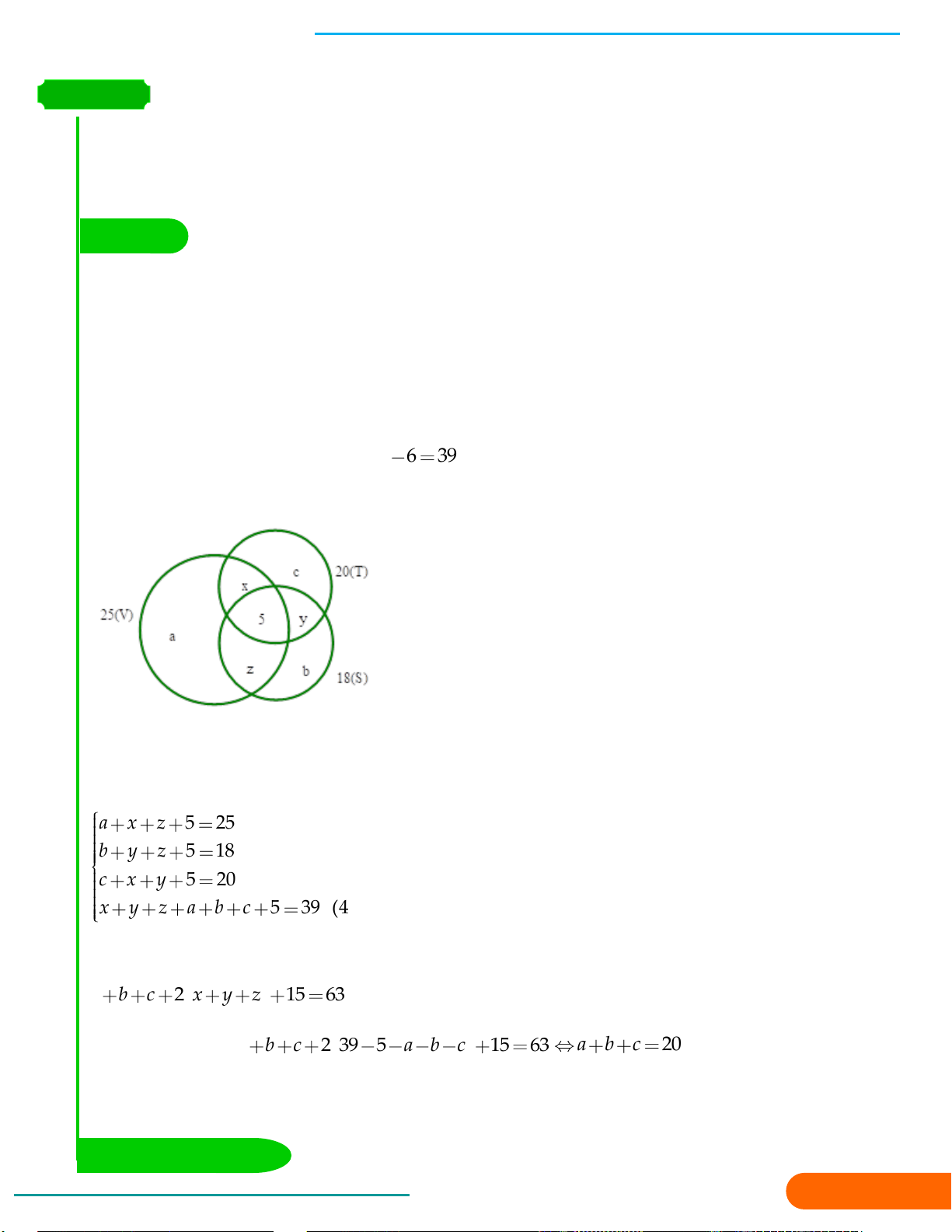
( Không chứa tập con của ℝ )
DẠNG 5: Sử dụng biểu đồ Ven để giải bài toán. 41
DẠNG 6: Chứng minh tập hợp bằng nhau, tập con 44
DẠNG 7: Phân biệt tập hợp và tập con của ℝ 45
Dạng 8: Các phép toán trên tập con của ℝ 46 Ⓒ
DẠNG 1: Xác định số phần tử của tập hợp 51
DẠNG 2: Xác định tập hợp bằng cách liệt kê hoặc chỉ ra tính chất 52
đặc trưng của các phần tử thuộc tập hợp.
DẠNG 3: Tìm tập con, số tập con của một tập hợp cho trước 56
DẠNG 4: Hai tập hợp bằng nhau. 58
DẠNG 5 : Giao của các tập hợp (Không chứa tập con của ℝ) 59
DẠNG 6: Hợp của các tập hợp (Không chứa tập con của ℝ) 60
DẠNG 7: Hiệu, phần bù của các tập hợp 62
(Không chứa tập con của ℝ)
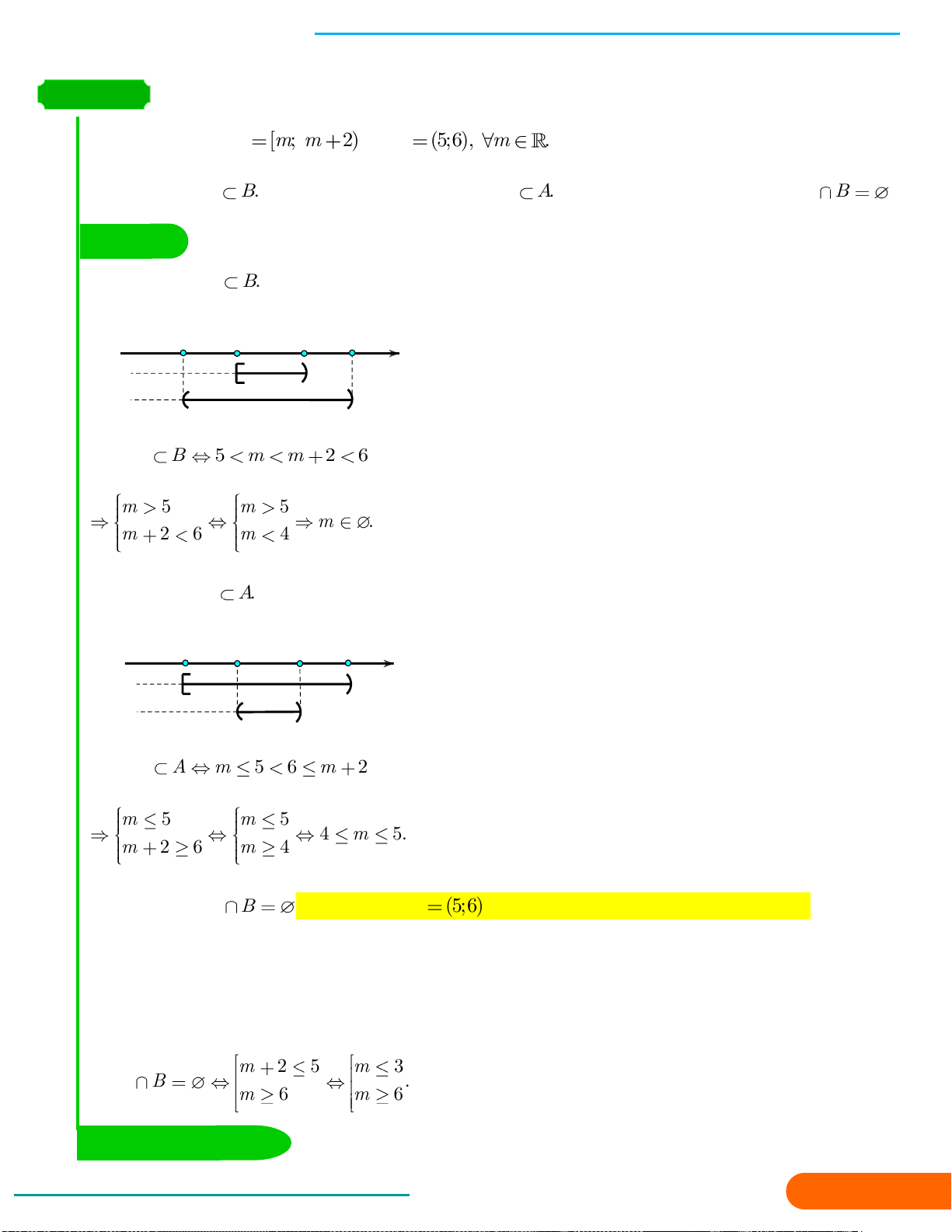
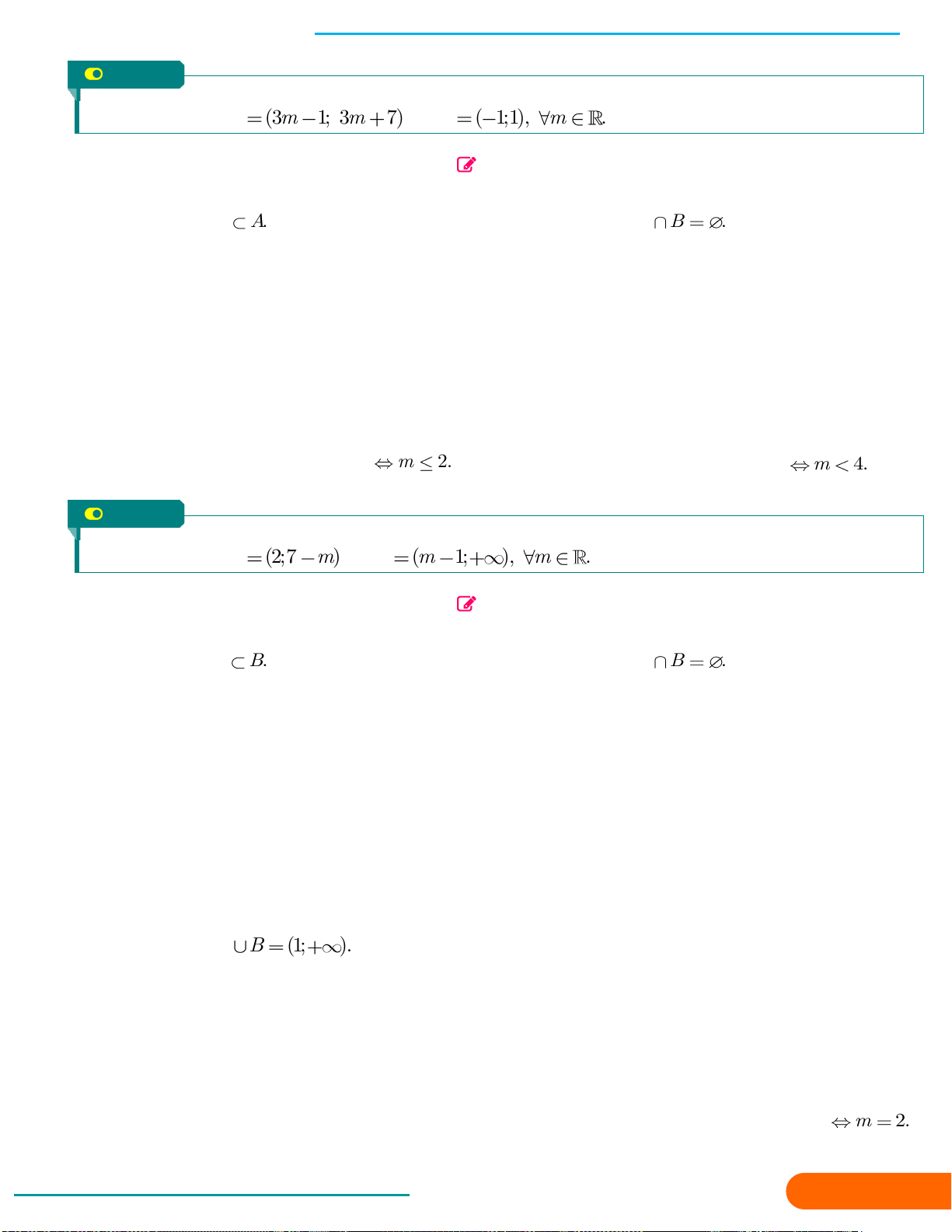
DẠNG 8: : Viết các tập con của ℝ dưới dạng đoạn; khoảng;… 63
DẠNG 9: Các phép toán trên tập con của ℝ 64
DẠNG 10: Tìm điều kiện của tham số m đê đoạn; khoảng; nửa 67
khoảng thỏa mản điều kiện cho trước
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10 Chương
1 MỆNH ĐỀ TOÁN HỌC TẬP HỢP Bài 1
MỆNH ĐỀ TOÁN HỌC
A TÓM TẮT LÝ THUYẾT
1. MỆNH ĐỀ, MỆNH ĐỀ CHỨA BIẾN a. Mệnh đề Định nghĩa
Mệnh đề là một câu khẳng định đúng hoặc một câu khẳng định sai.
Một mệnh đề Toán học không thể vừa đúng, vừa sai.
Người ta thường sử dụng các chữ cái: ; A ; B ; C ....; ; P ; Q ;
R .... để biểu thị các mệnh đề.
b. Mệnh đề chứa biến Định nghĩa
Mệnh đề chứa biến là một câu khẳng định chứa biến ( ; x ; y ;
n ... ). nhận giá trị trong
một tập X nào đó mà với mỗi giá trị của biến thuộc X ta được một mệnh đề.
Ta ký hiệu mệnh đề chứa biến n là P(n) ; mệnh đề chứa biến ( ; x y) là P( ; x y)
2. MỆNH ĐỀ PHỦ ĐỊNH Định nghĩa
Cho mệnh đề P.
Mệnh đề "không phải P " được gọi là mệnh đề phủ định của P và kí hiệu là . P
Nếu P đúng thì P sai, nếu P sai thì P đúng. 1
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
3. MỆNH ĐỀ KÉO THEO, MỆNH ĐỀ ĐẢO
a. Mệnh đề kéo theo Định nghĩa
Cho mệnh đề P và Q.
Mệnh đề "Nếu P thì Q " được gọi là mệnh đề kéo theo và kí hiệu là: P . Q Mệnh đề P
Q chỉ sai khi P đúng và Q sai.
Như vậy, ta chỉ cần xét tính đúng sai của mệnh đề P
Q khi P đúng.  Nhân xét:
Các định lý toán học là những mệnh đề đúng và thường phát biểu ở dạng P . Q Khi đó ta nói:
P là giả thiết, Q là kết luận.
P là điều kiện đủ để có Q.
Q là điều kiện cần để có P.
b. Mệnh đề đảo Định nghĩa
▶ Mệnh đề đảo: Cho mệnh đề kéo theo P Q Mệnh đề Q
P được gọi là mệnh đề đảo của mệnh đề P . Q
4. MỆNH ĐỀ TƯƠNG ĐƯƠNG Định nghĩa
▶ Mệnh đề “ nếu và chỉ nếu P ” được gọi là một mệnh đề tương đương. Kí hiệu: P Q.  Nhân xét:
Nếu cả hai mệnh để P Q và Q
P đều đúng thì mệnh đề tương đương P Q đúng. Mệnh đề P
Qcó thể phát biểu ở những dạng như sau:
Q" P tương đương Q.
Q" P là điều kiện cần và đủ để có Q.
Q" P khi và chỉ khi Q. 2
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
5. MỆNH ĐỀ CÓ CHỨA KÍ HIỆU: ∀ , ∃ Định nghĩa
• Kí hiệu  đọc là: “Với mọi”
• Kí hiệu  đọc là: “Tồn tại”. Khi đó:
"Với mọi x thuộc X ", ký hiệu là: " x X ".
"Tồn tại x thuộc X ", ký hiệu là: " x X ".
Mệnh đề phủ định của mệnh đề " x , X ( P x)" là " x
X, P(x)".
Mệnh đề phủ định của mệnh đề " x , X ( P x)" là " x
X, P(x)".
Mệnh đề chứa đúng khi ta chỉ ra một phần tử đúng.
Mệnh đề chứa sai khi ta chỉ ra một phần tử sai.
B BÀI TẬP TỰ LUẬN
Dạng 1: Xác định mệnh đề, tính đúng sai của mệnh đề Ví dụ 1
Các câu sau đây, câu nào là mệnh đề, câu nào không phải là mệnh đề? Nếu là mệnh đề hãy cho biết mệnh đề đó đúng hay sai. (1) Ở đây đẹp quá! (2) Phương trình 2 x 3x 1 0 vô nghiệm
(3) 16 không là số nguyên tố (4) Hai phương trình 2 x 4x 3 0 và 2 x x 3 1 0 có nghiệm chung.
(5) Số có lớn hơn 3 hay không?
(6) Italia vô địch Worldcup 2006
(7) Hai tam giác bằng nhau khi và chỉ khi chúng có diện tích bằng nhau.(8) Một tứ giác là hình thoi khi
và chỉ khi nó có hai đường chéo vuông góc với nhau. BÀI GIẢI
Câu (1) và (5) không là mệnh đề(vì là câu cảm thán, câu hỏi)
Các câu (3), (4), (6), (8) là những mệnh đề đúng
Câu (2) và (7) là những mệnh đề sai.
BÀI TẬP RÈN LUYỆN 3
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10 Bài 1
Các câu sau đây, câu nào là mệnh đề, câu nào không phải là mệnh đề? Nếu là mệnh đề hay cho
biết mệnh đề đó đúng hay sai.
a) Không được đi lối này!
b) Bây giờ là mấy giờ?
c) Chiến tranh thế giới lần thứ hai kết thúc năm 1946. d) 16 chia 3 dư 1.
e) 2023 không là số nguyên tố. f) 5 là số vô tỉ.
g) Hai đường tròn phân biệt có nhiều nhất là hai điểm chung. Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 4
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
Dạng 2: Lập mệnh đề phủ định, và xét tính đúng sai của mệnh đề phủ định đó? Ví dụ 2
Nêu mệnh đề phủ định của các mệnh đề sau, cho biết mệnh đề này đúng hay sai?
P : " Hình thoi có hai đường chéo vuông góc với nhau"
Q : " 6 là số nguyên tố"
R : " Tổng hai cạnh của một tam giác lớn hơn cạnh còn lại" S : " 5
3 "K : " Phương trình 4 2 x 2x 2 0 có nghiệm " BÀI GIẢI
Ta có các mệnh đề phủ định là:
P : " Hai đường chéo của hình thoi không vuông góc với nhau", mệnh đề này sai.
Q : " 6 không phải là số nguyên tố", mệnh đề này đúng.
R : " Tổng hai cạnh của một tam giác nhỏ hơn hoặc bằng cạnh còn lại", mệnh đề này sai. S : " 5 3 ", mệnh đề này sai. K : " phương trình 4 2 x 2x 2
0 vô nghiệm ", mệnh đề này đúng vì 2 4 2 2 x 2x 2 x 1 1 0
BÀI TẬP RÈN LUYỆN Bài 2
Nêu mệnh đề phủ định của các mệnh đề sau, cho biết mệnh đề này đúng hay sai? 2
P : " Trong tam giác tổng ba góc bằng 1800" Q : " 3 27 là số nguyên " 5
R : " Việt Nam vô địch Worldcup 2020" S : " 2 " 2
K : " Bất phương trình 2013 x 2030 vô nghiệm " Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 5
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
Dạng 3: Lập mệnh đề kéo theo, mệnh đề đảo và xét tính đúng sai của mệnh đề phủ định đó? Ví dụ 3
Phát biểu mệnh đề P
Q và phát biểu mệnh đề đảo, xét tính đúng sai của nó.
a) P : " Tứ giác ABCD là hình thoi" và Q : " Tứ giác ABCD AC và BD cắt nhau tại trung điểm mỗi đường"
b) P : "2 9" và Q: "4 3"
c) P : " Tam giác ABC vuông cân tại A" và Q : " Tam giác ABC có A 2B "
d) P :" Ngày 2 tháng 9 là ngày Quốc Khánh của nước Việt Nam" và Q :" Ngày 27 tháng 7 là ngày thương binh liệt sĩ" BÀI GIẢI a) Mệnh đề P
Q là " Nếu tứ giác ABCD là hình thoi thì AC và BD cắt nhau tại trung điểm mỗi đường", mệnh đề này đúng.
Mệnh đề đảo là Q
P : "Nếu tứ giác ABCD có AC và BD cắt nhau tại trung điểm mỗi đường thì ABCD là
hình thoi ", mệnh đề này sai. b) Mệnh đề P Q là " Nếu 2 9 thì 4
3", mệnh đề này đúng vì mệnh đề P sai.
Mệnh đề đảo là Q P : " Nếu 4 3 thì 2
9", mệnh đề này đúng vì mệnh đề Q sai. c) Mệnh đề P
Q là " Nếu tam giác ABC vuông cân tại A thì A
2B ", mệnh đề này đúng
Mệnh đề đảo là Q
P : " Nếu tam giác ABC có A
2B thì nó vuông cân tại A", mệnh đề này sai d) Mệnh đề P
Q là " Nếu ngày 2 tháng 9 là ngày Quốc Khánh của nước Việt Nam thì ngày 27 tháng 7 là
ngày thương binh liệt sĩ"
Mệnh đề đảo là Q
P : " Nếu ngày 27 tháng 7 là ngày thương binh liệt sĩ thì ngày 2 tháng 9 là ngày Quốc
Khánh của nước Việt Nam"Hai mệnh đề trên đều đúng vì mệnh đề P,Q đều đúng
BÀI TẬP RÈN LUYỆN 6
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10 Bài 3
Phát biểu mệnh đề P
Q và phát biểu mệnh đề đảo, xét tính đúng sai của nó.
a) P : “tam giác ABC đều” và Q : “tam giác ABC cân.”
b) P : “1= 2 ” và Q : “ 2 2 1 = 2 .”
c) P : “3  2 ” và Q : “3x  2x , x   .”
d) P : “Số chia hết cho 6” và Q : “số chia hết cho 3 .”
e) P : “Tứ giác ABCD là hình thoi” và Q : “Hai đường chéo của nó vuông góc với nhau”
f) P : “Số chia hết cho 2”và Q : “số đó là số chẵn.” g) P : “ ABC 
có AB = BC = CA” và Q : “ ABC  là tam giác đều.” Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 7
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
Dạng 4: Phát biểu mệnh đề tương đương Ví dụ 4 Cho ABC 
. Xét các mệnh đề sau: P : " ABC  là tam giác vuông " Q : " ABC 
có một góc bằng tổng hai góc còn lại "
Phát biểu mệnh đề P Q bằng 4 cách? BÀI GIẢI Q" ABC 
là tam giác vuông tương đương ABC 
có một góc bằng tổng hai góc còn lại. Q" ABC 
là tam giác vuông là điều kiện cần và đủ để ABC 
có một góc bằng tổng hai góc còn lại. Q" ABC 
là tam giác vuông khi và chỉ khi ABC 
có một góc bằng tổng hai góc còn lại Q" ABC 
là tam giác vuông nếu và chỉ nếu ABC 
có một góc bằng tổng hai góc còn lại
BÀI TẬP RÈN LUYỆN Bài 4
Phát biểu mệnh đề P
Q bằng bốn cách và và xét tính đúng sai của nó.
a) P : "Tứ giác ABCD là hình thoi" và Q :" Tứ giác ABCD là hình bình hành có hai đường chéo vuông góc với nhau"
b) P : " Tứ giác ABCD là hình vuông" và Q : " Tứ giác ABCD là hình chữ nhật có hai đường chéo bằng vuông góc với nhau ". Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 8
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 9
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
Dạng 5: Dùng kí hiệu ∀ và ∃ để viết mệnh đề Ví dụ 5
Dùng kí hiệu ∀ và ∃ để viết các mệnh đề và mệnh đề phủ định của các mệnh đề sau:
a) P: “Tích của ba số tự nhiên liên tiếp chia hết cho sáu.”
b) Q: “Có một số nguyên mà bình phương của nó bằng chính nó.” BÀI GIẢI
• Ta có P : n N, n n 1 n 2 6 , mệnh đề phủ định là P : n N, n n 1 n 2 6. • Ta có 2
Q : n Z, n
n , mệnh đề phủ định là 2
R : n Z, n n .
BÀI TẬP RÈN LUYỆN Bài 5
Dùng kí hiệu ∀ và ∃ để viết các mệnh đề và mệnh đề phủ định của các mệnh đề sau:
a) P : " Với mọi số thực bình phương của là một số không âm."
b) Q : " Có một số hữu tỉ mà nghịch đảo của nó lớn hơn chính nó." Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 10
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
Dạng 6: Phát biểu mệnh đề chứa kí hiệu ∀ và ∃ Ví dụ 6
Phát biểu các mệnh đề sau: a) P: “ 2 x , x 0 .” b) Q: “ x , x x 1 .” BÀI GIẢI
a) Cách 1: Với mọi số thực x thì bình phương của x lớn hơn hoặc bằng 0.
Cách 2: Bình phương của một số thực luôn là một số không âm.
b) Cách 1: Tồn tại số tự nhiên x sao cho x chia hết cho x +1.
Cách 2: Tồn tại số tự nhiên x sao cho x +1 là ước của x .
BÀI TẬP RÈN LUYỆN Bài 6
Phát biểu các mệnh đề sau và xét tính đúng sai của nó: a) " 4 2 n , n n 1 là hợp số " b) “ 3 2 x , x x 1 0 ” c) 2 x , n 3 4 d) 2 q , 2q 1 0 Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 11
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
Dạng 7: Lập mệnh đề phủ định của mệnh đề chứa kí hiệu ∀ và ∃ Ví dụ 7
Lập mệnh đề phủ định của các mệnh đề sau và xét tính đúng sai của các mệnh đề phủ định đó? a) 2 P : " x : x 1". b) 2 P : " x : x 3". BÀI GIẢI
a) Mệnh đề phủ định của mệnh đề P là 2 P : " x : x 1".
Mệnh đề P là mệnh đề đúng.
b) Mệnh đề phủ định của mệnh đề P là 2 P : " x : x 3".
Mệnh đề P là mệnh đề sai.
BÀI TẬP RÈN LUYỆN Bài 7
Lập mệnh đề phủ định của các mệnh đề sau và xét tính đúng sai của các mệnh đề phủ định đó?: a) 2 P : " x : x 0". b) 2 P : " x : x x ". c) 2 P : " x : 4x 1 0". d) 2 P : " x : x x 7 0". e) 2 P : " x : x x 2 0". f) P 2 : " x : (x 1) (x 1)". g) P : " x , x 2 hoặc x 7 ". h) 2 P : " x : x 5 0". Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 12
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 13
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
C BÀI TẬP TRẮC NGHIỆM distance
Dạng 1: Nhận biết mệnh đề – Mệnh đề chứa biến QUICK NOTE Phương pháp
Thà để giọt mồ hôi rơi trên
 Một câu mà chắc chắn là đúng hay chắc chắn là sai thì đó là một
trang sách còn hơn để nước mệnh đề
CÂU 1: Trong các câu sau, câu nào không phải là mệnh đề?
mắt rơi ướt cả đề thi A. Buồn ngủ quá!
..................................................
B. Hình thoi có hai đường chéo vuông góc với nhau.
..................................................
C. 8 là số chính phương.
D. Băng Cốc là thủ đô của Mianma.
..................................................
CÂU 2: Trong các câu sau, có bao nhiêu câu không phải là mệnh đề? ..................................................
a) Huế là một thành phố của Việt Nam.
..................................................
b) Sông Hương chảy ngang qua thành phố Huế.
..................................................
c) Hãy trả lời các câu hỏi này! d) 5+19 = 24.
..................................................
A. 1. B. 2. C. 3. D. 4.
..................................................
CÂU 3: Trong các câu sau, có bao nhiêu câu là mệnh đề?
.................................................. a) Hãy đi nhanh lên!
..................................................
b) Hà Nội là thủ đô của Việt Nam.
c) Năm 2018 là năm nhuận.
.................................................. d) 2 4 5 6 11.
..................................................
A. 1. B. 4. C. 3. D. 2.
..................................................
CÂU 4: Cho các phát biểu sau, có bao nhiêu phát biểu là mệnh đề?
..................................................
a) Hà Nội là thủ đô của Việt Nam. b) x , x 2 5.
.................................................. c) x 6 5.
.................................................. d) Phương trình 2 x 6x 5 0 có nghiệm.
..................................................
A. 1. B. 2. C. 3. D. 4. CÂU 5:
..................................................
Câu nào trong các câu sau không phải là mệnh đề? A. 3+ 2 = 7 . B. 2 x +1 > 0.
.................................................. C. 2 2 − − x  0. D. 4 + x .
..................................................
CÂU 6: Câu nào trong các câu sau không phải là mệnh đề?
.................................................. A. 3 + 2 = 7. B. 2 x +1 > 0 C.
.................................................. 2 - x < 0. D. 4 + x = 3.
.................................................. 14
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
Dạng 2: Xét tính ĐÚNG – SAI của mệnh đề
.................................................. Phương pháp
..................................................
 Sử dụng các định lý, tính chát đả học để nhạ n biết mê ̣nh đề đúng.
..................................................
 Láy mo ̣t vài ví dụ cụ thể để nhạ n biết mê ̣nh đề sai.
..................................................
CÂU 7: Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
..................................................
A. Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số .................................................. đều là số chẵn.
..................................................
B. Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều .................................................. là số chẵn.
..................................................
C. Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều .................................................. là số lẻ. D.
..................................................
Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.
..................................................
CÂU 8: Trong các câu sau, câu nào là mệnh đề đúng?
..................................................
A. Nếu a b thì 2 2 a b .
.................................................. B.
..................................................
Nếu a chia hết cho 9 thì a chia hết cho 3.
..................................................
C. Nếu em chăm chỉ thì em thành công.
..................................................
D. Nếu một tam giác có một góc bằng 0
60 thì tam giác đó đều.
..................................................
CÂU 9: Trong các phát biểu sau, phát biểu nào là mệnh đề đúng?
..................................................
A. π là một số hữu tỉ.
..................................................
B. Tổng của độ dài hai cạnh một tam giác lớn hơn độ dài cạnh thứ .................................................. ba.
..................................................
C. Bạn có chăm học không?
..................................................
D. Con thì thấp hơn cha.
..................................................
CÂU 10: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
.................................................. A. 2 2 2 4. B. 4 16.
.................................................. C. 23 5 2 23 2.5. D. 23 5 2 23 2.5.
..................................................
..................................................
.................................................. 15
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
Dạng 3: Mệnh đề chứa biến
.................................................. Phương pháp
..................................................
 Mệnh đề chứa biến là những câu chưa khẳng định được tính
..................................................
đúng sai. Nhưng với mỗi giá trị của biến sẽ cho ta một mệnh đề. CÂU 11:
..................................................
Trong các câu sau, câu nào không là mệnh đề chứa biến?
A. 15 là số nguyên tố.
B. a +b = c .
.................................................. C. 2 x + x = 0 .
D. 2n+1chia hết cho 3.
..................................................
CÂU 12: Với giá trị thực nào của x mệnh đề chứa biến .................................................. P(x) 2
: 2x −1 0 là mệnh đề đúng? A. 0 . B. 5 .
.................................................. 4 C.
.................................................. 1. D. . 5
..................................................
CÂU 13: Cho mệnh đề chứa biến P(x) 2
:"x +15  x " với x là số thực. ..................................................
Mệnh đề nào sau đây là đúng: A. P(0) . B. P( ) 3 .
.................................................. C. P(4). D. P( ) 5 .
..................................................
CÂU 14: Khẳng định nào sau đây sai?
..................................................
A. “Mệnh đề” là từ gọi tắc của “mệnh đề logic”.
..................................................
B. Mệnh đề là một câu khẳng đúng hoặc một câu khẳng định sai.
..................................................
C. Mệnh đề có thể vừa đúng hoặc vừa sai. D.
..................................................
Một khẳng định đúng gọi là mệnh đề đúng, một khẳng định sai gọi là mệnh đề sai.
..................................................
CÂU 15: Chọn khẳng định sai.
..................................................
A. Mệnh đề P và mệnh đề phủ định P , nếu P đúng thì P sai và ..................................................
điều ngược lại chắc đúng. B.
..................................................
Mệnh đề P và mệnh đề phủ định P là hai câu trái ngược nhau.
C. Mệnh đề phủ định của mệnh đề P là mệnh đề không phải P được .................................................. kí hiệu là P .
..................................................
D. Mệnh đề P : “ là số hữu tỷ” khi đó mệnh đề phủ định P là: “ .................................................. là số vô tỷ”.
..................................................
CÂU 16: Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng? A.
..................................................
Nếu a  b thì 2 2 a  b .
B. Nếu a chia hết cho 9 thì a chia hết cho 3 .
..................................................
C. Nếu em chăm chỉ thì em thành công.
..................................................
D. Nếu một tam giác có một góc bằng 60 thì tam giác đó là đều.
.................................................. 16
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
CÂU 17: Trong các phát biểu sau, phát biểu nào là mệnh đề đúng:
..................................................
A.  là một số hữu tỉ.
..................................................
B. Tổng của hai cạnh một tam giác lớn hơn cạnh thứ ba.
..................................................
C. Bạn có chăm học không?
..................................................
D. Con thì thấp hơn cha.
..................................................
CÂU 18: Cho n là số tự nhiên, mệnh đề nào sau đây đúng? A.  , n n(n + ) 1 là số chính phương.
.................................................. B.  , n n(n + ) 1 là số lẻ.
.................................................. C.
..................................................  , n n(n + )
1 (n + 2) là số lẻ.
.................................................. D.  , n n(n + )
1 (n + 2) là số chia hết cho 6 .
..................................................
CÂU 19: Trong các mệnh đề sau, mệnh đề nào sai? A. 2  −  2 −    4 . B. 2   4   16.
..................................................
C. 23  5  2 23  2.5.
D. 23  5  −2 23  2 − .5.
..................................................
CÂU 20: Cho x là số thực. Mệnh đề nào sau đây đúng?
.................................................. A. 2  ,
x x  5  x  5  x  − 5 . B. 2  ,
x x  5  − 5  x  5 .
.................................................. C. 2  ,
x x  5  x   5 . D. 2  ,
x x  5  x  5  x  − 5 .
..................................................
CÂU 21: Chọn mệnh đề đúng:
.................................................. A. * 2
n , n −1 là bội số của 3. B. 2
x , x = 3.
.................................................. C.   , 2n n
+1 là số nguyên tố. D.   , 2n n  n + 2.
..................................................
CÂU 22: Trong các mệnh đề nào sau đây mệnh đề nào sai? A.
..................................................
Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một góc bằng nhau.
..................................................
B. Một tứ giác là hình chữ nhật khi và chỉ khi chúng có 3 góc vuông. ..................................................
C. Một tam giác là vuông khi và chỉ khi nó có một góc bằng tổng hai .................................................. góc còn lại.
..................................................
D. Một tam giác là đều khi và chỉ khi chúng có hai đường trung tuyến ..................................................
bằng nhau và có một góc bằng 60 .
..................................................
CÂU 23: Các mệnh đề sau, mệnh đề nào có mệnh đề đảo là đúng?
A. Nếu a và b cùng chia hết cho c thì a +b chia hết cho c .
..................................................
B. Nếu hai tam giác bằng nhau thì diện tích bằng nhau.
..................................................
C. Nếu a chia hết cho 3 thì a chia hết cho 9 .
..................................................
D. Nếu một số tận cùng bằng 0 thì số đó chia hết cho 5 .
.................................................. 17
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
CÂU 24: Mệnh đề nào sau đây sai?
..................................................
A. Tứ giác ABCD là hình chữ nhật  tứ giác ABCD có ba góc vuông. ..................................................
B. Tam giác ABC là tam giác đều  A = 60. C.
..................................................
Tam giác ABC cân tại A  AB = AC .
D. Tứ giác ABCD nội tiếp đường tròn tâm O  OA = OB = OC = OD ..................................................
CÂU 25: Tìm mệnh đề đúng:
..................................................
A. Đường tròn có một tâm đối xứng và có một trục đối xứng. B.
..................................................
Hình chữ nhật có hai trục đối xứng.
C. Tam giác ABC vuông cân 0  A = 45 .
..................................................
D. Hai tam giác vuông ABC và A'B'C' có diện tích bằng nhau ..................................................
 ABC = A'B'C' .
..................................................
CÂU 26: Tìm mệnh đề sai:
A. 10 chia hết cho 5  Hình vuông có hai đường chéo bằng nhau .................................................. và vuông góc nhau.
..................................................
B. Tam giác ABC vuông tại 2 2 2
C  AB = CA +CB .
..................................................
C. Hình thang ABCD nội tiếp đường tròn (O)  ABCD là hình .................................................. thang cân.
D. 63 chia hết cho 7  Hình bình hành có hai đường chéo vuông .................................................. góc nhau.
..................................................
CÂU 27: Với giá trị thực nào của x mệnh đề chứa biến .................................................. P(x) 2
: 2x −1 0 là mệnh đề đúng: A. 0 . B. 5 .
.................................................. 4 C. 1. D. .
.................................................. 5 CÂU
..................................................
28: Cho mệnh đề chứa biến P(x) 2
:"x +15  x " với x là số thực.
Mệnh đề nào sau đây là đúng:
.................................................. A. P(0) . B. P( ) 3 .
.................................................. C. P(4). D. P( ) 5 .
..................................................
CÂU 29: Trong các mệnh đề sau, mệnh đề nào sai? A.
.................................................. A A .
B.   A.
C. A  A . D. A   A .
..................................................
CÂU 30: Cho biết x là một phần tử của tập hợp A , xét các mệnh đề .................................................. sau: (
..................................................
I ): x A. (II ): 
x  A. (III ): x  A.(IV ):  x  A.
..................................................
Trong các mệnh đề sau, mệnh đề nào là đúng
A. I và II .
B. I và III .
..................................................
C. I và IV .
D. II và IV .
.................................................. 18
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
CÂU 31: Cho mệnh đề chứa biến P(n) 2
: “n −1 chia hết cho 4” với n ..................................................
là số nguyên. Xét xem các mệnh đề P( )
5 và P(2) đúng hay sai?
.................................................. A. P( )
5 đúng và P(2) đúng. B. P( ) 5 sai và P(2) sai.
.................................................. C. P( ) 5 đúng và P(2) sai. D. P( ) 5 sai và P(2) đúng.
..................................................
CÂU 32: Cho tam giác ABC với H là chân đường cao từ A . Mệnh đề nào sau đây sai?
.................................................. 1 1 1
A. “ ABC là tam giác vuông ở A  = + ”.
.................................................. 2 2 2 AH AB AC B.
..................................................
“ ABC là tam giác vuông ở A 2
 BA = BH.BC ”.
C. “ ABC là tam giác vuông ở A 2  HA = H . B HC ”.
..................................................
D. “ ABC là tam giác vuông ở A 2 2 2
 BA = BC + AC ”.
..................................................
CÂU 33: Trong các mệnh đề sau, mệnh đề nào sai? A.
..................................................
Để tứ giác ABCD là hình bình hành, điều kiện cần và đủ là hai
cạnh đối song song và bằng nhau.
.................................................. B. Để 2
x = 25 điều kiện đủ là x = 2 .
..................................................
C. Để tổng a +b của hai số nguyên ,
a b chia hết cho 13, điều kiện cần ..................................................
và đủ là mỗi số đó chia hết cho 13. D.
..................................................
Để có ít nhất một trong hai số ,
a b là số dương điều kiện đủ là a +b  0.
..................................................
CÂU 34: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng? ..................................................
A. Nếu tổng hai số a +b  2 thì có ít nhất một số lớn hơn 1. B.
..................................................
Trong một tam giác cân hai đường cao bằng nhau.
C. Nếu tứ giác là hình vuông thì hai đường chéo vuông góc với nhau. ..................................................
D. Nếu một số tự nhiên chia hết cho 6 thì nó chia hết cho 3.
..................................................
CÂU 35: Mệnh đề nào sau là mệnh đề sai? A.
.................................................. n
  : n  2n . B. 2 n   :n = n. C. 2 x   : x  0. D. 2 x
  : x  x .
..................................................
CÂU 36: Trong các mệnh đề sau tìm mệnh đề đúng?
.................................................. A. 2
x : x  0.
B. x : x 3.
.................................................. C. 2 x   :−x  0 . D. 2
x : x  x .
CÂU 37: Trong các mệnh đề sau, mệnh đề nào đúng?
.................................................. A. 2
n , n +1 không chia hết cho 3.
.................................................. B. x
  , x  3  x  3.
.................................................. C. x (x− )2 , 1  x −1.
.................................................. D. 2 n
  ,n +1 chia hết cho 4 .
..................................................
.................................................. 19
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
Dạng 4: Phủ định mệnh đề
.................................................. Phương pháp
..................................................
 Thêm (hoặc bớt) từ “không” (hoặc “không phải”) vào trước vị
..................................................
ngữ của mệnh đề đó.
 Phủ định của “  ” là “  ”. Và ngược lại.
..................................................
 Phủ định của “ = ” là “  ”. Và ngược lại.
..................................................
 Phủ định của “ > ” là “  ”. Và ngược lại……………
..................................................
CÂU 38: Cho mệnh đề “Phương trình 2
x −4x + 4 = 0 có nghiệm”. ..................................................
Mệnh đề phủ định của mệnh đề đã cho là A. Phương trình 2
x −4x +4  0 có nghiệm.
.................................................. B. Phương trình 2
x −4x + 4 = 0 có vô số nghiệm.
.................................................. C. Phương trình 2
x −4x + 4 = 0 có hai nghiệm phân biệt.
.................................................. D. Phương trình 2
x −4x + 4 = 0 vô nghiệm.
..................................................
CÂU 39: Mệnh đề phủ định của mệnh đề “14 là số nguyên tố” là .................................................. mệnh đề:
A. 14 là số nguyên tố.
..................................................
B. 14 chia hết cho 2.
..................................................
C. 14 không phải là số nguyên tố.
..................................................
D. 14 chia hết cho 7.
..................................................
CÂU 40: Mệnh đề phủ định của mệnh đề: “ 5+ 4 =10 ” là mệnh đề:
.................................................. A. 5+4 10. B. 5+ 4 10 .
.................................................. C. 5+4 10. D. 5+ 4 10. CÂU
..................................................
41: Mệnh đề nào sau đây là phủ định của mệnh đề: “Mọi động vật đều di chuyển”.
..................................................
A. Mọi động vật đều không di chuyển.
..................................................
B. Mọi động vật đều đứng yên.
..................................................
C. Có ít nhất một động vật không di chuyển. D.
..................................................
Có ít nhất một động vật di chuyển.
CÂU 42: Phủ định của mệnh đề: “Có ít nhất một số vô tỷ là số thập ..................................................
phân vô hạn tuần hoàn” là mệnh đề nào sau đây:
..................................................
A. Mọi số vô tỷ đều là số thập phân vô hạn tuần hoàn.
..................................................
B. Có ít nhất một số vô tỷ là số thập phân vô hạn không tuần hoàn. C.
..................................................
Mọi số vô tỷ đều là số thập phân vô hạn không tuần hoàn.
D. Mọi số vô tỷ đều là số thập phân tuần hoàn.
..................................................
.................................................. 20
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
CÂU 43: Cho mệnh đề A: “ 2 x
  , x − x + 7  0” Mệnh đề phủ định .................................................. của A là:
.................................................. A. 2 x
  , x − x + 7  0 . B. 2 x
  , x − x + 7  0 . C.
.................................................. Không tồn tại 2
x: x − x +7  0. D. 2 x
  , x - x + 7  0.
.................................................. CÂU 2
44: Mệnh đề phủ định của mệnh đề P : "x +3x +1 0" với mọi x là:
..................................................
A. Tồn tại x sao cho 2 x +3x +1 0 .
..................................................
B. Tồn tại x sao cho 2 x +3x +1 0.
..................................................
C. Tồn tại x sao cho 2 x +3x +1= 0 .
..................................................
D. Tồn tại x sao cho 2 x +3x +1 0. CÂU
..................................................
45: Mệnh đề phủ định của mệnh đề P : “ 2
x: x +2x+5 là số nguyên tố” là :
.................................................. A. 2
x: x +2x+5không là số nguyên tố.
.................................................. B. 2
x: x +2x+5là hợp số.
.................................................. C. 2
x: x +2x+5là hợp số.
.................................................. D. 2
x: x +2x+5là số thực.
CÂU 46: Phủ định của mệnh đề 2 " x
  ,5x −3x =1" là:
.................................................. A. 2 " x
  ,5x −3x ". B. 2 " x
  ,5x −3x =1".
.................................................. C. 2
"x  ,5x−3x 1". D. 2 " x
  ,5x −3x 1".
.................................................. P(x) CÂU : 47: Cho mệnh đề 2 " x
  , x + x +1 0". Mệnh đề phủ .................................................. P(x) định của mệnh đề là:
.................................................. A. 2 " x
  , x + x +1 0" . B. 2 " x
  , x + x +1 0" .
.................................................. C. 2 " x
  , x + x +1 0" . D. "  2
x , x + x +1 0".
..................................................
CÂU 48: Trong các mệnh đề sau, mệnh đề nào đúng?
.................................................. 2 x 1
A. Phủ định của mệnh đề “x ,  ” là mệnh đề “ 2 2x +1 2
.................................................. 2 x 1 x ,  ”.
.................................................. 2 2x +1 2
..................................................
B. Phủ định của mệnh đề “ 2
k  , k + k +1 là một số lẻ” là mệnh đề
.................................................. “ 2
k  , k + k +1là một số chẵn”.
C. Phủ định của mệnh đề “n sao cho 2
n −1 chia hết cho 24” là ..................................................
mệnh đề “ n sao cho 2
n −1 không chia hết cho 24”.
..................................................
D. Phủ định của mệnh đề “ 3
x , x −3x +1 0 ” là mệnh đề “ .................................................. 3
x , x −3x +1 0 ”.
.................................................. 21
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
CÂU 49: Cho mệnh đề 2
A = “x : x  ”
x . Trong các mệnh đề sau, ..................................................
mệnh đề nào là phủ định của mệnh đề A ?
.................................................. A. 2
“x : x  ” x . B. 2
“x : x  ” x .
.................................................. C. 2
“x : x  ” x . D. 2
“x : x  ” x .
..................................................
CÂU 50: Cho mệnh đề 2 1
A = “x : x + x  − ”. Lập mệnh đề phủ .................................................. 4
..................................................
định của mệnh đề A và xét tính đúng sai của nó. A. 2 1
A = “x : x + x  − ” . Đây là mệnh đề đúng.
.................................................. 4
.................................................. B. 2 1
A = “x : x + x  − ” . Đây là mệnh đề đúng.
.................................................. 4
.................................................. C. 2 1
A = “x : x + x  − ” . Đây là mệnh đề đúng.
.................................................. 4
.................................................. D. 2 1
A = “x : x + x  − ” . Đây là mệnh đề sai. 4
..................................................
..................................................
CÂU 51: Cho mệnh đề “phương trình 2
x −4x + 4 = 0 có nghiệm”.
Mệnh đề phủ định của mệnh đề đã cho và tính đúng, sai của mệnh .................................................. đề phủ định là:
.................................................. A. Phương trình 2
x −4x + 4 = 0 có nghiệm. Đây là mệnh đề đúng.
.................................................. B. Phương trình 2
x −4x + 4 = 0 có nghiệm. Đây là mệnh đề sai.
.................................................. C. Phương trình 2
x −4x + 4 = 0 vô nghiệm. Đây là mệnh đề đúng.
..................................................
.................................................. D. Phương trình 2
x −4x + 4 = 0 vô nghiệm. Đây là mệnh đề sai.
..................................................
CÂU 52: Cho mệnh đề A = “n :3n+1là số lẻ”, mệnh đề phủ định ..................................................
của mệnh đề A và tính đúng, sai của mệnh đề phủ định là:
A. A = “n : 3n+1 là số chẵn”. Đây là mệnh đề đúng.
..................................................
..................................................
B. A = “n : 3n+1 là số chẵn”. Đây là mệnh đề sai.
..................................................
C. A = “n : 3n+1 là số chẵn”. Đây là mệnh đề sai.
.................................................. D.
..................................................
A = “n : 3n +1 là số chẵn”. Đây là mệnh đề đúng.
..................................................
.................................................. 22
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
Dạng 5: Mệnh đề kéo theo
..................................................
Phương pháp: Xét mệnh đề P  . Q ( Nếu P thì Q ).
..................................................
 Khi đó P là giả thiết, Q là kết luận.
..................................................
 P là điều kiện đủ để có Q hoặc Q là điều kiện cần để có . P
..................................................
CÂU 53: Cho mệnh đề: “Nếu a +b  2 thì một trong hai số a và b ..................................................
nhỏ hơn 1”. Phát biểu mệnh đề trên bằng cách sử dụng khái niệm .................................................. “điều kiện đủ”.
..................................................
A. a +b  2 là điều kiện đủ để một trong hai số a và b nhỏ hơn 1.
..................................................
B. Một trong hai số a và b nhỏ hơn 1 là điều kiện đủ để a +b  2.
..................................................
C. Từ a +b  2 suy ra một trong hai số a và b nhỏ hơn 1
..................................................
D. Tất cả các câu trên đều đúng.
..................................................
CÂU 54: Cho mệnh đề: “Nếu một tứ giác là hình thang cân thì tứ ..................................................
giác đó có hai đường chéo bằng nhau”. Phát biểu mệnh đề trên bằng
cách sử dụng khái niệm “điều kiện cần”.
..................................................
A. Điều kiện cần để tứ giác là hình thang cân là tứ giác đó có hai .................................................. đường chéo bằng nhau.
..................................................
B. Điều kiện cần để tứ giác có hai đường chéo bằng nhau là tứ giác .................................................. đó là hình thang cân.
..................................................
C. Tứ giác là hình thang cân kéo theo tứ giác đó có hai đường chéo .................................................. bằng nhau.
..................................................
D. Cả a, b đều đúng.
..................................................
..................................................
CÂU 55: Cho mệnh đề: “Nếu ABC là tam giác đều thì ABC là một
tam giác cân”. Tìm giả thiết và kết luận của định lí.
..................................................
A. “ ABC là tam giác cân” là giả thiết, “ ABC là tam giác đều ” là kết .................................................. luận.
..................................................
B. “ ABC là tam giác đều” là giả thiết, “ ABC là tam giác cân” là kết .................................................. luận.
..................................................
C. “Nếu ABC là tam giác đều” là giả thiết, “thì ABC là tam giác cân” là kết luận.
..................................................
D. “Nếu ABC là tam giác cân” là giả thiết, “thì ABC là tam giác đều” .................................................. là kết luận.
.................................................. 23
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
CÂU 56: Trong các mệnh đề sau, mệnh đề nào không phải là định lí? .................................................. A. 2 x
  , x chia hết cho 3 x chia hết cho3.
..................................................
.................................................. B. 2 x
  , x chia hết cho 6  x chia hết cho 3.
.................................................. C.
.................................................. 2 x
  , x chia hết cho 9 x chia hết cho 9.
.................................................. D. x
  , xchia hết cho 4 và 6  x chia hết cho 12.
..................................................
..................................................
CÂU 57: Trong các mệnh đề sau, mệnh đề nào là định lí?
.................................................. A. 2 x   , x  2 −  x  4.
.................................................. B. 2 x
  , x  2  x  4 .
..................................................
.................................................. C. 2 x
  , x  4  x  2 .
..................................................
D. Nếu a +b chia hết cho 3 thì a, b đều chia hết cho 3 .
..................................................
..................................................
CÂU 58: Cách phát biểu nào sau đây không thể dùng để phát biểu ..................................................
mệnh đề: A  B .
..................................................
A. Nếu A thì B .
..................................................
B. A kéo theo B .
..................................................
..................................................
C. A là điều kiện đủ để có B .
..................................................
D. A là điều kiện cần để có B .
..................................................
..................................................
..................................................
..................................................
..................................................
..................................................
..................................................
.................................................. 24
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
Dạng 6: Mệnh đề đảo
..................................................
Phương pháp: Xét mệnh đề P  . Q ( Nếu P thì Q ).
..................................................
 Khi đó P là giả thiết, Q là kết luận.
..................................................
 P là điều kiện đủ để có Q hoặc Q là điều kiện cần để có . P
..................................................
 Khi đó mệnh đề Q  P gọi là mệnh đề đảo của mệnh đề P  . Q
..................................................
CÂU 59: Cho mệnh đề: “Nếu 2 góc ở vị trí so le trong thì hai góc đó ..................................................
bằng nhau”. Trong các mệnh đề sau đây, đâu là mệnh đề đảo của .................................................. mệnh đề trên?
..................................................
A. Nếu 2 góc bằng nhau thì hai góc đó ở vị trí so le trong.
..................................................
B. Nếu 2 góc không ở vị trí so le trong thì hai góc đó không bằng .................................................. nhau.
..................................................
C. Nếu 2 góc không bằng nhau thì hai góc đó không ở vị trí so le .................................................. trong.
..................................................
D. Nếu 2 góc ở vị trí so le trong thì hai góc đó không bằng nhau.
.................................................. CÂU
..................................................
60: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo là
.................................................. sai? A.
..................................................
Tam giác cân có hai cạnh bằng nhau. B.
..................................................
x chia hết cho 6 thì x chia hết cho 2 và 3. C.
..................................................
ABCD là hình bình hành thì AB song song với CD .
..................................................
D. ABCD là hình chữ nhật thì A = B = C = 90 . 
..................................................
..................................................
..................................................
..................................................
..................................................
..................................................
..................................................
..................................................
.................................................. 25
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
Dạng 7: Mệnh đề tương đương
..................................................
Phương pháp: Xét mệnh đề P  . Q ( Nếu P thì Q ).
..................................................
 Nếu cả hai mệnh để P Q và Q
P đều đúng thì mệnh đề tương .................................................. đương đúng.
..................................................  Mệnh đề P
Qcó thể phát biểu ở những dạng như sau:
..................................................
Q" P tương đương Q.
..................................................
Q" P là điều kiện cần và đủ để có Q.
..................................................
Q" P khi và chỉ khi Q.
..................................................
CÂU 61: Cho a . Mệnh đề nào dưới đây đúng?
..................................................
A. a 2 và a 3  a 6 .
..................................................
B. a 3  a 9 .
..................................................
C. a 2  a 4 .
..................................................
D. a 3 và a 6 thì a 18 .
..................................................
CÂU 62: Mệnh đề nào dưới đây sai?
..................................................
A. Tứ giác ABCD là hình chữ nhật khi và chỉ khi ABCD có ba góc .................................................. vuông.
..................................................
B. Tứ giác ABCD là hình bình hành khi và chỉ khi ABCD có hai cạnh ..................................................
đối song song và bằng nhau.
..................................................
C. Tứ giác ABCD là hình thoi khi và chỉ khi ABCD có hai đường chéo ..................................................
vuông góc với nhau tại trung điểm mỗi đường.
..................................................
D. Tứ giác ABCD là hình vuông khi và chỉ khi ABCD có bốn góc .................................................. vuông.
..................................................
..................................................
..................................................
..................................................
..................................................
..................................................
..................................................
.................................................. 26
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
Dạng 8: Dùng kí hiệu ∀, ∃ để viết mệnh đề
..................................................
.................................................. Phương pháp:
 "Với mọi x thuộc
", ký hiệu là: " x X ".
..................................................
 "Tồn tại x thuộc
", ký hiệu là: " x X ".
.................................................. CÂU 63:
..................................................
Viết mệnh đề sau bằng cách sử dụng kí hiệu  hoặc  :
..................................................
“Mọi số nhân với 1 đều bằng chính nó”. A.
.................................................. x   , . x 1= x. B.
.................................................. x   , . x 1= x .
.................................................. C. x   , . x 1= x.
.................................................. D. x   , . x 1= x .
..................................................
CÂU 64: Viết mệnh đề sau bằng cách sử dụng kí hiệu  hoặc  : ..................................................
“Mọi số cộng với số đối của nó đều bằng 0”.
.................................................. A. x
  : x +(−x) = 0.
.................................................. B. x
  : x +(−x) = 0.
.................................................. C. x
  , x− x = 0.
..................................................
D. x , x +(−x) = 0.
..................................................
CÂU 65: Các kí hiệu nào sau đây dùng để viết đúng mệnh đề “ 7 là .................................................. một số tự nhiên”.
.................................................. A. 7  .
.................................................. B. 7 .
.................................................. C. 7  .
.................................................. D. 7  .
.................................................. CÂU 66:
..................................................
Kí hiệu nào sau đây dùng để viết đúng mệnh đề “ 2 không
.................................................. phải là số hữu tỉ”
.................................................. A. 2  . B. 2  .
.................................................. C. 2  .
D. 2 không trùng với .
..................................................
.................................................. 27
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
Dạng 9: Phát biểu mệnh đề chứa kí hiệu ∀, ∃
.................................................. Phương pháp:
..................................................
 Kí hiệu đọc là: “Với mọi”
..................................................
 Kí hiệu  đọc là: “Tồn tại”.
..................................................
.................................................. CÂU 67: Mệnh đề 2 " x
  , x = 3" khẳng định rằng:
..................................................
A. Bình phương của mỗi số thực bằng 3 .
..................................................
B. Có ít nhất một số thực mà bình phương của nó bằng 3 .
..................................................
C. Chỉ có một số thực có bình phương bằng 3 .
..................................................
D. Nếu x là số thực thì 2 x = 3.
..................................................
CÂU 68: Kí hiệu X là tập hợp các cầu thủ x trong đội tuyển bóng ..................................................
rổ, P( x) là mệnh đề chứa biến “ x cao trên 180 cm ”. Mệnh đề .................................................. "xX, ( P )
x "khẳng định rằng:
..................................................
A. Mọi cầu thủ trong đội tuyển bóng rổ đều cao trên 180 cm .
..................................................
B. Trong số các cầu thủ của đội tuyển bóng rổ có một số cầu thủ cao .................................................. trên 180 cm .
..................................................
C. Bất cứ ai cao trên 180 cm đều là cầu thủ của đội tuyển bóng rổ.
..................................................
D. Có một số người cao trên 180 cm là cầu thủ của đội tuyển bóng rổ. .................................................. CÂU 69: Mệnh đề 2 " x
  , x = 3" khẳng định rằng:
..................................................
A. Bình phương của mỗi số thực bằng 3 .
..................................................
B. Có ít nhất một số thực mà bình phương của nó bằng 3 .
..................................................
C. Chỉ có một số thực có bình phương bằng 3 .
..................................................
D. Nếu x là số thực thì 2 x = 3.
..................................................
..................................................
..................................................
..................................................
..................................................
..................................................
.................................................. 28
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10
Dạng 10: Phủ định mệnh đề chứa kí hiệu ∀, ∃
.................................................. Phương pháp:
..................................................
 Mệnh đề phủ định của mệnh đề "x X, ( P )
x " là "x X, ( P ) x ".
..................................................
 Mệnh đề phủ định của mệnh đề "x X, ( P )
x " là "x X, ( P ) x ".
..................................................
CÂU 70: Mệnh đề nào sau đây là phủ định của mệnh đề: “Mọi động ..................................................
vật đều di chuyển”. A.
..................................................
Mọi động vật đều không di chuyển. B. Mọi động vật đều đứng yên.
..................................................
C. Có ít nhất một động vật không di chuyển.
D. Có ít nhất ..................................................
một động vật di chuyển.
..................................................
CÂU 71: Phủ định của mệnh đề: “Có ít nhất một số vô tỷ là số thập ..................................................
phân vô hạn tuần hoàn” là mệnh đề nào sau đây:
A. Mọi số vô tỷ đều là số thập phân vô hạn tuần hoàn.
..................................................
B. Có ít nhất một số vô tỷ là số thập phân vô hạn không tuần hoàn. ..................................................
C. Mọi số vô tỷ đều là số thập phân vô hạn không tuần hoàn. D.
..................................................
Mọi số vô tỷ đều là số thập phân tuần hoàn.
CÂU 72: Cho mệnh đề A: “ 2 x
  , x − x + 7  0” Mệnh đề phủ định .................................................. của A là:
.................................................. A. 2 x
  , x − x + 7  0 . B. 2 x
  , x − x + 7  0 . C. Không tồn tại 2
x: x − x +7  0. D. 2 x
  , x - x + 7  0.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A C C B D D D B B A A A D C B B B D A A D A C B B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
D A D A C C D C B C D A D D D C C D B A C C C B C
51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75
D B A A B D B D A C A D B B B C B A B C C D 29
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ ÔN LUYỆN KNTT 10 30
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10 Bài 2
TẬP HỢP, CÁC PHÉP TOÁN TRÊN TẬP HỢP
A TÓM TẮT LÝ THUYẾT
1. CÁC KHÁI NIỆM CƠ BẢN VỀ TẬP HỢP a. Tập hợp
 Tập hợp là một khái niệm cơ bản của toán học, không định nghĩa mà chỉ mô tả.
 Có hai cách xác định tập hợp:
▶ Liệt kê các phần tử: viết các phần tử của tập hợp trong hai dấu móc {...;...;...;...}.  Ví dụ: X {0; 1; 2; 3; 4}.
▶ Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.  Ví dụ: 2 X {n | 3 n 36}.
 Tập rỗng: là tập hợp không chứa phần tử nào, kí hiệu .
 Ví dụ: Phương trình 2 x x 1 0 không có nghiệm.
Ta nói tập hợp các nghiệm của phương trình này là tập hợp rỗng, tức S . b. Tập hợp con  Cho 2 tập hợp : ; A B .
▶ Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói:
 Tập hợp A là một tập hợp con (tập con) của tập hợp B . Và ký hiệu làA B .
▶ Cách đọc khác:  Tập hợp A chứa trong tập hợp B .
 Tập hợp B chứa tập hợpA .
 Cách viết bằng ký hiệu: A B ( x A x ) B .
Nhận xét: ▶ A , A A và , A . A ▶ A , B B C A C.
 Nếu tập A có n phần tử
A có 2n tập hợp con.
 Người ta thường minh họa tập hợp bằng một hình Hình 1
phẳng, được bao quanh bởi 1 đường khép kín.
Gọi là biểu đồ Ven ( Hình 1 )
c. Hai tập hợp bằng nhau
 Nếu mổi phần tử của tập hợp A đều là phần tử của tập hợp B và ngược lại thì ta nói:
A và B là 2 tập hợp bằng nhau. Kí hiệu: A B A B Nhận xét: A B . B A 31
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
2. CÁC TẬP HỢP SỐ
a) Mối quan hệ giữa các tập hợp số
 Tập hợp các số tự nhiên :  =0;1;2;3;......
 Tập hợp các số tự nhiên khác không  * = 1;2;3;.....  .
 Tập hợp các số nguyên : *  * =....; 3 − ; 2 − ; 1 − ;0;1;2;3;..... .
 Tập hợp các số hữu tỉ : a   * =  ;
a b ;b  0 b 
 Tập hợp các số thực : gồm
các số hữu tỉ và vô tỉ.
 Số vô tỉ là các số thạ p phân
vô hạn không tuàn hoàn.
b) Các tập con thường dùng của ℝ  Khoảng ( ; a ) b {x |a x } b . a b Ví dụ: 2 x 3 x ( 2;3). ( ; a ) {x | x } a . a Ví dụ: x 3 x (3; ). ( ; ) b {x | x } b . b Ví dụ: x 3 x ( ;3).  Đoạn [ ; a b] {x |a x } b . a b  Nửa khoảng [ ; a ) b {x |a x } b . a b ( ; a b] {x |a x } b . a b [ ; a ) {x | x } a . a b ( ;b] {x | x } b . Kí hiệu
đọc là dương vô cực (cùng), kí hiệu
đọc là âm vô cực (cùng). Ta có thể viết ( ; ) và gọi là khoảng ( ; ). 32
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
3. CÁC PHÉP TOÁN TRÊN TẬP HỢP
a. Giao của hai tập hợp
 Tập hợp C gồm các phần tử vừa thuộc ,
A vừa thuộc B được gọi là giao của A và . B  Kí hiệu C
A B (phần gạch trong hình).  Vậy A B {x | x A và x }. B x A  x A B . x B B A
(Cách nhớ: giao là lấy phần chung)
b. Hợp của hai tập hợp
 Tập hợp C gồm các phần tử thuộc A hoặc thuộc B được gọi là hợp của A và . B  Kí hiệu: C
A B (phần gạch chéo trong hình).  Vậy A B {x | x A hoặc x }. B x A  x A B . x B
(Cách nhớ: hợp là lấy hết)
c. Hiệu của hai tập hợp
 Tập hợp C gồm các phần tử thuộc A nhưng không thuộc B gọi là hiệu của A và . B  Kí hiệu C
A\ B (phần gạch chéo trong hình).  Vậy A\ B {x | x A và x }. B x A  x A \ B . x B
(Cách nhớ: hiệu thuộc A mà không thuộc B)  Khi B
A thì A \ B gọi là phần bù của B trong . A  Kí hiệu C B
A \ B (phần gạch chéo trong hình). A
Tổng kết: Giao (A )
B là lấy phần chung, hợp (A )
B là lấy hết, trừ (A \ B) là thuộc A mà không thuộc , B phần bù C B
A \ B (dưới trừ trên và trên con dưới). A 33
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
B BÀI TẬP TỰ LUẬN
Dạng 1: Xác định tập hợp bằng cách liệt kê tất cả các phần tử của tập hợp Ví dụ 1
Viết tập hợp sau bằng cách liệt kê các phần tử của nó: A {x | x
20 và x chia hết cho 3}. BÀI GIẢI Ta có: A {0; 3; 6; 9; 12; 15; 18}.
BÀI TẬP RÈN LUYỆN Bài 1.1
Viết mỗi tập hợp sau bằng cách liệt kê các phần tử của nó.. a) A {x | 2 x 10}. b) A {x | 7 x 15}. c) A {x | 14 3x 0}. d) A {x | 15 2x 0}. e) A {x | x 1 3}. f) A {x | x 5}. 1 1 g) A {x | x 2 1}. h) A x x , n 2n 32 Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 34
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10 Bài 1.2
Viết mỗi tập hợp sau bằng cách liệt kê các phần tử của nó.. a) 2 2 A {x | (2x 5x 3)(4 x ) 0}. b) 2 A {x | (x 4x 3)(2x 1) 0}. c) 3 2 A {x | 2x 7x 5x 0}. d) A {x | 15 2x 0}. e) 4 2 2 A {x | (x 8x 9)(x 16) 0}. f) A {x | x 5}. g) 2 2 A {x | (3x 4x 7)(9 x ) 0}. h) 4 2 2 A {x | (x 3x 4)(x 25) 0}. Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 35
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 2: Xác định tập hợp bằng cách chỉ ra tính chất đặc trung Ví dụ 1
Viết tập hợp sau bằng cách nêu tính chất đặc trưng của nó: A {2; 6; 12; 20; 30}. BÀI GIẢI Cách 1:A { ( n n 1) 1 n 5;n }. Cách 2: A { ( n n 1) 0<n 6;n }.
BÀI TẬP RÈN LUYỆN Bài 1.1
Viết các tập hợp sau bằng cách nêu tính chất đặc trưng của nó: a) A {1; 3; 5; 7}. b) B 0 ; 2; 4; 6;...... 1 1 1 1 1 c) C = 0 { ;5;10;15;20 . } d) D ; ; ; ; 2 6 12 20 30 1 1 1 1 1 1 1 1 1 1 e) E 1; ; ; ; ; f) F ; ; ; ; 3 9 27 81 234 2 6 12 20 30 g) G =  4 − ; 3 − ; 2 − ; 1 − ;0;1;2;3;  4 . h) G {3; 6; 9; 12; 15}. Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 36
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 3: Xác định tập con của một tập hợp cho trước Ví dụ 1
Tìm tất cả các tập hợp con của tập hợp sau: a) A { ; a } b . b) B {0;1;2}. BÀI GIẢI
a) Các tập hợp con của tập hợp A { ; a } b là: ;  ; A { } a ; { } b .
b) Các tập hợp con của tập hợp B {0;1;2}. là: ;  ;
B {1}; {2}; {3}; {1;2}; {1;3}; {2;3}.
BÀI TẬP RÈN LUYỆN Bài 1.1
Tìm tất cả các tập hợp con của tập hợp sau: a) A = 1;2;3;  a b) B {x
sao cho x là ước của 8}. 2x 4 c) 2 C {k 1 k , k } 2 d) D (x;y) | x , y , y . x 3 1 1 1 1 1 1 1 1 1 1 e) E 1; ; ; ; ; f) F ; ; ; ; 3 9 27 81 234 2 6 12 20 30 1 1 g) G {x | 7 x 15}. h) H x x , n 2n 32 Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 37
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10 Ví dụ 2 Cho hai tập hợp A { 4; 2; 1;2;3;4} và B {x | x
4}. Tìm các tập hợp X sao cho A X . B BÀI GIẢI Ta có: x 4 4 x 4 và do x nên B { 4; 3; 2; 1;0;1;2;3;4}. Theo đề A X B { 4; 2; 1;2;3;4} X
{ 4; 3; 2; 1;0;1;2;3;4} nên tập hợp X là một
trong những tập hợp :
{ 4; 2; 1;2;3;4}, { 4; 3; 2; 1;2;3;4}, { 4; 2; 1;0;2;3;4},{ 4; 2; 1;1;2;3;4}, { 4; 2; 1;0;2;3;4},
{ 4; 3; 2; 1;1;2;3;4}, { 4; 2; 1;0;1;2;3;4}, { 4; 3; 2; 1;0;1;2;3;4}.
BÀI TẬP RÈN LUYỆN Bài 1.2 Cho A {1;2} và B
{1;2;3;4;5}. Tìm các tập hợp X sao cho A X . B Lời giải
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
.............................................................................................................................................................................................
............................................................................................................................................................................................. 38
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 4: Các phép toàn trên tập hợp ( Không chứa tập con của ℝ ) Ví dụ 1 Cho 2 tập hợp A {1; 2; 3} và B
{1; 3; 5; 7}.Tìm A B BÀI GIẢI Ta có: A B {1;3}.
BÀI TẬP RÈN LUYỆN Bài 1.1 Cho 2 tập hợp: A {1; 2; 3; 4; 5} và B
{1; 3; 5; 7; 9; 11}. Xác định các phép toán sau: Lời giải A B
.......................................................... A B
........................................................ …………… A\ B
........................................................... B \ A
......................................................... …………… (A ) B \(A ) B
..................................................................................................................... ………….. (A\ ) B (B \ ) A
........................................................................................................................................ Bài 1.2 Cho 2 tập hợp: A {1; 2; 3; 4}, B {2; 4; 6; 8} và C
{3; 4; 5; 6}.Xác định các phép toán sau: Lời giải A B
.......................................................... B C
........................................................ …………… C A
.......................................................... A B
........................................................ …………… B C
.......................................................... C
A ........................................................ …………… A\ B
........................................................... B \C
......................................................... ……………
C \ A ................................................................................................................................................... ….. (A ) B C
.............................................................................................................................................. .. 39
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10 Ví dụ 2
Xác định tập A và B đồng thời thỏa mãn: A B {1;2;3}; A\ B
{4;5} và B \ A {6;9}. BÀI GIẢI Vì A B
{1;2;3} nên hai tập hợp A và B sẽ có ba phần tử: 1, 2, 3. Vì A\ B
{4;5}, tức 4, 5 A mà 4, 5 B nên A {1; 2; 3; 4; 5}. Vì B \ A
{6;9}, ……………………………………………………………………………………………………………………………………………
BÀI TẬP RÈN LUYỆN Bài 1.1
Xác định tập A và B đồng thời thỏa mãn: A B
{0; 1; 2; 3; 4}, A\ B
{ 3; 2} và B \ A {6; 9; 10}. Lời giải
……………………………………………………………………………………………………………………………………………………………………………….
……………………………………………………………………………………………………………………………………………………………………………….
……………………………………………………………………………………………………………………………………………………………………………….
……………………………………………………………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………………………………………………………………. Bài 1.2
Xác định tập A và B đồng thời thỏa mãn: A\ B {1; 5; 7; 8}, A B {3; 6; 9} và A B {x | 0 x 10}. Lời giải
……………………………………………………………………………………………………………………………………………………………………………….
……………………………………………………………………………………………………………………………………………………………………………….
……………………………………………………………………………………………………………………………………………………………………………….
……………………………………………………………………………………………………………………………………………………………………………….
……………………………………………………………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………………………………………………………………. 40
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 5: Sử dụng biểu đồ Ven để giải bài toán. Ví dụ 1
Mỗi học sinh lớp 10C đều chơi bóng đá hoặc bóng chuyền. Biết rằng có 25 bạn chơi bóng đá, 20 bạn
chơi bóng chuyền và 10 bạn chơi cả 2 môn thể thao này. Hỏi lớp 10C có bao nhiêu học sinh ? BÀI GIẢI 10 bạn Kí hiệu:
A là tập các học sinh lớp 10C chơi bóng đá (có 25 người).
B là tập các học sinh lớp 10C chơi bóng chuyền (có 20 người).
Vì mỗi bạn lớp 10C đều chơi bóng đá hoặc bóng chuyền A B là t
ập các học sinh của lớp.
Để đếm số phần tử của A
B ta đếm số phần tử của A (25 phần tử) và đếm số phần tử của B (20
phần tử), nhưng khi đó số phần tử của A B được đếm 2 lần. (Những bạn chơi cả 2 môn thể thao)
Tức số học sinh của lớp là ( n A ) B ( n ) A ( n ) B ( n A ) B 25 20 10 35 học sinh.
BÀI TẬP RÈN LUYỆN Bài 1.1
Trong số 45 học sinh lớp 10A có 15 bạn được xếp loại học lực giỏi, 20 bạn xếp loại hạnh kiểm tốt, 1
trong đó có 10 bạn vừa học lực giỏi, vừa có hạnh kiểm tốt. Hỏi: Lời giải
a) Lớp 10A có bao nhiêu bạn được khen thưởng, biết rằng muốn được khen thưởng, bạn đó phải học 1
lực giỏi hoặc có hạnh kiểm tốt ?
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
.............................................................................................................................................................. 25 bạn.
b) Lớp 10A có bao nhiêu bạn chưa được xếp loại học lực giỏi và chưa có hạnh kiểm tốt ? 1
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
............................................................................................................................................................... 20 bạn. 41
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10 Ví dụ 2
Trong lớp 10A có 45 học sinh trong đó có 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Sử, 1
6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên. BÀI GIẢI
Gọi a,b,c theo thứ tự là số học sinh chỉ thích môn Văn, Sử, Toán:
x là số học sịnh chỉ thích hai môn là văn và toán.
y là số học sịnh chỉ thích hai môn là Sử và toán
z là số học sịnh chỉ thích hai môn là văn và Sử
Ta có số em thích ít nhất một môn là 45 6 39 . Ta có biểu đồ Ven:
Dựa vào biểu đồ ven ta có hệ phương trình a x z 5 25 (1) b y z 5 18 (2) c x y 5 20 (3) x y z a b c 5 39 (4)
Cộng vế với vế (1), (2), (3) ta có: a b c 2 x y z 15 63 (5)
Từ (4) và (5) ta có: a b c 2 39 5 a b c 15 63 a b c 20
Vậy chỉ có 20 em thích chỉ một môn trong ba môn trên.
BÀI TẬP RÈN LUYỆN 42
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10 Bài 1.2
Trong lớp 10A có 16 học sinh giỏi môn Toán, 15 học sinh giỏi môn Lý và 11 học sinh giỏi môn Hóa. Biết rằng 1
có 9 học sinh vừa giỏi Toán và Lý, 6 học sinh vừa giỏi Lý và Hóa, 8 học sinh vừa giỏi Hóa và Toán, trong đó
chỉ có 11 học sinh giỏi đúng hai môn. Hỏi có bao nhiêu học sinh của lớp: Lời giải
a) Giỏi cả ba môn Toán, Lý, Hóa?
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
........................................................................................................................................................ 4 học sinh.
b) Giỏi đúng một môn Toán, Lý hoặc Hóa.?
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
......................................................................................................................................................... 8 học sinh. Nhận xét: Với , A ,
B C là các tập bất kì khi đó ta luôn có n A B n A n B n A B ( n A B ) C n A n B n C ( n A ) B ( n B ) C ( n C ) A n A B C 43
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 6: Chứng minh tập hợp bằng nhau, tập con Ví dụ 1
Cho A và B là hai tập hợp. Chứng minh rằng: a) \ A B A b) A \ B A c) A \ B A A B BÀI GIẢI x A
a) Ta có x, x A\B x A . Suy ra \ A B A . x B x A x A b) Ta có x A B\A x B x . Suy ra A \ B A . x B\A x A x A x A x A c) Ta có x A B\A x B x A B x B\A x B x A
BÀI TẬP RÈN LUYỆN Bài 1.1 Cho các tập hợp ,
A B và C . Chứng minh rằng: Lời giải a) A B C A B A C
…………………………………………………………………………………………………………………….
……………………………………………………………………………………………………………………. b) A B C A B A C
…………………………………………………………………………………………………………………….
……………………………………………………………………………………………………………………. c) A \ B C A B \C
…………………………………………………………………………………………………………………….
……………………………………………………………………………………………………………………. 44
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 7: Phân biệt tập hợp và tập con của ℝ Ví dụ 1
Hãy phân biệt các tập hợp sau: { 1;2}, [ 1;2], ( 1;2), [ 1;2), ( 1;2]. BÀI GIẢI
{ 1;2} là tập hợp (dạng liệt kê) chỉ chứa 2 phần tử là số 1 và số 2. [ 1;2] {x | 1 x 2} là một đoạn từ 1 2 (lấy 1 và 2)
( gồm vô số các phần tử là số thực, chẳng hạn 1; 0,9; 0,89;.....;2.) ( 1;2) {x | 1 x 2} là một khoảng 1 2 (không lấy 1 và 2)
(gồm vô số các phần tử là số thực, chẳng hạn 0,9999;
0,98;.....;1,888; 1,9,..., nhưng không lấy 2.) [ 1;2) {x | 1 x
2} là nửa khoảng……………………………………………………………...................................................
………………………………………………………………………………………………………………………………………………………………………………. ( 1;2]
……………………………………………………………...................................................……………………………………………………………..
……………………………………………………………………………………………………………………………………………………………………………….
BÀI TẬP RÈN LUYỆN Bài 1.1
Hãy phân biệt tập hợp sau: A {x | 2 x 3} và B {x | 2 x 3}. Lời giải
…………………………………………………………………………………………………………………….
…………………………………………………………………………………………………………………….
…………………………………………………………………………………………………………………….
…………………………………………………………………………………………………………………….
…………………………………………………………………………………………………………………….
……………………………………………………………………………………………………………………. 45
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 8: Các phép toán trên tập con của ℝ Ví dụ 1 Cho A [ 4;4), B
[1;7). Hãy xác định các phép toán sau và biểu diễn kết quả của phép toán trên trục số ? BÀI GIẢI
Để tìm A B ta làm như sau:
- Sắp xếp theo thứ tự tăng dần các điểm đầu mút của các tập hợp ,
A B lên trục số. - Biểu diễn các tập ,
A B trên trục số(phần nào không thuộc các tập đó thì gạch bỏ).
- Phần không bị gạch bỏ chính là giao của hai tập hợp , A B
Để tìm A B ta làm như sau:
- Sắp xếp theo thứ tự tăng dần các điểm đầu mút của các tập hợp ,
A B lên trục số. - Tô đậm các tập ,
A B trên trục số.
- Phần tô đậm chính là hợp của hai tập hợp , A B .
Để tìm A\B ta làm như sau:
- Sắp xếp theo thứ tự tăng dần các điểm đầu mút của các tập hợp ,
A B lên trục số.
- Biểu diễn tập A trên trục số(gạch bỏ phần không thuộc tập A ), gạch bỏ phần thuộc tập B trên trục số .
- Phần không bị gạch bỏ chính là A\B . A B
[1;4), biểu diễn trên trục số: A B
[ 4;7), biểu diễn trên trục số: ………………………………………………………………………………………………………. A\ B
[ 4;1), biểu diễn trên trục số: ……………………………………………………………………………………………………….
B \ A [4;7), biểu diễn trên trục số: ………………………………………………………………………………………………………….. C A \ A ( ; 4) [4;
) :…………………………………………………………………………………………………………... C B \ B ( ;1) [7;
) : ……………………………………………………………………………………………………………...
BÀI TẬP RÈN LUYỆN 46
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10 Bài 1.1 Cho A [3; ), B
(0;4). Hãy xác định các phép toán sau và biểu diễn kết quả của phép toán trên trục số ? Lời giải
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. A B
............................................................................................................................................................. A B
.............................................................................................................................................................
A\ B ..............................................................................................................................................................
B \ A ..............................................................................................................................................................
C A ............................................................................................................................................................... C B
............................................................................................................................................................... Bài 1.2 Cho A ( ;10), B
\[0;1] Hãy xác định các phép toán sau và biểu diễn kết quả của phép toán trên trục số ? Lời giải
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. A B
............................................................................................................................................................. A B
.............................................................................................................................................................
A\ B ..............................................................................................................................................................
B \ A ..............................................................................................................................................................
C A ............................................................................................................................................................... C B
...............................................................................................................................................................
Nhận xét: Tập A (
;10)còn có thể viết dưới dạng: A x
................................... 47
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10 Ví dụ 2 Cho hai tập hợp A [ ;
m m 2) và B (5;6), m .
a) Tìm m để A .
B b) Tìm m để B .
A c) Tìm m để A B BÀI GIẢI
a) Tìm m để A . B 5 m m+2 6 -∞ +∞ A B • Để A B 5 m m 2 6 . m 5 m 5 m . m 2 6 m 4
b) Tìm m để B . A m 5 6 m+2 -∞ +∞ A B • Để B A m 5 6 m 2 m 5 m 5 4 m 5. m 2 6 m 4
c) Tìm m để A B
(Cố định tập B
(5;6) thì tập A nằm bên trái hoặc bên phải).
……………………………………………………………………………………………………………………………………………………………………………….
……………………………………………………………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………………………………………………………………. m 2 5 m 3 Để A B . m 6 m 6
BÀI TẬP RÈN LUYỆN 48
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10 Bài 1.1 Cho hai tập hợp A
(3m 1; 3m 7) và B ( 1;1), m . Lời giải
a) Tìm m để B . A
b) Tìm m để A B .
...........................................................................
............................................................................
...........................................................................
............................................................................
...........................................................................
............................................................................
...........................................................................
...........................................................................
...........................................................................
...........................................................................
...........................................................................
...........................................................................
.......................................................... m 2.
......................................................... m 4. Bài 1.2 Cho hai tập hợp A (2;7 ) m và B (m 1; ), m . Lời giải
a) Tìm m để A . B
b) Tìm m để A B .
...........................................................................
............................................................................
...........................................................................
............................................................................
...........................................................................
............................................................................
...........................................................................
...........................................................................
...........................................................................
...........................................................................
...........................................................................
...........................................................................
...........................................................................
............................................................................
c) Tìm m để A B (1; ).
............................................................................................................................................................................
............................................................................................................................................................................
............................................................................................................................................................................
............................................................................................................................................................................
………………………………………………………………………………………………………. m 2. 49
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10 Bài 1.3 Cho A , 2 , B [2m 1, ) . Tìm m để A B R . Lời giải
............................................................................................................................................................................
............................................................................................................................................................................ 3
…………………………………………………………………………………………………………. m 2 Bài 1.4 Tìm m để 1;m 2; . Lời giải
............................................................................................................................................................................
............................................................................................................................................................................
…………………………………………………………………………………………………………. m 2 Bài 1.5 x 3
Viết tập A gồm các phần tử x thỏa mãn điều kiện x 1 0 dưới dạng tập số. x 0 Lời giải
............................................................................................................................................................................
............................................................................................................................................................................
............................................................................................................................................................................
............................................................................................................................................................................
............................................................................................................................................................................
............................................................................................................................................................................
............................................................................................................................................................................
............................................................................................................................................................................
............................................................................................................................................................................ …
……………………………………………………………………………………………Vậy A 1; 0 . 50
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
C BÀI TẬP TRẮC NGHIỆM distance QUICK NOTE
Dạng 1: Xác định số phần tử của tập hợp Thà để giọt mồ hôi Phương pháp rơi trên trang sách
 a  A: phần tử a thuộc vào tập hợp A còn hơn để nước mắt
 a  A: phần tử a không thuộc vào tập hợp A rơi ướt cả đề thi distance CÂU 1:
.....................................
Trong các tập hợp sau đây, tập hợp nào có đúng một phần tử?
..................................... A.  ; x  y . B.   x .
.....................................
..................................... C.  ; x   . D. .
.....................................
.....................................
CÂU 2: Tập hợp X =2;  5 có bao nhiêu phần tử?
..................................... A. 4 . B. Vô số.
.....................................
..................................... C. 2 . D. 3 .
..................................... CÂU 3:
.....................................
Cho tập hợp A=x | x  
5 . Tập hợp A được viết dưới dạng liệt kê các ..................................... phần tử là
.....................................
A. A=1;2;3;  4 .
B. A=1;2;3;4;  5 .
.....................................
.....................................
C. A=0;1;2;3;4;  5 .
D. A=0;1;2;3;  4 .
.....................................
.....................................
CÂU 4: Cho tập hợp A . Trong các mệnh đề sau, mệnh đề nào sai?
..................................... A.   A. B. A    A .
.....................................
.....................................
C. A A.
D. A  A .
.....................................
.....................................
CÂU 5: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng?
.....................................
A. xN / x   1 . B.  2
xZ / 6x −7x +1=  0 .
.....................................
..................................... C.  2
xQ / x − 4x + 2 =  0 . D.  2
xR / x − 4x +3 =  0 .
.....................................
.....................................
CÂU 6: Trong các tập hợp sau đây, tập hợp nào có đúng một phần tử?
..................................... A.
.....................................  ; x  y . B.   x .
..................................... C.  ; x   . D. .
.....................................
.....................................
CÂU 7: Tập hợp X =2;  5 có bao nhiêu phần tử?
.....................................
..................................... A. 4 . B. Vô số.
..................................... C. 2 . D. 3 .
.....................................
..................................... 51
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 2: Xác định tập hợp bằng cách liệt kê hoặc chỉ ra tính
.....................................
.....................................
chất đặc trưng của các phần tử thuộc tập hợp.
..................................... Phương pháp
.....................................
 Xác định tạ p hợp bàng cách liê ̣t kê:
.....................................
 Bước 1: Xác định điều kiện của x . ( x thuộc tập số nào )
.....................................
 Bước 2: Giải phương trình, tìm các giá trị x . So sánh với điều kiện để chọn.
.....................................
 Xác định tạ p hợp bàng cách chỉ ra tính chát đạ c trưng của các phàn tử:
.....................................
 Bước 1: Liệt kê ra một vài phần tử thuộc tập hợp đả cho ở Đáp án.
.....................................  Bước 2: Kiểm tra
.....................................
.....................................
CÂU 8: Hãy liệt kê các phần tử của tập X =  2 x 
2x − 5x + 3 =  0 .
.....................................
..................................... A. X =  0 . B. X =   1 .
..................................... C. 3  3
..................................... X =  . D. X = 1  ; . 2  2
.....................................
.....................................
CÂU 9: Cho tập hợp A=x |x  
5 . Tập hợp A được viết dưới dạng liệt kê các ..................................... phần tử là
.....................................
A. A=1;2;3;  4 .
B. A=1;2;3;4;  5 .
.....................................
C. A=0;1;2;3;4;  5 .
D. A=0;1;2;3;  4 .
.....................................
.....................................
CÂU 10: Cho tập X = x ( 2
| x − 4)(x − ) 1 = 
0 . Tính tổng S các phần tử của tập ..................................... X
..................................... . 9
..................................... A. S = 4. B. S = . 2
.....................................
..................................... C. S = 9 . D. S =1.
.....................................
CÂU 11: Liệt kê phân tử của tập hợp B = 2 2 x | (2x − )
x (x −3x − 4) =  0 .
..................................... A. B = 1 − ;0;  4 . B. B =0;  4 .
.....................................
..................................... C.  1  B = 1 −  ; ;0;4.
D. B =0;1;  4 .  2 
.....................................
.....................................
CÂU 12: Cho X =  2
x R 2x −5x + 3 = 
0 , khẳng định nào sau đây đúng?
.....................................  3
..................................... A. X =   1 . B. X = 1  ; .  2
..................................... 3
.....................................
C. X =  . D. X =  0 .
..................................... 2
.....................................
CÂU 13: Có bao nhiêu cách cho một tập hợp?
..................................... A. 2 . B. 4 .
..................................... C. 3. D. 1.
.....................................
.....................................
..................................... 52
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10 CÂU 14:
.....................................
Cho hai tập hợp A = x ( 2 x − x − )( 2 | 2 3 x − 4) = 
0 , B = x | x  
4 . .....................................
Viết lại các tập A và B bằng cách liệt kê các phần tử.
..................................... A.  3 A =  2
− ;−1;2; , B =0;1;2;  3 .
.....................................  2
..................................... B.  3
..................................... A =  2
− ;−1;2; , B =1;2;3;  4 .  2
..................................... C. A = 2 − ; 1 − ;  2 , B =0;1;2;  3 .
.....................................
..................................... D. A = 2 − ; 1 − ;  2 , B =1;2;  3 .
.....................................
.....................................
CÂU 15: Cho tập hợp A =  2 * 2 x +1 x  , x  
5 . Khi đó tập A bằng tập hợp nào ..................................... sau đây?
.....................................
A. A =1;2;3;  4 .
B. A =0;2;  5 .
..................................... C.
..................................... A = 2;  5 .
D. A =0;1;2;3;4;  5 .
..................................... CÂU 16:
.....................................
Tìm số phần tử của tập hợp A = x (x− )(x+ )( 3 / 1
2 x − 4x) =  0 .
..................................... A. 5. B. 3 .
..................................... C. 2 . D. 4 .
.....................................
.....................................
CÂU 17: Cho tập hợp A =x ( 2 x + x + )( 2 | 2 5 2 x −16) = 
0 . Tập hợp A được .....................................
viết dưới dạng liệt kê là
.....................................  −
..................................... A. 1   4 − ; ; − 2; 4 . B.  4 − ; −  2 .  2 
..................................... C.
.....................................   4  . D.  4 − ; − 2;  4 .
.....................................
CÂU 18: Hãy liệt kê các phần tử của tập hợp: X =  2
x  / 2x − 5x + 2 =  0
.....................................
..................................... A. 1 X =   0 . B. X =  .
..................................... 2
..................................... C.  1 X =   2 . D. X = 2;  
.....................................  2
..................................... CÂU 19:
.....................................
Cho tập X = x
( 2x − )(x− )( 2 | 4
1 2x − 7x + 3) = 
0 . Tính tổng S các .....................................
phần tử của X .
..................................... A. 9 S = . B. S = 5.
..................................... 2
.....................................
C. S = 6. D. S = 4.
..................................... CÂU 20:
.....................................
Hãy liệt kê các phần tử của tập hợp X =  2
x | x + x +1=  0
.....................................
A. X = . B. X =    .
..................................... C. X =   0 . D. X = 0.
.....................................
..................................... 53
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
CÂU 21: Cho A =0;2;4; 
6 . Tập hợp A có bao nhiêu tập hợp con có 3 phần tử? .....................................
..................................... A. 4 . B. 6 .
..................................... C. 7 . D. 8 .
.....................................
CÂU 22: Cho tập hợp A =a,c, 
e . Có bao nhiêu tập con của tập hợp A .
.....................................
..................................... A. 3 . B. 5 .
..................................... C. 6 . D. 8 .
..................................... CÂU 23:
.....................................
Tính chất đặc trưng của tập hợp X = 1;2;3;4;  5 .
.....................................
A. x x   5 . B.  * x x   5 .
..................................... C.
.....................................
x x   5 .
D. x x   5 .
.....................................
CÂU 24: Tính chất đặc trưng của tập hợp X = 3 − ; 2 − ; 1 − ;0;1;2;  3 .
.....................................
.....................................
A. x x   3 .
B. x x   3 .
..................................... C.
..................................... x x   3 . D. x 3 −  x   3 .
..................................... CÂU 25: 1 1 1 1 
.....................................
Tính chất đặc trưng của tập hợp X =  ; ; ; ;..... 2 4 8 16 
.....................................  1   1 
.....................................
A. x x = ;n .
B. x x = ;n *.  2n   2n 
.....................................
.....................................  1   1  C.
..................................... x  x = ;n  *.
D. x x = ;n *.  2n +1   2n −1 
.....................................
..................................... CÂU 26: 1 1 1 1 
Tính chất đặc trưng của tập hợp X =  ; ; ; ;.....
..................................... 2 6 12 20 
.....................................  1   1 
A. x x =
;n *. B. x x = ;n *.
..................................... ( n n +1)   ( n n +1)  
..................................... 
..................................... 1   1 
C. x x =
;n *. D. x x = ;n *.
..................................... ( n n +1)   2 n (n +1)  
.....................................
CÂU 27: Tìm các phần tử của tập hợp: X = 2
x / 2x −5x +3 =  0 .
.....................................
..................................... A.  3 X = 1  ; . B. X =   1 .
.....................................  2
..................................... C. 3 X =   . D. X =  0 .
..................................... 2
..................................... CÂU 28:
.....................................
Hãy liệt kê các phần tử của tập hợp X =  2 x  x + x +1 =  0 :
.....................................
A. X = 0. B. X =  0 .
..................................... C.
.....................................
X =  . D. X =   .
..................................... 54
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
CÂU 29: Cho X =  2 x 
2x − 5x + 3 = 
0 , khẳng định nào sau đây đúng:
.....................................
..................................... A. X =  0 .
.....................................
..................................... B. X =   1 .
.....................................
..................................... C. 3
X =  . 2
.....................................
..................................... D.  3
..................................... X = 1  ; .  2
.....................................
.....................................
CÂU 30: Cho tập hợp B =xR ( 2 − x )( 2 9
x −3x + 2) = 
0 , tập hợp nào sau đây là .....................................
..................................... đúng?
.....................................
.....................................
A. Tập hợp B =3;9;1;  2 .
..................................... B.
.....................................
Tập hợp B =  3 − ; 9 − ;1;  2 .
.....................................
C. Tập hợp B = 9 − ;9;1;  2 .
.....................................
.....................................
D. Tập hợp B = 3 − ;3;1;  2 .
.....................................
.....................................
CÂU 31: Cho tập hợp S = 2
xR x − 2x −15 = 
0 . Hãy chọn kết quả đúng trong .....................................
.....................................
các kết quả sau đây
..................................... A. S = 3 − ;  5 .
.....................................
.....................................
B. S =3;−  5 .
.....................................
.....................................
C. S = .
.....................................
D. S = R .
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
..................................... 55
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 3: Tìm tập con, số tập con của một tập hợp cho trước.
.....................................
..................................... Phương pháp
.....................................
 A  B  x (x  A  x  B).
.....................................  A  A, A.
.....................................
 Nếu A  B và B  C thì A  C
.....................................    A, A.
.....................................
 Nếu A có n phần tử thì A có 2n tập con.
.....................................
.....................................
CÂU 32: Hình nào sau đây minh họa tập B
.....................................
là con của tập A ?
.....................................
.....................................
..................................... A. B.
.....................................
.....................................
.....................................
..................................... C. D.
.....................................
CÂU 33: Cho tập X =2;3;4; 
5 . Hỏi tập X có bao nhiêu tập hợp con?
..................................... A.
..................................... 16. B. 6.
..................................... C. 8. D. 9.
.....................................
CÂU 34: Cho hai tập hợp: X = n | n là bội số của 4 và 6} và Y = n | n .....................................
.....................................
là bội số của 12}. Trong các mệnh đề sau, tìm mệnh đề sai? A.
.....................................
X  Y .
B. Y  X . C.
..................................... X = Y . D. n
 :nX và nY .
.....................................
CÂU 35: Cho tập hợp A =1;2;  a , B =1;2; ; a ; b ; x 
y . Hỏi có bao nhiêu tập hợp ..................................... X
.....................................
thỏa A  X  B ? A.
..................................... 8 . B. 7 .
..................................... C. 6 . D. 2n .
.....................................
CÂU 36: Cho A là tập hợp có hai phần tử, số tập hợp con của tập A là
..................................... A. 4 . B. 1.
..................................... C. vô số. D. 2 .
.....................................
.....................................
CÂU 37: Số tập con của tập hợp có n (n 1,n ) phần tử là
..................................... A. 2 2n+ . B. 1 2n− .
..................................... C. 1 2n+ . D. 2n .
.....................................
.....................................
CÂU 38: Cách viết nào sau đây là đúng?
..................................... A. a  ; a b. B.   a   ; a  b .
..................................... C.   a  ; a b. D. a( ; a b.
.....................................
..................................... 56
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
CÂU 39: Cho tập hợp A =1;2;  a , B =1;2; ; a ; b ; x 
y . Hỏi có bao nhiêu tập hợp ..................................... X
.....................................
thỏa A  X  B ? A.
..................................... 8 .
..................................... B. 7 .
..................................... C. 6 .
..................................... D. 2n .
.....................................
.....................................
CÂU 40: Cho A là tập hợp có hai phần tử, số tập hợp con của tập A là
..................................... A. 4 .
..................................... B. 1.
..................................... C. vô số.
.....................................
..................................... D. 2 .
.....................................
CÂU 41: Cho tập hợp B = * x | 3 −  x  
4 . Tập hợp B có tất cả bao nhiêu tập ..................................... hợp con?
..................................... A. 16.
.....................................
..................................... B. 12 .
..................................... C. 8 .
..................................... D. 4 .
..................................... CÂU 42:
.....................................
Cho tập hợp A =  ; x ; y  z và B = ; x ; y ; z t; 
u . Có bao nhiêu tập X thỏa .....................................
mãn A  X  B ?
..................................... A. 16.
..................................... B. 4 .
..................................... C. 8 .
.....................................
..................................... D. 2 .
.....................................
CÂU 43: Có tất cả bao nhiêu tập X thỏa mãn 1; 
2  X 1;2;3;4;  5 ?
..................................... A. 8 .
..................................... B.
..................................... 1.
..................................... C. 3 .
..................................... D. 6 .
.....................................
CÂU 44: Trong các tập sau đây, tập hợp nào có đúng hai tập hợp con?
..................................... A.  ; x  y .
.....................................
..................................... B.   x .
..................................... C.
.....................................  ;   x .
..................................... D.  ;  ; x  y .
.....................................
.....................................
..................................... 57
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 4: Hai tập hợp bằng nhau.
.....................................
..................................... Phương pháp
.....................................
 A = B  ( x
  A  xB)
.....................................
.....................................
..................................... CÂU 45:
.....................................
Hai tập hợp nào dưới đây không bằng nhau?
..................................... A.  1 1 1 1 1
A = x | x =
,k  , x   và B =  ; ; .
.....................................  2k 8 2 4 8
.....................................
.....................................
B. A =3;9;27;8  1 và =3n B
| n ,1 n   4 .
..................................... C.
.....................................
A = x | 2 −  x   3 và B = 1 − ;0;1;2;  3 .
.....................................
D. A =x | x  
5 và B =0;1; 2; 3;  4 .
.....................................
.....................................
.....................................
CÂU 46: Khẳng định nào sau đây sai? Các tập A = B với ,
A B là các tập hợp sau? .....................................
..................................... A. A = 1 { ;3 ,
} B = x (x ) –1 (x − ) 3 =  0 .
.....................................
..................................... B. A = 1 { ;3;5;7;9 ,
} B =n n = 2k +1, k  ,0  k   4 .
.....................................
.....................................
C. A ={− } B =  2 1;2 , x 
x − 2x − 3 =  0 .
.....................................
.....................................
D. A =  B =  2 , x  x + x +1 =  0 .
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
..................................... 58
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 5: Giao của các tập hợp (Không chứa tập con của ℝ)
.....................................
..................................... Phương pháp
.....................................  x A
.....................................
 C = A B   x  C     x B
.....................................
.....................................
.....................................
CÂU 47: Cho hai tập hợp A = 7 − ;0;5;  7 , B =  3 − ;5;7;1 
3 khi đó tập A  B là
..................................... A. 5;  7 . B.  7 − ; 3 − ;0;5;7;1  3 .
.....................................
..................................... C.  7 − ;  0 . D. 1  3 .
..................................... CÂU 48:
.....................................
Cho hai tập hợp A =  2
x  2x − 3x +1 = 
0 , B = x 3x + 2  
9 khi đó: .....................................
A. A B =2;5;  7 .
B. A B =  1 .
.....................................
..................................... C.  1
A B = 0  ;1;2; .
D. A B =0;  2 .  2
.....................................
.....................................
CÂU 49: Cho hai tập hợp
..................................... A = x 2 x − x + 3 ( 10
21)(x − x) = 
0 ,B = x −3 2x +1  4 khi đó tập
.....................................
X = A B
..................................... là: A.
..................................... X =  . B. X =3;  7 .
..................................... C. X = 1 − ;0;  1 . D. X = 1 − ;0;1;3;  7 .
.....................................
..................................... CÂU 50: A =x 2
x − 4x +3 =  Cho ba tập hợp
0 , B =x −3 2x  
4 , ..................................... C
..................................... = x 5 x − 4 x = 
0 khi đó tập ABC là:
..................................... A.  1 − ;  3 . B.  1 − ;0;  3 .
..................................... C.
..................................... 1;  3 . D.   1 .
..................................... CÂU 51: Cho A ; a ; b ;
c d; m , B ; c d; ;
m k; l . Tìm A B .
..................................... A. A B ; a b . B. A B ;
c d; m .
..................................... C. A B ; c d . D. A B ; a ; b ; c d; ; m k; l .
..................................... CÂU 52:
.....................................
Cho A = 1;  5 ; B =1;3; 
5 .Chọn kết quả đúng trong các kết quả sau
.....................................
A. AB =  1 .
B. A B =1;  3 .
.....................................
C. A B =1;  5 .
D. A B =1;3;  5 .
..................................... CÂU 53:
.....................................
Chọn khẳng định sai trong các khẳng định sau: A.
.....................................  = . B.  = .
..................................... C. * *  = . D. * *  = .
..................................... CÂU 54: Cho A
. Trong các mệnh đề sau, mệnh đề nào sai?
..................................... A. A . B. A . A
..................................... C. . D. A A . A
..................................... 59
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 6: Hợp của các tập hợp (Không chứa tập con của ℝ)
.....................................
..................................... Phương pháp
.....................................  x A
.....................................
 Nếu C = A B   x  C     x B
.....................................
.....................................
.....................................
CÂU 55: Cho hai tập hợp A = 7 − ;0;5;  7 , B =  3 − ;5;7; 
8 khi đó tập A  B là
..................................... A. 5;  7 . B.  7 − ; 3 − ;0;5;7;  8 .
.....................................
..................................... C.  7 − ;  0 . D.   8 .
..................................... CÂU 56:
.....................................
Cho hai tập hợp A =  2 x 
2x − 3x +1 = 
0 , B = x 3x + 2 1 
0 khi ..................................... đó:
..................................... A.  1 
A B = 0  ;1; ;2.
B. A B =  1 .
.....................................  2 
.....................................
C. A B =0;1;  2 .
D. A B =0;  2 .
.....................................
.....................................
CÂU 57: Cho hai tập hợp
..................................... A = x 2 x − x + 3 ( 10
21)(x − x) = 
0 ,B = x −3 2x +1  5 khi đó tập
.....................................
X = A B
..................................... là: B.
..................................... X =  . B. X =3;  7 .
..................................... C. X = 1 − ;0;  1 . D. X = 1 − ;0;1;3;  7 .
.....................................
.....................................
CÂU 58: Cho ba tập hợp
..................................... A = x  2
x − x + =  B = x −  x   C =x 5 x − 4 5 4 0 , 3 2 4 , x = 
0 khi đó .....................................
.....................................
tập A B C là: A.
..................................... 1;  4 . B.  1 − ;0;1;  4 .
..................................... C. 0;  1 . D.   1 .
.....................................
.....................................
CÂU 59: Cho hai tập hợp A =1;3;5;  7 , B =5; 
7 . Tìm mệnh đề sai
..................................... A. B  . A B. A  . B
..................................... C. A  . A D. B  . B
..................................... CÂU 60:
.....................................
Cho tập hợp A =  ; a ; b 
c khi đó tập hợp A có tất cả bao nhiêu tập con. ..................................... A. 7 . B. 8 .
..................................... C. 10. D. 9 .
.....................................
.....................................
CÂU 61: Cho tập hợp A =x 2x−3 7. Tập hợp A có tất cả bao nhiêu tập ..................................... con khác rỗng.
..................................... A. 6. B. 7.
..................................... C.
..................................... 8. D. 9. 60
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
CÂU 62: Cho tập hợp  A 1;2;3; 
4 .Tập hợp A có tất cả bao nhiêu tập con có đúng .....................................
..................................... 3 phần tử.
..................................... A. 3.
..................................... B. 16.
..................................... C. 4.
..................................... D. 5.
.....................................
.....................................
CÂU 63: Cho tập hợp A =  B =
 C =x ( 2 1;3 , 0;1;3 , x − 4x + ) 3 = 
0 . Tập ..................................... mệnh đề đúng
..................................... A. A = . B
..................................... B. A = . C
..................................... C.
..................................... B = . C
.....................................
D. A = B = . C
.....................................
CÂU 64: Cho tập hợp
.....................................  
..................................... 2 15
A = x x  , B = 0;1;  3 ,C =  2
x  (2x − 3)(x − 4) =  0 . Khi đó  2 
.....................................
A(B C) là
.....................................
..................................... A. 0;1;  2 .
..................................... B.  2 − ;0;1;  2 .
.....................................
..................................... C.  1  2 −  ; ;1;2.  2 
.....................................
..................................... D.  1  3  ; ;1;2.
.....................................  2 
.....................................
CÂU 65: Cho hai tập hợp A 0;2 và B
0;1;2;3;4 .Có bao nhiêu tập hợp X
..................................... thỏa mãn A X . B
..................................... A. 3.
..................................... B.
..................................... 16.
..................................... C. 4.
..................................... D. 5.
.....................................
CÂU 66: Cho ba tập hợp
..................................... A =  2 x
x   B = −  C =x ( 2 x − x + )( 4 19 , 0;1; 3 , 4 3 x −16) =  0
..................................... . Khi đó tập
.....................................
hợp X = A(B \ C)
.....................................
A. X =0;1;−  3
..................................... B.
..................................... X =   1 .
..................................... C. X =2;  3 .
..................................... D. X = 3 − ;0;  3
.....................................
..................................... 61
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 7: Hiệu, phần bù của các tập hợp
.....................................
.....................................
(Không chứa tập con của ℝ)
..................................... Phương pháp
.....................................
 Tập hợp C gồm các phần tử thuộc A nhưng không thuộc B gọi là hiệu của A
..................................... và . B
..................................... x  A
.....................................  C A\ B Nếu x C thì  x  B
.....................................
.....................................  Khi B
A thì A \ B gọi là phần bù của B trong . A Kí hiệu C B A \ B . A
..................................... CÂU 67:
.....................................
Cho hai tập hợp A =  4 − ; 2 − ;5;  6 , B =  3 − ;5;7; 
8 khi đó tập A\ B là
..................................... A.  3 − ;7;  8 . B.  4 − ; 2 − ;  6 . C.   5 . D.  2 − ;6;7;  8 .
..................................... CÂU 68:
..................................... Cho ba tập hợp
..................................... A = x  2
x − x + =  B = x −  x   C =x ( 5x − 4 5 4 0 , 3 2 4 ,
x )(2x −6) = 
0 ..................................... khi đó tập (A\ )
B \ C là:
..................................... A. 1;  4 . B.  1 − ;0;1;  4 .
.....................................
..................................... C. 0;  1 . D.   4 .
..................................... CÂU 69:
.....................................
Cho hai tập hợp A = 1;2;4; 
6 , B =1;2;3;4;5;6;7;  8 khi đó tập C A B là
..................................... A. 1;2;4;  6 . B. 4;  6 . C. 3;5;7;  8 . D. 2;6;7;  8 .
..................................... CÂU 70:
.....................................
Cho tập hợp A =  * x 3x − 2 1  0 khi đó:
.....................................
A. C A =1;2;3; 
4 . B. C A =0;1;2;3; 
4 . C. C A =1;2; 
3 . D. C A =1;2;  4 .
.....................................
CÂU 71: Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp A =x 4  x  
9 : ..................................... A.
..................................... A = 4; 
9 . B. A = (4; 
9 . C. A = 4;9). D. A = (4;9).
.....................................
CÂU 72: Trong các khẳng định sau khẳng định nào đúng:
..................................... A. \ = . B. *  = .
..................................... C. *  = . D. * *  = .
.....................................
CÂU 73: Cho tập hợp C =x 3 −  x  
0 . Tập hợp C được viết dưới dạng nào? .....................................
..................................... A. C = ( 3
− ;0) . B. C = 3
− ;0) . C. C = ( 3 − ;  0 . D. C =  3 − ;  0 .
..................................... CÂU 74:
.....................................
Cho tập hợp C = xR 2  x  
7 . Tập hợp C được viết dưới dạng nào? .....................................
A. C = (2;7) .
B. C = 2;7).
.....................................
C. C = (2;7. D. C = 2;  7 .
.....................................
.....................................
CÂU 75: Cách viết nào sau đây là đúng:
..................................... A. a  ; a b. B.   a   ; a  b .
..................................... C.
.....................................   a  ; a  b . D. a( ; a b.
..................................... 62
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 8: Viết các tập con của ℝ dưới dạng đoạn; khoảng;…
.....................................
..................................... Phương pháp
.....................................  ( ; a ) b {x |a x } b .
.....................................  [ ; a b] {x |a x } b .
.....................................
.....................................  [ ; a ) b {x |a x } b .
.....................................
 (𝑎; 𝑏] = {𝑥 ∈ ℝ|𝑎 < 𝑥 ≤ 𝑏}.
.....................................
 [𝑎; +∞) = {𝑥 ∈ ℝ|𝑥 ≥ 𝑎}.
.....................................  ( ;b] {x | x } b .
.....................................
.....................................
CÂU 76: Sử dụng các kí hiệu khoảng, nửa khoảng, đoạn để viết tập hợp .....................................
A =x 4  x   9 :
..................................... A.
..................................... A = 4;  9 . B. A = (4;  9 .
..................................... C. A = 4;9). D. A = (4;9).
.....................................
.....................................
CÂU 77: Cho các tập hợp:
..................................... A x | R x 3 B x | R 1 x 5 C x | R 2 x 4 .
.....................................
Hãy viết lại các tập hợp , A ,
B C dưới kí hiệu khoảng, nửa khoảng, đoạn.
.....................................
..................................... A. A ; 3 B 1; 5 C 2; 4 .
..................................... B. A ; 3 B 1; 5 C 2; 4 .
.....................................
..................................... C. A ; 3 B 1; 5 C 2; 4 .
..................................... D. A ; 3 B 1; 5 C 2; 4 .
.....................................
.....................................
CÂU 78: Cho tập hợp: A =x x+3 4+2 
x . Hãy viết lại tập hợp A dưới kí .....................................
hiệu khoảng, nửa khoảng, đoạn.
..................................... A.
..................................... A 1; . B. A 1; .
..................................... C. A 1; . D. A ; 1 .
.....................................
.....................................
CÂU 79: Cho các tập hợp: B x | x
3 Hãy viết lại các tập hợp B .....................................
dưới kí hiệu khoảng, nửa khoảng, đoạn.
..................................... A. B 3;3 . B. B 3;3 .
..................................... C.
..................................... B ;3 . D. B 3;3 .
.....................................
.....................................
.....................................
.....................................
.....................................
.....................................
..................................... 63
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 9: Các phép toán trên tập con của ℝ Phương pháp
 Để tìm A B ta làm như sau
 Sắp xếp theo thứ tự tăng dần các điểm đầu mút của các tập hợp , A B lên trục số
 Biểu diễn các tập ,
A B trên trục số(phần nào không thuộc các tập đó thì gạch bỏ)
 Phần không bị gạch bỏ chính là giao của hai tập hợp , A B
 Để tìm A B ta làm như sau
 Sắp xếp theo thứ tự tăng dần các điểm đầu mút của các tập hợp , A B lên trục số  Tô đậm các tập ,
A B trên trục số
 Phần tô đậm chính là hợp của hai tập hợp , A B
 Để tìm A\B ta làm như sau
 Sắp xếp theo thứ tự tăng dần các điểm đầu mút của các tập hợp , A B lên trục số
 Biểu diễn tập A trên trục số(gạch bỏ phần không thuộc tập A ), gạch bỏ
phần thuộc tập B trên trục số
 Phần không bị gạch bỏ chính là A\B .
CÂU 80: Khẳng định nào sau đây sai? A. . B. * *. C. . D. * .
CÂU 81: Cho hai tập hợp A =  1
− ;5) và B =2;1 
0 . Khi đó tập hợp A B bằng A. 2; ) 5 . B.  1 − ;1  0 . C. (2;5) . D.  1 − ;10).
CÂU 82: Cho M = (−  ;5 và N =  2
− ;6) . Chọn khẳng định đúng
A. M  N =  2 − ;  5 .
B. M  N = (− ;6  ).
C. M  N = ( 2 − ;5).
D. M  N =  2 − ;6). 64
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10 CÂU 83: 1
Cho các khoảng A 2;2 ; B 1; ; C ; . Khi đó tập hợp 2 A B C bằng: A. 1 1 x 1 x . B. x 2 x . 2 2 C. 1 1 x 1 x . D. x 1 x . 2 2
CÂU 84: Cho các tập họp A = x 3 −  x   3 ; B = x 1 −  x  
5 ;C = x x   2 . Xác định các tập
hợp A B C A. 2; ) 3 . B. (2; ) 3 . C.  1 − ; ) 3 . D. .
CÂU 85: Sử dụng kí hiệu khoảng để viết các tập hợp sau đây: E 4; \ ;2 . A. 4;9 . B. ; . C. 1;8 . D. 4; .
CÂU 86: Cho A = (− ;  
5 ; B = (0;+) . Tập hợp A B là A. (0;  5 . B. 0; ) 5 . C. (0;5). D. (− ;  +) .
CÂU 87: Cho hai tập hợp C A =  9 − ;8 C B = − ;  7 −  8;+ R ) và R ( ) ( ). Chọn khẳng định đúng. A. A B =  8 .
B. AB = .
C. A  B = R .
D. A B =  9 − ; 7 − ) .
CÂU 88: Cho A 0;3 ; B 1;5 ;C
0;1 . Khẳng định nào sau đây sai? A. A B C .
B. A B C 0;5 .
C. A C \ C 1;5 .
D. A B \ C 1;3 .
CÂU 89: Tập hợp D = (− ;  2]( 6 − ;+ )
 là tập nào sau đây? A. ( 6 − ;2] B. ( 4 − ;9] C. (− ;  + )  D.  6 − ;  2
CÂU 90: Cho tập hợp A = (  ;5
− , B = xR/−1 x  
6 . Khi đó A\B là A. (− ;  − ) 1 B. (-1;5] C. (  ;6 − D. (− ;  −  1
CÂU 91: Cho tập hợp D = xR / 2 −  x  
4 , E = [-3; 1]. Khi đó D  E là: A. (-2;1] B. [-3;4] C.  1 − ;0;  1 D. 0;  1 65
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
CÂU 92: Cho tập hợp A 2; . Khi đó, tập A C là A. 2; B. 2; C. ; 2 D. ; 2
CÂU 93: Cho A = (−5; 
1 ; B = 3; +); C = (−;−  
2) . Câu nào sau đây đúng?
A. AC =[ −5; 2 − ]
B. AB = ( 5 − ;+ ) 
C. BC = (− ;  + ) 
D. BC =
CÂU 94: Cho A = 1; 
4 ; B = (2;6); C = (1;2). Tìm ABC ? A. 0;  4 . B. 5;+). C. ( ; − ) 1 . D. . 
CÂU 95: Cho A = (− ;  −  3 ; B = (2;+); C
= (0;4). Khi đó ( A B) C là:
A. x | 2  x   4
B. x | 2  x   4
C. x | 2  x   4
D. x | 2  x   4
CÂU 96: Cho tập C A =  3 − ; 8); C B = ( 5 − ;2) 
( 3; 11).Tập C (AB)là: A. ( 3 − ; 3) . B. . C. ( 5 − ; 11). D. ( 3 − ;2)( 3; 8). 66
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10
Dạng 10: Tìm điều kiện của tham số m đê đoạn; khoảng; nửa
khoảng thỏa mản điều kiện cho trước Phương pháp:
 Bước 1: Minh họa các tập đả cho trên trục số.
 Bước 2: Dựa vào yêu cầu bài toán. Xác định điều kiện của tham số.
Thường thì ta sẽ quy về việc giải BPT bậc nhất 1 ẩn.
 Bước 3: Giải BPT, kết luận. CÂU 97:  
Cho số thực a  0 .Điều kiện cần và đủ để (− a) 4 ;9  ;+     là  a  A. 2 2
−  a  0.
B. −  a  0. 3 3 C. 3 3
−  a  0.
D. −  a  0. 4 4
CÂU 98: Cho hai tập khác rỗng A = (m - 1;4] và B = (-2;2m + 2] với m thuộc R.
Xác định m để AB   A. ( 2 − ;5) B. ( 2 − ;5] C. [ −2;5] D. ( 2 − ;5]
CÂU 99: Cho hai tập khác rỗng A = (m - 1;4] và B = (-2;2m + 2] với m thuộc R.
Xác định m để B  A A. [-2;1) B. (−2;1]. C. [-2;1]. D. ( 2 − ;1)
CÂU 100: Cho hai tập hợp A ;m và B
3m 1;3m 3 . Tìm tất cả các giá trị
thực của tham số m để A C B . A. 1 1 m . B. m . 2 2 C. 1 1 m . D. m . 2 2 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 B C B C C B C D C D B B A C C D D C C A
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 A D B A B B A C D D A C A D C D D B A A
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 A B A B A C A B C D B C D A B A D B B B
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 B C B B C B B D C B A D A C B A A A D C
81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 A A D A D A A C A D B C D D A C A A D B 67
GV: Trương Việt Long – ĐT: 0569.59.79.99
CHUYÊN ĐỀ DẠY HỌC KNTT 10 68
GV: Trương Việt Long – ĐT: 0569.59.79.99