Chuyên đề quan hệ song song – Lê Minh Tâm

Tài liệu gồm 104 trang, được biên soạn bởi thầy giáo Lê Minh Tâm, trình bày lí thuyết, các dạng toán và phương pháp giải bài tập chuyên đề quan hệ song song, giúp học sinh lớp 11 tham khảo khi học chương trình Toán 11 phần Hình học chương 2

66 33 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

TÀI LIỆU LƯU HÀNH NỘI BỘ

LÊ MINH TÂM

Chuyên Đề.

QUAN HỆ

SONG SONG

Hình học 11 – Chương 02. QUAN HỆ SONG SONG 
 
  Trang 2 
Biên So
ạn: LÊ MINH TÂM
 
※※※MỤC LỤC※※※ 
BÀI 01. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG & MẶT PHẲNG .................................................. 4 
I. KHÁI NIỆM MỞ ĐẦU ................................................................................................................................ 4 
II. CÁC TÍNH CHẤT THỪA NHẬN ............................................................................................................... 6 
III. CÁC CÁCH XÁC ĐỊNH MẶT PHẲNG .................................................................................................... 7 
IV. HÌNH CHÓP VÀ TỨ DIỆN ...................................................................................................................... 7 
V. CÁC DẠNG TOÁN. ................................................................................................................................... 8 
 Dạng 01.
 
XÁC ĐỊNH GIAO TUYẾN CỦA HAI MẶT PHẲNG PHÂN BIỆT...................................... 8 
 Dạng 02.
 
TÌM GIAO ĐIỂM CỦA ĐƯỜNG THẲNG D VÀ MẶT PHẲNG (P). ............................... 10 
 Dạng 03.
 
CHỨNG MINH 03 ĐIỂM THẲNG HÀNG VÀ 03 ĐƯỜNG THẲNG ĐỒNG QUI.......... 11 
 Dạng 04.
 
THIẾT DIỆN CỦA HÌNH H KHI BỊ CẮT BỞI MẶT PHẲNG (P). .................................. 12 
VI. BÀI TẬP RÈN LUYỆN. .......................................................................................................................... 12 
BÀI 02. HAI ĐƯỜNG CHÉO NHAU – HAI ĐƯỜNG SONG SONG ............................................ 38 
I. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG TRONG KHÔNG GIAN: ........................................ 38 
II. TÍNH CHẤT: ............................................................................................................................................ 38 
III. CÁC DẠNG BÀI TẬP. ............................................................................................................................. 41 
 Dạng 01.
 
CHỨNG MINH HAI ĐƯỜNG THẲNG SONG SONG. .................................................... 41 
 Dạng 02.
 
TÌM GIAO TUYẾN CỦA HAI MẶT PHẲNG CHỨA HAI ĐƯỜNG THẲNG SONG 
SONG. ..................................................................................................................................................... 44 
 Dạng 03.
 
CHỨNG MINH HAI ĐƯỜNG THẲNG CHÉO NHAU. ................................................... 48 
 Dạng 04.
 
CHỨNG MINH MỘT ĐƯỜNG THẲNG DI ĐỘNG LUÔN ĐI QUA MỘT ĐIỂM CỐ 
ĐỊNH. ....................................................................................................................................................... 50 
BÀI 03. ĐƯỜNG THẲNG & MẶT PHẲNG SONG SONG............................................................. 52 
I. VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN .................. 52 
II. TÍNH CHẤT: ............................................................................................................................................ 52 
III. CÁC DẠNG BÀI TẬP. ............................................................................................................................ 55 
 Dạng 01.
 
CHỨNG MINH ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG. ........................... 55 
 Dạng 02.
 
TÌM GIAO TUYẾN CỦA HAI MẶT PHẲNG CHỨA MỘT ĐƯỜNG THẲNG SONG 
SONG VỚI MẶT PHẲNG. . ..................................................................................................................... 61 
BÀI 04. HAI MẶT PHẲNG SONG SONG ......................................................................................... 69 
I. ĐỊNH NGHĨA: ........................................................................................................................................... 69 

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 3

Biên So

ạn: LÊ MINH TÂM

II. TÍNH CHẤT: ............................................................................................................................................ 69

III. ĐỊNH LÝ THALES TRONG HÌNH HỌC KHÔNG GIAN: ................................................................... 72

IV. HÌNH LĂNG TRỤ VÀ HÌNH HỘP: ...................................................................................................... 73

V. HÌNH CHÓP CỤT: ................................................................................................................................. 75

III. CÁC DẠNG BÀI TẬP. ............................................................................................................................ 75

 Dạng 01.

CHỨNG MINH HAI MẶT PHẲNG SONG SONG. ......................................................... 75

 Dạng 02.

GIAO TUYẾN CỦA 2 MẶT PHẲNG CÓ 1 MẶT PHẲNG SONG SONG VỚI MẶT THỨ

BA . ............................................................................................................................................................ 79

 Dạng 03.

HÌNH LĂNG TRỤ - HÌNH HỘP . ................................................................................... 84

 Dạng 04.

ĐỊNH LÝ THALES TRONG KHÔNG GIAN . ................................................................ 90

BÀI 05. TỔNG ÔN TẬP CHƯƠNG ................................................................................................... 94

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 4

Biên So

ạn: LÊ MINH TÂM

BÀI 01

I. KHÁI NIỆM MỞ ĐẦU

1.1. Mặt phẳng

– Hình ảnh mô phỏng trong thực tế ví dụ: mặt gương phẳng, mặt hồ phẳng lặng được xem

là một phần của mặt phẳng.

 Chú ý :

– Mặt phẳng ko có bề dày và không bị giới hạn.

– Cách biểu diễn mặt phẳng lên mặt phẳng hình học:

dùng hình bình hành hay một góc và ghi tên của mặt

phẳng vào một góc của hình.

– Kí hiệu mặt phẳng:

       

,,, , .m mp mpp P mp Q 

1.2. Điểm thuộc mặt phẳng

Cho điểm

và

 

. Khi đó:

– Điểm

thuộc

 

hay

nằm trên

 

hay

 

chứa

hoặc đi qua

 Kí hiệu:

 

A

– Điểm

nằm ngoài

 

hay

 

không chứa

hoặc

không đi qua

 Kí hiệu:

 

A

1.3. Hình biểu diễn của một hình không gian.

Khi vẽ một hình không gian lên bảng, lên giấy ta tuân thủ nguyên tắc sau:

 Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.

 Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, hai

đường thẳng cắt nhau là hai đường thẳng cắt nhau.

 Giữ nguyên quan hệ thuộc giữa điểm với đường thẳng.

 Nét liền để vẽ đường nhìn thấy, nét đứt đọa để vẽ đường bị che khuất.

 Bảo toàn tỷ lệ giữa các đoạn thẳng song song, các đoạn thẳng cùng nằm trên một

đường thẳng. Không bảo toàn về góc.

 Một tam giác bất kỳ đều được coi là hình biểu diễn của tam giác có dạng tùy ý( vuông,

cân, đều).

ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG & MẶT PHẲNG

☆☆★☆☆

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 5

Biên So

ạn: LÊ MINH TÂM

 Hình bình hành là hình biểu diễn cho hình bình hành có dạng tùy ý (hình bình hành ,

vuông, chữ nhật, thoi) và kèm theo kí hiệu vuông, bằng nhau nếu là hình đặc biệt.

 Cho các hình 1 – 2 – 3 – 4 được đánh dấu như bên dưới.

 Hãy kể tên các mặt phẳng thấy hay không thấy trong các hình 1, 2, 3, 4.

Hình 1:

– Các mặt phẳng nhìn thấy là:

   

,SAB SBC

– Các mặt phẳng không nhìn thấy là:

   

,SAC ABC

Hình 2:

– Các mặt phẳng nhìn thấy là:

   

,SBC SCD

– Các mặt phẳng không nhìn thấy là:

     

,,SAB SAD ABCD

Hình 3:

– Các mặt phẳng nhìn thấy là:

     

,,ABCD ADD A DCC D

   

– Các mặt phẳng không nhìn thấy là:

     

,,A B C D ABB A BCC B

       

Hình 4:

– Các mặt phẳng nhìn thấy là:

     

,,SAB SBC SCD

– Các mặt phẳng không nhìn thấy là:

   

,SAD ABCD

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 6

Biên So

ạn: LÊ MINH TÂM

II. CÁC TÍNH CHẤT THỪA NHẬN

TÍNH CHẤT

HÌNH MINH HỌA

 Có một và chỉ một đường thẳng đi qua 02

điểm phân biệt.

 Có một và chỉ một mặt phẳng đi qua 3 điểm

không thẳng hàng.

 Kí hiệu:

 

ABC

 Nếu một đường thẳng có hai điểm phân biệt

thuộc một mặt phẳng thì mọi điểm của đường

thẳng đều thuộc mặt phẳng đó.

 

AB a







  









 Điểm

và đường thẳng

đều nằm trong

 

ABC

vì

thuộc đường thẳng

còn

trùng với đường thẳng

mà

nằm trong

 

ABC

 Tồn tại 04 điểm không cùng thuộc 01 mặt

phẳng.

 Nếu hai mặt phẳng phân biệt có 01 điểm

chung thì chúng còn có điểm chung khác nữa.

 Suy ra: Nếu hai mặt phẳng phân biệt có một

điểm chung thì chúng có một đường thẳng

chung chứa tất cả các điểm chung của hai mặt

phẳng.

 Đường thẳng chung đó gọi là giao tuyến của

hai mặt phẳng.

 Trong mỗi mặt phẳng, các kết quả của hình học phẳng đều đúng.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 7

Biên So

ạn: LÊ MINH TÂM

III. CÁC CÁCH XÁC ĐỊNH MẶT PHẲNG

MẶT PHẲNG ĐƯỢC XÁC ĐỊNH

HÌNH MINH HỌA

 Khi biết nó đi qua 3 điểm không thẳng

hàng cho trước.

 Kí hiệu:

 

mp ABC

hoặc

 

ABC

 Khi biết nó đi qua một đường thẳng và

một điểm không nằm trên đường thẳng đó.

 Kí hiệu:

 

;mp d A

hoặc

 

;mp A d

 Khi biết nó đi qua hai đường thẳng cắt

nhau.

 Kí hiệu:

 

;mp a b

hoặc

 

;mp b a

IV. HÌNH CHÓP VÀ TỨ DIỆN

Trong mặt phẳng

 

cho đa giác lồi

...

A A A

. Lấy

nằm ngoài

 

 Lần lượt nối

với

, ,...,

A A A

được

tam giác:

1 2 2 3 1

, ,..., .

SA A SA A SA A

 Hình gồm đa giác

...

A A A

và

tam giác:

1 2 2 3 1

, ,...,

SA A SA A SA A

gọi là hình chop.

 Kí hiệu:

. ...

S A A A

 Hình tứ diện là hình được tạo thành từ bốn tam

giác

, , ,ABC ABD ACD BCD

trong đó

,,B C D

không đồng phẳng.

– Đỉnh:

,,B C D

– Mặt bên:

;;ABC ABD ACD

– Cạnh bên:

;;AB AC AD

– Mặt đáy:

BCD

– Cạnh đáy:

;;BC BD CD

– Cặp cạnh đối diện:

;BC AD

và

;BD AC

và

;AB DC

– Đỉnh đối diện với mặt: đỉnh

đối diện

 

BCD

; đỉnh

đối diện

 

ACD

; đỉnh

đối

diện

 

ABD

; đỉnh

đối diện

 

ABC

 Lưu ý: Tứ diện đều là hình tứ diện

có bốn mặt là các tam giác đều.

 Các mặt bên, cạnh bên, cạnh đáy của hình chóp

.S ABCD

– Mặt bên:

; ; ;SBC SAD SCD SAB

– Cạnh bên:

; ; ;SA SB SC SD

– Cạnh đáy:

; ; ;AB BC AD CD

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 8

Biên So

ạn: LÊ MINH TÂM

V. CÁC DẠNG TOÁN.

 Dạng 01. XÁC ĐỊNH GIAO TUYẾN CỦA HAI MẶT PHẲNG PHÂN BIỆT.

 Giao tuyến của hai mặt phẳng phân biệt là đường thẳng chung (đường thẳng đi qua ít

nhất 2 điểm chung) của hai mặt phẳng đó.

Phương pháp giải

 Ta thường gặp:

Tình huống 01

Giả thiết

   

1 2 1 2

;;M d d d d   

Kết luận

   

M

Tình huống 02

Giả thiết

   

M

;

   

N

Kết luận

   

MN

 Kỹ thuật: Nối các đoạn hoặc kéo dài các đoạn thẳng có trong mặt phẳng để tìm điểm

chung và chú ý nét vẽ đứt hoặc liền.

 Ví dụ 01.

Cho

là một điềm không thuộc mặt phằng

 

chứa

tứ giác

ABCD

có

không song song

;

không song song

. Tìm giao tuyến của :

   

SAB SBC

   

SAB SCD

   

SAD SBC

   

SAC SBD

Lời giải

a. Tìm giao tuyến

   

SAB SBC

Hai mặt phẳng

( ),( )SAB SBC

có

chung. Suy ra

là giao tuyến,

Kí hiệu:

( ) ( )SAB SBC SB

b. Tìm giao tuyến

   

SAB SCD

Có:

 

1( ) ( )S SAB SBC 

Trong

 

ABCD

có

và

không song song. Gọi

F AB CD

 

     

F AB AB SAB

F SAB SCD

F CD CD SCD







  









Từ

       

12, SAB SCD SF  

c. Tìm giao tuyến

   

SAD SBC

Có:

 

1( ) ( )S SAD SBC 

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 9

Biên So

ạn: LÊ MINH TÂM

Trong

 

ABCD

có

và

không song song. Gọi

H AD BC

 

     

H AD AD SAD

H SAD SBC

H BC BC SBC







  









Từ

       

12, SAD SBC SH  

d. Tìm giao tuyến

   

SAC SBD

Có:

     

1S SAC SBD 

Trong

 

ABCD

có

và

không song song. Gọi

O AC BD

 

     

O AC AC SAC

O SAC SBD

O BD BD SBD







  









Từ

       

12, SAC SBD SO  

 Ví dụ 02.

Cho tứ diện

ABCD

. Gọi

,IJ

là các điềm lần lượt nằm trên

các cạnh

,AB AD

với

AI AB

AJ JD

. Tìm giao

tuyến của:

   

ACD CIJ

   

CIJ BCD

Lời giải

a. Tìm giao tuyến

   

ACD CIJ

Có:

 

1( ) ( )C ACD CIJ 

       

2,J AD AD ACD J ACD CIJ    

Từ

       

12, ACD CIJ CJ  

b. Tìm giao tuyến

   

CIJ BCD

Có:

     

1C CIJ BCD 

Trong

 

ABD

có

và

không song song. Gọi

M BD IJ

 

     

M BD BD BCD

M BCD CIJ

M IJ IJ CIJ







  









Từ

   

12 (), ()CMCIJ BCD

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 10

Biên So

ạn: LÊ MINH TÂM

 Dạng 02. TÌM GIAO ĐIỂM CỦA ĐƯỜNG THẲNG D VÀ MẶT PHẲNG (P).

Phương pháp giải

Bài toán: Tìm giao điểm của đường thẳng và mặt phẳng.

Giả thiết

   

,,d P M d M P  

Kết luận

 

M d P

 Ta có các trường hợp sau xảy ra.

Trường hợp 01

Trong

 

có sẵn đường thằng

cắt

tại

 Ta trình bày:

   

,a d M a P d P M     

Trường hợp 02

Trong mặt phẳng

 

chưa có đường

cắt

. Khi đó

 Bước 1: Chọn mặt phằng phụ

 

chứa

 Bước 2: Tìm giao tuyến

của

 

và

()

 Bước 3: Trong

 

, cho

cắt

tại

, khi đó

thuộc

mà

chứa trong

 

. Vậy

là điểm cần tìm.

 Ta trình bày:

 Chọn

 

chứa

 Tìm

   

Pa

 Trong

 

,P a d M

 

M a a







   









 Ví dụ 03.

Cho tứ diện

ABCD

. Trên cạnh

lấy điểm

thỏa

mãn

,AM AB G

là trọng tâm

BCD

. Tìm:

a. Giao điểm của

với

 

ABC

b. Giao điểm

với

()ACD

Lời giải

a. Giao điểm của

với

 

ABC

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 11

Biên So

ạn: LÊ MINH TÂM

Gọi

là trung điểm

là trọng tâm

BCD

nên

DG BC F

mà

 

BC ABC

 

DG ABC F  

b. Giao điểm

với

()ACD

Trong

 

ABH

với

là trung điểm

. Có

,AH MG

không song song.

Vì

;

BM BG

AB BH



. Gọi

P AH MG

. Mà

 

AH ACD

 

MG ACD P  

 Dạng 03. CHỨNG MINH 03 ĐIỂM THẲNG HÀNG VÀ 03 ĐƯỜNG THẲNG

ĐỒNG QUI.

Phương pháp giải

 Muốn chứng minh ba điểm

,,A B C

thẳng hàng:

 Ta chứng minh ba điểm đó đồng thời thuộc hai mặt phẳng phân biệt

 



và

 



suy

ra ba điểm

,,A B C

nằm trên giao tuyến của

 



và

 



nên chúng thẳng hàng.

 Cơ sở

   

B AB AC







     











 Muốn chứng minh ba đường

,,abc

thẳng đồng quy tại một điểm:

 Ta chọn một mặt phẳng

 

chứa đường thẳng

và

. Gọi

I a b

chứng minh

Ic

(chứng minh ba điểm thẳng hàng như trên).

 Ví dụ 04.

Cho 3 điểm

,,A B C

không thuộc mặt phằng

     

,,P BC P M CA P N   

 

.AB P Q

Chứng

minh , ,M N P

thẳng hàng.

Lời giải

       

1BC P M M ABC P    

       

2CA P N N ABC P    

       

3AB P Q Q ABC P    

Từ

     

1 2 3, , , ,M N Q

thẳng hàng.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 12

Biên So

ạn: LÊ MINH TÂM

 Dạng 04. THIẾT DIỆN CỦA HÌNH H KHI BỊ CẮT BỞI MẶT PHẲNG (P).

Phương pháp giải

 Khi cắt hình

bởi mặt phẳng

 

ta được phần chung

của

và

 

phần chung này gọi là thiết diện của hình

và

 

 Xem hình minh họa sau: Tứ giác

MNCP

là thiết diện của

hình chóp

.S ABCD

với

 

CHN

 Ví dụ 05.

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang, đáy lớn

2AD BC

không song song

. Lấy điểm

và

lần lượt là trung điểm của

,SA AB

Gọi

là giao điểm của

và

Tìm thiết diện tạo bởi

 

MNO

với hình

chóp

.S ABCD

Lời giải

Gọi

 

P NO CD CD MNO P    

Gọi

 

H NP AD H SAD   

Gọi

 

Q HM SD Q MNO SD    

Do đó thiết diện tạo bởi

 

MNO

với hình chóp

.S ABCD

là tứ giác

MNPQ

VI. BÀI TẬP RÈN LUYỆN.

 Bài 01.

Cho hình chóp

.S ABCD

, đáy

ABCD

là tứ giác có các cặp cạnh đối không song song, điểm

thuộc cạnh

. Tìm giao tuyến của các mặt phẳng:

.

 

SAC

và

 

SBD

. .

 

SAC

và

 

MBD

.

 

MBC

và

 

SAD

. .

 

SAB

và

 

SCD

Lời giải

.

 

SAC

và

 

SBD

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 13

Biên So

ạn: LÊ MINH TÂM

 Gọi

là giao điểm của

và

 Ta có

 

     

S SAC

S SAC SBD

S SBD







  









 Vì

O AC BD

 Nên

 

     

O SAC

O SAC SBD

O SBD







  









 Từ (1) và (2) suy ra

   

SAC SBD SO



 

SAC

và

 

MBD

 Vì

M SA

nên

 

M SAC

 Do đó

 

     

M SAC

M SAC MBD

M MBD







  









 Vì

O AC BD

 Nên

 

     

O SAC

O SAC MBD

O MBD







  









 Từ (3) và (4) suy ra

   

SAC MBD MO



 

MBC

và

 

SAD

 Gọi

là giao điểm của

và

 Vì

M SA

nên

 

M SAD

 Do đó

 

     

M SAD

M SAD MBC

M MBC







  









 Vì

E BC AD

 Nên

 

     

E MBC

E MBC SAD

E SAD







  









 Từ (5) và (6) suy ra

   

MBC SAD ME



 

SAB

và

 

SCD

 Gọi

là giao điểm của

và

 Ta có

 

     

S SAB

S SAB SCD

S SCD







  









 Vì

F AB CD

 Nên

 

     

F SAB

F SAB SCD

F SCD







  









 Từ (7) và (8) suy ra

   

SAB SCD SF

 Bài 02.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 14

Biên So

ạn: LÊ MINH TÂM

Cho tứ diện

ABCD

. Lấy các điểm

thuộc cạnh

sao cho

cắt

Gọi

là điểm nằm bên trong tam giác

BCD

. Tìm giao tuyến của hai mặt phẳng:

.

 

MNI

và

 

BCD

.

 

MNI

và

 

ABD

.

 

MNI

và

 

ACD

Lời giải

.

 

MNI

và

 

BCD

 Gọi

là giao điểm của

và

 Ta có

 

     

I IMN

I IMN BCD

I BCD







  









 Vì

E MN BC

 Nên

 

     

E IMN

E IMN BCD

E BCD







  









 Từ (1) và (2) suy ra

   

IMN ICD IE

.

 

MNI

và

 

ABD

 Gọi

là giao điểm của

và

 Vì

M AB

nên

 

M ABD

 

     

M ABD

M IMN ABD

M IMN







  









 Vì

F IE BD

 Nên

 

     

F IMN

F IMN ABD

F ABD







  









 Từ (3) và (4) suy ra

   

IMN ABD MF

.

 

MNI

và

 

ACD

 Gọi

là giao điểm của

và

 Vì

N AC

nên

 

N ACD

 

     

N ACD

N IMN ACD

N IMN







  









 Vì

P IE CD

 Nên

 

     

P IMN

P IMN ACD

P ACD







  









 Từ (5) và (6) suy ra

   

IMN ACD NP

 Bài 03.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 15

Biên So

ạn: LÊ MINH TÂM

Cho tứ diện

.S ABC

. Lấy

,,M SB N AC I SC  

sao cho

không song song với

không song

song với

. Tìm giao tuyến của mặt phẳng

 

MNI

với các mặt và .

.

 

MNI

và

 

ABC

.

 

MNI

và

 

SAB

Lời giải

.

 

MNI

và

 

ABC

 Trong mặt phẳng

 

SBC

, kéo dài

cắt

tại



 

G MI MI MNI

G BC BC ABC

















là điểm chung I của

 

MNI

và

 

ABC



 

N MNI

N AC AC ABC















N

là điểm chung II của

 

MNI

và

 

ABC

 Vậy giao tuyến của hai mặt phẳng

 

ABC

và

 

MNI

là

.

 

MNI

và

 

SAB

 Trong mặt phẳng

 

ABC

, nối

cắt

tại



 

D AB AB ABC

D NG NG MNI















D

là điểm chung I của hai mặt phẳng

 

MNI

và

 

SAB



 

M MNI

M SB SB SAB















M

là điểm chung II của hai mặt phẳng

 

MNI

và

 

SAB

Vậy giao tuyến của hai mặt phẳng

 

MNI

và

 

SAB

là

 Bài 04.

Cho tứ diện

ABCD

là một điểm bên trong tam giác

ABD

là một điểm bên trong tam giác

ACD

. Tìm giao tuyến của các cặp mặt phẳng sau:

.

 

AMN

và

 

BCD

.

 

DMN

và

 

ABC

Lời giải

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 16

Biên So

ạn: LÊ MINH TÂM

.

 

AMN

và

 

BCD

 Trong mặt phẳng

 

ABD

cắt

tại

;

 Trong mặt phẳng

 

BCD

cắt

tại



 

E AM AM AMN

E DB DB BCD

















là điểm chung I của

 

AMN

và

 

BCD



 

F EN EN AMN

F DC DC BCD

















là điểm chung II của

 

AMN

và

 

BCD

 Vậy

là giao tuyến của hai mặt phẳng

 

AMN

;

 

BCD

.

 

DMN

và

 

ABC

 Trong mặt phẳng

 

ABD

cắt

tại

;

 Trong mặt phẳng

 

BDC

cắt

tại



 

G DM DM DMN

G AB AB ABC

















là điểm chung I của 2 mặt phẳng

 

ABC

và

 

DMN



 

H DN DN DMN

H BC BC ABC

















là điểm chung II của 2 mặt phẳng

 

ABC

và

 

DMN

Vậy

là giao tuyến của hai mặt phẳng

 

DMN

;

 

ABC

 Bài 05.

Cho hình chóp

.S ABCD

đáy là hình bình hành tâm

. Gọi

,,M N P

lần lượt là trung điểm các cạnh

,,BC CD SA

. Tìm giao tuyến của:

.

 

MNP

và

 

SAB

.

 

MNP

và

 

SAD

.

 

MNP

và

 

SBC



 

MNP

và

 

SCD

Lời giải

Trong mặt phẳng

 

ABCD

, kéo dài

cắt

,AB AD

lần lượt tại

và

Trong mặt phẳng

 

SAB

nối

cắt

tại

Trong mặt phẳng

 

SAD

nối

cắt

tại

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 17

Biên So

ạn: LÊ MINH TÂM

.

 

MNP

và

 

SAB



 

H FP FP MNP

H SB SB SAB















H

là điểm chung thứ I của

 

MNP

;

 

SAB



là điểm chung thứ II của

 

MNP

;

 

SAB

 Vậy giao tuyến của

 

MNP

và

 

SAB

là

.

 

MNP

và

 

SAD



 

I GP GP MNP

I SD SD SAD















I

là điểm chung thứ I của

 

MNP

;

 

SAD



là điểm chung thứ II của

 

MNP

;

 

SAD

 Vậy giao tuyến của

 

MNP

và

 

SAD

là

.

 

MNP

và

 

SBC



 

H FP FP MNP

H SB SB SBC















H

là điểm chung thứ I của

 

MNP

;

 

SBC



là điểm chung thứ II của

 

MNP

;

 

SBC

 Vậy giao tuyến của

 

MNP

và

 

SBC

là



 

MNP

và

 

SCD



 

I GP GP MNP

I SD SD SCD















I

là điểm chung thứ I của

 

MNP

;

 

SCD



là điểm chung thứ II của

 

MNP

;

 

SCD

 Vậy giao tuyến của

 

MNP

và

 

SCD

là

 Bài 06.

Cho hình chóp

.S ABCD

đáy

ABCD

có các cạnh đối không song song. Hai điểm

;MG

lần lượt là

trọng tâm

 

; ; ,SAB SAD N SG N G P

nằm trong tứ giác

ABCD

. Tìm giao tuyến của:

.

 

MNP

và

 

ABCD

.

 

MNP

và

 

SAC

.

 

MNP

và

 

SCD

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 18

Biên So

ạn: LÊ MINH TÂM

Lời giải

.

 

MNP

và

 

ABCD

 Gọi

,EF

lần lượt là trung điển của

,AB AD

 Vì

'N G MN EF I   

   

I MN MN MNP I MNP

I EF EF ABCD I ABCD



   





   





   

I MNP ABCD  

 Lại có

   

P MNP ABCD

 Vậy

   

MNP ABCD IP

.

 

MNP

và

 

SAC

 Trong

 

ABCD

gọi

,J IP AC H EF AC   

 Trong

 

SEF

gọi

K MN SH

   

J AC AC SAC J SAC

J IP IP MNP J MNP



   





   





   

J MNP SAC  

   

K SH SH SAC K SAC

K MN MN MNP K MNP



   





   





   

K MNP SAC  

 Vậy

   

MNP SAC JK

.

 

MNP

và

 

SCD

 Trong

 

ABCD

gọi

,QR

lần lượt là giao điểm của

với

,CD AD

 Trong

 

SAD

gọi

là giao điểm của

với

 

Q CD CD SCD

Q IP IP MNP















   

Q MNP SCD  

 

T SD SD SCD

T NR NR MNP















   

T MNP SCD  

 Vậy

   

MNP SCD QT

 Bài 07.

Cho hình chóp

.S ABCD

với đáy

ABCD

là hình bình hành. Gọi

,'GG

lần lượt là trọng tâm của các

tam giác

SAD

và

SBC

. Tìm giao tuyến của các cặp mặt phẳng:

.

 

'SGG

và

 

ABCD

. .

 

CDGG



và

 

ABS

.

 

ADG



và

 

SBC

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 19

Biên So

ạn: LÊ MINH TÂM

Lời giải

.

 

'SGG

và

 

ABCD

 Gọi

,MN

lần lượt là trung điểm của

,AD BC

, ta có

 

   

M AD AD ABCD

M SGG ABCD

M SG SG SGG







  









 

   

', ' '

N BC BC ABCD

N SGG ABCD

N SG SG SGG







  









 Vậy

   

'SGG ABCD MN

.

 

CDGG



và

 

ABS

 Gọi

,EF

lần lượt là trung điểm của

,SA SB

, ta có

 

   

E SA SA SAB

E CDGG SAB

E DG DG CDGG







  









 

   

', ' '

F SB SB SAB

F CDGG SAB

F CG CG CDGG







  









 Vậy

   

'CDGG SAB EF

.

 

ADG



và

 

SBC

 Trong mp

 

ABCD

, gọi

O AC MN

 Trong mp

 

SMN

, gọi

'P G M SO

 Trong mp

 

SAC

, gọi

I AP SC

. Ta có

 

   

I AP AP ADG

I ADG SBC

I SC SC SBC







  









 Lại có

   

''G ADG SBC

 Vậy

   

''ADG SBC IG

 Bài 08.

Cho tứ diện

ABCD

. Trên hai đoạn

và

lấy hai điểm

,MN

sao cho



và



. Hãy

xác định giao điểm của đường thẳng

và mặt phẳng

 

DMN

Lời giải

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 20

Biên So

ạn: LÊ MINH TÂM

 Ta có

AM AN

AB AC

  

nên theo định lý

talet

MN BC I

 Vậy

 

I BC

I BC DMN

I DMN







  









 Bài 09.

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang, đáy lớn

. Gọi

,IJ

là trung điểm của

,SA SB

. Lấy điểm

tùy ý trên

. Tìm giao điểm của:

.

và

 

SBC

.

và

 

SAC

.

và

 

IJM

Lời giải

.

và

 

SBC

 Ta có

ABCD

là hình thang đáy lớn

nên gọi

Q BC AD

 Và

   

SBC SAD S

   

SBC SAD SQ  

 Trong

 

SAD

gọi

N IM SQ

 

N IM SBC  

.

và

 

SAC

 Gọi

   

O AC BD SAC SBD SO    

 Trong mặt phẳng

 

SAC

gọi

R JM SO

 

R SAC

R JM SAC

R JM







   









.

và

 

IJM

 Ta có

 

R JM

R JIM

JM JIM

















 Trong

 

SAC

gọi

 

P IJM

P IR SC P SC IJM

P SC







     









Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 21

Biên So

ạn: LÊ MINH TÂM

 Bài 10.

Cho hình chóp

SABCD

có đáy là hình bình hành

ABCD

tâm

. Gọi

là trung điểm

. Tìm giao tuyến của

 

BDE

và

 

SAC

. Tìm giao tuyến của

 

ABE

và

 

SBD

. Tìm giao điểm của

và

 

ABE

Lời giải

. Tìm giao tuyến của

 

BDE

và

 

SAC

 Ta có:

   

O BED SAC

E BED SAC















   

OE BED SAC  

. Tìm giao tuyến của

 

ABE

và

 

SBD

 Trong mp

 

SAC

, gọi

I SO AE

. Khi đó:

   

B ABE SBD

I ABE SBD















   

BI ABE SBD  

. Tìm giao điểm của

và

 

ABE

 Trong

 

SBD

, gọi

H SD IB

 

H SD ABE  

 Bài 11.

Cho hình chóp

SABCD

. Gọi

,MN

lần lượt là trung điểm

là điểm thuộc cạnh

sao

cho

3SP PB

.Tìm giao điểm

của

và

 

MNP

. Tìm giao tuyến của

 

MNP

và

 

ABCD

Lời giải

.Tìm giao điểm

của

và

 

MNP

 Gọi

là giao điểm của

và

là giao điểm của

và

 Ta có:

   

M SAC MNP

I SAC MNP















   

MI SAC MNP  

 Trong

 

SAC

, gọi

Q MI SC

 

Q SC MNP  

. Tìm giao tuyến của

 

MNP

và

 

ABCD

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 22

Biên So

ạn: LÊ MINH TÂM

 Trong

 

SAB

, gọi

E MP AB

   

E ABCD MNP  

(1).

 Trong

 

SAC

, gọi

F MQ AC

   

F ABCD MNP  

(2).

 Từ (1) và (2) suy ra

   

EF ABCD MNP

 Bài 07.

Cho tứ diện

ABCD

. Trên

và

lần lượt lấy các điểm

,MN

sao cho

không song song

với

. Gọi

là một điểm thuộc miền trong tam giác

BCD

. Tìm giao tuyến của

 

BCD

và

 

OMN

. . Tìm giao điểm của

và

 

OMN

. Tìm giao điểm của

và

 

OMN

. . Tìm giao điểm của

và

 

ABO

. Tìm giao điểm của

và

 

BMN

Lời giải

. Tìm giao tuyến của

 

BCD

và

 

OMN

 Trong mp

 

ABD

, gọi

E MN CD

 Ta có:

   

O OMN BCD

E OMN BCD















   

OE OMN BCD  

. Tìm giao điểm của

và

 

OMN

 Trong

 

BCD

, gọi

I OE BD

 

I BD

I BD OMN

I OE OE OMN







   









. Tìm giao điểm của

và

 

OMN

 Trong

 

BCD

, gọi

H OE BC

 

I BC

H BC OMN

H OE OE OMN







   









. Tìm giao điểm của

và

 

ABO

 Trong

 

BCD

, gọi

K OB CD

 Trong

 

ACD

, gọi

Q MN AK

 Suy ra

 

Q MN ABO

.Tìm giao điểm của

và

 

BMN

 Trong

 

ABK

, gọi

F AO BQ

 

F AO

F AO BMN

F BQ BQ OMN







   









Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 23

Biên So

ạn: LÊ MINH TÂM

 Bài 08.

Cho hình chóp

.S ABCD

có đáy là hình thang, đáy lớn

. Gọi

là ba điểm trên

. Tìm giao tuyến

với

 

SBD

. Tìm các giao điểm của

 

IJK

với

và

Lời giải

. Tìm giao tuyến

với

 

SBD

 Trong

 

ABCD

, vẽ

AK BD M

 Trong

 

SAK

, vẽ

SM IK N

 

N SM SBD

N IK



















 

IK SBD N  

. Tìm các giao điểm của

 

IJK

với

và

* Tìm giao điểm của

 

IJK

với

 Trong

 

ABCD

, vẽ

JK BD P



 

P BD SBD

P IK IJK















 Ta đã có

 

IK SBD N

(theo CMT)

 Trong

 

SBD

, vẽ

PN SD Q



 

Q SD

Q PN IJK



















 

SD IJK Q

* Tìm giao điểm của

 

IJK

với

 Trong

 

ABCD

, vẽ

AC BD R

 Trong

 

SBD

, vẽ

PQ SR U



 

U SR SAC

U PQ IJK















 Trong

 

SAC

, vẽ

IU SC T



 

T SC

T IU IJK



















 

SC IJK T

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 24

Biên So

ạn: LÊ MINH TÂM

 Bài 08.

Cho hình chóp

.S ABCD

có đáy là hình bình hành.

là trung điểm của

;

là trọng tâm tam

giác

SCD

. Xác định giao điểm của:

.

với

 

ABCD

.

với

 

SAC

.

với

 

AMN

.

với

 

CMN

Lời giải

.

với

 

ABCD

 Vì

là trọng tâm tam giác

SCD

 Nên trong

 

SCD

, vẽ

SN CD P

 Trong

 

SBP

, vẽ

MN BP Q

 

Q MN

Q BP ABCD



















 

MN ABCD Q  

.

với

 

SAC

 Trong

 

ABCD

, vẽ

BP AC T

 

T AC

T BP SBQ

















 Trong

 

SBQ

, vẽ

ST MN R

 

R ST SAC

R MN



















 

MN SAC T  

.

với

 

AMN

 Trong

 

SAC

, vẽ

AR SC D







 

D SC

D AR AMN























 

SC AMN D





.

với

 

CMN

 Trong

 

SAC

, vẽ

CR SA U



 

U SA

U CR SAC



















 

SA SAC U

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 25

Biên So

ạn: LÊ MINH TÂM

 Bài 09.

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

là trung điểm của cạnh

. Tìm giao điểm

của

với

 

SAC

. Chứng minh

2BI IM

. Tìm giao điểm

của

và

 

BCM

. Chứng minh

là trung điểm của

Lời giải

. Tìm giao điểm

của

với

 

SAC

. Chứng minh

2BI IM

 Gọi

O AC BD

 Ta có,

   

SO SAC SBD

 Trong

 

SBD

, gọi

I SO BM

 

I SO SAC

I BM

















 

I SAC

I BM

















 

I BM SAC  



SBD

có

và

là đường trung tuyến,

 Mà

I SO BM

 Nên

là trọng tâm của

SBD

 Do đó,

2BI IM

. Tìm giao điểm

của

và

 

BCM

. Chứng minh

là trung điểm của

 Tìm

   

SAD BCM

 Ta có

 

AD SAD

BC BCM

AD BC















và có chung điểm

 Nên giao tuyến của hai mặt phẳng

 

SAD

và

 

BCM

là đường thẳng đi qua

và song song

cắt

tại

 Suy ra,

là giao điểm của của

và

 

BCM

 Xét tam giác

SAD

có

//ME AD

 Mà

là trung điểm của cạnh

 Suy ra

là trung điểm của

 Bài 10.

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang,

là đáy lớn và

3AB CD

. Gọi

là trung

điểm

là điểm trên cạnh

thỏa mãn

3SM MB

;

là điểm trên cạnh

thỏa mãn

3AI IS

. Tìm giao điểm của

và

 

SAD

. Gọi

là giao điểm của

và

 

IMN

. Tính

Lời giải

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 26

Biên So

ạn: LÊ MINH TÂM

. Tìm giao điểm của

và

 

SAD

 Tìm giao tuyến của

 

SBN

và

 

SAD

 Trong

 

ABCD

, gọi

P BN AD

   

P SBN SAD  

   

SP SBN SAD  

 Trong

 

SBN

, gọi

K SP MN

 

K SP SAD

K MN

















 

K MN SAD  

. Gọi

là giao điểm của

và

 

IMN

. Tính

 Tìm giao tuyến của

 

ABCD

và

 

IMN

 Ta có,

N DC

   

N ABCD IMN  

(1).

 Trong

 

SAB

, gọi

Q IM AB

 

Q IM IMN

Q AB ABCD

















   

Q ABCD IMN  

(2).

 Từ (1) và (2) suy ra,

   

NQ ABCD IMN

 Trong

 

ABCD

, gọi

H CB NQ

 

H CB

H NQ IMN

















 

H CB IMN  

 Tính

 Xét tam giác

SAB

có

;;I SA M SB Q AB  

. Do 3 điểm

,,I M Q

thẳng hàng

 Nên theo định lý Menenauyt ta có:

1..

IS QA MB

IA QB MS





9QA QB

8AB QB

68NC QB

  

 Mặt khác,

//NC QB

HB QB

HC NC

  

 Bài 11.

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

, hai điểm

,MN

lần lượt là trung

điểm của

,SB SD

, điểm

P SC

và không là trung điểm của

. Tìm giao điểm của

với mặt phẳng

 

MNP

. Tìm giao điểm của

với mặt phẳng

 

MNP

. Gọi

,,F G H

lần lượt là giao điểm của

và

. Chứng minh

ba điểm

,,F G H

thẳng hàng.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 27

Biên So

ạn: LÊ MINH TÂM

Lời giải

. Tìm giao điểm của

với mặt phẳng

 

MNP

 Ta có

,MN SO

đều thuộc mặt phẳng

 

SBD

 Gọi

 

I MN SO I SO MNP    

. Tìm giao điểm của

với mặt phẳng

 

MNP

 Ta có

,IP SA

cùng thuộc mặt phẳng

 

SAC

 Gọi

   

, Q IP SA IP MNP Q SA MNP     

. Gọi

,,F G H

lần lượt là giao điểm của

và

Chứng minh ba điểm

,,F G H

thẳng hàng.

 Ta có

   

.F QM AB F MNP ABCD    



   

G QP AC G MNP ABCD    



   

H QN AD H MNP ABCD    

 Vậy

,,F G H

là ba điểm chung của

 

MNP

và

 

ABCD

Nên

,,F G H

thẳng hàng.

 Bài 12.

Cho hình chóp

.S ABCD

có

không song song với

. Gọi

là trung điểm của

và

là giao

điểm của

và

. Tìm giao điểm

của

với mặt phẳng

 

MAB

. Chứng minh:

,,SO AM BN

đồng quy.

Lời giải

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 28

Biên So

ạn: LÊ MINH TÂM

. Tìm giao điểm

của

với mặt phẳng

 

MAB

 Ta có

,AM SO

cùng thuộc mặt phẳng

 

SAC

 Gọi

   

.I SO AM I ABM BI ABM     

 Trong mặt phẳng

 

SBD

, gọi

N BI SD

 

N SD

N SD ABM

N BI ABM







  









. Chứng minh:

,,SO AM BN

đồng quy.

 Ta có

   

S SAC SBD

SO SAC SBD

O SAC SBD







  









 Lại có

 

I AM SAC

I BN AM

I BN SBD







  









   

I SAC SBD I SO    

,,SO AM BN

đồng quy tại

 Bài 13.

Cho hình chóp

.S ABCD

có đáy

ABCD

có các cạnh đối không song song

AC BD O

. Gọi

,,E F H

lần l;ượt là các điểm thuộc cạnh

,,SA SB SC

. Tìm giao điểm

 

K SD EFH

.

AC DB O

EH FK I

. Chứng minh

,,S I O

thẳng hàng.

.

AD BC M

EK FH N

. Chứng minh

,,S M N

thẳng hàng.

.

AB CD P

EF HK Q

. Chứng minh

,,A P Q

thẳng hàng.

Lời giải

. Tìm giao điểm

 

K SD EFH

 Trong

 

:SAC

   

I SO EH SBD EFH FI    

 Trong

   

:SDB K SD FI K SD EFH    

.

AC DB O

EH FK I

Chứng minh

,,S I O

thẳng hàng.



   

EH FK I I SAC SBD    

 Mặt khác

   

SBD SAC SO I SO   

,,S I O

thẳng hàng.

.

AD BC M

EK FH N

. Chứng minh

,,S M N

thẳng hàng.



   

EK FH N N d SAD SBC     

 Mặt khác

   

SAD SBC SM N SM   

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 29

Biên So

ạn: LÊ MINH TÂM

,,S M N

thẳng hàng.

.

AB CD P

EF HK Q

. Chứng minh

,,A P Q

thẳng hàng.



   

EF HK Q Q SAB SCD    

 Mặt khác

   

SAB SCD SP I SP   

,,S P Q

thẳng hàng.

 Bài 14.

Cho hình chóp

.S ABCD

, gọi

,IJ

là hai điểm trên hai cạnh

,AD SB

. Tìm giao tuyến của hai mặt phẳng

   

,SAC SBI

. Tìm giao tuyến của hai mặt phẳng

 

SAC

và

 

SBD

.

cắt

tại

cắt

tại

. Chứng minh

, , ,A K L M

thẳng hàng.

Lời giải

. Tìm giao tuyến của hai mặt phẳng

   

,SAC SBI

Tìm giao điểm

của

và

 

SAC

 Trong

 

ABCD

   

G AC BI SG SAC SBI    

 Ta có:

 

   

 

IJ SBI

SBI SAC SG

K IJ SAC





















 

K IJ SGtrong SAC  

. Tìm giao tuyến của hai mặt phẳng

 

SAC

và

 

SBD

. Tìm giao điểm

của

và

 

SAC

 Gọi

   

H AC BD SH SAC SDB    

 Ta có:

 

   

 

DJ SBD

SBD SAC SH

L DJ SAC



















 

L DJ SHtrong SAC  

.

cắt

tại

cắt

tại

. Chứng minh

, , ,A K L M

thẳng hàng.



, , ,A K L M

thuộc các đường thẳng

 

, , , , , ,OA IJ JD JO A K L M AOJ



, , ,A K L M

thuộc các đường thẳng

 

, , , , , ,AC SG SH SC A K L M SAC



   

, , ,I K L M SAC OAJ  

nên

, , ,A K L M

thẳng hàng.

 Bài 15.

Cho hình chóp

.S ABCD

có đáy là hình thang, đáy lớn

; lấy

,MN

lần lượt thuộc các cạnh

,SC SD

. Tìm thiết diện của hình chóp cắt bởi mặt phẳng

   

;ABM AMN

. Xác định thiết diện của hình chóp cắt bởi

 

ABM

. Xác định thiết diện của hình chóp với

 

AMN

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 30

Biên So

ạn: LÊ MINH TÂM

Lời giải

. Xác định thiết diện của hình chóp cắt bởi

 

ABM

 Gọi

O AC BD

 Trong

 

SAC

, gọi

I SO AM

 Trong

 

SCD

, gọi

P BI SD

   

P SCD ABM  

 Ta có :

   

ABM SBC BM

   

ABM SCD MP

   

ABM SAD AP

 Vậy thiết diện là hình thang

ABMP

( Vì

//AB MP

)

. Xác định thiết diện của hình chóp với

 

AMN

 Nếu

MN AB

   

AMN ABMN



thiết

diện cần tìm là từ giác

ABMN

 Nếu

không song song

 Trong mặt phẳng

 

SCD

, gọi

I MN CD

 Trong mặt phẳng

 

ABCD

, gọi

Q AI BC

 Ta có:

   

AMN SAD AN

   

AMN ABCD AQ

   

AMN SCD QM

   

AMN SCD MN

 Vậy thiết diện cần tìm là tứ giác

AQMN

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 31

Biên So

ạn: LÊ MINH TÂM

 Bài 16.

Hình chóp

.S ABCD

có đáy

ABCD

không là hình thang, điểm

nằm trong tam giác

SAB

và điểm

thuộc cạnh

sao cho

2MD MS

. Tìm giao tuyến của hai mặt phẳng

 

SAB

và

 

PCD

. Tìm giao điểm của

với mặt phẳng

 

ABM

. Gọi

là trung điểm của

, tìm thiết diện tạo bởi mặt phẳng

 

MNP

và hình chóp

.S ABCD

Lời giải

. Tìm giao tuyến của

 

SAB

và

 

PCD

 Ta có

là điểm chung thứ I.

 Gọi

E AB CD

Nên

là điểm chung thứ II.

   

PE SAB PCD  

. Tìm giao điểm của

với mặt phẳng

 

ABM

 Chọn

 

SCD SC

 Ta có:

   

M SCD ABM

 Nên

là điểm chung thứ I.

E AB CD

nên

là điểm chung thứ II.



   

SCD ABM ME  

 Gọi

   

G SC ME SC ABM G    

. Tìm thiết diện tạo bởi mặt phẳng

 

MNP

và hình chóp

.S ABCD

 Ta có

   

MNP SAD MN

 Gọi

F PE SB

H GF CB











và

 

I EH MP

J MNP

J AB NI













 Gọi

PJ SB L

MP FG K

O KL SC

















 Suy ra thiết diện của

 

MNP

và

.S ABCD

là ngũ giác

MNJLO

 Bài 17.

Hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành, gọi

là trọng tâm tam giác

SAC

và

,IJ

lần

lượt là trung điểm của

,CD SD

. Tìm giao điểm

của

với mặt phẳng

 

SAB

. Xác định thiết diện tạo bởi mặt phẳng

 

IJK

và hình chóp

.S ABCD

Lời giải

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 32

Biên So

ạn: LÊ MINH TÂM

. Tìm giao điểm

của

với

 

SAB

 Gọi

là tâm của hình bình hành

ABCD

 Vì

là trọng tâm tam giác

SAC

nên

K SO

 Gọi

E IO AB

 

IK SIE

 Ta có:

là điểm chung thứ I của

 

SAB

và

 

SIE

là điểm chung thứ II của

 

SAB

và

 

SIE

   

SAB SIE SE  

 Gọi

IK SE H

   

IK SIE H  

. Xác định thiết diện tạo bởi

 

IJK

và

.S ABCD

 Xét tam giác

SBD

có

là trung tuyến

SK SO

 Nên

là trọng tâm suy ra

B JK

 Gọi

G BH SA

 Ta có

   

IJK ABCD BI

IJK SAB BG

IJK SAD GJ

IJK SCD JI





















 Suy ra thiết diện là tứ giác

BIJG

 Bài 18.

Cho hình chóp

.S ABCD

. Gọi

,MN

là 2 điểm lần lượt nằm trên 2 cạnh

và

. Tìm giao điểm

của

và

 

SAC

. Tìm giao điểm

của

và

 

SAC

. Chứng minh

,,I J C

thẳng hàng.

. Xác định thiết diện của mặt phẳng

 

BCN

với hình chóp.

Lời giải

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 33

Biên So

ạn: LÊ MINH TÂM

. Tìm giao điểm

của

và

 

SAC

 Trong mp

 

ABCD

gọi

O AC BD

 Ta có:

   

S SAC SBD

 

   

;O AC AC SAC O SAC   

   

;O BD BD SBD O SBD   

 Do đó:

   

O SAC SBD

 



   

12&

SO SAC SBD  

 Trong

 

SBD

gọi

I SO BN

 Ta có:

I BN

   

;I SO SO SAC I SAC   

 Vậy

 

I BN SAC

. Tìm giao điểm

của

và

 

SAC

 Trong

 

ABCD

gọi

H AC MD

 Ta có:

   

S SAC SMD

 

   

;H AC AC SAC H SAC   

   

;H MD MD SMD H SMD   

 Do đó:

   

H SAC SMD

 



   

34&

SH SAC SMD  

 Trong

 

SMD

gọi

J SH MN

 Ta có:

J MN

   

;J SH SH SAC J SAC   

 Vậy

 

J MN SAC

. Chứng minh

,,I J C

thẳng hàng.

 Ta có:

   

C SAC BNC

 

   

     

;

I SAC

I SAC BNC

I BN BN BNC I BNC







  



   







   

56&

CI SAC BNC  

 

 Mặt khác:

 

   

     

;

J SAC

J SAC BNC

J MN MN BNC J BNC







   



   





 Từ

 

và

 

suy ra

,,I J C

thẳng hàng.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 34

Biên So

ạn: LÊ MINH TÂM

. Xác định thiết diện của mặt phẳng

 

BCN

với

hình chóp.

 Trong

 

SAC

gọi

Q SA CI

 Ta có:

   

SAB BCN BQ

   

SBC BCN BC

   

ABCD BCN BC

   

SCD BCN CN

   

SAD BCN NQ

 Vậy thiết diện cần tìm là tứ giác

BCNQ

 Bài 19.

Cho hình chóp

.S ABCD

. Lấy một điểm

thuộc miền trong tam giác

SBC

. Lấy một điểm

thuộc

miền trong tam giác

SCD

. Tìm giao điểm của

và

 

SAC

. Tìm giao điểm của

và

 

AMN

. Tìm thiết diện của hình chóp

.S ABCD

với

 

AMN

Lời giải

. Tìm giao điểm của

và

 

SAC

 Trong

 

SBC

gọi

Q SM BC

 Trong

 

SDC

gọi

P SN DC

 Trong

 

ABCD

gọi

O AC PQ

 Ta có:

     

1S SAC SPQ

   

;O AC AC SAC O SAC   

   

;O PQ PQ SPQ O SPQ   

 Do đó:

     

2O SAC SPQ

   

12&

SO SAC SPQ  

 Trong

 

SPQ

gọi

H MN SO

 Ta có:

   

;H SO SO SAC H SAC   

 Mà

H MN

nên:

 

H MN SAC

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 35

Biên So

ạn: LÊ MINH TÂM

. Tìm giao điểm của

và

 

AMN

 Trong mp

 

SAC

gọi

K AH SC

 Ta có:

K SC

   

;K AH AH AMN K AMN   

 Vậy

 

K SC AMN

. Tìm thiết diện của hình chóp với

 

AMN

 Trong

 

SBC

gọi

I MK SB

 Trong

 

SDC

gọi

J KN SD

 Ta có:

   

SAB AMN AI

   

SBC AMN IK

   

SCD AMN KJ

   

SAD AMN JA

 Vậy thiết diện cần tìm là tứ giác

AIKJ

 Bài 20.

Cho tứ diện

..S ABC

Gọi

,KN

lần lượt là trung điểm các cạnh

và

,BC

là điểm thuộc đoạn

sao cho

32.SM MC

. Tìm thiết diện tạo bởi mặt phẳng

 

KMN

và tứ diện

.S ABC

. Mặt phẳng

 

KMN

cắt

tại

. Tính tỉ số

Lời giải

. Tìm thiết diện tạo bởi mặt phẳng

 

KMN

và tứ

diện

.S ABC

 Trong

 

SAC

nối

cắt

tại

 Trong

 

ABC

nối

cắt

tại

Vậy tứ giác

KMNI

là thiết diện cần tìm.

. Mặt phẳng

 

KMN

cắt

tại

. Tính tỉ số

 BỔ ĐỀ:

Định lí Menelaus:

Cho tam giác ABC. Các điểm D, E, F lần lượt

nằm trên các đường thẳng BC, CA, AB.

Khi đó D, E, F thẳng hàng khi và chỉ khi

1..

FA DB EC

FB DC EA



 Phần thuận:

 Giả sử

,,D E F

thẳng hàng với nhau.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 36

Biên So

ạn: LÊ MINH TÂM

 Vẽ đường thẳng qua

và song song với

cắt đường thẳng

tại

 Vì

//CG AB

(cách dựng) nên theo định lý

Ta-lét, ta có:

DB FB

DC CG



(1) và

2()

EC CG

EA FA



 Nhân (1) và (2) vế theo vế

DB EC FB

DC EA FA



 Từ đó suy ra

1..

FA DB EC

FB DC EA



 Phần đảo:

 Giả sử

1..

FA DB EC

FB DC EA



 Khi đó gọi



là giao của đường thẳng

với đường thẳng

 Theo chứng minh ở trên, ta có

1..

F A DB EC

F B DC EA







 Kết hợp giả thuyết suy ra

FA F A

FB F B







 Hay

FA FB FA FB

F A F B F A F B



  

   



 Nên

F A FA





và

F B FB





. Do đó



trùng với

 Vậy định lí đã được chứng minh.

 Áp dụng:

 Vì

,,K M D

thẳng hàng nên

CM SK AD AD

MS KA DC DC

  

 Vì

,,D N I

thẳng hàng nên

AI BN CD AI AD

IB NC DA IB CD

   

 Bài 21.

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

Trên các cạnh

,SB SD

ta lần lượt lấy

các điểm

và

sao cho

SM SN

SB SD



. Tìm giao điểm

của

và mặt phẳng

 

AMN

. Suy ra thiết diện của mặt phẳng

 

AMN

và hình chóp

.S ABCD

. Gọi

là giao điểm của

và

.CD

Tính tỉ số

Lời giải

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 37

Biên So

ạn: LÊ MINH TÂM

. Tìm giao điểm

của

và mặt

 

AMN

Suy ra thiết diện của mặt phẳng

 

AMN

và hình

chóp.

 Trong

 

SBD

gọi

.H SO MN

 Ta có:

         

1;.A SAC A AMN A SAC AMN    

         

2;.H SAC H AMN H SAC AMN    

   

12&

.AH SAC AMN  

 Trong

 

SAC

gọi

I AH SC

Thì

 

.I SC AMN

 Khi đó thiết diện là tứ giác

.AMIN

. Gọi

là giao điểm của

và

.CD

Tính tỉ số

 Trong

 

mp SBD

gọi

.J BD MN

 p dụng định lí Menelaus cho các tam giác

; ; ;SBD SBO SCO SCD

ta có:



1 2 2 1 4. . . . .

MB NS JD JD

JB JD

MS ND JB JB

    



1 2 1

. . . . .

MB HS JO HS HS

MS HO JB HO HO

    



4 1 5

5 2 2

. . . . .

IC HS AO IC IC

IS HO AC IS IS

    



1 2 1 5

. . . . .

IC NS KD KD KC

IS ND KC KC KD

    

 Vậy



------------------ HẾT ------------------

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 38

Biên So

ạn: LÊ MINH TÂM

BÀI 02

I. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG TRONG KHÔNG GIAN:

//a b a

và

cùng nằm trong một mặt phẳng và không có

điểm chung.

cắt

hay

ab

và

cùng nằm trong một mặt phẳng

và có một điểm chung duy nhất.

a b a

và

cùng nằm trong một mặt phẳng và có từ hai

điểm chung trở lên.

chéo

b 

và

không cùng nằm trong một mặt phẳng.

II. TÍNH CHẤT:



Định lý 1

 Trong không gian, qua một điểm không nằm trên

đường cho trước, có một và chỉ một đường thẳng song

song song đường thẳng đã cho.

 Nhận xét:

Ta có thêm một cách để xác định mặt phẳng như sau:

Hai đường thẳng song song

và

xác định nên một mặt

phẳng ký hiệu

 

,ab

HAI ĐƯỜNG CHÉO NHAU – SONG SONG

☆☆★☆☆

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 39

Biên So

ạn: LÊ MINH TÂM



Định lý 2 (về giao tuyến của ba mặt phẳng)

 Nếu ba mặt phẳng đôi một cắt nhau theo ba giao

tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy

hoặc đôi một song song với nhau.

 Hệ quả:

 Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của

chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường

thẳng đó.

 Ví dụ 01.

Cho hình chóp

.S ABCD

có đáy là hình bình hành

ABCD

. Tìm giao tuyến của

 

SAD

và

 

SBC

 

SAB

và

 

SCD

. Gọi

,,M N H

.lần lượt là trung điểm của

,SA SB

và

. Tìm giao tuyến của hai mặt phẳng

 

MNH

và

 

ABCD

 

MDH

và

 

NAC

Lời giải

. Tìm giao tuyến của

 

SAD

và

 

SBC

 

SAB

và

 

SCD

 Ta có

   

S SAD SBC

và

//AD CB

 Nên

   

/ / / /SAD SBC m AD CB

 Ta có

   

S SAB SCD

và

//AB CD

 Nên

   

/ / / /SAB SCD d AB CD

. Tìm giao tuyến của

 

MNH

và

 

ABCD

 

MDH

và

 

NAC

 Ta có

   

H MNH ABCD

và

//MN AB

   

/ / / / ,MNH ABCD HK AB NM K AD  

 Gọi

,E AC HD F NC MD   

Suy ra

 

MDH 

 

NAC EF

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 40

Biên So

ạn: LÊ MINH TÂM

 Ví dụ 02.

Cho tứ diện

ABCD

. Gọi

,IJ

là trung điểm

,BC BD

. Mặt phẳng

 

qua

cắt

,AC AD

lần

lượt tại

,MN

. Chứng minh:

IJNM

là hình thang. Nếu

là trung điểm

thì

IJNM

là hình

gì?

Lời giải

 Ta có

là đường trung bình của tam giác

BCD

nên

//IJ CD



       

; ; / /P ACD MN IJ P CD ACD MN IJ    

 Do đó tứ giác

IJNM

là hình thang.

 Nếu

là trung điểm

thì

là trung điểm

 Khi đó

/ / / /

IM NJ AB

MN IJ CD







nên tứ giác

IJNM

là hình bình hành.



Định lý 3

 Hai đường thẳng phân biệt cùng song song với đường thẳng

thứ ba thì song song với nhau.

 Ví dụ 03.

Cho tứ diện

ABCD

. Gọi

, , , , ,M N P Q R S

lần lượt là trung điểm

, , , , ,AC BD AB CD AD BC

Chứng minh tứ giác

,PMQN MRNS

là các hình bình hành. Từ đó suy ra

,,MN PQ RS

đồng

quy tại

điểm.

Lời giải

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 41

Biên So

ạn: LÊ MINH TÂM

 Ta có

là đường trung bình của tam giác

ABC

nên

//MP BC

MP BC













 Tương tự

là đường trung bình của tam giác

DBC

nên

//NQ BC

NQ BC













 Suy ra tứ giác

PMQN

là hình bình hành.

 Ta có

là đường trung bình của tam giác

ACD

nên

//MR CD

MR CD













 Tương tự

là đường trung bình của tam giác

BCD

nên

//NS CD

NS CD













 Suy ra tứ giác

MRNS

là hình bình hành.

 Do tứ giác

,PMQN MRNS

là các hình bình hành

Nên các đường chéo

,,MN PQ RS

cắt nhau tại chung điểm

của mỗi đường.

 Suy ra

,,MN PQ RS

đồng quy tại

điểm.

III. CÁC DẠNG BÀI TẬP.

 Dạng 01. CHỨNG MINH HAI ĐƯỜNG THẲNG SONG SONG.

Phương pháp giải

 Ta có thể dùng một trong các cách sau

Xét mặt phẳng chứa

Dùng các định lý đường trung bình, Định lý Thales đảo,.... để chứng minh

//ab

Dùng định lý bắc cầu









Dùng định lý 4

   

// //

a b c

a b a b









   



















 Bài 01.

Cho hình chóp

.S ABCD

đáy là hình bình hành. Gọi

lần lượt là trọng tâm các tam giác

SAB

SBC

. Chứng minh

//IJ AC

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 42

Biên So

ạn: LÊ MINH TÂM

. Gọi

 

là mặt phẳng chứa

và cắt

lần lượt tại

. Chứng minh rằng

IJEF

là hình thang.

. Gọi

lần lượt là trung điểm

. Gọi

K AN BM

. Chứng minh

// //SK AD BC

. Tứ giác

SADK

là hình gì?

Lời giải

. Chứng minh

//IJ AC

 Gọi

lần lượt là trung điểm

 Trong

SPQ

có

SI SJ

SP SQ



nên

//IJ PQ

 Mà trong

BAC

có

là đường trung bình

nên

//PQ AC

 Do đó

// //IJ AC PQ

. Chứng minh rằng

IJEF

là hình thang.

 Ta có:

   

 

   

S SPQ SAC

PQ SPQ

SPQ SAC d

AC SAC

PQ AC











  









với

// //d PQ AC

 Xét

 

SPQ

 

SAC

 

có:

   

// //

SPQ IJ

SAC EF

IJ EF d

SAC SPQ d

d IJ





















Do đó

IJEF

là hình thang.

. Chứng minh

// //SK AD BC

. Tứ giác

SADK

là hình gì?

 Ta có

   

S SBC SAD

và

 

     

AN SAD

BM SBC K SAD SBC

K AN BM







   











 Do đó

   

SK SBC SAD

 Mặt khác

 

   

// //

AD SAD

BC SBC

SK AD BC

AD BC

SK SAD SBC





















 Tứ giác

SADK

có

//SK AD

và hai đường chéo giao nhau tại trung điểm mỗi đường nên là hình

bình hành.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 43

Biên So

ạn: LÊ MINH TÂM

 Bài 02.

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang đáy lớn

. Gọi

,EF

lần lượt là trung

điểm của

và

. Chứng minh rằng

//EF CD

. Tìm giao điểm

của

và

 

ADF

. Gọi

là giao điểm của

và

. Chứng minh rằng

// //SI AB CD

Lời giải

. Chứng minh rằng

//EF CD

 Xét

SAB

có

,EF

lần lượt là trung điểm của

,SA SB

(gt)

 Nên

là đường trung bình của tam giác

 Do đó

//EF AB

mà lại có

//AB CD

(gt)

 Suy ra

//EF CD

. Tìm giao điểm

của

và

 

ADF

 Trong

 

ABCD

gọi

O AC BD

Khi đó có

 

,SO FD SBD

 Trong

 

SBD

gọi

K SO FD

Khi đó có

 

,AK SC SAC

; gọi

I SC AK

 Khi đó có

 

I SC ADF

. Chứng minh rằng

// //SI AB CD

 Có

là giao điểm của

và

(gt) suy ra

 

   

J DI DI SCD

J SAB SCD

J AF AF SAB







  









(1).

 Lại có

   

S SAB SCD

(2).

 Từ (1) và (2) suy ra

   

SAB SCD SJ

 Lại có

//AB CD

;

   

,AB SAB CD SCD

;

 Suy ra

// //SI AB CD

(theo hệ quả).

 Bài 03.

Cho tứ diện

ABCD

. Gọi

,MN

lần lượt là trung điểm của

và

. Lấy

trên

. Gọi các

điểm

;I PD AN J PC AM   

. Chứng minh rằng

//IJ CD

Lời giải

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 44

Biên So

ạn: LÊ MINH TÂM

 Có

,MN

lần lượt là trung điểm của

và

(gt)

 Nên

là đường trung bình của

//BCD MN CD

(1).

 Xét

     

,,AMN BCD PCD

có

   

AMN BCD MN

;

   

AMN PCD IJ

;

   

PCD BCD CD

(2).

 Từ (1) và (2) suy ra

// //MN CD IJ

(Theo định

lý về giao tuyến của 3 mặt phẳng).

Hay

//IJ CD

(đpcm).

 Bài 03.

Cho hai hình vuông

ABCD

và

ABEF

không đồng phẳng. Trên các đường chéo

,AC BF

lấy

,MN

sao cho

AM BN

AC BF



. Chứng minh rằng

//MN DE

Lời giải

 Gọi

là trung điểm của đoạn thẳng

 Gọi

M DI AC





Ta có

AM AI AM

M C DC AC



   



 Lại có



suy ra





 Hay

,,D M I

thẳng hàng và



 Tương tự, ta có

,,I N E

thẳng hàng và



 Xét tam giác

IDE

có

IM IN

MN DE

ID IE



(Định lý Ta-let đảo) (đpcm).

 Dạng 02. TÌM GIAO TUYẾN CỦA HAI MẶT PHẲNG CHỨA HAI ĐƯỜNG

THẲNG SONG SONG.

Phương pháp giải

 Sử dụng định lí phương pháp giao tuyến thứ nhất.

   

       

, , // //

a b Sx Sx a b







    







Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 45

Biên So

ạn: LÊ MINH TÂM

 Bài 01.

Cho hình chóp

.S ABC

. Gọi

lần lượt là các điểm trên các cạnh

sao cho

AM BN

AC BC



. Gọi

lần lượt là các điểm trên cạnh

,AB

,SB

sao cho

AE SF SG

AB SB SC

  

. Tìm

   

SMN SAB

   

.SAC CEF

. Tìm

   

EFG SAC

, tìm

 

H AC EFG

. Tìm thiết diện

 

EFG

. Thiết diện là hình gì?

Lời giải

. Tìm

   

SMN SAB

   

.SAC CEF

 Ta có:

AM BN

MN AB

AC BC



 Nên

   

,MN

S SAB SMN

AB SAB SMN

AB MN















   

, // // .SAB SMN Sz Sz AB MN  

 Vì

AE SF

AB SB



//SA EF

(Định lí Ta-let)

   

C SAC CEF

SA SAC EF CEF

SA EF

















   

, // // .SAC CEF Cx Cx SA EF  

. Tìm

   

EFG SAC

, tìm

 

H AC EFG



   

       

, , // // .

G SAC EFG

SA SAC EF EFG SAC EFG Gy Gy SA EF

SA EF







    







 Vì

     

SAC EFG Gy AC EFG AC Gy     



 

.H AC Gy  

. Tìm thiết diện

 

EFG

. Thiết diện là hình gì?

 Ta có:

EB EF BF

AB SA SB

  

EF SA

(1)

 Do

//GH SA

CH GH CG

CA SA SC

   

GH SA

(2)



   

12&

EF GH 

, mà

//EF GH

FGHE

là hình bình hành



Thiết diện là hình bình

hành.

 Bài 02.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 46

Biên So

ạn: LÊ MINH TÂM

Cho tứ diện

ABCD

. Gọi

là trọng tâm

ABC

và

ABD

;

lần lượt là trung điểm

,BC

.AC

. Chứng minh rằng

//IJ CD

. Tìm giao tuyến

 

DEF

và

 

ABD

Lời giải

. Chứng minh rằng

//IJ CD

 Gọi

là trung điểm



là trọng tâm

ABC

C

thẳng hàng.



là trọng tâm

ABD

thẳng

hàng.

 Xét

DMC

có:

MI MJ

MC MD



(do

là trọng tâm

ABC

là

trọng tâm

ADB



//IJ DC

(Định lí Ta-lét).

. Tìm giao tuyến

 

DEF

và

 

ABD

 Chứng minh được

là đường trung bình

của

ABC

//EF AB



   

D DEF ABD

SA DEF EF ABD

EF AB

















   

, // // .DEF ABD Dx Dx EF AB  

 Bài 03.

Cho hình chóp

.S ABCD

có đáy là tứ giác lồi không có cặp cạnh nào song song. Gọi

,MN

lần

lượt là trọng tâm của hai tam giác

SAB

và

SAD

. Gọi

trung điểm của cạnh

. Chứng minh rằng

MN BD

. Xác định thiết diện của hình chóp với mặt phẳng

 

MNE

. Gọi

,OJ

lần lượt là các giao điểm của mặt phẳng

 

MNE

với các cạnh

,SB SD

. Chứng

minh rằng

OJ BD

Lời giải

. Chứng minh rằng

MN BD

 Gọi

là trung điểm của

Theo tính chất trọng tâm của tam giác ta có

FM FN

MN BD

FB FD

  

. Xác định thiết diện của hình chóp với mặt phẳng

 

MNE

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 47

Biên So

ạn: LÊ MINH TÂM

 Xét hai mặt phẳng

 

MNE

và

 

ABCD

có

   

E MNE ABCD

d MNE ABCD

MN BD

d MN BD











  







 Gọi

P d CD

G d AB

I d AD

















. Gọi

O MG SB

H MG SA

J HI SD

















 Vậy thiết diện cần tìm là ngũ giác

OHJPE

. Chứng minh rằng

OJ BD

 Ta có

 

   

BD MN

BD SBD

OJ BD MN

MN MNE

OJ MNE SBD





















 Bài 04.

Cho tứ diện

ABCD

có

,,I J K

là ba điểm lần lượt nằm trên các cạnh

,,AD AC BC

sao cho

AI AJ BK

AD AC BC

  

. Xác định giao tuyến của mặt phẳng

 

IJK

với các mặt phẳng

   

,BCD ABD

và xác định hình tính của thiết cắt bởi mặt

 

IJK

Lời giải

 Vì

AI AJ

AD AC



nên

IJ CD

 Ta có

 

   

IJ CD

d IJK BCD

IJ IJK

CD BCD

d IJ CD

K IJK BCD



























 Gọi

E d BD EK CD IJ  

 Theo chứng minh trên:

   

EK BCD IJK

 Vì

AJ BK

AC BC



CA CJ CB CK CJ CK CJ CK

AC BC AC BC AC BC



       

 Nên

JK AB

. Ta có

   

 

IE ABD IJK

JK IJK

IE JK AB

AB ABD

JK AB





















 Thiết diện cần tìm là tứ giác

IJKE

. Ta có

IJ EK

JK IE







nên

IJKE

là hình bình hành.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 48

Biên So

ạn: LÊ MINH TÂM

 Dạng 03. CHỨNG MINH HAI ĐƯỜNG THẲNG CHÉO NHAU.

Phương pháp giải

 (Chứng minh phản chứng) Giả sử hai đường thẳng đồng phẳng rồi suy ra điều vô lí.

 Bài 01.

Cho hình chóp

.S ABCD

có đáy

ABCD

là một tứ giác lồi. Chứng minh rằng các cặp đường

thẳng sau đây chéo nhau:

 

,;SA BC

 

,;SA CD

 

,;SB CD

 

,;SB DA

 

,;SC AD

 

,;SC AB

 

,SD AB

và

 

,.SD BC

Lời giải

 

,SA BC

 Giả sử

 

,SA BC

đồng phẳng, thì

, , ,S A B C

đồng phẳng.

 Nhưng rõ ràng

 

C SAB

, nên điều giả sử là sai.

 Vậy

 

,SA BC

chéo nhau.

 

,SA CD

 Giả sử

 

,SA CD

đồng phẳng, thì

, , ,S A C D

đồng phẳng.

 Nhưng rõ ràng

 

C SAD

, nên điều giả sử là sai.

 Vậy

 

,SA CD

chéo nhau.

 

,SB CD

 Giả sử

 

,SB CD

đồng phẳng, thì

, , ,S B C D

đồng phẳng.

 Nhưng rõ ràng

 

B SCD

, nên điều giả sử là sai.

 Vậy

 

,SB CD

chéo nhau.

 Các ý còn lại làm tương tự.

 Bài 02.

Cho hai đường thẳng chéo nhau

và

Trên đường thẳng

lấy hai điểm phân biệt

,AB

tùy

ý. Trên đường thẳng

lấy hai điểm phân biệt

,CD

tùy ý. Chứng minh hai đường thẳng

và

chéo nhau.

Lời giải

 Giả sử

,AC BD

đồng phẳng. Nghĩa là

, , ,A B C D

đồng

phẳng.

 Rõ ràng,

 

D ABC

nên điều giả sử là sai.

 Vậy

,AC BD

chéo nhau.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 49

Biên So

ạn: LÊ MINH TÂM

 Bài 03.

Cho tam giác

BCD

và điểm

 

A BCD

,MN

lần lượt là trung điểm của

,AB CD

. Chứng

minh

và

chéo nhau,

và

chéo nhau.

Lời giải

 Giả sử

và

đồng phẳng, thì

   

BCD ABCD

 Tức là

 

A BCD

(Vô lý).

 Do đó

và

chéo nhau.

 Giả sử

và

đồng phẳng,

 Mà

,MN

lần lượt thuộc

,AB CD

 Nên

   

;AB ADMN CD ADMN

 Suy ra

và

đồng phẳng (vô lý theo ý trên).

 Vậy

và

chéo nhau.

 Bài 04.

Cho hình thang

ABCD

có đáy lớn

,AD

đáy nhỏ

và điểm

 

S ABCD

. Gọi

là giao điểm

của

và

,MN

là hai điểm phân biệt trên đường thẳng

. Chứng minh

và

chéo nhau,

và

chéo nhau.

Lời giải

 Ta có

   

SI SAC SBD

,M N SI

 Nên

 

,,A M N SAC

 Giả sử

và

đồng phẳng,

 Suy ra

 

B SAC

nên

 

S ABC

(mâu thuẫn giả thiết

 

S ABC

 Vậy

và

chéo nhau.

 Chứng minh tương tự

và

chéo nhau.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 50

Biên So

ạn: LÊ MINH TÂM

 Dạng 04. CHỨNG MINH MỘT ĐƯỜNG THẲNG DI ĐỘNG LUÔN ĐI QUA MỘT

ĐIỂM CỐ ĐỊNH.

Phương pháp giải

 Sử dụng định lý về giao tuyến của ba mặt phẳng (ĐL3)

 Bài tập.

Cho tứ giác

ABCD

với

không song song với

và điểm

()S ABCD

. Mặt phẳng di động

 

qua

cắt

,SC SD

tại

,MN

. Mặt phẳng di động

 

qua

cắt

,SA SB

tại

,PQ

. Chứng minh đường thẳng

luôn đi qua một điểm cố định.

. Chứng minh nếu

và

cắt nhau tại

và

cắt nhau tại

thì đường thẳng

luôn đi qua một điểm cố định.

. Gọi

là giao điểm của

và

là giao điểm của

và

. Chứng minh đường

thẳng

qua một điểm cố định trong

 

ABCD

Lời giải

. Chứng minh

luôn đi qua một điểm cố định.

 Ta có

   

SCD MN

ABCD AB

ABCD SCD CD



















 Suy ra

,,MN AB CD

đồng quy tại

E AB CD

 Vậy

đi qua

cố định.

. Chứng minh nếu

và

cắt nhau tại

và

cắt nhau tại

thì đường thẳng

luôn đi

qua một điểm cố định.

 Ta có

AN BM I

 

I AN SAD

I BM SBC

















   

I SAD SBC  

 Lại có

CQ DP J

 

J DP SAD

J CQ SBC

















   

J SAD SBC  

 Mà

   

S SAD SBC

 Nên đường thẳng

luôn đi qua điểm

cố định.

. Chứng minh đường thẳng

qua một điểm cố định trong

 

ABCD

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 51

Biên So

ạn: LÊ MINH TÂM

 Ta có

AM BN K

 

K AM SAC

K BN SBD

















   

K SAC SBD  

 Lại có

CP DQ L

 

L DQ SBD

L CP SAC

















   

L SAC SBD  

 Gọi

O AC BD

   

O SAC SBD

 Nên đường thẳng

luôn đi qua điểm

cố định.

------------------ HẾT ------------------

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 52

Biên So

ạn: LÊ MINH TÂM

BÀI 03

I. VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN

Vị trí tương đối của đường thẳng và mặt phẳng được xét theo số điểm chung của chúng

và không có điểm chung.

Khi đó ta nói song song với hay song song với

và kí hiệu là hay

và có một điểm chung duy nhất

Khi đó ta nói và cắt nhau tại điểm và kí hiệu là

hay .

và có từ hai điểm chung trở lên.

Khi đó ta nói nằm trong hay chứa và kí hiệu

là hay

II. TÍNH CHẤT:



Định lý 1

 Nếu đường thẳng không nằm trong mặt phẳng và song song với đường thẳng

nằm trong mặt phẳng thì song song với .

 Tóm tắt định lý:

 Ví dụ 01.

Cho hình chóp có đáy là hình bình hành. Gọi là giao điểm của và

, các điểm , , lần lượt là trung điểm của .

. Chứng minh , .

. Chứng minh , .

Lời giải

 

//d

 

// .d

 

   

dM

 

dM

 

d 

 

d

 



 

// //

d d d





















.S ABCD

ABCD

,,SC AB AD

 

//AD SBC

 

//IK MBD

 

//CD ABM

 

//SA MBD

HAI ĐƯỜNG CHÉO NHAU – SONG SONG

☆☆★☆☆

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 53

Biên So

ạn: LÊ MINH TÂM

. Chứng minh ,

 Ta có: .

 .

. Chứng minh , .

 .

 Ví dụ 02.

Cho hình chóp có đáy là hình bình hành. Gọi là trọng tâm , là

một điểm trên cạnh sao cho , Chứng minh

. Chứng minh , .

. Chứng minh , .

Lời giải

 Gọi là trung điểm của .

 Do là trọng tâm tam giác , nên

 Trong , gọi

 Vì .



   

12&

HG HM

GM SK

HS HK

  

 Khi đó .



Định lý 2

 

//AD SBC

 

//IK MBD

 

// BC //

AD SBC

AD AD SBC

SBC

















 

// //

IK MBD

IK BD IK MBD

BD MBD

















 

//CD ABM

 

//SA MBD

 

// //

CD ABM

CD AB CD ABM

AB ABM

















 

// //

SA MBD

SA OM SA MBD

OM MBD

















.S ABCD

ABCD

SAB

3AD AM

 

// .MG SCD

 

//AD SBC

 

//IK MBD

 

//CD ABM

 

//SA MBD

SAB

 



 

ABCD

K HM CD

 

SK SCD

 

HM AM

AH DK

HK AD

  

 

// //

GM SCD

SGM SK MG SCD

SK SCD

















Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 54

Biên So

ạn: LÊ MINH TÂM

 Cho đường thẳng song song với mặt phẳng . Nếu mặt phẳng chứa và cắt

theo giao tuyến thì song song với

 Tóm tắt định lý:

 Ví dụ 03.

Cho tứ diện . Lấy điểm thuộc miền trong của tam giác . Gọi là mặt phẳng qua

và song song với , .

. Tìm giao tuyến của lần lượt với các mặt phẳng , , , .

. Mặt phẳng cắt tứ diện theo thiết diện là hình gì?

Lời giải

. Tìm giao tuyến của với các mặt phẳng

, , , .

 và có

Điểm chung,

   

P ABC IJ  

với

/ / , ,

IJ qua M

IJ AB I BC J AC









 và có

Điểm chung,

   

P BCD IH  

, với

 và có

Điểm chung,

   

P ACD JK  

, với

 và có điểm chung,

   

P ABD KH  

, với .

. Mặt phẳng cắt tứ diện theo thiết diện là hình gì?

 Mặt phẳng cắt tứ diện theo thiết diện là hình bình hành (vì và



Hệ quả

 

   

a a b

















ABCD

ABC

 

ABC

 

BCD

 

ACD

 

ABD

 

ABC

 

BCD

 

ACD

 

ABD

 

ABC

   

, / /AB ABC AB P

 

BCD

   

, / /CD BCD CD P

/ / ,IH CD H BD

 

ACD

   

, / /CD ACD CD P

/ / ,JK CD K AD

 

ABD

,KH

   

, / /AB ABD AB P

//KH AB

 

IJKH

/ / / /KH IJ AB

/ / / /IH JK CD

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 55

Biên So

ạn: LÊ MINH TÂM

 Hai mặt phẳng cùng song song với một đường thẳng thì giao tuyến của chúng nếu có cũng

song song với đường thẳng đó.

 Tóm tắt định lý:

   

/ / , / /

P d Q d

















Định lý 3

 Cho hai đường thẳng chéo nhau, có duy nhất một mặt phẳng

chứa đường thẳng này và song song với đường thẳng còn lại.

 Chú ý

Cho

và

là hai đường thẳng chéo nhau.

Cách dựng mặt

 

chứa đường

và song song với

đường

– Lấy

thuộc

– Qua

kẻ đường thẳng



song song với

– Mặt phẳng

 

chứa

và



III. CÁC DẠNG BÀI TẬP.

 Dạng 01. CHỨNG MINH ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG.

Phương pháp giải

 Ta có thể dùng một trong các cách sau

Dùng ĐL1

 

















– Xét mặt phẳng

 

chứa .

– Tìm giao tuyến

   

b 

– Chứng minh

 

// //a b a

 Bài 01.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 56

Biên So

ạn: LÊ MINH TÂM

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

,MN

lần lượt là trung điểm của

,AB CD

. Chứng minh

 

//MN SBC

 

//MN SAD

. Gọi

là trung điểm

. Chứng minh

 

//SB MNP

 

//SC MNP

. Gọi

là trọng tâm

SBC

thuộc cạnh

sao cho

BI BD

, Chứng minh

Lời giải

. Chứng minh

 

//MN SBC

 

//MN SAD

 Vì

,MN

lần lượt là trung điểm của

,AB CD

của

ABCD

 Nên

//BC//AD MN

 Ta có:

 

AD SAD MN SAD

MN SA

AD MN

















 Tương tự

 

BC SBC MN SBC

MN SB

BC MN

















. Gọi

là trung điểm

Chứng minh

 

//SB MNP

 

//SC MNP

 Ta có

 

// //SPMN SAD MN



 

MN MNP SP MNP

SP SA

SP MN

















 Tương tự

 

//SC MNP

. Chứng minh

 Gọi

là trung điểm

 Ta có

là trọng tâm tam giác ABC suy ra

IJ AJ

 G là trọng tâm

SBC

suy ra

JG JS



SAJ

có

IJ AJ

JG JS

nên

//GI SA

 Mà

 

SA SAB

suy ra

 

// .GI SAB

 Bài 02.

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang đáy lớn

, đáy nhỏ

với

2AB CD

. Gọi

là giao điểm của

và

là trung điểm của

là trọng tâm tam giác

SBC

và

là một

điểm trên cạnh

sao cho

23SE SD

. Chứng minh

. Chứng minh

 

//MN SBC

 

//MN SAD

. Gọi

là trung điểm

. Chứng minh

 

//SB MNP

 

//SC MNP

. Gọi

là trọng tâm

SBC

thuộc cạnh

sao cho

BI BD

, Chứng minh

Lời giải

 

// .GI SAB

 

// .GI SAB

 

// .GI SAB

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 57

Biên So

ạn: LÊ MINH TÂM

.

 

//DI SBC

 Gọi

là trung điểm

 Có

là trung điểm của



NI

là đường trung bình

SAB

//NI AB

NI AB















 Mà

CD AB

AB CD













suy ra

IN DC









 Tứ giác

NIDC

có

IN DC









 Nên

NIDC

là hình bình hành suy ra

//DI NC

 Ta có

 

DI NC

NC SBC DI SBC

DI SBC

















.

 

//GO SCD

 Gọi

là trung điểm của

 Có

là trọng tâm

SBC



 

 Ta có

//AB CD

OB OA AB OB

OD OC CD OD

     

 



   

12&

//OG BH

 Mà

   

//BH SCD OG SCD

.

 

// .SB ACE

 Ta có



nên



 Mặt khác vì

SE SD SE SD  

nên





OD DE

OE BS

BD DS

  

 Mà

 

OE ACE

suy ra

 

// .SB ACE

 Bài 03.

Cho hình chóp

.S ABCD

đáy là hình bình hành. Trên các cạnh

,SA SB

lần lượt lấy các điểm

,MN

sao

cho

SM SN

SA SB



. Chứng minh rằng:

.

   

// ; //AD SBC DC SAB

.

     

// ; // ; //MN ABCD AB MNCD MN SCD

Lời giải

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 58

Biên So

ạn: LÊ MINH TÂM

.

   

// ; //AD SBC DC SAB

 Do tứ giác

ABCD

là hình bình hành

 Suy ra

// ; //AD BC DC AB

 Mà

     

, //AD SBC BC SBC AD SBC  

 Chứng minh tương tự ta có

 

//DC SAB

.

     

// ; // ; //MN ABCD AB MNCD MN SCD

 Tam giác

SAB

có

SM SN

MN AB

SA SB



Mà

     

, //MN ABCD AB ABCD MN ABCD  

 Theo trên có

//MN AB

Mà

     

, //AB MNCD MN MNCD AB MNCD  

 Lại có

// //CD AB MN CD

Mà

     

, //MN SCD CD SCD MN SCD  

 Bài 04.

Cho hình chóp

.S ABCD

đáy là hình chữ nhật. Gọi

là trọng tâm tam giác

SAD

. Điểm

thuộc

sao cho

DE DC

và I là trung điểm của

. Tìm giao điểm của

và

 

SBC

. Chứng minh rằng:

 

//GE SBC

Lời giải

. Tìm giao điểm của

và

 

SBC

 Trong

 

ABCD

ta có

 

IE BC H IE SBC   

. Chứng minh rằng:

 

//GE SBC

 Trong

 

ABCD

ta có

DE IE IG IE

EG SH

DC EH SG EH

      

//ID CH

 Mà

     

, //EG SBC SH SBC EG SBC  

 Bài 05.

Cho tứ diện

ABCD

có

là trọng tâm tam giác

ABD

. Điểm

thuộc

sao cho

2BI IC

. Chứng

minh rằng:

 

//GI ACD

Lời giải

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 59

Biên So

ạn: LÊ MINH TÂM

 Gọi

là trung điểm của

 Trong

BCM

có

2 //

BG BI

IG CM

GM IC

  

 Mà

     

, //IG ACD CM ACD IG ACD  

 Bài 06.

Cho hình chóp

.S ABCD

có đáy là hình bình hành tâm

. Gọi

, MN

lần lượt là trung điểm các cạnh

, AB AD

. Gọi

, IJ

thuộc

, SM SN

sao cho

SI SJ

SM SN



. Chứng minh rằng

 

//MN SBD

;

 

//IJ SBD

;

 

//SC IJO

Lời giải



 

//MN SBD

 Trong

 

ABCD

//MN BD

mà

 

BD SBD

 Nên

 

//MN SBD



 

//IJ SBD

 Ta có

SI SJ

SM SN



nên

//IJ MN

( theo định lí

ta- lét)

 Suy ra

/ / / / BDIJ MN

mà

 

BD SBD

 Nên

 

//IJ SBD



 

//SC IJO

 Gọi

;H MN AC K IJ SH   

 Từ

SI SJ

IJ MN

SM SN

  

SK SI

SH SM

  

 Mà

là đường trung bình tam giác

ABD

AH AM

AH HO OC

HO MB

     

 Xét

SHC

SK CO

OK SC

SH CH

  

Mà

 

OK OIJ

 Suy ra

 

//SC OIJ

 Bài 07.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 60

Biên So

ạn: LÊ MINH TÂM

Cho hai hình bình hành

ABCD

và

ABEF

không đồng phẳng.

. Gọi

,PQ

là trọng tâm

ABD

và

ABE

. Chứng minh rằng

 

//PQ CEF

. Gọi

,MN

là trọng tâm

BCD

và

AEF

. Chứng minh rằng

 

//MN CEF

Lời giải

. Chứng minh rằng

 

//PQ CEF

 Gọi

là trung điểm của

 Xét tam giác

DEI

IQ IP

IE ID



//PQ DE

( theo định lí ta lét )

 Mà

   

DE DCEF CEF

 Nên

 

//PQ CEF

. Chứng minh rằng

 

//MN CEF

 Gọi

là trung điểm

là trọng tâm

AEF



là trọng tâm

BCD

MC AM

AC AC

  

 Xét

AKC

AN AM

AK AC



 Nên

//MN KC

( theo định lí ta lét)

 Mà

 

KC CEF

 Suy ra

 

//MN CEF

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 61

Biên So

ạn: LÊ MINH TÂM

 Dạng 02. TÌM GIAO TUYẾN CỦA HAI MẶT PHẲNG CHỨA MỘT ĐƯỜNG

THẲNG SONG SONG VỚI MẶT PHẲNG. .

Phương pháp giải

 Ta có thể dùng:

   

       

; / /

a b Mx a







    







 Bài 01.

Cho hình chóp

.S ABCD

đáy là hình bình hành tâm

. Gọi

 

là mặt phẳng qua

và song song với

,SA BC

. Tìm giao tuyến của

 

và

 

ABCD

. Xác định

,MN

lần lượt là giao điểm của

,AB CD

với

 

. Xác định giao điểm

của

và

 

. Tìm giao tuyến của

 

và

 

SAB

. Tìm thiết diện cắt bởi

 

. Thiết diện là hình gì ?

Lời giải

. Tìm giao tuyến của

 

và

 

ABCD

Xác định

,MN

lần lượt là giao điểm của

,AB CD

với

 

 Ta có:

 

   

ladiemchung cua va

ABCD BC

O ABCD















   

//ABCD BC

và đi qua

 Trong

 

ABCD

gọi

M AB

 Mà

   

M AB   

 Trong

 

ABCD

gọi

N CD

 Mà

   

N CD   

. Xác định giao điểm

của

và

 

. Tìm giao tuyến của

 

và

 

SAB

 Ta có:

   

 

P SBC

BC SBC

MN BC



















   

//SBC d BC  

và

đi qua

 Trong

 

SAB

gọi

 

Q d SB SB Q    

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 62

Biên So

ạn: LÊ MINH TÂM

 Dễ thấy

   

SAB MQ

. Tìm thiết diện cắt bởi

 

. Thiết diện là hình gì?

 Ta có:

   

ABCD MN

SAB MQ

SBC PQ

SCD NP























Thiết diện cần tìm là

MNPQ

 Có

//PQ MN

nên tứ giác

MNPQ

là hình thang

 Bài 02.

Cho hình chóp

.S ABC

. Gọi

là trung điểm

. Mặt phẳng

 

qua

và song song với

;SA BC

 

cắt

,,AB SB SC

lần lượt tại

;;N H K

. Chứng minh rằng

MNHK

là hình bình hành.

Lời giải



 

   

ladiemchungcua va

SAC SA

M SAC













   

//SAC MK SA  

 

K SC



 

   

ladiemchung cua va

SBC BC

K SBC













   

//SBC KH BC  

 

H SB



 

   

ladiem chungcua va

SAB SA

SA MK

H SAB

















   

// SAB HN SA  

 

N AB

 Ta có:

   

SBC KH

SAB HN

ABC NM

SAC MK























Thiết diện của hình chóp cắt bởi

 

là tứ giác

MNHK

 Ta có:

là trung điểm

//MK SA

MK

là đường trung bình của

SAC

 Nên

// MK SA

và

MK SA

(1)

 Chứng minh tương tự

// HN SA

HN SA

(2)

 Từ (1) (2) suy ra

MNHK

là hình bình hành.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 63

Biên So

ạn: LÊ MINH TÂM

 Bài 03.

Cho tứ diện

.SABC

Gọi

,MN

là trung điểm

,.AB SB

. Chứng minh

 

//SA CMN

. Tìm giao tuyến

 

CMN

và

()SAC

Lời giải

. Chứng minh

 

//SA CMN

 Xét

SAB

có

là đường trung bình

//MN SA

 Mà

   

//MN CMN SA CMN

. Tìm giao tuyến

 

CMN

và

()SAC

 Ta có :

()

C SAC

C CMN













là điểm chung của hai mặt

phẳng

 Mặt khác

//MN SA

 

MN CMN

 

SA SAC

 Nên

   

// //CMN SAC d MN SA

và

qua

 Bài 04.

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang đáy lớn

. Gọi

là trung điểm

 

là

mặt phẳng qua

song song với

và

. Tìm hình tính thiết diện của

 

và hình chóp

.S ABCD

Lời giải



 

   

//BC

ABCD BC

M ABCD

















   

//ABCD d BC  

với

qua

và cắt

tại



 

   

// SA

SA SAB

N SAB

















   

//SAB d SA



  

với



qua

và cắt

tại



 

   

BC SBC

BC MN

P SBC



















   

//SBC d SA



  

với



qua

và cắt

tại

 Vậy khi đó

 

cắt khối chóp

.S ABCD

theo thiết diện là hình thang

MNPQ

vì có

// //MN PQ BC

 Bài 05.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 64

Biên So

ạn: LÊ MINH TÂM

Cho hình chóp

.S ABCD

. Gọi

,MN

thuộc cạnh

,AB CD

. Gọi

 

là mặt phẳng qua

và song song

với

. Tìm thiết diện của hình chóp cắt bởi

 

. Tìm điều kiện của

để thiết diện là hình thang

Lời giải

. Tìm thiết diện của hình chóp cắt bởi

 



 

   

// SA

SA SAB

M SAB

















   

//SAB d SA  

với

qua

và cắt

tại

 Trong

 

ABCD

, gọi

O MN AC

 

O MN

O AC SAC

















 Ta có

 

   

// SA

SA SAC

O SAC

















   

//SAC d SA



  

với



qua

và cắt

tại

 Vậy khi đó thiết diện là tứ giác

MNPQ

. Tìm điều kiện của

để thiết diện là hình thang

 Nếu

// MQ PN

thì

// SA NP

 Mà

 

NP SCD

nên

 

//SA SCD

(vô lý).

 Do đó để

MNPQ

là hình thang thì

// QP MN

 Ta có

   

SBC PQ

ABCD MN

SBC ABCD BC



















 Mà

// PQ MN

nên

// MN BC

 Vậy để thiết diện là hình thang thì

// MN BC

 Bài 06.

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

. Gọi

là trung điểm

. Mặt phẳng

 

qua

, song song với

và

cắt

,,DC SC SB

lần lượt tại

,,N H K

. Chứng minh tứ giác

MNHK

là hình thang.

Lời giải

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 65

Biên So

ạn: LÊ MINH TÂM

 Ta có:

 

   

//BC

BC SBC

SBC HK

















//HK BC

 

 Lại có:

 

   

//BC

BC ABCD

ABCD MN

















//MN BC

 

 Từ

 

và

 

//HK MN



tứ giác

MNHK

là hình thang.

 Bài 07.

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang, đáy lớn

2AB CD

.Gọi

là trung điểm

Tìm thiết diện của mặt phẳng

 

với hình chóp

.S ABCD

biết mặt phẳng

 

qua

, song song với

và

. Chứng minh thiết diện là một hình thang.

Lời giải

 Có

   

 

M SAB

AB SAB

















   

, ( / / )SAB Mx Mx AB  

 Trong

 

SAB

gọi

N Mx SA

 Có:

   

 

N SAD

SD SAD

















     

, / /SAD Ny Ny SD  

 Trong

 

SAD

gọi

P Ny AD

 Có:

   

 

P ABCD

AB ABCD

















     

, / /ABCD Pz Pz AB  

 Trong

 

ABCD

gọi

Q Pz BC



   

SAB MN

SAD NP

ABCD PQ

SBC QM











 











Thiết diện cần tìm là tứ giác

MNPQ

, mà

//MN PQ

 

//AB

 Do đó tứ giác

MNPQ

là một hình thang.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 66

Biên So

ạn: LÊ MINH TÂM

 Bài 08.

Cho tứ diện

ABCD

. Hãy xác định thiết diện của hình tứ diện

ABCD

khi bị cắt bởi mặt phẳng

 

trong mỗi trường hợp sau:

. Mặt phẳng

 

đi qua trọng tâm

của tứ diện, qua

thuộc cạnh

và

 

//P AD

. Đi qua trọng tâm của tứ diện và song song với

và

Lời giải

. Mặt phẳng

 

đi qua trọng tâm

của tứ diện, qua

thuộc cạnh

và

 

//P AD

 Gọi

,IJ

lần lượt là trung điểm

,BC AD



G là trung điểm

( vì

là trọng tâm của tứ

diện).

 Trong

 

BCJ

gọi

M EG CJ

 

M EG EG P

M CJ CJ ACD

















   

M P ACD  

 Mà :

   

/ / ,P AD AD ACD

 Do đó

     

, / /P ACD Mx Mx AD

 Trong

 

ACD

gọi

;F Mx AC K Mx CD   

 Ta có:

   

P ABC FE

P BCD EK

P ACD KF



















 Vậy thiết diện cần tìm là

EFK

. Đi qua trọng tâm của tứ diện và song song với

và

 Gọi

, , ,L P Q O

lần lượt là trung điểm các cạnh

, , ,AB AC CD BD

 Theo tính chất trọng tâm của tứ diện và có mặt

phẳng

 

đi qua trọng tâm

của tứ diện và song

song với BC.

 Suy ra thiết diện cần tìm là hình bình hành

LPQO

 Bài 08.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 67

Biên So

ạn: LÊ MINH TÂM

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

là trung điểm của cạnh

 

là

mặt phẳng qua

và song song với

. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng

 

. Gọi

, EF

lần lượt là giao điểm của

 

với các cạnh

và

. Tính tỉ số diện tích của

SME

và

SBC

và tỉ số diện tích của

SFM

và

SCD

. Gọi

là giao điểm của

và

;

là giao điểm của

và

. Hãy chứng minh ba điểm

, , K A J

nằm trên đường thẳng song song với

và tìm tỉ số

Lời giải

. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng

 

 Trong

 

ABCD

, gọi

O AC BD

 Trong

 

SAC

, gọi

I SO AM

 Khi đó

 

   

I SO SBD

I SBD P

I AM P







  









 Ta có

 

   

// BD P

BD SBD

I SBD P

















   

//SBD P d BD  

và

qua

 Trong

 

SBD

có

E d SB

và

F SD d

 Ta có:

E d SB

 

   

E d P

E P SBC

E SB SBC







   









 

 Và

 

   

M AM P

M P SBC

M SC SBC







  









 

 Từ

   

ME P SBC

 

 Tương tự, ta cũng có

   

MF P SCD

 

 Ta có

 

   

E d P

E d SB E P SAB

E SB SAB







     









 

 Và

 

     

A AM P

A P SAB

A SAB







  









 Từ

   

34,

ta có

   

AE P SAB

 

III

 Tương tự, ta có

   

AF P SAD

 

 Từ

       

, , , I II III IV

ta có tứ giác

AFME

là thiết diện của hình chóp khi cắt bởi

 

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 68

Biên So

ạn: LÊ MINH TÂM

. Tính tỉ số diện tích của

SME

và

SBC

và tỉ số diện tích của

SFM

và

SCD



SAC

có

, SO AM

là hai đường trung tuyến cắt nhau tại

 Nên

là trọng tâm của tam giác

SAC



 Xét tam giác

SOB

có

// IE OB

nên

SE SI

SB SO



 Tương tự ta cũng có

SF SI

SD SO



 Ta có

1 2 1

2 3 3

1 2 1

2 3 3

. . .sin

SME

SBC

SFM

SCD

SM SE ESM

SM SE

S SC SB

SC SB CSB

SM SF MSF

SM SF

S SC SD

SC SD DSC





   







   





. Hãy chứng minh ba điểm

, , K A J

nằm trên đường thẳng song song với

và tìm tỉ số

 Ta có

 

     

K ME P

K ME CB K P ABCD

K CB ABCD







     









 Ta có

 

     

J MF P

J MF CD J P ABCD

J CD ABCD







     









 Và

 

     

A AM P

A P ABCD

A ABCD







  









 Từ

     

5 6 7, ,

ta được

, , A K J

cùng thuộc giao tuyến của

 

và

 

ABCD

nên

, , A J K

thẳng

hàng.

 Gọi

   

P ABCD

nên

, , A J K

thuộc .

 Ta có

 

   

BD P

BD ABCD BD

P ABCD

















 Mà

// EF BD

nên

// EF

 Vậy ba điểm

, , K A J

nằm trên đường thẳng song song với

 Ta có

// // EF BD JK

 Xét tam giác

AMK

có

// IE AK

nên

MI ME

MA MK



 Xét tam giác

JKM

có

// EF JK

nên

EF ME

JK MK



.Vậy



------------------ HẾT ------------------

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 69

Biên So

ạn: LÊ MINH TÂM

BÀI 04

I. ĐỊNH NGHĨA:

 Hai mặt phẳng

 

và

 

được gọi là song song với

nhau nếu chúng không có điểm chung.

 Ký hiệu:

   

//PQ

hoặc

   

//QP

 Nhận xét:

Nếu hai mặt phẳng

 

và

 

song song với nhau thì bất

kỳ đường thẳng nào nằm trong mặt phẳng này cũng song

song với mặt phẳng kia.

II. TÍNH CHẤT:

 Định lý 1:



Định lý 1

 Nếu mặt phẳng

 

chứa hai đường thẳng cắt nhau

,ab

và

,ab

cùng song song với mặt

phẳng

 

thì

 

song song với

 

 Tóm tắt định lý:

   

 

 

   

;

a P b P

a b M



















 Ví dụ 01.

Cho tứ diện

SABC

. Hãy dựng mặt phẳng

 

qua trung điểm

của đoạn

và song song với

mặt phẳng

 

ABC

Lời giải

 Cách dựng:

 Xét

 

SAB

, qua

dựng

//IK AB

 Xét

 

SAC

, qua

dựng

//IH AC

Vậy mặt phẳng

 

qua trung điểm

của đoạn

và song song với mặt phẳng

 

ABC

là

 

IHK

HAI MẶT PHẲNG SONG SONG

☆☆★☆☆

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 70

Biên So

ạn: LÊ MINH TÂM

 Chứng minh:

 Ta có:

 

IK AB

IK ABC

AB ABC

















 

IH AC

IH ABC

AC ABC















 Ta lại có:

 

 

 

   

IK IH IHK

IK IH I

IHK ABC

IK ABC

IH ABC



















 Ví dụ 02.

Cho tứ diện

ABCD

. Gọi

1 2 3

,,G G G

lần lượt là trọng tâm của

,,ABC ACD ABD  

. Chứng minh:

   

1 2 3

//GG G BCD

Lời giải

 Ta có:

1 2 3

,,G G G

lần lượt là trọng tâm của

,,ABC ACD ABD  

AG AG

AM AP AN

   

 Nên

1 2 1 3 2 3

// , // , //GG MP GG MN G G PN

 

   

) //

G G MP

G G BCD

MP BCD















 

   

//PN

) //

G G BCD

PN BCD















 Mà

   

1 2 2 3 2

3GG G G G

 Từ

 

suy ra

   

1 2 3

//GG G BCD



Định lý 2

 Qua một điểm nằm ngoài một mặt phẳng cho trước có một

và chỉ một mặt phẳng song song với mặt phẳng đã cho.

 Ta có các hệ quả sau:

 Nếu đường thẳng

song song với mặt phẳng

 

thì qua

có duy nhất một mặt phẳng song

song với

 

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 71

Biên So

ạn: LÊ MINH TÂM

 Hai mặt phẳng phân biệt cùng song song với

mặt phẳng thứ ba thì song song với nhau.

 Cho điểm

không nằm trên mặt phẳng

 

Mọi đường thẳng đi qua

và song song với

 

thì đều nằm trong mặt phẳng đi qua

song song

với

 

là

 

 Ví dụ 03.

Cho tứ diện

.S ABC

có

SA SB SC

. Gọi

lần lượt là phân giác ngoài của các góc

trong tam giác

SBC

SAC

SAB

. Chứng minh:

.

 

;Sx Sy

 

ABC

.

;

cùng nằm trên mặt phẳng

Lời giải

.

 

;Sx Sy

 

ABC

 Gọi

là đường phân giác trong của tam

giác

SBC

(với

M BC

)

 Mà

SBC

cân tại

(do

SC SB

)

SM BC

mà

Sx SM

Sx

 Ta có

 

Sx BC

BC ABC Sx ABC

Sx ABC

















 Chứng minh tương tự

 

//Sy ABC

 Ta có

 

 

   

// ; //

Sx ABC

Sy ABC Sx Sy ABC

Sx Sy S

















.

;

cùng nằm trên mặt phẳng

 Chứng minh tương tự

 

;Sy Sz

 

ABC

 Ta có

   

; //

;;

; //

Sx Sy ABC

Sx Sy Sy Sz

Sy Sz ABC













;;Sx Sy Sz

đồng phẳng

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 72

Biên So

ạn: LÊ MINH TÂM



Định lý 3

 Nếu một mặt phẳng thứ 3 cắt một trong hai mặt phẳng song song thì sẽ cắt mặt phẳng

còn lại và hai giao tuyến của chúng song song với nhau

 Tóm tắt định lý:

   

2 1 2

Q d d d







  







 Hệ quả: Hai mặt phẳng song song chắn trên hai cát tuyến song song những đoạn thẳng

bằng nhau.

III. ĐỊNH LÝ THALES TRONG HÌNH HỌC KHÔNG GIAN:

 Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương

ứng tỉ lệ.

1 1 1 1 1 1

2 2 2 2 2 2

A B BC C A

A B B C C A



Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 73

Biên So

ạn: LÊ MINH TÂM

IV. HÌNH LĂNG TRỤ VÀ HÌNH HỘP:

 Cho

 

Trên

 

cho đa giác

...

A A A

. Qua các đỉnh

, ,...,

A A A

ta vẽ các đường thẳng song song

với nhau và cắt

 

lần lượt tại

, ,...,

A A A

  

Hình lăng trụ gồm

– Hai đa giác

...

A A A

...

A A A

  

– Các hình bình hành

1 1 2 2

A A A A



2 2 3 3

A A A A



, …,

11nn

A A A A



 Hình lăng trụ có:

– Mặt đáy:

...

A A A

...

A A A

  

– Các cạnh bên:



, ...,



– Mặt bên:

1 1 2 2

A A A A



2 2 3 3

A A A A



, …,

11nn

A A A A



– Các đỉnh: là các đỉnh của đáy.

 Gọi tên lăng trụ: hình lăng trụ + tên đa giác

* Hình lăng trụ có đáy là tam giác gọi là hình lăng trụ tam giác .

* Hình lăng trụ có đáy là hình bình hành gọi là hình hộp.

 Ví dụ 04.

Cho hình lăng trụ

.ABC A B C

  

. Gọi

và



lần lượt là trung điểm của các cạnh

và



. Chứng minh

//AM A M



. Tìm giao điểm của

 

AB C



với



. Tìm giao tuyến

của

 

AB C



với

 

BA C



. Tìm giao điểm

của

với

 

AM M



. Chứng minh

là trọng tâm tam giác

AB C



Lời giải

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 74

Biên So

ạn: LÊ MINH TÂM

. Chứng minh

//AM A M



 Do

và



lần lượt là trung điểm của các

cạnh

và



 Nên

// CC

=CC











 Mà

// CC //

=CC =

AA AA MM

   







   





Tứ giác

AAMM



là hình bình hành

//A MAM





. Tìm giao điểm của

 

AB C



với



 Ta có



là trung điểm của cạnh



M B C

M AM

  















mà

 

B C AB C

M AA M M



   







  







     

AB C AA M M M

    

  

 Mặt khác

     

AB C AA M M A

   



 Nên ta có

   

AB C AA M M AM

    



 Trong

 

AA M M



gọi

là giao điểm của



và



   

A M AB C I

  

  

. Tìm giao tuyến

của

 

AB C



với

 

BA C



 Trong

 

ABA B



gọi

là giao điểm



và



D A B

D AB

















mà

 

A B BA C

AB AB C



  







  







     

AB C BA C D

   

  

 Ta lại có

         

AB C BA C C AB C BA C C D

         

    

 Vậy giao tuyến

của

 

AB C



với

 

BA C



là



. Tìm giao điểm

của

với

 

AM M



. Chứng minh

là trọng tâm tam giác

AB C



 Ta có

   

AM M AB C AM

   



 Mà

 

.C D AB C

  



 Trong

 

AB C



gọi

là giao điểm



và



. Suy ra

   

C D AM M G





 Ta có

là trung điểm





là đường trung tuyến của tam giác

C AB



 Tương tự ta có



là đường trung tuyến của tam giác

AB C



 Mà

là giao điểm



và



 Vậy

là trọng tâm tam giác

AB C



V. HÌNH CHÓP CỤT:

 Cắt hình chóp bởi mặt phẳng song song với đáy và không đi qua đỉnh ta được hình chóp

cụt.

Tính chất :

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 75

Biên So

ạn: LÊ MINH TÂM

 Hai đáy là hai đa giác có các cạnh tương ứng song song , các tỷ số các cặp cạnh tương

ứng bằng nhau.

 Các mặt bên là những hình thang.

 Các đường thẳng chứa các cạnh bên đồng quy tại một điểm.

III. CÁC DẠNG BÀI TẬP.

 Dạng 01. CHỨNG MINH HAI MẶT PHẲNG SONG SONG.

Phương pháp giải

 Chứng minh 2 mặt phẳngsong song:

 

   

a b I



















  





 Chứng minh đường thẳng song song với mặt phẳng:

   

 

//a















 Bài 01.

Cho hình chóp

.S ABCD

có đáy là hình bình hành tâm

. Gọi

,,M N P

lần lượt là trung điểm

,,SA SB SD

. Chứng minh

   

//PMN ABCD

   

//OMN SCD

. Gọi

,KJ

lần lượt là trung điểm

,BC OM

. Chứng minh

 

//KI SCD

Lời giải

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 76

Biên So

ạn: LÊ MINH TÂM

. Chứng minh

   

//PMN ABCD

 Ta có:

   

MN//AB, //AD

MN MNP MP MNP

AB ABCD AD ABCD

MN MP M

AB AD A























   

//MNP ABCD

 Chứng minh

   

//OMN SCD

 Ta có:

là đường trung bình của

SAB

 Nên

//MN AB

mà

//AB CD

hay

//MN CD



 

   

MN C D

MN SCD MN SCD

CD SCD

















 Tương tự

là đường trung bình của

SAC

 Nên

//OM SC



 

   

OM SC

OM SBC OM SBC

SC SBC



















MN OM M

trong

 

OMN

 

 Từ

     

1 2 3,,

suy ra

   

//SCD OMN

. Chứng minh

 

//KI SCD



   

 

O OMN ABCD

MN OMN

AB ABCD

MN AB



















   

//OMN ABCD Ox AB  

 Mặt khác

//OK AB

     

//OMN ABCD OK AB KI OMN    

 Ta có

   

 

OMN SCD

KI SCD

KI OMN















 Bài 02.

Cho tứ diện

ABCD

. Gọi

1 2 3

,,G G G

lần lượt là trọng tâm của

;;ABC ACD ABD

. Chứng

minh rằng

   

1 2 3

// GG G BCD

Lời giải

 Gọi

, ,PMN

lần lượt là trung điểm của

,,BC CD DB

 Theo tính chất của trọng tâm và định lý ta- lét:

AG AG

AM AN AP

  

G G MN

G G NP









 

G G MNP













(1)

 Mà

và

cắt nhau tại

và cùng nằm

trong

 

1 2 3

G G G

(2)

   

1 2 3

// G G G MNP

, hay

   

1 2 3

// GG G BCD

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 77

Biên So

ạn: LÊ MINH TÂM

 Bài 03.

Cho hai hình bình hành

ABCD

và

ABEF

không đồng phẳng.

. Chứng minh

 

// AB CDEF

. Chứng minh

   

// ADF BCE

. Gọi

, , ,M N P Q

lần lượt là trung điểm

, , ,AD BC BE AF

. Chứng minh

   

// MNPQ DCEF

Lời giải

. Chứng minh

 

// AB CDEF

 Ta có

// AB CD

(do tứ giác

ABCD

là hình

bình hành)



// AB FE

(do tứ giác

ABEF

là hình bình

hành)

// //AB FE CD

 

// AB CDEF

. Chứng minh

   

// ADF BCE

 Ta có

// AD BC

(do tứ giác

ABCD

là hình

bình hành),

 Mà

   

// BC BCE AD BCE

 Chứng minh tương tự ta có

 

// AF BCE

 Mà

và

cắt nhau tại

, và cùng nằm

trong mặt phẳng

 

ADF

 Suy ra

   

// ADF BCE

. Gọi

, , ,M N P Q

lần lượt là trung điểm

, , ,AD BC BE AF

. Chứng minh

   

// MNPQ DCEF

 Xét hình bình hành

ABEF

có

,PQ

là trung điểm

,BE AF

 Nên

là đường trung bình của hình bình hành

ABEF

// // , = PQ AB EF PQ AB EF

(3) (tính chất đường trung bình).

 Chứng minh tương tự ta có

// // , = MN AB CD MN AB CD

(4)

 Từ (3) và (4) suy ra

// , / / MN PQ EF CD

 Suy ra tồn tại mặt phẳng

 

MNPQ

và mặt phẳng

 

DCEF

 Ta có

// MN CD

   

// CD DCEF MN DCEF

(5)

 Xét

BCE

có

,PN

là trung điểm của

và

(gt),

 Suy ra

là đường trung bình của

// BCE PN EC

 Mà

 

EC DCEF

, suy ra

 

// PN DCEF

(6)

 Ta có

,MN PN

cùng nằm trong mặt phẳng

 

MNPQ

và cắt nhau tại

(7)

 Từ (5), (6) và (7) suy ra

   

// MNPQ DCEF

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 78

Biên So

ạn: LÊ MINH TÂM

 Bài 04.

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

là trọng tâm

ABS

và điểm

trên cạnh

sao cho

3AD AE

. Gọi

là trung điểm

. Tìm giao tuyến

 

SAB

và

 

SCD

. Đường thẳng qua

song song với

cắt

tại

. Chứng minh rằng

 

//GF SCD

. Chứng minh rằng

 

//EG SCD

Lời giải

. Tìm giao tuyến

 

SAB

và

 

SCD

 Ta có:

   

// ;

;

S SAB SCD

AB CD

AB SAB CD SCD















   

/ / / /SAB SCD Sx AB CD  

. Đường thẳng qua

song song với

cắt

tại

. Chứng minh rằng

 

//GF SCD

 Xét hình thang

AMCD

có

EF AM

Suy ra:

AE MF

AD MC



 Xét

SAB

là trung điểm

là trọng

tâm

ABC

suy ra:



 Xét

SCM

có

MG MF

GF SC

MS MC

  

 Ta có:

 

GF SC

GF SCD

SC SCD















. Chứng minh rằng

 

//EG SCD

 Ta có:

 

// //

GF SC cmt

EF CD AB











     

// //SCD EFG EG SCD

 Bài 05.

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

là trung điểm của

là

trọng tâm

SAB

và điểm

trên cạnh

sao cho

3AD AM

. Đường thẳng qua

song song

với

cắt

tại

. Chứng minh rằng

 

//GN SCD

và

 

//GM SCD

Lời giải

 Xét hình thang

AICD

có

//MN AI

, suy ra:

AM IN

AD IC



 Xét

SAB

có

là trung điểm

là trọng

tâm

ABC

Suy ra:



 Xét

SCM

có

IG IN

GN SC

IS IC

  

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 79

Biên So

ạn: LÊ MINH TÂM

 Ta có:

 

GN SC

GN SCD

SC SCD















 Ta có:

 

// //

GN SC cmt

MN CD AB











     

// //SCD GNM GM SCD

 Dạng 02. GIAO TUYẾN CỦA 2 MẶT PHẲNG CÓ 1 MẶT PHẲNG SONG

SONG VỚI MẶT THỨ BA .

Phương pháp giải

 Ta có thể dùng một trong các cách sau

   

// ; //b

Mx Mx







  











Đưa về dạng thiết diện song song với đường thẳng

   

 

, //















Như vậy thay vì tìm thiết diện song song với mặt phẳng

 

thì ta tìm thiết

diện song song với các đường thẳng

,ab

nằm trong

 

 Bài 01.

Cho hình chóp

.S ABCD

đáy là hình bình hành .Gọi

là trung điểm

,gọi

 

là mặt phẳng

qua

và

 

song song với

 

ABCD

. Tìm

   

SAB

 

N SB

.Tìm

     

,SBC P SC  

. Tìm thiết diện cắt bởi

 

.Thiết diện là hình gì ?

Lời giải

. Tìm

   

SAB

 

N SB

Tìm

     

,SBC P SC  



   

SAB

 Ta có

   

// ABCD

   

SAB ABCD AB

 Mà

   

SAB M

   

SAB d  

(với

là là đường thẳng đi qua

và song

song

 Do

là trung điểm của

d

cắt

tai

trung điểm

 

SB N  

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 80

Biên So

ạn: LÊ MINH TÂM



   

SBC

 Ta có

   

// ABCD

   

SBC ABCD BC

 Mà

   

SCB N

   

SCB  

(với là là đường thẳng đi qua

và song song

 Do

là trung điểm của



cắt

tai trung điểm

 

SC P  

. Tìm thiết diện cắt bởi

 

.Thiết diện là hình gì ?

 Ta có

   

// ABCD

   

SAD ABCD AD

 Mà

   

SAD M

   

SAD a  

(với

là đường thẳng đi qua

và song song

 Do

là trung điểm của

a

cắt

tai trung điểm

 Nối

, , ,M N P Q

ta được thiết diện là tứ giác

MNPQ

 Ta có

 

// // ; //

MN PQ MN AB PQ AB

NP MQ NP AD MQ AD











. Vậy tứ giác

MNPQ

là hình bình hành.

 Bài 02.

Cho hình chóp

.S ABCD

đáy là hình thang

 

//AB CD

là một điểm thuộc cạnh

 

,BC M B C

. Xác định thiết diện của hình chóp cắt bởi mặt

 

qua

và song song với

 

SAB

. Gọi

,,N E F

lần lượt là giao điểm của

 

và

,,AD SD SC

. Gọi

là giao điểm của

và

. Chứng minh rằng

chạy trên một đường thẳng cố định.

Lời giải

. Xác định thiết diện của hình chóp cắt bởi mặt

 

qua

và song song với

 

SAB

 Ta có:

 

đi qua

và song song với

 

SAB

   

//P ABCD d AB  

với

đi qua

và

d AD N



 

đi qua

và song song với

 

SAB

   

//P SAD d SA



  

với



đi qua

và

d SD E



 

đi qua

và song song với

 

SAB

   

//P SBC d SB



  

với



đi qua

và

d SC F

 Suy ra thiết diện tìm được là tứ giác

MNEF

 Vì

   

, / /P SCD EF CD AB

/ / / / / /EF AB CD MN

 Vậy thiết diện tìm được là hình thang

MNEF

. Chứng minh rằng

chạy trên một đường thẳng cố định.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 81

Biên So

ạn: LÊ MINH TÂM

 Ta có:

 

NE SAD



 

MF SBC



   

,SAD SBC SK K AD BC   

suy ra

cố định



là giao điểm của

và

I SK

(ĐPCM)

 Bài 03.

Cho hình chóp

.S ABCD

đáy là hình bình hành tâm

,AC a BD b

,tam giác

SBD

đều. Một

mặt phẳng

 

di động song song với mặt

 

SBD

và đi qua điểm

trên đoạn thẳng

 

,I A C

. Xác định thiết diện của hình chóp cắt bởi mặt phẳng

 

. Tính diện tích thiết diện theo

,ab

và

x AI

Lời giải

. Xác định thiết diện của hình chóp cắt bởi mặt phẳng

 

 Trường hợp 1:

I AO

 Ta có:

 

đi qua

và song song với

 

SBD

   

//P ABCD d BD  

với

đi qua

và

d AB M

d AD N













 

đi qua

và song song với

 

SBD

   

//P SAD d SD



  

với



đi qua

và

d SA P



   

SAB MP

mà

   

/ / / /SBD MP SB

 Suy ra thiết diện tìm được là tam giác

MNP

 Do tam giác

SBD

đều nên tam giác

MNP

đều.

 Trường hợp 2:

I CO

 Ta có:

 

đi qua

và song song với

 

SBD

   

//P ABCD d BD  

với

đi qua

và

d CB E

d CD F













 

đi qua

và song song với

 

SBD

   

//P SCD d SD



  

với



đi qua

và

d SC G



   

SBC EG

mà

   

/ / / /SBD EG SB

Suy ra thiết diện tìm được là tam giác

EFG

Do tam giác

SBD

đều nên tam giác

EFG

đều.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 82

Biên So

ạn: LÊ MINH TÂM

. Tính diện tích thiết diện theo

,ab

và

x AI

 Trường hợp 1:

I AO

, thiết diện tìm được là tam giác

MNP

đều



MNP SBD

nên

MNP SBD











MN AI x x

BD AO a

  

sin

SBD

S b b    

2 2 2

233

MNP

x b x b



   





 Trường hợp 2:

I CO

, thiết diện tìm được là tam giác

EFG

đều



EFG SBD

nên

EFG SBD











 

EF CI a x

BD CO a



  

sin

SBD

S b b    

   

EFG

a x a x b





   





 Bài 04.

Cho hình chóp

.S ABCD

đáy là hình bình hành tâm

. Gọi

là trung điểm của

. Biết tam

giác

ACE

đều và

AB OD a

. Một mặt phẳng

 

di động song song với mặt phẳng

 

ACE

và qua

trên đoạn

;

 

cắt

lần lượt tại

. Xác định thiết diện của hình chóp cắt bởi mặt phẳng

 

. Tính diện tích thiết diện theo

,ab

và

x AI

Lời giải

 Kẻ

với

Q SB

 Qua

kẻ

với

M AD

N AC

 Gọi

   

QR SAB

mà

   

AE CAE SAB

QR

 Gọi

   

PQ SAC

mà

   

CE CAE SAC

QP

   

P MNPQR

. Có nhận xét gì về

PQR

và tứ giác

MNPR

 Ta có

DI x

DO a



SQ x

SE a



QR PQ PR x

AE AE CA a

   

 Mà

CAE

đều

PQR

đều.

OE AC

(do

là đường trung tuyến trong

tam giác đều)

QI NM

PN NM

 Dễ thấy

PNMR

là hình bình hành

Mà

PN NM

PNMR

là hình chữ nhật.

. Tìm tập hợp giao điểm của

và

khi

di động trên đoạn

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 83

Biên So

ạn: LÊ MINH TÂM

 Gọi

 

K PM NR

KI PN

 Mà

PN SD





KI SD





 Gọi

là trung điểm

. Ta có

IK OI a x

GD OD a











 Mà

K GO

.Vậy khi

di động trên

thì

di động trên

. Tính diện tích đa giác

MNPQR

theo

và

x DI

. Tính

để diện tích ấy lớn nhất.

 Ta có

PR NM a x

  

1 3 3

2 2 4

PQR

Sx  

 Ta có

. . .

PRMN

S NM PN x SD





 

2 2 2. . . . .

a x a x

x OE x a a x x



   

 Vậy

 

MNPQR

S a x x  

(đvdt)

 Dạng 03. HÌNH LĂNG TRỤ - HÌNH HỘP .

Phương pháp giải

 Chú ý vào các đường thẳng và mặt phẳng song song của hình lăng trụ để áp dụng các định

lí song song đã học.

 Bài 01.

Cho lăng trụ tam giác

. ' ' 'ABC A B C

. Gọi

làn lượt là trung điểm của cạnh

và

''BC

. Chứng minh

// ' 'AM A M

. Tìm giao điểm

 

''AB C

và đường thẳng

'AM

. Tìm giao tuyến

của

 

''AB C

và

 

''BA C

. Tìm giao điểm

của

với

 

'AMA

. Chứng minh rằng

là trọng tâm

''AB C

Lời giải

. Chứng minh

// ' 'AM A M

 Xét tứ giác

''BCC B

có

là trung điểm

của

và

''BC

'MM

là đường trung bình của hình bình

hành

''BCC B

'// '// '; ' ' 'MM BB CC MM BB CC  

 Nên tứ giác

''AMA M

là hình bình hành

// ' 'AM A M

. Tìm giao điểm

 

''AB C

và đường thẳng

'AM

 Gọi

là trung điểm của

'AM

I

cũng là trung điểm của

'AM

 Mà



thuộc

 

''AB C

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 84

Biên So

ạn: LÊ MINH TÂM

 Do vậy I là giao điểm của

'AM

và

 

''AB C

. Tìm giao tuyến

của

 

''AB C

và

 

''BA C

 Trong

( ' ')ABB A

có

 

AB BA J





   

, ' ' ' 'J C AB C BA C  

   

' ' ' 'JC AB C BA C  

. Tìm giao điểm

của

với

 

'AMA

. Chứng minh rằng

là trọng tâm

''AB C

 Trong

 

''AB C

có

   

' ' ' ' 'JC IM G G JC AMM A    

 Xét

''AC B

có

'; 'AM C J

lần lượt là trung tuyến.

 Do vậy giao điểm

của chúng chính là trọng tâm

''AC B

 Bài 02.

Cho hình hộp

1 1 1 1

.DABCD A BC

. Gọi

là tâm hình bình hành

1 1 1 1

A B C D

;

là trung điểm

là trung điểm của

. Chứng minh

 

E ACB

. Xác định thiết diện của hình hộp với

 

đi qua

và song song với

 

EAC

Lời giải

. Chứng minh

 

E ACB

 Gọi giao điểm của hai hình bình hành

1 1 1 1

,A B BA BC BC

là

,PQ

 Ta có

;PE QE

lần lượt đường trung bình của

1 1 1 1;

BO A BOC

 Nên ta có

1 1 1 1

//A C ;A C //PE QE

 Do vậy

 

E PQ E ABC  

. Trong

 

ABCD

kẻ

 

//KI AC I AD

 Trong

 

A ADD

kẻ

 

1 1 1 1

// ; //IG A D G AA A D BC

 

// //IG BC IG B AC

 Trong

 

ABA B

kẻ

 

// 'GM AB M A B

 Trong

 

1 1 1 1

A BC D

kẻ

 

1 1 1 1

//HM AC H BC

 Trong

 

BBC C

kẻ

 

1 1 1

//HN AC N CC

 Do vậy giao tuyến cần tìm là ngũ giác

KIGMHN

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 85

Biên So

ạn: LÊ MINH TÂM

 Bài 03.

Cho lăng trụ tam giác

. ' ' 'ABC A B C

. Trên đường thẳng BA lấy điểm

sao cho

nằm giữa

đoạn thẳng

và

MA AB

. Xác định thiết diện của hình lăng trụ cắt bởi mặt

 

đi qua

và trung điểm

của

. Tính tỉ số

với

 

'D BC MB E

Lời giải

 Do

 

D BC MB E





;

 

,BC ME ABC

D BC ME  

. Xác định thiết diện của hình lăng trụ cắt bởi mặt

 

đi qua

và trung điểm

của

 Trong

( ')ABB

, gọi

''F MB AA

Như vậy, ta có:



   

P ABB FB

P BCC B B D

P ABC DE

P ACC A EF









  

















 Vậy thiết diện của hình lăng trụ cắt bởi mặt

phẳng

()P

là tứ giác

'B DEF

. Tính tỉ số

với

 

'D BC MB E

Kẻ

//AI DE

với

.I BC

 Mà

là trung điểm của

DE

là đường trung bình của

ACI

D

là trung điểm của

hay

CD DI

 Do

//AI DM

nên

BD BM BA AM AM AM

DI AM AM AM



   

3BD DI

. Vậy



 Bài 04.

Cho lăng trụ tam giác

. ' ' 'ABC A B C

. Gọi I, J, K lần lượt là tâm của các hình bình hành

''ACC A

''BCC B

''ABB A

. Chứng minh rằng:

 

//IJ ABB A



;

//( ' ')JK ACC A

;

//( ' ')IK BCC B

. Chứng minh rằng: Ba đường thẳng AJ, CK, BI đồng qui tại điểm O.

. Chứng minh rằng:

()IJK

song song với mặt đáy của lăng trụ.

. Gọi G,

là trọng tâm của các tam giác ABC và

' ' 'A B C

. Chứng minh G, O,

thẳng hàng

Lời giải

. Chứng minh rằng:

 

//IJ ABB A



;

//( ' ')JK ACC A

;

//( ' ')IK BCC B

 Ta có IJ là đường trung bình của

'C AB

 Nên

//IJ AB

. Mà

 

''AB ABB A

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 86

Biên So

ạn: LÊ MINH TÂM

Vậy

 

// ' 'IJ ABB A

 Chứng minh tương tự, ta có:

 

// ' 'JK ACC A

 

// ' 'IK BCC B

. Chứng minh rằng: Ba đường thẳng AJ, CK, BI

đồng qui tại điểm O.

 Xét ba mặt phẳng

     

:' , ' , 'C AB A BC B AC

   

C AB A BC BI   

;

   

C AB B AC AJ   

;

   

B AC A BC CK   

;

   

C AB A BC BI   

;

   

C AB B AC AJ   

;

   

B AC A BC CK   

 Suy ra, theo định lí giao tuyến: ba đường

thẳng

, , BI AJ CK

đồng quy tại một điểm.

. Chứng minh rằng:

()IJK

song song với mặt đáy của lăng trụ.

 Theo ý , ta có:

   

IJ AB

IJK ABC

JK AC









. Chứng minh

,,G O G



thẳng hàng

 Dễ thấy

là trọng tâm

’C AB

 Gọi

M ABCO





thì

là trung điểm của

 Vậy ba điểm

,,G M C

thẳng hàng.

 Vì

và

lần lượt là trọng tâm của hai

C AB



và

CAB

Nên ta có:

MO MG

OG CC

MC MC

   



(1)

 Chứng minh tương tự

'// 'OG CC

(2)

 Từ (1) và (2) suy ra ba điểm

,,G O G



thẳng hàng.

 Bài 05.

Cho hình hộp

.ABCD A B CD

   

. Chứng minh

 

BDA



song song với

 

B D C



. Chứng minh đường chéo



đi qua trọng tâm

của hai

BDA



và

B D C



. Chứng mình

chia đoạn



thành ba phần bằng nhau.

. Gọi

lần lượt là tâm các hình bình hành

ABCD

BCC B



. Xác định thiết diện của

 

A IK



với hình hộp.

Lời giải

. Chứng minh

 

BDA



song song với

 

B D C



Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 87

Biên So

ạn: LÊ MINH TÂM

 Gọi

lần lượt là tâm các hình bình hành

ABCD

AB C D

   

 Ta có:

 

 

BD B D

A I OC

BD A I BDA

OC B D B D C

BD A I I

OC B D O



















   











  





   

//BDA B D C

  



. Chứng minh đường chéo



đi qua trọng tâm

của hai

BDA



và

B D C



 Ta có:

   

ACC A BDA A I

  



và

AC A I G





   

AC BDA G



  

 Ta có:

//AI A C



G A G I

G C A C G A

   

   

G

là trọng tâm tam giác

BDA



 Ta có:

   

ACC A B D C CO

  



và

AC CO G





   

AC B D C G

  

  

 Ta có:

//OC AC



G O G C

G C G A AC



   

G

là trọng tâm tam giác

B D C



. Chứng mình

chia đoạn



thành ba phần bằng nhau.

 Theo ý  ta có:

AG AC C G







chia đoạn



thành ba phần bằng nhau.

. Xác định thiết diện của

 

A IK



với hình hộp.

 Ta có:

AI CC P





   

A IK BCC B KP



  

KP BC M

và

KP B C N





 Suy ra:

   

A IK A B C D A N

     



   

A IK ABCD IM





và

IM AD Q

 Suy ra:

   

A IK ADA D A Q

   



 Vậy thiết diện của

 

A IK



với hình hộp là tứ

giác

A NMQ



Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 88

Biên So

ạn: LÊ MINH TÂM

 Bài 06.

Cho hình hộp

.ABCD AB C D

   

. Gọi

, , ,P Q R S

lần lượt là tâm các mặt

ABB A



BCC B



CDD C



DAA D



. Chứng minh rằng:

 

//RQ ABCD

;

   

//PQRS ABCD

. Xác định thiết diện của hình hộp khi cắt bởi

 

AQR

.Gọi

là giao điểm của cạnh



với

 

AQR

. Tính tỉ số



Lời giải

. Chứng minh rằng:

 

//RQ ABCD

;

   

//PQRS ABCD



 

// //

RQ ABCD

RQ BD BD B D

















(1).



 

PQ ABCD

PQ AC















(2).

 Từ (1) và (2)

   

//PQRS ABCD

. Xác định thiết diện của hình hộp khi cắt bởi

 

AQR

 Gọi



là trung điểm



CO RQ E





AE CC M





MQ BB G





MR DD F





 Vậy thiết diện của hình hộp khi cắt bởi

 

AQR

là tứ giác

AGMF

.Tính tỉ số



 Theo ý 

E

là trung điểm

và



 Đặt

 

0CM xCC x





AM AC CM

AC xCC









AC x AC AC



  

 

1xAC AC x



  

AE AC AO









AC AC C O

  

  

1 1 1

2 2 2

AC AC AC





  





AC AC





 Vì

,,A M E

thẳng hàng

AE

cùng phương

xx



 

21xx  

x

 Vậy





Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 89

Biên So

ạn: LÊ MINH TÂM

 Dạng 04. ĐỊNH LÝ THALES TRONG KHÔNG GIAN .

Phương pháp giải

 Tìm 2 đường thẳng chéo nhau trên đó có các đoạn thẳng tỉ lệ.

 Bài 01.

Cho tứ diện

ABCD

là một điểm lưu động trên cạnh

;

là điểm lưu động trên cạnh

. Chứng tỏ rằng trung điểm

của đoạn

thuộc một mặt phẳng cố định.

Lời giải

 Kẻ

IK AB



là trung điểm

(do

là

trung điểm

 Qua

kẻ đường thẳng song song với

cắt

tại

, cắt

tại



là trung điểm



cố định.

 Kẻ hình bình hành

BEDC

()BE CD PQ PQ ABE

 

()IK AB IK ABE

 

   

12&

PQI ABE

 Do

 

ABE

là mặt phẳng cố định,

cố định



 

PQI

cố định.

 Vậy

thuộc mặt phẳng cố định qua

và song song

 

ABE

 Bài 02.

Cho hình vuông

ABCD

và

ABEF

nằm trong hai mặt phẳng phân biệt. Trên các đường chéo

và

lần lượt lấy hai điểm

và

sao cho

AM BN

. Chứng minh rằng

luôn

song song với một mặt phẳng cố định.

Lời giải

 Vẽ

NN AB



BN A N

CF AF





(1)

 Vẽ

MM AB CD



AM AM BN

AD AC BF



  

(do

,AM BN AC BF

)(2)

   

12&

A N AM

AF AD



 

 

M N DF M N DFEC

   



(3)

 Mà

 

M M CD M M DFEC





(4)

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 90

Biên So

ạn: LÊ MINH TÂM

   

34&

M N NM DFEC





, mà

   

MN M N NM MN DFEC





 Vậy

luôn song song mặt phẳng cố định

 

DFEC

 Bài 03.

Cho hình hộp

.ABCD A B CD

   

là điểm thuộc cạnh



sao

cho

AM D N

MD NC







. Chứng minh rằng

 

//MN C BD



. Xác định thiết diện cắt bởi mặt phẳng

()P

qua

và song song

 

C BD



Lời giải

. Chứng minh rằng

 

//MN C BD



 Theo giả thiết ta có

AM D N AM DM AD

MD NC D N C N D C



   

    

 Theo định lý Talet đảo ta có

,,MN AD DC



cùng song song với

 

 Khi đó

 

Q AD

Q DC















 Mà

//AD BC



 Nên

 

     

// //

Q BC

Q BDC MN BDC

Q DC



















(ĐPCM).

. Xác định thiết diện cắt bởi

()P

qua

và song song

 

C BD



 Ta có mặt phẳng

 

qua

và song song

 

C BD



Nên:

 Từ

kẻ

//MF BD

, cắt

tại

;

 Từ

kẻ đường thẳng

//EF AB



, cắt



tại

 Từ

kẻ đường thẳng

//EI BC



, cắt



tại

;

 Từ

kẻ đường thẳng

//NJ C D



cắt



tại

 Dễ thấy thiết diện là lục giác

MEFINJ

có các

cạnh đối lần lượt song song với ba cạnh của

tam giác

CBD



Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 91

Biên So

ạn: LÊ MINH TÂM

 Bài 04.

Cho hình lập phương

.ABCD AB C D

   

cạnh

,MN

lần lượt là các điểm trên

,AD DB



sao cho

 

02AM DN x x a   

. Chứng minh khi

thay đổi đường thẳng

luôn song song với một mặt phẳng cố định.

. Chứng minh khi

x 

thì

//MN A C



Lời giải

. Chứng minh khi

thay đổi đường thẳng

luôn song song với một mặt phẳng cố định.

 Kẻ

   

// ; //ME AD E AA NF AD F AB





, , ,M N E F

đồng phẳng.

 Áp dụng định lý Talet ta có:

;

AM AE DN AF

AD AA DB AB





 Mà

 

2 ;AD BD a gt





Theo gt:

AM DN x

nên

AE AF

EF A B

AA AB







 Ta có:

 

// //

EF A B

ME BC BC AD













     

// //MNFE A BC MN A BC





. Chứng minh khi

x 

thì

//MN A C



 Gọi

là giao điểm của

và

;

là giao điểm của



và





DO 

Mà

DN x

DN DO

hay

là trọng tâm

ADC

 Tương tự:

là trọng tâm

AA D



 Gọi

là trung điểm

 Khi đó ta có:

JM JN

JA JC





//MN A C





(ĐPCM).

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 92

Biên So

ạn: LÊ MINH TÂM

 Bài 05.

Cho tứ diện

ABCD

và 4 điểm

, , ,M N E F

lần lượt nằm trên các cạnh

,,AB BC CD

và

Dùng định lý đảo Thalès trong không gian chứng minh rằng:Nếu 4 điểm

, , ,M N E F

đồng

phẳng thì

1. . .

MA NB EC FD

MB NC ED FA



Lời giải

 Gọi

là đường thẳng bất kỳ cắt

 

MNEF

tại

 Từ các điểm

, , ,A B C D

vẽ các mặt phẳng song

song với

 

MNEF

và cắt đường thẳng

lần

lượt tại

, , ,A B C D

   

. Khi đó ta có:



   

MA OA

MNEF OA A

MB OB









   

NB OB

MNEF OB B

NC OC









   

EC OC

MNEF OC C

ED OD









   

EC OD

MNEF OD D

ED OA







 Do đó:

1. . . . . .

MA NB EC FD OA OB OC OD

MB NC ED FA OB OC OD OA

   



   

------------------ HẾT ------------------

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 93

Biên So

ạn: LÊ MINH TÂM

BÀI 05

 Bài 01.

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

. Gọi

,,M N P

lần lượt là

trung điểm

,,SA BC CD

. Tìm giao tuyến của hai mặt phẳng

 

SAD

và

 

MOP

. Chứng minh

   

//MOP SBC

. Gọi

là điểm bất kỳ trên

. Chứng minh

 

//KN SCD

. Mặt phẳng

 

qua

, song song với

và

. Tìm thiết diện của mp

 

và hình chóp

.S ABCD

. Xác định hình tính thiết diện.

Lời giải

. Tìm giao tuyến của

 

SAD

và

 

MOP

 Ta có

   

,M SA SA SAD M SAD   

;

 

M MOP

 Mặt khác

 

AD SAD

OP MOP

AD OP















   

// //SAD MOP d AD OP  

với

qua



d SD E

là trung điểm

nên

là trung điểm

 Vậy

   

SAD MOP ME

. Chứng minh

   

//MOP SBC

 Ta có:

ME AD

AD BC







     

1// ; // ME BC BC SBC ME SBC  



     

2// ; // EP SC SC SBC EP SBC



và

là hai đường thẳng cắt nhau

cùng nằm trong mặt phẳng

   

3 MOP

 Từ

 

và

 

suy ra

   

//MOP SBC

TỔNG ÔN TẬP CHƯƠNG

☆☆★☆☆

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 94

Biên So

ạn: LÊ MINH TÂM

. Gọi

là điểm bất kỳ trên

. Chứng minh

 

//KN SCD

 Ta có

     

4// ; // ON DC DC SCD ON SCD

     

5// ; // OM SC SC SCD OM SCD

và

là hai đường thẳng cắt nhau cùng nằm trong mặt phẳng

   

6 MON

 Từ

 

và

 

suy ra

   

//MON SCD

là điểm bất kỳ trên

nên

 

KN MON

mà

   

//MON SCD

nên

 

//KN SCD

. Tìm thiết diện của

 

và hình chóp

.S ABCD

Xác định hình tính thiết diện.

 Ta có

   

ABCD NO

và

NO AD Q

   

SAD QE

   

//SCD d CD





;



qua

và

d SC F







   

SBC FN



NQ CD

NQ EF

EF CD









Vậy thiết diện của mp

 

và hình chóp

.S ABCD

là hình thang

NQEF

 Bài 02.

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

. Tìm giao tuyến của hai mặt phẳng

 

SBC

và

 

SAD

. Trên các cạnh

,SB SD

ta lần lượt lấy các điểm

và

thỏa

;

SM SN

SB SD



. Tìm giao điểm

của

và mặt phẳng

 

AMN

. Suy ra thiết diện của mặt phẳng

 

AMN

và hình chóp

.S ABCD

. Gọi

là giao điểm của

và

. Tính tỉ số

Lời giải

. Tìm giao tuyến của hai mặt phẳng

 

SBC

và

 

SAD

 Ta thấy:

   

S SBC SAD

 Và

 

AD SAD

BC SBC

AD BC















 Nên

   

// //SBC SAD d AD BC

và

qua

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 95

Biên So

ạn: LÊ MINH TÂM

. Tìm giao điểm

của

và mặt phẳng

 

AMN

Suy ra thiết diện của mặt phẳng

 

AMN

và hình

chóp

.S ABCD

 Gọi

,E MN SO I SC AE   

I SC

I AE













 Mà

 

AE AMN

 

I SC

I SC AMN

I AMN







   









 Khi đó thiết diện của mặt phẳng

 

AMN

và

hình chóp

.S ABCD

là tứ giác

AMIN

. Tính tỉ số

 Gọi

là trung điểm

F OG AN

//OG SB



NF GF NG

NE SM SN

  

GF SM



1 1 1 1 5

2 4 2 4 4

.OF OG FG SB SM SM SM SM      



SME

đồng dạng với

OFE

OE OF

SE SM

  

 Gọi

là trung điểm

//OH AI



SI SE

IH OE



4 4 1 2 2

5 5 2 5 5

SI IH IC IC

     



J SD

sao cho

//IJ CD



SJ SI

JD IC





5 5 15 15

7 7 7 7

JD SD ND ND

     

 

15 8 7

1 1 1

7 7 8

IJ NJ JD ND JD

KD IJ

KD ND ND ND



         

 Mặt khác

IJ SI

CD SC



 

7 7 7 35

2 8 2 8

CD IJ KC KD CD IJ IJ IJ       

 Từ

 

và

 

suy ra



 Bài 03.

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành,

là giao điểm của hai đường chéo,

,AC a BD b

, tam giác

SBD

đều.

. Tìm giao tuyến của hai mặt phẳng

 

SAB

và

 

SCD

. Gọi

,GG

lần lượt là trọng tâm của các tam giác

,ACD SCD

. Chứng minh

song song

với mặt phẳng

 

SAC

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 96

Biên So

ạn: LÊ MINH TÂM

. Gọi

là điểm di động trên

với

AM x x



  





. Gọi

 

là mặt phẳng đi qua

và song song với mặt phẳng

 

SBD

. Tìm thiết diện tạo bởi

 

và hình chóp

.S ABCD

. Tính diện tích thiết diện tìm được ở ý  theo

,,a b x

Lời giải

. Tìm giao tuyến của

 

SAB

và

 

SCD

 Ta thấy:

   

S SAB SCD

 Và

 

AD SAB

BC SCD

AB CD















 Nên

   

// //SBC SAD AB CD

và qua

. Chứng minh

 

//GG SAC

 Gọi

là trung điểm

 Ta có

KG KG

G G SA

KA KS

  

 Mà

 

SA SAC

nên

 

//G G SAC

. Tìm thiết diện tạo bởi

 

và hình chóp

.S ABCD

 Ta có

   

// SBD

nên:

   

//ABCD d BD

và

qua

 Gọi

E d AB

F d AD











   

//SAB d SB





và



qua

 Gọi

là giao của



với

   

SAB PF

 Từ đó thiết diện là tam giác

PEF

. Tính diện tích thiết diện tìm được ở ý  theo

,,a b x

 Ta có

PEF

và

SBD

là hai tam giác đồng

dạng,



SBD

đều nên

PEF

đều.

2.EF AM AM BD xb

BD AO AO a

   

 Suy ra diện tích tam giác

PEF

là

2 2 2

3 2 3 3

PEF

EF xb x b





  





 Bài 04.

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành

. Tìm giao tuyến của hai mặt phẳng

 

SBC

và

 

SAD

. Gọi

là trọng tâm tam giác

SBD

. Trên các cạnh

và

lần lượt lấy các điểm

và

thoả

2MD MC

và

2NB NA

. Tìm giao tuyến của hai mặt phẳng

 

SND

và

 

BGM

Tìm giao điểm

của

và mặt phẳng

 

BGM

. Gọi

là giao điểm của

và mặt phẳng

 

BGM

. Tính tỷ số

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 97

Biên So

ạn: LÊ MINH TÂM

Lời giải

. Tìm giao tuyến của

 

SBC

và

 

SAD

 Ta có:

   

 

S SBC SAD

BC AD

BC SBC

AD SAD

















   

// //SBC SAD Sx BC AD  

. Tìm giao điểm

của

và mặt phẳng

 

BGM

 Trong

 

:ABCD H AC BM

L AC ND

 Trong

 

:SAC P GH SL

 

   

 

   

// //

P GH BGM

P SND BGM

P SL SND

SND BGM Px BM DN

BM DN

BM BGM

DN SND









   











  













 Tìm

 

I SN BGM

 Trong

 

I SN

SND I SN Px I SN BGM

I Px BGM







     









. Tính tỷ số

 Trong

 

:SAC K GH SA

 

K GH BGM

K SA BGM

K SA







   









Áp dụng định lý Menelaus

 Xét

ODC

, ta có:

1..

HC BO MD

HO BD MC



1 1 1

2 2 2

HC HO OC OA

     

 Xét

SOA

, ta có:

1..

KS GO HA

KA GS HO



 

HO OA

KA HO





1 3 2

2 1 3

. . .

KS KS

KA KA

   

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 98

Biên So

ạn: LÊ MINH TÂM

 Bài 05.

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành,

2,.AB a AD a

. Tìm giao tuyến của hai mặt phẳng

 

SAB

và

 

SCD

. Gọi M là điểm di động trên cạnh

với

 

0AM x x a  

. Gọi

 

là mặt phẳng đi qua

và song song với mặt phẳng

 

SAD

. Tìm thiết diện tạo bởi

 

và hình chóp

.S ABCD

. Cho

SA a

vuông góc với

. Tìm

để diện tích thiết diện bằng

Lời giải

. Tìm giao tuyến của

 

SAB

và

 

SCD

 Ta có:

   

 

S SAB SCD

AB CD

AB SAB

CD SCD

















   

// //SAB SCD Sx AB CD  

. Tìm thiết diện tạo bởi

 

và hình chóp

.S ABCD

 Vì mặt phẳng

     

//P SAD P

song song

với mọi đường thuộc mặt phẳng

 

.SAD

 Tìm giao tuyến của mặt phẳng

 

và mặt phẳng

 

.ABCD

 Ta có

   

M P ABCD

,vì

 

//P AD

nên

   

//ABCD P d AD

và

qua

Khi đó

 

1d CD Q

Tương tự:

 Ta có

   

M P SAB

,vì

 

//P SA

nên

   

// ;SAB P MN SA N SB  

 Ta có

   

N P SBC

,vì

 

// //P AD BC

nên

     

2//SBC P NP BC

 Ta có

   

P SCD PQ

Suy ra thiết diện cần tìm là

.MNPQ

Từ (1) và (2) thì

//MQ PN

. Vậy

MNPQ

là hình thang.

. Tìm

để diện tích thiết diện bằng

 Áp dụng Ta-lét cho

SAB

và

SBC

ta được:

x AM SN NP NP

NP x

a AB SB BC a

     

 Áp dụng Ta-lét cho

SAB

, ta có:

 

a x SA

MN BM a x

MN a x

SA AB a a



     

 Vì

SA AD MNPQ

là hình thang vuông .

     

MNPQ

S MN NP MQ a x x a a x       

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 99

Biên So

ạn: LÊ MINH TÂM

 Vì

2 2 2

3 3 3

()

(do )

()

MNPQ

a a a

S a x x x a







        









. Vậy

x 

 Bài 06.

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang, đáy lớn

,AB M

là trung điểm cạnh

. Tìm giao tuyến của hai mặt phẳng

 

SAD

và

 

SBC

. Tìm giao điểm

của

và mặt phẳng

 

ADM

. Xác định thiết diện của hình chóp

.S ABCD

khi cắt bởi mặt phẳng

 

CDM

. Gọi

là giao điểm của

và

. Chứng minh

// // .SI AB CD

Lời giải

. Tìm giao tuyến của

 

SAD

và

 

SBC

 Ta có:

     

1 S SAD SBC

 Trong

 

:ABCD J AD BC

 

     

J AD SAD

J SAD SBC

J BC SBC







   









 Từ

       

12,.SJ SAD SBC  

. Tìm giao điểm

của

và

 

ADM

 Tìm

 

N SC ADM

 Ta có:

   

ADM AJM

 Trong

 

:.SBJ N MJ SC

 

N SC

N SC ADM

N MJ ADM







   









. Xác định thiết diện của hình chóp

.S ABCD

khi

cắt bởi

 

CDM



   

 

M SAB CDM

AB CD

AB SAB

CD CDM

















   

// //SAB CDM Mx AB CD  

 Trong

 

:SAB

Kẻ

// // , .Mx AB CD P Mx SA

 Ta có:

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 100

Biên So

ạn: LÊ MINH TÂM

   

CDM ABCD CD

CDM SBC CM

CDM SAB PM

CDM SAD PD

CDM SCD CD



























Thiết diện cần tìm là

.CDPM

. Chứng minh

// // .SI AB CD

 Ta có:

     

1 S SAB SCD

 

     

I AM SAB

I AM DN I SAB SCD

I DN SCD







     









 Từ

       

12, SI SAD SCD  

 Ta có:

   

 

// //

SAD SCD SI

AB CD

SI AB CD

AB SAB

CD SCD



















 Bài 07.

Cho hình chóp

.S ABCD

, có đáy

ABCD

là hình bình hành tâm

. Gọi

, MN

lần lượt là trung

điểm của

và

. Chứng minh rằng :

.

   

//OMN SBC

. Mặt phẳng

 

qua

và song song

 

SAD

. Tìm thiết diện của

 

với hình chóp và xác

định hình tính của thiết diện.

. Giả sử

AS AD

AB AC

. Gọi

lần lượt là phân giác trong của tam giác

ACD

và

SAB

. Chứng minh

 

//EF SAD

Lời giải

.

   

//OMN SBC

 Vì

và

lần lượt là đường trung bình

của

ASC

và

DBC

 Nên

//MO SC

và

//ON BC

 

// ( ) //MO SC SBC MO SBC

 

// ( ) //ON BC SBC ON SBC

 Ta có:

   

// , //

( ), ( )

MO SBC ON SBC

MO ON O OMN SBC

MO OMN ON OMN





  









. Tìm thiết diện của

 

với hình chóp và xác định hình tính của thiết diện.

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 101

Biên So

ạn: LÊ MINH TÂM



     

// //SAD 

với



     

// // DSS d SCDD   

với

qua

và

d SC P

 Trong

 

ABCD

, kẻ

//Nx AD

Nx AB R









 Trong

 

SAB

, kẻ

//Ry AS

Ry SB Q









Nối

với

ta được thiết diện là tứ giác

NPQR

 Ba mặt phẳng phân biệt

 

ABCD

và

 

SBC

cắt nhau theo ba giao tuyến

và

. Mà

// //NR AD BC

nên

//NR PQ

hay thiết diện

NPQR

là hình thang.

. Chứng minh

 

//EF SAD

 Sử dụng tính chất đường phân giác, ta có

ED AD AS FS

EC AC AB FB

   

tồn tại duy nhất bộ ba

mặt phẳng song song lần lượt chứa

và

 Một trong ba mặt phẳng đó là

 

SAD

. Do đó

 

//EF SAD

 Bài 08.

Cho hình chóp

.S ABCD

, có đáy

ABCD

là hình thang,

2// ,AB CD AB CD

. Gọi

là trung

điểm của

và

là điểm thuộc cạnh

thỏa

2AP SP

. Tìm giao tuyến của hai mặt phẳng

 

SBA

và

 

SCD

. Tìm giao điểm

của

và mặt phẳng

 

SDC

. Tìm giao điểm

của

và mặt phẳng

 

PMD

. Tính

Lời giải

. Tìm giao tuyến của

 

SBA

và

 

SCD

 Ta có

   

DS SB CA S 



   

S SCD S

AB CD

A SA C

B D SCD

















   

// //SCD Sx AB CDSBA 

. Tìm giao điểm

của

và

 

SDC

 Trong

 

SAB

AM Sx I

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 102

Biên So

ạn: LÊ MINH TÂM

 Khi đó

 

I AM

I AM SC

I Sx SCD







  









. Tìm giao điểm

của

và mặt phẳng

 

PMD

. Tính

 Trong

 

SAB

, kéo dài

cắt

tại

, khi đó

 

K PMD

 Trong

 

ABCD

, kẻ đường thẳng

cắt

tại

 Khi đó

là điểm cần tìm.

 Ta có

EC DC

EB BK



 Kẻ

//BH AP

, ta có

1 1 1

2 2 2

BH KB BH EC

BH SP BK AB

AP AK AP EB

         

 Bài 09.

Cho hình chóp

.S ABCD

, có đáy

ABCD

là hình bình hành. Gọi

lần lượt là trung điểm

và

. Chứng minh

   

//IJK SAD

. Từ đó suy ra

 

//JK SAD

.

là một điểm trên

. Mặt phẳng

 

qua

và song song

 

SAB

cắt

và

lần lượt tại

và

. Hỏi

MNPQ

là hình gì?

Lời giải

. Chứng minh

   

//IJK SAD

. Từ đó suy ra

 

//JK SAD

 Vì

và

lần lượt là đường trung bình của

ASB

và

SBC

 Nên

//IJ SA

và

// // IK BC IK AD

   

// //IJ SA SAD IJ SAD

   

// // //IK BC AD SAD IK SAD

 Ta có

 

( ), ( ),

IJ SAD

IK SAD

IJ IJK IK IJK IJ IK I









   



( )//( )IJK SAD

. Suy ra

 

//JK SAD

. Hỏi

MNPQ

là hình gì?



     

//P SAB P

song song với

, và



     

// // BP AB P ABCD dA 

với

qua

 Trong

 

ABCD

, kẻ

//MN AB

MN BC N









 Trong

 

SBC

, kẻ

//Ny SB

Ny SC P









Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 103

Biên So

ạn: LÊ MINH TÂM

 Trong

 

SAD

, kẻ

//Mz SA

Mz SD Q









 Nối

với

ta được thiết diện là tứ giác

MNPQ

 Ba mặt phẳng phân biệt

 

SCD

 

và

 

ABCD

cắt nhau theo ba giao tuyến

và

. Mà

//MN CD

nên

//MN PQ

hay thiết diện

MNPQ

là hình thang.

 Bài 10.

Cho hình lập phương

.ABCD AB C D

   

cạnh

. Gọi

;;M N P

lần lượt là trung điểm của các cạnh

;;AB B C DD

  

. Chứng minh

 

MNP

song song với các mặt

 

AB D



và

 

BDC



. Xác định thiết diện của hình lập phương với mặt phẳng

 

MNP

. Thiết diện đó là hình gì ?

Tính diện tích của nó.

Lời giải

. Chứng minh

 

MNP

song song với các mặt

 

AB D



và

 

BDC



 Ta có

'PD MA

PD MB

  



,,MP AD DB



cùng song song với

 

(theo

định lý Ta-let đảo)



 

// //

, ( )

D B DB

AD AB D B D AB D













      







     

// //AB D MP AB D

   



 Tương tự,

 

//MN AB D



Suy ra

   

//MNP AB D



 Mặt khác

   

// .

BD B D

BDC AB D

BC AD





  









Vậy

     

// //MNP AB D BDC

  

. Xác định thiết diện của hình lập phương với mặt phẳng

 

MNP

 Gọi

,,E F K

lần lượt là trung điểm của các cạnh

,,C D AD BB

  

, ta có:



 

   

// //

NE B D NE AB D

N MNP

MNP AB D



   

















 

NE MNP

Tương tự

và

cũng chứa trong

 

MNP

 Suy ra thiết diện của

 

MNP

với hình lập

phương là lục giác

MNKEPF

Hình học 11 – Chương 02. QUAN HỆ SONG SONG

Trang 104

Biên So

ạn: LÊ MINH TÂM

 Hình tính thiết diện:



là đường trung bình

BCD

  

nên

NE B D





 Tương tự

cạnh của thiết diện đều bằng

 Mặc khác

// , // , //NE MF EP MK PF KN

 Vậy thiết diện là lục giác đều cạnh

Diện tích thiết diện:

 Gọi

là tâm đường tròn ngoại tiếp của thiết diện thì tam giác

ONE

là tam giác đều,

 Suy ra diện tích của thiết diện:

6 3 2 3 3 3

4 2 4 4

OEN

NE a a



   





------------------ HẾT ------------------

Bấm Tải xuống để xem toàn bộ.

| 1/104

| | Tải xuống

Preview text:

LÊ MINH TÂM Chuyên Đề. QUAN HỆ SONG SONG
TÀI LIỆU LƯU HÀNH NỘI BỘ
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
※※※MỤC LỤC※※※
BÀI 01. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG & MẶT PHẲNG .................................................. 4
I. KHÁI NIỆM MỞ ĐẦU ................................................................................................................................ 4
II. CÁC TÍNH CHẤT THỪA NHẬN ............................................................................................................... 6
III. CÁC CÁCH XÁC ĐỊNH MẶT PHẲNG .................................................................................................... 7
IV. HÌNH CHÓP VÀ TỨ DIỆN ...................................................................................................................... 7
V. CÁC DẠNG TOÁN. ................................................................................................................................... 8
 Dạng 01. XÁC ĐỊNH GIAO TUYẾN CỦA HAI MẶT PHẲNG PHÂN BIỆT...................................... 8
 Dạng 02. TÌM GIAO ĐIỂM CỦA ĐƯỜNG THẲNG D VÀ MẶT PHẲNG (P). ............................... 10 Bi
 Dạng 03. CHỨNG MINH 03 ĐIỂM THẲNG HÀNG VÀ 03 ĐƯỜNG THẲNG ĐỒNG QUI.......... 11 ê
 Dạng 04. THIẾT DIỆN CỦA HÌNH H KHI BỊ CẮT BỞI MẶT PHẲNG (P). .................................. 12 n So
VI. BÀI TẬP RÈN LUYỆN. .......................................................................................................................... 12 ạ
BÀI 02. HAI ĐƯỜNG CHÉO NHAU – HAI ĐƯỜNG SONG SONG ............................................ 38 n:
I. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG TRONG KHÔNG GIAN: ........................................ 38 LÊ MINH
II. TÍNH CHẤT: ............................................................................................................................................ 38
III. CÁC DẠNG BÀI TẬP. ............................................................................................................................. 41
 Dạng 01. CHỨNG MINH HAI ĐƯỜNG THẲNG SONG SONG. .................................................... 41
 Dạng 02. TÌM GIAO TUYẾN CỦA HAI MẶT PHẲNG CHỨA HAI ĐƯỜNG THẲNG SONG TÂM
SONG. ..................................................................................................................................................... 44
 Dạng 03. CHỨNG MINH HAI ĐƯỜNG THẲNG CHÉO NHAU. ................................................... 48
 Dạng 04. CHỨNG MINH MỘT ĐƯỜNG THẲNG DI ĐỘNG LUÔN ĐI QUA MỘT ĐIỂM CỐ
ĐỊNH. ....................................................................................................................................................... 50
BÀI 03. ĐƯỜNG THẲNG & MẶT PHẲNG SONG SONG............................................................. 52
I. VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN .................. 52
II. TÍNH CHẤT: ............................................................................................................................................ 52
III. CÁC DẠNG BÀI TẬP. ............................................................................................................................ 55
 Dạng 01. CHỨNG MINH ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG. ........................... 55
 Dạng 02. TÌM GIAO TUYẾN CỦA HAI MẶT PHẲNG CHỨA MỘT ĐƯỜNG THẲNG SONG
SONG VỚI MẶT PHẲNG. . ..................................................................................................................... 61
BÀI 04. HAI MẶT PHẲNG SONG SONG ......................................................................................... 69
I. ĐỊNH NGHĨA: ........................................................................................................................................... 69 Trang 2
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
II. TÍNH CHẤT: ............................................................................................................................................ 69
III. ĐỊNH LÝ THALES TRONG HÌNH HỌC KHÔNG GIAN: ................................................................... 72
IV. HÌNH LĂNG TRỤ VÀ HÌNH HỘP: ...................................................................................................... 73
V. HÌNH CHÓP CỤT: ................................................................................................................................. 75
III. CÁC DẠNG BÀI TẬP. ............................................................................................................................ 75
 Dạng 01. CHỨNG MINH HAI MẶT PHẲNG SONG SONG. ......................................................... 75
 Dạng 02. GIAO TUYẾN CỦA 2 MẶT PHẲNG CÓ 1 MẶT PHẲNG SONG SONG VỚI MẶT THỨ
BA . ............................................................................................................................................................ 79
 Dạng 03. HÌNH LĂNG TRỤ - HÌNH HỘP . ................................................................................... 84
 Dạng 04. ĐỊNH LÝ THALES TRONG KHÔNG GIAN . ................................................................ 90
BÀI 05. TỔNG ÔN TẬP CHƯƠNG ................................................................................................... 94 TÂM LÊ MINH n:ạ n SoêBi Trang 3
Hình học 11 – Chương 02. QUAN HỆ SONG SONG BÀI 01
ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG & MẶT PHẲNG ☆☆★☆☆
I. KHÁI NIỆM MỞ ĐẦU
1.1. Mặt phẳng Bi ê
– Hình ảnh mô phỏng trong thực tế ví dụ: mặt gương phẳng, mặt hồ phẳng lặng được xem n
là một phần của mặt phẳng. So  Chú ý : ạ
– Mặt phẳng ko có bề dày và không bị giới hạn. n:
– Cách biểu diễn mặt phẳng lên mặt phẳng hình học: LÊ MINH
dùng hình bình hành hay một góc và ghi tên của mặt
phẳng vào một góc của hình.
– Kí hiệu mặt phẳng: mpP , mpQ , .
 mp ,mp ,
1.2. Điểm thuộc mặt phẳng TÂM
Cho điểm A và mp  . Khi đó:
– Điểm A thuộc   hay A nằm trên   hay   chứa
A hoặc đi qua A .
 Kí hiệu: A 
– Điểm A nằm ngoài   hay   không chứa A hoặc không đi qua A .
 Kí hiệu: A .
1.3. Hình biểu diễn của một hình không gian.
Khi vẽ một hình không gian lên bảng, lên giấy ta tuân thủ nguyên tắc sau:
 Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.
 Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, hai
đường thẳng cắt nhau là hai đường thẳng cắt nhau.
 Giữ nguyên quan hệ thuộc giữa điểm với đường thẳng.
 Nét liền để vẽ đường nhìn thấy, nét đứt đọa để vẽ đường bị che khuất.
 Bảo toàn tỷ lệ giữa các đoạn thẳng song song, các đoạn thẳng cùng nằm trên một
đường thẳng. Không bảo toàn về góc.
 Một tam giác bất kỳ đều được coi là hình biểu diễn của tam giác có dạng tùy ý( vuông, cân, đều). Trang 4
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Hình bình hành là hình biểu diễn cho hình bình hành có dạng tùy ý (hình bình hành ,
vuông, chữ nhật, thoi) và kèm theo kí hiệu vuông, bằng nhau nếu là hình đặc biệt.
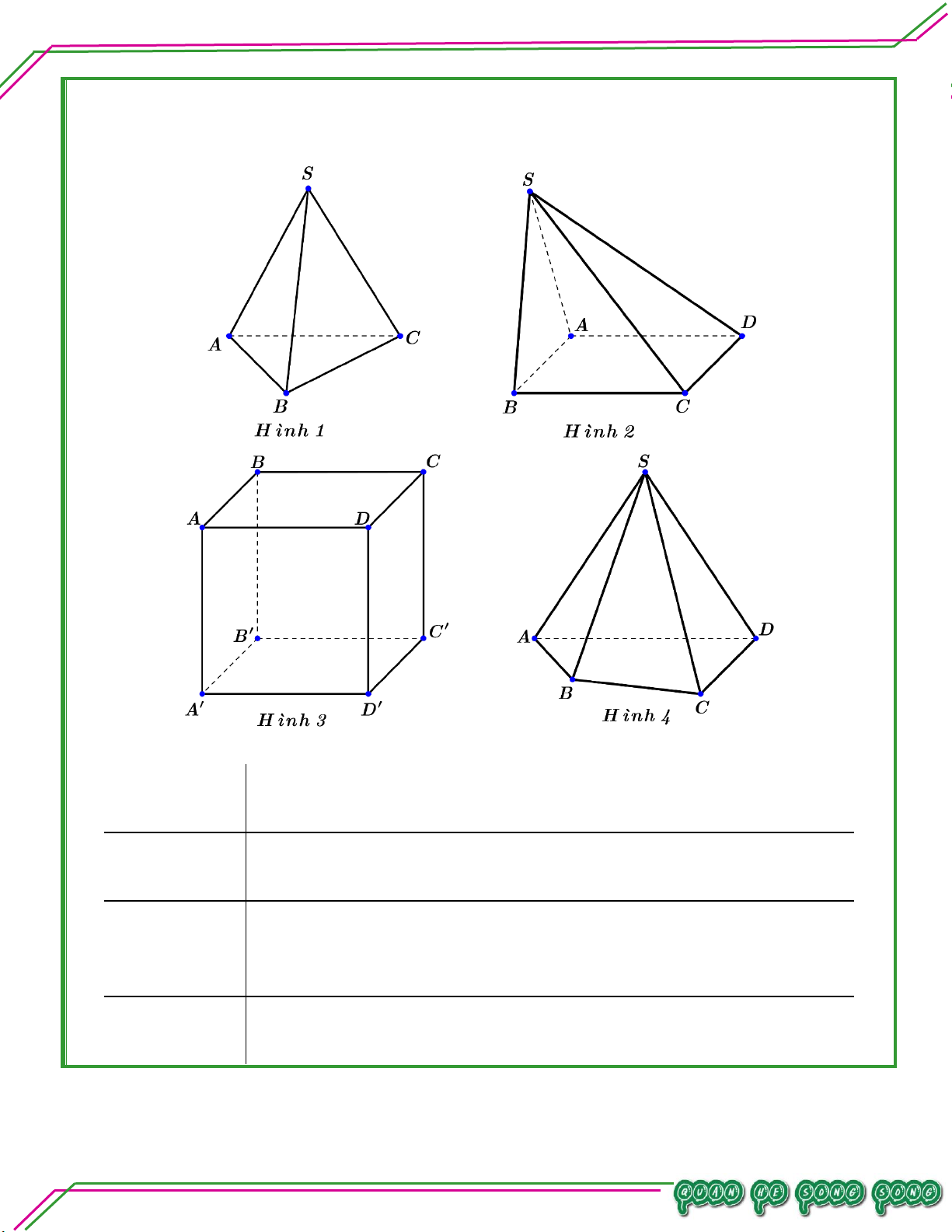
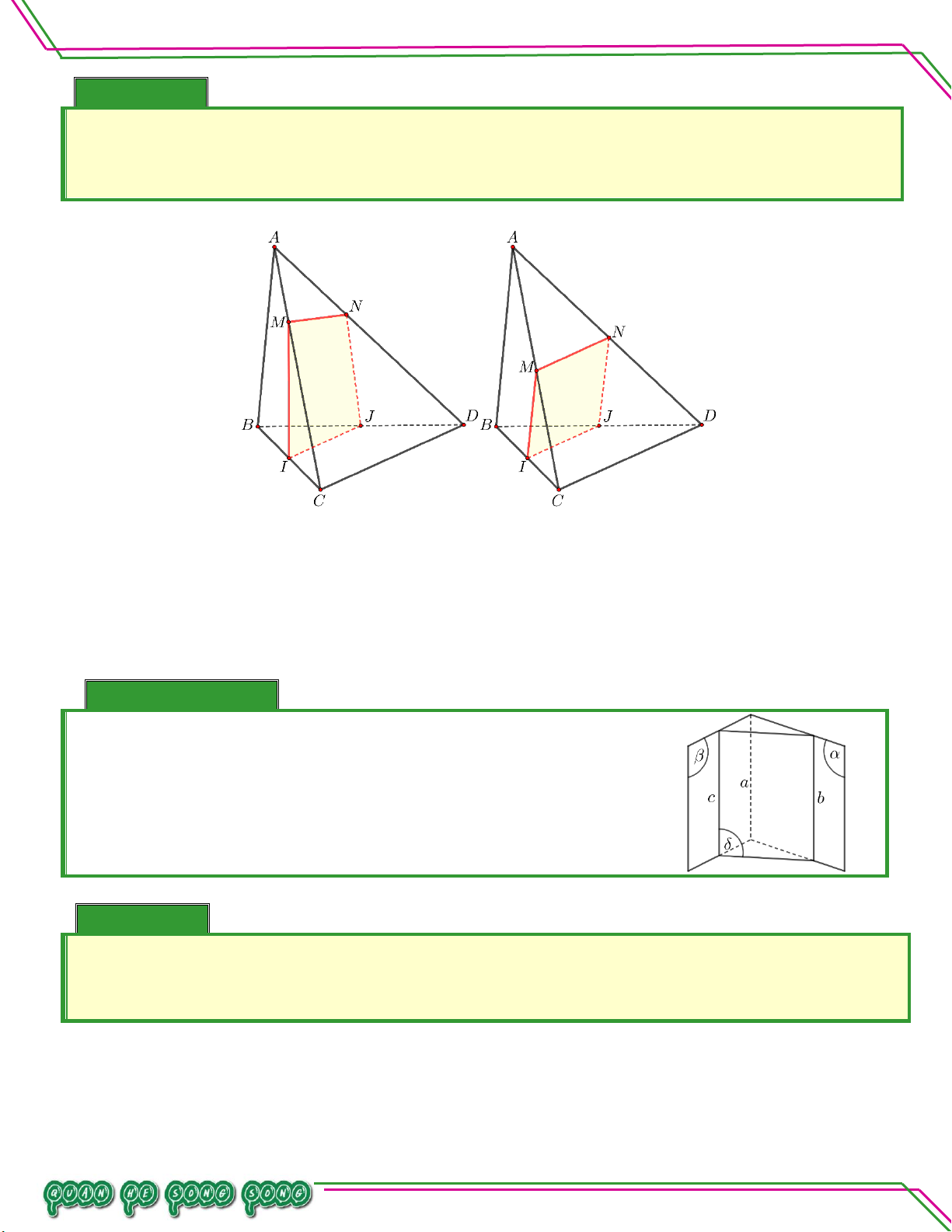
 Cho các hình 1 – 2 – 3 – 4 được đánh dấu như bên dưới. TÂM LÊ MINH n:ạ n Soê
 Hãy kể tên các mặt phẳng thấy hay không thấy trong các hình 1, 2, 3, 4. Bi
– Các mặt phẳng nhìn thấy là: SAB ,SBC. Hình 1:
– Các mặt phẳng không nhìn thấy là: SAC ,ABC .
– Các mặt phẳng nhìn thấy là: SBC ,SCD . Hình 2:
– Các mặt phẳng không nhìn thấy là: SAB ,SAD ,ABCD .
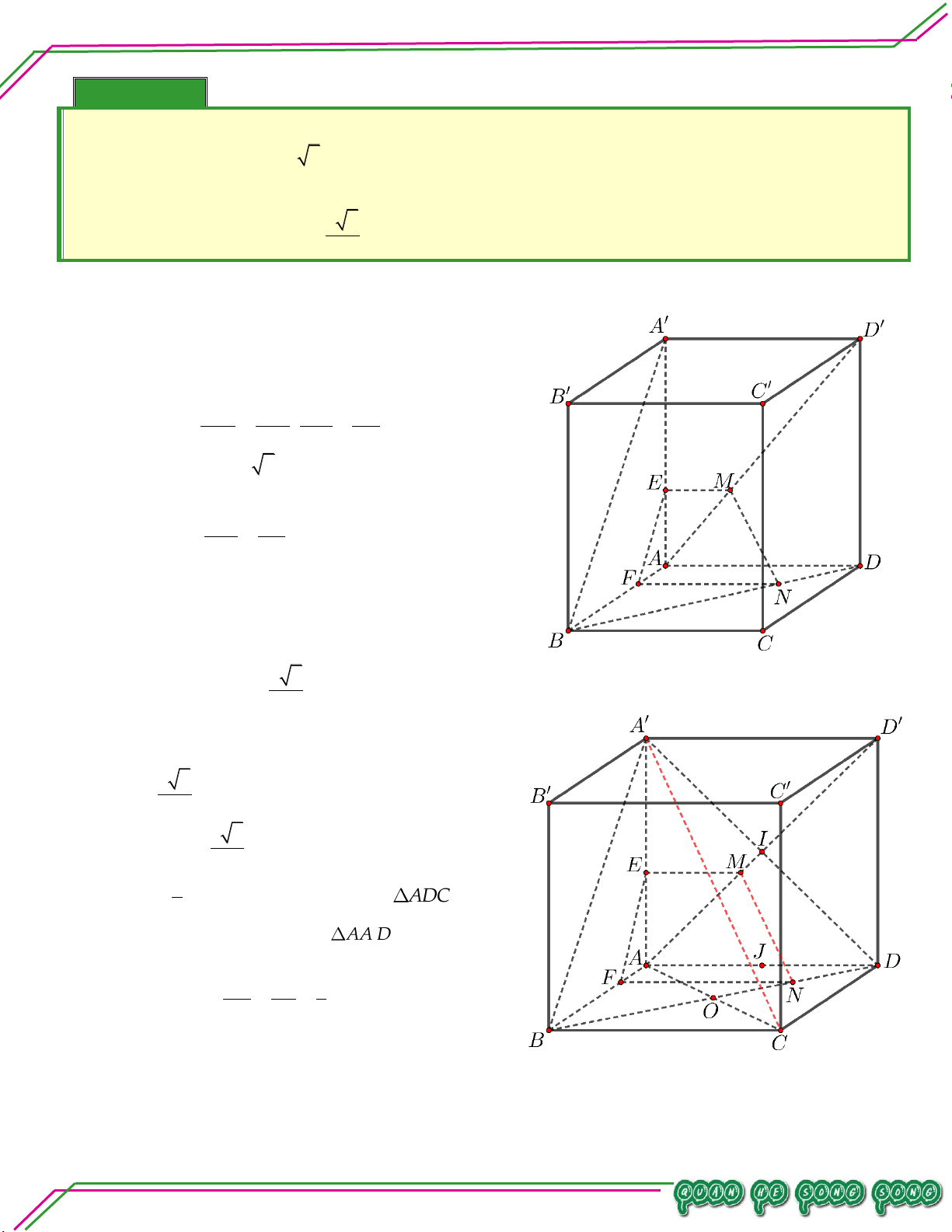
– Các mặt phẳng nhìn thấy là: ABCD ,ADD A  ,DCC D   . Hình 3:
– Các mặt phẳng không nhìn thấy là: A B  C  D  ,ABB A  ,BCC B   .
– Các mặt phẳng nhìn thấy là: SAB,SBC ,SCD . Hình 4:
– Các mặt phẳng không nhìn thấy là: SAD ,ABCD . Trang 5
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
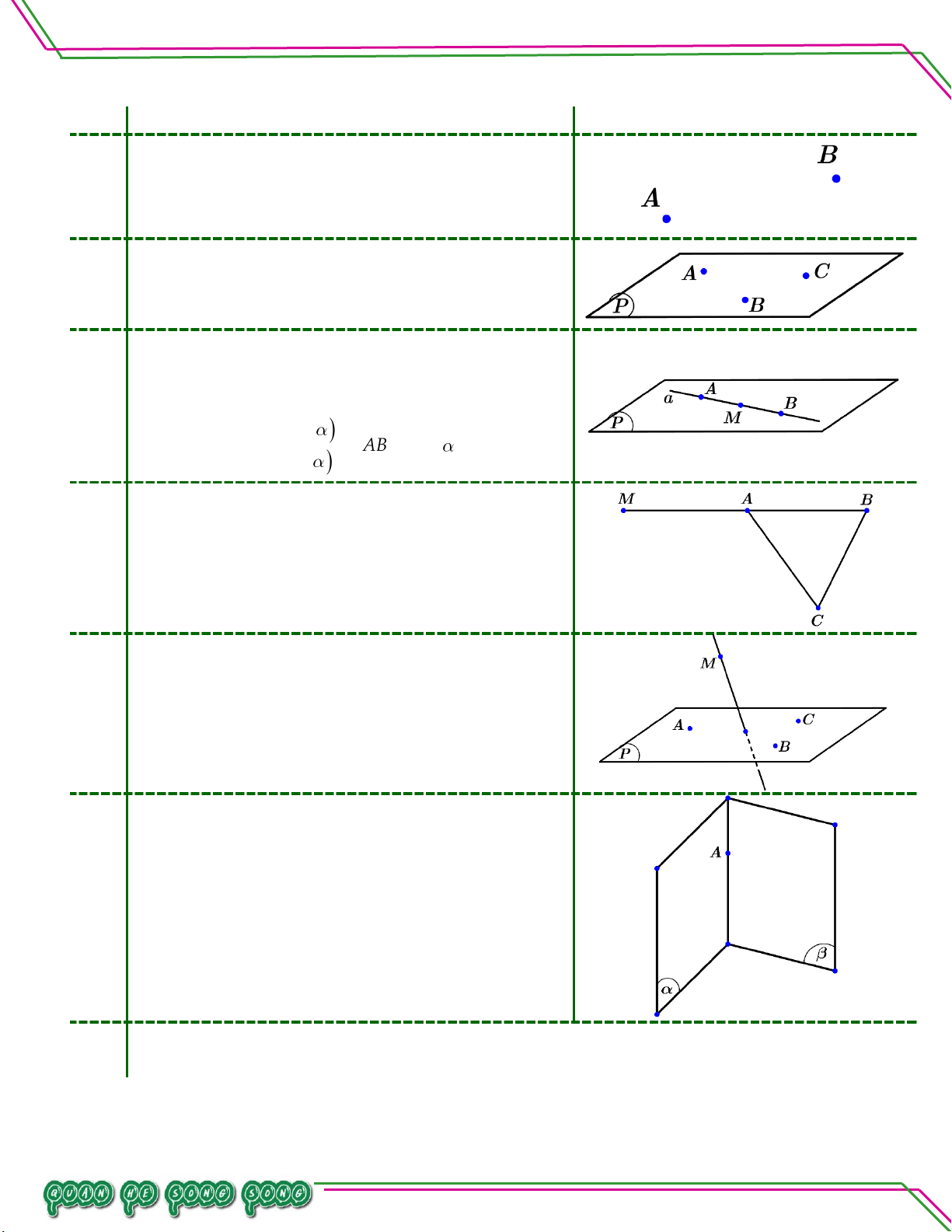
II. CÁC TÍNH CHẤT THỪA NHẬN TÍNH CHẤT HÌNH MINH HỌA
01  Có một và chỉ một đường thẳng đi qua 02 điểm phân biệt.
 Có một và chỉ một mặt phẳng đi qua 3 điểm Bi
02 không thẳng hàng. ê
 Kí hiệu: ABC . n So
 Nếu một đường thẳng có hai điểm phân biệt
thuộc một mặt phẳng thì mọi điểm của đường ạn:
03 thẳng đều thuộc mặt phẳng đó. Aa     LÊ MINH     B  a     AB a  
 Điểm M và đường thẳng AM đều nằm trong
ABCvì M thuộc đường thẳng AB còn AM
04 trùng với đường thẳng AB mà AB nằm trong TÂM ABC.
05  Tồn tại 04 điểm không cùng thuộc 01 mặt phẳng.
 Nếu hai mặt phẳng phân biệt có 01 điểm
chung thì chúng còn có điểm chung khác nữa.
 Suy ra: Nếu hai mặt phẳng phân biệt có một
06 điểm chung thì chúng có một đường thẳng
chung chứa tất cả các điểm chung của hai mặt phẳng.
 Đường thẳng chung đó gọi là giao tuyến của hai mặt phẳng.
07  Trong mỗi mặt phẳng, các kết quả của hình học phẳng đều đúng. Trang 6
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
III. CÁC CÁCH XÁC ĐỊNH MẶT PHẲNG
MẶT PHẲNG ĐƯỢC XÁC ĐỊNH HÌNH MINH HỌA
 Khi biết nó đi qua 3 điểm không thẳng 01 hàng cho trước.
 Kí hiệu: mpABC hoặcABC .
 Khi biết nó đi qua một đường thẳng và
02 một điểm không nằm trên đường thẳng đó.
 Kí hiệu: mp ;
d A hoặc mp ; A d .
 Khi biết nó đi qua hai đường thẳng cắt 03 nhau.
 Kí hiệu: mp ;ab hoặc mp ; b a .
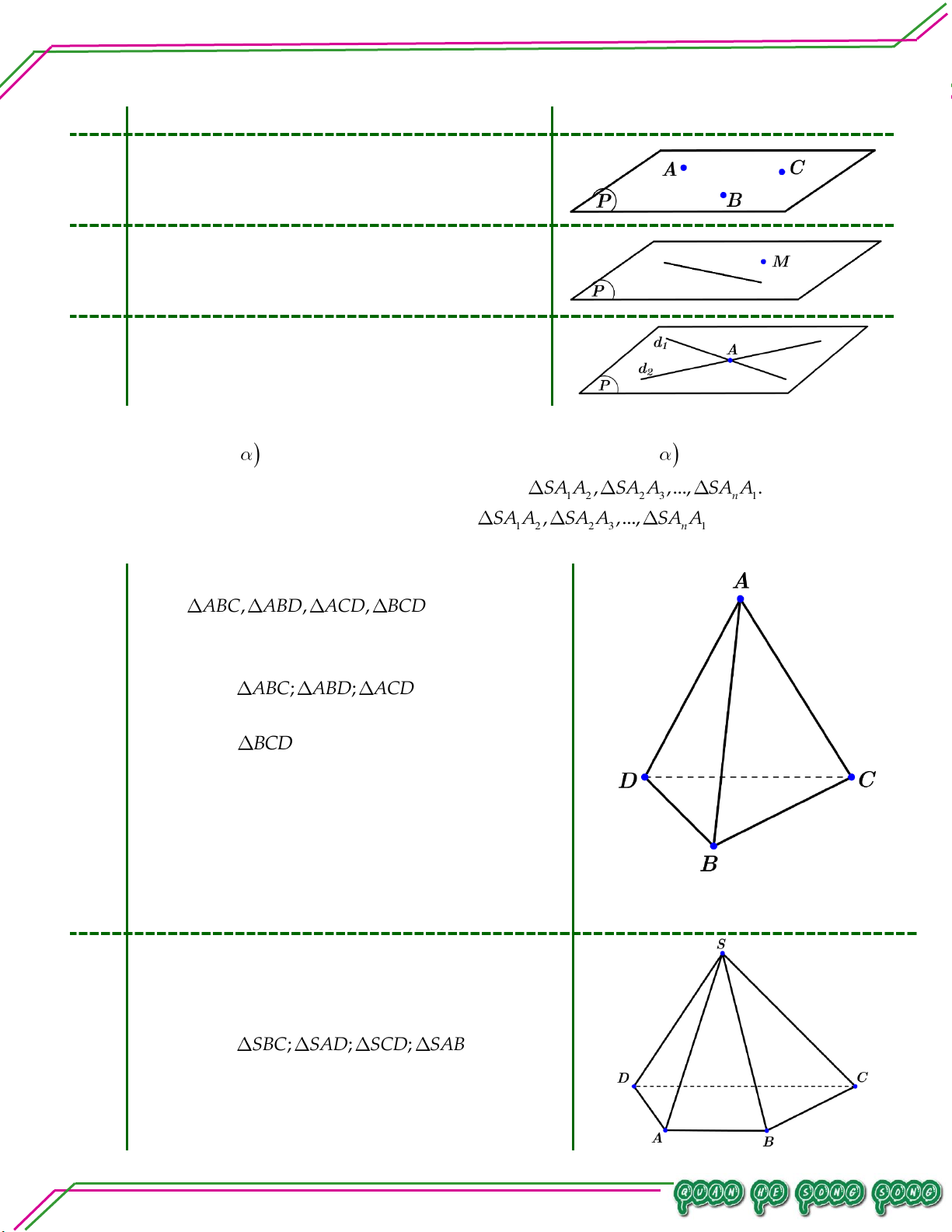
IV. HÌNH CHÓP VÀ TỨ DIỆN
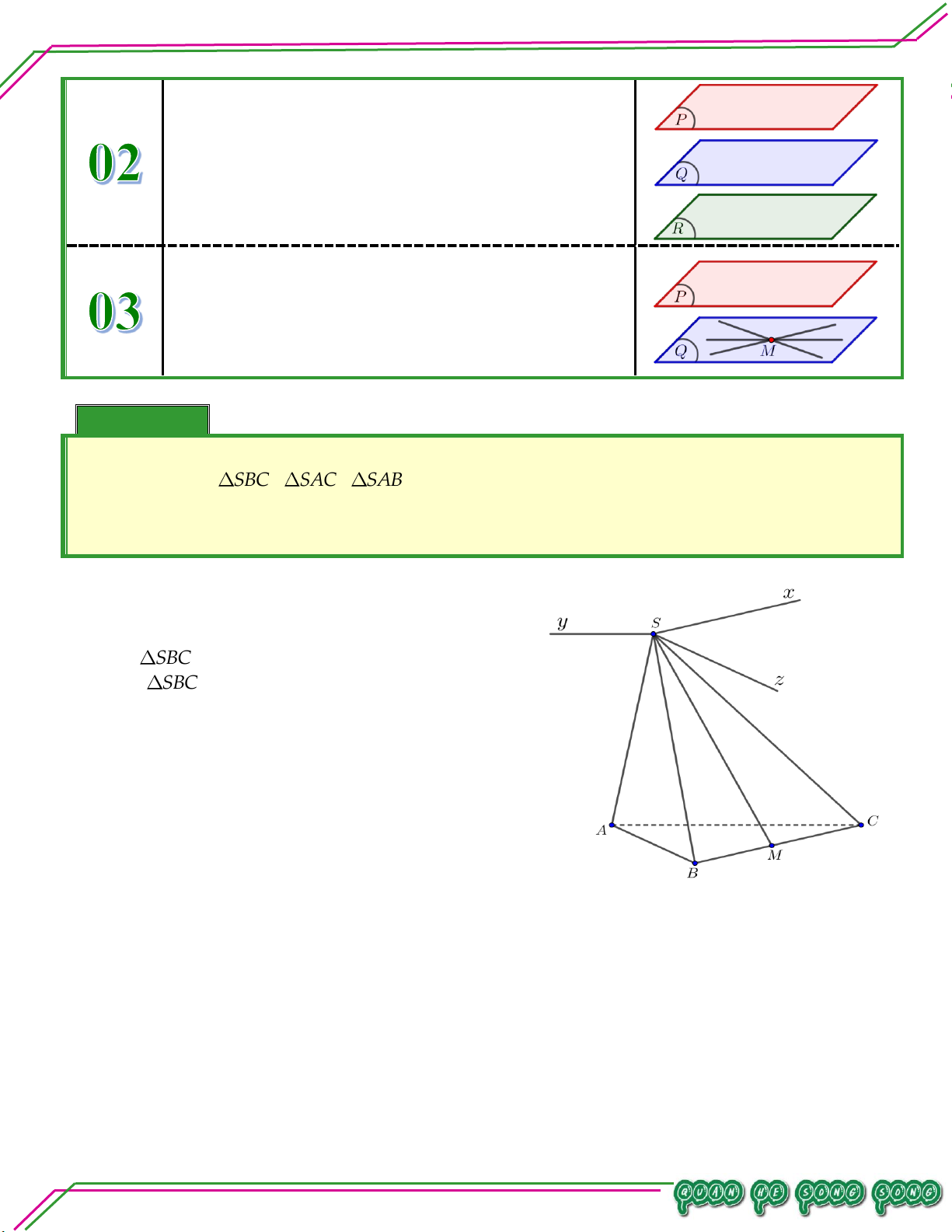
TÂM Trong mặt phẳng   cho đa giác lồi AA ...A . Lấy S nằm ngoài  . 1 2 n
 Lần lượt nối S với A , A ,..., A được n tam giác: SA A , SA A ,..., SA A . 1 2 n 1 2 2 3 n 1
 Hình gồm đa giác A A ...A và n tam giác: SA A , SA A ,..., SA A gọi là hình chop. 1 2 n 1 2 2 3 n 1  Kí hiệu: . S A A ...A . 1 2 n
 Hình tứ diện là hình được tạo thành từ bốn tam LÊ MINH giác
ABC, ABD, ACD, BCD trong đó A, n:
B,C, D không đồng phẳng. ạ
– Đỉnh: A, B,C, D
– Mặt bên: ABC; AB ; D ACD n So – Cạnh bên: A ; B AC; AD
ê 01 – Mặt đáy: BCD Bi
– Cạnh đáy: BC; B ; D CD
– Cặp cạnh đối diện: BC; AD và B ; D AC và A ; B DC .
– Đỉnh đối diện với mặt: đỉnh A đối diện 
BCD ; đỉnh B đối diện  ACD ; đỉnh C đối
 Lưu ý: Tứ diện đều là hình tứ diện
diện  ABD ; đỉnh D đối diện ABC .
có bốn mặt là các tam giác đều.
 Các mặt bên, cạnh bên, cạnh đáy của hình chóp . S ABCD.
02 – Mặt bên: SBC; SA ;D SC ;D SAB – Cạnh bên: S ; A S ; B SC;SD – Cạnh đáy: A ; B BC; A ; D CD Trang 7
Hình học 11 – Chương 02. QUAN HỆ SONG SONG V. CÁC DẠNG TOÁN.
 Dạng 01. XÁC ĐỊNH GIAO TUYẾN CỦA HAI MẶT PHẲNG PHÂN BIỆT.
 Giao tuyến của hai mặt phẳng phân biệt là đường thẳng chung (đường thẳng đi qua ít
nhất 2 điểm chung) của hai mặt phẳng đó.
Phương pháp giải  Ta thường gặp: Bi Giả thiết
M  d  d ; d  ; d  1 2 1   2   ê
Tình huống 01  n Kết luận M     So Giả thiết
M     ; N    
Tình huống 02 ạ Kết luận
    MN n: 
Kỹ thuật: Nối các đoạn hoặc kéo dài các đoạn thẳng có trong mặt phẳng để tìm điểm LÊ MINH
chung và chú ý nét vẽ đứt hoặc liền.  Ví dụ 01.
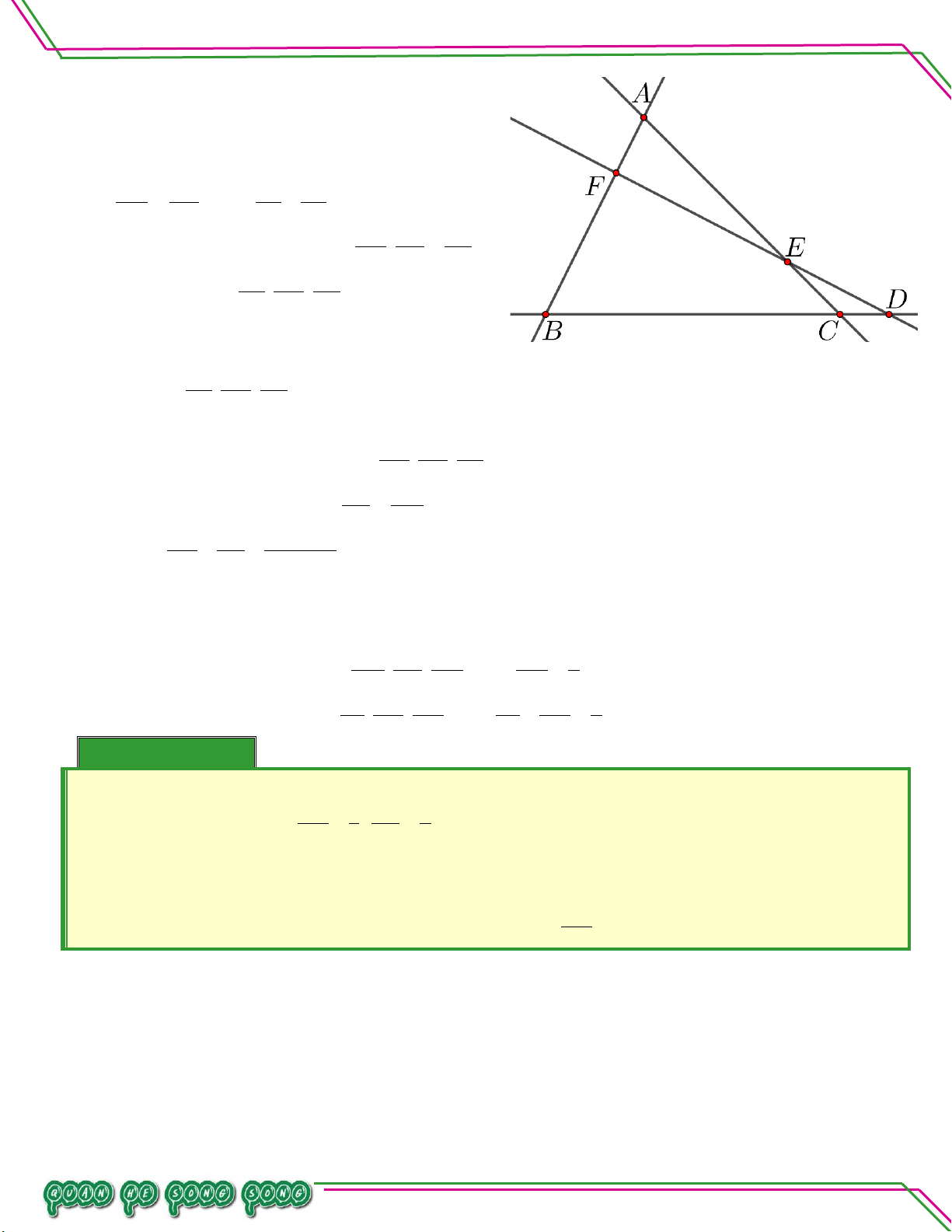
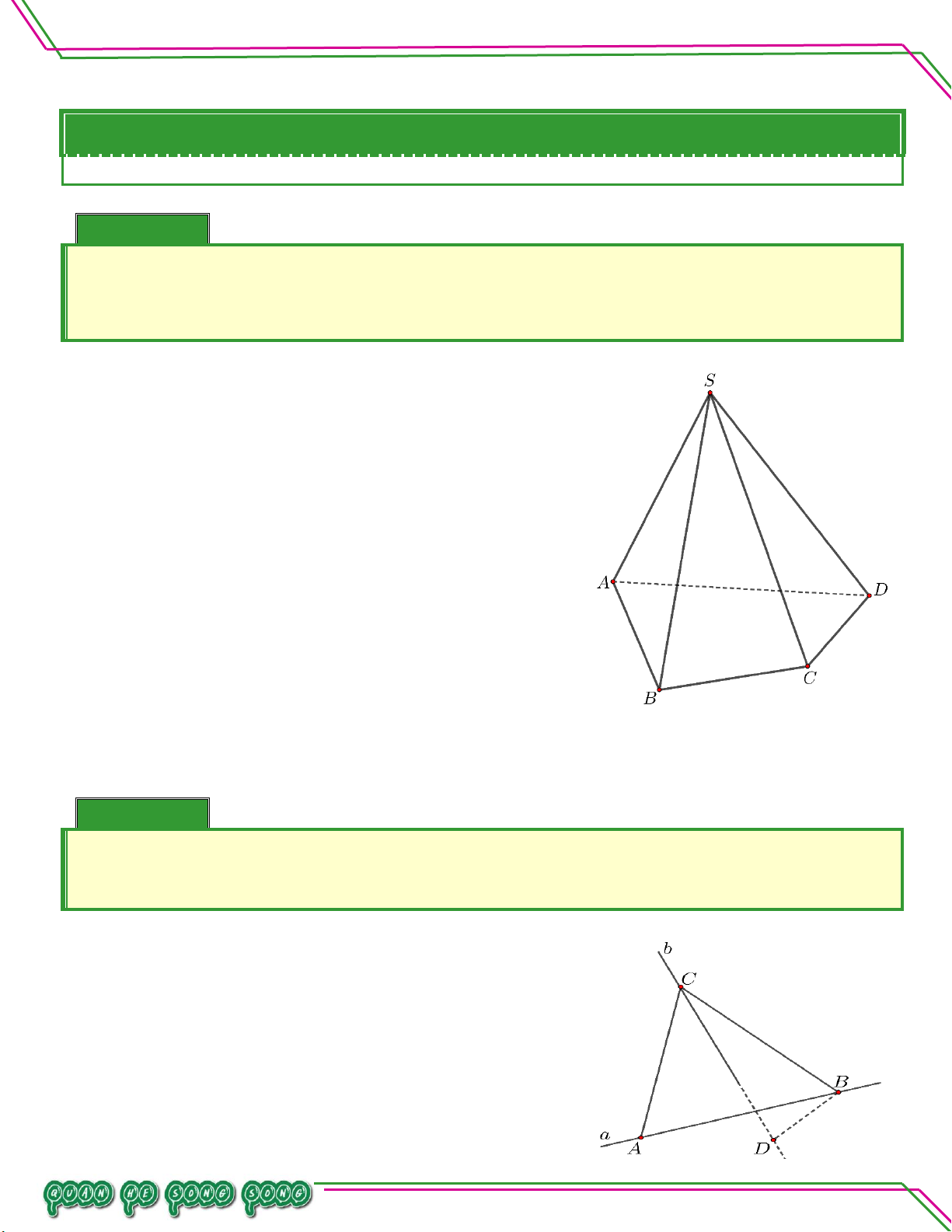
Cho S là một điềm không thuộc mặt phằng P chứa
tứ giác ABCD có AB không song song CD ; BC TÂM
không song song DA . Tìm giao tuyến của :
a. SAB SBC .
b. SAB SCD .
c. SAD SBC .
d. SAC SBD . Lời giải
a. Tìm giao tuyến SAB SBC .
Hai mặt phẳng (SA )
B ,(SBC) có SB chung. Suy ra SB là giao tuyến, Kí hiệu: (SA )
B  (SBC)  SB .
b. Tìm giao tuyến SAB SCD . Có: S(SA )
B (SBC)   1 .
Trong  ABCD có AB và CD không song song. Gọi F  ABCD .
F  AB, AB   SAB 
 F  SAB  SCD
F CD,CD   SCD     2 Từ  
1 ,2  SAB SCD  SF .
c. Tìm giao tuyến SAD SBC . Có: S(SA )
D (SBC)   1 . Trang 8
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
Trong  ABCD có AD và BC không song song. Gọi H  ADBC .
H  AD, AD   SAD 
 H  SAD  SBC
H  BC, BC   SBC     2 Từ  
1 ,2  SAD SBC  SH .
d. Tìm giao tuyến SAC SBD .
Có: SSAC SBD   1 .
Trong  ABCD có AC và BD không song song. Gọi O  AC BD. O
  AC, AC   SAC 
 O  SAC  SBD
O  BD, BD   SBD     2 Từ  
1 ,2  SAC SBD  SO .  Ví dụ 02. TÂM
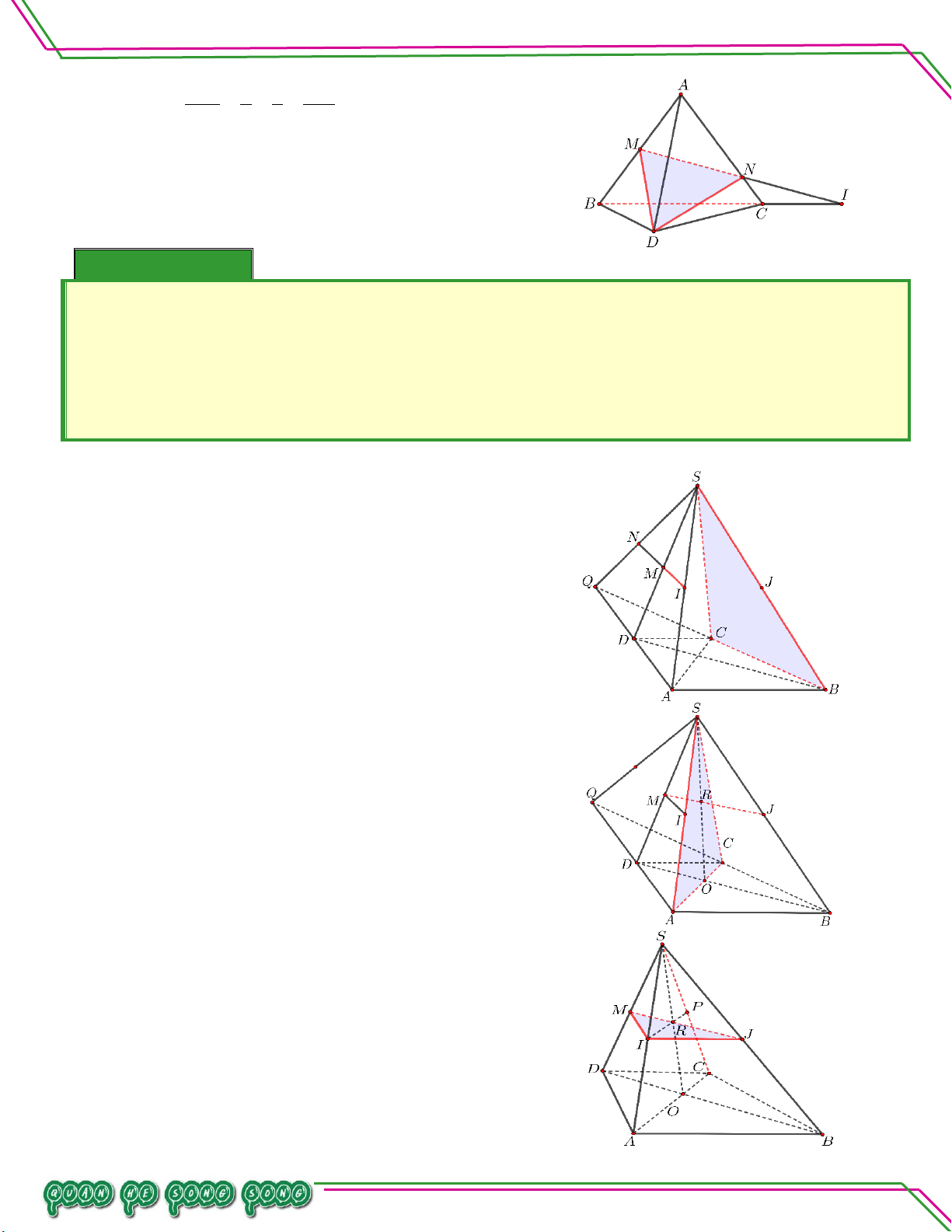
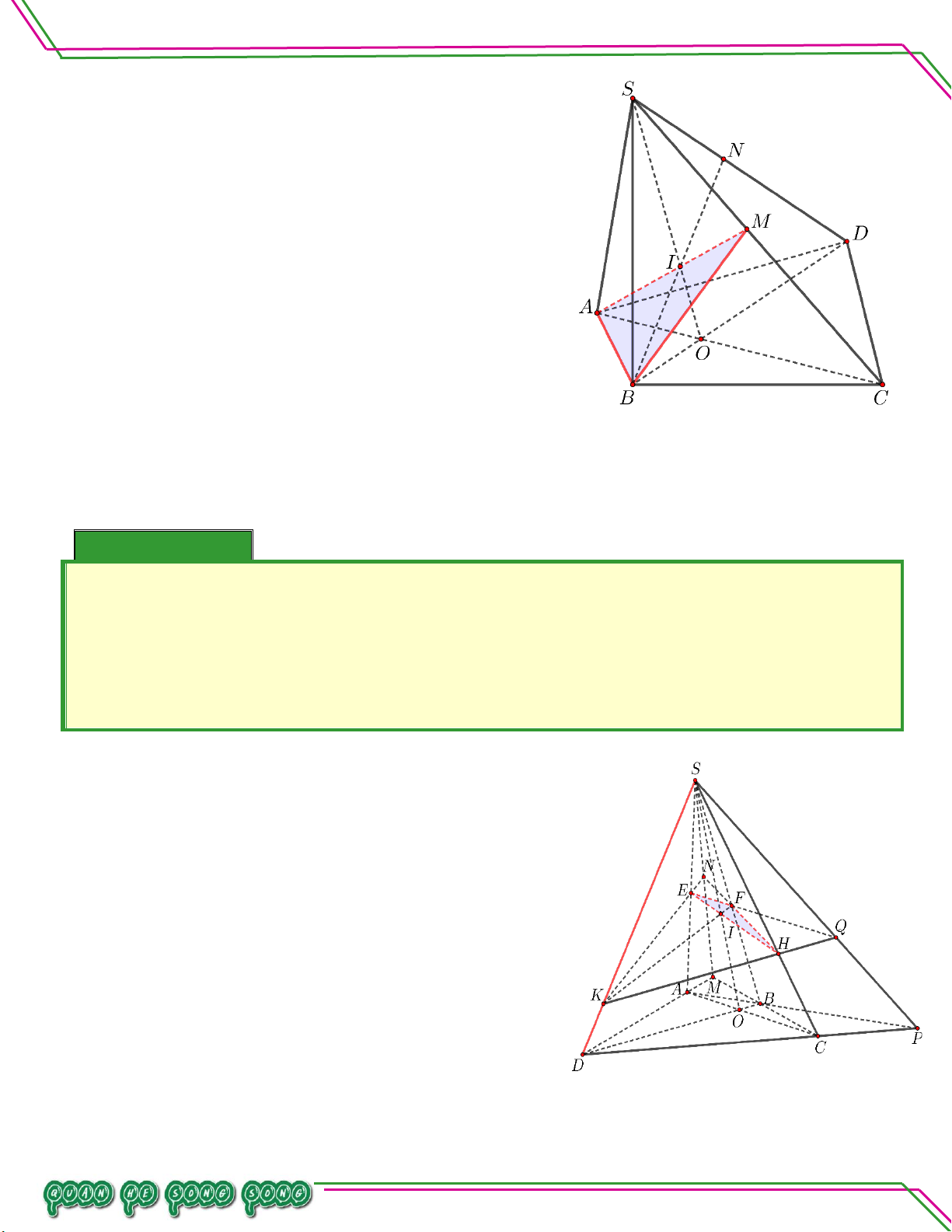
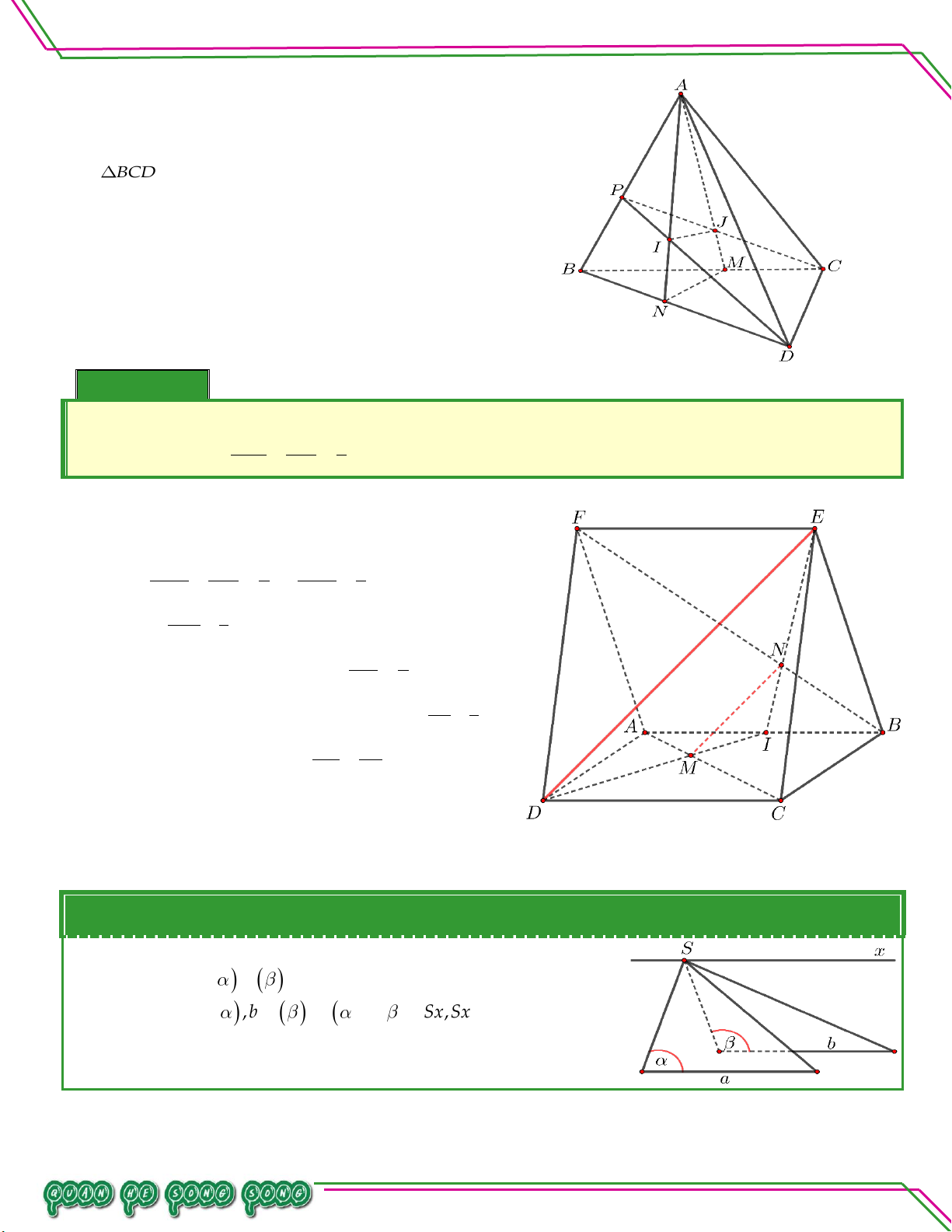
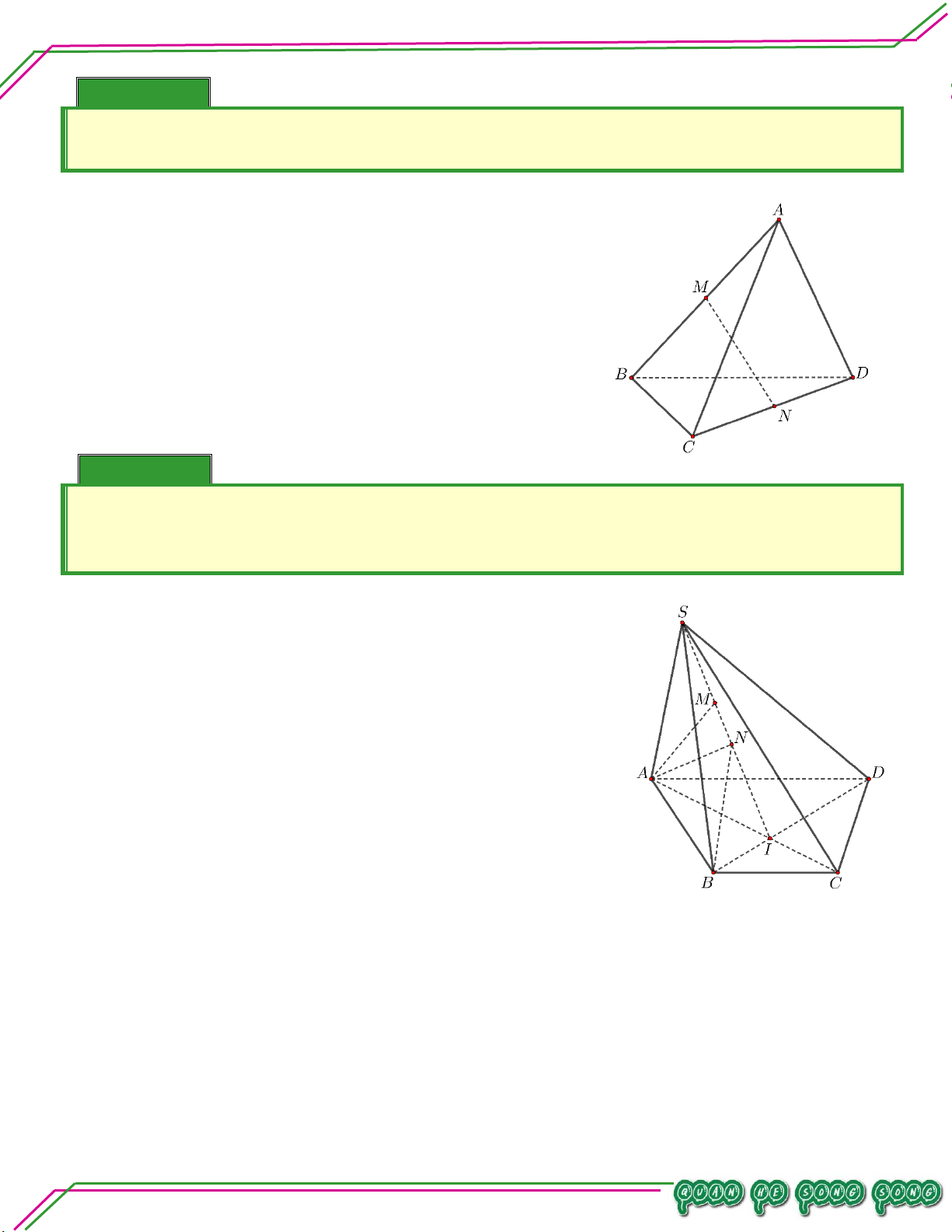
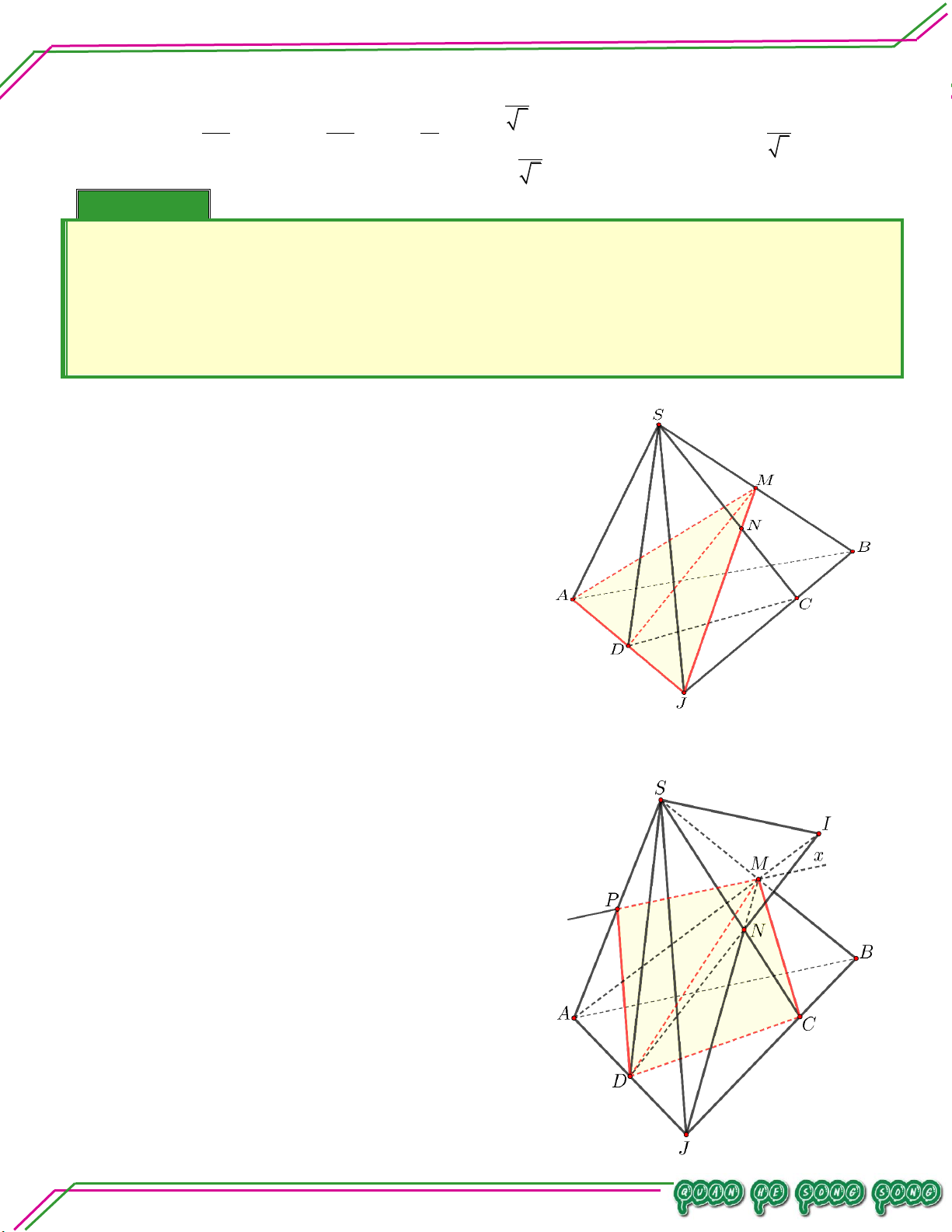
Cho tứ diện ABCD . Gọi I , J là các điềm lần lượt nằm trên 1 3
các cạnh AB, AD với AI  AB , AJ  JD . Tìm giao 2 2 tuyến của:
a. ACD CIJ . LÊ MINH
b. CIJ BCD . n:ạ n So ê Lời giải
Bi a. Tìm giao tuyến ACDCIJ. Có: C (AC )
D (CIJ)   1 .
J  AD, AD  ACD  J ACD CIJ 2 Từ  
1 ,2   ACD CIJ  CJ .
b. Tìm giao tuyến CIJ BCD .
Có: C CIJ BCD   1 .
Trong  ABD có BD và IJ không song song. Gọi M  BD  IJ .
M  BD,BD   BCD 
 M  BCD  CIJ
M  IJ, IJ   CIJ     2 Từ  
1 ,2  (CIJ) (BC ) D  CM Trang 9
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Dạng 02. TÌM GIAO ĐIỂM CỦA ĐƯỜNG THẲNG D VÀ MẶT PHẲNG (P).
Phương pháp giải
Bài toán: Tìm giao điểm của đường thẳng và mặt phẳng. Giả thiết
d  P , M d, M P Bi Kết luận
M  d  P ên So
 Ta có các trường hợp sau xảy ra. ạ
Trong P có sẵn đường thằng a cắt d tại M n:
Trường hợp 01
 Ta trình bày: a d  M,a  P  dP  M . LÊ MINH
Trong mặt phẳng   chưa có đường a cắt d . Khi đó
 Bước 1: Chọn mặt phằng phụ P chứa d .
 Bước 2: Tìm giao tuyến a của P và ( ).
 Bước 3: Trong P , cho a cắt d tại M, khi đó M thuộc d , M TÂM
thuộc a mà a chứa trong   . Vậy M là điểm cần tìm.
Trường hợp 02
 Ta trình bày:
 Chọn P chứa d .
 Tìm P   a .
 Trong P, ad  M M   d       a  
  d   M M a,  Ví dụ 03.
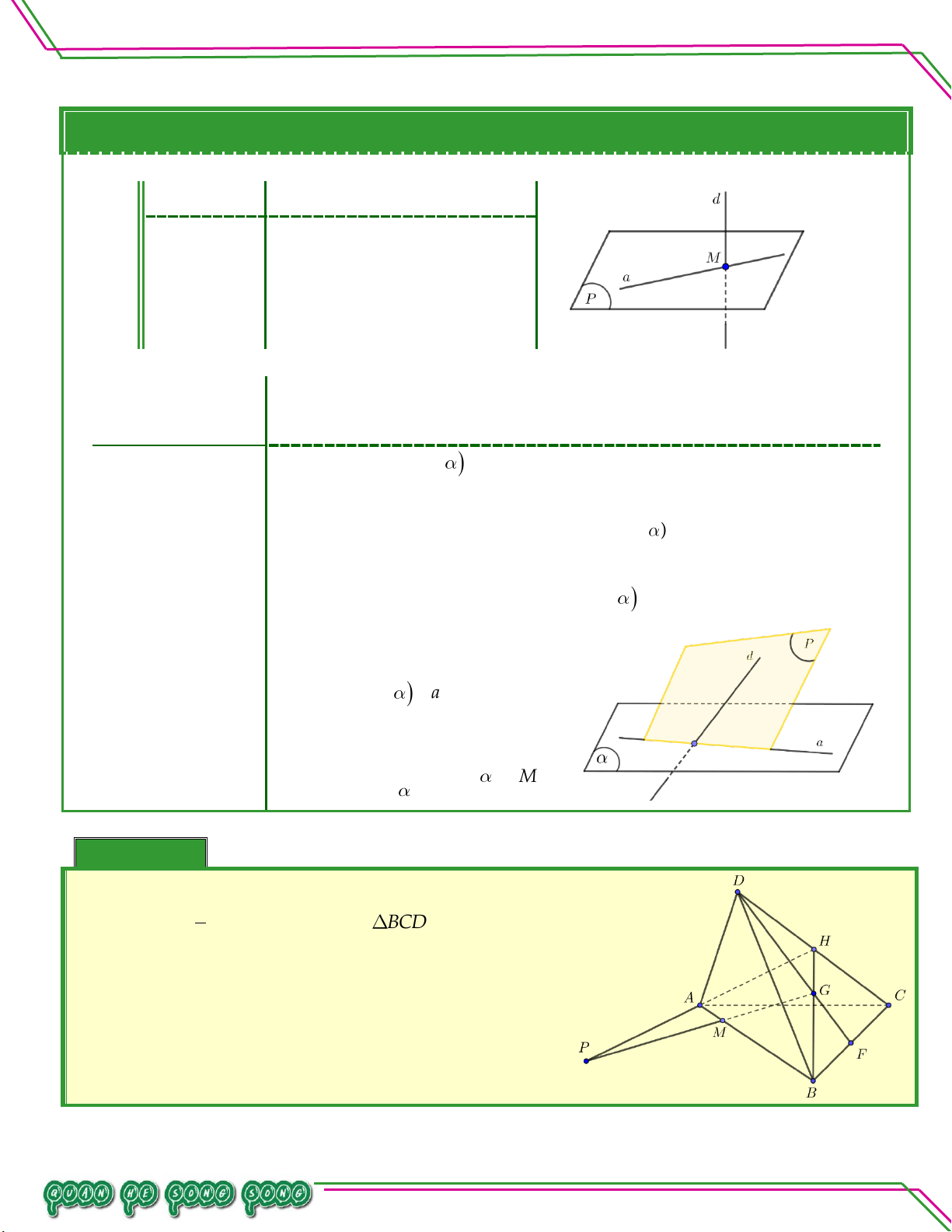
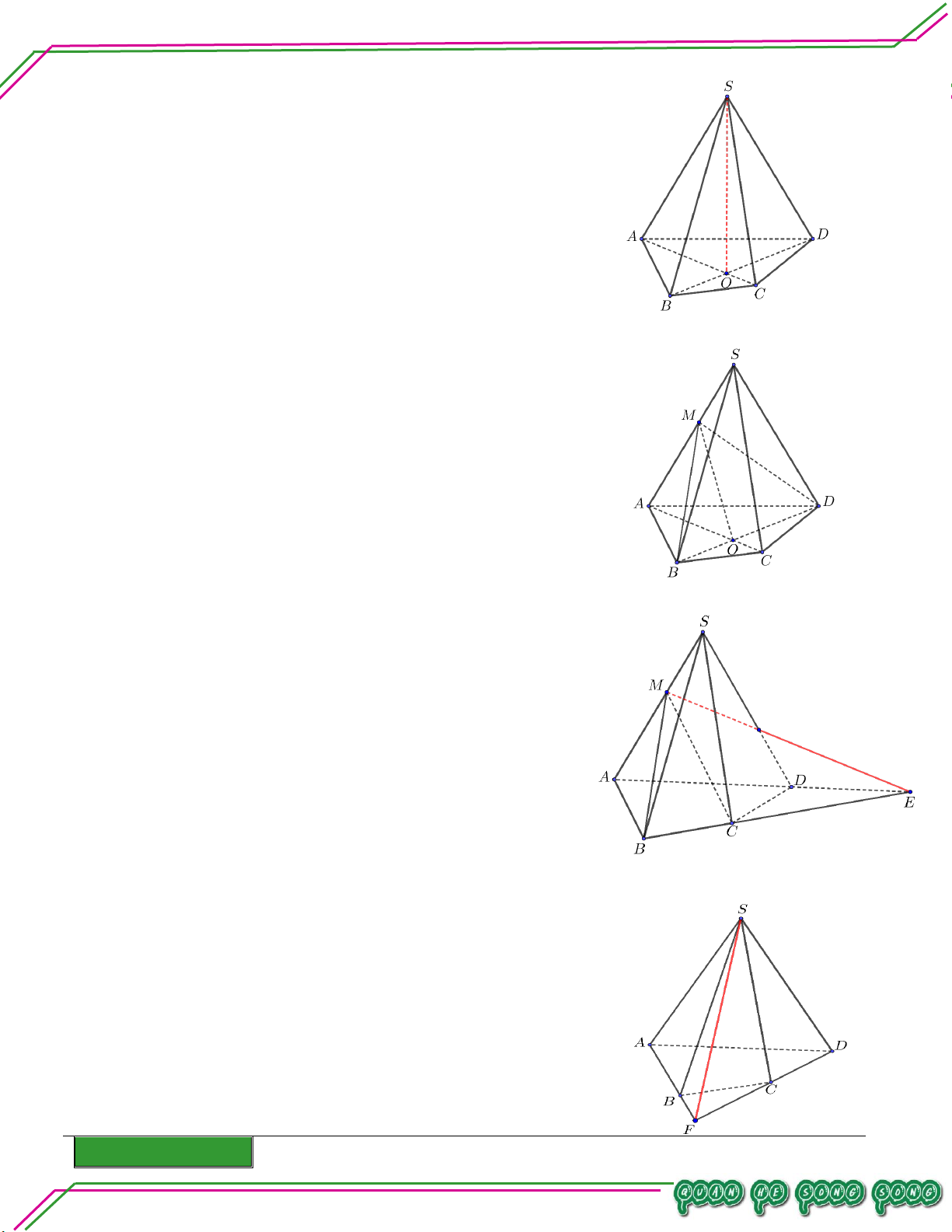
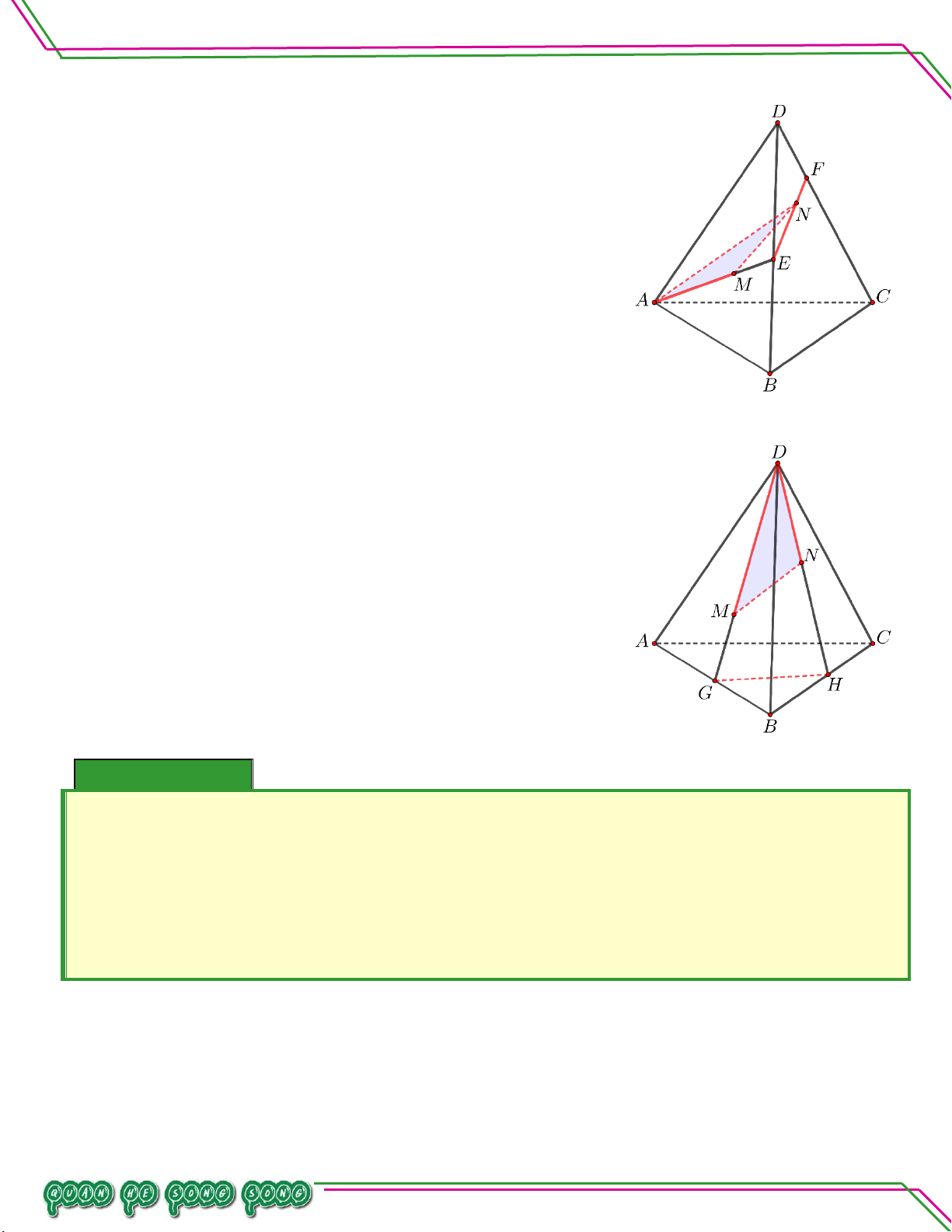
Cho tứ diện ABCD . Trên cạnh AB lấy điểm M thỏa 1 mãn AM 
AB,G là trọng tâm BCD. Tìm: 4
a. Giao điểm của GD với  ABC .
b. Giao điểm MG với (ACD) . Lời giải
a. Giao điểm của GD với  ABC . Trang 10
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
Gọi F là trung điểm BC . G là trọng tâm BCD nên DGBC  F mà BC  ABC
 DG ABC  F .
b. Giao điểm MG với (ACD) .
Trong  ABH với H là trung điểm DC . Có AH, MG không song song. BM 3 BG 2 Vì  ;
 . Gọi P  AHMG. Mà AH  ACD AB 4 BH 3
 MG ACD  P .
 Dạng 03. CHỨNG MINH 03 ĐIỂM THẲNG HÀNG VÀ 03 ĐƯỜNG THẲNG ĐỒNG QUI.
Phương pháp giải
 Muốn chứng minh ba điểm ,
A B, C thẳng hàng:
 Ta chứng minh ba điểm đó đồng thời thuộc hai mặt phẳng phân biệt   và   suy TÂM ra ba điểm ,
A B, C nằm trên giao tuyến của   và   nên chúng thẳng hàng.
A     
Cơ sở B      AB  AC       . C    
LÊ MINH  Muốn chứng minh ba đường a,b,c thẳng đồng quy tại một điểm:     n:
Ta chọn một mặt phẳng P chứa đường thẳng a và b . Gọi I a b chứng minh I c ạ
(chứng minh ba điểm thẳng hàng như trên). n So  Ví dụ 04. ê
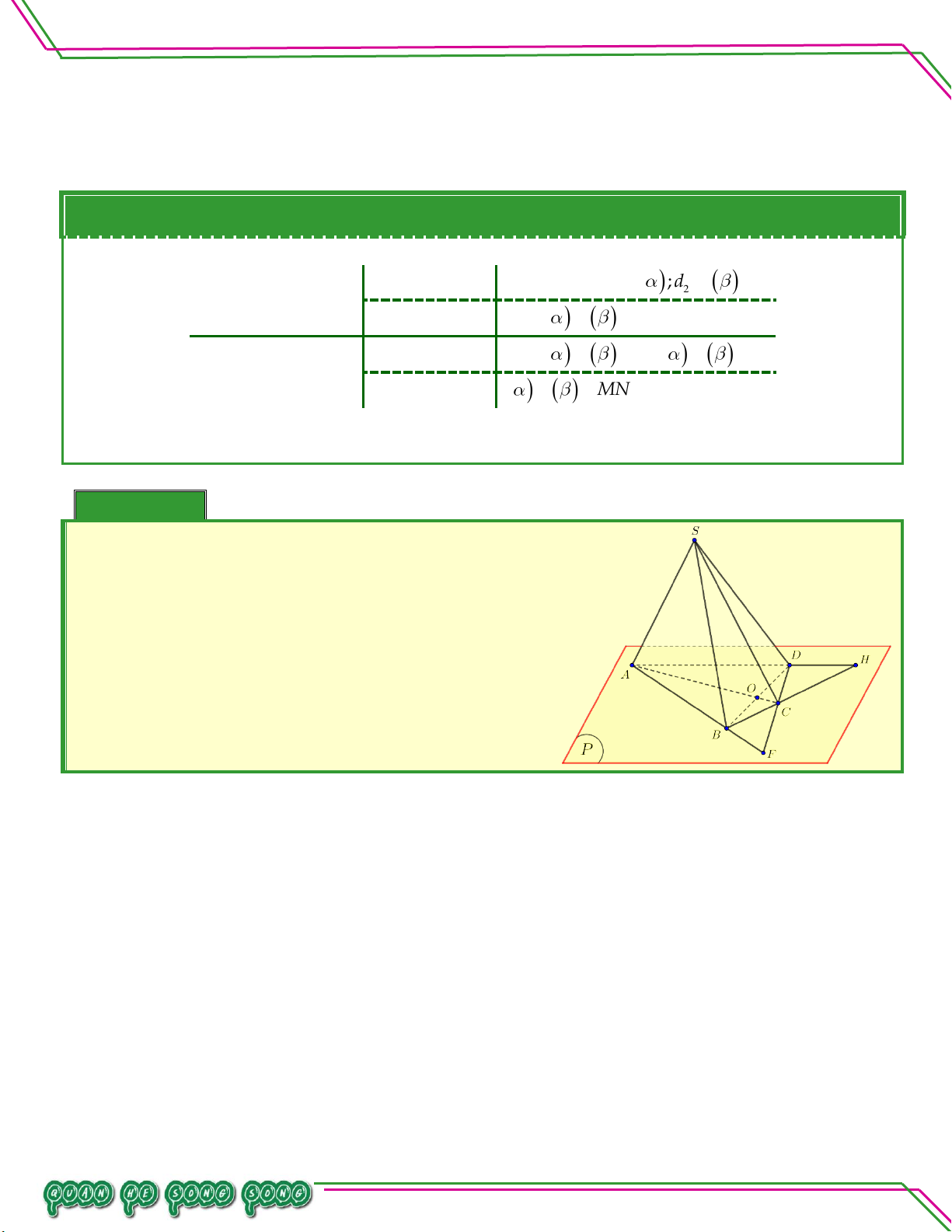
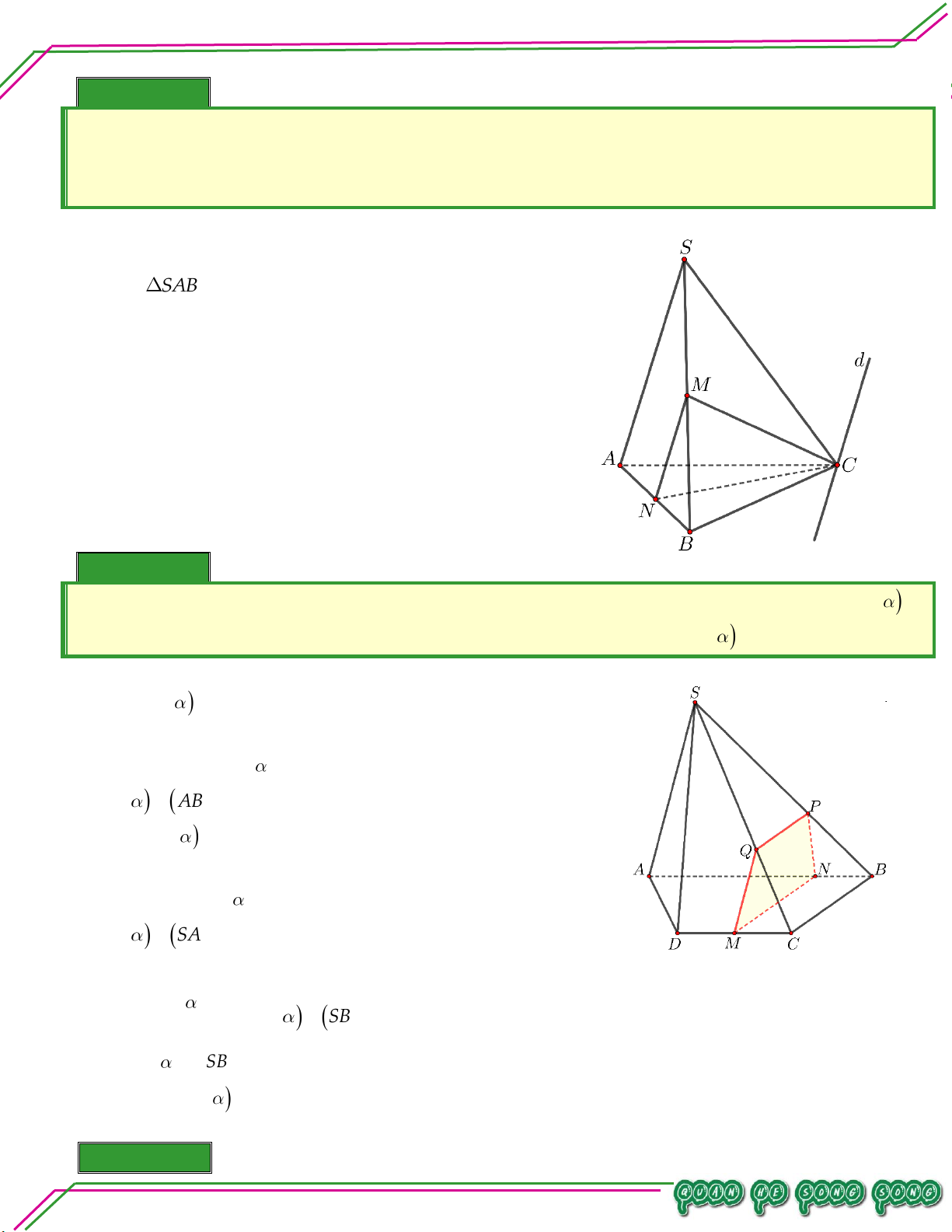
Cho 3 điểm A, B,C không thuộc mặt phằng P ,BC P  M,CAP  N , ABP  . Q Bi
Chứng minh M, N, P thẳng hàng. Lời giải
BC P  M  M ABC P   1
CA P  N  N ABC P 2
AB P  Q  QABC P   3 Từ   1 ,2 , 
3  M, N,Q thẳng hàng. Trang 11
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Dạng 04. THIẾT DIỆN CỦA HÌNH H KHI BỊ CẮT BỞI MẶT PHẲNG (P).
Phương pháp giải
 Khi cắt hình H bởi mặt phẳng P ta được phần chung
của H và P phần chung này gọi là thiết diện của hình H và P Bi
 Xem hình minh họa sau: Tứ giác MNCP là thiết diện của ên hình chóp .
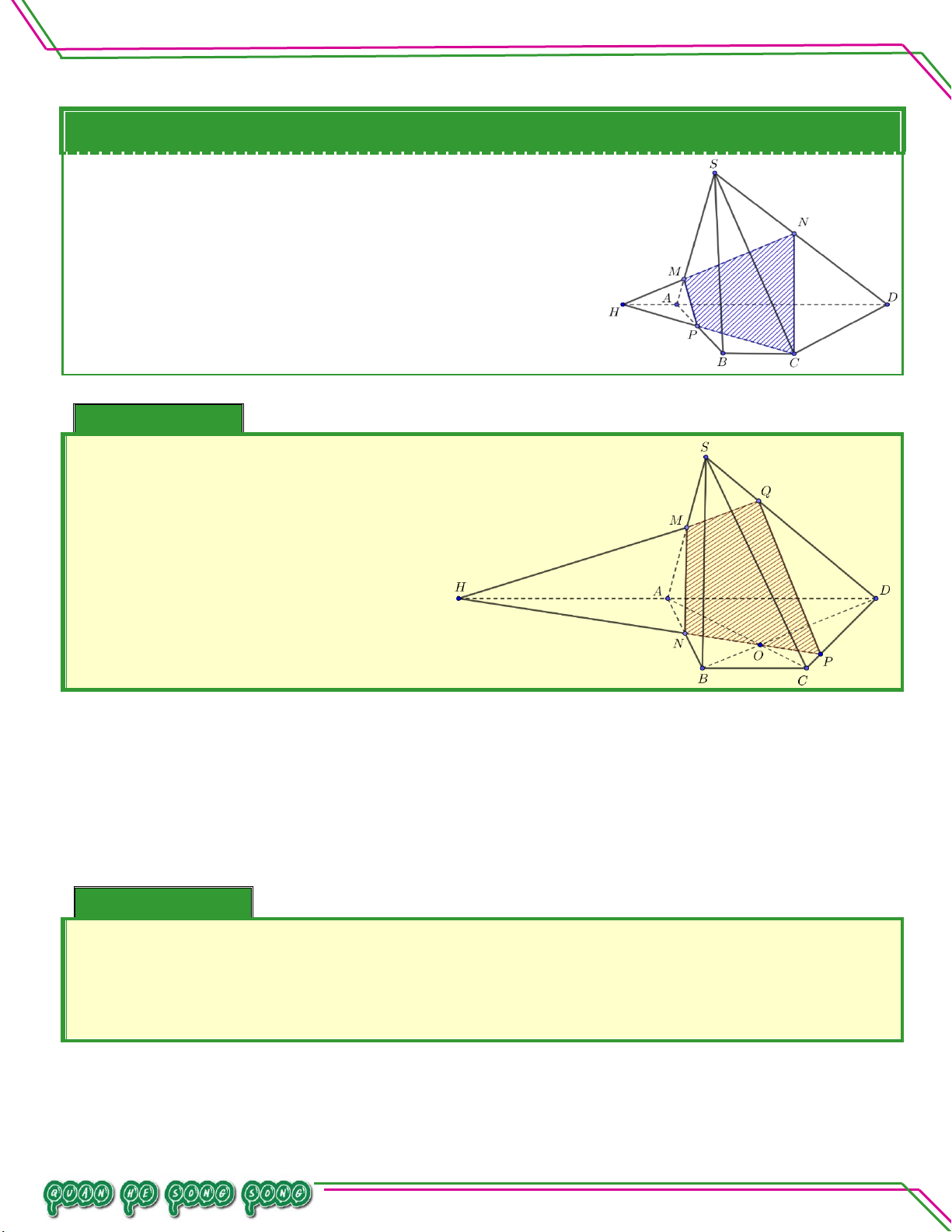
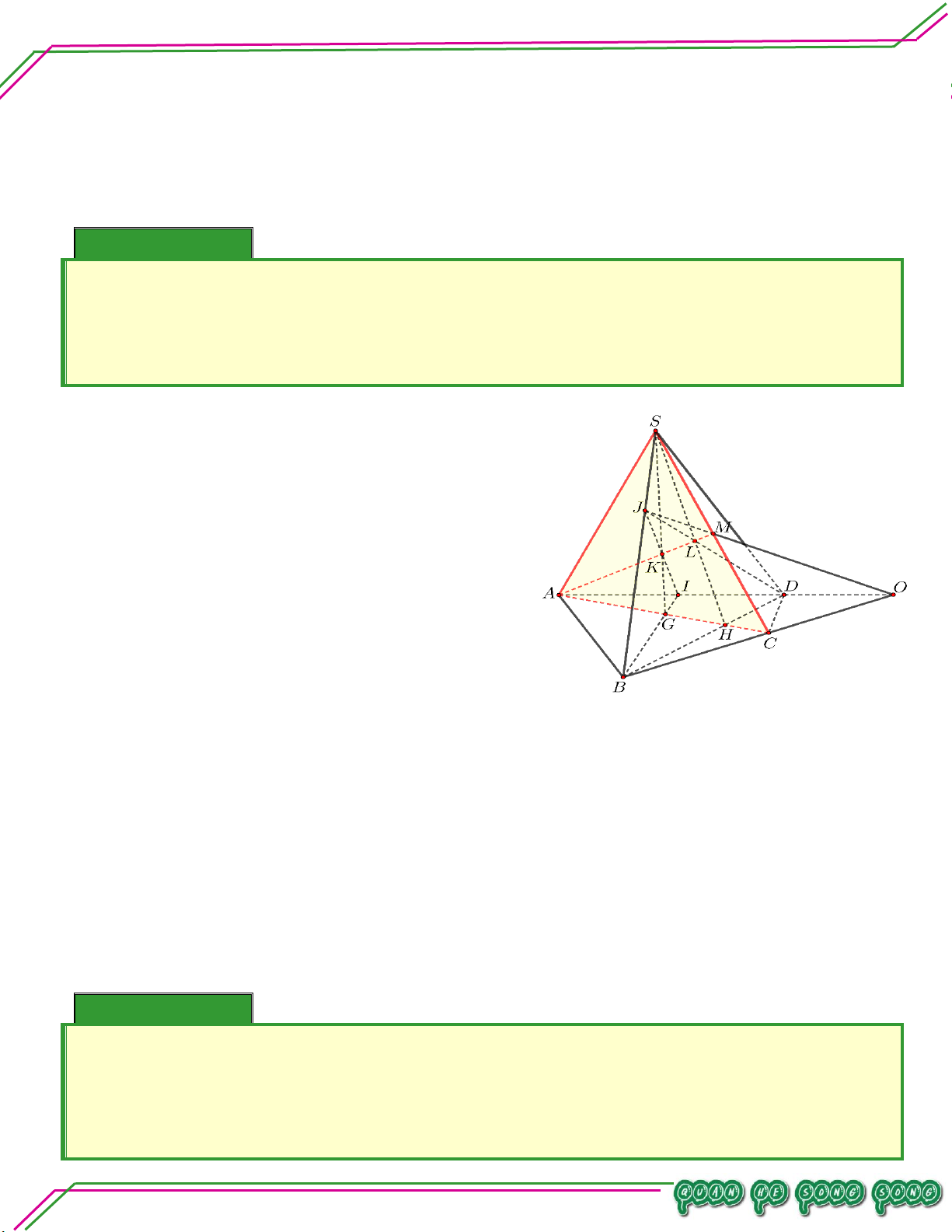
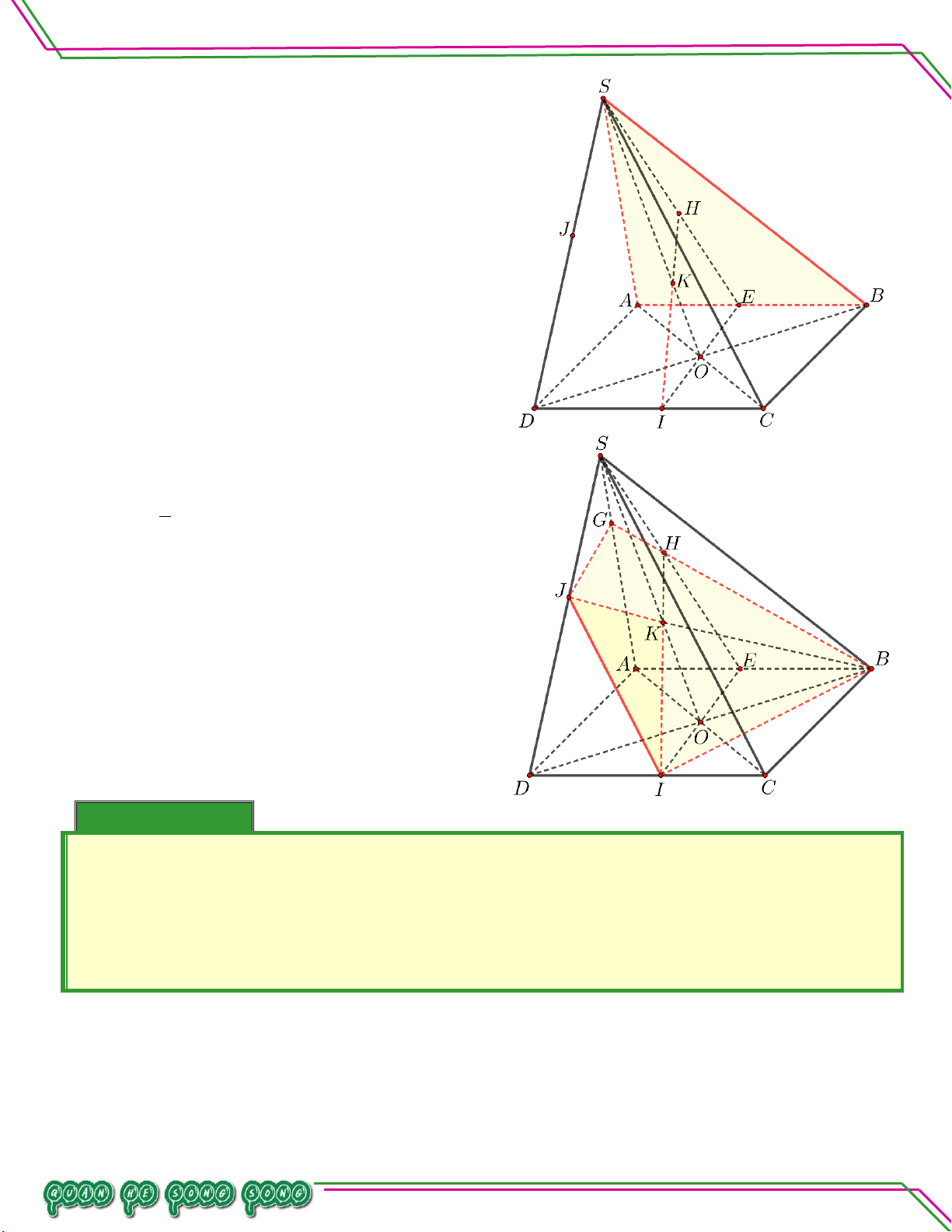
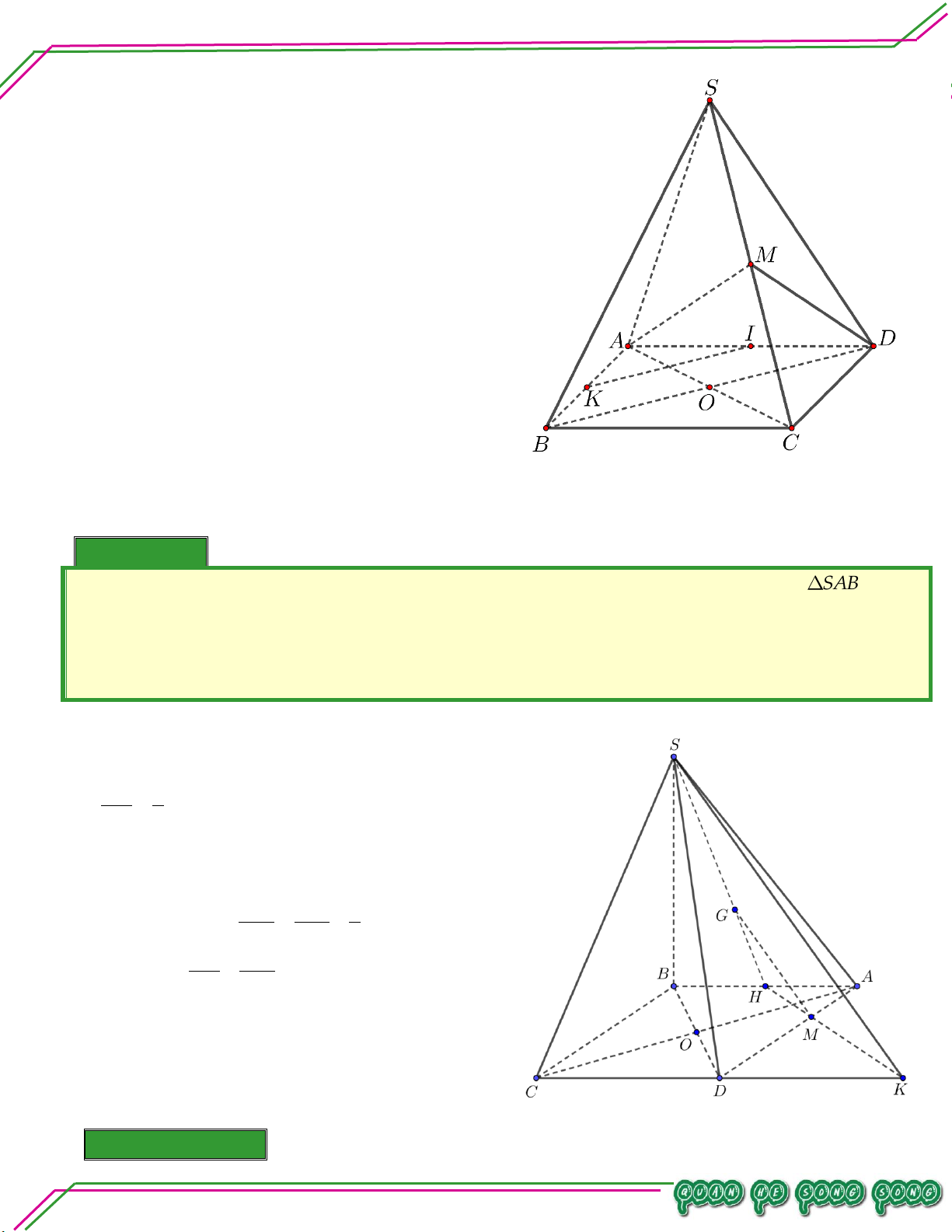
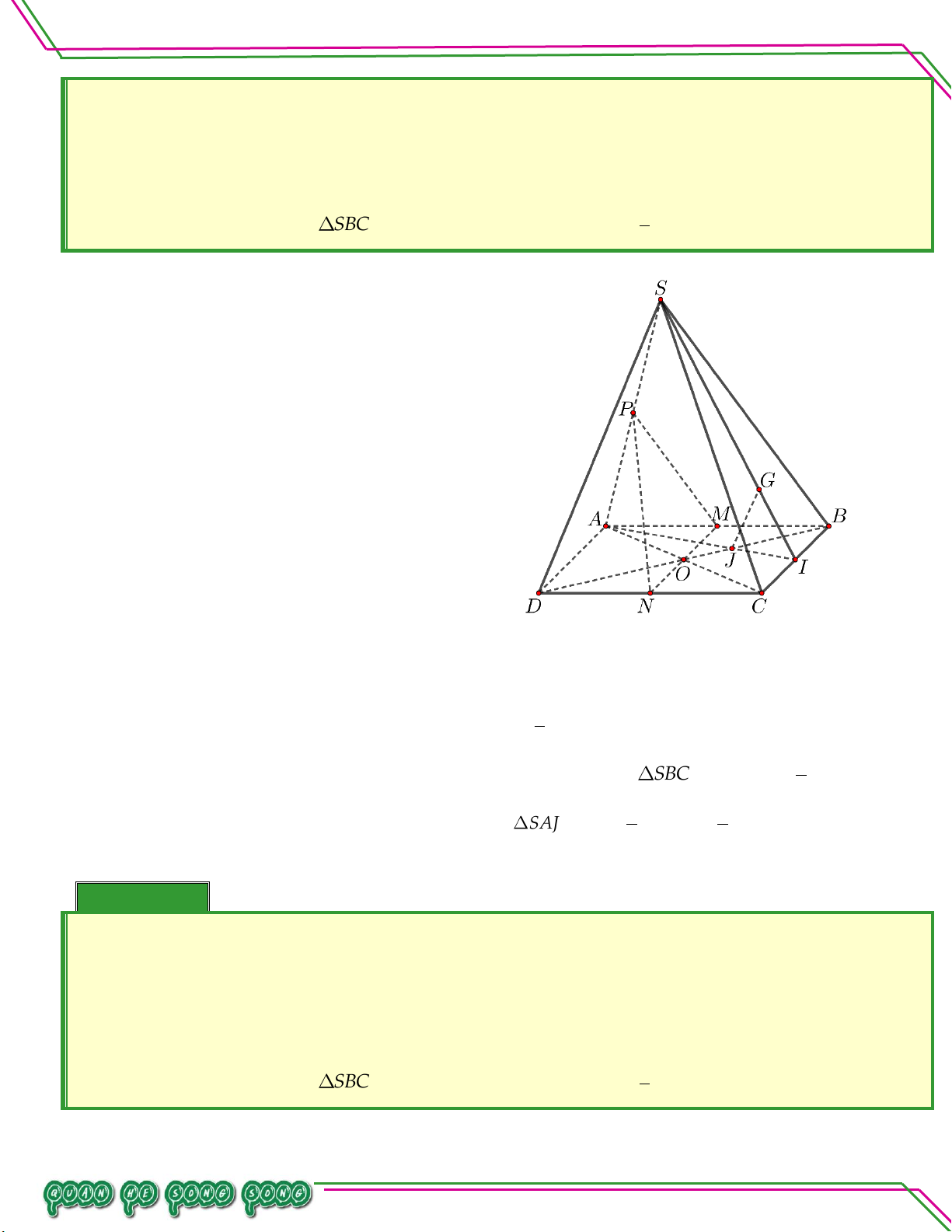
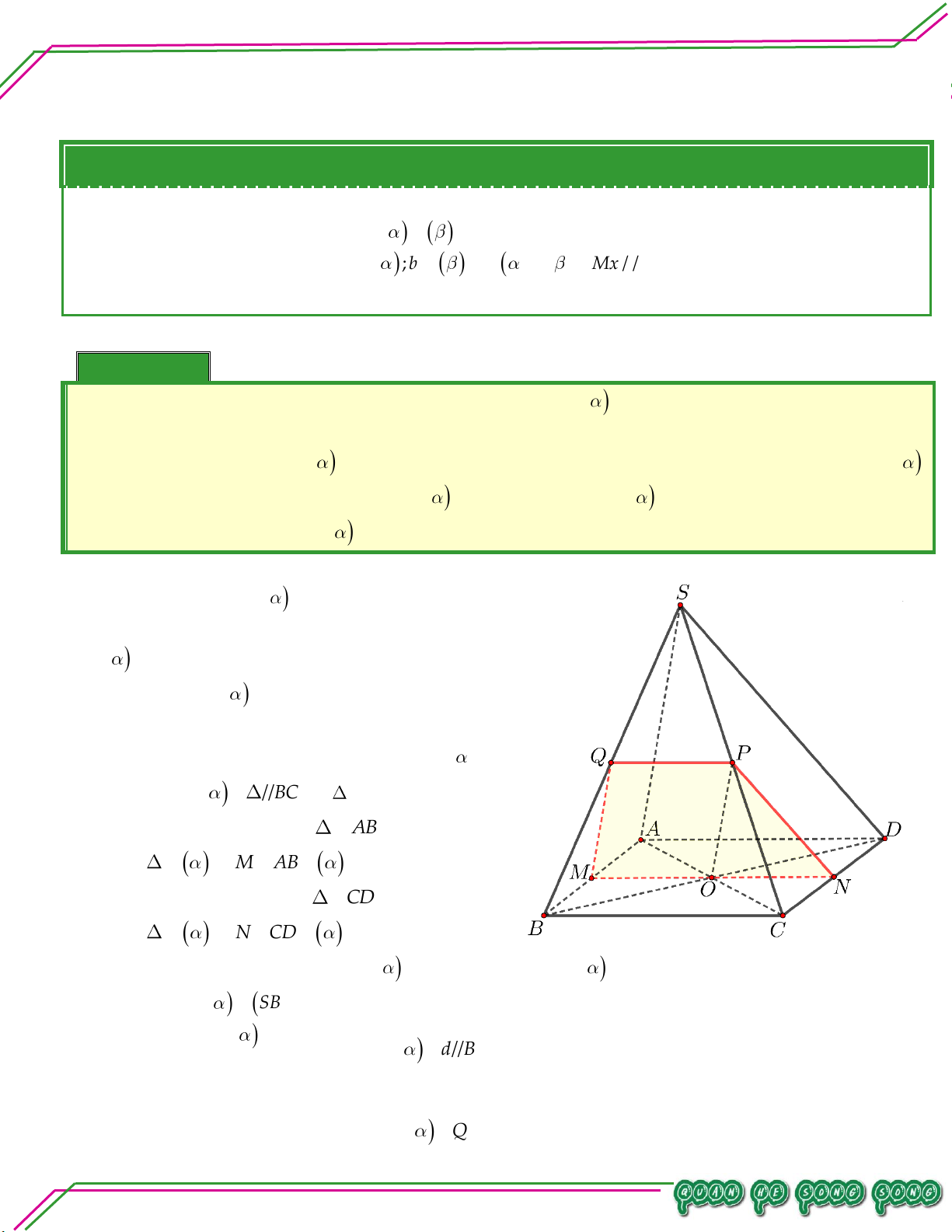
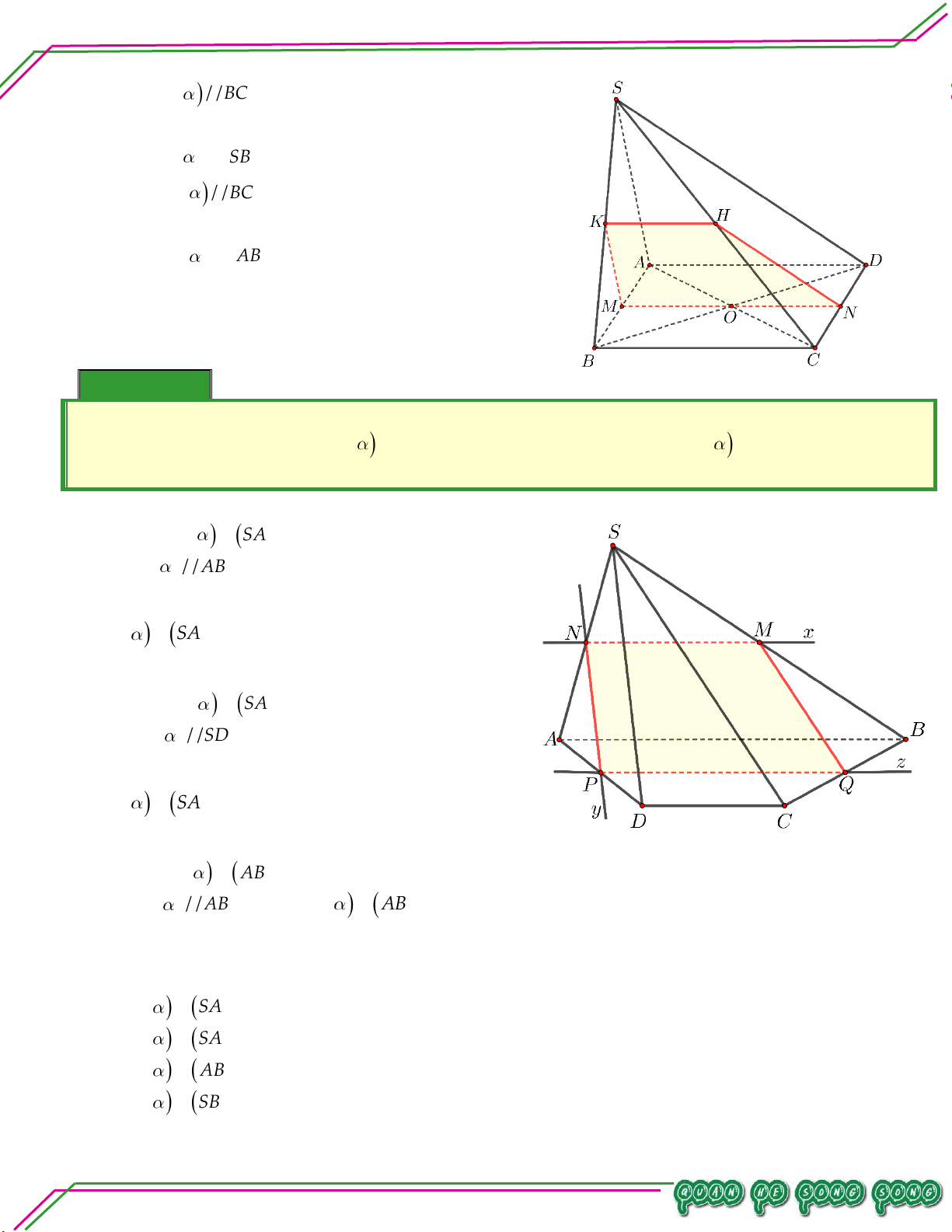
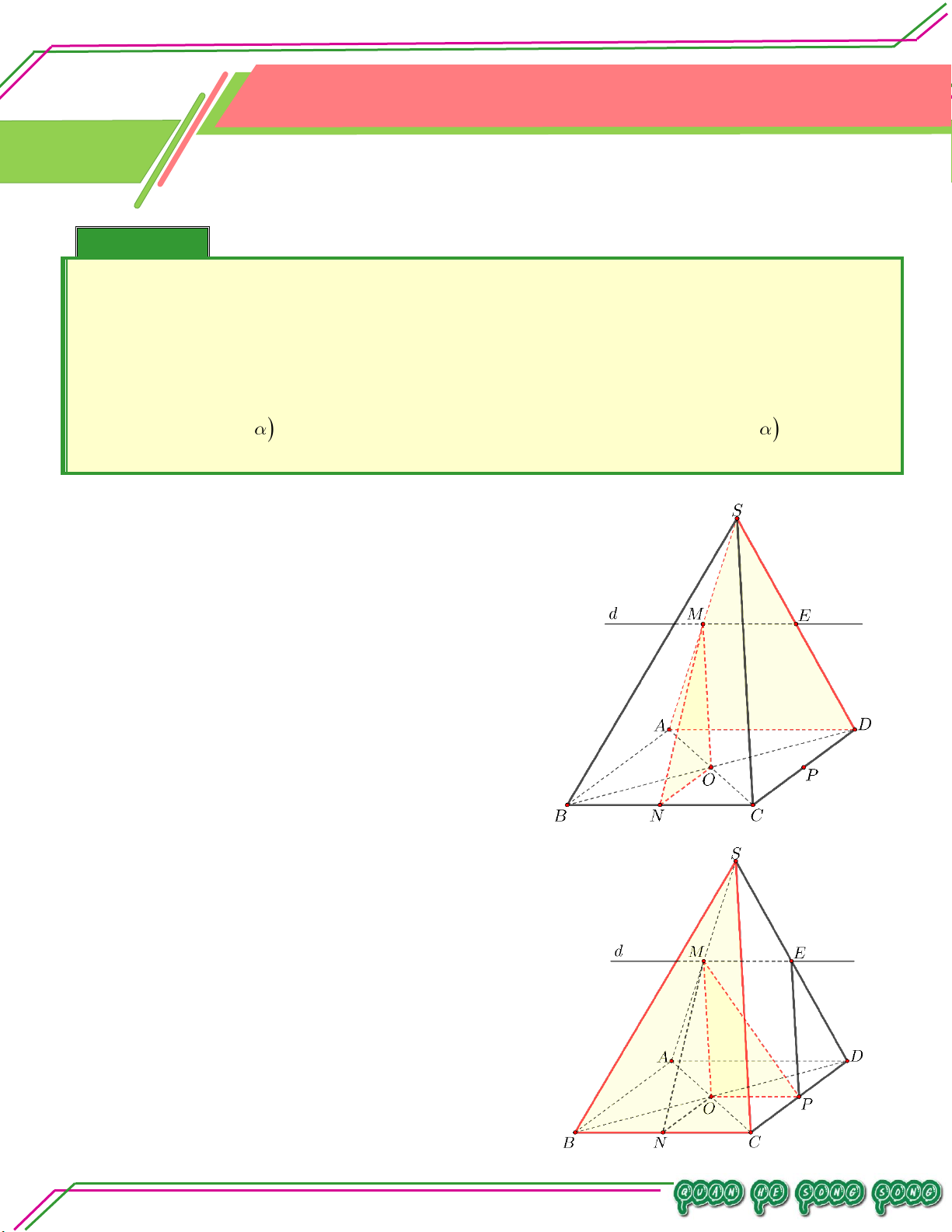
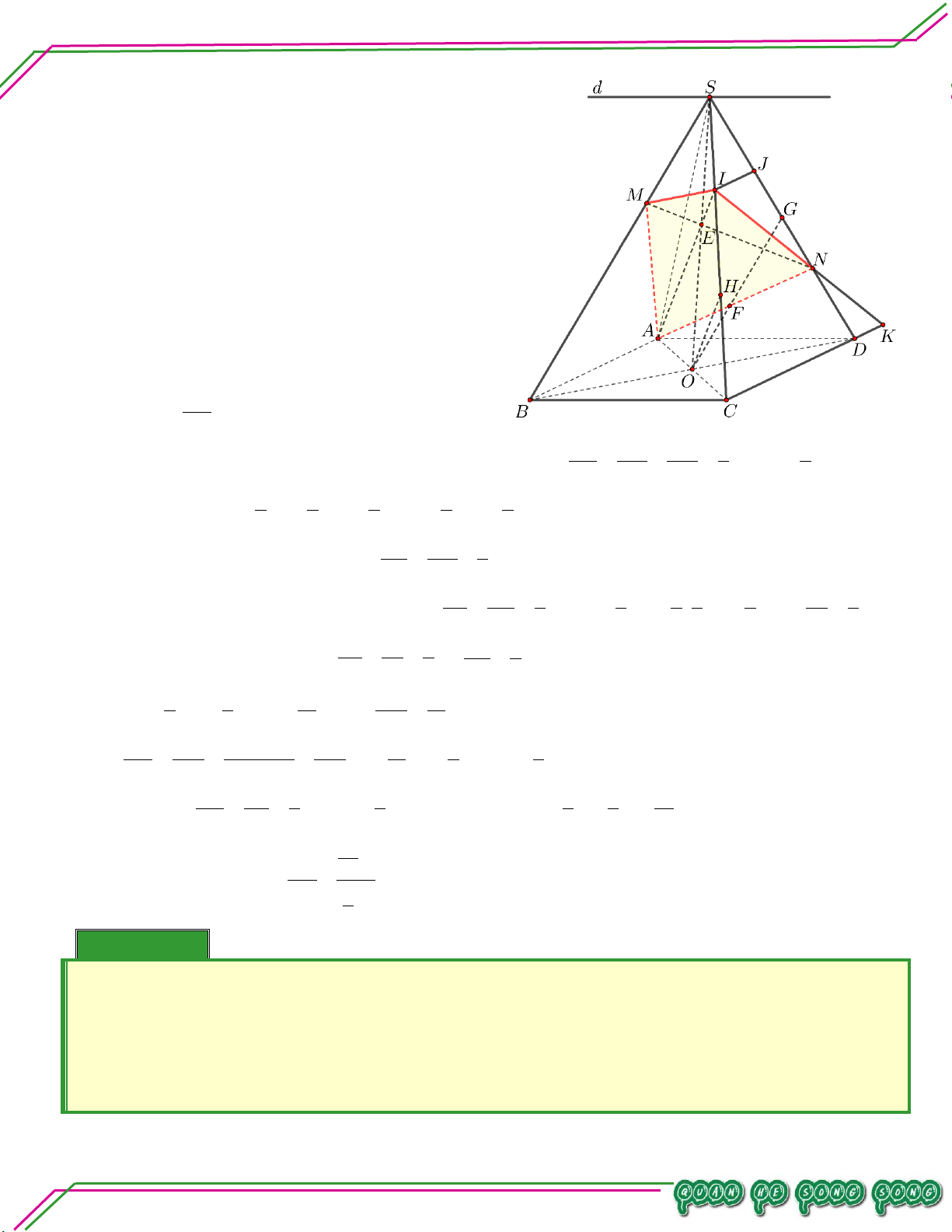
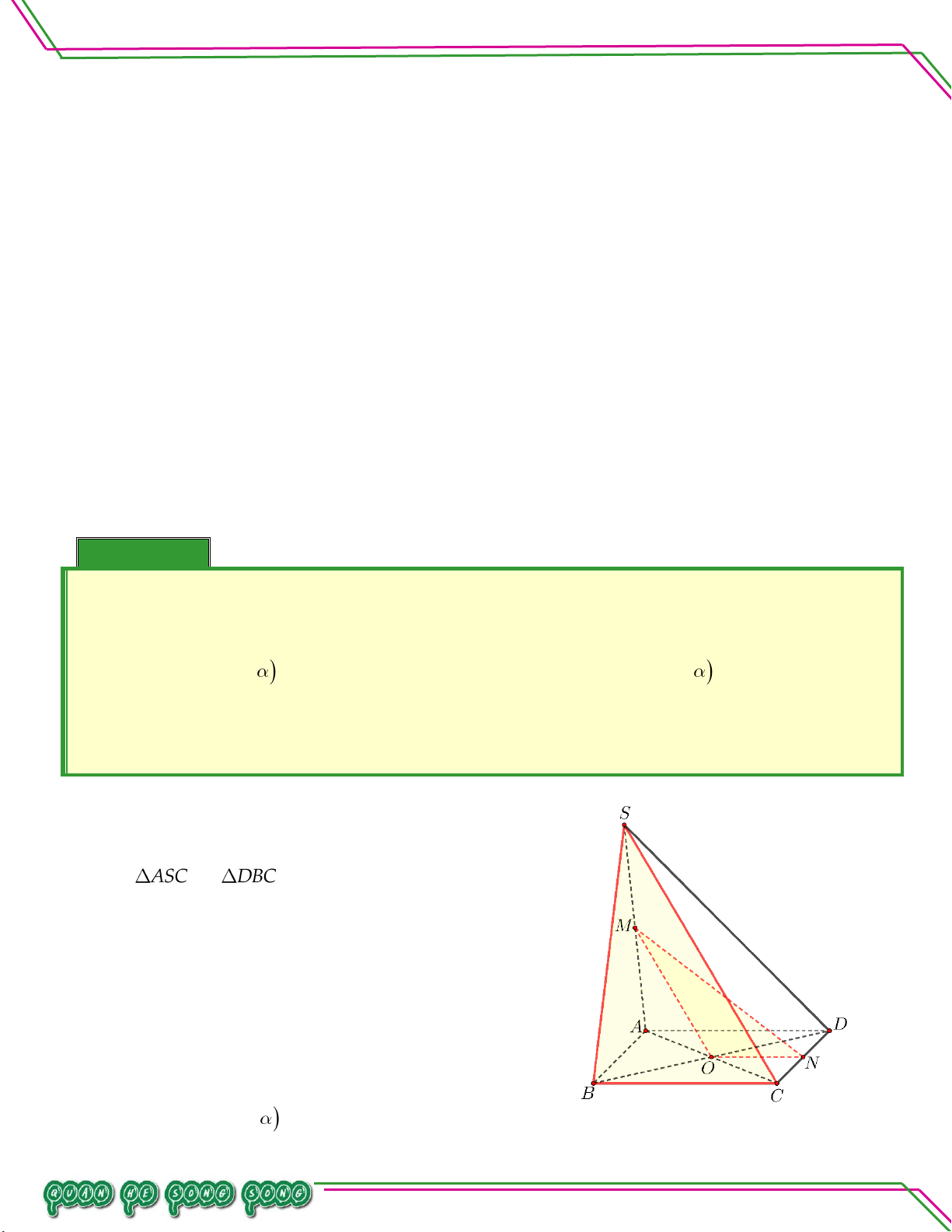
S ABCD với CHN . So ạ n:  Ví dụ 05. LÊ MINH Cho hình chóp .
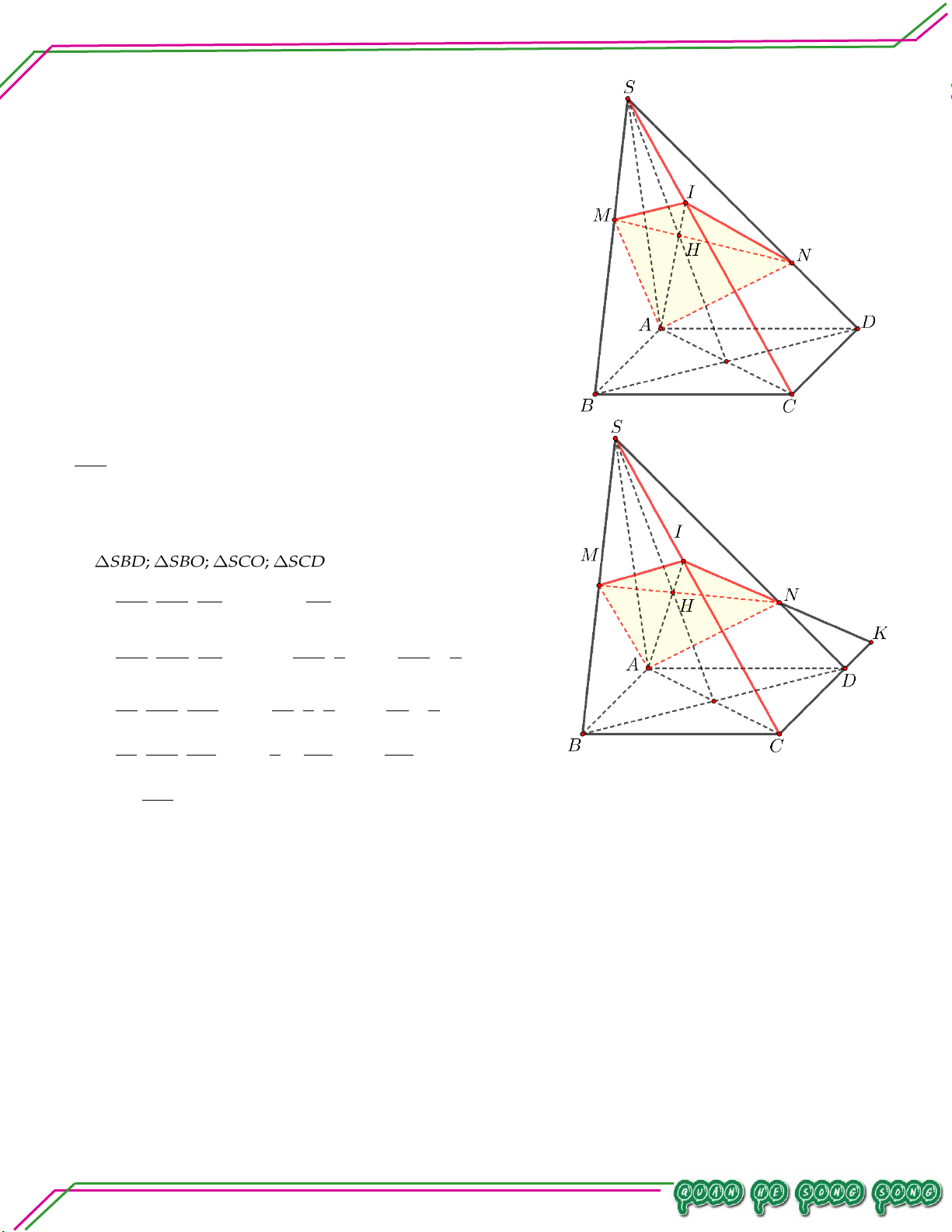
S ABCD có đáy ABCD
là hình thang, đáy lớn AD  2BC , AB
không song song CD . Lấy điểm M và
N lần lượt là trung điểm của SA, AB .
Gọi O là giao điểm của AC và BD . TÂM
Tìm thiết diện tạo bởi MNO với hình chóp . S ABCD. Lời giải
Gọi P  NO CD  CD MNO  P .
Gọi H  NP  AD  H SAD
Gọi Q  HM SD  Q  MNO SD
Do đó thiết diện tạo bởi MNO với hình chóp .
S ABCD là tứ giác MNPQ .
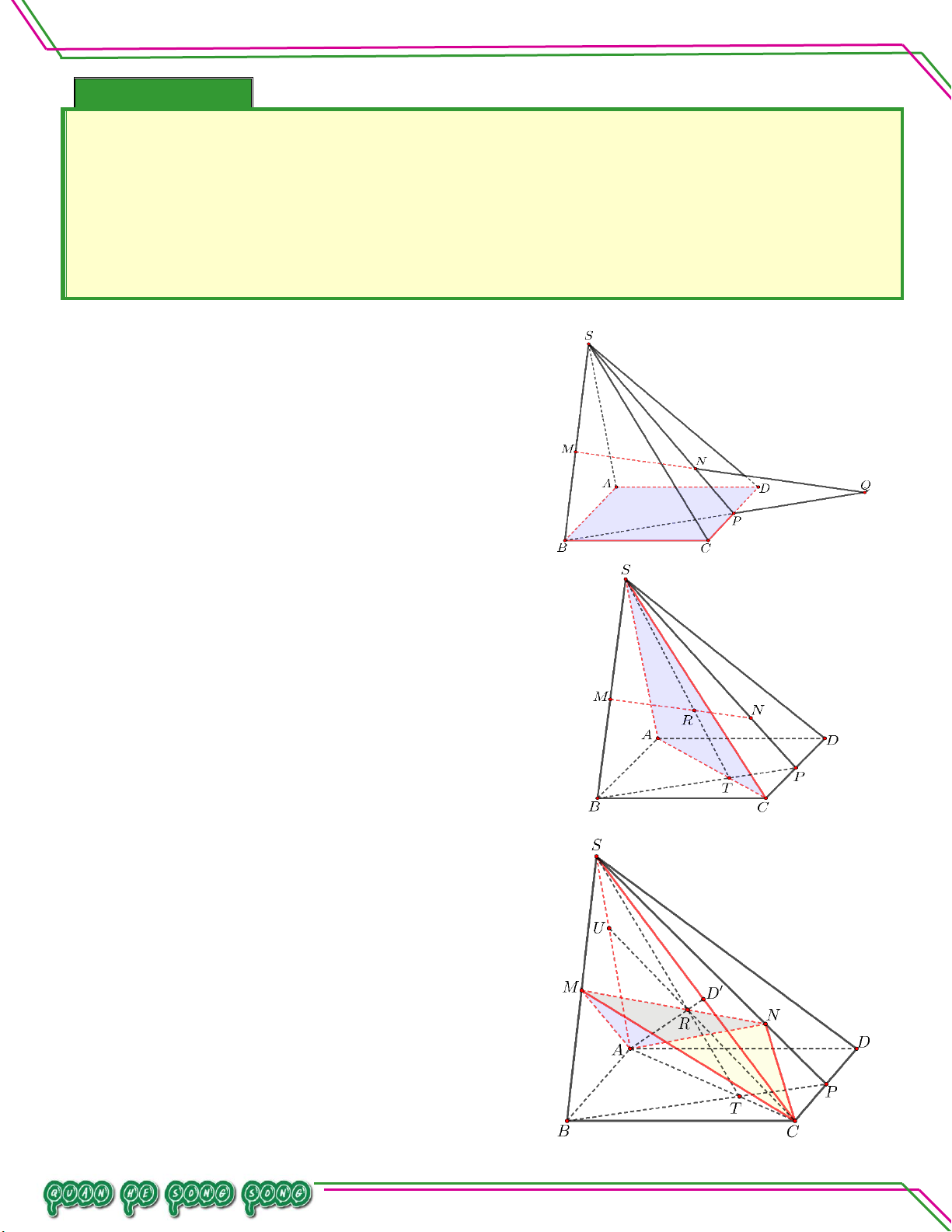
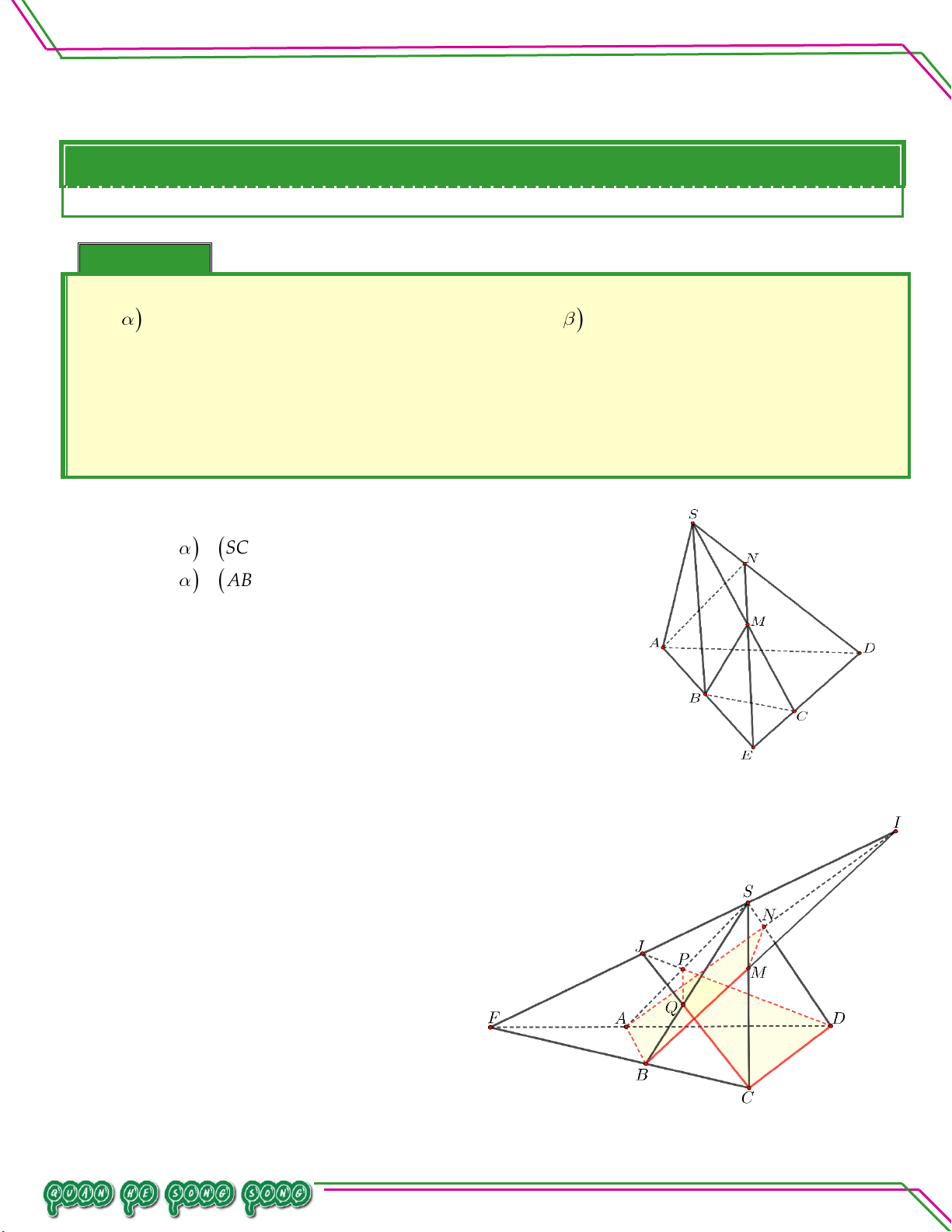
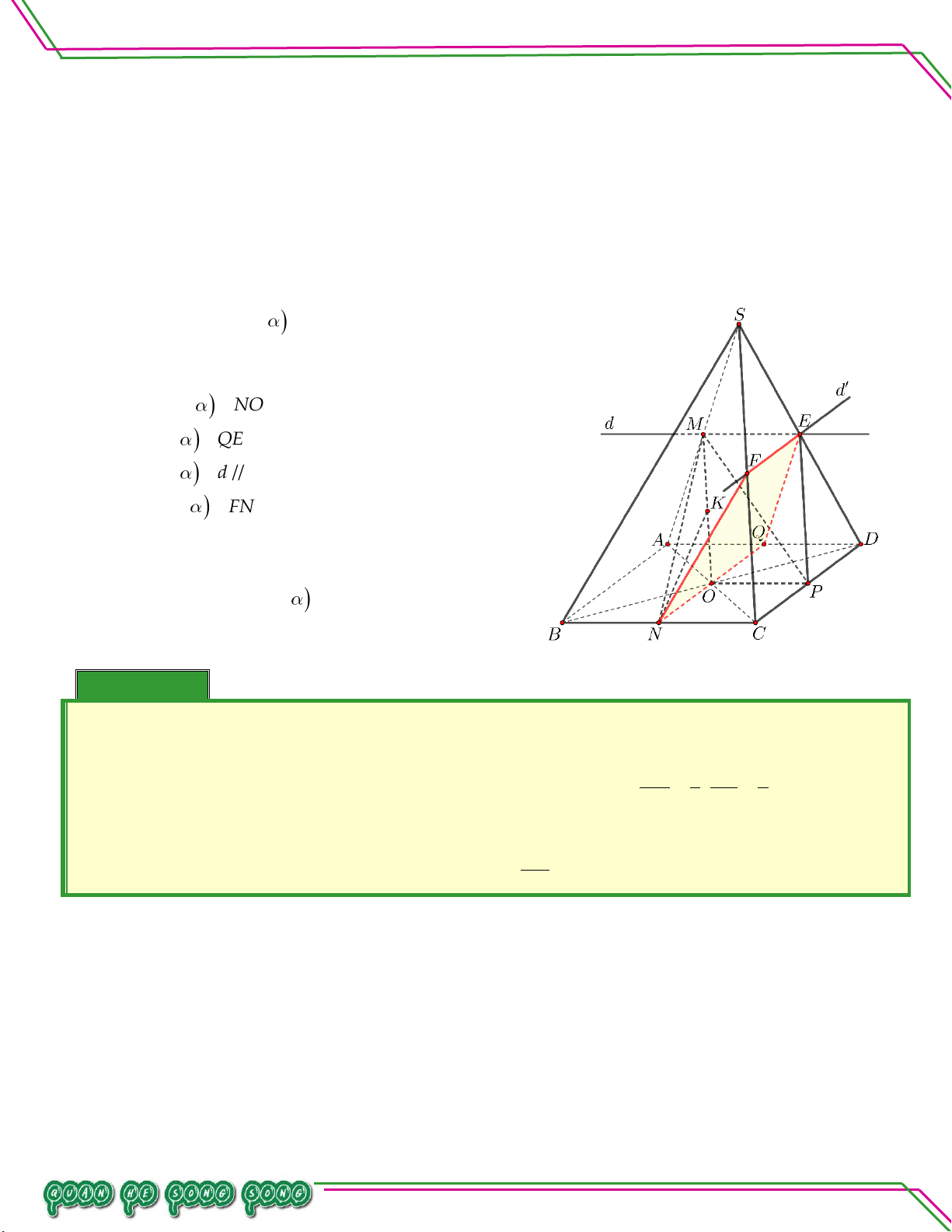
VI. BÀI TẬP RÈN LUYỆN.  Bài 01. Cho hình chóp .
S ABCD, đáy ABCD là tứ giác có các cặp cạnh đối không song song, điểm M
thuộc cạnh SA . Tìm giao tuyến của các mặt phẳng:
. SAC và SBD .
. SAC và MBD .
. MBC và SAD.
. SAB và SCD . Lời giải
. SAC và SBD . Trang 12
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Gọi O là giao điểm của AC và BD . S    SAC  Ta có     S  
SBD S SAC SBD  1
 Vì O  AC BD O    SAC  Nên     . O  
SBD O SAC SBD 2
 Từ (1) và (2) suy ra SACSBD  SO.
 SAC và MBD .
 Vì MSA nên M SAC . M   SAC  Do đó     M  
MBD M SAC MBD 3 TÂM
 Vì O  AC BD. O    SAC  Nên     . O  
MBD O SAC MBD 4
 Từ (3) và (4) suy ra SACMBD  MO .
 MBC và SAD. LÊ MINH
 Gọi E là giao điểm của BC và AD . n:  ạ
 Vì M SA nên MSAD M   SAD  Do đó 
 M  SAD  MBC 5 n So M   MBC       ê
 Vì E  BC  AD Bi E  MBC  Nên     . E   SAD
E  MBC SAD 6
 Từ (5) và (6) suy ra MBCSAD  ME .
 SAB và SCD .
 Gọi F là giao điểm của AB và CD . S    SAB  Ta có     S  
SCD S SAB SCD 7
 Vì F  ABCD F   SAB  Nên     . F  
SCD F SAB SCD 8
 Từ (7) và (8) suy ra SABSCD  SF .  Bài 02. Trang 13
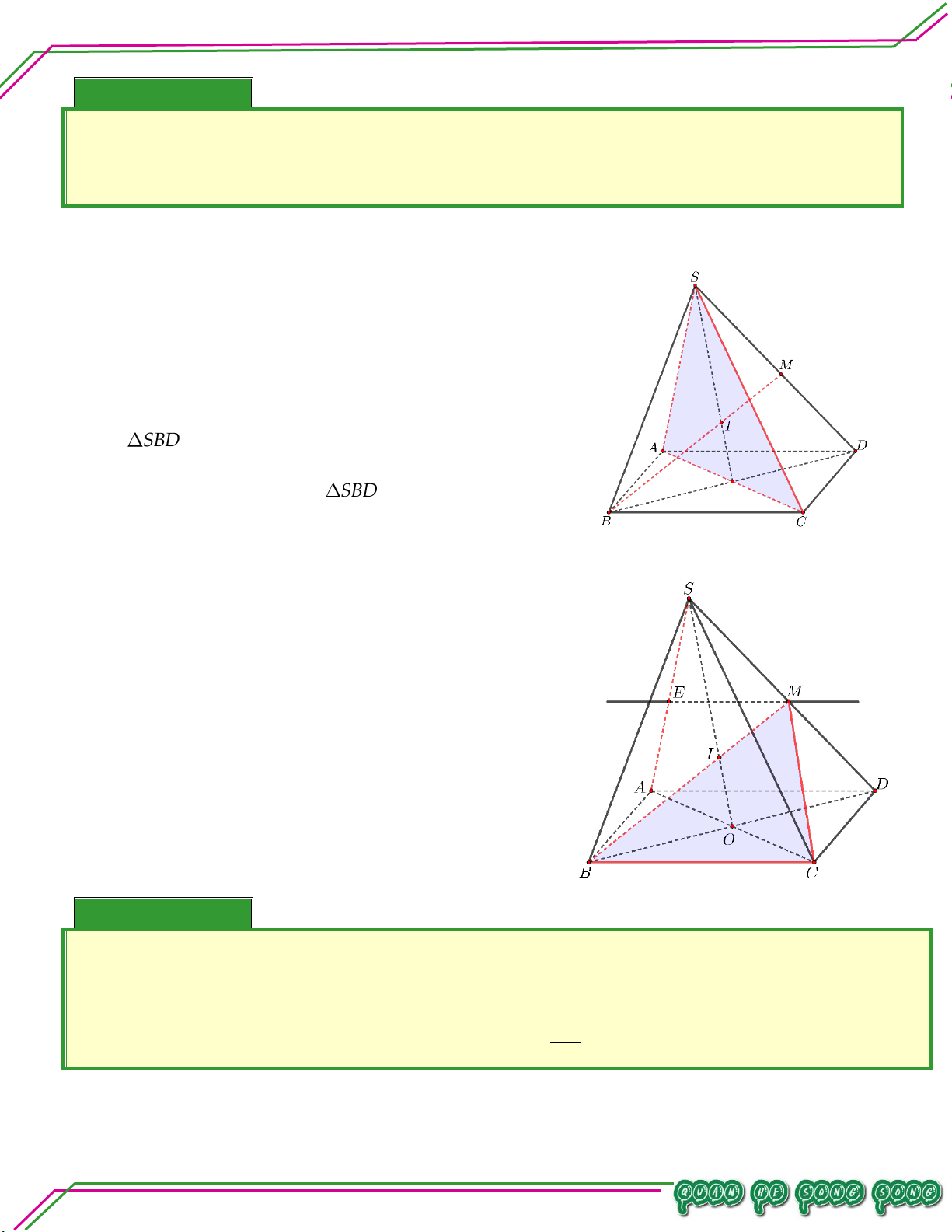
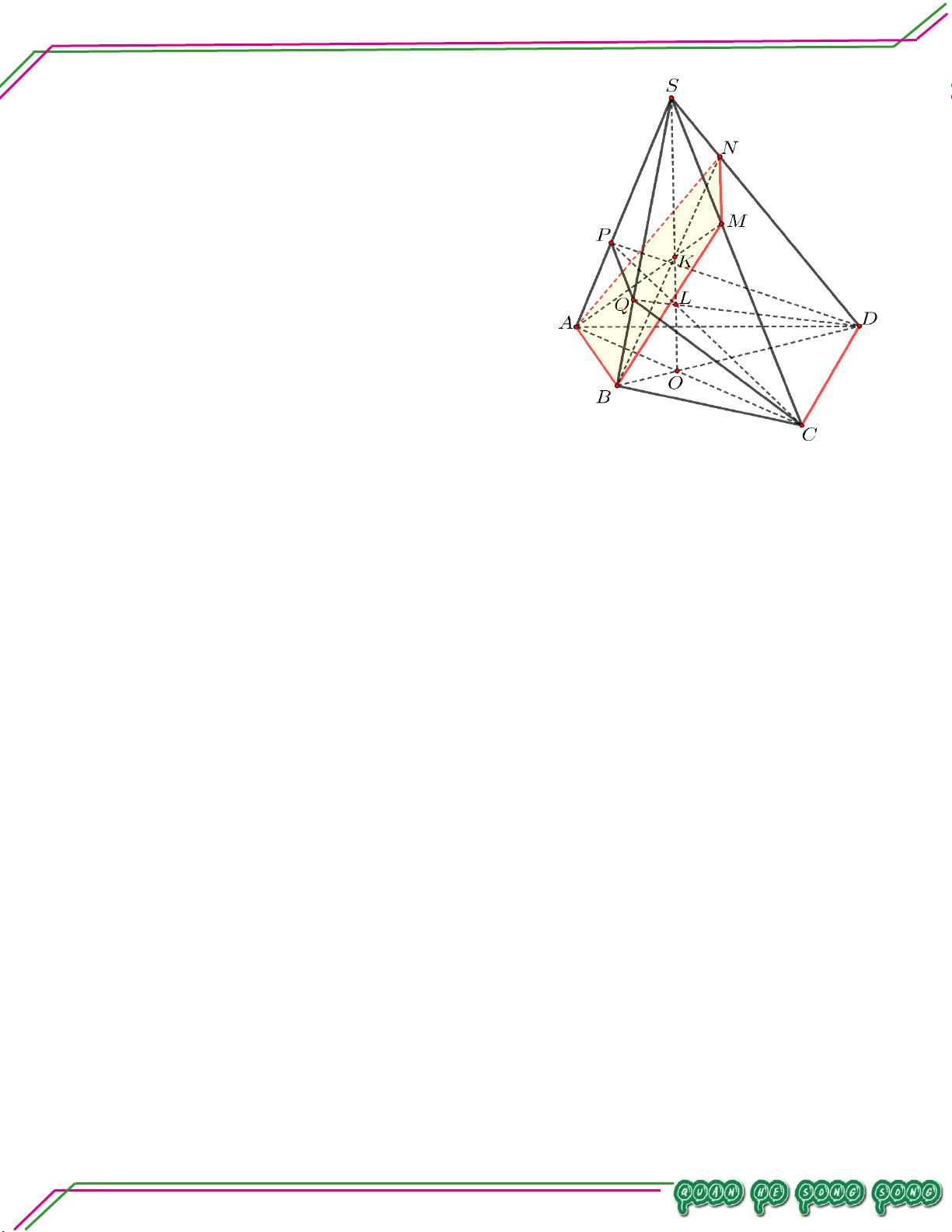
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
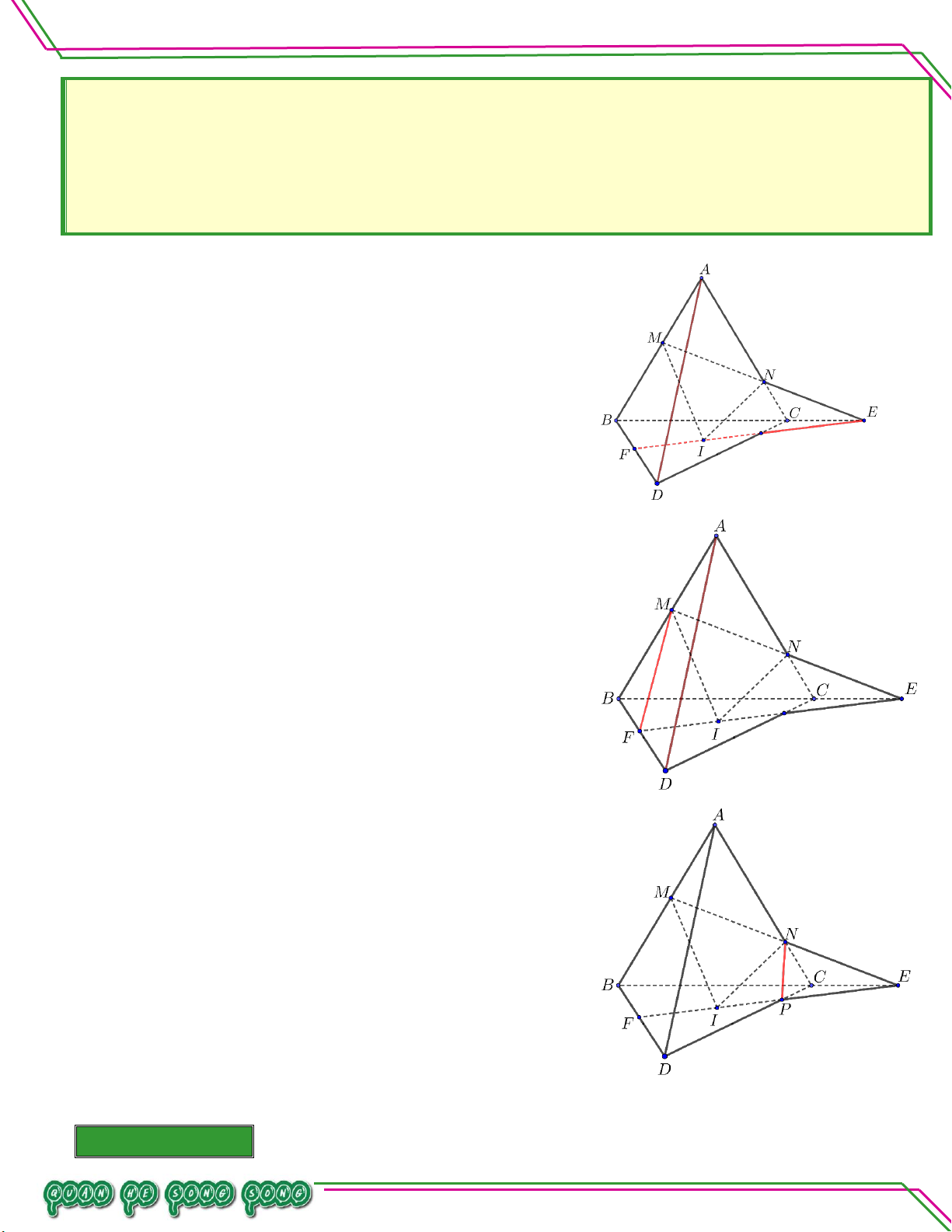
Cho tứ diện ABCD . Lấy các điểm M thuộc cạnh AB , N thuộc cạnh AC sao cho MN cắt BC .
Gọi I là điểm nằm bên trong tam giác BCD . Tìm giao tuyến của hai mặt phẳng:
. MNI và BCD .
. MNI và ABD .
. MNI và ACD . Lời giải Bi
. MNI và BCD . ê
 Gọi E là giao điểm của MN và BC . n I   IMN So  Ta có     . I   BCD
I IMN  BCD  1 ạn:
 Vì E  MN BC   LÊ MINH E IMN   Nên     . E  
BCD E IMN BCD 2
 Từ (1) và (2) suy ra IMNICD  IE.
. MNI và ABD .
 Gọi F là giao điểm của IE và BD . TÂM
 Vì M AB nên M ABD M   ABD 
 M  IMN  ABD 3  M  IMN      
 Vì F  IE  BD F   IMN  Nên     . F  
ABD F IMN ABD 4
 Từ (3) và (4) suy ra IMNABD  MF .
. MNI và ACD .
 Gọi P là giao điểm của IE và CD .
 Vì NAC nên N ACD N   ACD     . N   IMN
N IMN   ACD 5
 Vì P  IECD P   IMN  Nên     . P  
ACD P IMN ACD 6
 Từ (5) và (6) suy ra IMNACD  NP .  Bài 03. Trang 14
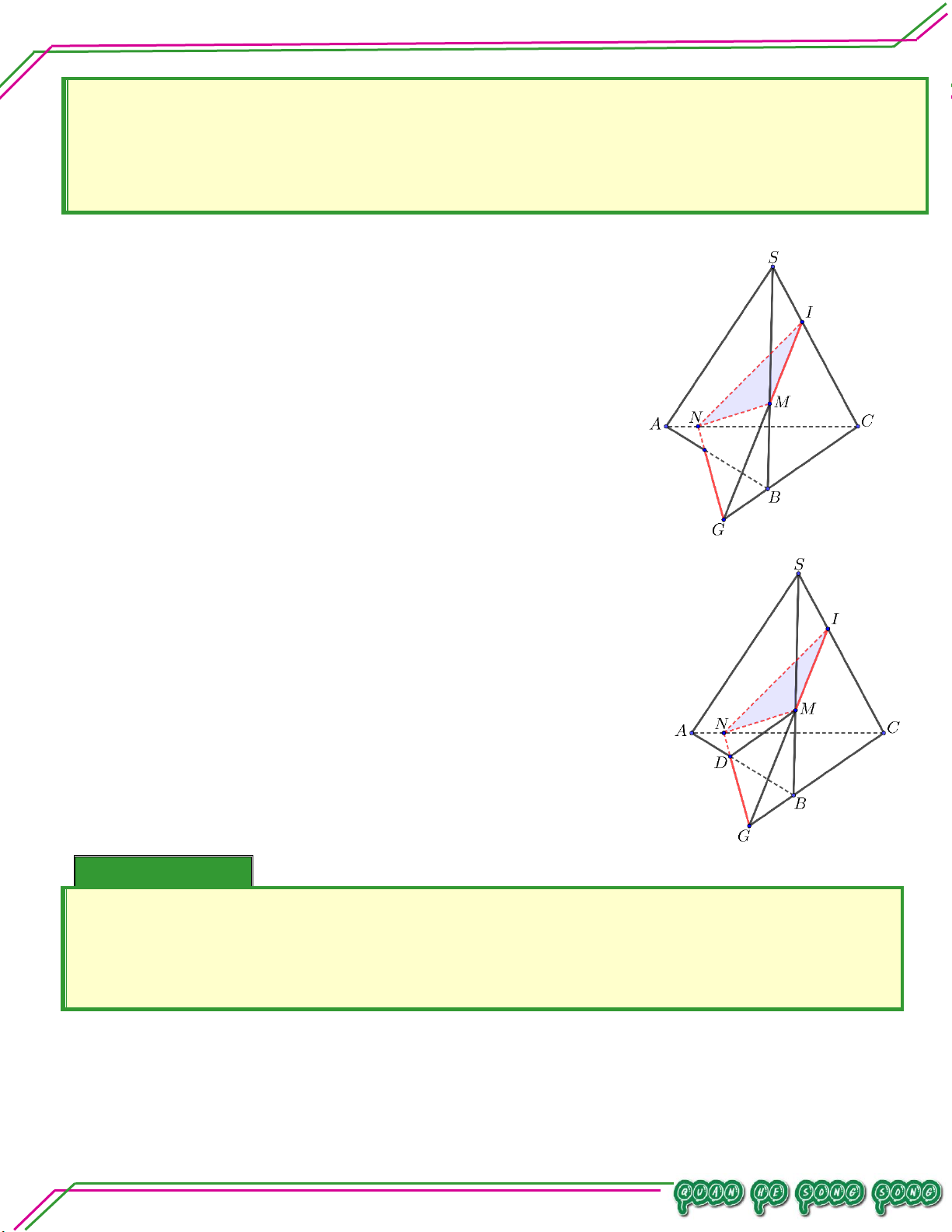
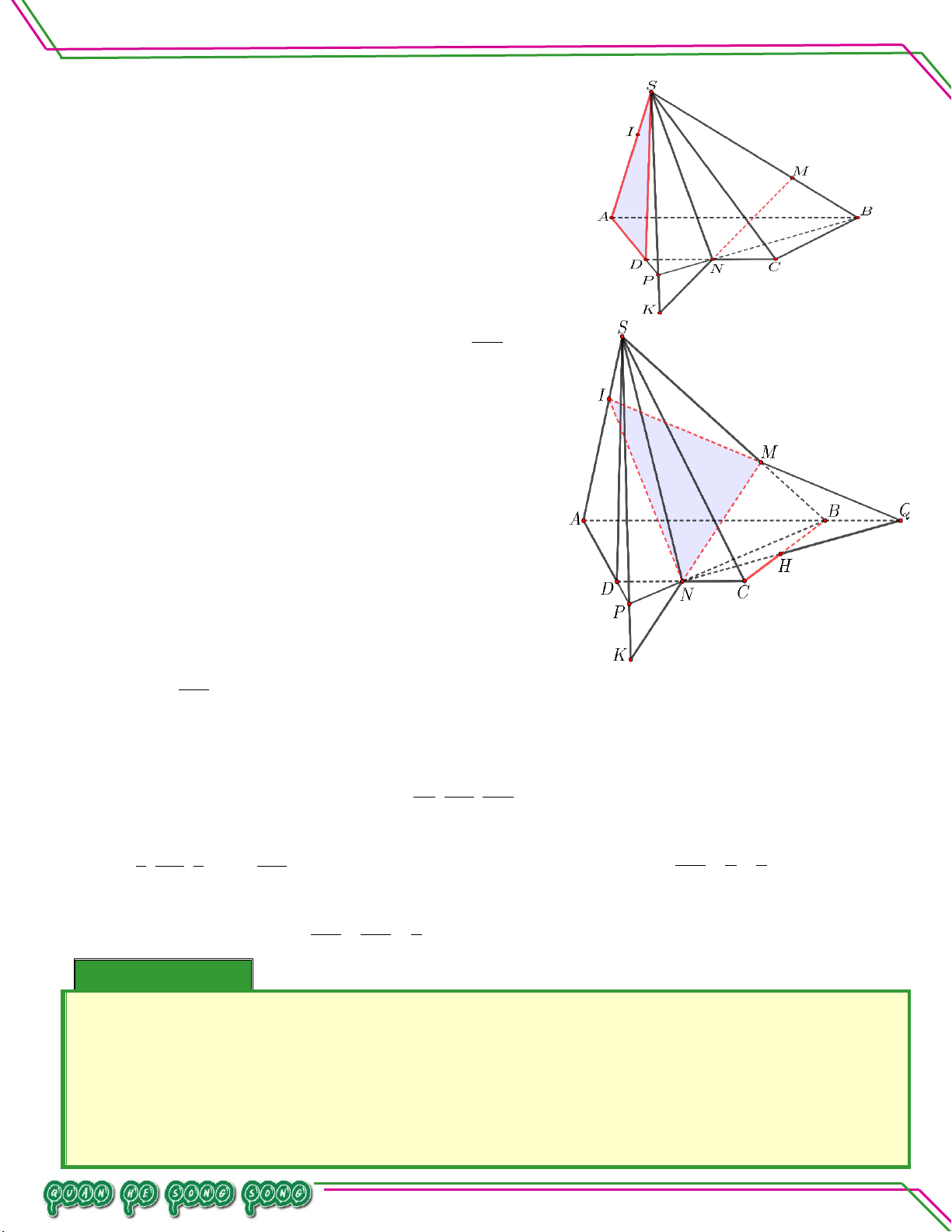
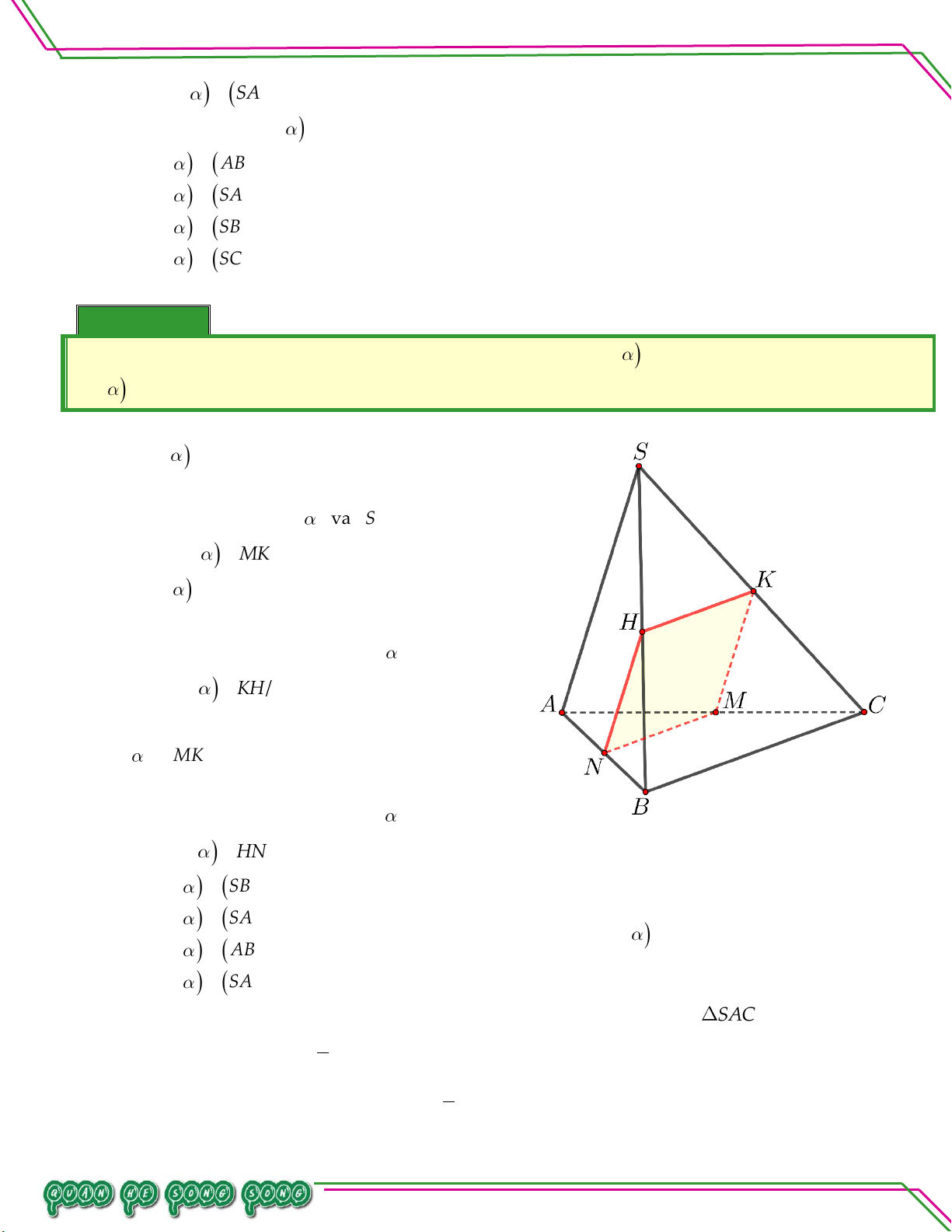
Hình học 11 – Chương 02. QUAN HỆ SONG SONG Cho tứ diện .
S ABC . Lấy M S ,
B N  AC,I SC sao cho MI không song song với BC , NI không song
song với SA . Tìm giao tuyến của mặt phẳng MNI  với các mặt và .
. MNI và ABC .
. MNI và SAB . Lời giải
. MNI và ABC .
 Trong mặt phẳng SBC , kéo dài IM cắt BC tại G . G
  MI, MI   MNI  
G  BC, BC   ABC
 G là điểm chung I của MNI và ABC . N   MNI   TÂM
N  AC, AC   ABC
 N là điểm chung II của MNI và ABC .
 Vậy giao tuyến của hai mặt phẳng ABC và MNI là NG.
. MNI và SAB .
 Trong mặt phẳng ABC , nối NG cắt AB tại D . LÊ MINH
D AB, AB   ABC n:   ạ
D  NG, NG   MNI
 D là điểm chung I của hai mặt phẳng MNI và SAB . n Soê M   MNI   Bi
M SB,SB   SAB
 M là điểm chung II của hai mặt phẳng MNI và SAB .
Vậy giao tuyến của hai mặt phẳng MNI  và SAB là MD .  Bài 04.
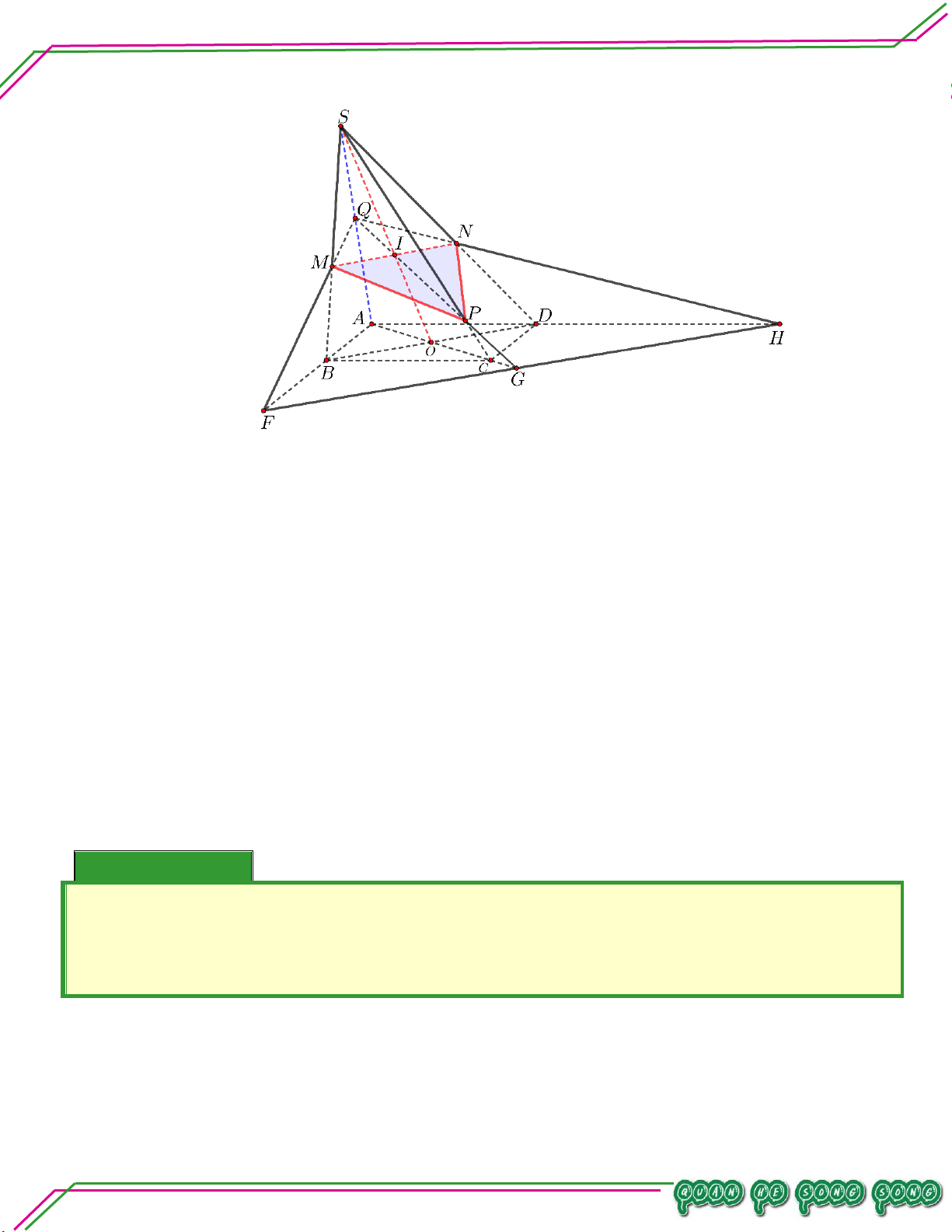
Cho tứ diện ABCD , M là một điểm bên trong tam giác ABD , N là một điểm bên trong tam giác
ACD . Tìm giao tuyến của các cặp mặt phẳng sau:
. AMN và BCD .
. DMN và ABC . Lời giải Trang 15
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
. AMN và BCD .
 Trong mặt phẳng ABD , AM cắt BD tại E ;
 Trong mặt phẳng BCD , EN cắt DC tại F .
E AM, AM   AMN  
E  DB, DB   BCD
 E là điểm chung I của AMN và BCD . Bi
F  EN,EN   AMN ê   n
F  DC, DC   BCD So
 F là điểm chung II của AMN và BCD ạ  n:
Vậy EF là giao tuyến của hai mặt phẳng AMN ; BCD  LÊ MINH
. DMN và ABC .
 Trong mặt phẳng ABD , DM cắt ABtại G ;
 Trong mặt phẳng BDC, DN cắt BC tại H G
  DM,DM   DMN  
G  AB, AB   ABC TÂM
 G là điểm chung I của 2 mặt phẳng ABC và DMN.
H  DN,DN   DMN  
H  BC, BC   ABC
 H là điểm chung II của 2 mặt phẳng ABC và DMN
Vậy GH là giao tuyến của hai mặt phẳng DMN ;  ABC  Bài 05.
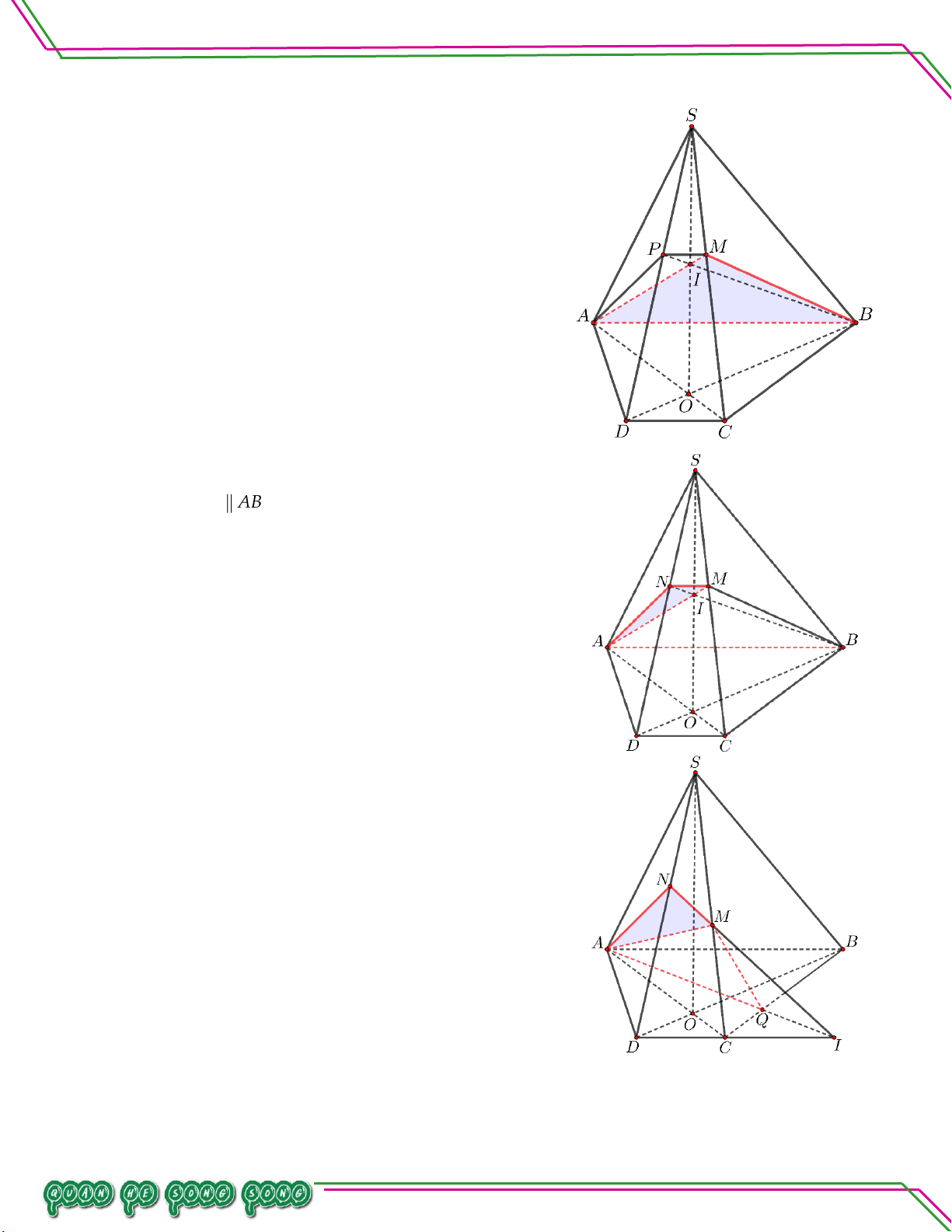
Cho hình chóp S.ABCD đáy là hình bình hành tâm O . Gọi M , N, P lần lượt là trung điểm các cạnh
BC, CD, SA . Tìm giao tuyến của:
. MNP và SAB .
. MNP và SAD.
. MNP và SBC .
 MNP và SCD Lời giải
Trong mặt phẳng  ABCD , kéo dài MN cắt AB, AD lần lượt tại F và G
Trong mặt phẳng SAB nối FP cắt SB tại H .
Trong mặt phẳng SAD nối GP cắt SD tại I . Trang 16
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
. MNP và SAB. H  F , P FP   MNP   H  S , B SB   SAB
 H là điểm chung thứ I của MNP ;SAB
 P là điểm chung thứ II của MNP ; SAB
 Vậy giao tuyến của MNP và SAB là PH
. MNP và SAD.
I GP,GP   MNP   I  S , D SD   SAD
 I là điểm chung thứ I của MNP ;SAD
 P là điểm chung thứ II của MNP ;SAD TÂM
 Vậy giao tuyến của MNP và SAD là PI
. MNP và SBC . H  F , P FP   MNP   H  S , B SB   SBC LÊ MINH
 H là điểm chung thứ I của MNP ;SBC
n:ạ  M là điểm chung thứ II của MNP;SBC
 Vậy giao tuyến của MNP vàSBC là MH n So
ê  MNP và SCD Bi
I GP,GP   MNP   I  S , D SD   SCD
 I là điểm chung thứ I của MNP ;SCD
 N là điểm chung thứ II của MNP ;SCD
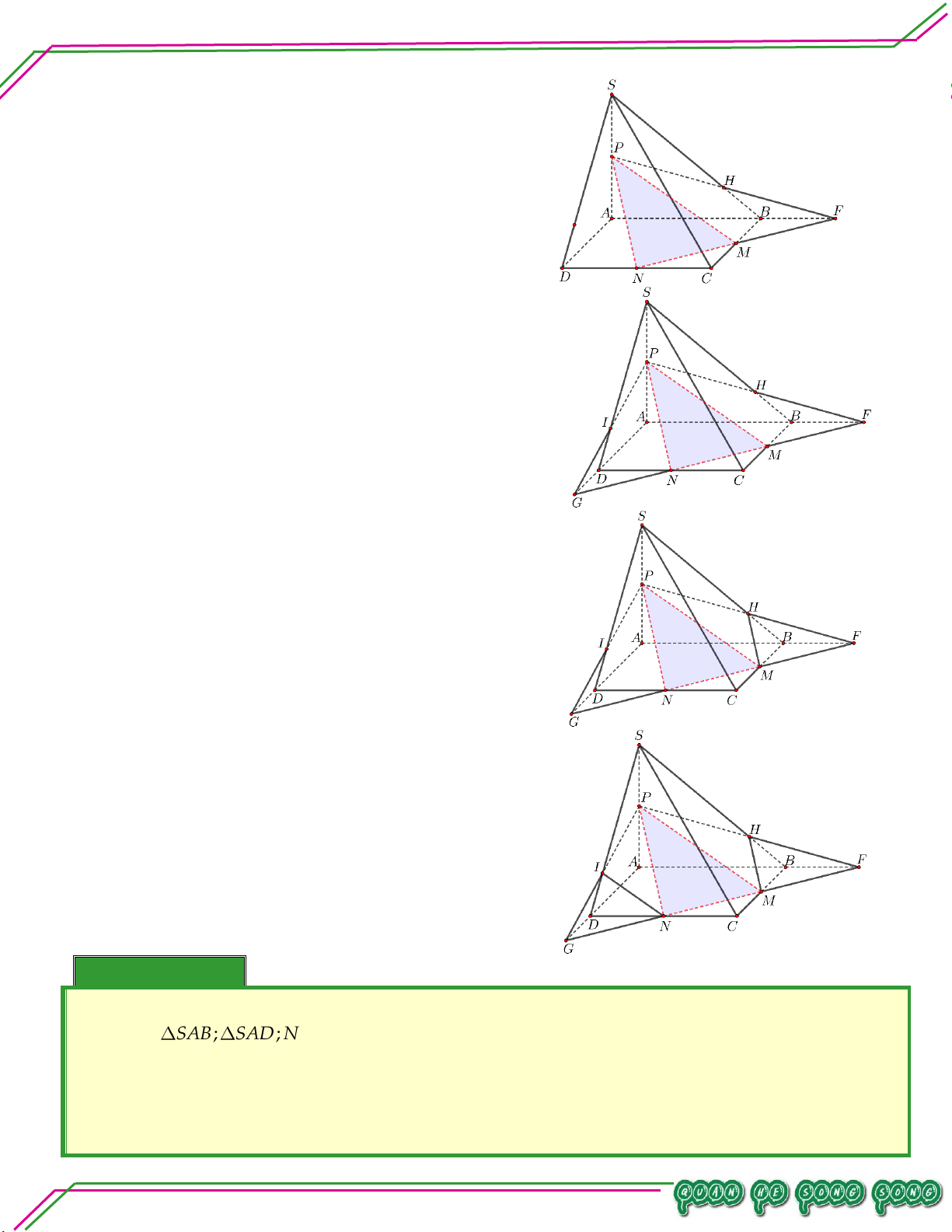
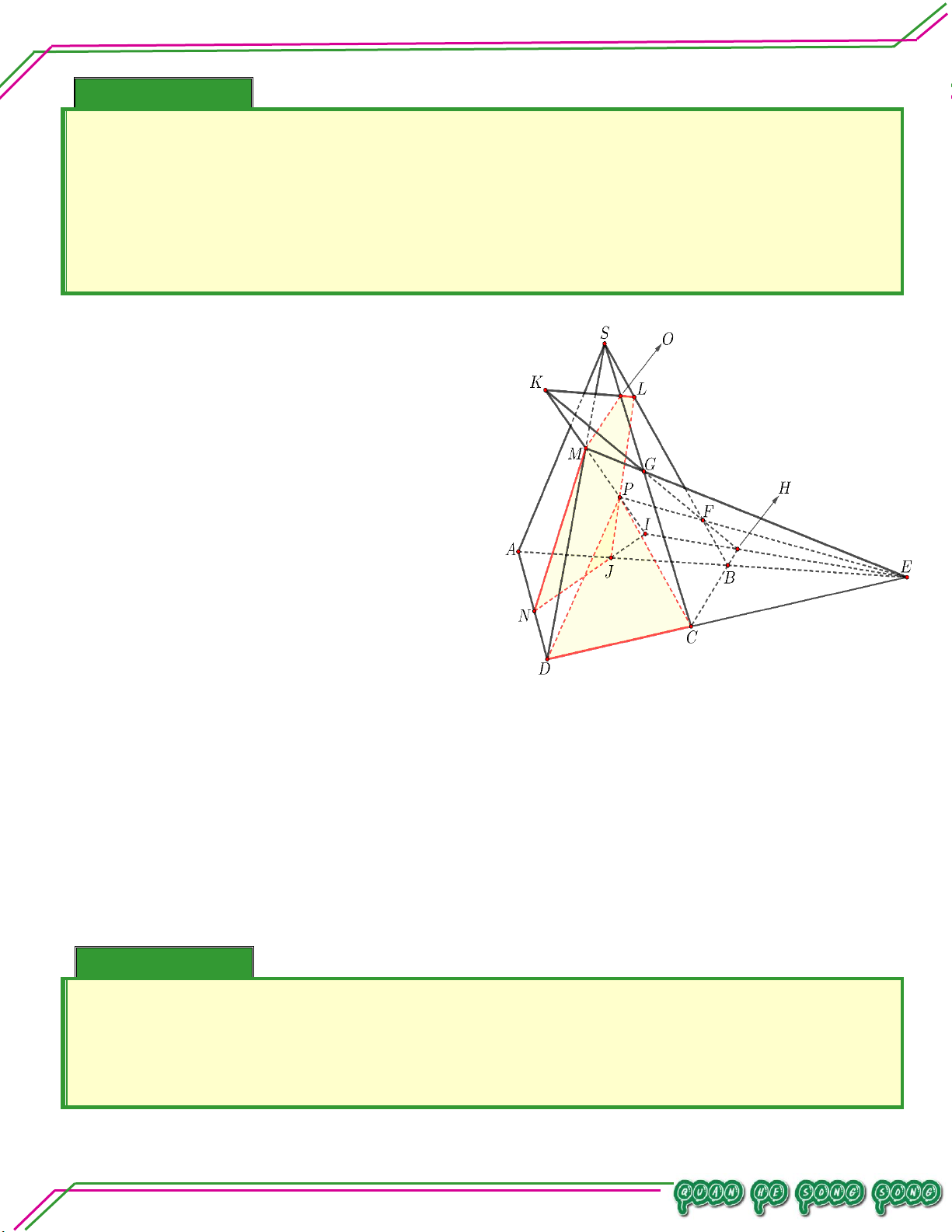
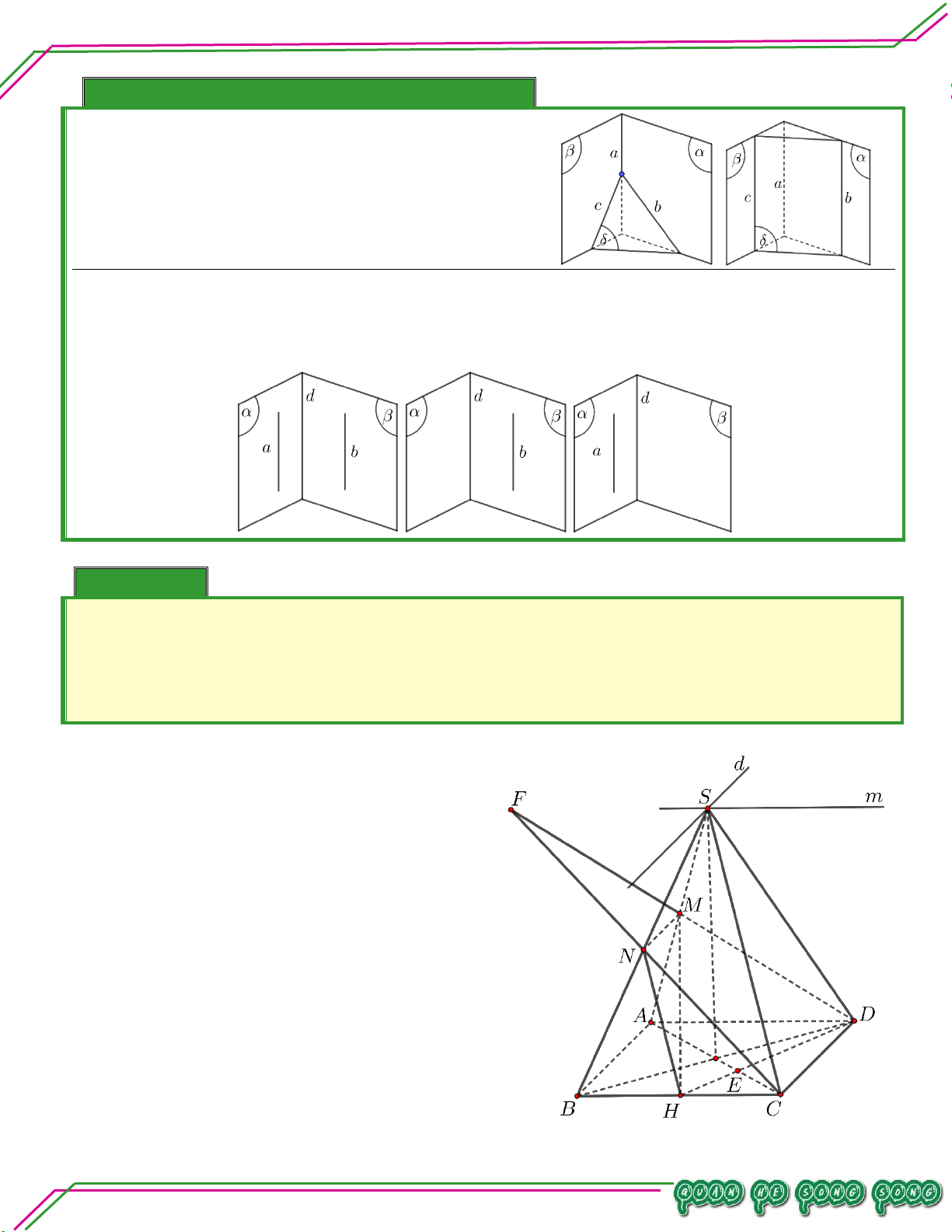
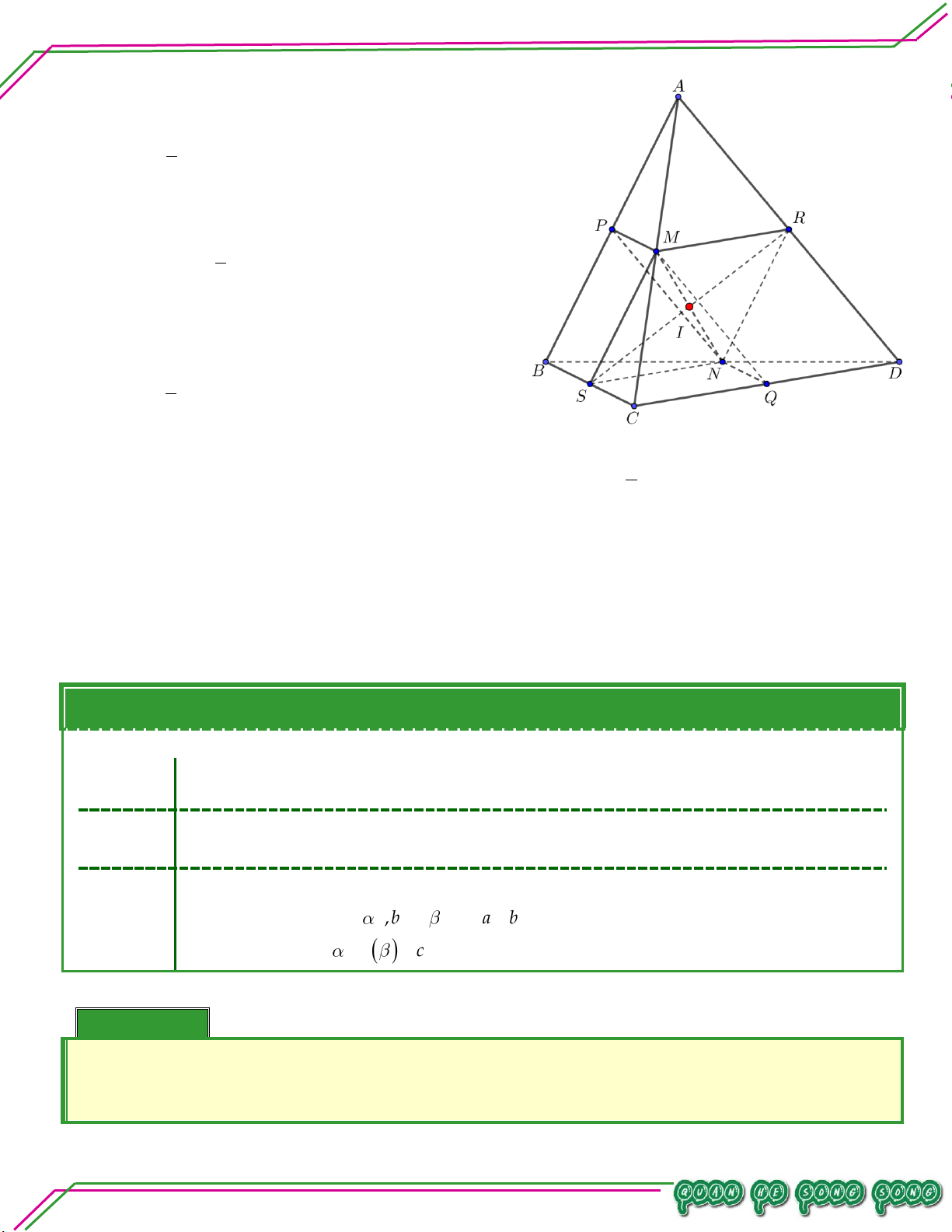
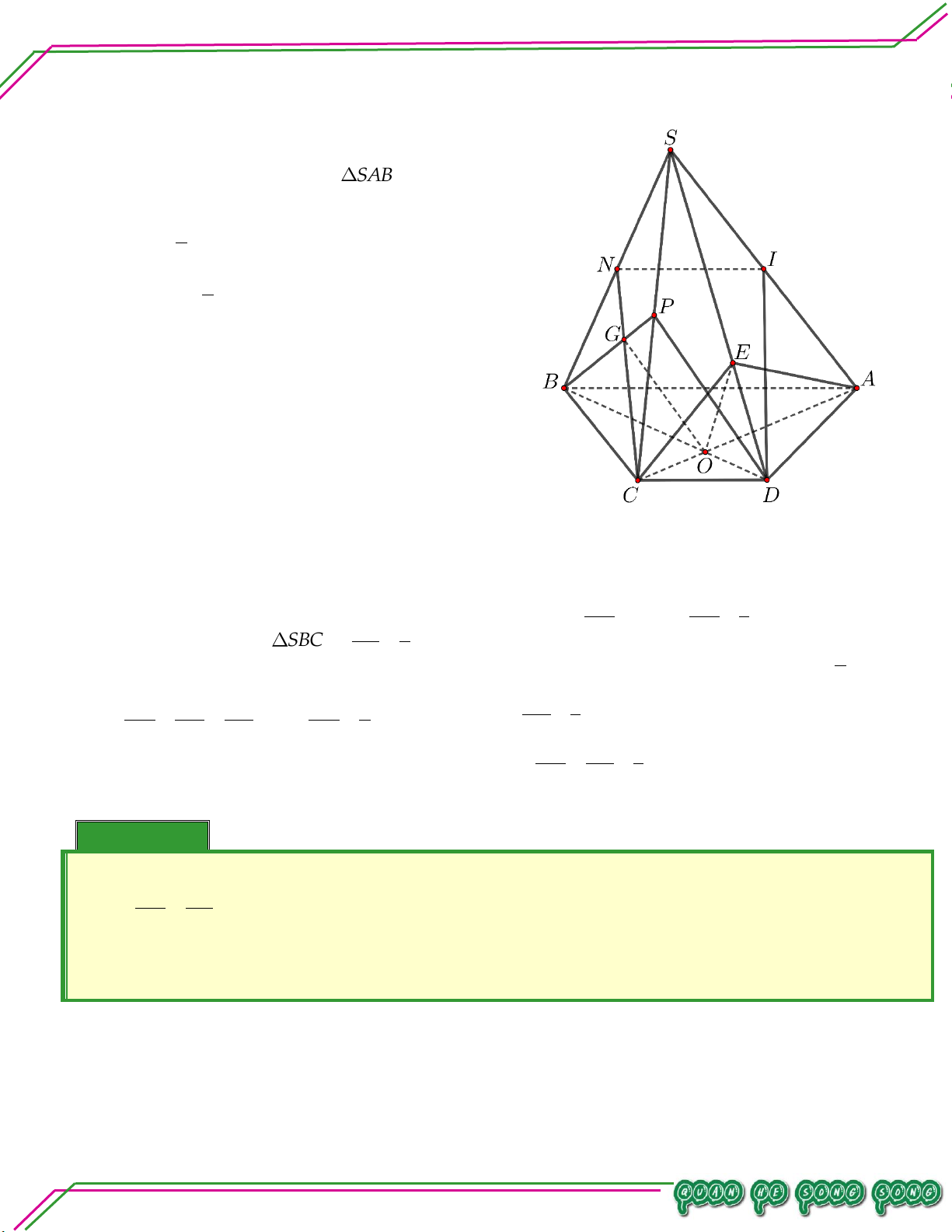
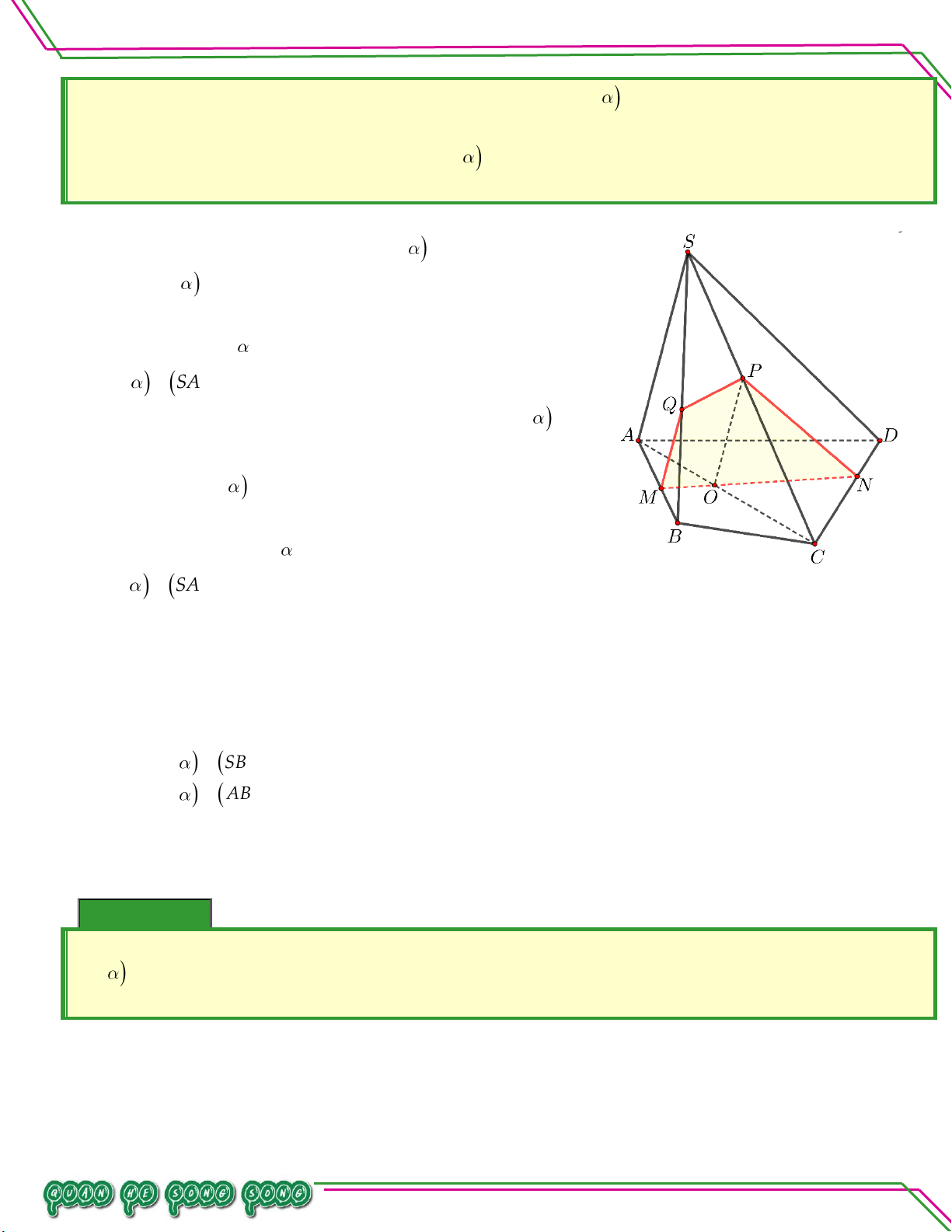
 Vậy giao tuyến của MNP và SCD là IN  Bài 06. Cho hình chóp .
S ABCD đáy ABCD có các cạnh đối không song song. Hai điểm M ;G lần lượt là
trọng tâm SAB; SAD; N SGN  G ,P nằm trong tứ giác ABCD . Tìm giao tuyến của:
. MNP và ABCD .
. MNP và SAC .
. MNP và SCD . Trang 17
Hình học 11 – Chương 02. QUAN HỆ SONG SONG Lời giải
. MNP và ABCD .
 Gọi E,F lần lượt là trung điển của AB, AD .
 Vì N  G'  MN EF  I .
I  MN , MN  MNP  I   MNP 
I  EF , EF   ABCD  I   ABCD Bi
 I MNPABCD ê
 Lại có PMNPABCD . n    So
Vậy MNP ABCD IP .
. MNP và SAC . ạn:
 Trong ABCD gọi J  IP  AC ,H  EF  AC . LÊ MINH
 Trong SEF gọi K  MN SH .
J  AC , AC  SAC  J   SAC 
J  IP , IP   MNP  J   MNP
 J MNPSAC TÂM
K SH ,SH  SAC  K   SAC 
K  MN , MN  MNP  K   MNP
 KMNPSAC
 Vậy MNPSAC  JK .
. MNP và SCD .
 Trong ABCD gọi Q ,R lần lượt là giao điểm của
IP với CD , AD .
 Trong SAD gọi T là giao điểm của NR với SD, Q
 CD ,CD   SCD 
 QMNPSCD
Q  IP , IP   MNP T
 SD ,SD   SCD 
 T MNPSCD
T  NR , NR   MNP
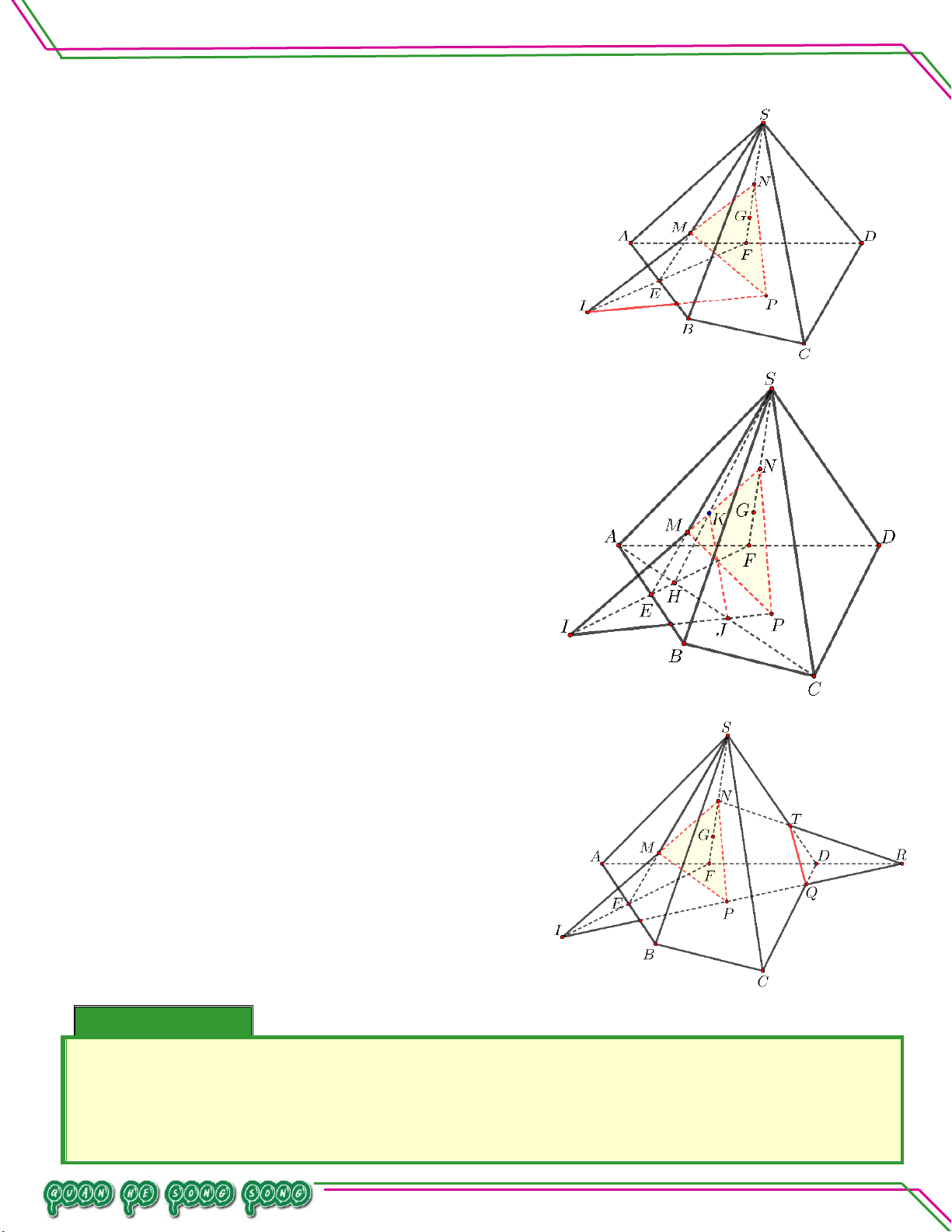
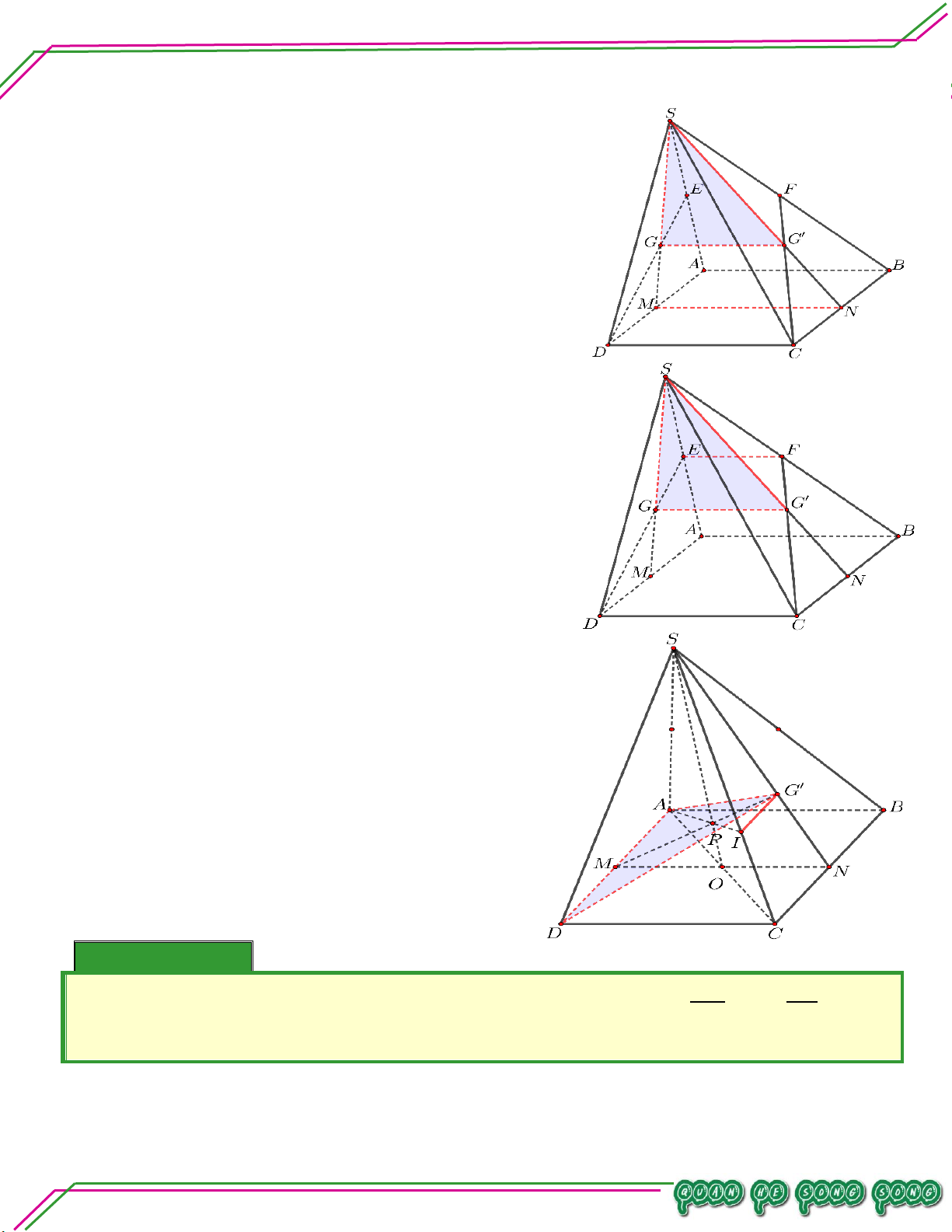
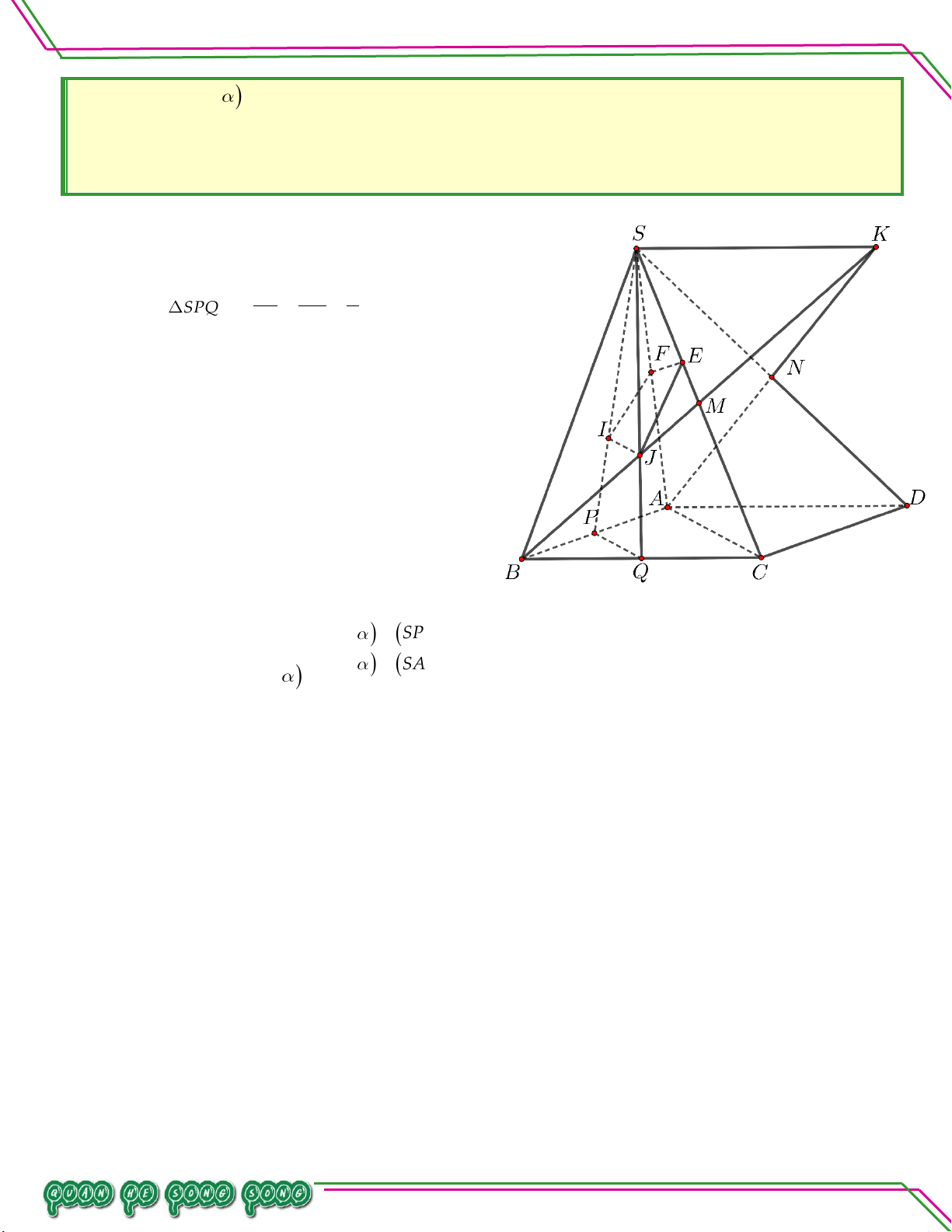
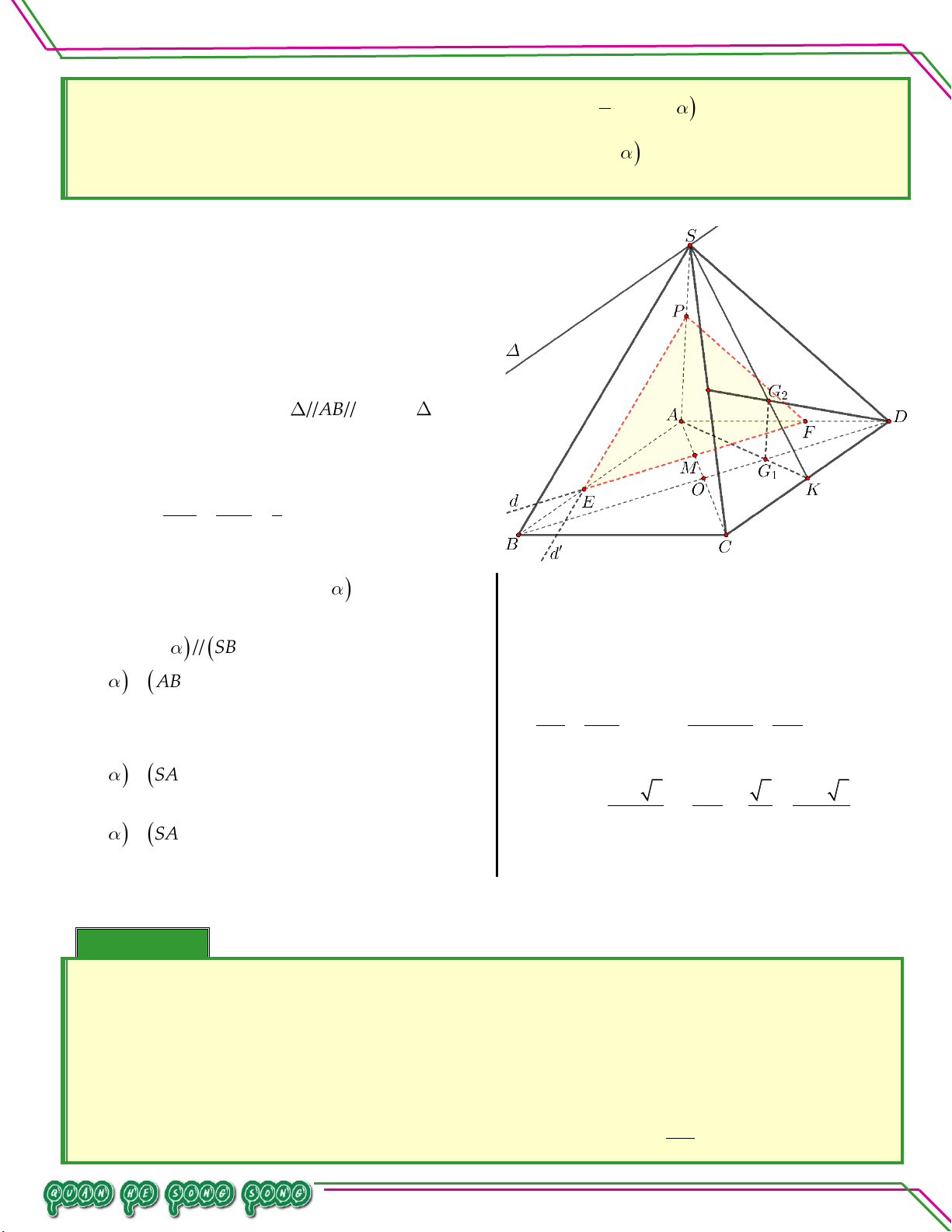
 Vậy MNPSCD  QT .  Bài 07. Cho hình chóp .
S ABCD với đáy ABCD là hình bình hành. Gọi G ,G' lần lượt là trọng tâm của các
tam giác SAD và SBC . Tìm giao tuyến của các cặp mặt phẳng:
. SGG' và ABCD .
. CDGG và ABS .
. ADG và SBC . Trang 18
Hình học 11 – Chương 02. QUAN HỆ SONG SONG Lời giải
. SGG' và ABCD .
 Gọi M , N lần lượt là trung điểm của AD ,BC , ta có
M  AD , AD   ABCD 
 M  SGG  ABCD
M SG ,SG   SGG'  '  
N  BC ,BC   ABCD 
 N  SGG  ABCD
N SG ' ,SG '   SGG'  '  
 Vậy SGG'ABCD  MN .
. CDGG và ABS .
 Gọi E,F lần lượt là trung điểm của SA,SB, ta có
ESA ,SA   SAB TÂM 
 E CDGG  SAB
E  DG , DG   CDGG'  '  
F SB ,SB   SAB 
 F  CDGG  SAB
F CG ' ,CG '   CDGG'  '  
 Vậy CDGG'SAB  EF . LÊ MINH
n: . ADG và SBC. ạ
 Trong mp ABCD , gọi O  AC MN .    n So
Trong mp SMN, gọi P G' M SO . ê
 Trong mp SAC , gọi I  APSC. Ta có Bi
I  AP , AP   ADG' 
 I  ADG  SBC
I SC ,SC   SBC  '  
 Lại có G'ADG'SBC .
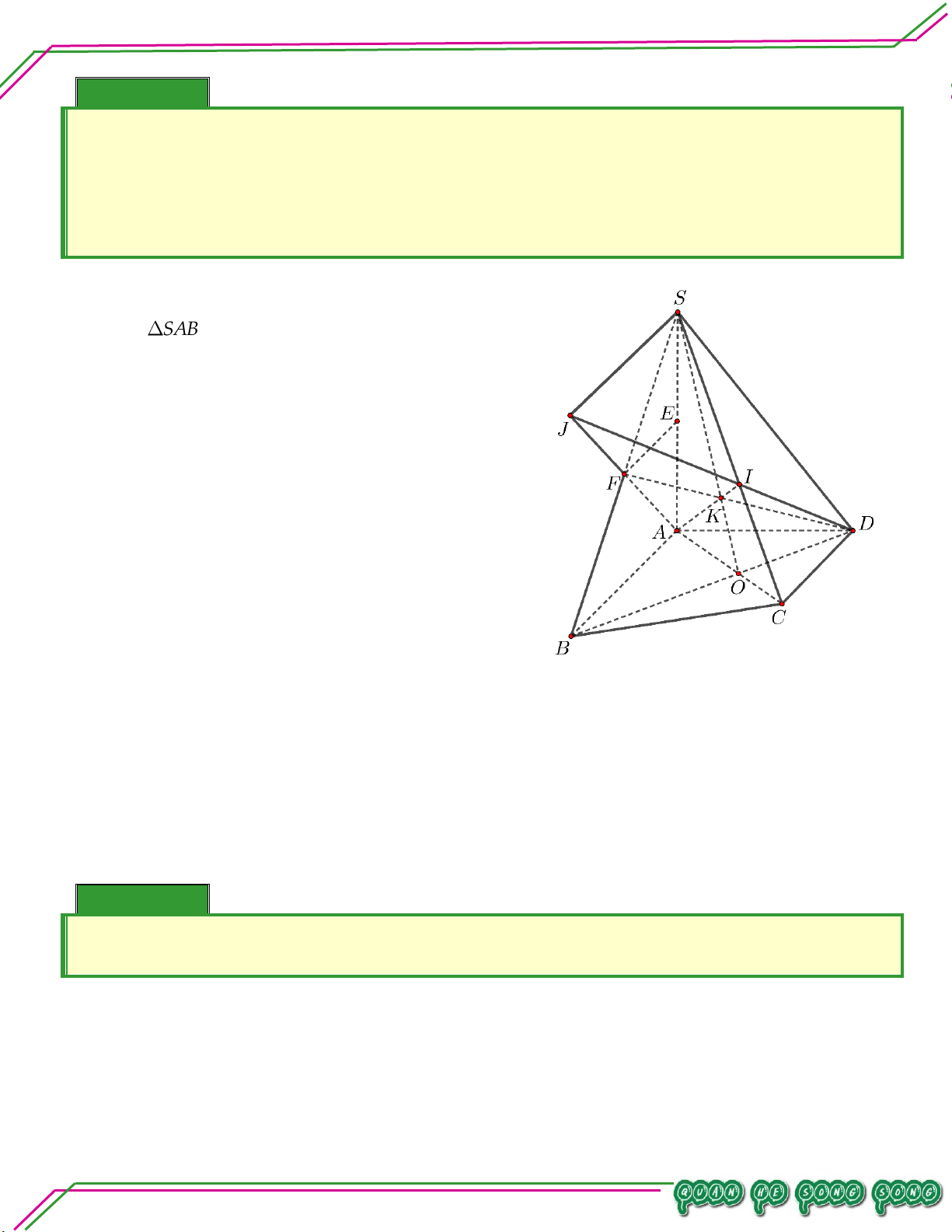
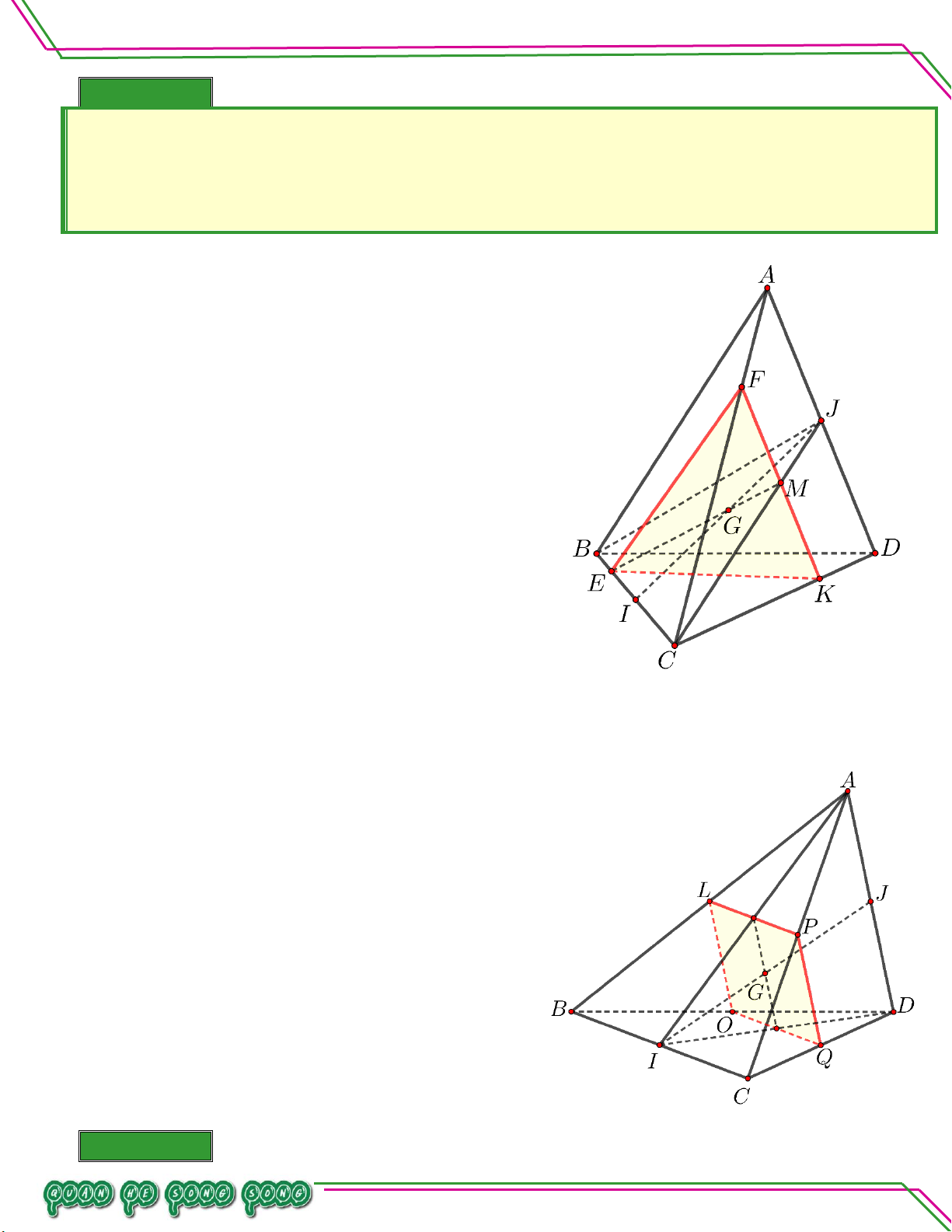
 Vậy ADG'SBC  IG' .  Bài 08. AM AN
Cho tứ diện ABCD . Trên hai đoạn AB và AC lấy hai điểm M, N sao cho 1 và  2 . Hãy BM NC
xác định giao điểm của đường thẳng BC và mặt phẳng DMN . Lời giải Trang 19
Hình học 11 – Chương 02. QUAN HỆ SONG SONG AM 1 2 AN  Ta có    nên theo định lý AB 2 3 AC
talet MN BC  I . I   BC  Vậy     . I   DMN I BC DMN  Bài 09. Bi Cho hình chóp .
S ABCD có đáy ABCD là hình thang, đáy lớn AB . Gọi I , J là trung điểm của SA,SB ên
. Lấy điểm M tùy ý trên SD. Tìm giao điểm của: So
. IM và SBC . ạ
. JM và SAC . n:
. SC và IJM . LÊ MINH Lời giải
. IM và SBC .
 Ta có ABCD là hình thang đáy lớn AB nên gọi
Q  BC  AD .
 Và SBCSAD  S TÂM
 SBCSAD  SQ
 Trong SAD gọi N  IM SQ
 N  IM SBC.
. JM và SAC .
 GọiO  AC  BD  SACSBD  SO.
 Trong mặt phẳng SAC gọi R  JM SO .
RSAC  
 R  JM SAC R JM
. SC và IJM . R  JM  Ta có    JM  
JIM R JIM
 Trong SAC gọi
PIJM
P  IR SC  
 P  SC IJM. PSC Trang 20
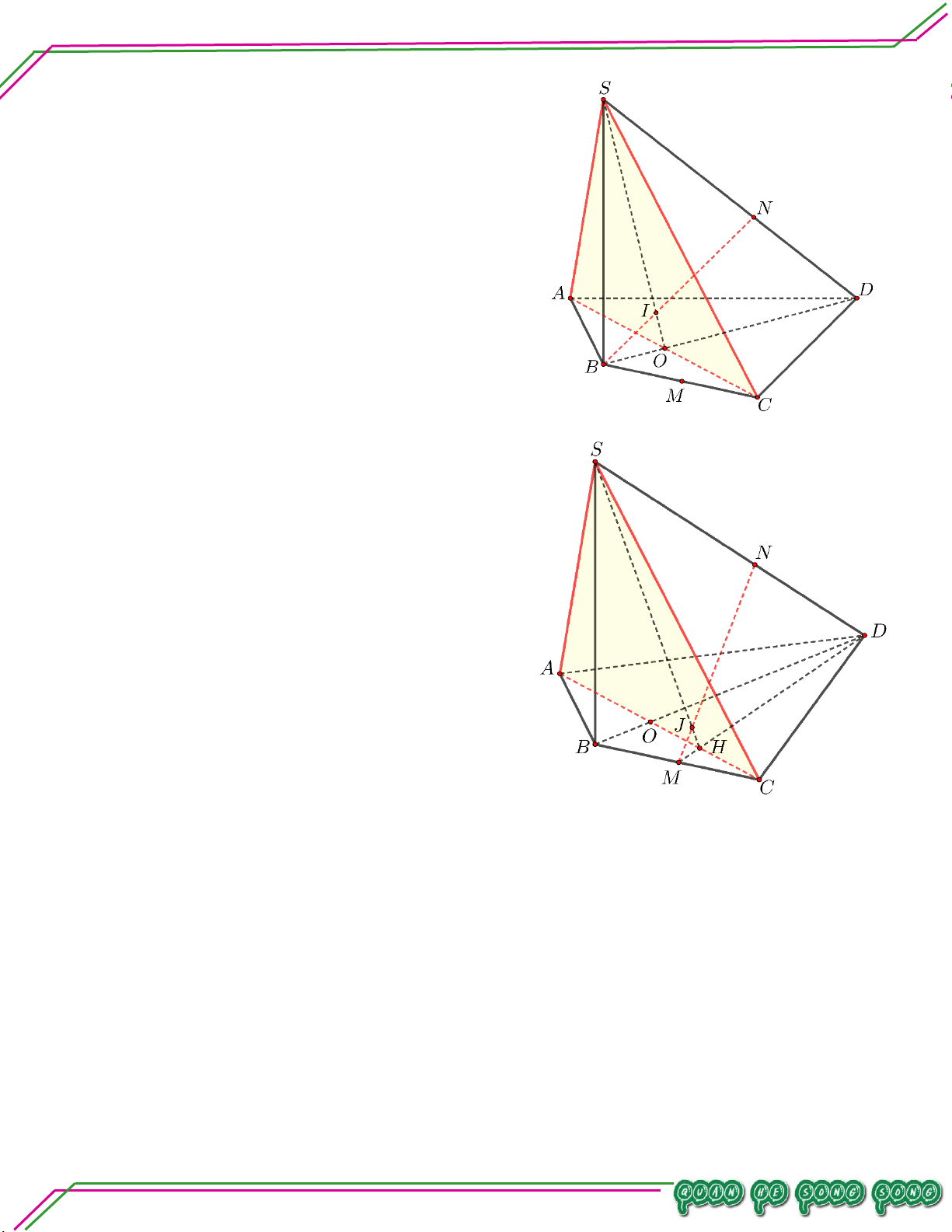
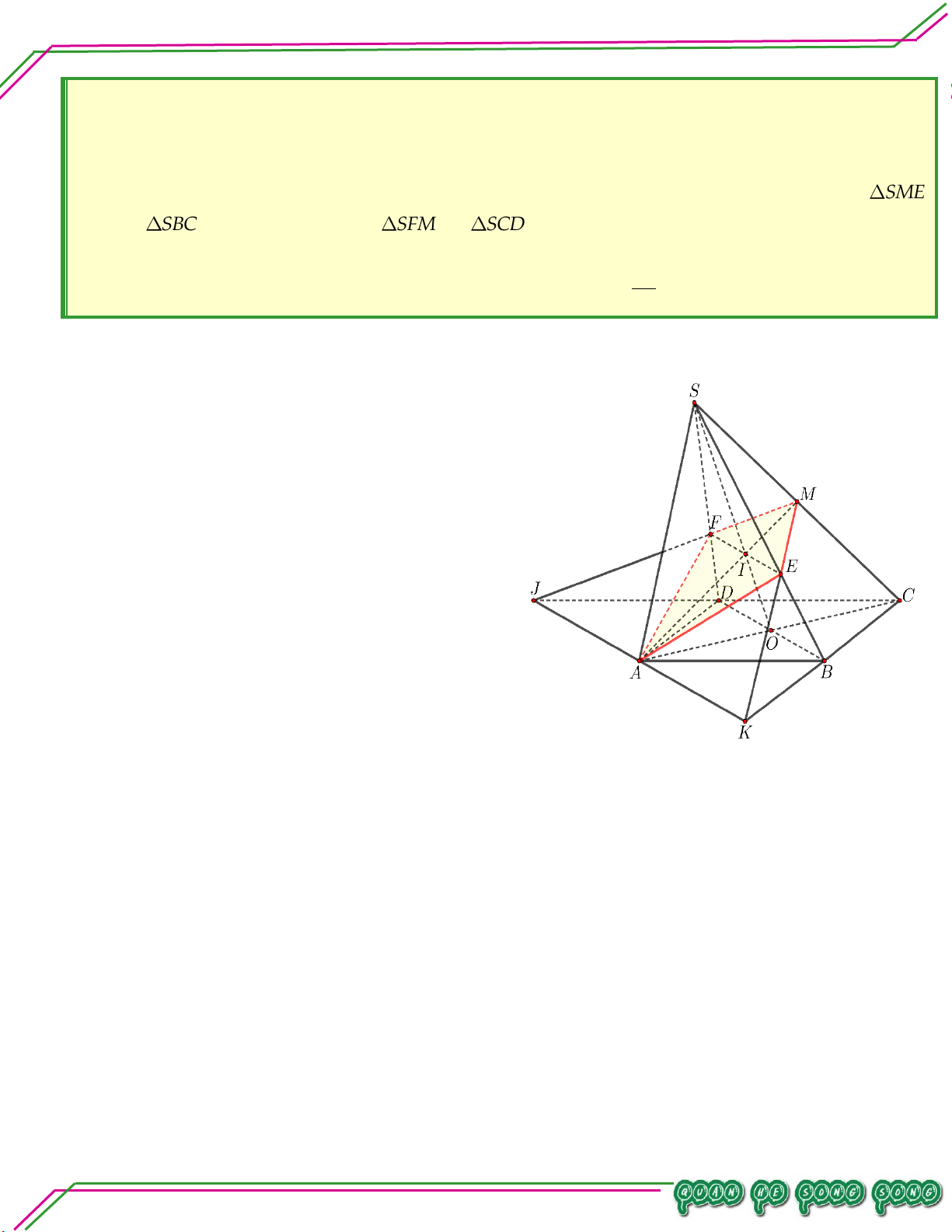
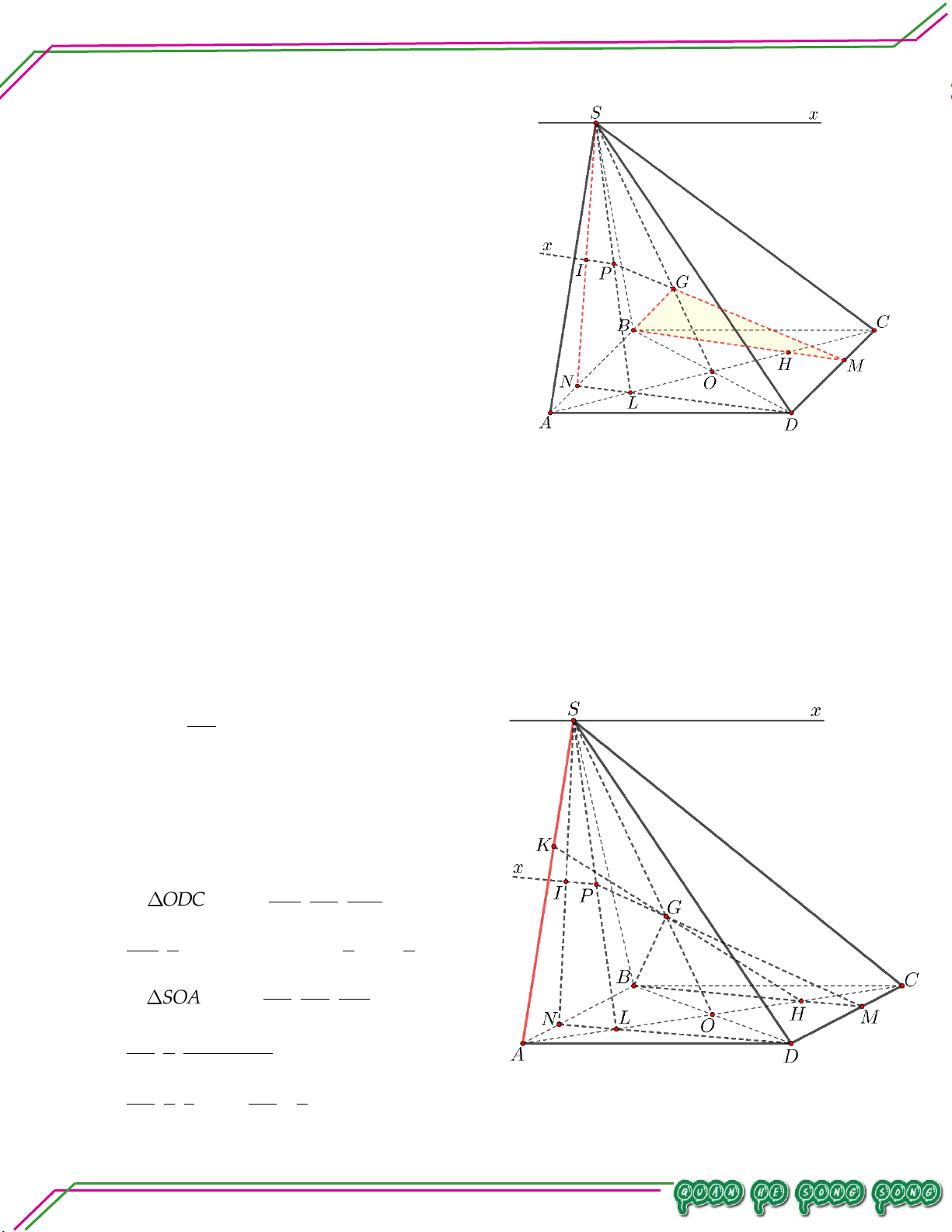
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Bài 10.
Cho hình chóp SABCD có đáy là hình bình hành ABCD tâm O . Gọi E là trung điểm SC .
. Tìm giao tuyến của BDE và SAC ..
. Tìm giao tuyến của ABE và SBD .
. Tìm giao điểm của SD và ABE . Lời giải
. Tìm giao tuyến của BDE và SAC . O  BED  SAC  Ta có: 
E  BED   SAC
 OE  BEDSAC .
. Tìm giao tuyến của ABE và SBD .   TÂM
 Trong mpSAC , gọi I SO AE . Khi đó:
BABE  SBD 
 BI  ABE SBD .
I   ABE   SBD
. Tìm giao điểm của SD và ABE .
 Trong SBD , gọi H SDIB LÊ MINH
 H  SDABE . n:ạ  Bài 11.
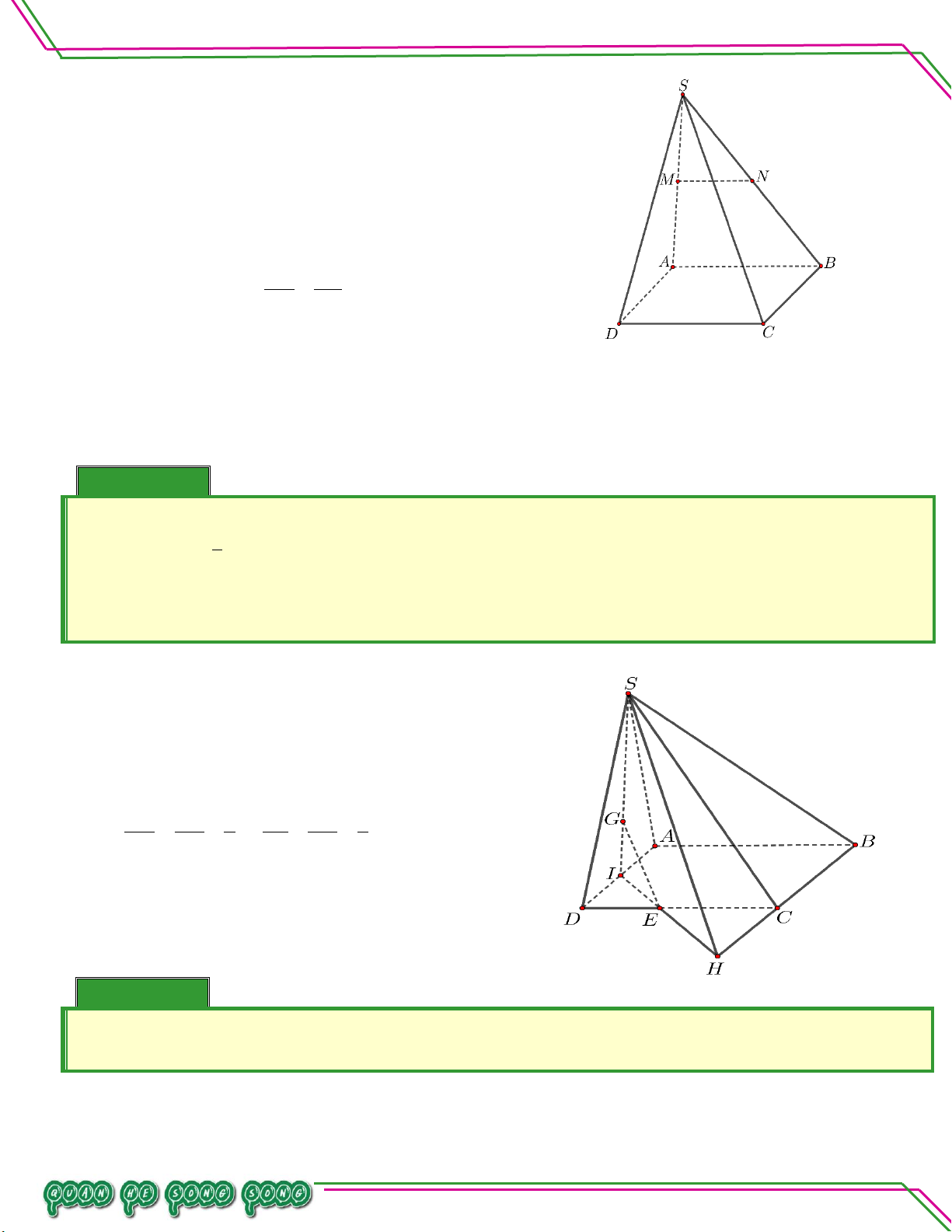
Cho hình chóp SABCD. Gọi M , N lần lượt là trung điểm SA , SD, P là điểm thuộc cạnh SB sao
n So cho SP3PB . ê
.Tìm giao điểm Q của SC và MNP . Bi
. Tìm giao tuyến của MNP và ABCD . Lời giải
.Tìm giao điểm Q của SC và MNP .
 Gọi O là giao điểm của AC và BD ,
I là giao điểm của SO và NP .
M SAC  MNP  Ta có: 
I  SAC   MNP
 MI  SACMNP .
 Trong SAC , gọi Q  MI SC
 Q  SC MNP.
. Tìm giao tuyến của MNP và ABCD . Trang 21
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Trong SAB , gọi E  MP AB  EABCDMNP (1).
 Trong SAC , gọi F  MQ  AC  FABCDMNP (2).
 Từ (1) và (2) suy ra EF  ABCDMNP.  Bài 07.
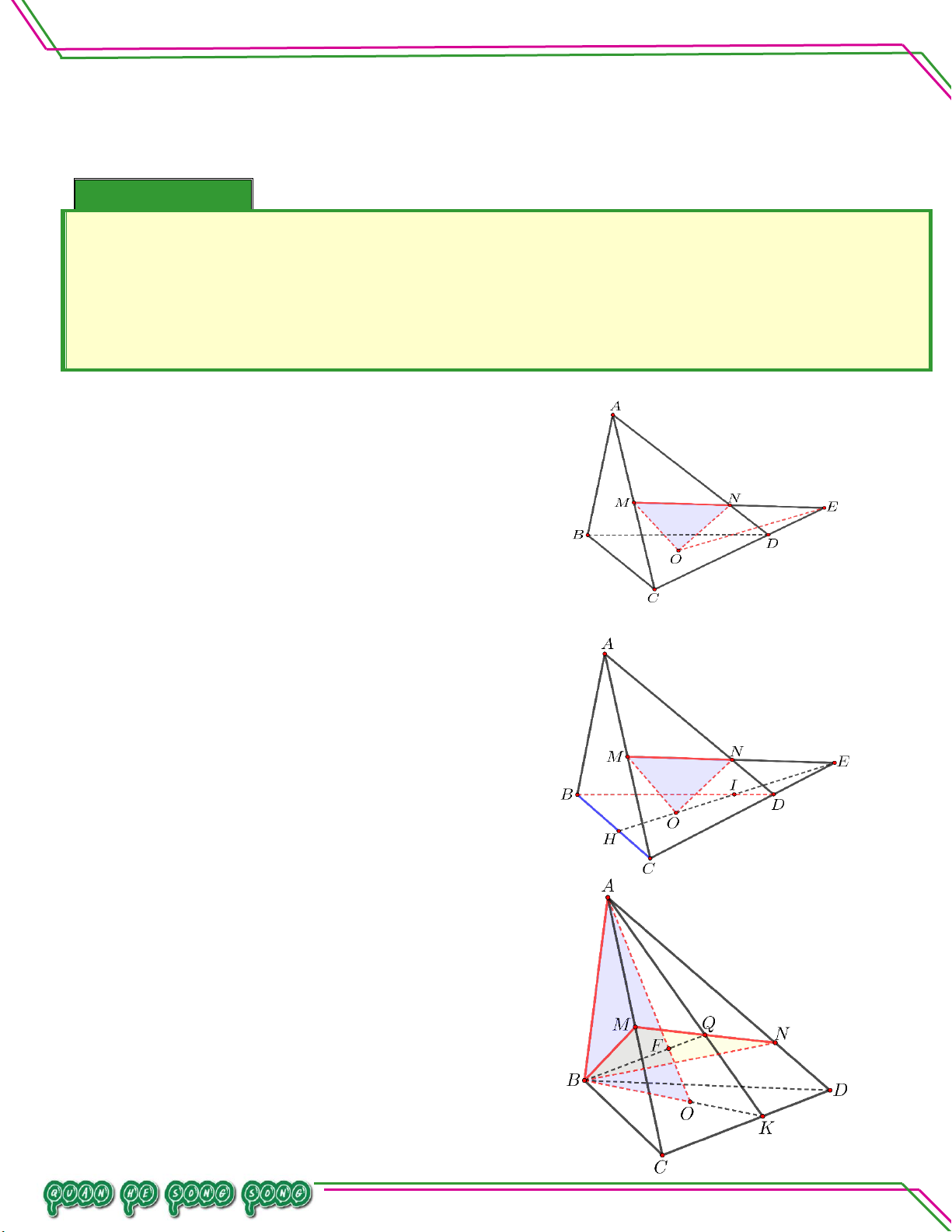
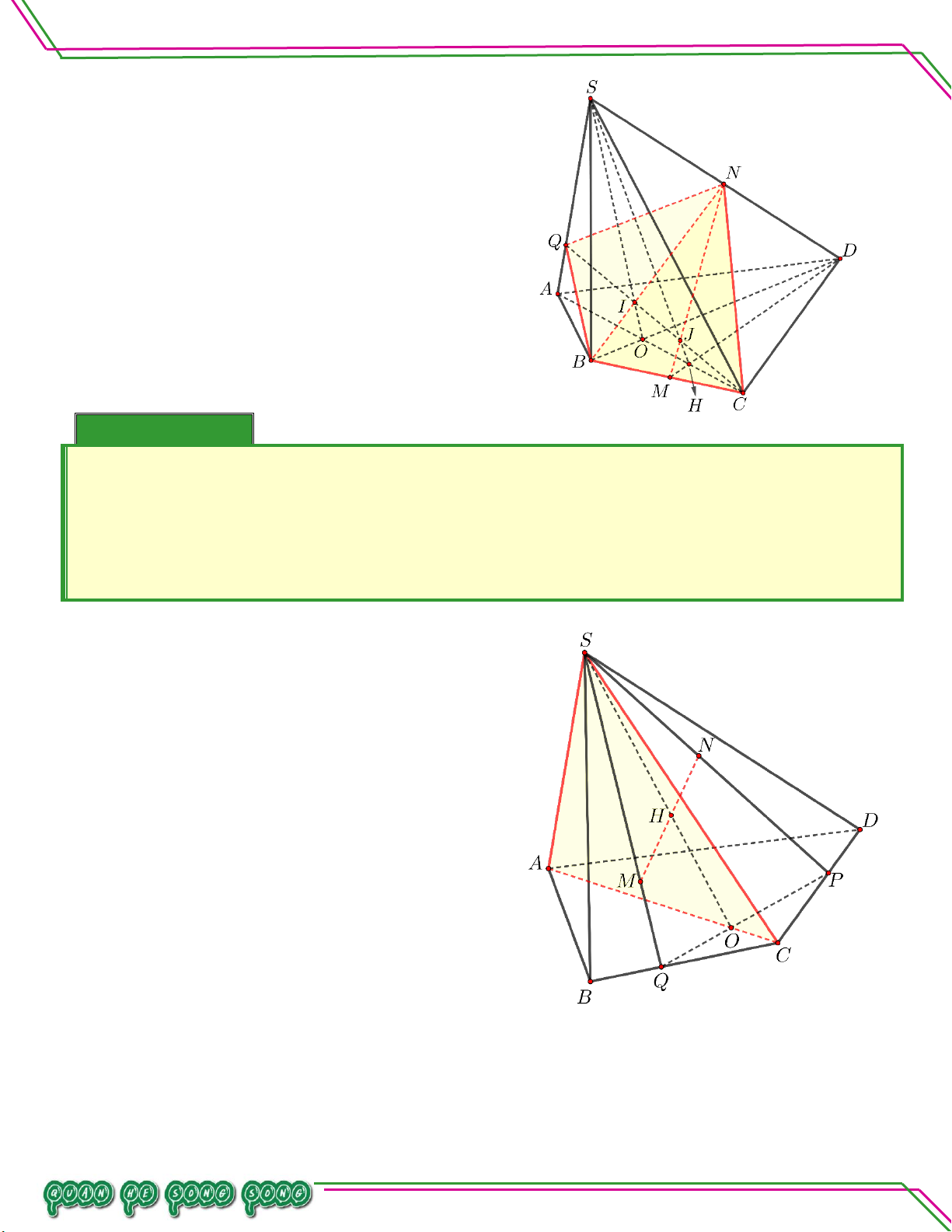
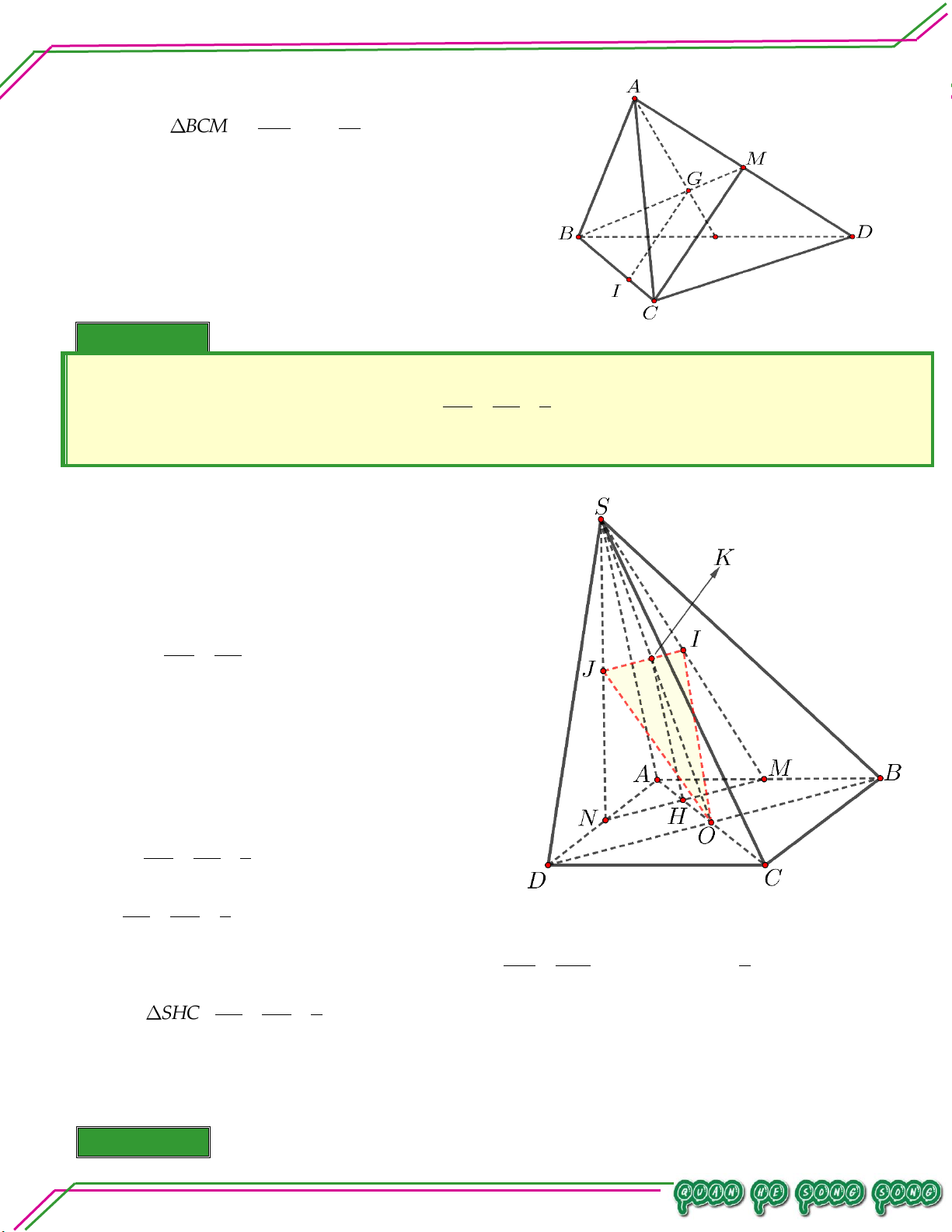
Cho tứ diện ABCD . Trên AC và AD lần lượt lấy các điểm M , N sao cho MN không song song
với CD . Gọi O là một điểm thuộc miền trong tam giác BCD . Bi
. Tìm giao tuyến của BCD và OMN . . Tìm giao điểm của BD và OMN . ê
. Tìm giao điểm của . . Tìm giao điểm của . n
BC và OMN
MN và  ABO So
. Tìm giao điểm của AO và BMN . ạ Lời giải n:
. Tìm giao tuyến của BCD và OMN . LÊ MINH
 Trong mpABD, gọi E  MN CD. O  OMN  BCD  Ta có: 
E  OMN    BCD
 OE  OMNBCD TÂM
. Tìm giao điểm của BD và OMN .
 Trong BCD , gọi I  OEBD. I   BD      . I OE OE 
OMN I BD OMN ,
. Tìm giao điểm của BC và OMN .
 Trong BCD , gọi H OEBC . I   BC      . H OE OE 
OMN H BC OMN ,
. Tìm giao điểm của MN và ABO .
 Trong BCD , gọi K OBCD.
 Trong ACD , gọi Q  MN  AK .
 Suy ra Q  MN ABO.
.Tìm giao điểm của AO và BMN .
 Trong ABK , gọi F  AO  BQ . F   AO      F  BQ BQ  
OMN F AO BMN , Trang 22
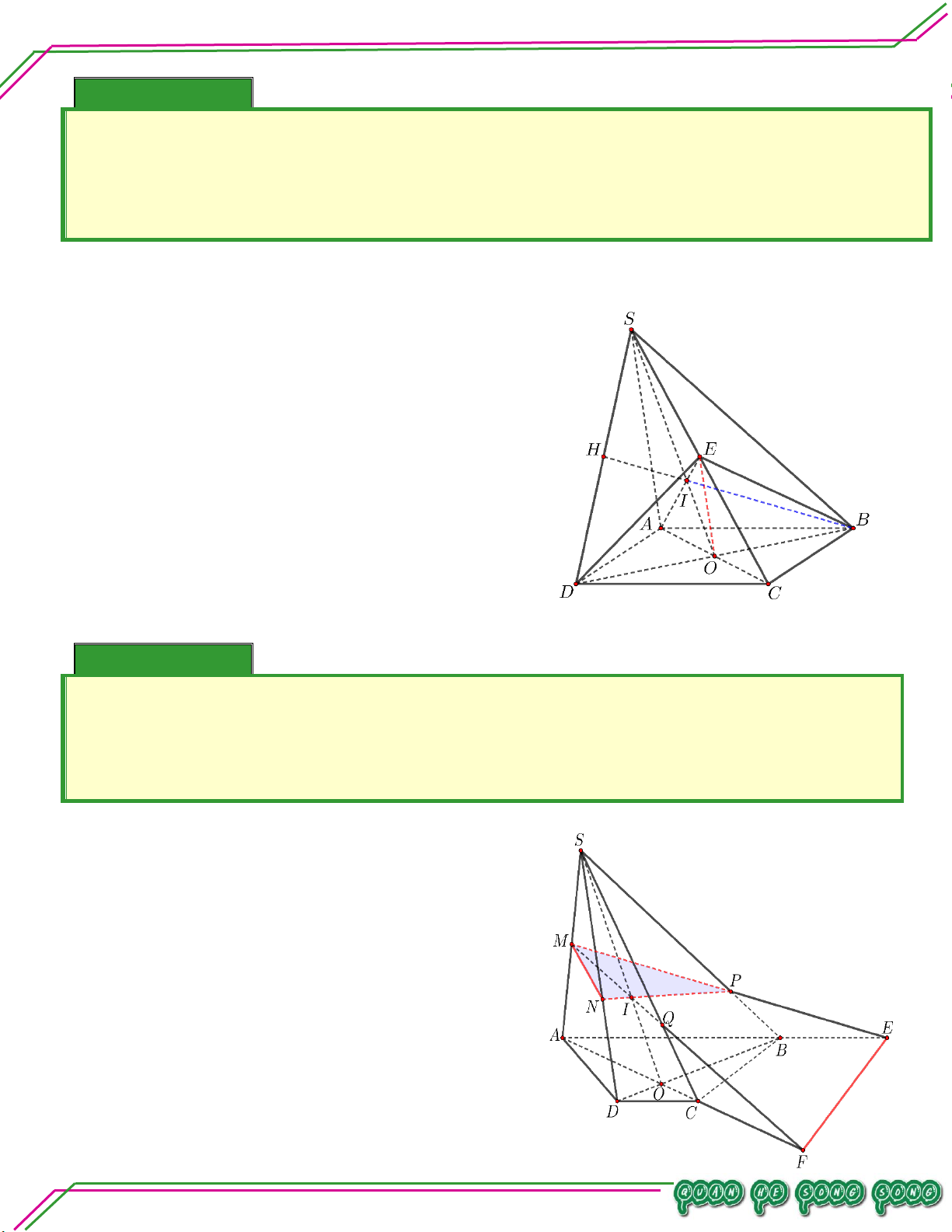
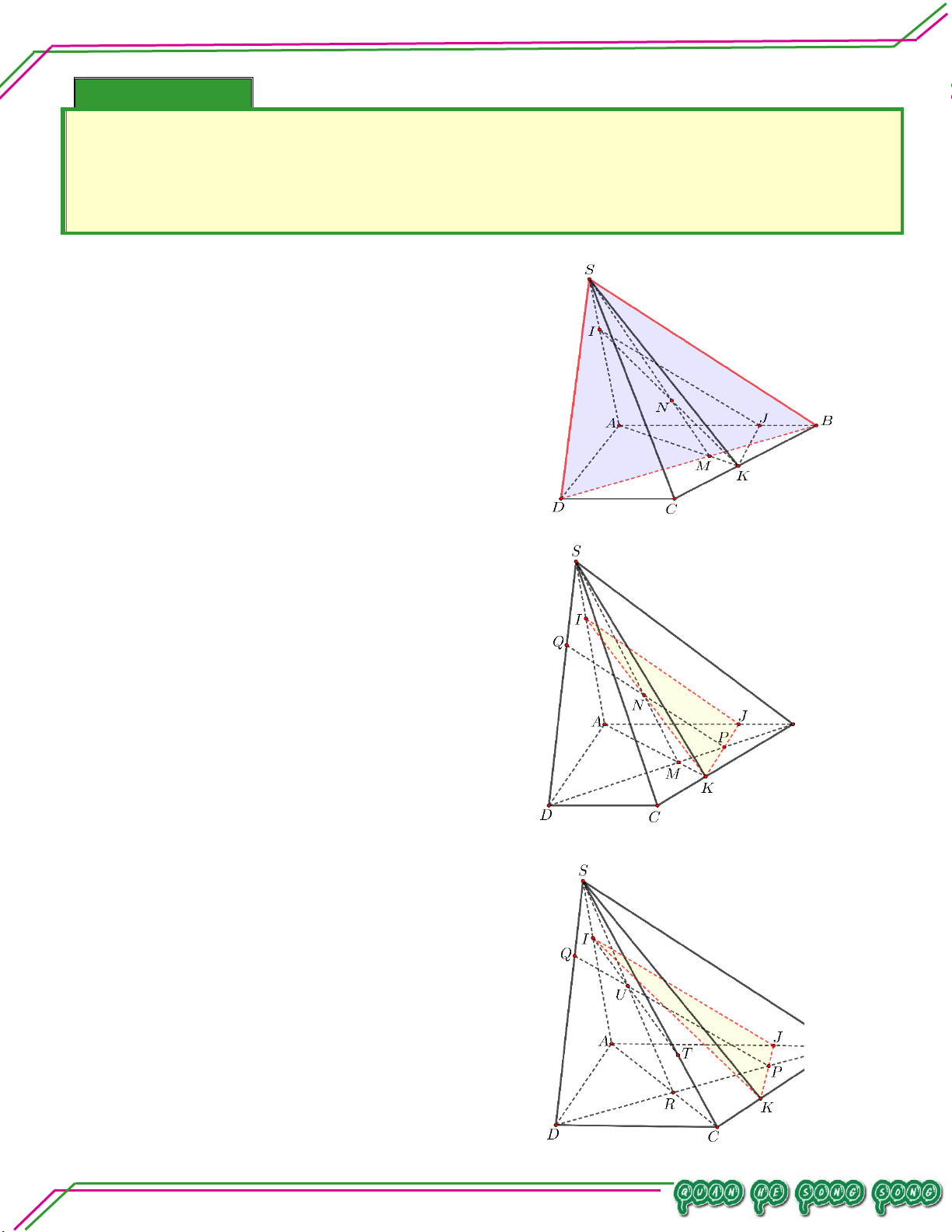
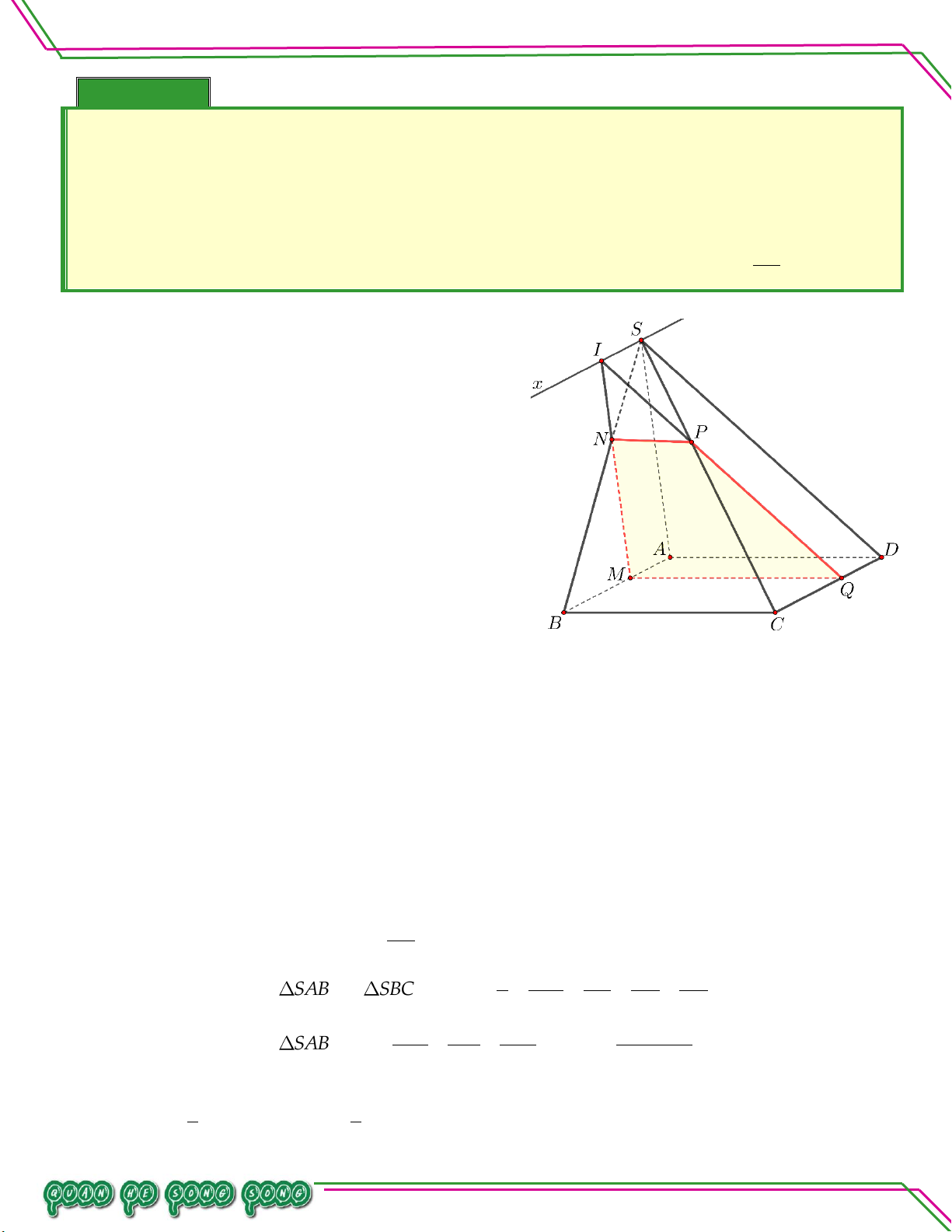
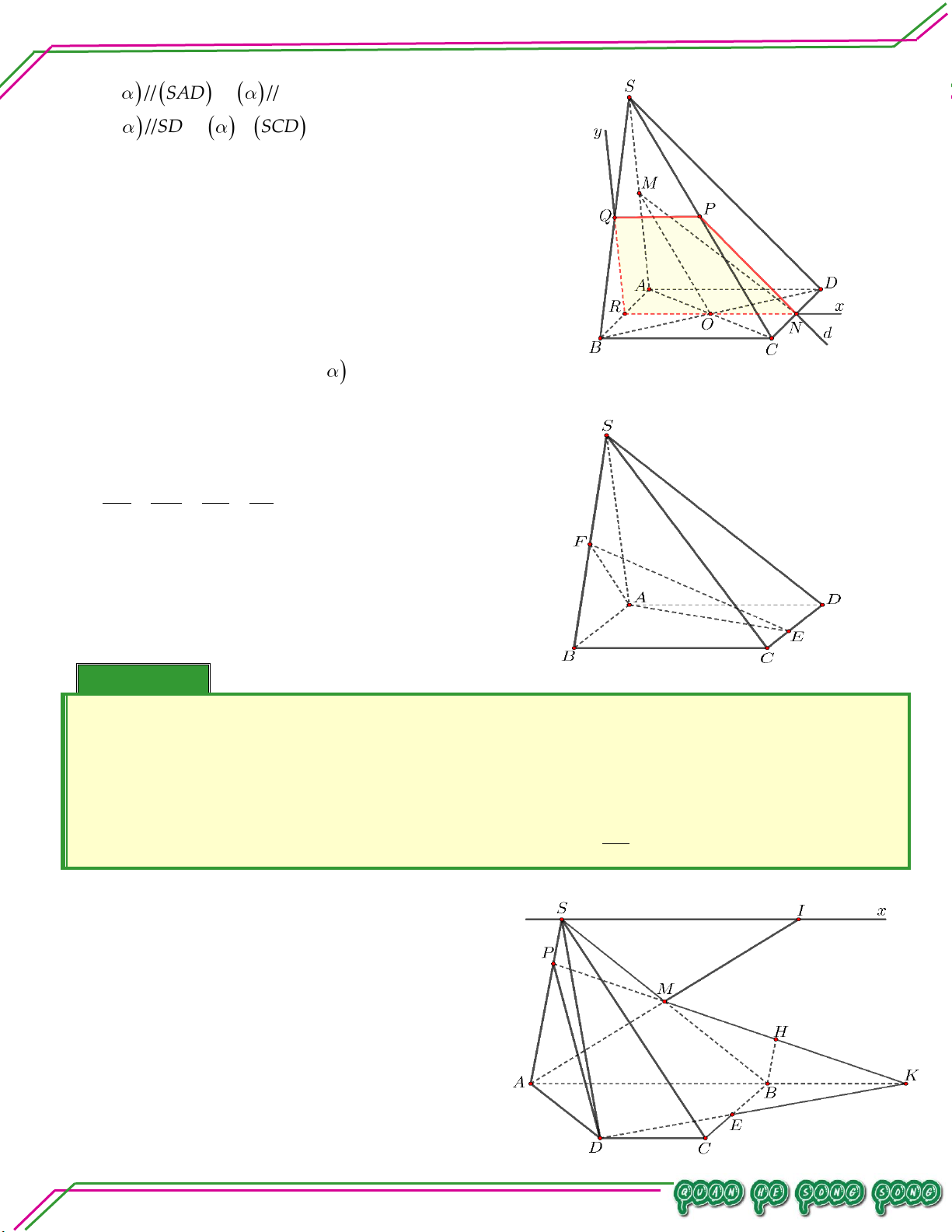
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Bài 08. Cho hình chóp .
S ABCD có đáy là hình thang, đáy lớn AB . Gọi I , J , K là ba điểm trên SA , AB , BC .
. Tìm giao tuyến IK với SBD .
. Tìm các giao điểm của IJK với SD và SC . Lời giải
. Tìm giao tuyến IK với SBD .
 Trong ABCD , vẽ AKBD  M
 Trong SAK , vẽ SMIK  N
N SM  SBD   N IK
  IK SBD  N . TÂM
. Tìm các giao điểm của IJK với SD và SC .
* Tìm giao điểm của IJK với SD
 Trong ABCD , vẽ JK  BD  P LÊ MINH P  BD   SBD n:   ạ P  IK   IJK
 Ta đã có IK SBD  N (theo CMT) n Soê
 Trong SBD , vẽ PN SD  Q Bi    Q  SD  Q  PN   IJK
  SD IJK  Q.
* Tìm giao điểm của IJK với SC
 Trong ABCD , vẽ AC BD  R
 Trong SBD , vẽ PQ SR  U U  SR   SAC   U  PQ   IJK
 Trong SAC , vẽ IU SC T    T  SC  T  IU   IJK
  SC IJK  T . Trang 23
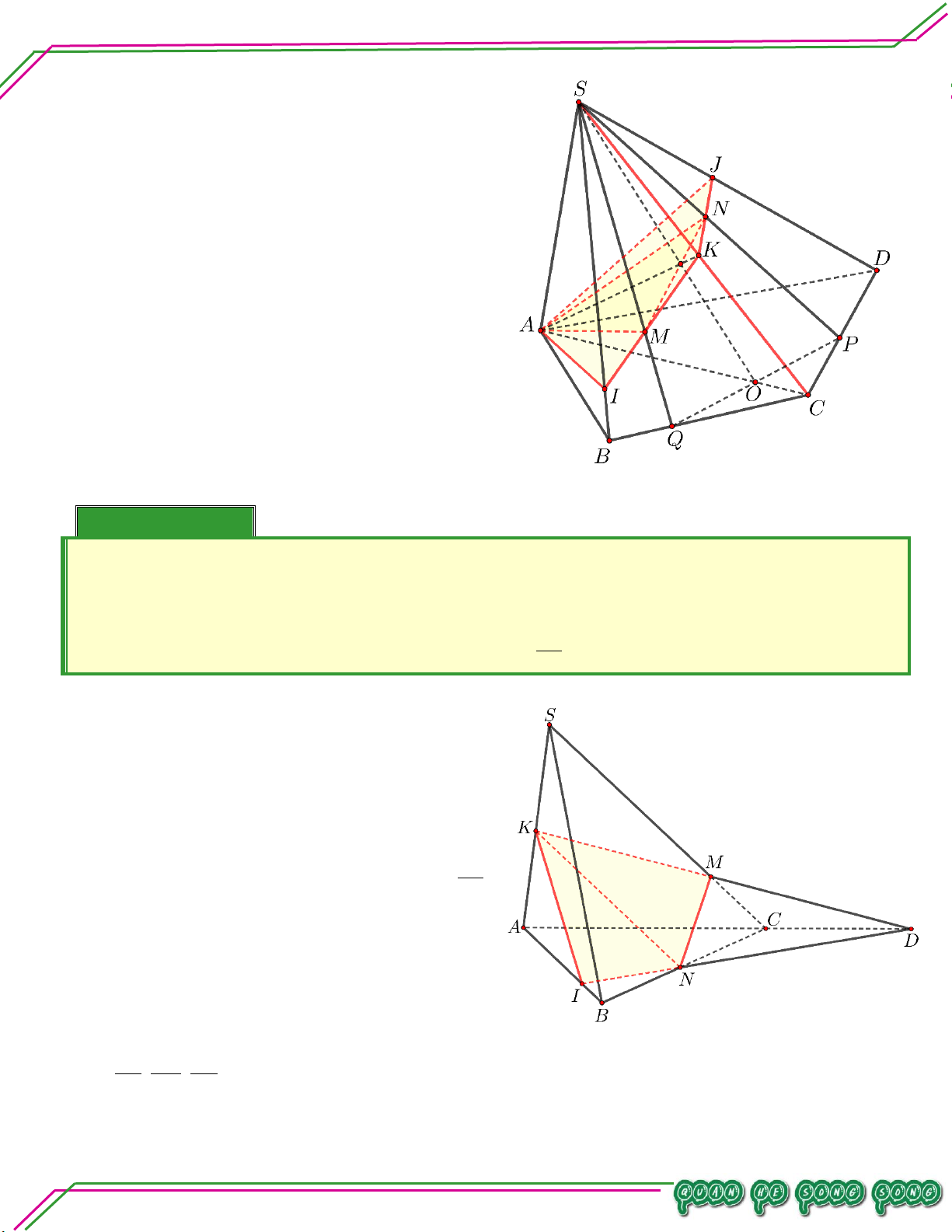
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Bài 08. Cho hình chóp .
S ABCD có đáy là hình bình hành. M là trung điểm của SB ; N là trọng tâm tam
giác SCD . Xác định giao điểm của:
. MN với ABCD .
. MN với SAC .
. SC với AMN. Bi
. SA với CMN . ê Lời giải n  So
. MN với  ABCD .
 Vì N là trọng tâm tam giác SCD . ạn:
 Nên trong SCD , vẽ SN CD  P LÊ MINH
 Trong SBP, vẽ MN  BP  Q Q    MN   Q  BP   ABCD
  MN ABCD  Q .
. MN với SAC . TÂM
 Trong ABCD , vẽ BP AC T T    AC   T  BP   SBQ
 Trong SBQ , vẽ ST MN  R
RST  SAC   R MN
  MN SAC  T .
. SC với AMN.
 Trong SAC , vẽ ARSC  D    D SC  D AR   AMN
  SC AMN  D.
. SA với CMN .
 Trong SAC , vẽ CRSA U    U  SA  U CR   SAC
  SA SAC U . Trang 24
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Bài 09. Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SD.
. Tìm giao điểm I của BM với SAC . Chứng minh BI  2IM.
. Tìm giao điểm E của SA và BCM. Chứng minh E là trung điểm của SA . Lời giải
. Tìm giao điểm I của BM với SAC . Chứng minh BI  2IM.
 Gọi O  AC BD.
 Ta có, SO  SACSBD.
 Trong SBD , gọi I  SOBM
I SO  SAC I SAC    
 I  BM SAC .  I  BM  I BM
 SBD có SO và BM là đường trung tuyến, TÂM
 Mà I  SOBM
 Nên I là trọng tâm của SBD.
 Do đó, BI  2IM.
. Tìm giao điểm E của SA và BCM. Chứng minh E là trung điểm của SA .
 Tìm SADBCM : LÊ MINH
AD  SAD  n:
 Ta có BC  BCM và có chung điểm M . ạ AD// BC 
 Nên giao tuyến của hai mặt phẳng SAD và n Soê
BCM là đường thẳng đi qua M và song song AD, Bi
BC cắt SA tại E .
 Suy ra, E là giao điểm của của SA và BCM.
 Xét tam giác SAD có ME//AD
 Mà M là trung điểm của cạnh SD, 
Suy ra E là trung điểm của SA .  Bài 10. Cho hình chóp .
S ABCD có đáy ABCD là hình thang, AB là đáy lớn và AB  3CD . Gọi N là trung
điểm CD , M là điểm trên cạnh SB thỏa mãn SM  3MB; I là điểm trên cạnh SA thỏa mãn AI  3IS .
. Tìm giao điểm của MN và SAD. HB
. Gọi H là giao điểm của CB và IMN. Tính ? HC Lời giải Trang 25
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
. Tìm giao điểm của MN và SAD.
 Tìm giao tuyến của SBN và SAD.
 Trong ABCD , gọi P  BNAD
 PSBNSAD SP  SBNSAD .
 Trong SBN, gọi K SPMN
KSP  SAD Bi  
 K  MN SAD .  K  MN ê n HB
. Gọi H là giao điểm của CB và IMN. Tính ? So HC ạ
 Tìm giao tuyến của ABCD và IMN. n:
 Ta có, N DC  N ABCDIMN (1). LÊ MINH
 Trong SAB , gọi Q  IM  AB
 QIM  IMN  
 QABCDIMN (2). Q  AB   ABCD
 Từ (1) và (2) suy ra, NQ  ABCDIMN. TÂM
 Trong ABCD , gọi H  CB  NQ  H CB  
 H  CBIMN. H  NQ   IMN HB  Tính : HC
 Xét tam giác SAB có I SA; MSB;Q AB. Do 3 điểm I , M ,Q thẳng hàng  IS QA MB
Nên theo định lý Menenauyt ta có: . .  1 IA QB MS 1 QA 1  QA QB . .  1 
 9  QA  9QB  AB  8QB  6NC  6 3 8QB    . 3 QB 3 QB NC 8 4 HB QB 3
 Mặt khác, NC//QB    . HC NC 4  Bài 11. Cho hình chóp .
S ABCDcó đáy ABCD là hình bình hành tâm O , hai điểm M, N lần lượt là trung
điểm của SB,SD , điểm PSC và không là trung điểm của SC .
. Tìm giao điểm của SOvới mặt phẳng MNP .
. Tìm giao điểm của SA với mặt phẳng MNP .
. Gọi F,G, H lần lượt là giao điểm của QM và AB , QP và AC , QN và AD . Chứng minh
ba điểm F,G, H thẳng hàng. Trang 26
Hình học 11 – Chương 02. QUAN HỆ SONG SONG Lời giải
. Tìm giao điểm của SOvới mặt phẳng MNP . TÂM
 Ta có MN,SO đều thuộc mặt phẳng SBD ,
 Gọi I  MN SO  I  SO MNP
. Tìm giao điểm của SA với mặt phẳng MNP .
 Ta có IP,SA cùng thuộc mặt phẳng SAC . LÊ MINH       
Gọi Q IP SA, IP
MNP Q SA MNP
n: . Gọi F,G,Hlần lượt là giao điểm của QM và AB, QPvà AC, QN và AD.
ạ Chứng minh ba điểm F,G,H thẳng hàng.
 Ta có F  QM  AB  F MNPABCD. n Soê
 G  QP  AC  GMNPABCD Bi
 H  QN  AD  H MNPABCD
 Vậy F,G, H là ba điểm chung của MNP và ABCD
Nên F,G, H thẳng hàng.  Bài 12. Cho hình chóp .
S ABCDcó AB không song song với AD . Gọi M là trung điểm của SC và O là giao
điểm của AC và BD .
. Tìm giao điểm N của SDvới mặt phẳng MAB.
. Chứng minh: SO, AM,BN đồng quy. Lời giải Trang 27
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
. Tìm giao điểm N của SDvới mặt phẳng MAB.
 Ta có AM,SO cùng thuộc mặt phẳng SAC ,
 Gọi I  SO  AM  I ABM  BI  ABM.
 Trong mặt phẳng SBD , gọi N  BI SD N   SD     . N  BI  
ABM N SD ABM Bi
. Chứng minh: SO, AM,BN đồng quy. ê  n Ta có  So
S  SAC   SBD    
O  SAC  
SBD SO SAC SBD ạn:  I  AM   SAC
 Lại có I  BN  AM  LÊ MINH IBN   SBD
 I SACSBD  I SO 
SO, AM,BN đồng quy tại I .  Bài 13. Cho hình chóp .
S ABCD có đáy ABCD có các cạnh đối không song song AC  BD  O. Gọi E, F, H TÂM
lần l;ượt là các điểm thuộc cạnh SA,S , B SC .
. Tìm giao điểm K  SD EFH .
. AC DB  O, EH  FK  I . Chứng minh S,I,O thẳng hàng.
. ADBC  M , EK FH  N . Chứng minh S, M,N thẳng hàng.
. ABCD  P , EF  HK  Q . Chứng minh A, P,Q thẳng hàng. Lời giải
. Tìm giao điểm K  SD EFH.  Trong SAC :
I  SO  EH  SBD EFH  FI  Trong
SDB:K SDFI K SDEFH
. AC DB  O, EH  FK  I .
Chứng minh S, I,O thẳng hàng.
 EH  FK  I  I SACSBD .
 Mặt khác SBDSAC  SO  I SO
 S,I,O thẳng hàng.
. ADBC  M , EK FH  N . Chứng minh S, M,N thẳng hàng.
 EK  FH  N  N d  SADSBC
 Mặt khácSADSBC  SM  N SM Trang 28
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 S,M,N thẳng hàng.
. ABCD  P , EF  HK  Q . Chứng minh A, P,Q thẳng hàng.
 EF  HK  Q  QSABSCD .
 Mặt khác SABSCD  SP  I SP
 S, P,Q thẳng hàng.  Bài 14. Cho hình chóp .
S ABCD, gọi I , J là hai điểm trên hai cạnh AD,SB
. Tìm giao tuyến của hai mặt phẳng SAC,SBI .
. Tìm giao tuyến của hai mặt phẳng SAC và SBD .
. AD cắt BC tại O, OJ cắt SC tại M . Chứng minh A,K, L, M thẳng hàng. Lời giải
. Tìm giao tuyến của hai mặt phẳng SAC,SBI .
TÂM Tìm giao điểm K của IJ và SAC.  Trong ABCD
G  AC  BI  SG  SAC SBI  .
IJ  SBI   Ta có: 
 SBI   SAC  SG LÊ MINH K  IJ   SAC n:ạ
  K  IJ SGtrongSAC .
. Tìm giao tuyến của hai mặt phẳng SAC và SBD . Tìm giao điểm L của DJ và SAC n Soê
 Gọi H  AC  BD  SH  SACSDB Bi
DJ  SBD   Ta có: 
 SBD SAC  SH  L  DJ SHtrongSAC . L  DJ   SAC
. AD cắt BC tại O, OJ cắt SC tại M . Chứng minh A,K, L, M thẳng hàng.
 A,K, L, M thuộc các đường thẳng OA,IJ, JD, JO  A,K, L, M AOJ
 A,K, L, M thuộc các đường thẳng AC,SG,SH,SC  A,K, L, M SAC
  I,K, L, M SACOAJ nên A,K,L,M thẳng hàng.  Bài 15. Cho hình chóp .
S ABCD có đáy là hình thang, đáy lớn AB ; lấy M, N lần lượt thuộc các cạnh
SC,SD . Tìm thiết diện của hình chóp cắt bởi mặt phẳng  ABM;AMN
. Xác định thiết diện của hình chóp cắt bởi ABM .
. Xác định thiết diện của hình chóp với AMN. Trang 29
Hình học 11 – Chương 02. QUAN HỆ SONG SONG Lời giải
. Xác định thiết diện của hình chóp cắt bởi ABM :
 Gọi O  AC BD
 Trong SAC , gọi I  SOAM
 Trong SCD , gọi P  BI SD
 PSCDABM . Bi  Ta có : ê
ABMSBC  BM. n So
ABMSCD  MP ạ
ABMSAD  AP. n:
 Vậy thiết diện là hình thang ABMP ( Vì LÊ MINH AB//MP )
. Xác định thiết diện của hình chóp với AMN.
 Nếu MN AB : AMN  ABMN  thiết
diện cần tìm là từ giác ABMN . TÂM
 Nếu MN không song song AB :
 Trong mặt phẳng SCD , gọi I  MN CD
 Trong mặt phẳng ABCD , gọi Q  AI  BC .  Ta có:
AMNSAD  AN
AMNABCD  AQ
AMNSCD QM
AMNSCD  MN
 Vậy thiết diện cần tìm là tứ giác AQMN . Trang 30
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Bài 16. Hình chóp .
S ABCD có đáy ABCD không là hình thang, điểm P nằm trong tam giác SAB và điểm
M thuộc cạnh SD sao cho MD  2MS.
. Tìm giao tuyến của hai mặt phẳng SAB và PCD .
. Tìm giao điểm của SC với mặt phẳng ABM .
. Gọi N là trung điểm của AD , tìm thiết diện tạo bởi mặt phẳng MNP và hình chóp . S ABCD. Lời giải
. Tìm giao tuyến của SAB và PCD .
 Ta có P là điểm chung thứ I.
 Gọi E  ABCD
Nên E là điểm chung thứ II.
 PE  SABPCD
TÂM . Tìm giao điểm của SC với mặt phẳng ABM
 Chọn SCD  SC .
 Ta có: M SCDABM
 Nên M là điểm chung thứ I. LÊ MINH
E  ABCD nên E là điểm chung thứ II. n:
  SCDABM  ME ạ
 Gọi G  SC  ME  SC ABM   G
. Tìm thiết diện tạo bởi mặt phẳng MNP và hình chóp . S ABCD. n Soê
 Ta có MNPSAD  MN Bi
F  PE SB
I  EH  MP  Gọi  và 
 J MNP H  GF   CB J  AB   NI
PJ SB  L 
 Gọi MP  FG  K .
O  KLSC 
 Suy ra thiết diện của MNP và .
S ABCD là ngũ giác MNJLO .  Bài 17. Hình chóp .
S ABCD có đáy ABCD là hình bình hành, gọi K là trọng tâm tam giác SAC và I , J lần
lượt là trung điểm của CD,SD .
. Tìm giao điểm H của IK với mặt phẳng SAB .
. Xác định thiết diện tạo bởi mặt phẳng IJK và hình chóp . S ABCD. Lời giải Trang 31
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
. Tìm giao điểm H của IK với SAB .
 Gọi O là tâm của hình bình hành ABCD .
 Vì K là trọng tâm tam giác SAC nên K SO .
 Gọi E  IOAB  IK  SIE  Ta có:
S là điểm chung thứ I của SAB và SIE Bi
E là điểm chung thứ II của SAB và SIE ên
 SABSIE  SE So
 Gọi IK SE  H ạ
 IK SIE   H . n: LÊ MINH
. Xác định thiết diện tạo bởi IJK và . S ABCD.
 Xét tam giác SBD có SO là trung tuyến 2 SK  SO , 3
 Nên K là trọng tâm suy ra B JK .  Gọi   . TÂM G BH SA
IJKABCD  BI
IJKSAB  BG  Ta có  .
IJKSAD   GJ IJK 
SCD  JI
 Suy ra thiết diện là tứ giác BIJG .  Bài 18. Cho hình chóp .
S ABCD. Gọi M,N là 2 điểm lần lượt nằm trên 2 cạnh BC và SD .
. Tìm giao điểm I của BN và SAC .
. Tìm giao điểm J của MNvà SAC .
. Chứng minh I, J,C thẳng hàng.
. Xác định thiết diện của mặt phẳng BCN với hình chóp. Lời giải Trang 32
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
. Tìm giao điểm I của BN và SAC .
 Trong mp ABCD gọi O  AC BD
 Ta có: SSACSBD   1
O AC; AC  SAC  OSAC O B ;
D BD  SBD  OSBD
 Do đó: OSACSBD 2   1&2
SO  SAC  SBD
 Trong SBD gọi I SOBN
 Ta có: I BN I S ;
O SO  SAC  I SAC
 Vậy I  BN SAC .  TÂM
. Tìm giao điểm J của MN và SAC .
 Trong ABCD gọi H  ACMD
 Ta có: SSACSMD 3
H  AC; AC  SAC  H SAC H  M ;
D MD  SMD  H SMD LÊ MINH
 Do đó: H SACSMD 4 n: 3 & 4 ạ     
SH  SAC  SMD
 Trong SMD gọi J  SH  MN n So
 Ta có: J  MN ê
J SH;SH  SAC  J SAC Bi
 Vậy J  MN SAC .
. Chứng minh I, J,C thẳng hàng.
 Ta có: C SACBNC 5 I   SAC 
 I  SAC  BNC
I  BN; BN  BNC  I   BNC     6  5&6
CI  SAC  BNC * J   SAC  Mặt khác:     
J  MN MN  BNC  J  
BNC J SAC BNC   ;
 Từ * và * * suy ra I, J,C thẳng hàng. Trang 33
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
. Xác định thiết diện của mặt phẳng BCN với hình chóp.
 Trong SAC gọi Q  SA CI
 Ta có: SABBCN  BQ
SBCBCN  BC
ABCDBCN  BC Bi
SCDBCN CN ên
SADBCN  NQ So
 Vậy thiết diện cần tìm là tứ giác BCNQ . ạn:  LÊ MINH Bài 19. Cho hình chóp .
S ABCD. Lấy một điểm M thuộc miền trong tam giác SBC . Lấy một điểm N thuộc
miền trong tam giác SCD .
. Tìm giao điểm của MNvà SAC .
. Tìm giao điểm của SC và AMN.  TÂM
. Tìm thiết diện của hình chóp .
S ABCD với AMN . Lời giải
. Tìm giao điểm của MNvà SAC .
 Trong SBC gọi Q  SM  BC .
 Trong SDC gọi P SN DC .
 Trong ABCD gọi O  AC  PQ
 Ta có: SSACSPQ   1
O AC; AC  SAC  OSAC O P ;
Q PQ  SPQ  OSPQ
 Do đó: OSACSPQ 2  1&2
SO  SAC  SPQ
 Trong SPQ gọi H  MN SO.
 Ta có: H S ;
O SO  SAC  H SAC
 Mà H MN nên: H  MN SAC Trang 34
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
. Tìm giao điểm của SC và AMN.
 Trong mpSAC gọi K  AHSC
 Ta có: KSC
K  AH; AH AMN  K AMN
 Vậy K  SC AMN .
. Tìm thiết diện của hình chóp với AMN
 Trong SBC gọi I  MKSB.
 Trong SDC gọi J  KN SD .
 Ta có: SABAMN  AI
SBCAMN  IK
SCDAMN  KJ TÂM
SADAMN  JA
 Vậy thiết diện cần tìm là tứ giác AIKJ .  Bài 20. Cho tứ diện .
S ABC . Gọi K, N lần lượt là trung điểm các cạnh SA và BC, M là điểm thuộc đoạn
SC sao cho 3SM  2M . C LÊ MINH
. Tìm thiết diện tạo bởi mặt phẳng KMN và tứ diện . S ABC . n:
. Mặt phẳng KMNcắt AB tại I . Tính tỉ số IA . ạ IB Lời giải
n So . Tìm thiết diện tạo bởi mặt phẳng KMN và tứ
ê diện .SABC. Bi
 Trong SAC nối KM cắt AC tại D .
 Trong ABC nối DN cắt AB tại I .
Vậy tứ giác KMNI là thiết diện cần tìm.
. Mặt phẳng KMNcắt AB tại I . Tính tỉ số IA IB .  BỔ ĐỀ:
Định lí Menelaus:
Cho tam giác ABC. Các điểm D, E, F lần lượt
nằm trên các đường thẳng BC, CA, AB.
Khi đó D, E, F thẳng hàng khi và chỉ khi FA DB EC . . 1. FB DC EA
 Phần thuận:
 Giả sử D,E,F thẳng hàng với nhau. Trang 35
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Vẽ đường thẳng qua C và song song với
AB cắt đường thẳng DE tại G .
 Vì CG / /AB (cách dựng) nên theo định lý Ta-lét, ta có: DB FB  (1) và EC CG  (2) . DC CG EA FA
 Nhân (1) và (2) vế theo vế DB EC FB .  . DC EA FA Bi
 Từ đó suy ra FA DB EC . . 1. ê FB DC EA n So
 Phần đảo: FA DB EC ạ  Giả sử . . 1. n: FB DC EA
 Khi đó gọi F là giao của đường thẳng ED với đường thẳng AB . LÊ MINH  
Theo chứng minh ở trên, ta có F A DB EC . . 1 F B  DC EA  
Kết hợp giả thuyết suy ra FA F A  . FB F B    Hay FA FB FA FB   1 . F A  F B  F A   F B  TÂM  Nên F A
  FA và F B
  FB . Do đó F trùng với F .
 Vậy định lí đã được chứng minh.  Áp dụng: CM SK AD AD
 Vì K, M,D thẳng hàng nên 2 . . 1  . MS KA DC DC 3
 Vì D,N,I thẳng hàng nên AI BN CD AI AD 2 . . 1   . IB NC DA IB CD 3  Bài 21. Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành tâm .
O Trên các cạnh SB, SD ta lần lượt lấy
các điểm M và N sao cho SM 1 SN 2  ;  . SB 3 SD 3
. Tìm giao điểm I của SC và mặt phẳng AMN. Suy ra thiết diện của mặt phẳng AMN và hình chóp . S ABCD.
. Gọi K là giao điểm của IN và .
CD Tính tỉ số KC . KD Lời giải Trang 36
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
. Tìm giao điểm I của SC và mặt AMN.
Suy ra thiết diện của mặt phẳng AMN và hình chóp.
 Trong SBD gọi H  SOM . N  Ta có:
ASAC; A AMN  ASAC  AMN   1 .
H SAC; H AMN  H SAC AMN 2.  1&2
 AH  SAC   AMN .
 Trong SAC gọi I  AHSC
Thì I  SC  AMN.
 Khi đó thiết diện là tứ giác AMI . N
. Gọi K là giao điểm của IN và . CD Tính tỉ số TÂM KC . KD
 Trong mpSBD gọi J  BD  MN.
 Áp dụng định lí Menelaus cho các tam giác SB ; D SB ; O SC ; O SCD ta có: MB NS JD JD      LÊ MINH  . . 1 2.2. 1 JB 4 . JD MS ND JB JB n: MB HS JO HS 5 HS 4 ạ  . .  1  2. .  1   . MS HO JB HO 8 HO 5  IC HS AO IC 4 1 IC 5 . . 1  . .  1  . n So IS HO AC IS 5 2 IS 2 ê  IC NS KD 5 KD KC . . 1  2 . . 1  5. Bi IS ND KC 2 KC KD  Vậy KC  5 . KD
------------------ HẾT ------------------ Trang 37
Hình học 11 – Chương 02. QUAN HỆ SONG SONG BÀI 02
HAI ĐƯỜNG CHÉO NHAU – SONG SONG ☆☆★☆☆
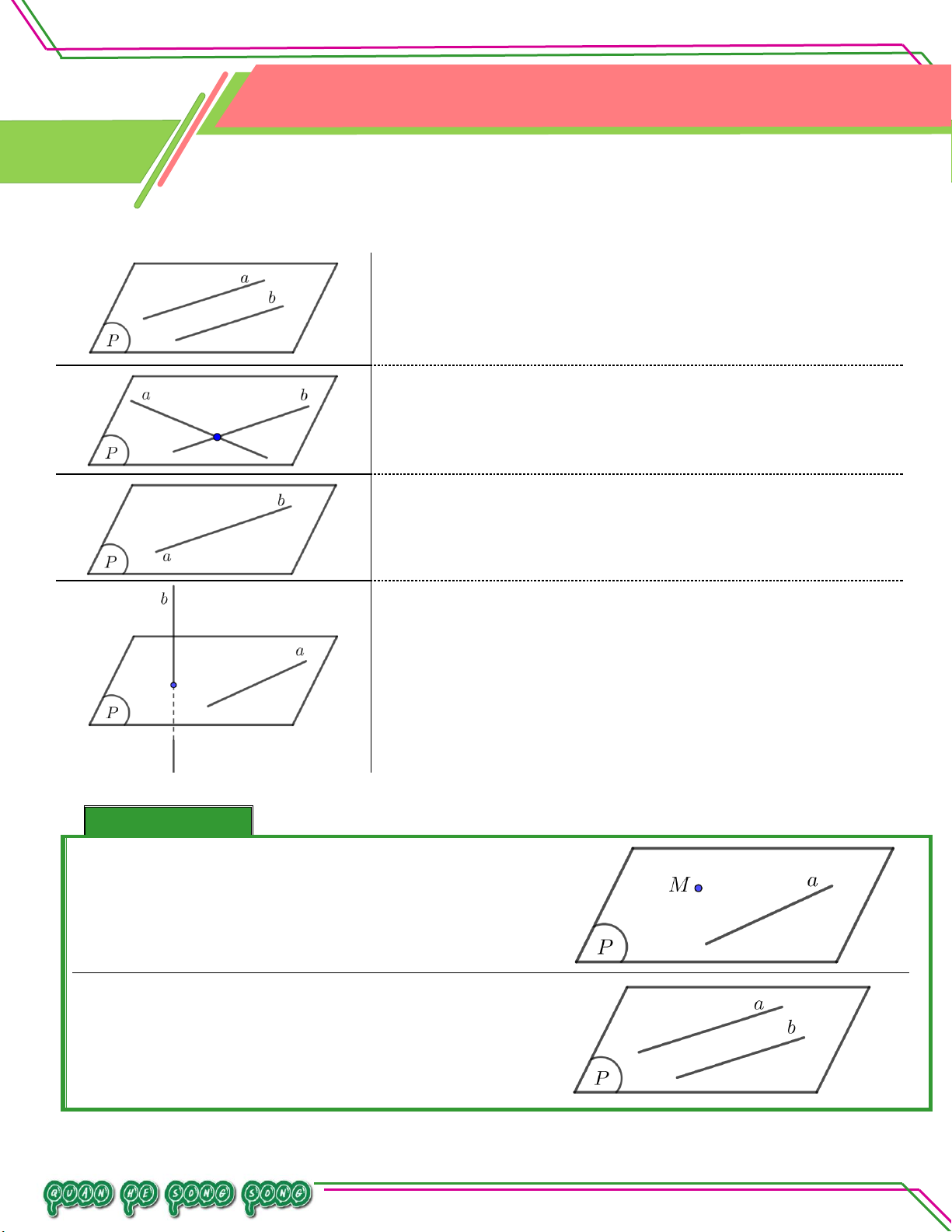
I. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG TRONG KHÔNG GIAN: Bi
a / / b  a và b ê
cùng nằm trong một mặt phẳng và không có n điểm chung. So ạn:
a cắt b hay a b  a và b cùng nằm trong một mặt phẳng LÊ MINH
và có một điểm chung duy nhất.
a  b  a và b cùng nằm trong một mặt phẳng và có từ hai
điểm chung trở lên. TÂM
a chéo b  a và b không cùng nằm trong một mặt phẳng. II. TÍNH CHẤT:
 Định lý 1
 Trong không gian, qua một điểm không nằm trên
đường cho trước, có một và chỉ một đường thẳng song
song song đường thẳng đã cho.
 Nhận xét:
Ta có thêm một cách để xác định mặt phẳng như sau:
Hai đường thẳng song song a và b xác định nên một mặt
phẳng ký hiệu a,b . Trang 38
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Định lý 2 (về giao tuyến của ba mặt phẳng)
 Nếu ba mặt phẳng đôi một cắt nhau theo ba giao
tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy
hoặc đôi một song song với nhau.
 Hệ quả:
 Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của
chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó. TÂM  Ví dụ 01. LÊ MINH Cho hình chóp .
S ABCD có đáy là hình bình hành ABCD n:
. Tìm giao tuyến của SAD và SBC , SAB và SCD . ạ
. Gọi M,N,H .lần lượt là trung điểm của SA,SB và BC . Tìm giao tuyến của hai mặt phẳng
MNH và ABCD, MDH và NAC . n Soê Lời giải
Bi . Tìm giao tuyến của SAD và SBC, SAB và SCD .
 Ta có SSADSBC và AD/ /CB
 Nên SADSBC  m / / AD/ /CB.
 Ta có SSABSCD và AB/ /CD
 Nên SABSCD  d / / AB/ /CD
. Tìm giao tuyến của MNH và ABCD ,
MDH và NAC
 Ta có H MNHABCD và MN / / AB
MNHABCD  HK / / AB/ /NM, KAD
 Gọi E  AC HD, F  NC  MD
Suy ra MDH  NAC  EF . Trang 39
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Ví dụ 02.
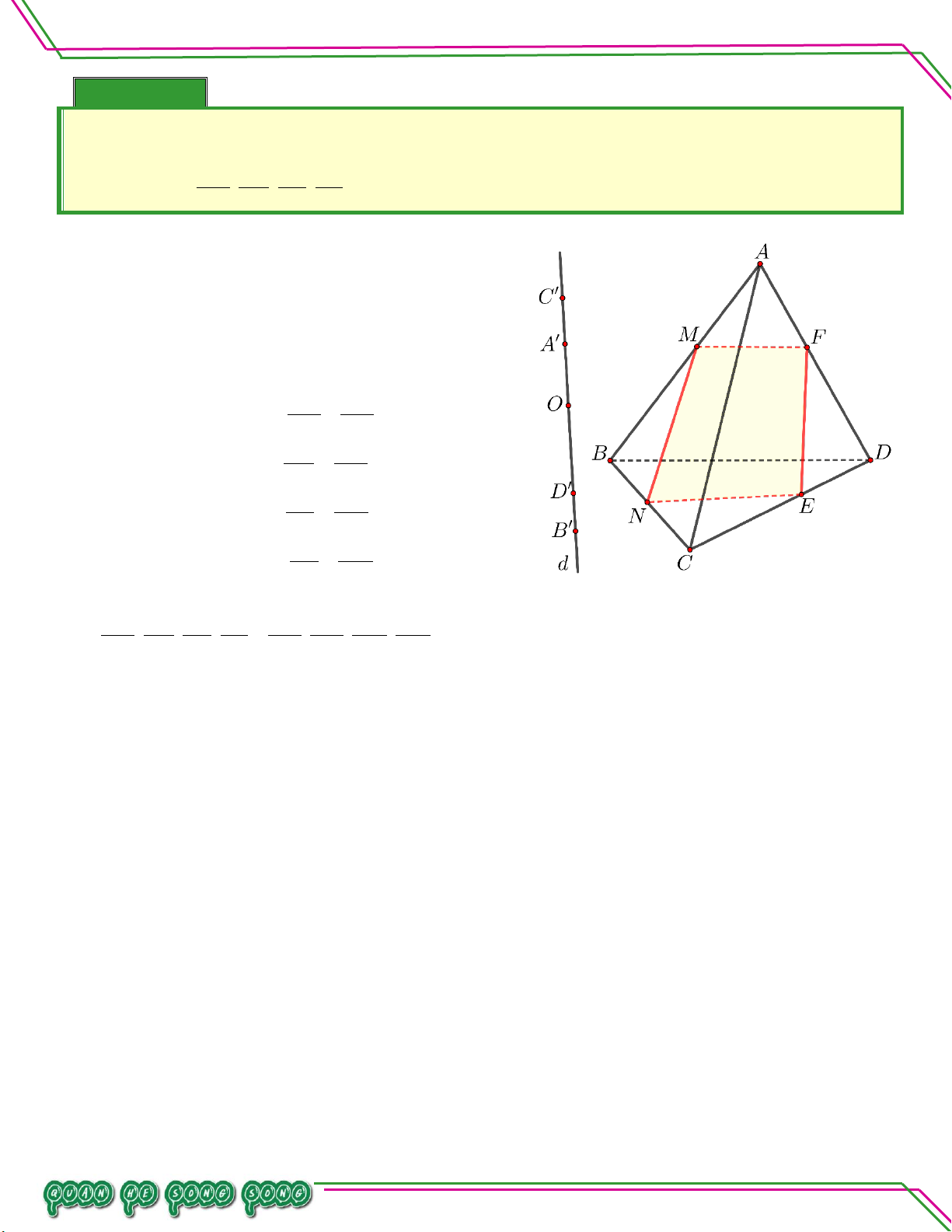
Cho tứ diện ABCD . Gọi I , J là trung điểm BC, BD . Mặt phẳng P qua IJ cắt AC , AD lần
lượt tại M,N . Chứng minh: IJNM là hình thang. Nếu M là trung điểm AC thì IJNM là hình gì? Lời giải Bi ên Soạn: LÊ MINH
 Ta có IJ là đường trung bình của tam giác BCD nên IJ / /CD .
 PACD  MN ; IJ  P; CD  ACD  MN / /IJ . TÂM
 Do đó tứ giác IJNM là hình thang.
 Nếu M là trung điểm AC thì N là trung điểm AD .  
IM / /NJ / / AB Khi đó 
nên tứ giác IJNM là hình bình hành.
MN / / IJ / / CD
 Định lý 3
 Hai đường thẳng phân biệt cùng song song với đường thẳng
thứ ba thì song song với nhau.  Ví dụ 03.
Cho tứ diện ABCD . Gọi M , N, P ,Q , R,S lần lượt là trung điểm AC , BD , AB,CD , AD , BC .
Chứng minh tứ giác PMQN , MRNS là các hình bình hành. Từ đó suy ra MN,PQ ,RS đồng quy tại 1 điểm. Lời giải Trang 40
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Ta có MP là đường trung bình của tam giác ABC MP / / BC  nên  1 . MP   BC  2
 Tương tự NQ là đường trung bình của tam giác NQ / / BC  DBC nên  1 . NQ   BC  2
 Suy ra tứ giác PMQN là hình bình hành.
 Ta có MR là đường trung bình của tam giác ACD MR / /CD  nên .  1 MR   CD  2 NS / / CD 
TÂM  Tương tự NS là đường trung bình của tam giác BCD nên  1 . NS   CD  2
 Suy ra tứ giác MRNS là hình bình hành.
 Do tứ giác PMQN , MRNS là các hình bình hành
Nên các đường chéo MN , PQ , RS cắt nhau tại chung điểm I của mỗi đường. 
LÊ MINH Suy ra MN,PQ,RS đồng quy tại 1 điểm.
III. CÁC DẠNG BÀI TẬP. n:ạ
 Dạng 01. CHỨNG MINH HAI ĐƯỜNG THẲNG SONG SONG.
Phương pháp giải
n Soê  Ta có thể dùng một trong các cách sau Bi
01 Xét mặt phẳng chứa a, b.
Dùng các định lý đường trung bình, Định lý Thales đảo,.... để chứng minh a//b .  02 a//c
Dùng định lý bắc cầu   a//b . b//c a//b
a//b//c  
03 Dùng định lý 4 a   ,b    a  b       a  c c   Bài 01. Cho hình chóp .
S ABCD đáy là hình bình hành. Gọi I , J lần lượt là trọng tâm các tam giác SAB , SBC .
. Chứng minh IJ//AC . Trang 41
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
. Gọi   là mặt phẳng chứa IJ và cắt SC , SA lần lượt tại E , F . Chứng minh rằng IJEF là hình thang.
. Gọi M , N lần lượt là trung điểm SC , SD. Gọi K  AN BM . Chứng minh
SK//AD//BC . Tứ giác SADK là hình gì? Lời giải
. Chứng minh IJ//AC .
 Gọi P , Q lần lượt là trung điểm AB , BC . Bi SI SJ 2 ê  Trong SPQ có 
 nên IJ//PQ . n SP SQ 3 So
 Mà trong BAC có PQ là đường trung bình nên PQ//AC . ạn:
 Do đó IJ//AC//PQ .
. Chứng minh rằng IJEF là hình thang. LÊ MINH  Ta có: S
 SPQSAC 
PQ  SPQ 
 SPQ SAC      d AC SAC  PQ//AC TÂM
với d // PQ // AC
 SPQ  IJ 
 SAC   EF
Xét SPQ , SAC ,   có:  .  
  IJ//EF//d SAC SPQ  d  d//IJ
Do đó IJEF là hình thang.
. Chứng minh SK//AD//BC . Tứ giác SADK là hình gì?
AN  SAD 
 Ta có SSBCSAD và BM  SBC  K SAD SBC .
K  AN BM 
 Do đó SK  SBCSAD .
AD  SAD 
BC  SBC  Mặt khác 
 SK//AD//BC . AD//BC
SK  SAD  SBC
 Tứ giác SADK có SK//AD và hai đường chéo giao nhau tại trung điểm mỗi đường nên là hình bình hành. Trang 42
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Bài 02. Cho hình chóp .
S ABCDcó đáy ABCD là hình thang đáy lớn AB . Gọi E,F lần lượt là trung
điểm của SA và SB.
. Chứng minh rằng EF // CD .
. Tìm giao điểm I của SC và ADF .
. Gọi J là giao điểm của AF và DI . Chứng minh rằng SI // AB//CD . Lời giải
. Chứng minh rằng EF // CD .
 Xét SAB có E,F lần lượt là trung điểm của SA,SB (gt)
 Nên EF là đường trung bình của tam giác
 Do đó EF // AB mà lại có AB// CD (gt)
 Suy ra EF // CD.
TÂM . Tìm giao điểm I của SC và ADF.
 Trong ABCD gọi O  AC BD
Khi đó có SO, FD  SBD
 Trong SBD gọi K  SOFD. LÊ MINH
Khi đó có AK,SC  SAC; gọi I  SC  AK . n:
 Khi đó có I  SC ADF . ạ
. Chứng minh rằng SI // AB//CD .
J  DI,DI   SCD n So
 Có J là giao điểm của AF và DI (gt) suy ra 
 J  SAB  SCD (1). ê
J  AF, AF   SAB     Bi
 Lại có SSABSCD (2).
 Từ (1) và (2) suy ra SABSCD  SJ .
 Lại có AB// CD ; AB  SAB,CD  SCD;
 Suy ra SI // AB//CD (theo hệ quả).  Bài 03.
Cho tứ diện ABCD . Gọi M,N lần lượt là trung điểm của BC và BD . Lấy P trên AB . Gọi các
điểm I  PD  AN; J  PC  AM . Chứng minh rằng IJ // CD . Lời giải Trang 43
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Có M,N lần lượt là trung điểm của BC và BD (gt)
 Nên MN là đường trung bình của
BCD  MN // CD (1).
 Xét AMN,BCD,PCD có
AMNBCD  MN ; AMNPCD  IJ ;
PCDBCD CD (2). Bi  ê
Từ (1) và (2) suy ra MN // CD // IJ (Theo định n
lý về giao tuyến của 3 mặt phẳng). So
Hay IJ // CD (đpcm). ạ  Bài 03. n:
Cho hai hình vuông ABCD và ABEF không đồng phẳng. Trên các đường chéo AC, BF lấy LÊ MINH AM BN M, N sao cho 1 
 . Chứng minh rằng MN // DE . AC BF 3 Lời giải
 Gọi I là trung điểm của đoạn thẳng AB .
 Gọi M  DI  AC .   Ta có AM AI 1 AM 1     TÂM M C  DC 2 AC 3  Lại có AM 1
 suy ra M  M . AC 3 IM
 Hay D, M,I thẳng hàng và 1  . ID 3  Tương tự, ta có IN
I, N, E thẳng hàng và 1  IE 3
 Xét tam giác IDE có IM IN   MN // DE ID IE
(Định lý Ta-let đảo) (đpcm).
 Dạng 02. TÌM GIAO TUYẾN CỦA HAI MẶT PHẲNG CHỨA HAI ĐƯỜNG THẲNG SONG SONG.
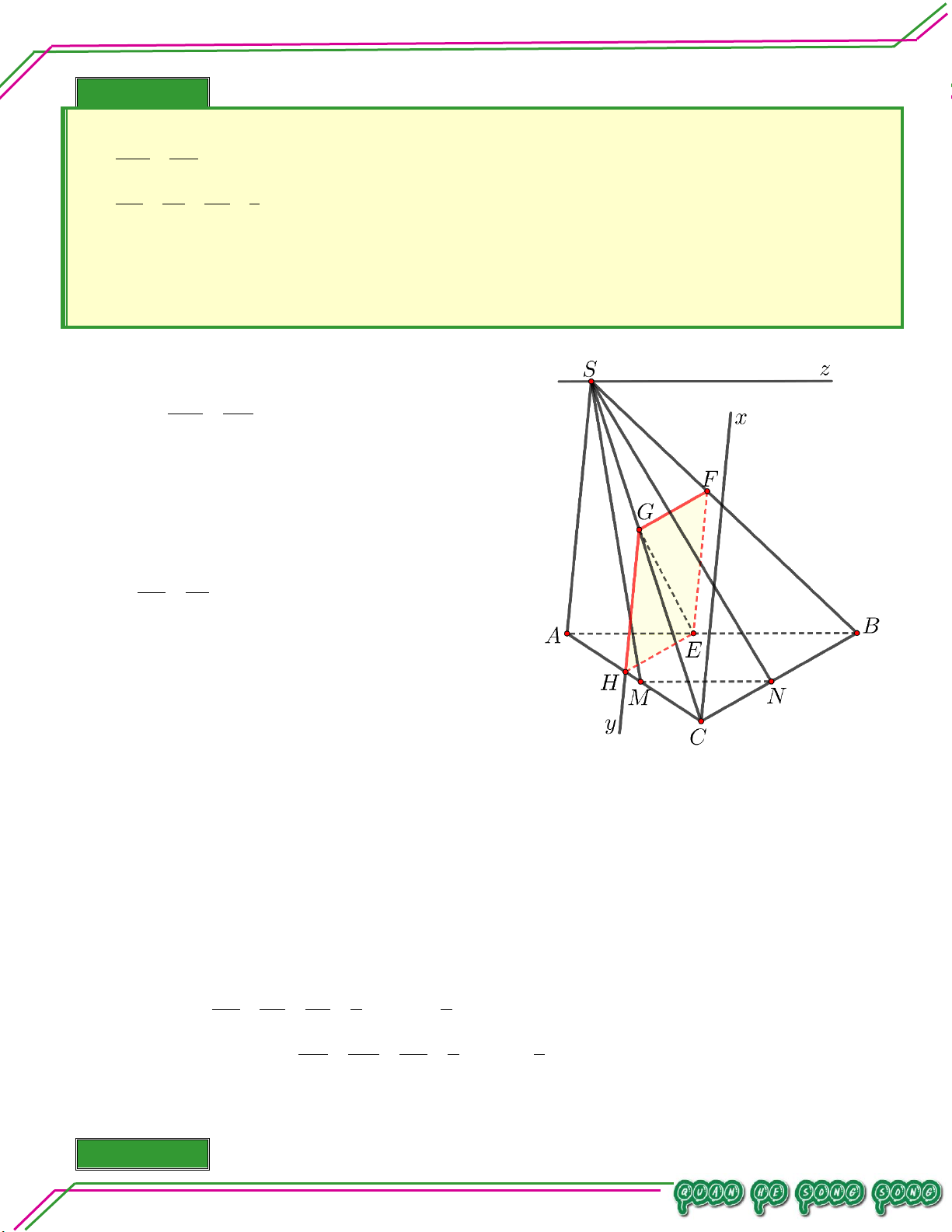
Phương pháp giải
 Sử dụng định lí phương pháp giao tuyến thứ nhất. S     
a    ,b           Sx,Sx//a//b a//b  Trang 44
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Bài 01. Cho hình chóp .
S ABC. Gọi M , N lần lượt là các điểm trên các cạnh AC , BC sao cho AM BN 
. Gọi E, F , G lần lượt là các điểm trên cạnh ,
AB SB, SC sao cho AC BC AE SF SG 1    . AB SB SC 3
. Tìm SMNSAB, SACCEF.
. Tìm EFGSAC, tìm H  AC EFG.
. Tìm thiết diện EFG . Thiết diện là hình gì? Lời giải
. Tìm SMNSAB, SACCEF.  Ta có: AM BN   MN / /AB AC BC S
 SABSMN TÂM 
 Nên AB  SAB ,MN  SMN  AB // MN 
 SABSMN  Sz, Sz // AB// MN.  Vì AE SF 
 SA // EF (Định lí Ta-let) LÊ MINH AB SB C
 SACCEF n:  ạ S
 A  SAC ,EF  CEF SA// EF  n So     ê
SAC CEF Cx, Cx//SA// E .F
Bi . Tìm EFGSAC, tìm H  ACEFG. G
 SACEFG   S
 A  SAC ,EF  EFG  SAC  EFG  Gy, Gy // SA // EF. SA// EF 
 Vì SACEFG  Gy  AC EFG  AC Gy   
H  AC G . y
. Tìm thiết diện EFG . Thiết diện là hình gì?  Ta có: EB EF BF 2    2
 EF  SA (1) AB SA SB 3 3  Do CH GH CG GH // SA 2     2
 GH  SA (2) CA SA SC 3 3  1&2
  EF  GH , mà EF // GH  FGHElà hình bình hành Thiết diện là hình bình hành.  Bài 02. Trang 45
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
Cho tứ diện ABCD . Gọi I , J là trọng tâm ABC và ABD ; E, F lần lượt là trung điểm BC, . AC
. Chứng minh rằng IJ//CD
. Tìm giao tuyến DEF và ABD. Lời giải
. Chứng minh rằng IJ//CD
 Gọi M là trung điểm AB ,
 I là trọng tâm A
 BC C , I , M thẳng hàng. Bi
 J là trọng tâm A
 BD  D , J , M thẳng ên hàng. So  Xét D  MC có: MI MJ 1 ạ 
 (do I là trọng tâm A  BC , J là MC MD 3 n: trọng tâm A  DB). LÊ MINH
 IJ // DC (Định lí Ta-lét).
. Tìm giao tuyến DEF và ABD.
 Chứng minh được EF là đường trung bình của A  BC EF // AB . TÂM
DDEFABD    S
 A  DEF ,EF   ABD EF // AB 
  DEFABD  Dx, Dx // EF // A . B  Bài 03. Cho hình chóp .
S ABCD có đáy là tứ giác lồi không có cặp cạnh nào song song. Gọi M,N lần
lượt là trọng tâm của hai tam giác SAB và SAD . Gọi E trung điểm của cạnh CB .
. Chứng minh rằng MN BD .
. Xác định thiết diện của hình chóp với mặt phẳng MNE .
. Gọi O, J lần lượt là các giao điểm của mặt phẳng MNE với các cạnh SB,SD . Chứng minh rằng OJ BD . Lời giải
. Chứng minh rằng MN BD .
 Gọi F là trung điểm của SA .
Theo tính chất trọng tâm của tam giác ta có FM FN 1    MN BD . FB FD 3
. Xác định thiết diện của hình chóp với mặt phẳng MNE . Trang 46
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Xét hai mặt phẳng MNE và ABCD có     Ed E MNE ABCD  
 d  MNE ABCD MN BD  d MN BD
P  d CD O   MG SB    Gọi G
  d  AB . Gọi H  MG SA .  
I  d  AD 
J  HI SD 
 Vậy thiết diện cần tìm là ngũ giác OHJPE .
. Chứng minh rằng OJ BD . BD MN  BD   SBD  Ta có  .      OJ BD MN MN MNE
OJ  MNE  SBD TÂM  Bài 04.
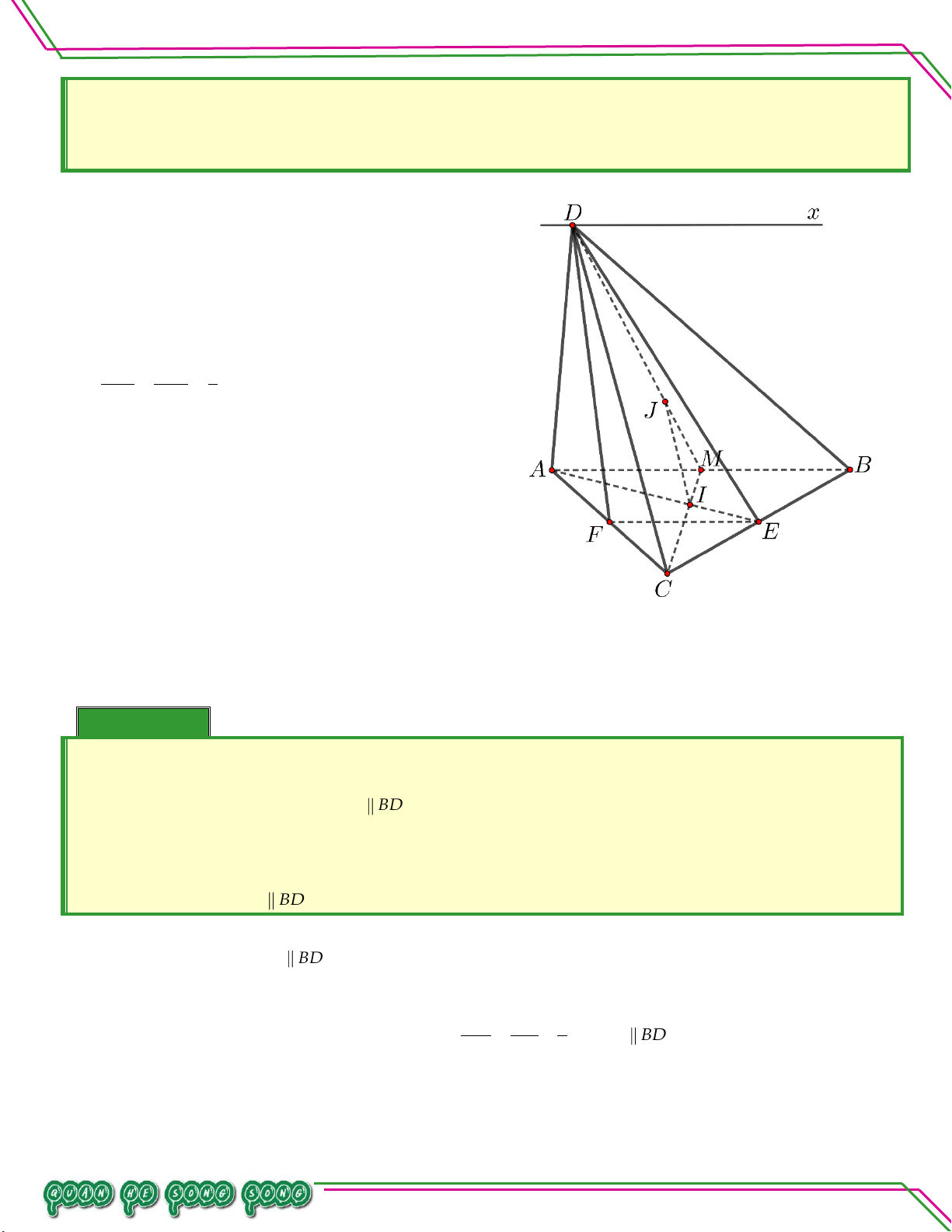
Cho tứ diện ABCD có I, J,K là ba điểm lần lượt nằm trên các cạnh AD, AC, BC sao cho AI AJ BK 1  
 . Xác định giao tuyến của mặt phẳng IJK với các mặt phẳng BCD ,ABD AD AC BC 3
và xác định hình tính của thiết cắt bởi mặt IJK LÊ MINH Lời giải n:ạ  Vì AI AJ 1   nên IJ CD . AD AC 3  Ta có n So IJ CD ê     IJ   IJK d
IJK BCD  Bi  .      K d CD BCD        d IJ CD  K IJK BCD
 Gọi E  d  BD  EK CD IJ .
 Theo chứng minh trên: EK  BCDIJK .    Vì AJ BK  CA CJ CB CK CJ CK CJ CK    1 1   AC BC AC BC AC BC AC BC
IE  ABDIJK 
JK  IJK
 Nên JK AB . Ta có  .      IE JK AB AB ABD  JK AB   IJ EK
Thiết diện cần tìm là tứ giác IJKE . Ta có 
nên IJKE là hình bình hành. JK IE Trang 47
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Dạng 03. CHỨNG MINH HAI ĐƯỜNG THẲNG CHÉO NHAU.
Phương pháp giải
 (Chứng minh phản chứng) Giả sử hai đường thẳng đồng phẳng rồi suy ra điều vô lí.  Bài 01. Cho hình chóp .
S ABCD có đáy ABCD là một tứ giác lồi. Chứng minh rằng các cặp đường Bi
thẳng sau đây chéo nhau: SA,BC; SA,CD; SB,CD; SB, DA; SC, AD; SC, AB; ên
SD,AB và SD,BC. So Lời giải ạ * SA, BC n:
 Giả sử SA,BC đồng phẳng, thì S, A,B,C đồng phẳng. LÊ MINH
 Nhưng rõ ràng C SAB, nên điều giả sử là sai.
 Vậy SA,BC chéo nhau. * SA,CD
 Giả sử SA,CD đồng phẳng, thì S, A,C,D đồng phẳng. TÂM
 Nhưng rõ ràng C SAD , nên điều giả sử là sai.
 Vậy SA,CD chéo nhau. * SB,CD
 Giả sử SB,CD đồng phẳng, thì S,B,C,D đồng phẳng.
 Nhưng rõ ràng BSCD , nên điều giả sử là sai.
 Vậy SB,CD chéo nhau.
 Các ý còn lại làm tương tự.  Bài 02.
Cho hai đường thẳng chéo nhau a và .
b Trên đường thẳng a lấy hai điểm phân biệt A,B tùy
ý. Trên đường thẳng b lấy hai điểm phân biệt C, D tùy ý. Chứng minh hai đường thẳng AC và BD chéo nhau. Lời giải
 Giả sử AC,BD đồng phẳng. Nghĩa là A,B,C,D đồng phẳng.
 Rõ ràng, DABC nên điều giả sử là sai.
 Vậy AC,BD chéo nhau. Trang 48
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Bài 03.
Cho tam giác BCD và điểm ABCD . M, N lần lượt là trung điểm của A , B CD . Chứng
minh AB và CD chéo nhau, AD và MN chéo nhau. Lời giải
 Giả sử AB và CD đồng phẳng, thì BCD  ABCD
 Tức là ABCD (Vô lý).
 Do đó AB và CD chéo nhau.
 Giả sử AD và MN đồng phẳng,
 Mà M,N lần lượt thuộc AB,CD
 Nên AB  ADMN;CD  ADMN,
 Suy ra AB và CD đồng phẳng (vô lý theo ý trên).
 Vậy AD và MN chéo nhau. TÂM  Bài 04.
Cho hình thang ABCD có đáy lớn AD, đáy nhỏ BC và điểm SABCD . Gọi I là giao điểm
của AC và BD . M,N là hai điểm phân biệt trên đường thẳng SI . Chứng minh AM và BN
chéo nhau, BM và AN chéo nhau. Lời giải LÊ MINH     Ta có SI
SAC SBD, M,N SI n:   ạ
Nên A, M, N SAC.
 Giả sử AM và BN đồng phẳng,
 Suy ra BSAC nên SABC (mâu thuẫn giả thiết n Soê
S ABC ). Bi
 Vậy AM và BN chéo nhau.
 Chứng minh tương tự AN và BM chéo nhau. Trang 49
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Dạng 04. CHỨNG MINH MỘT ĐƯỜNG THẲNG DI ĐỘNG LUÔN ĐI QUA MỘT ĐIỂM CỐ ĐỊNH.
Phương pháp giải
 Sử dụng định lý về giao tuyến của ba mặt phẳng (ĐL3)  Bài tập. Bi
Cho tứ giác ABCD với AB không song song với CD và điểm S (ABCD) . Mặt phẳng di động ên
  qua AB cắt SC,SD tại M,N . Mặt phẳng di động  qua CD cắt SA,SB tại P,Q. So
. Chứng minh đường thẳng MN luôn đi qua một điểm cố định.
. Chứng minh nếu AN và BM cắt nhau tại I , CQ và DP cắt nhau tại J thì đường thẳng IJ ạn:
luôn đi qua một điểm cố định.
. Gọi K là giao điểm của AM và BN , L là giao điểm của CP và DQ . Chứng minh đường LÊ MINH
thẳng KL qua một điểm cố định trong  ABCD Lời giải
. Chứng minh MN luôn đi qua một điểm cố định.
 SCD  MN     TÂM
 Ta có    ABCD AB ABCD  SCD   CD
 Suy ra MN, AB,CD đồng quy tại E  ABCD
 Vậy MN đi qua E cố định.
. Chứng minh nếu AN và BM cắt nhau tại I , CQ và DP cắt nhau tại J thì đường thẳng IJ luôn đi
qua một điểm cố định. I  AN   SAD
 Ta có AN BM  I   I  BM   SBC
 I SADSBC  Lại có J  DP   SAD
CQ  DP  J   J CQ   SBC
 J SADSBC
 Mà SSADSBC
 Nên đường thẳng IJ luôn đi qua điểm S cố định.
. Chứng minh đường thẳng KL qua một điểm cố định trong ABCD Trang 50
Hình học 11 – Chương 02. QUAN HỆ SONG SONG K  AM   SAC
 Ta có AMBN  K   K  BN   SBD
 KSACSBD L DQ   SBD
 Lại có CP  DQ  L   L CP   SAC
 LSACSBD
 Gọi O  AC BD OSACSBD
 Nên đường thẳng KL luôn đi qua điểm O cố định. TÂM
------------------ HẾT ------------------ LÊ MINH n:ạ n SoêBi Trang 51
Hình học 11 – Chương 02. QUAN HỆ SONG SONG BÀI 03
HAI ĐƯỜNG CHÉO NHAU – SONG SONG ☆☆★☆☆
I. VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN
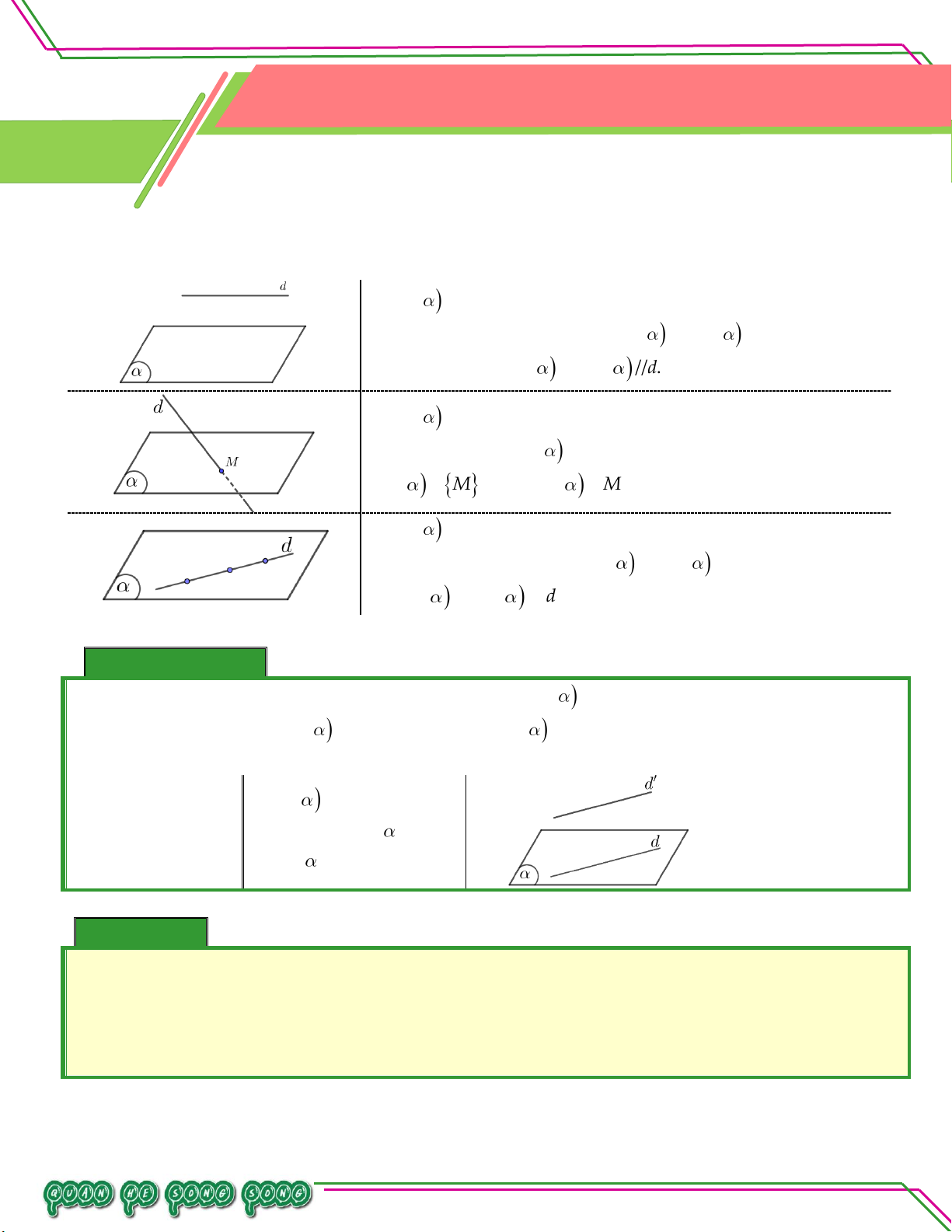
Vị trí tương đối của đường thẳng và mặt phẳng được xét theo số điểm chung của chúng Bi d ê
và   không có điểm chung. n
Khi đó ta nói d song song với   hay   song song với So
d và kí hiệu là d//   hay   // . d ạ n:
d và   có một điểm chung duy nhất . M LÊ MINH
Khi đó ta nói d và   cắt nhau tại điểm M và kí hiệu là
d     
M hay d    M .
d và   có từ hai điểm chung trở lên.
Khi đó ta nói d nằm trong   hay   chứa d và kí hiệu TÂM
là d    hay    d II. TÍNH CHẤT:
 Định lý 1
 Nếu đường thẳng d không nằm trong mặt phẳng   và d song song với đường thẳng d
nằm trong mặt phẳng   thì d song song với   .
 Tóm tắt định lý: d     d//d  d//   d      Ví dụ 01. Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của AC và
BD , các điểm M , I , K lần lượt là trung điểm của SC, A , B AD .
. Chứng minh AD // SBC , IK //MBD .
. Chứng minh CD // ABM , SA//MBD . Lời giải Trang 52
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
. Chứng minh AD // SBC , IK //MBD
AD SBC   Ta có: AD // BC
 AD// SBC . BC SBC 
IK  MBD   IK // BD
 IK // MBD .
BD  MBD 
. Chứng minh CD // ABM , SA// MBD . C
 D  ABM   C  D // AB
 CD // ABM .
AB  ABM  SA   MBD TÂM   SA  // OM
 SA // MBD .
OM  MBD   Ví dụ 02. Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm SAB , M là LÊ MINH
một điểm trên cạnh AD sao cho AD  3AM , Chứng minh MG // SCD. n:
. Chứng minh AD // SBC , IK //MBD . ạ
. Chứng minh CD // ABM , SA//MBD . n So Lời giải ê
 Gọi H là trung điểm của AB . Bi
 Do G là trọng tâm tam giác SAB , nên HG 2    1 . HS 3
 Trong ABCD , gọi K  HMCD
 SK  SCD .  HM AM 2 Vì AH// DK    2 . HK AD 3   1&2 HG HM    GM//SK . HS HK G
 M  SCD   Khi đó SG  M // SK
 MG // SCD.
SK  SCD 
 Định lý 2 Trang 53
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
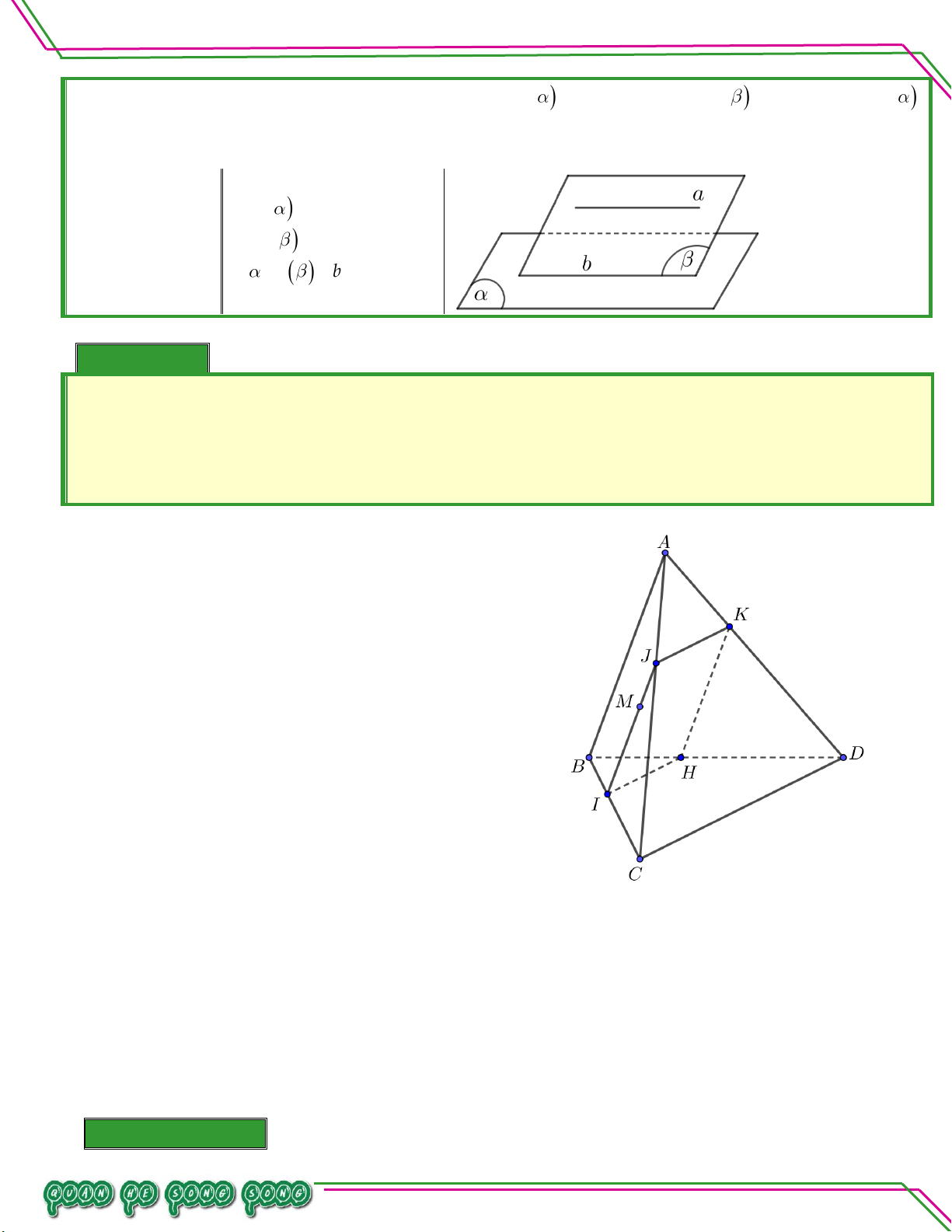
 Cho đường thẳng a song song với mặt phẳng   . Nếu mặt phẳng   chứa a và cắt  
theo giao tuyến b thì b song song với . a
 Tóm tắt định lý: a//    a     a//b      b Bi ê n So  Ví dụ 03. ạ
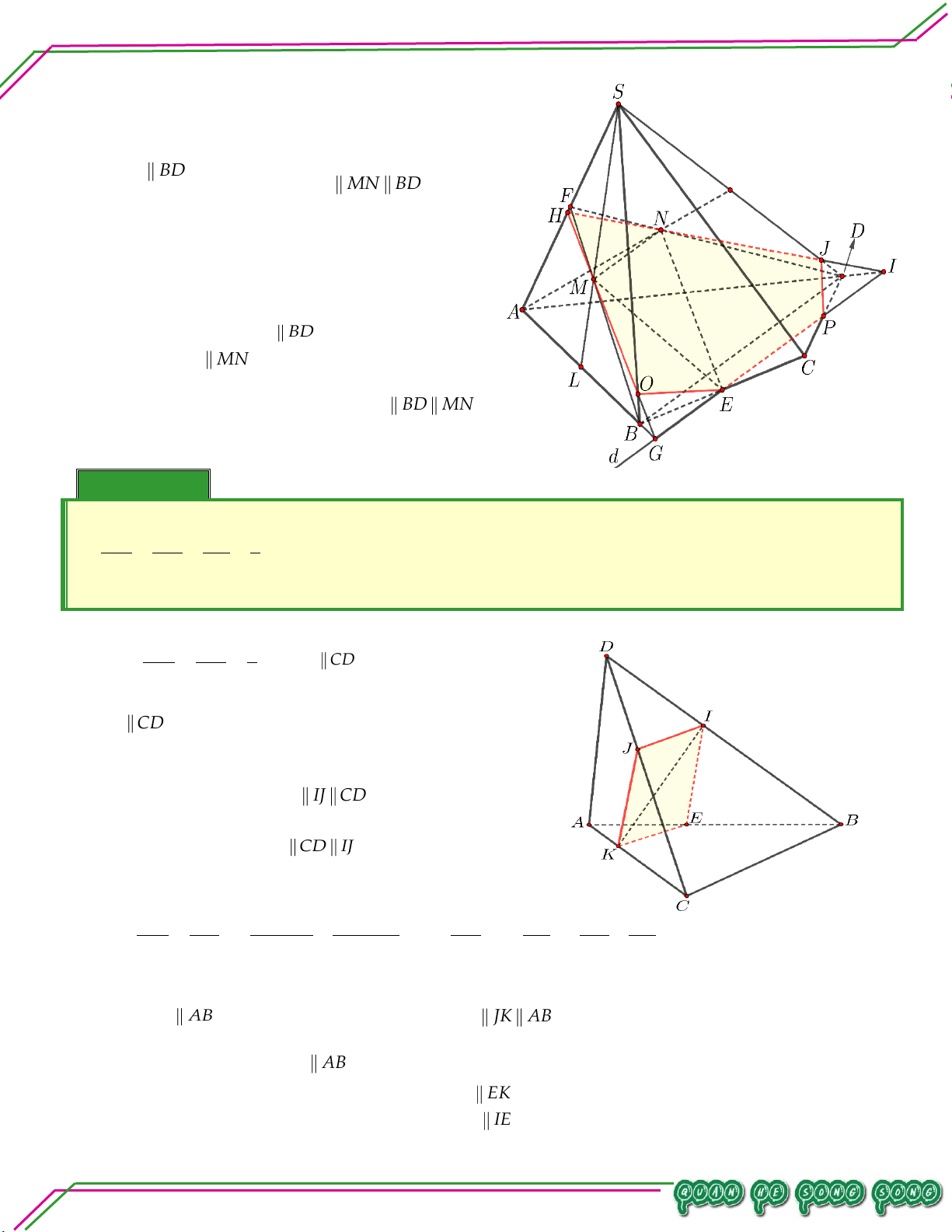
Cho tứ diện ABCD . Lấy điểm M thuộc miền trong của tam giác ABC . Gọi P là mặt phẳng n: qua AB M và song song với , CD . LÊ MINH
. Tìm giao tuyến của P lần lượt với các mặt phẳng ABC , BCD , ACD , ABD .
. Mặt phẳng P cắt tứ diện theo thiết diện là hình gì? Lời giải
. Tìm giao tuyến của P với các mặt phẳng TÂM
ABC , BCD , ACD, ABD.
 P và ABC có
Điểm M chung, AB  ABC , AB / / P    IJ qua M
P ABC  IJ với 
IJ / / AB, I  BC, J   AC
 P và BCD có
Điểm I chung, CD  BCD ,CD / / P
 PBCD  IH , với IH / /CD,HBD
 P và ACD có
Điểm J chung, CD  ACD ,CD / / P
 PACD  JK , với JK / /CD,KAD
 P và ABD có điểm K,H chung, AB  ABD, AB / / P
 PABD  KH , với KH / /AB .
. Mặt phẳng P cắt tứ diện theo thiết diện là hình gì?
 Mặt phẳng P cắt tứ diện theo thiết diện là hình bình hành IJKH (vì KH / /IJ / /AB và
IH / / JK / /CD ).  Hệ quả Trang 54
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Hai mặt phẳng cùng song song với một đường thẳng thì giao tuyến của chúng nếu có cũng
song song với đường thẳng đó.
 Tóm tắt định lý:
PQ       d Q / /d P / / , / /d
 Định lý 3
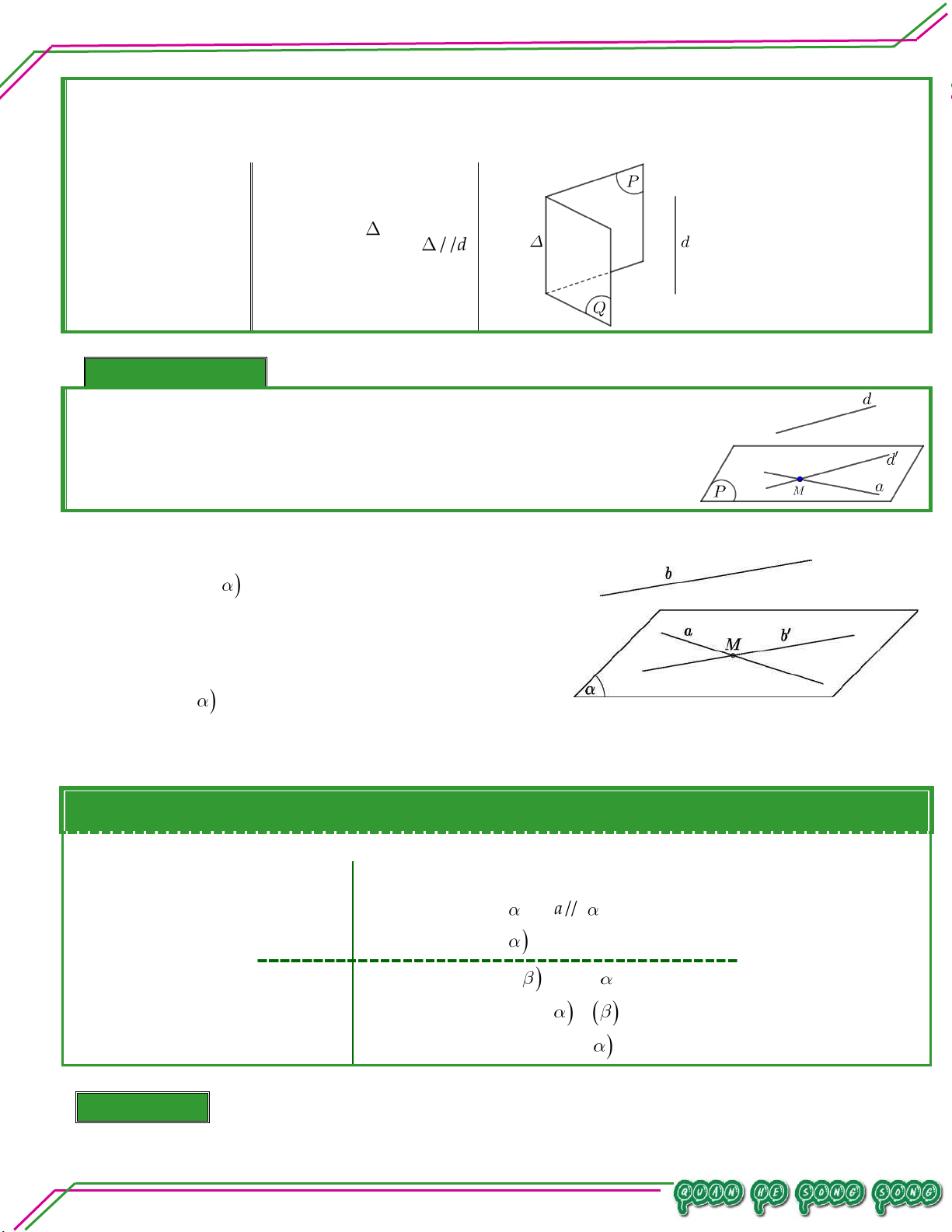
 Cho hai đường thẳng chéo nhau, có duy nhất một mặt phẳng
chứa đường thẳng này và song song với đường thẳng còn lại. TÂM  Chú ý
Cho a và b là hai đường thẳng chéo nhau.
Cách dựng mặt   chứa đường a và song song với
LÊ MINH đường b:
n: – Lấy M thuộc a.
ạ – Qua M kẻ đường thẳng b song song với b.
– Mặt phẳng   chứa a và b .
n Soê III. CÁC DẠNG BÀI TẬP. Bi
 Dạng 01. CHỨNG MINH ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG.
Phương pháp giải
 Ta có thể dùng một trong các cách sau a // b 
01 Dùng ĐL1 b    a//  a    
– Xét mặt phẳng   chứa .
02 – Tìm giao tuyến b   .
– Chứng minh a // b  a //    Bài 01. Trang 55
Hình học 11 – Chương 02. QUAN HỆ SONG SONG Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB,CD .
. Chứng minh MN // SBC, MN //SAD
. Gọi P là trung điểm SA . Chứng minh SB// MNP , SC // MNP .  1
. Gọi G là trọng tâm SBC , I thuộc cạnh BD sao cho BI  BD , Chứng minh GI // SAB. 3 Lời giải Bi
. Chứng minh MN // SBC, MN //SAD ên
 Vì M,N lần lượt là trung điểm của AB,CD So của ABCD
 Nên AD //BC//MN ạn: AD //MN  LÊ MINH
 Ta có: AD  SAD  MN // SAD MN   SAD BC //MN 
 Tương tự BC  SBC  MN // SBC MN   SBC TÂM
. Gọi P là trung điểm SA .
. Chứng minh GI // SAB.
Chứng minh SB // MNP , SC // MNP . 
Gọi J là trung điểm BC
 Ta có MN// SAD  MN//SP
 Ta có I là trọng tâm tam giác ABC suy ra 1 S  P //MN IJ  AJ .  3
 MN  MNP  SP // MNP 1 
 G là trọng tâm SBC suy ra JG  JS SP   SAD 3  1 1
Tương tự SC // MNP .
 SAJ có IJ  AJ , JG  JS nên GI //SA . 3 3
 Mà SA  SAB suy ra GI //SAB.  Bài 02. Cho hình chóp .
S ABCD có đáy ABCD là hình thang đáy lớn AB , đáy nhỏ CD với AB  2CD. Gọi
O là giao điểm của AC và BD , I là trung điểm của SA , G là trọng tâm tam giác SBC và E là một
điểm trên cạnh SD sao cho 2SE  3SD . Chứng minh
. Chứng minh MN // SBC, MN //SAD
. Gọi P là trung điểm SA . Chứng minh SB// MNP , SC // MNP .  1
. Gọi G là trọng tâm SBC , I thuộc cạnh BD sao cho BI  BD , Chứng minh GI // SAB. 3 Lời giải Trang 56
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
. DI // SBC .
 Gọi N là trung điểm SB.
 Có I là trung điểm của SA
  NI là đường trung bình SAB NI//AB    1 . NI   AB  2  1   IN  DC  CD AB Mà  2 suy ra  .  IN // DC AB // CD IN  DC  Tứ giác 
NIDC có IN //DC
 Nên NIDC là hình bình hành suy ra DI // NC TÂM DI // NC 
 Ta có NC  SBC  DI // SBC. DI   SBC
. GO // SCD .
. SB// ACE. LÊ MINH
 Gọi P là trung điểm của SC .  OB OD 1 Ta có  2 nên  . BG 2 OD BD 3 n:
 Có G là trọng tâm SBC     1 ạ BP 3  3
Mặt khác vì 2SE  3SD  SE  SD nên
 Ta có AB// CD 2 OB OA AB OB 2 DE 1  n So     2   2 DS 3 ê OD OC CD OD 3  1&2 OD DE 1 Bi
 OG // BH .  
  OE// BS BD DS 3
 Mà BH  SCD  OG//SCD.
 Mà OE  ACE suy ra SB//ACE.  Bài 03. Cho hình chóp .
S ABCD đáy là hình bình hành. Trên các cạnh SA ,SB lần lượt lấy các điểm M , N sao SM SN cho  . Chứng minh rằng: SA SB
. AD// SBC; DC// SAB .
. MN// ABCD; AB// MNCD; MN// SCD Lời giải Trang 57
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
. AD// SBC; DC//SAB .
 Do tứ giác ABCD là hình bình hành
 Suy ra AD//BC; DC//AB
 Mà AD  SBC,BC  SBC  AD//SBC .
 Chứng minh tương tự ta có DC// SAB
. MN// ABCD; AB// MNCD; MN// SCD Bi  SM SN Tam giác SAB có   MN//AB. ê SA SB n
Mà MN  ABCD , AB  ABCD  MN// ABCD. So
 Theo trên có MN//AB ạ
Mà AB  MNCD , MN  MNCD  AB// MNCD . n:
 Lại có CD//AB  MN//CD LÊ MINH
Mà MN  SCD ,CD  SCD MN// SCD .  Bài 04. Cho hình chóp .
S ABCD đáy là hình chữ nhật. Gọi G là trọng tâm tam giác SAD . Điểm E thuộc DC 1
sao cho DE  DC và I là trung điểm của AD . 3 TÂM
. Tìm giao điểm của IE và SBC .
. Chứng minh rằng:GE// SBC Lời giải
. Tìm giao điểm của IE và SBC .
 Trong ABCD ta có IE BC  H  IESBC
. Chứng minh rằng:GE// SBC
 Trong ABCD ta có DE IE 1 IG IE 1     
  EG//SH ID//CH DC EH 2 SG EH 2
 Mà EG  SBC,SH  SBC EG//SBC .  Bài 05.
Cho tứ diện ABCD có G là trọng tâm tam giác ABD . Điểm I thuộc BC sao cho BI  2IC . Chứng
minh rằng: GI// ACD . Lời giải Trang 58
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Gọi M là trung điểm của AD ,  BG BI Trong BCM có  2   IG//CM GM IC
 Mà IG  ACD,CM  ACD IG//ACD.  Bài 06. Cho hình chóp .
S ABCD có đáy là hình bình hành tâm O . Gọi M, N lần lượt là trung điểm các cạnh SI SJ 2 A ,
B AD . Gọi I, J thuộc SM, SN sao cho 
 . Chứng minh rằng MN / / SBD; IJ / / SBD SM SN 3
; SC / / IJO . TÂM Lời giải
 MN / / SBD
 Trong  ABCD : MN / /BD mà BD  SBD
 Nên MN / / SBD
LÊ MINH  IJ//SBD n: SI SJ ạ  Ta có 
nên IJ / /MN ( theo định lí SM SN ta- lét) n So
 Suy ra IJ / /MN / / BD mà BD  SBD . ê
 Nên IJ / / SBD
Bi  SC//IJO
 Gọi H  MN  AC; K  IJ SH  SI SJ 2 Từ 
  IJ / /MN SM SN 3 SK SI 2    SH SM 3  AH AM 1
Mà MN là đường trung bình tam giác ABD  
1 AH  HO  OC HO MB 2  SK CO 2 Xét SHC : 
  OK / /SC SH CH 3
Mà OK  OIJ
 Suy ra SC / / OIJ .  Bài 07. Trang 59
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
Cho hai hình bình hành ABCD và ABEF không đồng phẳng.
. Gọi P,Q là trọng tâm A  BD và ABE 
. Chứng minh rằng PQ / / CEF
. Gọi M,N là trọng tâm B  CD và AEF 
. Chứng minh rằng MN / / CEF Lời giải
. Chứng minh rằng PQ / / CEF
 Gọi I là trung điểm của AB . Bi  IQ IP 1 Xét tam giác DEI :   ê IE ID 3 n
 PQ / /DE ( theo định lí ta lét ) So
 Mà DE  DCEF  CEF ạ
 Nên PQ / / CEF n: LÊ MINH
. Chứng minh rằng MN / / CEF
 Gọi K là trung điểm EF . AN 2
N là trọng tâm AEF :  AK 3 MC 1 AM 2 TÂM
M là trọng tâm BCD:    AC 3 AC 3  AN AM Xét AKC :  AK AC
 Nên MN / /KC ( theo định lí ta lét)
 Mà KC  CEF .
 Suy ra MN / / CEF . Trang 60
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Dạng 02. TÌM GIAO TUYẾN CỦA HAI MẶT PHẲNG CHỨA MỘT ĐƯỜNG
THẲNG SONG SONG VỚI MẶT PHẲNG. .
Phương pháp giải  Ta có thể dùng:
M       
a   ; b           Mx / /a  a / /b   Bài 01. Cho hình chóp .
S ABCD đáy là hình bình hành tâm O . Gọi   là mặt phẳng qua O và song song với SA, BC . TÂM
. Tìm giao tuyến của   và ABCD . Xác định M,N lần lượt là giao điểm của AB,CD với  
. Xác định giao điểm Q của SB và   . Tìm giao tuyến của   và SAB .
. Tìm thiết diện cắt bởi   . Thiết diện là hình gì ? Lời giải
. Tìm giao tuyến của   và ABCD .
LÊ MINH Xác định M,N lần lượt là giao điểm của AB,CD
n:ạ với   . BC//   n So  Ta có: 
 ABCD  BC . ê O  la diem chung cua  ABCD va   Bi
 ABCD   //BC và đi qua O .
 Trong ABCD gọi M   AB
 Mà     M  AB  .
 Trong ABCD gọi N  CD
 Mà     N  CD  .
. Xác định giao điểm Q của SB và   . Tìm giao tuyến của   và SAB
P  SBC  MN     Ta có: 
 SBC   d//BC và d đi qua P .
BC  SBC  MN / /BC
 Trong SAB gọi Q  dSB  SB   Q Trang 61
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Dễ thấy  SAB  MQ
. Tìm thiết diện cắt bởi   . Thiết diện là hình gì?
 ABCD  MN    
 SAB  MQ   Ta có:  
Thiết diện cần tìm là MNPQ ,    SBC   PQ     
 SCD  NP  Bi
 Có PQ//MN nên tứ giác MNPQ là hình thang ên  Bài 02. So Cho hình chóp .
S ABC . Gọi M là trung điểm AC . Mặt phẳng   qua M và song song với S ; A B ạC ,
  cắt AB,SB,SC lần lượt tại N;H;K. Chứng minh rằng MNHK là hình bình hành. n: Lời giải LÊ MINH SA  //     
 SAC  SA  M la diem chung cua    va SAC
 SAC   MK//SA KSC . TÂM BC//     
 SBC  BC  K la diem chung cua  SBC va  
 SBC   KH//BC HSB .
SAB  SA    MK   S  A // MK H ladiemchungcua  SAB va  
 SAB   HN // SA NAB
 SBC  KH
 SAB  HN  Ta có:  
 Thiết diện của hình chóp cắt bởi   là tứ giác MNHK .  ABC   NM
 SAC  MK
 Ta có: M là trung điểm AC , MK//SA  MK là đường trung bình của SAC ,  1
Nên MK // SA và MK  SA (1) 2  1
Chứng minh tương tự HN // SA , HN  SA (2) 2
 Từ (1) (2) suy ra MNHK là hình bình hành. Trang 62
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Bài 03. Cho tứ diện SAB .
C Gọi M, N là trung điểm AB,S . B
. Chứng minh SA/ / CMN
. Tìm giao tuyến CMN và (SAC) Lời giải
. Chứng minh SA/ / CMN
 Xét SAB có MN là đường trung bình  MN //SA
 Mà MN CMN SA// CMN
. Tìm giao tuyến CMN và (SAC) C  (SAC)  Ta có : 
 C là điểm chung của hai mặt C   (CMN) phẳng TÂM
 Mặt khác MN // SA, MN  CMN, SA  SAC
 Nên CMNSAC  d//MN//SA và d qua C .  Bài 04. LÊ MINH Cho hình chóp .
S ABCD có đáy ABCD là hình thang đáy lớn AB . Gọi M là trung điểm CD ,   là n:
mặt phẳng qua M song song với SA và BC . Tìm hình tính thiết diện của   và hình chóp . S ABCD ạ Lời giải BC //   n So ABCD ê   BC  Bi
M   ABCD    
  ABCD  d//BC với d qua M và cắt AB tại N . SA  //     S
 A  SAB
NSAB   
  SAB  d//SA với d qua N và cắt SB tại P .
BC  SBC  MN     
  SBC  d//SA với d qua P và cắt SC tại Q BC // MN P   SBC
 Vậy khi đó   cắt khối chóp .
S ABCD theo thiết diện là hình thang MNPQ vì có MN//PQ//BC  Bài 05. Trang 63
Hình học 11 – Chương 02. QUAN HỆ SONG SONG Cho hình chóp .
S ABCD. Gọi M, N thuộc cạnh AB,CD . Gọi   là mặt phẳng qua MN và song song với SA
. Tìm thiết diện của hình chóp cắt bởi  
. Tìm điều kiện của MN để thiết diện là hình thang Lời giải
. Tìm thiết diện của hình chóp cắt bởi   Bi SA  //    ê   S
 A  SAB n  So
M  SAB     ạ
  SAB  d//SA với d qua M và cắt SB tại Q n: O   MN     LÊ MINH
 Trong ABCD , gọi O  MN AC   . O  AC   SAC SA  //     Ta có S
 A  SAC
OSAC    TÂM
  SAC  d//SA với d qua O và cắt SC tại P .
 Vậy khi đó thiết diện là tứ giác MNPQ
. Tìm điều kiện của MN để thiết diện là hình thang
 Nếu MQ // PN thì SA// NP
 Mà NP  SCD nên SA //SCD (vô lý).
 Do đó để MNPQ là hình thang thì QP // MN .
 SBC  PQ   Ta có 
   ABCD  MN SBC  ABCD   BC
 Mà PQ // MN nên MN // BC .
 Vậy để thiết diện là hình thang thì MN // BC .  Bài 06. Cho hình chóp .
S ABCDcó đáy ABCD là hình bình hành tâm O . Gọi M là trung điểm AB . Mặt phẳng
  qua M, song song với SA và BC cắt DC,SC,SBlần lượt tại N,H,K. Chứng minh tứ giác MNHK là hình thang. Lời giải Trang 64
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  / /BC 
 Ta có: BC  SBC
 HK / /BC   1 .
 SBC   HK   / /BC 
 Lại có: BC   ABCD
 MN / /BC 2 . 
    ABCD   MN  Từ  
1 và 2  HK / /MN
tứ giác MNHK là hình thang.  Bài 07. Cho hình chóp .
S ABCDcó đáy ABCD là hình thang, đáy lớn AB  2CD.Gọi M là trung điểm SB .
Tìm thiết diện của mặt phẳng   với hình chóp .
S ABCD biết mặt phẳng   qua M , song song với TÂM
SD và AB . Chứng minh thiết diện là một hình thang. Lời giải
M  SAB   Có    / /AB AB   SAB LÊ MINH
  SAB  n:
Mx , (Mx / /A ) B . ạ
 Trong SAB gọi N  MxSA.
N  SAD n So  ê  Có:    / /SD  Bi SD   SAD
  SAD  Ny, Ny / /SD.
 Trong SAD gọi P  Ny  AD .
P  ABCD 
 Có:   / /AB
  ABCD  Pz, Pz / /AB. AB   ABCD
 Trong ABCD gọi Q  Pz  BC .
 SAB  MN
 SAD  NP    
Thiết diện cần tìm là tứ giác MNPQ , mà MN / /PQ / / AB.     ABCD   PQ
 SBC QM
 Do đó tứ giác MNPQ là một hình thang. Trang 65
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Bài 08.
Cho tứ diện ABCD . Hãy xác định thiết diện của hình tứ diện ABCD khi bị cắt bởi mặt phẳng P
trong mỗi trường hợp sau:
. Mặt phẳng P đi qua trọng tâm G của tứ diện, qua E thuộc cạnh BC và P//AD.
. Đi qua trọng tâm của tứ diện và song song với BC và AD . Lời giải Bi
. Mặt phẳng P đi qua trọng tâm G của tứ diện, qua ê
E thuộc cạnh BC và P //AD . n So
 Gọi I , J lần lượt là trung điểm BC, AD
G là trung điểm IJ ( vìG là trọng tâm của tứ ạn: diện).
 Trong BCJ gọi M  EG CJ . LÊ MINH
M  EG,EG   P  
 MPACD.
M CJ,CJ   ACD
 Mà :P / /AD, AD  ACD .
 Do đó PACD  Mx, Mx / /AD . TÂM
 Trong ACD gọi F  Mx AC;K  MxCD .
PABC  FE   Ta có: 
 P BCD  EK . P
    ACD   KF
 Vậy thiết diện cần tìm là EF  K .
. Đi qua trọng tâm của tứ diện và song song với BC và AD .
 Gọi L, P,Q,O lần lượt là trung điểm các cạnh A ,
B AC,CD, BD
 Theo tính chất trọng tâm của tứ diện và có mặt
phẳng P đi qua trọng tâm G của tứ diện và song song với BC.
 Suy ra thiết diện cần tìm là hình bình hành LPQO  Bài 08. Trang 66
Hình học 11 – Chương 02. QUAN HỆ SONG SONG Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SC , P là
mặt phẳng qua AM và song song với BD .
. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng P .
. Gọi E, F lần lượt là giao điểm của P với các cạnh SB và SD. Tính tỉ số diện tích của SME
và SBC và tỉ số diện tích của SFM và SCD .
. Gọi K là giao điểm của ME và CB ; J là giao điểm của MF và CD . Hãy chứng minh ba điểm EF
K, A, J nằm trên đường thẳng song song với EF và tìm tỉ số . KJ Lời giải
. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng P .
 Trong ABCD , gọi O  AC BD
 Trong SAC , gọi I  SOAM TÂM I SO   SBD  Khi đó     . I  AM   P
I SBD P BD // P 
 Ta có BD  SBD
ISBD  P LÊ MINH
 SBDP n:
 d//BD và d qua I . ạ
 Trong SBD có E  dSB và F  SDd .
 Ta có: E  dSB n So Ed   P ê  
 E P  SBC   1 . Bi E SB   SBC     M  AM   P  Và     2 . M SC  
SBC M P SBC
 Từ ME  PSBC I .
 Tương tự, ta cũng có MF  PSCD II . Ed   P
 Ta có Ed SB      3 . E SB  
SAB E P SAB A AM   P  Và     . A   SAB
A P SAB 4
 Từ 3 , 4 ta có AE  PSAB III .
 Tương tự, ta có AF  PSAD IV  .
 Từ I, II, III, IV  ta có tứ giác AFME là thiết diện của hình chóp khi cắt bởi P . Trang 67
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
. Tính tỉ số diện tích của SME và SBC và tỉ số diện tích của SFM và SCD .
 SAC có SO, AM là hai đường trung tuyến cắt nhau tại I  SI 2
Nên I là trọng tâm của tam giác SAC   . SO 3  SE SI 2
Xét tam giác SOB có IE // OB nên   . SB SO 3  SF SI 2 Tương tự ta cũng có   . SD SO 3 Bi  1 ê .SM.S . E sin ESM S SM SE 1 2 1 SME 2 n    .  .  S 1 SC SB 2 3 3  SBC So .SC.S . B sin CSB   Ta có 2  ạ 1 
.SM.SF.sin MSF n: S SM SF 1 2 1 SFM 2   .  .  S 1 SC SD 2 3 3 LÊ MINH SCD  .SC.S . D sin DSC  2  EF
. Hãy chứng minh ba điểm K, A, J nằm trên đường thẳng song song với EF và tìm tỉ số . KJ K  ME   P
 Ta có K  ME CB      . K CB  
ABCD K P ABCD 5 TÂM J  MF   P
 Ta có J  MF CD      J CD  
ABCD J P ABCD 6 A AM   P  Và     . A   ABCD
A P  ABCD 7
 Từ 5, 6, 7 ta được A, K, J cùng thuộc giao tuyến của P và ABCD nên A, J, K thẳng hàng.
 Gọi  PABCD nên A, J, K thuộc . BD // P 
 Ta có BD  ABCD  BD // .
PABCD  
 Mà EF // BD nên // EF .
 Vậy ba điểm K, A, J nằm trên đường thẳng song song với EF .
 Ta có EF // BD // JK .  MI ME 1
Xét tam giác AMK có IE // AK nên   . MA MK 3  EF ME 1 EF 1
Xét tam giác JKM có EF // JK nên   .Vậy  . JK MK 3 JK 3
------------------ HẾT ------------------ Trang 68
Hình học 11 – Chương 02. QUAN HỆ SONG SONG BÀI 04
HAI MẶT PHẲNG SONG SONG ☆☆★ ☆☆ I. ĐỊNH NGHĨA:
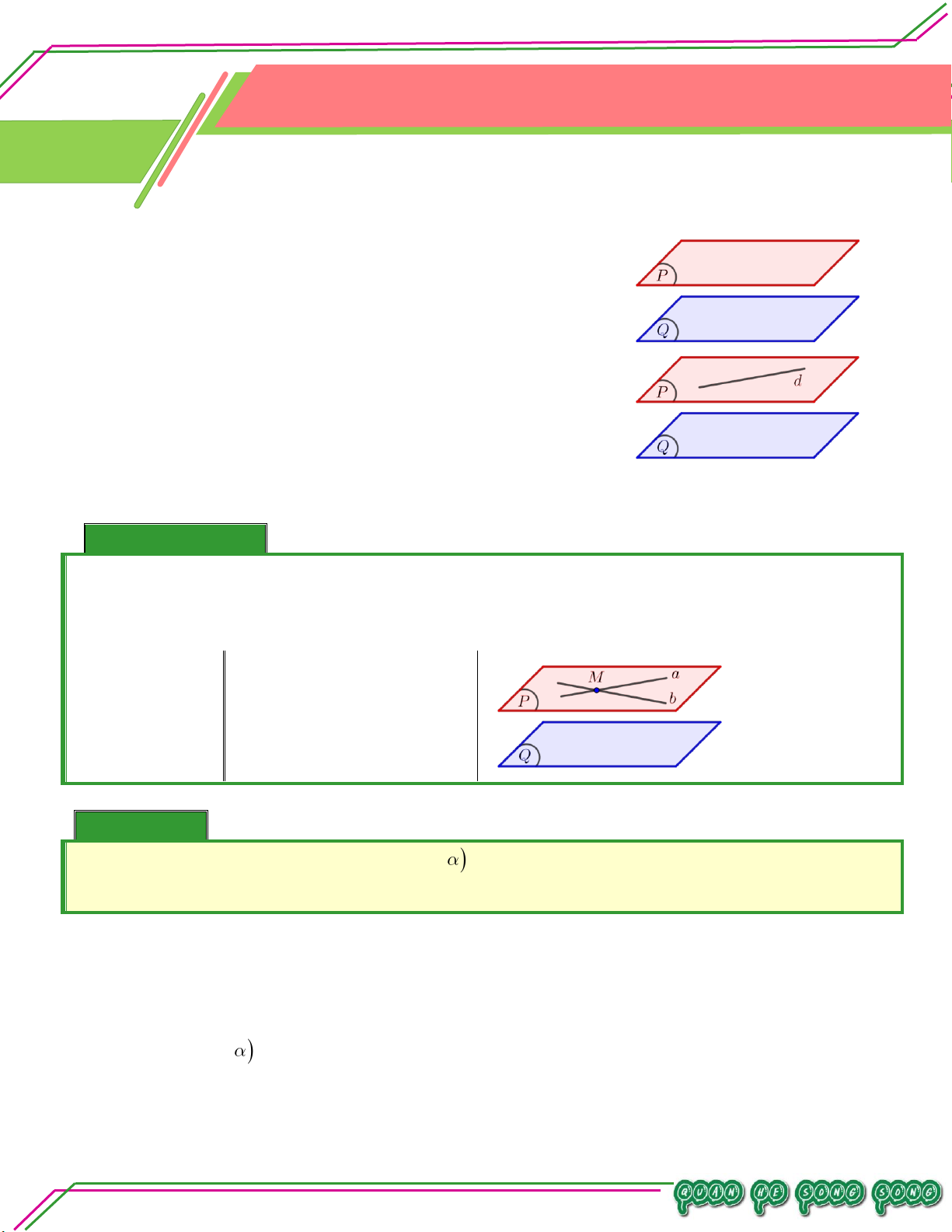
 Hai mặt phẳng P và Q được gọi là song song với
nhau nếu chúng không có điểm chung.
 Ký hiệu: P//Q hoặc Q//P.
 Nhận xét:
Nếu hai mặt phẳng P và Q song song với nhau thì bất
kỳ đường thẳng nào nằm trong mặt phẳng này cũng song
TÂM song với mặt phẳng kia. II. TÍNH CHẤT:
 Định lý 1:
 Định lý 1
 Nếu mặt phẳng P chứa hai đường thẳng cắt nhau a,bvà a,b cùng song song với mặt LÊ MINH
phẳng Q thì P song song với Q .
n:  Tóm tắt định lý: ạ
a  P;b  P 
a  b  M 
 P // Q n So a// Q ê  Bi b//  Q  Ví dụ 01.
Cho tứ diện SABC. Hãy dựng mặt phẳng   qua trung điểm I của đoạn SA và song song với
mặt phẳng  ABC . Lời giải  Cách dựng:
 Xét SAB , qua I dựng IK//AB .
 Xét SAC , qua I dựng IH//AC .
Vậy mặt phẳng   qua trung điểm I của đoạn SA và song song với mặt phẳng  ABC là IHK Trang 69
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Chứng minh: IK//AB  Ta có:   . AB  
ABC IK//ABC IH//AC    . AC  
ABC IH//ABC
IK ,IH  IHK  Bi
IK IH  I  Ta lại có: 
 IHK // ABC. ê
IK//  ABC n  So IH //  ABC  ạ Ví dụ 02. n:
Cho tứ diện ABCD . Gọi G ,G ,G lần lượt là trọng tâm của A  BC, A  CD, A  BD . Chứng minh: 1 2 3 LÊ MINH
GG G // BCD . 1 2 3    Lời giải
 Ta có: G ,G ,G lần lượt là trọng tâm của 1 2 3 A  BC, A  CD, A  BD AG AG AG 2 1 2 3     TÂM AM AP AN 3
 Nên G G //MP, G G //MN, G G //PN 1 2 1 3 2 3 G  G //MP 1 2 )
 G G // BCD 1 . MP   BCD 1 2     G  G //PN 2 3 )  . PN  
BCD G G // BCD 2 2 3    
 Mà G G G G  G 3 . 1 2 2 3  2    Từ  
1 , 2 , 3 suy ra G G G // BCD . 1 2 3   
 Định lý 2
 Qua một điểm nằm ngoài một mặt phẳng cho trước có một
và chỉ một mặt phẳng song song với mặt phẳng đã cho.
 Ta có các hệ quả sau:
 Nếu đường thẳng d song song với mặt phẳng
Q thì qua d có duy nhất một mặt phẳng song song với Q . Trang 70
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Hai mặt phẳng phân biệt cùng song song với
mặt phẳng thứ ba thì song song với nhau.
 Cho điểm A không nằm trên mặt phẳng P .
Mọi đường thẳng đi qua A và song song với P
thì đều nằm trong mặt phẳng đi qua A song song
với P là Q.  Ví dụ 03. Cho tứ diện .
S ABC có SA  SB  SC . Gọi Sx , Sy , Sz lần lượt là phân giác ngoài của các góc S TÂM
trong tam giác SBC , SAC , SAB . Chứng minh:
. Sx;Sy // ABC
. Sx ; Sy ; Sz cùng nằm trên mặt phẳng Lời giải  LÊ MINH
. Sx;Sy // ABC  n:
Gọi SM là đường phân giác trong của tam ạ
giác SBC (với M BC )
 Mà SBC cân tại S (do SC  SB)
SM  BC mà Sx SM n Soê Sx// BC Bi Sx//BC  
 Ta có BC  ABC  Sx// ABC 
Sx   ABC 
 Chứng minh tương tự  Sy// ABC
Sx//  ABC 
 Ta có Sy// ABC   Sx;Sy // ABC 
Sx  Sy    S 
. Sx ; Sy ; Sz cùng nằm trên mặt phẳng
 Chứng minh tương tự  Sy;Sz // ABC
Sx;Sy//ABC  Ta có 
  Sx Sy  Sy Sz  S ;
x Sy;Sz đồng phẳng
Sy;Sz //  ABC  ;   ;   Trang 71
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Định lý 3
 Nếu một mặt phẳng thứ 3 cắt một trong hai mặt phẳng song song thì sẽ cắt mặt phẳng
còn lại và hai giao tuyến của chúng song song với nhau
 Tóm tắt định lý:    Bi
  P d1  ê
 Q  d   d //d 2 1 2 n  P//Q  So  ạn: LÊ MINH
 Hệ quả: Hai mặt phẳng song song chắn trên hai cát tuyến song song những đoạn thẳng bằng nhau. TÂM
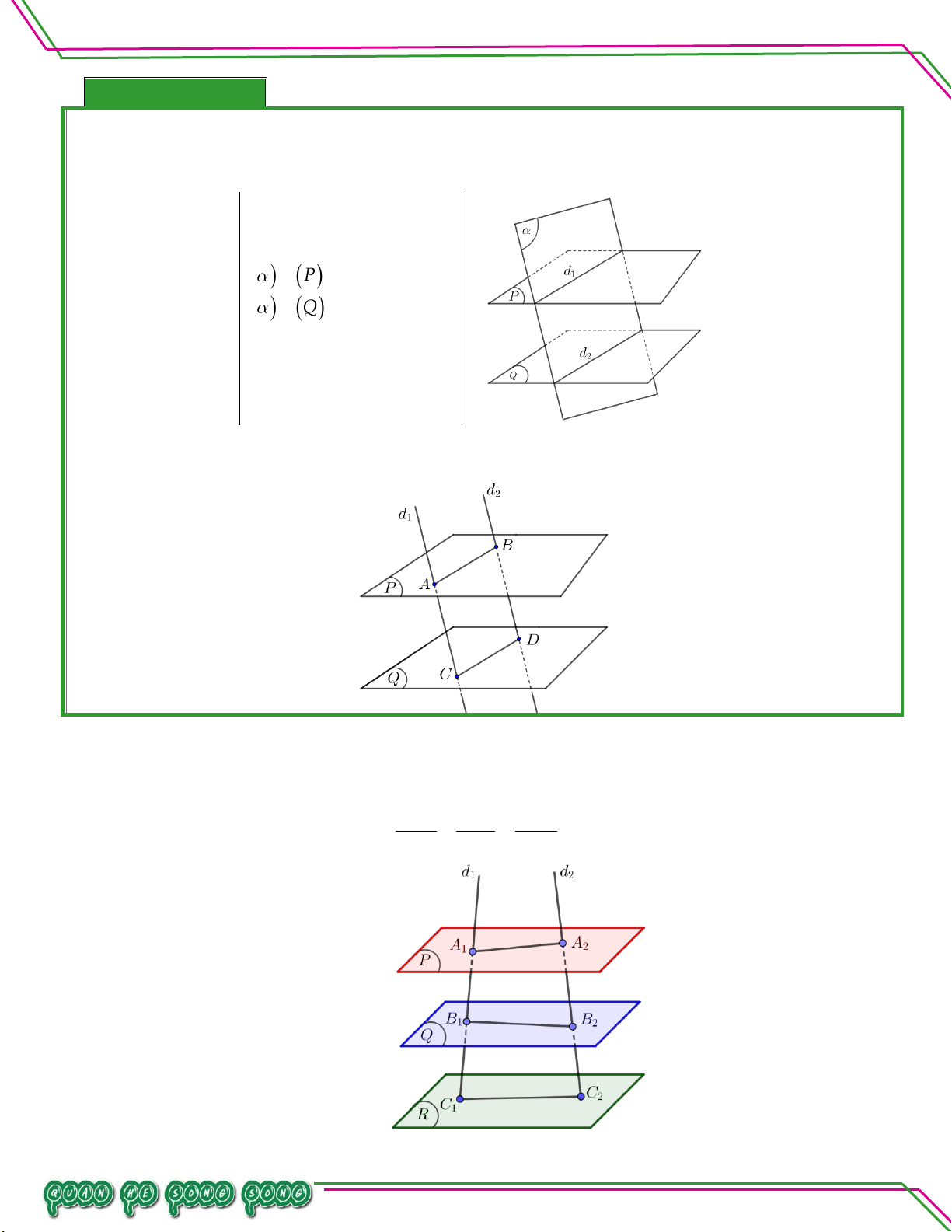
III. ĐỊNH LÝ THALES TRONG HÌNH HỌC KHÔNG GIAN:
 Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ. A B B C C A 1 1 1 1 1 1   . A B B C C A 2 2 2 2 2 2 Trang 72
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
IV. HÌNH LĂNG TRỤ VÀ HÌNH HỘP:
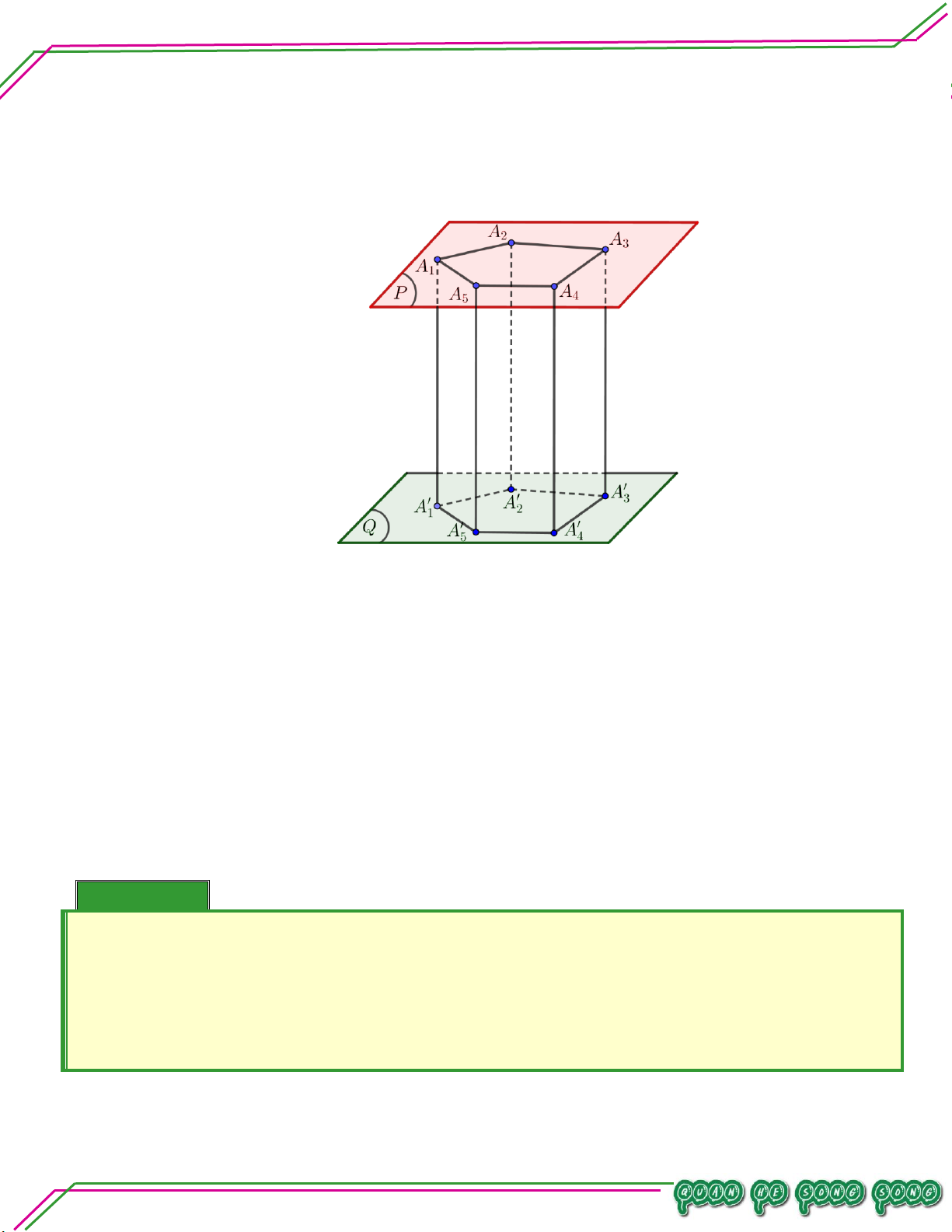
 Cho P // Q .
Trên P cho đa giác A A ...A . Qua các đỉnh A , A ,..., A ta vẽ các đường thẳng song song 1 2 n 1 2 n
với nhau và cắt Q lần lượt tại A , A ,..., A  . 1 2 n TÂM Hình lăng trụ gồm
– Hai đa giác A A ...A , A A ...A  LÊ MINH 1 2 n 1 2 n
– Các hình bình hành A AA A , A A A A , …, A A AA n: 1 1 2 2 2 2 3 3 n n 1 1
ạ  Hình lăng trụ có:
– Mặt đáy: A A ...A , A A ...A  1 2 n 1 2 n
n So – Các cạnh bên: A A, A A , ..., A A  ê 1 1 2 2 n n
– Mặt bên: A A A A , A A A A , …, A A A A Bi 1 1 2 2 2 2 3 3 n n 1 1
– Các đỉnh: là các đỉnh của đáy.
 Gọi tên lăng trụ: hình lăng trụ + tên đa giác
* Hình lăng trụ có đáy là tam giác gọi là hình lăng trụ tam giác .
* Hình lăng trụ có đáy là hình bình hành gọi là hình hộp.  Ví dụ 04.
Cho hình lăng trụ AB . C A B  C
 . Gọi Mvà Mlần lượt là trung điểm của các cạnh BC và B C  .
. Chứng minh AM // A M   .
. Tìm giao điểm của AB C  với A M  .
. Tìm giao tuyến d của AB C  với BA C   .
. Tìm giao điểm G của d với AM M
  . Chứng minh G là trọng tâm tam giác AB C  . Lời giải Trang 73
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
. Chứng minh AM // A M   .
 Do M và M lần lượt là trung điểm của các
cạnh BC và B C   MM // CC  Nên  . MM = CC  AA// CC AA// MM  Mà    AA = CC AA = MM   Bi Tứ giác AA M  M  là hình bình hành ê  AM//A M   . n
. Tìm giao điểm của AB C  với A M  . So
 Ta có M là trung điểm của cạnh B C   ạn: M B C   B C     AB C   mà       LÊ MINH M AM M  AA M M  AB C  AA M  M
  M .
 Mặt khác AB C  AA M  M     A .  Nên ta có AB C  AA M  M    AM.  Trong AA M  M
  gọi I là giao điểm của AM và A M   A M  AB C
  I . TÂM
. Tìm giao tuyến d của AB C  với BA C   .  Trong ABA B
  gọi D là giao điểm AB và A B  D A B  A B    BA C   mà   AB C  BA C     D . D   AB AB   AB C
 Ta lại có AB C  BA C
  C  AB C  BA C    C D  .
 Vậy giao tuyến d của AB C  với BA C   là C D  .
. Tìm giao điểm G của d với AM M
  . Chứng minh G là trọng tâm tam giác AB C  .  Ta có AM M  AB C    AM .  Mà C D   AB C  .  Trong AB C
  gọi G là giao điểm C D
 và AM . Suy ra C D  AM M     G .
 Ta có D là trung điểm AB C D
 là đường trung tuyến của tam giác C A  B.
 Tương tự ta có AM là đường trung tuyến của tam giác AB C  .
 Mà G là giao điểm C D  và AM .
 Vậy G là trọng tâm tam giác AB C  . V. HÌNH CHÓP CỤT:
 Cắt hình chóp bởi mặt phẳng song song với đáy và không đi qua đỉnh ta được hình chóp cụt. Tính chất : Trang 74
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Hai đáy là hai đa giác có các cạnh tương ứng song song , các tỷ số các cặp cạnh tương ứng bằng nhau.
 Các mặt bên là những hình thang.
 Các đường thẳng chứa các cạnh bên đồng quy tại một điểm. TÂM
III. CÁC DẠNG BÀI TẬP. LÊ MINH
 Dạng 01. CHỨNG MINH HAI MẶT PHẲNG SONG SONG. n:ạ
Phương pháp giải a//a n So b//b ê 
 Chứng minh 2 mặt phẳngsong song:     //     . Bi : a b I
 :abI  // 
 Chứng minh đường thẳng song song với mặt phẳng:   . a     a//    Bài 01. Cho hình chóp .
S ABCDcó đáy là hình bình hành tâm O . Gọi M, N, P lần lượt là trung điểm
SA,SB,SD .
. Chứng minh PMN// ABCD , OMN//SCD .
. Gọi K, J lần lượt là trung điểm BC,OM . Chứng minh KI// SCD . Lời giải Trang 75
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
. Chứng minh PMN//ABCD
MN  MNP,MP  MNP 
AB   ABCD , AD  ABCD 
 Ta có: MN  MP  M
AB AD  A  MN//AB, MP//AD  Bi
 MNP//ABCD ên
 Chứng minh OMN//SCD So
 Ta có: MN là đườ
ng trung bình của SAB
 Nên MN//AB mà A // B CD hay ạ MN// CD . n: MN//C D
. Chứng minh KI// SCD  LÊ MINH
 MN  SCD  MN// SCD   1 O
 OMNABCD   CD   SCD
MN  OMN   
 Tương tự OM là đường trung bình của SAC
AB   ABCD
 Nên OM//SC .  MN//AB O  M//SC 
 OMNABCD  Ox//AB TÂM   O
 M  SBC  OM// SBC 2  
Mặt khác OK//AB SC   SBC
 OMNABCD  OK//AB  KI  OMN   
MN OM M trong OMN 3
OMN//SCD    KI// SCD  Ta có Từ  
1 ,2 ,3 suy ra SCD // OMN . KI   OMN    Bài 02.
Cho tứ diện ABCD . Gọi G ,G ,G lần lượt là trọng tâm của ABC; AC ; D ABD . Chứng 1 2 3
minh rằng G G G // BCD . 1 2 3    Lời giải
 Gọi M,N,P lần lượt là trung điểm của
BC,CD, DB .
 Theo tính chất của trọng tâm và định lý ta- lét: AG AG AG 2 1 2 3    AM AN AP 3 G  G // MN G  G // MNP 1 2   1 2     (1) G G // NP  G  G // MNP  2 3   2 3
 Mà G G và G G cắt nhau tại G và cùng nằm 1 2 2 3 2 trong G G G (2) 1 2 3   1&2
G G G // MNP , hay G G G // BCD . 1 2 3    1 2 3    Trang 76
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Bài 03.
Cho hai hình bình hành ABCD và ABEF không đồng phẳng.
. Chứng minh AB // CDEF.
. Chứng minh ADF // BCE.
. Gọi M, N, P,Q lần lượt là trung điểm AD,BC,BE, AF . Chứng minh MNPQ // DCEF Lời giải
. Chứng minh AB // CDEF.
 Ta có AB // CD (do tứ giác ABCD là hình bình hành)
 AB // FE (do tứ giác ABEF là hình bình hành)
 AB // FE //CD  A
B // CDEF .  TÂM
. Chứng minh ADF // BCE .
 Ta có AD // BC (do tứ giác ABCD là hình bình hành),
 Mà BC  BCE  AD // BCE .
 Chứng minh tương tự ta có AF // BCE LÊ MINH
 Mà AD và AF cắt nhau tại A , và cùng nằm
trong mặt phẳng  ADF .
n:ạ  Suy ra ADF // BCE.
. Gọi M, N, P,Q lần lượt là trung điểm AD,BC,BE, AF . Chứng minh MNPQ // DCEF n So  ê
Xét hình bình hành ABEF có P,Q là trung điểm BE, AF  Bi
Nên PQ là đường trung bình của hình bình hành ABEF
 PQ // AB// EF, PQ = AB  EF (3) (tính chất đường trung bình).
 Chứng minh tương tự ta có  MN // A /
B / CD, MN = AB  CD (4)
 Từ (3) và (4) suy ra  MN // PQ, EF / / CD .
 Suy ra tồn tại mặt phẳng MNPQ và mặt phẳng DCEF .
 Ta có MN // CD, CD  DCEF  MN // DCEF(5)
 Xét BCE có P, N là trung điểm của BE và BC (gt),
 Suy ra PN là đường trung bình của BCE  PN // EC
 Mà EC  DCEF , suy ra PN // DCEF(6)
 Ta có MN,PN cùng nằm trong mặt phẳng MNPQ và cắt nhau tại N (7)
 Từ (5), (6) và (7) suy ra MNPQ // DCEF . Trang 77
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Bài 04. Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm A  BS và điểm
E trên cạnh AD sao cho AD  3AE. Gọi M là trung điểm AB .
. Tìm giao tuyến SAB và SCD .
. Đường thẳng qua E song song với AB cắt MC tại F . Chứng minh rằng GF// SCD.
. Chứng minh rằng EG// SCD. Bi Lời giải ê
. Tìm giao tuyến SAB và SCD . n    So
S SAB SCD 
 Ta có: AB//CD; ạ  n:
AB  SAB;CD  SCD  LÊ MINH
 SABSCD  Sx / /AB/ /CD.
. Đường thẳng qua E song song với AB cắt MC
tại F . Chứng minh rằng GF// SCD.
 Xét hình thang AMCD có EF AM , AE MF 1 Suy ra:   . TÂM AD MC 3
 Xét SAB : M là trung điểm AB , G là trọng . Chứng minh rằng EG// SCD. MG 1 tâm A  BC suy ra:  . GF
 //SCcmt MS 3  Ta có:  EF//CD  //AB  MG MF 1 Xét SCM có 
  GF//SC . MS MC 3
 SCD//EFG  EG//SCD . G  F//SC  Ta có:   SC  
SCD GF//SCD  Bài 05. Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành. Gọi I là trung điểm của AB , G là
trọng tâm SAB và điểm M trên cạnh AD sao cho AD  3AM . Đường thẳng qua M song song
với AB cắt IC tại N . Chứng minh rằng GN// SCD và GM// SCD . Lời giải
 Xét hình thang AICD có MN//AI , suy ra: AM IN 1   . AD IC 3
 Xét SAB có I là trung điểm AB , G là trọng tâm A  BC IG 1 Suy ra:  . IS 3  IG IN 1 Xét SCM có 
  GN//SC . IS IC 3 Trang 78
Hình học 11 – Chương 02. QUAN HỆ SONG SONG G  N//SC  Ta có:   . SC  
SCD GN//SCD G
 N//SCcmt  Ta có:  MN//CD  //AB
 SCD//GNM  GM//SCD.
 Dạng 02. GIAO TUYẾN CỦA 2 MẶT PHẲNG CÓ 1 MẶT PHẲNG SONG
SONG VỚI MẶT THỨ BA .
Phương pháp giải 
Ta có thể dùng một trong các cách sau
M     01  // 
      Mx; Mx//b TÂM      b  // 
Đưa về dạng thiết diện song song với đường thẳng   a b a,b     , //  
02 Như vậy thay vì tìm thiết diện song song với mặt phẳng   thì ta tìm thiết LÊ MINH
diện song song với các đường thẳng a,b nằm trong   n: ạ  Bài 01. Cho hình chóp .
S ABCD đáy là hình bình hành .Gọi M là trung điểm SA ,gọi   là mặt phẳng n Soê
qua M và   song song với  ABCD . Bi
. Tìm  SAB , N  SB .Tìm  SBC,P  SC   .
. Tìm thiết diện cắt bởi   .Thiết diện là hình gì ? Lời giải
. Tìm  SAB , N  SB .
Tìm   SBC ,P  SC   .
   SAB
 Ta có  // ABCD,SABABCD  AB.
 Mà SAB   M  SAB   d
(với d là là đường thẳng đi qua M và song song AB ).
 Do M là trung điểm của SA  d cắt SBtai trung điểm N .
 SB   N . Trang 79
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
  SBC .
 Ta có  // ABCD,SBCABCD  BC .
 Mà SCB   N  SCB   (với là là đường thẳng đi qua N và song song BC ).
 Do N là trung điểm của SB  cắt SC tai trung điểm P  SC    P .
. Tìm thiết diện cắt bởi   .Thiết diện là hình gì ?
 Ta có  // ABCD,SADABCD  AD. Bi ê
 Mà SAD   M  SAD   a (với a là đường thẳng đi qua M và song song AD ). n  
Do M là trung điểm của SA
a cắt SDtai trung điểm Q . So
 Nối M ,N ,P ,Q ta được thiết diện là tứ giác MNPQ . ạ
MN// PQ MN// AB;PQ// AB n:  Ta có 
. Vậy tứ giác MNPQ là hình bình hành. NP// MQ 
NP// AD;MQ// AD LÊ MINH  Bài 02. Cho hình chóp .
S ABCD đáy là hình thang AB / /CD , M là một điểm thuộc cạnh
BC M  B,C
. Xác định thiết diện của hình chóp cắt bởi mặt P qua M và song song với SAB . TÂM
. Gọi N,E,F lần lượt là giao điểm của P và AD,SD,SC . Gọi I là giao điểm của NE và
MF . Chứng minh rằng I chạy trên một đường thẳng cố định. Lời giải
. Xác định thiết diện của hình chóp cắt bởi mặt
Pqua Mvà song song với SAB.
 Ta có: P đi qua M và song song với SAB
 PABCD  d//AB với d đi qua M và
d  AD  N .
 P đi qua N và song song với SAB
 PSAD  d//SA với d đi qua N và
d SD  E .
 P đi qua M và song song với SAB
 PSBC  d//SB với d đi qua M và
d SC  F .
 Suy ra thiết diện tìm được là tứ giác MNEF
 Vì PSCD  EF,CD / /AB
 EF / /AB / /CD / /MN
 Vậy thiết diện tìm được là hình thang MNEF
. Chứng minh rằng I chạy trên một đường thẳng cố định. Trang 80
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Ta có: NE  SAD
 MF  SBC
 SADSBC  SK,K  AD BC suy ra SK cố định
 I là giao điểm của NE và MF
 I SK(ĐPCM)  Bài 03. Cho hình chóp .
S ABCD đáy là hình bình hành tâm O , AC  a, BD  b ,tam giác SBD đều. Một
mặt phẳng   di động song song với mặt SBD và đi qua điểm I trên đoạn thẳng AC
I  A,C 
. Xác định thiết diện của hình chóp cắt bởi mặt phẳng   .
. Tính diện tích thiết diện theo a,b và x  AI Lời giải
TÂM . Xác định thiết diện của hình chóp cắt bởi mặt phẳng  .
 Trường hợp 1: I  AO
 Ta có:   đi qua I và song song với SBD
 PABCD  d//BD với d đi qua I và
d  AB  M LÊ MINH  . d  AD   N
n:ạ   đi qua Nvà song song với SBD
 PSAD  d//SD với d đi qua N và n So
d SA  P. ê
  SAB  MP mà   / / SBD  MP / /SB Bi
 Suy ra thiết diện tìm được là tam giác MNP .
 Do tam giác SBD đều nên tam giác MNPđều.
 Trường hợp 2: I CO
 Ta có:   đi qua I và song song với SBD
 PABCD  d//BD với d đi qua I và
d CB  E  . d  CD   F
   đi qua F và song song với SBD
 PSCD  d//SD với d đi qua F và
d SC  G .
  SBC  EG mà   / / SBD  EG / /SB
Suy ra thiết diện tìm được là tam giác EFG .
Do tam giác SBD đều nên tam giác EFG đều. Trang 81
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
. Tính diện tích thiết diện theo a,b và x  AI
 Trường hợp 1:
 Trường hợp 2:
I  AO, thiết diện tìm được là tam giác MNPđều
I CO, thiết diện tìm được là tam giác EFG đều 2   2    MN EF MNP SBD nên S     S  EFG SBD nên S     S MNP SBD  BD  EFG SBD  BD   2 EF CI a x ax  MN AI x 2x    ,     BD AO a a , BD CO a a Bi 2 2 2 ê 1 b 3      2 1 b 3 n S b b sin 60 SBD S
 bbsin 60  2 4 SBD 2 4 So 2 2 2 2
 2x  b 3 x b 3 2 2  2 S   
 2a  x 2
 b 3 a  x b 3 MNP   2 ạ  a  4 a  S      . EFG 2   n: a 4 a   LÊ MINH  Bài 04. Cho hình chóp .
S ABCD đáy là hình bình hành tâm O . Gọi E là trung điểm của SB. Biết tam
giác ACE đều và AB  OD  a . Một mặt phẳng   di động song song với mặt phẳng  ACE
và qua I trên đoạn OD ;   cắt AD , CD , SC , SB, SA lần lượt tại M , N , P ,Q , R .
. Xác định thiết diện của hình chóp cắt bởi mặt phẳng   . TÂM
. Tính diện tích thiết diện theo a,b và x  AI Lời giải
 Kẻ QI // OE với Q SB .
 Qua I kẻ MN // AC với MAD, NAC .
 Gọi QR   SAB mà AE  CAESAB  QR // AE .
 Gọi PQ   SAC mà CE  CAESAC  QP //CE
 P  MNPQR.
. Có nhận xét gì về PQR và tứ giác MNPR  DI x Ta có  SQ x   DO a SE a QR PQ PR x     AE AE CA a
 Mà CAE đều  PQR đều.
OE  AC (do OE là đường trung tuyến trong tam giác đều)
 QI  NM  PN  NM.
 Dễ thấy PNMR là hình bình hành
Mà PN  NM  PNMR là hình chữ nhật.
. Tìm tập hợp giao điểm của MP và NR khi I di động trên đoạn OD . Trang 82
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Gọi   K  PM  1
NR  KI  PN 2    a x a x Mà PN  .SD  KI  .SD a 2a     IK OI a x
Gọi G là trung điểm SD. Ta có     GD OD  a 
 Mà IK // GD  KGO .Vậy khi I di động trên DO thì K di động trên GO.
. Tính diện tích đa giác MNPQR theo a và x  DI . Tính x để diện tích ấy lớn nhất. 2  x 1 x 3 x 3
Ta có PR  NM  .a  x  S  . . x  a PQR 2 2 4     a x a x a x Ta có S  N . M PN  . x .SD  . x 2 . OE  . x 2
. .a  2a  x x PRMN a a a  x Vậy S  a  x x  (đvdt) MNPQR   2 3 2 4 TÂM
 Dạng 03. HÌNH LĂNG TRỤ - HÌNH HỘP .
Phương pháp giải
 Chú ý vào các đường thẳng và mặt phẳng song song của hình lăng trụ để áp dụng các định lí song song đã học. LÊ MINH  Bài 01. n:ạ
Cho lăng trụ tam giác AB .
C A' B'C'. Gọi M, M ' làn lượt là trung điểm của cạnh BC và B'C' .
. Chứng minh AM // A' M' .
. Tìm giao điểm AB'C' và đường thẳng A' M. n Soê
. Tìm giao tuyến d của AB'C' và BA'C' . Bi
. Tìm giao điểm G của d với AMA'. Chứng minh rằng G là trọng tâm AB'C'
Lời giải
. Chứng minh AM // A' M' .
 Xét tứ giác BCC' B' có M , M' là trung điểm
của BC và B'C' .
 MM' là đường trung bình của hình bình hành BCC' B' .
 MM'//BB'//CC'; MM'  BB'  CC'
 Nên tứ giác AMA' M' là hình bình hành
AM // A' M' .
. Tìm giao điểm AB'C' và đường thẳng A' M.
 Gọi I là trung điểm của A' M
 I cũng là trung điểm của AM'.
 Mà AM thuộcAB'C' Trang 83
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Do vậy I là giao điểm của A' Mvà AB'C' .
. Tìm giao tuyến d của AB'C' và BA'C' .
 Trong (ABB' A') có AB BA    J
 J,C AB'C'BA'C'
 JC  AB'C'BA'C'
. Tìm giao điểm G của d với AMA'. Chứng minh rằng G là trọng tâm AB'C' Bi ê
 Trong AB'C' có JC'IM'  
G  G  JC'AMM' A' . n 
Xét AC' B' có AM';C' J lần lượt là trung tuyến. So
 Do vậy giao điểm G của chúng chính là trọng tâm AC'B' . ạ  Bài 02. n: Cho hình hộp ABC .
D A B C D . Gọi O là tâm hình bình hành A B C D ; K là trung điểm CD , 1 1 1 1 1 1 1 1 1 LÊ MINH
E là trung điểm của BO . 1
. Chứng minh EACB . 1 
. Xác định thiết diện của hình hộp với P đi qua K và song song với EAC .
Lời giải TÂM
. Chứng minh EACB . 1 
 Gọi giao điểm của hai hình bình hành A B B ,
A B C BC là P,Q 1 1 1 1
 Ta có PE;QE lần lượt đường trung bình của BO A BO C 1 1; 1 1
 Nên ta có PE//A C ;A C //QE 1 1 1 1
 Do vậy EPQ  EAB C 1 
. Trong ABCD kẻ KI//ACI  AD
 Trong A ADD kẻ 1 1 
IG//A D G  AA ; A D//B C 1  1  1 1
 IG//B C  IG// B AC 1  1 
 Trong ABA B kẻ GM//AB'M A B 1 1  1 1 
 Trong A BC D kẻ HM//A C H BC 1 1  1 1  1 1 1 1 
 Trong BB C C kẻ HN//A C N CC 1 1  1  1 1 
 Do vậy giao tuyến cần tìm là ngũ giác KIGMHN . Trang 84
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Bài 03.
Cho lăng trụ tam giác AB .
C A' B'C'. Trên đường thẳng BA lấy điểm M sao cho A nằm giữa 1
đoạn thẳng MB và MA  AB . 2
. Xác định thiết diện của hình lăng trụ cắt bởi mặt P đi qua M , B' và trung điểm E của AC .  BD . Tính tỉ số
với D  BC MB' E CD
Lời giải
 Do D  BC MB E
 ; BC,ME  ABC  D  BCME .
. Xác định thiết diện của hình lăng trụ cắt bởi mặt P đi qua M , B' và trung điểm E của AC .
 Trong (ABB') , gọi F  MB' AA' . Như vậy, ta có: TÂM
PABB  FB
PBCC B  B D   
P   ABC   DE P     ACC A    EF
 Vậy thiết diện của hình lăng trụ cắt bởi mặt LÊ MINH
phẳng (P) là tứ giác B' DEF . n: BD
ạ . Tính tỉ số với D BCMB'E CD
Kẻ AI//DE với I B . C n So
 Mà E là trung điểm của AC , ê
 DE là đường trung bình của ACI . Bi
 D là trung điểm của CI hay CD  DI    BD BM BA AM 2AM AM BD
Do AI//DM nên   
 3  BD  3DI . Vậy  3 . DI AM AM AM CD  Bài 04.
Cho lăng trụ tam giác AB .
C A' B'C'. Gọi I, J, K lần lượt là tâm của các hình bình hành ACC' A' ,
BCC' B' , ABB' A'
. Chứng minh rằng: IJ// ABB A
  ; JK//(ACC' A'); IK//(BCC'B').
. Chứng minh rằng: Ba đường thẳng AJ, CK, BI đồng qui tại điểm O.
. Chứng minh rằng: (IJK) song song với mặt đáy của lăng trụ.
. Gọi G, G' là trọng tâm của các tam giác ABC và A' B'C' . Chứng minh G, O, G' thẳng hàng Lời giải
. Chứng minh rằng: IJ// ABB A
  ; JK//(ACC' A'); IK//(BCC'B').
 Ta có IJ là đường trung bình của C' AB,
 Nên IJ//AB . Mà AB  ABB' A' Trang 85
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
Vậy IJ// ABB' A' .
 Chứng minh tương tự, ta có: JK// ACC' A' ,
IK// BCC' B' .
. Chứng minh rằng: Ba đường thẳng AJ, CK, BI
đồng qui tại điểm O.  Xét ba mặt phẳng Bi
C'AB, A'BC, B'AC: ê
CABABC  BI; CABBAC  AJ ; n         So
B AC A BC CK; C AB A BC BI;         ạ
C AB B AC AJ ;B AC A BC CK n:
 Suy ra, theo định lí giao tuyến: ba đường LÊ MINH
thẳng BI , AJ, CK đồng quy tại một điểm.
. Chứng minh rằng: (IJK) song song với mặt đáy của lăng trụ. IJ / / AB   Theo ý , ta có:
  IJK / /  ABC . JK / / AC TÂM
. Chứng minh G,O,G thẳng hàng
 Dễ thấy O là trọng tâm C’AB.
 Gọi M  C O
  AB thì M là trung điểm của AB.
 Vậy ba điểm G, M,C thẳng hàng.
 Vì O và G lần lượt là trọng tâm của hai C A  B và CAB MO MG 1 Nên ta có: 
  OG / /CC (1) MC MC 3
 Chứng minh tương tự OG' //CC' (2)
 Từ (1) và (2) suy ra ba điểm G,O,G thẳng hàng.  Bài 05. Cho hình hộp ABC . D A B  C  D   .
. Chứng minh BDA song song với B D  C   .
. Chứng minh đường chéo AC đi qua trọng tâm G , G của hai BDA và B D  C  . 1 2
. Chứng mình G , G chia đoạn AC thành ba phần bằng nhau. 1 2
. Gọi I , K lần lượt là tâm các hình bình hành ABCD , BCC B
  . Xác định thiết diện của
A IK với hình hộp.
Lời giải
. Chứng minh BDA song song với B D  C   . Trang 86
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Gọi I , O lần lượt là tâm các hình bình hành ABCD , A B  C  D  .  Ta có: BD//B D   A I//OC 
BD, A I  BDA  
 BDA//B D  C  . OC, B D    B D  C   
BD  A I I  OC   B D       O
. Chứng minh đường chéo AC đi qua trọng tâm G , G của hai BDA và B D  C  . 1 2  Ta có: ACC A
 BDA  A I và ACA I G  ACBDA G . 1 1 TÂM G A AI G I  1 Ta có: AI//A C   1 1   
  G là trọng tâm tam giác BDA. G C A C   G A 2 1 1 1  Ta có: ACC A  B D  C
  CO và ACCO  G  ACB D  C   G . 2 2 G O G C   OC 1
Ta có: OC//AC 2 2   
  G là trọng tâm tam giác B D  C  . G C G A AC 2 2 2 2
LÊ MINH . Chứng mình G , G chia đoạn AC thành ba phần bằng nhau. 1 2 n: 1 ạ
 Theo ý  ta có: AG  AC  C G  1 2 3
 G , G chia đoạn AC thành ba phần bằng nhau. 1 2
n So . Xác định thiết diện của AIK với hình hộp. ê Bi  Ta có: A I
 CC  P
 A IKBCC B    KP ,
KP BC  M và KP B C    N .
 Suy ra: A IKA B  C  D    A N  .
AIKABCD  IM và IM  AD Q.
 Suy ra: A IKADA D    A Q  .
 Vậy thiết diện của A IK với hình hộp là tứ giác A N  MQ . Trang 87
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Bài 06. Cho hình hộp ABC . D A B  C  D
  . Gọi P,Q,R,S lần lượt là tâm các mặt ABB A   , BCC B   , CDD C   , DAA D  .
. Chứng minh rằng: RQ// ABCD ; PQRS// ABCD.
. Xác định thiết diện của hình hộp khi cắt bởi AQR.   MC
.Gọi M là giao điểm của cạnh CC với  AQR. Tính tỉ số . Bi MC ê
Lời giải n
. Chứng minh rằng:
RQ// ABCD ; So
PQRS//ABCD. ạn: RQ   ABCD  
 RQ// ABCD (1). LÊ MINH
RQ//BD BD//B D      
PQ  ABCD  
 PQ// ABCD (2). PQ//AC
 Từ (1) và (2)  PQRS// ABCD TÂM
. Xác định thiết diện của hình hộp khi cắt bởi AQR.
 Gọi O là trung điểm B D   .
CO  RQ  E .
AECC  M .
MQ  BB  G .
MRDD  F .
 Vậy thiết diện của hình hộp khi cắt bởi AQR là tứ giác AGMF   MC .Tính tỉ số . MC
 Theo ý   E là trung điểm RQ và CO.
 Đặt CM  xCCx  0
AM  AC  CM  AC  xCC  AC  x AC AC  xAC  AC 1 x . 1 1 1 1 1 1  1  1 1 AE  AC  AO 
AC  ACC O
   AC  AC 
AC   AC  AC . 2 2 2 2 2 2  2  2 4   x 1 x 2
Vì A, M, E thẳng hàng  AE , AM cùng phương  
 x  21 x  x  . 1 1 3 2 4   MC 1 Vậy  . MC 2 Trang 88
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Dạng 04. ĐỊNH LÝ THALES TRONG KHÔNG GIAN .
Phương pháp giải
 Tìm 2 đường thẳng chéo nhau trên đó có các đoạn thẳng tỉ lệ.  Bài 01.
Cho tứ diện ABCD , M là một điểm lưu động trên cạnh AB ; N là điểm lưu động trên cạnh CD
. Chứng tỏ rằng trung điểm I của đoạn MN thuộc một mặt phẳng cố định.
Lời giải
 Kẻ IK AB  K là trung điểm BN (do I là trung điểm MN ).
 Qua K kẻ đường thẳng song song với CD ,
cắt BC tại P , cắt BD tại Q TÂM
 P là trung điểm BC , Q là trung điểm BD
 P ,Q cố định.
 Kẻ hình bình hành BEDC
 BE CD PQ  PQ (ABE)   1
IK AB  IK (AB ) E 2 LÊ MINH  1&2
PQI ABE n:
 Do ABE là mặt phẳng cố định, PQ cố định ạ
 PQI cố định. n So
 Vậy I thuộc mặt phẳng cố định qua PQ và song song ABE . ê  Bài 02. Bi
Cho hình vuông ABCD và ABEF nằm trong hai mặt phẳng phân biệt. Trên các đường chéo
AC và BF lần lượt lấy hai điểm M và N sao cho AM  BN . Chứng minh rằng MN luôn
song song với một mặt phẳng cố định. Lời giải   BN A N
Vẽ NN AB   (1) CF AF
 Vẽ MM AB CD AM AM BN    AD AC BF
(do AM  BN, AC  BF )(2)     1 &2 A N AM   AF AD  M N
  DF  M N   DFEC (3)  Mà M M  CD  M M  DFEC (4) Trang 89
Hình học 11 – Chương 02. QUAN HỆ SONG SONG 3&4 M N  N
 M DFEC , mà MN  M N  N
 M  MN DFEC.
 Vậy MN luôn song song mặt phẳng cố định DFEC .  Bài 03. Cho hình hộp ABC . D A B  C  D
  , M là điểm thuộc cạnh AD, N là điểm thuộc cạnh D C   sao AM D N  cho  MD NC .   Bi
. Chứng minh rằng MN // C BD . ê
. Xác định thiết diện cắt bởi mặt phẳng (P) qua MN và song song C B  D . n So
Lời giải
. Chứng minh rằng MN // C B  D. ạn:   AM D N AM DM AD Theo giả thiết ta có          . LÊ MINH MD NC D N C N D C
 Theo định lý Talet đảo ta có MN, AD,DC cùng song song với Q
Q// AD   Khi đó  Q // DC 
 Mà AD// BC TÂM
Q// BC   Nên      (ĐPCM). Q
Q//BDC  MN//BDC  // DC 
. Xác định thiết diện cắt bởi (P) qua MN và song song C B  D .
 Ta có mặt phẳng P qua MNvà song song C BD Nên:
 Từ M kẻ MF // BD , cắt AB tại F ;
 Từ F kẻ đường thẳng EF // AB, cắt BB tại E
 Từ E kẻ đường thẳng EI // BC, cắt BC tại I ;
 Từ N kẻ đường thẳng NJ // C D  cắt D D  tại J
 Dễ thấy thiết diện là lục giác MEFINJ có các
cạnh đối lần lượt song song với ba cạnh của tam giác C B  D . Trang 90
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Bài 04.
Cho hình lập phương ABC . D A B  C  D
  cạnh a , M,N lần lượt là các điểm trên AD,DB sao cho
AM  DN  x 0  x  a 2 .
. Chứng minh khi x thay đổi đường thẳng MN luôn song song với một mặt phẳng cố định.  a 2
. Chứng minh khi x  thì MN // A C  . 3
Lời giải
. Chứng minh khi x thay đổi đường thẳng MN luôn song song với một mặt phẳng cố định.
 Kẻ ME// ADE AA; NF // ADF  AB
 M,N,E,F đồng phẳng.
 Áp dụng định lý Talet ta có: AM AE DN AF  ;  AD AA . DB AB TÂM
 Mà AD  BD  a 2 gt;
Theo gt: AM  DN  x nên AE AF   EF // A B  AA AB EF // A B   Ta có:  LÊ MINH ME // BC  BC // AD n:
 MNFE//A B
 C  MN //A B  C ạ  a 2
. Chứng minh khi x  thì MN // A C  . 3 n So
 Gọi O là giao điểm của AC và BD ; ê
I là giao điểm của AD và A D  . Bi  a 2 DO  2 a 2 Mà DN  x  3 2
 DN  DO hay N là trọng tâm ADC . 3
 Tương tự: M là trọng tâm AA D  .
 Gọi J là trung điểm AD ,  JM JN 1 Khi đó ta có:   JA JC 3  MN // A C  (ĐPCM). Trang 91
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Bài 05.
Cho tứ diện ABCD và 4 điểm M, N, E, F lần lượt nằm trên các cạnh AB,BC,CD và DA .
Dùng định lý đảo Thalès trong không gian chứng minh rằng:Nếu 4 điểm M, N, E, F đồng MA NB EC FD phẳng thì . . . 1 MB NC ED FA
Lời giải
 Gọi d là đường thẳng bất kỳ cắt MNEF tại Bi O . ê
 Từ các điểm A,B,C,D vẽ các mặt phẳng song n So
song với MNEF và cắt đường thẳng d lần
lượt tại A, B,C, D . Khi đó ta có: ạn:   MA OA
MNEF // OA A     MB OB LÊ MINH   NB OB
MNEF // OB B     NC OC   EC OC
MNEF // OC C     ED OD   EC OD
MNEF // OD D     ED OA TÂM  Do đó: MA NB EC FD
OA OB OC OD . . .  . . . 1 MB NC ED FA
OB OC OD OA .
------------------ HẾT ------------------ Trang 92
Hình học 11 – Chương 02. QUAN HỆ SONG SONG BÀI 05
TỔNG ÔN TẬP CHƯƠNG ☆☆★ ☆☆  Bài 01. Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành tâm O . Gọi M, N, P lần lượt là
trung điểm SA, BC,CD .
. Tìm giao tuyến của hai mặt phẳng SAD và MOP .
. Chứng minh MOP// SBC.
. Gọi K là điểm bất kỳ trên OM . Chứng minh KN // SCD.
. Mặt phẳng   qua N , song song với SA và CD . Tìm thiết diện của mp   và hình chóp TÂM .
S ABCD. Xác định hình tính thiết diện. Lời giải
. Tìm giao tuyến của SAD và MOP .
 Ta có M SA,SA  SAD  MSAD ;
M MOP . LÊ MINH
AD  SAD n: O
 P  MOP ạ  Mặt khác AD//OP  n So
 SADMOP  d//AD//OP với d qua M. ê
 dSD  E Bi
M là trung điểm SA nên E là trung điểm SD . 
Vậy SAD MOP  ME .
. Chứng minh MOP// SBC. ME //AD  Ta có:  AD //BC
 ME//BC; BC  SBC  ME//SBC   1 .
 EP //SC;SC  SBC  EP // SBC 2 .
 ME và EP là hai đường thẳng cắt nhau
cùng nằm trong mặt phẳng MOP   3 .  Từ  
1 , 2 và 3 suy ra MOP // SBC Trang 93
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
. Gọi K là điểm bất kỳ trên OM . Chứng minh KN // SCD.  Ta có
ON // DC; DC  SCD  ON // SCD 4.
OM // SC;SC  SCD  OM // SCD 5 .
ON và OM là hai đường thẳng cắt nhau cùng nằm trong mặt phẳng MON 6 .
 Từ 4 ,5 và 6 suy ra MON// SCD . Bi
K là điểm bất kỳ trên OM nên KN  MON mà MON // SCD nên KN// SCD . ên
. Tìm thiết diện của   và hình chóp . S ABCD. So
Xác định hình tính thiết diện.  Ta có ạn:
ABCD   NO và NO AD  Q. LÊ MINH
SAD  QE.
SCD   d//CD ; d qua E và dSC  F.
 SBC   FN . NQ // CD    NQ // EF EF // CD TÂM
Vậy thiết diện của mp   và hình chóp .
S ABCD là hình thang NQEF .  Bài 02. Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành tâm O .
. Tìm giao tuyến của hai mặt phẳng SBC và SAD.  SM 1 SN 2
. Trên các cạnh SB,SD ta lần lượt lấy các điểm M và N thỏa  ;  . Tìm giao điểm SB 3 SD 3
I của SC và mặt phẳng AMN . Suy ra thiết diện của mặt phẳng AMN và hình chóp . S ABCD  KC
. Gọi K là giao điểm của IN và CD . Tính tỉ số . KD Lời giải
. Tìm giao tuyến của hai mặt phẳng SBC và SAD.
 Ta thấy: SSBCSAD
AD  SAD 
 Và BC  SBC AD//BC 
 Nên SBCSAD  d//AD//BC và d qua S Trang 94
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
. Tìm giao điểm I của SC và mặt phẳng AMN
Suy ra thiết diện của mặt phẳng AMN và hình chóp . S ABCD.  
 Gọi E  MN SO,I  SC  I SC AE   I   AE
 Mà AE  AMN I   SC      . I   AMN I SC AMN
 Khi đó thiết diện của mặt phẳng AMN và hình chóp .
S ABCD là tứ giác AMIN .  KC . Tính tỉ số . KD NF GF NG 1 TÂM
 Gọi G là trung điểm SD, F  OG AN  OG //SB     1  GF  SM NE SM SN 4 4  1 1 1 1 5
OF  OG  FG  SB  SM  3
. SM  SM  SM . 2 4 2 4 4  OE OF 5 S
 ME đồng dạng với O  FE    . SE SM 4 SI SE 4 4 1 2 SI 2 LÊ MINH
 Gọi H là trung điểm IC  OH // AI  4 
  SI  IH  . IC  IC   . IH OE 5 5 5 2 5 IC 5 n: SJ SI 2 JD ạ
 J SD sao cho IJ //CD    5   JD IC 5 SD 7 5 5 15 JD 15
 JD  SD  3 . ND  ND   n So 7 7 7 ND 7 ê IJ NJ JD  ND JD 15 8 7     1 
1   KD  IJ   Bi 1 KD ND ND ND 7 7 8  IJ SI 2 7 7 7 35 Mặt khác 
  CD  IJ  KC  KD CD  IJ  IJ  IJ 2 . CD SC 7 2 8 2 8 35 IJ  KC Từ   1 và 2 suy ra 8   5 . KD 7 IJ 8  Bài 03. Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành, O là giao điểm của hai đường chéo,
AC  a, BD  b , tam giác SBD đều.
. Tìm giao tuyến của hai mặt phẳng SAB và SCD .
. Gọi G ,G lần lượt là trọng tâm của các tam giác ACD,SCD . Chứng minh G G song song 1 2 1 2
với mặt phẳng SAC . Trang 95
Hình học 11 – Chương 02. QUAN HỆ SONG SONG    a
. Gọi M là điểm di động trên AO với AM  x 0  x  
 . Gọi   là mặt phẳng đi qua M  2 
và song song với mặt phẳng SBD . Tìm thiết diện tạo bởi   và hình chóp . S ABCD.
. Tính diện tích thiết diện tìm được ở ý  theo a,b,x . Lời giải
. Tìm giao tuyến của SAB và SCD . Bi
 Ta thấy: SSABSCD ê
AD  SAB n 
 Và BC  SCD So AB//CD  ạ  n:
 Nên SBCSAD  //A / B /CD và qua S LÊ MINH
. Chứng minh G G // SAC . 1 2  
 Gọi K là trung điểm CD . KG KG  1 Ta có 1 2 
  G G //SA 1 2 KA KS 3
 Mà SA  SAC nên G G // SAC 1 2   TÂM
. Tìm thiết diện tạo bởi   và hình chóp . Tính diện tích thiết diện tìm được ở ý  theo . S ABCD. a,b, x .    Ta có PEF  và là hai tam giác đồng Ta có   SBD // SBD nên:   dạng,
ABCD  d//BD và d qua M.  S
 BD đều nên PEF  đều.
E  d  AB EF AM A . M BD 2xb  Gọi    EF   . F  d   AD BD AO AO a    
Suy ra diện tích tam giác PEF là
SAB  d//SB và d qua E . 2 2 2 2 EF 3  2xb  3 x b 3
 Gọi P là giao của d với SA . S     .   . PEF   2 4  a  4  4a SAB  PF .
 Từ đó thiết diện là tam giác PEF .  Bài 04. Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành
. Tìm giao tuyến của hai mặt phẳng SBC và SAD.
. Gọi G là trọng tâm tam giác SBD . Trên các cạnh CD và AB lần lượt lấy các điểm M và
N thoả MD  2MC và NB  2NA. Tìm giao tuyến của hai mặt phẳng SND và BGM .
Tìm giao điểm I của SN và mặt phẳng BGM .  KS
. Gọi K là giao điểm của SA và mặt phẳng BGM . Tính tỷ số . KA Trang 96
Hình học 11 – Chương 02. QUAN HỆ SONG SONG Lời giải
. Tìm giao tuyến của SBC và SAD. S
 SBCSAD  BC//AD  Ta có:  BC   SBC AD   SAD
 SBCSAD  Sx//BC//AD.
. Tìm giao điểm I của SN và mặt phẳng BGM.
 Trong ABCD : H  AC  BM , L  ACND
 Trong SAC : P  GH SL TÂM P GH   BGM        P SL   SND
P SND BGM BM//DN
  SND BGM  Px//BM//DN  BM  BGM   DN  SND  LÊ MINH    Tìm I SN BGM n:   ạ I SN
 Trong SND : I  SN  Px      I  Px  
BGM I SN BGM n So  KS . Tính tỷ số . ê KA Bi
 Trong SAC : K  GH SA
KGH  BGM  
 K  SA BGM K SA
Áp dụng định lý Menelaus  HC BO MD Xét ODC , ta có: . . 1 HO BD MC HC 1 1 1  . 2
.  1  HC  HO  OC  OA HO 2 2 2  KS GO HA Xét SOA, ta có: . . 1 KA GS HO
KS 1 HO  OA  . . 1 KA 2 HO KS 1 3 KS 2  . .  1   . KA 2 1 KA 3 Trang 97
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  Bài 05. Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành, AB  a, AD  2 . a
. Tìm giao tuyến của hai mặt phẳng SAB và SCD .
. Gọi M là điểm di động trên cạnh AB với AM  x0  x  a . Gọi P là mặt phẳng đi qua
M và song song với mặt phẳng SAD . Tìm thiết diện tạo bởi P và hình chóp . S ABCD. 2  2a
. Cho SA  a , SA vuông góc với AD . Tìm x để diện tích thiết diện bằng . Bi 3 ê Lời giải n 
. Tìm giao tuyến của SAB và SCD . So S
 SABSCD ạ  n: AB//CD  Ta có:  AB   SAB LÊ MINH CD   SCD
 SABSCD  Sx//AB//CD.
. Tìm thiết diện tạo bởi P và hình chóp . S ABCD
 Vì mặt phẳng P//SAD  P song song TÂM
với mọi đường thuộc mặt phẳng SAD.
 Tìm giao tuyến của mặt phẳng P và mặt phẳng ABCD.
 Ta có MPABCD ,vì P//AD nên ABCDP  d//AD và d qua M
Khi đó d CD  Q   1 . Tương tự:
 Ta có M PSAB ,vì P//SA nên SABP  MN//SA ; N SB.
 Ta có N PSBC,vì P//AD//BC nên SBCP  NP//BC 2.
 Ta có PSCD  PQ
Suy ra thiết diện cần tìm là MNPQ.
Từ (1) và (2) thì MQ//PN . Vậy MNPQ là hình thang. 2  2a
. Tìm x để diện tích thiết diện bằng . 3  x AM SN NP NP
Áp dụng Ta-lét cho SAB và SBC ta được:      NP  2x a AB SB BC 2a MN BM a  x
axSA
 Áp dụng Ta-lét cho SAB , ta có:    MN   a  x . SA AB a a
 Vì SA  AD  MNPQ là hình thang vuông . 1  S
 MN.NP  MQ 1
 a  x. x  a  a  x . MNPQ 2 2  2 2 2 2 Trang 98
Hình học 11 – Chương 02. QUAN HỆ SONG SONG  a x  ( ) n  2 2 2  2a 2a a 3 a Vì 2 2 2 S   a  x   x   
( do 0  x  a ) . Vậy x  . MNPQ 3 3 3  a x   (l) 3   3  Bài 06. Cho hình chóp .
S ABCD có đáy ABCD là hình thang, đáy lớn AB, M là trung điểm cạnh SB.
. Tìm giao tuyến của hai mặt phẳng SAD và SBC .
. Tìm giao điểm N của SC và mặt phẳng ADM.
. Xác định thiết diện của hình chóp .
S ABCD khi cắt bởi mặt phẳng CDM .
. Gọi I là giao điểm của AM và DN . Chứng minh SI//AB//C . D Lời giải
. Tìm giao tuyến của SAD và SBC . TÂM
 Ta có: SSADSBC   1
 Trong ABCD : J  AD BC J  AD   SAD      J  BC   SBC
J SAD SBC 2  Từ  
1 ,2  SJ  SAD SBC.
LÊ MINH . Tìm giao điểm N của SC và ADM.
n:ạ  Tìm NSCADM.
 Ta có: ADM  AJM . n So N   SC ê
 Trong SBJ : N  MJ SC.      . N  MJ  
ADM N SC ADM
Bi . Xác định thiết diện của hình chóp .SABCD khi
cắt bởi CDM .
M  SAB  CDM  AB // CD    AB  SAB   CD  CDM 
 SABCDM  Mx// AB//CD .
 Trong SAB : Kẻ Mx//AB//CD, P  Mx S . A  Ta có: Trang 99
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
CDMABCD CD  
CDM   SBC  CM   
CDM   SAB  PM  Thiết diện cần tìm là CDP . M  
CDM   SAD  PD   
CDM   SCD  CD 
. Chứng minh SI//AB//C . D Bi
 Ta có: SSABSCD   1 ê  n I  AM   SAB        I AM DN I SAB SCD 2 So I  DN   SCD       ạ  Từ  
1 ,2  SI  SAD SCD n: .
SADSCD  SI LÊ MINH  AB//CD   Ta có:   
  SI // AB // CD . AB SAB   CD  SCD   Bài 07. TÂM Cho hình chóp .
S ABCD, có đáy ABCD là hình bình hành tâm O . Gọi M, N lần lượt là trung
điểm của SA và CD . Chứng minh rằng :
. OMN//SBC .
. Mặt phẳng   qua N và song song SAD. Tìm thiết diện của   với hình chóp và xác
định hình tính của thiết diện.
. Giả sử AS  AD, AB  AC . Gọi AE , AF lần lượt là phân giác trong của tam giác ACD và
SAB . Chứng minh EF// SAD Lời giải
. OMN//SBC .
 Vì MO và NO lần lượt là đường trung bình
của ASC và DBC
 Nên MO//SC và ON//BC .
MO // SC  (SBC)  MO // SBC
ON // BC  (SBC)  ON // SBC  Ta có:
MO // SBC,ON // SBC 
MO ON  O
 OMN // SBC
MO  (OMN),ON   (OMN)
. Tìm thiết diện của   với hình chóp và xác định hình tính của thiết diện. Trang 100
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
  //SAD   // với SD, AD, SA
  //SD   SCD  d// D
S với d qua N
và d SC  P Nx//AD
 Trong ABCD , kẻ  . Nx  AB   R Ry//AS
 Trong SAB , kẻ  . Ry  SB   Q
Nối P với Q ta được thiết diện là tứ giác NPQR .
 Ba mặt phẳng phân biệt   , ABCD và SBC cắt nhau theo ba giao tuyến NR, BC và
PQ . Mà NR // AD // BC nên NR // PQ hay thiết diện NPQR là hình thang.
. Chứng minh EF// SAD TÂM
 Sử dụng tính chất đường phân giác, ta có ED AD AS FS   
 tồn tại duy nhất bộ ba EC AC AB FB
mặt phẳng song song lần lượt chứa SD, EF và BC .
 Một trong ba mặt phẳng đó là SAD. Do đó LÊ MINH EF// SAD. n:ạ  Bài 08. Cho hình chóp .
S ABCD, có đáy ABCD là hình thang, A /
B /CD, AB  2CD . Gọi M là trung n Soê
điểm của SB và P là điểm thuộc cạnh SA thỏa AP  2SP . Bi
. Tìm giao tuyến của hai mặt phẳng SBA và SCD .
. Tìm giao điểm I của MA và mặt phẳng SDC .  EC
. Tìm giao điểm E của BC và mặt phẳng PMD . Tính . EB Lời giải
. Tìm giao tuyến của SBA và SCD .
 Ta có SSBAS D C  .
SBASCD S   AB//CD  B
A  SAB ,CD  SCD 
 SBASCD  Sx// AB//CD.
. Tìm giao điểm I của MA và SDC .
 Trong SAB , AMSx  I Trang 101
Hình học 11 – Chương 02. QUAN HỆ SONG SONG I   AM  Khi đó     . I Sx  
SCD I AM S D C   EC
. Tìm giao điểm E của BC và mặt phẳng PMD . Tính . EB
 Trong SAB , kéo dài PM cắt AB tại K , khi đó KPMD .
 Trong ABCD , kẻ đường thẳng DK cắt BC tại E .  Bi
Khi đó E là điểm cần tìm. EC DC ê  Ta có  . n EB BK So  BH 1 KB BH 1 EC 1
Kẻ BH//AP , ta có BH  SP    
  BK  AB    . AP 2 AK AP 2 EB 2 ạn:  Bài 09. Cho hình chóp .
S ABCD, có đáy ABCD là hình bình hành. Gọi I , J , K lần lượt là trung điểm LÊ MINH
SB, AB và SC .
. Chứng minh IJK//SAD . Từ đó suy ra JK//SAD .
. M là một điểm trên AD . Mặt phẳng P qua M và song song SAB cắt BC , SC và SD
lần lượt tại N , P và Q . Hỏi MNPQ là hình gì? TÂM Lời giải
. Chứng minh IJK//SAD . Từ đó suy ra JK//SAD .
 Vì IJ và IK lần lượt là đường trung bình của ASB và SBC
 Nên IJ//SA và IK//BC  IK// AD .
IJ // SA  SAD  IJ // SAD.
IK // BC // AD  SAD  IK // SAD .
IJ // SAD 
 Ta có IK // SAD
IJ (IJK),IK (IJK),IJ IK   I
 (IJK)//(SAD) . Suy ra JK// SAD
. Hỏi MNPQ là hình gì?
 P//SAB  P song song với AB , SB, và SA .
 P//AB  PABCD  d// B
A với d qua M . MN//AB
 Trong ABCD , kẻ  . MN  BC   N Ny//SB
 Trong SBC , kẻ  . Ny  SC   P Trang 102
Hình học 11 – Chương 02. QUAN HỆ SONG SONG Mz//SA
 Trong SAD, kẻ  . Mz  SD   Q
 Nối P với Q ta được thiết diện là tứ giác MNPQ .
 Ba mặt phẳng phân biệt SCD , P và ABCD cắt nhau theo ba giao tuyến MN, CD và PQ
. Mà MN//CD nên MN//PQ hay thiết diện MNPQ là hình thang.  Bài 10.
Cho hình lập phương ABC . D A B  C  D
  cạnh a . Gọi M;N;P lần lượt là trung điểm của các cạnh AB; B C  ; DD
. Chứng minh MNP song song với các mặt AB D
 và BDC
. Xác định thiết diện của hình lập phương với mặt phẳng MNP . Thiết diện đó là hình gì ? Tính diện tích của nó. Lời giải
TÂM . Chứng minh MNP song song với các mặt ABDvà BDC  PD ' MA Ta có   1 PD MB
 MP, AD,DB cùng song song với   (theo định lý Ta-let đảo) LÊ MINH D B  //DB//    AD//   n:  ạ AD   AB D  ,B D     (AB D  )  AB D
 //   MP//AB D  
n Soê  Tương tự, MN//ABD. Bi
Suy ra MNP //  AB D   BD//B D    Mặt khác 
 BDC// AB D
 . Vậy MNP//AB D
 //BDC BC//AD 
. Xác định thiết diện của hình lập phương với mặt phẳng MNP .
 Gọi E,F,K lần lượt là trung điểm của các cạnh C D
 , AD,BB , ta có: NE//B D
   NE// AB D   
 N MNP
 NE  MNP .
MNP//AB D    
Tương tự PF và MK cũng chứa trong MNP
 Suy ra thiết diện của MNP với hình lập
phương là lục giác MNKEPF Trang 103
Hình học 11 – Chương 02. QUAN HỆ SONG SONG
 Hình tính thiết diện:  1 a 2
NE là đường trung bình B C  D
  nên NE  B D    . 2 2  a 2
Tương tự 6 cạnh của thiết diện đều bằng 2
 Mặc khác NE//MF,EP//MK,PF//KN .  a 2
Vậy thiết diện là lục giác đều cạnh . Bi 2 ê
Diện tích thiết diện: n
 Gọi O là tâm đường tròn ngoại tiếp của thiết diện thì tam giác ONE là tam giác đều, So 2 2 2 6NE 3
 a 2  3 3a 3 ạ
 Suy ra diện tích của thiết diện: S  6S   6   . OEN 4  2  4 4 n:   LÊ MINH
------------------ HẾT ------------------ TÂM Trang 104

Chuyên đề quan hệ song song – Lê Minh Tâm

Thông tin :

Tài liệu liên quan:

Bộ đề đánh giá chất lượng Toán 11 chủ đề quan hệ song song trong không gian

Chuyên đề toán thực tế quan hệ song song trong không gian Toán 11

Quan hệ song song trong không gian Toán 11 KNTTVCS – Phan Nhật Linh

Toán 11 Bài tập cuối chương IX - sách Kết Nối Tri Thức

Toán 11 Bài 10: Đường thẳng và mặt phẳng trong không gian - sách Kết Nối Tri Thức