Chuyên đề rút gọn biểu thức và các bài toán liên quan – Trần Đình Cư

Tài liệu gồm 32 trang, được biên soạn bởi thầy giáo Trần Đình Cư, bao gồm kiến thức cần nắm, phân loại và phương pháp giải bài tập chuyên đề rút gọn biểu thức và các bài toán liên quan, có đáp án và lời giải chi tiết. Mời bạn đọc đón xem.

58 29 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 9

Môn: Toán 9

Thông tin:

32 trang 6 tháng trước

Tác giả:

Profile Hà Việt Anh
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 1
CHUYÊN ĐỀ 1: RÚT GỌN BIỂU THỨC VÀ CÁC BÀI TOÁN LIÊN QUAN
A. KIẾN THỨC CẦN NẮM
1. CĂN THỨC BẬC 2
Căn bậc hai của số thực
a
là số thực
x
sao cho
2
x a
.
Cho số thực
a
không âm. Căn bậc hai số học của
a
kí hiệu là
a
là một số thực không âm
x
mà
bình phương của nó bằng
a
:
2
0
a
x
x a
a x
Với hai số thực không âm
,
a b
ta có:
a b a b
.
Khi biến đổi các biểu thức liên quan đến căn thức bậc 2 ta cần lưu ý:
+
2
A
A A
A
nếu
0
0
A
A
+
2
A B A B A B
với
, 0
A B
;
2
A B A B A B
với
0; 0
A B
+
2
. .
A A B A B
B B B
với
0, 0
AB B
+
.
M M A
A
A
với
0
A
;(Đây gọi là phép khử căn thức ở mẫu)
+
M A B
M
A B
A B
với
, 0,
A B A B
(Đây gọi là phép trục căn thức ở mẫu)
2. CĂN THỨC BẬC 3.
Căn bậc 3 của một số
a
kí hiệu là
3
a
là số
x
sao cho
3
x a
Cho
3
3
3 3
;
a R a x x a a
Mỗi số thực
a
đều có duy nhất một căn bậc 3.
Nếu
0
a
thì
3
0
a
.
Nếu
0
a
thì
3
0
a
.
Nếu
0
a
thì
3
0
a
.
3
3
3
a a
b
b
với mọi
0
b
.
3 3 3
.
ab a b
với mọi
,
a b
.
3 3
a b a b
.
3
3
3
A B A B
.
3
2
3
A AB
B B
với
0
B
3
3
3
A A
B B
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 2
3 3
2 2
3
3 3
1
A AB B
A B
A B
với
A B
.
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Rút gọn biểu thức không chứa biến
1. Phương pháp
1.
2
nÕu A 0
nÕu A < 0
A
A A
A
2.
.
AB A B
(Với
0; 0
A B
)
3.
A A
B
B
(Với
0; 0
A B
)
4.
2
A B A B
(Với
0
B )
5.
2
A B A B
(Với
0; 0
A B
)
6.
2
A B A B
(Với
0; 0
A B
)
7.
1
A
AB
B B
(Với
0; 0
A B
)
8.
A A B
B
B
(Với
0
B )
9
2
C A B
C
A B
A B
(Với
2
0;A B
A
)
10
C A B
C
A B
A B
(Với
0; 0;A B
A B
)
11
3
3
3
3
A A A
2. Các ví dụ minh họa
Ví dụ 1: Rút gọn các biểu thức sau:
45 245 80
M
5 8 50 2 18
N
125 4 45 3 20 80
P
12 27 48
A
2 3 3 27 300
B
(2 3 5 27 4 12) : 3
C
Hướng dẫn giải
2
45 245 4 .5
M
2 2 2
3 .5 7 5 4 .5
3 5 7 5 4 5 6 5
5 8 50 2 18
N
5.2 2 5 2 2.3 2
10 2 5 2 6 2
(10 5 6) 2 9 2
5 5 12 5 6 5 4 5
P
5 5
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 3
12 27 48
2 3 3 3 4 3
3
A
2 2
2 3 3 27 300
2 3 3 3 .3 10 .3
B
2 3 3.3. 3 10 3
3
(2 3 5 27 4 12) : 3
(2 3 5.3 3 4.2 3) : 3
5 3 : 3 5
C
Nhận xét: Đây là một dạng toán dễ. Học sinh có thể bấm máy tính để kiểm tra kết quả, đa phần áp dụng
kiến thức đưa thừa số ra ngoài dấu căn để giải toán.
2
A B A B
(
0
B
)
Ví dụ 2: Rút gọn các biểu thức sau:
a)
2 2
3 2 2 3 2 2
b)
2 2
5 2 6 5 2 6
c)
2 2
2 3 1 3
d)
2 2
3 2 1 2
e)
2 2
5 2 5 2
f)
2 2
2 1 2 5
Hướng dẫn giải
a)
2 2
3 2 2 3 2 2 3 2 2 3 2 2 3 2 2 3 2 2 6
Lưu ý:
2
0
0
A nÕu A
A A
A nÕu A
Kết quả: b)
4 6
c) 1 d) 4 e)
2 5
f)
2 2 4
Ví dụ 3: Rút gọn biểu thức
a)
4 2 3
A
b)
8 2 15
B
c)
9 4 5
C
d)
7 13 7 13
D
e)
6 2 5 6 2 5
E
f)
1
7 2 10 20 8
2
F
Hướng dẫn giải
a)
2
4 2 3 3 1 3 1
A
b)
2
8 2 15 15 1 15 1
B
c)
2
9 4 5 2 5 5 2
C
d)
1
7 13 7 13 14 2 13 14 2 13
2
D
2 2
1
13 1 13 1 2
2
e)
6 2 5 6 2 5 5 2 5 1 5 2 5 1
E
2 2
( 5 1) ( 5 1) | 5 1| | 5 1| 5 1 5 1 2
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 4
f)
2
1 1
7 2 10 20 8 5 2 2 5 .2 2
2 2
F
5 2 2 5 2 5 2 2 5 2 3 5
Ví dụ 4: Rút gọn biểu thức: (áp dụng các kiến thức tổng hợp)
6 2 5 5 2 6
5 1 3 2
A
3 4 1
5 2 6 2 6 5
B
1 1 1 1
...
1 2 2 3 3 4 99 100
C
1
7 4 3
2 3
D
3 3 4 3 4
2 3 1 5 2 3
E
1 2 2
2 3 6 3 3
F
Hướng dẫn giải
a)
6 2 5 5 2 6 5 1 3 2
2
5 1 3 2 5 1 3 2
A
b)
3 5 2 4 6 2
3 4 1
6 5
3 4
5 2 6 2 6 5
B
5 2 6 2 6 5 2 6
c)
1 1 1 1
...
1 2 2 3 3 4 99 100
C
2 1 3 2 4 3 ... 100 99 9
d)
2
1 1 1
7 4 3 4 4 3 3 (2 3)
2 3 2 3 2 3
D
1 2 3 2 3
2 3 2 3 2 3 4
1
2 3 (2 3)(2 3)
e)
2 2
2
3 3 4 2 3 1 3 4 5 2 3
3 3 4 3 4
2 3 1 5 2 3
2 3 1 5 2 3
E
22 11 3 26 13 3
2 3 2 3
11 13
2 2
4 2 3 4 2 3 1
3 1 3 1
2 2
2
1 1
3 1 3 1 .( 2) 2
2 2
f)
1 2 2
2 3 6 3 3
F
1 1 2
2 3 3
3 3 1
3 3 1 2 3 3 1 2 2 3
3 3 1 2 3
2 3 2
2 3 4
3 3 1 2 3 3 3 1 2 3
2. 3 3 1
3 3 1 3 1
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 5
2 3 3 1 3 3 1
3 3 3
1
3 3 1 3 3 3
Kinh nghiệm: Đôi khi một số bài toán rút gọn căn thức sẽ thực hiện dễ dàng hơn nếu chúng ta trục căn
thức hoặc rút gọn được một hạng tử trong đề toán. Nếu quy đồng mẫu số thì việc thực hiện các phép tính
rất phức tạp. Vì vậy trước khi làm bài toán rút gọn, học sinh cần quan sát kỹ đề toán từ đó có định hướng
giải đúng đắn để lời giải được ngắn gọn, chính xác.
Ví dụ 5: Thu gọn các biểu thức sau
a)
18 2 50 3 8
A
b)
1 3 3
27 6
3
3
B
c)
5
8 2 7 2
7 2
C
Hướng dẫn giải
a)
18 2 50 3 8
A
2 2 2
3 .2 2 5 .2 3 2 .2
3 2 10 2 6 2 2
b)
2
1 3 3 3
27 6 3 .3 6. 1 3
3 3
3
B
3 3 2 3 1 3 1
c)
5
8 2 7 2
7 2
C
5 7 2
7 2 7 1 2
7 2 7 2
2
7 2 7 1 2
7 2 7 1 2
7 2 7 1 2
1
( Vì
7 1
)
Ví dụ 6: Thực hiện phép tính
a)
1 33 1
48 2 75 5 1
2 3
11
b)
3
6 2 5 6 2 5 8
c)
3
5 2 50 2 4 32
a a a a
với
0
a
Hướng dẫn giải
a)
1 33 1
48 2 75 5 1
2 3
11
2 2
1 3. 11 4
4 .3 2 5 .3 5
2 3
11
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 6
2
2
2 3 10 3 3 5
3
10 3 17 3
9 3
3 3
b)
3
6 2 5 6 2 5 8
3
3
5 2 5 1 5 2 5 1 2
2 2
5 1 5 1 2
5 1 5 1 2
5 1 5 1 2
( Vì
5 1
)
0
c)
3
5 2 50 2 4 32
a a a a
2 2 2
5 2 5 .2 2 . 4 4 .2
a a a a a
5 2 5 2 2 16 2
a a a a a
2 16 2
a a a
( Vì
0
a )
Ví dụ 7. (Đè thi năm học 2014 – 2015 Thành phố Hồ Chí Minh)
Thu gọn các biểu thức sau:
5 5 5 3 5
5 2 5 1 3 5
A
Lời giải
5 5 5 3 5
5 2 5 1 3 5
A
5 5 5 2 5 5 1 3 5 3 5
5 2 5 2 5 1 5 1 3 5 3 5
5 5 9 5 15 5 5 9 5 15
3 5 5 3 5 5
4 4 4
3 5 5 5 2 5 5
.
Ví dụ 8. Tính
2 2
21 2 3 3 5 6 2 3 3 5 15 15
B .
Lời giải
2 2
21
4 2 3 6 2 5 3 4 2 3 6 2 5 15 15
2
B
2 2
21
3 1 5 1 3 3 1 5 1 15 15
2
2
15
3 5 15 15 60
2
.
Dạng 2: Tìm điều kiện xác định của biểu thức
BIỂU THỨC - ĐKXĐ: VÍ DỤ
1.
A
ĐKXĐ:
0
A
Ví dụ:
2018
x
ĐKXĐ:
2018
x
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 7
2.
A
B
ĐKXĐ:
0
B
Ví dụ:
4
7
x
x
ĐKXĐ:
7
x
3.
A
B
ĐKXĐ:
0
B
Ví dụ:
1
3
x
x
ĐKXĐ:
3
x
4.
A
B
ĐKXĐ:
0; 0
A B
Ví dụ:
3
x
x
ĐKXĐ:
0
3
3
x
x
x
5.
A
B
ĐKXĐ:
0
0
0
0
A
B
A
B
Ví dụ:
1
2
x
x
ĐKXĐ:
1 0
2 0
2
1
1 0
2 0
x
x
x
x
x
x
6.
Cho a > 0 ta có:
2
x a
x a
x a
.
Ví dụ:
2
1
x
x a
x a
7.
Cho a > 0 ta có:
2
x a a x a
Ví dụ:
2
4 2 2
x x
Dạng 3: Rút gọn biểu thức chứa biến
1. Phương pháp
2. Các ví dụ
Ví dụ 1: Rút gọn
1 2 6
: 1
3 3 3
x
B
x x x x x x
0
x .
Hướng dẫn giải
1 2 6
: 1 0
3 3 3
x
B x
x x x x x x
1 2 6
:
3 3
3
x x
x x x
x x
2 3 6
1
: 1 . 1
3
3
x x
x x
x
x x x
x x
Ví dụ 2: (Đề thi năm 2014 – 2015 TP Đà Nẵng)
Rút gọn biểu thức
2 2 2
2
2 2
x x
P
x
x x
, với
0, 2
x x
7).
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 8
Lời giải:
Với điều kiện đã cho thì:
2 2
2 2
1
2 2
2 2 2 2
x
x x
P
x x
x x x x
.
Ví dụ 3: Thu gọn các biểu thức sau:
3 3
.
9
3 3
x x
A
x
x x
với
0, 9
x x
.
Hướng dẫn giải
Với
0
x
và
9
x
ta có:
3 3 9 3 1
. 3
9
3 3
x x x x
A
x
x
x x
.
Ví dụ 4: Rút gọn các biểu thức:
a)
1
4
A x x x
khi
0
x
.
b)
4 2 4 1 4 2 4 1
B x x x x
khi
1
4
x
.
Lời giải
a)
2
1 1 1
4 2 2
A x x x x x x x
+ Nếu
1 1
2 4
x x
thì
1 1 1
2 2 2
x x A
.
+ Nếu
1 1
0
2 4
x x
thì
1 1 1
2
2 2 2
x x A x
b)
4 2 4 1 4 2 4 1 4 1 2 4 1 1 4 1 2 4 1 1
B x x x x x x x x
Hay
2 2
4 1 1 4 1 1 4 1 1 4 1 1
B x x x x
4 1 1 4 1 1
x x
+ Nếu
1
4 1 1 0 4 1 1
2
x x x
thì
4 1 1 4 1 1
x x
suy ra
2 4 1
B x
.
+ Nếu
1 1
4 1 1 0 4 1 1
4 2
x x x
thì
4 1 1 4 1 1
x x
suy ra
2
B
.
Ví dụ 5. Cho các số thực dương
,
a b
;
a b
.
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 9
Chứng minh rằng:
3
3
2
3 3
0
a b
b b a a
a b
a ab
b a
a a b b
.
Lời giải
Ta có:
3
3
2
3 3
a b
b b a a
a b
a ab
Q
b a
a a b b
3 3
3
2
3
0
a b a b
b b a a
a b a a b
a b a ab b a b a b
3 3 2 3a a a b b a b b a a a
a b a ab b a b
3 3 3 3 3 3
0
a a a b b a a a a b b a
a b a ab b
Ví dụ 6. Rút gọn biểu thức
6 7 19 5
; 0, 9
9
12 4
x x x x x x
A x x
x
x x x x
.
Lời giải
6 7 19 5
9
12 4
x x x x x x
A
x
x x x x
2 7 19 5
3 4
3 4
x x x x
x x
x x
2 8 7 19 8 15
3 4
x x x x x x
x x
1 4
1
3
3 4
x x
x
x
x x
.
Dạng 4: Rút gọn biểu thức, biết biến thỏa mãn điều kiện cho trước
1. Phương pháp
2. Các ví dụ
Ví dụ 1: Cho
10 5
25
5 5
x x
A
x
x x
, với
0, 25
x x
.
1) Rút gọn biểu thức
A
2) Tính giá trị của A khi
9
x
.
Lời giải:
. 5 10 5. 5
10 5
25
5 5
5 5
x x x x
x x
A
x
x x
x x
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 10
5 10 5 25 10 25
5 5 5 5
x x x x x x
x x x x
2
5
5
5
5 5
x
x
A
x
x x
.
Với
9
x
ta có:
3
x
. Vậy
3 5 2 1
3 5 8 4
A
.
Ví dụ 2: Cho
2 3 9
9
3 3
x x x
P
x
x x
, với
0, 9
x x
.
1) Rút gọn
P
.
2) Tìm giá trị của
x
để
1
3
P
.
3) Tìm giá trị lớn nhất của
P
.
Lời giải
1)
3 2 3 3 9
3
3
3 3
x x x x x
P
x
x x
2)
1 3 1
3 9 36
3 3
3
P x x
x
(thỏa mãn ĐKXĐ)
3) Với
max
3 3
0, 1 1
0 3
3
x P P
x
khi
0
x
(TM).
Ví dụ 3: Cho biểu thức
3 3
2 2 2 2
. ,
x y x y
P x y
x xy y x y
.
1) Rút gọn biểu thức
P
.
2) Tính giá trị của
P
khi
7 4 3
x
và
4 2 3
y
.
Lời giải
1)
3 3
2 2
.
x y x y x y
P
x xy y x y x y x y
.
2) Với
7 4 3 2 3
x
và
4 2 3 3 1
y
Thay vào
P
ta được:
2 3 3 1 1 3 2 3
3
3 2 3
2 3 3 1
P
.
Ví dụ 4: Cho biểu thức
1 1 2
4
2 2
x
A
x
x x
0, 4
x x
.
Rút gọn
A
và tìm
x
để
1
3
A
.
Lời giải
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 11
2 2
1 1 2 4 2 2
4 4 4 4
2 2 2
x
x x
A
x x x x
x x x
. Với
1 2 1
3 3
2
A
x
4 16
x x
(nhận).
Vậy
1
3
A
khi
16
x
.
Ví dụ 5. Cho biểu thức
2 2
16
4 4
a
C
a
a a
.
1) Tìm điều kiện của
a
để biểu thức
C
có nghĩa và rút gọn
C
.
2) Tính giá trị của biểu thức
C
khi
9 4 5
a .
Lời giải
1) Biểu thức
C
có nghĩa khi:
0
0
16 0
16
0, 16
4 0 16
0
4 0
a
a
a
a
a a
a a
a
a
.
Rút gọn
2 2
16
4 4
a
C
a
a a
2 2
4 4
4 4
a
a a
a a
2 4 2 4
4 4
a a a
a a
2 8 2 8 4
4 4 4 4
a a a a a
a a a a
4
4
4 4
a a
a
a
a a
.
2) Giá trị của
C
khi
9 4 5
a
.
Ta có:
2
9 4 5 4 4 5 5 2 5
a a
2
2 5 5 2
a
Vậy
5 2 5 2
9 4 5
5 2 4 5 2
4
a
C
a
.
Ví dụ 6. (Đề thi năm 2014 – 2015 chuyên Thái Bình tỉnh Thái BÌnh)
Cho biểu thức
2 3 5 7 2 3
:
2 2 1 2 3 2 5 10
x x
A
x x x x x x
0, 4
x x
.
1) Rút gọn biểu thức
A
.
2) Tìm
x
sao cho
A
nhận giá trị là một số nguyên.
Lời giải
1) Với
0, 4
x x
biểu thức có nghĩa ta có:
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 12
2 3 5 7 2 3 3
:
2 2 1 2 3 2 5 10
x
A
x x x x x x
2 2 1 3 2 5 7
2 3
:
2 2 1 5 2
x x x
x
x x x x
5 2
2 3 5
.
2 3 2 1
2 2 1
x x
x x
x x
x x
.
Vậy với
0, 4
x x
thì
5
2 1
x
A
x
.
2) Ta có
0, 0, 4
x x x
nên
5
0, 0, 4
2 1
x
A x x
x
5 5 5 5
, 0, 4
2 2
2 1
2 2 1
x
A x x
x
x
5
0
2
A
, kết hợp với
A
nhận giá trị là một số nguyên
thì
1,2
A
.
1 1
1 5 2 1
3 9
A x x x x
thỏa mãn điều kiện.
2 5 4 2 2 4
A x x x x
không thỏa mãn điều kiện.
Vậy với
1
9
x
thì
A
nhận giá trị là nguyên.
Ví dụ 7. Cho biểu thức
2 1 1
.
2 2 1
x x
P
x x x x
với
0
x
và
1
x
.
a) Chứng minh rằng
1
x
P
x
.
b) Tìm các giá trị của
x
để
2 2 5
P x
.
Lời giải
1 . 2
2 1 1 1
. .
1 1
2 2
x x
x x x x x
P
x x x
x x x x
.
b) Theo câu a)
1
x
P
x
2 2
2 2 5 2 5
x
P x x
x
2 2 2 5 2 3 2 0
x x x x x
và
0
x
1 1 1
2 0
2 2 4
x x x x
.
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 13
Dạng 5: Các bài toán tổng hợp bao gồm các câu hỏi phụ
Bài 1: Cho biểu thức
2 10 2 1
0; 9
6 3 2
x x x
Q x x
x x x x
1. Rút gọn biểu thức
Q
2. Tính giá trị của
Q
khi
16
x
3. Tìm giá trị của
x
khi
1
3
Q
4. Tìm giá trị của
x
sao cho
1
9
Q
5. Tìm giá trị lớn nhất của
Q
.
Hướng dẫn giải
1. Với
0; 9
x x
thì
2 10 2 1
3 2 6 3 2
x x x
Q
x x x x x
2 10 2 1
3 2
3 2 3
x x x
x x
x x x
2 10 2 1
3 2
3 2
x x x
x x
x x
2 10 2 2 3
3 2
x x x x x
x x
2 10 4 3
3 2
x x x x
x x
3 1
2
3 2
x
x
x x
Vậy với
0; 9
x x
thì
1
2
Q
x
2. Thay
16
x
( thỏa mãn
0; 9
x x
) vào Q ta được:
1 1 1
4 2 6
16 2
Q
Vậy khi
16
x
thì
1
6
Q
3.
1 1 1
3 2 1 1
3 3
2
Q x x x
x
( thỏa mãn
0; 9
x x
)
Vậy với
1
x
thì
1
3
Q
4.
1 1 1 1 1
0
9 9 9
2 2
Q
x x
9 2 7
0
2
1
0
2
x x
x x
Vì
0
x
với mọi
0; 9
x x
nên
2 0
x
với mọi
0; 9
x x
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 14
7 0 7 49
1
x x x
Kết hợp với điều kiện
0; 9
x x
nên
0 49
9
x
x
Vậy với
0 49
9
x
x
thì
1
9
Q
5. Vì
0
x
với mọi
0; 9
x x
nên
2 2
x
với mọi
0; 9
x x
1 1
2
2x
với mọi
0; 9
x x
Vậy
Q
đạt giá trị lớn nhất bằng
1
2
khi
0
x
( thỏa mãn
0; 9
x x
)
Bài 2: Cho biểu thức
3 3 5
3 2 2 3
1 3 2 3
x
x x
P
x x x x
.
a) Rút gọn P;
b) Tìm giá trị của P, biết
4 2 3
x
;
c) Tìm giá trị nhỏ nhất của P.
Hướng dẫn giải
ĐKXĐ:
0; 9
x x
.
a)
3 3 5
3 2 2 3
1 3
1 3
x
x x
P
x x
x x
3 2 3 2 3 1 3 3 5
1 3
x x x x x
x x
3 9 2 6 2 2 3 3 9 15
1 3
x x x x x x x
x x
5 17 6
1 3
x x
x x
5 15 2 6
1 3
x x x
x x
5 2 3
5 2
1
1 3
x x
x
x
x x
.
b) Ta có
2
4 2 3 3 1 3 1
x x
;
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 15
Do đó:
5 3 1 2 5 3 3 2 3
5 3 3
7 3 9
3 2
3 1 1 3 2 2 3
P
.
c) Ta có
5 2 5 5 7
1 1
x x
P
x x
7
5
1
P
x
.
Vì
7
0
1x
nên P có giá trị nhỏ nhất
7
1
x
lớn nhất
1
x
nhỏ nhất
0
x
.
Khi đó min
5 7 2
P
.
Bài 3: Cho biểu thức
1 2 5 2 3
:
4
2 2 4 4
x x x x x
Q
x
x x x x
a) Rút gọn Q;
b) Tìm x để
2
Q
;
c) Tìm các giá trị của x để Q có giá trị âm.
Hướng dẫn giải
ĐKXĐ:
0; 4; 9
x x x
.
a)
1 2 5 2 3
:
4
2 2 4 4
x x x x x
Q
x
x x x x
2
1 2 2 2 5 2 3
:
2 2
2
x x x x x x x
x x
x
2
2
3 2 2 4 5 2
.
2 2 3
x
x x x x x
x x x x
2
2
2
.
2 2 3
x
x x
x x x x
2
2 2
2
.
3
2 2 3
x x x
x
x
x x x x
b)
2
2 2
3
x
Q
x
2 2 6
x x
8 8 64
x x x
.(Thỏa mãn ĐKXĐ).
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 16
c)
2
0 0
3
x
Q
x
3 0
x
(vì
2 0
x
)
3 9
x x
.
Kết hợp với điều kiện xác định ta có
0
Q
khi
0 9
x
và
4
x
.
Bài 4: Cho biểu thức
3 2
9
3 3
a a
B
a
a a
với
0; 9
a a
a) Rút gọn B.
b) Tìm các số nguyên
a
để B nhận giá trị nguyên
Hướng dẫn giải
a) Với
0; 9
a a
ta có:
3 2
9
3 3
a a
B
a
a a
=
3 2
3 3 ( 3)( 3)
a a
a a a a
( 3) 3( 3) 2
( 3)( 3) ( 3)( 3) ( 3)( 3)
a a a a
a a a a a a
3 3 9 2 11
9
3)( 3)
a a a a
a
a a
b) Để
11
11 ( 9) ( 9)
9
B Z Z a a
a
Ư (11)
Ư
(11) 1;11; 1; 11
. Khi đó ta có bảng giá trị
9
a
-11 -1 1 11
a -2 8 10 20
Không thoả mãn Thoả mãn Thoả mãn Thoả mãn
Vậy
8;10;20
a
thì
B Z
Bài 5: Cho biểu thức
2
2 1 1 2 2
1
x x x x x
A
x x x x x x x x
( Với
0, 1
x x
)
a) Rút gọn biểu thức A.
b) Tìm x để biểu thức A nhận giá trị là số nguyên.
Hướng dẫn giải
a)
2
.
1
x
A
x x
b) Cách 1: Với
0, 1 1 1 1.
x x x x x
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 17
Vậy
2 2 1
0 1 2.
1 1 1
x x
A
x x x x
Vì A nguyên nên A = 1
2
1 1
1
x
x
x x
( Không thỏa mãn).
Vậy không có giá trị nguyên nào của x để giả trị A là một số nguyên.
Cách 2: Dùng miền giá trị
2
Ax+(A 1) 2 0
1
x
A x A
x x
Trường hợp 1:
0 2A x x
Trường hợp 2:
2 2 2
1
0 (A 1) 4 ( 2) 3 6 1 0 2 0
3
A A A A A A A
2 2
4 4
2 1 (A 1) 1;2 , 0
3 3
A A A doA Z A
Với A = 1 => x = 1 ( loại)
Với A = 2
2
2 0
1
x
x
x x
( loại).
Bài 6: Cho biểu thức
3 2 9
2 3 6
x x x
P
x x x x
với
0; 4
x x
a) Rút gọn P
b) Tìm
x
để
7
12
P
c) Tìm
x
để
1
2
P
d) Tìm tất cả các giá trị nguyên của
x
để
1
P
nhận giá trị nguyên.
e) Tìm tất cả các giá trị hữu tỷ của của
x
để P nhận giá trị nguyên.
Hướng dẫn giải
a) Với
0; 4
x x
thì
3 2 9
2 3 3 2 6
x x x
P
x x x x x
3 2 9
2 3
3 2 3
x x x
x x
x x x
3 2 9
2 3
3 2 3
x x x
x x
x x x
3 2 9
2 3
3 2
x x x
x x
x x
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 18
2
3 3 2 9
3 2
x x x x
x x
2 2
9 2 9 2
2
3
3 2 3 2
x x x x
x
x
x x x x
Vậy với
0; 4
x x
thì
2
3
x
P
x
b)
7 2 7
12 24 7 21 5 45
12 12
3
x
P x x x
x
9 81
x x
( thỏa mãn
0; 4
x x
)
Vậy với
81
x
thì
7
12
P
c)
1 2 1 2 1 2 4 3
0 0
2 2 2
3 3
2 3
x x x x
P
x x
x
7
0
3
x
x
(3)
Vì
0
x
với mọi
0; 4
x x
nên
3 0
x
với mọi
0; 4
x x
Nên (3)
7 0 7 49
x x x
Kết hợp với điều kiện
0; 4
x x
.
Vậy
49
x
thì
1
2
P
d) Ta có
1 3 2 5 5
1
2 2 2
x x
P
x x x
1
P
nguyên
5
2
x
nguyên
5 2
x
2
x
là Ư (5)
1; 5
Lập bảng:
2
x
-1 1 -5 5
x
1 3 -3 7
x
1
9
49
Th
ỏ
a mãn
Th
ỏ
a mãn
Lo
ạ
i
Th
ỏ
a mãn
Vậy
1;9;49
x
thì
1
P
nguyên.
e) Ta có
2 3 2 2
1
3 3 3
x x
P
x x x
Vì
2
3
x
0
nên
1
P
với mọi
0; 4
x x
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 19
Mà
2 2 2 2 2 2 1
3 3 1 1
3 3 3 3
3 3 3
x
x x x
Do đó
1
1
3
P
. Vậy không có giá trị hữu tỷ nào của
x
để
P
nguyên.
Bài 7: Cho biểu thức
1 1 1
1 :
x x
P
x x x x
, (với
0
x
và
1
x
).
a) Rút gọn biểu thức
P
.
b) Tính giá trị của biểu thức
P
tại
2022 4 2018 2022 4 2018
x
.
Hướng dẫn giải
a) Ta có
1 1
1
x
x x
Và
1
1 1 1 1 1
1
1 1
x x
x x x x x
x x x x
x x x x
nên
1 1
.
1
x x
P
x x
1
x
x
.
b) Có
2022 4 2018 2022 4 2018
x
2 2
2018 2 2018 2
2018 2 2018 2 2018 2 2018 2 4
thỏa mãn điều kiện
0
x
và
1
x
.
+ Vậy giá trị của biểu thức
P
tại
4
x
là:
4 1 3
2
4
.
Bài 8: Cho hai biểu thức
2
5
x
A
x
và
3 20 2
25
5
x
B
x
x
với
0, 25
x x
.
a) Tính giá trị biểu thức
A
khi
9
x
.
b) Chứng minh rằng
1
5
B
x
.
c) Tìm tất cả các giá trị của
x
để
. 4
A B x
.
Hướng dẫn giải
a) Tính giá trị biểu thức
A
khi
9
x
.
Khi
9
x
ta có
9 2 3 2 5
3 5 2
9 5
A
b) Chứng minh rằng
1
5
B
x
.
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 20
Với
0, 25
x x
thì
3 20 2
15
5
x
B
x
x
3 20 2
5
5 5
x
x
x x
3 5 20 2
5 5
x x
x x
3 15 20 2
5 5
x x
x x
5
5 5
x
x x
1
5
x
(đpcm)
c) Tìm tất cả các giá trị của để
. 4
A B x
.
Với
0, 25
x x
Ta có:
. 4
A B x
2 1
. 4
5 5
x
x
x x
2 4 (*)
x x
Nếu
4, 25
x x
thì
(*)
trở thành :
2 4
x x
6 0
x x
3 2 0
x x
Do
2 0
x
nên
3
x
9
x
(thỏa mãn)
Nếu
0 4
x
thì
(*)
trở thành :
2 4
x x
2 0
x x
1 2 0
x x
Do
2 0
x
nên
1
x
1
x
(thỏa mãn)
Vậy có hai giá trị
1
x
và
9
x
thỏa mãn yêu cầu bài toán.
Bài 9: Cho biểu thức
2 4
8
3 4 1 4
x
x
B
x x x x
với
0; 16
x x
a) Rút gọn B.
b) Tìm giá trị của
x
để
1
B
c) Tính giá trị của
x
sao cho B không vượt quá
3
2
d) Tìm giá trị của B khi
x
thỏa mãn đẳng thức 2 1
x x
e) Tìm
x
để giá trị của B là một số nguyên.
Hướng dẫn giải
a) Với
0; 16
x x
thì
2 4
8
4 4 1 4
x
x
B
x x x x x
2 4
8
1 4
1 4 1
x
x
x x
x x x
2 4
8
1 4
4 1
x
x
x x
x x
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 21
2 8 4 8 1
4 1
x x x x
x x
2 8 4 8 8 3 12
4 1 4 1
x x x x x x
x x x x
3 4
4 1
x x
x x
3
1
x
x
Vậy với
0; 16
x x
thì
3
1
x
B
x
b)
3 1 1
1 1 3 1 2 1
2 4
1
x
B x x x x x
x
( thỏa mãn
0; 16
x x
). Vậy
1
4
x
thì
1
B
c)
B
không vượt quá
3
2
3 3 3
2 2
1
x
B
x
3 3
0
2
1
x
x
6 3 3
0
2 1
x x
x
3 3
0
2 1
x
x
1
0
1
x
x
(*)
Vì
0
x
với mọi
0; 16
x x
nên
1 0
x
với mọi
0; 16
x x
Suy ra (*)
1 0 1 1
x x x
Kết hợp với điều kiện
0; 16
x x
Vậy
0 1
x
thì
B
không vượt quá
3
2
d) Ta có
2 1
x x
(
0; 16
x x
)
2
2 2
2 1 2 1 0 1 0 1
x x x x x x
(
thỏa mãn
0; 16
x x
)
3 1 3
2
1 1
B
Vậy 2 1
x x
thì
3
2
B
e)
3 3 3 3 3
3 3
1 1 1
x x
B
x x x
( vì
3
0
1x
với
0; 16
x x
)
Vì
0
x
với mọi
0; 16
x x
nên
1 1
x
với mọi
0; 16
x x
3 3 3
3 3 3 0
1 1 1x x x
Suy ra
0 3
B
Mà
B Z
nên
0;1;2
B
TH1:
3
0 0 0
3
x
B x
x
( thỏa mãn)
TH2:
3 3 9
1 1 3 3
2 4
3
x
B x x x x
x
( thỏa mãn)
TH3:
3
2 2 3 2 6 6 36
3
x
B x x x x
x
( thỏa mãn)
Vậy
9
0; ;36
4
x
thì
B Z
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 22
Bài 10: Cho biểu thức
2 2 1 1
1:
1 1 1
x x x
P
x x x x x
với
0
x
a) Rút gọn
P
b) Tính giá trị của
P
biết
7 4 3
x
c) Tìm
x
để
2 1
P x
d) Tìm
m
để có giá trị
x
thoả mãn
P m
e) Tìm giá trị nhỏ nhất của
P
Hướng dẫn giải
a) Với
0
x
thì
2 2 1 1
1:
1 1 1
x x x
P
x x x x x
2 2 1 1
1:
1 1
1 1
x x x
x x x
x x x
1 1 1 1
2 2 1 1
x x x x x x
x x x x x x x
1 1
1
1
x x x
x x
x
x x
Vậy với
0
x
thì
1
x x
P
x
b) Với
2
7 4 3 4 2.2. 3 3 2 3
x thỏa mãn điều kiện
0
x
2
2 3 2 3 2 3
x
( vì
2 3
)
1 7 4 3 2 3 1 6 3 3
3
2 3 2 3
x x
P
x
Vậy với
7 4 3
x
thì
3
P
c)
1
2 1 2 1 1 2
x x
P x x x x x x
x
1
x
(thỏa mãn
0
x
)
Vậy với
1
x
thì
2 1
P x
d)
1
1 1 1 0
x x
P m x x m x x m x
x
(1)
Vì
1 0
nên (1) là phương trình bậc hai.
Đặt
0
t x t
(1) trở thành
2
1 1 0
t m t
(2)
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 23
Ta có
2
2 2
1 4 2 3 3 3
m m m m m m
1 3 1 1 3
m m m m m
Phương trình (1) có nghiệm
Phương trình (2) có nghiệm dương
TH1: Phương trình (2) có 2 nghiệm dương
1 0
1 3 0
1 0
1
1 0
1 0
1 0
m m
m
m
m
S m
P
TH2: Phương trình (2) có 2 nghiệm trái dấu
1 0
S
( vô lý)
Loại
TH3: Phương trình (2) có 1 nghiệm dương và 1 nghiệm bằng 0
Với
0
t
thay vào (2) ta được
2
0 1 .0 1 0 1 0
m
( vô lý )
Loại
Vậy
1
m
là giá trị cần tìm.
e)
1 1
1
x x
P x
x x
Vì
0
x
nên
1
0; 0
x
x
.
Áp dụng bất đẳng thức Cô si cho hai số dương
1
;
x
x
ta được:
1 1
2 . 2
x x
x x
Dấu “=” xảy ra
1
1
x x
x
( thỏa mãn
0
x
)
2 1 1
P
. Vậy giá trị nhỏ nhất của
1
P
khi
1
x
Bài 11: Cho biểu thức
2 3 2
1 :
1 3 2 6
x x x x
P
x x x x x
với
0; 4
x x
a) Rút gọn
P
b) Tính giá trị của
P
biết
3 5
2
x
c) Tìm
x Z
để
P Z
d) So sánh
P
với
1
e) Tìm các giá trị của
x
để
3
P x
.
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 24
Hướng dẫn giải
a) Với
0; 4
x x
2 3 2
1 :
1 3 2 6
x x x x
P
x x x x x
1 2 3 2
:
1 3 2 3 2 6
x x x x x
x x x x x x
1 2 3 2
:
1 3 2
3 2 3
x x x
x x x
x x x
1 2 3 2
:
1 3 2
3 2
x x x
x x x
x x
2 2 3 3 2
1
:
1
3 2
x x x x x
x
x x
3 2
1 4 9 2 1
: .
1 1 3
3 2
x x
x x x
x x x
x x
2
1
x
x
. Vậy với
0; 4
x x
thì
2
1
x
P
x
b) Với
2
5 1
3 5 6 2 5 5 2. 5.1 1
2 4 4 4
x
thỏa mãn
0; 4
x x
2
5 15 1
5 1
4 2 2
x
( vì
5 1
)
5 1
2
5 5 5 1
2 5 5
2
1 5 1 5 1
5 1 5 1
1
2
x
P
x
5 5 5 5 5 6 5 10 3 5 5
4 4 2
c)
2 1 3 3
1
1 1 1
x x
P
x x x
3
3 1 1
1
P Z Z x x
x
là Ư(3)
Ư(3)=
1; 3
Mà
0 0; 4 1 0 0; 4
x x x x x x
nên:
TH1:
1 1 0 0
x x x
( thỏa mãn)
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 25
TH2:
1 3 2 4
x x x
( loại)
Vậy
0
x
thì
P Z
d) Xét hiệu
2 2 1 3
1 1 0
1 1 1
x x x
P
x x x
0; 4
x x
Suy ra
1
P
e)
2
3 3 2 3 1
1
x
P x x x x x
x
2 3 3 3 1 0
x x x x x x
(2)
Đặt
0; 2
x t t t
(2) trở thành:
2
3 1 0
t t
2
3 4.1.( 1) 13
3 13
2
3 13
2
t TM
t loai
2
3 13 22 6 13
2 4
x
( thỏa mãn điều kiện)
Vậy
22 6 13
4
x
là giá trị cần tìm.
Bài 12: Cho biểu thức:
1
1
x
A
x
với
0
x
a) Khi
6 2 5
x
tính giá trị biểu thức
A
b) Rút gọn biểu thức
15 2 1
:
25
5 5
x x
B
x
x x
với
0; 5
x x
c) Tìm
x
để biểu thức
M B A
nhận giá trị nguyên.
Hướng dẫn giải
a) Với
6 2 5
x
thỏa mãn điều kiện
0
x
Ta có
2
6 2 5 5 2 5 1 5 1
x
2
5 1 5 1 5 1
x
( vì
5 1
)
1 5 1
2 5 2 5 5
5
1 5 1 5
A
b) Với
0; 5
x x
thì
15 2 1 15 2 1
: :
25
5 5 5 5
5 5
x x x x
B
x
x x x x
x x
15 2 10 1 5 5
: .
5 1
5 5 5 5
x x x x x
x x
x x x x
1
1
x
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 26
Vậy với
0; 5
x x
thì
1
1
B
x
c) Ta có
1 1 2 1 3
1 1 1 1
x x x
M B A
x x x x
3
1
1
x
Vì
0 0; 5 1 1 0; 5
x x x x x x
3 3
3 1 1 3 2
1 1
M
x x
Lại có
3 3
0 1 1
1 1x x
1 2
M
. Mà
M Z
0;1;2
M
TH1:
2
0 0 2 0 4
1
x
M x x TM
x
TH2:
2 1
1 1 2 1 2 1
4
1
x
M x x x x TM
x
TH3:
2
2 2 2 2 2 3 0 0
1
x
M x x x x TM
x
Vậy
1
0;4;
4
x
thì
M Z
Dạng 6: Bài tập chinh phục điểm 10
Bài 1. Cho
3 5 2 3 3 5 2 3
a
. Chứng minh rằng
2
2 2 0
a a
.
Giải
2
3 5 2 3 3 5 2 3 2 9 5 2 3 6 2 4 2 3
a
2 2
6 2 3 1 6 2 3 1 4 2 3 1 3
. Do
0
a
nên
3 1
a
. Do đó
2
1 3
a
hay
2
2 2 0
a a
.
Bài 2.
a) Cho
4 10 2 5 4 10 2 5
x
. Tính giá trị biểu thức:
4 3 2
2
4 6 12
2 12
x x x x
P
x x
.
b) Cho
3
1 2
x . Tính giá trị của biểu thức
4 4 3 2
2 3 1942
B x x x x
.(Trích đề thi vào lớp 10
Trường PTC Ngoại Ngữ - ĐHQG Hà Nội năm 2015-2016).
c) Cho
3 3
1 2 4
x . Tính giá trị biểu thức:
5 4 3 2
4 2 2015
P x x x x x
Giải
a) Ta có:
2
2
4 10 2 5 4 10 2 5 8 2 4 10 2 5 . 4 10 2 5
x
2 2
2
8 2 6 2 5 8 2 5 1 8 2 5 1 6 2 5 5 1
x
5 1
x
. Từ đó ta suy
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 27
ra
2
2
1 5 2 4
x x x
.
Ta biến đổi:
2
2 2
2
2
2 2 2 12
4 3.4 12
1
2 12 4 12
x x x x
P
x x
.
b) Ta có
3
3 2
3
1 2 1 2 3 3 3 0
x x x x x
. Ta biến đổi biểu thức
P
thành:
2 3 2 3 2 3 2
( 3 3 3) 3 3 3 3 3 3 1945 1945
P x x x x x x x x x x x
c) Để ý rằng:
3
2
3
2 2 1
x
ta nhân thêm 2 vế với
3
2 1
để tận dụng hằng đẳng thức:
3 3 2 2
a b a b a ab b
. Khi đó ta có:
3
2
3 3 3
2 1 2 1 2 2 1
x
3
3 3 2
3 3
2 1 1 2 1 2 1 3 3 1 0
x x x x x x x x
.
Ta biến đổi:
5 4 3 2 2 3 2
4 2 2015 1 3 3 1 2016 2016
P x x x x x x x x x x
Bài 3. Tính
9 5 3 5 8 10 7 4 3
C
Giải
Để ý rằng:
2
7 4 3 2 3 7 4 3 2 3
Suy ra
9 5 3 5 8 10(2 3) 9 5 3 5 28 10 3
C
2
9 5 3 5 5 3
.Hay
9 5 3 5(5 3) 9 25 9 5 4 2
C
Bài 4. Chứng minh:
a)
7 2 6 7 2 6
A
là số nguyên.
b)
3 3
84 84
1 1
9 9
B
là một số nguyên
Hướng dẫn giải
a) Dễ thấy
0,
A
Ta có
2
2
7 2 6 7 2 6 7 2 6 7 2 6 2 7 2 6. 7 2 6
A
14 2.5 4
Suy ra
2
A
.
b) Áp dụng hằng đẳng thức:
3
3 3
3
u v u v uv u v
. Ta có:
3
3
3 3 3 3
84 84 84 84 84 84
1 1 1 1 3 1 . 1
9 9 9 9 9 9
B
3 3
84 84
1 1
9 9
.
Hay
3 3 3 3
3
3
84 84 84
2 3 1 1 . 2 3 1 2 2 0
9 9 81
B B B B B B B B
2
1 2 0
B B B
mà
2
2
1 7
2 0
2 4
B B B
suy ra
1
B
. Vậy
B
là số nguyên.
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 28
Bài 5. Chứng minh rằng:
3 3
1 8 1 1 8 1
3 3 3 3
a a a a
x a a
với
1
8
a
là số tự nhiên.
Lời giải
Áp dụng hằng đẳng thức:
3
3 3
3
u v u v uv u v
Ta có
3 3 2
2 1 2 2 1 2 0 1 2 0
x a a x x a x a x x x a
Xét đa thức bậc hai
2
2
x x a
với
1 8 0
a
+ Khi
1
8
a
ta có
3 3
1 1
1
8 8
x
.
+ Khi
1
,
8
a
ta có
1 8
a
âm nên đa thức (1) có nghiệm duy nhất
1
x
Vậy với mọi
1
8
a
ta có:
3 3
1 8 1 1 8 1
1
3 3 3 3
a a a a
x a a
là số tự nhiên.
Bài 6. Tính
x y
biết
2 2
2015 2015 2015
x x y y
.
Lời giải
Nhận xét:
2 2 2 2
2015 2015 2015 2015
x x x x x x
.
Kết hợp với giả thiết ta suy ra
2 2
2015 2015
x x y y
2 2 2 2
2015 2015 2015 2015 0
y y x x x x y y x y
Bài 7.
a) Chứng minh rằng:
1 1 1
.... 4
1 2 3 4 79 80
.
b) Chứng minh rằng:
1 1 1 1 1
... 2 1
1 2 2 3 3 4 1 1
n n n
.
c) Chứng minh:
1 1 1 1 1
2 2 ... 2 1
1 2 3 4
n n
n
với mọi số nguyên dương
2
n
.
Lời giải
a) Xét
1 1 1
....
1 2 3 4 79 80
A
,
1 1 1
..
2 3 4 5 80 81
B
Dễ thấy
A B
.
Ta có
1 1 1 1 1
....
1 2 2 3 3 4 79 80 80 81
A B
Mặt khác ta có:
1
1
1
1
1 1
k k
k k
k k
k k k k
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 29
Suy ra
2 1 3 2 ... 81 80 81 1 8
A B
. Do
A B
suy ra
2 8 4
A A B A
.
b) Để ý rằng:
1 1 1 1
1 2 1
( 1) 1
k k k k
k k k k
với mọi
k
nguyên dương.
Suy ra
1 1 1 1 1 1
2 1 2 .. 2 2 1
2 2 3 1 1
VT
n n n
.
c) Đặt
1 1 1 1 1
...
1 2 3 4
P
n
Ta có:
2 1 2 2
1 2 1
n n n n n n
với mọi số tự nhiên
2
n
.
Từ đó suy ra
2 2 2
2 1 2 1
1 2 1
n n n n
n n n n n
hay
2
2 1 2 1
n n n n
n
Do đó:
2 2 1 3 2 ... 1
n n T
và
1 2 2 1 3 2 .... 1
T n n
.
Hay
2 2 2 1
n T n
.
Bài 8. Cho
1 1 1 1
...
1 2 2 3 3 4 120 121
A
và
1 1
1 ...
2 35
B
.
Chứng minh rằng
B A
.
Lời giải
Ta có:
1 1 1 1
...
1 2 2 3 3 4 120 121
A
1 2 2 3 120 121
...
1 2 1 2 2 3 2 3 120 121 120 121
1 2 2 3 120 121
...
1 1 1
2 1 3 2 ... 121 120 1 121 10
(1)
Với mọi
*
k
, ta có:
1 2 2
2 1
1
k k
k k k k k
Do đó
1 1
1 ...
2 35
B
2 2 1 3 2 4 3 ... 36 35
B
2 1 36 2 1 6 10
B
(2) . Từ (1) và (2) suy ra
B A
.
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 30
Ví dụ 9. Cho
2
4 4 4 4
8 16
x x x x x
A
x x
với
4
x
a) Rút gọn
A
.Tìm
x
để
A
đạt giá trị nhỏ nhất.
b) Tìm các giá trị nguyên của
x
để
A
có giá trị nguyên.
Lời giải
a) Điều kiện để biểu thức
A
xác định là
4
x
.
2 2
2
4 2 4 2
4 2 4 2
4
4
x x x
x x x
A
x
x
4 2 4 2
4
x x x
x
+ Nếu
4 8
x
thì
4 2 0
x
nên
4 2 2 4
4 16
4
4 4 4
x x x
x
A
x x x
Do
4 8
x
nên
0 4 4 8
x A
.
+ Nếu
8
x
thì
4 2 0
x
nên
4 2 4 2
2 4 2 8
2 4 2 16 8
4 4
4 4
x x x
x x x
A x
x x
x x
(Theo bất đẳng thức
Cô si). Dấu bằng xảy ra khi và chỉ khi
8
2 4 4 4 8
4
x x x
x
.
Vậy GTNN của
A
bằng
8
khi
8
x
.
b) Xét
4 8
x
thì
16
4
4
A
x
, ta thấy
A Z
khi và chỉ khi
16
4
4
Z x
x
là ước số nguyên
dương của
16
. Hay
4 1;2;4;8;16 5;6;8;12;20
x x đối chiếu điều kiện suy ra
x 5
hoặc
6
x
.
+ Xét
8
x
ta có:
2
4
x
A
x
, đặt
2
4
4
2
x m
x m
m
khi đó ta có:
2
2 4
8
2
m
A m
m m
suy
ra
2;4;8 8;20;68
m x .
Tóm lại để
A
nhận giá trị nguyên thì
5;6;8;20;68
x
.
Bài 10. Cho
4 10 2 5 4 10 2 5
a
.
Tính giá trị của biểu thức:
2 3 2
2
4 6 4
2 12
a a a a
T
a a
.
Giải
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 31
2
2
8 2 16 10 2 5 8 2 6 2 5 8 2 5 1
a
8 2 5 1 6 2 5
. Vì
0
a
nên
5 1
a
. Do đó
2
1 5
a
hay
2
2 4
a a
. Biểu diễn
2
2 2
2
2
2 3 2 4
4 3.4 4 1
2 12 4 12 2
a a a a
T
a a
.
Bài 11. Cho
3
2 7 61 46 5 1
a
.
a) Chứng minh rằng:
4 2
14 9 0
a a
.
b) Giả sử
5 4 3 2
2 14 28 9 19
f x x x x x x
. Tính
f a
.
Giải:
a) Vì
3
3
3
61 46 5 1 2 5 1 2 5
Từ đó
2 7 1 2 5 1 2 5
a
2
2 2 4 2
2 5 7 2 10 14 9 0
a a a a
.
b) Do
4 2
14 9 2 1
f x x x x
và
4 2
14 9 0
x a
nên ta được
1
f a
.
Bài 12. Cho
3 3
38 17 5 38 17 5
a
.
Giả sử có đa thức
2016
3
3 1940f x x x . Hãy tính
f a
.
Giải
Vì
3
3 3
38 17 5 38 17 5 3.3. 38 17 5. 38 17 5
a
2012
3 3 2016
76 3 3 76 76 1940 2016
a a a a f a
.
Bài 13. Chứng minh rằng với mọi số nguyên dương
3
n
, ta có
3 3 3 3
1 1 1 1 65
...
1 2 3 54
n
.
Giải:
Đặt
3 3 3 3
1 1 1 1
...
1 2 3
P
n
. Thực hiện làm trội mỗi phân số ở vế trái bằng cách làm giảm mẫu, ta có:
3 3
2 2 2 1 1
, 1
1 1 1 1
k
k k k k k k k k k
toanthaycu.com
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 32
Cho
4,5,...,
k n
thì
3 3 3
1 1 1 1 1 1 1 1 1
2 2 ...
1 2 3 3.4 4.5 4.5 5.6 1 1
P
n n n n
251 1 1 251 1 65
108 3.4 1 108 3.4 27
n n
. Do đó
65
64
P
(đpcm).
Bài 14. Chứng minh rằng:
43 1 1 1 44
...
44 45
2 1 1 2 3 2 2 3 2002 2001 2001 2002
Giải:
Đặt
1 1 1
...
2 1 1 2 3 2 2 3 1 1
n
S
n n n n
Để ý rằng :
2
2
1 1 1 1
1 1 1
, 1
1
1 1 1
1 1
k k k k k k k k
k
k k
k k k k k k
k k k k
Cho
1,2,...,
k n
rồi cộng vế với vế ta có:
1 1 1 1 1 1 1
... 1
1 2 2 3 1 1
n
S
n n n
Do đó
2001
1
1
2002
S
Như vậy ta phải chứng minh:
43 1 44 1 1 1
1
44 45 45 44
2002 2002
44 2002 45 1936 2002 2025
Bất đẳng thức cuối cùng đúng nên ta có điều phải chứng minh.
| 1/32
| | Tải xuống

Có thể bạn quan tâm:

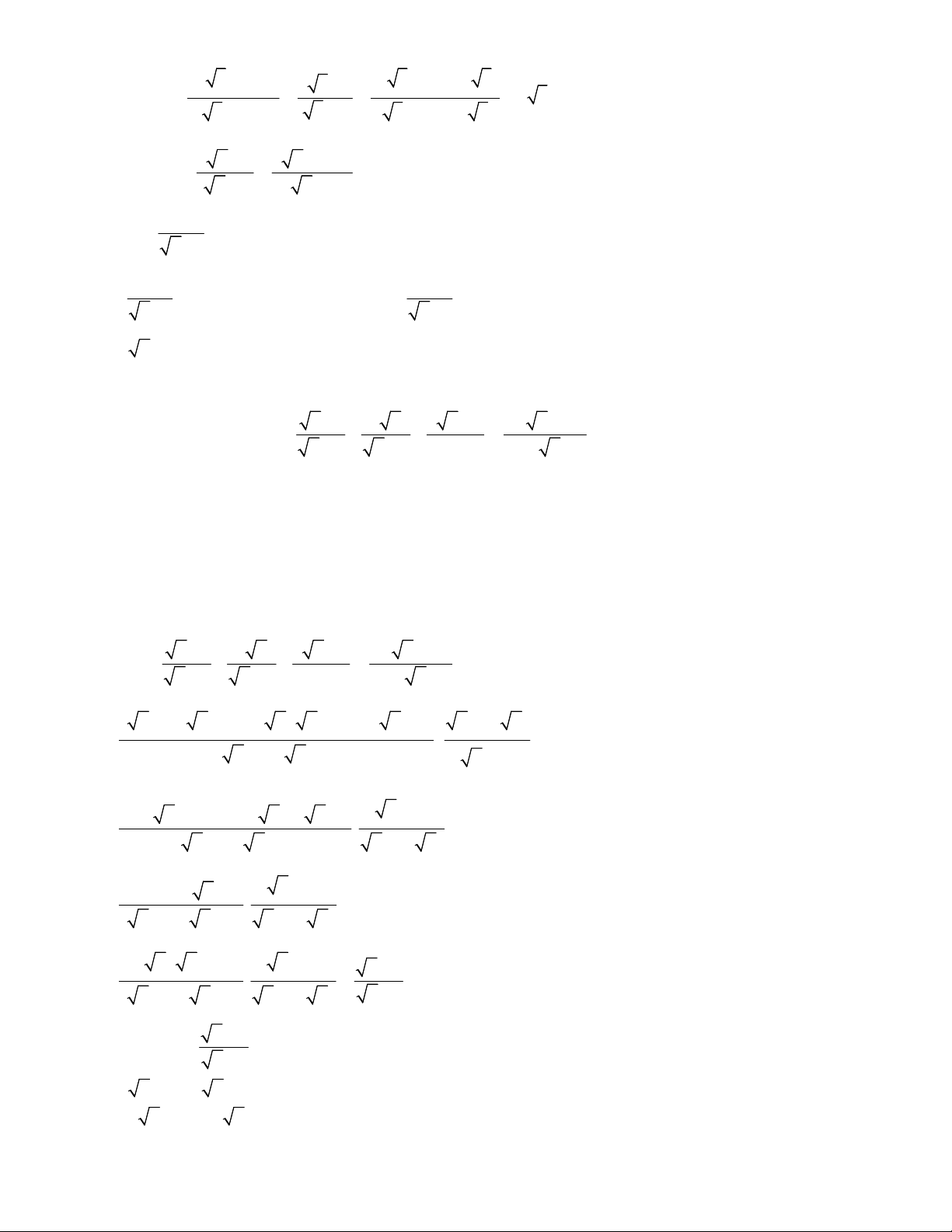
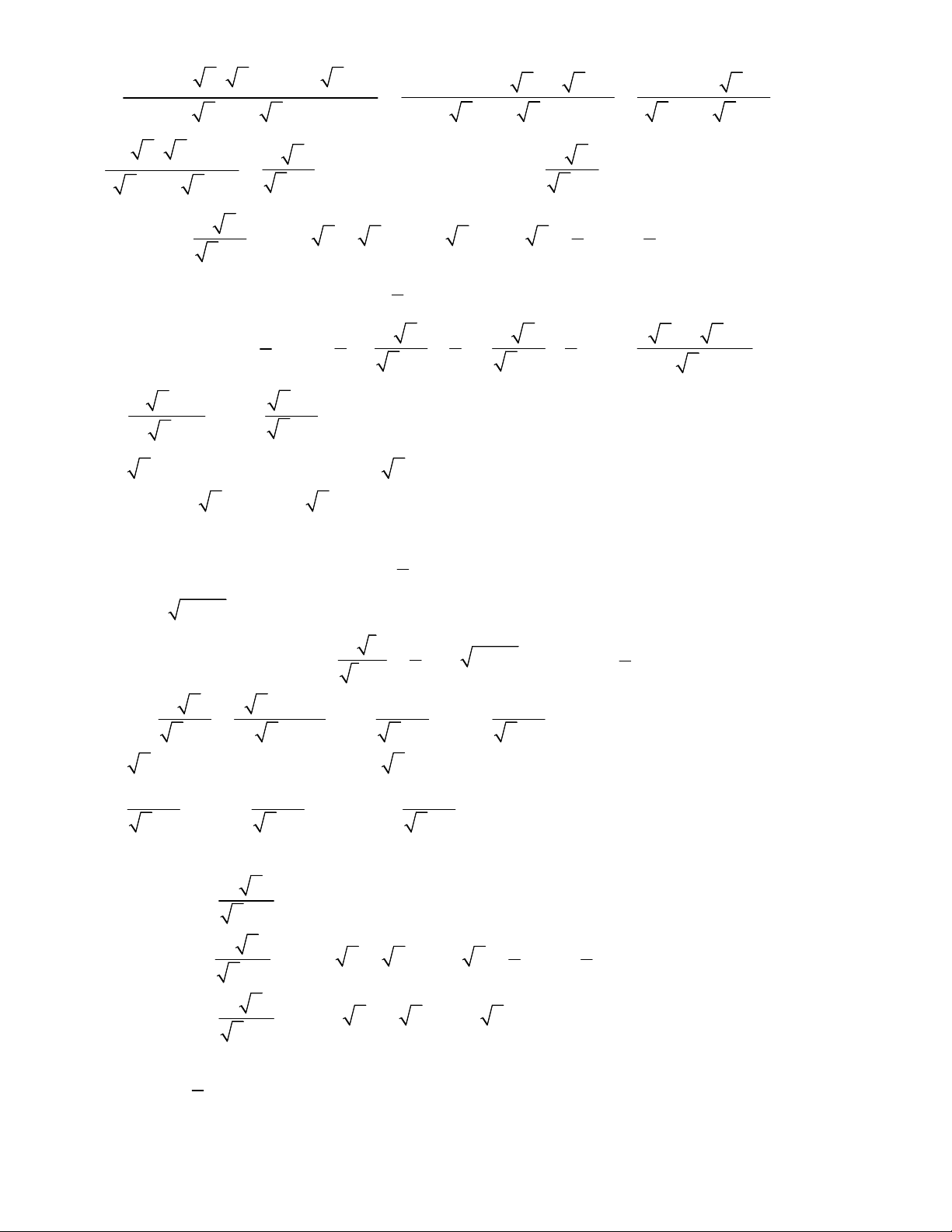
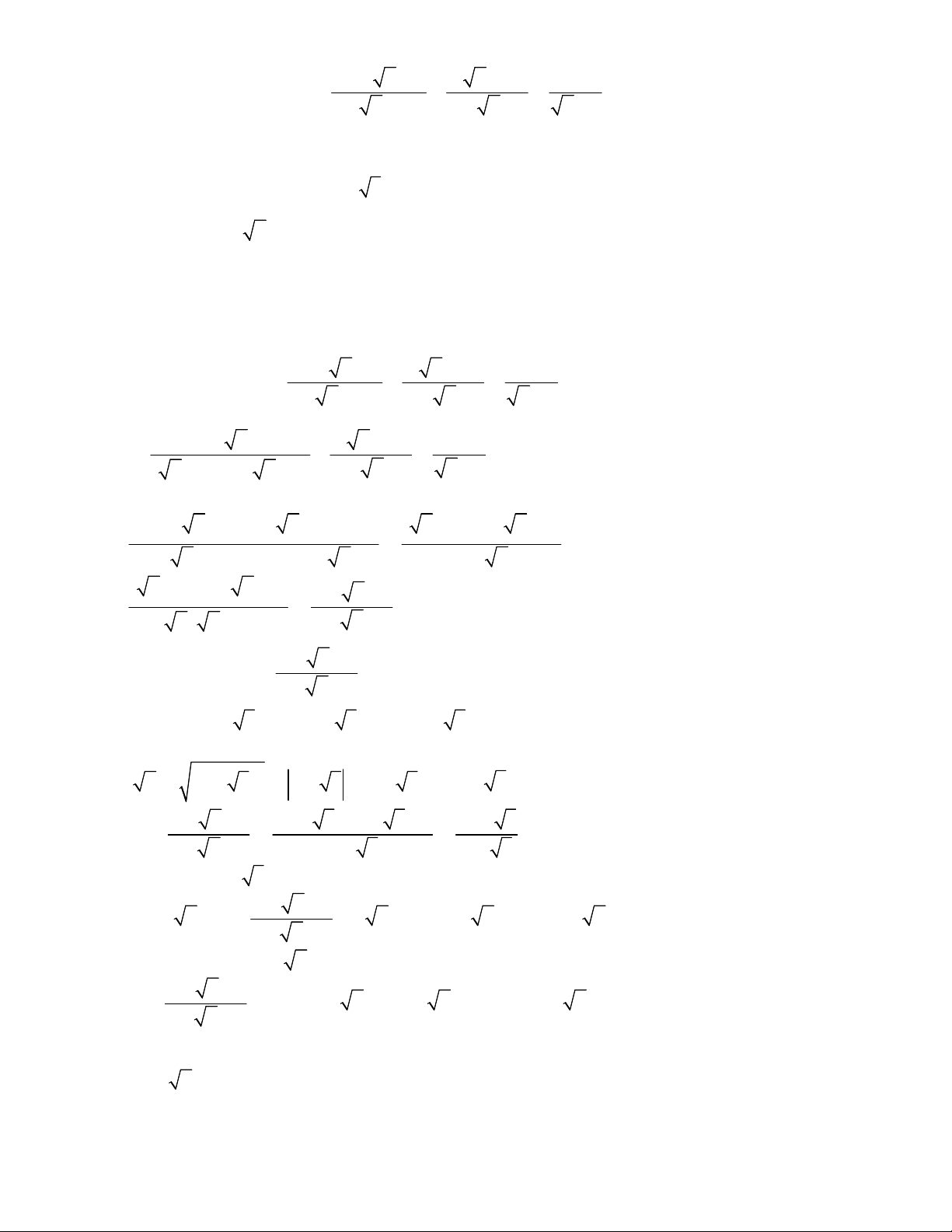
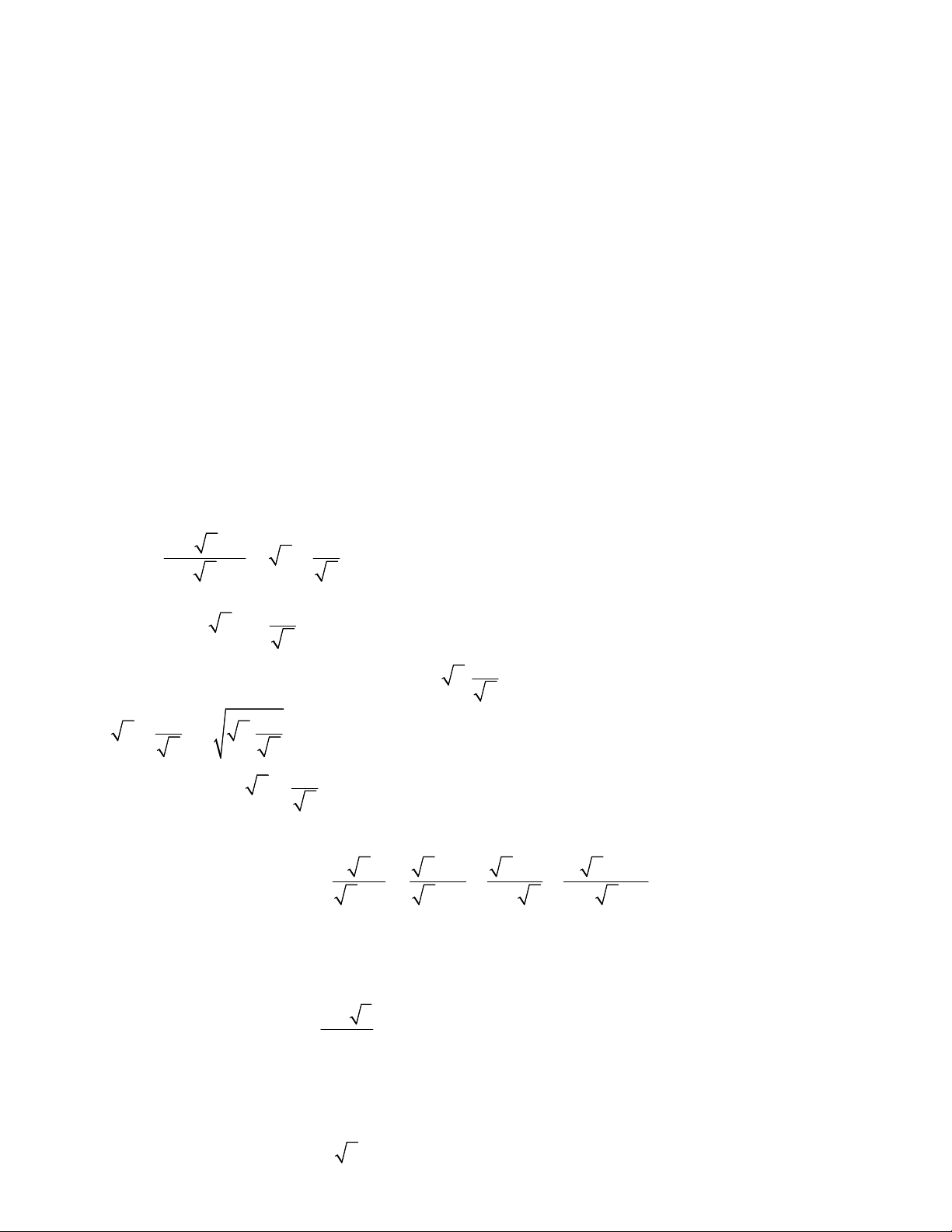
Preview text:

toanthaycu.com
CHUYÊN ĐỀ 1: RÚT GỌN BIỂU THỨC VÀ CÁC BÀI TOÁN LIÊN QUAN A. KIẾN THỨC CẦN NẮM 1. CĂN THỨC BẬC 2
 Căn bậc hai của số thực a là số thực x sao cho 2 x  a .
 Cho số thực a không âm. Căn bậc hai số học của a kí hiệu là a là một số thực không âm x mà
bình phương của nó bằng a : a  0  x  0    2  a  x x  a
 Với hai số thực không âm a,b ta có: a  b  a  b .
 Khi biến đổi các biểu thức liên quan đến căn thức bậc 2 ta cần lưu ý: A A  0 + 2 A  A   nếu A A  0 + 2 A B  A B  A B với , A B  0 ; 2
A B  A B   A B với A  0; B  0 A . A B . A B +   với AB  0, B  0 2 B B B M M . A + 
với A  0 ;(Đây gọi là phép khử căn thức ở mẫu) A A M  A  B M  +  với ,
A B  0, A  B (Đây gọi là phép trục căn thức ở mẫu) A  B A  B 2. CĂN THỨC BẬC 3.
 Căn bậc 3 của một số a kí hiệu là 3 a là số x sao cho 3 x  a  Cho 3
a  R a  x  x   3 ; a 3 3  a
 Mỗi số thực a đều có duy nhất một căn bậc 3.
 Nếu a  0 thì 3 a  0 .
 Nếu a  0 thì 3 a  0 .
 Nếu a  0 thì 3 a  0 . 3  a a 3  với mọi b  0 . 3 b b  3 3 3 ab  a. b với mọi a,b .  3 3 a  b  a  b .  3 3 3 A B  A B . 3 2  A AB 3  với B  0 B B 3  A A 3  3 B B
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 1 toanthaycu.com 3 2 3 3 2  1 A  AB  B  với A  B . 3 3 A  B A  B
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Rút gọn biểu thức không chứa biến 1. Phương pháp A nÕu A 0 2   1. A  A   A nÕu A < 0 2. AB  A. B (Với A  0; B  0 ) A A 3.  (Với A  0; B  0 ) B B 4. 2 A B  A B (Với B  0) 5. 2 A B  A B (Với A  0; B  0 ) 6. 2 A B   A B (Với A  0; B  0 ) A 1 7.  AB (Với A  0; B  0 ) B B A A B 8.  (Với B  0 ) B B C  A  B C  9  (Với 2 A  0; A  B ) 2 A  B A  B C  A  B C  10 
(Với A  0; B  0;A  B ) A  B A  B 11  3 A3 3 3  A  A 2. Các ví dụ minh họa
Ví dụ 1: Rút gọn các biểu thức sau: M  45  245  80 N  5 8  50  2 18
P  125  4 45  3 20  80 A  12  27  48 B  2 3  3 27  300
C  (2 3  5 27  4 12) : 3 Hướng dẫn giải 2 M  45  245  4 .5 N  5 8  50  2 18
P  5 5 12 5  6 5  4 5 2 2 2  3 .5  7 5  4 .5  5.2 2  5 2  2.3 2  5 5
 3 5  7 5  4 5  6 5  10 2  5 2  6 2  (10  5  6) 2  9 2
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 2 toanthaycu.com A  12  27  48 B  2 3  3 27  300
C  (2 3  5 27  4 12) : 3  2 3  3 3  4 3 2 2  2 3  3 3 .3  10 .3
 (2 3  5.3 3  4.2 3) : 3  3  2 3  3.3. 3 10 3     5 3 : 3 5  3
Nhận xét: Đây là một dạng toán dễ. Học sinh có thể bấm máy tính để kiểm tra kết quả, đa phần áp dụng
kiến thức đưa thừa số ra ngoài dấu căn để giải toán. 2 A B  A B ( B  0 )
Ví dụ 2: Rút gọn các biểu thức sau: 2 2 2 2 2 2
a) 3  2 2   3  2 2 
b) 5  2 6   5  2 6 
c) 2  3  1 3 2 2 2 2 2 2
d) 3  2   1 2 
e)  5  2    5  2  f)  2   1   2  5 Hướng dẫn giải 2 2
a) 3  2 2   3  2 2   3  2 2  3  2 2  3  2 2  3  2 2  6 A nÕu A 0 2   Lưu ý: A  A   A nÕu A  0 Kết quả: b) 4  6 c) 1 d) 4 e) 2 5 f) 2 2  4
Ví dụ 3: Rút gọn biểu thức a) A  4  2 3 b) B  8  2 15 c) C  9  4 5
d) D  7  13  7  13
e) E  6  2 5  6  2 5 1 f) F  7  2 10  20  8 2 Hướng dẫn giải a) A      2 4 2 3 3 1  3 1 b) B      2 8 2 15 15 1  15 1 c) C      2 9 4 5 2 5  5  2 1
d) D  7  13  7  13   142 13 142 13 2 2 2 1      13   1   13   1  2  2  
e) E  6  2 5  6  2 5  5  2 5 1  5  2 5 1 2 2  ( 5 1)  ( 5 1) |
 5 1|  | 5 1| 5 1 5 1  2
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 3 toanthaycu.com f) F        2 1 1 7 2 10 20 8 5 2  2 5  .2 2 2 2
 5  2  2 5  2  5  2  2 5  2  3 5
Ví dụ 4: Rút gọn biểu thức: (áp dụng các kiến thức tổng hợp) 6  2 5 5  2 6 3 4 1 A   B    5 1 3  2 5  2 6  2 6  5 1 1 1 1 1 C    ... D   7  4 3 1  2 2  3 3  4 99  100 2  3 3 3  4 3  4 1 2 2 E   F    2 3 1 5  2 3 2  3 6 3  3 Hướng dẫn giải 6  2 5 5  2 6 5 1 3  2 a) A      2 5 1 3  2 5 1 3  2 3 5  2 4 6  2 3 4 1  b) B        6  5 5  2 6  2 6  5 3 4
 5  2  6  2  6  5  2 6 1 1 1 1 c) C    ... 1  2 2  3 3  4 99  100   2  
1   3  2   4  3 ...  100  99   9 1 1 1 d) 2 D   7  4 3   4  4 3  3   (2  3) 2  3 2  3 2  3 1 2  3 2  3   2  3   2  3   2  3  4 2  3 (2  3)(2  3) 1  
3 342 3 1  3452 3 3 3 4 3 4  e) E     2 3 1 5  2 3 2 32 1 5  2 32 2 22 11 3 26 13 3    2  3  2  3 11 13    1 1      2     2 4 2 3 4 2 3 1  3 1 3 1  
 31 3 1 .( 2) 2 2 2 2   2 2 3  3  
1  2  3 3   1  22  3 1 2 2 1 1 2 f) F        2  3 6 3  3 2  3 3 3  3   1 3  3   1 2  3 2   32 2 3 4  2. 3  3   1    3  3   1 2  3 3  3   1 2  3 3 3   1  3   1
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 4 toanthaycu.com 2 3  3   1 3  3   1 3  3 3        1 3 3 1 3 3 3
Kinh nghiệm: Đôi khi một số bài toán rút gọn căn thức sẽ thực hiện dễ dàng hơn nếu chúng ta trục căn
thức hoặc rút gọn được một hạng tử trong đề toán. Nếu quy đồng mẫu số thì việc thực hiện các phép tính
rất phức tạp. Vì vậy trước khi làm bài toán rút gọn, học sinh cần quan sát kỹ đề toán từ đó có định hướng
giải đúng đắn để lời giải được ngắn gọn, chính xác.
Ví dụ 5: Thu gọn các biểu thức sau a) A  18  2 50  3 8 1 3  3 b) B  27  6  3 3 5 c) C   8  2 7  2 7  2 Hướng dẫn giải a) A  18  2 50  3 8 2 2 2
 3 .2 2 5 .2  3 2 .2  3 2  10 2  6 2   2 1 3  3 3 b) 2 B  27  6   3 .3  6.
 1 3  3 3  2 3  1  3  1 3 3 3 5 5 7  2 c) C   8  2 7  2   7  2 7  1  2 7  2  7  2 7  2      2 7 2
7 1  2  7  2  7 1  2
 7  2  7  1 2 1( Vì 7 1)
Ví dụ 6: Thực hiện phép tính 1 33 1 a) 48 2 75  5 1 2 11 3 b) 3 6  2 5  62 5  8 c) 3
5 2a  50a 2 a  4 32a với a  0 Hướng dẫn giải 1 33 1 1 3. 11 4 a) 48  2 75   5 1 2 2  4 .3  2 5 .3   5 2 11 3 2 11 3
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 5 toanthaycu.com 2 2  2 3 10 3  3  5 10 3 17 3  9 3   3 3 3 b) 3 6  2 5  6  2 5  8 3 3
 5  2 5  1  5  2 5  1  2
   2    2 5 1
5 1  2  5 1  5 1 2
 5 1 5 12( Vì 5 1)  0 c) 3 5 2a  50a  2 a  4 32a 2 2 2
 5 2a  5 .2a  2 a .a  4 4 .2a
 5 2a  5 2a  2 a a 16 2a  2a a 16 2a ( Vì a  0 )
Ví dụ 7. (Đè thi năm học 2014 – 2015 Thành phố Hồ Chí Minh) 5  5 5 3 5
Thu gọn các biểu thức sau: A    5  2 5 1 3  5 Lời giải 5  5 5 3 5 A    5  2 5 1 3  5 5 5 5 2 5  5   1 3 5 3 5    
5  2 5  2  5   1  5   1 3 53 5 5  5 9 5 15 5  5  9 5 15  3 5  5    3 5  5  4 4 4
 3 5  5  5  2 5  5 . 2 2
Ví dụ 8. Tính B  21 2 3  3 5  6 2 3  3 5  15 15 . Lời giải B 
    2     2 21 4 2 3 6 2 5 3 4 2 3 6 2 5 15 15 2 
    2      2 21 3 1 5 1 3 3 1 5 1 15 15    2 15 3 5 15 15  60 . 2 2
Dạng 2: Tìm điều kiện xác định của biểu thức BIỂU THỨC - ĐKXĐ: VÍ DỤ 1. A ĐKXĐ: A  0 Ví dụ: x  2018 ĐKXĐ: x  2018
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 6 toanthaycu.com A x  4 2. ĐKXĐ: B  0 Ví dụ: ĐKXĐ: x  7 B x  7 A x  3. ĐKXĐ: B  0 Ví dụ: 1 ĐKXĐ: x  3 B x  3 A x x  0 4. ĐKXĐ: A  0; B  0 Ví dụ: ĐKXĐ:   x  3 B x  3 x  3  x    1 0 A  0   x  2  0 x  2 A B  0 x 1  5. ĐKXĐ: Ví dụ: ĐKXĐ:  x 1 0 x 1 B A  0 x   2    x  2  0 B  0 Cho a > 0 ta có: x  a 6. x  a Ví dụ: 2 x 1   2 x  a   . x   a x   a Cho a > 0 ta có: 7. Ví dụ: 2 x  4  2  x  2 2 x  a   a  x  a
Dạng 3: Rút gọn biểu thức chứa biến 1. Phương pháp 2. Các ví dụ  x 1   2 6  Ví dụ 1: Rút gọn B   : 1       x  0 .  x  3 x x  3   x x  3 x  Hướng dẫn giải  x 1   2 6  B   : 1      x  0  x  3 x x  3   x x  3 x     x 1  x  2 6   :       x 3 x  3   x   x   x 3      x   x 2 x 3 6 1 x :       x   x  x     x 1. 1 3 3  x  x 
Ví dụ 2: (Đề thi năm 2014 – 2015 TP Đà Nẵng) x 2 2x  2 Rút gọn biểu thức P   , với x  0, x  2 7). 2 x  x 2 x  2
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 7 toanthaycu.com Lời giải:
Với điều kiện đã cho thì: 2 x  x  2 2  x 2 P      .
2x  2  x   x  2 x  2 1 2  x x  2  x 3  x  3
Ví dụ 3: Thu gọn các biểu thức sau: A    .  với x  0, x  9 . x  3 x  3  x  9   Hướng dẫn giải
Với x  0 và x  9 ta có:   x  3 x  3 x  9 x  3 1 A  .        x  3 x 3 . 3  x  9 x 
Ví dụ 4: Rút gọn các biểu thức: 1
a) A  x  x  x  khi x  0 . 4 1
b) B  4x  2 4x 1  4x  2 4x 1 khi x  . 4 Lời giải 2 1  1  1 a) A  x  x  x   x  x   x  x    4  2  2 1 1 1 1 1
+ Nếu x   x  thì x   x   A  . 2 4 2 2 2 1 1 1 1 1
+ Nếu x   0  x  thì x 
  x   A  2 x  2 4 2 2 2 b)
B  4x  2 4x 1  4x  2 4x 1  4x 1 2 4x 1 1  4x 1 2 4x 1 1 2 2 Hay B   4x 1   1   4x 1  
1  4x 1 1  4x 1 1  4x 1 1  4x 1 1 1
+ Nếu 4x 1 1  0  4x 1  1  x  thì 4x 1 1  4x 1 1 suy ra B  2 4x 1 . 2 1 1
+ Nếu 4x 1 1  0  4x 1  1   x  thì 4x 1 1   4x 1 1 suy ra B  2 . 4 2
Ví dụ 5. Cho các số thực dương a,b ; a  b .
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 8 toanthaycu.com a b3    a  b  b b 2a a 3 3a  3 ab Chứng minh rằng:   0 . a a  b b b  a Lời giải a b3    a  b  b b 2a a 3 3a  3 ab Ta có: Q   a a  b b b  a  a  b3 a  b3    a  b  b b 2a a 3 3 a   a  b    
a  b a  ab  b  a  b a  b 0
a a  3a b  3b a  b b  2a a 3 a   
a  b a  ab  b  a  b
3a a  3a b  3b a  3a a  3a b  3b a   
a  b a  ab  b 0 x  x  6 x  7 x 19 x  5 x
Ví dụ 6. Rút gọn biểu thức A    ; x  0, x  9 . x  9 x  x 12 x  4 x Lời giải x  x  6 x  7 x 19 x  5 x x  2 x  7 x 19 x  5 A       x  9 x  x 12 x  4 x
x  3  x 3 x  4 x  4
x  2 x  8  x  7 x 19  x  8 x 15  x  1 x 4   x 1    . x  3 x  4
 x 3 x 4 x 3
Dạng 4: Rút gọn biểu thức, biết biến thỏa mãn điều kiện cho trước 1. Phương pháp 2. Các ví dụ x 10 x 5 Ví dụ 1: Cho A    , với x  0, x  25 . x  5 x  25 x  5 1) Rút gọn biểu thức A
2) Tính giá trị của A khi x  9 . Lời giải: x. x x
 x 510 x 5. x 5 10 5  A     x  5 x  25 x  5  x 5 x 5
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 9 toanthaycu.com 2
x  5 x 10 x  5 x  25 x 10 x  25  x 5   x 5     A  . x  5 x  5
 x 5 x 5  x 5 x 5 x  5 3  5 2  1
Với x  9 ta có: x  3. Vậy A     . 3  5 8 4 x 2 x 3x  9 Ví dụ 2: Cho P    , với x  0, x  9 . x  3 x  3 x  9 1) Rút gọn P . 1
2) Tìm giá trị của x để P  . 3
3) Tìm giá trị lớn nhất của P . Lời giải
x  x 3  2 x  x  3 3x 9 3 1) P    x  3 x  3 x  3 1 3 1 2) P  
  x  3  9  x  36 (thỏa mãn ĐKXĐ) 3 x  3 3 3 3 3) Với x  0, P  
 1 P  1 khi x  0 (TM). max x  3 0  3 3 3 x  y x  y
Ví dụ 3: Cho biểu thức P  . , x  y . 2 2 2 2 x  xy  y x  y
1) Rút gọn biểu thức P .
2) Tính giá trị của P khi x  7  4 3 và y  4  2 3 . Lời giải 3 3 x  y x  y x  y 1) P  .  . 2 2
x  xy  y  x  yx  y x  y
2) Với x  7  4 3  2  3 và y  4  2 3  3 1 2  3  3 1 1 3  2 3
Thay vào P ta được: P      . 2  3    3   1 3  2 3 3 1 1 2 x
Ví dụ 4: Cho biểu thức A     x  0, x  4 . 2  x 2  x 4  x 1
Rút gọn A và tìm x để A  . 3 Lời giải
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 10 toanthaycu.com 22 1 1 2 4 2  x x x  2 1 2 1 A        . Với A    2  x 2  x 4  x 4  x 4  x 4  x 2  x 3 2  x 3
 x  4  x  16 (nhận). 1 Vậy A  khi x  16 . 3 a 2 2
Ví dụ 5. Cho biểu thức C    . a 16 a  4 a  4
1) Tìm điều kiện của a để biểu thức C có nghĩa và rút gọn C .
2) Tính giá trị của biểu thức C khi a  9  4 5 . Lời giải a  0 a  0 a 16 0     a  16
1) Biểu thức C có nghĩa khi:     a  0, a  16 . a  4  0 a  16          a  0 a 4 0 a 2 2 a 2 2 Rút gọn C       a 16 a  4 a  4
 a 4 a 4 a 4 a 4
a  2 a  4  2 a  4       a 2 a 8 2 a 8 a 4 a    a  4 a  4
 a 4 a 4  a 4 a 4 a  a  4 a    . a  4 a  4 a  4
2) Giá trị của C khi a  9  4 5 . Ta có: a  a         2 9 4 5 4 4 5 5 2 5  a    2 2 5  5  2 a 5  2 5  2 Vậy C       . a  4 9 4 5 5  2  4 5  2
Ví dụ 6. (Đề thi năm 2014 – 2015 chuyên Thái Bình tỉnh Thái BÌnh)  2 3 5 x  7  2 x  3 Cho biểu thức A      :   x  0, x  4 . x 2 2 x 1 2x 3 x 2      5x 10 x  
1) Rút gọn biểu thức A .
2) Tìm x sao cho A nhận giá trị là một số nguyên. Lời giải
1) Với x  0, x  4 biểu thức có nghĩa ta có:
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 11 toanthaycu.com  2 3 5 x  7  2 3  3 A      :  x 2 2 x 1 2x 3 x 2      5x 10 x   22 x  
1  3 x  2 5 x  7 2 x  3 5 x x   x 2 2 3   5 x   .  . x   x   : 2 2 1
5 x  x  2  x  22 x   1 2 x  3 2 x 1 5 x
Vậy với x  0, x  4 thì A  . 2 x 1 5 x
2) Ta có x  0,x  0, x  4 nên A   0, x  0, x  4 2 x 1 5 x 5 5 5 5 A     x 
x   0  A  , kết hợp với A nhận giá trị là một số nguyên 2 x 1 22 x   , 0, 4 2 1 2 2 thì A1,  2 . 1 1
A  1  5 x  2 x 1  x   x  thỏa mãn điều kiện. 3 9
A  2  5 x  4 x  2  x  2  x  4 không thỏa mãn điều kiện. 1
Vậy với x  thì A nhận giá trị là nguyên. 9  x  2 1  x 1
Ví dụ 7. Cho biểu thức P   .   với x  0 và x  1.  x  2 x x  2  x 1 x 1 a) Chứng minh rằng P  . x
b) Tìm các giá trị của x để 2P  2 x  5 . Lời giải       x   x x   x 1. x 2 2 1  x 1 x 1 P        .  x   x 2 . x   x    x 2 . 1  x 1 x  x 1 b) Theo câu a) P  x 2 x  2  2P  2 x  5 
 2 x  5 2 x  2  2x  5 x  2x  3 x  2  0 và x  0 x     x   1 1 1 2 x   0  x   x    .  2  2 4
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 12 toanthaycu.com
Dạng 5: Các bài toán tổng hợp bao gồm các câu hỏi phụ x  2 x 10 x 2 1
Bài 1: Cho biểu thức Q    x 0;x   9 x  x 6 x 3 x  2 1. Rút gọn biểu thức Q
2. Tính giá trị của Q khi x 16 1
3. Tìm giá trị của x khi Q  3 1
4. Tìm giá trị của x sao cho Q  9
5. Tìm giá trị lớn nhất của Q . Hướng dẫn giải
1. Với x  0; x  9 thì x  2 x 10 x 2 1 x  2 x 10 x 2 1 Q       x 3 x  2 x 6 x 3 x  2 x  x   3  2 x   3 x 3 x  2 x  2 x 10 x 2 1     x   3  x   2 x 3 x  2
x  2 x 10 x 2 x 2 x   3   x   3  x 2
x  2 x 10 x  4 x 3   x   3  x   2 x 3 1    x   3  x   2 x  2 1
Vậy với x  0; x  9 thì Q  x  2
2. Thay x 16( thỏa mãn x  0; x  9 ) vào Q ta được: 1 1 1 Q    16  2 4  2 6 1 Vậy khi x 16thì Q  6 1 1 1 3. Q  
  3  x  2  x 1 x 1( thỏa mãn x  0; x  9) 3 x  2 3 1 Vậy với x 1 thì Q  3 1 1 1 1 1 9 x 2 7  x 4. Q       0   0   0   1 9 x  2 9 x  2 9 x  2 x  2
Vì x  0với mọi x  0; x  9 nên x  2  0 với mọi x  0; x  9
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 13 toanthaycu.com   
1  7  x  0  x  7  x  49 0   x  49
Kết hợp với điều kiện x  0; x  9 nên  x  9  0   x  49 1 Vậy với  thì Q  x  9  9
5. Vì x  0với mọi x  0; x  9 nên x  2  2 với mọi x  0; x  9 1 1 
 với mọi x  0;x  9 x  2 2 1
Vậy Q đạt giá trị lớn nhất bằng khi x  0 ( thỏa mãn x  0; x  9 ) 2 3 x  x  3 x 5 3 2 2 3 
Bài 2: Cho biểu thức P    . x 1 3  x x  2 x  3 a) Rút gọn P;
b) Tìm giá trị của P, biết x  4  2 3 ;
c) Tìm giá trị nhỏ nhất của P. Hướng dẫn giải ĐKXĐ: x  0; x  9 . 3 x  x  3 x 5 3 2 2 3  a) P    x 1 x  3  x  1 x 3
3 x 2 x 32 x 3 x  133 x 5   x   1  x 3
3x  9 x  2 x  6  2x  2 x  3 x  3  9 x 15   x   1  x 3 5x 17 x  6   x   1  x 3 5x 15 x  2 x  6   x   1  x 3
5 x 2 x 3 5 x 2   . x    1  x 3 x 1 b) Ta có x      2 4 2 3 3 1  x  3 1 ;
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 14 toanthaycu.com 5 3   1  2  5 332 3 5 3 3  Do đó: P       . 3   1 1   322 3 7 3 9 3 2 5 x  2 5 x  5  7 c) Ta có P   x 1 x 1 7 P  5  x 1. 7 7 Vì
 0 nên P có giá trị nhỏ nhất  lớn nhất x 1 x 1
 x 1 nhỏ nhất  x  0 .
Khi đó min P  5  7  2 .  x 1 2 x 5 x  2  3 x  x
Bài 3: Cho biểu thức Q      :  x  2 x  2 4   x x  4 x  4   a) Rút gọn Q; b) Tìm x để Q  2 ;
c) Tìm các giá trị của x để Q có giá trị âm. Hướng dẫn giải
ĐKXĐ: x  0; x  4; x  9 .  x 1 2 x 5 x  2  3 x  x a) Q      :  x  2 x  2 4   x x  4 x  4  
 x  1 x 22 x x 25 x 2 x3 x   x   x   : 2 2  x 22 x x x x x  x        2 2 3 2 2 4 5 2   x   x   . 2 2 x 3 x  x x  x    2 2 2   x   x  . 2 2 x 3 x   x  x    x  2 2 2 x  2   
x  2 x  2 . x 3 x  x  3 x  2 b) Q  2   2 x  3  x  2  2 x  6
  x  8  x  8  x  64 .(Thỏa mãn ĐKXĐ).
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 15 toanthaycu.com x  2 c) Q  0   0 x  3
 x  3  0 (vì x  2  0 )  x  3  x  9 .
Kết hợp với điều kiện xác định ta có Q  0 khi 0  x  9 và x  4 . a 3 a  2
Bài 4: Cho biểu thức B    với a  0; a  9 a  3 a  3 a  9 a) Rút gọn B.
b) Tìm các số nguyên a để B nhận giá trị nguyên Hướng dẫn giải a)
Với a  0; a  9 ta có: a 3 a  2 a 3 a  2 B    =   a  3 a  3 a  9 a  3 a  3 ( a  3)( a  3) a ( a  3) 3( a  3) a  2   
( a  3)( a  3) ( a  3)( a  3) ( a  3)( a  3)
a  3 a  3 a  9  a  2 11   a  3)( a  3) a  9 11 b) Để B  Z 
 Z  11(a 9)  (a 9) Ư (11) a  9
Ư (11)  1;11;1;1 
1 . Khi đó ta có bảng giá trị a  9 -11 -1 1 11 a -2 8 10 20 Không thoả mãn Thoả mãn Thoả mãn Thoả mãn Vậy a 8;10;2  0 thì B  Z x  2 x x 1 1 2x  2 x
Bài 5: Cho biểu thức A    ( Với x  0, x  1) 2 x x 1 x x  x  x x  x
a) Rút gọn biểu thức A.
b) Tìm x để biểu thức A nhận giá trị là số nguyên. Hướng dẫn giải x  2 a) A  . x  x 1
b) Cách 1: Với x  0, x  1 x  x 1  x 1 1.
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 16 toanthaycu.com x  2 x  2 1 Vậy 0  A    1  2. x  x 1 x 1 x 1 x  2 Vì A nguyên nên A = 1 
 1  x  1( Không thỏa mãn). x  x 1
Vậy không có giá trị nguyên nào của x để giả trị A là một số nguyên.
Cách 2: Dùng miền giá trị x  2 A 
 Ax+(A  1) x  A  2  0 x  x  1
Trường hợp 1: A  0  x  2  x   Trường hợp 2: 2 2 2 1
A  0    (A1)  4 A( A  2)  3A  6A 1  0  A  2 A   0 3 2 4 2 4
 A  2A 1   (A1)   A1;  2 doA  Z , A  0 3 3
Với A = 1 => x = 1 ( loại) x  2 Với A = 2   2  x  0 ( loại). x  x 1 x 3 x 2 9 x
Bài 6: Cho biểu thức P    với x  0; x  4 2 x 3 x x  x 6 a) Rút gọn P 7 b) Tìm x để P  12 1 c) Tìm x để P  2 1
d) Tìm tất cả các giá trị nguyên của x để nhận giá trị nguyên. P
e) Tìm tất cả các giá trị hữu tỷ của của x để P nhận giá trị nguyên. Hướng dẫn giải x 3 x 2 9  x
a) Với x  0; x  4 thì P    2 x 3 x x 3 x 2 x 6 x  3 x  2 9  x    2  x 3  x
x  x  32 x  3 x  3 x  2 9  x    2  x 3  x
x  x  32 x  3 x  3 x  2 9  x    
x  2 3  x  x  3 x 2
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 17 toanthaycu.com
 x   x   x  2 3 3 2  9  x   x 3 x  2
 x   x  2  x  x  2 9 2 9 2 x  2     x  3 x 2
 x 3 x 2 x 3 x 2
Vậy với x  0; x  4 thì P  x 3 7 x 2 7 b) P   
12 x 24  7 x 21 5 x  45 12 x 3 12
 x  9  x 81 ( thỏa mãn x  0; x  4) 7
Vậy với x  81 thì P  12 1 x 2 1 x 2 1 2 x  4 x 3 x 7 c) P       0     0 (3) x 3 x 3 2 x   0 2 2 2 3 x 3
Vì x  0 với mọi x  0; x  4 nên x 3 0 với mọi x  0; x  4
Nên (3)  x 7  0  x  7  x  49
Kết hợp với điều kiện x  0; x  4 . 1 Vậy x  49 thì P  2 1 x 3 x 25 5 d) Ta có   1 P x 2 x 2 x 2
1 nguyên  5 nguyên  5  x 2  x2 là Ư (5) 1  ;  5 P x 2 Lập bảng: x 2 -1 1 -5 5 x 1 3 -3 7 x 1 9 49 Thỏa mãn Thỏa mãn Loại Thỏa mãn 1 Vậy x  1;9;4  9 thì nguyên. P x 2 x 32 2 e) Ta có P   1 x 3 x 3 x 3 2 Vì
 0 nên P 1 với mọi x  0; x  4 x 3
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 18 toanthaycu.com 2 2 2 2 2 2 1 Mà x  3  3      1 1  x 3 3 x 3 3 x 3 3 3 1
Do đó  P 1. Vậy không có giá trị hữu tỷ nào của xđể P nguyên. 3       Bài 7: 1 x 1 1 x Cho biểu thức P  1 :    
 , (với x  0 và x  1).  x   x x x    
a) Rút gọn biểu thức P .
b) Tính giá trị của biểu thức P tại x  2022  4 2018  2022  4 2018 . Hướng dẫn giải 1 x 1 a) Ta có 1  x x  x       1 1 1 1 1 x x x x x x 1 x 1 x 1 x 1 Và     nên P  .  . x x  x
 x  1 x  x  1 x x 1 x x 1 x 2 2
b) Có x  2022  4 2018  2022  4 2018   2018  2   2018  2
 2018  2  2018  2  2018  2  2018  2  4 thỏa mãn điều kiện x  0 và x  1. 4 1 3
+ Vậy giá trị của biểu thức P tại x  4 là:  . 4 2 x  2 3 20  2 x
Bài 8: Cho hai biểu thức A  và B   với x  0, x  25 . x  5 x  5 x  25
a) Tính giá trị biểu thức A khi x  9 . 1 b) Chứng minh rằng B  . x  5
c) Tìm tất cả các giá trị của x để A  . B x  4 . Hướng dẫn giải
a) Tính giá trị biểu thức A khi x  9 . 9  2 3  2 5 Khi x  9 ta có A     9  5 3  5 2 1 b) Chứng minh rằng B  . x  5
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 19 toanthaycu.com 3 20  2 x 3 20  2 x
Với x  0, x  25 thì B     x  5 x 15
x  5  x  5 x 5
3 x 5  20 2 x 3 x 15 20 2 x x  5 1      (đpcm) x  5 x 5
 x 5 x 5  x 5 x 5 x 5
c) Tìm tất cả các giá trị của để A  . B x  4 .
Với x  0, x  25 Ta có: A  . B x  4 x  2 1  
. x  4  x  2  x  4 (*) x  5 x  5
Nếu x  4, x  25 thì (*) trở thành : x  2  x  4
 x  x  6  0   x  3 x  2  0
Do x  2  0 nên x  3  x  9 (thỏa mãn)
Nếu 0  x  4 thì (*) trở thành : x  2  4  x
 x  x  2  0   x   1  x  2  0
Do x  2  0 nên x  1  x  1 (thỏa mãn)
Vậy có hai giá trị x  1 và x  9 thỏa mãn yêu cầu bài toán. 2x   4 x 8
Bài 9: Cho biểu thức B    với x  0; x 16 x 3 x 4 x 1 x 4 a) Rút gọn B.
b) Tìm giá trị của x để B 1 3
c) Tính giá trị của x sao cho B không vượt quá 2
d) Tìm giá trị của B khi x thỏa mãn đẳng thức 2x 1  x
e) Tìm x để giá trị của B là một số nguyên. Hướng dẫn giải 2x  4 x 8
a) Với x  0; x 16thì B    x  x 4 x 4 x 1 x 4 2x  4 x 8    2x  4 x 8   
x  x  14 x  1 x 1
x 4  x 4 x  1 x 1 x 4
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 20 toanthaycu.com
2x 8 x  x 48 x  1 
2x 8  x  4 x 8 x 8 3x 12 x     x  4 x  1  x4 x  1  x 4 x  1 3 x  x 4 3 x 3 x  
Vậy với x  0; x 16 thì B  x  4 x  1 x 1 x 1 3 x 1 1 b) B 1 
1 3 x  x 1 2 x 1 x   x  x 1 2 4 1
( thỏa mãn x  0; x 16). Vậy x  thì B 1 4 3 3 3 x 3 x 6 x 3 x 3
c) B không vượt quá  B     3 3   0   0 2 2 x 1 2 x 1 2 2 x  1 3 x 3  x 1     0 (*) x   0 2 1 x 1
Vì x  0 với mọi x  0; x 16nên x 1 0 với mọi x  0; x 16 Suy ra (*)  x 1  0  x 1 x 1
Kết hợp với điều kiện x  0; x 16 3
Vậy 0  x 1thì B không vượt quá 2
d) Ta có 2x 1  x ( x  0; x 16 )  x   x  x  x    x 2 2 2 2 1 2 1 0 1  0  x 1( 3 1 3 3
thỏa mãn x  0; x 16 ) B 
 Vậy 2x1  x thì B  1 1 2 2 3 x 3 x 33 3 3 e) B    3  3( vì  0với x  0; x 16) x 1 x 1 x 1 x 1
Vì x  0 với mọi x  0; x 16nên x 11với mọi x  0; x 16 3 3 3   3    3   3  0 x 1 x 1 x 1
Suy ra 0  B  3 Mà B  Z nên B  0;1;  2 3 x TH1: B  0 
 0  x  0 ( thỏa mãn) x  3 3 x 3 9 TH2: B 1
1 3 x  x 3  x   x  ( thỏa mãn) x 3 2 4 3 x TH3: B  2 
 2  3 x  2 x 6  x  6  x  36( thỏa mãn) x 3  9    Vậy x 0; ;36    thì B  Z 4    
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 21 toanthaycu.com x   2 x 2 x 1 1 
Bài 10: Cho biểu thức P 1:        x   với 0  x x 1 x  x 1 x 1 a) Rút gọn P
b) Tính giá trị của P biết x  74 3 c) Tìm x để P  2 x 1 
d) Tìm m để có giá trị x thoả mãn P  m
e) Tìm giá trị nhỏ nhất của P Hướng dẫn giải x 2 x 2 x 1 1      a) Với x  0 thì P 1:          x x 1 x  x 1 x 1    x  2 x 2 x 1 1  1:       x  1x x  
1 x x 1 x 1
 x  1x x  1
 x  1x x  1  
x  2 x  2 x 1 x  x 1 x  x
 x 1x x 1 x x1   x  x  1 x x  x 1 Vậy với x  0thì P  x b) Với x        2 7 4 3 4 2.2. 3 3 2
3 thỏa mãn điều kiện x  0  x    2 2
3  2 3  2 3 ( vì 2  3 )
x  x 1 74 3 2 3 1 63 3  P     3 x 2 3 2 3
Vậy với x  74 3 thì P  3 x  x 1 c) P  2 x 1 
 2 x 1 x x 1 2x x  x 1 (thỏa mãn x  0) x
Vậy với x 1thì P  2 x 1  x  x 1 d) P 
 m  x x 1 m x  xm  1 x 1 0 (1) x
Vì 1 0nên (1) là phương trình bậc hai. Đặt t  x t  0 (1) trở thành 2 t m   1 t 1 0 (2)
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 22 toanthaycu.com Ta có  m  2 2 2
1 4  m  2m3  m m 3m3  mm  1  3m   1  m   1 m   3
Phương trình (1) có nghiệm  Phương trình (2) có nghiệm dương
TH1: Phương trình (2) có 2 nghiệm dương 1   0    
m 1m 30 m10       m 1  S   m 1 0 m 1 0  P10 
TH2: Phương trình (2) có 2 nghiệm trái dấu
 S 1 0 ( vô lý) Loại
TH3: Phương trình (2) có 1 nghiệm dương và 1 nghiệm bằng 0
Với t  0thay vào (2) ta được 2 0 m  
1 .0 1 0  1 0( vô lý )Loại
Vậy m 1 là giá trị cần tìm. x  x 1 1 e) P   x  1 x x 1 Vì x  0 nên x  0;  0. x 1
Áp dụng bất đẳng thức Cô si cho hai số dương x; ta được: x 1 1 x   2 x.  2 x x 1
Dấu “=” xảy ra  x 
 x 1( thỏa mãn x  0) x
 P  211. Vậy giá trị nhỏ nhất của P 1 khi x 1  x   x 2 x 3 x 2       
Bài 11: Cho biểu thức P  1   :             
x 1  x 3 2 x x  x 6 với x  0; x  4 a) Rút gọn P 3 5
b) Tính giá trị của P biết x  2 c) Tìm x  Z để P  Z d) So sánh P với 1
e) Tìm các giá trị của x để P  x 3.
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 23 toanthaycu.com Hướng dẫn giải a) Với x  0; x  4  x   x 2 x 3 x 2        P  1   :            
x 1  x 3 2 x x  x 6 x 1 x  x 2 x 3 x 2         :        x 1
 x 3 2 x x3 x 2 x 6   1  x 2 x 3 x 2   :     x 1  x 3 2 x x   x  32 x  3   1  x 2 x 3 x 2   :     x 1  x 3 x 2   x  3 x  2
 x 2 x 2 x 3 x  3 x2 1  : x 1
 x 3 x2  x 3 x x x x       2 1 4 9 2 1  : x  x     3  x   . 1 2 x 1 x 3 x 2  x 2
. Vậy với x  0; x  4 thì P  x 1 x 1       2 5 1 3 5 6 2 5 5 2. 5.1 1 b) Với x     thỏa mãn x  0; x  4 2 4 4 4  5 21 51 51  x    ( vì 5 1) 4 2 2 5 12 x 5 5 5   1 2 5 5 2  P     x 1 5 1 5 1  5  1 5  1 1 2 5 5 55  5 6 5 10 3 5 5    4 4 2 x 2 x 13 3 c) P   1 x 1 x 1 x 1 3 P  Z 
 Z  3  x  1 x 1 là Ư(3) x 1 Ư(3)=1;  3
Mà x  0x  0; x  4  x 1 0x  0; x  4 nên:
TH1: x 11 x  0  x  0( thỏa mãn)
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 24 toanthaycu.com
TH2: x 1 3  x  2  x  4 ( loại) Vậy x    0 thì P  Z x 2 x 2 x 1 3 d) Xét hiệu P 1 1   0 x  0;x  4 x 1 x 1 x 1 Suy ra P 1 x 2 e) P  x 3 
 x 3  x 2  x  3 x  1 x 1
 x 2  x3 x  x 3  x3 x 1   0(2)
Đặt x  t t  0;t  2 (2) trở thành: 2 t 3t 1 0   2 3 4.1.(1) 13  3 13 t  TM  2 2     3   13 22  6 13   x      ( thỏa mãn điều kiện) 3 13   2  4   t  loai  2 22  6 13 Vậy x  là giá trị cần tìm. 4 1 x
Bài 12: Cho biểu thức: A  với x  0 1 x
a) Khi x  62 5 tính giá trị biểu thức A 1  5 x 2    x  1
b) Rút gọn biểu thức B    :  với x  0; x  5 x  25  x 5 x 5
c) Tìm x để biểu thức M  B  A nhận giá trị nguyên. Hướng dẫn giải
a) Với x  62 5 thỏa mãn điều kiện x  0 Ta có x        2 6 2 5 5 2 5 1 5 1  x    2
5 1  5 1  5 1 ( vì 5 1)
1 5  1 2 5 2 5 5  A    1 5 1 5 5
b) Với x  0; x  5 thì   1  5 x 2    x  1  15 x 2  x 1 B   :        x   x   x 
 x 5 x   : 25 5 5 5 x 5 x 5  15 x  2 x 10 x 1 5  x x 5  1    x   5  x   : 5 x   x 5 x . 5 5 x 1 x 1
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 25 toanthaycu.com 1
Vậy với x  0; x  5 thì B  x 1 1 1 x 2 x 1   x 3 3 c) Ta có M  B  A      1 x 1 1 x x 1 x 1 x 1
Vì x  0x  0; x  5  x 11x  0; x  5 3 3   3  M  1  1  3 2 x 1 x 1 3 3 Lại có  0  1 1 x 1 x 1  1
  M  2 . Mà M  Z  M  0;1;2 2 x TH1: M  0 
 0  2 x  0  x  4 TM  x 1 2 x 1 TH2: M 1
1 2 x  x 1 2 x 1 x  TM  x 1 4 2 x TH3: M  2 
 2  2 x  2 x  2  3 x  0  x  0 TM  x 1  1   Vậy x 0;4;    thì M  Z 4    
Dạng 6: Bài tập chinh phục điểm 10
Bài 1. Cho a  3  5  2 3  3  5  2 3 . Chứng minh rằng 2 a  2a  2  0 . Giải 2
a  3  5  2 3  3  5  2 3  2 9  5 2 3  6  2 4  2 3  
  2          2 6 2 3 1 6 2 3 1 4 2 3 1
3 . Do a  0 nên a  3 1. Do đó a  2 1  3 hay 2 a  2a  2  0 . Bài 2. 4 3 2 x  4x  x  6x 12
a) Cho x  4  10  2 5  4  10  2 5 . Tính giá trị biểu thức: P  . 2 x  2x 12 b) Cho 3
x  1 2 . Tính giá trị của biểu thức 4 4 3 2
B  x  2x  x  3x 1942 .(Trích đề thi vào lớp 10
Trường PTC Ngoại Ngữ - ĐHQG Hà Nội năm 2015-2016). c) Cho 3 3
x 1 2  4 . Tính giá trị biểu thức: 5 4 3 2
P  x  4x  x  x  2x  2015 Giải 2   a) Ta có: 2 x 
4  10  2 5  4  10  2 5
 8  2 4  10  2 5 . 4  10  2 5      x     
  2         2 2 8 2 6 2 5 8 2 5 1 8 2 5 1 6 2 5
5 1  x  5 1. Từ đó ta suy
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 26 toanthaycu.com ra  x  2 2 1  5  x  2x  4 . x 2x2 2  2 2 x  2x 2 12 4 3.4 12 Ta biến đổi: P   1. 2 x  2x 12 4 12 b) Ta có 3
x  1 2   x  3 3 2
1  2  x  3x  3x  3  0 . Ta biến đổi biểu thức P thành: 2 3 2 P  x x  x  x   x  3 2
x  x  x     3 2 ( 3 3 3) 3 3 3
x  3x  3x  3 1945  1945 c) Để ý rằng: 3 2 3
x  2  2 1 ta nhân thêm 2 vế với 3 2 1 để tận dụng hằng đẳng thức: 3 3      2 2 a b
a b a  ab  b  . Khi đó ta có:  3   x   3   3 2 3 2 1 2 1 2  2   1   3   3
2 1 x  1  2x  x 1  2x   x  3 3 3 2
1  x  3x  3x 1  0 . Ta biến đổi: 5 4 3 2
P  x  x  x  x  x    2 x  x   3 2 4 2 2015 1 x  3x  3x   1  2016  2016
Bài 3. Tính C  9  5 3  5 8 10 7  4 3 Giải Để ý rằng:     2 7 4 3 2 3  7  4 3  2  3
Suy ra C  9  5 3  5 8 10(2  3)  9  5 3  5 28 10 3      2 9 5 3 5 5 3 .Hay
C  9  5 3  5(5  3)  9  25  9  5  4  2 Bài 4. Chứng minh:
a) A  7  2 6  7  2 6 là số nguyên. 84 84 b) 3 3 B  1  1 là một số nguyên 9 9 Hướng dẫn giải a) Dễ thấy A  0, Ta có A      2 2 7 2 6 7 2 6
 7  2 6  7  2 6  2 7  2 6. 7  2 6 14  2.5  4 Suy ra A  2 .
b) Áp dụng hằng đẳng thức: u  v3 3 3
 u  v  3uv u  v . Ta có: 3  84 84  84 84  84 84   84 84  3 3 3 3 3 B   1  1  1 1  3 1 . 1  3 3  1  1  .  9 9  9 9  9 9        9 9    84  84  84 Hay 3 3 3 3 3 B  2  33 1 1 .B  B  2  3 1
B  B  2  B  B  B  2  0  9  9  81    2    1  7 B   2 1 B  B  2  0 mà 2 B  B  2  B    0  
suy ra B  1 . Vậy B là số nguyên.  2  4
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 27 toanthaycu.com a 1 8a 1 a 1 8a 1 1 Bài 5. Chứng minh rằng: 3 3 x  a   a 
với a  là số tự nhiên. 3 3 3 3 8 Lời giải
Áp dụng hằng đẳng thức: u  v3 3 3
 u  v  3uv u  v Ta có 3 x  a    a 3
x  x   a   x  a    x   2 2 1 2 2 1 2 0 1 x  x  2a  0 Xét đa thức bậc hai 2
x  x  2a với   1 8a  0 1 1 1 + Khi a  ta có 3 3 x   1 . 8 8 8 1 1
+ Khi a  , ta có  18a âm nên đa thức (1) có nghiệm duy nhất x  1 Vậy với mọi a  ta có: 8 8 a 1 8a 1 a 1 8a 1 3 3 x  a   a  1 là số tự nhiên. 3 3 3 3
Bài 6. Tính x  y biết  2 x  x   2
2015 y  y  2015   2015. Lời giải Nhận xét:  2x   x 2x   x 2 2 2015 2015
 x  2015  x  2015 .
Kết hợp với giả thiết ta suy ra 2 2
x  2015  x  y  2015  y 2 2 2 2
 y  2015  y  x  2015  x  x  2015  x  y  2015  y  x  y  0 Bài 7. 1 1 1 a) Chứng minh rằng:   ....  4 . 1  2 3  4 79  80 1 1 1 1  1  b) Chứng minh rằng:    ...  2 1   . 1 2 2 3 3 4 n n 1  n 1  1 1 1 1 1 c) Chứng minh: 2 n  2      ...
 2 n 1 với mọi số nguyên dương n  2 . 1 2 3 4 n Lời giải 1 1 1 1 1 1 a) Xét A   .... , B    .. 1  2 3  4 79  80 2  3 4  5 80  81 Dễ thấy A  B . 1 1 1 1 1 Ta có A  B     ....  1  2 2  3 3  4 79  80 80  81  k 1 1  k  Mặt khác ta có:       
k   k  k   k  k 1 k k k 1 1 1
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 28 toanthaycu.com
Suy ra A  B   2  1   3  2 ...  81  80  81 1  8 . Do A  B suy ra
2A  A  B  8  A  4 . 1 1 1 1 b) Để ý rằng:   
với mọi k nguyên dương. k k 1
k(k 1)  k 1  k  2k k 1  1   1 1   1 1   1  Suy ra VT  2 1  2   .. 2   2 1         .  2   2 3   n n 1   n 1  1 1 1 1 1 c) Đặt P      ... 1 2 3 4 n 2 1 2 2 Ta có:   
với mọi số tự nhiên n  2 . n  n 1 n 2 n n  n 1 2 2 2
Từ đó suy ra 2 n 1  n      2 n  n 1 hay n 1  n 2 n n  n 1  n  n 2 2 1   2 n  n 1 n
Do đó: 2  2  1 3  2... n1 n  T  và
T  1 2  2  1 3  2.... n  n1 .
Hay 2 n  2  T  2 n 1. 1 1 1 1 1 1 Bài 8. Cho A    ... và B  1  ... . 1 2 2  3 3  4 120  121 2 35 Chứng minh rằng B  A . Lời giải 1 1 1 1 Ta có: A     ... 1 2 2  3 3  4 120  121 1 2 2  3 120  121   
         ... 1 2 1 2 2 3 2 3
 120  121 120  121 1 2 2  3 120  121    ... 
 2 1 3  2 ... 121  120  1   121 10 (1) 1 1 1 1 2 2 Với mọi * k   , ta có:    2 k 1  k  k k  k k  k 1 1 1 Do đó B  1  ...
 B  2 2  1  3  2  4  3 ... 36  35 2 35
 B  2 1  36  21 6 10 (2) . Từ (1) và (2) suy ra B  A .
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 29 toanthaycu.com
x  x  4 x  4  x  4 x  4  Ví dụ 9. Cho A  với x  4 2 x  8x 16
a) Rút gọn A .Tìm x để A đạt giá trị nhỏ nhất.
b) Tìm các giá trị nguyên của x để A có giá trị nguyên. Lời giải
a) Điều kiện để biểu thức A xác định là x  4 .  
x   x  4  22   x  4  22  x
x  x  4  2  x  4  2     x42  x42 A    x  2 x  4 4 x  4
x  x  4  2  2  x  4 4x 16
+ Nếu 4  x  8 thì x  4  2  0 nên A    4  x  4 x  4 x  4
Do 4  x  8 nên 0  x  4  4  A  8 .
+ Nếu x  8 thì x  4  2  0 nên
x  x  4  2  x  4  2 2x x  4 2x 8 A     2 x  4 
 2 16  8 (Theo bất đẳng thức x  4 x  4 x  4 x  4 8
Cô si). Dấu bằng xảy ra khi và chỉ khi 2 x  4 
 x  4  4  x  8 . x  4
Vậy GTNN của A bằng 8 khi x  8 . 16 16
b) Xét 4  x  8 thì A  4 
, ta thấy A Z khi và chỉ khi
 Z  x  4 là ước số nguyên x  4 x  4
dương của 16 . Hay x  41;2;4;8;1  6  x  5;6;8;12;2 
0 đối chiếu điều kiện suy ra x  5 hoặc x  6 . 2x 2 x  m  4  2 2 m  4 8 + Xét x  8 ta có: A  , đặt x  4  m   khi đó ta có: A   2m  suy x  4 m  2 m m ra m 2;4;  8  x 8;20;6  8 .
Tóm lại để A nhận giá trị nguyên thì x 5;6;8;20;6  8 .
Bài 10. Cho a  4  10  2 5  4  10  2 5 . 2 3 2 a  4a  a  6a  4
Tính giá trị của biểu thức: T  . 2 a  2a 12 Giải
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 30 toanthaycu.com a     
        2 2 8 2 16 10 2 5 8 2 6 2 5 8 2 5 1  8  2 5  
1  6  2 5 . Vì a  0 nên
a  5 1. Do đó a  2 1  5 hay 2
a  2a  4 . Biểu diễn a 2a2 2  3 2 a  2a 2  4 4 3.4  4 1 T    . 2 a  2a 12 4 12 2 Bài 11. Cho 3
a  2  7  61 46 5 1. a) Chứng minh rằng: 4 2 a 14a  9  0 . b) Giả sử f  x 5 4 3 2
 x  2x 14x  28x  9x 19 . Tính f a. Giải: a) Vì     3 3 3 61 46 5 1 2 5  1 2 5
Từ đó a  2  7 1 2 5 1  2  5  a    2 2 2 4 2 2
5  a  7  2 10  a 14a  9  0 . b) Do f  x   4 2
x 14x  9 x  2 1 và 4 2
x 14a  9  0 nên ta được f a 1. Bài 12. Cho 3 3
a  38 17 5  38 17 5 .
Giả sử có đa thức f  x  x  x  2016 3 3 1940 . Hãy tính f a . Giải Vì 3 3 3
a  38 17 5  38 17 5  3.3. 38 17 5. 38 17 5  a   a  a  a   f a    2012 3 3 2016 76 3 3 76 76 1940  2016 .
Bài 13. Chứng minh rằng với mọi số nguyên dương n  3 , ta có 1 1 1 1 65    ...  . 3 3 3 3 1 2 3 n 54 Giải: 1 1 1 1 Đặt P     ...
. Thực hiện làm trội mỗi phân số ở vế trái bằng cách làm giảm mẫu, ta có: 3 3 3 3 1 2 3 n 2 2 2 1 1     , k  1 3 3 k k  k k  1k   1 k  1k k k   1
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 31 toanthaycu.com  1 1 1   1 1   1 1   1 1 
Cho k  4,5,..., n thì 2P  2        ...          3 3 3 1 2
3   3.4 4.5   4.5 5.6  n   1 n n n   1  251 1 1 251 1 65       65 . Do đó P  (đpcm). 108 3.4 n n   1 108 3.4 27 64 43 1 1 1 44 Bài 14. Chứng minh rằng:    ...  44 2 1 1 2 3 2  2 3 2002 2001  2001 2002 45 Giải: 1 1 1 Đặt S    ... n 2 1 1 2 3 2  2 3 n  1 n  n n 1 Để ý rằng : 1 k   1 k  k k 1 k   1 k  k k 1 1 1        k   , k 1 1 k  k k 1 k  2 2 1 k  k k   1 k k   1 k k 1
Cho k 1, 2,..., n rồi cộng vế với vế ta có: 1 1 1 1 1 1 1 S      ...  1 n 1 2 2 3 n n 1 n 1 1 Do đó S 1 2001 2002
Như vậy ta phải chứng minh: 43 1 44 1 1 1  1     44 2002 45 45 2002 44
 44  2002  45  1936  2002  2025
Bất đẳng thức cuối cùng đúng nên ta có điều phải chứng minh.
Thầy Trần Đình Cư. Gv chuyên luyện thi toán tại TP Huế. SĐT: 0834 332 133 Page 32