Chuyên Đề Tập Hợp Số Hữu Tỉ Toán 7 Có Lời Giải Chi Tiết

CHƯƠNG 1: SỐ HỮU TỈ
Bài 1: TẬP HỢP SỐ HỮU TỈ
I. LÍ THUYẾT TRỌNG TÂM
1. Khái niệm số hữu tỉ và biểu diễn số hữu tỉ trên trục số: a
a) Khái niệm: Số hữu tỉ là số viết được dưới dạng phân số với a,b  ;b  0 b
Tập hợp số hữu tỉ được kí hiệu là . a a
*) Chú ý: Mỗi số hữu tỉ đều có một số đối. Số đối của số hữu tỉ là − b b
*) Nhận xét: Các số thập phân đều viết được dưới dạng phân số thập phân nên chúng đều là các
số hữu tỉ. Số nguyên, hỗn số cũng là các số hữu tỉ
b) Biểu diễn số hữu tỉ trên trục số
+ Biểu diễn số hữu tỉ trên trục số: Tương tự như đối với số nguyên, ta có thể biểu diễn mọi số hữu tỉ trên trục số
+ Trên trục số, điểm biểu diễn số hữu tỉ a được gọi là điểm a
+ Nhận xét: Trên trục số, hai điểm biểu diễn hai số hữu tỉ đối nhau a và a
− nằm về hai phía khác
nhau só với điểm O và có cùng khoảng cách đến O
2. Thứ tự trong tập hợp các số hữu tỉ
+ Ta có thể so sánh hai số hũu tỉ bất kì bằngg cách viết chúng dưới dạng phân số rồi só sánh hai phân số đó
+ Với hai số hữu tỉ x, y ta luôn có hoặc x = y hoặc x  y hoặc x  y .
+ Cho ba số hữu tỉ a,b,c , ta có:
Nếu a  b và b  c thì a  c (tính chất bắc cầu)
+ Trên trục số, nếu a  b thì điểm a nằm trước điểm b *) Chú ý:
+ Số hữu tỉ lớn hơn 0 được gọi là số hữu tỉ dương;
+ Số hữu tỉ nhỏ hơn 0 được gọi là số hữu tỉ âm.
+ Số 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.
II. CÁC DẠNG BÀI TẬP
Dạng 1: Nhận biết các số hữu tỉ, quan hệ trên tập hợp số Phương pháp giải: Trang 1
+ Muốn xác định xem một số có là số hữu tỉ hay không, ta hãy biến đổi xem số đó có dạng a với b
a,b  ;b  0 hay không.
+ Mối quan hệ giữa các tập hợp số đã biết với tập hợp số hữu tỉ:   .
+ Sử dụng các kí hiệu ,  ,
 , , , , để biểu diễn mối quan hệ giữa số và tập hợp hoặc giữa các tập hợp với nhau. Bài 1: 5 2 2 − 1 − 3 0 3 9 − Cho các số sau: ;3 ; ; ; ; ;
;3,5;0;6, 25 , hãy cho biết số nào là số hữu tỉ, số nào không 4 5 7 17 3 0 9 − phải là số hữu tỉ? Lời giải 35 625 5 2 2 − 1 − 3 0 9 − Ta viết: 3,5 = ;0,625 =
. Vậy các số hữu tỉ là ;3 ; ; ; ; ;3,5;0;6, 25 100 1000 4 5 7 17 3 9 − 3
Số không phải số hữu tỉ là (vì có mẫu số là 0). 0 Bài 2: Số nguyên ...− 2; 1
− ;0;1;2;... có là số hữu tỉ không? Vì sao? Lời giải
Vì các số nguyên đề có thể viết được dưới dạng phân số với mẫu số là 1 nên các số nguyên đều là số hữu tỉ. Bài 3: Điền kí hiệu ( ;  )
 thích hợp vào ô trống: 6,5 6,5 4 2 0 -3,5 7 Lời giải Trang 2 6,5  6,5  4 2  0  -3,5  7 Bài 4: Điền kí hiệu (; )
 thích hợp vào ô trống: −5 −5 −5 1 0 − 5 8 Lời giải −5  −5  −5  1 0  −  5 8 Bài 5:
Điền các kí hiệu ¥ ,¤ ,¢ vào ô trống cho đúng (điền tất cả các khả năng có thể): a) 11..... b) 26 − ..... c) 1 ..... d) 3 − ..... 5 4 Lời giải
a) Có thể điền ¥ ,¢ ,¤ b) Có thể điền ¢ ,¤ c) Có thể điền ¤ d) Có thể điền ¤ Bài 6:
Điền các kí hiệu thích hợp ( ,  ,
 , , , , ) vào ô trống: 1 − 7 3 − ;  ;  . 2 9 Hướng dẫn giải 1 − 3 −   ; 2 7  ;   . 9 Trang 3 Bài 7:
Điền các kí hiệu thích hợp ( ,  ,
 , , , , ) vào ô trống: 10 3 1 ; −1 ; − ; ; 2 8 − 4 − 1 2 ;  ;  ;  . 9 4 5 Lời giải 10 10 1  ; −1  ; −  do − = − 5 ; 2 2 3 4 − 1 2  ;  ;  , ;  ;  ; . 8 − 9 4 5 Chú ý:
+ Kí hiệu  là “thuộc”.
+ Kí hiệu  là “không thuộc”.
+ Kí hiệu  là “tập hợp con”.
+ Kí hiệu  là “chứa trong” hoặc “chứa”.
+ Kí hiệu là “tập hợp các số tự nhiên”. Bài 8: Điền kí hiệu ( ,  ,
 ) thích hợp và ô trống: 5 − 2 − 4 − ; ; − 8 ; ; 3 9 1 2 2 − ; − ; − ; . 11 7 19 Lời giải 5 − 2 − 4 −  ;  ; −8 ;  ; 3 9 1 2 2 −  ; −  ; −  ;  . 11 7 19 Bài 9:
Điền các kí hiệu ; ; thích hợp vào ô trống (điền tất cả các khả năng có thể): 2 − 6 −  ; 22 ;  ;  ; 23 5 − 3  ;  ; − 21 ;; 1  . 7 4 Lời giải Trang 4 2 − 6 −  ; ; 22  ; ; ;  ;  ; ; 23 5 − 3  ;  ; ; − 21 ; 1  ; . 7 4 Bài 10:
Khẳng định nào dưới đây sai?
A. Số 19 là một số tự nhiên. B. Số 5
− là một số nguyên âm. 15 C. Số − là một số hữu tỉ.
D. Số 0 là một số hữu tỉ dương. 19 Lời giải Chọn đáp án D
Vì số 0 không là số hữu tỉ âm, cũng không là số hữu tỉ dương. Bài 11:
Viết Đ vào ô có khẳng định đúng và S vào ô có khẳng định sai:
1. Số nguyên là số hữu tỉ
2. Số nguyên âm không là số hữu tỉ âm
3. Tập hợp gồm các số hữu tỉ âm và các số hữu tỉ dương 1 4. Số 1 là số hữu tỉ 2 1 − 5. Số không là số hữu tỉ 5 − Lời giải 1. Đ 2. S 3. S 4. Đ 5. S Bài 12:
Các số hữu tỉ sau là âm hay dương? 5 4 3 − a) − b) c) 7 9 − 8 − 14 − 5 d) e) 9 8 − Lời giải 3 − Số hữu tỉ dương là 8 − 5 4 14 − 5 Số hữu tỉ âm là − ; ; ; 7 9 − 9 8 − Trang 5 Bài 13:
Các số hữu tỉ sau là âm hay dương? 3 − 2 a) − b) 5 9 0 c) −4 d) 3 − Lời giải 3 − a) − là số hữu tỉ dương 5 2
b) là số hữu tỉ dương 9
c) −4 là số hữu tỉ âm 0 d)
= 0 không là số hữu tỉ âm cũng không là số hữu tỉ dương. 3 − Bài 14: 11 7 − 5 − 1 1
Tìm số đối của các số sau: ; 4 − ; ;0; ; ; 2 6 7 3 2 Lời giải 11 7 − 5 − 1 1 11 7 5 1 1 Số đối của ; 4 − ; ;0; ; ; lần lượt là − ;4; ;0; ; − ; − 2 6 7 3 2 2 6 7 3 2 Bài 15: 1 3 −
Tìm số đối của các số sau: 3 ;( 5 − ); ; −( 8 − ) 2 4 − Lời giải 1 3 − 1 3 Số đối của 3 ;( 5 − ); ; −( 8 − ) lần lượt là 3 − ;5; − ; 8 − 2 4 − 2 4 Bài 16:
Dãy số nào dưới đây cùng biểu diễn một số hữu tỉ 3 − 6 5 − 1 − 0 a) 0 − ,3; ; b) 5; ; 10 20 1 − 2 2 7 − 1 − 4 9 6 − 3 c) ; ; d) ; ; 13 17 26 12 8 − 4 Lời giải Trang 6 3 − 6 a) Ta có: 0 − ,3 = 
. Dãy số này không biểu diễn một số hữu tỉ 10 20 5 − 10 − b) Ta có: 5 = 
. Dãy số này không biểu diễn một số hữu tỉ 1 − 2 2 7 − 14 − c)  =
. Dãy số này không biểu diễn một số hữu tỉ 13 17 26 9 6 − 3 d) ;
; . Dãy số này không biểu diễn một số hữu tỉ 12 8 − 4 Bài 17: 5 −
Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ
, từ đó rút ra dạng tổng quát của 4 5 −
các phân số bằng phân số . 4 1 − 0 15 2 − 0 1 − 9 25 12 , − , , , , 4 12 1 − 6 16 2 − 0 15 Lời giải 1 − 0 5 − 15 5 − 2 − 0 5 1 − 9 5 − 25 12 5
Rút gọn các phân số ta được: = , − = , = , = , , = 4 4 12 4 1 − 6 4 16 4 2 − 0 15 4 5 − 10 − 15 25
Vậy các phân số biểu diễn số hữu tỉ là , − , 4 8 12 20 − 5 − 5k
Dạng tổng quát của các phân số bằng phân số là −
(k  ,k  0) 4 4k Bài 18: 14
a) Tìm 3 phân số bằng cạc phân số 21 4
b) Tìm 3 phân số bằng cạc phân số 12 − Lời giải 14 2 4 16 a) Ta có: = = = 21 3 6 24 4 1 − 2 8 b) Ta có: = = − = 1 − 2 3 6 2 − 4 Bài 19:
Viết dạng chung của các số hữu tỉ bằng: 123123 − 434343 a) b) 164164 868686 Trang 7 Lời giải 1 − 23123 1 − 23.1001 1 − 23 a) Ta có: = = 164164 164.1001 164 123123 − 123. − m
Vậy dạng chung của số hữu tỉ là
với m  , m  0 164164 164.m 434343 1.434343 1 a) Ta có: = = 868686 2.434343 2 434343 1.m
Vậy dạng chung của số hữu tỉ là
với m  , m  0 868686 2.m 3 5 -2 -1 0 1 2 3 Bài 20: 2,3 3 5 − 12 0 2 3 − Cho các số sau: ; 1 ; ;− ; ; ;
; −1,6;0,35 . Hãy cho biết số nào là số hữu tỉ, số nào 5 4 9 7 8 0 3 −
không phải là số hữu tỉ? Lời giải 3 5 − 12 0 3 − Các số hữu tỉ là 1 ; ;− ; ; ;−1,6;0,35 4 9 7 8 3 − 2,3 2
Số không phải là số hữu tỉ là ; 5 0 Bài 21:
Các số hữu tỉ sau là âm hay dương? 1 − 3 − ; ; 2 ; −6 4 11 5 − Lời giải 3 − Số hữu tỉ dương là: ; 2 11 5 − 1
Số hữu tỉ âm là: − ; −6 4 Bài 22: 3 4 − 2
Tìm số đối của các số: 5 ;( 9 − ); ;−( 5 − );− ;0,56 . 7 1 − 1 3 Lời giải Trang 8 3 4 − 2 3 4 2 Số đối của 5 ;( 9 − ); ;−( 5
− );− ;0,56 lần lượt là: 5 − ;9;− ; 5 − ; ;− 0,56 7 1 − 1 3 7 11 3 Bài 23: 2
Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ ? 5 − 8 − 9 10 − 6 9 ; ; ; ; 20 12 − 25 15 − 15 − Lời giải 2 2 − Ta có =
. Rút gọn các phân số đã cho ta được: 5 − 5 8 − 4 − − − − − − = 9 3 10 2 6 2 9 3 ; = ; = ; = ; = 20 5 1 − 2 4 25 5 1 − 5 5 1 − 5 5 2 10 − 6
Vậy các phân số biểu diễn số hữu ti là: ; . 5 − 25 15 − Bài 24:
Biểu diễn các số hữu tỉ sau trên cùng một trục số. 1 − 3 − 3 a) b) c) 4 4 − 4 − 14 − 7 d) e) 9 4 Lời giải 3 − 3 3 3 − 1 − 4 5 7 3 Ta có: = ; = ; = 1 − ; = 1 . 4 − 4 4 − 4 9 9 4 4 -2 -1 0 1 2 -14 3 -1 -3 7 9 -4 4 -4 4 Bài 25: 2 −
Hãy tìm năm phân số bằng phân số . 7 Lời giải 2 − 4 − 6 − 8 − 1 − 0 1 − 2
Năm phân số bằng phân số là: ; ; ; ;  7 14 21 28 35 42 Bài 26: Trang 9
Tìm số nguyên x để các số sau là số hữu tỉ: x 3 − 7 a) b) c) 11 x 3 − x Lời giải x a) Để
là số hữu tỉ thì x  . 11 3 − b) Để
là số hữu tỉ thì x  và x  0 . Suy ra x là số nguyên khác 0 . x 7 c) Để
là số hữu tỉ thì −3x  và −3x  0 . Suy ra x là số nguyên khác 0 . 3 − x Bài 27:
Tìm số nguyên x để các số sau là số hữu tỉ: 5 4 − a) b) x − 3 5x +10 Lời giải 5 a) Để
là số hữu tỉ thì x − 3 và x − 3  0  x  3 . x − 3 5
Vậy khi x là số nguyên khác 3 thì là số hữu tỉ x − 3 4 − b) Để
là số hữu tỉ thì 5x +10 và 5x +10  0  x  −2 . 5x +10 4 −
Vậy khi x là số nguyên khác −2 thì là số hữu tỉ. 5x +10 Bài 28:
Tìm tất cả các số nguyên x để các phân số sau có giá trị là số nguyên: x −10 a) 10x −9 A = b) B = 2x −3 x − 5 Lời giải a) 10x −9 6 A = = 5+ 2x −3 2x − 3 6 A 
  2x − 3  Ư(6) 2x − 3  2x − 3  6
− ; − 3 ; − 2 ; −1; 1; 2; 3 ;  6
 x  0; 1 ; 2;  3 , ( x  ) Trang 10 x −10 5 b) B = =1−
. Làm tương tự câu a ta được x {4;6;0;10}. x − 5 x − 5 Bài 29:
Cho số x thỏa mãn 2
x = 5 . Hỏi số x có là số hữu tỉ không? Lời giải
x không thể là số hữu tỉ.
Dạng 2: Biểu diễn số hữu tỉ
Bài toán 1: Biểu diễn số hữu tỉ trên trục số *) Phương pháp giải:
Để biểu diễn một số hữu tỉ trên trục số, ta thường làm như sau:
Bước 1. Ta viết số đó dưới dạng phân số có mẫu dương. Khi đó mẫu của phân số sẽ cho ta biết
đoạn thẳng đơn vị được chia thành bao nhiêu phần bằng nhau.
Bước 2. Lấy đoạn thẳng mới làm đơn vị.
Bước 3. Số hữu tỉ dương (âm) nằm bên phải (trái) điểm 0 và cách điểm 0 một khoảng bằng giá trị
tuyệt đối của số hữu tỉ đó. Bài 1: 3
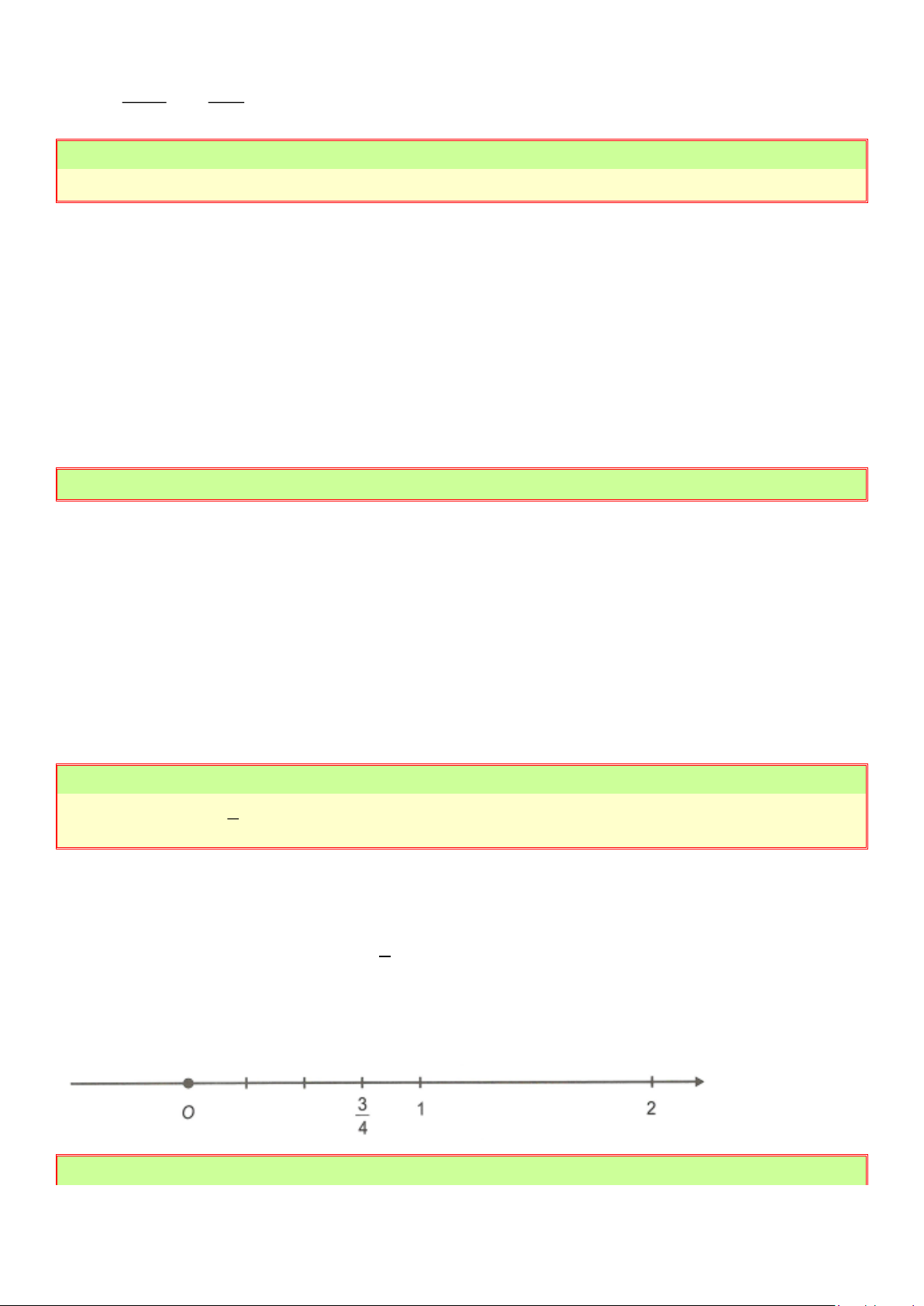
Biểu diễn số hữu tỉ trên trục số. 4 Lời giải
Chia các đoạn thẳng đơn vị ra làm 4 phần bằng nhau. 1
Lấy đoạn thẳng mới làm đơn vị (bằng đơn vị cũ). 4
Lấy điểm nằm bên trái điểm 0, cách điểm 0 một đoạn bằng 3 đơn vị mới.
Điểm vừa lấy là điểm phải tìm. Bài 2: Trang 11 3 Biểu diễn số hữu tỉ trên trục số. 5 − Lời giải 3 3 − Ta có = 5 − 5
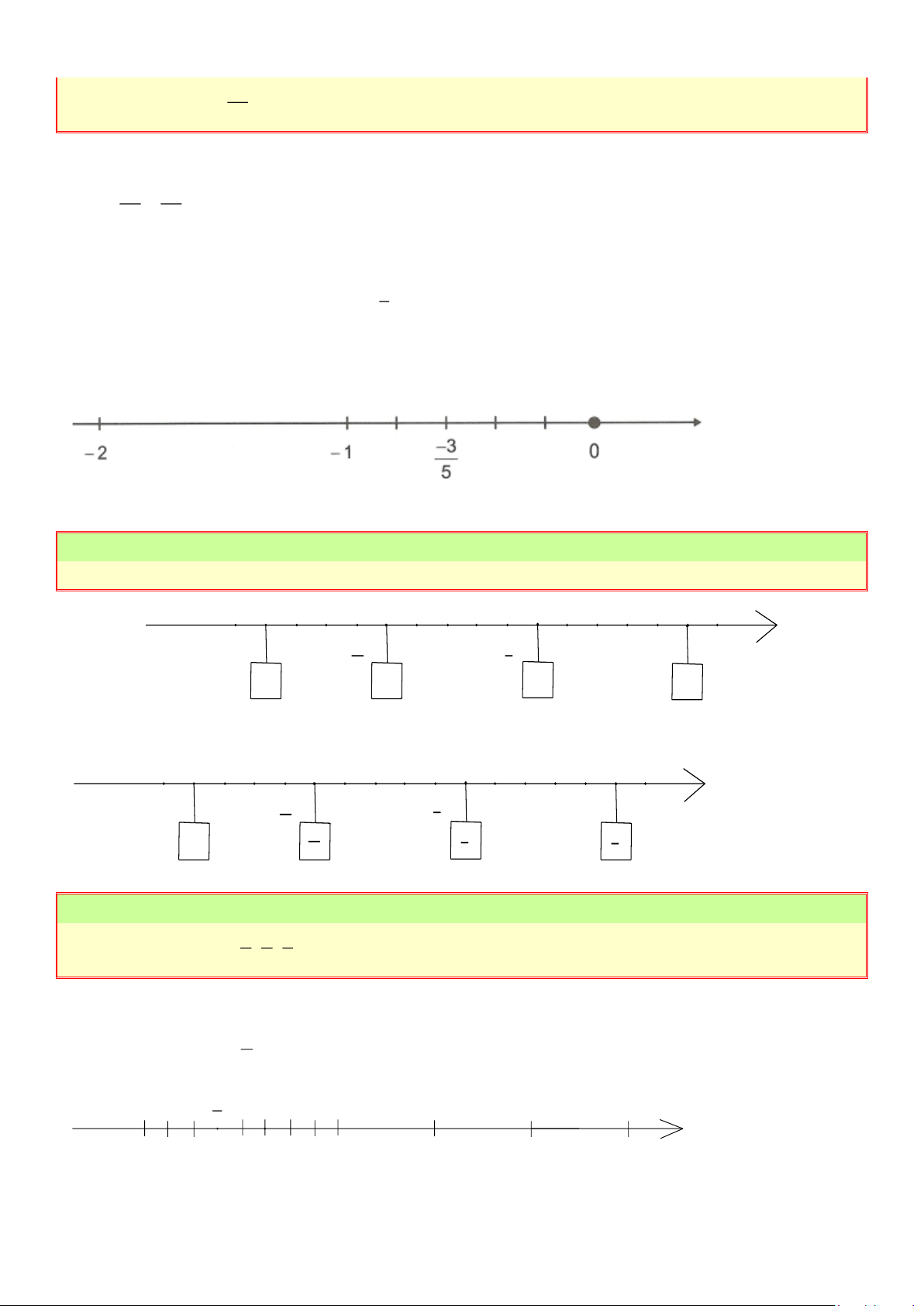
Chia các đoạn thẳng đơn vị ra làm 5 phần bằng nhau. 1
Lấy đoạn thẳng mới làm đơn vị (bằng đơn vị cũ). 5
Lấy điểm nằm bên trái điểm 0, cách điểm 0 một đoạn bằng 3 đơn vị mới.
Điểm vừa lấy là điểm phải tìm. Bài 3:
Điền số thích hợp vào chỗ trống: -1 -1 0 1 1 2 3 Lời giải -1 -1 0 1 1 2 -1 3 1 4 -1 3 2 3 Bài 4: 5 4 3
Biểu diễn số hữu tỉ − ; ; trên trục số. 4 4 5 Lời giải 5
Biểu diễn số hữu tỉ − 4 -5 4 -2 -1 0 1 2 3 Trang 12 4
Biểu diễn số hữu tỉ = 1 4 -2 -1 0 1 2 3 4 3 Biểu diễn số hữu tỉ 5
Bài toán 2: Biểu diễn số hữu tỉ dưới dạng các phân số bằng nhau *) Phương pháp giải: a
Số hữu tỉ thường được biểu diễn dưới dạng phân số tối giản với a,b  ;b  0 . b Bài 1 6 − 4 4 20 Cho các phân số sau: ; ; ; 15 1 − 2 1 − 0 8 − 2
Những phân số nào biểu diễn số hữu tỉ ? 5 − Hướng dẫn giải 2 2 − 6 − 2 − 4 1 − 4 2 − 20 5 − Ta có =
. Rút gọn các phân số đã cho ta được: = ; = ; = ; = 5 − 5 15 5 1 − 2 3 1 − 0 5 8 − 2 2 6 − 4
Vậy các phân số biểu diễn số hữu tỉ là: và . 5 − 15 10 − Bài 2: 3 − 1 1
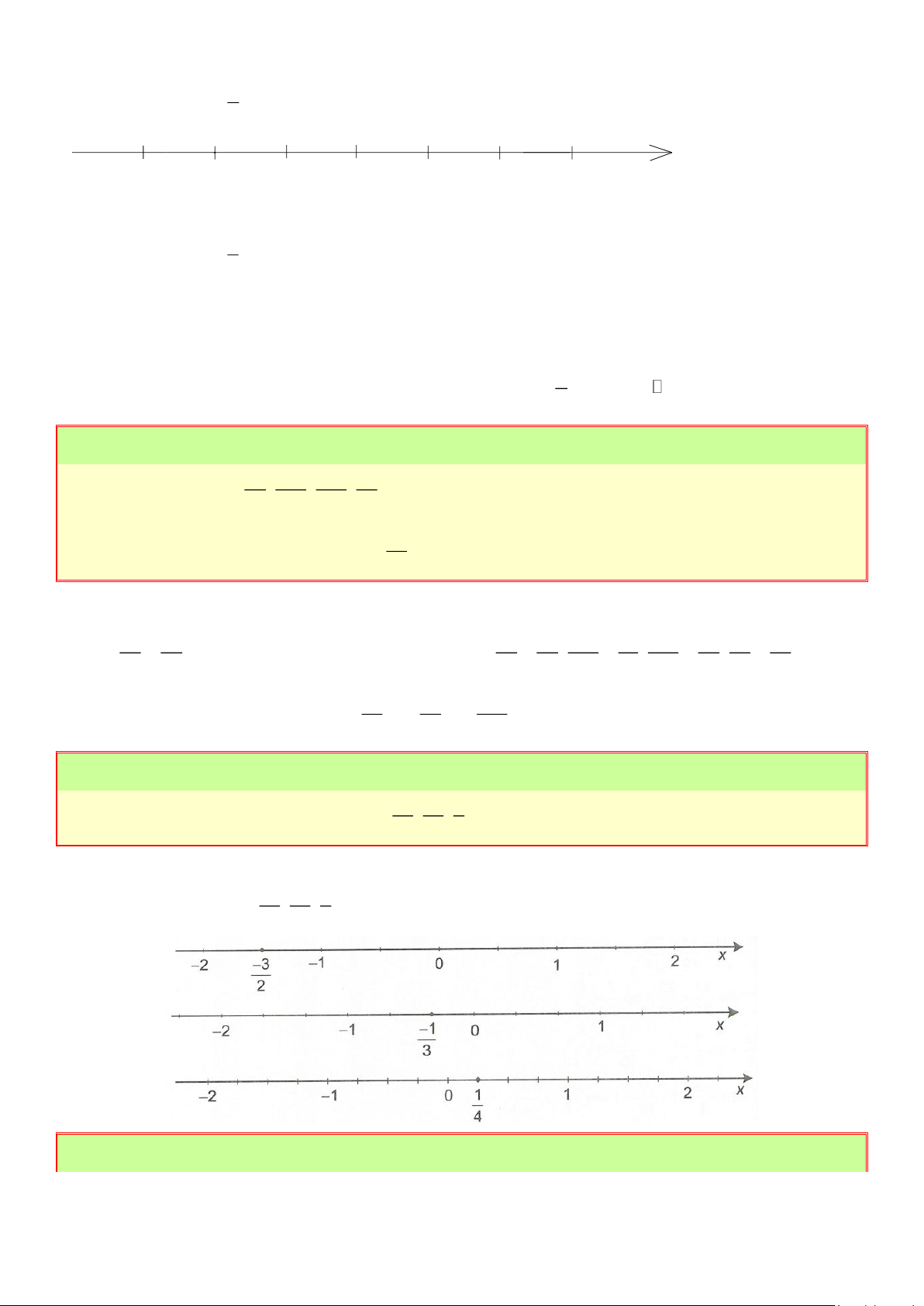
Biểu diễn các số hữu tỉ sau trên trục số: ; ; 2 3 − 4 Lời giải 3 − 1 1
Biểu diễn các số hữu tỉ ; ; trên trục số như sau: 2 3 − 4 Bài 3: Trang 13 9 − 1 − 4 4 12 2 Cho các phân số sau ; ; ;
. Những phân số nào biểu diễn số hữu tỉ ? 6 21 6 − 20 3 − Lời giải 2 −2 Ta có: = . 3 − 3 9 − 3 − 1 − 4 2 − 4 2 − 12 3 −
Rút gọn các phân số đã cho ta được: = ; = ; = ; = 6 2 21 3 6 − 3 2 − 0 5 2 14 − 4
Vậy các phân số biểu diễn số hữu tỉ là: và . 3 − 21 6 − Bài 4: 2 − 1 1 − 4 4 − 2 35 5 − 2 − 8 7 − a) Cho các phân số ; ; ; ; ;
. Những phân số nào biểu diễn số hữu tỉ ? 27 19 5 − 4 4 − 5 7 36 9 7 −
b) Biểu diễn số hữu tỉ trên trục số. 9 Lời giải 2 − 1 7 − 2 − 8 7 − 35 3 − 5 7 − a) Ta có: = ; = ; = = 27 9 36 9 4 − 5 45 9 7 − 2 − 1 2 − 8 35
Vậy các phân số biểu diễn số hữu tỉ là: ; và . 9 27 36 45 − 7 −
b) Biểu diễn các số hữu tỉ trên trục số như sau: 9 Bài 5: 3
Trong các phân số sau, phân số nào không bằng phân số ? 5 6 9 A. B. 11 15 6 − 3 − C. D. 10 − 5 − Lời giải 3
Các đáp án B, C, D sau khi rút gọn ta đều được phân số . 5 Bài 6: 1 2 − 5 5
Biểu diễn các số: ;0, 25; ;
bởi các điểm trên cùng một trục số ta được bao nhiêu điểm 4 1 − 00 20 phân biệt?
A. Một điểm. B. Hai điểm. Trang 14 C. Ba điểm. D. Bốn điểm. Lời giải 1 1 2 − 5 1 5 1
Đưa các số hữu tỉ về dạng phân số tối giản, ta có: ; 0, 25 = ; = ; = . 4 4 1 − 00 4 20 4 1
Vậy các số trên cùng biểu diễn bởi điểm trên trục số. 4 Bài 7: 14 24 26 2 − 8 72 12 Trong các phân số ; ; ; ;
có bao nhiêu phân số bằng phân số ? 18 26 2 − 8 30 78 13 A. 1. B. 2. C. 3. D. 4. Lời giải 14 7 24 12 26 13 2 − 8 1 − 4 72 12 = ; = ; = − ; = ; = . 18 9 26 13 2 − 8 14 30 15 78 13 12
Vậy có hai phân số biểu diễn phân số . 13
Dạng 3: So sánh hai số hữu tỉ *) Phương pháp giải:
+ Viết các số hữu tỉ dưới dạng phân số có cùng mẫu dương: So sánh các tử số, phân số nào có tử
nhỏ hơn thì phân số đó nhỏ hơn.
+ So sánh các số trung gian ( 0,1,... );
+ So sánh với phần hơn hoặc phần bù;
+ So sánh thương hai số hữu tỉ (khác 0 ) với 1;
+ Áp dụng tính chất bắc cầu và các bất đẳng thức đã chứng minh trong bài Bài 1: 11 − 8
So sánh các số hữu tỉ sau: và . 6 9 − Hướng dẫn giải 8 8 − = 9 − 9 1 − 1 3 − 3 8 8 − 1 − 6 Ta có = ; = = 6 18 9 − 9 18 3 − 3 1 − 6 1 − 1 8 Vì 33 −  −16 nên  hay  18 18 6 9 − Trang 15 Bài 2: So sánh các số sau: 25 − 20 15 21 19 − 23 − a) và ; b) và ; c) và . 20 25 21 49 49 47 Hướng dẫn giải 25 − 20 2 − 5 20 a) Ta có  0 và  0 nên  . 20 25 20 25 15 5 21 3 5 3 15 21 b) Ta có = ; = . Vì  nên  21 7 49 7 7 7 21 49 1 − 9 2 − 3 2 − 3 2 − 3 1 − 9 2 − 3 c) Ta có:  và  . Do đó  49 49 49 47 49 47 Bài 3:
So sánh các số hữu tỉ sau: 998 999 315 − 316 − 2020 2018 a) và ; b) và ; c) và . 555 556 380 381 2019 2019 Hướng dẫn giải
a) Ta thấy 998 − 555 = 999 − 556 = 443 nên ta so sánh hai phân số qua phần bù 998 443 999 443 Ta có −1 = ; −1 = 555 555 556 556 443 443 999 998 999 998 Vì  nên −1 −1 hay  556 555 556 555 556 555 b) Ta thấy 380 + ( 31 − 5) = 381+ ( 31
− 6) = 65 nên ta so sánh hai phân số bằng cách cộng thêm 1. 3 − 15 65 3 − 16 65 Ta có +1 = ; +1 = 380 380 381 381 65 65 3 − 15 3 − 16 31 − 5 31 − 6 Vì  nên +1  +1 hay  . 380 381 380 381 380 381 2020 c) Ta có 2020  2019 nên  1 2019 2018 Lại có 2018  2019 nên  1 2019 2020 2018 Do đó  . 2019 2019 Chú ý:
Ngoài phương pháp so sánh bằng cách quy đồng mẫu số, ta có thể sử dụng các phương pháp Trang 16 khác như:
+ So sánh qua một phân số trung gian. + So sánh qua phần bù.
+ Đưa về so sánh hai phân số có cùng tử số. Bài 4:
So sánh các số hữu tỉ sau: 7 11 5 − 7 a) và ; b) và ; 8 12 8 10 − 24 19 9 − 27 c) và ; d) và . 35 30 21 63 − Lời giải 7 21 11 22 a) Ta có = ; = 8 24 12 24 21 22 7 11 Vì 21  22 nên  hay  . 24 24 8 12 5 − 3 7 − 3 b) Ta có +1 = ; +1 = 8 8 10 10 3 3 5 − 7 − 5 − 7 Vì  nên +1  +1 hay  8 10 8 10 8 1 − 0 24 11 19 11 c) Ta có =1− ; =1− 35 35 30 30 11 11 11 11 24 19 Vì  nên 1− 1− hay  35 30 35 30 35 30 9 − 3 − 27 2 − 7 3 − d) Ta có = ; = = 21 7 6 − 3 63 7 9 − 27 Suy ra = . 21 6 − 3 Bài 5:
So sánh các số hữu tỉ sau: 9 5 4 − 15 a) và ; b) và ; 70 42 27 63 − 13 9 9 − 20 − c) và ; d) và . 15 11 17 21 − Lời giải Trang 17 9 27 5 25 a) Ta có = ; = 70 210 42 210 27 25 9 5 Vì 27  25 nên  hay  210 210 70 42 4 − 2 − 8 15 1 − 5 4 − 5 b) Ta có = ; = = 27 189 6 − 3 63 189 2 − 8 4 − 5 4 − 15 Vì 28 −  −45 nên  hay  189 189 27 6 − 3 13 2 9 2 c) Ta có =1− ; =1− 15 15 11 11 2 2 2 2 13 9 Vì  nên 1− 1− hay  15 11 15 11 15 11 9 − 2 − 0 20 9 − 2 − 0 d) Ta có  0; =  0 nên  . 17 2 − 1 21 17 2 − 1 Bài 6: 1 − 2 3 − 1 − 6 1 − 1 − 1 1 − 4 9 −
Sắp xếp các số hữu tỉ ; ; ; ; ; ;
theo thứ tự giảm dần. 19 19 19 19 19 19 19 Lời giải 1 − 6 1 − 4 1 − 2 1 − 1 9 − 3 − 1 − Vì 16
−  −14  −12  −11  −9  −3  −1 nên       19 19 19 19 19 19 19 1 − 3 − 9 − 1 − 1 1 − 2 1 − 4 1 − 6
Sắp xếp các số theo thứ tự giảm dần: ; ; ; ; ; ; 19 19 19 19 19 19 19 Bài 7: 1 − 6 1 − 6 19
Sắp xếp các số hữu tỉ ; ;− theo thứ tự tăng dần. 27 29 27 Lời giải 16 16 1 − 6 1 − 6 Có 27  29 nên  . Suy ra  27 29 27 29 1 − 6 1 − 9
Lại có −16  −19 nên  27 27 19 1 − 6 1 − 6 Vậy −   . 27 27 29 19 1 − 6 1 − 6
Sắp xếp các số theo thứ tự tăng dần: − ; ; 27 27 29 Bài 8:
So sánh các số hữu tỉ sau. 3 5 2 − 3 − a) và b) và 7 7 5 5 Trang 18 4 5 3 − 3 − c) và d) và 9 − 9 − 8 − 8 Lời giải 3 5 a) và 7 7 3 5 Vì 3  5 nên  7 7 2 − 3 − b) và 5 5 2 − 3 − Vì −2  −3 nên  5 5 4 5 c) và 9 − 9 − 4 4 − 5 5 − Ta có: = ; = 9 − 9 9 − 9 4 − 5 − 4 5 Vì  nên  9 9 9 − 9 − 3 − 3 − d) và 8 − 8 3 − 3 3 3 − Ta có: = ;  8 − 8 8 8 3 − 3 − Vậy  8 − 8 Bài 9:
So sánh các số hữu tỉ sau: 5 3 3 − 3 − 1 3 a) và b) và ; c) và . 4 4 5 4 21 27 Lời giải 5 3
a) Ta có 5  4 nên   4 4 3 3 3 − 3 − b) Ta có  nên   5 4 5 4 3 1 1 1 1 3 c) Ta có = mà  nên   27 9 21 9 21 27 Bài 10: Trang 19 1 − 2 3 − 1 − 6 1 − 1 − 1 1 − 4 1 − 9
Sắp xếp các số hữu tỉ sau theo thứ tự giảm dần: ; ; ; ; ; ; 17 17 17 17 17 17 17 Lời giải 1 − 3 − 1 − 1 1 − 2 1 − 4 1 − 6 1 − 9 Ta có :       17 17 17 17 17 17 17
Các số được sắp xếp theo thứ tự giảm dần là: 1 − 3 − 1 − 1 1 − 2 1 − 4 1 − 6 1 − 9 : : ; ; ; ; 17 17 17 17 17 17 17 Bài 11:
Sắp xếp các số hữu tỉ sau theo thứ tự tăng dần. 5 − 5 − 5 − 5 − 5 − 5 − 5 − ; ; ; ; ; ; 9 7 2 4 8 3 11 Lời giải 5 5 5 5 5 5 5 5 − 5 − 5 − 5 − 5 − 5 − 5 − Ta có :              11 9 8 7 4 3 2 11 9 8 7 4 3 2
Các số được sắp xếp theo thứ tự tăng dần là: 5 − 5 − 5 − 5 − 5 − 5 − 5 − ; ; ; ; ; ; 2 3 4 7 8 9 11 Bài 12:
So sánh các số hữu tỉ sau một cách nhanh nhất: 14 − 6 1 21 13 2019 2020 a) và ; b) và ; c) và . 43 89 23 12 2019 2019 Lời giải 1 − 46 1 1 − 46 1 a) Ta có:  0 và  0 nên   43 89 43 89 21 13 21 13 b) Ta có: <1 và 1 nên <  23 12 23 12 2019 2020 2019 2020 c) Ta có: =1 và 1 nên   2019 2019 2019 2019 Bài 13:
So sánh các số hữu tỉ sau một cách nhanh nhất: 1 a) x = 0 − ,125 và y = 8 − 5
b) b) x = 0,75 và y = 4 Trang 20