Chuyên đề tia phân giác của góc Toán 6

CHƯƠNG :
BÀI 5: TIA PHÂN GIÁC CỦA GÓC Mục tiêu  Kiến thức
+ Hiểu và phát biểu được định nghĩa tia phân giác của một góc.
+ Biết dùng thước đo góc và cách gấp giấy để vẽ tia phân giác của một góc cho trước.  Kĩ năng
+ Biết vẽ tia phân giác của một góc.
+ Nhận biết và chứng minh được tia phân giác của một góc.
+ Vận dụng định nghĩa tia phân giác của một góc để tính số đo góc. Trang 1 I. LÍ THUYẾT TRỌNG TÂM Định nghĩa
- Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với
hai cạnh ấy hai góc bằng nhau.
- Mỗi góc (không phải là góc bẹt) chỉ có một tia phân giác.
Oz là tia phân giác góc xOy II. CÁC DẠNG BÀI TẬP
Dạng 1: Vẽ tia phân giác của một góc Ví dụ mẫu
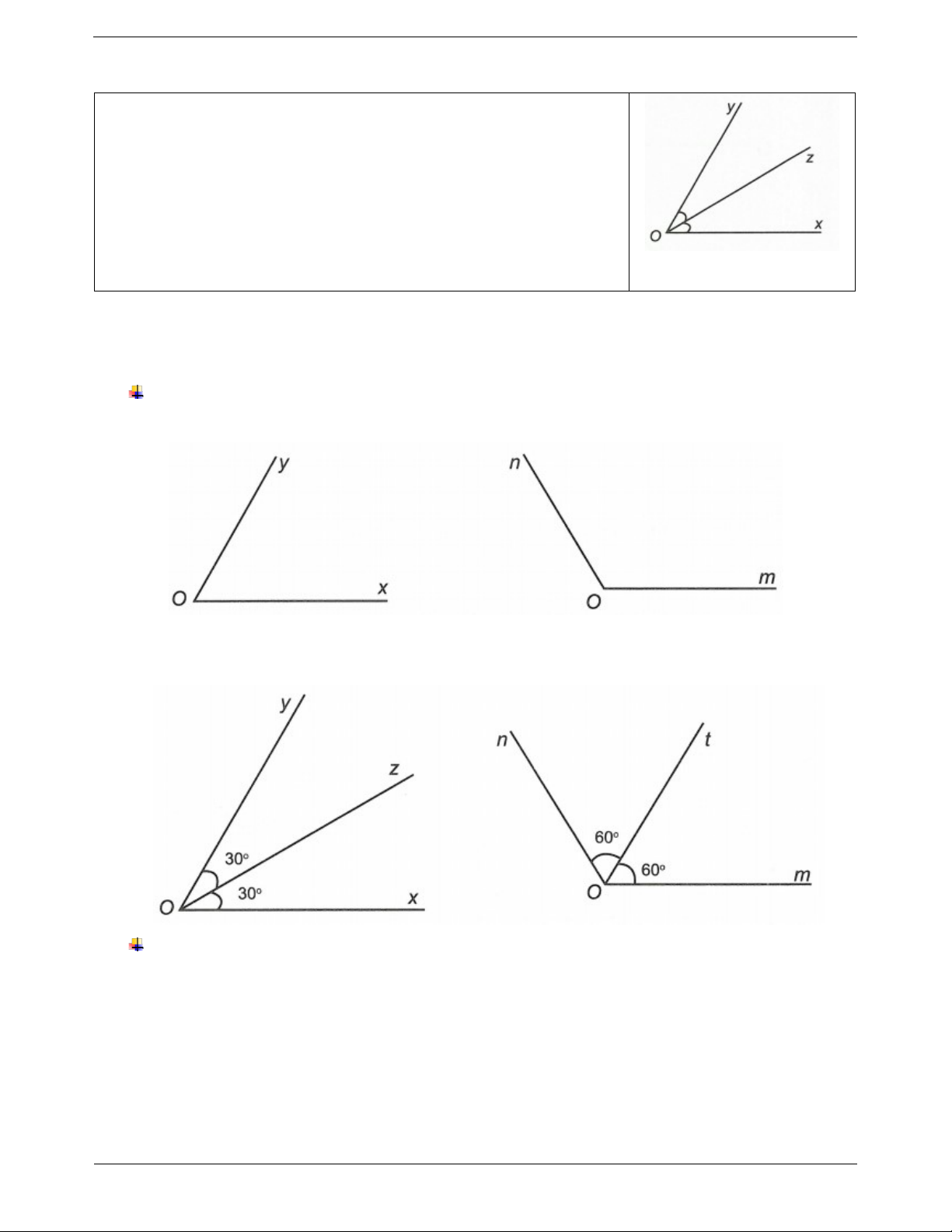
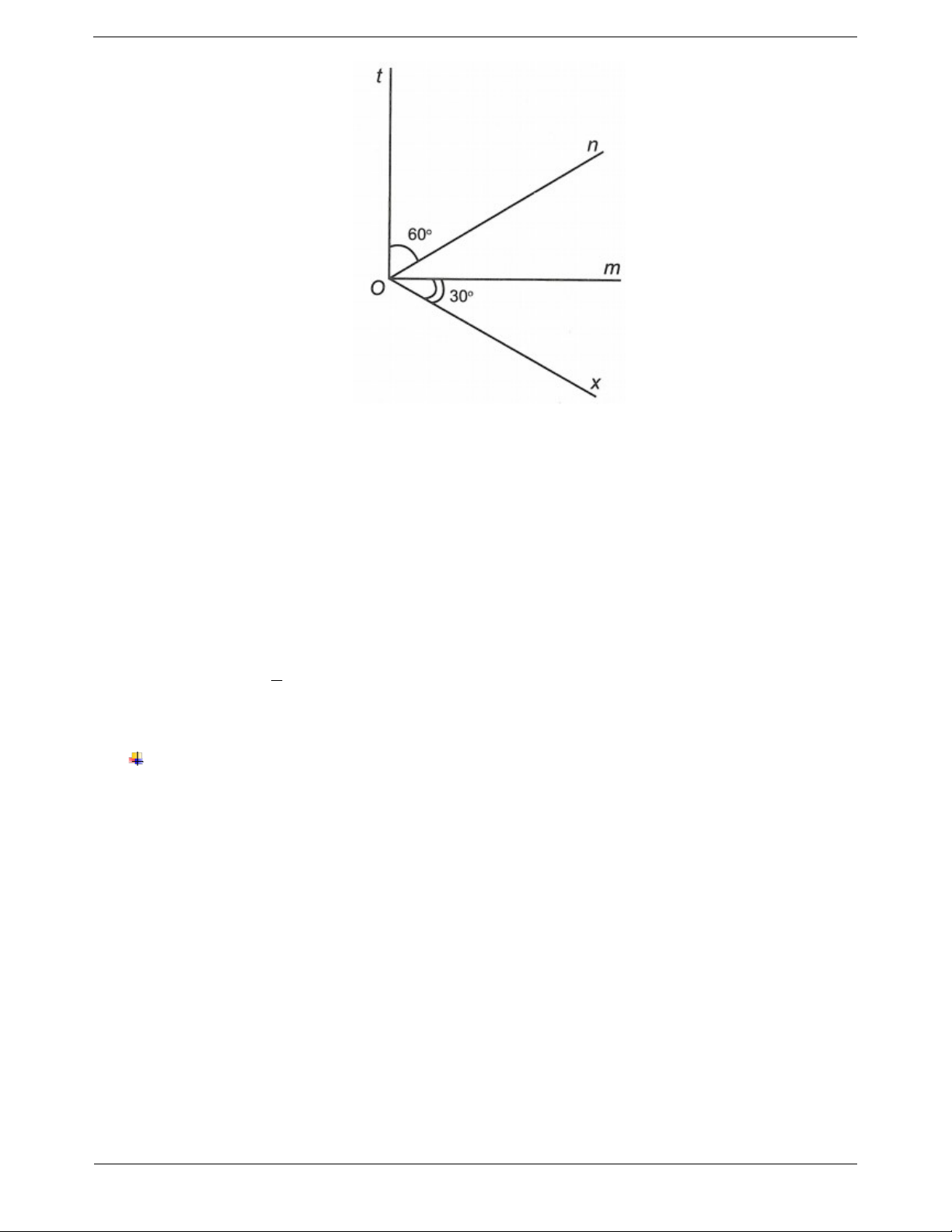
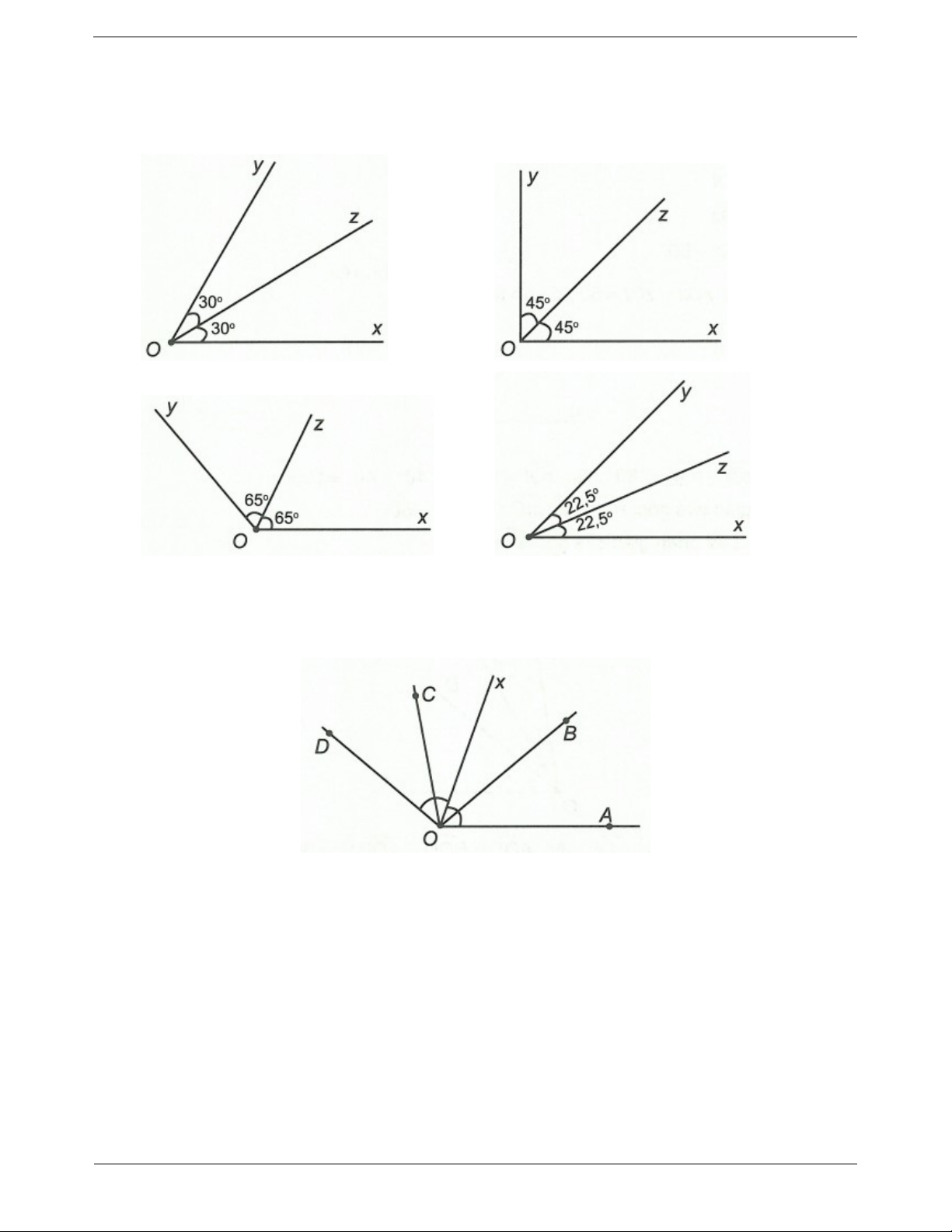
Ví dụ 1: Vẽ tia phân giác của các góc sau Hướng dẫn giải
Đo số đo các góc trên và vẽ tia phân giác tương ứng
Bài tập tự luyện dạng 1
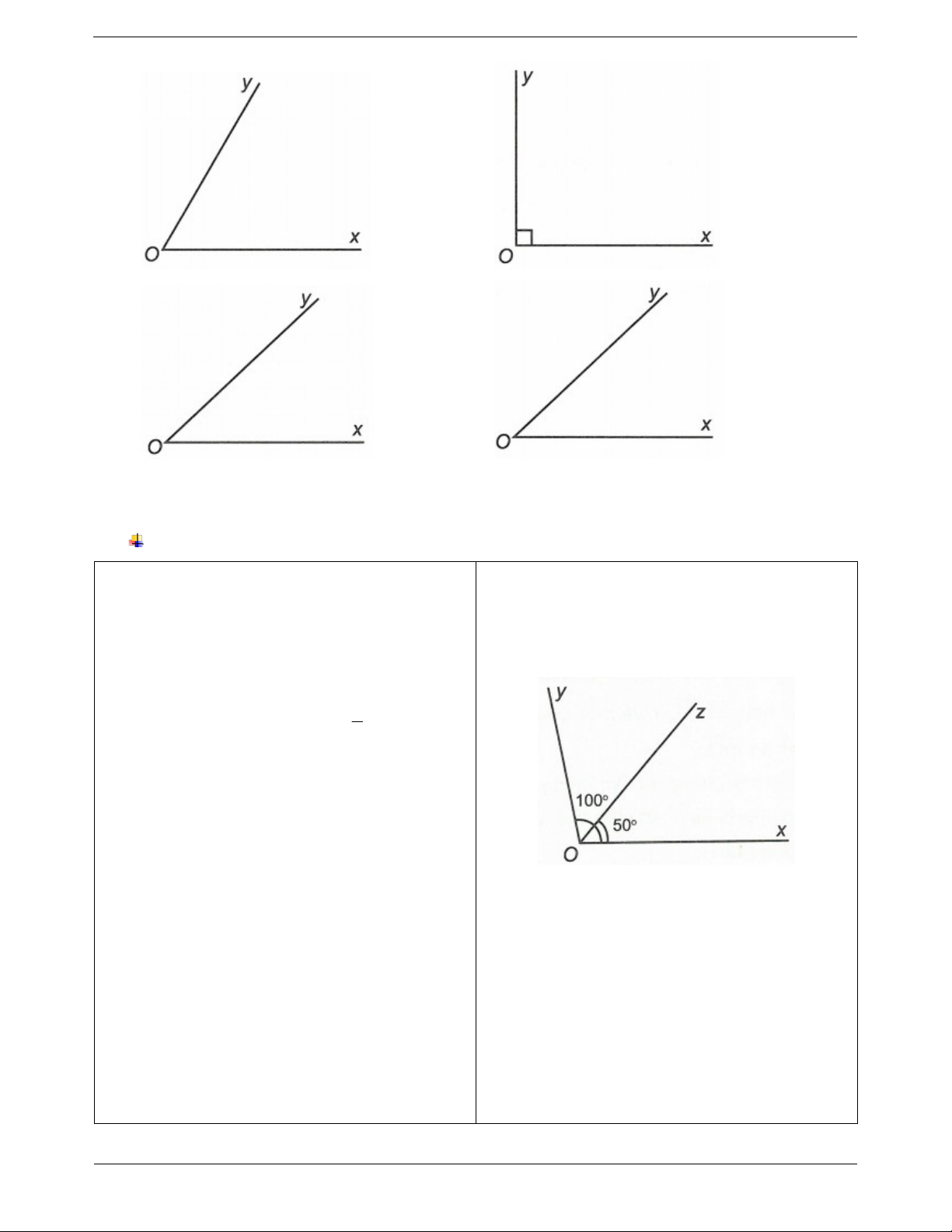
Câu 1: Vẽ tia phân giác của góc xOy trong các trường hợp sau Trang 2 a) b) c) d)
Dạng 2: Chứng minh một tia là phân giác của một góc cho trước Phương pháp giải
Chứng minh tia Oy là tia phân giác của  xOz . Ví dụ: Cho 
xOy  100 . Vẽ tia Oz nằm giữa hai tia Cách 1. Ox và Oy sao cho 
xOz  50 . Chứng tỏ rằng tia Oz
• Chứng minh tia Oy nằm giữa hai tia Ox và Oz. là tia phân giác của  xOy . • Chứng minh  xOy   yOz . 1 Cách 2. Chứng minh  xOy   yOz   xOz . 2 Hướng dẫn giải
Vì tia Oz nằm giữa hai tia Ox và Oy nên  xOz   zOy   xOy hay 50   zOy  100  zOy  100  50  zOy  50 .
Tia Oz nằm giữa hai tia Ox và Oy và Trang 3  xOz  
zOy  50 nên Oz là tia phân giác  xOy . Ví dụ mẫu
Ví dụ 1. Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ tia Oy, Ot sao cho  xOt  40 ,  xOy  80 .
a) Tia Ot có nằm giữa hai tia Ox và Oy không? b) So sánh  tOy và  xOt .
c) Tia Ot có là tia phân giác  xOy không? Vì sao? Hướng dẫn giải
a) Ta có tia Ot và tia Oy nằm trên cùng mặt phẳng bờ chứa tia Ox mà  xOt  
xOy 40  80 nên tia
Ot nằm giữa hai tia Ox và Oy.   1
b) Vì tia Ot nằm giữa hai tia Ox và Oy ta có  xOt   tOy   xOy 40   tOy  80  tOy  80  40  tOy  40   tOy   xOt  40 2 c) Từ  
1 và 2 suy ra Ot là tia phân giác của góc  xOy . Ví dụ 2. Cho hai góc  mOn và  nOt phụ nhau, biết  nOt  60 . a) Tính số đo  mOn .
b) Trên nửa mặt phẳng bờ Om không chứa tia On vẽ tia Ox sao cho 
mOx  30 . Tia On có phải là tia phân giác của  xOt không? Vì sao? Hướng dẫn giải Trang 4 a) Hai góc  mOn và  nOt phụ nhau nên  mOn   nOt  90 suy ra  mOn  90  
nOt  90  60  30 . Vậy  mOn  30 .
b) Tia Ox thuộc nửa mặt phẳng bờ Om không chứa tia On nên tia Om nằm giữa hai tia On và Ox. Khi đó  nOx   nOm  
mOx  30  30  60 .
Tương tự, tia Om nằm giữa hai tia Ot và Ox nên  tOx   tOm  
mOx  90  30  120 . 1 Do đó  nOx   nOt   tOx . 2
Vậy On là tia phân giác của  xOt .
Bài tập tự luyện dạng 2
Câu 1: Cho bốn tia OA, OB, OC, OD chung gốc O theo thứ tự đó sao cho  AOD  180 ;  AOB   COD .
Gọi Ox là tia phân giác của 
AOD . Chứng tỏ Ox cũng là tia phân giác của  BOC .
Câu 2: Trên cùng nửa mặt phẳng bờ chứa tia Ox, vẽ các tia Oy, Oz, Ot sao cho  xOy  30 ;  xOz  50 và  xOt  100 .
a) Trong ba tia Ox, Oy và Oz, tia nào nằm giữa hai tia còn lại? Tính số đo góc  yOz .
b) Trong ba tia Ox, Oz và Ot, tia nào nằm giữa hai tia còn lại? Tính số đo góc  zOt .
c) Tia Oz có là tia phân giác của góc  xOt không? Vì sao? Câu 3: Vẽ góc bẹt 
xOy . Trên cùng một nửa mặt phẳng bờ xy vẽ tia Oz và Ot sao cho  xOz   yOt  40 .
Vẽ tia phân giác Om của  zOt . a) Tính số đo  mOz và  mOt .
b) Tia Om có là tia phân giác của  xOy không? Vì sao? Trang 5 Câu 4: Cho 
AOB  80 . Vẽ tia OC nằm giữa hai tia OA và OB sao cho 
AOC  60 . Vẽ tia phân giác OD của  AOB . a) Tính số đo góc  COD .
b) Chứng tỏ rằng OC là tia phân giác của  BOD .
Câu 5: Trên cùng một nửa mặt phẳng bờ là đường thẳng xy đi qua O, vẽ các tia Om và On sao cho  xOm  40 ; 
yOn  160 . Chứng tỏ rằng On là tia phân giác của  xOm .
Câu 6: Trên cùng một nửa mặt phẳng bờ là đường thẳng xy đi qua O, vẽ các tia Om, On, Ot sao cho  xOm  55 ,  yOn  85 ,  yOt  45 .
a) Chứng tỏ rằng tia On nằm giữa hai tia Om và Ot.
b) Chứng tỏ rằng tia On là tia phân giác của góc  mOt . Dạng 3: Tính số đo góc Ví dụ mẫu Ví dụ 1. Cho hai góc  xOy và 
yOz là hai góc kề bù, biết  xOy  120 . a) Tính  yOz .
b) Gọi Om là tia phân giác của  xOy . Tính  zOm . Hướng dẫn giải a) Vì  xOy và 
yOz là hai góc kề bù nên ta có  xOy   yOz  180 hay  yOz  180  
xOy  180 120  60 . xOy 
b) Tia Om là tia phân giác của  xOy nên  xOm    120 mOy    60 . 2 2 Hai góc  xOm và  zOm kề bù nên  xOm   zOm  180 60   zOm  180 
zOm  180  60  120
Ví dụ 2. Trên một nửa mặt phẳng bờ chứa tia OA vẽ tia OB sao cho 
AOB  35 , vẽ tia OC sao cho  AOC  70 . Trang 6
a) Tia OB có phải là tia phân giác của  AOC không? Vì sao?
b) Vẽ OB là tia đối của tia OB. Tính số đo góc kề bù với  AOB . Hướng dẫn giải
a) OB và OC cùng nằm trên một nửa mặt phẳng bờ chứa tia OA mà  AOB  
AOC 35  70 nên tia
OB nằm giữa hai tia OA và OC.   1 Khi đó  AOB   BOC   AOC 35   BOC  70 
BOC  70  35  35 Do vậy  AOB   BOC  35 . 2 Từ  
1 và 2 suy ra OB là tia phân giác của  AOC .
b) Vì OB là tia đối của tia OB nên  AOB và 
AOB là hai góc kề bù nên  AOB   AOB  180 35   AOB  180 
AOB  180  35  145. Vậy  AOB  145 .
Ví dụ 3. Cho hai góc kề bù  xOy và  yOz biết 
xOy  78 , Ot là tia phân giác của góc  yOz . a) Tính  tOz .
b) Tia Oy có phải là tia phân giác của  xOt không? Vì sao? Hướng dẫn giải Trang 7 a) Vì  xOy và 
yOz là hai góc kề bù nên  xOy   yOz  180 78   yOz  180 
yOz  180  78  102 . yOz 
Vì Ot là tia phân giác của góc  yOt nên ta có  yOz    102 zOt    51 . 2 2 b) Nhận xét thấy  xOy  78 và  yOt  51  xOy   
yOt  nên Oy không phải là tia phân giác của  xOt .
Ví dụ 4. Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ hai tia Oy, Oz sao cho  xOy  50 ,  xOz  130 . a) Tính số đo góc  yOz .
b) Gọi Ot là tia phân giác của góc  yOz . Tính số đo góc  xOt .
c) Vẽ tia Oh là tia đối của tia Oy. So sánh  xOz và  xOh . Hướng dẫn giải
a) Hai tia Oy, Oz cùng nằm trên cùng một nửa mặt phẳng bờ chứa tia Ox mà  xOy   xOz 50 130
nên tia Oy nằm giữa hai tia Ox, Oz. Khi đó ta có  xOy   yOz   xOz 50   yOz  130 Trang 8 
yOz  130  50  80 .
b) Vì Ot là tia phân giác của góc  yOz nên yOz   yOt    80 zOt    40 . 2 2
Vì Oy nằm giữa hai tia Ox và Oz nên Oy nằm giữa hai tia Ox và Ot. Do đó  xOy   yOt   xOt 40  50   xOt  xOt  90
c) Vì Oh là tia đối của tia Oy nên  xOh và 
xOy là hai góc kề bù, ta có  xOh   xOy  180  xOh  50 180 
xOh  180  50  30 Vậy  xOz   xOh  130 . Ví dụ 5. Cho góc 
xOy có số đo là 160°, vẽ tia Oz bất kỳ nằm trong góc đó. Gọi Om, On lần lượt là các
tia phân giác của các góc  xOz và  yOz . Tính số đo góc  mOn . Hướng dẫn giải xOz
Do Om là tia phân giác của góc 
xOz nên Om nằm giữa hai tia Ox và Oz nên  xOm    zOm  . 2 yOz
Tương tự On là tia phân giác góc 
yOz nên On nằm giữa hai tia Oy và Oz nên  yOn    zOn  . 2
Lại có Oz nằm trong góc 
xOy nên Oz nằm giữa hai tia Ox và Oy.
Suy ra Oz nằm giữa hai tia Om và On.  xOz  yOz Khi đó ta có  mOz   nOz   mOn hay    mOn 2 2 Trang 9  xOy   mOn 2 160   mOn 2  mOn  80. Vậy  mOn  80 .
Bài tập tự luyện dạng 3 Câu 1: Cho góc tù  xOn . Bên trong góc 
xOy , vẽ tia Om sao cho góc 
xOm  90 , vẽ tia On sao cho  yOn  90 . a) Chứng minh  xOn   yOm .
b) Gọi Ot là tia phân giác của góc 
xOy . Chứng minh Ot cũng là tia phân giác của  mOn .
Câu 2: Cho hai góc kề nhau  AOB và  BOC sao cho  AOB  50 , 
BOC  80 . Gọi OD là tia đối của tia OC. a) Tính số đo góc  AOC .
b) Chứng tỏ tia OA nằm giữa hai tia OB và OD.
c) Tia OA có phải là phân giác của  BOD không? Vì sao?
Câu 3: Cho hai góc kề bù  AOB và  BOC trong đó  AOB  3 BOC . a) Tính  BOC .
b) Trên nửa mặt phẳng bờ AC có chứa tia OB, vẽ tia OD sao cho  AOD  
BOC . Hỏi tia OB có là tia phân giác của góc  COD không? Vì sao? Câu 4: Cho 
COD  80 . Vẽ tia OE trong góc  COD sao cho 
COE  60 . Vẽ tia phân giác OF của  COD . a) Tính  EOF .
b) Chứng tỏ OE là tia phân giác của  DOF . Trang 10 ĐÁP ÁN
Dạng 1: Vẽ tia phân giác của một góc
Câu 1. Đo số đo các góc xOy và dùng thước đo độ vẽ tia phân giác của từng trường hợp tương ứng. a) b) c) d)
Dạng 2: Chứng minh một tia là phân giác của một góc cho trước Câu 1.
Theo đề bài Ox là tia phân giác của góc  AOD nên ta có  AOx   DOx .   1 Mà  AOx   AOB   BOx ,  DOx   COD   COx . 2 Lại theo giả thiết  AOB   COD . 3 Từ  
1 , 2 và 3 suy ra  BOx   COx .
Vậy Ox là tia phân giác của góc  COB . Câu 2. Trang 11
a) Ta có số đo góc xOy nhỏ hơn số đo góc xOz nên tia Oy nằm giữa hai tia Ox và Oz.  xOz   xOy   yOz  yOz   xOz   xOy 
yOz  50  30  20 .
b) Ta có số đo góc xOz nhỏ hơn số đo góc xOt nên tia Oz nằm giữa hai tia Ox và Ot.  xOt   xOz   zOt  zOt   xOt   xOz 
zOt  100  50  50 . c) Từ câu trên ta có  xOz  
zOt  50 do đó tia Oz là tia phân giác của góc xOt. Câu 3. a) Ta có  xOz   zOt   tOy  180 nên  zOt  180   xOz  
tOy  180  40  40  100 .
Do Om là phân giác của góc  zOt nên  mOz   mOt  
zOt : 2  100 : 2  50 .
b) Tia Om cũng là tia phân giác của góc  xOy . Vì  xOm   xOz  
zOm  40  50  90 và  yOm   xOy  
xOm  180  90  90 nên  xOm   yOm . Câu 4. Trang 12
a) Ta có OD là phân giác của góc  AOB nên  AOD   BOD  
AOB : 2  80 : 2  40 . Do đó số đo góc 
AOD nhỏ hơn số đo góc 
AOC nên tia OD nằm giữa hai tia OA và OC. Suy ra  AOC   AOD   DOC  DOC   AOC   AOD 
DOC  60  40  20 b) Ta có  BOC   AOB  
AOC  80  60  20 . Do  AOC   AOD và  AOB  
AOC nên tia OC nằm giữa hai tia OB và OD. Như vậy  BOC  
DOC  20 nên OC là phân giác của góc  BOD . Câu 5. Ta có  xOn và 
yOn là hai góc kề bù nên  xOn   yOn  180  xOn 160  180 
xOn  180 160  20 .
Hai tia Om và On cùng nằm trên nửa mặt phẳng bờ là đường thẳng xy mà  xOn   xOm 20  40 tia
On nằm giữa hai tia Ox và Om.   1 Ta có  xOn   mOn   xOm 20   mOn  40 
mOn  40  20  20   mOn   xOn  20 2 Từ  
1 và 2 suy ra On là tia phân giác của  xOm . Câu 6. Trang 13 Ta có  xOm và 
yOm là hai góc kề bù nên  xOm   yOm  180 55   yOm  180 
yOm  180  55  125 .
Hai tia Om và Ot cùng nằm trên một nửa mặt phẳng bờ là đường thẳng xy mà  yOt   yOm
45 125 nên tia Ot nằm giữa hai tia Oy và Om. Khi đó ta có  yOt   tOm   yOm 45   tOm  125 
tOm  125  45  80 . Mặt khác  yOt  
yOn 45  85 nên tia Ot nằm giữa hai tia Oy và On. Ta có  yOt   tOn   yOn 45   tOn  85 
tOn  85  45  40 . Ta có  xOn và 
yOn là hai góc kề bù nên  xOn   yOn  180  xOn  85 180 
xOn  180  85  95 .
Hai tia Om và On cùng nằm trên một nửa mặt phẳng bờ là đường thẳng xy mà  xOm   xOn 55  95
nên tia Om nằm giữa hai tia Ox và On. Khi đó ta có  xOm   mOn   xOn 55   mOn  95 
mOn  95  55  40 . 1 Vậy  tOn   mOn  
tOm . Suy ra On là tia phân giác của 
tOm và tia On nằm giữa hai tia Om và Ot. 2 Dạng 3: Tính số đo góc Câu 1. Trang 14 a) Ta có:  yOn  90   mOn   yOm  xOm  90   mOn   xOn Do đó  mOn   xOn   mOn   yOm   xOn   yOm .
b) Ot là phân giác của góc  xOy nên  xOt   yOt . Mà  xOt   xOn   nOt ,  yOt   yOm   mOt suy ra  xOn   nOt   nOt   yOm   mOt  1 Từ   1 và a) ta suy ra  mOt   nOt * Do  xOy  180 nên  xOt   yOt  90 mà  xOm   yOn  90 nên  xOt   xOm ,  yOt   yOm . Từ đó suy
ra tia Ot nằm giữa hai tia Om và On. **
Từ * và ** suy ra Ot là phân giác của góc mOn. Câu 2: a)  AOC   AOB  
BOC  50  80  130 . b) Ta có  AOC  
COD 130 180 và  COB  
AOC 80 130 do đó tia OA nằm giữa tia OB và OD.
c) Tia OA nằm giữa hai tia OC và OD nên  COD   COA   AOD . 180  130   AOD 
AOD  180 130  50 Trang 15 Như vậy  AOD  
AOB  50 kết hợp với câu b) OA nằm giữa hai tia OB và OD nên OA là tia phân giác của góc  BOD . Câu 3.  AOB 3 a)  AOB  3 BOC suy ra   BOC 1  AOB và 
BOC là hai góc kề bù nên  AOB   BOC  180. Số đo góc 
AOB là 180 : 4.3  135 . Số đo góc 
BOC là 180 135  45 . b) Ta có  AOD   BOC  45 và  AOD   COD  180 nên 
COD  180  45  135 . Số đo góc 
COD lớn hơn số đo góc 
COB nên tia OB nằm giữa hai tia OC và OD.  COB   BOD   COD 45   BOD  135 
BOD  135  45  90 . Vậy số đo góc  BOD khác số đo góc 
COB nên OB không là tia phân giác của góc  COD Câu 4.
a) OF là tia phân giác của góc  COD nên  COF   DOF  
COD : 2  80 : 2  40 . Số đo góc 
COF nhỏ hơn số đo góc  COE nên OF nằm giữa hai tia OC và OE. Do đó  COF   EOF   COE 40   EOF  60 
EOF  60  40  20 .
b) OE nằm giữa hai tia OC và OD nên  COE   DOE   COD 60   DOE  80 
DOE  80  60  20 . Trang 16 Suy ra  DOE  
EOF  20 và số đo góc 
COE lớn hơn số đo góc  COF , số đo góc  COE nhỏ hơn số đo góc 
COD nên tia OE nằm giữa hai tia OD và OF.
Vậy OE là tia phân giác của góc DOF. Trang 17