CHUYÊN ĐỀ: TIẾP TUYẾN. HAI TIẾP TUYẾN CẮT NHAU
I. TÓM TẮT LÍ THUYẾT
1. Mở đầu về tiếp tuyến
Cho đường thẳng d và đường tròn O. Gọi A là một điểm nằm trên O.
Nếu d  OA tại A thì d gọi là tiếp tuyến của O , điểm A gọi là tiếp điểm.
 Dấu hiệu nhận biết tiếp tuyến:
 Nếu đường thẳng và đường tròn chỉ có 1 điểm chung thì đường thẳng đó là tiếp tuyến của đường tròn.
 Nếu khoảng cách từ tâm của đường tròn đến đường thẳng bằng độ dài bán kính của đường
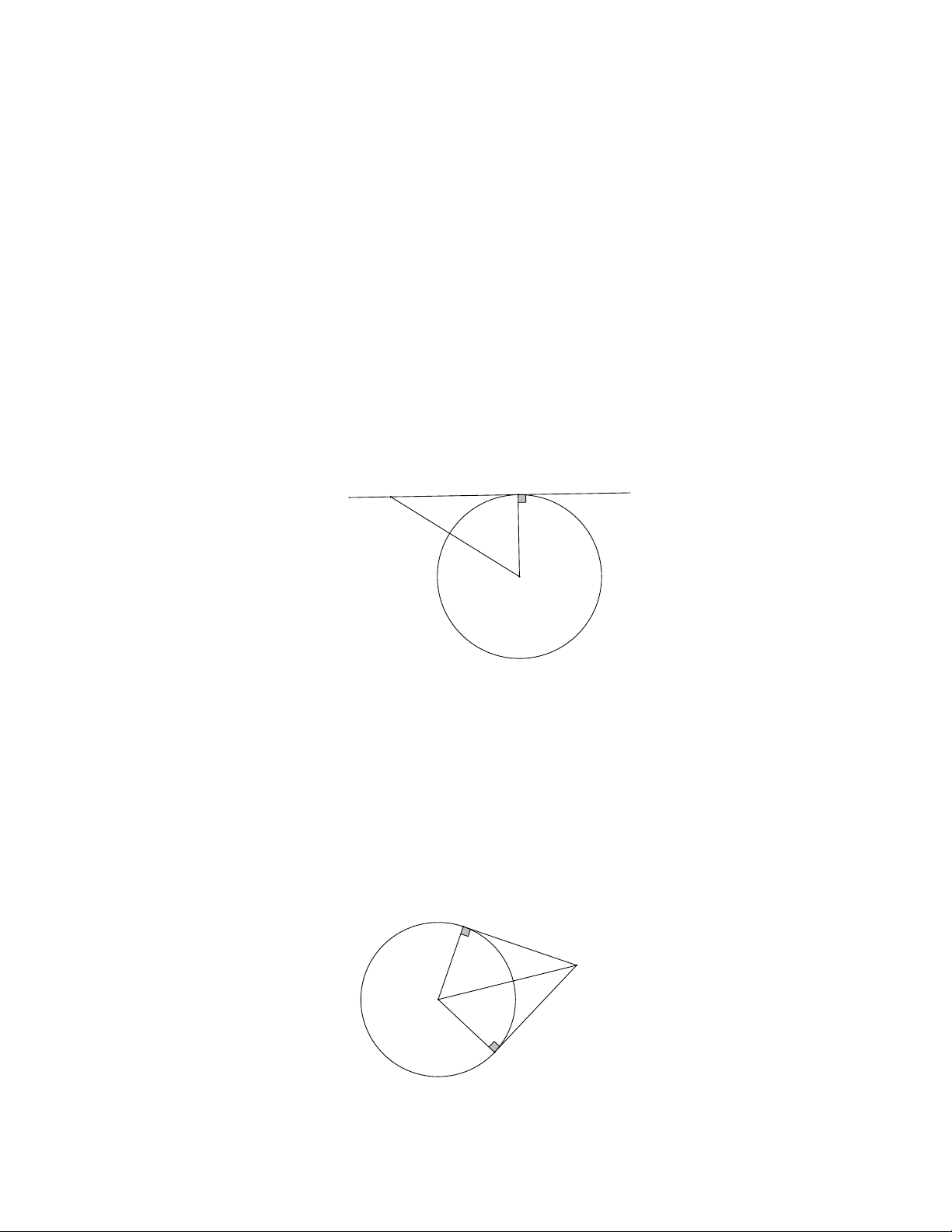
tròn thì đường thẳng đó là tiếp tuyến của đường tròn.  Hình minh họa: A d M O
2. Tính chất hai tiếp tuyến cắt nhau
Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì:
 Điểm đó cách đều hai tiếp điểm.
 Tia kẻ từ điểm đó qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
 Tia kẻ từ tâm qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm. Chứng minh:
Xét đường tròn O. M là một điểm nằm ngoài đường tròn. Từ M kẻ hai tiếp tuyến MA, MB tới đường
tròn (A, B là các tiếp điểm). A M O B Xét O  MA và O  MB có: OA  OB  R OM: cạnh chung 0
OAM  OBM  90 (do OA, OB là tiếp tuyến của O )  O  AM O
 BM(cạnh huyền – cạnh góc vuông)
 AM  BM, AMO  BMO, AOM  BOM . Từ đó, ta có điều phải chứng minh.
II. MỘT SỐ DẠNG BÀI TẬP
1. Dạng 1: Chứng minh một đường thẳng là tiếp tuyến của đường tròn. Bài 1: Cho ABC 
có độ dài các cạnh là AB  6cm, AC  8cm và 0
BAC  90 . Chứng minh rằng BC là  24 
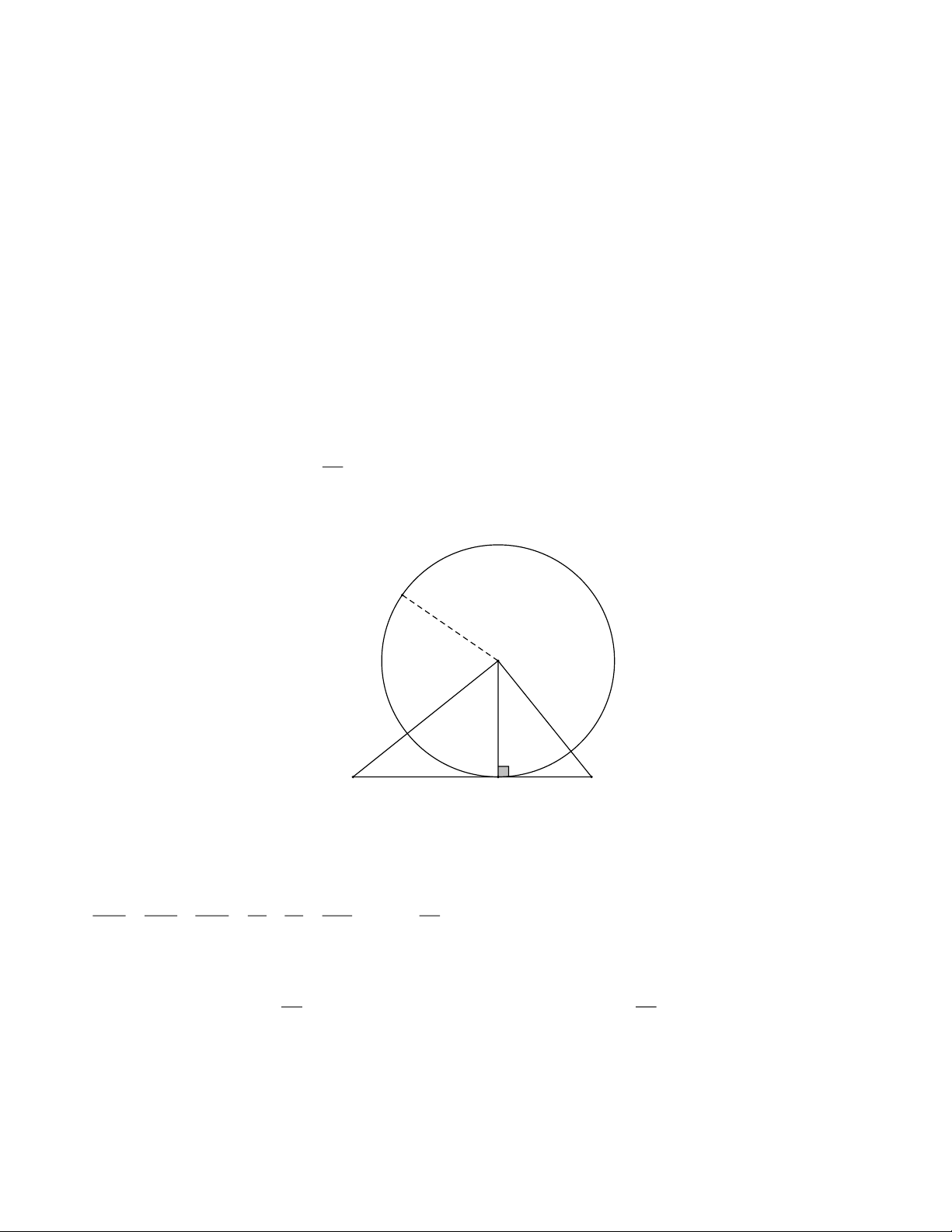
tiếp tuyến của đường tròn A ; cm   .  5  Giải R A C B H Từ A kẻ AH  BC tại H ABC 
vuông tại A có AH  BC tại H nên theo hệ thức lượng trong tam giác vuông, ta có: 1 1 1 1 1 25 24       AH  cm 2 2 2 2 2 AH AB AC 6 8 576 5
Vẽ đường tròn tâm A, bán kính AH. 24  24  Do BC  AH tại H, AH 
cm  BC là tiếp tuyến của đường tròn A ; cm   5  5 
Bài 2: Cho hình thang vuông ABCD  0
A  D  90  . Tia phân giác của góc C đi qua trung điểm I của
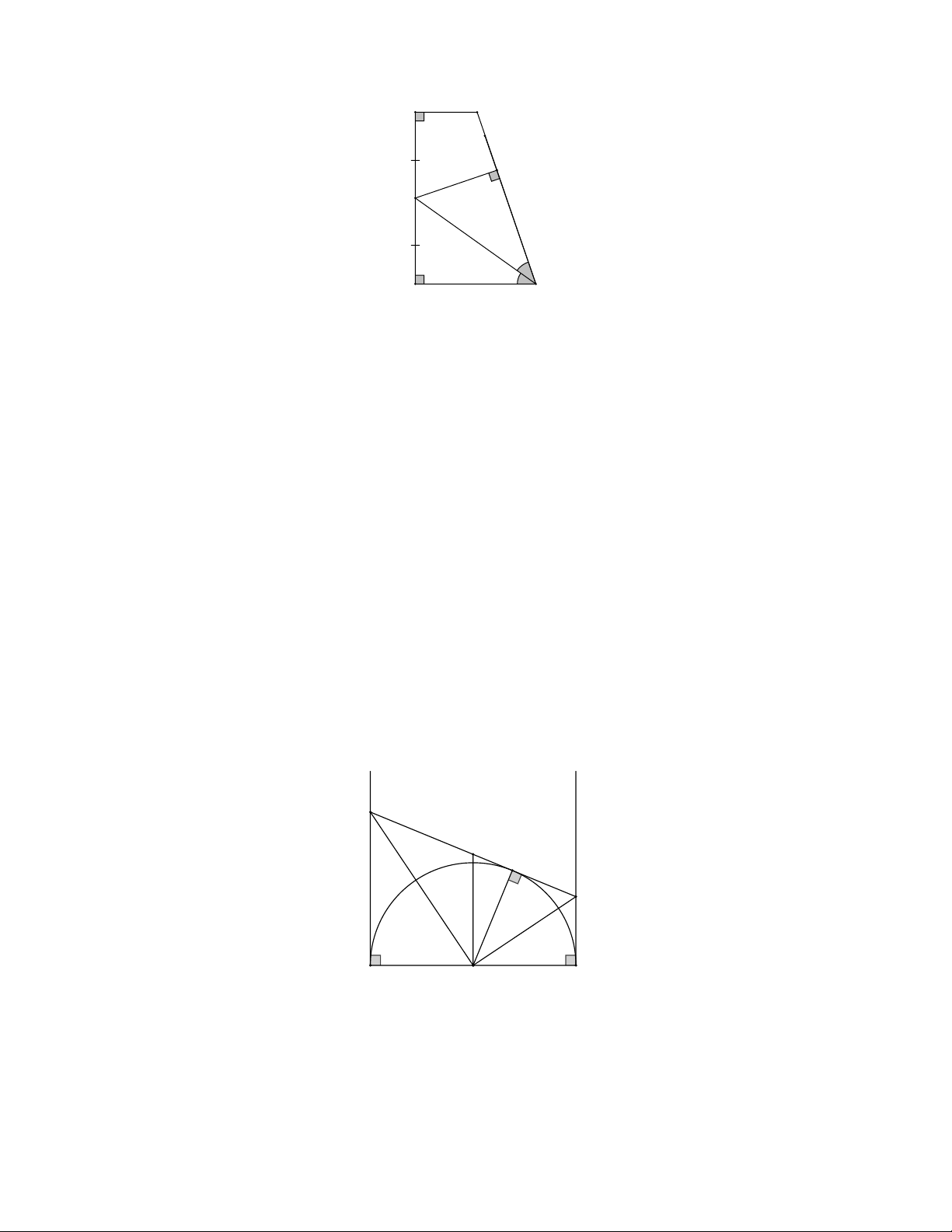
AD. Chứng minh rằng BC là tiếp tuyến của đường tròn I;IA Giải A B M I D C Từ I kẻ IM  BC tại M
Do CI là phân giác của DCM  DCI  MCI Xét I  CD và I  CM có: 0 IDC  IMC  90 (do 0 D  90 ,IM  BC ) IC: cạnh chung DCI  MCI  I  CD  I
 CM (cạnh huyền – góc nhọn)  IM  ID (2 cạnh tương ứng)
Lại có: ID  IA (I là trung điểm AD)  IM  IA
Xét I;IA có BC  IM tại M, IM  IA  BC là tiếp tuyến tại M của I;IA
Bài 3: Cho nửa O đường kính AB. Gọi Ax, By là các tiếp tuyến tại A và B của nửa đường tròn. Lấy
C là điểm bất kì trên Ax. Qua O kẻ đường thẳng vuông góc với OC, cắt By tại D. Chứng minh rằng CD
là tiếp tuyến của O . Giải x y C M H D A O B
Từ O kẻ OH  CD tại H. Gọi M là trung điểm của CD
Do Ax, By là tiếp tuyến của O  Ax  AB, By  AB  Ax / /By hay AC / /BD
Xét hình thang ABDC AC / /BD có O, M là trung điểm của AB và CD
 OM là đường trung bình của hình thang ABDC  OM/ /AC / /BD
Do OM / /AC  ACO  COM (2 góc sole trong) (1) 1 C
 OD vuông tại O OC  OD có OM là trung tuyến ứng với cạnh huyền  OM  CD  CM  DM 2 C  MO có OM  CM  C
 MO cân tại M  MCO  MOC (2)
Từ (1) và (2)  ACO  MCO hay ACO  HCO Xét A  CO và HCO  có: 0 CAO  CHO  90 CO: cạnh chung ACO  HCO  A  CO  H
 CO (cạnh huyền – góc nhọn)  AO  HO
Do OH  CD tại H, OH  AO với AO là bán kính của O  CD là tiếp tuyến của O
2. Dạng 2: Sử dụng tính chất hai tiếp tuyến cắt nhau để giải toán
Bài 1: Cho đường tròn O;R và một điểm A nằm ngoài đường tròn. Từ A kẻ các tiếp tuyến AB, AC
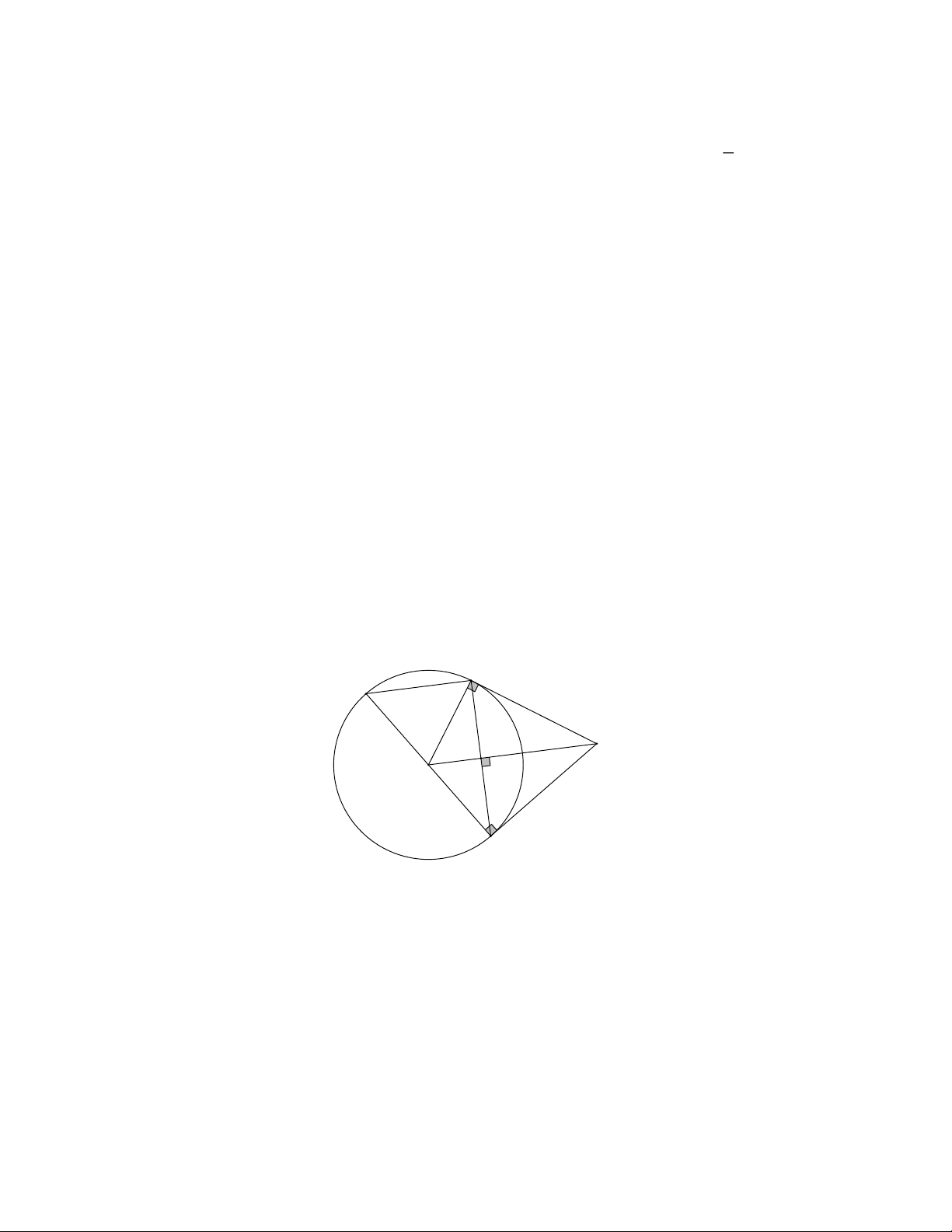
với O . Vẽ đường kính CD. Chứng minh rằng: a) OA  BC b) BD / /OA Giải B D I A O C
a) Do AB, AC là hai tiếp tuyến của đường tròn O và chúng cắt nhau tại A  AB  AC
Do AB  AC, OB  OC  OA là đường trung trực của BC  OA  BC
b) Do CD là đường kính của đường tròn O  O là trung điểm CD
Gọi I là giao điểm của OA và BC. Do OA là trung trực của BC  I là trung điểm BC B
 CD có I là trung điểm BC, O là trung điểm CD  OI là đường trung bình B  CD  OI / /BD Lại có IOA  OA / /BD
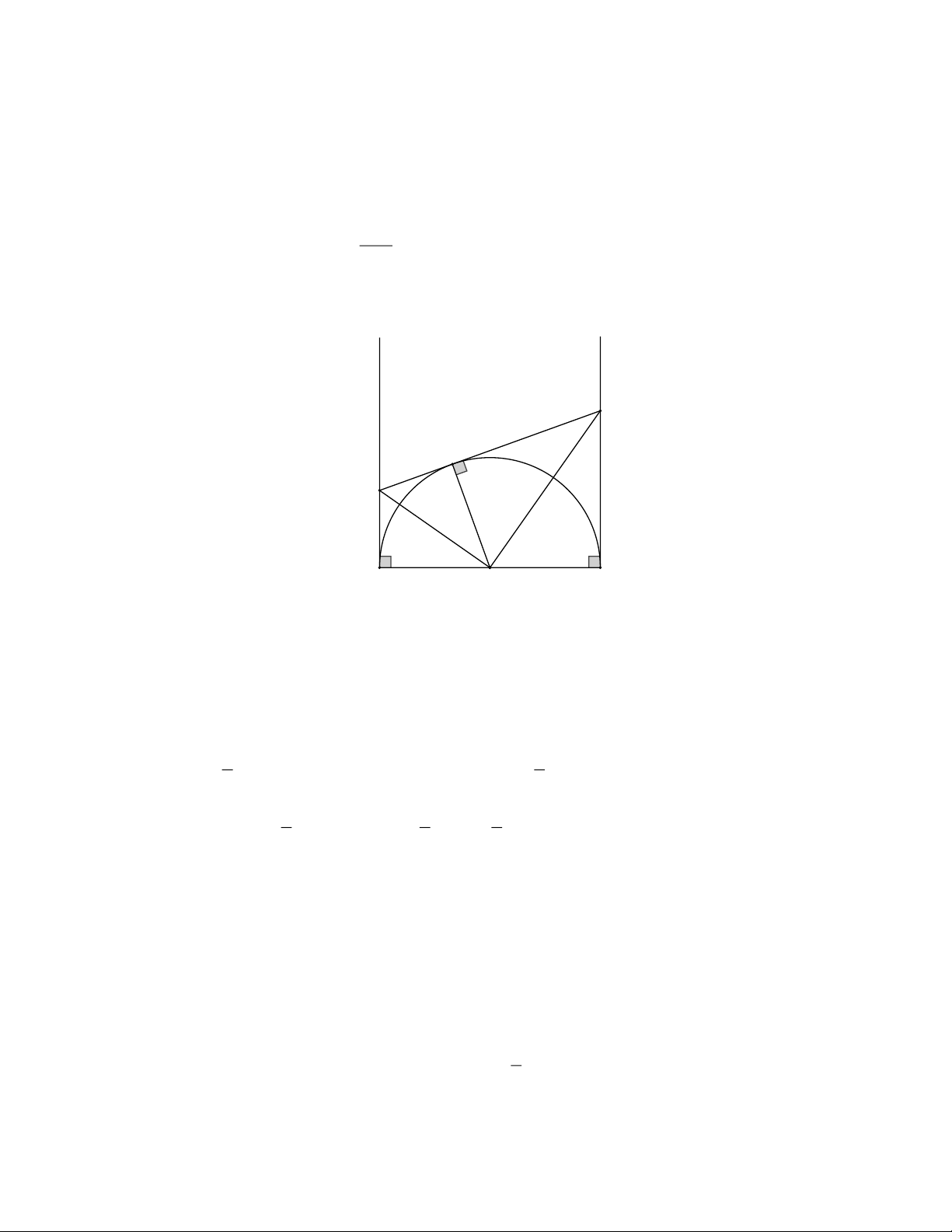
Bài 2: Cho nửa đường tròn O , đường kính AB. Trên nửa mặt phẳng bờ AB chứa nửa O , vẽ hai
tia Ax và By cùng vuông góc với AB. Trên nửa đường tròn, lấy điểm M không trùng với A và B. Qua M
vẽ tiếp tuyến d của O cắt Ax và By lần lượt tại C và D. a) Chứng minh C  OD vuông tại O.
b) Chứng minh rằng: AC  BD  CD 2 AB
c) Chứng minh rằng: AC.BD  4 Giải y x D M C A O B
Do Ax, By cùng vuông góc với đường kính AB của O  Ax, By là các tiếp tuyến của O
Do Ax và CM là 2 tiếp tuyến cắt nhau của O  CA  CM, OC là phân giác của AOM
Do By và DM là 2 tiếp tuyến cắt nhau của O  DB  DM, OD là phân giác của BOM 1 1 a) Ta có: COM 
AOM (OC là phân giác AOM ), DOM  BOM (OD là phân giác BOM ) 2 2 1
 COD  COM  DOM  AOMBO  1 1 0 0 M  .AOB  .180  90 2 2 2  C  OD vuông tại O.
b) Do AC  CM, BD  DM  AC  BD  CM  DM
Lại có M nằm giữa C và D  CM  DM  CD  AC  BD  CD (điều phải chứng minh) c) Xét C
 OD vuông tại O, OM  CD tại M 2
 CM.DM  OM (hệ thức lượng trong tam giác vuông)
Mà CM  CA,DM  DB (câu a) 2  CA.BD  OM (1)
Do AB là đường kính, OM là bán kính của   1 O  OM  AB (2) 2 1 Từ (1) và (2) 2  CA.BD  AB 4
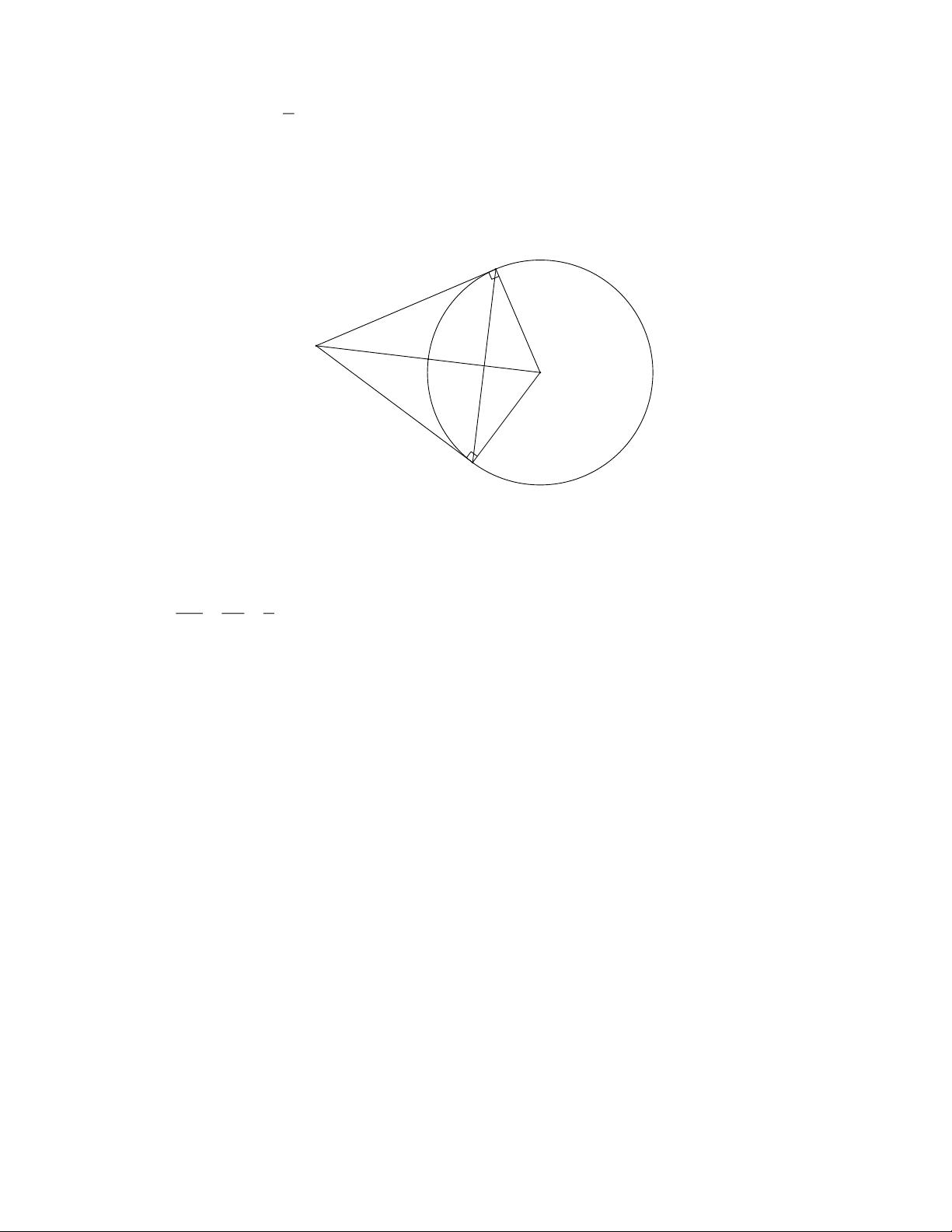
Bài 3: Cho đường tròn O;R . Từ một điểm A cách O một khoảng là 2R, ta vẽ hai tiếp tuyến AB, AC
với đường tròn (B, C là các tiếp điểm). Chứng minh rằng ABC  là tam giác đều. Giải B A O C
Do AB, AC là hai tiếp tuyến cắt nhau của O nên AB  AC, AO là phân giác góc BAC Xét ABO 
vuông tại B (do AB là tiếp tuyến của O nên AB  BO ), ta có: OB R 1 0 cos AOB     AOB  60 OA 2R 2 0 0 0 0
BAO  90  AOB  90  60  30 (do ABO  vuông tại B) Do AO là phân giác góc 0 0
BAC  BAC  2BAO  2.30  60 ABC 
cân tại A (do AB  AC ) mà 0 BAC  60  A
 BC đều (dấu hiệu nhận biết)
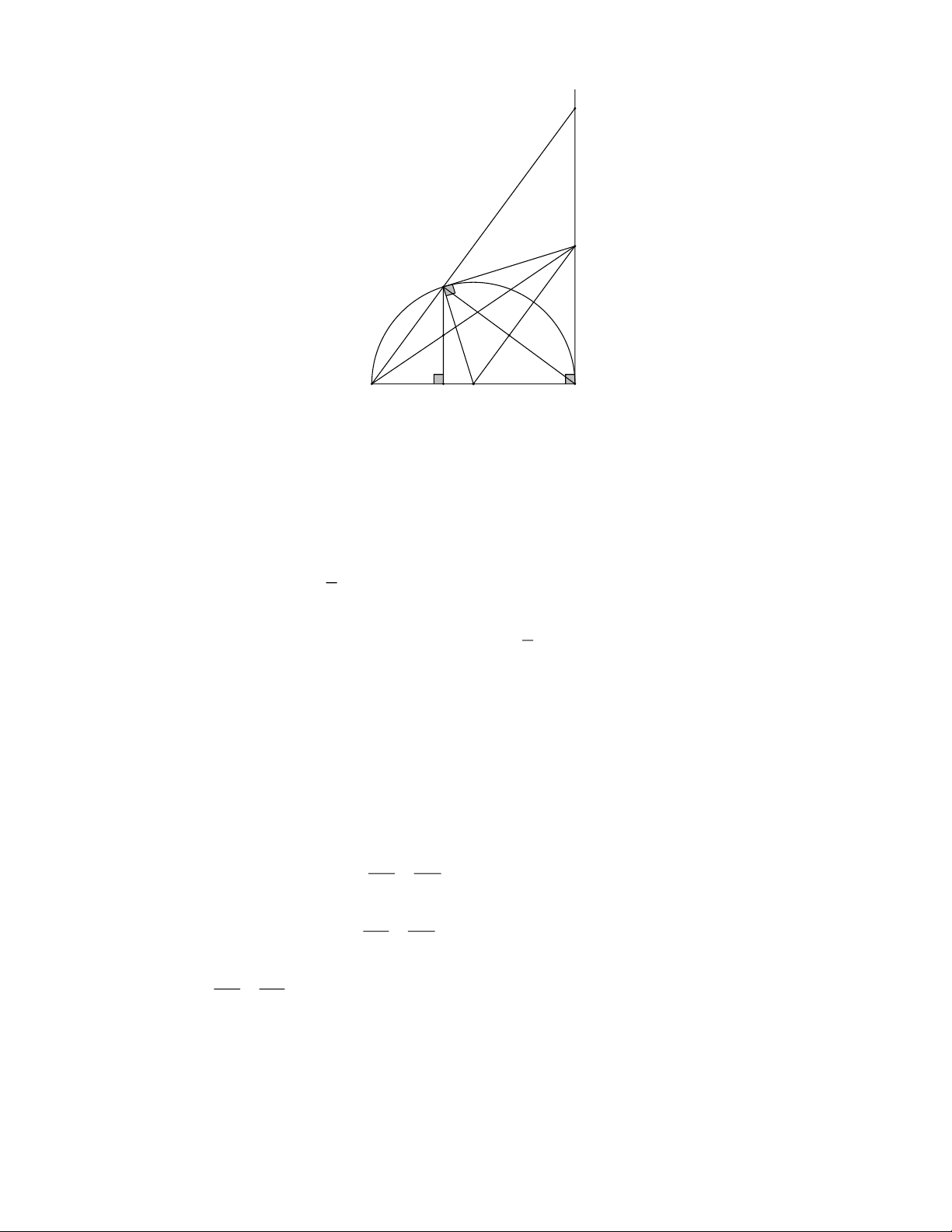
Bài 4: Cho nửa đường tròn O;R đường kính AB. Vẽ tiếp tuyến Bx với nửa đường tròn. Lấy điểm
C  O , kẻ tiếp tuyến tại C cắt Bx tại M. Tia AC cắt Bx tại N. a) Chứng minh: OM  BC
b) Chứng minh: M là trung điểm của BN
c) Kẻ CH  AB tại H. Gọi I là giao điểm của AM và CH.
Chứng minh I là trung điểm CH. Giải N M C I A H O B
a) Xét O có hai tiếp tuyến CM và Bx cắt nhau tại M  MC  MB
 M thuộc đường trung trực của BC
Lại có: OC  OB  R  O thuộc đường trung trực của BC
Do đó suy ra OM là đường trung trực của BC  OM  BC b) Do C thuộc   1 O  OC  R  AB 2 1 Xét ABC 
có CO là trung tuyến ứng với cạnh AB, CO  AB 2  ABC 
vuông tại C  BC  AC hay BC  AN
Có OM  BC (câu a), BC  AN  OM / /AN (từ vuông góc đến song song) Xét ABN 
có OM / /AN, O là trung điểm của AB  OM là đường trung bình của ABN   M là trung điểm BN.
c) Do CH  AB, BN  AB  CH / /BN (từ vuông góc đến song song)  CI / /MN, IH / /BM CI AI A
 MN có I AM,C AN,CI / /MN   (định lí Ta-let) (1) MN AM IH AI ABM 
có H AB,I AM,IH / /BM   (định lí Ta-let) (2) BM AM CI IH Từ (1) và (2)  
. Lại có MN  BM (M là trung điểm BN)  CI  IH MN BM
 I là trung điểm của CH.
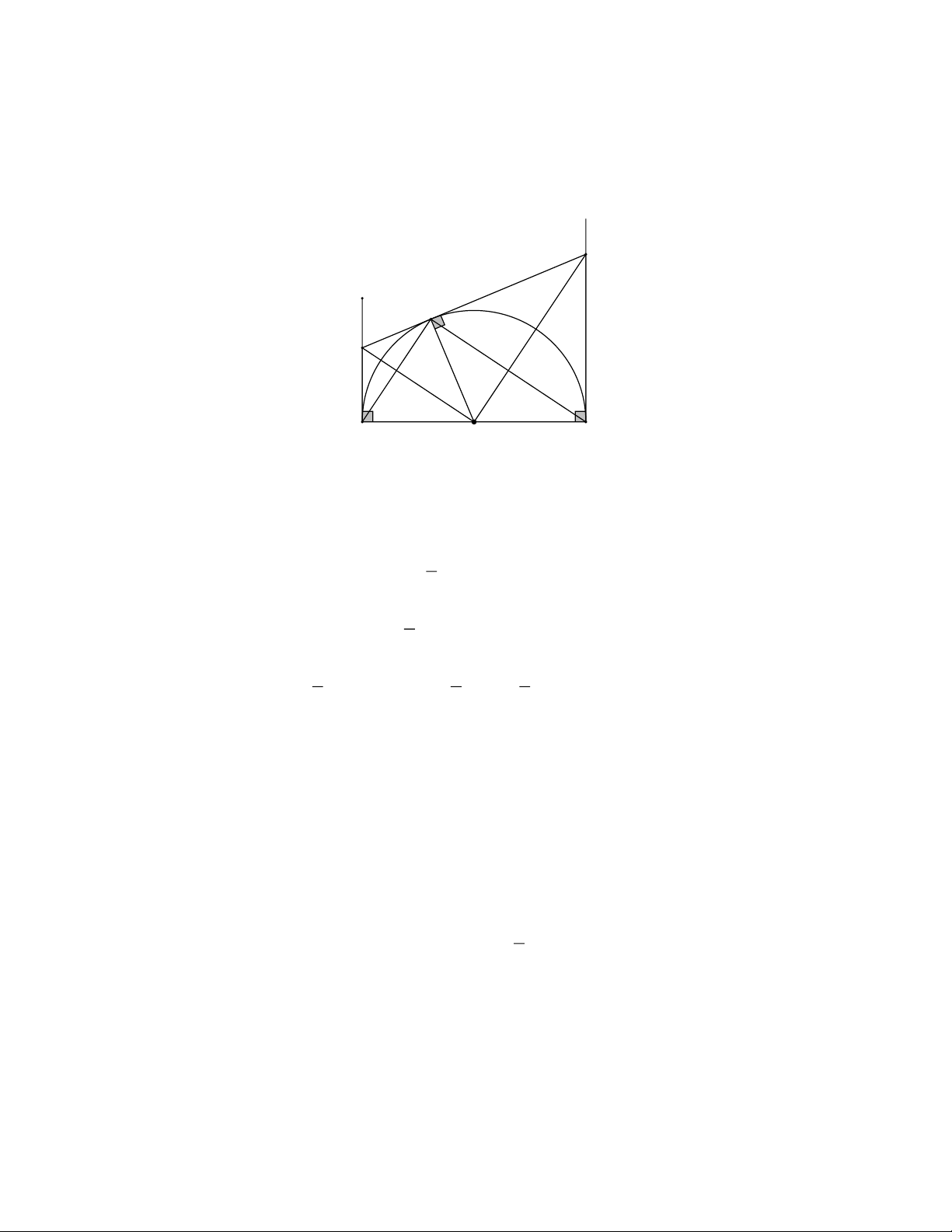
Bài 5: Cho nửa đường tròn O;R , đường kính AB. Vẽ các tiếp tuyến Ax, By cùng phía với nửa đường
tròn. Trên O lấy điểm M khác A và B. Tiếp tuyến tại M cắt Ax tại C, cắt By tại D. a) C
 OD là tam giác gì? Vì sao? b) Chứng minh: C  OD và A
 MB là hai tam giác đồng dạng.
c) Tìm vị trí của M trên nửa đường tròn O;R sao cho AC  BD đạt giá trị nhỏ nhất. Giải y D x M C A O B
O;R có 2 tiếp tuyến Ax cắt CM tại C  CA  CM, OC là phân giác của AOM
O;R có 2 tiếp tuyến By cắt DM tại D DB DM, OD là phân giác của BOM 1
a) Do OC là phân giác của AOM  COM  AOM 2 1
Do OD là phân giác của BOM  DOM  BOM 2 1 1 1
Ta có: COD  COM  DOM  AOMBO  0 0 M  AOB  .180  90 2 2 2  C  OD vuông tại O
b) Do CD là tiếp tuyến tại M của O  OM  CD tại M 0  MCO  MOC  90 (1)
Do OC là phân giác của AOM  MOC  AOC (2)
Do CA  CM, OA  OM  R  OC là đường trung trực của AM  AM  OC 0 MAO  AOC  90 (3)
Từ (1), (2) và (3)  MCO  MAO hay DCO  BAM 1 A
 MB có MO là trung tuyến ứng với cạnh AB và MO  AB  A  MB vuông tại M 0  AMB  90 2 Xét C  OD và A  MB có: 0 COD  AMB  90
DCO  BAM (chứng minh trên)  C  OD đồng dạng với A  MB (g.g) c) Xét C
 OD vuông tại O, có OM  CD tại M 2 2
 CM.DM  OM  R (hệ thức lượng trong tam giác vuông)
Do CA  CM,DB  DM  AC  BD  CM  DM
Áp dụng BĐT Cauchy cho 2 số dương, ta có: 2
CM  DM  2 CM.DM  2 R  2R
 AC  BD  2R  AC  BD  2R . min C  M  DM 
Dấu bằng xảy ra khi AC  BD  2R
 AC  CM  DM  BD  R AC  CM, BD  DM 
 M là điểm nằm trên nửa đường tròn và thỏa mãn OM  AB tại O.
III. BÀI TẬP LUYỆN TẬP
Bài 1: Cho đường tròn O;5cm , đường kính AB. Gọi E là điểm nằm trên đoạn AB sao cho BE  2cm.
Qua trung điểm H của AE vẽ dây cung CD  AB.
a) Tứ giác ADEC là hình gì? Vì sao?
b) Gọi I là giao của DE và BC. Chứng minh rằng I thuộc đường tròn tâm O’, đường kính EB.
c) Chứng minh HI là tiếp tuyến của đường tròn O' .
Bài 2: Cho nửa đường tròn tâm O, đường kính AB. Kẻ tiếp tuyến Ax, By cùng phía với nửa đường tròn
đối với AB. Vẽ bán kính OE bất kì. Tiếp tuyến của nửa đường tròn tại E cắt Ax và By theo thứ tự tại C và D. a) Chứng minh 0 COD  90
b) Gọi I là giao điểm của OC và AE, K là giao điểm của OD và BE. Tứ giác EIOK là hình gì? Vì sao?
c) Chứng minh rằng: OI.OC  OK.OD
Bài 3: Cho đường tròn tâm O và điểm M nằm ngoài đường tròn. Từ M kẻ hai tiếp tuyến MA, MB đến
đường tròn (A, B là tiếp điểm). Biết số đo 0 AMO  30 và OM  4.
a) Chứng minh OM là đường trung trực của A  MB và A  MB đều.
b) Tính độ dài bán kính OA và AB.
c) Từ M kẻ đường thẳng vuông góc với đường phân giác của góc MOB tại C.
Chứng minh tứ giác AMCO là hình chữ nhật. Bài 4: Cho ABC 
vuông tại A AB  AC , đường cao AH. Gọi E là điểm đối xứng với B qua H. Đường
tròn tâm đường kính EC cắt AC ở K. Chứng minh HK là tiếp tuyến của đường tròn O.
Bài 5: Cho nửa đường tròn O;R , đường kính AB. Vẽ 2 tiếp tuyến Ax, By cùng phía với nửa đường
tròn so với AB. Lấy điểm E bất kì trên nửa O . Tiếp tuyến tại E cắt Ax và By lần lượt tại C và D.
a) Chứng minh rằng khi E thay đổi trên nửa đường tròn thì tích AC.BD không đổi.
b) Tìm vị trí của điểm E trên nửa O sao cho tứ giác ACDB có diện tích nhỏ nhất.
Khi đó tứ giác ACDB là hình gì?