Thông tin
Quiz

Chuyên đề tổ hợp và xác suất – Dương Minh Hùng

Tài liệu gồm 87 trang, được biên soạn bởi thầy giáo Dương Minh Hùng, tóm tắt lý thuyết và hướng dẫn giải các dạng bài tập chuyên đề tổ hợp và xác suất, giúp học sinh học tốt chương trình Đại số và Giải tích 11 chương 2.

Chủ đề:

Chương 8: Các quy tắc tính xác suất (KNTT) 65 tài liệu

Môn:

Toán 11 3.3 K tài liệu

Thông tin:

87 trang 1 năm trước

Tác giả:

Kim Oanh

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Chuyên đề tổ hợp và xác suất – Dương Minh Hùng

108 54 lượt tải Tải xuống

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 1

①.Dạng 1: Sử dụng quy tắc cộng

. Bài tập minh họa:

Câu 1: Có

cây bút đỏ,

cây bút xanh trong một hộp bút. Hỏi có bao nhiêu cách lấy ra một cây

bút từ hộp bút?

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải

 Số cách lấy ra

cây bút là màu đỏ có

cách.

 Số cách lấy ra

cây bút là màu xanh có

cách.

 Theo quy tắc cộng, số cách lấy ra

cây bút từ hộp bút là:

3 4 7 

cách.

 Vậy có

cách lấy

cây bút từ hộp bút. Chọn đáp án A

Câu 2: Thầy giáo chủ nhiệm có

quyển sách khác nhau và

quyển vở khác nhau. Thầy chọn ra

một quyển sách hoặc một quyển vở để tặng cho học sinh giỏi. Hỏi có bao nhiêu cách chọn

khác nhau?

Ⓐ.

10.

Ⓑ.

Ⓒ.

80.

Ⓓ.

Lời giải

 Chọn một quyển sách có

cách chọn.

 Chọn một quyển vở có

cách chọn.

§➊. CÁC QUY TẮC ĐẾM

Chương ⓶

⓫

Tóm tắt lý thuyết

Ⓐ

➊.

Quy tắc cộng:



Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có

cách

thực hiện, hành động kia có

cách thực hiện không trùng với bất kì cách nào của hành động

thứ nhất thì công việc đó có

m n

cách thực hiện.

 Nếu

và

là các tập hợp hữu hạn không giao nhau thì:

     

n A B n A n B  

➋.

Quy tắc nhân:



Một công việc được hoành thành bởi hai hành động liên tiếp. Nếu có

cách thực hiện hành động

thứ nhất và ứng với mỗi cách đó có

cách thực hiện hành động thứ hai thì có

.m n

cách hoàn

thành công việc.

Dạng toán: tìm số các số tạo thành: Gọi số cần tìm có dạng:

...abc

, tuỳ theo yêu cầu bài toán:

 Nếu số lẻ thì số tận cùng là số lẻ.

 Nếu số chẵn thì số tận cùng là số chẵn.

Phân dạng bài tập

Ⓑ

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 2

Áp dụng quy tắc cộng có

cách chọn ra một quyển sách hoặc một quyển vở để tặng cho

học sinh giỏi.

②.Dạng 2: Sử dụng quy tắc nhân

. Bài tập minh họa:

Câu 1: Bạn muốn mua

cây bút gồm một cây bút mực và một cây bút chì. Các cây bút mực có

màu khác nhau, các cây bút chì có

màu khác nhau. Hỏi có bao nhiêu cách chọn để

mua?

Ⓐ.

8! 9!



. Ⓑ.

. Ⓒ.

. Ⓓ.

8!.9!

Lời giải

Số cách chọn một cây bút mực là

Số cách chọn một cây bút chì là

Áp dụng quy tắc nhân, ta có số cách chọn là

1 1

8 9

. 72

C C



Câu 2: Một đội văn nghệ chuẩn bị được 2 vở kịch, 3 điệu múa và 6 bài hát. Tại hội diễn văn nghệ,

mỗi đội chỉ được trình diễn một vở kịch, một điệu múa và một bài hát. Hỏi đội văn nghệ

trên có bao nhiêu cách chọn chương trình diễn, biết chất lượng các vở kịch, điệu múa, bài

hát là như nhau?

Ⓐ. 11. Ⓑ. 36. Ⓒ. 25. Ⓓ. 18.

Lời giải

Đội văn nghệ trên có 2 cách chọn trình diễn một vở kịch, có 3 cách chọn trình diễn một

điệu múa, có 6 cách chọn trình diễn một bài hát. Theo quy tắc nhân, đội văn nghệ trên có

2.3.6 36



cách chọn chương trình diễn.

③.Dạng 3: Sử dụng quy tắc cộng và quy tắc nhân

. Bài tập minh họa:

Câu 1: Một người có

chiếc áo trong đó có

chiếc áo trắng và

chiếc cà vạt trong đó có

chiếc

cà vạt màu vàng. Tìm số cách chọn một chiếc áo và một chiếc cà vạt sao cho đã chọn áo

trắng thì không chọn cà vạt màu vàng.

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Số cách chọn một chiếc áo và một chiếc cà vạt sao cho áo màu trắng và cà vạt không phải

màu vàng là

3.3 9



Số cách chọn một chiếc áo và một chiếc cà vạt sao cho áo không phải màu trắng và cà vạt

bất kì trong

cà vạt là

4.5 20



Số cách chọn một chiếc áo và một chiếc cà vạt sao cho đã chọn áo trắng thì không chọn cà

vạt màu vàng là

9 20 29

 

Câu 2: Từ một tập gồm 10 câu hỏi, trong đó có 4 câu lí thuyết và 6 câu bài tập, người ta tạo thành

các đề thi. Biết rằng một đề thi phải gồm 3 câu hỏi trong đó có ít nhất một câu lí thuyết

và 1 câu bài tập. Hỏi có thể tạo được bao nhiêu đề khác nhau?

Ⓐ.

100

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Trường hợp 1: 2 câu lí thuyết, 1 câu bài tập. Suy ra số đề tạo ra là

2 1

4 6

. 36

C C



Trường hợp 2: 1 câu lí thuyết, 2 câu bài tập. Suy ra số đề tạo ra là

1 2

4 6

. 60

C C



Vậy có thể tạo được số đề khác nhau là:

36 60 96

 

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 3

Câu 3: Từ tập

 

0;1;2;3;4;5X 

có thể lập được bao nhiêu số tự nhiên có ba chữ số khác nhau mà

số đó chia hết cho 5?

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải

* Th1: Số cần tìm có dạng

0ab

: có

20A 

số.

* Th2: Số cần tìm có dạng

5ab

: có

4.4 16

số.

Vậy có:

20 16 36 

số thỏa yêu cầu đề bài.

Câu 4: Lớp

12A

có

học sinh giỏi trong đó có

nam và

nữ. Lớp

12B

có

học sinh giỏi trong

đó có

nam và

nữ. Cần chọn mỗi lớp

học sinh giỏi đi dự Đại hội Thi đu

Ⓐ.

Hỏi có

bao nhiêu cách chọn sao cho trong

học sinh được chọn có

nam và

nữ?

Ⓐ.

1155

Ⓑ.

3060

Ⓒ.

648

Ⓓ.

594

Lời giải

Trường hợp 1: Chọn ở lớp

12 A

, 1 học sinh giỏi nam, 1 học sinh giỏi nữ.

Chọn ở lớp

12B

,1 học sinh giỏi nam, 1 học sinh giỏi nữ.

Số cách chọn là

1 1 1 1

1 9 6 2

. . . 108C C C C 

Trường hợp 2: Chọn ở lớp

12 A

, 2 học sinh giỏi nữ.

Chọn ở lớp

12B

,2 học sinh giỏi nam.

Số cách chọn là

2 2

9 6

. 540C C 

Vậy có

108 540 648 

Câu 1:Trên một bàn bi a có 15 quả bóng được đánh số lần lượt từ 1 đến 15, nếu người chơi đưa được quả bóng

nào vào lỗ thì sẽ được số điểm tương ứng với số điểm trên quả bóng đó. Hỏi người

Ⓐ.

120

Ⓑ.

Ⓒ.

100

Ⓓ.

150

Lời giải :......................................................................

......................................................................................

Câu 2:Cho hai tập hợp

,{ }, ,A a b c d



;

,{ },B c d e



. Chọn khẳng định sai trong các khẳng định sau:

Ⓐ.





4N A 

Ⓑ.

 

3N B 

Ⓒ.

7( )N A B 

Ⓓ.

2( )N A B 

Lời giải :......................................................................

......................................................................................

Câu 3:Có

học sinh giỏi gồm

học sinh khối

và

học sinh khối

. Hỏi có bao

nhiêu cách chọn ra

học sinh sao cho mỗi khối có ít nhất

học sinh?

Ⓐ.

4249

Ⓑ.

4250

Ⓒ.

5005

Ⓓ.

805

Lời giải :......................................................................

......................................................................................

Câu 4:Có bao nhiêu số tự nhiên có hai chữ số mà các chữ số hàng chục lớn hơn chữ số hàng đơn vị?

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải :......................................................................

......................................................................................

Bài tập rèn luyện

Ⓒ

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 4

......................................................................................

Câu 5:An muốn qua nhà Bình để cùng Bình đến chơi nhà Cường. Từ nhà An đến nhà Bình có bốn con đường

đi, t

ừ nh

à Bình

ến nh

à Cư

ờng có 6 con đ

ờng đi. Hỏi An có bao

nhiêu cách ch

ọn đ

ờng đi đến nh

à Cư

ờng?

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 6:Bạn muốn mua một cây bút mực và một cây bút chì. Các cây bút mực có

màu khác nhau, các cây

bút chì cũng có

màu khác nhau. Như vậy bạn có bao nhiêu cách chọn

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 7:Có

bông hồng đỏ,

bông hồng vàng và

bông hồng trắng, các bông hồng khác nhau từng đôi một.

Hỏi có bao nhiêu cách lấy

bông hồng có đủ ba màu.

Ⓐ.

319

Ⓑ.

3014

Ⓒ.

310

Ⓓ.

310

Lời giải :......................................................................

......................................................................................

Câu 8:Một liên đoàn bóng đá có

đội, mỗi đội phải đá

trận với mỗi đội khác,

trận ở sân nhà và

trận

ở sân khách. Số trận đấu được sắp xếp là:

Ⓐ.

180

. Ⓑ.

160

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 9:Có 7 bông hồng đỏ, 8 bông hồng vàng và 10 bông hồng trắng, mỗi bông hồng khác nhau từng đôi một.

Hỏi có bao nhiêu cách lấy 3 bông hồng có đủ ba màu.

Ⓐ. 560. Ⓑ. 310. Ⓒ. 3014.

Ⓓ. 319.

Lời giải :......................................................................

......................................................................................

Câu 10:Bạn muốn mua một cây bút mực và một cây bút chì. Các cây bút mực có

màu khác nhau, các cây

bút chì cũng có

màu khác nhau. Như vậy bạn có bao nhiêu cách chọn

Ⓐ.

. Ⓑ.

. Ⓒ.

Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 11:Có

cặp vợ chồng đi dự tiệc. Tổng số cách chọn một người đàn ông và một người phụ nữ trong bữa

tiệc phát biểu ý kiến sao cho hai người đó không là vợ chồng:

Ⓐ.

100

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 12:Bạn muốn mua một cây bút mực và một cây bút chì. Các cây bút mực có

màu khác nhau, các cây

bút chì cũng có

màu khác nhau. Như vậy bạn có bao nhiêu cách chọn?

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 5

......................................................................................

Câu 13:Trong đội văn nghệ nhà trường có 8 học sinh nam và 6 học sinh nữ. Hỏi có bao nhiêu cách chọn một

đôi song ca nam

ữ

Ⓐ.

. Ⓑ.

182

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 14:Có 10 quả cầu đỏ được đánh số từ 1 đến 10, 7 quả cầu xanh được đánh số từ 1 đến 7 và 8 quả cầu vàng

được đánh số từ 1 đến 8. Hỏi có bao nhiêu cách lấy ra 3 quả cầu khác màu và khác số.

Ⓐ. 392. Ⓑ. 1023.

Ⓒ. 3014. Ⓓ. 391.

Lời giải :......................................................................

......................................................................................

..............................

........................................................

Câu 15:Có bao nhiêu cách sắp xếp

nữ sinh,

nam sinh thành một hàng dọc sao cho các bạn nam và nữ

ngồi xen kẻ:

Ⓐ.

. Ⓑ.

Ⓒ.

720

. Ⓓ.

144

Lời giải :......................................................................

......................................................................................

Câu 16:Số các số tự nhiên gồm

chữ số chia hết cho

là:

Ⓐ.

3260

. Ⓑ.

3168

Ⓒ.

9000

. Ⓓ.

12070

Lời giải :......................................................................

......................................................................................

.......

...............................................................................

Câu 17:Một người có

cái áo trong đó có

áo trắng và

cái cà vạt trong đó có

cà vạt màu vàng. Tìm số

cách chọn một áo và một cà vạt sao cho đã chọn áo trắng thì không chọn cà vạt màu vàng.

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 18:Có 6 học sinh và 3 thầy giáo

, ,

A B C

được xếp vào một hàng ngang có 9 ghế. Hỏi có bao nhiêu cách

xếp chỗ cho 9 người đó sao cho mỗi thầy giáo ngồi giữa hai học sinh?

Ⓐ.

55012

Ⓑ.

94536

Ⓒ.

43200

Ⓓ.

35684

Lời giải :......................................................................

......................................................................................

Câu 19:Một liên đoàn bóng đá có

đội, mỗi đội phải đá

trận với mỗi đội khác,

trận ở sân nhà và

trận ở sân khách. Số trận đấu được sắp xếp là:

Ⓐ.

180

. Ⓑ.

160

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 20:Cho các số

1,5,6,7

có thể lập được bao nhiêu số tự nhiên có

chữ số với các chữ số khác nhau:

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

256

Lời giải :......................................................................

......................................................................................

Câu 21:Có bao nhiêu số tự nhiên có chín chữ số mà các chữ số của nó viết theo thứ tự giảm dần

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 6

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 22:Có bao nhiêu số tự nhiên có

chữ số được lập từ sáu chữ số

Ⓐ.

120

. Ⓑ.

216

Ⓒ.

256

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 23:Từ các chữ số

;

có thể lập được bao nhiêu số tự nhiên có

chữ số khác nhau đôi một?

Ⓐ.

. Ⓑ.

. Ⓒ.

Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 24:Có bao nhiêu số tự nhiên có hai chữ số mà các chữ số hàng chục lớn hơn chữ số hàng đơn vị?

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 25:Có bao nhiêu số tự nhiên lẻ có 4 chữ số khác nhau?

Ⓐ.

2240.

Ⓑ.

2520.

Ⓒ.

2016.

Ⓓ.

256.

Lời giải :......................................................................

......................................................................................

Câu 26:Từ các chữ số

2,3, 4,5

có thể lập được bao nhiêu số gồm

chữ số:

Ⓐ.

256

. Ⓑ.

120

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

........................................................................

..............

Câu 27:Cho các chữ số

1;2;3;4;5;6;9

hỏi có bao nhiêu số tự nhiên có 7 chữ số khác nhau và nhỏ hơn

7000.000

từ các số trên?

Ⓐ.

4320

. Ⓑ.

5040

Ⓒ.

8640

. Ⓓ.

720

Lời giải :......................................................................

......................................................................................

Câu 28:Có bao nhiêu số tự nhiên có

chữ số:

Ⓐ.

900

. Ⓑ.

901

Ⓒ.

899

. Ⓓ.

999

Lời giải :......................................................................

......................................................................................

Câu 29:Có bao nhiêu số có

chữ số, mà tất cả các chữ số đều lẻ:

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 30:Cho các số

1, 2,3,4,5,6,7

. Số các số tự nhiên gồm

chữ số lấy từ

chữ số trên sao cho chữ số đầu

tiên bằng

là:

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 7

Ⓐ.

. Ⓑ.

Ⓒ.

240

. Ⓓ.

2401

Lời giải :......................................................................

......................................................................................

Câu 31:Trong một tuần, bạn A dự định mỗi ngày đi thăm một người bạn trong

người bạn của mình. Hỏi

bạn A có thể lập được bao nhiêu kế hoạch đi thăm bạn của mình.

Ⓐ.

. Ⓑ.

35831808

Ⓒ.

12!

. Ⓓ.

3991680

Lời giải :......................................................................

......................................................................................

Câu 32:Có bao nhiêu số có

chữ số được tạo thành từ các chữ số

sao cho bất kì

chữ số nào đứng

cạnh nhau cũng hơn kém nhau

đơn vị?

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 33:Có bao nhiêu số tự nhiên chẵn gồm

chữ số khác nhau?

Ⓐ.

500

. Ⓑ.

328

Ⓒ.

360

. Ⓓ.

405

Lời giải :......................................................................

......................................................................................

Câu 34:Có bao nhiêu số tự nhiên có chín chữ số mà các chữ số của nó viết theo thứ tự giảm dần:

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 35:Có bao nhiêu chữ số chẵn gồm bốn chữ số đôi một khác nhau được lập từ các số

0,1, 2, 4,5, 6,8

Ⓐ. 252 Ⓑ. 520

Ⓒ. 480 Ⓓ. 368

Lời giải :......................................................................

......................................................................................

Câu 36:Từ các số

1,2,3

có thể lập được bao nhiêu số tự nhiên khác nhau và mỗi số có các chữ số khác nhau:

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 37:Từ các số

1, 2,3

có thể lập được bao nhiêu số tự nhiên khác nhau và mỗi số có các chữ số khác nhau:

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 38:Từ các chữ số

có thể lập được bao nhiêu số tự nhiên gồm

chữ số đôi một khác

nhau trong đó hai chữ số

và

không đứng cạnh nhau.

Ⓐ.

384

Ⓑ.

120

Ⓒ.

216

Ⓓ.

600

Lời giải :......................................................................

......................................................................................

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 8

Câu 39:Có bao nhiêu số tự nhiên có hai chữ số mà các chữ số hàng chục lớn hơn chữ số hàng đơn vị?

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 40:Cho tập hợp





1,2,3,...,20



. Hỏi

có bao nhiêu tập hợp con khác rỗng mà số phần tử là số

chẵn bằng số phần tử là số lẻ?

Ⓐ.

184755

. Ⓑ.

524288

Ⓒ.

524287

. Ⓓ.

184756

Lời giải :......................................................................

......................................................................................

BẢNG ĐÁP ÁN

1.A 2.C 3.B 4.B 5.C 6.A 7.D 8.A 9.A 10.A

11.D

12.A

13.C

14.A

15.B

16.C

17.A

18.C

19.A

20.B

21.D

22.B

23.B

24.B

25.A

26.A

27.A

29.A

30.D

31.B 32.D 33.B 34.D 35.B 36.A 37.A 38.A 39.B 40.A

Hướng dẫn giải

Câu 1.

Lời giải

Chọn A

Người chơi có thể đạt được số điểm tối đa là

1 2 ... 15 120

   

Câu 2.

Lờigiải

Chọn C

Ta có :









, , , , 5

A B a b c d e N A B

    

Câu 3.

Lời giải

Chọn B

Số cách chọn

học sinh bất kỳ trong

học sinh là

5005

C 

Số cách chọn

học sinh chỉ có khối

là



cách.

Số cách chọn

học sinh chỉ có khối

và

là



cách.

Số cách chọn

học sinh chỉ có khối

và

là

6 6

11 6

461

C C 

cách.

Số cách chọn

học sinh chỉ có khối

và

là

6 6

10 6

209

C C 

cách.

Do đó số cách chọn

học sinh sao cho mỗi khối có ít nhất

học sinh là

5005 1 84 461 209 4250

    

cách.

Câu 4.

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 9

Lời giải

Chọn B

Nếu chữ số hàng chục là

thì số có chữ số hàng đơn vị là



thì số các chữ số nhỏ hơn

năm ở

hàng đơn vị cũng bằng

. Do chữ số hang chục lớn hơn bằng

còn chữ số hàng đơn vị thi



Vậy số các số tự nhiên có hai chữ số mà các chữ số hàng chục lớn hơn chữ số hàng đơn vị là:

1 2 3 4 5 6 7 8 9 45

        

nên chọn

Câu 5.

Lời giải

Chọn C

Từ nhà An đến nhà Bình có bốn cách chọn đường.

Từ nhà Bình đến nhà Cường có sáu cách chọn đường.

Áp dụng quy tắc nhân ta có số cách chọn đường đi từ nhà An đến nhà Cường là:

4.6 24



(cách).

Câu 6.

Lờigiải

Chọn A

Chọn cây bút mực : có

cách

Chọn cây bút chì : có

cách

Theo quy tắc nhân, số cách mua là :

8.8 64



(cách )

Câu 7.

Lời giải

Chọn D

Só cách chọn là

7.8.10 560



Câu 8.

Lời giải

Chọn A

Mỗi đội sẽ gặp

đội khác trong hai lượt trận sân nhà và sân khách. Có

10.9 90



trận.

Mỗi đội đá

trận sân nhà,

trận sân khách. Nên số trận đấu là

2.90 180



trận.

Câu 9.

Lời giải

Chọn A

Số cách lấy 3 bông hồng bất kì:

2300

C

Số cách lấy 3 bông hồng chỉ có một màu:

3 3 3

7 8 10

211

  C C C

Số cách lấy 3 bông hồng có đúng hai màu:





3 3 3 3 3 3

15 17 18 7 8 10

2 1529

     C C C C C C

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 10

Vậy số cách chọn thỏa yêu cầu bài toán là:

2300 211 1529 560

  

Câu 10.

Lời giải

Chọn A

Chọn cây bút mực : có 8 cách

Chọn cây bút chì : có 8 cách

Theo quy tắc nhân, số cách mua là : 8.8 = 64 (cách )

Câu 11.

Lời giải

Chọn D

Có

cách chọn

người đàn ông.

Có

cách chọn

người phụ nữ.

Tổng số cách chọn một người đàn ông và một người đàn bà trong bữa tiệc phát biểu ý kiến sao cho

hai người đó không là vợ chồng:

10.10 10 90

 

Nên chọn

Theo em nên làm như thế này cho tiện

Chọn

người trong

người đàn ông có

cách.

Chọn

người trong

người phụ nữ không là vợ của người đàn ông đã chọn có

cách.

Vậy có

10.9 90



cách chọn

Câu 12.

Lời giải

Chọn A

Chọn cây bút mực : có

cách

Chọn cây bút chì : có

cách

Theo quy tắc nhân, số cách mua là :

8.8 64



(cách )

Câu 13.

Lời giải

Chọn C

Mỗi cách chọn ra một đôi song song nam-nữ được được hiện qua 2 công đoạn

-Công đoạn 1: Chọn 1 học sinh nữ từ 6 học sinh nữ có 6 cách.

-Công đoạn 2: Chọn 1 học sinh nam từ 8 học sinh nam có 8 cách.

Áp dụng quy tắc nhân có

6.8 48



cách chọn đôi song ca thỏa đề.

Câu 14.

Lời giải

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 11

Chọn A

Ta chọn các quả cầu theo trình tự sau:

Chọn quả xanh: 7 cách chọn.

Chọn quả cầu vàng: có 7 cách chọn.

Chọn quả cầu đỏ: có 8 cách chọn.

Vậy có tất cả

7.7.8 392



cách chọn.

Câu 15.

Lờigiải

Chọn B

Chọn vị trí

nam và

nữ:

2.1

cách chọn.

Xếp

nam có:

3.2.1

cách xếp.

Xếp

nữ có:

3.2.1

cách xếp.

Vậy có

 

2.1. 3.2.1 72



cách xếp.

Câu 16.

Lờigiải

Chọn C

Gọi số cần tìm có dạng :





abcde a



Chọn

: có

cách







Chọn

: có

cách







Chọn

bcd

: có

cách

Theo quy tắc nhân, có

1.9.10 9000



(số).

Câu 17.

Lời giải

Chọn A

TH1: Chọn một áo trắng trong

áo trắng thì có

cách chọn.

Chọn một cà vạt trong

cà vạt không phải màu vàng thì có

cách chọn.

Vậy có

3.3 9



chọn áo trắng và không chọn cà vạt màu vàng.

TH2: Chọn một áo trong

áo không phải áo trắng thì có

cách chọn.

Chọn một cà vạt trong

cà vạt bất kì thì có

cách chọn.

Vậy có

4.5 20



chọn một áo không phải áo trắng và chọn một cà vạt bất kì.

Do đó có

9 20 29

 

cách chọn thỏa mãn yêu cầu bài toán.

Câu 18.

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 12

Lời giải

Chọn C

Những vị trí có thể xếp cho 3 thầy giáo





2,4,6





2, 4, 7





2,4,8





2,5,7





2,5,8





2,6,8





3,5,7





3,5,8





3, 6,8





4,6,8

Mỗi một bộ vị trí có

cách xếp vị trí cho 3 thầy giáo

, ,

A B C

và

cách xếp vị trí cho 6 học sinh.

Vậy số cách xếp chỗ cho 9 người đó sao cho mỗi thầy giáo ngồi giữa hai học sinh là

10.3!6! 43200



Câu 19.

Lời giải

Chọn A

Mỗi đội sẽ gặp

đội khác (trong hai lượt trận sân nhà và sân khách) có

10.9 90



trận.

Mỗi đội đá

trận sân nhà,

trận sân khách. Nên số trận đấu là

2.90 180



trận.

Câu 20.

Lời giải

Chọn B

Gọi số tự nhiên có

chữ số cần tìm là:

, 0



abcd a , khi đó:

có

cách chọn

có

cách chọn

có

cách chọn

có

cách chọn

Vậy có:

4.3.2.1 24



số

Nên chọn

Câu 21.

Lời giải

Chọn D

Với một cách chọn

chữ số từ tập





0,1, 2,3,4,5,6,7,8,9

ta có duy nhất một cách xếp chúng theo thứ

tự giảm dần.

Ta có

cách chọn

chữ số từ tập





0,1, 2,3,4,5,6,7,8,9

Do đó có

số tự nhiên cần tìm. nên chọn

Câu 22.

Lời giải

Chọn B

Gọi số tự nhiên có ba chữ số là

abc

Có

cách chọn

Có

cách chọn

Có

cách chọn

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 13

Theo quy tắc nhân có

6.6.6 216



(số tự nhiên).

Câu 23.

Lời giải

Chọn B

Mỗi cách sắp thứ tự ba số

;

cho ta

số tự nhiên có

chữ số khác nhau đôi một.

Vậy số các chữ số thỏa yêu câu bài toán là

3! 6



cách.

Câu 24.

Lời giải

Chọn B

Nếu chữ số hàng chục là

thì số có chữ số hàng đơn vị là



thì số các chữ số nhỏ hơn

năm ở

hàng đơn vị cũng bằng

. Do chữ số hàng chục lớn hơn bằng

còn chữ số hàng đơn vị thi



Vậy số các số tự nhiên có hai chữ số mà các chữ số hàng chục lớn hơn chữ số hàng đơn vị là:

1 2 3 4 5 6 7 8 9 45

        

nên chọn

Câu 25.

Lời giải

Chọn A

Giả sử số tự nhiên lẻ có bốn chữ số khác nhau là

abcd

. Khi đó:

có

cách chọn.

có

cách chọn.

Số các số là:

5.8. 2240

A 

(số).

Vậy số các số tự nhiên lẻ có bốn chữ số khác nhau là

2240

số.

Câu 26.

Lời giải

Chọn Ⓐ.

Gọi số tự nhiên có

chữ số cần tìm là:

, 0

abcd a



, khi đó:

có

cách chọn

có

cách chọn

có

cách chọn

có

cách chọn

Vậy có:

4.4.4.4 256



số

Nên chọn

Câu 27.

Lời giải

Chọn A

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 14

Gọi số có dạng

1 2 3 4 5 6 7

a a a a a a a

Vì số đã cho có 7 chữ số phân biệt và nhỏ hơn

7000.000

nên



, vậy có 6 cách chọn

Các chữ số

2 3 4 5 6 7

; ; ; ; ;

a a a a a a

là hoán vị của 6 số còn lại.

Vậy có

6.6! 4320



số thỏa mãn bài toán.

Câu 28.

Lời giải

Chọn Ⓐ.

Cách 1: Số có

chữ số là từ

100

đến

999

nên có

999 100 1 900

  

số.

Cách 2:

Gọi số tự nhiên có

chữ số cần tìm là:

, 0

abc a



, khi đó:

có

cách chọn

có

cách chọn

có

cách chọn

Vậy có:

9.10.10 900



số

Nên chọn

Câu 29.

Lời giải

Chọn Ⓐ.

Gọi số tự nhiên cần tìm có dạng

Khi đó:

có 5 cách chọn,

có 5 cách chọn.

Nên có tất cả

5.5 25



số.

Câu 30.

Lờigiải

Chọn D

Gọi số cần tìm có dạng :

abcde

Chọn

: có

cách







Chọn

bcde

: có

cách

Theo quy tắc nhân, có

1.7 2401



(số)

Câu 31.

Lờigiải

Chọn B

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 15

Thứ

: có

cách chọn bạn đi thăm

Thứ

: có

cách chọn bạn đi thăm

Thứ

: có

cách chọn bạn đi thăm

Thứ

: có

cách chọn bạn đi thăm

Thứ

: có

cách chọn bạn đi thăm

Thứ

: có

cách chọn bạn đi thăm

Chủ nhật : có

cách chọn bạn đi thăm

Vậy theo quy tắc nhân, có

12 35831808



(kế hoạch)

Câu 32.

Lời giải

Chọn D

Gọi số tự nhiên cần tìm có dạng

1 2 3 10

...

a a a a

Bước 1: Xếp số

ở vị trí lẻ

, …,

hoặc vị trí chẵn

, …,

có

cách.

Bước 2: Xếp các số

hoặc

vào các vị trí còn lại có

cách.

Theo quy tắc nhân ta có

2.2 64



cách.

Câu 33.

Hướng dẫn giải

Chọn B

Gọi số tự nhiên chẵn cần tìm có dạng

abc





0;2;4;6;8

c  .

Xét các số có dạng

có tất cả



số thỏa yêu cầu bài toán.

Xét các số dạng

abc





2;4;6;8

c  có tất cả:

4.8.8 256



số thỏa yêu cầu bài toán.

Vậy số các số tự nhiên chẵn gồm

chữ số khác nhau là:

72 256 328

 

số.

Câu 34.

Lời giải

Chọn D

Với một cách chọn

chữ số từ tập





0,1,2,3,4,5,6,7,8,9

ta có duy nhất một cách xếp chúng theo

thứ tự giảm dần.

Ta có

cách chọn

chữ số từ tập





0,1,2,3, 4,5,6,7,8,9

Do đó có

số tự nhiên cần tìm. nên chọn

Câu 35.

Lời giải

Chọn B

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 16

Gọi





; , , , 0,1,2,4,5,6,8

 x abcd a b c d

Cách 1: Tính trực tiếp

Vì

là số chẵn nên





0, 2, 4, 6,8

d

TH 1:

 

d có 1 cách chọn

Với mỗi cách chọn

ta có 6 cách chọn





1, 2, 4,5,6,8

a

Với mỗi cách chọn

a d

ta có 5 cách chọn









1, 2, 4,5,6,8 \



b a

Với mỗi cách chọn

, ,

a b d

ta có

cách chọn









1, 2, 4,5,6,8 \ ,



c a b

Suy ra trong trường hợp này có

1.6.5.4 120



số.

TH 2:





0 2, 4, 6,8

   

d d

có 4 cách chọn d

Với mỗi cách chọn

, do



a nên ta có 5 cách chọn









1, 2, 4,5,6,8 \



a d

Với mỗi cách chọn

a d

ta có 5 cách chọn









1, 2, 4,5,6,8 \



b a

Với mỗi cách chọn

, ,

a b d

ta có

cách chọn









1, 2, 4,5,6,8 \ ,



c a b

Suy ra trong trường hợp này có

4.5.5.4 400



số.

Vậy có tất cả

120 400 520

 

số cần lập.

Cách 2: Tính gián tiếp ( đếm phần bù)

Gọi



{ số các số tự nhiên có bốn chữ số đôi một khác nhau được lập từ các số

0,1, 2, 4,5, 6,8

}



{ số các số tự nhiên lẻ có bốn chữ số đôi một khác nhau được lập từ các số

0,1, 2, 4, 5, 6,8

}



{ số các số tự nhiên chẵn có bốn chữ số đôi một khác nhau được lập từ các số

0,1, 2, 4,5, 6,8

}

Ta có:

 

C A B

Dễ dàng tính được:

6.6.5.4 720

 A

Ta đi tính



x abcd

là số lẻ





1,5

  

d d

có 2 cách chọn.

Với mỗi cách chọn

ta có 5 cách chọn

(vì

 

a a d

)

Với mỗi cách chọn

a d

ta có 5 cách chọn

Với mỗi cách chọn

, ,

a b d

ta có 4 cách chọn

Suy ra

2.5.5.4 200

 B

Vậy

520

C

Câu 36.

Lời giải

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 17

Chọn Ⓐ.

TH1: số có 1 chữ số thì có 3 cách.

TH2: số có 2 chữ số và mỗi số có các chữ số khác nhau thì có

3.2 6



số.

TH3: số có 3 chữ số và mỗi số có các chữ số khác nhau thì có

3.2.1 6



số

Vậy có

3 6 6 15

  

số.

BÀI 2: HOÁN VỊ – CHỈNH HỢP – TỔ HỢP

Câu 37.

Lờigiải

Chọn A

TH1: số có

chữ số thì có

cách.

TH2: số có

chữ số và mỗi số có các chữ số khác nhau thì có

3.2 6



số.

TH3: số có

chữ số và mỗi số có các chữ số khác nhau thì có

3.2.1 6



số

Vậy có

3 6 6 15

  

số.

BÀI2:HOÁNVỊ–CHỈNHHỢP–TỔHỢP

Câu 38.

Lời giải

Chọn A

Số các số có

chữ số được lập từ các chữ số

là

6! 5!



Số các số có chữ số

và

đứng cạnh nhau:

2.5! 4!



Số các số có chữ số

và

không đúng cạnh nhau là:





6! 5! 2.5! 4! 384

    .

Câu 39.

Lời giải

Chọn B

Nếu chữ số hàng chục là

thì số có chữ số hàng đơn vị là



thì số các chữ số nhỏ hơn

năm ở

hàng đơn vị cũng bằng

. Do chữ số hang chục lớn hơn bằng

còn chữ số hang đơn vị thi



Vậy số các số tự nhiên có hai chữ số mà các chữ số hàng chục lớn hơn chữ số hàng đơn vị là:

1 2 3 4 5 6 7 8 9 45

        

nên chọn

Câu 40.

Lời giải

Chọn A

có

phần tử là số chẵn và

phần tử là số lẻ nên số các phần tử là số chẵn trong các tập

con khác rỗng của

chỉ có thể là

1,2,3,...,10

Gọi

là tập con của

mà số các phần tử là số chẵn bằng số các phần tử là số lẻ và bằng

(với)

1 10

 

. Ta có:

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 18

- Số cách chọn ra

số chẵn trong các số

2,4,6,...,20

là

- Số cách chọn ra

số lẻ trong các số

1,3,5,...,19

là

- Số các tập con có số các phần tử là số chẵn bằng số các phần tử là số lẻ và bằng

là





Suy ra số tập hợp con khác rỗng của

mà số phần tử là số chẵn bằng số phần tử là số lẻ là

















2 2 2 2

1 2 3 10

10 10 10 10

...C C C C   

Cách 1: Bấm máy ta được

















2 2 2 2

1 2 3 10

10 10 10 10

... 184755

C C C C    

Cách 2: Xét biểu thức













10 10

1 . 1

f x x x  

Hệ số của số hạng chứa

trong khai triển





f x

là





















2 2 2 2 2

0 1 2 3 10

10 10 10 10 10

...C C C C C    

Mặt khác









f x x

 

, suy ra hệ số của số hạng chứa

trong khai triển





f x

là

Suy ra





















2 2 2 2 2

0 1 2 3 10 10

10 10 10 10 10 20

...

C C C C C C

     

Do đó





















2 2 2 2 2

1 2 3 10 10 0

10 10 10 10 20 10

... 184755

C C C C C C      

Vậy số tập hợp con cần tìm là

184755

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 19

§➋

. HOÁN V

Ị

Ỉ

NH H

Ợ

Ổ

Ợ

Chương ⓶

⓫

Tóm tắt lý thuyết

Ⓐ

➊.

Định nghĩa hoán vị:



Cho tập hợp A gồm n phần tử (n



1). Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập A được

gọi là một hoán vị của n phần tử đó.

①. Nhận xét: Hai hoán vị của n phần tử chỉ khác nhau ở thứ tự sắp xếp n phần tử.

Ví dụ: Hãy liệt kê tất cả các số gồm 3 chữ số khác nhau từ các số 1, 2, 3.

 Giải:

123, 132, 213, 231, 312, 321. Mỗi số là một hoán vị của 3 phần tử.

②.

Số các hoán vị:



Định lí: P

= n(n – 1) …2.1 = n!



Qui ước: 0! = 1

➋.

Định nghĩa chỉnh hợp:



Cho tập A gồm n phần tử (n



1). Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập A

và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã

cho.

①. Nhận xét:

Hai chỉnh hợp chập k của n phần tử đã cho khác nhau ở chỗ:

 Hoặc có phần tử ở chỉnh hợp này không ở chỉnh hợp kia;

 Hoặc thứ tự sắp xếp của các phần tử trong chúng khác nhau.

 Ví dụ

:Trên mặt phẳng, cho 4 điểm phân biệt A, B, C, D. Liệt kê tất cả các vectơ khác



mà

điểm đầu và điểm cuối của chúng thuộc tập điểm đã cho.

 Giải:

, , , , , ,AB AC AD BA BC BD

     

, , , , ,CA CB CD DA DB DC

     

. Mỗi vectơ là một chỉnh hợp chập 2

của 4 phần tử.

②.

Số các chỉnh hợp:

Định lí:

= n(n–1)…(n–k+1)

Chú ý: a)

( )!

n k





b) P

➌.

Định nghĩa tổ hợp:



Giả sử tập A có n phần tử (n



1). Mỗi tập con gồm k phần tử của A đgl một tổ hợp chập k của

n phần tử đã cho.

 Qui ước: Gọi tổ hợp chập 0 của n phần tử là tập rỗng.

 Nhận xét:

Trong một tổ hợp không có thứ tự sắp xếp. Hai tổ hợp trùng nhau nếu hai tập con đó

trùng nhau.

 Ví dụ

: Cho tập A = {1, 2, 3, 4, 5}. Hãy liệt kê các tổ hợp chập 3 của 5 phần tử của A.

 Giải:

{1, 2, 3}, {1, 2, 4}, {1, 2, 5}, {2, 3, 4}, {2, 3, 5}, {3, 4, 5}.

②.

Số các tổ hợp

 Định lí:

 



! !( )!

k k n k

 Tính chất 1: Cho số nguyên dương

và số nguyên

với

0 k n 

. Khi đó

k n k

n n

C C





 Tính chất 2: Cho các số nguyên

và

với

1 k n 

. Khi đó

k k k 1

n 1 n n

C C C





 

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 20

①.Dạng 1:

Bài toán chỉ sử dụng P hoặc C hoặc A

. Bài tập minh họa:

Câu 1: Cho tập hợp

có

phần tử. Số tập con gồm

phần tử của

là

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải

Số tập con gồm

phần tử của

chính là số tổ hợp chập

của

phần tử, nghĩa là bằng

Câu 2: Cho tập hợp

có

phần tử. Số chỉnh hợp chập

của

phần tử của

là

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải

Số chỉnh hợp chập

của

phần tử của

là:

Câu 3: Từ một nhóm có 10 học sinh nam và 8 học sinh nữ, có bao nhiêu cách chọn ra 5 học sinh

trong đó có 3 học sinh nam và 2 học sinh nữ?

Ⓐ.

3 2

10 8

C C

Ⓑ.

3 2

10 8

A A

Ⓒ.

3 2

10 8

A A

Ⓓ.

3 2

10 8

C C

Lời giải

Số cách chọn ra 3 học sinh nam từ 10 học sinh nam là:

Số cách chọn ra 2 học sinh nữ từ 8 học sinh nữ là:

Vậy số cách chọn thỏa yêu cầu là:

3 2

10 8

C C

②.Dạng 2:

Bài toán kết hợp P, C và A

. Bài tập minh họa:

Câu 1: Một nhóm có 6 học sinh gồm 4 nam và 2 nữ. Hỏi có bao nhiêu cách chọn ra 3 học sinh trong

đó có cả nam và nữ.

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải

Chọn 3 học sinh tùy ý từ nhóm 6 học sinh có:

cách.

Chọn 3 học sinh nam từ 4 học sinh nam có:

cách.

Do đó, số cách chọn ra 3 học sinh trong đó có cả nam và nữ là:

3 3

6 4

16C C 

cách.

Câu 2: Từ một tập gồm 10 câu hỏi, trong đó có 4 câu lí thuyết và 6 câu bài tập, người ta tạo thành

các đề thi. Biết rằng một đề thi phải gồm 3 câu hỏi trong đó có ít nhất một câu lí thuyết

và 1 câu bài tập. Hỏi có thể tạo được bao nhiêu đề khác nhau.

Ⓐ.

100

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải

Trường hợp 1: 2 câu lí thuyết, 1 câu bài tập. Suy ra số đề tạo ra là

2 1

4 6

. 36C C 

Trường hợp 2: 1 câu lí thuyết, 2 câu bài tập. Suy ra số đề tạo ra là

1 2

4 6

. 60C C 

Vậy có thể tạo được số đề khác nhau là:

36 60 96 

Câu 3: Cho tập hợp

có 26 phần tử. Hỏi

có bao nhiêu tập con gồm 6 phần tử?

Ⓐ.

Ⓑ.

26.

Ⓒ.

Ⓓ.

Phân dạng bài tập

Ⓑ

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 21

Lời giải

Số tập con có 6 phần tử của tập

là:

③.Dạng 3:

Bài toán liên quan đến hình học

. Bài tập minh họa:

Câu 1: Trong không gian cho

điểm trong đó không có

điểm nào cùng nằm trong một mặt

phẳng. Hỏi có bao nhiêu cách tạo mặt phẳng từ

điểm trong

điểm trên?

Ⓐ.

190

. Ⓑ.

6840

. Ⓒ.

380

. Ⓓ.

1140

Lời giải

Số cách tạo mặt phẳng là

1140

C 

Câu 2: Trong mặt phẳng có 5 điểm là các đỉnh của một hình ngũ giác đều. Hỏi tổng số đoạn thẳng

và tam giác có thể lập từ 5 điểm trên là

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Số tam giác được tạo thành là:

Số đoạn thẳng được tạo thành là:

Vậy tổng số tam giác và đoạn thẳng có thể lập từ 5 điểm trên là:

3 2

5 5

C C

 

Câu 3: Cho hình vuông

ABCD

. Trên cạnh

lấy

điểm khác nhau, không trùng với

A B

. Biết

có

tam giác được tạo thành từ



điểm. Giá trị của

bằng

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Số tam giác có

đỉnh là

C D

là:



Số tam giác có

đỉnh là

hoặc

, hai đỉnh còn lại thuộc cạnh



Ta có

2 2. 16 2

n C n



    

④.Dạng 4:

Giải phương trình, bất phương trình, hệ, chứng minh liên quan đến

P, C, A

. Bài tập minh họa:

Câu 1: Nghiệm của phương trình

2 1

x x

A A

 

là

Ⓐ.

 

. Ⓑ.



. Ⓒ.

 

và



. Ⓓ.



Lời giải

Điều kiện :













 





2 1

3 1 3

x x

x l

A A x x x

 

      







Vậy



Câu 2: Biết





2 3 *

n n

A C n  



, khi đó giá trị của

là

Ⓐ. 4. Ⓑ. 5. Ⓒ. 6. Ⓓ. 7

Lời giải

   

    

2 3

3 2

! ! 1

1 1 2 50

2 ! 3! 3 ! 6

3 4 300 0 6

n n

A C n n n n n

n n

n n n n

        

 

      

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 22

Câu 3: Số nguyên dương

thoả mãn

 

2 1

1 2

2 3

n n

A C P n





  

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải

Điều kiện:

1 1 0

n n











    

 













Ta có:

 

2 1

1 2

1 !

2 3 2! 2 3

2 ! 1 !2!

n n

A C P n n

n n





      

 

 

1 2 2 3 11 12 0

n l

n n

n n n n n

n n

 





         









Câu 1:Cho tập

có

phần tử (







là số nguyên thỏa mãn

0 k n

 

. Số các chỉnh hợp chập

của

phần tử trên là

Ⓐ.

Ⓑ.

 

! !

k n k

Ⓒ.

 

n k

Ⓓ.

 

! !k n k

Lời giải :......................................................................

......................................................................................

Câu 2:Khẳng định nào sau đây đúng?

Ⓐ.

 

! !

n n k





Ⓑ.

 

n k





Ⓒ.

 

n k





Ⓓ.

 

! !

k n k





Lời giải :......................................................................

......................................................................................

Câu 3:Có bao nhiêu số tự nhiên có

chữ số, các chữ số khác

và đôi một khác nhau?

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 4:Một tổ học sinh gồm có

nam và

nữ. Có bao nhiêu cách chọn

học sinh của tổ tham gia đội xung

kích?

Ⓐ.

4!.

Ⓑ.

4 4

5 7

.C C

Ⓒ.

Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 5:Số tập hợp con có

phần tử của một tập hợp có

phần tử là:

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải :......................................................................

......................................................................................

Mức độ nhận biết

⓵

BÀI T

Ậ

RÈN LUY

Ệ

Ⓒ

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 23

Câu 6:Từ các số

0,1, 2,7,8,9

tạo được bao nhiêu số lẻ có

chữ số khác nhau?

Ⓐ.

288

. Ⓑ.

360

Ⓒ.

312

. Ⓓ.

600

Lời giải :......................................................................

......................................................................................

Câu 7:Trong một buổi hoà nhạc, có các ban nhạc của các trường đại học từ Huế, Đà Nằng, Quy Nhơn, Nha

Trang, Đà Lạt tham dự. Tìm số cách xếp đặt thứ tự để các ban nhạc Nha Trang sẽ biểu diễn đầu tiên.

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

120

Lời giải :......................................................................

......................................................................................

Câu 8:Có bao nhiêu cách xếp

sách Văn khác nhau và

sách Toán khác nhau trên một kệ sách dài nếu các

sách Văn phải xếp kề nhau?

Ⓐ.

5!.7!

. Ⓑ.

2.5!.7!

Ⓒ.

5!.8!

. Ⓓ.

12!

Lời giải :......................................................................

......................................................................................

Câu 9:Có bao nhiêu cách sắp xếp

thí sinh vào một phòng thi có

bàn mỗi bàn một thí sinh.

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

18!

Lời giải :......................................................................

......................................................................................

Câu 10:Cho tập

có

phần tử. Tìm số tập con có

phần tử của tập

Ⓐ.

120

. Ⓑ.

126

Ⓒ.

15120

. Ⓓ.

216

Lời giải :......................................................................

......................................................................................

Câu 11:Trong một buổi hoà nhạc, có các ban nhạc của các trường đại học từ Huế, Đà Nằng, Quy Nhơn, Nha

Trang, Đà Lạt tham dự. Tìm số cách xếp đặt thứ tự để các ban nhạc Nha Trang sẽ biểu diễn đầu tiên.

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

120

Lời giải :......................................................................

......................................................................................

Câu 12:Cho tập hợp

có

phần tử, số tập con có hai phần tử của

là

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

................................................

......................................

Câu 13:Một hộp có

bi xanh,

bi đỏ và

bi vàng. Chọn ngẫu nhiên

bi sao cho có đủ ba màu. Số cách chọn

là

Ⓐ.

. Ⓑ.

220

Ⓒ.

360

. Ⓓ.

120

Lời giải :......................................................................

......................................................................................

Câu 14:Trong không gian cho bốn điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt

từ các điểm đã cho?

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải :......................................................................

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 24

......................................................................................

Câu 15:Cho tứ giác

ABCD

. Có bao nhiêu vectơ khác vectơ



có điểm đầu và điểm cuối là các đỉnh của tứ giác?

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 16:Chọn mệnh đề đúng trong các mệnh đề sau:

Ⓐ.

 

! !

k n k





Ⓑ.

 

! !

k n k





Ⓒ.

 

k n k





Ⓓ.

 

k n k





Lời giải :......................................................................

......................................................................................

Câu 17:Cho các số nguyên

,k n

thỏa mãn

0 k n

 

. Công thức nào dưới đây đúng ?

Ⓐ.



Ⓑ.

 

! !

k n k





Ⓒ.

 

n k





Ⓓ.

 

! !

k n

n k





Lời giải :......................................................................

......................................................................................

Câu 18:Nếu

110

thì:

Ⓐ.



Ⓑ.



Ⓒ.

11x

hay

10x

Ⓓ.

0x

Lời giải :......................................................................

......................................................................................

........................................................................

..............

Câu 19:Tìm số tự nhiên

thỏa

210

A 

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 20:Trong các câu sau câu nào sai?

Ⓐ.

3 11

14 14

C C

Ⓑ.

3 4 4

10 10 11

C C C 

Ⓒ.

0 1 2 3 4

4 4 4 4 4

16C C C C C    

Ⓓ.

4 4 5

10 11 11

C C C 

Lời giải :......................................................................

......................................................................................

BẢNG ĐÁP ÁN

1.C 2.D 3.D 4.D 5.A 6.A 7.C 8.C 9.D 10.B

11.C 12.C 13.A 14.B 15.A 16.B 17.C 18.B 19.A 20.D

Mức độ thông hiểu

Câu 1:Có tất cả bao nhiêu số tự nhiên có 3 chữ số và 3 chữ số đó đôi một khác nhau?

Ⓐ.

3 3

10 9

A A

Ⓑ.

Ⓒ.

Ⓓ.

9 9 8 

Lời giải :......................................................................

......................................................................................

⓶

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 25

......................................................................................

Câu 2:Trong mặt phẳng cho tập hợp

gồm

điểm, trong đó không có

điểm nào thẳng hàng. Có bao nhiêu

tam giác có

đỉnh đều thuộc

Ⓐ.

720

Ⓑ.

120

Ⓒ.

59049

Ⓓ.

3628800

Lời giải :......................................................................

......................................................................................

Câu 3:Có thể lập được bao nhiêu số tự nhiên có 3 chữ số khác nhau từ các chữ số





; ; ; ;

0 1 2 3 4

Ⓐ. 60. Ⓑ. 24.

Ⓒ. 48. Ⓓ. 11.

Lời giải :......................................................................

......................................................................................

Câu 4:Với các chữ số

2,3, 4,5,6

, có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau trong đó

hai chữ số

3,6

không đứng cạnh nhau?

Ⓐ.

120

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 5:Từ các số 1, 2, 3, 4, 5, 6 lập được bao nhiêu số tự nhiên

ồm 4 chữ số

Ⓐ. 1296. Ⓑ. 2019. Ⓒ. 2110. Ⓓ.

1297

Lời giải :......................................................................

......................................................................................

Câu 6:Từ các số

1,2,3

lập được bao nhiều số tự nhiên gôm

chữ số thỏa mãn đồng thời hai điều kiện sau: Trong

mỗi số, hai chữ số giống nhau không đứng cạnh nhau.

Ⓐ. 76. Ⓑ. 42.

Ⓒ. 80. Ⓓ. 68

Lời giải :......................................................................

......................................................................................

Câu 7:Cho tập hợp





1;2;3;...;19,20

S 

gồm 20 số tự nhiên từ 1 đến 20, lấy ngẫu nhiên 3 số thuộc

, xác suất

để 3 số lấy được lập thành một cấp số cộng là

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

114

Lời giải :......................................................................

......................................................................................

Câu 8:Cho tập





1,2,3,4,5,6,7,8

A 

Có bao nhiêu tập con của A chứa số 2 mà không chứa số 3

Ⓐ. 64. Ⓑ. 83.

Ⓒ. 13. Ⓓ. 41

Lời giải :......................................................................

......................................................................................

Câu 9:Lớp 11A1 có

học sinh trong đó có

bạn nam và

bạn nữ. Thứ hai đầu tuần lớp phải xếp hàng chào

cờ thành một hàng dọc. Hỏi có bao nhiêu cách sắp xếp để

bạn nam xen kẽ với

bạn nữ?

Ⓐ.

. Ⓑ.

21 20

. .

P P

Ⓒ.

21 20

2. .

P P

. Ⓓ.

21 20

P P



Lời giải :......................................................................

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 26

......................................................................................

Câu 10:Có bao nhiêu cách xếp

bạn A, B, C, D, E, F vào một ghế dài sao cho bạn A, F ngồi ở

đầu ghế?

Ⓐ.

120

. Ⓑ.

720

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 11:Tổ của An và Cường có

học sinh. Số cách xếp

học sinh ấy theo hàng dọc mà An đứngđầu hàng,

Cường đứng cuối hàng là:

Ⓐ. 120. Ⓑ. 100. Ⓒ. 110. Ⓓ.

125.

Lời giải :......................................................................

......................................................................................

Câu 12:Lớp

11 1

có

học sinh trong đó có

bạn nam và

bạn nữ. Thứ

đầu tuần lớp phải xếp hàng

chào cờ thành một hàng dọc. Hỏi có bao nhiêu cách sắp xếp để

bạn nam xen kẽ với

bạn nữ?

Ⓐ.

. Ⓑ.

21 20

P P

Ⓒ.

21 20

2. .

P P

. Ⓓ.

21 20

P P



Lời giải :......................................................................

......................................................................................

Câu 13:Trong tủ sách có tất cả

cuốn sách. Hỏi có bao nhiêu cách sắp xếp sao cho quyển thứ nhất ở kề quyển

thứ hai:

Ⓐ.

10!

. Ⓑ.

725760

Ⓒ.

. Ⓓ.

9! 2!



Lời giải :......................................................................

......................................................................................

Câu 14:Trong một lớp học có 20 học sinh nữ và 15 học sinh nam. Hỏi giáo viên chủ nhiệm có bao nhiêu cách chọn:

ốn học sinh l

àm t

ổ tr

ởng của 4 tổ sao cho trong 4 học s

inh đư

ợc chọn có cả nam v

à n

ữ.

Ⓐ. 1107600. Ⓑ. 246352.

Ⓒ. 1267463. Ⓓ. 1164776.

Lời giải :......................................................................

......................................................................................

Câu 15:Một nhóm học sinh có

người. Cần chọn

học sinh trong nhóm để làm

công việc là tưới cây, lau bàn

và nhặt rác, mỗi người làm một công việc. Số cách chọn là

Ⓐ.

. Ⓑ.

3 10



Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 16:Số cách sắp xếp

học sinh ngồi vào

trong

ghế trên một hàng ngang là

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 17:Có tất cả

120

cách chọn

học sinh từ nhóm

học sinh. Số

là nghiệm của phương trình nào sau đây?

Ⓐ.









1 2 120

n n n  

Ⓑ.









1 2 720

n n n  

Ⓒ.









1 2 120

n n n  

Lời giải :......................................................................

......................................................................................

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 27

Ⓓ.









1 2 720

n n n  

Câu 18:Một lớp học có 20 nam và 26 nữ. Giáo viên chủ nhiệm cần chọn một ban cán sự gồm 3 người. Hỏi có bao

nhiêu cách chọn nếu trong ban cán sự có cả nam và nữ.

Ⓐ. 11440. Ⓑ. 11242. Ⓒ. 24141. Ⓓ.

53342.

Lời giải :......................................................................

......................................................................................

Câu 19:Cho tập

có

phần tử. Số tập con gồm

phần tử của

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 20:Ông và bà An cùng có

đứa con đang lên máy bay theo một hàng dọⒸ. Có bao nhiêu cách xếp hàng

khác nhau nếu ông An hay bà An đứng ở đầu hoặc cuối hàng:

Ⓐ.

720

. Ⓑ.

1440

Ⓒ.

18720

. Ⓓ.

40320

Lời giải :......................................................................

......................................................................................

.......................................................

...............................

Câu 21:Một nhóm công nhân gồm 15 nam và 5 nữ. Người ta muốn chọn từ nhóm ra 5 người để lập thành một tổ

công tác sao cho phải có 1 tổ trưởng nam, 1 tổ phó nam và có ít nhất 1 nữ. Hỏi có bao nhiêu cách lập tổ công tác.

Ⓐ. 111300. Ⓑ. 233355.

Ⓒ. 125777. Ⓓ. 112342.

Lời giải :......................................................................

......................................................................................

Câu 22:Một hộp có

bi đen,

bi trắng. Chọn ngẫu nhiên

bi. Xác suất

bi được chọn cùng màu là:

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 23:Một trường cấp 3 của tỉnh Đồng Tháp có

giáo viên Toán gồm có

nữ và

nam, giáo viên Vật lý thì

có

giáo viên nam. Hỏi có bao nhiêu cách chọn ra một đoàn thanh tra công tác ôn thi THPTQG gồm

người có

ủ

môn Toán và V

ật lý v

à ph

ải

có giáo viên nam và giáo viê

n n

ữ trong đo

àn?

Ⓐ.

Ⓑ.

120

Ⓒ.

12960

Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 24:Có bao nhiêu cách chia hết

đồ vật khác nhau cho

người, biết rằng mỗi người nhận được ít nhất

đồ

vật.

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 25:Từ 6 điểm phân biệt thuộc đường thẳng



và một điểm không thuộc đường thẳng



ta có thể tạo được

tất cả bao nhiêu tam giác?

Ⓐ.

210

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

........................................................

..............................

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 28

Câu 26:Cho đa giác đều

đỉnh,





và



. Tìm

biết rằng đa giác đã cho có

135

đường chéo.

Ⓐ.



n . Ⓑ.



n .

Ⓒ.



n . Ⓓ.



n .

Lời giải :......................................................................

......................................................................................

Câu 27:Lục giác đều

ABCDEF

có bao nhiêu đường chéo

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 28:Cho các số nguyên dương

k n





k n



. Mệnh đề nào sau đây sai?:

Ⓐ.

 

n k





. Ⓑ.

!.C

k k

n n

A k

Ⓒ.

n k k

n n

C C





. Ⓓ.

1 1

k k k

n n n

C C C

 



 

Lời giải :......................................................................

......................................................................................

Câu 29:Cho

n 



thỏa mãn

2002

C 

. Tính

Ⓐ.

2007

. Ⓑ.

10010

Ⓒ.

40040

. Ⓓ.

240240

Lời giải :......................................................................

......................................................................................

Câu 30:Nếu một đa giác đều có

đường chéo, thì số cạnh của đa giác là:

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 31:Nếu

4 4

2 3

n n

A A



 thì

bằng:

Ⓐ.



. Ⓑ.



Ⓒ.



. Ⓓ.



Lời giải :......................................................................

......................................................................................

Câu 32:Nghiệm của phương trình

10 9 8

x x x

A A A

 

là

Ⓐ.



Ⓑ.



Ⓒ.

11 ; 5

x x

 

Ⓓ.

10 ; 2.

x x

 

Lời giải :......................................................................

......................................................................................

Câu 33:Giá trị của





thỏa mãn

3 3

8 6

n n

C A



 

 là

Ⓐ.



. Ⓑ.



Ⓒ.



. Ⓓ.



Lời giải :......................................................................

......................................................................................

BẢNG ĐÁP ÁN

1.D 2.B 3.C 4.D 5.A 6.A 7.C 8.A 9.B 10.D

11.A 12.B 13.B 14.A 15.D 16.C 17.D 18.A 19.B 20.C

21.A 22.B 23.D 24.D 25.C 26.D 27.C 28.A 29.D 30.A

31.B 32.B 33.B

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 29

Câu 1:Có bao nhiêu số tự nhiên gồm bảy chữ số khác nhau đôi một, trong đó chữ số

đứng liền giữa hai chữ số

và

Ⓐ.

6600

Ⓑ.

7440

Ⓒ.

8400

Ⓓ.

4560

Lời giải :......................................................................

......................................................................................

Câu 2:Biển số xe máy tỉnh

gồm hai dòng

- Dòng thứ nhất là

68 XY

, trong đó

là một trong

chữ cái,

là một trong

chữ số;

- Dòng thứ hai là

.abc de

, trong đó

là các chữ số.

Biển số xe được cho là

đẹp

khi dòng thứ hai có tổng các số là số có chữ số tận cùng bằng

và có đúng

chữ số

giống nhau. Hỏi có bao nhiêu cách chọn

biển số trong các biển số

đẹp

để đem bán đấu giá?

Ⓐ.

12000

Ⓑ.

143988000

Ⓒ.

4663440

Ⓓ.

71994000

Lời giải :......................................................................

......................................................................................

Câu 3:Mỗi bạn An và Bình chọn ngẫu nhiên ba số trong tập





0, 1, 2, 3, 4, 5, 6, 7, 8, 9

. Xác suất để trong hai bộ

số của An và Bình chọn ra có nhiều nhất một số giống nhau bằng

Ⓐ.

Ⓑ.

203

480

Ⓒ.

Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 4:Một người viết ngẫu nhiên một số có bốn chữ số. Tính xác suất để các chữ số của số được viết ra có thứ tự

tăng dần hoặc giảm dần.

Ⓐ.

125

Ⓑ.

375

Ⓒ.

250

Ⓓ.

375

Lời giải :......................................................................

......................................................................................

Câu 5:Hai nhóm người cần mua nền nhà, nhóm thứ nhất có 2 người và họ muốn mua 2 nền kề nhau, nhóm thứ hai

có 3 người và họ muốn mua 3 nền kề nhau. Họ tìm được một lô đất chia thành 7 nền đang rao bán. Tính số cách

chọn nền của mỗi người thỏa yêu cầu trên

Ⓐ.

144.

Ⓑ.

125.

Ⓒ.

140.

Ⓓ.

132

Lời giải :......................................................................

......................................................................................

Câu 6:Cho đa giác đều 20 cạnh nội tiếp đường tròn





. Xác định số hình thang có 4 đỉnh là các đỉnh của đa giác

đều.

Ⓐ.

720

Ⓑ.

765

Ⓒ.

810

Ⓓ.

315

Lời giải :......................................................................

......................................................................................

Câu 7:Ông và bà An cùng có

đứa con đang lên máy bay theo một hàng dọ

Ⓒ.

Có bao nhiêu cách xếp hàng khác

nhau nếu ông An hay bà An đứng ở đầu hoặc cuối hàng:

Ⓐ.

720

Ⓑ.

1440

Ⓒ.

18720

Ⓓ.

40320

Lời giải :......................................................................

Mức độ VD-VDC

⓷

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 30

......................................................................................

Câu 8:Giả sử rằng, trong Đại hội thể dục thể thao tỉnh Gia Lai năm

2018

có

đội bóng đăng ký tham gia giải,

được chia thành

bảng

, mỗi bảng gồm

đội. Cách thức thi đấu như sau:

Vòng

: Các đội trong mỗi bảng thi đấu vòng tròn một lượt, tính điểm và chọn ra đội nhất của mỗi bảng.

Vòng

: Đội nhất bảng

gặp đội nhất bảng

; Đội nhất bảng

gặp đội nhất bảng

Vòng

: Tranh giải ba: Hai đội thua trong bán kết; tranh giải nhất: Hai đội thắng trong bán kết.

Biết rằng tất cả các trận đấu đều diễn ra trên sân vận động Pleiku vào các ngày liên tiếp, mỗi ngày

trận. Hỏi

Ban t

ổ chức cần m

ợn sân vận động trong bao nhi

êu ngày?

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 9:Có

nam và

nữ. Có bao nhiêu cách chọn ra

người trong đó có ít nhất

nam và ít nhất

nữ (

, ; ; , 1

   

k m n a b k a b

) với

là số cách chọn có ít hơn

nam,

là số cách chọn có ít hơn

nữ.

Ⓐ. Số cách chọn thoả mãn điều kiện bài toán là:

1 2

2( )



 

m n

C S S

Ⓑ. Số cách chọn thoả mãn điều kiện bài toán là:

1 2

2 ( )



 

m n

C S S

Ⓒ. Số cách chọn thoả mãn điều kiện bài toán là:

1 2

3 2( )



 

m n

C S S

Ⓓ. Số cách chọn thoả mãn điều kiện bài toán là:

1 2

( )



 

m n

C S S

Lời giải :......................................................................

......................................................................................

Câu 10:Có bao nhiêu số tự nhiên có bẩy chữ số khác nhau từng đôi một, trong đó chữ số

đứng liền giữa hai chữ

số

và

Ⓐ.

3204

số. Ⓑ.

249

số.

Ⓒ.

2942

số. Ⓓ.

7440

số.

Lời giải :......................................................................

......................................................................................

Câu 11:Cho hai đường thẳng

và

song song với nhau. Trên

có

điểm phân biệt, trên

có

điểm

phân biệt







. Biết rằng có

2800

tam giác có đỉnh là

điểm trong số các điểm đã cho, tìm

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 12:Cho đa giác đều

đỉnh,





và



. Tìm

biết rằng đa giác đã cho có

135

đường chéo

Ⓐ.



. Ⓑ.



Ⓒ.



. Ⓓ.



Lời giải :......................................................................

......................................................................................

Câu 13:Tính giá trị của biểu thức:

0 1 2015 2016

2017 2017 2017 2017

2017 2016 2 1

...P

A A A A

    

Ⓐ.

2017

2018!

P   Ⓑ.

2017

2017!

P  

Ⓒ.

2018

2017!

P   Ⓓ.

2018

2018!

P  

Lời giải :......................................................................

......................................................................................

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 31

Câu 14:Giá trị của

thỏa mãn

2 2

3 42 0

n n

A A

  

là

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 15:Giá trị của

n 



thỏa mãn đẳng thức

6 7 8 9 8

3 3 2

n n n n n

C C C C C



   

là

Ⓐ.

18n



Ⓑ.

16n



Ⓒ.

15n 

Ⓓ.

14n 

Lời giải :......................................................................

......................................................................................

BẢNG ĐÁP ÁN

1.B 2.D 3.C 4.D 5.A 6.A 7.C 8.C 9.D 10.D

11.C 12.D 13.C 14.C 15.C

①. HƯỚNG DẪN GIẢI – NHẬN BIẾT

Câu 1.

Lời giải

Chọn C

Số các chỉnh hợp chập

của

phần tử là

 

n k

Câu 2.

Lời giải

Chọn D

Ta có:

 

! !

k n k





Câu 3.

Lời giải

Chọn D

Mỗi số tự nhiên có

chữ số, các chữ số khác

và đôi một khác nhau là một chỉnh hợp chập

của

phần tử.

Vậy số các số tự nhiên thỏa đề bài là

số.

Câu 4.

Lời giải

Chọn D

HƯ

Ớ

NG D

Ẫ

N GI

Ả

Ⓓ

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 32

Tổng cộng tổ đó có 12 học sinh, phép chọn là ngẫu nhiên cùng lúc không có sắp xếp nên số cách chọn là

Câu 5.

Lời giải

Chọn A

Đây là tổ hợp chập

của

phần tử. Vậy có

tập hợp con.

Câu 6.

Lời giải

Chọn A

Gọi

abcde

là số cần tìm.

Chọn

có

cách.

Chọn



và

a e



có

cách.

Chọn

trong

số còn lại sắp vào

, ,

b c d

có

cách.

Vậy có

3.4. 288

A 

số.

Câu 7.

Lời giải

Chọn C

Sắp xếp thứ tự biểu diễn của

ban nhạc còn lại có

4! 20

 

cách.

Câu 8.

Lời giải

Chọn C

Sắp

quyển văn có

cách sắp xếp.

Sắp

quyển toán và bộ

quyển văn có

cách sắp xếp.

Vậy có

5!.8!

cách sắp xếp.

Câu 9.

Lời giải

Chọn D

Số cách xếp là:

18!

Câu 10.

Lời giải

Chọn B

Từ tập

có

phần tử chọn ra

phần tử để hình thành nên tập con.

Vậy tập

có

126

C 

tập con chứa

phần tử.

Câu 11.

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 33

Lời giải

Chọn C

Sắp xếp thứ tự biểu diễn của

ban nhạc còn lại có

4! 20

 

cách.

Câu 12.

Lời giải

Chọn C

Số tập con có hai phần tử của

là

Câu 13.

Lời giải

Chọn A

Chọn ngẫu nhiên

bi sao có đủ ba màu có

1 1 1

3 4 5

. . 60

C C C



cách.

Câu 14.

Lời giải

Chọn B

Vì

điểm không đồng phẳng tạo thành một tứ diện mà tứ diện có

mặt (𝐶





= 4).

Câu 15.

Lời giải

Chọn A

Ta có mỗi vectơ được tạo thành từ

đỉnh của tứ giác là một chỉnh hợp chập

của

phần tử.

Vậy có

vectơ thỏa yêu cầu bài.

Câu 16.

Lời giải

Chọn B

Câu 17.

Lời giải

Chọn C

Câu 18.

Lời giải

Chọn B

Điều kiện:

, 2

 



x x

Ta có:

 

110 110 ( 1) 110

2 !





      



 





A x x

So sánh điều kiện ta nhận



Câu 19.

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 34

Lời giải

Chọn A

* PP tự luận:

210

A 

 

210, , 2

2 !

n n

   









1 210

n n  

210 0

n n

   





 

n nhan

n loai

 

  



 



* PP trắc nghiệm:

+ Nhập vào máy tính

210 0

 

+ Tính (CALC) lần lượt với



(thoả); với



(không thoả), với



(không thoả), với



(không thoả).

+ KL: Vậy



Câu 20.

Lời giải

Chọn D

Ta có công thức:

1 1

k k k

n n n

C C C

 



 

nên đáp án sai là

4 4 5

10 11 11

C C C

 

⓶. HƯỚNG DẪN GIẢI – THÔNG HIỂU

Câu 1.

Lời giải

Chọn D

Gọi số cần lập là

abc



nên

có

cách chọn

b a



nên

có

cách chọn

c a



và

c b



nên

có

cách chọn

Vậy có

9 9 8

 

cách chọn.

Câu 2.

Lời giải

Chọn B

Số tam giác có

đỉnh đều thuộc

bằng số tổ hợp chập

của

phần từ và bằng

120

C

Câu 3.

Lời giải

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 35

Chọn C

Số các chỉnh hợp chập 3 chữ số khác nhau từ các chữ số





; ; ; ;

0 1 2 3 4

là

số.

Số các chỉnh hợp chập 3 chữ số khác nhau từ các chữ số





; ; ; ;

0 1 2 3 4

và có số 0 đứng đầu là

số.

Vậy: số các số tự nhiên có 3 chữ số khác nhau từ các chữ số





; ; ; ;

0 1 2 3 4

là

A A

 

3 2

5 4

số.

Câu 4.

Lời giải

Chọn D

Số cách lập số tự nhiên gồm

chữ số đôi một khác nhau từ các chữ số đã cho:

Số cách lập số tự nhiên gồm

chữ số

2;4;5

và ký tự

(

đại diện cho

3;6

đứng cạnh nhau):

Số cách hoán đổi vị trí của

3;6

trong

Số cách lập số tự nhiên gồm

chữ số khác nhau từ các chữ số đã cho mà

và

đứng cạnh nhau:

4!.2!

Số cách lập số tự nhiên thỏa mãn

và

không cạnh nhau:

5! 4!.2! 72

 

Câu 5.

Câu 6.

Lời giải

Chọn A

Đặt

{1,2,3}



. Gọi

là tập các số thỏa yêu cầu thứ nhất của bài toán

Ta có số các số thỏa điều kiện thứ nhất của bài toán là



(vì các số có dạng

aabbcc

và khi hoán vị

hai số

a a

ta được số không đổi)

Gọi

1 2 3

, ,

S S S

là tập các số thuộc

mà có

1,2,3

cặp chữ số giống nhau đứng cạnh nhau.



Số phần tử của

chính bằng số hoán vị của 3 cặp

11,22,33

nên





Số phần tử của

chính bằng số hoán vị của 4 phần tử là có dạng

, , ,

a a bb cc

nhưng

a a

không đứng

cạnh nhau. Nên

6 6

  

phần tử.



Số phần tử của

chính bằng số hoán vị của các phần tử có dạng

, , , ,

a a b b cc

nhưng

a a

và

b b

không đứng cạnh nhau nên

6 12 12

   

Vậy số các số thỏa yêu cầu bài toán là:

90 (6 6 12) 76

   

Câu 7.

Lời giải

Chọn C

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 36





n C

 

Gọi A là biến cố “3 số lấy được lập thành 1 cấp số cộng”

Không mất tính tổng quát, gọi





, ,

a b c

là 3 số tự nhiên lập thành cấp số cộng với

a b c

 

là công sai

của cấp số cộng với

d N





: chọn

có 18 cách (

có thể chọn từ số 1 đến số 18)



: chọn

có 16 cách (

có thể chọn từ số 1 đến số 16)



: chọn

có 14 cách (

có thể chọn từ số 1 đến số 14)



: chọn

có 12 cách (

có thể chọn từ số 1 đến số 12)



: chọn

có 10 cách (

có thể chọn từ số 1 đến số 10)



: chọn

có 8 cách (

có thể chọn từ số 1 đến số 8)



: chọn

có 6 cách (

có thể chọn từ số 1 đến số 6)



: chọn

có 4 cách (

có thể chọn từ số 1 đến số 4)



: chọn

có 2 cách (

có thể chọn từ số 1 đến số 2)

 





18 2 9

18 16 ... 2 90

n A



     

 

90 3

P A

 

Câu 8.

Lời giải

Xét tập





1, 4,5,6, 7,8

B

, ta có B không chứa số 3.

là một tập con của A thỏa yêu cầu bài toán khi và chỉ khi





\ 2

là một tập con của

. Do đo, số tập

con của A thỏa yêu cầu bài toán bằng số tập con của B và bằng

2 64



Chọn A

Câu 9.

Lời giải.

Chọn B

Vì có

bạn nam và

bạn nữ nên để xếp nam nữ đứng xen kẽ thì số cách xếp là:

21 20

. .

P P

Câu 10.

Lời giải

Chọn D

Có

cách xếp bạn A, F ngồi ở

đầu ghế

Có

cách xếp

bạn vào

vị trí còn lại

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 37

Vậy: Có

2!.4! 48



(cách xếp).

Câu 11.

Lời giải.

Chọn A

Chọn An đứng đầu hàng có

cách, chọn Cường đứng cuối hàng có

cách.

Sắp xếp 5 bạn còn lại có:

5! 120

 

cách.

Vậy có:

1.1.120 120



cách.

Câu 12.

Lời giải

Chọn B

Có

bạn nam và

bạn nữ nên để nam mữ xen kẻ thì chỉ có thể nam đứng đầu hàng.

- Số cách xếp để nam đứng đầu và nam, nữ đứng xen kẽ nhau là:

21 20

P P

Câu 13.

Lời giải

Chọn B

Chọn

vị trí liên tiếp trong

vị trí, có

cách.

Hoán vị hai quyển sách có

cách.

Sắp

quyển sách còn lại vào

vị trí, có

cách.

Vậy có

9.2.8! 725760



cách.

Câu 14.

Lời giải

Chọn A

Số cách chọn 4 học sinh làm 4 tổ trưởng là:

Số cách chọn 4 học sinh làm tổ trưởng trong đó không có học sinh nam được chọn là:

Số cách chọn 4 học sinh làm tổ trưởng trong đó không có học sinh nữ được chọn là:

Vậy số cách chọn thỏa yêu cầu bài toán:





4 4 4

35 20 15

1107600

  A A A

Câu 15.

Lời giải

Chọn D

Số cách chọn

em học sinh là số cách chọn

phần tử khác nhau trong

phần tử có phân biệt thứ tự

nên số cách chọn thỏa yêu cầu là

Câu 16.

Lời giải

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 38

Chọn C

Mỗi cách chọn

ghế từ

ghế sắp xếp

người là một chỉnh hợp chập

của

phần tử.

Vậy có

cách chọn.

Câu 17.

Lời giải

Chọn D

Chọn

trong

học sinh có

 









1 2

3 !.3! 6

n n n

 

 



Khi đó









120 1 2 720

C n n n    

Câu 18.

Lời giải

Chọn A

Có

cách chọn ba học sinh trong lớp.

Có

cách chọn ban cán sự không có nam.

Có

cách chọn ban cán sự không có nữ.

Vậy có

3 3 3

46 26 20

( ) 11440

  C C C

cách chọn thỏa yêu cầu bài toán.

Câu 19.

Lời giải

Chọn B

Mỗi tập con gồm

phần tử của

là một tổ hợp chập

của

phần tử thuộc

và ngược lại. Nên số

các tập con gồm 3 phần tử của

bằng số các tổ hợp chập

của

phần tử thuộc

và bằng

Câu 20.

Lời giải

Chọn C

Ta dùng phần bù.

Sắp

người vào

vị trí theo hàng dọc có

cách sắp xếp.

Sắp ông và bà An vào

trong

vị trí (trừ vị trí đầu và cuối hàng) có

cách.

Sắp

người con vào

vị trí còn lại có

cách.

Vậy có

8! .6! 18720

A 

cách sắp xếp.

Câu 21.

Lời giải

Chọn A

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 39



Chọn 2 trong 15 nam làm tổ trưởng và tổ phó có

cách.



Chọn 3 tổ viên, trong đó có nữ.

+) chọn 1 nữ và 2 nam có

cách.

+) chọn 2 nữ và 1 nam có

13.

cách.

+) chọn 3 nữ có

cách.

Vậy có





2 2 2 3

15 13 5 5

5. 13. 111300

  A C C C

cách.

Câu 22.

Lời giải

Chọn B

Số phần tử không gian mẫu:





n C

 

Gọi

là biến cố: Hai bi được chọn cùng màu”.

Số phần tử của

là:





2 2

5 4

n A C C

 

Xác suất cần tìm là:

 





 

n A

P A





2 2

5 4

C C





Câu 23.

Lời giải

Chọn D

Vì chọn ra

người mà yêu cầu phải có giáo viên nam và giáo viên nữ trong đoàn nên số giáo viên nữ

được chọn chỉ có thể bằng

hoặc

. Ta xét hai trường hợp:

* Trường hợp 1: Chọn

giáo viên nữ: Có

cách. Khi đó:

- Chọn

giáo viên nam môn Toán và

nam môn Vật lý: Có

1 1

5 4

C C



cách.

- Chọn

giáo viên nam môn Vật lý: Có

cách.

Trường hợp này có





1 1 1 2

3 5 4 4

C C C C

 

cách chọn.

* Trường hợp 2: Chọn

giáo viên nữ: Có

cách chọn. Khi đó chọn thêm

giáo viên nam môn Vật lý:

Có

cách. Trường hợp này có

2 1

3 4

C C



cách chọn.

Vậy tất cả có





1 1 1 2 2 1

3 5 4 4 3 4

C C C C C C

   



cách chọn.

Câu 24.

Lời giải

Chọn D

Có hai người mà mỗi người nhận một đồ vật và một người nhận hai đồ vật.

Chọn hai người để mỗi người nhận một đồ vật: có

cách chọn.

Chọn hai đồ vật trao cho hai người: có

cách chọn.

Hai đồ vật còn lại trao cho người cuối cùng.

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 40

Vậy số cách chia là :



cách.

Câu 25.

Lời giải

Chọn C

Lấy 2 điểm trong 6 điểm trên đường thẳng



có



cách.

Vậy số tam giác được lập theo yêu cầu bài toán là: 15 tam giác.

Câu 26.

Lời giải

Chọn D

+ Tìm công thức tính số đường chéo: Số đoạn thẳng tạo bởi

đỉnh là

, trong đó có

cạnh, suy ra số

đường chéo là



C n

+ Đa giác đã cho có

135

đường chéo nên

135

 

C n

+ Giải PT :

 

135 , , 2

2 !2!

   





n n n





1 2 270

   n n n

3 270 0

   

n n





 

 





 



n nhan

n loai

 

n .

Câu 27.

Lời giải

Chọn C

Số đường chéo của lục giác đều (6 cạnh là):

6 9

 

Câu 28.

Hướng dẫn giải

Chọn A

Vì

 

!. !

k n k





Câu 29.

Lời giải

Chọn D

Ta có:

5 5

.5! 240240

n n

A C 

Câu 30.

Lời giải

Chọn A

Cứ hai đỉnh của đa giác





, 3

n n

 



đỉnh tạo thành một đoạn thẳng (bao gồn cả cạnh đa giác và

đường chéo).

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 41

Khi đó số đường chéo là:

 

44 44

2 !.2!

C n n

    



 

1 2 88 11

n n n n





      



 



(vì n





Câu 31.

Lời giải

Chọn B

Điều kiện:



;





Ta có:

 





 

4 4

1 !

! 2

2 3 2. 3. 3 12

4 ! 5 ! 4

n n

A A n

n n n



      

  

Câu 32.

Hướng dẫn giải.

Chọn B

Điều kiện:10

x N

 

Khi đó phương trình

10 9 8

! ! !

9 9

( 10)! ( 9)! ( 8)!

x x x

A A A

x x x

     

  

! ! !

( 10)! ( 9)( 10)! ( 8)( 9)( 10)!

x x x

x x x x x x

   

     

! 1 9 1 9

1 0 1 0

( 10)! ( 9) ( 8)( 9) ( 9) ( 8)( 9)

x x x x x x x

 

        

 

      

 

(do

( 10)!





)

 

Câu 33.

Lời giải

Chọn B

* PP tự luận:





 





 

8 ! 6 !

5. ,

5! 3 ! 3 !

n n

 

  

 























   

4 5 6 7 8

5. 4 5 6

n n n n n

n n n

    

    









7 8

n n 

 

15 544 0

n n

   





 

n nhan

n loai

 

  



 



* PP trắc nghiệm:

+ Nhập vào máy tính

3 3

8 6

5 0

n n

C A



 

 

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 42

+ Tính (CALC) lần lượt với



(không thoả); với



(thoả), với



(không thoả), với



(không thoả).

③. HƯỚNG DẪN GIẢI – VD, VDC

Câu 1.

Lời giải

Chọn B

Gọi số cần tìm có dạng

1 2 3 4 5 6 7

a a a a a a a

, (các chữ số

1 2 3 4 5 6 7

; ; ; ; ; ;

a a a a a a a

khác nhau).

 TH 1: Số có dạng

4 5 6 7

567

a a a a

+ Chọn bốn chữ số từ các chữ số

0;1;2;3;4;8;9

xếp vào các vị trí

4 5 6 7

; ; ;

a a a a

có

+ Đổi chỗ hai chữ số

và

có

cách.

Suy ra, TH 1 có

số.

 TH 2:





5;7

a 

+ Chọn một chữ số khác

vào vị trí

có

cách.

+ Xếp bộ

567

vào các vị trí

2 3 4 5 6 7

, , , , ,

a a a a a a

có

cách.

+ Đổi chỗ hai chữ số

và

có

cách.

+ Chọn ba chữ số từ sáu chữ số còn lại xếp vào các vị trí còn lại có

Suy ra, TH 2 có

6.4.2.

Vậy số các số cần tìm là:

4 3

7 6

2. 6.4.2. 7440

A A  .

Câu 2.

Lời giải

Chọn D

Chọn

từ

chữ cái và chọn

từ

chữ số, ta có

24.10 240



(cách chọn).

Chọn

chữ số giống nhau từ các chữ số ta có

cách chọn;

Mỗi bộ gồm

chữ số giống nhau, ta có một cách chọn duy nhất

chữ số còn lại để tổng các số là số có

chữ số tận cùng bằng

, chẳng hạn:

chữ số

, chữ số còn lại sẽ là

;

chữ số

, chữ số còn lại sẽ là

;…;

chữ số

, chữ số còn lại sẽ là

Sắp xếp

chữ số vừa chọn có

cách xếp.

Do đó, có tất cả

10.5 50



(cách chọn số ở dòng thứ hai).

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 43

Suy ra có tất cả

240.50 12000



(biển số đẹp).

Chọn

biển số trong các biển số

đẹp

ta có

12000

71994000

C 

(cách).

Câu 3.

Lời giải

Chọn C

Phép thử

:” An và bình chọn ngẫu nhiên ba số trong tập





0, 1, 2, 3, 4, 5, 6, 7, 8, 9

”

Số phần tử không gian mẫu

3 3

10 10

C C

 

Biến cố

:” Trong hai bộ số của An và Bình chọn ra có nhiều nhất một số giống nhau”.

Trường hợp 1: Trong hai bộ số không có số nào giống nhau.

Số các khả năng là

3 3

10 7

C C

Trường hợp 2: Trong hai bộ số có một số nào giống nhau.

Số các khả năng

3 1 2

10 3 7

. .

C C C

Số các kết quả thuận lợi của biến cố

là

3 3 3 1 2

10 7 10 3 7

. . .

C C C C C

  

Vậy xác suất của biến cố

là

 

3 1 2

7 3 7

C C C

P A





  



Câu 4.

Lời giải

Chọn D

Viết ngẫu nhiên một số có

chữ số nên số phần tử của không gian mẫu là





9.10.10.10 9000

n   

Gọi

là biến cố các chữ số của số được viết ra có thứ tự tăng dần hoặc giảm dần

Gọi số tự nhiên có

chữ số mà các chữ số của số được viết ra có thứ tự tăng dần hoặc giảm dần có dạng

abcd

Trường hợp 1: số tự nhiên có

chữ số mà các chữ số của số được viết ra có thứ tự giảm dần

Vì

a b c d

  

nên các chữ số đôi một khác nhau và các chữ số

lấy từ tập





1,2,3,4,5,6,7,8,9

X 

và với

chữ số lấy ra từ

thì chỉ lập được duy nhất một số thỏa yêu cầu bài

toán. Do đó số số tự nhiên có

chữ số mà các chữ số của số được viết ra có thứ tự tăng dần là

Trường hợp 2: số tự nhiên có

chữ số mà các chữ số của số được viết ra có thứ tự tăng dần

Vì

a b c d

  

nên các chữ số đôi một khác nhau và các chữ số

lấy từ tập





0,1,2,3,4,5,6,7,8,9

Y 

và với

chữ số lấy ra từ

thì chỉ lập được duy nhất mọt số thỏa yêu cầu bài

toán. Do đó số số tự nhiên có

chữ số mà các chữ số của số được viết ra có thứ tự giảm dần dần là

Vậy số phần tử của biến cố

là





4 4

9 10

336

n A C C  

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 44

Xác suất của biến cố

là:

 

336 14

9000 375

n A

P A

  



Câu 5.

Lời giải

Chọn A

Xem lô đất có 4 vị trí gồm 2 vị trí 1 nền, 1 vị trí 2 nền và 1 vị trí 3 nền.

Bước 1: nhóm thứ nhất chọn 1 vị trí cho 2 nền có 4 cách và mỗi cách có

2! 2

cách chọn nền cho mỗi người. Suy ra có

4.2 8

cách chọn nền.

Bước 2: nhóm thứ hai chọn 1 trong 3 vị trí còn lại cho 3 nền có 3 cách và mỗi cách có

3! 6

cách chọn

nền cho mỗi người.

Suy ra có

3.6 18

cách chọn nền.

Vậy có

8.18 144

cách chọn nền cho mỗi người.

Câu 6.

Lời giải

Chọn A

Gọi

là trục đối xứng của đa giác đều 20 cạnh.

TH1: Xét

đi qua hai đỉnh đối diện của đa giác đều (có 10 đường thẳng)

Chọn 2 đoạn thẳng trong 9 đoạn thẳng song song hoặc trùng với

thì sẽ tạo thành 1 hình thang hoặc

hình chữ nhật có các đỉnh là đỉnh của đa giác.



số hình thang là

(hình thang).

Vì vai trò của 10 đường thẳng

như nhau nên có

10C

(hình thang).

Mặt khác, trong số các hình trên có

hình thang (là hình chữ nhật) trùng nhau.



số hình thang có cạnh song song hoặc trùng với

là

2 2

9 10

10.C C

(hình thang).

TH2 : Xét

là đường trung trực của hai cạnh đối diện của đa giác (có 10 đường thẳng)

Chọn 2 đoạn thẳng trong 10 đoạn thẳng song song với

thì sẽ tạo thành 1 hình thang hoặc hình chữ nhật

có các đỉnh là đỉnh của đa giác.

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 45



số hình thang là

(hình).

Vì vai trò của 10 đường thẳng

như nhau nên có

(hình thang).

Mặt khác, trong số các hình trên có

hình thang (là hình chữ nhật) trùng nhau.



số hình thang là

2 2

9 10

10.

C C



(hình thang).

Vậy số hình thang cần tìm là





2 2 2

9 10 10

10 2 720

C C C  

(hình thang).

Câu 7.

Lời giải

Chọn C

Ta dùng phần bù.

Sắp

người vào

vị trí theo hàng dọc có

cách sắp xếp.

Sắp ông và bà An vào

trong

vị trí (trừ vị trí đầu và cuối hàng) có

cách.

Sắp

người con vào

vị trí còn lại có

cách.

Câu 8.

Lời giải

Chọn C

Số trận đấu diễn ra trong vòng

4. 24.

C 

Số trận đấu diễn ra trong vòng

Có tất cả

trận đấu.

Vậy ban tổ chức cần mượn sân trong



ngày.

Câu 9.

Lời giải

Chọn D

Số cách chọn

người trong



m n

người là:



m n

*Số cách chọn có ít hơn

nam là:

-1

1 1

    







a i k a i

S C C

m n

*Số cách chọn có ít hơn

nữ là:

1 1



    





b i k b i

n m

S C C

Số cách chọn thoả mãn điều kiện bài toán là:

1 2

( )



 

m n

C S S

Câu 10.

Lời giải

Chọn D

Vì chữ số

đứng liền giữa hai chữ số

và

nên số cần lập có bộ ba số

123

hoặc

321

TH1: Số cần lập có bộ ba số

123

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 46

Nếu bộ ba số

123

đứng đầu thì số có dạng 123

abcd

Có

840

A 

cách chọn bốn số

nên có

840

A 

số.

Nếu bộ ba số

123

không đứng đầu thì số có

vị trí đặt bộ ba số

123

Có

cách chọn số đứng đầu và có

120

A 

cách chọn ba số

Theo quy tắc nhân có

6.4. 2880

A 

số

Theo quy tắc cộng có

840 2880 3720

 

số.

TH2: Số cần lập có bộ ba số

321

Do vai trò của bộ ba số

123

và

321

như nhau nên có





2 840 2880 7440

 

Câu 11.

Lời giải

Chọn C

Một tam giác được tạo bởi ba điểm phân biệt nên ta xét:

TH1. Chọn

điểm thuộc

và

điểm thuộc



có

1 2

C C

tam giác.

TH2. Chọn

điểm thuộc

và

điểm thuộc



có

2 1

C C

tam giác.

Như vậy, ta có

1 2 2 1

10 10

. . 2800

n n

C C C C

 

   

 

! !

10. 45. 2800 5 1 45 2800

2! 2 ! 1! 1 !

20 ( )

5 40 2800 0

28 ( )

n n

n n n

n n

n tm

n n

n l

      

 





    



 



Vậy



Câu 12.

Lời giải

Chọn D

+ Tìm công thức tính số đường chéo: Số đoạn thẳng tạo bởi

đỉnh là

, trong đó có

cạnh, suy ra số

đường chéo là

C n



+ Đa giác đã cho có

135

đường chéo nên

135

C n 

+ Giải PT :

 

135 , , 2

2 !2!

n n n

   









1 2 270

n n n   

3 270 0

n n

   





 

n nhan

n loai

 





 



 

Câu 13.

Lời giải

Chọn C

2017.2017! 2016.2016! 2.2! 1.1! 2017.2017! 20

16.2016! ... 2.2! 1.1!

...

2017! 2017! 2017! 2017! 2017!

   

     

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 47

















2018 1 2017! 2017 1 2016! ... 3 1 2! 2 1 1!

2017!

       

 

















2018! 2017! 2017! 2016! ... 3! 2! 2! 1!

2018! 1! 1

2018

2017! 2017! 2017!

P P

       



     

Câu 14.

Lời giải

Chọn C

* PP tự luận:

+ PT

 





 

! 2 !

3. 42 0

2 ! 2 2 !

   

 

n n





, 2

 



n n









3 1 2 . 2 1 42 0

n n n n

     

42 0

n n

    





 

 





 



n nhan

n loai

 

* PP trắc nghiệm:

+ Nhập vào máy tính PT

2 2

3 42 0

n n

A A

  

+ Tính (CALC) lần lượt với



(không thoả); với



(không thoả), với



(thoả), với



(không thoả).

Câu 15.

Lời giải

Chọn C

PP sử dụng máy tính để chọn đáp số đúng (PP trắc nghiệm):

+ Nhập PT vào máy tính:

6 7 8 9 8

3 3 2 0

n n n n n

C C C C C



    

+ Tính (CALC) lần lượt với



(không thoả); với



(không thoả); với



(thoả), với



(không thoả)

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 48

①.Dạng 1:

Khai triển một nhị thức Newton

. Bài tập minh họa:

Câu 1: Viết khai triển theo công thức nhị thức Newton

( )x y .

Ⓐ.

5 4 3 2 2 3 4 5

5 10 10 5x x y x y x y xy y     .

Ⓑ.

5 4 3 2 2 3 4 5

5 10 10 5x x y x y x y xy y     .

Ⓒ.

5 4 3 2 2 3 4 5

5 10 10 5x x y x y x y xy y     .

Ⓓ.

5 4 3 2 2 3 4 5

5 10 10 5x x y x y x y xy y     .

ờ

i gi

ả

Ta có

( )x y

5 4 3 2 2 3 4 5

5 10 10 5x x y x y x y xy y    

Câu 2: Trong khai triển nhị thức Niu-tơn của

2019

(3 2 )x

có bao nhiêu số hạng?

§➌. NHỊ THỨC NEWTON

Chương ⓶

⓫

Tóm tắt lý thuyết

Ⓐ

➊.

Công thức nhị thức Newton

Định lý:

    



       



0 1 1 2 2 2 1 1

( ) ...

n k n k k n n n n n n n

n n n n n n

a b C a b C a C a b C a b C ab C b

(1)

Hệ quả:

 a = b = 1:

0 1

2 ...

n n

n n n

C C C

   

 a =1; b = –1:

0 1

0 ... ( 1)

n n

n n n

C C C

    



Ta có:

n 0 1 2 2 n n

n n n n

(1 x) C xC x C ... x C

     



   

0 1 n n

n n n

C C ... C 2



     

0 1 2 n n

n n n n

C C C ... ( 1) C 0

Chú ý: Trong công thức khai triển nhị thức Newton:

 Số các hạng tử là n + 1.

 Các hạng tử có số mũ của a giảm dần, số mũ của b tăng dần, nhưng tổng các số mũ bằng n.

 Các hệ số của các hạng tử cách đều hai hạng tử đầu và cuối thì bằng nhau.

 Hạng tử thứ k + 1:

k n k k

C a b



➋.

Tam giác Pascal



Trong công thức nhị thức Newton cho n = 0, 1, 2, … và xếp

các hệ số thành dòng ta nhận được tam giác sau đây, gọi là

tam giác Pascal.

Nhận xét:

 Từ công thức

1 1

k k k

n n n

C C C



 

 

suy ra cách tính các số ở mỗi

dòng dựa vào các số ở dòng trước nó.

Phân dạng bài tập

Ⓑ

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 49

Ⓐ.

2019

. Ⓑ.

2018

. Ⓒ.

2020

. Ⓓ.

2021

Lời giải

Ta có: Khai triển nhị thức Niu-tơn

( )

a b

 có



số hạng.

Vậy trong khai triển nhị thức Niu-tơn của

2019

(3 2 )

x có

2020

số hạng.

Câu 3: Từ khai triển biểu thức

 

x 

thành đa thức. Tổng các hệ số của đa

thức là

Ⓐ.

1023

. Ⓑ.

512

. Ⓒ.

1024

. Ⓓ.

2048

Lời giải

Xét khai triển

 

( ) 1 .

k k

f x x C x



  



Gọi

là tổng các hệ số trong khai triển thì ta có

 

(1) 1 1 2 1024

S f    

②.Dạng 2:

Tìm hệ số, số hạng trong khai triển nhị thức Newton

. Bài tập minh họa:

Câu 1: Hệ số của

trong khai triển của biểu thức

 



 

 

bằng

Ⓐ.

3124

. Ⓑ.

2268

. Ⓒ.

13440

. Ⓓ.

210

Lời giải

Số hạng tổng quát của khai triển:

 

2 20 3

1 10 10

2 0 10,

k k k k

T C x C x k k





 

     

 

 

Số hạng chứa

ứng với:

20 3 2 6

k k

   

Hệ số cần tìm là:

6 6

2 13440

C  .

Câu 2: Số hạng không chứa

trong khai triển

 



 

 

là

Ⓐ.

. Ⓑ.

5 5

C

. Ⓒ.



. Ⓓ.

5 5

Lời giải

Số hạng tổng quát trong khai triển

 



 

 

là:

10 10 2

1 10 10

. .2

k k k k k

T C x C x

 



 

 

 

 

Số hạng không chứa x trong khai triển tương ứng với

10 2 0 5

k k

   

Vậy số hạng không chứa x trong khai triển là:

5 5

Câu 3: Số hạng độc lập với x trong khai triển

 



 

 

là

Ⓐ.

8 4

2 .

. Ⓑ.

6 6

2 .

. Ⓒ.

4 4

2 .

. Ⓓ.

4 4

2 .



Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 50

Lời giải

Ta có:

 

12 12

2 2 3 12

12 12

0 0

1 1

2 2 2

k k k

k k

x C x C x

x x



 

   

    

   

   

 

Số hạng độc lập với x khi

3 12 0 4

k k

   

Vậy số hạng độc lập với x là:

4 4

2 .

=> chọn C

③.Dạng 3:

Chứng minh, tính giá trị của biểu thức đại số tổ hợp có sử dụng nhị

thức Newton

. Bài tập minh họa:

Câu 1: Cho

là số nguyên dương. Khi đó tổng

0 1 2

...

    

n n n n

S C C C C

là

Ⓐ.

. Ⓑ.

. Ⓒ.

. Ⓓ.

Lời giải

Xét:

 

0 1 1 2 2 0

1 ...

 

     

n n n n

x C x C x C x C x

Chọn



ta được:

0 1 2

2 ...

    

n n

n n n n

C C C C

Vậy



Câu 2: Cho

8 9 10 15

15 15 15 15

...

S C C C C

    

. Tính

Ⓐ.

S 

. Ⓑ.

S 

. Ⓒ.

S 

. Ⓓ.

S 

Lời giải

Khai triển nhị thức

 

0 1 2 2 7 7 8 8 15 15

15 15 15 15 15 15

1 ... ... .

x C C x C x C x C x C x

        

Thay



ta được:

15 0 1 2 7 8 15

15 15 15 15 15 15

2 ... ... .

C C C C C C

       

Mà

15 0 14 1 13 2 8 7

15 15 15 15 15 15 15 15

, , ,..., .

n k k

n n

C C C C C C C C C C



     





15 8 9 10 15

15 15 15 15

2 2 ...

2 2

2 .

C C C C

     

 

Câu 3: Tổng

1 2 2018

2018 2018 2018

...C C C  

bằng

Ⓐ.

2018

. Ⓑ.

2018

2 1



. Ⓒ.

2018

2 1



. Ⓓ.

2016

Lời giải

Ta có

 

2018

0 1 2 2018

2018 2018 2018 2018 2018

1 1 ...

C C C C C



      



Suy ra

1 2 2018 2018

2018 2018 2018

... 2 1

C C C

    

Câu 4: Cho một tập hợp có

phần tử (

là số tự nhiên). Số tập con khác

rỗng của nó là:

Ⓐ.

. Ⓑ.

2 1



. Ⓒ.

2 1



. Ⓓ.

2 1



Lời giải

Gọi

là tập hợp có

( )

n n





phần tử.

+ Số tập con có

phần tử của

là

+ Số tập con có

phần tử của

là

…

+ Số tập con có

phần tử của

là

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 51

Suy ra số tập con khác rỗng của

là

1 2

...

n n n

T C C C   

Xét nhị thức

 

0 1 2 2

1 ... (*)

n n

n n n n

x C C x C x C x     

Thay

1x 

vào ta được:

 

0 1 2

1 1 ... 2 1

n n

n n n n

C C C C T        

Câu 5: Tính tổng tất cả các số nguyên dương

thỏa mãn

2 2

3 15 5

n n

A C n  

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

ờ

i gi

ả

Điều kiện:

n 



2n 

Ta có:

2 2 2

( 1)

3 15 5 ( 1) 3. 5 15 0 11 30 0

n n

A C n n n n n n







             







Hai nghiệm đều thỏa mãn điều kiện, chúng có tổng bằng

Câu 1:Trong khai triển

 

2 1a 

, tổng ba số hạng đầu là:

Ⓐ.

6 5 4

2 6 15a a a 

Ⓑ.

6 5 4

2 15 30a a a 

Ⓒ.

6 5 4

64 192 480a a a 

Ⓓ.

6 5 4

64 192 240a a a 

ờ

i gi

ả

:......................................................................

......................................................................................

Câu 2:Ba số hạng đầu tiên theo lũy thừa tăng dần của x trong khai triển của

là

Ⓐ.

1, 45 , 120x x

Ⓑ.

1, 4 , 4x x

Ⓒ.

1,20 ,180x x

Ⓓ.

10, 45 , 120x x

ờ

i gi

ả

:......................................................................

......................................................................................

Câu 3:Ba số hạng đầu tiên theo lũy thừa tăng dần của x trong khai triển của

là:

Ⓐ.

1, 45 , 120 .x x

Ⓑ.

1, 4 , 4 .

x x

Ⓒ.

1, 20x, 180x

Ⓓ.

10, 45 , 120 .x x

ờ

i gi

ả

:......................................................................

......................................................................................

Câu 4:Trong khai triển





x y

, tổng hai số hạng cuối là

Ⓐ.

15 8

16x y y 

Ⓑ.

15 4

16x y y 

Ⓒ.

15 4

16xy y

Ⓓ.

15 8

16xy y

ờ

i gi

ả

:......................................................................

......................................................................................

Câu 5:Trong khai triển nhị thức:





2 1



. Ba số hạng đầu là:

Ⓐ.

6 5 4

2 6 15a a a

 

Ⓑ.

6 5 4

2 12 30a a a

 

Ⓒ.

6 5 4

64 192 480a a a

 

Ⓓ.

6 5 4

64 192 240 .a a a

 

ờ

i gi

ả

:......................................................................

......................................................................................

Bài tập rèn luyện

Ⓒ

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 52

Câu 6:Sau khi khai triển và rút gọn biểu thức

 

12 21

2 3

3 1

2f x x x

x x

   

   

   

   

thì





f x

có bao nhiêu số hạng?

Ⓐ.

. Ⓑ.

Ⓒ.

Ⓓ.

Lời giải :......................................................................

......................................................................................

.............

.........................................................................

Câu 7:Biểu thức

     

2 10

10 9 8

1 1 1

. . ...

10! 9! 1! 8! 2! 10!

x x x

  

   

bằng

Ⓐ.

10!

. Ⓑ.

20!

Ⓒ.

10!

. Ⓓ.

100!

Lời giải :......................................................................

......................................................................................

Câu 8:Cho khai triển

 

0 1 2 20 20

1 2

x a a x a x a x

     

. Giá trị của

0 1 2 20

a a a a

   



bằng:

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.



Lời giải :......................................................................

......................................................................................

Câu 9:Trong khai triển

 

x y



, hệ số của số hạng chứa

8 3

x y

là

Ⓐ

Ⓑ.



Ⓒ

C

Ⓓ

Lời giải :......................................................................

......................................................................................

Câu 10:Trong khai triển

 

2 1

x 

, hệ số của số hạng chứa

là:

Ⓐ.

11520



. Ⓑ.

Ⓒ.

256

. Ⓓ.

11520

Lời giải :......................................................................

......................................................................................

Câu 11:Trong khai triển







x y

, số hạng chứa

4 3

x y

là:

Ⓐ.



4 3

2835

x y

. Ⓑ.

4 3

2835

x y

Ⓒ.

4 3

945

x y

. Ⓓ.



4 3

945

x y

Lời giải :......................................................................

......................................................................................

Câu 12:Nếu khai triển nhị thức Niutơn:

 

5 4 3 2

5 4 3 2 1

a x a x a x a x a x a

    

 

thì tổng

5 4 3 2 1 0

a a a a a a

    

bằng

Ⓐ.

32.



Ⓑ.

Ⓒ.

Ⓓ

Lời giải :......................................................................

......................................................................................

Câu 13:Hệ số của

trong khai triển

 

x 

bằng

Ⓐ.

5 5

. Ⓑ.

5 5

C

Ⓒ.

3 3

. Ⓓ.

3 3

C

Lời giải :......................................................................

......................................................................................

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 53

......................................................................................

Câu 14:Tìm hệ số của số hạng chứa

trong khai triển

 



 

 

biết

là số nguyên dương thỏa mãn





4 3

7 3

n n

C C n



 

  

Ⓐ.

495

. Ⓑ.

313

. Ⓒ.

1303

. Ⓓ.

13129

Lời giải :......................................................................

......................................................................................

Câu 15:Tìm hệ số của

trong khai triển

 





P x x x

 

Ⓐ.

3630.

Ⓑ.

3360.

Ⓒ.

3330.

Ⓓ.

3260.

Lời giải :......................................................................

......................................................................................

Câu 16:Trong khai triển,

 

a b



hệ số của số hạng chứa

4 4

a b

là

Ⓐ.

1120

. Ⓑ.

560

Ⓒ.

140

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 17:Tính số hạng không chứa x trong khai triển

 



 

 

Ⓐ.

3300

. Ⓑ. -

3300

Ⓒ.

3003

 . Ⓓ.

3003

Lời giải :......................................................................

......................................................................................

...............................

.......................................................

Câu 18:Số hạng của

trong khai triển

 

 

 



là

Ⓐ.

5 4

C x

. Ⓑ.

4 4

C x

Ⓒ.

5 4

C x

 . Ⓓ.

3 4

C x

 .

Lời giải :......................................................................

......................................................................................

Câu 19:Tìm hệ số của

trong khai triển

 



 

 



Ⓐ.

120

. Ⓑ.

120



. Ⓒ.

210

. Ⓓ.

210



Lời giải :......................................................................

......................................................................................

Câu 20:Hệ số của

trong khai triển

 

x 

là

Ⓐ.

3 7

C . Ⓑ.

. Ⓒ.

3 3

C . Ⓓ.

7 3

C .

Lời giải :......................................................................

......................................................................................

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 54

Câu 21:Hệ số của

trong khai triển

 



 

 

là

Ⓐ.

. Ⓑ.



Ⓒ.

144

. Ⓓ.

672



Lời giải :......................................................................

......................................................................................

Câu 22:Cho số nguyên dương

thỏa mãn





1 2

2 3 ... 1 2621439

n n n

C C n C    

. Số hạng không chứa

trong

khai triển của biểu thức

 



 

 

bằng

Ⓐ.

43758

. Ⓑ.

31824

Ⓒ.

18564

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 23:Hệ số của

trong khai triển

 



 

 

bằng

Ⓐ. 792. Ⓑ. 252. Ⓒ. 165. Ⓓ.

210.

Lời giải :......................................................................

......................................................................................

Câu 24:Số hạng thứ

của khai triển

 



 

 

không chứa

. Tìm

biết rằng số hạng này bằng số hạng thứ

hai của khai triển







Ⓐ.



. Ⓑ.

. Ⓒ.



. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 25:Trong khai triển

 

a b



, hệ số của số hạng thứ

bằng:

Ⓐ.



. Ⓑ.

Ⓒ.



. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 26:Giả sử

0 1 2

(1 2 ) ...     

n n

x a a x a x a x

, biết rằng

0 1

... 729

   

a a a

. Tìm

và số lớn nhất

trong các số

0 1

, ,...,

a a a

Ⓐ. n=6,





max 240

 

a a .

Ⓑ. n=6,





max 240

 

a a

Ⓒ. n=4,





max 240

 

a a .

Ⓓ. n=4,





max 240

 

a a

Lời giải :......................................................................

......................................................................................

Câu 27:Cho

 

0 1

1 2 ...

x a a x a x

    

n 



. Biết

1 2

... 4096

2 2 2

aa a

a     

. Số lớn nhất trong các số

0 1 2

, , ,...,

a a a a

có giá trị bằng

Ⓐ.

126720

Ⓑ.

924

Ⓒ.

972

Ⓓ.

1293600

Lời giải :......................................................................

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 55

......................................................................................

Câu 28:Cho khai triển

 

0 1 2

1 2 ...

x a a x a x a x

     

, trong đó

n 



và các hệ số thỏa mãn hệ thức

... 4096

2 2

a    

. Tìm hệ số lớn nhất?

Ⓐ.

1293600

. Ⓑ.

126720

Ⓒ.

924

. Ⓓ.

792

Lời giải :......................................................................

......................................................................................

Câu 29:Tổng

0 1 2 3

...

n n n n n

T C C C C C

     

bằng

Ⓐ.



. Ⓑ.



Ⓒ.

2 1

 

. Ⓓ.

2 1

 

Lời giải :......................................................................

......................................................................................

Câu 30:Trong khai triển nhị thức

 

3 0,02



, tìm tổng số ba số hạng đầu tiên

Ⓐ.

2289, 3283

. Ⓑ.

2291,1012

Ⓒ.

2275,93801

. Ⓓ.

2291,1141

Lời giải :......................................................................

......................................................................................

Câu 31:Nếu khai triển nhị thức Niutơn

 

5 4 3 2

5 4 3 2 1

a x a x a x a x a x a

    

 

thì tổng

5 4 3 2 1 0

a a a a a a

    

bằng:

Ⓐ.



. Ⓑ.

Ⓒ.

. Ⓓ

Lời giải :......................................................................

......................................................................................

.............................................................

.........................

Câu 32:Khai triển

 

x y



rồi thay

bởi các giá trị thích hợp. Tính tổng

0 1 5

5 5 5

...S

C C C

  

 .

Ⓐ.

32

. Ⓑ.

Ⓒ.

. Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 33:Tính giá trị của tổng

0 1 6

6 6 6

C C C

  

 bằng

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

100

Lời giải :......................................................................

......................................................................................

Câu 34:Giả sử













2 2 2

0 1 2

1 1 ... 1 ... ...

n m

x x x x x x a a x a x a x

           

. Tính





Ⓐ.

Ⓑ.

Ⓒ.





1 !



Ⓓ.

Lời giải :......................................................................

......................................................................................

Câu 35:Nếu khai triển nhị thức Niutơn:

 

5 4 3 2

5 4 3 2 1

a x a x a x a x a x a

    

 

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 56

thì tổng

5 4 3 2 1 0

a a a a a a

    

bằng

Ⓐ.

32.



Ⓑ.

Ⓒ.

Ⓓ

Lời giải :......................................................................

......................................................................................

Câu 36:Tính các tổng sau:

0 1 2

1 1 1

...

2 3 1

    



n n n n

S C C C C

Ⓐ.

2 1



. Ⓑ.

2 1







Ⓒ.

2 1







. Ⓓ.

2 1







Lời giải :......................................................................

......................................................................................

Câu 37:Tính các tổng sau:

2 3 4

2.1. 3.2 4.3 ... ( 1)

     

n n n n

S C C C n n C

Ⓐ.

( 1)2



n n . Ⓑ.

( 2)2





n n .

Ⓒ.

( 1)2



n n . Ⓓ.

( 1)2





n n

Lời giải :......................................................................

......................................................................................

........................................

..............................................

Câu 38:Tính tổng

















2 2 2 2

0 1 2

...

n n n n

C C C C   

Ⓐ.

. Ⓑ.



Ⓒ.

. Ⓓ.

2 1



Lời giải :......................................................................

......................................................................................

Câu 39:Số tự nhiên

thỏa

1 2

1.C 2.C ... .C 1024

n n n

n   

thì

Ⓐ.



Ⓑ.



Ⓒ.



Ⓓ.

10.



Lời giải :......................................................................

......................................................................................

Câu 40:Tìm số nguyên dương

thỏa mãn





0 1 2

2 5 8 ... 3 2 1600

n n n n

C C C n C      .

Ⓐ.



. Ⓑ.



Ⓒ.



. Ⓓ.



Lời giải :......................................................................

......................................................................................

Câu 41:Cho số nguyên dương

thỏa mãn

1 3 2 1

2 2 2

512

n n n

C C C



   



. Tính tổng

 

2 2 2 3 2

2 3 1 . .

n n n

S C C n C

    

Ⓐ.



. Ⓑ.



Ⓒ.



. Ⓓ.



Lời giải :......................................................................

......................................................................................

Câu 42:Tính tổng sau:

0 1 3 4

1 1 1 1 ( 1)

...

2 4 6 8 2( 1)



     



n n n n n

S C C C C C

Ⓐ.

2( 1)



. Ⓑ. 1.

Ⓒ. 2. Ⓓ.

( 1)



Lời giải :......................................................................

......................................................................................

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 57

Câu 43:Trong các câu sau câu nào sai?

Ⓐ.

3 11

14 14



C C

Ⓑ.

3 4 4

10 10 11

 

C C C

Ⓒ.

0 1 2 3 4

4 4 4 4 4

    

C C C C C

Ⓓ.

4 4 5

10 11 11

 

C C C

Lời giải :......................................................................

......................................................................................

Câu 44:Biết hệ số của

trong khai triển của

 

1 3



là

. Tìm

Ⓐ.



. Ⓑ.



Ⓒ.



. Ⓓ.



Lời giải :......................................................................

......................................................................................

Câu 45:Biết rằng hệ số của

trong khai triển nhị thức Newton

 







n 



bằng

280

, tìm

Ⓐ.



. Ⓑ.



Ⓒ.



. Ⓓ.



Lời giải :......................................................................

......................................................................................

Câu 46:Biết





0 1 2 3

2 32768

n k k n n

n n n n n n

C iC C iC i C i C i

        

, với

là các số tổ hợp chập

của

và

 

. Đặt

k k

k n

T i C





, giá trị của

bằng

Ⓐ.

330



. Ⓑ.



Ⓒ.



. Ⓓ.

120



Lời giải :......................................................................

......................................................................................

Câu 47:Giá trị của

1 1 1 1 1

...

1!2018! 2!2017! 3!2016! 1008!1011! 1009!1010

A       bằng

Ⓐ.

2017

2 1

2018!



. Ⓑ.

2018

2019!

Ⓒ.

2018

2 1

2019!



. Ⓓ.

2017

2018!

Lời giải :......................................................................

......................................................................................

Câu 48:Số tự nhiên

thỏa

1 2

2. ... . 112641

n n n

C C n C   

thì

Ⓐ.



. Ⓑ.



Ⓒ.



. Ⓓ.



Lời giải :......................................................................

......................................................................................

..................

....................................................................

Câu 49:Tìm số tự nhiên

thỏa mãn

5 3

n n

C A

 



Ⓐ.



. Ⓑ.



Ⓒ.



. Ⓓ.



Lời giải :......................................................................

......................................................................................

Câu 50:Tìm số tự nhiên

thỏa mãn

     

0 1 2

100

2 3

...

1.2 2.3 3.4 1 2 1 2

n n n n

C C C C

n n n n

 

    

   

Ⓐ.

101



. Ⓑ.



Ⓒ.



. Ⓓ.

100



Lời giải :......................................................................

......................................................................................

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 58

ĐÁP ÁN TRẮC NGHIỆM

Dạng toán 01: Khai triển một nhị thức Newton cụ thể

1 2 3 4 5 6 7

D C C A D D C

Dạng toán 02: Tìm hệ số và số hạng trong khai triển

8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

A B D A B B A B A C A B C C C D D

Dạng toán 03: Hệ số lớn nhất, nhỏ nhất trong khai triển

25 26 27 28

B A A B

Dạng toán 04: Tính tổng hữu hạn các C (không đạo hàm, tích phân)

29 30 31 32 33 34 35 36 37 38

A B B A A C B B A A

Dạng toán 05: Tính tổng hữu hạn các C (Newton và đạo hàm)

39 40 41

B B B

Dạng toán 06: Tính tổng hữu hạn các C (Newton và tích phân)

Dạng toán 07: Toán về đẳng thức có dùng nhị thức Newton

43 44 45 46 47

D A C B C

Dạng toán 08: PT, BPT, HPT có dùng nhị thức Newton

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 59

48 49 50

B C B

HƯỚNG DẪN GIẢI - ĐÁP ÁN CHI TIẾT

Câu 1.

Lời giải

Chọn D

Ta có:

 

0 6 6 1 5 5 2 4 4

6 6 6

2 1 .2 .2 .2 ...

a C a C a C a

    

Vậy tổng 3 số hạng đầu là

6 5 4

64 192 240

a a a

 

Câu 2.

Lời giải

Chọn C

Ta có

 

10 0 1 2 2

20 10 10 10

(2 ) (2 )1 2

k k k

x C x y C C x C x





      



 



1 20 180 ...

x x

   

Vậy 3 số hạng đầu tiên theo lũy thừa tăng dần của x là:

1, 20 , 180

x x

Câu 3.

Lời giải

Chọn C

Ta có

 

10 0 1 2 2

20 10 10 10

(2 ) (2 )1 2

k k k

x C x y C C x C x





      







1 20 180 ...

x x

   

Vậy 3 số hạng đầu tiên theo lũy thừa tăng dần của x là:

1, 20 , 180

x x

Câu 4.

Lời giải

Chọn A

Ta có:













16 15 16

0 16 1 15 15 16

16 16 16 16

. ...

x y C x C x y C x y C y

     

Câu 5.

Lời giải

Chọn D

Ta có

 

6 0 6 1 5 2 4 2

6 6 6 6

(2 ) ( 1) .(2 ) (2 ) ( 1) (2 )2 1

( 1) ...

k k k

C a C a Ca C a a





       





Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 60

0 6 6 1 5 5 2 4 4 6 5 4

6 6 6

.2 2 2 ... 64 192 240 ...

C a C a C a a a a

       

Ba số hạng đầu là:

6 5 4

64 192 240 .

a a a

 

Câu 6.

Lời giải

Chọn D

 



 

 

 

C x





 



 

 



24 3

k k k

C x







 



 

 

 

C x





 



 

 



21 63 5

k k k

C x

 





Ta cho

chạy từ

đến

thì các số mũ của

không bằng nhau.

Với khai triển

 



 

 

ta có

số hạng; Với khai triển

 



 

 

ta có

số hạng. Vậy tổng số

hạng là:

Câu 7.

Lời giải

Chọn C

Ta có

 

! 10 !

k k



 

1 10!

. . . 1

10! ! 10 !

x x

k k



 



 

. . . 1

10!

k k

C x x



 

với

0 10

 

     

2 10

10 9 8

1 1 1

. . ...

10! 9! 1! 8! 2! 10!

x x x

  

   

 

. . 1

10!

k k

C x x





 



 

10!

x x

  

10!



Câu 8.

Lời giải

Chọn A

 

0 1 2 20 20

1 2

x a a x a x a x

     





Thay



vào





ta có:

 

0 1 2 20

1 1

a a a a

      



Câu 9.

Lời giải

Chọn B

Số hạng tổng quát trong khai triển trên là

 

1 11

. . 1 .

k k k

T C x y





 

Yêu cầu bài toán xảy ra khi



Khi đó hệ số của số hạng chứa

8 3

x y

là:



Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 61

Câu 10.

Lời giải

Chọn D

Số hạng tổng quát trong khai triển trên là

 

10 10

1 10

.2 . . 1

k k k

T C x

 



 

Yêu cầu bài toán xảy ra khi

10 8 2

k k

   

Khi đó hệ số của số hạng chứa

là:

2 8

.2 11520

C 

Câu 11.

Lời giải

Chọn A

Số hạng tổng quát trong khai triển trên là

 

7 7

1 7

.3 . 1 .

k k k k

T C x y

 



 

Yêu cầu bài toán xảy ra khi



Khi đó hệ số của số hạng chứa

4 3

x y

là:

3 4 4 3 4

.3 . . 2835. .

C x y x y

  

Câu 12.

Lời giải

Chọn B

Ta có





0 5 1 4 2 3 2 5 0 5

5 5 5 5

.( ) ( ) ( 1) ( ) ( 1) ... ( ) ( 1)

1 C x C x C x C xx

       



0 5 1 4 2 3 3 2 4 1 5 0

5 5 5 5 5 5

. . . . . .

C x C x C x C x C x C x

     

Khi đó tổng

5 4 3 2 1 0

a a a a a a

    

bằng:

0 1 2 3 4 5

5 5 5 5 5 5

C C C C C C

     

Câu 13.

Lời giải

Chọn B

Số hạng tổng quát của khai triển:

 

. 2

k k

C x



Số hạng chứa

ứng với

8 3 5

k k

   

Vậy hệ số của

là

5 5

C

Câu 14.

Lời giải

Chọn A

Ta có









1 3 3

4 3 4 3

7 3 7 3

n n

n n n n

C C n C C n



   

      

























 

4 3 2 3 2 1

7 3

3! 3!

n n n n n n

     

   

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 62

















4 2 2 1 42

n n n n

      

 

Số hạng thứ



trong khai triển

 



 

 

là





1 12 12

k k

T C x C x



 



 

 

 

 

Ta cần tìm

sao cho

36 8 8

k k

    

Do đó hệ số của số hạng chứa

là

495

C 

Câu 15.

Lời giải

Chọn B

Ta có

 

10 10

2 2 10 20

10 10

0 0

2 ( ) .( 2 ) ( 2)

k k k k k k

k k

P x x x C x x C x

 

 

     

 

Số hạng tổng quát là

1 10

( 2)

k k k

T C x





 

Để số hạng chứa

ta chọn k sao cho:

20 16 4

k k

   

Hệ số của

trong khai triển

 





P x x x

  là:

4 4

( 2) 3360

C  

Câu 16.

Lời giải

Chọn A.

Số hạng tổng quát trong khai triển trên là

 

1 8

. . 2 .

k k k

T C a b





 

Yêu cầu bài toán xảy ra khi



Khi đó hệ số của số hạng chứa

4 4

a b

là:

4 4

.2 1120

C 

Câu 17.

Lời giải

Chọn C

Ta có:

15 15

15 15 3

15 15

2 2

0 0

1 1 1

( ) .( ) ( )

2 2 2

k k k k k k

k k

x C x C x

x x

 

 

 

    

 

 

 

Số hạng tổng quát là

15 3

1 15

( )

k k k

T C x





 

Để số hạng không chứa

ta chọn k sao cho:

15 3 0 5

k k

   

Vậy số hạng không chứa x trong khai triển

 



 

 

là:

5 5

1 3003

( )

2 32

C   

Câu 18.

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 63

Lời giải

Chọn A

Số hạng tổng quát trong khai triển là

 

3 24 4

1 8 8

. . .

k k k

T C x C x





 

 

 

 

Ta cần tìm

sao cho:

24 4 4 4 20 5

k k k

     

Vậy số hạng của

trong khai triển là

5 24 4.5 5 4

8 8

. .

C x C x



 .

Câu 19.

Lời giải

Chọn B

Số hạng tổng quát của khai triển là

 

10 10 2

10 10

k k k k

C x C x

 



 

 

 

 

Số mũ

10 2 4 3

k k

   

. Vậy hệ số cần tìm là:

 

1 120

C  

Câu 20.

Lời giải

Chọn C

Công thức tổng quát của khai triển là:

k k k

C x



Số hạng chứa

khi

10 7 3

k k

   

, hệ số là:

3 3

C .

Câu 21.

Lời giải

Chọn C

Số hạng tổng quát trong khai triển

 

9 9 3

9 9

k k k k

T C x C x

 

 

   

 

 

chứa

khi và chỉ khi

9 3 3 2

k k

   

Suy ra hệ số của

trong khai triển là

 

2 144

C  

Câu 22.

Lời giải

Chọn C

Ta có:

 

0 1 2 2 3 1

1 ...

n n

n n n n

x x C x C x C x C x



     

Lấy đạo hàm hai vế ta được:

     

0 1 2 2

1 1 2 3 ... 1

n n

n n n n

x nx x C C x C x n C x



        

Cho



, ta có





0 1 2 1

2 3 ... 1 2 2

n n n

n n n n

C C C n C n



      





2 2



 





2 2 1 2621439



   





2 2 2621440



  

2621440

2 .2

 



. (*)

Xét





f n



là hàm số đồng biến trên







và

 

2621440

g n





là hàm số nghịch biến trên







Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 64

Ta có









18 18

f g

 

là nghiệm duy nhất của (*).

Khi đó số hạng tổng quát của khai triển

 



 

 

là:

36 3

k k

C x



với

, 0 18

k k

  



Vậy số hạng không chứa

là

18564

C 

Câu 23.

Lời giải

Chọn D

SHTQ:

104

kk

, cho

4 10 6 4

k k

    

hệ số của

là

210

C

Câu 24.

Lời giải.

Chọn D

2 2

1 1

2 .(2 ) .

n k

k n k

x C x

x x





   

 

   

   



Vì số hạng thứ ba của khai triển trên ứng với



nên số hạng thứ ba của khai triển là

2 2 6

.2 .

n n

C x

 

Mà số hạng thứ ba của khai triển không chứa

nên

6 0 6

n n

   

Số hạng thứ 2 của khai triển







là

1 3 3

. 30

C x x



Khi đó ta có

2 4 3

.2 30. 2

C x x

  

Câu 25.

Lời giải

Chọn B

Ta có:

       

5 5 4 3

0 1 2 2

5 5 5

2 2 2 2 ...

a b C a C a b C a b

    

Do đó hệ số của số hạng thứ

bằng

.8 80



Câu 26.

Lời giải.

Chọn A

Ta có:

0 1

... (1 2.1) 3 729 6

        

n n

a a a n



k k

a C

suy ra





max 240

 

a a .

Câu 27.

Lời giải

Chọn A

 

1 2 .2 .

k k k

x C x



  



0 0 0 1 1 1 2 2 2

.2 .2 .2 ... .2

n n n

n n n n

C x C x C x C x

   

0 1

...

a a x a x

   

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 65

Ta có:

1 2

... 4096

2 2 2

aa a

a     



0 1 2

... 4096

n n n n

C C C C    

2 4096

 

Ta có:

k k

a a







1 1

12 12

.2 .2

k k k k

C C

 





12 12

k k

C C





. Suy ra:

0 1 2 8

...

a a a a

   

Mặt khác:

k k

a a







1 1

12 12

.2 .2

k k k k

C C

 





12 12

k k

C C





. Suy ra:

8 9 10 12

...

a a a a

   

Vậy số lớn nhất trong các số

0 1 2

, , ,...,

a a a a

là

8 8

8 12

.2 126720

a C 

Câu 28.

Lời giải.

Chọn B

Số hạng tổng quát trong khai triển

 

1 2



là

.2 .

k k k

C x

, 0

k n

 

, k





. Vậy hệ số của số hạng chứa

là

.2 .2

k k k k

n k n

C a C 

Khi đó, ta có

 

0 1 2

... 4096 ... 4096

2 2

1 1 4096 12

n n n n

a C C C C

         

    

Dễ thấy

và

không phải hệ số lớn nhất. Giả sử





k n

 

là hệ số lớn nhất trong các hệ số

0 1 2

, , ,...,

a a a a

Khi đó ta có

     

1 1

1 12 12

1 1

12 12

12! 12!.2

!. 12 ! 1 !. 12 1 !

.2 .2

12! 12! 1

.2 .2

!. 12 ! 1 !. 12 1 ! 2

k k k k

k k

k k k k

k k

k k k k

a a

C C

a a

C C

k k k k

 



 









   







 

 

  















   



 

1 2 23

1 2 12 0

23 26

12 1 3

2 1 26

3 3

26 3 0

13 3

k k

 

 

 

   



  

 

     

  

 





 

 

 



 

k k

  



Vậy hệ số lớn nhất là

8 8

8 12

.2 126720

a C 

Câu 29.

Lời giải

Chọn A

Xét khai triển

0 1 1 1

( 1) . . . ... . .

n n n k n n n n

k n n n n

x C x C x C x C x C

  



      



Thay



vào khai triển trên ta được

0 1 1 0 1 1

(1 1) ... ... 2 .

n n n n n n

n n n n n n n n

C C C C C C C C

 

           

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 66

Câu 30.

Lời giải

Chọn B

Ta có

 

0 7 1 6 2 5 2

7 7 7

.(3) (3) (0,02) (3 0 3) (0,,02

02) ...

C C C

   

Tổng ba số hạng đầu tiên là:

0 7 1 6 2 5 2

7 7 7

.(3) (3) (0,02) (3) (0,02) 2291,1012

C C C  

Câu 31.

Lời giải

Chọn B

Ta có

 

0 5 1 4 2 3 2 5 0 5

5 5 5 5

.( ) ( ) ( 1) ( ) ( 1) ... ( ) ( 1)

1 C x C x C x C xx

       



0 5 1 4 2 3 3 2 4 1 5 0

5 5 5 5 5 5

. . . . . .

C x C x C x C x C x C x

     

Khi đó tổng

5 4 3 2 1 0

a a a a a a

    

bằng:

0 1 2 3 4 5

5 5 5 5 5 5

C C C C C C

     

Câu 32.

Lời giải

Chọn A

Với

1, 1

x y

 

ta có

  

0 1 5 5

5 5 5

C +C +...+C (1 1)S=

Câu 33.

Lời giải

Chọn A

0 1 6 6

6 6 6

C +C +..S =

.+C 2 64

 

Câu 34.

Lời giải

Chọn C

Cho



ta có





0 1

2.3.4.5... 1 ...

n a a a

    

Vậy

   

1.2.3... 1 1 !

a n n



   



Câu 35.

Lời giải.

Chọn B

Ta có

 

0 5 1 4 2 3 2 5 0 5

5 5 5 5

.( ) ( ) ( 1) ( ) ( 1) ... ( ) ( 1)

1 C x C x C x C xx

       



0 5 1 4 2 3 3 2 4 1 5 0

5 5 5 5 5 5

. . . . . .

C x C x C x C x C x C x

     

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 67

Khi đó tổng

5 4 3 2 1 0

a a a a a a

    

bằng:

0 1 2 3 4 5

5 5 5 5 5 5

C C C C C C

     

Câu 36.

Lời giải.

Chọn B

Ta có:

1 1 ! 1 ( 1)!

1 1 !( )! 1 ( 1)![( 1) ( 1))!



 

       

n n

k k k n k n k n k







(*)

1 0

1 1 1 1

0 0

1 1 2 1

1 1 1



  

 



 

    

 

  

 

 

n n

k k

n n n

k k

S C C C

n n n

Câu 37.

Lời giải.

Chọn A

Ta có

( 1) ( 1)

( 2)!( )!



   

 

k k

n n

k k C n n C

k n k

2 2

3 2

( 1) ( 1)2

 





    



k n

S n n C n n

Câu 38.

Lời giải.

Chọn A

Ta có:

     

1 1 1

n n n

x x x   

Vế trái của hệ thức trên chính là:









0 1 1 0 1

... ...

n n n n n

n n n n n n

C x C x C C C x C x



     

Và ta thấy hệ số của

trong vế trái là

















2 2 2 2

0 1 2

...

n n n n

C C C C   

Còn hệ số của

trong vế phải

 

x 

là

Do đó

















2 2 2 2

0 1 2

...

n n

n n n n n

C C C C C

     .

Câu 39.

Lời giải

Chọn B

Xét khai triển

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 68

 

0 1 2 2

1 C C C ... C

n n

n n n n

x x x x

     

. Lấy đạo hàm hai vế ta được:

 

1 2 1

1 C 2C ... C

n n

n n n

n x x n x



    

Cho



ta được:

1 1 2

.2 C 2C ... C

n n

n n n

n n



   

mà

1 2

1.C 2.C ... .C 1024

n n n

n   

Suy ra:

.2 1024





.2 1024 0



  

. Xét phương trình





.2 1024

g n n



  ,



Có





1 1

2 .2 .ln 2 0

n n

g n n

 



  

 

nên





g n

đồng biến







. Do đó phương trình





g n



có

nhiều nhất

nghiệm. Mà





8 1024

g  nên



Câu 40.

Lời giải

Chọn B

Biến đổi





0 1 2

2 5 8 ... 3 2

n n n n

C C C n C

    

















0 1 2

3.0 2 3.1 2 3.2 2 ... 3 2

n n n n

C C C n C

        









0 1 2 1 2

2 ... 3 2 ...

n n

n n n n n n n

C C C C C C nC

        

Ta có

0 1 2

... 2

n n

n n n n

C C C C

    

Xét hàm số

   

f x x

 

   

f x n x





  





1 .2

f n





 





Lại có

   

f x x

 

0 1 2 2 3 3

...

n n

n n n n n

C C x C x C x C x

     





1 2 2 3 1

2 3 ...

n n

n n n n

f x C xC x C nx C





     





1 2 3

1 2 3 ...

n n n n

f C C C nC



     





Từ





và





ta được

1 2 3 1

2 3 ... .2

n n

n n n n

C C C nC n



    

Do đó





0 1 2

2 5 8 ... 3 2

n n n n

C C C n C

    

2.2 3 .2

n n



 

2 .2

 

 

 

 

Bài ra





0 1 2

2 5 8 ... 3 2 1600

n n n n

C C C n C     

nên

2 .2 1600

 

 

 

 

Với



Loại.

Với

1 7

 

3 21

2 .2 2 .2 1600

2 2

   

     

   

   

Loại.

Do đó

2 .2 1600

 

 

 

 

 

Câu 41.

Lời giải

Chọn B

Ta có

 

0 1 2 2 3 3 2 1 2 1 2 2

2 2 2 2 2 2

1 . . . . .

n n n n

n n n n n n

x C C x C x C x C x C x

 

       





Thay



vào





ta có:

2 0 1 2 3 2 1 2

2 2 2 2 2 2

n n n

n n n n n n

C C C C C C



      







Thay

 

vào





ta có:

0 1 2 3 2 1 2

2 2 2 2 2 2

n n

n n n n n n

C C C C C C



      







Trừ từng vế của





và





ta có:





2 1 3 2 1

2 2 2

2 2.

n n

n n n

C C C



   

1 3 2 1 2 1

2 2 2

n n

n n n

C C C

 

    



Nên

1 3 2 1

2 2 2

512

n n n

C C C



   



2 1 9

2 2

n

 

2 1 9

  

 

Bởi vậy

2 2 2 3 2 4 2 5

5 5 5 5

2 3 4 5 .

S C C C C

   

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 69

Từ

 

0 1 2 2 3 3 4 4 5 5

5 5 5 5 5 5

1 . . . . .

x C C x C x C x C x C x

      

, lấy đạo hàm hai vế ta được:

 

1 2 3 2 4 3 5 4

5 5 5 5 5

5 1 2 . 3 . 4 . 5 .

x C C x C x C x C x

     

 

1 2 2 3 3 4 4 5 5

5 5 5 5 5

5 1 2 . 3 . 4 . 5 .

x x C x C x C x C x C x

      





Lại lấy đạo hàm hai vế





, ta có:

   

4 3

1 2 2 2 3 2 2 4 3 2 5 4

5 5 5 5 5

5 1 20 1 2 . 3 . 4 . 5 .

x x x C C x C x C x C x

       





Thay

 

vào





ta được:

1 2 2 3 2 4 2 5

5 5 5 5 5

0 2 3 4 5

C C C C C

    

2 2 3 2 4 2 5 1

5 5 5 5 5

2 3 4 5

C C C C C

    

Hay

2 2 2 3 2 4 2 5

5 5 5 5

2 3 4 5 . 5

S C C C C

    

Câu 42.

Lời giải

Chọn A

Ta có:

0 1 2

1 1 1 ( 1)

...

2 2 3 1

 



    

 



 

n n n n

S C C C C

Vì

( 1) ( 1)

1 1



 



 

k k

n n

C C

k n

nên:

( 1)

2( 1)





 





k k

S C

1 1

( 1)

2( 1) 2( 1)



 





 

   

 

 

 



k k

n n

C C

n n

Câu 43.

Lời giải

Chọn D

Ta có công thức:

1 1

 



 

k k k

n n n

C C C

nên đáp án sai là

4 4 5

10 11 11

 

C C C

Câu 44.

Lời giải

Chọn A

Số hạng tổng quát thứ



là

   

3 3

k k

k k k

k n n

T C x C x



   

Vì hệ số của

nên cho



Khi đó ta có

 

3 90

 

 





 

10 10

n n

n l





    



 





Vậy



Câu 45.

Lời giải

Chọn C

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 70

Ta có

   

2 2 . 1 .

n k

k n k k

x C x





  



Hệ số của

tương đương với



là

 

4 4

2 . 1 280



 













1 2 3

2 280

n n n n



  

 

   

4 4

6720 2 .3.5.7

1 2 3

2 2

n n

n n n n

 

     

Vì

là số tự nhiên nên

4 6

 

4 10

  

Lâp bảng giá trị được



Câu 46.

Lời giải

Chọn B

Ta có:





0 1 2 3

2 32768

n k k n n

n n n n n n

C iC C iC i C i C i

        





0 1 2 2 3 3

2 32768

n k k n n

n n n n n n

C iC i C i C i C i C i

         

 

2 1 2

i i

  





Ta có

 

1 2

i i

 

nên nếu

2 1

n k

 

, k





, thì

     

2 1

1 1 2 1

n k

k k

i i i i



    

nên không thỏa mãn





Xét

n k



, k





, thì

   

1 1 2

n k

k k

i i i

   

, nên:





2 15 3 15

* 2 .2 . 2 2 2

k k k k k

i i i i

   

5 10

k n

   

Từ đó ta có

7 7

8 8

T i C i

  

Câu 47.

Lời giải

Chọn C

Ta có

 

! ! !

k n k n





Do đó

1 2 3 1009

2019 2019 2019 2019

...

2019! 2019! 2019! 2019!

C C C C

A     

1 2 1009

2019 2019 2019

...

2019!

C C C  



0 1 2 1009

2019 2019 2019 2019

... 1

2019!

C C C C

    



2018

2 1

2019!





Câu 48.

Lời giải

Chọn B

Xét khai triển

 

0 1 2 2 3 3

1 ...

n n

n n n n n

x C C x C x C x C x

      

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 71

Đạo hàm hai vế ta được:

 

1 2 3 2 1

1 2 3 ...

n n

n n n n

n x C C x C x nC x



     

Thay



ở hai vế ta được

1 2 1

1. 2. ... . .2

n n

n n n

C C n C n



   

Do đó

.2 11264





Xét hàm số





f t t





trên





 

ta có:





1 1

2 .2 .ln 2 0 0

t t

f t t t

 



    

Do đó hàm số





f t t



 đồng biến trên





 

. Mà





11 11264

f  . Vậy



Câu 49.

Lời giải

Chọn C

Điều kiện:



n ,





n .

5 3

n n

C A

 











5 ! 3 !

!5! !

n n

 

 









5 4 600

n n    .

9 580 0

   

n n









 



 

Câu 50.

Lời giải

Chọn B

Cách 1: Ta có:

       





         

2 !

1 2 ! ! 1 2 ! 2 ! 1 2 1 2

k k

n n

C C

k k k n k k k n k k n n n n



  

          

Suy ra:

     

0 0

1 2 1 2

k k

n n

k k

C C

k k n n



 



   

 

     

0 1 2 2 3 4 2

2 2 2 2

...

1.2 2.3 3.4 1 2 1 2

n n

n n n n n n n n

C C C C C C C C

n n n n



   

     

   







Ta xét khai triển sau:

 

0 1 2 2 3 3 2 2

2 2 2 2 2

1 . . . ... .

n n

n n n n n

x C x C x C x C x C



 

    

      

Chọn

2 0 1 2 3 2

2 2 2 2 2

1 2 ...

n n

n n n n n

x C C C C C

 

    

       

Do đó:

 

     

2 0 1

100

100 2

2 2

2 3

2 2 98

1 2 1 2

n n

C C

n n n n



 

 

      

   

Cách 2: Ta có:

  

0 1 2

1 1 1 1 1 1 1 1

... .....

1.2 2.3 3.4 1 2 1 2 2 3 3 4 1 2

n n n n

C C C C

S C C C C

n n n n

       

             

       

   

       

0 1 2 0 1 2

1 1 1 1 1 1 1 1

..... .....

1 2 3 1 2 3 4 2

n n

n n n n n n n n

C C C C C C C C

n n

   

      

   

 

   

Lại có:

       

1 1 1 1

0 0 0 0

1 d 1 d 2 1 d 1 d

n n n n

x x x x x x x x x



      

   

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 72

   

1 1

1 2

0 1 2 0 1 2

0 0

1 1 1 1 1 1 1 1 2 1

..... ..... 1 1

1 2 3 1 2 3 4 2 1 2

n n

n n n n n n n n

C C C C C C C C x x

n n n n

 

   

           

   

   

   

  

1 2 2

2.2 2 2 1 2 3

1 2 1 2

n n n

n n n n

  

   

  

   

Kết hợp giả thiết có

     

2 100

2 3 2 3

1 2 1 2

n n

n n n n



   



   

 

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 73

§➍. PHÉP THỬ VÀ BIẾN CỐ

Chương ⓶

⓫

Tóm tắt lý thuyết

Ⓐ

➊.

Phép thử

Phép thử ngẫu nhiên:

 Là phép thử mà ta không đoán trước được kết quả của nó, mặc

dù đã biết tập hợp tất cả các kết quả có thể có của phép thử đó.



Chú ý: Ta chỉ xét các phép thử có một số hữu hạn kết quả.

➋.

Không gian mẫu



Tập hợp các kết quả có thể xảy ra của một phép thử đgl không

gian mẫu của phép thử và kí hiệu là .



Vi dụ: Mô tả không gian mẫu của phép thử gieo một đồng tiền.

 = {S, N}

➌. Biến cố



Mỗi biến cố liên quan đến một phép thử được mô tả bởi một

tập con của không gian mẫu.

 Biến cố là một tập con của không gian mẫu.

 Tập  đgl biến cố không thể.

 Tập  đgl biến cố chắc chắn.

Qui ước:

 Biến cố đôi khi được cho dưới dạng xác định tập hợp.

 Khi nói cho các biến cố A, B, .. mà không nói gì thêm thì ta

hiểu chúng cùng liên quan đến một phép thử.

 Ta nói biến cố A xảy ra trong một phép thử nào đó khi và

chỉ khi kết quả của phép thử đó là một phần tử của A (hay

thuận lợi cho A).

➍. Các phép toán trên các biến cố

Giả sử A và B là các biến cố liên quan đến một phép thử.

 Tập  \ A đgl biến cố đối của A

 Kí hiệu:

=  \ A .

xảy ra  A không xảy ra.

 Tập A  B đgl hợp của các biến cố A và B.

 Tập A  B đgl giao của các biến cố A và B. (còn kí hiệu

A.B)

 Nếu A  B =  thì ta nói A và B xung khắc.

 A và B xung khắc  A và B không cùng xảy ra.

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 74

①.Dạng 1: Mô tả không gian mẫu, biến cố

. Bài tập minh họa:

Câu 1: Gieo đồng tiền hai lần. Số phần tử của biến cố để mặt ngửa xuất hiện ít nhất một lần là

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải

Ta có số phần tử của biến cố để mặt ngửa xuất hiện ít nhất một lần là:

 

; ;SN NS NN

Câu 2: Gieo

đồng tiền là một phép thử ngẫu nhiên có không gian mẫu là

Ⓐ.

 

, , , , , ,NNN SSS NNS SSN NSN NSS SNN

Ⓑ.

 

, , ,NN NS SN SS

Ⓒ.

 

, , , , , , ,NNN SSS NNS SSN NSN SNS NSS SNN

Ⓓ.

 

, , , , ,NNN SSS NNS SSN NSN SNS

Lời giải

Số phần tử của không gian mẫu là

2 8

Câu 3: Gieo một đồng xu cân đối và đồng chất liên tiếp ba lần. Gọi

là biến cố “Có ít nhất hai

mặt sấp xuất hiện liên tiếp” và

là biến cố “Kết quả ba lần gieo là như nhau”. Xác định

biến cố

A B



Ⓐ.

 

, , , ,A B SSS SSN NSS SNS NNN 

Ⓑ.

 

,A B SSS NNN 

Ⓒ.

 

, , ,A B SSS SSN NSS NNN 

Ⓓ.

A B  

Lời giải

 

, ,A SSS SSN NSS

 

,B SSS NNN

. Suy ra

 

, , ,A B SSS SSN NSS NNN 

Câu 4: Gieo ngẫu nhiên một đồng tiền cân đối và đồng chất

lần. Tính số phần tử không gian

mẫu.

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

Lời giải

Mỗi lần gieo có hai khả năng nên gieo 5 lần theo quy tắc nhân ta có

2 32

Số phần tử không gian mẫu là

 

32n  

②.Dạng 2:

Các câu hỏi lý thuyết tổng hợp

. Bài tập minh họa:

Câu 1: Xét phép thử gieo một con súc sắc cân đối và đồng chất hai lần liên tiếp. Gọi

là biến cố

“Lần đầu xuất hiện mặt 6 chấm” và

là biến cố “Lần thứ hai xuất hiện mặt 6 chấm”.

Khẳng định nào sai trong các khẳng định sau?

Ⓐ.

A và B là hai biến cố xung khắ

Ⓑ.

A B



là biến cố “Ít nhất một lần xuất hiện mặt 6 chấm”.

Ⓒ.

A B



là biến cố “Tổng số chấm trên mặt xuất hiện của hai lần gieo bằng 12.

Ⓓ.

và

là hai biến cố độc lập.

Lời giải

Phân dạng bài tập

Ⓑ

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 75

Hai biến cố A và B có thể cùng xảy ra

Câu 2: Cho

A B

là hai biến cố của không gian mẫu



. Công thức nào sau đây sai?

Ⓐ.





 

P A P A

 

Ⓑ.













. .

P A B P A P B



nếu

A B

là hai biến cố độc lập.

Ⓒ.

















P A B P A P B P A B

    

Ⓓ.

 





 

P A

n A



 .

Lời giải

Ta có

 





 

n A

P A





nên D sai.

Câu 3: Xét một phép thử có không gian mẫu



và

là một biến cố của phép thử đó. Phát biểu

nào sau đây sai?

Ⓐ. Xác suất của biến cố

là

 





 

n A

P A





Ⓑ.





0 1

P A

 

Ⓒ.

 





P A P A

 

Ⓓ.





P A



khi và chỉ khi

là biến cố chắc chắn.

Lời giải

Theo định nghĩa biến cố chắc chắn ta có: Với

là biến cố chắc chắn thì









n A n

 

Suy ra:

 





 

1 0

n A

P A

  



Câu 4: Cho phép thử là “gieo

2019

đồng xu phân biệt” và xét sự xuất hiện mặt sấp và mặt ngửa

của các đồng xu. Khi đó số phần tử của không gian mẫu bằng

Ⓐ.

2019

. Ⓑ.

1 3 2019

2019 2019 2019

...C C C  

Ⓒ.

2020 2019

0 0

k k

C C

 



 

. Ⓓ.

Lời giải

Ta có

     

2020 2019

2020 2019 2019 2019

2020 2019

0 0

1 1 1 1 2 2 2 . 2 1 2

k k

C C

 

         

 

Vì một đồng xu có hai mặt nên khi gieo

2019

đồng xu phân biệt ta có

2019

kết quả có thể

xảy ra của phép thử. Vậy số phần tử của không gian mẫu là





2019

n  

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 76

Câu 1:Cho

là hai biến cố xung khắ

Đẳng thức nào sau đây đúng?

Ⓐ.













P A B P A P B  

Ⓑ.

     

.P A B P A P B 

Ⓒ.

     

P A B P A P B  

Ⓓ.

     

P A B P A P B  

:......................................................................

......................................................................................

Câu 2:Trong các thí nghiệm sau thí nghiệm nào không phải là phép thử ngẫu nhiên:

Ⓐ.

Gieo đồng tiền xem nó mặt ngửa hay mặt sấp

Ⓑ.

Gieo

đồng tiền và xem có mấy đồng tiền lật

ngửa

Ⓒ.

Chọn bất kì 1 học sinh trong lớp và xem là nam

hay nữ

Ⓓ.

Bỏ hai viên bi xanh và ba viên bi đỏ trong một

chiếc hộp, sau đó lấy từng viên một để đếm xem có

tất cả bao nhiêu viên bi.

:......................................................................

......................................................................................

.............................

.........................................................

Câu 3:Cho A là một biến cố liên quan phép thử T. Mệnh đề nào sau đây là mệnh đề đúng?

Ⓐ.

( )P A

là số lớn hơn

Ⓑ.

 

( ) 1P A P A 

Ⓒ.

( ) 0P A A   

Ⓓ.

( )P A

là số nhỏ hơn

:......................................................................

......................................................................................

Câu 4:Cho

và

là hai biến cố xung khắ

Mệnh đề nào dưới đây đúng?

Ⓐ.









1P A P B 

Ⓑ.

Hai biến cố

và

không đồng thời xảy r

Ⓒ.

Hai biến cố

và

đồng thời xảy r

Ⓓ.

   

1P A P B 

:......................................................................

......................................................................................

Câu 5:Rút ngẫu nhiên cùng lúc ba con bài từ cỗ bài tú lơ khơ

con thì





n 

bằng bao nhiêu?

Ⓐ.

140608

Ⓑ.

156

Ⓒ.

132600

Ⓓ.

22100

:......................................................................

......................................................................................

Câu 6:Gieo đồng tiền hai lần. Số phần tử của biến cố để mặt ngửa xuất hiện đúng

lần là

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

:......................................................................

......................................................................................

Câu 7:Gieo một con súc sắc

lần. Số phần tử của không gian mẫu là?

Ⓐ.

Ⓑ.

Ⓒ.

Ⓓ.

:......................................................................

......................................................................................

Câu 8:Gieo 3 đồng tiền là một phép thử ngẫu nhiên có không gian mẫu là:

Ⓐ.





, , ,NN NS SN SS

Ⓑ.

 

, , , , , NNN SSS NNS SSN NSN SNS

Ⓒ.

 

, , , , , , ,NNN SSS NNS SSN NSN SNS NSS SNN

:......................................................................

......................................................................................

Bài tập rèn luyện

Ⓒ

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 77

Ⓓ.





, , , , ,

NNN SSS NNS SSN NSS SNN

Câu 9:Gieo một đồng tiền liên tiếp

lần. Số phần tử của không gian mẫu

( )



là?

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

:......................................................................

......................................................................................

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

:......................................................................

......................................................................................

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

:......................................................................

......................................................................................

Câu 12:Gieo đồng tiền hai lần. Số phần tử của biến cố để mặt ngửa xuất hiện đúng

lần là:

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

:......................................................................

......................................................................................

..................................................

....................................

Câu 13:Gieo một đồng tiền liên tiếp

lần thì

( )



là bao nhiêu?

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

:......................................................................

......................................................................................

Câu 14:Gieo ngẫu nhiên

đồng tiền thì không gian mẫu của phép thử có bao nhiêu biến cố:

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

:......................................................................

......................................................................................

Câu 15:Một hộp chứa

quả cầu gồm

quả cầu màu xanh và

quả cầu màu đỏ. Chọn ngẫu nhiên lần lượt hai

quả cầu từ hộp đó. Xác suất để hai quả cầu được chọn ra cùng màu bằng

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

:......................................................................

......................................................................................

Câu 16:Gieo 2 con súc sắc và gọi kết quả xảy ra là tích số hai nút ở mặt trên. Số phần tử của không gian mẫu là

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

:......................................................................

......................................................................................

Câu 17:Cho phép thử có không gian mẫu





6,5,4,3,2,1

. Các cặp biến cố không đối nhau là:

Ⓐ.





A

và





2,3,4,5,6

B 

Ⓑ.





1,4,5

và





2,3,6

D 

:......................................................................

......................................................................................

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 78

Ⓒ.





1,4,6

E 

và





2,3

F 

Ⓓ.



và



......................................................................................

Câu 18:Một hộp đựng

thẻ, đánh số từ

đến

. Chọn ngẫu nhiên

thẻ. Gọi

là biến cố để tổng số của

thẻ được chọn không vượt quá

. Số phần tử của biến cố

là:

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

:......................................................................

......................................................................................

Câu 19:Gieo con súc sắc hai lần. Biến cố A là biến cố để sau hai lần gieo có ít nhất một mặt 6 chấm:

Ⓐ.

























1;6 , 2;6 , 3;6 , 4;6 , 5;6

A 

Ⓑ.





























1,6 , 2,6 , 3,6 , 4,6 , 5,6 , 6,6

A 

Ⓒ.

























         

1,6 , 2,6 , 3,6 , 4,6 , 5,6 , 6,6 ,

6,1 , 6,2 , 6,3 , 6,4 , 6,5

 

 



 

 

 

Ⓓ.

























6,1 , 6,2 , 6,3 , 6,4 , 6,5

A 

:......................................................................

......................................................................................

Câu 20:Một hộp đựng

thẻ, đánh số từ

đến

. Chọn ngẫu nhiên

thẻ. Gọi

là biến cố để tổng số của

thẻ

được chọn không vượt quá

. Số phần tử của biến cố

là

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

:......................................................................

......................................................................................

Ⓐ.

. Ⓑ.

Ⓒ.

. Ⓓ.

:......................................................................

......................................................................................

Câu 22:Cho

và

là hai biến cố đối nhau. Chọn câu đúng.

Ⓐ.









P A P A

 

Ⓑ.

 





P A P A



Ⓒ.

 





P A P A

 

Ⓓ.

 





P A P A

 

:......................................................................

......................................................................................

Câu 23:Cho A là một biến cố liên quan phép thử T. Mệnh đề nào sau đây là mệnh đề đúng?

Ⓐ.

( )

P A

là số lớn hơn 0.

Ⓑ.





( ) 1

P A P A

 

Ⓒ.

( ) 0P A A

   

Ⓓ.

( )

P A

là số nhỏ hơn 1.

:......................................................................

......................................................................................

Câu 24:Cho

và

là hai biến cố đối nhau. Chọn câu đúng.

Ⓐ.

 





1 .

P A P A

 

Ⓑ.

 





P A P A



Ⓒ.

 





1 .

P A P A

 

Ⓓ.

 





P A P A

 

:......................................................................

......................................................................................

Câu 25:Cho phép thử có không gian mẫu





6,5,4,3,2,1

. Các cặp biến cố không đối nhau là

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 79

Ⓐ.





A 

và





2,3,4,5,6

B 

Ⓑ.





1,4,5

và





2,3,6

D 

Ⓒ.





1,4,6

E 

và





2,3

F 

Ⓓ.



và



:......................................................................

......................................................................................

Câu 26:Cho hai biến cố

và

có

1 1 1

( ) , ( ) , ( )

3 4 2

P A P B P A B

   

. Ta kết luận hai biến cố

và

là:

Ⓐ. Độc lập.

Ⓑ. Không xung khắc

Ⓒ. Xung khắc

Ⓓ. Không rõ.

:......................................................................

......................................................................................

Câu 27:Trong các thí nghiệm sau thí nghiệm nào không phải là phép thử ngẫu nhiên:

Ⓐ. Gieo đồng tiền xem nó mặt ngửa hay mặt sấp.

Ⓑ. Gieo

đồng tiền và xem có mấy đồng tiền lật

ngửa

hay nữ.

Ⓓ. Bỏ hai viên bi xanh và ba viên bi đỏ trong một

chiếc hộp, sau đó lấy từng viên một để đếm xem có

tất cả bao nhiêu viên bi.

:......................................................................

......................................................................................

Câu 28:Xét một phép thử có không gian mẫu và là một biến cố của phép thử đó. Phát biểu nào dưới đây là

sai?

Ⓐ. khi và chỉ khi là chắc chắn.

Ⓑ. .

Ⓓ. .

:......................................................................

......................................................................................

Câu 29:Cho hai biến cố

và

có

1 1 1

( ) , ( ) , ( )

3 4 2

P A P B P A B

   

. Ta kết luận hai biến cố

và

là

Ⓐ. Độc lập.

Ⓑ. Không xung khắc

Ⓒ. Xung khắc

Ⓓ. Không rõ.

:......................................................................

......................................................................................

Câu 30:Cho phép thử có không gian mẫu





1,2,3, 4,5,6

 

. Các cặp biến cố không đối nhau là:

Ⓐ.





A 

và





2,3,4,5,6

B 

Ⓑ.





1,4,5

và





2,3,6

D 

Ⓒ.





1,4,6

E 

và





2,3

F 

Ⓓ.



và



:......................................................................

......................................................................................

BẢNG ĐÁP ÁN

1.A 2.D 3.B 4.B.D 5.D 6.A 7.D 8.C 9.C 10.B

11.B 12.A 13.C 14.A 15.D 16.B 17.C 18.C 19.C 20.C

21.B 22.C 23.B 24.C 25.C 26.B 27.D 28.A 29.B 30.C







P A



 





P A P A

 

 





 

n A

P A









0 1

P A

 

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 80

Hướng dẫn giải

Câu 1: Ta có

















P A B P A P B P A B

    

Vì

là hai biến cố xung khắc nên A B

  

. Từ đó suy ra













P A B P A P B

  

Câu 2: Phép thử ngẫu nhiên là phép thử mà ta chưa biết được kết quả là gì.

Đáp án D không phải là phép thử vì ta biết chắc chắn kết quả chỉ có thể là một số cụ thể

số bi xanh và số bi đỏ.

Câu 3: Loại trừ : A ; D ; C đều sai.

Câu 4: Vì

và

là hai biến cố xung khắc nên hai biến cố này không đồng thời xảy ra.

Câu 5: Ta có





22100

n C  

Câu 6: Liệt kê ta có:





A NS SN



Câu 7:

( ) 6.6 36

  

Câu 8: Liệt kê các phần tử.

Câu 9:

( ) 2.2 4

  

Câu 10: Mô tả không gian mẫu ta có:





1; 2; 3; 4; 5; 6; 1; 2; 3; 4; 5; 6

S S S S S S N N N N N N

 

Câu 11: Mô tả không gian mẫu ta có:





1; 2; 3; 4; 5; 6; 1; 2; 3; 4; 5; 6

S S S S S S N N N N N N

 

Câu 12: Liệt kê ta có:





A NS SN



Câu 13:

( ) 2.2.2 8

  

Câu 14: Mô tả không gian mẫu ta có:





; ; ;

SS SN NS NN

 

Câu 15: Gọi biến cố

: “Hai quả cầu được chọn ra cùng màu”.

Số phần tử của không gian mẫu là:





11.10 110

n   

Chọn hai quả cầu cùng màu xảy ra

trường hợp: hoặc

quả cùng màu xanh hoặc

quả

cùng màu đỏ. Khi đó





5.4 6.5

n A  



Xác suất để hai quả cầu được chọn ra cùng màu là

 





 

n A

P A







Câu 16: Mô tả không gian mẫu ta có:





1;2;3;4;5;6;8;9;10;12;15;16;18;20;24;25;

30;36

 

Câu 17: Cặp biến cố không đối nhau là





1,4,6

E 

và





2,3

F 

do E F

  

và

E F

  

Câu 18: Liệt kê ta có:





















1;2;3 ; 1;2;4 ; 1;2;5 ; 1;3;4

A 

Câu 19: Liệt kê ta có:

















































1,6 , 2,6 , 3,6 , 4,6 , 5,6 , 6,6 , 6,1 , 6,2 , 6,3 , 6,4 ,

6,5

A 

Câu 20: Liệt kê ta có:





















1;2;3 ; 1;2;4 ; 1;2;5 ; 1;3;4

A 

Câu 21: Mô tả không gian mẫu ta có:





1; 2; 3; 4; 5; 6; 1; 2; 3; 4; 5; 6

S S S S S S N N N N N N

 

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 81

Câu 22:

Câu 23:

Loại trừ :A ;B ;C đều sai

Câu 24: Câu 25: Cặp biến cố không đối nhau là





1,4,6

E 

và





2,3

F 

do E F

  

và

E F

  

Câu 26: Ta có:

















P A B P A P B P A B

    

nên

 

P A B

  

Suy ra hai biến cố

và

là hai biến cố không xung khắc.

Câu 27: Phép thử ngẫu nhiên là phép thử mà ta chưa biết được kết quả là gì.

Đáp án D không phải là phép thử vì ta biết chắc chắn kết quả chỉ có thể là một số cụ thể

số bi xanh và số bi đỏ.

Câu 28: Khẳng định A sai vì là biến cố chắc chắn thì .

Câu 29: Ta có:

















P A B P A P B P A B

    

nên

 

P A B

  

Suy ra hai biến cố

và

là hai biến cố không xung khắc.

Câu 30: Cặp biến cố không đối nhau là





1,4,6

E 

và





2,3

F 

do E F

  

và

E F

  





P A



Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 82

①.Dạng 1:

Tính xác suất bằng định nghĩa

. Bài tập minh họa:

Câu 1: Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là:

.B.

. C.

. D.

Lời giải

Không gian mẫu là:

 

1,2,3,4,5,6 

 

6  n

Gọi

là biến cố: “Mặt có số chấm chẵn xuất hiện”.

 

2,4,6 A

 

3 n A

§➎. XÁC SUẤT CỦA BIẾN CỐ

Chương ⓶

⓫

Tóm tắt lý thuyết

Ⓐ

➊. Định nghĩa cổ điển của xác suất

Định nghĩa

 Giả sử A là biến cố liên quan đến một phép thử chỉ có một số hữu hạn kết quả đồng khả

năng xuất hiện.

 Ta gọi tỉ số

( )

n A



là xác suất của biến cố A, kí hiệu P(A).

 Công thức tính: P(A) =

( )

n A



Chú ý:

 n(A) là số phần tử của A hay cũng là số kết quả thuận lợi của biến cố A

 n() là số kết quả có thể xảy ra của phép thử.

➋. Tính chất của xác suất

Định lí:

 P() = 0, P() = 1

 0  P(A)  1, với mọi biến cố A

 Nếu A và B xung khắc thì P(AB) = P(A) + P(B)

Hệ quả: Với mọi biến cố A, ta có

( ) 1 ( )P A P A

 

➌. Các biến cố độc lập và công thức nhân xác suất

 Hai biến cố được gọi là độc lập nếu sự xảy ra của biến cố này không ảnh hưởng đến xác suất xảy ra

của biến cố kia.

 A và B độc lập  P(A.B) = P(A).P(B)

Phân dạng bài tập

Ⓑ

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 83

Xác suất để mặt có số chấm chẵn xuất hiện là:

 





 

3 1

6 2

  



n A

P A

Câu 2: Trong giỏ có

đôi tất khác màu, các chiếc tất cùng đôi thì cùng màu. Lấy ngẫu nhiên ra

chiếc. Tính xác suất để

chiếc đó cùng màu.

. B.

. C.

. D.

Lời giải

Lấy

chiếc từ

chiếc tất, số cách lấy là:

  

Lấy

chiếc cùng màu từ

chiếc tất, số cách lấy là:

  

Xác suất để lấy được một đôi tất cùng màu:



 



Câu 3: Một lô hàng có

100

sản phẩm, trong đó có

sản phẩm tốt và

sản phẩm xấu. Lấy ngẫu

nhiên

sản phẩm từ hộp, tính xác suất để

sản phẩm lấy ra đều là sản phẩm tốt.

100

. B.

100

. C.

80!

100!

. D.

100

Lời giải

Số cách chọn ra

sản phẩm từ hộp là

100

Để

sản phẩm lấy ra đều là sản phẩm tốt thì số cách là

Vậy xác suất để

sản phẩm lấy ra đều là sản phẩm tốt là

100

Câu 4: Có 3 chiếc hộp. Mỗi hộp chứa 4 tấm thẻ được đánh số từ 1 đến 4. Lấy ngẫu nhiên từ mỗi

hộp một thẻ. Tính xác suất để 3 thẻ được lấy ra đều mang số chẵn.

. B.

. C.

. D.

Lời giải

Số phần tử của không gian mẫu:





1 1 1

4 4 4

. . 64

n C C C

  

Gọi A là biến cố 3 thẻ mang số chẵn:





1 1 1

2 2 2

. . 8

n A C C C

 

Xác suất cho biến cố A:

 

8 1

64 8

P A

 

Câu 5: Một hội nghị có 15 nam và 6 nữ. Chọn ngẫu nhiên 3 người vào ban tổ chức. Xác suất để 3

người lấy ra là nam:

. B.

266

. C.

. D.

Lời giải





1330

n C   .

Gọi A là biến cố: “3 người lấy ra là nam”. Khi đó,





455

n A C  .

Vậy xác suất để 3 người lấy ra là nam là:

 





 

13 91

38 266

n A

P A

  



Câu 6: Từ một hộp chứa

quả cầu màu đỏ và

quả cầu màu xanh, lấy ngẫu nhiên đồng thời

quả cầu. Xác suất để lấy được

quả cầu màu xanh bằng

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 84

165

. B.

455

. C.

. D.

455

Lời giải

Ta có:





455

n C  

Gọi

là biến cố “lấy được

quả cầu màu xanh”. Khi đó





n A C

 

Vậy

 

455

P A 

②.Dạng 2:

Tính xác suất bằng công thức cộng

. Bài tập minh họa:

Câu 1: Gieo đồng thời hai con súc sắc cân đối và đồng chất. Tính xác suất

để hiệu số chấm trên

các mặt xuất hiện của hai con súc sắc bằng 2.

. B.

. C.

. D.

Lời giải

Số phần tử của không gian mẫu:





6.6 36

  

Gọi

là biến cố thỏa mãn yêu cầu bài toán:





































1; 3 , 3; 1 , 4; 2 , 2; 4 , 3; 5 , 5; 3 , 4; 6

, 6; 4

A 

nên





n A



Vậy

 

8 2

36 9

P A

 

Câu 2: Người ta sử dụng

cuốn sách Toán,

cuốn sách Vật lí,

cuốn sách Hóa học để làm phần

thưởng cho

học sinh, mỗi học sinh được

cuốn sách khác loại. Trong số

học sinh

trên có hai bạn Thảo và Hiền. Tính xác suất để hai bạn Thảo và Hiền có phần thưởng giống

nhau.

. B.

. C.

. D.

Lời giải

Có

cuốn sách ghép cặp với nhau tạo thành

bộ sách.

Toán -

Lí có:

12 9 3

 

bộ.

Toán -

Hóa có:

12 8 4

 

bộ.

Lí -

Hóa có

12 7 5

 

bộ.

Số phần tử của không gian mẫu là:





n C

  

Gọi

là biến cố “ Thảo và Hiền có phần thưởng giống nhau”





2 2 2

3 4 5

3 6 10 19

n A C C C

      

 





 

  



n A

P A

Câu 3: Một lớp học có 20 học sinh nam và 15 học sinh nữ. Giáo viên chọn ngẫu nhiên 4 học sinh

lên bảng giải bài tập. Xác suất để 4 học sinh được chọn có cả nam và nữ là

4651

5236

4615

5236

4610

5236

4615

5263

Lời giải

Số cách chọn 4 học sinh trong số 35 học sinh lên bảng giải bài tập là:

 

Gọi A là biến cố: “có cả nam và nữ”.

Số cách chọn 4 học sinh nam là:

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 85

Số cách chọn 4 học sinh nữ là:

Do đó:

4 4 4

35 20 15

46150.

C C C    

Vậy xác suất cần tìm là:

 

4615

5236

P A



 



Câu 4: Một nhóm học sinh có học sinh nam và học sinh nữ. Từ nhóm học sinh này ta chọn

ngẫu nhiên học sinh. Tính xác suất để trong ba học sinh được chọn có cả nam và nữ.

A. . B. . C. . D. .

Lời giải

Số phần tử không gian mẫu là .

Gọi là biến cố trong ba học sinh được chọn có cả nam và nữ.

+Trường hợp 1: nam và nữ, ta có số cách chọn là

+ Trường hợp 2: nam và nữ, ta có số cách chọn là .

Số phần tử của là: .

Vậy xác suất càn tìm là .

Câu 5: Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3

quyển sách. Tính xác suất để 3 quyển được lấy ra có ít nhất một quyển là toán.

. B.

. C.

. D.

Lời giải

Trên giá có tất cả:

4 3 2 9

  

bao gồm cả 3 môn: toán, lý và hóa.

Lấy 3 quyển sách từ 9 quyển sách, số cách lấy ra là





84 84

C n

   

Gọi

là biến cố: “3 quyển lấy ra có ít nhất 1 quyển toán”.

Suy ra

: “3 quyển lấy ra không có quyển toán nào”





n A C

  

Vậy xác suất để 3 quyển được lấy ra có ít nhất một quyển sách toán là:

 

10 37

1 1

84 42

P A P A    

③.Dạng 3:

Tính xác suất bằng công thức nhân

. Bài tập minh họa:

Câu 1: Xác suất sút bóng thành công tại chấm

mét của hai cầu thủ Quang Hải và Văn Đức lần

lượt là

0,8

và

0, 7

. Biết mỗi cầu thủ sút một quả tại chấm

mét và hai người sút độc lập.

Tính xác suất để ít nhất một người sút bóng thành công.

0, 44

. B.

0,94

. C.

0,38

. D.

0,56

Lời giải

Xác suất sút không thành công tại chấm

của cầu thủ Quang Hải là

1 0,8 0,2

 

Xác suất sút không thành công tại chấm

của cầu thủ Văn Đức là

1 0,7 0,3

 



2 1 2 1

6 7 7 6

C C C C



3 3

6 7

C C







n C

 

2 1

6 7

C C

1 2

6 7

C C





2 1 2 1

6 7 7 6

n A C C C C

 

 





 

2 1 2 1

6 7 7 6

n A

C C C C

P A

n C



 



Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 86

Xác suất cả hai cầu thủ sút không thành công tại chấm

là

0,2.0,3 0,06



Suy ra: Xác suất để ít nhất một người sút bóng thành công là:

1 0,06 0,94

 

Câu 2: Xác suất bắn trúng mục tiêu của một vận động viên khi bắn một viên đạn là

0,3

. Người

đó bắn hai viên một cách độc lập. Xác suất để một viên trúng và một viên trượt mục tiêu

là

0,21

. B.

0,09

. C.

0,18

. D.

0, 42

Lời giải

Xác suất để một viên trúng và một viên trượt mục tiêu là:

0,3.0.7 0,7.0,3 0,42

 

Câu 3: Xác suất sút bóng thành công tại chấm 11 mét của hai cầu thủ Quang Hải và Văn Đức lần lượt là

0,8 và 0,7. Biết mỗi cầu thủ sút một quả tại chấm 11 mét và hai người sút độc lập. Tính xác suất để ít nhất

một người sút bóng thành công.

0, 44

. B.

0,94

. C.

0,38

. D.

0,56

Lời giải

Chọn B

Cách 1

Gọi A là biến cố cầu thủ Quang Hải sút bóng thành công, B là biến cố cầu thủ Văn Đức sút

bóng thành công, C là biến cố có ít nhất một người sút bóng thành công.

Suy ra

. . .

  

C A B A B A B

Do A, B là hai biến cố độc lập nên

 





. . . 0,8.0,3 0,2.0,7 0,8.0,7 0,94

      P C P A B A B A B

Cách 2

Gọi A là biến cố cầu thủ Quang Hải sút bóng thành công, B là biến cố cầu thủ Văn Đức sút

bóng thành công, C là biến cố có ít nhất một người sút bóng thành công. Khi đó

là biến cố

không cầu thủ nào sút bóng thành công.

Ta có:





 





. 0,2.0,3 0,06 1 0,94

       C A B P C P C P C

④.Dạng 4:

Bài toán kết hợp quy tắc cộng và quy tắc nhân xác suất

. Bài tập minh họa:

Câu 1: Trong một trò chơi, người chơi cần gieo cùng lúc ba con súc sắc cân đối đồng chất; nếu được ít

nhất hai con súc sắc xuất hiện mặt có số chấm lơn hơn thì người chơi đó thắng. Tính xác suất

để trong lần chơi, người đó thắng ít nhất lần.

386

729

. B.

. C.

11683

19683

. D.

Lời giải

Gọi

là biến cố trong lần chơi, người đó thắng ít nhất lần.

Khi đó:

là biến cố trong lần chơi, người đó toàn thua.

Tính xác suất để một lần chơi người đó thua:

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung

St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 87

Để chơi thua, thì ít nhất 2 trong ba con súc sắc người đó gieo xuất hiện số chấm bé hơn hoặc

bằng 4. Suy ra xác suất để người đó chơi thua một lần là:

4 4 2 4 4 4 20

. . .3 . . .

6 6 6 6 6 6 27

 

 

 

 

 

20 8000 8000 11683

27 19683 19683 19683

P A P A

 

     

 

 

Câu 2: Gieo hai đồng xu A và B một cách độc lập. Đồng xu A chế tạo cân đối. Đồng xu B chế tạo không

cân đối nên xác suất xuất hiện mặt sấp gấp 3 lần xác suất xuất hiện mặt ngửa. Tính xác suất để

khi gieo hai đồng xu cùng lúc được kết quả 1 sấp và 1 ngửa.

25%

. B.

50%

. C.

75%

. D.

60%

Lời giải

Gọi

là biến cố “đồng xu A xuất hiện mặt sấp”,

là biến cố “đồng xu B xuất hiện mặt sấp”;

là biến cố “có một sấp và một ngửa khi gieo cả hai đồng xu một lần”.

C AB AB

   , mà

AB AB

xung khắc và

, ; ,

A B A B

độc lập.

 

1 3 1 1 1

. . 50%

2 4 2 4 2

P C P AB P AB P A P B P A P B         .

Câu 3: Có hai hộp. Hộp I đựng 4 gói quà màu đỏ và 6 gói quà màu xanh, hộp II đựng 2 gói quà màu đỏ

và 8 gói quà màu xanh. Gieo một con súc sắc, nếu được mặt 6 chấm thì lấy một gói quà từ hộp

I, nếu được mặt khác thì lấy một gói quà từ hộp II. Tính xác suất để lấy được gói quà màu đỏ.

. B.

. C.

. D.

Lời giải

Ta có xác suất để gieo con súc sắc xuất hiện mặt 6 chấm là

 

P A



và xác suất để gieo con

súc sắc không xuất hiện mặt 6 chấm là

 

P A



Xác suất lấy từ hộp I được gói quà màu đỏ là

 

4 2

10 5

P B

 

Xác suất lấy từ hộp

được gói quà màu đỏ là

 

2 1

10 5

P B

 

Vậy xác suất để lấy được gói quà màu đỏ là

   

 

1 2

1 2 5 1 7

. . . .

6 5 6 5 30

P A P B P A P B    .

Bấm Tải xuống để xem toàn bộ.

| 1/87

| | Tải xuống

Preview text:

Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung GT Chương ⓶ §➊. CÁC QUY TẮC ĐẾM ⓫ Ⓐ Tóm tắt lý thuyết ➊. Quy tắc cộng:
 Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách
thực hiện, hành động kia có n cách thực hiện không trùng với bất kì cách nào của hành động
thứ nhất thì công việc đó có m  n cách thực hiện.
 Nếu A và B là các tập hợp hữu hạn không giao nhau thì: n  A  B  n A  n B ➋. Quy tắc nhân:
 Một công việc được hoành thành bởi hai hành động liên tiếp. Nếu có m cách thực hiện hành động
thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì có . m n cách hoàn thành công việc.
Dạng toán: tìm số các số tạo thành: Gọi số cần tìm có dạng: ab .
c .., tuỳ theo yêu cầu bài toán:
 Nếu số lẻ thì số tận cùng là số lẻ.
 Nếu số chẵn thì số tận cùng là số chẵn. Ⓑ Phân dạng bài tập
①.Dạng 1: Sử dụng quy tắc cộng . Bài tập minh họa:
Câu 1: Có 3 cây bút đỏ, 4 cây bút xanh trong một hộp bút. Hỏi có bao nhiêu cách lấy ra một cây bút từ hộp bút? Ⓐ. 7 . Ⓑ. 12 . Ⓒ. 3. Ⓓ. 4 . Lời giải
 Số cách lấy ra 1 cây bút là màu đỏ có 3 cách.
 Số cách lấy ra 1 cây bút là màu xanh có 4 cách.
 Theo quy tắc cộng, số cách lấy ra 1 cây bút từ hộp bút là: 3 4  7 cách.
 Vậy có 7 cách lấy 1 cây bút từ hộp bút. Chọn đáp án A
Câu 2: Thầy giáo chủ nhiệm có 10 quyển sách khác nhau và 8 quyển vở khác nhau. Thầy chọn ra
một quyển sách hoặc một quyển vở để tặng cho học sinh giỏi. Hỏi có bao nhiêu cách chọn khác nhau? Ⓐ. 10. Ⓑ. 8. Ⓒ. 80. Ⓓ. 18 . Lời giải
 Chọn một quyển sách có 10 cách chọn.
 Chọn một quyển vở có 8 cách chọn.
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 1
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Áp dụng quy tắc cộng có 18 cách chọn ra một quyển sách hoặc một quyển vở để tặng cho học sinh giỏi.
②.Dạng 2: Sử dụng quy tắc nhân . Bài tập minh họa:
Câu 1: Bạn muốn mua 2 cây bút gồm một cây bút mực và một cây bút chì. Các cây bút mực có
8 màu khác nhau, các cây bút chì có 9 màu khác nhau. Hỏi có bao nhiêu cách chọn để mua? Ⓐ. 8! 9!. Ⓑ. 72 . Ⓒ. 17 . Ⓓ. 8!.9!. Lời giải
Số cách chọn một cây bút mực là 1 C . 8
Số cách chọn một cây bút chì là 1 C . 9
Áp dụng quy tắc nhân, ta có số cách chọn là 1 1 C .C  72 . 8 9
Câu 2: Một đội văn nghệ chuẩn bị được 2 vở kịch, 3 điệu múa và 6 bài hát. Tại hội diễn văn nghệ,
mỗi đội chỉ được trình diễn một vở kịch, một điệu múa và một bài hát. Hỏi đội văn nghệ
trên có bao nhiêu cách chọn chương trình diễn, biết chất lượng các vở kịch, điệu múa, bài hát là như nhau? Ⓐ. 11. Ⓑ. 36. Ⓒ. 25. Ⓓ. 18. Lời giải
Đội văn nghệ trên có 2 cách chọn trình diễn một vở kịch, có 3 cách chọn trình diễn một
điệu múa, có 6 cách chọn trình diễn một bài hát. Theo quy tắc nhân, đội văn nghệ trên có
2.3.6  36 cách chọn chương trình diễn.
③.Dạng 3: Sử dụng quy tắc cộng và quy tắc nhân . Bài tập minh họa:
Câu 1: Một người có 7 chiếc áo trong đó có 3chiếc áo trắng và 5 chiếc cà vạt trong đó có 2 chiếc
cà vạt màu vàng. Tìm số cách chọn một chiếc áo và một chiếc cà vạt sao cho đã chọn áo
trắng thì không chọn cà vạt màu vàng. Ⓐ. 29 . Ⓑ. 36 . Ⓒ. 18. Ⓓ. 35 . Lời giải
Số cách chọn một chiếc áo và một chiếc cà vạt sao cho áo màu trắng và cà vạt không phải màu vàng là 3.3  9
Số cách chọn một chiếc áo và một chiếc cà vạt sao cho áo không phải màu trắng và cà vạt
bất kì trong 5 cà vạt là 4.5  20
Số cách chọn một chiếc áo và một chiếc cà vạt sao cho đã chọn áo trắng thì không chọn cà
vạt màu vàng là 9  20  29
Câu 2: Từ một tập gồm 10 câu hỏi, trong đó có 4 câu lí thuyết và 6 câu bài tập, người ta tạo thành
các đề thi. Biết rằng một đề thi phải gồm 3 câu hỏi trong đó có ít nhất một câu lí thuyết
và 1 câu bài tập. Hỏi có thể tạo được bao nhiêu đề khác nhau? Ⓐ. 100 . Ⓑ. 36 . Ⓒ. 96 . Ⓓ. 60 . Lời giải
Trường hợp 1: 2 câu lí thuyết, 1 câu bài tập. Suy ra số đề tạo ra là 2 1 C .C  36 4 6
Trường hợp 2: 1 câu lí thuyết, 2 câu bài tập. Suy ra số đề tạo ra là 1 2 C .C  60 4 6
Vậy có thể tạo được số đề khác nhau là: 36  60  96 .
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 2
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Câu 3: Từ tập X  0;1;2;3;4; 
5 có thể lập được bao nhiêu số tự nhiên có ba chữ số khác nhau mà số đó chia hết cho 5? Ⓐ. 4 . Ⓑ. 16 . Ⓒ. 20 . Ⓓ. 36 . Lời giải
* Th1: Số cần tìm có dạng ab0 : có 2 A  20 số. 5
* Th2: Số cần tìm có dạng ab5 : có 4.4  16 số.
Vậy có: 20 16  36 số thỏa yêu cầu đề bài.
Câu 4: Lớp 12 A có 10 học sinh giỏi trong đó có 1 nam và 9 nữ. Lớp 12B có 8 học sinh giỏi trong
đó có 6 nam và 2 nữ. Cần chọn mỗi lớp 2 học sinh giỏi đi dự Đại hội Thi đuⒶ. Hỏi có
bao nhiêu cách chọn sao cho trong 4 học sinh được chọn có 2 nam và 2 nữ? Ⓐ. 1155. Ⓑ. 3060. Ⓒ. 648 . Ⓓ. 594 . Lời giải
Trường hợp 1: Chọn ở lớp 12 A , 1 học sinh giỏi nam, 1 học sinh giỏi nữ.
Chọn ở lớp 12B ,1 học sinh giỏi nam, 1 học sinh giỏi nữ. Số cách chọn là 1 1 1 1 C .C .C .C  108 . 1 9 6 2
Trường hợp 2: Chọn ở lớp 12 A , 2 học sinh giỏi nữ.
Chọn ở lớp 12B ,2 học sinh giỏi nam. Số cách chọn là 2 2 C .C  540 9 6
Vậy có 108  540  648 . Ⓒ Bài tập rèn luyện
Câu 1:Trên một bàn bi a có 15 quả bóng được đánh số lần lượt từ 1 đến 15, nếu người chơi đưa được quả bóng
nào vào lỗ thì sẽ được số điểm tương ứng với số điểm trên quả bóng đó. Hỏi người Ⓐ. 120 . Ⓑ. 60 . Ⓒ. 100 . Ⓓ. 150 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 2:Cho hai tập hợp A  {a, b, c, d}; B  {c, d , }
e . Chọn khẳng định sai trong các khẳng định sau: Ⓐ. N  A  4 .
Lời giải :...................................................................... Ⓑ. N  B  3 .
...................................................................................... Ⓒ. N ( A  B)  7 . Ⓓ. N ( A  B)  2 .
......................................................................................
Câu 3:Có 15 học sinh giỏi gồm 6 học sinh khối 12 , 4 học sinh khối 11 và 5 học sinh khối 10 . Hỏi có bao
nhiêu cách chọn ra 6 học sinh sao cho mỗi khối có ít nhất 1 học sinh? Ⓐ. 4249 . Ⓑ. 4250 . Ⓒ. 5005 . Ⓓ. 805 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 4:Có bao nhiêu số tự nhiên có hai chữ số mà các chữ số hàng chục lớn hơn chữ số hàng đơn vị? Ⓐ. 40 . Ⓑ. 45 .
Lời giải :...................................................................... Ⓒ. 50 . Ⓓ. 55 .
......................................................................................
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 3
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
......................................................................................
Câu 5:An muốn qua nhà Bình để cùng Bình đến chơi nhà Cường. Từ nhà An đến nhà Bình có bốn con đường
đi, từ nhà Bình đến nhà Cường có 6 con đường đi. Hỏi An có bao nhiêu cách chọn đường đi đến nhà Cường? Ⓐ. 16 Ⓑ. 10 Ⓒ. 24 Ⓓ. 36
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 6:Bạn muốn mua một cây bút mực và một cây bút chì. Các cây bút mực có 8 màu khác nhau, các cây
bút chì cũng có 8 màu khác nhau. Như vậy bạn có bao nhiêu cách chọn Ⓐ. 64 . Ⓑ. 16 . Ⓒ. 32 . Ⓓ. 20 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 7:Có 7 bông hồng đỏ, 8 bông hồng vàng và 10 bông hồng trắng, các bông hồng khác nhau từng đôi một.
Hỏi có bao nhiêu cách lấy 3 bông hồng có đủ ba màu. Ⓐ. 319 Ⓑ. 3014 Ⓒ. 310 Ⓓ. 310
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 8:Một liên đoàn bóng đá có 10 đội, mỗi đội phải đá 4 trận với mỗi đội khác, 2 trận ở sân nhà và 2 trận
ở sân khách. Số trận đấu được sắp xếp là: Ⓐ. 180 . Ⓑ. 160 . Ⓒ. 90 . Ⓓ. 45 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 9:Có 7 bông hồng đỏ, 8 bông hồng vàng và 10 bông hồng trắng, mỗi bông hồng khác nhau từng đôi một.
Hỏi có bao nhiêu cách lấy 3 bông hồng có đủ ba màu. Ⓐ. 560. Ⓑ. 310. Ⓒ. 3014. Ⓓ. 319.
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 10:Bạn muốn mua một cây bút mực và một cây bút chì. Các cây bút mực có 8 màu khác nhau, các cây
bút chì cũng có 8 màu khác nhau. Như vậy bạn có bao nhiêu cách chọn Ⓐ. 64 . Ⓑ. 16 . Ⓒ. 32.
Lời giải :...................................................................... Ⓓ. 20 .
......................................................................................
......................................................................................
Câu 11:Có 10 cặp vợ chồng đi dự tiệc. Tổng số cách chọn một người đàn ông và một người phụ nữ trong bữa
tiệc phát biểu ý kiến sao cho hai người đó không là vợ chồng: Ⓐ. 100. Ⓑ. 91.
Lời giải :...................................................................... Ⓒ. 10 . Ⓓ. 90.
......................................................................................
......................................................................................
Câu 12:Bạn muốn mua một cây bút mực và một cây bút chì. Các cây bút mực có 8 màu khác nhau, các cây
bút chì cũng có 8 màu khác nhau. Như vậy bạn có bao nhiêu cách chọn? Ⓐ. 64 . Ⓑ. 16 . Ⓒ. 32 . Ⓓ. 20 .
Lời giải :......................................................................
......................................................................................
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 4
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
......................................................................................
Câu 13:Trong đội văn nghệ nhà trường có 8 học sinh nam và 6 học sinh nữ. Hỏi có bao nhiêu cách chọn một đôi song ca nam-nữ Ⓐ. 91. Ⓑ. 182 . Ⓒ. 48 . Ⓓ. 14 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 14:Có 10 quả cầu đỏ được đánh số từ 1 đến 10, 7 quả cầu xanh được đánh số từ 1 đến 7 và 8 quả cầu vàng
được đánh số từ 1 đến 8. Hỏi có bao nhiêu cách lấy ra 3 quả cầu khác màu và khác số. Ⓐ. 392. Ⓑ. 1023. Ⓒ. 3014. Ⓓ. 391.
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 15:Có bao nhiêu cách sắp xếp 3 nữ sinh, 3 nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẻ: Ⓐ. 6 . Ⓑ. 72 . Ⓒ. 720 . Ⓓ. 144 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 16:Số các số tự nhiên gồm 5 chữ số chia hết cho 10 là: Ⓐ. 3260 . Ⓑ. 3168 . Ⓒ. 9000 . Ⓓ. 12070.
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 17:Một người có 7 cái áo trong đó có 3 áo trắng và 5 cái cà vạt trong đó có 2 cà vạt màu vàng. Tìm số
cách chọn một áo và một cà vạt sao cho đã chọn áo trắng thì không chọn cà vạt màu vàng. Ⓐ. 29 Ⓑ. 36 Ⓒ. 18 Ⓓ. 35
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 18:Có 6 học sinh và 3 thầy giáo ,
A B,C được xếp vào một hàng ngang có 9 ghế. Hỏi có bao nhiêu cách
xếp chỗ cho 9 người đó sao cho mỗi thầy giáo ngồi giữa hai học sinh? Ⓐ. 55012 Ⓑ. 94536 Ⓒ. 43200 Ⓓ. 35684
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 19:Một liên đoàn bóng đá có 10 đội, mỗi đội phải đá 4 trận với mỗi đội khác, 2 trận ở sân nhà và 2
trận ở sân khách. Số trận đấu được sắp xếp là: Ⓐ. 180 . Ⓑ. 160 . Ⓒ. 90 . Ⓓ. 45 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 20:Cho các số 1,5, 6, 7 có thể lập được bao nhiêu số tự nhiên có 4 chữ số với các chữ số khác nhau: Ⓐ. 12 . Ⓑ. 24 . Ⓒ. 64 . Ⓓ. 256 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 21:Có bao nhiêu số tự nhiên có chín chữ số mà các chữ số của nó viết theo thứ tự giảm dần
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 5
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Ⓐ. 5. Ⓑ. 15 . Ⓒ. 55 . Ⓓ. 10 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 22:Có bao nhiêu số tự nhiên có 3 chữ số được lập từ sáu chữ số 1, 2 , 3 , 4 , 5 , 6 ? Ⓐ. 120 . Ⓑ. 216 . Ⓒ. 256 . Ⓓ. 20 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 23:Từ các chữ số 1; 2 ; 3 có thể lập được bao nhiêu số tự nhiên có 3 chữ số khác nhau đôi một? Ⓐ. 8 . Ⓑ. 6 . Ⓒ. 9 . Ⓓ. 3 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 24:Có bao nhiêu số tự nhiên có hai chữ số mà các chữ số hàng chục lớn hơn chữ số hàng đơn vị? Ⓐ. 40 . Ⓑ. 45 . Ⓒ. 50 . Ⓓ. 55 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 25:Có bao nhiêu số tự nhiên lẻ có 4 chữ số khác nhau? Ⓐ. 2240. Ⓑ. 2520. Ⓒ. 2016. Ⓓ. 256.
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 26:Từ các chữ số 2, 3, 4, 5 có thể lập được bao nhiêu số gồm 4 chữ số: Ⓐ. 256. Ⓑ. 120.
Lời giải :...................................................................... Ⓒ. 24 . Ⓓ. 16 .
......................................................................................
......................................................................................
Câu 27:Cho các chữ số 1; 2;3; 4;5; 6;9 hỏi có bao nhiêu số tự nhiên có 7 chữ số khác nhau và nhỏ hơn
7000.000 từ các số trên? Ⓐ. 4320 . Ⓑ. 5040 . Ⓒ. 8640 . Ⓓ. 720 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 28:Có bao nhiêu số tự nhiên có 3 chữ số: Ⓐ. 900. Ⓑ. 901.
Lời giải :...................................................................... Ⓒ. 899. Ⓓ. 999.
......................................................................................
......................................................................................
Câu 29:Có bao nhiêu số có 2 chữ số, mà tất cả các chữ số đều lẻ: Ⓐ. 25 . Ⓑ. 20 . Ⓒ. 30 . Ⓓ. 10 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 30:Cho các số1, 2,3, 4, 5, 6, 7 . Số các số tự nhiên gồm 5 chữ số lấy từ 7 chữ số trên sao cho chữ số đầu tiên bằng 3 là:
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 6
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Ⓐ. 5 7 . Ⓑ. 7!.
Lời giải :...................................................................... Ⓒ. 240 . Ⓓ. 2401.
......................................................................................
......................................................................................
Câu 31:Trong một tuần, bạn A dự định mỗi ngày đi thăm một người bạn trong 12 người bạn của mình. Hỏi
bạn A có thể lập được bao nhiêu kế hoạch đi thăm bạn của mình. Ⓐ. 7!. Ⓑ. 35831808 . Ⓒ. 12!. Ⓓ. 3991680 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 32:Có bao nhiêu số có 10 chữ số được tạo thành từ các chữ số 1, 2 , 3 sao cho bất kì 2 chữ số nào đứng
cạnh nhau cũng hơn kém nhau 1 đơn vị? Ⓐ. 32 Ⓑ. 16 Ⓒ. 80 Ⓓ. 64
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 33:Có bao nhiêu số tự nhiên chẵn gồm 3 chữ số khác nhau? Ⓐ. 500 . Ⓑ. 328 . Ⓒ. 360 . Ⓓ. 405 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 34:Có bao nhiêu số tự nhiên có chín chữ số mà các chữ số của nó viết theo thứ tự giảm dần: Ⓐ. 5 . Ⓑ. 15 . Ⓒ. 55 . Ⓓ. 10 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 35:Có bao nhiêu chữ số chẵn gồm bốn chữ số đôi một khác nhau được lập từ các số 0,1, 2, 4,5, 6,8 . Ⓐ. 252 Ⓑ. 520 Ⓒ. 480 Ⓓ. 368
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 36:Từ các số 1, 2,3 có thể lập được bao nhiêu số tự nhiên khác nhau và mỗi số có các chữ số khác nhau: Ⓐ. 15 . Ⓑ. 20 . Ⓒ. 72 . Ⓓ. 36
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 37:Từ các số 1, 2,3 có thể lập được bao nhiêu số tự nhiên khác nhau và mỗi số có các chữ số khác nhau: Ⓐ. 15 . Ⓑ. 20 . Ⓒ. 72 . Ⓓ. 36
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 38:Từ các chữ số 0 , 2 , 3 , 5 , 6 , 8 có thể lập được bao nhiêu số tự nhiên gồm 6 chữ số đôi một khác
nhau trong đó hai chữ số 0 và 5 không đứng cạnh nhau. Ⓐ. 384 Ⓑ. 120 Ⓒ. 216 Ⓓ. 600
Lời giải :......................................................................
......................................................................................
......................................................................................
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 7
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Câu 39:Có bao nhiêu số tự nhiên có hai chữ số mà các chữ số hàng chục lớn hơn chữ số hàng đơn vị? Ⓐ. 40 . Ⓑ. 45 . Ⓒ. 50 . Ⓓ. 55 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 40:Cho tập hợp A  1,2,3,...,2 
0 . Hỏi A có bao nhiêu tập hợp con khác rỗng mà số phần tử là số
chẵn bằng số phần tử là số lẻ? Ⓐ. 184755. Ⓑ. 524288 . Ⓒ. 524287 . Ⓓ. 184756 .
Lời giải :......................................................................
......................................................................................
...................................................................................... BẢNG ĐÁP ÁN 1.A 2.C 3.B 4.B 5.C 6.A 7.D 8.A 9.A 10.A 11.D 12.A 13.C 14.A 15.B 16.C 17.A 18.C 19.A 20.B 21.D 22.B 23.B 24.B 25.A 26.A 27.A 28.A 29.A 30.D 31.B 32.D 33.B 34.D 35.B 36.A 37.A 38.A 39.B 40.A Hướng dẫn giải Câu 1. Lời giải Chọn A
Người chơi có thể đạt được số điểm tối đa là 1 2  ... 15  120 . Câu 2. Lờigiải Chọn C
Ta có : A  B  a,b,c, d,  e  N  A B  5 . Câu 3. Lời giải Chọn B
Số cách chọn 6 học sinh bất kỳ trong 15 học sinh là 6 C  5005 . 15
Số cách chọn 6 học sinh chỉ có khối 12 là 6 C  1 cách. 6
Số cách chọn 6 học sinh chỉ có khối 10 và 11 là 6 C  84 cách. 9
Số cách chọn 6 học sinh chỉ có khối 10 và 12 là 6 6 C  C  461 cách. 11 6
Số cách chọn 6 học sinh chỉ có khối 11 và 12 là 6 6 C  C  209 cách. 10 6
Do đó số cách chọn 6 học sinh sao cho mỗi khối có ít nhất 1 học sinh là
5005 184  461 209  4250 cách. Câu 4.
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 8
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Lời giải Chọn B
Nếu chữ số hàng chục là n thì số có chữ số hàng đơn vị là n 1 thì số các chữ số nhỏ hơn n năm ở
hàng đơn vị cũng bằng n . Do chữ số hang chục lớn hơn bằng 1 còn chữ số hàng đơn vị thi  .
Vậy số các số tự nhiên có hai chữ số mà các chữ số hàng chục lớn hơn chữ số hàng đơn vị là:
1 23 456789  45 nên chọn B . Câu 5. Lời giải Chọn C
Từ nhà An đến nhà Bình có bốn cách chọn đường.
Từ nhà Bình đến nhà Cường có sáu cách chọn đường.
Áp dụng quy tắc nhân ta có số cách chọn đường đi từ nhà An đến nhà Cường là: 4.6  24 (cách). Câu 6. Lờigiải Chọn A
Chọn cây bút mực : có 8 cách
Chọn cây bút chì : có 8 cách
Theo quy tắc nhân, số cách mua là : 8.8  64 (cách ) Câu 7. Lời giải Chọn D
Só cách chọn là 7.8.10  560 Câu 8. Lời giải Chọn A
Mỗi đội sẽ gặp 9 đội khác trong hai lượt trận sân nhà và sân khách. Có 10.9  90 trận.
Mỗi đội đá 2 trận sân nhà, 2 trận sân khách. Nên số trận đấu là 2.90  180 trận. Câu 9. Lời giải Chọn A
Số cách lấy 3 bông hồng bất kì: 3 C  2300 . 25
Số cách lấy 3 bông hồng chỉ có một màu: 3 3 3 C  C  C  211 . 7 8 10
Số cách lấy 3 bông hồng có đúng hai màu: 3 3 3 C  C  C  2 3 3 3 C  C  C  1529 . 15 17 18 7 8 10 
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 9
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Vậy số cách chọn thỏa yêu cầu bài toán là: 2300  2111529  560 . Câu 10. Lời giải Chọn A
Chọn cây bút mực : có 8 cách
Chọn cây bút chì : có 8 cách
Theo quy tắc nhân, số cách mua là : 8.8 = 64 (cách ) Câu 11. Lời giải Chọn D
Có 10 cách chọn 1 người đàn ông.
Có 10 cách chọn 1 người phụ nữ.
Tổng số cách chọn một người đàn ông và một người đàn bà trong bữa tiệc phát biểu ý kiến sao cho
hai người đó không là vợ chồng:10.10 1  090 Nên chọn D .
Theo em nên làm như thế này cho tiện
Chọn 1 người trong 10 người đàn ông có 10 cách.
Chọn 1 người trong 9 người phụ nữ không là vợ của người đàn ông đã chọn có 9 cách.
Vậy có 10.9  90 cách chọn Câu 12. Lời giải Chọn A
Chọn cây bút mực : có 8 cách
Chọn cây bút chì : có 8 cách
Theo quy tắc nhân, số cách mua là : 8.8  64 (cách ) Câu 13. Lời giải Chọn C
Mỗi cách chọn ra một đôi song song nam-nữ được được hiện qua 2 công đoạn
-Công đoạn 1: Chọn 1 học sinh nữ từ 6 học sinh nữ có 6 cách.
-Công đoạn 2: Chọn 1 học sinh nam từ 8 học sinh nam có 8 cách.
Áp dụng quy tắc nhân có 6.8  48 cách chọn đôi song ca thỏa đề. Câu 14. Lời giải
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 10
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Chọn A
Ta chọn các quả cầu theo trình tự sau:
Chọn quả xanh: 7 cách chọn.
Chọn quả cầu vàng: có 7 cách chọn.
Chọn quả cầu đỏ: có 8 cách chọn.
Vậy có tất cả 7.7.8  392 cách chọn. Câu 15. Lờigiải Chọn B
Chọn vị trí 3 nam và 3 nữ: 2.1cách chọn.
Xếp 3 nam có: 3.2.1cách xếp.
Xếp 3nữ có: 3.2.1cách xếp. Vậy có  2
2.1. 3.2.1  72 cách xếp. Câu 16. Lờigiải Chọn C
Gọi số cần tìm có dạng : abcde a  0 .
Chọn e : có 1 cách e  0
Chọn a : có 9 cách a  0 Chọn bcd : có 3 10 cách Theo quy tắc nhân, có 3 1.9.10  9000 (số). Câu 17. Lời giải Chọn A
TH1: Chọn một áo trắng trong 3 áo trắng thì có 3 cách chọn.
Chọn một cà vạt trong 3 cà vạt không phải màu vàng thì có 3 cách chọn.
Vậy có 3.3  9 chọn áo trắng và không chọn cà vạt màu vàng.
TH2: Chọn một áo trong 3áo không phải áo trắng thì có 4 cách chọn.
Chọn một cà vạt trong 5 cà vạt bất kì thì có 5 cách chọn.
Vậy có 4.5  20 chọn một áo không phải áo trắng và chọn một cà vạt bất kì.
Do đó có 9  20  29 cách chọn thỏa mãn yêu cầu bài toán. Câu 18.
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 11
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Lời giải Chọn C
Những vị trí có thể xếp cho 3 thầy giáo 2,4,6 2, 4,7 2,4,8 2,5,7 2,5,8 2,6,8 3,5,7
3,5,8 3,6,8 4,6,8
Mỗi một bộ vị trí có 3! cách xếp vị trí cho 3 thầy giáo ,
A B,C và 6! cách xếp vị trí cho 6 học sinh.
Vậy số cách xếp chỗ cho 9 người đó sao cho mỗi thầy giáo ngồi giữa hai học sinh là 10.3!6!  43200 Câu 19. Lời giải Chọn A
Mỗi đội sẽ gặp 9 đội khác (trong hai lượt trận sân nhà và sân khách) có 10.9  90 trận.
Mỗi đội đá 2 trận sân nhà, 2 trận sân khách. Nên số trận đấu là 2.90  180 trận. Câu 20. Lời giải Chọn B
Gọi số tự nhiên có 4 chữ số cần tìm là: abcd, a  0 , khi đó: a có 4 cách chọn b có 3 cách chọn c có 2 cách chọn d có 1 cách chọn
Vậy có: 4.3.2.1  24 số Nên chọn B . Câu 21. Lời giải Chọn D
Với một cách chọn 9 chữ số từ tập 0,1, 2,3, 4,5,6,7,8, 
9 ta có duy nhất một cách xếp chúng theo thứ tự giảm dần.
Ta có 10 cách chọn 9 chữ số từ tập 0,1, 2,3, 4,5,6,7,8,  9
Do đó có 10 số tự nhiên cần tìm. nên chọn D . Câu 22. Lời giải Chọn B
Gọi số tự nhiên có ba chữ số là abc . Có 6 cách chọn a . Có 6 cách chọn b . Có 6 cách chọn c .
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 12
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Theo quy tắc nhân có 6.6.6  216 (số tự nhiên). Câu 23. Lời giải Chọn B
Mỗi cách sắp thứ tự ba số 1; 2 ; 3cho ta 1 số tự nhiên có 3chữ số khác nhau đôi một.
Vậy số các chữ số thỏa yêu câu bài toán là 3!  6 cách. Câu 24. Lời giải Chọn B
Nếu chữ số hàng chục là n thì số có chữ số hàng đơn vị là n 1 thì số các chữ số nhỏ hơn n năm ở
hàng đơn vị cũng bằng n . Do chữ số hàng chục lớn hơn bằng 1 còn chữ số hàng đơn vị thi  0.
Vậy số các số tự nhiên có hai chữ số mà các chữ số hàng chục lớn hơn chữ số hàng đơn vị là:
1 2  3  4  5  6  7  8  9  45 nên chọn B . Câu 25. Lời giải Chọn A
Giả sử số tự nhiên lẻ có bốn chữ số khác nhau là abcd . Khi đó: d có 5 cách chọn. a có 8 cách chọn. Số các số là: 2 5.8.A  2240 (số). 8
Vậy số các số tự nhiên lẻ có bốn chữ số khác nhau là 2240 số. Câu 26. Lời giải Chọn Ⓐ.
Gọi số tự nhiên có 4 chữ số cần tìm là: abcd, a  0 , khi đó: a có 4 cách chọn b có 4 cách chọn c có 4 cách chọn d có 4 cách chọn
Vậy có: 4.4.4.4  256 số Nên chọn A . Câu 27. Lời giải Chọn A
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 13
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Gọi số có dạng a a a a a a a . 1 2 3 4 5 6 7
Vì số đã cho có 7 chữ số phân biệt và nhỏ hơn 7000.000 nên a  7 , vậy có 6 cách chọn a . 1 1
Các chữ số a ;a ; a ; a ; a ;a là hoán vị của 6 số còn lại. 2 3 4 5 6 7
Vậy có 6.6! 4320 số thỏa mãn bài toán. Câu 28. Lời giải Chọn Ⓐ.
Cách 1: Số có 3 chữ số là từ 100 đến 999 nên có 999 1  00 1  900số. Cách 2:
Gọi số tự nhiên có 3 chữ số cần tìm là: ab , c a  0, khi đó: a có 9 cách chọn b có 10 cách chọn c có 10 cách chọn
Vậy có: 9.10.10 900 số Nên chọn A . Câu 29. Lời giải Chọn Ⓐ.
Gọi số tự nhiên cần tìm có dạng ab .
Khi đó: a có 5 cách chọn, b có 5 cách chọn.
Nên có tất cả 5.5  25 số. Câu 30. Lờigiải Chọn D
Gọi số cần tìm có dạng : abcde .
Chọn a : có 1 cách a  3 Chọn bcde : có 4 7 cách Theo quy tắc nhân, có 4 1.7  2401 (số) Câu 31. Lờigiải Chọn B
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 14
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Thứ 2 : có 12 cách chọn bạn đi thăm
Thứ 3 : có 12 cách chọn bạn đi thăm
Thứ 4 : có 12 cách chọn bạn đi thăm
Thứ 5 : có 12 cách chọn bạn đi thăm
Thứ 6 : có 12 cách chọn bạn đi thăm
Thứ 7 : có 12 cách chọn bạn đi thăm
Chủ nhật : có 12 cách chọn bạn đi thăm
Vậy theo quy tắc nhân, có 7
12  35831808 (kế hoạch) Câu 32. Lời giải Chọn D
Gọi số tự nhiên cần tìm có dạng a a a ...a 1 2 3 10
Bước 1: Xếp số 2 ở vị trí lẻ a , a , …, a hoặc vị trí chẵn a , a , …, a có 2 cách. 1 3 9 2 2 10
Bước 2: Xếp các số 1 hoặc 3 vào các vị trí còn lại có 5 2 cách. Theo quy tắc nhân ta có 5 2.2  64 cách. Câu 33. Hướng dẫn giải Chọn B
Gọi số tự nhiên chẵn cần tìm có dạng abc , c 0;2;4;6;  8 . Xét các số có dạng a 0 b có tất cả 2
A  72 số thỏa yêu cầu bài toán. 9
Xét các số dạng abc , c 2;4;6; 
8 có tất cả: 4.8.8  256 số thỏa yêu cầu bài toán.
Vậy số các số tự nhiên chẵn gồm 3 chữ số khác nhau là: 72  256  328 số. Câu 34. Lời giải Chọn D
Với một cách chọn 9 chữ số từ tập 0,1, 2,3,4,5,6,7,8, 
9 ta có duy nhất một cách xếp chúng theo thứ tự giảm dần.
Ta có 10 cách chọn 9 chữ số từ tập 0,1, 2,3, 4,5,6,7,8,  9
Do đó có 10 số tự nhiên cần tìm. nên chọn D . Câu 35. Lời giải Chọn B
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 15
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Gọi x  abcd; , a , b c, d 0,1,2,4,5,6,  8 . Cách 1: Tính trực tiếp
Vì x là số chẵn nên d 0, 2, 4,6,  8 .
TH 1: d  0  có 1 cách chọn d .
Với mỗi cách chọn d ta có 6 cách chọn a 1, 2,4,5,6,  8
Với mỗi cách chọn a, d ta có 5 cách chọn b 1, 2, 4,5,6,  8 \   a
Với mỗi cách chọn a,b, d ta có 4 cách chọn c 1, 2, 4,5,6,  8 \ a,  b
Suy ra trong trường hợp này có 1.6.5.4  120 số.
TH 2: d  0  d 2, 4,6,  8  có 4 cách chọn d
Với mỗi cách chọn d , do a  0 nên ta có 5 cách chọn a 1, 2, 4,5, 6,  8 \ d.
Với mỗi cách chọn a, d ta có 5 cách chọn b 1, 2, 4,5,6,  8 \   a
Với mỗi cách chọn a,b, d ta có 4 cách chọn c 1, 2, 4,5,6,  8 \ a,  b
Suy ra trong trường hợp này có 4.5.5.4  400 số.
Vậy có tất cả 120  400  520 số cần lập.
Cách 2: Tính gián tiếp ( đếm phần bù)
Gọi A  { số các số tự nhiên có bốn chữ số đôi một khác nhau được lập từ các số 0,1, 2, 4,5, 6,8 }
B  { số các số tự nhiên lẻ có bốn chữ số đôi một khác nhau được lập từ các số 0,1, 2, 4, 5, 6,8 }
C  { số các số tự nhiên chẵn có bốn chữ số đôi một khác nhau được lập từ các số 0,1, 2, 4,5, 6,8 } Ta có: C  A  B .
Dễ dàng tính được: A  6.6.5.4  720 . Ta đi tính B ?
x  abcd là số lẻ  d 1,  5  d có 2 cách chọn.
Với mỗi cách chọn d ta có 5 cách chọn a (vì a  0, a  d )
Với mỗi cách chọn a, d ta có 5 cách chọn b
Với mỗi cách chọn a,b, d ta có 4 cách chọn c Suy ra B  2.5.5.4  200 Vậy C  520 . Câu 36. Lời giải
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 16
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Chọn Ⓐ.
TH1: số có 1 chữ số thì có 3 cách.
TH2: số có 2 chữ số và mỗi số có các chữ số khác nhau thì có 3.2  6 số.
TH3: số có 3 chữ số và mỗi số có các chữ số khác nhau thì có 3.2.1  6 số
Vậy có 3  6  6  15 số.
BÀI 2: HOÁN VỊ – CHỈNH HỢP – TỔ HỢP Câu 37. Lờigiải Chọn A
TH1: số có 1 chữ số thì có 3 cách.
TH2: số có 2 chữ số và mỗi số có các chữ số khác nhau thì có 3.2  6 số.
TH3: số có 3 chữ số và mỗi số có các chữ số khác nhau thì có 3.2.1  6 số
Vậy có 3  6  6  15số.
BÀI2:HOÁNVỊ–CHỈNHHỢP–TỔHỢP Câu 38. Lời giải Chọn A
Số các số có 6 chữ số được lập từ các chữ số 0 , 2 , 3, 5, 6 , 8 là 6! 5!.
Số các số có chữ số 0 và 5 đứng cạnh nhau: 2.5! 4!.
Số các số có chữ số 0 và 5 không đúng cạnh nhau là: 6! 5! 2.5! 4 !  384 . Câu 39. Lời giải Chọn B
Nếu chữ số hàng chục là n thì số có chữ số hàng đơn vị là n 1 thì số các chữ số nhỏ hơn n năm ở
hàng đơn vị cũng bằng n . Do chữ số hang chục lớn hơn bằng 1 còn chữ số hang đơn vị thi  .
Vậy số các số tự nhiên có hai chữ số mà các chữ số hàng chục lớn hơn chữ số hàng đơn vị là:
1 2  3  4  5  6  7  8  9  45 nên chọn B . Câu 40. Lời giải Chọn A
Do A có 10 phần tử là số chẵn và 10 phần tử là số lẻ nên số các phần tử là số chẵn trong các tập
con khác rỗng của A chỉ có thể là 1,2 ,3,...,10 .
Gọi B là tập con của A mà số các phần tử là số chẵn bằng số các phần tử là số lẻ và bằng k (với) 1 k 10 . Ta có:
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 17
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
- Số cách chọn ra k số chẵn trong các số 2,4,6,...,20 là k C . 10
- Số cách chọn ra k số lẻ trong các số 1,3,5,...,19 là k C . 10
- Số các tập con có số các phần tử là số chẵn bằng số các phần tử là số lẻ và bằng k là  k C 2. 10
Suy ra số tập hợp con khác rỗng của A mà số phần tử là số chẵn bằng số phần tử là số lẻ là
C 2 C 2 C 2 ...C 2 1 2 3 10 . 10 10 10 10 2 2 2 2
Cách 1: Bấm máy ta được  1 C   2 C   3 C  ... 10 C 184755. 10 10 10 10  10 10
Cách 2: Xét biểu thức f x1 x .x   1 . 2 2 2 2 2
Hệ số của số hạng chứa 10
x trong khai triển f x là  0 C   1 C   2 C   3 C  ... 10 C . 10 10 10 10 10 
Mặt khác f x  x20 1
, suy ra hệ số của số hạng chứa 10
x trong khai triển f xlà 10 C . 20 2 2 2 2 2 Suy ra  0 C   1 C   2 C   3 C  ... 10 C  10  C . 10 10 10 10 10 20 2 2 2 2 2 Do đó  1 C   2 C   3 C  ... 10 C  10  C  0 C 184755 . 10 10 10 10 20 10 
Vậy số tập hợp con cần tìm là 184755.
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 18
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung GT Chương ⓶ ⓫
§➋. HOÁN VỊ-CHỈNH HỢP-TỔ HỢP Ⓐ Tóm tắt lý thuyết
➊. Định nghĩa hoán vị:
 Cho tập hợp A gồm n phần tử (n  1). Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập A được
gọi là một hoán vị của n phần tử đó.
①. Nhận xét: Hai hoán vị của n phần tử chỉ khác nhau ở thứ tự sắp xếp n phần tử.
Ví dụ: Hãy liệt kê tất cả các số gồm 3 chữ số khác nhau từ các số 1, 2, 3.
 Giải: 123, 132, 213, 231, 312, 321. Mỗi số là một hoán vị của 3 phần tử. ②. Số các hoán vị:
Định lí: Pn = n(n – 1) …2.1 = n! Qui ước: 0! = 1
➋. Định nghĩa chỉnh hợp:
 Cho tập A gồm n phần tử (n  1). Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập A
và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.
①. Nhận xét: Hai chỉnh hợp chập k của n phần tử đã cho khác nhau ở chỗ:
 Hoặc có phần tử ở chỉnh hợp này không ở chỉnh hợp kia;
 Hoặc thứ tự sắp xếp của các phần tử trong chúng khác nhau. 
 Ví dụ :Trên mặt phẳng, cho 4 điểm phân biệt A, B, C, D. Liệt kê tất cả các vectơ khác 0 mà
điểm đầu và điểm cuối của chúng thuộc tập điểm đã cho.
           
 Giải: AB, AC, AD, BA, BC, BD, CA,CB,CD, DA, DB, DC . Mỗi vectơ là một chỉnh hợp chập 2 của 4 phần tử. ②.Số các chỉnh hợp: Định lí: kn A = n(n–1)…(n–k+1) k n! Chú ý: a) n A  b) P (n  k)! n = nn A
➌. Định nghĩa tổ hợp:
 Giả sử tập A có n phần tử (n  1). Mỗi tập con gồm k phần tử của A đgl một tổ hợp chập k của n phần tử đã cho.
 Qui ước: Gọi tổ hợp chập 0 của n phần tử là tập rỗng.
 Nhận xét: Trong một tổ hợp không có thứ tự sắp xếp. Hai tổ hợp trùng nhau nếu hai tập con đó trùng nhau.
 Ví dụ : Cho tập A = {1, 2, 3, 4, 5}. Hãy liệt kê các tổ hợp chập 3 của 5 phần tử của A.
 Giải: {1, 2, 3}, {1, 2, 4}, {1, 2, 5}, {2, 3, 4}, {2, 3, 5}, {3, 4, 5}. ②. Số các tổ hợp k k n A n!  Định lí: C   n k! k!(n  k)!
 Tính chất 1: Cho số nguyên dương n và số nguyên k với 0  k  n . Khi đó k n k Cn C   n
 Tính chất 2: Cho các số nguyên n và k với 1  k  n . Khi đó k k k 1 C n 1  Cn  C   n
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 19
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Ⓑ Phân dạng bài tập
①.Dạng 1: Bài toán chỉ sử dụng P hoặc C hoặc A . Bài tập minh họa:
Câu 1: Cho tập hợp M có 30 phần tử. Số tập con gồm 5 phần tử của M là Ⓐ. 4 A . Ⓑ. 5 30 . Ⓒ. 5 30 . Ⓓ. 5 C . 30 30 Lời giải
Số tập con gồm 5 phần tử của M chính là số tổ hợp chập 5 của 30 phần tử, nghĩa là bằng 5 C . 30
Câu 2: Cho tập hợp M có 10 phần tử. Số chỉnh hợp chập 2 của 10 phần tử của M là Ⓐ. 2 A . Ⓑ. 10 C . Ⓒ. 2 C . Ⓓ. 10 A . 10 2 10 2 Lời giải
Số chỉnh hợp chập 2 của 10 phần tử của M là: 2 A . 10
Câu 3: Từ một nhóm có 10 học sinh nam và 8 học sinh nữ, có bao nhiêu cách chọn ra 5 học sinh
trong đó có 3 học sinh nam và 2 học sinh nữ? Ⓐ. 3 2 C C . Ⓑ. 3 2 A A . Ⓒ. 3 2 A  A . Ⓓ. 3 2 C  C . 10 8 10 8 10 8 10 8 Lời giải
Số cách chọn ra 3 học sinh nam từ 10 học sinh nam là: 3 C . 10
Số cách chọn ra 2 học sinh nữ từ 8 học sinh nữ là: 2 C . 8
Vậy số cách chọn thỏa yêu cầu là: 3 2 C C . 10 8
②.Dạng 2: Bài toán kết hợp P, C và A . Bài tập minh họa:
Câu 1: Một nhóm có 6 học sinh gồm 4 nam và 2 nữ. Hỏi có bao nhiêu cách chọn ra 3 học sinh trong đó có cả nam và nữ. Ⓐ. 6 . Ⓑ. 16 . Ⓒ. 20 . Ⓓ. 32 . Lời giải
Chọn 3 học sinh tùy ý từ nhóm 6 học sinh có: 3 C cách. 6
Chọn 3 học sinh nam từ 4 học sinh nam có: 3 C cách. 4
Do đó, số cách chọn ra 3 học sinh trong đó có cả nam và nữ là: 3 3 C  C  16 cách. 6 4
Câu 2: Từ một tập gồm 10 câu hỏi, trong đó có 4 câu lí thuyết và 6 câu bài tập, người ta tạo thành
các đề thi. Biết rằng một đề thi phải gồm 3 câu hỏi trong đó có ít nhất một câu lí thuyết
và 1 câu bài tập. Hỏi có thể tạo được bao nhiêu đề khác nhau. Ⓐ. 100 . Ⓑ. 36 . Ⓒ. 96 . Ⓓ. 60 . Lời giải
Trường hợp 1: 2 câu lí thuyết, 1 câu bài tập. Suy ra số đề tạo ra là 2 1 C .C  36 4 6
Trường hợp 2: 1 câu lí thuyết, 2 câu bài tập. Suy ra số đề tạo ra là 1 2 C .C  60 4 6
Vậy có thể tạo được số đề khác nhau là: 36  60  96
Câu 3: Cho tập hợp A có 26 phần tử. Hỏi A có bao nhiêu tập con gồm 6 phần tử? Ⓐ. 6 C . Ⓑ. 26. Ⓒ. P . Ⓓ. 6 A . 26 6 26
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 20
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Lời giải
Số tập con có 6 phần tử của tập A là: 6 C . 26
③.Dạng 3: Bài toán liên quan đến hình học . Bài tập minh họa:
Câu 1: Trong không gian cho 20 điểm trong đó không có 4 điểm nào cùng nằm trong một mặt
phẳng. Hỏi có bao nhiêu cách tạo mặt phẳng từ 3 điểm trong 20 điểm trên? Ⓐ. 190 . Ⓑ. 6840 . Ⓒ. 380 . Ⓓ. 1140 . Lời giải
Số cách tạo mặt phẳng là 3 C  1140 . 20
Câu 2: Trong mặt phẳng có 5 điểm là các đỉnh của một hình ngũ giác đều. Hỏi tổng số đoạn thẳng
và tam giác có thể lập từ 5 điểm trên là Ⓐ. 10 . Ⓑ. 80 . Ⓒ. 20 . Ⓓ. 40 . Lời giải
Số tam giác được tạo thành là: 3 C . 5
Số đoạn thẳng được tạo thành là: 2 C . 5
Vậy tổng số tam giác và đoạn thẳng có thể lập từ 5 điểm trên là: 3 2 C  C  20 . 5 5
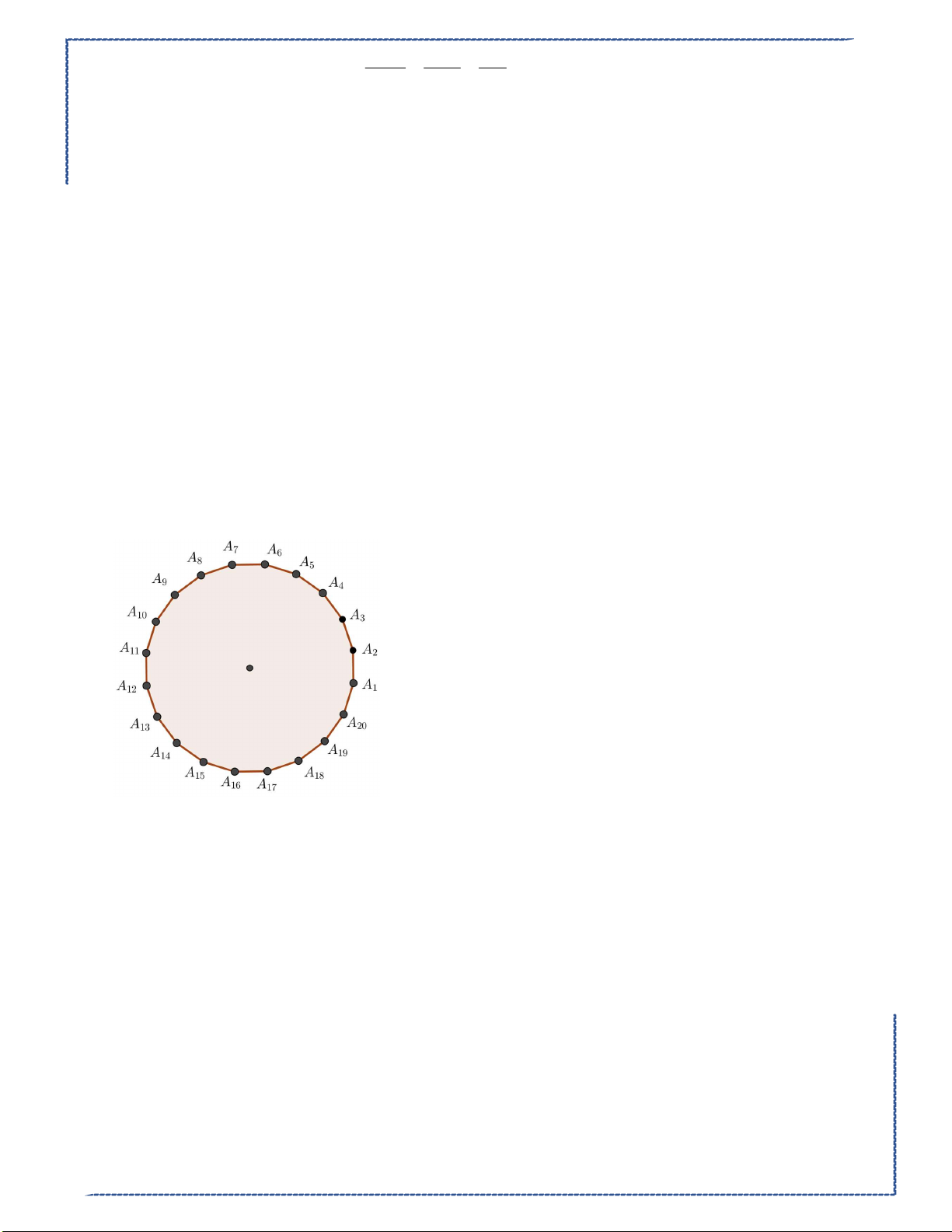
Câu 3: Cho hình vuông ABCD . Trên cạnh AB lấy n điểm khác nhau, không trùng với , A B . Biết
có 16 tam giác được tạo thành từ n  4 điểm. Giá trị của n bằng Ⓐ. 5 . Ⓑ. 3 . Ⓒ. 2 . Ⓓ. 4 . Lời giải
Số tam giác có 2 đỉnh là C, D là: n  2 .
Số tam giác có 1 đỉnh là C hoặc D , hai đỉnh còn lại thuộc cạnh AB : 2 2.C . n2 Ta có 2 n  2  2.C  16  n  2 . n2 ④
Giải phương trình, bất phương trình, hệ, chứng minh liên quan đến .Dạng 4: P, C, A . Bài tập minh họa:
Câu 1: Nghiệm của phương trình 2 1 A  A  3 là x x Ⓐ. x  1  . Ⓑ. x  3. Ⓒ. x  1  và x  3. Ⓓ. x 1. Lời giải x  Điều kiện :  x  2 x  1 l 2 1
A  A  3  x x   x   x x     1 3  x  3 Vậy x  3. Câu 2: Biết 2 3 A  C   *
50 n   , khi đó giá trị của n là n n  Ⓐ. 4. Ⓑ. 5. Ⓒ. 6. Ⓓ. 7 Lời giải n! n! 1 2 3 A  C    n n   n n  n   n n n   n     1  1 2 50 2 ! 3! 3 ! 6 3 2
 n  3n  4n  300  0  n  6
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 21
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Câu 3: Số nguyên dương n thoả mãn 2 n 1 A  C   P 2n  3 n n 1  2   Ⓐ. 12 . Ⓑ. 11. Ⓒ. 10 . Ⓓ. 15 . Lời giải n  2  n  2
Điều kiện: n 1  n 1  0   .  n   n      n n n ! 1 ! 2 1   Ta có: A  C  P 2n  3    2! 2n  3 n n 1  2   n2! n    1 !2! n n 1 n  1 l  n     1 n   22n  3 2
 n 11n 12  0   . 2 n  12  n Ⓒ BÀI TẬP RÈN LUYỆN ⓵ Mức độ nhận biết
Câu 1:Cho tập A có n phần tử ( n   , n  2 ), k là số nguyên thỏa mãn 0  k  n . Số các chỉnh hợp chập k của n phần tử trên là n! n! Ⓐ. . Ⓑ. .
Lời giải :...................................................................... k ! k  ! n  k ! n!
...................................................................................... Ⓒ.  . Ⓓ. k  ! n  k !. n  k !
......................................................................................
Câu 2:Khẳng định nào sau đây đúng? k k k ! k ! Ⓐ. C  . Ⓑ. C  . n n  ! n  k ! n n  k!
Lời giải :......................................................................
...................................................................................... k n! k n! Ⓒ. C  . Ⓓ. C  . n n  k! n k  ! n  k !
......................................................................................
Câu 3:Có bao nhiêu số tự nhiên có 5 chữ số, các chữ số khác 0 và đôi một khác nhau? Ⓐ. 5!. Ⓑ. 5 9 .
Lời giải :...................................................................... Ⓒ. 5 C . Ⓓ. 5 A . 9 9
......................................................................................
......................................................................................
Câu 4:Một tổ học sinh gồm có 5 nam và 7 nữ. Có bao nhiêu cách chọn 4 học sinh của tổ tham gia đội xung kích? Ⓐ. 4!. Ⓑ. 4 4 C  C . 5 7
Lời giải :...................................................................... Ⓒ. 4 A . Ⓓ. 4 C . 12 12
......................................................................................
......................................................................................
Câu 5:Số tập hợp con có 3 phần tử của một tập hợp có 7 phần tử là: Ⓐ. 3 C . Ⓑ. 3 A . 7 7
Lời giải :...................................................................... ! 7 Ⓒ. . Ⓓ. 7 . ! 3
......................................................................................
......................................................................................
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 22
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Câu 6:Từ các số 0,1, 2, 7,8,9 tạo được bao nhiêu số lẻ có 5 chữ số khác nhau? Ⓐ. 288 . Ⓑ. 360 . Ⓒ. 312 . Ⓓ. 600 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 7:Trong một buổi hoà nhạc, có các ban nhạc của các trường đại học từ Huế, Đà Nằng, Quy Nhơn, Nha
Trang, Đà Lạt tham dự. Tìm số cách xếp đặt thứ tự để các ban nhạc Nha Trang sẽ biểu diễn đầu tiên. Ⓐ. 4 . Ⓑ. 20 . Ⓒ. 24 . Ⓓ. 120 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 8:Có bao nhiêu cách xếp 5 sách Văn khác nhau và 7 sách Toán khác nhau trên một kệ sách dài nếu các
sách Văn phải xếp kề nhau? Ⓐ. 5!.7!. Ⓑ. 2.5!.7!. Ⓒ. 5!.8!. Ⓓ. 12!.
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 9:Có bao nhiêu cách sắp xếp 18 thí sinh vào một phòng thi có 18 bàn mỗi bàn một thí sinh. Ⓐ. 18 Ⓑ. 1
Lời giải :...................................................................... Ⓒ. 18 18 Ⓓ. 18!
......................................................................................
......................................................................................
Câu 10:Cho tập X có 9 phần tử. Tìm số tập con có 5 phần tử của tập X . Ⓐ. 120 . Ⓑ. 126 . Ⓒ. 15120 . Ⓓ. 216 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 11:Trong một buổi hoà nhạc, có các ban nhạc của các trường đại học từ Huế, Đà Nằng, Quy Nhơn, Nha
Trang, Đà Lạt tham dự. Tìm số cách xếp đặt thứ tự để các ban nhạc Nha Trang sẽ biểu diễn đầu tiên. Ⓐ. 4 . Ⓑ. 20 . Ⓒ. 24 . Ⓓ. 120 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 12:Cho tập hợp A có 20 phần tử, số tập con có hai phần tử của A là Ⓐ. 2 2C . Ⓑ. 2 2 A . 20 20
Lời giải :...................................................................... Ⓒ. 2 C . Ⓓ. 2 A . 20 20
......................................................................................
......................................................................................
Câu 13:Một hộp có 3 bi xanh, 4 bi đỏ và 5 bi vàng. Chọn ngẫu nhiên 3 bi sao cho có đủ ba màu. Số cách chọn là Ⓐ. 60 . Ⓑ. 220 . Ⓒ. 360 . Ⓓ. 120 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 14:Trong không gian cho bốn điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho? Ⓐ. 6 Ⓑ. 4 Ⓒ. 3 Ⓓ. 2
Lời giải :......................................................................
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 23
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
......................................................................................
...................................................................................... 
Câu 15:Cho tứ giác ABCD . Có bao nhiêu vectơ khác vectơ 0 có điểm đầu và điểm cuối là các đỉnh của tứ giác? Ⓐ. 2 A . Ⓑ. 2 C . 4 6
Lời giải :...................................................................... Ⓒ. 2 4 . Ⓓ. 2 C . 4
......................................................................................
......................................................................................
Câu 16:Chọn mệnh đề đúng trong các mệnh đề sau: n n k ! k ! Ⓐ. C  . Ⓑ. C  . n
Lời giải :...................................................................... k !n  k ! n k !n  k ! n n
...................................................................................... k ! k ! Ⓒ. C  . Ⓓ. C  . n k n  k ! n k !n  k 
......................................................................................
Câu 17:Cho các số nguyên k, n thỏa mãn 0  k  n . Công thức nào dưới đây đúng ? n n k ! k ! Ⓐ. A  . Ⓑ. A  . n
Lời giải :...................................................................... k ! n k  ! n  k ! n k n
...................................................................................... k ! ! k ! Ⓒ. A  . Ⓓ. A  . n n  k! n n  k!
...................................................................................... 2 A  Câu 18:Nếu 110 x thì: Ⓐ. x  10 . Ⓑ. x  11 . Ⓒ. x  11hay x 10 . Ⓓ. x  0 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 19:Tìm số tự nhiên n thỏa 2 A  210 . n Ⓐ. 15 . Ⓑ. 12. Ⓒ. 21 . Ⓓ. 18 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 20:Trong các câu sau câu nào sai? Ⓐ. 3 11 C  C . Ⓑ. 3 4 4 C  C  C . 14 14 10 10 11
Lời giải :...................................................................... Ⓒ. 0 1 2 3 4
C  C  C  C  C  16 4 4 4 4 4
...................................................................................... Ⓓ. 4 4 5 C  C  C . 10 11 11
...................................................................................... BẢNG ĐÁP ÁN 1.C 2.D 3.D 4.D 5.A 6.A 7.C 8.C 9.D 10.B 11.C 12.C 13.A 14.B 15.A 16.B 17.C 18.B 19.A 20.D ⓶ Mức độ thông hiểu
Câu 1:Có tất cả bao nhiêu số tự nhiên có 3 chữ số và 3 chữ số đó đôi một khác nhau? Ⓐ. 3 3 A  A . Ⓑ. 3 A . 10 9 9
Lời giải :...................................................................... Ⓒ. 3 A . Ⓓ. 9 98 . 10
......................................................................................
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 24
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
......................................................................................
Câu 2:Trong mặt phẳng cho tập hợp S gồm 10 điểm, trong đó không có 3 điểm nào thẳng hàng. Có bao nhiêu
tam giác có 3 đỉnh đều thuộc S ? Ⓐ. 720 Ⓑ. 120 Ⓒ. 59049 Ⓓ. 3628800
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 3:Có thể lập được bao nhiêu số tự nhiên có 3 chữ số khác nhau từ các chữ số  ; 0 ; 1 ; 2 ; 3  4 ? Ⓐ. 60. Ⓑ. 24. Ⓒ. 48. Ⓓ. 11.
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 4:Với các chữ số 2,3, 4,5, 6 , có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau trong đó
hai chữ số 3,6 không đứng cạnh nhau? Ⓐ. 120 Ⓑ. 96 Ⓒ. 48 Ⓓ. 72
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 5:Từ các số 1, 2, 3, 4, 5, 6 lập được bao nhiêu số tự nhiên Gồm 4 chữ số Ⓐ. 1296. Ⓑ. 2019. Ⓒ. 2110. Ⓓ. 1297
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 6:Từ các số 1, 2,3 lập được bao nhiều số tự nhiên gôm 6 chữ số thỏa mãn đồng thời hai điều kiện sau: Trong
mỗi số, hai chữ số giống nhau không đứng cạnh nhau. Ⓐ. 76. Ⓑ. 42. Ⓒ. 80. Ⓓ. 68
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 7:Cho tập hợp S  1;2;3;...;19, 2 
0 gồm 20 số tự nhiên từ 1 đến 20, lấy ngẫu nhiên 3 số thuộc S , xác suất
để 3 số lấy được lập thành một cấp số cộng là 7 5 Ⓐ. Ⓑ.
Lời giải :...................................................................... 38 38 3 1
...................................................................................... Ⓒ. Ⓓ. 38 114
...................................................................................... A  1,2,3,4,5,6,7,  8 Câu 8:Cho tập .
Có bao nhiêu tập con của A chứa số 2 mà không chứa số 3 Ⓐ. 64. Ⓑ. 83. Ⓒ. 13. Ⓓ. 41
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 9:Lớp 11A1 có 41 học sinh trong đó có 21 bạn nam và 20 bạn nữ. Thứ hai đầu tuần lớp phải xếp hàng chào
cờ thành một hàng dọc. Hỏi có bao nhiêu cách sắp xếp để 21 bạn nam xen kẽ với 20 bạn nữ? Ⓐ. P . Ⓑ. P .P . 41 21 20
Lời giải :...................................................................... Ⓒ. 2.P .P . Ⓓ. P  P . 21 20 21 20
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 25
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
......................................................................................
......................................................................................
Câu 10:Có bao nhiêu cách xếp 6 bạn A, B, C, D, E, F vào một ghế dài sao cho bạn A, F ngồi ở 2 đầu ghế? Ⓐ. 120 . Ⓑ. 720 . Ⓒ. 24 . Ⓓ. 48 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 11:Tổ của An và Cường có 7 học sinh. Số cách xếp 7 học sinh ấy theo hàng dọc mà An đứngđầu hàng,
Cường đứng cuối hàng là: Ⓐ. 120. Ⓑ. 100. Ⓒ. 110. Ⓓ. 125.
Lời giải :......................................................................
......................................................................................
...................................................................................... Câu 12:Lớp 11 1
A có 41 học sinh trong đó có 21 bạn nam và 20 bạn nữ. Thứ 2 đầu tuần lớp phải xếp hàng
chào cờ thành một hàng dọc. Hỏi có bao nhiêu cách sắp xếp để 21 bạn nam xen kẽ với 20 bạn nữ? Ⓐ. P . Ⓑ. P .P . 41 21 20
Lời giải :...................................................................... Ⓒ. 2.P .P . Ⓓ. P  P . 21 20 21 20
......................................................................................
......................................................................................
Câu 13:Trong tủ sách có tất cả 10 cuốn sách. Hỏi có bao nhiêu cách sắp xếp sao cho quyển thứ nhất ở kề quyển thứ hai: Ⓐ. 10!. Ⓑ. 725760 . Ⓒ. 9!. Ⓓ. 9! 2! .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 14:Trong một lớp học có 20 học sinh nữ và 15 học sinh nam. Hỏi giáo viên chủ nhiệm có bao nhiêu cách chọn:
Bốn học sinh làm tổ trưởng của 4 tổ sao cho trong 4 học sinh được chọn có cả nam và nữ. Ⓐ. 1107600. Ⓑ. 246352. Ⓒ. 1267463. Ⓓ. 1164776.
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 15:Một nhóm học sinh có 10 người. Cần chọn 3 học sinh trong nhóm để làm 3 công việc là tưới cây, lau bàn
và nhặt rác, mỗi người làm một công việc. Số cách chọn là Ⓐ. 3 10 . Ⓑ. 310 .
Lời giải :...................................................................... Ⓒ. 3 C . Ⓓ. 3 A . 10 10
......................................................................................
......................................................................................
Câu 16:Số cách sắp xếp 6 học sinh ngồi vào 6 trong 10 ghế trên một hàng ngang là Ⓐ. 10 6 . Ⓑ. 6!.
Lời giải :...................................................................... Ⓒ. 6 A . Ⓓ. 6 C . 10 10
......................................................................................
......................................................................................
Câu 17:Có tất cả 120 cách chọn 3 học sinh từ nhóm n học sinh. Số n là nghiệm của phương trình nào sau đây? Ⓐ. nn   1 n  2 120.
Lời giải :...................................................................... Ⓑ. nn   1 n  2  720 .
...................................................................................... Ⓒ. nn   1 n  2 120 .
......................................................................................
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 26
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Ⓓ. n n   1 n  2  720.
Câu 18:Một lớp học có 20 nam và 26 nữ. Giáo viên chủ nhiệm cần chọn một ban cán sự gồm 3 người. Hỏi có bao
nhiêu cách chọn nếu trong ban cán sự có cả nam và nữ. Ⓐ. 11440. Ⓑ. 11242. Ⓒ. 24141. Ⓓ. 53342.
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 19:Cho tập S có 20 phần tử. Số tập con gồm 3 phần tử của S . Ⓐ. 3 A . Ⓑ. 3 C 20 20
Lời giải :...................................................................... Ⓒ. 60 . Ⓓ. 3 20 .
......................................................................................
......................................................................................
Câu 20:Ông và bà An cùng có 6 đứa con đang lên máy bay theo một hàng dọⒸ. Có bao nhiêu cách xếp hàng
khác nhau nếu ông An hay bà An đứng ở đầu hoặc cuối hàng: Ⓐ. 720 . Ⓑ. 1440 . Ⓒ. 18720 . Ⓓ. 40320 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 21:Một nhóm công nhân gồm 15 nam và 5 nữ. Người ta muốn chọn từ nhóm ra 5 người để lập thành một tổ
công tác sao cho phải có 1 tổ trưởng nam, 1 tổ phó nam và có ít nhất 1 nữ. Hỏi có bao nhiêu cách lập tổ công tác. Ⓐ. 111300. Ⓑ. 233355. Ⓒ. 125777. Ⓓ. 112342.
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 22:Một hộp có 5 bi đen, 4 bi trắng. Chọn ngẫu nhiên 2 bi. Xác suất 2 bi được chọn cùng màu là: 1 4 1 5 Ⓐ. . Ⓑ. . Ⓒ. .
Ⓓ. . Lời giải :...................................................................... 4 9 9 9
......................................................................................
......................................................................................
Câu 23:Một trường cấp 3 của tỉnh Đồng Tháp có 8 giáo viên Toán gồm có 3 nữ và 5 nam, giáo viên Vật lý thì
có 4 giáo viên nam. Hỏi có bao nhiêu cách chọn ra một đoàn thanh tra công tác ôn thi THPTQG gồm 3 người có
đủ 2 môn Toán và Vật lý và phải có giáo viên nam và giáo viên nữ trong đoàn? Ⓐ. 60 Ⓑ. 120 Ⓒ. 12960 Ⓓ. 90
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 24:Có bao nhiêu cách chia hết 4 đồ vật khác nhau cho 3 người, biết rằng mỗi người nhận được ít nhất 1 đồ vật. Ⓐ. 72 Ⓑ. 18 Ⓒ. 12 Ⓓ. 36
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 25:Từ 6 điểm phân biệt thuộc đường thẳng  và một điểm không thuộc đường thẳng  ta có thể tạo được
tất cả bao nhiêu tam giác? Ⓐ. 210 . Ⓑ. 30 . Ⓒ. 15 . Ⓓ. 35 .
Lời giải :......................................................................
......................................................................................
......................................................................................
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 27
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Câu 26:Cho đa giác đều n đỉnh, n   và n  3 . Tìm n biết rằng đa giác đã cho có 135 đường chéo. Ⓐ. n  15. Ⓑ. n  27 . Ⓒ. n  8. Ⓓ. n  18.
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 27:Lục giác đều ABCDEF có bao nhiêu đường chéo Ⓐ. 15 . Ⓑ. 5 . Ⓒ. 9 . Ⓓ. 24 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 28:Cho các số nguyên dương k, n , k  n . Mệnh đề nào sau đây sai?: n k ! Ⓐ. C  . Ⓑ. k A  k !.Ck . n 
Lời giải :...................................................................... n  k ! n n Ⓒ. nk k C  C . Ⓓ. k k 1  k 1 C  C
 C  . ...................................................................................... n n n n n 1 
...................................................................................... 5 5 Câu 29:Cho *
n   thỏa mãn C  2002 A n . Tính n . Ⓐ. 2007 . Ⓑ. 10010 . Ⓒ. 40040 . Ⓓ. 240240 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 30:Nếu một đa giác đều có 44 đường chéo, thì số cạnh của đa giác là: Ⓐ. 11. Ⓑ. 10 . Ⓒ. 9 . Ⓓ. 8 .
Lời giải :......................................................................
......................................................................................
...................................................................................... Câu 31:Nếu 4 4 2 A  3A thì n bằng: n n 1  Ⓐ. n  11 . Ⓑ. n  12 . Ⓒ. n  13. Ⓓ. n  14 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 32:Nghiệm của phương trình 10 9 8 A  A  9 A là x x x Ⓐ. x  5. Ⓑ. x  11. Ⓒ. x  11 ; x  5 Ⓓ. x  10 ; x  2.
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 33:Giá trị của n   thỏa mãn n3 3 C  5A là n8 n6 Ⓐ. n  15 . Ⓑ. n  17 . Ⓒ. n  6 . Ⓓ. n  14 .
Lời giải :......................................................................
......................................................................................
...................................................................................... BẢNG ĐÁP ÁN 1.D 2.B 3.C 4.D 5.A 6.A 7.C 8.A 9.B 10.D 11.A 12.B 13.B 14.A 15.D 16.C 17.D 18.A 19.B 20.C 21.A 22.B 23.D 24.D 25.C 26.D 27.C 28.A 29.D 30.A 31.B 32.B 33.B
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 28
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung ⓷ Mức độ VD-VDC
Câu 1:Có bao nhiêu số tự nhiên gồm bảy chữ số khác nhau đôi một, trong đó chữ số 6 đứng liền giữa hai chữ số 5 và 7 . Ⓐ. 6600 Ⓑ. 7440 Ⓒ. 8400 Ⓓ. 4560
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 2:Biển số xe máy tỉnh K gồm hai dòng
- Dòng thứ nhất là 68 XY , trong đó X là một trong 24 chữ cái, Y là một trong 10 chữ số; - Dòng thứ hai là ab .
c de , trong đó a , b , c , d , e là các chữ số.
Biển số xe được cho là "đẹp" khi dòng thứ hai có tổng các số là số có chữ số tận cùng bằng 8 và có đúng 4 chữ số
giống nhau. Hỏi có bao nhiêu cách chọn 2 biển số trong các biển số "đẹp" để đem bán đấu giá? Ⓐ. 12000 . Ⓑ. 143988000 . Ⓒ. 4663440 . Ⓓ. 71994000 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 3:Mỗi bạn An và Bình chọn ngẫu nhiên ba số trong tập 0, 1, 2, 3, 4, 5, 6, 7, 8, 
9 . Xác suất để trong hai bộ
số của An và Bình chọn ra có nhiều nhất một số giống nhau bằng 21 203 Ⓐ. Ⓑ.
Lời giải :...................................................................... 40 480 49 17
...................................................................................... Ⓒ. Ⓓ. 60 24
......................................................................................
Câu 4:Một người viết ngẫu nhiên một số có bốn chữ số. Tính xác suất để các chữ số của số được viết ra có thứ tự
tăng dần hoặc giảm dần. 7 7 Ⓐ. . Ⓑ. .
Lời giải :...................................................................... 125 375 7 14
...................................................................................... Ⓒ. . Ⓓ. . 250 375
......................................................................................
Câu 5:Hai nhóm người cần mua nền nhà, nhóm thứ nhất có 2 người và họ muốn mua 2 nền kề nhau, nhóm thứ hai
có 3 người và họ muốn mua 3 nền kề nhau. Họ tìm được một lô đất chia thành 7 nền đang rao bán. Tính số cách
chọn nền của mỗi người thỏa yêu cầu trên Ⓐ. 144. Ⓑ. 125. Ⓒ. 140. Ⓓ. 132
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 6:Cho đa giác đều 20 cạnh nội tiếp đường tròn O . Xác định số hình thang có 4 đỉnh là các đỉnh của đa giác đều. Ⓐ. 720 . Ⓑ. 765 . Ⓒ. 810 . Ⓓ. 315 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 7:Ông và bà An cùng có 6 đứa con đang lên máy bay theo một hàng dọⒸ. Có bao nhiêu cách xếp hàng khác
nhau nếu ông An hay bà An đứng ở đầu hoặc cuối hàng: Ⓐ. 720 . Ⓑ. 1440. Ⓒ. 18720 . Ⓓ. 40320 .
Lời giải :......................................................................
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 29
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
......................................................................................
......................................................................................
Câu 8:Giả sử rằng, trong Đại hội thể dục thể thao tỉnh Gia Lai năm 2018 có 16 đội bóng đăng ký tham gia giải,
được chia thành 4 bảng A , B , C , D , mỗi bảng gồm 4 đội. Cách thức thi đấu như sau:
Vòng1 : Các đội trong mỗi bảng thi đấu vòng tròn một lượt, tính điểm và chọn ra đội nhất của mỗi bảng.
Vòng 2 : Đội nhất bảng A gặp đội nhất bảng C ; Đội nhất bảng B gặp đội nhất bảng D .
Vòng 3 : Tranh giải ba: Hai đội thua trong bán kết; tranh giải nhất: Hai đội thắng trong bán kết.
Biết rằng tất cả các trận đấu đều diễn ra trên sân vận động Pleiku vào các ngày liên tiếp, mỗi ngày 4 trận. Hỏi
Ban tổ chức cần mượn sân vận động trong bao nhiêu ngày? Ⓐ. 5 . Ⓑ. 6 .
Lời giải :...................................................................... Ⓒ. 7 . Ⓓ. 8 .
......................................................................................
......................................................................................
Câu 9:Có m nam và n nữ. Có bao nhiêu cách chọn ra k người trong đó có ít nhất a nam và ít nhất b nữ ( k  , m ; n a  b  k; ,
a b 1) với S là số cách chọn có ít hơn a nam, S là số cách chọn có ít hơn b nữ. 1 2
Ⓐ. Số cách chọn thoả mãn điều kiện bài toán là: k
Lời giải :...................................................................... C  2(S  S ) . mn 1 2
Ⓑ. Số cách chọn thoả mãn điều kiện bài toán là:
...................................................................................... 2 k C  (S  S ) . mn 1 2
......................................................................................
Ⓒ. Số cách chọn thoả mãn điều kiện bài toán là: 3 k C  2(S  S ) . mn 1 2
Ⓓ. Số cách chọn thoả mãn điều kiện bài toán là: k C  (S  S ) . mn 1 2
Câu 10:Có bao nhiêu số tự nhiên có bẩy chữ số khác nhau từng đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3 .
Ⓐ. 3204 số. Ⓑ. 249 số.
Ⓒ. 2942 số. Ⓓ. 7440 số.
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 11:Cho hai đường thẳng d và d song song với nhau. Trên d có 10 điểm phân biệt, trên d có n điểm 1 2 1 2
phân biệt n  2 . Biết rằng có 2800 tam giác có đỉnh là 3 điểm trong số các điểm đã cho, tìm n . Ⓐ. 30 . Ⓑ. 25 . Ⓒ. 20 . Ⓓ. 15 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 12:Cho đa giác đều n đỉnh, n   và n  3 . Tìm n biết rằng đa giác đã cho có 135 đường chéo Ⓐ. n  15 . Ⓑ. n  27 . Ⓒ. n  8 . Ⓓ. n  18 .
Lời giải :......................................................................
......................................................................................
...................................................................................... 2017 2016 2 1
Câu 13:Tính giá trị của biểu thức: P    ...  ? 0 1 2015 2016 A A A A 2017 2017 2017 2017 1 1 Ⓐ. P  2017  Ⓑ. P  2017 
Lời giải :...................................................................... 2018! 2017! 1 1
...................................................................................... Ⓒ. P  2018  Ⓓ. P  2018  2017! 2018!
......................................................................................
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 30
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
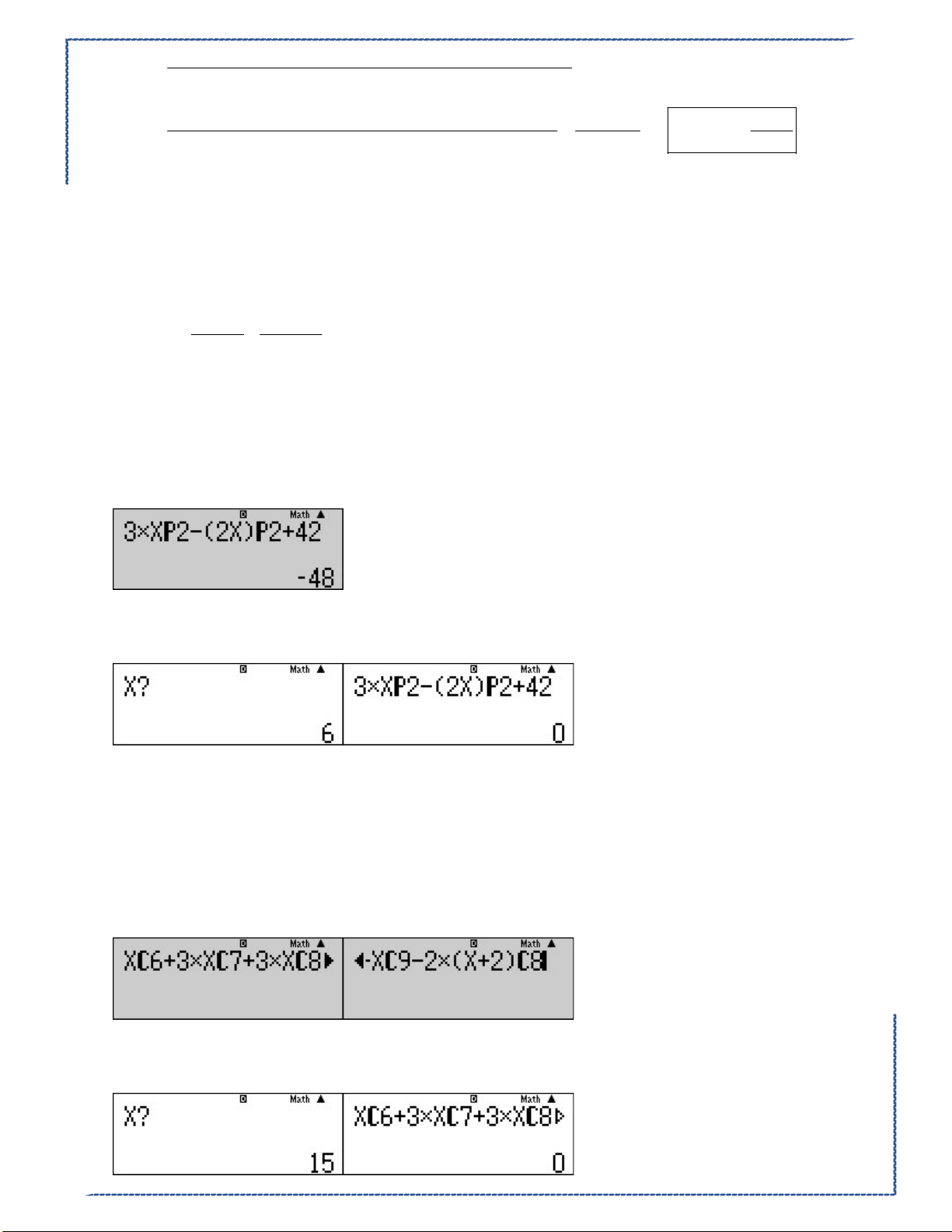
Câu 14:Giá trị của n thỏa mãn 2 2 3A  A  42  0 là n 2n Ⓐ. 9 . Ⓑ. 8 . Ⓒ. 6 . Ⓓ. 10 .
Lời giải :......................................................................
......................................................................................
......................................................................................
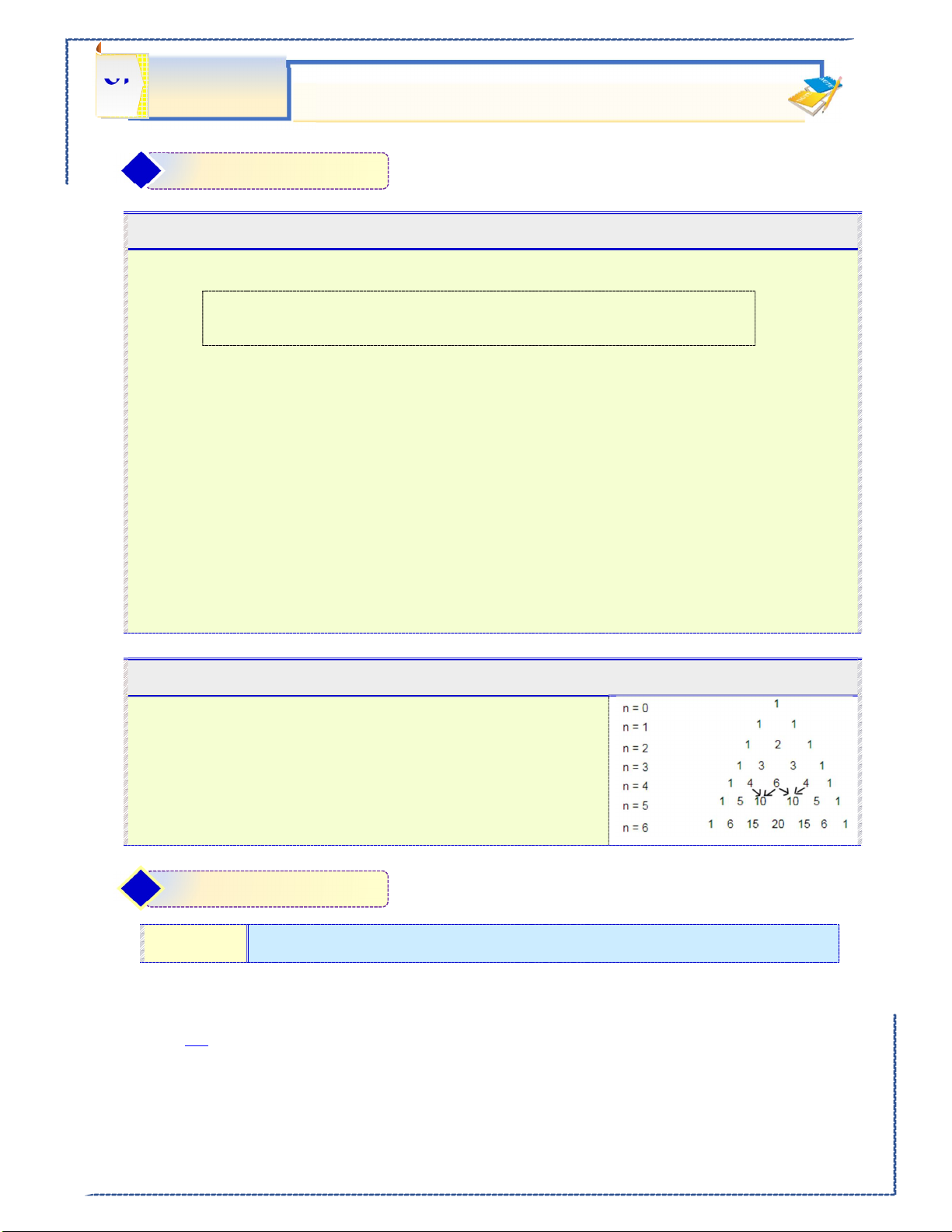
Câu 15:Giá trị của n   thỏa mãn đẳng thức 6 7 8 9 8 C  3C  3C  C  2C là n n n n n2 Ⓐ. n  18 . Ⓑ. n  16 . Ⓒ. n  15 . Ⓓ. n  14 .
Lời giải :......................................................................
......................................................................................
...................................................................................... BẢNG ĐÁP ÁN 1.B 2.D 3.C 4.D 5.A 6.A 7.C 8.C 9.D 10.D 11.C 12.D 13.C 14.C 15.C Ⓓ HƯỚNG DẪN GIẢI
①. HƯỚNG DẪN GIẢI – NHẬN BIẾT Câu 1. Lời giải Chọn C n!
Số các chỉnh hợp chập k của n phần tử là  . n  k ! Câu 2. Lời giải Chọn D n k ! Ta có: C  . n k  ! n  k ! Câu 3. Lời giải Chọn D
Mỗi số tự nhiên có 5 chữ số, các chữ số khác 0 và đôi một khác nhau là một chỉnh hợp chập 5 của 9 phần tử.
Vậy số các số tự nhiên thỏa đề bài là 5 A số. 9 Câu 4. Lời giải Chọn D
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 31
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Tổng cộng tổ đó có 12 học sinh, phép chọn là ngẫu nhiên cùng lúc không có sắp xếp nên số cách chọn là 4 C 12 Câu 5. Lời giải Chọn A
Đây là tổ hợp chập 3 của 7 phần tử. Vậy có 3 C tập hợp con. 7 Câu 6. Lời giải Chọn A
Gọi abcde là số cần tìm. Chọn e có 3 cách.
Chọn a  0 và a  e có 4 cách.
Chọn 3 trong 4 số còn lại sắp vào b, c, d có 3 A cách. 4 Vậy có 3 3.4.A  288 số. 4 Câu 7. Lời giải Chọn C
Sắp xếp thứ tự biểu diễn của 4 ban nhạc còn lại có 4 A  4!  20 cách. 4 Câu 8. Lời giải Chọn C
Sắp 5 quyển văn có 5! cách sắp xếp.
Sắp 7 quyển toán và bộ 5 quyển văn có 8! cách sắp xếp.
Vậy có 5!.8! cách sắp xếp. Câu 9. Lời giải Chọn D Số cách xếp là: 18 ! . Câu 10. Lời giải Chọn B
Từ tập X có 9 phần tử chọn ra 5 phần tử để hình thành nên tập con. Vậy tập X có 5
C  126 tập con chứa5 phần tử. 9 Câu 11.
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 32
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Lời giải Chọn C
Sắp xếp thứ tự biểu diễn của 4 ban nhạc còn lại có 4 A  4!  20 cách. 4 Câu 12. Lời giải Chọn C
Số tập con có hai phần tử của A là 2 C . 20 Câu 13. Lời giải Chọn A
Chọn ngẫu nhiên 3 bi sao có đủ ba màu có 1 1 1 C .C .C  60 cách. 3 4 5 Câu 14. Lời giải Chọn B
Vì 4 điểm không đồng phẳng tạo thành một tứ diện mà tứ diện có 4 mặt (𝐶 = 4). Câu 15. Lời giải Chọn A
Ta có mỗi vectơ được tạo thành từ 2 đỉnh của tứ giác là một chỉnh hợp chập 2 của 4 phần tử. Vậy có 2
A vectơ thỏa yêu cầu bài. 4 Câu 16. Lời giải Chọn B Câu 17. Lời giải Chọn C Câu 18. Lời giải Chọn B
Điều kiện: x  , x  2 . x! x  11 Ta có: 2 A  110  x x . x       x  2 110 ( 1) 110 !  x  10
So sánh điều kiện ta nhận x 11. Câu 19.
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 33
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Lời giải Chọn A * PP tự luận: n! PT 2 A  210 
 210, n  ,n  2  n   1 n  210 2  n  n  210  0 n n  2! n  15 nhan    n  15 . n  14 loai * PP trắc nghiệm: + Nhập vào máy tính 2 A  210  0 . n
+ Tính (CALC) lần lượt với X  15 (thoả); với X  12 (không thoả), với X  21 (không thoả), với X  18 (không thoả). + KL: Vậy n  15 . Câu 20. Lời giải Chọn D Ta có công thức: k k 1  k 1 C  C
 C  nên đáp án sai là 4 4 5 C  C  C . n n n 1  10 11 11
⓶. HƯỚNG DẪN GIẢI – THÔNG HIỂU Câu 1. Lời giải Chọn D
Gọi số cần lập là abc .
a  0 nên a có 9 cách chọn
b  a nên b có 9 cách chọn
c  a và c  b nên c có 8 cách chọn
Vậy có 9 98 cách chọn. Câu 2. Lời giải Chọn B
Số tam giác có 3 đỉnh đều thuộc S bằng số tổ hợp chập 3 của 10 phần từ và bằng 3 C  120 10 Câu 3. Lời giải
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 34
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Chọn C
Số các chỉnh hợp chập 3 chữ số khác nhau từ các chữ số  ; 0 ; 1 ; 2 ; 3  4 là A3 số. 5
Số các chỉnh hợp chập 3 chữ số khác nhau từ các chữ số  ; 0 ; 1 ; 2 ; 3 
4 và có số 0 đứng đầu là A3 số. 4
Vậy: số các số tự nhiên có 3 chữ số khác nhau từ các chữ số  ; 0 ; 1 ; 2 ; 3  4 là A3  A2  48 số. 5 4 Câu 4. Lời giải Chọn D
Số cách lập số tự nhiên gồm 5 chữ số đôi một khác nhau từ các chữ số đã cho: 5!
Số cách lập số tự nhiên gồm 3 chữ số 2; 4;5 và ký tự A ( A đại diện cho 3;6 đứng cạnh nhau): 4!
Số cách hoán đổi vị trí của 3;6 trong A: 2!
Số cách lập số tự nhiên gồm 5 chữ số khác nhau từ các chữ số đã cho mà 3 và 6 đứng cạnh nhau: 4!.2!
Số cách lập số tự nhiên thỏa mãn 3 và 6 không cạnh nhau: 5! 4!.2! 72 Câu 5. Câu 6. Lời giải Chọn A
Đặt A  {1, 2,3} . Gọi S là tập các số thỏa yêu cầu thứ nhất của bài toán 6!
Ta có số các số thỏa điều kiện thứ nhất của bài toán là
 90 (vì các số có dạng aabbcc và khi hoán vị 3 2
hai số a, a ta được số không đổi)
Gọi S , S , S là tập các số thuộc S mà có 1, 2,3 cặp chữ số giống nhau đứng cạnh nhau. 1 2 3
 Số phần tử của S chính bằng số hoán vị của 3 cặp 11, 22,33 nên S  6 3 3
 Số phần tử của S chính bằng số hoán vị của 4 phần tử là có dạng a, a,bb,cc nhưng a, a không đứng 2 4! cạnh nhau. Nên S   6  6 phần tử. 2 2
 Số phần tử của S chính bằng số hoán vị của các phần tử có dạng a, a,b,b,cc nhưng a, a và , b b 1 5!
không đứng cạnh nhau nên S   6 12 12 1 4
Vậy số các số thỏa yêu cầu bài toán là: 90  (6  6 12)  76 . Câu 7. Lời giải Chọn C
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 35
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung n 3  C 20
Gọi A là biến cố “3 số lấy được lập thành 1 cấp số cộng”
Không mất tính tổng quát, gọi a, , b 
c là 3 số tự nhiên lập thành cấp số cộng với a  b  c , d là công sai của cấp số cộng với * d  N
d 1: chọn a có 18 cách ( a có thể chọn từ số 1 đến số 18)
d  2 : chọn a có 16 cách ( a có thể chọn từ số 1 đến số 16)
d  3: chọn a có 14 cách ( a có thể chọn từ số 1 đến số 14)
d  4 : chọn a có 12 cách ( a có thể chọn từ số 1 đến số 12)
d  5: chọn a có 10 cách ( a có thể chọn từ số 1 đến số 10)
d  6 : chọn a có 8 cách ( a có thể chọn từ số 1 đến số 8)
d  7 : chọn a có 6 cách ( a có thể chọn từ số 1 đến số 6)
d  8: chọn a có 4 cách ( a có thể chọn từ số 1 đến số 4)
d  9 : chọn a có 2 cách ( a có thể chọn từ số 1 đến số 2)  n  A 18 29  18 16  ... 2   90 2 P  A 90 3   . 3 C 38 20 Câu 8. Lời giải
Xét tập B  1, 4,5,6,7, 
8 , ta có B không chứa số 3.
X là một tập con của A thỏa yêu cầu bài toán khi và chỉ khi X \  
2 là một tập con của B . Do đo, số tập
con của A thỏa yêu cầu bài toán bằng số tập con của B và bằng 6 2  64 . Chọn A Câu 9. Lời giải. Chọn B
Vì có 21 bạn nam và 20 bạn nữ nên để xếp nam nữ đứng xen kẽ thì số cách xếp là: P .P . 21 20 Câu 10. Lời giải Chọn D
Có 2! cách xếp bạn A, F ngồi ở 2 đầu ghế
Có 4! cách xếp 4 bạn vào 4 vị trí còn lại
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 36
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Vậy: Có 2!.4!  48 (cách xếp). Câu 11. Lời giải. Chọn A
Chọn An đứng đầu hàng có 1 cách, chọn Cường đứng cuối hàng có 1 cách.
Sắp xếp 5 bạn còn lại có: P  5!  120 cách. 5
Vậy có: 1.1.120  120 cách. Câu 12. Lời giải Chọn B
Có 21 bạn nam và 20 bạn nữ nên để nam mữ xen kẻ thì chỉ có thể nam đứng đầu hàng.
- Số cách xếp để nam đứng đầu và nam, nữ đứng xen kẽ nhau là: P .P . 21 20 Câu 13. Lời giải Chọn B
Chọn 2 vị trí liên tiếp trong 10 vị trí, có 9 cách.
Hoán vị hai quyển sách có 2 cách.
Sắp 8 quyển sách còn lại vào 8 vị trí, có 8! cách.
Vậy có 9.2.8!  725760 cách. Câu 14. Lời giải Chọn A
Số cách chọn 4 học sinh làm 4 tổ trưởng là: 4 A . 35
Số cách chọn 4 học sinh làm tổ trưởng trong đó không có học sinh nam được chọn là: 4 A . 20
Số cách chọn 4 học sinh làm tổ trưởng trong đó không có học sinh nữ được chọn là: 4 A . 15
Vậy số cách chọn thỏa yêu cầu bài toán: 4 A   4 4 A  A  1107600 . 35 20 15  Câu 15. Lời giải Chọn D
Số cách chọn 3 em học sinh là số cách chọn 3 phần tử khác nhau trong 10 phần tử có phân biệt thứ tự
nên số cách chọn thỏa yêu cầu là 3 A . 10 Câu 16. Lời giải
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 37
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Chọn C
Mỗi cách chọn 6 ghế từ 10 ghế sắp xếp 6 người là một chỉnh hợp chập 6 của 10 phần tử. Vậy có 6 A cách chọn. 10 Câu 17. Lời giải Chọn D n! n n 1 n  2 3   
Chọn 3 trong n học sinh có C   . n n 3!.3! 6 Khi đó 3 C  120  nn   1 n  2  720. n Câu 18. Lời giải Chọn A Có 3
C cách chọn ba học sinh trong lớp. 46 Có 3
C cách chọn ban cán sự không có nam. 26 Có 3
C cách chọn ban cán sự không có nữ. 20 Vậy có 3 3 3
C  (C  C )  11440 cách chọn thỏa yêu cầu bài toán. 46 26 20 Câu 19. Lời giải Chọn B
Mỗi tập con gồm 3 phần tử của S là một tổ hợp chập 3 của 20 phần tử thuộc S và ngược lại. Nên số
các tập con gồm 3 phần tử của S bằng số các tổ hợp chập 3 của 20 phần tử thuộc S và bằng 3 C . 20 Câu 20. Lời giải Chọn C Ta dùng phần bù.
Sắp 8 người vào 8 vị trí theo hàng dọc có 8! cách sắp xếp.
Sắp ông và bà An vào 2 trong 6 vị trí (trừ vị trí đầu và cuối hàng) có 2 A cách. 6
Sắp 6 người con vào 6 vị trí còn lại có 6! cách. Vậy có 2
8! A .6!  18720 cách sắp xếp. 6 Câu 21. Lời giải Chọn A
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 38
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
 Chọn 2 trong 15 nam làm tổ trưởng và tổ phó có 2 A cách. 15
 Chọn 3 tổ viên, trong đó có nữ.
+) chọn 1 nữ và 2 nam có 2 5.C cách. 13
+) chọn 2 nữ và 1 nam có 2 13.C cách. 5 +) chọn 3 nữ có 3 C cách. 5 Vậy có 2 A  2 2 3
5.C 13.C  C  111300 cách. 15 13 5 5  Câu 22. Lời giải Chọn B
Số phần tử không gian mẫu: n 2  C . 9
Gọi A là biến cố: Hai bi được chọn cùng màu”.
Số phần tử của A là: n A 2 2  C  C . 5 4 n A 2 2 C  C
Xác suất cần tìm là: P  A    5 4  4  . n  2 C 9 9 Câu 23. Lời giải Chọn D
Vì chọn ra 3 người mà yêu cầu phải có giáo viên nam và giáo viên nữ trong đoàn nên số giáo viên nữ
được chọn chỉ có thể bằng 1 hoặc 2 . Ta xét hai trường hợp:
* Trường hợp 1: Chọn 1 giáo viên nữ: Có 1 C cách. Khi đó: 3
- Chọn 1 giáo viên nam môn Toán và 1 nam môn Vật lý: Có 1 1 C  C cách. 5 4
- Chọn 2 giáo viên nam môn Vật lý: Có 2 C cách. 4 Trường hợp này có 1 C  1 1 2 C  C  C cách chọn. 3 5 4 4 
* Trường hợp 2: Chọn 2 giáo viên nữ: Có 2
C cách chọn. Khi đó chọn thêm 1 giáo viên nam môn Vật lý: 3 Có 1
C cách. Trường hợp này có 2 1 C  C cách chọn. 4 3 4 Vậy tất cả có 1 C  1 1 2 C  C  C  2 1
 C C  90 cách chọn. 3 5 4 4 3 4 Câu 24. Lời giải Chọn D
Có hai người mà mỗi người nhận một đồ vật và một người nhận hai đồ vật.
Chọn hai người để mỗi người nhận một đồ vật: có 2 C cách chọn. 3
Chọn hai đồ vật trao cho hai người: có 2 A cách chọn. 4
Hai đồ vật còn lại trao cho người cuối cùng.
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 39
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Vậy số cách chia là : 2 C . 2 A  36 cách. 3 4 Câu 25. Lời giải Chọn C
Lấy 2 điểm trong 6 điểm trên đường thẳng  có 2 C  15 cách. 6
Vậy số tam giác được lập theo yêu cầu bài toán là: 15 tam giác. Câu 26. Lời giải Chọn D
+ Tìm công thức tính số đường chéo: Số đoạn thẳng tạo bởi n đỉnh là 2
C , trong đó có n cạnh, suy ra số n đường chéo là 2 C  n . n
+ Đa giác đã cho có 135 đường chéo nên 2 C  n  135 . n n! + Giải PT :
 n  135 , n  ,n  2  n   1 n  2n  270 2  n  n    3 270 0 n  2!2! n 18nhan    n 18 . n  1  5loai Câu 27. Lời giải Chọn C
Số đường chéo của lục giác đều (6 cạnh là): 2 C  6  9 6 Câu 28. Hướng dẫn giải Chọn A n k ! Vì C  . n k !.n  k ! Câu 29. Lời giải Chọn D Ta có: 5 5 A  C .5!  240240 . n n Câu 30. Lời giải Chọn A
Cứ hai đỉnh của đa giác n n ,
 n  3 đỉnh tạo thành một đoạn thẳng (bao gồn cả cạnh đa giác và đường chéo).
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 40
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung n
Khi đó số đường chéo là: 2 ! C  n  44   n  n n   44 2 !.2!    nn   n 11 1  2n  88   n  11  (vì n   ). n  8  Câu 31. Lời giải Chọn B
Điều kiện: n  4 ; n   n! n 1 ! 2n 4 4   Ta có: 2A  3A  2.  3.   3  n  12 . n n 1  n  4! n 5! n 4 Câu 32. Hướng dẫn giải. Chọn B
Điều kiện:10  x  N . Khi đó phương trình 10 9 8 x! x! x! A  A  9A    9 x x x (x 10)! (x  9)! (x  8)! x! x! x!    9 (x 10)! (x  9)(x 10)! (x  8)(x  9)(x 10)! x!  1 9  1 9   1   0  1   0   (x 10)! 
(x  9) (x  8)(x  9)  (x  9) (x  8)(x  9) x! (do  0 )  x 11 (x 10)! Câu 33. Lời giải Chọn B * PP tự luận: n  8! n  6!
n  4n  5n  6n  7n  8 PT   5. , n    
 5.n  4n  5n  6 5  ! n  3! n  3! 5! n  7n  8 n  17 nhan   5 2
 n 15n  544  0    n  17 . 5! n  32 loai * PP trắc nghiệm: + Nhập vào máy tính n3 3 C  5A  0 . n8 n6
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 41
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
+ Tính (CALC) lần lượt với X  15 (không thoả); với X  17 (thoả), với X  6 (không thoả), với X  14 (không thoả).
③. HƯỚNG DẪN GIẢI – VD, VDC Câu 1. Lời giải Chọn B
Gọi số cần tìm có dạng a a a a a a a , (các chữ số a ; a ; a ;a ; a ; a ;a khác nhau). 1 2 3 4 5 6 7 1 2 3 4 5 6 7
 TH 1: Số có dạng 567a a a a 4 5 6 7
+ Chọn bốn chữ số từ các chữ số 0;1; 2;3; 4;8;9 xếp vào các vị trí a ;a ;a ;a có 4 A . 4 5 6 7 7
+ Đổi chỗ hai chữ số 5 và 7 có 2 cách. Suy ra, TH 1 có 4 2.A số. 7  TH 2: a  5;7 . 1  
+ Chọn một chữ số khác 0 vào vị trí a có 6 cách. 1
+ Xếp bộ 567 vào các vị trí a , a , a , a , a , a có 4 cách. 2 3 4 5 6 7
+ Đổi chỗ hai chữ số 5 và 7 có 2 cách.
+ Chọn ba chữ số từ sáu chữ số còn lại xếp vào các vị trí còn lại có 3 A . 6 Suy ra, TH 2 có 3 6.4.2.A . 6
Vậy số các số cần tìm là: 4 3 2.A  6.4.2.A  7440 . 7 6 Câu 2. Lời giải Chọn D
Chọn X từ 24 chữ cái và chọn Y từ 10 chữ số, ta có 24.10  240 (cách chọn).
Chọn 4 chữ số giống nhau từ các chữ số ta có 10 cách chọn;
Mỗi bộ gồm 4 chữ số giống nhau, ta có một cách chọn duy nhất 1 chữ số còn lại để tổng các số là số có
chữ số tận cùng bằng 8, chẳng hạn: 4 chữ số 0 , chữ số còn lại sẽ là 8; 4 chữ số 1, chữ số còn lại sẽ là
4 ;…; 4 chữ số 9, chữ số còn lại sẽ là 2 ).
Sắp xếp 5 chữ số vừa chọn có 5 cách xếp.
Do đó, có tất cả 10.5  50 (cách chọn số ở dòng thứ hai).
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 42
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Suy ra có tất cả 240.50  12000 (biển số đẹp).
Chọn 2 biển số trong các biển số "đẹp" ta có 2 C  71994000 (cách). 12000 Câu 3. Lời giải Chọn C
Phép thử T :” An và bình chọn ngẫu nhiên ba số trong tập 0, 1, 2, 3, 4, 5, 6, 7, 8,  9 ”
Số phần tử không gian mẫu 3 3   C .C . 10 10
Biến cố A :” Trong hai bộ số của An và Bình chọn ra có nhiều nhất một số giống nhau”.
Trường hợp 1: Trong hai bộ số không có số nào giống nhau. Số các khả năng là 3 3 C .C . 10 7
Trường hợp 2: Trong hai bộ số có một số nào giống nhau. Số các khả năng 3 1 2 C .C .C . 10 3 7
Số các kết quả thuận lợi của biến cố A là 3 3 3 1 2   C .C  C .C .C . A 10 7 10 3 7 3 1 2   A C C .C 49
Vậy xác suất của biến cố A là P  A 7 3 7    . 3  C 60 10 Câu 4. Lời giải Chọn D
Viết ngẫu nhiên một số có 4 chữ số nên số phần tử của không gian mẫu là n  9.10.10.10  9000 .
Gọi A là biến cố các chữ số của số được viết ra có thứ tự tăng dần hoặc giảm dần
Gọi số tự nhiên có 4 chữ số mà các chữ số của số được viết ra có thứ tự tăng dần hoặc giảm dần có dạng abcd .
Trường hợp 1: số tự nhiên có 4 chữ số mà các chữ số của số được viết ra có thứ tự giảm dần
Vì a  b  c  d nên các chữ số đôi một khác nhau và các chữ số a , b , c , d lấy từ tập X  1,2,3, 4,5,6,7,8, 
9 và với 4 chữ số lấy ra từ X thì chỉ lập được duy nhất một số thỏa yêu cầu bài
toán. Do đó số số tự nhiên có 4 chữ số mà các chữ số của số được viết ra có thứ tự tăng dần là 4 C . 9
Trường hợp 2: số tự nhiên có 4 chữ số mà các chữ số của số được viết ra có thứ tự tăng dần
Vì a  b  c  d nên các chữ số đôi một khác nhau và các chữ số a , b , c, d lấy từ tập
Y  0,1,2,3,4,5,6,7,8, 
9 và với 4 chữ số lấy ra từ Y thì chỉ lập được duy nhất mọt số thỏa yêu cầu bài
toán. Do đó số số tự nhiên có 4 chữ số mà các chữ số của số được viết ra có thứ tự giảm dần dần là 4 C . 10
Vậy số phần tử của biến cố A là n A 4 4  C  C  336 . 9 10
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 43
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung n A 336 14
Xác suất của biến cố A là: P  A      . n  9000 375 Câu 5. Lời giải Chọn A
Xem lô đất có 4 vị trí gồm 2 vị trí 1 nền, 1 vị trí 2 nền và 1 vị trí 3 nền.
Bước 1: nhóm thứ nhất chọn 1 vị trí cho 2 nền có 4 cách và mỗi cách có
2!  2 cách chọn nền cho mỗi người. Suy ra có 4.2  8 cách chọn nền.
Bước 2: nhóm thứ hai chọn 1 trong 3 vị trí còn lại cho 3 nền có 3 cách và mỗi cách có 3!  6 cách chọn nền cho mỗi người.
Suy ra có 3.6  18 cách chọn nền.
Vậy có 8.18  144 cách chọn nền cho mỗi người. Câu 6. Lời giải Chọn A
Gọi d là trục đối xứng của đa giác đều 20 cạnh.
TH1: Xét d đi qua hai đỉnh đối diện của đa giác đều (có 10 đường thẳng) d .
Chọn 2 đoạn thẳng trong 9 đoạn thẳng song song hoặc trùng với d thì sẽ tạo thành 1 hình thang hoặc
hình chữ nhật có các đỉnh là đỉnh của đa giác.  số hình thang là 2 C (hình thang). 9
Vì vai trò của 10 đường thẳng d như nhau nên có 2 10C (hình thang). 9
Mặt khác, trong số các hình trên có 2
C hình thang (là hình chữ nhật) trùng nhau. 10
 số hình thang có cạnh song song hoặc trùng với d là 2 2 10.C  C (hình thang). 9 10
TH2 : Xét d là đường trung trực của hai cạnh đối diện của đa giác (có 10 đường thẳng) d .
Chọn 2 đoạn thẳng trong 10 đoạn thẳng song song với d thì sẽ tạo thành 1 hình thang hoặc hình chữ nhật
có các đỉnh là đỉnh của đa giác.
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 44
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung  số hình thang là 2 C (hình). 10
Vì vai trò của 10 đường thẳng d như nhau nên có 2 10C (hình thang). 10
Mặt khác, trong số các hình trên có 2
C hình thang (là hình chữ nhật) trùng nhau. 10  số hình thang là 2 2 10.C  C (hình thang). 9 10
Vậy số hình thang cần tìm là 10  2 2 C  C  2  2C  720 (hình thang). 9 10 10 Câu 7. Lời giải Chọn C Ta dùng phần bù.
Sắp 8 người vào 8 vị trí theo hàng dọc có 8! cách sắp xếp.
Sắp ông và bà An vào 2 trong 6 vị trí (trừ vị trí đầu và cuối hàng) có 2 A cách. 6
Sắp 6 người con vào 6 vị trí còn lại có 6! cách. Câu 8. Lời giải Chọn C
Số trận đấu diễn ra trong vòng 1: 2 4.C  24. 4
Số trận đấu diễn ra trong vòng 2 : 2 .
Số trận đấu diễn ra trong vòng 3: 2 .
Có tất cả 28 trận đấu. 28
Vậy ban tổ chức cần mượn sân trong  7 ngày. 4 Câu 9. Lời giải Chọn D
Số cách chọn k người trong m  n người là: k C . m  n a-1
*Số cách chọn có ít hơn a nam là: ai 1  kai 1 S  C .   1 C .  m n i 0 1 
*Số cách chọn có ít hơn b nữ là:  1  k bi 1 S   b b i C .  C . 2 n m i0
Số cách chọn thoả mãn điều kiện bài toán là: k C  (S  S ) . mn 1 2 Câu 10. Lời giải Chọn D
Vì chữ số 2 đứng liền giữa hai chữ số 1 và3 nên số cần lập có bộ ba số 123 hoặc 321.
TH1: Số cần lập có bộ ba số 123 .
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 45
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Nếu bộ ba số 123 đứng đầu thì số có dạng 123abcd . Có 4
A  840 cách chọn bốn số a , b , c, d nên có 4 A  840 số. 7 7
Nếu bộ ba số 123 không đứng đầu thì số có 4 vị trí đặt bộ ba số 123 .
Có 6 cách chọn số đứng đầu và có 3
A  120 cách chọn ba số b , c , d . 6 Theo quy tắc nhân có 3 6.4.A  2880 số 6
Theo quy tắc cộng có 840  2880  3720 số.
TH2: Số cần lập có bộ ba số 321.
Do vai trò của bộ ba số 123 và 321 như nhau nên có 2840  2880  7440. Câu 11. Lời giải Chọn C
Một tam giác được tạo bởi ba điểm phân biệt nên ta xét:
TH1. Chọn 1 điểm thuộc d và 2 điểm thuộc d   có 1 2 C .C tam giác. 1 2 10 n
TH2. Chọn 2 điểm thuộc d và 1 điểm thuộc d   có 2 1 C .C tam giác. 1 2 10 n Như vậy, ta có 1 2 2 1 C .C C .C  2800 10 n 10 n n! n!  10.        n   45. n   2800 5nn  1 45n 2800 2! 2 ! 1! 1 ! n  20 (tm) 2
 5n  40n  2800  0  n  28 (l) Vậy n  20 . Câu 12. Lời giải Chọn D
+ Tìm công thức tính số đường chéo: Số đoạn thẳng tạo bởi n đỉnh là 2
C , trong đó có n cạnh, suy ra số n đường chéo là 2 C  n . n
+ Đa giác đã cho có 135 đường chéo nên 2 C  n  135 . n n! + Giải PT :
 n  135 , n  ,n  2  n   1 n  2n  270 2      n 3n 270 0 n  2!2! n 18nhan    n  18 . n  1  5loai Câu 13. Lời giải Chọn C 2017.2017! 2016.2016! 2.2! 1.1!
2017.2017! 2016.2016! ... 2.2!1.1! P   ...   2017! 2017! 2017! 2017! 2017!
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 46
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
2018 12017!2017   1 2016! ... 3  1 2! 2   1 1!  P  2017!
2018! 2017 ! 2017! 2016 ! ... 3!2 ! 2!1 ! 2018!1! 1  P    P  2018  . 2017! 2017! 2017! Câu 14. Lời giải Chọn C * PP tự luận: n! 2n! + PT  3.     3nn   1  2 . n 2n      , n  , n  2 1 42 0 n    n   42 0 2 ! 2 2 ! n  6 nhan 2
 n  n  42  0    n  6 . n  7  loai * PP trắc nghiệm: + Nhập vào máy tính PT 2 2 3A  A  42  0 . n 2n
+ Tính (CALC) lần lượt với X  9 (không thoả); với X  8 (không thoả), với X  6 (thoả), với X  10 (không thoả). Câu 15. Lời giải Chọn C
PP sử dụng máy tính để chọn đáp số đúng (PP trắc nghiệm): + Nhập PT vào máy tính: 6 7 8 9 8 C  3C  3C  C  2C  0 n n n n n2
+ Tính (CALC) lần lượt với X  18 (không thoả); với X  16 (không thoả); với X  15 (thoả), với X 14 (không thoả)
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 47
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung GT Chương ⓶ §➌. NHỊ THỨC NEWTON ⓫ Ⓐ Tóm tắt lý thuyết
➊. Công thức nhị thức Newton Định lý: n n k nk k 0 n 1 n1 2 n2 2 n1 n
(a  b)   C a b  C a C a b  C a b ... 1 C ab  n n n n n n n Cnb (1) k0 Hệ quả:  a = b = 1: n 0 1 2 C C . . n n n  n C  a =1; b = –1: 0 1 0  C C  . . ( 1  )n n n n Cn Ta có: n 0 1 2 2 n n
(1  x)  Cn  xCn  x Cn  . .  x Cn  0 C  1 C  . .  n C  n n n n 2  0 C  1 C  2 C  . .  ( n n 1) C  n n n n 0
Chú ý: Trong công thức khai triển nhị thức Newton:
 Số các hạng tử là n + 1.
 Các hạng tử có số mũ của a giảm dần, số mũ của b tăng dần, nhưng tổng các số mũ bằng n.
 Các hệ số của các hạng tử cách đều hai hạng tử đầu và cuối thì bằng nhau.
 Hạng tử thứ k + 1: k nk k n C a b ➋. Tam giác Pascal
 Trong công thức nhị thức Newton cho n = 0, 1, 2, … và xếp
các hệ số thành dòng ta nhận được tam giác sau đây, gọi là tam giác Pascal. Nhận xét:  Từ công thức k 1  k k n C 1  n C 1  n
C suy ra cách tính các số ở mỗi
dòng dựa vào các số ở dòng trước nó. Ⓑ Phân dạng bài tập
①.Dạng 1: Khai triển một nhị thức Newton . Bài tập minh họa:
Câu 1: Viết khai triển theo công thức nhị thức Newton 5 (x  y) . Ⓐ. 5 4 3 2 2 3 4 5
x  5x y 10x y 10x y  5xy  y . Ⓑ. 5 4 3 2 2 3 4 5
x  5x y 10x y 10x y  5xy  y . Ⓒ. 5 4 3 2 2 3 4 5
x  5x y 10x y 10x y  5xy  y . Ⓓ. 5 4 3 2 2 3 4 5
x  5x y 10x y 10x y  5xy  y . Lời giải Ta có 5 (x  y) = 5 4 3 2 2 3 4 5
x  5x y 10x y 10x y  5xy  y
Câu 2: Trong khai triển nhị thức Niu-tơn của 2019 (3  2x) có bao nhiêu số hạng?
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 48
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Ⓐ. 2019 . Ⓑ. 2018 . Ⓒ. 2020 . Ⓓ. 2021. Lời giải
Ta có: Khai triển nhị thức Niu-tơn (  )n a b có n 1 số hạng.
Vậy trong khai triển nhị thức Niu-tơn của 2019 (3  2x) có 2020 số hạng.
Câu 3: Từ khai triển biểu thức  x  10
1 thành đa thức. Tổng các hệ số của đa thức là Ⓐ. 1023 . Ⓑ. 512 . Ⓒ. 1024 . Ⓓ. 2048 . Lời giải
Xét khai triển f (x)   x   10 10 1 k  C . kx . 10 k 0
Gọi S là tổng các hệ số trong khai triển thì ta có S  f    10 10 (1) 1 1  2  1024 .
②.Dạng 2: Tìm hệ số, số hạng trong khai triển nhị thức Newton . Bài tập minh họa: 10  2  Câu 1: Hệ số của 2
x trong khai triển của biểu thức 2 x    bằng  x  Ⓐ. 3124 . Ⓑ. 2268 . Ⓒ. 13440 . Ⓓ. 210 . Lời giải
Số hạng tổng quát của khai triển:    T  C x  C x   k  k   . k    k 10 k k 2 2 k k 20 3 2 k 0 10, 1 10   10    x  Số hạng chứa 2
x ứng với: 20 3k  2  k  6 . Hệ số cần tìm là: 6 6 2 C  13440 . 10 10  2 
Câu 2: Số hạng không chứa x trong khai triển x    là  x  Ⓐ. 5 C . Ⓑ. 5 5 C .2 . Ⓒ. 5 C . Ⓓ. 5 5 C .2 . 10 10 10 10 Lời giải 10  2 
Số hạng tổng quát trong khai triển x    là:  x  k  2 k k 10  k k 102 T  C x .  C .2 k x k 1  10   10  x 
Số hạng không chứa x trong khai triển tương ứng với 10  2k  0  k  5.
Vậy số hạng không chứa x trong khai triển là: 5 5 C .2 . 10 12  1 
Câu 3: Số hạng độc lập với x trong khai triển 2  2x   là  x  Ⓐ. 8 4 2 .C . Ⓑ. 6 6 2 .C . Ⓒ. 4 4 2 .C . Ⓓ. 4 4 2 .C . 12 12 12 12
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 49
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Lời giải 12 12 12 k 12  1   1 k  Ta có: 2  2x  C      2 2x   C 2k k k 3k 1  2 x 12 12  x  k 0  x  k 0
Số hạng độc lập với x khi 3k  12  0  k  4
Vậy số hạng độc lập với x là: 4 4 2 .C => chọn C 12 ③
Chứng minh, tính giá trị của biểu thức đại số tổ hợp có sử dụng nhị .Dạng 3: thức Newton . Bài tập minh họa:
Câu 1: Cho n là số nguyên dương. Khi đó tổng 0 1 2
S  C  C  C  ...  n C là n n n n Ⓐ. 3n . Ⓑ. 2n . Ⓒ. 1. Ⓓ. 0 . Lời giải Xét:   xn 0 n 1 n 1  2 n2 n 0 1  C x  C x  C x  ... C x . n n n n Chọn x  1 ta được: n 0 1 2
2  C  C  C  ...  n C . n n n n Vậy  2n S . Câu 2: Cho 8 9 10 15
S  C  C  C  ...  C . Tính S . 15 15 15 15 Ⓐ. 14 S  2 . Ⓑ. 15 S  2 . Ⓒ. 13 S  2 . Ⓓ. 12 S  2 . Lời giải
Khai triển nhị thức 1 x15 0 1 2 2 7 7 8 8 15 15
 C  C x  C x  ... C x  C x  ... C x . 15 15 15 15 15 15 Thay x  1 ta được: 15 0 1 2 7 8 15
2  C  C  C  ...  C  C  ...  C . 15 15 15 15 15 15 Mà nk k 15 0 14 1 13 2 8 7 C
 C  C  C ,C  C ,C  C ,...,C  C . n n 15 15 15 15 15 15 15 15 15  2  2 8 9 10 15 C  C  C  ... C 15 15 15 15  15  2  2S . 14  S  2 . Câu 3: Tổng 1 2 2018 C  C  ... C bằng 2018 2018 2018 Ⓐ. 2018 2 . Ⓑ. 2018 2 1. Ⓒ. 2018 2 1. Ⓓ. 2016 4 . Lời giải Ta có 1  2018 2018 i 0 1 2 2018 1
  C  C  C  C ... C 2018 2018 2018 2018 2018 i0 Suy ra 1 2 2018 2018 C  C  ... C  2 1 . 2018 2018 2018
Câu 4: Cho một tập hợp có n phần tử ( n là số tự nhiên). Số tập con khác rỗng của nó là: Ⓐ. 2n . Ⓑ. 2n 1. Ⓒ. 2n 1. Ⓓ. 2n 1 Lời giải
Gọi X là tập hợp có n (n )  phần tử.
+ Số tập con có 1 phần tử của X là 1 C . n
+ Số tập con có 2 phần tử của X là 2 C . n …
+ Số tập con có n phần tử của X là n C . n
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 50
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Suy ra số tập con khác rỗng của X là 1 2 T  C  C  ... n  C . n n n
Xét nhị thức   xn 0 1 2 2 1  C  C x  C x  ... n n  C x (*) . n n n n
Thay x  1 vào ta được:   n 0 1 2 1 1  C  C  C  ... n  C  T  2n 1. n n n n
Câu 5: Tính tổng tất cả các số nguyên dương n thỏa mãn 2 2 A  3C  15  5n . n n Ⓐ. 13 . Ⓑ. 10 . Ⓒ. 12. Ⓓ. 11. Lời giải .
Điều kiện: n   , n  2 . ( n n 1) n  5 Ta có: 2 2 2
A  3C  15  5n  n(n 1)  3.
 5n 15  0  n 11n  30  0  . n n 2  n  6
Hai nghiệm đều thỏa mãn điều kiện, chúng có tổng bằng 11 Ⓒ Bài tập rèn luyện
Câu 1:Trong khai triển  a  6 2
1 , tổng ba số hạng đầu là: Ⓐ. 6 5 4 2a  6a 15a .
Lời giải :...................................................................... Ⓑ. 6 5 4 2a 15a  30a . Ⓒ. 6 5 4 64a 192a  480a .
...................................................................................... Ⓓ. 6 5 4 64a 192a  240a .
......................................................................................
Câu 2:Ba số hạng đầu tiên theo lũy thừa tăng dần của x trong khai triển của 10 là Ⓐ. 2 1, 45 , x 120x .
Lời giải :...................................................................... Ⓑ. 2 1, 4 , x 4x . Ⓒ. 2 1, 20x,180x .
...................................................................................... Ⓓ. 2 10, 45 , x 120x .
......................................................................................
Câu 3:Ba số hạng đầu tiên theo lũy thừa tăng dần của x trong khai triển của 10 là: Ⓐ. 2 1, 45x, 120x .
Lời giải :...................................................................... Ⓑ. 2 1, 4 , x 4x . Ⓒ. 1, 20x, 180x2.
...................................................................................... Ⓓ. 2 10, 45 , x 120x .
......................................................................................
Câu 4:Trong khai triển   16 x y
, tổng hai số hạng cuối là Ⓐ. 15 8 16x y  y .
Lời giải :...................................................................... Ⓑ. 15 4 16x y  y .
...................................................................................... Ⓒ. 15 4 16xy  y .
...................................................................................... Ⓓ. 15 8 16xy  y .
Câu 5:Trong khai triển nhị thức:  a  6 2
1 . Ba số hạng đầu là: Ⓐ. 6 5 4 2a  6a 15a .
Lời giải :...................................................................... Ⓑ. 6 5 4 2a 12a  30a . Ⓒ. 6 5 4 64a 192a  480a .
...................................................................................... Ⓓ. 6 5 4 64a 192a  240a .
......................................................................................
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 51
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung 12 21  3   1 
Câu 6:Sau khi khai triển và rút gọn biểu thức f  x 2 3  x   2x    
thì f  x có bao nhiêu số hạng? 2   x   x  Ⓐ. 30 . Ⓑ. 32 . Ⓒ. 29 . Ⓓ. 35 .
Lời giải :......................................................................
......................................................................................
...................................................................................... x x   x x   x2   x10 10 9 8 1 1 1 Câu 7:Biểu thức  .  . ... bằng 10! 9! 1! 8! 2! 10! Ⓐ. 10!. Ⓑ. 20!. 1 1
Lời giải :...................................................................... Ⓒ. . Ⓓ. . 10! 100!
......................................................................................
......................................................................................
Câu 8:Cho khai triển 1 2x20 2
 a  a x  a x  a x . Giá trị của a  a  a  a bằng: 0 1 2 20 20 0 1 2 20 Ⓐ. 1. Ⓑ. 20 3 . Ⓒ. 0 . Ⓓ. 1.
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 9:Trong khai triển   11 x y
, hệ số của số hạng chứa 8 3 x .y là Ⓐ 3 . C  C . 11 . Ⓑ. 3 11
Lời giải :...................................................................... 5 8 Ⓒ.  C C 11 . Ⓓ. 11 .
......................................................................................
......................................................................................
Câu 10:Trong khai triển  x  10 2
1 , hệ số của số hạng chứa 8 x là: Ⓐ. 1  1520. Ⓑ. 45 . Ⓒ. 256 . Ⓓ. 11520 .
Lời giải :......................................................................
......................................................................................
...................................................................................... 7
Câu 11:Trong khai triển 3x  y , số hạng chứa 4 3 x y là: Ⓐ.  4 3 2835x y . Ⓑ. 4 3 2835x y .
Lời giải :...................................................................... Ⓒ. 4 3 945x y . Ⓓ.  4 3 945x y .
......................................................................................
......................................................................................
Câu 12:Nếu khai triển nhị thức Niutơn:  x  5 5 4 3 2
1  a x  a x  a x  a x  a x  a . 5 4 3 2 1 0
thì tổng a  a  a  a  a  a bằng 5 4 3 2 1 0 Ⓐ. 32. Ⓑ. 0. Ⓒ. 1. Ⓓ. 32 .
Lời giải :......................................................................
......................................................................................
...................................................................................... Câu 13:Hệ số của 3
x trong khai triển  x  8 2 bằng Ⓐ. 5 5 C .2 . Ⓑ. 5 5 C .2 . 8 8
Lời giải :...................................................................... Ⓒ. 3 3 C .2 . Ⓓ. 3 3 C .2 . 8 8
......................................................................................
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 52
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
......................................................................................  1 n 
Câu 14:Tìm hệ số của số hạng chứa 8 x trong khai triển 5  x 
biết n là số nguyên dương thỏa mãn 3   x  n 1  n C  C  7 n  3 . n4 n3   Ⓐ. 495 . Ⓑ. 313 . Ⓒ. 1303 . Ⓓ. 13129 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 15:Tìm hệ số của 16
x trong khai triển Px  x  x10 2 2 Ⓐ. 3630. Ⓑ. 3360. Ⓒ. 3330. Ⓓ. 3260.
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 16:Trong khai triển, a  b8 2
hệ số của số hạng chứa 4 4 a b là Ⓐ. 1120 . Ⓑ. 560 . Ⓒ. 140 . Ⓓ. 70 .
Lời giải :......................................................................
......................................................................................
...................................................................................... 15  1 
Câu 17:Tính số hạng không chứa x trong khai triển x     2x  3300 3300 Ⓐ. . Ⓑ. - . 64 64
Lời giải :...................................................................... 3003 3003 Ⓒ.  . Ⓓ. .
...................................................................................... 32 32
...................................................................................... 8  1  Câu 18:Số hạng của 4 x trong khai triển 3 x    là  x  Ⓐ. 5 4 C x . Ⓑ. 4 4 C x . 8 8
Lời giải :...................................................................... Ⓒ. 5 4 C  x . Ⓓ. 3 4 C  x . 8 8
......................................................................................
...................................................................................... 10  1  Câu 19:Tìm hệ số của 4 x trong khai triển x    , x  0 .  x  Ⓐ. 120. Ⓑ. 1  20. Ⓒ. 210 . Ⓓ. 2  10.
Lời giải :......................................................................
......................................................................................
...................................................................................... Câu 20:Hệ số của 7
x trong khai triển  x  10 2 là Ⓐ. 3 7 C 2 . Ⓑ. 3 C . Ⓒ. 3 3 C 2 . Ⓓ. 10 10 10
Lời giải :...................................................................... 7 3 C 2 . 10
......................................................................................
......................................................................................
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 53
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung 9  2  Câu 21:Hệ số của 3 x trong khai triển x   là 2   x  Ⓐ. 1. Ⓑ. 1  8. Ⓒ. 144 . Ⓓ. 6  72.
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 22:Cho số nguyên dương n thỏa mãn 1 2
2C  3C ...  n  C 
. Số hạng không chứa x trong n n  1 n 2621439 n  1 n 
khai triển của biểu thức 2 x    bằng  x  Ⓐ. 43758 . Ⓑ. 31824 . Ⓒ. 18564 . Ⓓ. 1.
Lời giải :......................................................................
......................................................................................
...................................................................................... 10  1  Câu 23:Hệ số của 6 x trong khai triển 3  x   bằng  x  Ⓐ. 792. Ⓑ. 252. Ⓒ. 165. Ⓓ. 210.
Lời giải :......................................................................
......................................................................................
......................................................................................  1 n 
Câu 24:Số hạng thứ 3 của khai triển 2x  
không chứa x . Tìm x biết rằng số hạng này bằng số hạng thứ 2   x 
hai của khai triển   30 3 1 x . Ⓐ. 2  . Ⓑ. 1. Ⓒ. 1  .
Ⓓ. 2 . Lời giải :......................................................................
......................................................................................
...................................................................................... Câu 25:Trong khai triển   5
2a b , hệ số của số hạng thứ 3 bằng: Ⓐ. 8  0. Ⓑ. 80 . Ⓒ. 1  0. Ⓓ. 10 .
Lời giải :......................................................................
......................................................................................
...................................................................................... n 2
 x  a  a x  a x   n a  a  ... a  729 Câu 26:Giả sử (1 2 ) ... a x 0 1 2 n , biết rằng 0 1 n
. Tìm n và số lớn nhất a , a ,..., a trong các số 0 1 n . Ⓐ. n=6, maxa a . k    240 4
Lời giải :...................................................................... Ⓑ. n=6, maxa a . k    240 6
...................................................................................... Ⓒ. n=4, maxa a . k    240 4 Ⓓ. n=4, maxa a
...................................................................................... k    240 6 a a a Câu 27:Cho 1 2xn 1  a  a x  ... n  a x , * n   . Biết 1 2 a    ... n 
 4096 . Số lớn nhất trong các số 0 1 n 0 2 2 2 2n
a , a , a ,..., a có giá trị bằng 0 1 2 n Ⓐ. 126720 Ⓑ. 924 . Ⓒ. 972 Ⓓ. 1293600
Lời giải :......................................................................
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 54
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
......................................................................................
......................................................................................
Câu 28:Cho khai triển 1 2xn 2  a  a x  a x ... n  a x , trong đó *
n   và các hệ số thỏa mãn hệ thức 0 1 2 n a a 1 a   ... n 
 4096 . Tìm hệ số lớn nhất? 0 2 2n Ⓐ. 1293600 . Ⓑ. 126720 . Ⓒ. 924 . Ⓓ. 792 .
Lời giải :......................................................................
......................................................................................
...................................................................................... Câu 29:Tổng 0 1 2 3
T  C  C  C  C  ... n  C bằng n n n n n Ⓐ. 2n T  . Ⓑ. 4n T  .
Lời giải :...................................................................... Ⓒ. 2n T  1. Ⓓ. 2n T  1.
......................................................................................
......................................................................................
Câu 30:Trong khai triển nhị thức   7
3 0,02 , tìm tổng số ba số hạng đầu tiên Ⓐ. 2289, 3283 . Ⓑ. 2291,1012 . Ⓒ. 2275, 93801 . Ⓓ. 2291,1141 .
Lời giải :......................................................................
......................................................................................
...................................................................................... 5
Câu 31:Nếu khai triển nhị thức Niutơn  x   5 4 3 2
1  a x  a x  a x  a x  a x  a 5 4 3 2 1 0
thì tổng a  a  a  a  a  a bằng: 5 4 3 2 1 0 Ⓐ. 32 . Ⓑ. 0 . Ⓒ. 1. Ⓓ. 32 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 32:Khai triển   5
x y rồi thay x , y bởi các giá trị thích hợp. Tính tổng 0 1 5 S  C  C  ... C . 5 5 5 Ⓐ. 32 . Ⓑ. 64 . Ⓒ. 1. Ⓓ. 12 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 33:Tính giá trị của tổng 0 1 6
S  C  C  .. C bằng 6 6 6 Ⓐ. 64 . Ⓑ. 48 . Ⓒ. 72 . Ⓓ. 100 .
Lời giải :......................................................................
......................................................................................
...................................................................................... m
Câu 34:Giả sử 1 x 2 1 x  x ... 2 1 x  x  ... n  x  2  a  a x  a x  ... m  a x . Tính  a 0 1 2 m r r 0 Ⓐ. 1 Ⓑ. n . Lời giải
:...................................................................... Ⓒ. n   1 ! Ⓓ. n!
......................................................................................
......................................................................................
Câu 35:Nếu khai triển nhị thức Niutơn:  x  5 5 4 3 2
1  a x  a x  a x  a x  a x  a . 5 4 3 2 1 0
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 55
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
thì tổng a  a  a  a  a  a bằng 5 4 3 2 1 0 Ⓐ. 3  2. Ⓑ. 0.
Lời giải :...................................................................... Ⓒ. 1. Ⓓ. 32 .
......................................................................................
...................................................................................... 1 1 1
Câu 36:Tính các tổng sau: 0 1 2 S  C  C  C  ... n C 1 n 2 n 3 n n 1 n n 1 2  1 n 1 2  1 Ⓐ. . Ⓑ. .
Lời giải :...................................................................... n 1 n 1 n 1 2  1 n 1 2  1
...................................................................................... Ⓒ. 1. Ⓓ. 1 n 1 n 1
...................................................................................... Câu 37:Tính các tổng sau: 2 3 4
S  2.1.C  3.2C  4.3C  ...  n(n 1) n C . 3 n n n n Ⓐ. 2 ( 1)2   n n n . Ⓑ. 2 ( 2)2   n n n .
Lời giải :...................................................................... Ⓒ. 3 ( 1)2   n n n . Ⓓ. 2 ( 1)2   n n n
......................................................................................
...................................................................................... 2 2 2 2 Câu 38:Tính tổng  0 C    1 C    2 C  ...  n C n n n n  Ⓐ. n C . Ⓑ. n 1 C  . 2n 2n
Lời giải :...................................................................... Ⓒ. 2 n C . Ⓓ. n 1 C  2n 2n 1 
......................................................................................
......................................................................................
Câu 39:Số tự nhiên n thỏa 1 2 1.C  2.C  ...  . n Cn  1024 thì n n n Ⓐ. n  7. Ⓑ. n  8. Ⓒ. n  9. Ⓓ. n  10.
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 40:Tìm số nguyên dương n thỏa mãn 0 1 2
2C  5C  8C  ... n  C  . n n n 3 2 n 1600 n Ⓐ. n  5. Ⓑ. n  7 .
Ⓒ. n  10 . Ⓓ. n  8 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 41:Cho số nguyên dương n thỏa mãn 1 3 2n 1 C C  C      512 . Tính tổng 2n 2n 2n 2 2 2 3 S 
C  C   n 2 2 3 1 .n . n C . n n n Ⓐ. S  4 . Ⓑ. S  5. Ⓒ. S  6 . Ⓓ. S  7 .
Lời giải :......................................................................
......................................................................................
...................................................................................... 1 1 1 1 ( 1  )n Câu 42:Tính tổng sau: 0 1 3 4
S  C  C  C  C  ... n C 2 n 4 n 6 n 8 n 2(n 1) n 1 Ⓐ. . Ⓑ. 1. 2(n 1)
Lời giải :...................................................................... 1 Ⓒ. 2. Ⓓ.
...................................................................................... (n 1)
......................................................................................
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 56
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Câu 43:Trong các câu sau câu nào sai? Ⓐ. 3 11 C  C . 14 14
Lời giải :...................................................................... Ⓑ. 3 4 4 C  C  C . 10 10 11 Ⓒ. 0 1 2 3 4
C  C  C  C  C  16 .
...................................................................................... 4 4 4 4 4 Ⓓ. 4 4 5 C  C  C .
...................................................................................... 10 11 11
Câu 44:Biết hệ số của 2
x trong khai triển của 1 3 n x là 90 . Tìm n . Ⓐ. n  5. Ⓑ. n  8 . Ⓒ. n  6 . Ⓓ. n  7 .
Lời giải :......................................................................
......................................................................................
...................................................................................... n
Câu 45:Biết rằng hệ số của 4
x trong khai triển nhị thức Newton 2  x ,  *
n   bằng 280 , tìm n ? Ⓐ. n  8 . Ⓑ. n  6 . Ⓒ. n  7 . Ⓓ. n  5 .
Lời giải :......................................................................
......................................................................................
...................................................................................... Câu 46:Biết n  0 1 2 3 2 k k n n
C  iC  C  iC  i C   i C  i , với k
C là các số tổ hợp chập k của n và n n n n n n  32768 n 2 i  1. Đặt k k T
 i C , giá trị của T bằng k 1  n 8 Ⓐ. 3  30i . Ⓑ. 8  i . Ⓒ. 3  6i . Ⓓ. 1  20i .
Lời giải :......................................................................
......................................................................................
...................................................................................... 1 1 1 1 1 Câu 47:Giá trị của A     ...  bằng 1!2018! 2!2017! 3!2016! 1008!1011! 1009!1010! 2017 2 1 2018 2 Ⓐ. . Ⓑ. .
Lời giải :...................................................................... 2018! 2019! 2018 2 1 2017 2
...................................................................................... Ⓒ. . Ⓓ. . 2019! 2018!
......................................................................................
Câu 48:Số tự nhiên n thỏa 1 2 C  2.C  ...  . n n C  112641 thì n n n Ⓐ. n  10 . Ⓑ. n  11 . Ⓒ. n  12 . Ⓓ. n  9 .
Lời giải :......................................................................
......................................................................................
......................................................................................
Câu 49:Tìm số tự nhiên n thỏa mãn n 3 C  5A . n5 n3
Ⓐ. n 14 . Ⓑ. n 17 .
Ⓒ. n  20 . Ⓓ. n  15.
Lời giải :......................................................................
......................................................................................
...................................................................................... 0 1 2 n 100 C C C C 2  n  3
Câu 50:Tìm số tự nhiên n thỏa mãn n n n    ... n   . 1.2 2.3 3.4 n   1 n  2 n   1 n  2
Ⓐ. n  101. Ⓑ. n  98. Ⓒ. n  99 . Ⓓ. n  100 .
Lời giải :......................................................................
......................................................................................
......................................................................................
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 57
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung ĐÁP ÁN TRẮC NGHIỆM
Dạng toán 01: Khai triển một nhị thức Newton cụ thể 1 2 3 4 5 6 7 D C C A D D C
Dạng toán 02: Tìm hệ số và số hạng trong khai triển 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 A B D A B B A B A C A B C C C D D
Dạng toán 03: Hệ số lớn nhất, nhỏ nhất trong khai triển 25 26 27 28 B A A B
Dạng toán 04: Tính tổng hữu hạn các C (không đạo hàm, tích phân) 29 30 31 32 33 34 35 36 37 38 A B B A A C B B A A
Dạng toán 05: Tính tổng hữu hạn các C (Newton và đạo hàm) 39 40 41 B B B
Dạng toán 06: Tính tổng hữu hạn các C (Newton và tích phân) 42 A
Dạng toán 07: Toán về đẳng thức có dùng nhị thức Newton 43 44 45 46 47 D A C B C
Dạng toán 08: PT, BPT, HPT có dùng nhị thức Newton
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 58
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung 48 49 50 B C B
HƯỚNG DẪN GIẢI - ĐÁP ÁN CHI TIẾT Câu 1. Lời giải Chọn D Ta có: 2a  6 0 6 6 1 5 5 2 4 4
1  C .2 a  C .2 a  C .2 a ... 6 6 6
Vậy tổng 3 số hạng đầu là 6 5 4 64a 192a  240a . Câu 2. Lời giải Chọn C Ta có 1 2x 10 10 k 10k k 0 1 2 2
 C x y  C  C (2x)  C (2x)  20 10 10 10 k 0 2  1  20x 180x  ...
Vậy 3 số hạng đầu tiên theo lũy thừa tăng dần của x là: 2 1, 20 , x 180x Câu 3. Lời giải Chọn C 10 10 Ta có 1 2x k 10 k  k 0 1 2 2  C x y 
 C C (2x) C (2x)  20 10 10 10 k 0  2 1 20x 180x ...
Vậy 3 số hạng đầu tiên theo lũy thừa tăng dần của x là: 2 1, 20x, 180x Câu 4. Lời giải Chọn A 16 15 16 Ta có: x  y  0 16 1 15 15
 C x  C x . y  ... C x  y  16  C y 16 16 16 16   Câu 5. Lời giải Chọn D 6 Ta có 2a 6 k 6 k  k 0 6 1 5 2 4 2 1  C (2a) ( 1   ) C
 .(2a) C (2a) (1) C (2a) (1) ... 6 6 6 6 k0
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 59
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung 0 6 6 1 5 5 2 4 4 6 5 4
 C .2 a C 2 a  C 2 a ... 64a 192a  240a ... 6 6 6 Ba số hạng đầu là: 6 5 4 64a 192a  240a . Câu 6. Lời giải Chọn D 12  3 12 k k  3 k 2  12  x      12 C  2 x k k 24 3  C 3 k x  12     x  12 k 0  x  k 0 21  1 21 k k  1 k 3  21  2x     21 C  3 2x k 21k 635  C 2 k x 21  2     x  2 21 k 0  x  k 0
Ta cho k chạy từ 0 đến 12 thì các số mũ của x không bằng nhau. 12  3  21  1  Với khai triển 2 x  
 ta có 13 số hạng; Với khai triển 3 2x  
 ta có 22 số hạng. Vậy tổng số  x  2  x  hạng là: 35. Câu 7. Lời giải Chọn C  x   10 1 k k x 1 10! 1 Ta có .  . . . 1 k k x  x . . . 1 k k k C x x    với 0  k  10 . 10  10 k ! 10  k ! 10! k  ! 10  k   10 ! 10! x x   x x   x2   x10 10 9 8 1 1 1 10  1 1 .  .  ...  C .x . 1 k k k  x   x 1 1 x10  . 10  10 10! 9! 1! 8! 2! 10! 10! 10! 10! k 0 Câu 8. Lời giải Chọn A 1 2x20 2
 a  a x  a x  a x   1 . 0 1 2 20 20 Thay x  1 vào  
1 ta có: a  a  a  a   20 1  1. 0 1 2 20 Câu 9. Lời giải Chọn B
Số hạng tổng quát trong khai triển trên là 11 T  C .x  . 1 k k k . k y k 1  11  
Yêu cầu bài toán xảy ra khi k  3.
Khi đó hệ số của số hạng chứa 8 3 x .y là: 3 C . 11
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 60
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Câu 10. Lời giải Chọn D
Số hạng tổng quát trong khai triển trên là 10 10 T  C .2 .x  . 1 k k k k k 1  10  
Yêu cầu bài toán xảy ra khi 10  k  8  k  2 .
Khi đó hệ số của số hạng chứa 8 x là: 2 8 C .2  11520 . 10 Câu 11. Lời giải Chọn A
Số hạng tổng quát trong khai triển trên là 7 7 T  C .3 x  . 1 k k k k . k y k 1  7  
Yêu cầu bài toán xảy ra khi k  3.
Khi đó hệ số của số hạng chứa 4 3 x .y là: 3 4 4 3 4
C .3 .x .y  2835.x .y . 7 Câu 12. Lời giải Chọn B Ta có x  5 0 5 1 4 2 3 2 5 0 5
1  C .(x)  C (x) (1)  C (x) ( 1  ) ...C (x) ( 1  ) 5 5 5 5 0 5 1 4 2 3 3 2 4 1 5 0
 C .x C .x C .x C .x C .x C .x 5 5 5 5 5 5
Khi đó tổng a  a  a  a  a  a bằng: 0 1 2 3 4 5
C C  C C  C C  0 5 4 3 2 1 0 5 5 5 5 5 5 Câu 13. Lời giải Chọn B
Số hạng tổng quát của khai triển: 8 . 2 k k k C x   . 8   Số hạng chứa 3
x ứng với 8  k  3  k  5 . Vậy hệ số của 3 x là 5 5 C .2 . 8 Câu 14. Lời giải Chọn A Ta có n 1  n C  C  7 n   C  C  n  n n  3 3 3 7 3 4 3 n4 n3  
n  4n  3n  2 n  3n  2n   1    7n  3 3! 3!
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 61
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
 n  4n  2  n  2n   1  42  n  12 . 12  1  12k 11   k  1 k 36 k 
Số hạng thứ k 1 trong khai triển 5  x  là T  C . k x  C x . k 1  12  3   5 2 3   x  12  x  11 Ta cần tìm k sao cho 3  6  k  8  k  8 . 2
Do đó hệ số của số hạng chứa 8 x là 8 C  495 . 12 Câu 15. Lời giải Chọn B
Ta có P  x  x  2x 10 10 10 2 k 2 10k k k k 20
 C (x ) .(2x) C (2) k x 10 10 k 0 k 0 Số hạng tổng quát là k k 20 T C ( 2) k x  k 1    10 Để số hạng chứa 16
x ta chọn k sao cho: 20  k 16  k  4 Hệ số của 16
x trong khai triển Px  x  x10 2 2 là: 4 4 C (2)  3360 10 Câu 16. Lời giải Chọn A.
Số hạng tổng quát trong khai triển trên là 8 T  C .a  . 2 k k k . k b k 1  8  
Yêu cầu bài toán xảy ra khi k  4 .
Khi đó hệ số của số hạng chứa 4 4 a .b là: 4 4 C .2  1120 . 8 Câu 17. Lời giải Chọn C 15 15 15  1  k k 1 k k 1 Ta có: 15 k 153 x   C (x) .( ) C ( ) k x  2  15 2 15  2x  k 0 2x k 0 2 k 1 Số hạng tổng quát là k 15 3 T C ( ) k x  k 1    15 2
Để số hạng không chứa x ta chọn k sao cho:15 3k  0  k  5 15  1  1 3003
Vậy số hạng không chứa x trong khai triển x   là: 5 5 C ( )   2   2x  15 2 32 Câu 18.
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 62
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Lời giải Chọn A k   1 k k 
Số hạng tổng quát trong khai triển là T  C .  .  x 8 3 k 244 . C . k x k 1 8   8  x 
Ta cần tìm k sao cho: 24  4k  4  4k  20  k  5 . Vậy số hạng của 4
x trong khai triển là 5 244.5 5 4 C .x  C .x . 8 8 Câu 19. Lời giải Chọn B   1 k 
Số hạng tổng quát của khai triển là 10     k k k k 102 1 k C x C x . 10 10  x 
Số mũ 10  2k  4  k  3. Vậy hệ số cần tìm là:  3 3 1 C  120 . 10 Câu 20. Lời giải Chọn C
Công thức tổng quát của khai triển là: k k 10 2 k C x  . 10 Số hạng chứa 7
x khi 10  k  7  k  3 , hệ số là: 3 3 C 2 . 10 Câu 21. Lời giải Chọn C   2 k 
Số hạng tổng quát trong khai triển 9 T  C x   C 2 k k k k  k  x . k  2    9 3 9 9  x  T chứa 3
x khi và chỉ khi 9  3k  3  k  2. k Suy ra hệ số của 3
x trong khai triển là C 22 2  144 . 9 Câu 22. Lời giải Chọn C Ta có: x  xn 0 1 2 2 3 n n 1 1 C x C x C x ... C x        . n n n n
Lấy đạo hàm hai vế ta được:
x  n  nxx  n 1 0 1 2 2 1 1
 C  2C x  3C x  ... n   1 n n C x . n n n n Cho x  1, ta có 0 1 2 C C C n C n         n 1 2   2 n . n n n   n n n 1 2 3 ... 1 2 2 n n 1 2   2 n1 2621439 n 1 2   2 n  n 2621440 2621440  2  .2 . (*) 2  n Xét   2n f n 
là hàm số đồng biến trên 0; và g n 2621440  2.
là hàm số nghịch biến trên 0; 2  n
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 63
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung .
Ta có f 18  g 18  n 18 là nghiệm duy nhất của (*). 18  1 
Khi đó số hạng tổng quát của khai triển 2 x    là: k 36 3k
C x  với k  , 0  k  18.  x  18
Vậy số hạng không chứa x là 12 C  18564 . 18 Câu 23. Lời giải Chọn D SHTQ: k 4k 1  0 C x
, cho 4k 10  6  k  4 hệ số của 6 x là 4 C  210 . 10 10 Câu 24. Lời giải. Chọn D  1 n  k nk  1 k n  2x   C .(2x) .  . 2  n  2   x  k 0  x 
Vì số hạng thứ ba của khai triển trên ứng với k  2 n n
nên số hạng thứ ba của khai triển là 2 2 6 .2 . n C x .
Mà số hạng thứ ba của khai triển không chứa x nên n  6  0  n  6 .
Số hạng thứ 2 của khai triển   30 3 1 x là 1 3 3 C x  x . 30. 30 Khi đó ta có 2 4 3    . 6 C .2 30.x x 2 Câu 25. Lời giải Chọn B
Ta có: 2a  b5  C 2a5  C 2a4 b  C 2a3 0 1 2 2 b  ... 5 5 5
Do đó hệ số của số hạng thứ 3 bằng 2 C .8  80 . 5 Câu 26. Lời giải. Chọn A
Ta có: a  a  ...  a  (1 2.1)n  3n  729  n  6 0 1 n a  k C 2k suy ra maxa a . k    240 k 6 4 Câu 27. Lời giải Chọn A  n 1 2xn k  C .2k. kx  0 0 0 1 1 1 2 2 2
C .2 x  C .2 x  C .2 x  ... n  C .2n n x 1  a  a x  ... n  a x . n n n n n 0 1 n k 0
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 64
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung a a a Ta có: 1 2 a    ... n   4096  0 1 2 C  C  C  ... n  C  4096 2n   4096  n 12 . 0 2 2 2 2n n n n n Ta có: a  a  k k k 1 k 1 C .2 C  .2    k k 1 C 2C  
. Suy ra: a  a  a  ...  a . k k 1  12 12 12 12 0 1 2 8 Mặt khác: a  a  k k k 1 k 1 C .2 C  .2    k k 1 C 2C  
. Suy ra: a  a  a  ...  a . k k 1  12 12 12 12 8 9 10 12
Vậy số lớn nhất trong các số a , a , a ,..., a là 8 8 a  C .2  126720 . 0 1 2 n 8 12 Câu 28. Lời giải. Chọn B
Số hạng tổng quát trong khai triển 1 2 n x là k C .2k. k
x , 0  k  n , k   . Vậy hệ số của số hạng chứa n k x là k C .2k k  a  C .2k . n k n Khi đó, ta có a a 1 n 0 1 2 a  ...
 4096  C  C  C ... n  C  4096 0 2 2n n n n n  1  1 n  4096  n  12
Dễ thấy a và a không phải hệ số lớn nhất. Giả sử a 0  k  n là hệ số lớn nhất trong các hệ số 0 n k a , a , a ,..., a . 0 1 2 n Khi đó ta có  12! 12!.2  k k k 1  k 1 a  a C  .2  C .2 
k!. 12 k ! k 1 !. 12  k 1 ! k k 1  12 12             k k k 1  k 1 a  a     k k  C .2 C .2 12! 12! 1 1  12 12  
k   k k     k    . !. 12 ! 1 !. 12 1 ! 2  1 2  23      k 1 2 k 12 1 12  k k k   0  3 23 26         k  . 2 1  26  3k  0 26 3 3   k  k 13 k  3 Do k    k  8.
Vậy hệ số lớn nhất là 8 8 a  C .2  126720 . 8 12 Câu 29. Lời giải Chọn A n Xét khai triển n n nk 0 n 1 n 1  n 1
(x 1)  C .x  C .x C  .x  ... C  . n x  C . k n n n n k 0
Thay x  1 vào khai triển trên ta được n 0 1 n 1  n 0 1 n 1
(11)  C  C  ... C  C  C  C ...  n  C  C  2 .n n n n n n n n n
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 65
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Câu 30. Lời giải Chọn B Ta có 3 0,027 0 7 1 6 2 5 2
 C .(3)  C (3) (0,02)  C (3) (0,02) ... 7 7 7
Tổng ba số hạng đầu tiên là: 0 7 1 6 2 5 2
C .(3)  C (3) (0,02)  C (3) (0,02)  2291,1012 7 7 7 Câu 31. Lời giải Chọn B Ta có  x  5 0 5 1 4 2 3 2 5 0 5 1  C .(x)  C (x) ( 1  )  C (x) ( 1  ) ... C (x) ( 1  ) 5 5 5 5 0 5 1 4 2 3 3 2 4 1 5 0
 C .x  C .x  C .x  C .x  C .x  C .x 5 5 5 5 5 5
Khi đó tổng a  a  a  a  a  a bằng: 0 1 2 3 4 5
C  C  C  C  C  C  0. 5 4 3 2 1 0 5 5 5 5 5 5 Câu 32. Lời giải Chọn A Với x  1, y  1 ta có 0 1 5 S= C +C +...+C  (1 5 1)  32 . 5 5 5 Câu 33. Lời giải Chọn A 0 1 6 6 S = C +C +...+C  2  64 6 6 6 Câu 34. Lời giải Chọn C
Cho x  1 ta có 2.3.4.5...n   1  a  a  ...  a 0 1 m m
Vậy  a 1.2.3... n   n  . r   1   1 ! r 0 Câu 35. Lời giải. Chọn B Ta có  x  5 0 5 1 4 2 3 2 5 0 5
1  C .(x)  C (x) (1)  C (x) (1)  ... C (x) (1) 5 5 5 5 0 5 1 4 2 3 3 2 4 1 5 0
 C .x  C .x  C .x  C .x  C .x  C .x 5 5 5 5 5 5
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 66
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Khi đó tổng a  a  a  a  a  a bằng: 0 1 2 3 4 5
C  C  C  C  C  C  0 5 4 3 2 1 0 5 5 5 5 5 5 Câu 36. Lời giải. Chọn B Ta có: 1 n n k 1 ! 1 ( 1)! C   k 1 n
k 1 k !(n  k)! n 1 (k 1)![(n 1)  (k 1))! 1 k 1   C (*) n 1 n 1  n n 1  n 1 1 k  1  k  2  1 1 0  S  C  C C . n    1 1   n 1  n 1 n 1    k n   k  n  0 1 0 1 Câu 37. Lời giải. Chọn A n k ! Ta có k 2 k(k 1)C   n(n 1)C n n2 (k  2)!(n  k)! 2 n2  S  n(n 1)n k C  n(n 1)2 . 3 n2 k 2 Câu 38. Lời giải. Chọn A
Ta có:   n   n    2 1 1 1 n x x x .
Vế trái của hệ thức trên chính là:  0 n 1 n 1 n C x  C x   C  0 1 ... C  C x  ... n n  C x n n n n n n 
Và ta thấy hệ số của n x trong vế trái là
C 2 C 2 C 2  C 2 0 1 2 ... n n n n n Còn hệ số của n x trong vế phải  2 1 n x  là n C 2n 2 2 2 2 Do đó  0 C    1 C    2 C  ...  n C  n  C . n n n n 2n Câu 39. Lời giải Chọn B Xét khai triển
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 67
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung   xn 0 1 2 2 1
 C  C x  C x  ...  Cn n
x . Lấy đạo hàm hai vế ta được: n n n n n  xn 1 1 2 n n 1 1 C 2C x ... nC x       . n n n Cho x  1 ta được: n 1  1 2 . n 2
 C  2C  ...  nCn mà 1 2 1.C  2.C  ...  . n Cn  1024 . n n n n n n Suy ra: n 1 . n 2   1024 n 1 . n 2  
1024  0 . Xét phương trình g n n 1 . n 2   1024 , n 1. Có g n n 1  n 1 2 . n 2     .ln 2  0 , n
 1 nên g n đồng biến 1; . Do đó phương trình g n  0 có
nhiều nhất 1 nghiệm. Mà g 8 1024 nên n  8. Câu 40. Lời giải Chọn B Biến đổi 0 1 2
2C  5C  8C  ... 3n  2 n C n n n n     0 C     1 C     2 3.0 2 3.1 2
3.2 2 C ... 3n  2 n C n n n n   0 1 2 n
C  C  C   C    1 2 2 ... 3 C  2C  ... n  nC . n n n n n n n  Ta có 0 1 2 C  C  C  ... n  C  2n . n n n n
Xét hàm số    1 n f x x        1 1 n f x n x      1 1  .2n f n     1
Lại có    1 n f x x 0 1 2 2 3 3
 C  C x  C x  C x  ... n n  C x n n n n n  f x 1 2 2 3 1  C  2xC  3x C ... n n  nx C n n n n  f   1 2 3 1  C  2C  3C  ... n  nC 2 n n n n Từ   1 và 2 ta được 1 2 3 n n 1 C 2C 3C ... nC . n 2       . n n n n  n  Do đó 0 1 2
2C  5C  8C  ... 3n  2 n C n n 1 2.2 3 . n 2    3  2  .2n . n n n n    2   3n  Bài ra 0 1 2
2C  5C  8C  ... n  C  nên 2  .2n  1600 . n n n 3 2 n 1600 n    2  Với n  7 I Loại.  3n  n  21  Với 1 n  7 7  2  .2  2  .2  1600      Loại.  2   2   3n  Do đó 2  .2n  1600    n  7.  2  Câu 41. Lời giải Chọn B Ta có 1 x2n 0 1 2 2 3 3 2n 1  2n 1  2n 2
 C  C .x  C .x  C .x  C .x  C . n x   1 . 2n 2n 2n 2n 2n 2n Thay x  1 vào   1 ta có: 2 0 1 2 3 2 1  2 2 n n n
 C  C  C  C   C  C 2 . 2n 2n 2n 2n 2n 2n Thay x  1  vào   1 ta có: 0 1 2 3 2 1  2 0 n n
 C  C  C  C   C  C 3 . 2n 2n 2n 2n 2n 2 n
Trừ từng vế của 2 và 3 ta có: 2 2 n 2. 1 3 2n 1 C C  C      1 3 2 n 1 2n 1 C C  C  2       . 2n 2n 2n  2n 2n 2 n Nên 1 3 2n 1 C C  C      512 2n 1  9  2
 2  2n 1  9  n  5 . 2n 2n 2n Bởi vậy 2 2 2 3 2 4 2 5
S  2 C  3 C  4 C  5 .C . 5 5 5 5
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 68
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Từ 1 x5 0 1 2 2 3 3 4 4 5 5
 C  C .x  C .x  C .x  C .x  C .x , lấy đạo hàm hai vế ta được: 5 5 5 5 5 5 51 x4 1 2 3 2 4 3 5 4
 C  2C .x  3C .x  4C .x  5C .x 5 5 5 5 5  5x 1 x4 1 2 2 3 3 4 4 5 5
 C x  2C .x  3C .x  4C .x  5C .x 4 . 5 5 5 5 5
Lại lấy đạo hàm hai vế 4 , ta có:
51 x4  20x 1 x3 1 2 2 2 3 2 2 4 3 2 5 4
 C  2 C .x  3 C .x  4 C .x  5 C .x 5. 5 5 5 5 5 Thay x  1  vào 5 ta được: 1 2 2 3 2 4 2 5
0  C  2C  3 C  4 C  5 C 2 2 3 2 4 2 5 1
 2C  3 C  4 C  5 C  C 5 5 5 5 5 5 5 5 5 5 Hay 2 2 2 3 2 4 2 5
S  2 C  3 C  4 C  5 .C  5 . 5 5 5 5 Câu 42. Lời giải Chọn A 1  1 1 (1)n  Ta có: 0 1 2 S  C  C  C ...  n C n n n n  2  2 3 n 1  ( 1  )k k (1)k 1 Vì k 1  C  C nên: k k 1 S  n(1)  C n n 1 k 1 n 1  n 1 2(n 1)  k 0 1 1   k k  1 0   n ( 1  ) C  C   . n 1  n 1 2(n 1)     k  n  0 2( 1) Câu 43. Lời giải Chọn D Ta có công thức: k k 1  k 1  C  C  C nên đáp án sai là 4 4 5 C  C  C . n n n 1  10 11 11 Câu 44. Lời giải Chọn A
Số hạng tổng quát thứ k 1 là T  C 3 k x  C 3 k k k k x . k 1  n   n   Vì hệ số của 2 x nên cho k  2 . n n 1 n  5 n 2     Khi đó ta có C  2 2 3  90  C  10  10   . n n 2 n  4  l Vậy n  5. Câu 45. Lời giải Chọn C
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 69
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung n
Ta có 2  xn  C 2  .  1 k k n k . k x . n k 0 n n   1 n  2n  3 Hệ số của 4
x tương đương với k  4 là n C    n4  2  280 n  4 4 4 2 . 1 280 24 6
 n n  n  n   6720 2 .3.5.7 1 2 3   . n4 n4 2 2
Vì n là số tự nhiên nên n  4  6  4  n  10.
Lâp bảng giá trị được n  7 . Câu 46. Lời giải Chọn B Ta có: n  0 1 2 3 2 k k n n
C  iC  C  iC   i C  i C  i n n n n n n  32768 n   0 1 2 2 3 3 2 k k n n
C  iC  i C  i C  i C  i C  i n n n n n n  32768    in n 15 2 1  2 i * Ta có   i2 1
 2i nên nếu n  2k 1, k   , thì  n  2k 1 1 1      2k k i i
i 1 i nên không thỏa mãn * .
Xét n  2k , k   , thì   n    2 1 1 k  2k k i i i , nên:   2k k k 15 3k k 15
*  2 .2 .i  2 i  2 i  2 i  k  5  n  10 . Từ đó ta có 7 7 T  i C  8i . 8 8 Câu 47. Lời giải Chọn C 1 k C Ta có n  . k  ! n  k ! n! Do đó 1 2 3 1009 C C C C 1 2 1009 C  C  ... C 0 1 2 1009 C  C  C  ... C 1 2019 2019 2019 2019 A     ... 2019 2019 2019  2019 2019 2019 2019  2019! 2019! 2019! 2019! 2019! 2019! 2018 2 1  . 2019! Câu 48. Lời giải Chọn B
Xét khai triển  x  n 0 1 2 2 3 3
1  C  C x  C x  C x  ... n n  C x . n n n n n
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 70
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Đạo hàm hai vế ta được: n  x n 1 1 2 3 2 n n 1 1 C 2C x 3C x ... nC x        . n n n n
Thay x  1 ở hai vế ta được 1 2 n n 1 1.C 2.C ... . n C . n 2      . n n n Do đó n 1 . n 2   11264 . Xét hàm số   1 .2t f t t  
trên 0;  ta có: f t t 1  t 1 2 t.2     .ln 2  0 t   0 . Do đó hàm số   1 .2t f t t  
đồng biến trên 0;  . Mà f 1  1  11264 . Vậy n  11. Câu 49. Lời giải Chọn C
Điều kiện: n  0 , n   . n5! n3! n 3 C  5A   5.
 n 5n  4  600. n5 n3 n!5! n! n  20 2
 n 9n 580  0    n  20 . n  2  9 Câu 50. Lời giải Chọn B Cách 1: Ta có: k C n! n  C  n  2 k 2 ! n2     . k   1 k  2 k  ! n  k   ! k  
1 k  2 n  k   ! k  2  ! n   1 n  2 n   1 n  2 n k n k 2 C C Suy ra: n n2        k 0  k
1k 2 k0 n 1n 2 0 1 2 n 2 3 4 n2 C C C C C  C  C  ... C n n n n n2 n2 n2 n2     ...   . 1.2 2.3 3.4 n  1n  2 n  1n  2
Ta xét khai triển sau: 1 xn2 0 1 2 2 3 3 n2 n2  C  . x C  x .C  x .C  ... x .C . n2 n2 n2 n2 n2 Chọn n2 0 1 2 3 n2 x  1   2  C  C  C  C  ... C . n2 n2 n2 n2 n2 100 n2 0 1 2  n  3 2  C  C Do đó:  n2 n2 100 n2        . n  n   n  n   2 2 n 98 1 2 1 2 Cách 2: Ta có: 0 1 2 n C C C C 1 1   1 1   1 1   1 1  n n n n 0 1 2 S     ... n                    = n  n   C C C ..... C 1.2 2.3 3.4 1 2 1 2 n   2 3 n   3 4 n   n 1 n  2 n   1 1 1 1 n   1 1 1 1 0 1 2 0 1 2  C  C  C  ..... C  C  C  C  ..... n C      1 n 2 n 3 n n 1 n   2 n 3 n 4 n n  2 n  1 1 1 1 Lại có: 1 xndx x  1 xn dx 2
 1 xn dx 1 xn 1        dx 0 0 0 0
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 71
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung 1 1 1 1 1 1 n   1 1 1 1 n  2  C  C  C  C  C  C  C  C   x    x   n n n n   n n n n   n 1 1 ..... ..... 1 1 n 2 0 1 2 0 1 2 1 2 3 n 1   2 3 4 n  2  n 1 n  2 0 0 n 1  n2 n2 2.2  2 2 1 2  n  3 S    n 1 n  2 n   1 n  2 n2 100 2  n  3 2  n  3
Kết hợp giả thiết có    n  98 . n   1 n  2 n   1 n  2
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 72
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
GT Chương ⓶ §➍. PHÉP THỬ VÀ BIẾN CỐ ⓫ Ⓐ Tóm tắt lý thuyết ➊. Phép thử Phép thử ngẫu nhiên:
 Là phép thử mà ta không đoán trước được kết quả của nó, mặc
dù đã biết tập hợp tất cả các kết quả có thể có của phép thử đó.
Chú ý: Ta chỉ xét các phép thử có một số hữu hạn kết quả. ➋. Không gian mẫu
 Tập hợp các kết quả có thể xảy ra của một phép thử đgl không
gian mẫu của phép thử và kí hiệu là .
 Vi dụ: Mô tả không gian mẫu của phép thử gieo một đồng tiền.  = {S, N} ➌. Biến cố
 Mỗi biến cố liên quan đến một phép thử được mô tả bởi một
tập con của không gian mẫu.
 Biến cố là một tập con của không gian mẫu.
 Tập  đgl biến cố không thể.
 Tập  đgl biến cố chắc chắn. Qui ước:
 Biến cố đôi khi được cho dưới dạng xác định tập hợp.
 Khi nói cho các biến cố A, B, .. mà không nói gì thêm thì ta
hiểu chúng cùng liên quan đến một phép thử.
 Ta nói biến cố A xảy ra trong một phép thử nào đó khi và
chỉ khi kết quả của phép thử đó là một phần tử của A (hay thuận lợi cho A).
➍. Các phép toán trên các biến cố
Giả sử A và B là các biến cố liên quan đến một phép thử.
 Tập  \ A đgl biến cố đối của A
 Kí hiệu: A =  \ A . A xảy ra  A không xảy ra.
 Tập A  B đgl hợp của các biến cố A và B.
 Tập A  B đgl giao của các biến cố A và B. (còn kí hiệu A.B)
 Nếu A  B =  thì ta nói A và B xung khắc.
 A và B xung khắc  A và B không cùng xảy ra.
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 73
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Ⓑ Phân dạng bài tập
①.Dạng 1: Mô tả không gian mẫu, biến cố . Bài tập minh họa:
Câu 1: Gieo đồng tiền hai lần. Số phần tử của biến cố để mặt ngửa xuất hiện ít nhất một lần là Ⓐ. 6 . Ⓑ. 5 . Ⓒ. 3 . Ⓓ. 4 . Lời giải
Ta có số phần tử của biến cố để mặt ngửa xuất hiện ít nhất một lần là: SN ; NS ; NN .
Câu 2: Gieo 3 đồng tiền là một phép thử ngẫu nhiên có không gian mẫu là
Ⓐ. NNN, SSS, NNS, SSN, NSN, NSS,SNN. Ⓑ. NN, NS, SN, SS .
Ⓒ. NNN, SSS, NNS, SSN, NSN, SNS, NSS, SNN .
Ⓓ. NNN, SSS, NNS, SSN, NSN, SNS . Lời giải
Số phần tử của không gian mẫu là 3 2  8 .
Câu 3: Gieo một đồng xu cân đối và đồng chất liên tiếp ba lần. Gọi A là biến cố “Có ít nhất hai
mặt sấp xuất hiện liên tiếp” và B là biến cố “Kết quả ba lần gieo là như nhau”. Xác định biến cố A  . B
Ⓐ. A  B  SSS, SSN, NSS, SNS, NNN.
Ⓑ. A  B  SSS, NNN .
Ⓒ. A  B  SSS, SSN, NSS, NNN . Ⓓ. A  B   . Lời giải
A  SSS, SSN, NSS , B  SSS, NNN . Suy ra A B  SSS, SSN, NSS, NNN .
Câu 4: Gieo ngẫu nhiên một đồng tiền cân đối và đồng chất 5 lần. Tính số phần tử không gian mẫu. Ⓐ. 64 . Ⓑ. 10 . Ⓒ. 32 . Ⓓ. 16 . Lời giải
Mỗi lần gieo có hai khả năng nên gieo 5 lần theo quy tắc nhân ta có 5 2  32 .
Số phần tử không gian mẫu là n  32. ②.Dạng 2:
Các câu hỏi lý thuyết tổng hợp . Bài tập minh họa:
Câu 1: Xét phép thử gieo một con súc sắc cân đối và đồng chất hai lần liên tiếp. Gọi A là biến cố
“Lần đầu xuất hiện mặt 6 chấm” và B là biến cố “Lần thứ hai xuất hiện mặt 6 chấm”.
Khẳng định nào sai trong các khẳng định sau?
Ⓐ. A và B là hai biến cố xung khắc
Ⓑ. A  B là biến cố “Ít nhất một lần xuất hiện mặt 6 chấm”.
Ⓒ. A  B là biến cố “Tổng số chấm trên mặt xuất hiện của hai lần gieo bằng 12.
Ⓓ. A và B là hai biến cố độc lập. Lời giải
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 74
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Hai biến cố A và B có thể cùng xảy ra Câu 2: Cho ,
A B là hai biến cố của không gian mẫu  . Công thức nào sau đây sai?
Ⓐ. P  A 1 P A. Ⓑ. P  .
A B  P A.PB nếu ,
A B là hai biến cố độc lập.
Ⓒ. P  A B  P A  PB  P A B . n  Ⓓ. P  A    . n  A Lời giải n A Ta có P  A    nên D sai. n 
Câu 3: Xét một phép thử có không gian mẫu  và A là một biến cố của phép thử đó. Phát biểu nào sau đây sai? n A
Ⓐ. Xác suất của biến cố A là P  A    . n  Ⓑ. 0  P  A  1.
Ⓒ. P  A  1 P  A .
Ⓓ. P  A  0 khi và chỉ khi A là biến cố chắc chắn. Lời giải
Theo định nghĩa biến cố chắc chắn ta có: Với A là biến cố chắc chắn thì n A  n n A Suy ra: P  A      . n 1 0
Câu 4: Cho phép thử là “gieo 2019 đồng xu phân biệt” và xét sự xuất hiện mặt sấp và mặt ngửa
của các đồng xu. Khi đó số phần tử của không gian mẫu bằng Ⓐ. 2019 . Ⓑ. 1 3 2019 C  C ... C . 2019 2019 2019 2020 2019 Ⓒ. k k C C . Ⓓ. 2 . 2020 2019 k 0 k 0 Lời giải 2020 2019 Ta có k k
C C  1 2020 1  1 2019 2020 2019 2019 1  2  2  2 .2   2019 1  2 . 2020 2019 k 0 k 0
Vì một đồng xu có hai mặt nên khi gieo 2019 đồng xu phân biệt ta có 2019 2 kết quả có thể
xảy ra của phép thử. Vậy số phần tử của không gian mẫu là n 2019  2 .
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 75
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Ⓒ Bài tập rèn luyện
Câu 1:Cho A , B là hai biến cố xung khắc; Đẳng thức nào sau đây đúng?
Ⓐ. P  A B  P  A  P  B
:......................................................................
Ⓑ. P  A B  P A.P  B
......................................................................................
Ⓒ. P  A B  P A  PB
......................................................................................
Ⓓ. P  A  B  P A  P B
Câu 2:Trong các thí nghiệm sau thí nghiệm nào không phải là phép thử ngẫu nhiên:
Ⓐ. Gieo đồng tiền xem nó mặt ngửa hay mặt sấp
Ⓑ. Gieo 3 đồng tiền và xem có mấy đồng tiền lật
:...................................................................... ngửa
......................................................................................
Ⓒ. Chọn bất kì 1 học sinh trong lớp và xem là nam hay nữ
......................................................................................
Ⓓ. Bỏ hai viên bi xanh và ba viên bi đỏ trong một
chiếc hộp, sau đó lấy từng viên một để đếm xem có
tất cả bao nhiêu viên bi.
Câu 3:Cho A là một biến cố liên quan phép thử T. Mệnh đề nào sau đây là mệnh đề đúng?
Ⓐ. P( A) là số lớn hơn 0 .
:...................................................................... Ⓑ. P( ) A 1 P  A.
......................................................................................
Ⓒ. P( A)  0  A   .
Ⓓ. P( A) là số nhỏ hơn 1.
......................................................................................
Câu 4:Cho A và B là hai biến cố xung khắc; Mệnh đề nào dưới đây đúng?
Ⓐ. P  A  P B 1.
:......................................................................
Ⓑ. Hai biến cố A và B không đồng thời xảy ra
Ⓒ. Hai biến cố A và B đồng thời xảy ra
......................................................................................
Ⓓ. P  A  PB  1.
......................................................................................
Câu 5:Rút ngẫu nhiên cùng lúc ba con bài từ cỗ bài tú lơ khơ 52 con thì n bằng bao nhiêu? Ⓐ. 140608 . Ⓑ. 156 . Ⓒ. 132600 . Ⓓ. 22100 .
:......................................................................
......................................................................................
......................................................................................
Câu 6:Gieo đồng tiền hai lần. Số phần tử của biến cố để mặt ngửa xuất hiện đúng 1 lần là Ⓐ. 2 . Ⓑ. 4 . Ⓒ. 5 . Ⓓ. 6 .
:......................................................................
......................................................................................
......................................................................................
Câu 7:Gieo một con súc sắc 2 lần. Số phần tử của không gian mẫu là? Ⓐ. 6 . Ⓑ. 12 . Ⓒ. 18 . Ⓓ. 36 .
:......................................................................
......................................................................................
......................................................................................
Câu 8:Gieo 3 đồng tiền là một phép thử ngẫu nhiên có không gian mẫu là: Ⓐ. NN, NS, SN, S  S
:......................................................................
Ⓑ. NNN, SSS, NNS, SSN, NSN, SN  S .
......................................................................................
Ⓒ. NNN,SSS, NNS, SSN, NSN, SNS, NSS, SNN . ......................................................................................
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 76
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Ⓓ. NNN, SSS, NNS, SSN, NSS, SNN .
Câu 9:Gieo một đồng tiền liên tiếp 2 lần. Số phần tử của không gian mẫu ( n )  là? Ⓐ. 1. Ⓑ. 2 . Ⓒ. 4 . Ⓓ. 8 .
:......................................................................
......................................................................................
......................................................................................
Câu 10:Gieo một đồng tiền và một con súc sắⒸ. Số phần tử của không gian mẫu là: Ⓐ. 24 . Ⓑ. 12 . Ⓒ. 6 . Ⓓ. 8 .
:......................................................................
......................................................................................
......................................................................................
Câu 11:Gieo một đồng tiền và một con súcsắⒸ. Số phần tử của không gian mẫu là: Ⓐ. 24. Ⓑ. 12. Ⓒ. 6. Ⓓ. 8.
:......................................................................
......................................................................................
......................................................................................
Câu 12:Gieo đồng tiền hai lần. Số phần tử của biến cố để mặt ngửa xuất hiện đúng 1 lần là: Ⓐ. 2. Ⓑ. 4. Ⓒ. 5. Ⓓ. 6.
:......................................................................
......................................................................................
......................................................................................
Câu 13:Gieo một đồng tiền liên tiếp 3 lần thì n() là bao nhiêu? Ⓐ. 4 . Ⓑ. 6 Ⓒ. 8 . Ⓓ. 16 .
:......................................................................
......................................................................................
......................................................................................
Câu 14:Gieo ngẫu nhiên 2 đồng tiền thì không gian mẫu của phép thử có bao nhiêu biến cố: Ⓐ. 4 . Ⓑ. 8 . Ⓒ. 12 . Ⓓ. 16 .
:......................................................................
......................................................................................
......................................................................................
Câu 15:Một hộp chứa 11 quả cầu gồm 5 quả cầu màu xanh và 6 quả cầu màu đỏ. Chọn ngẫu nhiên lần lượt hai
quả cầu từ hộp đó. Xác suất để hai quả cầu được chọn ra cùng màu bằng 25 25 Ⓐ. . Ⓑ. .
:...................................................................... 33 66 5 5
...................................................................................... Ⓒ. . Ⓓ. . 22 11
......................................................................................
Câu 16:Gieo 2 con súc sắc và gọi kết quả xảy ra là tích số hai nút ở mặt trên. Số phần tử của không gian mẫu là Ⓐ. 9 . Ⓑ. 18 Ⓒ. 29 . Ⓓ. 39 .
:......................................................................
......................................................................................
......................................................................................
Câu 17:Cho phép thử có không gian mẫu   1,2,3,4,5,6. Các cặp biến cố không đối nhau là: Ⓐ. A   1 và B 2,3,4,5,  6 .
:...................................................................... Ⓑ. C 1, 4,  5 và D 2,3,  6 .
......................................................................................
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 77
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Ⓒ. E  1, 4,  6 và F 2,  3 .
...................................................................................... Ⓓ.  và  .
Câu 18:Một hộp đựng 10 thẻ, đánh số từ 1 đến 10 . Chọn ngẫu nhiên 3 thẻ. Gọi A là biến cố để tổng số của 3
thẻ được chọn không vượt quá 8 . Số phần tử của biến cố A là: Ⓐ. 2. Ⓑ. 3.
:...................................................................... Ⓒ. 4. Ⓓ. 5.
......................................................................................
......................................................................................
Câu 19:Gieo con súc sắc hai lần. Biến cố A là biến cố để sau hai lần gieo có ít nhất một mặt 6 chấm: Ⓐ. A  
 1;6,2;6,3;6,4;6,5;6.
:...................................................................... Ⓑ. A  
 1,6,2, 6,3, 6,4,6,5,6,6,6. ...................................................................................... 
 1,6,2,6,3,6,4,6,5,6,6,6,    Ⓒ. A   
......................................................................................  6,  
1 ,6,2,6,3,6,4,6,5  Ⓓ. A  
 6, 1,6,2,6, 3,6,4,6, 5.
Câu 20:Một hộp đựng 10 thẻ, đánh số từ 1 đến 10 . Chọn ngẫu nhiên 3 thẻ. Gọi A là biến cố để tổng số của 3 thẻ
được chọn không vượt quá 8 . Số phần tử của biến cố A là Ⓐ. 2 . Ⓑ. 3 . Ⓒ. 4 . Ⓓ. 5 .
:......................................................................
......................................................................................
......................................................................................
Câu 21:Gieo một đồng tiền và một con súc sắⒸ. Số phần tử của không gian mẫu là Ⓐ. 24 . Ⓑ. 12 . Ⓒ. 6 . Ⓓ. 8 .
:......................................................................
......................................................................................
......................................................................................
Câu 22:Cho A và A là hai biến cố đối nhau. Chọn câu đúng.
Ⓐ. P  A 1 P A .
:......................................................................
Ⓑ. P  A  P A.
......................................................................................
Ⓒ. P  A 1 P A .
......................................................................................
Ⓓ. P  A  P A  0 .
Câu 23:Cho A là một biến cố liên quan phép thử T. Mệnh đề nào sau đây là mệnh đề đúng?
Ⓐ. P( A) là số lớn hơn 0.
:...................................................................... Ⓑ. P( ) A 1 P  A.
......................................................................................
Ⓒ. P( A)  0  A   .
Ⓓ. P( A) là số nhỏ hơn 1.
......................................................................................
Câu 24:Cho A và A là hai biến cố đối nhau. Chọn câu đúng.
Ⓐ. P  A 1 P A.
:......................................................................
Ⓑ. P  A  P A.
......................................................................................
Ⓒ. P  A 1 P A.
......................................................................................
Ⓓ. P  A  P A  0.
Câu 25:Cho phép thử có không gian mẫu    , 1 , 3 , 2  6 , 5 , 4
. Các cặp biến cố không đối nhau là
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 78
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Ⓐ. A    1 và B  2,3,4,5,  6 .
:...................................................................... Ⓑ. C 1, 4,  5 và D  2,3,  6 .
...................................................................................... Ⓒ. E  1, 4,  6 và F  2,  3 . Ⓓ.  và .
......................................................................................
Câu 26:Cho hai biến cố A và B có 1 1 1
P( A)  , P(B)  , P( A  B) 
. Ta kết luận hai biến cố A và B là: 3 4 2 Ⓐ. Độc lập. Ⓑ. Không xung khắc
:...................................................................... Ⓒ. Xung khắc
...................................................................................... Ⓓ. Không rõ.
......................................................................................
Câu 27:Trong các thí nghiệm sau thí nghiệm nào không phải là phép thử ngẫu nhiên:
Ⓐ. Gieo đồng tiền xem nó mặt ngửa hay mặt sấp.
Ⓑ. Gieo 3 đồng tiền và xem có mấy đồng tiền lật
:...................................................................... ngửa
......................................................................................
Ⓒ. Chọn bất kì 1 học sinh trong lớp và xem là nam hay nữ.
......................................................................................
Ⓓ. Bỏ hai viên bi xanh và ba viên bi đỏ trong một
chiếc hộp, sau đó lấy từng viên một để đếm xem có
tất cả bao nhiêu viên bi.
Câu 28:Xét một phép thử có không gian mẫu  và A là một biến cố của phép thử đó. Phát biểu nào dưới đây là sai?
Ⓐ. P  A  0 khi và chỉ khi A là chắc chắn.
:......................................................................
Ⓑ. P  A  1 P  A .
...................................................................................... n A
Ⓒ. Xác suất của biến cố A là P  A    .
...................................................................................... n  Ⓓ. 0  P  A  1. 1 1 1
Câu 29:Cho hai biến cố A và B có P( )
A  , P(B)  , P(A  B)  . Ta kết luận hai biến cố A và B là 3 4 2 Ⓐ. Độc lập. Ⓑ. Không xung khắc
:...................................................................... Ⓒ. Xung khắc
...................................................................................... Ⓓ. Không rõ.
......................................................................................
Câu 30:Cho phép thử có không gian mẫu   1,2,3, 4,5, 
6 . Các cặp biến cố không đối nhau là: Ⓐ. A    1 và B  2,3,4,5,  6 .
:...................................................................... Ⓑ. C 1, 4,  5 và D  2,3,  6 .
...................................................................................... Ⓒ. E  1, 4,  6 và F  2,  3 . Ⓓ.  và .
...................................................................................... BẢNG ĐÁP ÁN 1.A 2.D 3.B 4.B.D 5.D 6.A 7.D 8.C 9.C 10.B 11.B 12.A 13.C 14.A 15.D 16.B 17.C 18.C 19.C 20.C 21.B 22.C 23.B 24.C 25.C 26.B 27.D 28.A 29.B 30.C
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 79
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Hướng dẫn giải
Câu 1: Ta có P  A B  P A  PB  P A B .
Vì A , B là hai biến cố xung khắc nên A  B   . Từ đó suy ra P  A B  P A  P B .
Câu 2: Phép thử ngẫu nhiên là phép thử mà ta chưa biết được kết quả là gì.
Đáp án D không phải là phép thử vì ta biết chắc chắn kết quả chỉ có thể là một số cụ thể
số bi xanh và số bi đỏ.
Câu 3: Loại trừ : A ; D ; C đều sai.
Câu 4: Vì A và B là hai biến cố xung khắc nên hai biến cố này không đồng thời xảy ra. Câu 5: Ta có n 3  C  22100 . 52
Câu 6: Liệt kê ta có: A  NS.SN
Câu 7: n()  6.6  36 . .
Câu 8: Liệt kê các phần tử. Câu 9: ( n )   2.2  4 . .
Câu 10: Mô tả không gian mẫu ta có:    1
S ; S2; S3; S4; S5; S6; N1; N 2; N3; N 4; N5; N  6 .
Câu 11: Mô tả không gian mẫu ta có:    1 S ; S2;S3;S4;S5;S6; 1 N ; N2; N3; N4; N5; N  6 .
Câu 12: Liệt kê ta có: A N . S S  N
Câu 13: n()  2.2.2  8 . .
Câu 14: Mô tả không gian mẫu ta có:   SS; SN; NS; NN
Câu 15: Gọi biến cố A : “Hai quả cầu được chọn ra cùng màu”.
Số phần tử của không gian mẫu là: n 11.10 110 .
Chọn hai quả cầu cùng màu xảy ra 2 trường hợp: hoặc 2 quả cùng màu xanh hoặc 2 quả
cùng màu đỏ. Khi đó n A  5.4  6.5  50 . n A 5
Xác suất để hai quả cầu được chọn ra cùng màu là P  A     . n  11
Câu 16: Mô tả không gian mẫu ta có:   1;2;3;4;5;6;8;9;10;12;15;16;18;20;24;25;30;3  6 .
Câu 17: Cặp biến cố không đối nhau là E 1,4,  6 và F 2, 
3 do E  F   và E  F  .
Câu 18: Liệt kê ta có: A  
 1;2; 3;1;2;4;1;2; 5;1;3;4
Câu 19: Liệt kê ta có: A  
 1,6,2,6,3,6,4,6,5,6,6,6,6, 1,6,2,6, 3,6, 4,6, 5
Câu 20: Liệt kê ta có: A  
 1;2;3;1;2;4;1;2;5;1;3;4
Câu 21: Mô tả không gian mẫu ta có:    1
S ; S2; S3; S4; S5; S6; N1; N 2; N3; N 4; N5; N  6 .
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 80
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung Câu 22: Câu 23:
Loại trừ :A ;B ;C đều sai
Câu 24: Câu 25: Cặp biến cố không đối nhau là E  1,4,  6 và F  2,  3 do E  F   và E  F   .
Câu 26: Ta có: P A B  P 
A  PB  P A B nên P  A  B 1   0 12
Suy ra hai biến cố A và B là hai biến cố không xung khắc.
Câu 27: Phép thử ngẫu nhiên là phép thử mà ta chưa biết được kết quả là gì.
Đáp án D không phải là phép thử vì ta biết chắc chắn kết quả chỉ có thể là một số cụ thể
số bi xanh và số bi đỏ.
Câu 28: Khẳng định A sai vì A là biến cố chắc chắn thì P  A 1.
Câu 29: Ta có: P A B  P A  PB  P A B nên P A B 1   0 12
Suy ra hai biến cố A và B là hai biến cố không xung khắc.
Câu 30: Cặp biến cố không đối nhau là E  1,4,  6 và F  2, 
3 do E  F   và E  F   .
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 81
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
GT Chương ⓶ §➎. XÁC SUẤT CỦA BIẾN CỐ ⓫ Ⓐ Tóm tắt lý thuyết
➊. Định nghĩa cổ điển của xác suất Định nghĩa
 Giả sử A là biến cố liên quan đến một phép thử chỉ có một số hữu hạn kết quả đồng khả năng xuất hiện. ( n A)  Ta gọi tỉ số
là xác suất của biến cố A, kí hiệu P(A). n() n(A)
 Công thức tính: P(A) = ( n ) Chú ý:
 n(A) là số phần tử của A hay cũng là số kết quả thuận lợi của biến cố A
 n() là số kết quả có thể xảy ra của phép thử.
➋. Tính chất của xác suất Định lí:  P() = 0, P() = 1
 0  P(A)  1, với mọi biến cố A
 Nếu A và B xung khắc thì P(AB) = P(A) + P(B)
Hệ quả: Với mọi biến cố A, ta có P(A)  1 P(A)
➌. Các biến cố độc lập và công thức nhân xác suất
 Hai biến cố được gọi là độc lập nếu sự xảy ra của biến cố này không ảnh hưởng đến xác suất xảy ra của biến cố kia.
 A và B độc lập  P(A.B) = P(A).P(B) Ⓑ Phân dạng bài tập
①.Dạng 1: Tính xác suất bằng định nghĩa . Bài tập minh họa:
Câu 1: Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là: 1 1 2 A. 1.B. . C. . D. . 2 3 3 Lời giải
Không gian mẫu là:   1,2,3,4,5,  6  n  6 .
Gọi A là biến cố: “Mặt có số chấm chẵn xuất hiện”.  A  2,4,  6  n A  3.
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 82
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung n A 3 1
Xác suất để mặt có số chấm chẵn xuất hiện là: P  A    . n      6 2
Câu 2: Trong giỏ có 5 đôi tất khác màu, các chiếc tất cùng đôi thì cùng màu. Lấy ngẫu nhiên ra
2 chiếc. Tính xác suất để 2 chiếc đó cùng màu. 1 1 1 1 A. . B. . C. . D. . 24 18 9 5 Lời giải
Lấy 2 chiếc từ 10 chiếc tất, số cách lấy là: 2   C  45 10
Lấy 2 chiếc cùng màu từ 10 chiếc tất, số cách lấy là: 1   C  5 A 5 A 1
Xác suất để lấy được một đôi tất cùng màu: P   .  9
Câu 3: Một lô hàng có 100 sản phẩm, trong đó có 80 sản phẩm tốt và 20 sản phẩm xấu. Lấy ngẫu
nhiên 4 sản phẩm từ hộp, tính xác suất để 4 sản phẩm lấy ra đều là sản phẩm tốt. 4 A 4 C 80! 4 C A. 80 . B. 80 . C. . D. 20 . 4 A 4 C 100! 4 C 100 100 100 Lời giải
Số cách chọn ra 4 sản phẩm từ hộp là 4 C . 100
Để 4 sản phẩm lấy ra đều là sản phẩm tốt thì số cách là 4 C . 80 4 C
Vậy xác suất để 4 sản phẩm lấy ra đều là sản phẩm tốt là 80 . 4 C100
Câu 4: Có 3 chiếc hộp. Mỗi hộp chứa 4 tấm thẻ được đánh số từ 1 đến 4. Lấy ngẫu nhiên từ mỗi
hộp một thẻ. Tính xác suất để 3 thẻ được lấy ra đều mang số chẵn. 2 3 1 1 A. . B. . C. . D. . 3 32 2 8 Lời giải
Số phần tử của không gian mẫu: n 1 1 1  C .C .C  64 4 4 4
Gọi A là biến cố 3 thẻ mang số chẵn: n A 1 1 1  C .C .C  8 2 2 2
Xác suất cho biến cố A: P  A 8 1   64 8
Câu 5: Một hội nghị có 15 nam và 6 nữ. Chọn ngẫu nhiên 3 người vào ban tổ chức. Xác suất để 3 người lấy ra là nam: 1 91 4 1 A. . B. . C. . D. . 2 266 33 11 Lời giải n 3  C  1330 . 21
Gọi A là biến cố: “3 người lấy ra là nam”. Khi đó, n  A 3  C  455 . 15 n A 13 91
Vậy xác suất để 3 người lấy ra là nam là: P  A      . n 38 266
Câu 6: Từ một hộp chứa 11 quả cầu màu đỏ và 4 quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3
quả cầu. Xác suất để lấy được 3 quả cầu màu xanh bằng
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 83
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung 4 4 33 24 A. . B. . C. . D. . 165 455 91 455 Lời giải Ta có: n 3  C  455 . 15
Gọi A là biến cố “lấy được 3 quả cầu màu xanh”. Khi đó n A 3  C  4 . 4 Vậy P  A 4  . 455
②.Dạng 2: Tính xác suất bằng công thức cộng . Bài tập minh họa:
Câu 1: Gieo đồng thời hai con súc sắc cân đối và đồng chất. Tính xác suất P để hiệu số chấm trên
các mặt xuất hiện của hai con súc sắc bằng 2. 1 2 1 A. . B. . C. . D. 1. 3 9 9 Lời giải
Số phần tử của không gian mẫu: n  6.6  36.
Gọi A là biến cố thỏa mãn yêu cầu bài toán: A  
 1; 3, 3; 1, 4; 2, 2; 4, 3; 5, 5; 3, 4; 6, 6; 4 nên n A 8. Vậy P  A 8 2   . 36 9
Câu 2: Người ta sử dụng 7 cuốn sách Toán, 8 cuốn sách Vật lí, 9 cuốn sách Hóa học để làm phần
thưởng cho 12 học sinh, mỗi học sinh được 2 cuốn sách khác loại. Trong số 12 học sinh
trên có hai bạn Thảo và Hiền. Tính xác suất để hai bạn Thảo và Hiền có phần thưởng giống nhau. 1 5 19 1 A. . B. . C. . D. . 22 18 66 11 Lời giải
Có 24 cuốn sách ghép cặp với nhau tạo thành 12 bộ sách.
1 Toán - 1 Lí có: 12  9  3 bộ.
1 Toán - 1 Hóa có: 12  8  4 bộ.
1 Lí - 1 Hóa có 12  7  5 bộ.
Số phần tử của không gian mẫu là: n 2  C  66 . 12
Gọi A là biến cố “ Thảo và Hiền có phần thưởng giống nhau” n A 2 2 2
 C  C  C  3 6 10 19. 3 4 5 n A  P A   19  . n     66
Câu 3: Một lớp học có 20 học sinh nam và 15 học sinh nữ. Giáo viên chọn ngẫu nhiên 4 học sinh
lên bảng giải bài tập. Xác suất để 4 học sinh được chọn có cả nam và nữ là 4651 4615 4610 4615 A. . B. . C. . D. . 5236 5236 5236 5263 Lời giải
Số cách chọn 4 học sinh trong số 35 học sinh lên bảng giải bài tập là: 4   C . 35
Gọi A là biến cố: “có cả nam và nữ”.
Số cách chọn 4 học sinh nam là: 4 C . 20
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 84
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Số cách chọn 4 học sinh nữ là: 4 C . 15 Do đó: 4 4 4
  C  C  C  46150. A 35 20 15 
Vậy xác suất cần tìm là: P  A A 4615   .  5236
Câu 4: Một nhóm học sinh có 6 học sinh nam và 7 học sinh nữ. Từ nhóm học sinh này ta chọn
ngẫu nhiên 3 học sinh. Tính xác suất để trong ba học sinh được chọn có cả nam và nữ. 3 C 3 C 2 1 2 1 C C  C C 3 3 C  C A. 7 1 . B. 6 1 . C. 6 7 7 6 . D. 6 7 . 3 C 3 C 3 C 3 C 13 13 13 13 Lời giải
Số phần tử không gian mẫu là n 3  C13 .
Gọi A là biến cố trong ba học sinh được chọn có cả nam và nữ.
+Trường hợp 1: 2 nam và 1 nữ, ta có số cách chọn là 2 1 C .C 6 7
+ Trường hợp 2: 1 nam và 2 nữ, ta có số cách chọn là 1 2 C C 6 7 .
Số phần tử của A là: n  A 2 1 2 1  C C  C C 6 7 7 6 . 2 1 2 1 n A C C  C C
Vậy xác suất càn tìm là P  A   6 7 7 6   . n 3 C13
Câu 5: Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3
quyển sách. Tính xác suất để 3 quyển được lấy ra có ít nhất một quyển là toán. A. 3 . B. 37 . C. 10 . D. 2 . 4 42 21 7 Lời giải
Trên giá có tất cả: 4  3 2  9 bao gồm cả 3 môn: toán, lý và hóa.
Lấy 3 quyển sách từ 9 quyển sách, số cách lấy ra là 3 C  84  n   84 9  
Gọi A là biến cố: “3 quyển lấy ra có ít nhất 1 quyển toán”.
Suy ra A : “3 quyển lấy ra không có quyển toán nào”  n A 3  C 10 . 5
Vậy xác suất để 3 quyển được lấy ra có ít nhất một quyển sách toán là: P  A   P  A 10 37 1  1  . 84 42
③.Dạng 3: Tính xác suất bằng công thức nhân . Bài tập minh họa:
Câu 1: Xác suất sút bóng thành công tại chấm 11 mét của hai cầu thủ Quang Hải và Văn Đức lần
lượt là 0,8 và 0, 7 . Biết mỗi cầu thủ sút một quả tại chấm 11 mét và hai người sút độc lập.
Tính xác suất để ít nhất một người sút bóng thành công. A. 0, 44 . B. 0,94 . C. 0,38 . D. 0,56 . Lời giải
Xác suất sút không thành công tại chấm 11 của cầu thủ Quang Hải là 1 0,8  0, 2
Xác suất sút không thành công tại chấm 11 của cầu thủ Văn Đức là 1 0,7  0,3
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 85
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Xác suất cả hai cầu thủ sút không thành công tại chấm 11 là 0, 2.0,3  0, 06
Suy ra: Xác suất để ít nhất một người sút bóng thành công là: 1 0,06  0,94 .
Câu 2: Xác suất bắn trúng mục tiêu của một vận động viên khi bắn một viên đạn là 0,3. Người
đó bắn hai viên một cách độc lập. Xác suất để một viên trúng và một viên trượt mục tiêu là A. 0, 21. B. 0, 09 . C. 0,18 . D. 0, 42 . Lời giải
Xác suất để một viên trúng và một viên trượt mục tiêu là: 0,3.0.7  0, 7.0,3  0, 42 .
Câu 3: Xác suất sút bóng thành công tại chấm 11 mét của hai cầu thủ Quang Hải và Văn Đức lần lượt là
0,8 và 0,7. Biết mỗi cầu thủ sút một quả tại chấm 11 mét và hai người sút độc lập. Tính xác suất để ít nhất
một người sút bóng thành công. A. 0, 44 . B. 0,94. C. 0,38. D. 0,56 . Lời giải Chọn B Cách 1
Gọi A là biến cố cầu thủ Quang Hải sút bóng thành công, B là biến cố cầu thủ Văn Đức sút
bóng thành công, C là biến cố có ít nhất một người sút bóng thành công. Suy ra C  . A B  . A B  . A B
Do A, B là hai biến cố độc lập nên P C  P  . A B  . A B  .
A B  0,8.0,3 0,2.0,7  0,8.0,7  0,94 . Cách 2
Gọi A là biến cố cầu thủ Quang Hải sút bóng thành công, B là biến cố cầu thủ Văn Đức sút
bóng thành công, C là biến cố có ít nhất một người sút bóng thành công. Khi đó C là biến cố
không cầu thủ nào sút bóng thành công. Ta có: C  .
A B  P C  0,2.0,3  0,06  PC 1 PC  0,94 .
④.Dạng 4: Bài toán kết hợp quy tắc cộng và quy tắc nhân xác suất . Bài tập minh họa:
Câu 1: Trong một trò chơi, người chơi cần gieo cùng lúc ba con súc sắc cân đối đồng chất; nếu được ít
nhất hai con súc sắc xuất hiện mặt có số chấm lơn hơn 4 thì người chơi đó thắng. Tính xác suất
để trong 3 lần chơi, người đó thắng ít nhất 1 lần. 386 7 11683 2 A. . B. . C. . D. . 729 27 19683 9 Lời giải
Gọi A là biến cố trong 3 lần chơi, người đó thắng ít nhất 1 lần.
Khi đó: A là biến cố trong 3 lần chơi, người đó toàn thua.
Tính xác suất để một lần chơi người đó thua:
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 86
Bài soạn giảng dạy ôn tập Lớp 11 năm 2021– FB Duong Hung
Để chơi thua, thì ít nhất 2 trong ba con súc sắc người đó gieo xuất hiện số chấm bé hơn hoặc  4 4 2  4 4 4 20
bằng 4. Suy ra xác suất để người đó chơi thua một lần là: . . .3  . .  .    6 6 6  6 6 6 27   P  A 3 20 8000    P  A 8000 11683  1    .  27  19683 19683 19683
Câu 2: Gieo hai đồng xu A và B một cách độc lập. Đồng xu A chế tạo cân đối. Đồng xu B chế tạo không
cân đối nên xác suất xuất hiện mặt sấp gấp 3 lần xác suất xuất hiện mặt ngửa. Tính xác suất để
khi gieo hai đồng xu cùng lúc được kết quả 1 sấp và 1 ngửa. A. 25% . B. 50%. C. 75% . D. 60% . Lời giải
Gọi A là biến cố “đồng xu A xuất hiện mặt sấp”, B là biến cố “đồng xu B xuất hiện mặt sấp”;
C là biến cố “có một sấp và một ngửa khi gieo cả hai đồng xu một lần”.
 C  AB  AB , mà AB, AB xung khắc và , A B; , A B độc lập.
 PC  P AB  P AB  P A PB  P A PB 1 3 1 1 1  .  .   50% . 2 4 2 4 2
Câu 3: Có hai hộp. Hộp I đựng 4 gói quà màu đỏ và 6 gói quà màu xanh, hộp II đựng 2 gói quà màu đỏ
và 8 gói quà màu xanh. Gieo một con súc sắc, nếu được mặt 6 chấm thì lấy một gói quà từ hộp
I, nếu được mặt khác thì lấy một gói quà từ hộp II. Tính xác suất để lấy được gói quà màu đỏ. 7 23 1 2 A. . B. . C. . D. . 30 30 3 3 Lời giải
Ta có xác suất để gieo con súc sắc xuất hiện mặt 6 chấm là P  A 1
 và xác suất để gieo con 6
súc sắc không xuất hiện mặt 6 chấm là P  A 5  . 6 4 2
Xác suất lấy từ hộp I được gói quà màu đỏ là P B   . 1  10 5 2 1
Xác suất lấy từ hộp II được gói quà màu đỏ là P B   . 2  10 5 1 2 5 1 7
Vậy xác suất để lấy được gói quà màu đỏ là P  A.PB  P A .P B  .  .  . 1     2 6 5 6 5 30
St-bs: FB: Duong Hung - Zalo: 0774860155 - Word xinh 2021 87