Chuyên Đề Ứng Dụng Đạo Hàm Để Khảo Sát Và Vẽ Đồ Thị Ôn Thi Tốt Nghiệp 2025 Giải Chi Tiết

CHƯƠNG I : ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
BÀI 1 TÍNH ĐƠN ĐIỆU VÀ CỰC TRỊ CỦA HÀM SỐ
1 MỨC ĐỘ CẦN ĐẠT : NHẬN BIẾT :
Yêu cầu cần đạt
– Nhận biết được tính đồng biến, nghịch biến của một hàm số trên một khoảng dựa vào dấu của đạo hàm cấp một của nó.
– Nhận biết được tính đơn điệu của hàm số thông qua bảng biến thiên hoặc thông qua hình ảnh hình học của đồ thị hàm số.
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
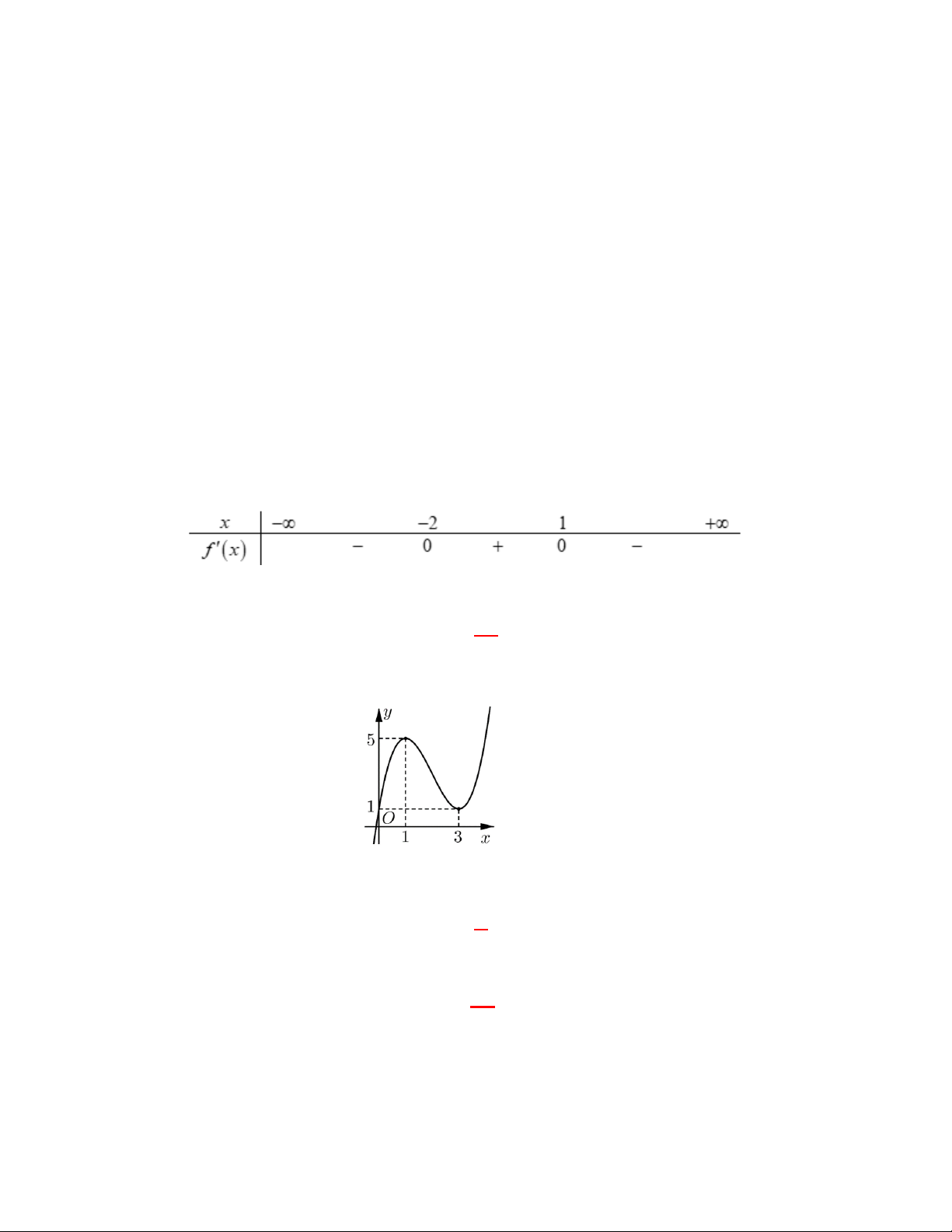
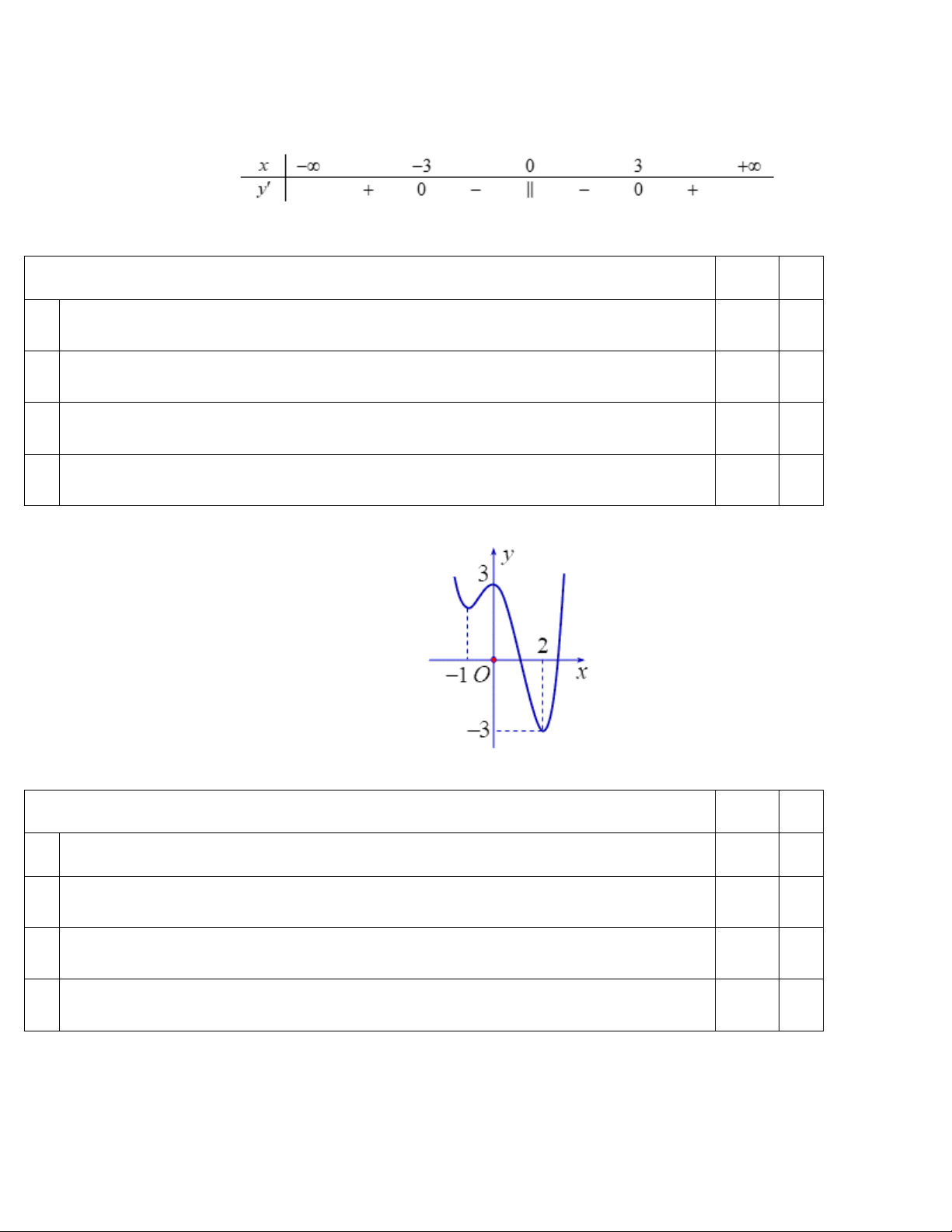
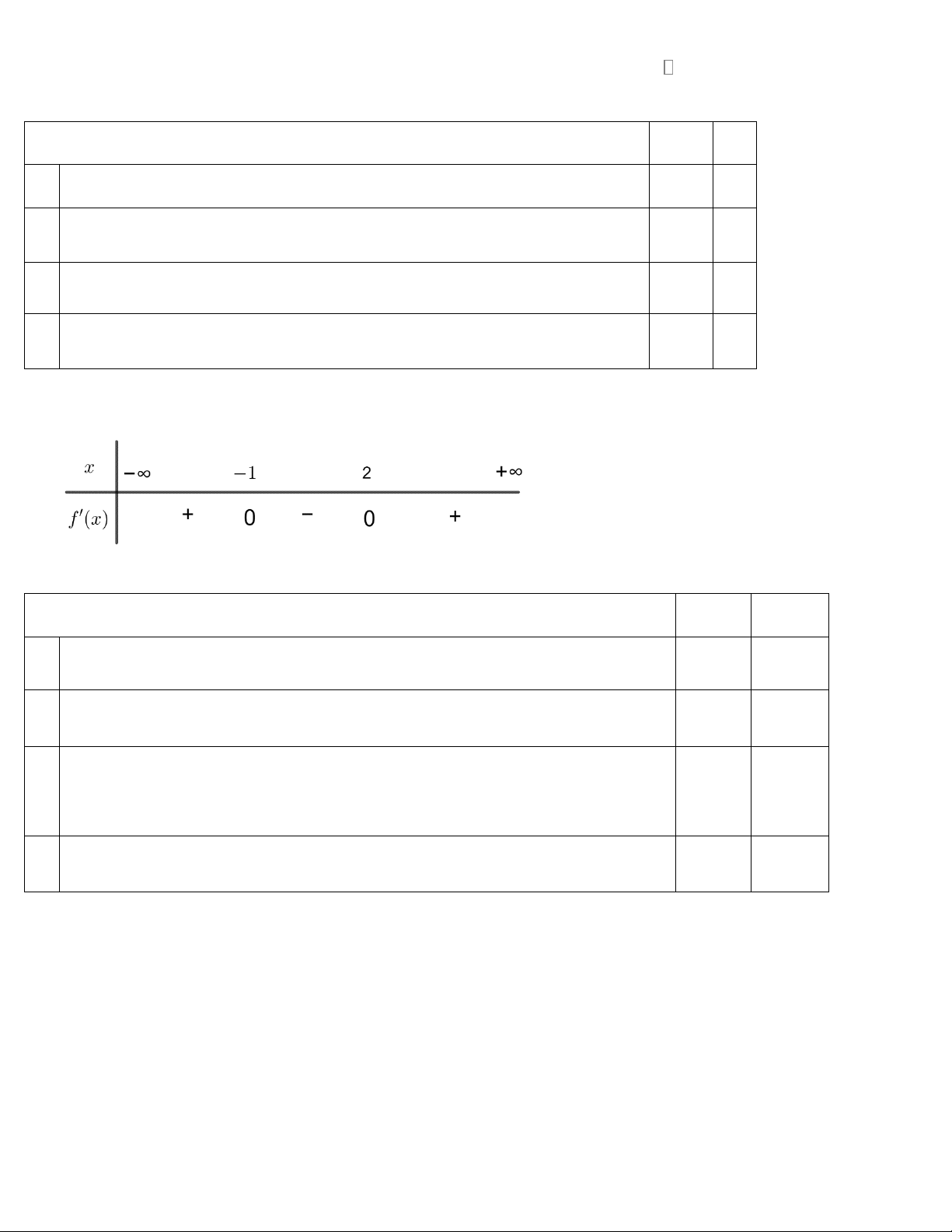
Câu 1: Cho hàm số f  x có bảng xét dấu của đạo hàm như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây A.  ;  2  .
B. 1; . C.  2  ;  1 . D.  2;  .
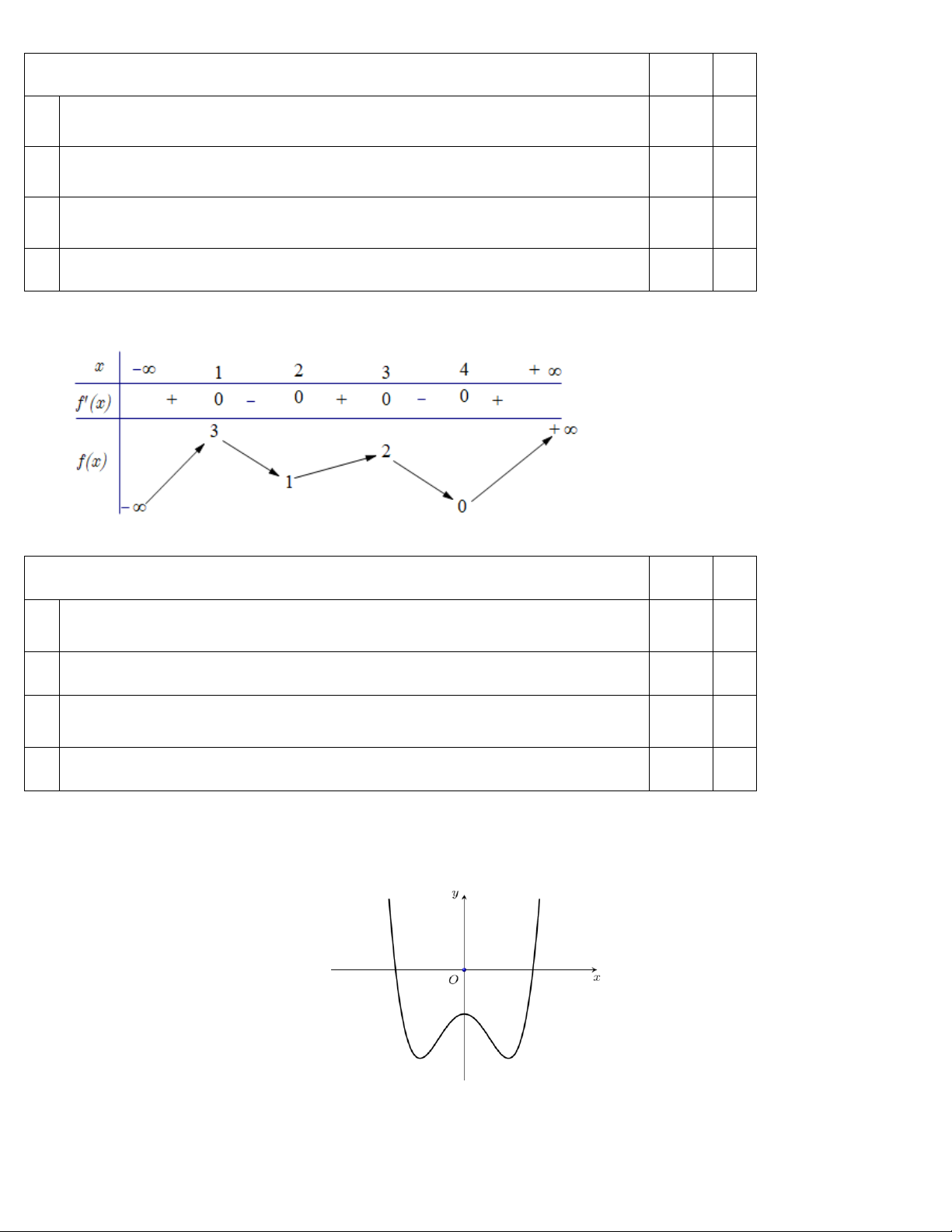
Câu 2: Cho hàm số y  f  x có đồ thị như hình vẽ.
Hàm số y  f  x nghịch biến trên khoảng A. 0;  1 .
B. 3; . C. 1;3 . D. 1;5.
Câu 3: Hàm số y= x3-3x2 nghịch biến trên khoảng nào dưới đây. A.  ;  0.
B. 2; . C. 0;2 . D.  ;   .
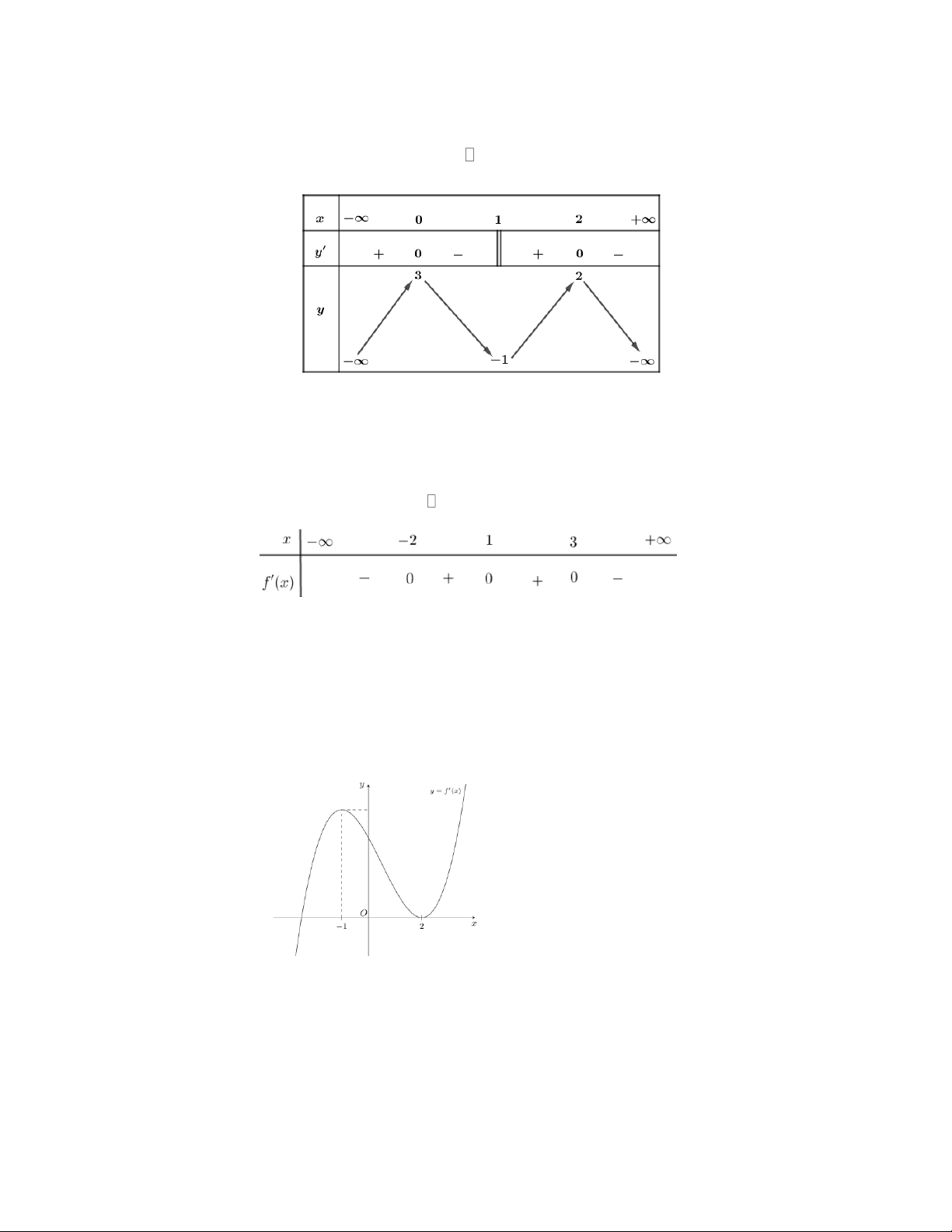
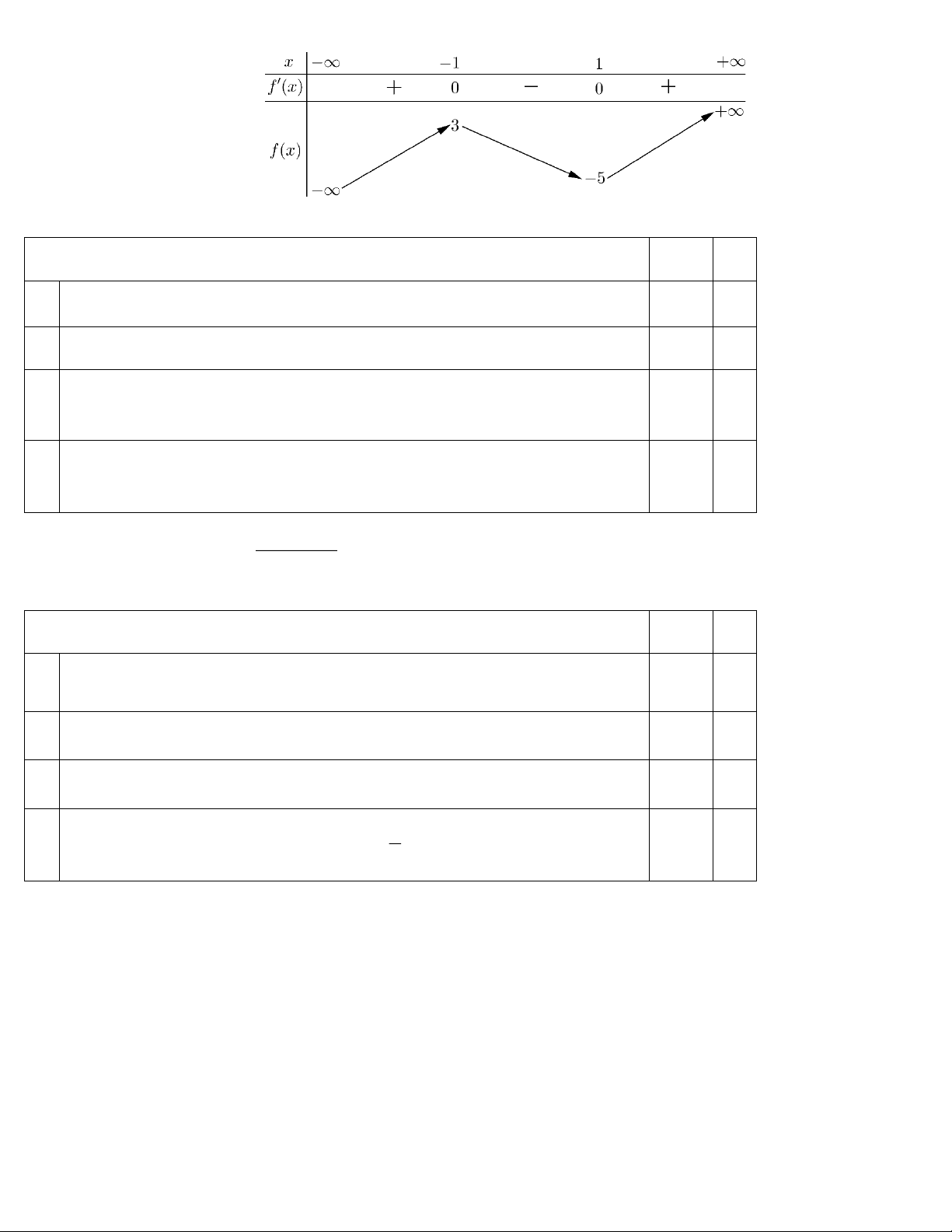
Câu 4: Cho hàm số y  f  x có bảng biến thiên như hình dưới đây. Mệnh đề nào sau đây là đúng? Trang 1
A. Hàm số đã cho đồng biến trên khoảng  1   ;   .  2 
B. Hàm số đã cho đồng biến trên khoảng  ;3   .
C. Hàm số đã cho nghịch biến trên khoảng 3; .
D. Hàm số đã cho nghịch biến trên các khoảng  1  ;     và 3; .  2 
PHẦN II. Câu trắc nghiệm đúng sai. x  Câu 1: Cho hàm số 1 y 
. Các mệnh đề sau đúng hay sai? x  2
a) Hàm số đã cho nghịch biến trên từng khoảng xác định.
b) Hàm số đã cho nghịch biến trên .
c) Hàm số đã cho nghịch biến trên tập  ;  22; .
d) Hàm số đã cho đồng biến trên từng khoảng xác định.
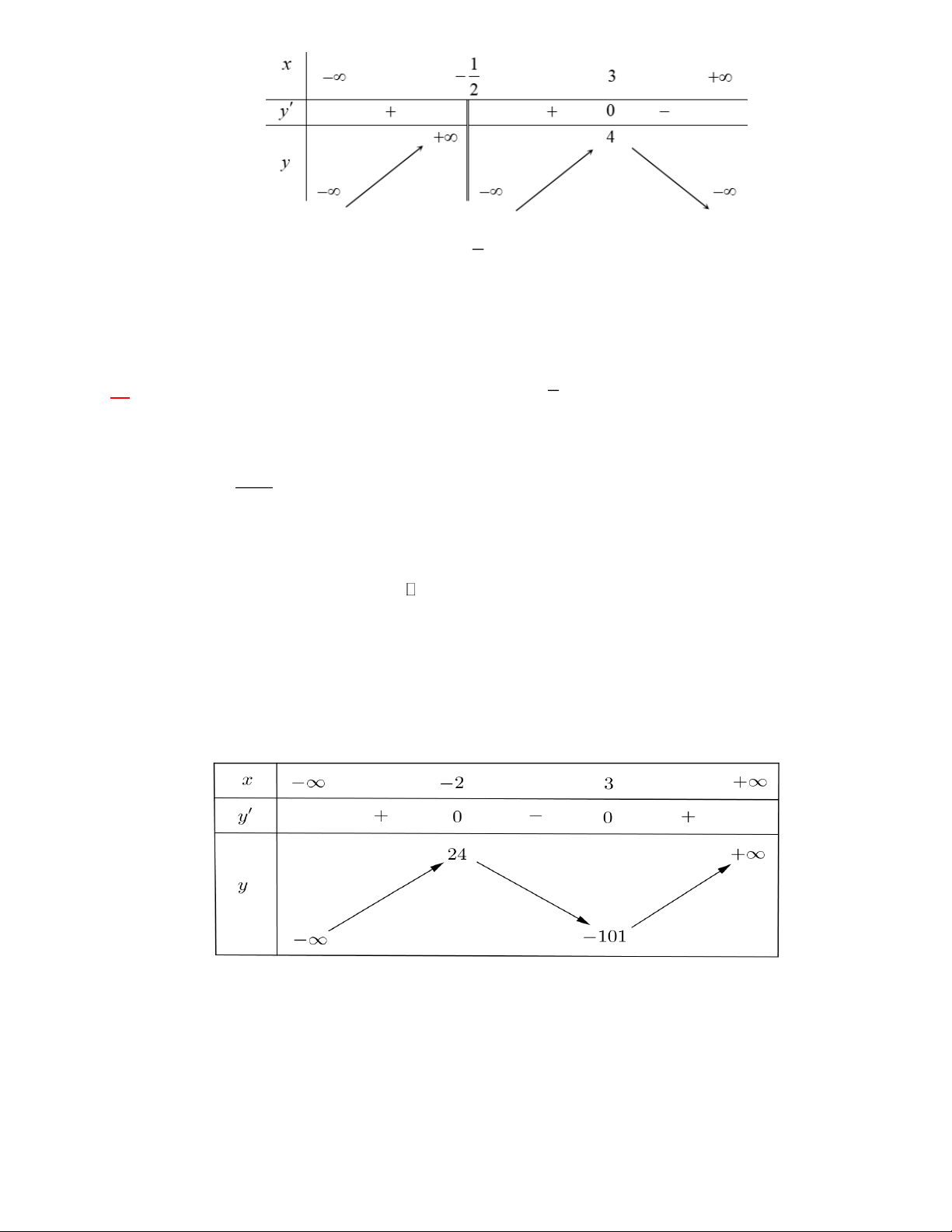
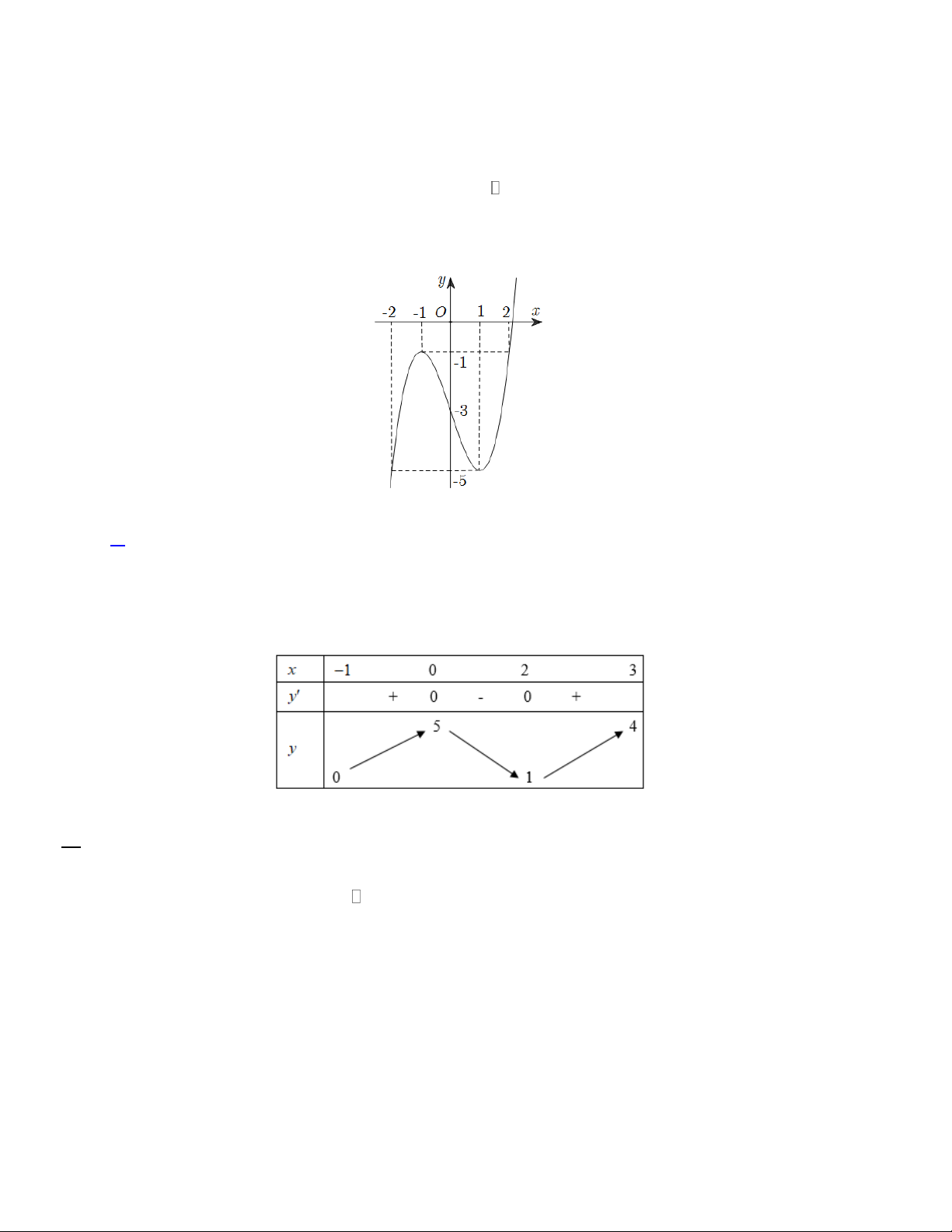
Câu 2: Cho hàm số y=f(x) có bảng biến thiên như hình vẽ. Các mệnh đề sau đúng hay sai
a) Hàm số đã cho nghịch biến trên  ;  2  
b) Hàm số đã cho nghịch biến trên (-2;3) .
c) Hàm số đã cho đồng biến trên 3; . Trang 2
d) Hàm số đã cho đồng biến trên  ;  24 .
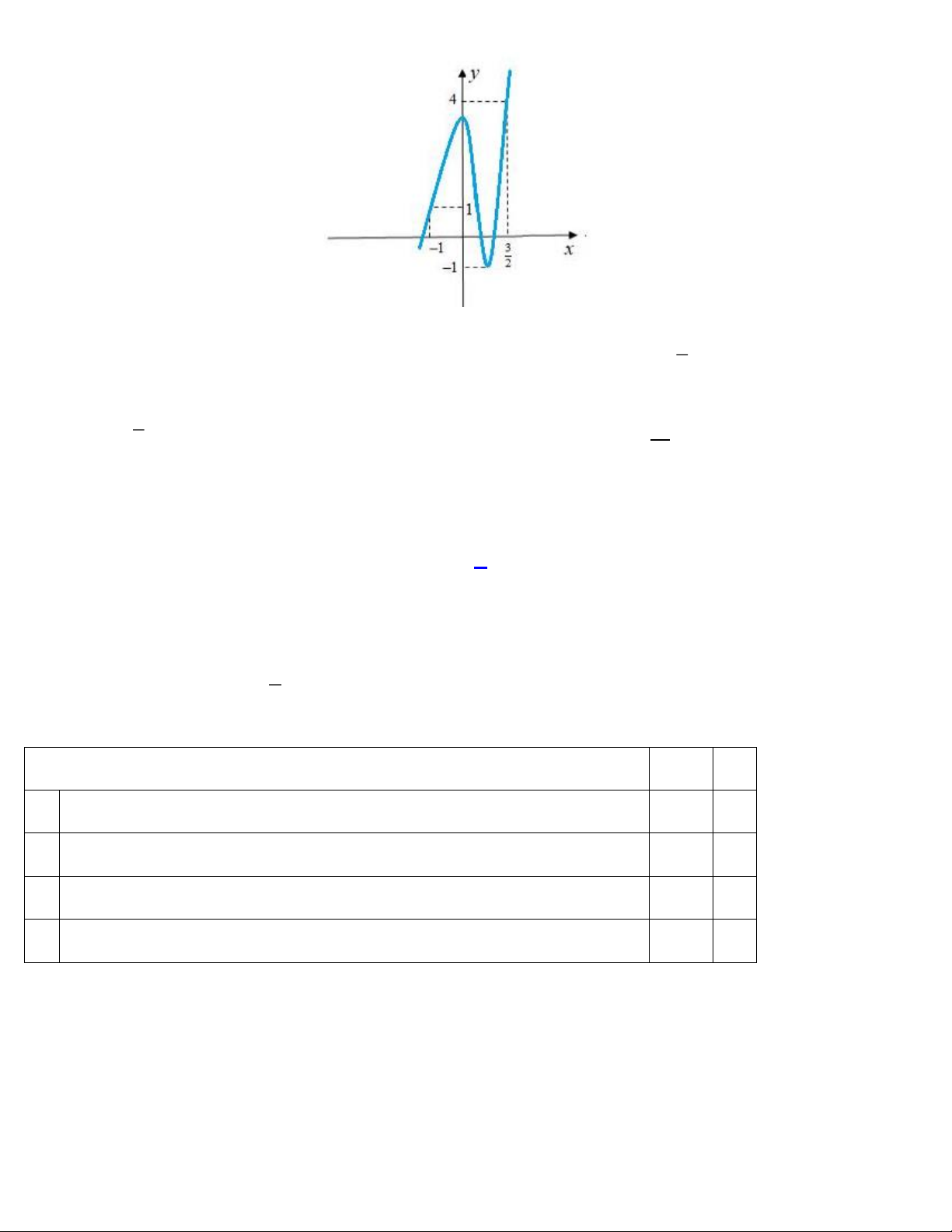
Câu 3: Cho hàm số y  f  x có đồ thị như hình vẽ. Các mệnh đề sau đúng hay sai? y 3 -1 O 1 x -1
a) Hàm số nghịch biến trên khoảng  1  ;  1 .
b) Hàm số đồng biến trên khoảng  1  ;  3 .
c) Hàm số đồng biến trên khoảng  ;    1 và 1; .
d) Hàm số đồng biến trên khoảng  1  ;  1 .
PHẦN III. Câu trắc nghiệm trả lời ngắn. x
Câu 1: Khoảng nghịch biến hàm số y  là ? x 1
Câu 2: Cho hàm số   3 2
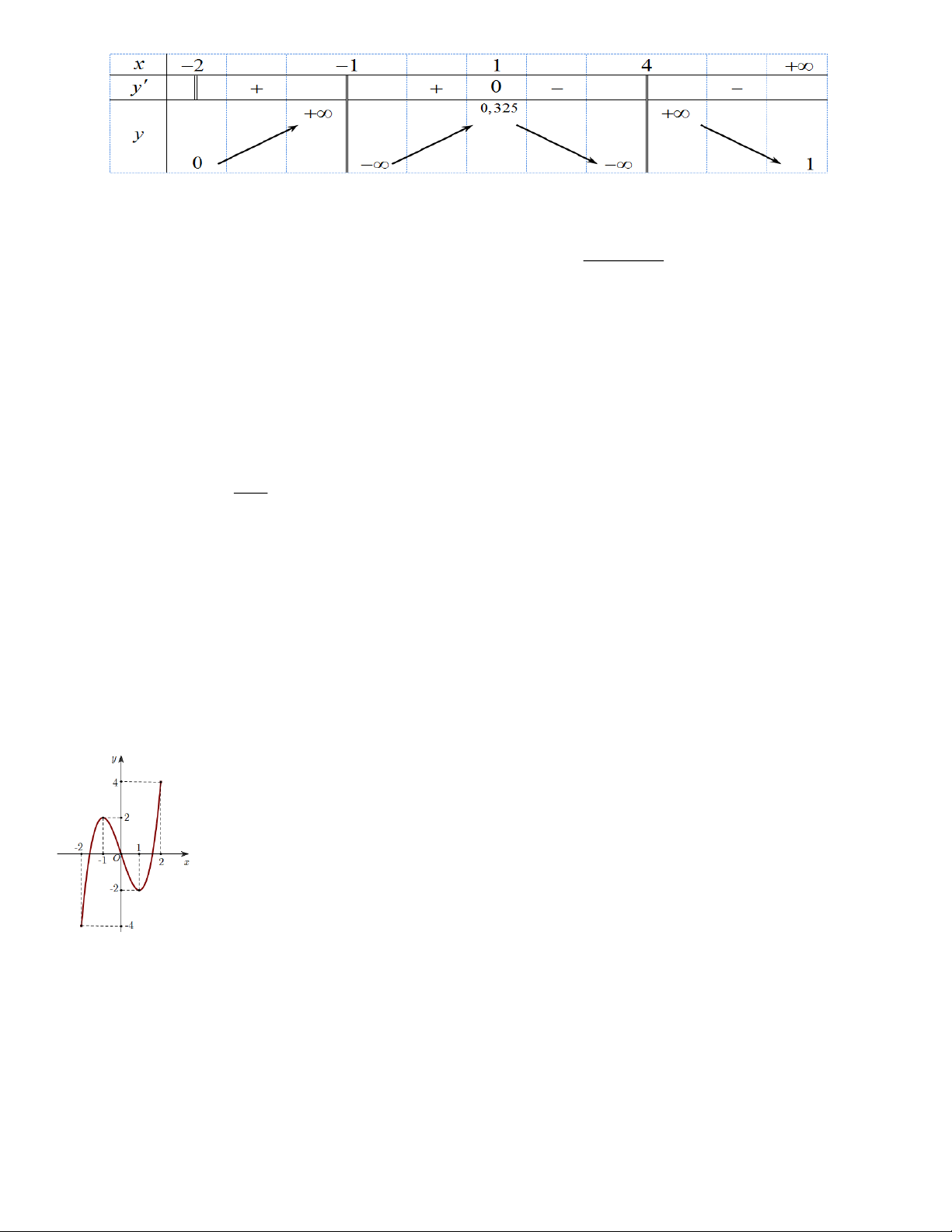
f x  ax  bx  cx  d có đồ thị như hình vẽ bên dưới . Hàm số đồng biến trên khoảng nào? y f(x)=x^3-3x^2+4 T ?p h?p 1 x - 2
Câu 3: Cho hàm số 𝑦 = 𝑓(𝑥) có bảng biến thiên như sau:
Hàm số nghịch biến trên khoảng ?
----------------------------------- Trang 3
MỨC ĐỘ CẦN ĐẠT : THÔNG HIỂU YÊU CẦU CẦN DẠT
– Hiểu được tính đồng biến, nghịch biến của hàm số trong bảng biến thiên của hàm số.
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
Câu 1: Cho hàm số y  f x có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 2 . B. 3 . C. 0 . D. 4  .
Câu 2. Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đạt cực đại tại A. x  2  .
B. x  2 .
C. x 1. D. x  1  .
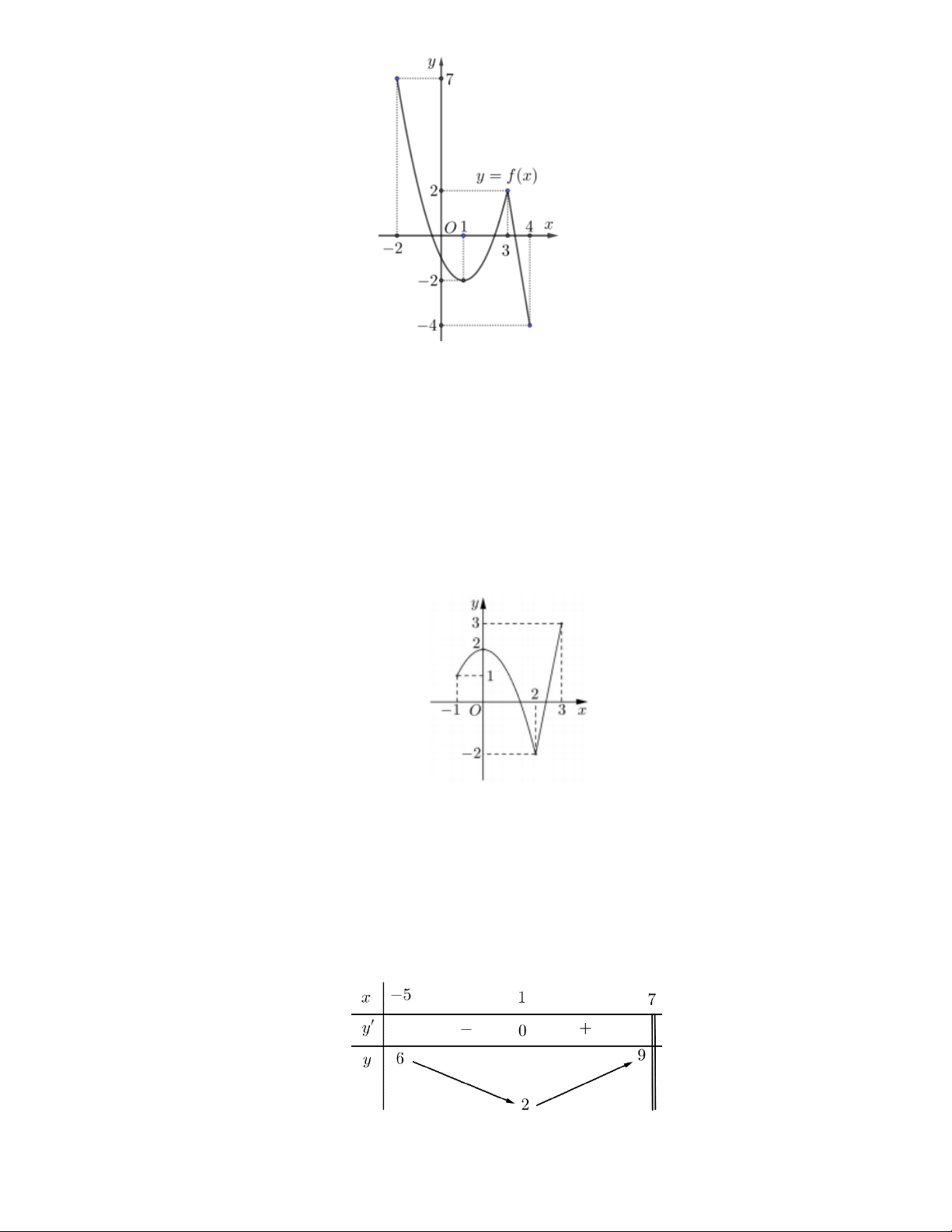
Câu 3. Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là: A. 3 B. 1 C. 2 D. 0
Câu 4. Hàm số nào dưới đây không có cực trị? 2   A. x 1 x y  B. 2 2 y  C. 2
y  x  2x 1 D. 3
y  x  x 1 x x 1 Trang 4
PHẦN II. Câu trắc nghiệm đúng sai.
Câu 1. Cho hàm số f  x có bảng xét dấu đạo hàm như sau
Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai
a) Hàm số đồng biến trên khoảng  3  ;0. X
b) Hàm số nghịch biến trên khoảng 0;  3 . X
c) Hàm số đồng biến trên khoảng  ;0  . X
d) Hàm số nghịch biến trên khoảng  ;    3 . X
Câu 2. Cho hàm số y  f  x có đồ thị như hình vẽ bên.
Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai
a) Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 3 X
b) Hàm số nghịch biến trên khoảng  3  ;0. X
c) Đồng biến trên khoảng  1  ;0 . X
d) Nghịch biến trên khoảng 0;  3 . X Câu 3. 2 3 4
Cho hàm số f  x có đạo hàm f ' x  x 1 x 3  x  x  2 với mọi x Î ¡ .
Các mệnh đề sau đúng hay sai? Trang 5 Mệnh đề Đúng Sai
a) Hàm số f  x đạt cực tiểu tại x  0 X
b) Hàm số f  x đạt cực tiểu tại x  2 X
c) Hàm số f  x đồng biến trên khoảng 3; X
d) Hàm số có hai điểm cực trị X
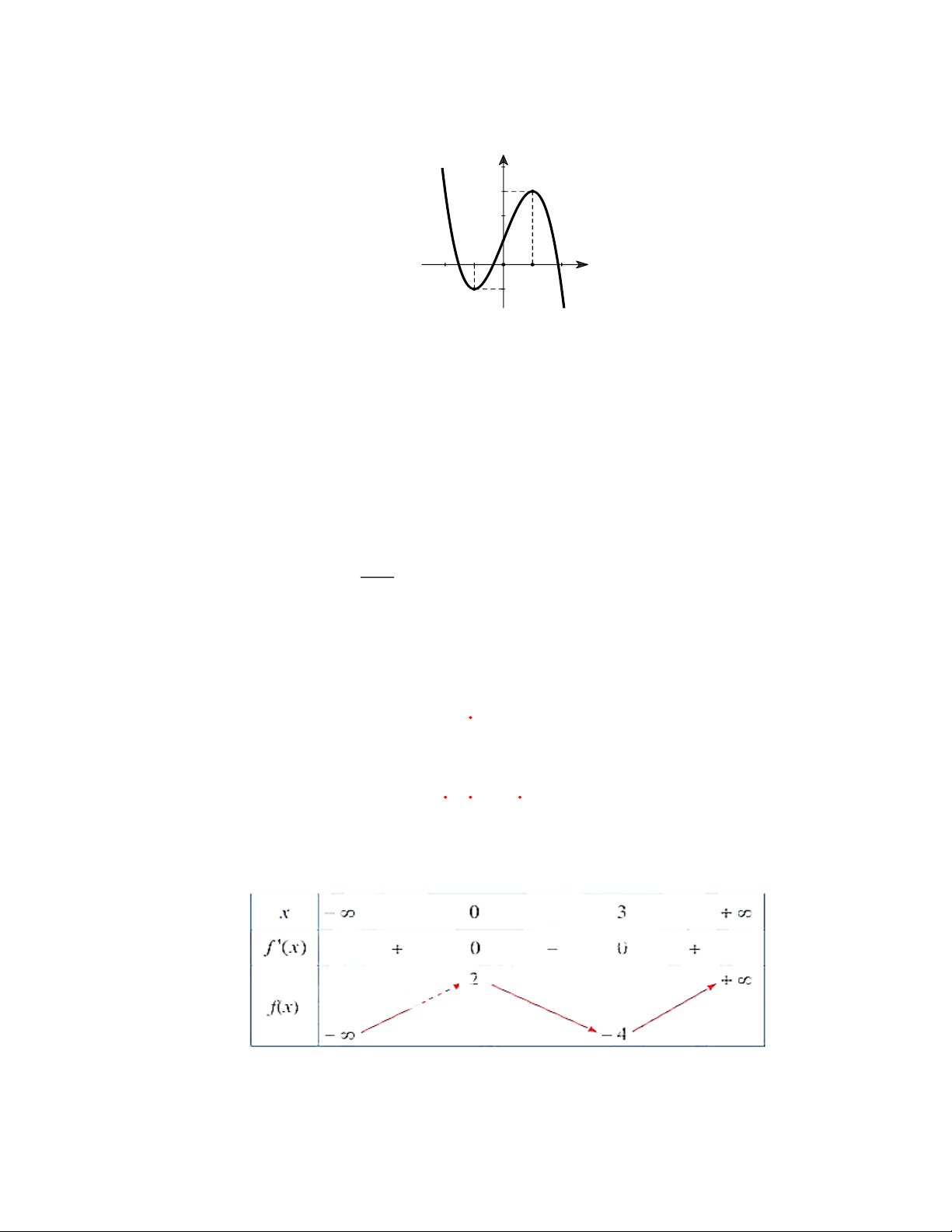
CÂU 4 Cho hàm số y  f x có bảng biến thiên như sau
Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai
a) Hàm số chỉ đồng biến trên khoảng   ;1  . X
b) Hàm số đạt cực đại tại x  3. X
c) Hàm số nghịch biến trên khoảng 1;2 . X
d) Hàm số chỉ đạt cực tiểu tại x  2 . X
PHẦN III. Câu trắc nghiệm trả lời ngắn. Câu 1. Cho hàm số 4 2
y  ax  bx  c có đồ thị như đường cong trong hình bên. Trang 6
Số điểm cực trị của hàm số đã cho là bao nhiêu? Đáp án: 3
Câu 2. Cho hàm số y  f x xác định, liên tục trên và có bảng biến thiên như sau ?
Hàm số y  f (x) có bao nhiêu điểm cực trị ? Đáp án: 3
Câu 3. Cho hàm số y  f x có đạo hàm trên và có bảng biến thiên như sau :
Có bao nhiêu khoảng mà hàm số y  f (x) tăng trên khoảng đó. Đáp á: 1
Câu 4. Cho hàm số y  f x có đồ thị y  f x như hình vẽ bên dưới. Số điểm cực trị của hàm số đã cho là Đáp án: 1
BÀI 2: GIÁ TRỊ LỚN NHÂT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
1 MỨC ĐỘ CẦN ĐẠT: NHẬN BIẾT : Trang 7 YÊU CẦU CẦN ĐẠT
Nhận biết được giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một tập xác định cho trước.
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
Câu 1: Cho hàm số y  f x xác định và liên tục trên có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất
m và giá trị lớn nhất M của hàm số y  f  x trên đoạn  2  ;2 . A. m  5  ;M  1  B. m  2
 ;M  2 . C. m  1;  M  0 . D. m  5  ;M  0 .
Câu 2. Cho hàm số y  f (x) liên tục và có bảng biến thiên trên đoạn  1  ; 
3 như hình vẽ bên. Khẳng định
nào sau đây đúng?
A. max f x  f 0.
B. max f x  f   3 .
C. max f x  f 2 .
D. max f x  f   1 .  1   ;3  1  ;  3  1  ;  3  1  ;  3
Câu 3. Cho hàm số f x liên tục trên và có đồ thị như hình vẽ sau: Trang 8  
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số f x trên 3 1; 
 . Giá trị của M  m bằng  2  1 A. . B. 5 . C. 4 . D. 3 . 2
Câu 4: Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3 2
y  2x  5x  3 trên đoạn  1  ; 
1 .Tính M  m. A. 4  . B. 1. C. 0 . D. 3.
PHẦN II. Câu trắc nghiệm đúng sai. Câu 1: Xét hàm số 4 y  x  trên đoạn  1  ;2 . x
Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai
a) Hàm số có giá trị nhỏ nhất là 4 và giá trị lớn nhất là 2.
b) Hàm số có giá trị nhỏ nhất là 4 và không có giá trị lớn nhất
c) Hàm số không có giá trị nhỏ nhất nhưng có giá trị lớn nhất là 2.
d) Hàm số không có giá trị nhỏ nhất và không có giá trị lớn nhất
Câu 2: Cho hàm số y = f (x ) có bảng biến thiên như sau: Trang 9
Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai
a) Hàm số không tồn tại giá trị nhỏ nhất trên tập xác định.
b) Hàm số đạt giá trị lớn nhất tại điểm x = - 1.
c) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-1; 1] bằng 3
d) Đường thẳng đi qua 2 điểm cực trị tạo với hai trục toạ độ một tam giác có diện tích bằng 8. 2   Câu 3. Cho hàm số x 2x 7 f (x)  . x  4
Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai a)
f ’(x)= có 2 nghiệm trên 4; .
b) Hàm số không tồn tại giá trị lớn nhất trên 4; 
c) Giá trị nhỏ nhất hàm số trên 4;  bằng 5. d) b
Biết rằng min f (x)  b tại x  a . Tỷ số bằng 2 4; a
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Câu 1. Cho hàm số y  f x liên tục và có đồ thị trên đoạn  2  ; 
4 như hình vẽ bên. Tổng giá trị lớn nhất
và nhỏ nhất của hàm số y  f x trên đoạn  2  ;  4 bằng Trang 10
Câu 2. Trên đoạn  1  ;2, hàm số 3 2
y  x  3x 1 đạt giá trị nhỏ nhất tại điểm có hoành độ bao nhiêu?
Câu 3. Người ta bơm xăng vào bình xăng của một xe máy Honda lead. Biết rằng thể tích V (lít) của
lượng xăng trong bình xăng được tính theo thời gian bơm xăng t (phút) cho bởi công thức:
V t    2 3
4 3t  2t  1 với 0  t 1Gọi Vt là tốc độ tăng thể tích tại thời điểm t với 0  t 1
Xăng chảy vào bình xăng vào thời điểm ở giây thứ bao nhiêu có tốc độ tăng thể tích là lớn nhất
Câu 4.Cho hàm số y  f x liên tục trên đoạn  1  ; 
3 và có đồ thị như hình vẽ bên. Gọi M và m lần lượt
là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn  1  ; 
3 . Giá trị của M  m bằng
1 MỨC ĐỘ CẦN ĐẠT : THÔNG HIỂU YÊU CẦU CẦN ĐẠT
Xác định được giá trị lớn nhất, giá trị nhỏ nhất của hàm số bằng đạo hàm trong những trường
hợp đơn giản. :
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
Câu 1. (Sở Hà Nội 2019) Cho hàm số y  f x có bảng biến thiên trên  5  ;7 như sau Trang 11
Mệnh đề nào dưới đây đúng?
A. Min f  x  6 .
B. Min f  x  2 .
C. Max f  x  9 .
D. Max f  x  6 .  5  ;7  5  ;7 -5;7  5  ;7
Câu 2. Cho hàm số f x liên tu ̣c trên đoa ̣n 0; 
3 và có đồ thi ̣ như hình vẽ bên. Go ̣i M và m lần lươ ̣t là
giá tri ̣ lớn nhất và nhỏ nhất của hàm số đã cho trên 0; 
3 . Giá tri ̣ của M  m bằng? A. 5 . B. 3 . C. 2 . D. 1.
Câu 3. Giá trị lớn nhất của hàm số f x 3
 x 3x  2 trên đoạn  3  ;  3 là A. 4 . B. 16  . C. 20 . D. 0 . Câu 4. 4
Tính giá trị nhỏ nhất của hàm số y  3x 
trên khoảng 0;. 2 x A. 33 min y  B. 3 min y  2 9 C. 3 min y  3 9
D. min y  7 0; 5 0; 0; 0;
PHẦN II. Câu trắc nghiệm đúng sai. f  x 2 Câu 1. Cho hàm số  x ln x .
Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai a) Trên đoạ 1  n ; e 
 , f e là giá trị lớn nhất của hàm số f  x . e  b)
min f  x  0 . 1  x ;e   e  c) max f  x 2  e 1  x ;e   e 
d) Trên đoạ 1   1  n ; e 
 , f   là giá trị nhỏ nhất của hàm số f  x . e   e  Trang 12
Câu 2. Cho hàm số y  f (x) có đạo hàm 2 f (
 x)  x(x 1)(x  2) với mọi x . Xét tính đúng sai của các mệnh đề sau. Mệnh đề Đúng Sai
a) Hàm số có 2 điểm cực trị
b) Hàm số đồng biến trên khoảng  1  ;2..
c) Giá trị nhỏ nhất của hàm số y  f (x) trên đoạn  1
 ;2 là f (0). d)
f 0  f 2.
Câu 3. Cho hàm số y  f x . Biết bảng xét dấu của f 'x như sau
Các khẳng định sau đúng hay sai? Mệnh đề Đúng Sai
a) Giá trị lớn nhất của hàm số hx  f (2 ) x trên đoạn  1
 ; 1 là f (1).
b) Giá trị lớn nhất của hàm số y  f (x) trên đoạn  1
 ;2 là f (1).
c) Giá trị lớn nhất của hàm số g  x  f  2 x  x 2 2
 3x  6x  5 trên 0;  2 là
f 0  2.
d) Giá trị nhỏ nhất của hàm số y  f (x) trên đoạn  1  ;  3 là f (3) .
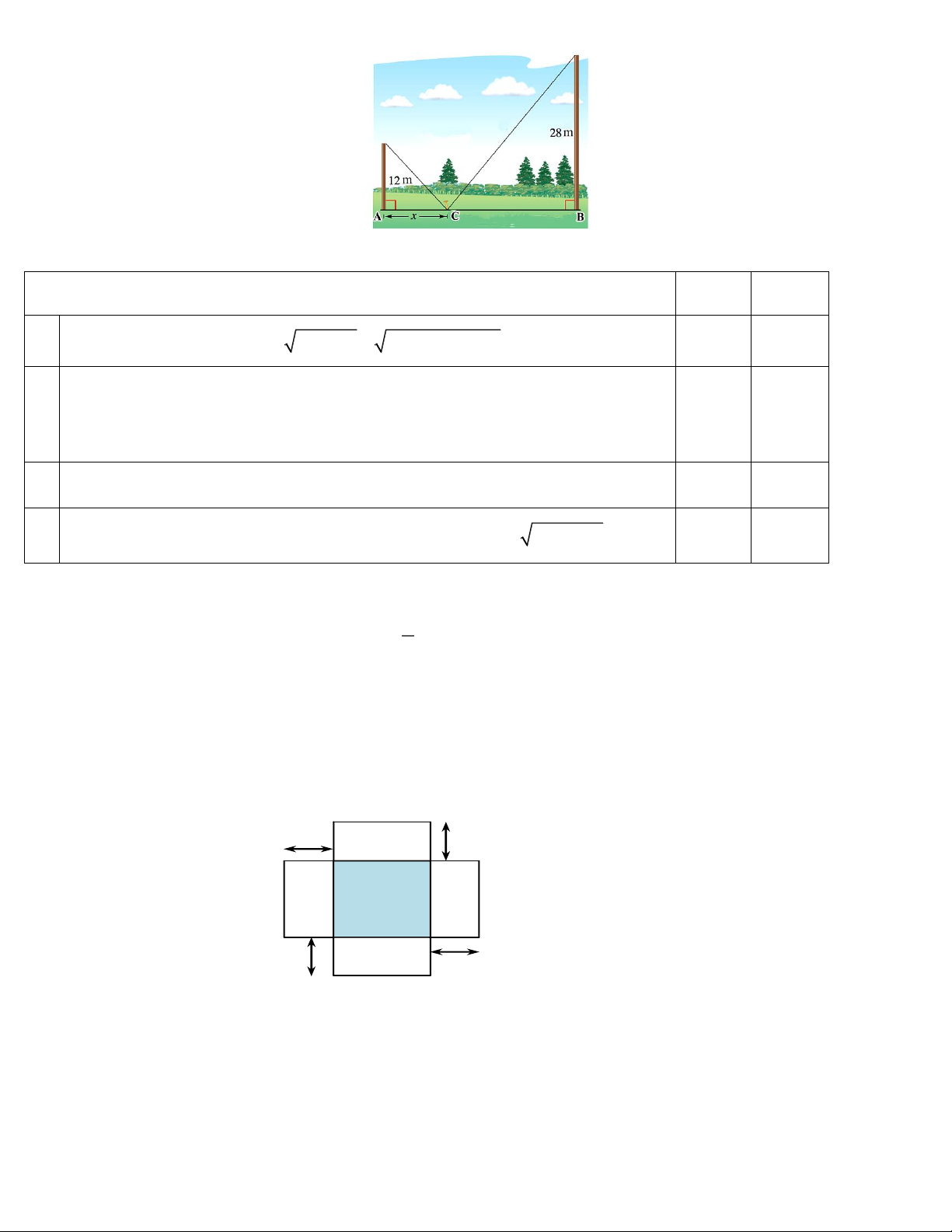
Câu 4. Có hai cây cột, một cây cao 12m và một cây cao 28m đứng cách nhau 30m.Chúng được giữ bằng
hai sợi dây, gắn vào một cọc duy nhất nối từ mặt đất đến đỉnh mỗi cột. Gọi x là khoảng cách từ cột cao 12 m  đến cọc. Trang 13
Các khẳng định sau đúng hay sai? Mệnh đề Đúng Sai
a) Tổng chiều dài của dây là 2 2
144  x  1684  60x  x .
b) Giá trị lớn nhất của hàm số g  x  f  2 x  x 2 2
 3x  6x  5 trên 0;  2 là
f 0  2.
c) Tổng chiều dài ngắn nhất của dây là 48,5 m  .
d) ) Chiều dài sợi dây nối từ cọc đến đỉnh cột cao 28m  là 2 1684  x .
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Câu 1. Biết rằng hàm số f  x 1
 x  2018  đạt giá trị lớn nhất trên đoạn 0;4 tại x . x 0
Tính P  x  2. 0
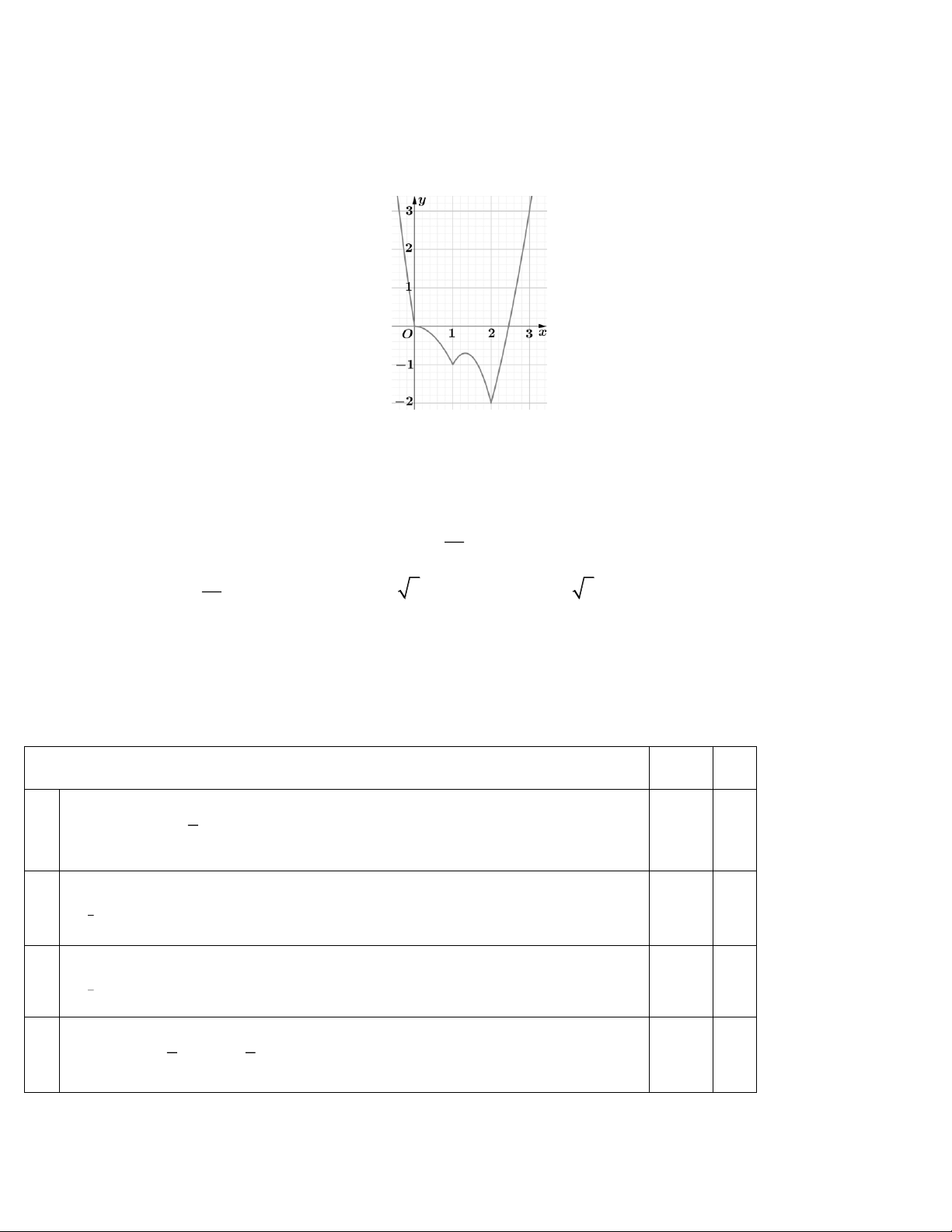
CÂU 2 Một hộp không nắp được làm từ một mảnh các tông theo mẫu như hình vẽ. Hộp có đáy là một hình
vuông cạnh x cm, chiều cao h cm và có thể tích 5 cm3. h h x x h h
Giá trị của x để diện tích của mảnh các tông nhỏ nhất bằng bao nhiêu? Trang 14
Câu 3. Một loại vi khuẩn được tiêm một loại thuốc kích thích sự sinh sản. Sau t phút, số vi khuẩn được xác định theo công thức 2 3
N (t)  1000  30t  t (0  t  30) . Hỏi sau bao giây thì số vi khuẩn lớn nhất?
BÀI 3 KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
MỨC ĐỘ CẦN ĐẠT: NHẬN BIẾT :
YÊU CẦU CẦN ĐẠT
– Nhận biết được hình ảnh hình học của đường tiệm cận ngang, đường tiệm cận đứng, đường tiệm cận
xiên của đồ thị hàm số.
– Nhận biết được tính đối xứng (trục đối xứng, tâm đối xứng) của đồ thị các hàm số.
. PHẦN I:Câu trắc nghiệm nhiều phương án lựa chọn.
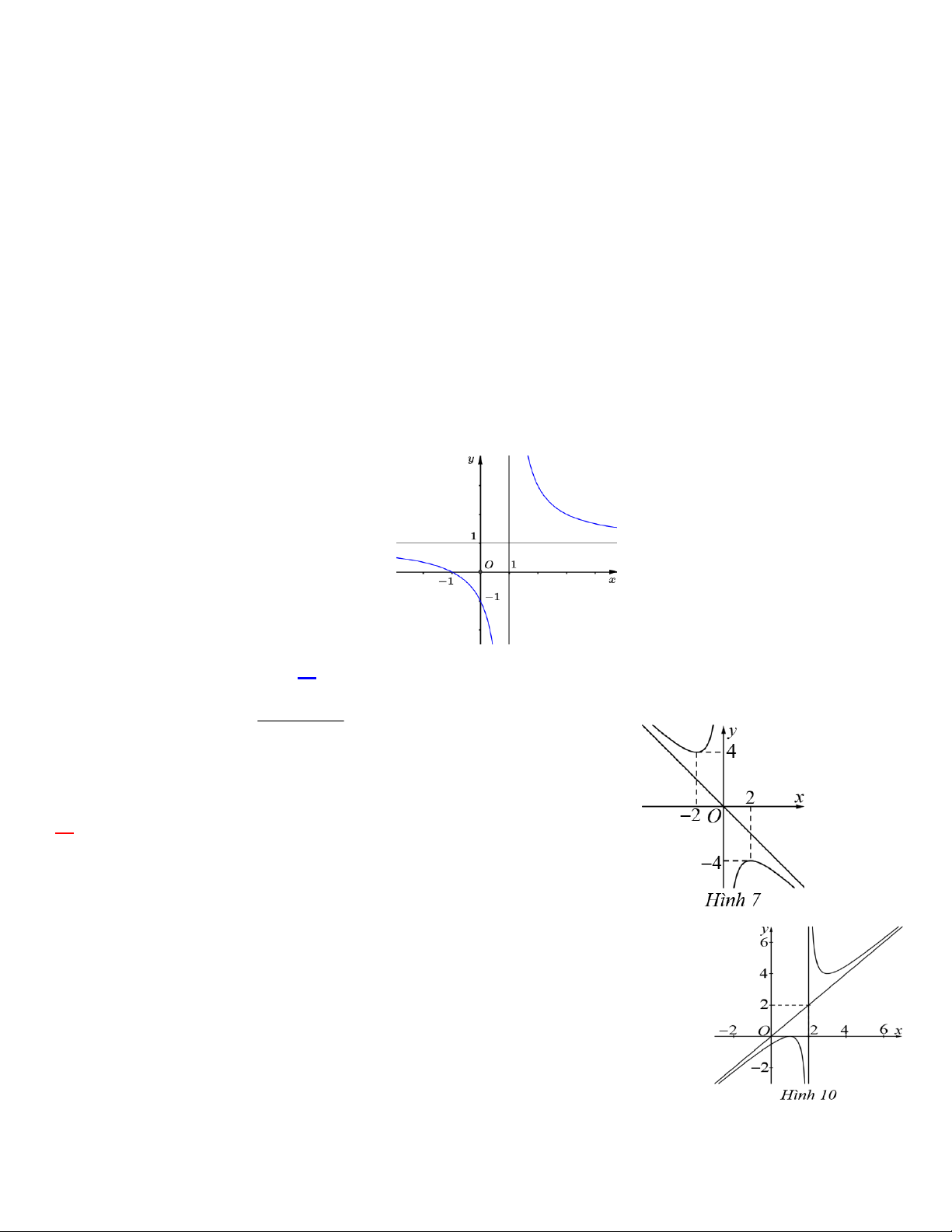
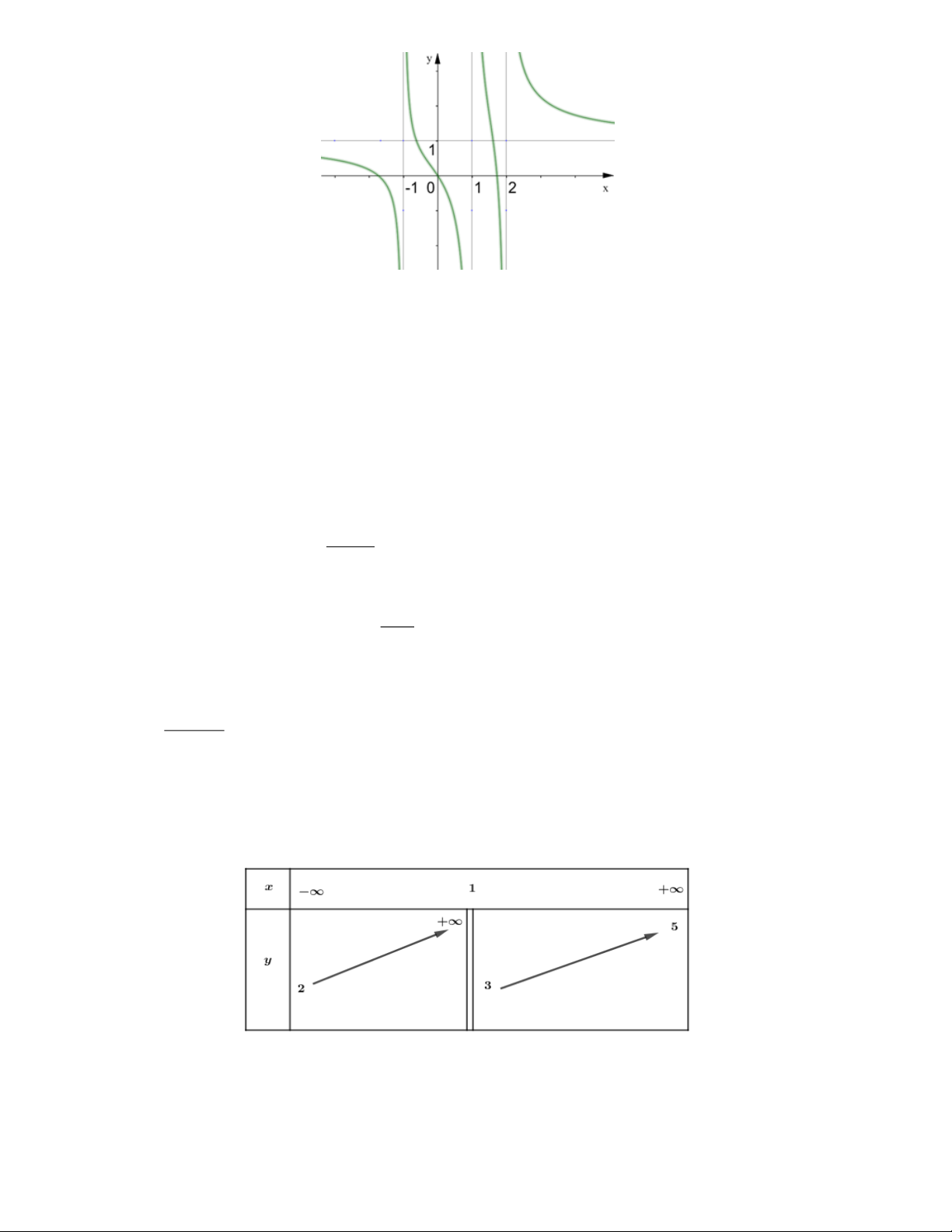
Câu 1: Cho hàm số y  f x có đồ thị như hình vẽ dưới đây. Tiệm cận đứng và tiệm cận ngang của đồ
thị hàm số theo thứ tự là A. x  1  ; y  1  .
B. x 1; y  1.
C. x 1; y  1  . D. x  1  ; y  1. 2
ax  bx  c
Câu 2: Cho hàm số y 
, (ac  0) có đồ thị như Hình 7. Đường x
tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng:
A. Đường thẳng y  . x
B. Đường thẳng y   . x
C. Đường thẳng x  0.
D. Đường thẳng y  2 . x
Câu 3: Cho hàm số y  f (x) có đồ thị ở Hình 10. Tâm đối xứng của đồ thị hàm số có toạ độ là A. (2; 2). B. ( 2  ; 2  ). C. ( 2  ; 2). D. (2; 2  ).
Câu 4. Cho hàm số y  f  x có báng biến thiên như sau: Trang 15
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là: A. 2. B. 3. C. 4. D. 1.
Câu 5. Cho hàm số y  f (x) có lim f (x) 1và. lim f (x)   Khẳng định nào sau đây là khẳng định x x 1  đúng?
A. Đồ thị hàm số đã cho có hai tiệm cận ngang
B. Đồ thị hàm số đã cho không có tiệm cận
C. Đồ thị hàm số đã cho có hai tiệm cận .
D. Đồ thị hàm số đã cho có hai tiệm cận đứng
PHẦN II. Câu trắc nghiệm đúng sai.
Câu 1: Cho đồ thị hàm số y  f x như hình bên. y 1 1  O x
Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai
a) Đồ thị hàm số có tiệm cận đứng x  0 , tiệm cận ngang y  1.
b) Hàm số có hai cực trị.
c) Đồ thị hàm số có một đường tiệm cận xiên. Trang 16
d) Đồ thị hàm số có tâm đối xứng
Câu 2. Cho hàm số y= f ( x ) có bảng biến như sau:
Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai
a) Đồ thị hàm số nhận đường thẳng y = 0 là tiệm cận ngang.
b) Đồ thị hàm số nhận đường thẳng x = - 3là tiệm cận đứng.
c) Số đường tiệm cận của đồ thị hàm số là 4.
d) Hàm số đồng biến trong khoảng ;  2 x  2x  2
Câu 3: Cho hàm số y  . x  2
Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai
a) Hàm số chỉ có 2 đường tiệm cận.
b) Giao điểm của hai tiệm cận là I (2; 6) .
c) Đồ thị hàm số không có tâm đối xứng.
d) Đường tiệm cận đi qua điểm M (0; 4  )
Câu 4. Cho hàm số y  f x . Có đồ thị như hình vẽ. Trang 17
A. Đồ thị hàm số y  f  x có hai đường tiệm cận đứng x  1  và x 1
B. Đồ thị hàm số y  f  x có một đường tiê ̣m câ ̣n ngang là y  1.
C. Đồ thị Hàm số y  f  x có 4 đường tiệm cận
D. Đường thẳng x = 2 là một tiệm cận đứng của đồ thị hàm số y  f  x
PHẦN III. Câu trắc nghiệm trả lời ngắn. 3x  5
Câu 1: Cho đồ thị hàm số f (x) 
có tâm đối xứng là I (a; b). Giá trị của biểu thức    là  B 4a b x  7 bao nhiêu? 8
Câu 2: Cho đồ thị hàm số f (x)  5x 1
có tâm đối xứng là I (a; b). Giá trị của biểu thức C  a 3b x 1 là bao nhiêu?
Câu 3: Số dân của một thị trấn sau t năm kể từ năm 197 được ước tính bởi công thức 26t 10 f (t) 
( f (t) được tính bằng nghìn người) (Nguồn: Giải tích 12 nâng cao, NXBGD Việt t  5
Nam, 2020). Xem y  f (t) là một hàm số xác định trên nửa khoảng [0; ). Đồ thị hàm số
y  f (t) có đường tiệm cận ngang là y  .
a Giá trị của a là bao nhiêu?
Câu 4. Cho hàm số y  f x có bảng biến thiên như sau
Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số đã cho là bao nhiêu?
Câu 5. Số tiệm cận đứng và số tiệm cận ngang của đồ thị hàm số y  f (x) có bảng biến thiên sau là Trang 18
Số đường tiệm cận đứng của đồ thị hàm số đã cho là bao nhiêu? 2 x  2x  5
Câu 4. Tìm tiệm cận đứng và tiệm cận xiên của đồ thị hàm số y  . x 1
MỨC ĐỘ CẦN ĐẠT: THÔNG HIỂU :
YÊU CẦU CẦN ĐẠT
– Mô tả được sơ đồ tổng quát để khảo sát hàm số (tìm tập xác định, xét chiều biến thiên, tìm cực trị, tìm
tiệm cận, lập bảng biến thiên, vẽ đồ thị).
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn.  Câu 1. Cho hàm số x 1 y 
. Khẳng định nào sau đây đúng? x 1
A. Hàm số nghịch biến trên \ R\   1  .
B. Hàm số đồng biến trên  ;    1 và  1  ;.
C. Hàm số có 2 cực trị
D. Đồ thị hàm số không có tâm đối xứng
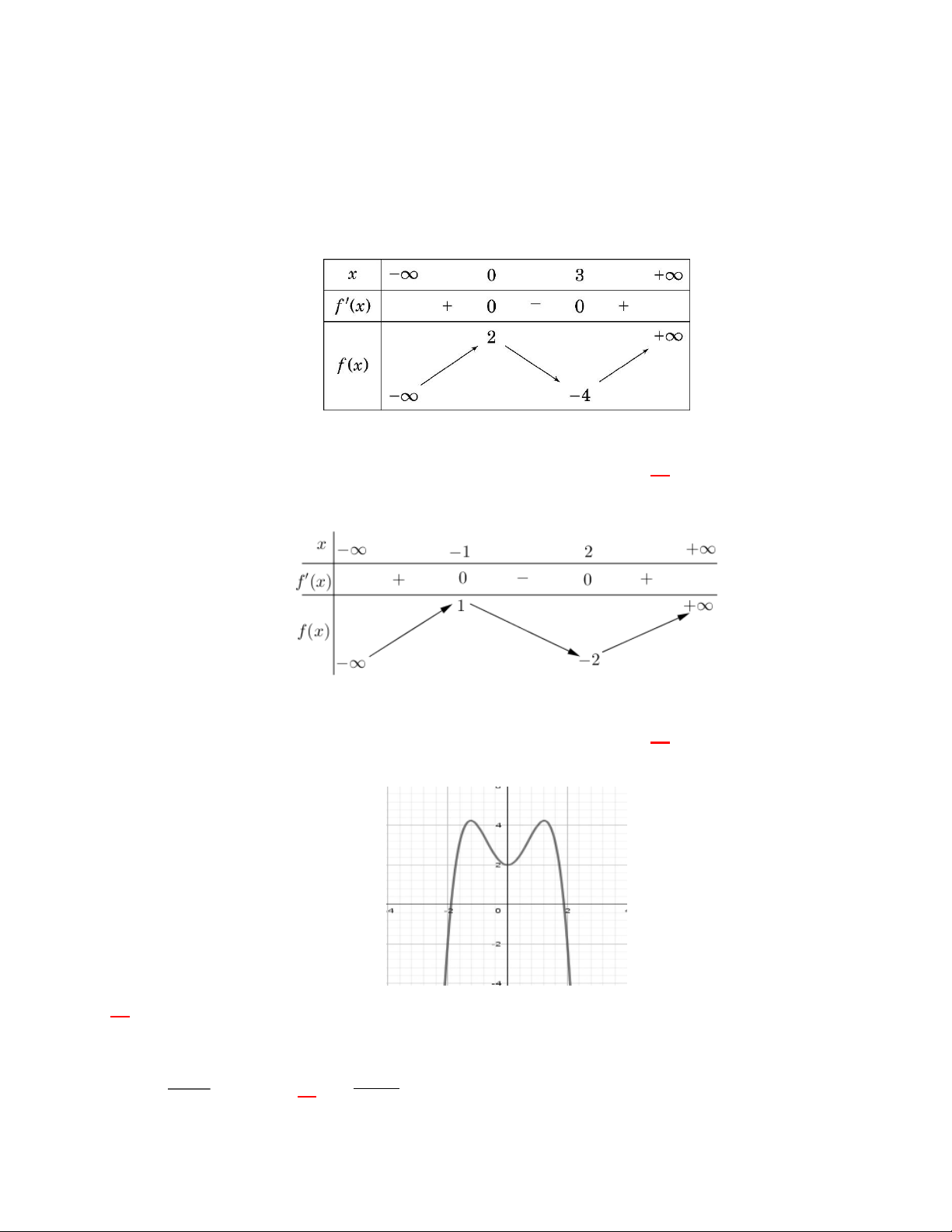
Câu 2. Cho hàm số y  f x xác định và liên tục trên đoạn  2
 ;2 và có đồ thị là đường cong trong hình vẽ sau.
A. hàm số đồng biến trên (-2; ). B. Đồ thị hàm số có đường tiệm cận.
C.giá trị lớn nhất băng 2. D. Điểm cực tiểu của đồ thị hàm số y  f x là M 1; 2 .
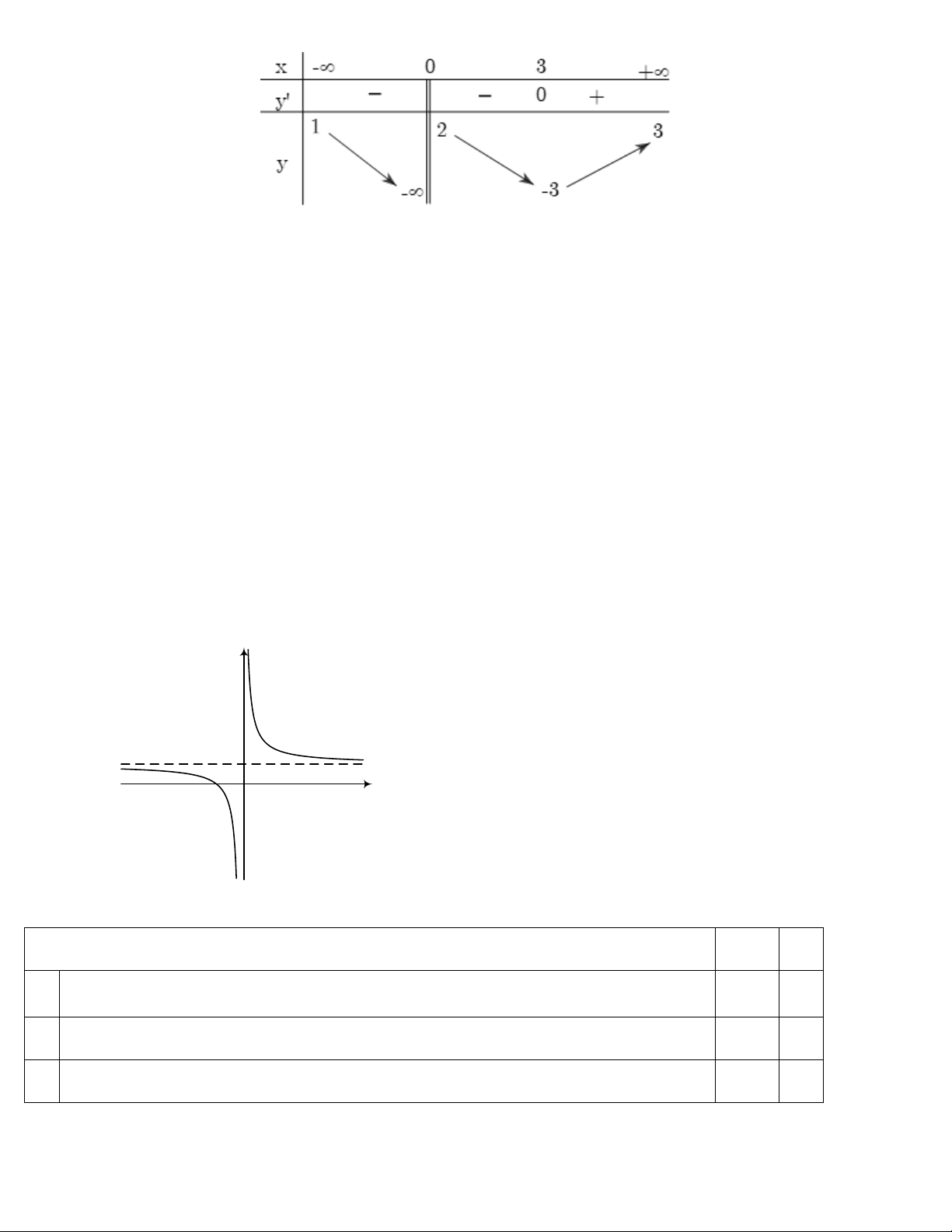
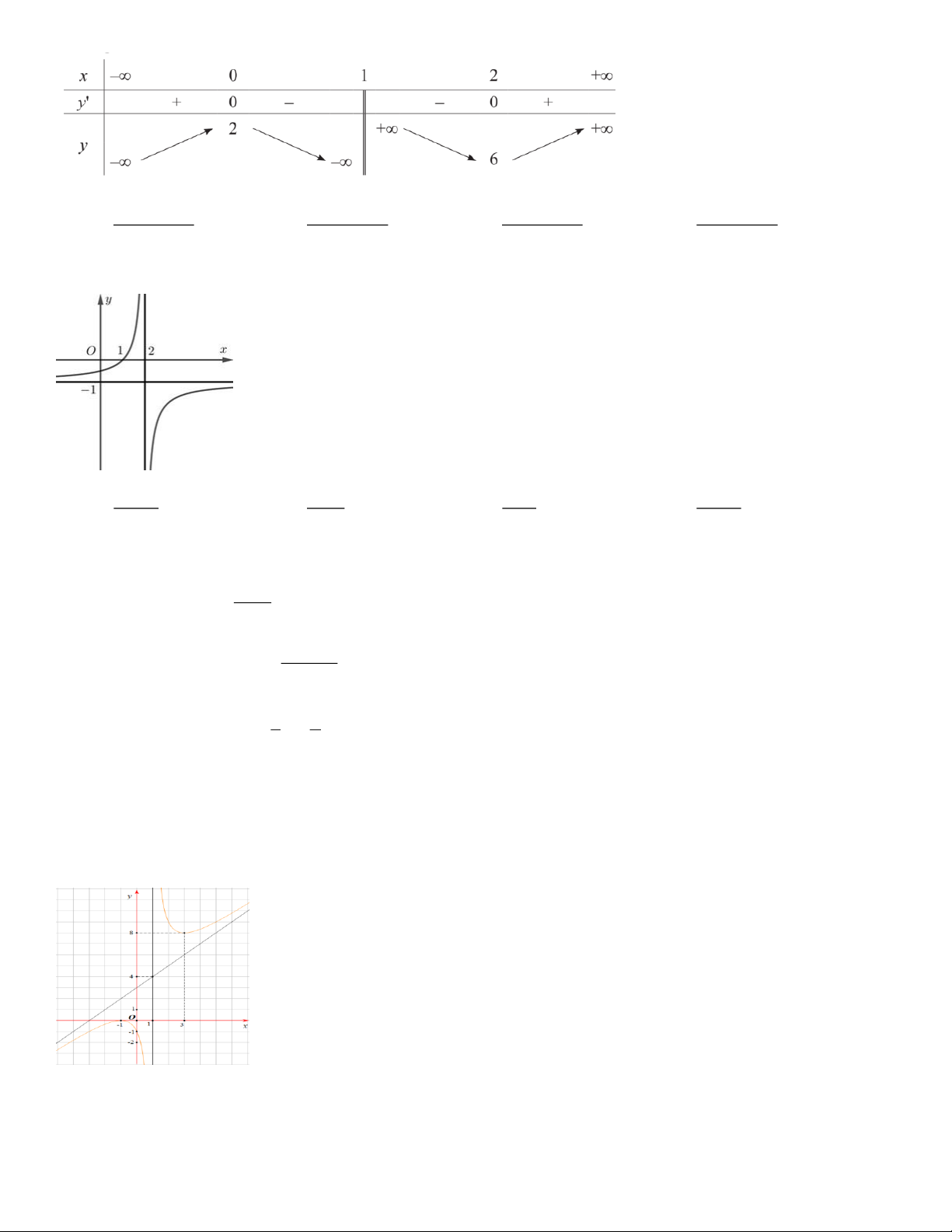
Câu 3. Bảng biến thiên sau là của hàm số nào dưới đây? Trang 19 2 x  2x  2 2 x  2x  2 2 x  2x  2 2 x  2x  2 A. y  . B. y  . C. y  . D. y  . x 1 x 1 x 1 x 1
Câu 4. Đường cong dưới đây là đồ thị hàm số nào x   x  x x  A. 1 y  . B. 1 y  . C. 1 y  . D. 1 y  . x  2 x  2 x 1 x  2
PHẦN II. Câu trắc nghiệm đúng sai.  Câu 1. Cho hàm số x 2 y  C. x 1 3
a) Hàm số có đạo hàm y   x  2 1
b) Đường thẳng d  1 2 : y   x 
luôn cắt đồ thị C tại 2 điểm phân biệt. 3 3
c) Phương trình tiếp tuyến của đồ thị C tại điểm có hoành độ bằng 2 là y  3  x 10 .
d) Đồ thị C đi qua điểm 2;4 .
Câu 2. Cho hàm số y  f x có đồ thị hàm số như hình bên dưới
a) Hàm số f x đạt cực đại tại x  1
 và đạt cực tiểu tại x  3. Trang 20