Chuyên Đề Vecto Trong Không Gian Ôn Thi Tốt Nghiệp Giải Chi Tiết
Một em nhỏ cân nặng 25 kg trượt trên cầu trượt dài 35m (như trong hình dưới đây). Biết rằng, cầu trượt có góc nghiêng so với phương nằm ngang là 30. Trong các khẳng định sau, có bao nhiêu khẳng định đúng? Với gia tốc rơi tự do g có độ lớn. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Tài liệu ôn thi THPTQG môn Toán 278 tài liệu
Môn: Toán 2.2 K tài liệu
Tác giả:
Preview text:
CHUYÊN ĐỀ VECTO TRONG KHÔNG GIAN
Câu hỏi – Trả lời trắc nghiệm 4 phương án
» Câu 1. Cho hình hộp chữ nhật ABC . D A B C D . uuur
Vectơ nào sau đây cùng phương với BC ? uuur uuur uuur uuur A. DC B. DA C. BB D. C C
Lời giải Chọn B uuur uuur
Vì BC // DA nên BC , DA là hai vectơ cùng phương.
» Câu 2. Trong các vectơ sau, vectơ nào sau đây có điểm đầu là A , điểm cuối là B ? uuur uuur uuur uur A. AA B. BA C. AB D. BB
Lời giải Chọn C uuur
Vectơ nào có điểm đầu A , điểm cuối B là AB
» Câu 3. Trong không gian cho 3 điểm phân biệt A , B , C . Vectơ nào trong các vec tơ sau đây là vectơ - không? uur uuur uuur uuur A. BB B. BA C. BA D. CA
Lời giải Chọn A uur r
Vì vectơ - không là vectơ có điểm đầu điểm cuối trùng nhau nên BB 0 .
» Câu 4. Cho hình hộp chữ nhật ABC . D A B C D . uuur
Vectơ BA bằng với vectơ nào sau đây? uuuur uuur uuur uuur A. A B B. CD C. BC D. AB
Lời giải Chọn B uuur uuur uuur uuur
Vì BA , CD là hai vectơ cùng hướng và BA CD nên BA , CD là hai vectơ bằng nhau uur uuur
» Câu 5. Cho hình chóp .
S ABC . Tìm vectơ tổng của hai vectơ SA và AB ? Trang 1 uur uuur uur uur A. BS B. BA C. SB D. SC
Lời giải Chọn C uur uuur uur
Theo quy tắc 3 điểm ta có, SA AB SB uuur uuur
» Câu 6. Cho hình hộp ABC . D A B C D
. Tìm vectơ tổng của hai vectơ AD và AB. uuur uuur uuur uuur A. DB B. BD C. AC D. CA
Lời giải Chọn C uuur uuur uuur
Theo quy tắc hình bình hành ta có, AD AB AC
» Câu 7. Cho hình hộp ABC . D A B C D
. Mệnh đề nào sau đây đúng? uuur uuur uuur uuur uuur uuur uuur uuur
A. AB AD AA AC .
B. AB AC AA AD . uuur uuur uuur uuur uuur uuur uuur uuur
C. AB AD AC AC .
D. AB AD AC AC .
Lời giải Chọn A uuur uuur uuur uuur
Theo quy tắc hình hộp ta có : AB AD AA AC .
» Câu 8. Cho hình chóp .
S ABC . Mệnh đề nào sau đây đúng? uur uuur uur uur uur uuur uur uur uuur uur uur uur
A. SA AB SB .
B. SA SB AB .
C. SA SB BA .
D. SA SB SC .
Lời giải Chọn C uur uur uuur
Theo quy tắc hiệu ta có: SA SB BA .
» Câu 9. Cho hình hộp ABC . D A B C D
. Mệnh đề nào sau đây đúng? Trang 2 uuur uuuur uuur uuur uuuur uuur uuur uuuur uuur uuur uuuur uuur
A. AB A D
AC . B. AB A D
BD . C. AB A D
AC. D. AB A D CA .
Lời giải Chọn A uuur uuuur uuur uuur uuur AB A D
AB AD AC (quy tắc hình bình hành).
» Câu 10. Cho hình chóp .
S ABCD có đáy là hình bình hành tâm O . Tính tổng uur uur uur uur
SA SB SC SD . uur uur uur r A. 2SO B. 4SO C. 3SO D. 0
Lời giải Chọn B uur uur uur uur uur uur
Vì O là trung điểm của AC, BD nên SA SC 2SO , SB SD 2SO . uur uur uur uur uur
Do đó SA SB SC SD 4SO .
» Câu 11. Cho tứ diện ABCD . Gọi M, N lần lượt là trung điểm của AD và BC . Tổng uuur uuur
AB DC bằng r uuur uuuur uuuur A. 0 B. 2AD C. 2NM D. 2MN
Lời giải Chọn C Ta có: uuur uuur uuuur uuuur uuur uuuur uuuur uuur uuuur uuuur uuuur uuur uuur
AB DC AM MN NB DM MN NC AM DM 2MN NB NC uuuur
2MN (vì M,N lần lượt là trung điểm của AD và BC nên uuuur uuuur r uuur uuur r
AM DM 0, NB NC 0 ). uuur uuur uuuur
» Câu 12. Cho hình hộp ABC . D A B C D
. Tính tổng AB AD A C . uuur r uuur uuuur A. 2AA B. 0 C. 2.AC . D. 2C A
Lời giải Chọn C uuur uuur uuur
Theo quy tắc hình bình hành ta có, AD AB AC . uuur uuur uuuur uuur uuuur uuur
AB AD A C
AC A C 2.AC . uuur uuur
» Câu 13. Cho khối lập phương ABC . D A B C D
. Khi đó, góc giữa vectơ AB và vectơ AD là: A. 90 B. 60 C. 45 D. 30 Trang 3
Lời giải Chọn A · uuur uuur · Ta có ; AB AD DAB · · uuur uuur
Ta thấy AB AD DAB 90 . Vậy ; AB AD 90
» Câu 14. Cho lăng trụ đứng AB . C A B C
. Đáy là tam giác ABC vuông tại B . Khi đó góc giữa uuur uuuur
vecto BA và vecto B C bằng bao nhiêu? A. 45 B. 120 C. 90 D. 30
Lời giải Chọn C uuuur uuur Ta có B C BC · uuur uuuur · uuur uuur · Do đó BA; B C
BA; BC ABC · · uuur uuuur
Mà tam giác ABC vuông tại B . Nên ABC 90 BA; B C 90 uuur
» Câu 15. Cho hình hộp chữ nhật ABC . D A B C D
. Khi đó, vectơ bằng vectơ AB là vectơ nào dưới đây? uuuur uuur uuur uuuur A. D C B. BA C. CD D. B A
Lời giải Chọn A Do ABC . D A B C D
là hinh hộp chữ nhật nên AB DC D C uuur uuuur Và A ; B D C
cùng phương, cùng chiều uuur uuuur
Từ đó AB D C Trang 4 uuur uuur r uuur uuur r r r
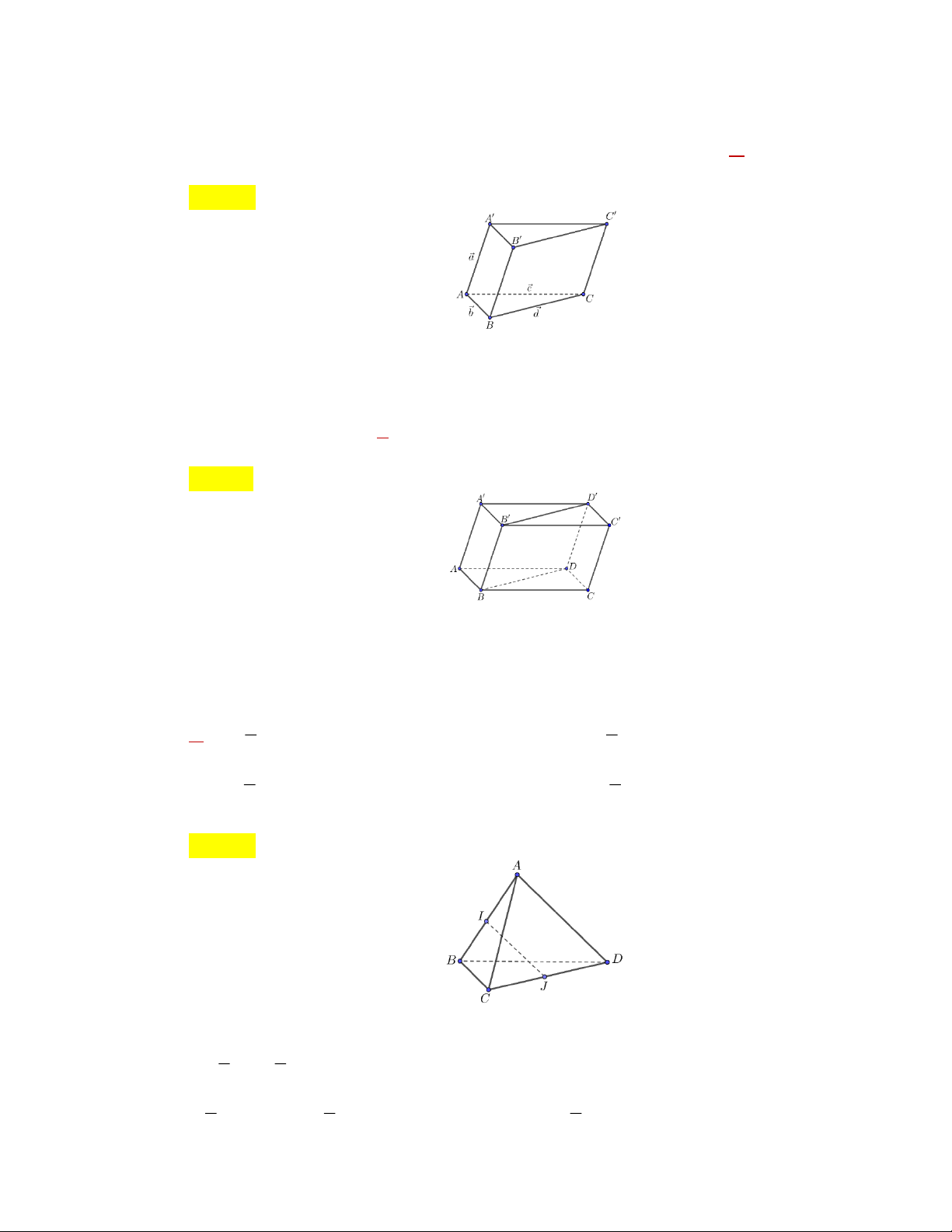
» Câu 16. Cho hình lăng trụ tam giác ABCA B C
. Đặt AA a, AB b,AC c,BC d . Trong
các biểu thức véctơ sau đây, biểu thức nào đúng? r r r r r r r r r r r r r r r r
A. a b c d
B. a b c
C. a b c d 0
D. b c d 0
Lời giải Chọn D r r uuur uuur uuur uur uuur r r
Ta thấy: b c d AB AC BC CB BC 0 .
» Câu 17. Cho hình hộp ABC . D A B C D
. Tìm giá trị của k thích hợp điền vào đẳng thức uuur uuuur uuuur uuur
vectơ: BD D D B D kBB A. k 4 B. k 1 C. k 0 D. k 2
Lời giải Chọn B uuur uuuur uuuur uuur uuuur uuuur uuur uuuur uuur
Đặt VT BD D D B D
BD DD D B
BD D B BB Vậy k 1
» Câu 18. Cho tứ diện ABCD , gọi I , J lần lượt là trung điểm của AB và CD ; Đẳng thức nào sai? ur 1 uuur uuur ur 1 uuur uuur
A. IJ AC BD
B. IJ AD BC 2 2 ur 1 uuur uuur uuur ur 1 uuur uuur uuur
C. IJ DC AD BD
D. IJ DC AD BD 2 2
Lời giải Chọn D ur uur uur
Ta có: IJ IA AJ 1 uuur 1 uuur uuur
AB AC AD 2 2 1 uuur uuur uuur uuur uuur uuur uuur uuur uuur uuur 1 1
BC AD AB BD CD DC BC ABCD 2BC . 2 2 2 Trang 5 ur 1 uuur uuur
Vậy đẳng thức sai là IJ ABCD. 2
» Câu 19. Cho hình hộp ABC .
D EFGH . Gọi O là trung điểm CH . Khẳng định nào sau đây là khẳng định đúng? uuur 1 uuur uuur 1 uur uuur uuur 1 uuur 1 uur
A. BO BA BC BF
B. BO BA BC BF . 2 2 2 2 uuur 1 uuur 1 uuur 1 uur uuur uuur uuur uur
C. BO BA BC BF .
D. BO BA BC BF . 2 2 2
Lời giải Chọn A uuur 1 uuur uuur 1 uuur uuur uuur uur 1 uuur uuur 1 uur
Ta có BO BC BH BC BA BC BF BA BC BF . 2 2 2 2
» Câu 20. Cho hình lập phương ABC . D A B C D
. Khẳng định nào sau đây là sai? uuur uuuur uuur uuuur A. A ; B A D 90. B. A ; B A C 45 . uuur uuuur uuur uuur
C. AC; B D 90. D. A A
;CB 45.
Lời giải Chọn D uuur uuuur uuur uuur A ; B A D
A ;B AD · BAD 90 uuur uuuur uuur uuur A ; B A C
A ;B AC · BAC 45 uuur uuuur uuur uuur AC; B D
AC;BD 90
uuur uuur uuur uuur uur uuur A A
;CB C C;CB ;
CE CB 135 trong đó E là điểm đối xứng với C qua C . uuur uuur
» Câu 21. Cho tứ diện đều ABCD có cạnh bằng a . Tính góc AB,CD . uuur uuur uuur uuur
A. AB,CD 60 .
B. AB,CD 90. Trang 6 uuur uuur uuur uuur
C. AB,CD 120.
D. AB,CD 180.
Lời giải Chọn B
Gọi M là trung điểm CD . uuur uuur uuuur uuur uuur uuuur uuur uuur uuur Khi đó, A .
B CD AM MB.CD AM.CD M . B CD uuuur uuur
Do tam giác ACD đều nên AM CD AM.CD 0 uuur uuur
Và tam giác BCD đều nên BM CD BM.CD 0 uuur uuur uuuur uuur uuur uuuur uuur uuur uuur uuur uuur Vậy A .
B CD AM MB.CD AM.CD M .
B CD 0 AB CD . uuur uuur
Kết luận AB,CD 90.
» Câu 22. Theo định luật II Newton: Gia tốc của một vật có cùng hướng với lực tác dụng lên
vật. Độ lớn của gia tốc tỉ lệ thuận với độ lớn của lực và tỉ lệ nghịch với khối lượng ur r r ur
của vật: F ma , trong đó a là vectơ gia tốc 2
m/s , F là vectơ lực N tác dụng lên
vật, m kg là khối lượng của vật. Muốn truyền cho quả bóng có khối lượng 0,5kg một gia tốc 20 2
m/s thì cần một lực đá có độ lớn là bao nhiêu?
A. 100 N . B. 20N . C. 25N .
D. 10 N .
Lời giải Chọn D ur r ur r
Ta có F ma F m a 0,5 2 . 0 10N .
Vậy muốn truyền cho quả bóng có khối lượng 0,5kg một gia tốc 20 2 m/s thì cần
một lực đá có độ lớn là 10 N .
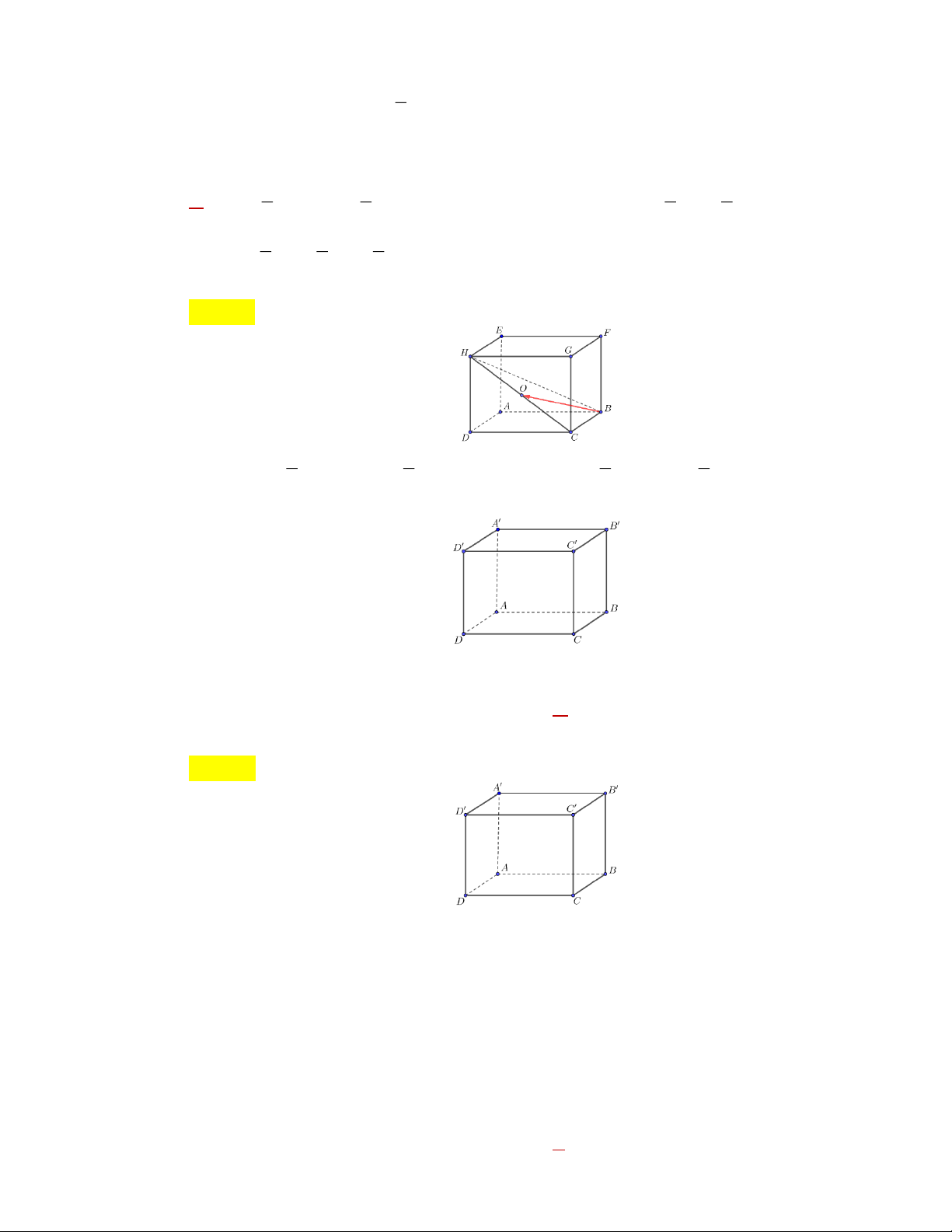
» Câu 23. Cho hình hộp đứng ABC . D A B C D
, trong đó mặt đáy là hình bình hành với ·
DAB 120 . Biết độ dài các cạnh AB 25c ,
m AD 12cm và AA 12cm. Tính uuur uuur uuur
AB AD AA . Trang 7 A. 12cm .
B. 469 cm .
C. 613 cm . D. 25cm .
Lời giải Chọn C uuur uuur uuur uuur
Theo quy tắc hình hộp, ta có AB AD AA AC , uuur uuur uuur uuur
Vậy AB AD AA AC AC Với 2 2
AC AC AA
Trong đó: AA 12cm ·
Do tổng hai góc kề của một hình bình hành là 180 nên ta có góc ABC 60
Áp dụng định lý cosin trong tam giác ABC , ta có 2 2 2 · 2 2
AC AB BC 2A .
B BC.cos ABC 25 12 2 2 . 5 1 . 2.cos 60 469 . Vậy 2 2
AC AC AA 469 144 613 cm.
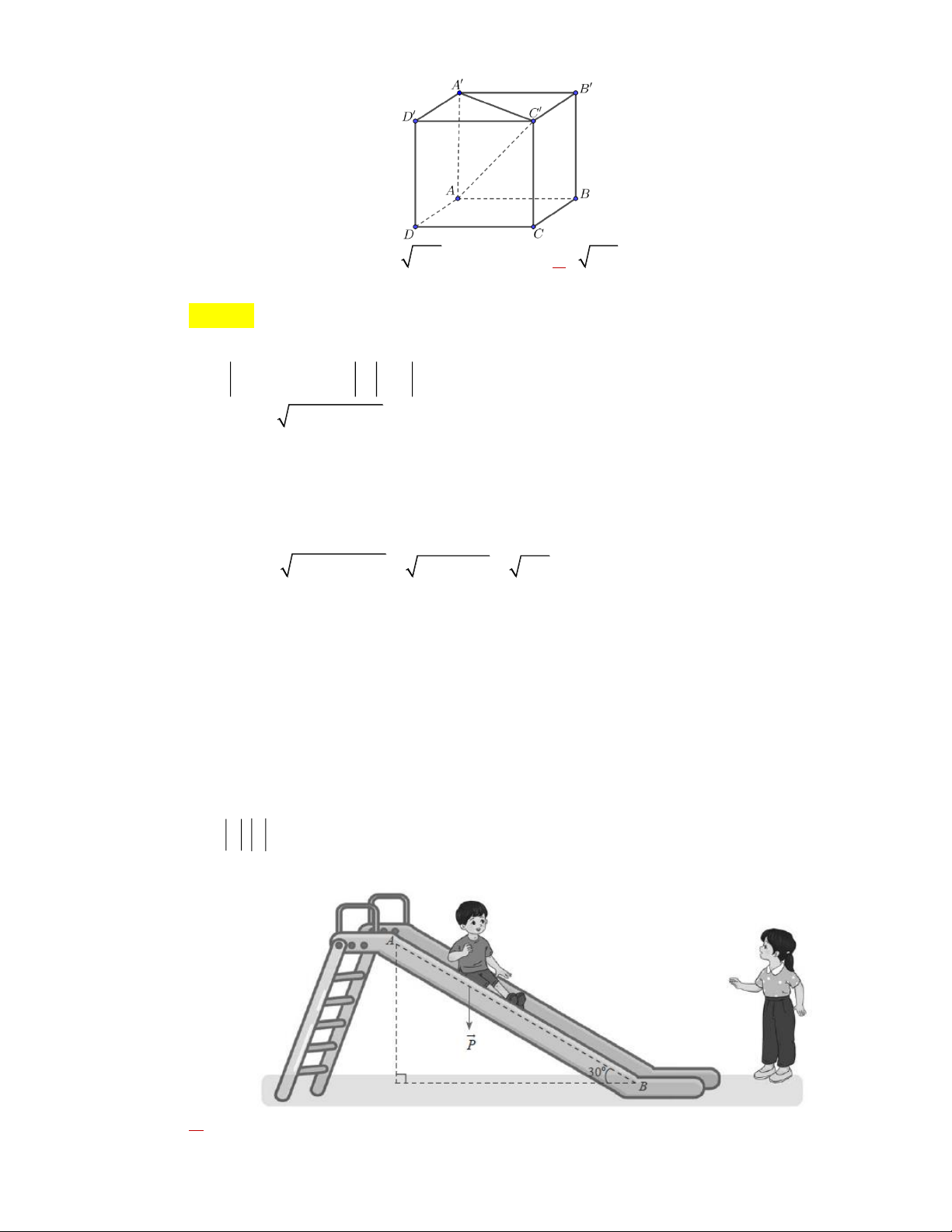
» Câu 24. Một em nhỏ cân nặng m 25kg trượt trên cầu trượt dài 3,5m (như trong hình
dưới đây). Biết rằng, cầu trượt có góc nghiêng so với phương nằm ngang là 30 .
Trong các khẳng định sau, có bao nhiêu khẳng định đúng? r r r
» Với gia tốc rơi tự do g có độ lớn là g 9 8 2 ,
m/s thì độ lớn của trọng lực P mg
tác dụng lên em nhỏ có độ lớn là 245N . r r
» Góc giữa độ dịch chuyển d so với trọng lực P là 30. r r
» Công A J sinh bởi một lực F có độ dịch chuyển d được tính bởi công thức r r r r r
A F . d .cosF;d thì công sinh bởi trọng lực P khi em nhỏ trượt hết chiều dài
cầu trượt là 428,75 J . A. 2 . B. 1. C. 3 . D. 0 .
Lời giải Trang 8 Chọn A r ur r
» Với gia tốc rơi tự do g có độ lớn là g 9 8 2 ,
m/s thì độ lớn của trọng lực P mg ur r
tác dụng lên em nhỏ có độ lớn là P m g 25 9 . ,8 245N . r
» Em nhỏ trượt từ điểm A tới điểm B nên khi đó góc giữa độ dịch chuyển d so với ur ur ur uuur ur
trọng lực P là d,P AB,P 60. ur r
» Ta có độ lớn của trọng lực P mg tác dụng lên em nhỏ có độ lớn là ur r ur
P m g 25 9
. ,8 245N nên công sinh bởi trọng lực P khi em nhỏ trượt hết ur r uur r
chiều dài cầu trượt là A P . d .cos P,d 245.3,5.cos60 428,75J .
Câu hỏi – Trả lời Đúng/sai
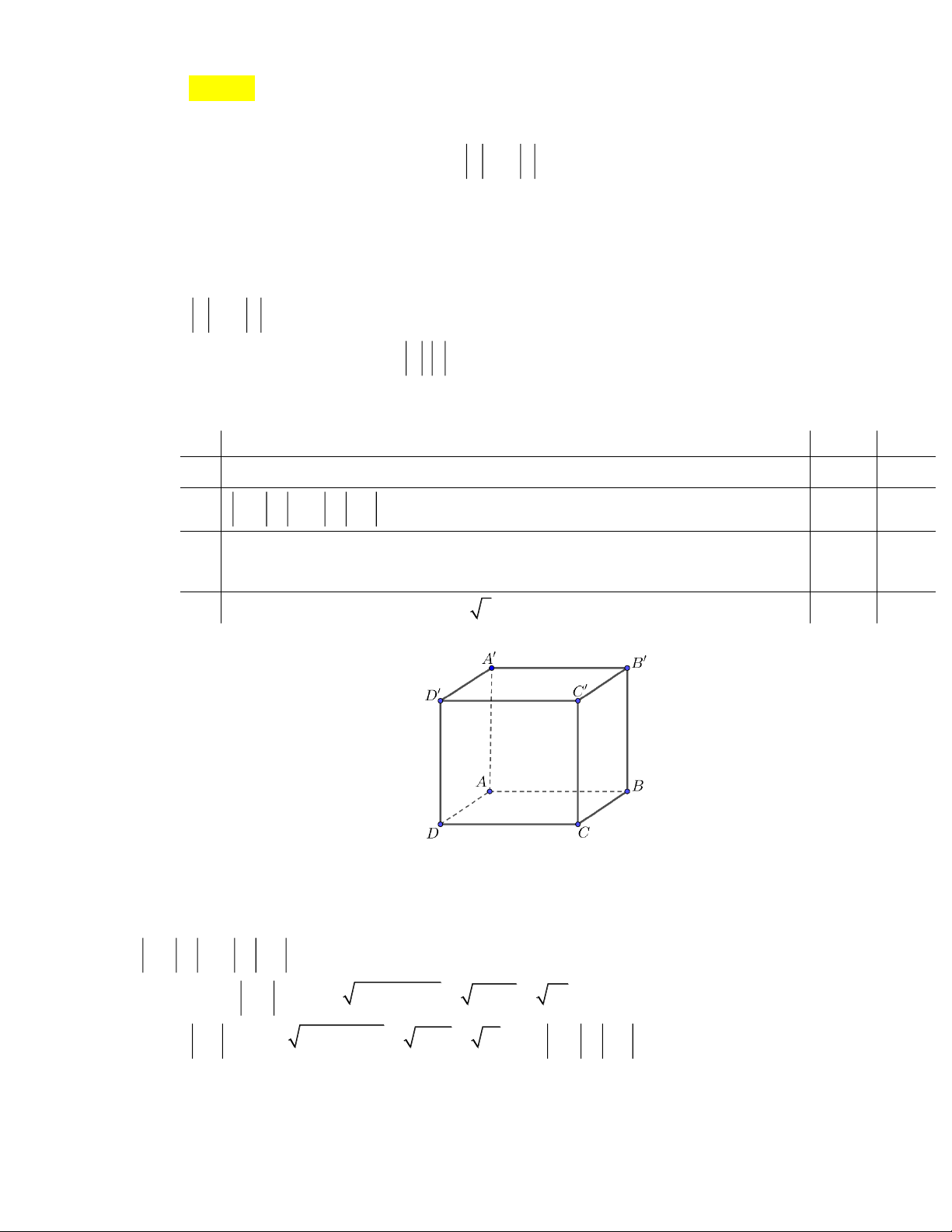
» Câu 25. Cho hình hộp chữ nhật ABC . D A B C D
có AB 2, AD 3, A A 4 . Mệnh đề Đúng Sai uuur uuur
(a) Vectơ BA bằng vectơ CD. uuur uuuur uuur
(b) BA A D DB r
Số các vectơ khác 0 có điểm đầu và điểm cuối là các đỉnh của hình (c) hộp là 2 A . 8 uuur
(d) Độ dài của vectơ BD bằng 3 3 .
Lời giải uuur uuur
(a) Vectơ BA bằng vectơ CD. uuur uuur
Vectơ BA bằng vectơ CD vì chúng cùng hướng và cùng độ dài.
» Chọn ĐÚNG. uuur uuuur uuur
(b) BA A D DB . uuur Ta có 2 2
BA BA BA BB 4 16 20 và uuur uuur uuur 2 2
BD BD BC BA 9 4 13 nên BA DB . » Chọn SAI. r
(c) Số các vectơ khác 0 có điểm đầu và điểm cuối là các đỉnh của hình hộp là 2 A . 8 r
Số các vectơ khác 0 có điểm đầu và điểm cuối là các đỉnh của hình hộp là 2 A . 8 Trang 9
» Chọn ĐÚNG. uuur
(d) Độ dài của vectơ BD bằng 3 3 . uuur
Độ dài của vectơ BD bằng 3 3 . uuur Ta có 2 2 2
BD BA BC BB 4 9 16 29 . » Chọn SAI.
» Câu 26. Cho hình hộp ABC . D A B C D . Mệnh đề Đúng Sai uuur uuuur uuur uuur
(a) AB A D B B A C uuur uuur uuur
(b) AB AA B A uuur uuur uuuur
(c) AB AD D B uuur uuur uuur uuur
(d) AB BD AC DC
Lời giải uuur uuuur uuur uuur
(a) AB A D B B A C . » Chọn ĐÚNG. uuur uuur uuur
(b) AB AA B A . uuur uuur uuur
Ta có: AB AA AB . » Chọn SAI. uuur uuur uuuur
(c) AB AD D B . uuur uuur uuur uuuur
AB AD DB D B » Chọn ĐÚNG. uuur uuur uuur uuur
(d) AB BD AC DC . uuur uuur uuur uuur uuur uuur
AB BD AC AD AC CD . » Chọn SAI.
» Câu 27. Cho hình lăng trụ AB . C A B C
. Gọi M là trung điểm của BB và G là trọng tâm tam giác ABC . Trang 10 Mệnh đề Đúng Sai uuur 1 uuur
(a) BM BB 2 uuuur uuur 1 uuur
(b) AM AB B B 2 uuuur 1 uuur 1 uuur (c) AM
AB AB 2 2 uuur uuur uuur uuur
(d) MA MB MC 3MG
Lời giải uuur 1 uuur
(a) BM BB . 2 » Chọn ĐÚNG. uuuur uuur 1 uuur
(b) AM AB B B . 2 uuuur uuur uuur uuur 1 uuur
AM AB BM AB BB . 2 » Chọn SAI. uuuur 1 uuur 1 uuur (c) AM
AB AB 2 2 uuuur 1 uuur 1 uuur AM AB AB 2 2 » Chọn ĐÚNG. uuur uuur uuur uuur
(d) MA MB MC 3MG . uuur uuur uuur uuur
MA MB MC 3MG » Chọn ĐÚNG.
» Câu 28. Cho hình hộp ABC . D A B C D . Khi đó Mệnh đề Đúng Sai Trang 11 uuur uuuur
(a) Hai vectơ AB và C D bằng nhau uuuur uuur
(b) Hai vectơ A D
và CB đối nhau uuuur uuur
(c) Hai vectơ A B
và AC cùng phương với nhau r uuur
(d) Có 3 vectơ khác vectơ 0 bằng vectơ BC
Lời giải uuur uuuur
(a) Hai vectơ AB và C D bằng nhau. uuur uuuur
Hai vectơ AB và C D
ngược hướng và có độ dài bằng nhau. uuur uuuur AB và C D đối nhau. » Chọn SAI. uuuur uuur
(b) Hai vectơ A D
và CB đối nhau. uuuur uuur
Ta có vectơ A D
và CB cùng độ dài và ngược hướng nhau uuuur uuur A D
và CB đối nhau.
» Chọn ĐÚNG. uuuur uuur
(c) Hai vectơ A B
và AC cùng phương với nhau. uuuur uuur Ta có A B
không song song với AC nên hai vectơ A B
và AC không cùng phương với nhau. » Chọn SAI. r uuur
(d) Có 3 vectơ khác vectơ 0 bằng vectơ BC . r uuur uuur uuuur uuuur
Ta có các vectơ khác 0 bằng với vectơ BC là AD, A D , B C
» Chọn ĐÚNG.
» Câu 29. Cho hình chóp tứ giác đều .
S ABCD có O là tâm của đáy ABCD , cạnh đáy bằng a,
cạnh bên bằng 2a (tham khảo hình bên). Mệnh đề Đúng Sai uuur uur
(a) Góc giữa hai vectơ AD và CB là 0. uuur uuur
(b) Góc giữa hai vectơ BD và BO là 180 . uuur uur 1
(c) Cosin của góc giữa hai vectơ BA và CS bằng . 4 uuur uur
(d) Góc giữa hai vectơ AO và SD bằng 60.
Lời giải uuur uur
(a) Góc giữa hai vectơ AD và CB là 0 . Trang 12 uuur uur
Hai vectơ AD và CB là hai vectơ ngược hướng nên góc giữa chúng bằng 180 .
» Chọn SAI. uuur uuur
(b) Góc giữa hai vectơ BD và BO là 180 . uuur uuur
Hai vectơ BD và BO là hai vectơ cùng hướng nên góc giữa chúng là 0 . » Chọn SAI. uuur uur 1
(c) Cosin của góc giữa hai vectơ BA và CS bằng . 4 uuur uur uuur uur
g BA CS CD CS · , , . SCD
g Áp dụng định lý cosin cho tam giác SCD có 2 2 2 · 2 2 2
SC CD SD
2a a 2a 1 cosSCD 2S . C CD 2 2 . . a a 4 » Chọn ĐÚNG. uuur uur
(d) Góc giữa hai vectơ AO và SD bằng 60. uuur uur uuur uuur uur uuur uuur uuur uur uuur
Ta có AO.SD .
OA OD OS . OA OD .
OA OS 0 nên góc giữa hai vectơ AO uur và SD bằng 90 . » Chọn SAI.
» Câu 30. Cho tứ diện đều .
S ABC có tất cả các cạnh bằng a , M là trung điểm của cạnh BC . Mệnh đề Đúng Sai uur uur uur uur uur uur (a) . SA SB . SB SC . SA SC uuuur uur 1 uur 1 uur
(b) AM S
A SB SC 2 2 uur uuur
(c) Góc giữa SA và BC bằng 90 uuuur uur
(d) AM.SC 0
Lời giải uur uur uur uur uur uur (a) . SA SB . SB SC . SA SC . uur uur · 2 a Ta có S . A SB S . A S . B cos ASB . a . a cos 60 . 2 uur uur 2 uur uur 2 a a uur uur uur uur uur uur Tương tự, S . B SC ;S . A SC nên . SA SB . SB SC . SA SC . 2 2 » Chọn ĐÚNG. Trang 13 uuuur uur 1 uur 1 uur
(b) AM S
A SB SC . 2 2 uuuur uuur uur uur 1 uur 1 uur
Ta có: AM SM SA S
A SB SC . 2 2 » Chọn ĐÚNG. uur uuur
(c) Góc giữa SA và BC bằng 90 . uur uuur
Góc giữa SA và BC bằng 90 . uur uur uur uur 2 a Ta có 2 SC.SA .
SB SA a .cos 60 . 2 uuur uur uur uur uur uur uur uur uur uur uuur
Suy ra BC.SA SC SB.SA SC.SA .
SB SA 0 nên góc giữa SA và BC bằng 90 . » Chọn ĐÚNG. uuuur uur
(d) AM.SC 0 . uuuur uur uur 1 uur 1 uur uur uur uur 1 uur uur 1 uur uur Ta có AM.SC S
A SB SC .SC S . A SC S .
B SC SC.SC 2 2 2 2 2 2 2 a 1 a 1 a 2 . a . 2 2 2 2 4 » Chọn SAI.
» Câu 31. Cho hình hộp chữ nhật ABC . D A B C D
có ABCD là hình vuông cạnh a và a 3 AA
. Gọi O là giao điểm của AC và BD . 2 Mệnh đề Đúng Sai uuur uuuur
(a) AC,C A
AC,C A uuur uuur r uuuur r r r
(b) Gọi u AB AD , v B C
. Ta có u;v 60. uuur uuur r uuuur r r r
(c) Gọi x BA BC , y A C
. Ta có x; y 90. uuur uuur
(d) OA,OC 90
Lời giải uuur uuuur
(a) AC,C A
AC,C A . uuur uuuur AC,C A
AC,C A . Trang 14 Ta có AC//C A
AC,C A 0. uuur uuuur uuur uuuur AC,C A
là hai vectơ ngược hướng nên AC,C A 180 . » Chọn SAI. uuur uuur r uuuur r r r
(b) Gọi u AB AD , v B C
. Ta có u;v 60. uuur uuur uuur r uuuur r uuur uuuur uuur uuur r r
Ta có u AB AD AC , v B C
u;v AC,B C
AC,AD · CAD 45. » Chọn SAI. uuur uuur r uuuur r r r
(c) Gọi x BA BC , y A C
. Ta có x; y 90. uuur uuur uuur r uuuur uuur r uuur uuur r r
Ta có x BA BC BD , y A C
AC suy ra x; y AC,BD 90.
» Chọn ĐÚNG. uuur uuur
(d) OA,OC 90 . 2 2 2 2 2 2 a 2 a 3 5 2 a
Ta có OA OC 2
AO AA A C 2 2a . 2 2 4 Suy ra tam giác OA C
không thể vuông tại O . » Chọn SAI.
» Câu 32. Cho hình lập phương ABC . D A B C D
có cạnh bằng a . Gọi O,O lần lượt là tâm
của hình vuông ABCD và A B C D . Mệnh đề Đúng Sai uuur uuur 2 a (a) A . B DC 2 uuur uuuur 2 a
(b) AB .B D 2 Trang 15 uuuur uuur uuur (c) D A C C
AB a 3 uuur uuur uuur uuuur
(d) OA OB OC OD 4a
Lời giải uuur uuur 2 a (a) A . B DC .
2 uuur uuur uuur uuur uuur uuur uuur uuur Ta có A . B DC A .
B AB AB . AB cos AB, AB 2 .
a a 2.cos 45 a . » Chọn SAI. uuur uuuur 2 a
(b) AB .B D . 2uuur uuuur
Ta có AB,B D · 180 AB D 120 , suy ra uuur uuuur uuur uuuur AB .B D
AB . B D
cos120 a 2.a 2 1 2 . a . 2 » Chọn SAI. uuuur uuur uuur (c) D A C C
AB a 3 uuuur uuur uuur uuuur uuuur uuuur uuur Ta có D A C C
AB D A D D D C D B uuuur uuur uuur uuur Suy ra D A C C
AB D B
BD a 3
» Chọn ĐÚNG. uuur uuur uuur uuuur
(d) OA OB OC OD 4a . uuur uuur uuur uuuur uuur uuur uuur uuuur uuuur uuuur uuuur
Ta có OA OB OC OD OAOC OBOD 2OO 2OO 4OO. uuur uuur uuur uuuur uuuur
Suy ra OA OB OC OD 4 OO 4a . » Chọn ĐÚNG.
Câu hỏi – Trả lời ngắn
» Câu 33. Cho hình hộp ABC . D A B C D
, từ các đỉnh của hình hộp đã cho, có bao nhiêu vectơ uuur
đối (khác vectơ không) của vectơ AB ?
Lời giải
Trả lời: 4 Trang 16 uuur uuur uuur uuuur uuuur
Ta có các vectơ đối của vectơ AB là B , A CD, B A ,C D .
Vậy số vectơ đối là 4 vectơ.
» Câu 34. Cho tứ diện ABCD , gọi M, N lần lượt là trung điểm của AB và CD . Biết rằng uuuur uuur uuur uuur
MN aAB bAC cAD . Giá trị của biểu thức a b c bằng:
Lời giải
Trả lời: 1,5 uuuur uuur uuur uuur 1 uuur uuur uuur 1 uuur
Ta có: MN MB BC CN
AB AB AC CD . 2 2 1 uuur uuur 1 uuur uuur uuur uuur uuur
AB AC AC AD 1 1 1
AB AC AD 2 2 2 2 2 3
Vậy a b c 1,5 2 uuuur
» Câu 35. Cho hình lập phương ABC . D A B C D
. Giá trị tan của góc giữa hai vectơ AD và uuuur A C
bằng (làm tròn tới hàng phần nghìn).
Lời giải
Trả lời: 1,732 uuuur uuuur uuuur uuur ·
Ta có AD, A C
AD,AC D A
C 60 (do tam giác DACD đều).
Vậy tan 60 3 1,732 Trang 17 r r
» Câu 36. Trong không gian với hệ toạ độ Oxyz , cho a và b tạo với nhau một góc 120o , đồng thời r r r r r r r r r r
a 2 và b 5 . Đặt u ka b và v a 2b . Để u v thì giá trị của k là
Lời giải
Trả lời: -4,5 r r r r 1 Ta có: .
a b a . b cos120 2 5 . . 5 . 2 r r r r r r r r
Để u v .
u v 0 ka ba 2b 0 r r r r
k a k 2 2 9 2
1 ab 2 b 0 6
k 45 0 k 4 ,5 . 2 r r r r r r r r r r r
» Câu 37. Cho ba vectơ a,b , c không đồng phẳng. Xét x 2a b c , y a 2b c , r r r r r r r
z a 4b mc . Giá trị của m để các vectơ x; y; z đồng phẳng bằng?
Lời giải
Trả lời: 1 r r r r r
Do y; z không cùng phương, để các vectơ x; y; z đồng phẳng r r r r r r r r r r r r
tồn tại a ,b ¡ : x a y b z 2a b c a a 2b c b a 4b mc 3 a 2 a b 2 1
2a 4b 1 b . 2
a mb 1 m 1 Vậy m 1
» Câu 38. Cho hình hộp chữ nhật ABC . D A B C D
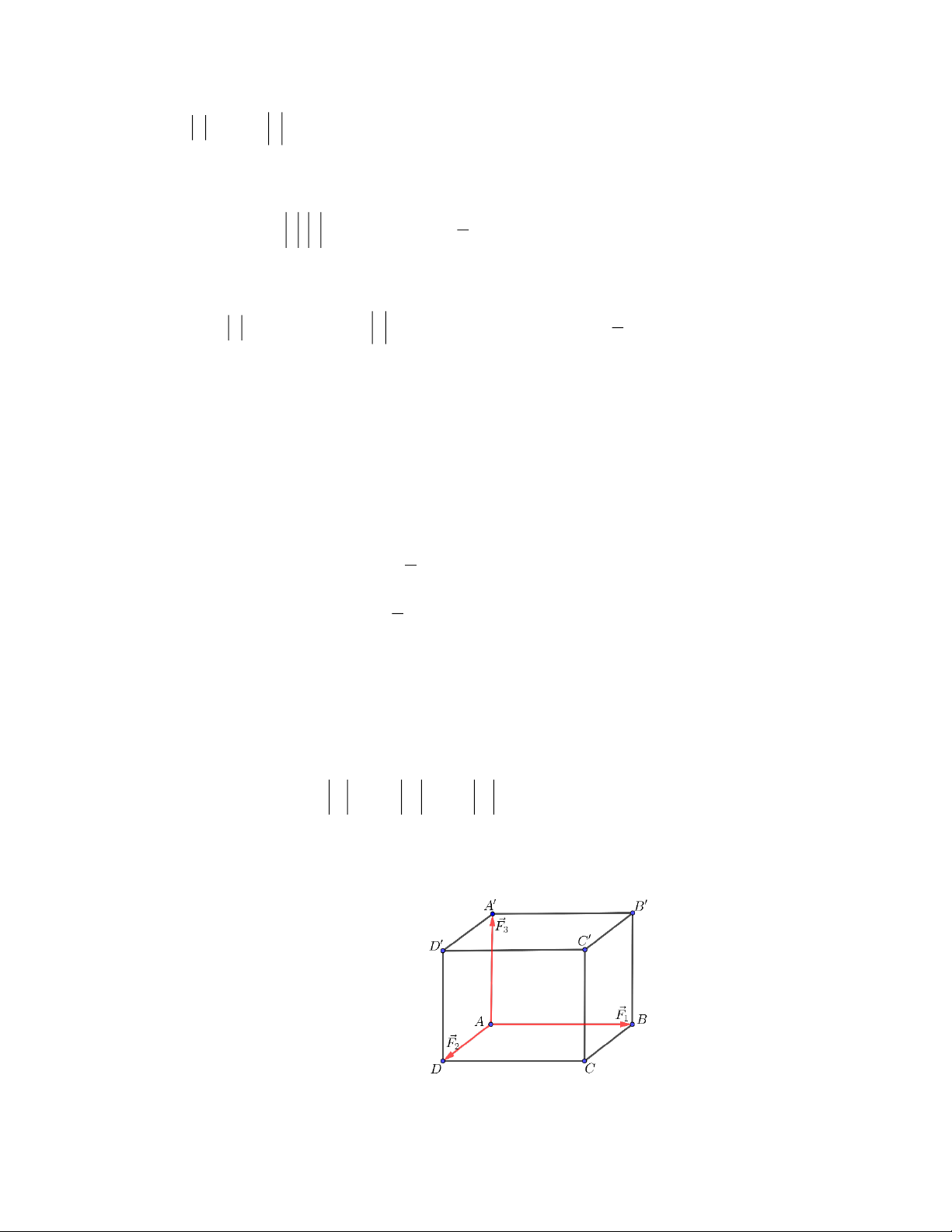
như hình vẽ. Đặt một vật tại đỉnh A , khi ur uur ur
đó tác động vào vật bởi những lực F , F , F có giá lần lượt nằm trên các cạnh 1 2 3 ur uur ur ur A ,
B AD, AA và F 2N, F 3N, F 4N . Hãy xác định độ lớn của hợp lực F tác 1 2 3
động lên vật (làm tròn đến hàng phần nghìn).
Lời giải
Trả lời: 5,385 ur ur uur ur
Ta có F F F F 1 2 3 ur
Theo quy tắc hình hộp ta có: F có giá là nằm trên cạnh AC Trang 18 ur ur 2 uur 2 ur 2 Do ABC . D A B C D
là hình hộp chữ nhật nên F F F F 29 5,385N 1 2 3 uuur r uuur r uuur r
» Câu 39. Cho tứ diện ABCD . Đặt AB a , AC b , AD c gọi G là trọng tâm của tam giác uuur r r r
BCD . Tìm giá trị thích hợp của k thỏa đẳng thức vectơ AG .
k c b a . (làm tròn
tới hàng phần nghìn).
Lời giải
Trả lời: 0,333
Gọi M là trung điểm BC . uuur uuur uuur 2 uuur 2 1 uuur uuur r r
AG AB BG a BM a . BC BD 3 3 2 1 uuur uuur uuur uuur r r r r r r r r
a AC AB AD AB 1
a a b c 1 2
c b a . 3 3 3 1 Vậy k ~ 0,333 . 3
» Câu 40. Cho tứ diện ABCD . Gọi G là trọng tâm tam giác ABC . Tìm giá trị thích hợp của k uuur uuur uuur uuur
thỏa đẳng thức vectơ: DA DB DC k.DG ?
Lời giải
Trả lời: 3 uuur uuur uuur uuur uuur uuur uur uuur uuur uuur
DA DB DC DG GA DG GB DG GC 3DG . Vậy k 3. · · ·
» Câu 41. Cho hình chóp .
S ABC có SA SB SC và ASB BSC CSA . Hãy xác định góc uur uuur
giữa cặp vectơ SC và AB ?
Lời giải
Trả lời: 90 Trang 19 uur uuur uur uur uur uur uur uur uur
Ta có: SC.AB SC.SB SA SC.SB SC.SA · · · ·
SC.SB cos BSC SC. .
SA cos ASC 0 (Vì SA SB SC và BSC ASC ) uur uuur
Do đó: SC AB 90o ,
» Câu 42. Cho hình chóp .
S ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên
đều bằng a . Gọi M và N lần lượt là trung điểm của AD và SD. Số đo của góc
MN,SC bằng:
Lời giải
Trả lời: 90
Ta có: AC a 2 2 2 2 2
AC 2a SA SC S
AC vuông tại S . uur uur Suy ra S . A SC 0 uuuur uur 1 uur uur uuuur uur Khi đó: N . M SC S .
A SC 0 NM,SC 90 2
MN,SC 90 .
» Câu 43. Cho hình chóp .
S ABC có SA SB và CA CB. Tính số đo của góc giữa hai đường
thẳng chéo nhau SC và . AB
Lời giải
Trả lời: 90 Trang 20