








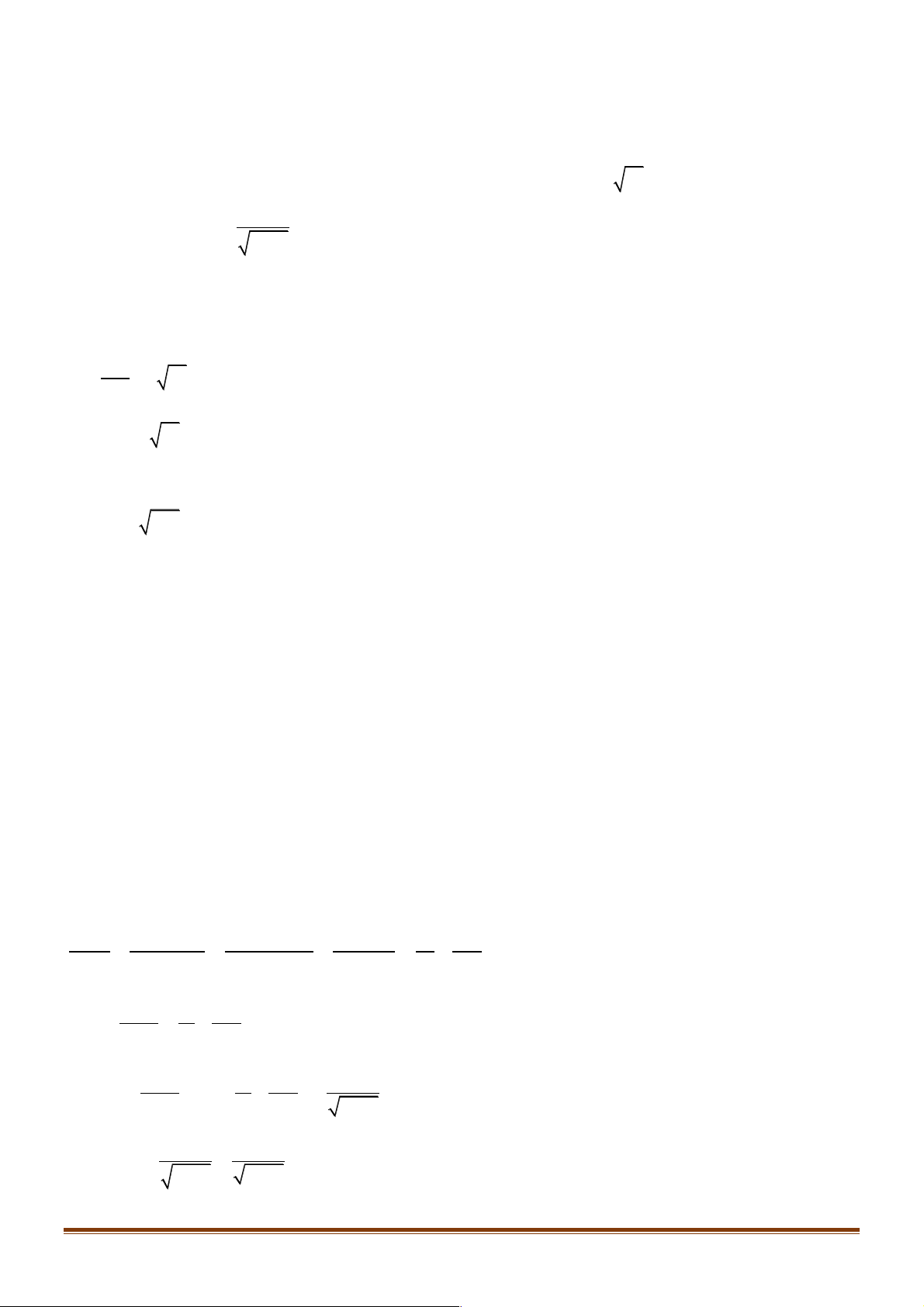








































Preview text:
CHUYÊN ĐỀ GIỚI HẠN CỦA DÃY SỐ BỒI DƯỠNG HỌC SINH GIỎI
3.1. TÍNH GIỚI HẠN BẰNG ĐỊNH NGHĨA. ì 1 a = a + ï 1 ï a Bài 1.
Cho dãy số (an ) xác định bởi : í
. Chứng minh rằng với mọi số thực 3 2 2a - 2a - 2 n n ïa = n 1 + 2 ï 3a - 4a -1 î n n
a ¹ 0 thì dãy (a a (an)
n ) hội tụ. Tùy theo
, hãy tìm giới hạn của dãy . Hướng dẫn giải Nếu a > 1
0 thì a + ³ 2 (do bất đẳng thức AM-GM). a 1 Nếu a < 1 0 thì -a +
³ 2 (do bất đẳng thức AM-GM) nên a + £ -2. -a a
Nếu a = 1 thì a = 2. Ta chứng minh: * a = 2, n " Î • . 1 n Hiển nhiên a = 2. 1 3 2 2.2 - 2.2 - 2
Giả sử a = 2 Þ a = = 2. k k 1 + 2 3.2 - 4.2 -1
Vậy lim a = lim 2 = 2 . n ìa > 0 . Nếu í
thì a > 2. Ta chứng minh * a > 2 n " Î • . îa ¹ 1 1 n Rõ ràng a > 2. . 1
Giả sử a > 2 . Ta chứng minh a > 2 . k k 1 + 3 2 2a - 2a - 2 a > 2 k k Û
> 2Û 2a a - 2 > 0 k 1 + 2 k ( k )2 ( đúng). 3a - 4a -1 k k
Ta chứng minh (an ) là dãy giảm, thật vậy :.
-a + 2a + a - 2 - a - a - n n n ( 2 3 2 n )1( 2 n ) " , n a - a = = < 0. n 1 + n 2 2 3a - 4a -1 3a - 4a -1 n n n n
( do tử âm, mẫu dương vì. é 2 + 7 êa > n 2 3
3a - 4a -1 > 0 Û ê . n n ê 2 - 7 êa < n ë 3 2 + 7 Mà 2 a > 2 >
Þ 3a - 4a -1 > 0). n 3 n n Trang 1 (a (a L n )
n ) giảm và bị chặn dưới Þ
có giới hạn là . 3 2 3 2 2a - 2a - 2 2L - 2L - 2 lim a = lim n n Þ n 1 + 2 2 3a - 4a -1 3L - 4L -1 . n n
Þ L = 2 (a > 2Þ L ¹ 1 - n ) Vậy lima = 2. n
. Nếu a > 0 thì a £ 2 - . Tương tự, ta có:. 1
-a + 2a + a - 2 - a - a - n n n ( 2 3 2 n )1( 2 n ) " , n a - a = = > 0. n 1 + n 2 2 3a - 4a -1 3a - 4a -1 n n n n nên (a (a 1 - n ) n ) tăng. Hơn nữa bị chặn trên bởi , thật vậy. 3 2 2a - 2a - 2 a < 1 k k - Û < 1
- Û a +1 (2a - 3)< 0 k 1 + 2 ( k )2 . 3a - 4a -1 k k Vậy (a (a L n )
n ) tăng và bị chặn trên Þ
có giới hạn là . a < 1, - n
" , a - a > 0, n " n n 1 + n 3 2 . 2L - 2L - 2 L = Þ L = 1
- a < -1Þ L ¹ 2 2 ( n ) 3L - 4L -1 Vậy lim a = 1 - . n
Tóm lại: + Nếu a = 1 thì lima = 2. n ìa > 0 + Nếu í thì lima = 2. îa ¹ 1 n
+ Nếu a < 0 thì lim a = 1 - . n ìx > 0 1 ï Bài 2. Cho dãy số (x í 1 2 3 2015
n ) được xác định bởi . Tìm giới x = x + + + +!+ n Î • n+ n ï ( * 1 2 3 2015 ) x x x x î n n n n
hạn của dãy nxa khi n ® +¥ , với a l à số thực cho trước. n Hướng dẫn giải
Dễ dàng chứng minh được x > 0, n " ³ 1 bằng qui nạp. n Ta có. 2 1 æ 1 ö 1 2 2 2 x > x + , n
" ³1 Þ x > ç x + ÷ = x + 2+ > x + 2 ; n " ³ . 1 n 1 + n n 1 + n n 2 n x x x n è n ø n Bởi vậy n " Î N, n ³ 2 thì 2 2 2 2
x > x + 2 > x
+ 4 >…> x + 2 n -1 n n 1 - n-2 1 ( ). Þ x >1, n
" ³ 2 và lim x = +¥. n n n®+¥ Trang 2 1 2 3 2015 Với *
n Î N , đặt x = x +
+ t trong đó t = + +…+ . n 1 + n n x n 2 3 2015 x x x n n n n t x > 1; n " ³ 2 Þ 0 < t <
, với t = 2 + 3 +…+ 2014 + 2015 (1), suy ra. n n 2 xn 2 æ 1 ö 1 2t 2 2 2 2
x - x = ç x +
+ t ÷ - x = +t + 2+ 2 n x t + ® 2. khi n ® +¥ . n 1 + n n n n 2 n n n x x x è n ø n n 2 ì b = x
Áp dụng định lý trung bình Cesaro cho dãy (b 1 1 í n ) vớ i . 2 2
b = x - x , n " ³ 2. î n n n 1 -
b + b +…+ b
ta có lim b = 2 suy ra 1 2 lim n = limb = 2.. n n n®+¥ n®+¥ n n®+¥ x x - x + x - x
+…+ x - x + x - - -
b + b +…+ b n 1 n ( 2 2 n n 1 ) ( 2 2 n 1 n 2 ) ( 2 2 2 1 ) 2 2 Mà 1 1 2 n = = s uy ra lim = .. n n n 2 n®+¥ x 2 n n 1
Thật vậy ta có thể chứng minh trực tiếp lim
= như sau (chứng minh định lý trung bình Cesaro). 2 n®+¥ x 2 n
Xét dãy (c c = x - c = x - x - n = 2,3… n ) 2 2 2 : 2; 2 với . 1 1 n n n 1 - e lim c = 0 nên e " > 0 t ồn tại *
m Î N sao cho c < , " n ³ . m . n n n®+¥ 2
Gọi M = max{c 1 £ i £ m -1 i } vớ i . é2(m - ) 1 M ù 2(m - ) 1 M (m- )1M e
Với e ở trên tồn tại m¢ = ú +1 thì < m' hay < . ê e ë û e m¢ 2
Xét n > max{ , m m }'. ta có. e n n m 1 - (n-m c c c + ) 1 | | | | å å å - - i i i m 1 M = = = e m 1 M e e i 1 i m i 1 2 ( ) ( ) £ + < + < +
< + = e. o đó theo định n n n n n 2 m¢ 2 2 | n c | å nghĩa 1 lim i i= = 0. n®+¥ n x ( 2 2 x - x + x - x
+…+ x - x + x n n- ) ( 2 2 n- n-
c + c +…+ c n 1 n ) ( 2 2) 2 2 1 1 2 2 1 1 1 2 n = = + 2 . s uy ra lim = .. n n n 2 n®+¥ x 2 n a - 1 Nếu a = 2 - thì 2 . n x = .
n x ® khi n ® +¥ . n n 2 Nếu a > 2 - thì a a +2 2 . n x x . . n x- = ® +¥ khi n ® +¥ . n n n Nếu a < 2 - thì a a +2 2 . n x x . . n x- = ® 0 khi n ® +¥ . n n n Trang 3
Cho hai số a ,b với 0 < b = < .L 1 ập hai dãy số (a (b n =1, 2,.. n ) n ) , với .Theo quy tắc Bài 3. 1 1 1 a1 1
sau: giải nghĩa cái đó là:. a
= (a + b ) b = a .b lim a limb n 1 + n n , n 1 + n 1 + n Tính: n n n®¥ và n®¥ . 2 . Hướng dẫn giải p
Tính a ,b với 0 < b = a < t
1 a có thể chọn 0 < a <
sao cho: b = cosa,. 2 2 1 1 2 1 Suy ra 2 a = cos a . 1 1 1 a 2 2
a = (cos a + cos a) = cos a(cos a +1) = cos a.cos . 2 2 2 2 a a 2 b = cos . a cos .cos a = cos . a cos . 2 2 2
Bằng quy nạp, chứng minh được:. a a a a a a = cos . a cos ...cos cos (1) b = cos . a cos ...cos (2). n n 1 - n 1 2 2 2 - n n 1 2 2 - a
Nhân hai vế của (1) và (2) cho sin
và áp dụng công thức sin 2a được:. 1 2n- a sin 2 . a cos n 1- sin 2 2 a a = , b = . n n a a 2 .nsin 2 .nsin n 1 - n 1 2 2 - Tính giới hạn:. sin 2a sin 2a lim a = , lim b = . n ®¥ 2 n n n a ®¥ 2a 1 a Bài 4. Cho dãy số (a a = a = a + lim n = 2 n ) , 1 và .Chứng minh: . 1 n 1 + n a n®¥ n n Hướng dẫn giải n n 1 - n 1 1 - 1 2 2 2 2 a = a +
+ 2 Þ åa = åa + å + 2(n -1).. k 1 + k 2 i j 2 a = = = a k i 2 j 1 j 1 j n 1 - 1 2 a = 2n -1+ V
å . ậy a > 2n-1 , n " ³ 2 .. n 2 n j 1 = a j 1 1 1 1 1 æ 1 1 2 ö a > 2k -1 k " ³ 2 Þ < < = = - . k 4 2 2 ç ÷ a (2k-1) (2k-1) -1 4k(k+1) 4 è k -1 k ø k n 1 - n 1 1 1 1 1 - 1 1 5 Suyra: å < (1- ) < Þ å <1+ = . 4 4 - k =2 a 4 n 1 4 = a k j 1 4 4 j Trang 4 n 1 - n 1 1 - 1 5
Suyra: å £ (n -1)å < (n -1) (n ³ 2).. 2 4 j 1 = a = a j j 1 4 j 5(n -1) Vậy: 2 a < 2n -1+ (n ³ 2) . n 2 5(n-1) 1 a 5(n-1) Suyra: n n ³ 2; 2n-1Þ 2- < < 2n-1+ . n 2 n n 2 a Dođó: lim n 2 . n®¥ n p p Bài 5.
Cho hai số a ,b với 2 a = cos , b = s co
. Lập hai dãy số (a ), b n = 1, 2,... n ( n) với theo quy 1 1 1 8 1 8 1 tắc sau:. a
= (a + b ) , b = a .b . Tính: lim a và limb . n 1 + 2 n n n 1 + n 1 + n n n n®¥ n®¥ Hướng dẫn giải +Tính a ,b :. 2 2 1 p p 1 p p p p 2 2 a = (cos
+ cos ) = cos (cos x +1) = cos .cos . 2 2 8 8 2 8 8 8 16 p p p p p 2 b = cos cos cos = cos cos . 2 8 16 8 8 16
+ Bằng quy nạp, chứng minh được:. p p p p p p p a = cos cos ...cos cos (1) b = cos cos ...cos (2). n 2 n 2.4 2 .4 2 .4 2 .n4 n 2 n 2.4 2 .4 2 .4 p
+Nhân hai vế của (1) và (2) cho sin
và áp dụng công thức sin 2a được:. n 2 .4 p p p sin .cos sin n 4 2 .4 4 a = , b = . n n p p 2 .nsin 2 .nsin n n 2 .4 2 .4 +Tính giới hạn:. p p 4sin 4sin 4 4 lim a = , limb = . n n n®¥ n p ®¥ p Bài 6.
Cho dãy số (un ) biết:. ì u = 1 1 ï * í u , n " Î N . n u = n 1 + ï 2 1+ u î n Hãy tính lim (u n). n n ®+¥ Trang 5 Hướng dẫn giải
Ta có: u > 0 => u > 0, * n " Î N . 1 n 2 3 2
un +1- un = u / (1+ u ) - un = ( u - ) / (1+ u ) < 0 * n " Î N . n n n n Þ (u 0
n ) là dãy số giảm và bị chặn dưới bởi .
Þ lim u = a (aÎ , R a ³ 0) n . n®+¥ Từ 2
un +1 = u / (1+ u ), cho n ® +¥ ta được:. n n 3
a = a / (1+ a ) Û a = 0. Vậy lim u = 0. n x®+¥ Đặt 2 2
v = 1/ (u +1) -1/ (u ), * n Î N . n n n Ta có 2 2 2 2
v = ((1+ u ) / u ) -1/ (u ) = 2 + u ® 2 khi n ® +¥? Áp dụng định lí trung bình Cesaro ta có:. n n n n n 1 1 - 2 2
v + v +…+ v u u 1 2 n n 1 + 1 lim = 2 Û lim = 2 . n® ¥ + n n ® ¥ + n æ 1 1 ö 1 1 ç - ÷ + - 2 2 2 2 u u u u è n 1+ n ø n 1 Û lim = 2. n® ¥ + n 1 1 - 1 2 2 u u v 2 u 1 Mà n 1 + n n lim = lim = 0; 1 lim = lim = 0. n® ¥ + n n® ¥ + n n® ¥ + n n® ¥ + n 1 2 Þ u 1 1 lim n = 2 Þ lim = 2 Þ lim (u n) = . 2 ® ¥ + n n ® ¥ + n.u n n n®+¥ 2 n U ì = 2 1 ï Bài 7. Cho dãy{U í + 2009 ( * 2 n Î N U U ) n} xác định bởi: . n n U = ï n 1+ î 2010 n ì U ü Ta lập dãy{S i íS = å lim S n} với ý.Tính . n - î n x®¥ i 1 = U 1 i 1 + þ Hướng dẫn giải a Tacó 0 a = - > 0. 1 2
Giả sử a , a ,..., a > 0. 1 2 n 1 - Tacó. Trang 6 ìa a a n n 1 - 0 + +...+ = 0 ïï 1 2 n +1 æ1 1 ö æ 1 1 ö æ 1 1 ö í Þ a = - a + - a +...+ - a . n ç ÷ n 1- ç ÷ n-2 ç ÷ 0 a a a ï è1 2 ø è 2 3 ø è n n +1ø n 1 - n-2 0 + +...+ = 0 ïî 1 2 n a a a a Hay n 1 - n-2 1 0 a = + +...+ + . n 1.2 2.3 (n -1)n ( n n +1)
Do a , a ,..., a > 0 nên. 1 2 n 1 - æ a a a öæ 2a 3a na ö n 1 - n-2 1 n 1 - n-2 1 + +...+ + + ...+ ç ÷ç ÷ è 1.2 2.3 (n -1)n øè 1 2 n -1ø . 2 2 æ a a a ö a n 1 - n-2 1 0 ³ + + ...+ = ç ÷ 2 è 1 2 (n -1) ø n 2 æ a a a ö a n 1 - n-2 1 0 Þ + +...+ ³ . ç ÷ è 1.2 2.3 (n -1)n ø 2 æ 2a 3a na ö n 1 - n-2 1 n + +...+ ç ÷ è 1 2 n -1ø Ta lại có. 2a 3a na æ 2a 3a a ö n 1 - n-2 1 n 1 - n-2 1 + +...+ = n + + ...+ ç ÷ 1 2 n -1 è n 2n n -1ø. æ a a a ö æ a ö n 1 - n-2 1 0 £ n + +...+ = n - = -a . ç ÷ ç ÷ 0 è 1 2 n -1ø è n ø æ a a a ö a n 1 - n-2 1 0 Þ + +...+ ³ - . ç ÷ 2 è 1.2 2.3 (n -1)n ø n a a a a a a n 1 - n-2 1 0 0 0 Þ a = + +...+ + ³ - + > 0. n 2 1.2 2.3 (n -1)n ( n n +1) n n(n +1)
Từ đó suy ra điều phải chứng minh. 2 1+ u -1 Bài 8. Cho dãy số (u u =1, n u = , n " ³1. n ) xác định bởi 1 n 1 + un a) Chứng minh:. p u = tan , n " ³1.. n n 1 2 +
b) Suy ra tính đơn điệu và bị chặn của (un ) . HƯỚNG DẪN GIẢI
a) Chứng minh bằng quy nạp toán học. p p æ p ö b) Nhận xét 0 < £ , n
" ³1 và hàm số tanx đồng biến trên 0; . n 1 ç ÷ 2 + 4 è 4 ø nên dãy số (u tan 0 = 0
n ) giảm và bị chặn dưới bởi số . Trang 7 p
và bị chặn trên bởi số tan =1. 4 . Bài 9.
Cho dãy số (xn ) xác định bởi:. 1 2 3 2014 2015 * x > 0; x = x + + + +...+ + , n " Î • .. 1 n 1 + n 2 3 2014 2015 x x x x x n n n n n n 1.Với mỗi *
n Î • ,đặt y =
.Chứng minh dãy số ( yn ) có giới hạn hữu hạn và tính giới hạn đó. n 2 xn
2.Tìm các số a để dãy (nxa 0
n ) có giới hạn hữu hạn và giới hạn là một số khác .
HƯỚNG DẪN GIẢI 1 1 1.Từ giả thiết suy ra 2 2 2 x > x +
> 0 Þ x > x + + 2 > x + 2 n 1 + n n 1 + n 2 n x x n n . Suy ra 2 2 2 2 x
> x + 2 > x + 2 > ... > x + 2n do đó lim x = +¥ n 1 + n n 1 - 1 n . Xét æ 1 2 3 2014 2015 öæ 1 2 3 2014 2015 ö 2 2
x - x = x + x
x - x = ç2x + + + +...+ + ÷ç + + +...+ + n 1 + n
( n 1+ n )( n 1+ n ) n 2 3 2014 2015 2 3 2014 2015 ÷ x x x x x x x x x x è n n n n n øè n n n n n ø . æ 1 2 3 2014 2015 öæ 2 3 2014 2015 ö = ç2+ + + +...+ + ÷ç1+ + +...+ + 2 3 4 2015 2016 2 2013 2014 ÷ x x x x x x x x x è n n n n n øè n n n n ø. Suy ra lim( 2 2 x - x = 2 n 1 + n ) . x x - x + x - x
+ + x - x + x n ( 2 2 ... n n 1 - ) ( 2 2 n 1 - n-2 ) ( 2 2 2 1 ) 2 2 Ta có 1 = . n n
Áp dụng định lý trung bình Cesaro ta có. x ( 2 2 x - x + x - x
+ + x - x + x n n- ) ( 2 2 n- n n - ) ... ( 2 2 ) 2 2 1 1 2 2 1 1 lim = lim = 2 . n n n 1 Do đó lim = 2 x 2 n . a n 2.Xét a +2 z = nx = x n n 2 n xn . Từ đó:. +) Nếu a > 2 - thì lim z = +¥ n . Trang 8 +)Nếu a < 2 - thì lim z = 0 n . +) Nếu a = 2 - 1 thì lim z = n 2 . Vậy a = 2
- là giá trị cần tìm thỏa mãn đề bài.
Bài 10. Cho dãy số {y 3 y > 0, y
= y + y +...+ y , n " ³ 1 n} thỏa mãn . 1 n 1 + 1 2 n ì y ü Chứng minh rằng dãy số n
í ý có giới hạn bằng 0 khi n ® +¥ . î n þ Hướng dẫn giải Từ giả thiết ta có 3 3 y
= y + y , n
" ³ 2, do đó dãy số {yn} là dãy tăng, vì. n 1 + n n n³2 vậy 3 3 2 2 y
= y + y = y (y +1) < y (y +1). n 1 + n n n n n 1 + n 2 2
Þ y < y +1, n " ³ 2 2 2 2
Þ y < y +1< ... < y + n - . 1 n 1 + n n 1 + n 2 2 2 æ y ö y + n -1 2 y + n -1 n 1 + 2 Þ < . Mà 2 lim
= 0 nên theo định lý kẹp ta có. ç ÷ 2 è n +1ø (n +1) 2 (n +1) 2 æ y ö y y n 1 + n 1 lim
= 0 Þ lim + = 0 Þ lim n = 0. ç ÷ è n +1ø n +1 n u ì Î(0;1)
Bài 11. Tìm tất cả các hằng số c > 0 sao cho mọi dãy số dãy số (u ) thỏa mãn: n í n " ³1 n
u (1- u ) > c î n 1+ n .
đều hội tụ. Với giá trị c tìm được hãy tính giới hạn của dãy (u ). n Hướng dẫn giải
Ta xét các trường hợp sau. 1 c cu
+ Nếu c > , thì từ giả thiết, ta có n u > = ³ 4cu ; n " ³1. 4 n 1 + 1- u u (1- u ) n n n n
Từ đây bằng quy nạp, ta suy ra 1 u (4c)n- >
u . Do 4c > 1 nên u ® +¥ khi n ® +¥ 1 . Do đó, c > n 1 n 4 không thỏa mãn. 1
æ - - c + - c ö
ìa(1- b) > c + Nếu 0 < c < 1 1 4 1 1 4
, thì tồn tại a,bÎç ;
÷, a < b sao cho í . Thật vây, lấy 4 ç 2 2 ÷ è ø b î (1- a) > c
æ1- 1- 4c 1+ 1- 4c ö a Îç ;
÷, đặt b = a + x (x > 0), thì. ç 2 2 ÷ è ø
a(1- a) - c
a(1- b) > c Û a(1- a - x) > c Û x < . a Trang 9
Chú ý là b(1- a) > a(1- a) > .
c Do đó, ta chỉ cần chọn x > 0 như trên và b = a + x, thì được 2 bất đẳng thức nêu trên.
Xét dãy số (u )xác định bởi. n ìa ê n u n = 2m u = í . n b î ê n u n = 2m +1 1
thì dãy (u ) thỏa mãn giả thiết nhưng không hội tụ. Thành thử, 0 < c < cũng không thỏa mãn. n 4 1 1 u + Nếu c = , thì n u > =
³ u . Suy ra dãy (u )tăng và bị chặn. Do đó, (u )hội tụ. 4 n 1 + 4(1- u ) 4u (1- u ) n n n n n n Đặt x = 1 m
li u ,thì từ giả thiết ta có x(1- 1 x) ³ hay x = 1 . Vậy limu = .. n 4 2 n 2 ì 1 x = ï 1 ï
Bài 12. Cho dãy số (x 2 n) thỏa mãn: í
. Chứng minh dãy số trên có giới hạn. 2 x ï n x = x + ; n " ³1 n 1 + n 2 ïî n Hướng dẫn giải n(n + ) 1 *) Ta chứng minh 2 x + n ³ với mọi n ³ 1 (1). n 2
Thật vậy: n = 1 đúng. k (k + ) 1
Giả sử (1) đúng với n = k ³ 2 1: x + k ³ . k 2 2 x Þ x x + k +1 k = x +
+ k +1 = k x + k + k +1 2 ( k ) ( )2 2 k 1 + ( )2 k 2 ( )2 . k k æ k +1 ö k (k + ) 1 (k + )2 3 1 k (k + ) 1 ³ -1 + (k + ç ÷ )2 1 ³ - . è k 2 ø 2 2 2 k +1æ 3(k + ) 1 ö (k + ) 1 (k + 2) ³ ç - k ³ (đpcm). ÷ 2 è 2 ø 2
*) Ta chứng minh (xn ) có giới hạn. NX: (x x > 0 n n ) tăng và với mọi . n 1 1 1 2 1 1 æ 1 ö 1 Ta có - = £ Þ - £ 2 1- < 2 Þ x < với mọi n ³1. 2 ç ÷ x x x + n n n +1 x x è n ø n 2 - 2 n n 1 + n ( ) 1 n
Vậy (xn ) có giới hạn. Trang 10 4 2 u + 2013
Bài 13. Cho dãy số (u u = 2014, n * u = , n " Ε n ) xác định bởi . Đặt 1 n 1 + 3 u - u + 4026 n n n 1 * v = å , n " Ε v n 3 . Tính lim n . + k 1 = u 2013 k Hướng dẫn giải 4 2 u + 2013 3
(u - 2013)(u + 2013) + Ta có u - 2013 = n - 2013 n n = (1). n 1 + 3 u - u + 4026 3
(u + 2013) - (u - 2013) n n n n
Từ đó bằng quy nạp ta chứng minh được * u > 2013, n " Î • . n 1 1 1 1 1 1 + Từ (1) suy ra = - Þ = - . 3 u
- 2013 u - 2013 u + 2013 3
u + 2013 u - 2013 u - 2013 n 1 + n n n n n 1 + n æ 1 1 ö 1 1 1 Do đó v = åç - ÷ = - =1- . n - - - - u - 2013 k 1 = u 2013 u 2013 u 2013 u 2013 è k k 1 + ø 1 k 1 + k 1 +
+ Ta chứng minh limu = +¥. n 2 2 2 u - 4026u + 2013 (u - 2013) Thật vậy, ta có n n n * u - u = = > 0, n " Î • . n 1 + n 3 3 u - u + 4026 u - u + 4026 n n n n Suy ra (u
2014 = u < u < ...
n ) là dãy tăng, ta có . 1 2 4 2 a + 2013 Giả sử (u limu = a a > 2014 a =
n ) bị chặn trên và thì . Khi đó . n 3 a - a + 4026
Þ a = 2013 < 2014 ( vô lí). Suy ra (u limu = +¥
n ) không bị chặn trên, do đó . n 1 Vậy limv = lim (1- ) = 1. n u - 2013 k 1 + u ì = 2013 2 u
Bài 14. Cho dãy số (u 1 n 1 lim +
n ) xác định bởi: í . Tìm . 2 * u = u - 2, n " Î î • 2 2 2
n®+¥ u .u ...u n 1 + n 1 2 n Hướng dẫn giải 1
- Vì u = 2013 > 2 nên đặt u = a + , a > 1. 1 1 a 2 æ 1 ö 1 Ta có 2 2
u = u - 2 = a + - 2 = a + . 2 1 ç ÷ 2 è a ø a
Bằng quy nạp, ta chứng minh được. n 1 2 u = a + " Î • n+ n , n . 1 2 a - Xét. Trang 11 1 - 1 n n n - i 1 - æ 1 ö æ 1 ö éæ 1 i 1 - ö æ 1 öù æ 1 n ö æ 1 ö 2 2 2 Õu = Õ a + = - - Õ + = - + ç - a a a ÷ ç ÷ êç ÷ ç - a a i i i ÷ú ç ÷ ç n 1.0 1 1 ÷ 2 2 2 = = è a ø è a ø ëè a ø = è a øû è a i 1 i 1 i 1 ø è a ø 2 æ 1 ö æ 2n 1 ö . a - a + 2 ç ÷ ç n ÷ 2 2 u 2 2 æ 1 ö æ 1 + è a ø è a ø u ö n 1 n 1 Þ = Þ lim + = 2 a - = a + - 4 = 2013 - 4 1.0 2 2 2 2 2 2 2 ç ÷ ç ÷ u .u ... n u ®+¥ æ ö u u u è a ø è a n ø n 1 . ... 1 2 2 1 2 n a - ç ÷ 2n è a ø
Bài 15. Cho dãy số (a )thỏa mãn: lim(5a - 3a ) = 4. Tính lim a . n n 1 + n n Hướng dẫn giải
Đặt a = 2 + b . Từ giả thiết suy ra lim(5b - 3b ) = 0 . n n n 1 + n
Với số dương e bé tùy ý, tồn tại số N sao cho với n > N thì ta có:. e
5b - 3b < (1). n 1 + n 5 e
- Nếu b .b £ 0thì từ (1) dẫn đến 5b
+ 3b < Þ b < e . n 1 + n n 1 + n 5 n
- Xét trường hợp b .b > 0 hay b , b cùng dấu, chẳng hạn chúng cùng dương. n 1 + n n 1 + n e e
. Nếu 2b - b £ 0 thì kết hợp với (1): 3(2b - b ) - b < dẫn đến b < . n 1 + n n 1 + n n 1 + 5 n 1 + 5 e
Mà từ (1) ta có 3b - 5b < Þ b < e . n n 1 + 5 n 5 1 e
. Nếu 2b - b > 0 thì kết hợp với (1): (b - b ) - b < dẫn đến b < e . n 1 + n n 1 2 + n 2 n 5 n
Tóm lại luôn có b < e , hay lim(b ) = 0. n n Vậy lim(a ) = 2 . n 2015 u + 2u + 4
Bài 16. Cho dãy (u )xác định như sau: u = 3 và n n u =
, n = 1, 2,3.... Với mỗi số n 1 n 1 + 2014 u - u + 6 n n n 1
nguyên dương n , đặt v = . Tìm v . å lim n 2014 n ®+¥ = u + n i 1 4 i Hướng dẫn giải 2015 u + 2u + 4 (u - 2)(ua + 4)
Đặt a = 2014 ta có u - 2 n n = - 2 n n = , (*). n 1 + 2014 u - u + 6
(ua + 4) - (u - 2) n n n n
Bằng quy nạp ta chứng minh được u > 3, n " >1. n a 1 u + + 2u + 4 2 (u - 2) Xét n n u - = - n = > 0, u " ³ 3 + u u . n 1 n ua -u + 6 n ua -u + 6 n n n n n
Do đó (u ) là dãy tăng và 3 = u < u <!< u < . ! n 1 2 n Trang 12 a 1 a + + a + 4
Giả sử (u ) bị chặn trên, suy ra lim u = a, a > 3. Khi đó ta có a =
Þ a = 2 < 3(vô lí), suy ra n n n®+¥ aa - a + 6 (u ) lim u = +¥
n không bị chặn trên. Vậy n n®+¥ . 1 1 1 1 1 1 Từ (*) suy ra = - , hay = - . u - 2 u - 2 ua + 4
ua + 4 u - 2 u - 2 n 1 + n n n n n 1 + n 1 n æ 1 1 ö 1 v = å = åç - =! =1- . n 2014 ÷ = u + = è u - u - u - 2 i 1 4 i i 1 2 2 i i 1 + ø n 1 + 1 Vậy lim v = lim 1 ( - ) = 1. n n®+¥ n®+¥ u - 2 n 1 + u ì = 3 ï
Bài 17. Cho dãy số (u 1 (un)
n ) được xác định bởi í . Chứng minh rằng dãy 3 u ï
- 3u = 2 + u , n " ³ 1 î n 1+ n 1 + n
có giới hạn hữu hạn và tìm giới hạn đó. Hướng dẫn giải u ì = 3 ï Dãy số (u 1
n ) được xác định bởi í . 3 u ï
- 3u = 2 + u , n " ³ 1 î n 1+ n 1 + n
Ta chứng minh u > 2, n " ³1. n
Thật vậy ta có u = 3 > 2. 1
Giả sử u > 2, k " ³ , khi 1 đó 3 u
- 3u = 2 + u > 2 + 2 = 2 nên. k k 1 + k 1 + k 3 u
- 3u - 2 > 0 Û (u + - > Û u > 2 + )2 1 u 2 0 k 1 ( k 1+ ) . k 1 + k 1 + k 1 +
Do đó theo nguyên lý quy nạp thì u > 2, n " ³1. n
Xét hàm số f (t) 3
= t -3t trên khoảng (2,+ ¥). Ta có f (t) 2 '
= 3t -3 > 0, t " > 2.
Do đó hàm số f (t) đồng biến trên khoảng (2,+ ¥). Mặt khác ta có 3 3
u -3u =18 > 5 = u -3u Û f (u > f u Þ u > u 1 ) ( 2) . 1 1 2 2 1 2
Giả sử u > u
k ³1 Þ 2 + u > 2 + u 3 3
Û u - 3u > u - 3u k k 1 + ( ) . k k 1 + k 1 + k 1 + k +2 k +2 Þ f (u > f u Þ u > u k 1 + ) ( k+2) . k 1 + k +2
Do đó u > u , n " ³ 1 Þ Dãy (u (un)
n ) là dãy giảm và bị chặn dưới bởi 2 nên dãy có giới hạn hữu n n 1 + hạn.
Giả sử limu = a (a ³ 2 3 u - 3u = 2 + u n
). Từ hệ thức truy hồi
chuyển qua giới hạn ta được:. n 1 + n 1 + n 3
a - 3a = 2 + a Û (a - a)2 3 3
= 2 + a Û (a - )( 5 4 3 2
2 a + 2a - 2a - 4a + a + ) 1 = 0. Trang 13 Û (a - )( 2 a ( 3 a - ) 3 2 4 + 2a (a - ) 1 + a + )
1 = 0 Û a = 2 (a ³ 2). Vậy limu = 2. n 2
Bài 18. Cho dãy số (x x = 2015 x = x . + " Î + ( x )1 n N n n n ( * 1 ) n ) thỏa mãn: và (*). 1 n 1 Tìm: lim . åi1= x +1 i Hướng dẫn giải * Ta có: * x > 0 n " Î N . n x Và: n 1 + = ( x + > n " Î N Þ (xn ) n )2 * 1 0 là dãy số tăng. xn
* Đặt u = x . n n Þ u xác định vì * x > 0 n
" Î N và u > 0 * n " Î N . n n n 2 Þ u = x Þ x = u . n 1 + n 1 + n 1 + n 1 +
Nên từ giả thiết (*) ta có:. u = u . u + = u u + + n ( n )2 2 2 1 . 1 n 1 ( n ( n ))2. 2
Þ u = u + u * n " Î N (1). n 1 + n n
* Xét dãy số (un ) ta có:. . 2 * u
- u = u > 0 n
" Î N Þ (un ) tăng. n 1 + n n . Giả sử (u a
n ) có giới hạn là . Từ (1) ta có:. 2
a = a + a Û a = 0 (loại). Þ (u Þ limu = +¥
n ) tăng và không bị chặn . n * Ta có:. 2 1 u u - u u - u 1 1 n n 1 + n n 1 + n = = = = - . u +1 u + u u + u u u u u u n ( n ) 2 1 n ( 2n n). . n n 1 + n n n 1 + n Þ 1 1 1 å = - . + 1 i 1 = u 1 u u i 1 n 1 + n 1 æ 1 1 ö 1 Þ limå = limç - ÷ = . + i 1 = u 1 u u i è n+ ø 2015 1 1 n 1 1 Vậy: lim å = .. i 1 = x +1 2015 i Trang 14 u ì = 5 ï
Bài 19. Cho dãy số {u 1 í . {un}
n} ; (n = 1; 2;.) được xác định bởi: Chứng minh dãy số có u ï = u +12 î n 1+ n
giới hạn. Tìm giới hạn đó. Hướng dẫn giải
Dự doán giới hạn của dãy số,bằng cách giải phương trình:. ìa ³ 0 a = a +12 Û í Þ a = 4. 2 îa = a +12 Nhận xét u = 5. 1
u = u +12 = 17 < u . 2 1 1 u = u +12 = 17 +12 < u .... 3 2 2
Ta dự đoán dãy số {u u ³ 4
n} là dãy số giảm và bị chặn dưới bởi 4 tức là . n
Chứng minh dãy số u bị chặn: tức là u ³ 4. n n
khi n = 1, u = 5 ³ 4 vậy n = 1 đúng. 1
Giả sử u ³ 4, ta chứng minh: u ³ 4. k k 1 + Thật vậy ta có:. u = u +12 > 0 2 2
Û u = u +12 Û u -12 = u ³ 4 2
Û u ³ 16 Þ u ³ 4. k 1 + k k 1 + k k 1 + k k 1 + k 1 +
Vậy dãy số u bị chặn dưới. n
Ta chứng minh dãy số {un} là dãy số giảm. Ta có:. 2 u - + u +12 -(u - 4)(u + 3) u - u = u +12 n n -u = n n Û u - u = £ 0 (vì u ³ 4). n 1 + n n n u +12 + u n 1 + n u +12 + u n n n n n
Vậy dãy số {un}giảm và bị chặn dưới nên có giới hạn.
Đặt limu = a thì limu = . a . n n 1 + Ta có:. u
= u +12 Û limu = lim u +12 Û a = a +12 Þ a = 4. n 1 + n n 1 + n Vậy limu = 4.. n
Bài 20. Cho dãy số (xn ) được xác định bởi. ìx = 2,1 1 ï 2 í .
x - 2 + x + 8x - 4 n n n ïx = * , n = 1, 2,... n 1 + ( ) î 2 Trang 15 n 1
Với mỗi số nguyên dương n, đặt y = . Tìm y . å lim n 2 - n i 1 = x 4 i Hướng dẫn giải
Ta có kết quả sau: với số thực a > 2 bất kì, ta có. 2 2 a - 2 + a + 8a - 4 a - 2 + a + 4a + 4 a - 2 + (a + 2) > = = a . 2 2 2
Do đó 2,1 < x < x < ... Þ ( x lim x = L > 2
n ) là dãy tăng, giả sử bị chặn trên tức là có giới hạn . 1 2 n
Chuyển qua giới hạn điều kiện (*) ta có phương trình. 2
x - 2 + x + 8x - 4 2 x =
Û x - 4 = (x + 3)(x - 2). 2
phương trình này không có nghiệm hữu hạn lớn hơn 2. Suy ra dãy ( x lim x = +¥
n ) tăng và không bị chặn trên nên . n 2
x - 2 + x + 8x - 4 Ta có n n n 2 x =
Û 2x - x + 2 = x + 8x - 4 . n 1 + n 1 2 + n n n
Û (2x - x + 2 = x + x - Û x - = x + x - + n )2 2 2 8 4 4 3 2 n 1 n n n+2 ( n )( n ). 1 x + 3 x + 2 + 1 1 1 n n Û = = = + . 2 2 2 x - 2 x - 4 x - 4 x - 2 x - 4 n n+1 n+1 n+1 n+1 1 1 1 Û = - . 2 x - 4 x - 2 x - 2 n+1 n n +1 n 1 1 1 1 Suy ra y = å = - = 10 - . n 2 - - - - = x x x x i 4 2 2 2 1 i 1 n+1 n+1 Vậy lim y =10. n
Bài 21. Cho dãy số (x 2 x = 2016, x
= x - x +1,n =1,2,3,...
n ) được xác định bởi . 1 n 1 + n n
a)Chứng minh rằng (x lim x = +¥ n ) tăng và . n æ 1 1 1 ö
b)Với mỗi số nguyên dương n , đặt y = 2016ç + +...+ ÷. Tính lim y .. n x x x è n 1 2 n ø Hướng dẫn giải
x - x = x - 2x +1= x -1 ³ 0 Þ x ³ x , n " ³1. (xn) n 1 + n n n ( n )2 2 a)Ta có n 1 + n Do đó tăng.
Ta chứng minh bằng quy nạp theo n rằng x > n +1, n " ³ 1 (1). n
Thật vậy, (1) đúng với n = 1.Giả sử (1) đúng với n (n > 1) thì. x
= x x -1 +1> n n +1 +1= n + n +1> n + 2 n 1 + n ( n ) ( ) 2 . Trang 16
Vậy (1) đúng với mọi n. Từ (x
x > n +1, n " ³1 lim x = + . ¥ n ) tăng ngặt và suy ra . n n 1 1 1 1
b)Ta có x -1 = x x -1 = = - n 1 + n ( n ). Suy ra . x -1 x x -1 x -1 x n 1 + n ( n ) n n 1 1 1 Từ đó = - x x -1 x -1 n n n 1 + . æ 1 1 1 ö æ 1 1 ö æ 1 1 ö
Þ y = 2016ç + +...+ ÷ = 2016ç - ÷ = 2016ç - n ÷ x x x x -1 x -1 2015 x -1 è 1 2 n ø è 1 n 1 + ø è n 1 + ø. 1 Từ lim x = +¥ Þ lim = 2016 0. Vậy lim y = .. n x n 2015 n 1 1 1 æ a ¥ ö
Bài 22. Cho dãy (a ¥ 2 2 2
a = sin1+ 2 sin + 3 sin +...+ n sin n " ³1 n n ) : . Chứng minh dãy n 1 = n 2 3 n ç 2 ÷ è n øn 1= a
hội tụ và tính lim n . 2 n Hướng dẫn giải 1 Bổ đề 1: 3
x > sin x > x - x x " > 0. 6 1 1 1 1+ + + ...+ Bổ đề 2: 2 3 lim n = 0. n 1 1 1 1 1 1 Đặt 2
x = n sin . Áp dụng bổ đề 1: > sin > -
Þ k > x > k - . n n 3 k k k 6 k k 6k 1 æ 1 1 ö
Þ1+ 2 +...+ n > a >1+ 2 + ...+ n - 1+ + ...+ . n ç ÷ 6 è 2 n ø 1 1 1+ +...+ 1 a 1 Chia các vế cho 2 n : n 2 n > > - . 2 2 2 n 2 6n a 1
Cho n ® ¥ , và lấy giới hạn, suy ra lim n = . 2 n 2 . (n + )2 1 u
Bài 23. Cho dãy số u = 2,u = n
" ³1. Tính giới hạn lim n . 1 n 1 + u +1 n®+¥ n n Hướng dẫn giải 2 n Ta chứng minh quy nạp
£ u £ n +1 , n " ³ . 1 n +1 n
Rõ ràng khẳng định đã đúng với u . 1 Trang 17 2 k (k + )2 1 Giả sử đã có
£ u £ k +1, k ³ . T 1 a chứng minh £ u £ k + 2. k +1 k 1 k + 2 k + (k +1) (k + )2 2 1
Thật vậy: u £ k +1 Þ u = ³ . k k 1 + u +1 k + 2 k k (k +1) (k + )2 2 2 1 1 u ³ Þ u = £ = k + 2 - £ k + 2 .. k k 1 + 2 2 k +1 u +1 k k + k +1 k +1 k +1 2 n u Vậy ta có
£ u £ n +1, n " ³1Þ lim n =1. n +1 n n®+¥ n ìx = a ï 1
Bài 24. Cho a > 2 và dãy số (x n ) với: . í 2 n + 3 ï2x = x 3 + * n N n+1 n ( Î ) î n
a) Chứng minh: x > 1 với * n " Î N . n
b) Chứng minh dãy số (xn ) có giới hạn và tìm giới hạn đó. Hướng dẫn giải
Ta chứng minh x > 1 với * n
" Î N bằng quy nạp. n Ta có: x = a nên x >1. 1 1 Giả sử: x > 1 với * k Î N . k n +1 n + 3 Ta có: x 3 2 > 3 và > 1 nên x 3 2 + > 2. Suyra: x > . 1 k n n n n 1 + Vậy x > 1 với * n " Î N . n
Ta chứng minh (x
n ) là dãy giảm bằng quy nạp. Vì a > 2 nên a 3 2 + 4 < a 2 .Ta có x < x . 2 1 n + 1 Giả sử: x < x . Ta có: 3 2 2 x < x 3 và f (n = )
là hàm nghịch biến nên:. k 1 + k k 1 + k n + + 2 k 4 2 k 3 x 3 + < x 3 + . k 1 + k +1 k k Suy ra: x < x . Vậy (x n ) là dãy giảm. k+2 k 1 + (x
n ) lả dãy giảm và bị chặn dưới bởi 1 nên hội tụ. ìx =1 1 ï
Đặt limx = a.Ta có 2a = 3 2 a +1 Û a =1. (x * í
3x + 4 (n Î N ) u u = x n Î N n ( n ) n n- ( * 2 1 ) n ) . n x = n 1 + ï x +1 î n Vậy lim x = . 1 n Trang 18 ïìu = 2011 1
Bài 25. Cho dãy số (un ) được xác định: í . ï n n * î2 u = 2 u -1 , n Î n+ N 1 n
Chứng minh rằng dãy số (un ) có giới hạn hữu hạn và tính giới hạn đó. Hướng dẫn giải 1 Ta có n n 2 u = 2 u . -1 Û u = u - . n 1 + n n 1 + n n 2 Chứng minh : 1–
u > 2 n (bằng quy nạp). n *với n = 1 ta có 0 u = 2011 > 2 . 1 *Giả sử 1–
u > 2 k (với k > 1 ). k *Cần chứng minh : – u > 2 k . k 1 + Ta có -k - 1 k -k -k u
= u - 2 > 2 - 2 = 2 . Suy ra điều phải chứng minh. k+1 k 1 Từ đó ta có –
u – 2 n > 0 với mọi n Þ u = u - . n n 1 + n n 2 1 1 1 1
Ta có u = u - ; u = u - ; u = u - ;...;u = u - . 2 1 3 2 2 4 3 3 n n 1 - n 1 2 2 2 2 - æ 1 1 1 1 ö Þ u = u - ... n 1 ç + + + + 2 3 n-1 ÷ . è 2 2 2 2 ø n 1 æ 1 - ö 1 - ç ÷ n 1 - Công thức tổng quát : 1 è 2 ø æ 1 ö u = 2011 - . = 2011 -1 + n ç ÷ . 2 1 è 2 ø 2 Vậy lim u = 2010. n u ì = a 1 ï
Bài 26. Cho số thực aÎ(0; )
1 , xét dãy số (un )với: í 1 2013 . 2 u = u + u , n * " Î N ï n 1+ î 2014 n 2014 n
a) Chứng minh rằng: 0 u 1, n * < < " Î N . n
b) Chứng minh rằng (un ) có giới hạn hữu hạn. Tìm giới hạn đó. Hướng dẫn giải
a) Chứng minh: 0 u 1, n * < < " ÎN n ( )1.
n =1: u = a Î 0;1 Þ 1 1 ( ) ( )đúng với n=1. 1 1
Giả sử 0 < u < 1với k " ³1,k Î N. Ta có: 2 2 0 < u <1Þ 0 < u < . k k 2014 k 2014 Trang 19 2013 2013 0 < u <1Þ 0 < u < . k 2014 k 2014 1 2013 2 Þ 0 < u +
u < 1 Þ 0 < u < . 1 2014 k 2014 k k 1 + Vậy: 0 u 1, n * < < " Î N . n
b) Chứng minh rằng (un ) có giới hạn hữu hạn. Tìm giới hạn đó.
Ta chứng minh: (un ) là dãy tăng. * 1 2013 1 2 n " Î N ,u - u = u + u - u = é
ë(u - u )(u + u - 2013)ù > 0. n 1 + n 2014 n 2014 n n 2014 n n n n û
Þ u > u , n *
" Î N hay (un )là dãy tăng.(2). n 1 + n Từ (1),(2) suy ra (u (u ,
a (o < a £ ) 1 n )
n ) có giới hạn hữu hạn.Giả sử có giới hạn là . 1 2013 Ta có: 2 a = a +
a Û a = 1. Vậy limu = 1. 2014 2014 n ì 3 u = ï 1 ï
Bài 27. Cho dãy số(u 2 n) xác định như sau: í . 1 2 3 u ï = u - , n " Î N* n 1 + ïî 3 n 3
a) Chứng minh rằng: 1 u 2, n * - < < " Î N . n
b) Chứng minh rằng (un ) có giới hạn hữu hạn. Tìm giới hạn đó. Hướng dẫn giải 3
a) Với: n = 1: u = Þ 1 1 ( )đúng với n=1. 2 Giả sử: 1
- < u < 2 với k " ³1,k Î N. k 1 8 1 Ta có: 3 u - 2 = u - = u - u + u + < Þ u < k + k ( 2 k )( 2 2 4 0 2 1 k k ) . k 1 3 3 3 + 1 u +1 = u + > Þ u > - k + ( 3 1 0 1 1 k ) . k 1 3 + Þ 1
- < u < 2. Vậy: 1 u 2, n * - < < " Î N . k 1 + n * 1 b) n " Î N ,u - u = u + u -
< Þ u < u , n * " Î N (un) n+ n ( n )2 1 2 0 1 ( n ) hay là dãy giảm (2). 3 n 1 + n
Từ (1),(2) suy ra (un ) có giới hạn hữu hạn.
Gọi a là giới hạn của (u 1 - £ a < 2 n ) , . 1 2 Ta có 3
a = a - Û a =1. Vậy limu = 1 - . 3 3 n Trang 20 2 u
Bài 28. Cho dãy số (u n * u =1;u =
+ u ,nÎ N
n ) xác định bởi: . Tìm giới hạn sau: 1 n 1 + 2015 n æ u u u ö 1 2 lim ç + +... n + ÷ n®+¥ . u u u è 2 3 n 1 + ø Hướng dẫn giải 2 u u æ 1 1 ö Từ đề bài ta có: n u -u = . Suy ra: n = 2015ç - . n 1 + n ÷ 2015 u u u n 1 + è n n 1 + ø u u u æ 1 1 ö æ 1 ö Ta có: 1 2 + +... k + = 2015ç - ÷ = 2015ç1- . ÷ u u u u u u 2 3 k 1 + è 1 k 1 + ø è k 1 + ø Ta có (u u =1
n ) là dãy đơn điệu tăng và . 1 2 a
Nếu lim u = a thì a = +a Þ a = 0. n n®+¥ 2015 ( vô lí vì (u u =1
n ) là dãy đơn điệu tăng và ). 1 Suy ra: lim u = +¥. n n®+¥ æ u u u ö Kết luận: 1 2 lim ç + +... n + ÷ = 2015. n®+¥ u u u è 2 3 n 1 + ø u ì = 2013
Bài 29. Cho dãy số (u 1 í ( * n Î N 2 ) n ) xác định bởi
. Chứng minh rằng dãy (un) có u - 2u .u + 2013 = 0 î n n n 1 +
giới hạn và tính giới hạn đó. Hướng dẫn giải
Từ hệ thức truy hồi suy ra 2 2u .u = u + 2013. n n 1 + n
Bằng quy nạp chứng minh được u > 0, với mọi n. n Do đó ta có:. 2 u + 2013 1 æ 2013 ö 2013 n 1 u - = = çu + ÷ ³ u . = 2013, n " ³ . 1 n n 1 2u 2 - n u u n 1 - è n 1 - ø n Mặt khác ta có :. 2 u u + 2013 1 2013 1 1 n 1 + n = = + £ + =1. 2 2 u 2u 2 2u 2 2 n n n
(un) là dãy số giảm và bị chặn dưới bởi 2013, do đó (un) có giới hạn hữu hạn.
Đặt limu = a. n 2 a + 2013 Ta có : a =
Þ a = 2013. Vậy limu = 2013. 2a n Trang 21 4 x + 9
Bài 30. Cho dãy số (x n * x = 4, x = , n " Ε
n ) xác định bởi: . 1 n 1 + 3 x - x + 6 n n
a) Chứng minh rằng lim x = +¥;. n n®+¥ n 1
b) Với mỗi số nguyên dương n , đặt y = . Tính y . å lim n 3 + n k 1 = x 3 k Hướng dẫn giải x + 9 (x -3 x + n )( 3 4 3 n n ) a) Xét x - 3 = = * n 1 + 3 ( ). x - x + 6 x + - x - n n ( 3 3 n ) ( 3 n )
Bằng quy nạp chứng minh được x > 3, n " ³1. n 4 2 x + 9 x - 6x + 9 Xét n n n x - x = - x = . n 1 + n 3 n 3 x - x + 6 x - x + 6 n n n n (x -3 n )2 * Þ x - x = > 0, n " Î • . n 1 + n 3 x - x + 6 n n Do đó (x
4 = x < x < x < ... n ) là dãy tăng và . 1 2 3 Giả sử (x Þ lim x = a n ) bị chặn trên . n 4 a + 9 Do đó: a =
Þ a = 3 < 4 (vô lý). Suy ra (x lim x = +¥
n ) không bị chặn trên. Vậy . 3 a - a + 6 n 1 1 1 1 1 1 b) Từ (*), suy ra: = - Þ = - . 3 3 x - 3 x - 3 x + 3 x + 3 x - 3 x - 3 n 1 + n n n n n 1 + n 1 n æ 1 1 ö 1 Suy ra: y = å = åç - ÷ =1- . n 3 + - - - k 1 = x 3 = x x x k k 1 3 3 3 è k k 1 + ø n 1 + æ 1 ö Vậy lim y = limç1- ÷ =1. n x - 3 è n 1 + ø ìx =1 1 ï 2014 2014 2014 x x x Bài 31. Cho dãy số 2015 í
. Tìm giới hạn của dãy số u với 1 2 u = + +... n + . xn x = + x n n ï x x x n 1 + î 2015 n 2 3 n 1 + Hướng dẫn giải 2015 2015 2015 x x x - x x n n n 1 + n n x =
+ x Û x - x = Û = n 1 + n n 1 2015 + n 2015 x x 2015x x n 1 + n n 1 + n . Trang 22 2014 2014 1 1 x æ 1 1 ö x n Û - = Û 2015 n ç - ÷ = x x 2015x x x x n n 1 + n 1 + è n n 1 + ø n 1 + . æ 1 ö Từ đó u = 2015ç1- . n ÷ x è n 1 + ø Dễ thấy (x
1 = x < x < x < ... n ) là dãy tăng và . 1 2 3 Giả sử (x Þ lim x = a n ) bị chặn trên . n 2015 a Do đó: a =
+ a Þ a = 0 < 1 (vô lý). Suy ra (x lim x = +¥
n ) không bị chặn trên. Vậy . 2015 n æ 1 ö Vậy limu = lim 2015ç1- ÷ = 2015. n x è n 1 + ø ìx =1 1 ï
Bài 32. Cho dãy số{x } xác định bởi 2 í
. Tìm giới hạn của dãy (S ) với n xn x = x + n ï n 1+ n î 2015 x x x 1 2 S = + +... n + . n x x x 2 3 n 1 + Hướng dẫn giải 2 x 2 x - x x x æ 1 1 ö n x = x +
Û 2015 x - x = x n 1 Û 2015 + n n n = Û = 2015ç - ÷. n 1 + n ( n 1+ n ) 2 . 2015 n x x x x x x x n 1 + n n 1 + n n 1 + è n n 1 + ø x x x æ 1 1 ö æ 1 ö Suy ra: 1 2 S = + +... n + = 2015ç - ÷ = 2015ç1- . n ÷ x x x x x x 2 3 n 1 + è 1 n 1 + ø è n 1 + ø Dễ thấy (x
1 = x < x < x < ... n ) là dãy tăng và . 1 2 3 Giả sử (x Þ lim x = a n ) bị chặn trên . n 2 a Do đó: a =
+ a Þ a = 0 < 1 (vô lý). Suy ra (x lim x = +¥
n ) không bị chặn trên. Vậy . 2015 n æ 1 ö Vậy limS = lim 2015ç1- ÷ = 2015. n x è n 1 + ø ìx =1 ï n 1
Bài 33. Cho dãy số (x ) xác định bởi 1 í . Đặt S = . å n
ïx = x (x +1)(x + 2)(x + 3) +1 n î + k = x 2 n 1 + n n n n 1 k Tìm limS . n Hướng dẫn giải 2 2 2 x
= x (x +1)(x + 2)(x + 3) +1 = (x + 3x )(x + 3x + 2) +1 = x + 3x +1 n 1 + n n n n n n n n n n . Trang 23 1 1 1 n 1 1 1 1 1 Ta có = - Þ S = å = - = - . x + 2 x +1 x +1 n + + + + k = x 2 x 1 x 1 2 x 1 n n n 1 + 1 k 1 n 1 + n 1 +
Dễ thấy: x - x = x +1 > 0, n " Î N (x
1 = x < x < x < ... n ) n 1 + n ( n )2 * suy ra là dãy tăng và . 1 2 3 Giả s ử (x Þ lim x = a n ) bị chặn trên . n Do đó: 2
a = a + 3a +1Þ a = 1
- <1 (vô lý). Suy ra (x lim x = +¥
n ) không bị chặn trên. Vậy . n æ 1 1 ö 1 Vậy limS = limç - ÷ = . n 2 x +1 2 è n 1 + ø ì 2016 u ï = 1 1 1
Bài 34. Cho dãy số (u 1 n) xác định bởi: í 2015 . Đặt S = + +. . .+ n u + 2 u + 2 u + 2 2
ï2u = u + 2u , n " Î * î • 1 2 n n 1 + n n Tính: limSn. Hướng dẫn giải u u + 1 1 1 1 1 1 2u = u u + Û u = Û = - Û = - n+ n ( 2 n ) n ( 2 n ) 1 n 1 + 2 u u u + 2 u + 2 u u n 1 + n n n n n 1 + . n 1 1 1 2015 1 Þ S = å = - = - . n + k 1 = u 2 u u 2016 u k 1 n 1 + n 1 +
Bằng quy nạp ta dễ dàng chứng minh được * u > 0, n " Î N . n 1 2016 Khi đó: 2 * u
- u = u > 0, n
" Î N suy ra (u
= u < u < u < ... n ) là dãy tăng và . n 1 + n 2 n 1 2 3 2015 Giả sử (u Þ limu = a n ) bị chặn trên . n 2016 Do đó: 2
2a = a + 2a Þ a = 0 <
(vô lý). Suy ra (un )không bị chặn trên. 2015 Vậy limu = +¥. n æ 2015 1 ö 2015 Vậy limS = limç - ÷ = . n 2016 u 2016 è n 1 + ø 4 x + 9
Bài 35. Cho dãy số (x n * x = 4, x = , n " Ε
n ) xác định bởi: . 1 n 1 + 3 x - x + 6 n n
a) Chứng minh rằng lim x = +¥;. n n®+¥ n 1
b) Với mỗi số nguyên dương n , đặt y = . Tính y . å lim n 3 + n k 1 = x 3 k Hướng dẫn giải Trang 24 x + 9 (x -3 x + n )( 3 4 3 n n ) a) Xét x - 3 = = * n 1 + 3 ( ). x - x + 6 x + - x - n n ( 3 3 n ) ( 3 n )
Bằng quy nạp chứng minh được x > 3, n " ³1. n 4 2 x + 9 x - 6x + 9 Xét n n n x - x = - x = . n 1 + n 3 n 3 x - x + 6 x - x + 6 n n n n (x -3 n )2 * Þ x - x = > 0, n " Î • . n 1 + n 3 x - x + 6 n n Do đó (x
4 = x < x < x < ... n ) là dãy tăng và . 1 2 3 Giả sử (x Þ lim x = a n ) bị chặn trên . n 4 a + 9 Do đó: a =
Þ a = 3 < 4 (vô lý). Suy ra (x lim x = +¥
n ) không bị chặn trên. Vậy . 3 a - a + 6 n 1 1 1 1 1 1 b) Từ (*), suy ra: = - Þ = - . 3 3 x - 3 x - 3 x + 3 x + 3 x - 3 x - 3 n 1 + n n n n n 1 + n 1 n æ 1 1 ö 1 Suy ra: y = å = åç - ÷ =1- . n 3 + - - - k 1 = x 3 = x x x k k 1 3 3 3 è k k 1 + ø n 1 + æ 1 ö Vậy lim y = limç1- ÷ =1. n x - 3 è n 1 + ø
3.2. TÍNH GIỚI HẠN BẰNG CÁC CÔNG THỨC CƠ BẢN u ì =1 1 ï Bài 1. Cho dãy số (a í 1 a n ) thỏa mãn
. Tìm tất cả các số thực sao cho dãy số u = u + n Î • * n 1 + n ( ) ï 3 u î n a ( u x n x = n Î • * n ) xác định bởi (
) hội tụ và giới hạn của nó khác 0. n n Hướng dẫn giải
Từ giả thiết ta có dãy số (un ) là dãy số dương và tăng(1). 1 Giả sử (u L = limu L = L +
n ) bị chặn trên suy ra nó hội tụ. Đặt , ta có ngay (vô lý). n 3 L
Vì vậy (un ) không bị chặn trên (2).
Từ (1) và (2) ta có limu = +¥. n 4 4 æ ö 1 Xét 3 3
limçu -u ÷. Đặt v =
( n Î • *), ta có limv = 0. n 1 + n n è ø 4 n 3 un Trang 25 4 3 æ ö 4 4 1 ç 1 ÷ 1 (1+ v -
v + v + v + n ) 4 3 2 3 1 4 6 4 3 3 4 n n n u - u = + v - = = . n 1 + n 3 n ç ÷ v v ç ÷ n n v (1+ v + + v + n )8 (1 n )4 4 3 3 1 è n ø 4 4 4 æ ö 4 3 u 4 Suy ra 3 3
limçu -u ÷ = . Từ đó lim n = (sử dụng trung bình Cesaro). n 1 + n 3 è ø n 3 ì 4 +¥ khi a > ï 4 3 æ ö ï a 4 3 u ç u a- ÷ ï 4 Ta có n n 3 lim = lim .u = í0 khi a < . n n ç n ÷ 3 ç ÷ ï è ø ï4 4 khi a = ïî3 3 4
Vậy a = là giá trị cần tìm. 3 ì 1 u = ;u = 3 ï 1 2 ï 2 Bài 2.
Cho dãy số (un ) xác định như sau: í u .u +1 n 1 + n * u ï = , n " Î N n+2 ï u + u î n 1 + n
a) Chứng minh rằng tồn tại vô số giá trị nguyên dương của n để u > . 1 n
b) Chứng minh rằng (un ) có giới hạn hữu hạn, tìm giới hạn đó. Hướng dẫn giải (u -1 u -1 1 + )( )
a) Trước hết ta luôn có u > 0, * n
" Î N . Xét u -1 n n = (1). n n+2 u + u n 1 + n
Bằng phương pháp quy nạp ta chứng minh được u , * u < 1, n " Î N và u >1, * n " Î N . 3n 3n 1 + 3n+2
Từ đó suy ra điều phải chứng minh. (u +1 u +1 1 + )( ) b) Ta có u +1 n n = (2). n+2 u + u n 1 + n u -1 u -1 u +1
Chia vế của (1) cho (2) có n+2 n 1 + n * = . , n " Î N . u +1 u +1 u +1 n+2 n 1 + n u -1 Đặt n * v = n " Î N , ta có * v = v .v n " Î N . n u +1 n+2 n 1 + n n
Bằng phương pháp quy nạp ta chứng minh được n F 1 - n F -2 v = v .v
, với (Fn ) là dãy số Phibonxi: n 2 1 ìF = F =1 1 2 í . * F
= F + F , n " Î N î n+2 n 1 + n n F 1 - n F -2 æ 1 ö æ 1 ö Hay v = . -
® 0 khi n ® +¥ , dẫn đến limu =1. n ç ÷ ç ÷ è 2 ø è 3 ø n Trang 26 Bài 3.
Cho dãy số (un ) được xác định như sau. u ì = 1 ï 1 í . u = u u + u + u + + n " Î ï + n ( 2 n )( 4 n )( 6 n ) * 16, n 1 î • n 1 Đặt v = , hãy tính v . å lim n + n i 1 = u 5 i Hướng dẫn giải Dễ thấy * u > 0, n " Î • . n Theo bài ra ta có. u = u + 6u u + 6u + 8 +16 =
u + 6u + 4 = u + 6u + 4 n 1 + ( n n ) ( n n ) ( n n )2 2 2 2 2 . n n 1 1 1 Suy ra u
+1 = u +1 u + 5 Û = - n 1 + ( n )( n ) . u +1 u +1 u + 5 n 1 + n n n 1 n æ 1 1 ö 1 1 1 1 Do đó v = å = åç - ÷ = - = - . n + + + + + + i 1 = u 5 = u u u u u i i 1 1 1 1 1 2 1 è i i 1 + ø 1 n 1 + n 1 + Mặt khác, từ 2 u
= u + 6u + 4 ta suy ra u > 6u . n 1 + n n n 1 + n
Kết hợp với u =1 ta có. 1 n- 1 1 * u > 6 , n
" Î • Þ limu = +¥ Þ lim = 0. n n u +1 n 1 + æ 1 1 ö 1
Từ đó ta có limv = limç - ÷ = . n 2 u +1 2 è n 1 + ø Bài 4. Cho dãy số thực (u * n Î • ( 2 +u + nu = n " Ε n ) * ln 1 1, n ) với thỏa mãn . n n(1- nu ) Tìm lim n . n®+¥ un Hướng dẫn giải Với mỗi *
n Î • , đặt f x =
+ x + nx - xÎ! n ( ) ( 2 ln 1 ) 1, . 2x x +1 Ta có f x = + n = + n - ³ n ( ) ( )2 ' 1 0 . 2 2 1+ x 1+ x ìx = 1 - ' f x = Û n ( ) 0 í . în =1 Do đó f x !
n ( ) là hàm tăng thực sự trên . ì f = - < n ( 0) 1 0 ï Ta có í . æ 1 ö æ 1 ö f = ln 1+ > 0 ï n ç ÷ ç 2 ÷ î è n ø è n ø Trang 27 Do đó !
$ u Î! sao cho f u = 1 0 < u < n ( n ) 0 và . n n n Ta thấy lim u = 0. n n®+¥ ì lim ln(1+u = ï n ) 1 2 2 un 1 Do đó: n®+¥ í . ï lim nu = lim 1 é - ln + u ù = n î ë ( 2 1 n ) 1 n®+¥ n®+¥ û n(1- nu ) nln ( 2 1+ un é ù n ) 1 Vậy lim = lim = lim nu ln + u = ê n ( 2 1 n ) 2n u 1.. ú n®+¥ n®+¥ n u u ®+¥ n n ë û ì 4 a = ï 1 Bài 5. Cho dãy số (a 3 í n " ³1,nΕ n ) thỏa mãn: . ( ï n + 2 î )2 2 a = n a - n +1 a a n n 1 + ( ) n n 1+ Tìm lim a . n Hướng dẫn giải (n + 2)2 2 n Dễ thấy * a ¹ 0, n
" Î • . Từ giả thiết ta có = - (n + ) 1 . n a a n 1 + n 1 1 Với mỗi *
n Î • , đặt y = + ta có y = 1 và. n a 4 1 n 2 ( + )2 æ 1 ö æ 1 ö n n 2 y - = n y -
- n +1 Þ n + 2 y = n y Þ y = y ç n 1+ ÷ ç n ÷ ( ) ( )2 2 2 . n 1 + n n 1 è 4 ø è 4 + ø (n + 2)2 n 2 2 2
æ n -1ö æ n - 2 ö æ 1 ö 4 4n (n + )2 2 1 Do đó y = ... y = Þ a = . n ç ÷ ç ÷ ç ÷ 1
è n +1ø è n -1 ø è 3 ø (n+ )2 2 1 n n 16 - n (n + )2 2 1 Vậy lima = 4. n Bài 6. Tính các giới hạn sau: 3 x - 8 2x +1 a) lim . b) lim . 2 x®2 x - 4 x 2- ® x - 2 Hướng dẫn giải x -8 ( 2 3 x + 2x + 4) a).lim = lim = 3. 2 x®2 x®2 x - 4 (x + 2) 2x +1 b) lim = -¥. x 2- ® x - 2 2 x + x +... n + x - n Bài 7. Tính giới hạn lim . x 1 ® x -1 Hướng dẫn giải Trang 28 2 n 2
x + x +...+ x - n
(x -1) + (x -1) +...+ ( n x -1) lim = lim x 1 ® x 1 x -1 ® x -1 2 n 1
(x -1)[1+ (x +1) + (x + x +1) +...+ (x - +...+1)] lim x 1 ® . x -1 2 n 1 lim 1
é + (x +1) + (x + x +1) +...+ (x - +...+1)ù. ë û x 1 ® n(n + ) 1 =1+ 2 + 3+…+ n = 2 . n 1+ ax -1 a Bài 8.
Cho n là số nguyên dương và a ¹ 0 .Chứng minh rằng: Lim = . x®0 x n Hướng dẫn giải Đặt n
y = 1+ ax , khi đó từ x ® 0 Þ y ®1.. n 1+ ax y -1 y -1 a Vậy Lim = aLim = a Lim = ... = .. n x® y x ® y -1 y® ( y - ) 1 ( n 1- n-2 0 1 1 y + y +...+ y +) n Bài 9. Tính các giới hạn sau:. 1 3 3 3 3
1 + 5 + 9 + ...+ (4n - 3) xsin æ cos5 x x ö a/ lim b/ lim . ç ÷
n®¥ [1+ 5 + 9 +...+ (4n - 3)]2 x®0 è cos3x ø Hướng dẫn giải Câu a. n n 3 3 3 3 3 3 2
1 + 5 + 9 + ...+ (4n - 3) = å(4i -3) = å(64i -144i +108i - 27). i 1 = i 1 = n n n 3 2
= 64åi -144åi +108åi - 27n. i 1 = i 1 = i 1 = n(4n - 2) 2
1+ 5 + 9 +...+ (4n - 3) = = 2n - n. 2 n n(n +1) n
n(n +1)(2n +1) 2 n é n(n +1) ù
Mà ta có các công thức: åi = ; 2 åi = ; 3 åi = . ê ú i 1 = 2 i 1 = 6 i 1 = ë 2 û Do đó: 3 3 3 3
P(x) =1 + 5 + 9 +...+ (4n -3) là một đa thức bậc 4 có hệ số bậc 4 là 64 / 4 =16.
Và Q x = [ + + + + n - ]2 ( ) 1 5 9 ... (4
3) là một đa thức bậc 4 có hệ số bậc 4 là 4 . 3 3 3 3
1 + 5 + 9 + ...+ (4n - 3) 16 Do đó: lim = = 4.
n®¥ [1+ 5 + 9 +...+ (4n - 3)]2 4 Câu b. Trang 29 cos5x-cos3x 1 cos3x
xsin x.cos3x é ù xsin æ cos5 x x ö cos5x-cos3 æ cos5x - cos3 x x ö lim = lim ê 1+ ú . ç ÷ ç ÷ x®0 è cos3x ø x®0 êè cos3x ø ú ë û cos5x - cos3x 2 - sin 4xsin x ésin 4x sin x 8 - ù Vì lim = lim = lim . . = 8 - . ê ú x®0 x®0 x®0 x sin . x cos3x x sin . x cos3x ë 4x x cos3x û 1 cos5x - cos3x xsin æ cos5 x x ö Vì lim
= 0và áp dụng công thức lim(1+ u)1u = e , nên 8 lim = e- . ç ÷ x®0 cos3x u®0 x®0 è cos3x ø ìx = 2 1 ï Bài 10. Cho dãy số (x í
x + 2x + 3x + ...+ (n -1)x limu n ) thỏa mãn . Tìm với 1 2 3 n 1 x - =
, n ³ 1, n Î • . n n ï 2 î n(n -1) 3
u = (n +1) x .. n n Hướng dẫn giải 1 Ta có x = . 2 3 Với n ³ 3: 3
x + 2x + 3x + ...+ nx = n x 1 2 3 n n (1). 3
x + 2x + 3x + ...+ (n -1)x
= (n -1) x (2). 1 2 3 n 1 - n 1 - Từ (1) và (2) ta có 3 3
nx = n x - (n -1) x . n n n 1 - 3 (n -1) x n -1 n Suy ra n 1 - 2 x = = ( ) . .x . n 3 n 1 n - n n n +1 - n -1 n - 2 2 n n -1 3 2 2 2 Þ x = ( ) .( ) ...( ) . . ... x . n 2 n n -1 3 n +1 n 4 4 2 + Þ 4(n 1) x = suy ra limu = lim = 4. n 2 n (n +1) n 2 n 3 3x +1. 2 - x - 2 Bài 11.
Tính giới hạn hàm số : L = lim . x 1 ® x -1 Hướng dẫn giải Ta có:. 3 3 3x +1. 2 - x - 2
3x +1. 2 - x - 3x +1 + 3x +1 - 2 lim = lim . x 1 ® x 1 x -1 ® x -1 3 2 - x -1 3x +1 - 2 = lim 3x +1 + lim . x 1 ® x 1 x -1 ® x -1 3 é 3 2 3 ( 2 x 1) (2 x) 2 x 1ù - - - + - + ë û
( 3x +1 - 2)( 3x +1 + 2) = lim 3x +1 + lim . x 1 ® é 3 2 3 x 1 (x -1)
(2 - x) + 2 - x +1 ® ù
(x -1)( 3x +1 + 2) ë û Trang 30 (2 - x -1) (3x +1- 4) = lim 3x +1 + lim . x 1 ® é 3 2 3 x 1 (x -1)
(2 - x) + 2 - x +1 ® ù
(x -1)( 3x +1 + 2) ë û ( - 3x +1) 3 1 = lim + lim = . x 1 ® é 3 2 3 x 1
(2 - x) + 2 - x +1 ® ù ( 3x +1 + 2) 12 ë û 2
x + 3 - 2011x + 2009 Lim Bài 12. Tính: x 1 ® x -1 . Hướng dẫn giải 2 2
x + 3 - 2 - 2011(x -1) x + 3 - 4 lim = lim[ - 2011] x 1 ® x 1 x -1 ®
(x -1)( x + 3 + 2) . x +1 4021 = lim( - 2011) = - x 1 ® x + 3 + 2 2 ì 4 a = ï Bài 13. Cho dãy số (a 1 3 í n " ³1,nΕ lim a n ) thỏa mãn: . Tìm . n ( ï n + 2 î )2 2 a = n a - n +1 a a n n 1 + ( ) n n 1+ Hướng dẫn giải (n + 2)2 2 n Dễ thấy * a ¹ 0, n
" Î • . Từ giả thiết ta có = - (n + ) 1 . n a a n 1 + n 1 1 Với mỗi *
n Î • , đặt y = + ta có y = 1 và. n a 4 1 n 2 ( + )2 æ 1 ö æ 1 ö n n 2 y - = n y -
- n +1 Þ n + 2 y = n y Þ y = y ç n 1+ ÷ ç n ÷ ( ) ( )2 2 2 . n 1 + n n 1 è 4 ø è 4 + ø (n + 2)2 n 2 2 2
æ n -1ö æ n - 2 ö æ 1 ö 4 4n (n + )2 2 1 Do đó y = ... y = Þ a = . n ç ÷ ç ÷ ç ÷ 1
è n +1ø è n -1 ø è 3 ø (n+ )2 2 1 n n 16 - n (n + )2 2 1 Vậy lima = 4. n 1 a Bài 14. Cho dãy số {x
x > 0, x = (3x + ), n = 2,3,... n} thỏa mãn . 1 n n 1 - 3 4 xn 1- Hướng dẫn giải 1 a Ta có 4
x = (x + x + x +
) ³ a với mọi n ³ 2 . n n 1 - n 1 - n 1 - 3 4 xn 1-
Do đó dãy {xn} bị chặn dưới. x 3 a 3 1
Với mọi n ³ 3 , ta có n = + £ + = 1 Þ x £ x . 4 x 4 4x 4 4 n n–1 n 1 - n 1 -
Do đó {xn} là dãy giảm. Trang 31
Từ đó suy ra dãy {x 4 lim x = a
n} có giới hạn và dễ dàng tìm được . n ìx = 3 1 ï Bài 15. Cho dãy số thực (x í 1 ( yn) n ) : . Xét dãy số cho bởi : x = 3 - , n " =1,2,3,... n 1 + ï x î n (3 + 5)n y = ; n
" = 1, 2,3,... Chứng minh dãy số ( yn )có giới hạn hữu hạn và tính giớn hạn đó. n
2 .nx .x .x ...x 1 2 3 n Hướng dẫn giải 1 § Ta có : x = 3-
Þ x .x = 3x -1 ; n " =1,2,3,.... n 1 + n n 1 + n xn
§ Đặt : z = x .x .x ...x thì ta có z
= x .x .x ...x .x .x . n 1 2 3 n n+2 1 2 3 n n 1 + n+2
= z .x .x . n n 1 + n+2 = z .(3x -1) . n n 1 + = 3z x - z . n n 1 + n = 3z - z . n 1 + n ìz = x = 3 1 1 ïï 8
Khi đó : íz = x .x = 3. = 8
. Suy ra (zn ) là dãy truy hồi tuyến tính cấp 2. 2 1 2 3 ï ïz
= 3z - z ; n " =1, 2,3,... î n+2 n 1 + n 3 ± 5
Xét phương trình đặc trưng : 2
t - 3t +1 = 0 Û t = . 2 n n æ 3- 5 ö æ 3+ 5 ö
Dãy có số hạng tổng quát dạng z = a ç ÷ + b ç ÷ . n ç 2 ÷ ç 2 ÷ è ø è ø ìæ 3- 5 ö æ 3+ 5 ö ïç ÷a + ç ÷ b = 3 ì 5 - 3 5 ç 2 ÷ ç 2 ÷ a ï = ïè ø è ø ï trong đó : 10 í Û í . æ ï 7 - 3 5 ö æ 7 + 3 5 ö ï 5 + 3 5 ç ÷a + ç ÷ b = 8 ïç b = 2 ÷ ç 2 ÷ ï è î ø è ø î 10 § Lúc này, ta có. n n æ 3+ 5 ö æ 3+ 5 ö ç ÷ ç ÷ (3 + 5)n 2 2 è ø è ø 1 y = = = = . n
2 .nx .x .x ... n n n x z 1 2 3 n n æ 3- 5 ö æ 3+ 5 ö æ 3- 5 ö a ç ÷ + b ç ÷ a ç ÷ + b 2 2 3 + 5 è ø è ø è ø Trang 32 1 1 1 3 5 - 5 Suy ra : lim y = = = = . n n æ - ö b 5 + 3 5 2 3 5 a.limç ÷ + b 10 3 + 5 è ø 3 5 - 5 § Vậy : y ® khi n ® +¥. n 2 u Bài 16. Cho dãy số (u u = 1 n u = n " Î • 3 lim n u = ?
n ) xác định bởi: , . Tìm . 0 n 1 + 2 2 n u + u +1 n n®+¥ n n Hướng dẫn giải u u 1 n Từ giả thiết n u = n " Î • ta có n * u < = n " Î • nên (v v = åu n ) xác định bởi có n 1 + 2 2 n u + u +1 n 1 + 2 2 n u n n k n n n k =0
giới hạn hữu hạn, giả sử lim v = c( c hữu hạn). n n®+¥ u 1 1 Cũng từ n u = n " Î • ta có 2 = n + u + n " Î • . n 1 + 2 2 n u + u +1 n u u n n n 1 + n 1 1 2 Û - = n + u n " Î • . n u u n 1 + n 1 1 Do đó 2 - = 0 + u . 0 u u 1 0 1 1 2 - =1 + u . 1 u u 2 1 …. 1 1 2 - = (n -1) + u . n 1 u u - n n 1 - n 1 1 1 (n -1) ( n 2n -1) -
Cộng theo vế ta được : - = + åu . u u 6 k n 0 k =0 1
(n -1)n(2n -1) v +1 n 1 - Þ = + . 3 3 3 n u 6n n n 1+ v Mà lim
n = 0 ( do lim v = c) nên. 3 n®+¥ n n n®+¥ 1
(n -1)n(2n -1) 1 Þ lim = lim = hay 3 lim n u = 3. 3 3 n®+¥ n n u ®+¥ 6n 3 n n®+¥ n 4 Bài 17. Cho dãy số (x x = 1, x =1+ , n " ³1 (xn)
n ) xác định bởi : . Chứng minh dãy có giới hạn hữu 1 n 1 + 1+ xn
hạn và tìm giới hạn đó. Hướng dẫn giải Trang 33 4 4 4
Ta có x =1+ = 3; x =1+ = 2 > x ; x =1+ < x . 2 3 1 4 2 2 4 3 4
Hàm số f (x) = 1+
liên tục và nghịch biến trên [0,+¥), 1 < f (x) £ 5. 1+ x 4 Ta có x =1+
= f (x ), n " Þ (x ) bị chặn. n 1 + 1 n + x n n
x < x Þ f (x ) > f (x ) Þ x > x Þ f (x ) < f (x ) Þ x < x Þ .... 1 3 1 3 2 4 2 4 3 5 suy ra dãy (x
) tăng và dãy (x ) giảm suy ra (x
),(x ) là các dãy hội tụ. 2n 1 + 2n 2n 1 + 2n Giả sử lim x = ; a lim x = b ( , a b ³1) . 2n 2n 1 + Từ x
= f (x ) Þ lim x
= lim f (x ) Þ b = f (a). 2n 1 + 2n 2n 1 + 2n Từ x = f (x ) Þ lim x = lim f (x ) Þ a = f ( ) b . 2n+2 2n 1 + 2n+2 2n 1 + ì 4 b = 1+ ïï Giải hệ phương trình 1+ a í
Û a = b = 4 = 2. Vậy lim x = 2. 4 n ïa =1+ ïî 1+ b 1 x Bài 18.
Cho x = 2014, x = 2013 và x = (1- ) n x + + +
, n = 2,3,.. .Tìm lim x . 1 2 n 2 n 1 n n n n®¥ Hướng dẫn giải x - x ( 1 - )n ( 1 - )n n ( 1 - )k Ta có n 1 + n x - x = - Þ x - x = (x - x ) = - và x = x - . å n+2 n 1 + n+2 n 1 + 2 1 n n! n! n+2 1 k 1 = k! ¥ ( 1 - )k ¥ ( 1 - )k 1
Dãy này rõ ràng hội tụ và có giới hạn là x - å = x +1- å = x +1- . 1 1 1 k 1 = k! k =0 k! e 1
Từ đó suy ra lim x = 2015 - . n n®+¥ e
3.3. TÍNH GIỚI HẠN BẰNG ĐỊNH LÍ KẸP 1 Bài 1. Tìm lim . n®¥ n n! Hướng dẫn giải n
Trước hết ta chứng minh bất đẳng thức : n! > ( ) n (*) (" n ÎN*). 3 1
Bằng phương pháp qui nạp. Thật vậy : với n =1, ta có 1 > (đúng). 3 k
Giả sử (*) đúng với n = k tức là : k! > ( )k. Ta đi chứng minh (*) đúng với. 3 Trang 34 n = k+1. k k +1 k +1
Ta có (k+1)! = k!(k+1) >( ) k (k+1) = ( )k+1. 3 > ( )k+1. 3 3 1 (1+ )k 3 k
Bất đẳng thức cuối này đúng vì :. 1 k k(k -1) 1
k(k -1)(k - 2)....(k - k +1) 1 (1+ )k =1+ + . +.+ . =. k k 2! 2 k k! k k 1 1 k - 1 1 1 = 1+1+ (1- 1 1 2 1 )+.+ (1- )(1- )...(1- 1 )< 1+1+ +… + <1+1+ +.+ <. 2! k k! k k k 2! n! 2 1 2n- 1 1 <1+1+ +.+ +.< 1+ 1 = 3. 2 1 2n- 1 1- 2 n æ n ö n
Vậy (*) đúng với n = k +1. Do đó , n! >
từ đây ta suy ra n n! > . ç ÷ è 3 ø 3 1 3 => 0 < < . n n! n 3 Vì lim = 0. n®¥ n 1
Do đó theo định lý về giới hạn kẹp giữa ta suy ra: lim = 0. n®¥ n n! 1 Vậy lim(2014 + ) =2014. n n! ìx =1; x = 2 1 2 ï Cho dãy số (x 5 í x n ) thoả mãn 2 . (x + = n " Î ï • n+ ) ( n 1) * ; 2 4 î (xn )2
Tính I = lim x . n
Từ giả thiết suy ra mội số hạng của dãy đều dương. ìy = 0; y =1
Đặt y = log x , ta có dãy 1 2 í . n 2 n * 2y
= 5y - 2y ; n " Î î • n+2 n 1 + n ì z = - , 2 z = -1 1 2 ìz = 2; - z = 1 - í2z = 5z -
Lại đặt y = z + 2, ta có dãy 1 2 z í î n+2 n+1 n . n n * 2z
= 5z - z ; n " Î î • n+2 n 1 + n 1
Tìm được số hạng tổng quát của dãy là z = 4. - . n 2n
Từ đó ta có lim y = 2 Þ lim x = 4 . n n Trang 35 2 a - 5a +10 Bài 2.
Cho dãy (a )¥ : a =1; n n a = , n " ³1. n n 1 = 1 n 1 + 5 - an
a) Chứng minh dãy (a ) hội tụ và tính lim a . n n
a + a + ...+ a 5 - 5 b) Chứng minh 1 2 n < , n " ³1.. n 2 Hướng dẫn giải 3
a) Bằng phương pháp chứng minh qui nạp ta có: 1 £ a £ , n " . n 2 5 - 5 2 x - 5x +10 10 Đặt A =
và xét hàm f (x) = = - , x (x ¹ 5) . 2 5 - x 5 - x 10 é 3ù é1 ù Suy ra f ( ¢ x) = -1< 0, x " Î 1;
., như vậy f (x) nghịch biến trên đoạn ;1 .. ( ê ú ê ú 5 - x)2 ë 2û ë 2 û
ìa < a < a < ... < a < ... < A ì$lim a = b £ A Dẫn đến 1 3 5 2k 1 - í 2k 1 - Þ í ..
a > a > a > ... > a > ... > A î
$lim a = c ³ A 2 4 6 2k î 2k
Kết hợp công thức xác định dãy ta được. 2 ì c - 5c +10 b = ïï 5 - c 5 - 5 í Û b = c = . 2 b ï - 5b +10 2 c = ïî 5 - b 5 - 5 Vậy lim a = .. n 2 é 5- 5 ö
b) Nhận xét: t " Î 1 ê ;
÷. thì t + f (t) < 5 - 5.. 2 ÷ ë ø Dẫn đến a + a < 5- 5, k " ³1. 2k 1 - 2k 5 - 5
Þ a + a +...+ a + a < 2k . (1). 1 2 2k 1 - 2k 2
Như vậy bất đẳng thức đúng với n = 2k . 5 - 5
Trường hợp n = 2k +1, chú ý a <
, kết hợp với (1) thu được:. 2k 1 + 2 5 - 5
a + a + ...+ a + a + a < (2k +1) . 1 2 2k 1 - 2k 2k 1 + 2
Vậy bất đẳng thức được chứng minh. 1 un u e Bài 3. Cho dãy số thực (u u = n * u = , n " Ε n ) : ,
. Chứng minh dãy trên có giới hạn hữu hạn, 1 2 n 1 + 1 un - e tìm giới hạn đó. Hướng dẫn giải Trang 36 Chứng minh 1
- < u < 0, n " ³ 2 n ( )1. 1 e Với n = 2, 2 u = Î -1;0 2 ( ) đúng. 1- e Giả sử ( )
1 đúng với n = k ³ 2 , ta chứng minh ( )
1 đúng với n = k +1. un u e Ta có u < 0 un
Þ e <1 Þ1 un - e > 0 n Þ < 0. n 1 un - e un u 1 u e u > 1 n - Þ e > ; n > 1 un un
- Û u e > e -1 n u Û e (u - > - n )1 (l 1 uôn đúng). n e 1 u n n - e
Vậy (1) được chứng minh. x xe x e (1 x + x - e )
Xét hàm f (x) = trên ( ;0
-¥ ). Ta có f '(x) = . 1 x - e (1 x - e )2 Hàm ( ) =1 x g x
+ x -e có '( ) =1 x g x
-e > 0 với mọi xÎ(- ;0
¥ )nên hàm này đồng biến trên ( ;0 -¥ ). x e (1 x + x - e )
Suy ra g (x) < g (0) = 0, suy ra f '(x) = < 0. (1 x - e )2
hay hàm f (x) nghịch biến trên ( ;0 -¥ ). e e 2(1- e) 1 e e e 2(1- e) Ta có 2 u = = , u = , u > u . 2 1- e 2(1- e) 3 e 4 2 2(1- e) 1- e
Suy ra f (u < f u Þ u < u < 0 < u 4 ) ( 2) . 5 3 1
Quy nạp ta được dãy (u (u2n ) 2n 1 + ) giảm và dãy tăng. Hơn nữa 1
- < u < 0, n
" ³ 2 nên mỗi dãy trên tồn tại giới hạn hữu hạn. n Giả sử limu = , a limu = b ( , a bÎ( 1
- ;0)), lấy giới hạn hai vế ta được. 2n 2n 1 + b ì be a a = ïï 1-e í Þ - e = e e - a ( ae b 1 a )2 a 1 a e . ae b ï = ïî 1 a - e æ æ öö t a 1
Đặt e = t t Î
;1 , ta được phương trình ( - )2 1 1 = . -t t t t
Û 2(1-t)ln(1-t) -(1-t)lnt -t lnt = 0. ç ç ÷ è e ÷ è øø
Hàm h(t) = 2(1-t)ln(1-t) -(1-t)lnt -t lnt nghịch biến nên phương trình có nhiều nhất 1 nghiệm, 1
nhận thấy t = là nghiệm nên nó là nghiệm duy nhất. 2 Trang 37 1 Suy ra a = 1
ln , thay vào được b = ln . 2 2 1 Vậy limu = ln . n 2 2n - 3 Bài 4. Cho dãy số (a n ³ a =1, a = a , n ³ 2 (b n ³ n ) , 1 n ) , 1 thỏa mãn và dãy thỏa mãn 1 n n 1 2n - n
b = åa ,n ³ . C
1 hứng minh dãy (bn ) có giới hạn và tìm giới hạn đó. n i i 1 = Hướng dẫn giải
Ta có 2na = (2n - )
3 a Û a = 2é n -1 a - na ù,n >1 n n 1 - n 1 - (ë ) . n 1 - n û n
Do đó b = å2éia - i + a ù = é - n + a ù n ë i ( )1 2 1 1 i 1 + û ë ( ) . n 1 + û i 1 = 1
Ta chứng minh bằng quy nạp rằng na £ , n ³ . 1 n n Thật vậy:.
- Với n = 1, ta có a =1 nên khẳng định đúng. 1 2(n + ) 1 - 3 æ 2n -1 öæ 1 ö
- Giả sử khẳng định đúng với n (n ³ ) 1 . Ta có a = a £ , ta cần chứng n 1 + ç ÷ 2(n )1 n è 2n 2 ç ÷ + + øè n n ø æ 2n -1 öæ 1 ö 1 minh £ Û ç ÷ç ÷
(2n- )1 n+1 £ 2n n .
è 2n + 2 øè n n ø (n + ) 1 n +1 Û ( 2
n - n + )(n + ) 3 4 4 1
1 £ 4n Û1£ 3n.
Bất đẳng thức cuối đúng nên khẳng định trên đúng với n +1.
Theo nguyên lí qui nạp thì khẳng định được chứng minh. æ 1 ö Ta có 2 1- £ 2 1 é - ç ÷ ë (n + )
1 a ù = b £ 2. 1 û è n +1 n+ n ø
Theo nguyên lí kẹp thì dãy (b limb = 2
n ) có giới hạn và . n ì 1 u = ï 1 2 ï Bài 5.
Cho dãy số (bn ) được xác định bởi: í . 1 æ 1 ö 2 u ï = çu + u + n 1 + ÷ 2 n n ç 4n ÷ ïî è ø
Chứng minh dãy số hội tụ và tìm limu . n x®¥ Hướng dẫn giải 1 p Ta chứng minh u = cot ; n " Ε (*). n n n 1 2 2 + Trang 38 1 p 1
Thật vậy: n = 1 : u = cot = . 1 1 1 1 2 2 + 2
Þ (*) đúng với n =1. 1 p
Giả sử (*) đúng tới n = k , k *
Î • , nghĩa là có : u = cot . k k k +1 2 2 1 æ 1 ö
Ta chứng minh (*) cũng đúng với n= k+1. Thật vậy 2 u = çu + u + ÷. k 1 + 2 k k ç 4k ÷ è ø 1 æ 1 p 1 p 1 ö 1 æ p p ö 2 = cot + cot + ç ÷ 2 = cot + cot +1 ç ÷. k k 1 + k k 1 2 2 2 4 2 + 4k ÷ è + + + ÷ ø k 1 k 1 k 1 2 è 2 2 ø æ ö 1 ç p 1 ÷ p = çcot +
÷ ( vì khi k ® +¥ thì ® 0; sin ® 0). k 1 + k 1 2 2 + p 1 + ç sin ÷ 2k k 1 è 2 + ø p p 2 cos +1 2cos k 1 + k +2 1 1 1 2 2 p = . = = cot . k 1 + k 1 + k 1 + k +2 2 p 2 p p 2 2 sin 2sin cos k 1 + k +2 k +2 2 2 2
Þ (*) cũng đúng với n = k +1. 1 p Vậy u = cot ; n " Ε . n n n 1 2 2 + æ p ö æ p ö cos ç n 1 + ÷ ç n 1 1 p + 2 ÷ 2 2 2 lim u = lim ç . ÷ = limçcos ÷ = . n n n 1 x x p 2 x 2 + ®¥ ®¥ ®¥ p p p ç ÷ ç ÷ n 1 + n 1 è 2 ø è 2 + ø 2
Vậy dãy hội tụ và có lim u = . n x®¥ p Bài 6. Cho phương trình: n 2
x - x - x -1 = 0 với nÎN, n > 2 .
1)Chứng minh rằng với mỗi số nguyên n > 2 , thì phương trình có một nghiệm dương duy nhất x . n
2)Xét dãy số sau đây: U = n x -1 n = 2,3, 4,... limU ? n ( n ), Tìm . n Hướng dẫn giải
Xét phương trình: f (x) = 2
xn - x - x -1 = 0, với n nguyên, n > 2 (1). +) Ta có: f (x) n 1 ’ nx - =
– 2x –1. Do n > 2 , nên khi x > 1 thì f ’(x) > 0. Vậy f (x) là hàm số đồng biến trên ( + ; 1 ¥ .) Lại có: f ( ) 1 = 2 - < 0 ; (2) 2n f =
– 7 > 0 ( vì n nguyên và n > 2 Þn ³3). Ta có: f ( )
1 f (2) < 0 và f (x) liên tục, đồng biến nên phương trình f (x) = 0 có nghiệm duy nhất trên ( + ; 1 ¥ .) Trang 39
+) Mặt khác với 0 < x < 1 thì n 2
x < x ( do n > 2 ) suy ra f (x) < 0 với mọi 0 < x <1.
Như vậy ta đã chứng minh được (1) có nghiệm dương duy nhất với mọi n nguyên, n > 2 .
Gọi x là nghiệm dương duy nhất của phương trình n 2
x – x – x –1 = 0. n Bây giờ xét dãy (U U = n(x - n = 3, 4,5, n )1 n ) với , . n Ta có: n 2
x - x - x -1 = 0 hay n
x = x2 + x +1. n n n n n n
Áp dụng bất đẳng thức AM – GM, ta có:.
x2 + x +1+1+ .... +1 n n ! $ ! # " n
x = x2 + x +1 = x2 + x +1 .... 1 . 1 . 1 n so 1 n n n n ( n n ) < (2). ! " # n n 1 - sô 1
(Chú ý rằng ở đây 1< x nên 2
x + x +1 ¹ 1, vì thế trong bất đẳng thức không có dấu bằng). n n n 6
+) Mặt khác do x < 2, nên 2
x + x < 6, nên từ (2) có: 1 < x < 1+ (3). n n n n n 6
Bất đẳng thức (3) đúng với mọi n ³ 3 và lim = 0 nên từ (3) ta có: lim x = . 1 n n ln(x2 + x +1 n n ) +) Ta có: n 2
x = x - x -1 Þ n ln x = ln x x Þ n = n ( 2 + + n n )1 . n n n ln xn x -1 Từ đó: n(x - x x n ) ( n ) 1 = ln( 2 + + n n )1 (5). ln xn
Đặt y = x -1Þ lim y = 0. n n n
Ta có: suy ra từ (5) limU = limn x - = n ( n )1 ln3. Vậy: limU = ln 3. n ln x ln y + t + n ( n )1 ln ( )1 Bài 7.
Cho số thực a, xét dãy số (x lim = lim = lim =1 n ) được xác định bởi n 1 ³ t®0 x -1 y t n n 3 x - 6x - 6 x = a, n n x = , n = 1, 2,.. .
.. Tìm tất cả các giá trị của a để dãy số có giới hạn hữu hạn, 1 n 1 + 2 3x + 9x + 7 n n tìm giới hạn đó?. Hướng dẫn giải Với a = 1 - thì x = 1, - n " ³ nê 1 n lim x = 1 - . n n n®+¥ (x +1 x + 2 n 1 - )3 ( n 1- )3 Với a Ï 1 - thì x +1 = , x + 2 = , n " ³ 2. n 2 n 2 3x + 9x + 7 3x + 9x + 7 n 1 - n 1 - n 1 - n 1 - n 1 3 3 -
x + 2 æ x + 2 ö æ a + 2 ö Do đó n n 1 - = ç ÷ = ... , n " ³ . 1 ç ÷ x +1 x +1 è ø è a +1 ø n n 1 - Trang 40 n- n- 2(a + ) 1 3 1 - (a + 2) 1 3
Từ đó, tính được x = " ³ - - n n n n , 1,. (a + 2) 1 3 - (a + ) 1 3 1 3
Kết luận + a < - Þ a +1 > a + 2 Þ lim x = 2 - . 2 n n®+¥ 3
+ a > - Þ a +1 < a + 2 Þ lim x = - . 1 2 n n®+¥ 3 3 3
+ a = - Þ x = - , n
" ³1Þ lim x = - .. 2 n 2 n n®+¥ 2 ì 2012 u ï = Bài 8.
Cho dãy số (u ) xác định như sau: 1 í 2013
. Tìm lim u . n n n®+¥ 2 u
ï - 2u -1= 0 , n " =1,2,3,... î n n 1 + Hướng dẫn giải 2 u 1 Ta có : 2 u - 2u -1 = 0 n Û u = - . n n 1 + n 1 + 2 2 2 2 x -1 x 1 1
Xét hàm số : f (x) = = - ³ - . 2 2 2 2
f '(x) = x. . x -1 0 1 2 Ta có :. f ¢(x) - 0 + f (x) -3 0 8 -1 2 1 - 1 - 1 - 3 < u <1Þ < u < 0 Þ < u < - < 0. 1 2 3 2 2 2 8 Vậy : n " ³ 2 thì 1 - < u < 0. n 2 u -1 2 u - 2u -1 = 0 n Û u = . n n 1 + n 1 + 2 2 x -1 1 - Gọi a là nghiệm của :
= x ( x Î( ;0)) Þ a =1- 2 . 2 2
Ta có : u - a = f (u ) - f (a) . n 1 + n
Theo định lí La-grăng : f (u ) - f (a) = f '(a) . u - a . n n Trang 41 1 1
Do f '(a) £ Þ f (u ) - f (a) £ u - a . 2 n 2 n 2 1 æ 1 ö æ 1 n ö
Þ u - a £ u - a £ u - a £ ... £ u - a . n 1 + n ç ÷ n 1- ç ÷ 1 2 è 2 ø è 2 ø æ 1 n ö Mà lim
= 0 Þ lim (u - a) = 0 Þ lim u = a = 1- 2 . ç ÷ n 1 + n 1 + n®+¥ è 2 n®+¥ n®+¥ ø Vậy : lim u = 1- 2 . n n®+¥ ì 1 u = ï 0 ï 2 Bài 9. Cho dãy số {u {un}
n} xác định như sau: í 2
. Chứng minh rằng dãy số có u + 5 n u ï = , n " Î • n 1 + ï 2 î (u + 2 n )
giới hạn và tìm giới hạn đó. Hướng dẫn giải
* Vì 0 < u ¹ 1 nên 0 < u ¹ 1, n " Ε . 0 n 9
* Áp dụng BĐT Cauchy ta có u + 2 +
³ 6. Dấu bằng xảy ra Û u = . 1 n u + 2 n n Þ 9 u + 2 + > 6 , n " Î • . n u + 2 n 2 u + 5 1 æ 9 ö * n u = = çu + 2+ ÷ - 2 >1, n " Ε . n 1 + 2(u + 2 u + n ) 2 n 2 è n ø 1 9
* u - u = - u -1+ . n 1 + n 2 n 2(u + 2 n ) 1 9
Xét hàm số f (x) = - x -1+ . 2 2(x + 2) f ( x) 1 9 ' = - - < 0, x
" > 1 Þ f (x) nghịch biến trên (1;+¥). 2 2(x + 2)2
* Vì u >1Þ f u < f = Þ u < u n " Ε n ( n) ( ) * 1 0 , . n 1 + n Þ {u Þ {un}
n}giảm và bị chặn dưới
có giới hạn hữu hạn. 2 u + 5
* Giả sử limu = a (1£ a < +¥). Từ n u =
chuyển qua giới hạn ta có. n n 1 + 2(u + 2 n ) 2 a + 5 éa =1 a = Û . 2(a + 2) ê ëa = 5( - loai) * Vậy limu =1. n u Bài 10.
Cho dãy số (u ) được xác định bởi: u = 4 và 2 u = u - 2, với * n Î • . Tìm n 1 lim + . n 1 n 1 + n
n®+¥ u .u ...u 1 2 n Trang 42 Hướng dẫn giải
Với mọi n = 1, 2,... ; ta có. u
- 4 = u - 2 - 4 = u - 4u = u u - 4 = u .u (u - 4) n 1 + ( n )2 2 2 4 2 2 n n n ( 2n ) 2 2 2 . n n 1 - n 1 -
= ... = u u ...u u (u - 4) =12 u .u ...u n n 1 - 2 1 1 ( n n 1- 1)2 2 2 2 2 2 (1). 2 æ u ö 4 Từ (1) ta có: n 1 + ç ÷ =12 + ; n " =1,2,...(2). u .u ...u è n ø
(u .u ...un )2 1 2 1 2
Mặt khác, vì u = 4 > 2 nên từ 2 u
= u - 2 và chứng minh bằng quy nạp ta thu được u > 2 với mọi 1 n 1 + n n n = 1, 2,.... 4 4 Do đó n *
u .u ...u > 2 ; n " Î • . Khi đó, 0 < < ; n " = 1, 2, . ... 1 2 n
(u .u ...un )2 2 2 n 1 2 4
nên theo nguyên lý kẹp giữa ta có: lim = 0.
n®+¥ (u .u ...un )2 1 2 2 æ u ö Vậy, từ (2) suy ra: n 1 lim + ç ÷ =12 . n®+¥ u .u ...u è 1 2 n ø
Mặt khác, hàm số f (x) = x liên tục trên nửa khoảng [0; + ¥) nên. 2 2 u æ u ö æ u ö n 1 + n 1 + n 1 lim = lim ç ÷ = lim + ç ÷ = 12 . n®+¥ u u ... n u ®+¥ u u ... n u ®+¥ u u ...u 1 2 n è 1 2 n ø è 1 2 n ø u Kết luận: n 1 lim + = 12 .
n®+¥ u .u ...u 1 2 n Bài 11.
a) Chứng minh rằng có đúng một dãy số thực (x ) thỏa mãn. n n³0 x + x
x =1, 0 £ x £1 n " ³1và 2 2 n n 1
(1- x ) - (1- x ) - = n " ³1.. 0 n n n 1 - 2
b) Với dãy (x ) xác định như trên, xét dãy ( y ) xác định bởi y = x + x +...+ x n " ³ 0. Chứng n n n³0 n 0 1 n
minh rằng dãy ( y ) có giới hạn hữu hạn khi n ® +¥ . Hãy tìm giới hạn đó. n n³0 Hướng dẫn giải
a) Bằng quy nạp ta sẽ chỉ ra rằng x xác định duy nhất với mỗi n ³ 0. Để làm được điều này ta cần dùng n
kết quả (chứng minh của nó là đơn giản) sau: Với mỗi số thực mÎ[ 1] 0; , phương trình t + m 2 2 (1- t) - (1- ) m =
có đúng một nghiệm trên [0;1]. 2 1 1 1 1 1
b) Để ý rằng y = x + (x + x ) + (x + x ) +!+ (x + x ) + x n " ³1.. n 0 0 1 1 2 n 1 2 2 2 2 - n 2 n 3
Ta có giới hạn cần tìm bằng .. 2 Trang 43 Bài 12. Giả sử (F n =
F = F =1; F = F + F n ) ( 1,2,.. ). là dãy Fibonacci (
với ). Chứng minh rằng nếu 1 2 n 1 + n n 1 - F 1 n 1 a + ¹ - (x x = a, x = n = 1, 2,3... , 1 n 1 + ( ) n )
với mọi n = 1, 2,3,...thì dãy số , trong đó là xác F 1+ x n n
định và nó có giới hạn hữu hạn khi n tăng lên vô hạn. Tìm giới hạn đó. Hướng dẫn giải
Giả sử x , x ,..., x đã được xác định. Khi đó x được xác định khi x ¹ - . 1 1 2 m m 1 + m 1 * Nếu x = 1 - thì do x = nên x = 2 - . m m 1+ x m 1 - m 1 - F F
Từ giả thiết F = F =1; F = F + F ta viết 2 x = - , 3 x = - . 1 2 n 1 + n n 1 - m F m 1 - F 1 2 F Giả sử i+2 x = -
, với i nào đó, 0 £ i £ m - 2 . m-i Fi 1+ 1 1 F F Vì x = nên i 1 + i+3 x = -1 = - -1 = - . m-i 1+ x m-i 1 - x F F m-i 1 - m-i i+2 i+2 F F Khi đó m 1 x + = -
. Mâu thuẫn với giả thiết m 1 x + ¹ -
. Như vậy (x ) là dãy số xác định. 1 F 1 F n m m 1 5 -1 - 5 -1 Phương trình 2 x =
Û x + x -1 = 0 có hai nghiệm u = ,v =
. Có hai trường hợp xảy ra:. 1+ x 2 2 - -
Trường hợp 1: x = v. Khi đó x = x , n " ³ 5 1 1. Do đó lim x = . 1 n 1 n n®+¥ 2 - v
Trường hợp 2: x ¹ 1 1 v . Chú ý = v Û x =
Û x = v. Do đó x ¹ v, n " ³ . 1 1 1 n n + x v n n x - u Đặt n z = , ta có. n x - v n 1 -u 2 x - u 1+ x (1- u) - ux u - ux u x - u u n 1 + n n n z = = - = = = . n = .z . n 1 + 2 x - v 1 (1- v) n - vx v - vx v x - v v n 1 + n n n - v 1+ xn n æ u ö u Từ đó có z =
.z nên z ® 0 khi n ® +¥ (vì < ). 1 n ç ÷ 1 è v ø n v x - u u - vz Từ n z = suy ra n x =
dần tới u khi n ® +¥ (do z ® 0). n x - v n 1- z n n n 5 -1
Tức là trong trường hợp này lim x = . n n®+¥ 2 Trang 44 ì y ü Bài 13. Cho dãy số {y 3 y > 0, y
= y + y +...+ y , n " ³ 1 n n} thỏa mãn
. Chứng minh rằng dãy số í ý 1 n 1 + 1 2 n î n þ
có giới hạn bằng 0 khi n ® +¥ . Hướng dẫn giải Từ giả thiết ta có 3 3 y
= y + y , n
" ³ 2, do đó dãy số {yn} là dãy tăng, vì. n 1 + n n n³2 vậy 3 3 2 2 y
= y + y = y (y +1) < y (y +1). n 1 + n n n n n 1 + n 2 2
Þ y < y +1, n " ³ 2 2 2 2
Þ y < y +1< ... < y + n - . 1 n 1 + n n 1 + n 2 2 2 æ y ö y + n -1 2 y + n -1 n 1 + 2 Þ < . Mà 2 lim
= 0 nên theo định lý kẹp ta có. ç ÷ 2 è n +1ø (n +1) 2 (n +1) 2 æ y ö y y n 1 + n 1 lim
= 0 Þ lim + = 0 Þ lim n = 0. ç ÷ è n +1ø n +1 n Bài 14. Cho (u 3 3 3
S = u + u + ...+ u n = 1, 2,...
n ) là một dãy số dương. Đặt với Giả sử n 1 2 n 1 u
£ S -1 u + u n = 2,3,.... limu n 1 + (( n ) n n 1-) với Tìm . S n n 1 + Hướng dẫn giải Ta có 3 S - S = u
> 0,n =1,2,...Þ S n 1 + n n 1 +
( n) là dãy số tăng. Nếu dãy số (S (S 3
limu = lim(S - S = 0 Þ limu = 0 n n 1 + n ) n )
n ) bị chặn trên thì là một dãy hội tụ và . n
Xét trường hợp dãy số (S lim S = +¥
n ) không bị chặn trên thì . n
Từ giả thiết ta có S u + u £ S u + u ,n = 2,3,.... n 1 + n 1 + n n n n 1 -
Từ đây ta thu được S u + u
£ S u + u ,n = 2,3,.. .. n n n 1 - 2 2 1 u S u + u S u + u Do đó n 1 - 2 2 1 2 2 1 u + £ Þ 0 < u < , n = 2,3,.... n n S S S n n n
Theo nguyên lí kẹp ta có limu = 0 . n
Vậy trong mọi trường hợp ta đều có limu = 0 . n u ì =1 1 ï Bài 15.
Cho dãy số (u ) xác định bởi công thức truy hồi: í 1 . Chứng minh rằng n * u = u + - 2, n " Î • n 1 + n ï u î n
dãy (u ) có giới hạn hữu hạn và tính giới hạn đó. n Hướng dẫn giải Đặt 1 1 1
f (x) = x + - 2; g(x) = f ( f (x)) - x = + - 2 2 . Khi đó. x x 1 x + - 2 x Trang 45 æ 2 ö 2 - ç x - ÷( 2 x + ) 1 2 è ø 1 1 g '(x) =
£ 0 Þ g(x) < g(
) = 0 Þ f ( f (x)) < x, x " Î( ;1) (*).. 2 æ 1 ö 2 2 4 x x + - 2 ç ÷ è x ø 1
Mặt khác f '(x) < 0, x " Î( ;1) nên. 2 1 1 1 1 1
f (x) < f ( ) =
Þ f ( f (x)) > f ( ) = , x " Î( ;1) (**).. 2 2 2 2 2 1 1 Từ (*) và (**) suy ra:
< f ( f (x)) < , x x " Î( ;1) .. 2 2 1 1
Vậy: 1 = u > u >
Þ1= u > u > u > ,... Do đó (u
) là đơn điệu giảm và bị chặn dưới nên tồn 1 3 1 3 5 2 2 2n 1 - 1 tại limu = .. 2n 1 - n®¥ 2 é 1 ù
Vì f (x) liên tục trên ;1 nên. ê 2 ú ë û 1 u = f (u
) Þ limu = f limu = .. 2n 2n 1 - 2n - n®¥ ( 2n 1 n®¥ ) 2
Vậy dãy (u ) được phân tích thành hai dãy con hội tụ tới cùng một giới hạn. Do đó dãy (u ) có giới hạn n n 1 bằng .. 2 Bài 16.
Tìm tất cả các hàm số f : ! ® ! thỏa mãn đồng thời các điều kiện sau đây:.
1. f (x + y) £ f (x) + f (y) với mọi x, y Î! . 2. ( ) x f x £ e - 1 với mỗi x Î ! . Hướng dẫn giải
f (x + 0) £ f (x) + f (0) Þ f (0) ³ 0 và bởi vì 0
f (0) £ e -1 = 0 nên f (0) = 0.
f (x + (-x)) £ f (x) + f (-x) Þ f (x) + f (-x) ³ 0 (1). x æ x ö æ x ö æ ö 2
f (x) £ f + f £ 2 ç ÷ ç ÷ çe -1 . ÷ è 2 ø è 2 ø è ø x x æ ö æ x ö æ x ö æ ö 2 4
f (x) £ 2çe -1÷ Þ f (x) £ f + f £ 4 ç ÷ ç ÷ çe -1 . ÷ è ø è 2 ø è 2 ø è ø x æ ö
Dùng quy nạp theo n =1, 2, … ta CM được 2 f (x) £ 2 n çe -1÷. ç ÷ è ø Trang 46 0 x æ ö
Cố định x Î ! ta có n 2 f (x ) £ 2 n çe -1÷. 0 0 ç ÷ è ø 0 x é ù 0 x æ ö 2n êe -1 Xét dãy n ú 2 a = 2 n
çe -1÷ ta có : lim a = lim x = x . n ç ÷ n x 0 0 ê ú è ø 0 2n ê ú ë û
Vậy f (x ) £ x , x " Î! (2). 0 0 0
Vậy f (x) + f (-x) £ x + (-x) = 0 (3).
Kết hợp ( 1) và (3) ta được f (x) + f (-x) = 0.
Từ (2) Þ f (-x) £ -x Þ f (x) ³ x (4). Kết hợp ( 2) và (4) ta được f (x) = , x x " Î! .
Thử lại f (x) = x ta thấy đúng. ìx =1, 1 ï Bài 17. Cho dãy số (x (xn)
n ) được xác định như sau 3 í . Chứng minh rằng có giới xn ïx = x + n " ³1 n 1 + n 2 î n
hạn hữu hạn khi n dần đến vô cùng. Hướng dẫn giải
Dễ thấy x > 0, với mọi n nguyên dương, nên dãy số đã cho là dãy tăng thực sự. n
Vậy để chứng minh dãy số có giới hạn hữu hạn ta chỉ cần chứng minh nó bị chặn trên. Ta chứng minh * x < 8, n " Î • . n
Thật vậy, với n =1Þ x =1< 8 nên điều cần chứng minh đúng. 1
Giả sử ta có: x < 8 , với n nguyên dương. Ta cần chứng minh x < 8. n n 1 + n 3 n xk 1
Theo công thức xác định dãy số có: x = x + å
< 1+ 2å <1+ 2.2 < 8. n 1 + 1 2 2 k 1 = k k 1 = k
Do đó x < 8 với mọi n nguyên dương từ đó suy ra điều phải chứng minh. n ì 1 3 a = ; a = ï 1 2 ï 4 10 Bài 18. Cho dãy số thực (a (an)
n ) xác định bởi í
. Chứng minh rằng dãy 2 1 a a ï n n 1 a - = + + , n " Î • ,n ³ 2 n ïî 2 6 3
có giới hạn hữu hạn. Hãy tìm giới hạn đó. Hướng dẫn giải Có a ,a Î 0;1
a ,a ,...,a Î 0;1 ,k Ε ,k ³ 2 1 2 k ( ) 1 2 ( ), giả sử
. Từ công thức truy hồi ta có:. 2 1 1 a a 1 1 1 k k 1 + 0 + 0 £ a - = + +
£ + + =1, vì 0 £ a ,a £1 Þ a Î 0;1 k 1 + ( ). k 1 2 + 2 6 3 2 6 3 k 1 - k
Vậy bằng phương pháp quy nạp ta chứng minh được a Î n " Ε n ( ) * 0;1 , . Trang 47 ì 1 ì 3 x = x = ï y = y = 1 2 ï ï 1 2 ï 10
Xét hai dãy số mới ( x ( y n " Ε ;n ³ 2 n ) : n ) 4 : í và í với . 2 1 x x ï 2 1 y y n n 1 x - = + + ï n n 1 y - = + + n 1 + ïî 2 6 3 n 1 + ïî 2 6 3 1
Có 0 < x £ x < < x < , gi 1
ả sử ta có 0 < x £ x £ ... £ x <1,k Ε ,k ³ 3, khi đó. 1 2 3 2 1 2 k 2 2 1 x x 1 x x k 1 - k -2 k k 1 x - = + + £ + + = x . k k 1 2 6 3 2 6 3 +
Vậy bằng phương pháp quy nạp ta chứng minh được (xn ) là dãy số tăng và bị chặn trên bởi 1, nên nó có
giới hạn hữu hạn lim x = a . n é 3 2 1 a a a =
Chuyển công thức truy hồi qua giới hạn tìm được a ê = + + Û 2 . 2 6 3 êa ë = 1 Do (x Ì a =1 n ) (0; )1 nên suy ra .
Chứng minh tương tự đối với dãy số ( y lim y = 1 n ) , ta cũng có . n Cuối cùng ta chứng minh *
x £ a £ y , n
" Î • (1) bằng phương pháp quy nạp:. n n n
Ta có x = a < y và a < x = y , với n = 1, 2 bất đẳng thức (1) đúng. Giả sử (1) đúng tới k Î • , k ³ 2, 1 1 1 2 2 2
tức là x £ a £ y , i
" =1,2,...,k . Khi đó. i i i 2 2 2 1 x x 1 a a 1 y y k k 1 - k k 1 - k k 1 x = + + £ a - = + + £ + + = y . k 1 + k 1 + k 1 2 6 3 2 6 3 2 6 3 +
Từ x £ a £ y , nÎ • ,n ³
1 và áp dụng định lý kẹp ta suy ra được lim a = . 1 n n n n Bài 19.
Cho hai dãy số (a ); b a = 3,b = 2 2 2 a = a + 2b b = 2a b n
( n) xác định bởi , và với n = 1, 2, 1 1 n 1 + n n n 1 + n n 3,…. Tìm 2 lim n b và 2
lim n a a ...a . n n®+¥ 1 2 n n®+¥ Hướng dẫn giải
Với mọi n = 1,2,3,… ta có. a + b
2 = a + 2b + 2 2a b = a + b 2 n 1 + n 1 + n n n n ( n n )2 2 2 . Do đó:. n- n- n
a + b 2 = a + b = a + b = = a + b = + = + n n ( 2 2 ... 2 3 2 2 2 1 n 1 - n 1 - ) ( n-2 n-2 ) 2 ( 1 1 ) 1 ( ) 1 2 2 2 2 ( )2 . n
Tương tự ta có: a - b = - n n ( )2 2 2 1 . 2n 2 1 n æ ö 2n 2 1 n æ ö Từ đó: a = + + - b = + - - n ç( 2 )1 ( 2 )1 n ç( 2 )1 ( 2 )1 ; . ÷ ÷ 2 è ø 2 2 è ø Trang 48 n n 2 +1 2 +1 2n ( )2 2n ( )2 Chú ý: 2n 2n
< b < a < 2 + 1 và lim = 2 + ,
1 nên theo nguyên lí kẹp ta có: 4 2 n n n®¥ 4 2 2n 2
lim b = lim n a = 2 + n n n®¥ n®¥ . 1 b b b b b
Mặt khác: b = 2a b hay n 1 a + = ( n " ³1). Suy ra: 2 3 n 1 + n 1 a a ...a . ... + = = . Do đó n 1 + n n n 2b 1 2 n 2b 2b 2b 2n n 1 2 n n 1 2
lim n a a ...a = lim n b = 2 +1 = 3 + 2 2 2 lim =1 n 1 + n®¥ ( )2 2 (vì ). 1 2 n n®+¥ 2n n®¥ ì 1 3 a = ; a = ï 1 2 ï 4 10 Bài 20. Cho dãy số thực (a (an)
n ) xác định bởi í . Chứng minh rằng dãy 2 1 a a ï n n 1 a - = + + , n " Î • ,n ³ 2 n ïî 2 6 3
có giới hạn hữu hạn. Hãy tìm giới hạn đó. Hướng dẫn giải
+ Ta Có a ,a Î 0;1
a ,a ,...,a Î 0;1 ,k Ε ,k ³ 2 1 2 k ( ) 1 2 ( ), giả sử
. Từ công thức truy hồi ta có:. 2 1 1 a a 1 1 1 k k 1 + 0 + 0 £ a - = + +
£ + + =1, vì 0 £ a ,a £1 Þ a Î 0;1 k 1 + ( ). k 1 2 + 2 6 3 2 6 3 k 1 - k
Vậy bằng phương pháp quy nạp ta chứng minh được a Î n " Ε n ( ) * 0;1 , . ì 1 x = x = ï 1 2 ï
+ Xét hai dãy số mới (xn ) 4 : í . 2 1 x x ï n n 1 x - = + + , n " Ε ,n ³ 2 n 1 + ïî 2 6 3 ì 3 y = y = ï 1 2 ï và ( yn ) 10 : í . 2 1 y y ï n n 1 y - = + + , n " Î • ,n ³ 2 n 1 + ïî 2 6 3 1
- Có 0 < x £ x < < x < , gi 1
ả sử ta có 0 < x £ x £ ... £ x <1,k Ε ,k ³ 3, khi đó. 1 2 3 2 1 2 k 2 2 1 x x 1 x x k 1 - k -2 k k 1 x - = + + £ + + = x . k k 1 2 6 3 2 6 3 +
Vậy bằng phương pháp quy nạp ta chứng minh được (xn ) là dãy số tăng và bị chặn trên bởi 1, nên nó có
giới hạn hữu hạn lim x = a . Chuyển công thức truy hồi qua giới hạn tìm được n é 3 2 1 a a a = a ê = + + Û 2 . Do ( x Ì a =1 n ) (0; )1 nên suy ra . 2 6 3 êa ë = 1
- Chứng minh tương tự đối với dãy số ( y lim y = 1 n ) , ta cũng có . n
- Cuối cùng ta chứng minh *
x £ a £ y , n
" Î • (1) bằng phương pháp quy nạp:. n n n Trang 49
Ta có x = a < y và a < x = y , với n = 1, 2 bất đẳng thức (1) đúng. Giả sử (1) đúng tới k Î • , k ³ 2, 1 1 1 2 2 2
tức là x £ a £ y , i " =1,2,...,k i i i . Khi đó. 2 2 2 1 x x 1 a a 1 y y k k 1 - k k 1 - k k 1 x = + + £ a - = + + £ + + = y . k 1 + k 1 + k 1 2 6 3 2 6 3 2 6 3 +
+ Từ x £ a £ y ,nΕ ,n ³
1 và áp dụng định lý kẹp ta suy ra được lim a = . 1 n n n n 1 Bài 21. Tìm giới hạn: lim(2014 + ) . n n! Hướng dẫn giải n æ n ö
Trước hết ta chứng minh bất đẳng thức: n! > (*) * n " Î N ). ç ÷ è 3 ø 1
Bằng phương pháp qui nạp. Thật vậy: với n = 1, ta có 1 > (đúng). 3 k æ k ö
Giả sử (*) đúng với n = k tức là: k ! >
. Ta đi chứng minh (*) đúng với. ç ÷ è 3 ø n = k +1. k æ k ö k +1 k +1 Ta có (k + ) 1 != k ( ! k + ) 1 > (k + )1 = ( 1 )k+ 3 . > ( 1 )k+ . ç ÷ è 3 ø 3 1 (1+ )k 3 k
Bất đẳng thức cuối này đúng vì:. æ 1 k ö k k(k -1) 1
k(k -1)(k - 2)....(k - k +1) 1 1+ = 1+ + . + ...+ . ç ÷ 2 2 è k ø k 2! k k ! k 1 1 1 1 2 k -1
=1+1+ (1- ) +...+ (1- )(1- )...(1- ) 2! k k! k k k 1 1 1 1 1 1 <1+1+ + ...+ < 1+1+ + ...+ < 1+1+ + ...+ + .. n 1 - n 1 2! n! 2 2 2 2 - 1 . <1+ = 3 1 1- 2 n æ n ö n
Vậy (*) đúng với n = k +1. Do đó n! >
, từ đây ta suy ra n n!> . ç ÷ è 3 ø 3 1 3 3 => 0 < < . Vì lim = 0. n n! n n®¥ n 1
Do đó theo định lý về giới hạn kẹp giữa ta suy ra: lim = 0. n®¥ n n! 1 Vậy lim(2014 + ) n =2014. n! Trang 50 3.4. CÁC DẠNG KHÁC ìx = 2016 1 ï Bài 1.
Tìm các giá trị thực của tham số m để dãy số (xn ) : í m
có giới hạn hữu hạn. * x = n " Î N ï n 1+ 2 1+ x î n Hướng dẫn giải
*) m > 0 Þ 0 < x < m n " >1. n m 2 - mx
Xét hàm số: f (x) = ta có f '(x) =
Þ f (x) nghịch biến trên (0;m). 2 x +1 2 2 (x +1) Suy ra (x ),(x
)đơn điệu và bị chặn. 2n 2n 1 + 2017
ìx > x > x > ... > + 1 3 5 0 < m <
Þ x > x , x Þ í . 1 2 3 2016
x < x < x < ... < î 2 4 6 4m m * f ( f (1)) = £1, x =
<1Þ x <1 n " Î N . 2 2 2 m + 4 2017 n 2
ìïa(1+b ) = m
Giả sử lim x = a,lim x
= b Þ a <1,í (I ). 2n 2n 1 + 2 b ïî (1+ a ) = m éìa = b êí (II ) 3
êîa + a = m ê Û ì 1 (I ) . ê b = ï êï a í (III ) ê 1 ï ê a + = m ëïî a
Khi o < m £ 2 hệ (I) có nghiệm duy nhất Þ (xn ) có giới hạn hữu hạn. 2017 Khi 2 < m <
hệ (II) có nghiệm duy nhất lớn hơn 1 và hệ (III) có nghiệm thỏa mãn a ¹ b . Do đó 2016
Þ lim x ¹ lim x
Þ (x ) không có giới hạn. 2n 2n 1 + n 2017
ìx £ x £ x £ ... 1 3 5 +
£ m < 2017 2016 Þ x > x , x £ x Þ í . 1 2 1 3 2016
x ³ x ³ x ³ ... î 2 4 6
Þ lim x < lim x
Þ (x ) không có giới hạn. 2n 2n 1 + n + *
m = 2017 2016 Þ x = 2016 n
" Î N Þ limx = 2016 . n n
ìx > x < x < ... + 1 3 5
m > 2017 2016 Þ x < x , x > x Þ í . 1 2 1 3
x < x < x < ... î 2 4 6
Þ lim x > lim x
Þ (x ) không có giới hạn. 2n 2n 1 + n
*) m < 0 tượng tự ta có 0 < m £ 2 và m = 2017 - 2016 . Trang 51 3 x - 6x - 6 Bài 2.
Cho số thực a, xét dãy số (x x = a, n n x = , n = 1, 2,.... n ) được xác định bởi . n 1 ³ 1 n 1 + 2 3x + 9x + 7 n n
Tìm tất cả các giá trị của a để dãy số có giới hạn hữu hạn, tìm giới hạn đó?. Hướng dẫn giải Với a = 1 - thì x = 1, - n " ³ nê 1 n lim x = 1 - . n n n®+¥ (x +1 x + 2 n 1 - )3 ( n 1- )3 Với a ¹ 1 - thì x +1 = , x + 2 = , n " ³ 2. n 2 n 2 3x + 9x + 7 3x + 9x + 7 n 1 - n 1 - n 1 - n 1 - n 1 3 3 -
x + 2 æ x + 2 ö æ a + 2 ö Do đó n n 1 - = ç ÷ = ... , n " ³ . 1 ç ÷ x +1 x +1 è ø è a +1 ø n n 1 - n- n- 2(a + ) 1 3 1 - (a + 2) 1 3
Từ đó, tính được x = " ³ - - n n n n , 1,. (a + 2) 1 3 - (a + ) 1 3 1 3
Kết luận + a < - Þ a +1 > a + 2 Þ lim x = 2 - . 2 n n®+¥ 3
+ a > - Þ a +1 < a + 2 Þ lim x = - . 1 2 n n®+¥ 3 3 3
+ a = - Þ x = - , n " ³1Þ lim x = - .. 2 n 2 n n®+¥ 2 ì 1+ an 1 a + b + = ï Bài 3.
Cho hai dãy số dương (a ) , b a = 3,b = 2 n n 1- a n ( í n³ n ) xác định bởi: và n 1 + . 0 n³0 0 0 ï 2 2 a +1 = b î n n
Với mọi n = 0,1, 2,.... Chứng minh rằng hai dãy trên hội tụ và tìm giới hạn của chúng. Hướng dẫn giải p
Ta chứng minh bằng quy nạp 1 a = tan ,b =
, n = 0,1, 2,... (*) . Thật vậy. n 3.2n n p cos 3.2n p p Với n = 0 , ta có 1 a = 3 = tan = tan ,b = 2 = , vậy ( ) * đúng. 0 0 0 3 3.2 p cos 0 3.2 p p Với n = 1, ta có 1 2 1 a = = tan = tan ,b = = , vậy ( ) * đúng. 1 1 1 3 6 3.2 3 p cos 1 3.2 p 1
Giả sử khẳng định đúng đến n = k, k ³1, tức là a = tan ,b = . n 3.2n n p cos 3.2n p 1 Ta chứng minh a = tan ,b = . Thật vậy. Từ ( ) 1 ta có. n 1 + n 1 + n 1 3.2 + p cos n 1 3.2 + Trang 52 p p p p p 2 2 sin +1 2sin cos + sin + cos n n 1 + n 1 + n 1 + n 1 1+ a + n 1 + 3.2 3.2 3.2 3.2 3.2 = = = 1- a p p p 2 2 n 1 + cos cos - sin n n 1 + n 1 3.2 3.2 3.2 + 2 æ p p ö sin + cos ç n 1 + n 1 ÷ è 3.2 3.2 + ø = æ p p öæ p p ö cos - sin cos + sin ç n 1 + n 1 + ÷ ç n 1 + n 1 ÷ è 3.2 3.2 øè 3.2 3.2 + ø p p p sin + cos tan +1 n 1 3.2 + n 1 + n 1 + p = 3.2 3.2 = Þ a = tan n 1 + n 1 p p p 3.2 + cos - sin 1- tan n 1 + n 1 + n 1 3.2 3.2 3.2 + p Khi đó từ ( 1 1 2), suy ra 2 2 2 b = a +1 = tan +1 = Þ b = . n 1 + n 1 + n 1 + n 1 3.2 p + p 2 cos cos n 1 + n 1 3.2 3.2 + p
Như vậy theo nguyên lý quy nạp thì 1 a = tan ,b = , n = 0,1, 2,... . n 3.2n n p cos 3.2n p Do đó 1 1 lim a = lim tan
= tan 0 = 0; lim b = lim = =1. n n®+¥ n®+¥ 3.2n n n®+¥ ®+¥ p n cos 0 cos 3.2n
Kết luận: lim a = 0; lim b = 1.■. n n n®+¥ n®+¥ u ì = 2014 Bài 4.
Cho dãy số (u ) xác định như sau : 1 í . Tìm điều kiện của n 2 2 u
= u + (1- 2a)u + a ; n " =1,2,... î n 1+ n n
a để dãy số (u ) có giới hạn hữu hạn khi n ® +¥ và tính giới hạn đó. n Hướng dẫn giải Ta có: 2 u
- u = (u - a) ³ 0 Þ u ³ u ; n " =1,2,3, . ... n 1 + n n n 1 + n
* Suy ra dãy số (u ) tăng knn ; từ đó dãy số (u ) có giới hạn hữu hạn khi và chỉ khi dãy bị chặn trên. n n
Giả sử lim u = L (LÎ! ), thì chuyển qua giới hạn hệ thức 2 2 u
= u + (1- 2a)u + a ta có: n n 1 + n n n®+¥ 2 2
L = L + (1- 2a)L + a Û L = a. - Nếu có chỉ số *
k Î • mà u > a thì u > ; a n
" ³ k trái với kết quả lim u = L = a. k n n n®+¥
Do đó: u £ a với mọi k = 1, 2,... hay 2 2
u - (1- 2a)u + a £ a, n " =1,2,3,.... k n n
Û a -1£ u £ a Û a -1£ 2014 £ a. 1
* Đảo lại: Nếu a -1£ 2014 £ a Þ a -1£ u £ a. 1 2 2
Þ (u - a +1)(u - a) £ 0 Þ u + (1- 2a)u + a - a £ 0 Þ u £ a . 1 1 1 1 2
và u £ u Þ a -1£ u £ a . 1 2 2 Trang 53
Bằng quy nạp ta chứng minh được a -1£ u £ , a n
" =1,2,3,... (H/s trình bày ra). n
Như vậy dãy (u ) tăng knn, bị chặn trên bới a , do đó dãy số (u ) có giới hạn hữu hạn. n n
Kết luận: Với điều kiện a -1 £ 2014 £ a thì dãy số (u ) có giới hạn hữu hạn khi n ® +¥ và lim u = a. n n n®+¥ ìx = a 1 ï Bài 5. Cho dãy số (x 3 n ) thỏa mãn í 2x
. Tìm a sao cho dãy số xác định và có n x = , n =1, 2,3,... ï n 1+ 2 3x -1 î n giới hạn hữu hạn. Hướng dẫn giải 3 2x 3 Đặt f ( x) = , x ¹ ± . Ta có x = , a x = f x 1 n 1 + ( n). Ta có. 2 3x -1 3 2 6x - 6x 6x ( 2 4 2 x - ) f '(x) 1 = = . (3x - )2 1 (3x - )2 2 2 1 Bảng biến thiên. 3
Ta xây dựng dãy số như sau a =
, a = f a , a = f a , a = f a ,... 0 0 ( 1) 1 ( 2) 2 ( 3) . 3
Nhận thấy a ,a ,...,a
,... < 0; a , a ,..., a ,... > 0 . 1 3 2k 1 + 0 2 2k æ 3 ö æ ö - 3
Dựa vào bảng biến thiên ta thấy 1 a Îç- ;0÷,a = f a Îç0; 1 2 ( 1) ÷. ç 3 ÷ ç 3 ÷ è ø è ø
Þ a < a Þ f a < f a Þ a > a Þ f a > f a Þ a < a 2 0 ( 3) ( 1) 3 1 ( 4) ( 2) . 4 2 3
Bằng quy nạp ta chứng minh được dãy (a (a2k 1+)
2k ) đơn điệu giảm, bị chặn bởi 0 và , dãy đơn điệu 3 3 tăng và bị chặn bởi -
và 0. Từ đó tồn tại lim (a , lim a 2k ) ( 2k 1+). 3 k®+¥ k®+¥
Ta có a = f (a = f f a
Þ lima = f f lima Þ l = f f l n n 1 + ) ( ( n+2)) n ( ( n+2 )) ( ( )). 3 3 æ 2l ö 2ç 2 ÷ è 3l -1ø æ 1 2 ö Û l = Û l l - ç ÷( 2 l - ) 1 ( 4 2 20l -15l + 5 = 0 2 ) (*). 3 æ ö è 5 2l ø 3 -1 ç 2 ÷ è 3l -1ø 3 2x 3 æ 3 ö æ 3 ö (do f ( x) = , x ¹ ± liên tục trên ç - ;0÷, ç0;
÷ và l = lim a ). 2 3x -1 3 ç 3 ÷ ç ÷ n è ø 3 è ø n®+¥ 3 Xét 0 < l <
. Ta có f ( f (a - a = a - a < ( ) 1 3 * Û < a < 5 l = n )) 0 nên . Vậy . 3 n n+2 n 5 n 3 5 Trang 54 5
Tương tự ta chứng minh được dãy (a - 2k 1
+ ) đơn điệu tăng, hội tụ về . 5 ì 5 n’ u n chΩn 5 ïï +) Nếu a =
thì x = -x , x = -x nên ta có dãy 5 x = í . 5 2 1 3 2 n ï 5 - n’ n ï u lŒ î 5 Dãy này không hội tụ. ì 5 ï- n’ u n chΩn 5 ï +) Nếu a = - ta có dãy 5 x = í . 5 n ï 5 n’ n ï u lŒ î 5 Dãy này không hội tụ.
+) Nếu tồn tại n sao cho a = a thì ta có. n 3
x = a Þ f x = f a Û x = a Þ f x = f a
Þ x = a ,..., x = a = 1 n ( 1) ( n ) 2 n 1 - ( 2) ( n 1-) . 3 n-2 n 1 + 0 3
Khi đó không tồn tại x . n+2
Vậy nếu a = a thì dãy không xác định. n 5 +) Nếu 0 < a <
thì hai dãy con (x , x 2k ) ( 2k 1
+ ) cùng hội tụ về 0 nên giới hạn của dãy là 0. 5
Nếu a > 1 thì x = f a < a = x 2 ( )
và hàm số đồng biến nên dãy đơn điệu giảm, bị chặn dưới bởi 1. Khi đó 1 dãy hội tụ về 1. 3 +) Nếu
< a < 1 thì x = f a >1 x 2
( ) . Khi đó ta có thể khảo sát dãy từ . Trường hợp này dãy đơn điệu 3 2
giảm và bị chặn dưới bởi 1 nên hội tụ về1.
+) Nếu a = 1 thì x =1 n
" nên dãy hội tụ về 1. n 5 3 5 3 +) Nếu < a < ta có = lim a và a =
nên tồn tại a ,a sao cho a
< a < a (Thật 5 3 2 5 n + + n®+¥ 0 3 2k 2k 2 2k 2 2k 3
vậy, các số hạng của (a a =
2k ) không thể cùng nằm bên trái a do
, chúng cũng không thể cùng nằm 0 3 3 5
bên phải a do nếu thế thì a < a < Þ lim a ¹ ). 2n 2 3 n n®+¥ 5 3 Vậy a Î(a ;a
Þ x Î a ;a
,..., x Î a ;a , x Î a ;+¥ Þ x > 2k +2 2k ) 2 ( 2k 2k-2 ) 2k ( 2 0 ) 2k+2 ( 0 ) . Khi đó ta lại có 2k +2 3
dãy đơn điệu giảm, bị chặn dưới bởi 1 nên hội tụ về 1. 5 3
Vì f(x) là hàm lẻ nên trường hợp -
< a < 0, -1< a < - , a < 1 - , a = 1
- ta khảo sát tương tự. 5 3 Trang 55
Kết luận: Điều kiện để dãy xác định và có giới hạn hữu hạn là. 3 5 a ¹ ± ; a ¹ ±
; a ¹ a , n " =1,2,3,.... 3 5 n n Bài 6. Cho dãy số {a 0 < a ¹ 1 a = a + , n " ³1 n} xác định bởi và . Chứng minh rằng 1 n 1 + n an lim(a - n = n ) 0. n®¥ Hướng dẫn giải 1
Áp dụng bất đẳng thức AM-GM ta có a = a + > 2 (do a ¹ ). 1 2 1 a 1 1 Nhận xét: a > , n n " ³ 2. n
Ta sẽ chứng minh nhận xét này bằng phương pháp quy nap. Thật vậy.
Với n = 2 ta có a > 2 (đúng). 2
Giả sử a > k . k k Ta có 2 a = a +
> k +1 Û a + k > k +1 a k 1 + k k ( ) . k ak 2
Û a - k + a + k > k ( )1 0. k Û (a - ) 1 a - k > k ( k ) 0 (đúng). Suy ra a > k + . 1 k 1 + Như vậy a > , n n
" ³ 2 (điều phải chứng minh). n n n
Mặt khác, a - n +1 = a +
- n +1 = a - n + -1 n 1 + ( ) n ( ) . n a a n n 2 a - (n + ) 1 a + n
(a - n)(a - )1 n n n n = = (1). a a n n Áp dụng (1) ta có. ì (a - 2 a -1 2 )( 2 ) a ï - 3 = 3 a2 ï ï (a -3 a -1 3 )( 3 ) ïa - 4 = 4 í a . 3 ï ... ï ï a - n a -1 ïa - n +1 n n = n 1 + ( ) ( )( ) a î n Trang 56
a - 2 a -1 a - 3 a -1 ... a - n a -1
Suy ra (a - 3 a - 4 ... a - n +1 n n = 3 )( 4 ) ( n 1+ ( )) ( 2 )( 2 )( 3 )( 3 ) ( )( ). a a ...a 2 3 n
a - 2 a -1 a -1 ... a -1 Û a - n +1 n = n 1 + ( ) ( 2 )( 2 )( 3 ) ( ) . a a ...a 2 3 n æ 1 öæ 1 ö æ 1 ö
Û a - n +1 = a - 2 ç1- ÷ç1- ÷...ç1- n 1 + ( ) ( 2 ) . ÷ a a a è 2 ø è 3 ø è n ø n æ 1 ö
Û a - n +1 = a - 2 Õç1- n 1 + ( ) ( 2 ) (2). ÷ = a i 2 è i ø n a + -1 1 a -1 n a a n Ta lại có n 1 1 + n n - = = < (do a > n Þ <1). a a a a n a n 1 + n 1 + n 1 + n 1 + n n æ 1 ö a a a a Suy ra 1 2 n 1 - 1 Õç1- ÷ < . ... = . = a a a a a i 2 è i ø 2 3 n n a a
Từ (2) Þ a - n +1 < a - 2 . < a - 2 . a > n n 1 + ( ) ( 2 ) 1 ( 2 ) 1 (vì ). a n n n a
Þ 0 < a - n +1 < a - 2 . n 1 + ( ) ( 2 ) 1 . n a a Mà 1 lim = 0 Þ lim(a - 2 = 0 2 ) 1 . n®¥ n n ®¥ n
Do đó lim(a - n +1 = 0 lim(a - n = n ) 0 n 1 + ( )) hay . n®¥ n®¥ 1 é a ù Bài 7. Cho *
p Ε , a > 0 và a > 0. Xét dãy số (a ) được xác định bởi: a = ( p -1)a + , 1 n n 1 + ê n p 1 ú p a - ë n û
với mọi n ³ 1. Chứng minh dãy số (a ) có giới hạn hữu hạn khi n ® + .
¥ Hãy tìm giới hạn đó. n Hướng dẫn giải
* Theo bất đẳng thức Côsi ta có:. 1 æ a ö 1 - a p 1 a
= ç a + a +...+ a + ÷ ³ . p p a . p
= a , với " n ³ . (1). 1 n 1 + n n n p 1 - n p 1 p ç !""#""$ a ÷ p a - è 1 n n p- ø 1 é a ù a - a = ( p -1)a + - a n 1 + n ê n p 1 - ú n p a Do đó: ë n û . p a a a - a n n = - + = - £ 0; " n ³ 2 (2) p 1 - p 1 p . p a . p a - n n
Từ (1) và (2) ta có dãy số (a ) giảm và bị chặn dưới bởi p a ;. n
suy ra dãy số (a ) có giới hạn hữu hạn khi n ® + . ¥ . n Trang 57
Giả sử lim a = L; ( p L ³ a ). n n®+¥ 1 é a ù
Chuyển qua giới hạn hệ thức a = ( p -1)a + . n 1 + ê n p 1 ú p a - ë n û 1 é a ù
ta có phương trình L = ( p -1) p L +
Û pL = ( p -1) p L + a. ê p 1 p L - ú ë û p p
Û L = a Û L = a (thỏa mãn điều kiện). Vậy lim p a = a . n n®+¥ a 1 a Bài 8.
Cho trước số thực dương a và xét dãy số dương (x x + < +1 a a a - + n 1 + ( ) 1 n ) thỏa mãn với xn mọi *
n Î • . Chứng minh rằng dãy (xn ) hội tụ và tìm giới hạn của nó. Hướng dẫn giải a 1
Xét hàm số f (x) = x + , x > 0. x a 1 + 1 a - 1 a x -1 Ta có 1
f '(x) = a x - = ; 1 f '(x) 0 x x a a- + = Û = = . 2 2 x x 0
Ta có bảng biến thiên của hàm f(x):. x x 0 0 +∞ f'(x) 0 + +∞ +∞ f(x) f(x0) . a 1 a - - Suy ra f (x) f (x a + a + ( 1) a a a a a + ³ = + = + 0 ) 1 1 1 . 1 a a a a 1 Do đó x + < a +1 a - + £ x + n 1 + ( ) 1 . n 1 x + x n n 1 + Suy ra x < x hay (x x > 0 (xn)
n ) là dãy giảm. Kết hợp với
với mọi n ta suy ra dãy hội tụ. n 1 + n n a 1 a -
Đặt lim x = b > 0. Chuyển qua giới hạn ta được a 1 b (a 1)a + + £ + Þ b = x . n 0 b 1 Vậy 1 lim x a a- + = . n Trang 58 u ì Î(0;1) Bài 9.
Tìm tất cả các hằng số c > 0 sao cho mọi dãy số dãy số (u ) thỏa mãn n í n " ³1 n
u (1- u ) > c î n 1+ n
đều hội tụ. Với giá trị c tìm được hãy tính giới hạn của dãy (u ) n . Hướng dẫn giải
Ta xét các trường hợp sau. 1 c cu
+ Nếu c > , thì từ giả thiết, ta có n u > = ³ 4cu ; n " ³1. 4 n 1 + 1- u u (1- u ) n n n n
Từ đây bằng quy nạp, ta suy ra 1 u (4c)n- >
u . Do 4c > 1 nên u ® +¥ khi n ® +¥ 1 . Do đó, c > n 1 n 4 không thỏa mãn. 1
æ - - c + - c ö
ìa(1- b) > c + Nếu 0 < c < 1 1 4 1 1 4
, thì tồn tại a,bÎç ;
÷, a < b sao cho í . Thật vây, lấy 4 ç 2 2 ÷ è ø b î (1- a) > c
æ1- 1- 4c 1+ 1- 4c ö a Îç ;
÷, đặt b = a + x (x > 0), thì. ç 2 2 ÷ è ø
a(1- a) - c
a(1- b) > c Û a(1- a - x) > c Û x < . a
Chú ý là b(1- a) > a(1- a) > .
c Do đó, ta chỉ cần chọn x > 0 như trên và b = a + x, thì được 2 bất đẳng thức nêu trên.
Xét dãy số (u )xác định bởi. n ìa khi n = 2m u = í . n b î khi n = 2m +1 1
thì dãy (u ) thỏa mãn giả thiết nhưng không hội tụ. Thành thử, 0 < c < cũng không thỏa mãn. n 4 1 1 u + Nếu c = , thì n u > =
³ u . Suy ra dãy (u )tăng và bị chặn. Do đó, (u )hội tụ. 4 n 1 + 4(1- u ) 4u (1- u ) n n n n n n Đặt x = 1 m
li u ,thì từ giả thiết ta có x(1- 1 x) ³ hay x = 1 . Vậy limu = .. n 4 2 n 2
Bài 10. Cho dãy số (u u = 2 2 u = u - u +1 * n Î •
n ) xác định như sau: , ,
. Tìm giới hạn của dãy 1 n 1 + n n ( 1 1 1 s * s = + +...+ , n Î • n ) với . n u u u 1 2 n Hướng dẫn giải
Bằng phép quy nạp đơn giản ta thấy rằng: u ³ 2. n
Xét tính đơn điệu của dãy (u 2 u = u - u +1 n ) . Từ hệ thức ta suy ra được n 1 + n n n
" Ε ,u -u = u -1 > 0 (un) n 1 + n ( n )2 * , vậy dãy số tăng. Trang 59
Tính tổng: Từ hệ thức truy hồi (1) ta suy ra được u -1 = u u -1 n 1 + n ( n ). 1 1 1 1 Þ = = - 1 1 1 Þ = - ( ) * với * n Î • . u -1 u u -1 u -1 u u u -1 u -1 n 1 + n ( n ) n n n n n 1 +
Thay n bởi 1, 2, 3,., n vào (*) và cộng vế với vế các đẳng thức ta suy ra :. 1 1 1 1 + +...+ =1- . u u u u -1 1 2 n n 1 +
Do dãy (un ) là dãy tăng nên có hai khả năng sau xảy ra:. 1) Dãy (u (un)
n ) bị chặn trên. Theo tiêu chuẩn Weierstrass, nên
tăng và bị chặn trên nên nó có giới hạn. Giả sử
lim u = a Þ a ³ 2 . Chuyển qua giới hạn hệ thức (1) khi n ® +¥ ta có: n n®+¥ 2 2
a = a - a +1 Û a - 2a +1 = 0 Û a = , vô l 1 ý. 2) Dãy không bị chặn trên, do
(un) tăng và không bị chặn trên nên u = +¥ Þ u - = +¥ Þ = n ( n ) 1 lim lim 1 lim 0. n®+¥ n®+¥ n®+¥ un æ 1 1 1 ö æ 1 ö
Vì thế từ (2) ta suy ra: lim ç + +...+ ÷ = lim ç1- ÷ = . 1 n®+¥ n u u u ®+¥ u è 1 2 n ø è n ø 1 3 u
Bài 11. Cho dãy số (un) thỏa mãn : u = 2016;u = u + . Tính lim n . 0 n 1 + n 2 u n®+¥ n n Hướng dẫn giải 3 æ 1 ö 3 1 3 3 (u ) = çu + ÷ = u + 3+ + . n 1 + n 2 n 3 6 u u u è n ø n n 3 1 Do u > 0 n " => 3 3 3 (u ) = u + 3 + + > u + 3 , n " . n n 1 + n 3 6 n u u n n suy ra 3 3 3
(u ) > u + 3n = 2016 + 3 , n n " Î • (1). n 0 Lại có. 3 æ 1 ö 3 1 3 3 (u ) = çu + ÷ = u + 3+ + n 1 + n 2 n 3 6 u u u è n ø n n . 3 1 1 1 3 3 < u + 3+ + < u + 3+ + n 3 2016 + 3n ( n 3 2016 + 3n)2 n (3n)2 1 1 => 3 3
(u ) < u + 3 + + n " Î • . n 1 + n n (3n)2 Suy ra. n 1 - n 1 1 - 1 n 1 n 1 3 3 3
(u ) < u + 3(n -1) + å + å
< u + 3n + å + . å n 1 2 1 2 k 1 = k k 1 = 9k k 1 = k k 1 = 9k Trang 60 n 1 1 1 1 1 Do å <1+ + +...+ = 2 - < 2. 2 - k 1 = k 1.2 2.3 (n 1)n n 2 n æ 1 n ö 1 và å
£ nå < 2n (Bất đẳng thức Bunhiacopxki). ç ÷ 2 è k 1= k ø k 1 = k 2 suy ra 3 3
(u ) < u + 3n + + 2n (2). n 1 9 Từ (1) và (2) suy ra. 2 3 3 3
2016 + 3n < (u ) < u + 3n + + 2n , n " Î • n 1 9 . 3 3 3 2016 (u ) u 2 2 n 1 Þ + 3 < < + 3+ + , n " Î • n n n 9n n 3 u Do đó lim n = 3. n®+¥ n Bài 12. Cho số thực a, xét dãy số (xn)xác định bởi: x = , a x
= ln 3+ cos x +sin x + 2014, n =1,2... 1 n 1 + ( n n )
Chứng minh rằng dãy số trên có giới hạn
hữu hạn khi n ® + . ¥ . Hướng dẫn giải
Đặt f (x) = ln(3+sin x + cos x) + 2014, x " Î! . ( - Þ x) cos x sin x f ' = .
3 + sin x + cos x æ p ö æ p ö
Þ 3 f '(x) = 2 cos x +
- 2 f '(x)sin x + ç ÷ ç ÷ è 4 ø è 4 ø .
Þ ( f (x))2 £ + ( f (x))2 Þ f (x) 2 9 ' 2 2 ' ' £ = q, x " Î ! 7
Áp dụng định lí Lagrange cho hàm số f (x)liên tục và có đạo hàm trên ! , thì với mọi số thực x,y tồn tại z Î ! sao cho:.
f (x) - f ( y) £ f '(z) x - y £ q x - y Þ f (x) - f ( y) £ q x - y , x " , y Î! . Với m > n( * ,
m nΕ ), ta có: x - x = f (x - f x £ q x - x £ ... m-n £ q - x - x m n m 1 - ) ( n 1-) 1 . m 1 - n 1 - m-n 1 + 1 Mặt khác: *
2014 < x < 2014 + ln5, n " Ε Þ x n ( n)bị chặn. Do đó: * m-n 1 e " > 0, N $ Ε : q - x - x < e, m " > n ³ N.. m-n 1 + 1
Vậy (xn ) là dãy Cauchy, nên dãy số đã cho hội tụ. u + v
Bài 13. Cho hai dãy số {u {v u =1,v = 2, n 1 - n 1 u - = ,v = u v n} n} và xác định như sau: và khi 1 1 n n n n 1 2 -
n ³ 2 . Chứng minh rằng hai dãy {u {vn} n} và
có giới hạn và tìm giới hạn đó. Trang 61 Hướng dẫn giải p 1 p a + b Ta có cos
= suy ra u = cos v mà n 1 - n 1 a - =
,b = a b khi n ³ 2 . 3 2 1 1 3 n n n n 1 2 - p p u + v Suy ra 1 1 2 3 3 u = = 2cos ,v = u v = 2cos . 2 2 2 1 2 2 2 p p p u + v p 2 2 3 2 3 3 u = = 2cos cos ,v = u v = 2cos cos . 3 3 3 2 2 2 4 2 3
bằng phương pháp quy nạp ta chứng minh được. p p p p u + v n 1 - n 1 - 3 3 3 2 3 u = = 2cos cos cos ....cos . n 2 3 n 1 2 2 2 2 2 - p p p p 3 3 3 3 v = u v = 2cos cos cos ....cos . n n n 1 - 2 3 n 1 2 2 2 2 - sin 2a Mặt khác cosa = nên ta có. 2sina p p p 3 p 2 3 sin sin sin n-2 1 3 2 2 p 3 u = 2 . .... = sin cot . n n-2 n 1 p p p 2 3 2 - 3 3 2 2 3 2sin 2sin 2 sin 2 n 1 2 2 2 - p p p 3 3 p sin sin sin sin n-2 1 3 2 2 3 v = 2 . ....... = . n n-2 p p p 2 p 3 3 3 3 2sin 2sin 2sin sin 2 n 1 - n 1 2 2 2 2 - Do đó. æ p ö æ p ö ç 3 ÷ ç ÷ ç cot n 1 1 p ÷ 3 p 2 - lim u = lim ç sin cot ÷ = 2sin lim ç ÷ n n-2 n 1 - n 1 n n 2 3 2 3 n ç ÷ ç 2 - ®¥ ®¥ ®¥ ÷ è ø ç ÷ ç ÷ è ø. p p 3 p 2sin 2sin n 1 - 3 3 3 2 3 = lim p = = n®¥ p p p 3 3 3 tan n 1 2 - Trang 62 n Bài 14. Với mỗi *
n Î • , đặt Q x = Õ x -i n ( ) ( 2). i=0
a) Chứng minh đa thức Q ¢ x x (0 ) ;1 n (
) có duy nhất 1 nghiệm thực thuộc . n
b) Chứng minh tồn tại giới hạn của dãy {xn}. Hướng dẫn giải a) Ta có Q = Q = Q = = Q n = n ( ) n ( ) n ( 2 ) n ( 2 0 1 2 ... ) 0. nên trong mỗi khoảng (0 ) ;1 , ( ) ( n- )2 2 1;4 ,...,
1 ;n ) có 1 nghiệm của phương trình Q ¢ x = n ( ) 0.
Mặt khác, ta có det Q ¢ x = n Q ¢ x x (0 ) ;1 . n ( ) n ( ) nên đa thức
có duy nhất 1 nghiệm thuộc khoảng . n æ 1 1 1 ö
b) Ta có Q ¢ x = Q x + + + n ( ) n ( ) ... . ç 2 2 ÷ è x x -1 x - n ø Do Q ¢ x Q x Q ¢ x = n ( ) 0 n ( ) n (
) có nghiệm không là nghiệm của
nên nghiệm của phương trình là nghiệm của phương trình:. f x = + + + = n ( ) 1 1 1 ... 0. 2 2 x x -1 x - n 1 1 1
Ta có: f ¢ x = - - + + < n ( ) ... 0. 2 x (x - )2 1 ( 2 x - n )2 Nên f x (0 ) ;1
n ( ) nghịch biến trên . 1 1 1 Lại có: f x = + + + = n ( n ) ... 0. 2 2 x x -1 x - n n n n Þ 1 1 1 1 1 = + + ...+ + < 0. x - (n + )2 2 2 1 x x -1 x - n - + n n n x n n n ( )2 1 Þ f
x < 0 = f x = f x Þ x > x n 1 + ( n ) n ( n ) n 1 + ( n 1 + ) . n n 1 +
Do đó dãy {xn} là dãy giảm. Lại có x Î {xn} n (0; )1. Vậy dãy có giới hạn.
Bài 15. Cho x = , a x = b , a bÎ! . n x
- (n -1).x - x = 0 n =1,2,... lim x 1 2 ( ) và , Tìm . n+2 n 1 + n n n®¥ Hướng dẫn giải x - x Ta có n 1 + n x - x = - . n+2 n 1 + n ( 1 - )n ( 1 - )n Þ x - x = (x - x ) = - . b - a n+2 n 1 + 2 1 ( ). n! n! n ( 1 - )k n ( 1 - )k Þ x = x - å
. b - a = x + a - b - å . b - a n+2 1 ( ) 1 ( ) ( ). k 1 = k! k =0 k! 1 1
Þ lim x = x + a - b - = 2a - b - . n 1 e e Trang 63
Bài 16. Cho dãy (u 2 * u = 2;u
= u - u +1, n " Î • M
n ) axác định bởi: . Tìm nhỏ nhất thỏa mãn 1 n 1 + n n 1 1 1 * + +...+ < M , n " Î • . u u u 1 2 n Hướng dẫn giải Ta có u = 2 >1 và 2 u
= (u -1) + u . Chứng minh bằng quy nạp ta được u > 2, n " Ε ,n ³ 2 (*). 1 n 1 + n n n Ta lại có: 2
u = u - u +1Þ u -1 = u (u -1) . i 1 + i i i 1 + i i 1 1 1 1 1 1 Þ = - Þ = - .
u -1 u -1 u u u -1 u -1 i 1 + i i i i i 1 + n (*) 1 1 1 1 Do đó: * å = - =1- <1, n " Ε . - - - i 1 = u u 1 u 1 u 1 i 1 n 1 + n 1 + Suy ra M £ 1.
Mặt khác, chứng minh bằng quy nạp ta được dãy (u ) tăng. Do đó nếu dãy có giới hạn hữu hạn L thì n
L > 2 . Vì phương trình 2
L = L - L +
1 có duy nhất nghiệm là L = 1, bởi vậy dãy (u ) không có giới hạn n n æ 1 ö
hữu hạn. Suy ra lim u = +¥ Þ limçå ÷ = 1(**). n è i 1= ui ø n æ 1 ö 0 n 1
Với mọi a < 1 thì từ limçå ÷ =
1 suy ra tồn tại n sao cho å > a. Do đó M ³1Þ M =1. 0 è i 1= u = u i ø i 1 i
Bài 17. Cho 4028 số thực: a ,a ,..., a
, b ,b ,...,b
. Xét dãy số (xn ) xác định như sau:. 1 2 2014 1 2 2014 2014
x = å[a .n + b ],(n =1,2,3,... n i i ). i 1 = 2014
Biết dãy số lập thành một cấp số cộng, chứng minh rằng å a là số nguyên (với [a] là phần nguyên của i i 1 =
số thực a – số nguyên lớn nhất không vượt quá a ). Hướng dẫn giải 2014 Đặt A = å 2014
a , B = å b . Gọi d là công sai của cấp số cộng (x .
n d = x - x n ) , thì: . i i n 1 + 1 i 1 = i 1 = Với mọi *
n Î • ta luôn có: a .n + b -1< a n + b £ a n + b i = i i [ .i i ] . , 1,2,...,2014. i i
Cộng vế với vế của 2014 bất đẳng thức cùng chiều, ta được:. .
A n + B - 2014 < x £ . A n + B. n
Thay n bởi n +1 và thay n bởi 1, có:. A(n + )
1 + B - 2014 < x £ A n +1 + B n 1 + ( ) .
A + B - 2014 < x £ A + B Þ -A- B £ -x < -A- B + 2014. 1 1
Cộng vế với vế của 2 bất đẳng thức cùng chiều nói trên thu được:. Trang 64 .
A n - 2014 < x - x < . A n + 2014. n 1 + 1 Û . A n - 2014 < . n d < . A n + 2014 . Û d.n - . A n < 2014. 2014 Û d - A < . n 2014 Vì lim
= 0 nên suy ra d = A. Mặt khác dãy (x d
n ) gồm toàn số nguyên nên công sai cũng là số n
nguyên. Vậy A nguyên. (đpcm). ì 1 x = ï 1 ï
Bài 18. Cho dãy số (x 2 n ) thỏa mãn: í
. Chứng minh dãy số trên có giới hạn. 2 x ï n x = x + ; n " ³1 n 1 + n 2 ïî n Hướng dẫn giải n(n + ) 1 *) Ta chứng minh 2 x + n ³ với mọi n ³ 1 (1). n 2
Thật vậy: n = 1 đúng. k (k + ) 1
Giả sử (1) đúng với n = k ³ 1 : 2 x + k ³ . k 2 2 x Þ x + k +1 k = x + + k +1 k 1 + ( )2 k 2 ( )2. k x
= k x + k + k +1 2 ( k ) ( )2 2 . k æ k +1 ö k (k + ) 1 ³ -1 + (k + ç ÷ )2 1 . è k 2 ø 2 (k + )2 3 1 k (k + ) 1 ³ - . 2 2 k +1æ 3(k + ) 1 ö (k + ) 1 (k + 2) ³ ç - k ÷ ³ (đpcm). 2 è 2 ø 2
*) Ta chứng minh (xn ) có giới hạn. NX: (x x > 0 n n ) tăng và với mọi . n 1 1 1 2 Ta có - = £ . 2 x x x + n n n +1 n n 1 + n ( ) 1 1 æ 1 ö Þ - £ 2 1- < 2 . ç ÷ x x è n ø 1 n Trang 65 1 Þ x < với mọi n ³ 1. n 2 - 2
Vậy (xn ) có giới hạn.
Bài 19. Cho dãy số (a a > 0 n " =1,2,3,.... a > 0 (xn) n ) tăng, và . Xét dãy số xác định bởi n n a - a i 1 + i x =
. Chứng minh rằng tồn tại x . å lim n n n®+¥ i 1 = a aa i 1 + i Hướng dẫn giải
Dễ dàng thấy rằng dãy (xn ) tăng ngặt.
Trường hợp 1. Nếu a > 1. a - a 1 1 1 1 1 i 1 + i = - < - Þ x < . a a a 1 a a a a a - aa aa n aa i 1 + i i i 1 + i i i 1 + 1 vậy dãy (x lim x
n ) bị chặn trên do đó tồn tại n n®+¥ .
Trường hợp 2. Nếu 0 < a < 1. a - a 1 æ 1 1 ö i 1 + i < ç - ( ) * a 1 Û a
a - a < aa - aa a - i 1 + ( i 1 + i ) a a a ÷ ( ) * thật vậy . a a a a a i 1 + i i 1 + i è i i 1 + ø aa - aa a 1 i 1 i Û > aa - + ** i 1 + ( ). a - a i 1 + i Ta chứng minh (**).
Xét hàm số f (x) xa
= Trên đoạn [a ;a i i 1 + ].
Hàm số thoả mãn điều kiện của định lí Lagrăng nên tồn tại số c Î(a ;a i i 1 + ) thoả mãn a a a a a a - - - f ¢(c) a a + a - a a + a - a a i 1 i 1 i 1 i 1 i 1 + i = Û ac = Þ aa < (đpcm). i 1 a - a a - a + a - a i 1 + i i 1 + i i 1 + i 1
Từ đó ta có Þ x < Þdãy (x lim x
n ) bị chặn trên do đó tồn tại n aa a n n®+¥ . 1 a a ...a n 1
Bài 20. Cho dãy số xác định bởi 1 2 a =1;a >1; n a = +1 n
" =1,2,3,.... Đặt S = . å 0 1 n 1 + a n = a a énù k 1 k 1 + ék ù ê2ú ë û ê 2ú ë û
Chứng minh tồn tại lim S ( trong đó [x] là phần nguyên của x ). n n®+¥ Hướng dẫn giải 1 1 a -1 1 1 Ta có k 1 + = = = - . a a a a ...a 1 2 k a a ...a a a ...a a a ...a k 1 + ék ù 1 2 k 1 + 1 2 k 1 2 k 1 a + ê ú k 1 + ë 2û a -1 k 1 + Trang 66 n æ 1 1 ö 1 1 Suy ra S = åç - ÷ = - . n k 1 = a a ...a a a ...a a a a ..a è 1 2 k 1 2 k 1 + ø 1 1 2 n 1 +
Chứng minh lim (a a ...a = +¥ 1 2 n 1 + ) . n®+¥ Ta có : a >1 n " ³ 2. n
én ù ¹ n Þ a > a +1 suy ra dãy đã cho là tăng. ê ú 1 ë 2 n+ n û
Như vậy a > a +1 > ... > a + n - . 1 n n 1 - 1 1
Vậy lim (a a ...a = +¥ lim S = 1 2 n 1 + ) , suy ra . n n®+¥ n®+¥ a1 u ì = 3, v = 2 1 1 ï
Bài 21. Cho dãy số (u ); v 2 2 u í = u + 2v n " Î N n 1 + n n ( ) n
( n) được xác định như sau ïv = 2u v î n 1+ n n . Tìm các giới hạn sau: 2 lim n v và 2
lim n u .u ...u n x®¥ 1 2 n x®¥ . Hướng dẫn giải Ta có: n
" Î N : u + 2.v = u + 2v + 2 2.u v = u + 2.v n 1 + n 1 + n n n n ( n n )2 2 2 (1).
Áp dụng (1) ta suy ra: u + 2.v = (u + 2.v n n n 1 - n 1 - )2. n 1 - n 1 2 2 - 2n
Theo quy nạp ta có: u + 2.v = u + v = + = + n n ( 2. 3 2 2 2 1 1 1 ) ( ) ( ) (2). n
Lập luận tương tự ta cũng có: u - v = - n n ( )2 2. 2 1 (3). ì 1 é ù u = + + - ï n ê( n n 2 )2 1 ( 2 )2 1 2 ú ï ë û Từ (2) và (3) ta suy ra: í . 1 ï é ù v = + - - n ï ê( n n 2 )2 1 ( 2 )2 1 î 2 2 ú ë û 2n 2n 2 1 n é ù Lại có: u = + + - < + 2n u < 2 +1 n ê( 2
)1 ( 2 )1 ú ( 2 )1 , từ đó suy ra: . 2 ë û n n n + n 2 1 n 2 ( )2 n n + é ù
Tương tự ta có : v = + - - > 2 Þ v > n (ê ) ( ) ( )2 2 2 2 1 1 2 1 2 1 . 2 2 ú ë û 8 n 8
Mặt khác ta có: v < u . Do đó ta có dãy bất đẳng thức sau:. n n n ( n + n æ ö 2 + ) ( 2 )2 1 1 1 2 2 2n 2 1 n =
< v < u < 2 +1. ç ÷ è 8 ø 8 n n Trang 67
Như vậy theo định lí kẹp ta suy ra 2n 2
lim u = lim n v = 2 + . 1 n n n®¥ n®¥ v
Hơn nữa theo đề bài ta có: n 1 v = 2u v Þ u + = . n 1 + n n n 2vn v v v v v Suy ra: 2 3 n 1 + n 1 + n 1
u .u ...u = . ... + = = . 1 2 n n n 1 2v 2v 2v 2 v 2 + 1 2 n 1 v n n n n+ n 1 Vậy 1 2 2 2 2
lim u .u ...u = lim = lim v .lim . 1 2 n n 1 + n 1 + n 1 n n 2 n n 2 + ®¥ ®¥ ®¥ ®¥ n 1 n n n n n 1 2 2 2 2 2 2 = lim 2u v .lim
= lim 2.lim u .lim v .lim . n n n 1 + n n n 1 n n 2 n n n n 2 + ®¥ ®¥ ®¥ ®¥ ®¥ ®¥ =1.( 2 + ) 1 .( 2 + ) 1 .1 = 3 + 2 2 . Tóm lại ta có: 2 lim n v = 2 +1 và 2
lim n u .u ...u = 3 + 2 2 . n n®¥ 1 2 n n®¥ n
Bài 22. Cho dãy số (a 0 < a ¹ 1 a = a + , n " ³1 n ) xác định bởi và . Chứng minh rằng 1 n 1 + n an lim(a - n = n ) 0. n®¥ Hướng dẫn giải 1
Áp dụng bất đẳng thức AM-GM ta có a = a + > 2 (do a ¹ ). 1 2 1 a 1 1 Nhận xét: a > , n n " ³ 2. n
Ta sẽ chứng minh nhận xét này bằng phương pháp quy nap. Thật vậy.
Với n = 2 ta có a > 2 (đúng). 2
Giả sử a > k . k k Ta có 2 a = a +
> k +1 Û a + k > k +1 a k 1 + k k ( ) . k ak 2
Û a - k + a + k > k ( )1 0. k Û (a - ) 1 a - k > k ( k ) 0 (đúng). Suy ra a > k + . 1 k 1 + Như vậy a > , n n
" ³ 2 (điều phải chứng minh). n n n
Mặt khác, a - n +1 = a +
- n +1 = a - n + -1 n 1 + ( ) n ( ) . n a a n n Trang 68 2 a - (n + ) 1 a + n
(a - n)(a - )1 n n n n = = (1). a a n n Áp dụng (1) ta có. ì (a - 2 a -1 2 )( 2 ) a ï - 3 = 3 a2 ï ï (a -3 a -1 3 )( 3 ) ïa - 4 = 4 í a . 3 ï ... ï ï a - n a -1 ïa - n +1 n n = n 1 + ( ) ( )( ) a î n
a - 2 a -1 a - 3 a -1 ... a - n a -1
Suy ra (a -3 a - 4 ... a - n +1 n n = 3 )( 4 ) ( n 1+ ( )) ( 2 )( 2 )( 3 )( 3 ) ( )( ). a a ...a 2 3 n
a - 2 a -1 a -1 ... a -1 Û a - n +1 n = n 1 + ( ) ( 2 )( 2 )( 3 ) ( ) . a a ...a 2 3 n æ 1 öæ 1 ö æ 1 ö
Û a - n +1 = a - 2 ç1- ÷ç1- ÷...ç1- n 1 + ( ) ( 2 ) . ÷ a a a è 2 ø è 3 ø è n ø n æ 1 ö
Û a - n +1 = a - 2 Õç1- n 1 + ( ) ( 2 ) (2). ÷ = a i 2 è i ø n a + -1 1 a -1 n a a n Ta lại có n 1 1 + n n - = = < (do a > n Þ <1). a a a a n a n 1 + n 1 + n 1 + n 1 + n n æ 1 ö a a a a Suy ra 1 2 n 1 - 1 Õç1- ÷ < . ... = . = a a a a a i 2 è i ø 2 3 n n a a
Từ (2) Þ a - n +1 < a - 2 . < a - 2 . a > n n 1 + ( ) ( 2 ) 1 ( 2 ) 1 (vì ). a n n n a
Þ 0 < a - n +1 < a - 2 . n 1 + ( ) ( 2 ) 1 . n a a Mà 1 lim = 0 Þ lim(a - 2 = 0 2 ) 1 . n®¥ n n ®¥ n
Do đó lim(a - n +1 = 0 lim(a - n = n ) 0 n 1 + ( )) hay . n®¥ n®¥ 1 a a
Bài 23. Cho trước số thực dương a và xét dãy số dương ( x x + < +1 a a a - + n 1 + ( ) 1 n ) thỏa mãn với xn mọi *
n Î • . Chứng minh rằng dãy (xn ) hội tụ và tìm giới hạn của nó. Hướng dẫn giải Trang 69 a 1
Xét hàm số f (x) = x + , x > 0. x a 1 + 1 a - 1 a x -1 Ta có 1 f ( ¢ x) = ax - = ; 1 f (x) 0 x x a a- + ¢ = Û = = . 2 2 x x 0
Ta có bảng biến thiên của hàm f (x) :. x x 0 0 +∞ f'(x) 0 + +∞ +∞ f(x) f(x0) . a 1 a - - Suy ra f (x) f (x a + a + ( 1) a a a a a + ³ = + = + 0 ) 1 1 1 . 1 a a a a 1 Do đó x + < a +1 a - + £ x + n 1 + ( ) 1 . n 1 x + x n n 1 + Suy ra x < x hay (x x > 0 (xn)
n ) là dãy giảm. Kết hợp với
với mọi n ta suy ra dãy hội tụ. n 1 + n n a 1 a -
Đặt lim x = b > 0. Chuyển qua giới hạn ta được a 1 b (a 1)a + + £ + Þ b = x . n 0 b 1 Vậy 1 lim x a a- + = . n u ì ,u Î(0;1) 1 2 ï
Bài 24. Cho dãy số thực (u (u ) n ) thỏa mãn í 1 4 . Chứng minh rằng dãy có 3 3 u = u + u , n " ³1 n ï n+2 n 1 î 5 + 5 n
giới hạn hữu hạn, tìm giới hạn đó. Hướng dẫn giải
ìx = min u ,u 1 { 1 2} ï Xét dãy (x ) : í . n 1 4 3 3 ïx = x + x n 1 + î 5 n 5 n Ta thấy x Î(0;1). n 3 13 3 3 3 3 1 4
x + x + x + x + x Ta có 3 n n n n n 5 3 3 x = x + x = ³ x > x . n 1 + 5 n 5 n 5 n n Vậy dãy (x
lim x = a (0 < a £1)
n ) tăng, bị chặn trên nên hội tụ, . n 1 4
Chuyển qua giới hạn ta được: 3 3 a = a + a Þ a = . 1 3 5
Ta sẽ chứng minh x £ u ; u <
1 (*) bằng quy nạp theo n. n 2n 1 - 2n Trang 70
Ta có x £ u ;u <1. Giả sử x £ u ;u < . 1 1 1 2 n 2n 1 - 2n 1 4 1 4 Suy ra 3 3 3 3 x = x + x £ u + u = u <1. n 1 + n n 2n 2n 1 - 2n 1 5 5 5 5 + 1 4 1 4 1 4 3 3 3 3 3 3 x = x + x £ x + x £ u + u = u <1. n 1 + n n n 1 + n 2n 1 + 2n 2n+2 5 5 5 5 5 5
Vậy (*) đúng với mọi n nguyên dương. Từ đó suy ra limu =1. n ìx = 2007 1 ï
Bài 25. Cho dãy số thực (x í x ( ) n ) xác định bởi: n . Chứng minh dãy số có x = 3 + n " ³1 n x n 1 + ï 2 x -1 î n
giới hạn và tìm giới hạn đó. Hướng dẫn giải
Dễ dàng quy nạp x > 3 . n x 1 Ta có: x = 3 n + = 3 + 1+ < 3 + 2 n " ³1. n 1 + 2 x -1 2 x -1 n n
Vậy x £ 2007 với mọi n nên dãy bị chặn. n x 1 1 Xét f (x) = 3 + Þ f ¢(x) = - Þ f ¢(x) < khi x > 3. 2 x -1 (x - )3 2 2 2 1 Ta có:. 2 f ( x) x x 2 = x Û x = 3 + Û (x - 3) = 2 2 x -1 x -1. 2 2 2
Û (x - 3x) - 2(x - 3x) - 3 = 0 2 éx - 3x = 1 - (L) Û ê 2 êëx - 3x = 3 . 3 + 15 x = = a 2
Áp dụng định lý Lagrang có:. 1 æ 1 n ö
x - a = f (x ) - f (a) = f '(q ) x - a <
x - a < ... < x - a ¾¾¾ ®0 Do đó n 1 + n n n n ç ÷ 1 2 2 è 2 2 n®¥ ø 3 + 15 lim x = a = . n 2 u ì = e 2 u
Bài 26. Cho dãy số (u 1 n 1 lim +
n ) xác định bởi: í . Tìm . 2 * u = u - 2, n " Î î • 2 2 2
n®+¥ u .u ...u n 1 + n 1 2 n Hướng dẫn giải Trang 71 1
Vì u = e > 2 nên đặt u = a + , a > 1. 1 1 a 2 æ 1 ö 1 Ta có 2 2
u = u - 2 = a + - 2 = a + . 2 1 ç ÷ 2 è a ø a n 1
Bằng quy nạp, ta có thể chứng minh được 2 u = a + " Î • n+ n , n . 1 2 a Xét. 1 - 1 n n n - i 1 - æ 1 ö æ 1 ö éæ 1 i 1 - ö æ 1 öù æ 1 n ö æ 1 ö 2 2 2 Õu = Õ a + = - - Õ + = - + ç - a a a ÷ ç ÷ êç ÷ ç - a a i i 1 i 1 ÷ú ç ÷ ç ÷ 2 2 2n = = è a ø è a ø ëè a ø = è a øû è a i 1 i 1 i 1 ø è a ø 2 æ 1 ö æ 2n 1 ö . a - a + 2 ç ÷ ç n ÷ 2 2 u 2 2 æ ö æ 1 + è a ø è a ø u 1 ö n 1 n 1 Þ = Þ lim + = a - 2 = a + - 4 = e - 4 2 2 2 2 2 2 2 ç ÷ ç ÷ u .u ... n u ®+¥ æ ö u u u è a ø è a n ø n 1 . ... 1 2 2 1 2 n a - ç ÷ 2n è a ø
Bài 1. Cho dãy số (xn ) xác định bởi. ìx = a 1 ï 2 í x + 7 . n x = , n =1, 2,3,... n 1 + ï 2 î (x +3 n )
Chứng minh rằng dãy số có giới hạn hữu hạn. Tính giới hạn đó. Hướng dẫn giải Theo Côsy thì. 1 æ 16 ö (x - x + n )1( 7 n ) x = ç x + 3+
- 6÷ ³1; x - x = - £ 0. n 2 n x + 3 n 1 + n è 2( x + 3 n ) n ø
dãy giảm, bị chặn bởi 1, vậy dãy có giới hạn.
Từ lim x = aÞ a = . 1 n ìx =1 1 ï
Bài 27. Cho dãy số {x í 2014 {xn}
n} , xác định bởi:
. Chứng minh rằng dãy số có x =1+ , n = 1, 2,3... n 1 + ï 1+ x î n
giới hạn hữu hạn và tìm giới hạn đó. Hướng dẫn giải 2014
Xét hàm số f (x) = 1+
trên [0;+¥). Ta thấy f (x) liên tục và nghịch biến trên [0;+¥) (Vì 1+ x 2014 - f '(x) =
< 0). Do đó 1< f (x) £ 2015. (1+ x)2 2014 Ta có x =1+
= f (x ) với mọi n Þ dãy (xn ) bị chặn. n 1 + 1 n + xn Trang 72
Mặt khác, ta có x < x Þ f (x ) > f (x ) Þ x > x Þ f (x ) < f (x ) Þ x < x Þ ... .Suy ra dãy (x2n 1+) 1 3 1 3 2 4 2 4 3 5 (x (x2n 1+) 2n )
là dãy đơn điệu tăng và bị chặn, còn dãy
là dãy đơn điệu giảm và bị chặn, nên các dãy ,
(x2n ) có giới hạn hữu hạn. Giả sử lim x
= a và lim x = b, ( a,b ³1). 2n 1 + 2n Từ x
= f (x ) Þ lim x
= lim f (x ) Û b = f (a). 2n 1 + 2n 2n 1 + 2n x = f (x ) Þ lim x = lim f (x
) Û a = f (b). 2n+2 2n 1 + 2n+2 2n 1 + ì 2014 b = 1+ ïï Vậy ta có hệ 1+ a í
Û a = b = 2015 . 2014 ïa =1+ ïî 1+ b Vậy lim x = 2015 . n ìx = 2,1 1 ï
Bài 28. Cho dãy số (x 2
n ) được xác định bởi í với mỗi số
x - 2 + x + 8x - 4 n n n ïx = * , n = 1, 2,... n 1 + ( ) î 2 n 1
nguyên dương n, đặt y = . Tìm y . å lim n 2 - n i 1 = x 4 i Hướng dẫn giải
Ta có kết quả sau: với số thực a > 2 bất kì, ta có. 2 2
a - 2 + a + 8a - 4
a - 2 + a + 4a + 4 a - 2 + (a + 2) > = = a. 2 2 2
Do đó 2,1 < x < x < ... Suy ra dãy (x lim x = L > 2
n ) là dãy tăng, giả sử bị chặn trên tức là có giới hạn . 1 2 n
Chuyển qua giới hạn điều kiện (*) ta có phương trình. 2
x - 2 + x + 8x - 4 2 x =
Û x - 4 = (x + 3)(x - 2). 2
phương trình này không có nghiệm hữu hạn lớn hơn 2. Suy ra dãy (x lim x = +¥
n ) tăng và không bị chặn trên nên . n 2
x - 2 + x + 8x - 4 Ta có n n n 2 x =
Û 2x - x + 2 = x + 8x - 4. n 1 + n 1 2 + n n n
Û (2x - x + 2 = x + x - Û x - = x + x - + n )2 2 2 8 4 4 3 2 n 1 n n n+2 ( n )( n ). 1 x + 3 x + 2 +1 1 1 n n Û = = = + . 2 2 2 x - 2 x - 4 x - 4 x - 2 x - 4 n n 1 + n 1 + n 1 + n 1 + 1 1 1 Û = - . 2 x - 4 x - 2 x - 2 n 1 + n n 1 + Trang 73 n 1 1 1 1 Suy ra y = å = - =10 - . n 2 - - - - i 1 = x 4 x 2 x 2 x 2 i 1 n 1 + n 1 + Vậy lim y =10. n ìx = a ï
Bài 29. Dãy số thực (x nΕ 0 í ( n " Ε ) n ) (
) được xác định bởi:
. Tìm tất cả các giá trị 2 ïx = 2x -1 î n 1+ n
của a để x < 0 với mọi số tự nhiên n. n Hướng dẫn giải
Giả sử x < 0 với n " Î • . n 2 Từ 2 x = 2x -1< 0 có - < x < 0. n+2 n 1 + 1 2 n+ 2 - - Lại từ 2 - < 2x -1< 2 2 2 1 0 có - < x < Þ 1
- < x < - , n " Î • . 2 n 2 n 2 n 4 1 3 Suy ra x - > 1 và x + <1, n " Î • . n 2 4 n 2 1 1 1 1 1 3 1 Từ đó 2 2 x +
= 2x -1+ = 2 x - = 2 x - . x + > x + , n " Î • . n 1 + 2 n 2 n 4 n 2 n 2 2 n 2
Áp dụng liên tiếp bất đẳng thức này, ta có:. 2 1 1 2 1 æ 2 ö 1 æ 2 n ö 1 æ 2 n ö a +
= x + < x + < x + < ... < x + < , n " Î • . 0 1 ç ÷ 2 ç ÷ ç ÷ 2 2 3 2 è 3 ø 2 è 3 n ø 2 è 3 ø æ 2 n ö 1 1 Mà lim
= 0 nên phải có a + = 0 Þ a = - . ç ÷ n®+¥ è 3 ø 2 2 1 Thử lại với a = - 1
thì x = - < 0, n " . 2 n 2 1
Vậy a = - là giá trị duy nhất cần tìm. 2 ìx = 2014 ï 1
Bài 30. Cho dãy số thực (xn) xác định bởi: í . * 3 ïx
= 6x -6sin x ,n î Ε n 1 + n n Hướng dẫn giải 3 x
Sử dụng bất đẳng thức x - £ sin x £ , x x " ³ 0. 6
Xét hàm số f (x) 3
= 6x -6sin x, x > 0. Trang 74 6 1- cos x Ta có: f '(x) ( ) = > 0, x
" > 0 Þ f(x) luôn đồng biến với mọi x > 0. 3 (6x -6sin x)2 3
Do đó: f (x) > f (0) = 0x > 0. mà x = f x > 0 x = 2014 > 0. 2 ( 1) vì . 1
Vậy ta có x = f x > 0, n " Î N n 1 + ( n) * . 3
6x - 6sin x - x Mặt khác: 3 x - x = 6x - 6sin n n n x - x = . n 1 + n n n n 3 (6x -6sin + - + n n x )2 2 3 x 6x 6sin n n n x n x 3 x Vì x - £ sin x £ , x x " ³ 0 Û 3
6x - x – 6sinx < 0, x " > 0. 6
Þ 6x – 6sinx - 3
x < 0 do x > 0 Þ x – x < 0. n n n n n 1 + n
Þ (xn ) là dãy giảm và bị chặn dưới bởi 0 nên tồn tại giới hạn hữu hạn.
Giả sử limx = x(x ³ 0), ta có phương trình:. n 3 3
x = 6x - 6sin x Û x - 6x + 6sin x = 0.
Xét hàm số g (x) = 3
x -6x +6sin x. g (x) 2 '
= 3x – 6 + 6cosx. ’’
g (x) = 6x – 6sinx ³ 0 x " ³ 0. Þ ’ g (x) ³ ’
g (0) = 0. Do đó g (x) luôn đồng biến và liên tục với mọi x ³ 0 .
Þ phương trình g (x) = 0 có nghiệm duy nhất x = 0 . Vậy limx = 0. n ì 1+ an 1 a + b + = ï
Bài 31. Cho hai dãy số dương (a ) , b a = 3,b = 2 n n 1- a n ( í n³ n ) xác định bởi: và n 1 + . 0 n³0 0 0 ï 2 2 a +1 = b î n n
Với mọi n = 0,1, 2,.... Chứng minh rằng hai dãy trên hội tụ và tìm giới hạn của chúng. Hướng dẫn giải p 1
Ta chứng minh bằng quy nạp a = tan ,b =
, n = 0,1, 2,... (*) . Thật vậy. n 3.2n n p cos 3.2n p p 1
Với n = 0 , ta có a = 3 = tan = tan ,b = 2 = , vậy ( ) * đúng. 0 0 0 3 3.2 p cos 0 3.2 Trang 75 1 p p 2 1
Với n = 1, ta có a = = tan = tan ,b = = , vậy ( ) * đúng. 1 1 1 3 6 3.2 3 p cos 1 3.2 p 1
Giả sử khẳng định đúng đến n = k, k ³1, tức là a = tan ,b = . n 3.2n n p cos 3.2n p 1 Ta chứng minh a = tan ,b = . Thật vậy. Từ ( ) 1 ta có. n 1 + n 1 + n 1 3.2 + p cos n 1 3.2 + p p p p p 2 2 sin +1 2sin cos + sin + cos n n 1 + n 1 + n 1 + n 1 1+ a + n 1 + 3.2 3.2 3.2 3.2 3.2 = = = 1- a p p p 2 2 n 1 + cos cos - sin n n 1 + n 1 3.2 3.2 3.2 + 2 æ p p ö sin + cos p p p ç ÷ + + n 1 + n 1 + sin cos tan 1 n 1 è 3.2 3.2 ø 3.2 + 3 n 1 + n 1 + = .2 3.2 = Khi đó từ (2), æ p p öæ p p ö p p p cos - sin cos + sin ç cos - sin 1- tan n 1 + n 1 + ÷ ç n 1 + n 1 ÷ è 3.2 3.2 øè 3.2 3.2 + ø n 1 + n 1 + n 1 3.2 3.2 3.2 + p Þ a = tan n 1 + n 1 3.2 + p 1 1 suy ra 2 2 2 b = a +1 = tan +1 = Þ b = . n 1 + n 1 + n 1 + n 1 3.2 p + p 2 cos cos n 1 + n 1 3.2 3.2 + p 1
Như vậy theo nguyên lý quy nạp thì a = tan ,b = , n = 0,1, 2,... . n 3.2n n p cos 3.2n p 1 1 Do đó lim a = lim tan
= tan 0 = 0; lim b = lim = =1. n n®+¥ n®+¥ 3.2n n n®+¥ ®+¥ p n cos 0 cos 3.2n
Kết luận: lim a = 0; lim b = 1.■. n n n®+¥ n®+¥ u ì = 2014
Bài 32. Cho dãy số (u ) xác định như sau:. 1 í . Tìm điều kiện của n 2 2 u
= u + (1- 2a)u + a ; n " =1,2,... î n 1+ n n
a để dãy số (u ) có giới hạn hữu hạn khi n ® +¥ và tính giới hạn đó. n Hướng dẫn giải Ta có: 2 u
- u = (u - a) ³ 0 Þ u ³ u ; n " =1,2,3, . ... n 1 + n n n 1 + n
* Suy ra dãy số (u ) tăng knn; từ đó dãy số (u ) có giới hạn hữu hạn khi và chỉ khi dãy bị chặn trên. n n
Giả sử lim u = L (LÎ! ), thì chuyển qua giới hạn hệ thức 2 2 u
= u + (1- 2a)u + a ta có: n n 1 + n n n®+¥ 2 2
L = L + (1- 2a)L + a Û L = a. - Nếu có chỉ số *
k Î • mà u > a thì u > ; a n
" ³ k trái với kết quả lim u = L = a. k n n n®+¥ Trang 76
Do đó: u £ a với mọi k = 1, 2,... hay 2 2
u - (1- 2a)u + a £ a, n " =1,2,3,.... k n n
Û a -1£ u £ a Û a -1£ 2014 £ a. 1
* Đảo lại: Nếu a -1£ 2014 £ a Þ a -1£ u £ a. 1 2 2
Þ (u - a +1)(u - a) £ 0 Þ u + (1- 2a)u + a - a £ 0 Þ u £ a . 1 1 1 1 2
và u £ u Þ a -1£ u £ a . 1 2 2
Bằng quy nạp ta chứng minh được a -1£ u £ , a n " =1,2,3,.... n
Như vậy dãy (u ) tăng knn, bị chặn trên bới a , do đó dãy số (u ) có giới hạn hữu hạn. n n
Kết luận: Với điều kiện a -1 £ 2014 £ a thì dãy số (u ) có giới hạn hữu hạn khi n ® +¥ và lim u = a. n n n®+¥ u ì =1 1 ï
Bài 33. Cho dãy số (u ) xác định bởi công thức truy hồi í 1 . Chứng minh n * u = u + - 2, n " Î • n 1 + n ï u î n
rằng dãy (u ) có giới hạn hữu hạn và tính giới hạn đó. n Hướng dẫn giải 1 1 1
Đặt f (x) = x + - 2; g(x) = f ( f (x)) - x = + - 2 2 . Khi đó. x x 1 x + - 2 x æ 2 ö 2 - ç x - ÷( 2 x + ) 1 2 è ø 1 1 g '(x) =
£ 0 Þ g(x) < g(
) = 0 Þ f ( f (x)) < x, x " Î( ;1) (*).. 2 æ 1 ö 2 2 4 x x + - 2 ç ÷ è x ø 1
Mặt khác f '(x) < 0, x " Î( ;1) nên. 2 1 1 1 1 1
f (x) < f ( ) =
Þ f ( f (x)) > f ( ) = , x " Î( ;1) (**).. 2 2 2 2 2 1 1 Từ (*) và (**) suy ra:
< f ( f (x)) < , x x " Î( ;1) .. 2 2 1 1
Vậy: 1 = u > u >
Þ1= u > u > u > ,... Do đó (u
) là đơn điệu giảm và bị chặn dưới nên tồn 1 3 1 3 5 2 2 2n 1 - 1 tại limu = .. 2n 1 - n®¥ 2 é 1 ù 1
Vì f (x) liên tục trên
;1 nên u = f (u
) Þ limu = f limu = . ê 2n 2n 1 - 2n - n®¥ ( 2n 1 n®¥ ) 2 ú ë û 2 Trang 77
Vậy dãy (u ) được phân tích thành hai dãy con hội tụ tới cùng một giới hạn. Do đó dãy (u ) có giới hạn n n 1 bằng .. 2 u ì = 2 1 ï n u
Bài 34. Cho dãy số (u lim k å n ) xác định í 1 . Tính . u - u = u - u n " ³ ï n®¥ - k = u 1 n+ n ( 2 , 1 1 n n ) î 2014 1 k 1 + Hướng dẫn giải u u - n ( n )1
Theo giả thiết ta có: u =
+ u mà u = 2 suy ra. n 1 + 2014 n 1
2 = u < u < u < ....... do đó dãy (un )là dãy tăng. 1 2 3 Giả sử dãy (u limu = L (L > 2)
n ) bị chặn trên suy ra với khi đó. n n®¥ 2 2 u + 2013u L + 2012L éL = 0 limu = lim n n Û L = Û . n 1 + ê n®¥ 2014 2014 ëL =1
Vô lý do L > 2 . Suy ra dãy (un )không bị chặn trên do đó. 1 lim u = ¥ Þ lim = 0. n n®¥ n®¥ un Ta có. 2 u + 2013u n n u =
Û u u -1 = 2014 u - u n 1 + n ( n ) ( n 1+ n ) 2014 . u æ 1 1 ö n Û = 2014ç - ÷ u -1 u -1 u -1 n 1 + è n n 1 + ø æ 1 1 ö Þ S = 2014ç - ÷ Þ lim S = 2014. n u -1 u -1 n x®¥ è 1 n 1 + ø ìx = 2014 ï 1
Bài 35. Cho dãy số thực (x í lim x ?
n ) xác định bởi: . Tính . * 3 n ïx
= 6x -6sin x ,n î Ε n 1 + n n Hướng dẫn giải 3 x
Sử dụng bất đẳng thức x - £ sin x £ , x x " ³ 0. 6
Xét hàm số f (x) 3
= 6x -6sin x, x > 0. 6 1- cos x Ta có: f '(x) ( ) = > 0, x
" > 0 Þ f(x) luôn đồng biến với mọi x > 0. 3 (6x -6sin x)2 3
Do đó: f (x) > f (0) = 0 x
" > 0. mà x = f x > 0 x = 2014 > 0. 2 ( 1) vì . 1 Trang 78 Vậy ta có x = f x > 0, n " Î N n 1 + ( n) *. . 3
6x - 6sin x - x Mặt khác: 3 x - x = 6x - 6sin n n n x - x = . n 1 + n n n n 3 (6x -6sin + - + n n x )2 2 3 x 6x 6sin n n n x n x 3 x Vì x - £ sin x £ , x x " ³ 0 3
Û 6x - x – 6sinx < 0. x " > 0. 6
Þ 6x – 6sinx - 3
x < 0 do x > 0 Þ x – x < 0. n n n n n 1 + n Þ (x 0
n ) là dãy giảm và bị chặn dưới bởi
nên tồn tại giới hạn hữu hạn. Giả sử im
l x = x(x ³ 0), ta có phương trình:. n 3 3
x = 6x - 6sin x Û x - 6x + 6sin x = 0.
Xét hàm số g (x) = 3
x -6x +6sin x. g (x) 2 '
= 3x – 6 + 6cosx.
g¢ (x) = 6x – 6sinx ³ 0,"x ³ 0.
Þ g¢(x) ³ g¢(0) = 0. Do đó g (x) luôn đồng biến và liên tục với mọi x ³ 0 Þ phương trình g (x) = 0
có nghiệm duy nhất x = 0 . Vậy limx = 0. n Trang 79




