Chuyển đổi hình thức một số đối tượng từ biểu đồ trình tự sang Queueing Petri Nets | Đại học Kinh tế Kỹ thuật Công nghiệp

BỘ CÔNG THƯƠNG
TRƯỜNG ĐẠI HỌC KINH TẾ - KHOA CÔNG NGHỆ
KỸ THUẬT CÔNG NGHIỆP THÔNG TIN BÁO CÁO TỔNG KẾT
ĐỀ TÀI NGHIÊN CỨU KHOA HỌC SINH VIÊN NĂM HỌC 2022 - 2023 Tên đề tài:
Chuyển đổi hình thức một số đối tượng từ
biểu đồ trình tự sang Queueing Petri Nets
Giảng viên hướng dẫn: ThS. Vũ Văn Đốc
Chủ nhiệm đề tài: Trần Huy Hoàng Lớp DHTI13A1ND Thành viên: Vũ Quang Ngọc Lớp DHTI15A2ND NAM ĐỊNH, 04/2023 BỘ CÔNG THƯƠNG lOMoAR cPSD| 46884348
TRƯỜNG ĐẠI HỌC KINH TẾ - KHOA CÔNG NGHỆ
KỸ THUẬT CÔNG NGHIỆP THÔNG TIN BÁO CÁO TỔNG KẾT
ĐỀ TÀI NGHIÊN CỨU KHOA HỌC SINH VIÊN NĂM HỌC 2022 - 2023 Tên đề tài:
Chuyển đổi hình thức một số đối tượng từ
biểu đồ trình tự sang Queueing Petri Nets
Giảng viên hướng dẫn: ThS. Vũ Văn Đốc
Chủ nhiệm đề tài: Trần Huy Hoàng Lớp DHTI13A1ND Thành viên: Vũ Quang Ngọc Lớp DHTI15A2ND NAM ĐỊNH, 04/2023 lOMoAR cPSD| 46884348
Danh sách những người thực hiện
Họ và tên Lớp Khoa Chức danh
Trần Huy Hoàng DHTI13A1ND Công nghệ thông tin Chủ nhiệm đề tài
Vũ Quang Ngọc DHTI15A2ND Công nghệ thông tin Thành viên
Danh sách các giảng viên hướng dẫn
Tên giảng viên hướng dẫn Khoa
ThS. Vũ Văn Đốc Công nghệ thông tin lOMoAR cPSD| 46884348 MỤC LỤC
CHƯƠNG 1. TỔNG QUAN .................................................................................... 1
1.1. Giới thiệu ý tưởng nghiên cứu ..................................................................... 1
1.2. Mục tiêu, đối tượng, phạm vi của đề tài ..................................................... 3
CHƯƠNG 2. BIỂU DIỄN HÌNH THỨC BIỂU ĐỒ TRÌNH TỰ VÀ
QUEUEING PETRI NETS ..................................................................................... 4
2.1. Biểu đồ trình tự ............................................................................................. 4
2.1.1. Biểu diễn hình thức biểu đồ trình tự ......................................................... 4
2.1.2. Một số đối tượng cơ bản trong biểu đồ trình tự ........................................ 7
2.2. Queueing Petri Nets ...................................................................................... 9
2.2.1. Metamodel .............................................................................................. 10
2.2.2. Ký pháp và ngữ nghĩa ............................................................................. 11
2.2.3. Định nghĩa hình thức .............................................................................. 15
CHƯƠNG 3. LUẬT CHUYỂN ĐỔI TỪ BIỂU ĐỒ TRÌNH TỰ SANG .......... 20
QUEUEING PETRI NETS ................................................................................... 20
3.1. Các luật chuyển đổi các thành phần cơ bản ............................................ 20
Chương 4. Xây dựng chương trình chuyển đổi ................................................... 25
4.1. Công cụ sử dụng .......................................................................................... 25
4.2. Sơ đồ khối hệ thống .................................................................................... 25
4.3. Cấu trúc của chương trình chuyển đổi ..................................................... 26
Chương 5: Kết Luận .............................................................................................. 54
Tài Liệu Tham Khảo ............................................................................................. 55 lOMoAR cPSD| 46884348 Danh Mục Hình Ả
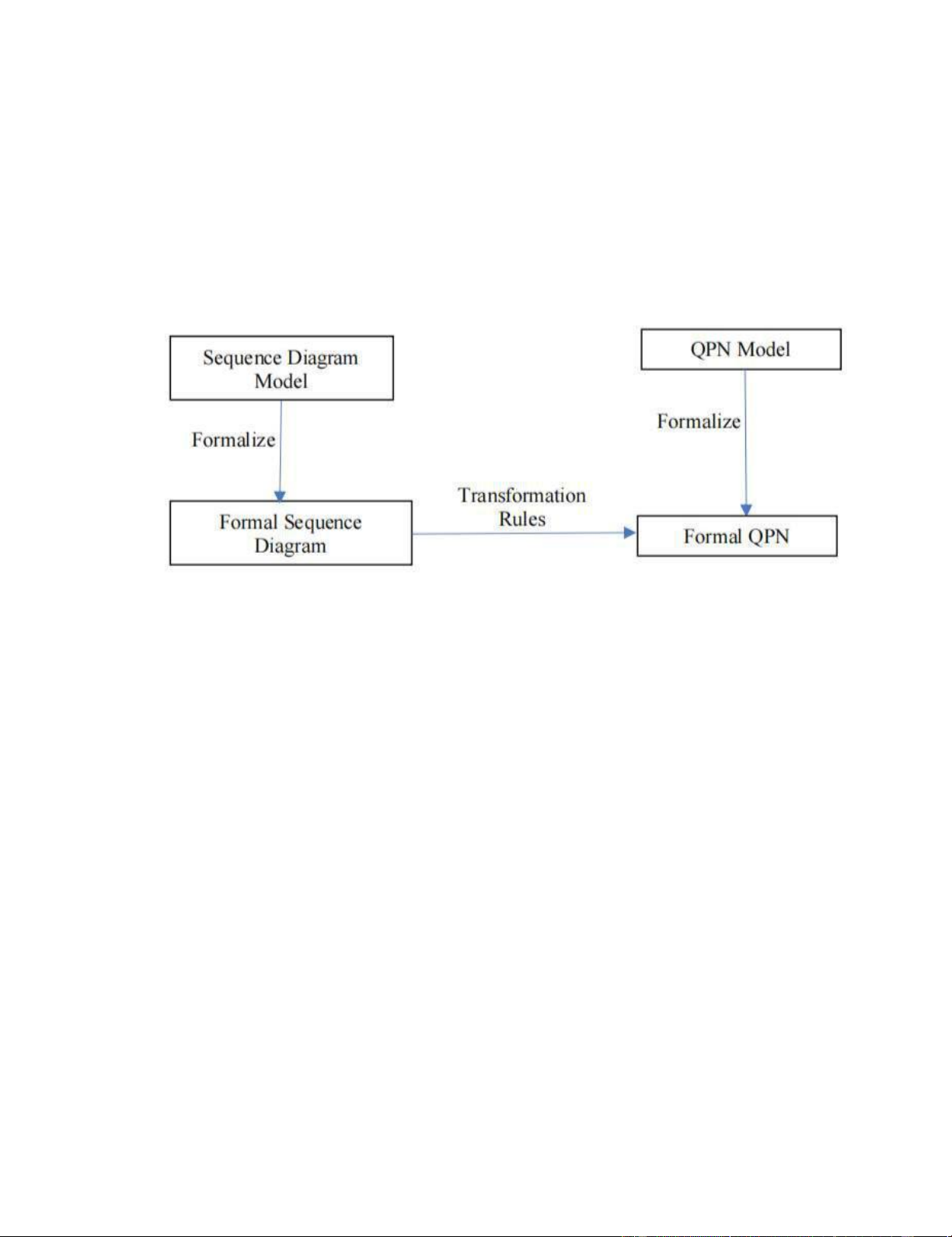
Hình 1. 1 Chuyển đổi từ hình thức SD tới hình thức QPN ........................................ 3 Y
Hình 2. 1 Ký pháp Interaction trong SD .................................................................... 8
Hình 2. 2 Ký pháp Lifeline trong SD ......................................................................... 8
Hình 2. 3 Ký pháp Message trong SD ........................................................................ 9
Hình 2. 4 QPN = PN + QN ........................................................................................ 9
Hình 2. 5 QPN metamodel ....................................................................................... 10
Hình 2. 6 Các ký pháp trong QPN ........................................................................... 11
Hình 2. 7 Một ví dụ về QPN .................................................................................... 12
Hình 2. 8 Một ví dụ về hàm tỷ lệ của transition ....................................................... 13
Hình 2. 9 Một góc nhìn về q-place và ký pháp của nó ............................................ 14
Hình 2. 10 Một góc nhìn về s-place và ký pháp của nó ........................................... 14
Hình 2. 11 Một ví dụ về QPN bên trong s-place ...................................................... 15
Hình 4. 1 minh họa khối mô hình đánh giá hiệu năng phần mềm ........................... 23 lOMoAR cPSD| 46884348 Danh Mục Bảng
Bảng 1. Các luật chuyển đổi..................................................................................... 21 lOMoAR cPSD| 46884348
Danh Mục Các Từ Viết Tắt SD Biểu đồ trình tự QPN Mạng Petri hàng đợi
UML Ngôn ngữ mô hình hóa thống nhất PN Mạng Petri QN Mạng hàng đợi XML Ngôn ngữ đánh dấu
API Giao diện lập trình ứng dụng lOMoAR cPSD| 46884348
CHƯƠNG 1. TỔNG QUAN
1.1. Giới thiệu ý tưởng nghiên cứu
Sự tiến triển về độ phức tạp của các hệ thống phần mềm yêu cầu một phương pháp thiết
kế cẩn thận và tinh vi hơn để thực hiện thành công. Biểu đồ trình tự (Sequence Diagram)
là một loại biểu đồ tương tác UML. Biểu đồ trình tự là biểu đồ hai chiều trong đó trục
thẳng đứng đại diện cho thời gian và trục ngang đại diện cho tương tác. Biểu đồ trình tự
thường được sử dụng để miêu tả dòng thông tin trong hệ thống thông qua sự giao tiếp
giữa các đối tượng. Ở đây, nhóm quan tâm đến mô hình, phân tích các hệ thống phần
mềm đáng tin cậy và sự kết hợp của thiết kế dựa trên UML và các kỹ thuật mô hình hóa
hình thức cho phân tích đáng tin cậy của các hệ thống này. Một Mạng Petri thông
thường là một ngôn ngữ mô hình hóa toán học để mô tả các hệ thống, bao gồm một tập
các places và một tập các transitions. Các places chứa một số lượng các mã thông báo
(token). Ở đầu phân tích, số lượng các mã thông báo được xác định bằng hàm đánh dấu
ban đầu. Hàm xảy ra chuyển tiếp định nghĩa số lượng các mã thông báo mà một
transition yêu cầu trong mỗi place kết nối để sẵn sàng đốt cháy (fire). Khi một transition
đốt cháy, nó trừ số lượng mã thông báo đó từ mỗi place đầu vào và gửi mã thông báo
mới vào các place khác nếu hàm xảy ra ngược được định nghĩa. Từ các biến thể mạng
Petri hiện có nhiều loại, QPN phù hợp với phương pháp của nhóm khi chuyển đổi các
mô hình hướng đối tượng vì Queueing Petri Nets (QPN) được xây dựng trên Colored,
một sự kết hợp của Colored Petri Nets và Generalized Stochastic Petri Nets. Hệ thống
mạng hàng đợi và mạng Petri stochastics tổng quát là hai trong số các hình thức mô hình
hóa phổ biến nhất đã được sử dụng trong thập kỷ qua, nhưng cả hai đều có một số hạn
chế. Thời gian một token chiếm đóng máy chủ được xác định thông qua phân phối thống
kê. Khi thời gian của một mã thông báo kết thúc, mã thông báo được đưa vào kho, sau
đó hoạt động như một immediate place cho các transition kết nối. Chỉ có các mã thông
báo trong kho được coi là có sẵn cho hàm xảy ra.
Tiến sĩ Meedeniya đề xuất một biểu diễn hính thức cho biểu đồ trình tự UML 2 với các
khái niệm bổ sung về các dấu vết và ngôn ngữ cùng các quy tắc biến đổi hình thức để
thu được một mạng Petri màu tương đương từ một biểu đồ trình tự UML 2 cho trước.
Đặc biệt, cô định nghĩa một cách hình thức biểu đồ trình tự và một tập hợp các vị trí
trạng thái liên quan đến một biểu đồ trình tự, các vị trí trạng thái tương ứng với các trạng
thái của các trường hợp đối tượng trước và sau sự kiện. Tác giả đã chỉ ra rằng các quy
tắc biến đổi được định nghĩa đảm bảo một mối tương ứng một-một giữa tập hợp các dấu
vết hợp lệ của cả hai mô hình. Đặc biệt, tác giả chia các quy tắc biến đổi từ SDs sang
CPN thành các quy tắc biến đổi chính, các quy tắc biến đổi bổ sung, quy tắc biến đổi của
đoạn tương tác và quy tắc biến đổi mô hình phức tạp.
Trong [3, 4, 5, 6], các tác giả định nghĩa QPN là một 8-tuple QPN = (P; T; C; I-; I+; M0;
Q; W). Tuy nhiên, đây chỉ là một định nghĩa hình thức cho một QPN đơn lẻ. Để có thể
phi tập trung hóa QPN, chúng ta cần thêm tham số S để biết liệu một nơi có phải là S- 1 lOMoAR cPSD| 46884348
place và cấu trúc bên trong của nó là gì. S-Place là một nơi có thể chứa một QPN con và
QPN này có thể có các s-place khác.
Dựa trên phân tích trên, nhóm đề ra các quy tắc hình thức để chuyển đổi biểu đồ trình tự
UML thành mạng Petri hàng đợi. Các quy tắc này được phân loại thành hai nhóm: (i)
Quy tắc chuyển đổi chung và (ii) Quy tắc đoạn tương tác. Trong các quy tắc chuyển đổi
chung, nhóm tập trung vào chuyển đổi SD-QPN bằng cách giải quyết tất cả các cấu trúc
quan trong sơ đồ trình tự. Trong khi đó, trong nhóm quy tắc đoạn tương tác, chúng tôi
mô tả các loại đoạn tương tác khác nhau có sẵn trong sơ đồ trình tự UML và cách tốt
nhất để đại diện cho chúng trong mạng Petri hàng đợi. Trong bài nghiên cứu này, chúng
tôi chỉ tập trung vào các quy tắc chuyển đổi chung.
Đóng góp chính trong bài nghiên cứu này như sau: Chúng tôi thêm tham số S vào định
nghĩa của QPN và giới thiệu QPN như một bộ 9-tuple. Chúng tôi phát triển một bộ quy
tắc chuyển đổi từ mô hình sơ đồ trình tự thành mô hình QPN, cho thấy rằng các quy tắc
đảm bảo các ngôn ngữ được phù hợp nhất. Các chuỗi hợp lệ của một sơ đồ trình tự có
một tương ứng một-một với các chuỗi hợp lệ của mô hình mạng Petri hàng đợi. Chúng
tôi áp dụng một nghiên cứu thực nghiệm để chứng minh tính hiệu quả của các quy tắc này.
Các công việc còn lại được tổ chức như sau: Các công trình liên quan được thảo luận
trong phần tiếp. Chúng tôi trình bày trong chương 2 biểu diễn hình thức của biểu đồ
trình tự và QPN, đưa ra một định nghĩa hình thức chi tiết về SD và QPN. Chương 3 thảo
luận về quy tắc chuyển đổi hình thức, xác định các quy tắc cho quá trình chuyển đổi hình
thức từ SD sang QPN. Chương 4 trình bày một nghiên cứu thực nghiệm chứng minh
phương pháp chuyển đổi mô hình của chúng tôi. Kết luận và công việc tương lai được
thảo luận trong chương 5.
Mạng hàng đợi và Mạng Petri là các mô hình phù hợp và phổ biến để phân tích [7,8,9].
Ví dụ, trong [10], mô hình hàng đợi đóng của SPECjAppServer2002 bao gồm máy
khách, cụm máy chủ ứng dụng, cơ sở dữ liệu và các trạm sản xuất được mô tả. Đôi khi,
các yếu tố của lý thuyết điều khiển được sử dụng để quản lý việc di chuyển các gói trong
các máy chủ web [11]. Nhiều phương pháp đã được đề xuất cho việc mô hình hóa hệ
thống hiệu suất: dựa trên các mô hình ngẫu nhiên như QN (hình thức sản phẩm cổ điển,
mở rộng hoặc lớp) hoặc PN ngẫu nhiên. Xây dựng các mô hình như vậy yêu cầu kinh
nghiệm trong mô hình và phân tích ngẫu nhiên. Cộng đồng nghiên cứu đã đề xuất các
phương pháp mô hình mạng cấp cao hỗ trợ tự động tạo ra các mô hình dự đoán cấp thấp.
Nhiều cuộc khảo sát gần đây đánh giá các công cụ mô hình hiệu suất, tập trung vào dự
đoán dựa trên mô hình [11], đánh giá các hệ thống dựa trên thành phần [12] và phân tích
kiến trúc phần mềm. Trong [10], các tác giả giải quyết vấn đề tính toán các giá trị hiệu
suất như thời gian phản hồi trong môi trường hệ thống web phân tán. Các tác giả đã
chứng minh tiềm năng trong việc mô hình hóa hệ thống web phân tán sử dụng QPN,
được hiểu là một kỹ thuật mô hình hóa toàn phần được sử dụng để đánh giá hiệu suất. 2 lOMoAR cPSD| 46884348
Trong [13,14,15], QPN được coi là phương pháp hiệu quả nhất để đánh giá hiệu suất
phần mềm. Tuy nhiên, do sự khác biệt về ngữ nghĩa giữa QPN và sơ đồ trình tự UML,
việc tạo tương ứng giữa chúng là thách thức và luôn yêu cầu nhiều can thiệp thủ công.
Do đó, cần xây dựng một mô hình trung gian để có thể giải quyết sự khác biệt ngữ nghĩa
giữa UML SD và QPN, đặt nền tảng cho việc chuyển đổi từ UML sang QPN.
Phương pháp của chúng tôi là cung cấp một định nghĩa hình thức chi tiết về SD và QPN,
sau đó chúng tôi phát triển các quy tắc cho việc chuyển đổi hình thức từ SD sang QPN như sau:
Hình 1. 1 Chuyển đổi từ hình thức SD tới hình thức QPN
1.2. Mục tiêu, đối tượng, phạm vi của đề tài - Mục tiêu:
Nghiên cứu cách biểu diễn bằng ngôn ngữ của một số đối tượng cơ bản trong biểu đồ
trình tự. Xây dựng các luật chuyển đổi chính thức các đối tượng đó sang ngôn ngữ tương
đương của Queueing Petri Nets và cuối cùng là xây dựng tool chuyển đổi tự động các
đối tượng trên sang Queueing Petri Nets bằng ngôn ngữ Java.
- Đối tượng nghiên cứu:
Các đối tượng cơ bản trong biểu đồ trình tự, Các cách biểu diễn bằng ngôn ngữ và chuyển sang Queueing Petri Nets. - Trong phạm vi: Nghiên cứu lý thuyết.
Mô phỏng kết quả chuyển đổi bằng ngôn ngữ Java. 3 lOMoAR cPSD| 46884348
CHƯƠNG 2. BIỂU DIỄN HÌNH THỨC BIỂU ĐỒ
TRÌNH TỰ VÀ QUEUEING PETRI NETS
2.1. Biểu đồ trình tự
2.1.1. Biểu diễn hình thức biểu đồ trình tự
Loại sơ đồ tương tác phổ biến nhất là biểu đồ trình tự UML [16]. Một tương tác được tạo
thành bởi các lifeline và các message giữa chúng, thứ tự này rất quan trọng để hiểu tình
huống. Mặc dù dữ liệu cũng có thể quan trọng, việc xử lý dữ liệu không phải là trọng
tâm của các tương tác. Dữ liệu được chuyển bằng các message và được lưu trữ trong các
lifeline, và có thể được sử dụng để trang trí các biểu đồ. Phần này cung cấp mô tả chi tiết
về biểu đồ trình tự UML. Ngữ nghĩa được mô tả trong phần này, tuân thủ tiêu chuẩn của
biểu đồ trình tự UML phiên bản 2.5 [1].
Biểu đồ trình tự là loại sơ đồ phổ biến dùng để ghi lại hành vi giữa các đối tượng [2,1].
Biểu đồ trình tự có hai chiều: một chiều ngang đại diện cho các thực thể tham gia vào
kịch bản, và một chiều dọc đại diện cho thời gian. Một thực thể có thể tương ứng với
một đối tượng cụ thể hoặc một vai trò trong tương tác. Một vai trò có thể là một phần
của sự cộng tác và/hoặc một phần bên trong của một lớp cấu trúc, một thành phần hoặc
một hệ thống phụ. Một thực thể có một đường kẻ đứt dọc gọi là "lifeline" đại diện cho sự
tồn tại của thực thể tại một thời điểm cụ thể; thứ tự các sự kiện dọc theo một lifeline là
quan trọng, nói chung, thứ tự các sự kiện này sẽ xảy ra. Một message được hiển thị dưới
dạng một đường thẳng từ MessageEnd của người gửi đến MessageEnd của người nhận
[16]. Đường này phải sao cho mỗi đoạn đường là ngang hoặc xuống khi đi từ sự kiện gửi
đến sự kiện nhận. Cả sự kiện gửi và nhận đều có thể trên cùng một lifeline. Một message
chỉ ra loại giao tiếp giữa các thực thể (đồng bộ hoặc không đồng bộ) và các sự kiện gửi
và nhận liên quan đến nó.
Một biểu đồ trình tự được bao quanh bởi một khung và hình hộp có năm mặt ở góc trên
bên trái đặt tên cho biểu đồ trình tự. Mỗi đoạn tương tác (interaction fragment) có ít nhất
một toán tử được giữ trong hộp năm mặt ở góc trên bên trái của đoạn đó. Có một số toán
tử khả dụng, ví dụ như alt (hành vi thay thế), par (hành vi song song), neg (hành vi cấm),
assert (hành vi bắt buộc), loop (hành vi lặp lại), ref (tham chiếu đến sơ đồ khác), và
nhiều hơn nữa. Tùy thuộc vào toán tử được sử dụng, một đoạn tương tác bao gồm một
hoặc nhiều toán hạng. Trong trường hợp của toán tử neg, assert, loop và ref, đoạn tương
tác chỉ có một toán hạng duy nhất, trong khi đối với hầu hết các toán tử khác, nó có nhiều toán hạng [2].
Để biểu diễn hình thức của biểu đồ trình tự, chúng ta sử dụng định nghĩa như trong [17]
với tên gọi d N hình thức là một bộ tổ hợp (tuple) SD. Để Ω là một tập hợp các toán tử
tương tác được cho bởi
Ω = {alt, par, loop, option, break, critical, assert, neg, strict, seq, consider, ignore, ref},
và Env là một tập hợp hữu hạn các thực thể môi trường. 4 lOMoAR cPSD| 46884348
Định nghĩa 1 (Một biểu đồ trình tự) Một biểu đồ trình tự là một bộ tổ hợp SD = (d, I, E,
<, M, T, F, X, Exp) trong đó
1. d N là tên của biểu đồ;
2. I là một tập hợp hữu hạn các thực thể đối tượng;
3. E = Ei là một tập các sự kiện sao cho với mọi i ≠ j ∈ I, Ei ∩ Ej = ;
4. < là một tập các thứ tự bộ phận
5. M là một tập hữu hạn các nhãn message;
6. T là một tập các transition cục bộ sao cho T E × M × E và đối với t1, t2 T, nếu t1 =
(e11, m1, e12) ≠ t2 = (e21, m2, e22) thì e11 ≠ e12 ≠ e21 ≠ e22,
7. F là tập các định danh đoạn tương tác (interaction fragment) trong d sao cho:
- f: F → Ω × N là một hàm liên kết một toán tử và một số tự nhiên (số lượng toán
hạng) với một định danh đoạn tương tác;
- g: F × N → là một hàm liên kết một tập các sự kiện với một cặp (id, n) trong đó id
là một định danh đoạn tương tác và n là toán hạng thứ n của đoạn đó. Nó chỉ được
định nghĩa nếu f(id) = (o, m) và n ≤ m. Đối với n ≠ k bất kỳ với n, k ≤ m, g(id, n) ∩ g(id, k) = ;
- h: F × N → là một hàm liên kết một tập hợp các định danh đoạn tương tác với một
cặp (id, n) trong đó id là định danh đoạn tương tác và n là toán hạng thứ n của đoạn
tương tác đó. Hàm này chỉ được định nghĩa nếu f(id) = (o, m) và n ≤ m, và đồng thời
thoả mãn các thuộc tính sau đây cho id1, id2 ∈ F với id1 ≠ id2, f(id1) = (o1, n1) và f(id2) = (o2, n2):
a. id1 h(id1, x) cho bất kỳ x ≤ n1;
b. nếu id1 h(id2, m2) và id2 h(id1, m1) với m1 ≤ n1 và m2 ≤ n2 bất kỳ, thì
g(id1, m1) ∩ g(id2, m2) = ∅;
c. nếu id2 ∈ h(id1, m1) thì g(id1, m1) ⊇ g(id2, n).
8. X = là một họ các biến địa phương có chỉ số I;
9. Exp là một tập hợp các biểu thức sao cho guard: T → Exp là một hàm ánh xạ
một biểu thức (guard) cho một transition địa phương.
Vị trí trạng thái miêu tả một tình huống trong suốt quá trình sống của một đối tượng sau
khi hoàn thành một số hoạt động hoặc đang chờ sự kiện. Trong biểu diễn hình thức,
chúng tôi sử dụng định nghĩa như trong [1] các vị trí trạng thái ban đầu, bên trong và kết thúc cho mỗi thực thể.
Định nghĩa 2. (Vị trí trạng thái) Cho là một biểu đồ trình tự cho biết tên
biểu đồ d. Tập hợp các vị trí trạng thái liên quan được cho bởi tập : 5 lOMoAR cPSD| 46884348
• = + trong đó là các vị trí trạng thái cho thực thể i và ∩ = ∅ cho i ≠ j ∈ ;
• = ∪ ∪ là tập hợp các vị trí trạng thái ban đầu khởi tạo, trong và kết thúc của thực thể i
∈ tương ứng. Mỗi thực thể chỉ có một vị trí trạng thái ban đầu và một
vị trí trạng thái kết thúc. Với i ∈ Env, = ∅;
•: M × → là một hàm với chỉ số mà cho một cặp (m, e) của
một message m và một event e, nó liên kết với một vị trí trạng thái kế tiếp của
thực thể i. Nó chỉ được xác định nếu tồn tại t ∈ T với t = (e, m, e’) hoặc t = (e’, m, e);
•: F × N → là một hàm với chỉ số mà cho một cặp (id, n) liên kết
với toán hạng thứ n của đoạn id với một tập hợp các vị trí trạng thái của
thực thể i ∈ j(id), chỉ ra tất cả các vị trí trạng thái của nó trong toán hạng;
•: F → là một hàm với chỉ số mà cho một đoạn tương tác id trả về
một vị trí trạng thái cho thực thể i ∈ j(id) liên kết với cuối đoạn.
Để tạo chỉ mục kế tiếp qua các thực thể trong và định nghĩa trên các sự kiện và
vị trí trạng thái, chúng ta sử dụng định nghĩa như trong [17] hàm kế tiếp.
Định nghĩa 3. (Hàm: next) Giả sử SD là một biểu đồ trình tự với tập các vị trí trạng thái
S. Chúng ta định nghĩa là một hàm được chỉ số hóa bởi được định nghĩa trên các vị trí
trạng thái và sự kiện sao cho : ∪ → Cho id thuộc F là một đoạn tương tác tùy ý trong
biểu đồ với f(id) = (o, m), và j là một số tự nhiên nằm trong khoảng 1 ≤ j ≤ m. 6 lOMoAR cPSD| 46884348 = { min() }x {} x
và định nghĩa cho những m M {,….., }
x ∈ , x = min((id)) và = min((id, j)) {(id)}
x ∈ , x = max((id)) và o ≠ break { max((id))}
x ∈ , x = max((id, j)) và o ≠ {par, loop}
{e’} x ∈ , không được bao phủ bởi những trường hợp trên với (m, e) = x
Với những m ∈ M, e ∈ và e → e’ ⊥ x ∈
Đối với các đoạn tương tác par, loop và break, chúng ta định nghĩa ) như sau: =
{e’} ∪ (id, p) x ∈ , x ∈ (id, j), o = par,
x ≠ min((id, j)), (m, e) = x cho những m ∈ M, e ∈ and e → e’
{ min((id)) ∪ max((id))} x ∈ , x = max((id, j)) và o = loop
{(id’)} x ∈ , x = max(), o = break,
f(id’) = (loop, 1) and h(id’, 1) = id
Tương tự, có thể định nghĩa một hàm (x) nhưng chúng tôi không mô tả nó trong bài nghiên cứu này.
2.1.2. Một số đối tượng cơ bản trong biểu đồ trình tự
2.1.2.1. Interaction (Frame)
Mỗi SD là sự kết hợp của một tập các nút (node) và các cạnh/đường đi (edgs/path).
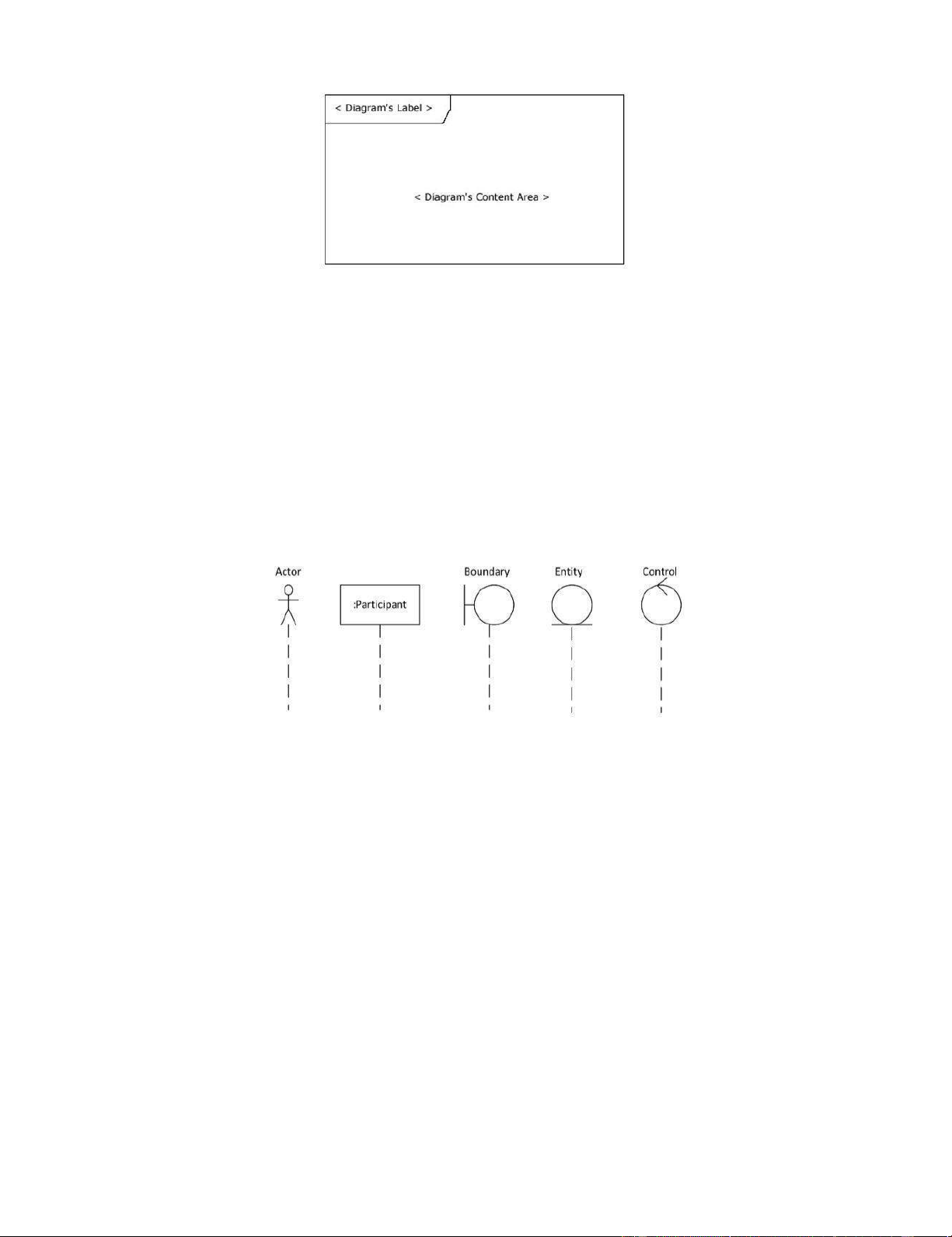
Interaction (Frame) là một node xác định ranh giới của SD, chứa các nút và cạnh khác trong SD. 7 lOMoAR cPSD| 46884348
Hình 2. 1 Ký pháp Interaction trong SD 2.1.2.2. Lifeline
Lifeline là một node biểu diễn một bên tham gia (participant) trong Interaction.
Participant có thể là các actor trong use case hay các object. Thứ tự của các participant
xác định thứ tự tham gia đầu tiên trong Interaction. Lifeline mô tả đường sống (time-line)
của một participant ở đó thời gian tăng dần từ trên xuống dưới. Khoảng cách giữa hai sự
kiện (event – một thời điểm theo thời gian) trên một time-line không đại diện cho bất kỳ
phép đo thời gian đúng nào mà chỉ hàm ý sự kiện ở dưới xảy ra sau sự kiện ở trên.
Hình 2. 2 Ký pháp Lifeline trong SD 2.1.2.3. Message
Message là một path xác định một loại giao tiếp cụ thể giữa các lifeline trong SD. Điểm
bắt đầu hoặc kết thúc của một message được gọi là message end.
Phụ thuộc vào loại hành động được dùng để sinh ra message, message có thể là lời gọi
đồng bộ (Synchronous Call), lời gọi không đồng bộ (Asynchronous Call), thông điệp khởi
tạo (Create Message), thông điệp hủy (Delete Message), thông điệp phản hồi (Reply Message).
- Synchronous Call là một message mà lifeline gửi đi nhưng block execution hiện tại
trên lifeline cho tới khi nhận được reply message.
- Asynchronous Call là một message mà lifeline gửi đi, sau đó lifeline vẫn có thể thực
hiện một path khác mà không cần đợi reply message. 8 lOMoAR cPSD| 46884348
- Create Message là một message gửi tới một lifeline và tạo ra lifeline đó.
- Delete Message là một message gửi đi để kết thúc một lifeline khác.
Phụ thuộc vào sự có mặt của sự kiện gửi (sending event) và sự kiện nhận (receiving
event) trên lifeline, message có thể là Complete Message, Lost Message, Found Message,
Unknown Message (mặc định).
- Complete Message là một message có thể xác định được cả sending event và receiving event.
- Lost Message là một message mà biết sending event nhưng không biết receiving event.
- Found Message là một message mà biết receiving event nhưng không biết sending event.
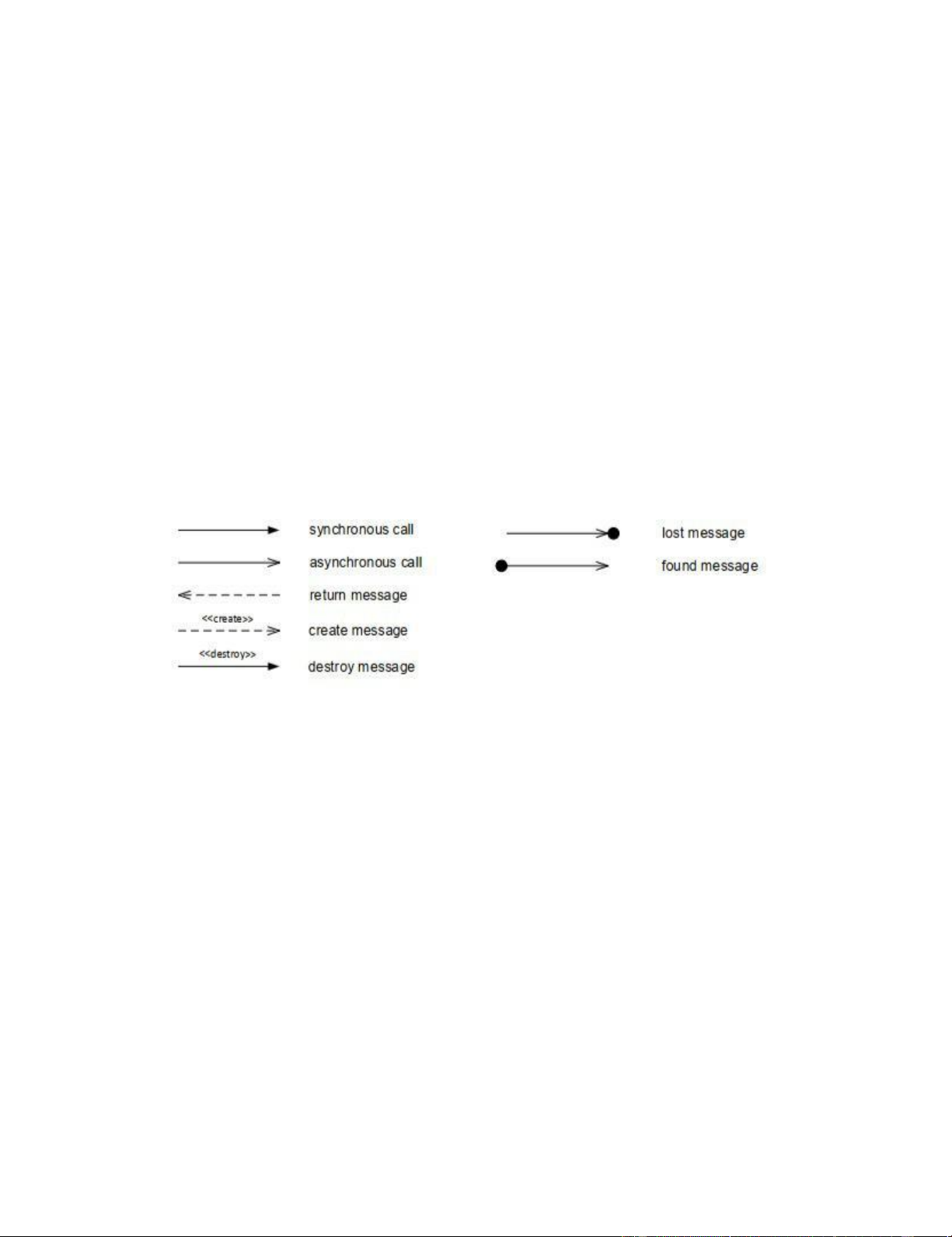
- Unknown Message là một message không xác định được cả sending event và receiving event.
Hình 2. 3 Ký pháp Message trong SD
2.2. Queueing Petri Nets 9 lOMoAR cPSD| 46884348
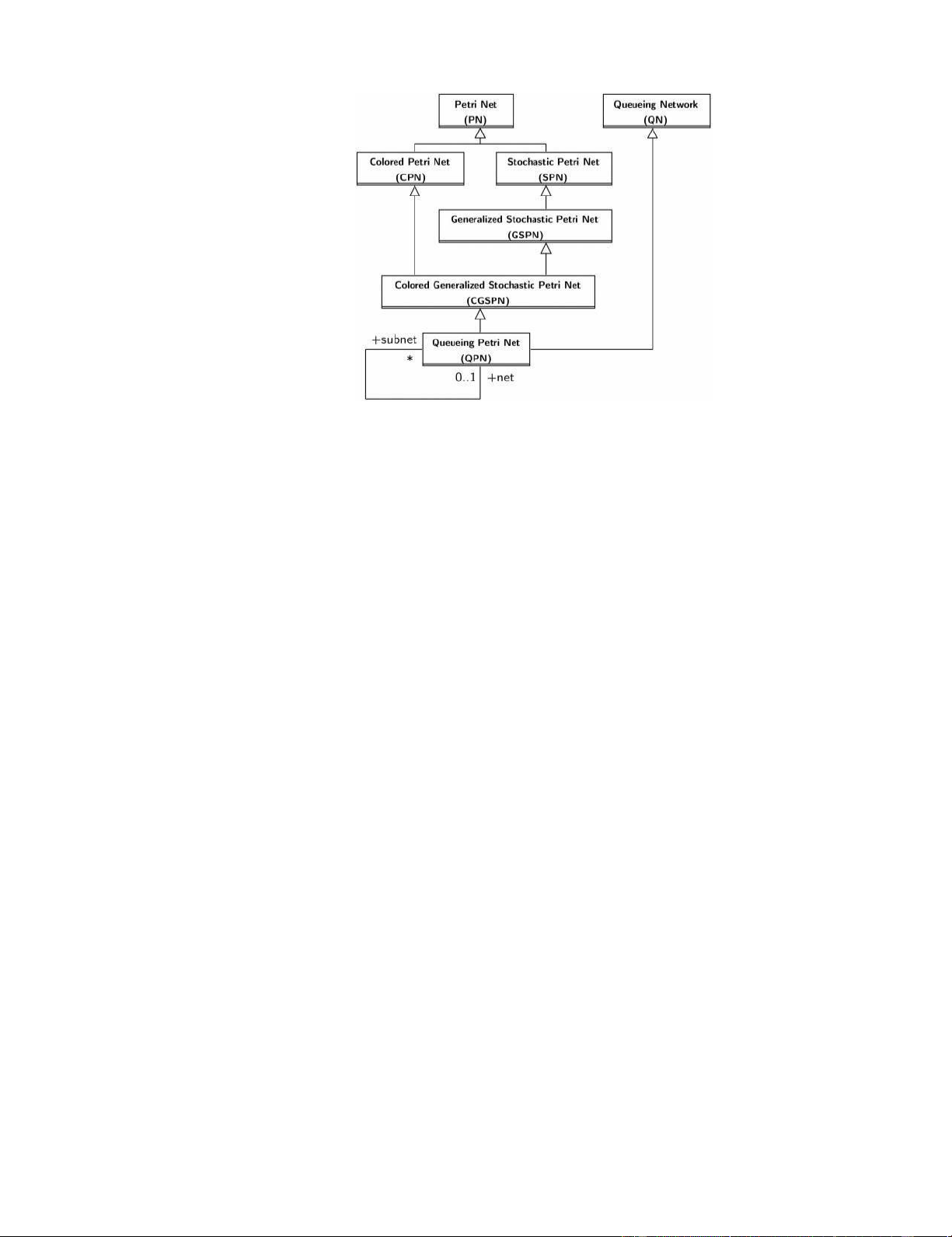
Hình 2. 4 QPN = PN + QN
QPN (Queueing Petri Net – mạng Petri hàng đợi) là một mô hình hiệu năng với cơ sở
toán học mạnh mẽ, được hình thành từ một số mở rộng của PN (Petri Net – mạng Petri)
như CPN, SPN, GSPN, CGSPN và được bổ sung thêm các tính chất về hàng đợi của QN
(Queueing Network – mạng hàng đợi). Một phương trình đơn giản để thể hiện điều này
là: QPN = PN + QN. (Hình 2.4)
QPN cho phép phân cấp cấu trúc bên trong, các QPN có thể lồng vào nhau.
Cấu trúc các tiểu mục sẽ gồm có metamodel của QPN, ký pháp, ngữ nghĩa và một ví dụ
minh hoạ, cuối cùng là định nghĩa hình thức cho QPN. 10 lOMoAR cPSD| 46884348 2.2.1. Metamodel
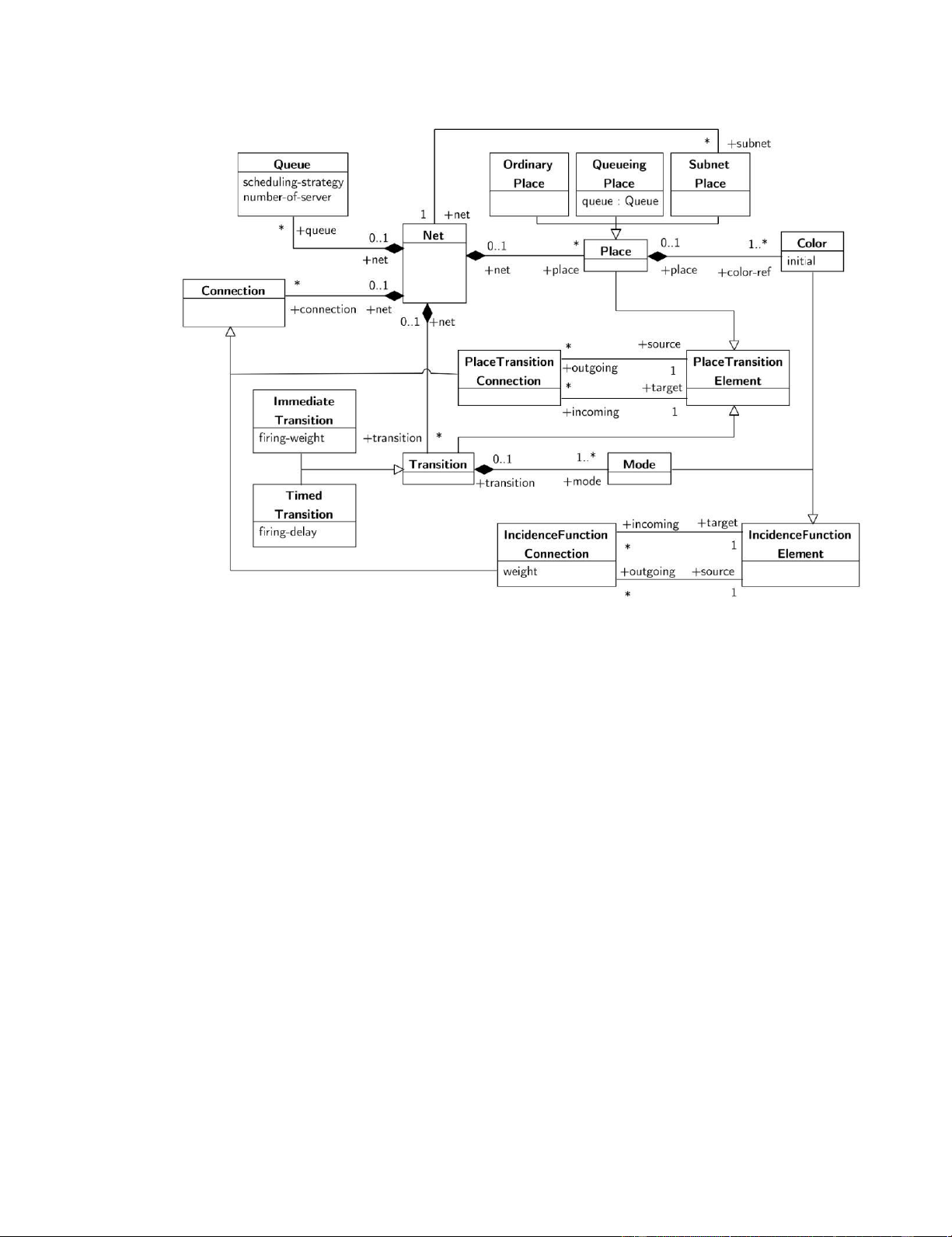
Hình 2. 5 QPN metamodel
Một metamodel cho QPN được giới thệu như trong Hình 2.5. Mỗi QPN là một tập hợp
của các Queue (hàng đợi), Place (vị trí), Transition (chuyển tiếp) và Connection (cung kết nối).
Mỗi Queue (tương tự khái niệm queue trong QN) có một khả năng nhất định và có chiến
lược để điều phối các yêu cầu truy cập trong mạng.
Một Place có thể chứa nhiều Color (màu) – là khái niệm mở rộng từ token (token trong
AD hoặc token trong PN) để phân biệt các token với nhau khi có nhiều loại. Có ba loại
place là OrdinaryPlace (o-place) là dạng place bình thường (tương tự place trong PN);
QueueingPlace (q-place) là dạng place được tích hợp thêm thành phần Queue, khi đó các
color trong place này sẽ được điều phối truy cập theo chiến lược của Queue; SubnetPlace
(s-place) là dạng place thay thế cho cả một QPN, là phần tử cho phép QPN có khả năng
phân cấp như đã nói tới.
Một Transition có thể có nhiều Mode (chế độ) – là khái niệm tương tự color dùng để
phân biệt các cách mà một transition có thể thực hiện. Có hai loại transition là
TimedTransition (t-transition) là dạng transition có liên quan đến yếu tố thời gian và 11 lOMoAR cPSD| 46884348
ImmediateTransition (i-transition) là dạng transition mà thời gian không phải nhân tố ảnh hưởng đến nó.
Có hai loại Connection, PlaceTransitionConnnection (pt-connection) dùng để kết nối một
place với một transition và ngược lại; IncidenceFunctionConnection (if-connection)
dùng để kết nối có trọng số một color với một mode và ngược lại.
Cách hoạt động của QPN sẽ được làm rõ trong báo cáo đồ án ở phần tiếp theo.
2.2.2. Ký pháp và ngữ nghĩa
Các ký pháp trong QPN được thể hiện như trong Hình 2.6. Một số ký pháp mở rộng tự
định nghĩa không ảnh hưởng đến ngữ nghĩa của mạng mà chỉ nhằm mục tiêu dễ dàng
hơn khi trình bày về sau.
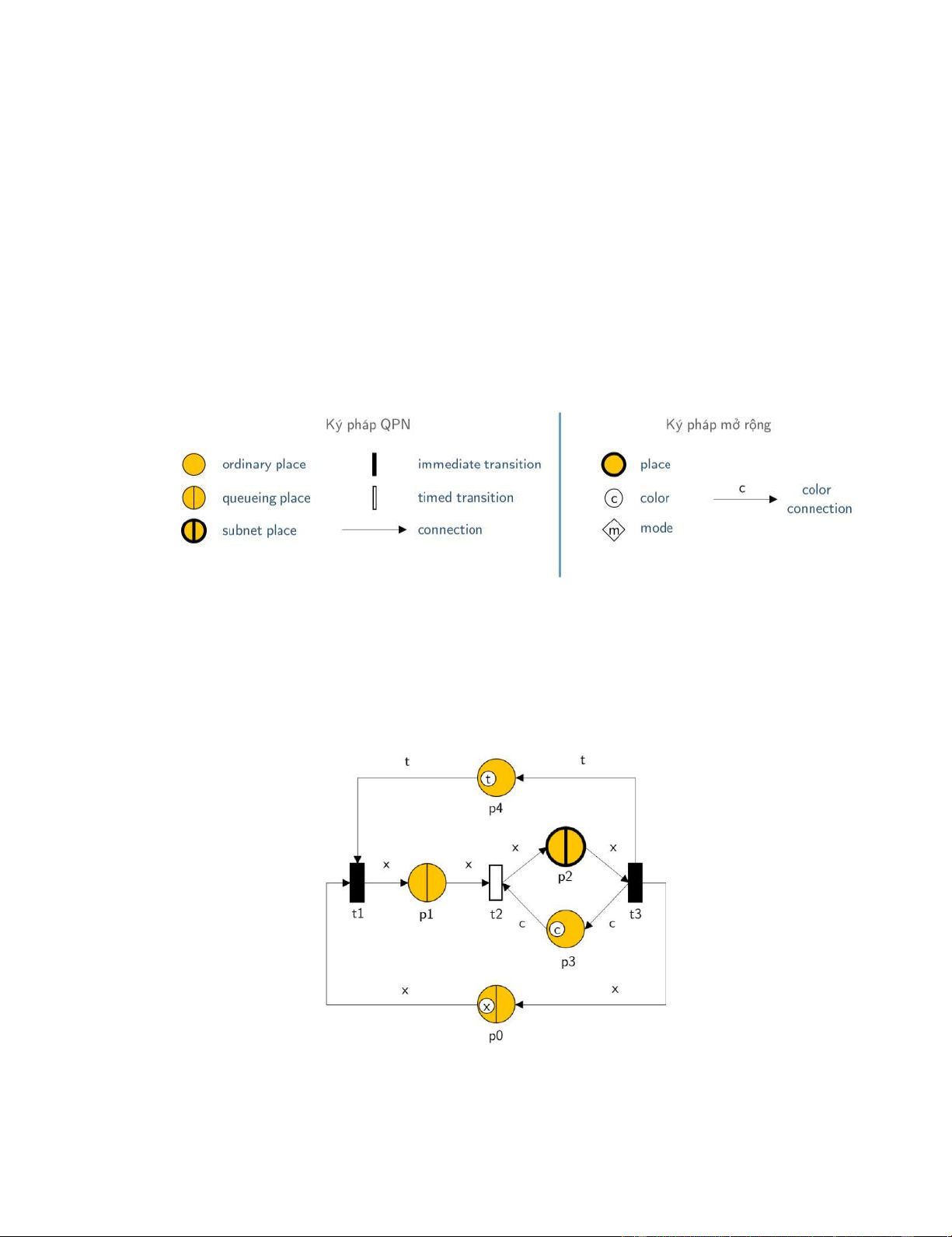
Hình 2. 6 Các ký pháp trong QPN
Hình 2.7 minh hoạ một ví dụ về QPN với năm place (p0, p1, p2, p3, p4), ba transition
(t1, t2, t3) và mười pt-connection trong đó: (p3, p4) là các o-place, (p0, p1) là các q-
place, p2 là một s-place, (t1, t3) là các i-transition, t2 là một t-transition.
Hình 2. 7 Một ví dụ về QPN 12 lOMoAR cPSD| 46884348
Nếu có một pt-connection đi từ place p đến transition t thì p được gọi là một inputplace
của transition t và t được gọi là một output-transition của place p. Nếu có một pt-
connection đi từ transition t đến place p thì p được gọi là một output-place của transition
t và t được gọi là một input-transition của của place p. Một place có thể không có, có một
hoặc nhiều input-transition hay output-transition. Một transition có thể không có, có một
hoặc nhiều input-place hay output-place.
Ví dụ, với Hình 2.7, t1 là input-transition của place p1, p1 là input-place của transition
t2, t2 là output-transition của place p3, p3 là output-place của transition t3. Transition t1
có hai input-place (p0, p4) và một output-place (p1). Transition t3 có một input-place
(p2) và ba output-place (p0, p3, p4). Mỗi place trong hình vẽ này đều có một input-
transition và một output-transition.
Ngoài những ký pháp thông thường, trong Hình 2.7 có xuất hiện các ký pháp mở rộng.
Các color x, c, t lần lượt được đặt nằm bên trong các place p0, p3, p4, thể hiện rằng: ở
thời điểm khởi tạo mạng (initial marking – hình trạng khởi tạo), những place này sẽ được
khởi tạo color tương ứng. Các place không có ký pháp color đặt bên trong sẽ không được
khởi tạo color tại thời điểm ban đầu (trong ví dụ này là p1, p2). Trên 10 pt-connection
cũng có các color, cho biết hướng đi của một hay nhiều color (hiểu tương tự như dòng
chảy token trong AD). Những connection loại này không chứa trọng số, chỉ nhằm xác
định hướng của các color đến và đi từ các input, output của mỗi place, transition.
Những connection chứa trọng số là những if-connection: kết nối color với mode và
ngược lại như đã nói từ trước. Một hàm tỷ lệ được liên kết với mỗi transition, xác định
cách thức transition hoạt động. Giả sử rằng transition t1 có ba mode là mode 1, mode 2
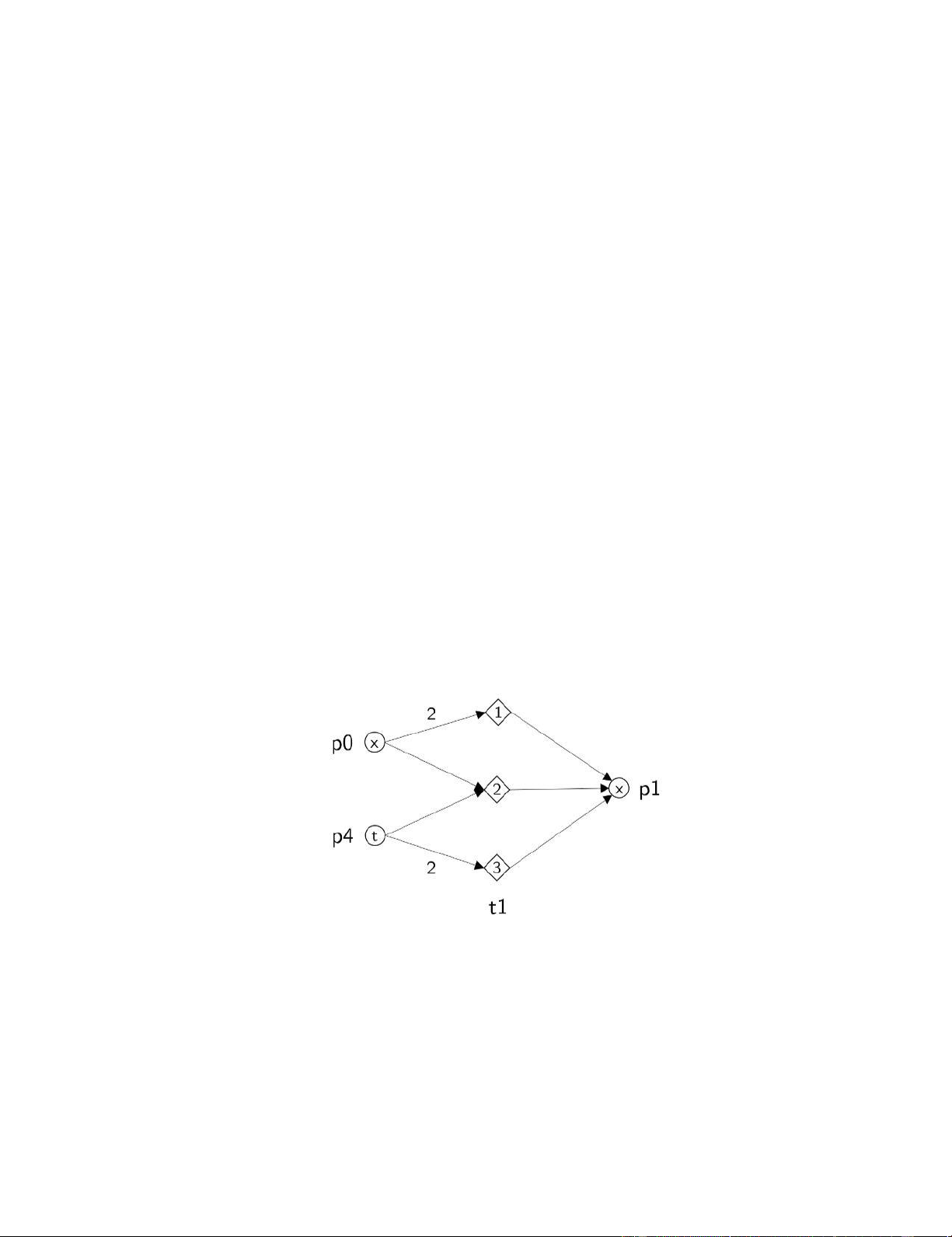
và mode 3. Hình 2.8 minh hoạ một ví dụ về hàm tỷ lệ liên kết với transition t1.
Hình 2. 8 Một ví dụ về hàm tỷ lệ của transition
Các color xuất hiện trong hình vẽ là các color có thể được chứa trong input-place và
output-place của transition t1, đó là color x trong place p0 là input-place của transition
t1, color t trong place p4 là input-place của transition t1 và color x trong place p1 là
output-place của transition t1. Các if-connection nối các color và mode với nhau chứa
trọng số mặc định là 1 nếu không biểu diễn trọng số khác. Trọng số trên if-connection 13