Comparison OF TWO Populations - Statistics for Business | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố HCM
Comparison OF TWO Populations - Statistics for Business | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố HCM được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Statistics for Business (BAO8OIU) 43 tài liệu
Trường: Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh 696 tài liệu
Tác giả:
Preview text:
International University IU
STATISTICS FOR BUSINESS [IUBA] CHAPTER 08 s
THE COM PARISON OF TW O POPULATIONS n tio la u p o P
STRUCTURE OF PAPER: o w f T o
PART I – THE COM PARISON OF TW O POPULATION M EANS n o ris a p M ETHOD 01 m o
THE COM PARISON OF TWO POPULATION M EANS USING PAIRED-OBSERVATION C e h : T M ETHOD 02 8 r 0
THE COM PARISON OF TWO POPULATION M EANS USING INDEPENDENT RANDOM SAM PLES te p a h C
PART II – THE COM PARISON OF TW O POPULATION PROPORTIONS ss | e sin
PART III – THE COM PARISON OF TW O POPULATION VARIANCES u r B s fo tistic ta S 1
Pow ered by sta tisticsforbusinessiuba.blogspot.com
International University IU PART I
COM PARISON OF TW O POPULATION M EANS s n tio M ETHOD 01 la u p o
COM PARISON OF TW O POPULATION M EANS USING PAIRED-OBSERVATION P o w HYPOTHESIS TESTING f T
Two – tailed Test ing
Right – tailed Testing
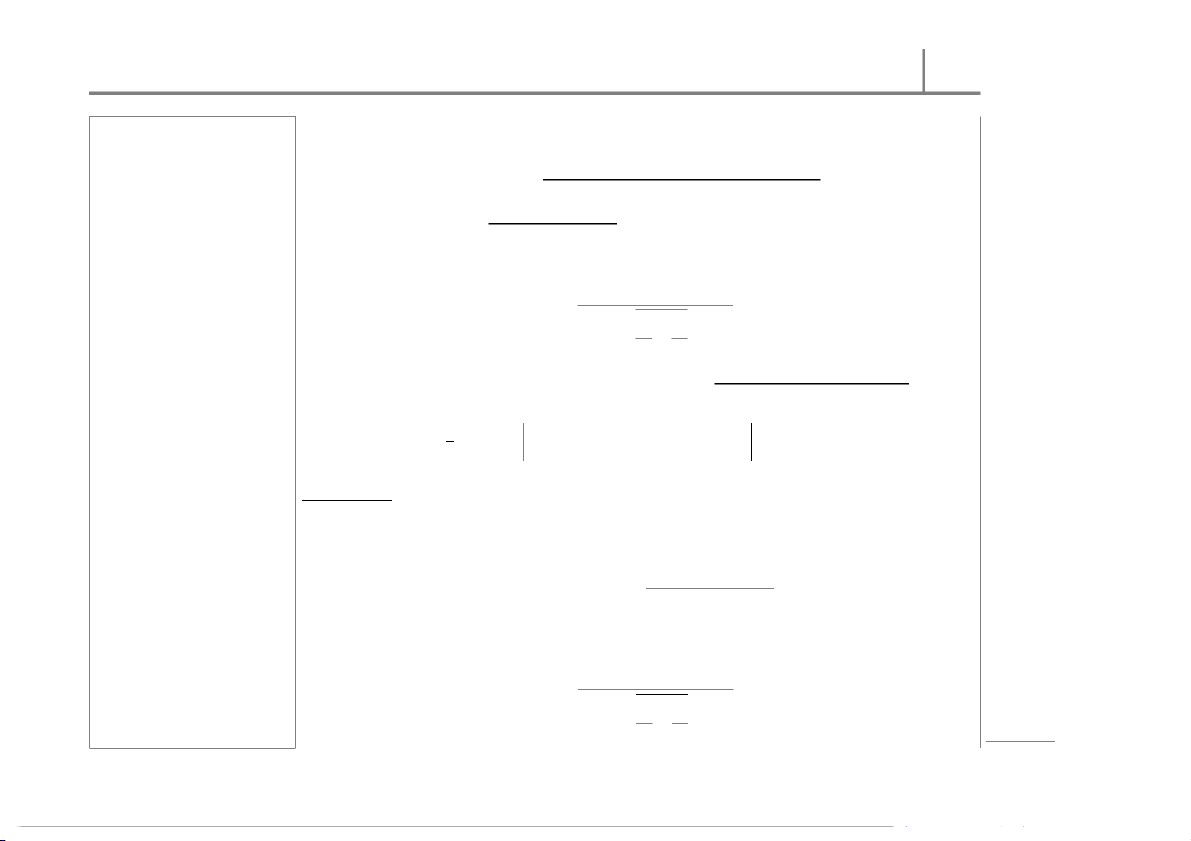
Left – tailed Test ing o PROCESS n o Step 01
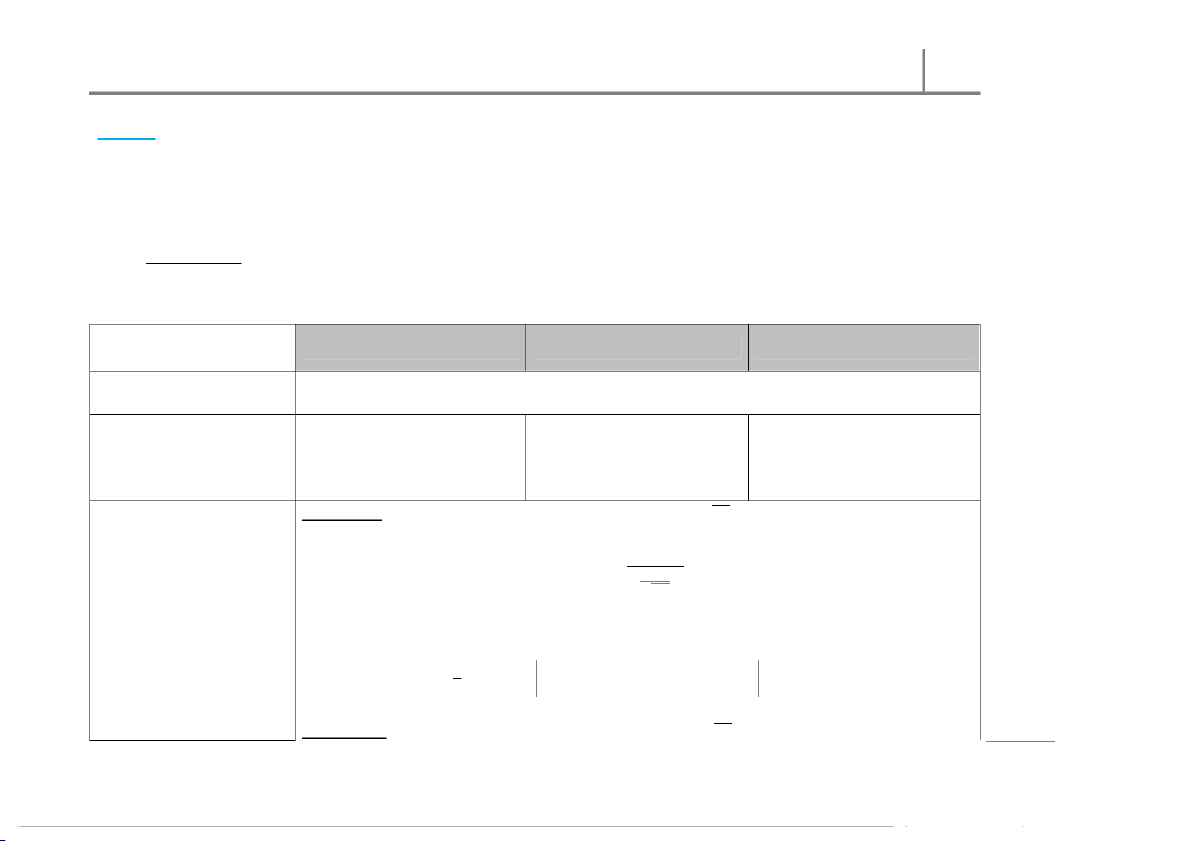
The population of differences is/ is assumed t o be normally distribut ed. ris a Condition p m Step 02 o Det ermine t he null and C : = : ≤ : ≥ e h alt ernative hypot heses : ≠ : > : < : T ( 8 and) r 0 Step 03
Situation I: When < 30, we use and ⁄√ te
Calculat e t he test stat istic The test st atistic value: p a h value. − C = ss | The crit ical-value √ e approach: sin At the level of significance, u
, the critical value(s): With = − 1 Det ermine the crit ical r B value(s). ± = ± = (,) = −(,) s fo (,)
The -value approach: tistic ta Calculat e t he -value. Situation II: When ⁄ S
≥ 30, we use and √ 2
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU The test st atistic value:
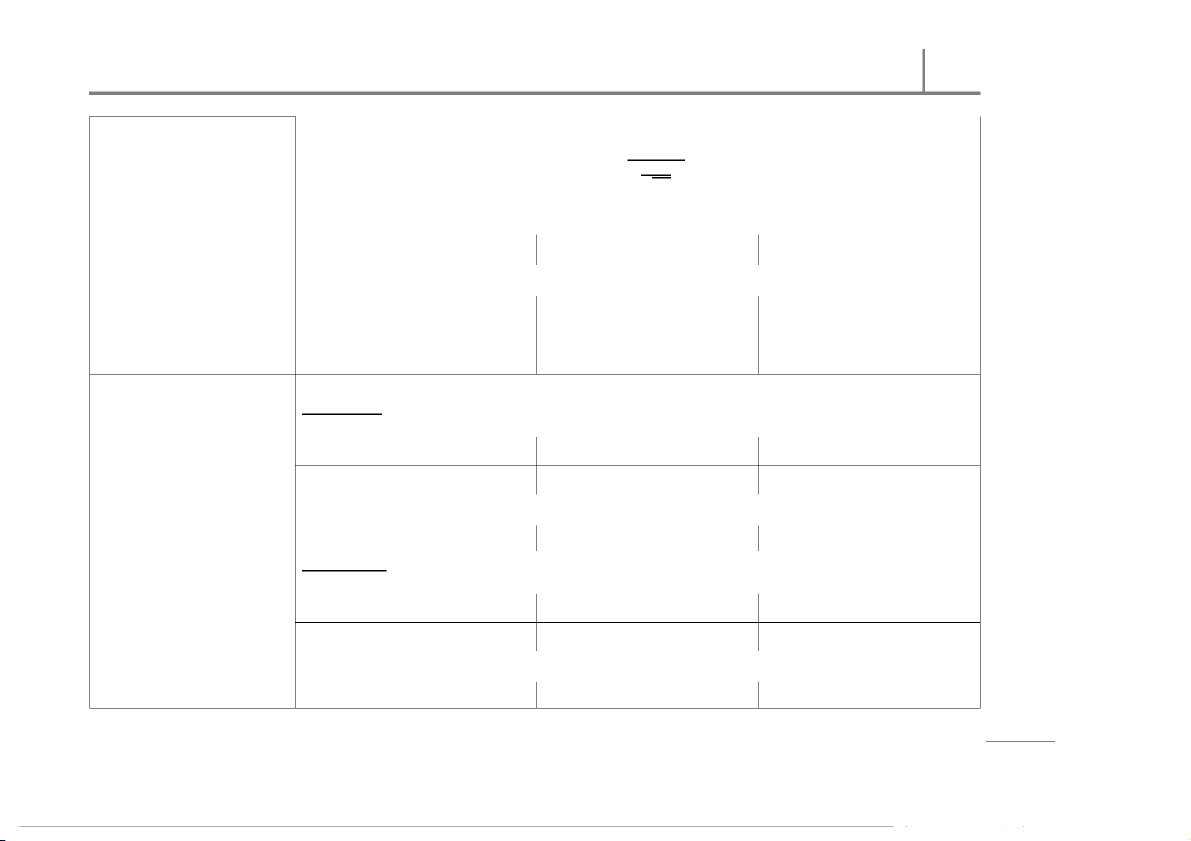
Note: The -value − =
approach is used for
√
The crit ical-value approach: s
At the level of significance, , t he crit ical value(s): n ± = ± / = = − tio la u The p-value approach: p o P If < 0, o w
− = ( < ) × 2
− = ( > )
− = ( < ) f T If > 0, o n
− = ( > ) × 2 o Step 04
Wit h the level of significance ( ) ris a M ake the decision
Situation I: We can reject when p m
The crit ical-value approach: o C [−,] > < e h [−,] > < : T 8 The p-value approach: r 0 te p
− <
− <
− < a h
Situation II: We cannot reject C w hen
The crit ical-value approach: ss | e ∈ [−,] < > sin u ∈ [−,] < > r B The p-value approach: s fo
− >
− >
− > tistic ta S 3
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU CONFIDENCE INTERVALS
Situat ion I: When , w e use and < 30
√ ⁄
= ± s ( ,) n √ tio la
Situat ion II: When , we use and ≥ 30
√ ⁄ u p o P ± o
= w √ f T o n o ris a p m o C e h : T 8 r 0 te p a h C ss | e sin u r B s fo tistic ta S 4
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU
Example I-01: (Case of the Comparison of Two Population M eans by using Pair-Observation) PROBLEM I-01A:
Recent advances in cell phone screen qualit y have enabled t he showing of movies and commercials on cell phone screens. (Situat ion I)
But according t o t he New York Tim es, advert ising is not as successf ul as movie view ing. Suppose t he follow ing dat a are
numbers of view ers for a movie (M ) and for a com mercial aired w it h t he movie (C). Test for equalit y of movie and s
commercial view ing, on average, using a tw o-t ailed t est at = 0.05 (dat a in thousands): n tio M : 15 17 25 17 14 18 17 16 14 la u C: 10 9 21 16 11 12 13 15 13 p o P o SOLUTION: M C
Score Differences w 15 10 5 f T 17 9 8 o n 25 21 4 o 17 16 1 ris a 14 11 3 p 18 12 6 m o 17 13 4 C e 16 15 1 h 14 13 1 : T 8 r 0 = 9, = 3.67, = 2.45, = 0.05 te p a h
We assum e t hat the population of score dif ferences is norm ally dist ribut ed. C ss | e
: = 0 sin : ≠ 0 u
The test st at istic value: r B − 3.67 − 0 = = ≈ 4.49 2.45 s fo √ √9 tistic
At = 0.05, the critical value(s): ta ± = = ± S = ± (,
( ,.) = ± 2 .306 ) 5
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU
Thus, at 0.05 level of significance, w e can reject since [− , ] . It means that based on the hypothesis testing we
have significant evidence to prove t he differences bet w een movie and com mercial viewing. PROBLEM I-01B:
A study is undert aken to det erm ine how consum ers react to energy conservation ef for ts. A random group of 60 families is s (Situat ion II)
chosen. Their consum pt ion of electricit y is monit ored in a period bef ore and a period af t er t he families are offered cert ain n
discount s t o reduce t heir energy consum pt ion. Bot h periods are t he same lengt h. The difference in elect ric consumpt ion tio
bet w een t he period before and t he period aft er the offer is recorded for each family. Then the average diff erence in la u
consumpt ion and t he st andard deviat ion of t he difference are comput ed. The result s are
= 0.2 kilowatt and sD = 1.0 p o
kilow at t . At = 0.01, is there evidence t o conclude that conservation effort s reduce consum ption? P o w SOLUTION:
Wit h = − f T = 60, = 0.2, = 1.0, = 0.01 o n o
We assum e t hat the population of score dif ferences is norm ally dist ribut ed. ris a p m : ≤ 0 o
: > 0 C e h
The test st at istic value: : T 8 − 0.2 − 0 = = ≈ 1.5492 r 0 1.0 te √ p √60 a
The critical-value approach: h C
At = 0.01, the critical value: = = 2.33 ss | e
Thus, at 0.01 level of significance, w e cannot reject since ∈ [−,]. It means that with the hypothesis testing we do sin
not have sufficient evidence to prove t hat conservat ion eff ort s reduce consumpt ion. u r B
The p-value approach: s fo
− = ( > 1.5492) ≈ 0.0607 tistic
Since − > , w e cannot reject since ∈ [−, ] . It means that with the hypothesis testing we do not have ta
suff icient evidence to pr ove that conservat ion effort s reduce consumpt ion. S 6
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU PART I
COM PARISON OF TW O POPULATION M EANS M ETHOD 02 s n tio
COM PARISON OF TW O POPULATION M EANS USING INDEPENDENT RANDOM SAM PLES la u p o HYPOTHESIS TESTING P
Two – tailed Test ing
Right – tailed Testing
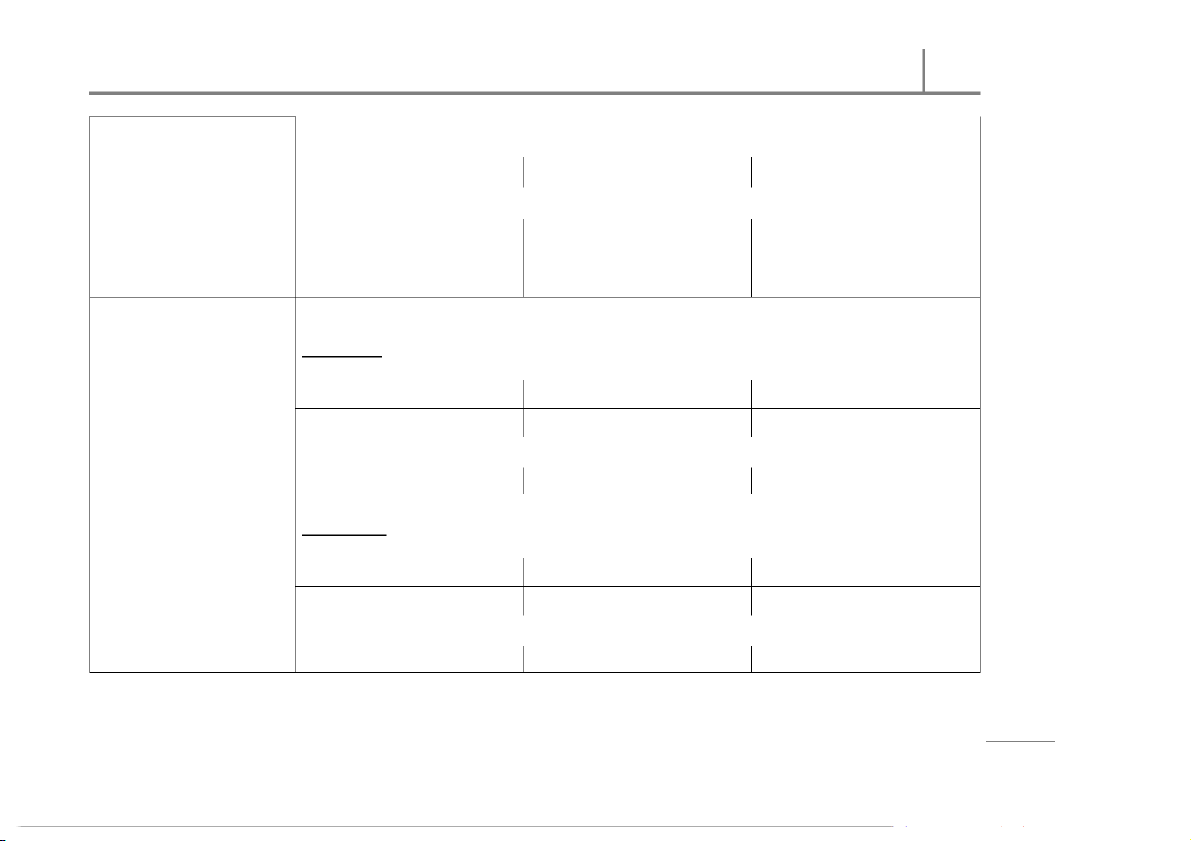
Left – tailed Test ing o PROCESS w Step 01 f T
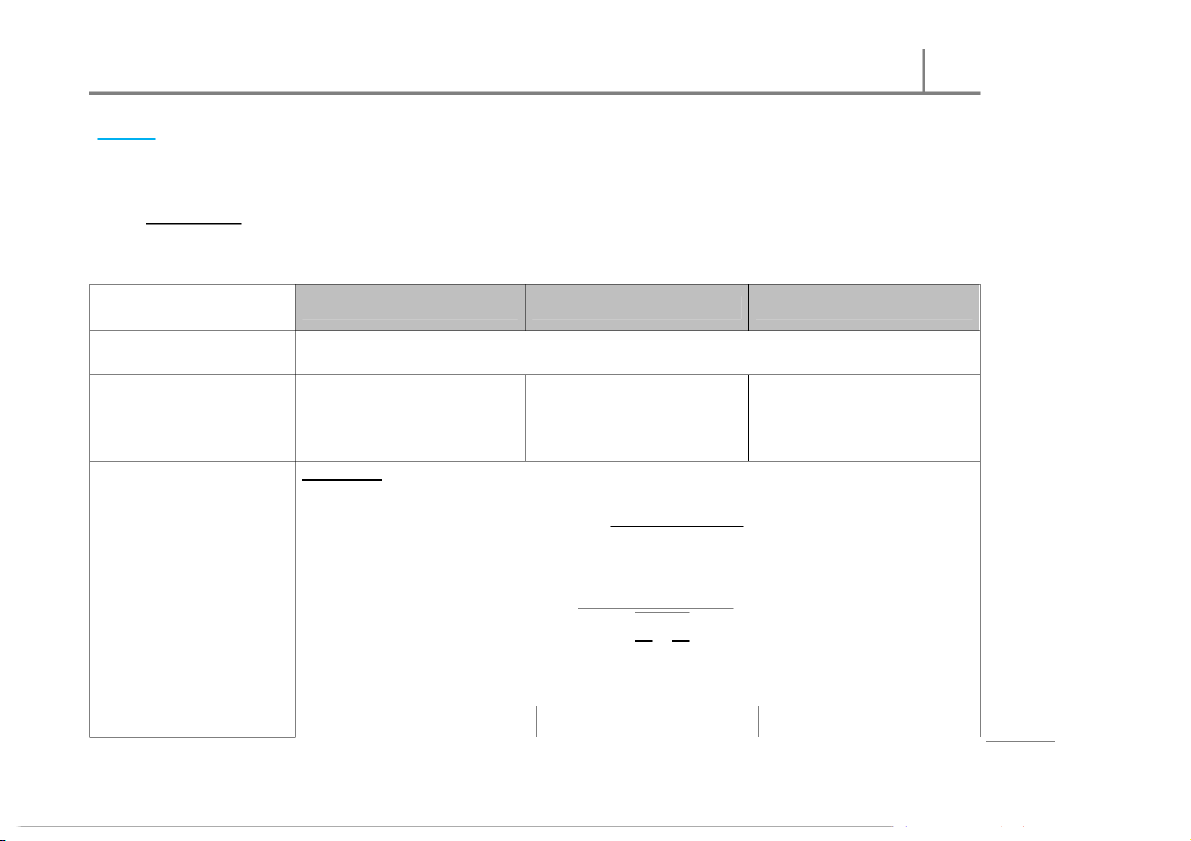
The populat ion from which the samples are select ed is/ is assumed to be normally dist ribut ed. o Conditions n o Step 02 ris a Det ermine t he null and
: − = ( − )
: − ≤ ( − )
: − ≥ ( − ) p m alt ernative hypot heses
: − ≠ ( − )
: − > ( −)
: − < ( − ) o C (and) e h Step 03 Situation I: : T 8
Calculat e t he test stat istic r 0 value.
Condition: and are known. te ) ) p
M ethod: We use and ( ⁄ + ( ⁄ a h The crit ical-value C approach: The test st atistic value: ss | Det ermine the crit ical
( − ) − ( − ) e = sin value(s). u + r B s fo
The crit ical-value approach:
At the level of significance, , t he crit ical value(s): tistic ± = ± / = = − ta S 7
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU
The -value approach: The p-value approach: Calculat e t he -value. If < 0,
− = ( < ) × 2
Note: The -value
− = ( > )
− = ( < ) If > 0,
approach is used for
− = ( > s ) × 2 n
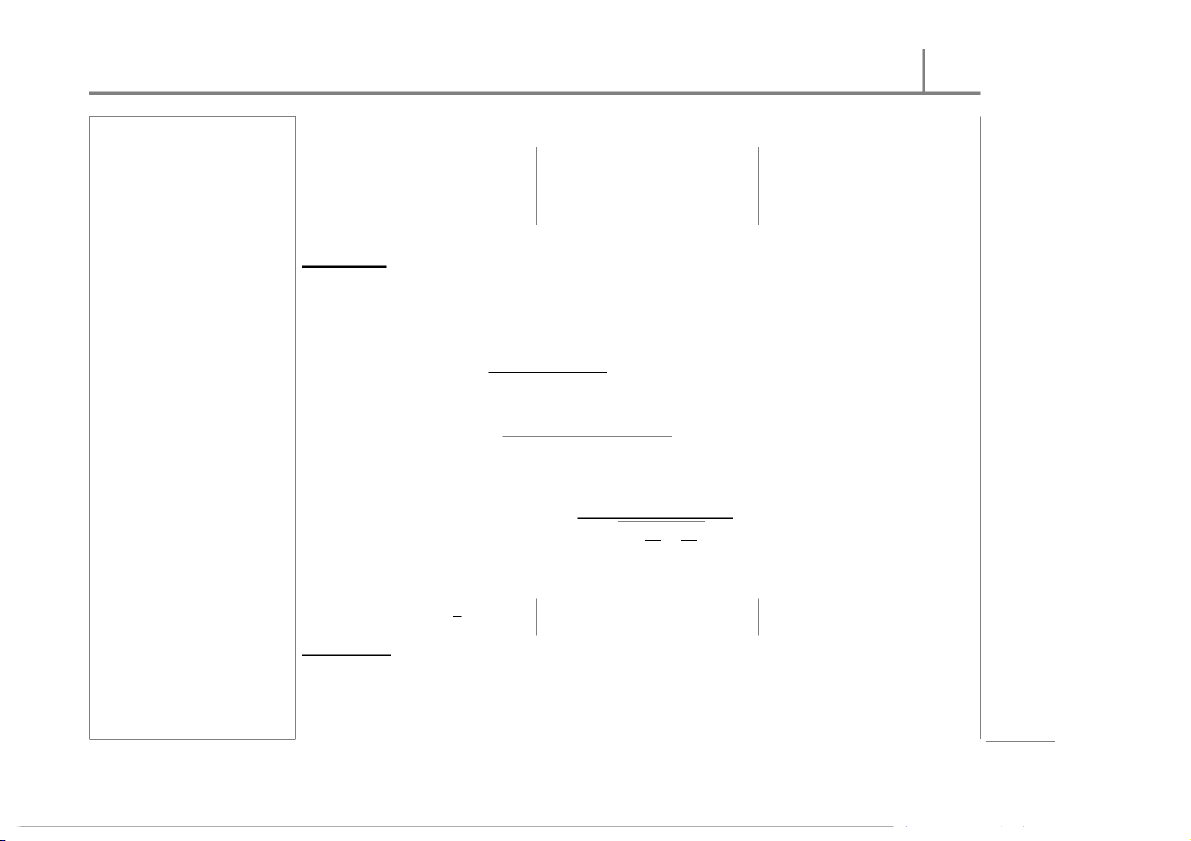
tio Situation II: la u p o Condition: P and are unknow n. o
= ( and are believed to equal (although unknown)) w f T o M ethod:
We use with = ( ) + ( − 1 1 − ) n o and (1 ⁄ + 1⁄) with ris a p ( + ( m − 1) − 1) o =
() ( ( C − 1) + − 1) e h : T The test st atistic value: 8
( − ) − ( − ) r 0 = te 1 p 1 + a h C
At the level of significance, , t he crit ical value(s): With = ( − 1) + ( − 1) , ss | e ± = ± = (,) (,) = −(,) sin u Situation III: r B s fo Condition:
and are unknown. tistic
≠ ( and are believed to unequal (although unknown)) ta S 8
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU M ethod:
We use w ith ( ⁄ ⁄ + ) = (
⁄ )/ ( − 1) + ( ⁄ )/ ( − 1) s n
and ( ⁄) + ( ⁄) tio la u The test st atistic value: p o
( − ) − ( − ) P = o w + f T o n ⁄ ⁄ o
At the level of significance, , t he crit ical values(s): With = ris
⁄ / () ⁄ / () a p m ± o = ± (, = ) (, ) = −(,) C e h : T 8 Situation IV: r 0 te p Condition:
and are unknown. a h
≥ 30and ≥ 30 (Large samples). C ss | M ethod:
We use and ( ⁄ ) + ( ⁄ ) e sin u r B The test st atistic value: s fo ( −
) − ( − ) = tistic + ta S 9
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU
The crit ical-value approach:
At the level of significance, , t he crit ical values(s): ± = ± / = = − The p-value approach: s n If < 0, tio
− = ( < ) × 2
− = ( > la )
− = ( < ) If u > 0, p o
− = ( > ) × 2 P Step 04
Wit h the level of significance ( ) o w M ake the decision f T
Situation I: We can reject when o n
The crit ical-value approach: o ris [−, ] > < a p [−, ] > < m o The p-value approach: C e h
− <
− <
− < : T 8 r 0 te
Situation II: We cannot reject when p a
The crit ical-value approach: h C
∈ [ −,] < > ss |
∈ [ −,] < > e sin The p-value approach: u r B
− >
− >
− > s fo tistic ta S 10
Pow ered by statisticsforbusinessiuba.blogspot.com
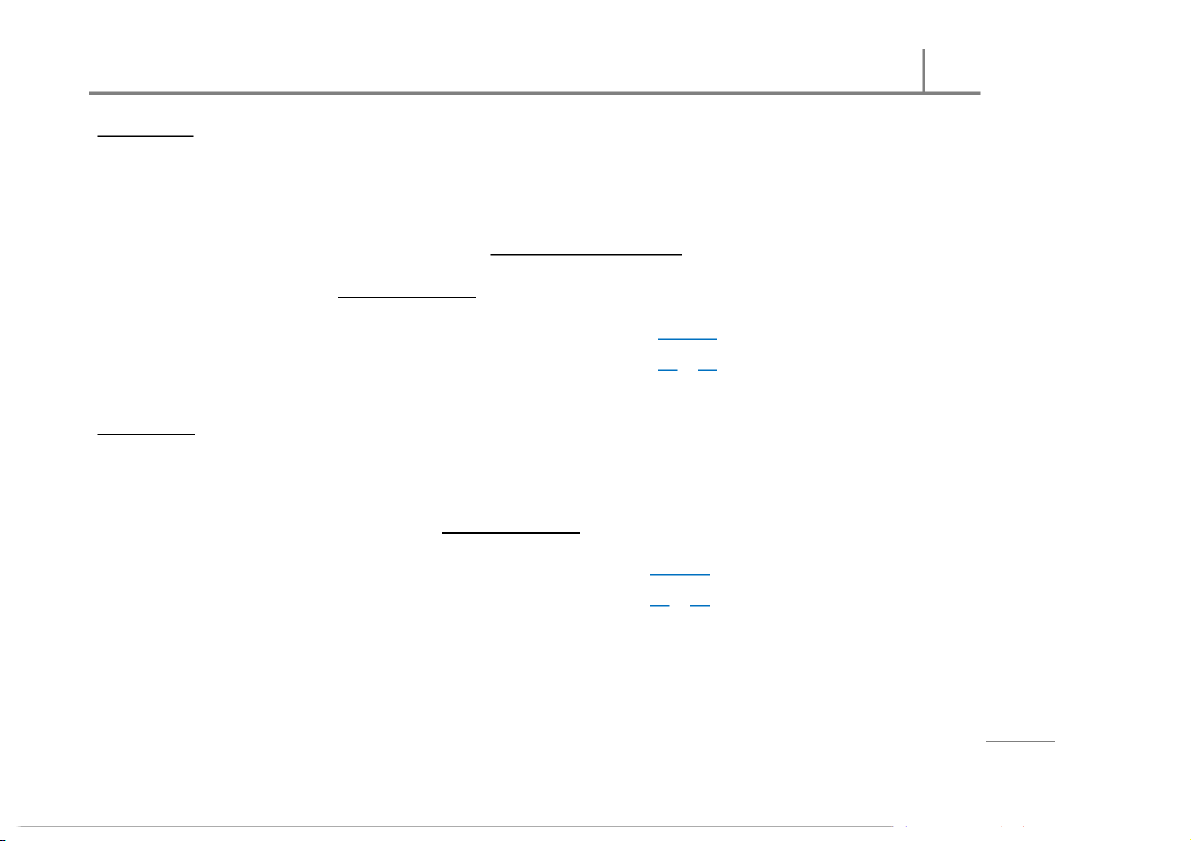
International University IU CONFIDENCE INTERVALS Situat ion I:
Condition: and are known. s n
M ethod: We use and ( ⁄ ) + ( ⁄ ) tio la u p o
( − ) = ( − ) ± / + P o w f T Situat ion II: o n o Condition: ris and are unknow n, a p m
= ( and are believed to equal (although unknown)) o C e h : T 8 M ethod:
We use with = ( − 1) + ( − 1) r 0 te p and (1 ⁄ + 1⁄) with a h C (
− 1) + ( − 1) =
() ss | ( ( e − 1) + − 1) sin u r B ( − ) = (
− ) ± ,/ + s fo tistic ta S 11
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU Situat ion III: Condition:
and are unknown.
≠ ( and are believed to unequal (although unknown)) sn 2 2 1 1+ 2 2 tio M ethod:
We use − with = 2 2 la 1 1
/ ( 1−1) 2 2 / (2−1) u p o P
And, = ( ⁄ ) + ( ⁄ ) o w f T o n
( − ) = ( − ) ± ,/ + o ris a p m Situat ion IV: o C e Condition: h
and are unknown. : T 8
≥ 30 and ≥ 30 (Large samples). r 0 te p M ethod:
We use and ) + ( ) a ( ⁄ ⁄ h C ss | e
( − ) = ( − ) ± / + sin u r B s fo tistic ta S 12
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU
Example I-02: (Case of the Comparison of Two Population M eans by using Independent Random Samples) PROBLEM I-02A:
Suppose t hat t he makers of Duracell bat t eries w ant t o dem onstrat e t hat t heir size AA bat t ery lasts an average of at least (Situation I)
45 minut es longer t han Duracell’s main compet it or, t he Energizer. Two independent random samples of 100 bat t eries of
each kind are select ed, and t he bat t eries ar e run cont inuously unt il t hey are no longer operational. The sample average
life f or Duracell is found to be s
= 308 minutes. The result for the Energizer batteries is = 254 minutes. Assume = n
84 minutes and = 67 minutes
. Is t here evidence to substant iate Dur acell’s claim t hat it s bat t eries last , on average, at tio
least 45 minut es longer than Energizer bat t eries of t he sam e size? la u p o SOLUTION: Duracell bat t eries Energizer batt eries P (1) (2) o w = 100 = 100 f T = 308 = 254 o n = 84 = 67 o
: − ≤ 45 ris a
: − > 45 p
The test st at istic value: m ( − ( 308 − 254) − 45 o
) − ( − ) = ≈ 0.8376 C = e 84 67 h + + 100 100 : T 8
The critical-value approach: r 0
At = 0.05, the critical value: te p a
= = . = 1.645 h C
Thus, at 0.05 level of significance, w e cannot reject since < . It means that with the hypothesis testing we do not ss |
have suf ficient evidence t o prove t hat Duracell bat t eries last , on average, at least 45 m inut es longer t han Energizer e
bat t eries of t he sam e size. sin u
The p-value approach: r B
− = ( > 0.8376) ≈ 0.2011 s fo
Since − > . we cannot reject . It means that with the hypothesis testing w e do not have sufficient evidence
t o prove that Duracell bat t eries last , on average, at least 45 minut es longer t han Energizer bat t eries of t he same size. tistic ta S 13
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU PROBLEM I-02B:
The pow er of supercomputers derives from t he idea of parallel processing. Engineers at Cr ay Research are int erest ed in (Situation II)
det erm ining whet her one of tw o par allel processing designs produces faster average com puting t ime, or whet her t he tw o
designs are equally fast. The follow ing are t he result s, in seconds, of independent random comput at ion t imes using t he t w o designs. Design 1 Design 2 2.1, 2.2, 1.9, 2.0, 1.8, 2.4, 2.6, 2.5, 2.0, 2.1, 2.6, 3.0, s n 2.0, 1.7, 2.3, 2.8, 1.9, 3.0,
2.3, 2.0, 2.4, 2.8, 3.1, 2.7, tio 2.5, 1.8, 2.2 2.6 la u p
Assume that the tw o populat ions of computing t ime are normally distributed a nd that t he tw o population variances o P
are equal. Is there evidence t hat one parallel processing design allow s for faster average comput at ion than t he ot her? o w f T SOLUTION: Design 1 Design 2 o (1) (2) n o = 15 = 13 ris = 2.173 = 2.515 a p = 0.375 = 0.351 m
: − = 0 o C
: − ≠ 0 e h ( + ( ( : T − 1) − 1)
15 − 1) 0.375 + (13 − 1)0.351 8 = = ≈ 0.1326
( − 1) + ( − 1) ( 15 − 1) + (13 − 1) r 0 te p
The test st at istic value: a h
( − ) − ( − ) ( 2.515 − 2.173) − 0 C = = ≈ 2.4785 1 1 1 + 0.1326 + ss | 1 15 13 e sin u
At = 0.05,with = ( − 1) + ( − 1) = (15 − 1) + (13 − 1) = 26, the critical value(s): r B ± = ± = ± ( ( , )
,.) = ± 2.056 s fo
Thus, at 0.05 level of significance, we can reject since [−,]. It means that based on the hypothesis testing we tistic
have suf ficient evidence t o prove t hat one parallel processing design allow s for faster average comput ation t han t he ta S ot her. 14
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU PROBLEM I-02C:
Air Transport W orld recent ly named t he Dut ch airline KLM “ Airline of t he Year.” One measure of t he airline’s excellent (Situation III)
managem ent is it s research effort in developing new rout es and improving service on existing rout es. The airline w anted
t o t est t he profitability of a certain transatlantic flight route and offered daily flights from Europe to the United States
over a period of 6 w eeks on t he new proposed rout e. Then, over a period of 9 w eeks, daily flights were offered from
Europe t o an alt ernat ive airport in t he Unit ed St at es. Weekly profitability data for the two samples were collected, under
t he assumpt ion t hat t hese may be view ed as independent random samples of w eekly profits from the two populations s n
(one populat ion is flights to the proposed airport , and t he ot her populat ion is flights to an alternative airport). Data are tio
as follow s. For t he proposed rout e, = $96,540 per week and
= $12,522. For the alternative route, = $85,991 and la u
= $19,548. Test the hypothesis that the proposed route is more profitable than the alternative route. Use a p o
significance level of your choice. P o w SOLUTION: Proposed Rout e Alt ernat ive Rout e (1) (2) f T o = 6 = 9 n o = 96,540 = 85,991 ris = 12,522 = 19,548 a p m
We assum e t hat tw o populat ions are normally dist ribut ed. o C
: − ≤ 0 e h
: − > 0
The test st at istic value: : T 8
( − ) − ( − ) ( 96,540 − 85,991) − 0 r 0 = = ≈ 1.2737 ( 19,548) te (12,522)+ p + 6 9 a h C ss |
At = 0.05 and e ( ⁄ + ⁄ ) ( 12,522 6 ⁄ + 19,548 9 ⁄ ) sin = = ≈ 12.9993 ≈ 12 u
( ⁄)/ ( − 1) + ( ⁄ ⁄ ⁄ )/ ( − 1) ( 12,522 6) ( 19,548 9 ) + ( 6 ( r B − 1) 9 − 1)
We have t he crit ical value: = (,) = (,.) = 1.782 s fo
Thus, at 0.05 level of significance, w e cannot reject since < . It means that with the hypothesis testing we do not tistic
have sufficient evidence to prove that t he proposed rout e is more profitable t han t he alt ernat ive rout e. ta S 15
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU PROBLEM I-02D:
The phot ography depart ment of a fashion magazine needs t o choose a cam era. Of t he t w o m odels t he depart ment is (Situation IV)
considering, one is made by Nikon and one by M inolt a. The depart ment cont ract s w it h an agency t o det ermine if one of
t he t w o models get s a higher average perfor mance rat ing by professional phot ographers, or whet her the average
perf orm ance ratings of t hese tw o cameras are not st at istically different . The agency asks 60 different professional
phot ographers t o rat e one of t he cameras (30 photographers rat e each m odel). The rat ings are on a scale of 1 t o 10. The
average sample rating for Nikon is 8.5, and t he sample standard deviat ion is 2.1. For t he M inolt a sample, t he average s n
sample rat ing is 7.8, and the st andard deviat ion is 1.8. Is t here a difference betw een t he average population r at ings of tio
t he tw o cam eras? If so, w hich one is rat ed higher? la u p o SOLUTION: Nikon M inolta P (1) (2) o w = 30 = 30 f T = 8.5 = 7 .8 o = 2 .1 = 1.8 n o ris
We assum e t hat tw o populat ions ar e norm ally dist ribut ed a p
: − = 0 m
: − ≠ 0 o
The test st at istic value: C e ( − ( 8.5 − 7.8) − 0 h
) − ( − ) = = ≈ 1.3862 : T ( 1.8) 8 (2.1) + + 30 30 r 0 te p a h
The critical-value approach: C
At = 0.05, the critical value(s): ± = ± / = ± 1.96 ss | e
Thus, at 0.05 level of significance, we cannot r eject since ∈ [−,]. It means that with the hypothesis testing we sin
do not have sufficient evidence t o prove the diff erence bet w een the average populat ion ratings of t w o cameras. u r B
The p-value approach: − = 2( > 1.3862) ≈ 0.1657 s fo
Since − > , w e cannot reject . It means that w ith the hypothesis testing w e do not have sufficient evidence tistic
t o prove the dif ference bet w een the average populat ion rat ings of t w o cameras. ta S 16
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU PART II
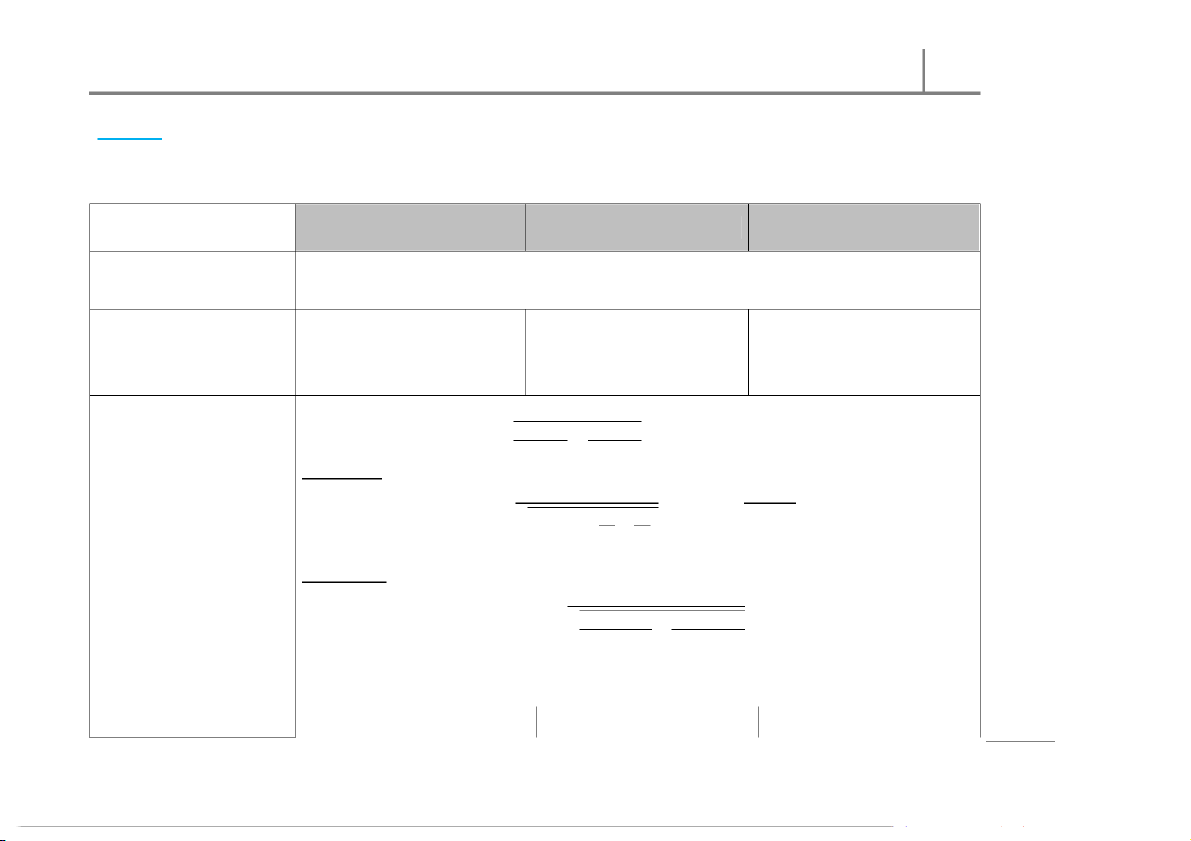
COM PARISON OF TW O POPULATION PROPORTIONS HYPOTHESIS TESTING s n
Two – tailed Test ing
Right – tailed Testing
Left – tailed Test ing PROCESS tio la
The populat ion from which the samples are selected is/ is assumed to be normally dist ribut ed. Step 01 u p o Conditions
:/ ℎ ≥ 5
≥ 5 P (1 − ) ≥ 5 ( 1 − ) ≥ 5 o Step 02 w Det ermine t he null and
: − = ( − )
: − ≤ ( − )
: − ≥ ( − ) f T o alt ernative hypot heses n
: − ≠ ( − )
: − > ( − )
: − < ( − ) o (and) ris a Step 03
In order t o perform a test of hypot hesis about the comparison of tw o populat ion proportions, p m
Calculat e t he test stat istic () o
w e use and () + C value. e h
Situation I: If ( − ) = 0, the test statistic value: : T The crit ical-value ( − 8 ) − 0 + = ℎ = r 0 approach: 1 + ( 1 ) + te − 1 Det ermine the crit ical p a h value(s). C
Situation II: If ( − ) = , the test statistic value: ss | The
( − ) − e -value approach: = sin Calculat e t he -value.
(1 − ) + (1 − ) u r B
Note: The -value s fo
The crit ical-value approach: approach is used for
At the level of significance, , t he crit ical value(s): tistic = ± / = = − ta S 17
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU The p-value approach: If < 0,
− = ( < ) × 2
− = ( > )
− = ( < ) If > 0,
− = ( > s ) × 2 n Step 04
Wit h the level of significance ( ), tio M ake the decision
Situation I: We can reject la w hen u
The crit ical-value approach: p o [ −,] > < P o w The p-value approach: f T o
− <
− <
− < n o
Situation II: We cannot reject when ris a
The crit ical-value approach: p m ∈ [−,] < > o C The p-value approach: e h : T
− >
− >
− > 8 r 0 te p a h CONFIDENCE INTERVALS C ss | () e
For all instances, w e alw ays use − / and = () + sin u r B
Situation I: If ( − ) = 0, s fo + tistic
( − ) = ( − ) ±
/ ( − ) + = ta + S 18
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU
Situation II: If ( − ) = , ( − ) ( − ) ( − ) = (
− ) ± + / sn
Example II: (Case of the Comparison of Tw o Population Proportions) tio la u p PROBLEM 01:
A physicians’ group is int erest ed in t esting t o det ermine w het her more people in small t ow ns choose a physician by word of o
mout h in comparison wit h people in large met ropolit an ar eas. A random sam ple of 1,000 people in small t ow ns reveals t hat P (Situat ion I) o
850 chose their physicians by w ord of mout h; a random sample of 2,500 people living in large met ropolit an areas reveals t hat w
1,950 chose a physician by w ord of mout h. Conduct a one-tailed t est aimed at proving t hat t he percent age of popular f T
recommendat ion of physicians is larger in small tow ns t han in large met ropolitan ar eas. Use = 0.01. o n o ris SOLUTION: Small Towns
Large met ropolit an areas a (1) (2) p m = 850 = 1,950 o C = 1,000 = 2,500 e h : T
:/ ℎ ≥ 5 ≥ 5 8 (1 − ) ≥ 5 (1 − ) ≥ 5 r 0 te p
: − ≤ 0 a h
: − > 0 C We have: ss | + 850 + 1,950 4 e = = = = 0.8 + 1,000 + 2,500 5 sin u r B
The test st at istic value: s fo ( − ( ) − ) − 0 0.85 − 0.78 0 = = ≈ 4.6771 tistic 1 1 ( 1 − ) 1 +
0.8(1 − 0.8) 1 + ta 1,000 2,500 S 19
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU
The critical- value approach:
At = 0.01, the critical value: = = . = 2.33
Thus, at 0.01 level of significance, w e can reject since < . It means that based on the hypothesis testing we have
suff icient evidence to prove t hat the percent age of popular recom mendation of physicians is larger t han in small t ow ns rather
t han in large met ropolit an areas. s n tio
The p-value approach: − = ( > 4.6771) ≈ 1.4566 × 10 la u p
Since − < , we can reject o
. It means that based on the hypothesis testing we have sufficient evidence to prove P
t hat t he percent age of popular recommendat ion of physicians is larger t han in small t owns rat her t han in large m et ropolit an o areas. w f T o PROBLEM 02:
A random sam ple of 2,060 consum ers show s t hat 13% pr efer California w ines. Over t he next t hr ee m ont hs, an advert ising n o (Situat ion II)
campaign is undert aken t o show that California w ines receive aw ards and win t ast e t est s. The organizers of t he cam paign ris
w ant t o prove t hat t he t hree-mont h campaign raised t he proport ion of people w ho prefer California w ines by at least 5%. At a p
t he end of t he campaign, a random sam ple of 5,000 consumers show s that 19% of t hem now prefer California w ines. Conduct m o
t he test at = 0.05. C e h SOLUTION: Before campaign Aft er cam paign : T (1) (2) 8 r 0 = 0.13 = 0.19 te = 2,060 = 5,000 p a h C
:/ ℎ ≥ 5
≥ 5 (1 − ) ≥ 5 (1 − ) ≥ 5 ss | e
: − ≤ 0.05 sin u
: − > 0.05 r B s fo
The test st at istic value: ( − ( ) − ) − 0.19 − 0.13 0.05 = = ≈ 1.0803 tistic (1 −) 0.13 ( 1 − 0.13) ta (1 − ) + 0.19(1 − 0.19) + S 5,000 2,060 20
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU
The critical- value approach:
At = 0.05, the critical value: = = . = 1.645( = 0.5 − 0.05 = 0.45 )
Thus, at 0.05 level of significance, w e cannot reject since > . It means that there is no evidence that the three-month
campaign raised t he proport ion of people w ho pr efer California w ines by at least 5%. s n
The p-value approach: tio
− = ( > 1.0803) ≈ 0.14 la u p o
Since − > , we cannot reject . It means that there is no evidence that the three-month campaign raised the P
proport ion of people who prefer California wines by at least 5%. o w f T o n PART III o ris a p
COM PARISON OF TW O POPULATION VARIANCES m o C e HYPOTHESIS TESTING h
Two – tailed Test ing
Right – tailed Testing : T PROCESS 8 Step 01 r 0
The populat ion from which the samples are selected is/ is assumed to be normally distribut ed. te Condition. p a Step 02 h = ≤ C Det ermine t he null and : : ss | alt ernative hypot heses : ≠ : > e (and) sin u Step 03 r B
Comput e t he test st at ist ic In order to perform a test of hypothesis about the comparison of two population variances, s fo
value(s) ( ) and the we use − . crit ical value(s) ( ) tistic ta S 21
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU The test st at ist ic = < ) = < ) value(s) ( ( ( ) () ( ) The crit ical value(s) = ( ) ( , ) ( = ( )
(,) s ) n tio Step 04
Wit h the level of significance ( la ), u p M ake the decision. o P
Situation I: We can reject when o > > w ( ) () () () f T o n o
Situation II: We cannot reject when ris < < a ( ) () () () p m o C e h
Example III: (Case of the Comparison of Two Population Variances) : T 8 r 0 PROBLEM :
The f ollow ing dat a are independent random samples of sales of t he Nissan Pulsar m odel made in a joint vent ure of Nissan te
and Alfa Romeo. The dat a represent sales at dealerships bef ore and aft er t he announcement t hat t he Pulsar m odel w ill no p a
longer be made in It aly. Sales num bers are monthly. h C
Before: 329, 234, 423, 328, 400, 399, 326, 452, 541, 680, 456, 220 ss | e
Aft er: 212, 630, 276, 112, 872, 788, 345, 544, 110, 129, 776 sin u
Do you believe t hat t he variance of t he number of car s sold per m ont h before t he announcement is equal to t he variance of r B
t he number of cars sold per mont h aft er t he announcement ? s fo tistic ta S 22
Pow ered by statisticsforbusinessiuba.blogspot.com
International University IU SOLUTION: Before Aft er (1) (2) = 12 = 11 = 128.03 = 294.70 = 16 ,384 = 86,849.09 s n
We assum e t hat tw o populat ions ar e norm ally dist ribut ed tio
: = la u ≠ p : o
The test st at istic value: P o 86,849.09 w = ≈ 5.3 ( ) = 16,384 f T
At = 0.05, the critical value o n = (
) = ( ,) = 3.53 o ( ) , ris a
Thus, at 0.05 level of significance, w e can reject p
since > . It means that based on the hypothesis testing we ( ) () m
have suf ficient evidence to prove t hat t he variance of t he number of cars sold per month before t he announcement is o C
differ ent from t he variance of t he number of cars sold per mont h af t er t he announcement . e h : T 8 r 0 te p a h C ss | e sin u r B s fo tistic ----- THE END ------ ta S 23
Pow ered by statisticsforbusinessiuba.blogspot.com