Công thức tính đường chéo hình thoi kèm bài tập ví dụ

Công thức tính đường chéo hình thoi kèm bài tập ví dụ
1. Giới thiệu về hình thoi
Hình thoi là một tứ giác đặc biệt có tất cả các cạnh bằng nhau. Điều này có
nghĩa là bốn cạnh của hình thoi đều có độ dài như nhau.
Đặc điểm cơ bản của hình thoi:
- Bốn cạnh bằng nhau: Đây là đặc điểm dễ nhận biết nhất của hình thoi.
- Hai đường chéo vuông góc: Hai đường chéo của hình thoi cắt nhau tại trung
điểm của mỗi đường và chúng vuông góc với nhau, tạo thành bốn góc vuông.
- Các góc đối bằng nhau: Giống như hình bình hành, các góc đối diện nhau
trong hình thoi có số đo bằng nhau.
- Các đường chéo là đường phân giác của các góc: Mỗi đường chéo của
hình thoi chia đôi các góc mà nó đi qua.
Ứng dụng của hình thoi trong thực tế
Hình thoi xuất hiện rất nhiều trong cuộc sống hàng ngày của chúng ta, đôi khi
bạn không để ý. Dưới đây là một số ví dụ:
- Biển báo giao thông: Nhiều biển báo có hình thoi để thu hút sự chú ý của người tham gia giao thông.
- Ô cửa sổ: Một số ô cửa sổ có hình thoi tạo nên vẻ đẹp độc đáo cho ngôi nhà.
- Hoa văn trang trí: Hình thoi thường được sử dụng để tạo ra các hoa văn
trang trí trên quần áo, vải, giấy dán tường,...
- Kim cương: Mặt cắt của một viên kim cương thường có hình dạng giống hình thoi.
- Cánh diều: Cánh diều truyền thống thường có hình dạng hình thoi.
- Các loại gạch lát nền: Nhiều loại gạch lát nền có hình dạng hình thoi.
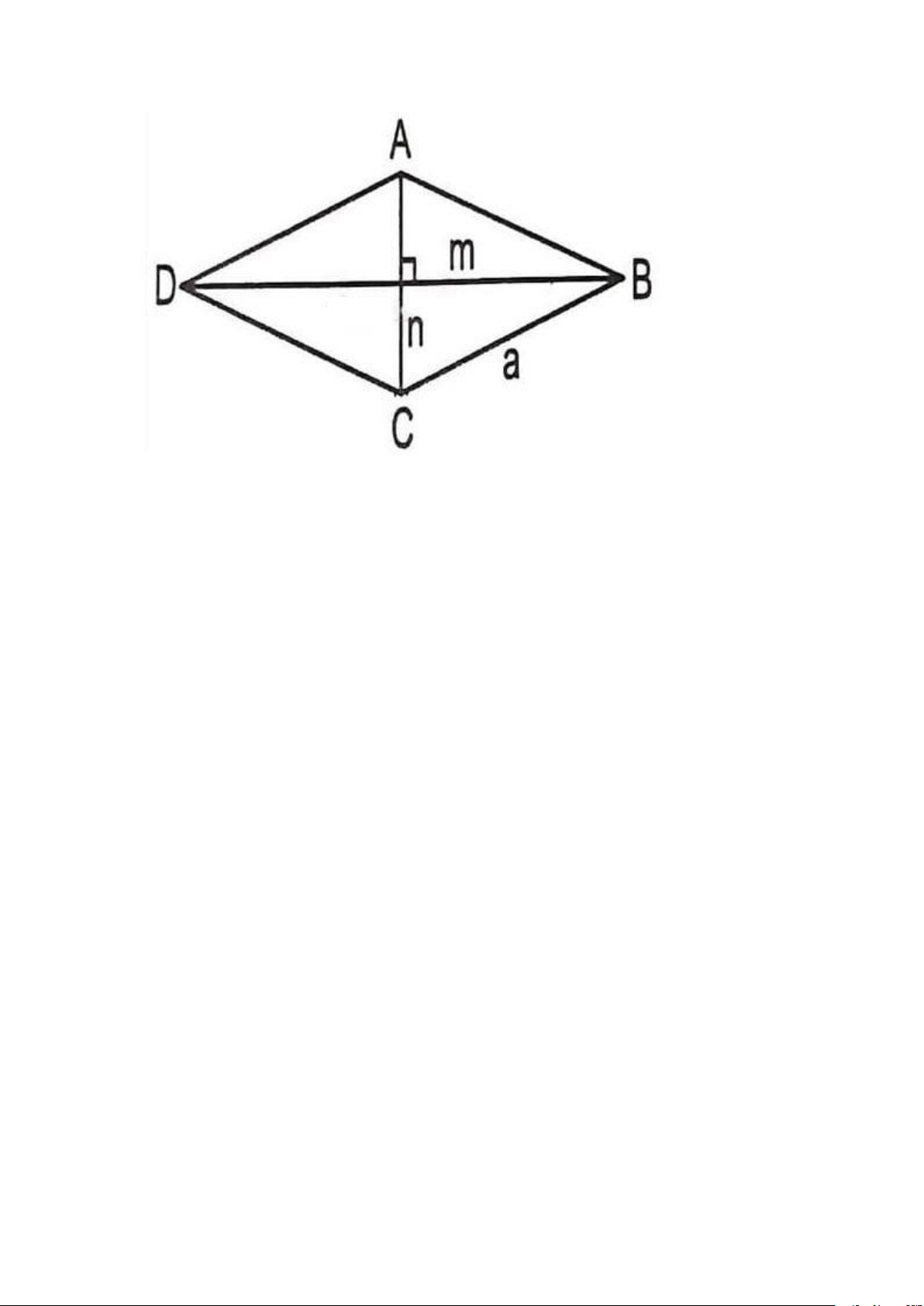
2. Công thức tính đường chéo hình thoi
Giả sử ta cần tính độ dài đường chéo hình thoi ABCD có cạnh a và một góc
ABC = 60 độ -> công thức tính đường chéo hình thoi trong trường hợp này như thế nào? Lời giải:
Vì ABCD là hình thoi nên các cạnh đều bằng a.
Xét tam giác ABC có: AB = BC = a
Lại có: ABC = 60 độ => Tam giác ABC là tam giác đều cạnh a. => AB = AC = BC = a
=> Độ dài đường chéo hình thoi chính là AC = BD = a.
Cách giải trên là một trong những công thức tính đường chéo hình thoi đơn giản và dễ hiểu nhất.
Công thức tính đường chéo hình thoi khi biết diện tích và đường chéo còn lại
Từ công thức tính diện tích hình thoi: S = (a x b) : 2
Ta có công thức độ dài đường chéo như sau : a = S x 2 : b hoặc b = S x 2 : a Trong đó: S là diện tích
a và b là độ dài 2 đường chéo 3. Bài tập ví dụ
Bài 1: Cho một hình thoi có diện tích là 360 cm vuông, độ dài một đường
chéo là 24 cm . Tính độ dài đường chéo thứ hai Lời giải :
Theo công thức diện tích hình thoi: a x b : 2
Ta có đường chéo thứ 2: 360 x 2 : 24 = 30cm Đáp án: 30cm
Bài 2: Hai đường chéo của hình thoi có độ dài là 160cm và 120 cm. Tính
chiều cao của hình thoi, biết tỉ số giữa chiều cao và độ dài cạnh hình thoi là 24:25. Lời giải:
Diện tích hình thoi là: 160.120:2 = 9 600 (cm2).
Vì tỉ số giữa chiều cao và độ dài cạnh hình thoi là 24:25 nên có thể coi chiều
cao hình thoi là 24a và cạnh hình thoi là 25a.
Khi đó ta có diện tích hình thoi là: 25a.24a = 9 600 a2 = 16 a = 4 cm.
Chiều cao của hình thoi là: 24.4 = 96 (cm).
Vậy chiều cao của hình thoi là 96cm.
Bài 3: Hình thoi ABCD có cạnh bằng 10 đơn vị. Tính độ dài đường chéo của hình thoi.
Giải: Độ dài đường chéo của hình thoi ABCD là:
Đường chéo = căn bậc hai của 2(10²) = căn bậc hai của 200 = 14.14 đơn vị độ dài.
Vậy độ dài đường chéo của hình thoi ABCD là 14.14 đơn vị độ dài.
Bài 4:Hình thoi ABCD có đường chéo bằng 12 đơn vị. Tính chu vi của hình thoi.
Giải: Vì hình thoi có bốn cạnh bằng nhau, chu vi của nó sẽ là tổng độ dài bốn cạnh, tức là:
Chu vi = 4 x độ dài cạnh = 4 x 6 = 24 đơn vị độ dài.
Vậy chu vi của hình thoi ABCD là 24 đơn vị độ dài Bài tập tự luyện tập Bài 1.
a) Cho hình thoi ABCD có hai đường cao AH, AK. Chứng minh AH = AK.
b) Cho hình bình hành ABCD có hai đường cao AH, AK bằng nhau. Chứng minh ABCD là hình thoi.
Bài 2. Hình thoi ABCD có góc A = 90 độ. Kẻ hai đường cao BE, BF. Tam giác
BEF là tam giác gì? Vì sao?
Bài 3. Cho tam giác ABC, phân giác AD. Qua D kẻ đường thẳng song song
với AC cắt AB tại E, qua D kẻ đường thẳng song song với AB cắt AC tại F.
Chứng minh EF là phân giác của góc AED.
Bài 4. Cho hình chữ nhật ABCD. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA.
a) EFGH là hình gì? Vì sao?
b) Chứng minh AC, BD, EG, FH đồng quy.
Bài 5. Cho tam giác ABC cân tại A, trung tuyến AM. Qua M kẻ đường thẳng
song song với AC cắt AB tại P và đường thẳng song song với AB cắt AC tại Q.
a) Tứ giác APMQ là hình gì? Vì sao? b) Chứng minh PQ // BC.
Bài 6. Cho hình bình hành ABCD. Trên các cạnh AB và CD lần lượt lấy các
điểm M và N sao cho AM = DN. Đường trung trực của BM lần lượt cắt các
đường thẳng MN và BC tại E và F.
a) Chứng minh E và F đối xứng nhau qua AB;
b) Chứng minh tứ giác MEBF là hình thoi;
c) Hình bình hành ABCD có thêm điều kiện gì để tứ giác BCNE là hình thang cân.
Bài 7. Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Gọi E, F, G,
H lần lượt là chân các đường vuông góc kẻ từ O đến AB, BC, CD, DA. Tứ
giác EFGH là hình gì? Vì sao?
Bài 8. Hình thoi ABCD có góc A = 60 độ. Trên cạnh AD lấy điểm M, trên cạnh
DC lấy điểm N sao cho AM = DN. Tam giác BMN là tam giác gì? Vì sao?
Bài 9. Dựng hình thoi ABCD biết cạnh bằng 2cm, một đường chéo bằng 3cm.
Bài 10. Cho tam giác ABC. Lấy các điểm D, E theo thứ tự trên các cạnh AB,
AC sao cho BD = CE. Gọi M, N, I, K theo thứ tự là trung điểm của BE, CD,
DE, BC. Chứng minh IK ⊥ MN .
Bài 11. Cho tam giác ABC nhọn, các đường cao BD, CE. Tia phân giác của
các góc ABD và ACE cắt nhau tại O và lần lượt cắt AC, BD tại N, M. Tia BN
cắt CE tại K, tia CM cắt BD tại H. Chứng minh: a) BN ⊥ CM ;
b) Tứ giác MNHK là hình thoi.
Bài 12. Cho tứ giác ABCD có AD = BC. Gọi I, J lần lượt là trung điểm của các
cạnh AB và CD; K, H theo thứ tự là trung điểm của hai đường chéo AC và BD. Chứng minh rằng: IJ ⊥ HK
Bài 13. Cho hình bình hành ABCD có AB = 2BC. Gọi M, N lần lượt là trung điểm của AB và CD.
a) Chứng minh tứ giác AMND là hình thoi.
b) Gọi E là giao điểm của AN và DM; F là giao điểm của BN và MC. Tứ
giác MENF là hình gì? Vì sao?
Bài 14. Cho hình thoi ABCD có AB = AC.
Kẻ AE ⊥ BC ( E ∈ BC); AF ⊥ CD (F ∈ CD). a) Chứng minh ΔAEF đều.
b) Biết AB = 4cm. Tính độ dài các đường chéo của hình thoi.
Bài 15. Cho tam giác ABC có ba góc nhọn, các đường cao AD, BE. Tia phân
giác của góc DAC cắt BE, BC theo thứ tự tại I và K. Tia phân giác của góc
EBC cắt AB, AC tại M và N. Chứng minh tứ giác MINK là hình thoi.
Bài 16. Cho hình bình hành ABCD, các đường chéo cắt nhau tại O. Gọi E, F,
G, H theo thứ tự là giao điểm của các đường phân giác của các tam giác
AOB, BOC, COD, DOA. Chứng minh EFGH là hình thoi.
Bài 17. Cho tam giác ABC, qua điểm D thuộc cạnh BC, kẻ các đường thẳng
song song với AB, AC cắt AC, AB theo thứ tự tại E và F.
a) Tứ giác AEDF là hình gì?
b) Điểm D ở vị trí nào trên BC thì AEDF là hình thoi?
Câu 18: Tính diện tích hình thoi có độ dài đường chéo là 14cm và 10cm.
Câu 19: Hình thoi có độ dài các đường chéo là 18dm và 5m. Diện tích hình
thoi đó bằng bao nhiêu đề-xi-mét vuông?
Câu 20: Một hình thoi có diện tích 4dm, độ dài một đường chéo là 3/5 dm.
Tính độ dài đường chéo thứ hai.
Câu 21: Một khu đất hình thoi có độ dài các đường chéo là 70m và 300m.
Tính diện tích khu đất đó.
Câu 22: Một hình thoi có diện tích 4dm2, độ dài một đường chéo là 3/5 dm.
Tính độ dài đường chéo thứ hai.
Document Outline

• Công thức tính đường chéo hình thoi kèm bài tập ví
  • 1. Giới thiệu về hình thoi
  • 2. Công thức tính đường chéo hình thoi
  • 3. Bài tập ví dụ