Công thức tính momen lực và bài tập có đáp án - Vật lý lớp 10

Công thức tính momen lực và bài tập có đáp án - Vật lý lớp 10 1. Momen lực là gì?
Moment lực là một khái niệm quan trọng trong vật lý và cơ học, liên quan đến
sự quay quanh một điểm hoặc một trục của một vật thể. Moment lực thể hiện
sự ảnh hưởng của lực đối với sự quay của vật thể, và nó liên quan đến cả lực
và cách lực được áp dụng.
Khi một vật có trục quay cố định nằm trong trạng thái cân bằng, quy tắc
momen lực cho chúng ta biết rằng tổng của các momen lực tạo ra sự xoay
cùng chiều kim đồng hồ phải cân bằng với tổng các momen lực tạo ra sự
xoay ngược chiều kim đồng hồ. Điều này có nghĩa là lực và khoảng cách từ
trục quay đến lực cần phải cân bằng với các lực và khoảng cách tương ứng ở hướng ngược chiều.
Tuy nhiên, quy tắc này vẫn áp dụng vào trường hợp vật không có trục quay
cố định. Khi vật không xuất hiện trục quay hoặc không bị ràng buộc bởi một
trục quay cố định, quy tắc momen lực vẫn giúp chúng ta hiểu rằng tổng
momen lực tạo ra xu hướng xoay của vật phải cân bằng với tổng momen lực
tạo ra xu hướng xoay ngược chiều. Điều này đảm bảo rằng vật duy trì trạng
thái cân bằng và không xoay theo một hướng cụ thể, dù trục quay có tồn tại
hay không. Như vậy, quy tắc momen lực không chỉ là một khía cạnh quan
trọng của cân bằng và chuyển động trong vật lý mà còn áp dụng rộng rãi
trong nhiều tình huống, bao gồm cả khi không có trục quay cố định.
2. Công thức tính momen lực
Momen lực là một trong những khái niệm quan trọng trong lĩnh vực vật lý, nó
là đại lượng mô tả tác động gây ra sự quay của một vật thể. Để hiểu rõ hơn
về momen lực, chúng ta cần xem xét cách tính toán nó và tại sao nó có tầm
quan trọng đặc biệt. Nói một cách đơn giản, momen lực (thường được ký
hiệu là M) được tính bằng cách nhân giữa lực tác động (F) và cánh tay đòn
(d). Cánh tay đòn chính là khoảng cách từ trục quay của vật thể đến điểm mà
lực tác động lên. Kết quả được đo bằng đơn vị N·m (Newton-mét), tức là một
Newton áp dụng lên một cánh tay đòn dài một mét.
Công thức momen lực: M = F * d Trong đó:
+ M là momen lực, đo lường bằng N·m.
+ F là giá trị của lực tác động lên vật thể, đo lường bằng N (Newton).
+ d là cánh tay đòn, tức khoảng cách từ trục quay đến điểm tác động của lực, đo lường bằng mét.
Một ví dụ cụ thể có thể giúp bạn hình dung sự áp dụng của momen lực. Khi
bạn cố gắng mở cửa sổ bằng cánh cửa sổ (lực tác động), cánh tay đòn là
khoảng cách từ bản lề cửa (trục quay) đến tay cửa. Điều này tạo ra momen
lực, nó cần phải được cân bằng với các yếu tố khác để mở cửa một cách dễ
dàng. Như vậy, momen lực là một khái niệm quan trọng giúp chúng ta hiểu và
dự đoán sự quay của các vật thể trong vật lý và cơ học, và nó có ứng dụng
rộng rãi trong thế giới thực.
3. Bài tập về momen lực và đáp án
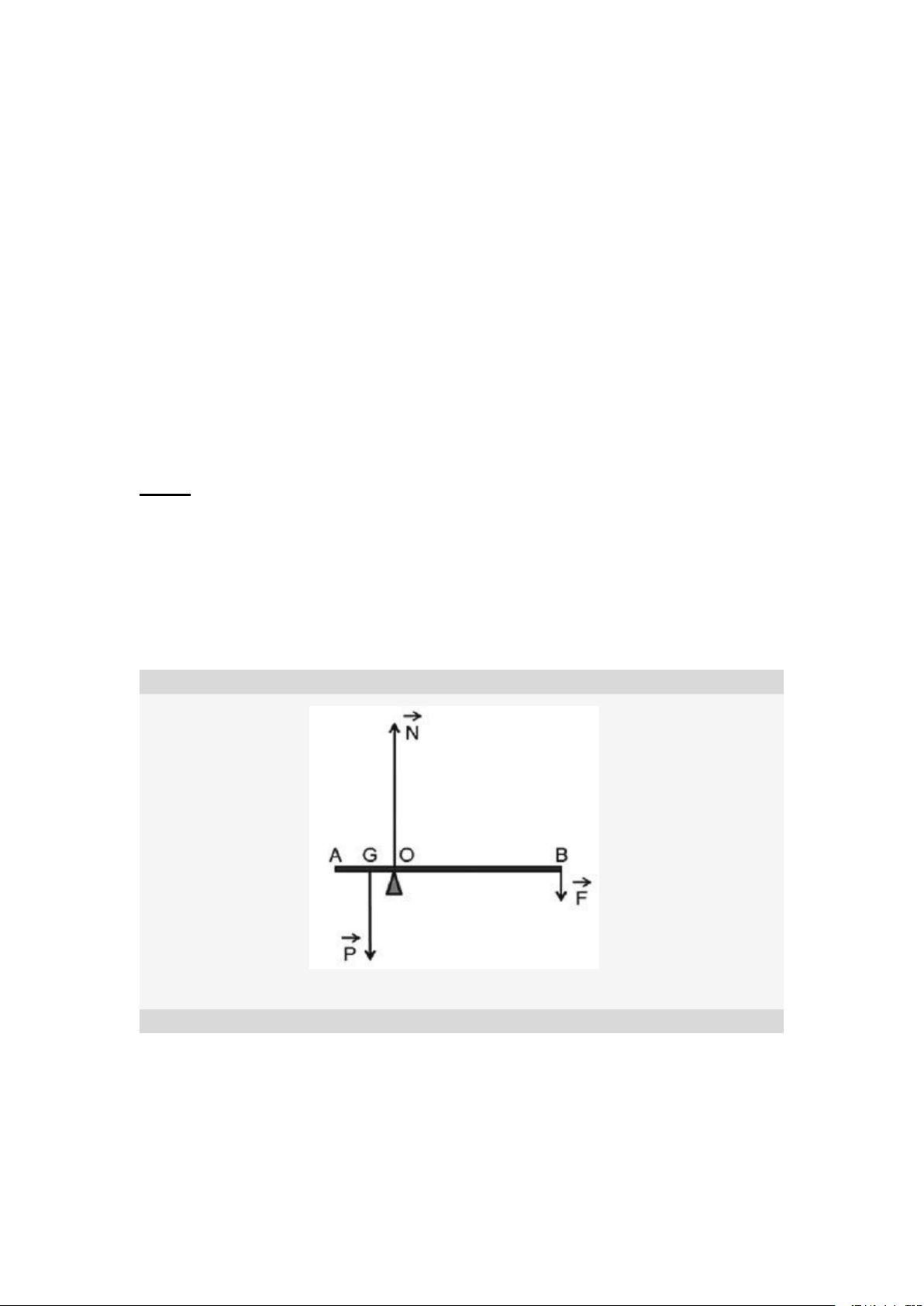
Câu 1:Thanh sắt AB có khối lượng 50 kg, chiều dài 15 m có trọng tâm tại G,
biết chiều dài GA=2,4 m. Thanh AB có thể quay quanh trục đi qua O, biết
chiều dài OA= 3 m. Khi ta tác động lực lên đầu B, trục quay sẽ tạo ra một lực
tác dụng lên thanh. Chúng ta cũng cần biết giá trị của lực tác động này. Vậy,
lực cần tác động lên đầu B để giữ cho thanh nằm ngang là bao nhiêu và lực
tác động của trục quay lên thanh sẽ có giá trị là bao nhiêu? Ta sẽ lấy g= 20 m/s2. Ta có:
GA= 2,4 m; m= 50 kg, AB=15 m, OA= 3 m; g= 20 m/s2
Trục quay đi qua điểm O vậy thanh nằm cân bằng Momen lực của G = Momen lực của B Cách giải:
MG = MB => mg.GO=F.OB => F=25 N. N=P + F= 525 N.
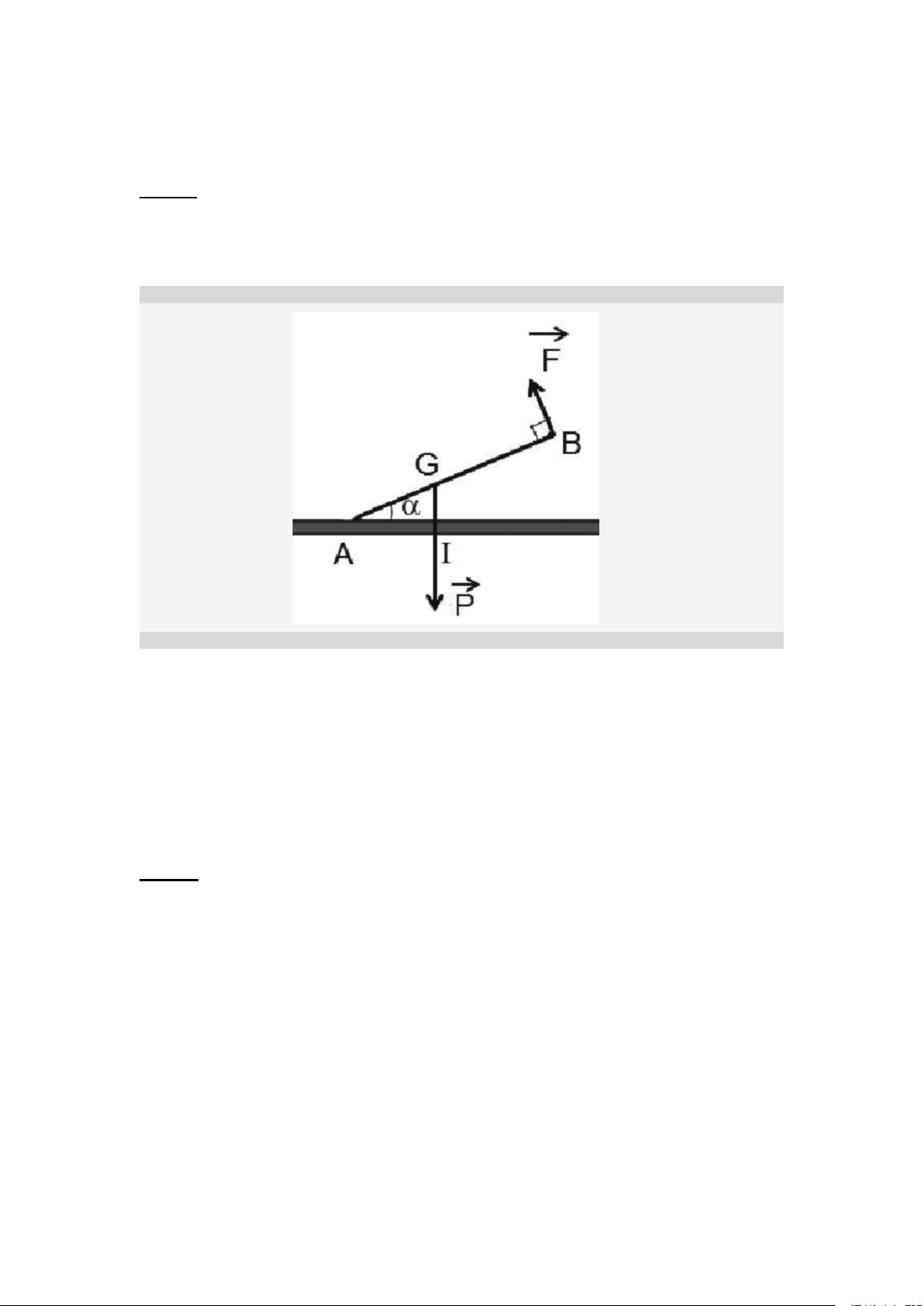
Câu 2: Một người đang nâng một khối sắt có khối lượng là 60kg và chiều dài
là 3m. Lực nâng vuông góc với khối sắt và giữ nó một góc α=60 độ so với
mặt đất. Biết rằng trọng tâm của khối sắt nằm cách đầu đầu của người đó
nâng là 240 cm. Tính lực nâng của người đó đang thực hiện. Ta có: m=60kg; AB=3m; α=60o; GB=2,4m
Cánh tay đòn của lực F: AB=3m
Cánh tay đòn của trọng lực P: AI=AGcosα Cách giải:
Xét trục quay đi qua A, ta có:
MP =MF => P.AGcosα=F.AB => F= ... N.
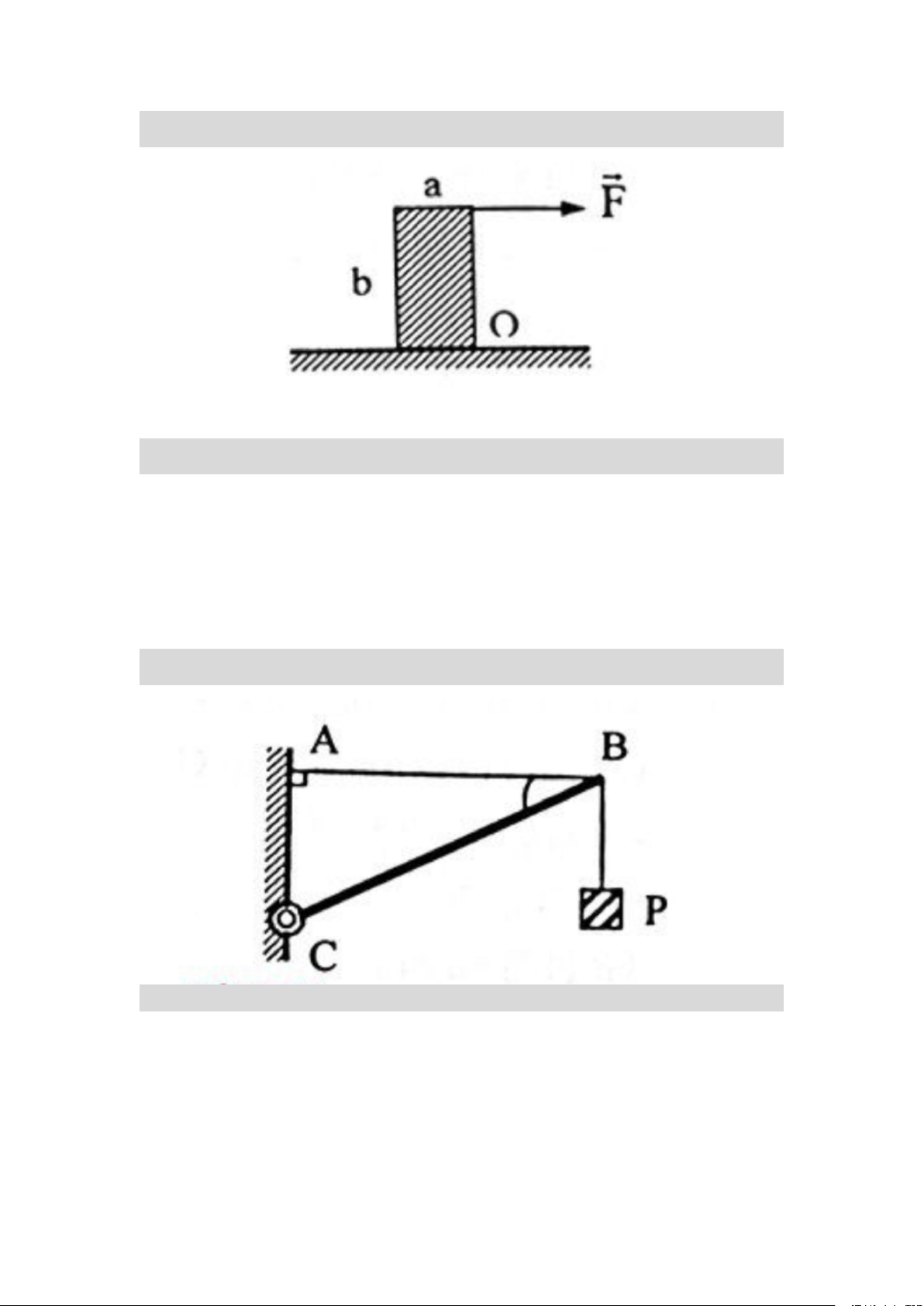
Câu 3: Để làm quay vật được hình hộp cùng một chất, cần có lực F là bao
nhiêu? Cho biết m = 20kg quay quanh tâm O. Chiều rộng hình hộp là a =
100cm, chiều dài hình hộp là b = 200cm.
Để hình hộp có thể quay quanh trục đi qua điểm O thì MF > MP
=> F.b > P.a/2 => F > P.a/2b = 50N
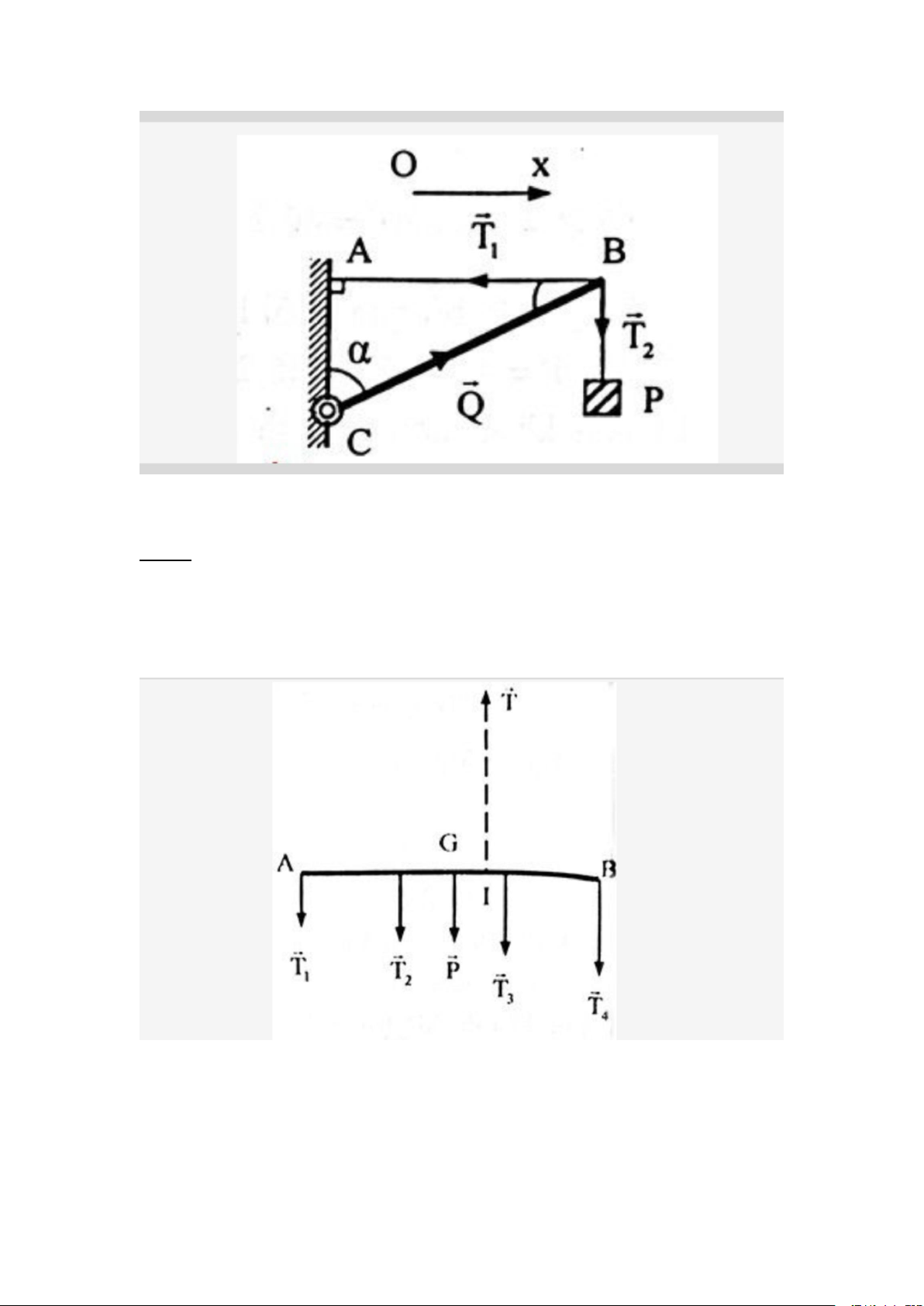
Câu 4: Cho một thanh đồng BC được gắn vào tường với bản lề C, đầu B treo
một chiếc túi có khối lượng m = 8kg và được giữ cân bằng nhờ dây treo AB.
Biết rằng, dây treo AB = 60cm, đoạn AC = 80cm. Xác định những lực nào tác dụng lên đoạn BC?
Theo thông tin từ đầu bài, ta áp dụng quy tắc momen đối với trục quay qua C như sau:
MT1 = MT2 => T1AC = T2AB => T1 = T2.AB/AC = mg.AB/AC = 60N Q = T1/sinα = T1.BC/AB = 100N
Câu 5: Treo bốn quả tạ trên một thanh sắt dài 6cm nằng 12kg, khoảng cách
giữa các quả tạ là bằng nhau. Trong đó có hai quả tạ treo ngoài cùng nằm ở
hai đầu thanh như hình vẽ. m1 = 4kg; mỗi quả tạ tiếp theo có khối lượng theo
thứ tự hơn vật trước 2kg. Cần phải treo các quả tạ trên thanh tại các điểm
nào, cách đầu trái một khoảng bao nhiêu để thanh sắt nằm cân bằng. Cách giải:
Gọi I là điểm treo quả tạ và đảm bảo thanh sắt nằm cân bằng.
Khi thanh sắt nằm cân bằng ta có: MP1 + MP2 + MP = MP3 + MP4
P1.AI + P2.CI + P.GI = P3.DI + P4.BI
4. Ứng dụng của momen lực
Momen lực là một khái niệm quan trọng có nhiều ứng dụng thực tế, giúp
người dùng thực hiện các nhiệm vụ hàng ngày một cách hiệu quả và dễ dàng
hơn. Momen lực là một khái niệm quan trọng và có ứng dụng rộng rãi trong
nhiều khía cạnh của cuộc sống và công nghiệp, giúp tối ưu hóa thiết kế, hiệu
suất và an toàn trong nhiều lĩnh vực khác nhau.
Tay nắm cửa: Momen lực làm cho việc mở và đóng cửa dễ dàng hơn, đặc
biệt là khi bạn cần áp dụng một lực nhỏ để tạo ra momen lực lớn và xoay cửa
mà không cần phải áp dụng một lực lớn trực tiếp lên cửa. Cánh tay đòn dài
hơn của tay nắm cửa tạo ra một momen lực lớn hơn, giúp bạn mở cửa dễ dàng hơn.
Cờ lê: Cờ lê là một công cụ được thiết kế dựa trên nguyên tắc của momen
lực. Khi bạn áp dụng một lực nhỏ ở một đầu cờ lê, nó tạo ra một momen lực
lớn ở đầu còn lại, giúp bạn tháo hoặc lắp đặt các ốc vít, đai ốc và bất kỳ phần
nào có độ khó trong việc vặn chặt hoặc nới lỏng chúng.
Mômen lực được sử dụng để kiểm tra độ bền của các công trình. Ví dụ, để
tính toán độ bền của một cây cầu, cần phải tính toán momen lực tác dụng lên
cây cầu do trọng lượng của cầu và trọng tải của các phương tiện qua lại.
Mômen lực được sử dụng để tính toán lực cần thiết để quay một vật thể. Ví
dụ, để nâng một vật nặng bằng cần cẩu, cần phải tính toán lực cần thiết để
tạo ra momen lực đủ lớn để thắng trọng lực của vật. Có thể được sử dụng để
thiết kế các chi tiết máy như trục, bánh răng,... Các chi tiết máy này phải chịu
được momen lực tác dụng lên chúng trong quá trình hoạt động.
Trong thiết kế cơ cấu của robot, momen lực được sử dụng để xác định cơ
cấu và cấu trúc cần thiết để tối ưu hóa hiệu suất và đáng tin cậy của robot.
Điều này đặc biệt quan trọng khi robot phải xử lý các vật thể nặng hoặc cần
độ chính xác cao. Momen lực là quan trọng để thiết kế và điều khiển cánh tay
robot. Các động cơ và ổ đĩa trong cánh tay robot tạo ra moment lực để làm
cho robot di chuyển và thực hiện các tác vụ như cắt, hàn, hay lắp ráp sản
phẩm. Trong quá trình điều khiển chuyển động của robot, momen lực được
sử dụng để đảm bảo rằng robot thực hiện các tác vụ một cách chính xác và
an toàn. Các hệ thống điều khiển sẽ tính toán và kiểm soát momen lực để
đảm bảo rằng robot không gây hỏng hoặc nguy hiểm cho môi trường xung quanh.
Document Outline

• Công thức tính momen lực và bài tập có đáp án - Vậ
  • 1. Momen lực là gì?
  • 2. Công thức tính momen lực
  • 3. Bài tập về momen lực và đáp án
  • 4. Ứng dụng của momen lực