CÔNG THỨC TÍNH NHANH DIỆN TÍCH PARABOL
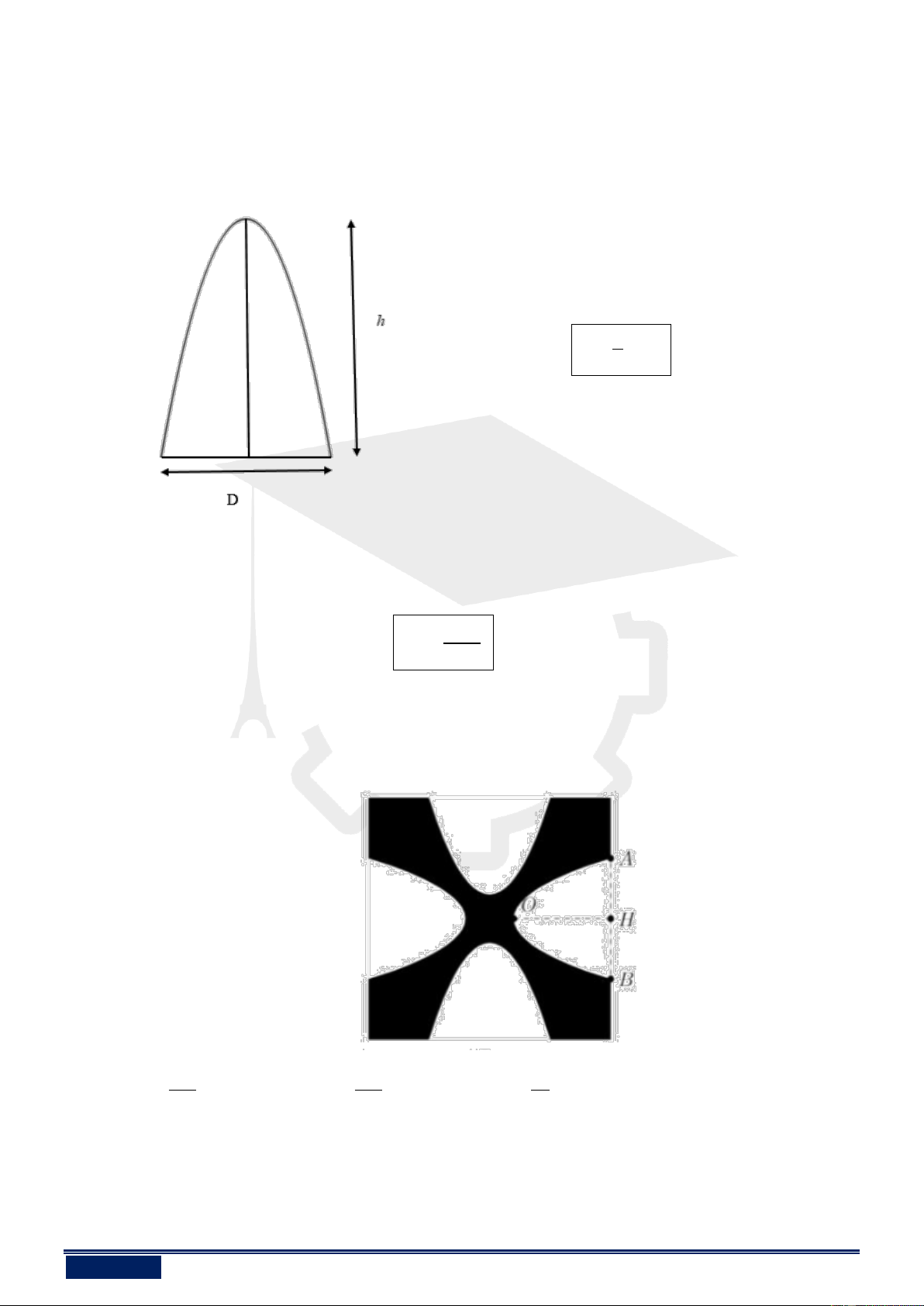
Công thức 1: Cho Parabol có phương trình 2
y = ax + bx + c và có đồ thị như hình vẽ:
Khi đó diện tích Parabol được tính theo công thức: 2 S = . . h D 3
Công thức 2: Cho Parabol có phương trình 2
y = ax + bx + c , khi đó diện tích hình phẳng bởi Parabol và trục hoành với 2
b − 4ac  0 được tính theo công thức: 3  2 S = 4 36a
Ví dụ 1: Một hoa văn trang trí được tạo ra từ một tấm bìa mỏng hình vuông cạnh bằng 10cm bằng cách
khoét đi bốn phần bằng nhau có hình dạng parabol như hình bên. Biết AB = 5c ,
m . OH = 4cm Tính diện
tích bề mặt hoa văn đó. 140 160 14 A. 2 cm B. 2 cm C. 2 cm D. 2 50cm 3 3 3 Lời giải Chọn A
Diện tích hình vuông bằng: 2 2 S = 10 = 100cm hv
Tài liệu KYS Education is the Key to Your Success 1 2 160
Diện tích 4 hình Parabol bằng: 2
S = 4. .OH.AB = cm P 3 3 140
Vậy diện tích hoa văn bằng: 2
S = S − S = cm hv P 3
Ví dụ 2: Một chiếc cổng bách khoa Hà Nội có hình dạng là Parabol, chiều rộng 8m , chiều cao 12,5m .
Diện tích của cổng là: 100 200 A. 2 100m B. 2 200m C. 2 m D. 2 m 3 3 Lời giải Chọn D 2 2 200
Áp dụng công thức tính diện tích Parabol ta được: 2 S = . . h D = .8.12, 5 = m 3 3 3
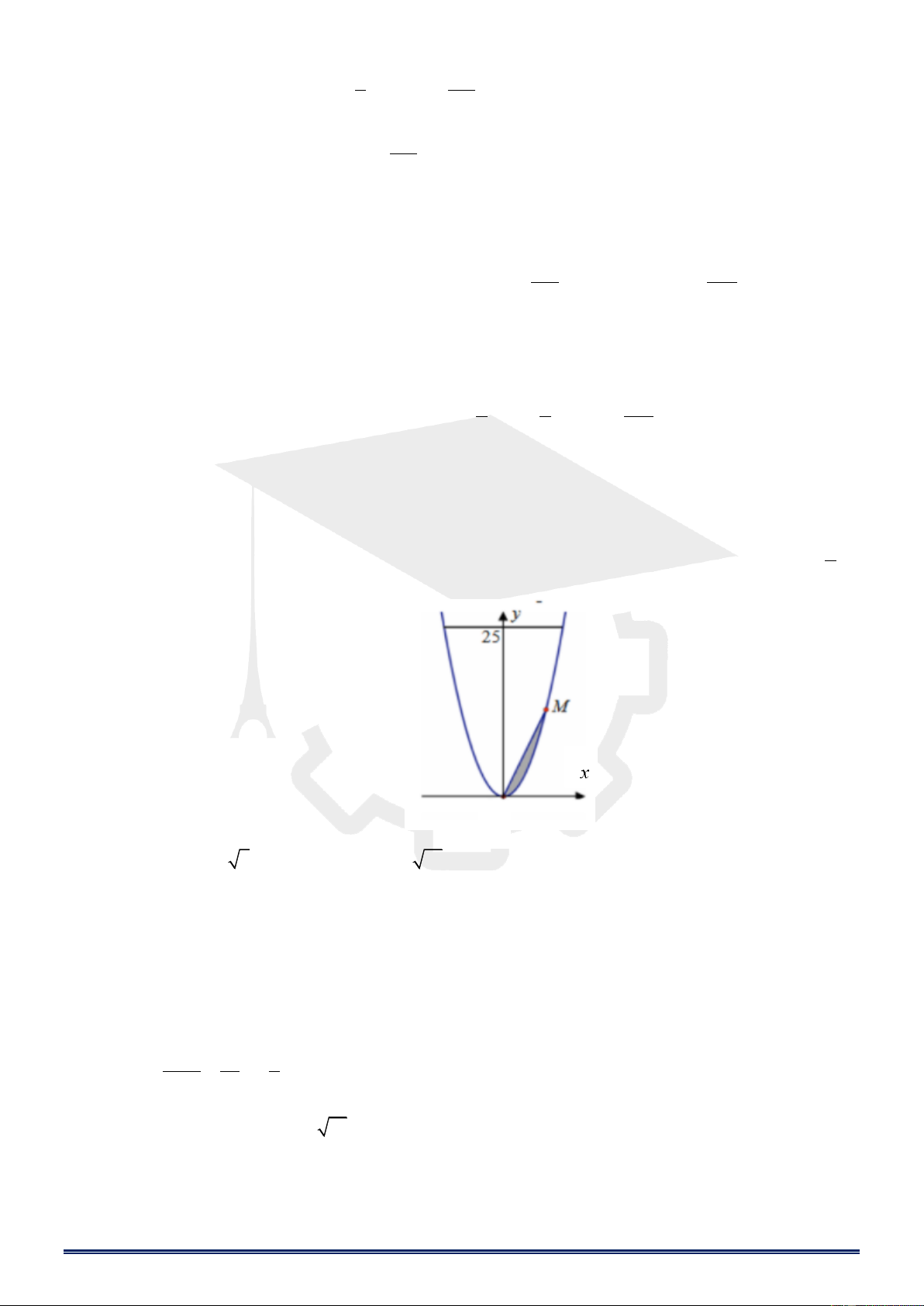
Ví dụ 3: Ông B có một khu vườn giới hạn bởi đường Parabol và một đường thẳng. Nếu đặt trong hệ tọa
độ Oxy như hình bên thì Parabol có phương trình 2
y = x và đường thẳng y = 25. Ông B đang dự định
dùng một mảnh vườn nhỏ được chia từ khu vườn bởi đường thẳng đi qua O và điểm M trên Parabol để 9
trồng hoa. Hãy giúp ông B xác định điểm M bằng cách tính độ dài OM để diện tích vườn nhỏ bằng 2 O
A. OM = 2 5
B. OM = 3 10
C. OM =15
D. OM =10 Lời giải Chọn B
Đường thẳng đi qua O nên có dạng y = kx Ta có: 2 2
x = kx  x − kx = 0 2 3 6    Do đó: k 9 2 S = = =  k = 3    4 36a 36  2  Khi đó M ( 3
 ;9) , suy ra OM = 3 10
Giáo viên: Đặng Mơ 2
Một số bài tập áp dụng Câu 1:
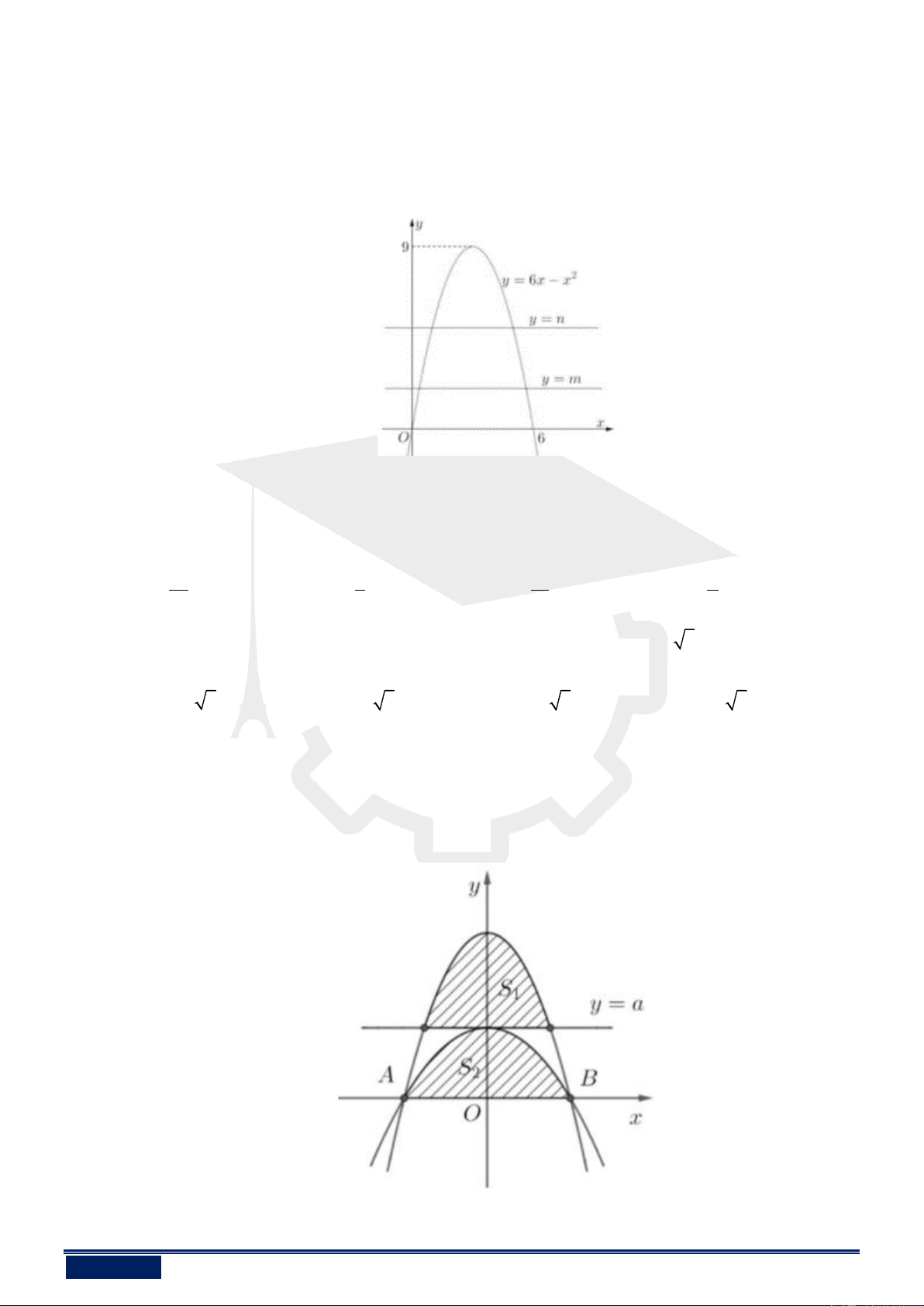
Gọi (H ) là diện tích hình phẳng giới hạn bởi Parabol 2
y = 6x − x . Các đường thẳng y = , m
y = n (0  m  n  6) . Gọi (H ) thành ba phần có diện tích bằng nhau như hình vẽ. Tính 3 3 T = (9 − ) m + (9 − ) n
A. T = 405
B. T = 407
C. T = 409
D. T = 403 Câu 2:
Với m là tham số thực thay đổi, hỏi diện tích hình phẳng giới hạn bởi Parabol 2 y = x +1 và
đường thẳng y = mx + 2 nhỏ nhất là? 64 8 16 4 A. B. C. D. 9 3 3 3 Câu 3: Xét hai điểm ,
A B phân biệt trên Parabol 2 ( )
P : y = x sao cho AB = 6 3 . Giá trị lớn nhất của
diện tích hình phẳng giới hạn bởi ( )
P và đường thẳng AB bằng A. 108 3 B. 48 3 C. 96 3 D. 72 3 Câu 4: Cho Parabol 2
(P ) : y = −x + 4 cắt trục hoành tại hai điểm phân biệt ,
A B và đường thẳng 1
d : y = a(0  a  4) . Xét Parabol (P ) có đỉnh thuộc đường thẳng d và đi qua hai điểm , A B . 2
Gọi S là diện tích hình phẳng giới hạn bởi (P ) và đường thẳng d ; (S ) là diện tích giới hạn 1 1 2
bởi (P ) và trục hoành. Biết rằng S = S . Giá trị của 3 2
a − 8a + 48a bằng 2 1 2 A. 96 B. 64 C. 72 D. 32
Tài liệu KYS Education is the Key to Your Success 3 Câu 5:
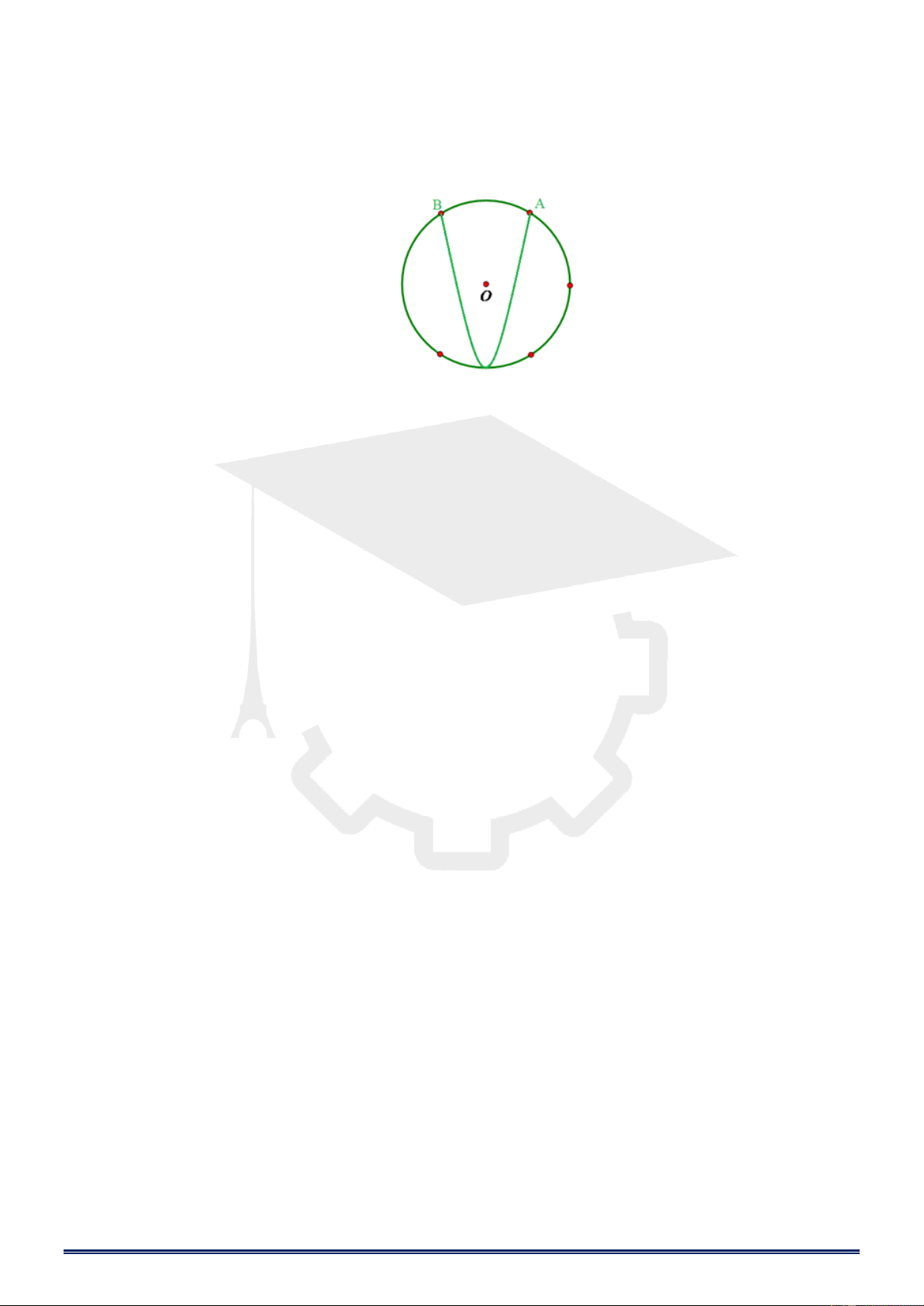
Bạn Dũng xây một bể cá hình tròn tâm 4 bán kính 3 và chia nó thành 2 phần như hình vẽ sau.
Bạn Dũng sẽ thả cá cảnh với mật độ 4 con cá cảnh trên S.ABCD ở phần bể giới hạn bởi đường
tròn tâm O và Parabol có trục đối xứng đi qua tâm O và chứa tâm O. Gọi S là phần nguyên của
diện tích phần thả cá. Hỏi bạn Dũng thả được bao nhiêu con cá cảnh trên phần bể có diện tích S,
biết ABCD và 2a ? A. 560 B. 650 C. 460 D. 640
Giáo viên: Đặng Mơ 4