CÔNG THỨC XÁC SUẤT THỐNG KÊ Y HỌC PHẦN I: XÁC SUẤT
1. Giải tích tổ hợp a. Hoán vị: Pn = n! b. Chỉnh hợp lặp: 𝐹" ! = n#
c. Chỉnh hợp không lặp:
𝐴"! = 𝑛(𝑛 − 1) … (𝑛 − 𝑘 + 1) = !! (!%")! d. Tổ hợp không lặp: 𝐶" ! – " ! = !! = 𝐶 "!(! – ")! ! (! ) " – +)! e. Tổ hợp lặp: 𝐶 ( " ((( " ! = 𝐶!)"*+ = "!(! – +)!
2. Các công thức tính xác suất !
a. Định nghĩa xác suất theo cổ điển: P(A) = ! !" b. Tính chất:
- 0 ≤ P(A) ≤ 1 P(F) = 0 P(W) = 1 - P(A .) = 1 - P(A)
- Công thức cộng xác suất:
• Trường hợp 2 biến cố bất kỳ:
P(A È B) = P(A) + P(B) - P(AB)
• Trường hợp n biến cố xung khắc từng đôi:
P(A1 A2… An) = P(A1) + P(A2) +…+ P(An)
c. Xác suất có điều kiện và định lý nhân xác suất "($%) "($%)
- Công thức xác suất có điều kiện: P(A\B) = P(B\A) = "(%) "($)
- Định lý nhân xác suất:
• Cho n biến cố bất kỳ:
P(A1 A2… An) = P(A1).P(A2\A1)…P(An\A1A2…An - 1)
d. Công thức xác suất đầy đủ và công thức Bayès
- Công thức xác suất đầy đủ: P(A) = ∑! P(A ()*
')P(A\A') = P(A1).P(A\A1) + P(A2).P(A\A2) +…+ P(An).P(A\An) 1 - Công thức Bayès
P(Ak \A) = ,(-!).,(-\-!) = ,(-!).,(-\-!) ∑# ,(- "$% "),(-\-") ,(-)
e. Tính độc lập của biến cố và công thức Bernoulli
- Công thức xác suất đầy đủ:
P(A1A2…An) = P(A1).P(A2)…P(An). - Công thức Bernoulli:
• Xác suất để biến cố A xuất hiện đúng k lần trong n phép thử với P(A) = p và q = 1 – p là P #
n (k ; p) = C1 . pk (1 - p) n – k
3. Biến ngẫu nhiên
a. Phân phối xác suất của biến ngẫu nhiên
- Bảng phân phối xác suất: mô tả luật phân phối của biến ngẫu nhiên rời rạc X X1 X2 … Xn P P1 P2 … Pn
- Hàm phân phối xác suất: F(x) = P (X < x) 0 khi x ≤ x ⎧ 1 ⎪ 𝑝* khi x1 < x ≤ x2 𝑝 F(x) = * + 𝑝+ khi x2 < x ≤ x3 ⎨ … …
⎪𝑝* + 𝑝+ + ⋯ + 𝑝 !%* ⎩
khi xn - 1 < x ≤ xn 1 khi x > xn
- Hàm mật độ xác suất của biến ngẫu nhiên liên lục:
• Hàm số p(x) xác định trên R được gọi là hàm mật độ xác suất của biến ngẫu nhiên liên lục X nếu: p(x) ≥ 0 với " x Î R P (X < x) = ∫- p(t)dt với " x Î R %-
• Với biến ngẫu nhiên liên lục X có hàm mật độ p và hàm phân phối là F thì:
F(x) = P (X < x) = ∫- p(t)dt với " x Î R %-
P(a < X < b) = P(a ≤ X ≤ b) = P(a ≤ X < b) = P(a < X ≤ b) = ∫. p(x)dx = F(b) – F(a) /
b. Các số đặc trưng của biến ngẫu nhiên 2
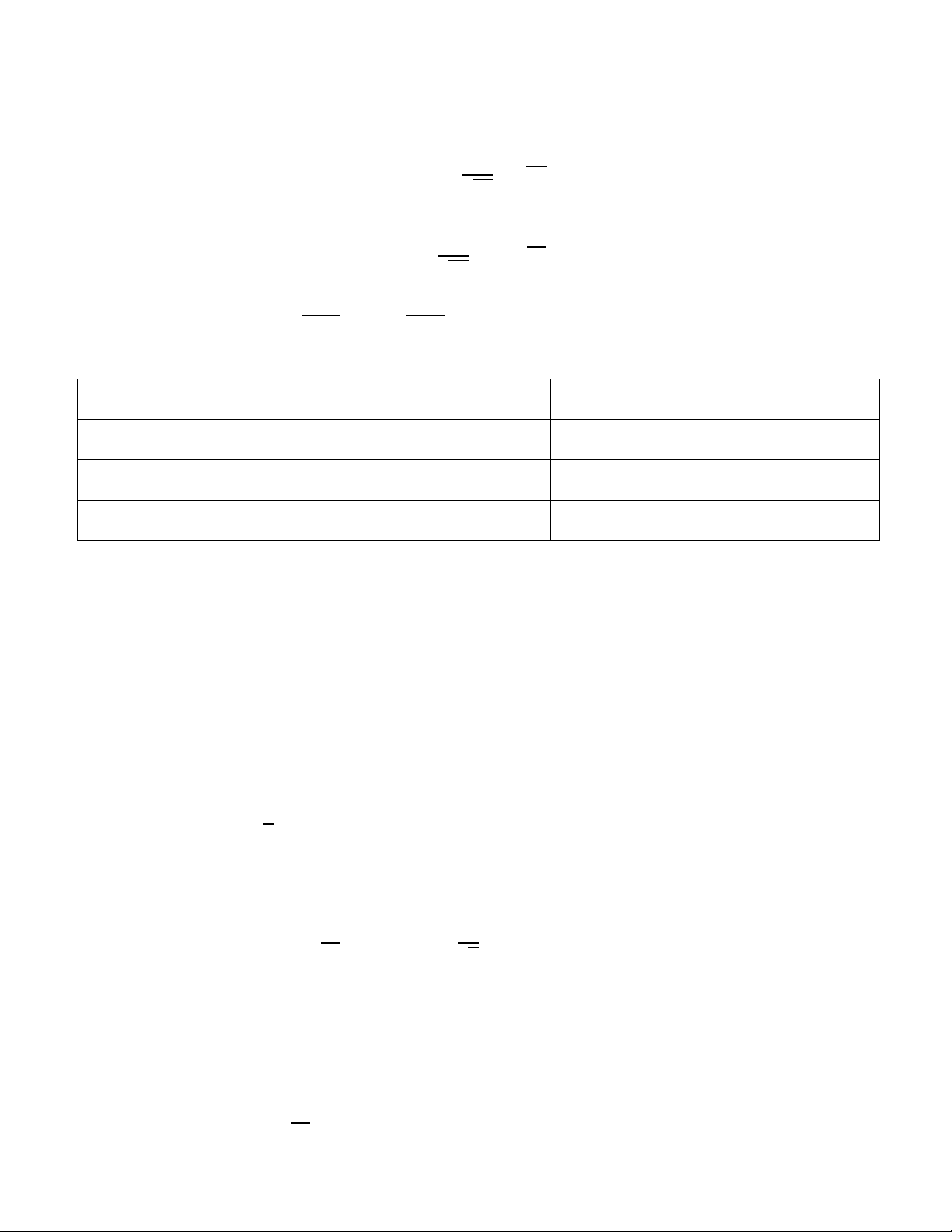
Phân loại Biến ngẫu nhiên rời rạc
Biến ngẫu nhiên liên tục Các số đặc trưng Kì vọng E(X) 01 E(X) = ∑1 𝑥 23+ 2𝑝2 E(X) =∫ x. p(x)dx %1 01 Phương sai V(X) = 𝜎5 1 5 4 V(X) = ∑ 𝑥 23+ 6 𝑝2 – [E(X)]2 V(X) = ∫ 𝑥+p(x)dx – [E(X)]2 %1 Độ lệch chuẩn 𝜎4 = .V(X)
4. Phân phối xác suất thường gặp
a. Phân phối không – một A(p) - Khái niệm: P(X = x) = px .q1 – x - Các số đặc trưng • E(X) = p E(X2) = p • V(X) = p.q 𝜎 = Bp. q
b. Phân phối Nhị thức B(n:p) - Khái niệm: P(X = x) = C#1 p k .q n – k - Các số đặc trưng • E(X) = n.p • V(X) = n.p.q 𝜎 = Bn. p. q
c. Phân phối Poisson P(𝜆) - Khái niệm: P(X = k) = 7! . e*8 k = 0; 1; …; n λ > 0 #!
- Hàm phân phối xác suất: F(x) = ∑ 7! "9 4 . e*8 #! - Các số đặc trưng • E(X) = n.p = λ • V(X) = λ 𝜎 = √λ
d. Phân phối Chuẩn N (𝜇, 𝜎5)
- Hàm mật độ xác suất: + p(x) = . e* (( – *), ,-, :.√2π
- Hàm phân phối xác suất: + 4 F(x) = ∫ e* (. – *), ,-, 𝑑𝑡 :.√2π *4 3
- Khi 𝜇 = 0 và 𝜎 =1, phân phối chuẩn N (0,1) được gọi là phân phối Chuẩn chuẩn tắc
• Hàm mật độ xác suất: 𝜑 + (x) = . e* (, , √5π
• Hàm phân phối xác suất: 𝜑 + 4 (x) = ∫ e* ., , 𝑑𝑡 √5π *4
• P(a ≤ X ≤ b) = 𝜑 ;< *= < − 𝜑 ;> *= < : : - Các số đặc trưng
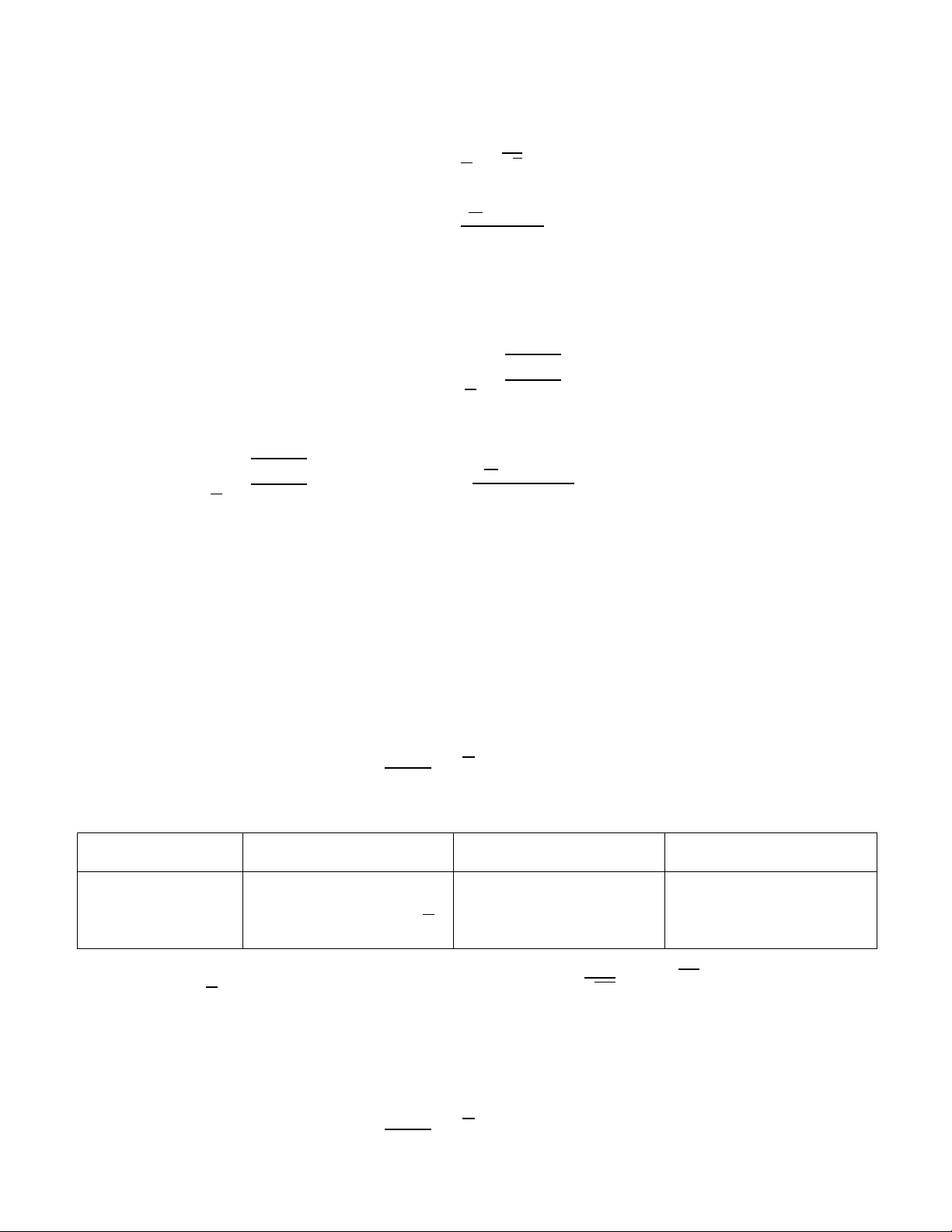
Phân phối Chuẩn N (𝜇, 𝜎5)
Phân phối Chuẩn chuẩn tắc N (0,1) Kỳ vọng E(X) E(X) = 𝜇 E(X) = 0 Phương sai V(X) V(X) = 𝜎5 V(X) = 1 Mode Mode X = 𝜇 Mode X = 0
- Quy tắc 3 xích ma – 3 𝜎
• Xác suất để biến ngẫu nhiên X có quy luật phân phối chuẩn (𝜇, 𝜎5) nhận giá trị trong khoảng
(𝜇 − 3𝜎; 𝜇 + 3𝜎) gần bằng 1
à Chắc chắn X nhận giá trị trong khoảng (𝜇 − 3𝜎; 𝜇 + 3𝜎) PHẦN II: THỐNG KÊ 1. Lý thuyết mẫu a. Trung bình mẫu - Khái niệm: 𝑋( = + ∑1 X ! 2 3 + 2
- Kỳ vọng và phương sai của trung bình mẫu • Kỳ vọng: E(X .) = 𝜇 • :, : Phương sai: V(X.) = 𝜎(X.) = ! √! b. Tần suất mẫu - P(A) = p - Kỳ vọng: E(X) = p - Phương sai: V(X) = p.q " - Thống kê mẫu: f = / trong đó k !
A là tần số của A, được gọi là tần suất mẫu. 4
c. Phương sai mẫu và độ lệch chuẩn mẫu - Phương sai mẫu • Phương sai mẫu: S2 = * ∑5 (X = * ∑5 X + − X.+ ! ' ) * ' − X .)+ ! ' ) * '
• Độ lệch chuẩn mẫu: S = √S6 !*+
• Kỳ vọng của phương sai mẫu theo phương sai V(X) = 𝜎+ của X: E(S2) = 𝜎2 !
- Phương sai mẫu hiệu chỉnh • !
Phương sai mẫu hiệu chỉnh: s’2 = S2 = * ∑5 (X !*+ !%* ' ) * ' − X .)+ B0
• Độ lệch chuẩn mẫu hiệu chỉnh: s’ = Bs6+ = S.O 𝑛 ð = C 𝑛−1 √! √!*+ !
• Kỳ vọng của phương sai mẫu hiệu chỉnh: E(s’2) = E(S2) = 𝜎+ !*+
2. Ước lượng tham số thống kế a. Ước lượng điểm - Trung bình mẫu X .: E(X) = 𝜇 - Tần suất mẫu f: P(A) = p
- Phương sai mẫu hiệu chỉnh s’2: V(X) = 𝜎5
b. Ước lượng tham số bằng khoảng tin cậy
- Khoảng tin cậy của kỳ vọng
• Trường hợp đã biết phương sai V(X) = 𝜎+
Khoảng tin cậy đối xứng của kỳ vọng 𝜇 với độ tin cậy 𝛾 = 1 − 𝛼 là: ; X
@ − 𝑢1 . : < 𝜇 < X@ + 𝑢1 . : < , √! , √! Trong đó + X @ : trung bình mẫu
+ 𝜎 : độ lệch chuẩn đã biết + D
+ 𝑢1 : được tra từ bảng Φ(u) = ∫ e* (, , 𝑑𝑥 = P(X < u)
PRX − 𝑢 T= 1− F = 𝜑 ;𝑢1 < *E 𝛼 , √5π ! 2 2
+ 𝜀 = 𝑢1 . : : độ chính xác của ước lượng , √! Ước lượng tối đa: 𝜇 < X@ + 𝑢F. : √!
Ước lượng tối thiểu: 𝜇 > X @ + 𝑢F. : √! 5
• Trường hợp chưa biết phương sai V(X) = 𝜎+ và kích thước mẫu lớn (n ≥ 30)
Khoảng tin cậy đối xứng của kỳ vọng 𝜇 với độ tin cậy 𝛾 = 1 − 𝛼 là: sG sG FX@ − 𝑢F . < 𝜇 < X@ + 𝑢F . I 5 √n 5 √n Trong đó + X @ : trung bình mẫu
+ s’ : độ lệch chuẩn mẫu hiệu chỉnh + D
+ 𝑢𝛼 : được tra từ bảng Φ(u) = ∫ e* (, , 𝑑𝑥 = P(X < u) ! √5π *E
+ 𝜀 = 𝑢1 . B0 : độ chính xác của ước lượng , √1 Ước lượng tối đa: 𝜇 < X@ + 𝑢F. B0 √1
Ước lượng tối thiểu: 𝜇 > X @ + 𝑢F. B0 √1
• Trường hợp chưa biết phương sai V(X) = 𝜎+ và kích thước mẫu nhỏ (n < 30)
Khoảng tin cậy đối xứng của kỳ vọng 𝜇 với độ tin cậy 𝛾 = 1 − 𝛼 là: sG sG FX@ − 𝑡F . < 𝜇 < X@ + 𝑡F . I 5 ; " √n 5 ; " √n Trong đó + X @ : trung bình mẫu
+ s’ : độ lệch chuẩn mẫu hiệu chỉnh
+ 𝑡1 ; " : được tra từ bảng giá trị 𝑡1 ; k của phân phối Student với k = n -1 bậc tự do , , + 𝜀 = 𝑡1 . B0 ; "
: độ chính xác của ước lượng , √1 Ước lượng tối đa: 𝜇 < X@ + 𝑡F; ". B0 √1
Ước lượng tối thiểu: 𝜇 > X @ + 𝑡F; ". B0 √1
- Ước lượng xác suất (p) của biến ngẫu nhiên có phân phối B(1; p)
• Với độ tin cậy 𝛾 = 1 − 𝛼 ta có khoảng tin cậy đối xứng của xác suất p của tổng thể là: 6
F𝑓 − 𝑢1 . KI (+*I) < 𝑝 < 𝑓 + 𝑢 . KI (+*I)I 1 , ! , ! Trong đó
+ 𝑓 = J : tần suất mẫu ! + D
+ 𝑢𝛼 : được tra từ bảng Φ(u) = ∫ e* (, , 𝑑𝑥 = P(X < u) *E , √5π + 𝜀 = 𝑢1 . KI (+*I)
: độ chính xác của ước lượng , ! Ước lượng tối đa:
𝑝 < 𝑓 + 𝑢7 . O8 (*%8) !
Ước lượng tối thiểu: 𝑝 < 𝑓 − 𝑢7 . O8 (*%8) !
- Ước lượng phương sai của biến ngẫu nhiên có phân phối chuẩn
• Trường hợp đã biết kỳ vọng E(X) = 𝜇
Với độ tin cậy 𝛾 ta có khoảng tin cậy đối xứng của tham số V(X) = 𝜎+ là: ∑! (𝑥 ∑! (𝑥
W ( ) * ( − 𝜇)+ < 𝜎+ < ( ) * ( − 𝜇)+ Y 𝑍+ 𝑍*
Tra bảng giá trị tới hạn của phân phối Khi bình phương c2 (n) ta xác định được: Z 5 5 2 = 𝜒(!) ;+ * K < Z ;+ ) K < 5 1 = 𝜒(!) 5
• Trường hợp chưa biết kỳ vọng E(X) = 𝜇
Với độ tin cậy 𝛾 ta có khoảng tin cậy đối xứng của tham số V(X) = 𝜎+ là: ∑ + ! + [𝑥 ∑! [𝑥 Z ( ) * ( − X
.\ < 𝜎+ < ( ) * ( −X.\ ] 𝑍+ 𝑍* hoặc
;(!*+).B0, < 𝜎5 < (!*+).B0, < L, L%
Tra bảng giá trị tới hạn của phân phối Khi bình phương c2 (n) ta xác định được: Z 5 5 2 = 𝜒(! * +) ;+ * K < Z ;+ ) K < 5 1 = 𝜒(! * +) 5 7
c. Phương pháp xác định kích thước mẫu cần thiết
- Với khoảng tin cậy của trung bình
• Độ chính xác của ước lượng: 𝜀 = 𝑡1 . B0 ; " với k = n – 1 , √1 '% . *)& ð n ≥ & ; (+& *
Vậy n là số nguyên dương nhỏ nhất thoả mãn điều kiện
- Với khoảng tin cậy của tỷ lệ
• Độ chính xác của ước lượng: 𝜀 = 𝑢1 . KI (+*I) , !
Muốn tăng độ chính xác sao cho: -% . .(/0.) 𝑢 & 1 . KI (+*I) ≤ 𝜀, ð n ≥ & , ! +*
Vậy n là số nguyên dương nhỏ nhất thoả mãn điều kiện
3. Kiểm định giả thuyết thống kê
a. Kiểm định giả thuyết với một mẫu thống kê
- Kiểm định tham số kỳ vọng
• Trường hợp đã biết phương sai V(X) = 𝜎+
+ Giả thuyết H0: µ = µ0 M N* =
+ Tiêu chuẩn kiểm định: Z = 3 . √𝑛 :
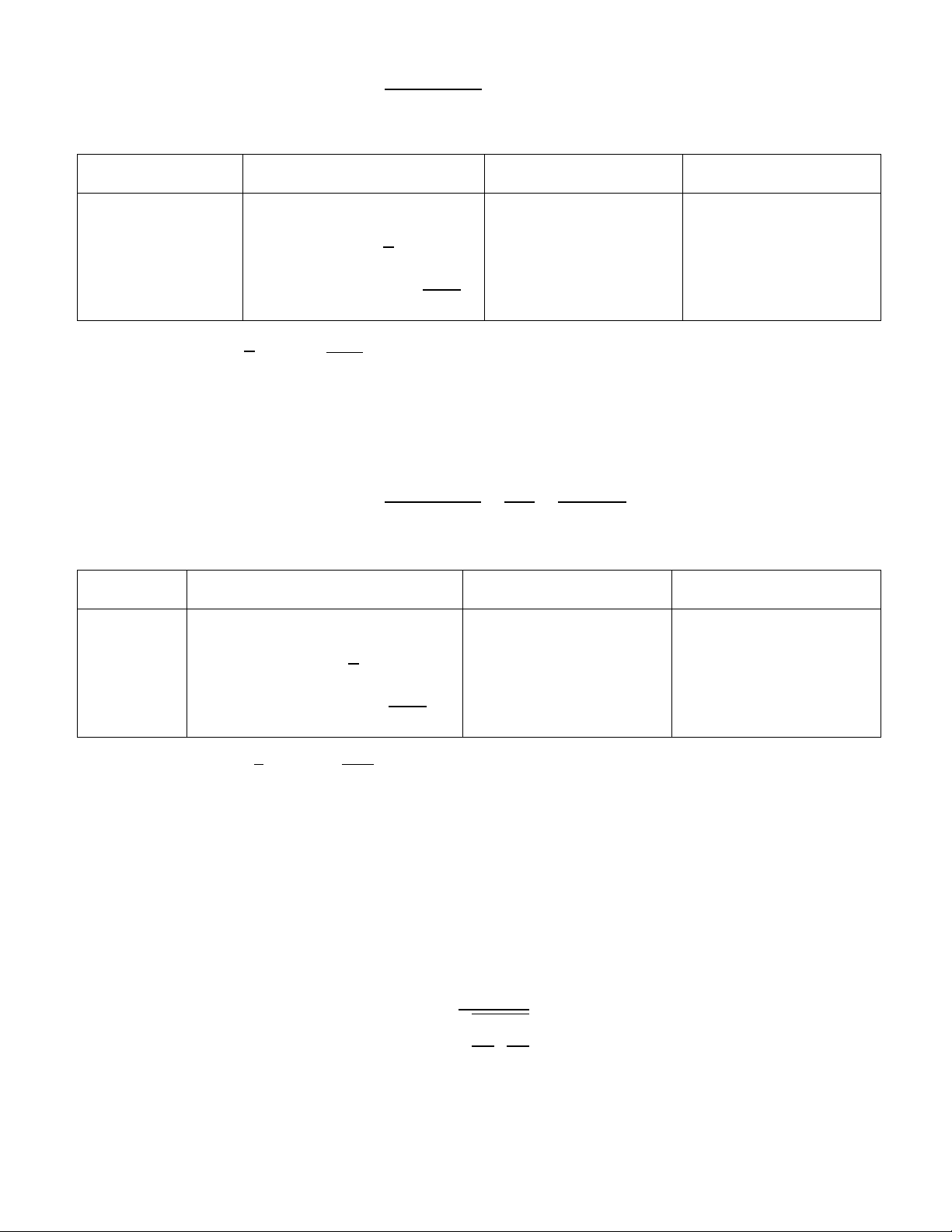
Với mức ý nghĩa a, ta phân chia miền bác bỏ theo các trường hợp của đối thuyết Đối thuyết
H1: µ ¹ µ0 H1: µ > µ0 H1: µ < µ0
Quy tắc kiểm định Bác bỏ H0 nếu |Ztn| > 𝑢1 Bác bỏ H0 nếu Ztn > 𝑢𝛼
Bác bỏ H0 nếu Ztn < −𝑢𝛼 , + D Giá trị của 𝑢1 𝑑𝑥
, 𝑢7 tra trong bảng hàm phân phối chuẩn Φ(u) = ∫ e* (, , *E , √5π
• Trường hợp chưa biết phương sai V(X) = 𝜎+ và n lớn
+ Giả thuyết H0: µ = µ0 M N* =
+ Tiêu chuẩn kiểm định: Z = 3 . √𝑛 BG 8
Với mức ý nghĩa a, ta phân chia miền bác bỏ theo các trường hợp của đối thuyết Đối thuyết
H1: µ ¹ µ0 H1: µ > µ0 H1: µ < µ0
Quy tắc kiểm định Bác bỏ H0 nếu |Ztn| > 𝑢1 Bác bỏ H0 nếu Ztn > 𝑢𝛼
Bác bỏ H0 nếu Ztn < −𝑢𝛼 , + D Giá trị của 𝑢1 𝑑𝑥
, 𝑢7 tra trong bảng hàm phân phối chuẩn Φ(u) = ∫ e* (, , *E , √5π
• Trường hợp chưa biết phương sai V(X) = 𝜎+ và n bé
+ Giả thuyết H0: µ = µ0 M N* =
+ Tiêu chuẩn kiểm định: T = 3 . √𝑛 BG
Với mức ý nghĩa a, ta phân chia miền bác bỏ theo các trường hợp của đối thuyết Đối thuyết
H1: µ ¹ µ0 H1: µ > µ0 H1: µ < µ0 Bác bỏ H0 nếu Bác bỏ H0 nếu Bác bỏ H0 nếu
Quy tắc kiểm định |Ttn| > 𝑡1 ,(!*+) Ttn > 𝑡𝛼,(𝑛−1)
Ttn < −𝑡𝛼,(𝑛−1) ,
Giá trị của 𝑡 1 ,(!*+), 𝑡𝛼,(𝑛−1) tra trong bảng phân phối Student ,
- Kiểm định giả thuyết về tỷ lệ
• Giả thuyết H0: µ = µ0 • I * Q
Tiêu chuẩn kiểm định: Z = 3 . √𝑛 BG
Với mức ý nghĩa a = 1− g , ta phân chia miền bác bỏ theo các trường hợp của đối thuyết Đối thuyết
H1: µ ¹ µ0 H1: µ > µ0 H1: µ < µ0 Bác bỏ H0 nếu Bác bỏ H0 nếu Bác bỏ H0 nếu
Quy tắc kiểm định |Ttn| > 𝑡1 ,(!*+) Ttn > 𝑡𝛼,(𝑛−1)
Ttn < −𝑡𝛼,(𝑛−1) , Trong đó: n : cỡ mẫu.
m : tần số xuất hiện dấu hiệu A.
𝑓 = J : tần suất mẫu ! + D Giá trị của 𝑢1 𝑑𝑥
, 𝑢7 tra trong bảng hàm phân phối chuẩn Φ(u) = ∫ e* (, , *E , √5π
- Kiểm định giả thuyết về phương sai
• Trường hợp đã biết kỳ vọng E(X) = 𝜇 + Giả thuyết H + 0: 𝜎+ = 𝜎9 9 ∑5 (R
+ Tiêu chuẩn kiểm định: Z = 4 $ % 4*=), :,
Với mức ý nghĩa a, ta phân chia miền bác bỏ theo các trường hợp của đối thuyết Đối thuyết H + + + 1: 𝜎+ ¹ 𝜎9 H1: 𝜎+ > 𝜎9 H1: 𝜎+ < 𝜎9 Bác bỏ H0 nếu Bác bỏ H0 nếu Bác bỏ H0 nếu 5 + +
Quy tắc kiểm định Ztn > Z2 = 𝜒(!) ;F< Z (𝛼) ( 5 tn > Z2 = 𝜒(!)
Ztn < Z1 = 𝜒(!) 1 − 𝛼) hoặc Z 5
tn < Z1 = 𝜒(!) ;5 * F< 5 Giá trị của 𝜒5 2 5 5 (!) ;F<, 𝜒 R2 − 𝛼T, 𝜒
(𝛼), 𝜒 (1 − 𝛼) tra trong bảng Khi bình phương 5 (𝑛) 2 (!) (!)
• Trường hợp chưa biết kỳ vọng E(X) = 𝜇 + Giả thuyết H + 0: 𝜎+ = 𝜎9 ∑5 (R
+ Tiêu chuẩn kiểm định: Z = 4 $ % 4*MN), = !.C, = (!*+).C0, :, , , 6 :6 :6
Với mức ý nghĩa a, ta phân chia miền bác bỏ theo các trường hợp của đối thuyết Đối thuyết H + + + 1: 𝜎+ ¹ 𝜎9 H1: 𝜎+ > 𝜎9 H1: 𝜎+ < 𝜎9 Bác bỏ H0 nếu Bác bỏ H0 nếu Bác bỏ H0 nếu Quy tắc Z 5 + tn > Z2 = 𝜒(!*+) ;F< Z + tn > Z2 = 𝜒(!%*)(𝛼)
Ztn < Z1 = 𝜒(!%*)(1 − 𝛼) kiểm định 5 hoặc Z 5
tn < Z1 = 𝜒(!*+) ;5 * F< 5 Giá trị của 𝜒+ + + + (!%*) R7T, 𝜒 R+ % 7T, 𝜒 (𝛼), 𝜒
(1 − 𝛼) tra trong bảng Khi bình phương + (!%*) + (!%*) (!%*)
b. Kiểm định giả thuyết với hai mẫu thống kê - So sánh hai kỳ vọng
• Trường hợp đã biết phương sai V(X + + A) = 𝜎:; V(XB) = 𝜎;
+ Giả thuyết H0: µA = µB
+ Tiêu chuẩn kiểm định: 1 2 Z = +012, & & 3-! - 4 / .+ .,
Với mức ý nghĩa a, ta phân chia miền bác bỏ theo các trường hợp của đối thuyết 10 Đối thuyết
H1: µA ¹ µB
H1: µA > µB
H1: µA < µB
Quy tắc kiểm định Bác bỏ H0 nếu |Ztn| > 𝑢1 Bác bỏ H0 nếu Ztn > 𝑢𝛼
Bác bỏ H0 nếu Ztn < −𝑢𝛼 , + D
Giá trị của 𝑢1 , 𝑢7 tra trong bảng hàm phân phối chuẩn Φ(u) = ∫ e* (, , 𝑑𝑥 *E , √5π
• Trường hợp chưa biết phương sai V(X + +
A) = 𝜎:; V(XB) = 𝜎; nhưng kích thước mẫu đủ lớn
+ Giả thuyết H0: µA = µB
+ Tiêu chuẩn kiểm định: 1 2 Z = +012, )& )& 30! 0 4 / .+ .,
Với mức ý nghĩa a, ta phân chia miền bác bỏ theo các trường hợp của đối thuyết Đối thuyết
H1: µA ¹ µB
H1: µA > µB
H1: µA < µB
Quy tắc kiểm định Bác bỏ H0 nếu |Ztn| > 𝑢1 Bác bỏ H0 nếu Ztn > 𝑢𝛼
Bác bỏ H0 nếu Ztn < −𝑢𝛼 , + D
Giá trị của 𝑢1 , 𝑢7 tra trong bảng hàm phân phối chuẩn Φ(u) = ∫ e* (, , 𝑑𝑥 *E , √5π
• Trường hợp chưa biết phương sai V(X + +
A) = 𝜎:; V(XB) = 𝜎; nhưng kích thước mẫu khá bé
+ Giả thuyết H0: µA = µB
+ Đối thuyết H1: µA ¹ µB
+ Tiêu chuẩn kiểm định: ! " T = !#! "" +, +,
%#$%&'( *% -#$.&'( *. & ' ' ' ( /!- /"&, /! /"
Với mức ý nghĩa a, ta phân chia miền bác bỏ theo các trường hợp của đối thuyết Đối thuyết
H1: µA ¹ µB
H1: µA > µB
H1: µA < µB Bác bỏ H0 nếu Bác bỏ H0 nếu Bác bỏ H0 nếu
Quy tắc kiểm định |Ttn| > 𝑡1 , 1 Ttn > 𝑡1 , 1 Ttn < − 𝑡1 , 1 , 7) 18*5 , 7) 18*5 , 7) 18*5 11 Giá trị của 𝑡1 , 1
tra trong bảng phân phối Student , 7) 18*5
• Trường hợp hai mẫu cho theo cặp
+ Thiết lập biến ngẫu nhiên D: Di = XAi – XBi (i = 1; 2;…n)
+ Giả thuyết H0: µD = µA – µB = 0
+ Đối thuyết H1: µD = µA – µB ¹ 0
Tiến hành tương tự kiểm định giả thuyết với một mẫu thống kê - So sánh hai tỷ lệ
• Giả thuyết H0: pA = pB
• Đối thuyết H1: pA ¹ pB )'#),
• Tiêu chuẩn kiểm định: Z = *+(-# +)/ ' ' ' 0 /' /,
Với mức ý nghĩa a, ta phân chia miền bác bỏ theo các trường hợp của đối thuyết Đối thuyết H1: pA ¹ pB H1: pA > pB H1: pA < pB
Quy tắc kiểm định Bác bỏ H0 nếu |Ztn| > 𝑢1 Bác bỏ H0 nếu Ztn > 𝑢𝛼
Bác bỏ H0 nếu Ztn < −𝑢𝛼 , 1 Trong đó: n %T% ) 1,T, 1, n2 : cỡ mẫu.
f1, f2 : tần suất mẫu. f = : tần suất mẫu chung 1% ) 1, + D
Giá trị của 𝑢1 , 𝑢7 tra trong bảng hàm phân phối chuẩn Φ(u) = ∫ e* (, , 𝑑𝑥 *E , √5π - So sánh hai phương sai • Cặp Giả thuyết H : : 0: 𝜎9 = 𝜎; Đối thuyết H : :
1: 𝜎9 ¹ 𝜎;
• Trường hợp 1: 𝑆<: <: 9 > 𝑆; U0,
+ Tiêu chuẩn kiểm định: Z = / U0, =
+ Với mức ý nghĩa a, tra bảng phân phối Fisher các giá trị 𝑓 % ;(6 = F1 & 10 /; 6&0 /)= F2 𝑓7/ 0 % 8 ;(6 & 10 /; 6&0 /) 12
+ Xây dựng miền bác bỏ giả thuyết H0 nếu Q L>5 V W, L>59 W%3 % ?,
• Trường hợp 2: 𝑆<: <: ; > 𝑆9 U0,
+ Tiêu chuẩn kiểm định: Z = = U0, /
+ Với mức ý nghĩa a, tra bảng phân phối Fisher các giá trị 𝑓% ;(6 = F1 & &0 /; 610 /)= F2 𝑓7/ 0 % 8 ;(6 & &0 /; 610 /)
+ Xây dựng miền bác bỏ giả thuyết H0 nếu Q L>5 V W, L>59 W%3 % ?, 13