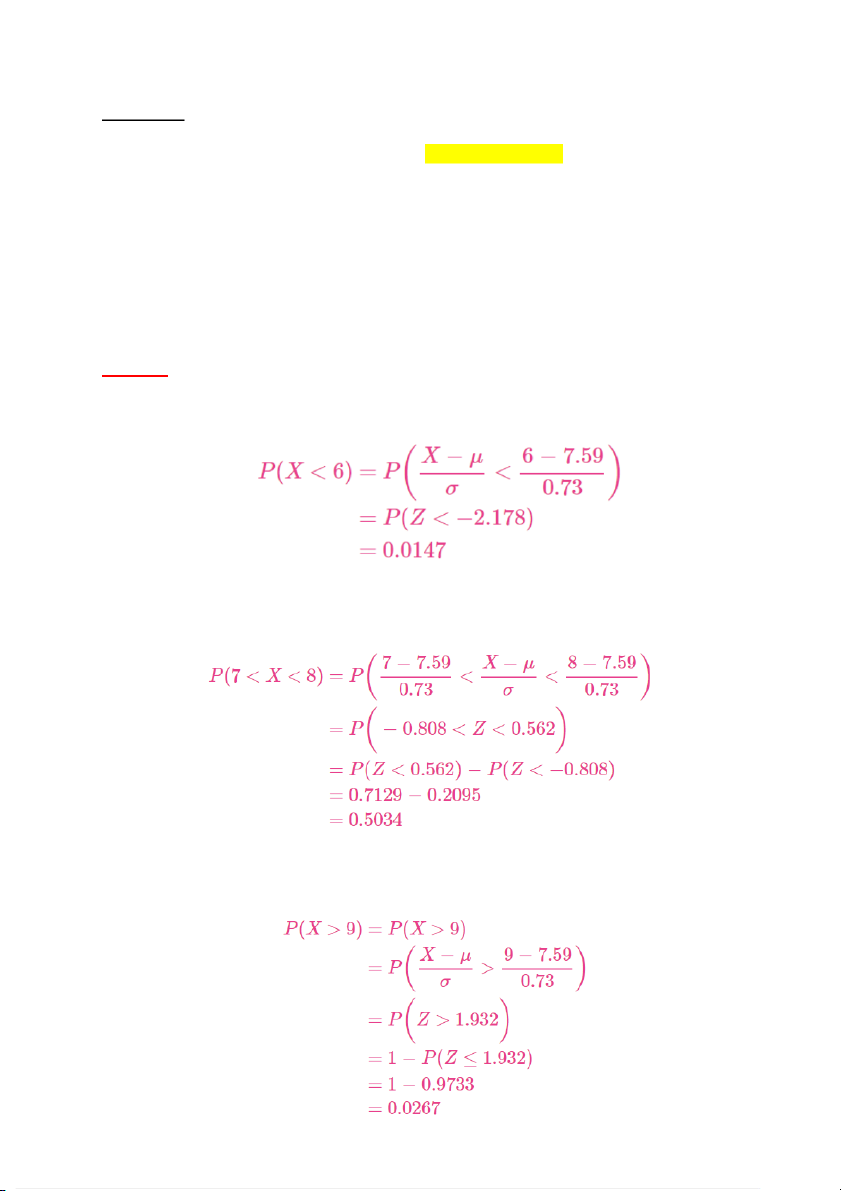




Preview text:
Ở chapter này mình sẽ không đi quá sâu về lí thuyết mà mình sẽ bà đi sâu về i tập nhé
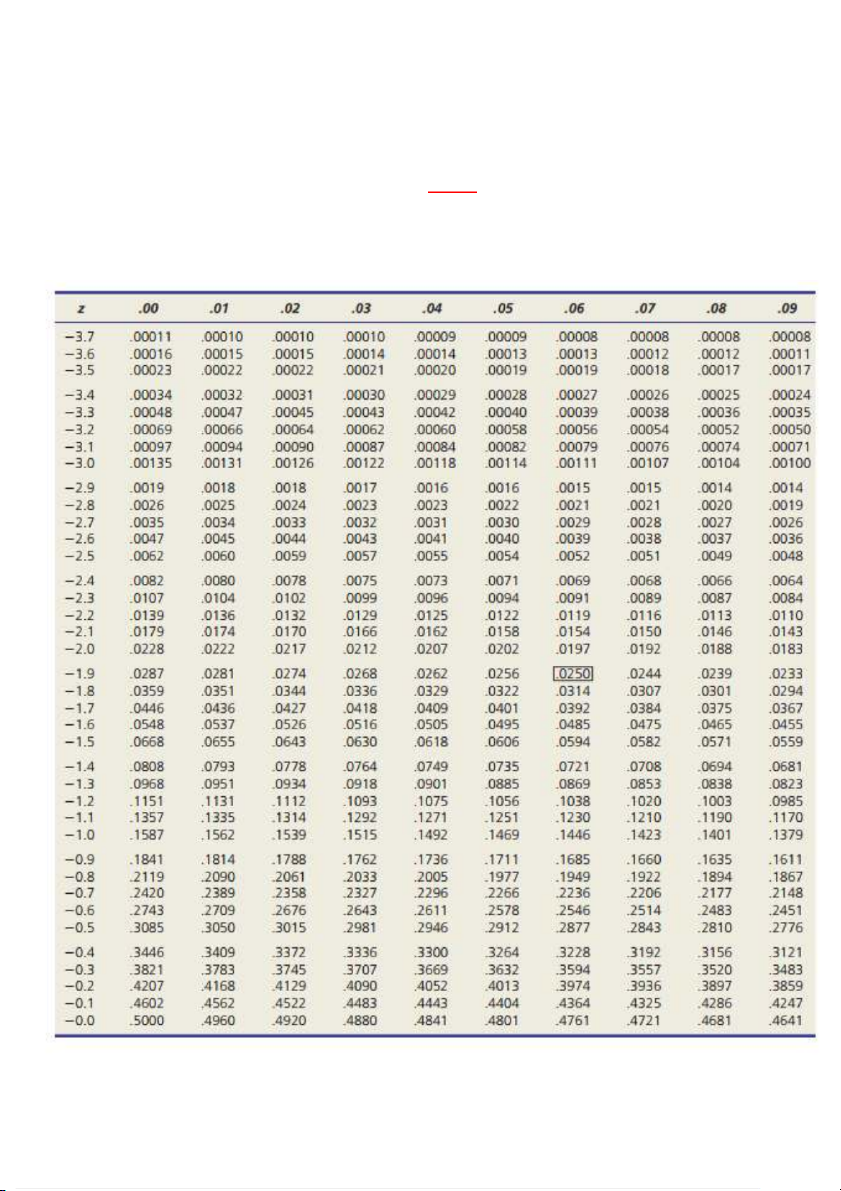
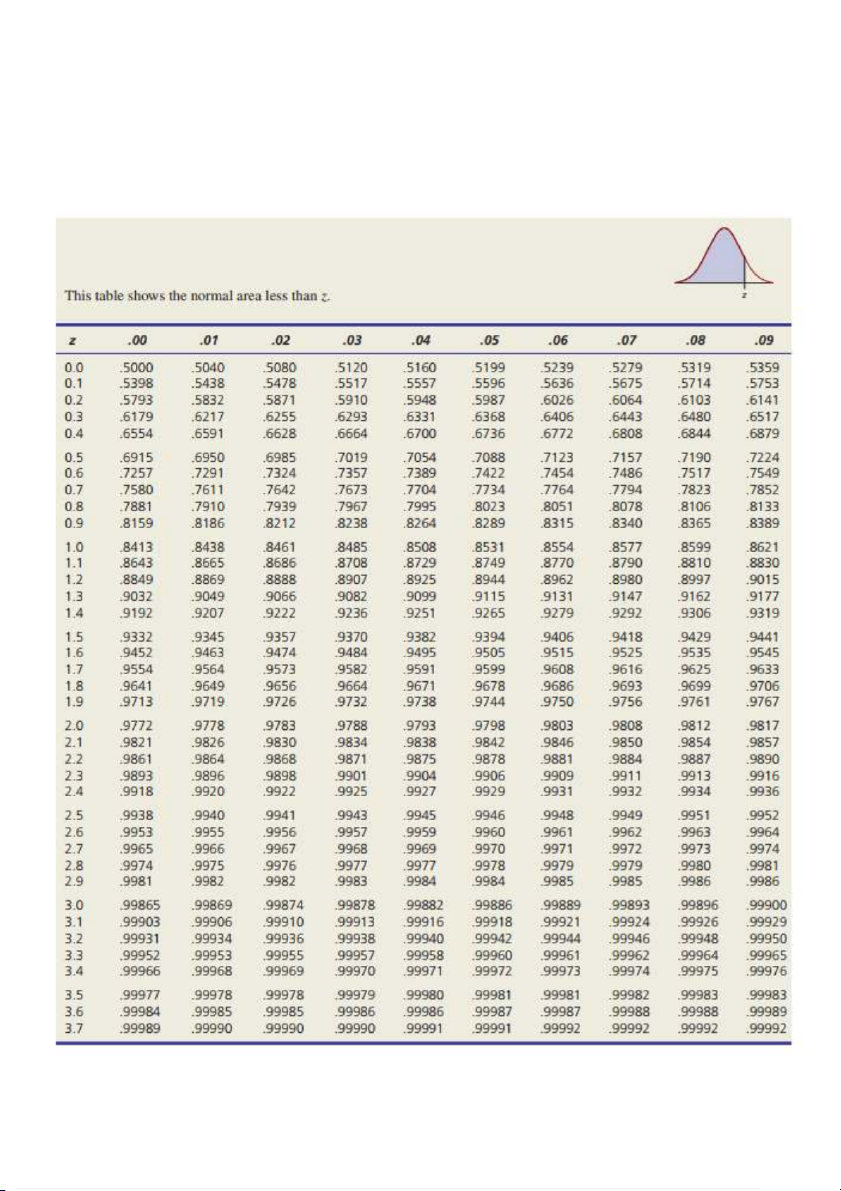
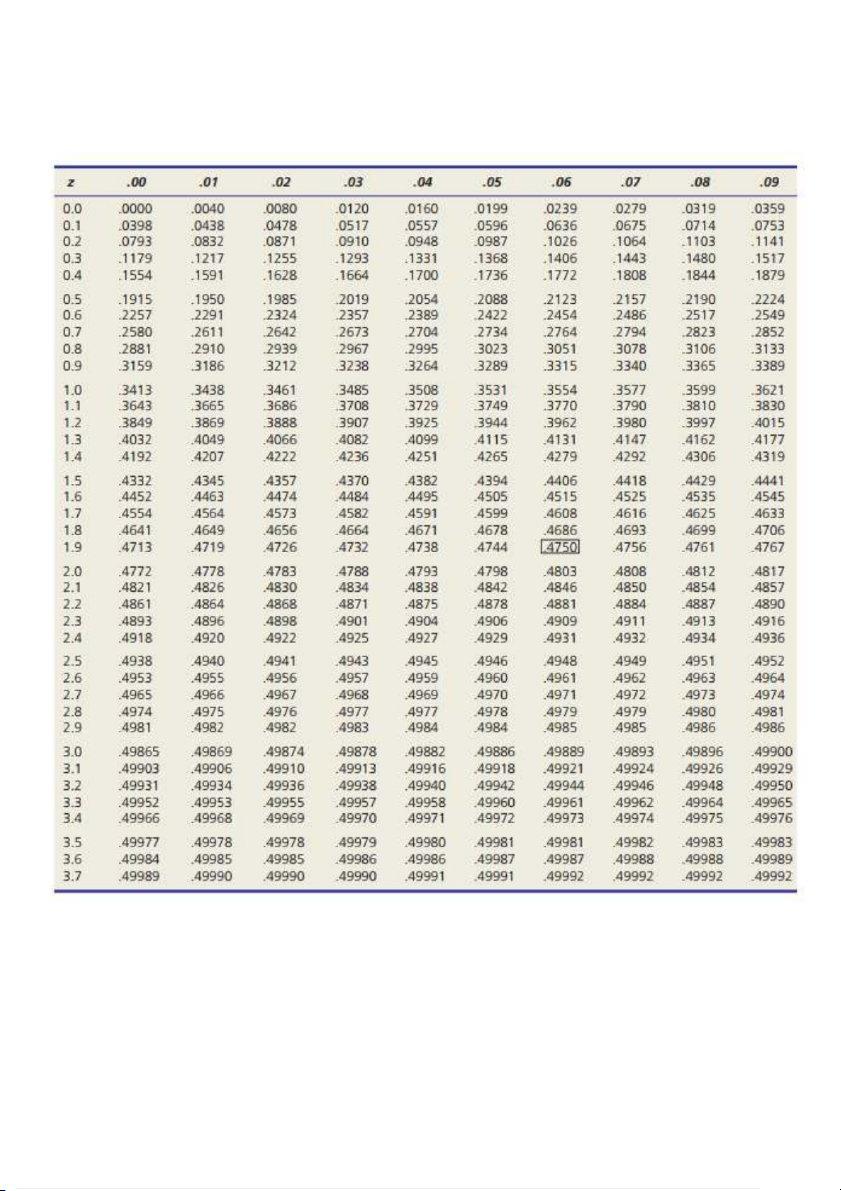
Công thức chuyển đổi X về Z 𝑿 − 𝝁 𝒁 = 𝝈 Bảng 1: P(Z
Bảng 2: P (0 < Z < X)
Example 1: A psychologist has devised a stress test for dental patients sitting in the waiting
rooms. According to this test, the stress scores (on a scale of 1 to 10) for patients waiting for root
canal treatments are found to be approximately normally distributed with a mean of 7.59 and a standard deviation of 0.73.
a. What percentage of such patients have a stress score lower than 6.0?
b. What is the probability that a randomly selected root canal patient sitting in the waiting room
has a stress score between 7.0 and 8.0?
c. The psychologist suggests that any patient with a stress score of 9.0 or higher should be given
a sedative prior to treatment. What percentage of patients waiting for root canal treatments
would need a sedative if this suggestion is accepted?
Solution: 𝜇 = 7.59, 𝜎 = 0.73
a) Probability that a patients have a stress score lower than 6.0 is
b) The probability that a randomly selected root canal patient sitting in the waiting room has a
stress score between 7.0 and 8.0 is
c) The probability that patients with stress score of 9.0 or higher is
Normal Approximation to the Binomial
Áp dụng công thức này khi thỏa tất cả các u ki điề ện sau + n > 20
+ n* 𝝅 > 5
+ n * (1- 𝝅 ) > 5 (một vài tài liệ ể u có th thay thế p và 𝜋 ạ nên các b n chú ý nhé ) • Note khi làm phần nà y (các bạn chú ý nhé )
+ X: a normal variable with mean and standard deviation + x: a given value
Example 2: A binomial probability distribution has p= 0.2 and n= 100.
a. What are the mean and standard deviation?
b. What is the probability of exactly 24 successes?
c. What is the probability of 18 to 22 successes?
d. What is the probability of 15 or fewer successes? Solution:
Mean: 𝜇 = 𝑛 ∗ 𝑝 = 100 ∗ 0.2 = 20
Standard deviation: 𝜎 = √𝑛 ∗ 𝑝 ∗ (1 − 𝑝) = √20 ∗ (1 − 0.2) = 4
b) Probability of exactly 24 successes: P (X= 24)
Apply the continuity correction factor), we have: P (23.5 ≤ 𝑥 ≤ 24.5)
c) Probability of 18 to 22 successes: P (18Apply the continuity correction factor, we have: P(17.5
d) Probability of 15 or fewer successes: P (X ≤ 15)
Apply the continuity correction factor, we have: P (X ≤ 15.5)
Exponential probability distribution
f(x) = 𝝀𝒆−𝝀/𝒙
Example 3: The time required to pass through security screening at the airport can be annoying
to travellers. The mean wait time during peak periods at Cincinnati/Northern Kentucky
International Airport is 12.1 minutes (The Cincinnati Enquirer, February 2, 2006). Assume the
time to pass through security screening follows an exponential distribution.
a. What is the probability it will take less than 10 minutes to pass through security screening
during a peak period? (0.5624)
b. What is the probability it will take more than 20 minutes to pass through security screening
during a peak period? (0.1915)
c. What is the probability it will take between 10 and 20 minutes to pass through security
screening during a peak period? (0.2461) EXERCISE:
Problem 1: CASIO Vietnam makes calculators. Consumer satisfaction is one of the top priorities
of the company’s management. The company guarantees the refund of money or a replacement
for any calculator that malfunctions within two years from the date of purchase. It is known from
past data that despite all efforts, 5% of the calculators manufactured by this company
malfunction within a 2-year period. The company recently mailed 500 such calculators to its customers.
a. Find the probability that exactly 29 of the 500 calculators will be returned for refund or
replacement within a 2-year period? (0.0584)
b. What is the probability that 27 or more of the 500 calculators will be returned for refund or
replacement within a 2-year period? (0.3791)
c. What is the probability that 15 to 22 of the 500 calculators will be returned for refund or
replacement within a 2-year period? (0.2884)
Problem 2: The average stock price for companies making up the S&P 500 is $30, and the
standard deviation is $8.20 (BusinessWeek, Special Annual Issue, Spring 2003). Assume the
stock prices are normally distributed.
a. What is the probability a company will have a stock price of at least $40? (0.1112)
b. How high does a stock price have to be to put a company in the top 10%? ($40.5) Problem 3:
Jim’s systolic blood pressure is a random variable with a mean of 145 mmHg and a
standard deviation of 20 mmHg. For Jim’s age group, 140 is the threshold for high blood pressure.
(a) If Jim’s systolic blood pressure is taken at a randomly chosen moment, what is the
probability that it will be 135 or less? (0.3085)
(b) 175 or more? (0.0668)
(c) Between 125 and 165? (0.6827)
Problem 4: In January 2003, the American worker spent an average of 77 hours logged on to the
Internet while at work (CNBC, March 15, 2003). Assume the population mean is 77 hours, the
times are normally distributed, and that the standard deviation is 20 hours.
a. What is the probability that in January 2003 a randomly selected worker spent fewer than 50
hours logged on to the Internet? (0.0885)
b. What percentage of workers spent more than 100 hours in January 2003 logged on to the Internet? (12.51%)
c. A person is classified as a heavy user if he or she is in the upper 20% of usage. In January
2003, how many hours did a worker have to be logged on to the Internet to be considered a
heavy user? (93.8 hours or more)
Problem 5: When you sign up for a credit card, do you read the contract carefully? In a
FindLaw.com survey, individuals were asked, “How closely do you read a contract for a credit
card?” (USA Today, October 16, 2003). The findings were that 44% read every word, 33% read
enough to understand the contract, 11% just glance at it, and 4% don’t read it at all. For a sample of 500 people,
a. How many would you expect to say that they read every word of a credit card contract? (220)
b. What is the probability that 200 or fewer will say they read every word of a credit card contract? (0.0392)
c. What is the probability that at least 15 say they don’t read credit card contracts? (0.8962)
Problem 6: The mean hourly pay rate for financial managers in the East North Central region is
$32.62, and the standard deviation is $2.32 (Bureau of Labor Statistics, September 2005).
Assume that pay rates are normally distributed.
a. What is the probability a financial manager earns between $30 and $35 per hour? (0.7193)
b. How high must the hourly rate be to put a financial manager in the top 10% with respect to pay? ($35.59)
c. For a randomly selected financial manager, what is the probability the manager earned less
than $28 per hour? (0.0233)
Problem 7: Comcast Corporation is the largest cable television company, the second largest
Internet service provider, and the fourth largest telephone service provider in the United States.
Generally known for quality and reliable service, the company periodically experiences
unexpected service interruptions. On January 14, 2009, such an interruption occurred for the
Comcast customers living in southwest Florida. When customers called the Comcast office, a
recorded message told them that the company was aware of the service outage and that it was
anticipated that service would be restored in two hours. Assume that two hours is the mean time
to do the repair and that the repair time has an exponential probability distribution.
a. What is the probability that the cable service will be repaired in one hour or less? (0.3935)
b. What is the probability that the repair will take between one hour and two hours? (0.2386)




