





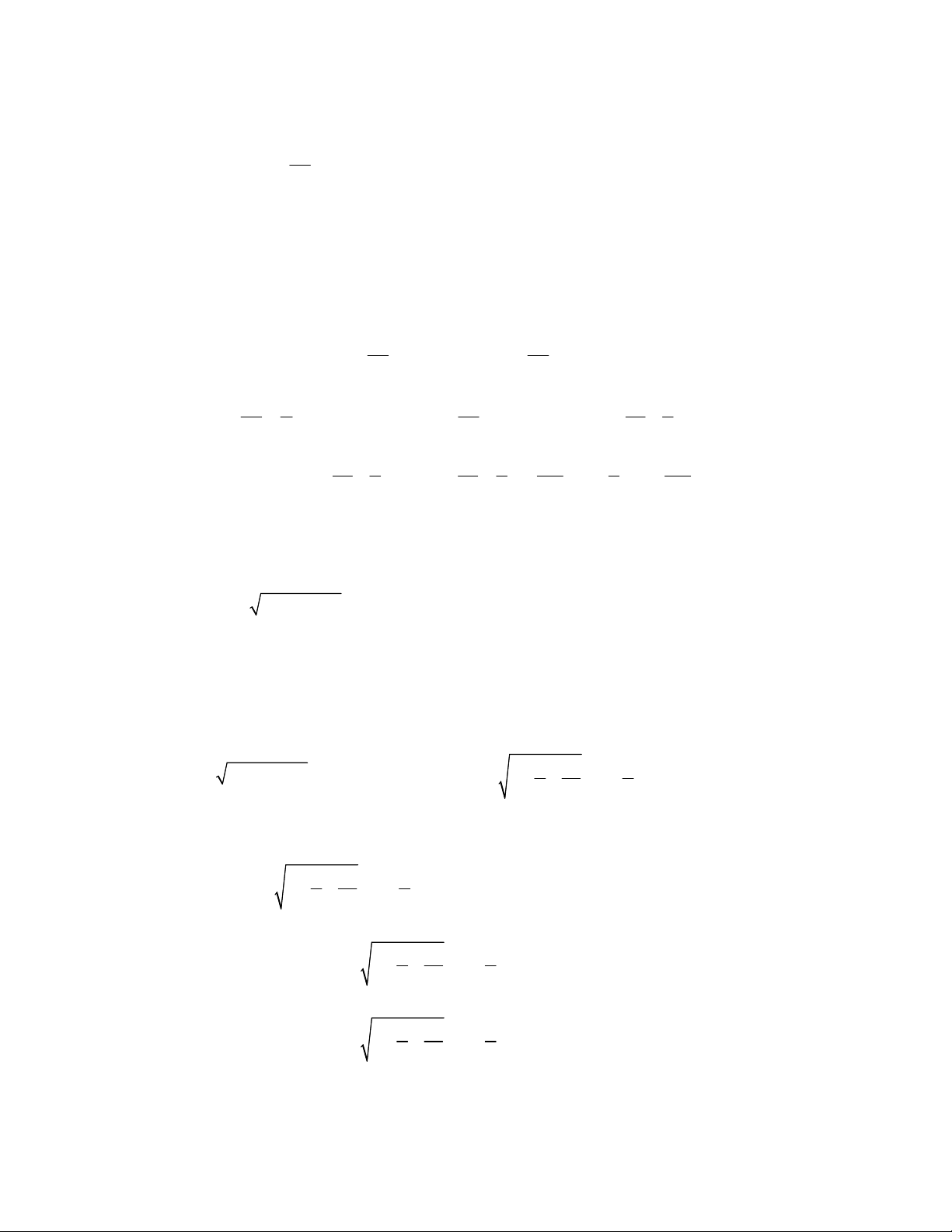




Preview text:
ĐÁP ÁN ĐỀ ÔN 2-KS TOÁN 11-NH
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí
sinh chỉ chọn một phương án
Câu 1:Một nhóm gom 6 học sinh nam và 4 học sinh nữ. Chọn ngau nhiên đong thời 3 học sinh trong
nhóm đó. Xác suat đe trong 3 học sinh được chọn luôn có học sinh nữ bang 1 5 2 1 A. . B. . C. . D. . 3 6 3 6 Lời giải
So phan từ của không gian mau n 3 C 120 . 10
Gọi A là bien co sao cho 3 học sinh được chọn có học sinh nữ,
A là bien co sao cho 3 học sinh được chọn không có học sinh nữ n A 3 C 20. 6 n A 5
Vậy xác suat can tı̀m P A 1 P A 1 . n 6
Câu 1: Tập xác định của hàm số y log 2 3 2x x 2 là A. D 1 ;3 B. D 0; 1 C. D 1 ; 1 D. D 3 ; 1 Lời giải Chọn D
Hàm số đã cho xác định 2
3 2x x 0 3 x 1. Vậy D 3 ; 1 . x
Câu 2: Với k , nghiệm của phương trình sin 1 là 2 A. x k4 B. x k2 C. x k2 D. x k2 2 Lời giải Chọn A x x Ta có sin 1
k2 x k4 , k . 2 2 2
Câu 3: Kết quả kì thi trắc nghiệm môn Toán với thang điểm 100 của 32 học sinh được cho trong bảng sau
Độ dài của nhóm 90;100 là A. 7. B. 8. C. 10. D. 9. Lời giải Chọn C
Độ dài của nhóm 90;100 là 100 90 10 .
Câu 4: Cho cấp số cộng u với u 5 2n . Tìm công sai của cấp số cộng. n n A. d 3. B. d 2 . C. d 1. D. d 2 . Lời giải Chọn B Ta có u
u 5 2 n 1 5 2n 5 2n 2 5 2n 2 d 2 . n 1 n Trang 8/29 – 3
Câu 5: Giá trị của giới hạn lim là: 2 4n 2n 1 3 A. . B. . C. 0. D. 1. 4 Lời giải Chọn C 3 2 3 0 Ta có lim lim n 0. 2 4n 2n 1 2 1 4 4 2 n n
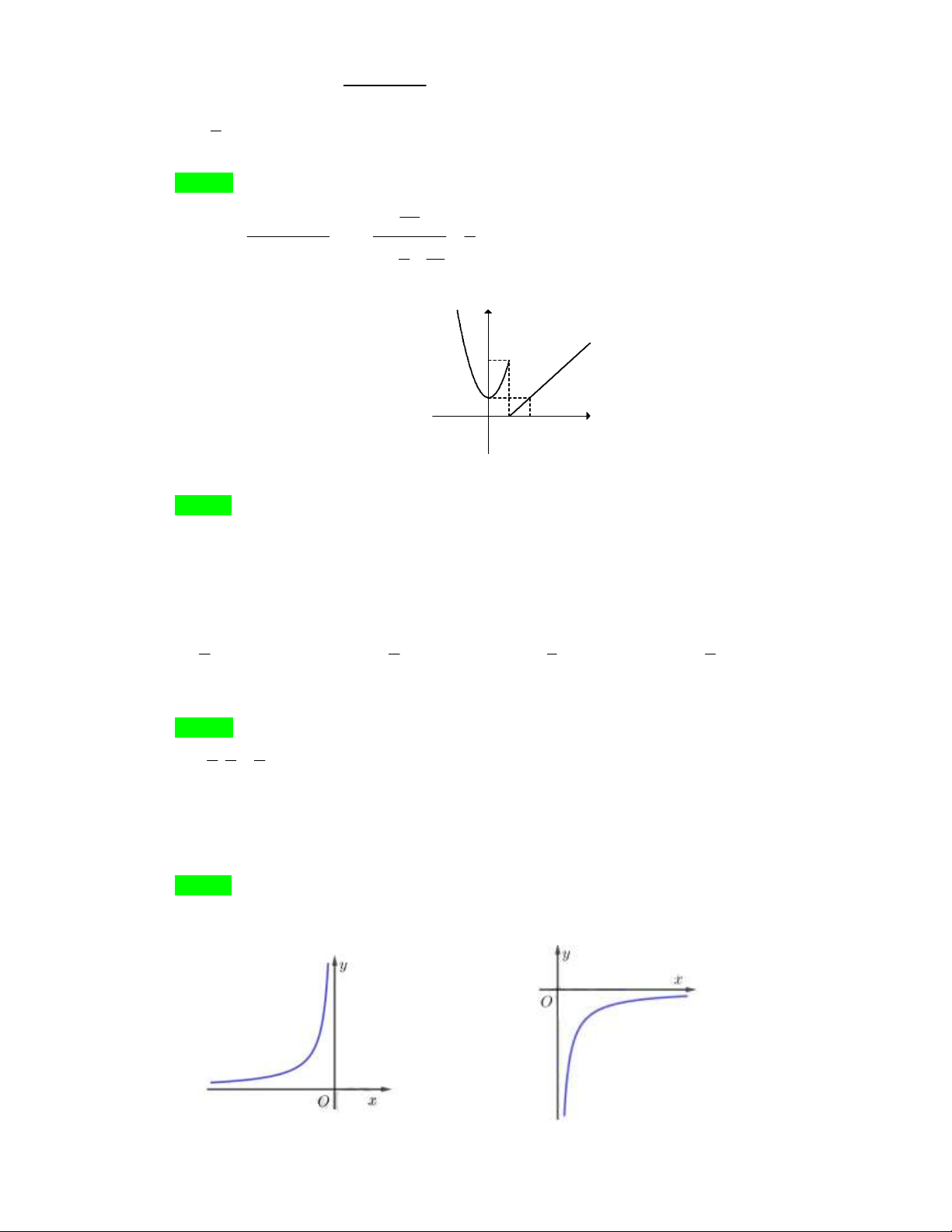
Câu 6: Hàm số f x có đồ thị như hình bên không liên tục tại điểm có hoành độ là bao nhiêu? y 3 1 x O 1 2 A. x 0. B. x 1. C. x 2. D. x 3. Lời giải Chọn B
Dễ thấy tại điểm có hoành độ x 1 đồ thị của hàm số bị ' đứt ' nên hàm số không liên tục tại đó.
Cụ thể: lim f x 0 3 lim f x nên f x gián đoạn tại x 1. x 1 x 1
Câu 7: Gieo 1 con súc sắc cân đối và đồng chất 2 lần. Tính xác suất để hai lần gieo đều xuất hiện mặt chẵn? 1 1 1 1 A. . B. . C. . D. . 4 2 3 6 Lời giải Lời giải Chọn A 1 1 1 P . 2 2 4
Câu 8: Khẳng định nào dưới đây sai? A. 2 2sin a 1 cos 2a . B. cos 2a 2 cos a 1.
C. sin a b sin a cosb sin .
b cos a . D. sin 2a 2sin a cos a . Lời giải Chọn B Ta có 2 cos 2a 2 cos a 1
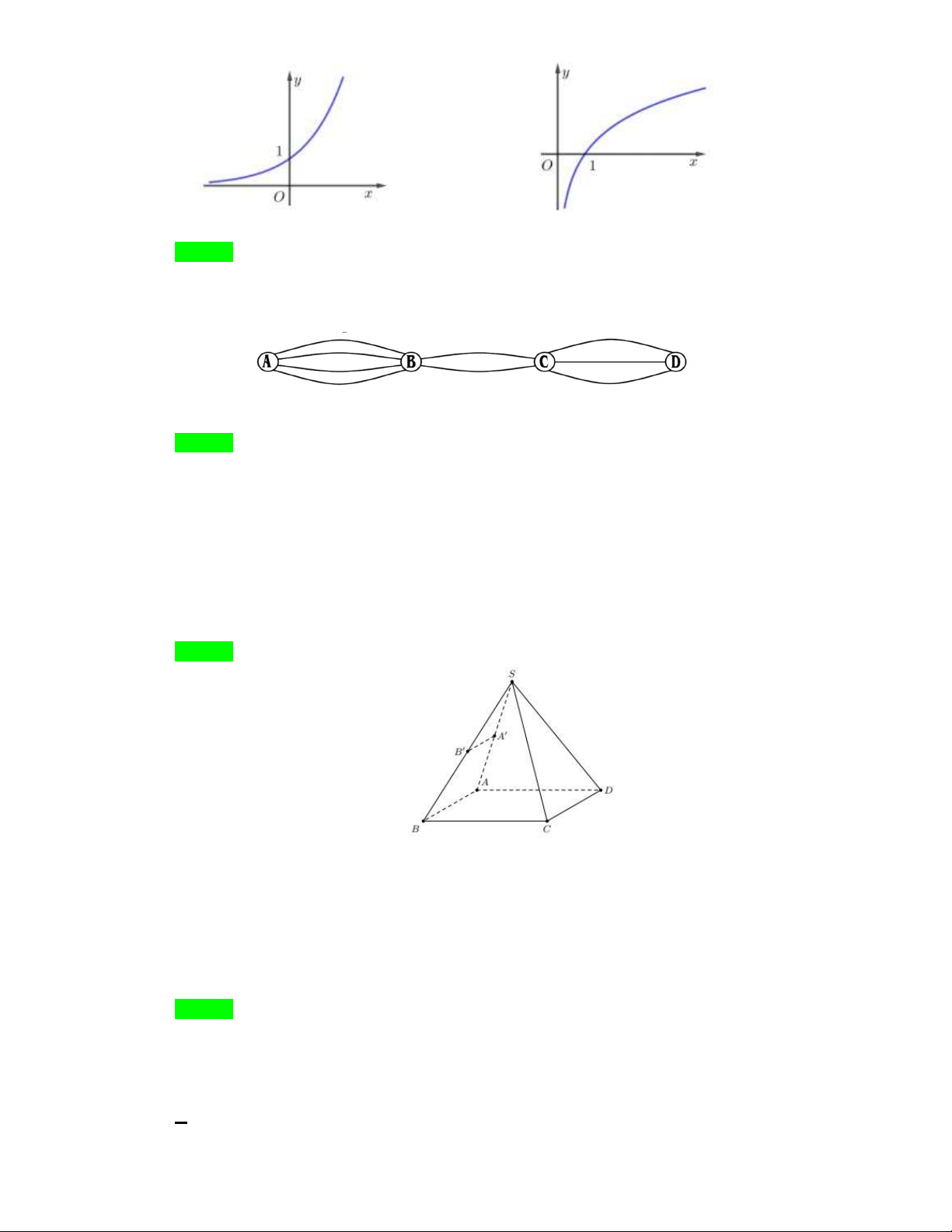
Câu 9: Cho a là số thực dương khác 1. Hình nào sau đây là đồ thị của hàm số mũ x y a ? A. B. Trang 9/29 - C. D. Lời giải Chọn C Hàm số x
y a có tập xác định là và tập giá trị là 0;
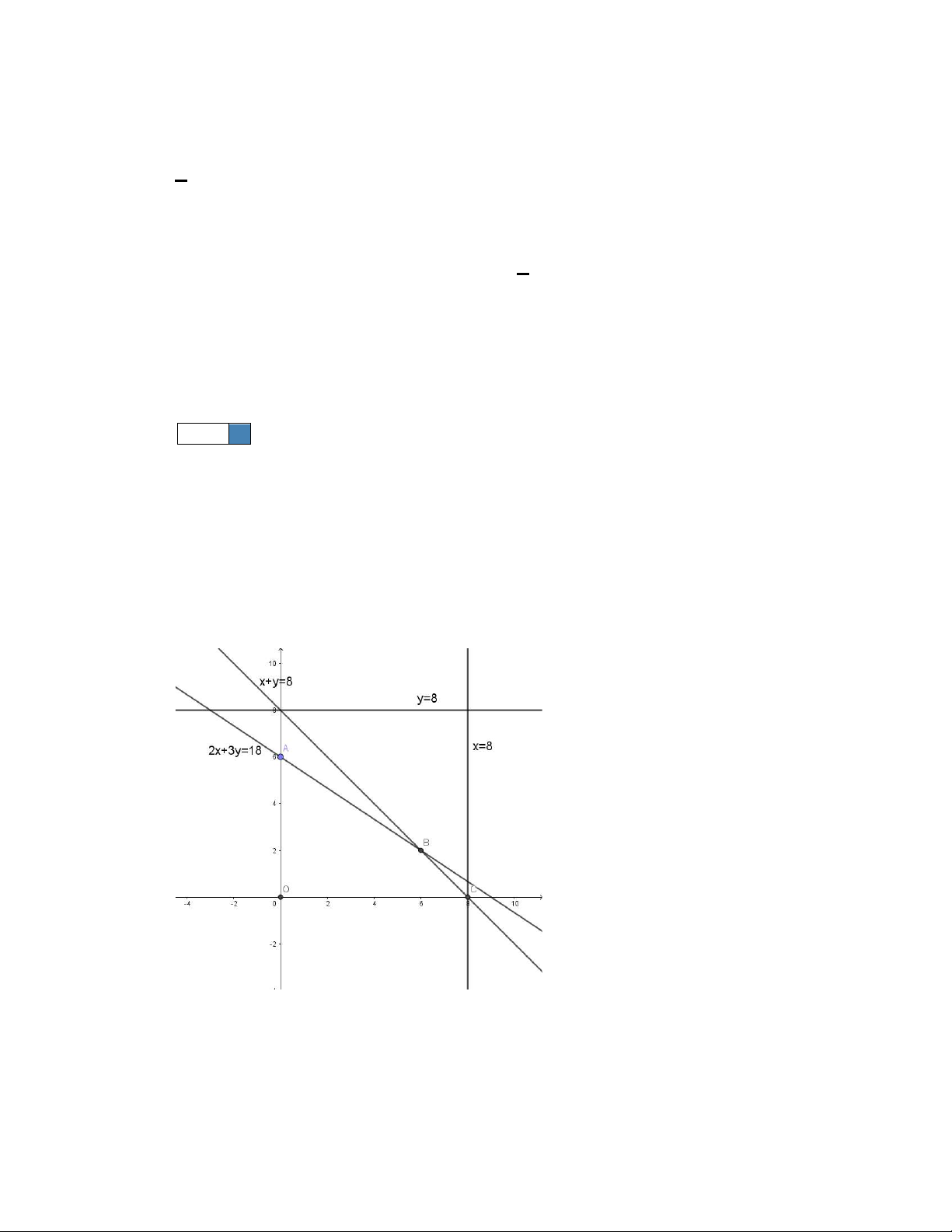
Câu 10: Các thành phố A, B, C, D được nối với nhau bởi các con đường như hình vẽ. Hỏi có bao nhiêu
cách đi từ A đến D mà qua B và C chỉ một lần? A. 9. B. 10. C. 18. D. 24. Lời giải Chọn D Từ A B có 4 cách. Từ B C có 2 cách. Từ C D có 2 cách.
Vậy theo qui tắc nhân ta có 4 2 3 24 cách.
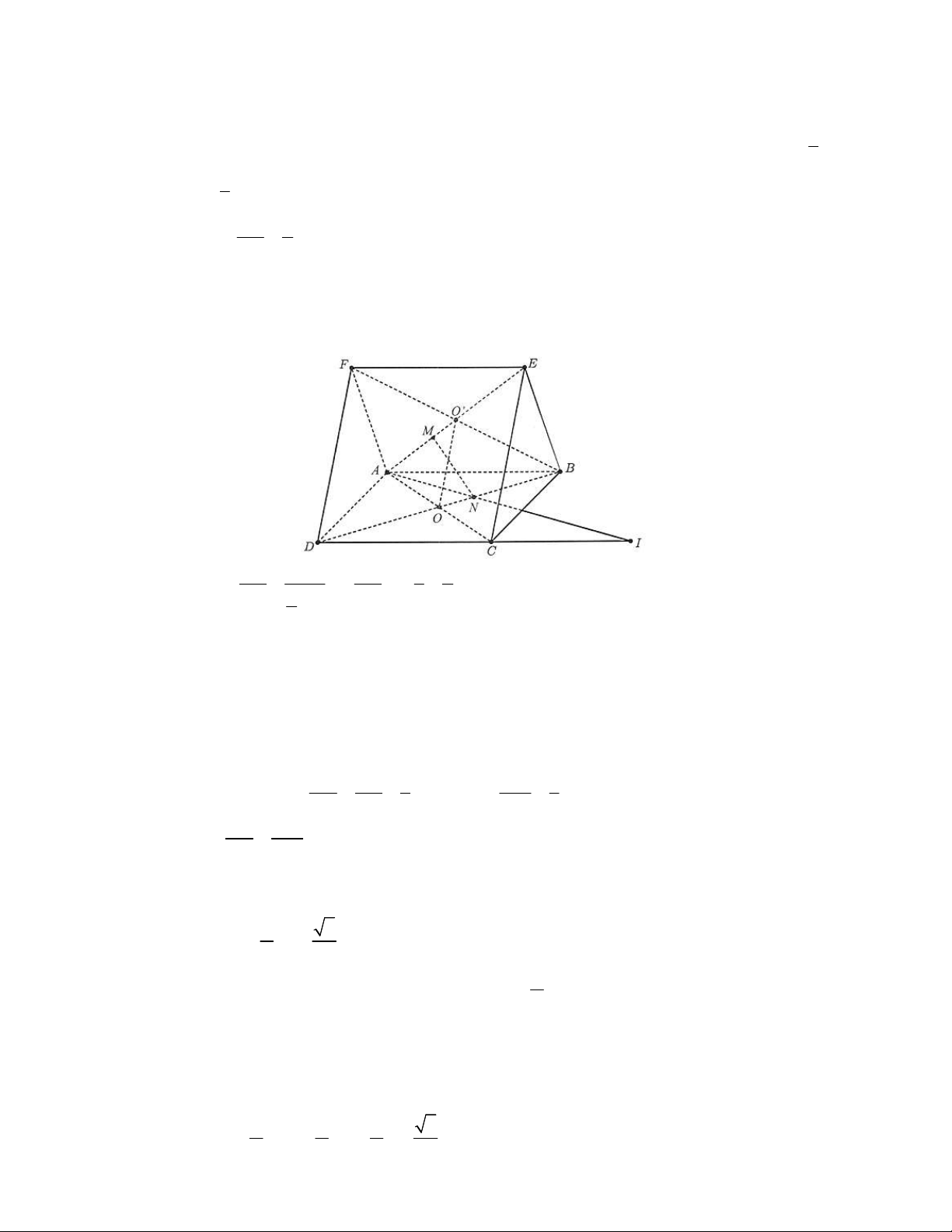
Câu 11: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi A , B lần lượt là trung điểm của S , A SB. Đường thẳng A B
song song với mặt phẳng nào sau đây? A. SAB . B. SBC . C. SCD . D. SAD . Lời giải Chọn C
Vì AB song song với AB và AB song song với CD nên A B song song với C . D
Hơn nữa, AB không chứa trong SCD nên A B
song song với SCD.
Câu 12: Cho hình chóp S.ABCD với ABCD là hình bình hành. Khi đó giao tuyến của hai mặt phẳng SAC và SAD là A. Đường thẳng SC . B. Đường thẳng SB . C. Đường thẳng SD . D. Đường thẳng SA . Lời giải Chọn D
Ta thấy SAC SAD SA .
Câu 13: [NB] Cho hai đường thẳng phân biệt không có điểm chung cùng nằm trong một mặt phẳng thì hai đường thẳng đó
A. song song. B. chéo nhau. C. cắt nhau. D. trùng nhau.
Câu 14: [NB] Một thùng trong đó có 12 hộp đựng bút màu đỏ, 18 hộp đựng bút màu xanh. Số cách khác
nhau để chọn được đồng thời một hộp màu đỏ, một hộp màu xanh là? Trang 10/29 –
A. 30 . B. 12. C. 18. D. 216 . Câu 15: [NB] Cho
. Kết quả đúng là 2
A. sin 0, cos 0 . B. sin 0, cos 0 .
C. sin 0, cos 0 . D. sin 0, cos 0 .
Câu 16: [NB] Cho đường thẳng a nằm trong mặt phẳng và đường thẳng b nằm trong mặt phẳng
. Mệnh đề nào sau đây SAI?
A. //( ) a//b. B. //( ) a// .
C. //( ) b// . D. a và b hoặc song song hoặc chéo nhau. 2 x 1
Câu 17: [TH] Cho hàm số f x và f 2
2 m 2 với x 2 . Giá trị của m để f x liên tục tại x 1 x 2 là:
A. 3 . B. 3 . C. 3 . D. 3 .
Câu 18: [TH] Có 5 tem thư khác nhau và 6 bì thư cũng khác nhau. Người ta muốn chọn ra từ đó 3 tem
thư và 3 bì thư. Có bao nhiêu cách như vậy? A. 3 3 C .C . B. 3 3 C C . C. 3 3.C . D. 3 3.C . 5 6 5 6 5 6
Câu 19: Chọn đáp án đúng trong các câu sau:
A. sin x 1 x k2, k . B. sin x 1 x k 2, k . C. sin x 1
x k, k . D. sin x 1
x k2, k . 2 2
Câu 20: Công thức nào sau đây là đúng với cấp số cộng có số hạng đầu u , công sai d, n 2.? 1 A. u u d .
B. u u n 1 d . C. u u n 1 d . D. u u n 1 d . n 1 n 1 n 1 n 1
Câu 21: Hàm số nào dưới đây gián đoạn tại điểm x 1. 0 2x 1 2x 1 x A. y . B. y . C. y . D. y x 2 1 x 2. 2 x 1 x 1 x 1
Câu 22: Cho A và B là hai biến cố đối nhau. Mệnh đề nào dưới đây đúng?
A. Hai biến cố A và B đồng thời xảy ra.
B. P A P B 1.
C. P A P B 1.
D. P A P B 1.
Câu 23: Cho bảng phân bố thực nghiệm sau: Các lớp 40;42 42;44 44;46 46;48 48;50 Tần số 5 10 26 5 4
Số trung vị thuộc lớp nào: A. 42;44 . B. 44;46 . C. 46;48 . D. 48;50 . Trang 11/29 -
Câu 24: Cho hình bình hành EFGH và một điểm b không nằm trong mặt phẳngEFGH . Giao tuyến
của hai mặt phẳng SEF và SGH là một đường thẳng song song với đường thẳng nào sau đây? A. GH . B. EG . C. EH . D. SG .
Câu 25: Cho hình chóp S.ABCD . Gọi I là trung điểm của SD , J là điểm trên SC và không trùng
trung điểm SC . Gọi F là giao điểm của IJ với CD . Tìm giao điểm của BC và AIJ ?. B. I AI SD . B. J AJ SC .
C. M AF BC . D. F IJ CD
Câu 26. Một hộ nông dân định trồng dứa và củ đậu trên diện tích 8ha . Trên diện tích mỗi ha , nếu
trồng dứa thì cần 20 công và thu 3 triệu đồng, nếu trồng củ đậu thì cần 30 công và thu 4 triệu
đồng. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu ha để thu được nhiều tiền
nhất, biết rằng tổng số công không quá 180.
A. 1 ha dứa và 7 ha củ đậu.
B. 6 ha dứa và 2 ha củ đậu. C. 8 ha củ đậu.
D. 2 ha dứa và 6 ha củ đậu. Lời giải Chọn B Gọi ,
x y lần lượt là số ha trồng dứa và củ đậu.
Có 0 x 8;0 y 8 ; x y 8 ; 20x 30y 180 2x 3y 18 .
Số tiền thu được là T x, y 3x 4y . 0 x 8 0 y 8 Ta có hệ x y 8 2x 3y 18
Miền nghiệm của hệ là miền tứ giác OABC với A0;6, B6;2,C 0;8 .
Khi đó T x, y đạt cực đại tại một trong các đỉnh của OABC .
Có T 0,0 0;T 0;6 24;T 6;2 26;T 8;0 24 .
Vậy cần trồng 6 ha dứa và 2 ha củ đậu. Trang 12/29 –
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S)
Câu 1: Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng và có tâm lần 1
lượt là O và O . Gọi M , N lần lượt là hai điểm trên các cạnh AE, BD sao cho AM AE 3 1
BN BD . Khi đó, Các mệnh đề sau đúng hay sai? 3 BN 2 a) [NB] . BO 3
b) [TH] OO song song với mặt phẳng (ADF).
c) [TH] OO cắt mặt phẳng (BCE) .
d) [VD] MN song song với mặt phẳng (CDFE) . Lời giải BN BN BN 1 2 a) Ta có 2
2. , suy ra mệnh đề đúng. BO 1 BD 3 3 BD 2
b) Ta có OO là đường trung bình của tam giác BDF nên OO / /DF , mà DF (ADF ) suy
ra OO / /(ADF) , suy ra mệnh đề đúng
c) Ta có OO là đường trung bình của tam giác ACE nên OO / /CE , mà CE (BCE) suy ra
OO / /(BCE) suy ra mệnh đề sai.
d) Chứng minh MN song song với mặt phẳng (CDFE) :
Trong mặt phẳng (ABCD) , gọi I AN CD . AN BN 1 AM 1 Do AB / /CD nên . Mặt khác: . AI BD 3 AE 3 AN AM Do đó MN / /IE AI AE
Mà IE (CDFE) , suy ra MN / /(CDFE) . suy ra mệnh đề đúng.
Câu 2: Cho hàm số f x cos 2x cos x . Xét tính đúng sai của các khẳng định sau đây: 2 a) [NB] f 4 2
b) [TH] Phương trình f x 0 có nghiệm là x k k . 2
c) [TH] Tập giá trị của hàm số f x cos 2x cos x là đoạn 1; 1 .
d) [VD,VDC] Phương trình f x 0 có tất cả ba nghiệm thuộc đoạn 0;2 . Lời giải a) Đúng. 2 Ta có: f cos cos . 4 2 4 2 b) Sai. Trang 13/29 - x x k Ta có: f x 2 2
0 cos 2x cos x 0 cos 2x cos x 2x x k2 x k2 k2 k2 x k . x 3 3 c) Sai. Ta có: f x 2
cos 2x cos x 2cos x cos x 1.
Đặt t cos x với 1 t 1. Xét hàm số g t 2
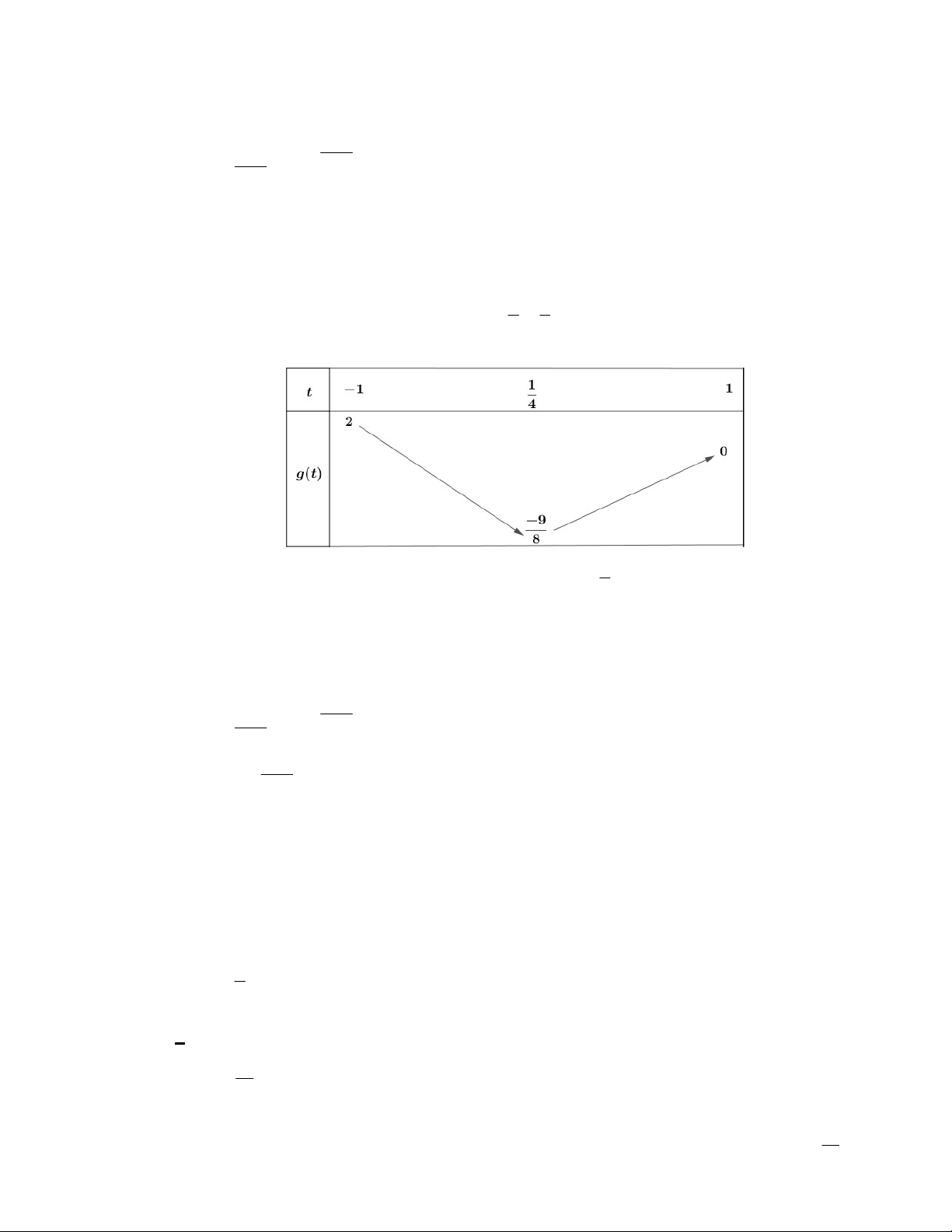
2t t 1 với t 1; 1 . 1 9
Đồ thị của hàm số là một parabol có đỉnh là I ; . 4 8 Bảng biến thiên: 9
Vậy tập giá trị của hàm số f x cos 2x cos x là đoạn ;2 . 8 d) Sai. x x k Ta có: f x 2 2
0 cos 2x cos x 0 cos 2x cos x 2x x k2 x k2 k2 k2 x k . x 3 3 k2 Khi đó: 0 2 0 k 3 . 3
Vì k nên k 0; 1; 2; 3 .
Vậy phương trình f x 0 có tất cả bốn nghiệm thuộc đoạn 0;2 .
Câu 3: Một người vừa gieo một con xúc xắc để ghi lại số chấm xuất hiện, sau đó người này tiếp tục chọn
ngẫu nhiên một lá bài từ bộ bài 52 lá. Các khẳng đinh sau đúng hay sai?
a) [NB] Gọi A là biến cố: "Số chấm của xúc xắc lớn nhất", khi đó xác suất của biến cố A là 1 P A . 2
b) [TH] Gọi B là biến cố: "Chọn được một lá bài tây", khi đó xác suất của biến cố B là P B 3 . 13 1
c) [TH] Xác suất để số chấm trên con xúc xắc là lớn nhất và chọn được một lá bài tây bằng . 12 Trang 14/29 – 1
d) [VD,VDC] Xác suất để số chấm trên con xúc xắc và số của lá bài là giống nhau bằng . 16 Lời giải a) Sai.
Gọi A là biến cố: "Số chấm của xúc xắc lớn nhất". Suy ra
A P A 1 1; 2;3;4;5;6 , 6 . 6 b) Đúng.
B là biến cố: "Chọn được một lá bài tây".
Trong bộ bài 52 là có 12 lá bài tây, nên xác suất chọn được một lá bài tây là P B 3 . 13 c) Sai. Vì ,
A B là hai biến cố độc lập.
Suy ra P AB P A P B 1 3 1 . 6 13 26 d) Sai.
Khi tung con xúc xắc một lần, và lấy một lá bài trong bộ bài, số khả năng có thể xảy ra là: 6.52 312 khả năng.
+ Ứng với một kết quả tung con xúc xắc, có 4 cách tìm được một lá bài có cùng số với số xuất
hiện trên mặt con xúc xắc, do đó có tất cả 6.4 24 khả năng để số chấm trên con xúc xắc và số
của lá bài là giống nhau . 24 1
Vậy xác suất để số chấm trên con xúc xắc và số của lá bài là giống nhau là: . 312 13
Câu 4: Người ta đo đường kính của 57 cây gỗ được trồng sau 10 năm (đơn vị: centimét), họ thu được
bảng tần số ghép nhóm sau: Đường kính [20; 25) [25;30) [30;35) [35; 40) [40; 45) Số cây 4 10 24 13 6
a) [NB] Cỡ mẫu của mẫu số liệu là n 57 .
b) [TH] Đường kính trung bình của 57 cây gỗ là 33,11cm (kết quả làm tròn đến hai chữ số thập phân).
c) [TH] Số cây có đường kính khoảng 31,8 cm là nhiều nhất Trang 15/29 -
d) [VD] Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: Q 36,38 33,11cm (kết quả làm 3
tròn đến hai chữ số thập phân). Lời giải
a) Cỡ mẫu của mẫu số liệu là n 57 , suy ra mệnh đề đúng.
22,5.4 27,5.10 32,5.4 37,5.13 42,5.6
b) Giá trị trung bình: x 33,11 57
Vậy đường kính trung bình của 57 cây gỗ xấp xỉ 33,11cm , suy ra mệnh đề đúng.
c) Nhóm có tần số lớn nhất là 30;35 . 24 10
Ta đi tính mốt của mẫu số liệu ghép nhóm này: M 30 e
.35 30 32,8 24 10 24 13
Suy ra mốt của mẫu số liệu bằng 32,8 . Do đó số cây có chiều cao 32,5cm là nhiều nhất, suy ra mệnh đề sai. x x
d) Xét nửa mẫu số liệu bên phải x , x , , x có trung vị 43 44 [35;40) . 30 31 7 5 2 3.57 38 1915
Suy ra tứ phân vị thứ ba của mẫu số liệu là: 4 Q 35 (40 35) 36,83( cm) , suy ra 3 13 52 mệnh đề sai.
Câu 5: Vào năm con gái được 4 tuổi, một người chuẩn bị gửi tiết kiệm đầu mỗi năm một số tiền x (triệu
đồng) x để đến năm 18 tuổi sẽ có được 200 triệu cho con gái đi học đại học. Hiện tại lãi suất tiền
gửi hàng năm là 4,8% /năm. Giả sử lãi suất này được giữ ổn định Mệnh đề Đúng Sai
a) Tổng số tiền thu về sau 14 năm là một cấp số nhân có q 1 4,8% .
b) Tổng số tiền thu về sau 14 năm là một cấp số nhân có u x . 1 3. x 10(triệu đồng)
4. Đến năm con gái được 10 tuổi, người này dự định khi con gái được
18 tuổi sẽ mua thêm cho con gái một chiếc xe máy trị giá 50 triệu
đồng. Do đó, kể từ thời điểm đầu năm con gái được 10 tuổi người này
cần gửi tiết kiệm y triệu đồng đến khi con gái 18 tuổi y . Giá trị nhỏ nhất của y 15 . Lời giải a) Đúng b) Sai c) Đúng d) Đúng
Số tiền người đó nhận được sau năm thứ nhất là: A x 1 4,8% . 1
Số tiền người đó nhận được sau năm thứ hai là: A x14,8% x14,8% 2 . 2 Số tiền người đó nhận được sau năm thứ 14 là:
A x14,8% x14,8% 2... x14,8%14 . 14 Trang 16/29 – u x 14,8% n 1 q 1 1 4,8% 1 Khi đó: A có nên A u x 14,8% . 14 1 14 14 q 1 4,8% q 1 4,8% 200.4,8% Suy ra: x
9,873336 10 (triệu đồng).
1 4,8% 1 4,8%14 1 Khi x 10(triệu đồng).
Gọi z y x là số tiền mà người đó phải gửi thêm mỗi năm kể từ năm con gái 10 tuổi (năm
thứ 6) và P z14,8% z14,8 2
% ... z14,8%8 là số tiền nhận được sau 8 8 năm.
Khi đó để nhận được số tiền 250 triệu đồng vào năm con gái 18 tuổi ( 8 năm kể từ con gái 10 tuổi) thì: P 1 4,8%14 1 250 10 1 4,8% 47,43 (triệu đồng). 8 4,8% 47, 43.4,8% Suy ra z
4,77 5(triệu đồng).
1 4,8% 1 4,8%8 1
Vậy y 15 (triệu đồng).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. ĐỀ 1
Câu 1: Phương trình 2sin 2x 3 0
có mấy nghiệm thuộc khoảng 0;3 ? 3 Lời giải Đáp án: 6 2x k2 3 Ta có 3 3 2sin 2x 3 0 sin 2x sin 3 3 2 3 2x k2 3 3 1 8 x k 0 k 3 k 3 k 0;1;2
, k . Vì x 0;3 nên 3 3 3 1 5 k 0;1;2 x k 0 k 3 k 2 2 2 2
4 7 3 5 x ; ; ; ; ; . 3 3 3 2 2 2
Câu 2: Gọi S là tập các số tự nhiên gồm 6 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số từ tập
S . Xác suất để số được chọn có đúng 3 chữ số chẵn bằng bao nhiêu (làm tròn đến hàng phần trăm)? Lời giải Đáp án: 0,48
Số phần tử của không gian mẫu: n 5 9.A . 9
Tập các chữ số A 0;1;2;3;4;5;6;7;8; 9
Gọi x abcdef a 0 là số cần lập. Ta có: TH1: Có chữ số 0
Xếp chữ số 0 : có 5 cách; Chọn 2 chữ số chẵn: 2 C 6 cách; 4 Trang 17/29 - Chọn 3 chữ số lẻ: 3 C 10 cách; 5
Xếp 5 chữ số vừa chọn: 5! 120 .
Trường hợp này có: 120.10.6.5 36000 số. TH2: Không có chữ số 0
Chọn 3 chữ số chẵn có 3 C 4 cách; 4 Chọn 3 chữ số lẻ có 3 C 10 cách; 5
Xếp 6 chữ số đó có 6! 720 cách;
Trường hợp này có: 720.10.4 28800 số.
Suy ra n A 36000 28800 64800 số.
Vậy xác suất là: P A 64800 10 0,48 136080 21
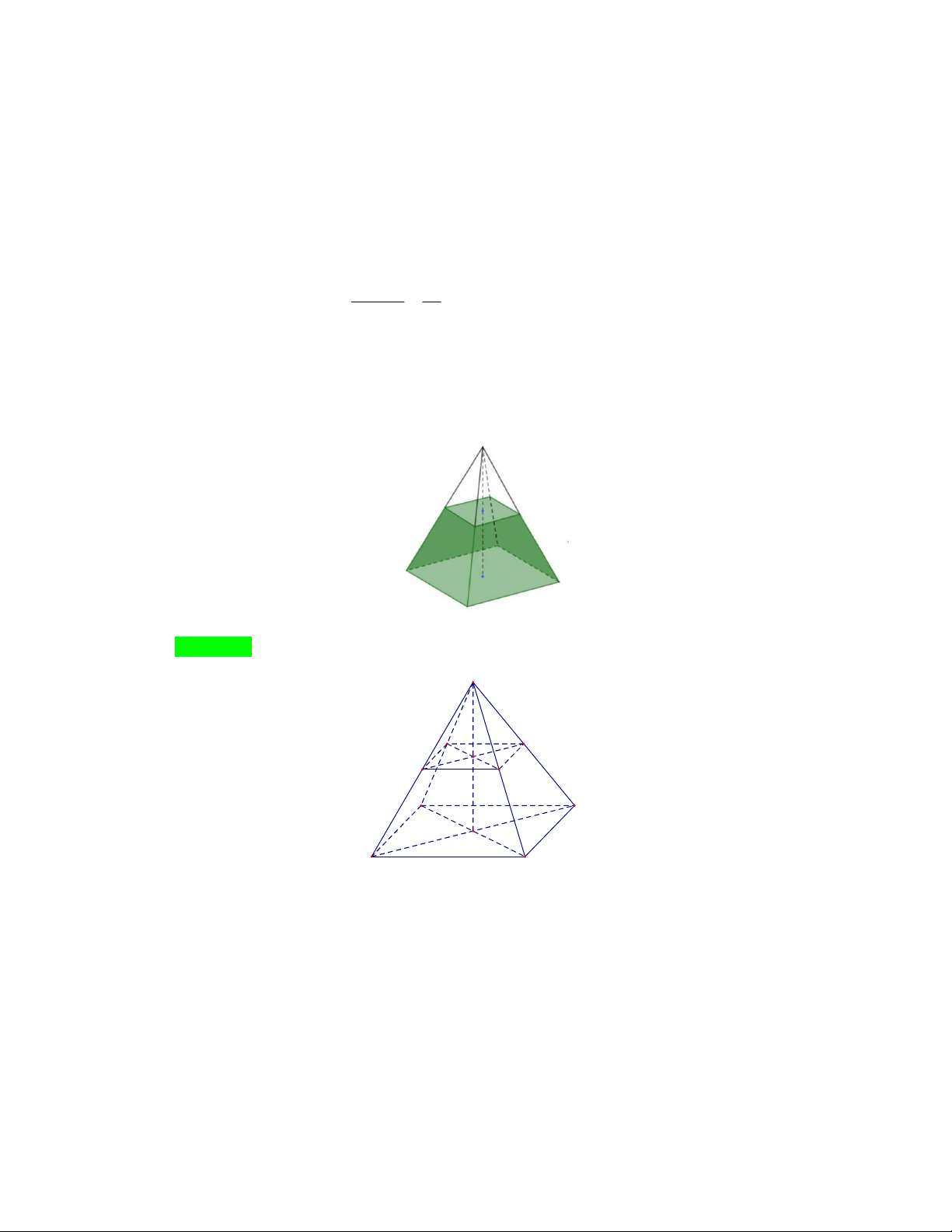
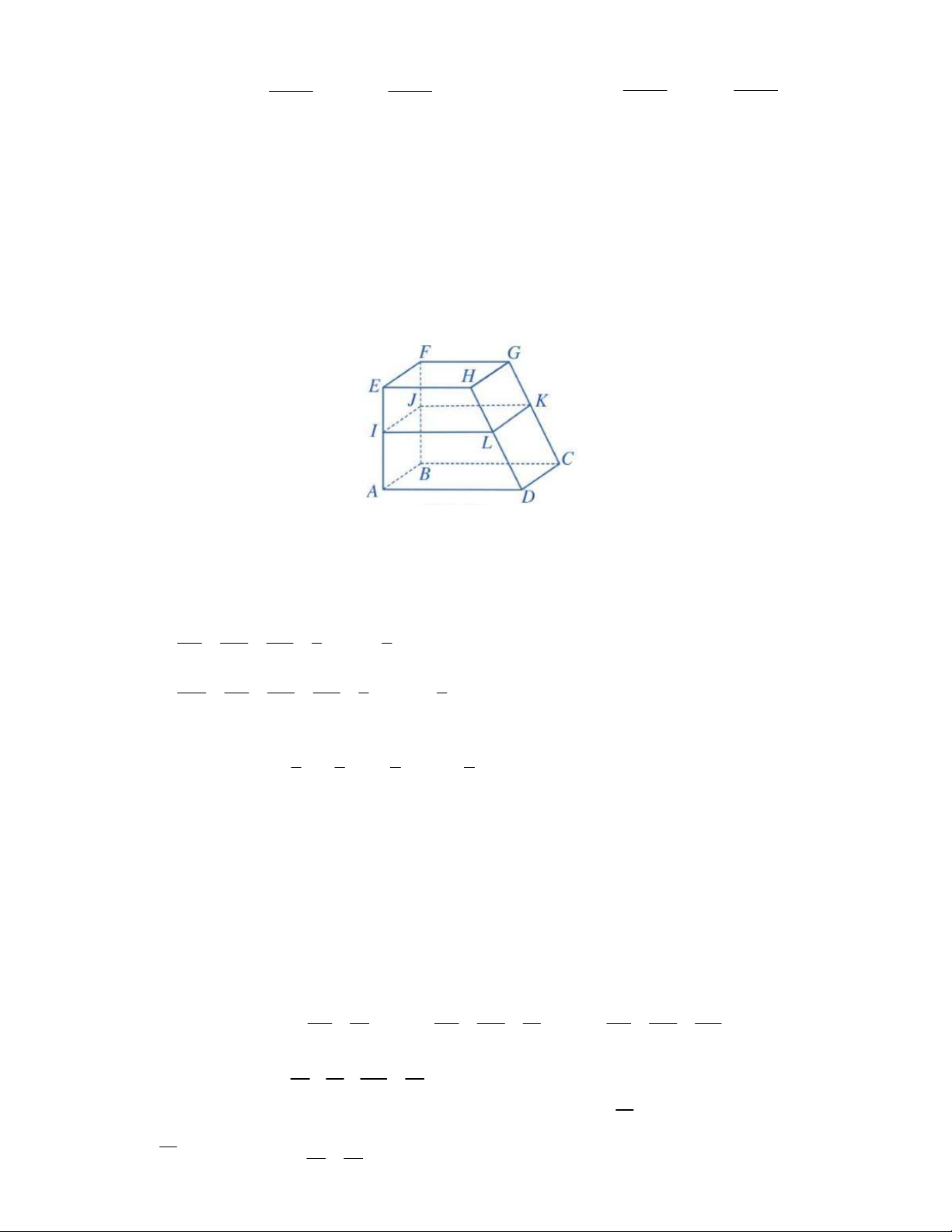
Câu 3: Một khối gỗ có dạng hình chóp có đáy là hình vuông và tất cả các cạnh bằng 0,5 m . Một người
muốn thiết kế thành đồ trang trí bằng cách cưa đi phần đỉnh của khối gỗ này và gắn dây đèn
trang trí theo cách cạnh của khối hình mới (tham khảo hình bên dưới). Biết rằng lưỡi cưa đi qua
3 trung điểm của ba cạnh bên của khối gỗ. Chiều dài của dây đèn trang trí là bao nhiêu m (làm
tròn đến hàng đơn vị). Lời giải Đáp án: 4. S D' C' A' O' B' D C A O B
Hình chóp S.ABCD mô tả khối gỗ.
Cưa đi phần đỉnh của khối gỗ, lưỡi cưa đi qua các trung điểm của ba cạnh bên của khối gỗ
nghĩa là cắt hình chóp bởi một mặt phẳng đi qua các điểm A , B ,C ( A , B ,C là trung điểm của S , A SB, SC ).
Trong mặt phẳng ABCD : gọi O là giao điểm của AC, BD .
Trong mặt phẳng SAC : gọi O là giao điểm của A C , SO .
Trong mặt phẳng SBD : gọi D là giao điểm của B O , SD .
Suy ra mặt phẳng cắt các mặt của hình chóp theo các giao tuyến là A B , B C ,C D , D A .
Dây đèn trang trí được gắn vào cách cạnh AB, BC,CD, D , A AB , B C ,C D , D A , AA , BB , CC , DD nên tổng chiều dài sợi dây bằng
l AB BC CD DA AB B C C D D A
AA BB CC DD.
Dễ dàng chứng minh được D là trung điểm của SD . Trang 18/29 – 1 Do
A , B là trung điểm của S , A SB nên A B
AB 0, 25m . Tương tự 2 B C C D D A 0, 25m .
Do A , B ,C , D là trung điểm của S ,
A SB, SC, SD nên AA BB CC DD 0, 25 m Vậy
l AB BC CD DA AB B C C D D A
AA BB CC DD l 0,5.4 0.25.8 4 m Câu 4: Cho 2 lim x ax 5 x và x bx
x thì giá trị của biểu thức x 2 lim 10 0 1012 x T a b là Lời giải Đáp án: 2024 2 2 x ax 5 x ax 5 Ta có: lim lim 2 lim x ax 5 x x x 2
x ax 5 x x 2 x ax 5 x 5 a a lim x x a 5 2 1 1 2 x x a Do giả thiết 2 lim x ax 5 x 1012 a 2024 . 1012 x 2
Do đó giá trị của a là 2024 . 2 2 x bx 10 x bx 10 Ta có: lim lim 2 lim x bx 10 x x x 2
x bx 10 x x 2 x bx 10 x 10 b b lim x x b 10 2 1 1 2 x x b Do giả thiết 2 lim
x bx 10 x 0 b 0 . 0 x 2
Do đó giá trị của b là 0 . Vậy T a b 2024
Câu 5: Sau khi tốt nghiệp đại học, bạn Nam được hai công ty mời về làm việc với yêu cầu là phải làm
ít nhất 3 năm và cách trả lương như sau: Công ty A: Mức lương tháng đầu tiên
20.000.000/tháng. Từ tháng thứ hai, mức lương tăng thêm 300.000 đồng mỗi tháng. Công ty
B: Mức lương tháng đầu tiên là 15.000.000/tháng. Từ tháng thứ hai, lương mỗi tháng tăng
3,5% trên mỗi tháng so với tháng trước đó. Sau thời gian suy nghĩ, Nam quyết định chọn công
ty có tổng thu nhập sau 3 năm cao hơn công ty còn lại. Hỏi tổng thu nhập sau 3 năm của Nam
là bao nhiêu triệu đồng (làm tròn đến hàng đơn vị)? Lời giải Đáp án: 1050.
Gọi u là mức lương của Nam ở tháng làm việc thứ n tại Công ty A. Khi đó u là cấp số n n
cộng với u 20 (triệu) và công sai d 0,3(triệu). Khi đó, sau 3 năm (36 tháng) Nam nhận 1 362u 35d 1 được số tiền là S 909 (triệu) 36 2 Trang 19/29 -
Gọi v là mức lương của Nam ở tháng làm việc thứ n tại Công ty B. Khi đó v là cấp số n n
nhân với v 15 (triệu) và công bội q 1,035 . Khi đó, sau 3 năm (36 tháng), Nam nhận được 1 v 36 q 1 1 số tiền là S 1050 (triệu). 36 q 1
Vậy Nam chọn công ty B để làm việc và số tiền nhận được sau 3 năm làm việc là 1050 triệu đồng.
Câu 6. Một xí nghiệp may áo vest và quần âu để chuẩn bị cho dịp cuối năm. Biết may 1 áo vest hết 2m
vải và cần 20 giờ; may 1 quần âu hết 1,5m vải và cần 5 giờ. Xí nghiệp được giao sử dụng
không quá 920m vải và số giờ công không vượt quá 6400 giờ. Theo khảo sát thị trường, số
lượng quần âu bán ra không nhỏ hơn số lượng áo vest bán ra và số lượng quần âu bán ra không
vượt quá 2 lần số lượng áo vest bán ra. Khi xuất ra thị trường, 1 chiếc áo vest lãi 350 nghìn
đồng, 1 chiếc quần âu lãi 100 nghìn đồng. Gọi ,
x y lần lượt là số áo vest và quần âu xí nghiệp
cần may và bán ra thị trường để xí nghiệp có số tiền lãi cao nhất. Tính giá trị của biểu thức T 2x 3y ? Lời giải Trả lời 1 3 4 Gọi , x y ,
x y lần lượt là số áo vest và quần âu xí nghiệp cần may và bán ra thị trường
Số vải cần thiết để may số áo vest và quần âu đó là 2x 1,5y .
Thời gian cần thiết để may số áo vest và quần âu đó là 20x 5y .
Theo bài ra ta có hệ bất phương trình: 3 2x y 920 4x 3y 1840 2 4x y 1280 20x 5y 6400 x y 0 y x * 2x y 0 y 2x x 0 x 0 y 0 y 0
Biểu diễn miền nghiệm của hệ bất phương trình
* lên mặt phẳng tọa độ Oxy ta được miền tứ
giác OABC trong đó O0;0, A184;368, B250;280, C 256;256 . Số tiền lãi là L ;
x y 350x 100y , đơn vị: nghìn đồng.
Ta có L0;0 0, L184;368 101200, L250;280 115500, L256;256 115200 .
Ta thấy số tiền lãi đạt cao nhất khi x 250, y 280 .
Khi đó T 2.250 3.280 1340 . Trang 20/29 – ĐỀ 2
Câu 1: Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương trình 2 x 3cos 4t
, với t là thời gian tính bằng giây và x là quãng đường tính bằng cm. 3
Hãy cho biết trong khoảng thời gian từ 0 đến 5 giây, vật đi qua vị trí cân bằng bao nhiêu lần? Lời giải Đáp số: 20 .
Yêu cầu bài toán ⇔ Tìm t sao cho x 0, với 0 t 5 2 Ta có x 2 0 3cos 4t 0 cos 4t 0 . 3 3 2 7 7 1 4 t
k k 4 t
k k t k k . 3 2 6 24 4 7 1 7 113 Ta có 0 ≤ t ≤ 5 0 k 7 1 113 5 k k . 24 4 24 4 24 6 6
Mà k nên k 1;0;1;...;17;1
8 , có 20 giá trị k thỏa mãn.
Vậy trong khoảng thời gian từ 0 đến 5 giây, vật đi qua vị trí cân bằng 20 lần. Câu 2: Biết . Tính a 4b . 2 lim 4x 3x 1 ax b 0 x Lời giải Đáp số: 1. Ta có: 3 1 b lim x 4 a 0 (*) 2 lim 4x 3x 1 ax b 0 x 2 x x x x lim x x Ta có: 3 1 b lim 4 a 2 a 2 x x x x 3 1 b
Nếu 2 a 0 thì lim x 4
a nên không thỏa mãn (*) 2 x x x x 3 1 b
Nếu 2 a 0 thì lim x 4
a nên không thỏa mãn (*) 2 x x x x
Nếu 2 a 0 a 2 thì (*) trở thành Trang 21/29 - 1 3 1 3 3 3 lim x 4 2 b 0 lim x b 0 b 0 b 2 x x x x 3 1 4 4 4 2 2 x x Vậy a 4b 1 .
Câu 3: Anh An đi làm với mức lương khởi điểm là x (triệu đồng)/ tháng, và số tiền lương này được
nhận vào ngày đầu tháng. Vì làm việc chăm chỉ và có trách nhiệm nên sau 12 tháng kể từ ngày
đi làm, anh An được tăng lương thêm 10% . Mỗi tháng, anh ta giữ lại 20% số tiền lương để gửi
tiết kiệm ngân hàng với kì hạn 1 tháng và lãi suất là 0,5% /tháng, theo hình thức lãi kép (tức
tiền lãi của tháng này được nhập vào vốn để tính lãi cho tháng tiếp theo). Sau 24 tháng kể từ
ngày đi làm, anh An nhận được số tiền cả gốc và lãi là 100 triệu đồng. Hỏi mức lương khởi
điểm của anh An là bao nhiêu triệu đồng(làm tròn kết quả đến một chữ số thập phân)? Lời giải Đáp án: 18,7
Gọi số tiền mỗi tháng anh gửi tiết kiệm ngân hàng trong 12 tháng đầu là A (triệu đồng); số tiền
mỗi tháng anh gửi tiết kiệm sau 12 tháng là B (triệu đồng)
Đặt q 1 0,5% 1,005
Gọi S là số tiền sau tháng thứ n ta có n S A . A 0,5% . A q 1
S S A S A.0,5% S A 2 .q Aq Aq . 2 1 1 1 …. 12
q S S A S A .0,5% S A 1 12 11
.q Aq Aq Aq A . q . 12 11 11 11 q 1
S S B S B .0,5% S B .q S .q . B q . 13 12 12 12 12
S S B S B.0,5% S B 2 2 .q S q Bq Bq . 14 13 13 13 12 …. 12 12 q 1 q 1 12 12 11 13
S S .q Bq Bq ... Bq Aq . B . q 24 12 q 1 q 1
Theo giả thiết ta có A 20%x 0, 2x ; B 20% x 10%x 0,22x ; S 100. 24 Trang 22/29 – 12 12 q 1 q 1 12 12 q 1 q 1 Vậy 13 0, 2xq . 0, 22 . x . q 100 13 x 100 : 0,2q . 0,22. . q q 1 q 1 q 1 q 1
x 18,7 triệu đồng.
Câu 5: Một kệ để đồ bằng gỗ có mâm tầng dưới ABCD và mâm tầng trên EFGH song song với
nhau. Bác thợ mộc đo được AE 180 cm và muốn đóng thêm một mâm tầng giữa IJKL
song song với hai mâm tầng trên và dưới sao cho khoảng cách EI 60cm (Hình dưới). Hãy tính số 2
m gỗ cần dùng để làm mâm gỗ của tầng giữa biết rằng mâm gỗ dưới cùng là hình chữ nhật có diện tích là 2 7, 2 m . Lời giải
Ta có cát tuyến AE cắt ba mặt phẳng song song EFGH , IJKL, ABCD lần lượt tại
E, I , A ; cát tuyến GC cũng cắt ba mặt phẳng trên theo thứ tự tại G, K , C .
Áp dụng định lí Ta-lét trong không gian, ta có: EI IL 60 1 1 IL AD EA AD 180 3 3 GK EI LK 60 1 1 LK CD GC EA CD 180 3 3
Khi đó diện tích hình chữ nhật IJLK là: 1 1 1 1 S I . L LK A . D CD .S .7, 2 0,8 . IJLK ABCD 2 m 3 3 9 9
Câu 6: Một hộp đựng 5 viên bi trắng, 7 viên bi đỏ và 4 viên bi vàng. Chọn ngẫu nhiên 3 viên bi
trong hộp. Tính xác suất để 3 viên bi được chọn không cùng một màu. Lời giải Đáp án:0,91 Gọi , A ,
B C lần lượt là 3 biến cố “chọn được ba viên bi trắng”, “chọn được ba viên bi đỏ”,
“chọn được ba viên bi vàng”. M là biến cố: “chọn được viên bi cùng một màu”. Ta có: , A ,
B C đôi một xung khắc và M A B C P M P A P B P C . 3 3 3 C 1 C 35 1 C 4 1 Trong đó: P A 5 ; PB 7 ; PC 4 . 3 3 3 C 56 C 560 16 C 560 140 16 16 16 Suy ra P M 1 1 1 7 . 56 16 140 80
Biến cố “chọn ba viên bi không cùng một màu” là biến cố đối M .
Vậy P M PM 7 73 1 1 0,91 80 80 Trang 23/29 - ĐỀ 3 Câu 1: Cho hàm số 2 2
y sin x 2sinx cosx cos x 5. Gọi M,m lần lượt là giá trị lớn nhất, giá trị
nhỏ nhất của hàm số. Tính M m ? (Kết quả làm tròn đến hàng phần mười). Lời giải Đáp án: 10, 0 . TXĐ: . Ta có 2 2
y sin x 2sinx cosx cos x 5 y sin 2x cos2x 5 y 2 sin2x 5 4 1 sin 2x 1, x 4
5 2 2 sin 2x 5 5 2 4 5 2 y 5 2
M 5 2;m 5 2 M m 10 Ghi 10,0
Câu 2: Trong một căn phòng có 36 người, trong đó có 25 người họ Nguyễn và 11 người họ Trần. Chọn
ngẫu nhiên hai người trong phòng đó. Tính xác suất để hai người được chọn cùng họ. (Kết quả
làm tròn đến hàng phần mười). Lời giải Đáp án: 0,6 .
A : " Hai người được chọn cùng họ Nguyễn ".
B : " Hai người được chọn cùng họ Trần ".
C : " Hai người được chọn cùng họ ". C A B
Do A và B xung khắc nên P C P A B P A P B Ta có: n 2 C 630 n A 36 2 C 300;n B 2 C 55 25 11 300 55 P A ;P B 630 630
P C P A P B 300 55 0,56 630 630 Ghi : 0,6
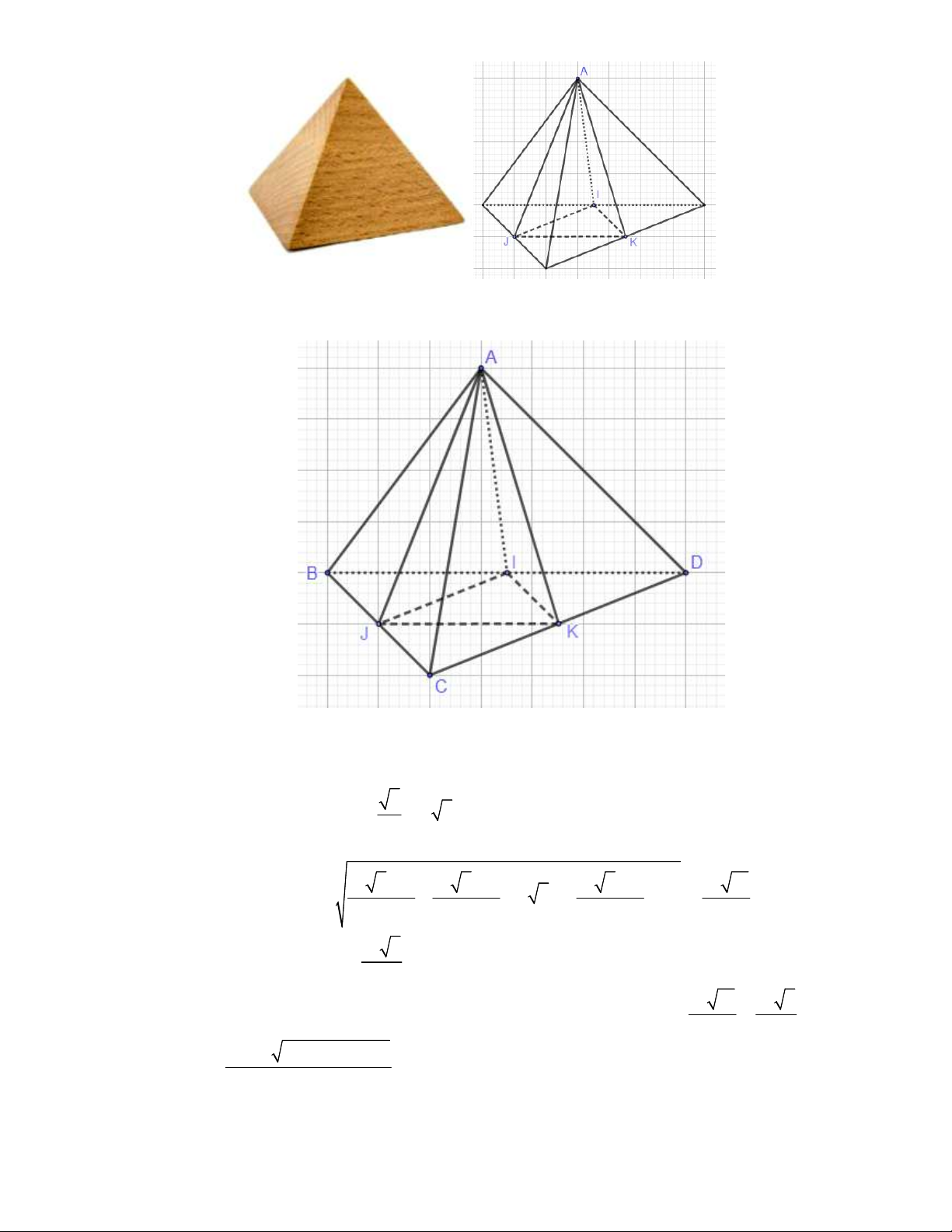
Câu 3: Anh Bình mua một cục chắn giấy có bốn mặt là bốn tam giác đều cạnh bằng 10cm như hình
vẽ. Tuy nhiên khi sử dụng, Anh thấy hơi quá cỡ nên quyết định cắt bớt bằng cách cắt theo các
mặt phẳng tạo bởi các đường nối từ đỉnh xuống trung điểm của các cạnh đáy (tham khảo hình vẽ).
Tính tổng diện tích các mặt của cục chặn giấy mới sau khi được cắt (làm tròn đến hàng đơn vị). Trang 24/29 – Lời giải Đáp án: 73.
Sau khi cắt theo các mặt AIJ ,AIK ,AKJ ta được khối AIJK . 3 Ta có AI AJ AK 10
5 3 , IJ JK KI 5 . 2
Áp dụng công thức Hê-rông: 2 10 3 5 10 3 5 10 3 5 25 11 S S S . 5 3 5 . AIJ AIK AJK 2 2 2 4 25 3 Diện tích tam giác S . IJK 4 25 11 25 3
Vậy tổng diện tích các mặt của cục chặn giấy mới sau khi được cắt là: 3. 73 4 4 2 2ax x 3x 2024 Câu 4: Biết lim
20 . Khi đó giá trị 1 2a bằng bao nhiêu? x x 3 Lời giải Đáp án: 20. Trang 25/29 - Ta có: 3 2024 3 2024 2 2ax x 1 2ax x 1 2 2 2ax x 3x 2024 lim lim x x lim x x x x 3 x x 3 x x 3 3 2024 2a 1 2 lim x x 2a 1 . x 3 1 x
Theo giả thiết: 2a 1 20 1 2a 2 0.
Câu 5: Một cửa hàng nhập về một thùng táo Envy size 5 (1kg có 5 quả táo). Vị khách đầu tiên mua nửa
số táo trong thùng, người thứ hai mua nửa số táo còn lại, người thứ ba mua nửa số táo còn lại,…. Đến
người thứ tám cửa hàng cũng bán nửa số táo còn lại và còn lại 3kg. Hỏi thùng táo bán được bao nhiêu tiền
(đơn vị triệu đồng, làm tròn đến hàng đơn vị), biết rằng cửa hàng bán táo với giá 75 nghìn đồng một kilogam. Lời giải Đáp án: 57,6.
Mỗi quả táo có khối lượng là 1kg : 5 0,2kg
Số táo còn lại sau khi bán 3kg tức là còn 15 quả. Gọi *
x x là số quả táo mà cửa hàng đã nhập về để bán. x
Người thứ nhất đã mua: quả, 2 1 x x
Người thứ hai đã mua: . quả, 2 2 2 2 x Người thứ ba đã mua: quả, 3 2 …………………. x Người thứ tám đã mua: quả. 8 2
Sau khi người thứ tám mua thì còn lại 15 quả nên ta có phương trình: x x x x 1 1 1 1 . . x 15 x
. . x 15 * 2 3 8 2 3 8 2 2 2 2 2 2 2 2 8 1 1 8 1 1 1 1 1 2 1 255 Lại có .. . 1 . 2 3 8 2 2 2 2 2 1 2 256 1 2 Do đó 255 * x x 15 x 3840. 256
Thùng táo có số kilogam là : 3840.0,2 768 kg.
Vậy cửa hàng đã thu được số tiền là 768.75000 57600000 đồng hay . 57,6triệu đồng.
Câu 6: Một bệnh truyền nhiễm có xác suất lây bệnh là 0,95 nếu tiếp xúc với người bệnh mà không đeo
khẩu trang; là 0,2 nếu tiếp xúc với người bệnh mà có đeo khẩu trang. Anh Thành tiếp xúc với một người
bệnh hai lần, trong đó có một lần đeo khẩu trang và một lần không đeo khẩu trang. Tính xác suất anh
Thành bị lây bệnh từ người bệnh mà anh tiếp xúc. Trang 26/29 – Lời giải Đáp án: 0,96 .
Gọi A là biến cố “anh Thành bị lây bệnh từ người bệnh nếu tiếp xúc với người bệnh mà không đeo khẩu trang". P( ) A 0,95 .
Khi đó A là biến cố “anh Thành không bị lây bệnh từ người bệnh nếu tiếp xúc với người bệnh
mà không đeo khẩu trang". P( ) A 1 0,95 0,05.
Gọi B là biến cố “anh Thành bị lây bệnh từ người bệnh nếu tiếp xúc với người bệnh mà có đeo khẩu trang". P(B) 0,2 .
Khi đó B là biến cố “anh Thành không bị lây bệnh từ người bệnh nếu tiếp xúc với người bệnh
mà có đeo khẩu trang". P( ) A 1 0,2 0,8.
Vì A và B là 2 biến cố độc lập nên xác suất của biến cố "anh Thành không bị lây bệnh từ
người bệnh mà anh tiếp xúc đó” là:
P(AB) 0,050,8 0,04 .
Xác suất anh Thành bị lây bệnh từ người bệnh mà anh tiếp xúc là 1 0, 04 0,96 HẾT Trang 27/29 -



