


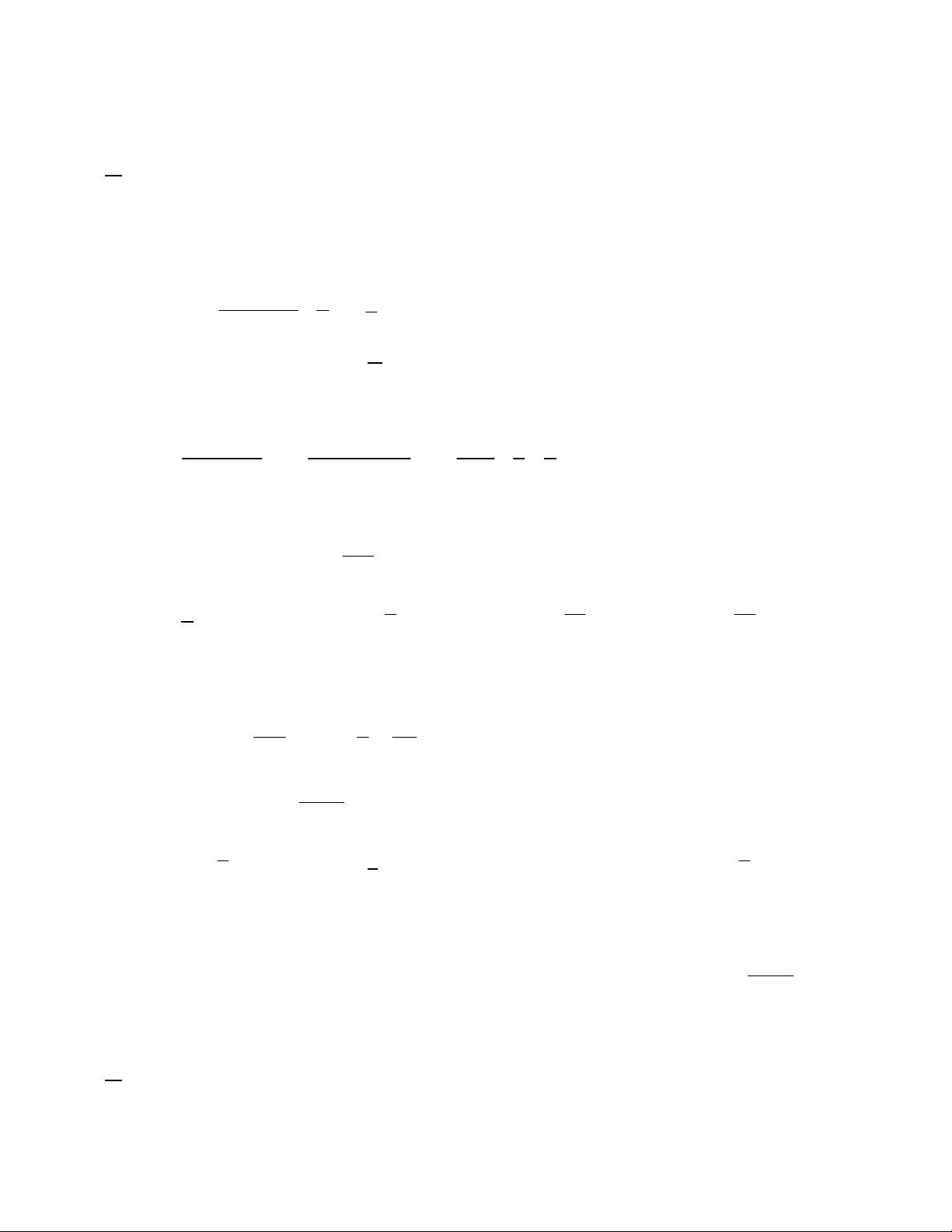











Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI KHẢO SÁT ĐỢT 1 - NĂM 2025 LIÊN TRƯỜNG THPT CỤM 09
Đáp án khối: 11 Môn: TOÁN Câu Mã đề
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. 0101 0 102 0 103 0104 1 B A D B 2 D B C B 3 B C A A 4 A C C C 5 B A C C 6 D B B D 7 B B A B 8 C D D A 9 A A D C 10 D B D C 11 A A C D 12 C D C C
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu thí sinh chọn đúng hoặc sai Câu . Mã đề 0101 0 102 0 103 0104 1 D S D D D D S S D D S D S D S D 2 S D S D D D S S S S D D D D S S 3 S D D D D S D D S S D D D D S D 4 D S D S D D S D D S D D D S D D Câu Mã đề
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6. 0101 0 102 0 103 0104 1 48 10 0,16 0,16 2 5,96 0,29 0,29 5,96 3 20,2 48 48 0,29 4 0,16 0,16 20,2 20,2 5 0,29 5,96 5,96 48 6 10 20,2 10 10
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI KHẢO SÁT ĐỢT 1 - NĂM 2025 LIÊN TRƯỜNG THPT CỤM 09
Hướng dẫn giải môn: TOÁN
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Phủ định của mệnh đề “ 2 x | x x 2
026 0 ” là mệnh đề A. “2 x | x x 2 026 0 ”. B. “2 x | x x 2 026 0 ”. C. “2 x | x x 2 026 0 ”. D. “2x | x x 2 026 0 ”. Lời giải Đáp án: A
Phủ định của mệnh đề 2 x | x x 2
026 0 là mệnh đề 2 x | x x 2 026 0 . x y
Câu 2. Trong mặt phẳng với hệ tọa độ Oxy , cho đường thẳng d 4 5 :
. Vectơ nào sau đây là một 3 2
vectơ chỉ phương của đường thẳng d ? A. u 3;2 u 4;5 u 3; 2 u 4;5 4 3 2 1 . B. . C. . D. . Lời giải: Đáp án: C x y Đường thẳng d 4 5 :
có vectơ chỉ phương là u 3; 2 . 3 3 2
Câu 3. Giải phương trình 2 cos x 1
ta được tập nghiệm là kk A. , . B. 3k k , . 3 2 kk 2 2 , C. , . D. 3 k k . 3 3 Lời giải Đáp án : D Ta có 1 2 2 cos x 1 cos x x k2k , . 2 3 Câu 4.
Cho hai góc lượng giác ; thỏa mãn
. Khẳng định nào sau đây đúng? 2 A. sin si n . B. sin co s . C. sin co s . D. sin si n . Lời giải Đáp án: B Vì nên sin si n c o s . 2 2 Câu 5. Cho dãy số u u. Số hạng u n biết 5.5n n n 2 của dãy số là A. 2 5 5 n . B. 2 125.5 1 n . C. 25.5n . D. 25.5n . Lời giải: Đáp án: C Số hạng n2 1 u 5.5 12 5.5 2 n 5 n .5. n 2
Câu 6: Cho cấp số cộng u biết u , u . Công sai d của cấp số cộng đó là n 2 5 5 8 A. d 1. B. d 3 . C. d 2 . D. d 8 . Lời giải: Đáp án: A Ta có: 5 u 2
u 3d 3d u 52u 3 d 3 d 1 . 2 x x 5 6 a a Câu 7. Cho lim với a b b 2
là phân số tối giản và , , 0 . Tính a b . x3 x b 9 b A. 5 . B. 7 . C. 6 . D. 0 . Lời giải Đáp án: B 2 x 5x 6 x x2 3 x 2 1 a a b Ta có: lim lim lim 1, 6. 2 x x3 3 x 9 xx 3x3 3 x 3 6b Vậy: a b 7 . n 1 4 Câu 8. Cho dãy số u u. Tính lim nn u n với 2 . 5 n n 4 4 25 A. 0 . B. . C. . D. . 5 25 4 Lời giải Đáp án: A n 1 1 4 4 4 n Ta có: lim li um . lim . 0 nn 2 2 n n n 5 5 5 3 2 x Câu 9. Tìm giới hạn lim . x 3 x 3 1 7 A. . B. . C. . D. . 4 4 Lời giải Đáp án: B 3 2 x Ta có x l x im , x lxim và khi x 3 thì x 3 0 nên lim 3 . 3 0 3 2 3 3 3 x 3 x
Câu 10: Cho tứ diện ABCD. Gọi I ,J lần lượt là trọng tâm các tam giác ABC và ABD. Chọn khẳng định
đúng trong các khẳng định sau? A. IJ song song với CD. B. IJ song song với AB. C. IJ chéo CD. D. IJ cắt AB. Lời giải Đáp án: A
Gọi M ,N lần lượt là trung điểm của B C B , D .
MN là đường trung bình của tam giác BCD M N CD 1 . AI AJ 2IJ MN
I,J lần lượt là trọng tâm các tam giác ABC và ABD 2 AM AN 3
Từ 1 và 2 suy ra : IJ CD .
Câu 11: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng S AD và S
BC . Khẳng định nào sau đây đúng ?
A. d qua S và song song với BC. B. d qua S và song song với DC.
C. d qua S và song song với AB. D. d qua S và song song với BD. Lời giải Đáp án: A S d A D B C S S AD S B C Ta có AD S AD ,BC SBC SA D
SBC d với d là đường thẳng qua S và song song AD BC với BC . Câu 12: Cho hình hộp .
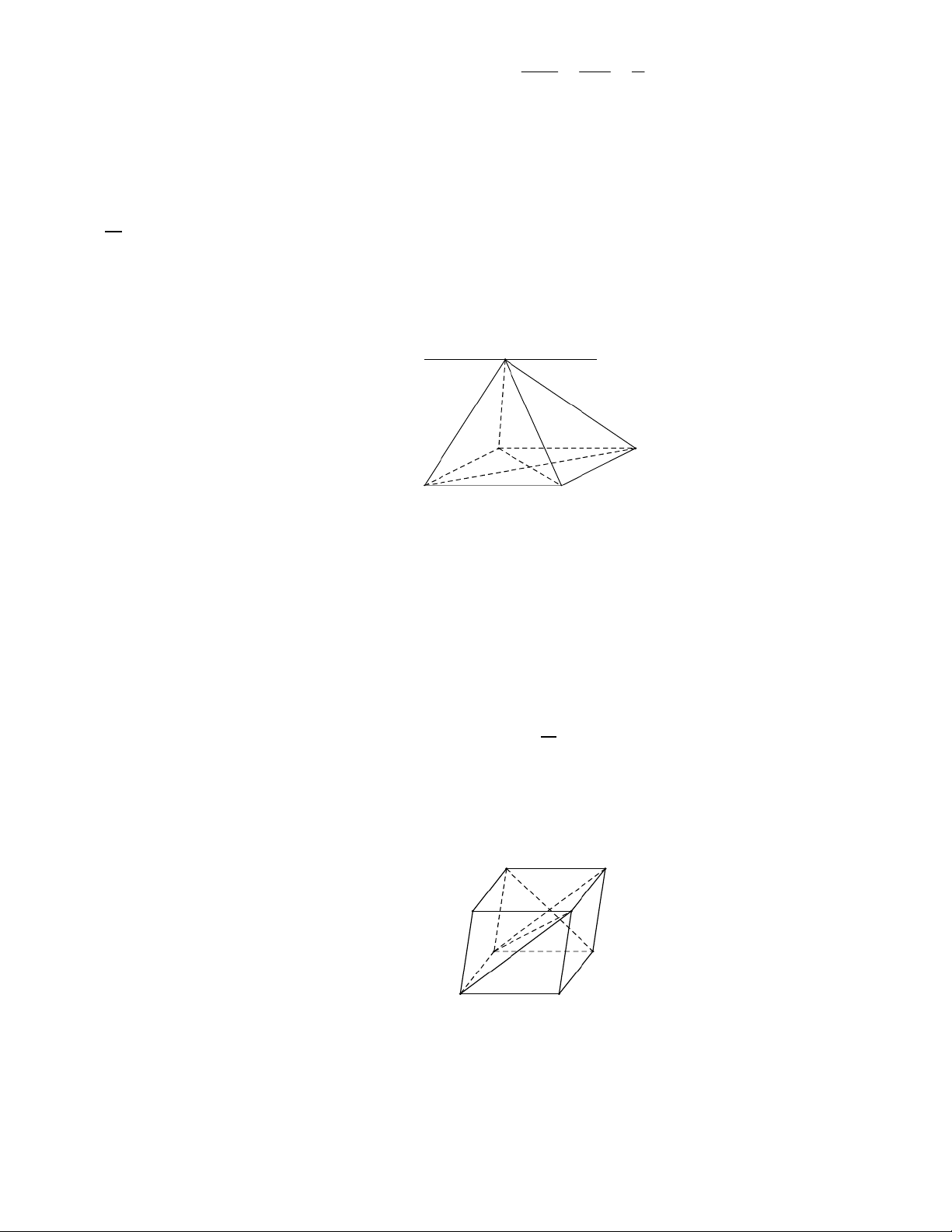
ABCD ABCD có các cạnh bê An A BB, , CC ,DD .
Khẳng định nào dưới đây sai? A. A A BB //D DC C . B. B AD //A DC . C. AB CD là hình bình hành. D. BB D D là một tứ giác. Lời giải Đáp án: B D C A B D' C' A' B'
Dựa vào hình vẽ dưới và tính chất của hình hộp, ta thấy rằng: Hai mặt bên A A BB và D D C C
đối diện, song song với nhau.
Hình hộp có hai đáy ABCD , ABCD là hìn h bình hành AB
CD và AB //CD suy ra AB CD là hình hình hành. BD //B D suy ra B , B ,D ,D đồng phẳng BB D D là tứ giác. Mặt phẳng B
AD chứa đường thẳng CD mà CD cắt C D suy ra B
AD không song song với A DC .
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu thí sinh chọn đúng hoặc sai.
Câu 1. Theo nghiên cứu, một gia đình 4 người cần ít nhất 200 gam chất đạm protein và 200 gam chất béo lipit
trong thức ăn mỗi ngày. Biết rằng trong 100 g thịt bò chứa khoảng 20 gam protein và 5 gam lipit, trong 100 gam
thịt lợn (ba chỉ) chứa khoảng 15 gam protein và 30 gam lipit. Giả sử gia đình này chỉ mua nhiều nhất 1,2 kg thịt bò
và 1 kg thịt lợn và giá thịt bò là 250 000 đồng/kg, giá thịt lợn là 120 000 đồng/kg. Để đảm bảo nhu cầu về protein
và lipit gia đình này mua x kg thịt bò và y kg thịt lợn. Khi đó 0 1, 2x 0 1 y a)
là hệ bất phương trình biểu thị các điều kiện của bài toán. 4 3 x y 4 x y6 4
b) Miền nghiệm của hệ trên là miền của tam giác.
c) Gọi T là số tiền phải trả khi mua x kg thịt bò và y kg thịt lợn. Khi đó: T 25x0y 120 (nghìn đồng).
d) Gia đình đó mua 0, 57 kg thịt bò và 0,57 kg thịt lợn thì chi phí là ít nhất. Lời giải a) Đúng
Giả sử gia đình đó mua x kg thịt bò và y kg thịt lợn. Đi ều kiện: x 0y 1 ,2;0 1 .
Khi đó lượng protein có được là 20% x y 15%
và lượng lipit có được là 5% x y 30% .
Vì gia đình đó cần ít nhất 0, 2 kg protein và 0, 2 kg lipit trong thức ăn mỗi ngày nên điều kiện tương ứng là: 20% x y15% 0, 2 x; 5% y30% 0, 2. 0 1, 2 x 0 1y
Ta có hệ bất phương trình: . 4 3 x y 4 x y 6 4 b) Sai
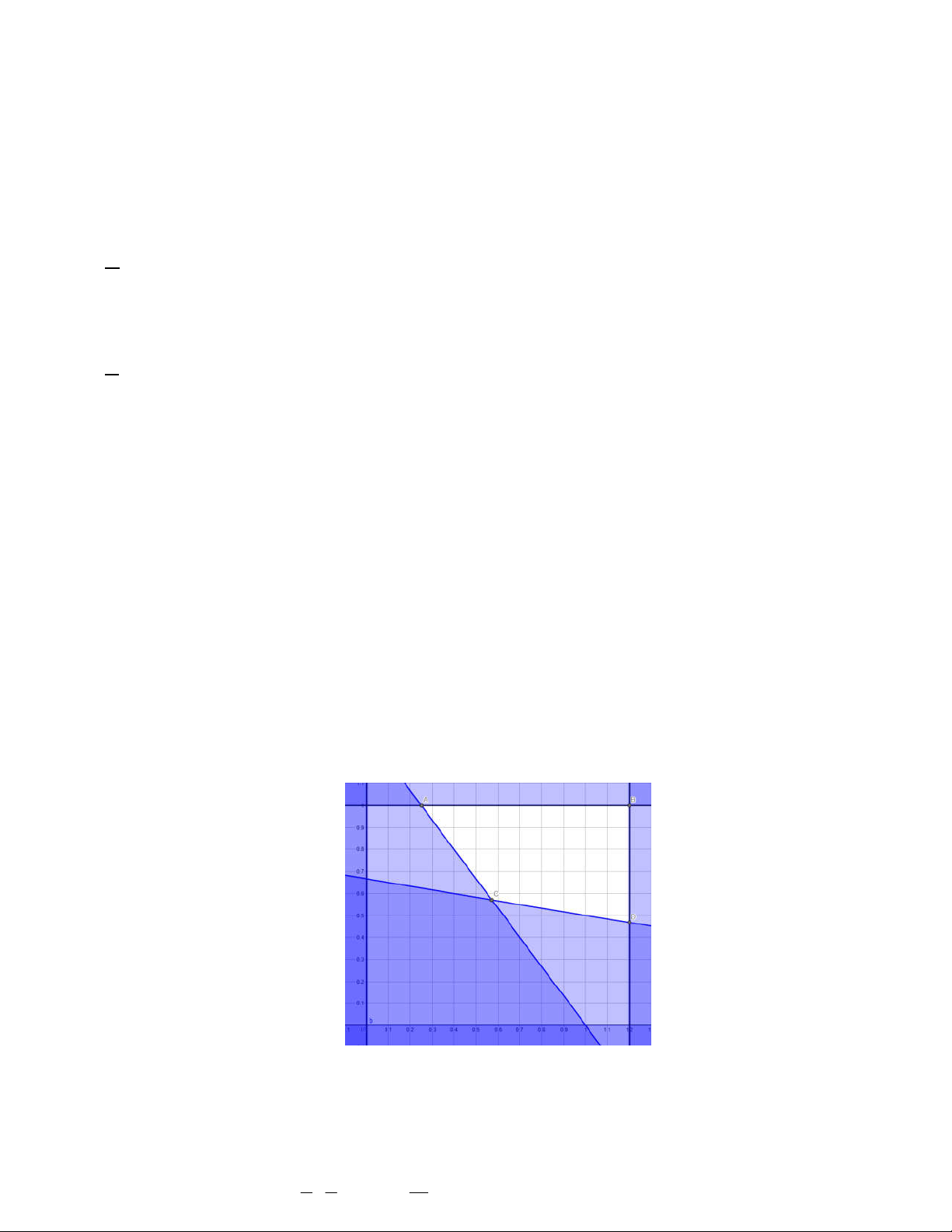
Miền nghiệm của hệ trên là miền của tứ giác lồi ABCD (kể cả biên) được mô tả ở hình vẽ. c) Đúng
Chi phí để mua x kg thịt bò và y kg thịt lợn là: T 25x0y 120 (nghìn đồng). d) Sai
Ta đã biết T đạt giá trị nhỏ nhất tại một trong các đỉnh tứ giác ABCD trong đó: A B C 4 4 7 0,25; 1 ; 1,2; 1 ; D; ; 1, 2; . 7 7 15 Với A t0a, 2 c 5 ó ; 1 T 250.0, 25 1 20.1 182,5 . Với B t1a, c 2; ó 1 T 250.1, 2 1 20.1 420 . 4 4 Với C t0 a ,c 57 ó ; 0, 57 T 250. 12 0. 211, 4 . 7 7 7 7 Với D 1, 2; ta có T 250.1, 2 1 20 . 356 . 15 15 x 0,25
So sánh ta được T đạt giá trị nhỏ nhất bằng 182,5 (nghìn đồng) khi . (tức là gia đình đó mua 0, 25 kg y 1
thịt bò và 1kg thịt lợn thì chi phí là ít nhất).
Câu 2: Anh Linh là một cầu thủ bóng đá chuyên nghiệp. Anh vừa kí hợp đồng 5 năm với một câu lạc bộ với mức
lương khởi điểm là 300 triệu đồng mỗi năm, tiền lương được trả đều hàng tháng. Chủ tịch câu lạc bộ đưa ra cho ba
phương án về lương như sau:
Phương án 1: Mỗi năm ngoài mức lương cố định như trên, sẽ được thưởng thêm 50 triệu đồng.
Phương án 2: Mỗi năm lương sẽ tăng thêm 10% so với lương năm trước đó, bắt đầu tính từ năm thứ hai.
Phương án 3: Mỗi năm lương sẽ tăng thêm 30 triệu so với lương năm trước đó, bắt đầu tính từ năm thứ hai.
Xét tính đúng sai của các mệnh đề sau:
a) Lương khởi điểm của anh Linh mỗi tháng là 25 triệu đồng.
b) Theo phương án 2 thì đến năm thứ 3 lương mỗi tháng của anh Linh là 30 triệu đồng.
c) Theo phương án 3 thì tổng số tiền lương anh nhận được sau 5 năm là: 1800 triệu đồng.
d) Trong ba phương án: Phương án 2 giúp anh có tổng thu nhập sau 5 năm là cao nhất. Lời giải a) Đúng 300
Tiền lương khởi điểm mỗi tháng là: 12 25 triệu đồng. b) Sai
Theo phương án 2, tiền lương hàng tháng là một cấp số nhân với 1 u q 25, 1,1
. Do đó, đến năm thứ 3 tiền lương mỗi tháng là L 25 .1, 2 1 3 0 tr ,i2 ệ 5 u đồng. 3 c) Đúng
Phương án 3: Mỗi năm lương sẽ tăng thêm 30 triệu so với lương năm trước đó, nên tiền lương hàng năm là một cấp số cộng với 1 u d 300 , 30
. Vậy sau 5 năm tổng số tiền lương là n 5 S 2u n 1 d 2.3 00 4.30 1800 (triệu đồng). 5 1 2 2 d) Đúng
Ta tính tổng tiền lương theo từng phương án:
Phương án 1: Mỗi năm ngoài mức lương cố định như trên, sẽ được thưởng thêm 50 triệu đồng thì sau 5 năm tổng số tiền lương là 5.300 5.5 0 1750 (triệu đồng).
Phương án 2: Mỗi năm lương sẽ tăng thêm 10% so với lương năm trước đó, nên tiền lương hàng năm là một cấp số nhân với 1 u q 300 , 1,1
. Do đó, sau 5 năm tổng số tiền lương là 1n u q 300 1 5 1,1 1 Sq (1t8 ri 3 ệ 1 u , 5 đ 3 ồng). 5 1 1 1,1
Phương án 3: Mỗi năm lương sẽ tăng thêm 30 triệu so với lương năm trước đó, nên tiền lương hàng năm là một cấp số cộng với 1 u d 300 , 30
bắt đầu kể từ năm thứ hai thì sau 5 năm tổng số tiền lương là n 5 S 2u n 1 d 2.3 00 4.30 1800 (triệu đồng). 5 1 2 2
Vậy anh Linh nên sử dụng Phương án 2 để nhận được tổng lương sau 5 năm là cao nhất. xkh 3i 2 x , 1
Câu 3. Cho hàm số f x x 1
. Xét tính đúng sai của các mệnh đề sau? 2 x m , 1khi x
a) Hàm số xác định trên . b) f 1 m 1 . c) lim 1f x m . x 1 3
d) Hàm số liên tục tại x 1 khi m . 4 Lời giải a) Đúng.
Hàm số xác định trên . b) Đúng. Ta có: f 2 1 1 1 m m c) Sai. Ta có: lim lif . m x x 2 1m m x x 1 1 d) Sai. Ta có: +) f 1 m 1 . +) lim lif mx x 2 1m m x x 1 1 x x32 3 2 x x 3 22 2 3 2 +) lim lif m x xx lim x x x lim x x1 1 x 1 1 1 x 1 3 2 1 3 2 x 1 1 1 lim lim . x x 1 1 x x1 3 2 x 3 2 4 1 5
Hàm số liên tục tại x 1 khi và chỉ khi lim f . x limf x f 1 1 m m x x 1 1 4 4
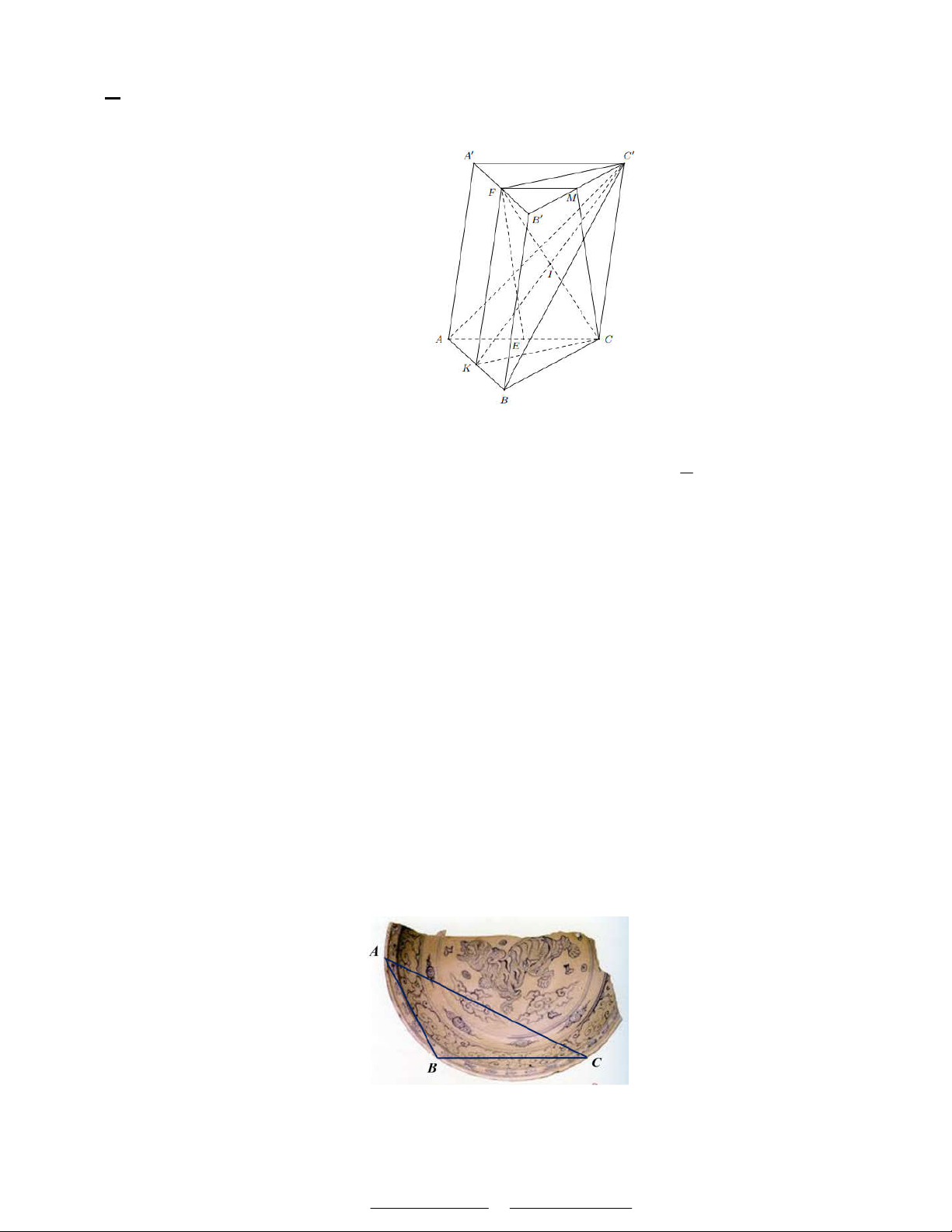
Câu 4: Cho hình lăng trụ tam giác ABC.AB C
. Gọi E,F lần lượt là trung điểm của các cạnh AC và AB .
Xét tính đúng sai của các khẳng định sau: 1
a) Nếu gọi M là trung điểm của B C
thì FM AC . 2 b) EF B CC B ∥ . )
c) Nếu gọi K là trung điểm của AB thì tứ giác CC FK là hình thang vuông. d) Gọi I CF A C B
thì khi đó I là trung điểm đoạn thẳng CF . Lời giải a) Đúng 1 Gọi M là trung điểm B C
ta có FM là đường trung bình của A
B C FM A' 'C . 2 b) Đúng
Ta có FM song song và bằng EC , nên CEFM là hình bình hành.
Do đó EF song song với MC mà MC nằm trong B CCB nên EF B CC B . c) Sai
Gọi K là trung điểm AB , vì F là trung điểm AB và ABBA là hình bình hành nên FK song song và bằng
AA. Do đó FK song song và bằng CC, suy ra CC FK là hình bình hành. d) Đúng
Khi đó gọi I là giao điểm của CF và KC thì I là trung điểm CF .
Mặt khác KC A C B nên điểm I CF A C'B .
Phần III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Trong các cổ vật gốm sứ thu được từ con tàu đắm vùng biển Cù lao Chàm Hội An, thành phố Đà Nẵng các
nhà khảo cổ đã tìm thấy một chiếc đĩa cổ hình tròn bị vỡ, khi lấy ba điểm A, B, C trên chiếc đĩa và tiến hành đo đạc thu được kết qu A ả: B c5, m 5 ; BC 8 ,5 c ; m CA 11, 4cm
. Tính bán kính của chiếc đĩa? (Kết quả viết dưới
dạng số thập phân và quy tròn đến hàng phần trăm). Lời giải: Đáp án: 5,96
Bán kính của chiếc đĩa bằng bán kính đường tròn ngoại tiếp tam giác ABC. AB BC C A 5,5 8,5 11,4
Nửa chu vi của tam giác ABC là: p 12,7. 2 2
Diện tích của tam giác ABC là S p p a p b p c 22,3.4 A . B .BC CA
Bán kính của đường tròn ngoại tiếp tam giác ABC là R 5,96 4.S
Vậy bán kính của chiếc đĩa là R 5,96 .
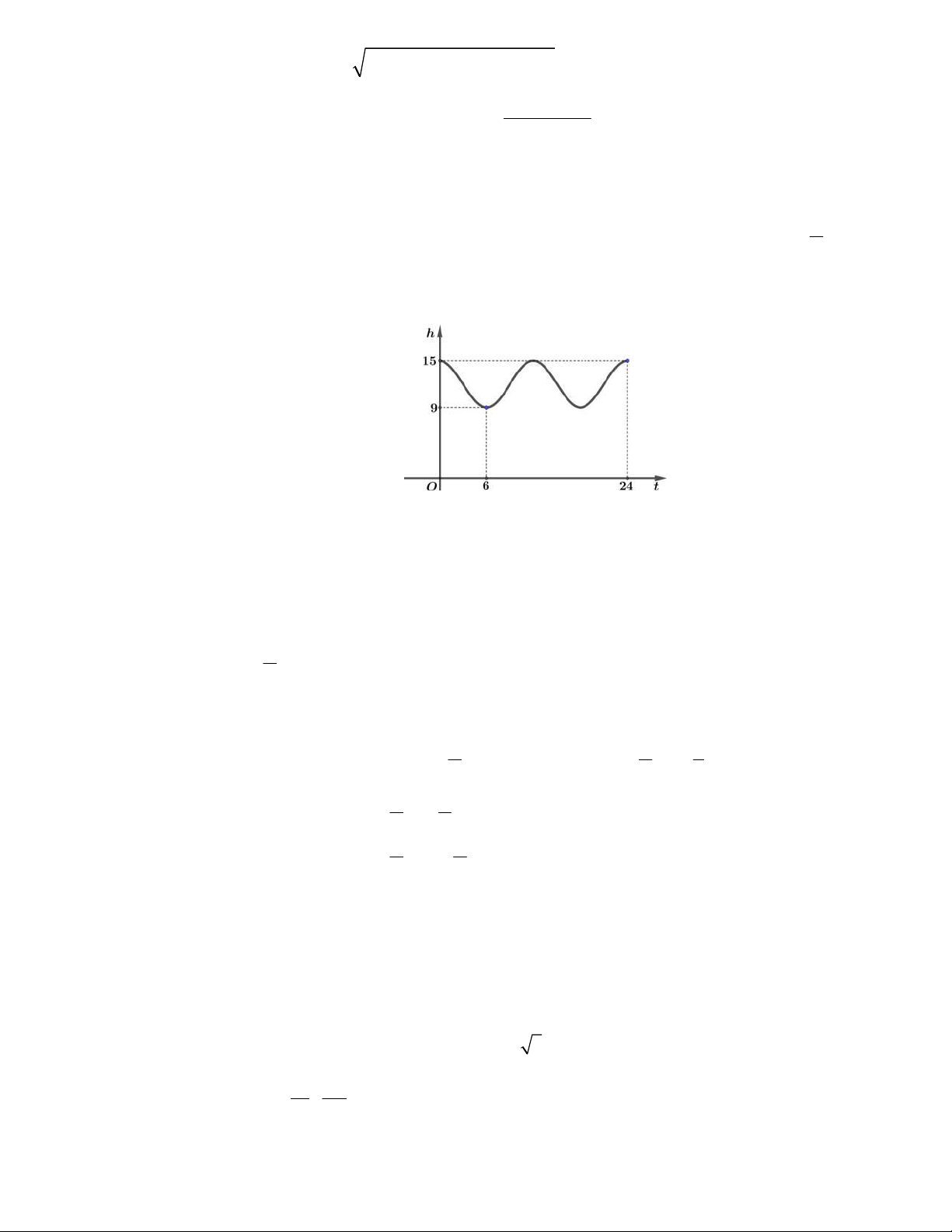
Câu 2. Hằng ngày, mực nước của một con sông ở khu vực gần cửa biển lên xuống theo thủy triều. Độ sâu h (mét)
của mực nước tính theo thời gian t (giờ) trong một ngày 0 24t
cho bởi hàm số ht a c os 6 t b
có đồ thị như hình bên dưới ( ,
a b là các số thực dương). Gọi S là tập hợp tất cả các thời điểm t trong ngày để
chiều cao của mực nước biển là 13, 5mét. Tính tổng tất cả phần tử của S ? Lời giải Đáp án: 48 h 6 9 a b 9 a 3
Theo đồ thị ta có: h 2 4 15 a b 15 12b Suy ra: h t 3 c os t 12 . 6 Theo đề bài yêu cầu: h t 1
13, 5 3 cos t 12 13, 5 cos t 6 6 2 t k 22t 12 k 6 3 , k t k 2 12 t k 2 6 3 Vì: t 0 24 t n t ên t 2, 10, t 14, 22 Suy ra: S 2; 10;14;22
Tổng các phần tử của S bằng: 2 1 0 14 22 48 .
Câu 3. Tính tổng các giá trị nguyên của tham số m và m 5, để phương trình m1 tan 2x m 3 tan 2 x 2 có đúng 2 nghiệm thuộc ; . 12 3 Lời giải Đáp số: 10 Ta có: m m 1 tan 2x m 3 3 tan 2 x m 2 tan 2x m 3 tan 2x m 2 . m 2 2 2 4 Do x ; hay x x 2
. Dựa vào đường tròn lượng giác ta thấy phương trình đã 12 3 12 3 6 3 2 3 3 m
cho có đúng 2 nghiệm thuộc ; khi 3 1 2 3 3 2 m m 3 20 3 m 2 m 2 m 2 m 2 m 1 . 3 3 m m 1 0 m 1 3 2 m m 2 3 m Vì nên m 1 n ;ên 2; 3;4 1 2 3 4 10 . m 5
Câu 4: Trong quá trình tham gia giao thông bằng ôtô, anh A không tập trung nên vi phạm lỗi vượt đèn đỏ và bị
phạt với mức phạt 20 triệu đồng. Anh A phải nộp phạt trong thời hạn 10 ngày kể từ thời điểm bị phạt. Theo thông
tư số 18/2023/TT-BTC ngày 21/3/2023 của Bộ Tài chính, cứ mỗi ngày chậm nộp phạt, cá nhân phải nộp thêm
0,05 % trên tổng số tiền phạt chưa nộp của ngày hôm trước. Vì bận công việc nên sau khi vi phạm 30 ngày anh A
mới đến cơ quan chức năng để nộp phạt được. Tại thời điểm này số tiền mà anh A phải chuẩn bị để nộp phạt cho cơ
quan chức năng là bao nhiêu triệu đồng? (Viết kết quả dưới dạng số thập phân và quy tròn đến hàng phần chục). Lời giải: Đáp số: 20,2
Nếu nộp phạt quá thời hạn thì số tiền anh A phải nộp vào ngày thứ 10 n là: 20 T 1 0,05% n . n
Đến ngày thứ 30 anh A mới đến nộp phạt, thì số tiền anh phải chuẩn bị là: T 2 01 20 0,05% 2 ( 0 T ,r2 iệu đồng). 20 f x 20 3 6 f x 5 5
Câu 5. Cho f x là đa thức thỏa mãn lim 10 . Tín h T l im . x 2 x 2 2 x 2 x x 6 Lời giải: Đáp án: 0,16
Theo giả thiết có lim f x 20 0 hay lim 2f 0x * x 2 x 2 3 6 f x 5 5 6 f x 5 12 5 Khi đó Tx l x im lim x x f x f x 22 x x 2 2 6 233 6 6 5 5 6 5 25



