









Preview text:
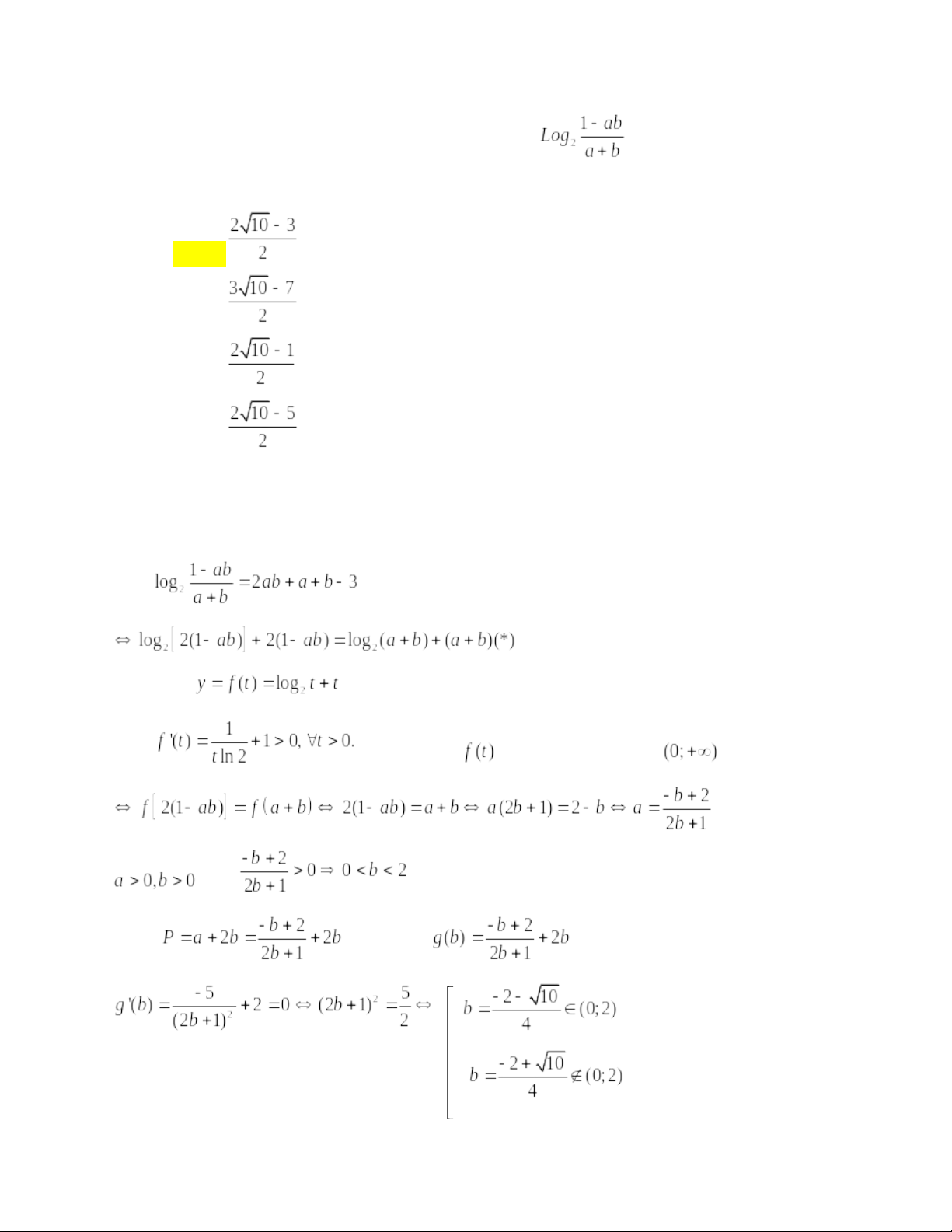
Câu 1: Xét các số thực dương a,b thỏa mãn = 2ab+a+b-3. Tìm giá trị nhỏ nhất Pmin của P = a + 2b.
- Pmin =
- Pmin =
- Pmin =
- Pmin =
Bài giải
Điều kiện : ab<1.
Ta có
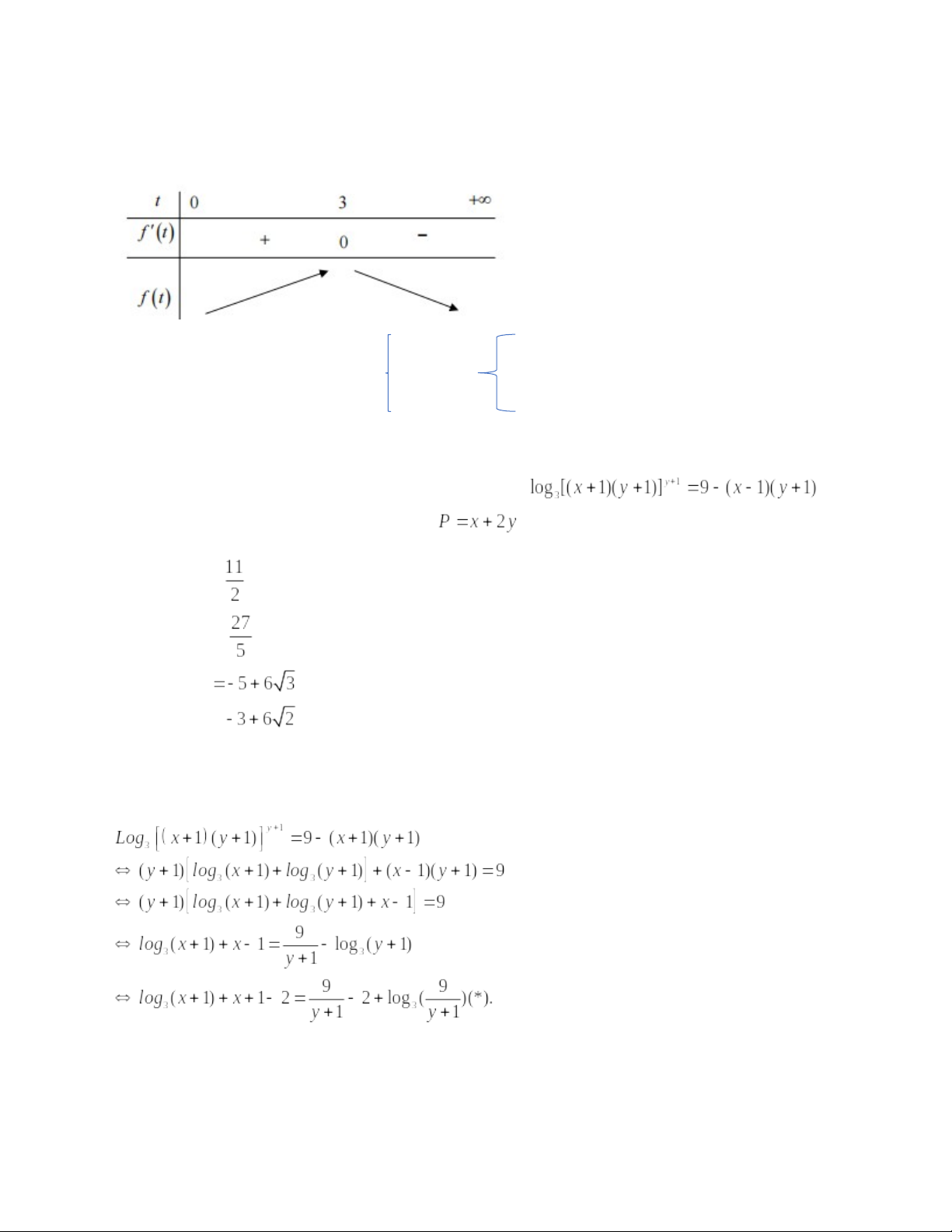
Xét hàm số trên khoảng (0,)
Ta có Suy ra hàm số
đồng biến trên khoảng
.
, nên
Khi đó .Xét hàm số
trên khoảng (0;2).
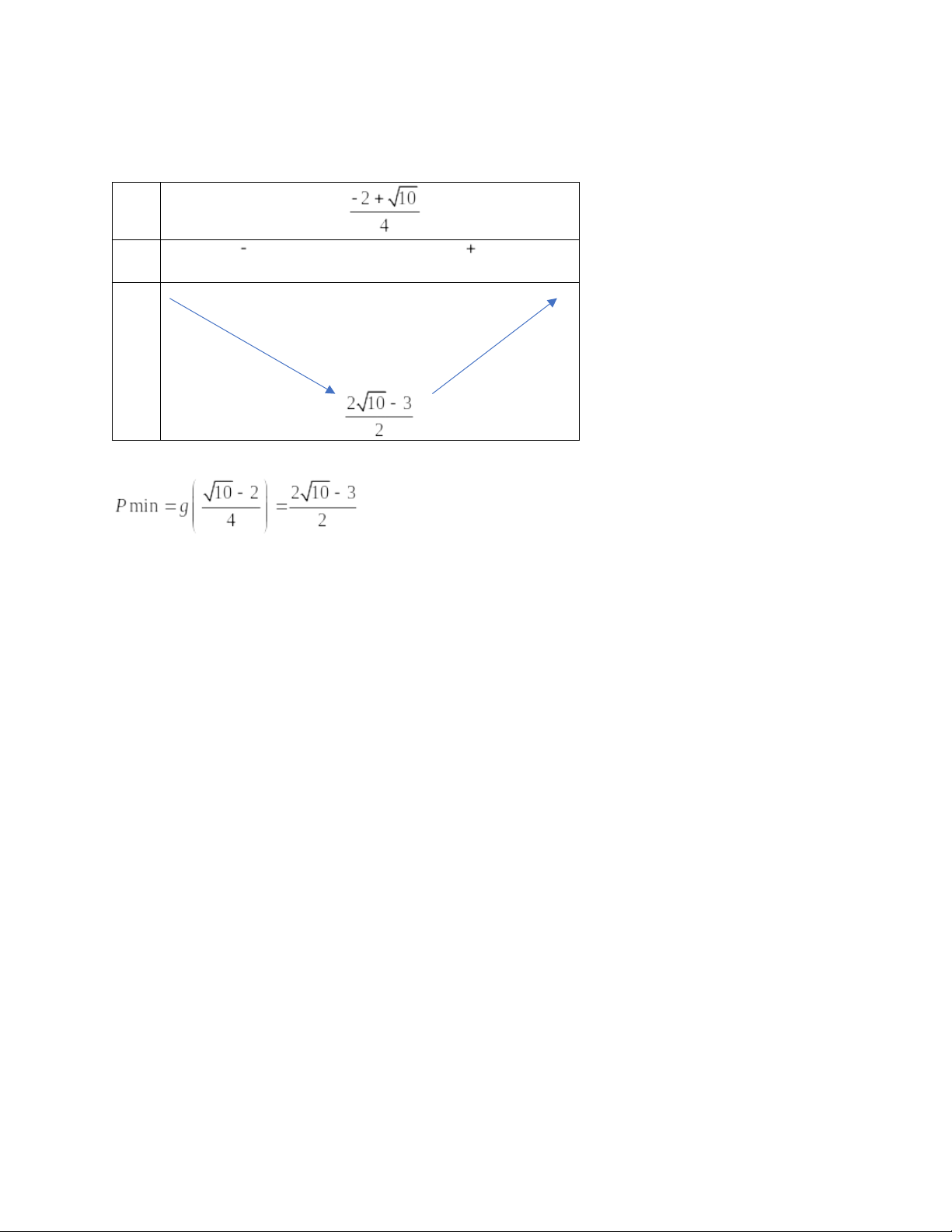
Lập bảng biến thiên
x | 0 |
g’(b) | |
g(b) |
|
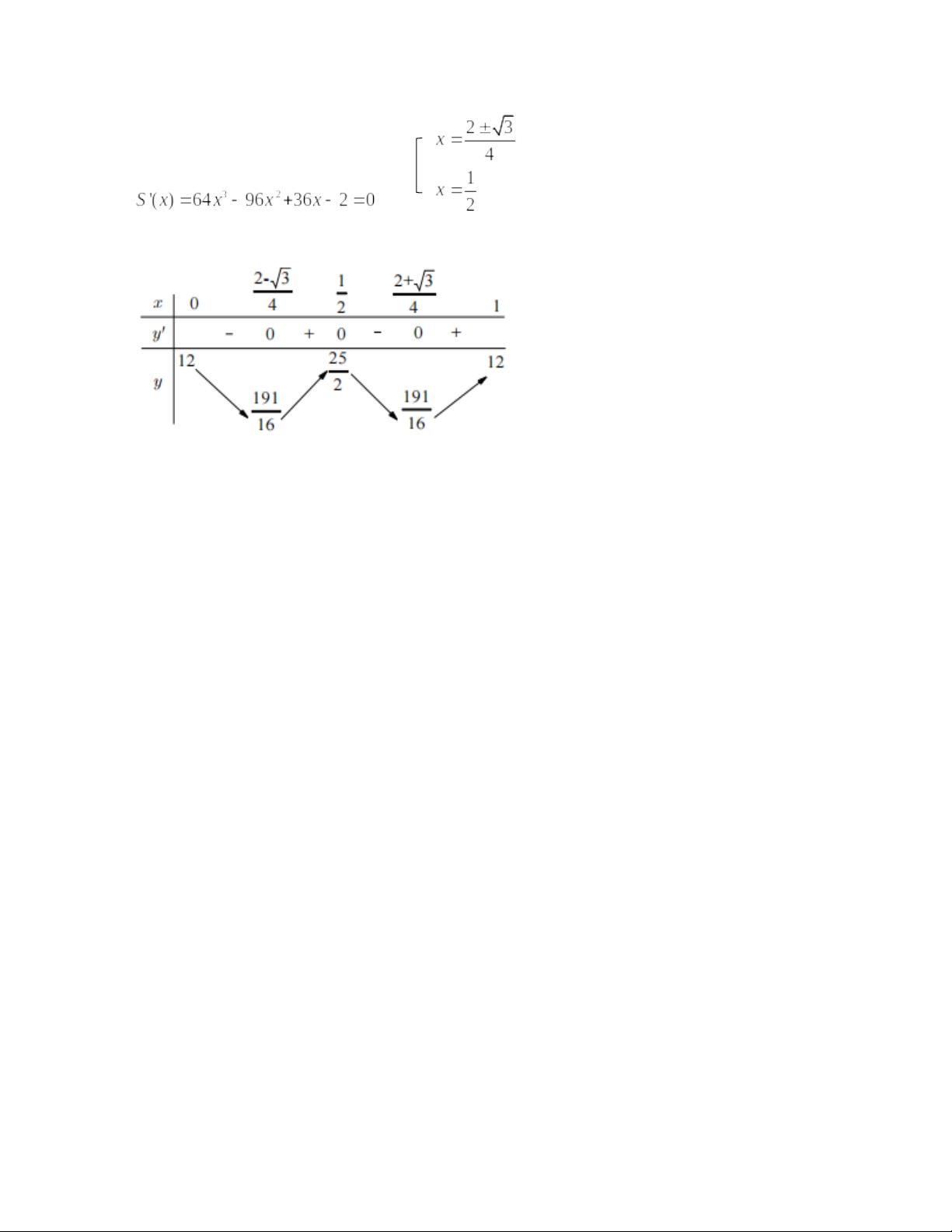
Câu 2: Cho x ≥ 0, y ≤ 1 thỏa mãn . Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức S =
. Khi đó M + m bẳng
- 136/3
- 391/16
- 381/16
- 25/2
Bài giải
Ta có
Xét hàm số với
=>
=> hàm số đồng biến trên
=>
Theo giả thiết
Xét hàm số với
=> ⬄
Bảng biến thiên
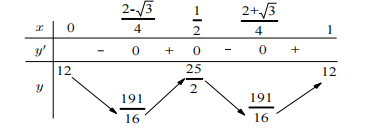
Từ bbt suy ra max của hàm số là : M=25/2
Min của hàm số : m = 191/16
M+m=391/16
Câu 3: Xét các số thực dương x,y thỏa mãn . Tìm giá trị lớn nhất của P=
- 2
- 3
- 1
- 4
Ta có
Xét hàm số
Có
Vậy hàm số liên tục và đồng biến trên khoảng
Do đó :
Từ
Ta có
Đẳng thức xảy ra khi và chỉ khi
Do đó từ (1) suy ra
Đặt
Suy ra
Ta có
Bbt
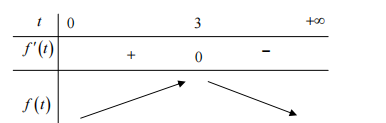
Max P =max f(t) =f(3)=1 khi và chỉ khi x=y+1 x=2
X+y=3 y=1
Câu 4 : Xét các số thực dương x,y thỏa mãn . Tìm giá trị nhỏ nhất của biểu thức
- Pmin =
- Pmin =
- Pmin
- Pmin =
Ta có
Xét hàm số với
có
với mọi t>0 nên hàm số luôn đồng biến và liên tục trên
Từ (*) suy ra do
nên
Vậy
khi
Câu 5: Xét các số thực dương x,y thỏa mãn . Giá trị nhỏ nhất của
bằng
- 19
Điều kiện
Ta có
Xét hàm số đồng biến trên
Ta có
Mặt Khác Ta có
Vậy GTNN Của A=19, dấu “=” xảy ra ⬄ ⬄
(N)
PHÁT TRIỂN CÂU 47 ( Max Min số phức)
Câu 1: Giả sử Z1,Z2 là hai số phức Z thỏa mãn ( z-6)(8+) là số thực .Biết rằng
= 4 , giá trị nhỏ nhất của
bằng :
Đặt
Ta có :
Gọi M ,N là điểm biểu diễn của z1,z2 nên M,N thuộc đường tròn tâm I(3,4), R=5
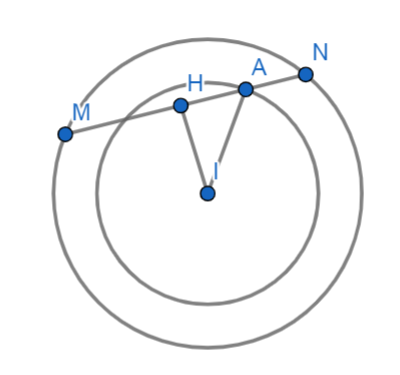
IM=5
MH=2=HN
HA=1
Ta có
Lấy điểm A sao cho thỏa mãn
Mà
Câu 2: Xét các số phức z, w thỏa mãn . Giá trị nhỏ nhất của
T = bằng
- 1
ĐẶT
Sử dụng bổ đề
Đặt
Thì suy ra
Điểm thuộc đường tròn có tâm
gọi
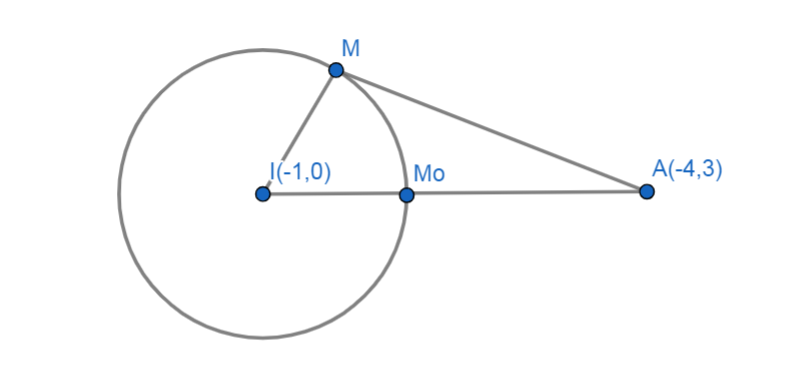
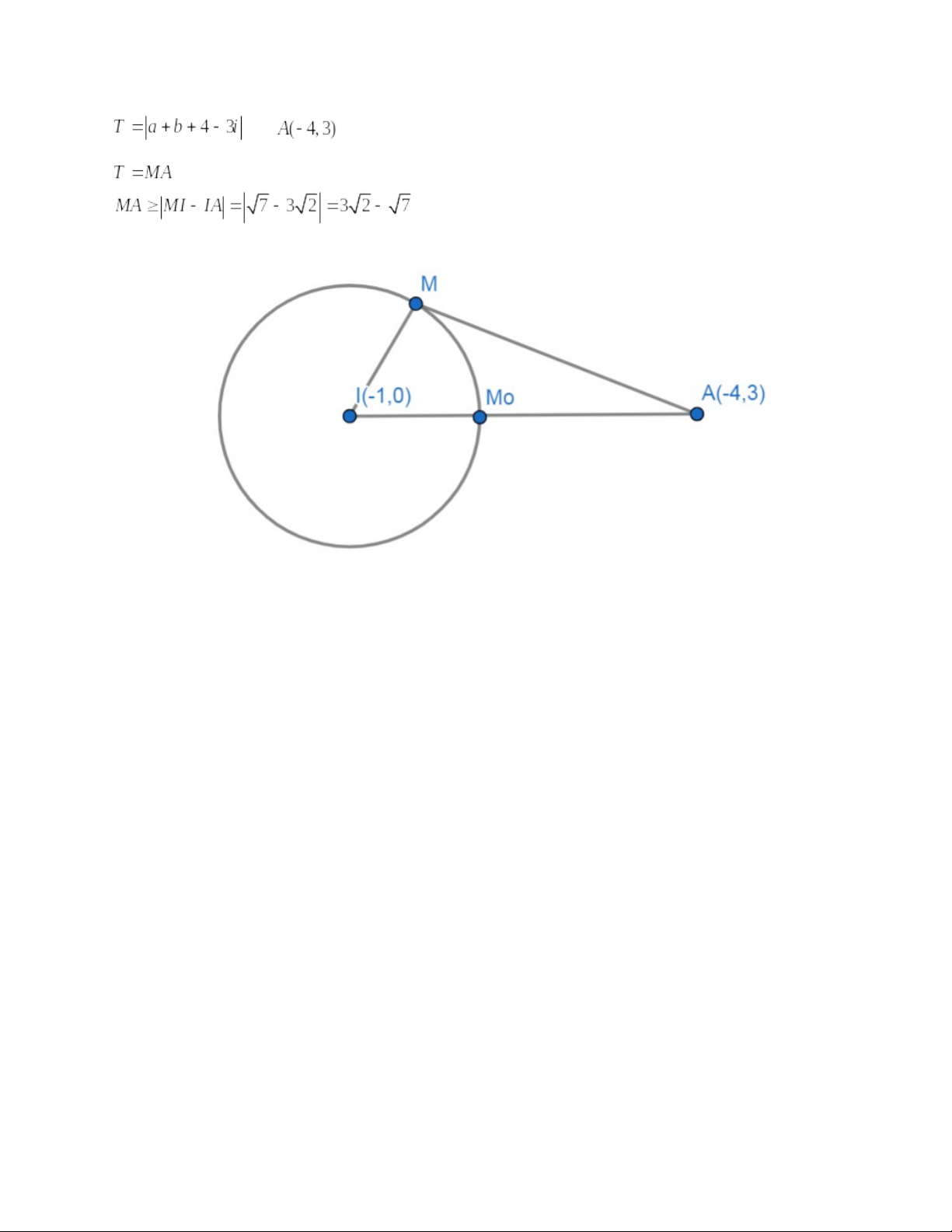
Câu 3: Cho số phức z thỏa mãn điều kiện . Tìm giá trị lớn nhất của
T= bằng:
- Max T= 8
- Max T= 4
- Max T= 6
- Max T= 10
Đặt . Ta có
và
Đặt . Khi đó
Câu 4: Với hai số phức Z1 và Z2 thỏa mãn Z1 + Z2 = 8+ 6i và= 2. Tìm giá trị lớn nhất của P =
+
A. P = 5
B. P =
C. P = 4
D. P = 8/20
Sử dụng bổ đề
Chứng minh sử dụng ct và
Áp dụng (*) ta có
Bunhiacopxki ta có
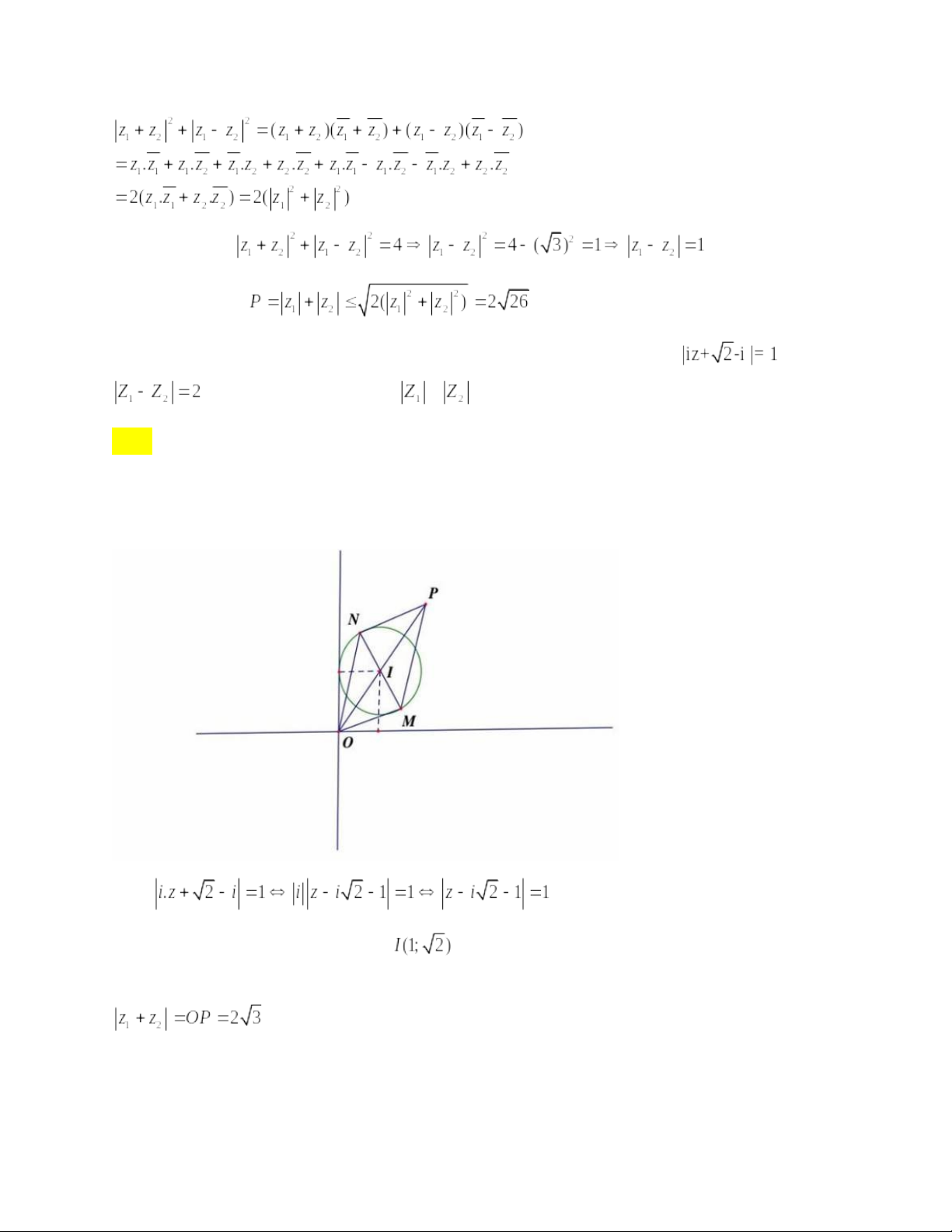
Câu 5: Giả sử Z1 và Z2 hai trong số các số phức Z thỏa mãn và
. Giá trị lớn nhất của
+
bằng
A. 4
B. 2
C. 3
D. 10
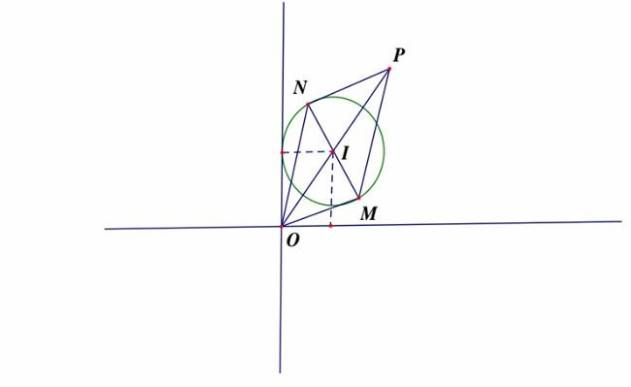
Ta có
Điểm biểu diễn z thuộc đường tròn tâm ,R=1
Gọi M ,N là điểm biểu diễn của z1,z2 nên MN =2 là đường kính dựng hình bình hành OMNP có
Ta có
MN vuông góc với OI




