











Preview text:
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2021 BÀI THI: TOÁN THỜI GIAN: 90 PHÚT
SẢN PHẨM CỦA TẬP THỂ THẦY CÔ 26 TỔ NHÓM TOÁN
“STRONG TEAM TOÁN VD-VDC”
STRONG TEAM TOÁN VD-VDC
*Là Group Toán THPT, thành lập đầu năm 2018 bởi 1 nhóm giáo viên yêu toán: cô Lưu Thêm,
Trần Hồng Minh, Nguyễn Kim Duyên cùng các thầy Nguyễn Văn Quý, Nguyễn Việt Hải, Nguyễn
Hưng, Trần Hùng Quân, Võ Quang Mẫn và Nguyễn Đăng Ái. Đây là nhóm toán trao đổi, làm, soạn
tài liệu chuyên môn dành riêng cho các thầy cô dạy toán THPT.
*Group hiện có 26 tổ chuyên môn, mỗi tổ 60-80 thành viên (hiện vẫn tiếp tục mở rộng) chuyên làm
tài liệu, đề thi và các dự án liên quan đến toán. (Nếu có nhu cầu tham gia các tổ xin liên hệ các Admin nhóm).
*Group không dành cho học sinh. Mọi thành viên tham gia Group đều cần dùng nick thật, nick
facebook chính của mình.
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 1
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101
PHẦN I. ĐỀ BÀI MÃ 101 Câu 1.
Tập nghiệm của bất phương trình 3x 2 là A. ; log 2 . B. log 2; . C. ; log 3 . D. log 3; . 2 2 3 3 4 4 4 Câu 2. Nếu f
xdx 3 và gxdx 2
thì f x g xdx bằng 1 1 1 A. 1. B. 5 . C. 5 . D. 1. Câu 3.
Trong không gian Oxyz , cho mặt cầu S có tâm I 1; 4;0 và bán kính bằng 3 . Phương
trình của S là 2 2 2 2
A. x y 2 1 4 z 9 .
B. x y 2 1 4 z 9 2 2 2 2
C. x y 2 1 4 z 3 .
D. x y 2 1 4 z 3 . Câu 4.
Trong không gian Oxyz , cho đường thẳng d đi qua điểm M 3; 1; 4 và có một vectơ chỉ phương u 2
; 4;5 . Phương trình của d là: x 2 3t
x 3 2t
x 3 2t x 3 2t A.
y 4 t .
B. y 1 4t
C. y 1 4t .D. y 1 4t . z 5 4t z 4 5t z 4 5t z 4 5t Câu 5.
Cho hàm số y f x có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là A. 5 . B. 3 . C. 2 . D. 4 . Câu 6.
Đồ thị nào của hàm số dưới đây có dạng như đường cong trong hình bên? A. 4 2 y 2
x 4x 1. B. 3
y x 3x 1. C. 4 2
y 2x 4x 1. D. 3
y x 3x 1 . Câu 7. Đồ thị của hàm số 4 2 y x 4x
3 cắt trục tung tại điểm có tung độ bằng. A. 0 . B. 3 . C. 1 D. 3 . Câu 8.
Với n là số nguyên dương bất kì, n 4 , công thức nào dưới đây đúng? n 4 ! 4! n! n! 4 A. A . B. 4 A 4 A 4 A n n n n n! n C. 4! 4 ! n . D. 4! n . 4!
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 2
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101 Câu 9.
Phần thực của số phức z 5 2i bằng A. 5 . B. 2 . C. 5 . D. 2 . 5
Câu 10. Trên khoảng 0; , đạo hàm của hàm số 2 y x là: 7 2 3 2 3 5 3 5 A. 2 y x . B. 2 y x . C. 2 y x . D. 2 y x . 7 5 2 2
Câu 11. Cho hàm số f x 2
x 4 . Khẳng định nào dưới đây đúng? A. f
xdx 2xC . B. f x 2
dx x 4x C . x C. f x 3 dx 4x C . D. f x 3
dx x 4x C 3
Câu 12. Trong không gian Oxyz , cho điểm A2;3;5 . Toạ độ của vectơ OA là A. 2;3;5 . B. 2; 3;5 . C. 2 ; 3 ;5 . D. 2; 3 ; 5 .
Câu 13. Cho hàm số y f x có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 1. B. 5 . C. 3 . D. 1.
Câu 14. Cho hàm số y f x có đồ thị là đường cong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 0; 1 . B. ; 0 . C. 0; . D. 1; 1 .
Câu 15. Nghiệm của phương trình log 5x 2 là 3 8 9 A. x . B. x 9 . C. x . D. x 8 . 5 5 3 3 Câu 16. Nếu f
xdx 4 thì 3f xdx bằng 0 0
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 3
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101 A. 36 . B. 12 . C. 3 . D. 4 .
Câu 17. Thể tích của khối lập phương cạnh 5a bằng A. 3 5a . B. 3 a . C. 3 125a . D. 3 25a .
Câu 18. Tập xác định của hàm số 9x y là A. . B. 0; . C. \ 0 . D. 0; .
Câu 19. Diện tích S của mặt cầu bán kính R được tính theo công thức nào dưới đây? 4 A. 2 S 16 R . B. 2 S 4 R . C. 2 S R . D. 2 S R . 3 2x 1
Câu 20. Tiệm cận đứng của đồ thị hàm số y x là đường thẳng có phương trình 1 1 A. x 1. B. x 1 . C. x 2 . D. x . 2
Câu 21. Cho a 0 và a 1, khi đó 4 log a bằng a 1 1 A. 4 . B. . C. . D. 4 . 4 4
Câu 22. Cho khối chóp có diện tích đáy 2
B 5a và chiều cao h a . Thể tích khối chóp đã cho bằng 5 5 5 A. 3 a . B. 3 a . C. 3 5a . D. 3 a . 6 2 3
Câu 23. Trong không gian Oxyz , cho mặt phẳng (P) : 3x y 2z 1 0 . Vectơ nào dưới đây là một
vectơ pháp tuyến của (P) ? A. n 3 ;1;2 . B. n 3;1;2 . C. n 3;1;2 . D. n 3;1; 2 . ( p) ( p) ( p) ( p )
Câu 24. Cho khối trụ có bán kính đáy r 6 và chiều cao h
3 . Thể tích của khối trụ đã cho bằng A. 108 . B. 36 . C. 18 . D. 54 .
Câu 25. Cho hai số phức z 4 2i và w 3 4i . Số phức z w bằng A. 1 6i . B. 7 2i . C. 7 2i . D. 1 6i .
Câu 26. Cho cấp số nhân u với u 3 và u
9 . Công bội của cấp số nhân đã cho bằng n 1 2 1 A. 6 . B. . C. 3 . D. 6 . 3 Câu 27. Cho hàm số x
f x e 2 . Khẳng định nào sau đây đúng? A. 2 d x f x x e C . B. d x
f x x e 2x C . C. d x
f x x e C . D. d x
f x x e 2x C .
Câu 28. Trên mặt phẳng tọa độ, điểm M
3; 4 là điểm biểu diễn của số phức nào dưới đây? A. z 3 4i . B. z 3 4i . C. z 3 4i . D. z 3 4i . 2 3 4 1 x a
Câu 29. Biết hàm số y
a ) có đồ thị như hình vẽ sau:
x ( a là số thực cho trước, 1 1
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 4
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101
Mệnh đề nào dưới đây đúng?
A. y ' 0, x 1.
B. y ' 0, x 1.
C. y ' 0, x .
D. y ' 0, x .
Câu 30. Từ một hộp chứa 12 quả bóng gồm 5 quả màu đỏ và 7 quả màu xanh, lấy ngẫu nhiên đồng thời
3 quả. Xác suất để lấy được 3 quả màu xanh bằng 7 2 1 5 A. . B. . C. . D. . 44 7 22 12
Câu 31. Trên đoạn 0; 3 , hàm số 3
y x 3x đạt giá trị lớn nhất tại điểm A. x 0 . B. x 3. C. x 1. D. x 2 .
Câu 32. Trong không gian Oxyz , cho điểm M 1;3; 2 và mặt phẳng
P: x 2y 4z 1 0 . Đường thẳng đi qua M và vuông góc với P có phương trình là x 1 y 3 z 2 x 1 y 3 z 2 A. 1 2 . B. 1 1 2 . 1 x 1 y 3 z 2 x 1 y 3 z 2 C. 1 2 . D. 4 1 2 . 4
Câu 33. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AB 2a và SA vuông góc với mặt
phẳng đáy. Khoảng cách từ C đến mặt phẳng SAB bằng A. 2a . B. 2a . C. a . D. 2 2a .
Câu 34. Trong không gian Oxyz , cho hai điểm A1; 0; 0 và B 4;1; 2 . Mặt phẳng đi qua A và vuông
góc với AB có phương trình là
A. 3x y 2z 17 0 .
B. 3x y 2z 3 0 .
C. 5x y 2z 5 0 .
D. 5x y 2z 25 0 .
Câu 35. Cho số phức z thỏa mãn iz 5 4i . Số phức liên hợp của z là:
A. z 4 5i .
B. z 4 5i . C. z 4 5i . D. z 4 5i .
Câu 36. Cho hình lăng trụ đứng AB . C A B C
có tất cả các cạnh bằng nhau (tham khảo hình bên).
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 5
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101
Góc giữa hai đường thẳng AA và BC bằng A. 30 . B. 90 . C. 45 . D. 60 .
Câu 37. Với mọi a, b thỏa mãn 3
log a log b 6 , khẳng định nào sau đây đúng? 2 2 A. 3 a b 64 . B. 3 a b 36 . C. 3
a b 64 . D. 3
a b 36 . 2 2 Câu 38. Nếu f
xdx 5 thì 2 f
x1dx bằng 0 0 A. 8 . B. 9 . C. 10 . D. 12 .
2x 5 khi x 1
Câu 39. Cho hàm số f (x)
. Giả sử F là nguyên hàm của f trên thỏa mãn 2 3
x 4 khi x 1
F (0) 2 . Giá trị của F ( 1 ) 2F(2) bằng A. 27. B. 29. C. 12. D. 33. 2
Câu 40. Có bao nhiêu số nguyên x thỏa mãn 3x 9x .log x 25 3 0? 3 A. 24. B. Vô số. C. 26. D. 25.
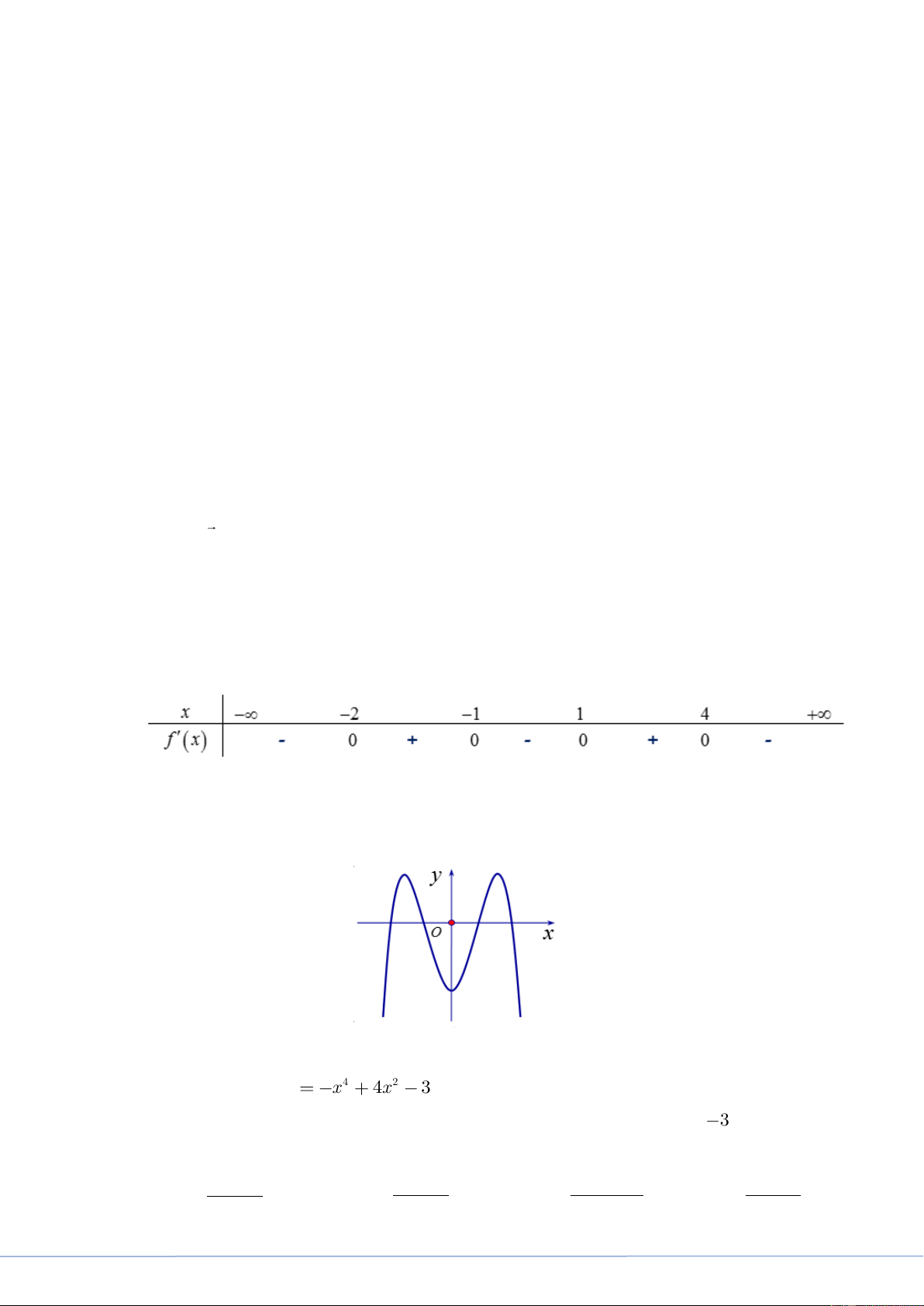
Câu 41. Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình bên.
Số nghiệm thực phân biệt của phương trình f f x 1 là A. 9 . B. 3 . C. 6 D. 7 .
Câu 42. Cắt hình nón N bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng một góc bằng 60 ta được
thiết diện là tam giác đều cạnh 4a . Diện tích xung quanh của N bằng A. 2 8 7 a . B. 2 4 13 a . C. 2 8 13 a . D. 2 4 7 a .
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 6
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101
Câu 43. Trên tập hợp các số phức, xét phương trình z2 m z m2 2 1
0 ( m là tham số thực). Có
bao nhiêu giá trị của m để phương trình đó có nghiệm z thỏa mãn z 7 ? o o A. 2 . B. 3 . C. 1. D. 4 .
Câu 44. ét các số phức z, w thỏa mãn z 1 và w 2 . Khi z iw 6 8i đạt giá trị nhỏ nhất, z w bằng? 221 29 A. . B. 5 . C. 3 . D. . 5 5 x y 1 z 2
Câu 45. Trong không gian Oxyz , cho đường thẳng d : 1 1 1 và mặt phẳng
P: x 2y z 4 0 . Hình chiếu vuông góc của d trên P là đường thẳng có phương trình x y 1 z 2 x y 1 z 2 x y 1 z 2 x y 1 z 2 A. 2 1 4 . B. 3 2 . C. 1 2 1 4 . D. 3 2 . 1 Câu 46. Cho hàm số 3 2
f x x ax bx c với a, , b c là các số thực. Biết hàm số
g x f x f x f x có hai giá trị cực trị là 3
và 6 . Diện tích hình phẳng giới hạn f x
bởi các đường y và y 1 bằng g x 6 A. 2 ln 3 . B. ln 3 . C. ln18 . D. 2 ln 2 . 1 2
Câu 47. Có bao nhiêu số nguyên y sao cho tồn tại x ;3
thỏa mãn 3x xy 9 27 1 .27 x xy ? 3 A. 27 . B. 9 . C. 11. D. 12 .
Câu 48. Cho khối hộp chữ nhật ABC . D A B C
D có đáy là hình vuông, BD 2a , góc giữa hai mặt phẳng
A BD và ABCD bằng 30 . Thể tích của khối hộp chữ nhật đã cho bằng 2 3 2 3 A. 3 6 3a . B. 3 a . C. 3 2 3a . D. 3 a . 9 3
Câu 49. Trong không gian Oxyz, cho hai điểm A1; 3 ; 4
và điểm B2;1;2 . ét hai điểm M và
N thay đổi thuộc mặt phẳng Oxy sao cho MN 2 . Giá trị lớn nhất của AM BN bằng A. 3 5 . B. 61 . C. 13 . D. 53 .
Câu 50. Cho hàm số y f x có đạo hàm f x x 2 ' 7 x 9, x
. Có bao nhiêu giá trị
nguyên dương của tham số m để hàm số g x f 3
x 5x m có ít nhất 3 điểm cực trị? A. 6 . B. 7 . C. 5 . D. 4 . HẾT
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 7
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101
PHẦN II. BẢNG ĐÁP ÁN 1.A 2.C 3.B 4.D 5.D 6.A 7.D 8.D 9.A 10.C 11.C 12.A 13.C 14.A 15.C 16.B 17.C 18.A 19.B 20.A 21.B 22.D 23.B 24.A 25.B 26.C 27.B 28.B 29.B 30.A 31.C 32.D 33.B 34.B 35.A 36.C 37.A 38.A 39.A 40.C 41.D 42.D 43.B 44.D 45.C 46.D 47.C 48.D 49.D 50.A
PHẦN III. HƯỚNG DẪN GIẢI CHI TIẾT Câu 1.
Tập nghiệm của bất phương trình 3x 2 là A. ; log 2 . B. log 2; . C. ; log 3 . D. log 3; . 2 2 3 3 Lời giải
FB tác giả: Nguyễn Hưng
Ta có 3x 2 x log 2 . 3
Vậy tập nghiệm của bất phương trình đã cho là S ; log 2 . 3 4 4 4 Câu 2. Nếu f
xdx 3 và gxdx 2
thì f x g xdx bằng 1 1 1 A. 1. B. 5 . C. 5 . D. 1. Lời giải
FB tác giả: Ngoclan Nguyen 4 4 4 Ta có
f x gxdx f xdx
gxdx 32 5. 1 1 1 Câu 3.
Trong không gian Oxyz , cho mặt cầu S có tâm I 1; 4;0 và bán kính bằng 3 . Phương
trình của S là 2 2 2 2
A. x y 2 1 4 z 9 .
B. x y 2 1 4 z 9 2 2 2 2
C. x y 2 1 4 z 3.
D. x y 2 1 4 z 3 . Lời giải
FB tác giả: Vu Thi Thanh Huyen
Do mặt cầu S có tâm I 1; 4;0 và bán kính bằng 3 nên phương trình mặt cầu S là:
x 2 y 2 2 1 4 z 9. Câu 4.
Trong không gian Oxyz , cho đường thẳng d đi qua điểm M 3; 1; 4 và có một vectơ chỉ phương u 2
; 4;5 . Phương trình của d là: x 2 3t
x 3 2t x 3 2t x 3 2t A.
y 4 t . B. y 1 4t C. y 1 4t .D. y 1 4t . z 5 4t z 4 5t z 4 5t z 4 5t Lời giải
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 8
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101
FB tác giả: Phuong Nguyen
Vì đường thẳng d đi qua điểm M 3;1;4 và có một vectơ chỉ phương u 2 ; 4;5 nên
x 3 2t phương trình của đườ
ng thẳng d là: y 1 4t .
z 4 5t Câu 5.
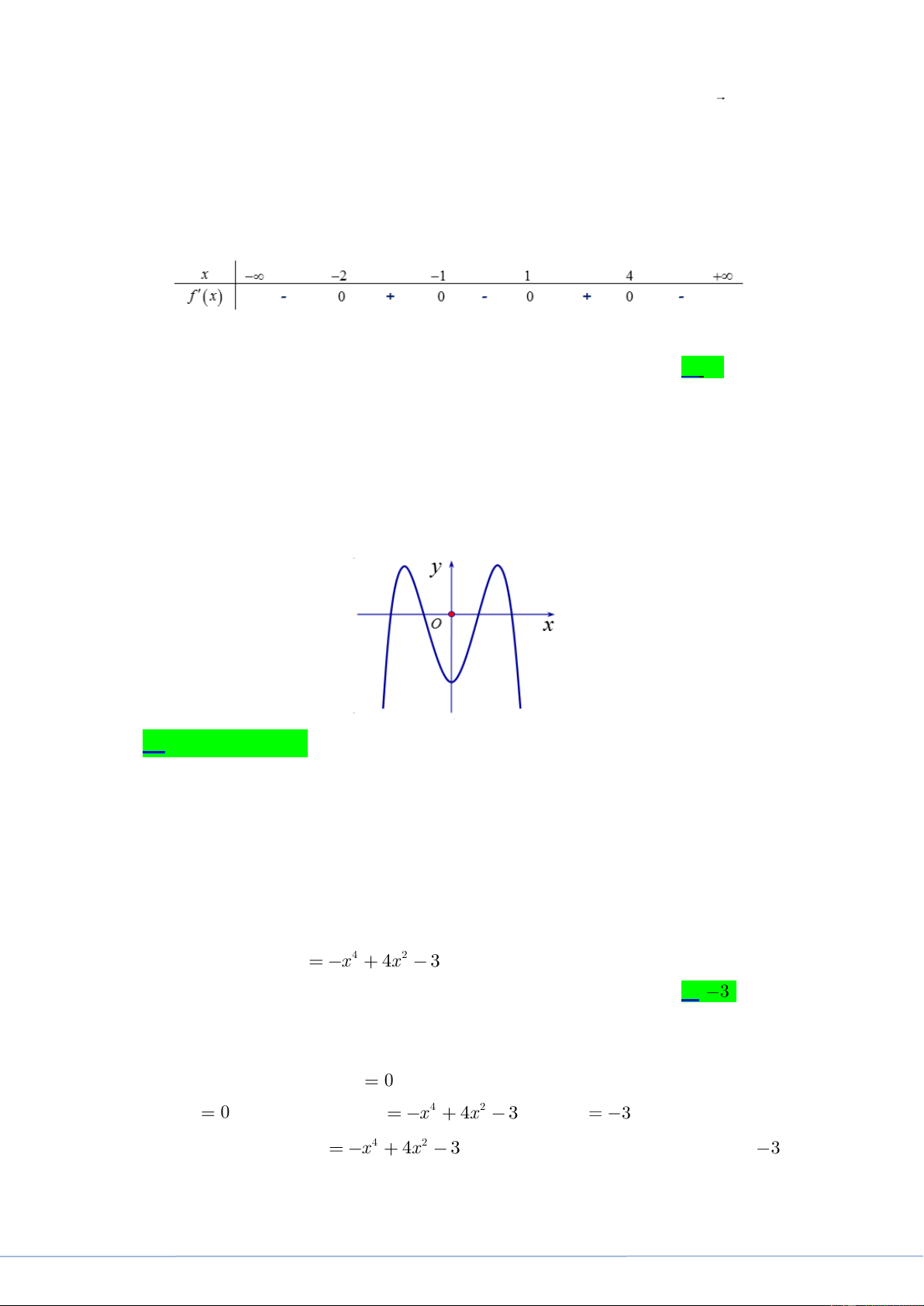
Cho hàm số y f x có bảng xét dấu của đạo hàm như sau :
Số điểm cực trị của hàm số đã cho là A. 5 . B. 3 . C. 2 . D. 4 . Lời giải
FB tác giả: Ngọc Quách
Từ bảng biến thiên ta thấy f x 0 có 4 nghiệm và đổi dấu qua các nghiệm này nên hàm số
y f x có 4 điểm cực trị. Câu 6.
Đồ thị nào của hàm số dưới đây có dạng như đường cong trong hình bên ? A. 4 2 y 2
x 4x 1. B. 3
y x 3x 1. C. 4 2
y 2x 4x 1. D. 3
y x 3x 1 . Lời giải
FB tác giả: Ngọc Quách
Dựa trên hình dạng đường cong đã cho và các phương án, ta suy ra đường cong trên là đồ thị
của hàm số trùng phương 4 2
y ax bx c với a 0 .
Do đó chọn đáp án A. Câu 7.
Đồ thị của hàm số 4 2 y x 4x
3 cắt trục tung tại điểm có tung độ bằng. A. 0 . B. 3 . C. 1 D. 3 . Lời giải
FB tác giả: Ngoclan Nguyen
Trục tung có phương trình: x 0 . Thay x 0 vào phương trình 4 2 y x 4x 3 y ta có: 3 .
Vậy đồ thị của hàm số 4 2 y x 4x
3 cắt trục tung tại điểm có tung độ bằng 3 . Câu 8.
Với n là số nguyên dương bất kì, n 4 , công thức nào dưới đây đúng?
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 9
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101 n 4 ! 4! n! n! 4 A. A . B. 4 A C. 4 A . D. 4 A . n n! n n 4! n 4 ! n 4! n n 4! Lời giải
FB tác giả: Vu Thi Thanh Huyen n!
Ta có số các chỉnh hợp chập 4 của n phần tử là: 4 A n n . n n , , 4 4! Câu 9.
Phần thực của số phức z 5 2i bằng A. 5 . B. 2 . C. 5 . D. 2 . Lời giải
FB tác giả: Thanh Tâm Trần
Phần thực của số phức z 5 2i bằng 5 . 5 Câu 10.
Trên khoảng 0; , đạo hàm của hàm số 2 y x là: 7 2 3 2 3 5 3 5 A. 2 y x . B. 2 2 2 y x . C. y x . D. y x . 7 5 2 2 Lời giải 5 3 5 Với x 0 , ta có 2 2
y x x . 2 Câu 11.
Cho hàm số f x 2
x 4 . Khẳng định nào dưới đây đúng? A. f
xdx 2xC . B. f x 2
dx x 4x C . x C. f x 3 dx 4x C . D. f x 3
dx x 4x C 3 Lời giải
FB tác giả: Thúy Minh x Ta có f
x x x 3 2 d 4 dx 4x C . 3 Câu 12.
Trong không gian Oxyz , cho điểm A2;3;5 . Toạ độ của vectơ OA là A. 2;3;5 . B. 2; 3;5 . C. 2 ; 3 ;5 . D. 2; 3 ; 5 . Lời giải
FB tác giả: Hương Ly
Ta có A2;3;5 nên toạ độ của vectơ là OA = 2;3;5 . Câu 13.
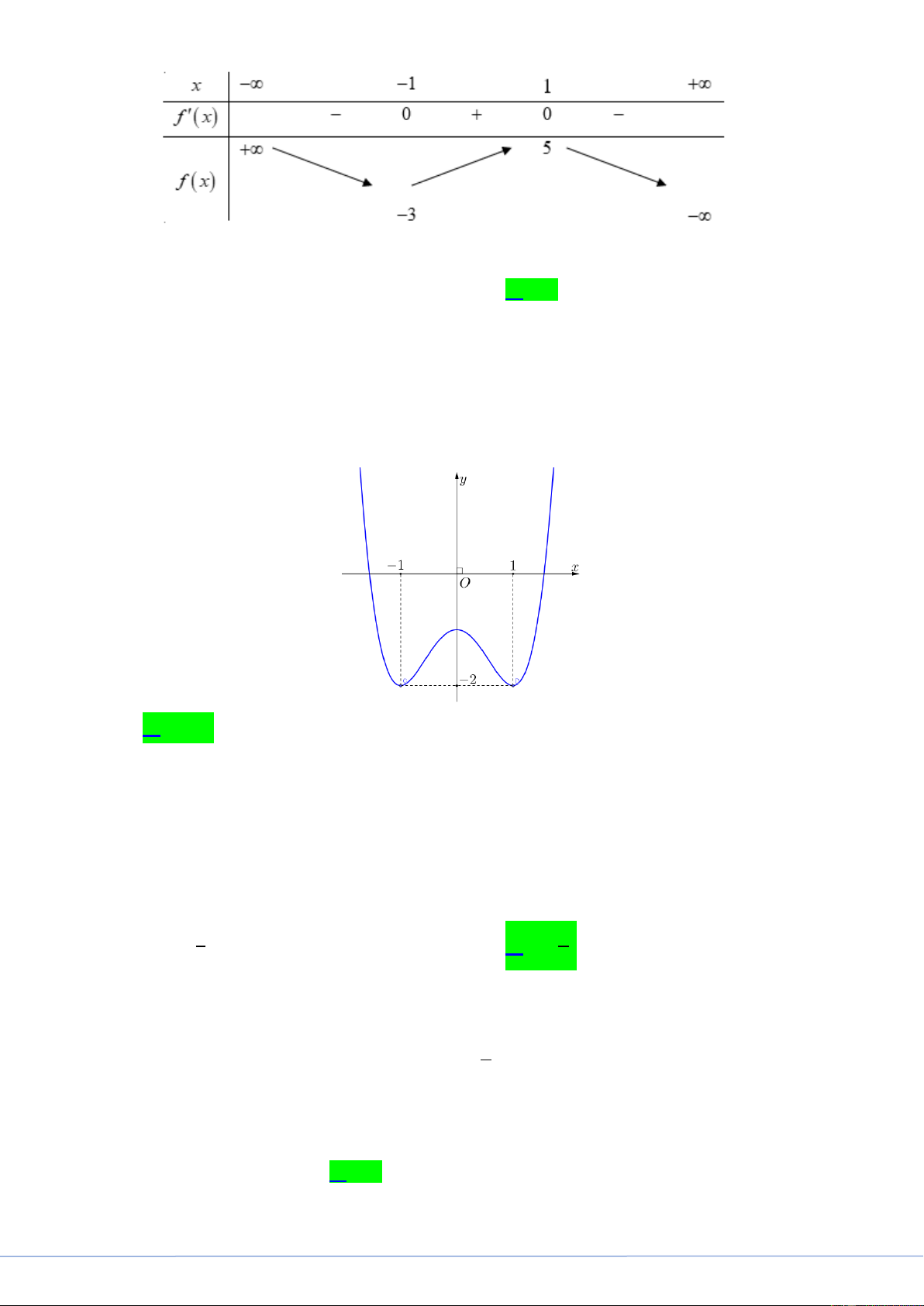
Cho hàm số y f x có bảng biến thiên như sau:
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 10
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101
Giá trị cực tiểu của hàm số đã cho bằng A. 1. B. 5 . C. 3 . D. 1. Lời giải
FB tác giả: Đặng Hương
Giá trị cực tiểu của hàm số đã cho là y 3 . CT Câu 14.
Cho hàm số y f x có đồ thị là đường cong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 0; 1 . B. ; 0 . C. 0; . D. 1; 1 . Lời giải
FB tác giả: Ngọc Thanh
Dựa vào đồ thị hàm số y f x , ta thấy hàm số y f x nghịch biến trên các khoảng ; 1 và 0; 1 .
Câu 15. Nghiệm của phương trình log 5x 2 là 3 8 9 A. x . B. x 9 . C. x . D. x 8 . 5 5 Lời giải
FB tác giả: Dieuptnguyen 9
Phương trình log 5x 2
2 5x 3 x . 3 5 3 3 Câu 16. Nếu f
xdx 4 thì 3f xdx bằng 0 0 A. 36 . B. 12 . C. 3 . D. 4 . Lời giải
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 11
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101
FB tác giả: Đoàn Thanh Huyền 3 3 Ta có 3 f
xdx 3 f
xdx 3.4 12. 0 0
Câu 17. Thể tích của khối lập phương cạnh 5a bằng A. 3 5a . B. 3 a . C. 3 125a . D. 3 25a . Lời giải
FB tác giả: Minh Ngoc
Thể tích của khối lập phương cạnh 5a là V a3 3 5 125a .
Câu 18. Tập xác định của hàm số 9x y là A. . B. 0; . C. \ 0 . D. 0; . Lời giải
FB tác giả: Hằng Nguyễn Tập xác định hàm số 9x y là .
Câu 19. Diện tích S của mặt cầu bán kính R được tính theo công thức nào dưới đây? 4 A. 2 S 16 R . B. 2 S 4 R . C. 2 S R . D. 2 S R . 3 Lời giải
FB tác giả: Kim Huệ
Diện tích S của mặt cầu bán kính R là: 2 S 4 R . 2x 1
Câu 20. Tiệm cận đứng của đồ thị hàm số y x là đường thẳng có phương trình 1 1 A. x 1 . B. x 1 . C. x 2 . D. x . 2 Lời giải
FB tác giả: Nguyễn Hữu Kính 2x 1 2x 1 Vì lim
x là tiệm cận đứng của đồ thị hàm số y x 1 x nên đường thẳng 1 1 x . 1
Câu 21. Cho a 0 và a 1, khi đó 4 log a bằng a 1 1 A. 4 . B. . C. . D. 4 . 4 4 Lời giải
FB tác giả: Hong Chau Tran. 1 1 1
Với a 0 và a 1 ta có: 4 4 log
a log a log a . a a 4 a 4
Câu 22. Cho khối chóp có diện tích đáy 2
B 5a và chiều cao h a . Thể tích khối chóp đã cho bằng 5 5 5 A. 3 a . B. 3 a . C. 3 5a . D. 3 a . 6 2 3
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 12
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101 Lời giải
Fb tác giả: Len Nguyen Thi 1 5
Ta có thể tích khối chóp là 3 V Bh a . 3 3
Câu 23. Trong không gian Oxyz , cho mặt phẳng (P) : 3x y 2z 1 0 . Vectơ nào dưới đây là một
vectơ pháp tuyến của (P) ? A. n 3 ;1;2 . B. n 3;1;2 . C. n 3;1;2 . D. n 3;1; 2 . ( p) ( p) ( p) ( p ) Lời giải
FB tác giả: Lương Công Bằng
Một vectơ pháp tuyến của mặt phẳng (P) là: n 3;1;2 . ( p)
Câu 24. Cho khối trụ có bán kính đáy r 6 và chiều cao h
3 . Thể tích của khối trụ đã cho bằng A. 108 . B. 36 . C. 18 . D. 54 . Lời giải
FB tác giả: La Nguyễn Ta có 2 2 V
r h .6 .3 108 .
Câu 25. Cho hai số phức z 4 2i và w 3 4i . Số phức z w bằng A. 1 6i . B. 7 2i . C. 7 2i . D. 1 6i . Lời giải
FB tác giả: Đỗ Hằng
Ta có z w 4 2i 3 4i 7 2i .
Câu 26. Cho cấp số nhân u với u 3 và u
9 . Công bội của cấp số nhân đã cho bằng n 1 2 1 A. 6 . B. . C. 3 . D. 6 . 3 Lời giải
FB tác giả: La Nguyễn u Ta có u u .q 2 q 3 . 2 1 u1 Câu 27. Cho hàm số x
f x e 2 . Khẳng định nào sau đây đúng? A. 2 d x f x x e C . B. d x
f x x e 2x C . C. d x
f x x e C . D. d x
f x x e 2x C . Lời giải
FB tác giả: Nguyễn Huyền Nga
Ta có d x 2d x f x x e
x e 2x C .
Câu 28. Trên mặt phẳng tọa độ, điểm M
3; 4 là điểm biểu diễn của số phức nào dưới đây? A. z 3 4i . B. z 3 4i . C. z 3 4i . D. z 3 4i . 2 3 4 1 Lời giải
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 13
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101
FB tác giả: Nguyễn Đức Thắng
Điểm M a;b trong mặt phẳng tọa độ được gọi là điểm biểu diễn số phức z a bi . Do đó điểm M 3; 4
điểm là điểm biểu diễn số phức z 3 4 . i x a
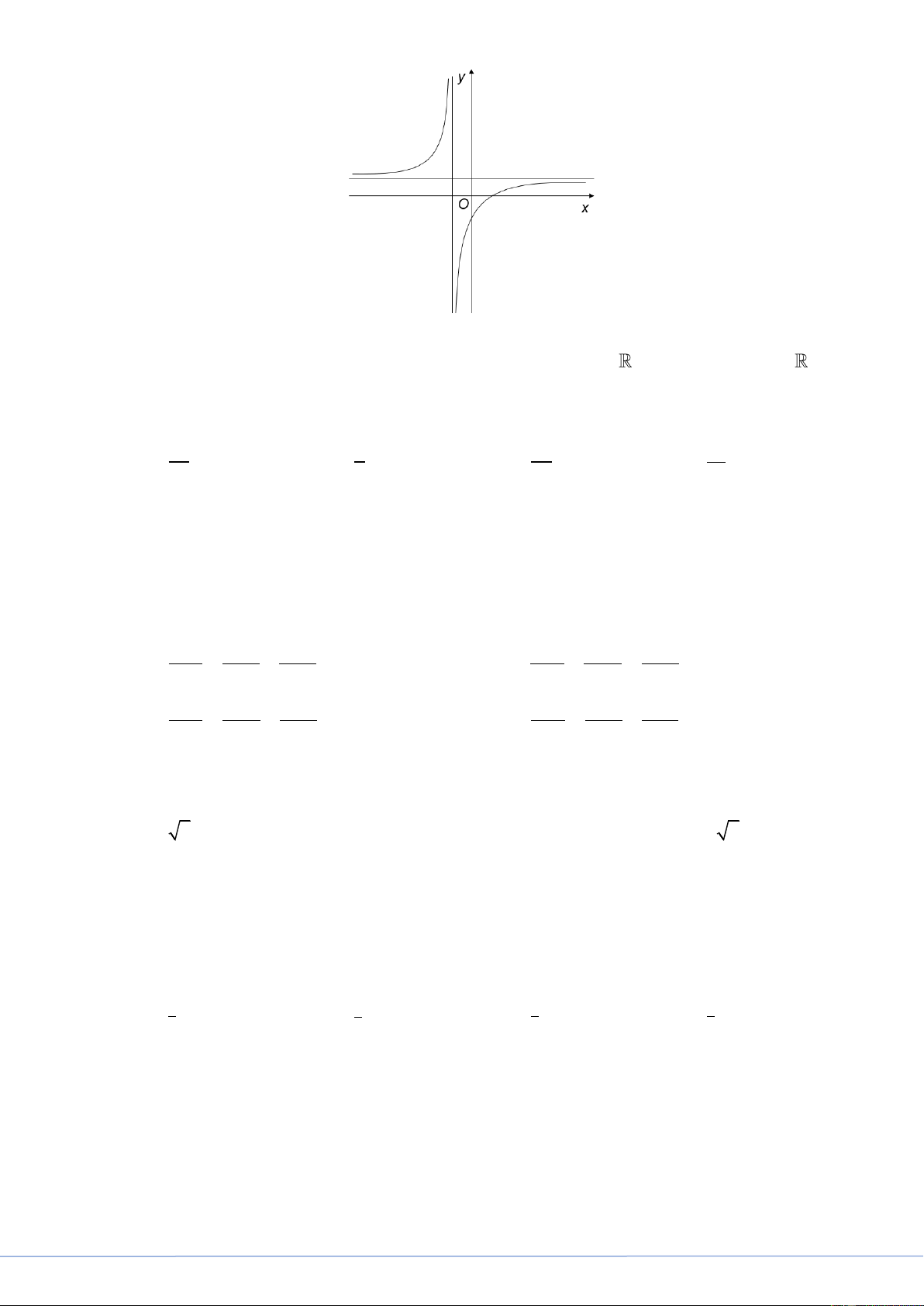
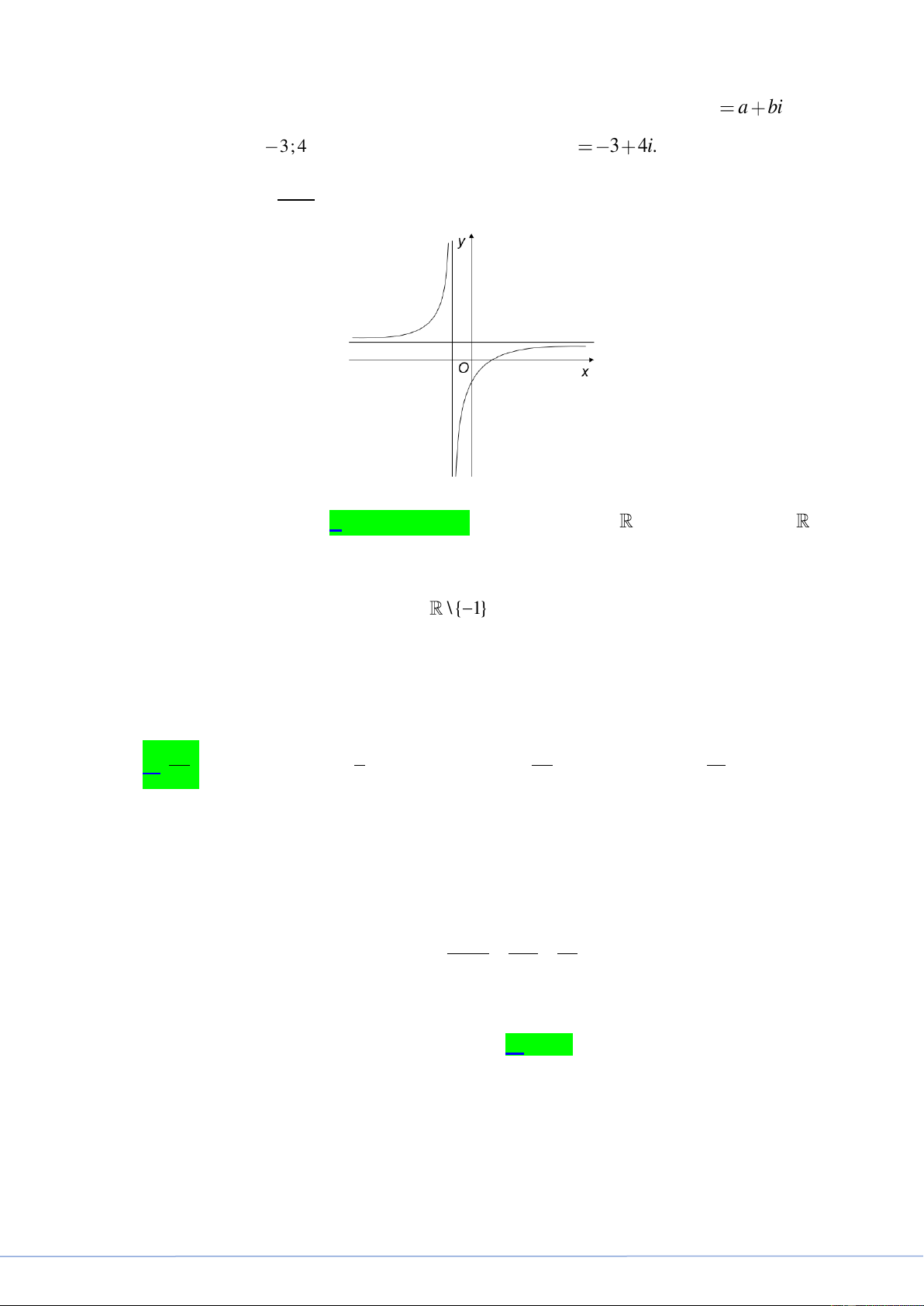
Câu 29. Biết hàm số y
a ) có đồ thị như hình vẽ sau:
x ( a là số thực cho trước, 1 1
Mệnh đề nào dưới đây đúng?
A. y ' 0, x 1.
B. y ' 0, x 1.
C. y ' 0, x .
D. y ' 0, x . Lời giải
FB tác giả: Mỳ Nguyễn Thị
Hàm số đã cho có tập xác định là D \ { 1 }.
Dựa vào đồ thị ta thấy hàm số đã cho đồng biến trên mỗi khoảng xác định.
Do đó y ' 0, x 1.
Câu 30. Từ một hộp chứa 12 quả bóng gồm 5 quả màu đỏ và 7 quả màu xanh, lấy ngẫu nhiên đồng
thời 3 quả. Xác suất để lấy được 3 quả màu xanh bằng 7 2 1 5 A. . B. . C. . D. . 44 7 22 12 Lời giải
FB tác giả: Trọng Luân
Số phần tử của không gian mẫu là: n 3 C 220 . 12
Gọi A là biến cố: “Lấy được 3 quả màu xanh” . Ta có n A 3 C 35. 7 n A 35 7
Vậy xác suất của biến cố A là : P A . n 220 44 Câu 31. Trên đoạn 0; 3 , hàm số 3
y x 3x đạt giá trị lớn nhất tại điểm A. x 0 . B. x 3. C. x 1. D. x 2 . Lời giải
FB tác giả: Nguyễn Thành Trung Hàm số 3
y x 3x xác định và liên tục trên đoạn 0; 3 . x 10; 3 2 y 3 x 3 ; 2
y 0 3x 3 0 . x 1 0; 3
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 14
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101
Ta có: f 0 0 ; f 3 18 ; f 1 2 .
Vậy max f x 2 đạt tại x 1. 0;3 Câu 32.
Trong không gian Oxyz , cho điểm M 1;3; 2 và mặt phẳng P : x 2 y 4z 1 0 .
Đường thẳng đi qua M và vuông góc với P có phương trình là x 1 y 3 z 2 x 1 y 3 z 2 A. 1 2 . B. 1 1 2 . 1 x 1 y 3 z 2 x 1 y 3 z 2 C. 1 2 . D. 4 1 2 . 4 Lời giải
FB tác giả: Trần Mạnh Nguyên
Mặt phẳng P có một vectơ pháp tuyến là n 1; 2 ;4 . P
Gọi d là đường thẳng qua M 1;3; 2 và vuông góc với P .
Vì d P nên d nhận vectơ n 1; 2
;4 làm vectơ chỉ phương. P x 1 y 3 z 2
Vậy phương trình đường thẳng d là : 1 2 . 4
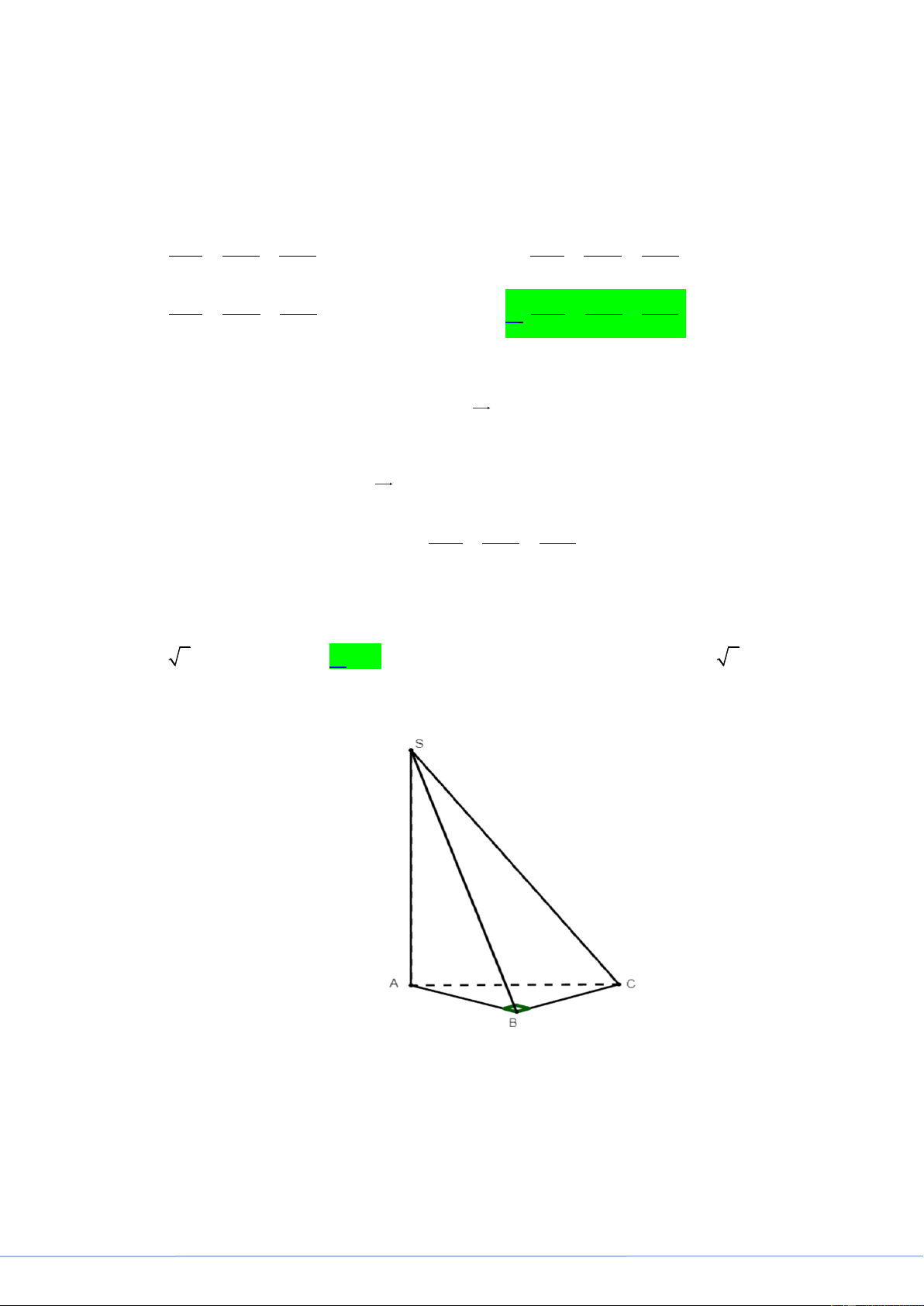
Câu 33. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AB 2a và SA vuông góc với mặt
phẳng đáy. Khoảng cách từ C đến mặt phẳng SAB bằng A. 2a . B. 2a . C. a . D. 2 2a . Lời giải
FB tác giả: Trương Huyền
SA ABC SA CB . C B AB Ta có
CB SAB . C B SA
Do đó d C,SAB CB AB 2a .
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 15
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101 Câu 34.
Trong không gian Oxyz , cho hai điểm A1; 0; 0 và B 4;1; 2 . Mặt phẳng đi qua A và vuông
góc với AB có phương trình là
A. 3x y 2z 17 0 .
B. 3x y 2z 3 0 .
C. 5x y 2z 5 0 .
D. 5x y 2z 25 0 . Lời giải
FB tác giả: Nguyễn Ngọc Nam
Gọi P là mặt phẳng đi qua A1; 0; 0 và vuông góc với AB .
Do P AB nên vectơ n AB 3;1; 2 là một vectơ pháp tuyến của P .
Vậy phương trình mặt phẳng P cần lập là: 3x y 2z 3 0 .
Câu 35. Cho số phức z thỏa mãn iz 5 4i . Số phức liên hợp của z là:
A. z 4 5i .
B. z 4 5i . C. z 4 5i . D. z 4 5i . Lời giải
FB tác giả: Chương Huy i Ta có iz 5 5 4 4i z 4 5i . i
Vậy số phức liên hợp của z là: z 4 5i .
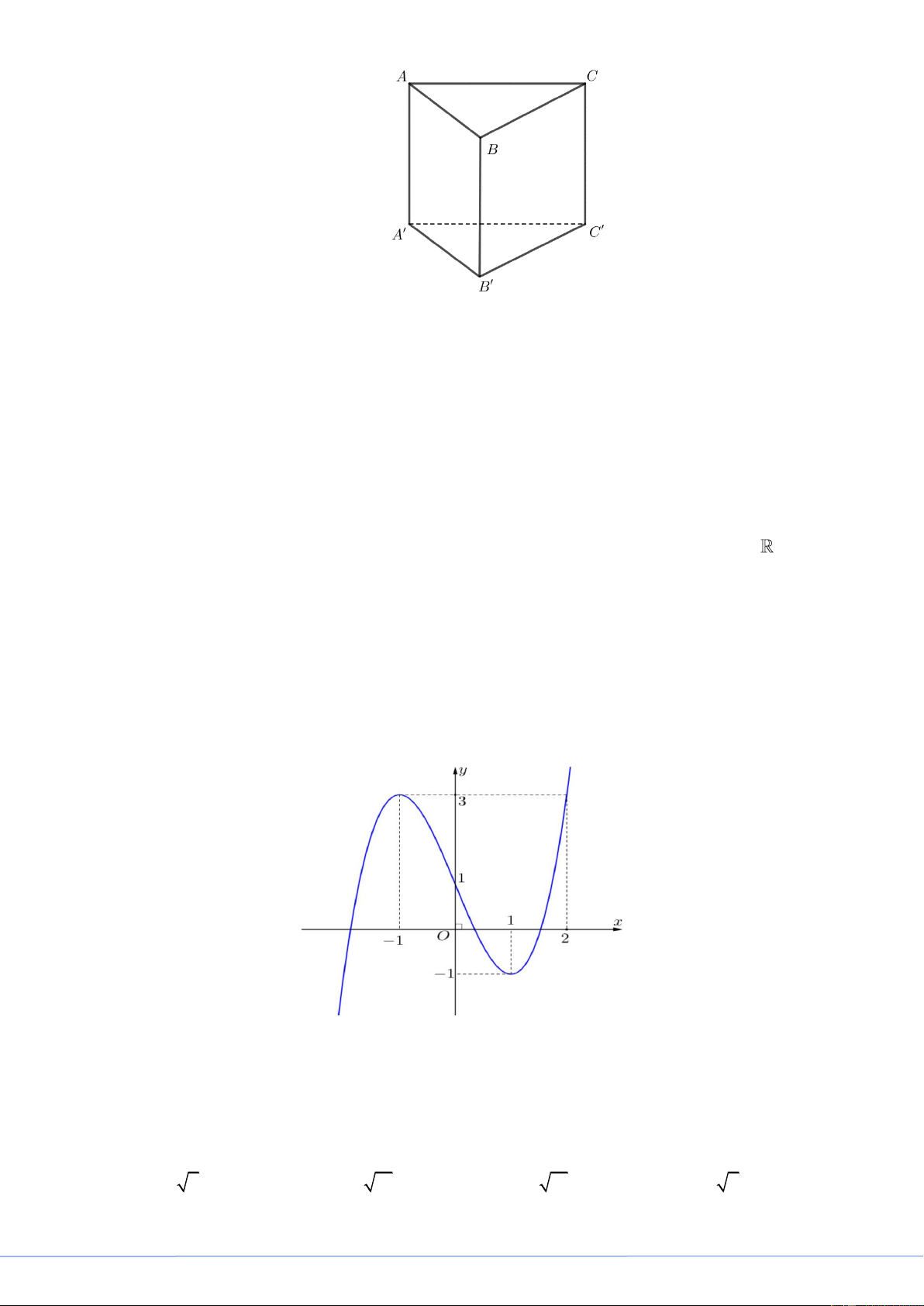
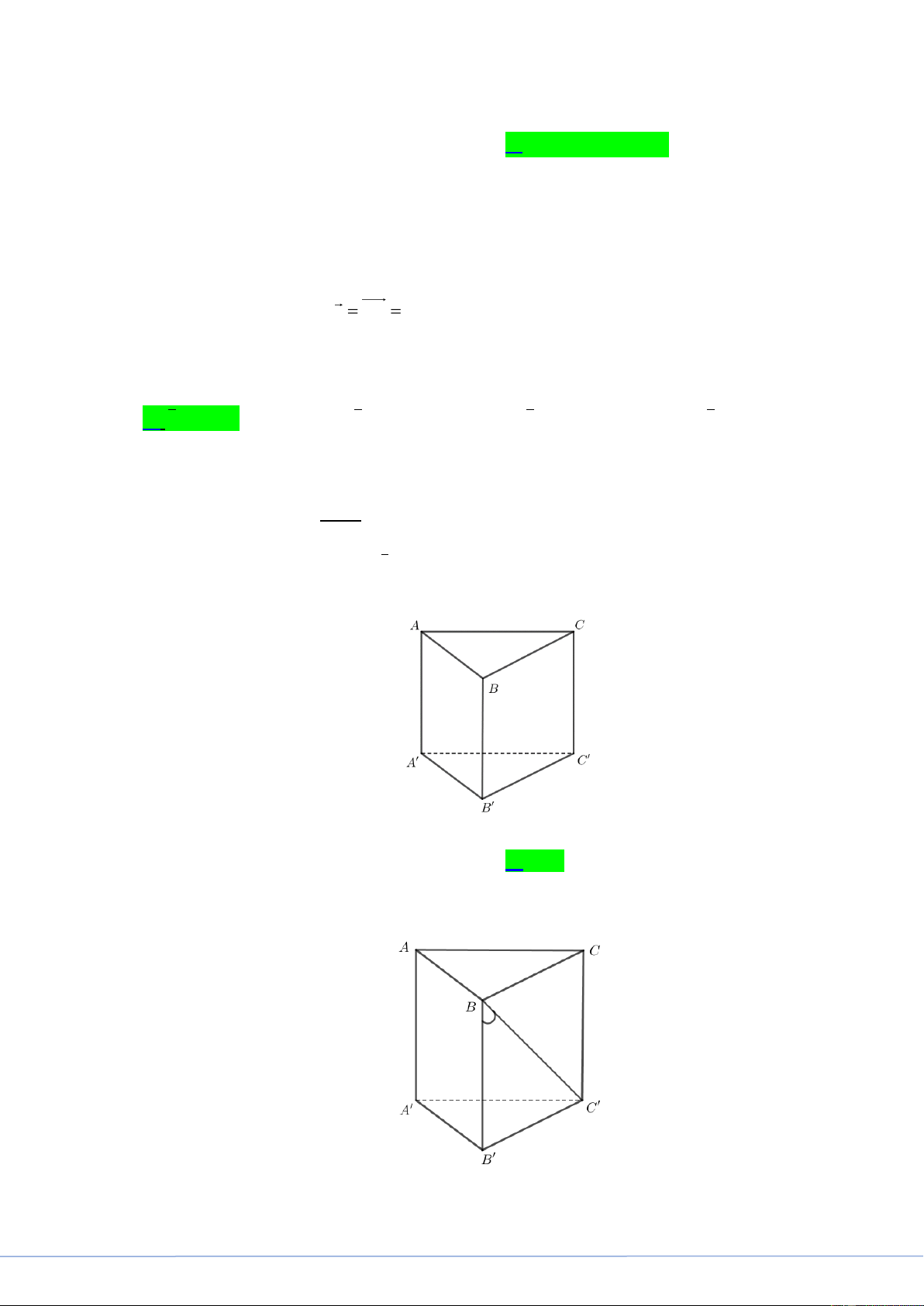
Câu 36. Cho hình lăng trụ đứng AB . C A B C
có tất cả các cạnh bằng nhau (tham khảo hình bên).
Góc giữa hai đường thẳng AA và BC bằng A. 30 . B. 90 . C. 45 . D. 60 . Lời giải
FB tác giả: Lê Mỹ Dương
Ta có: AA // BB nên góc giữa hai đường thẳng AA và BC là góc giữa hai đường thẳng BB
và BC và bằng góc B B C (do B B C nhọn).
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 16
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101 Tam giác BB C
vuông cân tại B nên B B C 45.
Vậy góc giữa hai đường thẳng AA và BC bằng 45 .
Câu 37. Với mọi a, b thỏa mãn 3
log a log b 6 , khẳng định nào sau đây đúng? 2 2 A. 3 a b 64 . B. 3 a b 36 . C. 3
a b 64 . D. 3
a b 36 .
FB tác giả: Lê Đức Hiền Lời giải Ta có: 3
log a log b 6 log 3 a b 3 6
6 a b 2 64 . 2 2 2 2 2 Câu 38. Nếu f
xdx 5 thì 2 f
x1dx bằng 0 0 A. 8 . B. 9 . C. 10 . D. 12 . Lời giải
FB tác giả: Phạm Quốc Hưng 2 2 2 Ta có: 2 f
x1dx 2 f
xdx dx 2.52 8. 0 0 0
2x 5 khi x 1
Câu 39. Cho hàm số f (x)
. Giả sử F là nguyên hàm của f trên thỏa mãn 2 3
x 4 khi x 1
F (0) 2 . Giá trị của F ( 1 ) 2F(2) bằng A. 27. B. 29. C. 12. D. 33. Lời giải
FB tác giả: Thy Nguyen Vo Diem 1 2 Ta có I
f (x)dx 2 f (x)dx F ( 1
) F(0) 2F(2) 2F(0) . 0 0
Do đó I F( 1
) 2F(2) 3F(0) F( 1
) 2F(2) 6 F( 1
) 2F(2) I 6 . 1 0 2 1 2 Mà
f (x)dx 2
3x 4dx 5
và 2 f (x)dx 2 2
3x +4dx 2x 5dx 26 . 0 1 0 0 1
Suy ra I 26 5 21. Vậy F ( 1 ) 2F(2) 21 6 27 . 2 Câu 40.
Có bao nhiêu số nguyên x thỏa mãn 3x 9x .log x 25 3 0? 3 A. 24. B. Vô số. C. 26. D. 25. Lời giải
FB tác giả: Thành Luân
Điều kiện: x 25 *. Trường hợp 1: x 0 2 2 x x x 2 x 2 3 9 0 3 3 x 2x x 0 x 2 .
log x 25 3 0 log x 25 3 x 25 27 x 2 3 3 x 2
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 17
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101
Kết hợp với điều kiện * ta được x 25;0 2 . Mà x
x 24;23;...;1;0;
2 có 26 giá trị nguyên của x thỏa mãn. Trường hợp 2: 2 2 x x x 2 x 2 3 9 0 3 3 x 2x 0 x 2
x 2 tm.
log x 25 3 0 log x 25 3 x 25 27 x 2 3 3
Kết hợp các trường hợp, ta có tất cả 26 giá trị nguyên của của x thỏa mãn đề.
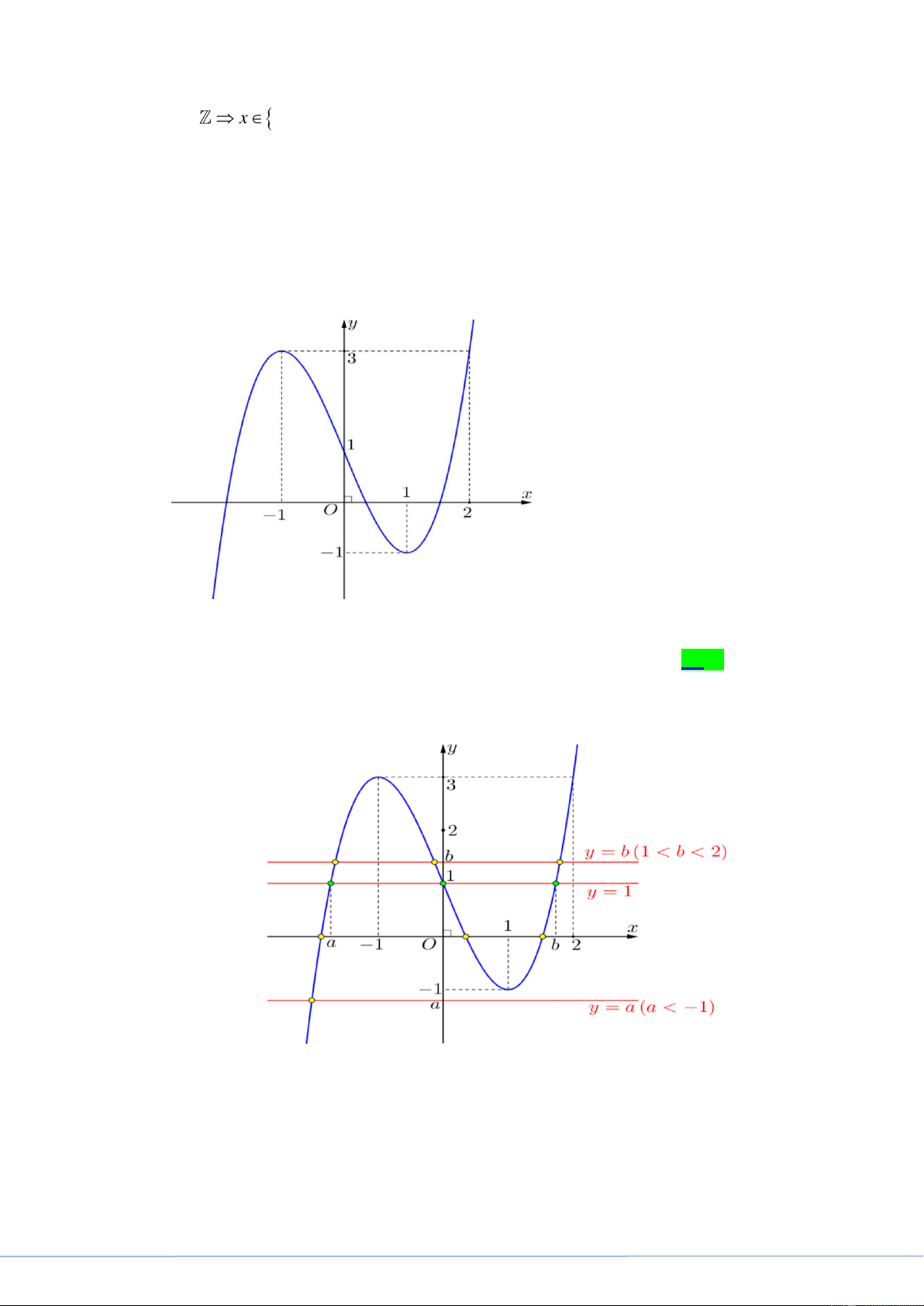
Câu 41. Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình bên.
Số nghiệm thực phân biệt của phương trình f f x 1 là A. 9 . B. 3 . C. 6 D. 7 . Lời giải
FB tác giả: Nguyễn Tuyết Lê
Căn cứ vào đồ thị hàm số đã cho ta thấy:
f x a a 1
f f x 1 f x 0 .
f x b 1 b 2
Căn cứ vào đồ thị hàm số y f x ta có:
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 18
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101 + Với a 1
, phương trình f x a có 1 nghiệm.
+ Phương trình f x 0 có ba nghiệm thực phân biệt.
+ Với 1 b 2 , phương trình f x b có ba nghiệm thực phân biệt.
Các nghiệm của các phương trình f x a ; f x 0 ; f x b là các nghiệm phân biệt.
Vậy phương trình đã cho có 7 nghiệm thực phân biệt. Câu 42.
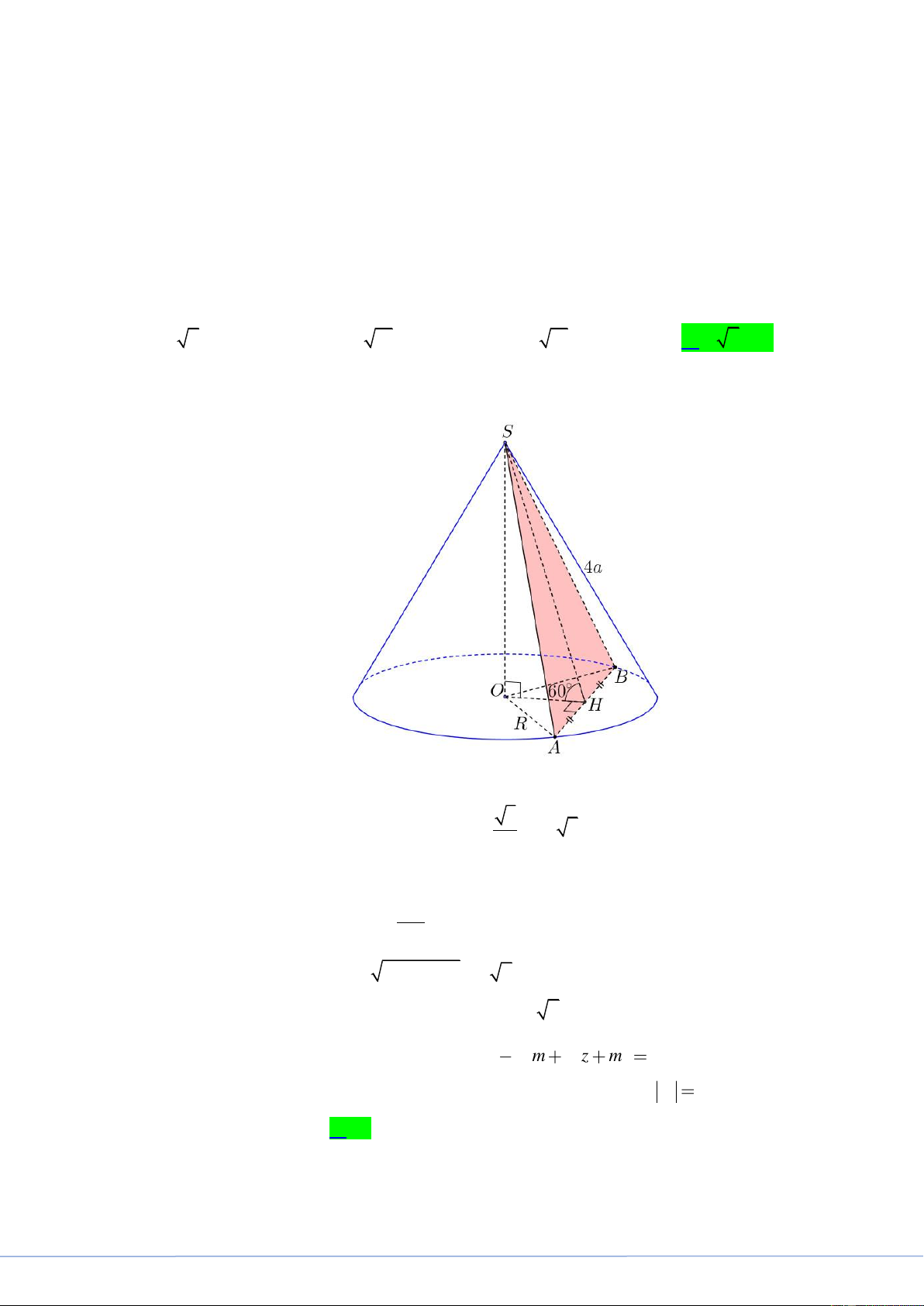
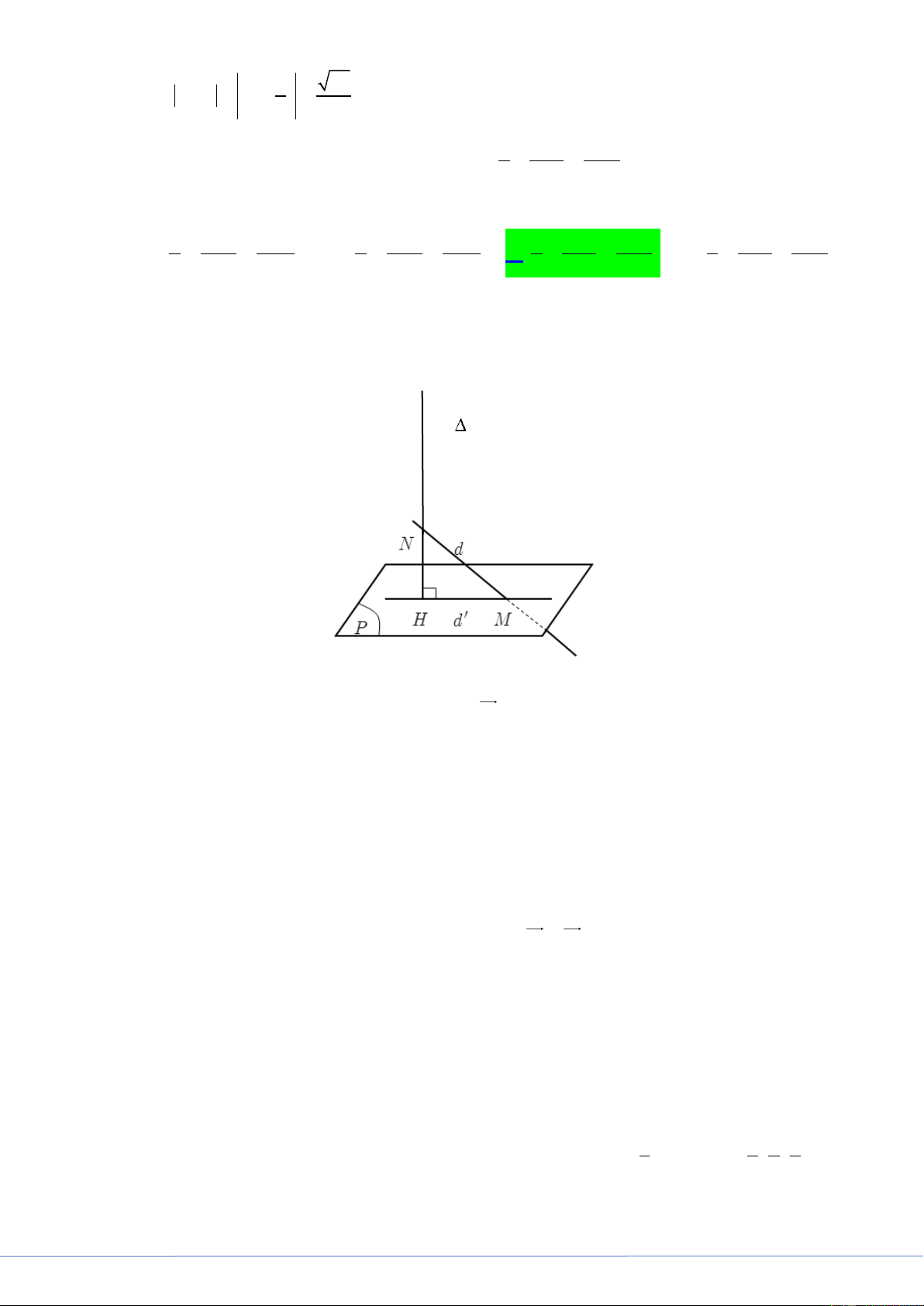
Cắt hình nón N bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng một góc bằng 60 ta được
thiết diện là tam giác đều cạnh 4a . Diện tích xung quanh của N bằng A. 2 8 7 a . B. 2 4 13 a . C. 2 8 13 a . D. 2 4 7 a . Lời giải
FB tác giả: Thanh Tâm Trần
Gọi O là tâm đường tròn đáy và thiết diện là S
AB đều cạnh 4a . 3
Gọi H là trung điểm của AB . Ta có SH . SA 2a 3 . 2
Khi đó góc giữa hai mặt phẳng SAB và OAB là SHO SHO 60 . SO
Trong tam giác SHO có sin 60
SO SH sin 60 3a . SH
Trong tam giác SOA có 2 2 OA
SA SO a 7 .
Vậy diện tích xung quanh của N là 2 S
rl 4 7a . xq
Câu 43. Trên tập hợp các số phức, xét phương trình z2 m z m2 2 1
0 ( m là tham số thực). Có
bao nhiêu giá trị của m để phương trình đó có nghiệm z thỏa mãn z 7 ? o o A. 2 . B. 3 . C. 1. D. 4 . Lời giải
FB tác giả: Thượng Đàm
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 19
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101 Phương trình z2 m z m2 2 1 0 1 có m 2 1. 1 +Trường hợp 1: 0 m . 2
Phương trình 1 có nghiệm z thỏa mãn z 7 suy ra z 7 hoặc z 7 . o o o o m 7 14 Nếu z 7 suy ra 49 14 m 1 m2 0 m2 14m 35 0 , (chọn). o m 7 14 Nếu z 7 suy ra m m2 m2 49 14 1 0 14m 63 0 vô nghiệm. o 1 + Trường hợp 2: 0 m
. Khi đó phương trình 1 có hai nghiệm phức z ; z 2 1 2 thỏa mãn z z z o 1 2 . 2 Suy ra z 7 z .z 49 z .z 49 m 49 m 7 . o o o 1 2 1
Kết hợp điều kiện m suy ra m 7 . 2
Vậy có 3 giá trị của m thỏa mãn.
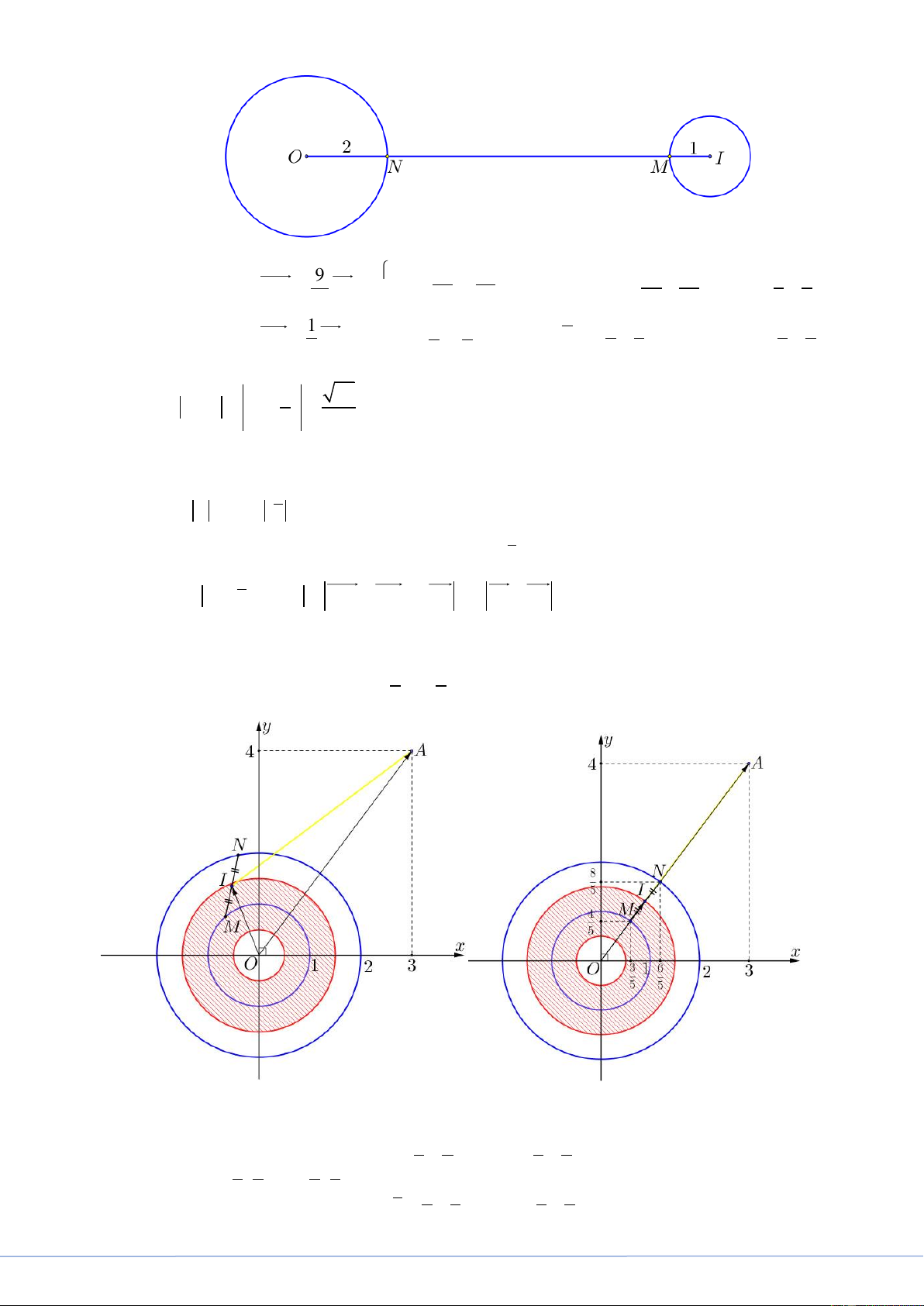
Câu 44. ét các số phức z, w thỏa mãn z 1 và w 2 . Khi z iw 6 8i đạt giá trị nhỏ nhất,
z w bằng? 221 29 A. . B. 5 . C. 3 . D. . 5 5 Lời giải
Fb tác giả: Lưu Thêm
Gọi M , N lần lượt là các điểm biểu diễn số phức z 6 8i và iw .
Ta có z 1 z 6 8i 6 8i 1 MI 1, với I 6; 8 .
Suy ra tập hợp điểm M là đường tròn T
tâm I 6; 8 và bán kính R 1. 1 1 Ta có i w i
. w 2 . Suy ra tập hợp điểm N là đường tròn T2 tâm O và bán kính R 2 . 2
Ta có P z iw 6 8i MN .
min P OI R R 10 1 2 7 (do T và T rời nhau). 2 1 1 2
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 20
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101 9 27 36 27 36 3 4 OM OI M ; z 6 8i i z i 10 5 5 , đạt đượ 5 5 5 5 c khi 1 6 8 6 8 8 6 ON OI N ; iw i w i 5 5 5 5 5 5 5 2 29
Vậy z w 1 i . 5 5
Cách 2: Đoàn Trí Dũng
Ta có w 2 iw 2 .
Gọi M , N là điểm biểu diễn của các số phức z,iw và A3; 4 .
Khi đó z iw 6 8i OM ON 2OA 2 OI OA 2AI , với I là trung điểm MN .
Do M , N thuộc hai đường tròn tâm O , bán kính 1 và 2 nên I thuộc hình vành tròn được giới 1 3
hạn bởi hai đường tròn bán kính và . 2 2
Suy ra AI nhỏ nhất O, M , N , A thẳng hàng. 3 4 3 4 z i z i Khi đó 3 4 6 8 5 5 5 5 M ; , N ; 5 5 5 5 6 8 8 6 iw i w i 5 5 5 5
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 21
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101 2 29
Vậy z w 1 i . 5 5 x y 1 z 2
Câu 45. Trong không gian Oxyz , cho đường thẳng d : 1 1 1 và mặt phẳng
P: x 2y z 4 0 . Hình chiếu vuông góc của d trên P là đường thẳng có phương trình x y 1 z 2 x y 1 z 2 x y 1 z 2 x y 1 z 2 A. 2 1 4 . B. 3 2 . C. 1 2 1 4 . D. 3 2 . 1 Lời giải
FB tác giả: Ngọc Thanh
Mặt phẳng P có một vec tơ pháp tuyến là n 1; 2; 1 . P
Gọi M là giao điểm của d và P .
M d M ;
m m 1; m 2 .
M P m 2m
1 m 2 4 0 m 0 . Suy ra M 0;1; 2 .
Lấy N 1;2;1 d .
Gọi là đường thẳng qua N và vuông góc với P .
Suy ra đường thẳng có một vectơ chỉ phương là u n 1;2; 1. P x 1 t
Do đó phương trình đường thẳng là: y 2 2t . z 1t
Gọi H là giao điểm của và P .
H H 1 ; h 2 2 ; h 1 h . 2 4 2
H P h h h 1 1 2 2 2 1
4 0 6h 2 0 h . Suy ra H ; ; . 3 3 3 3
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 22
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101 2 1 4 Ta có MH ; ; . 3 3 3
Gọi d là hình chiếu vuông góc của d trên P .
Suy ra đường thẳng d qua M 0;1; 2 có một vectơ chỉ phương là u 3MH 2;1; 4 . d x y 1 z 2
Vậy phương trình hình chiếu vuông góc d của d trên P là: 2 1 4 . Câu 46. Cho hàm số 3 2
f x x ax bx c với a, ,
b c là các số thực. Biết hàm số
g x f x f x f x có hai giá trị cực trị là 3
và 6 . Diện tích hình phẳng giới hạn f x
bởi các đường y và y 1 bằng g x 6 A. 2 ln 3 . B. ln 3 . C. ln18 . D. 2 ln 2 . Lời giải
FB tác giả: Lưu Thêm
Xét hàm số g x f x f x f x
Ta có g x f x f x f x f x f x 6 . g m 3
Theo giả thiết ta có phương trình g x 0 có hai nghiệm , m n và . g n 6 f x ét phương trình
g x 6 f x 0 f x f x 6 x m 0 . g x 1 6 x n
Diện tích hình phẳng cần tính là: n f x
n g x 6 f x
n f x f x 6 n g x S 1 x dx dx x g x g x g x g x m d 6 m 6 m 6 m d 6
ln g x 6 n ln g n 6 ln g m 6 ln12 ln 3 ln 4 2ln 2 . m 1 2
Câu 47. Có bao nhiêu số nguyên y sao cho tồn tại x ;3
thỏa mãn 3x xy 9 27 1 .27 x xy ? 3 A. 27 . B. 9 . C. 11. D. 12 . Lời giải
FB tác giả: Lưu Thêm +) Ta có 2
1 3x xy log 1 xy 9x 27 2
3x 9x 1 log t t , với t 1 xy 0. 27
+) Xét hàm số f x 2
3x 9x 1. 31 Ta có
f x 1 1 x ;3 . 4 3
+) Xét hàm số g t log t t, t 0 . 27
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 23
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101 gt 1
1; gt 1 0 t t ln 27 ln 27 12 31
t 8,07.10 ; 0,04 31 Ta có
f x 1 1 x ;3 . Suy ra
g t 1 4 3 4 t 1; 8,4 12 1 8, 07.10 1 0,04 12 y 8, 07.10 1 xy 0,04 x x hay 1
1 xy 8, 4 7, 4 0 y x 1 3 y 1 3 , ( x ;3 , y nguyên). 3 0 y 22
+) Nhận thấy y 2 ; y 1 thỏa mãn đề.
+) Với 0 y 22 , ta có 1 2
3x 9x 1 log 1 xy 1 xy 0 . 27 1
Nhập hàm, thay các giá trị nguyên của y, kiểm tra nghiệm x ;3
dẫn đến chọn 1 y 9 . 3 1
(Chú ý hàm số f t t nghịch biến trên khoảng ; nên y 10 , ta có: 3 2
3x 9x 1 log 1 xy 1 xy 2
3x 9x 1 log 110x 110x 1 0 x ;3 . 27 27 3
Do đó loại y 10 ). Vậy y 2 ; 1 ;1;2;...;
9 nên có 11 giá trị nguyên của y thỏa mãn đề.
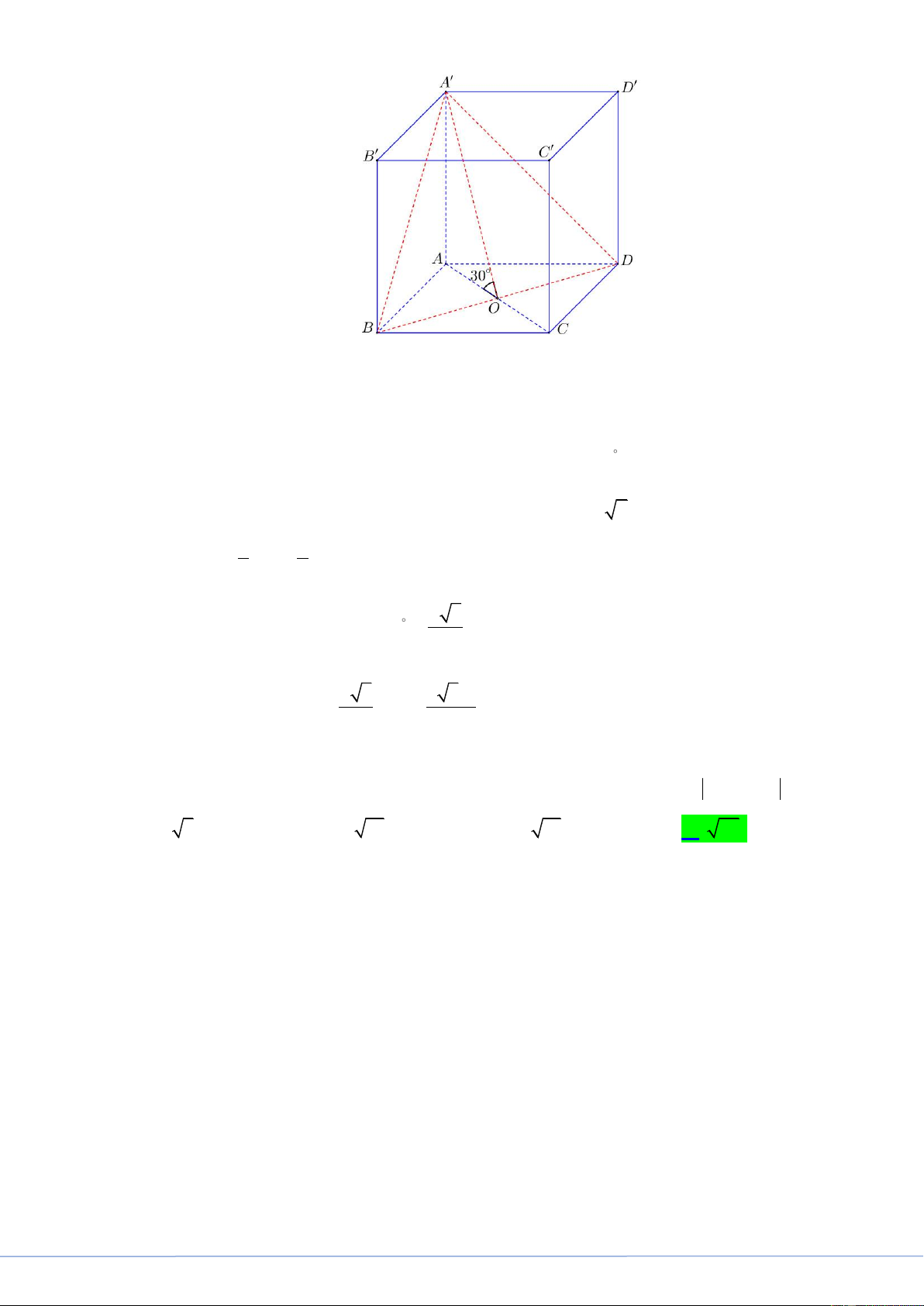
Câu 48. Cho khối hộp chữ nhật ABC . D A B C
D có đáy là hình vuông, BD 2a , góc giữa hai mặt phẳng
A BD và ABCD bằng 30 . Thể tích của khối hộp chữ nhật đã cho bằng 2 3 2 3 A. 3 6 3a . B. 3 a . C. 3 2 3a . D. 3 a . 9 3 Lời giải
FB tác giả: Phùng Hoàng Cúc
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 24
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101
Gọi là góc giữa hai mặt phẳng
A BD và ABCD .
Gọi O AC BD . AO BD Ta có A O A ; O A O
AOA 30 . A BD A BD
Ta có đáy ABCD là hình vuông có BD 2a AB AD a 2 . 1 1 Ta có AO AC BD a . 2 2 3 Trong AO A có AA . AO tan 30 a . 3
Vậy thể tích khối hộp chữ nhật ABC . D A B C D là: 3 a 3 2 3a 2 V A A S a . ABCD
A BCD . .2 . ABCD 3 3 Câu 49.
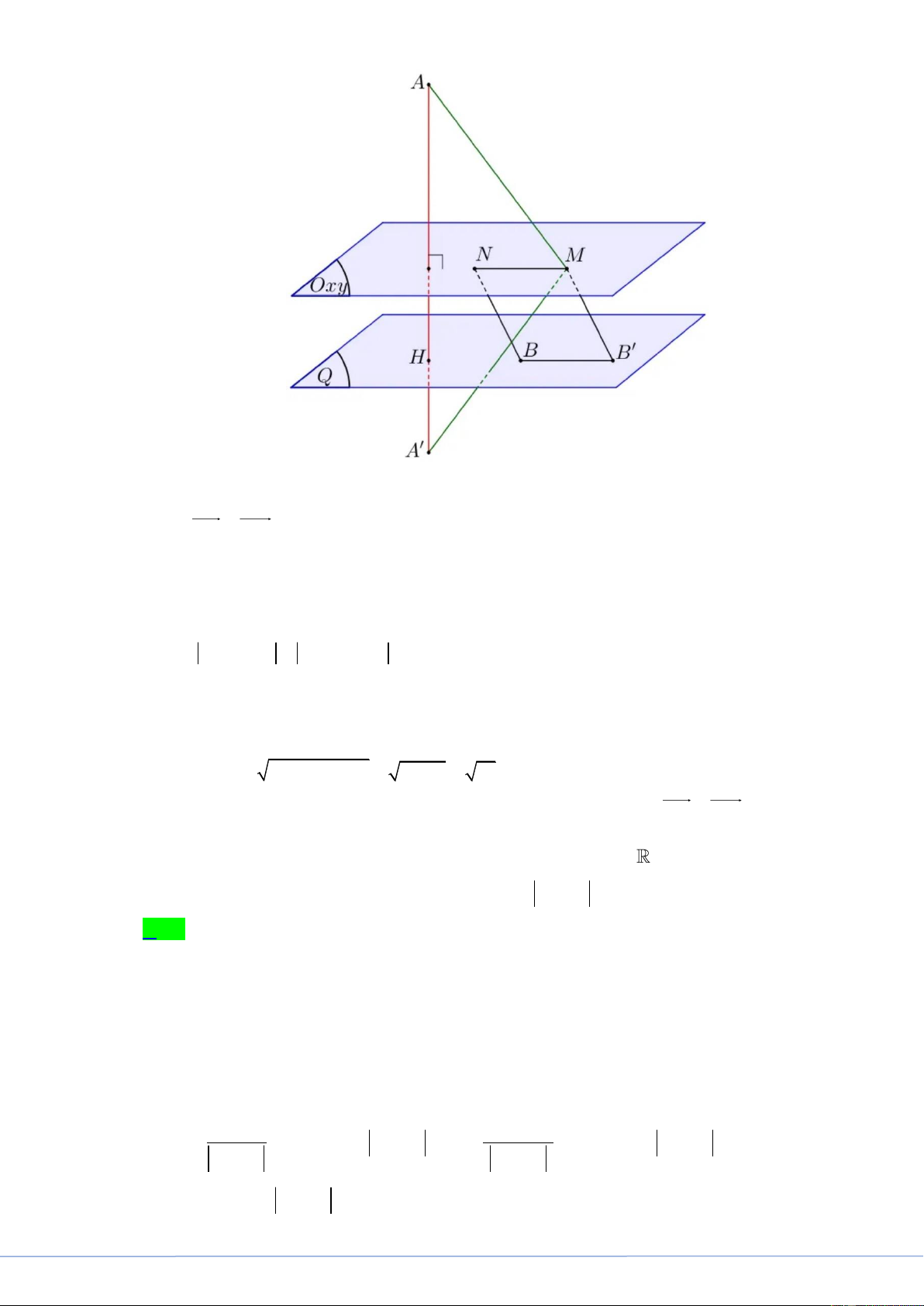
Trong không gian Oxyz, cho hai điểm A1; 3 ; 4
và điểm B2;1;2 . ét hai điểm M và
N thay đổi thuộc mặt phẳng Oxy sao cho MN 2 . Giá trị lớn nhất của AM BN bằng A. 3 5 . B. 61 . C. 13 . D. 53 . Lời giải
FB tác giả: Nguyễn Thị Thúy
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 25
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101
Gọi A ' đối xứng với A qua mặt phẳng Oxy . Suy ra A'1; 3 ;4 .
Dựng BB ' NM . Khi đó B ' thuộc mặt phẳng Q qua B và song song Oxy .
Phương trình Q : z 2 . Và BB' 2.
Suy ra B ' thuộc đường tròn tâm B , bán kính R 2 trong Q .
Ta có: AM BN A ' M MB ' A ' B '. Trong đó A '; B ' cùng phía so với Oxy .
Gọi H là hình chiếu của A ' trên Q . Suy ra H 1; 3 ;2 .
Suy ra A' H 2; HB ' HB BB ' 5 2 7 . Khi đó 2 2 A ' B '
A ' H HB ' 4 49 53 .
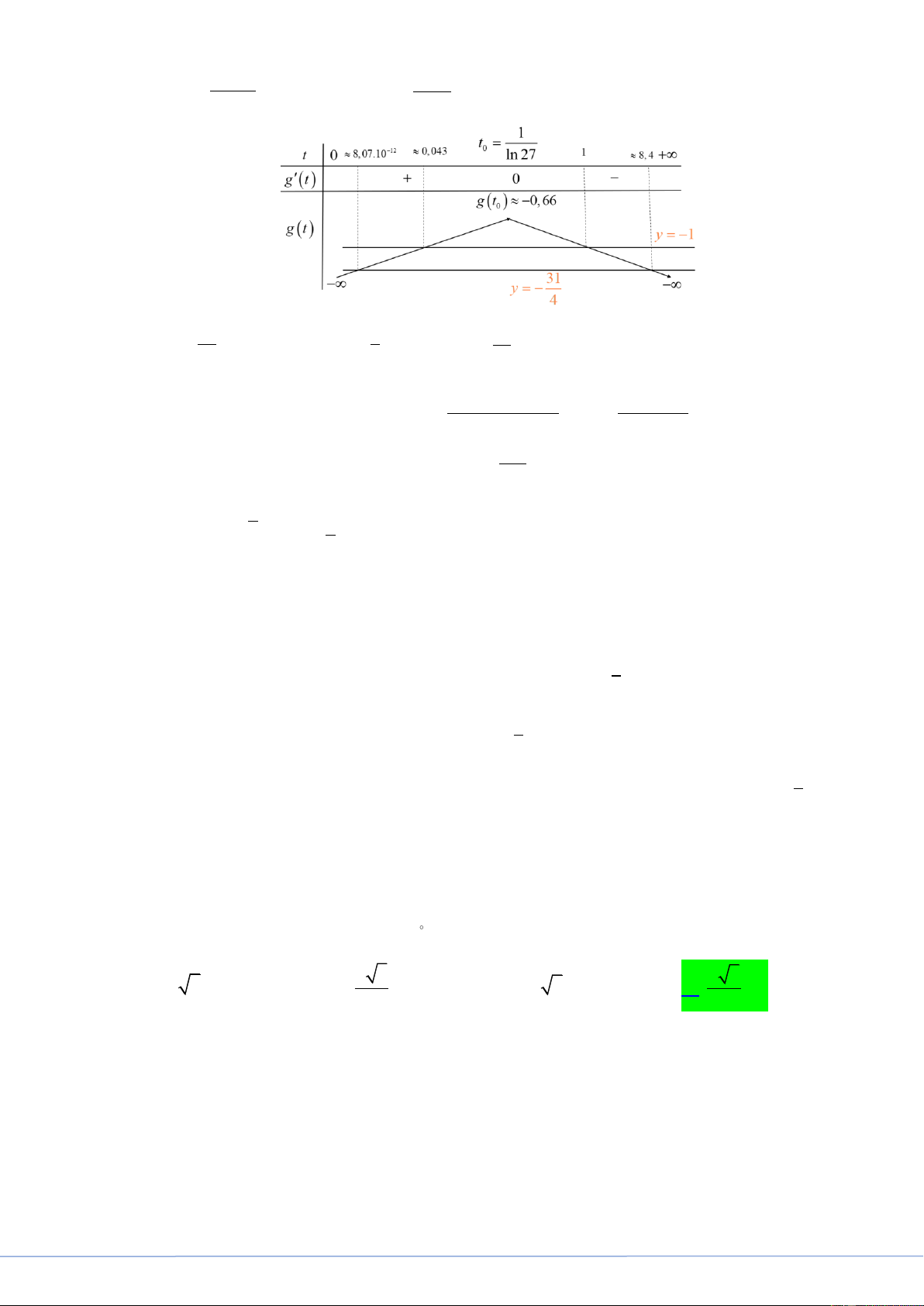
Dấu bằng xảy ra khi B nằm giữa B ' và H và M A ' B ' Oxy và BB ' NM . Câu 50.
Cho hàm số y f x có đạo hàm f x x 2 ' 7 x 9, x
. Có bao nhiêu giá trị
nguyên dương của tham số m để hàm số g x f 3
x 5x m có ít nhất 3 điểm cực trị? A. 6 . B. 7 . C. 5 . D. 4 . Lời giải
Fb tác giả: Đoàn Trí Dũng x 7
Ta có f x x 7 x 3 x 3 f x 0 x 3 . x 3 2 3 x x x x g x . 5 5 2
3x 5 f 3
x 5x m . 2
3x 5 f 3
x 5x m . 3 3 x 5x x 5x
g x 0 f 3
x 5x m 0 .
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 26
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101
Đạo hàm không xác định tại x 0 .
Do đó điều kiện để g x có ít nhất 3 điểm cực trị là phương trình f 3
x 5x m 0 có ít
nhất 2 nghiệm đơn hoặc bội lẻ khác 0. 3
x 5x m 7 3
x 5x 7 m f 3
x 5x m 0 3
x 5x m 3 3
x 5x 3 m 3
x 5x m 3 3
x 5x 3 m
Phương trình f 3x 5x m 0 có ít nhất 2 nghiệm bội lẻ khác 0 m 7 m 7
Vậy có tất cả 6 giá trị nguyên m thỏa mãn. HẾT
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 27
STRONG TEAM TOÁN VD-VDC
Key 24 Mã Đề Và Giải Chi Tiết Mã Đề 101
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 28