







Preview text:
lOMoAR cPSD| 59735516
Đáp án và Thang iểm (D) 1− n (1+ kx)
1.(2,5 ) limx 0 k 1=n có dạng vô ịnh (0,25 ) → n − (1+ kx) k 1=
- Ta thấy n (kx +1) là a thức bậc n, tức là n (kx + =1) n a x k
k , nên nếu thực hiện các phép nhân k 1= k 1= k 1= n a0 =1 n n
+1) thì nhận ược k 1= (kx a1 = n i k 1= (kx + = +1) 1 x i 1= i + x P2 n 2− (x) , trong ó P (x)n 2− là a thức bậc i 1= n = (n–2), tức là P k 2− n 2− (x) a xk
, hơn nữa Pn(0) = a2 có giá trị hữu hạn.(0,75 ) k 2= n n 2 n 2 n 2
−1 (1+ kx) = − +1 1x i + x Pn 2− (x) =−x i − x P − (x) (0,25 ) k 1= i 1= i 1=
- Ta có n (1+ kx) = n 1+ n kx = +nx n k(0,25 ) k 1= k 1= k 1= k 1= n n n
−n (1+ kx) = −n n + x k =−x k (0,25 ) k 1= k 1= k 1= −
1 n (1+ kx) − x n i − x P2n 2− (x) xP (x) xP (x) xP (x) k
k 1=n = i 1= n = +1 n 2n− n − (1+ kx) − x k 2 k 1= k 1= k 1=
= +1 n 2− = +1 2 n 2− (0,5 ) n(n +1) n(n +1) n 1− (1+ kx) lOMoAR cPSD| 59735516
limx→0 n − k 1 =n (1+ kx) = lim 1x→0 + 2 xPn(nn 2−+(1)x) = +1 2 0n(n.Pn 2++(0)1) = + =1 0 1.(0,25 ) k 1= 1− n (1+ kx)
Cách khác. lim
k 1=n có dạng vô ịnh (0,25 ) x→0 n − (1+ kx) k 1= n n , n , 1− (1+ kx) (L') 1− (1+ kx) (1+ kx) = = limx 0 k 1=n= limx 0 k 1n, = limx 0 k 1n , (0,5 ) = → − + → → n k 1 (1 kx) n − k 1= (1+ kx) k 1= (1+ kx)
- Theo công thức ạo hàm của một tích n thừa số ta ược n , n n n n
(1+ kx) = (1+ kx)' (1+ ix) = k (1+ ix) (0,5 ) k 1= k 1= i 1(i k)= k 1= i 1(i k)= n , n n
- Theo công thức ạo hàm của một tổng n số hạng ta ược (1+ kx) = (1+ kx)' = k (0,5 ) k 1= k 1= k 1=
n (1+ kx) , n k n (1+ ix) n k n(1+ i.0) n (k.1) n k limx k 1n= , = limx 0 k 1= i 1(i= nk)
= k 1= i 1(i= nk) = k 1= n = k 1n= = 1(0,5 )
→0 k 1 (1+ kx) → k 1= k k 1= k k 1= k k 1= k = 2 lOMoAR cPSD| 59735516
1− n (1+ kx) limx 0 k 1=n = 1.(0,25 ) → n − (1+ kx) k 1= 1+ x 2 khi x 0 khi 0 khi
x 2 là D(f) = R.(0,25 ) x
2.(2,5 ) Tập xác ịnh của hàm số f(x) = 2− x 2 (x − 2)2
2.1. Khảo sát tính liên tục/gián oạn của f(x) trên D(f) và phân loại iểm gián oạn 1+ x 2 khi x 0
- Hàm số f(x) = 2− x khi
0 x 2 liên tục trong trong các khoảng mở (– ,0), (0,2), (2,+ ) (x − 2)2 khi x 2
vì trong mỗi khoảng này, biểu thức tương ứng của f(x) là hàm sơ cấp.(0,5 )
- Tại iểm x = 0 ta có xlim f(x)lim f(x)→ −0 0
== xlim (1lim (2→ −0 0 + x )2 =1 xlim f(x)→ −0 0
xlim f(x)→ +0 0 nên f(x) gián oạn loại 1 x→ +0 0 x→ +0 0 − =x) 2
tại iểm này và có bước nhảy lim f(x) − lim f(x) = − =2 1 1.(0,5 ) x→ +0 0 x→ −0 0
lim f(x) = lim (2− =x) 0
- Tại iểm x = 2 ta có x 2 0x 2 0lim f(x)→ −→ + = x 2 0x 2 0lim (x→ −→ + − 2)2 = 0 x 2 0lim f(x)→ − = x 2 0lim f(x)→ + = f(2) f(2) = − =2 2 0
limf(x) = f(2) nên f(x) liên tục tại iểm này.(0,5 ) x→2 1+ x2 khi x 0
Kết luận: Hàm số f (x) = 2 − x khi 0 x
2 liên tục trong miền mở (– ,0) (0,+ ), gián (x − 2)2 khi x 2
oạn loại 1 tại iểm x = 0 và tại iểm này hàm số có bước nhảy lim f(x)− lim f(x) =1.(0,25 ). x 0 0→ + x 0 0→ − lOMoAR cPSD| 59735516 1+ x2 khi x 0
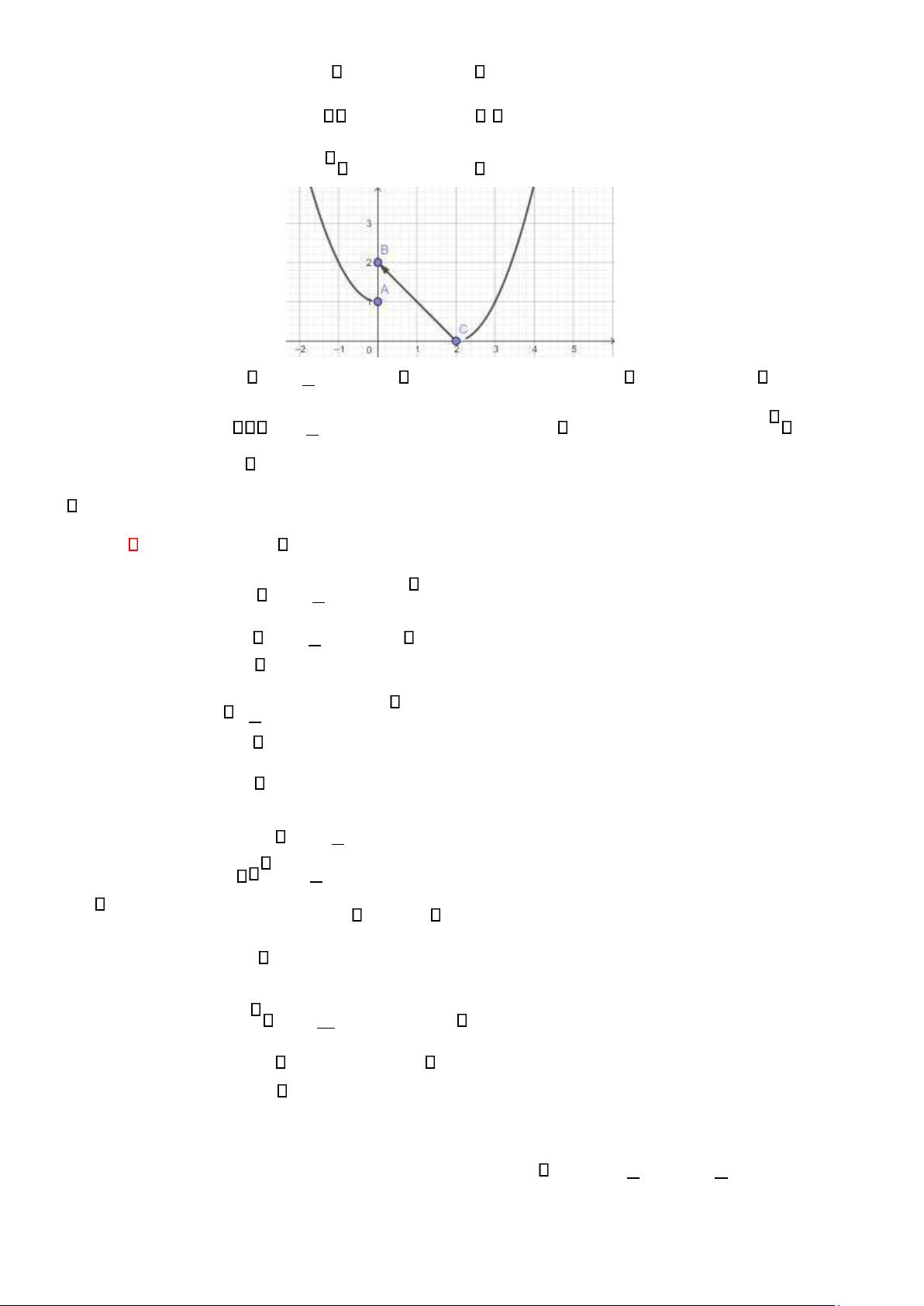
2.2. Đồ thị của hàm số f (x) = 2 − x khi 0 x 2 là (x − 2)2 khi x 2 (0,5 ) x +1 1 R khi b 1
3.(2,5 ) Hàm số f(x) = xlnx − a 2 khikhi
xx 1 có tập xác ịnh là D(f) = R \{b} khi b 1.(0,5 ) x −b
- Khi b 1: D(f) = R với b 1 x +1 1 x +1 x 1 xln 2 khi
khả vi trên tập xác ịnh D(f) của nó thì f(x) phải khả vi tại x Do ó, ể f(x) = x −a 1 khi x −b iểm x = 1. x +1
+ Hàm số f(x) = xlnx − a 2 khikhi
xx 1 khả vi trong các khoảng mở (− ,1) , (1,+ ) vì trong mỗi x −b
khoảng này, biểu thức tương ứng của f(x) là hàm sơ cấp.(0,25 ) 2
+ Để hàm số f (x) = x lnx − a khi
x 1 khả vi tại iểm x = 1 thì f(x) phải ồng thời thỏa mãn 2 khi x 1 x − b iều kiện:
(1) f(x) liên tục tại iểm x = 1, tức là lim f(x) = lim f(x) lim xln x +1 = lim x −a 4 lOMoAR cPSD| 59735516 x 1 0→+ x 1 0→− x 1 0→+ 2 x 1 0→− x − b −a a =1
xln x 12+ khi x 1.(0,25 ) =0 11
1 f(x) = x 1− khi x 1 −b b x−b
(2) f’(x) tồn tại hữu hạn tại iểm x = 1, tức là f '(1+ =0)
f '(1− 0) và là một số hữu hạn.
Theo ịnh nghĩa ạo hàm một phía của hàm số f(x) tại iểm x = 1 thì x→+1 0 f
(x)x −−1f (1) x→+1 0 x ln x 2+x1
−−11.ln1+21 = xlim→+1 0 x lnx −x12+1 f '(1+ 0) = lim= lim − f (1)
xx−−1b −1.ln1+21 = lim 1 = 1 f '(1− 0) = lim f (x)= lim x→−1 0 x −1 x→−1 0 x −1 x→−1 0 x − b 1− b x +1 x ln 2 = 1 (0,25 ) x lim − x→+1 0 1 1− b Bây giờ, ta tìm lim 2 = lim x +1 ln xln x x +1 x→+1 0
x −1 x→+1 0 x −1 2 t → +0 0 x → +1 0 1 Đổi biến t = −x
xx−1ln x 2+1 t +t 1 2t + 2t 2 t = t +2 1ln
1 + 2t 2 t = ln 1 lim
x ln x +1 = lim t +1ln 1 + t 2 t = lim t +1 ln lim 1 + t 2 t = 0 1+ lne = 1 →+ → + → + → + x 1 0 x −1 2 t 0 0 2 2 t 0 0 2 t 2 0 0 2 2 2 lOMoAR cPSD| 59735516 =1 1 =−b
1 iều này mâu thuẫn với trường hợp ang xét là b 1 nên không tìm ược 2 1− b
tham số b ể hàm số f (x) = x ln x −1x 2+1
khikhi xx 11 với b 1, khả vi tại iểm x = 1.(0,25 ) x − b
- Khi b < 1: D(f) = R\{b} với b < 1 xln + Hàm số f(x) = x −ax2+1 khikhi
xx 11 khả vi trong các khoảng mở (−, b) ,(b,1) , (1,+) vì trong x −b
mỗi khoảng này, biểu thức tương ứng của f(x) là hàm sơ cấp.(0,25 ) x 1 x 1 xln 2 khi
khả vi trên tập xác ịnh D(f) của nó thì f(x) phải khả vi tại x 1 Do ó, ể f(x) = x −a khi x −b iểm x = 1. x +1 + 2
+ Để hàm số f (x) = x lnx − a khikhi xx 11 khả vi tại iểm x = 1 thì f(x) phải ồng thời thỏa mãn 2 x − b iều kiện:
(1) f(x) liên tục tại iểm x = 1, tức là lim f(x) = lim f(x) lim xln x +1 = lim x −a x 1 0→+ x 1 0→− x 1 0→+ 2
x 1 0→− x − b −a a =1 xln x 12+ khi x 1.(0,25 ) 6 lOMoAR cPSD| 59735516
=0 11−b b 1 f(x) = x 1− khi x 1 x−b
(2) f’(x) tồn tại hữu hạn tại iểm x = 1, tức là f '(1+ =0)
f '(1− 0) và là một số hữu hạn.
Theo ịnh nghĩa ạo hàm một phía của hàm số f(x) tại iểm x = 1 thì f (x) x ln x +1 −1.ln1+1 x ln x +1 −
f '(1+ 0) = xlim→+1 0
x −1f (1) = xlim→+1 02 x −12 = xlim→+1 0 x −12 f '(1− 0) = lim f (x) = lim x +1 x→−1 0 x −−1f (1) x→−1 0 xx−−1b x ln −x1−.ln1 2
1+21 = xlim→−1 0 x 1− b = 1−1b = 1 (0,25 ) x lim − x→+1 0 1 1− b x +1 xln x x +1 Bây giờ, ta tìm lim 2 = lim ln x→+1 0 x −1 x→+1 0 x −1 2 t → +0 0 x → +1 0 Đổi biến t 1 = −x
x−1ln x 2+1 = t +t 1 2t ln 1 + 2t 2 t = t +2
1ln 1 + 2t 2 t x
lim x ln x +1 = lim t +1ln 1 + t 2 t = lim t +1 ln lim 1 + t →+ → + → + → + 2 t = 0 1+ lne = 1 x 1 0 x −1 2 t 0 0 2 2 t 0 0 2 t 2 0 0 2 2 2 =1
1 =−b1 iều này phù hợp với trường hợp ang xét là b < 1. 2 1− b x 1 x ln x 2+1 x +1 x 1 khi = x −1 khả vi khi x 1 x 1 x +1 lOMoAR cPSD| 59735516
+ Như vậy, khi ab ==−1 1 thì hàm số f (x) = x lnx − a 2 khikhi x − b
trên tập xác ịnh D(f) = R\{–1} của nó.(0,25 ) x5 sin 1 khi x 0
4.(2,5 ) Hàm số f (x) = x
có tập xác ịnh D(f) = R.(0,25 ) x2 sin3 x khi x 0
- Tính f’(0): Theo ịnh nghĩa ạo hàm một phía của hàm số f(x) tại iểm x = 0 thì 5 1 2 3 + f '(0 − 0) = lim f (x) − f (0) = lim x
sin x − 0 .sin 0 = lim x 4 sin 1 = 0 vì sin 1
1(0,25 ) x→ −0 0 x − 0 x→ −0 0 x x→ −0 0 x x f (x) − f (0) x2 sin3 x − 02.sin3 0 3 3 3 + f '(0 + 0) = lim = lim
= lim x sin x = 0.sin 0 = 0.0 = 0 (0,25 ) x→
+0 0 x − 0 x→ +0 0 x x→ +0 0
f '(0 − =0) f '(0 + =0) 0 f '(0) = 0.(0,25 )
- Tính f”(0): Để tính f”(0) chúng ta tính f’(x) khi x < 0 và f’(x) khi x > 0 theo quy tắc tính
ạo hàm, sau ó chúng ta tính f”(0) theo ịnh nghĩa, khi sử dụng f’(0) = 0 tìm ược ở trên.
x5 sin 1x , = 5x 4 sin 1x − x3 cos x1 khi x 0
(0,5 ) Chúng ta có f '(x) =
(x 2 sin3 x)'= 2x sin3 x + 3x 2 sin2 x cosx khi x 0
Theo ịnh nghĩa, ạo hàm một phía của hàm số f’(x) tại iểm x = 0 là
5x4 sin 1 − x3 cos 1 − 0 + f"(0 − 0) = lim
f '(x) − f '(0) = lim x x = lim 5x3 sin 1 − x2 cos 1 x
0 0→ − x − 0 x 0 0→ − x x 0 0→ − x x 1 1 3 2 sin(1 x) 1
= 5x 0 0lim x sin→ − x − x 0 0lim x cos→ −
x = 5.0 − =0 0 vì cos(1 x) 1 (0,5 ) + f"(0 + 0) = lim
f '(x) − f '(0) = lim (2x sin3 x + 3x2 sin2 x cosx) − 0 8 lOMoAR cPSD| 59735516 x→ +0 0 x − 0 x→ +0 0 x
= lim (2x sin3 x + 3x2 sin2 x cosx) = 2 lim x sin3 x + 3 lim x2 sin2 x cosx x 0 0→ + x 0 0→ + x 0 0→ +
= 2.0.sin3 0 +3.02.sin 0.cos2 0 = 2.0 + 3.0.1= 0(0,25 )
f"(0 − =0) f"(0 + =0) 0 f"(0) = 0.(0,25 )




