Đề chọn đội tuyển HSG Toán 9 năm 2022 – 2023 phòng GD&ĐT Kim Thành – Hải Dương

UBND HUYỆN KIM THÀNH
ĐỀ THI CHỌN ĐỘI TUYỂN CHÍNH THỨC
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HỌC SINH GIỎI THAM DỰ KỲ THI CẤP TỈNH
NĂM HỌC 2022 – 2023 ĐỀ CHÍNH THỨC MÔN: TOÁN - LỚP 9
Thời gian làm bài: 150 phút
(Không kể thời gian giao đề)
(Đề bài gồm 05 câu, 01 trang) Câu 1. (2,0 điểm). 2 2
a) Cho M = x + 5 x −1 + x . Rút gọn và tính giá trị của M khi x = 1 − − 2 2
5x − 5 + x x −1
b) Cho a,b,c là các số thực dương thỏa mãna +b + c =14 và a + b + c = 6 . Chứng minh rằng: a b c 22 + + =
a +11 b +11 c +11
(a +11)(b +11)(c +11) Câu 2. (2,0 điểm).
a) Giải phương trình: 2x x + x(1− x) =1 x + 1− x 2 2 
b) Giải hệ phương trình: x + y + 3 = 4x  . 3 3 2
x +12x + y = 6x +9 Câu 3 (2,0 điểm).
a) Cho a, b, c, k là các số tự nhiên thỏa mãn: 3 3 3 2
a + b + c = a + b + c + k − 2k +1.
Chứng minh rằng k −1 chia hết cho 3. b) Tìm x, y nguyên biết: 2 2
7x + y + 4xy +12x + 5 = 0 Câu 4: (3 điểm).
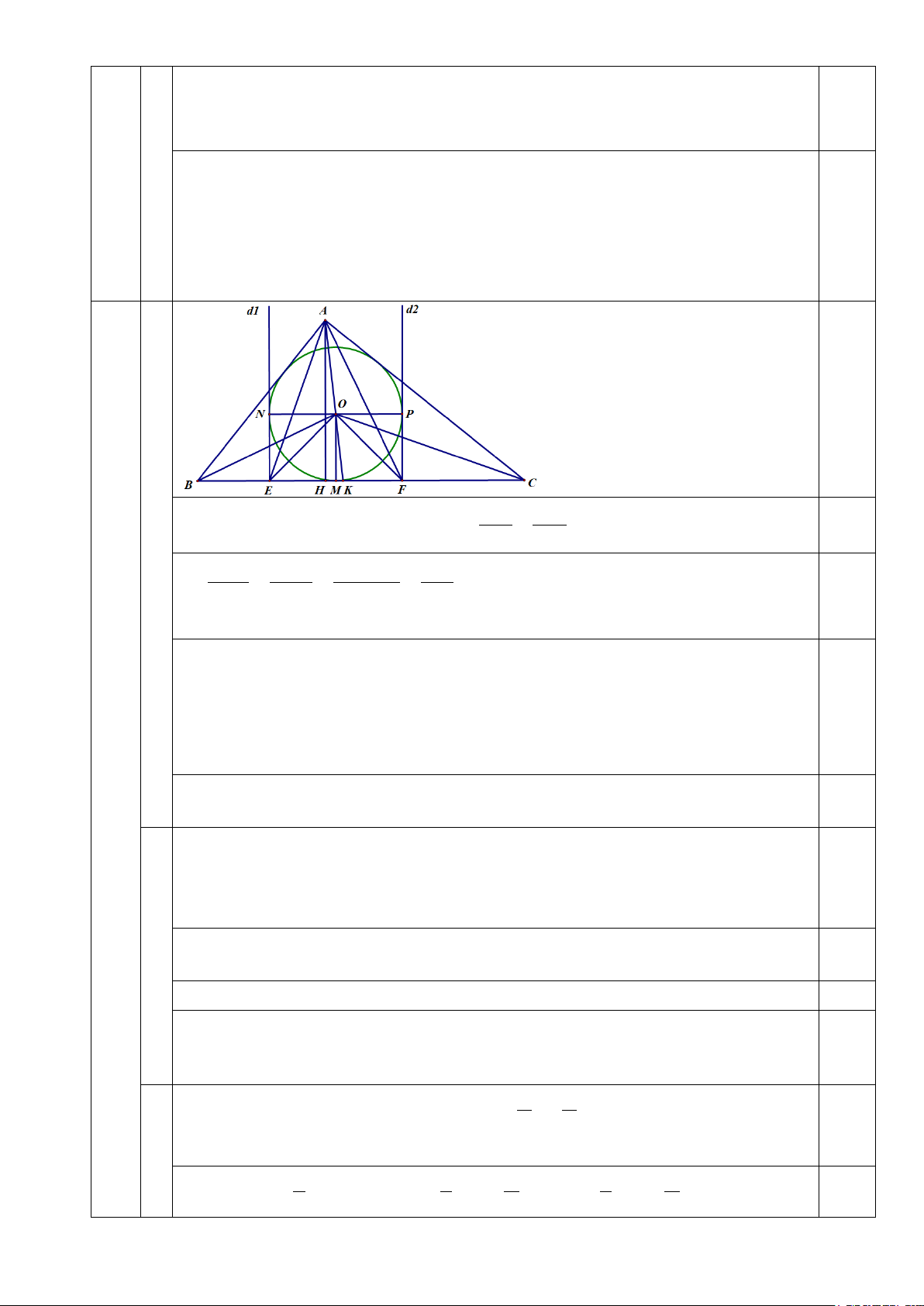
1) Cho ∆ABC vuông tại A, đường cao AH. Các đường phân giác của góc BAH,
CAH cắt BC lần lượt tại E, F. a) Chứng minh: 2 2
BC.EH = CH.BE và tâm đường tròn ngoại tiếp ∆AEF trùng với
tâm đường tròn nội tiếp ∆ABC .
b) Kí hiệu d ,d lần lượt là các đường thẳng vuông góc với BC tại E, F. Chứng minh 1 2
rằng d ,d tiếp xúc với đường tròn nội tiếp ∆ABC . 1 2
2) Cho tam giác ABC. Gọi l l l lần lượt là độ dài các đường phân giác trong của A , B , C
góc A, B, C. Chứng minh rằng 2bc A l = và 1 1 1 1 1 1 + + > + + A .cos b + c 2 l l l a b c A B C
Câu 5 (1,0 điểm). Cho x, y, z là các số thực dương thay đổi thỏa mãn: x + y + z = 9 3 3 3 3 3 3
Tìm giá trị nhỏ nhất của biểu thức x + y y + z z + = + + x M xy + 9 yz + 9 xz + 9
---------------HẾT----------------
Họ và tên học sinh................................................Số báo danh.....................................
Chữ kí của giám thị 1.................................... Chữ kí của giám thị 2............................ 2 UBND HUYỆN KIM THÀNH HƯỚNG DẪN CHẤM
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI CHỌN ĐỘI TUYỂN CHÍNH THỨC
HỌC SINH GIỎI THAM DỰ KỲ THI CẤP TỈNH NĂM HỌC 2022- 2023
MÔN: TOÁN – LỚP 9
(Hướng dẫn chấm gồm 04 trang) Câu Ý Nội dung Điểm 2
x(x +1) + 5 x −1 M =
(ĐK: x>1 hoặc x ≤ 1 − ) 2
5(x −1) + x x −1 0.25 A x >1 =>
x +1(x x +1 + 5 x −1) x +1 M = =
x −1(5 x −1 + x x +1) x −1 0.25 1 x − − − − − + − + − − ≤ 1 −
x 1( x x 1 5 x 1) x 1 ⇒ M = = − −x +1( 5
− −x +1 + x −x −1) −x +1 0.25
khi x = -1- 2 < -1 => M = −x −1 − − = 2 2(2 2) − = − = − 2 −1 −x +1 2 + 2 2 0,25 Ta có
a + b + c = 6 ⇔ a + b + c + 2( ab + bc + ca ) = 36 0,25
⇔ ab + bc + ca =11
Do đó:a +11= a + ab + bc + ca = ( a + b)( a + c) 0,25 b Tươngtự ta có:
b +11 = b + ab + bc + ca = ( b + c )( b + a )
c +11 = c + ab + bc + ca = ( c + a )( c + b) Suy ra: 0,25 a b c a b c + + = + +
a +11 b +11 c +11 ( a + b)( a + c) ( b + c)( b + a) ( c + a)( c + b)
a( b + c )+ b( c + a )+ c( a + b) = (
a + b)( b + c )( c + a )
2( ab + bc + ca ) 22 0,25 = =
(a +11)(b +11)(c +11)
(a +11)(b +11)(c +11)
Điều kiện xác định 0 ≤ x ≤1 0.25
Phương trình đã cho ⇔ 2x x +( x + 1− x) x(1− x) = x + 1− x 2
⇔ (a −b)(ab + ) 1 = 0
Đặt x = a (a ≥ 0) 1− x = b (b ≥ 0) khi đó 2 x =1− b 0.25
Ta có phương trình 2( 2
1− b )a + (a + b)ab = a + b
a Vì ab+1>0 nên a = b 0.25
Khi đó ta được phương trình x = 1− x 3 Tìm được 1
x = thỏa mãn điều kiện nên là nghiệm của pt đã cho 0.25 2
Từ phương trình (1) ta suy ra: 2 2
9 =12x − 3x − 3y thế vào phương trình (2) thu b gọn ta được: 0.25 x + y = 0 3 3 2 2 2 2
x + y = 3(x − y ) ⇔ (x + y)(x − xy + y −3x + 3y) = 0 ⇔  2 2
x − xy + y − 3x + 3y = 0 * Nếu 2 2
x + y = 0 ⇔ y = −x ⇒ y = x thế vào phương trình (1) ta được 0.25 2 2
2x + 3 = 4x ⇔ 2(x −1) +1 = 0 phương trình này vô nghiệm. * Nếu 2 2
x − xy + y − 3x + 3y = 0 , trừ vế theo vế của phương này với phương trình (1) ta được: 0.25 x = 3
−xy − 3x + 3y − 3 = 4
− x ⇔ xy − x −3y + 3 = 0 ⇔ (x −3)(y −1) = 0 ⇔   y =1
+ Nếu x =3 thay vào phương trình (1) ta suy y2 = 0 suy ra y = 0
=> (x;y) = (3; 0) thoả mãn phương trình (2). 0.25
+ Nếu y =1 thay vào phương trình (1) ta suy (x - 2)2 = 0
=> x = 2 => (x;y) = (2; 1) thoả mãn phương trình (2).
Vậy nghiệm của hệ đã cho là (x; y) = (3;0), (2; 1).
Bài toán phụ: Với x là số tự nhiên.
Chứng minh rằng: x3 – x luôn chia hết cho 3
Chứng minh: Ta có: x3 – x = x(x – 1)(x + 1) 0,25
Do đó: x3 – x luôn chia hết cho 3 Ta có : 3 3 3 2
a + b + c = a + b + c + k − 2k +1 Hay 3 3 3 2 a − a + b −b +
c − c = k − 2k +1 0,25 Hay: (k − )2 3 3 3
1 = a − a + b −b + c − c Áp dụng bài toán ta có: 3 a − a3 3 b − b3 0,25 3 c − c3 Nên: (k − )2 1 3 Mà 3 là số nguyên tố
Nên : k −13 (đpcm) 0,25 Ta có: 2 2
7x + y + 4xy +12x + 5 = 0 2 2 2
⇔ 4x + 4xy + y + 3x +12x +12 − 7 = 0 0,25
⇔ ( x + y)2 + (x + )2 2 3 2 = 7 Suy ra: ≤ (x + )2 0 3 2 ≤ 7 Hay: ≤ (x + )2 0 2 ≤ 2 0,25 Do đó: (x + )2 2 ∈{0; } 1 Ta có các trường hợp: +) (x + )2
2 = 0 Khi đó ( x + y)2 2 = 7 (Loại) 0,25 4 +) (  + =  = − x + )2 x 2 1 x 1 2 =1 ⇔ ⇔  x 2 1  + = − x = 3 − Khi đó: (  + = x + y)2 2x y 2 2 = 4 ⇔  2x + y = 2 −
Nên: x = –1 y = 4  y = ⇒ 0,25  hoặc x = –3 8 ⇒   y = 0  y = 4
Nghiệm của phương trình ( ;x y)∈{( 1 − ;4);( 1 − ;0);( 3 − ;8);( 3 − ;4 } );
Vì AE là phân giác góc BAH, ta có: EB AB = 0.25 1. EH AH a 2 2 EB AB BH.BC BC ⇒ = = = 2 2 EH AH BH.CH CH 0.25 2 2
⇒ BC.EH = CH.BE
Gọi O là giao điểm 2 đường phân giác trong góc B, C.
⇒ O là tâm đường tròn nội tiếp ABC ∆ 0.25
Ta có:  =  +  =  +  =  AEC B BAE HAC EAH EAC ⇒ AEC ∆
cân tại C⇒ CO là phân giác góc ACE đồng thời là trung trực của AE 4
CMTT: BO là trung trực của AE
⇒ O là tâm đường tròn ngoại tiếp AEF ∆ ⇒ ĐPCM 0.25
1. Kẻ OM, ON, OP lần lượt vuông góc với BC, d ,d , gọi K là giao điểm của 1 2 b AO với BC. 0.25
Có:  =  +  =  +  ( )=  =  2 2 = 90o EOF EOK FOK EAO FAO EAF BAC
Mà OE = OF ⇒ EOF ∆ vuông cân tại O
⇒ OM = EM = FM 0.25
Chứng minh được: ON = ME;OP = MF 0.25
⇒ OM = ON = OP
⇒ d ,d tiếp xúc với đường tròn nội tiếp 0.25 1 2
Chứng minh được công thức α α sinα = 2sin cos
bằng sử dụng tam giác cân 2 2 0,25
tại đỉnh A có A = 2α thông qua công thức diện tích để đi đến kết luận trên. A A Ta có: 1 S = , 1 S = , 1 S = ∆ bl ACD A sin ∆ cl ABD A sin ∆ bc A ABC sin 0,25 2 2 2 2 2 5 2 Mà 2bc A S = + ⇒ = ∆ S∆ S∆ l ABC ABD ACD A cos b + c 2
cos A2 1b+c 1 1 = = +   l  bc  b c A 2 2 2 cos B cos C Tương tự: 2 1 1 2 1 1 = + , = + 0,25 l a c l a b B 2 2 C 2 2
cos A cos B cos C 2 2 2 1 1 1 ⇒ + + = + + l l l a b c A B C
cos A cos B cos C Ta có 2 2 2 1 1 1 + + < + + l l l l l l A B C A B C 0,25 1 1 1 1 1 1 ⇒ + + > + + l l l a b c A B C 3 3 1
Ta chứng minh được : với a, b là các số dương ta có a + b ≥ (a + b)3 và 4 1 0.25
ab ≤ (a + b)2. 4 Dấu bằng xảy ra khi a=b 5 x + y (x + y)3 3 3 36(x + y) Khi đó ta có ≥ = x + y −
xy + 9 (x + y)2 + 36
(x + y)2 + 36
Áp dụng BĐT Cô-si ta được ( 0.25
x + y)2 + 36 ≥12(x + y) 3 3 x + y (x + y) 3 3 36 x + ⇒ ≥ + − y x y x y x y xy +
(x + y) = + − 3 ⇔ ≥ + − 3 9 12 xy + 9
Chứng minh tương tự ta được 3 3 3 3 y + z 3 ; z + ≥ + − x y z ≥ z + x − 3 yz + 9 xz + 9 0.25
Cộng ba BĐT cùng chiều ta được
M ≥ x + y − 3 + y + z − 3 + z + x − 3
⇔ M ≥ 2(x + y + z) − 9 ⇔ M ≥ 2.9 − 9 ⇔ M ≥ 9 Dấu bằng xảy ra khi
x = y = z 
⇔ x = y = z = 3 0.25
x + y + z = 9
Vây GTNN của M là 9 đạt được khi x = y = z = 3
Document Outline

• ĐỀ THI CHỌN ĐỘI TUYỂN CHÍNH THỨC
• HƯỚNG DẪN CHẤM
• ĐỀ THI CHỌN ĐỘI TUYỂN CHÍNH THỨC