Đề chọn đội tuyển HSG Toán 9 vòng 1 năm 2023 – 2024 trường THCS Cầu Giấy – Hà Nội

PHÒNG GD & ĐT QUẬN CẦU GIẤY
ĐỀ KIỂM TRA CLB VĂN HÓA LỚP 9
TRƯỜNG THCS CẦU GIẤY
VÀ CHỌN ĐỘI TUYỂN HỌC SINH GIỎI LỚP 9 VÒNG I Môn kiểm tra: Toán ĐỀ CHÍNH THỨC Ngày thi: 07/09/2023
Thời gian làm bài: 120 phút
(Không tính thời gian phát đề)
Bài 1. (5,0 điểm) 2 2 2 2   1. Cho 2  x y  x y  x  y P      . 
với x  0,y  0,x  y  . 2 2  2 2 x x  xy xy
xy  y  x  xy  y
a) Rút gọn biểu thức P.
b) Tính giá trị của biểu thức P biết x,y thỏa mãn đẳng thức: 2 2
x  y  10  2x  3y.
2. Tìm tất cả các số nguyên tố ,
p q,r thỏa mãn 2 2 2
(p  1)(q  1)  r  1.
Bài 2. (4,0 điểm)   
1. Giải phương trình 3  x   3  x x   x        2. x  1  x  1
2. Tìm các cặp số nguyên dương (x;y) thỏa mãn 2
xy  2xy  x  9y.
Bài 3. (4,0 điểm)
1. Cho x và y là các số nguyên dương thỏa mãn 3 x  y và 3
x  y cùng chia hết cho 2 2 x  y .
Chứng minh rằng 2x  2y là số chính phương.
2. Cho các số dương a, , b c thỏa mãn 2 2 2
a  b  c  3. Tìm giá trị nhỏ nhất của biểu thức: 1 1 1 P    . 2 a 2 b 2 c
Bài 4. (6,0 điểm) Cho tam giác ABC vuông tại A (AB  AC). Vẽ đường cao AH (H  BC).
Trên tia đối của tia BC lấy điểm K sao cho KH  H .
A Qua K kẻ đường thẳng song song
với AH, cắt đường thẳng AC tại P.
1. Chứng minh rằng tam giác AKC đồng dạng với tam giác BPC.
2. Gọi Q là trung điểm của BP. Chứng minh   BQH  BCP. 3. Tia AH BC
AQ cắt BC tại I. Chứng minh   1. HB IB
Bài 5. (1,0 điểm)
1. Xét tập T  1,2,3, ,  1 
3 . Lập tất cả các tập con hai phần tử trong T sao cho hiệu của hai
phần tử đó là 5 hoặc 8.
2. Cho M là tập con của S  1,2,3, ,  86 
9 có tính chất hiệu hai số bất kỳ của M không là
5 hoặc 8. Hỏi M có nhiều nhất bao nhiêu phần tử ?
-----------HẾT-----------
Họ và tên thí sinh: ………………………………………………… Số báo danh: …………………….
PHÒNG GD & ĐT QUẬN CẦU GIẤY ĐÁP ÁN
TRƯỜNG THCS CẦU GIẤY
ĐỀ KIỂM TRA CLB VĂN HÓA LỚP 9
VÀ CHỌN ĐỘI TUYỂN HỌC SINH GIỎI LỚP 9 VÒNG I ĐỀ CHÍNH THỨC Môn thi: Toán Ngày thi: 07/09/2023
Thời gian làm bài: 120 phút
(Không tính thời gian phát đề) BÀI Ý HƯỚNG DẪN CHẤM ĐIỂM 2 2 2 2   1. Cho 2  x y  x y  x  y P      .  với 2 2  2 2 x x  xy xy
xy  y  x  xy  y
x  0,y  0,x  y  1
a) Rút gọn biểu thức P . 1,5
b) Tính giá trị của biểu thức P biết x,y thỏa mãn đẳng thức: 2 2
x  y  10  2x  3y 1.0 2 2 2 2   a) 2  x y  x y  x  y P      .  2 2  2 2 x x  xy xy
xy  y  x  xy  y 2 2 x y   2 2
y  x x  y 2  xy x  y 1 P   x
xy x  y . 2 2
x  xy  y 1,0 2 2 3 3 2 2 2
x y  xy  y  x  x y  xy x  y P   . 2 2 x
xy x  y
x  xy  y 2
y x 2 2
x  xy  y  x  y P   x
xy x  y . 2 2
x  xy  y 2 y  x    0,5 P   2y y x P  x y P 
với x  0,y  0,x  y  x xy xy xy BÀI Ý HƯỚNG DẪN CHẤM ĐIỂM
b)Tính giá trị của biểu thức P biết x,y thỏa mãn đẳng thức: 2 2
x  y  10  2x  3y Ta có 2 2
x  y  10  2x  3y 2 2
 x  2x  1  y  6y  9  0
 x  2  y  2 1 3  0 Vì x  2 
x y  2 1 0 ; 3  0 y 0,5 x  1  0 x   1       (TMĐK) y   3  0 y   3    1  3 Tại 2
x  1,y  3 thì P   1.3 3 Vậy 2 P  khi 2 2
x  y  10  2x  3y 3 0,5
Tìm tất cả các số nguyên tố ,
p q,r thỏa mãn 2 2 2
(p  1)(q  1)  r  1. 2,5
Do vai trò p và q như nhau nên ta có thể giả sử p  q.
Nếu p và q cùng lẻ thì vế trái chia hết cho 4. Suy ra 2
r chia cho 4 dư 3: vô lý. 1,0
Do đó có ít nhất một số chẵn trong p và q. Suy ra p  2. Khi đó có 2 2
5(q  1)  r  1 2 2
 5q  4  r 2 0,5 2
q  2  r  24 : loại 2
q  3  r  49  r  7 : thỏa mãn 0,5 2 2
q  3  r  5q  4 chia hết cho 3  r  3 2
 9  5q  4  49 : vô lý
p  2;q  3;r  7 0,5 Vậy 
p  3;q  2;r  7  ĐKXĐ: x  1 2,0 1 3 x    3 x    2 x   x        2 x  1  x  1 BÀI Ý HƯỚNG DẪN CHẤM ĐIỂM C1 2 2
3x  x x  x  3  x  .  2 x  1 x  1  0,5 2
3x  x  2 x   3   2 x  2 1 3 4 2 2
 3x  9x  x  3x  2x  4x  2 4 3 2
 x  3x  5x  5x  2  0 2 1,0  x   1 . 2 x  x   2  0 x  1  0 x   1(tm)      2 x x 2 0 VN         0,5 Vậy S    1     C2 Đặt A = 3  x  x x        ;B = 3 x  
 . Ta có A+B = 3 ; A.B = 2 và tìm được A = 1; B= x  1  x  1
2 hoặc ngược lại và tìm được x = 1
Tìm các cặp số nguyên dương(x;y) thỏa mãn : 2
xy  2xy  x  9y 2,0 2
xy  2xy  x  32y 2
 x(y  1)  9y 0,5 Do y nguyên dương 9y
 y  1  0  x  2 (y  1) 2 Vì 2 ( ,
y y  1)  1  (y  1) U(9) 0,5 Do 2
(y  1)  1 và là số chính phương nên 2 (y  1)  9 0,5 2
(y  1)  9  y  2;x  2 x   2 0,5
Vậy nghiệm nguyên dương của phương trình là:  y   2 
1 Cho x và y là các số nguyên dương thỏa mãn 3
x  y và 3
x  y cùng chia hết cho 2,0 2 2
x  y . Chứng minh rằng 2x  2y là số chính phương.
Đặt a  (x;y)  chứng minh được a  1. 3 3 2 2 x
  y x  y 0,5  2 2 2 2 
 (x  y)(x  xy  y  1)x  y 3 2 2 x
  yx  y  2 x
  y(modd) 2  x d Đặt 2 2 d (x , y x y )         0,5 2 2  2 x   y d 2  y d   BÀI Ý HƯỚNG DẪN CHẤM ĐIỂM
Do (x;y)  1  d  1;  2 . +) Nếu 3 3
x  y  x  y  x  x chia hết cho 2 2 2
x  y  2x . Từ đây tìm được x  y  1. Nếu 2 2
d  1  (x  ,
y x  y )  1 khi đó 2 2 2 2 2 2
 x  xy  y  1x  y  xy  1x  y 0,5
Từ đây chỉ ra xy 1  0  x  y  1 2 2  (x  ,
y x  y )  (0;2)  2 loại 2 2 2 2 2 2 Nếu
x  y x  y   2 2 x y x y d  2  ( ,
)  1  x  xy  y  1  xy  1 2 2 2 2 Từ đây chỉ ra 0,5
xy  1  0  x  y  1 : thỏa mãn
Vậy x  y  1  2x  2y  4 là số chính phương
Cho các số dương a, ,
b c thỏa mãn 2 2 2
a  b  c  3. Tìm giá trị nhỏ nhất của biểu thức: 2,0 1 1 1 P    . 2 a 2 b 2 c 2 2 1 a a 2 a  1   1   0,5 2 2 2 a  1 a  1 2a 2 2 1 a  1   0,5 2 a 2 2 2 2 Tương tự suy ra
a  b  c  3 P   3 0,5 2 Suy ra P  3 min 0,5
Dấu “=” xảy ra khi a  b  c  1. I
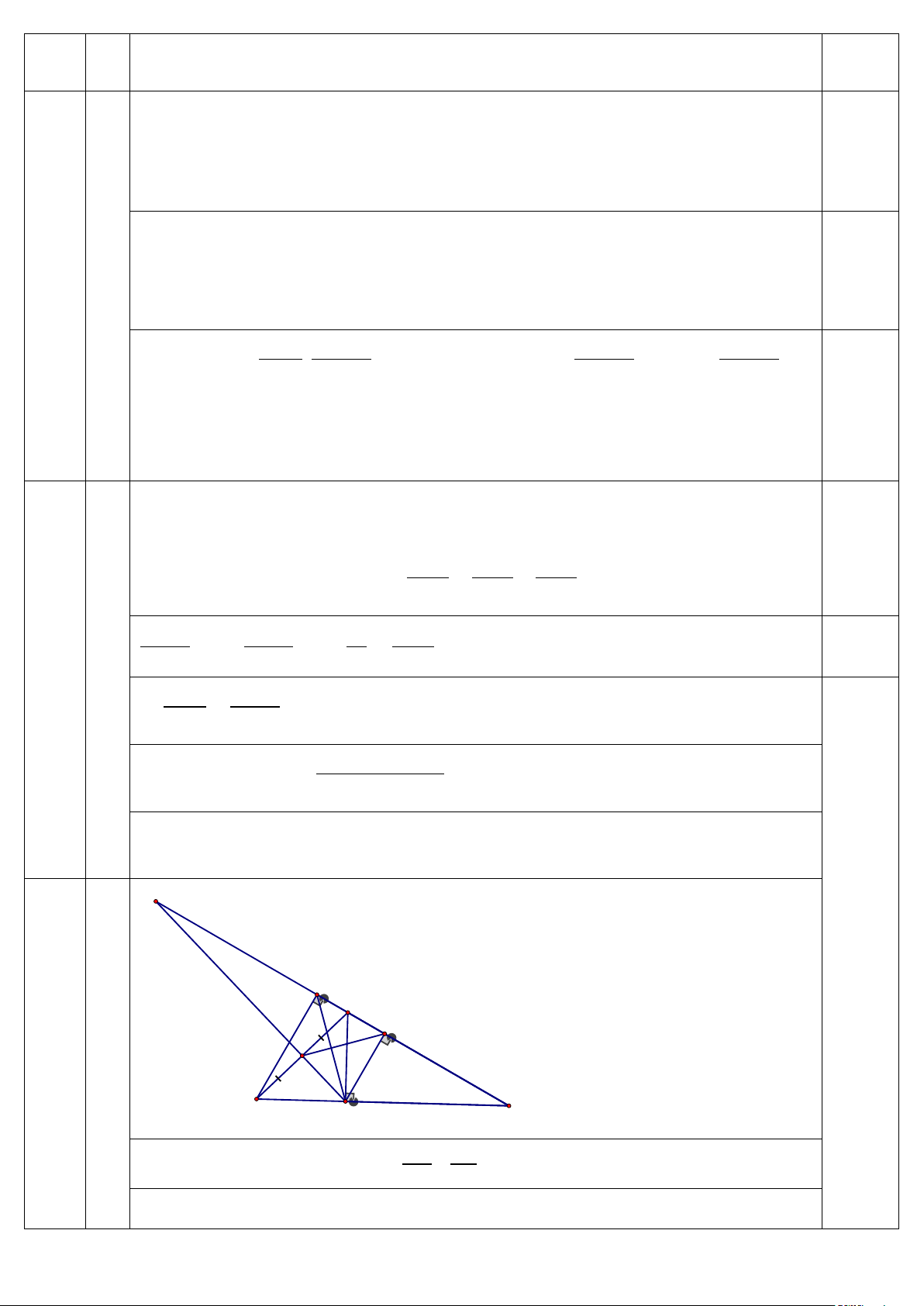
K 1 B H 4 1 Q 1 P A C a) / / CK CA PK AH ⇒ C ∆ KP  C ∆ AB ⇒ = 2,0 CP CB Suy ra A ∆ KC  B ∆ PC ( . c g.c)(1) 1,0 BÀI Ý HƯỚNG DẪN CHẤM ĐIỂM A
∆ KH vuông cân tại H ⇒  0 K = 45 . ⇒  =  0 K P = 45 ⇒ B ∆ AP 1 Từ (1) 1 1 vuông cân tại A ⇒ BP = AB 2 0,5 Chứng minh BH AB B ∆ HA  B ∆ AC ⇒ = AB BC BH 2AB BH AB BH 2AB ⇒ = ⇒ = ⇒ = 2 AB 2BC 2AB 2BC 2AB 2BC 1,0 BH BP BH BQ ⇒ = ⇒ = (BP = 2BQ) BP 2BC BP BC B ∆ HQ và B
∆ PC có: BH BQ = 
; PBC chung ⇒ B ∆ HQ  B ∆ PC ( . c g.c) BP BC 0,5 Suy ra   BQH  BCP B
∆ AP vuông cân tại A, AQ là trung tuyến nên cũng là phân giác ⇒ AI là phân giác ngoài của IC AC A ∆ BC ⇒ = (2) 0,5 IB AB AC AH A ∆ BC  H ∆ BA ⇒ = (3) 3 AB HB Từ (2) và (3) ta có: IC AH IB + BC AH BC AH = ⇒ = ⇒ 1+ = 0,5 IB HB IB HB IB HB AH BC ⇒ − = 1(dfcm) HB IB
1. Xét tập T  1,2,3,1 
3 . Lập tất cả các tập con hai phần tử trong T sao cho
hiệu của hai phần tử đó là 5 hoặc 8. 1,0
2. Cho M là tập con của S  1,2,3, ,  86 
9 có tính chất hiệu hai số bất kỳ của M
không là 5 hoặc 8. Hỏi M có nhiều nhất bao nhiêu phần tử ?
Xét T = {1, 2, 3, …, 13} có 13 tập con {1,6} {2,7} {3,8} {4,9} {5,10} {6,11} {7,12} {8,13} 1 0,25
{1,9} {2,10} {3,11} {4,12} {5,13} mà hiệu các phần tử của mỗi tập này chỉ là 5 hoặc 8.
Đồng thời mỗi phần tử của T luôn nằm trong đúng 2 tập con như trên. Nếu N là 5
một tập con của T có ít nhất 7 phần tử thì mỗi phần tử của N sẽ nằm trong đúng 2
tập con trong 13 tập kể trên. Do đó 7 phần tử sẽ nằm trong 14 tập con. Vậy phải 0,25
có 2 phần tử trong 7 phần tử phải cùng nằm trong 1 tập con trong 13 tập kể trên,
khi đó hiệu của 2 phần tử đó là 5 hoặc 8.
2 Do đó, nếu T’ là 1 tập con của T có tính chất như M thì T’ chỉ có nhiều nhất 6 phần
tử, dễ thấy T’ = {1,2,4,5,8,11} có tính chất là 2 phần tử bất kỳ có hiệu không là 5 0,25
hoặc 8 và có 6 phần tử.
Chú ý 869 chia 13 được thương 66 và dư 11 nên M sẽ có nhiều nhất 6*66 + 6 = 402 0,25 phần tử.