Đề chọn đội tuyển HSG Toán 9 vòng 2 năm 2023 – 2024 trường THCS Cầu Giấy – Hà Nội

PHÒNG GD & ĐT QUẬN CẦU GIẤY ĐỀ KIỂM TRA CLB VĂN HÓA LỚP 9 VÀ CHỌN ĐỘI
TRƯỜNG THCS CẦU GIẤY
TUYỂN HỌC SINH GIỎI LỚP 9 VÒNG II Môn kiểm tra: Toán Ngày thi: 21/09/2023 ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút
(Không tính thời gian phát đề)
Bài 1. (5,0 điểm)   1. − + Cho biểu thức 2 3 5 x 7 2 x 3 A =  + −  : 
với x > 0, x ≠ 4. x
2 2 x 1 2x 3 x 2  − + − − 5x −   10 x a. Rút gọn biểu thức . A
b. Tìm x sao cho A nhận giá trị là một số nguyên.
2. Cho các số thực a, , b c thỏa mãn 2 2
2a − 3ab + 2b = 1, 2 2
b − 3bc + 4c = 2 và 2 2
c + 3ca − a = 3. Tính giá trị của biểu thức 4 4 4
B = a + b + c .
Bài 2. (4,0 điểm)
1. Giải phương trình 2
4x − 9 = 5x + 6 x + 1.
2. Tìm tất cả các cặp số nguyên dương (a;b) thỏa mãn 2
7a − 1 chia hết cho 7ab − 1 và 2
a + b + 2 là số chính phương
Bài 3. (4,0 điểm)
1. Cho các số hữu tỉ x,y thỏa mãn 3 3
x − 2x = y − 2y. Chứng minh rằng x = y.
2. Cho các số thực không âm a, ,
b c thỏa mãn a + b + c = 4. Tìm giá trị lớn nhất của biểu thức:
P = 3a + ab + ab . c
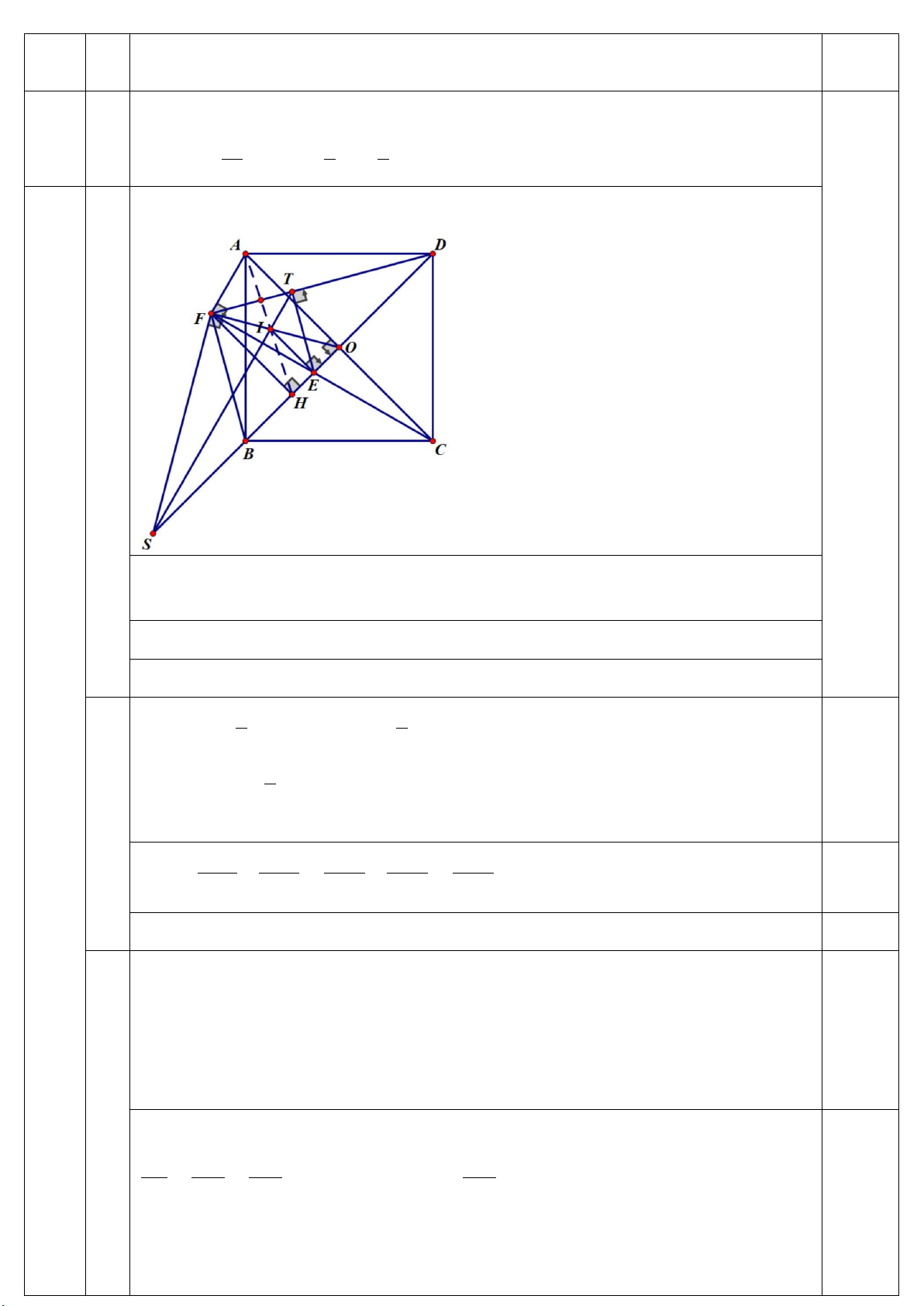
Bài 4. (6,0 điểm) Cho hình vuông ABC ,
D gọi O là giao điểm của hai đường chéo. E là điểm
bất kì thuộc đoạn OB, trên tia đối của tia EC lấy điểm F sao cho OF = OC. Đường thẳng
qua F vuông góc với FO cắt đường thẳng BD tại S. Kẻ FH vuông góc với BD (H ∈ BD).
1. Chứng minh S ∆ FB ∽ S
∆ DF và SB ⋅ SD = SH ⋅ SO. 2. Chứng minh rằng 1 1 2
FE là phân giác của  BFD. Từ đó suy ra + = . 2 2 2 BE DE EF
3. Kẻ ET vuông góc với FD tại T. Chứng minh rằng FO, AH và ST đồng quy.
Bài 5. (1,0 điểm)
1. Xét tập T = {1,2,3,,1 }
0 . Chỉ ra một tập con U có 4 phần tử của T thỏa mãn với mọi
x,y ∈U, x ≠ y thì x + y không chia hết cho x − y.
2. Cho M là tập con chứa n phần tử của S = {1,2,3,, }
2023 . Tìm n lớn nhất để mọi
x,y ∈ M, x ≠ y thì x + y không chia hết cho x − y.
-----------HẾT-----------
Họ và tên thí sinh: ………………………………………………… Số báo danh: …………………….
PHÒNG GD & ĐT QUẬN CẦU GIẤY ĐÁP ÁN
TRƯỜNG THCS CẦU GIẤY
ĐỀ KIỂM TRA CLB VĂN HÓA LỚP 9
VÀ CHỌN ĐỘI TUYỂN HỌC SINH GIỎI LỚP 9 VÒNG II ĐỀ CHÍNH THỨC Môn kiểm tra: Toán Ngày thi: 21/09/2023
Thời gian làm bài: 120 phút
(Không tính thời gian phát đề) BÀI Ý HƯỚNG DẪN CHẤM ĐIỂM   Cho biểu thức 2 3 5 x − 7 2 x + 3 A =  + −  : 
với x > 0, x
2 2 x 1 2x 3 x 2  − + − − 5x −   10 x 1 x ≠ 4. 1,5
a. Rút gọn biểu thức . A 1,5
b. Tìm x sao cho A nhận giá trị là một số nguyên.  2 3 5 x 7  − 2 x + 3 A =  + −  :
 x 2 2 x 1 2x 3 x 2  − + − − 5x −   10 x
2 (2 x + 1) + 3( x − 2) − (5 x − 7) 5x −10 x = ( 1,5
x − 2)(2 x + 1) . 2 x + 3 5 x x + ( x −2 2 3 ) 5 x = ( =
x − 2)(2 x + 1) . 2 x + 3 2 x + 1
1 Vìx > 0 ⇒ 5 x > 0;2 x +1 > 0 ⇒ A > 0
5 x − 3 (2 x + 1) 0,5 − − Mặt khác, xét x 3 A − 3 = = < 0 x
∀ > 0 ⇒ A < 3 + + 0,5 2 x 1 2 x 1 Vậy 0 < A < 3
Do đó A nguyên ⇔ A = 1 hoặc A = 2. 5 x 1 1 A = 1 ⇔
= 1 ⇔ 5 x = 2 x + 1 ⇔ 3 x = 1 ⇔ x = ⇔ x = (thỏa 2 x + 1 3 9 mãn) 5 x A = 2 ⇔
= 2 ⇔ 5 x = 2(2 x + 1) ⇔ x = 2 ⇔ x = 2 ⇔ x = 4 0,5 2 x + 1 (loại) Vậy 1
A ∈  ⇔ x = 9
2. Cho các số thực a, , b c thỏa mãn 2 2 2 2
2a − 3ab + 2b = 1;b − 3bc + 4c = 2 và 2 2 2
c + 3ca − a = 3 . 2,0
Tính giá trị của biểu thức 4 4 4
B = a + b + c BÀI Ý HƯỚNG DẪN CHẤM ĐIỂM Ta có : 2 2 2 2 2
 a − 3ab + 2b = 1 2
 a − 3ab + 2b = 1   2 2 2 2 2 2 2 b
 − 3bc + 4c = 2 ⇔ b
 − 3bc + 4c = 2 → 3a + 3b + 3c − 3 (ab + bc + ca) = 1  2 2  2 2
c + 3ca − a = 3 c
− − 3ca + a = 3 −  
⇒ a + b + c − ab − bc − ca = ⇔ (a −b)2 + (b −c)2 + (c −a)2 2 2 2 0
= 0 ⇔ a = b = c 0,5 2 2 2 2
 a − 3ab + 2b = 1 a  = 1   2 2 2 ⇒ b
 − 3bc + 4c = 2 ⇔ b  = 1 ⇒ B = 3 0,5  2 2  2
c + 3ca − a = 3 c = 1   2
Giải phương trình 2
4x − 9 = 5x + 6 x + 1 2,0 1 Đk: x ≥ 1. − 1,0 Pt ⇔ x + = ( x + + )2 2 (2 1) 3 1 1 x  = 3(TM)
TH1: 2x 1 3 x 1 1  + = + + ⇔ 3 0,5 x  = − (TM)  4 TH2: 2x + 1 = 3
− x + 1 − 1 ⇔ x = 1( − TM)   0,5 Vậy 3 x ∈  1; − − ;3  4 
Chú ý: có thể giải bằng cách đặt y = x + 1 ≥ 0 và đưa về phương trình bậc 4 phân tích được.
Tìm tất cả các cặp số nguyên dương (a;b)thỏa mãn: 2
7a − 1 chia hết cho 7ab − 1 2,0 và 2
a + b + 2 là số chính phương
Vì a,b là các số nguyên dương nên 2
7a − 1 và 7ab − 1 là các số nguyên dương. Vì 0,5 2
7a − 17ab − 1 nên 2 2
7a − 1 ≥ 7ab − 1 ⇒ 7a ≥ 7ab ⇒ a ≥ b . 2 Lại có: 2 7a − 1 − 
(7ab −1)(7ab −1) nên 2
7a − 7ab7ab − 1 ⇒ 7a (a −b)7ab − 1. mà (7a,7ab − 1) = 1 nên (a −b)7ab − 1 0,5 .
Nếu a > b thì a −b ≥ 7ab − 1 ⇒ a (1 − 7b) + 1 −b ≥ 0 điều này là vô lý do 0,5
1 − 7b < 0,1 − b < 0 vậy nên chỉ có thể xảy ra a = b . BÀI Ý HƯỚNG DẪN CHẤM ĐIỂM
Ta cần tìm a để 2
a + a + 2 là số chính phương. Nếu a > 1 thì 2 2 2
a < a + a + 2 < a + 2a + 1 nên 2
a + a + 2 không thể là số chính phương. 0,5 Với a = 1 thì 2 2
a + a + 2 = 4 = 2 là số chính phương.
Vậy a = b = 1 là giá trị cần tìm
1 Cho các số hữu tỉ x,y thỏa mãn 3 3
x − 2x = y − 2y. Chứng minh rằng x = y. 2,0 Giả sử 2 2
x ≠ y ⇒ x + xy + y = 2 0,5 a c x = ,y = với * a, , b ,
c d ∈  ,(a,b) = ( , c d) = 1 b d 2 2 a  a c  c  2 2 2 2 2 2
  + ⋅ +   = 2 ⇔ a d + abcd + c b = 2b d  b  b d d  0,5 (
 a,b) = 1 ⇒ (a,x) = 1 u = ( ,
b d) ⇒ b = ux,d = uy,(x,y) = 1. Có  ( , c d) = 1 ⇒ ( , c y) = 1  3 x  y 2 2 2 2 2 2
a y + acxy + c x = 2x y ⇒ 
⇒ x = y ⇒ b = d = u y  x  2 2 2
⇒ a + ac + c = 2u
Nếu a chia hết cho 2 thì c chia hết cho 2 và ngược lại 0,5
Nếu a và c cùng không chia hết cho 2 thì VT lẻ và VP chẵn, vô lý
Vậy a và c cùng chia hết cho 2. Khi đó 2 2 2
2u = a + ac + c chia hết cho 4. Suy ra
u chia hết cho 2. Điều này trái với (a,u) = (a,b) = 1. 0,5 Vậy x = y
Cho các số thực không âm a, ,
b c thỏa mãn a + b + c = 4. Tìm giá trị lớn nhất của biểu thức: 2,0
P = 3a + ab + ab . c a   2 b  2 ( 3 ) (7 c)
P  a(3  b)  abc   abc   abc 4 4 0,5 2 2
c  2(2ab  7)c  49 f (c)  P   4 4
Chứng minh nếu f(x) là đa thức bậc hai với hệ số cao nhất dương và m  x  n
thì max f(x)  max f(m); f(n  ) 0,5
Áp dụng: max f(c)  max f(0); f(4  )  49; f(4  ) 0,5 f
  ab   a  2 b    2 (4) 9 8 9 2( ) 9 2(4 c)  41 BÀI Ý HƯỚNG DẪN CHẤM ĐIỂM
 max f(0); f(4  )  49 0,5 49 7 1  P 
, khi a  ,b  ,c  0 max 4 2 2 1 Ta có 
OF = OC = OB = OD ⇒ BFD = 90 . ° 1,0 Suy ra  
SFB = SDF (cùng phụ với   BFO = OBF ) ⇒ ∆SBF∽∆SFD (g.g) ⇒ 2
SB.SD = SF 1,0 Lại có: 2
SH.SO = SF (hệ thức lượng) ⇒ (đpcm) 1,0 1 1 4 Có  
OFD = FOB và  
OFE = FOA (góc ngoài tại đỉnh cân của tam giác cân) 2 2 1,0 Suy ra  1 
EFD = AOB = 45° 2
2 Suy ra FE là phân giác  BFD. 2 2 2 2 2 Suy ra EF EF DF BF BD + = + = = 2 (đpcm) 1,0 2 2 2 2 2 BE DE BC BC BC
Gọi I là giao của FO và ST. Từ câu a) ⇒    
SFB = SDF ⇒ SEF = SFE
⇒ SE = SF mà TE = TF (do ∆ ETF vuông cân) ⇒ TS trung trực EF mà I 0,5 thuộc ST ⇒   IFS IES 90 = = ⇒ IE ∥ FH
3 Xét hình thang AOHF (AO ∥ FH ) FI HE FH = =
(Talet CO ∥ FH ) = AO IO EO OC FH 0,5 ⇒ ,
A I,H thẳng hang ⇒ đpcm BÀI Ý HƯỚNG DẪN CHẤM ĐIỂM
1. Xét tập T = {1,2,3,,1 }
0 . Chỉ ra một tập con U có 4 phần tử của T thỏa
mãn với mọi x,y ∈U, x ≠ y thì x + y không chia hết cho x − y. 1,0
2. Cho M là tập con chứa n phần tử của S = {1,2,3,, }
2023 . Tìm n lớn nhất
để mọi x,y ∈ M, x ≠ y thì x + y không chia hết cho x − y. 1 U = {1,4,7,1 } 0 0,25
Xét M = {3k + 1 với k = 0, 1, 2, ..., 674 thì A là tập con của S và A có 675 phần tử.
Dễ thấy hiệu 2 số bất kỳ của A là bội của 3 còn tổng của 2 số bất kỳ của M không 0,25 5
chia hết cho 3. Do đó với 2 số bất kỳ trong M thì tổng của chúng không chia hết cho hiệu của chúng.
Xét N là tập con của S có ít nhất 676 phần tử. Chia S thành 675 tập con như sau {1,
2, 3} {4, 5, 6} … {2020, 2021, 2022} {2023}. Khi đó sẽ có ít nhất 2 phần tử của N, 0,25
2 giả sử là a và b, thuộc 1 trong các tập con 3 phần tử kể trên.
Chú ý rằng hiệu 2 phần tử bất kỳ trong mỗi tập 3 phần tử kể trên không lớn hơn 2.
Vậy ta có a – b = 1 hoặc 2. Nếu a – b = 1 thì a + b chia hết cho a – b, nếu a – b = 2
thì a và b cùng tính chẵn lẻ nên a + b chẵn và chia hết cho a – b. Vậy N không thỏa 0,25 mãn yêu cầu bài toán.
Do đó n lớn nhất = 675.