Đề chọn đội tuyển thi HSG tỉnh Toán 9 năm 2025 – 2026 xã Quảng Bình – Thanh Hóa

UỶ BAN NHÂN DÂN
KÌ THI CHỌN ĐỘI TUYỂN DỰ THI HỌC SINH XÃ QUẢNG BÌNH
GIỎI LỚP 9 CẤP TỈNH NĂM HỌC: 2025-2026 MÔN: TOÁN Ngày thi: 01/10/2025 ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề) (Đề gồm 01 trang).  2 2  x +1  x −1
Câu 1.(2,0 điểm )Cho biểu thức: A = −  . − x −  1 :
với x ≠ 0;x ≠ 1 ± .
3x x +1  3x  x
Rút gọn biểu thức A, tìm giá trị nguyên của x để A nguyên.
Câu 2. (2,0 điểm) Cho a +b + c = 0 . Tính: 3 3 2 2
A = a + b + c(a + b ) − abc 2
Câu 3. (2,0 điểm) Giải phương trình: x −16x − 25 31+ 6x − = 4 * 2 ( ) 1− 2x x +1
Câu 4. (2,0 điểm) Đội tuyển học sinh giỏi Toán gồm 10 em: 9 nam và 1 nữ. Muốn dự
đoán 1 em giải nhất, 1 em giải nhì và 1 em giải ba. Tính xác suất để dự đoán được 3 em
mà trong đó giải nhất và giải nhì phải là hai người khác giới. Biết khả năng đạt giải của các bạn là như nhau.
Câu 5. (1,5 điểm). Một người dự định đi xe đạp từ A đến B cách nhau 60 km trong một
thời gian nhất định. Sau khi đi được 30 km người đó đã dừng lại nghỉ 30 phút . Do đó, để
đến B đúng thời gian dự định người đó phải tăng vận tốc thêm 2 km/h. Tính vận tốc dự định của người đó.
Câu 6. (2,0 điểm) Tìm tất cả các cặp số nguyên (𝑥𝑥; 𝑦𝑦) thỏa mãn phương trình
(𝑥𝑥 + 𝑦𝑦)(2𝑥𝑥 + 3𝑦𝑦)2 + 2𝑥𝑥 + 𝑦𝑦 + 2 = 0.
Câu 7. (1.5 điểm) Gia đình Bác Tuấn muốn cải tạo một cái hồ nước nhỏ thành một hồ
nước đẹp hơn để nuôi cá. Trong bản thiết kế hồ nước có dạng hình hộp chữ nhật với
chiều dài gấp hai lần chiều rộng. Sau khi thiết kế xong, kĩ sư tính được thể tích bằng 62 500 3
m . Theo thị trường xây dựng hiện nay, giá tiền xây dựng bình quân là 400000 3
đồng/m2 (bao gồm cả đáy và thành hồ). Hỏi chi phí thấp nhất mà gia đình Bác Tuấn phải
trả để xây dựng hồ nước trên là bao nhiêu tiền.
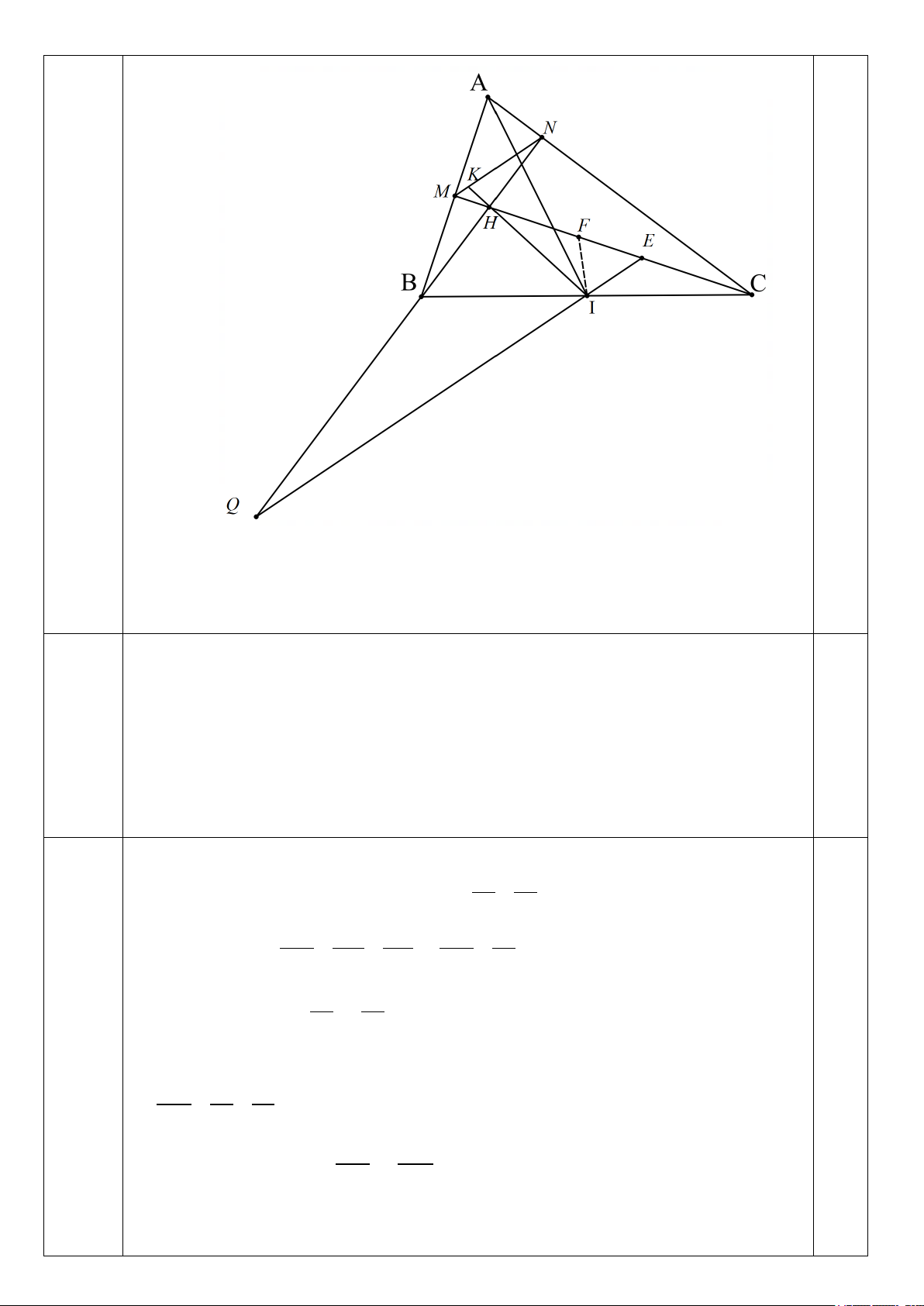
Câu 8. (5.5 điểm) Cho tam giác ABC nhọn (ABnhau tại H. Gọi I là trung điểm của BC, K là giao điểm của đường thẳng IH và đường
thẳng MN. Qua I kẻ đường thẳng song song với MN, đường thẳng này cắt đường thẳng
CM và đường thẳng BN lần lượt tại E và Q. a) Chứng minh :  =  BQI ECI 2 b) Chứng minh rằng 2 .
IQ IE = IC và KN  HN  = KM  HM   
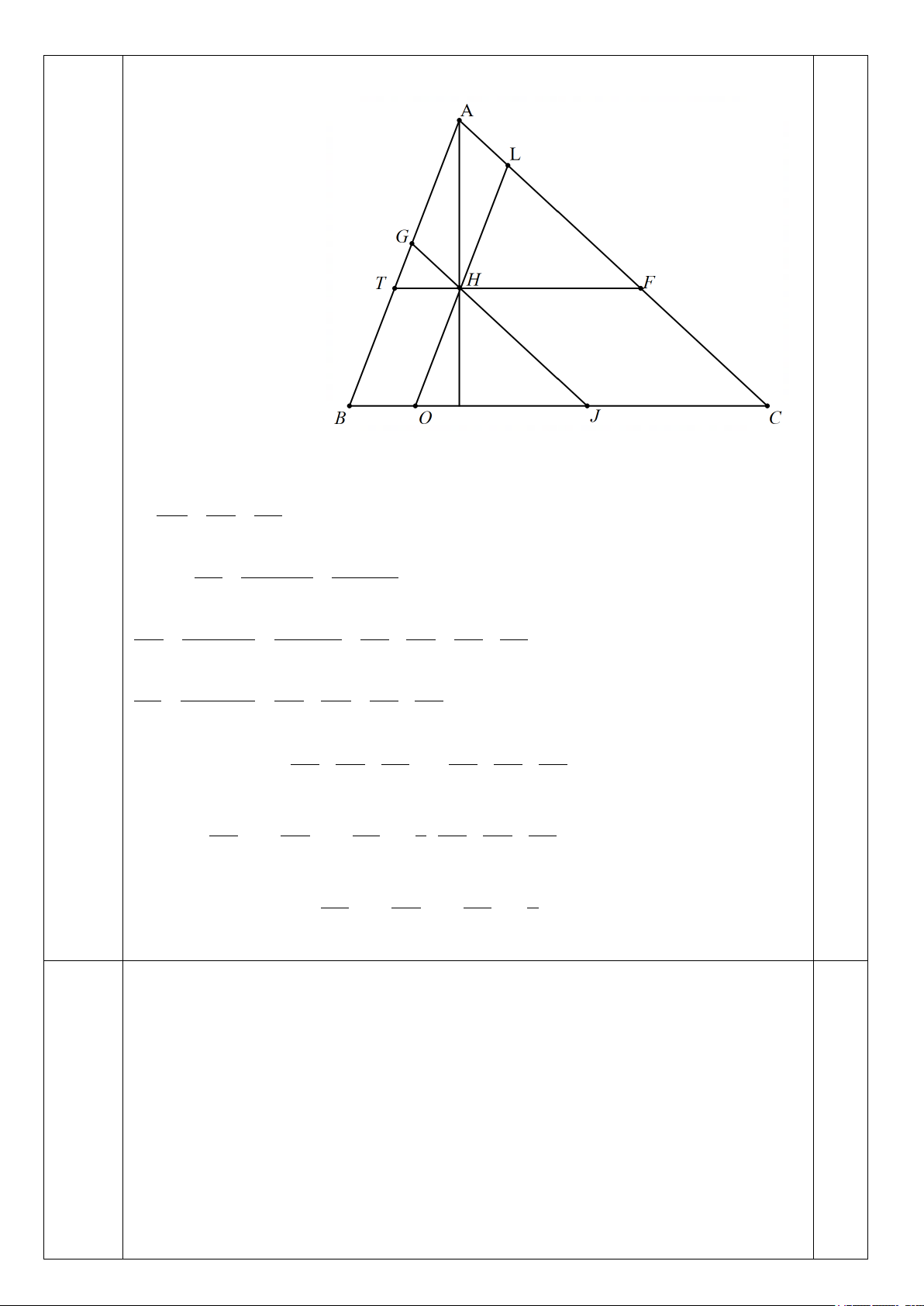
c) Qua H kẻ các đường thẳng TF;JG;LO lần lượt song song với BC, AC, AB ( với 2 2 2  TF   JG   LO  4
T ∈ AB, F ∈ AC, J ∈ BC,G ∈ AB, L ∈ AC,O ∈ BC) . Chứng minh: + + ≥ 
BC   AC   AB        3
Câu 9. (1.5 điểm) Cho một mảnh giấy hình vuông. Mảnh giấy này dược chia thành hai
mảnh giấy bằng một đường cắt thẳng. Lấy một trong hai mảnh có được, ta lại làm như
trên nhiều lần. Hỏi số lần cắt ít nhất phải là bao nhiêu đế có thẻ nhận được 100 đa giác 20 cạnh. - HẾT - UỶ BAN NHÂN DÂN
KÌ THI CHỌN ĐỘI TUYỂN DỰ THI HỌC SINH XÃ QUẢNG BÌNH
GIỎI LỚP 9 CẤP TỈNH NĂM HỌC: 2025-2026 MÔN: TO ÁN
HƯỚNG DẪN CHẤM KHẢO SÁT CHỌN ĐỘI TUYỂN
HỌC SINH GIỎI LỚP 9 CẤP TỈNH NĂM HỌC 2025-2026 MÔN TOÁN Câu Hướng dẫn giải
Với x ≠ 0;x ≠ 1 ±  2 2  x +1  x −1  2
2 (x +1) − 3x(x +1) x −1 A = −  . − x −1  : = −   . : 0,5 3x x 1  3x  x 3x x 1 3x  + +  x 0,5 Câu 1  2 2(1− 3x)  − = − . x A 2 2(1 3x) = − . x 2x = (2.0 3x 3x  x −1 3x 3x  x −1 x −1 điểm) Với x x ≠ 0; x ≠ 1 ± Ta có 2 2 A = = 2 + 0.25 x −1 x −1
A∈ Z ⇔ x −1∈Ư(2) ⇔ x −1∈{ 1; ± ± } 2 0.25 x-1 -2 -1 1 2 0,25 x -1 (Loại) 0 (Loại) 2 (T/M) 3 (T/M) Vậy 2x A =
với x ≠ 0;x ≠ 1
± , Khi x = 2 hoặc x = 3 thì A nguyên 0,25 x −1
Ta có: a +b + c = 0 ⇒ a +b = −c 0,5 Câu 2 3 3 2 2 3 2 2
A = a + b + c(a + b ) − abc = (a + b) − 3ab(a + b) + c(a + b ) − abc 0,5 (2 3 2 2 3 2 2 3 2 2
= −c + 3abc + c(a + b ) − abc = −c + 2abc + c(a + b ) = −c + c(a + 2ab + b ) 0,5 điểm) 3 2 2 2
= −c + c(a + b) = c (a + b) − c  = c(a + b + c)(a + b − c) = 0 0,5   ĐKXĐ: 1 x ≠ 0.25 2 Đặt 2
a = x +1, b =1− 2x Khi đó: 2 2
x −16x − 25 = x +1+ 8(1− 2x) −34 = a +8b −34
Câu 3 31+ 6x = 34−3(1− 2x) = 34−3b 0.25 (2 Khi đó (*) trở thành:
điểm) a +8b−34 34−3b −
= 4 ⇒ a(a + 8b − 34) − b(34 − 3b) = 4ab 0.25 b a 2 2
⇒ a + 4ab + 3b − 34a − 34b = 0 0.25 ⇒ (  + =
a + b)(a + b − ) a b 0 3 34 = 0 ⇒ 
a + 3b − 34 = 0 0.25 0.25 +) 2
a + b = 0 ⇒ x − 2x + 2 = 0 ⇒ (x − )2 1 +1 = 0 . Vô nghiệm  0.25 +) x = + 2
a + 3b − 34 = 0 ⇒ x − 6x − 30 = 0 ⇒ (x − )2 3 39 3 = 39 ⇒  x = 3− 39 0.25
Vậy x∈{3+ 39;3− 39}
Dự đoán 1 bạn giải nhất có 10 cách
Dự đoán 1 bạn giải nhì có 9 cách
Dự đoán 1 bạn giải ba có 8 cách
Số cách dự đoán 3 bạn đạt giải là : 10.9.8=720 cách 0,5
Để dự đoán được 3 em mà trong đó giải nhất và giải nhì phải là hai người
Câu 4 khác giới ta xét (2
TH1: Dự đoán 1 giải nhất là nam, 1 giải nhì là nữ và 1 bạn giải ba có 9.1.8 = 72 cách.
điểm) TH2: Dự đoán 1 giải nhất là nữ, 1 giải nhì là nam và 1 bạn giải ba có 0,5 1.9.8 = 72 cách. 0,5 ⇒ có 72 + 72 =144 cách.
Xác suất cần tìm là 144 1 = 720 5 0,5 Đổi 30 phút = 1 giờ 2
Gọi vận tốc dự định là x ( km/h). Điều kiện: x > 0
Thời gian dự định là 60 (giờ) 0,25 x
Câu 5 Thời gian người đó đi 30 km đầu là 30 (giờ). 0.25 x (1,5 0.25
Thời gian người đó đi 60 – 30 = 30 km còn lại là 30 ( giờ). điểm) x + 2
Do xe đến B đúng hạn nên ta có phương trình 30 + 30 + 1 = 60 0.25 ⇔ 30 - 30 = 1 60 1 ⇔ = x x + 2 2 x x x + 2 2 x(x + 2) 2 0,25
⇔ x2 + 2x - 120 = 0 ⇔ x2 + 2x + 1 – 121= 0 ⇔ (x+1)2 = 121 ⇔ x+ 1= 11
± ⇔ x= 10 ( thỏa mãn), x= -12 (loại) 0,25
Vậy vận tốc dự định là 10 ( km/h)
Đặt 𝑎𝑎 = 𝑥𝑥 + 𝑦𝑦 �
𝑏𝑏 = 2𝑥𝑥 + 3𝑦𝑦 0,25
Khi đó 2𝑥𝑥 + 𝑦𝑦 + 2 = 4𝑥𝑥 + 4𝑦𝑦 − 2𝑥𝑥 − 3𝑦𝑦 + 2
= 4(𝑥𝑥 + 𝑦𝑦) − (2𝑥𝑥 + 3𝑦𝑦) + 2 = 4𝑎𝑎 − 𝑏𝑏 + 2 0,25
Câu 6 Ta có : (𝑥𝑥 + 𝑦𝑦)(2𝑥𝑥 + 3𝑦𝑦)2 + 2𝑥𝑥 + 𝑦𝑦 + 2 = 0 ⇔ 𝑎𝑎𝑏𝑏2 + 4𝑎𝑎 − 𝑏𝑏 + 2 = 0 0,25 (2
⇔ 𝑎𝑎(𝑏𝑏2 + 4) = 𝑏𝑏 − 2 ⇒ 𝑏𝑏 − 2 ⋮ 𝑏𝑏2 + 4 ⇒ (𝑏𝑏 − 2)(𝑏𝑏 + 2) ⋮ (𝑏𝑏2 + 4) điểm)
⇒ (𝑏𝑏2 + 4) − (𝑏𝑏 − 2)(𝑏𝑏 + 2) ⋮ (𝑏𝑏2 + 4) ⇒ 8 ⋮ (𝑏𝑏2 + 4) ⇒ (𝑏𝑏2 + 4) ∈ {4,8} 0,25  3 −
Nếu 𝑏𝑏2 + 4 = 4 ⇒ 𝑏𝑏 = 0 ⇒ 𝑎𝑎 = − 1 ⇒ �𝑥𝑥 + 𝑦𝑦 = − 1 x = 2 ⇒  2 (Loại) 2 2𝑥𝑥 + 3𝑦𝑦 = 0 y =1 0,25 𝑏𝑏 = 2 ⇒ 𝑎𝑎 = 0
Nếu 𝑏𝑏2 + 4 = 8 ⇒ �𝑏𝑏 = −2 ⇒ 𝑎𝑎 = −1 2 0,25  + =  = − 𝑏𝑏 = 2 ⇒ 𝑎𝑎 = 0 x y 0 x 2 ⇒  ⇒ (T/M) 2x 3y 2  + = y = 2 0,25  1 −  1
𝑏𝑏 = −2 ⇒ 𝑎𝑎 = − 1 x + y = x = ⇒  2 ⇒  2 (Loại) 2 2x +3y = 2 − y = 1 − 0,25
Vậy (−2; 2) thỏa mãn pt đã cho
Gọi chiều rộng của hình chữ nhật đáy hồ là x (m) (điều kiện x > 0 )
Suy ra chiều dài của hình chữ nhật là 2x (m).
Gọi y là chiều sâu của hồ (điều kiện y > 0) 0,25 Thể tích của hồ là 2
V = 2x.x.y = 2x y (m3).
Theo bài ra ta có phương trình 2 62500 2x y = , suy ra 31250 y = 3 2 3x
Diện tích xây dựng của hồ nước là S 0,25
= x.x + . ( x + x) 2 2 31250 2 62500 2 2 2
.y = 2x + 6xy = 2x + 6 ⋅x⋅ = 2x + 2 3x x
Câu 7. Áp dụng bất đẳng thức AM −GM,với hai số dương a , b ta có a +b ≥ 2 ab .
dấu bằng xảy ra khi a = b . (1,5 điểm) Ta có 2 62500 S = x + = ( 2x + ) 62500 2 62500 62500 2 2 1250 +
−1250 ≥ 2 2x .1250 + −1250 =100x + −1250 x x x x 0,25 62500 62500 S ≥100x + −1250 ≥ 2 100x⋅ −1250 = 3750 x x 0,25 2  2x =1250 Khi đó S =
. Dấu = xảy ra khi  min 3750  62500 ⇒ x = 25 100x = 0,25  x
Vậy chi phí thấp nhất mà gia đình bác Tuấn phải trả để xây dựng hồ nước là
3750.400000 =1500000000 đồng ( một tỉ rưỡi ) 0,25 Câu 8 (5,5 điểm)
Vì QI//MN nên BQI=MNB (hai góc so le trong) (1) 0,5
Vì BN và CM là 2 đường cao nên ta chứng minh được A ∆ MC  A
∆ NB(g.g) .
Từ đó ta chứng minh được ∆  ∆ ⇒  =  (Góc tương 0,5 a) ABC
ANM ( .cg.c) ANM ABC ứng) Lại có  0,5 +  0 =  +  0 = ⇒  = 
MCB MBC 90 ; ANM MNB 90 ; MBC MNB (2) 0,5
Từ (1)&(2) suy ra  =  BQI ECI . (đpcm) Theo câu a)  =  =  BI IE 2
IQB MNB ECI ⇒ IQ ∆ B  IC
∆ E(g.g) ⇒ = ⇒ . IQ IE = . IB IC = IC 1,0 IQ IC
Vì MN//QE nên KM KH KN KN IQ = = ⇒ = (3) 0,25 IE HI IQ KM EI 2 Lại có 2 . IQ  IC IQ IE IC  = ⇒ = 0,25   (4) IE  IE b) 
Lấy F trên HC sao cho  = 
IFE IEF ⇒ IF = IE ⇒ C ∆ IF  N
∆ HM (g.g) 0,25 HN IC IC ⇒ = = (5) HM FI IE 2
Từ (3);(4)và (5) suy ra KN  HN  0,25 = KM  HM   
Vì HO//AB; HJ//AC.Ta chứng minh được HOJ ∆  A
∆ BC(g.g) 0.25 c) OH HJ OJ 0,25 ⇒ = = AB AC BC
Ta có: TF TH + HF OB + JC = = (1) BC BC BC JG GH + JH AL + HJ AL HJ BO JO = = = + = + (2) AC AC AC AC AC BC BC OL LH + OH AG HO JC JO = = + = + (3) 0,25 AB AB AB AB BC BC
TỪ (1);(2)&(3) TF JG LO 2 OB JO JC  ⇒ + + = + + = 2.1 =   2 (*) BC AC AB  BC BC BC  0,25 2 2 2 2
Lại có:  TF   JG   LO  1 TF JG LO  + + ≥ + +  (**)
BC   AC   AB  3  BC AC AB          0,25 2 2 2
Từ (*) &(**) suy ra  TF   JG   LO  4 + + ≥  (đpcm)
BC   AC   AB        3 0,25
Trước tiên ta đưa ra một số nhận xét sau:
Nhận xét 1: Mỗi nhóm cắt, số mảnh giấy tăng đúng 1. Mỗi mảnh giấy được 0,25
cắt ra đều là một đa giác lồi.
Điểu này hiển nhiên, có thế chứng minh bằng quy nạp.
Câu 9 Nhận xét 2: Mỗi nhát cắt, tống số cạnh của tất cả các mảnh giáy tăng lên tối 0,25 (1,5 đa 4.
điểm) Điều này suy ra từ nhận xét 1, ta thấy một đường cắt chỉ đi qua tối đa 2 cạnh
của mảnh giấy đa giác lồi, thêm cạnh sinh ra từ đường cắt được tính 2 lần, thì
chỉ có tới đa 4 cạnh tăng thêm.
Từ 2 nhận xét trên, ta biết rằng qua 𝑘𝑘 lần cắt, thì sẽ có đúng 𝑘𝑘 + 1 mảnh
giấy và tối đa 4 + 4𝑘𝑘 cạnh trong tất cả các mảnh giấy.
Vậy để có 100 đa giác 20 cạnh, ta cần số lần cắt 𝑘𝑘 ≥ 99, và đồng thời 0,25
sẽ có ít nhất 𝑘𝑘 + 1 − 100 = 𝑘𝑘 − 99 đa giác khác ngoài 100 da giác 20 cạnh
đang xét. Ta có bất đẳng thức: 0,25
4 + 4𝑘𝑘 ≥ 100 ⋅ 20 + 3(𝑘𝑘 − 99) ⇒ 𝑘𝑘 ≥ 1699 0,25
Đến đây, ta chỉ ra cách cắt, không quá phức tạp như sau. Với đa giác 𝑛𝑛 cạnh,
ta cắt đường đi qua 2 cạnh kề nhau, sẽ sinh ra được đa giác 𝑛𝑛 + 1 cạnh và 1
tam giác. Theo cách này, sau 16 bước cắt đầu, ta ra được 1 đa giác 20 cạnh
và 16 tam giác. Mỗi lần sau, ta dùng 17 bước cắt sẽ tạo ra thêm được 1 đa
giác 20 cạnh. Tức cuối cùng sẽ cần: 16 + 17 ⋅ 99 = 1699, thỏa mãn dấu
bằng. Vậy cần ít nhất 1699 bước cắt dế thỏa mãn bài toán. 0,25
Xem thêm: ĐỀ THI HSG TOÁN 9
https://thcs.toanmath.com/de-thi-hsg-toan-9
Document Outline

• TOÁN 9
  • KÌ THI CHỌN ĐỘI TUYỂN DỰ THI HỌC SINH GIỎI LỚP 9 CẤP TỈNH NĂM HỌC: 2025-2026
  • KÌ THI CHỌN ĐỘI TUYỂN DỰ THI HỌC SINH GIỎI LỚP 9 CẤP TỈNH NĂM HỌC: 2025-2026
• HSG 9