Đề chọn học sinh giỏi Toán 7 năm 2024 – 2025 phòng GD&ĐT Lâm Thao – Phú Thọ

PHÒNG GD&ĐT LÂM THAO KỲ THI CHỌN HỌC SINH GIỎI LỚP 6,7,8 CẤP HUYỆN
NĂM HỌC 2024 – 2025 ĐỀ CHÍNH THỨC MÔN THI: TOÁN 7
Thời gian làm bài: 90 phút không kể thời gian phát đề
(Đề thi gồm 02 trang)
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN: (6,0 điểm)
Câu 1. Giá trị của x trong biểu thức: ( x − )2 1 = 0,25 là A. 9 1 ; . B. 9 1 − ;− . C. 9 1 ;− . D. 9 1 − ; . 4 4 4 4 4 4 4 4
Câu 2. Cho x, y là các số thỏa mãn 2024
(x − 3) + | 2x + 3y − 9 |= 0 . Giá trị của biểu thức
A = 3x − 4y là A. 3. B. 5 . C. 9 . D. 13.
Câu 3. Biết 50 người thợ may xong một lượng quần áo trong 12 ngày. Hỏi 30 người thợ
may hết lượng quần áo đó trong bao nhiêu ngày? (Giả sử năng suất làm việc của mỗi người thợ là như nhau). A. 10 ngày.
B. 15 ngày. C. 20 ngày. D. 25 ngày. Câu 4. Cho x y + + ; y z x y z =
= . Giá trị của biểu thức 2 3 4 M = là 3 4 5 6
3x + 4y + 5z A. 168 . B. 186 . C. 168 . D. 186 . 254 254 245 245
Câu 5. Cho đa thức F (x) thỏa mãn điều kiện F (x .x = F x .F x và F (2) = 5. Khi đó 1 2 ) ( 1) ( 2) F (16) bằng A. 5 . B. 25. C. 125 . D. 625 . Câu 6. Cho đa thức 2
f (x) = x − 3x + a . Giá trị của a để đa thức f (x) chia hết cho đa thức x − 2 là A. 2 − . B. 10 − . C. 2. D. 10.
Câu 7. Cho hình vẽ, biết AB / /EF và B  0 =  0 =  0
ABC 60 , BCD 130 ,CDE =140 . Số đo 600 D  DEF bằng 1400 1300 C E A. 0 105 . B. 0 110 . C. 0 115 . D. 0 120 . A F
Câu 8. Cho tam giác ABC . Vẽ đoạn thẳng AD vuông góc với AB ( D và C nằm khác phía
với AB ), AD = AB . Vẽ đoạn thẳng AE vuông góc với AC ( E và B nằm khác phía với AC
), AE = AC . Biết rằng DE = BC . Khi đó  BAC bằng A. 0 90 . B. 0 60 . C. 0 45 . D. 0 120 .
Câu 9. Cho tam giác ABC cân tại A, có  0
A =120 ;BC = 6cm . Đường vuông góc với AB tại
A cắt BC ở D . Độ dài đoạn thẳng BD bằng A. 2cm . B. 4cm . C. 5cm . D. 6cm. 2
Câu 10. Cho tam giác ABC có ba đường phân giác cắt nhau tại I . Khẳng định nào sau đây đúng? A.   90 A
BIC = ° + ⋅ B.   90 A
BIC = ° − ⋅ C.   90 B
BIC = ° + ⋅ D.   90 C BIC = ° + ⋅ 2 2 2 2
Câu 11. Cho tam giác ABC vuông tại A, có trọng tâm G . Biết BC = 6cm. Khi đó AG bằng A. 1,5c . m B. 2c . m C. 1c . m D. 3c . m
Câu 12. Gieo ngẫu nhiên một con xúc xắc một lần. Gọi a (với a,b nguyên tố cùng nhau) là b
xác suất của biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chia hết cho 2”. Giá trị của
biểu thức 2025a + 4b − 4 là A. 2029. B. 4029. C. 2024. D. 2025.
II. PHẦN TỰ LUẬN: (14,0 điểm)
Câu 1. (3,0 điểm)
1.1. Chứng minh rằng A = ( 2025 2024 2 75 4 + 4 + ...+ 4 + 4 + ) 1 + 25 chia hết cho 100 .
1.2. Tìm các số nguyên tố p thỏa mãn 2
2p + p là số nguyên tố.
Câu 2. (4,0 điểm)
2.1. Cho dãy tỉ số 2a + b + c + d a + 2b + c + d a + b + 2c + d a + b + c + 2d = = = (với a b c d + + + +
a,b,c,d ≠ 0 ). Chứng minh rằng biểu thức a b b c c d d a Q = + + + có giá trị là số
c + d d + a a + b b + c nguyên. 2.2. Cho đa thức ( ) 3 2
f x = ax + bx + cx + d với a,b,c,d ∈. Biết f (x)5 với mọi x ∈ .
Chứng minh rằng a,b,c,d đều chia hết cho 5.
Câu 3. (5,0 điểm)
Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm BC . Lấy điểm D trên
đoạn thẳng AB ( D khác A và B ), trên tia đối của tia CA lấy điểm K sao cho CK = BD ;
DK cắt BC tại I . Kẻ DP vuông góc với BC tại P và KQ vuông góc với BC tại Q .
a) Chứng minh rằng: BDP ∆ = C
∆ KQ và I là trung điểm DK .
b) Đường vuông góc với DK tại I cắt AM tại S . Tính góc  SCK ?
c) Đường thẳng vuông góc với MD tại M cắt AC tại E .
Chứng minh rằng: MD + ME ≥ AD + AE .
Câu 4. (2,0 điểm)
Tìm các cặp số nguyên ( ;
x y) thỏa mãn (x + y − )2 14 2 + 7 = y −1 + y − 3
------------------------------ Hết-----------------------------
Họ và tên thí sinh :............................................................... Số báo danh ..................
Cán bộ coi thi không giải thích gì thêm. 3
PHÒNG GD&ĐT LÂM THAO
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM MÔN TOÁN
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN: (6,0 điểm) Mỗi câu đúng được 0,5 điểm 1 2 3 4 5 6 7 8 9 10 11 12 A B C D D C B A B A B A
II. PHẦN TỰ LUẬN: (14,0 điểm)
Câu 1. (3,0 điểm)
1.1. Chứng minh rằng A = ( 2025 2024 2 75 4 + 4 + ...+ 4 + 4 + ) 1 + 25 chia hết cho 100 .
1.2. Tìm các số nguyên tố p thỏa mãn 2
2p + p là số nguyên tố.
1.1 (1,5 điểm). Chứng minh rằng A = ( 2025 2024 2 75 4 + 4 + ...+ 4 + 4 + ) 1 + 25 chia hết 1,5 cho 100 . Đặt 2025 2024 2 B = 4 + 4 + ...+ 4 + 4 +1 Ta có 2026 2025 3 2 4B = 4 + 4 + ...+ 4 + 4 + 4 0,75 2026 Lấy 2026 4 1 4B B 4 1 B − − = − ⇒ =
thay vào biểu thức A ta được 3 2026 4 −1 A = 75. + 25 = 25( 2026 4 − ) 2026 2025 1 + 25 = 25.4 = 100.4 100  0,75 3
1.2 (1,5 điểm). Tìm các số nguyên tố p thỏa mãn 2
2p + p là số nguyên tố. 1,5 Với p 2 2 2
p = 2 ⇒ 2 + p = 2 + 2 = 8 là hợp số => loại 0,5 Với p 2 3 2
p = 3 ⇒ 2 + p = 2 + 3 =17 là số nguyên tố => thỏa mãn
Với p > 3, vì p là số nguyên tố nên p lẻ, do đó p = 2k +1 (k ∈ ,k > ) 1 0,25 p 2k 1 2 2 +  = ≡  2(mod3) Ta có:  0,25 2  p ≡ 1  (mod3) p 2 0,25 ⇒ + p ≡ ( ) p 2 2
0 mod3 ⇒ 2 + p 3 và lớn hơn 3 nên 2
2p + p là hợp số => loại Vậy p = 3 0,25
Câu 2. (4,0 điểm)
2a + b + c + d a + 2b + c + d a + b + 2c + d a + b + c + 2 2.1. d Cho dãy tỉ số = = = (với a b c d
a,b,c,d ≠ 0
a + b b + c c + d d + a
). Chứng minh rằng biểu thức Q = + + + có giá trị là số
c + d d + a a + b b + c nguyên. 2.2. Cho đa thức ( ) 3 2
f x = ax + bx + cx + d với a,b,c,d ∈. Biết f (x)5 với mọi x ∈ . Chứng
minh rằng a,b,c,d đều chia hết cho 5. 3 4
2a + b + c + d a + 2b + c + d a + b + 2c + d a + b + c + 2 2.1. d Cho dãy tỉ số = = = a b c d
a + b b + c c + d d + a 2,0
(với a,b,c,d ≠ 0 ). Chứng minh rằng biểu thức Q = + + + có
c + d d + a a + b b + c giá trị là số nguyên.
2a + b + c + d a + 2b + c + d a + b + 2c + d a + b + c + 2d Từ = = = suy ra a b c d
2a + b + c + d
a + 2b + c + d
a + b + 2c + d
a + b + c + 2 −1 = −1 = −1 d = −1 0,5 a b c d
a + b + c + d a + b + c + d a + b + c + d a + b + c + d = = = = k a b c d
- Nếu a + b + c + d ≠ 0 ⇒ a = b = c = d
Khi đó Q = 1+1+1+1 = 4∈ 0,75
a + b = −(c + d )
b+c = −(d +a)
- Nếu a + b + c + d = 0 ⇒ 
c + d = −(a +  b) 0,75 d + a = −  (b + c) Khi đó Q = 1 − −1−1−1 = 4 − ∈
Vậy giá trị của biểu thức Q là số nguyên 2.2. Cho đa thức ( ) 3 2
f x = ax + bx + cx + d với a,b,c,d ∈. Biết f (x)5 với mọi 2,0
x ∈ . Chứng minh rằng a,b,c,d đều chia hết cho 5.
Vì f (x)5 với mọi x ∈ nên
Với x = 0 ⇒ f (0) = d5 0,25
Với x =1⇒ f ( )
1 = a + b + c + d5 mà d5 ⇒ a + b + c5 (1) 0,25 Với x = 1 − ⇒ f ( )
1 = −a + b − c + d5 mà d5 ⇒ −a + b − c5 (2) 0,25
Từ (1) và (2) say ra 2b5 mà (2,5) =1⇒ b5 0,25
Với x = 2 ⇒ f (2) = 8a + 4b + 2c + d5 mà b,d5 ⇒ 8a + 2c5 (3) 0,25
Từ (1) suy ra a + c5 ⇒ 2a + 2c5 (4) 0,25
Từ (3) và (4) suy ra 6a5, mà (5,6) =1⇒ a5 ⇒ c5 0,25
Vậy a,b,c,d đều chia hết cho 5. 0,25
Câu 3. (5,0 điểm)
Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm BC . Lấy điểm D trên đoạn
thẳng AB ( D khác A và B ), trên tia đối của tia CA lấy điểm K sao cho CK = BD ; DK cắt BC
tại I . Kẻ DP vuông góc với BC tại P và KQ vuông góc với BC tại Q .
a) Chứng minh rằng: BDP ∆ = C
∆ KQ và I là trung điểm DK .
b) Đường vuông góc với DK tại I cắt AM tại S . Tính  SCK ? 4 5
c) Đường thẳng vuông góc với MD tại M cắt AC tại E . Chứng minh rằng:
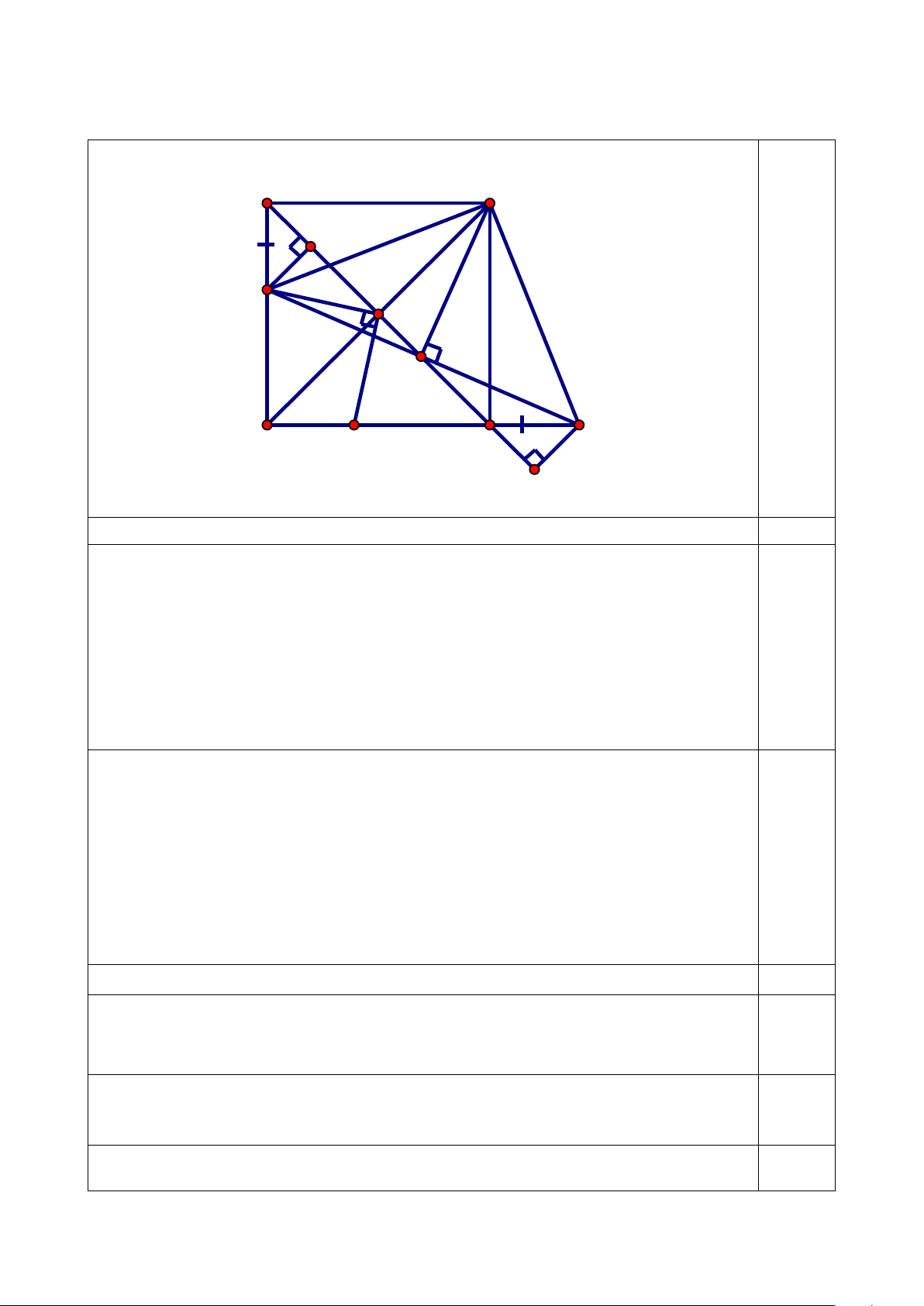
MD + ME ≥ AD + AE . Vẽ hình, viết GT, KL B S 1 P D M 0,25 I 1 2 1 C 2 A E K Q
a) Chứng minh rằng: BDP ∆ = C
∆ KQ và I là trung điểm DK . 1,75
Vì tam giác ABC vuông cân tại A nên  =  0
B C = 45 , mà  =  C
C (2 góc đối đỉnh) nên 1 1 2 1  =  B C 1 2
Xét tam giác BDP và tam giác CKQ, ta có BD = CK (gt)  =  0 BPD CQK = 90  =  B C 1 2 1,0 Suy ra B ∆ DP = CKQ ∆ (CH-GN)
=> DP = KQ (cạnh tương ứng)
Ta có DP // KQ (cùng vuông góc với BC) =>  =  PDI QKI
Xét tam giác DPI và tam giác KQI, ta có DP = KQ (cmt)  =  0 DPI KQI = 90 0,75  =  PDI QKI (cmt) Suy ra DP ∆ I = K
∆ QI (g.c.g) => DI = KI (cạnh tương ứng)
=> DI = KI (cạnh tương ứng) => I là trung điểm của DK
b) Đường vuông góc với DK tại I cắt AM tại S . Tính  SCK ? 2,0
Vì AM là trung tuyến trong tam giác cân nên AM cũng là phân giác của góc A Chứng minh ABS ∆ = AC ∆
S ( .cg.c) ⇒  =  ABS ACS ( )1 và SB = SC 1,0
Vì S thuộc trung trực của DK => SD = SK Chứng minh SB ∆ D = SC
∆ K ( .c .cc) ⇒  =   = 
SBD SCK hay ABS SCK (2) 1,0
Từ (1) và (2) suy ra  =   +  0 = ⇒  =  0
ACS SCK ,mà ACS SCK 180 ACS SCK = 90
c) Đường thẳng vuông góc với MD tại M cắt AC tại E . Chứng minh rằng:
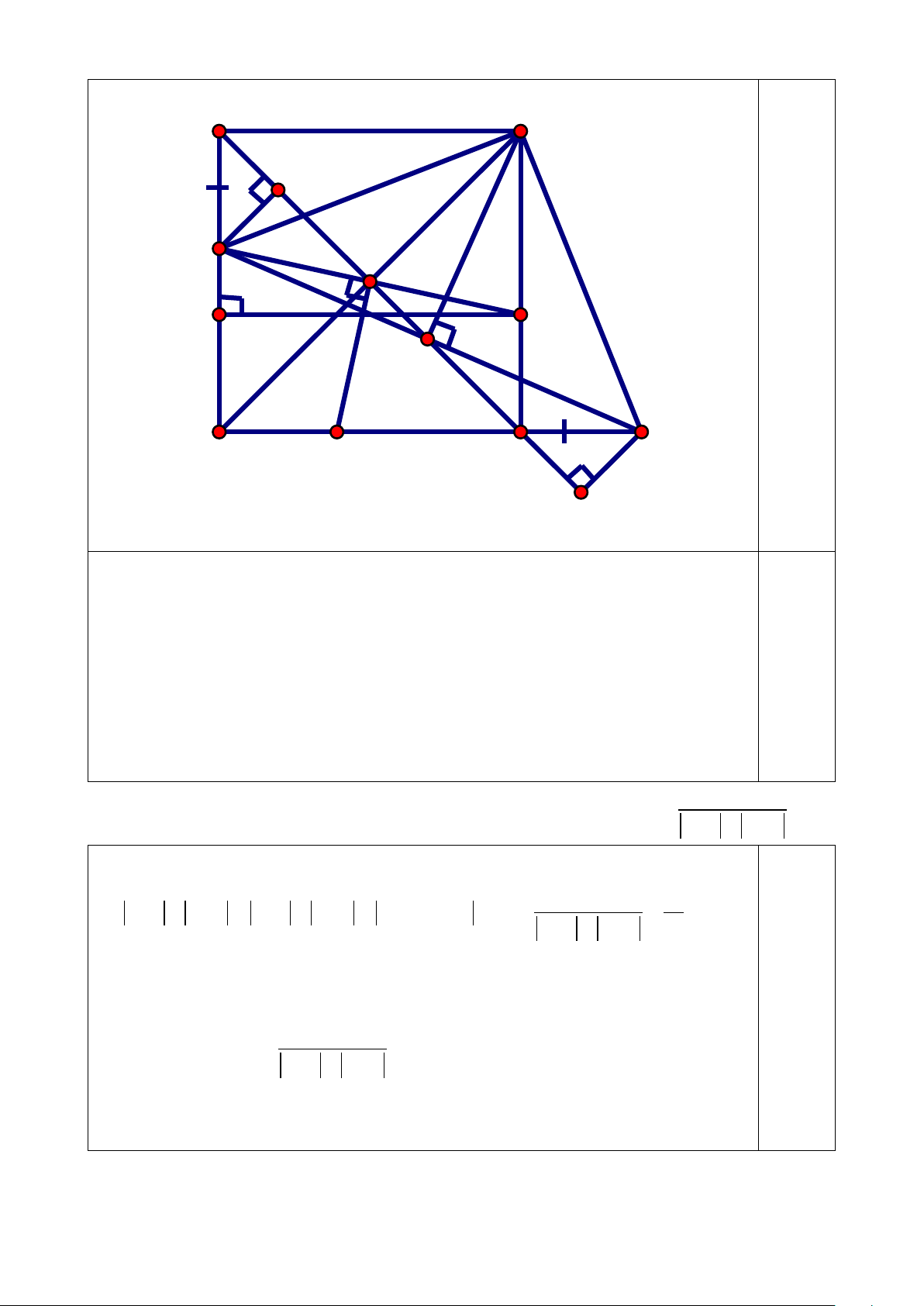
MD + ME ≥ AD + AE 1,0 . 5 6 B S 1 P D M H F I 1 2 1 C 2 A E K Q
Gọi giao điểm của DM với SC là F.
Chứng minh ∆ MDB = ∆ MFC ⇒ MD = MF ⇒ M là trung điểm của DF
Từ F kẻ FH ⊥ AB tại H. 0,25
Chứng minh ∆ FAH = ∆ AFC⇒ FH = AC 0,25
Do ∆ AMD = ∆ CME ⇒ AD = CE ⇒ AD + AE = AC.
Do MD = ME nên MD + ME = 2MD = DF 0,25
Mặt khác DF ≥ HF ⇒ DF ≥ AC hay MD + ME ≥ AD + AE
Dấu “=” khi MD ⊥ AB. 0,25
Câu 4. (2,0 điểm). Tìm các cặp số nguyên ( ;
x y) thỏa mãn (x + y − )2 14 2 + 7 = y −1 + y − 3
Vì (x + y − )2 ≥ ⇒ (x + y − )2 2 0 2 + 7 ≥ 7 và 14 14
y −1 + y − 3 = y −1 + 3 − y ≥ y −1+ 3 − y = 2 ⇒ ≤ = 7 y −1 + y − 3 2
dấu “=” xảy ra khi ( y − )
1 (3− y) ≥ 0 ⇔ 1≤ y ≤ 3 1,0 (  x + y − )2 2 + 7 = 7 
x + y − 2 = 0
x = 2 − y nên theo bài ra ta có:  14 ⇔  ⇔  (do x, =  7 1  ≤ y ≤ 3 y ∈  {1;2; } 3 y −1 + y − 3  y nguyên) 1,0 Vậy ( ; x y)∈ ( { 1; )1;(0;2);( 1; − 3)}
------------------------------ Hết-----------------------------
Lưu ý: HS làm cách khác đúng vẫn cho điểm tối đa 6
Xem thêm: ĐỀ THI HSG TOÁN 7
https://thcs.toanmath.com/de-thi-hsg-toan-7
Document Outline

• 1. Toán 7-Lâm Thao
  • Câu 4. Cho . Giá trị của biểu thức là
• HSG 7