Đề chọn học sinh giỏi Toán 9 năm 2025 – 2026 xã Hải Châu – Nghệ An

UBND XÃ HẢI CHÂU
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP XÃ, LỚP 9 NĂM HỌC 2025 - 2026
Môn: Toán (Thời gian làm bài 150 phút) Câu 1. (2,5 điểm)
a) Cho các số nguyên dương a, b, c, d thỏa mãn: 3 3 3 3
2018a  2021b  c  d . Chứng minh
rằng a  b  c  d là hợp số.
b) Thực hiện chính quyền địa phương hai cấp, mỗi hộ gia đình trong tổ dân cư đều
được gắn một số tự nhiên khác 0 (gọi là số nhà). Số nhà của bác An là một số tự nhiên
có hai chữ số. Biết rằng bình phương của số nhà bằng lập phương của tổng các chữ số
của số nhà. Tìm số nhà của bác An. Câu 2. (6,0 điểm)
a) Giải phương trình: (x  7)(x  5)(x  4)(x  2)  72 x  y  xy  1 
b) Giải hệ phương trình:  2 2 x   y  xy  7 Câu 3. (1,5 điểm)
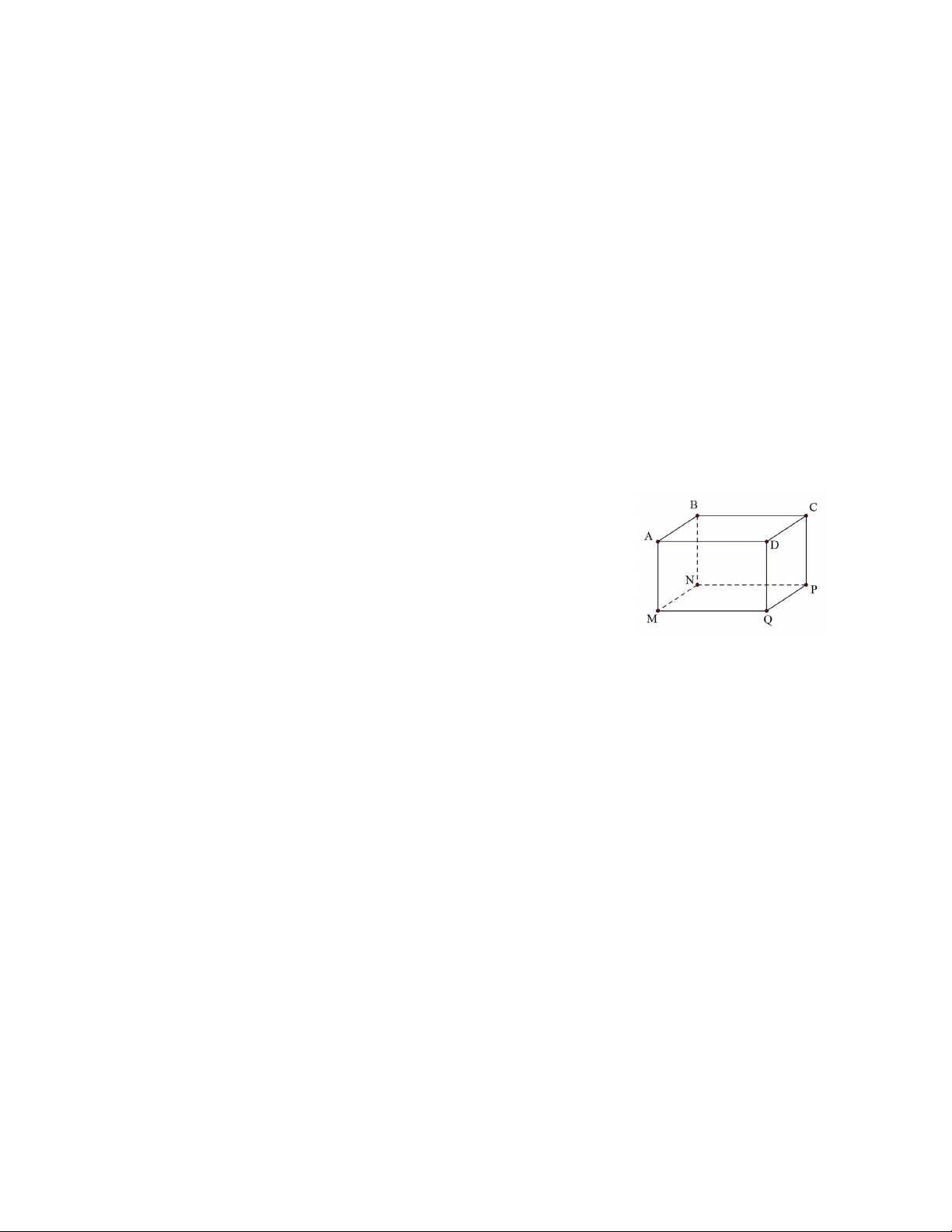
Bác Bình muốn làm một cái bể nuôi cá bằng kính có
dạng hình hộp chữ nhật có đáy là hình vuông (như hình
bên) có thể tích 0,5 m3. Hãy tìm độ dài cạnh MN và chiều
cao AM của bể nước sao cho tổng diện tích các mặt bên và
mặt đáy (không tính mặt nắp) của bể nước nhỏ nhất. Câu 4. (2,0 điểm)
Trong một hộp đựng những chiếc kẹo giấy màu xanh lá, đỏ, trắng, vàng và xanh
dương. Số kẹo giấy màu trắng nhiều gấp ba lần số kẹo giấy màu đỏ, số kẹo giấy màu
vàng gấp đôi số kẹo giấy màu đỏ, số kẹo giấy màu xanh lá bằng số kẹo giấy màu xanh
dương và bằng số kẹo giấy màu đỏ. Chọn ngẫu nhiên một chiếc kẹo giấy. Tính xác
suất của biến cố A: “Chọn được chiếc kẹo giấy màu vàng hoặc màu đỏ”. Câu 5. (7,0 điểm)
Cho tam giác nhọn ABC. Các đường cao AD, BE, CF cắt nhau tại H. a) Chứng minh:  AEF =  ABC .
b) Chứng minh rằng điểm H cách đều ba cạnh của tam giác DEF.
c) Cho B và C cố định, A di chuyển sao cho góc BAC không đổi. Chứng minh rằng
khi điểm A di chuyển thì độ dài đoạn thẳng EF không đổi. Câu 6. (1,0 điểm)
Cho một đa giác đều có 2025 đỉnh. Tô màu các đỉnh của đa giác bằng một trong
hai màu xanh hoặc đỏ. Chứng minh rằng luôn tồn tại một tam giác cân có ba đỉnh được tô cùng một màu.
.................Hết.................
Họ và tên thí sinh : ......................................................Số báo danh: ................. HƯỚNG DẪN GIẢI Câu 1 a) gt: 3 3 3 3 2018a  2021b  c  d 3 3 3 3 3 3
2019a  2022b  (a  b )  c  d 3 3 3 3 3 3
a  b  c  d  2019a  2022b 3 (vì 20193,20223) (1) Xét 3
a  a  a(a 1)(a 1)3 (vì a 1,a,a 1 là 3 so nguyên liên tiep) Tương tự: 3 b  b3 3 c  c3 3 d  d 3 3 3 3 3
 a  b  c  d  (a  b  c  d )3 (2)
Từ (1) và (2)  a  b  c  d3 mà *
a  1,b  1,c  1,d  1 (a,b,c,d   )
 a  b  c  d  4  3
Vậy a  b  c  d là hợp số.
b) Gọi số nhà: n  ab , ta có: 2 3 ab  (a  b) (gt) Đặt 2 3 6 ab  (a  b)  x (x ) 2 x  a  b   (I ) 3 x  ab  Do 3 x  ab  10 nên x  3 2
x  a  b  18 nên x  4  x {3;4}
Xét x  3 từ (I) ta có: a  b  9,ab  27 (nhận)
Xét x  4 , từ (I) ta có: a  b  16,ab  64 (loại) Vậy n  27 Câu 2.
a) Giải phương trình: (x  7)(x  5)(x  4)(x  2)  72 2 2
(x  9x 14)(x  9x  20)  72 (t 14)(t  20)  72 (t  8)(t  26)  0 t  8  0 t  8     t  26  0 t  2  6  
Tập nghiệm của phương trình là S  {1,8}. x  y  xy  1
b) Giải hệ phương trình:  2 2 x  y  xy  7  Đặt S = x+y và P  xy . Ta có hệ: S  P  1   2 S  3P  7  2 S  3  3S  7 2 S  3S  4  0
Có hai nghiệm: S  1 và S  4  . 1 2
Trường hợp 1: S  1, P  1 S  11  2
Vậy ta có hai cặp nghiệm (x, y) là (2, -1) và (-1, 2).
Trường hợp 2: S  4 , P  1   S  1   ( 4  )  3 .
Vậy ta có hai cặp nghiệm (x, y) là (-1, -3) và (-3, -1).
Hệ phương trình có 4 cặp nghiệm là (2, -1), (-1, 2), (-1, -3), (-3, -1). Câu 3:
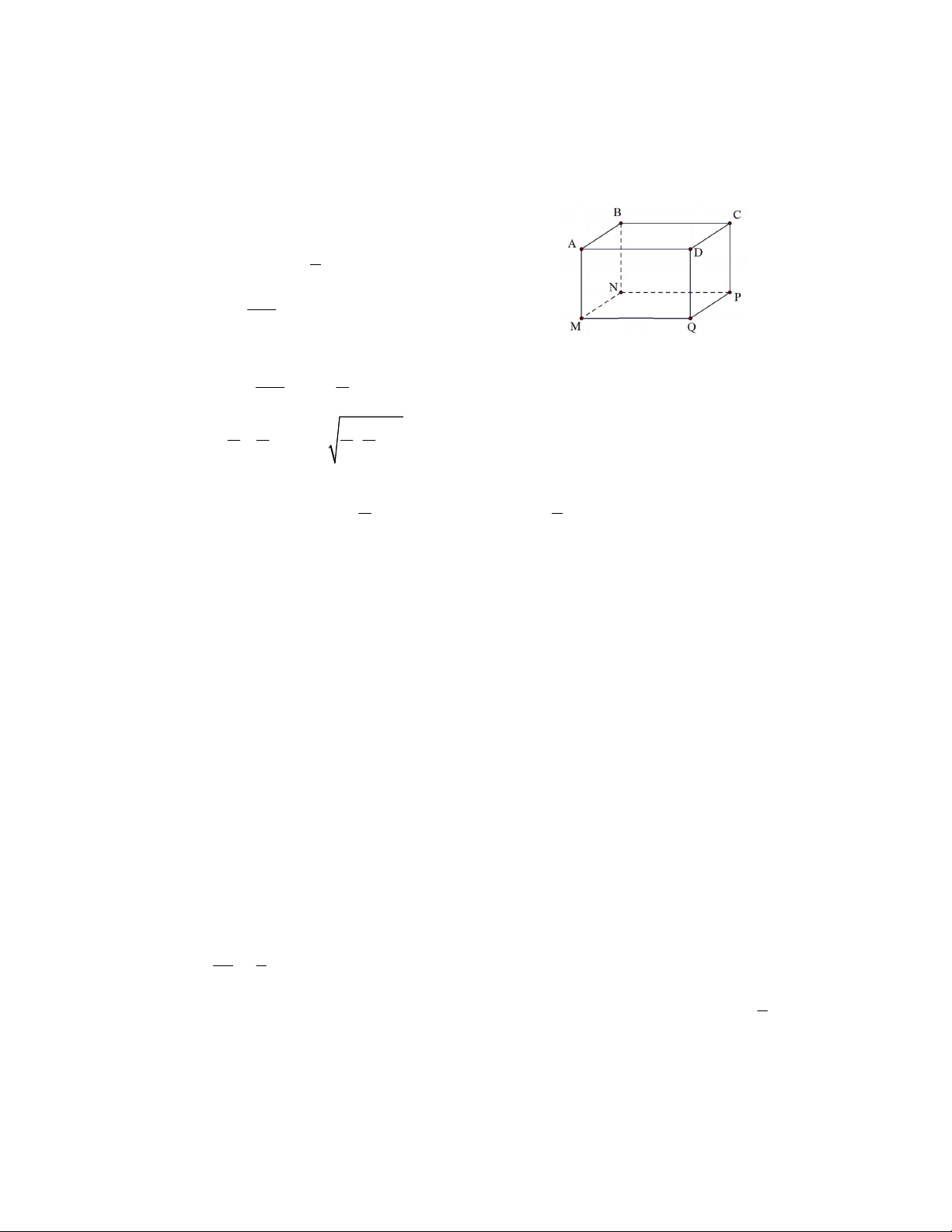
Đặt: Chiều cao AM  x (x  0)
cạnh đáy MN  MQ  y ( y  0) 1 2 V  xy  0,5  2 x 1 y  x  2 2 y y 2
S  S  S  4 y  x  y xq d 1 2 2 2 S  4 y   y   y 2 2 y y 1 1 1 1 2 2 S 
  y  33   y  3. y y y y Dấu "=" xảy ra khi 1 1 2  y  y  1 mà 2 xy   x  0,5 y 2 Vậy 2 S  3 (m ) khi x  0,5 , m y  1 m min Câu 4. (2,0 điểm) HD:
Gọi số kẹo giấy màu Đ là x (chiếc).
Điều kiện: x là số nguyên dương
Ta có: Số kẹo màu T là: 3x (chiếc)
Số kẹo màu V là: 2x (chiếc)
Số kẹo màu XL là: x (chiếc)
Số kẹo màu XD là: x (chiếc)
Tổng số kẹo trong hộp là tổng số kẹo của tất cả các màu:
Tổng số kẹo = x + 3x + 2x + x + x = 8x (chiếc)
Số phần tử của không gian mẫu là  = 8x.
Biến cố A là "Chọn được chiếc kẹo giấy màu V hoặc màu Đ".
Số kết quả thuận lợi cho biến cố A là tổng số kẹo màu V và số kẹo màu Đ:
Số kẹo V hoặc Đ = 2x + x = 3x (chiếc)
Số phần tử của biến cố A là A = 3x.
Xác suất của biến cố A được tính bằng công thức: P(A) = 3x = 3 8x 8
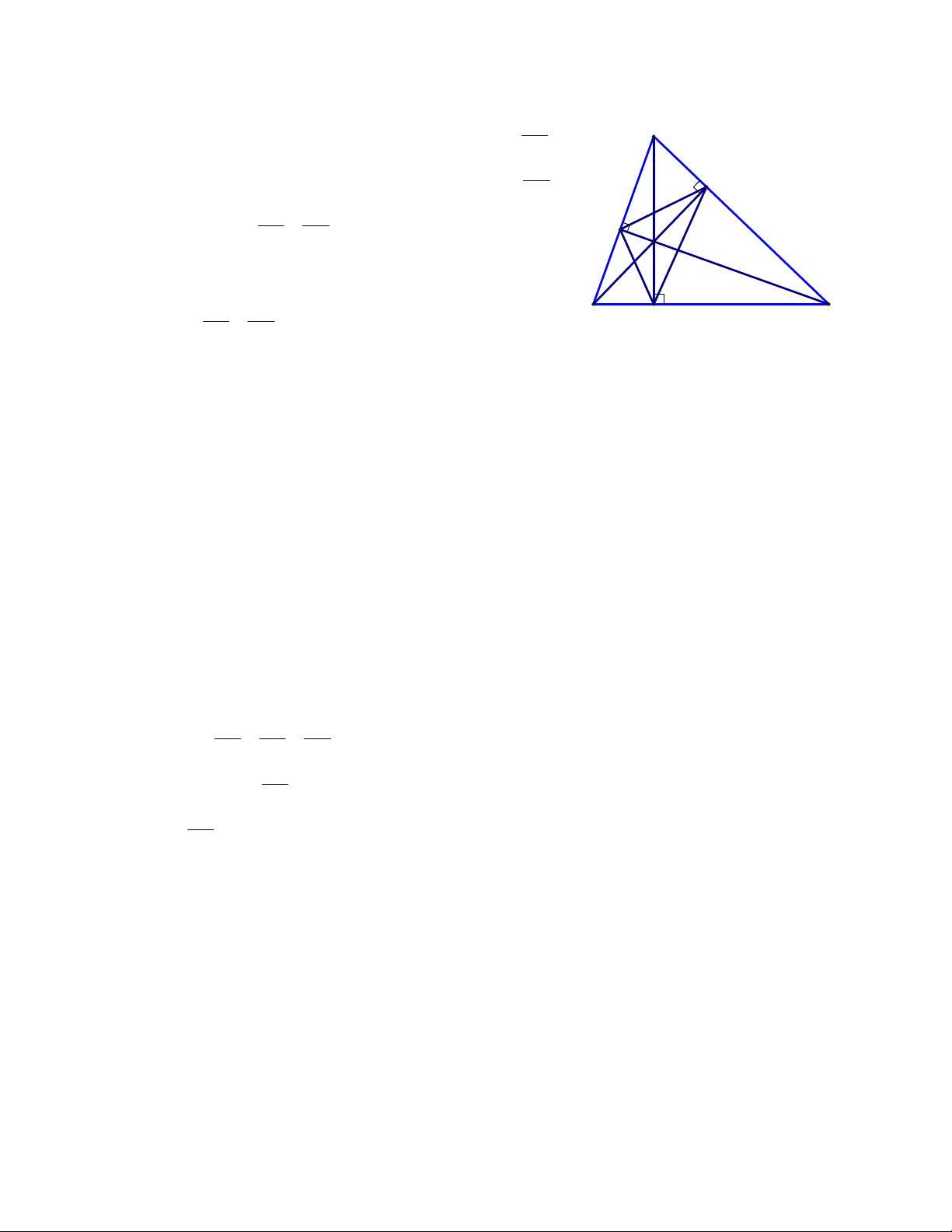
Xác suất của biến cố A "Chọn được chiếc kẹo giấy màu V hoặc màu Đ" là 3 . 8 Câu 5. (7,0 điểm) a) Chứng minh:  AEF   ABC Trong AE
AEB vuông tại E, ta có: cos  BAC  A AB Trong AF
AFC vuông tại F, ta có: cos  BAC  E AC Suy ra: AE AF  F AB AC H
Tam giác AEF và ABC có:  BAC chung. AE AF  (chứng minh trên). B C D AB AC Do đó, AEF 
 ABC (theo trường hợp cạnh - góc - cạnh). Vậy,  AEF  
ABC (điều phải chứng minh).
b) Chứng minh rằng điểm H cách đều ba cạnh của tam giác DEF. Theo câu a)  AEF  
ABC , Chứng minh tương tự:  DEC   ABC Suy ra:  AEF   DEC Mà  AEF   0 FEH  90 và  DEC   0 DEH  90 =>  FEH   DEH
=> EH là tia phân giác của góc  FDE .
Chứng minh tương tự: FH là tia phân giác của góc  EFD .
Vì H là giao điểm của ba đường phân giác trong của tam giác DEF,
Do đó, H cách đều ba cạnh của tam giác DEF (đpcm).
c) Cho B và C cố định, A di chuyển sao cho góc BAC không đổi. Chứng minh rằng
khi điểm A di chuyển thì độ dài đoạn thẳng EF không đổi.
Ở câu a, ta đã chứng minh AEF   ABC . EF AE AF k    BC AB AC AE EF  BC  AB AE  cos  BAC AB
Thay tỉ số này vào biểu thức của EF, ta được: EF  BC cos  BAC
Vì hai điểm B và C là cố định, nên độ dài đoạn thẳng BC không đổi.
Theo giả thiết, A di chuyển nhưng góc  BAC không đổi. Do đó, giá trị cos  BAC cũng không đổi.
Vậy, khi điểm A di chuyển sao cho góc BAC không đổi thì độ dài đoạn thẳng EF
không đổi (điều phải chứng minh).
Document Outline

• Đề HSG Toán 9 (xã Hải Châu) 2025
• HD GIAI DE HSG CAP XA