Đề cuối học kỳ 1 Toán 10 năm 2022 – 2023 trường THPT Quế Sơn – Quảng Nam

TRƯỜNG THPT QUẾ SƠN
KIỂM TRA CUỐI KỲ 1- NĂM HỌC 2022-2023 TỔ:TOÁN - TIN
Môn: TOÁN – Lớp 10
Thời gian: 60 phút (Không kể thời gian giao đề) ĐỀ CHÍNH THỨC
(Đề gồm có 02 trang) MÃ ĐỀ 101
I. PHẦN TRẮC NGHIỆM (15 câu x 1/3 điểm = 5,0 điểm)
Học sinh chọn câu trả lời đúng và tô vào ô tương ứng trong phiếu làm bài riêng.
Câu 1: Trong các câu sau, câu nào không phải là mệnh đề?
A. Hãy làm bài kiểm tra thật nghiêm túc!
B. Hà Nội là thủ đô của Việt Nam.
C. 7 là số nguyên tố. D. 8 + 2 = 11.
Câu 2: Cho tập hợp M = 2
{x ∈ | x + 3x − 4 = 0}. Tập M được viết lại là: A. M ={ 1; − 4}. B. M = { 4 − ;1}. C. M = ( 1; − 4) . D. M = ( 4 − ;1) .
Câu 3: Cho 2 tập hợp M = (–∞ ;–1], N= ( –2;4]. Mệnh đề nào sau đây đúng?
A. M∩ N = (–∞ ; 4]. B. M∩ N = (–∞ ; 4). C. M∩ N = [–2; –1). D. M∩ N = (–2; –1].
Câu 4: Trong mặt phẳng tọa độ, điểm nào sau đây thuộc miền nghiệm của bất phương trình bậc nhất hai ẩn x + 2y ≥ 3?
A. A (–2; –1). B. B (–1; 2). C. C (1; –2). D. D(2; 0).  − <
Câu 5: Cho hệ bất phương trình bậc nhất 2 ẩn: x y 0 
. Cặp số nào sau đây không phải là x + 2y ≥ 0
nghiệm của hệ đã cho?
A. (x; y) = (0; 1). B. (x; y) = (1; 2). C. (x; y) = (–2; 1). D. (x; y) = (0; –3).
Câu 6: Cho α và β là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai?
A. sinα = sin β . B. cosα = −cos β . C. tanα = − tan β . D. cotα = cot β .
Câu 7: Trong tam giác ABC, gọi p, R, r, S lần lượt là nửa chu vi, bán kính đường tròn ngoại
tiếp, bán kính đường tròn nội tiếp và diện tích của tam giác ABC, khẳng định nào sau đây đúng? A. S = 2 . a .
b sin C . B. S = . a .
b c . C. b = 2R . D. S = .pR . 4r sin B
Câu 8: Trên đoạn thẳng MN , lấy điểm P nằm giữa 2 điểm M , N . Phát biểu nào sau đây đúng?    
A. Hai vectơ MN và MP ngược hướng. B. Hai vectơ PN và MP ngược hướng.    
C. Hai vectơ NM và MP cùng phương. D. Hai vectơ PM và PN cùng hướng.
Câu 9: Cho 3 điểm A, B, C tùy ý, khẳng định nào sau đây sai?
  
  
  
  
A. CA+ AB = CB . B. AB − AC = CB . C. BA+ AC = BC .
D. CA−CB = AB . Câu 10: Cho A
∆ BC có G là trọng tâm, I là trung điểm BC . Đẳng thức nào sau đây đúng?       
  
A. GA = 2GI . B. 1
IG = − IA . C. GB + GC = 2GI . D. GB + GC = GA . 3
Câu 11: Trên đoạn thẳng AC, cho điểm B nằm giữa hai điểm A và C, với AB = 2a, AC = 8a.
Đẳng thức nào dưới đây đúng?         A. BC = 3
− BA. B. AB = 4CA .
C. BC = 4AB . D. AC = 4 − AB .
Trang 1/2 - Mã đề 101     
Câu 12: Trong mặt phẳng tọa độ Oxy, cho a = (1; 2), b = (3;8). Tọa độ c = 2a −b là:     A. c = ( 1;
− − 4). B. c = (5; 12) . C. c = (2; 5).
D. c = (2; 6) . 
Câu 13: Trong mặt phẳng tọa độ Oxy, cho 2 điểm M ( 2; − 3
− ) , N (4; 5) . Tìm tọa độ vectơ MN     A. MN =(1; )
1 . B. MN =(2; 2). C. MN =(6; 8) . D. MN =( 6; − 8 − ) .
Câu 14: Trong mặt phẳng tọa độ Oxy, cho A(2; 3
− ) , B(2; 7) . Tọa độ trung điểm I của đoạn thẳng AB là:
A. I(4; 4). B. I(2; 2). C. I(0; −10) . D. I(0;10) .  
Câu 15: Cho tam giác ABC vuông tại A và có  0
B = 60 . Tính góc giữa hai vectơ CA và CB .         A. (CA CB) 0 ,
=150 . B. (CA CB) 0 ,
= 60 . C. (CA CB) 0 , =120 . D. (CA CB) 0 , = 30 .
II. PHẦN TỰ LUẬN (5, 0 điểm)
Câu 1(1,0 điểm): Hai chiếc tàu thủy cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo
với nhau một góc 1200. Tàu thứ nhất chạy với vận tốc 50km/h, tàu thứ hai chạy với vận tốc
40km/h. Hỏi sau 1 giờ hai tàu cách nhau bao nhiêu km?  
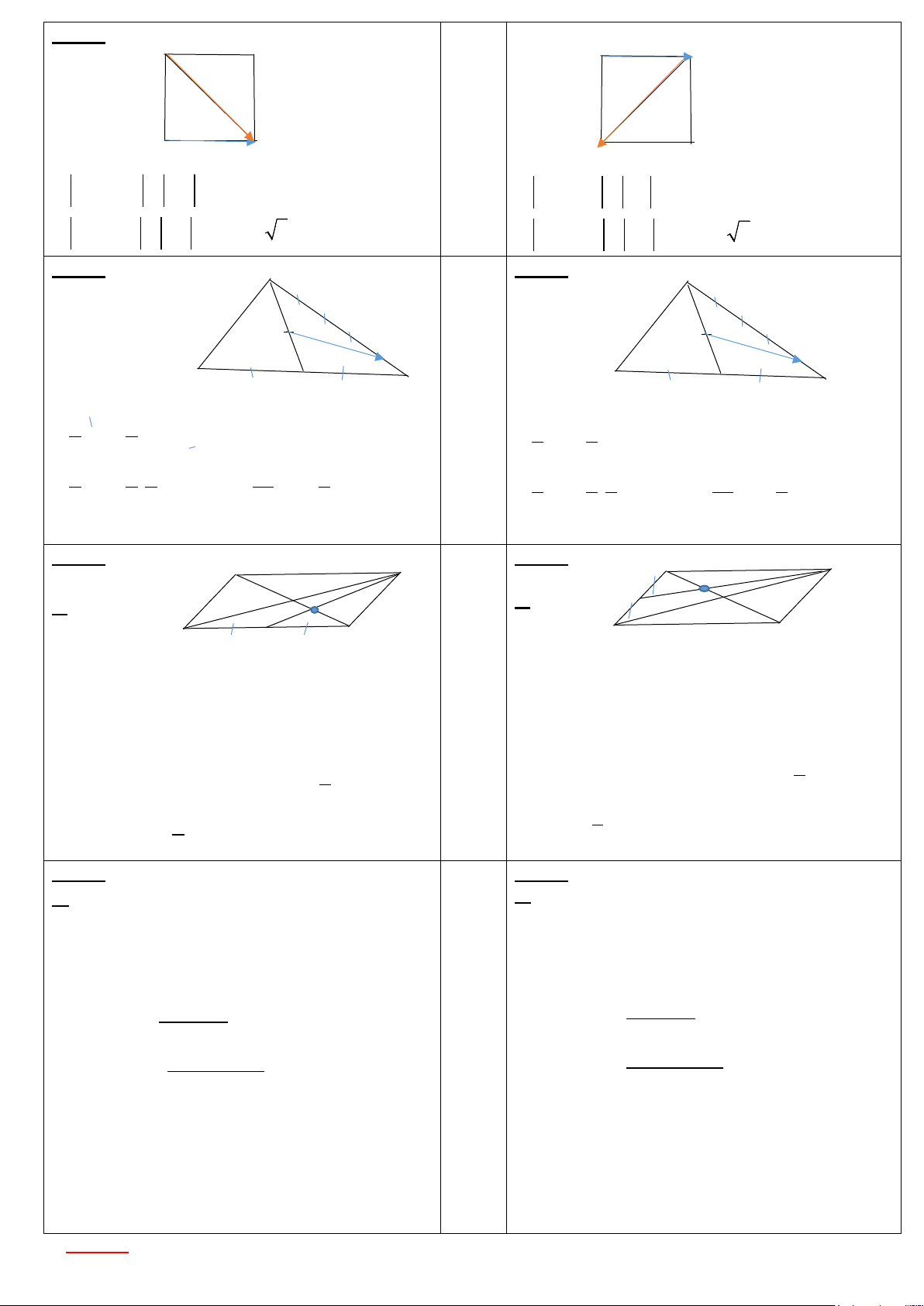
Câu 2(1,0 điểm): Cho hình vuông ABCD có cạnh bằng a. Tính độ dài các vectơ AC − AD ,  
AB + BC theo a.
Câu 3(1,0 điểm): Cho tam giác ABC có trung tuyến AI . Gọi M là trung điểm của AI , H là   
điểm cạnh AC sao cho AH = 4HC . Chứng minh rằng: 20MH =11AC −5AB .
Câu 4(2,0 điểm): Trong mặt phẳng tọa độ Oxy , cho hình bình hành ABCD có B(1;2), D(3; 1) − .
a) Tìm tọa độ điểm P trên trục Ox sao cho tam giác BDP vuông tại D .
b) Gọi Q là trung điểm của cạnh BC , N là giao điểm của AC và DQ . Biết N(2; 1) − , tìm
tọa độ các điểm A , C .
-----------Hết-----------
Trang 2/2 - Mã đề 101 Trường THPT Quế Sơn HƯỚNG DẪN CHẤM Tổ: Toán-Tin
KIỂM TRA CUỐI HỌC KỲ 1 -NĂM HỌC 2022-2023
------------------------ MÔN: TOÁN -Lớp 10 I/TRẮC NGHIỆM 101
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 A x x x B x x x C x x x x D x x x x x 102
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 A x x x B x x x x x x x C x x x D x x
103 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 A x x x B x x x C x x x x x x D x x x
104 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 A x x x x B x x x x x x C x D x x x x II/TỰ LUẬN MÃ ĐỀ 101-103 ĐIỂM MÃ ĐỀ 102-104 Câu 1 (1,0đ): Câu 1 (1,0đ): B 30 B 50 A A 60 120 40 30 C C
+ Gọi B, C lần lượt là vị trí của tàu thứ nhất và
+ Gọi B, C lần lượt là vị trí của tàu thứ nhất và tàu
tàu thứ hai đến sau 1 giờ. Khoảng cách giữa 2 tàu
thứ hai đến sau 1 giờ. Khoảng cách giữa 2 tàu sau
sau một giờ là độ dài BC
0,25 một giờ là độ dài BC
+Ta có AB = c = 50, AC = b = 40,  =  0 BAC A =120
0,25 +Ta có AB = c = 30, AC = b = 40,  =  0 BAC A = 60
+ Áp dụng định lý côsin trong tam giác ABC, ta
+ Áp dụng định lý côsin trong tam giác ABC, ta
có: BC2 = a2 = b2 + c2 – 2bc.cosA
có: BC2 = a2 = b2 + c2 – 2bc.cosA
= 502 + 302 – 2.50.4. cos1200 = 6100
0,25 = 302 + 402 – 2.30.40. cos600 = 1300 + Suy ra BC = 10 61 (km) 0,25 + Suy ra BC = 10 13 (km) Câu 2: A B A B D C D C
  
  
+ AC − AD = DC = DC = a 0,5
+ AC + CB = AB = AB = a
  
  
+ AB + BC = AC = AC = a 2 0,5
+ AD − AB = BD = BD = a 2 Câu 3: A Câu 3: A M H I K
   B C B I B
MH = AH − AM
0,25    M
IK = AK − AI 4  1  = AC − AI
4  1  5 2 0,25 = AB − AM 5 2
4  1 1   11  1 
= AC − . (AB + AC)= AC − AB
4  1 1   11  1  5 2 2 20 4
0,25 = AB − . (AB + AC)= AB − AC    5 2 2 20 4   
Suy ra: 20MH =11AC − 5AB
0,25 Suy ra 20IK =11AB −5AC Câu 4: Câu 4: A A D D I N Q a) a) I N B B Q C C
+) P ∈Ox ⇒ P( ; x 0)
+) P ∈Oy ⇒ P(0; y)   0,25   +) DB = ( 2;
− 3) ; DP = (x −3;1) +) BD = (2; 3) − ; BP = ( 1; − y − 2)
+) Tam giác BDP vuông tại D
0,25 +) Tam giác BDP vuông tại B        
khi và chỉ khi DB ⊥ DP ⇔ . DB DP = 0 ⊥ ⇔ = 0,25 khi và chỉ khi BD BP B . D BP 0 4 +) ⇔ 2(
− x − 3) + 3.1 = 0 ⇔ x = 9 +) ⇔ 2( 1
− ) − 3(y − 2) = 0 ⇔ y = 2 3 Vậy P( 9 ; 0) 0,25 Vậy P( 4 0; ) 2 3 Câu 4: Câu 4: b) b)
+ Gọi I là tâm của hình bình hành ABCD , xét
+ Gọi I là tâm của hình bình hành ABCD , xét
tam giác BCD có CI , DQ là hai đường trung 0,25
tam giác ABD có AI , DQ là hai đường trung
tuyến nên N là trọng tâm.
tuyến nên N là trọng tâm.  1+ x +  1+ x + A 3 C 3 2 =  2 =  3 x =  3 x = A 2 C 2 + Do đó  ⇔ + Do đó  ⇔  2 y  + + −   y = − 2 + y + −   y = A ( 1) A 5 C ( 1) C 4 1 − = 2 =  3 0,25  3 ⇒ C (2;− 4). ⇒ A(2;5) .   0,25  
+ Ta có ⇒ CA = 3CN
+ Ta có ⇒ AC = 3AN 0,25 + Tìm được A(2;5)
Tìm được C (2;− 4)
Ghi chú: Học sinh giải theo cách khác mà đúng thì thầy cô cho điểm tối đa theo thang điểm đã qui định.
Document Outline

• MADE 101
• Đáp án Toán 10- HK1 22-23