Đề cuối kì 1 Toán 11 năm 2024 – 2025 trường THPT Chế Lan Viên – Quảng Trị

TRƯỜNG THPT CHẾ LAN VIÊN
ĐỀ KIỂM TRA CUỐI KÌ I - NĂM HỌC 2024 - 2025 TỔ TOÁN Môn: Toán, Lớp 11 MÃ ĐỀ 101
Thời gian làm bài: 90 phút, không tính thời gian phát đề
( Đề thi gồm có 04 trang)
PHẦN I. (5 điểm) Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời câu 1 đến câu 20.
Câu 1. Khẳng định nào dưới đây là đúng? A. sin 2x  sin .c x os . x B. 2 cos2x  2sin x 1. C. 2
cos 2x  2sin x 1. D. sin 2x  2sin . x c osx .
Câu 2. Hàm số nào sau đây là hàm số chẵn? A. y  cos . x
B. y  tan x  cot x . C. y  sin 2x .
D. y  sin x  cos x .
Câu 3. Trong các mệnh đề sau, mệnh đề nào là sai ? 
A. sin x  1  x   k2 .
B. sin x  0  x  k . 2 C. cos x  1
  x    k .
D. cosx  1  x  k 2 .
Câu 4. Trong các dãy số hữu hạn được cho dưới đây, dãy số nào là dãy số tăng? A. 3;5;8;9;10. B. 6 ;4 ;2 ;1. C. 1 ;-1 ;2 ;-5 ;3. D. 1 1 1 1 ; ; ; . 2 4 8 16
Câu 5. Cho cấp số cộng u thỏa mãn u  4;d  2
 . Số hạng thứ 6 của cấp số cộng là n  1 A. 8. B. 6. C. 18.  D. 18.
Câu 6. Trong các dãy số sau, dãy số nào là cấp số nhân? A. 128;64;32;16;4. B. 1;3;3 3;9;27 . C. 5 1; 4;7;10;13 . D. 5 10;5; ; . 2 4
Câu 7. Cho mẫu số liệu ghép nhóm về thống kê điểm số của học sinh tham dự kỳ thi học sinh
giỏi toán, ta có bảng số liệu sau: Điểm [8; 10) [10; 12) [12; 14) [14; 16) [16; 18) [18; 20) Số học sinh 3 5 4 2 6 5
Giá trị trung vị của mẫu số liệu ghép nhóm trên là A.14,25. B. 14,5. C. 15. D. 15,5.
Câu 8. Số cuộc gọi điện thoại một người thực hiện mỗi ngày trong 30 ngày được lựa chọn ngẫu
nhiên và được thống kê trong bảng sau:
Giá trị đại diện của nhóm [5,5;8,5) là A. 4. B. 8. C. 7. D. 13.
Câu 9. Khẳng định nào dưới đây là đúng?
A. Nếu hai mặt phẳng phân biệt có hai điểm chung thì chúng có vô số đường thẳng chung.
B. Nếu hai mặt phẳng phân biệt có hai điểm chung thì chúng có vô số điểm chung.
C. Qua hai điểm phân biệt có vô số đường thẳng.
D. Có vô số mặt phẳng đi qua ba đỉnh của một tam giác.
Câu 10. Trong các hình chóp, hình chóp có ít cạnh nhất có số cạnh là bao nhiêu? A. 3 . B. 4 . C. 5 . D. 6 .
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm
AD và BC. Giao tuyến của hai mặt phẳng SMN và SAC là A. . SD
B. SO (O là tâm hình bình hành ABCD).
C. SG (G là trọng tâm tam giác ABC).
D. SF (F là trung điểm CD).
Câu 12. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau.
B. Hai đường thẳng chéo nhau thì chúng có điểm chung.
C. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau hoặc trùng nhau.
D. Hai đường thẳng song song khi và chỉ khi chúng không điểm chung.
Câu 13. Cho tứ diện ABCD. Gọi M và N theo thứ tự là trung điểm của AD và AC. Giao tuyến
của hai mặt phẳng (BMN) và (BCD) là
A. Đường thẳng qua G và song song với BC. B. Đường thẳng qua M và song song với AB.
C. Đường thẳng qua N và song song với BD.
D. Đường thẳng qua B và song song với CD.
Câu 14. Cho hình chóp tứ giác S.ABCD . Gọi M và N lần lượt là trung điểm của SA và SC .
Khẳng định nào sau đây đúng?
A. MN // mp ABCD .
B. MN // mp SAB .
C. MN // mp SCD .
D. MN // mp SBC .
Câu 15. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt đáy của hình lăng trụ là hai đa giác đều và nằm trên hai mặt phẳng song song.
B. Các mặt bên của hình lăng trụ là các hình chữ nhật.
C. Các cạnh bên của hình lăng trụ bằng nhau và song song với nhau.
D. Các mặt bên của hình lăng trụ song song với nhau.
Câu 16. Cho hình hộp ABCD.A B C D có các cạnh bên AA , BB , CC , DD . Khẳng định nào dưới đây sai ?
A. mp ABB ' A' // mp DD C C .
B. Tứ giác ABCD là hình chữ nhật.
C. AA' // mp DD C C .
D. BD // B' D'.
Câu 17. Cho hình hộp AB .
CD EFGH . Mặt phẳng  ABCD song song với mặt phẳng nào sau đây? A. mp EFGH  . B. BCGF mp . C. mp DCGH  . D. mp DFH  .
Câu 18. Chọn khẳng định đúng trong các khẳng định sau
A. Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song.
B. Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng trùng nhau.
C. Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.
D. Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng chéo nhau.
Câu 19. Công thức nào dưới đây là đúng? A. 1 lim
 0 (với k  Z ). B. lim n
q  0 (với q  1 ). k n n n 1 C. lim   . D. lim k n   . n n n
Câu 20. Cho lim f (x)  L  0 và limg(x)   . Kết quả nào dưới đây là đúng? xx xx 0 0
A. lim f (x).g(x)   .
B. lim f (x).g(x)   . xx xx 0 0 C. l m i f (x).g( ) x  M  0 .
D. lim f (x).g(x)  L xx xx 0 0
PHẦN II. (2 điểm) Câu trắc nghiệm đúng sai. Thí sinh trả lời câu 1 và câu 2. Trong mỗi ý a),
b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm đoạn SB, H và
K lần lượt là trọng tâm tam giác SAB và SBC (Tham khảo hình vẽ dưới đây). Khi đó: S M H K B A D C a. AB / /C . D
b. SC và AB cắt nhau.
c. HK / /(ABCD). d. (MHK) / /(SAC). 3x 1  
Câu 2. Cho hàm số y f (x) x  . Khi đó: 1
a. lim f (x)   .   x 1  b. lim f(x)  4. x
c. Hàm số y  f (x) liên tục tại điểm x 1. 0
d. Hàm số y  f (x) liên tục trên từng khoảng ( ;  1) và 1;.
PHẦN III. (3,0 điểm) Tự luận
Câu 1 ( 1,0đ) . Cho hình chóp S.ABCD đáy là hình bình hành, O là giao điểm của AC và BD.
a. Tìm giao tuyến của hai mặt phẳng SAD và SBC.
b. Trên các cạnh S ,
B SD lần lượt lấy điểm M , N sao cho SM  2M ;
B SD  2SN . Tìm hình chiếu
của tam giác AMN qua phép chiếu song song lên mặt phẳng (ABC )
D theo phương chiếu . SO 2 2n 3n 2  3x 1
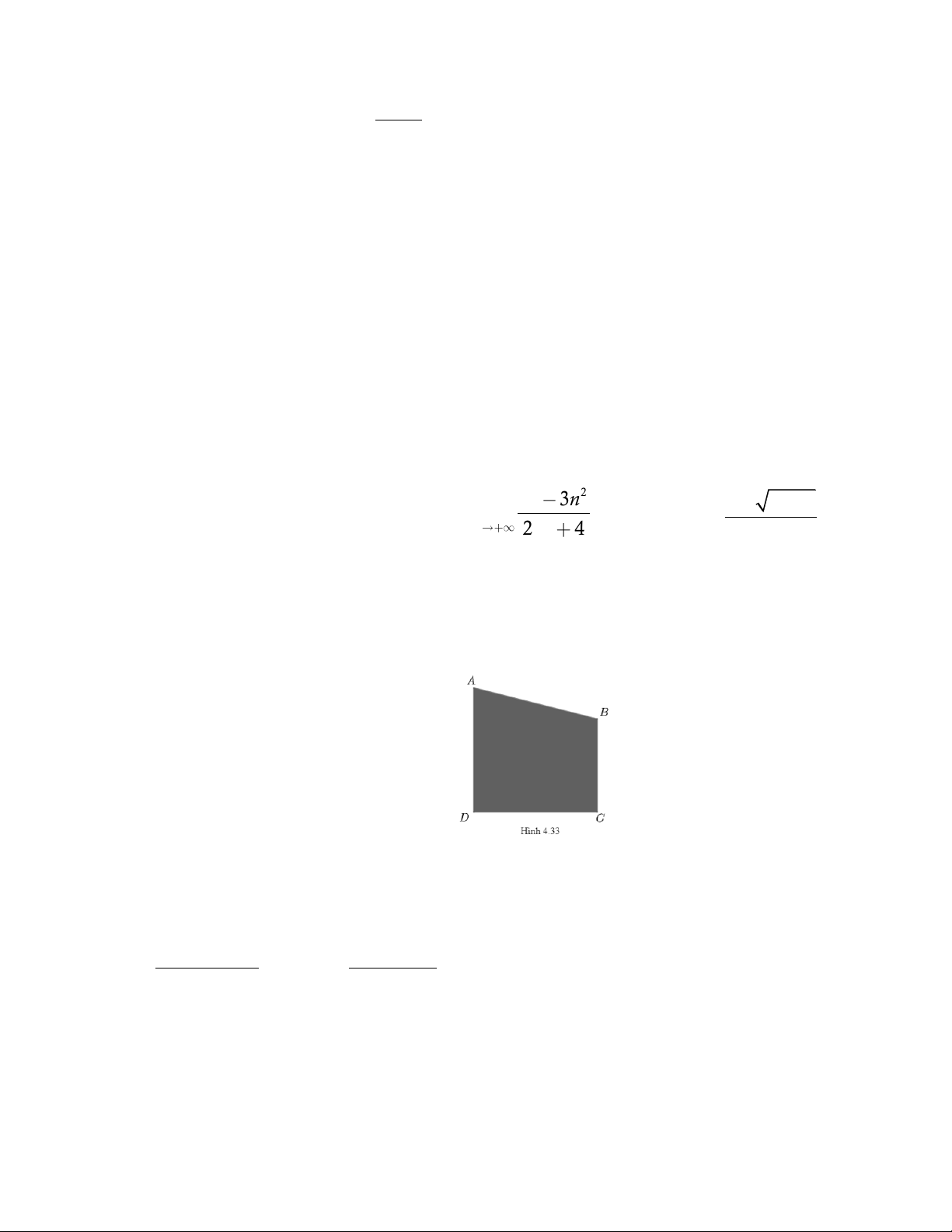
Câu 2 ( 1,0đ) . Tính các giới hạn sau : a. lim 2 b. lim n 2n 4 2 x 1
 2x  x  1
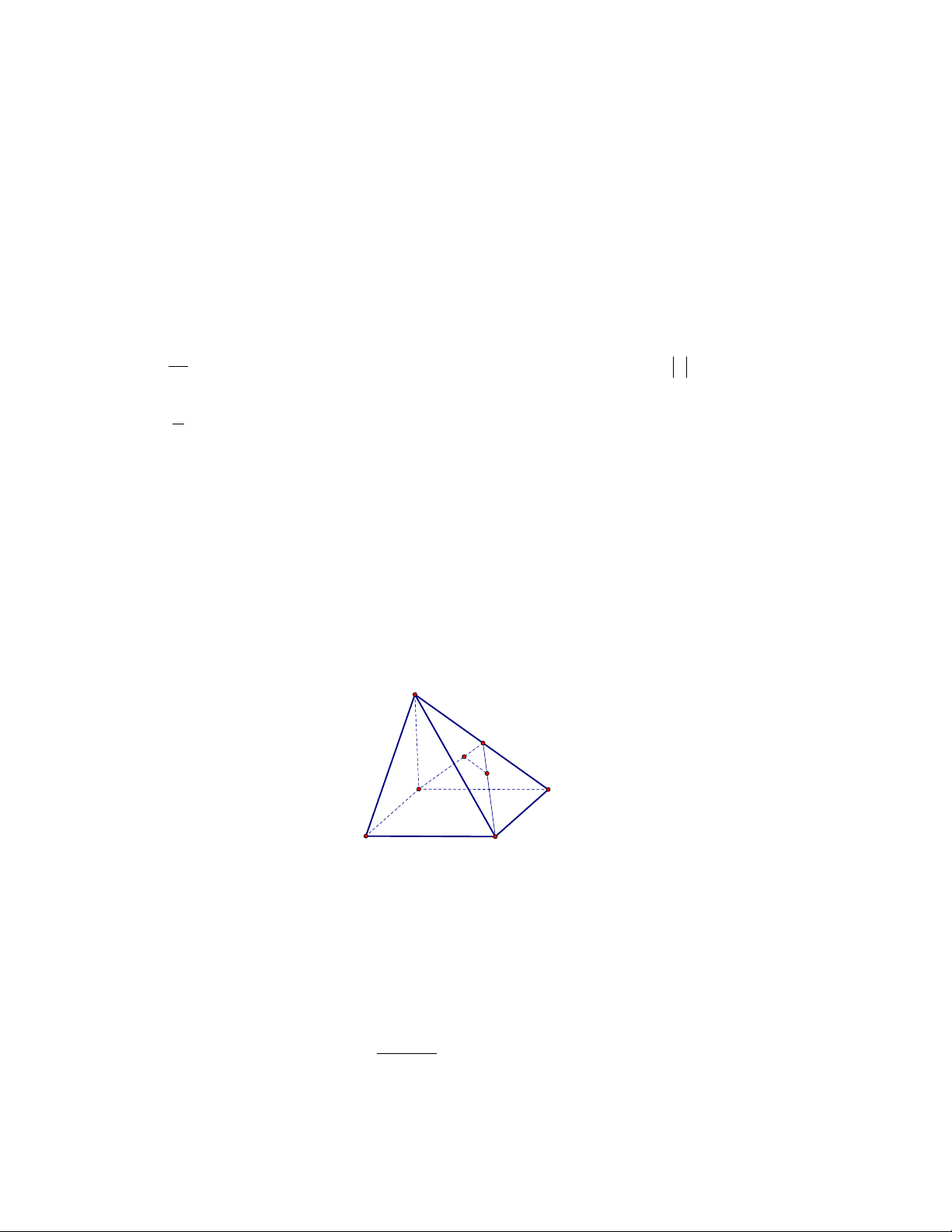
Câu 3 ( 0,5 đ) . Một người thợ đang cố gắng đặt tấm kính ABCD (mép AB không song song với
CD ) dựa vào tường sao cho mép kính CD song song với đường chân tường, còn mép kính AB
nằm hoàn toàn trên tường. Sau một hồi loay hoay, người thợ vẫn không thể đặt được tấm kính
như mong muốn. Hãy giải thích tại sao. Có cách nào đặt tấm kỉnh để một mép kính song song với
đường chân tường, một mép kính khác nằm hoàn toàn trên tường không?
Câu 4 ( 1,0đ) . Trong đợt dịch bệnh covid vừa qua, các chuyên gia y tế ước tính số người nhiễm
bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên biến đổi theo một hàm số thời gian (tính theo ngày) là 2 3
g(t)  15t  t (người). Tốc độ trung bình gia tăng người bệnh giữa hai thời điểm t ,t là 1 2
g t  g t  2   1 g(t) g(5) V  . Tính lim
và cho biết ý nghĩa của kết quả tìm được. tb t  t t 5  t  5 2 1
------------HẾT--------------------
TRƯỜNG THPT CHẾ LAN VIÊN
ĐỀ KIỂM TRA CUỐI KÌ I - NĂM HỌC 2024 - 2025 TỔ TOÁN Môn: Toán, Lớp 11 MÃ ĐỀ 102
Thời gian làm bài: 90 phút, không tính thời gian phát đề
( Đề thi gồm có 04 trang)
PHẦN I. (5 điểm) Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời câu 1 đến câu 20.
Câu 1. Khẳng định nào dưới đây là đúng ? A. sin 2x  sin .c x os . x B. 2 cos2x  2sin x 1. C. 2
cos2x  2cos x 1 .
D. sin 4x  4sinx.cosx .
Câu 2. Hàm số nào sau đây là hàm số lẻ?
A. y  cos x .
B. y  tan x  cos x . C. y  sinx .
D. y  3sin x  cos x .
Câu 3. Mệnh đề nào dưới đây là mệnh đề đúng ? 
A. sin x  1  x   k .
B. sin x  0  x  k 2 . 2  C. cos x  1
  x    k .
D. cosx  0  x   k . 2
Câu 4. Trong các dãy số hữu hạn được cho dưới đây, dãy số nào là dãy số giảm? A. 0;2;3;5; 1  . B. 6 ;4 ;2 ;1. C. 1 ;-1 ;2 ;-5 ;3. D. 8  ; 6  ; 2  ;0;3 .
Câu 5. Cho CSC u có số hạng đầu u  3  u bằng n  1
, công sai của cấp số cộng là 5. Khi đó 8 A. 35. B. 37. C. 32. D. 40.
Câu 6. Trong các dãy số sau, dãy số nào là cấp số nhân? A. 2; 4  ;8; 1  6; 3  2. B. 2;2;2 2;4;4 2. C. 5 1; 4;7;10;13 . D. 5 20;5; ; . 2 4
Câu 7. Thống kê điểm trung bình môn Toán của một số học sinh lớp 11 được cho ở bảng sau:
Giá trị trung vị của mẫu số liệu ghép nhóm trên gần bằng giá trị nào dưới đây? A. 8,15. B. 8,2. C. 8,3. D. 8,4.
Câu 8. Tuổi thọ (năm) của 50 bình ắc quy ô tô được cho như sau:
Giá trị đại diện của nhóm [3,5;4) là A. 14. B. 3,5. C. 3,75. D. 4.
Câu 9. Khẳng định nào dưới đây là đúng?
A. Nếu hai mặt phẳng phân biệt có hai điểm chung thì chúng có vô số điểm chung.
B. Nếu hai mặt phẳng phân biệt có hai điểm chung thì chúng có vô số đường thẳng chung.
C. Qua hai điểm phân biệt có vô số đường thẳng.
D. Có duy nhất một mặt phẳng đi qua bốn điểm bất kì.
Câu 10. Hình chóp có đáy là tứ giác có số cạnh là bao nhiêu? A.6. B.7. C.8. D. 9.
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm
AD và BC. Giao tuyến của hai mặt phẳng SMN và SAC là A. . SD
B. SF (F là trung điểm CD).
C. SG (G là trọng tâm tam giác ABC).
D. SO (O là tâm hình bình hành ABCD).
Câu 12. Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai đường thẳng không có điểm chung thì chéo nhau.
B. Hai đường thẳng chéo nhau thì không có điểm chung.
C. Hai đường thẳng phân biệt không cắt nhau và không song song thì chéo nhau.
D. Hai đường thẳng phân biệt không chéo nhau thì hoặc cắt nhau hoặc song song.
Câu 13. Cho tứ diện ABC .
D Gọi I,J lần lượt là trung điểm của các cạnh AC và . AD Chọn khẳng
định đúng trong các khẳng định sau? A. IJ song song với . AB B. IJ song song với . CD C. IJ chéo . CD
D. IJ song song với BC.
Câu 14. Cho hình chóp tứ giác S.ABCD . Gọi M và N lần lượt là trung điểm của SA và AB.
Khẳng định nào sau đây đúng?
A. MN // mp ABCD .
B. MN // mp SAD .
C. MN // mp SCD .
D. MN // mp SBC .
Câu 15. Trong các mệnh đề sau, mệnh đề nào đúng ?
A. Hai mặt phẳng không cắt nhau thì song song.
B. Hai mặt phẳng cùng song song với một đường thẳng thì cắt nhau.
C. Qua một điểm nằm ngoài một mặt phẳng cho trước có duy nhất một mặt phẳng song song với mặt phẳng đó.
D. Qua một điểm nằm ngoài một mặt phẳng cho trước có vô số mặt phẳng song song với mặt phẳng đó.
Câu 16. Cho hình lăng trụ ABC.A B C . Trong các khẳng định sau, khẳng định nào sai? 1 1 1
A. ABC // A B C . AA // BCC . 1 1 1 B. 1 1 C. AB // A B C .
AA B B là hình chữ nhật. 1 1 1 D. 1 1
Câu 17. Cho hình hộp ABC .
D ABC D
  . Mặt phẳng  AB D
  song song với mặt phẳng nào sau đây? A. BA C   . B. C B  D . C. BDA . D.  ACD .
Câu 18. Hình chiếu song song của hình chữ nhật không thể là hình nào trong các hình sau? A. Hình thang. B. Hình bình hành. C. Hình chữ nhật. D. Hình thoi
Câu 19. Công thức nào dưới đây là đúng? A. 1 lim  0 (với k Z  ). B. lim n
q  0 ( q  1) . k n n n 1 C. lim   . D. lim k n  0 (với k Z   ). n n n
Câu 20. Cho lim f (x)  L  0 và limg(x)   . Kết quả nào dưới đây là đúng? xx xx 0 0 A. l m i f (x).g( ) x  M  0 .
B. lim f (x).g(x)   . xx xx 0 0
C. lim f (x).g(x)   .
D. lim f (x).g(x)  L . xx xx 0 0
PHẦN II. (2 điểm) Câu trắc nghiệm đúng sai. Thí sinh trả lời câu 1 và câu 2. Trong mỗi ý a),
b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm của đoạn thẳng
SC, H và K lần lượt là trọng tâm tam giác SBC và trọng tâm tam giác SBC và SCD . Tham S M H K C B A
khảo hình vẽ bên ). Khi đó: D a. SD cắt AC.
b. SC và AB chéo nhau. c. HK / /(SBD).
d. (MHK) / /(SAC). 2  x 1  
Câu 2. Cho hàm số y f (x) x  . Khi đó: 2
a. lim f (x)   .   x2 lim f(x)  2  . b. x
c. Hàm số y  f (x) liên tục tại điểm x  2. 0
d. Hàm số y  f (x) liên tục trên từng khoảng ( ;
 2) và 2; .
PHẦN III. (3,0 điểm) Tự luận
Câu 1 ( 1,0đ) . Cho hình chóp S.ABCD đáy là hình bình hành, O là tâm của đáy.
a. Tìm giao tuyến của hai mặt phẳng SAC và SBD b. Trên cạnh S ,
A SC lần lượt lấy điểm M , N sao cho SM  3MA và SC  3SN . Tìm hình chiếu
của tam giác DMN qua phép chiếu song song lên mặt phẳng (ABC )
D theo phương chiếu . SO
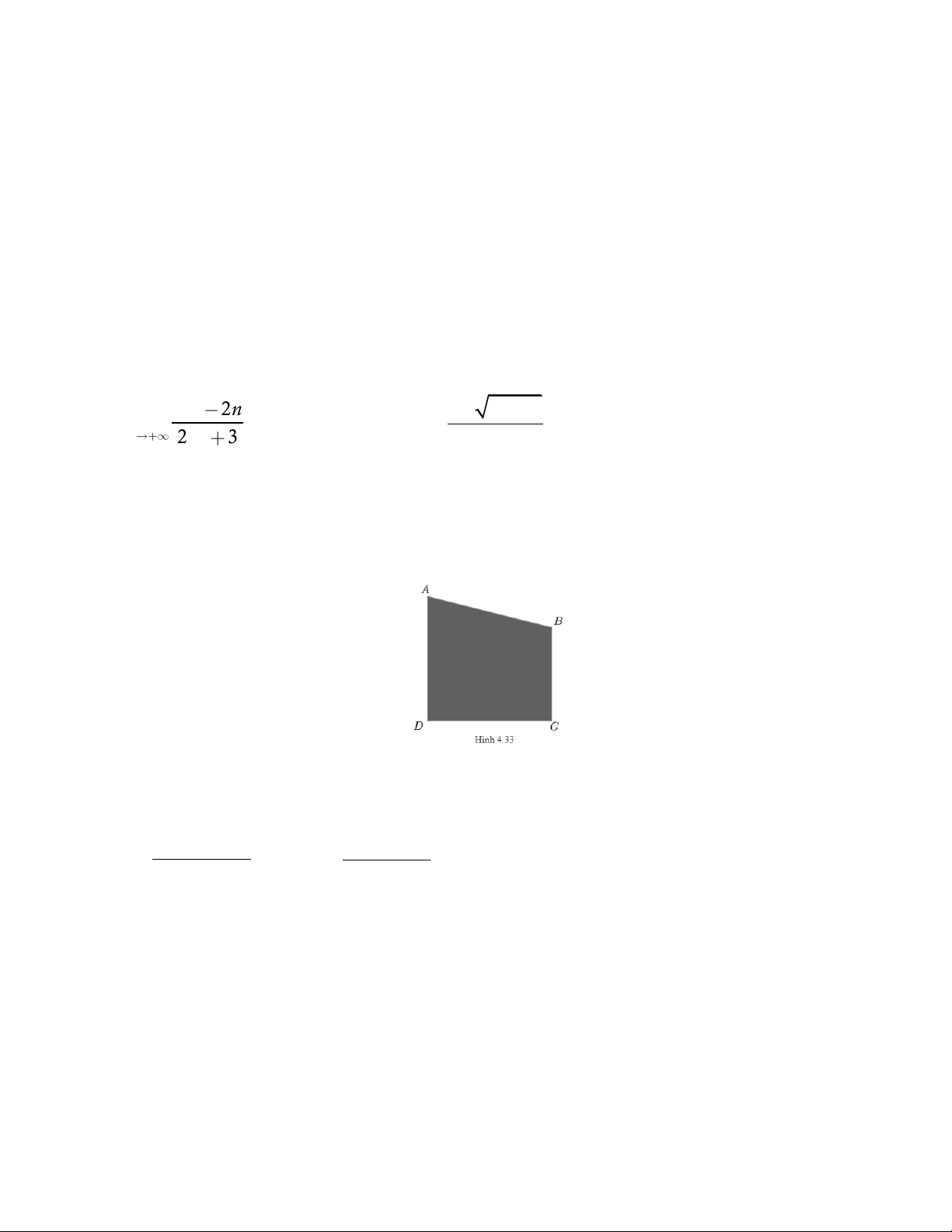
Câu 2 ( 1,0đ) . Tính các giới hạn sau : 2 5n 2n 1 4x  3 a. lim 2 . b. lim n 2n 3 x 1 2
 2x  x  3
Câu 3 ( 0,5đ). Một người thợ đang cố gắng đặt tấm kính ABCD (mép AB không song song với
CD ) dựa vào tường sao cho mép kính CD song song với đường chân tường, còn mép kính AB
nằm hoàn toàn trên tường. Sau một hồi loay hoay, người thợ vẫn không thể đặt được tấm kính
như mong muốn. Hãy giải thích tại sao. Có cách nào đặt tấm kỉnh để một mép kính song song với
đường chân tường, một mép kính khác nằm hoàn toàn trên tường không?
Câu 4 ( 0,5đ). Một vật chuyển động thẳng xác định bởi phương trình 3 2
S (t)  t  2t (S tính
bằng mét, thời gian t tính bằng giây.) Vận tốc tức thời của chuyển động giữa hai thời điểm t ,t là 1 2
S t  S t
S t   S 3 2   1 V  . Tính lim
và cho biết ý nghĩa của kết quả tìm được? tt t  t t 3 t  3 2 1
---------------HẾT-------------
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn (mỗi câu 0.25 đ) CÂU 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20
ĐỀ 1 D A C A B D B C B D B C D A C B A C B B
ĐỀ 2 C C D B C B A C A C D A B D C D B A A C
Phần II. Câu trắc nghiệm đúng sai (mỗi câu 0.25 đ) ĐỀ CÂU A B C D ĐỀ 1 1 Đ S Đ S 2 Đ S S Đ ĐỀ 2 1 S Đ Đ S 2 S Đ S Đ Phần III. Tự luận ĐỀ 1 Câu Đáp án Điểm
Câu 1 a.Tìm giao tuyến của hai mặt phẳng SAD và SBC Ta có
S SAD  (SBC) 0,5
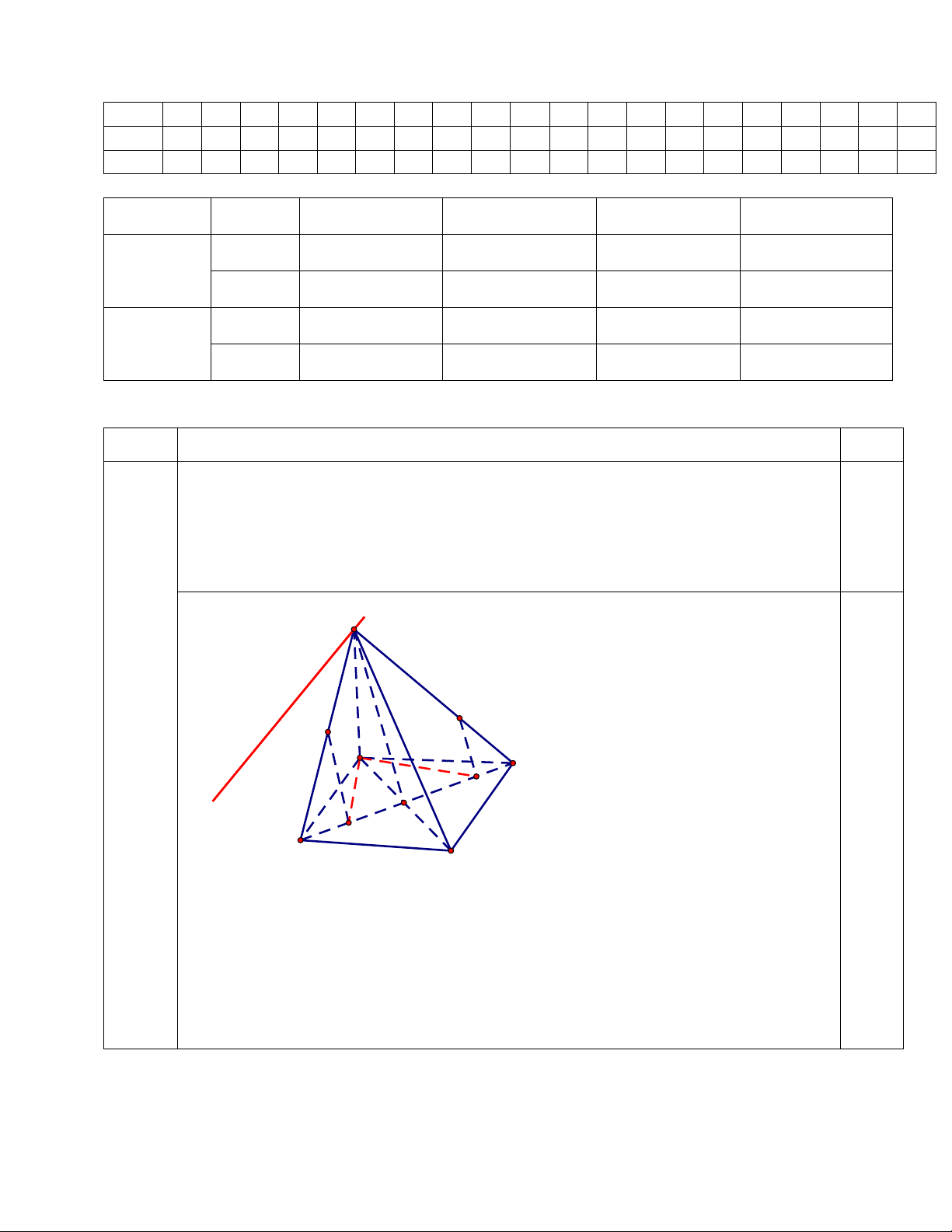
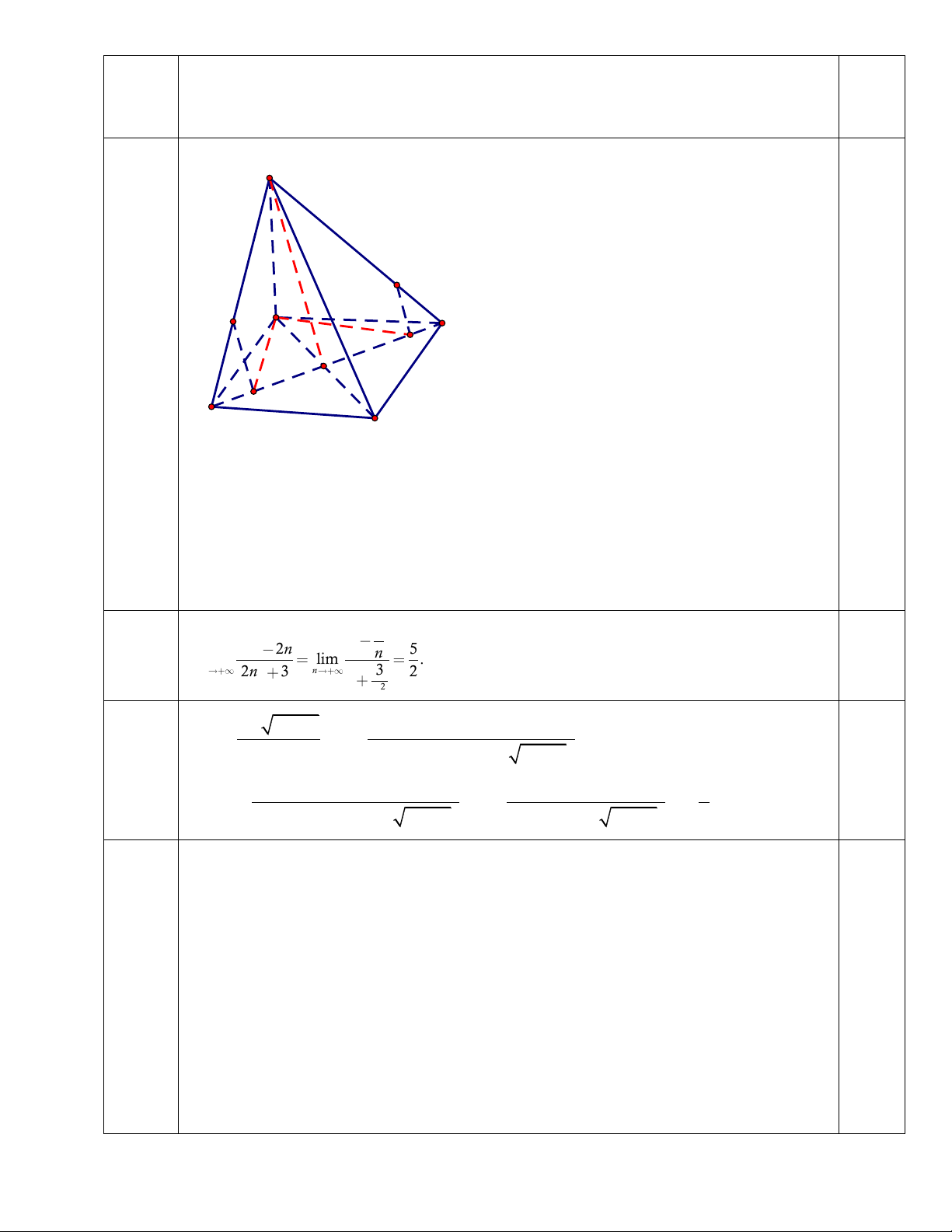
Do AD// BC nên giao tuyến là đường thẳng d đi qua S và song song với AD. S M N A B M' O N' D C b. Vẽ hình (0,25 điểm)
Trong tam giác SBO, từ M dựng MM’ // SO.
Trong tam giác SDO, từ N dựng NN’ // SO. 0,25
Khi đó, hình chiếu của tam giác AMN qua phép chiếu song song lên mặt phẳng (ABC )
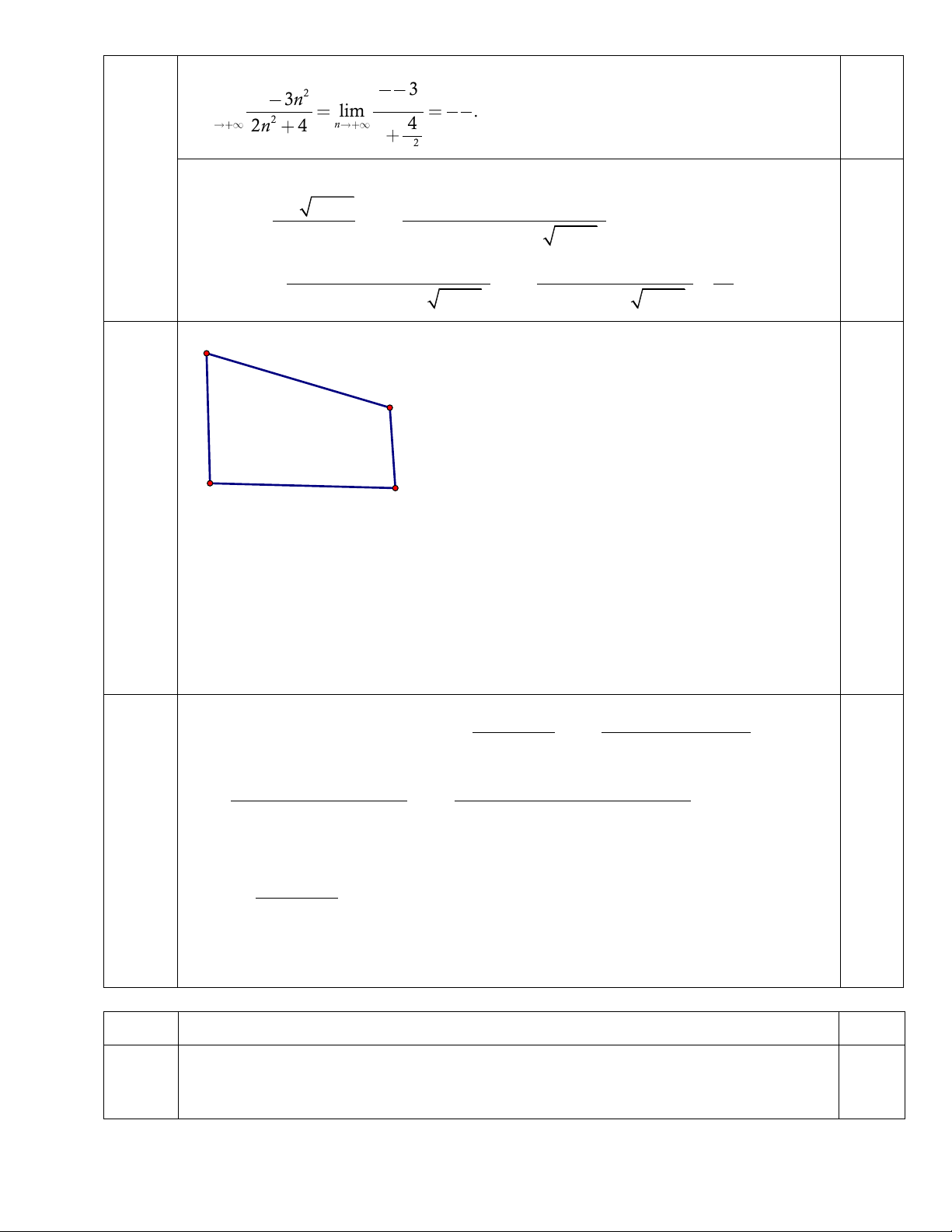
D theo phương SO là tam giác AM’N’ Câu 2 2 0,5 2 3 2n 3n 3 lim lim n . 2 n 2n 4 n 4 a. 2 2 2 n b. 0,25 2  3x 1 4  (3x 1) lim  lim 2 x 1  x 1 2x  x 1
 (x 1)2 x  1 2  3x 1 0,25 3(1 x) 3  1   lim  lim  x 1
 (x 1)2x  
1 2  3x 1 x 1  2 x  1 2  3x 1 4 Câu 3 A B D C
Giải thích: Áp dụng định lí ba đường giao tuyến cho ba mặt phẳng gồm: mặt
đất, mặt tường và mặt kính. Khi đó ba giao tuyến là mép chân tường và hai mép kính A ,
B CD . Mà AB không song song với CD nên ba giao tuyến này 0,25
đồng quy, vì vậy không thể đặt tấm kính sao cho mép CD song song với đường chân tường.
Có thể đặt tấm kính sao cho mép kính BC nằm trên tường và mép kính AD
nằm trên mặt đất. Khi đó cả hai mép kính đều song song với đường chân tường. 0,25 Câu 4 2 3 2 3
g(t)  g(5)
15t  t 15.5  5 2 3
. Ta có g(5) 155  5 . Khi đó lim  lim t 5 t 5 t  5 t  5  2 2
15t 15.5    3 3 t  5  (t  5) 15  t 5    2 2
t  5t  5  0,25  lim  lim t 5 t 5 t  5 t  5  lim 15  t  5    2 2
t  5t  5   5 7  t 5  Vậy g(t) g(5) lim  75 . t 5  t  5
Từ kết quả trên, ta thấy tốc độ tăng người bệnh ngay tại thời điểm t = 5 ngày là 0,25 75 người/ngày. ĐỀ 2 Câu Đáp án Điểm Câu 1
a. Tìm giao tuyến của hai mặt phẳng SAC và SBD 0,5
Ta có S SAC(SBD)
Gọi AC  BD  O , khi đó O  AC và O  BD nên OSAC(SBD)
Vậy giao tuyến của hai mặt phẳng SAC và SBD là SO. S M 0,25 D A N M' O N' C B Vẽ hình (0,25 điểm)
Trong tam giác SAO, từ M dựng MM’ // SO.
Trong tam giác SCO, từ N dựng NN’ // SO.
Khi đó, hình chiếu của tam giác DMN qua phép chiếu song song lên mặt phẳng (ABC )
D theo phương SO là tam giác DM’N’ Câu 3 2 0,5 2 5 5n 2n 5 lim lim n . a. 2 n 2n 3 n 3 2 2 2 n Câu 4 1 4x  3 1 4x  3 0,25 lim  lim x 1 2  x 1 2x  x  3  x  
1 2x  31 4x  3 b. 4(1 x) 4  2  lim  lim   x 1  x  
1 2x  31 4x  3 x 1
 2x  31 4x 3 5 0,25 Câu 3 Như trên. 0,5 Câu 4 Ta có: 3 2 3 2 S(t)  S(3)
t  2t  3  2.3 lim  lim t 3  t 3 t  3  t  3 3 2 0,25
S (3)  3  2.3 Khi đó  3 3 t  3  2 2  2(t  3 )  lim  lim   2 2
t  3t  3   2(t  3) 15  t 3  t 3 t  3   Vậy S(t) S(3) lim 15 t 3  t  3 0,25
Từ kết quả trên, ta thấy vận tốc tức thời của chuyển động giữa hai thời điểm t = 3(s) là 15 m/s.