Đề cuối kì 1 Toán 12 năm 2023 – 2024 trường THPT chuyên Hạ Long – Quảng Ninh

HƯỚNG DẪN GIẢI
PHẦN 1. TRẮC NGHIỆM (7 ĐIỂM) 1A 2D 3B 4D 5B 6C 7C 8D 9D
10D 11B 12D 13C 14A 15A
16A 17A 18A 19A 20C 21D 22C 23A 24A 25D 26A 27C 28A 29A 30A 31B 32A 33A 34A 35A Câu 1:
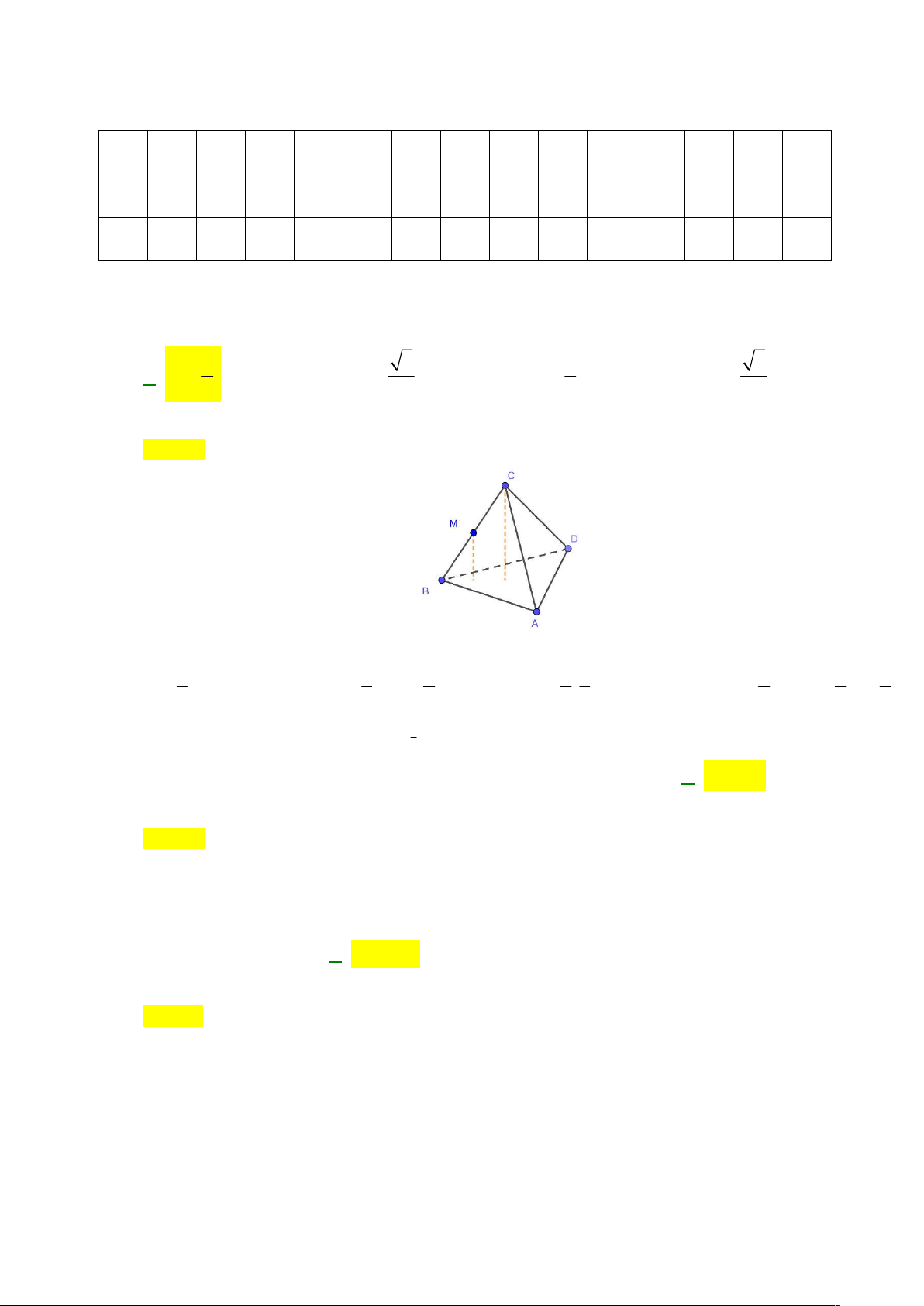
Cho khối tứ diện đều ABCD có thể tích bằng 1, M là trung điểm BC . Thể tích V của khối
chóp M .ABD bằng bao nhiêu? 1 3 1 3 A. V  . B. V  . C. V  . D. V  . 2 2 3 24 Lời giải Chọn A Ta có 1 V  S d M ABD  S d C ABD  S d C ABD  V   AB  D  1 1 1 1 1 1 1 . . ,  . . . A  BD  ,  . . . A  BD  ,  . .1 3 3 2 2 3 2 ABCD 2 2 1 Câu 2:
Tập xác định của hàm số y   x  5 1 là A.  .
B. 0;  .
C. 1;  . D. 1;   . Lời giải Chọn D
Hàm số xác định khi x 1  0  x  1 Câu 3:
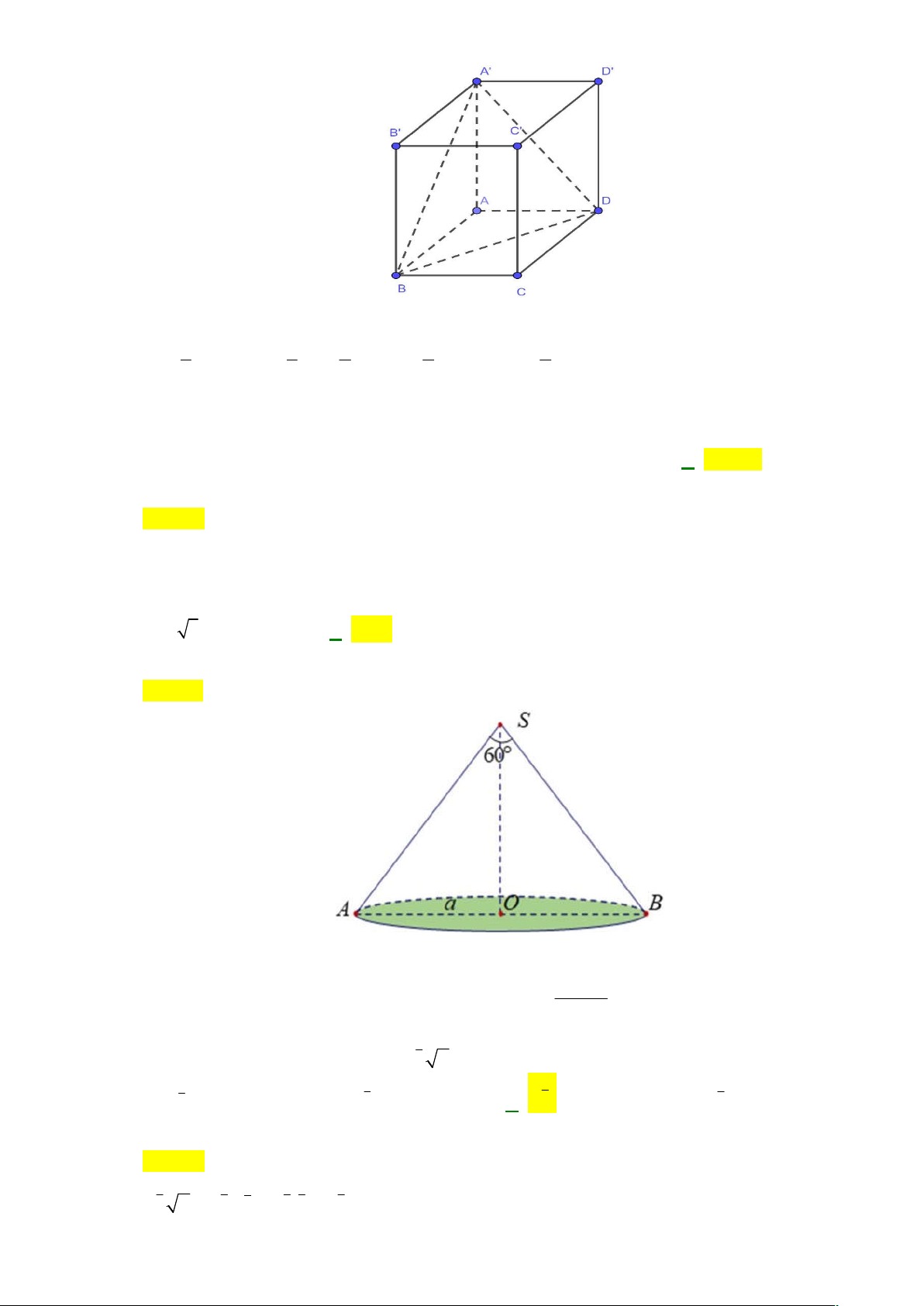
Gọi V là thể tích của khối lập phương ABCD.AB C  D
  , V là thể tích khối tứ diện AABD . Hệ 1 2
thức nào sau đây là đúng?
A. V  8V .
B. V  6V .
C. V  2V .
D. V  4V . 1 2 1 2 1 2 1 2 Lời giải Chọn B Ta có: 1 1 1 1 1
V  .AA' S  .AA'. .S  .AA'.S  .V 2 AB  D A  BCD AB  CD 1 3 3 2 6 6  V  6V 1 2 Câu 4:
Thể tích V của khối lăng trụ có diện tích đáy bằng 3 và độ dài đường cao bằng 4 là
A. V  4 .
B. V  6 .
C. V  8 . D. V  12 . Lời giải Chọn D Ta có V  . B h  3.4  12 Câu 5:
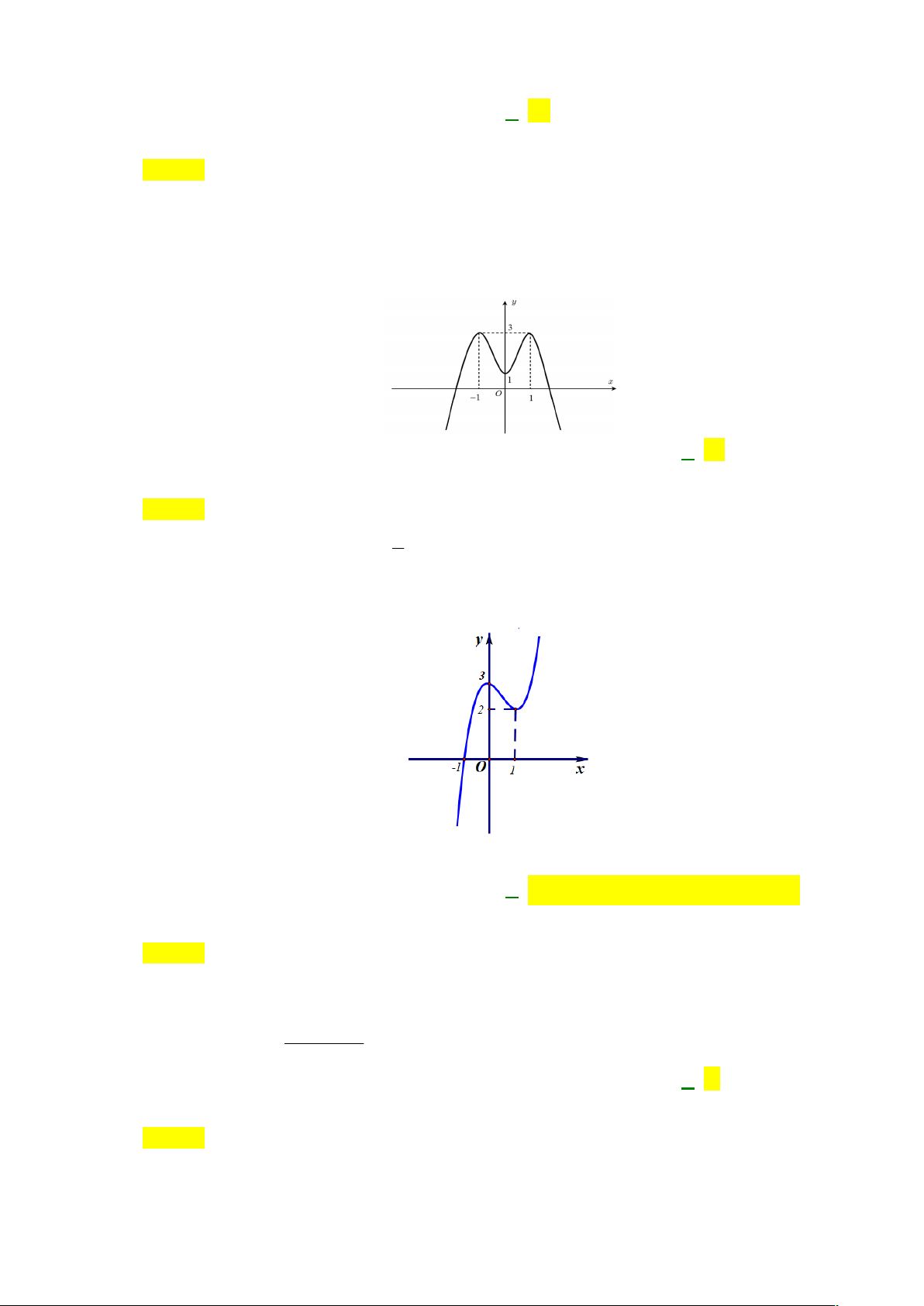
Một hình nón có góc ở đỉnh bằng 60 và bán kính đáy bằng 4 . Diện tích xung quanh của hình nón đó bằng: A. 9 3 . B. 32 . C. 64 . D. 3 . Lời giải Chọn B
Giả sử hình nón có đỉnh là S, O là tâm của đường tròn đáy và AB là một đường kính của đáy.  OA o 
Ta có r  OA  4, ASB  60  ASO  30o  l  SA   8  S   rl  32 sin 30o xq 2 Câu 6:
Cho a là một số dương, biểu thức 3 a
a viết dưới dạng lũy thừa với số mũ hữu tỉ là 5 6 7 4 A. 6 a . B. 7 a . C. 6 a . D. 3 a . Lời giải Chọn C 2 2 1 2 1 7  3 3 2 3 2 6 a
a  a .a  a  a . Câu 7:
Cho hàm số f  x có đạo hàm 3 f (
 x)  x(x  2) . Số điểm cực trị của hàm số đã cho là A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn C
Số điểm cực trị của hàm số đã cho là 2 . Câu 8:
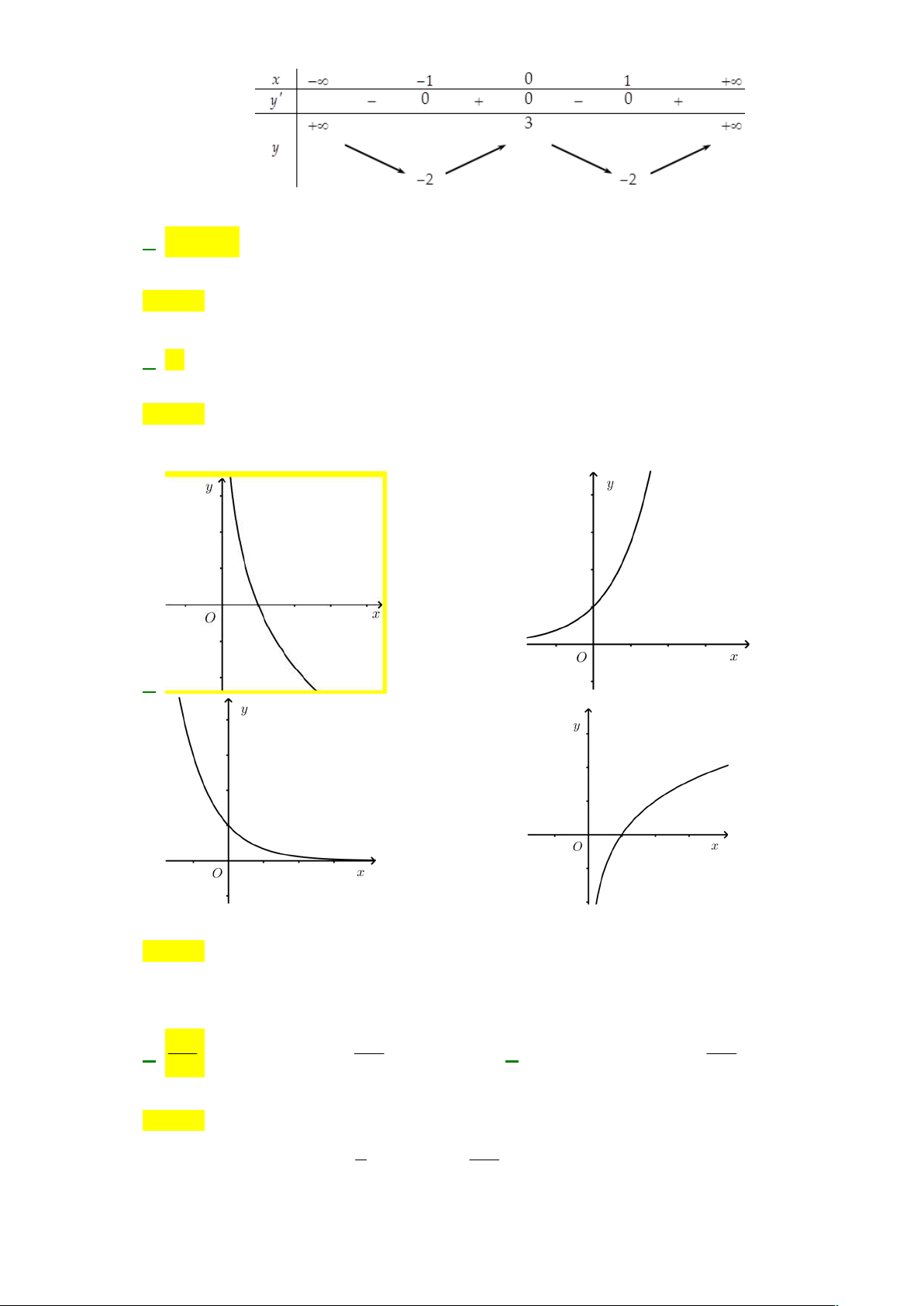
Cho hàm số bậc bốn y  f  x có đồ thị như hình vẽ bên. Số nghiệm của phương trình
2 f  x  5  0 là A. 4 . B. 3 . C. 1. D. 2 . Lời giải Chọn D 5
Ta có 2 f  x  5  0  f  x   . Dựa vào đồ thị hàm số ta thấy phương trình có hai nghiệm. 2 Câu 9:
Cho hàm số f  x . Hàm số y  f (x) có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây là đúng?
A. Hàm số f  x đạt cực tiểu tại x  1 .
B. Hàm số f  x đạt cực tiểu tại x  0 .
C. Hàm số f  x đạt cực đại tại x 1.
D. Hàm số f  x đạt cực tiểu tại x  1 . Lời giải Chọn D
Dựa vào đồ thị hàm số ta thấy hàm số f  x đạt cực tiểu tại x  1 . x 1
Câu 10: Đồ thị hàm số y 
có bao nhiêu tiệm cận đứng? 2 x  3x  2 A. 2 . B. 3. C. 0 . D. 1. Lời giải Chọn D
Tập xác định D   \ 1;  2 . Ta có
lim y  lim y  1
 nên x 1 không là tiệm cận đứng; x 1  x 1  lim y   x 2  
nên x  2 là tiệm cận đứng. lim y     x 2 
Vậy đồ thị hàm số đã cho có một đường tiệm cận đứng.
Câu 11: Cho hình chóp S.AB D
C có đáy AB D
C là hình vuông cạnh a . Cạnh bên SA vuông góc với mặt
đáy và SB tạo với mặt đáy một góc 45o . Thể tích V của khối chóp S.A D
O , với O là tâm của hình vuông AB D C là 3 a 3 a A. 3
V  a . B. V  . C. V  . D. 3 4a . 12 2 Lời giải Chọn B
+) Tam giác SAB vuông cân tại A  SA  AB  a 3 1 1 1 a Vậy V  S .SA  . S .SA  AOD ABCD 3 3 4 12 2x  4
Câu 12: Đường thẳng y  4  2x cắt đường cong y  tại mấy điểm? x 1 A. 2 . B. 3 . C. 0 . D. 1. Lời giải Chọn D Xét phương trình hoành độ giao điểm  x  1 2x 4    4  2x   x 1 2x  4  
4  2x x   2
1  2x  0  x  0  Vậy có 1 giao điểm
Câu 13: Diện tích xung quanh của hình trụ có độ dài đường sinh l và bán kín là r bằng 1
A. 4 rl .
B.  rl .
C. 2 rl . D.  rl . 3 Lời giải Chọn C
Câu 14: Diện tích mặt cầu S  có tâm I bán kính bằng a là 2  a A. 2 4 a . B. . C. 2  a . D. 2 2 a . 4 Lời giải Chọn A
Câu 15: Cho hàm số f  x có bảng biến thiên như hình bên.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. ; 2 .
B. ; 0 .
C. 0;  . D. 1  ;1 . Lời giải Chọn A
Câu 16: Khối lập phương có số đỉnh là A. 8 . B. 6 . C. 4 . D. 10 . Lời giải Chọn A
Câu 17: Cho số thực a  0; 
1 . Đồ thị hàm số y  log x là đường cong nào dưới đây? a A. . B. . C. . D. . Lời giải Chọn A
Câu 18: Cho tứ diện OABC có O ,
A OB, OC đôi một vuông góc và OA  a, OB  b, OC  c . Tính thể tích
khối tứ diện OABC . abc abc abc A. . B. . C. abc . D. . 6 2 3 Lời giải Chọn A 1 abc
Thể tích khối tứ diện là V  O . A O . B OC  . 6 6
Câu 19: Cho hình nón có bán kính đáy bằng r , đường sinh bằng l và chiều cao bằng h . Diện tích xung
quanh của hình nón đó bằng
A.  rl .
B. 2 rh .
C. 2 rl . D.  rh . Lời giải Chọn A Câu 20: Hàm số 4 2
y  x  2x 1 đồng biến trên khoảng nào dưới đây?
A. 1;  .
B. 0;  . C.  ;    1 . D.  ;  0 . Lời giải Chọn C  x  0
Tập xác định của hàm số là D   . Có 3 
y  4x  4x; y  0  x  1 .  x  1 
Xét dấu y ta thấy y  0 khi x  ;   1  0; 
1 nên hàm số đã cho đồng biến trên các khoảng ;   1 và 0;  1 .
Câu 21: Tổng các nghiệm của phương trình 2
log x  7 log x 12  0 bằng 1 2 2 A. 7. B. 25. C. 20. D. 24. Lời giải Chọn D Với x  0 ta có: log x  4 x  16 2 2 2
log x  7 log x 12  0  log x  7 log x 12  0   1 2 2 2   log x  3 x  8 2  2 
Vậy tổng các nghiệm của phương trình là 24.
Câu 22: Cho a  1. Mệnh đề nào sau đây đúng? 1 1 3 2 a 1  1 A. 2016 2017 a  a . B.  1. C. 3 a  . D. 3 a  a . a 5 a Lời giải Chọn C  1
Do  3   5 và a  1 nên  3  5 a  a hay 3 a  5 a
Câu 23: Tính tổng các nghiệm của phương trình log x 1  log
x  2  1 là 2   2   A. 0. B. 1. C. 3. D. 3.  Lời giải Chọn A
Điều kiện: x  1   x  0(tm)
Ta có: log  x  
1  log  x  2 2
 1  log (x 1)(x  2)  1  x  3x  0  2 2 2  x  3  (l) 
Vậy tổng các nghiệm của phương trình bằng 0
Câu 24: Cho hàm số y x 
với x  0,   R . Phát biểu nào sau đây đúng về hàm số đã cho?
A. Đồ thị hàm số luôn đi qua điểm (1;1) .
B. Hàm số nghịch biến trên khoảng (0; ) .
C. Đồ thị hàm số y x 
luôn có đường tiệm cận ngang.
D. Hàm số đồng biến trên khoảng (0; ) . Lời giải Chọn A
Câu 25: Số nghiệm thực của phương trình x x2 4  2  3  0 là A. 1. B. 0. C. 3. D. 2. Lời giải Chọn D 2x  3  x  log 3 x x2 2 x x 2 4  2
 3  0  2  4.2  3  0     . 2x  1 x  1  
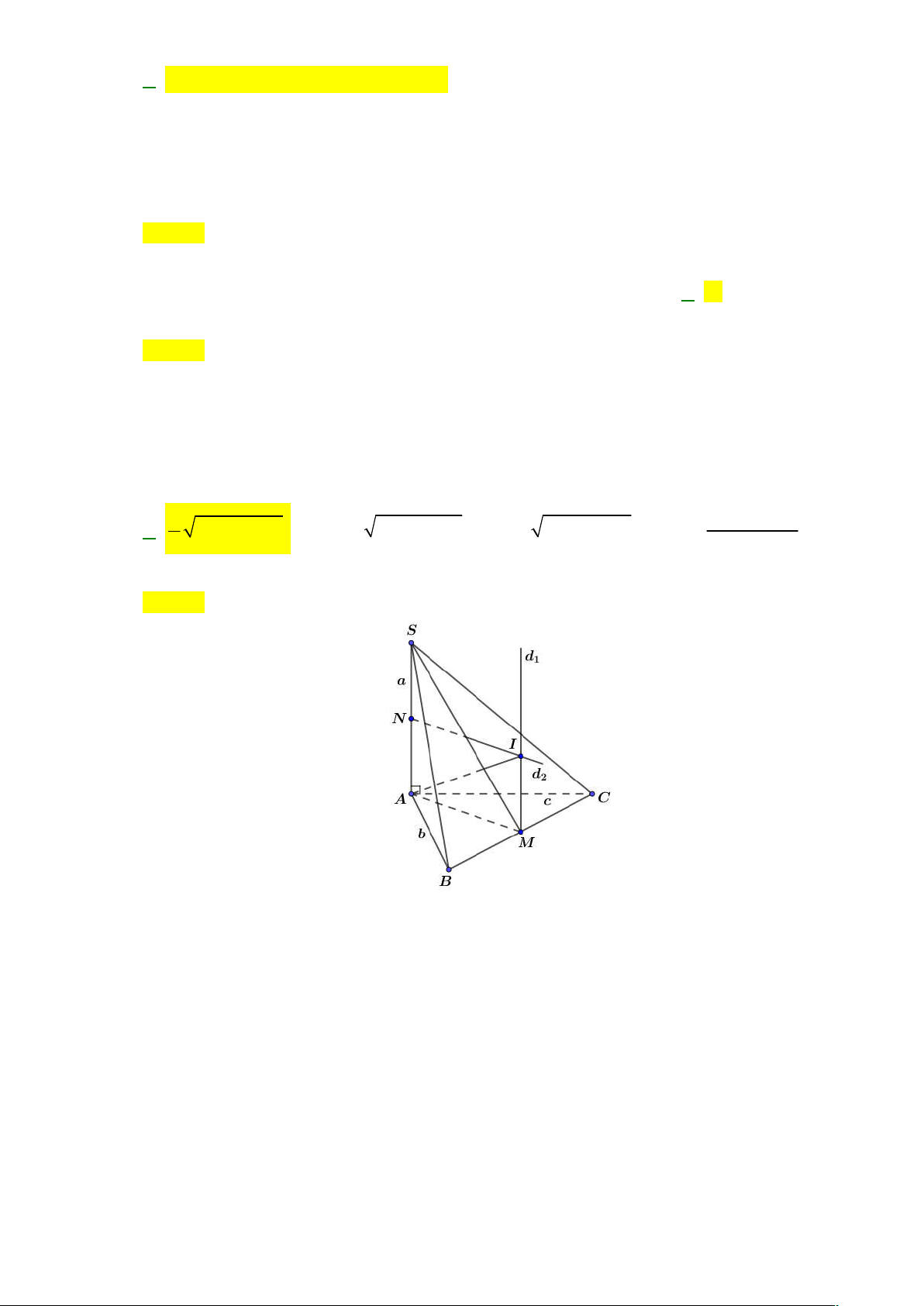
Câu 26: Hình chóp S.ABC có đáy là tam giác ABC vuông tại A , có SA vuông góc với mặt phẳng
 ABC và có SA  a, AB  b, AC  c . Mặt cầu đi qua các đỉnh ,
A B, C, S có bán kính bằng 1
2 a  b  c A. 2 2 2
a  b  c . B. 2 2 2
2 a  b  c . C. 2 2 2
a  b  c . D. . 2 3 Lời giải Chọn A
Gọi M , N lần lượt là trung điểm của BC, SA. Vì tam giác ABC vuông tại A nên M là tâm
đường tròn ngoại tiếp tam giác ABC .
Dựng đường thẳng d vuông góc với  ABC tại M . 1
Các điểm nằm trên đường thẳng d cách đều , A ,
B C . Đường thẳng d là trục đường tròn của tam 1 1
giác ABC . Do SA   ABC, d  ABC  SA / /d , SA và d đồng phẳng. 1   1 1
Dựng đường thẳng d vuông góc với SAtại N cắt d tại I . 2 1
I  d  IA  IB  IC , I  d  IA  IS . 1 2
Vì vậy I cách đều các đỉnh của hình chóp S.ABC nên I là tâm mặt cầu ngoại tiếp hình chóp 1 a
S.ABC và bán kính mặt cầu là 2 2
R  IA  IN  NA , mà AN  SA  2 2
Do tam giác ABC vuông tại A nên 2 2 2 2 BC 
AB  AC  b  c . 2 2 1 b  c Mà AM  BC  AM  . 2 2
Khi đó mặt cầu đi qua các đỉnh ,
A B, C, S có bán kính là: 1 2 2 2 2 2 R  IA  IN  NA 
a  b  c . 2 2
Câu 27: Đặt log 2  a , khi đó log bằng 3 3 27 2 2  1  A. a  2 .
B. 2a  4 .
C. a  3 .
D.  a  2 . 4  2  Lời giải Chọn C 2 Ta có log
 log 2  log 27  a  3 3 3 3 27
Câu 28: Cho hình lập phương cạnha. Tính thể tích khối cầu ngoại tiếp hình lập phương đó. 3 3 4 a 3 4 a 2 A. 3  a . B. . C. 3 4 a 2 . D. . 2 3 3 Lời giải Chọn A a 3
Bán kính khối cầu ngoại tiếp hình lập phương cạnh a là r  . 2 3 3 4 4  a 3   a 3
Thể tích khối cầu ngoại tiếp hình lập phương là: 3 V   r      . 3 3  2  2  
Câu 29: Tính thể tích V của khối trụ có bán kính đáy r  4 và chiều cao h  4 2 .
A. V  64 2 .
B. V  32 .
C. V 128 .
D. V  32 2 . Lời giải Chọn A
Thể tích V của khối trụ có bán kính đáy r  4 và chiều cao h  4 2 là
V  r h    2 2 4 4 2  64 2 .
Câu 30: Xét các số thực a, b thỏa mãn log 2a.8b   2 . Mệnh đề nào là đúng? 2
A. a  3b  2 .
B. a  3b  4 .
C. a  3b  6 .
D. a  3b  8 . Lời giải Chọn A 3b Ta có log 2a.8b 2 log 2a log 2 2 a 3b 2 . 2      2 2      
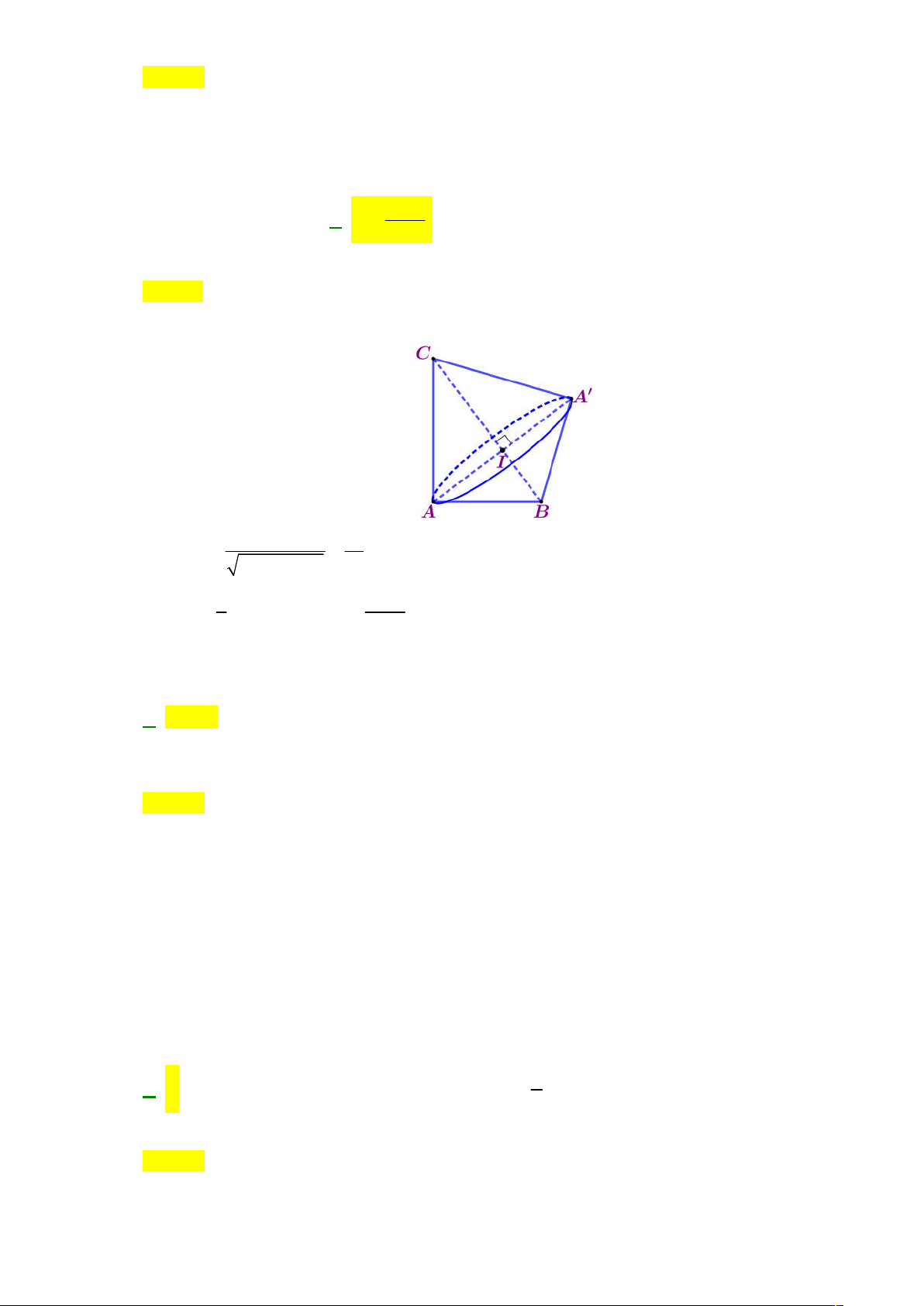
Câu 31: Cho tam giác ABC có AB  3; AC  4; BC  5 . Quay tam giác ABC xung quanh cạnh BC ta
được khối tròn xoay có thể tích V bằng: 144
A. V  20 . B. V  .
C. V  16 .
D. V  12 . 15 Lời giải Chọn B Ta có: 2 2 2
AB  AC  BC  25  ABC  tại A . . AB AC 12 Tính AI   . 2 2 5 AB  AC 1 144 Tính 2
V   AI .CI  BI   . 3 15
Câu 32: Tìm giá trị thực của tham số m để phương trình 2
log x  m log x  m 1  0 có hai nghiệm thực 5 5
x , x thỏa mãn x x  625 . 1 2 1 2
A. m  4 .
B. m  44 . C. m  4  .
D. Không có giá trị nào của m . Lời giải Chọn A
Điều kiện x  0 . Đặt  log   5t t x x
, phương trình ban đầu trở thành 2
t  mt  m  1  0   1 . 5
Điều kiện bài toán   
1 có 2 nghiệm t , t thỏa t  t  log 625  4 1 2 1 2 5 2
  m  4m  4  0    m  4 . m  4 
Câu 33: Biết phương trình log
3x 1 . 1 log 3x 
1   0 có hai nghiệm x , x trong đó x  x . Tính 3   3     1 2 1 2
2x  x . 2 1 2 A. 1. B. 2 . C. . D. 1. 3 Lời giải Chọn A
Điều kiện 3x 1  0  x  0 . x log 3x 1  0 3 1  1 3  
Phương trình log 3x 1 . 1
  log 3x 1   0     3   3     x 1 1
  log 3x 1  0 3 1  3     3  x  log 2 3   4 .  x  log3  3 4
Ta có 2x  x  2 log 2  log  1. 2 1 3 3 3
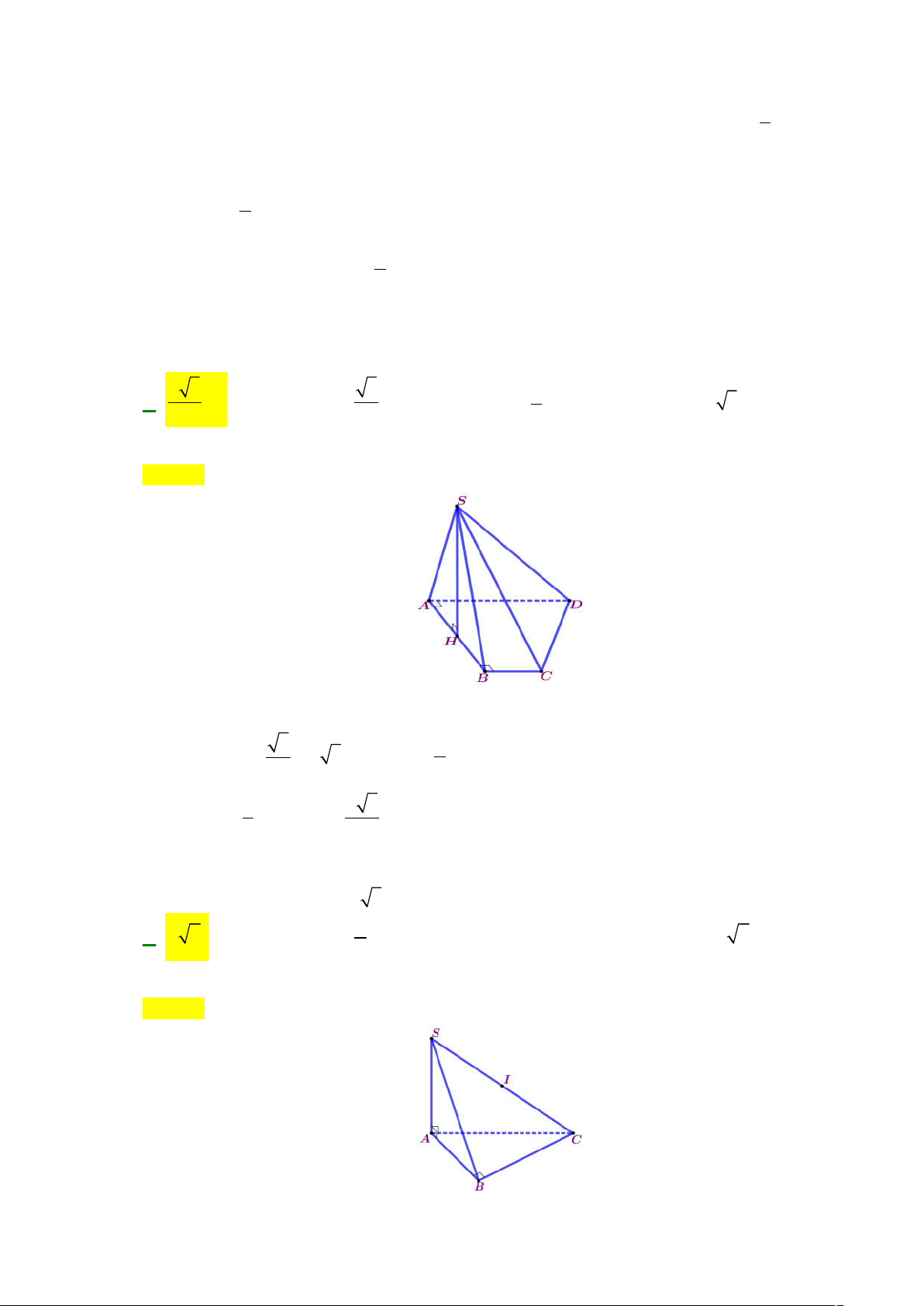
Câu 34: Cho hình chóp tứ giác S.ABCD , ABCD là hình thang vuông tại A và B biết AB  2a ,
AD  3BC  3a . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy.Tính
thể tích khối chóp S.ABCD theo a . 4 3 3 8 A. 3 a . B. 3 a . C. 3 a . D. 3 2 3a . 3 3 3 Lời giải Chọn A
Gọi H là trung điểm AB . Vì SAB   ABCD  SH   ABCD . 3 1 Ta có: SH  2 . a  a 3 và S  .2 . a
a  a  a . ABCD 3  2 4 2 2 1 4 3 Thể tích 3 V  SH .S  a . 3 ABCD 3
Câu 35: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC  , tam giác ABC vuông tại B .
Biết SA  2a, AB  a, BC  a 3 . Tính bán kính R của mặt cầu ngoại tiếp hình chóp. a A. a 2 . B. . C. a . D. 2a 2 . 2 Lời giải Chọn A
Gọi I là trung điểm BC . Ta có:  
SAC  SBC  90  4 điểm S, ,
A B, C nằm trên mặt cầu tâm I , bán kính 2 2 2 SC
SA  AB  AC R    2a 2 2
PHẦN 2. TRẮC NGHIỆM (3 ĐIỂM)
Câu 36: Giải các phương trình
a. log x  log  2 x
 log (2x)  3 . b. log 5x  1 log  x 1 5     5  1. 5 25  2 2  2 Lời giải
a. Điều kiện: x  0. Do x  0  x  . x x  0  x  0 log x  log  2 x
 log (2x)  3    2 2  2 
log x  2 log x  log 2  log x  3 4 log x  2   2 2 2 2  2 x  0 x  0     1    x 
2. Tập nghiệm của phương trình là S   2. log x   x  2 2   2 5  x  1  0
b. Điều kiện của phương trình:   x  0. x 1 5    5  0  x  0 x  0 x x   log 5   1 1  log 5   5  1    5 25   x x  log 5 1  1   log 5 1   2 log
5x 1  log 5x 1  2  0 5    5   2 5       5    x  0 x  x  0 0 x  0   x x  x    log 6 5  x  5 1  5   5  6 x  log 6 log 5 1  1   5      5         26 .      x x  x 1  x 26 26  log  log 5 1  2  5 1   5   x  log  25 5       5 5    25  25   25  26 
Tập nghiệm của phương trình là S  log 6;log . 5 5  25 
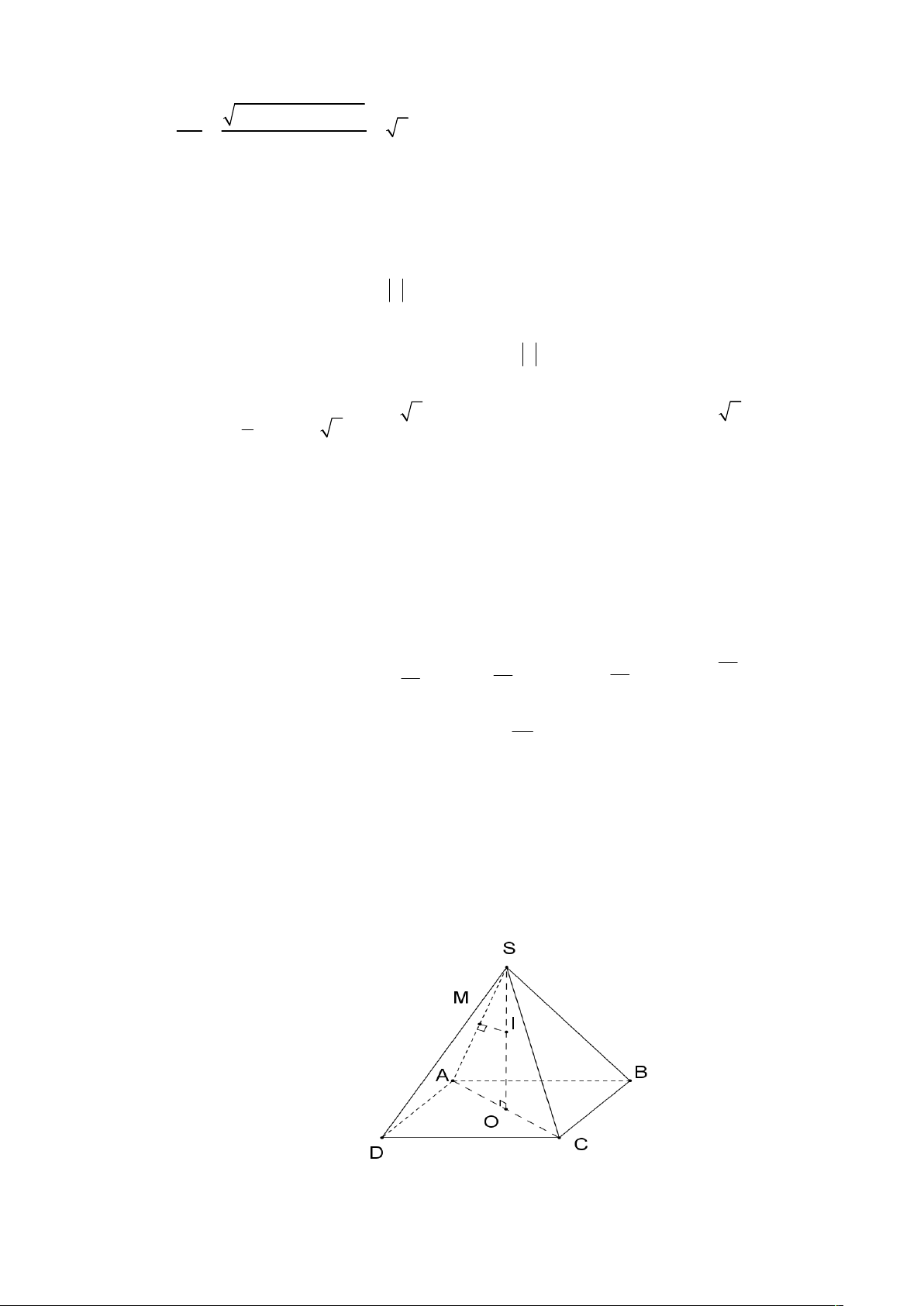
Câu 37: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O , cạnh AB  4, BC  2, SO vuông
góc với mặt đáy (ABCD) và cạnh bên SA  3 .
a. Hình nón (N) đỉnh S và có đáy là đường tròn qua các điểm A, B, C, D . Tính thể tích khối nón (N).
b. Tính bán kính mặt cầu đi qua các điểm S, A, B, C, D . Giải
a. Hình nón có đường cao, bán kính đáy, độ dài đường sinh lần lượt là h  SO, r  O , A SA  3. 2 2 2 2 AC AB  BC 4  2
Bán kính đáy của nón là r     5. 2 2 2 Chiều cao nón 2 2 2
h  SO  SA  OA  3  5  2. 1 1 10 Thể tích khối nón là 2 V 
 r h   .5.2  . 3 3 3
b. Gọi M là trung điểm của S .
A Trong mặt phẳng SOA , kẻ
MI  SO, I  SO  IA  IB  IC  ID  IS  I là tâm mặt cầu đi qua các điểm S, A, B, C, D.
Khi đó bán kính mặt cầu bằng R  IS. 2 . 9 Ta có   SI SM SM SA SA SMI SOA    R  SI    . SA SO SO 2SO 4 3
Câu 38: Cho phương trình 2x .3x.4x  m
a. Giải phương trình với m  1.
b. Tìm các giá trị của m để phương trình có ít nhất một nghiệm lớn hơn 2. Lời giải 3
a. Ta có: 2x .3 .4 x x  m  1 . 3 3 3 Với m  1,   1 2x .3x.4x 1 log 2x .3x.4x log 1 log 2x log 3x log 4x         0 2   2 2 2 2 3
 x  x log 3  2x  0  x  2
x  log 12  0  x  0 .Vậy S    0 . 2 2  3 3 3 b. x x x x x log 3 2 x
x  xlog 32 2 2  2 .3 .4  m  2 .2 .2  m  2  m * 3 Xét hàm số   log2 3 2 2x x f x    trên 2;  3
Ta có: f  x
x  xlog2 32  2  2
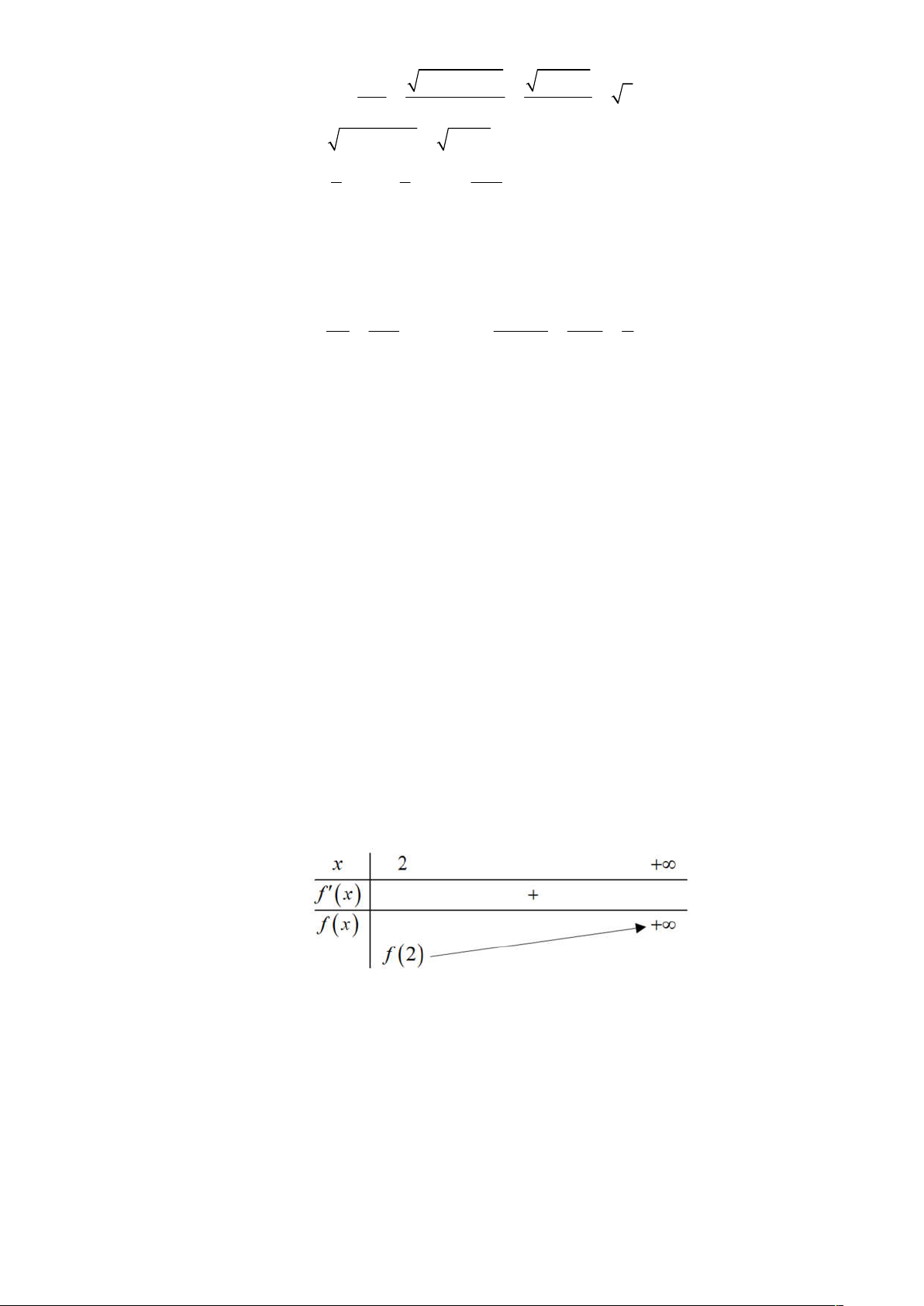
3x  log 3  2 ln 2  0, x   2;  . 2    Bảng biến thiên: Phương trình  
* có ít nhất một nghiệm trên 2;  khi m  f 2 82log2 32  2  36864
---------- HẾT ----------
Document Outline

• de-cuoi-ki-1-toan-12-nam-2023-2024-truong-thpt-chuyen-ha-long-quang-ninh
• TOÁN-LỚP12-CKI-THPT-CHUYÊN-HẠ-LONG-QUẢNG-NINH-NH-23-24