Đề cuối kỳ 1 Toán 10 năm 2024 – 2025 trường THPT chuyên Trần Phú – Hải Phòng

SỞ GD & ĐT HẢI PHÒNG
ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2024 - 2025
Môn: TOÁN; Khối: 10
Ngày thi: ………….
Thời gian làm bài: 90 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC
(Đề thi có 04 trang) Mã đề thi 101
Họ, tên thí sinh:.......................................................................................
Số báo danh:............................................................................................
PHẦN I (4 điểm). Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu
16. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Trên đoạn thẳng AB lấy điểm I sao cho AB = 4AI . Đẳng thức nào sau đây đúng?         A. 4 IB = − AB . B. 4 IB = AB .
C. IB = 3IA . D. IB = 3 − IA . 3 3  
Câu 2. Cho tam giác đều ABC có cạnh bằng .
a Tính tích vô hướng A . B AC. 2   2   A. . a AB AC = − . B. . a AB AC = . 2 2 2     C. a 3 A . B AC = − . D. 2 A . B AC = 2a . 2
Câu 3. Cho tam giác ABC có =  0 =  0
AB 3, A 30 , B =120 . Hãy chọn khẳng định đúng. A. AC = 4 3 . B. AC = 3 3 . C. AC = 3 . D. AC = 2 3 . Câu 4. Cho góc α ( 0 0
0 < α <180 ) thỏa mãn 1
cotα = − . Giá trị cosα bằng 2 A. 5 ± . B. 5 − . C. 5 − . D. 5 . 5 2 5 5  
Câu 5. Cho tam giác ABC vuông tại A có AB = 3c ,
m BC = 5cm . Khi đó AB + BC là: A. 4. B. 13 . C. 2 13 . D. 8.       
Câu 6. Cho hai vectơ a và b khác 0 . Xác định góc α giữa hai vectơ a và b khi .
a b = − a . b . A. o α = 45 . B. o α =180 . C. o α = 90 . D. o α = 0 .
Câu 7. Cho hai tập hợp A = ( ; −∞ ]
3 ; B = (1;5] . Khi đó, tập A∪ B là A. (1;3] . B. ( ; −∞ 5] . C. ( ; −∞ 1) . D. (3;5].
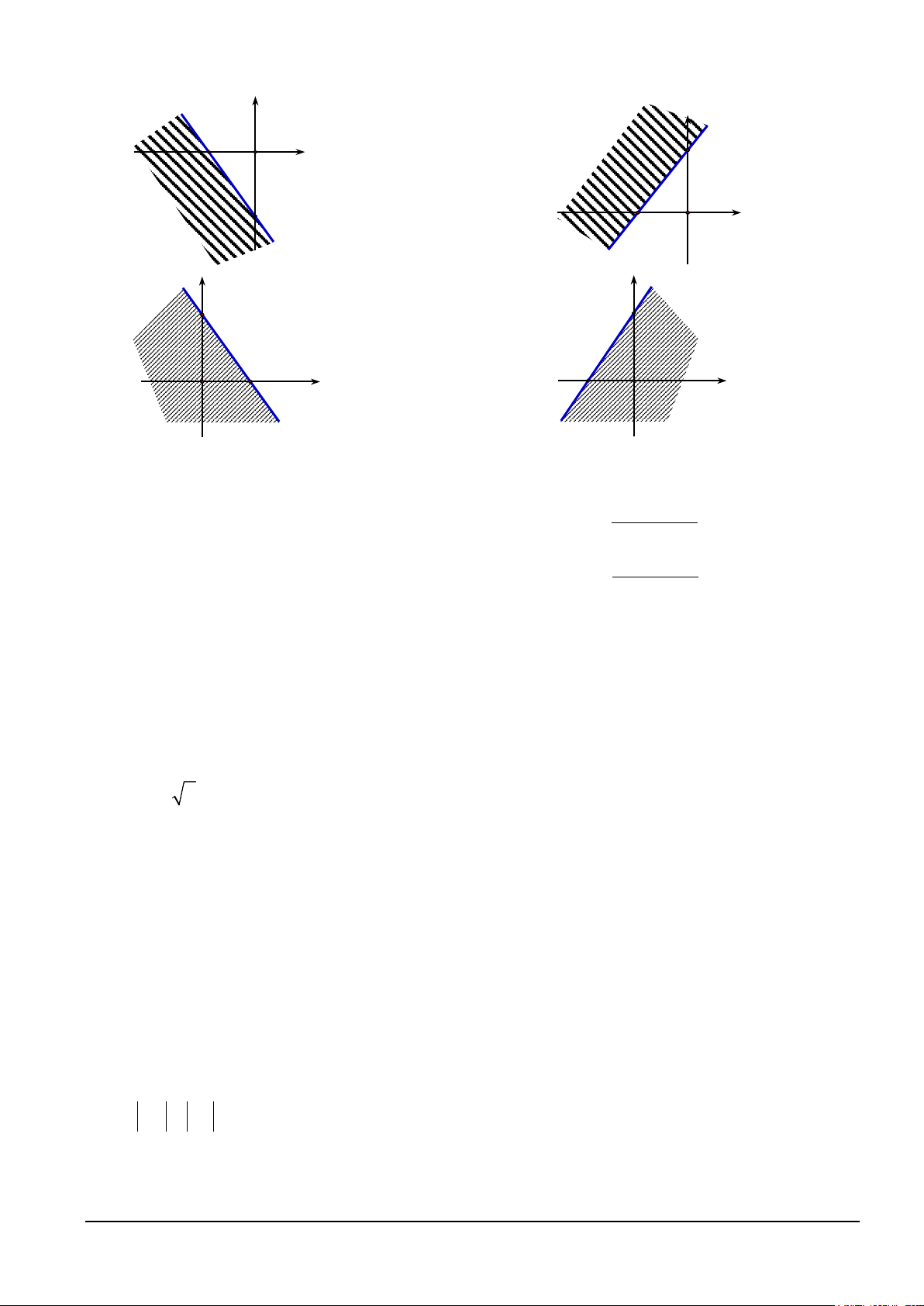
Câu 8. Miền không bị gạch kể cả bờ trong hình vẽ nào dưới đây là miền nghiệm của bất phương trình 3x − 2y ≥ 6 − ? Mã đề 101 Trang 1/4 y y 2 − 3 O x 3 2 − O x A. . B. . y y 3 3 2 x 2 − O O x C. . D. .
Câu 9. Cho tam giác ABC . Mệnh đề nào dưới đây sai ? 2 2 2 A. 2 2 2 a + −
= b + c + 2bc cos A. B. cos a c b B = . 2ac 2 2 2 C. 2 2 2 a + −
= b + c − 2bc cos A. D. cos b c a A = . 2bc
Câu 10. Cho hai tập hợp A = {2;3;4; } 5 và B = {1;2; }
3 . Có tất cả bao nhiêu tập X thỏa mãn: X ⊂ A và X ⊂ B ? A. 2. B. 6. C. 4. D. 8.    
Câu 11. Trong mặt phẳng tọa độ Oxy , cho a = 4 j − i . Tọa độ của vectơ a là:     A. a = (4;− ) 1 . B. a = ( 1; − 4 − ) . C. a = ( 1; − 4) . D. a = ( 4; − ) 1 .
Câu 12. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?  2 3
 x − 20y > 7
A. x + y > 3  . B.  .
x − y ≥ 2 − 2
x + y ≤100 x >5
x + y + z <10 C.   y + 2 < 0 .
D. x + y <5 . x + y≥   100 2x +3y ≥  20
Câu 13. Cho a là một phần tử của tập hợp S . Mệnh đề nào dưới đây đúng? A. { } a ∈ S .
B. a ⊂ S .
C. S ⊃ a .
D. a ∈ S .
Câu 14. Gọi O là tâm hình bình hành ABCD. Đẳng thức nào sau đây sai?
   
  
A. OB − OC = OD − . OA
B. OA − OB = C . D
   
  
C. BC − BA = DC − . DA
D. AB − AD = D . B
Câu 15. Mệnh đề nào sau đây sai?   
A. AB = BA .
B. Vectơ 0 cùng hướng với mọi vectơ.   C. AA = 0 .
D. Vectơ 0 cùng phương với mọi vectơ.
Câu 16. Cho 90° < α <180° . Mệnh đề nào sau đây đúng? A. tanα > 0. B. cotα > 0 . C. sinα > 0. D. cosα > 0 . Mã đề 101 Trang 2/4
Phần II (2 điểm). Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a),
b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Trong mặt phẳng với hệ tọa độ Oxy , cho ∆ABC với ( A 2; − 5), B( 4; − 2
− ),C(1;5). Các khẳng định sau đây là đúng hay sai?   
a) Toạ độ véc tơ u = 2AB + AC là (1;14) .
b) Trọng tâm G của tam giác có tọa độ là  5 8 ;  − −  . 3 3   
c) Độ dài A B = 53 .  
d) cos( AB,CG) > 0,8 với G là trọng tâm của tam giác ABC .
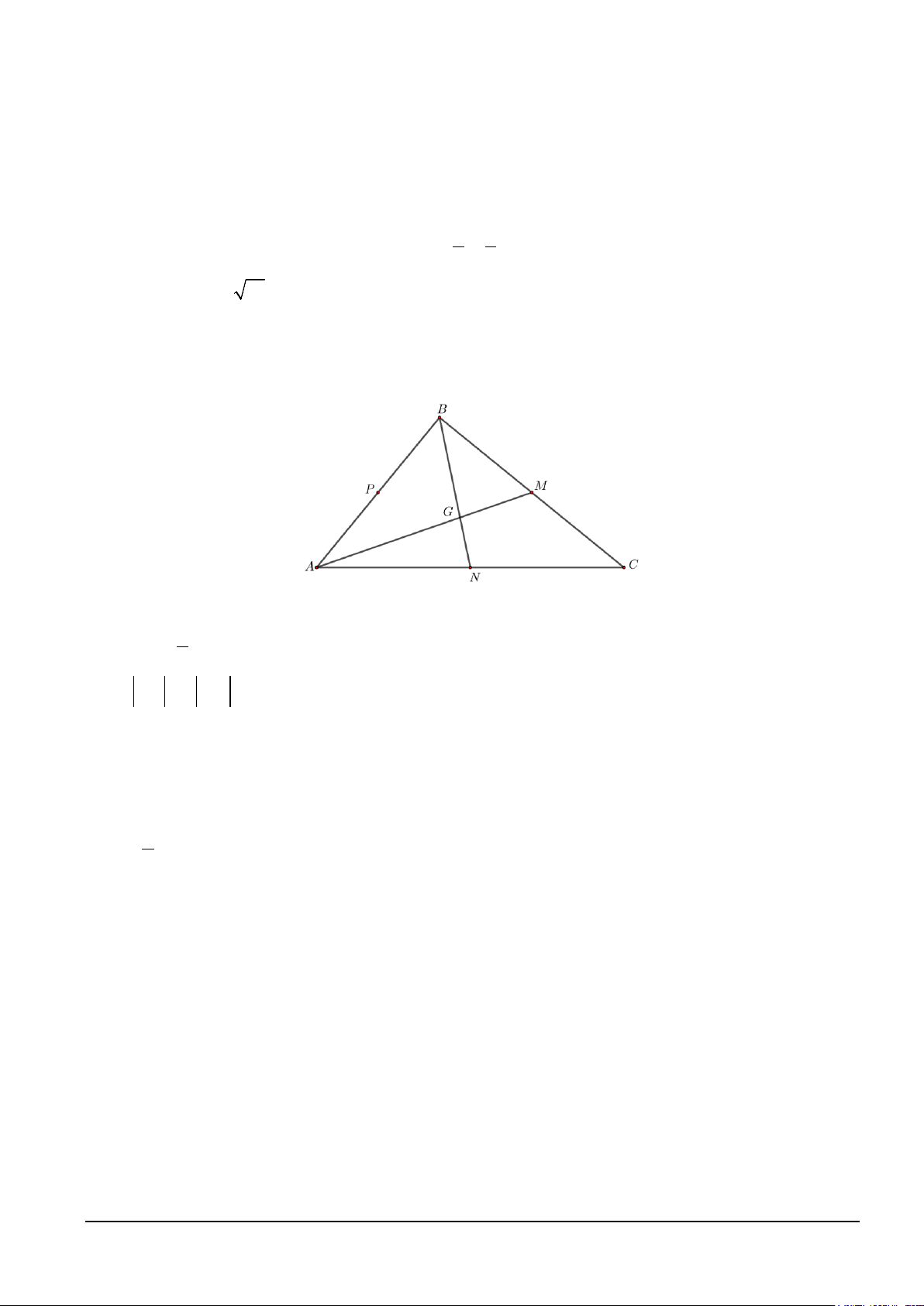
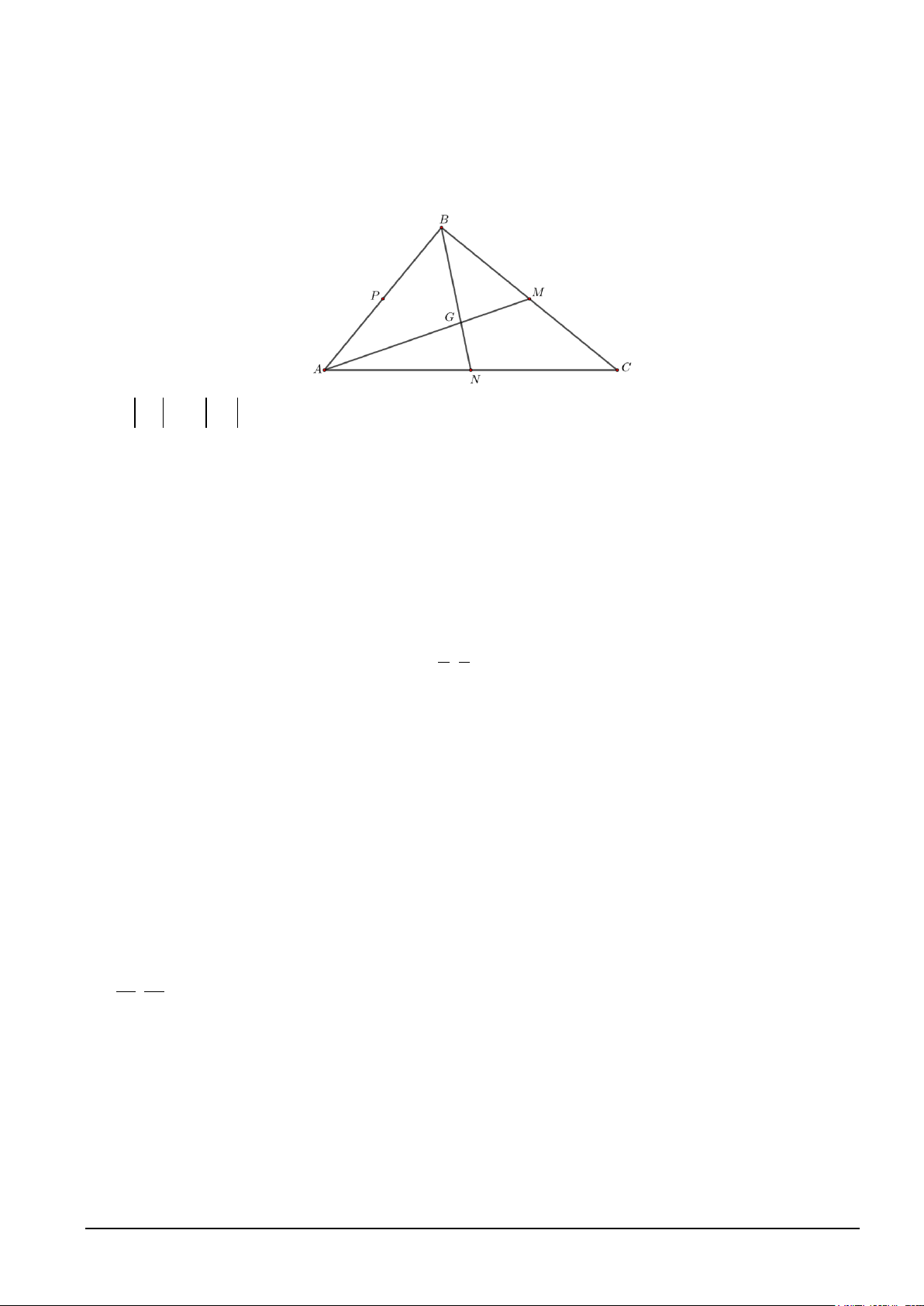
Câu 2. Cho tam giác ABC có M , N, P lần lượt là trung điểm của BC,C ,
A AB . Gọi G là giao điểm của
AM và BN . Các khẳng định sau đây là đúng hay sai?   
a) GA+ GB = 2GC .    b) 1
AP + BC = NA . 2  
c) AG = 3 MG .
  
d) MB + MC = 0 .
Phần III (2 điểm). Câu trả lời ngắn.Thí sinh trả lời đáp án từ câu 1 đến câu 4.
Câu 1. Trong mặt phẳng với hệ trục tọa độ Oxy , cho tam giác ABC có A( 1; − )
1 , B(1;3) và trọng tâm 2 G  2;  − 
. Điểm H trên trục Oy thỏa mãn tam giác HBC vuông cân tại H . Tìm tung độ điểm H . 3   
Câu 2. Cho tam giác ABC có M là điểm thuộc cạnh BC sao cho MB = 2MC , N là trung điểm của
      
cạnh AC . Giả sử AB = a, AC = b , ta có MN = xa + yb . Khi đó tổng 3x + 6y bằng bao nhiêu?
Câu 3. Đợt cuối năm, do nhu cầu tiêu dùng tăng cao, một cửa hàng kinh doanh xe máy dự định kinh
doanh bổ sung hai loại xe máy của Honda là xe máy Lead và xe máy Vision, với số vốn ban đầu không
vượt quá 36 tỉ đồng. Giá nhập về một chiếc xe máy Lead là 40 triệu đồng, lợi nhuận dự kiến là 5 triệu
đồng một chiếc. Giá nhập về một chiếc xe máy Vision là 30 triệu đồng, lợi nhuận dự kiến là 3,2 triệu
đồng một chiếc. Cửa hàng ước tính rằng tổng nhu cầu thị trường không vượt quá 1100 chiếc xe cả hai
loại và nhu cầu xe Lead không vượt quá 1,5 lần nhu cầu xe Vision.
Hỏi lợi nhuận có thể thu được lớn nhất của cửa hàng là bao nhiêu tiền? (viết câu trả lời theo đơn vị triệu đồng)
Câu 4. Cho hai tập hợp A = [7;2m −5], B =(9;12] với A là tập hợp khác rỗng. Có bao nhiêu giá trị
nguyên của m thuộc [0;2024] để B ⊂ A? Mã đề 101 Trang 3/4
PHẦN IV (2 điểm). Tự luận. Thí sinh trình bày lời giải Câu 1 và Câu 2 vào giấy thi.
Câu 1. Cho tam giác ABC , biết các cạnh a = 3,b = 4,c = 6 . Tính độ đài đường cao hạ từ đỉnh C của
tam giác (làm tròn kết quả đến hàng phần trăm). Câu 2.
a) Trong mặt phẳng với hệ tọa độ Oxy , cho ba điểm A(1;− 2) , B(0;4) ,C (3;2). Tìm tọa độ điểm N    
sao cho AN + 2BN − 4CN = 0 .
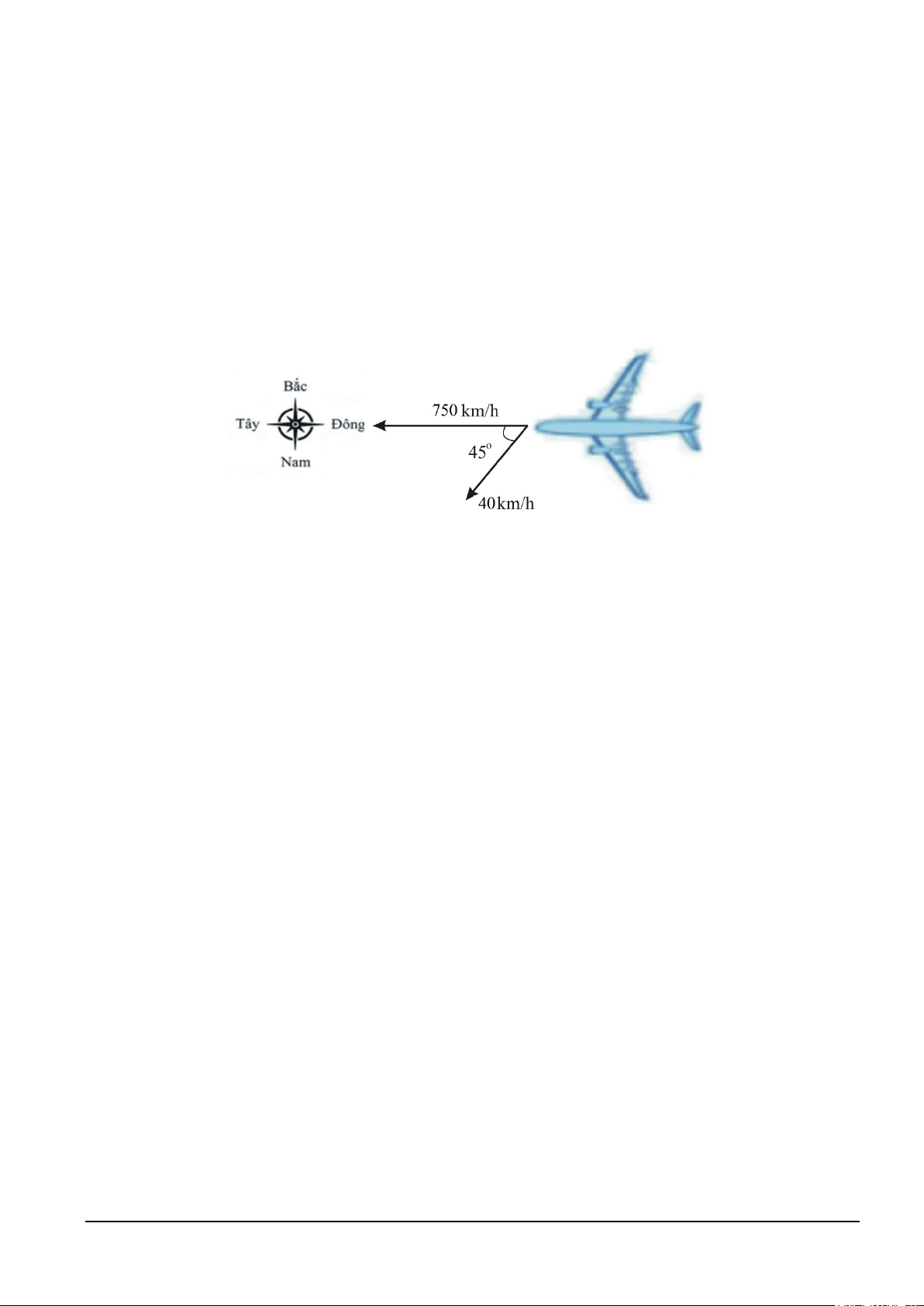
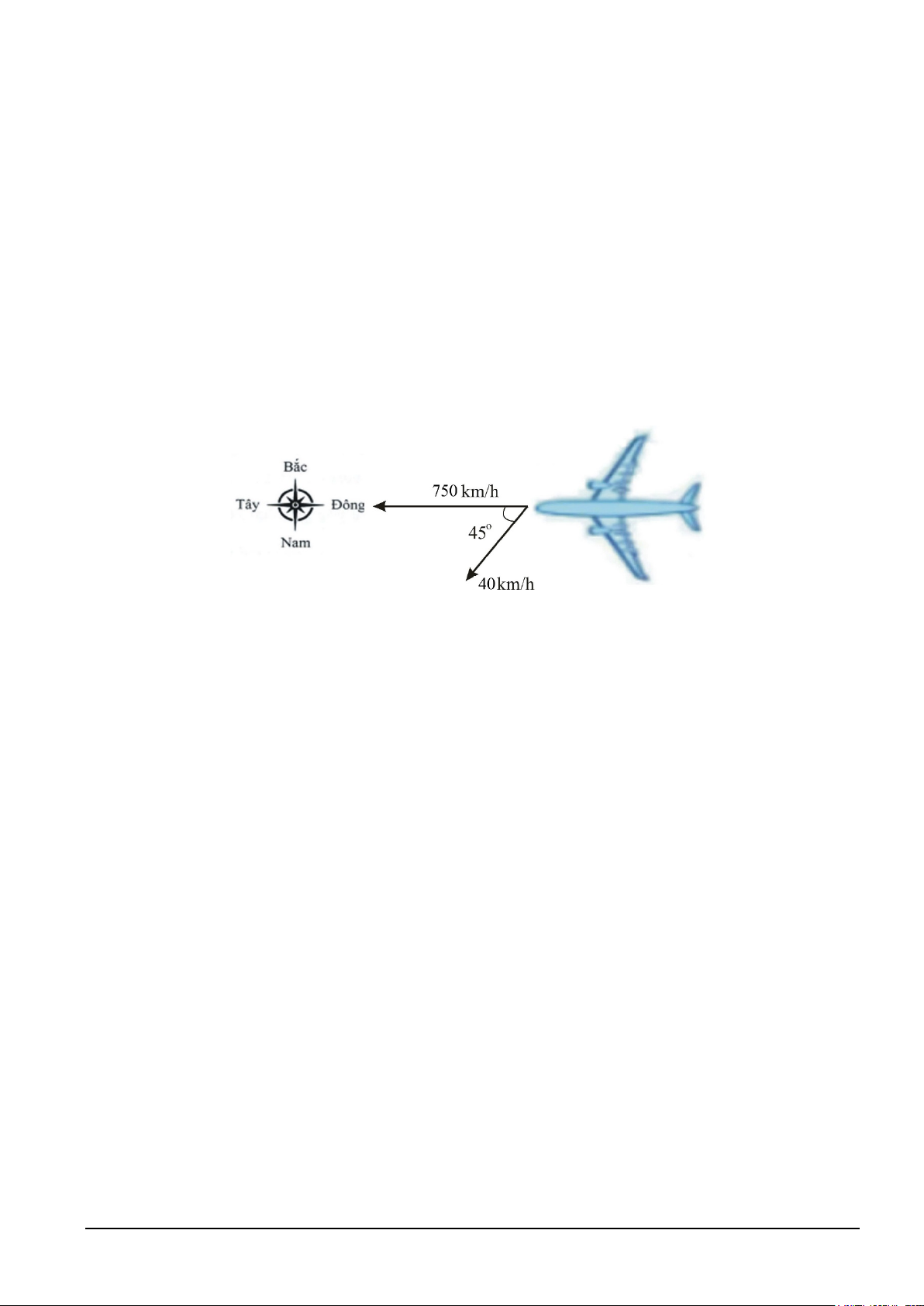
b) Một máy bay đang bay từ hướng Đông sang hướng Tây với vận tốc 750
km / h thì gặp luồng gió
thổi từ hướng Đông Bắc sang hướng Tây Nam với vận tốc 40km / h ( hình vẽ dưới) . Máy bay bị thay
đổi vận tốc sau khi gặp gió thổi. Hãy tìm vận tốc mới của máy bay (làm tròn kết quả đến hàng phần
chục theo đơn vị km / h ). ----HẾT---- Mã đề 101 Trang 4/4
SỞ GD & ĐT HẢI PHÒNG
ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2024 - 2025
Môn: TOÁN; Khối: 10
Ngày thi: ………….
Thời gian làm bài: 90 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC
(Đề thi có 04 trang) Mã đề thi 102
Họ, tên thí sinh:.......................................................................................
Số báo danh:............................................................................................
PHẦN I (4 điểm). Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu
16. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Cho tam giác ABC . Mệnh đề nào dưới đây sai ? 2 2 2 A. cos
b + c − a A = . B. 2 2 2
a = b + c + 2bccos A. 2bc 2 2 2 C. cos
a + c − b B = . D. 2 2 2
a = b + c − 2bccos A. 2ac Câu 2. Cho góc α ( 0 0
0 < α <180 ) thỏa mãn 1
cotα = − . Giá trị cosα bằng 2 A. 5 − . B. 5 − . C. 5 . D. 5 ± . 2 5 5 5
Câu 3. Cho tam giác ABC có =  0 =  0
AB 3, A 30 , B =120 . Hãy chọn khẳng định đúng. A. AC = 2 3 . B. AC = 3 3 . C. AC = 3 . D. AC = 4 3 .  
Câu 4. Cho tam giác ABC vuông tại A có AB = 3c ,
m BC = 5cm . Khi đó AB + BC là: A. 2 13 . B. 8. C. 13 . D. 4.  
Câu 5. Cho tam giác đều ABC có cạnh bằng .
a Tính tích vô hướng A . B AC.   2   A. 2 a A . B AC = 2a . B. A . B AC = . 2 2   2   C. . a AB AC a 3 = − . D. A . B AC = − . 2 2    
Câu 6. Trong mặt phẳng tọa độ Oxy , cho a = 4 j − i . Tọa độ của vectơ a là:     A. a = ( 4; − ) 1 . B. a = (4;− ) 1 . C. a = ( 1; − 4) . D. a = ( 1; − 4 − ) .
Câu 7. Cho hai tập hợp A = {2;3;4; } 5 và B = {1;2; }
3 . Có tất cả bao nhiêu tập X thỏa mãn: X ⊂ A và X ⊂ B ? A. 4. B. 8. C. 6. D. 2.
Câu 8. Cho hai tập hợp A = ( ; −∞ ]
3 ; B = (1;5] . Khi đó, tập A∪ B là A. (1;3]. B. ( ; −∞ 5] . C. ( ; −∞ 1). D. (3;5]. Mã đề 102 Trang 1/4
Câu 9. Cho a là một phần tử của tập hợp S . Mệnh đề nào dưới đây đúng?
A. a ∈ S . B. { } a ∈ S .
C. S ⊃ a .
D. a ⊂ S .
Câu 10. Trên đoạn thẳng AB lấy điểm I sao cho AB = 4AI . Đẳng thức nào sau đây đúng?         A. 4 IB = − AB . B. IB = 3 − IA .
C. IB = 3IA . D. 4 IB = AB . 3 3
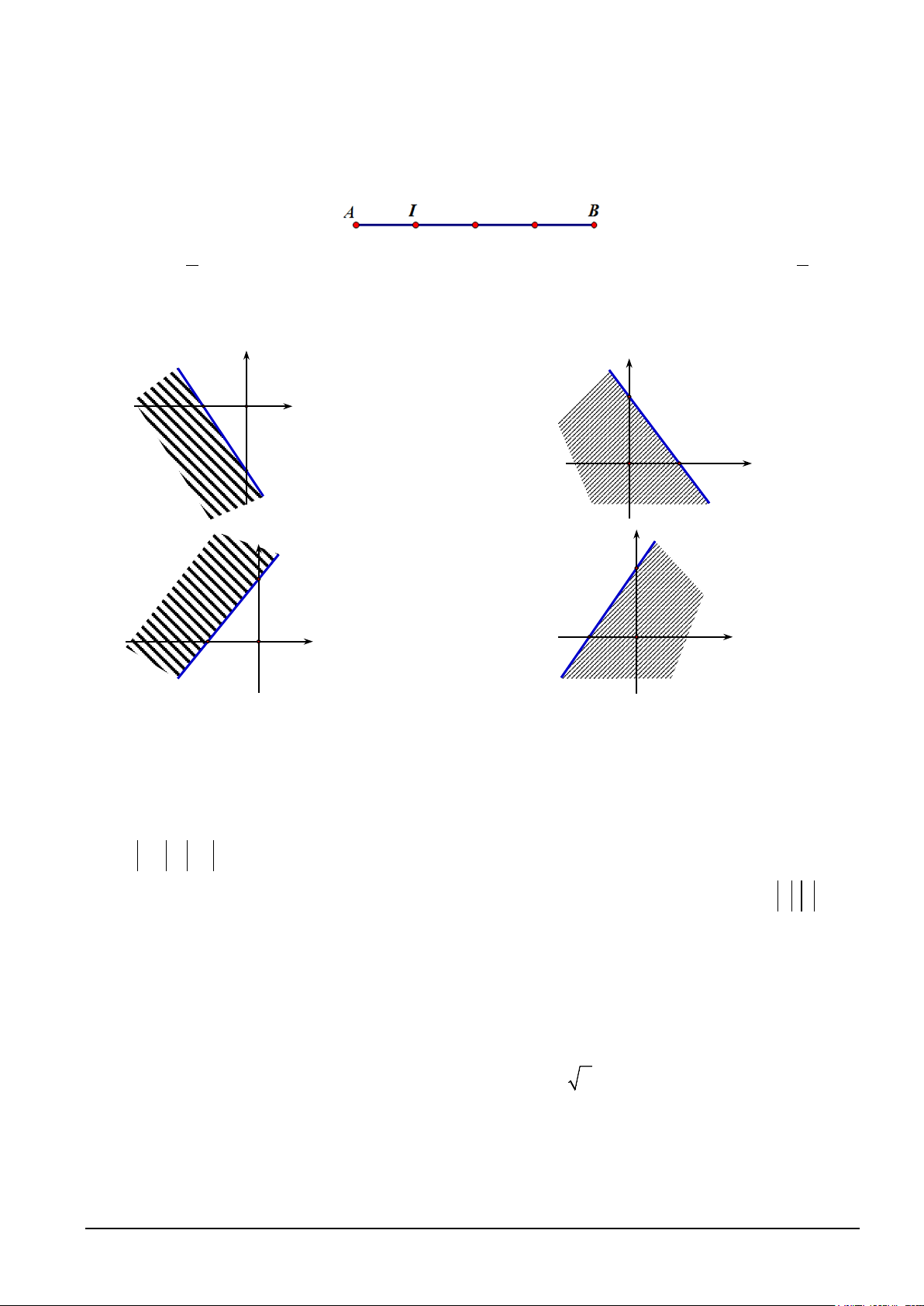
Câu 11. Miền không bị gạch kể cả bờ trong hình vẽ nào dưới đây là miền nghiệm của bất phương trình 3x − 2y ≥ 6 − ? y y 3 2 − O x 2 x 3 O A. . B. . y y 3 3 2 − 2 − O x O x C. . D. .
Câu 12. Gọi O là tâm hình bình hành ABCD. Đẳng thức nào sau đây sai?
  
   
A. OA − OB = C . D
B. OB − OC = OD − . OA
  
   
C. AB − AD = D . B
D. BC − BA = DC − . DA
Câu 13. Mệnh đề nào sau đây sai?  
A. Vectơ 0 cùng phương với mọi vectơ. B. AA = 0 .   
C. AB = BA .
D. Vectơ 0 cùng hướng với mọi vectơ.       
Câu 14. Cho hai vectơ a và b khác 0 . Xác định góc α giữa hai vectơ a và b khi .
a b = − a . b . A. o α = 45 . B. o α = 90 . C. o α = 0 . D. o α =180 .
Câu 15. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn? x >5
x + y + z <10 A.   y + 2 < 0 .
B. x + y <5 . x + y≥   100 2x +3y ≥  20 2 3
 x − 20y > 7
x + y > 3 C.  . D.  . 2
x + y ≤100
x − y ≥ 2 −
Câu 16. Cho 90° < α <180°. Mệnh đề nào sau đây đúng? A. cosα > 0 . B. tanα > 0. C. sinα > 0. D. cotα > 0 . Mã đề 102 Trang 2/4
PHẦN II (2 điểm). Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a),
b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho tam giác ABC có M , N, P lần lượt là trung điểm của BC,C ,
A AB . Gọi G là giao điểm của
AM và BN . Các khẳng định sau đây là đúng hay sai?   a) GB = 2 − GN .
   
b) AG + BG + CG = 0 .
  
c) PB + MC = NA.  
d) NA = NC .
Câu 2. Trong mặt phẳng với hệ tọa độ Oxy cho ∆ABC với ( A 2; − 5), B( 4; − 2
− ),C(1;5). Các khẳng định sau đây là đúng hay sai?   
a) Toạ độ véc tơ u = 2AB + AC là ( 1; − 14) .
b) Độ dài AC = 3.
c) Trọng tâm G của tam giác có tọa độ là  5 8 ;   . 3 3     
d) cos( AB,GC) > 0,8 với G là trọng tâm của tam giác ABC .
PHẦN III (2 điểm). Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Đợt cuối năm, do nhu cầu tiêu dùng tăng cao, một cửa hàng kinh doanh xe máy dự định kinh
doanh bổ sung hai loại xe máy của Honda là xe máy Lead và xe máy Vision, với số vốn ban đầu không
vượt quá 27 tỉ đồng. Giá nhập về một chiếc xe máy Lead là 40 triệu đồng, lợi nhuận dự kiến là 5 triệu
đồng một chiếc. Giá nhập về một chiếc xe máy Vision là 30 triệu đồng, lợi nhuận dự kiến là 3,2 triệu
đồng một chiếc. Cửa hàng ước tính rằng tổng nhu cầu thị trường không vượt quá 800 chiếc xe cả hai
loại và nhu cầu xe Lead không vượt quá 1,5 lần nhu cầu xe Vision. Hỏi lợi nhuận có thể thu được lớn
nhất của cửa hàng là bao nhiêu tiền?( viết câu trả lời theo đơn vị triệu đồng)
Câu 2. Trong mặt phẳng với hệ trục tọa độ Oxy , cho tam giác ABC có A(5;8), B(7;6) và trọng tâm 10 17 G  ;  
. Điểm H trên trục Ox thỏa mãn tam giác HBC vuông cân tại H . 3 3   
Tìm hoành độ điểm H .
Câu 3. Cho tam giác ABC có M là điểm thuộc cạnh BC sao cho MC = 2MB , N là trung điểm của
      
cạnh AC . Giả sử AB = a, AC = b , ta có MN = xa + yb . Khi đó tổng 3x + 6y bằng bao nhiêu?
Câu 4. Cho hai tập hợp A = [7;2m −5], B =(9;14] với A là tập hợp khác rỗng. Có bao nhiêu giá trị
nguyên của m thuộc [0;2024] để B ⊂ A? Mã đề 102 Trang 3/4
PHẦN IV (2 điểm). Tự luận. Thí sinh trình bày lời giải Câu 1 và Câu 2 vào giấy thi.
Câu 1 (1.0 điểm). Cho tam giác ABC , biết các cạnh a = 3,b = 4,c = 6 . Tính độ đài đường cao hạ từ
đỉnh C của tam giác (làm tròn kết quả đến hàng phần trăm).
Câu 2 (1.0 điểm).
a) Trong mặt phẳng với hệ tọa độ Oxy , cho ba điểm A(1;− 2) , B(0;4) ,C (3;2). Tìm tọa độ điểm N    
sao cho AN + 2BN − 4CN = 0 .
b) Một máy bay đang bay từ hướng Đông sang hướng Tây với vận tốc 750
km / h thì gặp luồng gió
thổi từ hướng Đông Bắc sang hướng Tây Nam với vận tốc 40km / h ( hình vẽ dưới) . Máy bay bị thay
đổi vận tốc sau khi gặp gió thổi. Hãy tìm vận tốc mới của máy bay (làm tròn kết quả đến hàng phần
chục theo đơn vị km / h ). ----HẾT---- Mã đề 102 Trang 4/4
SỞ GD & ĐT HẢI PHÒNG
ĐÁP ÁN ĐỂ KIỂM TRA HỌC KỲ I NĂM HỌC 2024 - 2025
Môn: TOÁN; Khối: 10
Ngày thi: …………. ĐỀ CHÍNH THỨC
I. TRẮC NGHIỆM (8 ĐIỂM) Mã đề thi Câu hỏi 101 102 103 104 1 D B A A 2 B B B B 3 B B D D 4 C D D C 5 A B C D 6 B C C C 7 B A A C 8 B B A B PHẦN I. 9 A A B A 10 C B D D 11 C C C C 12 C B C D 13 D B C C 14 A D A D 15 C A D B 16 C C D C 1 SSĐĐ SĐSS ĐSSS SSSĐ PHẦN II. 2 SSSĐ SĐSS SĐSĐ SSĐS 1 −3 3210 4280 −1 2 −2 4 −2 4 PHẦN III. 3 4280 −1 −3 3210 4 2016 2015 2016 2015 1
II. TỰ LUẬN (2 ĐIỂM) Câu Nội dung Điểm
Ta gọi h là đường cao ứng với đỉnh C . Theo công thức Hê-rông c a b c
S = p( p − a)( p − b)( p − c) với 13 p + + = = . 0,25đ 2 2 1.    (1,0 đ) Nên 13 13 13 13 455 S  = −  3 −  4 −  6 = . 2 2 2 2  0,25đ     4 Ta có 2S 455 455 h = = = ≈ . c 1,78 0,5đ c 2.6 12    
AN + 2BN − 4CN = 0 2a
⇔ (x −1; y + 2) + 2(x ; y − 4) − 4(x −3; y − 2) = 0,25đ N N N N N N (0;0) (0,5 đ) x = N 11
⇔ (−x + − y + = ⇔  ⇔ N (11;2) . . N 11; N 2) (0;0) y = 0,25đ  N 2 0,25đ
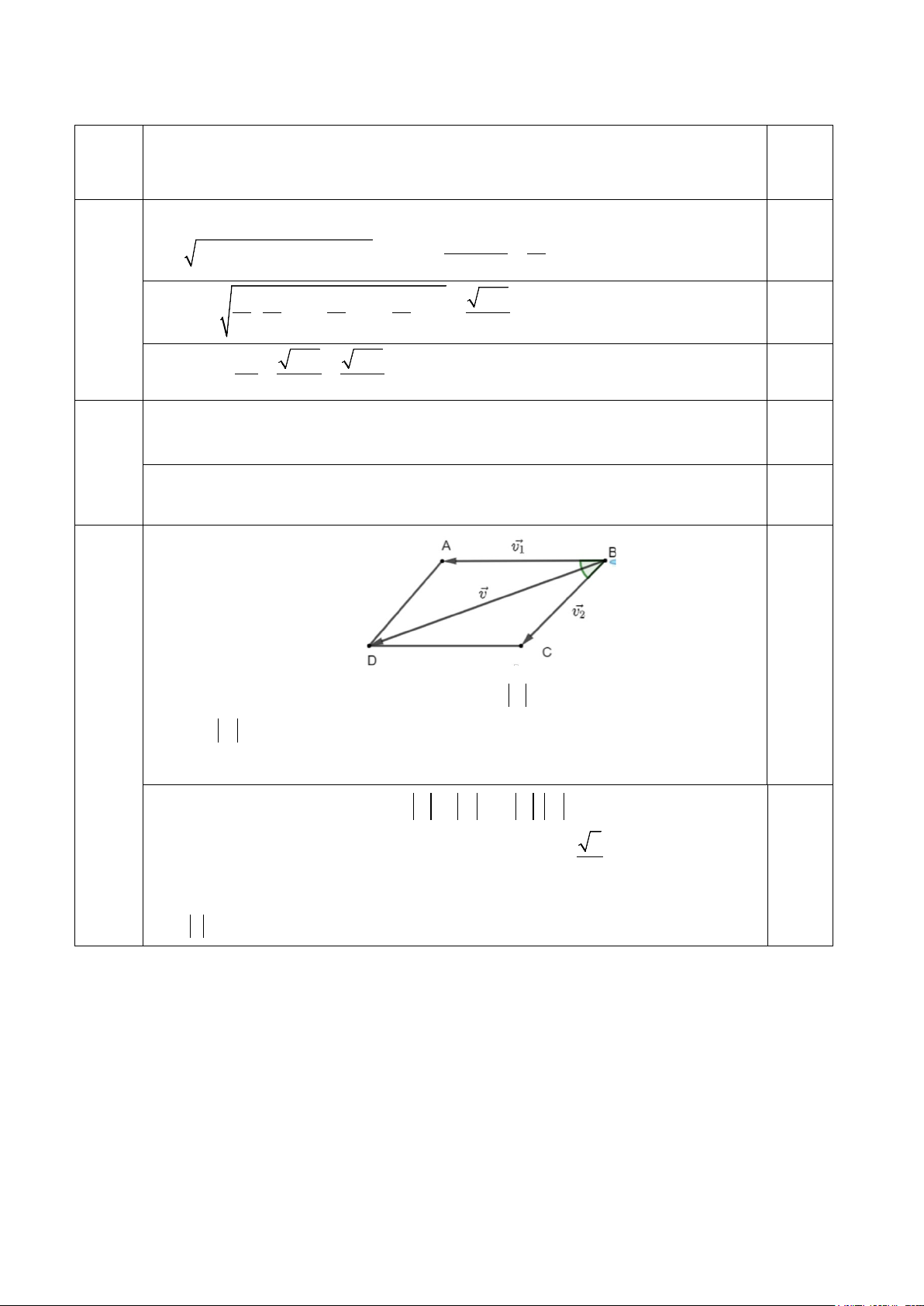
Gọi v là vận tốc của máy bay khi chưa có gió, v = 750 ( km / h) ; v là vận tốc 1 1 2 2b
của gió, v = 40 ( km / h) ;  2
v là vận tốc của máy bay khi gặp gió.
(0,5đ) Ta có:  =  +  v v v và (  ,  v v 45° = . 1 2 ) 1 2 v (  v v v v 2v v v v 2 v v cos45 1 2 )2      2  2 2 2 2   ° = + = + + ⋅ = + + ⋅ ⋅ 1 2 1 2 1 2 1 2 2 2 2 = 750 + 40 + 2.750.40. ≈ 606526,4068 2 0.25đ
Vậy v ≈ 778,8( km / h). 2
Xem thêm: ĐỀ THI HK1 TOÁN 10
https://toanmath.com/de-thi-hk1-toan-10
Document Outline

• MÃ 101 - Copy
• MÃ 102 - Copy
• ĐÁP ÁN TOÁN 10 HK1 (2024 -2025)
• Đề Thi HK1 Toán 10