Đề cuối kỳ 1 Toán 12 năm 2023 – 2024 trường THPT chuyên Hùng Vương – Phú Thọ

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra cuối học kỳ 1 môn Toán 12 năm học 2023 – 2024 .Mời bạn đọc đón xem.

29 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

15 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Trang 1/5 - Mã đề thi 125
SỞ GD&ĐT PHÚ THỌ
TRƯỜNG THPT CHUYÊN
HÙNG VƯƠNG
(Đề gồm: 05 trang)
ĐỀ KIỂM TRA CUỐI HỌC KỲ I
LỚP: 12 - MÔN: TOÁN
CHƯƠNG TRÌNH: Không chuyên
Ngày 15 tháng 12 năm 2023
Thời gian làm bài: 90 phút.
(35 câu TNKQ- 4 câu TL)
Mã đề 125
Họ và tên thí sinh………………………………………………SBD………………………………………………….
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (35 CÂU, 7.0 ĐIỂM)
Câu 1: Cho hàm số
()
fx
liên tục trên
và có bảng xét dấu của
()
fx
′
như sau:
Số điểm cực tiểu của hàm số đã cho là
A.
3.
B.
1.
C.
D.
Câu 2: Cho khối lăng trụ đứng
.ABC A B C
′′′
có
3BC a
′
=
, đáy
ABC
là tam giác vuông cân tại
và
2AC a=
. Tính thể tích
của khối lăng trụ đứng
.ABC A B C
′′′
.
A.
3
2.Va=
B.
3
.
62
a
V =
C.
3
2.Va=
D.
3
2
.
3
a
V =
Câu 3: Cho khối chóp
.S ABC
có tam giác
ABC
vuông tại
,
3
AB=
,
3
BC =
,
(
)
SA ABC⊥
và góc
giữa
SC
với đáy bằng
0
45
. Thể tích của khối chóp
.
S ABC
bằng
A.
2 3.
B.
C.
D.
3.
Câu 4: Cho hàm số
( )
y fx=
liên tục trên
và có đồ thị như hình bên. Hàm số đồng biến trên khoảng
nào dưới đây?
A.
( )
1; 2 .−
B.
(
)
1; 0 .
−
C.
( )
2; .+∞
D.
( )
0; 2 .
Câu 5: Cho khối hộp hình chữ nhật có ba kích thước
2; 4; 6
. Thể tích của khối hộp đã cho bằng
A.
16.
B.
12.
C.
48.
D.
Câu 6: Cho hình lăng trụ tứ giác
.
ABCD A B C D
′′′′
có đáy
ABCD
là hình vuông cạnh
a
và thể tích bằng
3
3a
. Tính chiều cao
h
của hình lăng trụ đã cho.
A.
.ha=
B.
3.ha=
C.
9.ha=
D.
.
3
a
h =
Câu 7: Phương trình
(
)
3
log 3 2 3x −=
có nghiệm là
A.
29
.
3
x =
B.
11
.
3
x =
C.
87.x
=
D.
25
.
3
x =
Câu 8: Cho các số thực
, , ( 0; 1).ab a b
αα
>> ≠
Mệnh đề nào sau đây đúng?
Trang 2/5 - Mã đề thi 125
A.
() .
ab a b
α αα
+=+
B.
.
aa
bb
α
α
α
−

=


C.
() .ab a b
α αα
−=−
D.
() .ab a b
α αα
=
Câu 9: Giả sử
,xy
là các số thực dương. Mệnh đề nào sau đây sai?
A.
3 33
log log log .
x
xy
y
= −
B.
(
)
3 33
1
log log log .
2
xy x y= +
C.
3 33
log log log .xy x y= +
D.
( )
3 33
log log log .xy x y+= +
Câu 10: Tập xác định của hàm số
(
)
1
3
5
yx= −
là
A.
( )
;5 .−∞
B.
( )
5; .+∞
C.
{ }
\5.
D.
( )
;.
−∞ +∞
Câu 11: Đồ thị hàm số
( )
( )
2
2
93
yx x=−+
cắt trục hoành tại bao nhiêu điểm phân biệt?
A.
1.
B.
C.
D.
Câu 12: Cho
a
là số thực dương,
1a
≠
, khi đó
3log 2
a
a
bằng
A.
8.
B.
3
.a
C.
D.
3.a
Câu 13: Cho hàm số bậc ba
( )
y fx=
có đồ thị là đường cong trong hình bên.
Số nghiệm thực của phương trình
( )
1
2023
fx=
là
A.
2.
B.
C.
1.
D.
Câu 14: Tính đạo hàm của hàm số
( )
3
log 2 1yx= +
.
A.
( )
2
.
2 1 ln 3
y
x
′
=
+
B.
(
)
2 1 .ln 3.yx
′
= +
C.
(
)
1
.
2 1 ln 3
y
x
′
=
+
D.
1
.
21
y
x
′
=
+
Câu 15: Tiệm cận ngang của đồ thị hàm số
2024 1
1
x
y
x
+
=
−
là
A.
2024.y = −
B.
2024.y =
C.
1
.
2024
y =
D.
1
.
2024
y
−
=
Câu 16: Cho
a
là một số dương bất kỳ, biểu thức
2
3
aa
viết dưới dạng lũy thừa với số mũ hữu tỷ là
A.
5
6
.a
B.
6
5
.a
C.
7
6
.a
D.
11
6
.a
Câu 17: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên dưới?
A.
3
3.yx x= −
B.
42
2.yx x= −
C.
42
2.yx x=−+
D.
3
3.yx x=−+
Trang 3/5 - Mã đề thi 125
Câu 18: Giả sử
,ab
là các số thực dương bất kỳ. Biểu thức
2
ln
a
b
bằng
A.
ln 2 ln .ab−
B.
1
ln ln .
2
ab−
C.
ln 2 ln .ab+
D.
1
ln ln .
2
ab+
Câu 19: Nghiệm của phương trình
2
3 27
x+
=
là
A.
1.
x = −
B.
2.x = −
C.
2.x =
D.
1.x =
Câu 20: Cho hàm số
(
)
fx
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
A.
2.
B.
3.−
C.
D.
2.−
Câu 21: Cho hàm số
()y fx=
liên tục và có bảng biến thiên trên đoạn
[ ]
1;3−
như hình vẽ bên. Khẳng
định nào sau đây đúng?
A.
[ ]
1;3
min ( ) (0).fx f
−
=
B.
[ ]
( ) ( )
1;3
min 1 .fx f
−
= −
C.
[ ]
( ) ( )
1;3
min 3 .fx f
−
=
D.
[ ]
( ) ( )
1;3
min 2 .fx f
−
=
Câu 22: Cho khối lập phương có cạnh bằng
6
. Thể tích của khối lập phương đã cho bằng
A.
216.
B.
18.
C.
36.
D.
72.
Câu 23: Tiệm cận đứng của đồ thị hàm số
2 2023
1
x
y
x
−
=
+
là
A.
2.
x =
B.
2.x = −
C.
1.x =
D.
1.x = −
Câu 24: Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng đáy và
2SA a
=
. Thể tích khối chóp đã cho bằng
A.
2.a
B.
3
2
.
3
a
C.
3
4
.
3
a
D.
3
.a
Câu 25: Hàm số
3
yx=
có đạo hàm là
A.
31
' 3. .yx
−
=
B.
3
' ln .yx x=
C.
31
'.
31
x
y
−
=
+
D.
3
' ln 3.yx
=
Trang 4/5 - Mã đề thi 125
Câu 26:
Cho ba số thực dương
,,abc
khác
1
. Đồ thị các
hàm số
,,
xxx
y ayby c
= = =
được cho trong hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A.
.cab<<
B.
.bca<<
C.
.
acb<<
D.
.abc<<
Câu 27: Cho hàm số
(
)
fx
liên tục trên
[ ]
1; 5−
và có đồ thị trên đoạn
[ ]
1; 5
−
như hình vẽ bên dưới. Tổng
giá trị lớn nhất và giá trị nhỏ nhất của hàm số
(
)
fx
trên đoạn
[ ]
1; 5
−
bằng
A.
2.
B.
C.
1.
D.
1.−
Câu 28: Cho khối hộp chữ nhật
.ABCD A B C D
′′′′
, biết
; 2 ; 21
AB a BC a AC a
′
= = =
. Tính thể tích
của
khối hộp đó?
A.
3
4.a
B.
3
16 .a
C.
3
8
.
3
a
D.
3
8.a
Câu 29: Cho hàm số
( )
y fx=
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( )
4; .+∞
B.
( )
;2 .
−∞
C.
( )
1;1 .−
D.
( )
0;1 .
Câu 30: Khối lăng trụ có chiều cao bằng
h
và diện tích đáy bằng
S
thì có thể tích bằng
A.
.Sh
B.
1
.
3
Sh
C.
3.Sh
D.
1
.
2
Sh
Câu 31: Gọi
,
,
là các điểm cực trị của đồ thị hàm số
42
24yx x=−+
. Bán kính đường tròn ngoại
tiếp tam giác
ABC
bằng
A.
2 1.+
B.
1.
C.
D.
2 1.−
Câu 32: Cho hình lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông tại
,
AC a=
,
60 .ACB = °
Đường chéo
BC
′
của mặt bên
( )
BCC B
′′
tạo với mặt phẳng
( )
ACC A
′′
một góc
30°
. Tính
thể tích của khối lăng trụ theo
a
.
A.
3
6.Va=
B.
3
6
.
3
a
V =
C.
3
26
.
3
a
V
=
D.
3
46
.
3
a
V =
Câu 33: Cho
,ab
là số thực dương thỏa mãn
23
1
2
a b ab
ab
ab
++ −
−
=
+
. Giá trị nhỏ nhất của biểu thức
22
ab+
là:
Trang 5/5 - Mã đề thi 125
A.
( )
2
51.−
B.
C.
51
.
2
−
D.
3 5.−
Câu 34: Cho phương trình
2
55
log 3log 4 7 0
x xm− + −=
có hai nghiệm thực phân biệt
12
,xx
thỏa mãn
( )( )
12
1 5 180.xx+ +=
Khẳng định nào dưới đây đúng?
A.
( )
1; 2 .m∈
B.
5
; ;.
2
m

∈ +∞


C.
7
;3 .
4
m

∈


D.
(
)
;0 .m
∈ −∞
Câu 35: Cho hàm số
32
() ay f x x bx cx d= = + ++
có đồ thị
là đường cong trong hình vẽ bên.Tổng giá trị lớn nhất và
giá trị nhỏ nhất của hàm số
2
( 3sin 1)yf x=−+
bằng
A.
33.
B.
832
.
27
C.
31.
D.
896
.
27
-----------------------------------------------
II. PHẦN TỰ LUẬN ( 4 CÂU, 3.0 ĐIỂM)
Câu 1 (1 điểm). Giải phương trình
a)
31
5
1
3
9
x
x
−
−

=


b)
( ) ( )
22
log 1 log 1 3xx−+ +=
Câu 2 (0,5 điểm). Cho hình lăng trụ đứng
.' ' 'ABC A B C
có đáy
ABC
là tam giác vuông cân tại
,A
2,BC a=
' 6.AB a=
Tính thể tích của khối lăng trụ
.' ' 'ABC A B C
theo
a
.
Câu 3 (1,0 điểm). Có bao nhiêu giá trị nguyên
0m ≠
thuộc đoạn
[ ]
5; 5 ,
−
để đường thẳng
1
y mx= +
cắt đồ thị hàm số
21
1
x
y
x
−+
=
−
tại hai điểm phân biệt.
Câu 4 (0,5 điểm). Cho các số thực
, ab
thỏa mãn
2
1 ab<≤
.
Tìm giá trị nhỏ nhất của biểu thức
2
2 2log log 8log
aa a
bb
a
P ab
b


= −+




.
-------------------- HẾT --------------------
Lưu ý:
- Cán bộ coi thi không giải thích gì thêm.
- Học sinh không được sử dụng tài liệu trong thời gian làm bài.
Trang 1/5 - Mã đề thi 126
SỞ GD&ĐT PHÚ THỌ
TRƯỜNG THPT CHUYÊN
HÙNG VƯƠNG
(Đề gồm: 05 trang)
ĐỀ KIỂM TRA CUỐI HỌC KỲ I
LỚP: 12 - MÔN: TOÁN
CHƯƠNG TRÌNH: Không chuyên
Ngày 15 tháng 12 năm 2023
Thời gian làm bài: 90 phút.
(35 câu TNKQ- 4 câu TL)
Mã đề 126
Họ và tên thí sinh………………………………………………SBD………………………………………………….
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (35 CÂU, 7.0 ĐIỂM)
Câu 1: Tính đạo hàm của hàm số
( )
3
log 2 1yx= +
.
A.
(
)
2
.
2 1 ln 3
y
x
′
=
+
B.
1
.
21
y
x
′
=
+
C.
(
)
2 1 .ln 3.yx
′
= +
D.
( )
1
.
2 1 ln 3
y
x
′
=
+
Câu 2: Cho hàm số
()fx
liên tục trên
và có bảng xét dấu của
()
fx
′
như sau:
Số điểm cực tiểu của hàm số đã cho là
A.
4.
B.
C.
1.
D.
Câu 3: Cho
a
là số thực dương,
1a ≠
, khi đó
3log 2
a
a
bằng
A.
8.
B.
3
.a
C.
3.a
D.
Câu 4: Cho hình lăng trụ tứ giác
.ABCD A B C D
′′′′
có đáy
ABCD
là hình vuông cạnh
a
và thể tích bằng
3
3a
. Tính chiều cao
h
của hình lăng trụ đã cho.
A.
.ha=
B.
.
3
a
h =
. C.
3.ha=
D.
9.ha=
Câu 5: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
3
3.yx x= −
B.
42
2.
yx x=−+
C.
42
2.yx x= −
D.
3
3.
yx x=−+
Câu 6: Cho hàm số
(
)
fx
liên tục trên
[ ]
1; 5
−
và có đồ thị trên đoạn
[ ]
1; 5−
như hình vẽ bên dưới. Tổng
giá trị lớn nhất và giá trị nhỏ nhất của hàm số
(
)
fx
trên đoạn
[ ]
1; 5−
bằng
Trang 2/5 - Mã đề thi 126
A.
4.
B.
1.
C.
D.
1.−
Câu 7: Cho khối lập phương có cạnh bằng
6
. Thể tích của khối lập phương đã cho bằng
A.
72.
B.
18.
C.
36.
D.
216.
Câu 8: Giả sử
,
xy
là các số thực dương. Mệnh đề nào sau đây sai?
A.
3 33
log log log .
x
xy
y
= −
B.
( )
3 33
1
log log log .
2
xy x y= +
C.
3 33
log log log .xy x y= +
D.
( )
3 33
log log log .xy x y+= +
Câu 9: Tiệm cận ngang của đồ thị hàm số
2024 1
1
x
y
x
+
=
−
là
A.
2024.y =
B.
2024.y = −
C.
1
.
2024
y
=
D.
1
.
2024
y
−
=
Câu 10: Cho hàm số bậc ba
( )
y fx=
có đồ thị là đường cong trong hình bên.
Số nghiệm thực của phương trình
( )
1
2023
fx=
là
A.
1.
B.
C.
D.
Câu 11: Cho hàm số
(
)
y fx
=
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( )
4; .+∞
B.
( )
;2 .−∞
C.
( )
1;1 .−
D.
( )
0;1 .
Câu 12: Cho khối chóp
.S ABC
có tam giác
ABC
vuông tại
B
,
3AB=
,
3BC =
,
(
)
SA ABC⊥
và góc
giữa
SC
với đáy bằng
0
45
. Thể tích của khối chóp
.S ABC
bằng
A.
3.
B.
C.
D.
2 3.
Câu 13: Tập xác định của hàm số
( )
1
3
5yx
= −
là
A.
{ }
\5.
B.
( )
5; .+∞
C.
( )
;5 .−∞
D.
( )
;.−∞ +∞
Câu 14: Nghiệm của phương trình
2
3 27
x+
=
là
A.
1.x = −
B.
2.x = −
C.
2.x =
D.
1.x
=
Câu 15: Giả sử
,ab
là các số thực dương bất kỳ. Biểu thức
2
ln
a
b
bằng
A.
ln 2 ln .
ab
−
B.
1
ln ln .
2
ab−
C.
ln 2 ln .ab+
D.
1
ln ln .
2
ab+
Trang 3/5 - Mã đề thi 126
Câu 16: Phương trình
( )
3
log 3 2 3x −=
có nghiệm là
A.
87.x =
B.
11
.
3
x =
C.
29
.
3
x =
D.
25
.
3
x =
Câu 17: Cho các số thực
, , ( 0; 1).
ab a b
αα
>> ≠
Mệnh đề nào sau đây đúng?
A.
() .
ab a b
α αα
−=−
B.
.
aa
bb
α
α
α
−

=


C.
() .ab a b
α αα
+=+
D.
() .ab a b
α αα
=
Câu 18: Đồ thị hàm số
( )
( )
2
2
93yx x=−+
cắt trục hoành tại bao nhiêu điểm phân biệt?
A.
2.
B.
1.
C.
D.
Câu 19: Cho hàm số
(
)
fx
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
A.
2.
B.
3.−
C.
D.
2.
−
Câu 20: Cho hàm số
()y fx=
liên tục và có bảng biến thiên trên đoạn
[
]
1;3
−
như hình vẽ bên. Khẳng
định nào sau đây đúng?
A.
[ ]
1;3
min ( ) (0).fx f
−
=
B.
[ ]
( ) ( )
1;3
min 1 .fx f
−
= −
C.
[ ]
( ) ( )
1;3
min 3 .fx f
−
=
D.
[ ]
(
) ( )
1;3
min 2 .fx f
−
=
Câu 21: Hàm số
3
yx=
có đạo hàm là
A.
3
' ln .yx x
=
B.
3
' ln 3.yx=
C.
31
' 3. .yx
−
=
D.
31
'.
31
x
y
−
=
+
Câu 22: Cho
a
là một số dương bất kỳ, biểu thức
2
3
aa
viết dưới dạng lũy thừa với số mũ hữu tỷ là
A.
5
6
.
a
B.
11
6
.
a
C.
7
6
.a
D.
6
5
.a
Câu 23: Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng đáy và
2SA a=
. Thể tích khối chóp đã cho bằng
A.
2.a
B.
3
2
.
3
a
C.
3
4
.
3
a
D.
3
.a
Câu 24: Cho khối hộp hình chữ nhật có ba kích thước
2; 4; 6
. Thể tích của khối hộp đã cho bằng
A.
16.
B.
C.
48.
D.
12.
Trang 4/5 - Mã đề thi 126
Câu 25: Cho ba số thực dương
,,abc
khác
1
.
Đồ thị các hàm số
,,
xxx
y ayby c= = =
được
cho trong hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A.
.
bca
<<
B.
.cab
<<
C.
.
acb<<
D.
.abc<<
Câu 26:
Cho hàm số
( )
y fx
=
liên tục trên
và có đồ thị như hình bên. Hàm số đồng biến trên khoảng
nào dưới đây?
A.
(
)
1; 0 .
−
B.
( )
0; 2 .
C.
( )
2; .+∞
D.
(
)
1; 2 .
−
Câu 27: Cho khối hộp chữ nhật
.ABCD A B C D
′′′′
, biết
; 2 ; 21AB a BC a AC a
′
= = =
. Tính thể tích
của
khối hộp đó?
A.
3
4.a
B.
3
16 .a
C.
3
8
.
3
a
D.
3
8.a
Câu 28: Cho khối lăng trụ đứng
.ABC A B C
′′′
có
3BC a
′
=
, đáy
ABC
là tam giác vuông cân tại
và
2AC a
=
. Tính thể tích
của khối lăng trụ đứng
.
ABC A B C
′′′
.
A.
3
2.Va=
B.
3
2
.
3
a
V =
C.
3
2.Va=
D.
3
.
62
a
V =
Câu 29: Tiệm cận đứng của đồ thị hàm số
2 2023
1
x
y
x
−
=
+
là
A.
2.x
=
B.
2.x = −
C.
1.x
=
D.
1.x = −
Câu 30: Khối lăng trụ có chiều cao bằng
h
và diện tích đáy bằng
S
thì có thể tích bằng
A.
1
.
2
Sh
B.
.Sh
C.
3.Sh
D.
1
.
3
Sh
Câu 31: Cho hàm số
32
() ay f x x bx cx d= = + ++
có đồ thị
là đường cong trong hình vẽ bên.Tổng giá trị lớn nhất và
giá trị nhỏ nhất của hàm số
2
( 3sin 1)yf x=−+
bằng
A.
33.
B.
832
.
27
C.
31.
D.
896
.
27
Câu 32: Gọi
,
,
là các điểm cực trị của đồ thị hàm số
42
24yx x=−+
. Bán kính đường tròn ngoại
tiếp tam giác
ABC
bằng
A.
1.
B.
C.
2 1.−
D.
2 1.+
Câu 33: Cho phương trình
2
55
log 3log 4 7 0x xm− + −=
có hai nghiệm thực phân biệt
12
,xx
thỏa mãn
( )( )
12
1 5 180.xx+ +=
Khẳng định nào dưới đây đúng?
Trang 5/5 - Mã đề thi 126
A.
( )
1; 2 .m∈
B.
5
; ;.
2
m

∈ +∞


C.
7
;3 .
4
m

∈


D.
( )
;0 .
m
∈ −∞
Câu 34: Cho hình lăng trụ đứng
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông tại
,
AC a=
,
60 .ACB = °
Đường chéo
BC
′
của mặt bên
(
)
BCC B
′′
tạo với mặt phẳng
( )
ACC A
′′
một góc
30°
. Tính
thể tích của khối lăng trụ theo
a
.
A.
3
6
.
3
a
V =
B.
3
6.Va=
C.
3
26
.
3
a
V
=
D.
3
46
.
3
a
V =
Câu 35: Cho
,ab
là số thực dương thỏa mãn
23
1
2
a b ab
ab
ab
++ −
−
=
+
. Giá trị nhỏ nhất của biểu thức
22
ab+
là
A.
3 5.−
B.
51
.
2
−
C.
D.
( )
2
51.−
-----------------------------------------------
II. PHẦN TỰ LUẬN ( 4 CÂU, 3.0 ĐIỂM)
Câu 1 (1 điểm). Giải phương trình
a)
31
5
1
3
9
x
x
−
−

=


b)
( ) ( )
22
log 1 log 1 3xx−+ +=
Câu 2 (0,5 điểm). Cho hình lăng trụ đứng
.' ' 'ABC A B C
có đáy
ABC
là tam giác vuông cân tại
,A
2,
BC a=
' 6.AB a=
Tính thể tích của khối lăng trụ
.' ' 'ABC A B C
theo
a
.
Câu 3 (1,0 điểm). Có bao nhiêu giá trị nguyên
0m ≠
thuộc đoạn
[ ]
5; 5 ,−
để đường thẳng
1y mx= +
cắt đồ thị hàm số
21
1
x
y
x
−+
=
−
tại hai điểm phân biệt.
Câu 4 (0,5 điểm). Cho các số thực
, ab
thỏa mãn
2
1 ab<≤
.
Tìm giá trị nhỏ nhất của biểu thức
2
2 2 log log 8log
aa a
bb
a
P ab
b


= −+




.
-------------------- HẾT --------------------
Lưu ý:
- Cán bộ coi thi không giải thích gì thêm.
- Học sinh không được sử dụng tài liệu trong thời gian làm bài.
mamon
made cautron dapan
TOAN 125 1 D
TOAN 125 2 C
TOAN 125 3 C
TOAN 125 4 D
TOAN 125 5 C
TOAN 125 6 B
TOAN 125 7 A
TOAN 125 8 D
TOAN 125 9 D
TOAN 125 10 B
TOAN 125 11 D
TOAN 125 12 A
TOAN 125 13 B
TOAN 125 14 A
TOAN 125 15 B
TOAN 125 16 C
TOAN 125 17 C
TOAN 125 18 A
TOAN 125 19 D
TOAN 125 20 B
TOAN 125 21 B
TOAN 125 22 A
TOAN 125 23 D
TOAN 125 24 B
TOAN 125 25 A
TOAN 125 26 C
TOAN 125 27 C
TOAN 125 28 D
TOAN 125 29 D
TOAN 125 30 A
TOAN 125 31 B
TOAN 125 32 A
TOAN 125 33 D
TOAN 125
34 C
TOAN 125 35 B
TOAN 126 1 A
TOAN 126 2 D
TOAN 126 3 A
TOAN 126 4 C
TOAN 126 5 B
TOAN 126 6 B
TOAN 126 7 D
TOAN 126 8 D
TOAN
126 9 A
TOAN 126 10 B
TOAN 126 11 D
TOAN 126 12 C
TOAN 126 13 B
TOAN 126 14 D
TOAN 126 15 A
TOAN 126 16 C
TOAN 126 17 D
TOAN 126 18 A
TOAN 126 19 B
TOAN 126 20 B
TOAN 126 21 C
TOAN 126 22 C
TOAN 126 23 B
TOAN 126 24 C
TOAN 126 25 C
TOAN 126 26 B
TOAN 126 27 D
TOAN 126 28 A
TOAN 126 29 D
TOAN 126 30 B
TOAN 126 31 B
TOAN 126 32 A
TOAN 126 33 C
TOAN 126 34 B
TOAN 126 35 A
Xem thêm: ĐỀ THI HK1 TOÁN 12
https://toanmath.com/de-thi-hk1-toan-12
ĐÁP ÁN TỰ LUẬN ĐỀ KI ỂM TRA CUỐI HỌC KỲ 1 TOÁN 12 NĂM HỌC 23-24
Câu 1 (1 điểm). Giải phương trình
a)
31
5
1
3
9
x
x
−
−

=


b)
( )
(
)
22
log 1 log 1 3xx
−+ +=
Câu 2 (0,5 điểm). Cho hình lăng trụ đứng
.' ' '
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
,
A
2,BC a=
' 6.AB a=
Tính thể tích của khối lăng trụ
.' ' 'ABC A B C
theo
a
.
Câu 3 (1,0 điểm). Có bao nhiêu giá trị nguyên
0m ≠
thuộc đoạn
[
]
5; 5−
để đường thẳng
1y mx= +
cắt đồ thị
hàm số
21
1
x
y
x
−+
=
−
tại hai điểm phân biệt.
Câu 4 (0,5 điểm). Cho các số thực
, ab
thỏa mãn
2
1 ab<≤
.
Tìm giá trị nhỏ nhất của biểu thức
2
2 2log log 8log
aa a
bb
a
P ab
b


= −+




.
ĐÁP ÁN
Câu
Đáp án
Điểm
1
Câu 1 (1 điểm). Giải phương trình
1
a
Giải phương trình
31
5
1
3
9
x
x
−
−

=


0,5
Ta có:
31
5
1
3
9
x
x
−
−

=


5 62
33
xx− −+
⇔=
0,25
562xx⇔−=− +
1.
x⇔=
Tập nghiệm của phương trình là
{ }
1S =
0,25
b
Giải phương trình
(
) ( )
22
log 1 log 1 3xx
−+ +=
0,5
Điều kiện
1x >
.
Phương trình đã cho trở thành
( )
2
2
log 1 3x −=
0,25
2
18x⇔ −=
3x⇔=±
Đối chiếu điều kiện. Tập nghiệm của phương trình là
{ }
3S =
0,25
2
Câu 2 (0,5 điểm). Cho hinh lăng trụ đứng
.' ' 'ABC A B C
có đáy
ABC
là tam giác
vuông cân tại
, 2 , ' 6.A BC a A B a= =
Tính thể tích của khối lăng trụ
.' ' 'ABC A B C
theo
a
.
0,5
Tam giác
ABC
vuông cân tại
2.
2
BC
A AB AC a⇒== =
Tam giác
'A AB
vuông tại
2 2 22
' ' 6 2 2.A A A A B AB a a a⇒ = − = −=
0,25
Diện tích đáy
ABC
là:
2
11
. 2. 2 .
22
ABC
S AB AC a a a= = =
Thể tích của khối lăng trụ là
23
.'''
' . 2. 2 .
ABC A B C ABC
V A AS aa a
= = =
0,25
3
Câu 3 (1,0 điểm). Có bao nhiêu giá trị nguyên
0
m ≠
thuộc đoạn
[ ]
5; 5 ,−
để đường
thẳng
1
y mx= +
cắt đồ thị hàm số
21
1
x
y
x
−+
=
−
tại hai điểm phân biệt.
1,0
Xét phương trình hoành độ giao điểm:
21
1
1
x
mx
x
−+
= +
−
;
( 1).x ≠
⇔
( ) ( )
2
3 20g x mx m x= + − −=
;
( 1).x ≠
0,25
Để đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt khi và chỉ khi phương trình
trên có
2
nghiệm phân biệt khác
1
( )
( )
2
0
3 80
10
3 20
mm
g
mm
∆>
− +>

⇔⇔

≠
+− −≠
0,25
2
2 90 0mm m⇔ + + > ⇔∀ ≠
0,25
Mà
[
]
5; 5m ∈−
,
mZ∈
⇒
{ }
5; 4; 3; 2; 1;1; 2; 3; 4; 5m ∈−−−−−
⇒
có 10 giá trị
m
.
Lưu ý: Thiếu đk
1x ≠
dẫn đến thiếu đk
(1) 0g ≠
thì -0,25
0,25
4
Câu 4 (0,5 điểm). Cho các số thực
, ab
thỏa mãn
2
1 ab<≤
.
Tìm giá trị nhỏ nhất của biểu thức
2
2 2log log 8log
aa a
bb
a
P ab
b


= −+




.
0,5
Ta có
log log . log 1
aa a
bb b
b
ba a
a

= = −


.
Do đó
2
2
88
2 2log log 1 2 log 1
log log
aa a
aa
bb b
bb
P aa a
aa


= − − + = ++





.
Lưu ý: HS có thể biến đổi nhiều cách khác nhau cứ rút gọn để đặt được ẩn phụ
thì dều cho 0,25 ( HS thường sẽ biến đổi về
log
a
tb=
)
0,25
Đặt
log
a
b
ta=
. Do
2
1 ab ab< ≤ → ≤
, suy ra
1 1 11
log 1 log 1 log 1 2
log 2 2
a aa
a
b
a
ba t
t ab
= = = − ≤ − = − = → ≥
.
Khi đó
( ) ( )
2
8
21P t ft
t
= + +=
.
Khảo sát
( )
ft
( )
2
8
21t
t
= ++
trên
[
)
2; +∞
Ta được
(
)
[
)
( )
2;
min 2 22.
ft f
+∞
= =
Với
2
2 log 2 .
a
b
t a ab= → = ↔ =
Vậy giá trị nhỏ nhất của biểu thức
22P = ⇔
2
.ab=
0,25
| 1/15
| | Tải xuống

Có thể bạn quan tâm:

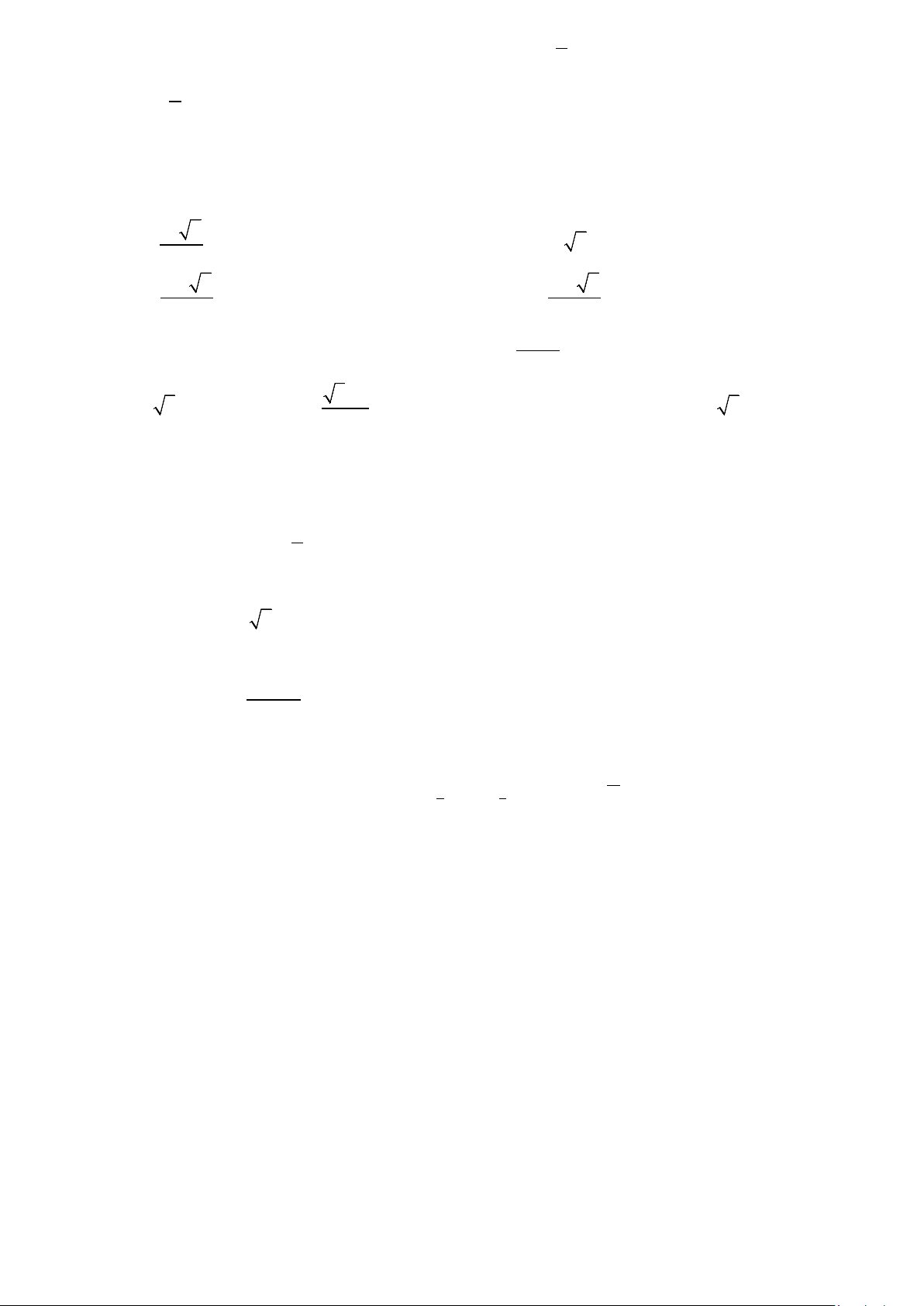
Preview text:

SỞ GD&ĐT PHÚ THỌ
ĐỀ KIỂM TRA CUỐI HỌC KỲ I TRƯỜNG THPT CHUYÊN
LỚP: 12 - MÔN: TOÁN HÙNG VƯƠNG
CHƯƠNG TRÌNH: Không chuyên
Ngày 15 tháng 12 năm 2023
(Đề gồm: 05 trang)
Thời gian làm bài: 90 phút.
(35 câu TNKQ- 4 câu TL) Mã đề 125
Họ và tên thí sinh………………………………………………SBD………………………………………………….
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (35 CÂU, 7.0 ĐIỂM)
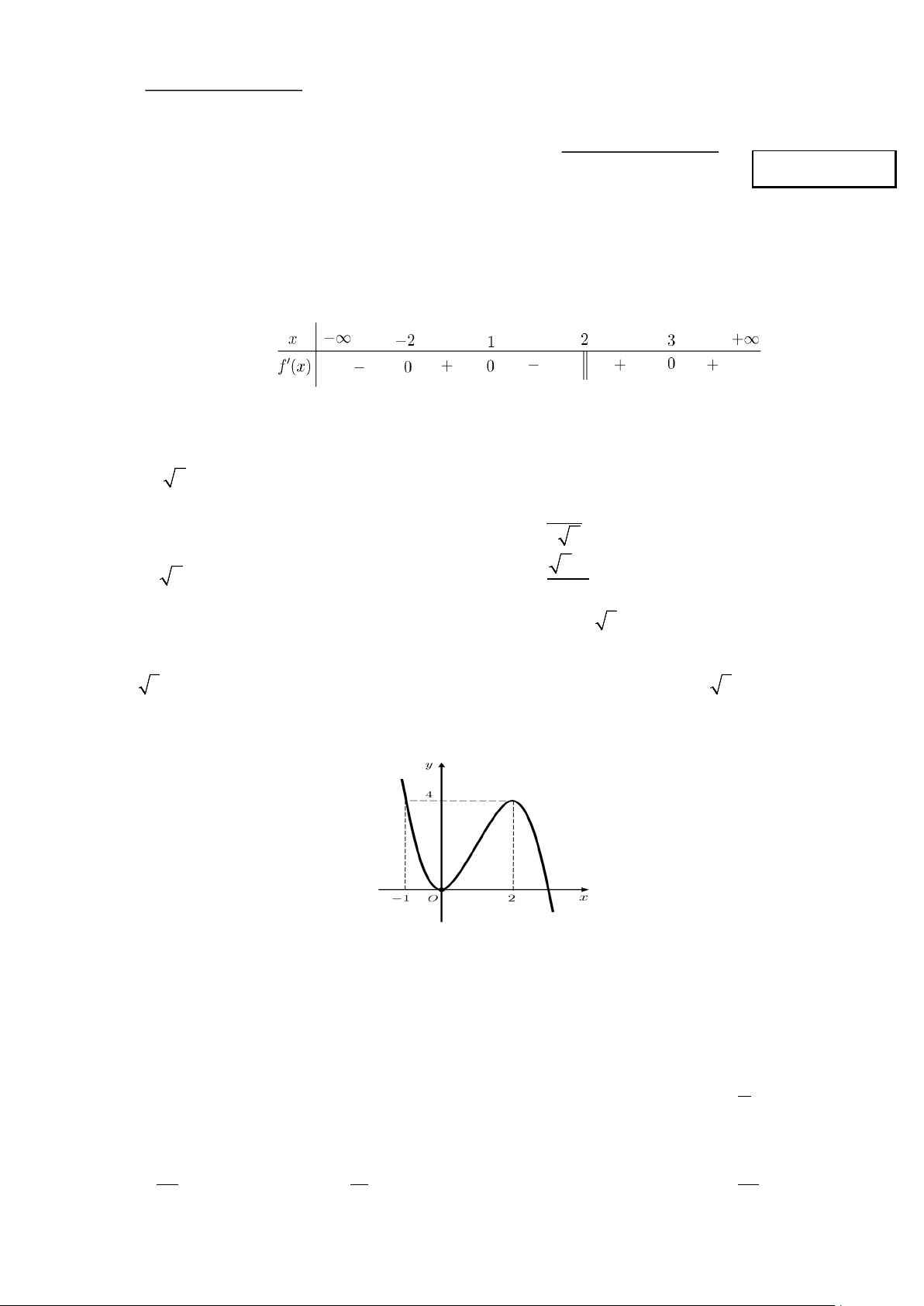
Câu 1: Cho hàm số f (x) liên tục trên  và có bảng xét dấu của f (′x) như sau:
Số điểm cực tiểu của hàm số đã cho là A. 3. B. 1. C. 4. D. 2.
Câu 2: Cho khối lăng trụ đứng ABC.A′B C ′ ′ có B C
′ = 3a , đáy ABC là tam giác vuông cân tại B
và AC = a 2 . Tính thể tích V của khối lăng trụ đứng ABC.A′B C ′ ′. 3 A. 3 V = 2a . B. a V = . 6 2 3 C. 3 2 V a = 2a . D. V = . 3
Câu 3: Cho khối chóp S.ABC có tam giác ABC vuông tại B , AB= 3 , BC = 3, SA ⊥ ( ABC) và góc
giữa SC với đáy bằng 0
45 . Thể tích của khối chóp S.ABC bằng A. 2 3. B. 6. C. 3. D. 3.
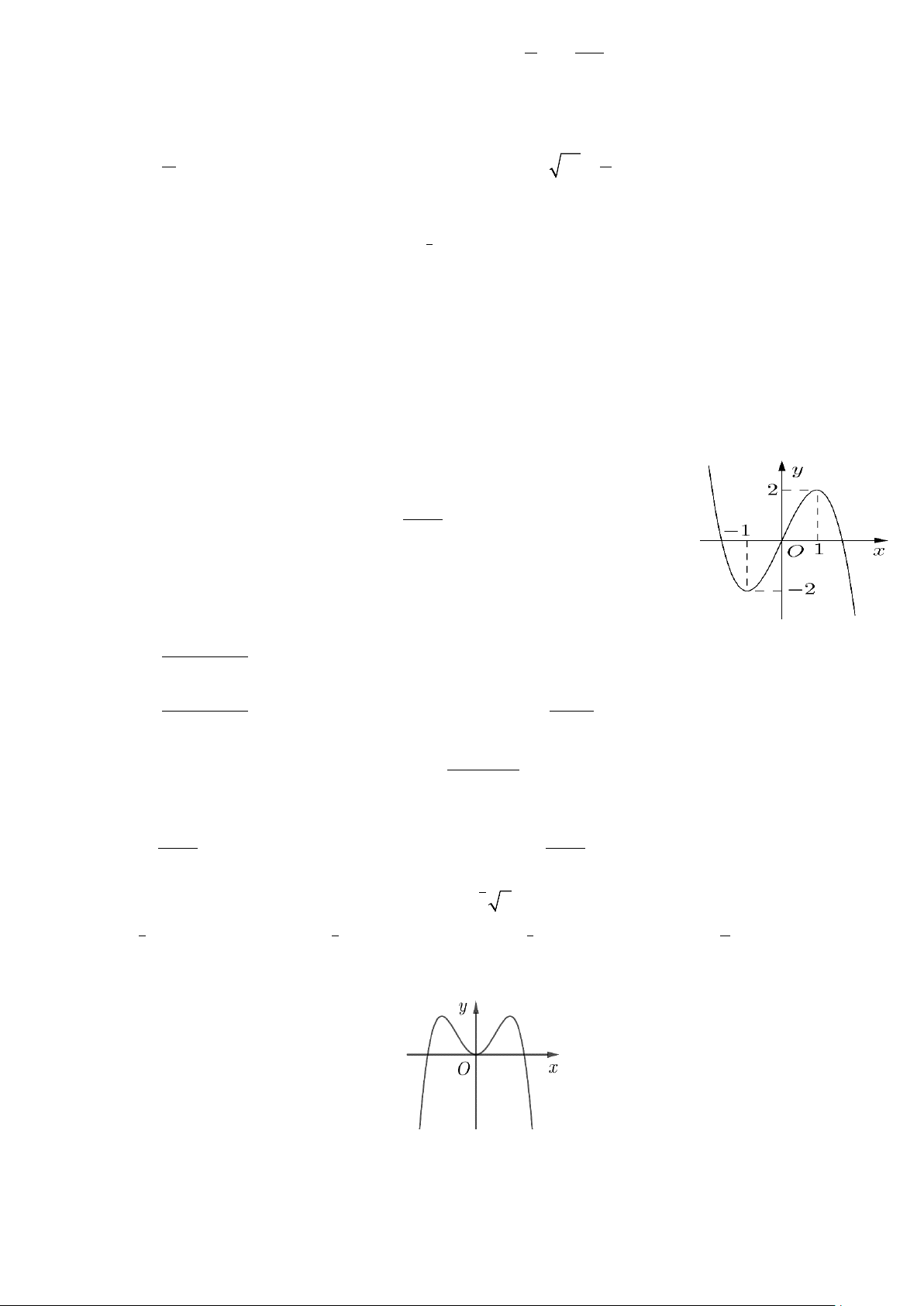
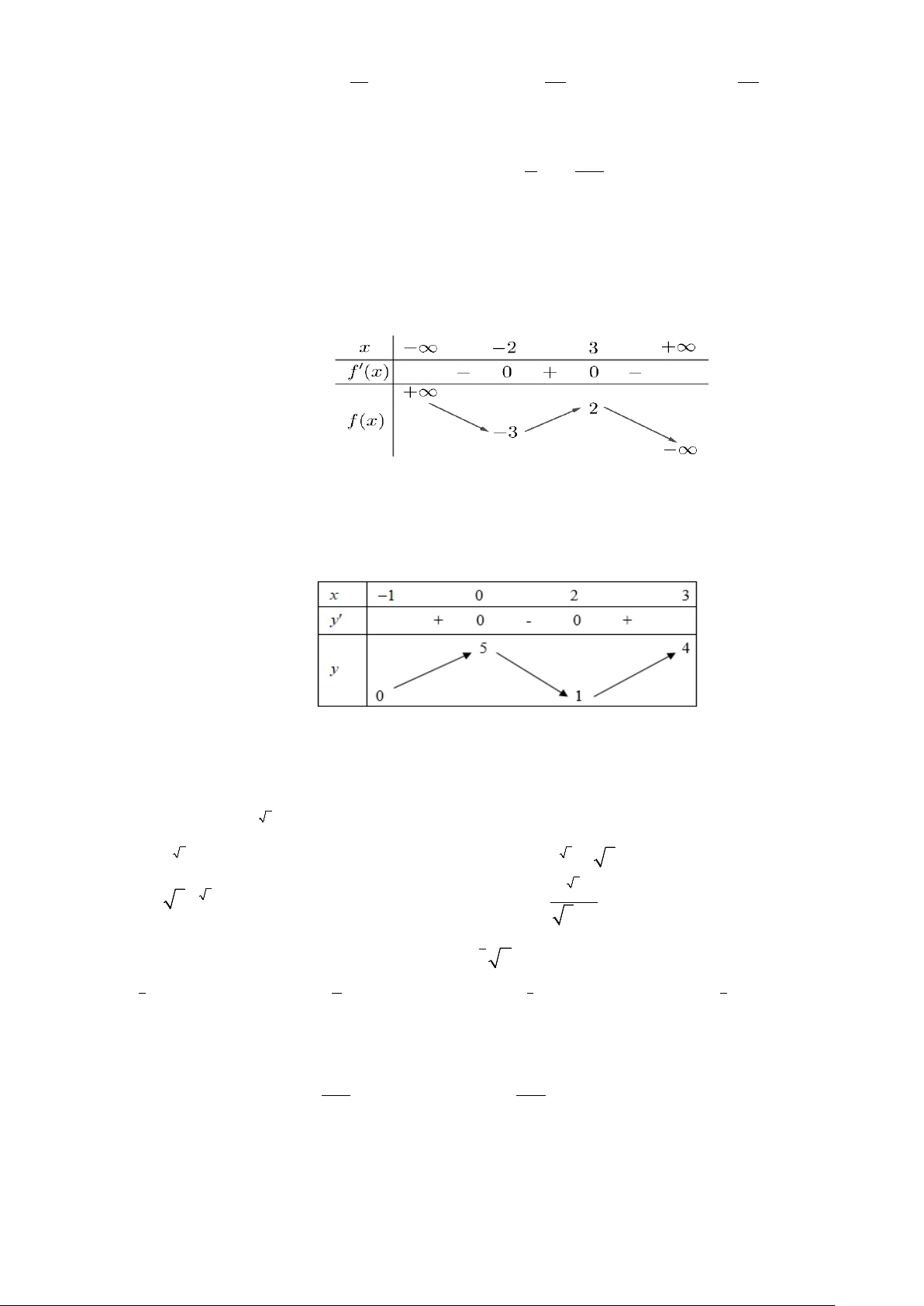
Câu 4: Cho hàm số y = f (x) liên tục trên  và có đồ thị như hình bên. Hàm số đồng biến trên khoảng nào dưới đây? A. ( 1; − 2). B. ( 1; − 0). C. (2;+∞). D. (0;2).
Câu 5: Cho khối hộp hình chữ nhật có ba kích thước 2; 4; 6 . Thể tích của khối hộp đã cho bằng A. 16. B. 12. C. 48. D. 8.
Câu 6: Cho hình lăng trụ tứ giác ABC . D A′B C ′ D
′ ′ có đáy ABCD là hình vuông cạnh a và thể tích bằng 3
3a . Tính chiều cao h của hình lăng trụ đã cho. A. h a = . a B. h = 3 . a C. h = 9 . a D. h = . 3
Câu 7: Phương trình log 3x − 2 = 3 có nghiệm là 3 ( ) A. 29 x = . B. 11 x = . C. x = 87. D. 25 x = . 3 3 3
Câu 8: Cho các số thực a,b,α (a > b > 0;α ≠ 1). Mệnh đề nào sau đây đúng?
Trang 1/5 - Mã đề thi 125 α α
A. (a b)α aα bα + = + . B. a a =   .  b b−α
C. (a b)α aα bα − = − .
D. (ab)α aαbα = .
Câu 9: Giả sử x, y là các số thực dương. Mệnh đề nào sau đây sai? A. log x 1 = log x − log .
y B. log xy = log x + log y . 3 ( 3 3 ) 3 3 3 y 2
C. log xy = log x + log .
y D. log x + y = log x + log . y 3 ( ) 3 3 3 3 3
Câu 10: Tập xác định của hàm số y = (x − )13 5 là A. ( ; −∞ 5). B. (5;+∞). C.  \{ } 5 . D. ( ; −∞ +∞).
Câu 11: Đồ thị hàm số y = ( 2
x − 9)(x + 3)2 cắt trục hoành tại bao nhiêu điểm phân biệt? A. 1. B. 3. C. 4. D. 2.
Câu 12: Cho a là số thực dương, a ≠1, khi đó 3loga 2 a bằng A. 8. B. 3 a . C. 6. D. 3 . a
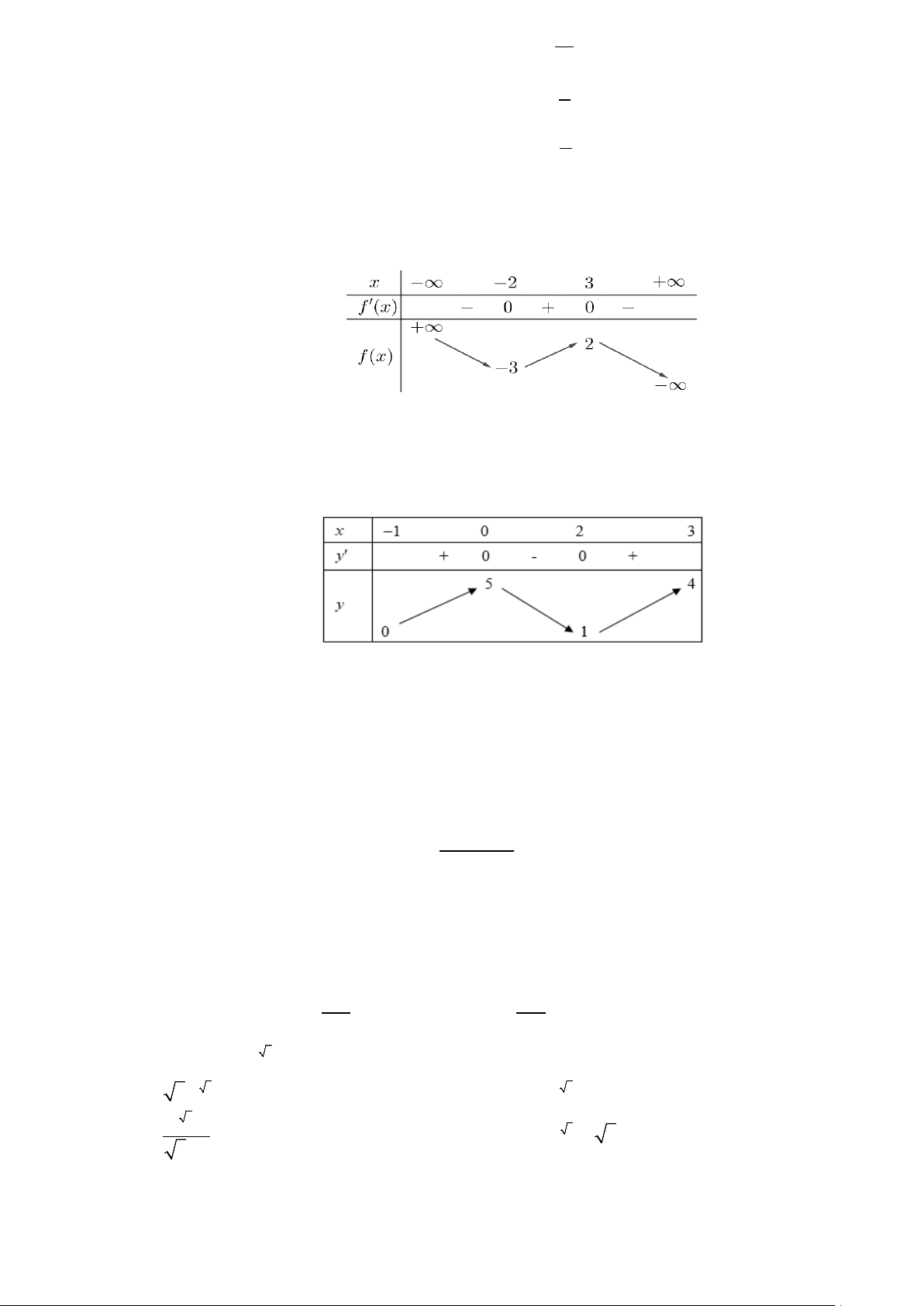
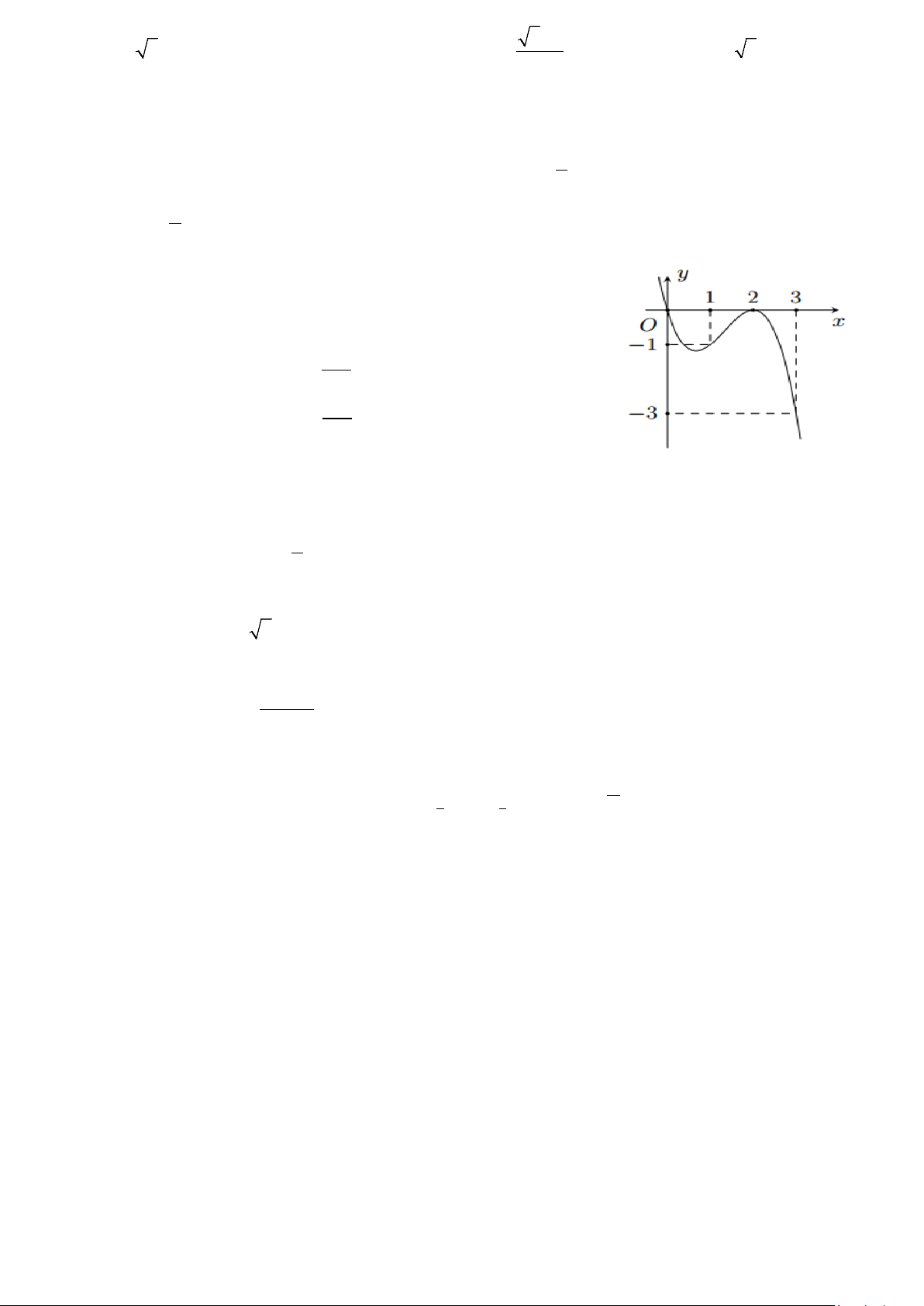
Câu 13: Cho hàm số bậc ba y = f (x) có đồ thị là đường cong trong hình bên.
Số nghiệm thực của phương trình f (x) 1 = là 2023 A. 2. B. 3. C. 1. D. 0.
Câu 14: Tính đạo hàm của hàm số y = log 2x +1 . 3 ( ) A. 2 y′ = (
B. y′ = (2x + ) 1 .ln 3. x + ) . 2 1 ln 3 C. 1 y′ = ′ ( D. 1 y = . x + ) . 2 1 ln 3 2x +1
Câu 15: Tiệm cận ngang của đồ thị hàm số 2024x +1 y = là x −1 A. y = 2024. − B. y = 2024. C. 1 y = . D. 1 y − = . 2024 2024 2
Câu 16: Cho a là một số dương bất kỳ, biểu thức 3
a a viết dưới dạng lũy thừa với số mũ hữu tỷ là 5 6 7 11 A. 6 a . B. 5 a . C. 6 a . D. 6 a .
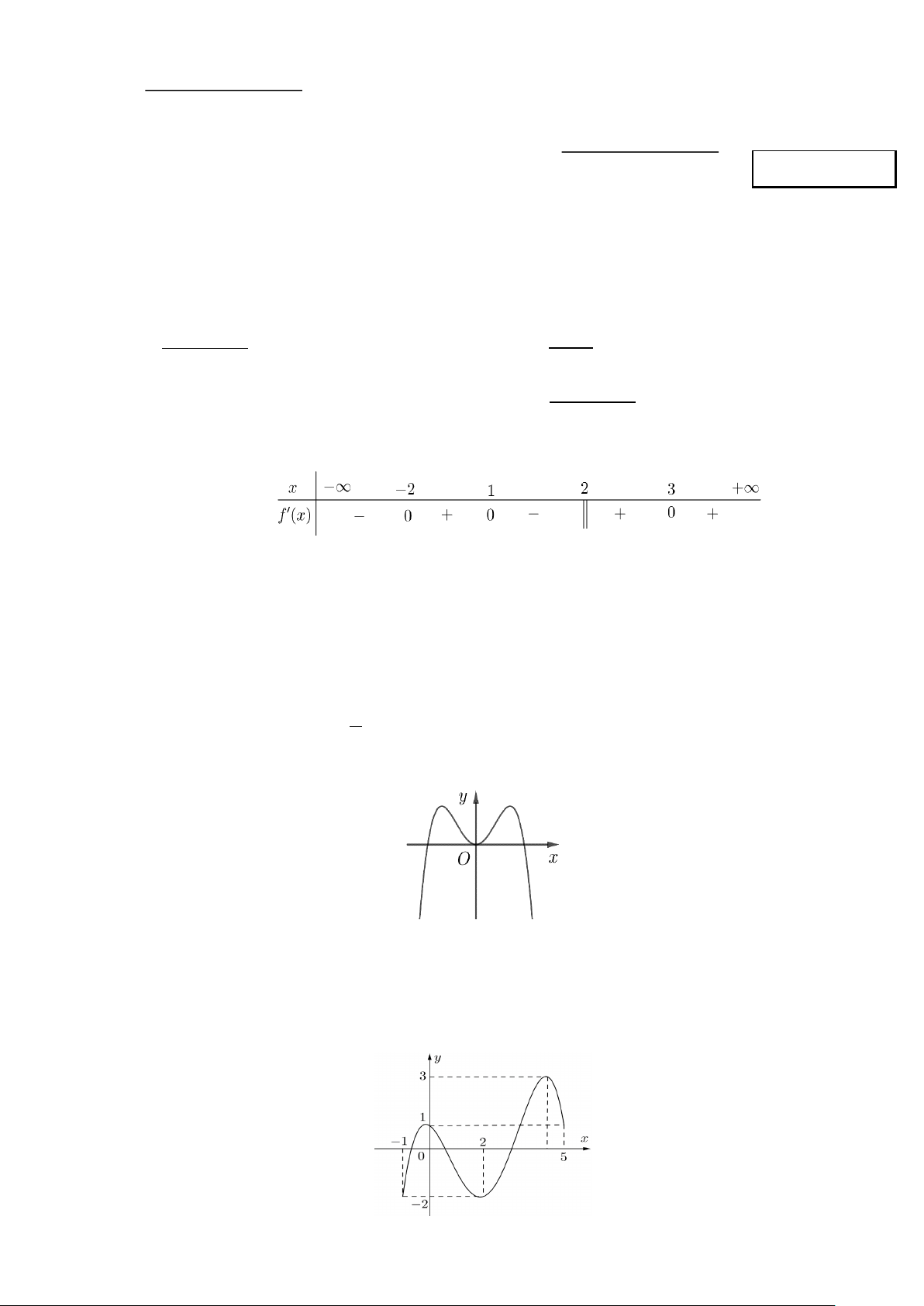
Câu 17: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên dưới? A. 3 y = x − 3 . x B. 4 2
y = x − 2x . C. 4 2
y = −x + 2x . D. 3 y = −x + 3 . x
Trang 2/5 - Mã đề thi 125
Câu 18: Giả sử a,b là các số thực dương bất kỳ. Biểu thức ln a bằng 2 b
A. ln a − 2ln . b B. 1 ln a − ln . b 2 C. ln a + 2ln . b D. 1 ln a + ln . b 2
Câu 19: Nghiệm của phương trình x+2 3 = 27 là A. x = 1. − B. x = 2. − C. x = 2. D. x =1.
Câu 20: Cho hàm số f (x) có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 2. B. 3. − C. 3. D. 2. −
Câu 21: Cho hàm số y = f (x) liên tục và có bảng biến thiên trên đoạn [ 1; −
]3 như hình vẽ bên. Khẳng
định nào sau đây đúng?
A. min f (x) = f (0).
B. min f (x) = f (− ) 1 . [ 1 − ; ] 3 [ 1 − ; ] 3
C. min f (x) = f (3).
D. min f (x) = f (2). [ 1 − ; ] 3 [ 1 − ; ] 3
Câu 22: Cho khối lập phương có cạnh bằng 6 . Thể tích của khối lập phương đã cho bằng A. 216. B. 18. C. 36. D. 72.
Câu 23: Tiệm cận đứng của đồ thị hàm số 2x − 2023 y = là x +1 A. x = 2. B. x = 2. − C. x =1. D. x = 1. −
Câu 24: Cho khối chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy và
SA = 2a . Thể tích khối chóp đã cho bằng 3 3 A. 2 . a B. 2a . C. 4a . D. 3 a . 3 3 Câu 25: Hàm số 3
y = x có đạo hàm là A. 3 1 y ' 3.x − = . B. 3 y ' = x ln . x 3 1 − C. ' x y = . D. 3 y ' = x ln 3. 3 +1
Trang 3/5 - Mã đề thi 125
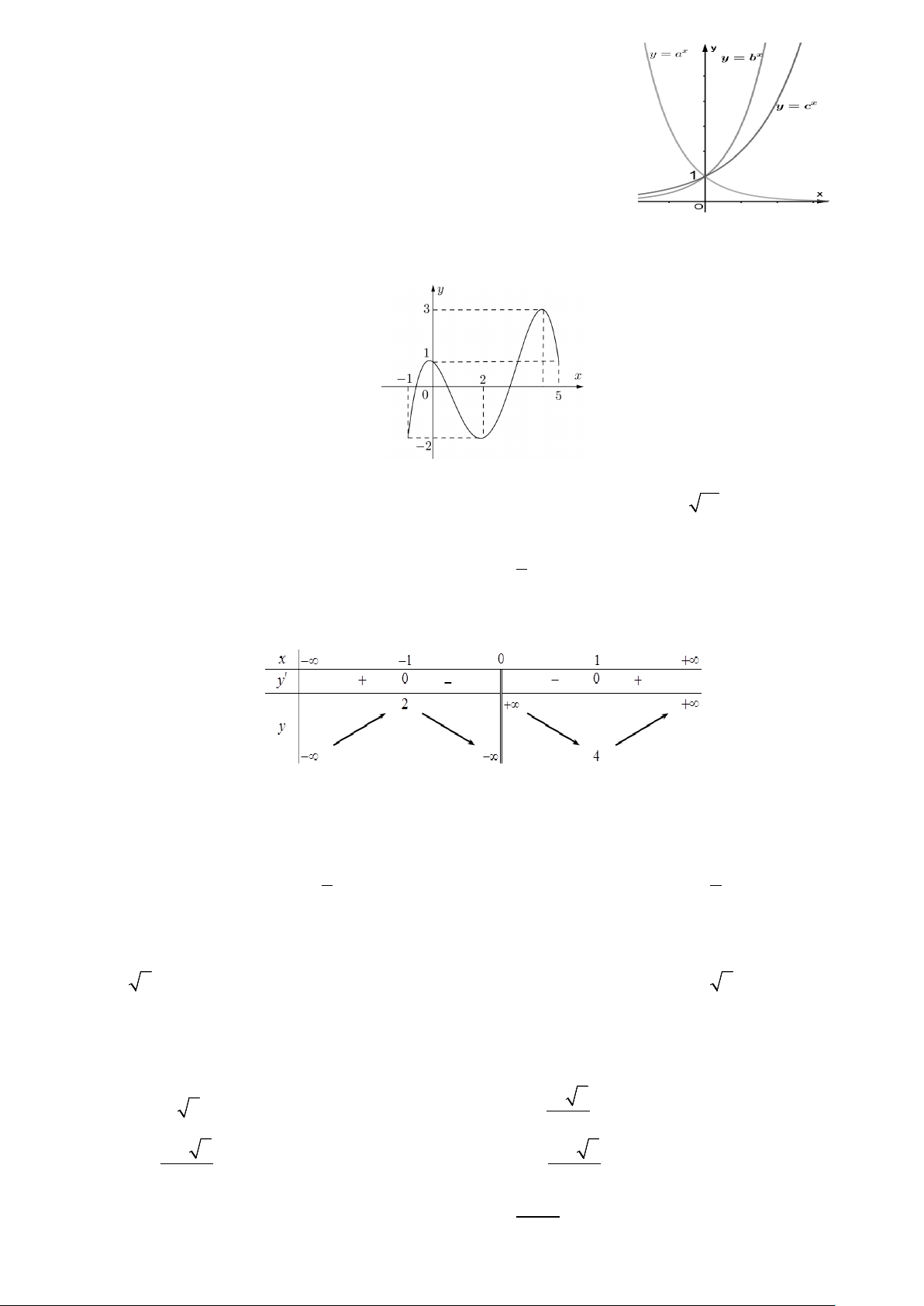
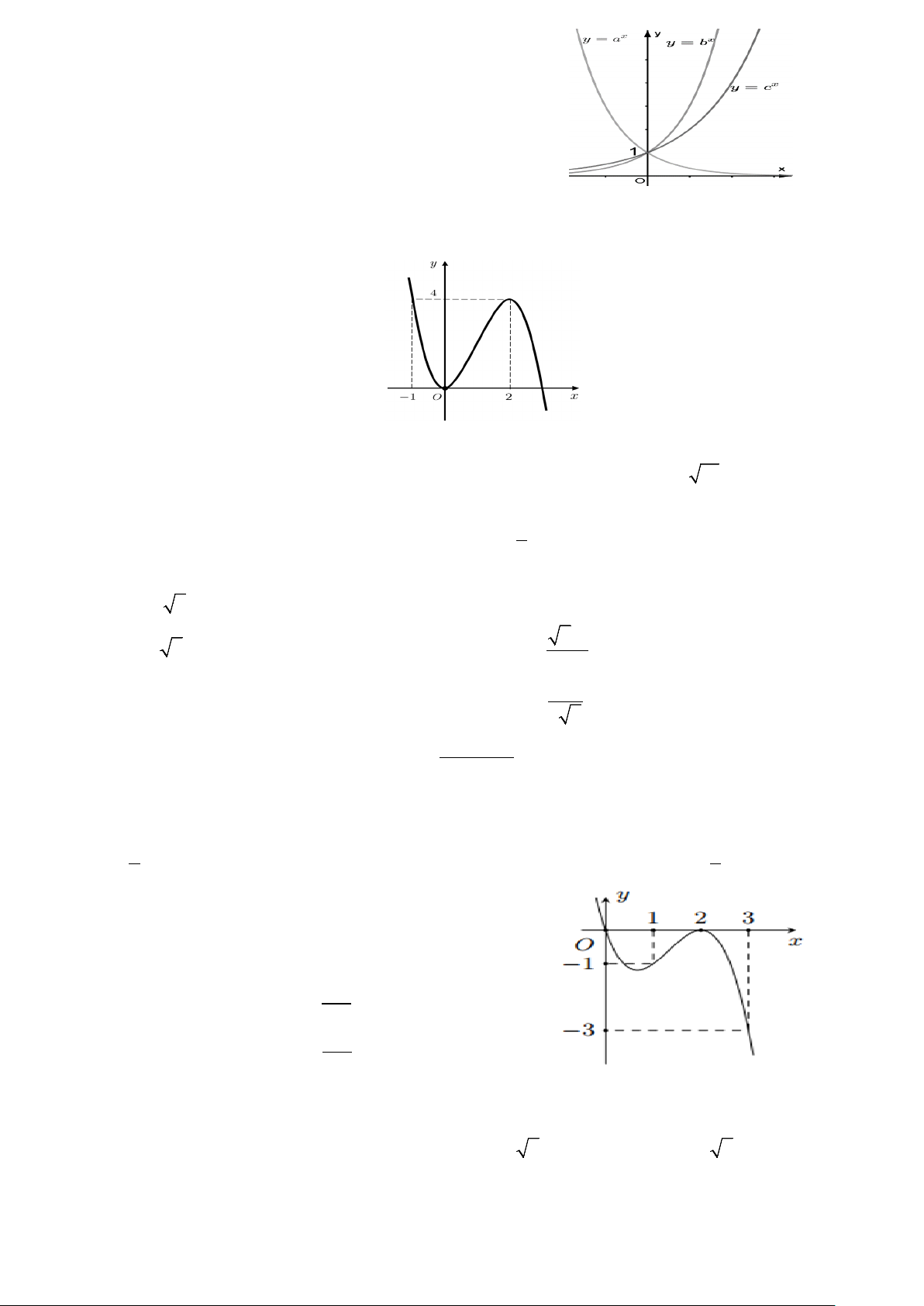
Câu 26: Cho ba số thực dương a,b,c khác 1. Đồ thị các hàm số x = , x = , x
y a y b y = c được cho trong hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A. c < a < . b
B. b < c < . a
C. a < c < . b
D. a < b < .c
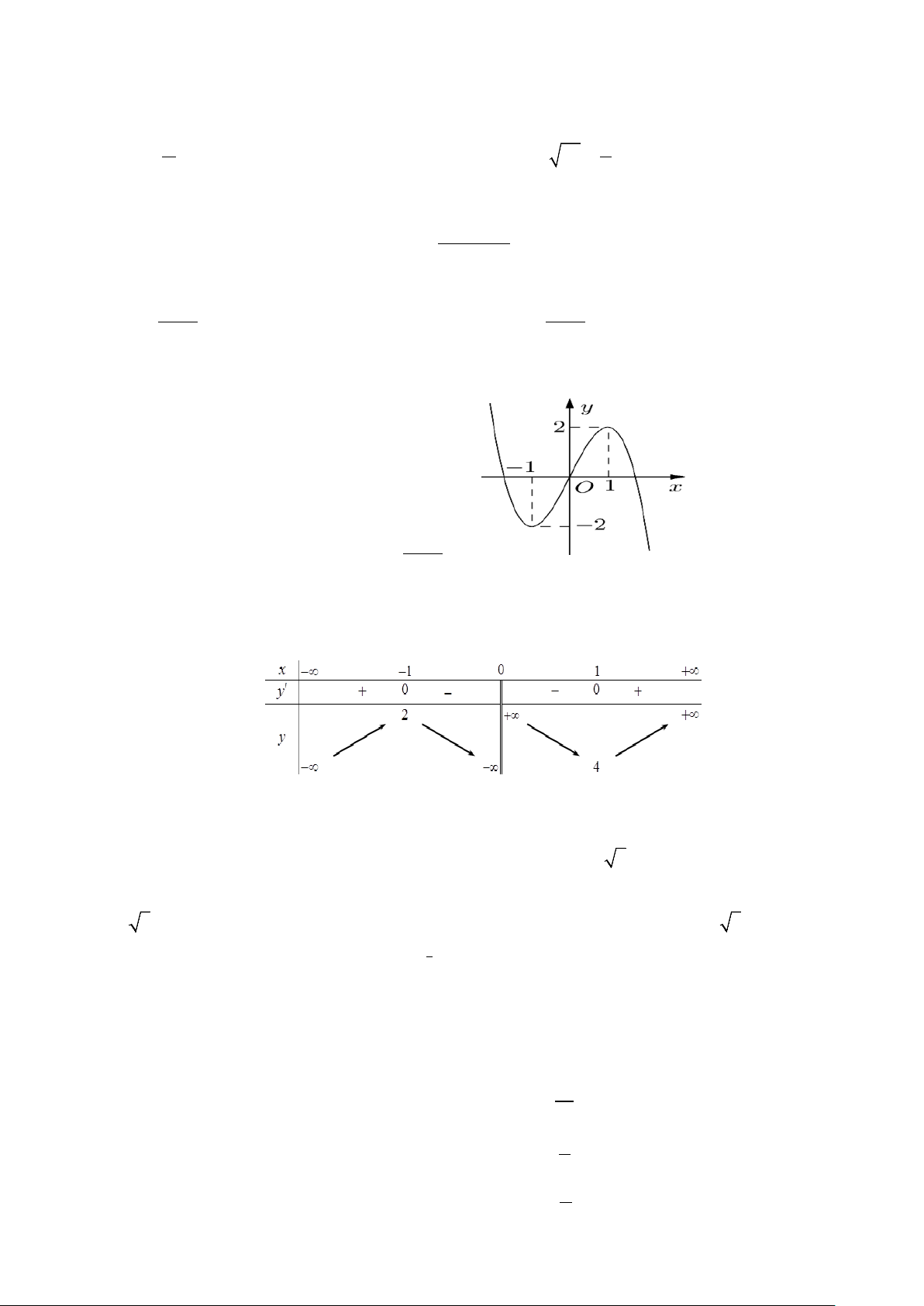
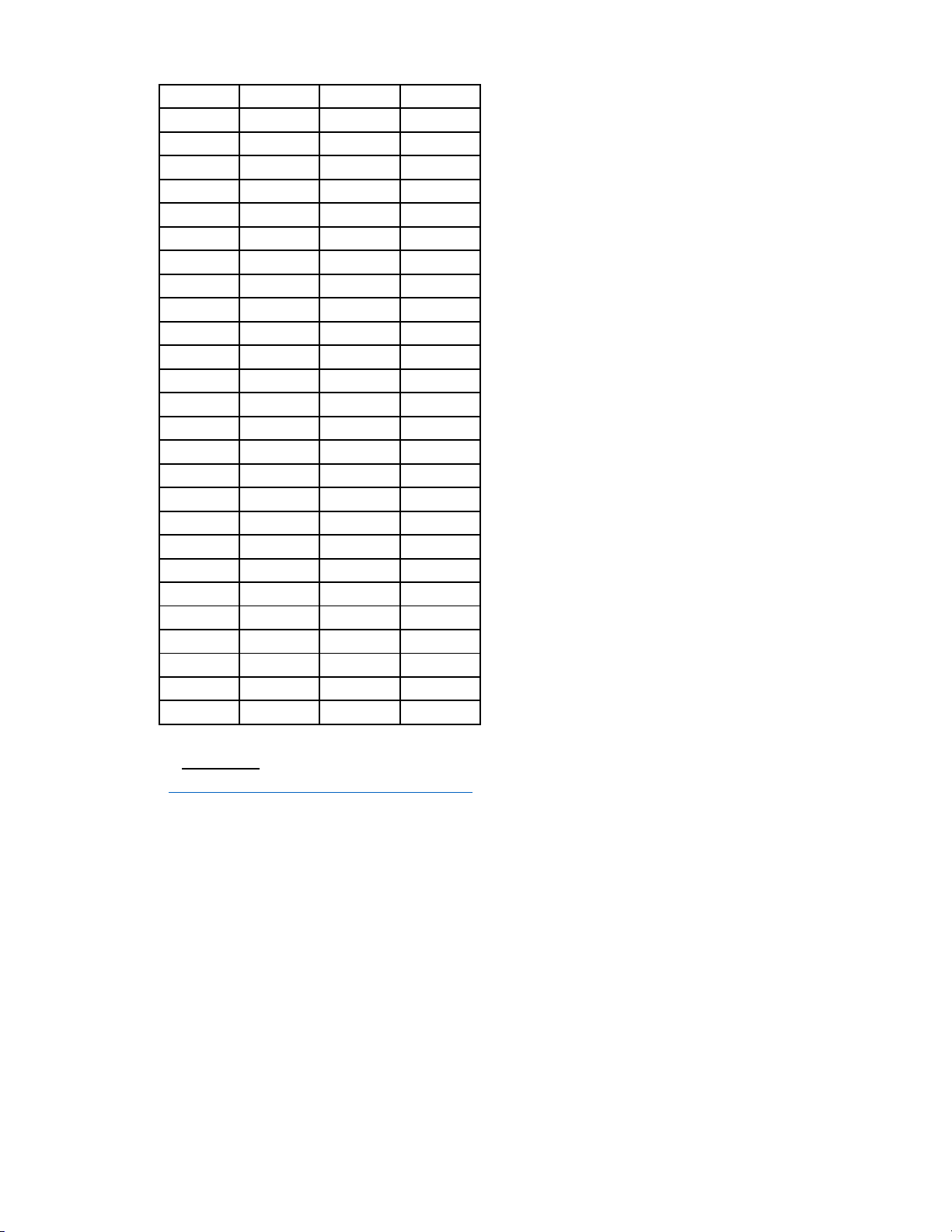
Câu 27: Cho hàm số f (x) liên tục trên [ 1;
− 5] và có đồ thị trên đoạn [ 1;
− 5] như hình vẽ bên dưới. Tổng
giá trị lớn nhất và giá trị nhỏ nhất của hàm số f (x) trên đoạn [ 1; − 5] bằng A. 2. B. 4. C. 1. D. 1. −
Câu 28: Cho khối hộp chữ nhật ABCD. A′B C ′ D
′ ′ , biết AB = a; BC = 2a; AC′ = a 21 . Tính thể tích V của khối hộp đó? A. 3 8 4a . B. 3 16a . C. 3 a . D. 3 8a . 3
Câu 29: Cho hàm số y = f (x) có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. (4;+ ∞). B. (−∞;2). C. ( 1; − ) 1 . D. (0 ) ;1 .
Câu 30: Khối lăng trụ có chiều cao bằng h và diện tích đáy bằng S thì có thể tích bằng A. . Sh B. 1 . Sh C. 3 . Sh D. 1 . Sh 3 2
Câu 31: Gọi A , B , C là các điểm cực trị của đồ thị hàm số 4 2
y = x − 2x + 4 . Bán kính đường tròn ngoại
tiếp tam giác ABC bằng A. 2 +1. B. 1. C. 2. D. 2 −1.
Câu 32: Cho hình lăng trụ đứng ABC.A′B C
′ ′ có đáy ABC là tam giác vuông tại A , AC = a , 
ACB = 60 .° Đường chéo BC′ của mặt bên (BCC B
′ ′) tạo với mặt phẳng ( ACC A
′ ′) một góc 30° . Tính
thể tích của khối lăng trụ theo a . 3 A. 3 V = a 6. B. a 6 V = . 3 3 3 C. 2a 6 V = . D. 4a 6 V = . 3 3 Câu 33: Cho −
a,b là số thực dương thỏa mãn + +2 −3 1 2a b ab ab =
. Giá trị nhỏ nhất của biểu thức 2 2 a + b là: a + b
Trang 4/5 - Mã đề thi 125 A. ( − − )2 5 1 . B. 2. C. 5 1. D. 3− 5. 2
Câu 34: Cho phương trình 2
log x − 3log x + 4m − 7 = 0 có hai nghiệm thực phân biệt x , x thỏa mãn 5 5 1 2
(x +1 x +5 =180. Khẳng định nào dưới đây đúng? 1 )( 2 ) A. m∈(1;2). B. 5 m  ; ; ∈ +∞  .  2  C. 7 m  ;3 ∈ . D. m∈( ;0 −∞ ).  4 
Câu 35: Cho hàm số 3 2
y = f (x) = ax + bx + cx + d có đồ thị
là đường cong trong hình vẽ bên.Tổng giá trị lớn nhất và
giá trị nhỏ nhất của hàm số 2 y = f ( 3 − sin x +1) bằng A. 33. B. 832 . 27 C. 31. D. 896 . 27
-----------------------------------------------
II. PHẦN TỰ LUẬN ( 4 CÂU, 3.0 ĐIỂM)
Câu 1 (1 điểm). Giải phương trình 3x 1 − a) x−5  1 3  = 
b) log x −1 + log x +1 = 3 2 ( ) 2 ( ) 9   
Câu 2 (0,5 điểm). Cho hình lăng trụ đứng ABC.A'B 'C ' có đáy ABC là tam giác vuông cân tại ,
A BC = 2a, A'B = a 6. Tính thể tích của khối lăng trụ ABC.A'B 'C ' theo a .
Câu 3 (1,0 điểm). Có bao nhiêu giá trị nguyên m ≠ 0 thuộc đoạn [ 5;
− 5], để đường thẳng y = mx +1 − + cắt đồ thị hàm số 2x 1 y =
tại hai điểm phân biệt. x −1
Câu 4 (0,5 điểm). Cho các số thực a, b thỏa mãn 2 1< a ≤ b . 2  
Tìm giá trị nhỏ nhất của biểu thức 22log  a P a b  = −  + . a loga 8loga     b b b
-------------------- HẾT -------------------- Lưu ý:
- Cán bộ coi thi không giải thích gì thêm.
- Học sinh không được sử dụng tài liệu trong thời gian làm bài.
Trang 5/5 - Mã đề thi 125 SỞ GD&ĐT PHÚ THỌ
ĐỀ KIỂM TRA CUỐI HỌC KỲ I TRƯỜNG THPT CHUYÊN
LỚP: 12 - MÔN: TOÁN HÙNG VƯƠNG
CHƯƠNG TRÌNH: Không chuyên
Ngày 15 tháng 12 năm 2023
(Đề gồm: 05 trang)
Thời gian làm bài: 90 phút.
(35 câu TNKQ- 4 câu TL) Mã đề 126
Họ và tên thí sinh………………………………………………SBD………………………………………………….
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (35 CÂU, 7.0 ĐIỂM)
Câu 1: Tính đạo hàm của hàm số y = log 2x +1 . 3 ( ) A. 2 y′ = ′ ( B. 1 y = . x + ) . 2 1 ln 3 2x +1
C. y′ = (2x + ) 1 .ln 3. D. 1 y′ = ( x + ) . 2 1 ln 3
Câu 2: Cho hàm số f (x) liên tục trên  và có bảng xét dấu của f (′x) như sau:
Số điểm cực tiểu của hàm số đã cho là A. 4. B. 3. C. 1. D. 2.
Câu 3: Cho a là số thực dương, a ≠1, khi đó 3loga 2 a bằng A. 8. B. 3 a . C. 3 . a D. 6.
Câu 4: Cho hình lăng trụ tứ giác ABC . D A′B C ′ D
′ ′ có đáy ABCD là hình vuông cạnh a và thể tích bằng 3
3a . Tính chiều cao h của hình lăng trụ đã cho. A. h a = . a B. h = .. C. h = 3 . a D. h = 9 . a 3
Câu 5: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3 y = x − 3 . x B. 4 2
y = −x + 2x . C. 4 2
y = x − 2x . D. 3 y = −x + 3 . x
Câu 6: Cho hàm số f (x) liên tục trên [ 1;
− 5] và có đồ thị trên đoạn [ 1;
− 5] như hình vẽ bên dưới. Tổng
giá trị lớn nhất và giá trị nhỏ nhất của hàm số f (x) trên đoạn [ 1; − 5] bằng
Trang 1/5 - Mã đề thi 126 A. 4. B. 1. C. 2. D. 1. −
Câu 7: Cho khối lập phương có cạnh bằng 6 . Thể tích của khối lập phương đã cho bằng A. 72. B. 18. C. 36. D. 216.
Câu 8: Giả sử x, y là các số thực dương. Mệnh đề nào sau đây sai? A. log x 1 = log x − log .
y B. log xy = log x + log y . 3 ( 3 3 ) 3 3 3 y 2
C. log xy = log x + log .
y D. log x + y = log x + log . y 3 ( ) 3 3 3 3 3
Câu 9: Tiệm cận ngang của đồ thị hàm số 2024x +1 y = là x −1 A. y = 2024. B. y = 2024. − C. 1 y = . D. 1 y − = . 2024 2024
Câu 10: Cho hàm số bậc ba y = f (x) có đồ thị là đường cong trong hình bên.
Số nghiệm thực của phương trình f (x) 1 = là 2023 A. 1. B. 3. C. 2. D. 0.
Câu 11: Cho hàm số y = f (x) có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. (4;+ ∞). B. (−∞;2). C. ( 1; − ) 1 . D. (0 ) ;1 .
Câu 12: Cho khối chóp S.ABC có tam giác ABC vuông tại B , AB= 3 , BC = 3, SA ⊥ ( ABC) và góc
giữa SC với đáy bằng 0
45 . Thể tích của khối chóp S.ABC bằng A. 3. B. 6. C. 3. D. 2 3.
Câu 13: Tập xác định của hàm số y = (x − )13 5 là A.  \{ } 5 . B. (5;+∞). C. ( ; −∞ 5). D. ( ; −∞ +∞).
Câu 14: Nghiệm của phương trình x+2 3 = 27 là A. x = 1. − B. x = 2. − C. x = 2. D. x =1.
Câu 15: Giả sử a,b là các số thực dương bất kỳ. Biểu thức ln a bằng 2 b
A. ln a − 2ln . b B. 1 ln a − ln . b 2 C. ln a + 2ln . b D. 1 ln a + ln . b 2
Trang 2/5 - Mã đề thi 126
Câu 16: Phương trình log 3x − 2 = 3 có nghiệm là 3 ( ) A. x = 87. B. 11 x = . C. 29 x = . D. 25 x = . 3 3 3
Câu 17: Cho các số thực a,b,α (a > b > 0;α ≠ 1). Mệnh đề nào sau đây đúng? α α
A. (a b)α aα bα − = − . B. a a =   .  b b−α
C. (a b)α aα bα + = + .
D. (ab)α aαbα = .
Câu 18: Đồ thị hàm số y = ( 2
x − 9)(x + 3)2 cắt trục hoành tại bao nhiêu điểm phân biệt? A. 2. B. 1. C. 4. D. 3.
Câu 19: Cho hàm số f (x) có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 2. B. 3. − C. 3. D. 2. −
Câu 20: Cho hàm số y = f (x) liên tục và có bảng biến thiên trên đoạn [ 1; −
]3 như hình vẽ bên. Khẳng
định nào sau đây đúng?
A. min f (x) = f (0).
B. min f (x) = f (− ) 1 . [ 1 − ; ] 3 [ 1 − ; ] 3
C. min f (x) = f (3).
D. min f (x) = f (2). [ 1 − ; ] 3 [ 1 − ; ] 3 Câu 21: Hàm số 3
y = x có đạo hàm là A. 3 y ' = x ln . x B. 3 y ' = x ln 3. 3 1 − C. 3 1 y ' 3.x − = . D. ' x y = . 3 +1 2
Câu 22: Cho a là một số dương bất kỳ, biểu thức 3
a a viết dưới dạng lũy thừa với số mũ hữu tỷ là 5 11 7 6 A. 6 a . B. 6 a . C. 6 a . D. 5 a .
Câu 23: Cho khối chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy và
SA = 2a . Thể tích khối chóp đã cho bằng 3 3 A. 2 . a B. 2a . C. 4a . D. 3 a . 3 3
Câu 24: Cho khối hộp hình chữ nhật có ba kích thước 2; 4; 6 . Thể tích của khối hộp đã cho bằng A. 16. B. 8. C. 48. D. 12.
Trang 3/5 - Mã đề thi 126
Câu 25: Cho ba số thực dương a,b,c khác 1. Đồ thị các hàm số x = , x = , x
y a y b y = c được cho trong hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A. b < c < . a
B. c < a < . b
C. a < c < . b
D. a < b < .c
Câu 26: Cho hàm số y = f (x) liên tục trên  và có đồ thị như hình bên. Hàm số đồng biến trên khoảng nào dưới đây? A. ( 1; − 0). B. (0;2). C. (2;+∞). D. ( 1; − 2).
Câu 27: Cho khối hộp chữ nhật ABCD. A′B C ′ D
′ ′ , biết AB = a; BC = 2a; AC′ = a 21 . Tính thể tích V của khối hộp đó? A. 3 8 4a . B. 3 16a . C. 3 a . D. 3 8a . 3
Câu 28: Cho khối lăng trụ đứng ABC.A′B C ′ ′ có B C
′ = 3a , đáy ABC là tam giác vuông cân tại B
và AC = a 2 . Tính thể tích V của khối lăng trụ đứng ABC.A′B C ′ ′. 3 A. 3 2 V a = 2a . B. V = . 33 C. 3 V = 2a . D. a V = . 6 2
Câu 29: Tiệm cận đứng của đồ thị hàm số 2x − 2023 y = là x +1 A. x = 2. B. x = 2. − C. x =1. D. x = 1. −
Câu 30: Khối lăng trụ có chiều cao bằng h và diện tích đáy bằng S thì có thể tích bằng A. 1 . Sh B. . Sh C. 3 . Sh D. 1 . Sh 2 3
Câu 31: Cho hàm số 3 2
y = f (x) = ax + bx + cx + d có đồ thị
là đường cong trong hình vẽ bên.Tổng giá trị lớn nhất và
giá trị nhỏ nhất của hàm số 2 y = f ( 3 − sin x +1) bằng A. 33. B. 832 . 27 C. 31. D. 896 . 27
Câu 32: Gọi A , B , C là các điểm cực trị của đồ thị hàm số 4 2
y = x − 2x + 4 . Bán kính đường tròn ngoại
tiếp tam giác ABC bằng A. 1. B. 2. C. 2 −1. D. 2 +1.
Câu 33: Cho phương trình 2
log x − 3log x + 4m − 7 = 0 có hai nghiệm thực phân biệt x , x thỏa mãn 5 5 1 2
(x +1 x +5 =180. Khẳng định nào dưới đây đúng? 1 )( 2 )
Trang 4/5 - Mã đề thi 126 A. m∈(1;2). B. 5 m  ; ; ∈ +∞  .  2  C. 7 m  ;3 ∈ . D. m∈( ;0 −∞ ).  4 
Câu 34: Cho hình lăng trụ đứng ABC.A′B C
′ ′ có đáy ABC là tam giác vuông tại A , AC = a , 
ACB = 60 .° Đường chéo BC′ của mặt bên (BCC B
′ ′) tạo với mặt phẳng ( ACC A
′ ′) một góc 30° . Tính
thể tích của khối lăng trụ theo a . 3 A. a 6 V = . B. 3 V = a 6. 3 3 3 C. 2a 6 V = . D. 4a 6 V = . 3 3 Câu 35: Cho −
a,b là số thực dương thỏa mãn + +2 −3 1 2a b ab ab =
. Giá trị nhỏ nhất của biểu thức 2 2 a + b là a + b A. 3 − − 5. B. 5 1. C. 2. D. ( − )2 5 1 . 2
-----------------------------------------------
II. PHẦN TỰ LUẬN ( 4 CÂU, 3.0 ĐIỂM)
Câu 1 (1 điểm). Giải phương trình 3x 1 − a) x−5  1 3  = 
b) log x −1 + log x +1 = 3 2 ( ) 2 ( ) 9   
Câu 2 (0,5 điểm). Cho hình lăng trụ đứng ABC.A'B 'C ' có đáy ABC là tam giác vuông cân tại ,
A BC = 2a, A'B = a 6. Tính thể tích của khối lăng trụ ABC.A'B 'C ' theo a .
Câu 3 (1,0 điểm). Có bao nhiêu giá trị nguyên m ≠ 0 thuộc đoạn [ 5;
− 5], để đường thẳng y = mx +1 2 − x +1
cắt đồ thị hàm số y =
tại hai điểm phân biệt. x −1
Câu 4 (0,5 điểm). Cho các số thực a, b thỏa mãn 2 1< a ≤ b . 2  
Tìm giá trị nhỏ nhất của biểu thức 22log  a P a b  = −  + . a loga 8loga     b b b
-------------------- HẾT -------------------- Lưu ý:
- Cán bộ coi thi không giải thích gì thêm.
- Học sinh không được sử dụng tài liệu trong thời gian làm bài.
Trang 5/5 - Mã đề thi 126 mamon made cautron dapan TOAN 125 1 D TOAN 125 2 C TOAN 125 3 C TOAN 125 4 D TOAN 125 5 C TOAN 125 6 B TOAN 125 7 A TOAN 125 8 D TOAN 125 9 D TOAN 125 10 B TOAN 125 11 D TOAN 125 12 A TOAN 125 13 B TOAN 125 14 A TOAN 125 15 B TOAN 125 16 C TOAN 125 17 C TOAN 125 18 A TOAN 125 19 D TOAN 125 20 B TOAN 125 21 B TOAN 125 22 A TOAN 125 23 D TOAN 125 24 B TOAN 125 25 A TOAN 125 26 C TOAN 125 27 C TOAN 125 28 D TOAN 125 29 D TOAN 125 30 A TOAN 125 31 B TOAN 125 32 A TOAN 125 33 D TOAN 125 34 C TOAN 125 35 B TOAN 126 1 A TOAN 126 2 D TOAN 126 3 A TOAN 126 4 C TOAN 126 5 B TOAN 126 6 B TOAN 126 7 D TOAN 126 8 D TOAN 126 9 A TOAN 126 10 B TOAN 126 11 D TOAN 126 12 C TOAN 126 13 B TOAN 126 14 D TOAN 126 15 A TOAN 126 16 C TOAN 126 17 D TOAN 126 18 A TOAN 126 19 B TOAN 126 20 B TOAN 126 21 C TOAN 126 22 C TOAN 126 23 B TOAN 126 24 C TOAN 126 25 C TOAN 126 26 B TOAN 126 27 D TOAN 126 28 A TOAN 126 29 D TOAN 126 30 B TOAN 126 31 B TOAN 126 32 A TOAN 126 33 C TOAN 126 34 B TOAN 126 35 A
Xem thêm: ĐỀ THI HK1 TOÁN 12
https://toanmath.com/de-thi-hk1-toan-12
ĐÁP ÁN TỰ LUẬN ĐỀ KIỂM TRA CUỐI HỌC KỲ 1 TOÁN 12 NĂM HỌC 23-24
Câu 1 (1 điểm). Giải phương trình 3x 1 − a) x−5  1 3  = 
b) log x −1 + log x +1 = 3 2 ( ) 2 ( ) 9   
Câu 2 (0,5 điểm). Cho hình lăng trụ đứng ABC.A'B 'C ' có đáy ABC là tam giác vuông cân tại , A BC = 2a,
A'B = a 6. Tính thể tích của khối lăng trụ ABC.A'B 'C ' theo a .
Câu 3 (1,0 điểm). Có bao nhiêu giá trị nguyên m ≠ 0 thuộc đoạn [ 5;
− 5] để đường thẳng y = mx +1cắt đồ thị hàm số 2 − x +1 y =
tại hai điểm phân biệt. x −1
Câu 4 (0,5 điểm). Cho các số thực a, b thỏa mãn 2 1< a ≤ b . 2  
Tìm giá trị nhỏ nhất của biểu thức 22log  a P a b  = −  + . a loga 8loga     b b bĐÁP ÁN Câu Đáp án Điểm 1
Câu 1 (1 điểm). Giải phương trình 1 3x 1 −   a
Giải phương trình x−5 1 3 =  9  0,5   3x 1 − Ta có: x−5  1 3  =  x−5 6 − x+2 ⇔ 3 = 3 9    0,25 ⇔ x − 5 = 6
− x + 2 ⇔ x =1.
Tập nghiệm của phương trình là S = { } 1 0,25 b
Giải phương trình log x −1 + log x +1 = 3 2 ( ) 2 ( ) 0,5
Điều kiện x >1.
Phương trình đã cho trở thành log ( 2 x −1 = 3 2 ) 0,25 2
⇔ x −1 = 8 ⇔ x = 3 ±
Đối chiếu điều kiện. Tập nghiệm của phương trình là S = { } 3 0,25
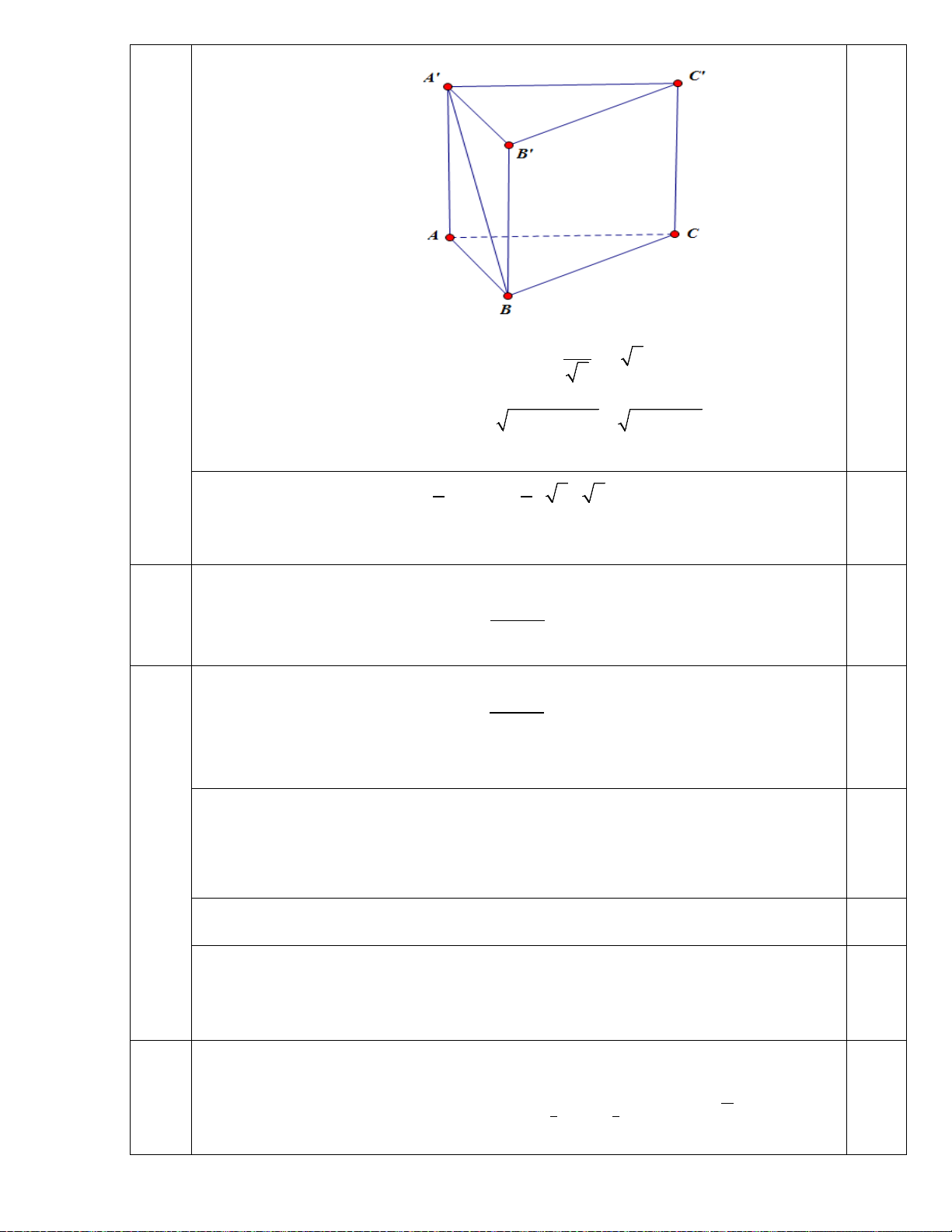
Câu 2 (0,5 điểm). Cho hinh lăng trụ đứng ABC.A'B 'C ' có đáy ABC là tam giác 2 vuông cân tại ,
A BC = 2a, A'B = a 6. Tính thể tích của khối lăng trụ ABC.A'B 'C ' 0,5 theo a . 0,25
Tam giác ABC vuông cân tại BC
A ⇒ AB = AC = = a 2. 2
Tam giác A' AB vuông tại 2 2 2 2
A ⇒ A' A = A' B − AB = 6a − 2a = 2 . a Diện tích đáy 1 1 ABC là: 2 S = AB AC = a a = a ABC . 2. 2 . 2 2 0,25
Thể tích của khối lăng trụ là 2 3 V = A A S = a a = a ABC A B C ' . ABC 2 . 2 . . ' ' '
Câu 3 (1,0 điểm). Có bao nhiêu giá trị nguyên m ≠ 0 thuộc đoạn [ 5; − 5], để đường 3 thẳng − x +
y = mx +1cắt đồ thị hàm số 2 1 y =
tại hai điểm phân biệt. 1,0 x −1
Xét phương trình hoành độ giao điểm: 2
− x +1 = mx+1; (x ≠1). x −1 0,25 ⇔ g (x) 2
= mx + (3− m) x − 2 = 0 ; (x ≠ 1).
Để đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt khi và chỉ khi phương trình ∆ >  (  − m)2 0 3 + 8m > 0
trên có 2 nghiệm phân biệt khác 1 ⇔  ⇔ 0,25 g  ( ) 1 0  ≠
m + 3− m − 2 ≠ 0 2
⇔ m + 2m + 9 > 0 ⇔ m ∀ ≠ 0 0,25 Mà m∈[ 5;
− 5] , m∈ Z ⇒ m∈{ 5 − ; 4; − 3 − ; 2; − 1 − ;1;2;3;4; }
5 ⇒ có 10 giá trị m . 0,25
Lưu ý: Thiếu đk x ≠ 1 dẫn đến thiếu đk g(1) ≠ 0 thì -0,25
Câu 4 (0,5 điểm). Cho các số thực a, b thỏa mãn 2 1< a ≤ b . 2 4  
Tìm giá trị nhỏ nhất của biểu thức 22log  a P a b  = −  + . 0,5 a loga 8loga     b b b  Ta có log  b ba  = =  a − . a loga . loga 1  a b bb 2 2      Do đó 8 8
P = 2 2log a − a −  + =  a +  + . a loga 1 2 loga 1 0,25    log a    a b b a log b a b b
Lưu ý: HS có thể biến đổi nhiều cách khác nhau cứ rút gọn để đặt được ẩn phụ
thì dều cho 0,25 ( HS thường sẽ biến đổi về t = log b a )
Đặt t = log a . Do 2
1< a ≤ b 
→ a ≤ b , suy ra a b 1 1 a 1 1 = = log = − b ≤ − a = − =  →t ≥ . a 1 loga 1 loga 1 2 t log a b a 2 2 b
Khi đó P = (t + )2 8 2 1 + = f (t). t
Khảo sát f (t) = (t + )2 8 2 1 + trên [2; 0,25 +∞) t
Ta được min f (t) = f (2) = 22. [2;+∞) Với 2 t = 2 
→log a = ↔ a = b a 2 . b
Vậy giá trị nhỏ nhất của biểu thức P = 22 ⇔ 2 a = b .
Document Outline

  • TOAN 12 HK 1_TOAN_125
  • TOAN 12 HK 1_TOAN_126
  • TOAN 12 HK 1_TOAN_dapancacmade
    • Table1
  • ĐÁP ÁN ĐỀ KIỂM TRA CUỐI HỌC KỲ 1 TOÁN 12-KO CHUYÊN (1)