Đề cương bài giảng Lý thuyết mạch 2 - Biên soạn: Bùi Thị Kim Thoa-Nguyễn Thị Huyền Linh | Trường Đại học sư phạm kỹ thuật TP Hồ Chí Minh

1.1. Định nghĩa: Mạch bốn cực là phần mạch có bốn đầu dẫn ra 1,1’,2,2’. Trạng thái của nó được xác định bởi các điện áp U1 , U2 ở từng cặp đầu dây dẫn (mỗi cặp đầu dây làm thành một cửa) và các dòng điện I1,I2 ở các cửa (hình 1.1.1). Các điều kiện về dòng điện được thoã mãn trong hai trường hợp…Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

13 7 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: lý thuyết mạch 1,2

Trường: Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

Thông tin:

73 trang 2 tuần trước

Tác giả:

Profile Lê Kim Dung
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 1ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
MỤC LỤC
CHƯƠNG 1. B ẾN TÍNH TƯƠNG HỖN CC TUY .......................................................... 4
1.1. Định nghĩa ..................................................................................................................... 4
1.2. Cá ........................................................................................ 5c hệ phương trình đặc tính
1.2.1. H kháng ....................................................................... 5ệ phương trình đặc tính trở
1.2.2. H n n p .......................................................................... 6ệ phương trình đặc tính dẫ ạ
1.2.3. H t ...................................................................... 7ệ phương trình đặc tính truyền đạ
1.2.4. H c ......................................................................... 8ệ phương trình truyền đạt ngượ
1.2.5. H n h p ......................................................................... 9ệ phương trình đặc tính hỗ ợ
1.2.6. H n h c ............................................................ 10ệ phương trình đặc tính hỗ ợp ngượ
1.2.7. Quan h gi a các thông s c n c c ............................................................... 12ệ ữ ố ủa bố ự
1.3. Các b n c ng .................................................................................................. 13ố ực đối xứ
1.3.1. Khái ni ng .............................................................................................. 13ệm đối xứ
1.3.2. Định lý Bartlett dùng cho bốn cực đối xứng ....................................................... 16
1.4. Các cách ghép n i nhi u b n c c ................................................................................ 18ố ề ố ự
1.4.1. Ghép n p n p (N - ...................................................................... 18ối n i tiố ế – ối tiế N)
1.4.2. Ghép n i song song-song song (S- ................................................................... 19ố S)
1.4.3. Ghép n p song song (N - .................................................................. 20ối n i tiố ế – S)
1.4.4. Ghép n i song song n i ti p (S - .................................................................. 21ố – ố ế N)
1.4.5. Ghép n i dây chuy n ............................................................................................ 21ố ề
1.5. B n c c có t i .............................................................................................................. 22ố ự ả
1.5.1. Tr kháng vào ...................................................................................................... 22ở
1.5.2. Hàm truy t ..................................................................................................... 23ền đạ
1.6. H s truy n c c ...................................................................................... 23ệ ố ền đạt của bố ự
1.7. Các thông s ....................................................................................................... 25ố sóng
1.7.1. Tr kháng sóng ..................................................................................................... 25ở
1.7.2. C nh thông s sóng ................................................................................ 27ách xác đị ố
1.8. Sơ đồ tương đương củ ến tính tương hỗ a bốn cực tuy . ................................................ 28
1.8.1. Sơ đồ tương đương hình chữ T ............................................................................ 28
1.8.2. Sơ đồ tương đương hình ................................................................................... 29
CHƯƠNG 2. B ÍNH KHÔNG TƯƠNG HỖN CC TUYẾN T ......................................... 33
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 2ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
2.1. Định nghĩa bố ến tính không tương hỗn cực tuy .......................................................... 33
2.2. Các sơ đồ tương đương củ ực không tương hỗ a bốn c ................................................ 33
2.2.1. Sơ tương đương hì đồ nh T ................................................................................... 34
2.2.2. Sơ đồ tương đương hì nh Π ................................................................................... 34
2.3. M v d v b n c c tuy .................................................. 35ột số í ề ố ự ến tính không tương hỗ
2.3.1. Giratơ .................................................................................................................... 36
2.3.2. M ch bi kháng âm (NIC-Negative Impedancce Converter) ................. 37ạ ến đổi trở
2.3.3. Transistor .............................................................................................................. 38
2.3.4. M ch khu i thu ................................................................................. 40ạ ếch đạ ật toán
CHƯƠNG 3. NG DNG CA BN CC-B LC TH ĐNG LC ............................ 42
3.1. Nhi v phân lo l c...................................................................................... 42ệm v à ại bộ
3.1.1. Nhi c l c............................................................................................. 42ệm v ủa bộ
3.1.2. Phân lo l c .................................................................................................... 42ại bộ
3.2. C u tr l c ...................................................................................................... 43 c c a bủ ộ
3.3. Tr ng s ng Z ....................................................................................................... 43ở khá
0
3.4. D i thông, d i ch n và t n s c c hình T và ................................................ 44ả ả ắ ầ ố ắt của l
3.5. B l c lo ............................................................................................................... 45ộ ại K
3.5.1. B l c thông th p ................................................................................................. 46ộ
3.5.2. B l c thông cao ................................................................................................... 47ộ
3.5.3. B l c thông d i ................................................................................................... 48ộ ả
3.5.4. B l n d i ..................................................................................................... 49ộ c chắ ả
3.6. M i M .......................................................................................................... 50ạch l c lo ạ
3.6.1. Chuy n t b l c lo i K sang b l c lo i M ........................................................ 50ể ừ ộ ạ ộ ạ
3.6.2. Xây d ng các b l i M t b l c lo ....................................................... 51ự ộ c loạ ừ ộ ại K
CHƯƠNG 4. MẠCH PHI TUYẾN ........................................................................................ 53
4.1. Khái ni m v m ch phi tuy n ...................................................................................... 53ệ ề ạ ế
4.1.1. Định nghĩa ............................................................................................................ 53
4.1.2. So sánh m ch phi tuy n và m ch tuy n tính ........................................................ 53ạ ế ạ ế
4.2. Phân lo i các ph n t phi tuy n .................................................................................. 53ạ ầ ử ế
4.3. Các thông s c a ph n t phi tuy n ............................................................................ 56ố ủ ầ ử ế
4.3.1. Các thông s m u ........................................................................................ 56ố ột chiề
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 3ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
4.3.2. Các thông s vi phân ............................................................................................ 57ố
4.3.3. Các thông s trung bình ....................................................................................... 57ố
4.4. H s méo phi tuy n .................................................................................................... 57ệ ố ế
4.5. Các phương pháp thông dng phân tích mạch phi tuyến ............................................ 58
4.5.1. Phương pháp đồ thị .............................................................................................. 58
4.5.2. Phương pháp dò .................................................................................................... 60
4.5.3. Phương pháp lặp ................................................................................................... 61
4.5.4. Phương pháp cân bằng điều hòa .......................................................................... 62
4.6. Phương pháp tuyến tính ha quy ướ ần đngc tính g .................................................. 64
4.7. Nh ng quá trình tuy n c a h ng phi tuy n ........................................ 65ữ ến tính cơ bả ủ ệ thố ế
4.8. B t u hòa ............................................................................................ 68ộ ạo dao động điề
4.8.1. Định nghĩa về ổn đị độ nh ..................................................................................... 68
4.8.2. B t ng có ph n h i ................................................................................ 70ộ ạo dao độ ả ồ
4.8.3. Điều kiện tự kích – Tiêu chuẩn Nyquist .............................................................. 72
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 4ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
CHƯƠNG 1. BN C C TUYẾN TÍNH TƯƠNG HỖ
1.1. Định nghĩa
M
ạch bốn c c là ph n m ch có b u dây d n ra 1, 1 , 2, 2 . Tr ng thái c a nó ự ầ ạ ốn đầ ẫ
’ ’
ạ ủ
được xác đị ởi các điệ ặp đầ ặp đầnh b n áp U , U
1 2
ở từng c u dây dẫn (mỗi c u dây làm thành
một cửa) và các dòng điện I , I
1 2
ở a (hình 1.1.1). các cử
Hình 1.1.1
Đi
ều kiệ ền v dòng điện: I = I
1 1
’
; I = I
2 2
’
(1)
Các điề dòng điện được thoã mãn trong hai trườu kiện về ng hợp:
- ng h p 1: C hai c u m c t i, trên các t u ki c thoã mãn Trườ ợ ả ửa đề ắ ả ải này điề ện (1) đượ
(hình 1.1.2a).
- ng h p 2: C u t o bên trong c a b n c m b u ki n (1) (hình Trườ ợ ạ ủ ố ực đả ảo thoã mãn điề ệ
1.1.2b).
Hình 1.1.2 a, b
Các chi ều dòng điện và điện áp như trên hình vẽ là các chiều quy ước dương.
Để ủ tính toán thuận ti ng cện, người ta thường tưởng tượ u tạo bên trong c a bốn cực
sao cho các đ
ầu 1
’
, 2
’
được nối chung (hình 1.1.3 ).
Hình 1.1.3
V
ới b n c ng ký hi u c u 1,1 là c a vào (hay c p) ố ực chng ta thườ ệ ặp đầ
’
ử ửa sơ c ở đ
thư
ờ ởng mắc ngu ng, còn c u 2,2ồn tác độ ặp đầ
’
là cửa ta (hay cửa thứ cp) đ thường mắc
tải.
Các ký hi u U,I là các ký hi u t ng quát, chúng có th n áp ệ ệ ổ ể là các đại lượng điệ hoặc
dòng điện 1 chiều, có thể là các giá trị hiệu dng trong mạch xoay chiều ho c có thặ ể là nh ả
Laplace trong trường hợp tổng quát tín hiệu là hàm thời gian bt kỳ.
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 5ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
1.2. Các hệ phương trình đặc tính
Phương trình đặ ải là phương trình tuyếc tính của bốn cực tuyến tính th động ph n
tính thuần nht.
Dạng t ng quát c c tính: ổ ủa phương trình đặ
.0
.0
222121222121
212111212111
IbIbUaUa
IbIbUaUa
Từ h y có th ng b t kệ phương trình trên ta th ể rt ra hai đại lượ ỳ theo hai đại lượng
còn l y, ta có 6 t h ng b t k t i ng trên, t 6 t hại. Như vậ ổ ợp hai đại lượ ỳ ừ bốn đạ lượ ừ ổ ợp đ ta
sẽ có 6 hệ phương trình đặc tính khác nhau.
Chúng ta s xét l t các h a các h ẽ ần lượ ệ phương trình đặc tính đ cùng với ý nghĩa củ ệ
số trong các phương trình đ (đượ ực) và cách xác địc gi là các thông số của bốn c nh
chúng. S d chúng ta ph c tính khác nhau vì trong th c t ng ở ĩ ải đưa ra các phương trình đặ ự ế ứ
với t ng d ng cừ ạ ủa b n c c ta có th phân tích chúng d a vào m t lo i h ố ự ể ễ dàng hơn dự ộ ạ ệ
phương trình đặc tính nht định.
1.2.1. Hệ phương trình đặc tính trở kháng
Giả thiết dòng điệ đã biế ửa đ, như vận ở cửa 1 và cửa 2 t ta tìm điện áp ở hai c y ta
nhận đượ phương trình đặc hệ c tính trở kháng với các thông số trở kháng z :
ij
2221212
2121111
IzIzU
IzIzU
.2.1.1) (1
Hệ phương trình trên được gi là hệ phương trình đặc tính trở kháng vì các thông số
z
ij
c đơn vị là ; z
ij
i là các thông scòn được g ố trở kháng.
Hệ phương trình trên được viết dưới dạng ma tr ận như sau:
2
1
2
1
I
I
Z
U
U
Trong đ:
2221
1211
z z
z z
Z
được gi là ma tr n tr kháng. ậ ở
* Ý a các thông s kháng: nghĩa vật lý củ ố trở
- N u m c ngu n c mế ắ ồ ở ửa 1 và hở ạch c a 2: ử
0
1
1
11
2
I
I
U
z
và
0
1
2
21
2
I
I
U
z
Ta thy:
z
11
là tr kháng vào c a c a 1 khi h mở ủ ử ở ạch ở c a 2 nên zử
11
được g i là tr kháng vào ở
hở mạch của c a 1.ử
z
21
là t s gi n áp c a 2 và dòng c a 1 khi c a 2 h mỉ ố ữa điệ ở ử ở ử ử ở ạch nên z
21
được gi
là trở kháng truy t h m ền đạ ở ạch c a c a 1.ủ ử
- N u m c ngu n c mế ắ ồ ở ửa 2 và hở ạch c a 1: ử
0
2
1
12
1
I
I
U
z
và
.
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 6ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
z
12
kháng truy t h m được gi là trở ền đạ ở ạch c a c a 2.ủ ử
z
22
kháng vào h m a c được gi là trở ở ạch củ ửa 2.
Tóm l i, các thông s z c g i là các thông s kháng h m ạ ố
ij
đượ ố trở ở ạch, do đ hệ
phương trình (1 1) còn đượ phương trình đặ.2.1. c gi là hệ c tính trở kháng hở mạch.
Với b : zốn c c tuyự ến tính tương hỗ
12
= z .
21
Ví d 1.2.1.1:
Cho b n c c tuy n t nh T) c nh 1.2.1.1. ố ự ế ính tương hỗ (hì sơ đồ như hì
Hãy x c á định c c thông s á ố trở kh ng h m ch c n c c trên. á ở ạ ủa bố ự
Gi i:
21
0
1
1
11
2
ZZ
I
U
z
I
;
2
0
1
2
21
2
Z
I
U
z
I
2
0
2
1
12
1
Z
I
U
z
I
;
32
0
2
2
22
1
ZZ
I
U
z
I
1.2.2. Hệ phương trình đặc tính dẫn nạp
Giả thiết các điện áp đã biết ta tìm dòng điện theo điện áp, như vậy ta nh c h ận đượ ệ
phương trình đặc tính dẫn nạp với các thông số dẫn nạp y :
ij
2221212
2121111
UyUyI
UyUyI
.2.2.1) (1
Hệ phương trình trên được gi là hệ phương trình đặc tính dẫn nạp vì các thông s y ố
ij
c đơn vị còn đượ là S; y
ij
c gi là các thông số dẫn nạp.
Hệ phương trình trên được viết dưới dạng ma tr ận như sau:
2
1
2
1
U
U
Y
I
I
Trong đ:
1121
12221
2221
1211
ZZ-
Z-
1
y y
y Z
Z
Z
y
Y
được gi là ma tr n d n n p. ậ ẫ ạ
* a các thông s d n n p: ý nghĩa vật lý củ ố ẫ ạ
- N u m c ngu n c n mế ắ ồ ở ửa 1 và ngắ ạch c a 2ử :
0
1
1
11
2
U
U
I
y
và
0
1
2
21
2
U
U
I
y
y
11
là d n n p vào ng n m ẫ ạ ắ ạch c a c a 1.ủ ử
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 7ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
y
21
là d n n p truy n ẫ ạ ề đạt ngắn m ch c a 1. ạ ủa cử
- N u m c ngu n c n mế ắ ồ ở ửa 2 và ngắ ạch c a 1ử :
0
2
1
12
1
U
U
I
y
và
0
2
2
22
1
U
U
I
y
y
12
được g n n p truy t ng n m ch c i là dẫ ạ ền đạ ắ ạ ủa c a 2.ử
y
22
được g n n p vào ng n mi là dẫ ạ ắ ạch của c ửa 2.
Tóm l i, các thông s y c g i là các thông s d n n p ng n m ạ ố
ij
đượ ố ẫ ạ ắ ạch, do đ hệ
phương trình (1 ) còn đượ phương trình đặ.2.2.1 c gi là hệ c tính dẫn nạp ngắn mạch.
Với bốn c c tuy : y = y . ự ến tính tương hỗ
12 21
Ví d 1.2.2.1:
Cho bốn c c tuy n t nh nh 1.2.2.1. ự ế ính tương hỗ (hì Π) c sơ đồ như hì
Tính c c thông s d n n p ng n m n c c á ố ẫ ạ ắ ạch c a ủ bố ự trên.
Gii:
21
0
1
1
11
11
2
RRU
I
y
U
;
2
0
1
2
21
1
2
RU
I
y
U
2
0
2
1
12
1
1
RU
I
y
U
;
32
0
2
2
22
11
1
RRU
I
y
U
1.2.3. Hệ phương trình đặc tính truyền đạt
Giả thiết điện áp và dòng điệ đã biế điện áp và dòng điệ , như n ở cửa 2 t ta tìm n cửa 1
vậy ta nh c tính truy t v truy t aận được hệ phương trình đặ ền đạ ới các thông số ền đạ
ij
:
2222211
2122111
IaUaI
IaUaU
.2.3.1) (1
a
21
c đơn vị là S, a
12
c đơn vị là , a và a
11 22
ng không th nguyên. là các đ i lưạ ợ ứ
Hệ phương trình trên được viết dưới dạng ma tr ận như sau:
2
2
1
1
I
U
A
I
U
Trong đ:
2221
1211
a a
a a
A
được gi là ma tr n truy t thu n. ậ ền đạ ậ
* Cách tính các thông s truy t thu n ố ền đạ ậ
ij
a
:
- N u m c ngu n c mế ắ ồ ở ửa 1 và hở ạch c a 2ử :
0
2
1
11
2
I
U
U
a
và
0
2
1
21
2
I
U
I
a
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 8ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
- N u m c ngu n c n m a 2: ế ắ ồ ở ửa 1 và ngắ ạch cử
0
2
1
12
2
U
I
U
a
và
0
2
1
22
2
U
I
I
a
Điều kiện b n cố ực tuyến t : -1. ính tương hỗ ΔA =
Ví d 1.2.3.1:
Cho bốn c c tuy n t nh T) c nh 1.2.3.1. ự ế ính tương hỗ (hì sơ đồ như hì
Hãy x c á định c c thông s truy n c c á ố ền đạt của bố ự trên.
Gi i:
2
21
0
2
1
11
2
R
RR
U
U
a
I
;
2
0
2
1
21
1
2
RU
I
a
I
2
323121
0
2
1
12
...
2
R
RRRRRR
I
U
a
U
;
2
32
0
2
1
22
2
R
RR
I
I
a
U
1.2.4. Hệ phương trình truyền đạt ngược
Giả thiết điện áp và dòng điệ đã biế điện áp và dòng điệ , như n ở cửa 2 t ta tìm n cửa 2
vậy ta nh c h c tính truy c v i các thông sận đượ ệ phương trình đặ ền đạt ngượ ớ ố truyền đạt
ngược b
ij
:
1221212
1121112
IbUbI
IbUbU
(1.2.4.1)
b
21
c đơn vị là S, b
12
là , b và bc đơn vị
11 22
ng không th nguyên. là các đ i lưạ ợ ứ
Hệ phương trình trên được viết dưới dạng ma tr ận như sau:
1
1
2
2
I
U
B
I
U
Trong đ:
1
2221
1211
b b
b
A
b
B
được gi là ma tr n truy c. ậ ền đạt ngượ
* Cách tính các thông s truy c ố ền đạt ngượ
ij
b
:
- N u m c ngu n c 2 và h mế ắ ồ ở ửa ở ạch c a ử 1:
0
1
2
11
1
I
U
U
b
và
0
1
2
21
1
I
U
I
b
- N u m c ngu n c 2 và ng n mế ắ ồ ở ửa ắ ạch c a ử 1:
0
1
2
12
1
U
I
U
b
và
0
1
2
22
1
U
I
I
b
Điều kiện b n cố ực tuyến t : B = -1. ính tương hỗ Δ
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 9ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
Ví d 1.2.4.1:
Cho bốn c c tuy n t nh nh 1.2.4.1. ự ế ính tương hỗ (hì Π) c sơ đồ như hì
T bính c c thông s truy c cá ố ền đạt ngượ ủa ốn c c ự trên.
Gii:
1
21
0
1
2
11
1
R
RR
U
U
b
I
;
31
321
0
1
2
21
.
1
RR
RRR
U
I
b
I
2
0
1
2
12
1
R
I
U
b
U
;
3
32
0
1
2
22
1
R
RR
I
I
b
U
1.2.5. Hệ phương trình đặc tính hỗn hợp
Giả thiết dòng điệ ửa 1 và điệ đã n ở c n áp ở cửa 2 biết ta tìm điện áp ở cửa 1 và dòng
điệ ớn ở cửa 2 y ta nh c h, như vậ ận đượ ệ phương trình đặc tính hỗn hợp v i các thông số hỗn
hợp h
ij
:
2221212
2121111
UhIhI
UhIhU
(1.2.5.1)
Hệ phương trình trên được gi là hệ phương trình đặc tính hỗn hợp vì: h
11
c đơn vị
là , h là S, h và h
22
c đơn vị
12 21
là các đ i lưạ ợng không th nguyên. ứ
Hệ phương trình trên được viết dưới dạng ma tr ận như sau:
2
1
2
1
U
I
H
I
U
Trong đ:
2221
1211
h h
h h
H
i là ma tr n h n h p thu được g ậ ỗ ợ ận.
* a các thông s h n h p: ý nghĩa vật lý củ ố ỗ ợ
- N u m c ngu n c n m a 2: ế ắ ồ ở ửa 1 và ngắ ạch cử
0
1
1
11
2
U
I
U
h
và
0
1
2
21
2
U
I
I
h
h
11
kháng vào ng n mlà trở ắ ạch của c ửa 1.
h
21
slà hệ ố truy n ng n m c n c ền đạt dòng điệ ắ ạch từ ửa 1 đế ửa 2.
- N u m c ngu n c m ế ắ ồ ở ửa 2 và hở ạch c a 1:ử
0
2
1
12
1
I
U
U
h
và
0
2
2
22
1
I
U
I
h
h
12
được gi là hệ số truy n áp h m c n c ền đạt điệ ở ạch từ ửa 2 đế ửa 1.
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 10ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
V -hới b n c c tuy n t ố ự ế ính tương hỗ thì điều ki l h ện tương hỗ à
12
=
21
.
Ví d 1.2.5.1:
Cho b n c c tuy n t nh h nh gamma hay g xuôi) cố ự ế ính tương hỗ (hì Γ – ì sơ đồ như
hình 1.2.5.1.
Hãy xác định c c thông s h n há ố ỗ ợp c n c c ủa bố ự trên.
Gi i:
21
21
0
1
1
11
.
2
RR
RR
I
U
h
U
;
21
1
0
1
2
21
2
RR
R
I
I
h
U
21
1
0
2
1
12
1
RR
R
U
U
h
I
;
21
0
2
2
22
1
1
RRU
I
h
I
1.2.6. Hệ phương trình đặc tính hỗn hợp ngược
Giả thiết điện áp c n c a 2 t ta tìm c a 1 và ở ửa 1 và dòng điệ ở ử đã biế dòng điện ở ử
điệ ở ớn áp cửa 2 y ta nh c h, như vậ ận đượ ệ phương trình đặ ợp ngược tính hỗn h c v i các
thông số h n h c gỗ ợp ngượ
ij
:
2221212
2121111
IgUgU
IgUgI
(1.2.6.1)
g
11
c đơn vị là S, g
22
c đơn vị là , h
12
và h
21
ng không th nguyên. là các đ i lưạ ợ ứ
Hệ phương trình trên được viết dưới dạng ma tr ận như sau:
2
1
2
1
I
U
G
U
I
Trong đ:
1
2221
1211
g g
g
H
g
G
được gi là ma tr n h n hậ ỗ ợp ngược.
* a các thông s h n h ý nghĩa vật lý củ ố ỗ ợp ngược:
- N u m c ngu n c mế ắ ồ ở ửa 1 và hở ạch c a 2: ử
0
1
1
11
2
I
U
I
g
và
0
1
2
21
2
I
U
U
g
g
11
n n p vào h m ch clà dẫ ạ ở ạ ủa c a 1.ử
g
21
slà hệ ố truy n áp h m c n c ền đạt điệ ở ạch từ ửa 1 đế ửa 2.
- N u m c ngu n c n m a 1: ế ắ ồ ở ửa 2 và ngắ ạch cử
0
2
1
12
1
U
I
I
g
và
0
2
2
22
1
U
I
U
g
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 11ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
g
12
được gi là hệ số truy n ng n m c n c ền đạt dòng điệ ắ ạch từ ửa 2 đế ửa 1.
g
22
được gi là trở kháng vào ng n mắ ạch của c ửa 2.
B -gốn c c tuy n t ng hự ế ính tươ ỗ: g
12
=
21
.
Ví d 1.2.6.1:
Cho bốn c c tuy n t s nh 1.2.6.1. ự ế ính tương hỗ (hình g ngược) c ơ đồ như hì
Hãy x c á định c c thông s h n h n c c á ố ỗ ợp ngược c a ủ bố ự trên.
Gi i:
21
0
1
1
11
1
2
RRU
I
g
I
;
21
2
0
1
2
21
2
RR
R
U
U
g
I
21
2
0
2
1
12
1
RR
R
I
I
g
U
;
21
21
0
2
2
22
.
1
RR
RR
I
U
g
U
Lưu : Đối v i c c m ch c h c m th s không p d ng c c công th c trên m ng ớ á ạ ỗ ả ì ẽ á á ứ à ch
ta s p d ng c p gi i m h c p nh ẽ á ác phương phá ả ạch điện đã c trướ đây để đưa ra hệ hương trì
đặ đc ttrưng và ừ suy ra các thông số cần tìm.
Ví d 1.2.6.2:
Cho bốn c c tuy n t c h c m c nh 1.2.6.2. ự ế ính tương hỗ ỗ ả sơ đồ như hì
Hãy xác định c c thông s z cá ố
ij
ủa bốn c c trên. ự
Gii:
p d p d n v ng v i hai v h nh 1.2.6.3, ta ng phương phá òng điệ ò ớ òng như trên sơ đồ ì
được:
1212
2111
)()(
)()(
IjXRIjXRU
IjXRIjXRU
LM
ML
Vây: z = R + jX = z = R + jX = R + jX
11 L1
; z
12 21 M
; z
22 L2
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 12ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
1.2.7. Quan hệ giữa các thông số của bốn cực
Với 6 h nh trên ta th y t m t h nh b t kì có th suy ra các h ệ phương trì ừ ộ ệ phương trì ể ệ
phương trình còn lại. Các bộ thông số Z, Y, A, B, H, G có mối quan hệ với nhau, nếu biết
đượ ộc m t bộ ố thông s ta sẽ suy ra được các bộ thông số còn lại.
Ví d 1.2.7.1:
Từ h p c tệ hương trình đặ ính trở ng suy ra h pkhá ệ hương trình đặc tính truy ền đạt.
Gi i:
2222211
2122111
2
21
22
2
21
1
2
21
2
21
11
1
2221212
2121111
1
IaUaI
IaUaU
I
Z
Z
U
Z
I
I
Z
Z
U
Z
Z
U
IzIzU
IzIzU
V .z .zới ΔZ = z
11 22
– z
12 21
.
Với cách chuy ta cển đổi đ được bảng mối quan h gi c thông sệ ữa cá ố:
Bảng m i quan h gi a c : ố ệ ữ ác thông số
Trở ở kháng h mạch
1
z
11
z
12
z
21
z
22
z
Truyền đạt
a
21
a
11
-a
1
-a
22
-a
12
Hỗn hợp
h
22
h
h
12
-h
21
1
h
11
Dẫn n p ng n m ạ ắ ạch
y
y
22
-y
12
-y
21
y
11
1
Từ m i thông s bột loạ ố t kỳ ta có th suy ra các thông s khác. ể ố
a) a các thông sTìm m i quan h giố ệ ữ ố:
1. Các hàng t l v i nhau, n u bi t c thông s c a m t hàng có thỷ ệ ớ ế ế đượ ố ủ ộ ể tìm được
thông số của các hàng còn lại.
Bộ thông số đã bi t: M u s T s ế ẫ ố ử ố
↑ ↑
Bộ thông s c n t m: 1 X ố ầ ì
Ví d 1.2.7.2:
Biết
Z
c n tầ ìm
H
.
Gi i:
Từ b ng m i quan h gi c ả ố ệ ữa cá thông số ta c :
1 z-
z
1
21
12
22
Z
z
H
Ví d 1.2.7.3:
Cho bốn c c tuy n t c nh 1.2.7.3. ự ế ính tương hỗ sơ đồ như hì
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 13ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
Biết: X
L1
= = = 2Ω; X
L2
4Ω; X
C
1Ω. Tìm
A
.
Gi i:
Ta c: Z ; Z
a
= j2
b
-j; Z = j4 =
c
z
11
= Z + Z = j; z
a b 12
= z
21
= Z
b
= -j; z
22
= j3
Từ b ng m i quan h : ả ố ệ giữa c c thông sá ố
3 j
2j 1
z- 1
Z-
1
22
11
21
A
z
z
A
2. Các c t t l v i nhau, n u bi c thông s c a m t c t có th c thông ộ ỷ ệ ớ ế ết đượ ố ủ ộ ộ ể tìm đượ
số c ủa các cột còn lại.
Bộ thông số đã bi t B thông s c n t m ế ộ ố ầ ì
M u s 1 ẫ ố ←
T s X ử ố ←
3. Trong m t hình ch nh t b t k , tích s các thông s ng chéo b ng nhau. ộ ữ ậ ỳ ố ố trên đườ ằ
Ví d: ; b-g .z
12
= g
11 12 21
.(-a
22
) = a
21
.b
11
.
b) u ki ng h Tìm điề ện tươ ỗ
Điều ki c rút ra tện tương hỗ đượ ừ ữ c t 3 và 4 trong bộ ảng mối quan hệ gi a các thông
số, ta có:
z
12
= z
21
; y
12 12
= y
21
; h = -h
21
; g
12
= -g
21
; ∆A B = -1; ∆ = -1.
c) Tìm điề ện đốu ki i xứng
Điề ệu ki i x c rút ra tện đố ứng đượ ừ cộ ộ ủ ốt 2 và c t 5 c a bảng m i quan h giữa các thông
số:
z
11
= z
22
; y
11 11 11
= y
22
; ∆H = 1 G = 1; ∆ ; a = -a
22
; b = -b
22
.
1.3. Các bốn cực đối xứng
1.3.1. Khái niệm đối xứng
a. Khái ni m a b c ệm đối xứng về ặt điện củ ốn cự
Một b n c c g i x ng v m n khi c a 1 và c a 2 có thố ực đượ i là đố ứ ề ặt điệ ử ử ể đổi l n cho ẫ
nhau mà các thông s c n c ố ủa bố ực hoàn toàn không đổi.
Phương trình trở kháng của bốn cực:
2221212
2121111
IzIzU
IzIzU
Nếu b n c ng v m n: ố ực đối xứ ề ặt điệ
1222211
1122112
IzIzU
IzIzU
Như vậy rõ ràng: z = z và z = z .
12 21 11 22
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 14ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
Điều ki i xện đố ứ ự ứng về m n là z = z , mặt điệ
11 22
ộ ốt b n c c tuy i xến tính tương hỗ đố ng
về m n ch c n hai thông s zặ ệt đi ỉ ần quan tâm đế ố
11
(hoặc z
22
) và z
12
(hoặc z
21
).
b. Khái ni m a b c ệm đối xứng về ặt hình học củ ốn cự
Sự đối x ng v m t hình h c cứ ề ặ ủa một m c bi u di n là sạch điện thường đượ ễ ễ ự đối x ng ứ
qua tr ng chia b n c n gi ng h c đứ ố ực thành hai phầ ố ệt như nhau.
Một b i xốn cực đố ứng có th bi u di 1.3.1.1. ể ễ ễn như hình
Nhận xét:
Các b n c i x ng v m t hình h i x ng v m n cố ực đố ứ ề ặ c thì cũng đố ứ ề ặt điện nhưng các bố ực
đố i xứng về mặ ểt điện thì có th không đối xứng về mặt hình h c.
Ví d 1.3.1.1 : Cho b n c i x ng v m ng h p ố ực đố ứ ề ặt điện như hình 1.3.1.2. Trong trườ ợ
nào thì b n c ng v m t hình h ố ực đối xứ ề ặ c.
Gi i:
432
423
0
2
2
22
1
432
243
0
1
1
11
).(
).(
1
2
RRR
RRR
I
U
z
R
RRR
RRR
I
U
z
I
I
Do bốn c ng v m n nên z = z . ực là đối xứ ề ặt điệ
11 22
Ta có:
432
24
31
.
RRR
RR
RR
Nếu R = R n c i x ng c v m t hình h
4 2
thì R
1
= 0 khi đ bố ực sẽ đố ứ ả ề ặ c.
Nếu R = R n c ng c v m t hình h
4
thì R
1 3
khi đ bố ực cũng sẽ đối xứ ả ề ặ c.
Hình 1.3.1.1
U
1
U
2
I
1
I
2
R
1
R
1
R
2
U
1
U
2
I
1
I
2
R
1
R
1
2R
2
2R
2
U
1
U
2
I
1
I
2
R
1
R
2
R
2
U
1
U
2
I
1
I
2
R
1
/2
R
2
R
2
R
1
/2
U
1
U
2
I
1
I
2
Hình 1.3.1.2
R
1
R
2
R
3
R
4
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 15ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
Các b n c i x ng v m i hai thông s z và z , s kh o sát ố ực đố ứ ề ặt điện được đặc trưng bở ố
11 12
ự ả
chúng s kh o sát m hình 1.3.1.3. được đưa về ự ả ạch cầu như
Mạch hình 1.3.1.3a được gi là mạch cầu vì khi mắc nguồn vào cửa 1 và tải 2 thì mạch
đ đượ ến đổ ầu đặc bi i thành dạng mạch hình 1.3.1.3b. Hình 1.3.1.3b là một mạch c c biệt có
từng c p tr kháng b u ki n cân b ng c u là tích các trặ ở ằng nhau. Điề ệ ằ ầ ở kháng n i di n ằm đố ệ
nhau b ng h p Z = Z kháng Z s n áp, s ằng nhau, trong trườ ợ
I II
, lc đ trên trở
2
ẽ không c điệ ự
truyền đạt củ ốa b n cực bằng 0.
Tính các thông số trở kháng h m u: ở ạch c ch của mạ ầ
2
0
1
1
11
2
III
I
ZZ
I
U
z
Khi hở m c nh lu p II, ta có: ạch ở ửa 2, theo đị ật Kiếckhố
2
)(0
22
1
2
1
2
1
I
ZZU
I
ZU
I
Z
IIIIII
Do đ:
2
0
1
2
12
2
III
I
ZZ
I
U
z
Như vậy: Z = z
I 11
– z v
12
à Z
II
= z + z .
11 12
Một b i xốn cực đố ứng bao giờ u cũng c sơ đồ tương đương là hình cầ (hình X).
Ví d 1.3.1.2 :
Cho b n c ng c nh 1.3.1.4. ố ực đối xứ sơ đồ như hì
Hãy chuy n b n c c sang ể ố ự thành sơ đồ ương đương hì t nh cầu.
Hình 1.3.1.4
R
1
R
2
R
1
Z
I
Z
I
U
1
Z
II
Z
II
U
2
a)
Z
I
Z
II
Z
I
Z
II
Z
2
E
b)
Z
1
U
2
Hình 1.3.1.3
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 16ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
Gi i:
Ta c: z ; z
11
= z = R + R
22 1 2 12
= z = R
21 2
Hình c = zầu tương đương c: Z
I 11
z–
12
= R v Z
1
à
II
= R .
1
+ 2R
2
Đố ớ ởi v i bốn c i xực đố ứng c sơ đồ xác đị phức tạp sự nh tr kháng cầu trong sơ đồ tương
đương đượ dàng theo địc thực hiện dễ nh lý Bartlett-Brune.
1.3.2. Định lý Bartlett dùng cho bốn cực đối xứng
Định lý Bartlett-Bru ne được phát biểu như sau:
“Bốn c i xực đố ứng có thể chứa bi ng 1:1, hoến áp lý tưở ặ ặ ẫc 1:-1, ho c các dẫy d n chéo
nhau trên tr i x ng, có th c thay th b c kháng Z c đố ứ ể đượ ế ởi sơ đồ ầu tương đương c trở
I
bằng tr kháng vào c a n a bở ủ ử ốn c i x ng khi ng n m ch các dây d n nực đố ứ ắ ạ ẫ ối hai n a bử ốn
cực và cu n dây th c p c a bi i v i bi n áp 1:-1 ho c hai dây d n chéo ộ ứ ủ ến áp 1:1, còn đố ớ ế ặ ẫ
nhau thì ph i h m ch; có tr kháng c u Z b ng tr kháng vào c a n a b n c i x ng ả ở ạ ở ầ
II
ằ ở ủ ử ố ực đố ứ
khi h m ch các dây n i hai n a b n c c và cu n c p c a bi n áp 1:1, ng n m ch cuở ạ ố ử ố ự ộ thứ ủ ế ắ ạ ộn
thứ c p bi n áp 1:-1 ho ế ặc hai dây dẫn chéo nhau.”
Nội dung đị Brune đượnh lý Bartlett- c minh hoạ trên hình 1.3.2.1.
Hình 1.3.2.1
Để đượ hi nh lý trên, chúng ta xét các biểu rõ đị ến áp. Bi ng là mến áp lý tưở ột bốn cực, c
coi là m t trong các ph n t b n c n c a m n. ộ ầ ử ố ực cơ bả ủ ạch điệ
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 17ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
Biến áp lý tưởng theo định nghĩa là mộ ực được cách điệt bốn c n 1 chiều giữa các cửa
vào và ra, có h ệ phương trình đặc trưng sau:
12
12
1
I
n
I
nUU
Ký hiệu bi n áp lý a. ế tưởng như trên hình 1.3.2.2
Bộ ph n ch y u c a bi n áp th c g m hai cu n dây ghép h c m vậ ủ ế ủ ế ự ồ ộ ỗ ả ới nhau. N u b qua ế ỏ
các điệ ến áp đượ như trên hình n trở của các cuộn dây thì bi c vẽ 1.3.2.2b (n là tỷ s gi a các ố ữ
vòng dây c p c n th c p c ủa cuộn sơ c ở ửa 1 và cuộ ứ ở ửa 2).
Đố ới v i bi ng nến áp lý tưở ếu n = 1 thì: U = U , I .
2 1 2
= -I
1
Vậy bi i b n c c có hai dây d n song song n i t c n cến áp 1:1 tương đương vớ ố ự ẫ ố ừ ửa 1 đế ửa
2 như hình 1.3.2.3a.
Nếu n = -1 thì bi ng 1:-1 có : U , I = I . ến áp lý tưở
2
= -U
1 2 1
Vậy bi n áp 1:-1 t n c hình 1.3.2.3b. ế ương đương với bố ực c hai dây chéo nhau như
Hình 1.3.2.3
Ví d 1.3.2.1: ng d nh lý Bartlett-Brune trên m u hình 1.3.2.3a. ng đị ạch cầ
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 18ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
Gi i:
Theo đị ệt nhau như hình nh lý Bartlett-Brune ta chia mạch cầu ra hai nửa giống h
1.3.2.3b. Ta nh c Z n u ng n m ch các dây d n th ng, h m ch các dây dận đượ
1
ế ắ ạ ẫ ẳ ở ạ ẫn chéo như
hình 1.3.2.3c. Còn Z s nh c khi h m ch các dây d n th ng và ng n m ch các dây
2
ẽ ận đượ ở ạ ẫ ẳ ắ ạ
dẫn chéo hình 1.3.2.3d. như
Ví d 1.3.2.2:
Cho bốn cực đối xứng c sơ đồ như hì nh 1.3.2 , bi.4 ết R
i
= iΩ. Hãy tìm các thông số z
ij
.
Gi i:
Do b n c c h nh 1.3.2.4 l i x ng nên ta c t ch b n c c l m hai ph n gi ng ố ự ì à đố ứ thể á ố ự à ầ ố
hệt nhau v ng v i nhau, mà đối xứ ớ ỗi phần c nh 1.3.2.5. sơ đồ như hì
p d nh lng đị ý Bartlett- ta chuy nh cBrune ển sang sơ đồ tương đương hì ầu.
Để tìm Z ta ng
I
ắn mạch các điểm 1, 2, 3 khi đ trở ng vkhá ào c a phủ ần mạch chính là Z
I
:
)(545,0
3
1
2
1
1
11111
321
I
I
Z
RRRZ
Để tìm Z ta h
II
ở mạch các điểm 1, 2, 3 khi đ trở kháng vào của phần mạch chính l Z : à
II
)(2
9
6.3).(
423
423
RRR
RRR
Z
II
Vây:
)(728,0
2
);(273,1
2
21122211
IIIIII
ZZ
zz
ZZ
zz
1.4. Các cách ghép nối nhiều bốn cực
Khi g p các h ng ph c t p, m t trong nh u l c ặ ệ thố ứ ạ ộ ững phương pháp phân tích c hiệ ự
là coi n như đượ ống đơn giản hơn nốc hợp thành bởi nhiều hệ th i ghép với nhau theo
những cách khác nhau. Đố phương trình và mội với mỗi hình thức ghép nối sẽ có một hệ t hệ
thông số thích h p nh ợ t.
1.4.1. Ghép nối nối tiếp – nối tiếp (N -N)
Hình N v1.4.1 v hai b n c c N-ẽ ố ực mắ ới nhau.
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 19ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
Hình 1.4.1
Ta có:
.;
;;
''
2
'
22
''
1
'
11
''
2
'
22
''
1
'
11
UUUUUU
IIIIII
Hệ c tính trphương trình đặ ở kháng c a hai b n củ ố ực được viết dưới d ng ma tr n: ạ ậ
' '
1 1
1
' '
2 2
U I
Z
U I
và
'' ''
1 1
2
'' ''
2 2
U I
Z
U I
Đặt
2
1
''
2
''
1
'
2
'
1
I
I
I
I
I
I
và c ng hai h heo t ng v ộ ệ phương trình t ừ ế ta có:
' ''
1 1 1 1 1
1 2
' ''
2 2
2 2 2
U U U I I
Z Z Z
I I
U U U
Như vậy:
1 2
Z Z Z
Tổng quát: Với n b n c c N N v i nhau ta có ố ực mắ – ớ
1
n
k
k
Z Z
.
Phát bi u: Ma tr n tr kháng c a h ng nhi u b n c c n i N N v i nhau b ng ể ậ ở ủ ệ thố ề ố ự ố – ớ ằ
tổng các ma tr n tr kháng cậ ở ủa các bốn c c thành ph n. ự ầ
1.4.2. Ghép nối song song-song song (S- S)
Hình 1.4.2 v hai b n c c S- ẽ ố ực mắ S với nhau.
Hình 1.4.2
Ta có:
.;;;
''
2
'
22
''
1
'
11
''
2
'
22
''
1
'
11
IIIIIIUUUUUU
Hệ c tính d n n p c a hai b n c i d ng ma tr n: phương trình đặ ẫ ạ ủ ố ực được viết dướ ạ ậ
' '
1 1
1
' '
2 2
I U
Y
I U
'' ''
1 1
2
'' ''
2 2
I U
Y
I U
Đề cương bài giảng Lý thuyết mạch 2
Biên so n: Page 20ạ Bùi Th Kim Thoa -ị Nguyễn Thị Huyền Linh
Đặt
2
1
''
2
''
1
'
2
'
1
U
U
U
U
U
U
và c ng hai h ng v ộ ệ phương trình theo từ ế ta có:
' ''
1 1 1 1 1
1 2
' ''
2 2
2 2 2
I I I U U
Y Y Y
U U
I I I
Như vậy:
1 2
Y Y Y
Tổng quát: V i n b n c c N N v i nhau ta có ớ ố ực mắ – ớ
1
n
k
k
Y Y
.
Phát bi u: Ma tr n d n n p c a h ng nhi u b n c i S S v i nhau b ng t ng các ma ể ậ ẫ ạ ủ ệ thố ề ố ực nố – ớ ằ ổ
trận d n n p c a các b n c n. ẫ ạ ủ ố ực thành phầ
1.4.3. Ghép nối nối tiếp – song song (N - S)
Hình 1.4.3 vẽ hai b n c c N- ố ực mắ S với nhau.
Hình 1.4.3
Ta có:
.;;;
''
2
'
22
''
1
'
11
''
2
'
22
''
1
'
11
IIIUUUUUUIII
Hệ c tính h n h p c a hai b n c i d ng ma tr n: phương trình đặ ố ợ ủ ố ực được viết dướ ạ ậ
' '
1 1
1' '
2 2
U I
H
I U
'' ''
1 1
2'' ''
2 2
U I
H
I U
Đặt
2
1
''
2
''
1
'
2
'
1
U
I
U
I
U
I
và c ng hai h ng v ộ ệ phương trình theo từ ế ta có:
' ''
1 1 1 1 1
1 2' ''
2 2
2 2 2
U U U I I
H H H
U U
I I I
Như vậy:
1 2
H H H
Tổng quát: V i n b n c c N S v i nhau ta có ớ ố ực mắ – ớ
1
n
k
k
H H
.
Phát bi u: Ma tr n h n h p c a h ng nhi u b n c c n i N S v i nhau b ng t ng các ể ậ ố ợ ủ ệ thố ề ố ự ố – ớ ằ ổ
ma tr n h n h p c a các b n c c thành ph n. ậ ố ợ ủ ố ự ầ
| 1/73
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Đề cương bài giảng Lý thuyết mạch 2
MỤC LỤC CHƯƠNG 1. BN CC TU Ế
Y N TÍNH TƯƠNG HỖ .......................................................... 4
1.1. Định nghĩa ..................................................................................................................... 4
1.2. Các hệ phương trình đặc tính ........................................................................................ 5
1.2.1. Hệ phương trình đặc tính trở kháng ....................................................................... 5
1.2.2. Hệ phương trình đặc tính dẫn nạp .......................................................................... 6
1.2.3. Hệ phương trình đặc tính truyền đạt ...................................................................... 7
1.2.4. Hệ phương trình truyền đạt ngược ......................................................................... 8
1.2.5. Hệ phương trình đặc tính hỗn hợp ......................................................................... 9
1.2.6. Hệ phương trình đặc tính hỗn hợp ngược ............................................................ 10
1.2.7. Quan hệ giữa các thông số của bốn cực ............................................................... 12
1.3. Các bốn cực đối xứng .................................................................................................. 13
1.3.1. Khái niệm đối xứng .............................................................................................. 13
1.3.2. Định lý Bartlett dùng cho bốn cực đối xứng ....................................................... 16
1.4. Các cách ghép nối nhiều bốn cực ................................................................................ 18
1.4.1. Ghép nối nối tiếp – nối tiếp (N -N) ...................................................................... 18
1.4.2. Ghép nối song song-song song (S-S) ................................................................... 19
1.4.3. Ghép nối nối tiếp – song song (N - S) .................................................................. 20
1.4.4. Ghép nối song song – nối tiếp (S - N) .................................................................. 21
1.4.5. Ghép nối dây chuyền ............................................................................................ 21
1.5. Bốn cực có tải .............................................................................................................. 22
1.5.1. Trở kháng vào ...................................................................................................... 22
1.5.2. Hàm truyền đạt ..................................................................................................... 23
1.6. Hệ số truyền đạt của bốn cực ...................................................................................... 23
1.7. Các thông số sóng ....................................................................................................... 25
1.7.1. Trở kháng sóng ..................................................................................................... 25
1.7.2. Cách xác định thông số sóng ................................................................................ 27
1.8. Sơ đồ tương đương của bốn cực tuyến tính tương hỗ. ................................................ 28
1.8.1. Sơ đồ tương đương hình chữ T ............................................................................ 28
1.8.2. Sơ đồ tương đương hình  ................................................................................... 29
CHƯƠNG 2. BN CC TUYẾN TÍNH KHÔNG TƯƠNG HỖ ......................................... 33
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 1
Đề cương bài giảng Lý thuyết mạch 2
2.1. Định nghĩa bốn cực tuyến tính không tương hỗ .......................................................... 33
2.2. Các sơ đồ tương đương của bốn cực không tương hỗ ................................................ 33
2.2.1. Sơ đồ tương đương hình T ................................................................................... 34
2.2.2. Sơ đồ tương đương hình Π ................................................................................... 34
2.3. Một số ví d về bốn cực tuyến tính không tương hỗ .................................................. 35
2.3.1. Giratơ .................................................................................................................... 36
2.3.2. Mạch biến đổi trở kháng âm (NIC-Negative Impedancce Converter) ................. 37
2.3.3. Transistor .............................................................................................................. 38
2.3.4. Mạch khuếch đại thuật toán ................................................................................. 40
CHƯƠNG 3. NG DNG CA BN CC-B LC TH ĐNG LC ............................ 42
3.1. Nhiệm v và phân loại bộ lc...................................................................................... 42
3.1.1. Nhiệm v của bộ lc............................................................................................. 42
3.1.2. Phân loại bộ lc .................................................................................................... 42
3.2. Cu trc của bộ lc ...................................................................................................... 43
3.3. Trở kháng sng Z0 ....................................................................................................... 43
3.4. Dải thông, dải chắn và tần số cắt của lc hình T và  ................................................ 44 3.5. Bộ lc loại
K ............................................................................................................... 45
3.5.1. Bộ lc thông thp ................................................................................................. 46
3.5.2. Bộ lc thông cao ................................................................................................... 47
3.5.3. Bộ lc thông dải ................................................................................................... 48
3.5.4. Bộ lc chắn dải ..................................................................................................... 49
3.6. Mạch lc loại M .......................................................................................................... 50
3.6.1. Chuyển từ bộ lc loại K sang bộ lc loại M ........................................................ 50
3.6.2. Xây dựng các bộ lc loại M từ bộ lc loại K ....................................................... 51
CHƯƠNG 4. MẠCH PHI TUYẾN ........................................................................................ 53
4.1. Khái niệm về mạch phi tuyến ...................................................................................... 53
4.1.1. Định nghĩa ............................................................................................................ 53
4.1.2. So sánh mạch phi tuyến và mạch tuyến tính ........................................................ 53
4.2. Phân loại các phần tử phi tuyến .................................................................................. 53
4.3. Các thông số của phần tử phi tuyến ............................................................................ 56
4.3.1. Các thông số một chiều ........................................................................................ 56
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 2
Đề cương bài giảng Lý thuyết mạch 2
4.3.2. Các thông số vi phân ............................................................................................ 57
4.3.3. Các thông số trung bình ....................................................................................... 57
4.4. Hệ số méo phi tuyến .................................................................................................... 57
4.5. Các phương pháp thông dng phân tích mạch phi tuyến ............................................ 58
4.5.1. Phương pháp đồ thị .............................................................................................. 58
4.5.2. Phương pháp dò .................................................................................................... 60
4.5.3. Phương pháp lặp ................................................................................................... 61
4.5.4. Phương pháp cân bằng điều hòa .......................................................................... 62
4.6. Phương pháp tuyến tính ha quy ước tính gần đng .................................................. 64
4.7. Những quá trình tuyến tính cơ bản của hệ thống phi tuyến ........................................ 65
4.8. Bộ tạo dao động điều hòa ............................................................................................ 68
4.8.1. Định nghĩa về độ ổn định ..................................................................................... 68
4.8.2. Bộ tạo dao động có phản hồi ................................................................................ 70
4.8.3. Điều kiện tự kích – Tiêu chuẩn Nyquist .............................................................. 72
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 3
Đề cương bài giảng Lý thuyết mạch 2
CHƯƠNG 1. BN CC TUYẾN TÍNH TƯƠNG HỖ
1.1. Định nghĩa
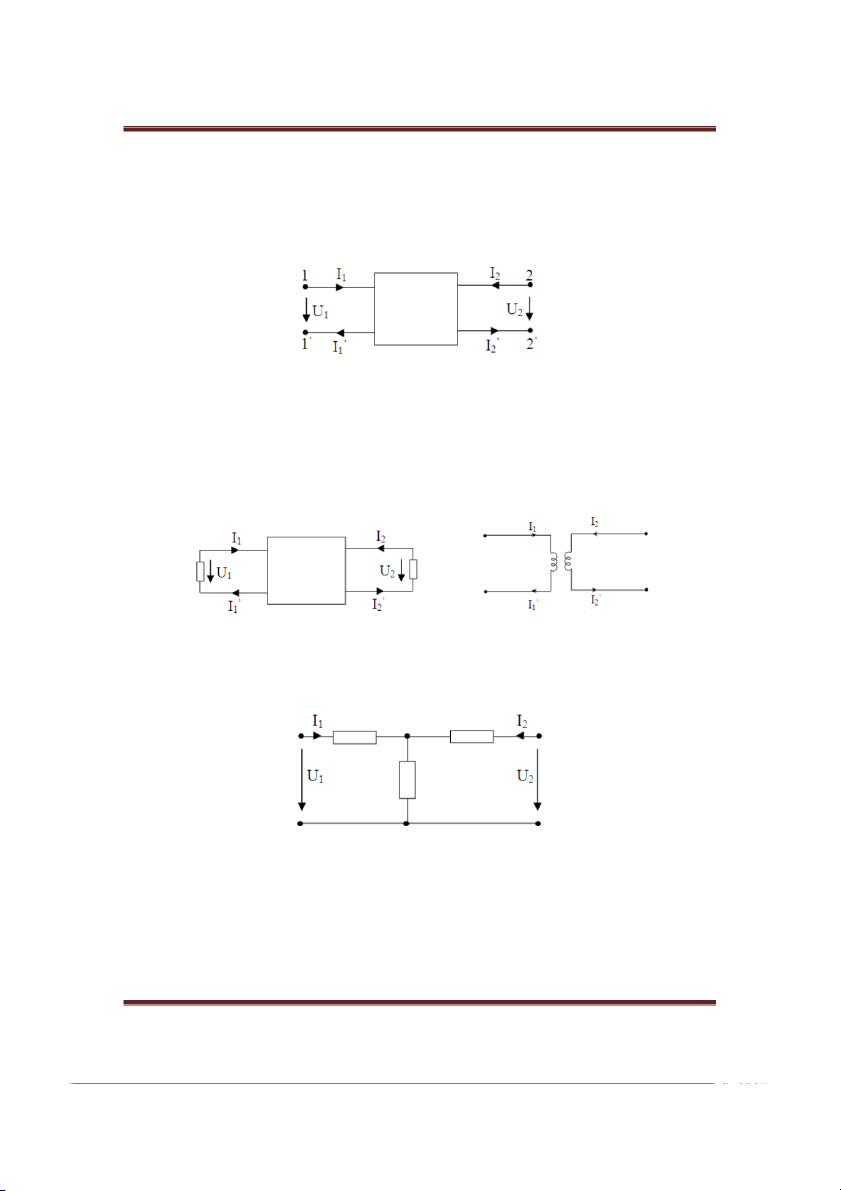
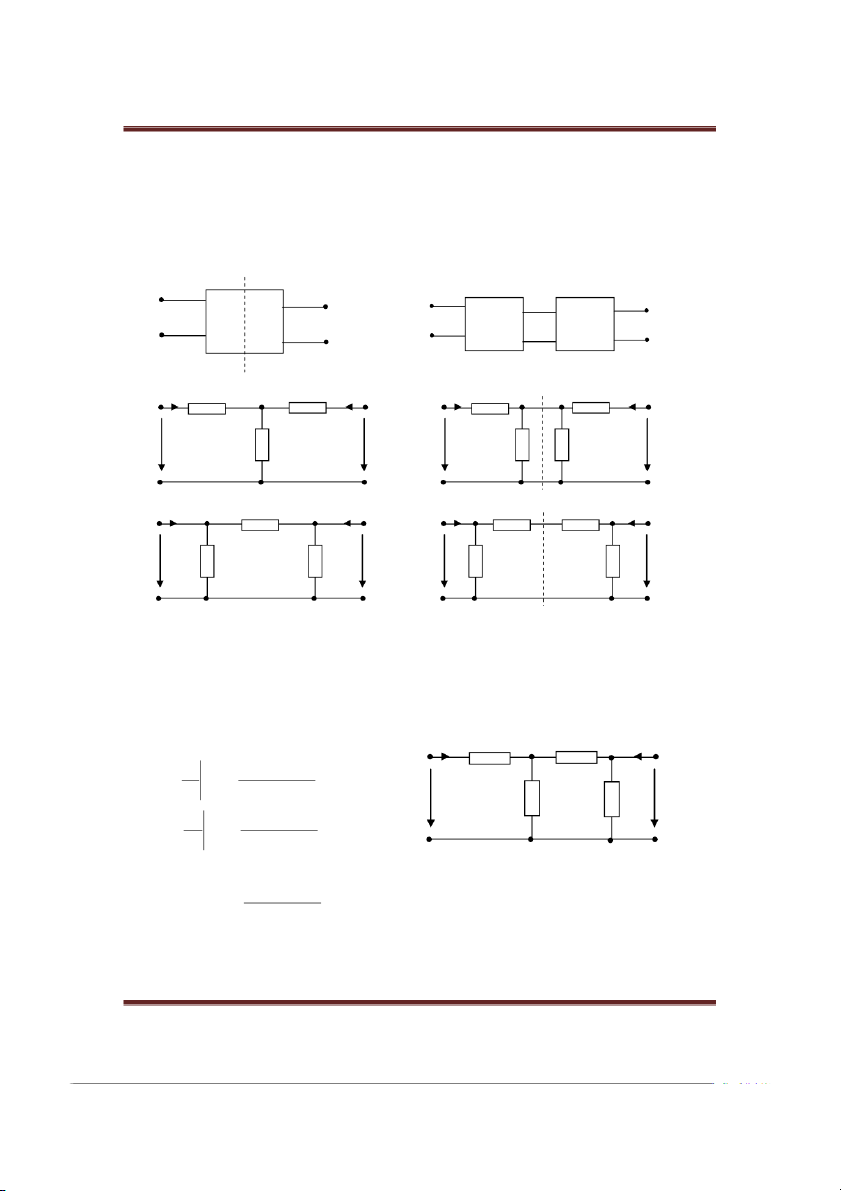
Mạch bốn cực là phần mạch có bốn đầu dây dẫn ra 1, 1’, 2, 2’. Trạng thái của nó
được xác định bởi các điện áp U1, U2 ở từng cặp đầu dây dẫn (mỗi cặp đầu dây làm thành
một cửa) và các dòng điện I1, I2 ở các cửa (hình 1.1.1). Hình 1.1.1
Điều kiện về dòng điện: I ’ ’ 1 = I1 ; I2 = I2 (1)
Các điều kiện về dòng điện được thoã mãn trong hai trường hợp:
- Trường hợp 1: Cả hai cửa đều mắc tải, trên các tải này điều kiện (1) được thoã mãn (hình 1.1.2a).
- Trường hợp 2: Cu tạo bên trong của bốn cực đảm bảo thoã mãn điều kiện (1) (hình 1.1.2b). Hình 1.1.2 a, b
Các chiều dòng điện và điện áp như trên hình vẽ là các chiều quy ước dương.
Để tính toán thuận tiện, người ta thường tưởng tượng cu tạo bên trong của bốn cực
sao cho các đầu 1’, 2’ được nối chung (hình 1.1.3). Hình 1.1.3
Với bốn cực chng ta thường ký hiệu cặp đầu 1,1’ là cửa vào (hay cửa sơ cp) ở đ
thường mắc nguồn tác động, còn cặp đầu 2,2’ là cửa ta (hay cửa thứ cp) ở đ thường mắc tải.
Các ký hiệu U,I là các ký hiệu tổng quát, chúng có thể là các đại lượng điện áp hoặc
dòng điện 1 chiều, có thể là các giá trị hiệu dng trong mạch xoay chiều hoặc có thể là ảnh
Laplace trong trường hợp tổng quát tín hiệu là hàm thời gian bt kỳ.
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 4
Đề cương bài giảng Lý thuyết mạch 2
1.2. Các hệ phương trình đặc tính
Phương trình đặc tính của bốn cực tuyến tính th động phải là phương trình tuyến tính thuần nht.
Dạng tổng quát của phương trình đặc tính:  1 a 1U1  1 a 2U2  1 b 1I1  1 b 2 I2  . 0 
a U a U b I b I  . 0 21 1 22 2 21 1 22 2
Từ hệ phương trình trên ta thy có thể rt ra hai đại lượng bt kỳ theo hai đại lượng
còn lại. Như vậy, ta có 6 tổ hợp hai đại lượng bt kỳ từ bốn đại lượng trên, từ 6 tổ hợp đ ta
sẽ có 6 hệ phương trình đặc tính khác nhau.
Chúng ta sẽ xét lần lượt các hệ phương trình đặc tính đ cùng với ý nghĩa của các hệ
số trong các phương trình đ (được gi là các thông số của bốn cực) và cách xác định
chúng. Sở dĩ chúng ta phải đưa ra các phương trình đặc tính khác nhau vì trong thực tế ứng
với từng dạng của bốn cực ta có thể phân tích chúng dễ dàng hơn dựa vào một loại hệ
phương trình đặc tính nht định.
1.2.1. Hệ phương trình đặc tính trở kháng
Giả thiết dòng điện ở cửa 1 và cửa 2 đã biết ta tìm điện áp ở hai cửa đ, như vậy ta
nhận được hệ phương trình đặc tính trở kháng với các thông số trở kháng zij:
U z I z I  1 11 1 12 2 (1.2.1.1)
U2  z21I1  z22 I2
Hệ phương trình trên được gi là hệ phương trình đặc tính trở kháng vì các thông số
zij c đơn vị là ; zij còn được gi là các thông số trở kháng.
Hệ phương trình trên được viết dưới dạng ma trận như sau: U 1  1I     Z   U 2  I2  z z 11 12  Trong đ: Z  
 được gi là ma trận trở kháng. z z 21 22 
* Ý nghĩa vật lý của các thông số trở kháng:
- Nếu mắc nguồn ở cửa 1 và hở mạch cửa 2: U1 U z  và 2 z  11 21 I1 I I 0 1 2  I 0 2  Ta thy:
z11 là trở kháng vào của cửa 1 khi hở mạch ở cửa 2 nên z11 được gi là trở kháng vào hở mạch của cửa 1.
z21 là tỉ số giữa điện áp ở cửa 2 và dòng ở cửa 1 khi cửa 2 hở mạch nên z21 được gi
là trở kháng truyền đạt hở mạch của cửa 1.
- Nếu mắc nguồn ở cửa 2 và hở mạch cửa 1: U 1 U z  và 2 z  . 12 I 22 2 I2 1 I  0 I 1 0 
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 5
Đề cương bài giảng Lý thuyết mạch 2
z12 được gi là trở kháng truyền đạt hở mạch của cửa 2.
z22 được gi là trở kháng vào hở mạch của cửa 2.
Tóm lại, các thông số zij được gi là các thông số trở kháng hở mạch, do đ hệ
phương trình (1.2.1.1) còn được gi là hệ phương trình đặc tính trở kháng hở mạch.
Với bốn cực tuyến tính tương hỗ: z12 = z21.
Ví d 1.2.1.1:
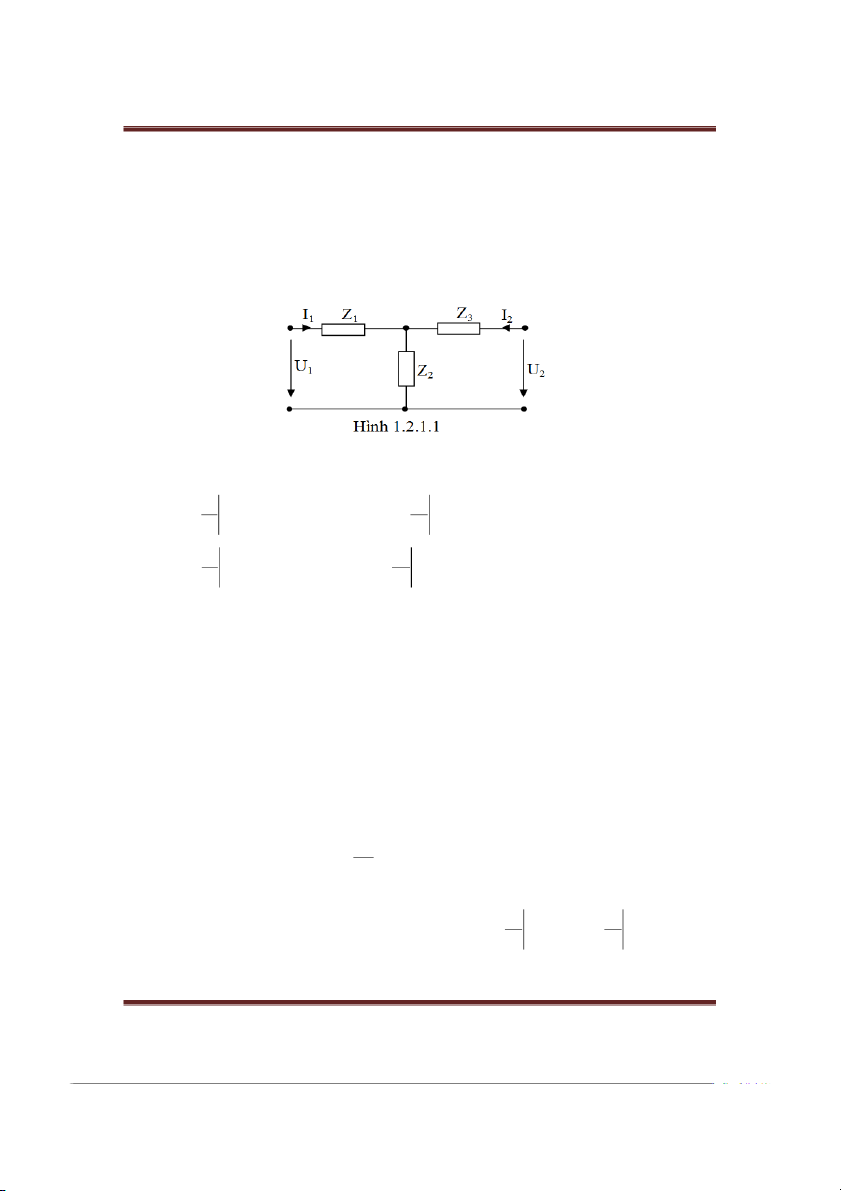
Cho bốn cực tuyến tính tương hỗ (hình T) c sơ đồ như hình 1.2.1.1.
Hãy xác định các thông số trở kháng hở mạch của bốn cực trên. Gii: U 1    ; U 2   1 z 1 1 Z Z2 z21 Z2 1 I I I 0 1 2 I  0 2 U1   ; U 2    1 z 2 Z 2 z 22 Z2 Z3 I 2 I I  0 2 1 I  0 1
1.2.2. Hệ phương trình đặc tính dẫn nạp
Giả thiết các điện áp đã biết ta tìm dòng điện theo điện áp, như vậy ta nhận được hệ
phương trình đặc tính dẫn nạp với các thông số dẫn nạp yij:
I y U y U  1 11 1 12 2 (1.2.2.1) I y U  2 21 1 y 22U 2
Hệ phương trình trên được gi là hệ phương trình đặc tính dẫn nạp vì các thông số yij
c đơn vị là S; yij còn được gi là các thông số dẫn nạp.
Hệ phương trình trên được viết dưới dạng ma trận như sau:  1 I   1 U     Y   I 2   2 U   y y 1 Z - Z 11 12   1  22 12  Trong đ: Y   Z    
 được gi là ma trận dẫn nạp. y y   Z - Z Z 21 22   21 11 
* ý nghĩa vật lý của các thông số dẫn nạp:
- Nếu mắc nguồn ở cửa 1 và ngắn mạch cửa 2: 1 I yI và 2 y  11 21 1 U U U 1 2 0 2 U  0
y11 là dẫn nạp vào ngắn mạch của cửa 1.
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 6
Đề cương bài giảng Lý thuyết mạch 2
y21 là dẫn nạp truyền đạt ngắn mạch của cửa 1.
- Nếu mắc nguồn ở cửa 2 và ngắn mạch cửa 1: 1 I yI và 2 y  12 U 22 2 U U 0 2 1  U 0 1 
y12 được gi là dẫn nạp truyền đạt ngắn mạch của cửa 2.
y22 được gi là dẫn nạp vào ngắn mạch của cửa 2.
Tóm lại, các thông số yij được gi là các thông số dẫn nạp ngắn mạch, do đ hệ
phương trình (1.2.2.1) còn được gi là hệ phương trình đặc tính dẫn nạp ngắn mạch.
Với bốn cực tuyến tính tương hỗ: y12 = y21.
Ví d 1.2.2.1:
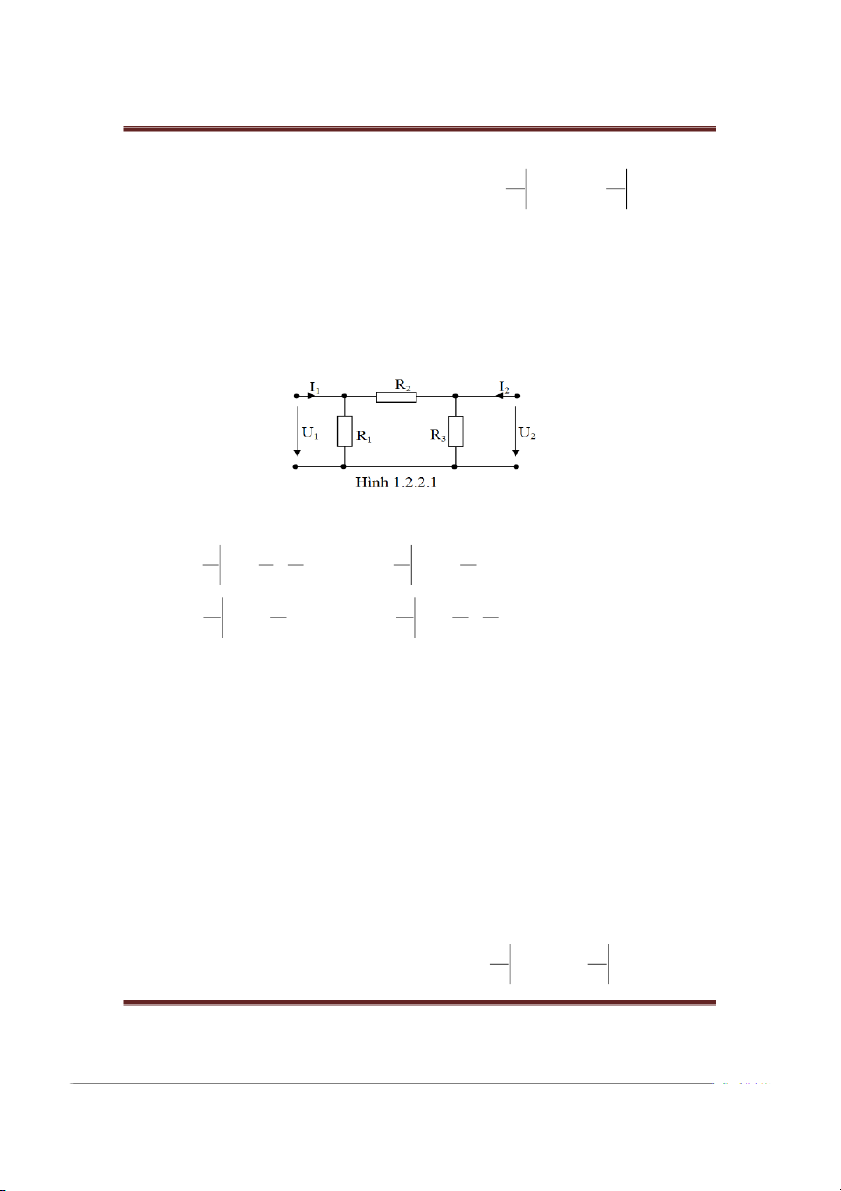
Cho bốn cực tuyến tính tương hỗ (hình Π) c sơ đồ như hình 1.2.2.1.
Tính các thông số dẫn nạp ngắn mạch của bốn cực trên. Gii: I 1 1 I 1 1    ; 2    1 y 1 2 y 1 1 U R R U R U  0 1 2 1 U 0  2 2 2 I 1 I 1 1 1    ; 2    1 y 2 2 y 2 U 2 2 R U R R U 0  2 2 3  1 U 0 1
1.2.3. Hệ phương trình đặc tính truyền đạt
Giả thiết điện áp và dòng điện ở cửa 2 đã biết ta tìm điện áp và dòng điện cửa 1, như
vậy ta nhận được hệ phương trình đặc tính truyền đạt với các thông số truyền đạt aij:
U a U a I  1 11 2 12 2 (1.2.3.1) I a U  1 21 2 a 22I 2
a21 c đơn vị là S, a12 c đơn vị là , a11 và a22 là các đại lượng không thứ nguyên.
Hệ phương trình trên được viết dưới dạng ma trận như sau: U  1 U 2     A   1 I  I 2  a a 11 12  Trong đ: A  
 được gi là ma trận truyền đạt thuận. a a 21 22 
* Cách tính các thông số truyền đạt thuận a : ij
- Nếu mắc nguồn ở cửa 1 và hở mạch cửa 2: U1 I a  và 1 a  11 21 U 2 U I 0 2 2  I 0 2 
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 7
Đề cương bài giảng Lý thuyết mạch 2
- Nếu mắc nguồn ở cửa 1 và ngắn mạch cửa 2: 1 I aU và 1 a  12 I 22 2 I U 0 2 2  U 0 2 
Điều kiện bốn cực tuyến tính tương hỗ: ΔA = -1.
Ví d 1.2.3.1:
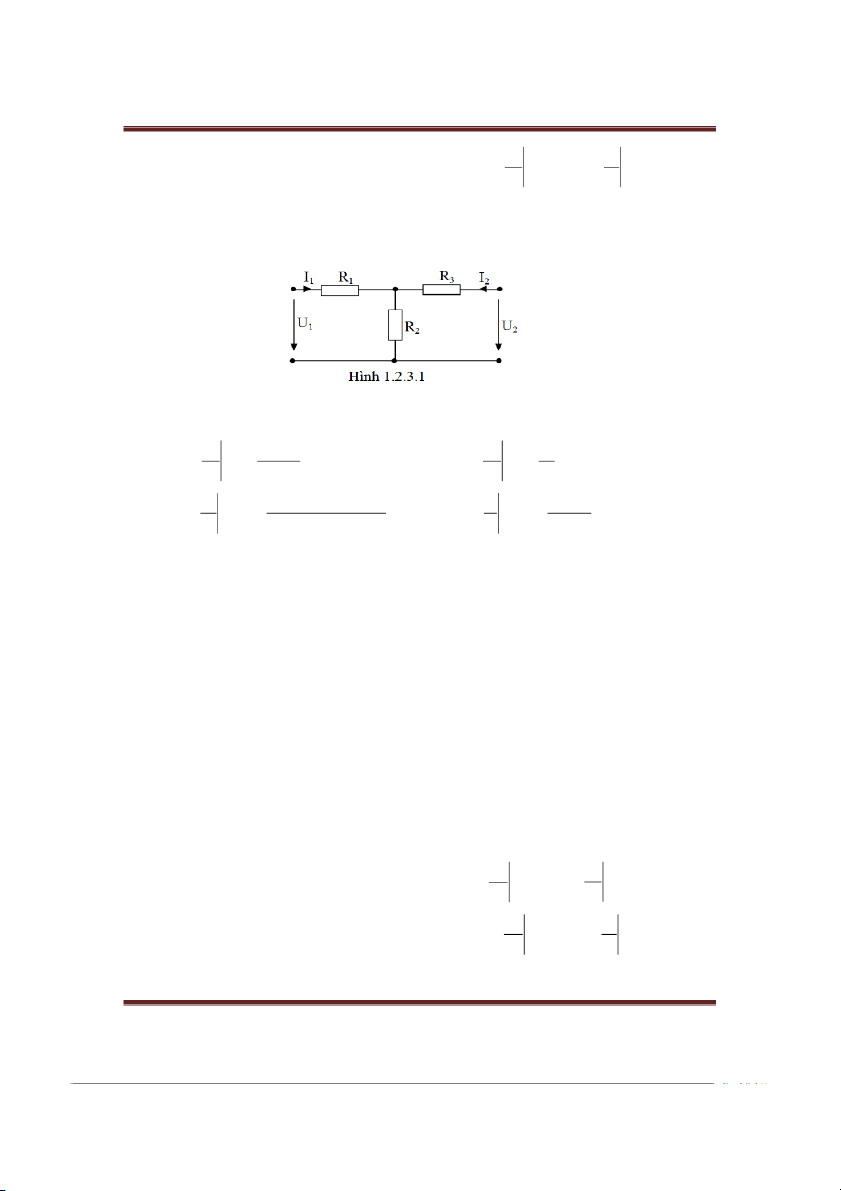
Cho bốn cực tuyến tính tương hỗ (hình T) c sơ đồ như hình 1.2.3.1.
Hãy xác định các thông số truyền đạt của bốn cực trên . Gii: I 1 1 U 1 R 2 R   ; 1   1 a 1 a U 21 2 2 R U2 2 R 2 I  0 I 2 0    U R .R R .R R . 1 1 2 1 3 2 3 R    ; 1 I 2 R 3 R    1 a 2 a I 22 2 2 R I R U 2 2 2  0 U 2  0
1.2.4. Hệ phương trình truyền đạt ngược
Giả thiết điện áp và dòng điện ở cửa 2 đã biết ta tìm điện áp và dòng điện cửa 2, như
vậy ta nhận được hệ phương trình đặc tính truyền đạt ngược với các thông số truyền đạt ngược bij: U2  1
b 1U1  b I  12 1 (1.2.4.1) I b U  2 21 1 2 b 2 1 I
b21 c đơn vị là S, b12 c đơn vị là , b11 và b22 là các đại lượng không thứ nguyên.
Hệ phương trình trên được viết dưới dạng ma trận như sau: U 2  U1      B   2 I   1I  b b  Trong đ: 11 12 1  B
A được gi là ma trận truyền đạt ngược. b  b   21 22 
* Cách tính các thông số truyền đạt ngược b : ij
- Nếu mắc nguồn ở cửa 2 và hở mạch cửa 1: U I 2 b  và 2 b  11 21 U U 1 1 I I  1 0  1 0
- Nếu mắc nguồn ở cửa 2 và ngắn mạch cửa 1: U2 I b  và 2 b  12 I 22 1 1 I 1 U 0  1 U  0
Điều kiện bốn cực tuyến tính tương hỗ: ΔB = -1.
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 8
Đề cương bài giảng Lý thuyết mạch 2
Ví d 1.2.4.1:
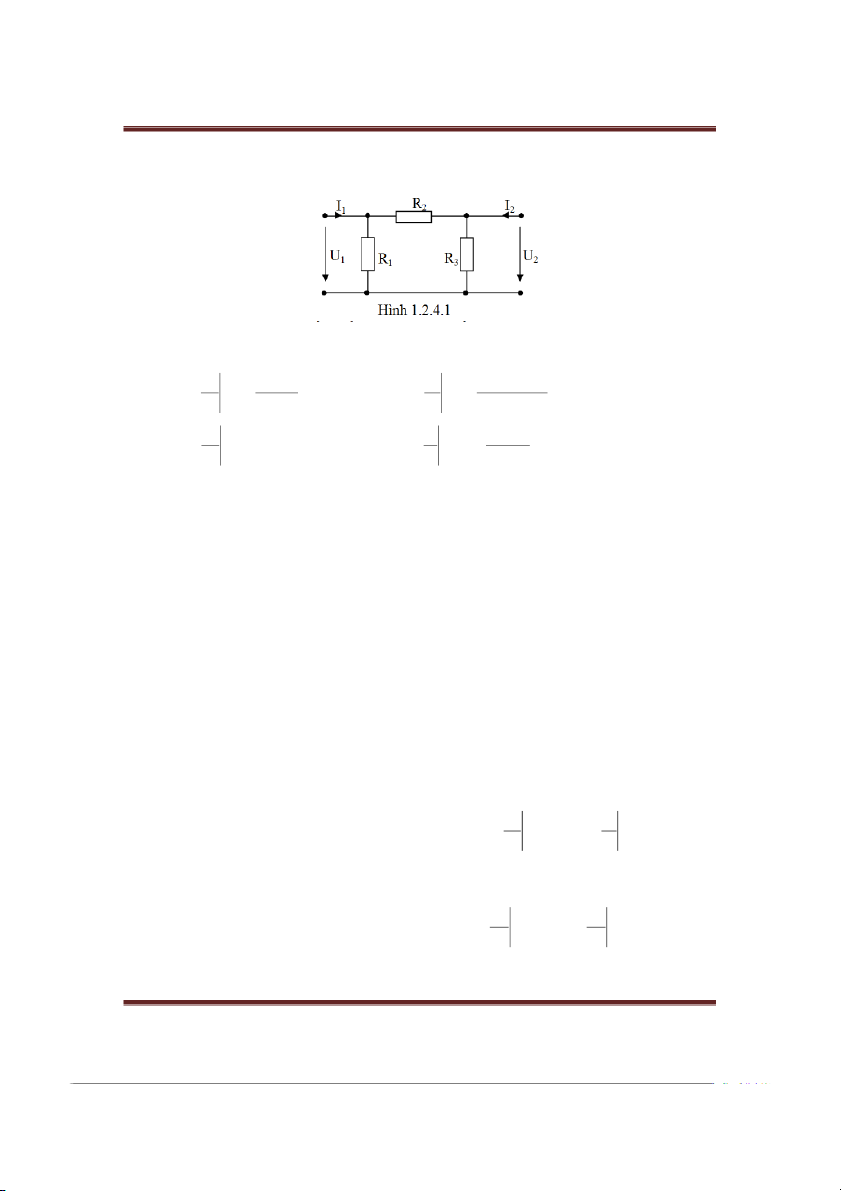
Cho bốn cực tuyến tính tương hỗ (hình Π) c sơ đồ như hình 1.2.4.1.
Tính các thông số truyền đạt ngược của bốn cực trên. Gii: U    2 1 R 2 R   ; 2 I R1 R2 R3   1 b 1 2 b 1 U U R . 1 R R I 0 1 1 I  0 1 3 1 1 U  2    ; 2 I 2 R 3 R    1 b 2 2 R 2 b 2 I1 I R U 0 1 U 0 3 1 1
1.2.5. Hệ phương trình đặc tính hỗn hợp
Giả thiết dòng điện ở cửa 1 và điện áp ở cửa 2 đã biết ta tìm điện áp ở cửa 1 và dòng
điện ở cửa 2, như vậy ta nhận được hệ phương trình đặc tính hỗn hợp với các thông số hỗn hợp hij:
U h I h U  1 11 1 12 2 (1.2.5.1)  2 I  2 h 1 1 I  2 h 2U2
Hệ phương trình trên được gi là hệ phương trình đặc tính hỗn hợp vì: h11 c đơn vị
là , h22 c đơn vị là S, h12 và h21 là các đại lượng không thứ nguyên.
Hệ phương trình trên được viết dưới dạng ma trận như sau: U  1  1 I     H    2 I  U2  h h 11 12  Trong đ: H  
 được gi là ma trận hỗn hợp thuận. h h 21 22 
* ý nghĩa vật lý của các thông số hỗn hợp:
- Nếu mắc nguồn ở cửa 1 và ngắn mạch cửa 2: U 1 I h  và 2 h  11 I 21 1 I U 0 1 2  U 0 2 
h11 là trở kháng vào ngắn mạch của cửa 1.
h21 là hệ số truyền đạt dòng điện ngắn mạch từ cửa 1 đến cửa 2.
- Nếu mắc nguồn ở cửa 2 và hở mạch cửa 1: U1 I h  và 2 h  12 U 22 2 U2 1 I  0 1 I  0
h12 được gi là hệ số truyền đạt điện áp hở mạch từ cửa 2 đến cửa 1.
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 9
Đề cương bài giảng Lý thuyết mạch 2
Với bốn cực tuyến tính tương hỗ thì điều kiện tương hỗ là h12 = -h21.
Ví d 1.2.5.1:
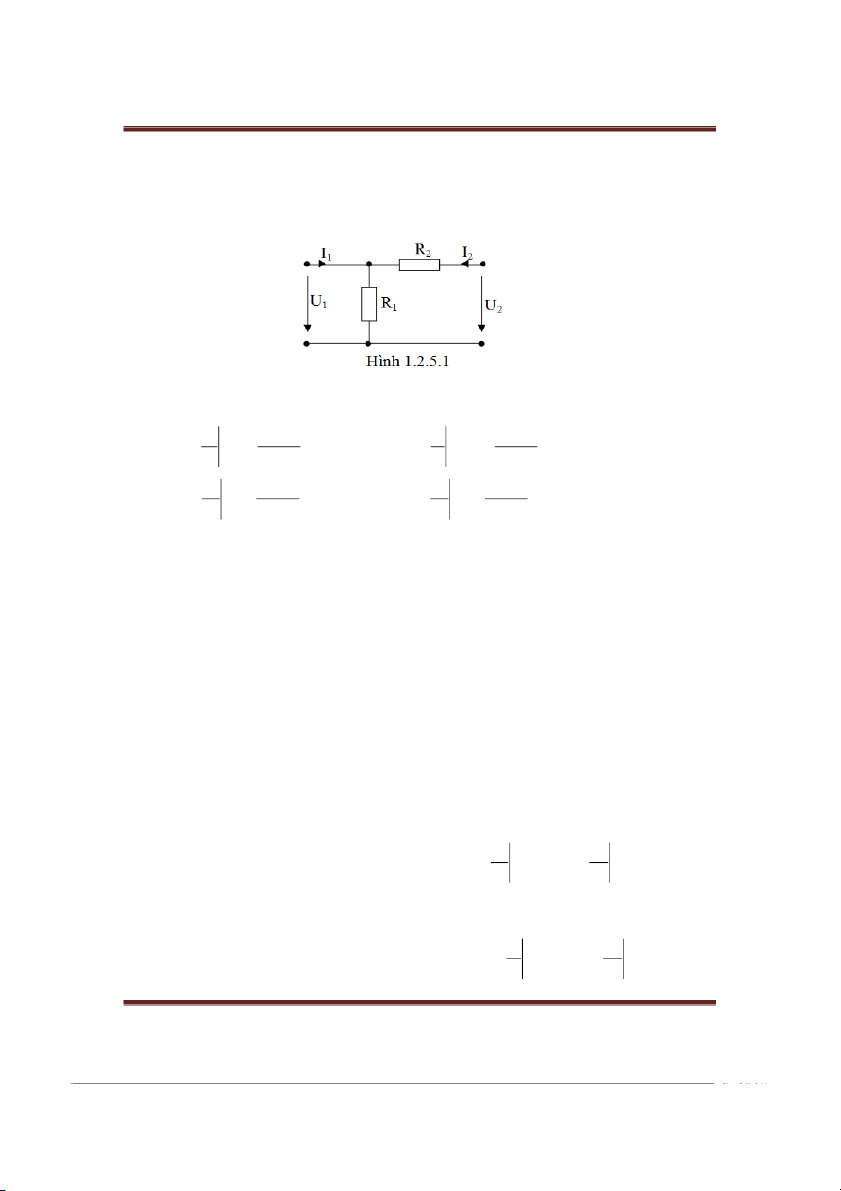
Cho bốn cực tuyến tính tương hỗ (hình Γ – hình gamma hay g xuôi) c sơ đồ như hình 1.2.5.1.
Hãy xác định các thông số hỗn hợp của bốn cực trên. Gii: U R . 1 1 2 R   ; 2 I 1 R    1 h 1 h  21  1 I 1 R R2 I R R U 1 1 2 2  0 U 20 U I 1 1 R1   ; 2   1 h 2 2 h 2 U   2 R1 R2 U 2 1 R 2 R 1 I  0 I 1 0 
1.2.6. Hệ phương trình đặc tính hỗn hợp ngược
Giả thiết điện áp ở cửa 1 và dòng điện ở cửa 2 đã biết ta tìm dòng điện ở cửa 1 và
điện áp ở cửa 2, như vậy ta nhận được hệ phương trình đặc tính hỗn hợp ngược với các
thông số hỗn hợp ngược gij:
I g U g I  1 11 1 12 2 (1.2.6.1) U g U  2 21 1 g22 I2
g11 c đơn vị là S, g22 c đơn vị là , h12 và h21 là các đại lượng không thứ nguyên.
Hệ phương trình trên được viết dưới dạng ma trận như sau:  1 I  U1     G  U 2  I2  g g  Trong đ: 11 12 1  G
H được gi là ma trận hỗn hợp ngược. g  g   21 22 
* ý nghĩa vật lý của các thông số hỗn hợp ngược:
- Nếu mắc nguồn ở cửa 1 và hở mạch cửa 2: 1 U gI và 2 g  11 U 21 1 U I 0 1 2  I 0 2 
g11 là dẫn nạp vào hở mạch của cửa 1.
g21 là hệ số truyền đạt điện áp hở mạch từ cửa 1 đến cửa 2.
- Nếu mắc nguồn ở cửa 2 và ngắn mạch cửa 1: 1 U gI và 2 g  12 I 22 2 2 I 1 U  0 1 U 0 
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 10
Đề cương bài giảng Lý thuyết mạch 2
g12 được gi là hệ số truyền đạt dòng điện ngắn mạch từ cửa 2 đến cửa 1.
g22 được gi là trở kháng vào ngắn mạch của cửa 2.
Bốn cực tuyến tính tương hỗ: g12 = -g21.
Ví d 1.2.6.1:
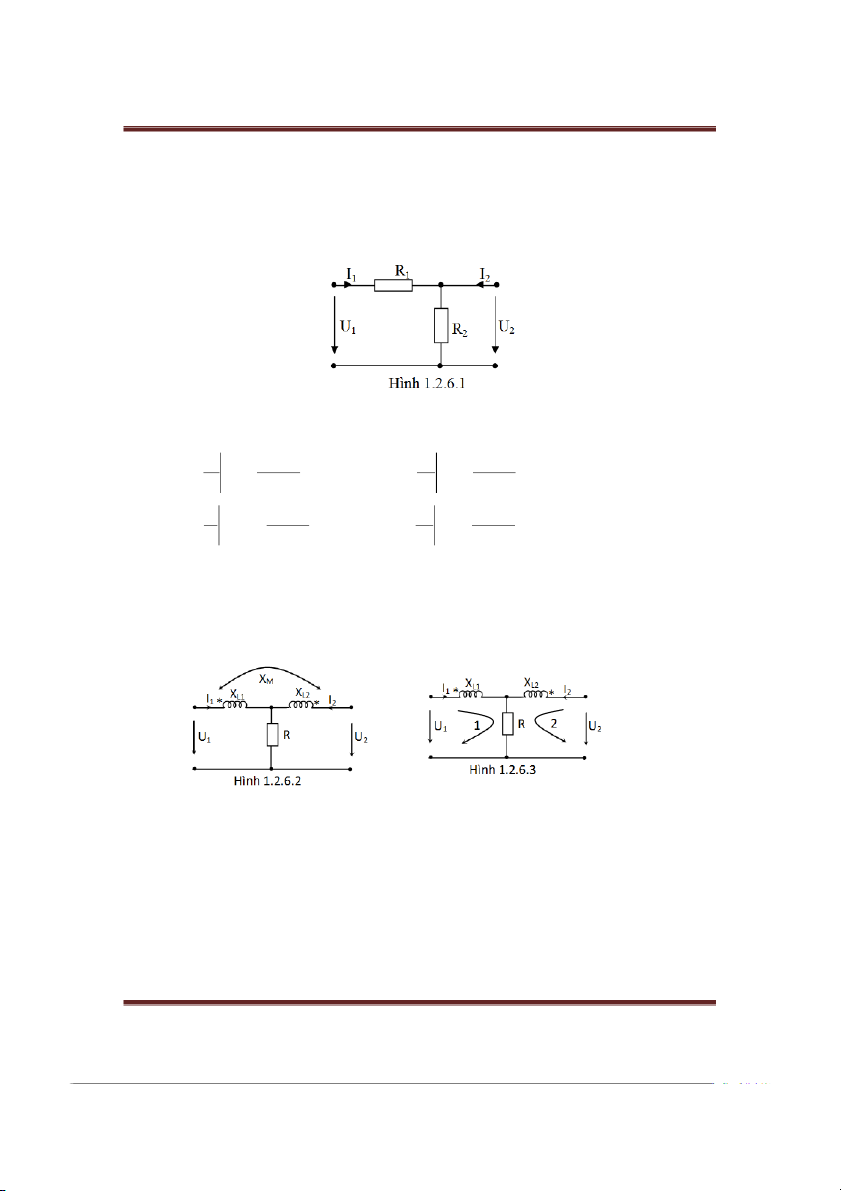
Cho bốn cực tuyến tính tương hỗ (hình g ngược) c sơ đồ như hình 1.2.6.1.
Hãy xác định các thông số hỗn hợp ngược của bốn cực trên. Gii: I 1 1 U R g   ; 2 2   11 g  21  1 U R R U R R I 0 1 2 1 I 0 1 2 2 2 I U R . 1 2 R R g    ; 2 1 2   12 2 g 2 I   2 R R I R R U 0 1 2 2 U 0 1 2 1 1
Lưu : Đối với các mạch c hỗ cảm thì sẽ không áp dng các công thức trên mà chng
ta sẽ áp dng các phương pháp giải mạch điện đã hc trước đây để đưa ra hệ phương trình
đặc trưng và từ đ suy ra các thông số cần tìm.
Ví d 1.2.6.2:
Cho bốn cực tuyến tính tương hỗ c hỗ cảm c sơ đồ như hình 1.2.6.2.
Hãy xác định các thông số zij của bốn cực trên. Gii:
p dng phương pháp dòng điện vòng với hai vòng như trên sơ đồ hình 1.2.6.3, ta được: U (R jX ) L I (R jX ) 1   1 1   M I  2
U  (R jX )I  (R jX ) 2 M 1 L 2 1 I
Vây: z11 = R + jXL1; z12 = z21 = R + jXM; z22 = R + jXL2
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 11
Đề cương bài giảng Lý thuyết mạch 2
1.2.7. Quan hệ giữa các thông số của bốn cực
Với 6 hệ phương trình trên ta thy từ một hệ phương trình bt kì có thể suy ra các hệ
phương trình còn lại. Các bộ thông số Z, Y, A, B, H, G có mối quan hệ với nhau, nếu biết được một bộ thông ố
s ta sẽ suy ra được các bộ thông số còn lại.
Ví d 1.2.7.1:
Từ hệ phương trình đặc tính trở kháng suy ra hệ phương trình đặc tính truyền đạt . Gii: ZZU  11 1 U2  IU z I  1 11 1 z12I 2  2 Z Z  21 21 1 U  1
a 1U2  a I      12 2
U z I z I 1 2 21 1 22 2  Z 22
I a U a I I1  U 2  1 21 2 22 2  I2  Z21 Z21 Với ΔZ = z11.z22 – z1 . 2 z21.
Với cách chuyển đổi đ ta c được bảng mối quan hệ giữa các thông số:
Bảng mối quan hệ giữa các thông số: Trở kháng hở mạch 1 z11 z12 z21 z22 z Truyền đạt a21 a11 -a 1 -a22 -a12 Hỗn hợp h22 h h12 -h21 1 h11 Dẫn nạp ngắn mạch y y22 -y12 -y21 y11 1
Từ một loại thông số bt kỳ ta có thể suy ra các thông số khác.
a) Tìm mối quan hệ giữa các thông số:
1. Các hàng tỷ lệ với nhau, nếu biết được thông số của một hàng có thể tìm được
thông số của các hàng còn lại.
Bộ thông số đã biết: Mẫu số Tử số ↑ ↑
Bộ thông số cần tìm: 1 X
Ví d 1.2.7.2:
Biết Z cần tìm H . Gii:
Từ bảng mối quan hệ giữa các thông số ta c: 1 Z z 12  H    z 22 - z 21  1
Ví d 1.2.7.3:
Cho bốn cực tuyến tính tương hỗ c sơ đồ như hình 1.2.7.3.
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 12
Đề cương bài giảng Lý thuyết mạch 2
Biết: XL1 = 2Ω; XL2 = 4Ω; XC = 1Ω. Tìm A . Gii:
Ta c: Za = j2; Zb = -j; Zc = j4
z11 = Za + Zb = j; z12 = z21 = Zb = -j; z22 = j3
Từ bảng mối quan hệ giữa các thông số: 1 z -  11  Z  1 2  j A   A      2 z 1  1 - z22  j 3 
2. Các cột tỷ lệ với nhau, nếu biết được thông số của một cột có thể tìm được thông
số của các cột còn lại.
Bộ thông số đã biết Bộ thông số cần tìm Mẫu số ← 1 Tử số ← X
3. Trong một hình chữ nhật bt kỳ, tích số các thông số trên đường chéo bằng nhau. Ví d: -g12 = g11.z1 ; 2 b21.(-a22) = a21.b11.
b) Tìm điều kiện tương hỗ
Điều kiện tương hỗ được rút ra từ cột 3 và 4 trong bảng mối quan hệ giữa các thông số, ta có: z12 = z21; y12 = y21; 1
h 2 = -h21; g12 = -g21; ∆A = -1; ∆B = -1.
c) Tìm điều kiện đối xứng
Điều kiện đối xứng được rút ra từ cột 2 và cột 5 của bảng mối quan hệ giữa các thông số:
z11 = z22; y11 = y22; ∆H = 1; ∆G = 1; a11 = -a22; b11 = -b22.
1.3. Các bốn cực đối xứng
1.3.1. Khái niệm đối xứng
a. Khái niệm đối xứng về mặt điện của bốn cực
Một bốn cực được gi là đối xứng về mặt điện khi cửa 1 và cửa 2 có thể đổi lẫn cho
nhau mà các thông số của bốn cực hoàn toàn không đổi.
U z I z I
Phương trình trở kháng của bốn cực:  1 11 1 12 2
U 2  z 21I1  z 22I 2
U z I z I
Nếu bốn cực đối xứng về mặt điện:  2 11 2 12 1
U1  z21I2  z22 1 I
Như vậy rõ ràng: z12 = z21 và z1 1 = z22.
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 13
Đề cương bài giảng Lý thuyết mạch 2
Điều kiện đối xứng về mặt điện là z11 = z22, một bốn cực tuyến tính tương hỗ đối xứng về mặt đ ệ
i n chỉ cần quan tâm đến hai thông số z11(hoặc z22) và z12 (hoặc z21).
b. Khái niệm đối xứng về mặt hình học của bốn cực
Sự đối xứng về mặt hình hc của một mạch điện thường được biễu diễn là sự đối xứng
qua trc đứng chia bốn cực thành hai phần giống hệt như nhau.
Một bốn cực đối xứng có thể biễu diễn như hình 1.3.1.1. I R R 1 1 R1 I2 I1 1 R1 I2 U  1 U R 2 U 2 1 U 2R 2 2 2R2 I R R R 1 1 I2 I1 1/2 1/2 I2 U  U 1 U R2 R 2 2 1 U R2 R 2 2 Hình 1.3.1.1 Nhận xét:
Các bốn cực đối xứng về mặt hình hc thì cũng đối xứng về mặt điện nhưng các bốn cực
đối xứng về mặt điện thì có thể không đối xứng về mặt hình hc.
Ví d 1.3.1.1: Cho bốn cực đối xứng về mặt điện như hình 1.3.1.2. Trong trường hợp
nào thì bốn cực đối xứng về mặt hình hc. Gii: I R 1 R1 3 I2 U ( R R ). 1 3 4 2 R z    11 1 R I   1 R R R I 0 2 3 4 U R R 2 1 U2 2 4 U ( R R ). 2 3 2 4 R z   22 I   2 R R R I  0 2 3 4 1 Hình 1.3.1.2
Do bốn cực là đối xứng về mặt điện nên z 11 = z22.  Ta có: 4 R 2 R R R . 1 3   2 R 3 R 4 R
Nếu R4 = R2 thì R1 = 0 khi đ bốn cực sẽ đối xứng cả về mặt hình hc.
Nếu R4   thì R1 = R3 khi đ bốn cực cũng sẽ đối xứng cả về mặt hình hc.
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 14
Đề cương bài giảng Lý thuyết mạch 2
Các bốn cực đối xứng về mặt điện được đặc trưng bởi hai thông số z11 và z12, sự khảo sát
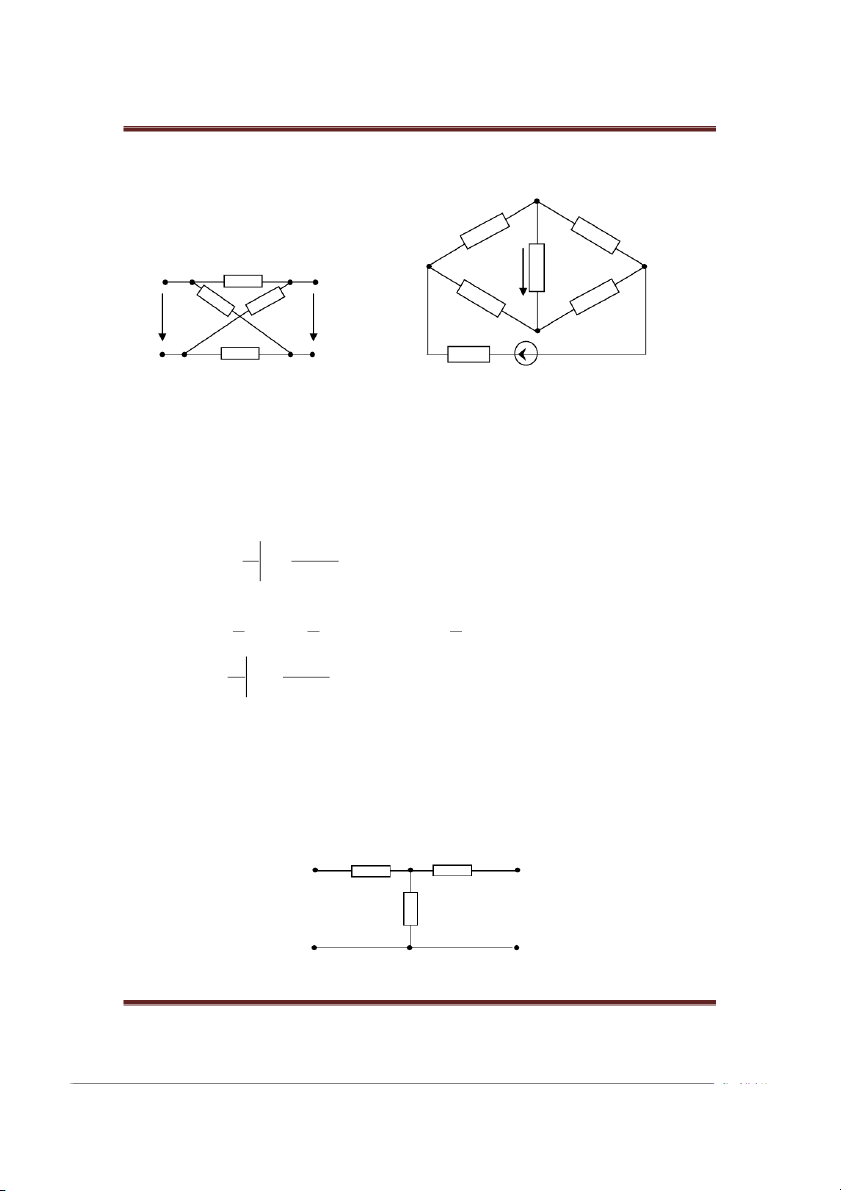
chúng được đưa về sự khảo sát mạch cầu như hình 1.3.1.3. Z I ZII Z U2 Z I 2 ZII Z ZII U II U ZI 1 2 Z  I Z1 E b) Hình 1.3.1.3 a)
Mạch hình 1.3.1.3a được gi là mạch cầu vì khi mắc nguồn vào cửa 1 và tải 2 thì mạch
đ được biến đổi thành dạng mạch hình 1.3.1.3b. Hình 1.3.1.3b là một mạch cầu đặc biệt có
từng cặp trở kháng bằng nhau. Điều kiện cân bằng cầu là tích các trở kháng nằm đối diện
nhau bằng nhau, trong trường hợp ZI = ZII, lc đ trên trở kháng Z2 sẽ không c điện áp, sự
truyền đạt của bốn cực bằng 0.
Tính các thông số trở kháng hở mạch của mạch cầu:  1 U Z Z I II z   11 I 2 1 I 0 2
Khi hở mạch ở cửa 2, theo định luật Kiếckhốp II, ta có: I1 1 I I ZU Z
 0 U  (Z Z ) 1 I 2 2 II 2 2 II I 2  Do đ: U 2 Z Z II I z   12 I 2 1 I 0 2
Như vậy: ZI = z11 – z12 và ZII = z11 + z12.
Một bốn cực đối xứng bao giờ cũng c sơ đồ tương đương là hình cầu (hình X).
Ví d 1.3.1.2:
Cho bốn cực đối xứng c sơ đồ như hình 1.3.1.4.
Hãy chuyển bốn cực sang thành sơ đồ tương đương hình cầu. R1 R1 R2 Hình 1.3.1.4
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 15
Đề cương bài giảng Lý thuyết mạch 2 Gii:
Ta c: z11 = z22 = R1 + R2; z12 = z2 1 = R2
Hình cầu tương đương c: ZI = z11 – z12 = R1 và ZII = R1 + 2R2.
Đối với bốn cực đối xứng c sơ đồ phức tạp sự xác định trở kháng cầu trong sơ đồ tương
đương được thực hiện dễ dàng theo định lý Bartlett-Brune.
1.3.2. Định lý Bartlett dùng cho bốn cực đối xứng
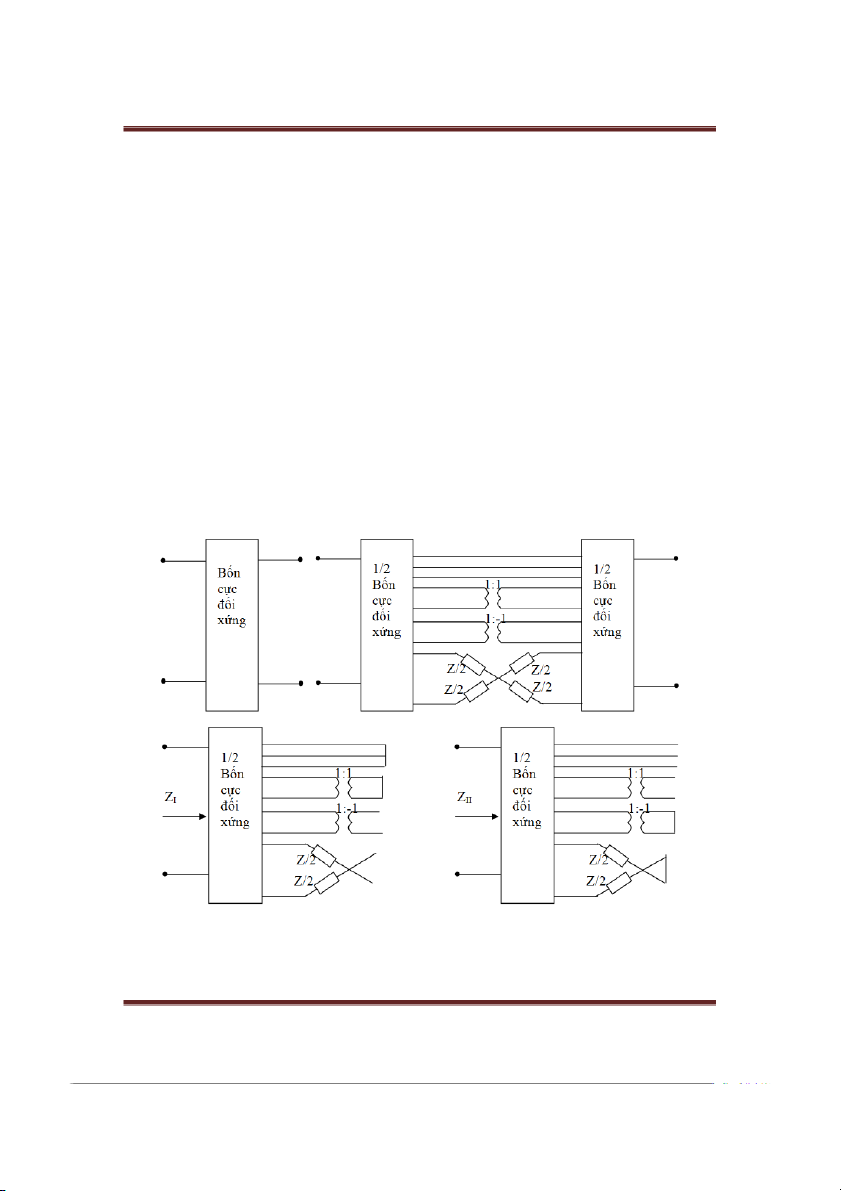
Định lý Bartlett-Brune được phát biểu như sau:
“Bốn cực đối xứng có thể chứa biến áp lý tưởng 1:1, hoặc 1:-1, hoặc các dẫy dẫn chéo
nhau trên trc đối xứng, có thể được thay thế bởi sơ đồ cầu tương đương c trở kháng ZI
bằng trở kháng vào của nửa bốn cực đối xứng khi ngắn mạch các dây dẫn nối hai nửa bốn
cực và cuộn dây thứ cp của biến áp 1:1, còn đối với biến áp 1:-1 hoặc hai dây dẫn chéo
nhau thì phải hở mạch; có trở kháng cầu ZI Ibằng trở kháng vào của nửa bốn cực đối xứng
khi hở mạch các dây nối hai nửa bốn cực và cuộn thứ cp của biến áp 1:1, ngắn mạch cuộn
thứ cp biến áp 1:-1 hoặc hai dây dẫn chéo nhau.”
Nội dung định lý Bartlett-Brune được minh hoạ trên hình 1.3.2.1. Hình 1.3.2.1
Để hiểu rõ định lý trên, chúng ta xét các biến áp. Biến áp lý tưởng là một bốn cực, được
coi là một trong các phần tử bốn cực cơ bản của mạch điện.
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 16
Đề cương bài giảng Lý thuyết mạch 2
Biến áp lý tưởng theo định nghĩa là một bốn cực được cách điện 1 chiều giữa các cửa
vào và ra, có hệ phương trình đặc trưng sau: U  2 nU 1 1 I   2 I1 n
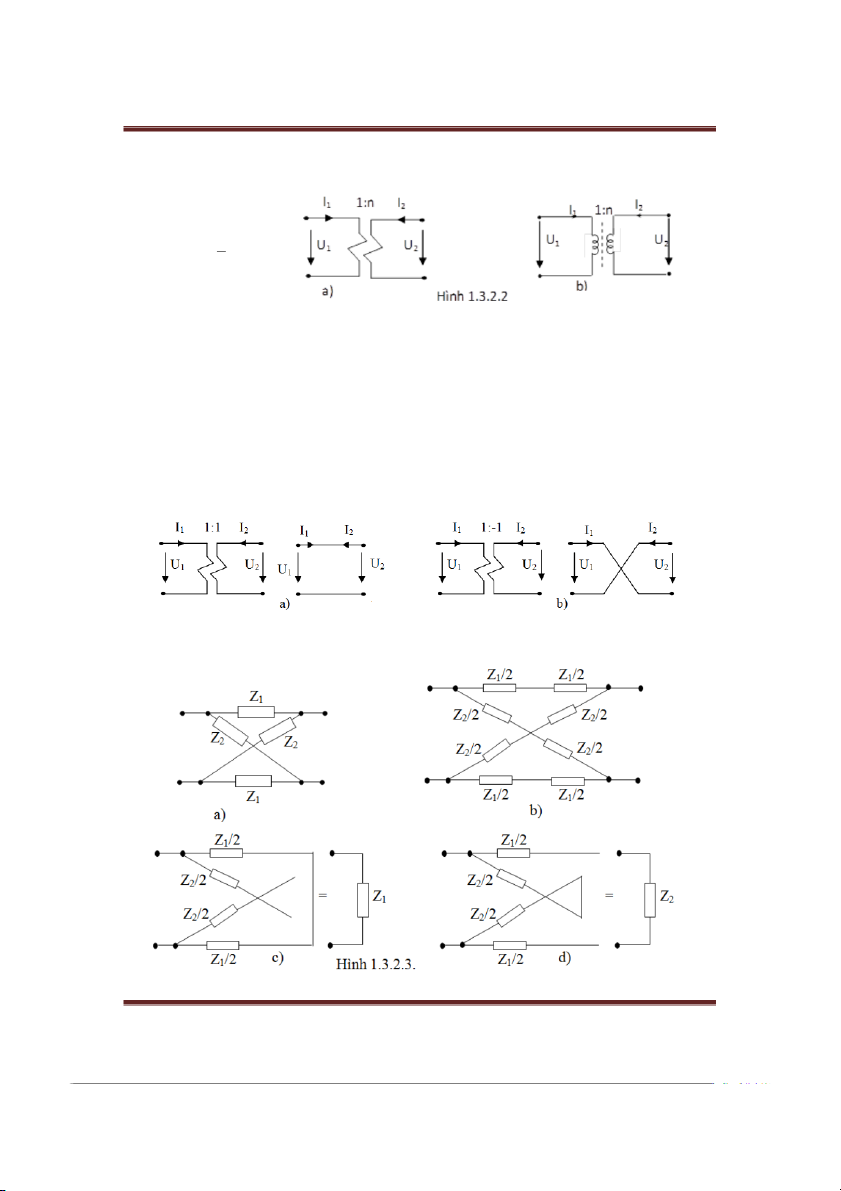
Ký hiệu biến áp lý tưởng như trên hình 1.3.2.2a.
Bộ phận chủ yếu của biến áp thực gồm hai cuộn dây ghép hỗ cảm với nhau. Nếu bỏ qua
các điện trở của các cuộn dây thì biến áp được vẽ như trên hình 1.3.2.2b (n là tỷ số giữa các
vòng dây của cuộn sơ cp ở cửa 1 và cuộn thứ cp ở cửa 2). Đối ớ
v i biến áp lý tưởng nếu n = 1 thì: U2 = U1, I2 = -I1.
Vậy biến áp 1:1 tương đương với bốn cực có hai dây dẫn song song nối từ cửa 1 đến cửa 2 như hình 1.3.2.3a.
Nếu n = -1 thì biến áp lý tưởng 1:-1 có : U2 = -U1, I2 = I1.
Vậy biến áp 1:-1 tương đương với bốn cực c hai dây chéo nhau như hình 1.3.2.3b. Hình 1.3.2.3
Ví d 1.3.2.1: ng dng định lý Bartlett-Brune trên mạch cầu hình 1.3.2.3a.
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 17
Đề cương bài giảng Lý thuyết mạch 2 Gii:
Theo định lý Bartlett-Brune ta chia mạch cầu ra hai nửa giống hệt nhau như hình
1.3.2.3b. Ta nhận được Z1 nếu ngắn mạch các dây dẫn thẳng, hở mạch các dây dẫn chéo như
hình 1.3.2.3c. Còn Z2 sẽ nhận được khi hở mạch các dây dẫn thẳng và ngắn mạch các dây
dẫn chéo như hình 1.3.2.3d.
Ví d 1.3.2.2:
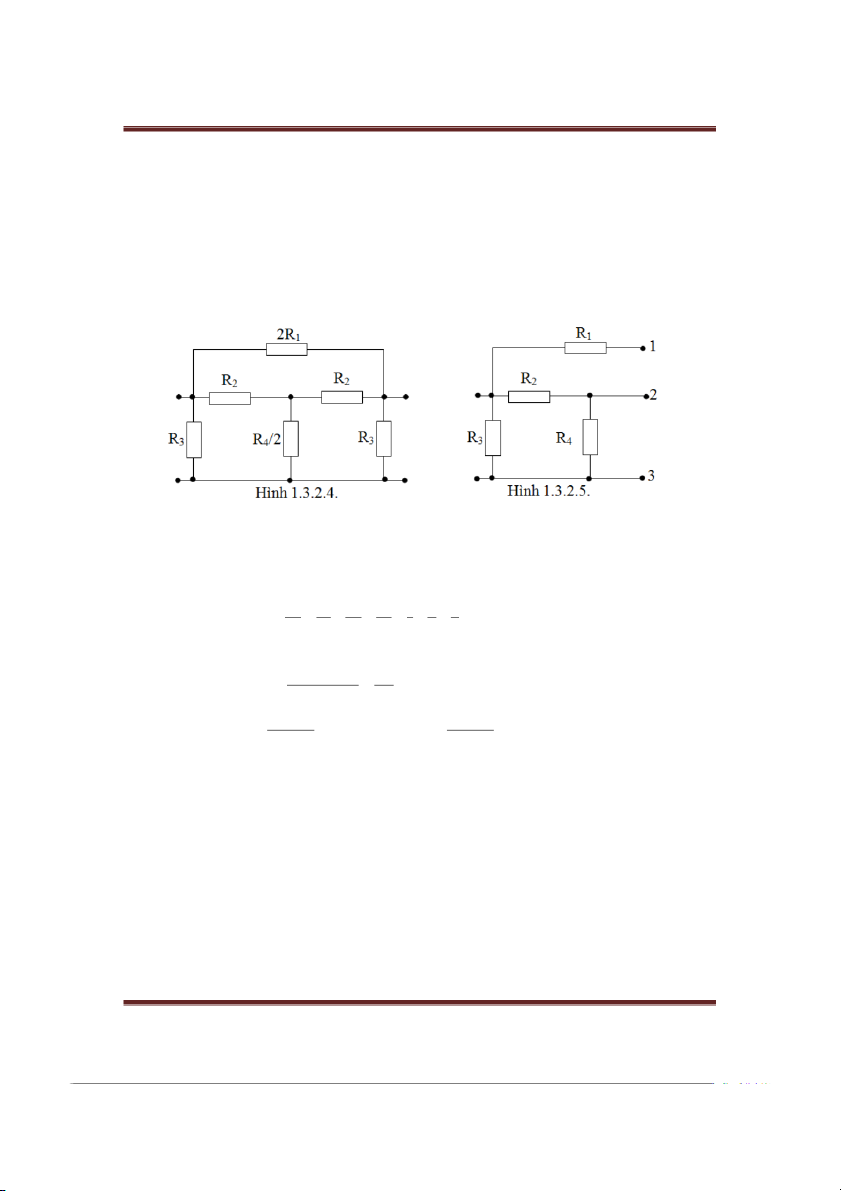
Cho bốn cực đối xứng c sơ đồ như hình 1.3.2. ,
4 biết Ri = iΩ. Hãy tìm các thông số zij. Gii:
Do bốn cực hình 1.3.2.4 là đối xứng nên ta c thể tách bốn cực làm hai phần giống
hệt nhau và đối xứng với nhau, mỗi phần c sơ đồ như hình 1.3.2.5.
p dng định lý Bartlett-Brun
e ta chuyển sang sơ đồ tương đương hình cầu.
Để tìm ZI ta ngắn mạch các điểm 1, 2, 3 khi đ trở kháng vào của phần mạch chính là ZI: 1 1 1 1 1 1 1        Z  , 0 54 ( 5 )  Z R R R 1 2 3 I I 1 2 3
Để tìm ZI Ita hở mạch các điểm 1, 2, 3 khi đ trở kháng vào của phần mạch chính là ZI :I R R  .( R ) 6 . 3 3 2 4 Z II    ( 2 )
R R R 9 3 2 4 Z Z Z
Vây: z z Z I II
z z II I   11 22 , 1 27 ( 3 ); 12 , 0 72 ( 8 ) 2 21 2
1.4. Các cách ghép nối nhiều bốn cực
Khi gặp các hệ thống phức tạp, một trong những phương pháp phân tích c hiệu lực
là coi n như được hợp thành bởi nhiều hệ t ố
h ng đơn giản hơn nối ghép với nhau theo
những cách khác nhau. Đối với mỗi hình thức ghép nối sẽ có một hệ phương trình và một hệ
thông số thích hợp nht.
1.4.1. Ghép nối nối tiếp – nối tiếp (N -N)
Hình 1.4.1 vẽ hai bốn cực mắc N-N với nhau.
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 18
Đề cương bài giảng Lý thuyết mạch 2 Hình 1.4.1 ' '
I I I ; ' '
I I I ; Ta có: 1 1 1 2 2 2 ' '
U U U ; ' '
U U U . 1 1 1 2 2 2
Hệ phương trình đặc tính trở kháng của hai bốn cực được viết dưới dạng ma trận: ' ' U     ' '     1 I1 U I    1 1 Z và    1   Z   ' ' 2 U     ' '     2 I2  U2 I2   ' I   ' I  I
Đặt  1    1    1  và cộng hai hệ phương trình theo từng vế ta có :
 '2I   '
I2  I2  ' ' U          1 U1 U1 I1 I1           1 Z 2 Z Z       ' ' U   U   U   I I   2 2 2   2   2  Như vậy: Z   1 Z 2 Z n
Tổng quát: Với n bốn cực mắc N – N với nhau ta có Z   Z . k k 1
Phát biểu: Ma trận trở kháng của hệ thống nhiều bốn cực nối N – N với nhau bằng
tổng các ma trận trở kháng của các bốn cực thành phần.
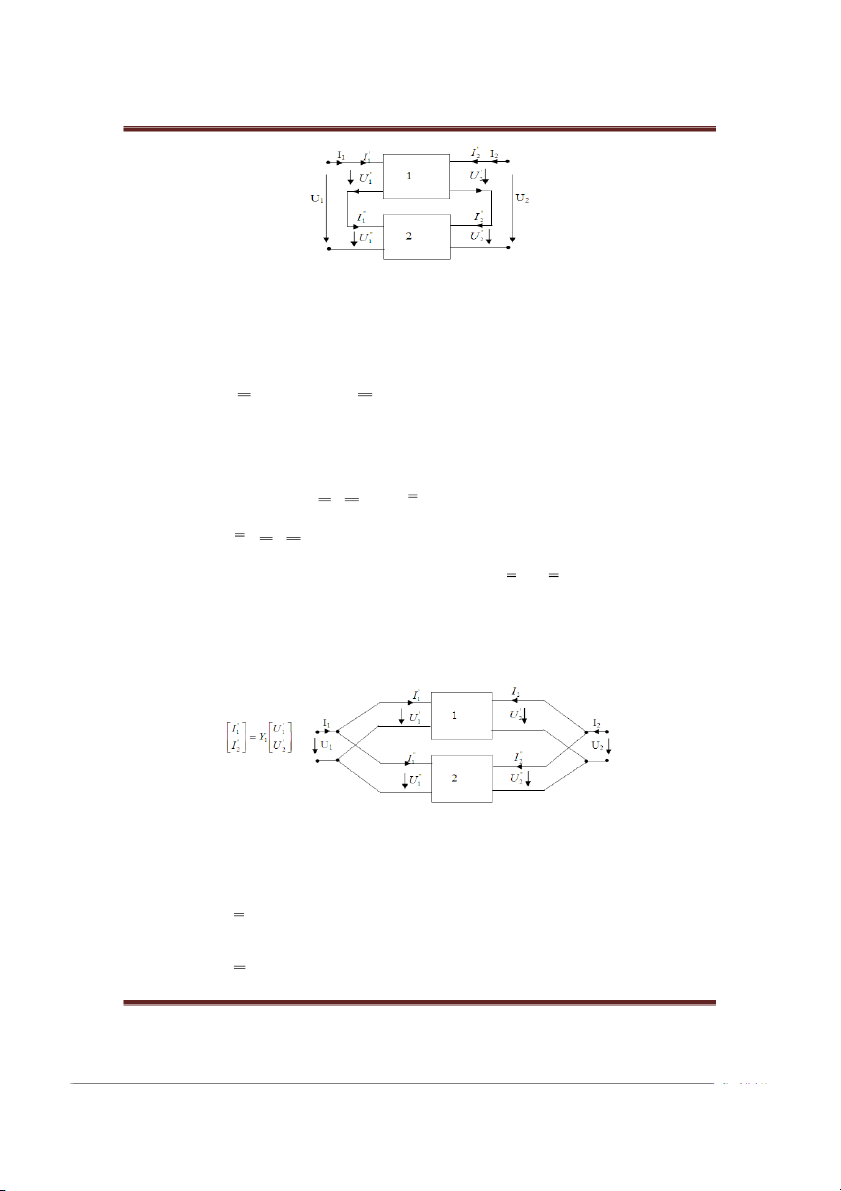
1.4.2. Ghép nối song song-song song (S-S )
Hình 1.4.2 vẽ hai bốn cực mắc S-S với nhau. Hình 1.4.2 Ta có: ' ' U         1 U1 U1 ; ' ' U 2 U 2 U 2 ; ' ' I1 I1 I 1 ; ' ' I 2 I 2 I 2 .
Hệ phương trình đặc tính dẫn nạp của hai bốn cực được viết dưới dạng ma trận: ' '     1 I 1 U    1 Y   ' '  2I U   2  ' '     1 I 1 U    2 Y   ' '     2 I U2 
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 19
Đề cương bài giảng Lý thuyết mạch 2  ' U   ' U  U
Đặt  1    1    1  và cộng hai hệ phương trình theo từng vế ta có:  ' U 2   ' U2  U2  ' '      1 I 1 I 1 I  1 U   1 U            1 Y 2 Y Y ' '       I   I I      2 U   2 U 2 2 2  Như vậy: Y   1 Y 2 Y n
Tổng quát: Với n bốn cực mắc N – N với nhau ta có Y  Y . k k 1 
Phát biểu: Ma trận dẫn nạp của hệ thống nhiều bốn cực nối S – S với nhau bằng tổng các ma
trận dẫn nạp của các bốn cực thành phần.
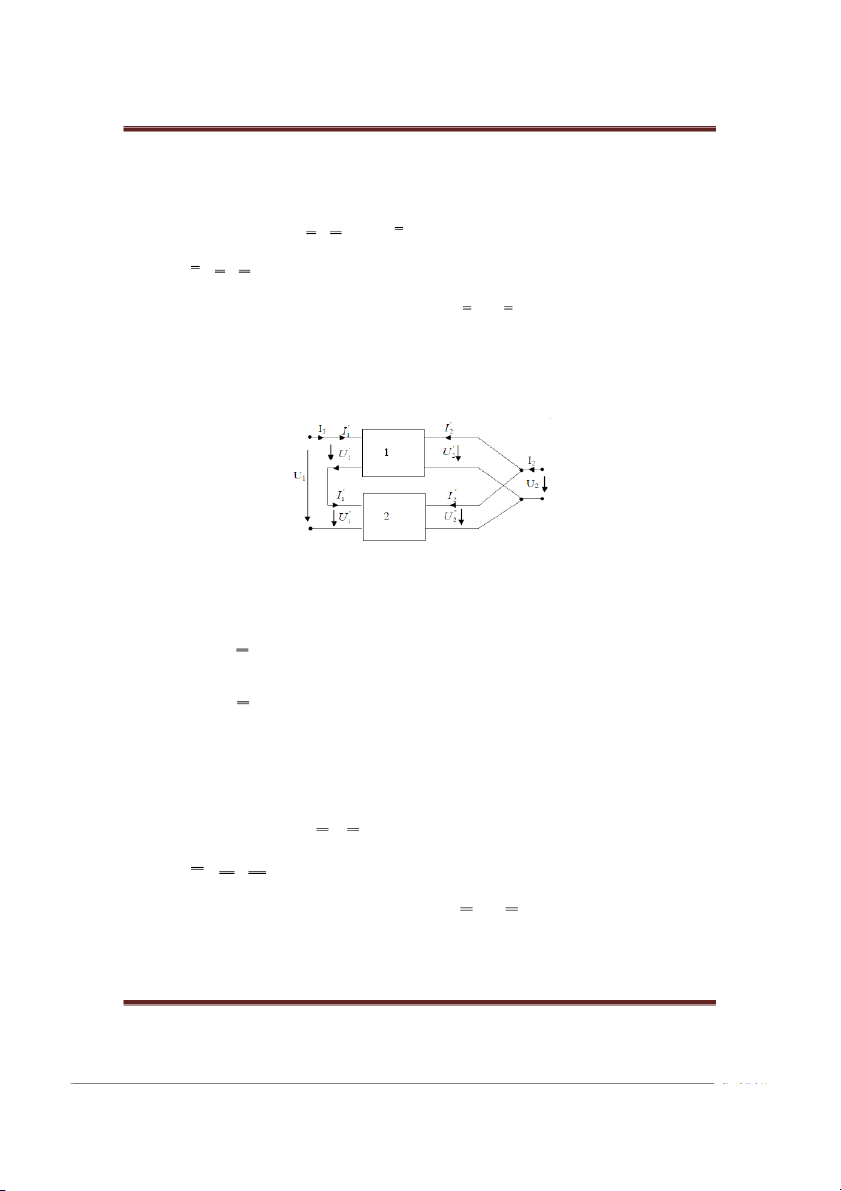
1.4.3. Ghép nối nối tiếp – song song (N - S)
Hình 1.4.3 vẽ hai bốn cực mắc N-S với nhau. Hình 1.4.3 Ta có: ' '
I I I ; ' '
U U U ; ' '
U U U ; ' '
I I I . 1 1 1 2 2 2 1 1 1 2 2 2
Hệ phương trình đặc tính hốn hợp của hai bốn cực được viết dưới dạng ma trận: ' ' U     1 I1    H   ' 1 ' I  2  U   2  ' ' U     1 I1    H   ' 2 ' I   U    2 2   ' I   ' I  I
Đặt  1    1    1  và cộng hai hệ phương trình theo từng vế ta có:  ' U 2   '
U2  U2  ' ' U   U  U  I  I 1 1 1 1 1     
  H H   H ' '  1 2      I
 I I U    2 U   2 2 2 2 
Như vậy: H H  1 H 2 n
Tổng quát: Với n bốn cực mắc N – S với nhau ta có H  H . k k 1 
Phát biểu: Ma trận hốn hợp của hệ thống nhiều bốn cực nối N – S với nhau bằng tổng các
ma trận hốn hợp của các bốn cực thành phần.
Biên soạn: Bùi Thị Kim Thoa - Nguyễn Thị Huyền Lin h Page 20