
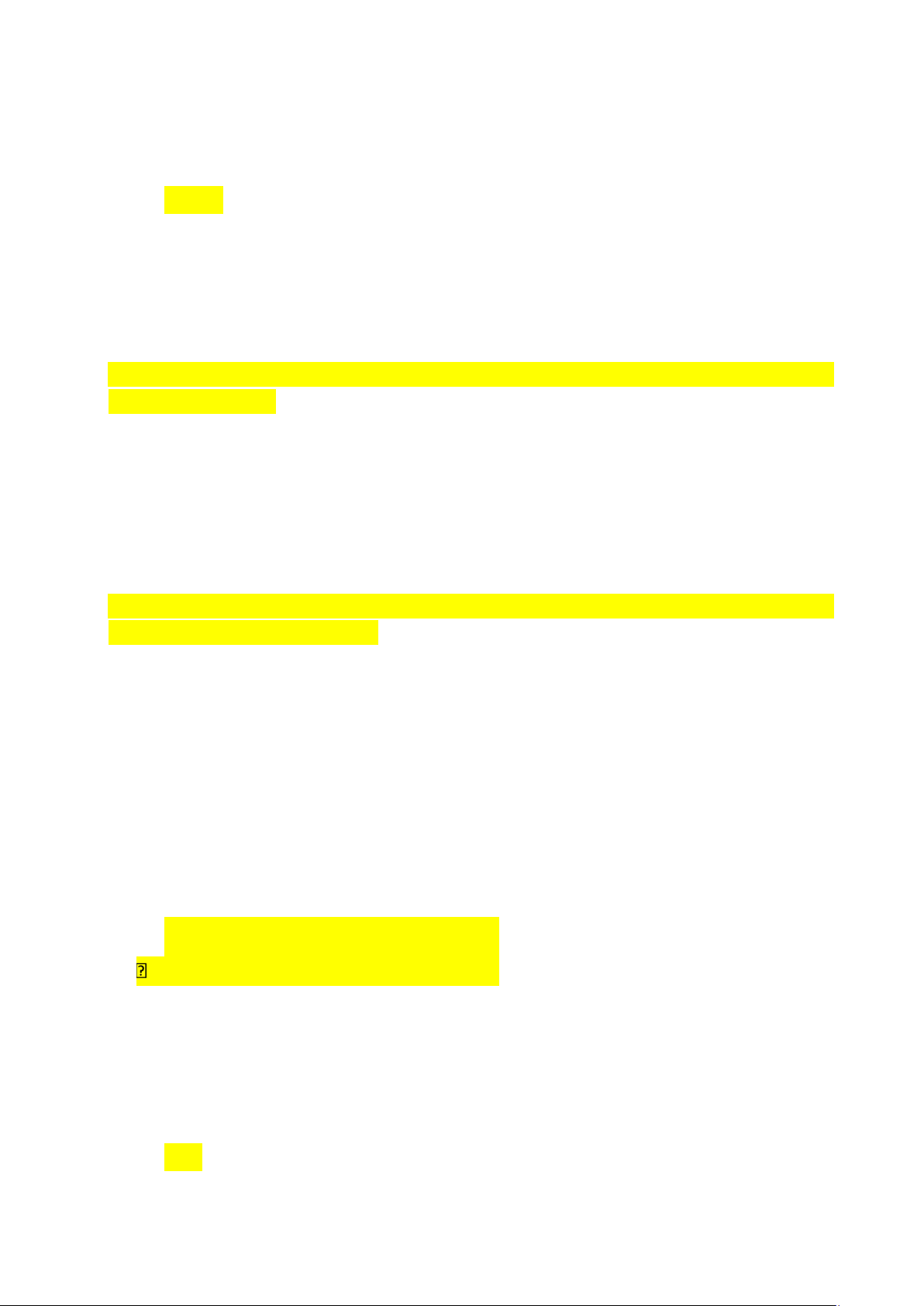
















Preview text:
lOMoAR cPSD| 58794847
ĐỀ CƯƠNG PPDH TOÁN Ở TIỂU HỌC 1
1. Trình bày đặc điểm của cấu trúc nội dung môn Toán ở tiểu học. Cho ví dụ minh họa.
- Môn Toán ở Tiểu học là một môn thống nhất, không chia thành phân môn.
+ Hạt nhân của nội dung môn Toán là số học.
+ Sự sắp xếp các nội dung trong mối quan hệ gắn bó, hỗ trợ nhau với hạt nhân
số học không làm mất đi hoặc mờ nhạt đi đặc trưng của từng nội dung.
- Cấu trúc nội dung môn Toán ở Tiểu học quán triệt các tư tưởng của toán
học hiệnđại và phù hợp với từng giai đoạn phát triển của HS Tiểu học.
- Các kiến thức, kĩ năng của môn Toán ở Tiểu học được hình thành chủ yếu
bằngthực hành, luyện tập và thường xuyên được ôn tập củng cố, phát triển, vận
dụng trong học tập và đời sống.
Ví dụ: Ở vòng số đến 100, sau khi giới thiệu về chục (1 chục = 10 đơn vị) thì
giới thiệu đơn vị đo độ dài đê-xi-mét (dm) và giới thiệu đê-xi-mét trong mối quan hệ
với đơn vị đo độ dài xăng-ti-mét (1dm = 10cm).
2. Trình bày những điểm mới trong cấu trúc nội dung chương trình môn
Toán cấp tiểu học (Chương trình 2018). Cho ví dụ minh họa.
- Cấu trúc chương trình môn Toán 2006 gồm 4 mạch kiến thức: + Số học + Yếu tố hình học
+ Đại lượng và đo đại lượng
+ Giải bài toán có lời văn
- Cấu trúc chương trình môn Toán 2008 gồm 3 mạch kiến thức:
+ Số, Đại số và Một số yếu tố giải tích
+ Hình học và Đo lường + Thống kê và Xác suất
- Điểm mới trong chương trình 2018 môn Toán cấp Tiểu học:
+ Số lượng từ 4 mạch kiến thức giảm xuống còn 3 mạch kiến thức ⇒ Tinh giảm
trong cấu trúc chương trình.
+ Tích hợp (nội môn) của mạch kiến thức; của nội dung và mạch kiến thức.
+ Chú ý tiếp cận nối với Chương trình GD mầm non.
+ Chú ý rèn luyện kĩ năng tính nhẩm.
+ Giảm độ khó của kĩ thuật tính viết. lOMoAR cPSD| 58794847
+ Tăng cường thực hành, luyện tập, ứng dụng trong thực tiễn.
+ Chú ý kĩ năng tiến trình trong thiết kế chương trình.
+ Bổ sung mạch kiến thức mới: Thống kê và Xác suất.
Ví dụ: Ở lớp 4 chỉ yêu cầu: “Thực hiện được phép chia cho số có không quá
hai chữ số”; “Thực hiện được phép cộng, phép trừ phân số trong những trường hợp
đơn giản”. Ở lớp 5, trong chủ đề Tỉ số phần trăm chỉ yêu cầu: “Thực hành giải quyết
vấn đề gắn với việc giải các bài toán liên quan đến: Tính tỉ số phần trăm của hai số;
Tìm giá trị phần trăm của một số cho trước”.
3. Phân tích một ví dụ để minh họa đặc điểm:
a, Số và phép tính là nội dung “hạt nhân”, trọng tâm của chương trình môn
Toán cấp tiểu học.
- Từ lớp 1, học sinh được giới thiệu với các số đếm và phép tính cộng, trừ đơngiản.
Từ đó, học sinh sẽ có khả năng tính toán cơ bản để giải quyết các vấn đề thực tế đơn
giản. Khi sang lớp 2, học sinh được học khái niệm về nhân và chia, giúp họ có khả
năng tính toán phức tạp hơn. Lớp 3 là giai đoạn quan trọng để giới thiệu cho học
sinh về phần trăm, phân số và tỷ lệ, giúp học sinh hiểu rõ hơn về các mối quan hệ giữa các con số.
b, Nội dung chương trình môn Toán cấp tiểu học phù hợp với các giai đoạn phát
triển nhận thức của học sinh.
- Trong lớp 1, trẻ em được giới thiệu với các số đếm, các phép tính đơn giản
vàhình học cơ bản. Trong khi đó, lớp 2 tập trung vào việc xây dựng khả năng tính
toán của học sinh thông qua các bài toán cộng, trừ và nhân đơn giản, cùng với các
khái niệm về đo lường và thời gian.
- Lớp 3 là giai đoạn quan trọng trong việc phát triển khả năng tính toán của
họcsinh, đồng thời đưa ra các khái niệm mới như phân số và tỷ lệ. Các bài tập cũng
trở nên phức tạp hơn, yêu cầu học sinh phải suy nghĩ sáng tạo để giải quyết các vấn đề toán học.
4. Trình bày biểu hiện của các năng lực thành tố sau:
Năng lực tư duy và lập luận toán học
- Thực hiện được các thao tác tư duy (ở mức độ đơn giản), đặc biệt biết quan
sát,tìm kiếm sự tương đồng và khác biệt trong những tình huống quen thuộc và mô
tả được kết quả của việc quan sát.
- Nêu được chứng cứ, lí lẽ và biết lập luận hợp lí trước khi kết luận.
- Nêu và trả lời được câu hỏi khi lập luận, giải quyết vấn đề. Bước đầu chỉ ra
đượcchứng cứ và lập luận có cơ sở, có lí lẽ trước khi kết luận. VD:
(Sách HS Toán 2, tập 2, trang 17, sách Chân trời sáng tạo).
Mỗi chậu cây có 5 bông hoa. Hỏi 4 chậu cây như thế có bao nhiêu bông
hoa? Bước 1: Tìm hiểu bài toán + GV: Bài toán cho biết gì? lOMoAR cPSD| 58794847
+ HS: Cho biết mỗi chậu cây có 5 bông hoa. + GV: Bài toán hỏi gì?
+ HS: Hỏi 4 chậu cây như thế có bao nhiêu bông hoa?
Bước 2: Tìm cách giải bài toán
+ GV: Muốn tìm số bông hoa của 4 chậu làm thế nào?
+ HS 1: Lấy số bông hoa của từng chậu cộng lại với nhau.
+ HS 2: Lấy số bông hoa của một chậu nhân với số chậu.
Bước 3: Giải bài toán
+ HS tổng hợp các việc cần thực hiện: viết lời giải, phép tính, đáp số.
Bước 4: Kiểm tra lại
Năng lực mô hình hóa toán học
- Lựa chọn được các phép toán, công thức số học, sơ đồ, bảng biểu, hình vẽ đểtrình
bày, diễn đạt (nói hoặc viết) được các nội dung, ý tưởng của tình huống xuất hiện
trong bài toán thực tiễn đơn giản.
- Giải quyết được những bài toán xuất hiện từ sự lựa chọn trên.
- Nêu được câu trả lời cho tình huống xuất hiện trong bài toán thực tiễn. VD:B
ài 40 “Chia cho số có hai chữ số” lớp 4
- GV nêu vấn đề, làm tròn số được sử dụng như thế nào khi thực hiện phép
chia?Câu trả lời sẽ có trong bài học “Chia cho số có hai chữ số”.
- Tạo tình huống kết nối vào bài và làm nảy sinh vấn đề cần giải quyết bằng kiếnthức toán học.
- GV tổ chức HS đọc tình huống và trả lời câu hỏi: Muốn biết 76 kg cỏ đàn bò
ăntrong mấy ngày thực hiện phép tính gì?
- HS trả lời thực hiện phép tính chia, 76 : 19.
- Tổ chức HS hoạt động nhóm, tìm kết quả của phép tính 76 : 19. HS thảo luận
dựatrên kiến thức đã biết về phép cộng, phép trừ, phép nhân để tìm ra kết quả của
phép tính. HS có thể thực hiện theo cách sau:
+ Cách 1: Lấy 19 + 19 = 38; 38 + 19 = 57; 57 + 19 = 76. Từ đó cho kết quả thương tìm được là 4.
+ Cách 2. Lấy 76 – 19 = 57; 57 – 19 = 38; 38 – 19 = 19; 19 – 19 = 0. Từ đó cho
kết quả thương tìm được là 4.
+ Cách 3. Lấy 19 × 1 = 19; 19 × 2 = 38; 19 × 3 = 57; 19 × 4 = 76. Từ đó cho kết
quả thương tìm được là 4. lOMoAR cPSD| 58794847
- HS sử dụng các kiến thức toán học để tìm được thương của phép chia đó. Từ
đóHS có được câu trả lời cho thực tiễn là 76kg cỏ đàn bò ăn trong 4 ngày.
- GV nêu vấn đề, cách tìm ra thương của các nhóm đề đúng, tuy nhiên, nếu
vớinhững số bị chia lớn, thì việc làm như vậy rất mất thời gian. Do đó, cần có một
thuật toán để thực hiện tìm thương của phép chia trên. Cách thực hiện như sau:
+ Làm tròn số 76 và 19 đến tròn chục thì được số 80 và 20.
+ Lấy 80 : 20 = 4. Dự đoán thương là 4.
+ Kiểm tra HS nêu được cách thực hiện phép chia cho số có hai chữ số: Làm tròn
– dự đoán – kiểm tra. HS biết được kĩ thuật thực hiện phép chia cho số có hai chữ số
và tìm được câu trả lời cho tình huống thực tiễn.
Năng lực giải quyết vấn đề toán học
- Nhận biết được vấn đề cần giải quyết và nêu được thành câu hỏi.
- Nêu được cách thức giải quyết vấn đề.
- Thực hiện và trình bày được cách thức giải quyết vấn đề ở mức độ đơn giản.-
Kiểm tra được giải pháp đã thực hiện.
VD: Bài “Phép cộng có 2 chữ số với số có một chữ số” tập 2 lớp 1 KNTT
- Tình huống có vấn đề: Mình có 41 cái kẹo. Nam cho Minh them 5 cái kẹo
nữa.Hỏi Minh có tất cả bao nhiêu cái kẹo? - GQVĐ:
+ HS sử dụng bộ đồ dùng học tập: Lấy 4 thanh chục và 1 que tính, lấy them 5 que tính.
+ GV hỏi: Trên bàn có tất cả bao nhiêu que tính? => HS trả lời: Có tất cả 46 que tính.
+ GV hỏi: Làm thế nào m biết có 46 que tính? => HS trả lời: 4 thanh chục có 40
que tính, 40 chính là 4 chục. Có 1 que tính rời, thêm 5 que tính rời nữa nên có tất cả
6 que tính, 6 que tính chính là 6 đơn vị. 4 chục và 6 đơn vị chính là 46 que tính. Vậy 41+5=46.
+ GV hướng dẫn HS đặt tính: 41 + 5 _______________ 46
Năng lực giao tiếp toán học lOMoAR cPSD| 58794847
- Nghe hiểu, đọc hiểu và ghi chép (tóm tắt) được các thông tin toán học trọng
tâmtrong nội dung văn bản hay do người khác thông báo (ở mức độ đơn giản), từ đó
nhận biết được vấn đề cần giải quyết.
- Trình bày, diễn đạt (nói hoặc viết) được các nội dung, ý tưởng, giải pháp toán
họctrong sự tương tác với người khác (chưa yêu cầu phải diễn đạt đầy đủ, chính xác).
Nêu và trả lời được câu hỏi khi lập luận, giải quyết vấn đề.
- Sử dụng được ngôn ngữ toán học kết hợp với ngôn ngữ thông thường, động
táchình thể để biểu đạt các nội dung toán học ở những tình huống đơn giản.
- Thể hiện được sự tự tin khi trả lời câu hỏi, khi trình bày, thảo luận các nội
dungtoán học ở những tình huống đơn giản.
VD: Dạy học hình thành quy tắc tính diện tích hình chữ nhật, GV tổ chức HS
đọc hiểu nội dung toán học. Tính diện tích hình chữ nhật ABCD
- HS quan sát hình vẽ, huy động các kiến thức đã biết: biểu tượng về hình chữ
nhật,biết được đặc điểm của hình chữ nhật, đơn vị đo độ dài xăng-ti-mét.
- GV hỗ trợ học HS bằng cách đưa ra những câu hỏi gợi ý:
+ Hình chữ nhật ABCD có mấy cạnh dài? mấy cạnh ngắn?
(Hình chữ nhật ABCD có cạnh dài AB, DC, cạnh ngắn AD, BC)
+ Nêu tên của các cạnh dài, cạnh ngắn. (Hình chữ nhật ABCD có cạnh dài AB, DC, cạnh ngắn AD, BC)
+ Hình chữ nhật ABCD được tạo bởi mấy ô vuông có cạnh 1 cm? (Hình chữ nhật
ABCD được tạo bởi 10 ô vuông có cạnh 1 cm)
+ Chiều dài hình chữ nhật bằng bao nhiêu? (Chiều dài của hình chữ nhật ABCD là 5 cm)
+ Chiều rộng của hình chữ nhật bằng bao nhiêu? (Chiều rộng của hình chữ nhật ABCD là 2 cm)
- HS thảo luận nhóm đề xuất cách giải quyết vấn đề.
+ Phương án 1. Đếm lần lượt số ô vuông 1 cm2 rồi tìm diện tích hình chữ nhật.
=> Diện tích mỗi ô vuông là 1 cm2 . Diện tích hình chữ nhật ABCD là: 1 × 10 = 10 (cm2 )
+ Phương án 2. Đếm số ô vuông 1 cm2 theo hàng, đếm số hàng rồi tìm số ô vuông
của hình chữ nhật, tính diện tích hình chữ nhật.
=> Hình chữ nhật ABCD có số ô vuông là: 5 × 2 = 10 (ô vuông)
Diện tích mỗi ô vuông là 1 cm2 . Diện tích hình chữ nhật ABCD là: 1 × 10 = 10 (cm2 )
+ Phương án 3. Đếm số ô vuông 1 cm2 theo cột, đếm số cột rồi tìm số ô vuông của
hình chữ nhật, tính diện tích hình chữ nhật.
=> Hình chữ nhật ABCD có số ô vuông là: 2 × 5 = 10 (ô vuông) Diện tích mỗi ô
vuông là 1 cm2 . Diện tích hình chữ nhật ABCD là: 1 × 10 = 10 (cm2 ) lOMoAR cPSD| 58794847
- GV hướng dẫn để HS phát hiện ra diện tích hình chữ nhật ABCD có mối liên hệ
vớichiều dài và chiều rộng của hình chữ nhật (10 cm2 = 5 cm × 2 cm).
=> Từ đó, HS dự đoán cách tính diện tích hình chữ nhật (lấy chiều dài nhân với chiều rộng)
- HS nêu cách tính diện tích hình chữ nhật: lấy chiều dài nhân với chiều rộng
(cùngđơn vị đo). Giáo viên chính xác lại quy tắc tính diện tích hình chữ nhật.
Năng lực sử dụng công cụ, phương tiện học toán
- Nhận biết được tên gọi, tác dụng, quy cách sử dụng, cách thức bảo quản các
côngcụ, phương tiện học toán đơn giản (que tính, thẻ số, thước, compa, êke, các mô
hình hình phẳng và hình khối quen thuộc…).
- Sử dụng được các công cụ, phương tiện học toán để thực hiện những nhiệm
vụhọc tập toán đơn giản.
- Làm quen với máy tính cầm tay, phương tiện công nghệ thông tin hỗ trợ học tập.
- Nhận biết được (bước đầu) một số ưu điểm, hạn chế của những công cụ,
phươngtiện hỗ trợ để có cách sử dụng hợp lí. VD:
“Làm quen với phép tính chia – Dấu chia”
- GV hướng dẫn HS thực hiện thao tác “chia đều”:
+ Lấy ra 6 hình tròn, chia đều cho 2 bạn (đưa cho bạn thứ nhất 1 hình tròn, đưa
cho bạn thứ 2 1 hình tròn, cứ như vậy cho đến khi hết số hình tròn) + Mỗi bạn đc bao nhiêu chấm tròn?
- GV thực hiện thao tác trực quan:
+ 6 hình tròn chia đều cho 2 bạn
+ mỗi bạn đc 3 hình tròn + ta đc phép chia 6 : 2 = 3
5. Trình bày yêu cầu cần đạt trong dạy học các nội dung sau trong Chương
trình môn Toán 2018: LỚP 1
Phép tính với số tự nhiên (lớp 1)
- Phép cộng, phép trừ lOMoAR cPSD| 58794847
+ Nhận biết được ý nghĩa của phép cộng, phép trừ.
+ Thực hiện được phép cộng, phép trừ (không nhớ) các số trong phạm vi 100.
+ Làm quen với việc thực hiện tính toán trong trường hợp có hai dấu phép tính
cộng, trừ (theo thứ tự từ trái sang phải). - Tính nhẩm
+ Thực hiện được việc cộng, trừ nhẩm trong phạm vi 10.
+ Thực hiện được việc cộng, trừ nhẩm các số tròn chục.
- Thực hành giải quyết vấn đề liên quan đến các phép tính cộng, trừ
+ Nhận biết được ý nghĩa thực tiễn của phép tính (cộng, trừ) thông qua tranh
ảnh, hình vẽ hoặc tình huống thực tiễn.
+ Nhận biết và viết được phép tính (cộng, trừ) phù hợp với câu trả lời của bài
toán có lời văn và tính được kết quả đúng.
VD: Bài 10. Phép cộng trong phạm vi 10 (Toán 1-Tập 1, sách Kết nối tri thức với cuộc sống).
- Nhận biết được ý nghĩa của phép cộng là “gộp lại”, là “thêm vào”. Biết
tìm kếtquả phép cộng trong phạm vi 10 bằng cách đếm tất cả hoặc đếm thêm.
- Bước đầu nhận biết được đặc điểm của phép cộng với 0: số nào cộng với
0 cũngbằng chính số đó, 0 cộng với số nào cũng bằng chính số đó. Vận dụng đặc
điểm này trong thực hành tính.
- Thực hiện được phép cộng trong phạm vi 10.
- Biết tính và tính được giá trị của biểu thức số có hai dấu phép tính cộng
(theo thứtự từ trái qua phải).
- Bước đầu nhận biết tính chất giao hoán của phép cộng qua các công thức
số(dạng 3 + 4 = 4 + 3). Vận dụng tính chất này trong thực hành tính.
- Phát triển năng lực:
+ Năng lực giải quyết vấn đề toán học: Viết được phép cộng phù hợp với tranh
ảnh, hình vẽ hoặc tình huống thực tế có vẫn đề cần giải quyết bằng phép cộng.
+ Năng lực tư duy và lập luận toán học: Nêu được bài toán phù hợp với tranh
vẽ, mô hình đã có; trả lời được câu hỏi của bài toán. LỚP 2
Phép tính với số tự nhiên (lớp 2)
- Phép cộng, phép trừ
+ Nhận biết được các thành phần của phép cộng, phép trừ.
+ Thực hiện được phép cộng, phép trừ (không nhớ, có nhớ không quá một lượt)
các số trong phạm vi 1000. lOMoAR cPSD| 58794847
+ Thực hiện được việc tính toán trong trường hợp có hai dấu phép tính cộng,
trừ (theo thứ tự từ trái sang phải).
- Phép nhân, phép chia
+ Nhận biết được ý nghĩa của phép nhân, phép chia.
+ Nhận biết được các thành phần của phép nhân, phép chia.
+ Vận dụng được bảng nhân 2 và bảng nhân 5 trong thực hành tính.
+ Vận dụng được bảng chia 2 và bảng chia 5 trong thực hành tính. - Tính nhẩm
+ Thực hiện được việc cộng, trừ nhẩm trong phạm vi 20.
+ Thực hiện được việc cộng, trừ nhẩm các số tròn chục, tròn trăm trong phạm vi 1000.
- Thực hành giải quyết vấn đề liên quan đến các phép tính đã học
+ Nhận biết ý nghĩa thực tiễn của phép tính (cộng, trừ, nhân, chia) thông qua
tranh ảnh, hình vẽ hoặc tình huống thực tiễn.
+ Giải quyết được một số vấn đề gắn với việc giải các bài toán có một bước tính
(trong phạm vi các số và phép tính đã học) liên quan đến ý nghĩa thực
tế của phép tính (ví dụ: bài toán về thêm, bớt một số đơn vị; bài toán về nhiều hơn,
ít hơn một số đơn vị).
VD: Bài 7. Phép cộng (qua 10) trong phạm vi 20 (Toán 2-Tập 1)
- Nhận biết được phép cộng (qua 10) trong phạm vi 20, tính được phép cộng
(qua10) bằng cách nhẩm hoặc tách số.
- Hình thành được bảng cộng (qua 10).
- Vận dụng vào giải các bài tập, bài toán thực tế liên quan đến phép cộng (qua 10).
- Phát triển năng lực:
+ Thông qua hoạt động khám phá, lựa chọn để tự tìm ra các cách tính thích hợp,
HS phát triển năng lực giải quyết vấn đề toán học.
+ Thông qua hệ thống giải các bài tập vận dụng, bổ sung, nâng cao (cộng bằng
cách đếm tiếp, tách số…) HS phát triển năng lực tư duy và lập luận toán học, năng
lực giao tiếp toán học.
Yếu tố Hình học (lớp 2)
- Quan sát, nhận biết, mô tả hình dạng của một số hình phẳng và hình khối đơn giản
+ Nhận biết được điểm, đoạn thẳng, đường cong, đường thẳng, đường gấp khúc,
ba điểm thẳng hàng thông qua hình ảnh trực quan.
+ Nhận dạng được hình tứ giác thông qua việc sử dụng bộ đồ dùng học tập cá nhân hoặc vật thật.
+ Nhận dạng được khối trụ, khối cầu thông qua việc sử dụng bộ đồ dùng học
tập cá nhân hoặc vật thật.
- Thực hành đo, vẽ, lắp ghép, tạo hình gắn với một số hình phẳng
và hình khối đã học
+ Thực hiện được việc vẽ đoạn thẳng có độ dài cho trước. lOMoAR cPSD| 58794847
+ Nhận biết và thực hiện được việc gấp, cắt, ghép, xếp và tạo hình gắn với việc
sử dụng bộ đồ dùng học tập cá nhân hoặc vật thật.
+ Giải quyết được một số vấn đề thực tiễn đơn giản liên quan đến hình phẳng và hình khối đã học.
VD: Bài 25. Điểm, đoạn thẳng, đường thẳng, đường cong, ba điểm thẳng hàng (Toán 2-Tập 1)
- Nhận biết được điểm, đoạn thẳng, đường thẳng, đường cong, ba điểm
thẳng hàngthông qua hình ảnh trực quan.
- Đọc được tên điểm, đoạn thẳng, đường thẳng, đường cong cho trước.
- Giải quyết được một số vẫn đề thực tiễn đơn giản liên quan đến hình
phẳng.- Phát triển năng lực:
+ Qua hoạt động quan sát, nhận biết hình ảnh điểm, đoạn thẳng, liên hệ nhận
dạng điểm, đoạn thẳng trong thực tế, HS bước đầu hình thành năng lực mô hình hóa toán học.
+ Cùng với hoạt động trên, qua hoạt động diễn đạt, trả lời câu hỏi (bằng cách
nói hoặc viết) mà GV đặt ra sẽ giúp HS phát triển năng lực giao tiếp toán học.
Biểu tượng về đại lượng và đơn vị đo đại lượng (lớp 2)
- Nhận biết được về “nặng hơn”, “nhẹ hơn”.
- Nhận biết được đơn vị đo khối lượng: kg (ki-lô-gam); đọc và viết được số
đo khối lượng trong phạm vi 1000kg.
- Nhận biết được đơn vị đo dung tích: l (lít); đọc và viết được số đo dung
tích trong phạm vi 1000 lít.
- Nhận biết được các đơn vị đo độ dài dm (đề-xi-mét), m (mét), km (ki-lô-
mét) và quan hệ giữa các đơn vị đo độ dài đã học.
- Nhận biết được một ngày có 24 giờ; một giờ có 60 phút.
- Nhận biết được số ngày trong tháng, ngày trong tháng (ví dụ: tháng Ba có
31 ngày; sinh nhật Bác Hồ là ngày 19 tháng 5).
- Nhận biết được tiền Việt Nam thông qua hình ảnh một số tờ tiền. VD: Bài
15. Ki-lô-gam (Toán 2-Tập 1)
- Bước đầu cảm nhận, nhận biết về nặng hơn, nhẹ hơn, về biểu tượng đơn
vị đokhối lượng ki-lô-gam (kg).
- Đọc, viết tắt kí hiệu ki-lô-gam.
- Thực hiện phép tính cộng, trừ với số đo ki-lô-gam.
- Vận dụng giải các bài toán thực tế liên quan đến nặng hơn, nhẹ hơn, liên
quanđến đơn vị đo khối lượng ki-lô-gam.
- Phát triển năng lực:
+ Thông qua hoạt động khám phá (nhận biết, so sánh) về nặng hơn, nhẹ hơn,
hình thành biểu tượng về đại lượng và đơn vị đo đại lượng (kg), HS phát triển năng
lực tư duy và lập luận toán học. lOMoAR cPSD| 58794847
+ Thông qua trao đổi, diễn đạt (nói, viết) về giải quyết “tình huống” ở các bài
tập, bài toán thực tế, về tinh toán, so sánh số đo đại lượng, HS phát triển năng lực
giải quyết vẫn đè và năng lực giao tiếp toán học. LỚP 3
Số tự nhiên (lớp 3)
- Số và cấu tạo thập phân của một số
+ Đọc, viết được các số trong phạm vi 10 000; trong phạm vi 100 000.
+ Nhận biết được số tròn nghìn, tròn mười nghìn.
+ Nhận biết được cấu tạo thập phân của một số.
+ Nhận biết được chữ số La Mã và viết được các số tự nhiên trong phạm vi 20
bằng cách sử dụng chữ số La Mã. - So sánh các số
+ Nhận biết được cách so sánh hai số trong phạm vi 100 000.
+ Xác định được số lớn nhất hoặc bé nhất trong một nhóm có không quá 4 số (trong phạm vi 100 000).
+ Thực hiện được việc sắp xếp các số theo thứ tự (từ bé đến lớn hoặc ngược lại)
trong một nhóm có không quá 4 số (trong phạm vi 100 000). - Làm tròn số
+ Làm quen với việc làm tròn số đến tròn chục, tròn trăm, tròn nghìn, tròn mười
nghìn (ví dụ: làm tròn số 1234 đến hàng chục thì được số 1230).
VD: Bài 59. Các số có năm chữ số. Số 100 000 (Toán 3-Tập 2).
- Biết cách phân tích cấu tạo số, cách đọc và cách viết các số có năm chữ số và số 100 000.
- Làm quen với cách làm tròn số và làm tròn được một số đến hàng nghìn và hàng chục nghìn.
- Phát triển năng lực:
+ Năng lực mô hình hóa thông qua sử dụng biểu tượng khối lập phương 10 × 10
× 10, bảng 10 × 10, cột 10 × 1 và các khối lập phương đơn vị để biểu diễn số.
+ Năng lực giao tiếp toán học thông qua rèn luyện kĩ năng đọc và viết số.
+ Năng lực tu duy khi áp dụng yêu cầu làm tròn số vào các bài toán thực tế.
Yếu tố Hình học (lớp 3)
- Quan sát, nhận biết, mô tả hình dạng và đặc điểm của một số hình phẳng
và hìnhkhối đơn giản.
+ Nhận biết được điểm ở giữa, trung điểm của đoạn thẳng.
+ Nhận biết được góc, góc vuông, góc không vuông.
+ Nhận biết được tam giác, tứ giác.
+ Nhận biết được một số yếu tố cơ bản như đỉnh, cạnh, góc của hình chữ nhật,
hình vuông; tâm, bán kính, đường kính của hình tròn.
+ Nhận biết được một số yếu tố cơ bản như đỉnh, cạnh, mặt của khối lập phương, khối hộp chữ nhật. lOMoAR cPSD| 58794847
- Thực hành đo, vẽ, lắp ghép, tạo hình gắn với một số hình phẳng và hình khối đãhọc.
+ Thực hiện được việc vẽ góc vuông, đường tròn, vẽ trang trí.
+ Sử dụng được êke để kiểm tra góc vuông, sử dụng được compa để vẽ đường tròn.
+ Thực hiện được việc vẽ hình vuông, hình chữ nhật bằng lưới ô vuông.
+ Giải quyết được một số vấn đề liên quan đến gấp, cắt, ghép, xếp, vẽ và tạo hình trang trí.
VD: Bài 18. Góc, góc vuông, góc không vuông (Toán 3-Tập
1) - Làm quen với khái niệm góc.
- Nhận dạng được góc; phân biệt được góc vuông và góc không vuông.
- Sử dụng được ê ke để kiểm tra góc vuông.
- Phát triển năng lực:
+ Sử dụng công cụ toán học.
+ Thông qua nhận dạng hình, HS phát triển năng lực quan sát, mô hình hóa và
phát triển trí tưởng tượng hình học phẳng.
6. Trình bày cách hình thành và củng cố tính chất sau:
a, “Khi thực hiện phép cộng hai số, ta có thể đổi chỗ các số hạng mà tổng không
thay đổi” (Tính chất giao hoán của phép cộng).
- Con đường hình thành: Con đường suy đoán - Quy trình:
+ Giáo viên yêu cầu học sinh tính và so sánh kết quả của phép tính. 20 + 30 và 30 + 20
+ Giáo viên cho học sinh nêu nhận xét: Tổng của 2 phép cộng bằng nhau.
+ Cho học sinh thể hiện bằng lời: Khi đổi chỗ các số hạng trong một tổng thì tổng không thay đổi.
+ Giáo viên giới thiệu: Tính chất giao hoán của phép cộng.
+ Giáo viên phát biểu tính chất: “Khi thực hiện phép cộng hai số, ta có thể đổi
chỗ các số hạng mà tổng không thay đổi” - Hoạt động củng cố:
Bài 1: Nêu kết quả tính: a, 46 + 23 = 69 b, 15 + 82 = … c, 100 + 350 =… 23 + 46 = … 82 + 15 = … 300 + 100 =…
Bài 2: Viết số hoặc chữ thích hợp vào chỗ chấm: a, 24 + 56 = 56 +… b, m + n = n + … 150 + … = 270 + 150 a + 0 = … + a lOMoAR cPSD| 58794847
b, “Khi cộng một tổng hai số với số thứ ba, ta có thể cộng số thứ nhất với tổng của
số thứ hai và số thứ ba” (Tính chất kết hợp của phép cộng).
- Con đường hình thành: Con đường suy đoán. - Quy trình:
+ Giáo viên yêu cầu học sinh tính và so sánh kết quả của phép tính. (5 + 4) + 6 với 5 + (4 + 6)
+ Giáo viên cho học sinh nêu nhận xét: Tổng của 2 phép cộng bằng nhau.
+ Giáo viên giới thiệu: Tính chất kết hợp của phép cộng.
+ Giáo viên phát biểu tính chất: “Khi cộng một tổng hai số với số thứ ba, ta có
thể cộng số thứ nhất với tổng của số thứ hai và số thứ ba” - Hoạt động củng cố:
Bài 1: Tính bằng cách thuận tiện nhất: a, 145 + 357 + 463 b, 921 + 275 + 279 468 + 199 + 502 467 + 145 + 325
Bài 2: Viết số hoặc chữ thích hợp vào chỗ chấm: a, a + 0 = … + a b, 5 + a = … + 5 c, (a + 28) + 2 = a + (28 + …)
c, “Khi thực hiện phép nhân hai số, ta có thể đổi chỗ các thừa số mà tích không
thay đổi” (Tính chất giao hoán của phép nhân).
- Con đường hình thành: Con đường suy đoán. - Quy trình:
+ Giáo viên yêu cầu học sinh tính và so sánh kết quả của phép tính. 4 × 8 = 8 × 4
+ Giáo viên cho học sinh nêu nhận xét: Tích của 2 phép nhân bằng nhau.
+ Cho học sinh thể hiện bằng lời: đổi vị trí các thừa số trong phép nhân nhưng
kết quả không thay đổi.
+ Giáo viên giới thiệu: Tính chất giao hoán của phép nhân.
+ Giáo viên phát biểu tính chất: “Khi thực hiện phép nhân hai số, ta có thể đổi
chỗ các thừa số mà tích không thay đổi”. - Hoạt động củng cố:
Bài 1. Viết số thích hợp vào ô trống: a, 45 x 2 = 2 x …
b. 15 x 8 = 8 x … 207 x 7 = … x 207 2136 x 9 = … x 2136 lOMoAR cPSD| 58794847 Bài 2: Tính: a, 4 x 56 b, 27 x 8 c. 51 x 6
d, “Khi nhân một tích hai số với số thứ ba, ta có thể nhân số thứ nhất với tích của
số thứ hai và số thứ ba” (Tính chất kết hợp của phép nhân).
- Con đường hình thành: con đường quy nạp. - Cách tiến hành:
+ GV yêu cầu HS tính và so sánh kết quả của các phép tính:
(17 x 6) x 3 và 17 x (6 x 3); (207 x 7) x 4 và 207 x (7 x 4).
+ Từ việc tính giá trị của biểu thức, GV yêu cầu HS nhận xét về kết quả, đặc điểm,
vị trí các thừa số trong tích.
+ GV hướng dẫn HS phát biểu tính chất kết hợp của phép nhân bằng lời và biểu thức chứa chữ.
+ Hoạt động củng cố: đề xuất 2 – 3 bài tập phù
hợp BT1: Viết số thích hợp vào chỗ trống a) 16 x 8 x 2 = 16 x ... x 8
b) ... ( tự nghĩ các phép tính tương
tự) BT2: Tính bằng cách thuận tiện nhất a) 3 x 5 x 2 b) 2 x 17 x 5 c) 12 x 3 x 5 d) 2 x 3 x 4 x 5
e, “Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng
một đơn vị đo) rồi chia cho 2”.
- Gợi động cơ phát biểu vấn đề: Biết tính các diện tích hình nào
rồi? HS trả lờihình chữ nhật.
- Con đường dạy học quy tắc: Con đường suy diễn- Quy trình:
+ GV hướng dẫn HS cắt ghép 2 hình tam giác:
• Yêu cầu HS lấy 1 trong 2 hình tam giác bằng nhau. Vẽ một đường cao lên hình tam giác đó.
• Dùng kéo cắt theo đường cao, được hai mảnh tam giác ghi là 1 và 2.
• Ghép hai mảnh 1 và 2 vào hình tam giác còn lại để thành 1 hình chữ nhật.
+ GV hướng dẫn HS so sánh, đối chiếu các yếu tố hình học trong hình vừa ghép.
• Hình chữ nhật có chiều dài bằng độ dài cạnh đáy của hình tam giác.
• Hình chữ nhật có chiều rộng bằng đường cao của hình tam giác.
• Diện tích hình chữ nhật gấp 2 lần diện tích hình tam giác. lOMoAR cPSD| 58794847
+ GV hình thành công thức tính diện tích hình tam giác.
• Tính diện tích hình chữ nhật?
• Tính diện tích hình tam giác?
+ GV hướng dẫn HS phát biểu quy tắc và ghi công thức.
• HS phát biểu quy tắc: “Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với
chiều cao (cùng một đơn vị đo) rồi chia cho 2”. • GV ghi công thức: a×h
S = 2 hoặc S = a × h : 2
(S là diện tích, a là độ dài đáy, h là chiều cao). - Hoạt động củng cố:
Bài 1: Tính diện tích hình tam giác có:
a, Độ dài đáy là 8cm và chiều cao là 6cm.
b, Độ dài đáy là 2,3dm và chiều cao là 1,2dm.
Bài 2: Tính diện tích hình tam giác có: a,
Độ dài đáy là 5m và chiều cao là 24dm.
b, Độ dài đáy là 42,5m và chiều cao là 5,2m.
f, “Diện tích hình thang bằng tổng độ dài hai đáy nhân với chiều cao (cùng một
đơn vị đo) rồi chia cho 2”.
- Gợi động cơ phát biểu vấn đề: Biết tính các diện tích hình nào rồi? HS trả lờihình tam giác.
- Con đường dạy học quy tắc: Con đường suy diễn - Quy trình:
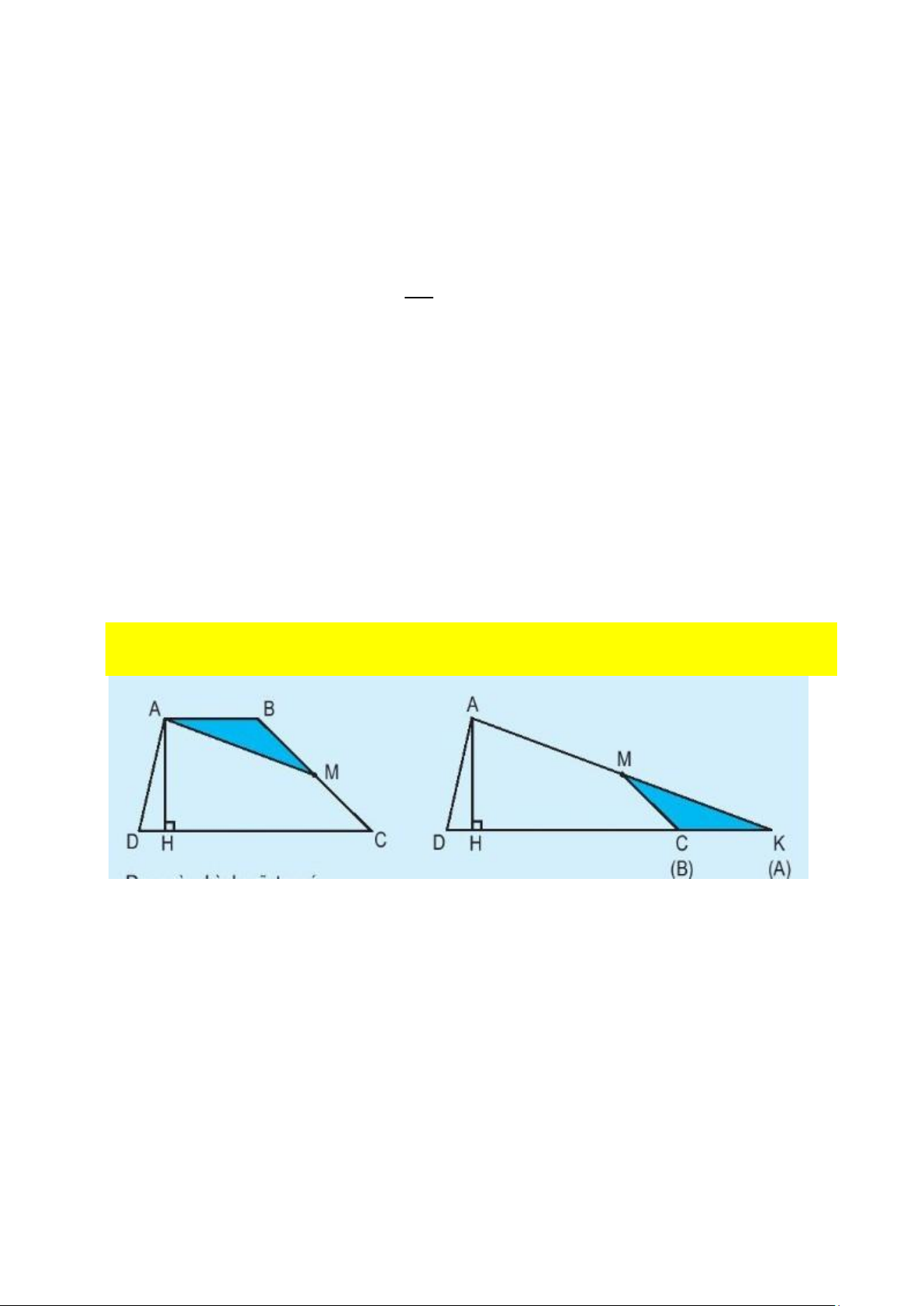
+ GV hướng dẫn HS cắt ghép hình thang.
• GV yêu cầu HS lấy 1 hình thang đã chuẩn bị để lên bàn.
• Yêu cầu HS vẽ đường cao AH cho hình thang ABCD.
• GV dẫn dắt để HS xác định trung điểm M của cạnh BC, rồi cắt rời hình tam giác
ABM; sau đó ghép lại như hướng dẫn trong SGK để được hình tam giác ADK. +
GV tổ chức hoạt động so sánh hình.
• So sánh diện tích hình thang ABCD và diện tích hình tam giác ADK vừa tạo thành? ( lOMoAR cPSD| 58794847
SABCD = SADK) S = ADK DK×2 AH)
• Tính diện tích hình tam giác ADK? (
• So sánh chiều cao của hình thang ABCD và chiều cao của tam giác ADK? (Bằng nhau)
• So sánh độ dài đáy DK của tam giác AGK và tổng độ dài 2 đáy AB và CD của hình thang ABCD?¿DK = AB + CD)
• GV kết luận: SABCD = (AB+CD2 )×AH
+ GV hướng dẫn HS phát biểu quy tắc và ghi công thức.
• HS phát biểu quy tắc: “Diện tích hình thang bằng tổng độ dài hai đáy nhân với chiều
cao (cùng một đơn vị đo) rồi chia cho 2”. • GV ghi công thức:
S = (a+b)×h 2
(S là diện tích; a, b là độ dài các cạnh đáy; h là chiều cao). - Hoạt động củng cố:
Bài 1: Tính diện tích hình thang, biết:
a, Độ dài hai đáy lần lượt là 12cm và 8cm; chiều cao là 5cm.
b, Độ dài hai đáy lần lượt là 9,4m và 6,6m; chiều cao là 10,5m.
Bài 2: Một thửa ruộng hình thang có độ dài hai đáy lần lượt là 110m và 90,2m. Chiều
cao bằng trung bình cộng của hai đáy. Tính diện tích thửa ruộng đó.
g. Trình bày cách hình thành khái niệm toán học: trung điểm của đoạn thẳng
- Gợi động cơ phát biểu vấn đề:
- Con đường dạy học khái niệm: Con đường quy nạp: Xuất phát từ những
đối tượng riêng lẻ, GV dẫn dắt HS tìm ra dấu hiệu đặc trưng của khái niệm, từ đó
đi đến định nghĩa hoặc hiểu biết về khái niệm. - Quy trình:
+ GV đưa ra ví dụ: So sánh độ dài AB và BC.
+ Gv dẫn dắt học sinh tìm ra đặc điểm chung: B ở giữa; AB = BC.
+ HS phát biểu khái niệm: Trung điểm là điểm nằm chính giữa đoạn thẳng, chia
đoạn thẳng ra làm hai đoạn dài bằng nhau. - Hoạt động củng cố:
Bài 2 (trang 50, sách kết nối tri thức): Trong hình bên:
a, Tìm 3 điểm thẳng hàng.
b, Điểm H ở giữa hai điểm nào? c, Điểm M là trung
điểm của đoạn thẳng nào? lOMoAR cPSD| 58794847
Bài 3 (trang 50): Nêu tên trung điểm của
cácđoạn thẳng AC, BD trong hình vẽ:
7. Trình bày cách sử dụng các phép suy luận toán học để hướng dẫn học sinh:
a, So sánh các số trong phạm vi 100 000.
Tìm quy tắc bằng phép quy nạp không hoàn toàn và suy diễn.
VD: So sánh hai số 35378 và 35498.
- GV hướng dẫn HS so sánh từ trái qua phải:
+ Hàng chục nghìn đều là 3.
+ Tiếp tục hàng nghìn cũng bằng nhau và bằng 5.
+ Tiếp theo hàng trăm thì 3 < 4. Vậy 35378 < 35498.
b, Qui tắc: “Muốn tính giá trị số hạng có thứ tự n của một dãy số cách đều, ta lấy
số thứ tự đã cho trừ đi 1, được bao nhiêu nhân với khoảng cách, rồi cộng với số
hạng đầu của dãy số.”
Tìm quy tắc bằng phép suy luận quy nạp.
VD: Cho dãy số cách đều 2, 5, 8, 11… Tìm số hạng 30 của dãy số.
- GV hướng dẫn HS phân tích các số hạng của dãy: 5 = (2 – 1) × 3 + 2 8 = (3 – 1) × 3 + 2
11 = (4 – 1) × 3 + 2 …
- GV hướng dẫn HS nhận xét các số hạng của dãy dựa trên số thứ tự, khoảng
cáchvà số hạng đầu tiên.
- GV hướng dẫn HS phát biểu quy tắc “Muốn tính giá trị số hạng có thứ tự
n của một dãy số cách đều, ta lấy số thứ tự đã cho trừ đi 1, được bao nhiêu nhân
với khoảng cách, rồi cộng với số hạng đầu của dãy số.”
- Tìm số hạng bất kì của dãy, dựa trên số thứ tự của số hạng bằng phép suy diễn.
Số hạng số 30 của dãy:
(30 – 1) × 3 + 2 = 89 lOMoAR cPSD| 58794847
10. Hướng dẫn học sinh tiểu học giải bài toán sau:
10.1. Mẹ mua 3 kg cam hết 81000 đồng. Bố mua 2 kg cam cùng loại hết 56000
đồng. Hỏi bố và mẹ ai mua cam giá rẻ hơn, mỗi ki-lô-gam rẻ hơn bao nhiêu tiền.
- Bước 1: Tìm hiểu đề bài
GV yêu cầu HS đọc đề và trả lời câu hỏi: + Bài toán cho biết gì?
+ Bài toán hỏi gì? (Mẹ mua … Bố mua…ai rẻ hơn).
- Bước 2: Xây dựng kế hoạch giải
GV đưa ra hệ thống câu hỏi hướng dẫn HS giải bài toán.
+ Tính giá tiền mẹ mua 1 kg cam? (81000 : 3 = 27000 (đồng))
+ Tính giá tiền bố mua 1 kg cam? (56000 : 2 = 28000 (đồng))
+ So sánh số tiền mẹ mua 1 kg cam và bố mua 1 kg cam? (Vì 27000 ¿ 28000 nên mẹ mua rẻ hơn bố)
+ Tính giá tiền mẹ mua 1 kg cam mẹ mua rẻ hơn bố mua? (28000 – 27000 = 1000 (đồng))
- Bước 3: Trình bày lời giải Bài
giải Số tiền mẹ mua 1 kg cam là: 81000 : 3 = 27000
(đồng) Số tiền bố mua 1 kg cam là: 56000 : 2 = 28000 (đồng)
Mẹ mua 1kg cam rẻ hơn bố mua 1 kg cam số
tiền là: 28000 – 27000 = 1000 (đồng) Đáp số: 1000 đồng.
- Bước 4: Kiểm tra, nghiên cứu sâu lời giải+ GV yêu cầu HS kiểm tra lại kết quả phép tính.
+ Già soát lại cách diễn đạt, lời giải bài toán.
10.2. Một xe tải đang ở trên bàn cân (không có người trên xe). Đồng hồ cân cho
biết khối lượng xe và hàng hóa là 3 tấn 100 kg. Biết khối lượng xe là 1500 kg và
khối lượng hàng mà xe được phép chở nặng nhất là 850 kg. Khối lượng hàng
hóa xe đã chở quá mức qui định là bao nhiêu ki-lô-gam?
- Bước 1: Tìm hiểu đề bài lOMoAR cPSD| 58794847
GV yêu cầu HS đọc đề và trả lời câu hỏi: + Bài toán cho biết gì? + Bài toán hỏi gì?
- Bước 2: Xây dựng kế hoạch giải
GV đưa ra hệ thống câu hỏi hướng dẫn HS giải bài toán:
+ Đổi đơn vị: 3 tấn 100 = 3100 kg.
+ Tính khối lượng hành hóa xe đã chở? (3100 – 1500 = 1600 kg)
+ Tính khối lượng hàng hóa xe đã chở vượt quá mức quy định? (1600 – 850 = 750 kg)
- Bước 3: Trình bày lời giải Bài giải Đổi
đơn vị: 3 tấn 100 kg = 3100 kg
Khối lượng hàng hóa xe đã chở là: 3100 – 1500 = 1600 (kg)
Khối lượng hàng hóa xe đã chở quá mức quy định là: 1600 – 850 = 750 (kg) Đáp số: 750 kg
- Bước 4: Kiểm tra, nghiên cứu sâu lời giải
+ GV yêu cầu HS kiểm tra lại kết quả phép tính.
+ Già soát lại cách diễn đạt, lời giải bài toán. + Tìm cách giải khác:
Đổi đơn vị: 3 tấn 100 kg = 3100 kg
Khối lượng xe và hàng hóa được phép chở là: 1500 + 850 = 2350 (kg)
Khối lượng hàng hóa xe chở vượt quy định là: 3100 – 2350 = 750 (kg) Đáp số: 750 kg
10.3. Mẹ đem ra chợ bán 60 quả trứng vịt và trứng gà, trong đó trứng gà nhiều
hơn trứng vịt 10 quả. Hỏi mẹ đem ra chợ bán bao nhiêu quả trứng gà, bao nhiêu quả trứng vịt? Tóm tắt: ? quả trứng lOMoAR cPSD| 58794847 Trứng gà: 60 quả trứng Trứng 10 quả vịt: ? quả trứng
- Bước 1: Tìm hiểu đề bài
GV yêu cầu HS đọc đề và trả lời câu hỏi: + Bài toán cho biết gì? + Bài toán hỏi gì?
- Bước 2: Xây dựng kế hoạch giải
GV đưa ra hệ thống câu hỏi hướng dẫn HS giải bài toán:
+ Tính hai lần số quả trứng vịt? (60 – 10 = 50 (quả))
+ Tính số quả trứng vịt mẹ đem ra chợ bán? (50 : 2 = 25 (quả))
+ Tính số quả trứng gà mẹ đem ra chợ bán? (60 – 25 = 35 (quả))
- Bước 3: Trình bày lời giải Bài giải
Hai lần số quả trứng vịt là: 60 – 10 = 50 (quả)
Mẹ đem ra chợ bán số quả trứng vịt là: 50 : 2 = 25 (quả)
Mẹ đem ra chợ bán số quả trứng gà là: 60 – 25 = 35 (quả)
Đáp số: Trứng gà: 35 quả Trứng vịt: 25 quả
- Bước 4: Kiểm tra, nghiên cứu sâu lời giải
+ GV yêu cầu HS kiểm tra lại kết quả phép tính.
+ Già soát lại cách diễn đạt, lời giải bài toán.
10.4. Một cửa hàng hoa quả nhập về 15 thùng xoài nặng như nhau, cân nặng
tất cả 375 kg. Cửa hàng đã bán hết 7 thùng. Hỏi cửa hàng còn lại bao nhiêu ki- lôgam xoài?
- Bước 1: Tìm hiểu đề bài
GV yêu cầu HS đọc đề và trả lời câu hỏi: + Bài toán cho biết gì? + Bài toán hỏi gì? lOMoAR cPSD| 58794847
- Bước 2: Xây dựng kế hoạch giải
GV đưa ra hệ thống câu hỏi hướng dẫn HS giải bài toán:
+ Tính cân nặng của một thùng xoài: 375 :15 = 25 (kg)
+ Tính cân nặng của 7 thùng xoài đã bán: 25 × 7 = 175 (kg)
+ Tính số kg xoài còn lại của cửa hàng: 375 – 175 = 200
(kg) - Bước 3: Trình bày lời giải: Bài giải
Cân nặng của một thùng xoài là: 375 :15 = 25 (kg)
Cân nặng của 7 thùng đã bán là: 25 × 7 = 175 (kg)
Số kg xoài cửa hàng còn lại là: 375 – 175 = 200 (kg) Đáp án: 200 kg
- Bước 4: Kiểm tra, nghiên cứu sâu lời giải
+ GV yêu cầu HS kiểm tra lại kết quả phép tính.
+ Già soát lại cách diễn đạt, lời giải bài toán.
10.5. Người ta dùng loại gạch men hình vuông có cạnh 60 cm để lát nền một
phòng học hình chữ nhật có chiều dài 9 m, chiều rộng 4 m. Hỏi cần bao nhiêu
viên gạch men loại đó để vừa đủ lát kín nền phòng học? (Diện tích phần mạch
vữa không đáng kể).
- Bước 1: Tìm hiểu đề bài
GV yêu cầu HS đọc đề và trả lời câu hỏi: + Bài toán cho biết gì? + Bài toán hỏi gì?
- Bước 2: Xây dựng kế hoạch giải
GV đưa ra hệ thống câu hỏi hướng dẫn HS giải bài toán:
+ Đổi đơn vị: 60 cm = 0,6 m
+ Tính diện tích một viên gạch men:



