Đề cương Môn Phương pháp dạy học toán | Đại học Sư phạm Hà Nội 2

lOMoAR cPSD| 58794847
ĐỀ CƯƠNG - PHƯƠNG PHÁP DẠY HỌC TOÁN Ở TH GDTH2. K21 A. LÝ THUYẾT
Câu 1.Thiết kế 1 bài toán bằng Phương Pháp khử. Các bước tiến hành
Đề toán : Mua 2 bút xanh và 7 bút đỏ hết 25000 Đồng. Mua 2 bút xanh và 3 bút
đỏ như thế hết 13000 Đồng. Tìm giá mua 1 bút xanh , 1 bút đỏ.
Giải: Số bút đỏ lần 1 mua nhiều hơn số bút đỏ lần 2 là: 7-3=4 ( bút)
Số tiền lần 1 mua nhiều hơn số tiền lần 2 là
25000 – 13000 = 12000 ( đồng) Giá tiền 1 bút đỏ là 12000 : 4 = 3000 ( đồng) Giá tiền 1 bút xanh là
( 25000 – ( 3000 x 7 )) : 2 = 2000 ( đồng)
Đáp số: 1 bút đỏ: 3000 đồng
1 bút xanh: 2000 đồng Các
bước tiến hành:
B1: Điều chỉnh số liệu để đưa về 2 đại lượng bằng nhau.
B2: Tính giá trị 1 phần( 1 đơn vị còn lại)
B3: Tìm giá trị tương ứng.
Câu 2: Thiết kế 1 đề toán giải bằng phương pháp giả thiết tạm. Trình bày các
bước hướng dẫn học sinh tiểu học giải bài toán đó.
Thiết kế bài toán ( lớp 4,5): May 45 cái áo gồm hai loại, loại 1 may hết 1,3m vải, loại 2 may
hết 1,8m vải. Tổng số vải may cả hai áo là 68,5m. Hỏi mỗi loại áo có bao nhiêu cái?
- Bước 1: tìm hiểu kĩ đề bài:
+ Bài toán cho biết: May 45 cái áo gồm hai loại, loại 1 may hết 1,3m vải, loại 2 may hết 1,8m
vải. Tổng số vải may cả hai áo là 68,5m.
+ Bài toán hỏi: Hỏi mỗi loại áo có bao nhiêu cái?
- Bước 2: Lập kế hoạch giải lOMoAR cPSD| 58794847 + Dạng toán
+ Phương pháp: giả thiết tạm -Bước
3: Thực hiện kế hoạch giải Giải:
Giả sử nếu may 45 cái áo loại 1,8m, ta tốn hết:
Số m vải là: 45 x 1,8 = 81(m) Vậy ta thừa số m vải là: 81- 68,5 = 19,5 (m)
Vậy ta làm được số áo loại 1,3 m là: 19,5 : 1,3 = 15( chiếc áo)
Số áo loại 1,8 m may được là: 45-15=30( chiếc áo)
Vậy may được 15 chiếc áo loại 1,3m và 30 chiếc áo loại 1,8 m
-Bước 4: Kiểm tra lời giải và khai thác bài toán
Câu 3: An, Bình, Chi sưu tầm được 108 con tem. Nếu An cho Bình 10 con tem,
Bình cho Chi 8 con tem, Chi lại cho An 6 con tem thì lúc đó số tem của 3 bạn
bằng nhau. Hỏi lúc đầu mỗi bạn có bao nhiêu con tem? Cách giải:
Bước 1: Tìm hiểu kĩ đề bài
- Bài toán cho biết: An, Bình, Chi sưu tầm được 108 con tem. Nếu An cho Bình 10 con
tem, Bình cho Chi 8 con tem, Chi lại cho An 6 con tem thì lúc đó số tem của 3 bạn bằng nhau.
- Bài toán hỏi: Hỏi lúc đầu mỗi bạn có bao nhiêu con tem?
Bước 2: Lập kế hoạch giải
- Phương pháp giải: Tính ngược từ cuối
+ Đầu tiên ta đi tìm số tem của mỗi bạn sau khi cho nhau: 108:3=36.
+ Số tem lúc đầu của An được tính như sau, ta lấy số tem của mỗi bạn sau khi cho cộng
với số tem An cho Bình và trừ đi số tem An được Chi cho: 36+10-6= 40
+ Số tem lúc đầu của Bình được tính như sau, ta lấy số tem của mỗi bạn sau khi cho
trừ đi số tem mà Bình được An cho sau đó cộng với số tem mà Bình cho An: 36-10+8= 34
+ Số tem lúc đầu của Chi được tính như sau, ta lấy số tem của mỗi bạn sau khi cho trừ
đi số tem Chi được Bình cho sau đó cộng với số tem Chi cho An: 36-8+6= 34 Bước 3:
Thực hiện kế hoạch giải
Sau khi cho nhau, mỗi bạn có số tem là: lOMoAR cPSD| 58794847 108 : 3 = 36 (con tem)
Số tem lúc đầu của An là: 36 + 10 – 6 = 40 (con tem)
Số tem lúc đầu của Bình là: 36 – 10 + 8 = 34 (con tem)
Số tem lúc đầu của Chi là: 36 – 8 + 6 = 34 (con tem)
Đáp số: An: 40 con tem, Bình: 34 con tem, Chi: 34 con tem
Bước 4: Kiểm tra lời giải: 40 + 34 + 34 = 108
Câu 4: Thiết kế 1 đề toán giải bằng phương pháp đồ thị. Trình bày các
bước hướng dẫn học sinh Tiểu học giải được bài đó. Toán lớp 4
Đề bài: Tổ 1 lớp 4A có 6 bạn. Hỏi cô giáo có bao nhiêu cách chọn 2 bạn của tổ 1 làm trực nhật ?
Bước 1: Tìm hiểu đề bài
- Bài toán hỏi gì và cho biết điều gì? – Hỏi: Có bao nhiêu cách chọn 2 bạn của tổ 1 làm trực nhật
Cho: Tổ 1 lớp 4A có 6 bạn
Bước 2: Lập kế hoạch giải
- Sử dụng phương pháp đồ thị Dữ kiện đã cho: biểu diễn nét liền
Dữ kiện cần tìm: biểu diễn nét đứt
- Gọi 6 bạn lần lượt là: A, B, C, D, E, F
- Bạn A là đối tượng ghép cặp đầu tiên nên ghép được với tất cả các bạn khác (biểu diễn nét liền)
- Tìm được số cách để ghép cặp với bạn A thì tương tự sẽ tìm được số cách ghép cặp
với các bạn còn lại (biểu diễn nét đứt) - Sau đó cộng tất cả các cách lại với nhau.
- F là bạn cuối cùng nên không có cách nào.
Bước 3: Thực hiện lời giải A A B B C C lOMoAR cPSD| 58794847 D D E E F F
Có 5 cách cử nhóm 2 bạn, trong đó có bạn A
Có 4 cách cử nhóm 2 bạn, trong đó có bạn B (không có bạn A)
Có 3 cách cử nhóm 2 bạn, trong đó có bạn C (không có bạn A, B)
Có 2 cách cử nhóm 2 bạn, trong đó có bạn D (không có bạn A, B, C)
Có 1 cách cử nhóm 2 bạn, trong đó có bạn E (không có bạn A,B,C và D)
Vậy số cách chọn 2 bạn của tổ 1 làm trực nhật là:
5 + 4 + 3 + 2 + 1 = 15 (cách) Đáp số: 15 cách
Bước 4: Kiểm tra lời giải
Câu 5. Thiết kế 1 đề toán bằng phương pháp đại số. Các bước tiến hành.
Đề toán: Tìm số có 4 chữ số biết rằngtổng các chữ số bằng 24. Nếu viết số đó theo
thứ tự ngược lại thì nó không thay đổi. Nhóm 2 chữ số bên trái > nhóm 2 chữ số bên phải 36 đơn vị.
Giải: Gọi số cần tìm là abba a + b + b + a = 24 ab - ba = 36
Theo bài ra ta có: a + b + b + a = 24 a x 2 + b x 2 = 24 (a + b) x 2 = 24 a + b = 12 Ta có: 12 = 8 + 4 = 4 + 8 12 = 7 + 5 = 5 + 7 12 = 6 + 6
Xét: a = 8, b = 4 có: a + b + b + a = 24 8 + 4 + 4 + 8 = 24
ab - ba = 36 84 - 48 = 36(đúng) a = 7, b = 5 a +
b + b + a = 24 7 + 5 + 5 + 7 = 24 ab - lOMoAR cPSD| 58794847
ba = 36 75 - 57 = 18(loại) a = 6, b = 6 a + b
+ b + a = 24 6 + 6 + 6 + 6 = 24 ab - ba = 36 66 - 66 = 0(loại)
Vậy số có 4 chữ số là: 8448 Các bước tiến hành:
B1: Biểu diễn phép tính. Số cần tìm được kí hiệu bởi 1 biểu tượng bất kỳ.
B2: Tìm đại lượng đó dựa vào dữ liệu đã biết B3: Kết luận.
Câu 6: Thiết kế 1 đề toán giải bằng phương pháp thay thế. Trình bày các bước
hướng dẫn học sinh tiểu học giải bài toán đó.
Đề bài: Hai đội công nhân sửa đường trong 1 ngày đã sửa được tất cả 1km đường. Đội
Một sửa được nhiều hơn đội Hai 146m. Hỏi mỗi đội đã sửa được bao nhiêu mét đường? (Lớp
4, M1; mục đích tìm hai số khi biết tổng và hiệu của chúng) Hướng dẫn HS giải:
- Bước 1: Tìm hiểu kĩ đề bài:
+ Bài toán cho biết: Hai đội công nhân sửa đường một ngày sửa tất cả 1km; Đội một sửa
nhiều hơn đội hai 146m.
+ Bài toán hỏi: Mỗi đội sửa được bao nhiêu mét đường?
- Bước 2: Lập kế hoạch giải
+ Dạng toán: Tìm hai số khi biết tổng và hiệu + Phương pháp thay thế
- Bước 3: Thực hiện kế hoạch giải: Ta có sơ đồ sau: ?m Đội Một: 1km Đội Hai: ?m 146 m Bài giải Đổi 1km = 1000m
Đội Một sửa được số mét đường là: (1000 + 146) : 2 = 573 (m)
Đội Hai sửa được số mét đường là: 1000 – 573 = 427 (m)
Đáp số: Đội Một: 573m; Đội Hai: 427m
- Bước 4: Kiểm tra lời giải và khai thác bài toán. lOMoAR cPSD| 58794847
Câu 7: Trên bàn là 3 cuốn sách giáo khoa: Văn, Toán và Địa lí được bọc 3 màu
khác nhau: Xanh, đỏ, vàng. Cho biết cuốn bọc bìa màu đỏ đặt giữa 2 cuốn Văn
và Địa lí, cuốn Địa lí và cuốn màu xanh mua cùng 1 ngày. Bạn hãy xác định mỗi
cuốn sách đã bọc bìa màu gì? Cách giải:
Bước 1: Tìm hiểu kĩ đề bài
- Bài toán cho biết: Trên bàn là 3 cuốn sách giáo khoa: Văn, Toán và Địa lí được
bọc 3 màu khác nhau: Xanh, đỏ, vàng. Cho biết cuốn bọc bìa màu đỏ đặt giữa
2 cuốn Văn và Địa lí, cuốn Địa lí và cuốn màu xanh mua cùng 1 ngày. -
Bài toán hỏi: Bạn hãy xác định mỗi cuốn sách đã bọc bìa màu gì?
Bước 2: Lập kế hoạch giải
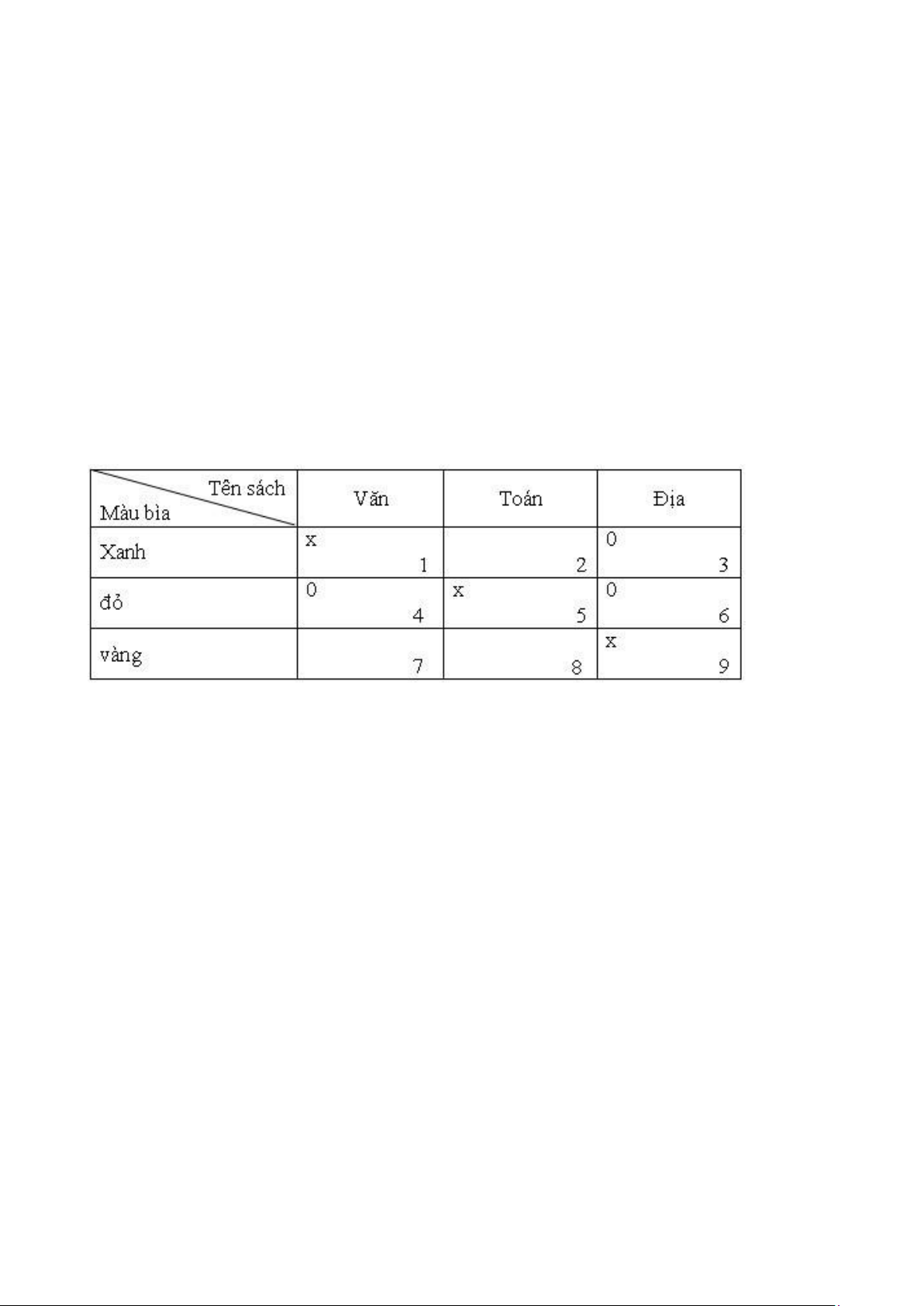
- Phương pháp giải: Lập bảng Ta có bảng sau:
Bước 3: Thực hiện kế hoạch giải:
Theo đề bài “Cuốn bìa màu đỏ đặt giữa 2 cuốn Văn và Địa lí”. Vậy cuốn sách Văn và
Địa lí đều không đặt màu đỏ cho nên cuốn toán phải bọc màu đỏ. Ta ghi số 0 vào ô 4
và 6, đánh dấu x vào ô 5.
Mặt khác, “Cuốn Địa lí và cuốn màu xanh mua cùng ngày”. Điều đó có nghĩa rằng
cuốn Địa lí không bọc màu xanh. Ta ghi số 0 vào ô 3. –
Nhìn vào cột thứ 4 ta thấy cuốn địa lí không bọc màu xanh, cũng không bọc màu đỏ.
Vậy cuốn Địa lí bọc màu vàng. Ta đánh dấu x vào ô 9. –
Nhìn vào cột 2 và ô 9 ta thấy cuốn Văn không bọc màu đỏ, cũng không bọc
màu vàng. Vậy cuốn Văn bọc màu xanh. Ta đánh dấu x vào ô 1.
Kết luận: Cuốn Văn bọc màu xanh, cuốn Toán bọc màu đỏ, cuốn Địa lí bọc màu vàng. lOMoAR cPSD| 58794847
Bước 4: Kiểm tra lời giải:
Dùng phương pháp suy luận đơn giản :
Vì cuốn màu đỏ đặt giữa cuốn Văn và Địa lý, mà cuốn Địa lý mua cùng ngày với
cuốn màu xanh nên cuốn Địa Lý bọc màu VÀNG
Ta đã biết cuốn Địa Lý màu vàng, mà cuốn đỏ nằm giữa cuốn Văn và Địa lý nên cuốn Văn bọc màu xanh
Vậy cuốn Toán bọc màu đỏ
Câu 8: Thiết kế 01 đề toán giải bằng phương pháp lựa chọn tình huống. Trình
bày các bước hướng dẫn học sinh Tiểu học giải bài toán đó. Toán lớp 5
Đề bài: Trong kì thi học sinh giỏi tỉnh có 4 bạn Phương, Dương, Hiếu, Hằng tham
gia. Được hỏi quê mỗi người ở đâu ta nhận được các câu trả lời sau:
Phương: Dương ở Thăng Long còn tôi ở Quang Trung.
Dương : Tôi cũng ở Quang Trung còn Hiếu ở Thăng Long.
Hiếu : Không, tôi ở Phúc Thành còn Hằng ở Hiệp Hoà.
Hằng : Trong các câu trả lời trên đều có 1 phần đúng 1 phần sai.
Em hãy xác định quê của mỗi bạn.
Bước 1: Tìm hiểu đề bài: - Cho gì.... - Hỏi gì.....
Bước 2: Lập kế hoạch giải:
- Sử dụng phương pháp lựa chọn tình huống: chia 2 tình huống: + Dương ở TL là đúng + Dương ở TL là sai
Bước 3: Thực hiện lời giải:
- Vì trong mỗi câu trả lời đều có 1 phần đúng và 1 phần sai nên có các trường hợp:
+ Giả sử Dương ở Thăng Long là đúng thì Phương ở Quang Trung là sai.
Suy ra Dương ở Quang Trung là sai.
Vậy Hiếu ở Thăng Long là đúng. lOMoAR cPSD| 58794847
Điều này vô lý vì Dương và Hiếu cùng ở Thăng Long.
+ Giả sử Dương ở Thăng Long là sai.
Suy ra Phương ở Quang Trung và do đó Dương ở Quang Trung là sai.
Suy ra Hiếu ở Thăng Long.
Vậy Hiếu ở Phúc Thành là sai.
Suy ra Hằng ở Hiệp Hòa.
Còn lại Dương ở Phúc Thành.
Bước 4: Kiểm tra lời giải
Câu 9. Thiết kế 1 đề toán bằng phương pháp biểu đồ ven. Các bước tiến hành.
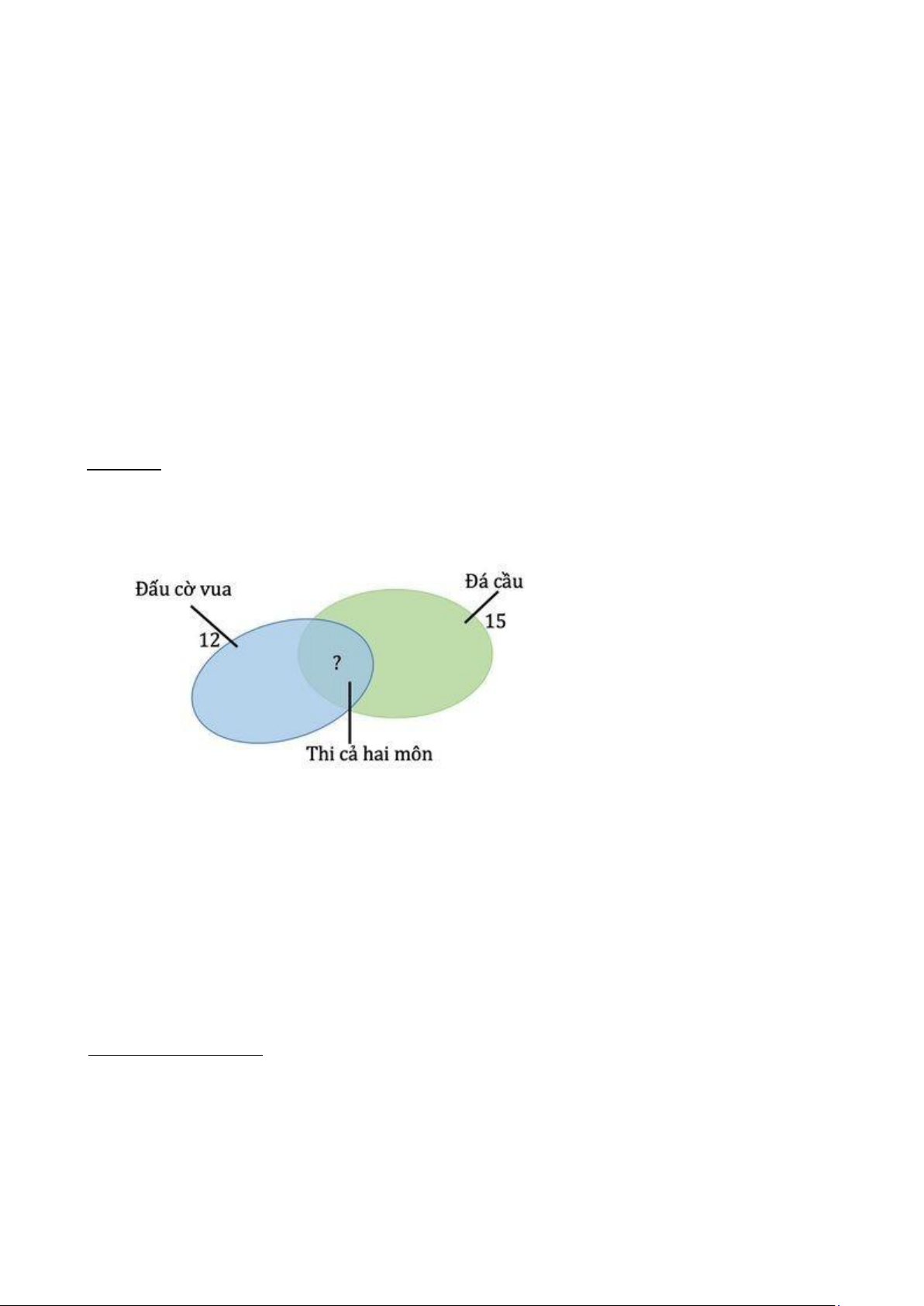
Đề toán: Đội tuyển thi đá cầu và đấu cờ vua của Trường Tiểu học Võ Thị Sáu có 22
em, trong đó có 15 em thi đá cầu và 12 em thi đấu cờ vua. Hỏi có bao nhiêu em trong
đội tuyển thi đấu cả hai môn ? Giải:
Dựa vào hình vẽ, ta thấy Số em chỉ thi đá cầu là: 22 – 12 = 10 (em)
Số em trong đội tuyển thi đấu cả hai môn là: 15 – 10 = 5 (em) Đáp số: 5 em Các bước tiến hành:
B1: Chuyển Bài tập về các tập hợp
B2: Sử dụng sơ đồ ven để minh họa các tập hợp
B3: Thiết lập công thức. Tìm ra các đại lượng lOMoAR cPSD| 58794847
Câu 10: Thiết kế 1 đề toán giải bằng phương pháp suy luận đơn giản. Trình bày
các bước hướng dẫn học sinh tiểu học giải bài toán đó.
Bài toán: Trong một cuộc thi vẽ, ba bạn Hoa – Mai – Lan đạt ba giải cao nhất. Mai không
đạt giải Nhất, Lan không đạt giải Nhì, Hoa không đạt giải Nhất và giải Ba. Hỏi ai đạt giải
Nhất – Nhì – Ba? (Lớp 4, 5 – M2 - Phát triển tư duy và bồi dưỡng phương pháp suy luận) Hướng dẫn giải:
- B1: Tìm hiểu kĩ đề bài:
+ Bài toán cho biết: ba bạn Hoa – Mai – Lan đạt ba giải cao nhất. Mai không đạt giải Nhất,
Lan không đạt giải Nhì, Hoa không đạt giải Nhất và giải Ba.
+ Bài toán hỏi: ai đạt giải Nhất – Nhì – Ba?
- B2: Lập kế hoạch giải
+ Dạng toán: suy luận logic.
+ Phương pháp: suy luận đơn giản.
- B3: Thực hiện kế hoạch giải:
Hoa không đạt giải Nhất và giải Ba suy ra Hoa đạt giải Nhì.
Mai không đạt giải Nhất, mà Hoa đã đạt giải Nhì, suy ra Mai đạt giải Ba.
Lan không đạt giải Nhì, mà Hoa và Mai đã lần lượt đạt các giải Nhì, Ba. Suy ra Lan đạt giải Nhất.
Vậy Lan đạt giải Nhất, Hoa đạt giải Nhì, Mai đạt giải Ba.
- B4: Kiểm tra lại lời giải. lOMoAR cPSD| 58794847 B. BÀI TẬP
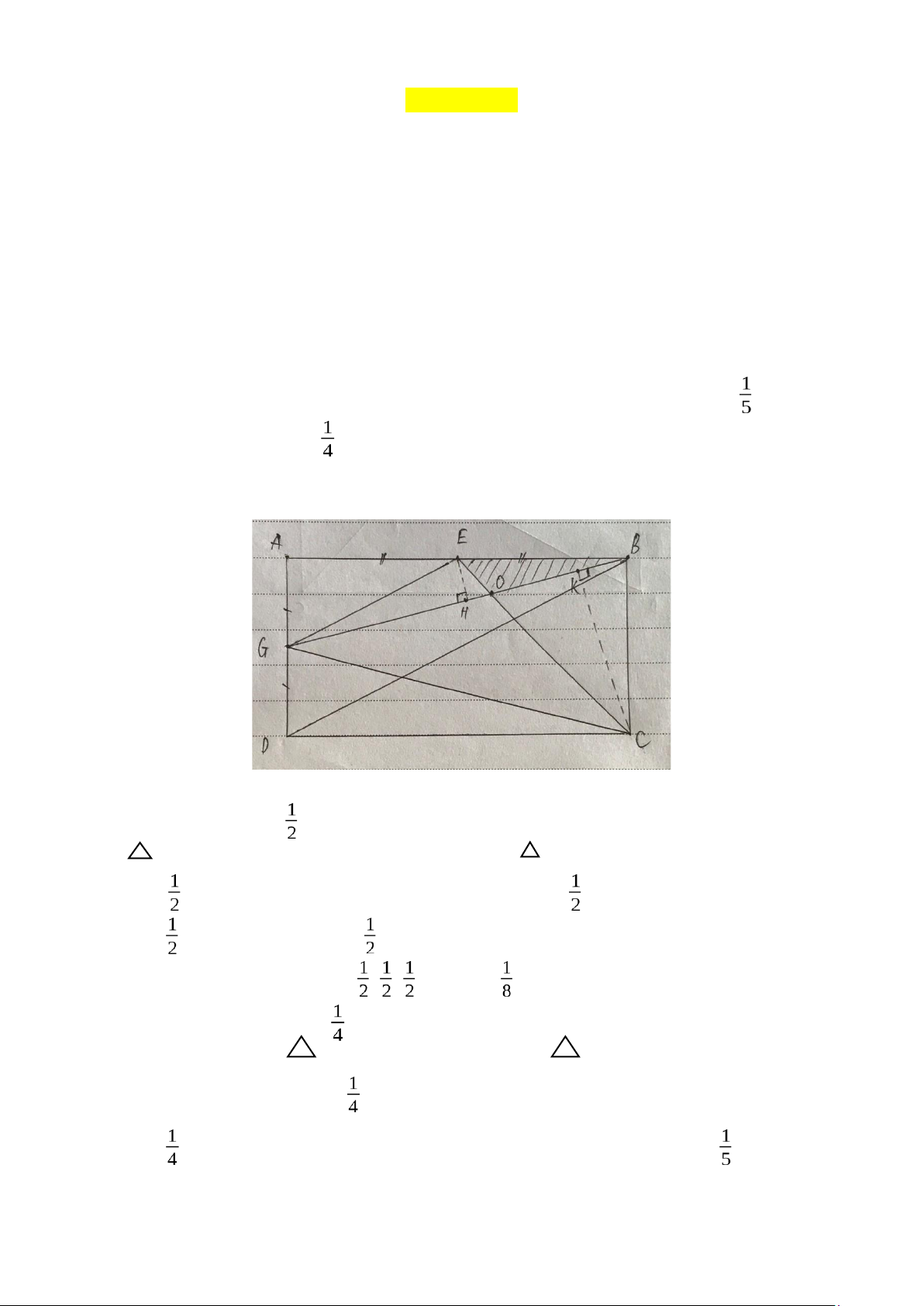
Câu 1. Cho HCN ABCD, trên AB lấy trung điểm E, trên AD lấy trung điểm G.
Nối B với G, C với E cắt nhau tại O. Biết diện tích tam giác OEB là 8cm2.
Tính diện tích hình chữ nhật ABCD. Bước 1: Tìm hiểu kĩ đề bài
- Bài toán cho biết: cho HCN ABCD. Trên AB lấy trung điểm E, trên AD lấy
trungđiểm G. Nối B với G, C với E cắt nhau tại O. Biết diện tích tam giác OEB là 8cm2.
- Bài toán hỏi: Tính diện tích hình chữ nhật ABCD.
Bước 2: Lập kế hoạch giải
Phương pháp giải: Phương pháp diện tích
Để tính diện tích hình chữ nhật ABCD, ta cần chứng minh được SOEB = . SCEB, và
dễ nhận thấy được SCEB = .SABCD. Từ đó tính được SCEB dựa vào SOEB mà đề bài đã cho là 8cm2
Bước 3: Thực hiện lời giải
Nối E với G; B với D; G với C
Ta có: SABD=SGBC= .SABCD (vì đáy AD = BC, độ dài đường cao hạ từ B của
ABD bằng độ dài đường cao hạ từ G của GBC) (1)
SBAG = .SABD (vì chung đáy AB, đường cao AG = .AD) (2)
SGEB = .SBAG (vì đáy EB = .AB, chung đường cao hạ từ G) (3)
Từ (1), (2), (3) suy ra SGEB = . . .SGBC = .SABCD (4)
Từ (1) và (4) ta có: SGEB= .SGBC
Kẻ đường cao EH của GEB, đường cao CK của GBC.
Có: CK = 4. EH ( vì SGEB = .SGBC)
SOEB = .SOBC (chung đáy OB; đường cao CK = 4. EH) nên SOEB = .SCBE lOMoAR cPSD| 58794847
Suy ra: SCBE = SOEB : = 8: = 40 (cm2)
Mà SCEB = .SABCD nên SABCD = SCEB : = 40 : = 160 (cm2) Đáp số: 160 cm
Bước 4: Kiểm tra lời giải.
Câu 2: Năm nay tuổi em bằng tuổi anh. Tính tuổi của mỗi người hiện nay biết
rằng tổng số tuổi của anh và em 5 năm trước đây bằng tổng số tuổi của anh và
em sau đây 5 năm nữa.
Câu 4: Hiện nay gia đình Nam có 3 người. Tổng số tuổi của 3 người là 66 tuổi.
Cách đây 4 năm tổng số tuổi của những người trong gia đình là 55 tuổi. Tính
tuổi hiện nay của mỗi người. Biết rằng 3 năm trước bố Nam hơn mẹ Nam là 3 tuổi.
o Phương pháp Tính ngược từ cuối Giải lOMoAR cPSD| 58794847
Tổng số tuổi của những người trong gia đình Nam hiện nay hơn tổng số tuổi của những người
trong gia đình Nam cách đây 4 năm là : 66 - 55 = 11 ( tuổi )
Nếu 4 năm trước gia đình nhà Nam có 3 người thì tổng số tuổi của họ hiện nay phải hơn tổng
số tuổi của họ 4 năm trước là : 4 × 3 = 12 ( tuổi )
Vì 12 tuổi > 11 tuổi nên cách đây 4 năm Nam chưa được sinh ra và 55 tuổi chính là tổng số
tuổi của bố và Nam lúc đó.
Vì hiệu số tuổi không thay đổi theo thời gian nên lúc nào bố Nam cũng hơn mẹ Nam 3 tuổi.
Tuổi của mẹ Nam cách đây 4 năm là :
( 55 - 3 ) ÷ 2 = 26 ( tuổi )
Tuổi của mẹ Nam hiện nay là : 26 + 4 = 30 ( tuổi )
Tuổi của bố Nam hiện nay là : 30 + 3 = 33 ( tuổi )
Tuổi của Nam hiện nay là :
66 - ( 30 + 33 ) = 3 ( tuổi )
Đáp số : Mẹ: 30 tuổi, Bố: 33 tuổi, Nam: 3 tuổi
Câu 5: Tìm một số có bốn chữ số abcd (c>b), biết rằng nếu viết các chữ số theo
thứ tự ngược lại ta được số mới dcba lớn hơn số ban đầu 90 đơn vị và tổng là 5
o Sử dụng phương pháp thử chọn để giải bài toán như sau:
*Bước 1: Từ dữ liệu ban đầu, tìm và liệt kê các số thỏa mãn
Gọi số có 4 chữ số cần tìm là: abcd (a khác 0)
Vì khi viết ngược lại thì được số mới dcbalớn hơn số cũ là 90. Ta có:
dcba - abcd = 90
Tức là: a – d = 0 hay a = d (a, d #0)
Xét hàng chục của phép tính được kết quả là 9. Suy ra c phải lớn b 1 đơn vị(c – b = 1) Do a+b+c+d =5 mà a=d
Nên: 2×a +b +c =5 (b #c, 2×a <5) (1)
Để 2×a<5Xảy ra 2 trường hợp: a=1 hoặc a= 2 lOMoAR cPSD| 58794847
*Bước 2:Kiểm tra và kết luận các trường hợp thỏa mãn
* Xét trường hợp a=1 thay vào (1) ta được: 2 × 1 +b+c = 5 2 +b+c=5 2-2+b+c=5-2 b+c=3
Vậy b+c=3 mà c-b =1. Nên b = 1, c = 2 và a = d = 1.
Ta tìm được số ban đầu là 1121, số ngược lại 1211.
Hiệu hai số là 1211-1121 = 90 (thỏa mãn)
* Xét trường hợp a=2 thay vào (1) ta được: 2 × 2 +b+c = 5 4 +b+c=5 4-4 +b+c=5-4 b+c=1
Vậy b+c =1 mà c-b =1. Nên b = 0, c = 1 và a = d = 1.
Ta tìm được số ban đầu là 2012, số ngược lại 2102. Hiệu hai số 2012-2102=90 (thỏa mãn)
Kết luận: có 2 số thỏa mãn là 1121 và 2012
Câu 6: Tùng có ba hộp đựng số viên bi bằng nhau. Tùng lấy ra từ hộp thứ nhất
một số viên bi, lấy gấp đôi số viên bi đó từ hộp thứ hai và lấy gấp ba số viên bi đó
từ hộp thứ ba thì cả ba hộp còn lại 30 viên và hộp thứ ba chỉ còn đúng 1 viên.
Tính tổng số bi ban đầu ở cả ba hộp. lOMoAR cPSD| 58794847
Câu 7: Năm học 2015 – 2016, một trường tiểu học có số học sinh nam nhiều hơn
số học sinh nữ là 80 học sinh. Năm học 2016 – 2017 số học sinh nữ giảm 25% so
với năm học trước, số học sinh nam giảm so với năm học trước nên số học
sinh nam bằng số học sinh nữ. Tính số học sinh nam và số học sinh nữ năm
học 2015 – 2016. o Phương pháp sơ đồ đoạn thẳng Giải Đổi
Năm học 2016 – 2017 số học sinh nam còn :
( số học sinh nam năm trước )
Năm học 2016 – 2017 số học sinh nữ còn :
( số học sinh nữ năm trước )
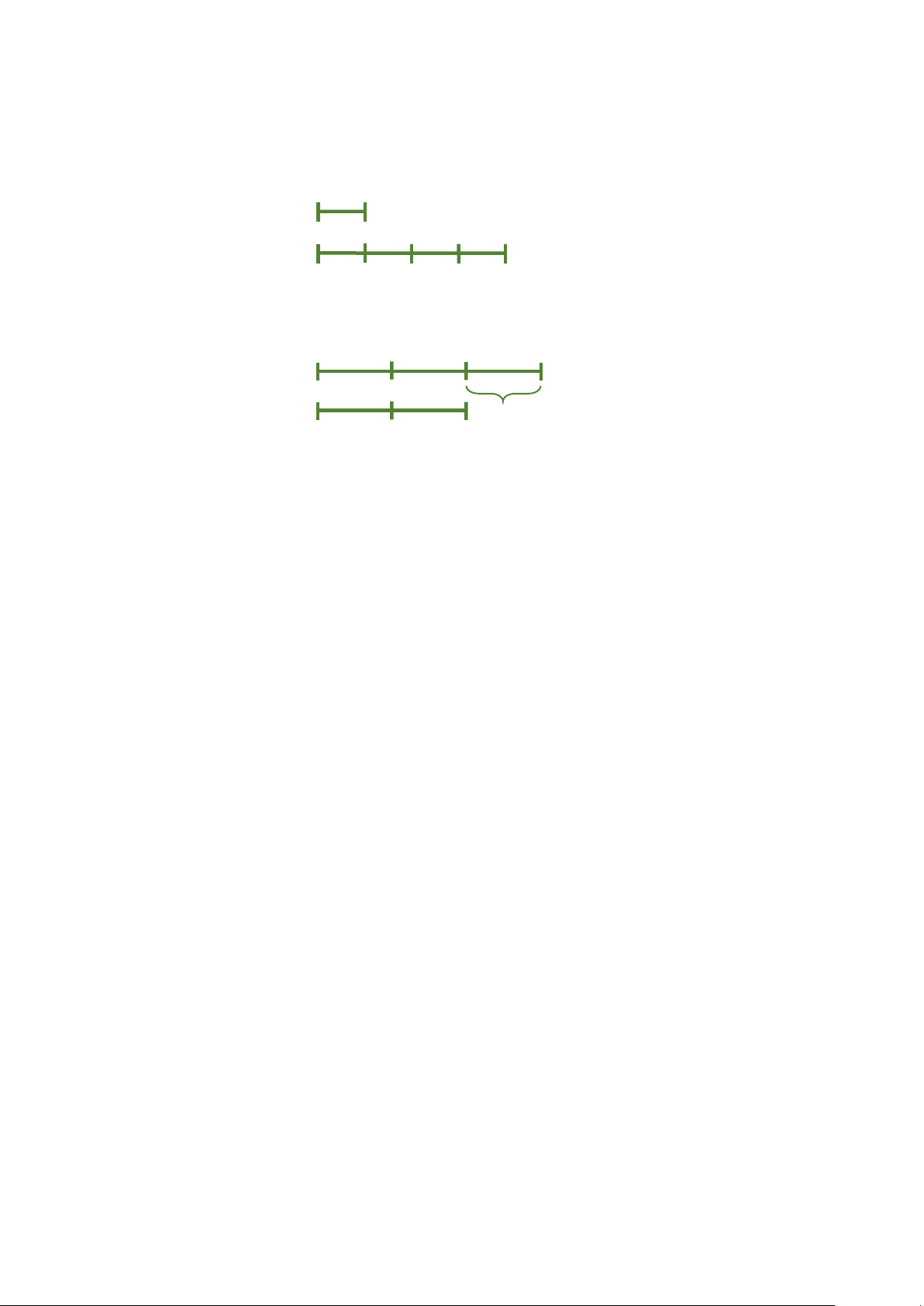
Vì số học sinh nam bằng số học sinh nữ nên nếu coi số học sinh nam là 5
phần thì số học sinh nữ là 4 phần như thế.
Ta có sơ đồ đoạn thẳng: lOMoAR cPSD| 58794847 HS nam: HS nữ:80 HS
Hiệu số phần bằng nhau là: (phần)
Số HS nam năm 2015 – 2016 là: (HS)
Số HS nữ năm 2015 – 2016 là: (HS)
Đáp số: HS nam: 400 HS HS nữ: 320 HS
Câu 8: Năm 2009 tuổi của mẹ gấp 7 lần tuổi của Hương. Đến năm 2014 tuổi của
Hương bằng tuổi mẹ. Hỏi Hương sinh năm nào? Mẹ sinh năm nào? o (Phương pháp chia tỉ lệ) Giải
Tuổi của Hương năm 2009: Tuổi của mẹ năm 2009:
Tuổi của Hương năm 2014: Tuổi của mẹ năm 2014
Từ năm 2009 đến năm 2014 mỗi người tăng số tuổi là
2014 – 2009 = 5 ( tuổi )
Coi tuổi Hương năm 2009 là 1 phần thì tuổi mẹ là 7 phần bằng nhau như thế:
Hiệu số phần bằng nhau lúc đó là: 7 – 1 = 6 ( phần )
Xem tuổi Hương 2014 là 1 phần thì tuổi mẹ là 4 phần như thế:
Hiệu số phần bằng nhau của mẹ và Hương năm 2014 là: 4 – 1 = 3 ( phần )
Hiệu tuổi mẹ và tuổi Hương luôn không thay đổi nên 3 phần tuổi Hương năm 2014 bằng 6
phần tuổi Hương lúc năm 2009
Vậy 1 phần tuổi Hương 2009 + 5 tuổi = 1 phần tuổi Hương năm 2014 lOMoAR cPSD| 58794847
Vậy 1 phần tuổi Hương năm 2009 là 5 tuổi Vậy tuổi mẹ năm 2009 là: 5 x 7 = 35 ( tuổi)
Mẹ sinh năm là : 2009 – 35 = 1974
Hương sinh năm là: 2009 – 5 = 2004
Đáp số: Hương sinh năm 2004 Mẹ sinh năm 1974
Câu 9: Bốn bạn Xuân, Hạ, Thu, Đông có tất cả 61 viên bi. Xuân có số bi ít nhất,
Đông có số bi nhiều nhất và là số lẻ, Thu có số bi gấp 9 lần của Hạ. Hãy tính xem
mỗi bạn có bao nhiêu viên bi.
Số bi của Thu gấp 9 lần số bi của Hạ nên tổng số bi của Thu và Hạ là một số chẵn.
Tổng số bi của bốn bạn là số lẻ, số bi của Đông là số lẻ, tổng số bi của Hạ và Thu là
số lẻ do đó số bi của Xuân phải là số chẵn.
Số bi của Hạ phải là số bé hơn 4 vì nếu số đó là 4 thì số bi của Thu là 4 x 9 = 36.
Khi đó ít nhất Đông có số bi là 37 thì chỉ riêng tổng số bi của Thu và Đông đã vượt quá
tổng số bi của bốn bạn: 36 + 37 = 73 > 61
Nếu số bi của Xuân là 2 thì số bi của Hạ là 3, số bi của Thu là 27 (3 x 9 = 27) Số bi của Đông là:
61 - (2 + 3 + 27) = 29 (viên)
Câu 10: Một hình chữ nhật có chiều dài gấp rưỡi chiều rộng. Kéo dài chiều dài
thêm chiều dài và kéo dài chiều rộng thêm chiều rộng thì được hình chữ nhật
mới có diện tích lớn hơn diện tích hình cũ là 132 cm2. Tính diện tích hình chữ nhật ban đầu. lOMoAR cPSD| 58794847
Câu 11: Có một can 10 lít và một cái can 20 lít, trong mỗi can đó có đựng một
lượng dầu không biết là bao nhiêu. Nếu đổ dầu từ can lớn sang can nhỏ cho đầy
thì số dầu còn lại của can lớn bằng lượng dầu lúc đầu của nó. Nếu đổ dầu từ
can nhỏ sang can lớn cho đầy thì trong can nhỏ còn lại 2 lít. Hỏi lúc đầu trong
mỗi can có bao nhiêu lít dầu? Giải
Nếu đổ dầu từ can nhỏ sang can lớn cho đầy: Can lớn đầy nên can lớn chứa 20
lít và 2 lít còn lại ở can nhỏ. Vậy tổng số lít dầu trong 2 can là 22 lít
Nếu đổ dầu từ can lớn sang can nhỏ cho đầy: Can nhỏ đầy thì can nhỏ chứa 10
lít dầu. Vậy can lớn chứa (lít)
Mà số dầu của can lớn sau khi đổ từ can lớn sang can nhỏ bằng lượng dầu lúc
đầu của nó nên số dầu ban đầu trong can lớn là: (lít)
Vậy số dầu ban đầu trong can nhỏ ( lít ) là:
Đáp số: can lớn: 14 lít Can nhỏ: 8 lít
Câu 12: Peter có một ngời bạn là người Việt Nam. Khi hai người gặp nhau, tay
bắt mặt mừng. Peter hỏi bạn mình: “Các con anh bao nhiêu tuổi rồi?”. Ông bạn
đáp: “ Sắp nghỉ hưu rồi mà con út vẫn còn bé, chỉ bằng tuổi bố. Tuổi đứa kia thì
bằng tuổi bố”. Hỏi ông bạn của Peter bao nhiêu tuổi và mỗi con của ông ta bao nhiêu tuổi? Bài giải
Vì ông bạn của Peter người VN sắp được nghỉ hưu nên:
50 < tuổi bố < 62 tuổi
Mà tuổi đứa con út bằng tuổi bố. Tuổi đứa kia thì bằng tuổi bố
Nên tuổi của bố vừa phải chia hết cho 4 và 7 lOMoAR cPSD| 58794847
Suy ra tuổi của bố là 56 Tuổi của con út là: 56 : 7= 8 (tuổi) Tuổi của con lớn là: 56 : 4 = 14 (tuổi)
Đáp số: bố 56 tuổi, con út 8 tuổi, con lớn 14 tuổi
Câu 13: Ba tổ thu nhặt giấy vụn. Biết tổ 1 thu được số giấy vụn bằng 3/4 số giấy
vụn tổ 2 và bằng 9/10 số giấy vụn tổ 3. Sau đó tổ 1 thu nhặt thêm được số giấy
vụn đúng bằng số giấy vụn tổ mình đã thu nhặt được, tổ 2 thu nhặt thêm 27 kg
nữa thì lúc đó số giấy vụn của tổ 1 bằng 6/7 số giấy vụn của tổ 2. Hỏi cả ba tổ đã
thu nhặt được bao nhiêu ki –lô – gam giấy vụn? o Sử dụng phương pháp thay
thế để giải bài toán
Gọi số giấy vụn đã thu nhặt được của cả 3 tổ lần lượt là a,b,c (a,b,c>0) Theo bài ra ta có:
+ Tổ 1 thu được số giấy vụn bằng số giấy vụn tổ 2 a= b
+ Bằng số giấy vụn tổ 3  a = c
+ Sau đó tổ 1 thu được số giấy vụn bằng đúng số giấy vụn tổ mình : a + a = 2a
+ Tổ 2 thu nhặt thêm 27kg : b + 27
Tổ 1 lúc bấy giờ thu nhặt được số giấy vụn là:
2 ×a= ×(b+27)
Thay a = b vào 2×a= ×(b+27) ta được:
2 × b= × (b+27 ) b = b+ lOMoAR cPSD| 58794847 b = b =36
Số giấy vụn tổ 1 thu nhặt được là : ×36=27 (kg )
Số giấy vụn tổ 3 thu nhặt được là: 27: =30(kg) Đáp số : tổ 1 : 27 kg Tổ 2: 36 kg Tổ 3: 30 kg
Câu 14: Hai thùng chứa đầy dầu. Biết số dầu thùng thứ nhất bằng số dầu thùng
thứ hai và số dầu ở thùng thứ nhất ít hơn số dầu ở thùng thứ hai là 36 lít. Tính
số dầu mỗi thùng ban đầu? o Sử dụng phương pháp tính ngược từ cuối
3/10 số dầu ở thùng thứ nhất bằng:
3/10 x 5/6 =1/4 (số dầu thùng thứ hai) 36 lít tương ứng với
3/4 -1/4 =1/2 (số dầu thùng thứ hai)
Số dầu thùng thứ hai là 36 : 1/2 =72 (l)
Số dầu thùng thứ nhất là 72 x 5/6 =60 (l)
Đáp số: Số dầu thùng 1: 60 lít Số dầu thùng 2: 72 lít
Câu 15: Bình và Dương chơi bi. Đầu cuộc chơi hai bạn có số bi bằng nhau. Sau
ván thứ nhất Bình thắng được 20 viên bi của Dương, nhưng đến ván thứ hai
Dương lại thắng được số bi đang có của Bình nên số bi của Dương gấp 4 lần số
bi của Bình. Hỏi lúc đầu mỗi bạn có bao nhiêu viên bi? Sau ván đầu tiên Bình
hơn Dương số viên bi là: 20 + 20 = 40 (viên)
Sau ván thứ hai Dương lại thắng được 2/3 số bi đang có của Bình . Như vậy số bi của Bình sau ván thứ hai là: 3 – 2 = 1 (phần) lOMoAR cPSD| 58794847
Số bi của Dương sau ván thứ hai là: 1 x 4 = 4 (phần)
Ta có sơ đồ ván thứ 2: Số bi của Bình ván 2: Số bi của Dương ván 2:
Số bi của Dương sau ván thứ nhất là:
4 – 2 = 2 (phần) Số bi của Bình ván 1: Số bi của Dương ván 1: 40 Viên
Số bi của Dương sau ván 1 là: 40 : (3-2) x 3 = 120 (viên)
Số bi của mỗi bạn lúc đầu là: 120- 20 = 100 (viên) Đáp số: 100 viên bi.