Đề cương giữa học kỳ 1 Toán 12 năm 2024 – 2025 trường THPT Hoàng Văn Thụ – Hà Nội

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề cương ôn tập giữa học kỳ 1 môn Toán 12 năm học 2024 – 2025 trường THPT Hoàng Văn Thụ, quận Hoàng Mai, thành phố Hà Nội. Mời bạn đọc đón xem!

20 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK1 Toán 12

Môn: Toán 12

Thông tin:

15 trang 1 tuần trước

Tác giả:

Profile Lê Phương
TRƯỜNG THPT HOÀNG VĂN THỤ
TỔ TOÁN
ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KỲ I
MÔN TOÁN – KHỐI 12
NĂM HỌC 2024 – 2025
1. MỤC TIÊU
1.1. Kiến thức: Học sinh ôn tập các kiến thức về:
- Tính đồng biến, nghịch biến của một hàm số.
- Cực trị của một hàm số.
- Gi trị ln nht, gi trị nh nht của hm số.
- Đường tiệm cận ngang, đường tiệm cận đứng, đường tiệm cận xiên của đồ thị hm số.
- Vectơ trong không gian: hai vectơ cùng phương, hai vectơ cùng hưng/ngược hưng, hai vectơ bằng
nhau.
- Các phép ton vectơ trong không gian.
1.2. Kĩ năng: Học sinh rèn luyện cc kĩ năng:
- Rèn luyện năng lực tư duy v lập luận toán học, năng lực mô hình hoá toán học v năng lực giải quyết
vn đề toán học thông qua việc mô hình hoá những vn đề thực tiễn liên quan đến tính đơn điệu và cực trị
của hàm số, giá trị ln nht và GTNN của hàm số, đường tiệm cận của đồ thị hàm số.
- Rèn luyện cc năng lực toán học, nói riêng là năng lực mô hình hoá toán học (thông qua việc sử dụng
các kiến thức về vectơ trong không gian để trả lời các câu hi trong phần Vận dụng).
- Bồi dưỡng hứng thú học tập, ý thức làm việc nhóm, ý thức tìm tòi, khám phá và sáng tạo cho HS.
2. NỘI DUNG
2.1. Các câu hỏi và bài tập minh họa
2.1.1. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hi, học sinh chỉ chọn một phương n.
Câu 1. Cho hàm số có đồ thị l đường cong trong hình vẽ dưi đây:
Hàm số đồng biến trên khoảng no sau đây?
A. B. C. D.
Câu 2. Cho hm số vi l tham số. Gọi l tập hợp tt cả cc gi trị nguyên của để
hm số nghịch biến trên cc khoảng xc định. Tm số phần tử của .
A. . B. . C.Vô số. D. .
Câu 3. Hàm số
2
2
1
=
+
y
x
nghịch biến trên khoảng no dưi đây?
A.
( 1;1)−
. B.
( ; )− +
. C.
(0; )+
. D.
( ;0)−
Câu 4. Cho hàm số . Mệnh đề no dưi đây đúng?
A.Cực tiểu của hàm số bằng . B.Cực tiểu của hàm số bằng .
C.Cực tiểu của hàm số bằng . D.Cực tiểu của hàm số bằng
Câu 5. Cho hàm số . Biết đồ thị của hàm số như hnh bên.
( )
y f x
=
O
-
y=f '(x)
( )
y f x=
( )
; 1 .− −
( )
1;1 .−
( )
1;4 .
( )
1; .+
4mx m
y
xm
+
=
+
m
S
m
S
5
4
3
2
3
1
+
=
+
x
y
x
3−
1
6−
2
( )
y f x=
( )
'
y f x=
Tìm số điểm cực tiểu của hàm số
A. . B. . C. . D. .
Câu 6. Cho hàm số liên tục trên v có đồ thị như hnh vẽ. Hi hàm số có bao nhiêu điểm
cực trị?
A. 4. B. 5. C. 2. D. 3.
Câu 7. Cho hàm số có bảng biến thiên như hnh bên.
Giá trị ln nht của hàm số đã cho trên đoạn bằng
A. . B. . C. . D. .
Câu 8. Cho hàm số
( )
y f x=
có bảng biến thiên trên
)
5;7−
như sau
Mệnh đề no dưi đây đúng?
A.
)
( )
5;7
min 6fx
−
=
. B.
)
( )
5;7
min 2fx
−
=
. C.
)
( )
5;7
max 9fx
−
=
. D.
)
( )
5;7
max 6fx
−
=
.
Câu 9. Giá trị ln nht của hàm số
2
3
1
+
=
−
x
y
x
trên đoạn
2;4
là
A.
2;4
max 7y =
B.
2;4
max
19
3
y =
C.
2;4
max 6y =
. D.
2;4
max 8y=
( )
y f x=
5
4
3
2
( )
=y f x
( )
y f x=
3;3−
0
3
1
8
Câu 10. Cho hm số
( )
y f x=
có đạo hm
( )
fx
tại mọi
x
. Đồ thị của hm số
( )
y f x
=
được
cho như hnh vẽ dưi đây.
Biết rằng
( ) ( ) ( ) ( )
0 3 2 5f f f f+ = +
. Hãy tìm giá trị nh nht, giá trị ln nht của
( )
y f x=
trên đoạn
0;5
?
A.
( ) ( )
0;5
5Max f x f=
. B.
( ) ( )
0;5
0Max f x f=
.
C.
( ) ( )
0;5
2Max f x f=
. D.
( ) ( )
0;5
3Max f x f=
.
Câu 11. Cho hm số
()y f x=
xc định v liên tục trên có đồ thị bên dưi. Gọi
, Mm
lần lượt l gi
trị ln nht v nh nht của hm số trên đoạn
[1;3].
Gi trị của
Mm+
bằng:
A.
2Mm+=
. B.
4Mm+ = −
. C.
3Mm+ = −
. D.
1Mm+=
.
Câu 12. Cho hàm số
2 4 ln2
x
yx=−
. Giá trị nh nht của hàm số trên đoạn
0;4
có dạng
lna b c−
.
Tính
abc++
?
A.
2−
. B.
14.
C.
34.
D.
0
.
Câu 13. Gọi
,mM
lần lượt l gi trị nh nht, ln nht của hm số
lny x x=−
trên đoạn
1
;
2
e



. Gi trị
của
Mm−
là
A.
1
ln2
2
e −−
. B.
1e −
. C.
1
ln2
2
−
. D.
2e −
.
Câu 14. Cho hàm số
( )
2
4.y f x x= = −
Khẳng định no sau đây l sai?
A. Hàm số có GTLN là 2. B. Hàm số có GTNN là 0.
C. Hàm số đạt GTLN tại
2.x =
D. Hàm số đạt GTNN tại
2.x =
Câu 15. Đồ thị hàm số
33
1
x
y
x
−
=
−
có tiệm cận ngang là
A.
1x =
. B.
1y =
. C.
2x =
. D.
3y =
.
Câu 16. Cho hàm số
( )
y f x=
có bảng biến thiên như sau'
x
y
5
2
O
Phương trnh đường tiệm cận đứng của đồ thị hàm số đã cho l
A.
1x =
. B.
1y =
. C.
1x =−
. D.
1y =−
.
Câu 17. Cho đồ thị của hàm số
( )
fx
như hnh bên dưi?
Số đường tiệm cận của đồ thị của hàm số
( )
fx
là
A. 1. B. 2. C. 0. D. 3.
Câu 18. Cho hàm số
( )
y f x=
có
( )
2
lim
x
fx
→−
= 
và
( )
2
lim
x
fx
→
= 
. Chọn mệnh đề đúng?
A. Đồ thị hàm số đã cho có đúng một tiệm cận đứng.
B. Đồ thị hàm số đã cho không có tiệm cận đứng.
C. Đồ thị hàm số đã cho có hai tiệm cận đứng l cc đường thẳng
2y =
và
2y =−
.
D. Đồ thị hàm số đã cho có hai tiệm cận đứng l cc đường thẳng
2x =
và
2x =−
.
Câu 19. Cho đồ thị hàm số
( )
y f x=
như hnh bên. Khẳng định no sau đây l đúng?
A. Đồ thị hàm số đã cho có một tiệm cận đứng và một tiệm cận ngang
B. Đồ thị hàm số đã cho không có tiệm cận đứng.
C. Đồ thị hàm số đã cho có một tiệm cận ngang và một tiệm cận xiên
D. Đồ thị hàm số đã cho có một tiệm cận đứng và một tiệm cận xiên
Câu 20. Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Tổng số tiệm cận của đồ thị hàm số đã cho l
A. 1. B. 2. C. 3. D. 0.
Câu 21. Cho hàm số
2
3 5 4
54
xx
y
x
+−
=
−+
. Đường tiệm cận xiên của đồ thị hàm số đã cho l
A.
3 37
5 25
yx= − −
. B.
3 37
5 25
yx= − −
. C.
3 37
5 25
yx= − −
. D.
3 37
5 25
yx= − −
.
Câu 22. Đồ thị sau là của hàm số no dưi đây?
A.
2
2 9 10
2
xx
y
x
−+
=
−+
. B.
2
2 9 10
2
xx
y
x
−+
=
+
. C.
2
57
2
xx
y
x
−+
=
+
. D.
2
57
2
xx
y
x
−+
=
−+
.
Câu 23. Cho hình chóp
.S ABCD
có đy
ABCD
l hnh bnh hnh. Đặt
SA a=
;
SB b=
;
SC c=
;
SD d=
. Khẳng định no sau đây đúng?
A.
0a b c d+ + + =
. B.
a b c d+ = +
. C.
a d b c+ = +
. D.
a c d b+ = +
.
Câu 24. Cho hnh lăng trụ
.ABC A B C
vi
G
là trọng tâm của tam giác
.ABC
Đặt
AA a
=
,
AB b=
,
.AC c=
Khi đó
AG
bằng:
A.
( )
1
.
3
a b c++
B.
( )
.
1
4
a b c++
C.
( )
1
.
6
a b c++
D.
( )
1
.
2
a b c++
Câu 25. Cho tứ diện
ABCD
. Đặt
,,DA a DB b DC c= = =
. Gọi
,MN
lần lượt l trung điểm của hai
cạnh
AD
và
BC
. Biểu diễn vectơ
MN
qua cc vectơ
,,abc
.
A.
1
()
2
MN a b c= + +
. B.
1
()
2
MN a b c= − + +
. C.
1
()
2
MN a b c−=+
. D.
1
()
2
MN a b c−=+
.
Câu 26. Cho hnh lăng trụ
.ABC A B C
, M l trung điểm của
BB
. Đặt
CA a=
,
CB b=
,
AA c
=
(Tham
khảo hình vẽ).
Khẳng định no sau đây đúng?
A.
1
2
AM a c b= + −
. B.
1
2
AM a c b= − +
. C.
1
2
AM b c a= + −
. D.
1
2
AM b a c= − +
.
Câu 27. Cho hình lập phương có cạnh bằng (tham khảo hình vẽ). Tính
.'AB DC
.
A. . B. . C. . D. .
Câu 28. Cho hai vectơ
a
và
b
tha mãn điều kiện
1ab==
và
. 2.ab=
Độ di vectơ
23ab+
bằng
A.
5 5.
B.
37.
C. 8. D. 5.
Câu 29. Cho hnh lập phương
ABCD A B C D
. Gọi
,MN
lần lượt l trung điểm của
AD

và
CD

.
Gọi
l góc giữa hai vectơ
MN
và
AB
. Số đo của góc
bằng bao nhiêu độ?
A.
0
45 .
B.
0
30 .
C.
0
90 .
D.
0
60 .
2.1.2. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu hỏi, học sinh chọn đúng hoặc sai.
Câu 30. Cho hàm số xc định, liên tục trên và có bảng biến thiên dưi đây:
a) Hàm số đạt cực đại tại
4x =
.
b) Hàm số có giá trị cực tiểu là .
c) Hàm số có hai cực trị tri du.
d) Số điểm cực trị của hàm số
là 2.
Câu 31. Cho hm số có bảng biến thiên như sau:
.ABCD A B C D
a
A
D
B
C
B'
C'
D'
A'
2
2
a
2a
0
2
a
( )
y f x=
\2
( )
y f x=
( )
2024y f x=+
2025
( )
y f x=
( )
1y f x=+
( )
y f x=
a) Hm số đồng biến trên khoảng
( )
;2− −
b) Cực tiểu của hàm số bằng
c) Đường thẳng
21yx= − −
đi qua hai điểm cực trị của đồ thị hm số
d) Hàm số
đồng biến trên .
Câu 32. Cho hàm số
( )
32
6 2 9 4.= − − − + +y x x m x
a)
( )
12ym
− = −
b) Vi
4m =
thì hàm số đã cho nghịch biến trên
.
c) Tập hợp tt cả các giá trị của tham số
m
để hàm số đã cho nghịch biến trên là
3
;.
2

+

d) Có 7 giá trị nguyên của tham số
m
thuộc đoạn
8;8−
để hàm số đã cho nghịch biến trên khoảng
( )
; 2 .− −
Câu 33. Cho hàm số
( )
=y f x
. Biết hàm số
( )
=y f x
có đồ thị như hnh vẽ bên dưi:
a) Phương trnh
( )
0
=fx
có 3 nghiệm phân biệt. b) Hàm số đồng biến trên khoảng
( )
+2; .
c) Hàm số có 3 điểm cực trị.
d) Hàm số
( )
2
1y f x=−
đồng biến trên khoảng
( )
0;1 .
Câu 34. Cho hàm số
2
500
2f x x
x
.
Khẳng định
Đúng
Sai
a)
05f x x
.
b)
( )
lim 0
x
fx
→+
=
.
c)
Giá trị nh nht của hàm số trên
( )
0;5
là 150.
d)
Giá trị nh nht của hàm số trên
( )
0;+
là 150.
Câu 35. Cho hàm số
( )
fx
có bảng biến thiên như sau:
1
( )
2y f x=−
( )
1;3
x
y
-1
O
1
x
−
1−
0
1
+
( )
fx
+
0
−
0
+
0
−
( )
fx
−
5
2
3
−
Khẳng định
Đúng
Sai
a)
( )
max 5.
x
fx
=
b)
( )
min 2.
x
fx
=
c)
Tổng gi trị ln nht v gi trị nh nht của hm số
( )
fx
trên
1;1−
là 7
d)
( )
0;
2
max sin 5.
x
fx



=
Câu 36. Cho hàm số
()y f x=
xc định trên và có bảng biến thiên như hnh vẽ.
Khẳng định
Đúng
Sai
a)
Giá trị ln nht của hàm số
()y f x=
trên bằng 21.
b)
Giá trị nh nht của hàm số
()y f x=
trên bằng 12.
c)
Giá trị ln nht của hàm số
( )
( ) 2h x f x m=+
trên đoạn
0;5
bằng 34 khi
15m =
.
d)
Hàm số
( )
(2 2)g x f x=−
đạt giá trị ln nht trên khoảng
( ;4)−
tại
3x =
.
Câu 37. Cho hàm số
42
( ) 2 2y f x x x= = − −
.
Khẳng định
Đúng
Sai
a)
Giá trị nh nht của hàm số trên đoạn
1;1−
là
3−
.
b)
Gi trị ln nht của hm số trên nửa khoảng
)
1;− +
là
2−
.
c)
Tổng gi trị nh nht v gi trị ln nht của hm số trên
đoạn
2;2−
là
3
.
d)
Nếu
0; 2
min ( )
AA
y f x y==
,
0;2
max ( )
BB
y f x y==
thì
2AB =
Câu 38. Cho hàm số
2
ax bx c
y
mx n
++
=
+
có đồ thị
( )
C
như hnh vẽ bên dưi.
a) Đồ thị
( )
C
có một tiệm cận đứng. b) Đồ thị
( )
C
có tiệm cận xiên là
1yx=+
.
c) Đồ thị
( )
C
đi qua điểm
( )
2;2−
. d) Giao điểm của hai tiệm cận là
( )
1;0E −
Câu 39. Cho hàm số
2
2
32
1
xx
y
x
++
=
−
.
a) Đường thẳng
1x =
l đường tiệm cận đứng của đồ thị hàm số.
b) Đường thẳng
1y =
l đường tiệm cận ngang của đồ thị hàm số.
c) Đồ thị hàm số đã cho có
1
tiệm cận ngang,
2
tiệm cận đứng.
d) Đồ thị hàm số đã cho có 2 đường tiệm cận.
Câu 40. Cho hm số
( )
y f x=
có bảng biến thiên như hnh dưi đây, trong đó
.m
a) Đồ thị hm số có đúng 2 đường tiệm cận đứng v 1 đường tiệm cận ngang vi mọi
.m
b) Đồ thị hàm số có đúng 2 đường tiệm cận đứng v 2 đường tiệm cận ngang vi mọi
\ 2 .m
c) Đồ thị hàm số có đúng 2 đường tiệm cận đứng v 2 đường tiệm cận ngang vi mọi
.m
d) Đồ thị hàm số có đúng 1 đường tiệm cận đứng v 2 đường tiệm cận ngang vi mọi
.m
Câu 41. Cho hàm số
( )
1
2
x
fx
x
−+
=
−
.
a)Tiệm cận đứng của đồ thị hàm số trên có phương trnh l
2x =
.
b)Tiệm cận ngang của đồ thị hàm số trên có phương trnh l
1y =
.
c)Đồ thị hàm số trên có hai đường tiệm cận tạo vi hai trục tọa độ một tam giác có diện tích bằng 2.
d)Đồ thị hàm số
( ) ( )
.g x x f x=
có tiệm cận xiên song song vi đường phân giác của góc phần tư thứ
2.
Câu 42. Cho tứ diện
ABCD
có
,MN
lần lượt l trung điểm các cạnh
AC
và
.BD
Gọi
G
là trung
điểm của đoạn thẳng
.MN
a)
2GA GC GM+=
. b)
GB GD MN+=
.
c)
0GA GB GC GD+ + + =
. d)
2NM AB CD=+
.
Câu 43. Cho hình hộp
.ABCD A B C D
vi tâm O.
a)
+ + .AB AA AD DD

=
b)
++.AC AB AD AA

=
c)
+.AB BC CC AD D O OC
+ + = +
d)
=0.AB BC C D D A
+ + +
Câu 44. Cho tứ diện đều
ABCD
,
M
và
N
theo thứ tự l trung điểm của cạnh
AB
và
CD
.
a)
AC BD AD BC+ = +
. b)
( )
1
2
MN AD BC=+
.
c)
4AC BD AD BC NM+ + + = −
. d)
40MC MD MN+ − =
.
Câu 45. Cho hình chóp
.S ABC
có và .
a)
. 0.AB AC
b)
0
, 120 .SA AB
c)
2
..
2
a
SC AB
d)
1
cos , .
2
SC AB
2.1.3 Câu trắc nghiệm trả lời ngắn.
Câu 46. Cho hàm số liên tục trên v có đạo hàm . Hàm số
có bao nhiêu điểm cực trị?
Câu 47. Có bao nhiêu giá trị nguyên của tham số để hàm số nghịch biến trên khoảng
?
Câu 48. Biết rằng đồ thị hàm số có một điểm cực trị là . Tính khoảng cách giữa
điểm cực đại v điểm cực tiểu của đồ thị hàm số đã cho (quy tròn đến hàng phần trăm).
Câu 49. Cho hàm số , bảng biến thiên của hàm số như sau:
Hàm số có bao nhiêu điểm cực trị?
A. . B. . C. . D. .
Câu 50. Tm gi trị nh nht của hm số
3
34y x x= − +
trên đoạn
0;2 .
Câu 51. Gọi
,mM
lần lượt là giá trị nh nht và giá trị ln nht của hàm số
32
4
sin 4cos 5sin 1
3
y x x x= + − +
. Tính giá trị của
Mm−
.
Câu 52. Cho các số thực dương
x
,
y
tha mãn
5
2
4
xy+=
. Tìm giá trị nh nht
min
P
của biểu thức
21
4
P
xy
=+
.
Câu 53. Đường tiệm cận xiên của đồ thị hàm số
2
32
4
xx
y
x
−+
=
+
có dạng
y ax b=+
. Tìm tổng
23ab+
?
SA SB SC AB AC a= = = = =
2BC a=
( )
y f x=
( ) ( )( )( )
1 3 5f x x x x
= − − −
( )
( )
2
y g x f x==
m
1
3
+
=
+
x
y
xm
( )
6;+
42
2y x ax b= − +
( )
1;2
( )
fx
( )
fx
( )
2
44y f x x=−
9
5
7
3
Câu 54. Vi giá trị nào của tham số
m
th đường tiệm cận ngang của đồ thị hàm số
( )
( )
2 1 3
2024
mx
fx
x
−+
=
−
đi qua điểm
( )
1;2 ?M
Câu 55. Biết đường tiệm cận xiên của đồ thị hàm số
2
2
1
xx
y
x
+
=
+
cắt trục hoành và trục tung lần lượt tại
hai điểm
,AB
. Tính diện tích tam giác
OAB
(vi
O
là gốc tọa độ).
Câu 56. Nồng độ oxygen trong hồ theo thời gian
t
cho bởi công thức
( )
2
15
5
91
t
yt
t
=−
+
, vi
y
được
tính theo
/mg l
và
t
được tính theo giờ,
0t
. Đường tiệm cận ngang của đồ thị hàm số
( )
y y t=
khi
t → +
có dạng
ya=
. Tính giá trị của
a
Câu 57. Cho tứ diện đều
ABCD
,
M
l trung điểm của cạnh
BC
. Khi đó
( )
cos ,AB DM
bằng
a
b
.
Tính giá trị của biểu thức
.T a b
Câu 58. Cho hnh lâp phương
ABCD A B C D
có cạnh bằng
a
. Gọi
,MN
lần lượt l trung điểm của
AD

và
CD

. Tích vô hưng
2
MN C B na
=
(
n
l số thập phân). Gi trị của
n
bằng bao nhiêu?
Câu 59. Cho ba vectơ , , tha mãn , , . Tính .
Câu 60. Một tm gỗ tròn được treo song song vi mặt phẳng nằm ngang bởi ba sợi dây không giãn xut
pht từ điểm
O
trên trần nh v lần lượt buộc vo ba điểm
,,A B C
trên tm gỗ tròn sao cho cc lực căng
1 2 3
,,F F F
lần lượt trên mỗi dây
,,OA OB OC
đôi một vuông góc vi nhau v có độ ln
( )
1 2 3
10F F F N= = =
(xem hnh vẽ).
Tính trọng lượng
P
của tm gỗ tròn đó (lm tròn đến hng phần mười).
a
b
c
1a =
2b =
3ab−=
( ) ( )
2 . 2a b a b−+
2.2. MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KỲ I
MÔN: TOÁN, LỚP 12 – THỜI GIAN LÀM BÀI: 90 phút
STT
NỘI DUNG
HÌNH THỨC
TN
4 lựa
chọn
(mức
độ 1,
2)
TN
Đúng –
Sai
(mức độ
1, 2, 3)
TL ngắn
(mức độ
2,3,4)
1
Tính đơn điệu và cực trị của hàm số
4
3
2
2
Giá trị ln nht giá trị nh nht của
hàm số
2
2
3
Đường tiệm cận của đồ thị hàm số
2
1
4
Véc tơ trong không gian
4
1
1
Tổng
12
4
6
ĐỀ MINH HỌA
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hi, học sinh chỉ chọn một phương n.
Câu 1. Cho hàm số đồng biến trên khoảng .Khẳng định no sau đây đúng?
A. . B. . C. . D. .
Câu 2. Cho hàm số có bảng biến thiên như sau :
Hàm số đã cho đồng biến trên khoảng no dưi đây?
A. B. C. D.
Câu 3. Cho hàm số xc định, liên tục trên và có bảng biến thiên
Khẳng định no sau đây l khẳng định đúng?
A. Hàm số có giá trị cực tiểu bằng 1.
B. Hàm số có giá trị ln nht bằng 0 và giá trị nh nht bằng -1.
C. Hàm số đạt cực đại tại v đạt cực tiểu tại .
( )
fx
( )
0;+
( ) ( )
21ff−
( ) ( )
13ff
( ) ( )
3ff
23
34
ff
( )
y f x=
( )
1;0−
( )
1; +
( )
;1−
( )
0;1
y f x
y f x
y f x
y f x
0x
1x
D. Hàm số có đúng một cực trị.
Câu 4. Cho hàm số
( )
fx
có đạo hàm
( ) ( )( )
3
12
= − +f x x x x
,
x
. Số điểm cực trị của hàm số l:
A.
3
. B.
2
. C.
5
. D.
1
.
Câu 5. Cho hàm số
( )
y f x=
liên tục trên tha mãn giá trị nh nht của hàm số trên là
5
. Khẳng
định no sau đây l đúng?
A.
( )
5fx
x
. B.
5fx
x
,
0
x
,
0
5fx
.
C.
( )
5fx
x
. D.
5fx
x
,
0
x
,
0
5fx
.
Câu 6. Cho hàm số liên tục trên v có đồ thị như hnh vẽ bên. Khi đó
bằng
A. . B. . C. . D. .
Câu 7. Đường tiệm cận đứng của đồ thị hàm số
34
4
x
y
x
−
=
+
có phương trnh l
A. . B.
4x =
. C.
4y =−
. D.
3y =
.
Câu 8. Đường tiệm cận xiên của đồ thị hàm số
21
4
5
yx
x
= + −
+
cắt trục hoành tại điểm
A.
( )
2;1A
. B.
( )
2;0B
. C.
( )
1;3C
. D.
1
;0
2
D

−


.
Câu 9. Cho tứ diện
ABCD
. Mệnh đề no dưi đây l mệnh đề đúng?
A.
BC AB DA DC+=−
. B.
AC AD BD BC− = −
.
C.
AB AC DB DC− = −
. D.
AB AD CD BC− = +
.
Câu 10. Cho hình hộp chữ nhật
ABCD A B C D
. Tính góc giữa hai vectơ
AA
và
CC
.
A.
0
45
. B.
0
30
. C.
0
90
. D.
0
180
.
Câu 11. Cho tứ diện đều
ABCD
có cạnh bằng
a
. Tính
.AB BC
theo
a
A.
2
2
a
. B.
2
2
a
−
. C.
2
3
2
a
. D.
2
3
2
a
.
Câu 12. Cho hình lập phương
.ABCD A B C D
cạnh
a
. Đặt
x AA AC

=+
. Độ dài của
x
bằng
A.
( )
13a+
. B.
6
2
a
. C.
6a
. D.
2a
.
y f x
( )
y f x=
4;2−
( )
( )
4;2
4; 1
max minf x f x
−
−−
+
1
0
2
5
4x =−
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu hi, học sinh chọn đúng hoặc
sai.
Câu 1. Cho hàm số .
a) Hàm số nghịch biến trên khoảng .
b) Hàm số đồng biến trên khoảng .
c) Hàm số có giá trị cực tiểu .
d) Hàm số có 2 điểm cực trị.
Câu 2. Cho hàm số
()y f x=
xc định trên
\{ 2}−
và có bảng biến thiên như sau:
a) Hàm số có giá trị cực tiểu ln hơn gi trị cực đại.
b)
2x =−
đường tiệm cận đứng của đồ thị hàm số.
c) Đồ thị hàm số có một đường tiệm cận ngang
d) Biết hàm số
()fx
có dạng
2
()
x bx c
fx
xn
++
=
+
khi đó
( )
5
1
3
f =
Câu 3. Một cơ sở sản xut khăn mặt đang bn mỗi chiếc khăn vi giá
30.000
đồng một chiếc và mỗi
thng cơ sở bn được trung bình
3000
chiếc khăn. Cơ sở sản xut đang có kế hoạch tăng gi bn để có lợi
nhận tốt hơn. Sau khi tham khảo thị trường, người quản lý thy rằng nếu từ mức giá
30.000
đồng mà cứ
tăng gi thêm
1000
đồng thì mỗi tháng sẽ bn ít hơn
100
chiếc. Biết vốn sản xut một chiếc khăn không
thay đổi là
18.000
.
Khẳng định
Đúng
Sai
a)
Nếu cơ sở bn mỗi chiếc khăn vi gi
37000
th số tiền lãi
sau 1 tháng là
44
.
b)
Sau khi cơ sở tăng gi mỗi chiếc khăn thêm
x
thì tổng số
lợi nhuận một tháng của cơ sở được tính theo công thức
( )
2
100 1800 36000f x x x= − + +
.
c)
Để đạt lợi nhuận ln nht thì số khăn bn ra giảm
800
chiếc.
d)
Để đạt lợi nhuận ln nht thì mỗi chiếc khăn cần bán vi
giá
39000
đồng.
Câu 4. Cho hình lập phương
.ABCD A B C D
có cạnh bằng
a
.
a)
20AB B C CD D A
+ + + =
. b)
2
.AD AB a

=
. c)
.0AB CD

=
.
d) Gọi
M
,
N
lần lượt l trung điểm của
AD
,
.BB
Cosin của góc hợp bởi
MN
và
AC
bằng
3
3
.
Phần III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 1 đến câu 6.
2
13
3
4
2
xx
y
−+
=
( )
1;0−
( )
0;1
2
CT
y =
Câu 1. Tìm giá trị cực đại của hàm số
2
29
21
xx
y
x
−+
=
−
.
Câu 2. Cho hàm số . Tm số giá trị nguyên của thuộc
khoảng để hàm số đồng biến trên đoạn ?
Câu 3. Tìm giá trị nh nht của hàm số
2
9
()
x
fx
x
+
=
trên khoảng
(0; )+
.
Câu 4. Cho hàm số
( )
23
f x ax bx cx d= + + +
,
( , , , )a c b d
có đồ thị như hnh vẽ.
Tìm số đường tiệm cận đứng của đồ thị của hàm số
( )
2
1
1
x
y
fx
−
=
−
.
Câu 5. Một màn hình
BC
có chiều cao
1,4m
được đặt thẳng đứng v mép dưi của màn hình cách mặt
đt một khoảng
1,8BA m=
. Một chiếc đèn quan st mn hnh được đặt ở vị trí
O
trên mặt đt. Hãy xác
định khoảng cách
AO
sao cho góc quan sát
BOC
là ln nht. Kết quả lm tròn đến hàng phần chục và
dùng đơn vị m.
Câu 6. Một chiếc ô tô được đặt trên mặt đy dưi một khung sắt có dạng hnh hộp chữ nhật vi đy trên
l hnh chữ nhật
ABCD
, mặt phẳng
( )
ABCD
song song vi mặt mặt phẳng nằm ngang. Khung sắt đó
được buộc vo móc
E
của chiến cần cẩu sao cho cc đoạn dây cp
, , ,EA EB EC ED
có độ di bằng nhau
v cùng tạo vi mặt phẳng
( )
ABCD
một góc
0
60
như hnh vẽ. Chiếc cần cẩu kéo khung sắt lên theo
phương thẳng đứng. Biết lực căng
1 2 3 4
, , ,F F F F
đều có cường độ
( )
3000 N
v trọng lượng khung sắt l
( )
1000 N
. Tính trọng lượng của chiếc xe ô tô (lm tròn đến hng đơn vị).
( ) ( )
32
1
3 2024
3
x x x
y f x e me m e= = + + − +
m
( )
2024;2024−
( )
y f x=
0;ln2
| 1/15
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT HOÀNG VĂN THỤ
ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KỲ I TỔ TOÁN
MÔN TOÁN – KHỐI 12
NĂM HỌC 2024 – 2025 1. MỤC TIÊU
1.1. Kiến thức: Học sinh ôn tập các kiến thức về:
- Tính đồng biến, nghịch biến của một hàm số.
- Cực trị của một hàm số.
- Giá trị lớn nhất, giá trị nhỏ nhất của hàm số.
- Đường tiệm cận ngang, đường tiệm cận đứng, đường tiệm cận xiên của đồ thị hàm số.
- Vectơ trong không gian: hai vectơ cùng phương, hai vectơ cùng hướng/ngược hướng, hai vectơ bằng nhau.
- Các phép toán vectơ trong không gian.
1.2. Kĩ năng: Học sinh rèn luyện các kĩ năng:
- Rèn luyện năng lực tư duy và lập luận toán học, năng lực mô hình hoá toán học và năng lực giải quyết
vấn đề toán học thông qua việc mô hình hoá những vấn đề thực tiễn liên quan đến tính đơn điệu và cực trị
của hàm số, giá trị lớn nhất và GTNN của hàm số, đường tiệm cận của đồ thị hàm số.
- Rèn luyện các năng lực toán học, nói riêng là năng lực mô hình hoá toán học (thông qua việc sử dụng
các kiến thức về vectơ trong không gian để trả lời các câu hỏi trong phần Vận dụng).
- Bồi dưỡng hứng thú học tập, ý thức làm việc nhóm, ý thức tìm tòi, khám phá và sáng tạo cho HS. 2. NỘI DUNG
2.1. Các câu hỏi và bài tập minh họa
2.1.1. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi, học sinh chỉ chọn một phương án.
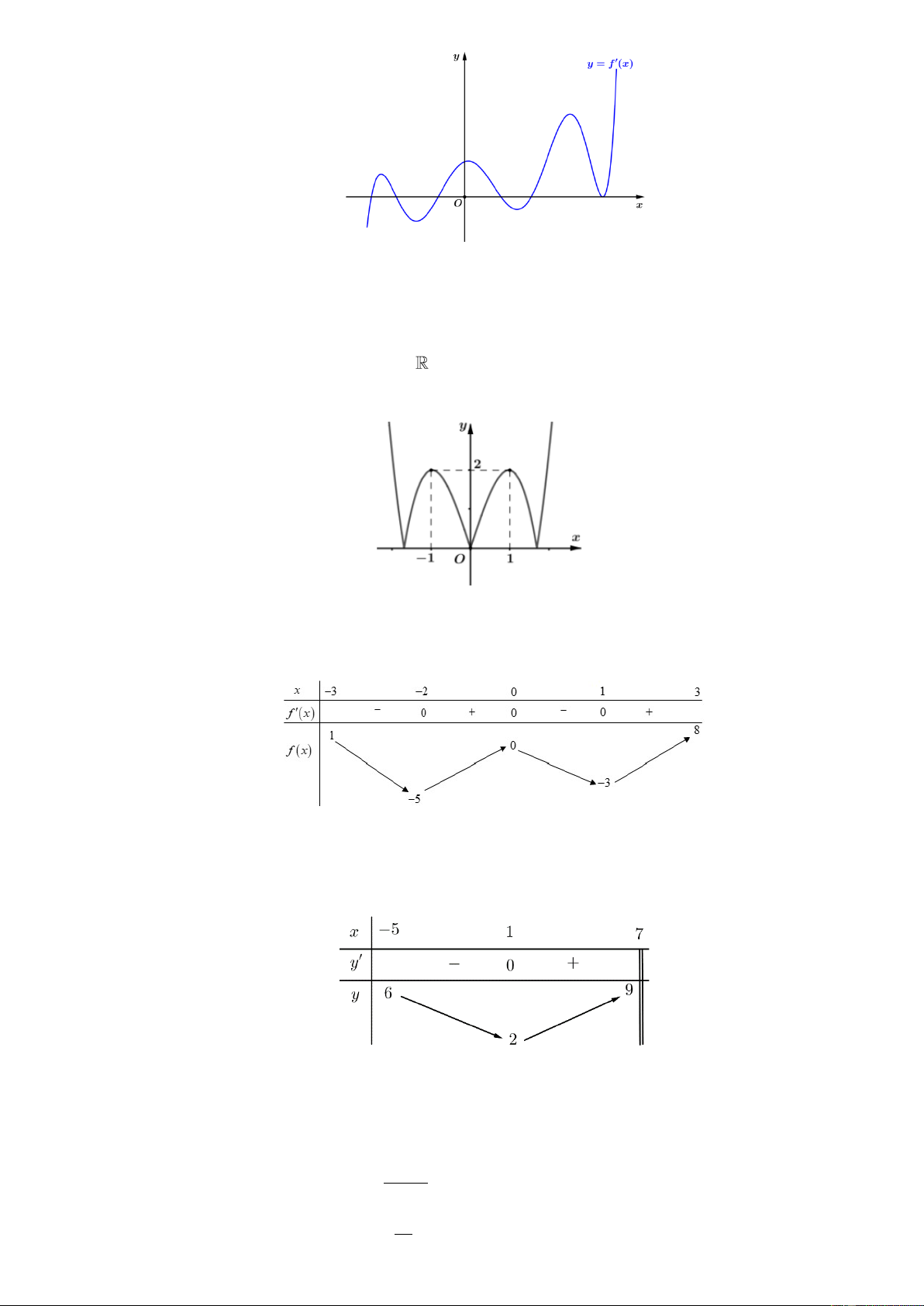
Câu 1. Cho hàm số y = f ( x) có đồ thị là đường cong trong hình vẽ dưới đây: y y=f '(x) x - O
Hàm số y = f ( x) đồng biến trên khoảng nào sau đây? A. (− ;  − ) 1 . B. ( 1 − ) ;1 . C. (1; 4). D. (1; +). mx + 4m
Câu 2. Cho hàm số y =
với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để x + m
hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của S . A. 5 . B. 4 . C.Vô số. D. 3 . 2
Câu 3. Hàm số y =
nghịch biến trên khoảng nào dưới đây? 2 x +1 A. ( 1 − ;1) . B. (− ;  +) . C. (0; +) . D. ( ; − 0) 2 x + Câu 4. Cho hàm số 3 y =
. Mệnh đề nào dưới đây đúng? x +1
A.Cực tiểu của hàm số bằng 3 − .
B.Cực tiểu của hàm số bằng 1.
C.Cực tiểu của hàm số bằng 6 − .
D.Cực tiểu của hàm số bằng 2
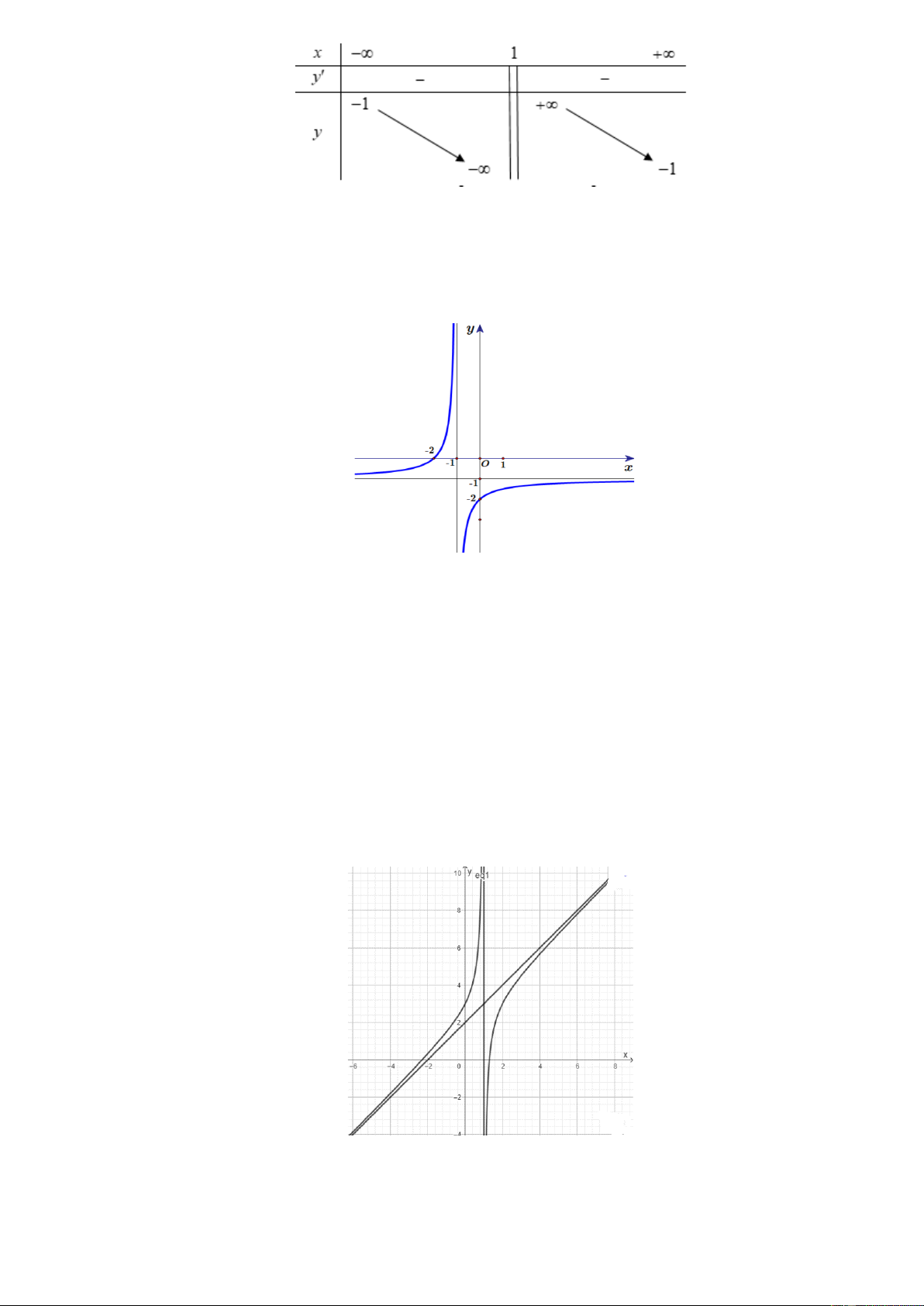
Câu 5. Cho hàm số y = f ( x) . Biết đồ thị của hàm số '
y = f ( x) như hình bên.
Tìm số điểm cực tiểu của hàm số y = f ( x) A. 5 . B. 4 . C. 3 . D. 2 .
Câu 6. Cho hàm số y = f (x) liên tục trên và có đồ thị như hình vẽ. Hỏi hàm số có bao nhiêu điểm cực trị? A. 4. B. 5. C. 2. D. 3.
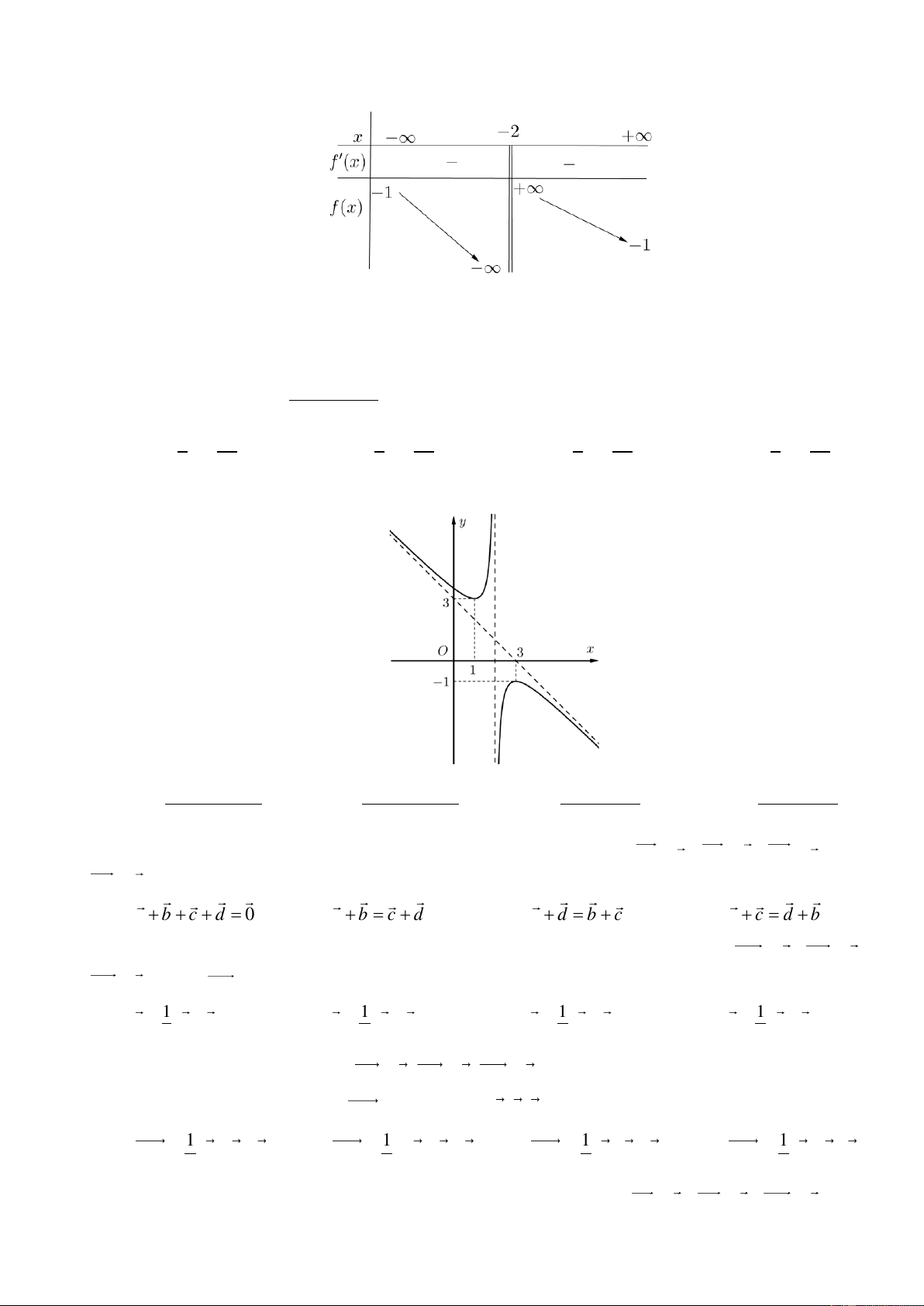
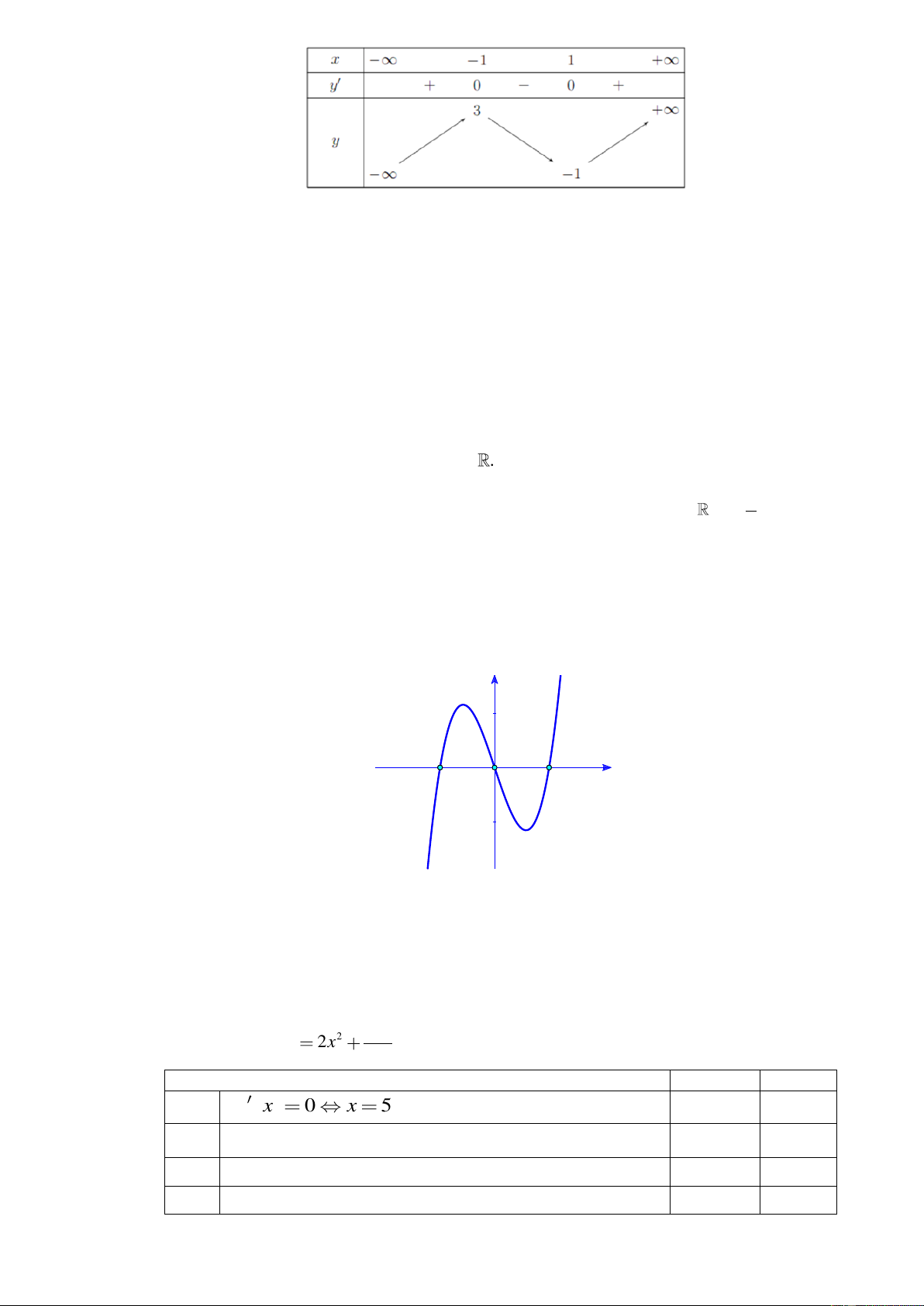
Câu 7. Cho hàm số y = f ( x) có bảng biến thiên như hình bên.
Giá trị lớn nhất của hàm số đã cho trên đoạn  3 − ;  3 bằng A. 0 . B. 3 . C. 1. D. 8 .
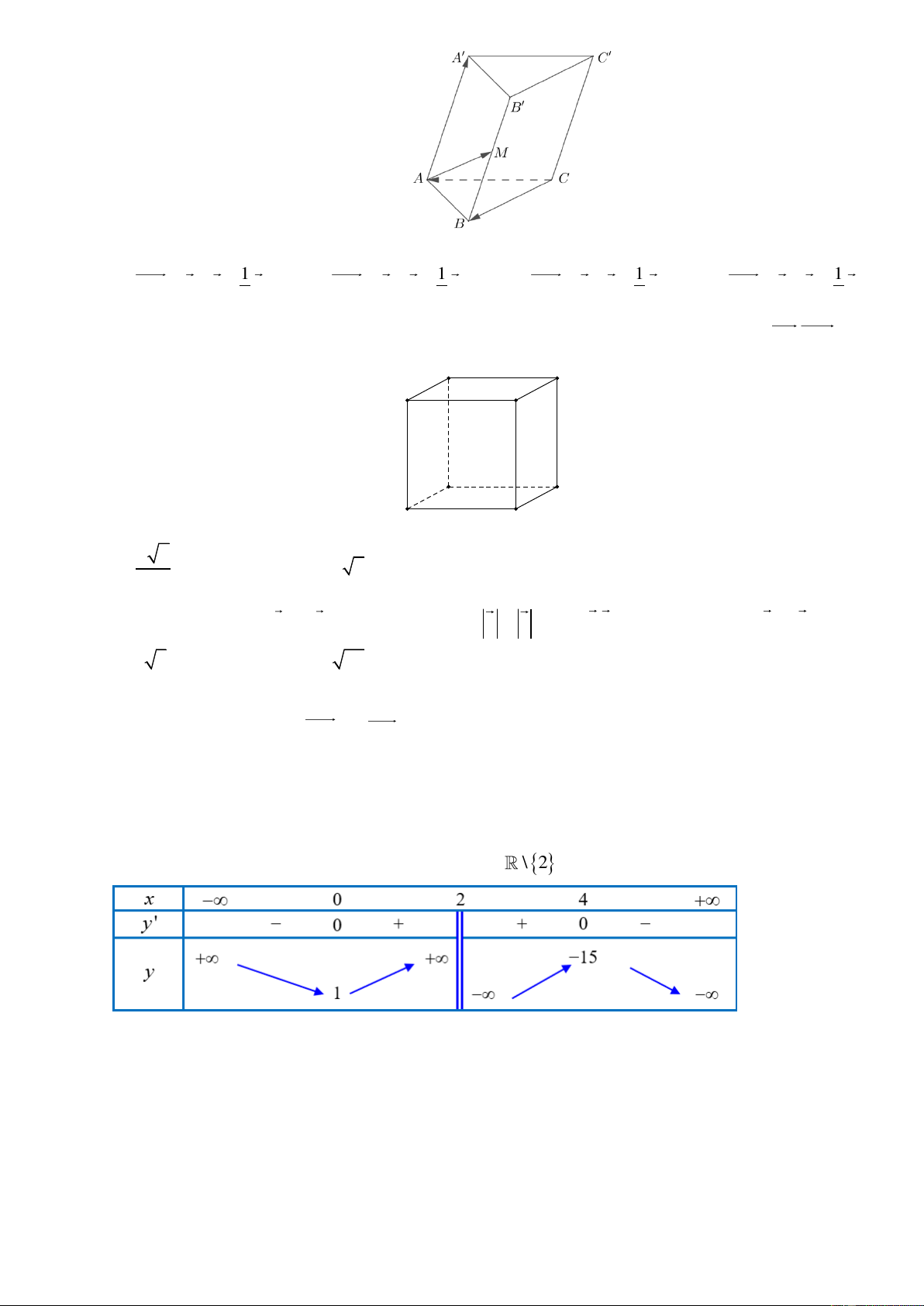
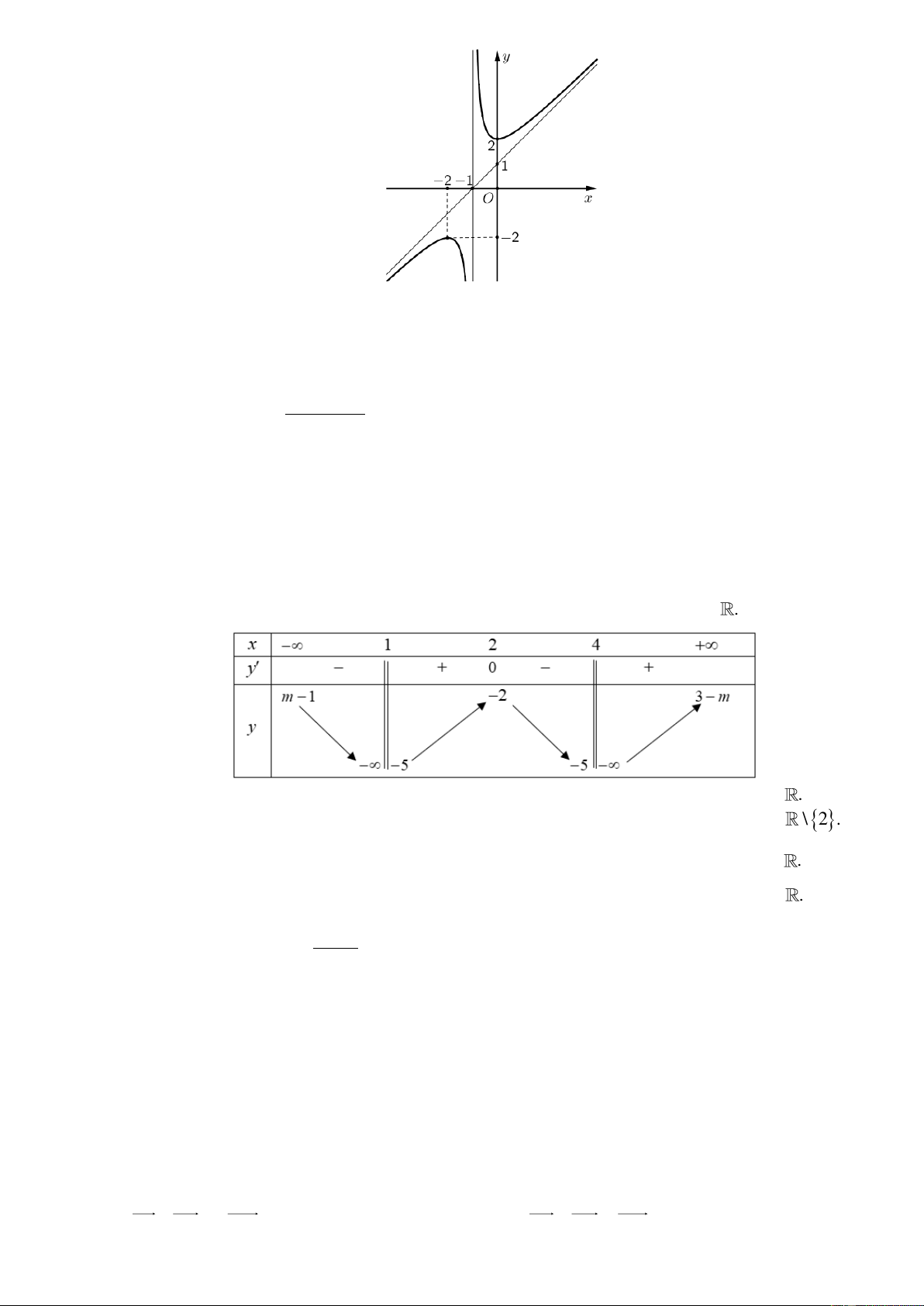
Câu 8. Cho hàm số y = f ( x) có bảng biến thiên trên  5 − ;7) như sau
Mệnh đề nào dưới đây đúng?
A. min f ( x) = 6.
B. min f ( x) = 2 .
C. max f ( x) = 9 .
D. max f ( x) = 6 .  5 − ;7)  5 − ;7)  5 − ;7)  5 − ;7) 2 x + 3
Câu 9. Giá trị lớn nhất của hàm số y =
trên đoạn 2;4 là x −1 19
A. max y = 7 B. max y =
C. max y = 6 .
D. max y= 8 2;4 2;4 3 2;4 2;4
Câu 10. Cho hàm số y = f ( x) có đạo hàm f ( x) tại mọi x  . Đồ thị của hàm số y = f ( x) được
cho như hình vẽ dưới đây. y x O 2 5
Biết rằng f (0) + f (3) = f (2) + f (5) . Hãy tìm giá trị nhỏ nhất, giá trị lớn nhất của y = f ( x) trên đoạn 0; 5?
A. Max f ( x) = f (5) .
B. Max f ( x) = f (0) . 0;  5 0;  5
C. Max f ( x) = f (2) .
D. Max f ( x) = f (3) . 0;  5 0;  5
Câu 11. Cho hàm số y = f (x) xác định và liên tục trên
có đồ thị bên dưới. Gọi M , m lần lượt là giá
trị lớn nhất và nhỏ nhất của hàm số trên đoạn [1;3]. Giá trị của M + m bằng:
A. M + m = 2 .
B. M + m = 4 − .
C. M + m = 3 − .
D. M + m = 1. Câu 12. Cho hàm số = 2x y
− 4xln 2 . Giá trị nhỏ nhất của hàm số trên đoạn 0;4 có dạng a −blnc .
Tính a + b + c ? A. 2 − . B. 14. C. 34. D. 0 . 1 
Câu 13. Gọi m, M lần lượt là giá trị nhỏ nhất, lớn nhất của hàm số y = x − ln x trên đoạn ;e   . Giá trị 2 
của M − m là 1 1
A. e − ln 2 − .
B. e −1. C. ln 2 − . D. e − 2 . 2 2
Câu 14. Cho hàm số y = f ( x) 2
= 4 − x . Khẳng định nào sau đây là sai?
A. Hàm số có GTLN là 2.
B. Hàm số có GTNN là 0.
C. Hàm số đạt GTLN tại x = 2.
D. Hàm số đạt GTNN tại x = 2.  3x − 3
Câu 15. Đồ thị hàm số y = x −
có tiệm cận ngang là 1
A. x = 1.
B. y = 1.
C. x = 2 . D. y = 3 .
Câu 16. Cho hàm số y = f ( x) có bảng biến thiên như sau'
Phương trình đường tiệm cận đứng của đồ thị hàm số đã cho là
A. x = 1.
B. y = 1. C. x = 1 − . D. y = 1 − .
Câu 17. Cho đồ thị của hàm số f ( x) như hình bên dưới?
Số đường tiệm cận của đồ thị của hàm số f ( x) là A. 1. B. 2. C. 0. D. 3.
Câu 18. Cho hàm số y = f ( x) có lim f ( x) =  và lim f ( x) =  . Chọn mệnh đề đúng? x 2 →− x→2
A. Đồ thị hàm số đã cho có đúng một tiệm cận đứng.
B. Đồ thị hàm số đã cho không có tiệm cận đứng.
C. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng y = 2 và y = 2 − .
D. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng x = 2 và x = 2 − .
Câu 19. Cho đồ thị hàm số y = f ( x) như hình bên. Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số đã cho có một tiệm cận đứng và một tiệm cận ngang
B. Đồ thị hàm số đã cho không có tiệm cận đứng.
C. Đồ thị hàm số đã cho có một tiệm cận ngang và một tiệm cận xiên
D. Đồ thị hàm số đã cho có một tiệm cận đứng và một tiệm cận xiên
Câu 20. Cho hàm số y = f ( x) có bảng biến thiên như sau:
Tổng số tiệm cận của đồ thị hàm số đã cho là A. 1. B. 2. C. 3. D. 0. 2 3x + 5x − 4
Câu 21. Cho hàm số y =
. Đường tiệm cận xiên của đồ thị hàm số đã cho là 5 − x + 4 3 37 3 37 3 37 3 37 A. y = − x − . B. y = − x − . C. y = − x − . D. y = − x − . 5 25 5 25 5 25 5 25
Câu 22. Đồ thị sau là của hàm số nào dưới đây? 2 2x − 9x +10 2 2x − 9x +10 2 x − 5x + 7 2 x − 5x + 7 A. y = . B. y = . C. y = . D. y = . −x + 2 x + 2 x + 2 −x + 2
Câu 23. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đặt SA = a ; SB = b ; SC = c ;
SD = d . Khẳng định nào sau đây đúng?
A. a + b + c + d = 0 .
B. a + b = c + d .
C. a + d = b + c .
D. a + c = d + b .
Câu 24. Cho hình lăng trụ AB . C A BC
  với G là trọng tâm của tam giác A BC
 . Đặt AA = a , AB = b , AC = .
c Khi đó AG bằng: 1 1 1 1
A. a + (b + c). B. a + (b+c).
C. a + (b + c).
D. a + (b + c). 3 4 6 2
Câu 25. Cho tứ diện ABCD . Đặt DA = a, DB = ,
b DC = c . Gọi M , N lần lượt là trung điểm của hai
cạnh AD và BC . Biểu diễn vectơ MN qua các vectơ a, , b c . 1 1 1 1 A. MN =
(a + b + c) . B. MN =
(−a + b + c) . C. MN =
(a − b + c) . D. MN =
(a + b − c) . 2 2 2 2
Câu 26. Cho hình lăng trụ AB . C AB C
 , M là trung điểm của BB . Đặt CA = a , CB = b , AA = c (Tham khảo hình vẽ).
Khẳng định nào sau đây đúng? 1 1 1 1
A. AM = a + c − b .
B. AM = a − c + b .
C. AM = b + c − a .
D. AM = b − a + c . 2 2 2 2
Câu 27. Cho hình lập phương ABC . D A BCD
  có cạnh bằng a (tham khảo hình vẽ). Tính . AB DC ' . A' D' B' C' A D B C a 2 A. . B. a 2 . C. 0 . D. 2 a . 2
Câu 28. Cho hai vectơ a và b thỏa mãn điều kiện a = b = 1 và .
a b = 2. Độ dài vectơ 2a + 3b bằng A. 5 5. B. 37. C. 8. D. 5.
Câu 29. Cho hình lập phương ABCD A BCD
 . Gọi M , N lần lượt là trung điểm của A D   và C D   .
Gọi  là góc giữa hai vectơ MN và AB . Số đo của góc  bằng bao nhiêu độ? A. 0 45 . B. 0 30 . C. 0 90 . D. 0 60 .
2.1.2. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu hỏi, học sinh chọn đúng hoặc sai.
Câu 30. Cho hàm số y = f ( x) xác định, liên tục trên \  
2 và có bảng biến thiên dưới đây:
a) Hàm số y = f ( x) đạt cực đại tại x = 4 .
b) Hàm số y = f ( x) + 2024 có giá trị cực tiểu là 2025 .
c) Hàm số y = f ( x) có hai cực trị trái dấu.
d) Số điểm cực trị của hàm số y = f ( x + ) 1 là 2.
Câu 31. Cho hàm số y = f ( x) có bảng biến thiên như sau:
a) Hàm số đồng biến trên khoảng (− ;  2 − )
b) Cực tiểu của hàm số bằng 1
c) Đường thẳng y = 2
− x −1 đi qua hai điểm cực trị của đồ thị hàm số
d) Hàm số y = f (2 − x) đồng biến trên (1;3) .
Câu 32. Cho hàm số 3 2
y = −x − 6x − (2m + 9) x + 4. a) y(− ) 1 = 2 − m
b) Với m = 4 thì hàm số đã cho nghịch biến trên .  3 
c) Tập hợp tất cả các giá trị của tham số m để hàm số đã cho nghịch biến trên là ; +  . 2 
d) Có 7 giá trị nguyên của tham số m thuộc đoạn  8 − ; 
8 để hàm số đã cho nghịch biến trên khoảng (− ;  2 − ).
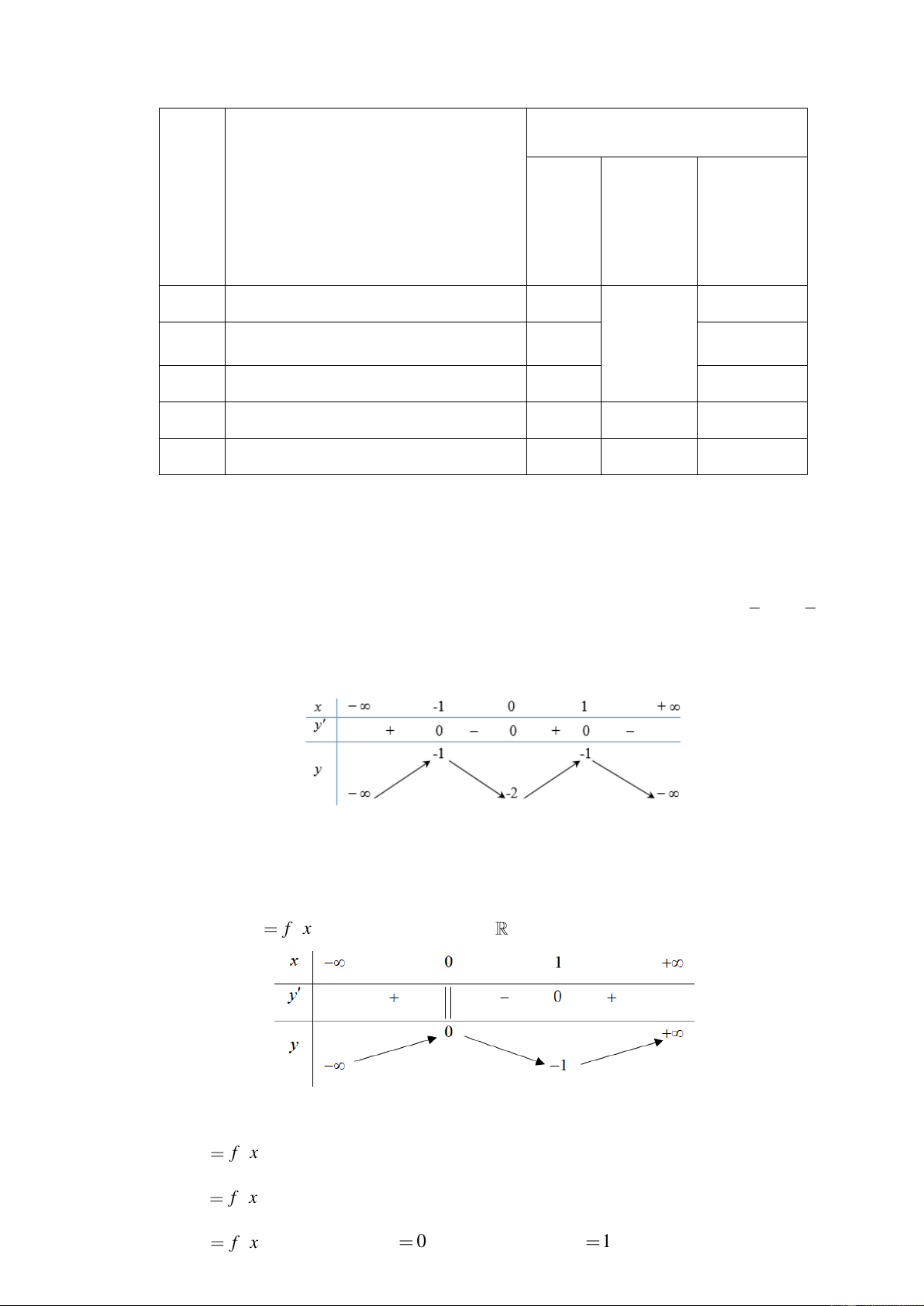
Câu 33. Cho hàm số y = f (x) . Biết hàm số y = f (x) có đồ thị như hình vẽ bên dưới: y -1 1 x O
a) Phương trình f ( x) = 0 có 3 nghiệm phân biệt. b) Hàm số đồng biến trên khoảng (2; +).
c) Hàm số có 3 điểm cực trị.
d) Hàm số y = f ( 2
x − 1) đồng biến trên khoảng (0;1). 500
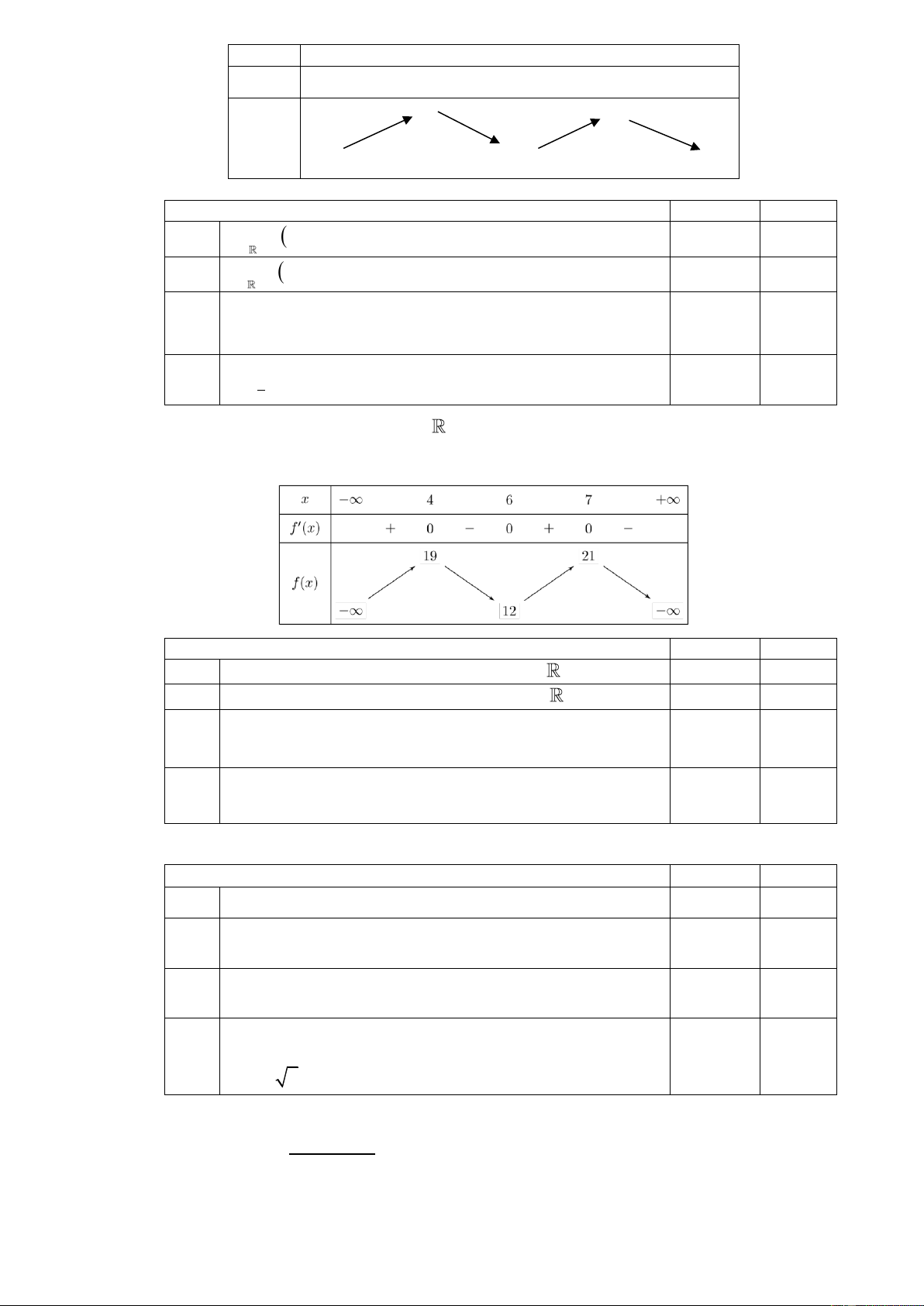
Câu 34. Cho hàm số 2 f x 2x . x Khẳng định Đúng Sai a) f x 0 x 5 . b)
lim f ( x) = 0 . x→+ c)
Giá trị nhỏ nhất của hàm số trên (0;5) là 150. d)
Giá trị nhỏ nhất của hàm số trên (0;+) là 150.
Câu 35. Cho hàm số f ( x) có bảng biến thiên như sau: x − 1 − 0 1 + f ( x) + 0 − 0 + 0 − 5 3 f ( x) − − 2 Khẳng định Đúng Sai a) max f ( x) = 5. x b) min f ( x) = 2. x c)
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số f ( x) trên  1 −  ;1 là 7 d)
max f (sin x) = 5.    x 0;    2 
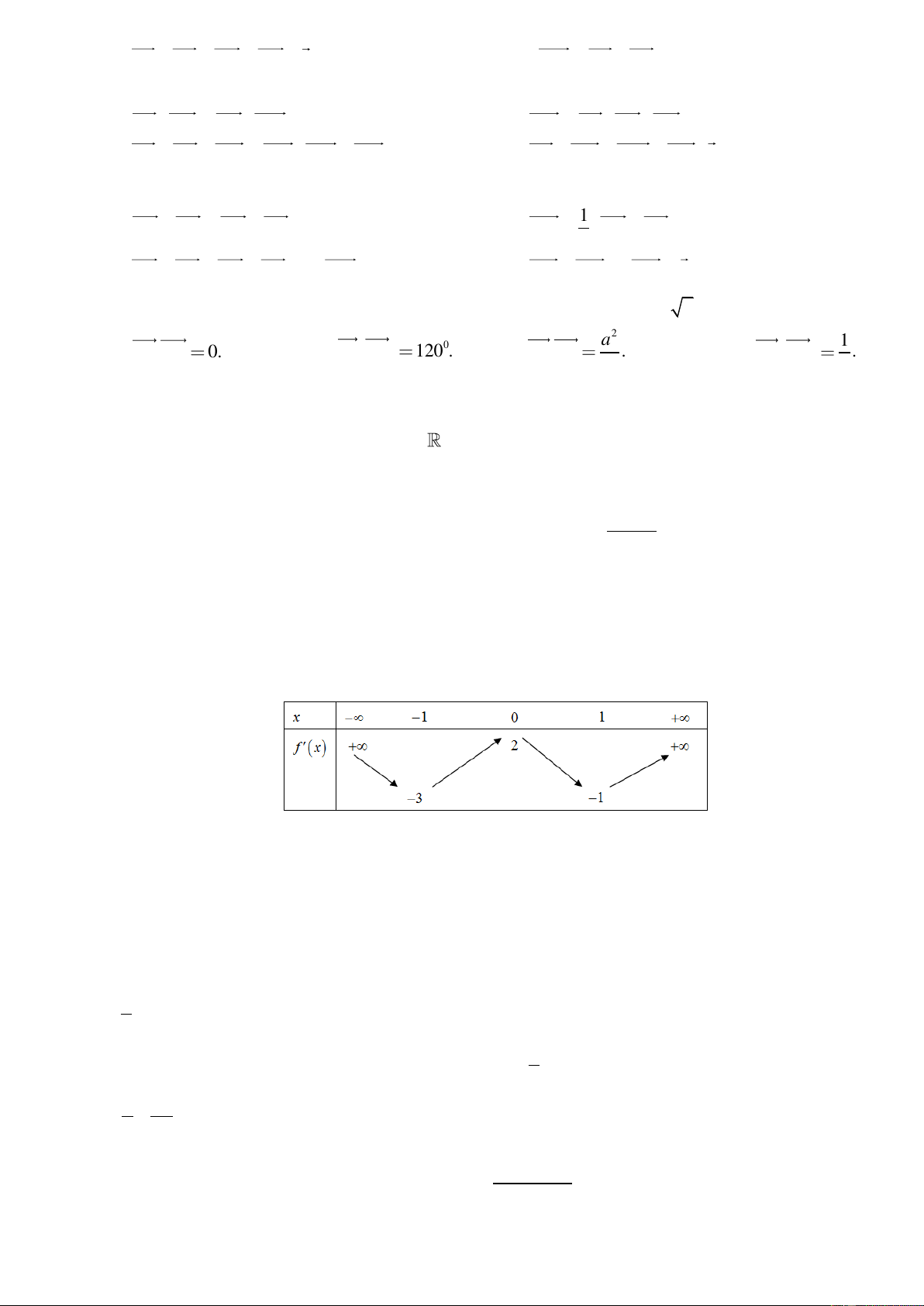
Câu 36. Cho hàm số y = f (x) xác định trên
và có bảng biến thiên như hình vẽ. Khẳng định Đúng Sai a)
Giá trị lớn nhất của hàm số y = f (x) trên bằng 21. b)
Giá trị nhỏ nhất của hàm số y = f (x) trên bằng 12. c)
Giá trị lớn nhất của hàm số h ( x) = f (x) + 2m trên đoạn 0; 
5 bằng 34 khi m = 15 . d)
Hàm số g ( x) = f (2x − 2) đạt giá trị lớn nhất trên khoảng ( ; − 4) tại x = 3. Câu 37. Cho hàm số 4 2
y = f (x) = x − 2x − 2. Khẳng định Đúng Sai a)
Giá trị nhỏ nhất của hàm số trên đoạn  1 − ;  1 là 3 − . b)
Giá trị lớn nhất của hàm số trên nửa khoảng  1; − + ) là 2 − . c)
Tổng giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn  2 − ;2 là 3. d)
Nếu min y = f (x ) = y , max y = f ( x ) = y thì  A A B B 0; 2 0;2 AB = 2 2
ax + bx + c
Câu 38. Cho hàm số y =
C như hình vẽ bên dưới. mx + có đồ thị ( ) n
a) Đồ thị (C ) có một tiệm cận đứng. b) Đồ thị (C ) có tiệm cận xiên là y = x +1.
c) Đồ thị (C ) đi qua điểm ( 2
− ;2) . d) Giao điểm của hai tiệm cận là E ( 1 − ;0) 2 x + 3x + 2
Câu 39. Cho hàm số y = 2 x − . 1
a) Đường thẳng x = 1 là đường tiệm cận đứng của đồ thị hàm số.
b) Đường thẳng y = 1 là đường tiệm cận ngang của đồ thị hàm số.
c) Đồ thị hàm số đã cho có 1 tiệm cận ngang, 2 tiệm cận đứng.
d) Đồ thị hàm số đã cho có 2 đường tiệm cận.
Câu 40. Cho hàm số y = f ( x) có bảng biến thiên như hình dưới đây, trong đó m .
a) Đồ thị hàm số có đúng 2 đường tiệm cận đứng và 1 đường tiệm cận ngang với mọi m .
b) Đồ thị hàm số có đúng 2 đường tiệm cận đứng và 2 đường tiệm cận ngang với mọi m  \   2 .
c) Đồ thị hàm số có đúng 2 đường tiệm cận đứng và 2 đường tiệm cận ngang với mọi m .
d) Đồ thị hàm số có đúng 1 đường tiệm cận đứng và 2 đường tiệm cận ngang với mọi m . −x +
Câu 41. Cho hàm số f ( x) 1 = x− . 2
a)Tiệm cận đứng của đồ thị hàm số trên có phương trình là x = 2 .
b)Tiệm cận ngang của đồ thị hàm số trên có phương trình là y = 1.
c)Đồ thị hàm số trên có hai đường tiệm cận tạo với hai trục tọa độ một tam giác có diện tích bằng 2.
d)Đồ thị hàm số g ( x) = .
x f ( x) có tiệm cận xiên song song với đường phân giác của góc phần tư thứ 2.
Câu 42. Cho tứ diện ABCD có M , N lần lượt là trung điểm các cạnh AC và .
BD Gọi G là trung
điểm của đoạn thẳng MN.
a) GA + GC = 2GM .
b) GB + GD = MN .
c) GA + GB + GC + GD = 0 .
d) 2NM = AB + CD .
Câu 43. Cho hình hộp ABC . D A BCD
  với tâm O.
a) AB+ AA = AD+DD .
b) AC = AB+ AD+ AA .
c) AB + BC + CC = AD+D O  + OC .
d) AB + BC + C D   + D = A 0.
Câu 44. Cho tứ diện đều ABCD , M và N theo thứ tự là trung điểm của cạnh AB và CD . 1
a) AC + BD = AD + BC . b) MN = (AD+BC). 2
c) AC + BD + AD + BC = −4NM .
d) MC + MD − 4MN = 0 .
Câu 45. Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a và BC = a 2 . 2 a 1 a) A . B AC 0. b) 0 , SA AB 120 . c) SC.AB .
d) cos SC, AB . 2 2
2.1.3 Câu trắc nghiệm trả lời ngắn.
Câu 46. Cho hàm số y = f ( x) liên tục trên
và có đạo hàm f ( x) = ( x − )
1 ( x − 3)( x − 5) . Hàm số = ( ) = ( 2 y g x
f x ) có bao nhiêu điểm cực trị? x +1
Câu 47. Có bao nhiêu giá trị nguyên của tham số m để hàm số y =
nghịch biến trên khoảng x + 3m (6;+) ?
Câu 48. Biết rằng đồ thị hàm số 4 2
y = x − 2ax + b có một điểm cực trị là (1;2) . Tính khoảng cách giữa
điểm cực đại và điểm cực tiểu của đồ thị hàm số đã cho (quy tròn đến hàng phần trăm).
Câu 49. Cho hàm số f ( x) , bảng biến thiên của hàm số f ( x) như sau:
Hàm số y = f ( 2
4x − 4x) có bao nhiêu điểm cực trị? A. 9 . B. 5 . C. 7 . D. 3 .
Câu 50. Tìm giá trị nhỏ nhất của hàm số 3
y = x − 3x + 4 trên đoạn 0; 2.
Câu 51. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số 4 3 2 y =
sin x + 4 cos x − 5sin x +1. Tính giá trị của M − m . 3 5
Câu 52. Cho các số thực dương x , y thỏa mãn 2x + y =
. Tìm giá trị nhỏ nhất P của biểu thức 4 min 2 1 P = + . x 4 y 2 x − 3x + 2
Câu 53. Đường tiệm cận xiên của đồ thị hàm số y =
có dạng y = ax + b . Tìm tổng 2a + 3b ? x + 4
Câu 54. Với giá trị nào của tham số m thì đường tiệm cận ngang của đồ thị hàm số − +
f ( x) (2m ) 1 x 3 =
đi qua điểm M (1; 2)? x − 2024 2 2x + x
Câu 55. Biết đường tiệm cận xiên của đồ thị hàm số y =
cắt trục hoành và trục tung lần lượt tại x +1 hai điểm ,
A B . Tính diện tích tam giác OAB (với O là gốc tọa độ). 15t
Câu 56. Nồng độ oxygen trong hồ theo thời gian t cho bởi công thức y (t ) = 5 − 2
9t + , với y được 1
tính theo mg / l và t được tính theo giờ, t  0 . Đường tiệm cận ngang của đồ thị hàm số y = y (t ) khi
t → + có dạng y = a . Tính giá trị của a a
Câu 57. Cho tứ diện đều ABCD , M là trung điểm của cạnh BC . Khi đó cos ( A , B DM ) bằng . b
Tính giá trị của biểu thức T a . b
Câu 58. Cho hình lâp phương ABCD A BCD
  có cạnh bằng a . Gọi M , N lần lượt là trung điểm của A D   và C D   . Tích vô hướng 2 MN C B
 = na ( n là số thập phân). Giá trị của n bằng bao nhiêu?
Câu 59. Cho ba vectơ a , b , c thỏa mãn a = 1, b = 2 , a − b = 3 . Tính (a − 2b).(2a + b) .
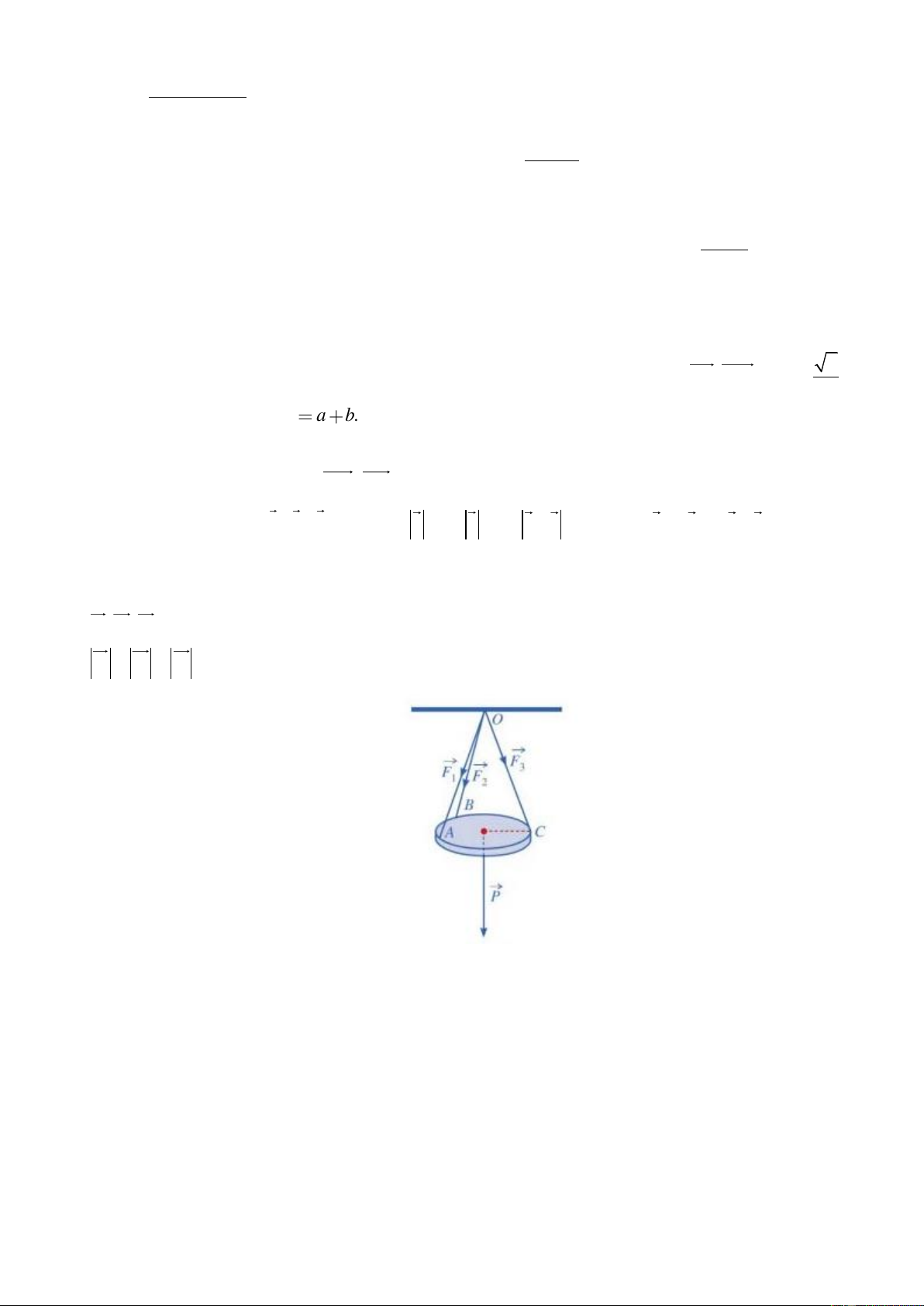
Câu 60. Một tấm gỗ tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không giãn xuất
phát từ điểm O trên trần nhà và lần lượt buộc vào ba điểm ,
A B,C trên tấm gỗ tròn sao cho các lực căng F , F , F OA OB OC 1 2
3 lần lượt trên mỗi dây , ,
đôi một vuông góc với nhau và có độ lớn
F = F = F = 10 N (xem hình vẽ). 1 2 3 ( )
Tính trọng lượng P của tấm gỗ tròn đó (làm tròn đến hàng phần mười).
2.2. MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KỲ I
MÔN: TOÁN, LỚP 12 – THỜI GIAN LÀM BÀI: 90 phút HÌNH THỨC TN TN STT NỘI DUNG 4 lựa Đúng – TL ngắn chọn Sai (mức độ (mức 2,3,4) độ (mức độ 1, 1, 2, 3) 2) 1
Tính đơn điệu và cực trị của hàm số 4 2
Giá trị lớn nhất giá trị nhỏ nhất của 2 2 3 2 hàm số 3
Đường tiệm cận của đồ thị hàm số 2 1 4 Véc tơ trong không gian 4 1 1 Tổng 12 4 6 ĐỀ MINH HỌA
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi, học sinh chỉ chọn một phương án.
Câu 1. Cho hàm số f ( x) đồng biến trên khoảng (0; + ) .Khẳng định nào sau đây đúng?    
A. f (2)  f (− ) 1 . B. f ( ) 1  f (3) .
C. f (3)  f ( ) . D. 2 3 ff .      3   4 
Câu 2. Cho hàm số y = f ( x) có bảng biến thiên như sau :
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ( 1 − ;0) B. (1; +) C. ( ) ;1 − D. (0 ) ;1
Câu 3. Cho hàm số y
f x xác định, liên tục trên và có bảng biến thiên
Khẳng định nào sau đây là khẳng định đúng? A. Hàm số y
f x có giá trị cực tiểu bằng 1. B. Hàm số y
f x có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -1. C. Hàm số y
f x đạt cực đại tại x
0 và đạt cực tiểu tại x 1 . D. Hàm số y
f x có đúng một cực trị.
Câu 4. Cho hàm số f ( x) có đạo hàm f ( x) = x ( x − )( x + )3 1 2 , x
. Số điểm cực trị của hàm số là: A. 3 . B. 2 . C. 5 . D.1.
Câu 5. Cho hàm số y = f ( x) liên tục trên
thỏa mãn giá trị nhỏ nhất của hàm số trên là 5 . Khẳng
định nào sau đây là đúng?
A. f ( x)  5 x . B. f x 5 x , x , f x 5 . 0 0
C. f ( x)  5 x . D. f x 5 x , x , f x 5 . 0 0
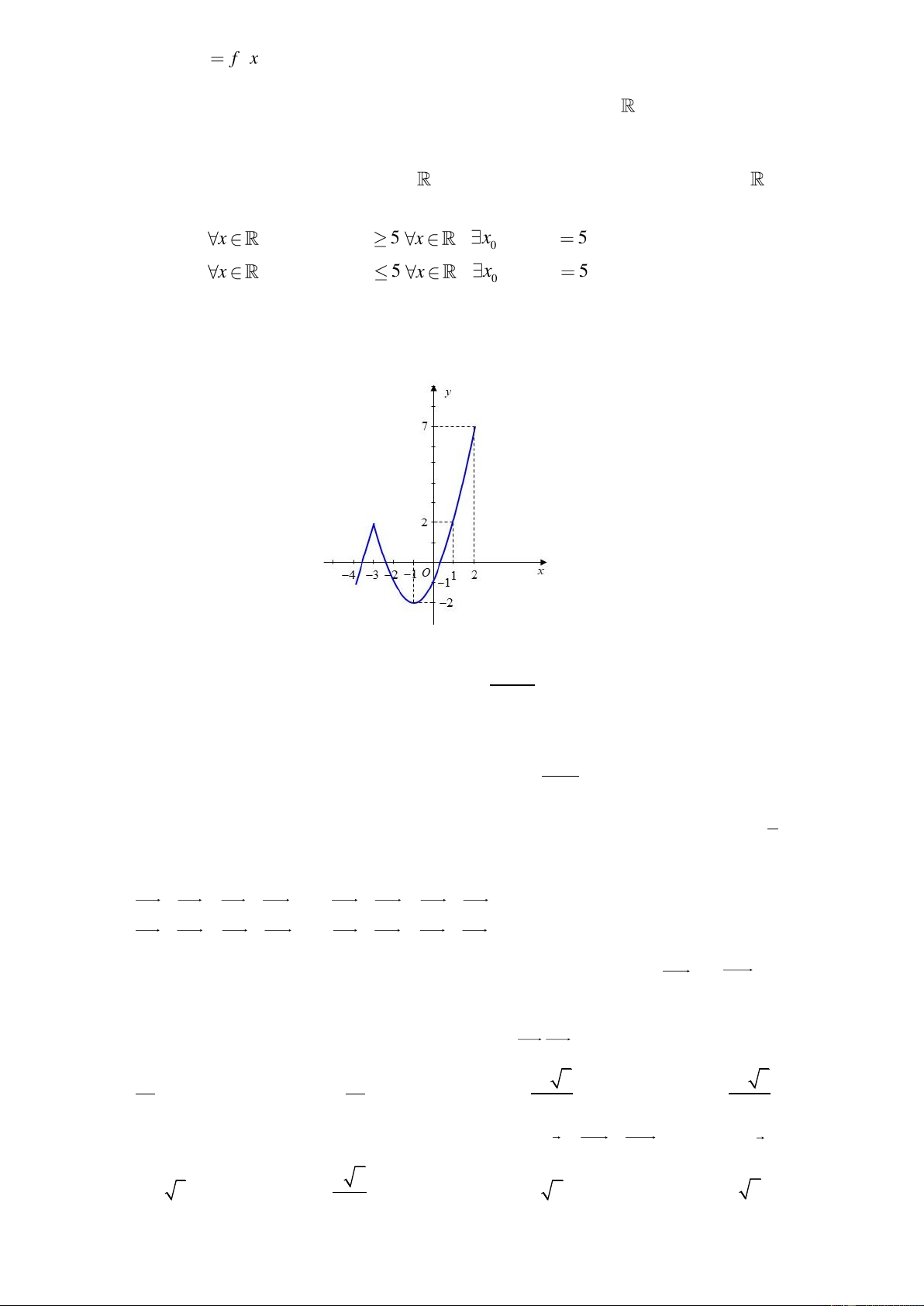
Câu 6. Cho hàm số y = f ( x) liên tục trên  4
− ;2 và có đồ thị như hình vẽ bên. Khi đó
max f ( x) + min f ( x) bằng  4 − ;−  1  4 − ;2 A. 1. B. 0 . C. 2 . D. 5 . 3x − 4
Câu 7. Đường tiệm cận đứng của đồ thị hàm số y = x + có phương trình là 4 A. x = 4 − .
B. x = 4 . C. y = 4 − . D. y = 3 . 5
Câu 8. Đường tiệm cận xiên của đồ thị hàm số y = 2x +1− x + cắt trục hoành tại điểm 4  1  A. A(2 ) ;1 .
B. B (2;0) .
C. C (1;3) . D. D − ;0   .  2 
Câu 9. Cho tứ diện ABCD . Mệnh đề nào dưới đây là mệnh đề đúng?
A. BC + AB = DA − DC . B. AC − AD = BD − BC .
C. AB − AC = DB − DC . D. AB − AD = CD + BC .
Câu 10. Cho hình hộp chữ nhật ABCD A BCD
 . Tính góc giữa hai vectơ AA và C C  . A. 0 45 . B. 0 30 . C. 0 90 . D. 0 180 .
Câu 11. Cho tứ diện đều ABCD có cạnh bằng a . Tính A .
B BC theo a 2 a 2 a 2 a 3 2 a 3 A. . B. − . C. . D. . 2 2 2 2
Câu 12. Cho hình lập phương ABC . D A BCD
  cạnh a . Đặt x = AA + AC . Độ dài của x bằng a 6
A. (1+ 3)a . B. . C. a 6 . D. a 2 . 2
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu hỏi, học sinh chọn đúng hoặc sai. 2 13 x −3x+ Câu 1. Cho hàm số 4 y = 2 .
a) Hàm số nghịch biến trên khoảng ( 1 − ;0) .
b) Hàm số đồng biến trên khoảng (0 ) ;1 .
c) Hàm số có giá trị cực tiểu y = 2 . CT
d) Hàm số có 2 điểm cực trị.
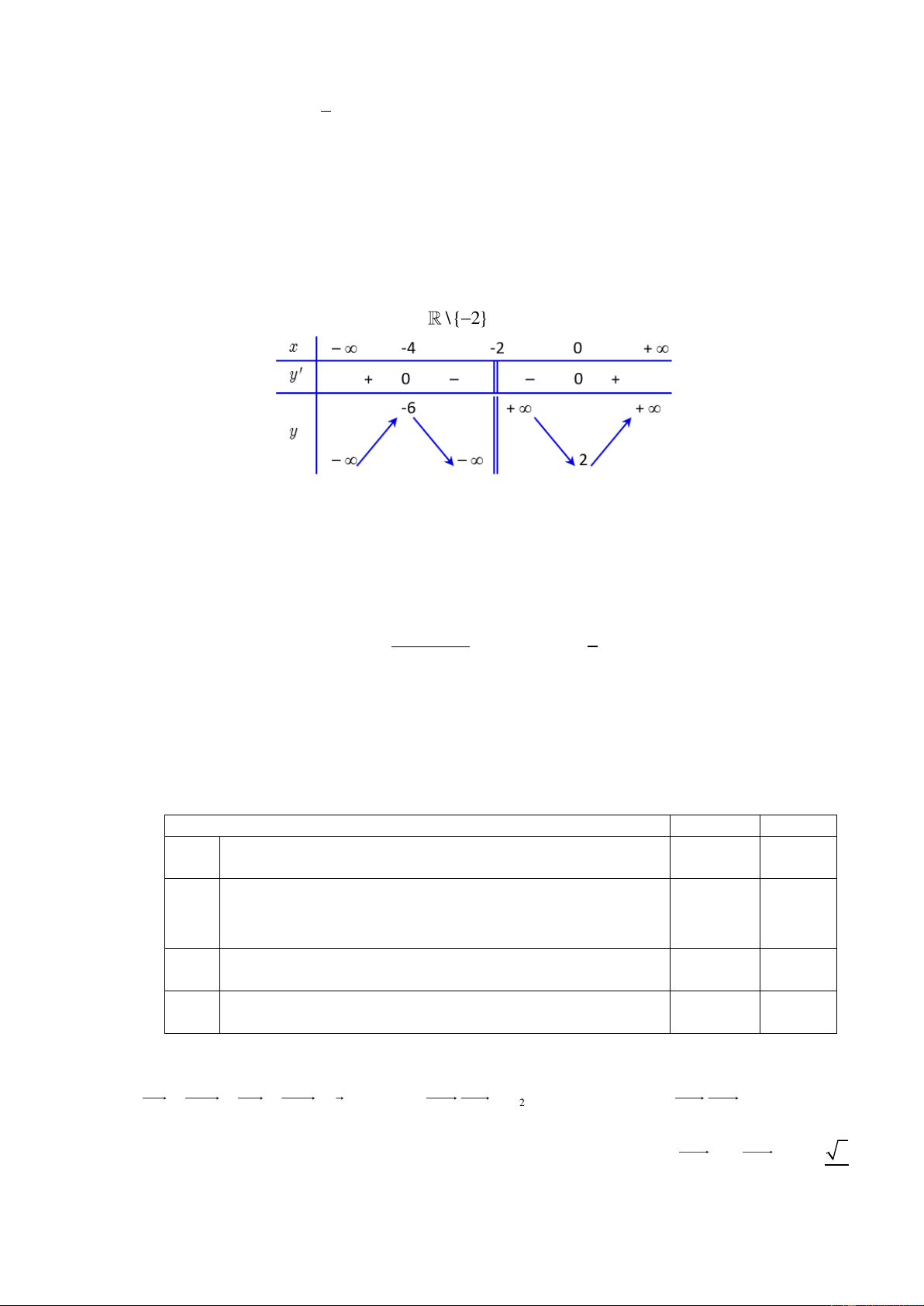
Câu 2. Cho hàm số y = f (x) xác định trên \ { 2
− } và có bảng biến thiên như sau:
a) Hàm số có giá trị cực tiểu lớn hơn giá trị cực đại. b) x = 2
− đường tiệm cận đứng của đồ thị hàm số.
c) Đồ thị hàm số có một đường tiệm cận ngang 2
x + bx + c
d) Biết hàm số f (x) có dạng f (x) = khi đó f ( ) 5 1 = x + n 3
Câu 3. Một cơ sở sản xuất khăn mặt đang bán mỗi chiếc khăn với giá 30.000 đồng một chiếc và mỗi
tháng cơ sở bán được trung bình 3000 chiếc khăn. Cơ sở sản xuất đang có kế hoạch tăng giá bán để có lợi
nhận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá 30.000 đồng mà cứ
tăng giá thêm 1000 đồng thì mỗi tháng sẽ bán ít hơn 100 chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là 18.000. Khẳng định Đúng Sai a)
Nếu cơ sở bán mỗi chiếc khăn với giá 37000 thì số tiền lãi sau 1 tháng là 44 . b)
Sau khi cơ sở tăng giá mỗi chiếc khăn thêm x thì tổng số
lợi nhuận một tháng của cơ sở được tính theo công thức f ( x) 2 = 1
− 00x +1800x + 36000 . c)
Để đạt lợi nhuận lớn nhất thì số khăn bán ra giảm 800 chiếc. d)
Để đạt lợi nhuận lớn nhất thì mỗi chiếc khăn cần bán với giá 39000 đồng.
Câu 4. Cho hình lập phương ABC . D A BCD
  có cạnh bằng a .
a) 2 AB + B C
  + CD + D A   = 0 . b) 2
AD .AB = a . c) AB .CD = 0 . 3
d) Gọi M , N lần lượt là trung điểm của AD , BB . Cosin của góc hợp bởi MN và AC bằng . 3
Phần III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 1 đến câu 6. 2 2x − x + 9
Câu 1. Tìm giá trị cực đại của hàm số y = . 2x −1 1 Câu 2. Cho hàm số = ( ) 3x 2 x = + + ( − 3) x y f x e me m
e + 2024 . Tìm số giá trị nguyên của m thuộc 3 khoảng ( 2
− 024;2024) để hàm số y = f (x) đồng biến trên đoạn 0;ln 2 ? 2 x + 9
Câu 3. Tìm giá trị nhỏ nhất của hàm số f (x) = trên khoảng (0; +) . x
Câu 4. Cho hàm số f ( x) 3 2
= ax + bx + cx + d , (a,c, , b d
) có đồ thị như hình vẽ. 2 x −1
Tìm số đường tiệm cận đứng của đồ thị của hàm số y = f (x)− . 1
Câu 5. Một màn hình BC có chiều cao 1, 4m được đặt thẳng đứng và mép dưới của màn hình cách mặt
đất một khoảng BA = 1,8m . Một chiếc đèn quan sát màn hình được đặt ở vị trí O trên mặt đất. Hãy xác
định khoảng cách AO sao cho góc quan sát BOC là lớn nhất. Kết quả làm tròn đến hàng phần chục và dùng đơn vị m.
Câu 6. Một chiếc ô tô được đặt trên mặt đáy dưới một khung sắt có dạng hình hộp chữ nhật với đáy trên
là hình chữ nhật ABCD , mặt phẳng ( ABCD) song song với mặt mặt phẳng nằm ngang. Khung sắt đó
được buộc vào móc E của chiến cần cẩu sao cho các đoạn dây cáp E ,
A EB, EC, ED có độ dài bằng nhau
và cùng tạo với mặt phẳng ( ABCD) một góc 0
60 như hình vẽ. Chiếc cần cẩu kéo khung sắt lên theo
phương thẳng đứng. Biết lực căng F , F , F , F
3000 N và trọng lượng khung sắt là 1 2 3 4 đều có cường độ ( )
1000( N ) . Tính trọng lượng của chiếc xe ô tô (làm tròn đến hàng đơn vị).