UBND QUẬN HOÀNG MAI
TRỌNG TÂM ÔN TẬP GIỮA HỌC KỲ II - LỚP 7
TRƯỜNG THCS VĨNH HƯNG
Năm học: 2023 - 2024 MÔN: TOÁN A. LÝ THUYẾT I. ĐẠI SỐ
1) Thu thập, phân loại và biểu diễn dữ liệu.
2) Phân tích và xử lí dữ liệu.
3) Biểu đồ đoạn thẳng.
4) Biểu đồ hình quạt tròn.
5) Biến cố trong một số trò chơi đơn giản.
6) Xác xuất của biến cố ngẫu nhiên trong một số trò chơi đơn giản. II. HÌNH HỌC 1) Hai tam giác bằng nhau.
2) Trường hợp bằng nhau thứ nhất của tam giác cạnh – cạnh – cạnh.
3) Trường hợp bằng nhau thứ hai của tam giác cạnh – góc – cạnh.
4) Trường hợp bằng nhau thứ ba của tam giác góc – cạnh – góc. B. BÀI TẬP
Dạng 1. Các bài toán về thống kê
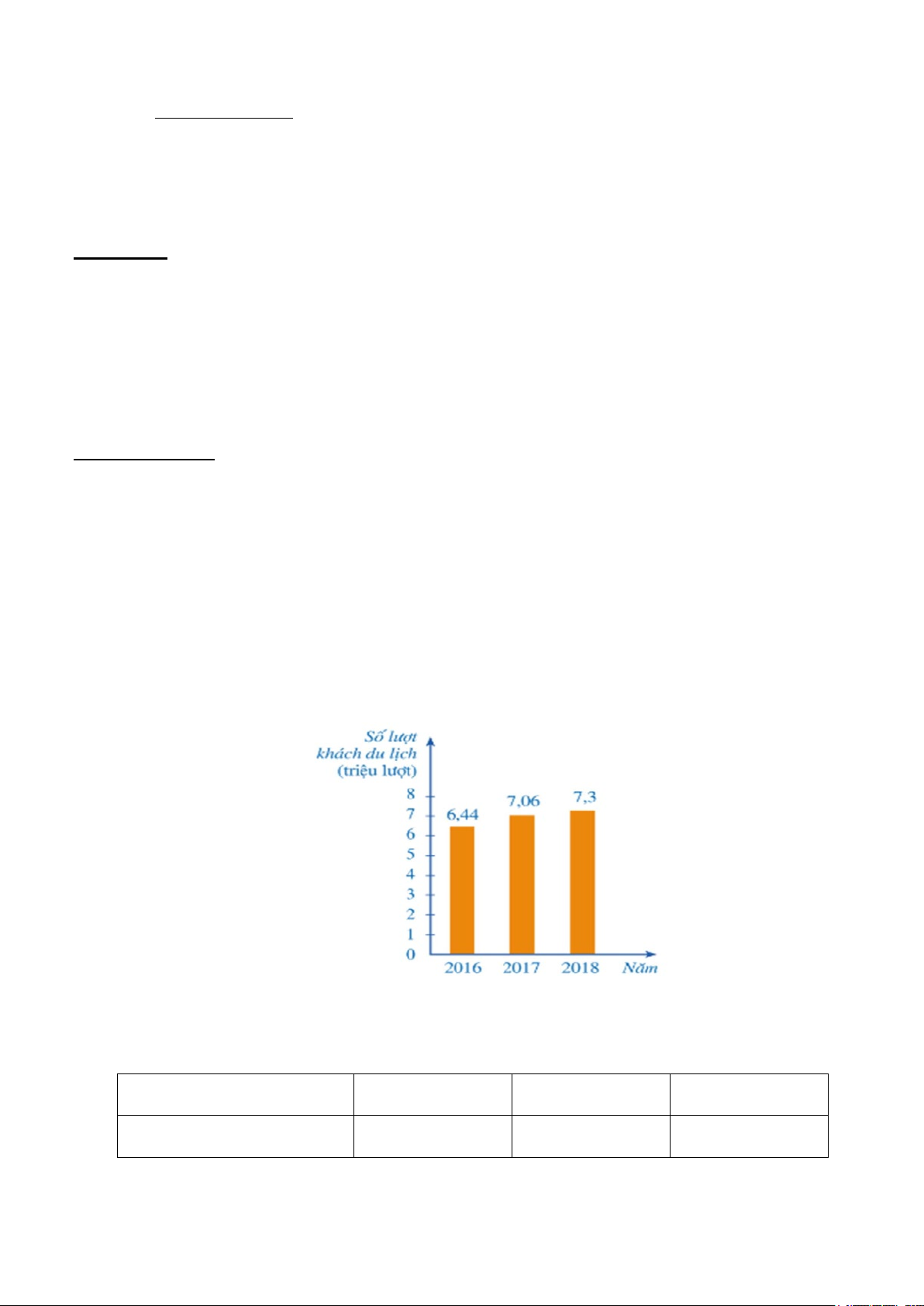
Bài 1. Biểu đồ cột sau biểu diễn số lượt khách du lịch (ước đạt) đến Ninh Bình trong các năm 2016,2017, 2018.
a) Nêu đối tượng thống kê và tiêu chí thống kê.
b) Lập bảng số liệu thống kê lượt khách du lịch đến Ninh Bình theo mẫu sau: Năm 2016 2017 2018 Số lượt khác ? ? ?
c) Tính số lượt khách du lịch chênh lệch giữa các năm. Năm nào có nhiều lượt khách du
lịch nhất? Năm nào có ít khách du lịch nhất?
Bài 2. Để bố trí đội ngũ nhân viên, phục vụ, số sản phẩm quản lí của một nhà hàng đã tiến
hành đếm số khách đến cửa hàng đó vào một số thời điểm trong ngày và được biểu diễn
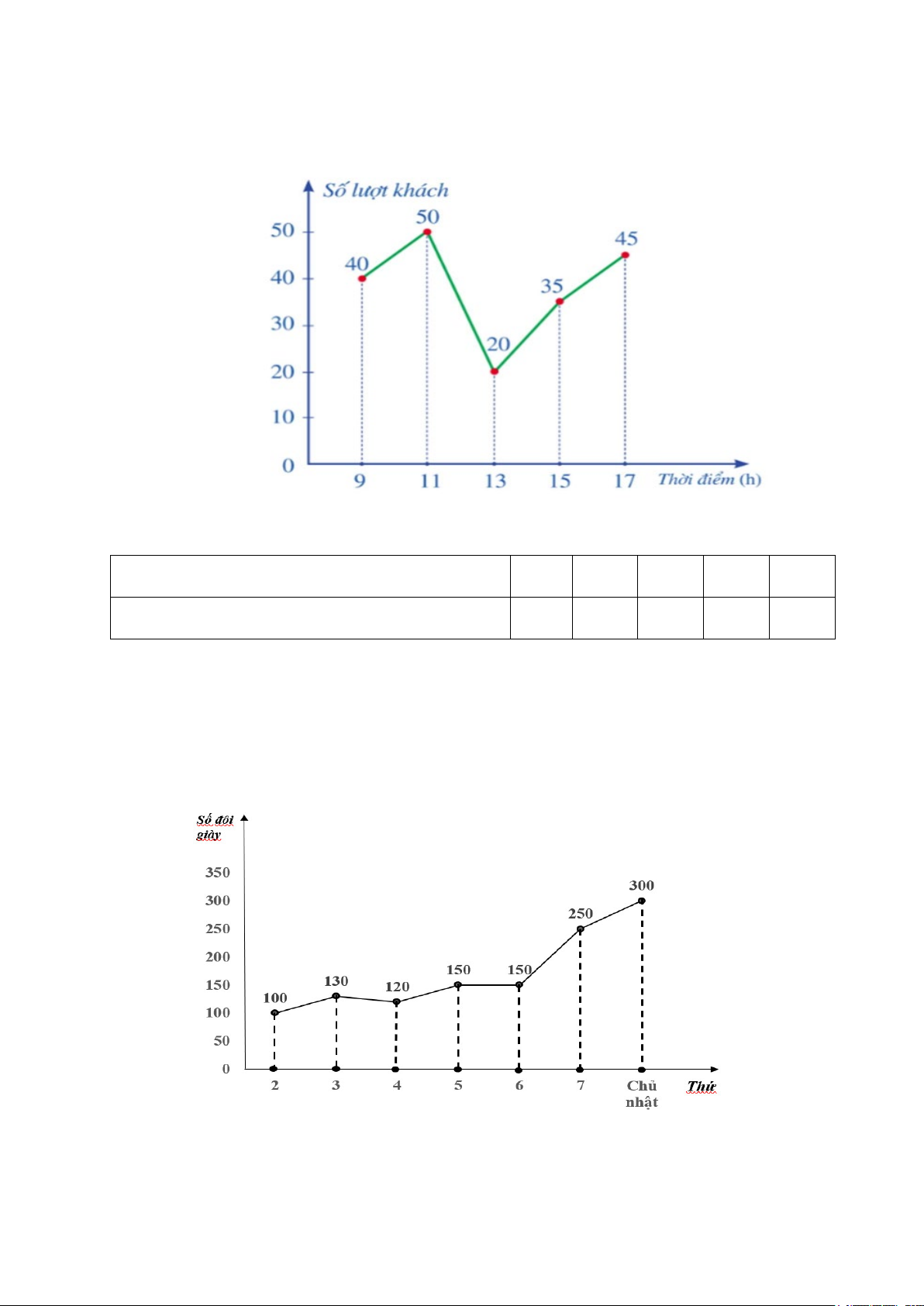
bằng biểu đồ đoạn thẳng sau:
a) Lập bảng thống kê số lượt khách hàng đến nhà hàng theo mẫu sau: Thời điểm (h) 9 11 13 15 17 Số lượt khách ? ? ? ? ?
b) Trong các thời điểm này, thời điểm nào có nhiều khách hàng nhất? Thời điểm nào có ít khách hàng nhất?
c) Tính tổng số lượt khách trong cả 5 thời điểm của cửa hàng?
Bài 3. Biểu đồ đoạn thẳng ở hình vẽ sau biểu diễn số đôi giày cửa hàng Thành Phát đã bán trong một tuần.
Số đôi giày cửa hàng Thành Phát đã bán trong một tuần
a)Lập bảng số liệu thống kê số đôi giày cửa hàng Thành Phát đã bán trong một tuần theo mẫu sau: Thứ 2 3 4 5 6 7 Chủ nhật Số đôi giày ? ? ? ? ? ? ?
b) Tính tổng số đôi giày cửa hàng Thành Phát đã bán trong một tuần?
c) Tính tỉ số phần trăm số đôi giày cửa hàng Thành Phát đã bán trong ngày chủ nhật so
với số đôi giày cửa hàng đã bán trong một tuần?
Bài 4. Số truyện đóng góp được trong một tuần lễ của các bạn học sinh lớp 7A về thư
viện trường cho trong bảng thống kê sau: Ngày
Số truyện đóng góp được Thứ Hai 50 Thứ Ba 45 Thứ Tư 19 Thứ Năm 17 Thứ Sáu 13 Thứ Bảy 8
a) Vẽ biểu đồ đoạn thẳng biểu diễn dữ liệu trong bảng thống kê trên.
b) Cho biết xu hướng tăng, giảm về số sách góp được trong tuần.
c) Ngày nào trong tuần các bạn học sinh đóng góp được nhiều truyện nhất?
d) Số truyện đóng góp được vào ngày thứ Năm và thứ Sáu chiếm bao nhiêu phần trăm
tổng số truyện đã quyên góp được trong tuần?
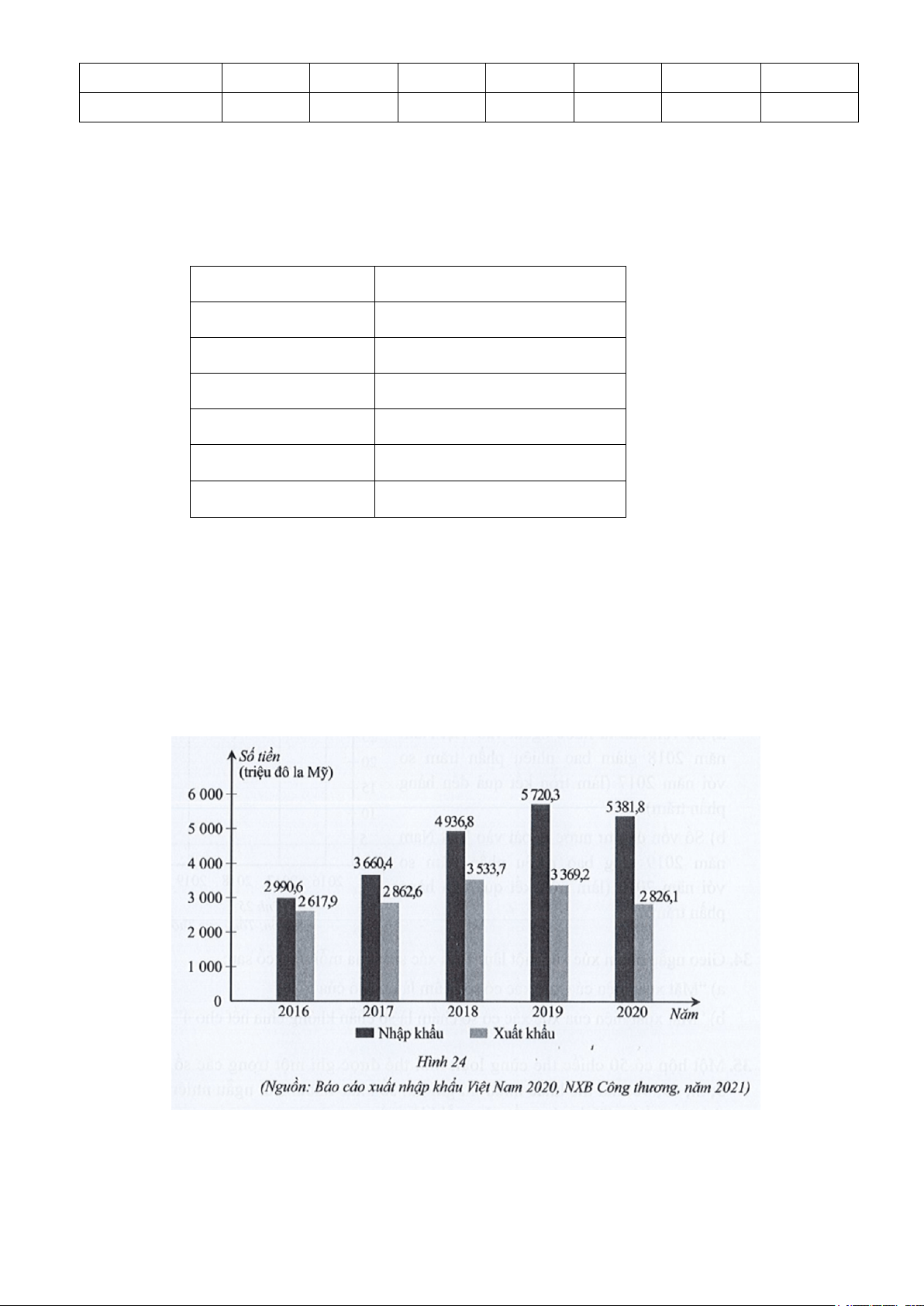
Bài 5. Biểu đồ cột kép ở Hình 24 biểu diễn kim ngạch xuất nhập khẩu của Việt Nam với
Indonesia trong các năm 2016, 2017, 2018, 2019, 2020.
a) Lập bảng số liệu thống kê kim ngạch xuất nhập khẩu của Việt Nam với Indonesia theo mẫu sau: Năm
2016 2017 2018 2019 2020 Kim ngạch nhập khẩu ? ? ? ? ? (triệu đô la Mỹ) Kim ngạch xuất khẩu ? ? ? ? ? (triệu đô la Mỹ)
b) Trong năm 2020, kim ngạch nhập khẩu của Việt Nam từ Indonesia gấp bao nhiêu lần
kim ngạch xuất khẩu của Việt Nam sang Indonesia (làm tròn kết quả đến hàng đơn vị)?
c) Hãy cho biết tổng kim ngạch xuất khẩu của Việt Nam sang Indonesia trong giai đoạn
từ năm 2016 đến năm 2020 bằng bao nhiêu phần trăm tổng kim ngạch nhập khẩu của
Việt Nam từ Indonesia trong giai đoạn từ năm 2016 đến năm 2020 (làm tròn kết quả đến hàng đơn vị)?
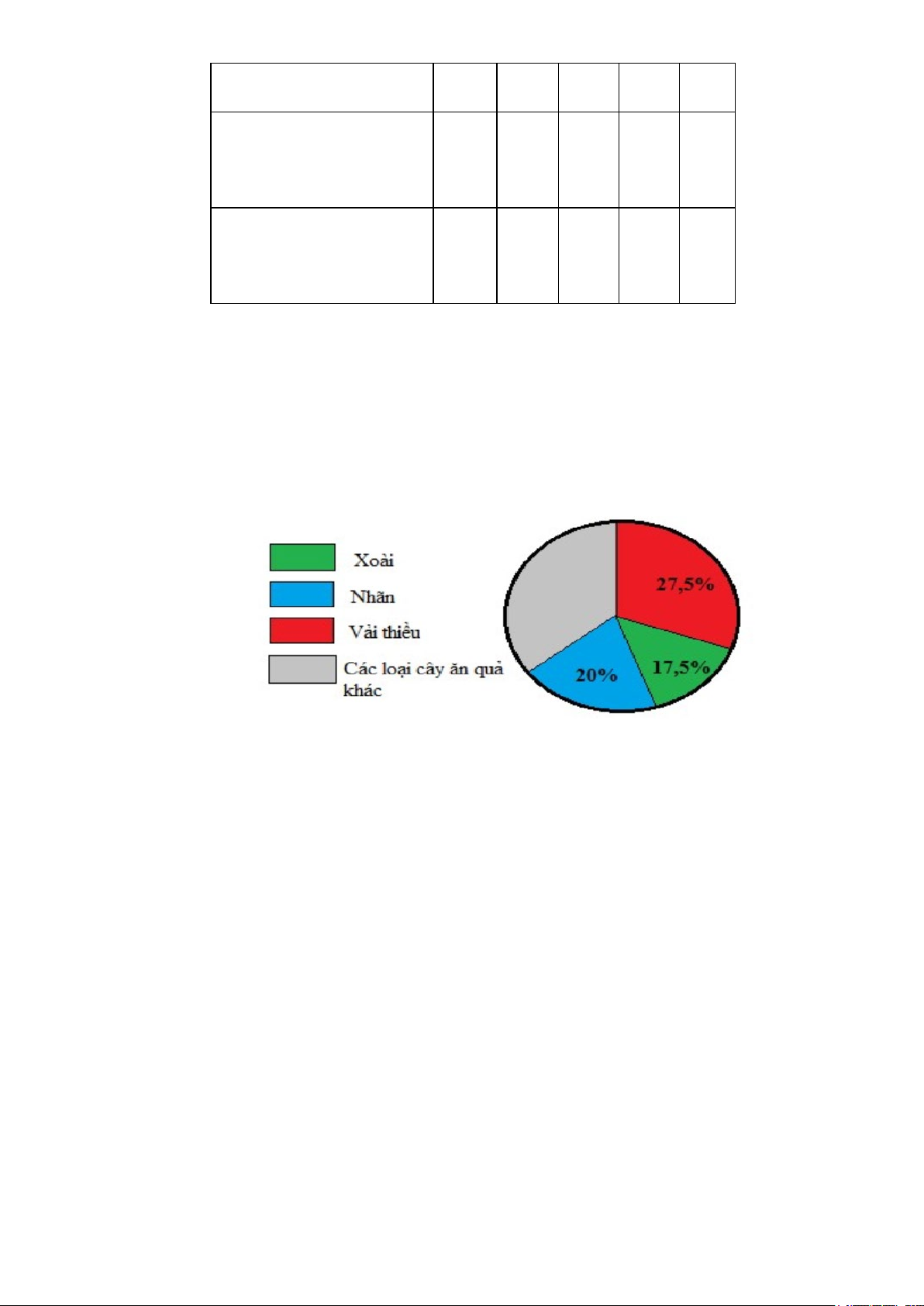
Bài 6. Khối lượng các loại quả siêu thị T nhập về bán được thể hiện bằng biểu đồ sau:
a) Tính tỉ số phần trăm khối lượng các loại quả khác mà siêu thị T nhập về bán.
b) Biết siêu thị T nhập về 44kg vải thiều. Hỏi siêu thị T nhập bao nhiêu ki-lô-gam xoài, bao nhiêu ki-lô-gam nhãn?
Dạng 2. Các bài toán về xác suất
Bài 1. Gieo ngẫu nhiên xúc xắc một lần. Tính xác suất của biến cố:
a) “Mặt xuất hiện của xúc xắc có số chấm là số lẻ”.
b) “Mặt xuất hiện của xúc xắc có số chấm là số chia 3 dư 1”.
c) “Mặt xuất hiện của xúc xắc có số chấm là số nguyên tố”.
d) “Mặt xuất hiện của xúc xắc có số chấm là số lớn hơn 2”.
Bài 2. Một hộp có 20 chiếc thẻ, mỗi thẻ được ghi một trong các số 1, 2, 3, ..., 20; hai thẻ
khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp.
a) Tìm số phần tử của tập hợp A gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra?
b) Tính xác suất của biến cố “Số xuất hiện trên thẻ được rút ra chia hết cho 3”?
Bài 3. Một hộp có 100 chiếc thẻ cùng loại, mỗi thẻ được ghi một số trong các số
1,2,3,. .,99,100 (hai thẻ khác nhau ghi hai số khác nhau). Rút ngẫu nhiên một thẻ trong
hộp. Tìm số phần tử của tập hợp C gồm các kết quả có thể xảy ra đối với số xuất hiện
trên thẻ được rút ra. Sau đó, hãy tính xác suất của mỗi biến cố sau:
a)” Số xuất hiện trên thẻ được rút ra là số chia hết cho 3”.
b) “Số xuất hiện trên thẻ được rút ra là số khi chia cho 2 và 5 đều dư 1”.
c) “Số xuất hiện trên thẻ được rút ra là số có tổng các chữ số bằng 6”.
Bài 4. Lớp 7A có 15 học sinh nữ và 25 học sinh nam. Chọn ngẫu nhiên một học sinh
trong lớp. Tìm số phần tử của tập hợp E gồm các kết quả có thể xảy ra đối với học sinh
được chọn ra. Sau đó, hãy tính xác xuất của mỗi biến cố sau:
a) “Học sinh được chọn ra là học sinh nữ”.
b) “Học sinh được chọn ra là học sinh nam”.
Dạng 3. Một số bài toán hình
Bài 1. Cho tam giác ABC, gọi D, E lần lượt là trung điểm của AB và AC, lấy F sao cho E
là trung điểm của DF. Chứng minh rằng: a) DB = CF b) B ∆ DC = F ∆ CD
Bài 2. Cho tam giác ABC, gọi M, N lần lượt là trung điểm của AC, AB. Trên tia đối của
tia NC lấy E sao cho NE = NC, trên tia đối của tia MB lấy D sao cho MD = MB. Chứng minh rằng: a) A ∆ MD = C ∆ MB b) AD // BC
c) A là trung điểm của DE.
Bài 3. Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Trên tia đối của tia
MA lấy sao cho AM = MD. Chứng minh rằng: a) AC ⊥ CD b) BC AM = 2
Bài 4. Cho tam giác ABC. Trên tia đối của tia AB, AC lần lượt lấy các điểm D và E sao
cho AD = AB và AE = AC. Gọi M, N lần lượt là trung điểm của BC và DE. Chứng minh rằng: a) A ∆ BC = A ∆ DE
b) DE = BC và DE song song với BC c) A ∆ EN = A ∆ CM d) M, A, N thẳng hàng. Bài 5. Cho AB ∆
C vuông tại A, AB = AC . Kẻ CE ⊥ AB,(E∈AB). Kẻ BD ⊥ AC
(D∈AC). Gọi O là giao điểm của BD và CE. Chứng minh rằng: a) BD = CE b) OE = OD và OB = OC
c) OA là tia phân giác của góc BAC.
Bài 6. Cho tam giác ABC vuông tại A có AB < AC, đường phân giác BD. Từ D vẽ DE vuông góc với BC tại E. a) Chứng minh A ∆ BD = E ∆ BD b) Chứng minh AD < DC
Dạng 4. Một số bài tập nâng cao
Bài 1. Cho tam giác ABC vuông ở A, M là trung điểm AC. Kẻ tia Cx vuông góc CA (tia
Cx và điểm B ở hai nửa mặt phẳng đối nhau bờ AC). Trên tia Cx lấy điểm D sao cho
CD = AB. Chứng minh ba điểm B, M, D thẳng hàng.
Bài 2. Cho hai đoạn thẳng AC và BD cắt nhau tại trung điểm O của mỗi đoạn. Trên tia
AB lấy điểm M sao cho B là trung điểm AM, trên tia AD lấy điểm N sao cho D là trung
điểm AN. Chứng minh ba điểm M, C, N thẳng hàng.
Bài 3. Cho tam giác ABC cân ở A. Trên cạnh AB lấy điểm M, trên tia đối tia CA lấy
điểm N sao cho BM = CN. Gọi K là trung điểm MN.
Chứng minh ba điểm B, K, C thẳng hàng.
-------------------- HẾT --------------------