28 trang 4 lượt tải

Đề cương giữa kỳ 2 Toán 10 năm 2024 – 2025 trường THPT Kiến Thụy – Hải Phòng

8

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề cương ôn tập kiểm tra giữa học kỳ 2 môn Toán 10 năm học 2024 – 2025 trường THPT Kiến Thụy, thành phố Hải Phòng.

Chủ đề: Đề giữa HK2 Toán 10 235 tài liệu

Môn: Toán 10 3.1 K tài liệu

Tác giả:

Profile

Linh Đan

1 tuần trước
Danh sách Quiz
/28
TRƯỜNG THPT KIẾN THỤY
TỔ TOÁN - TIN
MA TRẬN NỘI DUNG, NĂNG LỰC VÀ CẤP ĐỘ TƯ DUY MÔN TOÁN LỚP 10
NĂM HỌC 2024 – 2025
1. MA TRẬN ĐỀ KIỂM TRA ĐỊNH KÌ GIỮA HỌC KÌ II
TT
Chương/
chủ đề
Nội dung/
đơn vị
kiến thức
Mức độ đánh giá
Tổng
Tỉ lệ
%
điểm
TNKQ Tự luận
Nhiều lựa chọn
Đúng - Sai
Trả lời ngắn
Biết Hiểu VD Biết Hiểu VD Biết Hiểu VD Biết Hiểu VD Biết Hiểu VD
1
Hàm số,
đồ thị và
ứng dụng
Hàm số
2
45
Hàm số bậc
hai
Câu 13
a,b,c
Câu 15 2,75 1
Dấu của
tam thức
bậc hai
Câu 5
Câu 13
d
Câu
19
1 1,25
Phương
trình quy
về phương
trình bậc
hai
Câu 6
Câu
16
1 1
2
Phương
pháp tọa
độ trong
mặt
phẳng
Phương
trình đường
thẳng
Câu
7,8
Câu 14
a,b,c,d
Câu 17
Câu
20
3 1
55
Vị trí tương
đối giữa hai
đường
thẳng. Góc
và khoảng
cách
Câu
9.10
Câu
18
2 2
Đường tròn
trong mặt
phẳng tọa
độ
Câu
11,12
Câu
21
2 1
Tổng số câu
1,75
0,25
2
2
2
1
13,75
4,25
3
Tổng số điểm
1,75
0,25
1,0
1,0
2,0
1,0
4,5
3,5
2
Tỉ lệ %
30
20
20
30
45
35
20
2. BẢN ĐẶC TẢ ĐỀ KIỂM TRA ĐỊNH KÌ GIỮA HỌC KÌ II
TT
Chương/
Chủ đề
Nội dung/
Đơn vị kiến
thức
Yêu cầu cần đạt
Dạng thức câu hỏi
TNKQ
Tự luận
Nhiều lựa chọn
Đúng - Sai
Trả lời ngắn
Nhiều lựa chọn
Biết
Hiểu
VD
Biết
Hiểu
VD
Biết
Hiểu
VD
Biết
Hiểu
VD
1
Hàm số, đồ
thị và ứng
dụng
Hàm số
Nhận biết: (Câu 1,2)
-
Nhận biết được những mô hình thực tế (dạng
bảng, biểu đồ, công thức) dẫn đến khái niệm hàm
số.
- Nhận biết được khoảng đồng biến, nghịch biến
dựa vào đồ thị hàm số
Câu
1,2
Hàm số bậc
hai
Nhận biết: (Câu 3,4; Câu 13: a, b, c)
-
Nhận biết được hàm số bậc hai. Nhận dạng
được đồ thị hàm số bậc hai.
-
Nhận biết được trục đối xứng, tọa độ đỉnh, giao
điểm của đồ thị với trục
hoành từ đồ thị.
-
Các công thức tìm tọa độ đỉnh, phương trình
trục đối xứng.
-
Kiểm tra điểm thuộc đồ thị hàm số bậc hai
Vận dụng:
(Câu 15)
-
Vận dụng được kiến thức về hàm số bậc hai và
đồ thị vào giải quyết một số bài toán thực tiễn.
Câu
3,4
Câu 13
a,b,c
Câu
15
Dấu của tam
thức bậc hai
Nhận biết: (Câu 5)
-
Nhận biết được dạng của tam thức bậc hai.
Thông hiểu:
(Câu 13d; Câu 19)
-
Giải thích được định lí về dấu tam thức bậc hai
từ việc quan sát đồ thị của hàm số.
- Giải được bài toán về bất phương trình bậc hai
Câu 5
Câu 13
d
Câu
19
Phương trình
quy về
phương trình
bậc hai
Nhận biết: (Câu 6)
-
Nhận biết nghiệm của phương trình dạng:
2
ax bx c dx e+ += +
;
22
ax bx c dx ex f+ += + +
Thông hi
ểu: (Câu 16)
Giải được phương
trình quy về phương trình bậc
hai
dạng:
2
ax bx c dx e+ += +
;
22
ax bx c dx ex f+ += + +
Câu 6
Câu
16
2
Phương
pháp
tọa độ
trong
mặt
phẳng
Phương trình
đường thẳng
Nhận biết: (Câu 7; 8; Câu 14: a, b, c, d)
-
Xác định được vectơ pháp tuyến, vectơ chỉ
phương c
ủa một đường thẳng
-
Điểm thuộc (không thuộc) đường thẳng.
-
Nhận dạng PTTS của đường thẳng khi biết
đư
ờng thẳng đó đi qua 1 điểm và nhận 1 vectơ
chỉ phương.
-
Nhận biết được PTTQ của đường thẳ
ng khi biết
đư
ờng thẳng đó đi qua 1 điểm và nhận 1 vectơ
pháp tuyến cho trước
Thông hi
ểu: (Câu 20)
L
ập được phương trình tổng quát của đường
th
ẳng
Vận dụng:
(Câu 17)
Vận dụng kiến thức về đường thẳng để giải bài
toán có liên quan đến thực tiễn
Câu 7,
Câu 8
Câu 14
a, b, c, d
Câu
17
Câu
20
Vị trí tương
đối giữa hai
đường
thẳng. Góc
và khoảng
cách
Nhận biết: (Câu 9; 10)
-
Xác định được vị trí tương đối của hai đường
th
ẳng
-
Chỉ ra được công thức tính khoảng cách từ một
điểm đến một đường thẳng;
công thức tính góc
gi
ữa hai đường thẳng
Thông hi
ểu: (Câu 18)
-
Tính khoảng cách từ một điểm đến một đường
thẳng.
-
Tính góc giữa hai đường thẳng.
-
Xác định vị trí tương đối giữa hai đường thẳng.
- Tìm giao điểm của 2 đường thẳng.
Câu
9,10
Câu
18
Đường tròn
trong mặt
phẳng tọa độ
Nhận biết: (Câu 11; 12)
-
Lập được phương trình đường tròn khi biết tâm
và bán kính
-
Xác định được tâm và bán kính của đường tròn
khi bi
ết phương trình của nó
V
ận dụng: (Câu 21)
Vận dụng kiến thức về đường tròn để
giải bài
toán liên quan đến thực tiễn
Câu
11,12
Câu
21
Tổng số câu
12
1,75
0,25
2
2
2
1
Tổng số điểm
3,0
2,0
2,0
3,0
Tỉ lệ %
3,0
2,0
2,0
3,0
3. TỰ LUẬN
Câu 19 (1,0 điểm): (Hiểu)
- Tìm tập xác định của hàm số dạng
2
y ax bx c= ++
Câu 20 (1,0 điểm ): (Hiểu)
a) Viết phương trình tổng quát của đường thẳng đi qua 2 điểm
b) Tính khoảng cách từ một điểm đến một đường thẳng
Câu 21 (1 điểm ): (VD)
- Bài toán thực tế
……… HẾT ……….
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
1
ĐỀ CƯƠNG ÔN TẬP KIỂM TRA GIỮA HỌC KỲ 2 - TOÁN 10
NĂM HỌC 2024 - 2025
PHẦN I. CÂU HỎI TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
Thí sinh trả lời từ câu 1 đến câu …. Mỗi câu thí sinh chỉ chọn một phương án.
Câu 1: Cho bảng các giá trị đo nhiệt độ trong ngày tại Hải Phòng tương ứng của hai đại lượng
,xy
.
Thời điểm (giờ)
6
9
12
15
18
21
Nhiệt độ (
C
)
15
17
21
20
15
11
Nhiệt độ tại thời điểm nào là thấp nhất:
A. 6h. B. 15h.
C. 18h. D. 21h.
Câu 2: Bảng mô tả thu nhập bình quân đầu người của nước ta từ năm 1995 đến 2004
Năm
1995
1996
1997
1998
1999
2000
2001
2002
2004
TNBQĐN
(tính theo USD)
200 282 295 311 339 363 375 394 564
Thu nhập bình quân đầu người của nước ta năm nào là thấp nhất:
A. 1995. B. 1997.
C. 2024. D. 2000.
Câu 3: Biểu đồ mô tả số công trình khoa học kĩ thuật đăng kí dự giải thưởng Sáng tạo Khoa học công
nghệ Việt Nam và một số công trình đoạt giải hàng năm từ 1995 đến 2001
Tổng số công trình đoạt giải thưởng năm nào là cao nhất:
A. 2001. B. 1997.
C. 1995. D. 2000.
Câu 4: Cho hàm số
( )
y fx=
có tập xác định là
[ ]
3; 3−
và có đồ thị được biểu diễn bởi hình bên.
Khẳng định nào sau đây là đúng?
A. Hàm số
( )
2018y fx= +
đồng biến trên các khoảng
( )
3; 1−−
và
( )
1; 3
.
B. Hàm số
( )
2018y fx= +
đồng biến trên các khoảng
( )
2;1−
và
( )
1; 3
.
C. Hàm số
( )
2018y fx= +
nghịch biến trên các khoảng
( )
2; 1−−
và
( )
0;1
.
D. Hàm số
( )
2018
y fx= +
nghịch biến trên khoảng
( )
3; 2−−
.
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
2
Câu 5: Cho hàm số có đồ thị như hình bên dưới.
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng
( )
0;3
. B. Hàm số đồng biến trên khoảng
( )
;1−∞
.
C. Hàm số nghịch biến trên khoảng
( )
0; 2
. D. Hàm số đồng biến trên khoảng
( )
;3−∞
.
Câu 6: Hàm số nào sau đây có đồ thị như hình dưới đây
A.
2
31yx x=−+
. B.
2
31yx x=−+ −
.
C.
2
2 31y xx=− +−
. D.
2
2 31yx x= −+
.
Câu 7: Đồ thị của hàm số
( )
2
f x ax bx c= ++
như hình vẽ bên.
Tìm mệnh đề đúng?
A.
0
0
a >
∆≤
. B.
0
0
a >
∆<
. C.
0
0
a >
∆>
. D.
0
0
a <
∆<
.
Câu 8: Hình vẽ bên là đồ thị của hàm số nào?
A.
2
21yx x=−− −
. B.
2
21
yx x=−+
.
C.
2
21yx x
=−+
. D.
2
21
yx x=−+ −
.
Câu 9: Cho hàm số
2
y ax bx c= ++
có đồ thị như hình vẽ. Khẳng định nào su đây đúng?
4
2
0
y
x
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
3
A.
0, 0, 0ab
> > ∆>
. B.
0, 0, 0ab< > ∆>
.
C.
0, 0, 0ab
< < ∆>
. D.
0, 0, 0ab
> < ∆<
.
Câu 10: Tìm khẳng định đúng trong các khẳng định sau?
A.
( )
2
3 25fx x x= +−
là tam thức bậc hai. B.
(
)
24
fx x= −
là tam thức bậc hai.
C.
( )
3
3 21fx x x= +−
là tam thức bậc hai. D.
(
)
42
1
fx x x=−+
là tam thức bậc hai.
Câu 11: Biểu thức nào sau đây là tam thức bậc hai?
A.
( )
22fx x= −
. B.
( )
21
x
fx
x
=
−
.
C.
( )
2
1
34
fx
xx
=
−−
. D.
( )
2
43fx x x=−+
.
Câu 12: Cho
(
)
2
4
fx x= +
. Khẳng định nào sau đây là đúng?
A.
( )
0,fx x> ∀∈
. B.
(
)
0,
fx x
< ∀∈
.
C.
( )
0,fx x= ∀∈
. D.
(
) ( ) ( )
0, ; 2 2;
fx x< ∀ ∈ −∞ − +∞
.
Câu 13: Nghiệm của phương trình
3 52x +=
là
A.
1x = −
. B.
0x =
. C.
4x =
. D.
1
3
x = −
.
Câu 14: Tập nghiệm
S
của phương trình và
2
42xx−=−
là
A.
{ }
0S =
. B.
{ }
2S =
. C.
{ }
0; 2S =
. D.
S = ∅
.
Câu 15: Tập nghiệm
S
của phương trình
23 3xx−=−
là
A.
.
S = ∅
B.
{ }
6.
S
=
C.
{ }
6; 2 .S =
D.
{ }
2.S =
Câu 16: Một vectơ chỉ phương của đường thẳng
23
3
xt
yt
= +
=−−
là:
A.
( )
1
2; –3 .u =

B.
( )
2
3; –1 .u =

C.
( )
3
3; 1 .u
=

D.
( )
4
3; –3u =

Câu 17: Một vectơ pháp tuyến của đường thẳng
2 3 60xy− +=
là :
A.
( )
4
2; 3n = −

B.
( )
2
2;3n =

C.
( )
3
3; 2n =

D.
( )
1
3; 2n = −

Câu 18: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm
( )
3; 2A −
và
( )
?
1; 4B
A.
( )
1
1; 2 .u −=

B.
(
)
2
2 .;1u =

C.
( )
3
2; 6 .u =
−

D.
( )
4
1;1 .u =

Câu 19: Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng đi qua hai điểm
( )
2;3A
và
( )
4;1 ?B
A.
( )
1
22.;n = −

B.
( )
2
2; 1 .n = −

C.
( )
3
1 .;1n =

D.
( )
4
1; 2 .n = −

Câu 20: Cho đường thẳng
( )
23
:
12
= −
=−+
xt
d
yt
và điểm
7
;2.
2

−


A
Điểm
( )
∈Ad
ứng với giá trị nào của
t?
A.
3
.
2
=t
B.
1
.
2
=
t
C.
1
.
2
= −t
D.
2t =
Câu 21: Cho
( )
23
:
54
= +
= −
xt
d
yt
. Điểm nào sau đây không thuộc
( )
?d
A.
( )
5; 3 .A
B.
( )
2;5 .B
C.
( )
1; 9 .−C
D.
( )
8; 3 .−D
Câu 22: Xét vị trí tương đối của hai đường thẳng
1
: 2 10dx y− +=
và
2
: 3 6 10 0d xy−+ −=
.
A. Trùng nhau. B. Song song.
C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau.
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
4
Câu 23: Xét vị trí tương đối của hai đường thẳng
1
:3 2 6 0dxy
− −=
và
2
:6 2 8 0dxy− −=
.
A. Trùng nhau. B. Song song.
C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau.
Câu 24: Xét vị trí tương đối của hai đường thẳng
1
34
:
26
xt
d
yt
=−+
= −
và
2
22
:
84
xt
d
yt
′
= −
′
=−+
.
A. Trùng nhau. B. Song song.
C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau.
Câu 25: Hai đường thẳng
( )
1
25
:
2
=−+
=
xt
d
yt
và
( )
2
: 4 3 18 0+−=d xy
. Cắt nhau tại điểm có tọa độ:
A.
(
)
2;3 .
B.
( )
3; 2 .
C.
( )
1; 2 .
D.
( )
2;1 .
Câu 26: Góc giữa hai đường thẳng
:3 7 0a xy−+=
và
: 3 10bx y− −=
là:
A.
30°
. B.
90°
. C.
60°
. D.
45°
.
Câu 27: Cho hai đường thẳng
1
:2 5 2 0dxy+ −=
và
2
:3 7 3 0dxy− +=
. Góc tạo bởi đường thẳng
1
d
và
2
d
bằng
A.
0
30
. B.
0
135
. C.
0
45
. D.
0
60
.
Câu 28: Tìm côsin góc giữa hai đường thẳng
1
:2 1 0xy∆ + −=
và
2
2
:
1
xt
yt
= +
∆
= −
A.
10
10
. B.
3
10
. C.
3
5
. D.
3 10
10
.
Câu 29: Cho hai điểm
( ) (
)
3; 1 , 0; 3AB−
. Tìm tọa độ điểm
M
thuộc
Ox
sao khoảng cách từ
M
đến
đường thẳng
AB
bằng
1
.
A.
7
;0
2
M



và
( )
1; 0M
. B.
( )
13;0M
.
C.
( )
4; 0M
. D.
( )
2; 0M
.
Câu 30: Trong mặt phẳng với hệ tọa độ
Oxy
, cho hai điểm
( )
1;1A
,
( )
4; 3B −
và đường thẳng
: 2 10dx y
− −=
. Tìm điểm
M
thuộc
d
có tọa độ nguyên và thỏa mãn khoảng cách từ
M
đến đường
thẳng
AB
bằng
6
.
A.
( )
3; 7 .M
B.
( )
7;3 .
M
Câu 31: Đường tròn
22
2 2 –8 4 1 0x y xy+ + −=
có tâm là điểm nào sau đây?
A.
( )
8; 4−
. B.
( )
2; 1−
. C.
( )
8; 4−
. D.
( )
2;1−
.
Câu 32: Đường tròn tâm
(3; 1)
I −
và bán kính
2R =
có phương trình là
A.
22
( 3) ( 1) 4xy
+ +− =
. B.
22
( 3) ( 1) 4xy− +− =
.
C.
22
(3)(1)4xy− ++ =
. D.
22
( 3) ( 1) 4xy
+ ++ =
.
Câu 33: Đường tròn tâm
( 1; 2)I −
và đi qua điểm
(2;1)M
có phương trình là
A.
22
2 4 50xy xy+ + − −=
. B.
22
2 4 3 0.xy xy+ + − −=
C.
22
2 4 50xy xy+ − − −=
. D.
22
2 4 5 0.xy xy+ + + −=
Câu 34: Trong mặt phẳng
Oxy
, đường tròn
( )
22
: 4 6 12 0Cx y x y+++ −=
có tâm là.
A.
( )
2; 3I −−
. B.
( )
2;3I
. C.
( )
4; 6I
. D.
( )
4; 6I −−
.
PHẦN II. CÂU HỎI TRẮC NGHIỆM ĐÚNG - SAI
Trong mỗi ý a, b, c, d ở mỗi câu, hãy chọn đúng hoặc sai
Câu 1: Xét tính đúng, sai của các khẳng định sau
a) Hàm số
2
1
23
2
=− +−y xx
là hàm số bậc hai
b) Hàm số
42
8 5 0,5=−+yx x
là hàm số bậc hai
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
5
c) Hàm số
32
1
93
2
= + −−y x xx
là hàm số bậc hai
d) Hàm số
( )
22 2
6 10 ( 1) 3 1= + + ++− +ym m x m xm
(
m
là tham số
)
là hàm số bậc hai
Câu 2: Xét đồ thị của hàm số
2
2 41= ++
yx x
. Khi đó:
a) có tọa độ đỉnh
( 1; 1)I
−−
b) trục đối xứng là
1x =
.
c) Giao điểm của đồ thị với trục tung là
(0;1)
M
.
d) Đồ thị đi qua các điểm
( )
1; 6Q
và
( 3; 6)P −
.
Câu 3: Xét đồ thị của hàm số
2
54=−+ −yx x
. Khi đó:
a) có toạ độ đỉnh
59
;
24
I



b) trục đối xứng là
5
2
x =
.
c) Giao điểm của đồ thị với trục tung là
(0; 4)C −
.
d) Giao điểm của đồ thị với trục hoành là
(2; 0)
A
và
(3; 0)
B
.
Câu 4: Cho đồ thị hàm số bậc hai
()=y fx
có dạng như hình sau:
a) Trục đối xứng của đồ thị là đường thẳng
2x
= −
.
b) Đỉnh
I
của đồ thị hàm số có tọa độ là
(2; 2)−
.
c) Đồ thị hàm số đi qua điểm
(0; 6)A
d) Hàm số đã cho là
2
2 26yx x= −+
.
Câu 5: Các mệnh đề sau đúng hay sai?
Mệnh đề
Đúng
Sai
a)
2
4 30+ +<xx
khi
( 3; 1)
x ∈− −
.
b)
2
6 80− +≥xx
khi
( ; 2] [4; )x
∈ −∞ ∪ +∞
.
c)
2
() 5= −+
fx x x
luôn âm với mọi
x
thuộc
d)
2
( ) 36 12 1
=− +−fx x x
luôn nhỏ hơn hoặc bằng 0 với mọi
∈x
Câu 6: Cho hai đường thẳng
1
: 20∆ −+=xy
và
2
13
:
2
= +
∆
=−+
xt
yt
. Khi đó:
a) Đường thẳng
1
∆
có vectơ pháp tuyến
(1; 1)n
b) Đường thẳng
2
∆
có vectơ pháp tuyến là
(1; 3)n −
c) Phương trình tham số của đường thẳng
1
∆
là
2.
xt
yt
=
= +
d) Phương trình tổng quát của đường thẳng
2
∆
là
3 70xy− −=
Câu 7: Trong mặt phẳng toạ độ
Oxy
, cho hai điểm
( 2; 2), (3; 4)−
AB
. Khi đó:
a) Đường thẳng
AB
có vectơ chỉ phương là
(2; 5)AB

b) Đường thẳng
AB
có vectơ pháp tuyến là
(2; 5)n −
c) Phương trình tổng quát của đường thẳng
AB
là
2 5 14 0xy−+=
d) Phương trình tham số của đường thẳng đi qua
( 1;1)−M
và song song với
AB
là
12
15
xt
yt
=−+
= +
Câu 8: Xác định tính đúng, sai của các khẳng định sau:
a)
∆
qua
(1; 0 )A
, có vectơ pháp tuyến
(3; 2)= −
n
, khi đó phương trình tổng quát của
∆
là :
3 2 30− −=xy
b)
∆
qua
( 1; 0 )−A
và vuông góc với đường thẳng
AB
biết
(1; 4)B
, khi đó phương trình tổng quát của
∆
là :
2 10+ +=xy
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
6
c)
∆
là đường trung trực của đoạn thẳng
MN
với
(0; 3), (2; 5)−MN
, khi đó phương trình tổng quát
của
∆
là :
4 30xy+ −=
d)
∆
là đường cao xuất phát từ điểm
A
trong tam giác
ABC
biết rằng
(1; 1), (1; 2), (3; 3)
−−A BC
,khi đó
phương trình tổng quát của
∆
là :
2 3 50xy− −=
PHẦN III. CÂU HỎI TRẮC NGHIỆM TRẢ LỜI NGẮN
Thí sinh viết kết quả vào phần trả lời (kết quả làm tròn tối đa gồm 4 kí tự)
Câu 1: Tìm giá trị lớn nhất của hàm số
2
25=− ++y xx
.
Câu 2: Tìm giá trị nhỏ nhất của hàm số
2
31=+−yx x
.
Câu 3: Một người nông dân thả 1000 con cá giống vào hồ nuôi vừa mới đào. Biết rằng sau mỗi năm
thì số lượng cá trong hồ tăng thêm
x
lần số lượng cá ban đầu và
x
không đổi. Bằng cách thay đổi kĩ
thuật nuôi và thức ăn cho cá. Hỏi sau hai năm để số cá trong hồ là 36000 con thì tốc độ tăng số lượng
cá trong hồ là bao nhiêu? Biết tốc độ tăng mỗi năm là không đổi.
Câu 4: Tìm số nghiệm phương trình sau:
2
3 9 1 | 2|− += −xx x
;
Câu 5: Số nghiệm của phương trình
2
43 2 1xx−=−
là:
Câu 6: Phương trình
2
4 22x xx−+ = −
có bao nhiêu nghiệm?
Câu 7: Số nghiệm của phương trình
− + −+=
2
4 352xx x
là?
Câu 8: Trong mặt phẳng toạ độ
Oxy
, cho hình vuông
ABCD
và các điểm
(0; 2)M
,
(5; 3), ( 2; 2), (2; 4)− −− −NP Q
lần lượt thuộc các đường thẳng chứa các cạnh
,,,AB BC CD DA
. Lập
phương trình đường thẳng
AB
và tính diện tích hình vuông
ABCD
.
Câu 9: Trong mặt phẳng toạ độ
Oxy
, cho tam giác
ABC
có
(1;1), (5; 2)−
AB
, đỉnh
C
thuộc đường
thẳng
40
−=y
, trọng tâm
G
thuộc đường thẳng
3 2 60− +=xy
. Tính diện tích tam giác
ABC
.
Câu 10: Trong mặt phẳng toạ độ
Oxy
, cho các đường thẳng
1
: 2 30+ +=dx y
,
2
:3 5 0−+=d xy
và
điểm
( 2;1)−P
. Đường thẳng
∆
đi qua
P
và cắt
12
,dd
lần lượt tại
,
AB
sao cho
P
là trung điểm của
AB
. Tính khoảng cách từ
(3; 2)−M
đến đường thẳng
∆
.
Câu 11: Tìm
m
để hai đường thẳng sau vuông góc với nhau:
12
: 1 0 ; : 2 3 0.x my x y m
∆ − += ∆ + + =
Câu 12: Tìm tham số
m
để các đường thẳng sau đây song song:
( )
2
1
:2 1 3 0∆ + + −=xm y
và
2
: 100 0∆ +− =x my
.
Câu 13: Cho hai đường thẳng
1
: 10 0
∆ +− =xy
và
1
: 2 999 0
∆ ++ =x my
. Tìm
m
để góc tạo bởi hai
đường thẳng trên bằng
45°
.
Câu 14: Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
, biết
(1;1), (3; 2), (1;3)AB C
. Tính góc giữa
hai đường thẳng
,AB AC
.
PHẦN IV. TỰ LUẬN
Câu 19 (1,0 điểm): (Hiểu)
- Tìm tập xác định của hàm số dạng
2
y ax bx c= ++
Câu 20 (1,0 điểm ): (Hiểu)
a) Viết phương trình tổng quát của đường thẳng đi qua 2 điểm
b) Tính khoảng cách từ một điểm đến một đường thẳng
Câu 21 (1 điểm ): (VD)
- Bài toán thực tế
……… HẾT ……….
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
1
ĐỀ CƯƠNG ÔN TẬP KIỂM TRA GIỮA HỌC KỲ 2 - TOÁN 10
NĂM HỌC 2024 - 2025
PHẦN I. CÂU HỎI TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
Thí sinh trả lời từ câu 1 đến câu …. Mỗi câu thí sinh chỉ chọn một phương án.
Câu 1: Cho bảng các giá trị đo nhiệt độ trong ngày tại Hải Phòng tương ứng của hai đại lượng
,xy
.
Thời điểm (giờ)
6
9
12
15
18
21
Nhiệt độ (
C
)
15
17
21
20
15
11
Nhiệt độ tại thời điểm nào là thấp nhất:
A. 6h. B. 15h.
C. 18h. D. 21h.
Câu 2: Bảng mô tả thu nhập bình quân đầu người của nước ta từ năm 1995 đến 2004
Năm
1995
1996
1997
1998
1999
2000
2001
2002
2004
TNBQĐN
(tính theo USD)
200
282
295
311
339
363
375
394
564
Thu nhập bình quân đầu người của nước ta năm nào là thấp nhất:
A. 1995. B. 1997.
C. 2024. D. 2000.
Câu 3: Biểu đồ mô tả số công trình khoa học kĩ thuật đăng kí dự giải thưởng Sáng tạo Khoa học công
nghệ Việt Nam và một số công trình đoạt giải hàng năm từ 1995 đến 2001
Tổng số công trình đoạt giải thưởng năm nào là cao nhất:
A. 2001. B. 1997.
C. 1995. D. 2000.
Câu 4: Cho hàm số
( )
y f x=
có tập xác định là
3;3−
và có đồ thị được biểu diễn bởi hình bên.
Khẳng định nào sau đây là đúng?
A. Hàm số
( )
2018y f x=+
đồng biến trên các khoảng
( )
3; 1−−
và
( )
1;3
.
B. Hàm số
( )
2018y f x=+
đồng biến trên các khoảng
( )
2;1−
và
( )
1;3
.
C. Hàm số
( )
2018y f x=+
nghịch biến trên các khoảng
( )
2; 1−−
và
( )
0;1
.
D. Hàm số
( )
2018y f x=+
nghịch biến trên khoảng
( )
3; 2−−
.
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
2
Lời giải
Chọn A
Gọi
( ) ( )
:C y f x=
,
( ) ( )
2018C y f x
=+
. Khi tịnh tiến đồ thị
( )
C
theo phương song song trục tung
lên phía trên
2018
đơn vị thì được đồ thị
( )
C
. Nên tính đồng biến, nghịch biến của hàm số
( )
y f x=
,
( )
2018y f x=+
trong từng khoảng tương ứng không thay đổi.
Dựa vào đồ thị ta thấy:
Hàm số
( )
2018y f x=+
đồng biến trên các khoảng
( )
3; 1−−
và
( )
1;3
(đúng).
Hàm số
( )
2018y f x=+
đồng biến trên các khoảng
( )
2;1−
và
( )
1;3
(sai).
Hàm số
( )
2018y f x=+
nghịch biến trên các khoảng
( )
2; 1−−
và
( )
0;1
(sai).
Hàm số
( )
2018y f x=+
nghịch biến trên khoảng
( )
3; 2−−
(sai).
Câu 5: Cho hàm số có đồ thị như hình bên dưới.
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng
( )
0;3
. B. Hàm số đồng biến trên khoảng
( )
;1−
.
C. Hàm số nghịch biến trên khoảng
( )
0;2
. D. Hàm số đồng biến trên khoảng
( )
;3−
.
Lời giải
Chọn C
Trên khoảng
( )
0;2
, đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến.
Câu 6: Cho hàm số
( )
y f x=
xác định trên khoảng
( )
;− +
có đồ thị như hình vẽ dưới đây.
Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên khoảng
( )
0;2
B. Hàm số nghịch biến trên khoảng
( )
3;0−
C. Hàm số đồng biến trên khoảng
( )
1;0−
D. Hàm số nghịch biến trên khoảng
( )
0;3
Lời giải
Đáp án C.
Quan sát trên đồ thị ta thấy đồ thị hàm số đi lên trên khoảng
( )
1;0−
. Vậy hàm số đồng biến trên
khoảng
( )
1;0−
.
Câu 7: Hàm số nào sau đây có đồ thị như hình dưới đây
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
3
A.
2
31y x x= − +
. B.
2
31y x x= − + −
.
C.
2
2 3 1y x x= − + −
. D.
2
2 3 1y x x= − +
.
Lời giải
Chọn D
Bề lõm của parabol hướng lên trên suy ra
0a
, nên loại A và
Đồ thị đi qua điểm
( )
1;0
nên)Chọn D.
Câu 8: Đồ thị của hàm số
( )
2
f x ax bx c= + +
như hình vẽ bên.
Tìm mệnh đề đúng?
A.
0
0
a

. B.
0
0
a

. C.
0
0
a

. D.
0
0
a

.
Lời giải
Chọn B
Parabol có bề lõm hướng lên nên
0a
. Parabol không cắt trục
Ox
nên phương trình
2
0ax bx c+ + =
vô nghiệm, tức là
0
.
Câu 9: Hình vẽ bên là đồ thị của hàm số nào?
A.
2
21y x x= − − −
. B.
2
21y x x= − +
.
C.
2
21y x x= − +
. D.
2
21y x x= − + −
.
Lời giải
Chọn D.
Câu 10: Cho hàm số
2
y ax bx c= + +
có đồ thị như hình vẽ. Khẳng định nào su đây đúng?
A.
0, 0, 0ab
. B.
0, 0, 0ab
.
C.
0, 0, 0ab
. D.
0, 0, 0ab
.
Lời giải
Chọn B
4
2
0
y
x
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
4
Dựa vào đồ thị ta thấy bề lõm quay xuống nên
0a
, đồ thị cắt trục hoành tại 2 điểm phân biệt nên
0
, tọa độ đỉnh nằm bên phải trục tung nên
00
2
b
b
a
−
.
Câu 11: Tìm khẳng định đúng trong các khẳng định sau?
A.
( )
2
3 2 5f x x x= + −
là tam thức bậc hai. B.
( )
24f x x=−
là tam thức bậc hai.
C.
( )
3
3 2 1f x x x= + −
là tam thức bậc hai. D.
( )
42
1f x x x= − +
là tam thức bậc hai.
Lời giải
Chọn A
* Theo định nghĩa tam thức bậc hai thì
( )
2
3 2 5f x x x= + −
là tam thức bậc hai.
Câu 12: Biểu thức nào sau đây là tam thức bậc hai?
A.
( )
22f x x=−
. B.
( )
21
x
fx
x
=
−
.
C.
( )
2
1
34
fx
xx
=
−−
. D.
( )
2
43f x x x= − +
.
Lời giải
Chọn D
Theo định nghĩa tam thức bậc hai.
Câu 13: Cho
( )
2
4f x x=+
. Khẳng định nào sau đây là đúng?
A.
( )
0,f x x
. B.
( )
0,f x x
.
C.
( )
0,f x x=
. D.
( ) ( ) ( )
0, ; 2 2;f x x − − +
.
Lời giải
Chọn A
Cách 1: Ta có:
22
0, 4 0,x x x x +
.
Cách 2:
( )
2
4f x x=+
là tam thức bậc hai có
1a =
,
16 0 = −
( )
0,f x x
.
Câu 14: Nghiệm của phương trình
3 5 2x +=
là
A.
1x =−
. B.
0x =
. C.
4x =
. D.
1
3
x =−
.
Lời giải
Chọn D
Phương trình
1
3 5 2 3 5 4
3
x x x+ = + = = −
.
Câu 15: Tập nghiệm
S
của phương trình và
2
42xx− = −
là
A.
0S =
. B.
2S =
. C.
0;2S =
. D.
S =
.
Lời giải
Chọn B
2
42xx− = −
( )
2
2
20
42
x
xx
−
− = −
2
4 8 0
x
x
−=
2
2
x
x
=
2x=
.
Vậy tập nghiệm của phương trình
2S =
.
Câu 16: Tập nghiệm
S
của phương trình
2 3 3xx− = −
là
A.
.S =
B.
6.S =
C.
6;2 .S =
D.
2.S =
Lời giải
Chọn B
Ta có
( )
2
2
3
3
2 3 3 6
8 12 0
2 3 3
x
x
x x x
xx
xx

− = − =

− + =
− = −
Vậy tập nghiệm của phương trình là
6.S =
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
5
Câu 17: Giải phương trình
3 2 3 2x x x− + = −
.
A.
3
2
x
. B.
3
2
x =
. C.
3
2
x
. D.
0x =
.
Lời giải
Chọn D
Điều kiện:
3
3 2 0
2
xx−
.
Với điều kiện trên, phương trình
3 2 3 2x x x− + = −
0x=
.
Vậy phương trình đã cho có một nghiệm
0x =
.
Câu 18: Phương trình sau có bao nhiêu nghiệm:
22xx− = −
?
A.
0
. B.
1
. C.
2
. D. Vô số.
Lời giải
Chọn B
Điều kiện:
20
20
x
x
−
−
2
2
x
x
2x=
.
Thay
2x =
vào phương trình ta được
00=
hay
2x =
là nghiệm của phương trình.
Câu 19: Một vectơ chỉ phương của đường thẳng
23
3
xt
yt
=+
= − −
là:
A.
( )
1
2; –3 .u =
B.
( )
2
3; –1 .u =
C.
( )
3
3; 1 .u =
D.
( )
4
3; –3u =
Lời giải
Chọn B
Từ phương trình tham số của đường thẳng ta có một VTCP của đường thẳng là
( )
2
3; –1 .u =
Câu 20: Một vectơ pháp tuyến của đường thẳng
2 3 6 0xy− + =
là :
A.
( )
4
2; 3n =−
B.
( )
2
2;3n =
C.
( )
3
3;2n =
D.
( )
1
3;2n =−
Lời giải
Chọn A
Từ PTTQ ta thấy một VTPT của đường thẳng là
( )
4
2; 3n =−
Câu 21: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm
( )
3;2A −
và
( )
?1;4B
A.
( )
1
1;2 .u −=
B.
( )
2
2 .;1u =
C.
( )
3
2;6 .u = −
D.
( )
4
1;1 .u =
Lời giải
Chọn B
Ta có
( )
4;2AB =
một VTCP của đường thẳng
AB
cùng phương với
( )
4;2AB =
.
Ta thấy
( )
2
1
2
2;1u AB==
vậy
( )
2
2;1u =
là một VTCP của
AB
Câu 22: Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng đi qua hai điểm
( )
2;3A
và
( )
4;1 ?B
A.
( )
1
22.;n =−
B.
( )
2
2; 1 .n =−
C.
( )
3
1 .;1n =
D.
( )
4
1; 2 .n =−
Lời giải
Chọn C
Ta có
( )
2; 2AB =−
một VTPT
n
của đường thẳng
AB
thì vuông góc với
AB
Suy ra
( )
. 0 .2 . 2 0n AB x y= + − =
chọn
( )
1, 1 1;1x y n= = =
Chú ý: Ta hoàn toàn có thể dùng nhận xét nêu ở mục 2.3.2 để giải quyết nhanh bài toán này.
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
6
Câu 23: Cho đường thẳng
( )
23
:
12
=−
= − +
xt
d
yt
và điểm
7
; 2 .
2

−


A
Điểm
( )
Ad
ứng với giá trị nào của
t?
A.
3
.
2
=t
B.
1
.
2
=t
C.
1
.
2
=−t
D.
2t =
Lời giải
Chọn C
Ta có
( )
1
7
23
71
2
;2
2
1
22
2 1 2
2
t
t
A d t
t
t
=−
=−


− = −




− = − +
=−
Câu 24: Cho
( )
23
:
54
=+
=−
xt
d
yt
. Điểm nào sau đây không thuộc
( )
?d
A.
( )
5;3 .A
B.
( )
2;5 .B
C.
( )
1;9 .−C
D.
( )
8; 3 .−D
Lời giải
Chọn B
Thay
( )
2 2 3 0
2;5 0
5 5 4 0
tt
Bt
tt
= + =

=

= − =

Câu 25: Xét vị trí tương đối của hai đường thẳng
1
: 2 1 0d x y− + =
và
2
: 3 6 10 0d x y− + − =
.
A. Trùng nhau. B. Song song.
C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau.
Lời giải
Chọn B
1
2
12
1
|| .
: 2 1 0
12
: 3 6 10
10
0
36
d x y
d x y
dd
− + =
−
→=
− + − =
−
−
= ⎯⎯→
Câu 26: Xét vị trí tương đối của hai đường thẳng
1
:3 2 6 0d x y− − =
và
2
:6 2 8 0d x y− − =
.
A. Trùng nhau. B. Song song.
C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau.
Lời giải
Chọn D
( )
( )
1
11
2
12
2
2
3
:3 2 6 0 3; 2
6
:6 2 8 0 6;
2
0
2
2
,
d x y n
dd
n
n
x
n
dy
−
=
⎯⎯→
−
=
− − = → = −

→

− − = → = −
cắt nhau nhưng không vuông góc.
Câu 27: Xét vị trí tương đối của hai đường thẳng
1
34
:
26
xt
d
yt
= − +
=−
và
2
22
:
84
xt
d
yt
=−
= − +
.
A. Trùng nhau. B. Song song.
C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau.
Lời giải
Chọn B
( ) ( )
( )
1 1 1
12
2
2
2
34
: 3;2 , 2; 3
23
26
|| .
23
12
: 2;3
43
xt
dA
yt
d
d
d
x
u
t
d
y
d
u
t
A
= − +
→ − = −
−
=−
=
→→
−

=−

→ = −
=+
Câu 28: Hai đường thẳng
( )
1
25
:
2
= − +
=
xt
d
yt
và
( )
2
:4 3 18 0+ − =d x y
. Cắt nhau tại điểm có tọa độ:
A.
( )
2;3 .
B.
( )
3;2 .
C.
( )
1;2 .
D.
( )
2;1 .
Lời giải
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
7
Chọn A
Ta có
( ) ( )
11
25
: :2 5 4 0
2
xt
d d x y
yt
= − +
− + =
=
Gọi
( ) ( )
12
M d d=
M
là nghiệm của hệ phương trình
2 5 4 0 2
4 3 18 0 3
x y x
x y y
− + = =


+ − = =

Câu 29: Tính góc giữa hai đường thẳng
: 3 2 0xy − + =
và
: 3 1 0xy
+ − =
.
A.
90
. B.
120
. C.
60
. D.
30
.
Lời giải
Chọn C
Đường thẳng
có vectơ pháp tuyến
( )
1; 3n =−
, đường thẳng
có vectơ pháp tuyến
( )
1; 3n
=
.
Gọi
là góc giữa hai đường thẳng
,.

( )
13
1
cos cos , 60
2
1 3. 1 3
nn

−
= = = =
++
.
Câu 30: Góc giữa hai đường thẳng
: 3 7 0a x y−+=
và
: 3 1 0b x y− − =
là:
A.
30
. B.
90
. C.
60
. D.
45
.
Lời giải
Chọn A
Đường thẳng
a
có vectơ pháp tuyến là:
( )
1
3; 1n =−
;
Đường thẳng
b
có vectơ pháp tuyến là:
( )
2
1; 3n =−
.
Áp dụng công thức tính góc giữa hai đường thẳng có:
( )
( )
( )
12
12
1. 3 1 3
.
3
cos ,
2.2 2
.
nn
ab
nn
+ − −
= = =
. Suy ra góc giữa hai đường thẳng bằng
30
.
Câu 31: Cho hai đường thẳng
1
:2 5 2 0d x y+ − =
và
2
:3 7 3 0d x y− + =
. Góc tạo bởi đường thẳng
1
d
và
2
d
bằng
A.
0
30
. B.
0
135
. C.
0
45
. D.
0
60
.
Lời giải
Chọn C
Đường thẳng
1
:2 5 2 0d x y+ − =
có vectơ pháp tuyến
( )
1
2;5n =
.
Đường thẳng
2
:3 7 3 0d x y− + =
có vectơ pháp tuyến
( )
2
3; 7n =−
.
Góc giữa hai đường thẳng được tính bằng công thức
( )
( )
( )
12
12
12
12
2
2 2 2
.
2.3 5.( 7)
29 1
cos , cos ,
29 2 2
.
2 5 . 3 7
nn
d d n n
nn
+−
= = = = =
+ + −
( )
0
12
; 45dd=
Vậy góc tạo bởi đường thẳng
1
d
và
2
d
bằng
0
45
.
Câu 32: Tìm côsin góc giữa hai đường thẳng
1
:2 1 0xy + − =
và
2
2
:
1
xt
yt
=+
=−
A.
10
10
. B.
3
10
. C.
3
5
. D.
3 10
10
.
Lời giải
Chọn D
Véctơ pháp tuyến của đường thẳng
1
là
( )
2;1n =
nên véctơ chỉ phương
( )
1; 2u =−
Véctơ chỉ phương của đường thẳng
2
là
( )
1; 1u
=−
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
8
Khi đó
( )
( )
12
.
3 3 10
cos ; cos ;
10
5. 2
.
uu
uu
uu
= = = =
Câu 33: Cho hai điểm
( ) ( )
3; 1 , 0;3AB−
. Tìm tọa độ điểm
M
thuộc
Ox
sao khoảng cách từ
M
đến
đường thẳng
AB
bằng
1
.
A.
7
;0
2
M



và
( )
1;0M
. B.
( )
13;0M
.
C.
( )
4;0M
. D.
( )
2;0M
.
Lời giải
Chọn A
Gọi
( )
;0Mx
.
Ta có
( )
3;4AB =−
Phương trình đường thẳng
( )
:4 3 3 0AB x y+ − =
4 3 9 0xy + − =
.
( )
49
; 5 4 9
5
x
d M AB x
−
= = −
7
2
1
x
x
=
=
Vậy
( )
7
;0 ; 1;0
2
MM



.
Câu 34: Trong mặt phẳng với hệ tọa độ
Oxy
, cho hai điểm
( )
1;1A
,
( )
4; 3B −
và đường thẳng
: 2 1 0d x y− − =
. Tìm điểm
M
thuộc
d
có tọa độ nguyên và thỏa mãn khoảng cách từ
M
đến đường
thẳng
AB
bằng
6
.
A.
( )
3;7 .M
B.
( )
7;3 .M
C.
( )
43; 27 .M −−
D.
.
27
11
3;M



−
Lời giải
( )
: 2 1 0 2 1; ,
.
:4 3 7 0
M d x y M m m m
AB x y
− − = → +
+ − =
Khi đó
( )
( )
( )
3
8 4 3 7
6 ; 11 3 30 7;3 .
27
5
l
11
m
mm
d M AB m M
m
=
+ + −
= = − = →
=
Chọn B
Câu 35: Đường tròn
22
2 2 – 8 4 1 0x y x y+ + − =
có tâm là điểm nào sau đây?
A.
( )
8;4−
. B.
( )
2; 1−
. C.
( )
8; 4−
. D.
( )
2;1−
.
Lời giải
Chọn B
22
2 2 – 8 4 1 0x y x y+ + − =
22
1
– 4 2 0
2
x y x y + + − =
.
Vậy tâm là:
( )
2; 1I −
.
Câu 36: Đường tròn tâm
(3; 1)I −
và bán kính
2R =
có phương trình là
A.
22
( 3) ( 1) 4xy+ + − =
. B.
22
( 3) ( 1) 4xy− + − =
.
C.
22
( 3) ( 1) 4xy− + + =
. D.
22
( 3) ( 1) 4xy+ + + =
.
Lời giải
Chọn C
Phương trình đường tròn có tâm
( )
3; 1I −
, bán kính
2R =
là:
( ) ( )
22
3 1 4xy− + + =
Câu 37: Đường tròn tâm
( 1;2)I −
và đi qua điểm
(2;1)M
có phương trình là
A.
22
2 4 5 0x y x y+ + − − =
. B.
22
2 4 3 0.x y x y+ + − − =
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
9
C.
22
2 4 5 0x y x y+ − − − =
. D.
22
2 4 5 0.x y x y+ + + − =
Lời giải
Chọn A
Đường tròn có tâm
( )
1;2I −
và đi qua
( )
2;1M
thì có bán kính là:
( )
2
2
3 1 10R IM= = + − =
Khi đó có phương trình là:
( ) ( )
22
22
1 2 10 2 4 5 0x y x y x y+ + − = + + − − =
Câu 38: Trong mặt phẳng
Oxy
, đường tròn
( )
22
: 4 6 12 0C x y x y+ + + − =
có tâm là.
A.
( )
2; 3I −−
. B.
( )
2;3I
. C.
( )
4;6I
. D.
( )
4; 6I −−
.
Lời giải
Chọn A
Ta có phương trình đường tròn là:
( ) ( )
22
2 3 25xy+ + + =
.
Vậy tâm đường tròn là:
( )
2; 3I −−
.
Câu 39: Đường tròn
22
10 24 0x y y+ − − =
có bán kính bằng bao nhiêu?
A.
49
. B.
7
. C.
1
. D.
29
.
Lời giải
Chọn B
Đường tròn
22
10 24 0x y y+ − − =
có tâm
( )
0;5I
, bán kính
( )
22
0 5 24 7R = + − − =
.
Câu 40: Xác định tâm và bán kính của đường tròn
( ) ( ) ( )
22
: 1 2 9.C x y+ + − =
A. Tâm
( )
1;2 ,I −
bán kính
3R =
. B. Tâm
( )
1;2 ,I −
bán kính
9R =
.
C. Tâm
( )
1; 2 ,I −
bán kính
3R =
. D. Tâm
( )
1; 2 ,I −
bán kính
9R =
.
Lời giải
Chọn A
Câu 41: Tìm tọa độ tâm
I
và bán kính
R
của đường tròn
( )
C
:
22
2 4 1 0x y x y+ − + + =
.
A.
( )
1;2 ; 4IR−=
. B.
( )
1; 2 ; 2IR−=
. C.
( )
1;2 ; 5IR−=
. D.
( )
1; 2 ; 4IR−=
.
Lời giải
Chọn B
( )
C
có tâm
( )
1; 2I −
, bán kính
( )
2
2
1 2 1 2R = + − − =
.
Câu 42: Trong mặt phẳng
Oxy
, cho đường tròn
( ) ( ) ( )
22
: 2 3 9C x y− + + =
. Đường tròn có tâm và
bán kính là
A.
( )
2;3 , 9IR=
. B.
( )
2; 3 , 3IR−=
. C.
( )
3;2 , 3IR−=
. D.
( )
2;3 , 3IR−=
.
Lời giải
Chọn B
Đường tròn
( )
C
có tâm
( )
2; 3I −
và bán kính
3R =
.
Câu 43: Tìm tọa độ tâm
I
và tính bán kính
R
của đường tròn
( ) ( )
22
( ): 2 5 9C x y+ + − =
.
A.
( 2;5), 81.IR−=
. B.
(2; 5), 9.IR−=
. C.
(2; 5), 3.IR−=
. D.
( 2;5), 3.IR−=
Lời giải
Chọn D
Theo bài ra ta có tọa độ tâm
( 2;5)I −
và bán kính
3R =
.
Câu 44: Đường tròn
( )
22
: 2 4 3 0C x y x y+ − + − =
có tâm
I
, bán kính
R
là
A.
( )
1;2 , 2IR−=
. B.
( )
1;2 , 2 2IR−=
. C.
( )
1; 2 , 2IR−=
. D.
( )
1; 2 , 2 2IR−=
.
Lời giải
Chọn D
Tâm
( )
1; 2I −
, bán kính
( ) ( )
2
2
1 2 3 8 2 2R = + − − − = =
.
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
10
Câu 45: Phương trình đường tròn có tâm
( )
1;2I
và bán kính
5R =
là
A.
22
2 4 20 0x y x y+ − − − =
. B.
22
2 4 20 0x y x y+ + + + =
.
C.
22
2 4 20 0x y x y+ + + − =
. D.
22
2 4 20 0x y x y+ − − + =
.
Lời giải
Chọn A
Phương trình đường tròn có tâm
( )
1;2I
và bán kính
5R =
là
( ) ( )
22
2
1 2 5xy− + − =
22
2 1 4 4 25x x y y − + + − + =
22
2 4 20 0x y x y + − − − =
.
Câu 46: Đường tròn tâm
( )
1;2I −
, bán kính
3R =
có phương trình là
A.
22
2 4 4 0x y x y+ + + − =
.
B.
22
2 4 4 0x y x y+ − − − =
.
C.
22
2 4 4 0x y x y+ + − − =
.
D.
22
2 4 4 0x y x y+ − + − =
.
Lời giải
Chọn C
Đường tròn tâm
( )
1;2I −
, bán kính
3R =
có phương trình là
( ) ( )
22
22
1 2 9 2 4 4 0x y x y x y+ + − = + + − − =
.
Câu 47: Phương trình nào sau đây là phương trình của đường tròn tâm
( )
1;2I −
, bán kính bằng
3
?
A.
( ) ( )
22
1 2 9xy− + + =
. B.
( ) ( )
22
1 2 9xy+ + + =
.
C.
( ) ( )
22
1 2 9xy− + − =
. D.
( ) ( )
22
1 2 9xy+ + − =
.
Lời giải
Chọn D
Phương trình đường tròn tâm
( )
1;2I −
và bán kính
3R =
là:
( ) ( )
22
1 2 9xy+ + − =
.
PHẦN II. CÂU HỎI TRẮC NGHIỆM ĐÚNG - SAI
Trong mỗi ý a, b, c, d ở mỗi câu, hãy chọn đúng hoặc sai
Câu 1: Xét tính đúng, sai của các khẳng định sau
a) Hàm số
2
1
23
2
= − + −y x x
là hàm số bậc hai
b) Hàm số
42
8 5 0,5= − +y x x
là hàm số bậc hai
c) Hàm số
32
1
93
2
= + − −y x x x
là hàm số bậc hai
d) Hàm số
( )
2 2 2
6 10 ( 1) 3 1= + + + + − +y m m x m x m
(
m
là tham số
)
là hàm số bậc hai
Lời giải
a) Đúng
b) Sai
c) Sai
d) Đúng
a) Là hàm số bậc hai với
1
2, 3,
2
= − = = −a b c
.
b) Không phải là hàm số bậc hai vì chứa
4
x
.
c) Không phải là hàm số bậc hai vì chứa
3
x
.
d) Là hàm số bậc hai với
22
6 10 ( 3) 1 0, 1= + + = + + = +a m m m b m
,
2
31= − +cm
.
Câu 2: Xét đồ thị của hàm số
2
2 4 1= + +y x x
. Khi đó:
a) có tọa độ đỉnh
( 1; 1)I −−
b) trục đối xứng là
1x =
.
c) Giao điểm của đồ thị với trục tung là
(0;1)M
.
d) Đồ thị đi qua các điểm
( )
1;6Q
và
( 3;6)P −
.
Lời giải

Tài liệu khác của Toán 10

Preview text:

TRƯỜNG THPT KIẾN THỤY
MA TRẬN NỘI DUNG, NĂNG LỰC VÀ CẤP ĐỘ TƯ DUY MÔN TOÁN LỚP 10 TỔ TOÁN - TIN
NĂM HỌC 2024 – 2025
1. MA TRẬN ĐỀ KIỂM TRA ĐỊNH KÌ GIỮA HỌC KÌ II
Mức độ đánh giá Tỉ lệ Nội dung/ Tổng % TT Chương/ TNKQ Tự luận điểm chủ đề đơn vị kiến thức Nhiều lựa chọn Đúng - Sai Trả lời ngắn
Biết Hiểu VD Biết Hiểu VD
Biết Hiểu VD
Biết Hiểu VD
Biết Hiểu VD Hàm số Câu 1,2 2 Hàm số bậc Câu hai 3,4 Câu 13 a,b,c Câu 15 2,75 1 Hàm số, Dấu của 1
đồ thị và tam thức Câu 5 Câu 13 d Câu 19 1 1,25 45 ứng dụng bậc hai Phương trình quy về phương Câu 6 Câu trình bậc 16 1 1 hai Phương trình đường Câu 3 1 thẳng 7,8 Câu 14 a,b,c,d Câu 17 Vị trí tương Phương Câu đối giữa hai pháp tọa 20 đường Câu 2
độ trong thẳng. Góc 9.10 Câu 18 2 2 55 mặt và khoảng phẳng cách Đường tròn trong mặt Câu phẳng tọa 11,12 Câu 21 2 1 độ Tổng số câu 12 1,75 0,25 2 2 2 1 13,75 4,25 3 Tổng số điểm 3,0 1,75 0,25 1,0 1,0 2,0 1,0 4,5 3,5 2 Tỉ lệ % 30 20 20 30 45 35 20
2. BẢN ĐẶC TẢ ĐỀ KIỂM TRA ĐỊNH KÌ GIỮA HỌC KÌ II
Dạng thức câu hỏi Nội dung/ TT Chương/ TNKQ Tự luận
Chủ đề Đơn vị kiến
Yêu cầu cần đạt thức
Nhiều lựa chọn Đúng - Sai
Trả lời ngắn
Nhiều lựa chọn Biết Hiểu VD
Biết Hiểu VD Biết Hiểu VD Biết Hiểu VD
Nhận biết: (Câu 1,2)
- Nhận biết được những mô hình thực tế (dạng Hàm số
bảng, biểu đồ, công thức) dẫn đến khái niệm hàm Câu số. 1,2
- Nhận biết được khoảng đồng biến, nghịch biến
dựa vào đồ thị hàm số
Nhận biết: (Câu 3,4; Câu 13: a, b, c)
- Nhận biết được hàm số bậc hai. Nhận dạng
được đồ thị hàm số bậc hai.
- Nhận biết được trục đối xứng, tọa độ đỉnh, giao
Hàm số bậc điểm của đồ thị với trục hoành từ đồ thị. Câu hai
- Các công thức tìm tọa độ đỉnh, phương trình trục đối xứng. 3,4 Câu 13 a,b,c Câu 15
-Kiểm tra điểm thuộc đồ thị hàm số bậc hai Hàm số, đồ
Vận dụng: (Câu 15) 1 thị và ứng
- Vận dụng được kiến thức về hàm số bậc hai và dụng
đồ thị vào giải quyết một số bài toán thực tiễn.
Nhận biết: (Câu 5)
- Nhận biết được dạng của tam thức bậc hai.
Dấu của tam Thông hiểu: (Câu 13d; Câu 19)
thức bậc hai - Giải thích được định lí về dấu tam thức bậc hai Câu 5 Câu 13 d Câu 19
từ việc quan sát đồ thị của hàm số.
- Giải được bài toán về bất phương trình bậc hai
Nhận biết: (Câu 6)
- Nhận biết nghiệm của phương trình dạng: Phương trình 2
ax + bx + c = dx + e ; quy về 2 2
ax + bx + c = dx + ex + f
phương trình Thông hiểu: (Câu 16) Câu 6 Câu 16 bậc hai
Giải được phương trình quy về phương trình bậc hai dạng: 2
ax + bx + c = dx + e ; 2 2
ax + bx + c = dx + ex + f
Nhận biết: (Câu 7; 8; Câu 14: a, b, c, d)
- Xác định được vectơ pháp tuyến, vectơ chỉ
phương của một đường thẳng
- Điểm thuộc (không thuộc) đường thẳng.
- Nhận dạng PTTS của đường thẳng khi biết
đường thẳng đó đi qua 1 điểm và nhận 1 vectơ chỉ phương.
Phương trình - Nhận biết được PTTQ của đường thẳng khi biết Câu 7,
đường thẳng đường thẳng đó đi qua 1 điểm và nhận 1 vectơ Câu 8 Câu 14 a, b, c, d Câu 17 Câu 20 pháp tuyến cho trước
Thông hiểu: (Câu 20)
Lập được phương trình tổng quát của đường thẳng
Vận dụng: (Câu 17)
Vận dụng kiến thức về đường thẳng để giải bài Phương
toán có liên quan đến thực tiễn pháp
Nhận biết: (Câu 9; 10) 2 tọa độ
- Xác định được vị trí tương đối của hai đường trong thẳng mặt
Vị trí tương - Chỉ ra được công thức tính khoảng cách từ một
phẳng đối giữa hai điểm đến một đường thẳng; công thức tính góc đường giữa hai đường thẳng Câu
thẳng. Góc Thông hiểu: (Câu 18) 9,10 Câu 18
và khoảng - Tính khoảng cách từ một điểm đến một đường cách thẳng.
- Tính góc giữa hai đường thẳng.
- Xác định vị trí tương đối giữa hai đường thẳng.
- Tìm giao điểm của 2 đường thẳng.
Nhận biết: (Câu 11; 12)
- Lập được phương trình đường tròn khi biết tâm
Đường tròn và bán kính
trong mặt - Xác định được tâm và bán kính của đường tròn Câu
phẳng tọa độ khi biết phương trình của nó 11,12 Câu 21
Vận dụng: (Câu 21)
Vận dụng kiến thức về đường tròn để giải bài
toán liên quan đến thực tiễn Tổng số câu 12 1,75 0,25 2 2 2 1 Tổng số điểm 3,0 2,0 2,0 3,0 Tỉ lệ % 3,0 2,0 2,0 3,0 3. TỰ LUẬN
Câu 19 (1,0 điểm): (Hiểu)
- Tìm tập xác định của hàm số dạng 2
y = ax + bx + c
Câu 20 (1,0 điểm ): (Hiểu)
a) Viết phương trình tổng quát của đường thẳng đi qua 2 điểm
b) Tính khoảng cách từ một điểm đến một đường thẳng
Câu 21 (1 điểm ): (VD)
- Bài toán thực tế
……… HẾT ……….
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
ĐỀ CƯƠNG ÔN TẬP KIỂM TRA GIỮA HỌC KỲ 2 - TOÁN 10 NĂM HỌC 2024 - 2025
PHẦN I. CÂU HỎI TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
Thí sinh trả lời từ câu 1 đến câu …. Mỗi câu thí sinh chỉ chọn một phương án.
Câu 1: Cho bảng các giá trị đo nhiệt độ trong ngày tại Hải Phòng tương ứng của hai đại lượng x, y . Thời điểm (giờ) 6 9 12 15 18 21
Nhiệt độ (C ) 15 17 21 20 15 11
Nhiệt độ tại thời điểm nào là thấp nhất: A. 6h. B. 15h. C. 18h. D. 21h.
Câu 2: Bảng mô tả thu nhập bình quân đầu người của nước ta từ năm 1995 đến 2004 Năm
1995 1996 1997 1998 1999 2000 2001 2002 2004 TNBQĐN (tính theo USD) 200 282 295 311 339 363 375 394 564
Thu nhập bình quân đầu người của nước ta năm nào là thấp nhất: A. 1995. B. 1997. C. 2024. D. 2000.
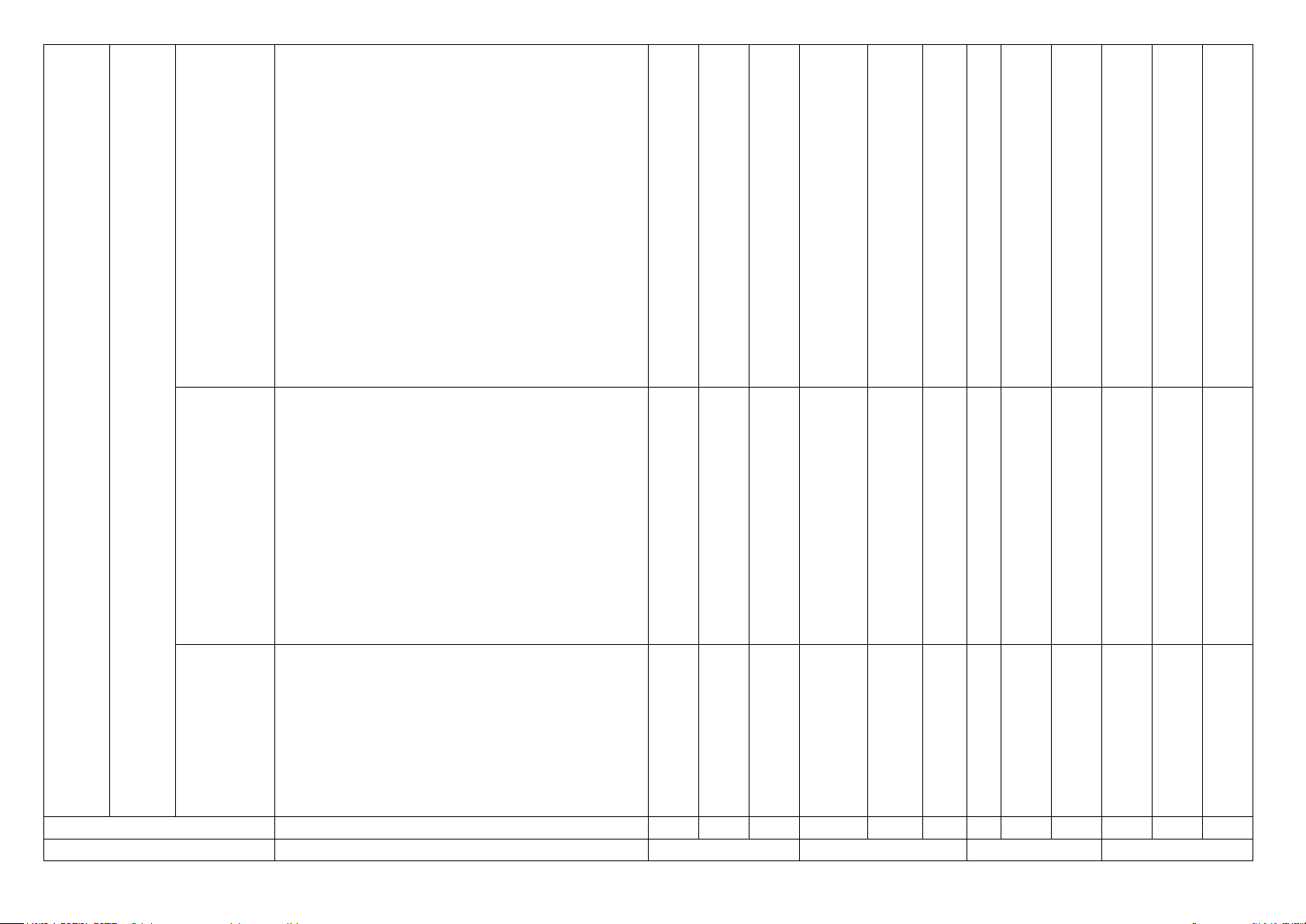
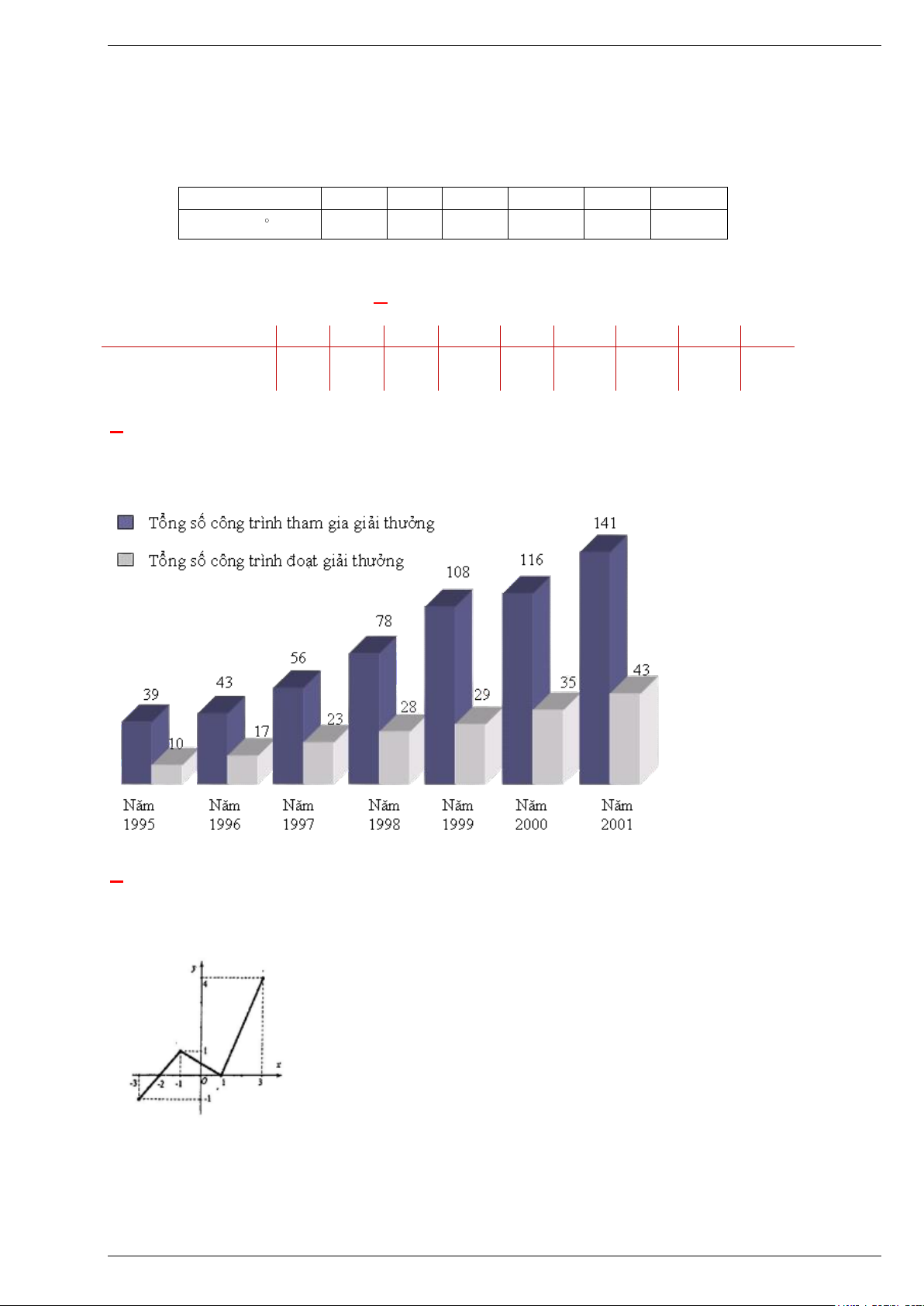
Câu 3: Biểu đồ mô tả số công trình khoa học kĩ thuật đăng kí dự giải thưởng Sáng tạo Khoa học công
nghệ Việt Nam và một số công trình đoạt giải hàng năm từ 1995 đến 2001
Tổng số công trình đoạt giải thưởng năm nào là cao nhất: A. 2001. B. 1997. C. 1995. D. 2000.
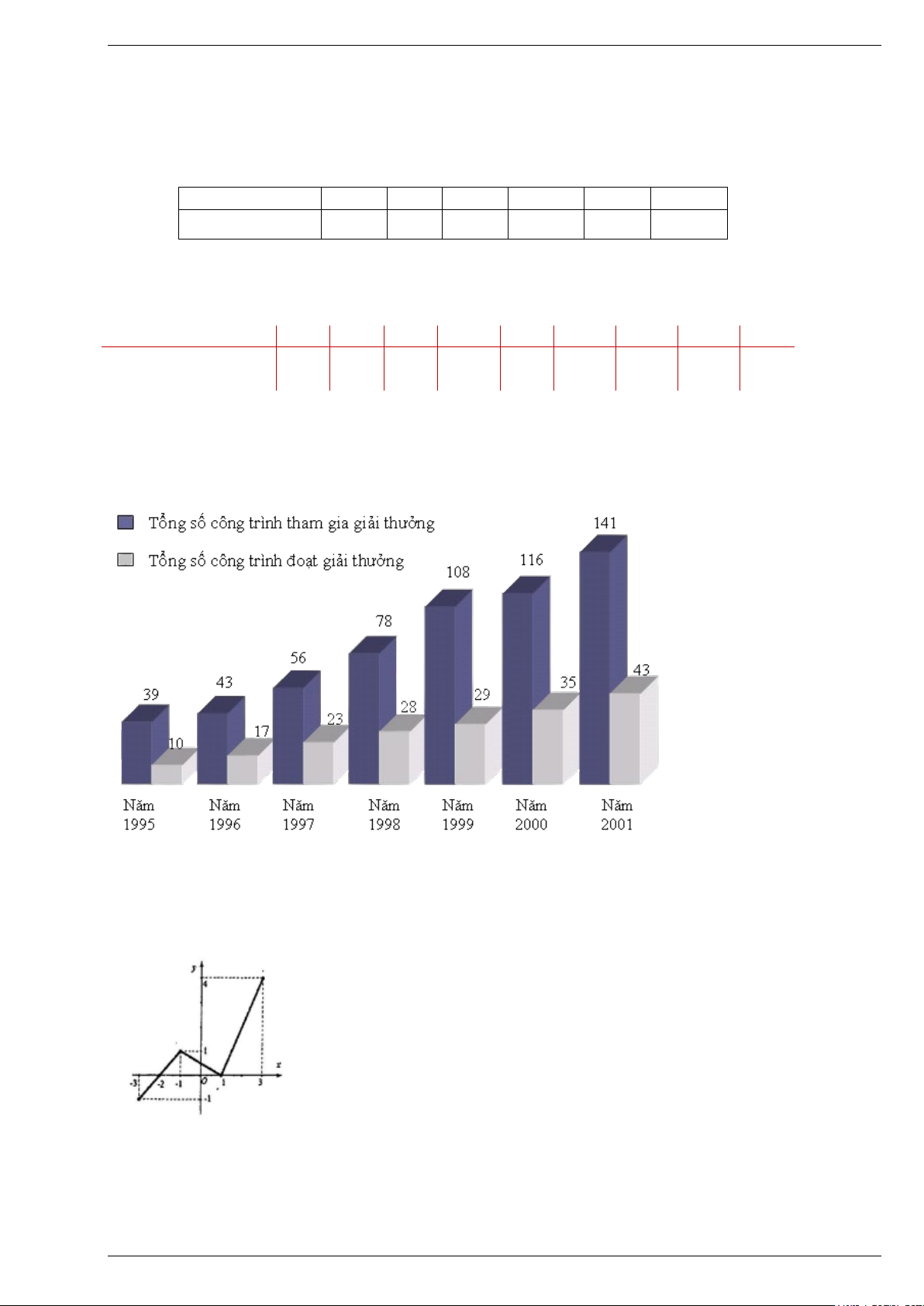
Câu 4: Cho hàm số y = f (x) có tập xác định là [ 3 − ; ]
3 và có đồ thị được biểu diễn bởi hình bên.
Khẳng định nào sau đây là đúng?
A. Hàm số y = f (x) + 2018 đồng biến trên các khoảng ( 3 − ;− ) 1 và (1;3).
B. Hàm số y = f (x) + 2018 đồng biến trên các khoảng ( 2; − ) 1 và (1;3).
C. Hàm số y = f (x) + 2018 nghịch biến trên các khoảng ( 2; − − ) 1 và (0; ) 1 .
D. Hàm số y = f (x) + 2018 nghịch biến trên khoảng ( 3 − ; 2 − ) . 1
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
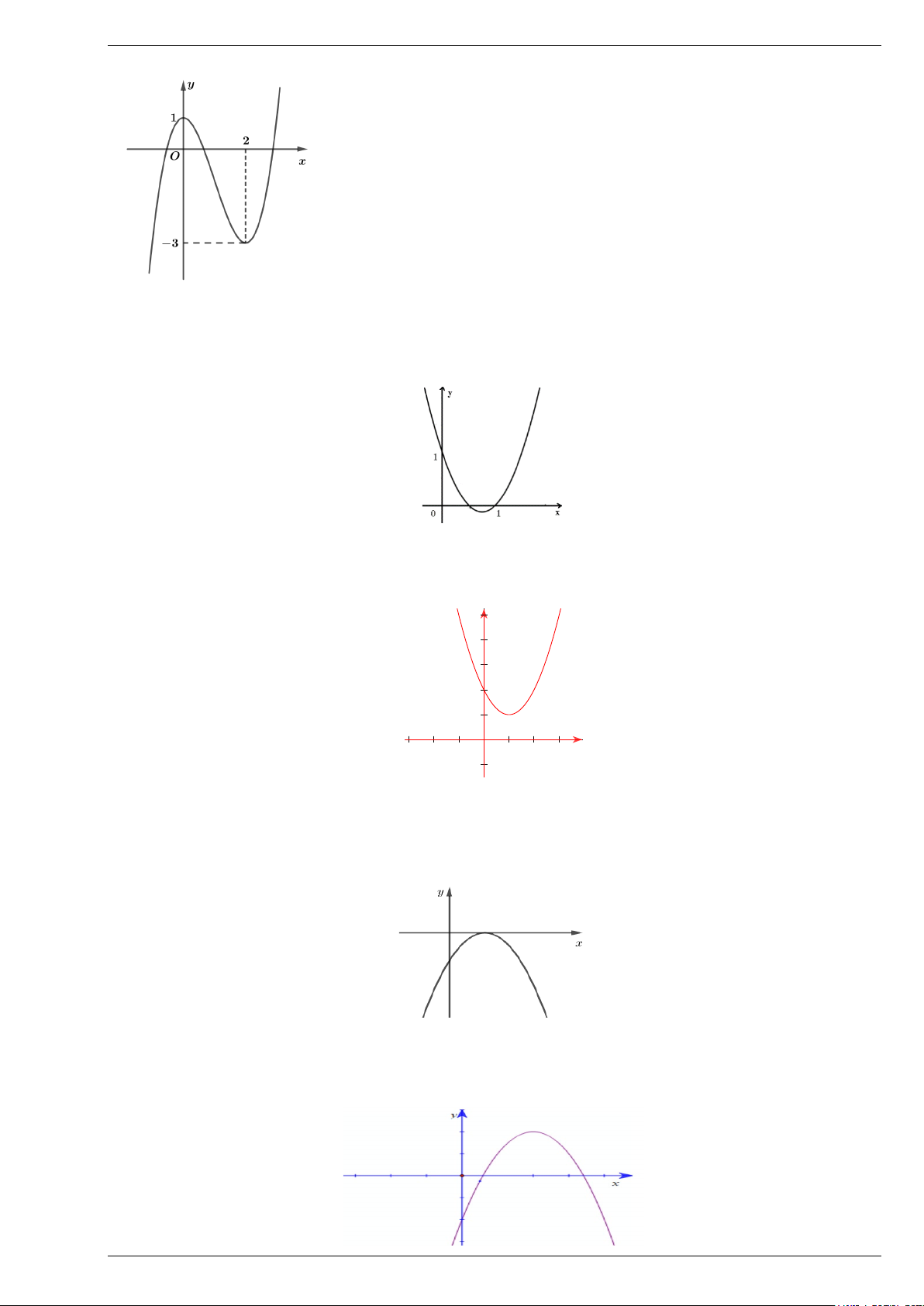
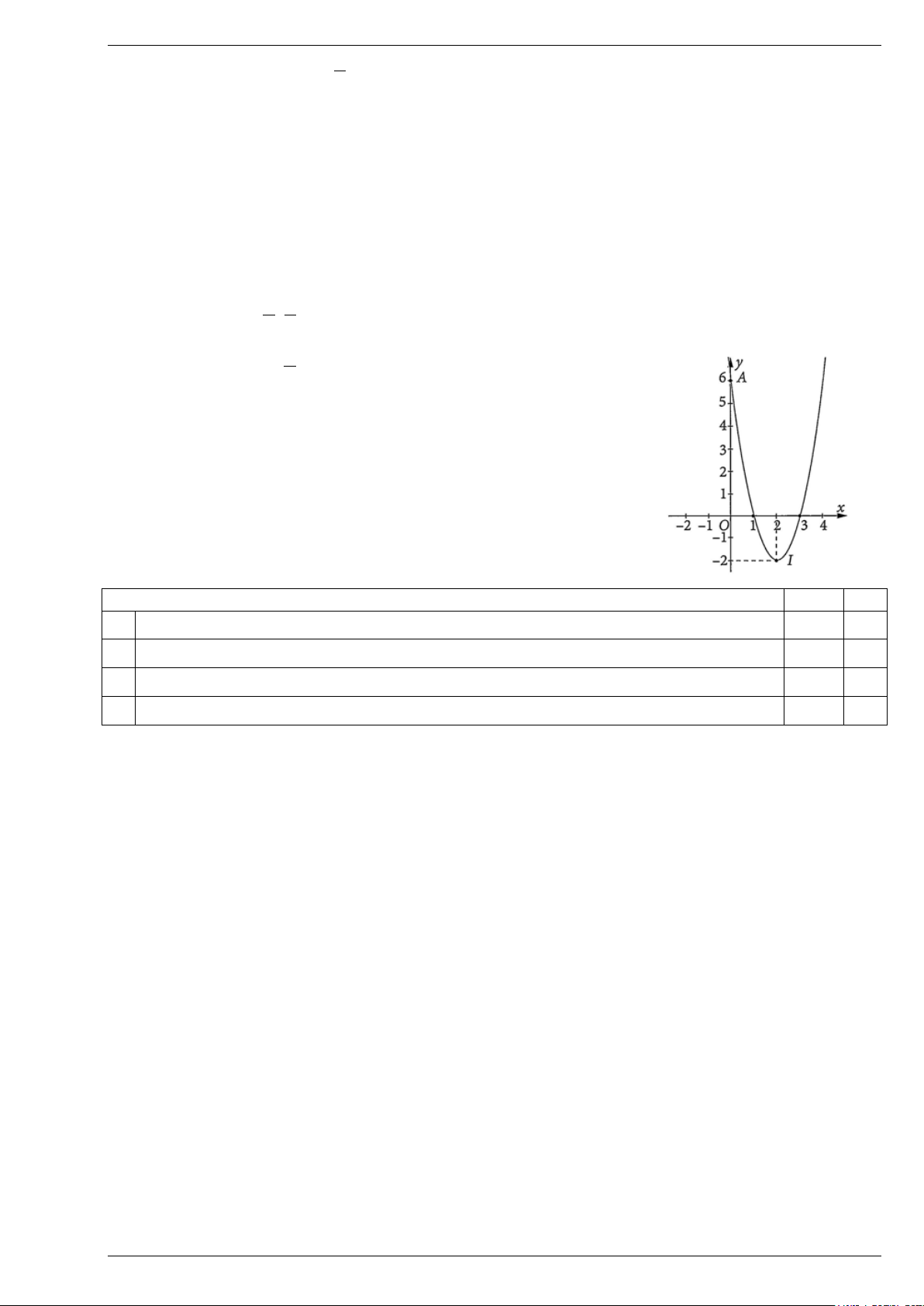
Câu 5: Cho hàm số có đồ thị như hình bên dưới.
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng (0;3).
B. Hàm số đồng biến trên khoảng ( ) ;1 −∞ .
C. Hàm số nghịch biến trên khoảng (0;2) .
D. Hàm số đồng biến trên khoảng ( ; −∞ 3) .
Câu 6: Hàm số nào sau đây có đồ thị như hình dưới đây A. 2
y = x − 3x +1. B. 2
y = −x + 3x −1. C. 2 y = 2
− x + 3x −1. D. 2
y = 2x − 3x +1.
Câu 7: Đồ thị của hàm số ( ) 2
f x = ax + bx + c như hình vẽ bên. y 4 2 0 x Tìm mệnh đề đúng? A. a > 0 a > a > a <  . B. 0  . C. 0  . D. 0  . ∆ ≤ 0 ∆ < 0 ∆ > 0 ∆ < 0
Câu 8: Hình vẽ bên là đồ thị của hàm số nào? A. 2
y = −x − 2x −1. B. 2
y = x − 2x +1. C. 2
y = x − 2x +1. D. 2
y = −x + 2x −1. Câu 9: Cho hàm số 2
y = ax + bx + c có đồ thị như hình vẽ. Khẳng định nào su đây đúng? 2
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
A. a > 0,b > 0,∆ > 0 .
B. a < 0,b > 0,∆ > 0.
C. a < 0,b < 0,∆ > 0.
D. a > 0,b < 0,∆ < 0.
Câu 10: Tìm khẳng định đúng trong các khẳng định sau? A. f (x) 2
= 3x + 2x − 5 là tam thức bậc hai.
B. f (x) = 2x − 4 là tam thức bậc hai. C. f (x) 3
= 3x + 2x −1là tam thức bậc hai. D. f (x) 4 2
= x − x +1là tam thức bậc hai.
Câu 11: Biểu thức nào sau đây là tam thức bậc hai? x
A. f (x) = 2x − 2 .
B. f (x) = . 2x −1 1
C. f (x) = . D. f (x) 2
= x − 4x + 3. 2 x − 3x − 4
Câu 12: Cho f (x) 2
= x + 4 . Khẳng định nào sau đây là đúng?
A. f (x) > 0, x ∀ ∈  .
B. f (x) < 0, x ∀ ∈  .
C. f (x) = 0, x ∀ ∈  .
D. f (x) < 0, x ∀ ∈( ; −∞ 2 − )  (2;+∞) .
Câu 13: Nghiệm của phương trình 3x + 5 = 2 là A. x = 1 − .
B. x = 0 .
C. x = 4 . D. 1 x = − . 3
Câu 14: Tập nghiệm S của phương trình và 2
x − 4 = x − 2 là A. S = { } 0 . B. S = { } 2 . C. S = {0; } 2 .
D. S = ∅ .
Câu 15: Tập nghiệm S của phương trình 2x − 3 = x − 3 là A. S = . ∅ B. S = { } 6 . C. S = {6; } 2 . D. S = { } 2 . x = 2 + 3t
Câu 16: Một vectơ chỉ phương của đường thẳng  là: y = 3 − − t    
A. u = 2; –3 .
B. u = 3; –1 . C. u = 3; 1 . D. u = 3; –3 4 ( ) 3 ( ) 2 ( ) 1 ( )
Câu 17: Một vectơ pháp tuyến của đường thẳng 2x − 3y + 6 = 0 là :     A. n = 2;− 3 B. n = 2;3
C. n = 3;2 D. n = 3 − ;2 1 ( ) 3 ( ) 2 ( ) 4 ( )
Câu 18: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm A( 3 − ;2) và B(1;4)?     A. u = 1; − 2 .
B. u = 2;1 . C. u = 2;
− 6 . D. u = 1;1 . 4 ( ) 3 ( ) 2 ( ) 1 ( )
Câu 19: Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng đi qua hai điểm A(2;3) và B(4; ) 1 ?     A. n = 2; 2 − . B. n = 2; 1
− . C. n = 1;1 . D. n = 1; 2 − . 4 ( ) 3 ( ) 2 ( ) 1 ( ) x = − t
Câu 20: Cho đường thẳng (d ) 2 3 :    và điểm 7 A ; 2 − 
. Điểm A∈(d ) ứng với giá trị nào của y = 1 − + 2t  2  t? A. 3 t = . B. 1 t = . C. 1 t = − . D. t = 2 2 2 2 x = + t Câu 21: Cho(d ) 2 3 : 
. Điểm nào sau đây không thuộc (d )? y = 5 − 4t
A. A(5;3).
B. B(2;5). C. C ( 1; − 9). D. D(8; 3 − ).
Câu 22: Xét vị trí tương đối của hai đường thẳng d : x − 2y +1 = 0 d : 3
− x + 6y −10 = 0 1 và 2 . A. Trùng nhau. B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau. 3
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
Câu 23: Xét vị trí tương đối của hai đường thẳng d :3x − 2y − 6 = 0 và d : 6x − 2y −8 = 0. 1 2 A. Trùng nhau. B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau. x = 3 − + 4t
x = 2 − 2t′
Câu 24: Xét vị trí tương đối của hai đường thẳng d : và d : . 1   y = 2 − 6t 2 y = 8 − + 4t′ A. Trùng nhau. B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau. x = 2 − + 5t
Câu 25: Hai đường thẳng (d :
và (d : 4x + 3y −18 = 0. Cắt nhau tại điểm có tọa độ: 2 ) 1 )  y = 2t A. (2;3). B. (3;2). C. (1;2). D. (2; ) 1 .
Câu 26: Góc giữa hai đường thẳng a : 3x − y + 7 = 0 và b : x − 3y −1 = 0 là: A. 30° . B. 90° . C. 60°. D. 45°.
Câu 27: Cho hai đường thẳng d : 2x + 5y − 2 = 0 và d :3x − 7y + 3 = 0 . Góc tạo bởi đường thẳng d 1 2 1 và d bằng 2 A. 0 30 . B. 0 135 . C. 0 45 . D. 0 60 . x = 2 + t
Câu 28: Tìm côsin góc giữa hai đường thẳng ∆ : 2x + y −1 = 0 và ∆ : 1 2  y =1− t A. 10 . B. 3 . C. 3 . D. 3 10 . 10 10 5 10
Câu 29: Cho hai điểm A(3;− )
1 , B(0;3). Tìm tọa độ điểm M thuộc Ox sao khoảng cách từ M đến
đường thẳng AB bằng 1. A. 7 M  ;0  và M (1;0).
B. M ( 13;0). 2   
C. M (4;0) . D. M (2;0) .
Câu 30: Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A(1; ) 1 , B(4; 3 − ) và đường thẳng
d : x − 2y −1 = 0 . Tìm điểm M thuộc d có tọa độ nguyên và thỏa mãn khoảng cách từ M đến đường thẳng AB bằng 6 . A. M (3;7). B. M (7;3).
Câu 31: Đường tròn 2 2
2x + 2y – 8x + 4y −1= 0 có tâm là điểm nào sau đây? A. ( 8; − 4). B. (2; ) 1 − . C. (8; 4 − ) . D. ( 2; − ) 1 .
Câu 32: Đường tròn tâm I(3; 1)
− và bán kính R = 2 có phương trình là A. 2 2
(x + 3) + (y −1) = 4. B. 2 2
(x −3) + (y −1) = 4. C. 2 2
(x −3) + (y +1) = 4. D. 2 2
(x + 3) + (y +1) = 4 .
Câu 33: Đường tròn tâm I( 1;
− 2) và đi qua điểm M (2;1) có phương trình là A. 2 2
x + y + 2x − 4y − 5 = 0 . B. 2 2
x + y + 2x − 4y − 3 = 0. C. 2 2
x + y − 2x − 4y − 5 = 0 . D. 2 2
x + y + 2x + 4y −5 = 0.
Câu 34: Trong mặt phẳng Oxy , đường tròn (C) 2 2
: x + y + 4x + 6y −12 = 0 có tâm là. A. I ( 2; − 3 − ).
B. I (2;3) .
C. I (4;6). D. I ( 4; − 6 − ) .
PHẦN II. CÂU HỎI TRẮC NGHIỆM ĐÚNG - SAI
Trong mỗi ý a, b, c, d ở mỗi câu, hãy chọn đúng hoặc sai
Câu 1: Xét tính đúng, sai của các khẳng định sau a) Hàm số 2 1 y = 2
− x + 3x − là hàm số bậc hai 2 b) Hàm số 4 2
y = 8x − 5x + 0,5là hàm số bậc hai 4
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10 c) Hàm số 3 2 1
y = 9x + 3x − x − là hàm số bậc hai 2 d) Hàm số y = ( 2 m + m + ) 2 2 6
10 x + (m +1)x − 3m +1 ( m là tham số ) là hàm số bậc hai
Câu 2: Xét đồ thị của hàm số 2
y = 2x + 4x +1. Khi đó:
a) có tọa độ đỉnh I( 1; − 1 − )
b) trục đối xứng là x =1.
c) Giao điểm của đồ thị với trục tung là M (0;1) .
d) Đồ thị đi qua các điểm Q(1;6) và P( 3 − ;6) .
Câu 3: Xét đồ thị của hàm số 2
y = −x + 5x − 4 . Khi đó: a) có toạ độ đỉnh 5 9 I  ;   2 4    b) trục đối xứng là 5 x = . 2
c) Giao điểm của đồ thị với trục tung là C(0; 4 − ) .
d) Giao điểm của đồ thị với trục hoành là (
A 2;0) và B(3;0) .
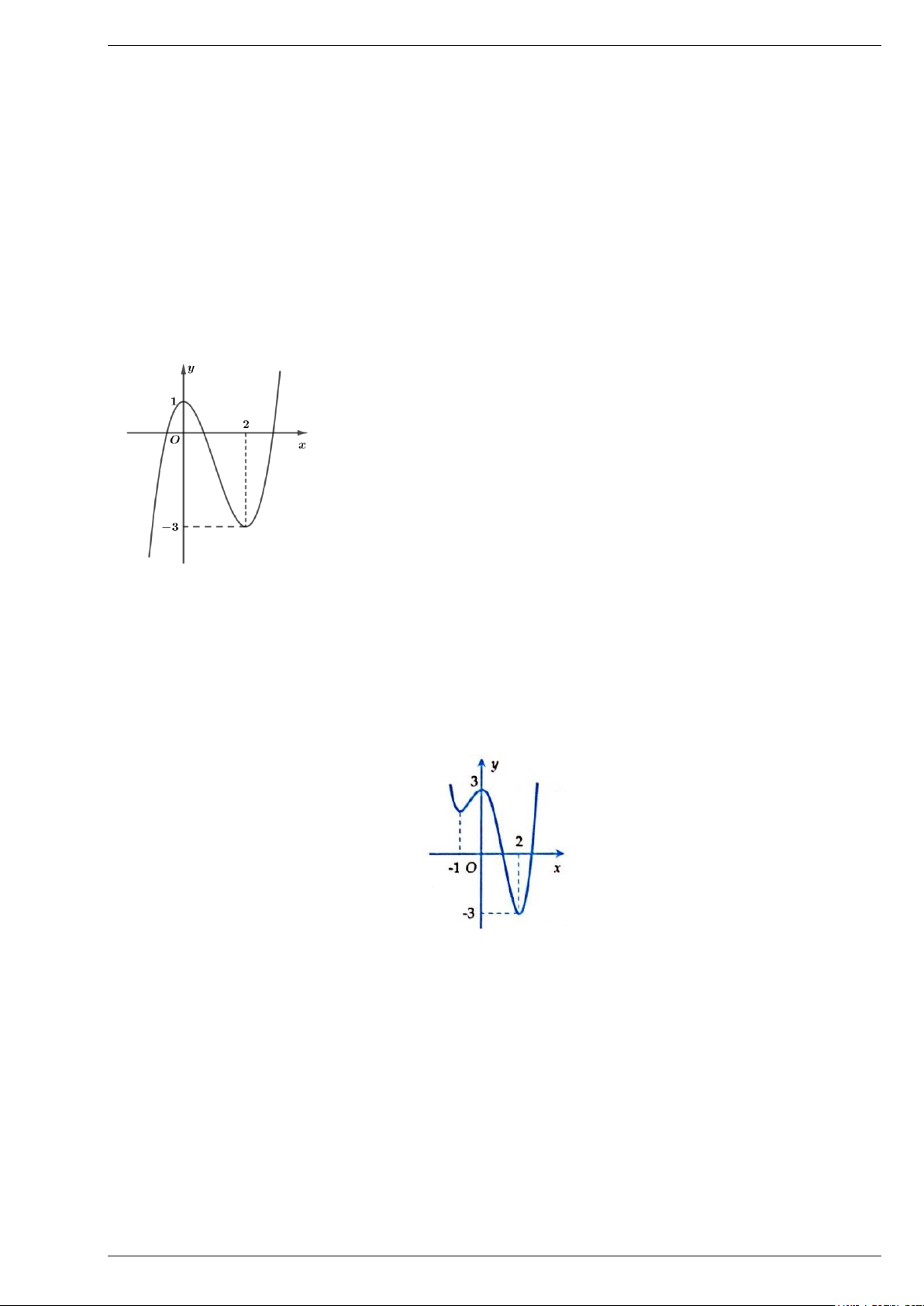
Câu 4: Cho đồ thị hàm số bậc hai y = f (x) có dạng như hình sau:
a) Trục đối xứng của đồ thị là đường thẳng x = 2 − .
b) Đỉnh I của đồ thị hàm số có tọa độ là (2; 2 − ) .
c) Đồ thị hàm số đi qua điểm ( A 0;6) d) Hàm số đã cho là 2
y = 2x − 2x + 6 .
Câu 5: Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai a) 2
x + 4x + 3 < 0 khi x ∈( 3 − ; 1) − . b) 2
x − 6x + 8 ≥ 0 khi x ∈( ; −∞ 2]∪[4;+∞) . c) 2
f (x) = x − x + 5 luôn âm với mọi x thuộc  d) 2 f (x) = 36
− x +12x −1 luôn nhỏ hơn hoặc bằng 0 với mọi x ∈ x =1+ 3t
Câu 6: Cho hai đường thẳng ∆ : x − y + 2 = 0 và ∆ : . Khi đó: 1 2  y = 2 − + t
a) Đường thẳng ∆ có vectơ pháp tuyến n(1;1) 1
b) Đường thẳng ∆ có vectơ pháp tuyến là n(1; 3 − ) 2 x = t
c) Phương trình tham số của đường thẳng ∆ là 1  y = 2 + t.
d) Phương trình tổng quát của đường thẳng ∆ là x − 3y − 7 = 0 2
Câu 7: Trong mặt phẳng toạ độ Oxy , cho hai điểm ( A 2
− ;2), B(3;4). Khi đó: 
a) Đường thẳng AB có vectơ chỉ phương là AB(2;5)
b) Đường thẳng AB có vectơ pháp tuyến là n(2; 5 − )
c) Phương trình tổng quát của đường thẳng AB là 2x − 5y +14 = 0 x = 1 − + 2t
d) Phương trình tham số của đường thẳng đi qua M ( 1;
− 1) và song song với AB là  y = 1+ 5t
Câu 8: Xác định tính đúng, sai của các khẳng định sau: a) ∆ qua (
A 1;0) , có vectơ pháp tuyến n = (3; 2
− ) , khi đó phương trình tổng quát của ∆ là :
3x − 2y − 3 = 0 b) ∆ qua ( A 1;
− 0) và vuông góc với đường thẳng AB biết B(1;4) , khi đó phương trình tổng quát của
∆ là : x + 2y +1 = 0 5
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
c) ∆ là đường trung trực của đoạn thẳng MN với M (0; 3)
− , N(2;5) , khi đó phương trình tổng quát
của ∆ là : x + 4y − 3 = 0
d) ∆ là đường cao xuất phát từ điểm A trong tam giác ABC biết rằng ( A 1; 1
− ), B(1;2),C(3; 3 − ) ,khi đó
phương trình tổng quát của ∆ là : 2x − 3y − 5 = 0
PHẦN III. CÂU HỎI TRẮC NGHIỆM TRẢ LỜI NGẮN
Thí sinh viết kết quả vào phần trả lời (kết quả làm tròn tối đa gồm 4 kí tự)
Câu 1: Tìm giá trị lớn nhất của hàm số 2 y = 2 − x + x + 5 .
Câu 2: Tìm giá trị nhỏ nhất của hàm số 2
y = x + 3x −1.
Câu 3: Một người nông dân thả 1000 con cá giống vào hồ nuôi vừa mới đào. Biết rằng sau mỗi năm
thì số lượng cá trong hồ tăng thêm x lần số lượng cá ban đầu và x không đổi. Bằng cách thay đổi kĩ
thuật nuôi và thức ăn cho cá. Hỏi sau hai năm để số cá trong hồ là 36000 con thì tốc độ tăng số lượng
cá trong hồ là bao nhiêu? Biết tốc độ tăng mỗi năm là không đổi.
Câu 4: Tìm số nghiệm phương trình sau: 2 3x − 9x +1 | = x − 2 | ;
Câu 5: Số nghiệm của phương trình 2
4 − 3x = 2x −1là:
Câu 6: Phương trình 2
−x + 4x = 2x − 2 có bao nhiêu nghiệm?
Câu 7: Số nghiệm của phương trình − 2
x + 4x − 3 + 5 = 2x là?
Câu 8: Trong mặt phẳng toạ độ Oxy , cho hình vuông ABCD và các điểm M (0;2), N(5; 3) − , P( 2; − 2 − ),Q(2; 4
− ) lần lượt thuộc các đường thẳng chứa các cạnh AB, BC,CD, DA . Lập
phương trình đường thẳng AB và tính diện tích hình vuông ABCD .
Câu 9: Trong mặt phẳng toạ độ Oxy , cho tam giác ABC có ( A 1;1), B(5; 2
− ) , đỉnh C thuộc đường
thẳng y − 4 = 0 , trọng tâm G thuộc đường thẳng 3x − 2y + 6 = 0 . Tính diện tích tam giác ABC .
Câu 10: Trong mặt phẳng toạ độ Oxy , cho các đường thẳng d : x + 2y + 3 = 0, d :3x − y + 5 = 0 và 1 2 điểm P( 2
− ;1) . Đường thẳng ∆ đi qua P và cắt d ,d lần lượt tại , 1 2
A B sao cho P là trung điểm của
AB . Tính khoảng cách từ M (3; 2
− ) đến đường thẳng ∆ .
Câu 11: Tìm m để hai đường thẳng sau vuông góc với nhau: ∆ : x − my +1 = 0 ;∆ : 2x + 3y + m = 0. 1 2
Câu 12: Tìm tham số m để các đường thẳng sau đây song song: ∆ : 2x + ( 2
m +1 y − 3 = 0 và ∆ : x + my −100 = 0 . 1 ) 2
Câu 13: Cho hai đường thẳng ∆ : x + y −10 = 0 và ∆ : 2x + my + 999 = 0 . Tìm m để góc tạo bởi hai 1 1
đường thẳng trên bằng 45°.
Câu 14: Trong mặt phẳng tọa độ Oxy , cho tam giác ABC , biết (
A 1;1), B(3;2),C(1;3) . Tính góc giữa
hai đường thẳng AB, AC . PHẦN IV. TỰ LUẬN
Câu 19 (1,0 điểm): (Hiểu)
- Tìm tập xác định của hàm số dạng 2
y = ax + bx + c
Câu 20 (1,0 điểm ): (Hiểu)
a) Viết phương trình tổng quát của đường thẳng đi qua 2 điểm
b) Tính khoảng cách từ một điểm đến một đường thẳng
Câu 21 (1 điểm ): (VD)
- Bài toán thực tế
……… HẾT ………. 6
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
ĐỀ CƯƠNG ÔN TẬP KIỂM TRA GIỮA HỌC KỲ 2 - TOÁN 10 NĂM HỌC 2024 - 2025
PHẦN I. CÂU HỎI TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
Thí sinh trả lời từ câu 1 đến câu …. Mỗi câu thí sinh chỉ chọn một phương án.
Câu 1: Cho bảng các giá trị đo nhiệt độ trong ngày tại Hải Phòng tương ứng của hai đại lượng , x y . Thời điểm (giờ) 6 9 12 15 18 21
Nhiệt độ ( C ) 15 17 21 20 15 11
Nhiệt độ tại thời điểm nào là thấp nhất: A. 6h. B. 15h. C. 18h. D. 21h.
Câu 2: Bảng mô tả thu nhập bình quân đầu người của nước ta từ năm 1995 đến 2004 Năm 1995 1996 1997 1998 1999 2000 2001 2002 2004 TNBQĐN 200 282 295 311 339 363 375 394 564 (tính theo USD)
Thu nhập bình quân đầu người của nước ta năm nào là thấp nhất: A. 1995. B. 1997. C. 2024. D. 2000.
Câu 3: Biểu đồ mô tả số công trình khoa học kĩ thuật đăng kí dự giải thưởng Sáng tạo Khoa học công
nghệ Việt Nam và một số công trình đoạt giải hàng năm từ 1995 đến 2001
Tổng số công trình đoạt giải thưởng năm nào là cao nhất: A. 2001. B. 1997. C. 1995. D. 2000.
Câu 4: Cho hàm số y = f ( x) có tập xác định là  3 − ; 
3 và có đồ thị được biểu diễn bởi hình bên.
Khẳng định nào sau đây là đúng?
A. Hàm số y = f ( x) + 2018 đồng biến trên các khoảng ( 3 − ;− ) 1 và (1;3) .
B. Hàm số y = f ( x) + 2018 đồng biến trên các khoảng ( 2 − ; ) 1 và (1;3) .
C. Hàm số y = f ( x) + 2018 nghịch biến trên các khoảng ( 2 − ;− ) 1 và (0 ) ;1 .
D. Hàm số y = f ( x) + 2018 nghịch biến trên khoảng ( 3 − ; 2 − ) . 1
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10 Lời giải Chọn A
Gọi (C) : y = f ( x) , (C) y = f ( x) + 2018. Khi tịnh tiến đồ thị (C) theo phương song song trục tung
lên phía trên 2018 đơn vị thì được đồ thị (C) . Nên tính đồng biến, nghịch biến của hàm số y = f ( x)
, y = f ( x) + 2018 trong từng khoảng tương ứng không thay đổi.
Dựa vào đồ thị ta thấy:
Hàm số y = f ( x) + 2018 đồng biến trên các khoảng ( 3 − ;− ) 1 và (1;3) (đúng).
Hàm số y = f ( x) + 2018 đồng biến trên các khoảng ( 2 − ; ) 1 và (1;3) (sai).
Hàm số y = f ( x) + 2018 nghịch biến trên các khoảng ( 2 − ;− ) 1 và (0 ) ;1 (sai).
Hàm số y = f ( x) + 2018 nghịch biến trên khoảng ( 3 − ; 2 − ) (sai).
Câu 5: Cho hàm số có đồ thị như hình bên dưới.
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng (0;3) .
B. Hàm số đồng biến trên khoảng ( ) ;1 − .
C. Hàm số nghịch biến trên khoảng (0;2) .
D. Hàm số đồng biến trên khoảng ( ;3 − ) . Lời giải Chọn C
Trên khoảng (0;2) , đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến.
Câu 6: Cho hàm số y = f ( x) xác định trên khoảng (− ;
 +) có đồ thị như hình vẽ dưới đây.
Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên khoảng (0;2)
B. Hàm số nghịch biến trên khoảng ( 3 − ;0)
C. Hàm số đồng biến trên khoảng ( 1 − ;0)
D. Hàm số nghịch biến trên khoảng (0;3) Lời giải Đáp án C.
Quan sát trên đồ thị ta thấy đồ thị hàm số đi lên trên khoảng ( 1
− ;0) . Vậy hàm số đồng biến trên khoảng ( 1 − ;0) .
Câu 7: Hàm số nào sau đây có đồ thị như hình dưới đây 2
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10 A. 2
y = x − 3x +1 . B. 2
y = −x + 3x −1. C. 2 y = 2
− x + 3x −1. D. 2
y = 2x − 3x +1 . Lời giải Chọn D
Bề lõm của parabol hướng lên trên suy ra a  0 , nên loại A và
Đồ thị đi qua điểm (1;0) nên)Chọn D.
Câu 8: Đồ thị của hàm số ( ) 2
f x = ax + bx + c như hình vẽ bên. y 4 2 0 x
Tìm mệnh đề đúng? a  0 a  0 a  0 a  0 A.  . B.  . C.  . D.  .   0   0   0   0 Lời giải Chọn B
Parabol có bề lõm hướng lên nên a  0 . Parabol không cắt trục Ox nên phương trình 2
ax + bx + c = 0
vô nghiệm, tức là   0 .
Câu 9: Hình vẽ bên là đồ thị của hàm số nào? A. 2
y = −x − 2x −1. B. 2
y = x − 2x +1. C. 2
y = x − 2x +1. D. 2
y = −x + 2x −1. Lời giải Chọn D. Câu 10: Cho hàm số 2
y = ax + bx + c có đồ thị như hình vẽ. Khẳng định nào su đây đúng?
A. a  0,b  0,   0 .
B. a  0,b  0,   0 .
C. a  0,b  0,   0 .
D. a  0,b  0,   0 . Lời giải Chọn B 3
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
Dựa vào đồ thị ta thấy bề lõm quay xuống nên a  0 , đồ thị cắt trục hoành tại 2 điểm phân biệt nên   b
0 , tọa độ đỉnh nằm bên phải trục tung nên −  0  b  0 . 2a
Câu 11: Tìm khẳng định đúng trong các khẳng định sau? A. f ( x) 2
= 3x + 2x − 5 là tam thức bậc hai.
B. f ( x) = 2x − 4 là tam thức bậc hai. C. f ( x) 3
= 3x + 2x −1là tam thức bậc hai. D. f ( x) 4 2
= x − x +1là tam thức bậc hai. Lời giải Chọn A
* Theo định nghĩa tam thức bậc hai thì f (x) 2
= 3x + 2x − 5 là tam thức bậc hai.
Câu 12: Biểu thức nào sau đây là tam thức bậc hai? x
A. f ( x) = 2x − 2 .
B. f ( x) = 2x − . 1 1
C. f ( x) =
f x = x − x + . 2
x − 3x − . D. ( ) 2 4 3 4 Lời giải Chọn D
Theo định nghĩa tam thức bậc hai.
Câu 13: Cho f ( x) 2
= x + 4 . Khẳng định nào sau đây là đúng?
A. f ( x)  0, x   .
B. f ( x)  0, x   .
C. f ( x) = 0, x   .
D. f ( x)  0, x  (− ;  2 − ) (2;+) . Lời giải Chọn A Cách 1: Ta có: 2 2 x  0, x
   x + 4  0, x   . Cách 2: f ( x) 2
= x + 4 là tam thức bậc hai có a = 1,  = 1
− 6  0  f (x)  0, x   .
Câu 14: Nghiệm của phương trình 3x + 5 = 2 là 1 A. x = 1 − .
B. x = 0 .
C. x = 4 .
D. x = − . 3 Lời giải Chọn D 1
Phương trình 3x + 5 = 2  3x + 5 = 4  x = − . 3
Câu 15: Tập nghiệm S của phương trình và 2
x − 4 = x − 2 là A. S =   0 . B. S =   2 . C. S = 0;  2 .
D. S =  . Lời giải Chọn B x − 2  0  x  2 x  2 2
x − 4 = x − 2        x = 2. x − 4 =  (x − 2)2 2 4x −8 = 0 x = 2
Vậy tập nghiệm của phương trình S =   2 .
Câu 16: Tập nghiệm S của phương trình 2x − 3 = x − 3 là A. S = .  B. S =   6 . C. S = 6;  2 . D. S =   2 . Lời giải Chọn B x  3   x  3 
Ta có 2x − 3 = x − 3      x =  2x − 3 =  (x −3) 6 2 2
x −8x +12 = 0
Vậy tập nghiệm của phương trình là S =   6 . 4
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
Câu 17: Giải phương trình 3 − 2x + x = 3 − 2x . 3 3 3 A. x  . B. x = . C. x  .
D. x = 0 . 2 2 2 Lời giải Chọn D Điề 3
u kiện: 3 − 2x  0  x  . 2
Với điều kiện trên, phương trình 3 − 2x + x = 3 − 2x x = 0 .
Vậy phương trình đã cho có một nghiệm x = 0 .
Câu 18: Phương trình sau có bao nhiêu nghiệm: x − 2 = 2 − x ? A. 0 . B. 1. C. 2 . D. Vô số. Lời giải Chọn Bx − 2  0 x  2 Điều kiện:     x = 2. 2 − x  0 x  2
Thay x = 2 vào phương trình ta được 0 = 0 hay x = 2 là nghiệm của phương trình. x = 2 + 3t
Câu 19: Một vectơ chỉ phương của đường thẳng  là: y = 3 − − t
A. u = 2; –3 .
B. u = 3; –1 . C. u = 3; 1 . D. u = 3; –3 4 ( ) 3 ( ) 2 ( ) 1 ( ) Lời giải Chọn B
Từ phương trình tham số của đường thẳng ta có một VTCP của đường thẳng là u = 3; –1 . 2 ( )
Câu 20: Một vectơ pháp tuyến của đường thẳng 2x − 3y + 6 = 0 là : A. n = 2; − 3 B. n = 2;3 C. n = 3; 2 D. n = −3; 2 1 ( ) 3 ( ) 2 ( ) 4 ( ) Lời giải Chọn A
Từ PTTQ ta thấy một VTPT của đường thẳng là n = 2; − 3 4 ( )
Câu 21: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm A( 3 − ;2) và B (1;4)?
A. u = −1; 2 . B. u = 2;1 . C. u = 2
− ;6 . D. u = 1;1 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) Lời giải Chọn B
Ta có AB = (4; 2) một VTCP của đường thẳng AB cùng phương với AB = (4; 2) . 1 Ta thấy u = 2;1 =
AB vậy u = 2;1 là một VTCP của AB 2 ( ) 2 ( ) 2
Câu 22: Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng đi qua hai điểm A(2;3) và B (4; ) 1 ? A. n = 2; 2 − .
B. n = 2; −1 . C. n = 1;1 .
D. n = 1; −2 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) Lời giải Chọn C Ta có AB = (2; 2
− ) một VTPT n của đường thẳng AB thì vuông góc với AB Suy ra . n AB = 0  .2 x + .
y (−2) = 0 chọn x = 1, y = 1  n = (1; ) 1
Chú ý: Ta hoàn toàn có thể dùng nhận xét nêu ở mục 2.3.2 để giải quyết nhanh bài toán này. 5
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10 x = − t  7 
Câu 23: Cho đường thẳng (d ) 2 3 :  và điểm A ; 2 − . 
 Điểm A(d ) ứng với giá trị nào của y = 1 − + 2t  2  t? 3 1 1 A. t = . B. t = .
C. t = − . D. t = 2 2 2 2 Lời giải Chọn C  1 7 t = −  7   = 2 − 3t  2 1 Ta có A ; 2 −    (d )  2    t = −  2  1 2  2 − = 1 − + 2t t  = −  2 x = + t
Câu 24: Cho (d ) 2 3 : 
. Điểm nào sau đây không thuộc (d )? y = 5 − 4t
A. A(5;3).
B. B (2;5). C. C ( 1 − ;9). D. D (8; 3 − ). Lời giải Chọn B  = + t t  = Thay B ( ) 2 2 3 0 2;5      t = 0 5  = 5 − 4t t  = 0
Câu 25: Xét vị trí tương đối của hai đường thẳng d : x − 2 y +1 = 0 d : 3
− x + 6y −10 = 0 1 và 2 . A. Trùng nhau. B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau. Lời giải Chọn B
d : x − 2y +1 = 0 − 1 1 2 1  → = = ⎯⎯ →d || d . 1 2 d : 3
− x + 6y −10 = 0  3 − 6 10 − 2
Câu 26: Xét vị trí tương đối của hai đường thẳng d : 3x − 2 y − 6 = 0 và d : 6x − 2 y − 8 = 0 . 1 2 A. Trùng nhau. B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau. Lời giải Chọn D 3 2 −
d : 3x − 2y − 6 = 0 → n = 3; 2 −   = 1 1 ( )  → 6 2 − ⎯⎯
→ d , d cắt nhau nhưng không vuông góc. 1 2
d : 6x − 2y − 8 = 0 → n = 6;−2  2 2 ( ) n n =   0 1 2 x = 3 − + 4t
x = 2 − 2t
Câu 27: Xét vị trí tương đối của hai đường thẳng d :  và d :  . 1 y = 2 − 6t 2 y = 8 − + 4tA. Trùng nhau. B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau. Lời giải Chọn B x = 3 − + 4td :  → A 3
− ;2  d , u = 2; 3 −   − 1 ( ) 1 1 ( ) 2 3 y = 2 − 6t   =  →  2 − 3 → d || d . 1 2
x = 1− 2t   d :  → = 2 − ;3 A    d u 2 ( ) 2 2 y = 4 + 3t  x = 2 − + 5t
Câu 28: Hai đường thẳng (d : 
và (d : 4x + 3y −18 = 0. Cắt nhau tại điểm có tọa độ: 2 ) 1 ) y = 2t A. (2;3). B. (3; 2). C. (1;2). D. (2; ) 1 . Lời giải 6
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10 Chọn A x = 2 − + 5t Ta có (d : 
d : 2x − 5y + 4 = 0 1 ) ( 1) y = 2t
2x −5y + 4 = 0 x = 2
Gọi M = (d d M là nghiệm của hệ phương trình    1 ) ( 2)
4x + 3y −18 = 0 y = 3
Câu 29: Tính góc giữa hai đường thẳng  : x − 3y + 2 = 0 và  : x + 3y −1 = 0 . A. 90 . B. 120 . C. 60 . D. 30 . Lời giải Chọn C
Đường thẳng  có vectơ pháp tuyến n = (1;− 3), đường thẳng 
 có vectơ pháp tuyến n = (1; 3) . −
Gọi  là góc giữa hai đường thẳng ,  .  = (n n) 1 3 1 cos cos , = =   = 60 . 1+ 3. 1+ 3 2
Câu 30: Góc giữa hai đường thẳng a : 3x − y + 7 = 0 và b : x − 3y −1 = 0 là: A. 30 . B. 90 . C. 60 . D. 45 . Lời giải Chọn A
Đường thẳng a có vectơ pháp tuyến là: n = 3; −1 ; 1 ( )
Đường thẳng b có vectơ pháp tuyến là: n = 1;− 3 . 2 ( )
Áp dụng công thức tính góc giữa hai đường thẳng có: 1. 3 + − − n n ( ) 1 ( 3 . ) cos (a,b) 3 1 2 = = =
. Suy ra góc giữa hai đường thẳng bằng 30 . n . n 2.2 2 1 2
Câu 31: Cho hai đường thẳng d : 2x + 5y − 2 = 0 và d : 3x − 7 y + 3 = 0 . Góc tạo bởi đường thẳng d 1 2 1 và d bằng 2 A. 0 30 . B. 0 135 . C. 0 45 . D. 0 60 . Lời giải Chọn C
Đường thẳng d : 2x + 5y − 2 = 0 có vectơ pháp tuyến 1 n = (2;5) . 1
Đường thẳng d : 3x − 7 y + 3 = 0 có vectơ pháp tuyến n = − 2 (3; 7) . 2
Góc giữa hai đường thẳng được tính bằng công thức ( n .n 2.3 + 5.( 7 − ) 29 1 cos d , d = cos n ,n = = = = 1 2 ) ( ) 1 2 1 2 2 2 2 2 n . n 29 2 2 + + − 1 2 2 5 . 3 ( 7)  (d ;d ) 0 = 45 1 2
Vậy góc tạo bởi đường thẳng d và d bằng 0 45 . 1 2 x = 2 + t
Câu 32: Tìm côsin góc giữa hai đường thẳng  : 2x + y −1 = 0 và  :  1 2 y = 1− t 10 3 3 3 10 A. . B. . C. . D. . 10 10 5 10 Lời giải Chọn D
Véctơ pháp tuyến của đường thẳng  là n = (2; )
1 nên véctơ chỉ phương u = (1; − 2) 1
Véctơ chỉ phương của đường thẳng  là u = (1;− ) 1 2 7
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10 . u u Khi đó ( 3 3 10 cos  ;  = cos u;u = = = 1 2 )
( ) u.u 5. 2 10
Câu 33: Cho hai điểm A(3;− )
1 , B (0;3) . Tìm tọa độ điểm M thuộc Ox sao khoảng cách từ M đến
đường thẳng AB bằng 1.  7  A. M ; 0 
 và M (1;0).
B. M ( 13;0) .  2 
C. M (4;0) . D. M (2;0) . Lời giải Chọn A Gọi M ( ;0 x ) . Ta có AB = (−3; 4)
Phương trình đường thẳng AB : 4x + 3( y −3) = 0  4x + 3y −9 = 0 . −  7 x = d (M AB) 4x 9 ; =  5 = 4x − 9   2 5   x = 1  7  Vậy M ; 0 ; M   (1;0) .  2 
Câu 34: Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A(1; ) 1 , B (4; 3 − ) và đường thẳng
d : x − 2y −1 = 0 . Tìm điểm M thuộc d có tọa độ nguyên và thỏa mãn khoảng cách từ M đến đường thẳng AB bằng 6 . A. M (3;7). B. M (7;3).  27  C. M ( 4 − 3; 2 − 7). D. M 3; − .    11  Lời giải
M d : x − 2y −1= 0 → M (2m +1;m), m  . Khi đó
AB : 4x + 3y − 7 = 0 m = 3 + + − d (M AB) 8m 4 3m 7 6 ; 11m 3 30  = =  − =  27
→ M (7;3) Chọn B 5 m = (l) .  11
Câu 35: Đường tròn 2 2
2x + 2y – 8x + 4y −1 = 0 có tâm là điểm nào sau đây? A. ( 8 − ;4). B. (2; )1 − . C. (8; 4 − ) . D. ( 2 − ; ) 1 . Lời giải Chọn B 2 2 2 1
x + 2 y – 8x + 4 y −1 = 0 2 2
x + y – 4x + 2y − = 0 . 2
Vậy tâm là: I (2;− ) 1 .
Câu 36: Đường tròn tâm I (3; 1
− ) và bán kính R = 2 có phương trình là A. 2 2
(x + 3) + ( y −1) = 4 . B. 2 2
(x − 3) + ( y −1) = 4 . C. 2 2
(x − 3) + ( y +1) = 4 . D. 2 2
(x + 3) + ( y +1) = 4 . Lời giải Chọn C
Phương trình đường tròn có tâm 2 2 I (3;− )
1 , bán kính R = 2 là: ( x − 3) + ( y + ) 1 = 4
Câu 37: Đường tròn tâm I ( 1
− ;2) và đi qua điểm M (2;1) có phương trình là A. 2 2
x + y + 2x − 4 y − 5 = 0 . B. 2 2
x + y + 2x − 4 y − 3 = 0. 8
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10 C. 2 2
x + y − 2x − 4 y − 5 = 0 . D. 2 2
x + y + 2x + 4 y − 5 = 0. Lời giải Chọn A
Đường tròn có tâm I ( 1
− ;2) và đi qua M (2; )
1 thì có bán kính là: R = IM = + (− )2 2 3 1 = 10
Khi đó có phương trình là: ( x + )2 + ( y − )2 2 2 1 2
=10  x + y + 2x − 4y − 5 = 0
Câu 38: Trong mặt phẳng Oxy , đường tròn (C) 2 2
: x + y + 4x + 6y −12 = 0 có tâm là. A. I ( 2 − ; 3 − ).
B. I (2;3) .
C. I (4;6) . D. I ( 4 − ; 6 − ) . Lời giải Chọn A
Ta có phương trình đườ 2 2
ng tròn là: ( x + 2) + ( y + 3) = 25 .
Vậy tâm đường tròn là: I ( 2 − ; 3 − ).
Câu 39: Đường tròn 2 2
x + y −10 y − 24 = 0 có bán kính bằng bao nhiêu? A. 49 . B. 7 . C. 1. D. 29 . Lời giải Chọn B Đường tròn 2 2
x + y −10 y − 24 = 0 có tâm I (0;5) , bán kính 2 2 R = 0 + 5 − ( 2 − 4) = 7 . 2 2
Câu 40: Xác định tâm và bán kính của đường tròn (C ) : ( x + ) 1 + ( y − 2) = 9. A. Tâm I ( 1
− ;2), bán kính R = 3 . B. Tâm I ( 1
− ;2), bán kính R = 9 . C. Tâm I (1; 2
− ), bán kính R = 3. D. Tâm I (1; 2
− ), bán kính R = 9. Lời giải Chọn A
Câu 41: Tìm tọa độ tâm I và bán kính R của đường tròn (C) : 2 2
x + y − 2x + 4 y + 1 = 0 . A. I ( 1 − ; 2); R = 4 . B. I (1; 2 − ); R = 2 .
C. I (−1; 2) ; R = 5 . D. I (1; 2 − ); R = 4 . Lời giải Chọn B
(C) có tâm I (1; 2 − ) , bán kính R = + (− )2 2 1 2 −1 = 2. 2 2
Câu 42: Trong mặt phẳng Oxy , cho đường tròn (C ) : ( x − 2) + ( y + 3) = 9 . Đường tròn có tâm và bán kính là
A. I (2;3), R = 9 . B. I (2; 3 − ), R = 3. C. I ( 3 − ;2), R = 3 . D. I ( 2 − ;3), R = 3 . Lời giải Chọn B
Đường tròn (C) có tâm I (2; 3
− ) và bán kính R = 3 . 2 2
Câu 43: Tìm tọa độ tâm I và tính bán kính R của đường tròn (C) : ( x + 2) + ( y − 5) = 9 . A. I ( 2 − ;5), R = 81.. B. I (2; 5 − ), R = 9.. C. I (2; 5 − ), R = 3.. D. I ( 2 − ;5), R = 3. Lời giải Chọn D
Theo bài ra ta có tọa độ tâm I ( 2
− ;5) và bán kính R = 3 .
Câu 44: Đường tròn (C) 2 2
: x + y − 2x + 4y − 3 = 0 có tâm I , bán kính R là A. I ( 1
− ;2), R = 2 .
B. I (−1; 2), R = 2 2 . C. I (1; − 2), R = 2 . D.
I (1; − 2), R = 2 2 . Lời giải Chọn D 2
Tâm I (1; − 2) , bán kính 2 R = 1 + ( 2 − ) − ( 3 − ) = 8 = 2 2 . 9
TRƯỜNG THPT KIẾN THỤY NỘI DUNG ÔN TẬP KIỂM TRA GIỮA HK2 TOÁN 10
Câu 45: Phương trình đường tròn có tâm I (1;2) và bán kính R = 5 là A. 2 2
x + y − 2x − 4 y − 20 = 0 . B. 2 2
x + y + 2x + 4 y + 20 = 0 . C. 2 2
x + y + 2x + 4 y − 20 = 0 . D. 2 2
x + y − 2x − 4 y + 20 = 0 . Lời giải Chọn A Phương trình đườ 2 2
ng tròn có tâm I (1;2) và bán kính R = 5 là ( x − ) + ( y − ) 2 1 2 = 5 2 2
x − 2x +1+ y − 4y + 4 = 25 2 2
x + y − 2x − 4y − 20 = 0 .
Câu 46: Đường tròn tâm I ( 1
− ;2) , bán kính R = 3 có phương trình là A. 2 2
x + y + 2x + 4 y − 4 = 0 . B. 2 2
x + y − 2x − 4 y − 4 = 0 . C. 2 2
x + y + 2x − 4 y − 4 = 0 . D. 2 2
x + y − 2x + 4 y − 4 = 0 . Lời giải Chọn C Đường tròn tâm I ( 1 − ;2) , bán kính R = 3 có phương trình là
(x + )2 +( y − )2 2 2 1 2
= 9  x + y + 2x − 4y − 4 = 0 .
Câu 47: Phương trình nào sau đây là phương trình của đường tròn tâm I ( 1
− ;2) , bán kính bằng 3 ? 2 2 2 2 A. ( x − ) 1 + ( y + 2) = 9 . B. ( x + ) 1 + ( y + 2) = 9 . 2 2 2 2 C. ( x − ) 1 + ( y − 2) = 9. D. ( x + ) 1 + ( y − 2) = 9 . Lời giải Chọn D Phương trình đườ 2 2 ng tròn tâm I ( 1
− ;2) và bán kính R = 3 là: (x + ) 1 + ( y − 2) = 9 .
PHẦN II. CÂU HỎI TRẮC NGHIỆM ĐÚNG - SAI
Trong mỗi ý a, b, c, d ở mỗi câu, hãy chọn đúng hoặc sai
Câu 1: Xét tính đúng, sai của các khẳng định sau 1 a) Hàm số 2 y = 2
− x + 3x − là hàm số bậc hai 2 b) Hàm số 4 2
y = 8x − 5x + 0, 5 là hàm số bậc hai 1 c) Hàm số 3 2
y = 9x + 3x − x − là hàm số bậc hai 2 d) Hàm số y = ( 2 m + m + ) 2 2 6
10 x + (m +1)x − 3m +1 ( m là tham số ) là hàm số bậc hai Lời giải a) Đúng b) Sai c) Sai d) Đúng 1
a) Là hàm số bậc hai với a = 2
− ,b = 3,c = − . 2
b) Không phải là hàm số bậc hai vì chứa 4 x .
c) Không phải là hàm số bậc hai vì chứa 3 x .
d) Là hàm số bậc hai với 2 2
a = m + 6m +10 = (m + 3) +1  0, b = m +1, 2 c = 3 − m +1.
Câu 2: Xét đồ thị của hàm số 2
y = 2x + 4x +1 . Khi đó:
a) có tọa độ đỉnh I ( 1 − ; 1 − )
b) trục đối xứng là x = 1 .
c) Giao điểm của đồ thị với trục tung là M (0;1) .
d) Đồ thị đi qua các điểm Q(1;6) và P( 3 − ;6) . Lời giải 10

Tài liệu liên quan: