ĐỀ CƯƠNG ÔN TẬP HỌC KÌ II - NĂM HỌC 2023 - 2024 MÔN: TOÁN 7 PHẦN I - ĐẠI SỐ I. Trắc nghiệm
Câu 1. Cho x và y là 2 đại lượng tỉ lệ thuận. Biết x  3thì y  6
 , nếu y  4 thì x bằng A. 2 . B. 2 . C. 8 . D. 8 .
Câu 2. Cho x và y là 2 đại lượng tỉ lệ nghịch. Biết khi x  0,4 thì y  15 . Khi x  6 thì y bằng A. 1. B. 0 . C. 6 . D. 0,6
Câu 3. Cho tỉ lệ thức 3x  y 3
 . Giá trị của tỉ số x bằng x  y 4 y 3 2 1  5 7 A. . B. . C. . D. . 4 9 4 9 x y z Câu 4. Cho
  và x  y  z  1
 2. Số lớn nhất trong 3 số x, y, z là 7  4 3 A. 1  4 . B. 14 . C. 8 . D. 6 .
Câu 5. Một người đi xe máy với vận tốc 40km / h trong x giờ, sau đó tăng vận tốc thêm
5km / h trong y giờ. Tổng quãng đường người đó đi được (tính theo km ) là A. 40x  5y .
B. 40 x  y  45y . C. 40x  45x  y . D. 40x  45y .
Câu 6. Đa thức nào sau đây là đa thức một biến? A. 2 1 x  1. B. 3 2 x  2x  3. C. 2 xy  x  3 . D. xyz  yz  3. x
Câu 7. Giá trị của biểu thức 2
A  x 1 tại x  1 là A. 2 . B. 0 . C. 1. D. 1. Câu 8. Cho 4 3 2
P(x)  5x  4x  3x  2x 1 và 4 3 2 Q(x)  2
 x  2x  3x  4x  5 .
Đa thức K(x)  P(x)  Q( )
x . Khi đó, phát biểu nào dưới đây đúng?
A. K (x) có bậc là 3, hệ số tự do bằng 6  .
B. K (x) có bậc là 4 , hệ số cao nhất bằng 6 .
C. K (x) có bậc là 4 , hệ số tự do bằng 6  .
D. K (x) có bậc là 3, hệ số cao nhất bằng 3.
Câu 9. Kết quả của phép tính (2x  3)(2x  3) là A. 2 4x 12x  9 . B. 2 4x  9. C. 2 2x  3. D. 2 4x  9 .
Câu 10. Phép chia đa thức 4 3
2x  3x  3x  2 cho đa thức x 1 được đa thức dư là A. 0 . B. 1. C. 2 . D. 10 . Câu 11. Đa thức 2
3  x có tối đa bao nhiêu nghiệm? A. 1. B. 2 . C. 3. D. 0 .
Câu 12. Giá trị của đa thức 3 5 99
x  x  x  ...  x tại x  1 là A. 100 . B. 1  01. C. 51. D. 50 .
Câu 13. Một thùng kín đựng 7 quả bóng màu đỏ, 12 quả bóng màu xanh, 18 quả bóng màu
vàng, 15 quả bóng màu trắng có cùng kích thước. Nam lấy ngẫu nhiên một quả bóng trong
thùng. Hỏi khả năng Nam lấy được quả bóng màu gì lớn nhất? A. Đỏ. B. Xanh. C. Vàng. D. Trắng.
Câu 14. Có hai chiếc hộp, mỗi hộp đựng 6 tấm thẻ ghi các số 1;2;3;4;5;6. Rút ngẫu nhiên một
tấm thẻ từ mỗi hộp. Biến cố “Chênh lệch giữa hai số ghi trên hai tấm thẻ bằng 6 ” là A. Biến cố ngẫu nhiên. B. Biến cố chắc chắn. C. Biến cố không thể. D. Biến cố có thể.
Câu 15. Một túi đựng các tấm thẻ được ghi các số 0;4;8;12;16;20 . Rút ngẫu nhiên một tấm thẻ
trong túi. Hỏi trong các biến cố dưới đây, biến cố nào là biến cố chắc chắn?
Biến cố A: “Rút được thẻ ghi số là số chia hết cho 4 ”
Biến cố B: “Rút được thẻ ghi số là số nguyên dương”
Biến cố C: “Rút được thẻ ghi số nhỏ hơn 30 ”. A. B. B. A. C. A và B. D. A và C.
Câu 16. Đáp án đúng nhất khi nói về giá trị của xác suất P của một biến cố? A. 0  P  1. B. 0  P  1. C. 0  P  1. D. 0  P  1.
Câu 17. Xác suất của biến cố “Tháng 5 dương lịch có 31 ngày” bằng A. 0% . B. 50% . C. 100% . D. 8,33% .
Câu 18. Gieo một con xúc xắc cân đối. Xác suất của biến cố “Số chấm xuất hiện là số chẵn” là 1 1 1 A. . B. . C. . D. 0 . 2 3 6
Câu 19. Tổ I lớp 7A có 5 học sinh nữ và 5 học sinh nam. Chọn ngẫu nhiên một học sinh trong
tổ I lớp 7A. Xác suất của biến cố “Học sinh được chọn là học sinh nữ” là 1 1 1 1 A. . B. . C. . D. . 2 5 10 25
Câu 20. Một chuyến xe khách có 28 hành khách nam và 31 hành khách nữ. Đến một bến xe,
có một số hành khách nữ xuống xe. Chọn ngẫu nhiên một hành khách trong các hành khách 1
còn lại trên xe. Biết rằng, xác suất để chọn được hành khách nữ là . Hỏi có bao nhiêu hành 2 khách nữ đã xuống xe? A. 1. B. 2 . C. 3. D. 4 . II. Tự luận: Bài 1. Thu gọn:  1  1 a) 2 3 3  x 4x  2x    b) 3 4x  x 2 2x  x  5  3  5 c) 2 2
(x  x 1)(x 1)  x(x  3) 15 d) 2 2 2 1
 5x  5x(x  7x  3)  x (5x  8)  27x Bài 2. Làm tính chia: a) 3 2
(x  6x 11x  6) : (x  3) b) 4 3 2 2
(x  3x  4x  x  3) : (x  2x  3) c) 3 2 (x 1) : (x  x 1) d) 3 2 2
(4x  2x  x  3) : (x  2x ) Bài 3. Cho hai đa thức: f  x 2 2 3 5 3
 3x  7  5x  6x  4x  8  5x  x g  x 2 2 3 5 3
 x  7x  5x  7x  2x  7x 10x  x  2
a) Thu gọn các đa thức trên rồi sắp xếp theo lũy thừa giảm của biến. Tìm bậc, hệ số cao
nhất, hệ số tự do của mỗi đa thức.
b) Tính h x  f x  g x và k  x  2 f x  g  x .
c) Tính giá trị của hx tại x  1.
d) Tìm nghiệm của đa thức k x . Bài 4. Cho hai đa thức: f  x 4 3 4
 2x  3x  4x  9  xx  5 2 3  3x  4x  6 g  x 2  2  x  2 x   2 3 1  x  2x  x  3 .
a) Thu gọn và sắp xếp đa thức f  x và g x theo lũy thừa giảm dần của biến.
b) Tìm đa thức hx sao cho h x  f  x  g x.
c) Tìm nghiệm của đa thức hx.
d) Tìm đa thức thương và dư trong phép chia đa thức hx cho đa thức  x 1.
Bài 5. Cho hai đa thức Ax 2  x  x  x 3 2 3 2
 3x : x và B x  2x 1.
a) Thu gọn đa thức Ax rồi tìm nghiệm của nó.
b) Tính giá trị của đa thức Ax tại x thỏa mãn x  2  3 .
c) Thực hiện phép chia đa thức Ax cho đa thức B x, tìm thương Q x và dư R x. Bài 6. a) Cho đa thức f  x 2
 x  mx  6 ( m là hệ số). Tìm hệ số m biết đa thức f  x có nghiệm x  2. b) Cho đa thức g x 2
 2x  mx  n ( m,n là các hệ số). Tìm m,n biết g 0  2 và đa thức
g  x có nghiệm x  1. Bài 7. a) Cho đa thức hx 3 2
 x  3x  5x  m ( m là hệ số). Tìm m để đa thức chia hết cho đa thức x 1.
b) Tìm các giá trị nguyên của x để giá trị của đa thức k  x 3 2
 x  x  x  3 chia hết cho giá
trị của đa thức s x  x  2.
Bài 8. Cho đa thức f  x 2
 ax  bx  c trong đó a, ,
b c  . Biết rằng giá trị của f (x) chia hết
cho 3 với mọi giá trị nguyên của x . Chứng minh rằng a, , b c đều chia hết cho 3.
Bài 9. Cho đa thức f  x 3 2  x  ax  9x  b .
a) Tìm a và b để đa thức có hai nghiệm là 1 và 3.
b) Với hai giá trị a và b tìm được của câu a, hãy tìm nghiệm còn lại của đa thức f x.
Bài 10. Cho đa thức f  x thỏa mãn  2
x  4x  3 f x  
1   x  2 f  x   1 . Chứng tỏ rằng đa
thức f  x có ít nhất 3 nghiệm.
Bài 11. Cho đa thức f  x 3 2
 ax  2bx  3cx  4d với các hệ số a, , b , c d là các số nguyên.
Chứng minh rằng không thể đồng thời tồn tại f 7  73 ; f 3  58 . Bài 12. Cho f  x 2
 ax  bx  ca  0 và f x 1với mọi x thỏa mãn x  1. Chứng minh rằng: a  2 . Bài 13. Cho đa thức 2
f (x)  ax  bx  c có 2 ;
a a  b và c là các số nguyên. Chứng minh f (x)
nhận giá trị nguyên với mọi số nguyên . x x  y y  z
Bài 14. Chứng minh rằng nếu 2 x  y  5 y  z  3 z  x thì  . 4 5 Bài 15. Cho a, ,
b c  0 thỏa mãn a  2b  2c  0;2a  b  2c  0;2a  2b  c  0 và a b c   .
a  2b  2c 2a  b  2c 2a  2b  c  b  a  c 
Tính giá trị của biểu thức: P  1 1 1 .      a  c  b  PHẦN II – HÌNH HỌC I. Trắc nghiệm
Câu 1. Một tam giác cân có số đo góc ở đỉnh bằng 50 thì số đo góc ở đáy là A. 120 . B. 65 . C. 60 . D. 70 .
Câu 2. Cho tam giác MNP có  P  N 90  
. Kẻ MH vuông góc với NP tại H . Trên tia đối
của tia HM lấy điểm D sao cho HD  HM . Khẳng định nào sau đây sai? A. MP  MN . B. DN  DP . C. DP  MN . D. MP  MH .
Câu 3. Cho I là giao điểm của ba đường phân giác trong của một tam giác. Kết luận nào là đúng?
A. I cách đều 3 cạnh của tam giác.
B. I cách đều 3 đỉnh của tam giác.
C. I là trọng tâm của tam giác. 2
D. I cách đỉnh một khoảng bằng độ dài đường phân giác. 3
Câu 4. Biết điểm I nằm trên đường trung trực của đoạn thẳng MN ; MN  6cm , IM  5cm ,
O là trung điểm của MN . Kết quả nào dưới đây sai? A. IO vuông góc với MN . B. 2cm  IO  8cm .
C. IO là phân giác của góc MIN . D. IM  IO  IN .
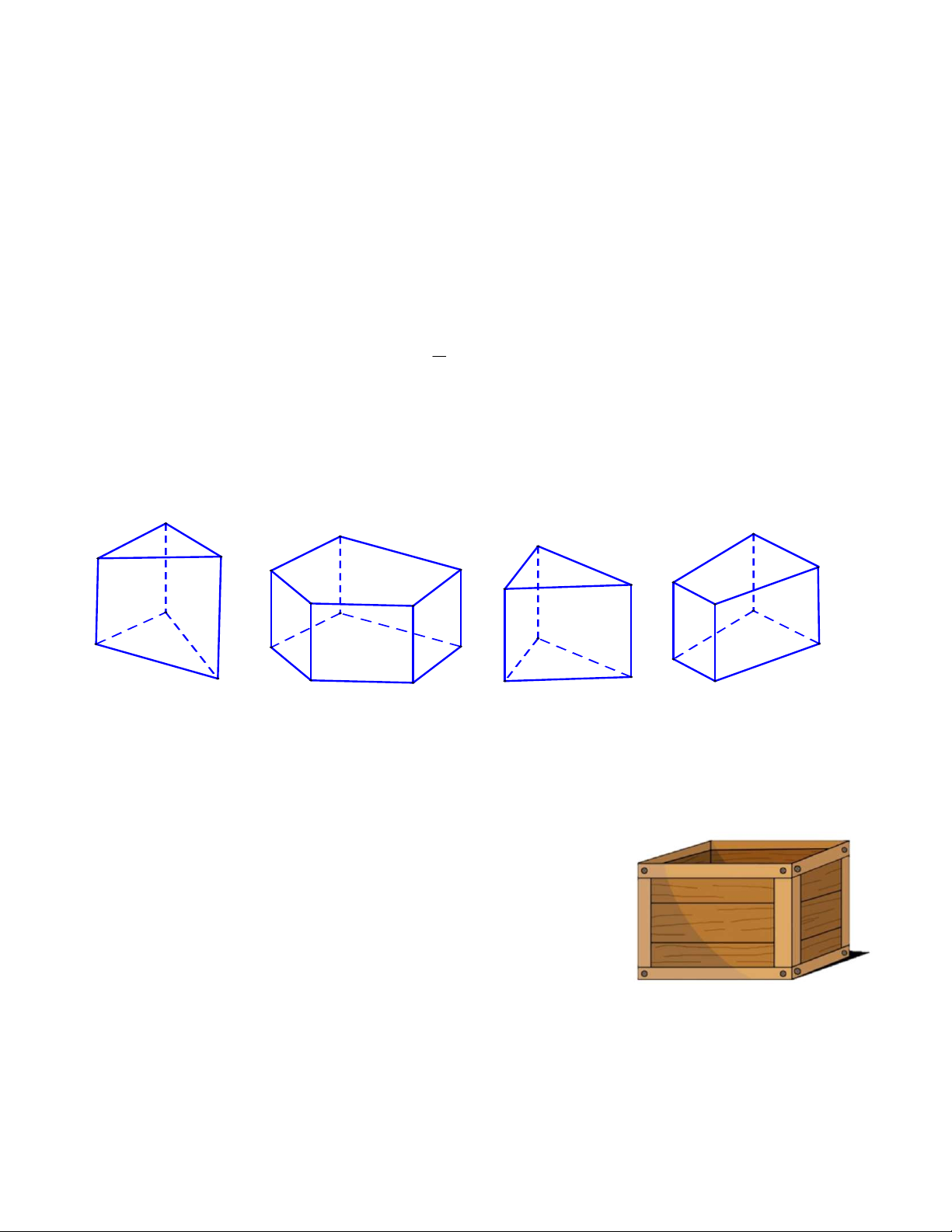
Câu 5. Trong các hình sau, đâu là hình lăng trụ đứng tam giác?
Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 3. B. Hình 2. C. Hình 1. D. Hình 4.
Câu 6. Số mặt, đỉnh, cạnh, đường chéo của hình hộp chữ nhật lần lượt là A. 4;8;12;2 . B. 6;8;12;2 . C. 6;8;12;4 . D. 6;8;8;1.
Câu 7. Một người thợ đóng một thùng bằng gỗ có dạng hình
hộp chữ nhật không có nắp, chiều dài 2,1m , chiều rộng 1,6m ,
chiều cao 1,3m . Người thợ đó cần ít nhất bao nhiêu mét
vuông gỗ để đóng chiếc thùng đó? A. 2 9,62 m . B. 2 12,98m . C. 2 16,34 m . D. 2 8,17m .
Câu 8. Một khối sắt hình lập phương có cạnh 0,2dm. Biết mỗi xăng-ti-mét khối sắt nặng 8g .
Khối lượng khối sắt trên bằng A. 0,064g . B. 0,64g . C. 8g . D. 64g .
Câu 9. Gàu xúc của một máy xúc có dạng gần như
một hình lăng trụ đứng tam giác với kích thước
như hình bên. Để xúc hết 3 112 m cát, máy xúc
đó phải xúc ít nhất bao nhiêu gàu? A. 58 . B. 59 . C. 116 . D. 117 .
Câu 10. Một ngôi nhà đồ chơi có kích thước như hình dưới đây. Thể tích của ngôi nhà bằng A. 3 4500cm . B. 3 2400cm . C. 3 3450cm . D. 3 1800cm . II. Tự luận: Bài 1. Cho A
 BC, AB  AC, AB  BC,H là trung điểm của BC .
a) Chứng minh ABH  ACH . Từ đó suy ra AH vuông góc với BC .
b) Tia phân giác của góc B cắt AH tại I . Chứng minh tam giác BIC cân.
c) Đường thẳng đi qua A và song song với BC cắt BI,CI lần lượt tại M , N . Chứng
minh A là trung điểm của đoạn MN .
d) Kẻ IE vuông góc với AB tại E , IF vuông góc với AC với F . Chứng minh: IH  IE  IF .
e) Chứng minh IC vuông góc với MC .
Bài 2. Cho ABC . Gọi E, F theo thứ tự là trung điem của các cạnh AB và AC . Trên tia đoi
của tia FB lay điem D sao cho DF  FB . Trên tia đoi của tia EC lay điem H sao cho HE  EC . a) Chứng minh AD  BC .
b) Chứng minh A là trung điem của HD . c) Chứng minh CD / / A . B
d) Gọi P là giao của DC và HB . Chứng minh A ; P B ; D CH đong quy.
Bài 3. Cho ABC cân tại A, và điểm M là trung điểm của cạnh BC . Vẽ tia Ax / /BC ,
Cy / / AB sao cho Ax cắt Cy tại D . Kéo dài AM cắt tia đối của tia Cy tại E .
a) Chứng minh ACB  CAD ; AB  CD .
b) Chứng minh MBA  MCE ; MA  ME ; CE  CD .
c) Trên tia Ax lấy điểm N sao cho AN  BM và G là giao điểm của AC và MD .
Chứng minh rằng E,G, N thẳng hàng.
d) Gọi P là trọng tâm của tam giác ABC . Chứng minh rằng NG  AP .
Bài 4. Cho ABC vuông cân tại A. Gọi BE là đường phân giác của góc B ( E  AC ). Đường
thang vuông góc với BC vẽ từ E cat BC tại D .
a) Chứng minh BAD cân, từ đó suy ra BE là trung trực của đoạn thẳng AD . b) So sánh AE và EC .
c) Gọi H là giao của BE và AD . Trên tia AD lấy điểm K sao cho BH  AK .
Chứng minh BAH  ACK và AH  CK .
d) Cho M là trung điểm của BC , AM cắt BE tại I , AM cắt CK tại F . Xác định dạng của F  DI .
Bài 5. Cho tam giác ABC vuông tại A, có AB  AC , đường cao AH . Tia phân giác của  CAH
cắt cạnh BC tại E . Đường thẳng qua E vuông góc với BC cắt AC tại D . Gọi I là giao điểm của AH và BD . a) Chứng minh:  BAH   ACB và tam giác ADE cân.
b) Chứng minh: Tia BD là tia phân giác của 
ABC và BD là đường trung trực của AE .
c) Chứng minh: BC  2BH . d) Chứng minh: EI / / AC .
e) Khi tam giác ADI cân tại D , tı́nh so đo các góc của tam giác ABC .
f) Chứng minh: AH  BC  AB  AC . ----- HẾT -----
Chúc các con ôn tập và thi đạt kết quả cao!